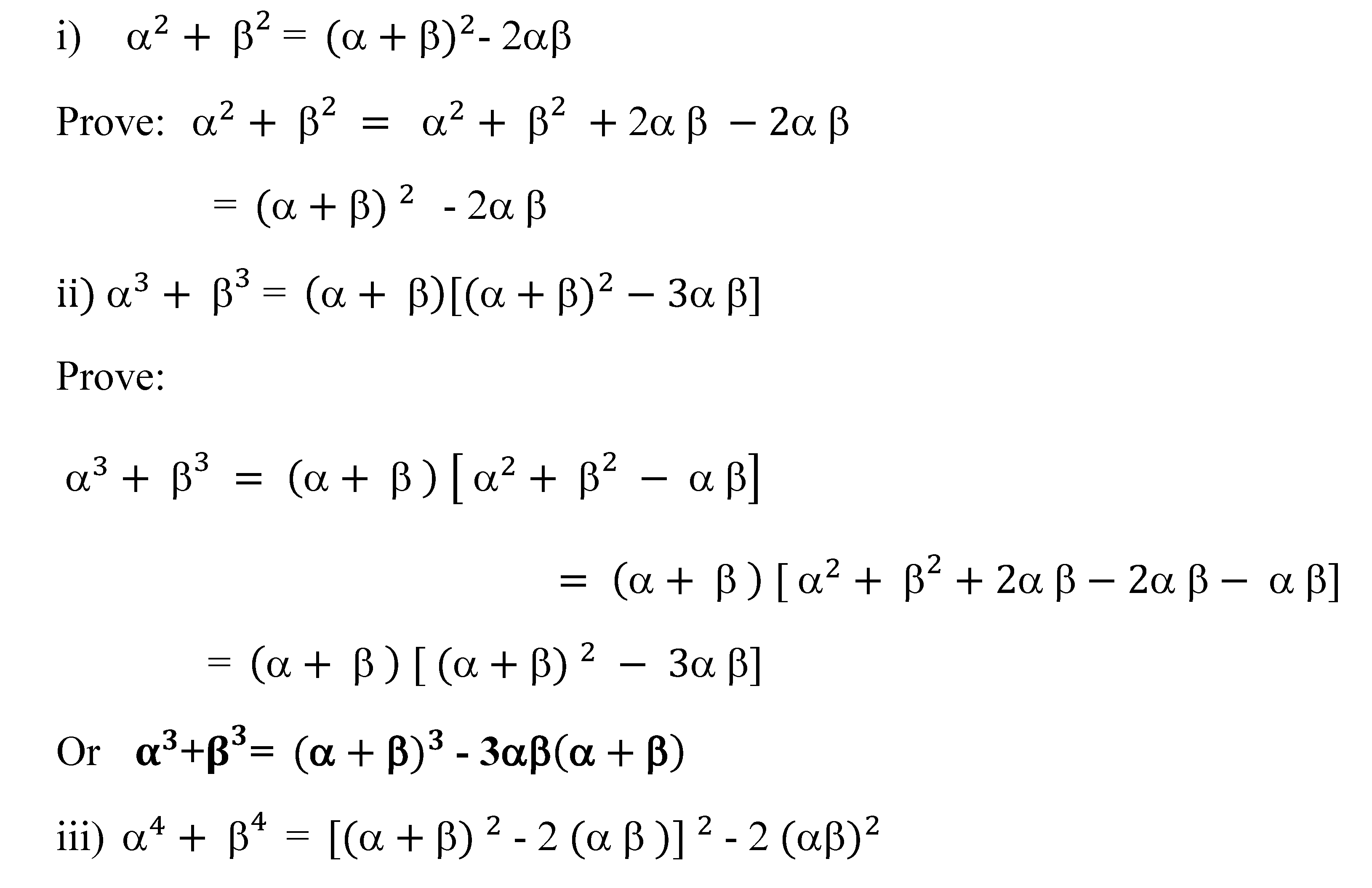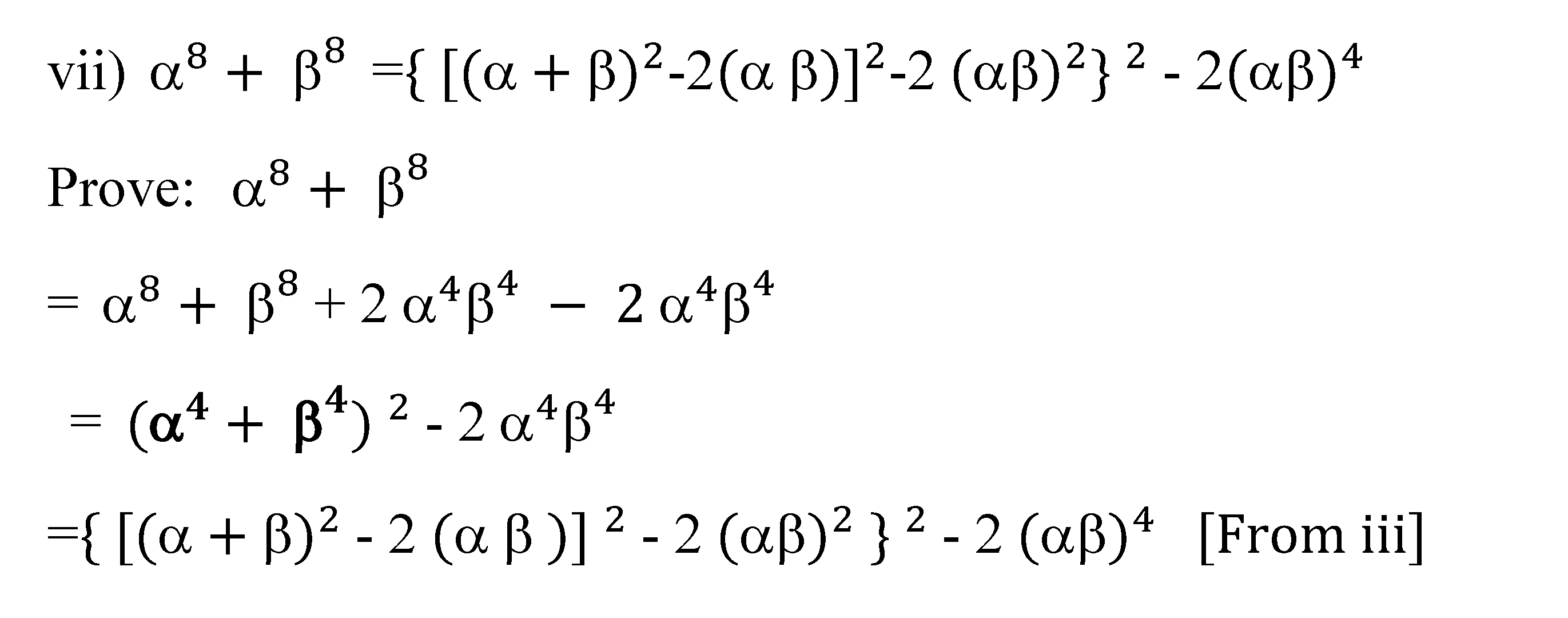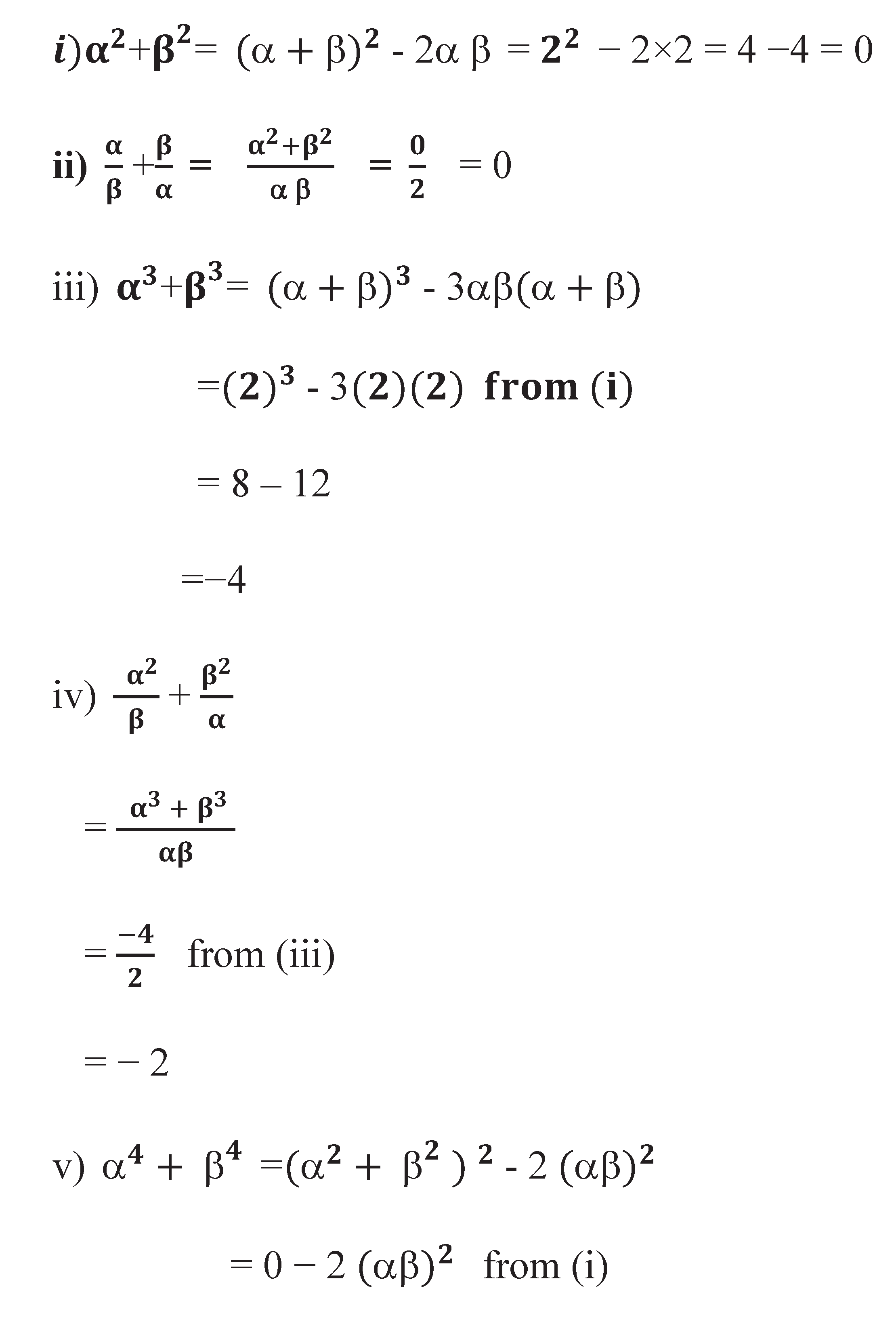Peter Chew Sum: Beyond Newton Sum in Quadratic Root Function Computations

Preprint

Article

Peter Chew Sum: Beyond Newton Sum in Quadratic Root Function Computations

Altmetrics

Downloads

205

Views

Comments

Peter Chew^*

This version is not peer-reviewed

Submitted:

29 March 2024

Posted:

05 April 2024

You are already at the latest version

Alerts

Abstract

This study provides a comprehensive comparison of the Peter Chew Sum method and Newton's Sum in Quadratic Root Function Computations. Both methods offer significant advancements by alleviating the need for memorization of multiple formulas. However, when confronted with higher-order quadratic root functions such as the calculation of power 33. Newton's Sum method proves cumbersome due to its requirement of all previous answers for final computation, leading to increased steps and error risks. In contrast, the Peter Chew Sum method simplifies the computational process by requiring only a few previous answers, resulting in a more straightforward series of operations. We contextualize our analysis within the historical progression of mathematical techniques, highlighting the transformative leap represented by the Peter Chew Sum method in quadratic root function computations. Peter Chew Sum addressing the limitations of Newton's Sum , especially concerning higher-order functions such as the calculation of power 256. Furthermore, study demonstrates that the innovative approach of the Peter Chew Sum method not only simplifies complex computations but also fosters enhanced conceptual understanding among students. In conclusion, study findings underscore the profound impact of the Peter Chew Sum method on quadratic root function computations.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

1.1. Algebra Formula: Symmetric ${F u n c t i o n}^{1, 2, 3}$ Of A Quadratic’s Roots

1.2. Example Quadratic Root function Calculation [Algebra Formula]

{E x a m p l e}^{4}

: If α, β are the zeroes of the polynomial

x^{2}

− 2x + 2 . find the value of i)

α^{2}

β^{2}

, ii)

\frac{α}{β}

\frac{β}{α}

,iii)

α^{3}

β^{3}

, iv)

\frac{α^{2}}{β}

\frac{β^{2}}{α}

α^{4}

β^{4}

Solution

Sum of the roots = α + β = − (−

\frac{2}{1}

)=2 , Product of the roots = αβ =

\frac{c}{a}

= 2

2. Peter Chew Sum.

P_{n} = P_{a} P_{b}

- (

{α β)}^{a} P_{b - a}

, where

a + b = n

, b

If a = b or n =

2 a

P_{n}

= {(P}_{a})^{2}

- 2 (

{α β)}^{a}

2.1. Prove $^{2, 3}$ of Peter Chew Sum.

L {e t P}_{n} = α^{n} + β^{n} a n d a + b = n, b a

α^{n} + β^{n} = α^{a + b} + β^{a + b}

= {(α}^{a} + β^{a}) {(α}^{b} + β^{b})

α^{a} β^{b} - β^{a} α^{b}

= P_{a} P_{b}

- (

{α β)}^{a} (\frac{β^{b}}{β^{a}} + \frac{α^{b}}{α^{a}})

= P_{a} P_{b}

- (

{α β)}^{a} (β^{b - a} + α^{b - a})

= P_{a} P_{b}

- (

{α β)}^{a} P_{b - a}

(Prove)
If a = b , n =

a + a = 2 a

P_{n} = P_{a} P_{a}

- (

{α β)}^{a} P_{a - a}

= {(P}_{a})^{2}

- (

{α β)}^{a}

P_{0}

= {(P}_{a})^{2}

- 2 (

{α β)}^{a}

2.2. Example using Peter Chew Sum Method

Example : If the roots of the equation

x^{2}

- 3x + 2 =0 are α and β , find the

α^{8} + β^{8}

Solution:

P_{i} = α^{i}

β^{i}

, So,

P_{0} = α^{0}

β^{0}

= 2.

P_{1} = α^{1}

β^{1}

= 3 , αβ = 2.

P_{2}

{(P}_{1})^{2}

- 2 (

{α β)}^{1}

(3)^{2}

- 2 (

{2)}^{1}

= 5

P_{4}

{(P}_{2})^{2}

- 2 (

{α β)}^{2}

(5)^{2}

- 2 (

{2)}^{2}

= 17

P_{8}

{(P}_{4})^{2}

- 2 (

{α β)}^{4}

(17)^{2}

- 2 (

{2)}^{4}

= 257

3. Newton Sum ( Newton's Identities $)^{5,6}$

Newton's identities, also known as Newton-Girard formulae, is an efficient way to find the power sum of roots of polynomials without actually finding the roots. If

x_{1}, x_{2}, \dots . . x_{n}

are the roots of a polynomial equation, then Newton's identities are used to find the summations like

It is mainly used in conjunction with Vieta's formula while working with the (complex) roots (say

a_{1}, a_{2}, \dots . . a_{k}

) of a

k^{t h}

degree polynomial. The main idea is that the elementary symmetric polynomials form an algebraic basis to produce all symmetric polynomials. Newton's identity gives us the calculation via a recurrence relation with known coefficients.

Newton's Identities for a Quadratic Polynomial

Suppose that you have a quadratic polynomial P(x) with (complex) roots

α_{1}

and

α_{2}

. Now, you are asked to find the value of

{α_{1}}^{2} + {α_{2}}^{2}

This seems very easy since you can use Vieta's formula along with the identity

{(a + b)}^{2}

a^{2}

b^{2}

+ 2ab to find the required result. But what if you need to find

({α_{1}}^{10} + {α_{2}}^{10})

? This would take a while if you were to simply use algebraic manipulations. But there's a clever way, using Newton's sums.

Let P(x) =

{a x}^{2}

+ bx + c . Then using Vieta`s formula,
we can get

α_{1} + α_{2}

= -

\frac{b}{a}

and

α_{1} α_{2}

\frac{c}{a} .

Denote

P_{i} a s t h e i^{t h} p o w e r s u m o f t h e r o o t s, n a m e l y

P_{i} = {α_{1}}^{i} + {α_{2}}^{i}

.
Then we can obtain

P_{i} r e c u r s i v e l y a s f o l l o w s .

P_{0} = {α_{1}}^{0} + {α_{2}}^{0}

= 2

P_{1} = {α_{1}}^{1} + {α_{2}}^{1} = - \frac{b}{a}

P_{2} = {α_{1}}^{2} + {α_{2}}^{2}

= ({α_{1}}^{} + α_{2}) ({α_{1}}^{1} + {α_{2}}^{1}) - 2 α_{1} α_{2}

= - \frac{b}{a} P_{1} - \frac{c}{a} P_{0}

P_{3} = {α_{1}}^{3} + {α_{2}}^{3}

= ({α_{1}}^{} + α_{2}) ({α_{1}}^{2} + {α_{2}}^{2}) - α_{1} α_{2} (α_{1} {+ α}_{2})

= - \frac{b}{a} P_{2} - \frac{c}{a} P_{1}

P_{i} = {α_{1}}^{i} + {α_{2}}^{i}

= ({α_{1}}^{} + α_{2}) ({α_{1}}^{i - 1} + {α_{2}}^{i - 1}) - α_{1} α_{2} ({α_{1}}^{i - 2} + {α_{2}}^{i - 2})

= - \frac{b}{a} P_{i - 1} - \frac{c}{a} P_{i - 2}

This is a linear recurrence relation that gives us the

i^{t h}

power sum. Note that solving this recurrence to get a closed-form solution is equivalent to finding the roots of the quadratic polynomial.

Full Calculation;

P(x) =

x^{2}

- 2x + 6 , A=2 , B= 6.

P_{i}

A P_{i - 1} - B P_{i - 2}

2 P_{i - 1} - 6 P_{i - 2}

P_{0} = {α_{1}}^{0} + {α_{2}}^{0} = 2

P_{1} = {α_{1}}^{} + α_{2} = A = 2

P_{2} = 2 P_{2 - 1} - 6 P_{2 - 2}

= 2 P_{1} - 6 P_{0}

= 2(2) - 6(2)
= - 8

P_{3} = 2 P_{3 - 1} - 6 P_{3 - 2}

= 2 P_{2} - 6 P_{1}

= 2(-8) - 6(2)
= - 28

P_{4} = 2 P_{4 - 1} - 6 P_{4 - 2}

= 2 P_{3} - 6 P_{2}

= 2(-28) - 6(-8)
= - 8

P_{5} = 2 P_{5 - 1} - 6 P_{5 - 2}

= 2 P_{4} - 6 P_{3}

= 2(-8) - 6(-28)
= 152

P_{6} = 2 P_{5} - 6 P_{4}

= 2(152) - 6(-8)
= 352

P_{7} = 2 P_{6} - 6 P_{5}

= 2(352) - 6(152)
= -208

P_{8} = 2 P_{7} - 6 P_{6}

= 2(-208) - 6(352)
= -2528

P_{9} = 2 P_{8} - 6 P_{7}

= 2(-2528) - 6(-208)
= -3808

P_{10} = 2 P_{9} - 6 P_{8}

= 2(-3808) - 6(-2528)
= 7 552

4. Peter Chew Sum and Newton Sum free students from the arduous task of memorizing various formulas for Calculating Quadratic Root Functions

4.1. Real Root Quadratic Equation

Example : If the roots of the equation

x^{2}

- 6x + 5 = 0 are α and β , find the value of i)

α^{2}

β^{2}

, ii)

α^{3}

β^{3}

, iii)

α^{4}

β^{4}

iv)

α^{5}

β^{5}

, v)

α^{6}

β^{6}

, vi)

α^{7}

β^{7}

and vii)

α^{8}

β^{8}

Solution:

Sum of the roots = α + β

= -

\frac{b}{a}

= − (

\frac{- 6}{1}

)
= 6

Product of the roots = αβ

\frac{c}{a}

\frac{5}{1}

= 5

Let A= α + β = 6 and B = αβ = 5

P_{n} = α^{n}

β^{n}

P_{0} = α^{0}

β^{0}

= 2.

P_{1} = α^{1}

β^{1}

= 6 .

Newton Sum Method

L e t P_{i}

A P_{i - 1} - B P_{i - 2}

6 P_{i - 1} - 5 P_{i - 2}

Peter Chew Sum Method

P_{n} = P_{a} P_{b}

- (

{α β)}^{a} P_{b - a}

, where

a + b = n

, b a .

i)

α^{2}

β^{2}

a)Algebraic formulas Method:

Note: The significant advantages of Newton's Sum and Peter Chew Sum method are obvious, such as freeing students from the burden of memorizing a large number of formulas. As shown above, if the algebraic formula method is used to calculate the quadratic root function, students need to remember a large number of formulas.

4.2. Complex Root Quadratic Equation

Example : If the roots of the equation

x^{2}

- 4x + 5 = 0 are α and β , find the value of i)

α^{2}

β^{2}

, ii)

α^{3}

β^{3}

, iii)

α^{4}

β^{4}

iv)

α^{5}

β^{5}

, v)

α^{6}

β^{6}

, vi)

α^{7}

β^{7}

and vii)

α^{8}

β^{8}

Solution:

Sum of the roots = α + β

= -

\frac{b}{a}

= − (

\frac{- 4}{1}

)
= 4

Product of the roots = αβ

\frac{c}{a}

\frac{5}{1}

= 5

Let A= α + β = 4 and B = αβ = 5

$P_{n} = α^{n}$ + $β^{n}$ . $P_{0} = α^{0}$ + $β^{0}$ = 2. $P_{1} = α^{1}$ + $β^{1}$ = 4 .
Newton Sum Method $L e t P_{i}$ = $A P_{i - 1} - B P_{i - 2}$ = $4 P_{i - 1} - 5 P_{i - 2}$

Peter Chew Sum Method

P_{n} = P_{a} P_{b}

- (

{α β)}^{a} P_{b - a}

, where

a + b = n

, b a .

i) α^{2}

β^{2}

5. The Peter Chew Sum method is more simple (fewer computational steps) than Newton Sum to calculate higher order quadratic root functions.

Example 1: If the roots of the equation

x^{2}

- 4x + 3 = 0 are α and β , find the value

α^{16}

β^{16} b y u s i n g {N e w t o n}^{'} s S u m m e t h o d a n d P e t e r C h e w S u m M e t h o d .

Solution: i)Newton's Sum method. Let A= α + β = -

\frac{- 4}{1} =

4 and B = αβ =

\frac{3}{1} =

P_{i} = α^{i}

β^{i}

, So,

P_{0} = α^{0}

β^{0}

= 2.

P_{1} = α^{1}

β^{1}

= 3

P_{i}

A P_{i - 1} - B P_{i - 2}

4 P_{i - 1} - 3 P_{i - 2}

P_{2}

4 P_{1} - 3 P_{0}

= 4 (4) – 3(2)
= 10

P_{3}

4 P_{2} - 3 P_{1}

= 4 (10) – 3 (4)
= 28

P_{4}

4 P_{3} - 3 P_{2}

= 4 (28) – 3 (10)
= 82

P_{5}

4 P_{4} - 3 P_{3}

= 4 (82) – 3 (28)
= 244

P_{6}

4 P_{5} - 3 P_{4}

= 4 (244) – 3 (82)
= 730

P_{7}

4 P_{6} - 3 P_{5}

= 4 (730) – 3(244)
= 2 188

P_{8}

4 P_{7} - 3 P_{6}

= 4 (2 188) – 3 (730)
= 6 562

P_{9}

4 P_{8} - 3 P_{7}

= 4(6 562) – 3(2 188)
= 19 684

P_{10}

4 P_{9} - 3 P_{8}

= 4 (19 684) – 3 (6 562)
= 59 050

P_{11}

4 P_{10} - 3 P_{9}

= 4 (59 050) – 3 (19 684)
= 177 148

P_{12}

4 P_{11} - 3 P_{10}

= 4 (177 148) – 3 (59 050)
= 531 442

P_{13}

4 P_{12} - 3 P_{11}

= 4 (531 442) – 3 (177 148)
= 1 594 324

P_{14}

4 P_{13} - 3 P_{12}

= 4 (1 594 324) – 3 (531 442)
= 4 782 970

P_{15}

4 P_{14} - 3 P_{13}

= 4 (4 782 970) – 3 (1 594 324)
= 14 348 908

P_{16}

4 P_{15} - 3 P_{14}

= 4 (14 348 908) – 3 (4 782 970)
= 43 046 722

Note: As shown above, Newton's Sum is a historical calculation method that relies on all previous results for subsequent calculations. This common historical basis reveals a limitation, particularly when dealing with higher-order quadratic root functions involving exponents such as

^{16}

^{16}

. For higher-order quadratic root functions, using Newton's Sum involves many steps that can lead to calculation errors.

ii) Peter Chew Sum Method. If a = b 0r n = $2 a$ ${. P}_{n} = {(P}_{a})^{2}$ - 2 ( ${α β)}^{a}$ $P_{i} = α^{i}$ + $β^{i}$ , So, $P_{0} = α^{0}$ + $β^{0}$ = 2. $P_{1} = α^{1}$ + $β^{1}$ = 4 , αβ = 3. $P_{2}$ = ${(P}_{1})^{2}$ - 2 ( ${α β)}^{1}$ = $(4)^{2}$ - 2 ( ${3)}^{1}$ = 16 – 6 = 10
$P_{4}$ = ${(P}_{2})^{2}$ - 2 ( ${α β)}^{2}$ = $(10)^{2}$ - 2 ( ${3)}^{2}$ = 82 $P_{8}$ = $P_{4} P_{4}$ - ( ${α β)}^{4} P_{4 - 4}$ = (82) (82) – ( ${3)}^{4}$ (2) = 6562 $P_{8}$ = $P_{4} P_{4}$ - ( ${α β)}^{4} P_{4 - 4}$ = (82) (82) – ( ${3)}^{4}$ (2) = 6562 $P_{16}$ = $P_{8} P_{8}$ - ( ${α β)}^{8} P_{8 - 8}$ = (6562) (6562) – ( ${3)}^{8}$ (2) = 43 046 722

Note: As shown above, using Peter Chew Sum involves a few steps compare using Newton Sum. This can prevent calculation errors.

Example 2: If the roots of the equation

x^{2}

- x - 2 = 0 are α and β , find the value

α^{33}

β^{33} b y u s i n g {N e w t o n}^{'} s S u m m e t h o d a n d P e t e r C h e w S u m M e t h o d .

Solution:

i)Newton's Sum method. Let A= α + β =- $\frac{- 1}{1} =$ 1 and B = αβ = $\frac{- 2}{1} =$ -2 $P_{i} = α^{i}$ + $β^{i}$ , So, $P_{0} = α^{0}$ + $β^{0}$ = 2. $P_{1} = α^{1}$ + $β^{1}$ = 1 $P_{i}$ = $A P_{i - 1} - B P_{i - 2}$ = $P_{i - 1} + 2 P_{i - 2}$ $P_{2}$ = $P_{1} + 2 P_{0}$ = 1 + 2(2)
= 5 $P_{3}$ = $P_{2} + 2 P_{1}$ = 5 + 2 (1) = 7 $P_{4}$ = $P_{3} + 2 P_{2}$ = 7 + 2 (5) = 17 $P_{5}$ = $P_{4} + 2 P_{3}$ = 17 + 2 (7) = 31 $P_{6}$ = $P_{5} + 2 P_{4}$ = 31 + 2 (17) = 65 $P_{7}$ = $P_{6} + 2 P_{5}$ = 65 + 2 (31) = 127 $P_{8}$ = $P_{7} + 2 P_{6}$ = 127 + 2 (65) = 257 $P_{9}$ = $P_{8} + 2 P_{7}$ = 257 + 2 (127) = 511
$P_{10}$ = $P_{9} + 2 P_{8}$ = 511 + 2 (257) = 1 025 $P_{11}$ = $P_{10} + 2 P_{9}$ = 1 025 + 2 (511) = 2 047 $P_{12}$ = $P_{11} + 2 P_{10}$ = 2 047 + 2 (1 025) = 4 097 $P_{13}$ = $P_{12} + 2 P_{11}$ = 4 097 + 2 (2 047) = 8 191 $P_{14}$ = $P_{13} + 2 P_{12}$ = 8 191 + 2 (4 097) = 16 385 $P_{15}$ = $P_{14} + 2 P_{13}$ = 16 385 + 2 (8 191) = 32 767 $P_{16}$ = $P_{15} + 2 P_{14}$ = 32 767 + 2 (16 385) = 65 537 $P_{17}$ = $P_{16} + 2 P_{15}$
= 65 537 + 2 (32 767) = 131 071 $P_{18}$ = $P_{17} + 2 P_{16}$ = 131 071 + 2 (65 537) = 262 145 $P_{19}$ = $P_{18} + 2 P_{17}$ = (262 145) + 2(131 071) = 524 287 $P_{20}$ = $P_{19} + 2 P_{18}$ = (524 287) + 2(262 145) = 1 048 577 $P_{21}$ = $P_{20} + 2 P_{19}$ = (1048577) + 2(524 287) = 2 097 151 $P_{22}$ = $P_{21} + 2 P_{20}$ = (2 097 151) + 2(1 048 577) = 4194305 $P_{23}$ = $P_{22} + 2 P_{21}$ = (4 194 305) +2(2 097 151) = 8 388 607 $P_{24}$ = $P_{23} + 2 P_{22}$ = (8 388 607) +2(4194305) = 16 777 217 $P_{25}$ = $P_{24} + 2 P_{23}$ = (16 777 217) +2 (8 388 607) = 33 554 431 $P_{26}$ = $P_{25} + 2 P_{24}$ = (33 554 431) + 2 (16 777 217) = 67 108 865 $P_{27}$ = $P_{26} + 2 P_{25}$ = (67 108 865) + 2(33 554 431) = 134 217 727 $P_{28}$ = $P_{27} + 2 P_{26}$ = (134 217 727) + 2(67 108 865) = 268 435 457 $P_{29}$ = $P_{28} + 2 P_{27}$ = (268 435 457) + 2(134 217 727) = 536 870 911 $P_{30}$ = $P_{29} + 2 P_{28}$ = (536 870 911) + 2(268 435 457) = 1 073 741 825 $P_{31}$ = $P_{30} + 2 P_{31}$ = (1 073 741 825) + 2(536 870 911) = 2 147 483 647 $P_{32}$ = $P_{31} + 2 P_{30}$ = (2 147 483 647) + 2 (1 073 741 825) = 4 294 967 297 $P_{33}$ = $P_{32} + 2 P_{31}$ = (4 294 967 297)+ 2 (2 147 483 647) = 8 589 934 591

Note: As shown above, Newton's Sum is a historical calculation method that relies on all previous results for subsequent calculations. For higher-order quadratic root functions such as

^{33}

^{33}

, using Newton's Sum involves many steps that can lead to calculation errors.

ii) Peter Chew Sum Method. If a = b 0r n =

2 a

{. P}_{n} = {(P}_{a})^{2}

- 2 (

{α β)}^{a}

i f b a, P_{n} = P_{a} P_{b}

- (

{α β)}^{a} P_{b - a}

, where

a + b = n

P_{i} = α^{i}

β^{i}

, So,

P_{0} = α^{0}

β^{0}

= 2.

P_{1} = α^{1}

β^{1}

= 1, αβ =

\frac{- 2}{1} =

-2

P_{2}

{(P}_{1})^{2}

- 2 (

{α β)}^{1}

(1)^{2}

- 2 (

{- 2)}^{1}

= 5

P_{3}

P_{1} P_{2}

- (

{α β)}^{1} P_{2 - 1}

(1) (5)

- (

{- 2)}^{1}

(1)
= 7

P_{4}

{(P}_{2})^{2}

- 2 (

{α β)}^{2}

(5)^{2}

- 2 (

{- 2)}^{2}

= 17

P_{4}

{(P}_{2})^{2}

- 2 (

{α β)}^{2}

(5)^{2}

- 2 (

{- 2)}^{2}

= 17

P_{7}

P_{3} P_{4}

- (

{α β)}^{3} P_{4 - 3}

(7) (17)

- (

{- 2)}^{3}

(1)
= 127

P_{8}

{(P}_{4})^{2}

- 2 (

{α β)}^{4}

(17)^{2}

- 2 (

- 2)^{4}

= 257

P_{9}

P_{1} P_{8}

- (

{α β)}^{1} P_{8 - 1}

(1) (257)

- (

{- 2)}^{1}

(127)

= 511

P_{16}

{(P}_{8})^{2}

- 2 (

{α β)}^{8}

(257)^{2}

- 2 (

{- 2)}^{8}

= 65 537

P_{17}

P_{8} P_{9}

- (

{α β)}^{8} P_{9 - 8}

(257) (511)

- (

{- 2)}^{8}

(1)
= 131 071

P_{33}

P_{16} P_{17}

- (

{α β)}^{16} P_{17 - 16}

(65 537) (131 071)

- (

{- 2)}^{16} (

1)
= 8 589 934 591.

Note: Peter Chew Sum Method involves fewer steps than using Newton Sum Method, preventing calculation errors.

6. Limitation ${N e w t o n}^{'} s S u m$

Example : If the roots of the equation

x^{2}

- 2x + 2 = 0 are α and β , find the value

α^{256}

β^{256} b y u s i n g {N e w t o n}^{'} s S u m m e t h o d a n d P e t e r C h e w S u m M e t h o d .

Solution: i)

{N e w t o n}^{'} s S u m m e t h o d, n o t s u i t a b l e .

ii) Peter Chew Sum Method. If a = b 0r n =

2 a

{. P}_{n} = {(P}_{a})^{2}

- 2 (

{α β)}^{a}

P_{i} = α^{i}

β^{i}

, So,

P_{0} = α^{0}

β^{0}

= 2.

P_{1} = α^{1}

β^{1}

= 2 , αβ = 2.

P_{2}

{(P}_{1})^{2}

- 2 (

{α β)}^{1}

(2)^{2}

- 2 (

{2)}^{1}

= 0

P_{4}

{(P}_{2})^{2}

- 2 (

{α β)}^{2}

(0)^{2}

- 2 (

{2)}^{2}

= - 8

P_{8}

{(P}_{4})^{2}

- 2 (

{α β)}^{4}

(- 8)^{2}

- 2 (

{2)}^{4}

= 32

P_{16}

{(P}_{8})^{2}

- 2 (

{α β)}^{8}

(32)^{2}

- 2 (

{2)}^{8}

= 512

P_{32}

{(P}_{16})^{2}

- 2 (

{α β)}^{16}

(512)^{2}

- 2 (

{2)}^{16}

= 131072

P_{64}

{(P}_{32})^{2}

- 2 (

{α β)}^{32}

(131072)^{2}

- 2 (

{2)}^{32}

= 8 589 934 592

P_{128}

{(P}_{64})^{2}

- 2 (

{α β)}^{64}

(8 589 934 592)^{2}

- 2 (

{2)}^{64}

= 36893488147419103232

P_{256}

{(P}_{128})^{2}

- 2 (

{α β)}^{128}

(36893488147419103232)^{2}

- 2 (

{2)}^{128}

= 680564733841876926926749214863536422912

Note: Newton's sum method is not suitable for solving this problem because it involves too much steps. The Peter Chew Sum Method involves fewer steps so this problem can be calculated.

6. Conclusion

In conclusion, this study provides a thorough examination and comparison of the Peter Chew Sum method and Newton's Sum in quadratic root function computations. It is evident that both methods offer advancements by eliminating the need for memorization of numerous formulas. However, when faced with higher-order quadratic root functions, such as

α^{33}

β^{33}

. Newton's Sum method becomes cumbersome due to its reliance on all previous answers for final computation, resulting in increased steps and error risks.

In contrast, the Peter Chew Sum method streamlines the computational process by requiring only a few previous answers, leading to a more straightforward series of operations. Through contextualizing our analysis within the historical progression of mathematical techniques, we underscore the transformative leap represented by the Peter Chew Sum method in quadratic root function computations.

Furthermore, study demonstrates the Peter Chew Sum method's ability to address the limitations of Newton's Sum, particularly concerning higher-order functions like

α^{256}

β^{256} .

In summary, the findings of this study emphasize the profound impact of the Peter Chew Sum method on quadratic root function computations, highlighting its potential to revolutionize mathematical education and problem-solving approaches in this domain.

References

UTKARSH UJJWAL. Symmetric Functions of Roots, Unacademy https://player.uacdn.net/lesson-raw/MO7GCNCM3QUZNFJKYT48/pdf/2934554061.pdf .
Symmetric Functions of Roots of a Quadratic Equation. Math-Only-Math.com https://www.math-only-math.com/symmetric-functions-of-roots-of-a-quadratic-equation.html .
SkanCity Academy Solved Example 1 - Symmetric Functions of Roots of a Quadratic Equation | SHS 1 ELECTIVE MATH Youtube. https://youtu.be/6pd6j-7Nid8?si=6A1D7fo3P1IOnjCQ .
BYJUS: https://byjus.com/question-answer/if-alpha-beta-are-the-zeroes-of-the-polynomial-x-2-2x-2-find-the/.
Prasun Biswas et al. Newton's Identities. BRILLIANT. https://brilliant.org/wiki/newtons-identities/.
Polynomial Maths Newton’s Sums - Finding the Sum of the Nth powers of the Roots of a Polynomial. https://youtu.be/1Pd4HgI1bOQ?si=VFRa0XX1WD-hwqs3.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Peter Chew Sum: Beyond Newton Sum in Quadratic Root Function Computations

Abstract

1. Introduction

1.1. Algebra Formula: Symmetric F u n c t i o n 1 , 2 , 3 Of A Quadratic’s Roots

2. Peter Chew Sum.

2.1. Prove 2 , 3 of Peter Chew Sum.

3. Newton Sum ( Newton's Identities ) 5,6

4. Peter Chew Sum and Newton Sum free students from the arduous task of memorizing various formulas for Calculating Quadratic Root Functions

4.1. Real Root Quadratic Equation

4.2. Complex Root Quadratic Equation

5. The Peter Chew Sum method is more simple (fewer computational steps) than Newton Sum to calculate higher order quadratic root functions.

6. Limitation N e w t o n ' s S u m

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

1.1. Algebra Formula: Symmetric ${F u n c t i o n}^{1, 2, 3}$ Of A Quadratic’s Roots

2.1. Prove $^{2, 3}$ of Peter Chew Sum.

3. Newton Sum ( Newton's Identities $)^{5,6}$

6. Limitation ${N e w t o n}^{'} s S u m$