Prerpints.org logo
Preprint
Article

Parkinson's Disease Recognition using Decorrelated Convolutional Neural Networks: Addressing Imbalance and Scanner Bias in rs-fMRI Data

This version is not peer-reviewed.

Submitted:

21 March 2024

Posted:

22 March 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Parkinson’s Disease (PD) is a neurodegenerative and progressive disease that impacts the nerve cells in the brain and varies from person to person. The exact cause of PD is still unknown, and the diagnosis of PD does not include a specific objective test with certainty. Although deep learning has made great progress in medical neuroimaging analysis, these methods are very susceptible to biases present in neuroimaging datasets. An innovative decorrelated deep learning technique is introduced to mitigate class bias and scanner bias while simultaneously focusing on finding distinguishing characteristics in resting-state functional MRI (rs-fMRI) data, which assist in recognizing the PD with good accuracy. The decorrelation function reduces the non-linear correlation between features and bias in order to learn bias-invariant features. The Parkinson’s Progression Markers Initiative (PPMI) dataset, referred to as a single scanner imbalanced dataset in this study used to validate our method. The imbalanced dataset problem affects the performance of the deep learning framework by overfitting to the majority class. To resolve this problem, we propose a new Decorrelated Convolutional Neural Networks (DcCNN) framework by applying decorrelation-based optimization to Convolutional Neural Networks(CNN). An analysis of evaluation metrics comparisons shows that integrating the decorrelation function boosts the performance of PD recognition by removing class bias. Specifically, our DcCNN model performs significantly better than existing traditional approaches to tackle the imbalance problem. Finally, the same framework can be extended to create scanner invariant features without significantly impacting the performance of a model. The obtained dataset is a multi-scanner dataset which leads to scanner bias due to the differences in acquisition protocols and scanners. The multi-scanner dataset is a combination of two datasets, namely PPMI and FTLDNI - frontotemporal lobar degeneration neuroimaging initiative (NIFD) dataset. The results of t-distributed stochastic neighbor embedding (t-SNE) and scanner classification accuracy of our proposed Feature Extraction-DcCNN (FE-DcCNN) model validated the effective removal of scanner bias. Our method achieves an average accuracy of 77.80% on a multi-scanner dataset for differentiating PD from healthy control, which is superior to the DcCNN model trained on a single scanner imbalanced dataset.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Parkinson’s disease (PD) is characterized by the lack of dopamine transmitters due to the degeneration of melanin cells in the pars compacta (posterior part) of the substantia nigra, and PD patients show several cognitive deficits which include executive functioning, visuospatial abilities, and memory loss. The symptoms of PD include shaking, slow movements, walking problems, behavioral problems, speech problems, etc. Diagnosis of PD generally includes assessment of behavior, neuroimaging, physical, biological sampling, and clinical data. The false-positive rate for PD is higher in the early stage and high at the final diagnostic stage. In the past few years, studies in neuroimaging modalities have provided more profound and valuable insights into the underlying mechanism of PD.
Parkinson’s disease remains the second most common neurodegenerative disorder. But still, there is an unknown factor in the cause of PD, which makes PD a very important area of study. Motor symptoms, along with cognitive impairment, are also found as common disabling symptoms in PD. The mechanism underlying cognitive dysfunction PD remains ambiguous, unlike motor symptoms. Many studies have been conducted on PD using clinical and biomarker data. Most of them are driven by hypotheses and hand-crafted feature extraction methods which are based on pathology-related background knowledge. Recently, neuroimaging has been considered an important information source for neurodegenerative disease. Hence, it has also arisen considerable interest from the PD community. Diagnosing Parkinson’s disease based on diagnostic tests and radiologists’ reading on neuro-images is oftentimes prone to mistakes. So there is a gray area in the PD diagnosing research field where the unknown cause of PD, no precise test for PD, and a high misdiagnosis rate is present. There is a need for highly accurate and reliable results. This research may be of use to the medical community in a screening setting and to understand how and why PD develops and search for solutions to stop or avoid the progression of the disease.
Currently, no specific test exists to diagnose Parkinson’s disease. There are a few diagnostics tests that Physicians use to diagnose Parkinson’s disease based on medical history, review of signs and symptoms, physical examination, blood test, and neuroimaging tests. As PD progresses, it becomes harder to prevent or slow the changes through medication. For this reason, in 2016, experts developed new criteria [1]. These include three steps. The first step includes accessing the probability based on the age that the diagnosis will be PD. In the second step, physicians access the information based on variables such as whether the person is male or female, environmental risks, caffeine use and smoking, genetic factors, family history, or genetic test. Sometimes findings based on these results of scans and other diagnostic tests show early signs and symptoms, which include constipation, loss of a sense of smell, and difficulty with movement. The third and final step consists of calculating the outcome by multiplying all the factors together and then comparing this total likelihood ratio with a threshold measure. If the comparison indicates a total likelihood ratio higher than 80 percent that PD is present, the physicians will diagnose that patient with the early stages of PD. Most commonly, a patient with a 75–80 percent total likelihood will have symptoms that may or may not relate to PD, e.g., constipation and depression, whereas a patient with a 95–97 percent total likelihood will have symptoms that are closely related to PD, e.g., Rapid eye movement (REM) sleep behavior disorder where a person experiences sudden and rapid movements and vocalizations during vivid dreams.
Deaths caused by PD have increased significantly over the years. The diagnosis of PD used in hospitals relies mainly on a combination of different diagnostic tests and symptoms assessment. It is still difficult to make an accurate prediction of PD. Neuroimaging data such as Magnetic Resonance Imaging (MRI), Resting-State Functional Magnetic Resonance Imaging (rs-fMRI), Single-photon emission tomography (SPECT), Dopamine transporter imaging (DAT), 123I-ioflupane-SPECT (DaTscan), Diffusion tensor imaging (DTI), A positron emission tomography (PET), Computed tomography (CT) scans can be used to diagnose PD. However, CT scans and MRI images sometimes do not show patterns in images to distinguish PD from a healthy patient. Whereas SPECT is a commonly used method but suffers from high cost and time issues and requires injection of radioactive material. Radiologists generally use one of these neuroimages to diagnose PD disease, but it is proven to be more prone to mistakes. Recent research and studies have shown that DTI and rs-fMRI can be used to predict PD and are found to be promising methods for the diagnosis of PD. But in order to capture DTI images, the patient will have to remain still for a longer period, i.e., half an hour. Since DTI is a relatively new technique, it is difficult to find hospitals equipped with DTI scanners.
Current existing methodologies such as [2,3] do not use rs-fMRI using CNN to detect PD. Therefore, the processing of rs-fMRI with a single scanner and multi-scanner settings using CNN techniques to diagnose PD is not yet explored. This novel research study will evaluate the prediction of PD on noninvasive and comparatively less expensive neuroimaging data such as rs-fMRI in a single scanner and multi-scanner settings using a model that uses the convolutional neural network. Since available neuroimaging data is limited and the majority of the data is class imbalanced, this study will also provide a novel decorrelation-based deep learning fusion approach to mitigate class bias. Further, we will also explore the use of multi-scanner rs-fMRI data, which is obtained by combining different datasets from different scanners not only to balance the dataset but also to increase the size of the dataset and to improve the performance of the model. But this leads to an undesirable increase in variance caused by scanner and acquisition protocol differences, including scanner upgrade, scanner drift, and gradient nonlinearities. The same framework of decorrelation-based deep learning is used to produce features that are invariant to scanner and acquisition protocol while still capable of not impacting the performance of the PD recognition task.
The rest of this paper is structured as follows: Section 2 briefly reviews the related work, whereas Section 3 provides a brief description of the proposed methodologies, involved PD datasets, and preprocessing techniques; Section 4 reports the results and comparison with existing methodologies and Section 5 discusses the performance of our proposed method for the PD detection. Lastly, Section 6 concludes the research and provides opportunities for future work.

2. Prior Work

Two centuries ago, James Parkinson presented the first medical description of Parkinson’s disease in 1817. Today, Parkinson’s disease is the second most common neurodegenerative disorder. The pathophysiology of Parkinson’s disease (PD) is the study of the functional processes that occur in a PD which is only partially understood. Currently, what we know about PD is that the loss of neurons in the Substantia Nigra pars compacta part of the brain and the presence of Lewy bodies leads to the loss of dopamine (a neurotransmitter). This damaged neurotransmitter ultimately prevents normal function in the basal ganglia, which causes the motor symptoms of PD and cognitive impairment. Common motor symptoms observed in PD include tremors, slowness, stiffness, rigidity, swallowing problems, balance problems, unpredictable movements, difficulty initiating or controlling movement, cramping, and speech problems. Cognitive issues, such as short-term memory loss, difficulty following complicated instructions, or a loss of multitasking ability, may also occur in PD patients. Some people will have several symptoms, whereas others will have only a few. It has been observed that deaths caused by PD have increased significantly over the years. This is mainly because PD is difficult to diagnose and can be caused by a combination of environmental, genetic, or lifestyle factors. Male gender, gait disorder, and absent rest tremor are generally associated with poorer long-term survival. According to NIH, approximately 50,000 to 60,000 Americans are diagnosed with PD each year. Because of a lack of knowledge regarding which symptoms develop and how severely and quickly symptoms develop, and since the symptoms of Parkinson’s vary from patient to patient and often overlap with other medical conditions, PD is misdiagnosed as up to 30 percent of the time. It has been observed that misdiagnosis of PD is very common. So there is a need for an automated diagnostic tool.

2.1. Pathology Driven Hypothesis

In the past few years, several studies have been done to explore the connection between clinical, biological, and imaging data to achieve an accurate diagnosis and early detection of PD. Most of these studies are driven by pathology or the underlying biology of PD and use hypotheses. According to [4,5], the α -Synuclein protein, which is a major component of Lewy pathology, accumulates and originates from cells in the gut and transmits to the brain via a vague nerve in the patient with Parkinson’s disease. The authors performed this study on a mouse model and supported the Braak hypothesis. This research might help to prevent or halt PD progression by blocking the vagal transmission pathway in an early stage. From a genetic contribution point of view, a paper published by [6] suggests that protein products of genes help to identify the functionality of PD whereas [7] have investigated the use of α -Synuclein protein as a biomarker for PD using hypothesis testing with around 85% specificity and 52% sensitivity. In [8] the paper, an innovative approach, such as the use of sebum to diagnose PD was used since a change in skin microflora, and skin physiology can cause a change in odor in PD patients. The results (AUC 78%) to support this theory were achieved by collecting sebum samples from the participant’s upper back and using a combination of data processing techniques, such as olfactogram and chromatogram, and performing partial least-squares-discriminant analysis on this preprocessed data. The main limitation of this study is the smaller sample size. There are quite a few studies conducted to diagnose PD by using neuroimaging and clinical data.
Several papers such as [9,10,11,12,13,14] have suggested the use of DTI metrics can provide distinguishing features to detect PD or be used as imaging biomarkers for PD. In recent years, there have been studies [15,16] in rs-fMRI, which is a fast-developing research field and helps in revealing cognitive dysfunction or increasing motor connectivity for early PD detection. All these studies perform hypothesis testing such as t-test, two-way mixed model ANOVA, comprehensive meta-analysis, etc., to find significant group differences between PD and control healthy groups. The cross-sectional study [17] claimed that serotonergic pathology plays a vital early role in the progression of PD. This study provided evidence that loss in serotonin function is observed in the very early stages of PD by using PET and SPECT scans. To access molecular, clinical, and structural pathology, PET imaging was used. ANOVA and t-test were used for comparisons between the groups and suggested that serotonergic malfunction precedes the development of other PD symptoms, such as motor, and is related to the dopaminergic deficit by using the Braak staging scheme.

2.2. Data-Driven Models

Data-driven approaches, such as deep learning and machine learning, are different than conventional statistical analyses. DaTscan SPECT image analysis with the one-layer artificial neural network is developed to classify PD versus normal with around 94% accuracy [18]. Machine learning-based approaches such as a support vector machine [19], a Naive Bayes classifier [20], and a boosted logistic regression model [2] were also used for PD classification using rs-fMRI data, but it was tested on very small datasets.
To overcome the drawback of feature-engineering or hand-crafted features, a few deep learning techniques have been deployed in the past decade. [21] used SPECT data to detect PD over normal using deep 3D CNN architecture which achieved around 96%, far higher than human evaluation accuracy, and could be used for the SWEDD group. Another study in deep learning is carried out by [22] using graph convolutional deep networks (GCN) to fuse multiple modalities of MRI and DTI to detect PD cases and achieved around 95% AUC. In this study, a Brain Geometry graph (BGG) is obtained from the Region of Interest of MRI and Brain Connectivity Graphs (BCGs) from the tractography of DTI and used as input to GCN to explore spatial and frequency spectrum information. Laplacian and Fourier transform-based graph convolution are performed on BGG and BCGs, and then the multi-view pooling is done to aggregate multi-view outputs of GCNs together. The authors also used pairwise matching between outputs of multi-view GCN to increase the amount of data. In the final step, a fully connected softmax network is used for classification by using pairwise matching layer output. [23] performed PD diagnosis using a 3D Convolutional Neural Network(3D CNN) deep learning framework on 3D MRI and patient personal information such as age and gender. This work is primarily compared with [24,25] work for performance comparison. The main goal of this pilot study is to integrate feature extraction and model learning into one framework to improve performance. Skull stripping by using the Brain Extraction Technique (BET) with Statistical Parametric Mapping (SPM) algorithms were used to remove non-cerebral tissue in order to improve the speed and accuracy of this study. Flipping of the right and left hemispheres was done in the data augmentation process. In their study, the authors claimed that using age alone in logistic regression to predict PD achieved 72% accuracy. The authors also performed image occlusion analysis to study important parts of the brain in PD diagnosis and suggested those parts are the Basal Ganglia and Substantia Nigra, along with the Superior Parietal part on the right hemisphere of the brain. Their proposed approach achieved 100% accuracy in distinguishing PD from healthy. The limitation of this study is that methodology has been tested on a small sample size dataset.
In the [15] paper, the authors suggested that rs-fMRI can differentiate patients with early PD from healthy controls. Their study primarily consists of calculating connectivity scores based on three regions of interest such as the caudate, putamen, and pallidum. This paper also recommended the use of rs-fMRI as a biomarker for early PD detection. Recently, rs-fMRI data was used in the early diagnosis of PD using a long short-term memory (LSTM) model by [3]. This model achieved around 72% accuracy with a small size of a dataset consisting of only 84 subjects. All the above studies are performed using identical data acquisition conditions and on a single scanner at the same site. However, larger multi-scanner and multi-site data are required to achieve higher generalization by building a more robust model. There are a few multi-site research [26,27,28] which are based on fMRI. These studies are focused on controlling scanner variations, but these studies are performed using very small datasets and not for PD diagnosis. In addition to these studies, the ComBat harmonization approach [29] is also used for fMRI-derived connectivity measures in a multi-site study but can be used only on image-derived values and predefined relationships. Deep learning methods with the attention-based channel are used on large multi-site resting-state fMRI datasets without explicitly applying any scanner bias mitigation method [30] to generalize models to multi-site datasets. The federated learning approach [31] with two domain adaptation techniques, such as a mixture of experts domain adaptation to reduce the effect of a new domain on the global model and adversarial domain alignment to reduce the discrepancy between the source and target domains, are used to resolve domain shift issue observed in multi-site fMRI datasets.
There have been many methods proposed for classifying PD using machine learning and deep learning. However, class imbalance and scanner bias remain issues in PD classification. Moreover, a minimal amount of previous research has used rs-fMRI to classify PD based on data-driven models. To the best of our knowledge, the proposed approach is the first to use a convolutional neural network and convolutional-gated recurrent unit-convolutional neural network (ConvGRU-CNN) to identify Parkinson’s disease using Resting-State Functional Magnetic Resonance Imaging (rs-fMRI) data and patient information such as age and gender. Furthermore, a simple and effective distance correlation technique was used for the first time to address class imbalance and scanner bias issues in neuroimaging data which allows us to generalize the proposed model to larger multi-site and multi-scanner settings.

3. Materials and Methods

Deep learning techniques in the medical domain have received increasing interest due to their ability of accurately performing tasks and for extracting meaningful features in neuroimaging datasets. However, the performance of the deep learning models is impacted by the imbalanced and multi-scanner datasets issues. Imbalanced datasets exhibit skewed class distributions, whereas multi-scanner datasets exhibit data bias or confounding effects due to variance caused by differences in scanner and acquisition protocols. In this study, we aim to resolve two issues associated with rs-fMRI datasets of PD.
  • The dataset is highly imbalanced, which introduces a class bias issue. Hence, deep learning models trained on this dataset are biased towards the majority class. In our study, the majority class is PD patients.
  • In order to improve the performance of deep learning, the datasets from two different scanners and different studies and sites are combined. But this leads to scanner-variant features, and hence model predictions are dependent on a scanner.
Our proposed method focuses on using distance correlation in the objective function to mitigate bias toward majority class and scanner dependencies from features learned by deep learning. In this method, we improve the classification performance on the imbalanced dataset by decorrelating class bias from learned features by model. Scanner dependencies on model performance are mitigated by decorrelating scanner configuration information from learned features to create scanner-invariant features. The proposed method is simple yet more effective and can be applied to the mitigation of a wide range of data bias, confounders, class bias, or a combination of all bias issues, as shown in our previous work [32]. The proposed DcCNN framework in this study, on the other hand, is specifically designed to address scanner dependency and imbalance issues that are common in large clinical trials involving neuroimaging data. The proposed DcCNN model framework is shown in Figure 1. The framework mainly consists of three steps: data preprocessing, balancing the dataset using different sampling techniques and adding a new dataset, and classification using DcCNN. Finally, the model is evaluated using different evaluation metrics and t-distributed stochastic neighbor embedding (t-SNE) plots.

3.1. Decorrelated Convolutional Neural Networks

Decorrelated Convolutional Neural Networks (DcCNN) are implemented by applying the decorrelation loss function to CNN architectures. We propose our DcCNN architecture as in Figure 2. We can use one or combinations of any layer outputs and concatenate them as features for the decorrelation function depending on the complexity of the task. Distance correlation is used as a decorrelation function.
Distance correlation calculates the association between two arbitrary dimension variables using the distances. In our proposed approach, B 1 , . . . , p is the bias variable. F 1 , . . . , p is features extracted from DNN, and p is the total number of samples. The distance correlation is the square root of:
DC 2 ( B , F ) = V 2 ( B , F ) V 2 ( B , B ) V 2 ( F , F ) if V 2 ( B , B ) V 2 ( F , F ) > 0 0 else 0
where D C ( B , F ) is bounded between 0 and 1. D C ( B , F ) = 0 only if the variables B and F are independent. v 2 ( B , F ) is the distance covariance between a pair of variables, and v 2 ( B , B ) , v 2 ( F , F ) is the distance variance as defined in [33]. The distance covariance is normalized by the distance variances. The Pearson correlation coefficient [34] measures only linear dependencies but features extracted from CNN can have non-linear dependencies and hence distance correlation is more preferable since it measures not only linear but also non-linear dependencies between two random variables.
In our study, we use the squared distance correlation. Class weights are also used in the distance correlation loss function in some of the models to tackle the imbalance problem of scanner data. This function is minimized to reduce the distance correlation between features learned by the networks and the biases. This means that we want to find parameters of the network such that F features have a minimal distance correlation with the B bias variable. The decorrelation function term is added to the standard objective function for optimization.

3.2. Mitigation of Class Bias

Previous research work has shown that imbalanced datasets have a negative impact on the performance of CNNs due to bias towards the majority class. The PPMI dataset used in this study is highly imbalanced, and hence learning discriminating boundaries between Parkinson’s Disease (PD) subjects and healthy control subjects could be more challenging. Our DcCNN models introduce the idea of using the decorrelation loss function along with a data sampling technique to address the class bias problem in deep learning due to an imbalanced dataset.

3.2.1. PPMI Dataset and Preprocessing

The PPMI dataset consists of around 183 subjects with follow-up visits. This dataset includes 164 PD patients and 19 healthy control subjects. The demographic information and box plot for the PPMI dataset is shown in Table 1 and Figure 3, respectively. The time required to collect the rs-fMRI data for each subject is around 8 min 4 sec. During data collection, subjects are instructed to minimize all movements as well as to rest quietly with eyes open with a clear mind during the scan. They also instructed to not to fall asleep during this process. For a few subjects, data has been collected up to 1 to 3 years. In this study, imaging data associated with follow-ups are considered independent since they were scanned at different points in time. The size of each rs-fMRI slice is 68 x 66, and these images are grayscale. A total of 40 axial slices are captured for each subject. The scanner used to collect this dataset is the Tesla scanner manufactured by Siemens Medical Solutions. Functional scans are acquired using EPI sequence (Field Strength=3.0 tesla; Flip Angle=80.0 degree; Matrix X=476.0 pixels; Matrix Y=462.0 pixels; Mfg Model=TrioTim; Pixel Spacing X=3.2941 mm; Pixel Spacing Y=3.2941 mm; Pulse Sequence=EP; Volumes=210.0 time series ; Slice Thickness=3.2999 mm; TE=25.0 ms; TR=2400.0 ms).
The preprocessing of rs-fMRI is done using FSL v6.0 [35]. An FSL-BET extraction tool [36] is used to extract brain regions and remove skull and neck voxels. Motion correction is performed with the help of the FSL-MCFLIRT toolbox [37] to remove motion artifacts introduced by head movement over time. Spatial smoothing of each volume is implemented using a gaussian kernel of 5 mm full width at half maximum to reduce noise without reducing the true underlying signal. High-pass temporal filtering with a cut-off frequency of 0.01 HZ (sigma = 90 seconds) is also applied to remove low-level noise. Since the first ten slices and the last five slices of each subject contains no functional information, they are removed. The end results of this prepossessing for each subject are 66 x 66 PNG images with 25 slices and 210 volumes. The dataset is trained, validated, and tested using 70%, 15%, and 15% of the dataset, respectively. To improve the generalization ability of DcCNN models, data augmentation methods such as random rotation, random translation, and elastic deformations [38] are applied to the training dataset, which helps to make the model shift, rotation, and deformation invariant.
Since the number the subjects are less and to minimize the overfitting issue, we use each slice and volume as independent 2D images. Table 2 provides the number of 2D images in the PPMI datasets before oversampling, which clearly indicates an imbalanced dataset since the number of images for PD subjects is more as compared to healthy subjects. In order to resolve the class imbalance problem, different data oversampling techniques such as Random over-sampling (ROS), Synthetic Minority Over-Sampling Technique (SMOTE), and Stratified sampling are used. ROS [39] is a simple method in which samples from the monitory class are randomly increased by making exact copies of existing samples, whereas SMOTE synthetically creates new minority samples by interpolating between minority class samples [40] to balance class distribution. Disproportionate or Balanced Stratified Sampling is a sampling technique that randomly divides the data into different strata in such a way that it samples more data from the minority class samples to balance the samples in the strata [41]. The total number of 2D rs-fMRI images after applying oversampling techniques is shown in Table 2. We also implement CNN as a feature extraction technique before applying data sampling methods to evaluate the performance of the model on a class-imbalanced dataset [42]. A simple method, such as the weighted cross-entropy loss function, is also implemented to boost the performance of the DcCNN model by providing more emphasis on the minority class. Our proposed method is a fusion model (Oversampling + Weighted loss + Decorrelation Loss) which applies oversampling technique and includes weighted cross-entropy along with a decorrelation loss function to mitigate class bias.

3.2.2. Decorrelation and Weighted Loss in Objective Function

The models tend to predict most images and subjects as PD patients due to class bias. This class bias is mainly caused by the higher number of PD patients compared to healthy control subjects. In order to represent the class bias condition quantitatively and to use it as a bias variable in the decorrelation function, we use a dummy bias variable based on discrete uniform distribution. PD patients group will have a wider discrete uniform distribution than the healthy control group, which means the dummy variable would bias the classification results towards PD patients and create class bias. Minimizing the distance correlation between this dummy bias variable and features will result in balanced true positive and true negative rates.
We introduce the objective function, which consists of three main functions, namely, weighted cross entropy, decorrelation function, and regularizer L2 loss function to mitigate class bias, and is defined as:
J ( θ ) = min θ L W C E ( Y , Y ^ ) + λ DC 2 ( B , F ) + | | θ | | 2
L W C E in Equation 2 represents the weighted binary cross-entropy, and Y and Y ^ are true and classifier outputs, respectively. The weighted binary cross-entropy simply uses class weights to place more emphasis on minority class so that model learns equally from both classes. The decorrelation function is D C 2 ( B , F ) where B is the dummy class bias variable and F is features extracted from the model. The λ in the objective function is a hyperparameter that determines the relative importance of the decorrelation function in relation to the weighted cross-entropy loss function. The last term | | θ | | 2 is a regularizer L2 loss function in the objective function for weight decay purposes which helps to avoid overfitting issues. Optimizing the decorrelation function along with the weighted cross-entropy loss helps to mitigate class bias.

3.2.3. Experimental Setup

The DcCNN model is built by applying decorrelation-based optimization to customized CNN architecture and is trained from scratch. It consists of stacks of 3 convolutional and max-pooling layers with ReLU activation and batch normalization layer, two fully connected layers, and SoftMax as the classifier. These three convolutional layers have 32, 64, and 128 filters, respectively. We use a random oversampling technique to have an equal number of samples between two classes, i.e., PD and healthy control. We use the root means square propagation (RMSprop) optimizer for optimization and weighted cross-entropy and decorrelation function with λ = 0.2 as the loss function, as mentioned in the Section 3.2.2. Mini-batch size of 4000 and an exponential cyclical learning policy[43] which increases and decreases the learning rate by an exponential factor during the training is used. We observe that an exponential decaying learning rate leads to better generalization. For the decorrelation loss function, we use the outputs of fully connected layers and the softmax layer as features F. For the evaluation of the DcCNN model, we use different evaluation metrics such as sensitivity, specificity, precision, and balanced accuracy (BC) calculated from the confusion matrix.
All models in this study are implemented in python using the TensorFlow platform [44] and cuDNN library [45] on a Linux instance. These experiments are conducted on the AWS Deep Learning AMIs [46] to accelerate deep learning in the cloud using an Amazon EC2 P2 Instance. We use eight high-speed GPUs, parallel processing cores, and single and double-precision floating-point performance to train the dataset using deep learning. This helps to speed up the training processes.

3.3. Mitigation of Scanner Dependencies

A large and balanced neuroimaging dataset is important for deep learning and to improve its generalization ability. Hence, combining all available data from different sites and different scanners plays a vital part in achieving high performance. But it leads to an increase in variance due to differences in acquisition protocols and scanners. This includes scanner upgrades, scanner manufacturers, scanner strength, etc. We combine PPMI and healthy control subjects from the NIFD dataset to balance the dataset and improve the performance of deep learning to detect PD. The idea behind the proposed DcCNN models is to decorrelate the scanner information and features extracted from models to create scanner-invariant features. Three different variations of DcCNN models such as DcCNN, feature extraction + DcCNN(FE-DcCNN), which extracts features from scanner classifier and use it as bias variable in DcCNN, and decorrelated convolutional-gated recurrent unit DcCNN (ConvGRU-DcCNN) which performs temporal processing are proposed to mitigate the scanner dependencies.

3.3.1. NIFD Datasets and Preprocessing

We use only rs-fMRI data for healthy controls from the NIFD dataset, and this dataset consists of 215 healthy control subjects with follow-up visits. Just like the PPMI dataset, the demographic information and box plot for the NIFD dataset is shown in Table 1 and Figure 3, respectively. We can see that there is no significant difference in age distribution between PPMI and NIFD datasets. The size of the rs-fMRI slice is 92 x 92, and the slices are grayscale. A total of 36 axial slices are captured for each subject. The scanner used to collect this dataset is the Tesla scanner manufactured by Siemens Medical Solutions. Functional scans are acquired using EPI sequence (Field Strength=3.0 tesla; Flip Angle=80.0 degree; Matrix X=552.0 pixels; Matrix Y=552.0 pixels; Mfg Model=TrioTim; Pixel Spacing X=2.5 mm; Pixel Spacing Y=2.5 mm; Pulse Sequence=EP; Volumes=240.0 time series ; Slice Thickness=3.0 mm; TE=27.0 ms; TR=2000.0 ms). As we can see, the scanner manufacturer for the NIFD dataset is the same as the PPMI dataset. However, scanner configurations such as TE, TR, slice thickness, voxel size, and the total number of slices and volumes are different. This might introduce the variance related to scanners which will ultimately mask the discriminating features between PD and healthy controls. The rs-fMRI data were preprocessed using the same library and steps as the PPMI dataset. Since the first five slices and the last six slices of each subject contains no functional information in the NIFD dataset, they are removed. In order to have the same and fixed size as the PPMI dataset, we also deleted the first 30 volumes in the NIFD dataset. So the preprocessed NIFD dataset has 66 x 66 PNG images with 25 slices and 210 volumes for each subject. The NIFD dataset is also divided into 70% training, 15% validation, and 15% testing dataset. After combing the PPMI and NIFD datasets, a total of 2346750 images were produced, and the class distribution of the combined dataset is provided in Table 3.

3.3.2. Decorrelation in Objective Function

Deep learning models are extremely sensitive to non-biological variabilities, such as acquisition and scanner settings in the field of neuroimaging data. One of the important problems in large clinical trials is the scanner dependencies/bias. To deal with the scanner dependencies issue, we introduce three types of scanner bias variables which contain: (i) scanner voxel size, i.e., slice thickness and pixel spacing [47], (ii) features extracted from scanner classifier, and (iii) temporal standard deviation to represent scanner-to-scanner variability [28].
The models are trained with a combination of cross entropy loss L ( Y , Y ^ ) , the decorrelation loss D C c o n t r o l 2 ( B , F ) , and the regularizer L2 Loss | | θ | | 2 functions. This objective function can be expressed as:
J ( θ ) = min θ λ 1 L ( Y , Y ^ ) + λ 2 DC c o n t r o l 2 ( B , F ) + | | θ | | 2
where L is the softmax cross-entropy loss and | | θ | | 2 is regularizer L2 loss function. The decorrelation function is D C c o n t r o l 2 ( B , F ) where B is the scanner bias variable, and F is features extracted from the model, and subscript c o n t r o l indicates the decorrelation function is only applied to control subjects since the healthy control subjects had been scanned using both the scanners with different acquisition protocols, i.e., present in PPMI as well as NIFD datasets whereas PD subjects had been scanned using only one scanner out of two scanners, i.e., present in only PPMI dataset. This will help models to remove scanner-related information than removing the main task, i.e., PD detection-related information. The λ 1 and λ 2 in the objective function are hyperparameters that control the trade-off between the cross-entropy loss function and the decorrelation function. Since the number of healthy controls in the PPMI dataset is less compared to NIFD dataset, higher class weights are assigned to PPMI controls than NIFD controls to make decorrelation loss for PPMI controls larger than NIFD controls. This will help models to decorrelate features equally from both scanners and ultimately to resolve imbalanced scanner data problems for healthy controls.

3.3.3. Experimental Setup

We train three different DcCNN models with different architectures and scanner bias variables. The first model, abbreviated as DcCNN, has the same architecture as the DcCNN model used to mitigate class bias except for changes in the objective function to mitigate scanner dependencies, and there are three stack convolutional layers with 32,16, and 16 filters and followed by two hidden layers with 40 and 100 neurons. We train DcCNN with a mini-batch size of 4000 and an exponential cyclical leaning policy using an RMSProp optimizer for optimization with a decay of 0.005. Hyperparameters λ 1 = 0.5 for cross-entropy loss and λ 2 = 5.0 for decorrelation function are used to control the trade-off between two loss functions as mentioned in Section 3.3.2. The output of the first convolutional layer and fully connected layers are used as feature F, whereas slice thickness and pixel spacing are considered as scanner information and used as scanner bias variable B.
The second model (FE-DcCNN) has two models. The first model is built to predict the scanner, which we refer it as Feature Extraction(FE) model. The dataset used to train this model consists of only healthy control subjects from PPMI and NIFD datasets. Once the training is done, features are extracted from the FE model and used as a scanner bias variable in the second, i.e., the DcCNN model. Both FE and DcCNN models have the same architecture and the same training dataset. These models have five stacks of convolution, batch normalization, and max-pooling layers with ReLU activation, as shown in Figure 4 followed by two fully connected layers with 40 and 100 neurons. Both models use 32, 16, 16, 8, and 8 filters to extract discriminative features for the detection of PD. The output of the fifth convolutional layer in the FE model is used as scanner bias variable B, whereas the outputs of the fifth convolutional layer, along with fully connected layers in the DcCNN model, are used as feature F. The hyperparameters used in objective function are λ 1 = 0.05 and λ 2 = 0.95 . We have used the dropout of 0.2 in the first four convolutional layers to reduce the overfitting problem in the model, and the rest of the training configuration is the same as the first model DcCNN.
To make use of temporal information present in rs-fMRI, we implement the third model (ConvGRU-DcCNN) as shown in Figure 5. ConvGRU-DcCNN performs temporal processing first and uses a 3D image of size 66 x 66 x 210 as the input. Since we have to use temporal information for this model, we have to convert 2D images to 3D images, and that produces a total of 11175 images, including 5450 PD and 5725 healthy control PNG samples. The core architecture consists of convolutional gated recurrent operations (convGRU)[48] as the first layer and followed by the DcCNN architecture. ConvGRU is used to perform temporal processing. The DcCNN part consists of three convolutional layers with filters 16, 32, and 32, followed by two fully connected layers with 1000 and 500 neurons. The model is trained using an Adam optimizer with a mini-batch size of 256 and a learning rate (lr) scheduler with an initial lr of 0.001 with a decay of 0.5. In addition to this, an optimizer weight decay of 0.005 is used. We use λ 1 = 0.2 and λ 2 = 0.6 in objective function. For decorrrelation loss, we use the output of the second convolutional layer and first fully connected layer as features F, whereas temporal standard deviation (temporal fluctuations) is used as scanner bias B.

4. Results

In order to access whether DcCNN models perform better to mitigate class bias and scanner bias, we apply our method and baseline model to the single scanner imbalanced PPMI dataset and combination of multi-scanner PPMI and NIFD datasets, respectively.

Single Scanner Imbalanced Dataset

We access the performance of DcCNN to classify PD on PPMI imbalanced dataset. Our proposed fusion method aims to mitigate class bias. In order to show that DcCNN reduces the statistical dependence between features and class bias variables, we plot the distance correlation against iterations as shown in Figure 6. The plot shows that distance correlation decreases as the iteration increases for our fusion model as opposed to the oversampling method. We compare our fusion model with different CNN models and existing data-sampling techniques. The baseline model is a simple CNN model and has the same architecture as DcCNN, where no data-sampling technique and class bias mitigation methods are applied. The existing data-sampling techniques, [49] such as smote and oversampling, are implemented to address the class imbalance issue. We have also compared our model with a fusion of different combinations of existing class bias mitigation techniques, such as a fusion of oversampling and weighted loss functions, a fusion of feature extraction (FE) and smote, and stratified sampling.
The results of the holdout testing dataset for each method are displayed in Table 4 and the performance of imbalanced classification is measured specifically by sensitivity, specificity, precision, and balanced accuracy (BA). As we can see from the results, our proposed fusion method significantly increases balanced accuracy as compared to other methods. This, therefore, suggests that by using the decorrelation function along with oversampling technique and weighted loss function creates features that are invariant to class bias. The precision and specificity are higher for our fusion model compared to other methods. Lower sensitivity and higher specificity for our fusion model indicate that model prediction is not biased towards the majority class, i.e., PD subjects, whereas higher sensitivity and lower specificity for methods such as baseline, smote, FE+smote, stratified sampling, and oversampling indicate model prediction is highly biased towards PD class. The lower values of specificity for these model clearly demonstrates that the classification of control subjects are almost based on random chance. For all these existing models, we notice that the weighted loss function helps the model to improve balanced accuracy. Figure 7 shows the confusion matrix of the baseline model and our proposed DcCNN model to classify slices into the PD and healthy controls. The confusion matrix for the baseline model clearly indicates that all subjects are classified as PD due to the presence of class bias, while our proposed model classifies both classes almost equally by mitigating this class bias. Figure 8 illustrates the ROC curve of different methods. From this graph, we observe the superior performance of our fusion DcCNN model over traditional data-sampling methods. In both balanced accuracy and ROC metrics, our DcCNN fusion method clearly outperforms other methods.
Due to a few labeled rs-fMRI images available at the subject level in the PPMI dataset, we train the models at the slice level, which increase the data and avoid overfitting issue. The above reported results are for the slice-level classification. Since in the medical field, subject-level PD classification is important, we propose a global subject-level classification by using a max-wins voting strategy. In this strategy, all slices for each subject are classified, and then the class with the maximum votes for a given subject determines the global subject classification. This will allow to classify and assign PD or healthy control labels to a given subject. As shown in Table 5, applying the max-wins voting strategy for subject-level classification significantly improved accuracy by correcting a small number of misclassified slices. Our fusion DcCNN model achieves a subject-level balanced accuracy of 67% after applying a max-wins voting strategy.

Multi-Scanner Datasets

A DcCNN, an FE-DcCNN, and a ConvGRU-DcCNN are the three main models presented in this subsection to create features that are invariant to scanner and acquisition protocols while maintaining the performance of PD classification. This will reduce the influence of the scanner on model predictions. We compare our proposed models with baseline models. In a similar way to the previous imbalanced dataset experiment, baseline models such as CNN and ConvGRU-CNN share the same architecture as DcCNN and ConvGRU-DcCNN, respectively, without any scanner bias mitigation methods being incorporated. Figure 9 shows that statistical dependence between learned features and scanner bias decreases as iteration increases for ConvGRU-DcCNN as opposed to the baseline ConvGRU-CNN model. The purpose of this plot is to observe the trend rather than to show the true difference between the distance correlation values of the ConvGRU-DcCNN model and the baseline model since weights have been assigned to calculate the decorrelation function used in ConvGRU-DcCNN versus the baseline model. We also evaluate the performance of scanner bias mitigation techniques using accuracy, scanner classification accuracy, and error rate for each dataset/scanner (since each dataset represents one scanner). The scanner classification accuracy indicates the scanner information present in features that influence the decision of model prediction.
Table 6 presents the performance of different types of DcCNN models on a multi-scanner testing dataset. As expected, the scanner classification accuracy for baseline models is 100% which means models make predictions based on features that are dependent on the scanner and not on the main task of PD recognition. With the FE model, the scanner classification was performed using only healthy control groups, and scanner-relevant features were extracted for the FE-DcCNN model to use as scanner bias variables. FE model results in an accuracy of 92.6% at the slice level and 100% at the subject level. All three types of DcCNN models reduce the scanner classification accuracy compared to baseline models indicating that DcCNN reduces scanner dependencies fairly with a slight reduction in accuracy. Accuracy for baseline models is high due to the fact that all PD subjects in the dataset had been scanned on one scanner, and the majority of the healthy control subjects had been scanned on another scanner. Thus, it makes the task more harder, and we can see a reduction in accuracy for DcCNN when compared with baseline models. Hence, for our multi-scanner dataset, we can say that raw classification accuracy is not only a consideration. The error rates for both datasets (i.e., both scanners) increase for DcCNN models indicating scanner bias removal is performed. ConvGRU-DcCNN model performs poorer compared to the DcCNN and FE-DcCNN models in terms of accuracy, possibly because it removes information related to the main task while reducing scanner dependencies. The ConvGRU-DcCNN performs poorly, most likely due to four factors: removal of PD-relevant features, decorrelation penalization leading to a negative influence on predictive accuracy, reduction in data size, and inclusion of PD information in scanner bias variable. DcCNN and FE-DcCNN models have similar accuracy while substantially decreasing the scanner dependencies.
Finally, these above results are further supported by t-distributed stochastic neighbor embedding (t-SNE) visualizations of the learned fully connected layer features as shown in Figure 10. Since only healthy control subjects had been scanned using both scanners and present in both datasets, we plot tSNE visualization for the healthy control group. We observe that the baseline models, such as CNN and ConvGRU-CNN, have a clear association with the scanner since the PPMI dataset is grouped on the right side, while the NIFD dataset is grouped on the left side of Figure 10. But scanner features become jointly embedded for DcCNN, FE-DcCNN, and ConvGRU-DcCNN models, which indicate no apparent bias towards the scanner. This suggests that our proposed DcCNN models successfully create features that are invariant with respect to scanners without compromising the performance of PD classification. For the FE-DcCNN model, data points in Figure 10 are largely indistinguishable across all two scanners compared to the DcCNN model in Figure 10. This can also be confirmed by scanner classification accuracy for FE-DcCNN is lower than the DcCNN model. Similar to FE-DcCNN, the features learned by the ConvGRU-DcCNN model spread uniformly across all scanners, indicating successful mitigation of scanner dependencies, but the ConvGRU-DcCNN model results in a drastic loss in accuracy, indicating the removal of information related to the main task.
For subject-level classification, we use the same max-wins voting strategy as defined for a single scanner imbalanced dataset. The above-reported results for multi-scanner datasets are for the subject-level classification. The evaluation metrics for slice-level and subject-level classification are summarized in Table 7. All these results show that the FE-DcCNN model not only successfully mitigates the scanner bias but also achieves high performance in comparison with DcCNN and ConvGRU-DcCNN models, respectively. FE-DcCNN model achieves a subject-level accuracy of 78% after applying a max-wins voting strategy and scanner classification accuracy of 80%.

5. Discussion

This study presents a decorrelation-based bias mitigation technique that can be applied to deep learning architectures such as CNN, ConvGRU, and fusion methods to mitigate not only class bias but also scanner bias by creating class and scanner invariant features. We have demonstrated that our decorrelation technique can be applied to any architecture and provides a high level of flexibility. The hyperparameter λ > 0 plays a vital role in deciding the importance of decorrelation and regular loss function. When λ = 0 , it means it is a baseline model with no bias mitigation technique applied. Extreme high values of λ will cause unstable training and poor classification performance. Hence, finding optimal values for hyperparameters λ is crucial and can be achieved by trying different values of λ . We notice that increasing the batch size improves the stability of the decorrelation function during training. In addition, it provides unbiased estimates of distance covariance when the batch size is larger. Similar to hyperparameter λ , we experience that finding the optimal combination of the output of layers as feature F helps in improving the performance of the bias mitigation technique. The choice of feature F depends on the type of bias mitigation technique and model architecture. As stated in our previous work [32], the bias variable B should provide more precise bias-relevant information.
The rs-fMRI original imaging data is organized in 4D matrices, which contain spatial as well as temporal information. Due to high dimensionality and small dataset size, deep learning models face problems like overfitting when 4D data is used. This would only be solved by adding more data. However, 2D and 3D rs-fMRI data used in this study show the applicability of using this data for PD classification while significantly mitigating the class and scanner bias. We also find that the ConvGRU-DcCNN model almost exhibits similar performance with and without class weights for the decorrelation function since using temporal information reduces the size of the dataset and, ultimately, the imbalance ratio between PPMI controls and NIFD controls. Out of the three types of scanner bias variables used to mitigate scanner bias, features extracted from the scanner classifier bias variable provide more accurate scanner-relevant information since the FE-DcCNN model yields optimal results, which reduces scanner dependence without removing much PD-specific information.
The results from the class bias mitigation study show that not only we are able to achieve high performance than existing traditional approaches but also successfully mitigate bias towards the majority class. We have also shown that the same decorrelation function technique can be used to remove scanner dependencies. The scanner classification accuracy and tSNE plots confirm that scanner dependencies have been reduced. Since existing harmonization and domain adaptation methods approach scanner mitigation differently than our method, we do not directly compare them to our method. Additionally, our proposed model differs from previous methods in that it is designed for rs-fMRI data collected from a single scanner with identical acquisition protocols and a single site rather than from multi-scanner and multi-site data. The presented method also suggests that combining multi-scanner data and increasing the size of the dataset improve the performance of PD classification compared to single scanner imbalanced data.

6. Conclusions

The performance of deep learning models is highly impacted by bias variability and class imbalance present in data. We introduce a novel decorrelation approach, which reduces the distance correlation between the features learned by deep learning models and biases. The main goal of this approach is to mitigate scanner dependencies and class bias which will help the model to generalize to multi-scanner and multi-center datasets. The proposed framework includes extensive data preprocessing modules and decorrelated deep learning-based classifiers to distinguish PD patients from healthy controls using rs-fMRI data. We evaluated our four different models on single scanner imbalanced and multi-scanner datasets. On a single scanner imbalanced PPMI datasets, our proposed DcCNN model significantly improves performance by alleviating bias toward the majority class, whereas our proposed FE-DcCNN model produces scanner-invariant features without affecting accuracy much on multi-scanner PPMI and NIFD datasets. Furthermore, the rs-fMRI dataset is used for the first time to train CNN models for PD classification. These simple yet efficient proposed DcCNN models perform better than previous approaches and baseline models to mitigate the bias and require fewer hyperparameters to optimize. We additionally verify from the results that using a multi-scanner and larger dataset results in significantly better performance when compared with a single scanner imbalanced dataset. This study also demonstrated that subject-level classification results in an even more robust model and improves accuracy using a max-wins voting strategy.
An immediate next step would be using advanced visualization techniques such as saliency maps, DeepLIFT, and occlusion maps. A combination of these precise and detail-oriented visualization techniques may help in characterizing fMRI biomarkers for PD. Our proposed models also demonstrate the potential for predicting stages in the progression of PD, which could be addressed in future studies. Additional future direction works also include collecting a larger dataset and more information related to patients along with individual rs-fMRI slices and temporal information to achieve higher accuracy and reliability. A larger dataset and increased computation complexity will also enhance the overall performance of 4D-DcCNN models by taking advantage of using the inherent spatial-temporal information in 4D rs-fMRI data. Moreover, it would be interesting to investigate how by applying the proposed decorrelation approach to pre-trained models and to different types of data variations and biases would impact performance.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, P.P.; methodology, P.P.; software, P.P.; validation, P.P.; formal analysis, P.P.; investigation, P.P..; resources, P.P.; data curation, P.P.; writing—original draft preparation, P.P.; writing—review and editing, P.P and R.F..; visualization, P.P.; supervision, R.F.; funding acquisition, P.P and R.F.. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Harrisburg University of Science and Technology.

Acknowledgments

We are grateful to PPMI and NIFD consortium for making the imaging data available. We thank Harrisburg University of Science and Technology for their support and AWS funding.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PD Parkinson’s Disease
rs-fMRI resting-state functional MRI
CNN Convolutional Neural Networks
DcCNN Decorrelated Convolutional Neural Networks
PPMI Parkinson’s Progression Markers Initiative
NIFD FTLDNI - frontotemporal lobar degeneration neuroimaging initiative
t-SNE t-distributed stochastic neighbor embedding
t-SNE t-distributed stochastic neighbor embedding
FE-DcCNN Feature Extraction-DcCNN

References

  1. Postuma, R.B.; Berg, D.; Adler, C.H.; Bloem, B.R.; Chan, P.; Deuschl, G.; Gasser, T.; Goetz, C.G.; Halliday, G.; Joseph, L.; others. The new definition and diagnostic criteria of Parkinson’s disease. The Lancet Neurology 2016, 15, 546–548. [Google Scholar] [CrossRef]
  2. Rubbert, C.; Mathys, C.; Jockwitz, C.; Hartmann, C.J.; Eickhoff, S.B.; Hoffstaedter, F.; Caspers, S.; Eickhoff, C.R.; Sigl, B.; Teichert, N.A.; others. Machine-learning identifies Parkinson’s disease patients based on resting-state between-network functional connectivity. The british journal of radiology 2019, 92, 20180886. [Google Scholar] [CrossRef] [PubMed]
  3. Guo, X.; Tinaz, S.; Dvornek, N.C. Early Disease Stage Characterization in Parkinson’s Disease from Resting-state fMRI Data Using a Long Short-term Memory Network. arXiv preprint, arXiv:2202.12715 2022.
  4. Kim, S.; Kwon, S.H.; Kam, T.I.; Panicker, N.; Karuppagounder, S.S.; Lee, S.; Lee, J.H.; Kim, W.R.; Kook, M.; Foss, C.A.; Shen, C.; Lee, H.; Kulkarni, S.; Pasricha, P.J.; Lee, G.; Pomper, M.G.; Dawson, V.L.; Dawson, T.M.; Ko, H.S. Transneuronal Propagation of Pathologic α-Synuclein from the Gut to the Brain Models Parkinson’s Disease. Neuron 2019, pp. 1–15. [CrossRef]
  5. Braak, H.; Del Tredici, K.; Rüb, U.; De Vos, R.A.; Steur, E.N.J.; Braak, E. Staging of brain pathology related to sporadic Parkinson’s disease. Neurobiology of aging 2003, 24, 197–211. [Google Scholar] [CrossRef] [PubMed]
  6. Beilina, A.; Cookson, M.R. Genes associated with Parkinson’s disease: regulation of autophagy and beyond. Journal of neurochemistry 2016, 139, 91–107. [Google Scholar] [CrossRef] [PubMed]
  7. El-Agnaf, O.M.; Salem, S.A.; Paleologou, K.E.; Curran, M.D.; Gibson, M.J.; Court, J.A.; Schlossmacher, M.G.; Allsop, D. Detection of oligomeric forms of α-synuclein protein in human plasma as a potential biomarker for Parkinson’s disease. The FASEB journal 2006, 20, 419–425. [Google Scholar] [CrossRef] [PubMed]
  8. Trivedi, D.K.; Sinclair, E.; Xu, Y.; Sarkar, D.; Walton-Doyle, C.; Liscio, C.; Banks, P.; Milne, J.; Silverdale, M.; Kunath, T. ; others. Discovery of volatile biomarkers of Parkinson’s disease from sebum. ACS Central Science, 2019. [Google Scholar]
  9. Son, S.J.; Kim, M.; Park, H. Imaging analysis of Parkinson’s disease patients using SPECT and tractography. Scientific reports 2016, 6, 38070. [Google Scholar] [CrossRef] [PubMed]
  10. Cochrane, C.J.; Ebmeier, K.P. Diffusion tensor imaging in parkinsonian syndromes: a systematic review and meta-analysis. Neurology 2013, 80, 857–864. [Google Scholar] [CrossRef] [PubMed]
  11. Atkinson-Clement, C.; Pinto, S.; Eusebio, A.; Coulon, O. Diffusion tensor imaging in Parkinson’s disease: Review and meta-analysis. NeuroImage: Clinical 2017, 16, 98–110. [Google Scholar] [CrossRef] [PubMed]
  12. Vaillancourt, D.; Spraker, M.; Prodoehl, J.; Abraham, I.; Corcos, D.; Zhou, X.; Comella, C.; Little, D. High-resolution diffusion tensor imaging in the substantia nigra of de novo Parkinson disease. Neurology 2009, 72, 1378–1384. [Google Scholar] [CrossRef]
  13. Zheng, Z.; Shemmassian, S.; Wijekoon, C.; Kim, W.; Bookheimer, S.Y.; Pouratian, N. DTI correlates of distinct cognitive impairments in Parkinson’s disease. Human brain mapping 2014, 35, 1325–1333. [Google Scholar] [CrossRef]
  14. Saeed, U.; Compagnone, J.; Aviv, R.I.; Strafella, A.P.; Black, S.E.; Lang, A.E.; Masellis, M. Imaging biomarkers in Parkinson’s disease and Parkinsonian syndromes: current and emerging concepts. Translational neurodegeneration 2017, 6, 8. [Google Scholar] [CrossRef]
  15. Rolinski, M.; Szewczyk-Krolikowski, K.; Menke, R.A.; Filippini, N.; Heise, V.; Zamboni, G.; Wilcock, G.; Talbot, K.; Hu, M.; Mackay, C. Resting State Fmri Discerns Early Parkinson’s From Controls. J Neurol Neurosurg Psychiatry 2014, 85, e4–e4. [Google Scholar] [CrossRef]
  16. Li, K.; Su, W.; Li, S.H.; Jin, Y.; Chen, H.B. Resting State fMRI: A Valuable Tool for Studying Cognitive Dysfunction in PD. Parkinson’s Disease 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
  17. Wilson, H.; Dervenoulas, G.; Pagano, G.; Koros, C.; Yousaf, T.; Picillo, M.; Polychronis, S.; Simitsi, A.; Giordano, B.; Chappell, Z. ; others. Serotonergic pathology and disease burden in the premotor and motor phase of A53T α-synuclein parkinsonism: a cross-sectional study. The Lancet Neurology, 2019. [Google Scholar]
  18. Zhang, Y.C.; Kagen, A.C. Machine learning interface for medical image analysis. Journal of digital imaging 2017, 30, 615–621. [Google Scholar] [CrossRef] [PubMed]
  19. Shi, D.; Zhang, H.; Wang, G.; Wang, S.; Yao, X.; Li, Y.; Guo, Q.; Zheng, S.; Ren, K. Machine Learning for Detecting Parkinson’s Disease by Resting-State Functional Magnetic Resonance Imaging: A Multicenter Radiomics Analysis. Frontiers in aging neuroscience 2022, 14, 806828. [Google Scholar] [CrossRef] [PubMed]
  20. Jiji, W.; Rajesh, A.; Lakshmi, M.M. Diagnosis of Parkinson’s Disease Using EEG and fMRI 2022.
  21. Choi, H.; Ha, S.; Im, H.J.; Paek, S.H.; Lee, D.S. Refining diagnosis of Parkinson’s disease with deep learning-based interpretation of dopamine transporter imaging. NeuroImage: Clinical 2017, 16, 586–594. [Google Scholar] [CrossRef] [PubMed]
  22. Zhang, X.; He, L.; Chen, K.; Luo, Y.; Zhou, J.; Wang, F. Multi-View Graph Convolutional Network and Its Applications on Neuroimage Analysis for Parkinson’s Disease. arXiv preprint, arXiv:1805.08801 2018.
  23. Esmaeilzadeh, S.; Yang, Y.; Adeli, E. End-to-End Parkinson Disease Diagnosis using Brain MR-Images by 3D-CNN. arXiv preprint, arXiv:1806.05233 2018.
  24. Ahmed, M.N.; Farag, A.A. Two-stage neural network for volume segmentation of medical images. Proceedings of International Conference on Neural Networks (ICNN’97). IEEE, 1997, Vol. 3, pp. 1373–1378.
  25. Gil, D.; Manuel, D.J. Diagnosing Parkinson by using artificial neural networks and support vector machines. Global Journal of Computer Science and Technology 2009, 9. [Google Scholar]
  26. Stöcker, T.; Schneider, F.; Klein, M.; Habel, U.; Kellermann, T.; Zilles, K.; Shah, N.J. Automated quality assurance routines for fMRI data applied to a multicenter study. Human brain mapping 2005, 25, 237–246. [Google Scholar] [CrossRef] [PubMed]
  27. Friedman, L.; Glover, G.H.; Krenz, D.; Magnotta, V.; BIRN, T.F. Reducing inter-scanner variability of activation in a multicenter fMRI study: role of smoothness equalization. Neuroimage 2006, 32, 1656–1668. [Google Scholar] [CrossRef]
  28. Friedman, L.; Glover, G.H.; Consortium, F.; others. Reducing interscanner variability of activation in a multicenter fMRI study: controlling for signal-to-fluctuation-noise-ratio (SFNR) differences. Neuroimage 2006, 33, 471–481. [Google Scholar] [CrossRef]
  29. Yu, M.; Linn, K.A.; Cook, P.A.; Phillips, M.L.; McInnis, M.; Fava, M.; Trivedi, M.H.; Weissman, M.M.; Shinohara, R.T.; Sheline, Y.I. Statistical harmonization corrects site effects in functional connectivity measurements from multi-site fMRI data. Human brain mapping 2018, 39, 4213–4227. [Google Scholar] [CrossRef] [PubMed]
  30. Zhang, T.; Li, C.; Li, P.; Peng, Y.; Kang, X.; Jiang, C.; Li, F.; Zhu, X.; Yao, D.; Biswal, B.; others. Separated channel attention convolutional neural network (SC-CNN-attention) to identify ADHD in multi-site rs-fMRI dataset. Entropy 2020, 22, 893. [Google Scholar] [CrossRef] [PubMed]
  31. Li, X.; Gu, Y.; Dvornek, N.; Staib, L.H.; Ventola, P.; Duncan, J.S. Multi-site fMRI analysis using privacy-preserving federated learning and domain adaptation: ABIDE results. Medical Image Analysis 2020, 65, 101765. [Google Scholar] [CrossRef] [PubMed]
  32. Patil, P.; Purcell, K. Decorrelation-Based Deep Learning for Bias Mitigation. Future Internet 2022, 14, 110. [Google Scholar] [CrossRef]
  33. Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. The annals of statistics 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
  34. Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. The American Statistician 1988, 42, 59–66. [Google Scholar] [CrossRef]
  35. Smith, S.M.; Jenkinson, M.; Woolrich, M.W.; Beckmann, C.F.; Behrens, T.E.; Johansen-Berg, H.; Bannister, P.R.; De Luca, M.; Drobnjak, I.; Flitney, D.E.; others. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004, 23, S208–S219. [Google Scholar] [CrossRef]
  36. Smith, S.M. Fast robust automated brain extraction. Human brain mapping 2002, 17, 143–155. [Google Scholar] [CrossRef]
  37. Jenkinson, M.; Bannister, P.; Brady, M.; Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002, 17, 825–841. [Google Scholar] [CrossRef] [PubMed]
  38. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.
  39. Batista, G.E.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD explorations newsletter 2004, 6, 20–29. [Google Scholar] [CrossRef]
  40. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research 2002, 16, 321–357. [Google Scholar] [CrossRef]
  41. Saleema, J.; Bhagawathi, N.; Monica, S.; Shenoy, P.D.; Venugopal, K.; Patnaik, L.M. Cancer prognosis prediction using balanced stratified sampling. arXiv preprint, arXiv:1403.2950 2014.
  42. Salekshahrezaee, Z.; Leevy, J.L.; Khoshgoftaar, T.M. Feature extraction for class imbalance using a convolutional autoencoder and data sampling. 2021 IEEE 33rd International Conference on Tools with Artificial Intelligence (ICTAI). IEEE, 2021, pp. 217–223.
  43. Smith, L.N. Cyclical learning rates for training neural networks. 2017 IEEE winter conference on applications of computer vision (WACV). IEEE, 2017, pp. 464–472.
  44. Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Goodfellow, I.; Harp, A.; Irving, G.; Isard, M.; Jia, Y.; Jozefowicz, R.; Kaiser, L.; Kudlur, M.; Levenberg, J.; Mané, D.; Monga, R.; Moore, S.; Murray, D.; Olah, C.; Schuster, M.; Shlens, J.; Steiner, B.; Sutskever, I.; Talwar, K.; Tucker, P.; Vanhoucke, V.; Vasudevan, V.; Viégas, F.; Vinyals, O.; Warden, P.; Wattenberg, M.; Wicke, M.; Yu, Y.; Zheng, X. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software available from tensorflow.org.
  45. Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. cudnn: Efficient primitives for deep learning. arXiv preprint, arXiv:1410.0759 2014.
  46. Deep learning ami - Developer Guide.
  47. Shafiq-ul Hassan, M.; Zhang, G.G.; Latifi, K.; Ullah, G.; Hunt, D.C.; Balagurunathan, Y.; Abdalah, M.A.; Schabath, M.B.; Goldgof, D.G.; Mackin, D.; others. Intrinsic dependencies of CT radiomic features on voxel size and number of gray levels. Medical physics 2017, 44, 1050–1062. [Google Scholar] [CrossRef] [PubMed]
  48. Bengs, M.; Gessert, N.; Schlaefer, A. 4d spatio-temporal deep learning with 4d fmri data for autism spectrum disorder classification. arXiv preprint, arXiv:2004.10165 2020.
  49. Leevy, J.L.; Khoshgoftaar, T.M.; Bauder, R.A.; Seliya, N. A survey on addressing high-class imbalance in big data. Journal of Big Data 2018, 5, 1–30. [Google Scholar] [CrossRef]
Preprints 101996 g001
Figure 1. General Framework of the proposed method for classification of Parkinson’s Disease.
Figure 1. General Framework of the proposed method for classification of Parkinson’s Disease.
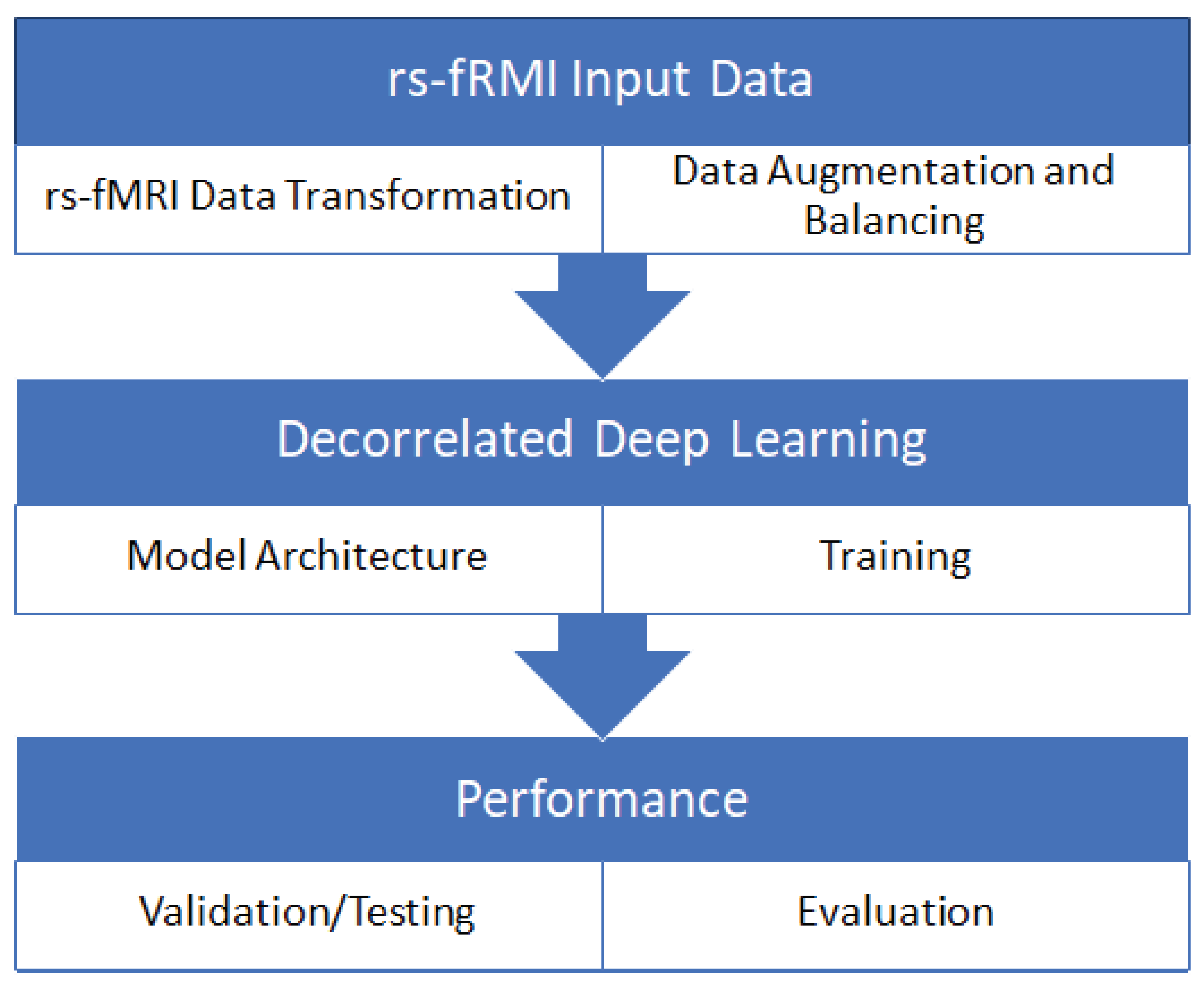
Preprints 101996 g001
Preprints 101996 g002
Figure 2. Proposed DcCNN architecture. Red dashed lines denote the output of convolutional layers l, which are combined together to represent learned features. Green dashed lines indicate the start of the learning process, where backward arrows show back-propagation using their respective gradient values, while forward arrows show forward paths with updated parameters. Network parameters are updated as per the objective function.
Figure 2. Proposed DcCNN architecture. Red dashed lines denote the output of convolutional layers l, which are combined together to represent learned features. Green dashed lines indicate the start of the learning process, where backward arrows show back-propagation using their respective gradient values, while forward arrows show forward paths with updated parameters. Network parameters are updated as per the objective function.
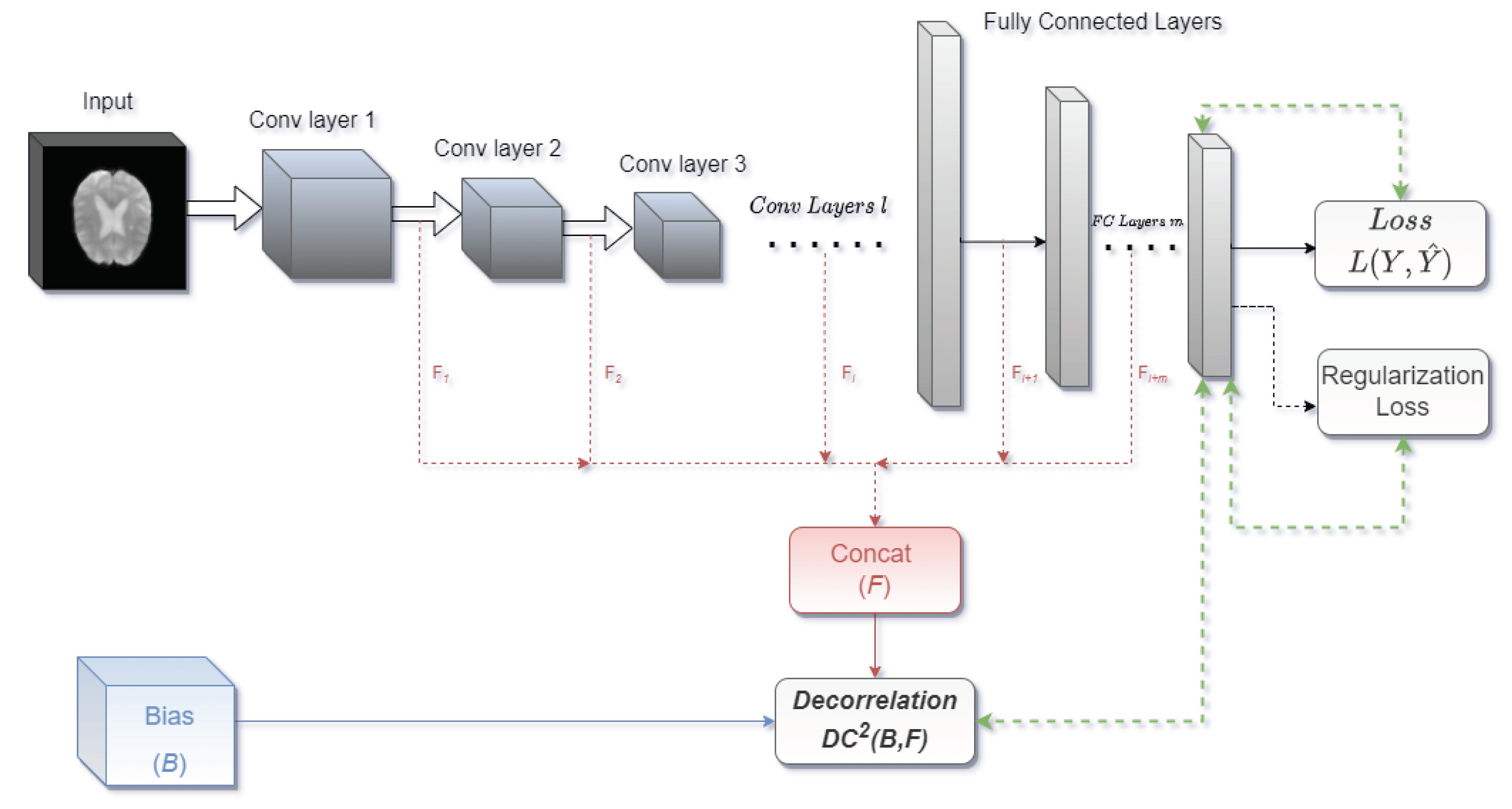
Preprints 101996 g002
Preprints 101996 g003
Figure 3. The boxplot of Age for Male and Female for PPMI and NIFD Datasets.
Figure 3. The boxplot of Age for Male and Female for PPMI and NIFD Datasets.
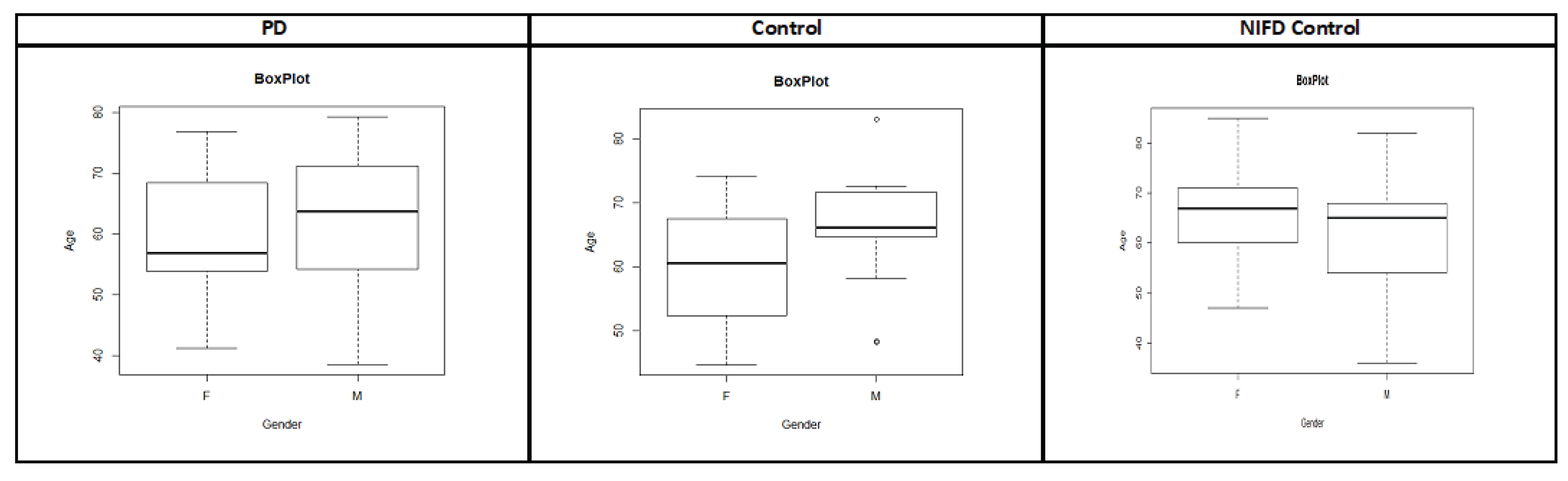
Preprints 101996 g003
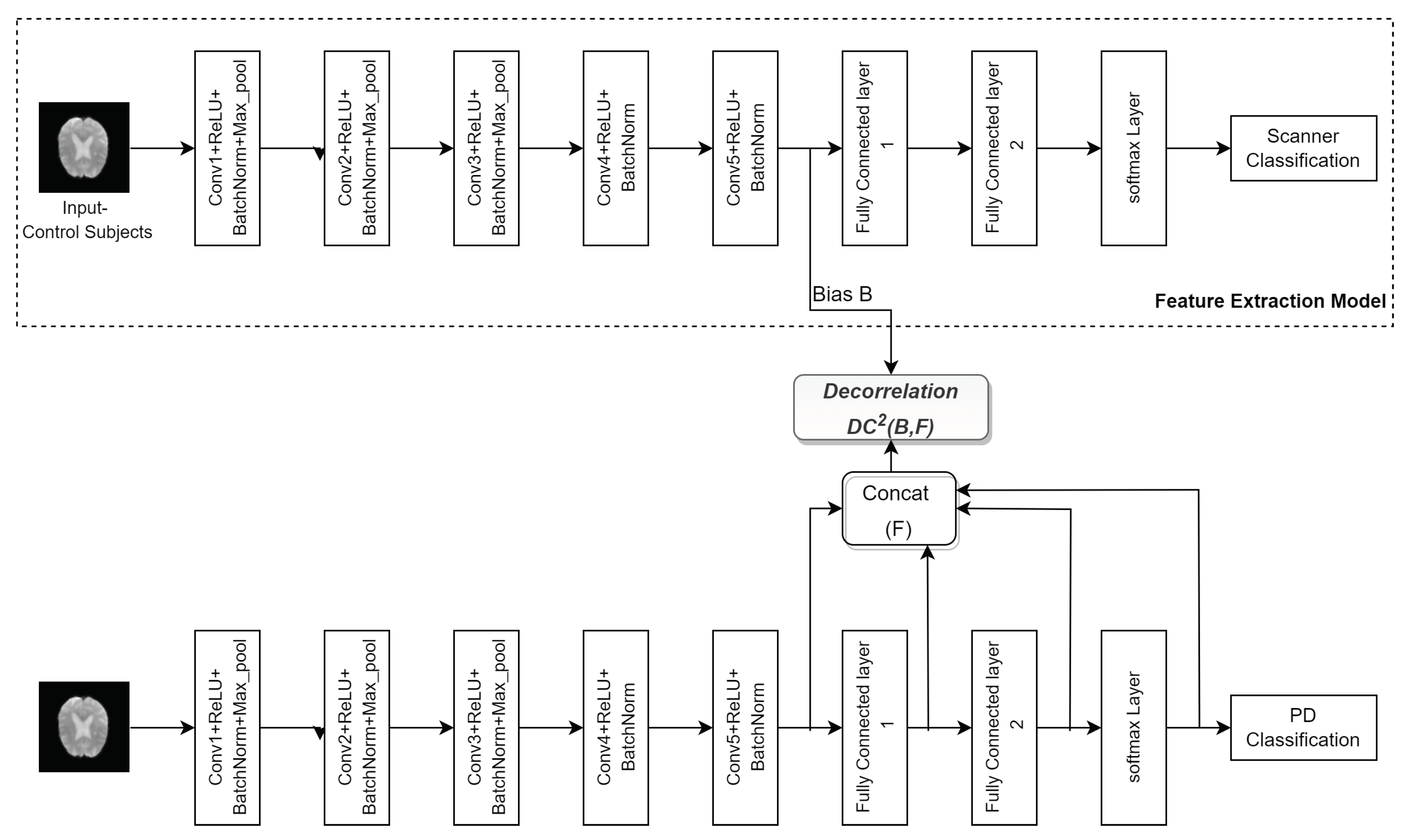
Preprints 101996 g004
Figure 4. The architecture of the FE-DcCNN model.
Figure 4. The architecture of the FE-DcCNN model.
Preprints 101996 g004
Preprints 101996 g005
Figure 5. The architecture of the ConvGRU-DcCNN model.
Figure 5. The architecture of the ConvGRU-DcCNN model.
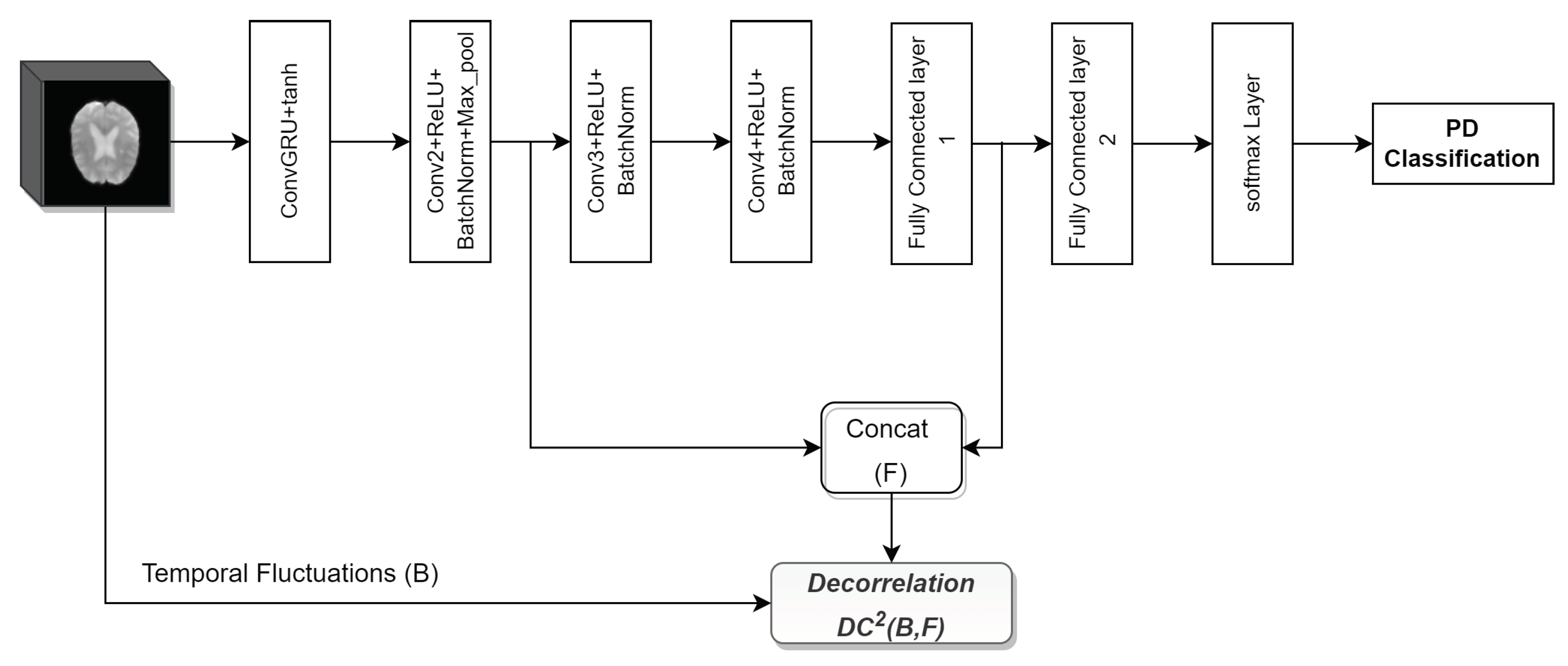
Preprints 101996 g005
Preprints 101996 g006
Figure 6. Distance correlation between learned features and class bias for the imbalanced dataset.
Figure 6. Distance correlation between learned features and class bias for the imbalanced dataset.
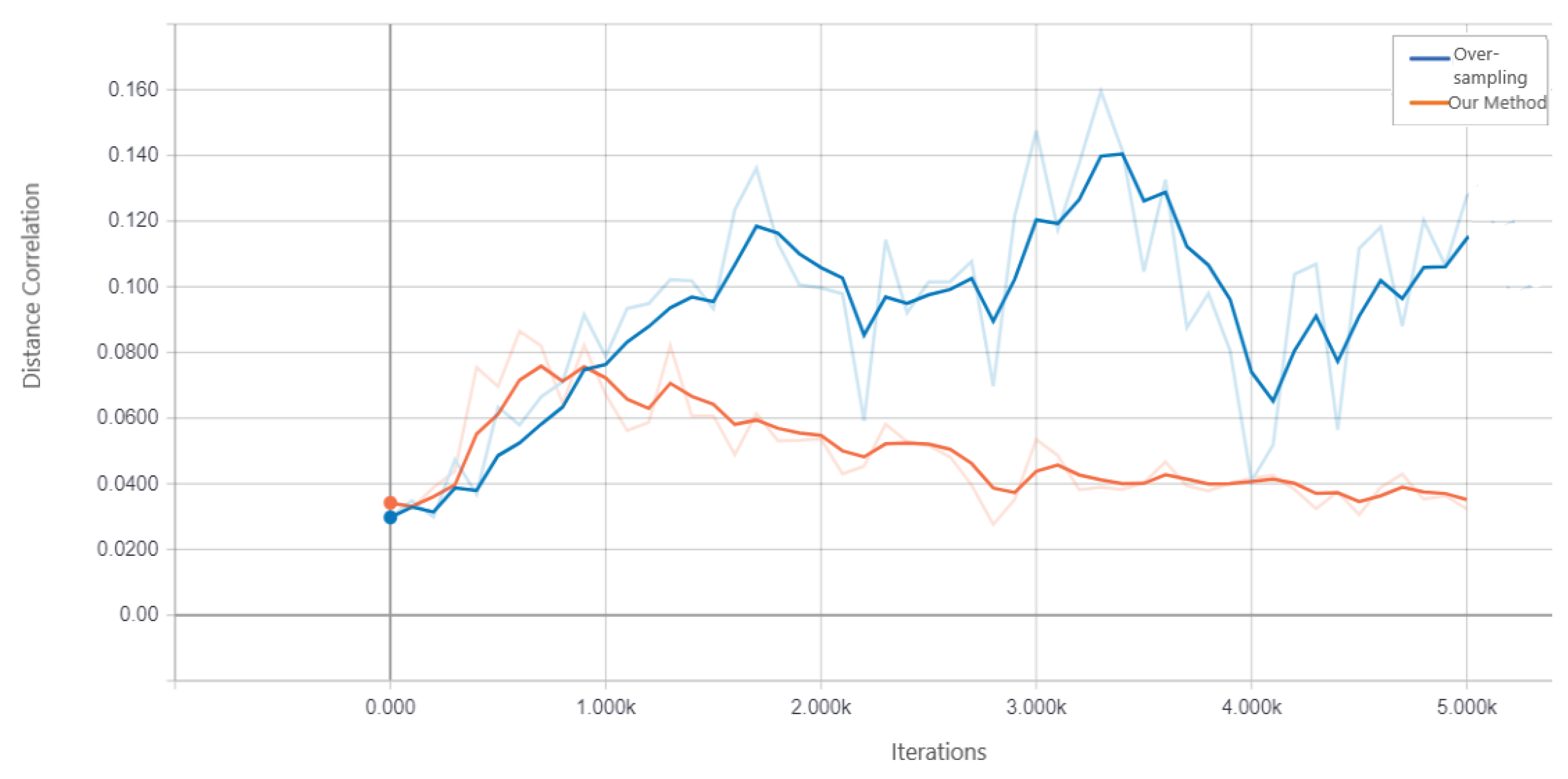
Preprints 101996 g006
Preprints 101996 g007
Figure 7. Confusion matrix of baseline and our method(ROS + weighted loss + DcCNN) with two classes for imbalanced PPMI testing dataset(Slice-level PD recognition).
Figure 7. Confusion matrix of baseline and our method(ROS + weighted loss + DcCNN) with two classes for imbalanced PPMI testing dataset(Slice-level PD recognition).
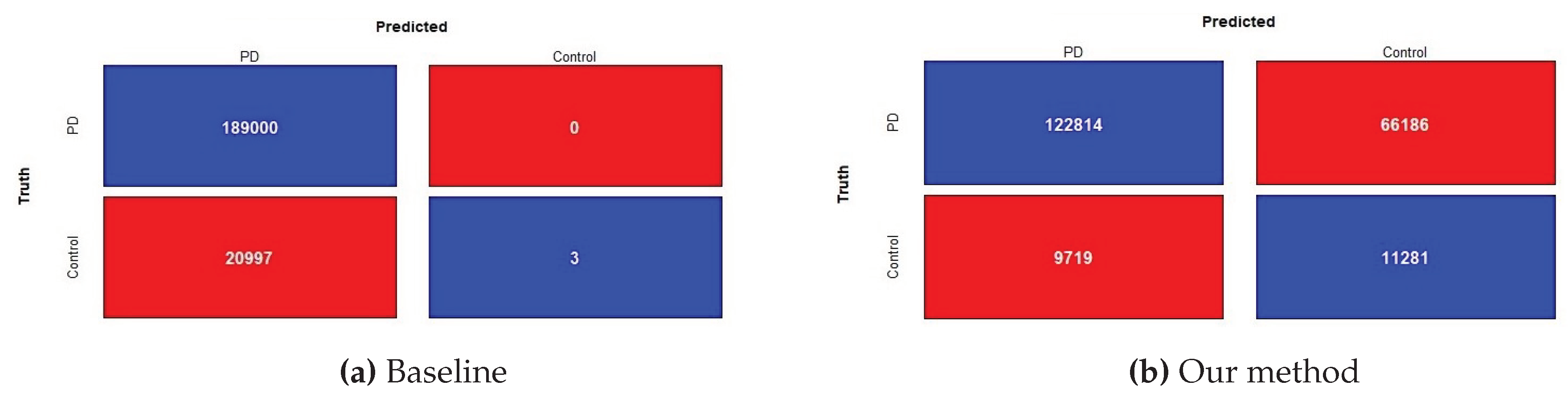
Preprints 101996 g007
Preprints 101996 g008
Figure 8. ROC curves of different methods for imbalanced dataset. The X-axis represents the False Positive Rate, and Y-axis represents the True Positive Rate.
Figure 8. ROC curves of different methods for imbalanced dataset. The X-axis represents the False Positive Rate, and Y-axis represents the True Positive Rate.
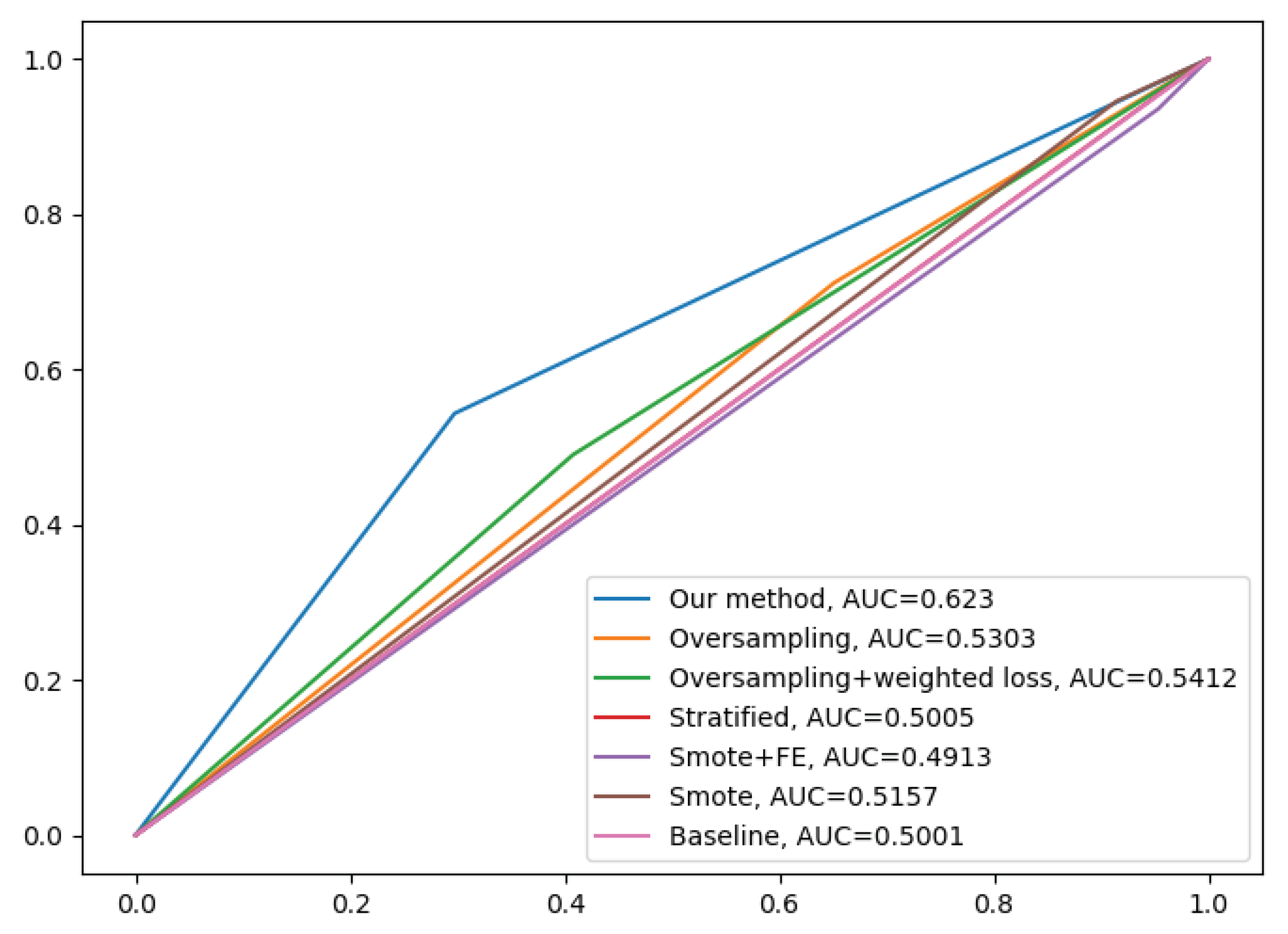
Preprints 101996 g008
Preprints 101996 g009
Figure 9. Decorrelation between learned features and scanner bias for baseline ConvGRU-CNN and ConvGRU-DcCNN models.
Figure 9. Decorrelation between learned features and scanner bias for baseline ConvGRU-CNN and ConvGRU-DcCNN models.
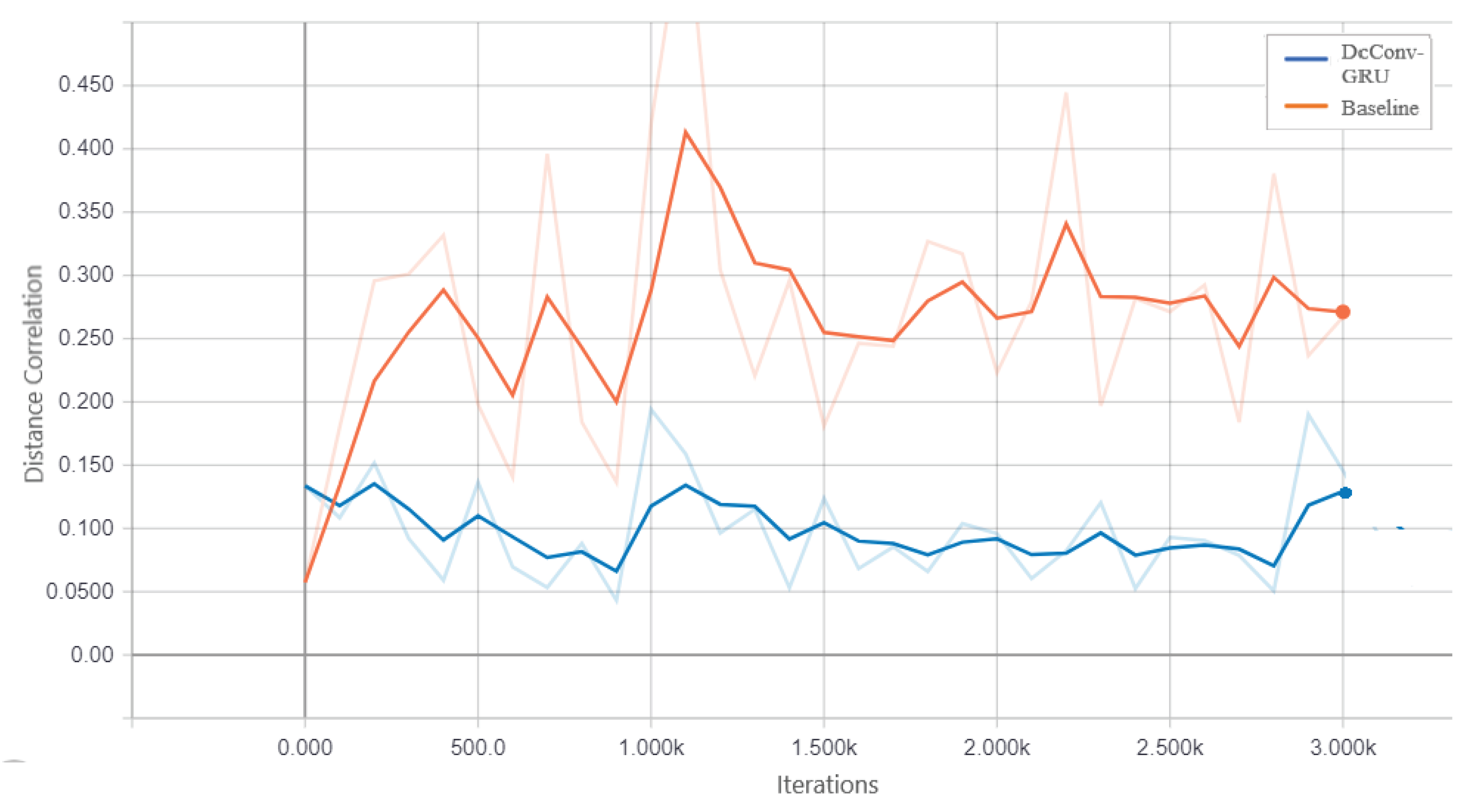
Preprints 101996 g009
Preprints 101996 g010
Figure 10. tSNE plot of the learned fully connected layer features for healthy control data. The yellow color indicates the NIFD dataset scanner, and the purple color indicates the PPMI dataset scanner.
Figure 10. tSNE plot of the learned fully connected layer features for healthy control data. The yellow color indicates the NIFD dataset scanner, and the purple color indicates the PPMI dataset scanner.
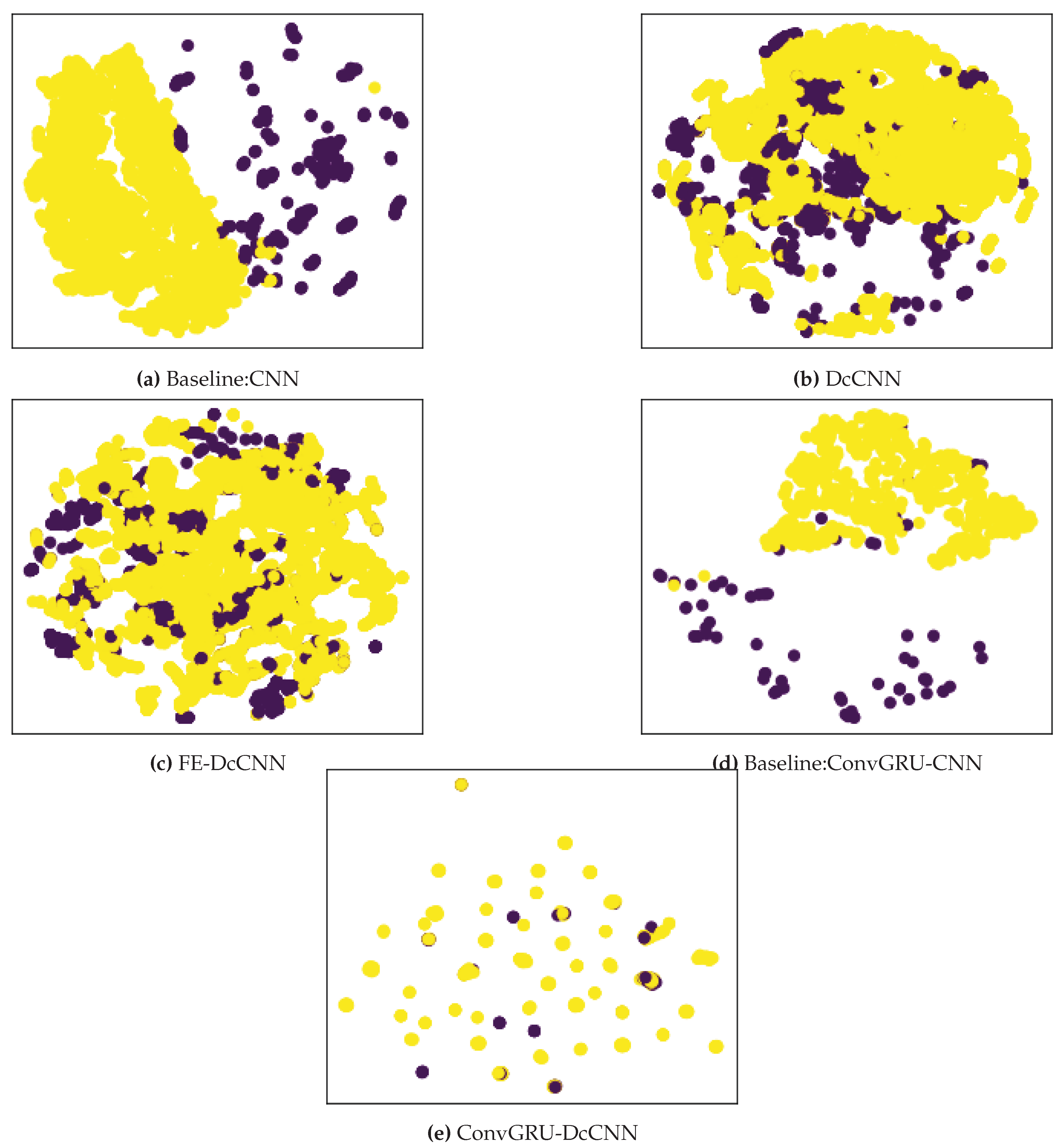
Preprints 101996 g010
Table 1. Demographic information of Two datasets, PPMI and NIFD.
Table 1. Demographic information of Two datasets, PPMI and NIFD.
Datasets Total Subjects Group Subjects Gender Subjects Mean of Age SD of Age Min of Age Max of Age
PPMI 183 PD 164 Male 111 62.55 10.53 38.6 79.3
Female 53 59.65 9.36 41.2 76.9
Control 19 Male 15 65.98 9.04 48.1 83.1
Female 4 59.95 12.1 44.6 74.2
NIFD 215 Control 215 Male 129 62.6 8.45 36 82
Female 86 65.9 7.95 47 85
Table 2. Class Distribution of PPMI training dataset Before and After Oversampling.
Table 2. Class Distribution of PPMI training dataset Before and After Oversampling.
Class Number of Images
Before OverSampling After OverSampling
PD 818,790 818,790
Control 90,930 818,790
Table 3. Class Distribution of Combined PPMI and NIFD datasets.
Table 3. Class Distribution of Combined PPMI and NIFD datasets.
Class Number of Images
Training Validation Testing
PD 813,750 141,750 189,000
Control 819,000 178,500 204,750
Table 4. Performance Evaluation of PD Classification for imbalanced PPMI Dataset using different methods.
Table 4. Performance Evaluation of PD Classification for imbalanced PPMI Dataset using different methods.
Methods Sensitivity Specificity Precision BA
Baseline 100.00% 0.01% 90.00% 50.01%
Smote 94.60% 8.60% 90.30% 51.60%
FE + Smote 93.60% 4.70% 89.80% 49.15%
Stratified 95.60% 4.50% 90.00% 50.05%
Oversampling 71.20% 34.90% 90.80% 53.05%
Oversampling + weighted loss 49.00% 59.20% 91.50% 54.10%
Our method 58.47% 60.37% 93.07% 59.42%
Table 5. Sensitivity(%), Specificity(%), Precision(%), and Balanced accuracies(%) of slicewise and subjectwise PD recognition for imbalanced PPMI testing dataset. Results are mean across three initializations with a 95% confidence interval.
Table 5. Sensitivity(%), Specificity(%), Precision(%), and Balanced accuracies(%) of slicewise and subjectwise PD recognition for imbalanced PPMI testing dataset. Results are mean across three initializations with a 95% confidence interval.
Methods Sensitivity Specificity Precision BA
Slice-level 58.47±0.05 60.37±0.08 93.07±0.01 59.42±0.03
Subject-level 66.67±0.08 66.67±0.20 95.13±0.03 66.67±0.10
Table 6. Performance Evaluation of Baseline Models and DcCNN models using PPMI and NIFD datasets.
Table 6. Performance Evaluation of Baseline Models and DcCNN models using PPMI and NIFD datasets.
Models Accuracy Scanner
Classification
Accuracy		 NIFD
Error rate		 PPMI
Error rate
Baseline Models:
CNN 94.70% 100.00% 0.00 0.00
ConvGRU-CNN 94.70% 100.00% 0.00 0.00
Our Models:
DcCNN 80.47% 83.10% 0.25 0.06
FE-DcCNN 77.80% 80.43% 0.30 0.17
ConvGRU-DcCNN 65.77% 63.13% 0.46 0.28
Table 7. Sensitivity(%), Specificity(%), Precision(%), F1(%), and accuracies(%) of slicewise and subjectwise PD recognition for PPMI and NIFD testing Datasets. Results are mean across three initializations with a 95% confidence interval.
Table 7. Sensitivity(%), Specificity(%), Precision(%), F1(%), and accuracies(%) of slicewise and subjectwise PD recognition for PPMI and NIFD testing Datasets. Results are mean across three initializations with a 95% confidence interval.
Models Methods Sensitivity Specificity Precision F1 Accuracy
DcCNN Slicewise 76.87+0.06 78.00±0.08 76.90±0.05 76.60±0.01 77.47±0.02
Subjectwise 79.63+0.09 81.20±0.10 80.43±0.06 79.57±0.03 80.47±0.03
FE-DcCNN Slicewise 83.40+0.14 71.00±0.06 72.70±0.02 77.20±0.05 76.95±0.03
Subjectwise 80.53+0.16 75.20±0.05 75.03±0.01 77.13±0.07 77.80±0.05
ConvGRU-DcCNN Slicewise/
Subjectwise		 74.07+0.03 58.13±0.01 62.00±0.002 67.50±0.01 65.77±0.01
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated