Efficient Pipeline Conflict Resolution for Layered QC-LDPC Decoders in OFDM-PON

Preprint

Article

Efficient Pipeline Conflict Resolution for Layered QC-LDPC Decoders in OFDM-PON

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhijie Wang

,Zhengjun Xu,Kun Chen,Yuanzhe Qu,Xiaoqun Liu,Yingchun Li,

Junjie Zhang^*

Zhijie Wang

,Zhengjun Xu,Kun Chen,Yuanzhe Qu,Xiaoqun Liu,Yingchun Li,

Junjie Zhang^*

This version is not peer-reviewed

Submitted:

21 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts

Abstract

Pipeline conflicts arising from data dependencies are a common issue encountered in the hardware implementation of layered QC-LDPC decoders. This paper proposes an efficient layered decoding architecture to reduce pipeline conflicts without introducing stall cycles, by reordering the processing order offline and using the patch method based on variable-to-check message. The experimental results on the LDPC code of the IEEE802.16 standard in the OFDM-PON system demonstrate that the proposed architecture has a sensitivity improvement of 0.125 dBm and 0.375 dBm, respectively, compared with our previous work and the method described in the other work.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The explosive growth of bandwidth-intensive services such as ultra-high definition live streaming, Cloud Office applications, and 5G technology has posed further challenges to the "last mile" optical access network of the information superhighway. Orthogonal Frequency Division Multiplexing Passive Optical Access Network (OFDM-PON) [1] is considered one of the reliable solutions for the next-generation optical access network due to its cost-effectiveness, high-frequency spectral efficiency, flexible bandwidth allocation, and robustness to dispersion. However, during high-speed data transmission, signal attenuation and noise interference are unavoidable issues. To further enhance transmission reliability, we can introduce forward error correction (FEC) codes.

The low-density parity-check (LDPC) code exhibits the remarkable property of approaching the Shannon limit, making it one of the most promising forward error correction codes currently available [2]. Thus it is widely used in many fields, such as deep-space communications [3], storage devices [4], and 5G NR [5]. Many works have also introduced its practical applications in optical access networks [6,7,8,9]. LDPC codes can be divided into random code, cyclic code, and quasi-cyclic code (QC-LDPC) based on their type characteristics. The original LDPC code is random, and its parity-check matrix (PCM) rarely has structural characteristics, leading to highly complex encoding and decoding procedures. Cyclic code has obvious structural characteristics and can theoretically greatly simplify the hardware implementation process. However, existing cyclic code generally has a large row weight, which makes the implementation of the decoder complex and subtle. And it generally has a high minimum distance, resulting in a very low decoding threshold. QC-LDPC is composed of zero submatrices of the same size and cyclic shift submatrices, which offers favorable structural characteristics and can simplify the design of encoders and decoders. Therefore, QC-LDPC is a popular choice for the OFDM-PON system currently.

Among numerous decoding algorithms, the layered decoding schedule is more popular due to its superior decoding convergence [10]. During the hardware implementation process, the quasi-cyclic characteristic of QC-LDPC code is highly suitable for partially parallel layered decoding architectures [11], which can achieve a compromise between hardware resource consumption and throughput. However, certain QC-LDPC decoders aim to further improve the throughput by increasing the system's operation frequency, which can be achieved by inserting more pipeline stages. Yet, the presence of data dependencies in the iterative decoding process across contiguous layers poses a challenge, as the introduction of pipelines significantly exacerbates the issue of data updating conflicts in message memory [12]. When the next layer needs to utilize the updated messages, the corresponding update process for the previous layer has not yet been completed. This dilemma is recognized as the pipeline conflict problem.

1.1. Related Works

Traditional processing schemes merely introduce multiple stall cycles during the processing stage and wait for the completion of the update of log-likelihood ratios (LLRs) at the previous layer before proceeding to the next layer. The number of stall cycles inserted is often substantial, leading to a significant reduction in decoding throughput.

In [13,14], partial pipeline conflicts can be reduced by rearranging the processing order of the submatrix using techniques such as graph coloring or solving the traveling salesman problem. Although these methods can reduce the corresponding stall cycles, complete elimination is not achievable. To completely eliminate the stall cycles, the method from [15] employs a flooding decoding mechanism when pipeline conflicts occur, while using a layered mechanism at other times. However, this approach incurs a significant performance loss compared to the theoretical layered decoding algorithm, necessitating more iterations. Similarly, the residue-based layered schedule [16] continuously accumulates and stores the contributions in registers when pipeline conflicts arise, adding them to the corresponding LLRs at the end of the pipeline problem. [17] proposes to split the matrix for the LDPC codes in the DVB-T2 protocol, which can reduce the degree of parallelism and significantly reduce the number of conflicts. The remaining conflicts are avoided by adding the equivalent matrix of puncture sites. However, decreased parallelism translates to lower throughput.

In our previous work [18], we introduced a priority-based layered decoder with a double update queue. The occurrence of conflicts is reduced by reordering the submatrix processing within each layer. Additionally, the processing is divided into overlapping and non-overlapping paths in parallel according to the arrangement order, greatly reducing the processing delay. For unavoidable conflicts, corresponding gains will be calculated and added to recent usage to minimize performance losses. However, when the number of pipeline stages inserted into the decoder exceeds the maximum check node weight, the double update queue will be completely invalidated.

1.2. Overview and Contribution

To address the aforementioned issues, building upon our previous work, this paper introduces an ideal pipeline QC-LDPC layered decoder without a stall cycle. The main contributions are:

(1): A decoding method based on patched variable-to-check message is proposed. When necessary, it is preferable to read the un-updated LLR and apply a patch to the variable-to-check message, rather than waiting to read the updated LLR. This approach effectively reduces pipeline conflicts.
(2): The proposed hardware structure allows the sequence of LLR reading and LLR writing back to be different during each layer’s decoding, effectively eliminating pipeline conflicts caused by overlapping submatrices among three or more successive layers of traditional decoding.
(3): We implement the proposed decoding architecture on hardware and conduct experiments on the OFDM-PON platform. The experimental results demonstrate that the proposed architecture has a performance improvement of 0.125 dBm compared to our previous work [17] and 0.375 dBm compared to the residual-based decoder in literature [18] under the maximum 10 iterations of decoding and a 64-QAM modulation format.

The content is organized as follows: In the second section, a brief overview of the layered decoding algorithm and the pipeline conflict issue encountered during hardware implementation is provided. The third section delves into the detailed design of the proposed decoder architecture. The fourth section outlines the experiment conducted on the OFDM-PON platform and presents an analysis of the experimental results. Finally, a brief summary of this article is provided in the fifth section.

2. Conflict Problems in Pipelined Layered Decoders

2.1. Layered Decoding Algorithm

The layered decoding is adopted by most practical systems because each layer can utilize the latest a-posteriori(AP) LLR when updating, which shows better decoding convergence performance.

For the layered decoding algorithm, each row of the check matrix

H_{(N - K) \times N}

can be viewed as a component code, and each component code shares the same variable node information. Each component code is decoded in turn, and each decoding process includes three steps: variable node update, check node update, and a-posteriori(AP) LLR update.

In an additive white Gaussian noise (AWGN) channel, the initialization of LLR of the variable node

V_{i}

is given as

{L L R}_{v}^{i n i t} = l o g \frac{P (x_{v} = 0 | y_{v})}{P (x_{v} = 1 | y_{v})} = \frac{2 y_{v}}{σ^{2}}

(1)

where

x_{v}

represents the transmitted bit of variable node

V_{i}

σ^{2}

represents the noise variance,

P (x_{v} = x | y_{v})

represents the probability that

x_{v}

is equal to the value x (x = 0 or x = 1), and

y_{v}

represents the received symbol.

The check-to-variable message(

L_{i \to j}

) is initialized to 0.

L_{i \to j}^{(0, i)} = 0

(2)

During the update process of i-th layer in the it-th iteration, the variable-to-check messages(

L_{j \to i}

) are calculated using the check-to-variable message(

L_{i \to j}

) from the previous (it-1)-th iteration and a posteriori probability LLR.

L_{j \to i}^{(i t, i)} = L L R (j) - L_{i \to j}^{(i t - 1, i)}

(3)

When all the variable-to-check messages(

L_{j \to i}

) in a layer are available, check-to-variable message(

L_{i \to j}

) can be generated with MSA by the following equation (4)

L_{i \to j}^{(i t, i)} = \prod_{j^{'} \in V_{i} \ j} s g n (L_{j^{'} \to i}^{(i t, i)}) \cdot m a x (\min_{j^{'} \in V_{i} \ j} (| L_{j^{'} \to i}^{(i t, i)} |))

(4)

Although MSA reduces the complexity of hardware implementation, it causes a degradation in decoding performance. To compensate for the loss of performance, the magnitude of the check-to-variable message(

L_{i \to j}

) can be multiplied with a normalization factor α or subtracted an offset factor β, which are referred to as OMSA and NMSA algorithms respectively, as proposed in (5) and (6).

L_{i \to j}^{(i t, i)} = α \cdot \prod_{j^{'} \in V_{i} \ j} s g n (L_{j^{'} \to i}^{(i t, i)}) \cdot m a x (\min_{j^{'} \in V_{i} \ j} (| L_{j^{'} \to i}^{(i t, i)} |))

(5)

L_{i \to j}^{(i t, i)} = \prod_{j^{'} \in V_{i} \ j} s g n (L_{j^{'} \to i}^{(i t, i)}) \cdot m a x (\min_{j^{'} \in V_{i} \ j} (| L_{j^{'} \to i}^{(i t, i)} |) - β, 0)

(6)

The LLR for variable node

V_{i}

can be updated once the corresponding check-to-variable message(

L_{i \to j}

) have been calculated as given by (7)

L L R (j) = L_{j \to i}^{(i t, i)} + L_{i \to j}^{(i t, i)}

(7)

When an iteration is done, the codeword is judged with the soft decision based on the sign of LLR. The decided codeword C and the parity-check matrix H are used to calculate the syndrome

S = C \times H^{T}

. If

C \times H^{T} = 0

or the decoding has reached the set maximum number of iterations, then this decoding will end.

To sum up, the decoding pseudocode based on OMSA used in this article is shown as follows.

Initialization:

set LLR(j)(j = 1,2,…,N) to Channel LLR

set

L_{i \to j}^{(0, i)}

to 0

set it and syndrome to 1

While (it >

i t_{m a x}

) or (syndrome = 0)

For it = 1 : (N - K)

For

j \in V_{i}

L_{j \to i}^{(i t, i)} = L L R (j) - L_{i \to j}^{(i t - 1, i)}

End for

For

j \in V_{i}

L_{i \to j}^{(i t, i)} = \prod_{j^{'} \in V_{i} \ j} s g n (L_{j^{'} \to i}^{(i t, i)}) \cdot m a x (\min_{j^{'} \in V_{i} \ j} (| L_{j^{'} \to i}^{(i t, i)} |) - β, 0)

L L R (j) = L_{j \to i}^{(i t, i)} + L_{i \to j}^{(i t, i)}

End for

Hard decision: C = -sign(

L L R

)

Compute syndrome =

C \times H^{T}

it = it +1

End for

End while

2.2. Pipeline Conflict Problem

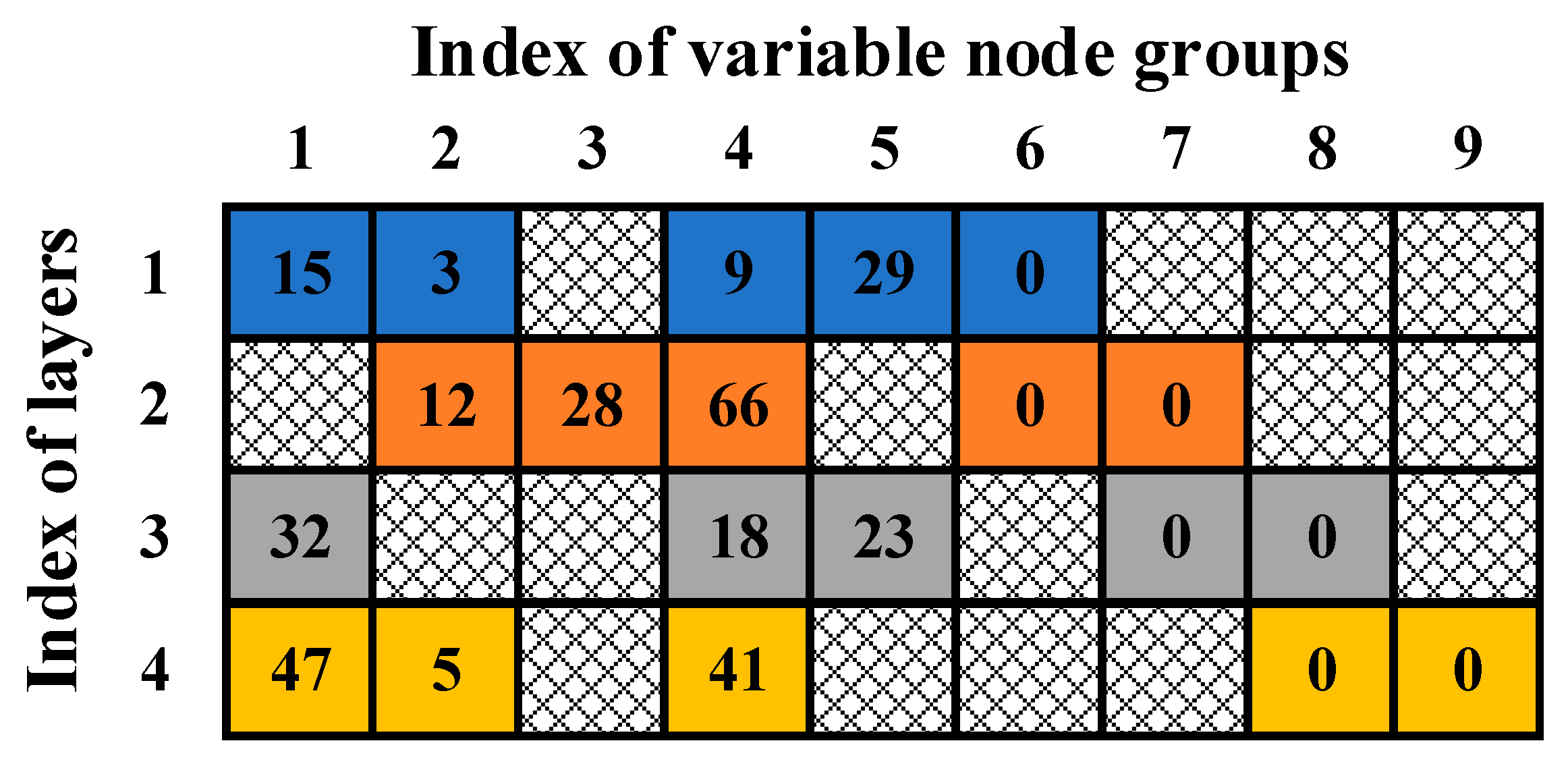
Figure 1 illustrates an example of a QC-LDPC PCM consisting of 4×9 cyclic submatrices. The grid boxes represent the zero matrices, while the other boxes represent the matrices offset according to the standard matrix. To fully leverage the cyclic characteristics of submatrices in QC-LDPC, partially parallel layered decoders with parallelism equal to the submatrix size are commonly employed. In hardware implementation, incorporating pipeline operations is an effective approach to enhance the system's operating frequency.

According to Chapter 2.1, the layered decoder algorithm can be divided into several main steps based on the processing sequence. These steps include obtaining LLR, updating variable-to-check messages, updating check-to-variable messages, and updating LLR. Usually, several pipeline stages are inserted between these steps. As shown in Figure 2, reading LLRs from the hardware storage space and writing updated LLRs back to the corresponding storage space are the first and last stage of the pipeline, respectively. In theory, the previous layer should provide updated values for the next layer. The corresponding submatrix of the lines in the diagram shows that the next layer needs to read the update value, but the update value in the previous layer has not been calculated. This situation leads to the pipeline conflict that we mentioned above.

3. Reordered QC_LDPC Decoder with Patched Variable-to-Check Message

3.1. Inter-Layer and Intra-Layer Processing Scheduling

In essence, the pipeline conflict problem is caused by the overlap of non-zero submatrices in the PCM. Therefore, the primary approach to resolving pipeline conflicts is to minimize the number of overlapping submatrices as much as possible. According to the principle of layered decoding, the adjustment of the processing order between layers does not change the decoding performance of the decoder. The number of overlapping submatrices can be reduced by adjusting the processing order between layers properly. Especially for those PCMs whose non-zero submatrices are not particularly dense, reasonable adjustment of the processing order between the layers can even completely eliminate pipeline conflicts. 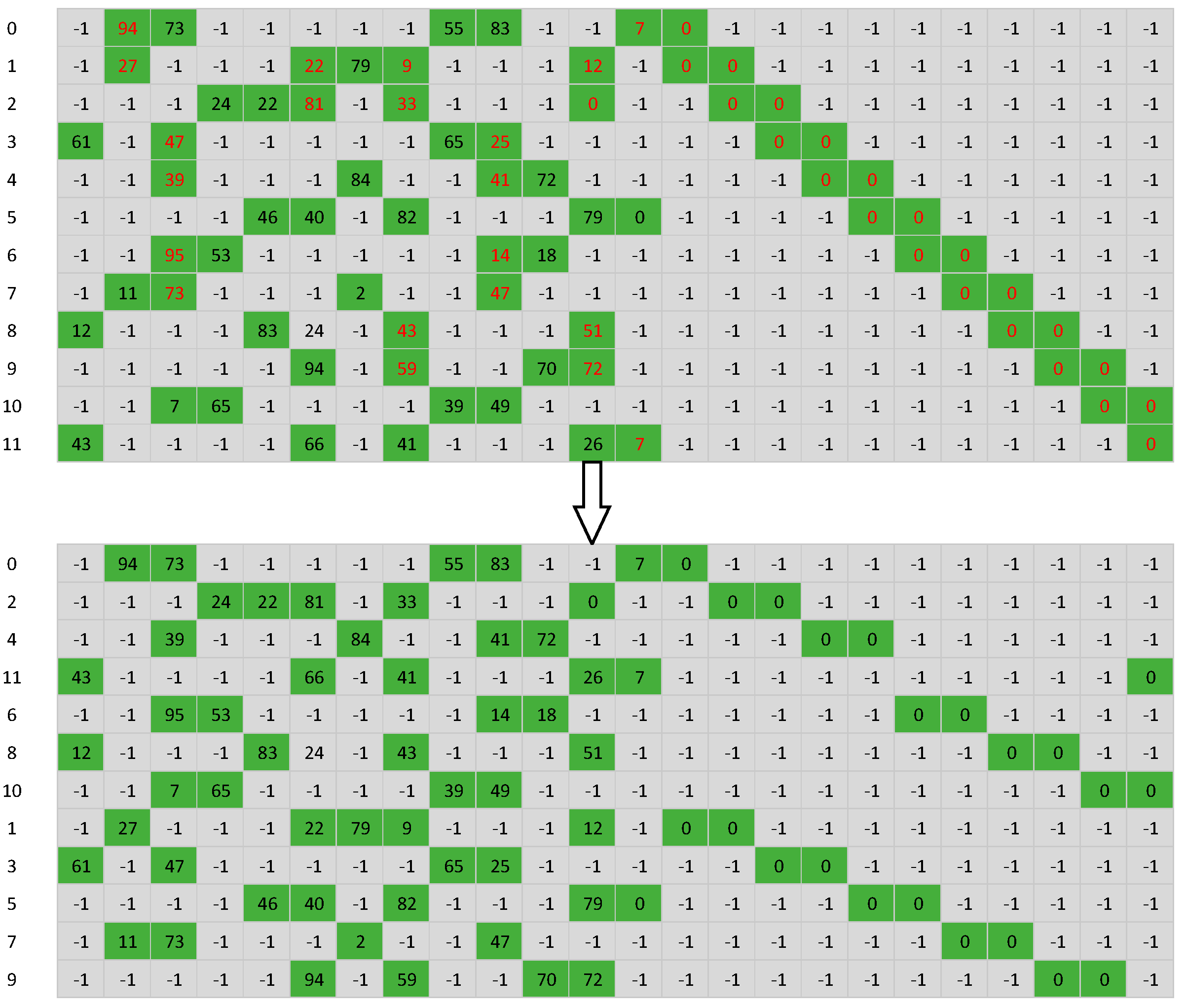Figure 3 below shows the check matrix of the WiMAX QC-LDPC code with a rate of 1/2. By adjusting the processing order between layers to 0, 2, 4, 11, 6, 8, 10, 1, 3, 5, 7, 9, it can be observed that the overlapping submatrices in the check matrix have been entirely eliminated.

The intra-layer processing order can also be rearranged to reduce pipeline conflicts, in addition to the inter-layer processing order. Within a layer's processing sequence, two main processes are involved: reading the LLRs from memory and writing the updated LLRs back to memory.

During the reading process, it is preferential to read the non-overlapping submatrix between the current layer and the preceding layer first, followed by the reading of the overlapping submatrix.

Conversely, in the write-back process, priority is given to writing back the overlapping submatrix between the current layer and the subsequent layer, followed by writing back the non-overlapping submatrix.

This allows the LLR of the overlapping submatrix to be updated at an earlier time as much as possible, and to be read and used at a later time. It can minimize the occurrence of pipeline conflicts.

Like other works, the hardware implementation of layered decoders in [15,16,18], due to the fact that many intermediate process variables are stored in FIFO, the read order and write-back order of each layer of LLR RAM must be consistent. It causes some contradictions in the rearrangement of the reading and writing order of multi-layer overlapping submatrices. In Figure 1, there is an overlapping submatrix (specifically, the fourth submatrix) that exists at the same position across consecutive first, second, and third layers. When analyzing the sequential arrangement of LLR reads and writes for this submatrix in the second layer, several considerations arise. Firstly, since the first layer supplies updated LLRs for the second layer, it is desirable to arrange the reading order of the submatrix's LLR in the second layer to occur later, allowing sufficient time for the updated LLR to be read. Secondly, as the second layer provides updated values for the third layer, there is a need for the LLR of the submatrix in the second layer to be updated promptly, necessitating an earlier write-back order. Consequently, the reading and writing order of the fourth submatrix in the second layer presents a contradiction: the need for a delayed read to accommodate updated LLR from the first layer versus the need for an early write-back to ensure timely updates for the third layer. This conflict highlights the complexities involved in optimizing the reading and writing orders of overlapping submatrices in layered decoders.

In our proposed hardware architecture, it is supported that each layer has a different order of reading and updating LLRs. This approach effectively reduces the pipeline conflicts caused by the above situation. Details of the specific hardware structure are provided in Chapter 3.3.

3.2. Patch Method Based on Variable-to-Check Message

Some pipeline conflicts can be avoided by rescheduling the processing order of inter-layer and intra-layer submatrices. However, the remaining part will still cause great performance loss. Especially for those PCMs with dense non-zero submatrices, pipeline conflicts are severe, and rescheduling is basically ineffective.

By combining formulas (7) and (3), the updated formula for LLR can be rewritten as follows:

{L L R}^{i} (j) = L_{j \to i}^{(i t, i)} + L_{i \to j}^{(i t, i)} = {(L L R}^{i - 1} (j) - L_{i \to j}^{(i t - 1, i)}) + L_{i \to j}^{(i t, i)} = {L L R}^{i - 1} (j) + (L_{i \to j}^{(i t, i)} - L_{i \to j}^{(i t - 1, i)}) = {L L R}^{i - 1} (j) + ∆ L_{i \to j}^{i}

(8)

where

∆ L_{i \to j}^{i}

is defined as residue or gain, representing the difference before and after the update of the check-to-variable messages. It reflects the decision information newly contributed by the check node during the iteration process. Therefore, in the layered decoding algorithm, it effectively obtains new gains from the check node through continuous layer traversal.

To achieve the ideal pipeline effect, when pipeline conflicts occur, the only option is to read the un-updated LLRs. However, this results in the loss of the gain generated by the corresponding check node, which cannot positively impact subsequent iterations. Referring to formula (8), many references [15,16,18] suggest that, in such instances, the corresponding gain can be calculated and stored in the corresponding memory space. The gain will not be read and stacked until the LLR is updated at the same position. This way, the gain will only be temporarily disregarded during conflicts but will be incorporated in the subsequent iteration process, thereby positively contributing to convergence acceleration. We refer to this type of decoding architecture as the patch method based on LLR.

However, shifting the patching position from the LLR to the variable-to-check message reveals that reading the un-updated LLR may not necessarily induce pipeline conflicts. This adjustment can further reduce pipeline conflicts. We refer to this proposed architecture as the patch method based on variable-to-check message. As formula (4) is rewritten, the variable-to-check messages will be updated to:

\begin{matrix} L_{j \to i}^{(i t, i)} = ({L L R}^{o l d} (j) - L_{i \to j}^{(i t - 1, i)}) + ∆ L_{i \to j}^{i - 1} \end{matrix}

(9)

From another perspective, for those overlapping submatrices where the gain of the previous layer has already been calculated before calculating the variable-to-check messages in the next layer, there will be no pipeline conflicts caused by reading the old LLRs. Because we replace reading updated LLRs by reading old LLRs and patching variable-to-check message. As shown in Figure 4, in our proposed architecture, although the un-updated LLRs were read, no pipeline conflicts were generated.

Figure 5 shows the main process flow charts of the patch method based on LLR and the patch method based on variable-to-check message, respectively. The letters on the arrow lines represent the number of pipeline stages inserted in the hardware implementation.

Assuming there is an overlapping non-zero submatrix between two adjacent layers, and the moment when the LLR is read by the two layers is

N_{1}

and

N_{2}

, respectively.

For the patch method based on LLR, when there is no pipeline conflict,

N_{1}

and

N_{2}

need to meet the following requirements:

N_{2} \geq N_{1} + X_{1} + X_{2} + X_{3} + X_{4} + X_{5}

(10)

For our proposed scheme, We only need to ensure that the gain of the first layer is calculated before the second layer finishes calculating the variable-to-check message. So we need to meet:

N_{2} + X_{1} + X_{2} \geq N_{1} + X_{1} + X_{2} + X_{3} + Y_{1} + Y_{2} \to N_{2} \geq N_{1} + X_{3} + Y_{1} + Y_{2}

(11)

Since

{(Y}_{1} + Y_{2})

is always less than

{(X}_{1} + X_{2} + X_{4} + X_{5})

during the design process, the condition for the patch method based on LLR to avoid pipeline conflicts is more stringent than that for the patch method based on variable-to-check message. When the number of pipeline stages and overlapping submatrices is sufficiently high, the patch method based on variable-to-check message can reduce the number of pipeline conflicts by

{(X}_{1} + X_{2} + X_{4} + X_{5} - {(Y}_{1} + Y_{2}))

in each layer iteration compared to the patch method based on LLR.

3.3. Proposed Hardware Implementation Structure

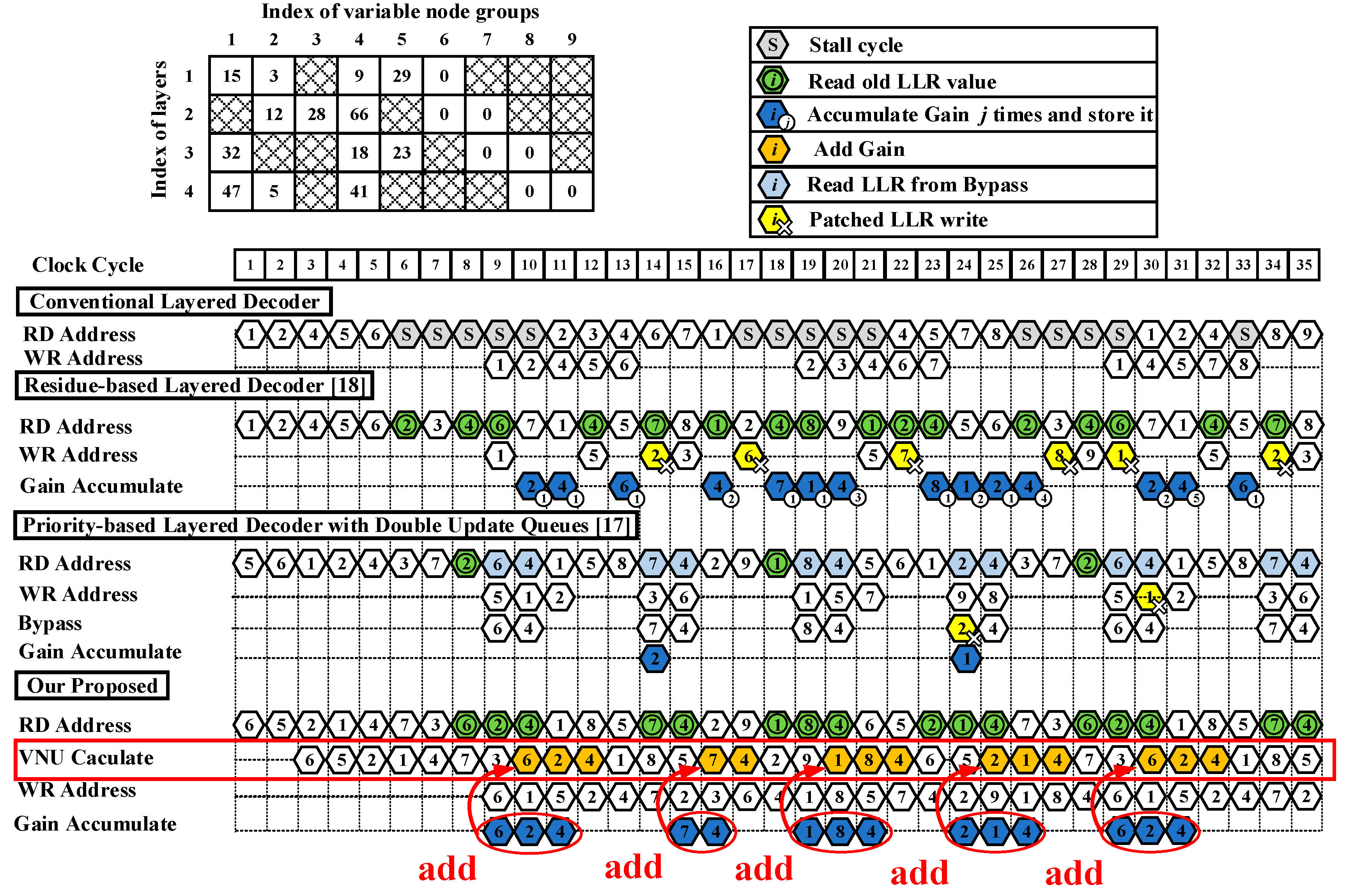
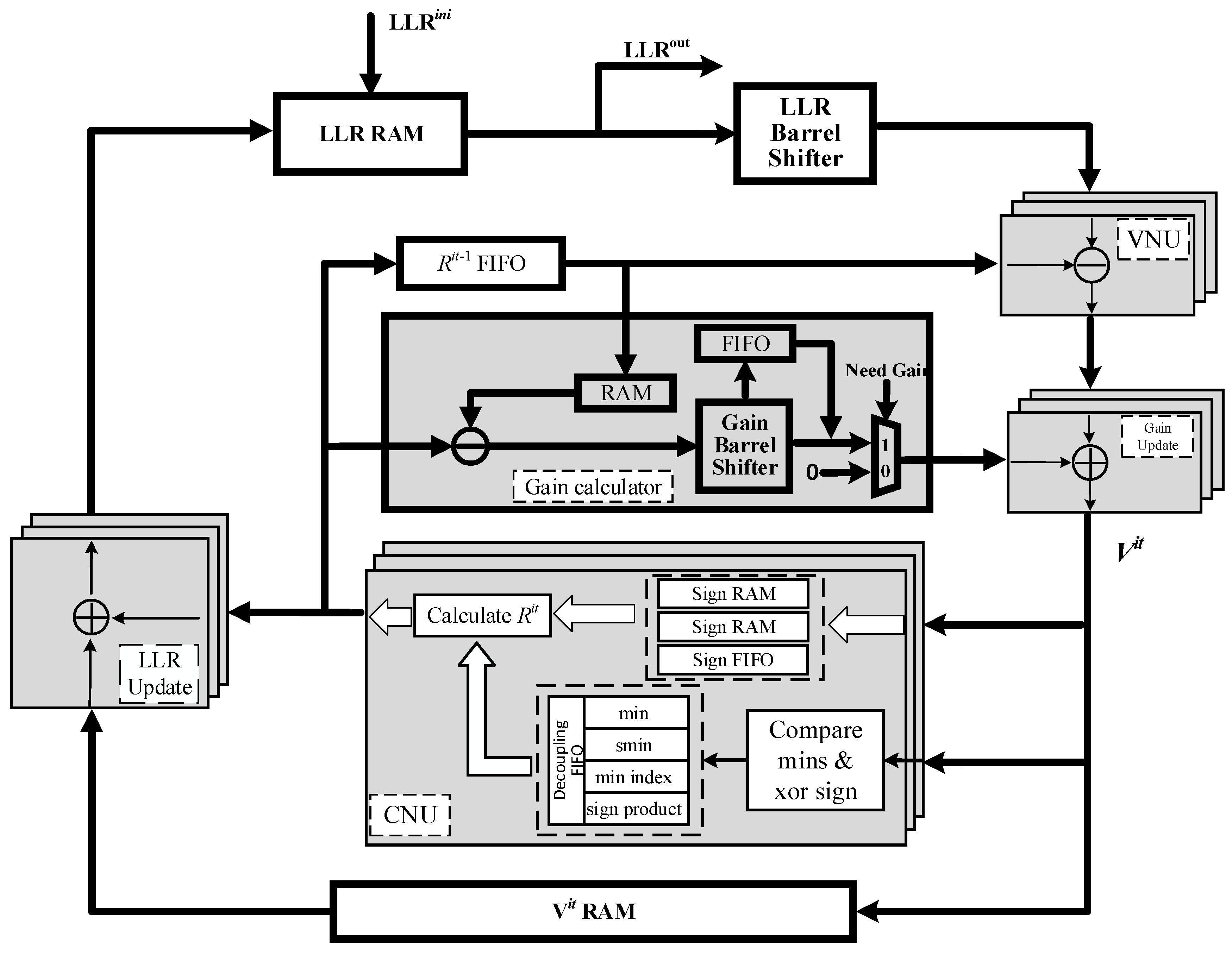
Figure 6 shows the hardware design details of the layered decoder that we propose. The decoder mainly consists of LLR RAM, Variable Node Unit (VNU), Check Node Unit (CNU), LLR update Unit (LU), Gain generate Unit (GU), other auxiliary units (barrel shifter, cache, etc.), and control modules. The parallelism of the decoder is equal to the size Z of the submatrix, which means that there will be Z VNUs, CNUs, LUs and GUs working simultaneously.

To begin with, the initialized channel LLRs are written into LLR RAM. The depth of LLR RAM is the number of recurrent submatrices in a layer, and each storage space contains LLR information for Z variable nodes.

When decoding begins, the LLRs of the corresponding addresses in RAM are sequentially read and fed into the barrel shifter according to the rearrangement order of inter-layer and intra-layer submatrix processing in Chapter 3.1. The barrel shifter is responsible for adjusting the order of information during decoding.

In the VNU, the variable-to-check messages are obtained by subtracting the check-to-variable messages of the previous iteration from the LLRs. If the LLRs previously read are not up-to-date and the corresponding gain of the last layer can be obtained at this moment, then the variable-to-check messages obtained here need to be patched with gain. At this point, it is still believed that no pipeline conflict has occurred. Only when the gain of the last layer lags behind the end time of variable-to-check message calculation, will it be considered that pipeline conflict has truly occurred. And the gain will be cached until the next time when the same variable-to-check message is recalculated, and patches will be applied to compensate for the loss caused by reading the un-updated LLR. The updated variable-to-check messages are fed into the CNU. On the other hand, they are cached and read out for computation during LLR updates. But unlike other architectures, the hardware used for caching here is RAM rather than FIFO, as there is a need for different write and read orders.

In the CNU, the sign bits and amplitudes of variable-to-check messages are separated. By comparing the amplitudes of variable-to-check messages, the minimum and second minimum values in a layer, as well as the positional index corresponding to the minimum value, are obtained. Concurrently, the sign product of all variable-to-check messages in the same layer is calculated. Afterward, by comparing the positional index of the submatrices that need to be processed with the position index of the minimum value, one can determine whether to use the minimum value or the second minimum value as the amplitude of the updated check-to-variable messages (because the OMSA algorithm is used, further amplitude processing is required for the minimum and second minimum values). The signs for check-to-variable messages are obtained by the sign product and the sign of the corresponding variable-to-check messages. There are three directions to the updated check-to-variable messages: one is directly used to add the updated LLR with variable-to-check messages. Another is cached into the FIFO for the next iteration of the variable-to-check messages update. The rest is used to generate gains to compensate for the loss caused by reading un-updated LLRs. Because the order of the check-to-variable messages in these three directions is different, the check-to-variable messages in these three ways need to be calculated separately. This is why the signs of the variable-to-check messages are originally cached in three memory spaces.

In the GU, the gains of the overlapping submatrices are obtained by subtracting the check-to-variable message of the current iteration and the previous iteration. These gains are aligned by barrel shifters and then patched into the corresponding variable-to-check messages.

In the LU, the updated LLRs are obtained by variable-to-check messages and check-to-variable messages. Then they are rewritten into the LLR RAM.

4. Results and Analysis

4.1. Experimental Setup

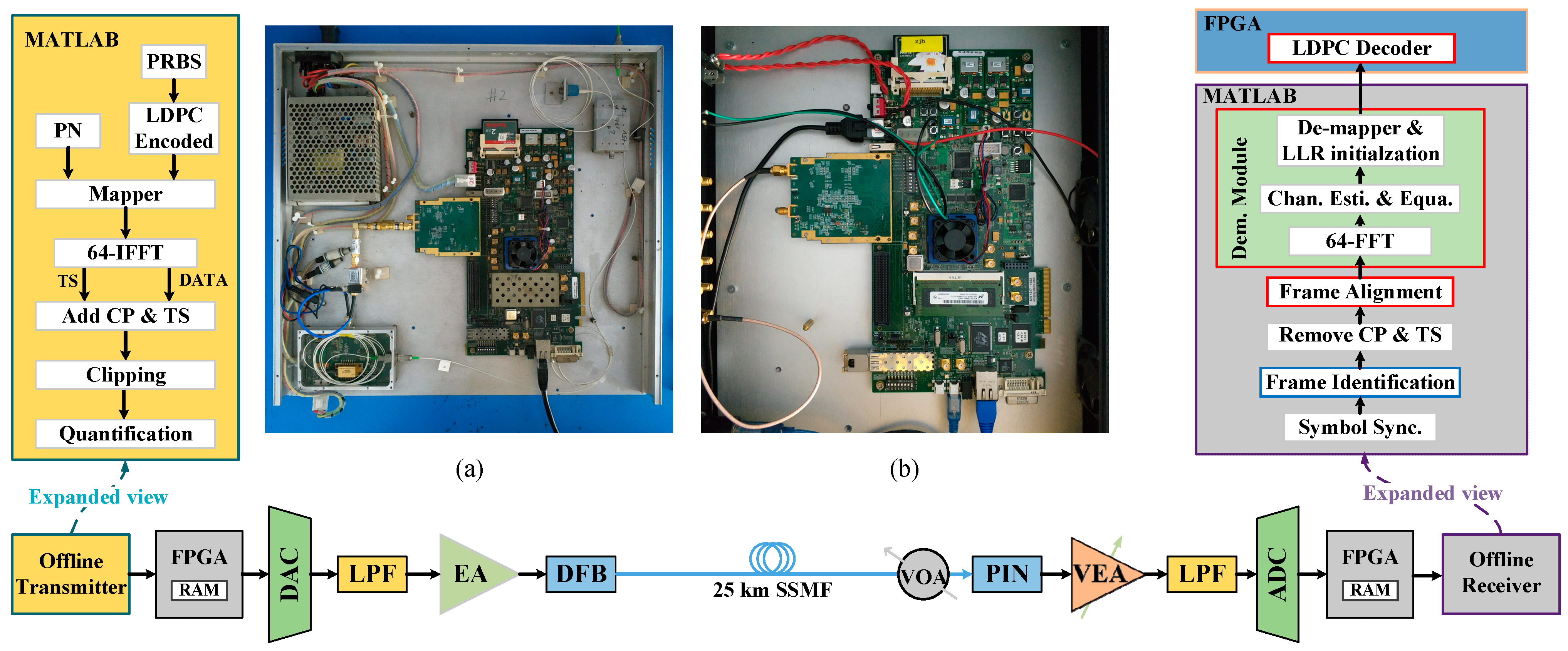
To verify the performance of the layered LDPC decoder with the proposed architecture in OFDM-PON, experiments are undertaken by an FPGA-based OFDM-PON platform previously used in [19,20,21] and an FPGA-based LDPC decoder, as shown in Figure 7. In this paper, two Xilinx FPGA boards (ML605) with Virtex-6 XC6VLX240T are used in the implementation of the OFDM-PON platform. The key parameters of the platform are summarized in Table 1. To maximize the throughput and operating frequency, another Xilinx FPGA board (VC709) with xc7vx690t is independently used for the LDPC decoder.

At the OFDM transmitter side, the data is generated by pseudo-random binary sequence (PRBS) and then encoded with the LDPC code. Its mother code parity-check matrix is composed of an array of 6×24 circulant 96×96 submatrices. The code rate is 3/4 with a code length of 2304 bits. Among them, the first 1728 bits of the codeword are information bits and the rest 576 bits are parity-check bits. The whole OFDM modulation is completely done offline by MATLAB software. The FFT size is set to 64. Considering the code length and for the convenience of modulation, 16-QAM and 64-QAM are chosen as the signal modulation formats. Here we turn on 2 to 28 subcarriers to carry the encoded data, following the approach in our previous work [20].

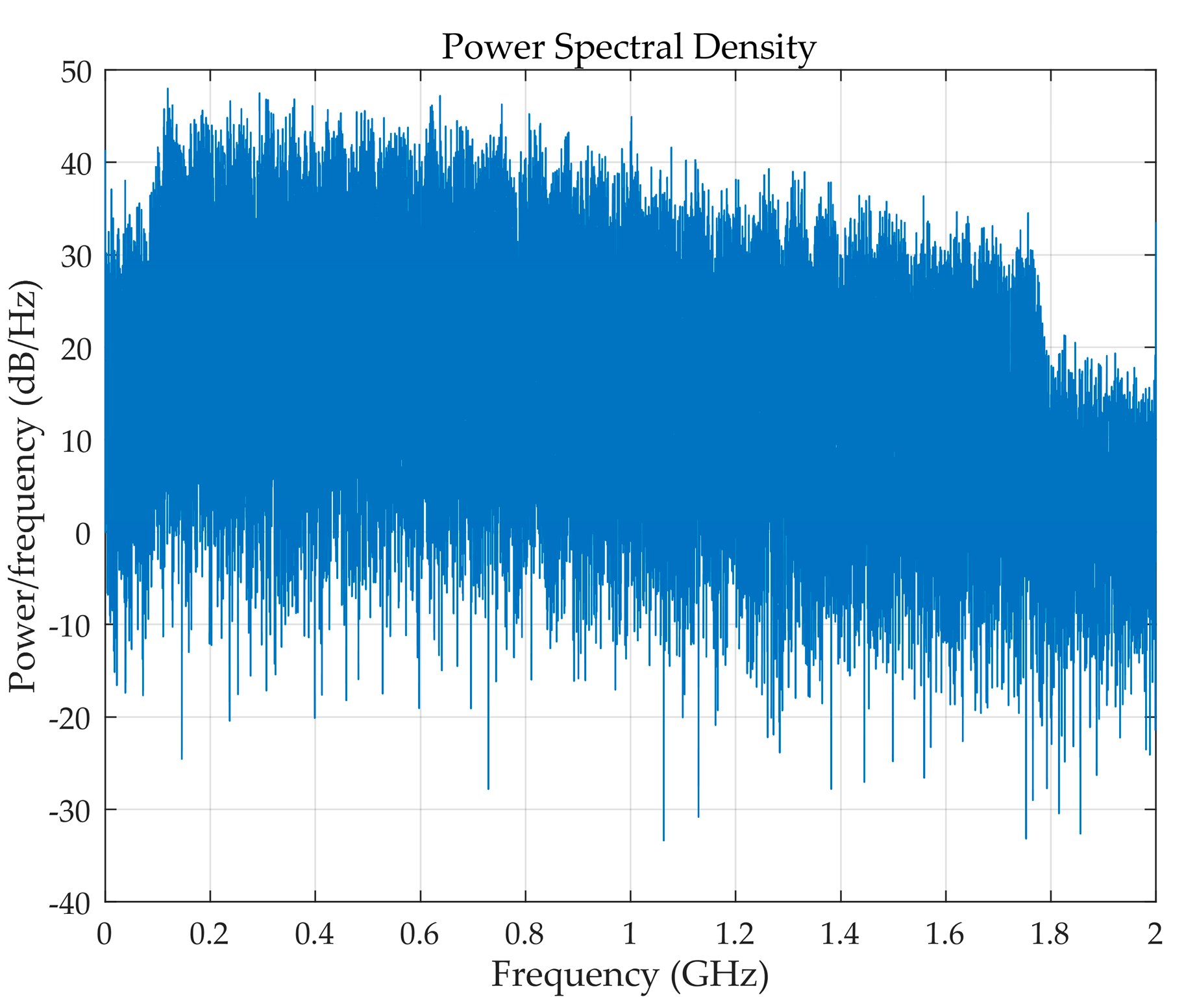
Figure 8. The power spectral density when 2 to 28 subcarriers are turned on.

All these 27 subcarriers need to satisfy the Hermitian symmetry to obtain the real-valued IFFT outputs. Then a 16-sample cyclic prefix, two FFT-sized sample TSs and M (M is 22 for 16-QAM or 15 for 64-QAM) OFDM symbols carrying data are together to form a complete OFDM frame. The generated OFDM frames are sent to the Xilinx ML605 FPGA board via UDP protocol and stored into the internal BRAMs of the FPGA board. The analog signal is outputted by a 4GS/s DAC with a resolution of 12 bits and directly modulated by a narrow bandwidth distributed feedback laser (DFB-LD). The optical signals pass through a 25 km standard single-mode fiber (SSMF).

At the OFDM receiver side, a variable optical attenuator (OA) is set before the 2.7 GHz PIN detector to adjust the optical power. A PIN is used to convert the optical signal to electrical domain and then a 10-bit ADC is applied to quantify the received analog OFDM signal. Digital signals are de-multiplexed into 32-parallel samples and buffered into BRAMs. Then the digital signals will be wrapped into UDP packages and transmitted to MATLAB. The following signal processing is all done offline in MATLAB, including symbol synchronization, 64-point FFT, channel equalization and bit log-likelihood ratio (LLR) calculation. LLRs are re-initialized according to the modulation format.

The initialized LLRs are quantized and then transmitted to the VC709 FPGA board via UDP. The decoding process is executed. And calculate the bit error rate (BER) after decoding is completed.

4.2. Schedule Optimization Results

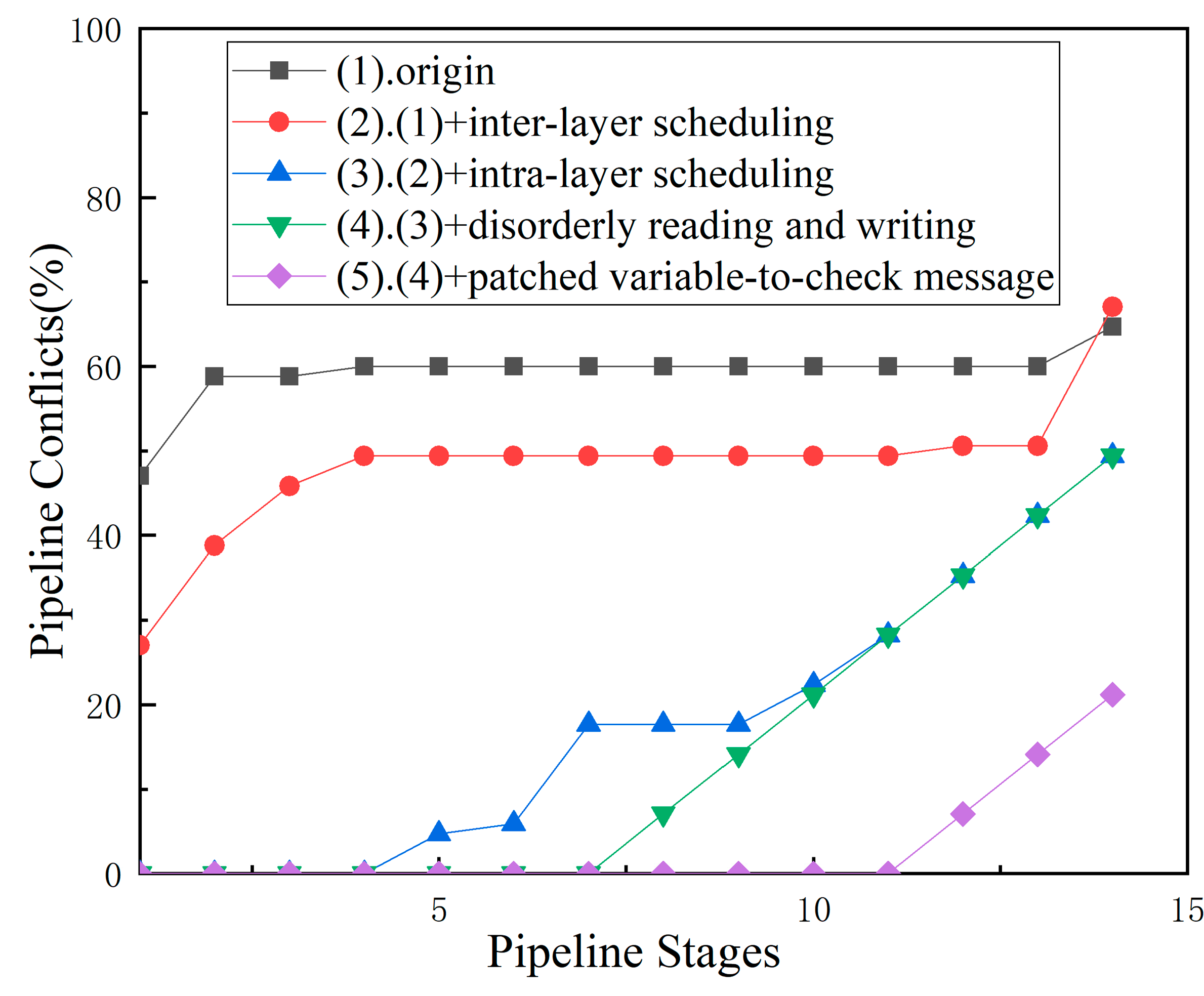
To demonstrate our proposed schedule optimization results clearly, we broke down the proposed method into four points that are beneficial for reducing pipeline conflicts:

(1): Reorder the processing of the inter-layer.
(2): Reorder the processing of the intra-layer.
(3): Allow each layer to read and write back LLRs in a different order.
(4): Use the patch method based on variable-to-check message.

To demonstrate the optimization process more intuitively, we compare the optimization structure of each step with the original decoding method. The original decoding method refers to the patch method based on LLR without any optimization in the processing order. We calculate the proportion of pipeline conflicts generated by the different decoding methods under different pipeline settings and show it in Figure 9.

In the original method represented by line (1), when the number of pipeline stages exceeds 3, overlapping submatrices between adjacent layers in the PCM will all experience pipeline conflicts. Thus, the proportion of pipeline remains stable at around 60%. As the number of pipeline stages gradually increases, it is also necessary to consider the possibility of conflicts between the two layers of the interval. When 14 pipeline stages are set, the proportion of pipeline conflicts further increases.

In line (2), a reordering of the inter-layer processing of decoding is used based on (1) and the number of overlapping submatrices is reduced by 10.59%. It can be seen that between the 4~11 pipeline stages, (2) has reduced the pipeline conflict ratio by 10.59% compared to (1).

Line (3) is a further reordering of the intra-layer processing based on (2). A reasonable reordering of the intra-layer processing order can prevent some overlapping submatrices from colliding with the pipeline when the number of pipeline stages is not set too high. However, when the number of the pipeline stages approaches the row weight of the check matrix, the proportion of pipeline conflicts also approaches (1) and (2).

Line (4) allows each decoding layer to have a different order when reading LLR and writing LLR back to the RAM based on (3). This method solves the contradiction problem of read-and-write order rearrangement caused by overlapping submatrices with more than two consecutive layers connecting the same set of variable nodes.

Line (5) uses the patch method based on variable-to-check message applied on the basis of (4). According to formula (10) (11) and the actual hardware structure in Figure 6, it can be inferred that the patch method based on variable-to-check message can reduce the number of pipeline conflicts for each layer at most, which is equal to the total number of pipeline stages for reading and writing LLR as well as computing variable-to-check message. In practical design, LLR writing back to RAM and reading out of RAM each requires one pipeline stage. The calculation of the variable-to-check message requires one subtraction and one supersaturation process, assuming a two-stage pipeline is required here. Therefore, curve (5) is equivalent to a horizontal shift of 4 units to the right compared to (4).

4.3. Comparison of Decoding Performance

To compare the decoding performance of the proposed architecture, the priority-based with double update queue (PD) architecture in [18] and the residue-based scheme (RS) architecture in [16], we did the experiment. For a fair comparison, LLR, variable-to-check message, and check-to-variable message are quantified as 8-bit, 8-bit, and 6-bit in these three decoding architectures, respectively. And the decoders with three decoding architectures are all inserted with 11 pipeline stages. On the OFDM-PON platform, 1,000,000 OFDM frames are sent out for each received optical power (ROP) to calculate the BER. The BER curves of the decoder with proposed architecture, PD and RS depending on the ROP are shown in Figure 10. The maximum number of decoding iterations is set to 10. It can be observed that with our proposed architecture, the decoder outperforms the decoder with PD by 0.125 dBm, and outperforms the decoder with RS by 0.375 dBm when the BER is

1 \times 10^{- 6}

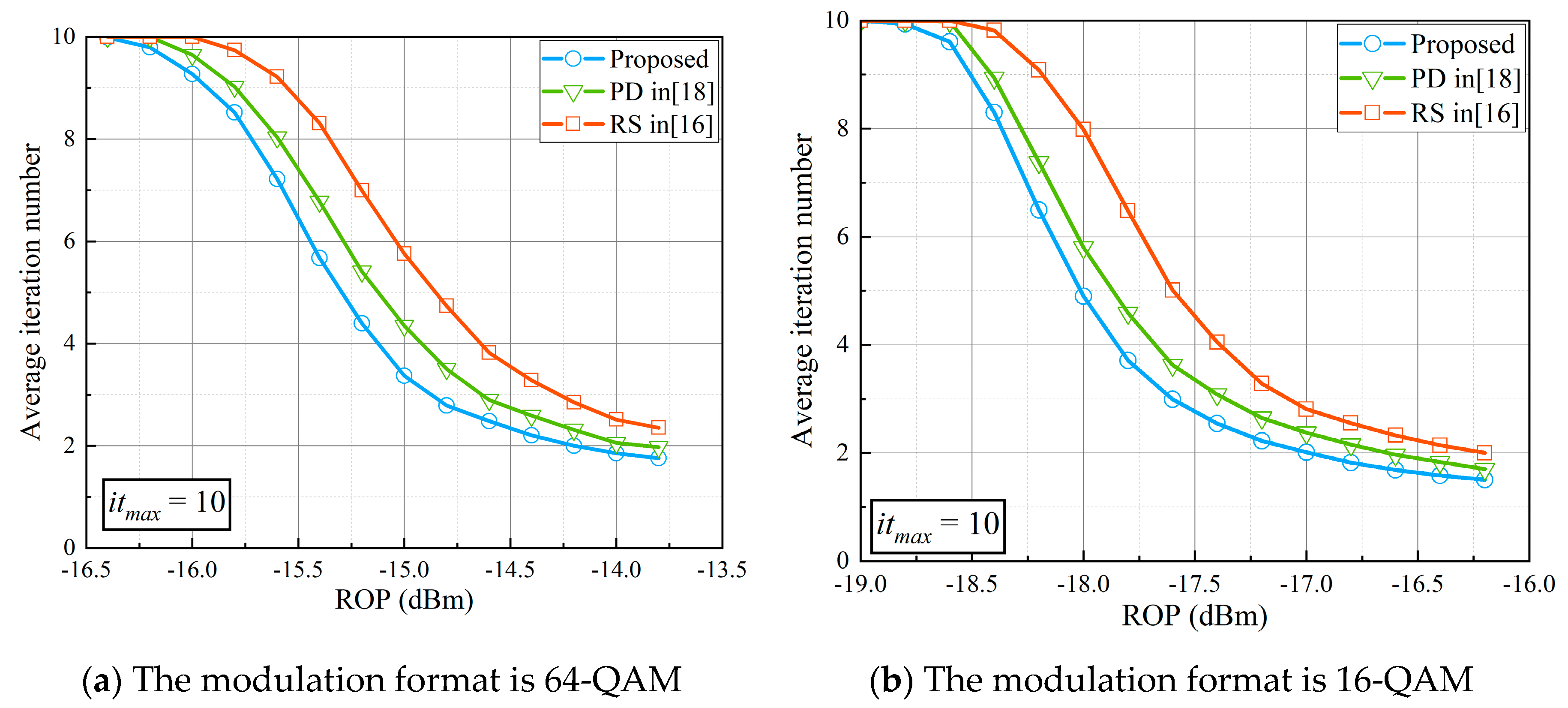
Further, we investigate the average iteration number among the three algorithms, as shown in Figure 11. The maximum iteration number is set to 10 and the iteration finishes once the codeword C and PCM H satisfy

C \times H^{T} = 0

or the decoding has reached the maximum iteration number. It can be seen that compared to our proposed architecture, the decoders based on PD and RS require an increase in the average number of iterations to achieve the same decoding performance.

4.4. Hardware Implementation

As shown in Table 2, we conducted a comparison of the hardware resources utilized by the proposed decoding architecture with the priority-based architecture in our previous work [18] and the residue-based architecture in reference [16]. Compared with our previous work [18], the proposed architecture does not require two update queues, resulting in a slight reduction in LUTs and FFs. However, to ensure that each layer of the layered decoder can read and write LLRs in a different order during the decoding process, we replaced some FIFOs in other architectures with BRAM. Consequently, there is a slightly excessive use of BRAM.

5. Conclusions

In this paper, a reordered QC_LDPC decoder with a patched variable-to-check message is proposed to solve the pipeline conflict problem in the OFDM-PON platform. The effectiveness of the proposed architecture for resolving pipeline conflicts consists of four components: reordering of inter-layer processing, reordering of intra-layer submatrices, allowing for different read and write orders at each layer and the patch method based on variable-to-check message. For the rate 3/4 LDPC code of the IEEE802.16 standard, the traditional patch method based on LLR achieves a conflict rate of about 60% when inserting more than 2 pipeline stages. However, our proposed architecture can achieve the effect of no pipeline conflicts when inserting fewer than 11 pipeline stages. Compared with our previous work and the method in other paper, the sensitivity is improved by 0.125 dBm and 0.375 dBm respectively at a bit error rate of

10^{- 6}

. And our proposed architecture also shows a significant reduction in average number of iterations. We believe that the proposed LDPC decoding architecture can further improve the system performance of OFDM-PON.

Author Contributions

Conceptualization, Z.J.W. and J.J.Z.; methodology, Z.J.W. and Z.J.X.; software, Z.J.W.; validation, Z.J.W., K.C. and X.Q.L; formal analysis, Y.Z.Q.; investigation, Y.C.L.; resources, J.J.Z.; data curation, K.C.; writing—original draft preparation, Z.J.W.; writing—review and editing, Z.J.W., J.J.Z., Y.Z.Q. and Y.C.L.; supervision, J.J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by National Key Research and Development Program 483 of China (2021YFB2900800), the Science and Technology Commission of Shanghai Municipality 484 (Project No. 20511102400, 20ZR1420900) and 111 project (D20031).

Conflicts of Interest

The authors declare no conflicts of interest.

References

Cheng, L.; Wen, H.; Zheng, X.; Zhang, H.; Zhou, B. Channel characteristic division OFDM-PON for next generation optical access. Opt. Express 2011, 19, 19129–19134. [Google Scholar] [CrossRef] [PubMed]
Gallager, R. Low-Density Parity-Check Codes. IEEE Trans. Inform. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
Ten Brink, S.; Kramer, G.; Ashikhmin, A. Design of Low-Density Parity-Check Codes for Modulation and Detection. IEEE Trans. Commun. 2004, 52, 670–678. [Google Scholar] [CrossRef]
Li, M.; Chou, H.; Ueng, Y.; Chen, Y. A low-complexity LDPC decoder for NAND flash applications. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, Australia, 1–5 June 2014; pp. 213–216. [Google Scholar]
3rd Generation Partnership Project. Technical Specification Group Radio Access Network; NR; Multiplexing and Channel Coding (Release 16), 3GPP TS 38.212 V16.5.0 (2021-03); 3GPP: Valbonne, France, 2021. [Google Scholar]
Yang, M.; Li, L.; Liu, X.; Djordjevic, I. B. Real-time verification of soft-decision LDPC coding for burst mode upstream reception in 50G-PON. J. Light. Technol. 2020, 38, 1693–1701. [Google Scholar] [CrossRef]
Mo, W.; Zhou, J.; Liu, G.; Huang, Y.; Li, L.; Cui, H.; Wang, H.; Lu, Q.; Liu, W.; Yu, C. Simplified LDPC-assisted CNC algorithm for entropy-loaded discrete multi-tone in a 100G flexible-rate PON. Opt. Express 2023, 31, 6956–6964. [Google Scholar] [CrossRef] [PubMed]
Gong, X.; Guo, L.; Wu, J.; Ning, Z. Design and performance investigation of LDPC-coded upstream transmission systems in IM/DD OFDM-PONs. Opt. Commun. 2016, 380, 154–160. [Google Scholar] [CrossRef]
Djordjevic, I. B.; Batshon, H. G. LDPC-coded OFDM for heterogeneous access optical networks. IEEE Photonics J. 2010, 2, 611–619. [Google Scholar] [CrossRef]
Sharon, E.; Litsyn, S.; Goldberger, J. Convergence analysis of serial message-passing schedules for LDPC decoding. In Proceedings of the 4th International Symposium on Turbo Codes & Related Topics, Munich, Germany, 03–07 April 2006; pp. 1–6. [Google Scholar]
Shimizu, K.; Ishikawa, T.; Togawa, N.; Ikenaga, N. Partially-parallel LDPC decoder based on high-efficiency message-passing algorithm. In Proceedings of the 2005 International Conference on Computer Design. San Jose, CA, USA, 02–05 October 2005; pp. 503–510. [Google Scholar]
Kumawat, S.; Shrestha, R.; Daga, N.; Paily, R. High-throughput LDPC-decoder architecture using efficient comparison techniques & dynamic multi-frame processing schedule. IEEE Trans. Circuits Syst. I 2015, 62, 1421–1430. [Google Scholar]
Lee, H.C.; Li, M.R.; Hu, J.K.; Chou, P.C.; Ueng, Y.L. Optimization Techniques for the Efficient Implementation of High-Rate Layered QC-LDPC Decoders. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 457–470. [Google Scholar] [CrossRef]
Marchand, C.; Dore, J.; Conde-Canencia, L.; Boutillon, E. Conflict resolution for pipelined layered LDPC decoders. In Proceedings of the IEEE Workshop on Signal Processing Systems, Tampere, Finland, 7–9 October 2009; pp. 220–225. [Google Scholar]
Petrovic, V.L.; Markovic, M.M.; Mezeni, D.M.E.; Saranovac, L.V.; Radosevic, A. Flexible High Throughput QC-LDPC Decoder with Perfect Pipeline Conflicts Resolution and Efficient Hardware Utilization. IEEE Trans. Circuits Syst. I 2020, 67, 5454–5467. [Google Scholar] [CrossRef]
Boncalo, O.; Kolumban-Antal, G.; Amaricai, A.; Savin, V.; Declercq, D. Layered LDPC Decoders with Efficient Memory Access Scheduling and Mapping and Built-In Support for Pipeline Hazards Mitigation. IEEE Trans. Circuits Syst. I 2019, 66, 1643–1656. [Google Scholar] [CrossRef]
Marchand, C.; Dore, J.-B.; Conde-Canencia, L.; Boutillon, E. Conflict Resolution by Matrix Reordering for DVB-T2 LDPC Decoders. In Proceedings of the GLOBECOM 2009 - 2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 2009; pp. 1–6. [Google Scholar]
Li, Y.; Li, Y.; Ye, N.; Chen, T.; Wang, Z.; Zhang, J. High Throughput Priority-Based Layered QC-LDPC Decoder with Double Update Queues for Mitigating Pipeline Conflicts. Sensors 2022, 22, 3508. [Google Scholar] [CrossRef] [PubMed]
Zhang, J.; Zhao, J.; Huang, H.; Ye, N.; Giddings, R.P.; Li, Z.; Qin, D.; Zhang, Q.; Tang, J. A Clock-Gating-Based Energy-Efficient Scheme for ONUs in Real-Time IMDD OFDM-PONs. J. Light. Technol. 2020, 38, 3573–3583. [Google Scholar] [CrossRef]
Peng, J.; Sun, Y.; Chen, H.; Xu, T.; Li, Z.; Zhang, Q.; Zhang, J. High-Precision and Low-Complexity Symbol Synchronization Algorithm Based on Dual-Threshold Amplitude Decision for Real-Time IMDD OFDM-PON. IEEE Photonics J. 2019, 11, 1–14. [Google Scholar] [CrossRef]
Chen, L.; Halabi, F.; Giddings, R. P.; Zhang, J.; Tang, J. Subcarrier Index-Power Modulated-Optical OFDM With Dual Superposition Multiplexing for Directly Modulated DFB-Based IMDD PON Systems. IEEE Photonics J. 2018, 10, 1–13. [Google Scholar] [CrossRef]

Figure 1. An example of a base graph matrix schematic diagram.

Figure 2. The conflicts of inter-layer memory access.

Figure 3. The inter-layer reordering for LDPC check matrix of WiMAX protocol with a 1/2 rate.

Figure 4. Comparison diagram between different decoding architectures.

Figure 5. The main process flow charts of the patch method based on LLR and variable-to-check message.

Figure 6. Proposed hardware architecture of layered QC-LDPC decoder.

Figure 7. Experimental system and transceiver DSP block of off-line OFDM-PON and FPGA-based LDPC decoder.

Figure 9. The Pipeline Conflicts comparison among different decoders.

Figure 10. The BER comparison among decoders with different decoder architecture.

Figure 11. Average iteration number necessary for decoding with different architectures.

Table 1. OFDM-PON system and LDPC decoder parameters.

Parameter	Value
FFT/IFFT points	64
Data-carrying subcarriers	From 2 to 28
Modulation format	16-QAM\64-QAM
ADC/DAC resolution	10/12-bit
ADC & DAC sample rate	4 GS/s
OFDM frame CP	16 samples (4ns)
Transmitter output power	+7.75 dBm
DFB wavelength	1549.98 nm
DFB modulation bandwidth	2.7 GHz
DFB bias current	45 mA
DFB driving voltage	2 Vpp
PIN detector bandwidth	40 MHz~3 GHz
PIN responsivity	0.9 mA/mW
Standard	802.16
Code rate	3/4
Code length	2304
Size of submatrices	96×96
Parallelism	96

Table 2. Implementation results for LDPC decoders with different architectures.

	Resource Utilization			f_max [MHz]	T_norm [Gbps]	HUE (T_norm/Resources)
Algorithm	LUTs	FFs	36k BRAMs	f_max [MHz]	T_norm [Gbps]	Mbps/kLUT	Mbps/kFF	Mbps/BRAM
[16]	40700	26925	40.5	142.8	10.8	265.3	401.1	266.7
[18]	26744	19594	27	310.0	8.2	306.3	418.5	303.7
This work	24985	15688	41	350.0	9.3	372.2	592.8	226.7

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Efficient Pipeline Conflict Resolution for Layered QC-LDPC Decoders in OFDM-PON

Abstract

1. Introduction

1.1. Related Works

1.2. Overview and Contribution

2. Conflict Problems in Pipelined Layered Decoders

2.1. Layered Decoding Algorithm

2.2. Pipeline Conflict Problem

3. Reordered QC_LDPC Decoder with Patched Variable-to-Check Message

3.1. Inter-Layer and Intra-Layer Processing Scheduling

3.2. Patch Method Based on Variable-to-Check Message

3.3. Proposed Hardware Implementation Structure

4. Results and Analysis

4.1. Experimental Setup

4.2. Schedule Optimization Results

4.3. Comparison of Decoding Performance

4.4. Hardware Implementation

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe