Prerpints.org logo
Preprint
Article

Conceptualizing an Interferometer with Multiple Beams Splitting and Multiple Interference

Altmetrics

Downloads

122

Views

57

Comments

0

This version is not peer-reviewed

Submitted:

20 March 2024

Posted:

22 March 2024

Read the latest preprint version here

Alerts
Abstract
ABSTRACTThis article proposes an interferometer which should in principle split further an initially split beam to yield new sets of beams, effectively multiplying the number of beams that can be subjected to detectable interference. It can be considered a modification to the Michelson interferometer that introduces additional arrays of beam splitters, mirrors and detectors. It is expected of the interferometer to provide us with a set or sets of data holding details of phase changes in multiple interference patterns detectable by multiple detectors, enabling comparative analysis of data for multiple interference patterns recorded from a single measurement or activity. The number of multiplied beams possible is not limited, as it only depends on the specific amount of beam splitters required for certain experiments and practicals. The interference of multiple beams may improve sensitivity and detection for instrumentation purposes. The use of multiplied beam interferometry may also extend to quantum computation, particularly in linear optical quantum computation scheme as it enable production of multiple coherent beams which may exhibit properties of entanglement, making it suitable for developing optical multi-qubit systems.
Keywords: 
Subject: Physical Sciences  -   Other

Introduction

The Michelson interferometer was developed by Albert-A-Michelson as the central apparatus of the famed Michelson-Morley experiment [1,2] which was performed in 1887, meant to test the aether hypothesis but turned out to disprove the existence of aether and its dynamic properties.
Aether was initially believed to be the medium through which light travels, it was also believed that what is observed as vacuum had to be filled with this Aether medium allowing for the propagation of light waves. It was theorized that if the earth’s motion or light itself travels through the aether medium, and this medium also flows in a given direction, then the relative motion of the earth or light in same direction with the aether flow would be different from the motion of the earth or light in a direction opposite or perpendicular to the direction of aether flow. Hence if there is to be an interference of light from perpendicular directions, a small difference in path length or difference in velocity will be expected. This is because one of the light would arrive later than the other, as the aether flow will exercise drag on the light that is in a different direction relative to the flow.
To test for the properties of this hypothetical aether there was a need for a device that could measure the speed of light in the relative directions with great level of accuracy, and also detect small phase differences. Considering these needs, Michelson developed an interferometer that could do serve these purposes. A collaboration between Albert Michelson and Edward Morley was later made on an experiment to detect the differences in velocity between two light waves of different directions in the aether medium now known as the Michelson-Morley experiment [1,2]. However the results coming from the experiment performed using Michelson’s interferometer showed no difference in velocities, or any change in path length, annulling the hypothesis of an aethereal medium for the propagation of light. But this result aligned well with the theory of relativity that was later developed by Albert-Einstein, stating that the speed of light remains the same at all frames, positions and directions from which it is being observed.
The Michelson interferometer uses two beams both derived from a single beam splitted to two new sets of beams in perpendicular directions through the use of beam splitters, which are then interfered with a detector set to read the interference patterns. However the Michelson-Morley interferometer detects only a single interference pattern.
Apart from the Michelson-Morley experiment, the Michelson interferometer has found applications in the field of instrumentation, especially for practicals and experiments requiring the detection of small changes and micro-scale effects [3,4]. It is also applied in astronomical observations such as in LIGO (laser interferometer gravitational wave observatory). [5,6,7]
As stated previously, the Michelson interferometer is known to detect a single interference pattern/ fringes. But advances in interferometry led to the development of an interferometer that allowed the detection of two interference patterns, which is now known as the Mach Zehnder interferometer [8,9]. The fact that the Mach-Zehnder interferometer could detects two separate fringes produced from a single interference made it suitable for experimentations involving entangled states [10,11,12,13]. It is also considered for its potentials in quantum computation [14,15,16], particularly in optical quantum computation [17,18] schemes such as the KLM protocol [27].
While the Mach Zehnder interferometer has proven to be useful the entanglement of two quantum mechanical system, referred to as multi-partite entanglement [25,26] doesn’t appear to be a straight forward possibility using a typical Mach-Zehnder interferometer.
In search for an interferometer device with multiple detectable interference patterns, a potential interferometer design based on a modified Michelson interferometer is being presented, one that would multiply the beams and interference patterns, by splitting an already split beam into more amount of beams and reflecting them back using mirrors such that the beams will interfere perpendicularly before reaching their respective detectors.
The proposed interferometer would be useful in the detection of n-number of interference patterns arising from the crossed paths of multiple beams. Where the multiple beams originate from a single light source/ laser beam that is first split into two and then to higher numbers.
Splitting of beams are achieved through the use of beam splitters that partially reflects light coming from a source. The number of split beams that can be used in this interferometer is not fixed and is only dependent on the specific requirement of the experiment or its practical applications.

How the Michelson Interferometr Works

Michelson interferometry basically starts with a light source, preferably a laser which emits light in the form of a beam that is directed towards a single beam splitter. This partially reflects the beam in one direction and at the same time allows some of the beam to pass through it. The partially reflected beam and the one that passes through the splitter will be perpendicular to each other, as they are both directed towards respective mirrors. The beams reflected by both mirrors will cross paths perpendicularly (this is how interference occurs). And finally one of the interfered beams will head towards a photo-detector that detects the fringes produced from interference and provides details of the phase changes and changes in optical path length.
Mathematically we may define the difference in optical path length as;
∆ x = ∆ λ 2 π n   ( Δ φ )
Where ∆ x defines the difference in optical path length and Δ φ is the phase difference.
What we have below is a diagram showing how a michelson intrferometer is being set up and how the beams are being splitted, reflected, interfered and detected.
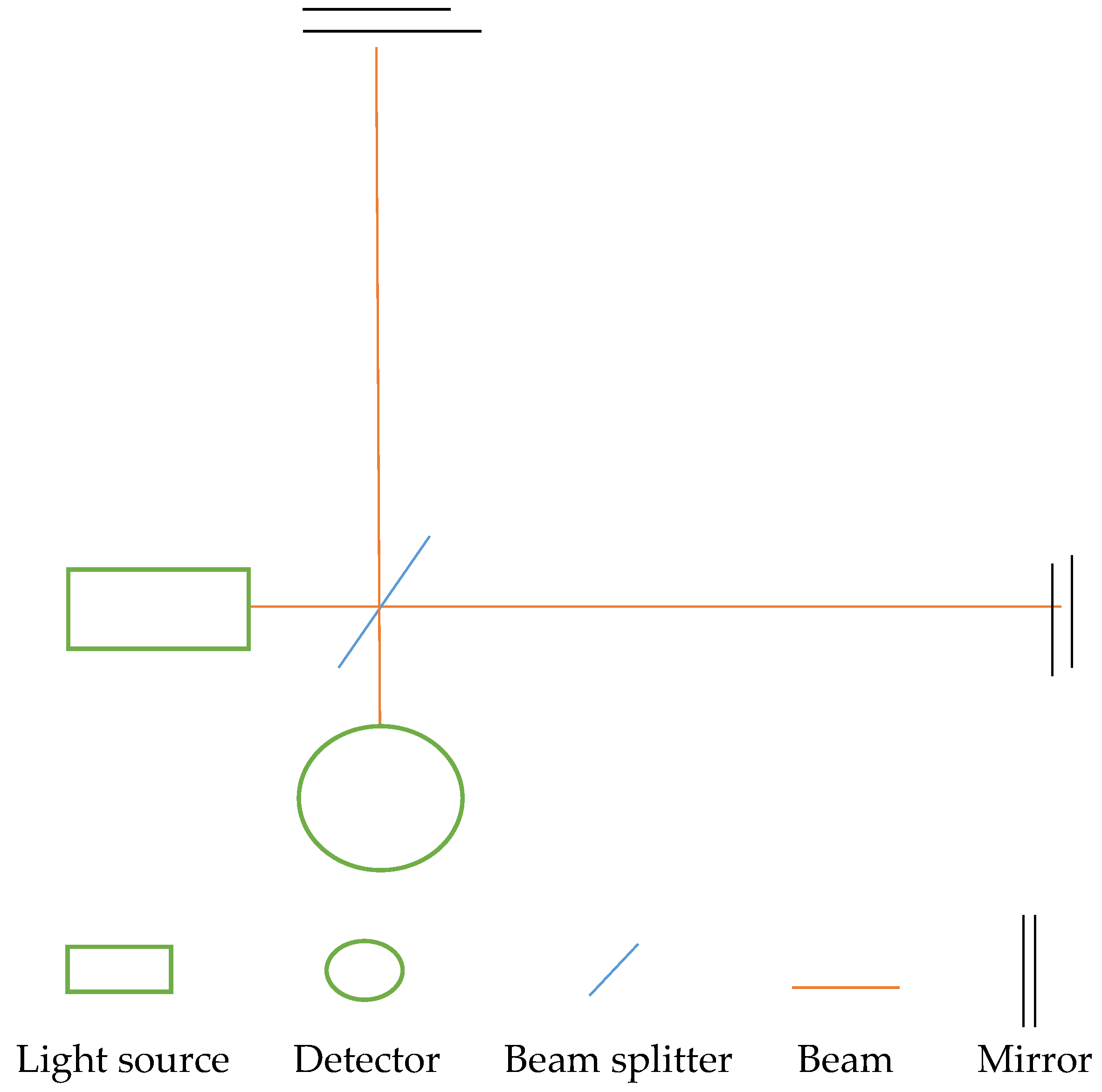
Preprints 101892 g001
Figure 1. XX.
Figure 1. XX.
Preprints 101892 g001
The michelson interferometer is very versatile and its applications spans across various fields and disciplines as an instrumentation device for detecting very small scale quantites and measurables with high level of precision. For example; the field of medicine optical coherence tomography (OCT) [22] is based on a device that is actually based on michelson interferometry, large scale applications of michlson interferometry in astronomy via. gravitational wave detector (LIGO) also shows more of its versatility. Many other disciplines including Engineering have utilized setups and devices based on the michelson interferometer for instrumentations involving microscale physical quantities and chnges where great precision is needed.

The Mach Zehnder Interferometer

The Mach Zehnder interferometer named after Ludwig Mach and Ludwig Zehnder, was first prroposed in an article by Zehnder in 1892 and the proposed interferometer was further refined in another article by Mach in 1892.
This interferometer had unique differences in its design compared to the michelson interferometer, in that it employs a closed geometry in its configauration of beam paths. Unlike the michelson interferometer having open perpendiular paths. It also ensured that the beams cross paths in such a way that two interference patterns/fringes can be generated and detected separately.
One merit of this interferometer that interested physicists was that it could help to practcially study quantum mechanical phenomanas such as Superpositoning, quantum enttanglement, quantum zeno effects, and other interesting areas of quantum physics. It also led to developments in technological fields such as holography.
The Mach zehnder interferometer is one of the most popular interferometers, and like the michelson interferometer is also very versatile as an instrumentation device. Laboratories and institutions often apply interferometry to research and studies, with the mach zender interferometer as a preferred choice for instrumentation.
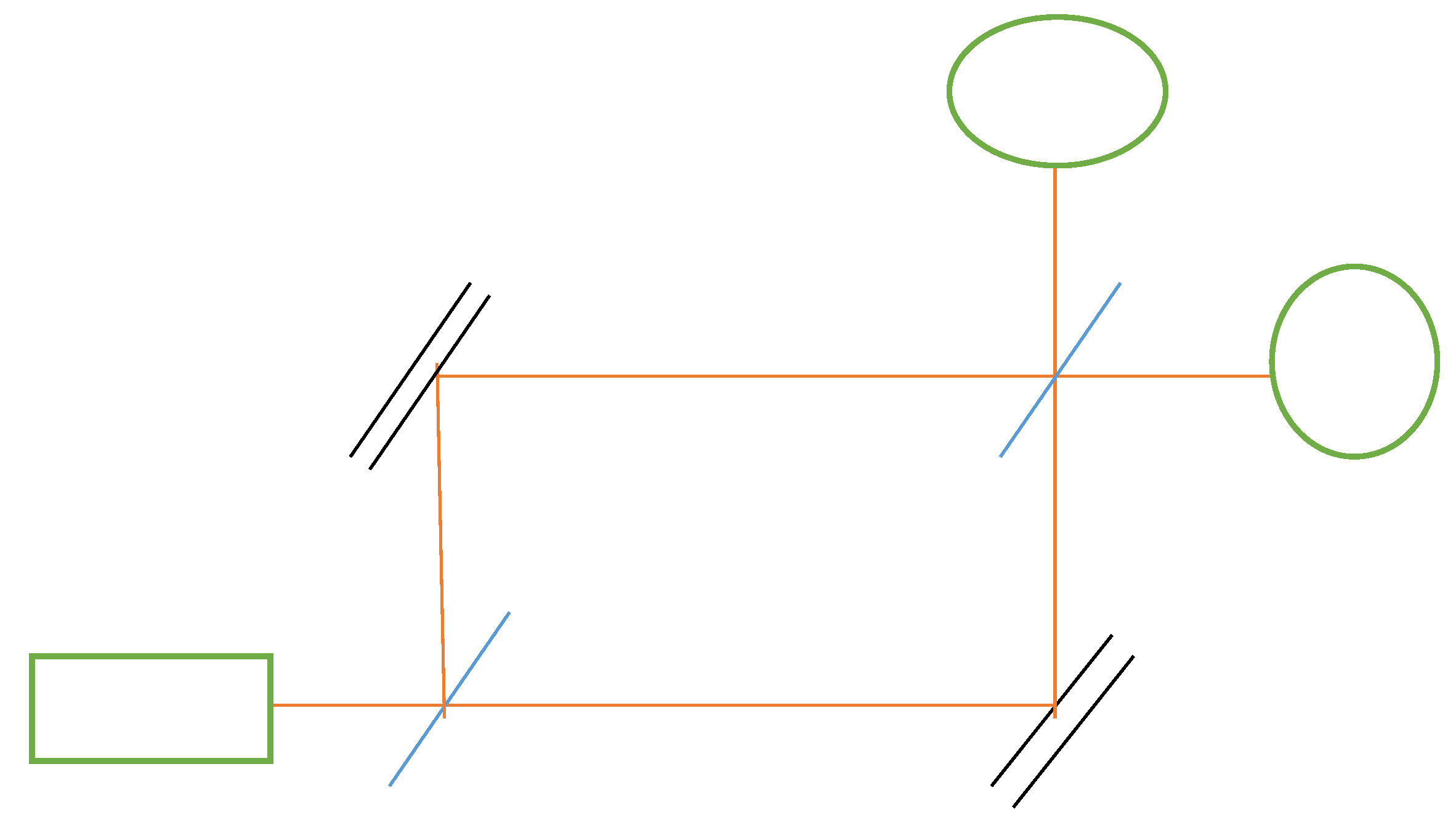
Preprints 101892 g002
Figure 2. XX.
Figure 2. XX.
Preprints 101892 g002
Another applications of Mach Zender interferommeter is in the field of optcal quantum computation. The polarization state of light was considered to be a suitable representation of qubit states, and that by appling phase shifts to a light beam, we can perform a probability rotation of states, and also apply gate operations to the qubit states. These are all posssible in interferometric systems or other optical devices. But applying these gates to multi-qubit systems seemed most viable through a mach zender inteferometer, since both beams in their distinct paths mach zender interferometer exhibits properties of entanglement.
The superposed quantum states for both optical paths are given by;
ψ 1 = | 0 ± 1 2 … … p a t h   1       a n d       ψ 2 = | 0 ± 1 2 … … ( p a t h   2 )
Where the state “1” is represnted by vertical polarization of the light and “0” is represnted by the horizontal polarization of state.
Lineary the states are defined as;
| 0 = 1 0   | 1 = 0 1
A linear transformtion [23,24] applied on these states would yield an output, depending on the particular transformation matrix corresponding to a given quantum gate.

Multiple Beam Splitting and Multiple Intereference

Although the Mach Zehnder interferometer detects two fringes, an alternative interferometric system which may detect higher number of fringes is being proposed in this section, one which may be considered a modification of the michelson interferometer. Such that the michelson interferometer will detect more than just one or two fringes.
Two digrams are given illustrating possible configaurations for the proposed device.
In Figure 3 it can be seen that the first beam splitter just after the light source splits the incoming beams from the source into two beams in perpendicular paths. Let one path be referred to as an x1 path; this is the path on vertical axis of the diagram, and the other path referred to as an x2 path on the horizontal axis of the diagram.
Additional beam splitters in array are introduced between the beam splitter and the mirror in the x2 path, the number of beam splitters that can be added is not limited. But for the simplicity of the diagram only two additional beam splitters are used. The additional beam splitters may require adjustments of the distance between the first beam splitter and the mirror, likewise the gaps between the beam-splitters in the array would also have to be considered.
Each additional beam splitters is splitting the beam in the x2 path further, and just like the first beam splitter, the additional beam splitters will also split the beams perpendicularly, into more x1 and x2 paths. All the beams in the x2 path will overlap in the same direction and still remain a single beam, but the new sets of x1 paths will be parallel to each other.
Like the Michelson interferometer, the beams in the x1 path will each be directed towards the mirrors in their paths, which then reflects them to their respective detectors. But before each of them must have intersected with the x2 beam leading to interference that will generate individual fringes for each interference which will be detected using the photo-detectors.
The phase difference for a single interference between two beams is typically given as;
∆ φ = φ x 2 − φ x 1
However the sum of phase differences for multiple interference would be;
φ x 2 − φ a x 1 + φ x 2 − φ b x 1 + … φ x 2 − φ n x 1
This sum would have to be redefined for the multiple x1 paths, and the single overlapped x2 path, that the phase difference for the multiple interference is;
∆ φ = N φ x 2 − ( φ a x 1 + φ b x 1 + …   φ n x 1 )
  w h i c h   c a n   a l s o   b e   w r i t t e n   a s ;           ∆ φ = N φ x 2 − ∑ i = a n φ i x 1   Where “N” is the number of interference.
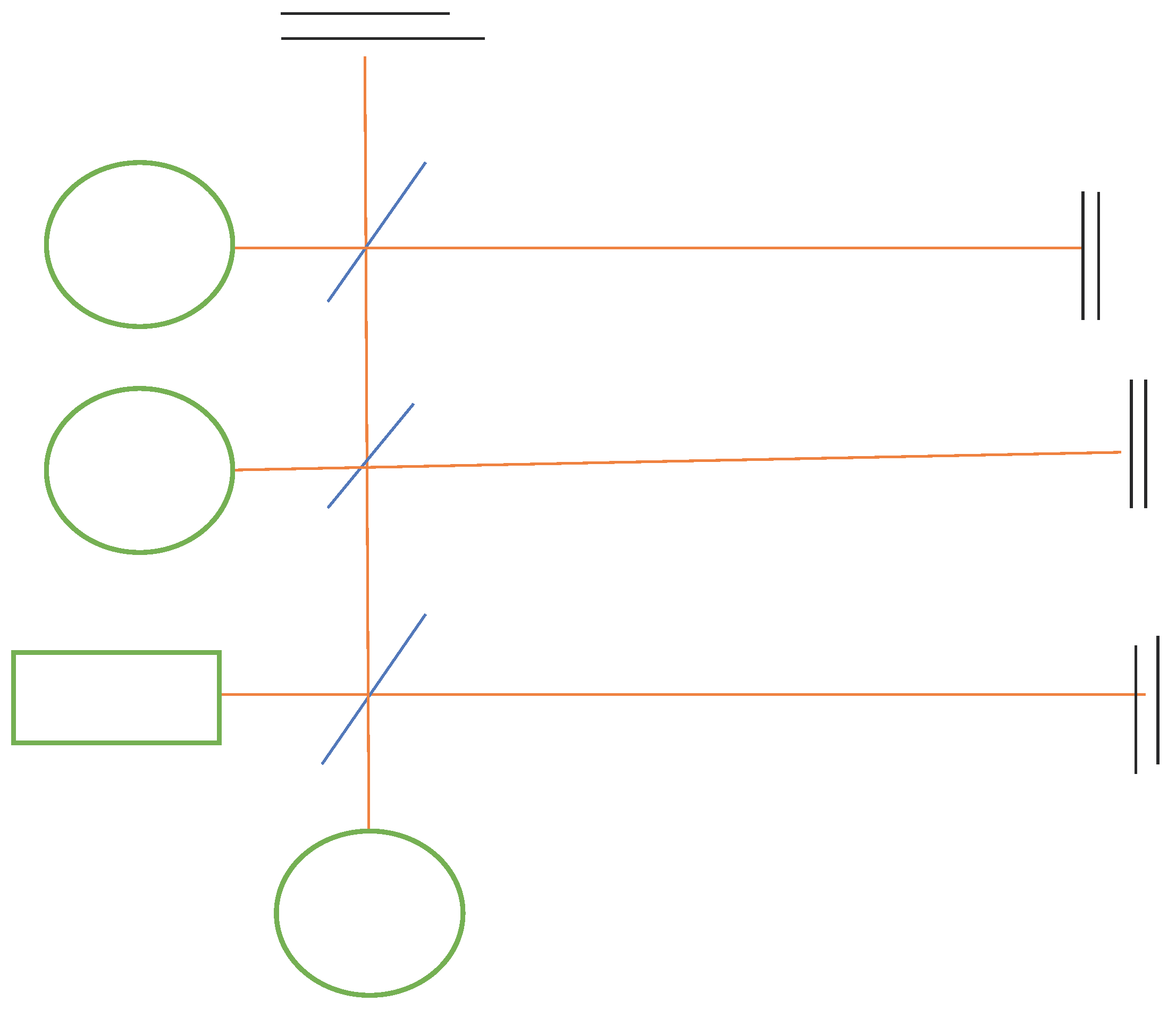
Figure 4 is another configuration but based on the same principle, the first beam splitter also splits the beams into two paths x1 and x2. However the additional beam splitters are on the x1 path, unlike the previous configuration where it’s on the x2 path. This leads to an overlapping of all the x1 beams in form of a single beam, and a parallel set of x2 beams, with mirrors and detectors for each x2 that would interfere with the x1 beam. Hence it can be said that;
[ ∆ φ = ( φ a x 2 + φ b x 2 + …   N φ n x 2 ) − N φ x 1 ]
a l t e r n a t i v e l y   e x p r e s s e d   a s ;           ∆ φ = ( ∑ i = a n φ i x 2 ) − N φ x 1
It is seen that both configurations still modifies the Michelson interferometer in the same manner but with different setups. These configurations would allow us to have multiple detectable fringes, providing separate patterns of interference that can be compared and analyzed, which may reveal more details of the interference, and may enhance sensitivity. It also gives us multiple choices of reference beams, or even allow us to have more than one reference beams at the same time.
Just like a Mach-Zender interferometer, it may also be applicable to quantum entanglement and other quantum mechanical phenomena.

Merits of Multiple Beam Splitting Interferometry in Instrumentation

The proposed interferometer would be an improvement to interferometry as instrumentation device. If one were to consider a parameter to be measured with an interferometer, and that parameter requires an interaction with the beams of a Michelson or a Mach Zehnder interferometer, the presence of the parameter would lead to a detectable, phase shifts between the beams. However these are just two beams, and the difference in their path length would be given as;
∆ x = ∆ λ 2 π n   ( φ 2 − φ 1 )
Though the difference in path length between the two beams and phase shifts incurred by an interaction with the given parameter can be sensed by the photodetector, but the difference in path length for n-number of coherent beams would be more pronounced.
The difference in path length for n-number of beams would be given as;
∆ x = ∆ λ 2 π n   | N φ x 2 − ∑ i = a n φ i x 1 |
w h e r e   d i f f e r e n c e   i n   w a v e l e n g t h   λ   i s   n o w   g i v e n   a s ;
  Δ λ = N λ x 2 − ∑ i = a n λ i x 1  
Leading us to; ∆ x = 1 2 π n | N λ x 2 − ∑ i = a n λ i x 1 | | N φ x 2 − ∑ i = a n φ i x 1 |
This optical path-length would be more noticeable to the detector, as the parameter is interacting with higher number of beams which are all at interference with the beam in the x2 direction. Hence we would record significant phase shifting, difference in wavelength, and optical path length between the n-number of beams.
The interferometer also allows relative detection of fringes, as individual detectors would be detecting individual fringes relative to other fringes. This way a parameter or sample can be studied or measured from different paths and perspectives. This is very useful for analysis as one can compare the data gotten from each detectors, revealing useful informations about the system.
Instrumentation involves measurement, detection and control of parameters, and the various interferometric system have been used for these purposes [19,20,21], particularly in terms of detection with high level of sensitivity and precision. It also has analytical advantage and freedom to vary the number of fringes according to experimental or practical needs, which is a level of control over the instrumentation system.

Quantum Computational Advantages of the Proposed Interferometer

Interferometry has found a place in the field of quantum information processing and quantum computation, particularly the Mach-Zehnder interferometer as stated in pervious sections of this article. The use of interferometers in quantum information processing and computational falls under the general umbrella of linear optical quantum computing (LOQC).
LOQC is one out of the many approaches in the development of a true universal quantum computer. LOQC involves the use of photons as carriers of quantum information, which can be manipulated using optical instruments like wave plates, mirrors, beam splitters etc. as ways of processing these informations.
In optical quantum computation, photon represents a qubit state which is a superposition of quantum states representing informations. Just as classical computation utilizes bits to represent informations, quantum computation also uses a superposition of two or more bits represented by quantum mechanical states to represent information. In optics the quantum states are represented by the polarization states
Qubits can be processed through quantum gates, such as the CNOT-gate, CPHASE-gate, and Toffoli-gate etc. in optical quantum computations these gates are implemented using wave-plates that alters the polarization states of the light beams, thereby applying a transformation to the information and eventually yield an output.
These operations can be carried out with a Mach Zehnder interferometer, and even more the Mach Zehnder interferometer performs the operations for entangled system (the two coherent light beams to be precise) with their quantum state being detected by the photodetectors. This makes the Mach Zehnder interferometer very suitable for processing two qubit systems.
In previous sections it was stated that the proposed interferometric system modifies the Michelson interferometer to extend the number of coherent beams and interference patterns, and that more than one fringes can be detected, akin to a Mach Zehnder’s interferometer. But the difference is that the number of beams and fringes that are be produced are limited to two in a Mach-Zender interferometer, but are not directly limited in this proposed interferometer as the number of beams only depends on the specific practical requirements. Making it possible to have multiple number of coherent beams.
This implies that the proposed modification may enable multi-partite entanglement, or a multi-qubit system. Implementing quantum logic gates and transformations may be possible through the use of similar linear optical elements used with the Mach-Zehnder interferometer to alter the polarization states of the beams, such as the wave plate mentioned earlier. This is clearly an advantage in the field of quantum computation, indicating that the proposed interferometer to be just as useful as a Mach-Zehnder interferometer for quantum computation.

Conclusion

The Michelson and Mach Zehnder interferometer are very versatile instrumentation devices, the proposed interferometric system which multiplies beams and produces multiple interference would also be another interferometer that would be useful for instrumentation and computation, while providing other benefits such as enhanced sensitivity and the multiplicity of interferometric data. Expectations are that the interferometer if fully developed and properly engineered would facilitate progress in the field interferometry, instrumentation, physics, optics, and quantum information processing. Further research and development may be necessary to take the proposed interferometer from a simple stage of conceptualization to reality, it would be interesting to see it function in real time as there might be other merits it may have.

Declarations

I hereby declare that this article, titled; “conceptualizing an interferometer with multiple beams splitting and multiple interference”.
  • Is written with no conflicting interest, neither is there any existing or pre-existing affiliation with any institution.
  • No prior funds is received by the author from any organization, individual or institution.
  • The content of the article is written with respect to ethics.
  • The content of the article does not involve experimentation with human and/or animal subjects.
  • Data-availability; no data, table or software prepared by an external body or institution is directly applicable to this article.

References

  1. Wikipedia.org. https://en.m.wikipedia.org/wiki/Michelson-Morley-experiment.
  2. Shankland, R.S. Michelson-Morley experiment. American journal of physics 1964, 32, 16–35. [Google Scholar] [CrossRef]
  3. Lawal, J.; Kessler, E. Michelson interferometry with 10pm accuracy. Review of Scientific Instruments 2000, 71, 2669–2676. [Google Scholar] [CrossRef]
  4. Ikram, M.; Hussain, G. Michelson interferometer for precision angle measurements. Applied Optics 1999, 38, 113–120. [Google Scholar] [CrossRef] [PubMed]
  5. Alex Abramovici et-al. LIGO the Laser interferometer gravitational wave observatory. Science 1992, 256, 325–333. [Google Scholar] [CrossRef] [PubMed]
  6. Junaid Aasi, Thomas abbot et-al. Advanced LIGO. Classical and quantum gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
  7. Gregory. M. Harry Advanced LIGO: the next generational wave detectors. Classical and quantum gravity 2010, 27, 084006. [Google Scholar] [CrossRef]
  8. Adams, S.F. ; et-al. How does a Mach-Zender interferometer work? Physics Education 2000, 35, 46. [Google Scholar]
  9. JG Rarity et-al. Two photon interference in a Mach-Zender interferometer. Physical review letters 1990, 65, 1348. [Google Scholar] [CrossRef]
  10. Ryzard Horodecki et-al. Quantum entanglement. Review of modern physics 2009, 81, 865. [Google Scholar] [CrossRef]
  11. Karol Zyczkowski et-al. Dynamics of quantum entanglement. Physical Review ‘A’ 2001, 65, 012101. [Google Scholar] [CrossRef]
  12. Vlatko Vedral. Quantum entanglement. Nature physics 2014, 10, 256–258. [Google Scholar] [CrossRef]
  13. Barbara M Terhal. Detecting quantum entanglement. Theoretical computer science 2002, 287, 313–335. [Google Scholar] [CrossRef]
  14. Vlatko Vedral and Martin. B. Pleino. Basics of quantum computation. Progress in quantum electronics 1998, 22, 1–39.
  15. Chris Bernhardt. Quantum computing for everyone, MIT Press, (2020).
  16. Robert. S. Sutor, Dancing with qubits; how quantum computing works and how it can change the world, Packt Publishing, (2019).
  17. Ralph, T.C.; Pryde, G.J. Optical quantum computing. Progress in Optics 2010, 54, 209–269. [Google Scholar]
  18. Jeremy. L. O’Brien. Optical quantum computing. Science 2007, 318, 1567–1570. [Google Scholar] [CrossRef] [PubMed]
  19. Yang, S.; Zhang, G. A review of interferometry for geometric measurement. Measurement and science technology 2018, 29, 102001. [Google Scholar] [CrossRef]
  20. Donati, S. Developing self-mixing interferometry for instrumentation and measurements. Laser & Photonics reviews 2012, 6, 393–417. [Google Scholar]
  21. Nicusor. V. iftima et-al. A portable low coherence interferometry based instrument for fine needle aspiration biopsy guidance, Review of scientific instruments, 76(6), (2005). [CrossRef]
  22. Wikipedia.org. https://en.m.wikipedia.org/wiki/Optical-coherence-tomography-(OCT).
  23. Charles. G. Cullen, Matrices and linear transformation, Courier-Corporation, (2012).
  24. Daniel. T. Finkbeiner, Introduction to matrices and transformations, Courier-Corporation, (2013).
  25. Jinhyoung-Lee et-al. Multipartite, entanglement for entanglement teleportation. Physical Review “A” 2002, 66, 052318. [Google Scholar] [CrossRef]
  26. Andrew. C. Doherty et-al. Detecting Multipartite Entanglement. Physical Review ‘A’ 2005, 71, 032333. [Google Scholar]
  27. Emmanuel Knill et-al. A Scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
Preprints 101892 g003
Figure 3. XX.
Figure 3. XX.
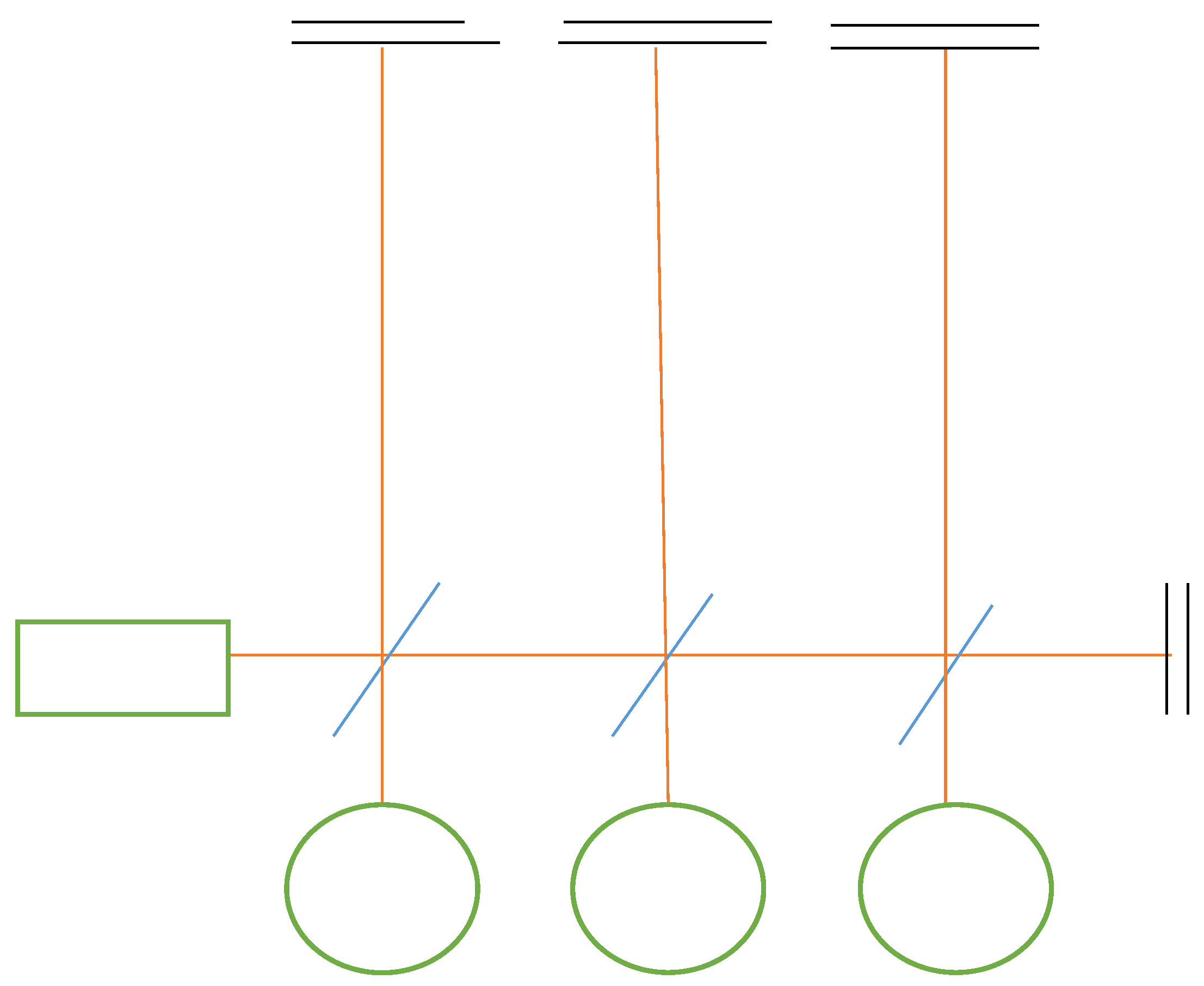
Preprints 101892 g003
Preprints 101892 g004
Figure 4. XX.
Figure 4. XX.
Preprints 101892 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated