Prerpints.org logo
Preprint
Article

Modelling of the Evapotranspiration Portion Calculation of the Water Footprint: A Global Sensitivity Analysis in the Brazilian Serra Gaúcha

Altmetrics

Downloads

109

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 March 2024

Posted:

25 March 2024

You are already at the latest version

Alerts
Abstract
Water footprint has been widely used to illustrate the consumption of water in many situations; for instance, in products, processes or regions of interest. In this work, we analyzed – using a sensitivity analysis approach – the effect of some variables in the calculation of the water footprint in the viticulture in Brazilian Serra Gaúcha (the major producing region of Brazilian Wine).The classical Penman-Monteith model for evapotransporation was considered, with uncertainties in some parameters (dead mulch covering fraction in the vineyard, maximum temperatures for some months, altitudes and latitudes of the site). The sensitivity analysis was conducted using the SAFE toolbox under Octave framework. The results indicated that the the portion of the water footprint corresponding to the evapotranspiration is more sensitive to the values of mulch covering fraction and the altitude of the site in comparison with the latitude and the maximum temperatures.
Keywords: 
Subject: Environmental and Earth Sciences  -   Sustainable Science and Technology

1. Introduction

Water consumption in the viticulture is gaining more attention every year [1,2]. Thus, it is necessary to understand the factors that affect it and on which ones we can interfere to reduce the water use. In the last decades, Brazil has been getting attention on it is capacity to produce wine [3]. Furthermore, the most traditional and main wine hub in Brazil is the Brazilian Serra Gaúcha [4,5,6].
A well-established measure of the water consumption is called water footprint. The water footprint concept was introduced by Hoekstra and Hung [7] and represents the consumption of water of a crop, product, region or nation (for instance). The water footprint is usually classified as green, blue and gray water. In essence, the green water indicates the portion of water arising from rain and snow, whereas the blue water corresponds to the water coming from irrigation. Finally, the gray portion refers to the necessary quantity of water employed in dilution processes (in order to achieve the concentration of each pollutant in a river, for instance). In the wine industry, the study of the water footprint is fairly recent, with calculations presented for New Zealand, Italy, South Africa and Portugal, for instance [8,9,10,11]. The water consumption in the winery and in the vineyard must be considered. The water is consumed through evapotranspiration, irrigation, use of fertilizers and agrochemicals, among others [9].
An important part of water footprint calculation of a crop is usually conducted considering the evapotranspiration concept. The evapotranspiration is a combined process of evaporation and transpiration by a crop. The initial step in the calculation of the evapotranspiration is the determination of the reference evapotranspiration ( E T 0 ). The reference evapotranspiration is commonly calculated using the Penman-Monteith model [12], a well-established methodology. Using a small set of parameters (latitude, altitude, wind speed, temperatures of the site), this model permits the evaluation of the reference evapotranspiration E T 0 . The crop evapotranspiration ( E T c ) is calculated using the value of E T 0 and a crop coefficient, which considers the different growth stages of a particular crop and the existence of dead mulch (for instance) [12]. Clearly, the different quantities employed in the calculation of the parameters E T 0 and E T c are subject to uncertainty (for instance, temperatures and wind speeds). Thus, the main objective of the sensitivity analysis is to evaluate the effect of these uncertainties in the calculated values of the evapotranspiration. Furthermore, the productivity of the crop are also subject to uncertainty, which can have a direct impact on the calculation of the water footprint.

1.1. Previous Related Works

Many researches deal with sensitivity analysis in the Penman-Monteith model for the reference evapotranspiration, considering different parameters and locations. Beven [13] studied the sources of errors and presented a sensitivity analysis study for the Penman-Monteith equation for three meteorological sites in England and Wales. The author observed a higher dependence of the vegetation type on the evapotranspiration, in comparison with climatic differences between the three sites analyzed. Ndiaye et al. [14] analyzed the effects of maximum/minimum temperatures, solar radiation, wind speeds and maximum/minimum relative humidity on evapotranspiration in different localities in Burkina Faso. Irmak et al. [15] conducted a sensitivity analysis study of several parameters (maximum/minimum wind speeds, maximum/minimum air temperatures, vapor pressure deficit and solar radiation) in some regions of United States of America, concluding that E T 0 is more sensitive to variations in the vapor pressure deficit. Debnath et al. [16] conducted a sensitivity analysis study for the reference evapotranspiration value in India, indicating that E T 0 is more sensitive to the solar radiation. Furthermore, Debnath et al. [16] noted a linear relationship between the value of E T 0 and the variables under consideration (maximum and minimum temperatures, solar radiation, relative humidity and wind speed). Biazar et al. [17] conducted a sensitivity analysis study for the reference evapotranspiration E T 0 , using different models, in a humid region of Iran. The findings of Biazar et al. [17] indicate a high sensitivity of E T 0 for the maximum temperatures and number of sunshine hours, and some lower sensitivities with respect to the minimum temperatures and wind speeds. Arunrat et al. [18] analyzed the impact of the climate change on the water footprint for rice, cassava, maize, soybean and mung bean in Thailand. The authors considered changes in demography and economics, as well as the greenhouse effect, in the studied scenarios (Shared Socioeconomic Pathways – SSPs). Arunrat et al. [18] concluded that the water footprint for the studied crops in the future will be closely related to the yields, considering the greenhouse effect. Furthermore, some crops (maize, soybean, mung bean and cassava) appear as alternatives to rice during the dry seasons. Rossi et al. [19] studied the water footprints for olive production in Italy (considering the green, blue and gray portions of the water footprint). The authors observed a predominance of the green water footprint in comparison to the blue and gray portions. Furthermore, it was observed by Rossi et al. [19] that the water footprint was severely influenced by the productivity, even in some years with low precipitation, what is in agreement with the results of Arunrat et al. [18] (i.e., the effects of some parameters in the reference evapotranspiration can be compensated by an increase in the productivity, considering the calculation of the water footprint). Arunrat et al. [20] presented a study analyzing the nitrogen, carbon and water footprints of organic and conventional rice in Thailand in the 2018-2021 period. The authors highlighted that the water footprint for the conventional crop is higher than the value for the organic rice (mainly with respect to the gray water footprint). Recently, Yong et al. [21] presented a review study concerning the different sensitivity analysis techniques applied in the calculation of the reference evapotransporation. The results obtained by Yong et al. [21] indicated that the global sensitivity analysis studies are recent and restricted to some few countries (Australia, Malaysia, United States, and China).
Considering specifically the calculation of the water footprint, Zhuo et al. [22] presented a study of uncertainty and sensitivity analysis in the water footprint for the production of maize, soybean, rice and wheat in China (Yellow River Basin). Recently, Li et al. [23] conducted a sensitivity analysis study in the production of wheat, rice, maize, and soybean in China. In this study, the authors considered the value of the reference evapotranspiration E T 0 as one of the parameters.

1.2. Proposal of This Work

In this work, we propose a detailed sensitivity analysis procedure in the water footprint calculation for the viticulture in Serra Gaúcha, Brazil, located in the Rio Grande do Sul state. As pointed previously, the Serra Gaúcha is Brazil’s main wine producing region. We consider, as parameters, the altitude and the latitude of the site (which impacts in the reference evapotranspiration) and the existence of dead mulch in the vineyard (affecting the crop evapotranspiration). In addition to these, the maximum temperatures for the months of October, November and December are also considered as parameters. Obviously, there is a huge scope for choosing other parameters for the sensitivity analysis (for instance, wind speeds and humidities). On the other hand, the main focus of this work is to detail the influence of some parameters which can be object of decision (for instance, the place to set up a vineyard and the use of a soil management technique in order to minimize the water consumption). Thus, the results of the water footprint sensitivity analysis provide supplementary data for decision-making purposes. Moreover, considering the rising temperatures in the Rio Grande do Sul state (Brazil) [24,25], the effects of maximum temperatures in the water footprint are also taken into account. Moreover, Biazar et al. [17] indicated that the most sensitive parameter for E T 0 in a humid region in Iran is the maximum temperature, which justifies this choice. It should be noted that this study only covers the portion of the water footprint that refers to crop evapotranspiration.
Although the analysis is specific to a particular region, the procedures used are applicable to any location worldwide. Here, we employ the SAFE toolbox (under Octave [26]) for sensitivity analysis developed by Pianosi et al. [27]. Global sensitivity analysis tools are also available in other platforms; see, for instance, Borges et al. [28]. Finally, it should be emphasized that the use of global sensitivity analysis techniques in water footprint calculations has not been frequently found in the literature.

2. Modelling

In this section, the mathematical models under consideration were detailed, namely: the reference evapotransporation model (Penman-Monteith model) ( E T 0 ), the crop evapotranspiration model ( E T c ), and the water footprint model ( W F ).

2.1. The Reference Evapotranspiration Model

The reference evapotranspiration ( E T 0 , in mm/day or mm/month, depending on the time step employed) was represented by the Penman-Monteith model [12]:
E T 0 = 0.408 Δ ( R n − G ) + γ p 900 T + 273 u 2 ( e s 0 − e a ) Δ + γ p ( 1 + 0.34 u 2 ) ,
where R n is the net flux of solar radiation (MJ/ m 2 /day) , G is the heat flux in the soil (MJ/ m 2 /day), T is the mean air temperature at 2 m height (°C), e s 0 is the saturation vapor pressure (kPa), e a is the actual vapor pressure (kPa), Δ is the slope of the vapor pressure curve, γ is the psychrometric constant (kPa/K) and u 2 is the wind speed at 2m (m/s).
In order to clarify the objectives of the sensitivity analysis study, the main terms of Equation (1) must be detailed. Even though this equation is well-known, a detailed analysis of the model permits a clear understanding of the nonlinearities of the equations involved in the problem. Therefore, the calculations of e s 0 , Δ , γ , R n and G will be explained in detail, as well as the correlated quantities.
In Equation (1), e s 0 was determined by [12]:
e s 0 = e 0 ( T m a x ) + e 0 ( T m i n ) 2 ,
where the saturation pressure is calculated by an Antoine-type equation [12]:
e 0 ( T ) = 0.6108 exp 17.27 T T + 237.3 ,
with the temperature expressed in °C and the vapor pressure calculated in kPa. T m i n and T m a x refer, respectively, to the monthly average daily minimum and maximum temperatures for the months of the year (in °C).
Parameter Δ represents the slope of the saturation pressure curve [12]:
Δ = 4098 0.6108 exp 17.27 T m e a n T m e a n + 237.3 ( T m e a n + 237.3 ) 2 ,
where T m e a n is the mean monthly average temperature.
γ p refers to the psychrometric constant [12]:
γ p = 0.000665 P ,
where P is the local atmospheric pressure (kPa). Here, it was considered that the atmospheric pressure depends on the altitude:
P = 101.3 293 − 0.0065 z 293 5.26 ,
where z is the site elevation above sea level (m).
The net flux of solar radiation ( R n ) was determined by:
R n = R n s − R n l ,
where R n s and R n l refer, respectively, to the net short-wave radiation and the net long-wave radiation.
For short-wave radiation, the following expression was employed:
R n s = ( 1 − α ) R s ,
where α is the albedo coefficient ( α = 0.23 , as pointed by [12]) and R s is the incident solar radiation.
The long-wave radiation was calculated by [12]:
R n l = σ f c d 0.34 − 0.14 e a T K , m a x 4 + T K , m i n 4 2 ,
where σ is the Stefan-Boltzmann constant, and f c d is the cloudiness function. T K , m a x and T K , m i n , respectively, refer to the monthly average daily maximum and minimum absolute temperatures (for a specific month of the year). The cloudiness function f c d was evaluated by:
f c d = 1.35 R s R s 0 − 0.35 ,
where R s 0 is the solar radiation in the absence of clouds (clear sky). Values of R s 0 can be obtained by using information regarding the extraterrestrial radiation ( R a ). For instance, R s 0 = ( 0.75 + 2 × 10 − 5 z ) R a , where z is the site elevation with respect to the sea level.
The extraterrestrial radiation R a (short-wave radiation in the absence of atmosphere, or solar radiation at the top of the atmosphere) was calculated by:
R a = 24 × 60 π G s c d r ω s sin ( γ ) sin ( δ ) + cos ( γ ) cos ( δ ) sin ( ω s ) ,
where γ is the latitude (rad) and δ represents the declination (rad). In Equation (11), G s c is the solar constant 0.0820 M J m 2 m i n , d r is the inverse relative distance earth-sun, calculated by:
d r = 1 + 0.033 cos 2 π 365 J ,
where J = i n t ( 30.4 M − 15 ) (Julian day). Moreover, J is the day of the half of the month, i n t is the integer function, and M is the month under consideration. The solar declination δ was calculated by:
δ = 0.409 sin 2 π 365 J − 1.39 ,
The incident solar radiation was evaluated by:
R s = a s + b s n N R a ,
where a s = 0.25 and b s = 0.50 [29]. Furthermore, n is the number of hours of sunlight per day and N is the maximum number of sunlight per day N = 24 π ω s . The parameter ω s (solar angle at the end of the day) was calculated by ω s = arccos − tan ( γ ) tan ( δ ) .
The actual vapor pressure ( e a ) can be obtained using relative humidity data ( U R ) [12], according to:
e a = U R m e a n 100 e 0 ( T m a x ) + e 0 ( T m i n ) 2 ,
Finally, in Equation (1), G is the heat flux in the soil, calculated by [12]:
G = 0.07 T m o n t h , i + 1 − T m o n t h , i − 1 ,
where T m o n t h , i refers to the mean air temperature of the month i. It can be noted that the calculation of the soil heat flux G demands an information regarding the mean air temperature of every month of the year. On the other hand, as pointed by Martins [30], the value of G can be approximated using the simple arithmetic mean between the maximum and minimum temperatures for a month as a good approach. In fact, in many cases, is reasonable to accept that G ≈ 0 [12].

2.2. Crop Evapotranspiration Model

The crop evapotranspiration can be obtained using the value of the reference evapotranspiration, considering the different development stages of the crop, according to [12]:
E T c = E T 0 K c ,
where K c is the crop coefficient. Usually, three different stages are considered (initial, mid-season and late season stages), with three values for K c . The FAO [12] recommendation for grape wines are K c i n i t = 0.30 , K c m i d = 0.70 and K c l a t e = 0.45 , where the subscripts init, mid and late refer, respectively, to the initial, mid and late stages of the development of the crop. On the other hand, some parameters can affect the values of K c , such as the existence of dead mulch [31]. According to Fonseca [32], the effect of dead mulch in the value of K c i n i t can be represented by the following expression:
K c i n i t , d c = K c i n i t 1 − 0.50 f d m ,
where f d m is the dead mulch coverage fraction. K c i n i t , d c represents the crop coefficient considering the existence of dead mulch.Thus, an obvious effect of the use of dead mulch is the reduction in the values of the crop evapotranspiration ( E T c ). It must be emphasized that the use of mulch is a common practice in the Brazilian Serra Gaúcha, as pointed by Rosa et al. [33], which justifies the study of the impact of this parameter in the water footprint. The use of organic mulching in vineyards to reduce E T c was also reported by López-Urrea et al. [34]. Furthermore, Fonseca [32] points out that although the use of mulch is very common for wine production in the Brazilian tropical regions, this practice has also been observed in temperate regions.

2.3. Water Footprint Model

In this work, it was assumed that the water demand by the crop was fully attended. Thus, the water footprint can be calculated as [7]:
W F = 10 × ∑ E T c Y ,
where Y is the grape productivity by hectare (ton/ha) and E T c is in mm/month. The factor 10 converts the evapotranspiration into m 3 /ha. The sum refers to the months of the year. We are not differing between the types of water footprint (green and blue).

3. Materials and Methods

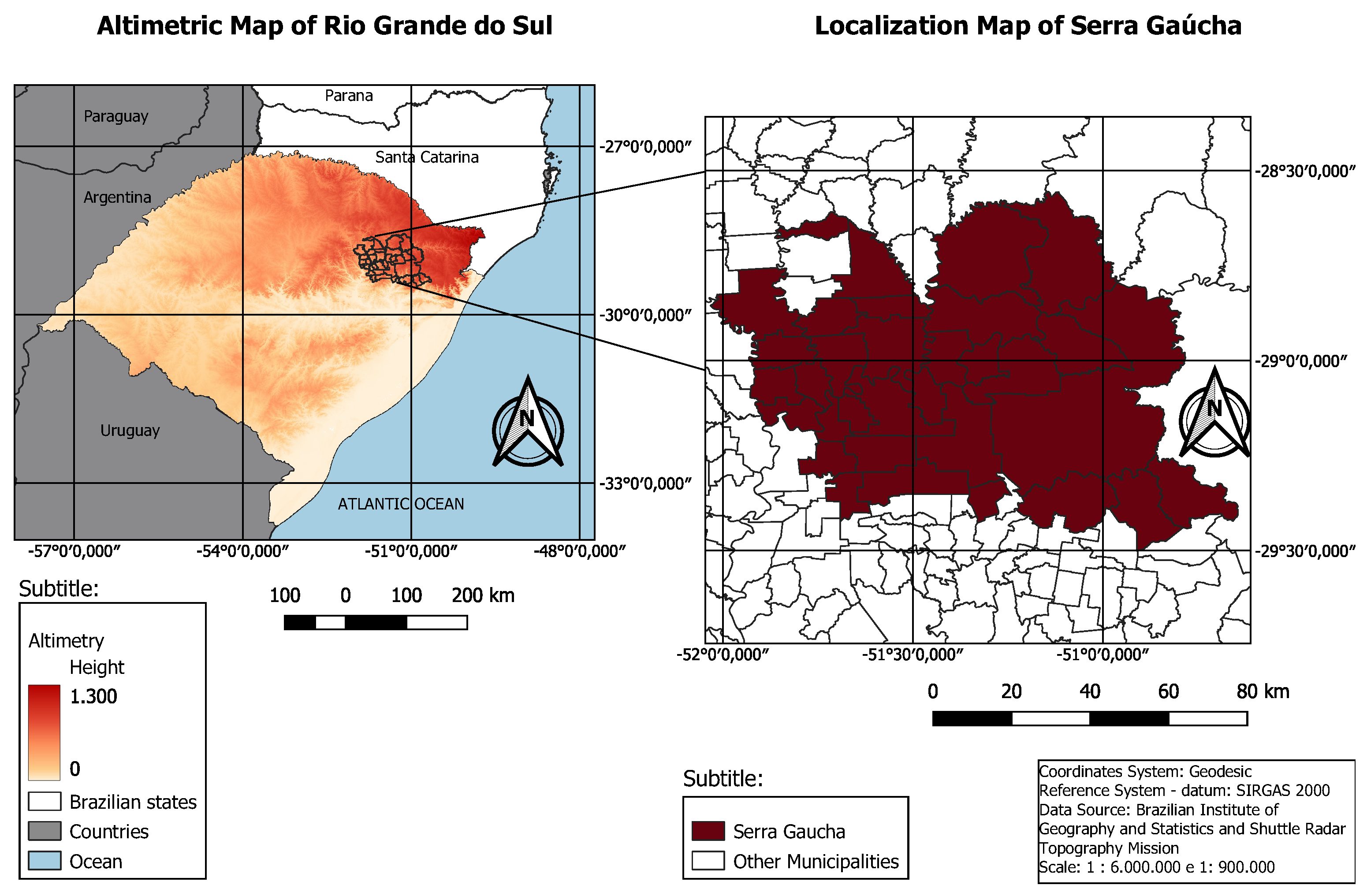
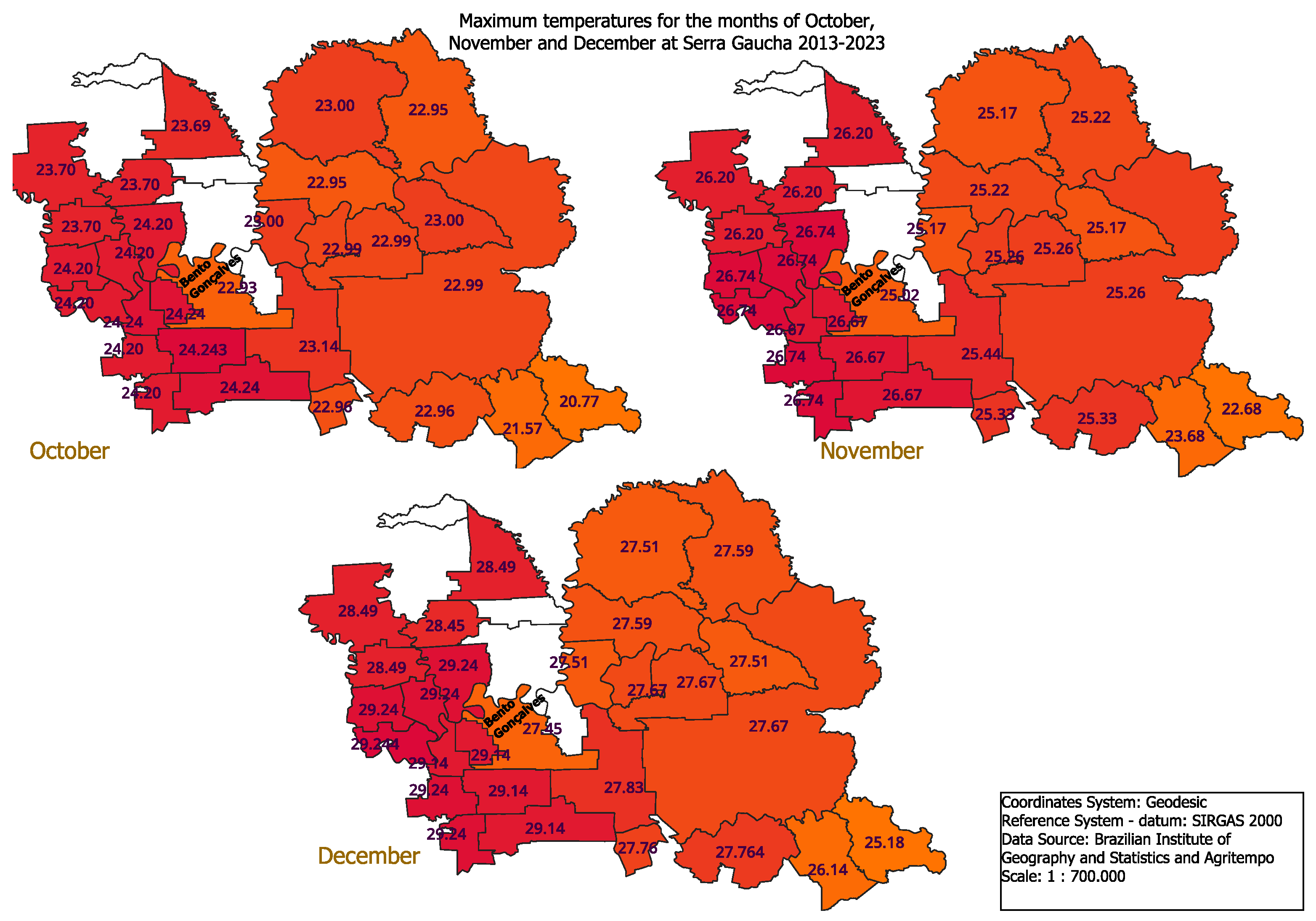
3.1. The Brazilian Serra Gaúcha

We considered the latitudes between the cities of Nova Araçá (-28.654549°) and Gramado (-29.433653°). Figure 1 presents an altimetric map of the Rio Grande do Sul State, in Brazil, as well as the localization of Serra Gaúcha, the region under study. The main objective of these maps is to detail the ranges of latitudes and longitudes for the sensitivity analysis. In the Serra Gaúcha, the elevations are in the range from 206m to 926m (considering the existence of valleys in the region). In recent years, there has been an increase in the production of wine at altitudes above 700 m (for example, the so-called Altos de Pinto Bandeira wine). Furthermore, the soil management techniques in vineyards usually employ mulching practices [35]. With respect to the dead mulch covered fraction, f d m , this parameters is in the interval 0 , 1 .
Calculations were conducted using information from the municipality of Bento Gonçal-ves – Brazil, the main wine-producing city in the Serra Gaúcha. Data of temperatures, relative humidities and number of hours of sunlight per day were obtained from https://pt.climate-data.org/america-do-sul/brasil/rio-grande-do-sul/bento-goncalves-1386/. Wind velocities are obtained by https://pt.weatherspark.com/y/29709/Clima-caracter%C3%ADstico-em-Bento-Gon%C3%A7alves-Brasil-durante-o-ano. We considered variations of 3 °C in the maximum temperatures of the months of October, November and December (an arbitrary choice, in order to evaluate the effect of the maximum temperatures on the water footprint). These variations are far greater than the differences of the maximum temperatures in the region under study (even considering the differences of altitude and latitude). Figure 2 presents the maximum temperatures in the Serra Gaúcha for October, November and December (2013-2023). We can observe that the maximum temperatures for these months are in the interval T b a s e ± 3 °C, where T b a s e refers to the temperature in the city of Bento Gonçalves.
A medium productivity value Y for grape production was assumed, Y = 10 ton/ha. Usually, three scenarios may be considered for the grape production in the Serra Gaúcha: Y m a x = 12 ton/ha, Y a v g = 10 ton/ha and Y m i n = 8 ton/ha [36] (obviously, the effect of the productivity exhibits a direct effect on the water footprint, and a sensitivity analysis is not necessary for this variable). Furthermore, we used a typical conversion factor of 70% to calculate the number of liters of wine by ton of grape, i.e., a ton of grape is capable to produce 700 L of wine.

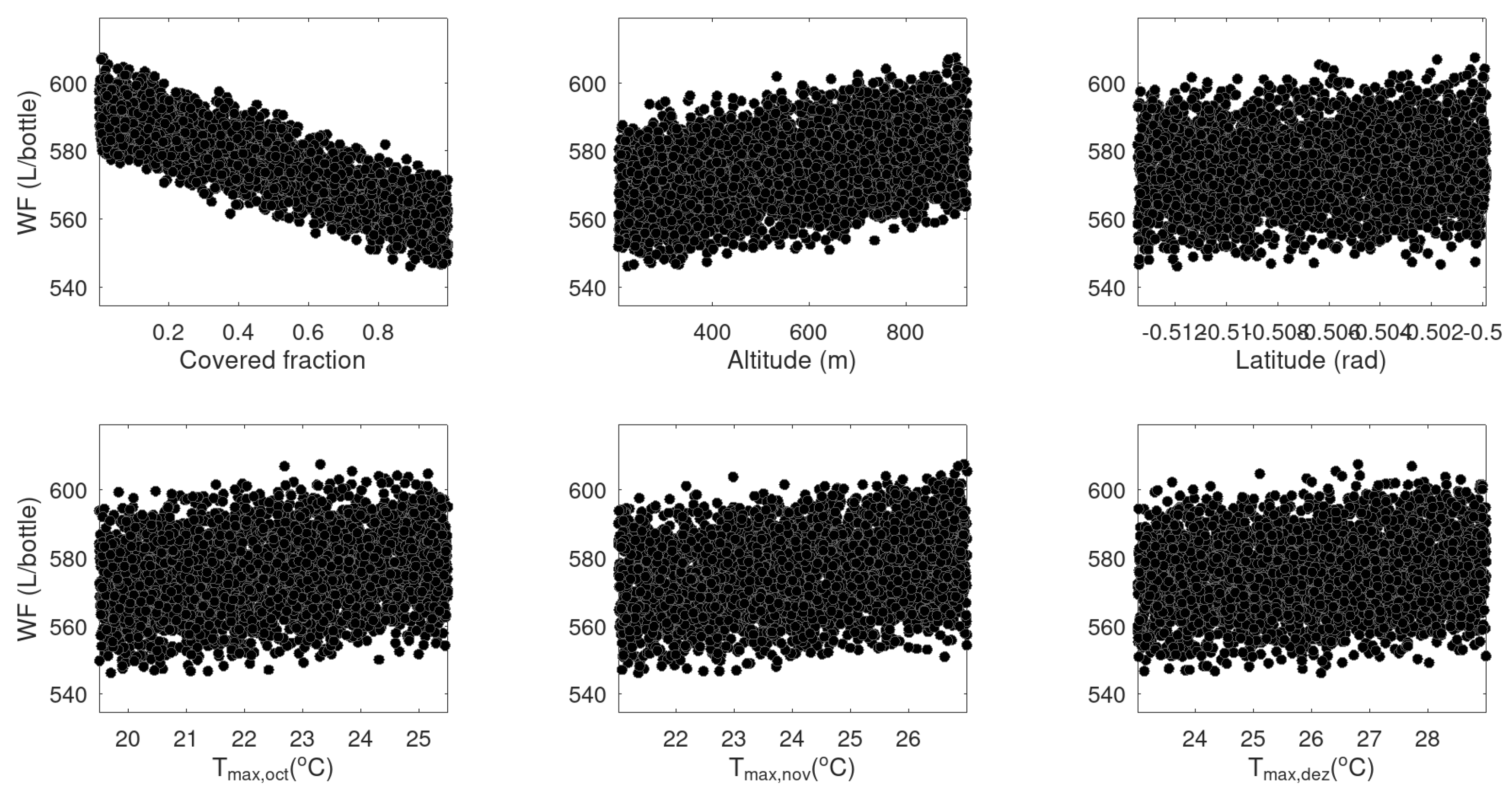
3.2. Global Sensitivity Analysis Techniques

As pointed previously, we employed the SAFE package [27,37], under Octave, to perform the sensitivity analysis. Here, some of the steps proposed by Noacco et al. [37] in the conduction of the sensitivity analysis were taken.

3.2.1. Sampling Strategy

The most popular sampling strategy is the Latin Hypercube Sampling [38]. Considering that each coordinate of a vector is in the interval [ 0 , 1 ] , a Latin Hypercube Sample with N intervals shows a random distribution of N values, with one value in each of the intervals 0 , 1 N , 1 N , 2 N , … , 1 − 1 N , 1 . In practice, the Latin Hypercube strategy has been optimized, for instance with random permutations of the values (coordinate exchange) and with a maximization of the minimum distance between sample points (called maximin criterion), as implemented in SAFE toolbox [27]. The sampling strategy employed here was the Latin Hypercube Sampling (LHS) [39,40], with N = 3000 .
A simple substitution of the Latin Hypercube sample in the model (in our work, the calculation of the water footprint in the wine viticulture) permits to obtain the responses of the model using, for instance, scatter plots.

3.2.2. Analysis of Elementary Effects (EEs)

The first global sensitivity analysis technique applied in our computational experiments is the analysis of the elementary effects (EEs). As pointed by Morris [41], the main objective of the analysis of elementary effects (also called Morris’ method [41]) is to determine whether an effect of a such variable in the response of the model is (i) negligible, (ii) linear and additive, (iii) nonlinear, or (iv) involved in interactions with other variables.
An elementary effect E E i for a input i is defined by [41]:
E E i ( X ) = ( y ( X 1 , … , X i − 1 , X i + Δ X , X i + 1 , … , X k ) − y ( X ) ) Δ X ,
where X is the vector representing the variables of the problem and Δ X is a perturbation in the vector X (only in the position i). Each value of X i may vary in some levels. We aim to compute r EEs, using r trajectories [42]. The mean of the effects for r trajectories is then calculated by [42]:
μ i = 1 r ∑ i = 1 r E E i .
The standard deviation is represented by [42]:
σ i = ∑ i = 1 r E E i − μ i 2 r ,
In our computations, we computed 500 elementary effects ( r = 500 ). A bootstraping approach (i.e., a resampling strategy) is also applied [43], with N b o o t = 100 . Furthermore, the SAFE package employs the “revised version” of μ , represented by μ * (using the absolute values of the elementary effects) [44]. Considering r elementary effects, the number of evaluations of the model is n = r ( M + 1 ) = 500 ( 6 + 1 ) = 3500 , where M is the number of variables considered in the analysis [45].

3.2.3. Fourier Amplitude Sensitivity Testing – FAST

The Fourier Amplitude Sensitivity Testing (FAST) is a variance-based global sensitivity test [46], as well as the Variance Based Sensitivity Analysis (VBSA, or Sobol’ method [47]). The so-called first order FAST sensitivity index is calculated by:
S i = V i V ( y ) ,
where V i is the first-order conditional variance of Y considering the input X i with a value x i * ( V i = V ( E ( Y | X i = x i * ) ) ) and V ( y ) is the total variance of the model output [48].

3.3. Assumptions of the Study

The following assumptions have been made in the present study:
  • The analysis considers only latitude, altitude, fraction of mulch covering in the soil and the temperatures of three months (October, November and December) in the water footprint for the wine production;
  • The water footprint considers only the evapotranspiration portion of the viticulture of the wine production;
  • Temperatures, relative humidities, and wind speeds are considered the same for the different latitudes and altitudes (this assumption may be reasonable considering the small size of the region under consideration; on the other hand, new studies can be conducted considering the uncertainties in temperatures and wind speeds, for instance). Besides, as pointed previously, the range of variation in the maximum temperatures is higher than the real differences in the regions under study.
As pointed previously, a large number of studies analyzed the effects of temperatures, relative humidities and wind speeds in the reference evapotranspiration calculated by the Penman-Monteith model. In our study, we focused on the sensitivity of the model with respect to the parameters that can be effectively chosen by the decision makers, i.e., the site (latitude and altitude) and the use of a mulch covering.

4. Results

In this section, the results of the computational experiments using SAFE toolbox applied in the water footprint for the wine production in the Serra Gaúcha were presented.
The first analysis was conducted only with the sampling strategy and the evaluation of the model, producing a set of scatter plots. Figure 3 presents the scatter plots for the water footprint ( W F , in L/bottle of wine) with respect to the covered fraction, the altitude and the latitude of the site, and to the temperatures of three months. A clear effect of the covered fraction in the water footprint can be observed. We also noticed that the water footprint was directly affected by the altitude (even considering the nonlinear relationship between altitude and the reference evapotranspiration). On the other hand, the effects of latitude and of the maximum temperatures for October, November and December seemed to be less important, according to the Figure 3. On the other hand, a direct comparison of the effects is not possible using only the scatter plots. On account of that, the global sensisity analysis tools must be employed.
First, we considered the calculation of the EE (Morris’ indexes). Figure 4 illustrates the convergence of the Morris’ indexes as a function of the number of model evaluations. The convergence with respect to the screening, to the ranking and to the sensitivity indexes [45] is obtained with a low number of the model evaluations.
Figure 5 presents the means and standard deviations of the EEs for the water footprint calculation. It was observed that the model is more sensitive to the covered fraction in a comparison with the geographical data. Furthermore, the altitude of the site was more important, for the region under study, than the latitude (the parameter with the least impact in the model) in the evaluation of the water footprint. The EEs for the maximum temperatures of the months under consideration were also smaller than those for covered fraction and altitude.
An important feature of sensitivity analysis is the identification of interactions between parameters. In this sense, Figure 6 presents the interaction effects between the parameters under study, in order to highlight pairwise interactions. As pointed by Noacco et al. [37], the existence of clear patterns (a separation of the colors used in the figure colorbars) in the two-dimensional scatter plots indicates an interaction between the corresponding parameters. We observed more expressive interactions between the covered fraction and the other parameters (indicated by the yellow points at the left-upper corner of the first line of the figure). The other parameters did not show an important correlation , i. e., the points/colors are essentially dispersed in the diagrams.
In order to corroborate the results obtained by the EE, we also employed the FAST sensitivity technique. Figure 7 illustrates the convergence pattern for the FAST-indexes for each variable considered in our computations. Clearly, a convergence of the FAST-indexes was achieved. In accordance to the results obtained, for instance, in the elementary effects, one can note that the main effect for the covered fraction and for the altitude were more important when compared to the maximum temperatures and to the latitude of the site. The accordance of the results obtained by Morris method and by a variance-based sensitivity analysis technique (such as FAST) is expected, as pointed by Campolongo and Cariboni [49].
comparison presents the numerical values for the Morris EE (using μ * ) and the FAST-indices.

5. Discussion

The results obtained indicate that the water footprint in the viticulture in the Serra Gaúcha (under all the hypotheses considered) is more affected by two parameters – the covered fraction and the altitude – when compared to the other quantities evaluated in the study (latitude and maximum temperatures of the months of October, November and December). This situation is clearly supported by the results of Figure 3, Figure 5 and Figure 7. These findings are compatible, for instance, with the conclusions of Debnath et al. [16], which obtained an important influence of solar radiation in the reference evapotranspiration (in our computational experiments, this can be noted by the high sensitivity to the altitude of the site). This situation indicates that this kind of approach can be extended to other crops/regions, with the necessary adjustments, in order to predict the particular response (in terms of water footprint), for instance, to severe temperature variations.
It must be emphasized that the effect of the temperatures in the reference evapotranspiration model is absolutely nonlinear, as indicated, for instance, by the Equations (3) and (9). In the same way, the altitude and latitude of the site also appear in a nonlinear form in the reference evapotranspiration model. Considering this fact, it is clear that some parameters which can be manipulated by the decision-maker are able, for instance, to compensate the effect of temperature variations with respect to the water footprint. In some degree, this situation is similar to that described by Arunrat et al. [18], with respect to some crops in Thailand. As discussed previously, Arunrat et al. [18] argue that the greenhouse effect on the water footprint can be offset by an increase in crop productivity. In our numerical experiments, it was shown that this effect (a reduction in the water footprint) can also be produced by an increase in the fraction of vegetation cover, even considering an increase in the temperatures.
With regard to the variables related to a possible decision-making process (covered fraction, altitude and latitude of the site), one can observe that the effect of altitude can be mitigated by the extent of coverage, but only up to a certain threshold (see Figure 6). Secondly, as anticipated, the fraction of mulch covering plays a decisive role across the investigated latitude range. Lower altitudes can decrease water footprint, even at different latitudes.

6. Conclusions

In this work, we conducted a global sensitivity analysis study regarding to the water footprint in the viticulture in Brazilian Serra Gaúcha (considering only the contribution of the evapotranspiration in the water footprint). The results indicated that the mulch fraction and the altitude of the site are the two most important parameters in the calculation of the water footprint (under the assumptions of the study). Furthermore, the numerical values obtained using different global sensitivity methods (Morris’ method and FAST) are consistent and convergent.

Author Contributions

Conceptualization, G.M. Platt; methodology, G.M. Platt, R.F. Corrêa, F.B.S. Oliveira, P.R. Martins and V.K. Nunes; software, G.M. Platt and P.R. Martins; validation, G.M. Platt, R.F. Côrrea and F.B.S. Oliveira; formal analysis, G.M. Platt, R.F. Côrrea, F.B.S. Oliveira; investigation, G.M. Platt, R.F. Corrêa, F.B.S. Oliveira, P.R. Martins and V.K. Nunes; resources, G.M. Platt, P.R. Martins and V.K. Nunes; data curation, G.M. Platt, P.R. Martins and V.K. Nunes ; writing—original draft preparation, G.M. Platt, R.F. Côrrea, F.B.S. Oliveira; writing—review and editing, G.M. Platt, R.F. Côrrea, F.B.S. Oliveira; visualization, G.M. Platt; supervision, G.M. Platt and F.B.S. Oliveira; project administration, G.M. Platt and F.B.S. Oliveira. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
EE Elementary Effects
FAO Food and Agriculture Organization
FAST Fourier Amplitude Sensitivity Test
LHS Latin Hypercube Sampling
VBSA Variance Based Sensitivity Analysis
WF Water footprint

References

  1. Finco, A.; Bentivoglio, D.; Chiaraluce, G.; Alberi, M.; Chiarelli, E.; Maino, A.; Mantovani, F.; Montuschi, M.; Raptis, K.G.C.; Semenza, F.; Strati, V.; Vurro, F.; Marchetti, E.; Bettelli, M.; Janni, M.; Anceschi, E.; Sportolaro, C.; Bucci, G. Combining Precision Viticulture Technologies and Economic Indices to Sustainable Water Use Management. Water 2022, 14. [Google Scholar] [CrossRef]
  2. Saraiva, A.; Presumido, P.; Silvestre, J.; Feliciano, M.; Rodrigues, G.; Silva, P.O.e.; Damásio, M.; Ribeiro, A.; Ramôa, S.; Ferreira, L.; Gonçalves, A.; Ferreira, A.; Grifo, A.; Paulo, A.; Ribeiro, A.C.; Oliveira, A.; Dias, I.; Mira, H.; Amaral, A.; Mamede, H.; Oliveira, M. Water Footprint Sustainability as a Tool to Address Climate Change in the Wine Sector: A Methodological Approach Applied to a Portuguese Case Study. Atmosphere 2020, 11. [Google Scholar] [CrossRef]
  3. Wurz, D.A. .; Brighenti, A.F.. Analysis of Brazilian wine competitiveness. BIO Web Conf. 2019, 12, 03015. [Google Scholar] [CrossRef]
  4. Alderete, M.V. The Wine Clusters of Mendoza and Serra Gaúcha: A Local Development Perspective. Frontera Norte 2014, 26, 179–204. (In Spanish) [Google Scholar]
  5. Zen, A.C.; Fensterseifer, J.E.; Prévot, F. The influence of resources on the internationalisation process of clustered wine companies. International Journal of Business and Globalisation 2012, 8, 30–48. [Google Scholar] [CrossRef]
  6. Fensterseifer, J.E. The emerging Brazilian wine industry: Challenges and prospects for the Serra Gaúcha wine cluster. International Journal of Wine Business Research 2007, 19, 187–206. [Google Scholar] [CrossRef]
  7. Hoekstra, A.; Hung, P. Virtual water trade: a quantification of virtual water flows between nations in relation to international crop trade. Value of Water. Research Report Series No.11; 2002.
  8. Herath, I.; Green, S.; Singh, R.; Horne, D.; van der Zijpp, S.; Clothier, B. Water footprinting of agricultural products: a hydrological assessment for the water footprint of New Zealand’s wines. Journal of Cleaner Production 2013, pp. 232–243. [CrossRef]
  9. Bonamente, E.; Scrucca, F.; Asdrubali, F.; Cotana, F.; Presciute, A. The Water Footprint of the Wine Industry: Implementation of an Assessment Methodology and Application to a Case Study. Sustentability 2015, 7, 12190–12208. [Google Scholar] [CrossRef]
  10. Jairman, C. Water footprint as an indicator of sustainable table and wine grape production. Technical Report 2020. [Google Scholar]
  11. Saraiva, A.; Rodrigues, G.; Silvestre, J.; Feliciano, M.; Silva, P.; Oliveira, M. A pegada hídrica na fileira vitivinícola portuguesa. Agrotec 2019, pp. 68–70. (In Portuguese).
  12. Allen, R.; Walter, I.; Elliot, R.; Howell, T.; Itenfisu, D.; Jensen, M. The ASCE Standardized Reference Evapotranspiration Equation; 2005.
  13. Beven, K. A Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Estimates. Journal of Hydrology 1979, 44, 169–190. [Google Scholar] [CrossRef]
  14. Ndiaye, P.; Bodian, A.; Diop, L.; Djaman, K. Sensitivity Analysis of the Penman-Monteith Reference Evapotranspiration to Climatic Variables: Case of Burkina Faso. Journal of Water Resource and Protection 2017, 9, 1364–1376. [Google Scholar] [CrossRef]
  15. Irmak, S.; Payero, J.O.; Martin, D.L.; Irmak, A.; Howell, T.A. Sensitivity Analyses and Sensitivity Coefficients of Standardized Daily ASCE-Penman-Monteith Equation. Journal of Irrigation and Drainage Engineering 2006, 132, 564–578. [Google Scholar] [CrossRef]
  16. Debnath, S.; Adamala, S.; Raghuwanshi, N. Sensitivity Analysis of FAO-56 Penman-Monteith Method for Different Agro-ecological Regions of India. Environmental Processes 2015, 2, 689–704. [Google Scholar] [CrossRef]
  17. Biazar, S.M.; Dinpashoh, Y.; Singh, V.P. Sensitivity analysis of the reference crop evapotranspiration in a humid region. Environmental Science and Pollution Research 2019, 26, 32517–32544. [Google Scholar] [CrossRef]
  18. Arunrat, N.; Sereenonchai, S.; Chaowiwat, W.; Wang, C. Climate change impact on major crop yield and water footprint under CMIP6 climate projections in repeated drought and flood areas in Thailand. Science of The Total Environment 2022, 807, 150741. [Google Scholar] [CrossRef]
  19. Rossi, L.; Regni, L.; Rinaldi, S.; Sdringola, P.; Calisti, R.; Brunori, A.; Dini, F.; Proietti, P. Long-Term Water Footprint Assessment in a Rainfed Olive Tree Grove in the Umbria Region, Italy. Agriculture 2020, 10. [Google Scholar] [CrossRef]
  20. Arunrat, N.; Sereenonchai, S.; Chaowiwat, W.; Wang, C.; Hatano, R. Carbon, Nitrogen and Water Footprints of Organic Rice and Conventional Rice Production over 4 Years of Cultivation: A Case Study in the Lower North of Thailand. Agronomy 2022, 12. [Google Scholar] [CrossRef]
  21. Yong, S.L.S.; Ng, J.L.; Huang, Y.F.; Ang, C.K.; Mirzaei, M.; Ahmed, A.N. Local and global sensitivity analysis and its contributing factors in reference crop evapotranspiration. Water Supply 2023, 23, 1672–1683. [Google Scholar] [CrossRef]
  22. Zhuo, L.; Mekonnen, M.M.; Hoekstra, A.Y. Sensitivity and Uncertainty in Crop Water Footprint Accounting: A Case Study for the Yellow River Basin. Value of Water Research Report Series no. 62 62, UNESCO – IHE, Enschede, the Netherlands, 2013.
  23. Li, Z.; Feng, B.; Wang, W.; Yang, X.; Wu, P.; Zhuo, L. Spatial and temporal sensitivity of water footprint assessment in crop production to modelling inputs and parameters. Agricultural Water Management 2022, 271, 107805. [Google Scholar] [CrossRef]
  24. Conceição, M.A.F.; Mandelli, F. Climate trends in the Serra Gaúcha region. XV Brazilian Congress on Agrometereology;, 2007. (in Portuguese).
  25. Cardoso, I.P.; Siqueira, T.M.; Timm, L.C.; Rodrigues, A.A.; Nunes, A.B. Analysis of average annual temperatures and rainfall in southern region of the state of Rio Grande do Sul, Brazil. Brazilian Journal of Environmental Sciences (RBCIAMB) 2022, 57, 58–71. [Google Scholar] [CrossRef]
  26. Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave version 8.3.0 manual: a high-level interactive language for numerical computations, 2023.
  27. Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environmental Modelling & Software 2015, 70, 80–85. [Google Scholar] [CrossRef]
  28. Borges, L.F.A.; Ferreira, F.F.; Gonçalves, F.; Espósito Junior, A.; Oliveira, A.F.d.S.; Telles, W.R. IPSAL: Implementation of the module to generate the Sobol sequence and indices. VETOR 2023, 33, 60–69. [Google Scholar] [CrossRef]
  29. Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56 – Crop Evapotranspiration (guidelines for computing crop water requirements). Technical report, FAO, Roma, Itália, 1998.
  30. Martins, P.R. Water Footprint Modelling in Viticulture for the Wine Production in the Serra Gaúcha. Master’s thesis, Graduate Program in Agroindustrial Systems and Processes, Federal University of Rio Grande, Santo Antônio da Patrulha, Brazil, 2023. Available at https://argo.furg.br/?BDTD13706 (in Portuguese).
  31. Li, S.; Li, Y.; Lin, H.; Feng, H.; Dyck, M. Effects of different mulching technologies on evapotranspiration and summer maize growth. Agricultural Water Management 2018, 201, 309–318. [Google Scholar] [CrossRef]
  32. Fonseca, M.A. Models to estimate the crop coefficients (Kc) for irrigated grapevines; Embrapa – Brazil, 2016. in Portuguese.
  33. Rosa, J.D.; Álvaro Luiz Mafra. ; Nohatto, M.A.; Ferreira, E.Z.; de Oliveira, O.L.P.; Miquelluti, D.J.; Cassol, P.C.; Medeiros, J.C. Soil chemical properties and grapevine yield affected by cover crop management in Serra Gaúcha, Southern Brazil. Revista Brasileira de Ciência do Solo 2009, 33, 179–187. (in Portuguese). [Google Scholar] [CrossRef]
  34. López-Urrea, R.; Sánchez, J.; Montoro, A.; Mañas, F.; Intrigliolo, D. Effect of using pruning waste as an organic mulching on a drip-irrigated vineyard evapotranspiration under a semi-arid climate. Agricultural and Forest Meteorology 2020, 291, 108064. [Google Scholar] [CrossRef]
  35. Mirás-Avalos, J.M.; Araujo, E.S. Optimization of Vineyard Water Management: Challenges, Strategies, and Perspectives. Water 2021, 13. [Google Scholar] [CrossRef]
  36. Lazzarotto, J.J.; Protas, J.F.S. Capital costs and demands for the production of vineyards for processing in Bento Gonçalves on a Spaleswood. Observatórios Agropensa 2020, pp. 1–10. (in Portuguese).
  37. Noacco, V.; Sarrazin, F.; Pianosi, F.; Wagener, T. Matlab/R workflows to assess critical choices in Global Sensitivity Analysis using the SAFE toolbox. MethodsX 2019, 6, 2258–2280. [Google Scholar] [CrossRef]
  38. Viana, F.A.C. A Tutorial on Latin Hypercube Design of Experiments. Quality and Reliability Engineering International 2016, 32, 1975–1985. [Google Scholar] [CrossRef]
  39. Pang, M.; Xu, R.; Hu, Z.; Wang, J.; Wang, Y. Uncertainty and Sensitivity Analysis of Input Conditions in a Large Shallow Lake Based on the Latin Hypercube Sampling and Morris Methods. Water 2021, 13. [Google Scholar] [CrossRef]
  40. Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environmental Modelling & Software 2017, 93, 109–126. [Google Scholar] [CrossRef]
  41. Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
  42. Campolongo, F.; Saltelli, A.; Cariboni, J. From screening to quantitative sensitivity analysis. A unified approach. Computer Physics Communications 2011, 182, 978–988. [Google Scholar] [CrossRef]
  43. Tian, W.; Song, J.; Li, Z.; de Wilde, P. Bootstrap techniques for sensitivity analysis and model selection in building thermal performance analysis. Applied Energy 2014, 135, 320–328. [Google Scholar] [CrossRef]
  44. Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environmental Modelling & Software 2007, 22, 1509–1518 Modelling, computer-assisted simulations, and mapping of dangerous phenomena for hazard assessment. [Google Scholar] [CrossRef]
  45. Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environmental Modelling & Software 2016, 79, 135–152. [Google Scholar] [CrossRef]
  46. Saltelli, A.; Bolado, R. An alternative way to compute Fourier amplitude sensitivity test (FAST). Computational Statistics & Data Analysis 1998, 26, 445–460. [Google Scholar] [CrossRef]
  47. Sobol<i>´</i>, I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation 2001, 55, 271–280. [Google Scholar] [CrossRef]
  48. Yan, M.; Tian, X.; Li, Z.; Chen, E.; Wang, X.; Han, Z.; Sun, H. Simulation of Forest Carbon Fluxes Using Model Incorporation and Data Assimilation. Remote Sensing 2016, 8. [Google Scholar] [CrossRef]
  49. Campolongo, F.; Cariboni, J. On the Relationship Between the Sensitivity Measures Proposed by Morris and the Variance Based Measures. Probabilistic Safety Assessment and Management; Spitzer, C., Schmocker, U., Dang, V.N., Eds.; Springer London: London, 2004; pp. 2030–2035. [Google Scholar] [CrossRef]
Preprints 102055 g001
Figure 1. Altimetric map of Rio Grande do Sul – Brazil and localization map of Serra Gaúcha.
Figure 1. Altimetric map of Rio Grande do Sul – Brazil and localization map of Serra Gaúcha.
Preprints 102055 g001
Preprints 102055 g002
Figure 2. Maximum temperatures for the months of October, November and December (2013-2023).
Figure 2. Maximum temperatures for the months of October, November and December (2013-2023).
Preprints 102055 g002
Preprints 102055 g003
Figure 3. Scatter plots (inputs-output) for the water footprint (L/bottle of wine) considering the uncertainties in soil covered fraction (dimensionless), altitude (m) and latitude. N = 3000 .
Figure 3. Scatter plots (inputs-output) for the water footprint (L/bottle of wine) considering the uncertainties in soil covered fraction (dimensionless), altitude (m) and latitude. N = 3000 .
Preprints 102055 g003
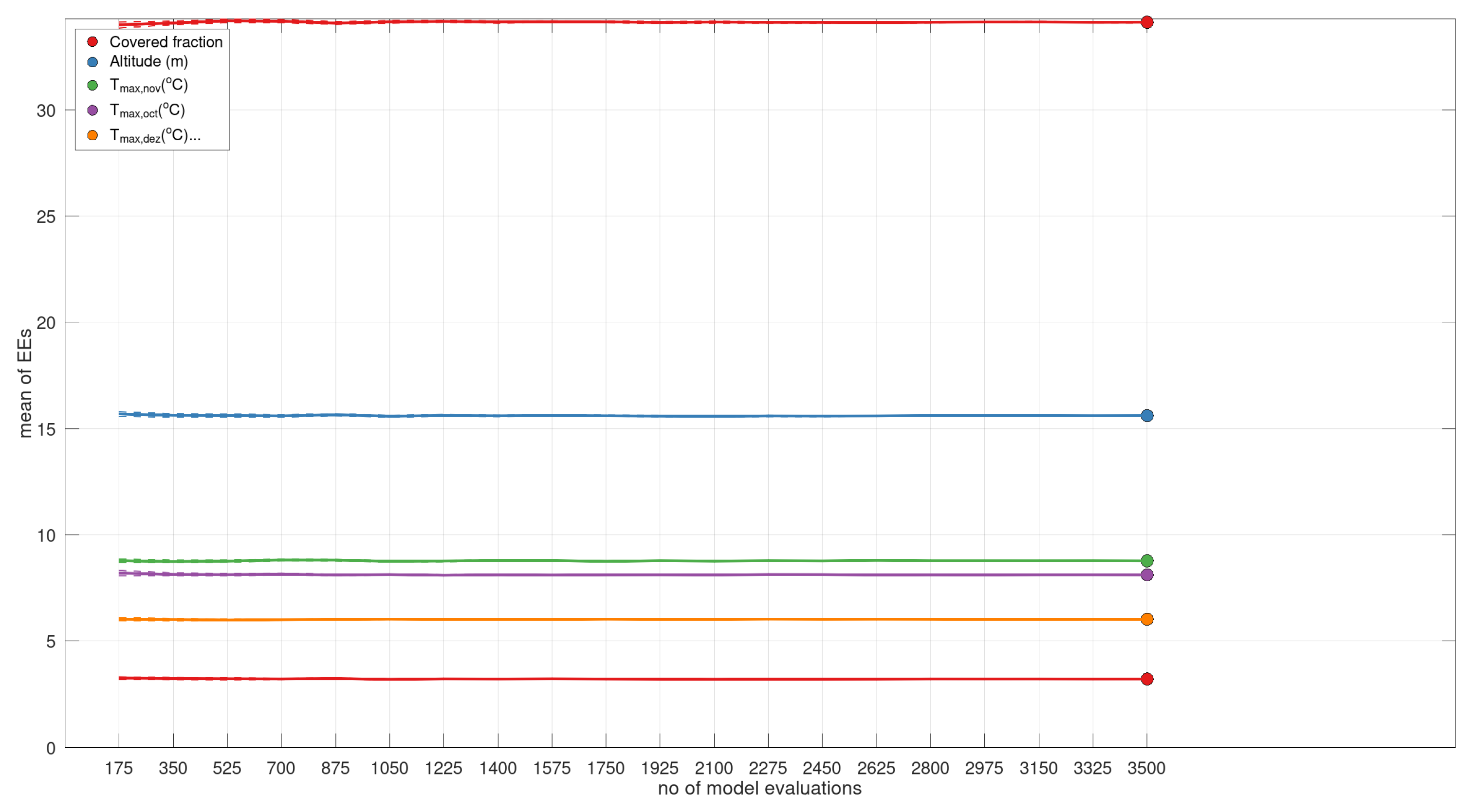
Preprints 102055 g004
Figure 4. Means of Morris’ Elementary Effects (EEs) convergence pattern.
Figure 4. Means of Morris’ Elementary Effects (EEs) convergence pattern.
Preprints 102055 g004
Preprints 102055 g005
Figure 5. Elementary Effects (EEs) for the water footprint (L/bottle of wine) with r = 500 and N b o o t = 100 .
Figure 5. Elementary Effects (EEs) for the water footprint (L/bottle of wine) with r = 500 and N b o o t = 100 .
Preprints 102055 g005
Preprints 102055 g006
Figure 6. Scatter plots (interaction effects) for the water footprint (L/bottle of wine).
Figure 6. Scatter plots (interaction effects) for the water footprint (L/bottle of wine).
Preprints 102055 g006
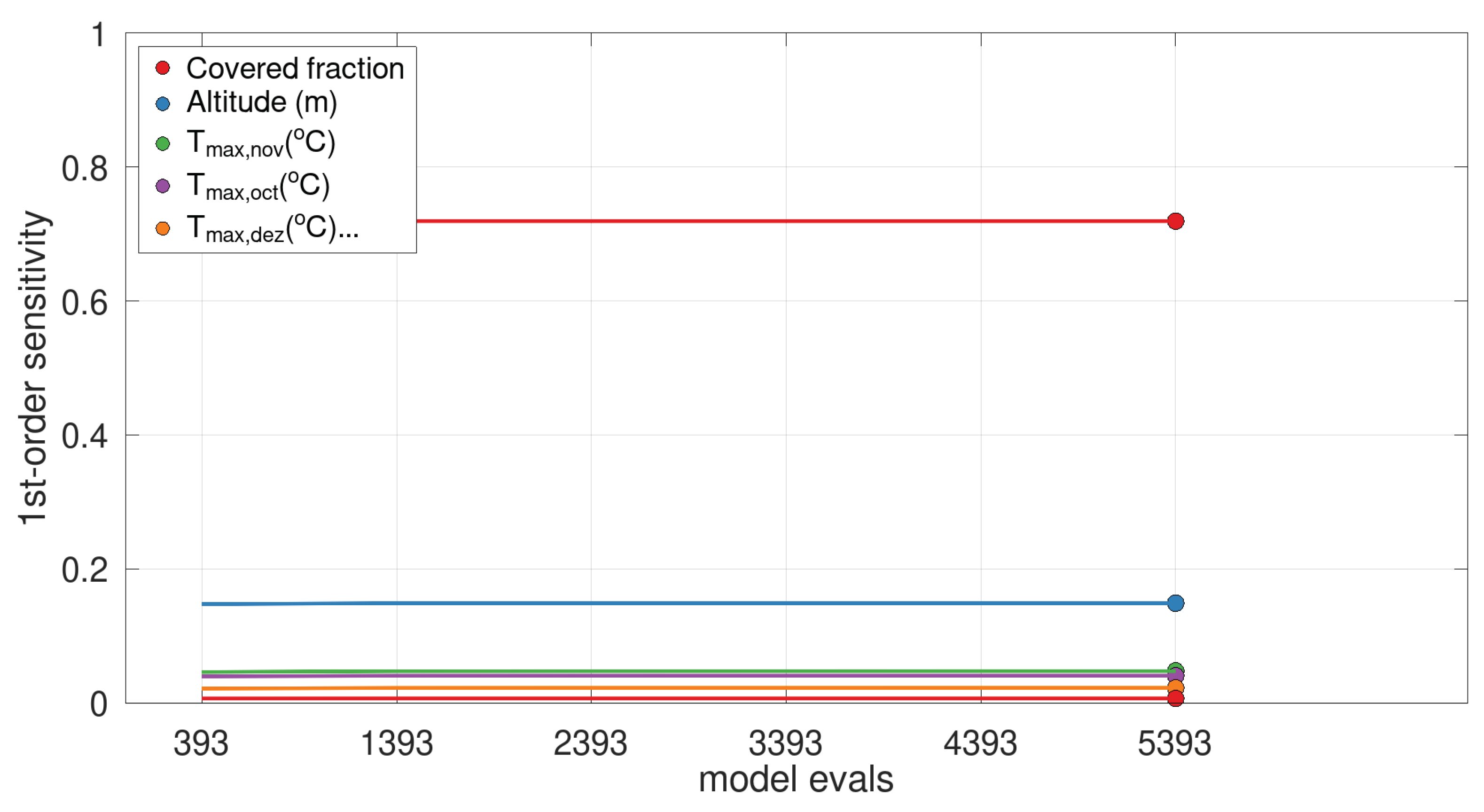
Preprints 102055 g007
Figure 7. Main effects or first order effects convergence pattern using FAST .
Figure 7. Main effects or first order effects convergence pattern using FAST .
Preprints 102055 g007
Table 1. Morris EE effects and FAST-indices for the water footprint
Table 1. Morris EE effects and FAST-indices for the water footprint
Morris EE ( μ * ) FAST-index
Covered fraction 34.2017 7.1938e-01
Altitude 15.2832 1.4891e-01
Latitude 2.9088 6.5333e-03
T m a x , o c t 7.6636 4.0507e-02
T m a x , n o v 8.3152 4.7451e-02
T m a x , d e c 5.9991 2.2368e-02
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated