Kazakhstan’s extensive railway network plays a pivotal role in its economy, offering vital connections for both domestic and international trade. Despite its significance, the network faces challenges in maintenance efficiency and safety management, heightened by the vast geographical span it covers. The proposed Digital Track Model (DTM) stands as a transformative solution, aiming to revolutionize maintenance practices through enhanced precision and predictive analytics. This paper delineates the economic, safety, and operational benefits of integrating DTM into Kazakhstan’s railways. The subsequent sections detail the current landscape, the methodology of our study, followed by a comprehensive analysis of the DTM’s potential impact, culminating in a discussion of our findings and concluding remarks.

The urgency for digital innovation within JSC NC KTZ is driven by the escalating costs associated with traditional track maintenance methods and the ever-present imperative to enhance safety measures. A meticulously designed DTM can serve as a cornerstone for achieving these objectives, offering a leap towards predictive maintenance strategies and thus, significantly reducing unplanned downtime and associated costs. This section explores the strategic importance of adopting DTM, supported by a domestically developed mathematical model, to underscore its feasibility and substantial benefits in the context of Kazakhstan’s unique railway challenges. The economy of the Republic of Kazakhstan, like any country’ s economy, significantly relies on the state of the railway industry, which, in the RK, determines the country’ s transit potential. Therefore, the need for railway transportation by neighboring countries is a key component of JSC NC KTZ. However, at the same time, the presence of other transit carriers leads to fierce competitive struggle. Naturally, the problem of survival and prosperity of JSC NC KTZ arises. Current global trends in railway development [1] have led to the need for creating digital analogs of assets for their optimal management. Undoubtedly, to find optimal management of railway assets, it is necessary to translate all objects of the railway industry into the language of mathematics. In the current global practice, this is solved by digitizing assets and synchronizing digital model assets with real-existing objects. Naturally, the task of optimally constructing a digital twin arises. At the same time, the cost of digitization must be justified, which, undoubtedly, will lead to economic benefits. Today, there are many methods and companies that create digital models of railway assets. Unfortunately, due to economic problems in JSC NC KTZ at the moment, imported road digitization technologies are expensive. Moreover, currently, in the short term of creating DTM, there still isn’ t a good justification for economic feasibility. Developed countries, having a large investment potential, consider such tasks as strategic with a payback horizon of several decades. Therefore, the choice of our digitization technology is in difficult economic conditions and requirements for quick payback. Considering the above.

This section introduces a mathematical model to quantify the relationship between track curvature errors and maintenance costs. By examining two scenarios of curvature errors at various points along the track, we demonstrate how increased error margins can significantly escalate repair costs. The analysis concludes that a reduction in curvature error can lead to substantial savings, thereby justifying the investment in DTM.

Let us present a mathematical model of the economic efficiency of digitization. Let’ s introduce the following concepts: A - the number of works to maintain the track in a normal state. $A^{\ast }$- the number of works performed by compositions over railway tracks. It is known that they are in direct proportion The cost of works is proportional to the volume of works performed Consider the structure of works performed by compositions over iron roads, as is known [2], . the work represents an integral along the trajectory from forces, so where L is the length of the path s. Let Let’ s use the following acceleration formula then where m, v –mass and speed of the composition respectively, R – radius of curvature of the path. Since we cannot affect the speed and mass of the composition in optimal management, the only control parameter remains the curvature of the path. Therefore, the criterion for minimizing path maintenance costs will be educing the curvature of the path. How does one reduce the path’ s curvature? The curvature of the path is set by the project’ s alignment. The question arises whether there is an exact project alignment of the path and with what accuracy and optimality does this project alignment of the path exist. Reiterating in terms of DTM, we come to the questions of its accuracy, optimality, and creation cost. Obviously, the more accurate a model we want to build, the more expensive it will be. We considered the question of increasing repair work costs with an increase in the path’s curvature. For this, we considered two variants of curvature at each point of the railway track trajectory:Under the first variant of curvature, we understand the project alignment, then the costs of repair works, respectively, will be determined as follows: Accordingly, the increase in the cost of works in the presence of curvature will be calculated by the formula: Assuming the mass and speed of the composition are constants, we come to the following formula:

Since relative to railways all significant characteristics are determined on a per-picket basis, the last expression will be written per-picket as well: where P is the length of the i-th picket , $i=1\dots N$. According to Lagrange’ s Theorem 3, within pickets, there exist points $\theta$ , for which Let’ s adopt the hypothesis: the disturbance of the path on average goes equally across pickets, and eventually we get Thus, with some assumptions, we obtained that the excess cost of repair work is proportional to the excess curvature. Let’ s estimate the proportionality coefficient From the last formulas, it follows that an increase in curvature by one percent results in an increase in the cost of repair work by one percent. Therefore, the calculations of the economic feasibility of DTM depend on the percentage of the road’ s curvature in its current state and the possibility of controlling repair work. Let’ s consider what curvature error occurs on a section L=100 meters.

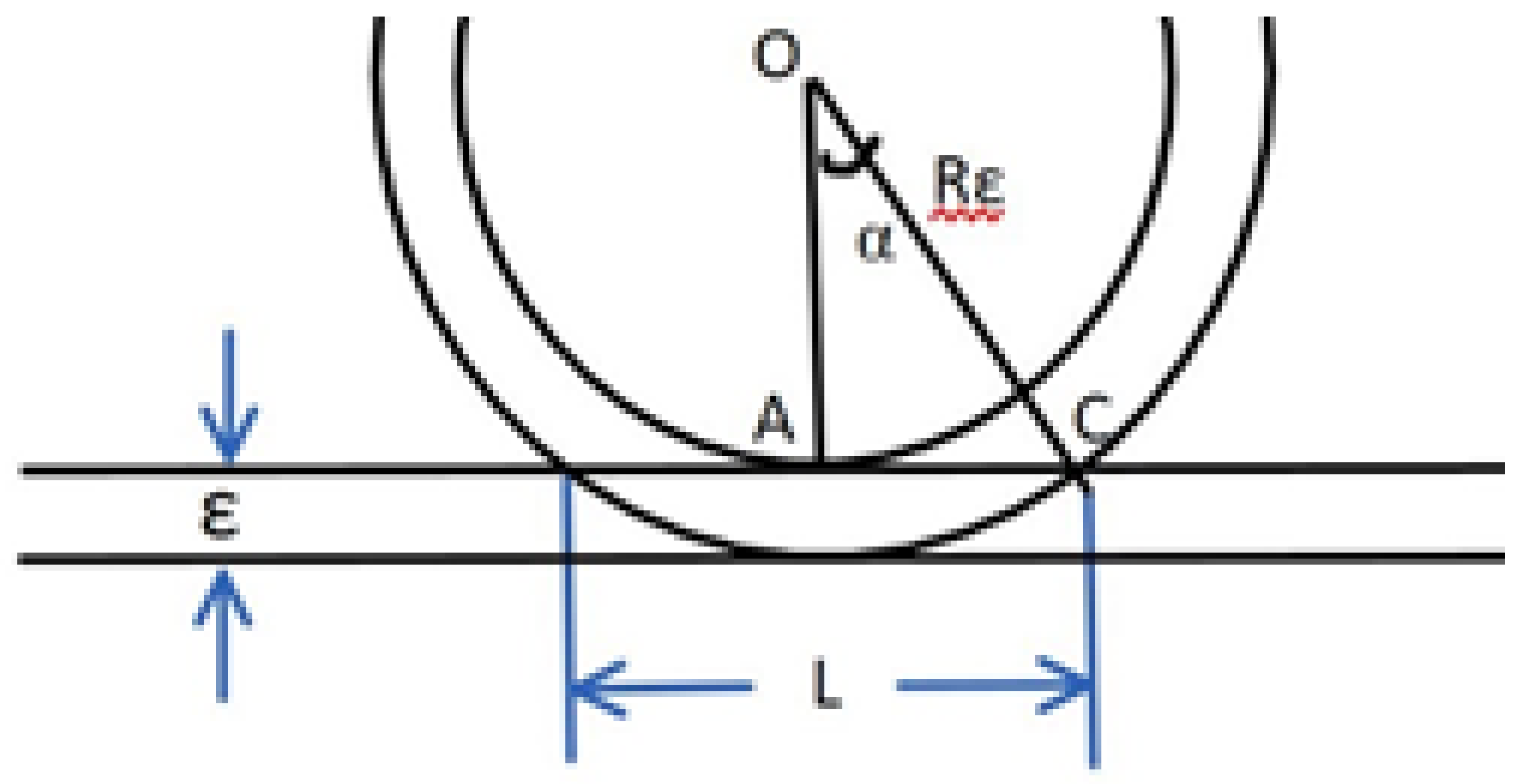
According to Figure 1, we have the following equations: from which it follows In the last expression, due to the smallness of $ϵ$, we can neglect the term ${ϵ}^2/2$, then we get Taking as a standard error m, then for the error m we get

After performing simple calculations of the proportionality coefficient, it follows that when moving from an error of 1 cm to an error of 2 cm, the cost of repair work will increase by 100 percent, i.e., it will double. Similarly, moving from an error of 1 cm to an error of 5 cm, the cost of maintenance and repair of the track will increase fivefold, or lead to a deterioration of the track condition, which will result in reduced established speeds and a significant decrease in the transit potential.

Our reasoning leads to the conclusion that the cost of producing such a Digital Track Model (DTM), which would amount to 1 percent of the repair work costs, along with the maintenance and control of repair work transitioning from a 2 cm error to a 1 cm error, will save funds by reducing costs by half. It can be added that if our assumptions about the uniformity of error per kilometer are accurate within 50 percent, then in this case, the cost of track maintenance will decrease by 20 percent, which aligns well with global results of using DTM, significantly reducing the cost of track maintenance. These results demonstrate an improvement in the quality of road repairs with curvature control, or equivalently, project alignment control.

Another important fact is the reduction of "windows" due to the longevity of road quality when adhering to a high-precision project alignment. A third significant factor is the reduction in wear and tear of rolling stock since the forces acting on wheel pairs and the wagon as a whole also depend on the curvature of the track according to this scheme, which should lead to a 20-percent reduction in the cost of repairing rolling stock. A fourth important factor in favor of using DTM is the possibility of optimally adjusting the curvature of the curve to increase permissible speeds. The last factor is the cumulative synergistic effect, which will increase the competitiveness of our roads in the global market for transit transportation.

Based on the above, we conclude that annual expenditures on DTM with an error of no more than 1 cm, amounting to 1 percent of the repair costs, will not only save funds but also improve the quality of repairs, serving as a significant economically justified driver for the growth of the economy both for JSC NC KTZ and for the economy of the Republic of Kazakhstan.

The findings suggest that the implementation of a DTM, accurate within 1 cm, could halve maintenance costs, based on certain assumptions about error distribution. Additionally, DTM adoption is expected to enhance rolling stock durability, optimize track maintenance, and potentially increase train speeds through better curvature adjustment.

Investing in DTM technology, despite its initial costs, is economically justified given the potential for considerable savings on track maintenance and improvements in system reliability and efficiency. This initiative represents a significant opportunity for JSC NC KTZ and Kazakhstan’s economy at large, promising to bolster the railway system’s competitiveness and sustainability.