On δP-approximation Spaces

Preprint

Article

On δP-approximation Spaces

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

23 March 2024

Posted:

25 March 2024

You are already at the latest version

Alerts

Abstract

In order to deal with imprecision, ambiguity, and uncertainty in data analysis, Pawlak introduced rough set theory in 1982. This paper aims to expand the scope of basic set theory developed by presenting the notions of δP-upper and δP-lower approximations, that are based on the notion of δP-open sets, we additionally examine a few of their fundamental characteristics.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

The "rough set theory" [1], a mathematical technique for coping with ambiguity or uncertainty, is attributed to Pawlak. Rough set theory and applications have substantially advanced since 1982. Rough set theory has several uses, particular, when analyzing data both cognitive sciences and artificial intelligence [2,3,4]. Pawlak and Skowron have recently published several fundamental ideas in rough set research as well as a number of applications [5,6]. An extension of set theory known as rough set theory [5,8] describes a portion of the universe as being described by two ordinary sets known as the lower and upper approximation. Initially, an equivalence was used to introduce Pawlak provides definitions for both upper and lower approximations. Pawlak and Skowron [5,6] derived numerous intriguing characteristics of the lower and upper approximations in accordance with the equivalence relations, the equivalence relation, on the other hand, seems to be a strict requirement that might restrict the suitability of the rough set model proposed by Pawlak. Equivalence relation or partition have undergone numerous extensions in recent years by being replaced by concepts like binary relations [10,12], neighborhood systems, by using a general relation, Abu-Donia [17] talked about three distinct upper(lower) approximation types based on the appropriate neighborhood. These types were then used to create a collection of limited binary relationships in in two different methods. This theory, which primarily depends on a specific topological structure, has been extremely successful in many fields of real-world applications. Numerous papers on generalizing and interpreting rough sets have been written [13,14,15,18,20,21,23,24,25]. Weginger’s generalization of rough sets is among the most important [16] in 1989 when he introduced the idea of topological rough sets. The closure and interior operators of topological spaces were used to define the approximation in this generalization, which began with a topological space. The notion of

δ P

-open sets was first presented in [11]. This work presents and investigates the concept of the

δ P

-approximation space. These areas aid in the development of a new categorization for the cosmos. Additionally, we explore the idea of "

δ P

-lower" furthermore "

δ P

-upper" approximation. Rough sets are compared to this idea as part of our study of

δ P

-rough sets. we also provide some opposition examples.

2. Fundamental Concepts $δ P$ -Open Sets and Topology

A pair

(Y, τ)

that consists of a set

Y

and family

τ

of subset of

Y

that match the following criteria is topological space [10]:

$\emptyset, Y \in τ$ ,
$τ$ is closed under an arbitrary union,
$τ$ is closed Under finite intersection .

The pair

(Y, τ)

is referred to as a topological space, and the subset of

Y

that belongs to

τ

is referred to as open sets in the space. The opposite of the pair is called the closed subsets of

Y

are those that fall into the family

τ

, the family

τ

of open subsets of

Y

is often referred to as topology of

Y

\bar{S} = ⋂ {W \subseteq Y : S \subseteq W

and W is closed } is known as

τ

-closure of a subset

S \subset Y

It appears that the smallest closed subset of

Y

that contains S is

\bar{S}

. Keep in mind that S is only closed if and when

S = \bar{S}

S^{\cdot} = ⋃ {V \subseteq Y : V \subset S

and V is open } is known

τ

-interior of a subset

S \subseteq Y

It appears that

S^{\cdot}

is the union of all

Y

open subsets that contain in S. Keep in mind that S is only open if and when

S = S^{\cdot}

. Additionally, the

τ

boundary of a subset

S \subseteq Y

is denoted as

b (S) = \bar{S} - S^{\cdot}

Assume that S is a subset of

Y

, a topological space. Let

S^{\cdot}

\bar{S}

, and

b (S)

be interior, closure, and boundary of S, In that order . If

b (S) = \emptyset

then S is exact , if not, S is rough. If and only if

\bar{S} = S^{\cdot}

, then it is evident that S is exact.

Definition 1

([3]). Let

(Y, τ)

be a topological space the subset

S \subseteq Y

is referred to as Preopen if

S \subseteq I n t (C l (S))

The opposite of Preopen set is Preclosed set. As we that indicate the set of all Preopen and Preclosed sets by

P O (Y)

and

P C (Y)

Remark 1.

Every topological space

(Y, τ)

, has the property

τ \subseteq P O (Y)

Definition 2

([9]). Let S be a subset of a topological space

(Y, τ)

. The δ- closure of S is defined as follow

c l_{δ} (S) = {x \in Y : S \cap i n t (c l (A)) \neq \emptyset, A \in τ

and

y \in A}

. A set S is referred to as δ-closed if

S = c l_{δ} (S)

.The opposite of a δ-closed set is δ-open.

Observe that

i n t_{δ} (S) = Y ∖ c l_{δ} (Y ∖ S)

Definition 3

([11]). If S is a subset of a topological space

(Y, τ)

and

S \subseteq i n t (c l_{δ} (S))

, then S is

δ P

-open.

δ P O (Y)

is the family of all

δ P

-open sets of

Y

δ P

-closed is the complement of

δ P

-open.

The

δ P

-closure of S is

P

_{δ} (S)

, which is the intersection of all

δ P

-closed sets that contain S.

The

δ P

-interior of S is represented by

P

int

_{δ} (S)

and is the union of all

δ P

-open sets that are contained in S.

Lemma 1

([17]). The following hold for a subset S of a topological space

(X, τ)

$P c l_{δ} (S) = S \cup c l (i n t_{δ} (S))$ .
$P i n t_{δ} (S) = S \cap i n t (c l_{δ} (S))$ .
$P c l_{δ} (P i n t_{δ} (S)) = P i n t_{δ} (S) \cup c l (i n t_{δ} (S))$ .
$P i n t_{δ} (P c l_{δ} (S)) = P c l_{δ} (S) \cap i n t (c l_{δ} (S))$ .

3. Rough Set

Rough set theory was inspired by the necessity of express subsets of a universe in terms of equivalency classes of a partition of that universe. A topological space known as approximation space

K = (X, τ)

is characterized by the partition, where

R

is an equivalency relation and

X

is a set known as the universe [1]. The terms chunks, granules, and elementary sets are also used to describe the equivalency classes of

R

. To denote that an equivalency class contains an

x \in X

, we will use

R_{x} \subseteq X

. Two operators in the approximation space are considered.

$\underset{̲}{R} (S) = {x \in X : R_{x} \subseteq S}$ .
$\bar{R} (S) = {x \in X : R_{x} \cap S \neq \emptyset}$ .

Referred to as, respectively, the lower and upper approximations of S⊆

X

. Furthermore, let

N E G_{R} (S) = X - \bar{R} (S)

represent the negative region of S, and

P O S_{R} (S) = \underset{̲}{R} (S)

represent the positive region of S,

B N_{R} (S) = \bar{R} (S) - \underset{̲}{R} (S)

represent the boundary region of

X

If we assume that

X

is a finite, nonempty universe and that

S \subseteq X

, then the accuracy measure can also be used to quantify the degree of completeness as follows:

$\propto_{R} (S) = \frac{∣ \underset{̲}{R} (S) ∣}{∣ \bar{R} (S) ∣}, S \neq \emptyset$ ,

Where

| \cdot |

the set’s cardinality is represented. The degree of knowledge completeness is attempted to be expressed via accuracy metrics.

\propto_{R} (S)

is capable to depict the size of the data sets boundary region, but the knowledge’s organizational structure is more difficult to depict. Rough set theory has the essential advantage of being able to handle categories that, given a knowledge basis, cannot be properly specified. The rough sets framework can be used to measure the properties of potential data sets, we may quantify imprecision and convey topological characterization of it, with the help of the following.

If $\underset{̲}{R} (S) \neq \emptyset$ and $\bar{R} (S) \neq X$ , then S is roughly $R$ - definable, and indicated by $R D (X)$ .
If $\underset{̲}{R} (S) = \emptyset$ and $\bar{R} (S) \neq X$ , then S is internally $R$ -undefinable, and indicated by $I U D (X)$ ,
If $\underset{̲}{R} (S) \neq \emptyset$ and $\bar{R} (S) = X$ , then S is externally $R$ - undefinable, and indicated by $E U D (X)$ ,
If $\underset{̲}{R} (S) = \emptyset$ and $\bar{R} (S) = X$ , then S is totally $R$ - undefinable, and indicated by $T U D (X)$ .

We can characterize rough sets in terms of the boundary region’s size and structure by utilizing

\propto_{R} (S)

and the previously given categories. Viewed as a particular instance of relative sets, rough sets are associated with the notion of Belnap’s logic [7].

Remark 2.

We indicate the relationship between a class of Preopen sets

P

(X)

and a topology τ on

X

that was utilized to obtain a subbase using

R_{P}

. Furthermore, we represent

P

- approximation space by

(X, R_{P})

Definition 4.

(X, R_{P})

be a

P

-approximation space, then the

P

-lower (resp.,

P

-upper) approximation of each nonempty subset S of

X

follows: as:

${\underset{̲}{R}}_{P} (S) = ⋃ {V \in P O (X) : V \subseteq S}$ ,
${\bar{R}}_{P} (S) = ⋂ {W \in P C (X) : W \supseteq S}$ .

We are able to obtain the

P

-approximation operator as shown below.

From the provided relation $R$ , find the right neighborhood $x R$ , where $x R = {y : x R y}$ .
Taking right neighborhoods $x R$ as a sub-base to obtain the topology τ.
Preopen set family obtained by using open sets in topology τ "from Definition 1."
To obtain $P$ - approximation operators, use the set of all Preopen sets ( see Definition 4).

Proposition 1.

For every

S \subseteq X

in any

P

- approximation space

(X, R_{P})

the following are hold :

$b (S) = \underset{̲}{E d g} (S) \cup \bar{E d g} (S)$ .
$P b (S) = P \underset{̲}{E d g} (S) \cup P \bar{E d g} (S)$ .

Proof.

(2) It the follows from

P b (S) = {\bar{R}}_{P} (S) - {\underset{̲}{R}}_{P} (S) = ({\bar{R}}_{P} (S) - S) \cup (S - {\underset{̲}{R}}_{P} (S)) = P \underset{̲}{E d g} (S) \cup P \bar{E d g}

. □

Definition 5.

Assume that S

\subseteq Y

and that

(Y, R_{P})

is a

P

- approximation space and. Then there are the memberships

\underset{̲}{\in}

\bar{\in}

{\underset{̲}{\in}}_{P}

, and

{\bar{\in}}_{P}

, which are defined as , strong, weak,

P

-strong, and

P

-weak memberships respectively.

$y \underset{̲}{\in} S$ iff $y \in \underset{̲}{R} (S)$ ,
$y \bar{\in} S$ iff $y \in \bar{R} (S)$ ,
$y {\underset{̲}{\in}}_{P} S$ iff $y \in {\underset{̲}{R}}_{P} (S)$ ,
$y {\bar{\in}}_{P} S$ iff $y \in {\bar{R}}_{P} (S)$ .

Remark 3.

As stated by Definition 5,

P

- lower and

P

- upper approximation of a set

S \subseteq Y

is possible to write as

${\underset{̲}{R}}_{P} (S) = {y \in S : y {\underset{̲}{\in}}_{P} S}$ ,
${\bar{R}}_{P} (S) = {y \in S : y {\bar{\in}}_{P} S}$ .

Definition 6.

Assume that

S \subseteq Y

and that

(Y, R_{p})

is a

P

- approximation space. the

P

- accuracy measure of S, defined as follows;

$\propto_{R_{P} (S)} = \frac{| {\underset{̲}{R}}_{P} (S) |}{| {\bar{R}}_{P} (S) |}, S \neq \emptyset$ .

Definition 7.

The subset

N \subseteq Y

of any

P

- approximation space

(Y, R_{P})

is referred to as;

If ${\underset{̲}{R}}_{P} (N) \neq \emptyset$ and ${\bar{R}}_{P} (N) \neq Y$ , then roughly $R_{P}$ - definable, and indicated by $P R D (Y)$ ,
If ${\underset{̲}{R}}_{P} (N) = \emptyset$ and ${\bar{R}}_{P} (N) \neq Y$ , then internally $R_{P}$ - undefinable, and indicated by $P I U D (Y)$ ,
if ${\underset{̲}{R}}_{P} (N) \neq \emptyset$ and ${\bar{R}}_{P} (N) = Y$ , then externally $R_{P}$ - undefinable, and indicated by $P E U D (Y)$ ,
If ${\underset{̲}{R}}_{P} (N) = \emptyset$ and ${\bar{R}}_{P} (N) = Y$ , then totally $R_{P}$ - undefinable, and indicated by $P T U D (Y)$ .

Remark 4.

For any

P

- approximation space

(Y, R_{P})

the following hold:

$P R D (Y) \supseteq R D (Y)$ ,
$P I U D (Y) \subseteq I U D (Y)$ ,
$P E U D (Y) \subseteq E U D (Y)$ ,
$P T U D (Y) \subseteq T U D (Y)$ .

4. A Novel Approach to Rough Categorization Using the $δ P$ -Open Set

Remark 5.

A subbase for a topology τ on

X

and a class of

δ P O (X)

of all

δ P

-0pen sets by

R_{δ_{P}}

are indicated, along with the relationship that was utilized to obtain them. Furthermore, we designate the approximation space

δ P

(X, R_{δ P})

Example 1.

Assume a universe

X = {u_{1}, u_{2}, u_{3}, u_{4}}

and a relation

R

defined as

R = {(u_{1}, u_{1}), (u_{1}, u_{2}), (u_{1}, u_{3}), (u_{2}, u_{3}), (u_{3}, u_{4})}

thus

u_{1} R = {u_{1}, u_{2}, u_{3}}, u_{2} R = {u_{3}}, u_{3} R = {u_{4}}

as well

u_{4} R = \emptyset

. Consequently, the topology related to this relationship is

τ = {\emptyset, X, {u_{3}}, {u_{4}}, {u_{3}, u_{4}}, {u_{1}, u_{2}, u_{3}}}

as well

δ P O (X) = {\emptyset, X, {u_{1}}, {u_{2}}, {u_{3}}, {u_{4}}, {u_{1}, u_{2}}, {u_{1}, u_{3}}, {u_{1}, u_{4}}, {u_{2}, u_{3}}, {u_{2}, u_{4}}, {u_{3}, u_{4}}, {u_{1}, u_{2}, u_{3}}, {u_{1}, u_{3}, u_{4}}, {u_{1}, u_{2}, u_{4}}, {u_{2}, u_{3}, u_{4}}}

.is a

δ P

- approximation space.

Definition 8.

Assume that (

X, R_{δ}

_{P}

) is

δ P

- lower approximation as well

δ P

- upper approximation for every nonempty subset S of

X

, the definition is:

${\underset{̲}{R}}_{δ P} (S) = ⋃ {V : V \in δ P O (X), V \subseteq S}$ ,
${\bar{R}}_{δ P} (S) = ⋂ {W : W \in δ P C (X), W \supseteq S}$ .

Definition 9.

Assume that(

X, R_{δ P}

) is

δ P

- accuracy measure of S specified as follows

$\propto_{R_{δ P}} (S) = \frac{∣ {\underset{̲}{R}}_{δ P} (S) ∣}{∣ {\bar{R}}_{δ P} (S) ∣}, S \neq \emptyset$ .

Theorem 1.

Given any binary relation

R

X

, which generates a topological space

(X, τ)

, we obtain

\underset{̲}{R} (S) \subseteq {\underset{̲}{R}}_{P} (S) \subseteq {\underset{̲}{R}}_{δ}_{P} (S) \subseteq S \subseteq {\bar{R}}_{δ}_{P} (S) \subseteq {\bar{R}}_{P} (S) \subseteq \bar{R} (S)

Proof.

\underset{̲}{R} (S) = ⋃ {V \in τ : V \subseteq S} \subseteq ⋃ {V \in P O (X) : V \subseteq S} = {\underset{̲}{R}}_{P} (S) \subseteq ⋃ {V \in δ P O (X) : V \subseteq S} = {\underset{̲}{R}}_{δ}_{P} (S) \subseteq S

, that is,

\underset{̲}{R} (S) \subseteq {\underset{̲}{R}}_{P} (S) \subseteq {\underset{̲}{R}}_{δ}_{P} (S) \subseteq S

Furthermore,

\bar{R} (S) = ⋂ {W \in τ^{c} : W \supseteq S} \supseteq ⋂ {W \in P C (X) : W \supseteq S} = {\bar{R}}_{P} (S) \supseteq ⋂ {W \in δ P C (X) : W \supseteq S} = {\bar{R}}_{δ}_{P} (S) \supseteq S

, that is,

\bar{R} (S) \supseteq {\bar{R}}_{P} (S) \supseteq {\bar{R}}_{δ}_{P} (S) \supseteq S

Consequently,

\underset{̲}{R} (S) \subseteq {\underset{̲}{R}}_{P} (S) \subseteq {\underset{̲}{R}}_{δ}_{P} (S) \subseteq S \subseteq {\bar{R}}_{δ}_{P} (S) \subseteq {\bar{R}}_{P} (S) \subseteq \bar{R} (S)

. □

Definition 10.

Assume that the

δ P

- approximation space is (

X, R_{δ P})

. With consider to any

S \subseteq X

, the universe

X

can be divided into 24 areas as follows.

$\underset{̲}{E d g} (S) = S - \underset{̲}{R} (S)$ , which is the internal edg of S.
$P \underset{̲}{E d g} (S) = S - \underset{̲}{R}_{P} (S)$ , which is the $P$ -internal edg of S.
$δ P \underset{̲}{E d g} (S) = S - {\underset{̲}{R}}_{δ}_{P} (S)$ , which is the $δ P$ - internal edg of S .
$\bar{E d g} (S) = \bar{R} (S) - S$ , which is the external edg of S.
$P \bar{E d g} (s) = {\bar{R}}_{P} (S) - S$ , which is the $P$ - external edg of S.
$δ P \bar{E d g} (S) = {\bar{R}}_{δ}_{P} (S) - S$ , which is the $δ P$ - external edg of S.
b(S) = $\bar{R} (S) - \underset{̲}{R} (S)$ , which is the boundary of S.
$P b (S)$ = ${\bar{R}}_{P} (S) - {\underset{̲}{R}}_{P} (S)$ , which is the $P$ - boundary of S.
$δ P b (S) = {\bar{R}}_{δ}_{P} (S) - {\underset{̲}{R}}_{δ}_{P} (S)$ , which is the $δ P$ - boundary of S.
$e x t (S) = X - \bar{R} (S)$ , which is the exterior of S.
$P e x t (S) = X - {\bar{R}}_{P} (S)$ , which is the $P$ - exterior of S.
$δ P e x t (S) = X - {\bar{R}}_{δ}_{P} (S)$ , which is the $δ P$ - exterior of S.
$\bar{R} (S) - {\underset{̲}{R}}_{P} (S)$ .
$\bar{R} (S) - {\underset{̲}{R}}_{δ}_{P} (S)$ .
$\bar{R} (S) - {\bar{R}}_{δ}_{P} (S)$ .
${\bar{R}}_{P} (S) - \underset{̲}{R} (S)$ .
${\bar{R}}_{P} (S) - {\underset{̲}{R}}_{δ_{P}} (S)$ .
${\bar{R}}_{P} (S) - {\bar{R}}_{δ}_{P} (S)$ .
${\underset{̲}{R}}_{P} (S) - \underset{̲}{R} (S)$ .
${\bar{R}}_{δ}_{P} (S) - {\underset{̲}{R}}_{P} (S)$ .
${\bar{R}}_{δ}_{P} (S) - \underset{̲}{R} (S)$ .
${\underset{̲}{R}}_{δ}_{P} (S) - {\underset{̲}{R}}_{P} (S)$ .
${\underset{̲}{R}}_{δ}_{P} (S) - \underset{̲}{R} (S)$ .
$\bar{R} (S) - {\bar{R}}_{P} (S)$ .

Remark 6.

An extension of the study of approximation space is the study of

δ P

- approximation space (Figure 1). Due to the components of the areas [

{\underset{̲}{R}}_{P} (S) - \underset{̲}{R} (S)

], [

{\underset{̲}{R}}_{δ}_{P} (S) - {\underset{̲}{R}}_{P} (S)

], and[

{\underset{̲}{R}}_{δ}_{P} (S) - \underset{̲}{R} (S)

] will be defined well in S, In Pawlak’s approximation, however, this point was undefinable. Additionally, the component of the areas [

\bar{R} (S) - {\underset{̲}{R}}_{δ}_{P} (S)

],[

{\bar{R}}_{P} (S) - {\bar{R}}_{δ}_{P} (S)

],additionally [

\bar{R} (S) - {\bar{R}}_{P} (S)

] don’t belong in S, even though Pawlak’s approximation space doesn’t provide these components a clear definition.

Figure 1 shows the above 24 areas.

Proposition 2.

If S is any subset of

X

, then the following holds for any

δ P

- approximation space

(X, R_{δ}_{P})

$b (S) = \underset{̲}{E d g} (S) \cup \bar{E d g} (S)$ .
$δ P b (S) = δ P \underset{̲}{E d g} (S) \cup δ P \bar{E d g} (S)$ .

Proof.

(2) It the follows from

δ P b (S) = {\bar{R}}_{δ}_{P} (S) - {\underset{̲}{R}}_{δ}_{P} (S) = ({\bar{R}}_{δ}_{P} (S) - S) \cup (S - {\underset{̲}{R}}_{δ}_{P} (S)) = δ P \underset{̲}{E d g} (S) \cup δ P \bar{E d g} (S)

. □

Definition 11.

Assume that

S \subseteq Y

and that (

X, R_{δ P})

is a

δ P

- approximation space. Then there are the memberships

{\underset{̲}{\in}}_{δ P}

{\bar{\in}}_{δ P}

, which are defined as,

δ P

- strong and

δ P

- weak membership respectively

$y {\underset{̲}{\in}}_{δ P} S$ iff $y \in {\underset{̲}{R}}_{δ P} (S)$ ,
$y {\bar{\in}}_{δ P} S$ iff $y \in {\bar{R}}_{δ P} (S)$ .

Remark 7.

As stated by definition 10 ,

δ P

- lower and

δ P

- upper approximations of a set

S \subseteq Y

is possible to write as:

${\underset{̲}{R}}_{δ P} (S) = {y \in S : y {\underset{̲}{\in}}_{δ P} S}$ ,
${\bar{R}}_{δ P} (S) = {y \in S : y {\bar{\in}}_{δ P} S}$ .

Remark 8.

Assume that (

X, R_{δ P})

is a

δ P

- approximation space,

S \subseteq Y

. Then

$y \underset{̲}{\in} S \Rightarrow y {\underset{̲}{\in}}_{P} S \Rightarrow y {\underset{̲}{\in}}_{δ P} S$ ,
$y {\bar{\in}}_{δ P} S \Rightarrow y {\bar{\in}}_{P} S \Rightarrow y \bar{\in} S$ .

The converse of Remark 8 It might not always be the case, as demonstrated by the example below.

Example 2.

In example 1. Let N=

{u_{2}, u_{4}}

, we have

u_{2}

{\underset{̲}{\in}}_{δ}_{P}

N but

u_{3}

{\underset{̲}{\notin}}_{P}

N. Let N =

{u_{1}, u_{3}}

u_{1}

{\underset{̲}{\in}}_{P}

N but

u_{1}

\underset{̲}{\notin}

N. Let N =

{u_{1}, u_{4}}

then we have

u_{2}

\bar{\in}

N but

u_{2}

{\bar{\notin}}_{P}

N. Let N =

{u_{3}}

u_{1}

{\bar{\in}}_{P}

N but

u_{1}

{\bar{\notin}}_{δ}_{P}

Example 3.

We can deduce from example 1 with the following table, which displays the degree of accuracy measure

\propto_{R}

(S)

P

-accuracy measure

\propto_{R_{P}}

(S)

additionally

δ P

- accuracy measure

\propto_{R_{δ P}}

(S)

for some subset of

X

The set

S = {u_{3}, u_{4}}

has a degree of precision of 50% according to the accuracy measure, and 100% according to the

δ P

- accuracy measure. Furthermore, the set

N = {u_{1}, u_{3}, u_{4}}

according to

P

- accuracy measure equal to 75% and according to

δ P

- accuracy measure equal to 100%. Thus,

δ P

-accuracy measures are superior to accuracy and

P

-accuracy metrics.

We study

δ P

- rough inclusion, using the rough inclusion method that Novotny and Pawlak developed in [19,20].

Definition 12.

Assume that (

X, R_{δ}_{P})

is a

δ P

approximation space where S,

N \subseteq X

. Then we state:

S is $δ P$ - roughly bottom included in N if ${\underset{̲}{R}}_{δ P} (S) \subseteq {\underset{̲}{R}}_{δ P} (N)$ ,
S is $δ P$ - roughly top included in N if ${\bar{R}}_{δ P} (S) \subseteq {\bar{R}}_{δ P} (N)$ ,
S is $δ P$ - roughly included in N if (1) and (2).

Example 4.

As shown in Example 1,

{u_{2}, u_{4}}

δ P

- roughly bottom included in

{u_{1}, u_{2}, u_{4}}

Furthermore

{u_{2}, u_{4}}

δ P

- roughly top included in

{u_{1}, u_{2}, u_{4}}

. Additionally

{u_{2}, u_{4}}

δ P

- roughly included in

{u_{1}, u_{2}, u_{4}} .

Definition 13.

Assume that (

X, R_{δ P})

δ P

- approximation space, a subset S of

X

is referred to as

$R_{δ P}$ - definable $(δ P - e x a c t)$ when ${\bar{R}}_{δ P} (S) = {\underset{̲}{R}}_{δ P} (S)$ ,
$δ P$ - rough when ${\bar{R}}_{δ P} (S) \neq {\underset{̲}{R}}_{δ P} (S) .$

Example 5.

For any

δ P

- approximation space

(X, R_{δ P})

as in Example 1. We have the set

{u_{2}, u_{3}, u_{4}}

δ P

- exact.

Definition 14.

The subset

S \subseteq X

of any

δ P

- approximation space

(X, R_{δ P})

is referred to as;

If ${\underset{̲}{R}}_{δ P} (S) \neq \emptyset$ and ${\bar{R}}_{δ P} (X) \neq X$ , then roughly $R_{δ P}$ - definable, and indicated by $δ P R D (X)$ ,
If ${\underset{̲}{R}}_{δ P} (S) = \emptyset$ and ${\bar{R}}_{δ P} (S) \neq X$ , then internally $R_{δ P}$ - undefinable, and indicated by $δ P I U D (X)$ ,
if ${\underset{̲}{R}}_{δ P} (S) \neq \emptyset$ and ${\bar{R}}_{δ P} (S) = X$ , then externally $R_{δ P}$ - undefinable, and indicated by $δ P E U D (X)$ ,
If ${\underset{̲}{R}}_{δ P} (S) = \emptyset$ and ${\bar{R}}_{δ P} (S) = X$ , then totally $R_{δ P}$ - undefinable, and indicated by $δ P T U D (X)$ .

Remark 9.

Assume that

(Y, R_{δ}_{P})

is a

δ P

- approximation space. These are on hold :

$δ P R D (Y) \supseteq P R D (Y) \supseteq R D (Y)$ ,
$δ P I U D (Y) \subseteq P I U D (Y) \subseteq I U D (Y)$ ,
$δ P E U D (Y) \subseteq P E U D (Y) \subseteq E U D (Y)$ ,
$δ P T U D (Y) \subseteq P T U D (Y) \subseteq T U D (Y)$ .

Example 6.

As shown in Example 1, the set

{u_{1}, u_{2}} \in δ P R D (X)

but

{u_{1}, u_{2}} \notin p R D (X)

.The set

{u_{2}} \in P I U D (X)

but

{u_{2}} \notin δ P I U D (X)

. The set

{u_{2}} \in P I U D (X)

and

{u_{2}} \in δ P I U D (X)

. the set

{u_{1}, u_{3}, u_{4}} \in P E U D (X)

but

{u_{1}, u_{3}, u_{4}} \notin δ P E U D (X)

Proposition 3.

Assume that the

δ P

- approximation space is

(Y, R_{δ}_{P})

. After that

Each $P$ - exact set in $Y$ is $δ P$ - exact
Each $δ P$ - rough set in $Y$ is $P$ - rough

Proof.

Evident.

As demonstrated by the example that follows, the converse of every part of proposition 3, might not always hold. □

Example 7.

Consider

(X, R_{δ}_{P})

as an

δ P

- approximation space for in example 1. Consequently the subset

{u_{1}, u_{2}}

δ P

- exact but not

P

-exact, while

{u_{2}, u_{3}, u_{4}}

is P-rough but not

δ P

-rough.

Proposition 4.

Assuming that

S, N \subseteq X

and any

δ P

- approximation space

(X, R_{δ P})

.Next

${\underset{̲}{R}}_{δ P} (S) \subseteq S \subseteq {\bar{R}}_{δ P} (S)$ ,
${\underset{̲}{R}}_{δ}_{P} (\emptyset) = {\bar{R}}_{δ}_{P} (\emptyset) = \emptyset, {\underset{̲}{R}}_{δ}_{P} (X) = {\bar{R}}_{δ}_{P} (X) = X$ ,
If $S \subseteq N$ then ${\underset{̲}{R}}_{δ}_{P} (S) \subseteq {\underset{̲}{R}}_{δ}_{P} (N)$ and ${\bar{R}}_{δ}_{P} (S) \subseteq {\bar{R}}_{δ}_{P} (N)$

Proof.

Assume $x \in {\underset{̲}{R}}_{δ}_{P} (S)$ , meaning that $x \in ⋂ {V \in δ P O (X), V \subseteq S}$ . And after that, there $V_{0} \in δ P O (X)$ in such a manner that $x \in V_{0} \subseteq S$ . So $x \in S$ , therefore ${\underset{̲}{R}}_{δ}_{P} (S) \subseteq S$ , furthermore, assume $x \in X$ additionally, by definition of ${\bar{R}}_{δ}_{P} (S) = ⋃ {W \in δ P C (X), S \subseteq W}$ , then $x \in W$ for everyone $W \in δ P C (X)$ . Therefore $S \subseteq {\bar{R}}_{δ}_{P} (S)$ .
Adheres directly.
Assume $x \in {\underset{̲}{R}}_{δ}_{P} (S)$ , meaning that $x \in ⋃ {V \in δ P O (X), V \subseteq S}$ however $S \subseteq N$ , so $V \subseteq N$ and $x \in V$ , then $x \in {\underset{̲}{R}}_{δ}_{P} (N)$ . Additionally let $x \notin {\bar{R}}_{δ}_{P} (N)$ this implies that $x \notin ⋂ {W \in δ P C (X), N \subseteq W}$ afterward, there are $W \in δ P C (X), N \subseteq W$ and $x \notin W$ meaning that, there is $W \in δ P C (X), S \subseteq N \subseteq W$ and $x \notin W$ which suggest $x \notin ⋂ {W \in δ P C (X), S \subseteq W}$ , so $x \notin {\bar{R}}_{δ}_{P} (S)$ . Consequently ${\bar{R}}_{δ}_{P} (S) \subseteq {\bar{R}}_{δ}_{P} (N)$ .

□

Proposition 5.

Assuming that

S, N \subseteq X

and any

δ P

- approximation space

(X, R_{δ}_{P})

.Next:

${\underset{̲}{R}}_{δ}_{P} (X ∖ S) = X ∖ {\bar{R}}_{δ}_{P} (S)$ ,
${\bar{R}}_{δ}_{P} (X ∖ S) = X ∖ {\underset{̲}{R}}_{δ}_{P} (S)$ ,
${\underset{̲}{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S)) = {\underset{̲}{R}}_{δ}_{P} (S)$ ,
${\bar{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)) = {\bar{R}}_{δ}_{P} (S)$ ,
${\underset{̲}{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S)) \subseteq {\bar{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S))$ ,
${\underset{̲}{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)) \subseteq {\bar{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)$ .

Proof.

Assume $x \in {\underset{̲}{R}}_{δ}_{P} (X ∖ S)$ meaning that $x \in ⋃ {V \in δ P O (X), V \subseteq X ∖ S}$ . Consequently, there $V_{0} \in δ P O (X)$ in such a manner that $x \in V_{0} \subseteq X ∖ S$ . And after that, there $V_{0}^{c}$ such that $S \subset V_{0}^{c}, V_{0}^{c} \in δ P C (X)$ . So $x \notin {\bar{R}}_{δ}_{P} (S)$ . So $x \in X ∖ {\bar{R}}_{δ}_{P} (S)$ . Consequently ${\underset{̲}{R}}_{δ}_{P} (X ∖ S) = X ∖ {\bar{R}}_{δ}_{P} (S)$ .
Comparable to (1).
By definition ${\underset{̲}{R}}_{δ}_{P} (S) = ⋃ {V \in δ P O (X), V \subseteq S}$ , That suggests that ${\underset{̲}{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S)) = ⋃ {V \in δ P O (X), V \subseteq {\underset{̲}{R}}_{δ}_{P} (S) \subseteq S}} = ⋃ {V \in δ P O (X), V \subseteq S} = {\underset{̲}{R}}_{δ}_{P} (S)$ .
${\bar{R}}_{δ P} ({\bar{R}}_{δ P} (S)) = {\bar{R}}_{δ P} (X ∖ {\underset{̲}{R}}_{δ P} (X ∖ S)) = X ∖ {\underset{̲}{R}}_{δ P} (X ∖ {\underset{̲}{R}}_{δ P} (X ∖ S))$ . From (1), (2) and (3), we get ${\bar{R}}_{δ P} ({\bar{R}}_{δ P} (S)) = X ∖ {\underset{̲}{R}}_{δ P} (X ∖ S) = X ∖ (X ∖ {\bar{R}}_{δ P} (S)) = {\bar{R}}_{δ P} (S)$ .
Since ${\underset{̲}{R}}_{δ}_{P} (S) \subseteq {\bar{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S))$ and by (3) we have ${\underset{̲}{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S)) = {\underset{̲}{R}}_{δ}_{P} (S)$ , then ${\underset{̲}{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S)) \subseteq {\bar{R}}_{δ}_{P} ({\underset{̲}{R}}_{δ}_{P} (S))$ .
Since ${\underset{̲}{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)) \subseteq {\bar{R}}_{δ}_{P} (S)$ and by (4), we have ${\bar{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)) = {\bar{R}}_{δ}_{P} (S)$ , then ${\underset{̲}{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S)) \subseteq {\bar{R}}_{δ}_{P} ({\bar{R}}_{δ}_{P} (S))$ .

□

Proposition 6.

Assume that

(X, R_{δ}_{P})

is a

δ P

- approximation apace and

S, N \subseteq X

. Then

${\underset{̲}{R}}_{δ}_{P} (S \cup N) \supseteq {\underset{̲}{R}}_{δ}_{P} (S) \cup {\underset{̲}{R}}_{δ}_{P} (N)$ ,
${\bar{R}}_{δ}_{P} (S \cup N) \supseteq {\bar{R}}_{δ}_{P} (S) \cup {\bar{R}}_{δ}_{P} (N)$ ,
${\underset{̲}{R}}_{δ}_{P} (S \cap N) \subseteq {\underset{̲}{R}}_{δ}_{P} (S) \cap {\underset{̲}{R}}_{δ}_{P} (N)$ ,
${\bar{R}}_{δ}_{P} (S \cap N) \subseteq {\bar{R}}_{δ}_{P} (S) \cap {\bar{R}}_{δ}_{P} (N)$ .

Proof.

Given that we have $S \subseteq S \cup N$ and $N \subseteq S \cup N$ . And after that ${\underset{̲}{R}}_{δ}_{P} (S) \subseteq {\underset{̲}{R}}_{δ}_{P} (S \cup N)$ and ${\underset{̲}{R}}_{δ}_{P} (N) \subseteq {\underset{̲}{R}}_{δ}_{P} (S \cup N)$ by (3) in the Proposition 4, then ${\underset{̲}{R}}_{δ}_{P} (S \cup N) \supseteq {\underset{̲}{R}}_{δ}_{P} (S) \cup {\underset{̲}{R}}_{δ}_{P} (N)$ .
(2), (3) and (4) the same as (1).

□

Theorem 2.

Assuming that

S, N \subseteq X

and any

δ P

- approximation space

(X, R_{δ}_{P})

If S is

R_{δ}_{P}

-definable. The next items are then held.

(1): ${\underset{̲}{R}}_{δ}_{P} (S \cup N) = {\underset{̲}{R}}_{δ}_{P} (S) \cup {\underset{̲}{R}}_{δ}_{P} (N)$ .
(2): ${\bar{R}}_{δ}_{P} (S \cap N) = {\bar{R}}_{δ}_{P} (S) \cap {\bar{R}}_{δ}_{P} (N)$ .

Proof.

Evidently ${\underset{̲}{R}}_{δ}_{P} (S) \cup {\underset{̲}{R}}_{δ}_{P} (N) \subseteq {\underset{̲}{R}}_{δ}_{P} (S \cup N)$ . To include the opposite, assume $x \in {\underset{̲}{R}}_{δ}_{P} (S \cup N)$ , that implies $x \in ⋃ {V$ is $δ P O (X), V \subseteq S \cup N}$ . And after that, there $V_{0} \in δ P O (X)$ in such a manner that $x \in V_{0} \subset \cup N$ . We present three instances:

(a)

If $V_{0} \subset S, x \in V_{0}$ and $V_{0}$ is a $δ P$ -open the set, then $x \in {\underset{̲}{R}}_{δ}_{P} (S)$ .

(b)

If $V_{0} \cap S = \emptyset$ , then $V_{0} \subseteq N$ and $x \in V_{0}$ , thus $x \in {\underset{̲}{R}}_{δ}_{P} (N)$ .

(c)

If $V_{0} \cap S \neq \emptyset$ . Since $x \in V_{0}$ and $V_{0}$ is an $δ P$ -open the set, then $x \in δ P c l (S)$ , each $V_{0}$ in the previously mentioned condition, therefore $x \in {\bar{R}}_{δ P} (S)$ , then $x \in {\underset{̲}{R}}_{δ P} (S)$ , since S is $δ P$ - definable. Thus, in three instances $x \in {\underset{̲}{R}}_{δ P} (S) \cup {\underset{̲}{R}}_{δ P} (N)$ .
Evidently ${\bar{R}}_{δ}_{P} (S \cap N) \subseteq {\bar{R}}_{δ}_{P} (S) \cap {\bar{R}}_{δ}_{P} (N)$ . We demonstrate the opposite inclusion, assume $x \in {\bar{R}}_{δ}_{P} (S) \cap {\bar{R}}_{δ}_{P} (N)$ , then $x \in {\bar{R}}_{δ}_{P} (S)$ denotes $x \in {\underset{̲}{R}}_{δ}_{P} (S)$ and $x \in V \subseteq X$ , in which V is an $δ P$ -open the set and $x \in {\bar{R}}_{δ P} (N)$ suggests for every $V \in δ P O (X), V \cap N \neq \emptyset$ . Consequently $V \cap (S \cap N) = (V \cap S) \cap N = V \cap Y \neq \emptyset$ . Therefore $x \in {\bar{R}}_{δ}_{P} (S \cap N)$ .

□

Theorem 3.

Assuming that

S, N \subseteq X

and any

δ P

- approximation space

(X, R_{δ}_{P})

. Afterwards, the following are held.

${\bar{R}}_{δ}_{P} (c l (S) \cup N) = c l (S) \cup {\bar{R}}_{δ}_{P} (N)$ ,
${\underset{̲}{R}}_{δ}_{P} (i n t (S) \cap N) = i n t (S) \cap {\underset{̲}{R}}_{δ}_{P} (N)$ .

Proof.

In accordance with propositions 4 (1) and 6 (2), we $c l (S) \subset {\bar{R}}_{δ P} (c l (S))$ . Then $c l (S) \cup {\bar{R}}_{δ P} (N) \subset {\bar{R}}_{δ P} (c l (S)) \cup {\bar{R}}_{δ P} (N) \subset {\bar{R}}_{δ P} (c l (S) \cup N)$ . However, since $c l (S) \cup M \subset c l (S) \cup {\bar{R}}_{δ P} (N)$ and the union of an $δ P$ -open set and a closed set is $δ P$ -closed, and after that ${\bar{R}}_{δ P} (c l (S) \cup N) \subset {\bar{R}}_{δ P} (c l (S) \cup {\bar{R}}_{δ P} (N)) = c l (S) \cup {\bar{R}}_{δ P} (N)$ . Consequently ${\bar{R}}_{δ P} (c l (S) \cup N) = c l (S) \cup {\bar{R}}_{δ P} (N)$ .
Given that an open set’s intersection with $i n t (S)$ and an $δ P$ -open set ${\underset{̲}{R}}_{δ}_{P} (N)$ is $δ P$ -open, $i n t (S) \cap {\underset{̲}{R}}_{δ}_{P} (N) = {\underset{̲}{R}}_{δ}_{P} (i n t (S) \cap {\underset{̲}{R}}_{δ}_{P} (N)) \subset {\underset{̲}{R}}_{δ}_{P} (i n t (S) \cap N)$ . However, by applying proposition 6 (3), ${\underset{̲}{R}}_{δ}_{P} (i n t (S) \cap N) \subset {\underset{̲}{R}}_{δ}_{P} (i n t (S)) \cap {\underset{̲}{R}}_{δ}_{P} (N) \subset i n t (S) \cap {\underset{̲}{R}}_{δ}_{P} (N)$ . Consequently ${\underset{̲}{R}}_{δ}_{P} (i n t (S) \cap N) = i n t (S) \cap {\underset{̲}{R}}_{δ}_{P} (N)$ .

□

Lemma 2.

For any

δ P

-approximation space

(X, R_{δ}_{P})

furthermore, for everyone

c, d \in X

, the state of

c \in {\bar{R}}_{δ}_{P} ({d})

and

d \in {\bar{R}}_{δ}_{P} ({c})

infers

{\bar{R}}_{δ}_{P} ({c}) = {\bar{R}}_{δ}_{P} ({d})

Proof.

According to the definition of

δ P

-upper approximation a set is a

δ P

-closure of this set, furthermore

δ P c l ({d})

is a

δ P

-closed set containing c (according to the condition) but

δ P c l ({c})

is the tiniest

δ P

-closed set containing c, thus

δ P c l ({c}) \subseteq δ P c l ({d})

. Therefore

{\bar{R}}_{δ}_{P} ({c}) \subseteq {\bar{R}}_{δ}_{P} ({d})

By symmetry, the opposite inclusion occurs

δ P c l ({d}) \subseteq δ P c l ({c})

. therefore

{\bar{R}}_{δ}_{P} ({d}) \subseteq {\bar{R}}_{δ}_{P} ({c})

we obtain

{\bar{R}}_{δ}_{P} ({c}) = {\bar{R}}_{δ}_{P} ({d})

. □

Lemma 3.

Assume that

(X, R_{δ}_{P})

be a

δ P

-approximation space, where each

δ P

-open subset S of

X

δ P

-closed, Then

d \in {\bar{R}}_{δ}_{P} ({c})

therefore

c \in {\bar{R}}_{δ}_{P} ({d})

for every

c, d \in X

Proof.

c \notin {\bar{R}}_{δ}_{P} ({d})

, then there is a

δ P

-open set V include c such that

V \cap {d} = \emptyset

which suggests that

{d} \subseteq (X ∖ V)

but

(X ∖ V)

is a

δ P

-closed set additionally is a

δ P

-open set does not include c, thus

(X ∖ V) \cap {c} = \emptyset

. Therefore

d \notin {\bar{R}}_{δ}_{P} ({c})

. □

Proposition 7.

Assume that

(X, R_{δ P})

be a

δ P

- approximation space, and all of them

δ P

-open subset S of

X

δ P

-closed. After that, the family of sets

{{\bar{R}}_{δ}_{P} ({c}) : c \in S}

is a division of the set

X

Proof.

c, d, f \in S

furthermore

f \in {\bar{R}}_{δ}_{P} ({c}) \cap {\bar{R}}_{δ}_{P} ({d})

, then

f \in {\bar{R}}_{δ}_{P} ({c})

furthermore

f \in {\bar{R}}_{δ}_{P} ({d})

. Consequently, by Lemma 3,

c \in {\bar{R}}_{δ}_{P} ({f})

and

d \in {\bar{R}}_{δ}_{P} ({f})

furthermore by Lemma 2, as we have

{\bar{R}}_{δ}_{P} ({c}) = {\bar{R}}_{δ}_{P} ({f})

and

{\bar{R}}_{δ}_{P} ({d}) = {\bar{R}}_{δ}_{P} ({f})

. Consequently

{\bar{R}}_{δ}_{P} ({c}) = {\bar{R}}_{δ}_{P} ({d}) = {\bar{R}}_{δ}_{P} ({f})

. Therefore either

{\bar{R}}_{δ}_{P} ({c}) = {\bar{R}}_{δ}_{P} ({d})

{\bar{R}}_{δ}_{P} ({c}) \cap {\bar{R}}_{δ}_{P} ({d}) = \emptyset

□

5. Conclusions

This paper introduces the

δ P

- approximation operator, a new class of approximations that we introduced using the

δ P

-open sets class. Furthermore, the

δ P

- approximation yields 24 unique granules of the discourse universe. The most extensive granulation based on closure and interior operator in topological spaces is used in our method, which is the class of

δ P

- open sets. Because of this, the accuracy measurements are higher than when using any kind of near-open sets, like

α

-open, etc. There are some generalizations of significant characteristics of the traditional Pawlak’s rough sets. Additionally, we used our approach to define the notion of rough membership function. It is an extension of the traditional rough membership function of Pawlak rough sets. In a decision information system, depending on a conditional attribute. The decision that has to be made can be done using the generalized rough membership function. Intelligent computational versions of granular beneficial computing is generated by the rough set approach to approximation of sets.

References

Z. Pawlak, "Rough sets". Int. J. Inf. Comput. Sci. 1982, 11, 341-356.
Z. Pawlak, Rough Sets, Theoretical Aspects of Reasoning about Data, Kluwer Academic, Boston, Mass, USA, 1991.
A.S. Mashhour, M.E. Abd El-Monsef, S.N. El-Deeb. On pre-continuous and week pre-continuous mappings. Proc. Math. Phys. Soc. Egypt, 1982, 53, 47–53. [Google Scholar]
R. Slowinski and D.Vanderpooten. "A generalized definition of rough approximations based on similarity", IEEE Transactions on Knowledge and Data Engineering, 2000, 12, 331–336. [Google Scholar] [CrossRef]
Z. Pawalk and A. Skowron, "Rough sets: some extensions",Information Sciences, 2007, 177, 28-40.
Z. Pawalk and A. Skowron,"Rudiments of rough sets",Information Sciences, 2007, 177, 3-27.
A.Mousavi, PJ. Maralani, Relative sets and rough sets, Int. J. Appl. Math. Comput. Sci. 2001, 11, 637-654.
P. Pattaraintakorn and N. Cercone, "A foundation of rough sets theoretical and computational hybrid intelligent system for survival analysis",Computers mathematics with Applications, 2008, 56, 1699-1708.
N.V. Velicko, H-closed topological spaces, Am. Math. Soc. Transl, 1968, 78, 103-118.
J.L. Kelley, General topology, D.Van Nostrand Company, London, UK, 1955.
D.S. Sivaraj, Extremally Disconnected Space, Indian J.Pure APPl. Math. 1986, 17, 1374-1375.
Y.Y. Yao, "Relational interpretations of neighborhood operators and rough set approximation operators", International Sciences, 1998, 111, 239-259.
M. Chuchro, On rough sets in topological Boolean algebras,Rough sets and Knowledge Discovery Baff AB, 1993, 157-160.
J. James, Alpigini, F. James, Peters, Andrzej Skowron and Ning zhong, Rough set elements, Rough sets and Current trends in compuring, 5th Int.conf. Malvern, PA. USA. Proc. Springer, 2002, 12-16.
E.F. Lashin, A.M.Kozae, A.A. Abo Khadra,T. Medhat, Rough set theory for topological space,Int.J.of approximation reasoning, 2005, 40, 35-43.
A. Wiweger, On topological rough sets, Bull. Pol. Acad. Math, 1989, 37, 89-93.
S. Raychaudhuri and M.N.Mukherjee, On δ-almost continuity and δ-preopen sets, Bull. Inst. Math. Acad. Sinica, 1993, 4, 357-366.
Z. Pawlak, Rough sets, Int.J.of computer and information sciences, 1982, 11, 341-356.
M. Novotny, Z. Pawlak, Characterization of rough top equalities and rough bottom equalities, Bull. Polish. Acad. of Sci, Math, 1985, 33, 92-97.
M. Novotny, Z. Pawlak, On rough equalities, Bull. Polish. Acad. Sci. Math. 1985, 33, 99-104.
K. Qin, Z. Pei, On the topological properties of Fuzzy rough sets, fuzzy sets and systems to Appear, 2005.
A. Wasilewska, L.Vigneron. On generalized rough sets, In Proc. of 5th work shop on Rough sets and soft of compiding at the 3rd joint Conf. On Information Sci, 1997, 20-24.
Y.Y. Yao,Two views of the theory of rough sets in finite Universes, Int. J. of Approximation Reasoning, 1997, 15, 291-317.
Y.Y. Yao, Generalized rough set models, in: Rough Sets in Knowledge Discovery,, Physica-Verlag, Heidelberg, 1998, 286-318.
Y.Y. Yao, On Generalized rough set theory,Rough sets,fuzzy sets,Data Mining and Granular computing, Proc. Of the 9th Int.Conf.1999, 44-51.

Figure 1. Showing the 24 areas given in Definition 10.

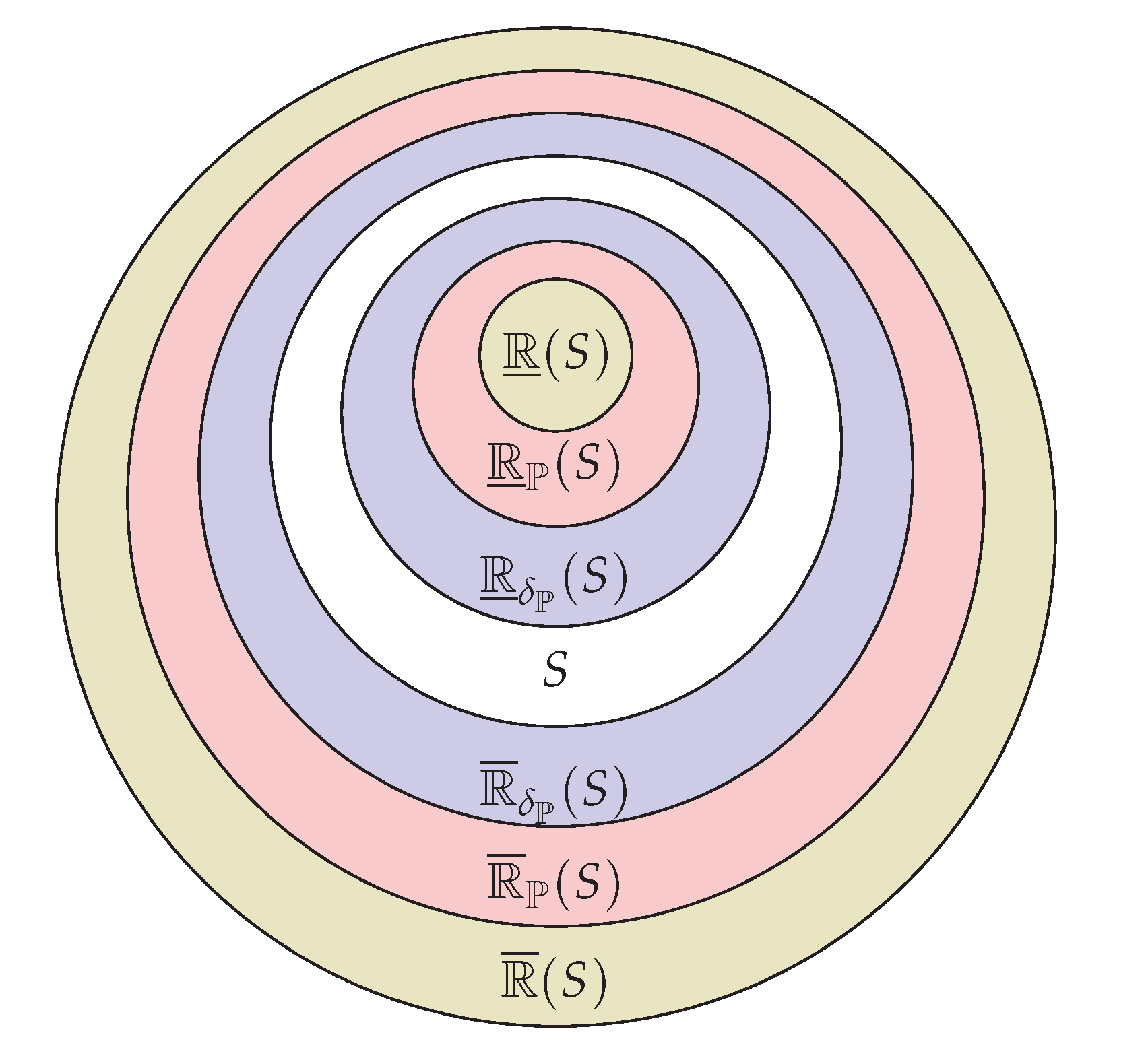
Table 1. Showing the degree of accuracy measure

\propto_{R}

(S)

\propto_{R_{P}}

(S)

and

\propto_{R_{δ}_{P}}

(S)

Table 1. Showing the degree of accuracy measure

\propto_{R}

(S)

\propto_{R_{P}}

(S)

and

\propto_{R_{δ}_{P}}

(S)

Power Set	$\propto_{R}$ $(S)$	$\propto_{R_{P}}$ $(S)$	$\propto_{R_{δ}_{P}}$ $(S)$
${u_{1}}$	0	0	1
${u_{2}}$	0	0	1
${u_{3}}$	$1 / 3$	$1 / 3$	1
${u_{4}}$	1	1	1
${u_{1}, u_{2}}$	0	0	1
${u_{1}, u_{3}}$	$1 / 3$	$2 / 3$	1
${u_{1}, u_{4}}$	$1 / 3$	$1 / 2$	1
${u_{2}, u_{3}}$	$1 / 3$	$2 / 3$	1
${u_{2}, u_{4}}$	$1 / 3$	$1 / 2$	1
${u_{3}, u_{4}}$	$1 / 2$	$1 / 2$	1
${u_{1}, u_{2}, u_{3}}$	1	1	1
${u_{1}, u_{2}, u_{4}}$	$1 / 3$	$1 / 3$	1
${u_{1}, u_{3}, u_{4}}$	$1 / 2$	$3 / 4$	1
${u_{2}, u_{3}, u_{4}}$	$1 / 2$	$3 / 4$	1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On δP-approximation Spaces

Abstract

1. Introduction

2. Fundamental Concepts δ P -Open Sets and Topology

3. Rough Set

4. A Novel Approach to Rough Categorization Using the δ P -Open Set

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe

2. Fundamental Concepts $δ P$ -Open Sets and Topology

4. A Novel Approach to Rough Categorization Using the $δ P$ -Open Set