The Clique Width of Two Classes of Series-Parallel Digraphs

Preprint

Article

The Clique Width of Two Classes of Series-Parallel Digraphs

This version is not peer-reviewed.

Ruzayn Quaddoura^*

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

21 March 2024

Posted:

26 March 2024

You are already at the latest version

Abstract

The concept of graphs with clique-width at most was first introduced by Courcelle et al.to be the graphs that can be characterized using -expressions derived from graph operations that use labels of vertices. If the clique-width for some graph is bounded then a grand number of algorithmic problems, in general NP-hard, can be solved in polynomial time when restricted to this graph. This important fact motivated the researchers to prove that the clique-width of certain graphs is bounded. Following this research direction, we prove in this paper that the clique-width of series-parallel digraphs is at most 6 and we present an time algorithm to construct a 6-expression for this class of digraphs. In another part, we present a linear time recognition algorithm for a similar class of series-parallel digraphs and prove that the clique-width of this class is at most 3.

Keywords:

Subject:

Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

Courcelle et al. in [1] characterized graphs with clique-width at most k as those graphs that can be generated through expressions involving graph operations utilizing

k

vertex labels. Clique width generalizes another significant graph parameter, tree-width, in the sense that any graph has a bounded tree-width also has a bounded clique width [6]. The concept of clique width was established in 1993 [1], and since then a large number of studies concerning this concept have been published. The subjects in the literature that concern clique width have a theoretical or an algorithmic standpoint and can be summarized by one of the following questions:

What is the complexity of computing the clique width?
When the clique width of a graph is unbounded?
Is there a general algorithm to recognize a graph of bounded clique width?
Are there general algorithms to solve some optimization problems in a graph of bounded clique width?
How to construct the clique width of a given graph?

The subject of complexity of computing the clique width has been resolved by Fellows et. al. in [14]. They proved that the problem of determining the clique width of a graph is NP-complete in general. The subject of determining the necessary and /or sufficient conditions to be the clique width of a graph unbounded is till now an open question. This question is motivated from the fact that the clique width for certain class of graphs can be unbounded, for example the class of

(4 k_{1}, C_{4}, C_{5}, C_{7})

-free graphs and not chordal [8]. The subject of recognizing a class of graphs of bounded clique width is resolved partially; for example, it is proved in [5] that any graph of clique width at most 3 can be recognized in

O (n^{2} m)

time. The subject of solving some optimization problems in a graph of bounded clique width is the significance of these graph invariants. It stems from the fact that many problems that are NP-hard in general admit polynomial-time solutions when restricted to graphs with bounded clique width (see for example [2,3,15]). Among these problems are Hamiltonian path or Hamiltonian cycle problems, computing the minimum size of a maximal matching and several partition problems (partition into cliques or triangles or complete bipartite sub-graphs or perfect matching's or forests) [16], computing the chromatic number and computing the minimum size of a dominating set of vertices or edges [4], computing the maximum size of a cut [7], finding vertex-disjoint Paths [13]. The construction of the clique width for a given graph has been studied extensively. For example, in [9], it is proved that the clique width of Cactus graphs is at most 4 and the construction of 4-expression of these graphs can be done in polynomial time. Also in [10] it is proved that the clique width of polygonal tree graphs can be done by constructing a 5-expression in a polynomial time. Recently, the clique width for series parallel undirected graphs is studied in [12], where it is proved that the clique width of these graphs is at most 5 and an

O (n^{2})

algorithm is presented to construct a 5-expression. Following this last direction of research, we prove that the clique width of the famous class of series parallel directed graphs (digraphs) is at most 6 and we propose an

O (n)

time algorithm to compute a 6-expression of this class. From other part, we introduce a new definition of a similar class of series parallel digraphs and present for which a linear time recognition algorithm. We prove that the clique width of this new class of digraphs is at most 3.

2. Preliminaries

A directed graph (or a digraph for short)

G = (V, E)

is defined by two sets,

V (G)

or simply

V

is the vertices set and

E (G)

or simply

E

is the arcs set. Every arc of

E

is an ordered pairs of vertices of

V

. The number

n

indicates to the number of vertices of

G

and the number

m

indicates to the number of edges of

G

.If

(x, y) \in E

then

x

is called a predecessor of

y

and

y

is called a successor of

x

. The set of all predecessors of a vertex

x

is denoted by

N^{+} (x)

, and the set of all successors of

x

is denoted by

N^{-} (x)

). The set of neighbors of

x

is the set

N (x) = N^{+} (x) \cup N^{-} (x)

. The number

{| N}^{+} (x) |

is called the positive degree of

x

and denoted by

d^{+} (x)

, and the number

{| N}^{-} (x) |

is called the negative degree of

x

and denoted by

d^{-} (x)

, the degree of a vertex x is the number

d (x) = | N (x) |

. A vertex

x

is called a source if

{| N}^{+} (x) | = 0

and is called a sink if

{| N}^{-} (x) | = 0

. Given a subset

X

of the vertices set

V

, the sub-graph induced by

X

will be denoted by

G [X]

. A path of length

k

is a sequence of vertices

x_{1}, x_{2}, . . ., x_{k}

such that any two consecutive vertices form an arc. A path

x_{1}, x_{2}, . . ., x_{k}

is called a circuit if

x_{1}, = x_{k}

and

k \geq 2

. A directed acyclic graph denoted by DAG is a digraph with no circuit. A chain of length

k

is a sequence of vertices

x_{1}, x_{2}, . . ., x_{k}

such that

(x_{i}, x_{i + 1})

(x_{i + 1}, x_{i})

is an arc. If

x_{1} = x_{k}

and

k \geq 2

the chain is called a cycle. An arc

(x, y)

is called transitive arc if there is a path from

x

y

of length at least 2. A bipartite graph

G = (B \cup W, E)

is given by a set of black vertices

B

and a set of white vertices

W

and a set of edges

E \subseteq B \times W

. A graph

G

is called

F

-free where

F

is a set of graphs when

G

does not contain an induced sub-graph isomorphic to a graph of

F

The clique width of a graph G is the smallest number of labels required to construct

G

using the four operations listed below:

The operation $i (v)$ ) to create a new vertex $v$ has the label $i$ .
The operation $G ⨁ H$ to make a union of two disjoint labeled graphs $G$ and $H$ .
The operation $η_{i, j} (G)$ to add in the labeled graph $G$ an edge (or an arc in case of digraphs) from each vertex with label $i$ to each vertex with label $j$ ( $i \neq j$ ).
The operation $ρ_{i \to j} (G)$ to change in the labeled graph $G$ every label $i$ to label $j$ .

Using these four operations, any graph may be defined by an algebraic expression. For example, the graph

G = (V, E)

where

V = {a, b, c, d}

and

E = {a b,, b c, c d, d a, d b}

can be defined by the following expression:

{{{η_{3,1} (d (3) ⨁ (ρ}_{3 \to 2} {(ρ}_{2 \to 1} (η}_{2,3} (3 (c) (η}_{1,2} (2 (b) ⨁ 1 (a)))))))

If an expression uses at most k different labels, it is referred to as a k-expression.

3. Clique Width of Series Parallel Digraphs (SP DAGs)

Series-parallel digraphs, or SP DAGs for short, are a class of directed graphs that play a significant role in graph theory and find extensive applications in various real-world scenarios. It has been defined by Tarjan et al. in [11] to be the digraph that can be constructed starting of the vertices set and recursively using two fundamental operations: series composition and parallel composition. More precisely:

Definition 1: A SP DAG is defined recursively as follows:

A DAG containing only one vertex is a SP DAG.

G_{1} = (V_{1}, E_{1})

and

G_{2} = (V_{2}, E_{2})

are two SP DAGs then the DAG constructed by each of the following operations is also a SP DAG :

Parallel composition:

G = G_{1} P G_{2} = (V_{1} \cup V_{2}, E_{1} \cup E_{2})

Series composition:

G = G_{1} S G_{2} = (V_{1} \cup V_{2}, E_{1} \cup E_{2} \cup T_{1} \times S_{2})

where

T_{1}

is the set of sink vertices of

G_{1}

and

S_{2}

is the set of source vertices of

G_{2}

A SP DAG

G

can be represented by a binary decomposition tree

T (G)

that reflects the construction of

G

starting of its vertices using series and parallel operations as following:

The leaves correspond to the vertices of $G$ .
Let $α$ be An internal node and $α_{1}, α_{1}$ are respectively the left and right child of $α$ , then $α$ is labeled by $P$ (resp. $S$ ) if $G [α] = G [α_{1}] P G [α_{2}]$ (resp. $G [α] = G [α_{1}] S G [α_{2}]$ ) where $G [α_{i}], i = 1,2$ is the sub-graph of $G$ induced by the set of vertices having $α_{i}$ as their least common ancestor.

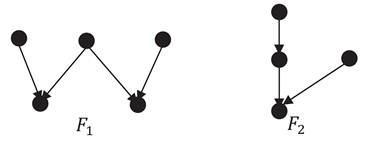
Figure 1 illustrates an example of a SP DAG and its binary decomposition tree. It is worthy mentioned that the two children of a

S

-node are ordered according to the series operation of that node. Tarjan et. al. in [11] proved that the construction of

T (G)

when

G

is a SP DAG can be done in

O (n + m)

time complexity. This binary decomposition tree of a SP DAG is the key of our computing to its clique width.

Theorem 1: The clique width of a SP DAG

G

is at most 6.

Proof: Let

α

be an internal node of

T (G)

and

α_{1}

α_{2}

are respectively the left and right child of

α

. We will construct a 6-expression of

G [α]

starting of a similar 6-expression of

G [α_{1}]

and 6-expression of

G [α_{2}]

For

i = 1,2

, we can partition the vertices set of

G [α_{i}]

into at most four sets

S (α_{i}), T (α_{i}), X (α_{i})

and

Y (α_{i})

, where

S (α_{i})

is the set of non-isolated sources of

G [α_{i}]

, T (α_{i})

is the set of non-isolated sinks of

G [α_{i}]

X (α_{i})

contains the set of isolated vertices of

G [α_{i}]

, and

Y (α_{i})

is the set of vertices that are not sources, not sinks, and not isolated in

G [α_{i}]

. We suppose that the label of every vertex of

S (α_{1})

is 1, the label of every vertex of

T (α_{1})

is 2, the label of every vertex of

X (α_{1})

is 1, and the label of every vertex of

Y (α_{1})

is 5.We express this in notation by

1 (S (α_{1})), 2 (T (α_{1})), 1 (X (α_{1}))

and

5 (Y (α_{1}))

. Similarly, we suppose that the label of every vertex of

S (α_{2})

is 3, the label of every vertex of

T (α_{2})

is 4, the label of every vertex of

X (α_{2})

is also 4, and the label of every vertex of

Y (α_{2})

is 6. We can express the sub-graph

G [α_{1}]

H_{1} ⨁ H_{2}

where:

H_{1} = G [1 (S (α_{1})) ⨁ 5 (Y (α_{1})) ⨁ 2 (T (α_{1}))]

H_{2} = G [1 (X (α_{1}))]

Similarly, we can express the sub-graph

G [α_{2}]

H_{3} ⨁ H_{4}

where:

H_{3} = G [3 (S (α_{2})) ⨁ 6 (Y (α_{2})) ⨁ 4 (T (α_{2}))]

H_{4} = G [4 (X (α_{2}))]

Figure 2.a illustrates this decomposition of

G [α_{i}]

. Without loss of generality, and for simplification of reading, we represented in this Figure each set of

S (α_{i}), T (α_{i}), X (α_{i})

and

Y (α_{i})

i = 1,2

, by a single vertex. To construct a 6-expression for

G [α]

we distinguish two cases according to the type of

α

Suppose that

α

is a

P

-node. In this case, the set

S (α_{1}) \cup S (α_{2})

is the set of non-isolated sources of

G [α]

, the set

T (α_{1}) \cup T (α_{2})

is the set of non-isolated sinks of

G [α]

, the set

X (α_{1}) \cup X (α_{2})

is the set of isolated vertices of

G [α]

, and the set

Y (α_{1}) \cup Y (α_{2})

is the set of vertices that are not sources, not sinks, and not isolated in

G [α]

. Hence, the expression

t_{1} ⨁ t_{2}

constructs

G [α]

using 6 labels where:

t_{1} = H_{1} ⨁ ρ_{3 \to 1} (ρ_{6 \to 5} (ρ_{4 \to 2} (H_{3})))

t_{2} = H_{2} ⨁ ρ_{4 \to 1} (H_{4})

Figure 2.b, illustrate the construction of

G [α]

using the expressions

t_{1}

and

t_{2}

. Suppose that

α

is a

S

-node. Since

G [α]

is connected, it does not contain isolated vertices. Since

α_{1}, α_{2}

are respectively the left child and right child of

α

then, every vertex of

X (α_{1})

must be a sink in

G [α_{1}]

and every vertex of

X (α_{2})

must be a source in

G [α_{2}]

, thus every vertex of

X (α_{1})

would be a source in

G [α]

and every vertex of

X (α_{2})

would be a sink in

G [α]

. Therefore,

S (α_{1}) \cup X (α_{1})

is the set of sources of

G [α]

, the set

X (α_{2}) \cup T (α_{2})

is the set of sinks of

G [α]

, and the set

Y (α_{1}) \cup T (α_{1}) \cup S (α_{2}) \cup Y (α_{2})

is the set of vertices that are not sources, not sinks, and not isolated in

G [α]

. Hence, the following ordered series of expressions constructs

G [α]

using 6 labels:

t_{1} = η_{3,4} (ρ_{1 \to 3} (H_{2}) ⨁ H_{4}), t_{2} = η_{2,4} (t_{1} + H_{1}), t_{3} = ρ_{3 \to 6} (ρ_{6 \to 5} (H_{3})),

t_{4} = η_{2,6} (η_{3,6} (t_{3} ⨁ t_{2})), t_{5} = ρ_{3 \to 1} (ρ_{6 \to 5} (ρ_{2 \to 5} (ρ_{4 \to 2} (t_{4}))))

Figure 2.c illustrate the construction of

G [α]

using the expressions

t_{1}, t_{2}, t_{3}, t_{4}

and

t_{5}

. Now, by traversing

T (G)

in post order and calculating a 6-expression for every internal node of

T (G)

, we conclude that the whole digraph

G

represented by the root of

T (G)

can be constructed by a 6-expression.

The construction a SP DAG by a 6-expression using the method described in the proof of Theorem 1 can be translated into the Algorithm Construction a 6-expression of a SP DAG. In this Algorithm, we define an empty expression, denoted by

\emptyset

, to be an expression of an empty set of vertices. For any expression

t

, we consider that

t ⨁ \emptyset = t

, so

η_{i, j} (t ⨁ \emptyset) = η_{i, j} (t)

and

ρ_{i \to j} (t ⨁ \emptyset) = ρ_{i \to j} (t)

. Our Algorithm associates with every node

α

T (G)

two expressions

t_{1} (α)

and

t_{2} (α)

, where

t_{1} (α)

represents the construction of the sub-graph induced by the non-isolated vertices of

G [α]

and

t_{2} (α)

represents the construction of isolated vertices of

G [α]

. It may be at most one of

t_{1} (α)

and

t_{2} (α)

empty. The labels in the end of computing

t_{1} (α)

t_{2} (α)

represent implicitly whether the corresponding vertices are non-isolated sources (labeled by 1), non-isolated sinks (labeled by 2), isolated vertices (labeled by 1), or vertices that are not sources, not sinks and not isolated in

G [α]

(labeled by 5). Initially, in step 1, every vertex is labeled by 1 since the sub-graph induced by a leaf consists only of one isolated vertex that consider as a source. Step 2 determines the left child

α_{1}

and the right child

α_{2}

of an internal node

α

. Step 3 constructs the expression

t_{1} (α)

and

t_{2} (α)

for a

P

-node

α

to be respectively the disjoint union of

t_{1} (α_{1}), t_{1} (α_{2})

and the disjoint union of

t_{2} (α_{1}), t_{2} (α_{2})

. Steps 4 to 13 constructs the expressions

t_{1} (α)

and

t_{2} (α)

for a

S

-node

α

as following: Step 5 changes the label of non- isolated sources of

G [α_{2}]

from 1 to 3, the label of non-isolated sinks from 2 to 4, and the other non-isolated vertices from 5 to 6; Step 6, changes the label of isolated vertices of

G [α_{2}]

from 1 to 4 as these vertices are sinks in

G [α_{2}]

. Step 7 changes the label of isolated vertices of

G [α_{1}]

from 1 to 3. The steps from 8 to13 construct the expression

t_{1} (α)

in the same way as in Figure 2c. The expression

t_{2} (α)

must be empty because of

G [α]

is connected. Since the number of nodes in

T (G)

O (n)

and every step can be done in

O (1)

time, the total time complexity of this Algorithm is

O (n)

Figure 3 illustrates an example of the application of Algorithm Construction a 6-expression of a SP DAG for the digraph

G

and its binary decomposition tree

T (G)

shown in Figure 1. The visited nodes according to post order traversal of

T (G)

is defined by the symbols

α_{i}, 1 \leq i \leq 9

, written near every internal node of

T (G)

. Every line in Figure 3 shows the executed steps for constructing

G [α_{i}], 1 \leq i \leq 9

. The vertices of left and right children of

α_{i}, 1 \leq i \leq 9

are represented respectively by a black color and a white color. The arrow and the number above it indicates the result of the corresponding step of the Algorithm. The absence of a result for a specific step means that this step has no effect on the construction.

3. Similar Series Parallel Digraphs (SSP DAGs)

Definition 1: A SSPDA G is defined recursively as follows:

A DAG having a single vertex is a SSP.

G_{1} = (V_{1}, E_{1})

and

G_{2} = (V_{2}, E_{2})

are two SSP DAGs then the DAG constructed by each of the following operations is also a SSP:

Parallel composition:

G = G_{1} P G_{2} = (V_{1} \cup V_{2}, E_{1} \cup E_{2})

Series composition:

G = G_{1} S G_{2} = (V_{1} \cup V_{2}, E_{1} \cup E_{2} \cup S_{1} \times S_{2})

where

S_{i}

is the set of source vertices of

G_{i}, i = 1,2

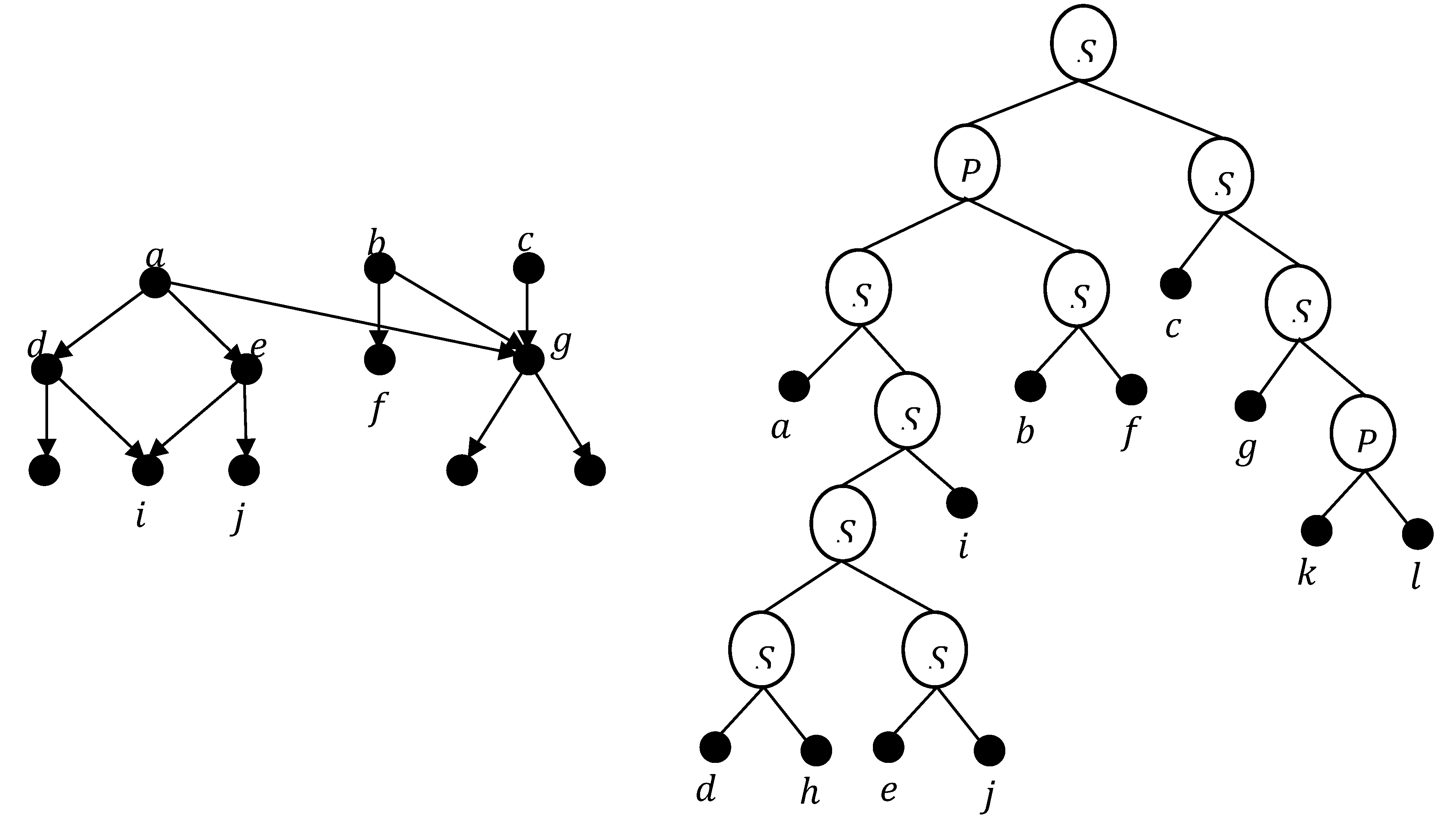
It is obvious that a SSP DAG is without transitive arcs. In the same way as in the class of SP DAGs, a SSP DAG

G

can be represented by a binary decomposition tree

T (G)

that reflects the construction of

G

starting of its vertices using series and parallel operations. Also as in the binary decomposition tree of a SP DAG, the two children of a

S

-node are ordered according to the series operation of that node. Figure 4 represents a SSP DAG

G

and its binary decomposition tree

T (G)

The following theorem is the key of our recognition algorithm of SSP DAGs.

Theorem 2: Let G be a connected DAG without transitive arcs.

G

is a SSP if and only

G

{F_{1}, F_{2}}

-free.

Proof: Suppose that

G

is a SSPDAG and let’s show that

G

{{F}_{1}, F_{2}}

-free.

Claim 1: Let

y_{1}, y_{2} \in V (G)

such that

N^{-} (y_{1}) \cap N^{-} (y_{2}) \neq \emptyset

then

N^{-} (y_{1}) \subseteq N^{-} (y_{2})

N^{-} (y_{2}) \subseteq N^{-} (y_{1})

Proof: Since

G

is a SSP, every arc in

G

is created by a series operation. According to the series operation, for any vertex

y

, all the arcs

{({x, y) | x \in N}^{-} (y)}

are created by the same series operation. So, if there is two vertices

y_{1}, y_{2}

such that

N^{-} (y_{1}) \cap N^{-} (y_{2}) \neq \emptyset

then if the two sets of arcs

{({x, y_{1}) | x \in N}^{-} (y_{1})}

and

{({x, y_{2}) | x \in N}^{-} (y_{2})}

are created by the same series operation then

N^{-} (y_{1}) = N^{-} (y_{2})

.Suppose that the set of arcs

{({x, y_{1}) | x \in N}^{-} (y_{1})}

is created by a series operation

S_{1}

and the set of arcs

{({x, y_{2}) | x \in N}^{-} (y_{2})}

is created by a series operation

S_{2}

where

S_{1}

precedes

S_{2}

. Since

N^{-} (y_{1}) \cap N^{-} (y_{2}) \neq \emptyset

, the vertex

y_{2}

was a source during the operation

S_{2}

, so

N^{-} (y_{1}) \subseteq N^{-} (y_{2})

. If

S_{2}

precedes

S_{1}

then

N^{-} (y_{2}) \subseteq N^{-} (y_{1})

. ■

By Claim 1,

G

F_{1}

-free.

Claim 2: Let

y \in V (G)

, for every

x_{1}, x_{2} \in N^{-} (y), N^{-} (x_{1}) = N^{-} (x_{2})

Proof: Let

x \in N^{-} (x_{1})

. By the definition of the series operation, the arc

(x_{1}, y)

has been created by a series operation

S_{1}

that precedes the series operation

S_{2}

for which the arc

(x, x_{1})

has been created. Since the arcs

(x_{1}, y), (x_{2}, y)

have been created by the same series operation

S_{1}

then during the series operation

S_{2}

there was as sources

x_{1}

and

x_{2}

, therefore

(x, x_{2}) \in E

, this implies that

N^{-} (x_{1}) = N^{-} (x_{2})

. ■

By Claim 2,

G

F_{2}

-free suppose now

G

is a connected DAG without transitive arcs and

{{F}_{1}, F_{2}}

-free. Let’s show that

G

is SSP DAG. Let

S

be the set of all sources of

G

and

Q = G [V - S]

Claim 3: Every vertex of

Q

that is a successor of a vertex of

S

is a source of

Q

Proof:Let

y

be a vertex of

Q

that is not a source and a successor to a vertex

x \in S

. Let

z

be a source in

Q

such that

z

is an ancestor of

y

. Since

G

does not contain transitive arcs,

(x, u) \notin E

for every vertex

u

located on the path going from

z

y

. Suppose that

z

is a predecessor of

y

. Since

S

is the set of all sources of

G

, there is a source

t \in S

such that

(t, z) \in E

. Since

G

does not contain transitive arcs, the set

{t, z, y, x}

induces the configuration

F_{2}

, a contradiction. Suppose that

z

is not a predecessor of

y

, let

u_{1}

be a predecessor of

y

Q

and

u_{2}

is a predecessor of

u_{1}

. Since

G

does not contain transitive arcs then

{x, y, u_{1}, u_{2}}

induces the configuration

F_{2}

, a contradiction. ■

Let

C_{1}, . . ., C_{k}

be the connected components of

Q

and

S'

is the set of sources of

Q

Claim 4: If a source

x \in S

is a predecessor to a source

y

of some connected component

C_{i}, 1 \leq i \leq k

then

x

is a predecessor to every source of

C_{i}

Proof: Suppose the contrary, then there a source

y'

C_{i}

such that

(x, y') \notin E

. Since

y

and

y'

are sources in

C_{i}

and

{G [C}_{i}]

is connected there is a chain in

{G [C}_{i}]

that connects

y

and

y'

. Without loss of generality, let

z \in C_{i}

such that

(y, z), (y^{'}, z) \in E

. Now the set

{x, y^{'}, y,, z}

induces the configuration

F_{2}

, a contradiction. ■

k = 1

then by Claim 4,

G [S \cup S^{'}]

is a bipartite complete. It is clear that

G

admit a series decomposition into

S

and

V (G) - S

Suppose

k \geq 2

and

G [S \cup S']

is not abipartite complete. Since

G

is connected,

G [S \cup S']

must be also connected. We claim that there is a vertex

y \in S

' such that for every

x \in S

(x, y) \in E .

Suppose the contrary, then for every vertex

y \in S

' there is avertex

x \in S

such that

(x, y) \notin E

. Let

y_{1}, y_{2} \in S'

and

x_{1}, x_{2} \in S

such that

(x_{1}, y_{1}), (x_{2}, y_{2}) \in E

and

(x_{1}, y_{2}), (x_{2}, y_{1}) \notin E

. Since

G [S \cup S']

is connected, there is a chain in

G [S \cup S']

that connects

(x_{1}, y_{1})

and

(x_{2}, y_{2})

. Without loss of generality, let

x \in S

such that

(x, y_{1}), (x, y_{2}) \in E

, then

{x, x_{1}, y_{1}, x_{2}, y_{2}}

induces the configuration

F_{1}

, a contradiction. Let

Y = {y \in S^{'} : \forall x \in S, (x, y) \in E

and

C_{1}, . . ., C_{r}

be the connected components of

Q

that contain the vertices of

Y

. It is proved in Claim 4 that every source of every connected component

C_{i} (1 \leq i \leq r)

is a successor of every source in

S

. Therefore

G

admit a series decomposition into

V (G) - (C_{1}, . . ., C_{r})

and

C_{1}, . . ., C_{r}

. It follows that we can always reduce

G

to its vertices set by a parallel decomposition and a series decomposition, this implies that

G

is a SSP DAG.

4. Recognition of SSP DAGs

We present in this section a linear Algorithm to recognize if an arbitrary DAG is SSP or not. We will take into account the following sort of the vertex set for a DAG

G

Definition 3: Let

G

be a DAG and

S

is the set of sources of

G

, let

A_{1} = S, A_{2} = N^{+} (A_{1}), \dots, A_{p} = N^{+} (A_{p - 1})

. The sort

ρ = {A_{1}, . . ., A_{p}}

is called a topologically sort of

V (G)

Our Algorithm uses the following result:

Lemma 4: Let

G

be a DAG and let

ρ = {A_{1}, . . ., A_{p}}

be the topologically sort of

V (G)

. Then

G

is a SSP DAG if and only if the following conditions are verified:

a): For every $(x, y) \in E (G)$ there is $1 \leq i \leq p - 1$ such that $x \in A_{i}, y \in A_{i + 1}$ ;
b): For every $2 \leq i \leq p, G [A_{i - 1} \cup A_{i}]$ is a bipartite $F_{1}$ -free graph;
c): Let $C = (C_{i}, C_{i + 1})$ be a connected component of $G [A_{i} \cup A_{i + 1}]$ , $2 \leq i \leq p - 1$ then for every $x, y \in C_{i}, N^{-} (x) = N^{-} (y)$ .

Proof: We can remark that

y \in A j, j > i + 1

if and only if

G

contains a transitive arc or

G

contains the configuration

F_{2}

. The conditions a and b assure that

G

F_{1}

-free, the conditions a and c assure that

G

F_{2}

-free.

The following Lemma provides a simple method for verifying the condition b of Lemma 4.

Lemma 5: Let

G = (B \cup W, E)

be a bipartite DAG of depth one.

G

F_{1}

-free if and only if for every

x, y \in W, N^{-} (x) \subseteq N^{-} (y)

N^{-} (x) \cap N^{-} (y) = \emptyset

Proof: Obviously if

G

F_{1}

-free then the conditions of Lemma must be verified. On the contrary, if one of these conditions is verified then every connected component of

G

contains an isolated vertex or a universal vertex. Therefore we can reduce

G

to its vertices set by a parallel and series decomposition.

The following Algorithm contains the procedures for detecting the conditions of Lemma 4. Step 1 tests whether

G

contains a transitive arc or the configuration

F_{1}

. Step 2 tests whether

G

contains the configuration

F_{2}

or not. Step 3 tests whether

G

contains between two consecutive levels of

ρ

the configuration

F_{1}

or not. Let’s show that the time complexity of this algorithm is

O (n + m)

. The determination of

ρ

and testing whether every arc of

G

is located between two consecutive levels of

ρ

requires

O (n + m)

time. The success of first step guarantees that the sets of edges

E (G_{i}), i = 1, . . ., p - 1

, constitute a partition of

E (G)

. Therefore, testing the inclusion relation of the vertices

N^{-} (y_{j}), j = 1, \dots, r

for every

A_{i + 1} = {y_{1}, \dots, y_{r}}, i = 1, . . ., p - 1

, using the mark procedure described in step 2, can be executed in time

O (V (G_{i}) + E (G_{i}))

, so the second step also requires

O (n + m)

time. The non-empty sets

C_{1}, \dots C_{k}

produced in step 2 are the input of step 3 for every

G_{i}, i = 1, . . ., p - 1

. Indeed

C_{i} \cup \{N^{+} (x) : x \in C_{i}\}

are the connected components of

G_{i}, i = 1, . . ., p - 1

. Now, to test the condition c of Lemma 4, it is enough to compare for every

x \in C_{i}

, the set

N^{-} (x)

with

N^{-} (x_{1})

where

x_{1}

is an arbitrary vertex of

C_{i}

. This can be done in

O (V (G_{i}) + E (G_{i}))

time. Hence the total time complexity of this Algorithm is

O (n + m)

5. Clique Width of SSP DAGs

The computation of clique width of SSP DAGs can be done in a similar way to the one we did for computing the clique width of SP DAGs. The following theorem shows this computation.

Theorem 1: The clique width of a SSP DAG

G

is at most 3.

Proof: Let

T (G)

be a binary decomposition tree of a SSP DAG

G

. Let

α

be an internal node of

T (G)

and

α_{1}

α_{2}

are respectively the left and right children of

α

. We will construct a 3-expression of

G [α]

starting of a similar 3-expression of

G [α_{1}]

and 3-expression of

G [α_{2}]

For

i = 1,2

, we can partition the vertices set of

G [α_{i}]

into at most two sets

S (α_{i})

and

Y (α_{i})

, where

S (α_{i})

is the set of sources of

G [α_{i}]

and

Y (α_{i})

is the set of remaining vertices of

G [α_{i}]

. We must point out here that if

G [α_{i}]

contains an isolated vertex then this vertex is considered as a source in

G [α_{i}]

. We suppose that the label of every vertex of

S (α_{1})

is 1 and the label of every vertex of

Y (α_{1})

is 2. Similarly, we suppose that the label of every vertex of

S (α_{2})

is 3 and the label of every vertex of

Y (α_{2})

is 2. So we can express the sub-graph

G [α_{1}]

and

G [α_{2}]

as:

G [α_{1}] = G [1 (S (α_{1}) ⨁ 2 (Y (α_{1}))]

G [α_{2}] = G [3 (S (α_{1}) ⨁ 2 (Y (α_{1}))]

Suppose that

α

is a

P

-node. The set

S (α_{1}) \cup S (α_{2})

is the set of sources of

G [α]

, and the set

Y (α_{1}) \cup Y (α_{2})

is the set of remaining vertices of

G [α]

. Hence, the expression

t

constructs

G [α]

using 3 labels where:

t = G [α_{1}] ⨁ ρ_{3 \to 1} (G [α_{2}])

Suppose that

α

is a

S

-node. By the definition of series operation, the set of sources of

G [α]

is the set

S (α_{1})

, and the set of remaining vertices of

G [α]

is the set

S (α_{2}) \cup Y (α_{1}) \cup Y (α_{2})

. Hence the expression

t

constructs

G [α]

using 3 labels where:

t = ρ_{3 \to 1} (η_{1,3} (G [α_{1}] ⨁ G [α_{2}]))

6. Conclusion

We show in this paper that the clique width of a SP DAG

G

is at most 6 and the construction of a 6-expression of

G

can be done in

O (n)

time complexity using a binary decomposition tree

T (G)

. On other hand, we defined the class of digraphs SSP as a similar class of SP DAGs and proved that this new class can be recognized in linear time complexity. We proved that the clique width of a SSP DAG is at most 3. The construction of a 3-expression of a SSP DAG

G

requires to construct a binary decomposition tree

T G)

that we believe to be done in linear time.

References

Courcelle, B.; Engelfriet, J. Rozenberg. Handle-rewriting hypergraph grammars. Journal of Computer and System Sciences 1993, 46, 218–270. [Google Scholar] [CrossRef]
Courcelle, B.; Makowsky, J.A.; Rotics, U. Linear time solvable optimization problems on graphs of bounded clique width. Theory of Computing Systems 2000, 33, 125–150. [Google Scholar] [CrossRef]
Courcelle, B. The expression of graph properties and graph transformations in monadic second-order logic, in: Handbook of Graph Grammars and Computing by Graph Transformation, vol. 1, World Sci. Publishing, River Edge, NJ, 1997, pp. 313_400.
Kobler, D.; Rotics, U. Edge dominating set and colorings on graphs with fixed clique width. Discrete Applied Mathematics 2003, 126, 197–221. [Google Scholar] [CrossRef]
Corneil, D.G.; Habibb, M.; Lanlignel, J.M.; Reedd, B.; Rotics, U. Polynomial-time recognition of clique width ≤ 3 graphs. Discrete Applied Mathematics 2012, 160, 834–865. [Google Scholar] [CrossRef]
Corneil, D.G.; Rotics, U. On the relationship between clique-width and treewidth. SIAM Journal on Computing 2005, 34, 825_847. [Google Scholar] [CrossRef]
Wanke, E. k-NLC graphs and polynomial algorithms. Discrete Applied Mathematics 1994, 54, 251–266. [Google Scholar] [CrossRef]
Penev, I. On the clique width of (4k1,C4,C5,C7)-free graphs. Discrete Applied Mathematics 2020, 285, 688–690. [Google Scholar] [CrossRef]
Gonzalez-Ruiz, J.L.; Marcial-Romero, J.R.; Hernandez-Servın, J. Computing the clique width of cactus graphs. Electronic Notes in Theoretical Computer Science 2016, 328, 47–57. [Google Scholar] [CrossRef]
Gonzalez-Ruiz, J.L.; Marcial-Romero, J.R.; Hernandez, J.A.; De Ita, G. Computing the clique width of polygonal tree graphs, Advances in Soft Computing, Springer International Publishing, Cham, (2017) pp. 449–459.
Valdes, J.; Tarjan, R.E.; Lawler, E.L. The Recognition of Series Parallel Digraphs. SIAM Journal on Computing 1982, 2, 298–313. [Google Scholar] [CrossRef]
López-Medina, M.A.; González-Ruiz, J.L.; Marcial-Romero, J.R.; Hernández, J.A. Computing the Clique-Width on Series-Parallel Graphs. Computación y Sistemas 2022, 26. [Google Scholar] [CrossRef]
Kurt, M.; Berberler, M.; Ugurlu, O. A New Algorithm for Finding Vertex-Disjoint Paths. The International Arab Journal of Information Technology 2015, 12. [Google Scholar]
Fellows, M.R.; Rosamond, F.A.; Rotics, U.; Szeider, S. Clique-width is NP-complete. SIAM Journal on Discrete Mathematics 2009, 23, 909–939. [Google Scholar] [CrossRef]
Oum, S.I.; Seymour, P. Approximating clique width and branch-width. Journal of Combinatorial Theory Series B 2006, 94, 514–528. [Google Scholar] [CrossRef]
Espelage, W.; Gurski, F.; Wanke, E. How to solve NP-hard graph problems on clique width bounded graphs in polynomial time. Lecture Notes in Computer Science 2001, 2204, 117–128. [Google Scholar]

Figure 1. A SP DAG and its decomposition binary tree.

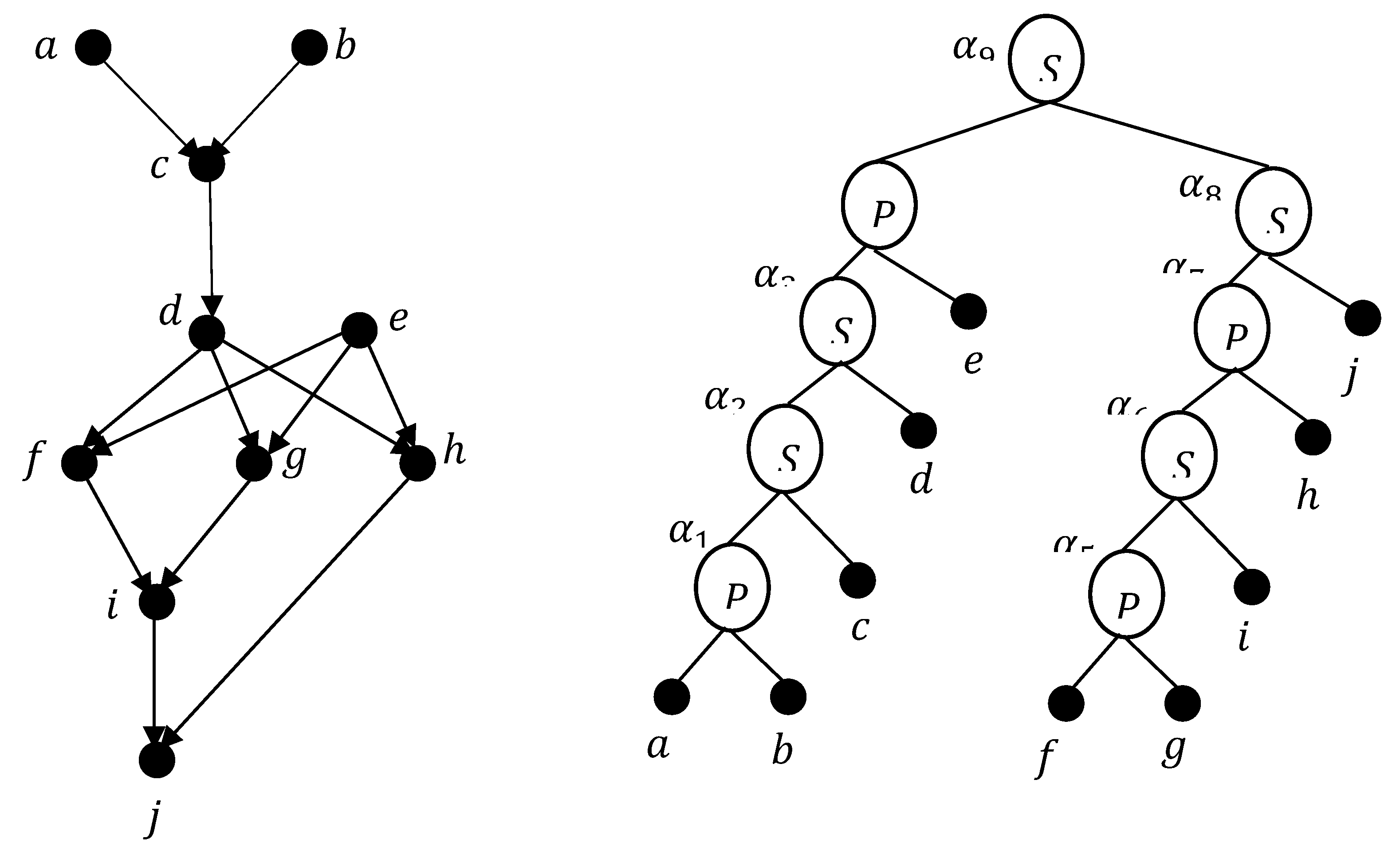
Figure 2. a) The sub-graphs

G [α_{1}]

and

G [α_{2}]

, b) the construction of

G [α] = G [α_{1}] P G [α_{2}]

, c) the construction of

G [α] = G [α_{1}] S G [α_{2}]

Figure 2. a) The sub-graphs

G [α_{1}]

and

G [α_{2}]

, b) the construction of

G [α] = G [α_{1}] P G [α_{2}]

, c) the construction of

G [α] = G [α_{1}] S G [α_{2}]

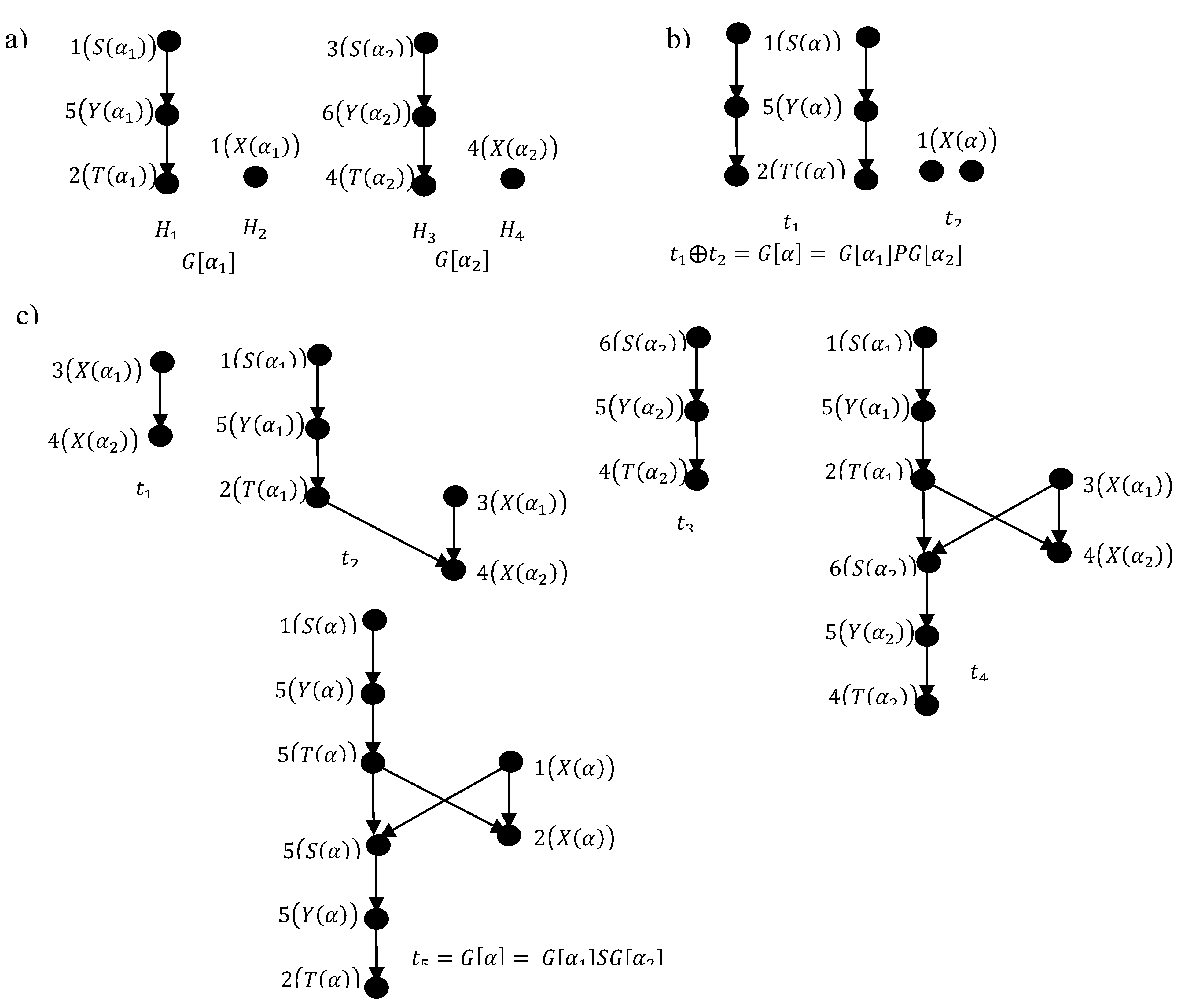
Figure 3. application of Algorithm Construction a 6-expression of a SP DAG for the digraph

G

in Figure 1.

Figure 3. application of Algorithm Construction a 6-expression of a SP DAG for the digraph

G

in Figure 1.

Figure 4. A SSP DAG and its binary decomposition tree.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Clique Width of Two Classes of Series-Parallel Digraphs

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminaries

3. Clique Width of Series Parallel Digraphs (SP DAGs)

3. Similar Series Parallel Digraphs (SSP DAGs)

4. Recognition of SSP DAGs

5. Clique Width of SSP DAGs

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe