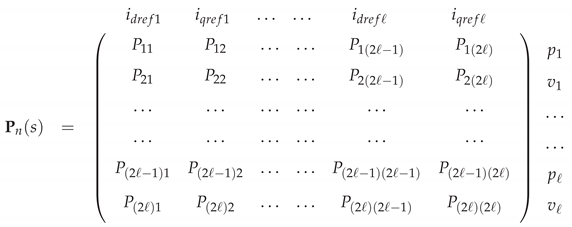Local DER Control with Reduced Loop Interactions in Active Distribution Networks

1. Introduction

In the last decade, electric distribution systems are undergoing deep changes to allow large penetration of Distributed Generation (DG) exploiting Renewable Energy Sources (RESs). Their configuration has changes from passive to Active Distribution Networks (ADNs) and new Distributed Energy Sources (DERs) are being connected, which include, in addition to DG, Battery Energy Storage Systems (BESSs), controllable loads and Electric Vehicles (EVs).

A key issue in ADNs is the regulation of the voltage profiles which are no longer monotonic along the feeders and can violate the quality limits of over and under voltage. In distribution systems voltage regulation is traditionally poorly automated and essentially centralized. Then, the new ADNs require all the DERs to support the voltage regulation. In particular, it is possible to act on the inverters interfacing the DERs to grid so as to vary their reactive power injections with no impact on the operation of the DC bus of the DER and, consequently, on the RES generator. However due to the high $R/X$ ratio of distribution lines the control of the reactive power injection is not enough effective to assure an adequate voltage regulation. In this view, Active Power Curtailment (APC) has been proposed as an additional tool for voltage regulation. In [1] the control system prioritizes the use of reactive power, while APC is performed only as a last resort; the controllers switch to active power curtailment only if all the reactive power capability has been exploited. In [2] a method that includes APC in coordination with reactive power control for voltage control in distribution networks is presented: APC is applied if the inverter rated apparent power is reached.

However, the approaches exploiting APC generally present two drawbacks. The first one is the non linear behavior of the control systems which often adopt a switching strategy between reactive power control and APC. To overcome this issue, the proposed voltage control methods typically use different control layers, that are adequately coordinated to manage both reactive power and APC [3,4,5]. The second important drawback is the economical impact of APC: it wastes energy produced from RESs and reduces revenues [6]. To reduce the economical impact, some methods use the voltage-active sensitivity factors to define the optimal APC strategy with respect to some chosen objectives, such as acting with priority on the most voltage-effective PV system [7] so as to limit the overall curtailment. To really overcome this problem, BESS should be installed to store excessive PV produced energy during peak generation periods and then use it to supply active power for voltage regulation [8]. But the BESS equipment is usually expensive, making it difficult to be justified from the cost-benefit point of views [9].

Recently, the asset of distribution systems with DERs is significantly changing because of the environmental requirements that push towards the complete substitution of conventional energy sources with RESs. To allow a further increase of RESs in distribution systems two main innovations are being introduced:

• new Ancillary Services (ASs) provided by DERs at ADN level are being defined [10] and commercialized in the deregulated markets [9];
• new market agents can aggregate [11] to provide ASs at transmission system level, as well as new entities, such as energy communities [12], are being introduced to promote the power balance and the AS provision at distribution system level.

Such innovations are favouring the installation of BESSs in conjunction with RES generators because ASs can provide additional incomes that justify the cost of BESSs. For this reason, the present paper focuses attention on DERs composed of DG exploiting RESs, equipped with BESS and interfaced to the ADN by an inverter. Such a type of DER is commonly equipped with a local controller that guarantees voltage regulation at node of connection with the network.

As well known, any local controller interacts with each other through the distribution lines of the ADN when they act on multiple DERs connected to the same feeder [13]. This mutual interaction leads to system operating conflicts and also to voltage instability [14,15,16]. The techniques employed to address this problem are categorized in two main approaches [17,18]. The first is based on centralized and/or distributed techniques which guarantee optimal solutions to the voltage control problem, for example, in term of power loss minimization [19,20,21,22]. A general issue with the aforementioned techniques is that they are based on field network’s measurements in a closed loop real time control system [23,24]. However, the implementation of the communication-based control strategies may not be practical in active distribution networks that lack of information infrastructures or the whole control scheme fails to work if a communication failure occurs [25]. The main drawback of the centralized solutions is the computational cost to handle a big amount of data measured by the ADN. On the contrary, distributed control algorithms require less information, coming from the neighboring DERs, with respect to centralized solutions but may suffer from a slow convergence rate [26]. The second approach relies on the use of decentralized techniques. Generally they do not give optimal solutions since use only local information and measurements. However, as previously noted, due to the requirement of a large amount of information exchanges and increased needed computing capacity, decentralized techniques are usually preferred since they can be implemented in the existing distribution networks easily. Furthermore, they are less complex and more reliable compared to centralized/distributed techniques [27].

Keeping the simplicity of a completely decentralized architecture, our contribution to the voltage control problem is the design that we present in this paper applicable to local control of DERs composed of DG exploiting RESs and equipped with BESS. Each local controller acts on the reactive power of the inverter and, if necessary, provides an additional AS by varying the active power injected by the DER. In particular, the AS is defined by its droop characteristic and by the range of power variation allowed by the BESS. Moreover, the local control scheme should both avoid the introduction of any switching mechanism between reactive and active power control and mitigate the interaction’s level.

To pursue this objective, in the proposed approach each DER is equipped with a double IMC-based PI local control loop, which regulates the voltage and active power to the desired set-point, respectively. Moreover, the two control loops are coupled by a filtered droop control law which realizes the AS. Based on the Relative Gain Matrix (RGA) matrix of the adopted Multi-Input Multi-Output (MIMO) system dynamically coupled of the ADN, we propose a design method articulated in two sequential steps. In the first one, each PI-IMC voltage controller is designed for the corresponding Effective Open-Loop Transfer Function (EOTF) [28], where the free parameters of all controllers are designed to mitigate the interactions among the voltage control loops in a frequency range of interest (external interaction). In the second step, due to the reduced external interaction, the free parameters of all PI-IMC active-power controllers and the cut off frequency of all filters are designed to mitigate the interaction between voltage and active power control loop of any DER (internal interaction). The robust stability of the IMC-PI controllers is also investigated in presence of model parameter uncertainty modeling unknown scenarios of the ADN.

Summarizing, the contributions of this paper can be synthesized into: i. the AS of voltage regulation provided by DERs locally varying, primarily, their reactive power injection according to an integral law, and, in case of reactive current saturation, their active power injection according to a given droop law; ii. decentralized approach without any need of communication among DERs; iii. a single parameter to design each IMC-PI controller; iv. reduction of the internal and external interaction level; v. robust stability without any need of communication among local controllers; v. simplicity of the controller’s structure easily implementable in real distribution systems.

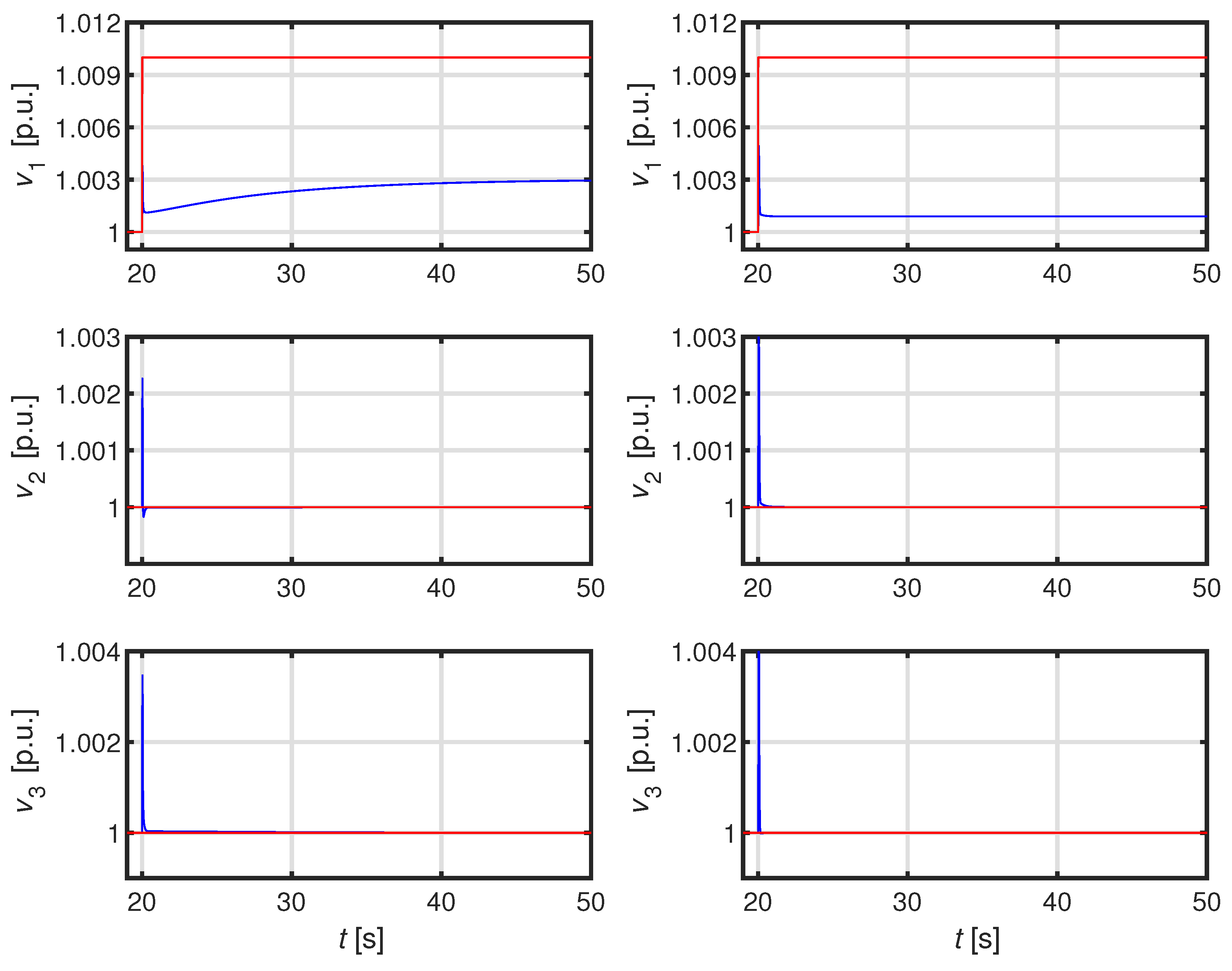
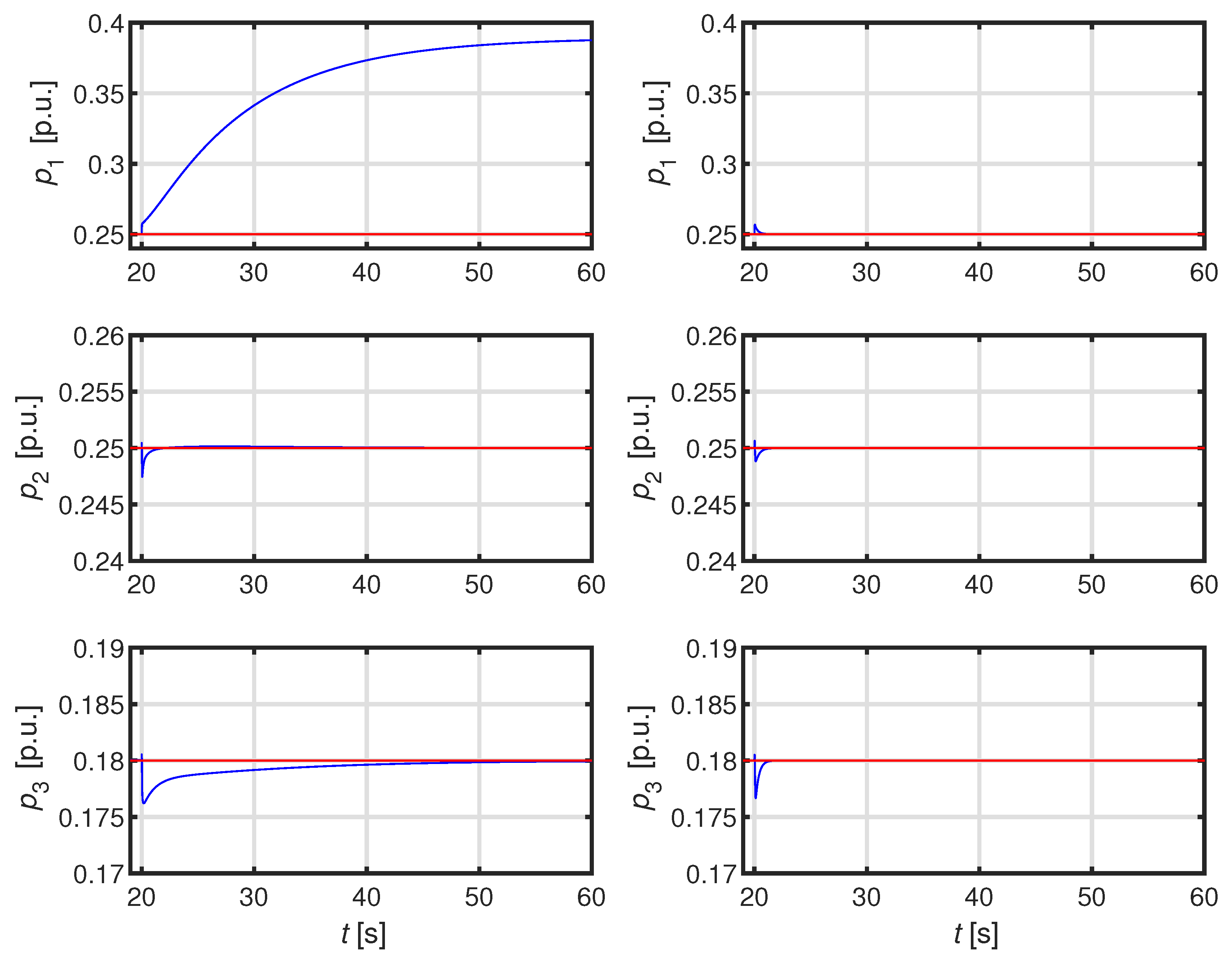
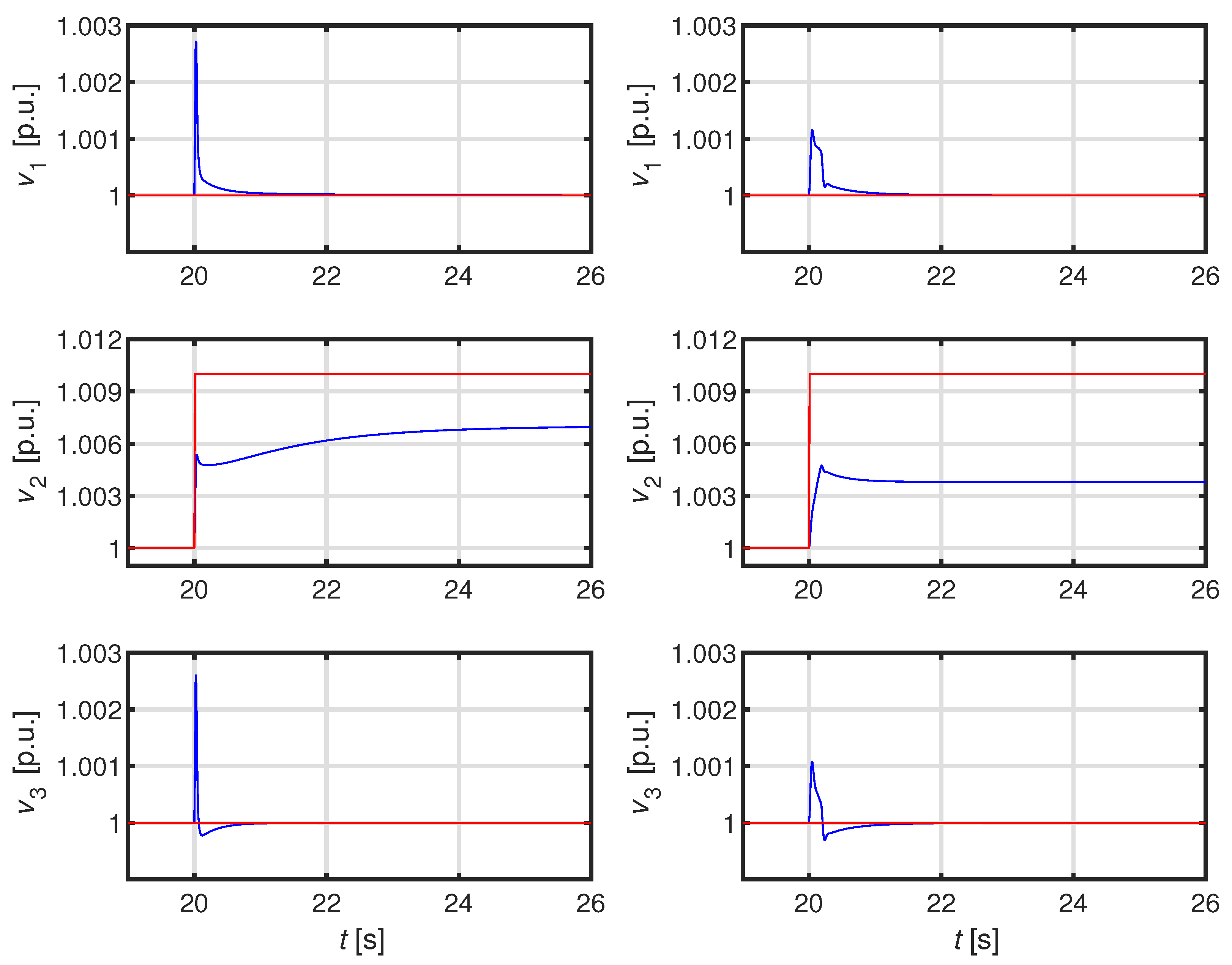
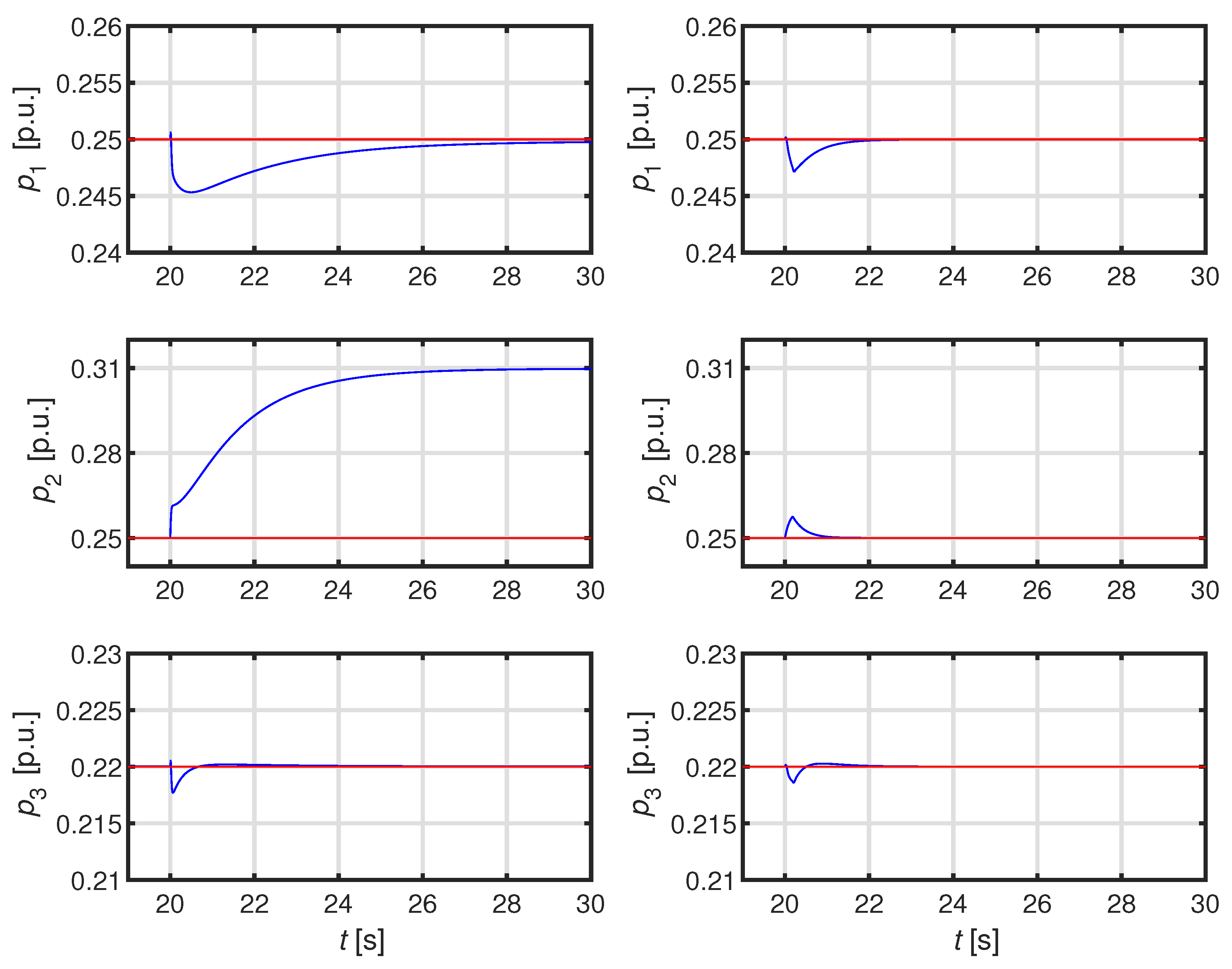
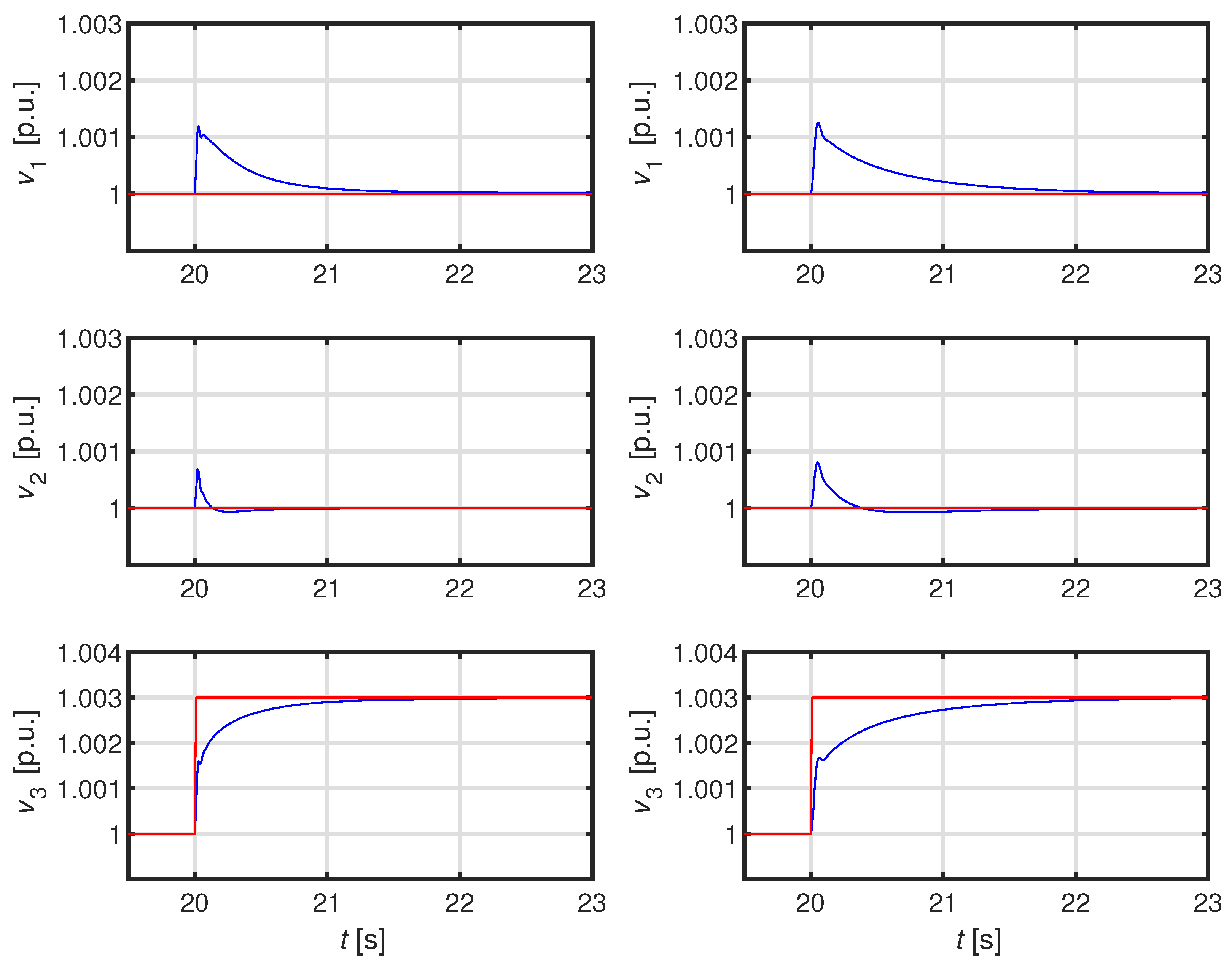
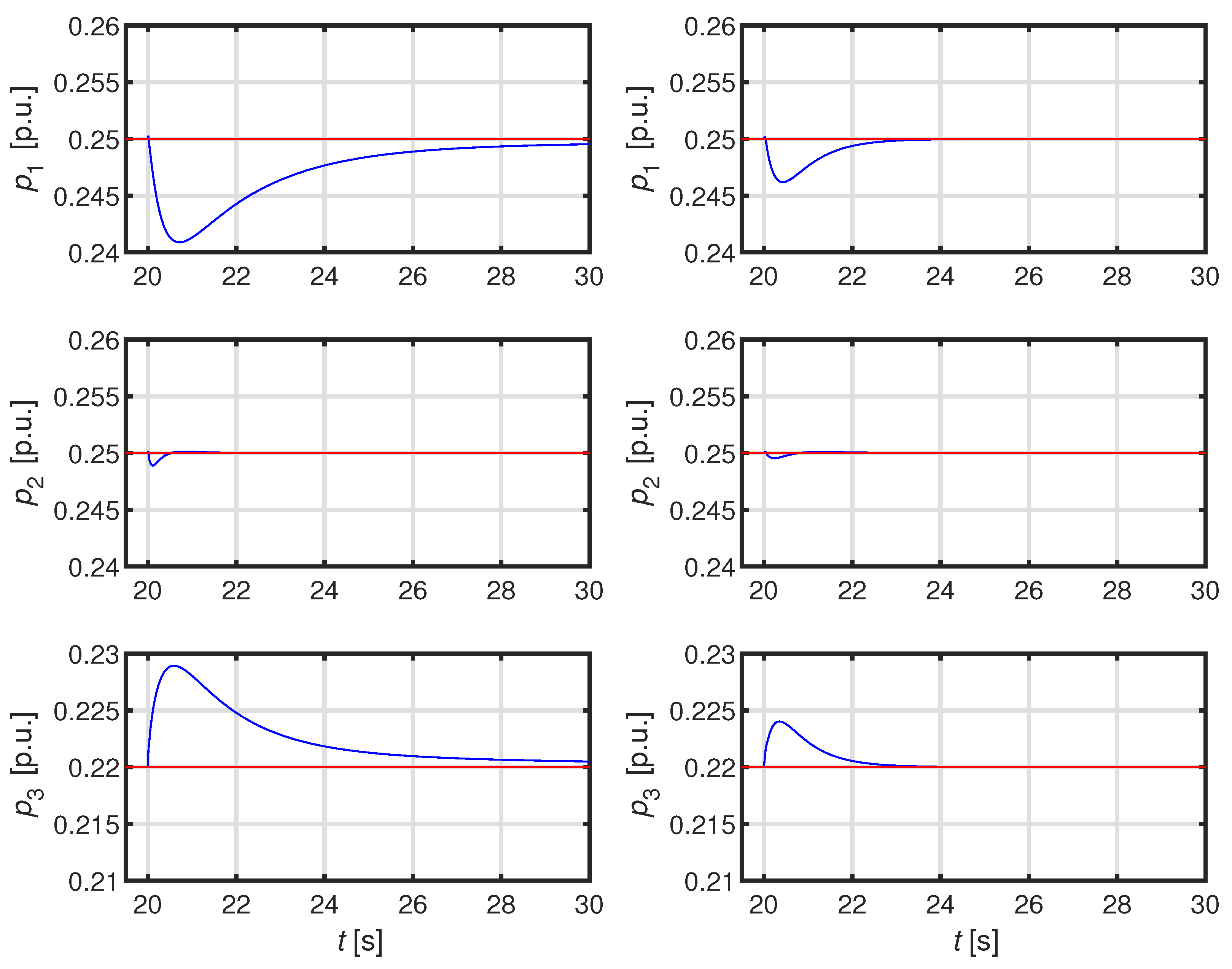
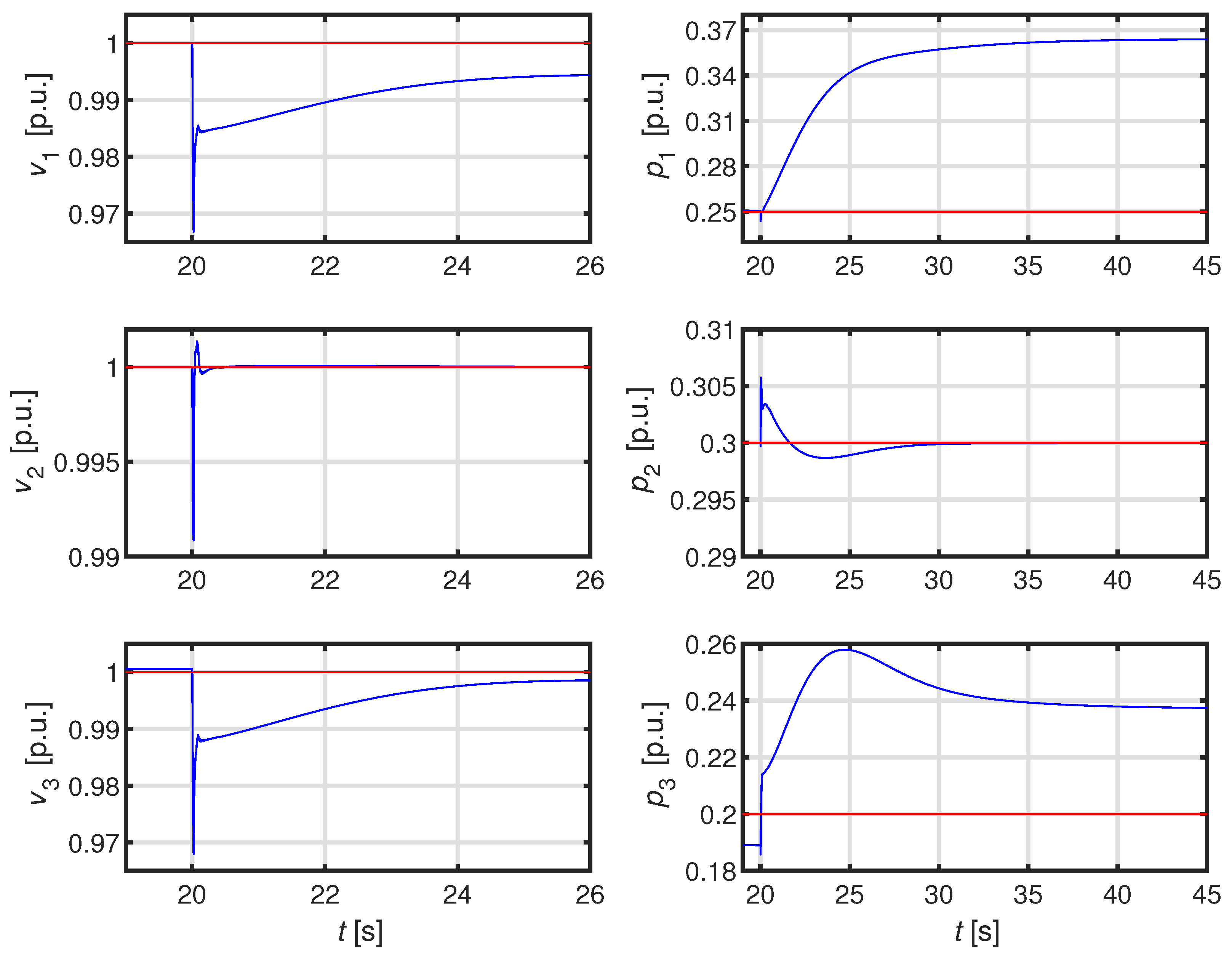
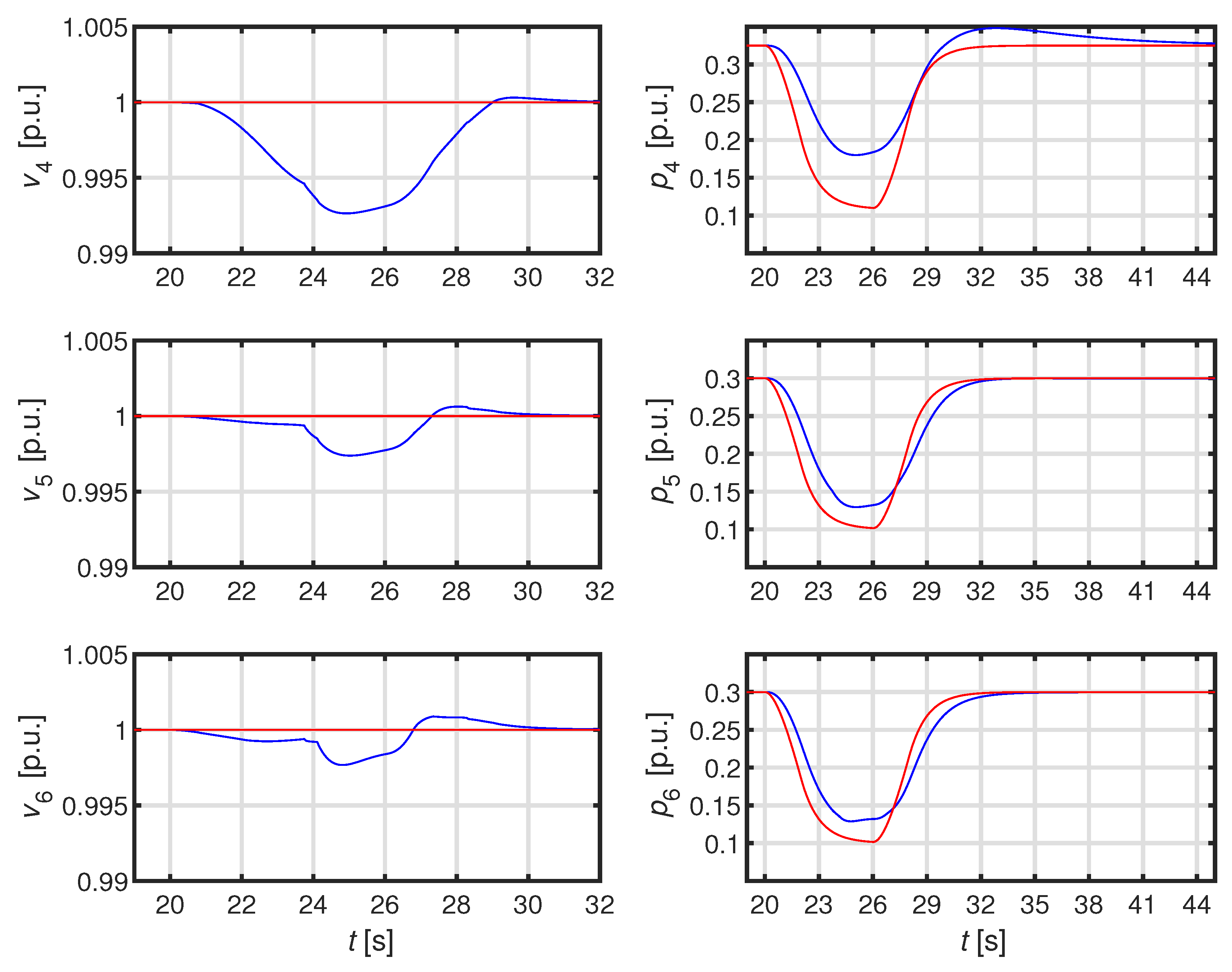
The paper is organized as follows. In Section II we firstly recall the adopted model of the ADN; subsequently we illustrate the proposed technique and validate the robust stability. Finally Section III is devoted to the development of a detailed numerical case studies aimed at validating the performance of our technique also in comparison with the technique proposed in [29].

2. The proposed control design

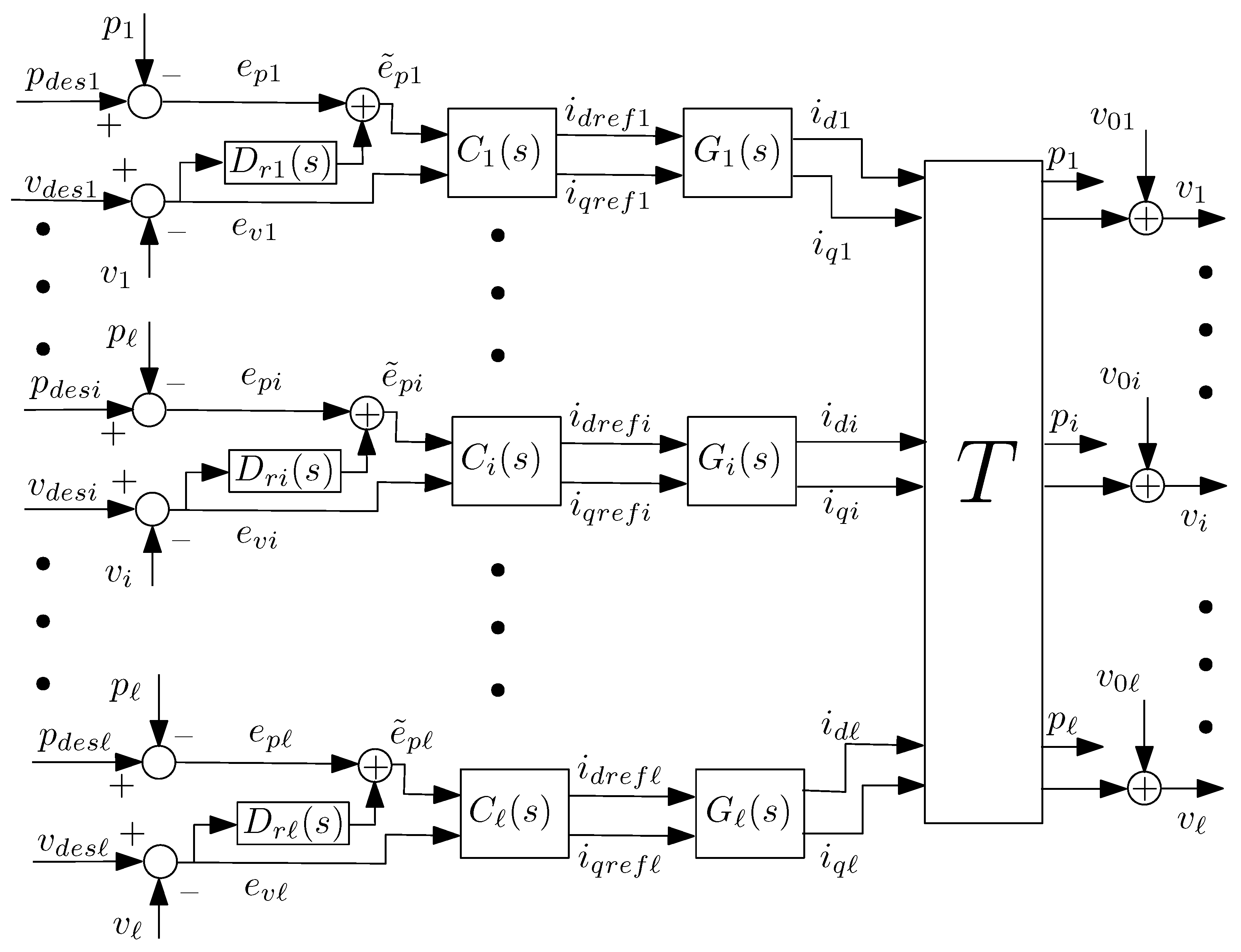
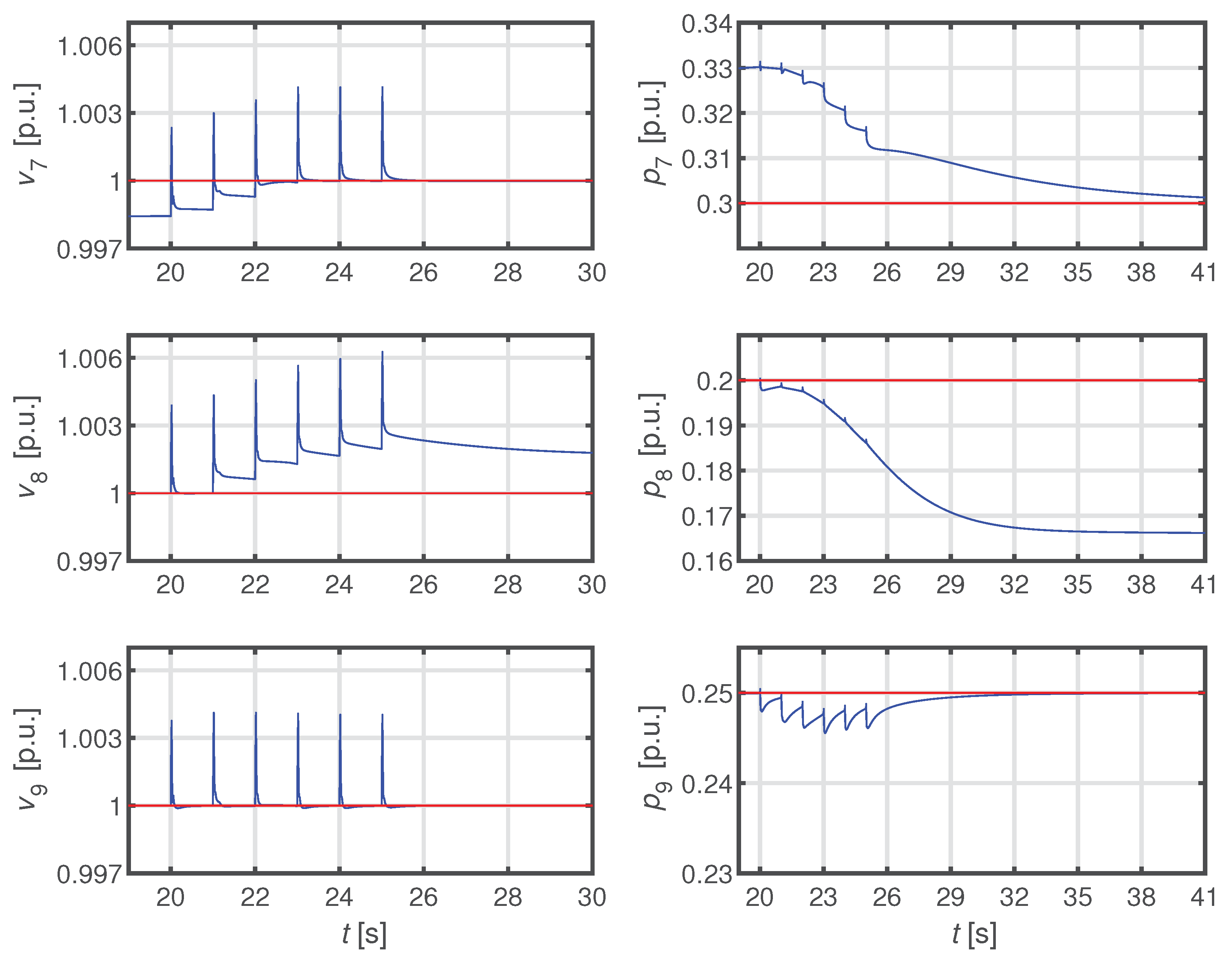
The scope of this section is to illustrate the design methodology for the decentralized voltage control with reduced loop interactions. The control scheme is shown in Figure 1.

Any DER is equipped with two control loops; the former controls the active power $p_i$ while the latter the voltage $v_i$ ($i=1,\dots ,\ell$). The i-th decentralized control matrix is ${\mathbf{C}}_i\left(s\right)=\mathrm{diag}\left\{C_{pi}\left(s\right)C_{vi}\left(s\right)\right\}$. As it can be observed from Figure 1, the two loops are coupled by the filtered voltage error $D_{ri}\left(s\right)e_{vi}$ which realizes the AS of voltage regulation by active power. In practice, in absence of saturation of $i_{qi}$, the integral action of $C_{vi}$ imposes $e_{vi}(\infty )=0$; hence the contribution of active power to voltage regulation is null at steady-state. Conversely, if $i_{qi}$ saturates, $(e_{vi}(\infty )\ne 0)$, the signal $D_{ri}\left(s\right)e_{vi}$ acts with the scope of varying the active power $p_i$ in order to reduce the steady-state voltage error.

The transfer function $D_{ri}\left(s\right)$ is given by:

$$D_{ri}\left(s\right)=d_{ri}\frac{\frac{s}{\beta {\omega }_{fi}}+1}{\frac{s}{{\omega }_{fi}}+1}=d_{ri}{B}_i\left(s\right)$$

(1)

where the value of the droop constant $d_{ri}$ is chosen according to the AS that is agreed to be provided by the active power of each DER according to economical/commercial criteria. The mission of the first-order low pass filter $B_i\left(s\right)$ is to reduce the effect of the filtered voltage error on the active power during the transient.

In the following, after briefly recalling the plant model of the ADN with DERs, the design of $\mathbf{C}\left(s\right)=\mathrm{diag}\{{\mathbf{C}}_1\left(s\right)\dots {\mathbf{C}}_{\ell }\left(s\right)\}$ and ${\omega }_{f1},\dots {\omega }_{f\ell }$ is presented, starting from the nominal plant matrix ${\mathbf{P}}_n\left(s\right)$ obtained assuming that the ADN operates in a known operating condition.

2.1. ADN Model

Concerning the ADN, it is composed of the local transfer functions $G_i\left(s\right)$ which represent the generic ${\mathrm{DER}}_{\mathrm{i}}$ and the matrix $\mathbf{T}$ that represents the distribution grid. The model is briefly recalled in the following; refer to [30] for its foundation.

Concerning the DERs, they are assumed to be composed of a renewable energy generator and a battery energy storage system, connected on a DC bus, which is interfaced to the distribution grid by an inverter, an AC filter and a transformer. According to [31], the following TITO model is adopted to represent the closed-loop transfer function of the current control loops of the inverter, acting on the $d-q$ components

$${\left(i_{id}{i}_{iq}\right)}^T={\mathbf{G}}_i\left(s\right){\left(i_{drefi}{i}_{drefi}\right)}^T$$

(2)

where the transfer functions matrix ${\mathbf{G}}_i\left(s\right)$ is expressed by

$${\mathbf{G}}_i\left(s\right)=\left(\begin{array}{cc}{\displaystyle \frac{1}{1+s{\tau }_{id}}}& {\displaystyle \frac{-k_{i1}s}{(1+s{\tau }_{i1})(1+s{\tau }_{i2})}}\\ {\displaystyle \frac{k_{i2}s}{(1+s{\tau }_{i3})(1+s{\tau }_{i4})}}& {\displaystyle \frac{1}{1+s{\tau }_{iq}}}\end{array}\right)j=1,\dots \ell$$

(3)

Concerning the distribution grid, it is modelled by the full $2\ell x2\ell$ algebraic matrix $\mathbf{T}$, which linearly represents the effect of the vector $(i_{d1},i_{q1},\dots ,i_{d\ell },i_{q\ell })$ of the currents injected by the DERs on the output vector $y=(p_1,v_1,\dots ,p_{\ell },v_{\ell })$ of the injected active powers and of the DERs nodal voltages.

The resulting model of the ADN, including both the DERs and the distribution grid, is

$$y=y^0+\mathbf{P}\left(s\right)u\mathrm{with}\mathbf{P}\left(s\right)=\mathbf{T}\mathbf{G}\left(s\right)$$

(4)

where $\mathbf{P}\left(s\right)$ is the MIMO model with $2\ell$ inputs $u=(i_{dref1},i_{qref1},\dots ,i_{dref\ell },i_{qref\ell })$, and outputs y and $\mathbf{G}\left(s\right)=diag{G}_i\left(s\right)$. Moreover $\mathbf{P}\left(0\right)=\mathbf{T}\mathbf{G}\left(0\right)=\mathbf{T}$, see (3), where $\mathbf{P}\left(0\right)$ is the matrix that represents the steady-state ($\omega =0$) model.

Before illustrating the design technique, it is necessary to discuss about the mutual interaction among the control loops of DERs. For any DER there are two types of interaction. The former is the internal interaction, represented by the TITO model (2)-(3); the latter is an external interaction caused by other DERs through the distribution grid, represented by the matrix $\mathbf{T}$.

One of the most popular tools used to quantify the degree of interaction is the Relative Gain Array (RGA) defined as [32]

$$\mathrm{RGA}=\mathbf{P}\left(0\right)\otimes {\left(\mathbf{P}{\left(0\right)}^{-1}\right)}^T$$

(5)

where the operator ⊗ denotes element-by-element multiplication or Schur product and $\mathbf{P}\left(0\right)$ is the matrix that represents the steady-state ($\omega =0$) model.

From the analysis of the RGA matrix, paper [30] has shown that the external interaction exists only between the voltage control loops. That is the regulation of $v_i$ is affected by the regulation of all other $(\ell -1)$ voltages and vice-versa. This means that the voltage control loops are fully coupled. Conversely, the interaction between the active power control loops is weak. Hence the regulation of $p_i$ does not affect the regulation of all other $(\ell -1)$ active powers and vice-versa. As concerns the internal interaction, the regulation of $p_i$ does not influence the regulation of $v_i$; but, in the case of this paper, the converse is not true. In fact the regulation of $v_i$ affects that of $p_i$ by means of the filtered voltage error $D_{ri}\left(s\right)e_{vi}$.

Summarizing, external interaction exists only between the voltage control loops, whereas it has internal interaction from the voltage control loop to the active power one. Based on this result, we present a design procedure formed by two sequential steps. In both steps the Internal Model Control (IMC) technique is adopted since exhibits robustness to model parameter uncertainty. In particular, in the first step, control matrix ${\mathbf{C}}_v\left(s\right)=\mathrm{diag}\{C_{v1}\left(s\right)\dots C_{v\ell }\left(s\right)\}$ is designed for achieving voltage regulation and reduction of the external interactions. Conversely, in the subsequently second step, control matrix ${\mathbf{C}}_p\left(s\right)=\mathrm{diag}\{C_{p1}\left(s\right)\dots C_{p\ell }\left(s\right)\}$ is designed for achieving active power regulation and reduction of the internal interaction.

2.2. First Step of the Design

Let now address the problem of designing ${\mathbf{C}}_v\left(s\right)$. Since the active power control loops are decoupled, it is possible to consider only the transfer functions corresponding to the pairings $(i_{qrefi},v_i)$, see Figure 1. To this scope the matrix plant ${\mathbf{P}}_n\left(s\right)$ is written by evidencing the $2\ell$ inputs and outputs as follows

The square matrix plant with inputs $i_{qrefi}$ and outputs $v_i$ used in this step is then given by.

$$\begin{array}{ccc}\hfill {\mathbf{P}}_n^v\left(s\right)& =& \left(\begin{array}{cccccc}{P}_{22}& P_{24}& P_{26}& \dots & \dots & P_{2(2\ell )}\\ P_{42}& P_{44}& P_{46}& \dots & \dots & P_{4(2\ell )}\\ \dots & \dots & \dots & \dots & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots & \dots \\ P_{(2\ell -2)2}& P_{(2\ell -2)4}& P_{(2\ell -2)6}& \dots & \dots & P_{(2\ell -2)(2\ell )}\\ P_{(2\ell )2}& P_{(2\ell )4}& P_{(2\ell )6}& \dots & \dots & P_{(2\ell )(2\ell )}\end{array}\right)\hfill \end{array}$$

Employing the method of the Effective Open-Loop Transfer Function (EOTF), $P_i^{eotf}\left(s\right)$, the design of the IMC controller $C_{vi}^{imc}\left(s\right)$ is developed for model $P_i^{eotf}\left(s\right)$ rather than ${\mathbf{P}}_n^v\left(s\right)$, thus avoiding a more complex MIMO design.

The expression of $P_i^{eotf}\left(s\right)$ is given by [28]

$$P_i^{eotf}\left(s\right)=\frac{{\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}}{DRG{A}_{ii}\left(s\right)}$$

(6)

where ${\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}$ and $DRG{A}_{ii}\left(s\right)$ denote, respectively, the i-th diagonal element of ${\mathbf{P}}_n^v\left(s\right)$ and of the Dynamic Relative Gain Array (DRGA) calculated by

$$DRG{A}_{ii}\left(s\right)={[{\mathbf{P}}_n^v\left(s\right)\otimes {\left({\mathbf{P}}_n^v{\left(s\right)}^{-1}\right)}^T]}_{ii}$$

The IMC voltage control matrix is

$${\mathbf{C}}_v^{imc}\left(s\right)=\mathrm{diag}\left\{\underset{C_{v1}^{imc}\left(s\right)}{\underbrace{\frac{1}{P_1^{eotf}\left(s\right){(1+s{\lambda }_{v1})}^{q_{v1}}}}}\dots \dots \underset{C_{v\ell }^{imc}\left(s\right)}{\underbrace{\frac{1}{P_{\ell }^{eotf}\left(s\right){(1+s{\lambda }_{v\ell })}^{q_{v\ell }}}}}\right\}$$

where $q_{v1},\dots q_{v\ell }$ are positive integers chosen to make ${\mathbf{C}}_v^{imc}\left(s\right)$ realizable.

From ${\mathbf{C}}_v^{imc}\left(s\right)$ it is obtains the feedback control matrix

$${\mathbf{C}}_v\left(s\right)=\mathrm{diag}\left\{\frac{1}{s{\lambda }_{v1}{P}_1^{eotf}\left(s\right)}\dots \dots \frac{1}{s{\lambda }_{v\ell }{P}_{\ell }^{eotf}\left(s\right)}\right\}$$

(7)

The adjustable control parameters ${\lambda }_{v1},\dots {\lambda }_{v\ell }$ are selected with the objective of reducing the external interactions. To this scope we formulate the controller design problem into an optimization framework. In details, ${\lambda }_{v1},\dots {\lambda }_{v\ell }$ are obtained by solving the following problem

$$\underset{{\lambda }_{v1},\dots {\lambda }_{v\ell }}{min}\left|\right|{\mathbf{W}}_d(j\omega ){\left|\right|}_{\infty }\omega \in {\mathsf{\Omega }}_v$$

(8)

subject to

$${\lambda }_{vi}^m\le {\lambda }_{vi}\le {\lambda }_{vi}^M$$

where ${\mathsf{\Omega }}_v$ is a a frequency range of interest and ${\mathbf{W}}_d(j\omega )$ is the interaction matrix obtained from the following closed voltage control matrix

$${\mathbf{W}}_v(j\omega )={\left({\mathbf{I}}_{\ell \times \ell }+{\mathbf{P}}_n^v(j\omega ){\mathbf{C}}_v(j\omega )\right)}^{-1}{\mathbf{P}}_n^v(j\omega ){\mathbf{C}}_v(j\omega )$$

by setting ${\left[{\mathbf{W}}_v(j\omega )\right]}_{ii}=0$. In this way the response $v_i$ due to a change of $v_{desj}$ ($j\ne i$) is effectively attenuated.

Remark 1.

As above described, the design of ${\mathbf{C}}_v\left(s\right)$ uses model in (6). The EOTF relates $i_{qrefi}$ to $v_i$ when the i-th loop is open while all other loops are closed under the condition of perfect control. To explain this concept, let consider the actual relationship between $i_{qrefi}$ to $v_i$ given by [28]

$$v_i=\left[{\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}-{\mathbf{p}}^{ir}\left(s\right){\tilde{\mathbf{C}}}_{vi}\left(s\right){\left({\mathbf{I}}_{(\ell -1)\times (\ell -1)}+{\mathbf{P}}_n^{vi}\left(s\right){\tilde{\mathbf{C}}}_{iv}\left(s\right)\right)}^{-1}{p}^{ic}\left(s\right)\right]i_{qrefi}$$

(9)

where ${\tilde{\mathbf{C}}}_{vi}=\mathrm{diag}\{C_{v1},C_{v2},\dots C_{v(i-1)},C_{v(i+1)},\dots C_{v\ell }\}$, ${\mathbf{P}}_n^{vi}\left(s\right)$ denotes a transfer functions matrix where both the i-th row and column are removed from ${\mathbf{P}}_n^v\left(s\right)$, ${\mathbf{p}}^{ir}\left(s\right)$ and ${\mathbf{p}}^{ic}\left(s\right)$ are the i-th row and column vector of matrix ${\mathbf{P}}_n^v\left(s\right)$ where ${\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}$ is discarded, respectively.

If the following approximation

$${\mathbf{H}}_i(j\omega )={\mathbf{P}}_n^{vi}(j\omega ){\tilde{\mathbf{C}}}_{vi}(j\omega ){\left({\mathbf{I}}_{(\ell -1)\times (\ell -1)}+{\mathbf{P}}_n^{vi}(j\omega ){\tilde{\mathbf{C}}}_{vi}(j\omega )\right)}^{-1}\simeq {\mathbf{I}}_{(\ell -1)\times (\ell -1)}$$

(10)

holds in the frequencies range smaller than the cross-over frequency ${\omega }_{ci}$, then eq. (9) can be reasonably simplified as follows

$$v_i=\left({\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}-{\mathbf{p}}^{ir}\left(s\right){\left({\mathbf{P}}_n^{vi}\right)}^{-1}\left(s\right){\mathbf{p}}^{ic}\right)i_{iqrefi}=\frac{{\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{ii}}{DRG{A}_{ii}\left(s\right)}{i}_{iqrefi}=P_i^{eotf}\left(s\right)i_{iqrefi}$$

Condition (10) guarantees the perfect control and it is fulfilled if $C_{vj}\left(s\right)$, ($j=1,\dots \ell$, $j\ne i$) has a pole in $s=0$ and its gain is greater than that of ${\left[{\mathbf{P}}_n^v\left(s\right)\right]}_{jj}$, respectively.

2.3. Second Step of the Design

In the second step of the procedure, any controller $C_{pi}\left(s\right)$ is independently designed from all the others since the active control loos are decoupled. The expression of the i-th IMC active power controller is

$$C_{pi}^{imc}\left(s\right)=\frac{1}{={\left[{\mathbf{P}}_n\left(s\right)\right]}_{(2i-1)(2i-1)}\left(s\right){(1+s{\lambda }_{pi})}^{q_{pi}}}$$

with $q_{pi}$ a positive integer chosen to make $C_{pi}^{imc}\left(s\right)$ realizable. The corresponding feedback controller is

$$C_{pi}\left(s\right)=\frac{1}{s{\lambda }_{pi}{\left[{\mathbf{P}}_n\left(s\right)\right]}_{(2i-1)(2i-1)}\left(s\right)}$$

(11)

Since the external interactions have been minimized in the first step of the design procedure, the relationship between $v_{desi}$ and $p_i$ (internal interaction), can be modeled by the element $W_i^{(1,2)}$ of the following TITO closed transfer matrix

$${\mathbf{W}}_i\left(s\right)={\left({\mathbf{I}}_{2\times 2}+{\mathbf{P}}_i\left(s\right){\mathbf{C}}_i\left(s\right){\mathbf{D}}_{ri}\left(s\right)\right)}^{-1}{\mathbf{P}}_i\left(s\right){\mathbf{C}}_i\left(s\right){\mathbf{D}}_{ri}\left(s\right)$$

(12)

with

$$\begin{array}{ccc}\hfill {\mathbf{D}}_{ri}\left(s\right)& =& \left(\begin{array}{cc}1& D_{ri}\left(s\right)\\ 0& 1\end{array}\right)\hfill \\ \hfill {\mathbf{P}}_i\left(s\right)& =& \left(\begin{array}{cc}{P}_{(2i-1)(2i-1)}\left(s\right)& P_{(2i-1)\left(2i\right)}\left(s\right)\\ P_{\left(2i\right)(2i-1)}\left(s\right)& P_{\left(2i\right)\left(2i\right)}\left(s\right)\end{array}\right)\hfill \end{array}$$

The internal interaction can be reduced by finding parameters ${\lambda }_{pi}$ and ${\omega }_{fi}$ which solve the following problem

$$\underset{{\lambda }_{pi},{\omega }_{fi}}{min}\left|\right|W_i^{\left(12\right)}(j\omega ){\left|\right|}_{\infty }$$

(13)

subject to

$$\begin{array}{ccc}\hfill {\alpha }_1^i{\lambda }_{vi}\le & {\lambda }_{pi}& \le {\alpha }_2^i{\lambda }_{vi}\hfill \\ \hfill \frac{{\alpha }_3^i}{{\lambda }_{vi}}\le & {\omega }_{fi}& \le \frac{{\alpha }_4^i}{{\lambda }_{vi}}\hfill \end{array}$$

with ${\alpha }_k^i$ ($k=1,2,3,4$) positive quantities.

The described design technique assumes that ${\mathbf{T}}_n$ is a constant matrix; however, its value depends on factors such as the power injected through the DERs, the power consumed by the loads at each node, the topology of the distributions system, etc... Hence in presence of uncertainty in the elements of matrix ${\mathbf{T}}_n$ it is necessary to investigate the robust stability of the control system. 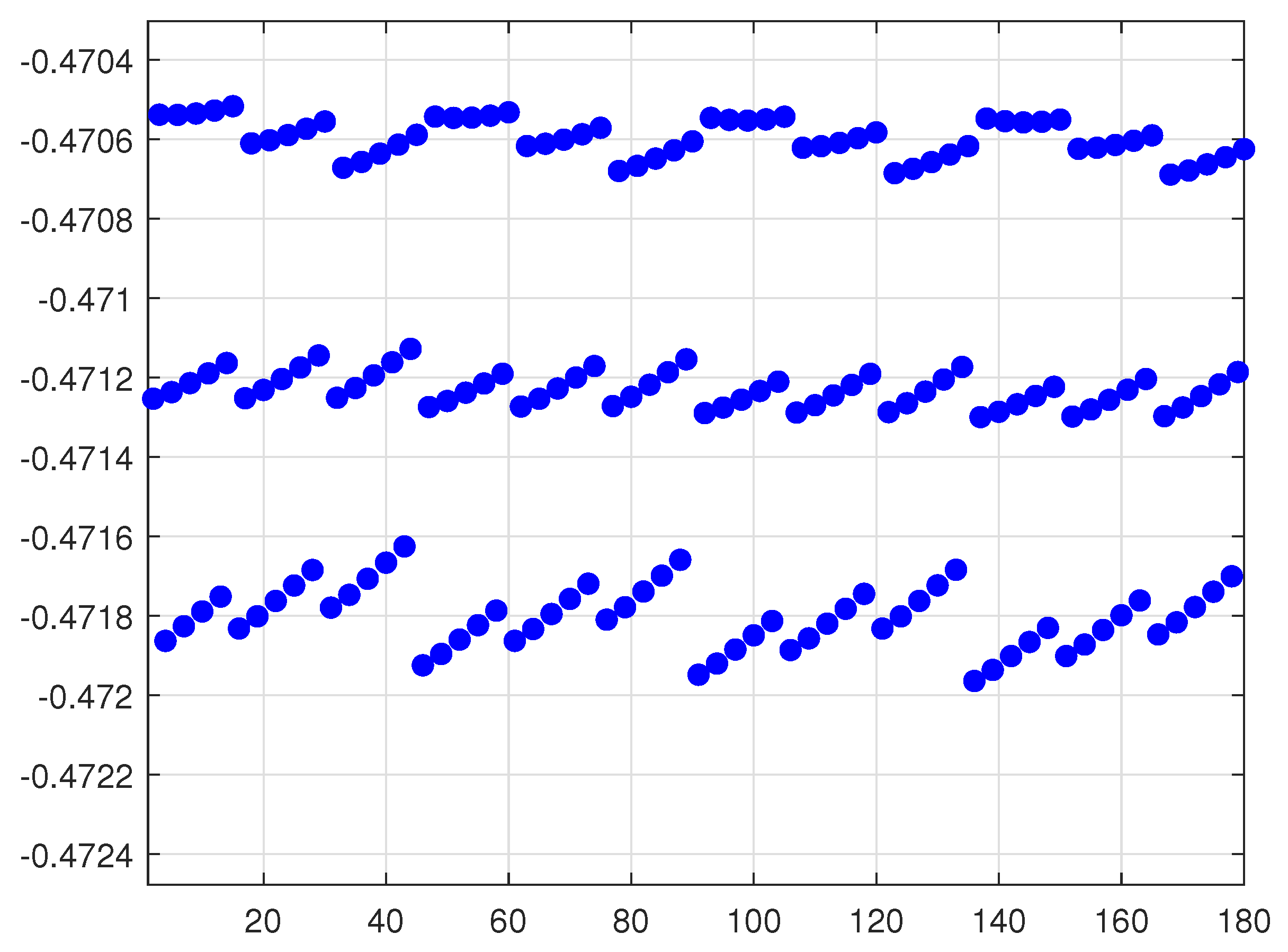To this aim, we have determined a matrix plant $\mathbf{P}\left(s\right)$ for each of the considered operating conditions. In particular, the following ones have been considered: the reactive power ranges in the interval $[-0.0150.015]$ pu; the voltage at the slack bus varies in the interval $[0.981.02]$ pu; loads in the range $[0.31.2]$. At the end of the procedure, a set formed by 180 different matrices $\mathbf{P}\left(s\right)$ has been created. Subsequently, for any $\mathbf{P}\left(s\right)$ the corresponding MIMO closed-loop matrix $\mathbf{W}\left(s\right)$ is built and the largest pole computed. The obtained set formed by the 180 poles is shown in Figure 2. One can see that the requirement of robust stability is fulfilled.

3. Cases Study and Simulation Results

The proposed control is tested for two different ADNs. In particular, the first case study considers an ADN with 3 DERs while the second case study a larger ADN with 3 feeders, multiple sub-feeders, 36 nodes and 9 DERs.

3.1. First Case Study: ADN with 3 DERs

The ADN depicted in Figure 3 is considered. A 250 kVA 20/0.4 kV transformer, connected to the MV busbar (slack bus), supplies the LV substation busbar (node 2), from which a single LV feeder with three laterals departs. The electrical parameters of the lines are derived from the ones of existing LV feeders.

The rated loading of the feeder is equal to 39.0 kW and 66 kVAR of reactive power. Each DER is composed of a 35 kWp PV equipped with a battery storage system sized 24 kWh/1h and connected to the grid by a single inverter with rated power equal to 50 kVA. The DER provides flexibility to the DSO by varying the injected active power with respect to the one generated by the PV through the storage, and by varying the reactive power within the rectangular capability curve of the inverter, that is within the range $\pm 30$ kVAR. Each DER is connected to the distribution system through an AC filter, equipped with 4 kVAR capacitor, and a 50 kVA transformer .

To apply the proposed design procedure, an operating condition of the ADN is assumed; in details: null power injections of DERs; $70\%$ loading conditions and balanced loads; unitary per-unit values for both voltage at the slack node and ratio of the substation transformer. In this condition the ADN model is derived yielding the nominal plant matrix ${\mathbf{P}}_n\left(s\right)$. Then, the first step of design is performed to obtain the voltage control matrices: each $C_{vi}\left(s\right)$ is designed for model $P_i^{eotf}\left(s\right)$ ($i=1,2,3$) obtained by (6). However, $P_i^{eotf}\left(s\right)$ shows a complicated dynamic form that can be reduced by using the Hankel-norm approximation with balanced realization available in the Control Toolbox of Matlab. Parameters ${\lambda }_{v1}$, ${\lambda }_{v2}$ and ${\lambda }_{v3}$ are obtained by solving problem (8) with ${\lambda }_{vi}^m=0.06$, ${\lambda }_{vi}^M=0.3$ and ${\mathsf{\Omega }}_v=[0.0150]$. In particular the imposed values for ${\lambda }_{vi}^m$ and ${\lambda }_{vi}^M$ guarantee typical values of the pulse bandwidth. Problem (8) is solved by the sequential quadratic programming algorithm of the fmincon function available in MATLAB library. This function realizes nonlinear programming and treats all variables as continuous. The voltage control matrix obtained by (7) is as follows

$${\mathbf{C}}_v\left(s\right)=\mathrm{diag}\left\{14.195\frac{(s+83.95)}{s}17.287\frac{(s+78.06)}{s}13.768\frac{(s+79.78)}{s}\right\}$$

(14)

which is indeed a PI control.

With regard to the design of $C_{pi}\left(s\right)$ and ${\omega }_{fi}$, it is set $d_{ri}=20$, $\beta =10$; ${\alpha }_1^i=2$, ${\alpha }_2^i=6$, ${\alpha }_3^i=2{10}^{-2}$ and ${\alpha }_4^i=1$. Subsequently, parameters ${\lambda }_{p1}$ and ${\omega }_{f1}$ are obtained by solving problem (13). The same design procedure is repeated for ${\lambda }_{p2}$, ${\omega }_{f2}$ and ${\lambda }_{p3}$, ${\omega }_{f3}$. The active power control matrix calculated using (11) is

$${\mathbf{C}}_p\left(s\right)=\mathrm{diag}\left\{0.0074595\frac{(s+90.92)}{s}0.03014\frac{(s+88.51)}{s}0.010391\frac{(s+83.34)}{s}\right\}$$

which is indeed a PI control. Moreover, it is obtained

$$\begin{array}{ccc}\hfill D_{r1}\left(s\right)& =& 20\frac{1.183s+1}{11.83s+1}\hfill \\ \hfill D_{r2}\left(s\right)& =& 20\frac{0.3s+1}{3.0s+1}\hfill \\ \hfill D_{r3}\left(s\right)& =& 20\frac{0.909s+1}{9.09s+1}\hfill \end{array}$$

To give evidence of the performance of the proposed control design (briefly referred to as proposed control), simulation results are compared with the ones obtained from the application of the method presented in [29] in absence of the active power ancillary service, that is $d_{ri}=0$ (briefly referred to as standard control). The time evolution of DERs nodal voltages and injected active powers is analyzed when imposing, for each DER at a time, a step variation of the desired voltage signal $v_{desi}$ at simulation time instant $t=20s$. In particular, Figure 4 and Figure 5 refer to a step variation of $v_{des1}$ of ${\mathrm{DER}}_1$ from 1.0 to 1.01 p.u., Figure 6 and Figure 7 to a step variation of $v_{des2}$ of ${\mathrm{DER}}_2$ from 1.0 to 1.01 p.u. and Figure 4 and Figure 5 refer to a step variation of $v_{des3}$ of ${\mathrm{DER}}_3$ from 1.0 to 1.003 p.u.. Each figure reports the time evolution of either the voltages or the active powers for the three DERs, comparing the responses of the proposed control on the left side with the corresponding ones of the standard control on the right side.

From the analysis of Figure 4 and Figure 5, focusing on ${\mathrm{DER}}_1$, it is apparent that the voltage $v_1$ does not reach the new desired value equal to 1.01 p.u. due to reactive power saturation. Comparing the two controls, the proposed control guarantees a smaller voltage error, reaching the value of about 1.003 p.u., with respect to the standard control, which reaches the value of about 1.001. It is thanks to the action of active power according to the ancillary service characterized by $d_{ri}=20$; in fact the active power varies from 0.25 p.u., which is the desired value, to about 0.39 p.u. which is the new final value, so as to reduce the voltage error. Concerning the other DERs it is evident that the voltage control promptly reacts to the variation of the reactive power injection by ${\mathrm{DER}}_1$ in the first instants, before its saturation. Then, the standard control is practically inactive whereas the proposed control presents a slight reaction in terms of active power in response to the slow voltage variation of $v_1$; it is more evident for ${\mathrm{DER}}_3$ which is more strongly coupled with ${\mathrm{DER}}_1$ than ${\mathrm{DER}}_2$.

Similar considerations derive from the analysis of Figure 6 and Figure 7, in the case of step variation of $v_{des2}$ of ${\mathrm{DER}}_2$. Also in this case, the voltage $v_2$ does not reach the new desired value equal to 1.01 p.u. due to reactive power saturation and the proposed control guarantees a smaller voltage error than the one obtained by the standard control, due to the action of active power which varies from 0.25 p.u. to about 0.31 p.u.. Concerning the other DERs the voltage control promptly reacts to the variation of the reactive power injection by ${\mathrm{DER}}_2$ in the first instants, before its saturation. In this case the smaller scale on the time axis allows to compare the voltage transients in details: for the proposed control the voltage response is slightly faster but the variation is slightly larger with respect to the standard control. Concerning the active powers of the other DERs, the presence of the ancillary service causes, as expected, a slightly larger and slower perturbation of the active powers (it is more evident for ${\mathrm{DER}}_1$). However it can be stated that the variation is well limited by the filter and by the action of the active power controller. As a general consideration, it can be stated that the response of the controllers of ${\mathrm{DER}}_2$ are faster than the ones of ${\mathrm{DER}}_1$ analysed in the previous case; it is due to the weak coupling of ${\mathrm{DER}}_2$ with the other two DERs that allows the design procedure to give smaller values of ${\lambda }_{vi}$, ${\lambda }_{pi}$ and a larger value of ${\omega }_{fi}$

Finally in the case of ${\mathrm{DER}}_3$ (Figure 8 and Figure 9) a smaller step variation of $v_{des3}$ is imposed to avoid reactive power saturation and analyse the transient responses of the controllers in linear operation. In fact, the voltage $v_3$ reaches the new desired value equal to 1.003 p.u. and both the proposed and the standard control guarantee null steady-state voltage error. Then, the active power does not provide any ancillary service to voltage regulation, and all the active powers return to their desired values at steady-state. Analysing the transients, Figure 8 gives evidence of the faster voltage response guaranteed by the proposed control with respect to the standard control. It is due the active power which gives a contribution to the voltage regulation during the transient response, as evidenced by Figure 9. It is important to note from this figure that the active power contribution during transient is negligible in terms of energy injected/absorbed by the storage system; in fact, the energy is represented by the integral of the active power whose variation is limited to less than 0.01 p.u. and lasts for few seconds.

3.2. Second Case Study: ADN with 3 Feeders and 9 DERs

To give evidence of the applicability of the proposed control, a larger distribution network (0.4 kV – 50 Hz) is considered, see [30]: it has three feeders, 36 nodes and 9 DERs connected. Each DER presents the same size and characteristics as the ones described in the previous subsection. The results obtained in three simulations are reported to analyse the effects of, respectively, a load insertion (Simulation 1), variations of the desired active power signals due to changes of the solar radiation (Simulation 2) and the On-Load Tap Changer (OLTC) operation in the MV/LV substation (Simulation 3).

3.2.1. Simulation 1

At simulation time instant $t=20s$ a load of 20 kW – 10 kVAR is connected at the end of the first feeder. Figure 10 reports the time evolution of nodal voltages (left-hand side) and active powers (right-hand side) for ${\mathrm{DER}}_1$, ${\mathrm{DER}}_2$ and ${\mathrm{DER}}_3$, which are connected along the first feeder. The response of the proposed control to the sudden decrease of the nodal voltages due to the load connection is stable and fast, reaching the new steady-state operation in few seconds. In particular, ${\mathrm{DER}}_1$ and ${\mathrm{DER}}_3$ saturates their reactive powers and consequently, the ancillary service acts by increasing the injected active power thus reducing the steady-state voltage error.

3.2.2. Simulation 2

In this simulation a variation of the desired active power signal is imposed during the simulation time interval $t=20-30s$. In particular, due to the shading effect of a cloud, it is assumed that the signal $v_{des4}$, $v_{des5}$ and $v_{des6}$ of, respectively, ${\mathrm{DER}}_4$, ${\mathrm{DER}}_5$ and ${\mathrm{DER}}_6$ along the second feeder are temporarily reduced down to 0.1 p.u.. Figure 11 reports the time evolution of nodal voltages (left-hand side) and active powers (right-hand side) for the three considered DERs. In the case of ${\mathrm{DER}}_4$, the voltage decreases down to about 0.993: it is due to saturation of reactive power as evidenced by the active power which decreases but keeps larger values than the desired signal so as to support the voltage and limit its decrease. On the contrary, in the case of ${\mathrm{DER}}_5$ and ${\mathrm{DER}}_6$, the reactive power does not saturate, except for the very small time interval around $t=24-26s$, when the active power is very low. Consequently, with respect to ${\mathrm{DER}}_4$, the voltage variations are more limited and the injected active powers better follow the desired signals.

3.2.3. Simulation 3

In this simulation step variations of the MV/LV transformer ration are operated by the OLTC in the feeding substation. In particular, during the simulation time interval $t=20-25s$ six step increases of the OLTC take place, one per second, causing an overall variation of the transformer ratio from 1.0 to 1.0375 p.u.. Figure 12 reports the time evolution of nodal voltages (left-hand side) and active powers (right-hand side) for the three considered DERs, that are ${\mathrm{DER}}_7$, ${\mathrm{DER}}_8$ and ${\mathrm{DER}}_9$. Also this simulation gives evidence of the stable fast responses of the proposed controllers. Concerning the ancillary service, ${\mathrm{DER}}_7$ starts from an operating condition of reactive power saturation: the nodal voltage is smaller that the desired value equal to 1.0 p.u. and the injected active power is equal to 0.33 p.u. which is larger than the desired value equal to 0.3 p.u.. Then, the effect of the OLTC operation causes an increase of the nodal voltage and allows the voltage regulation to guarantee the desired value without the need of the ancillary service; in fact, the active power injection reaches the final steady-state value equal to the desired one. Concerning ${\mathrm{DER}}_8$ its behaviour is the opposite: it starts from null voltage and active power errors but the voltage increase due to the OLTC operation causes the reactive power to decrease and reach its negative saturation. Consequently, the final steady-state operation shows a voltage which is larger than the desired value equal to 1.0 p.u. and the action of the ancillary service which causes the active power to reach a steady-state value of about 0.167 p.u., which is smaller than the desired value equal to 0.2 p.u.. Eventually, ${\mathrm{DER}}_9$ does not reach reactive power saturation and shows null steady-state errors for both voltage and active power and both before and after OLTC operation.

4. Conclusions

This paper has proposed a decentralized control of DERs providing the ancillary service of voltage regulation. The goal is to achieve local voltage regulation by each DER, which acts on its reactive power injection and, in case of the inverter current saturation, on its active power injection. The proposed procedure is based on the sequential design, for each DER, of two free parameters of a double IMC-PI control loop and the cut-off frequency of a low pass filter. The design robustly guarantees voltage and active power regulation with attenuation of the coupling level due to both the internal and the external interactions among the other control loops. The results of different numerical case studies have confirmed the effectiveness of the design technique.