Prerpints.org logo
Preprint
Article

All-Solid-State Post-Compression of Low Energy Pulses at High Repetition Rate

Altmetrics

Downloads

126

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 March 2024

Posted:

26 March 2024

You are already at the latest version

Alerts
Abstract
We demonstrate a proof-of-principle of simple all-solid-state post-compression setup for low energy, high repetition rate laser pulses, where spectral broadening was performed using a combination of highly nonlinear bulk materials in a simple single pass geometry. 75 fs, 210 nJ pulses from an amplified 76 MHz, 15.7 W Yb:KGW oscillator after sequential spectral broadening in ZnS and YAG samples of 2 mm and 15 mm thickness, respectively, were compressed to 37 fs by means of Gires–Tournois interferometric mirrors. The post-compressed pulses with an average power of 11.47 W demonstrated reasonable spatial-spectral homogeneity of the beam with the spectral overlap parameter V>83% and good beam quality with Mx2=1.28 and My2=1.14.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Extracavity compression, or post-compression of laser pulses that relies on increasing the spectral bandwidth via self-phase modulation (SPM) in a nonlinear bulk medium and subsequent removal of the frequency modulation by using an appropriate dispersive delay line constitutes a simple and very efficient method for generation of ultrashort pulses whose spectral bandwidths extend well beyond the gain bandwidths supported by the driving laser sources [1,2]. Among various pulse compression methods developed so far, pulse compression based on SPM-induced spectral broadening in bulk solid-state materials offers the advantages of technical simplicity, low cost, and easy implementation to virtually any existing ultrashort pulse laser system [3].
At present, all-solid-state pulse post-compression technique widely attracts a renewed practical interest, and to date, was demonstrated in a variety of setups, unveiling the potential of scalability to very high peak [4,5] and average [6,7,8] powers, as well as for achieving huge compression factors [9]. In particular, all-solid-state pulse post-compression emerges as very attractive and useful technique to compress the relatively long femtosecond and sub-picosecond pulses delivered by various rapidly developing high average power Yb-laser sources. Multi-plate [10,11,12], multi-pass [6,13,14] techniques, as well as multistage [15] and hybrid [16,17] approaches were recently developed to achieve large compression factors and provide few optical cycle pulses. In contrast to conventional single- or few-pass geometry, these geometries ensure excellent beam quality and uniform spectral distribution across the beam thanks to sequential spectral broadening and careful management of unwanted spatial nonlinear effects, i.e., onset of self-focusing of the beam and spectral variations across the spatial profile.
These techniques are perfectly suited to compress the ultrashort pulses from Yb thin-disc oscillators and pulses from amplified Yb-laser systems, with energies from several microjoules to several hundreds of microjoules, respectively. However, SPM-induced spectral broadening of pulses with an energy of several hundreds of nanojoules is usually performed in highly nonlinear fibers [18,19,20], while spectral broadening of such pulses in solid-state bulk materials remains elusive due to their low nonlinearity. To this end, high repetition rate, low threshold filamentation and supercontinuum generation was recently demonstrated in narrow bandgap dielectric materials, such as undoped KGW and YVO4 crystals, owing to their resistance to multiple pulse-induced optical damage and relatively large nonlinear indexes of refraction [21,22]. These findings suggest that bulk solid-state materials exhibiting similar nonlinear properties could be readily employed for SPM-induced spectral broadening and post-compression of low energy laser pulses and may operate at very high laser repetition rates.
In this Paper, we demonstrate a proof-of-principle of simple all-solid-state post-compression setup for low energy (210 nJ), high repetition rate (76 MHz) pulses from an amplified Yb:KGW oscillator, which is based on sequential spectral broadening in highly nonlinear materials (ZnS, YAG and KGW) and compression of spectrally broadened pulses using Gires-Tournois interferometric (GTI) mirrors.

2. Materials and Methods

The laser source we used was a commercial 4.3 W average power, 76 MHz repetition rate Yb:KGW oscillator (FLINT, Light Conversion) that provided 90 fs pulses with a central wavelength of 1036 nm. The oscillator pulses were amplified in a home-built pre-chirp managed (PCMA) rod-type single pass fiber amplifier, which after GTI mirror compression delivered 210 nJ, 75 fs pulses with an average power of 15.7 W and a peak power of 2.5 MW [23]. The experimental setup is depicted in Figure 1. The SPM-induced spectral broadening was performed in a two stage arrangement, combining sequential propagation of several highly nonlinear materials: ZnS (uncoated, 2 mm-thick, n 2 = 68 × 10 − 16 cm2/W [24]), KGW (uncoated, 6 mm-thick, n 2 = 11 × 10 − 16 cm2/W [25]) and YAG (uncoated, 15 mm-thick, n 2 = 6 . 13 × 10 − 16 cm2/W [26]).
In the first stage, the laser beam with a diameter of 1.6 mm (at the 1 / e 2 intensity level) was focused using an anti-reflection (AR) coated lens L1 with a focal length of f = + 150 mm onto 2 mm-thick ZnS crystal. The crystal was tilted at 50 ∘ angle with respect to beam incidence in a compromise of minimizing the reflection losses (the calculated Brewster`s angle is 66 ∘ ) and at the same time keeping the ellipticity of the beam and so the peak intensity at still acceptable level to induce spectral broadening of the pulse [28,29]. Under these settings, the optimal position of the crystal was found at the geometrical focus of the lens without incurring any distortion of the beam shape. The average power of the output beam was 14.2 W, as measured with a thermal power sensor (F80(120)A-CM-17, Ophir Optronics), suggesting 90.5% transmission of the first stage of spectral broadening.
In the second stage, the beam was then focused with an AR-coated lens L2 ( f = + 100 mm) onto the second nonlinear crystal (2 mm-thick ZnS, 6 mm-thick KGW or 15 mm-thick YAG). Here ZnS crystal was tilted at the same 50 ∘ angle with respect to the beam incidence, while KGW and YAG crystals were placed at normal incidence due to their relatively small transverse dimensions. The position of the lens L2 was found experimentally to achieve the desired dimensions of the beam waist and achieve the SPM-induced spectral broadening in a diverging beam, locating the samples ∼ 5 mm behind the geometrical focus of the lens, thus avoiding very high intensity, which may lead to beam filamentation and eventually optical damage of the sample due to high repetition rate multi pulse exposure. Thereafter AR-coated lens L3 ( f = + 200 mm) was used to collimate the output beam after the second stage of spectral broadening.
The spectrally broadened pulse was directed to the compression stage consisting of a pair of GTI mirrors (with 99.5% reflectivity per bounce) with a group delay dispersion (GDD) of − 1230 fs2 at a wavelength of 1036 nm (see [23] for full spectral characteristics of GTI mirrors). A set of AR-coated fused silica slabs of different thicknesses was used for fine dispersion compensation.
A small part of radiation, which was reflected from 20% beam splitter BS and fused silica wedges WP, was sent for diagnostics. The beam profile measurements were performed using a CCD camera (Spiricon SP620U, Ophir Optronics). The spectral measurements were performed with a portable spectrometer (AvaSpec-ULS2048CL-EVO, Avantes), which for the characterization of spatial-spectral structure of the beam was mounted on a motorized translation stage. The temporal characterization of the compressed pulses was performed with the homemade second harmonic generation frequency-resolved optical gating (SHG-FROG) setup, which used a 50 μ m-thick BBO crystal. The FROG traces were retrieved using a standard FROG pulse retrieval algorithm.

3. Results

The spectra of the laser pulses after each stage of spectral broadening are presented in Figure 2a, while Figure 2b shows the intensity profile of the input beam and Figure 2c–e show the collimated beam profiles after passing the investigated combinations of nonlinear materials. Only a slight spectral broadening was recorded after the propagation in the first 2 mm-thick ZnS crystal (black curve to be compared with grey curve showing the spectrum of the input pulse), producing the spectrum ranging from 1002 nm to 1077 nm (evaluated at the 10 − 2 intensity level). The pulse duration after the crystal was 103 fs, indicating a slight temporal broadening of the pulse due to group velocity dispersion, as verified by the SHG-FROG measurements. The spectrum extending 990 nm to 1100 nm was measured after passing the second 2 mm-thick ZnS crystal (this configuration is further referred to as ZnS+ZnS) and shown by magenta curve. Zero-phase Fourier transform yielded 37 fs transform limited (TL) pulse duration, however, the beam profile measurements shown in Figure 2c revealed the occurrence of a characteristic low-intensity ring, which is a signature of nonlinear spatial effects, i.e., self-focusing. A combination of 2 mm-thick ZnS and 6 mm-thick KGW crystals (referred to as ZnS+KGW) produced a slightly narrower spectrum, extending from 994 nm to 1088 nm and shown by red curve, corresponding to TL pulses of 39 fs. However, the output beam showed an even more pronounced ring structure, as illustrated in Figure 2d. These measurements imply that an appreciable spectral broadening in the above configurations of nonlinear materials could be achieved only at the cost of deterioration of the output beam profile. Finally, the widest spectrum extending from 986 nm to 1100 nm (blue curve) was measured using 2 mm-thick ZnS and 15 mm-thick YAG crystals (referred to as ZnS+YAG), potentially yielding 32 fs TL pulses. Moreover, a smooth, distortion-free Gaussian beam profile was measured at the output, as shown in Figure 2e.
In what follows, we examined the compressibility of spectrally broadened pulses in ZnS+YAG and characterized the overall performance of this particular combination in more detail. The pulse compression was performed using 3 reflections from the GTI mirrors with an additional passage through the AR-coated 27 mm-thick fused silica slab for fine-matching of GDD. The compression results are presented in Figure 3. The measured SHG-FROG trace is shown in Figure 3a, while Figure 3b shows the reconstructed trace with a retrieval root mean square error of 0.13%. Figure 3c compares the measured and reconstructed spectra, showing an excellent agreement of spectral profiles over 4 orders of magnitude. The retrieved temporal profile of the compressed pulse is presented in Figure 3d, yielding pulse duration of 37 fs, which is close to the TL pulse duration of 32 fs, which was obtained by zero-phase Fourier transform of the measured spectrum. The satellite post-pulses are likely due to large GDD imposed by GTI mirrors (close to the boundary of their specified operation interval). Nevertheless, we estimated that 85% of the pulse energy is contained in the main peak.
The measured average power at the output of the entire setup was 11.47 W, indicating the energy throughput of 73%. It is important to notice that the overall 27% energy losses were of solely linear character, as introduced by Fresnel reflections in uncoated ZnS sample (9.5%) and in uncoated YAG sample at normal incidence (16.5%), and 1.5% energy losses after by 3 reflections from GTI mirrors, suggesting the absence of any detectable nonlinear energy losses in the samples due to multiphoton absorption, ionization, etc. Assuming these energy losses, the estimated peak power of the post-compressed pulses was 3.26 MW. Finally, we note that the energy throughput of the overall post-compression setup could be improved significantly just by minimizing the reflection losses using AR-coated samples of nonlinear materials.
A more detailed characterization of the compressed pulses was carried out by evaluating spatial-spectral homogeneity of the beam. This is an important characteristic, since typically, SPM-induced spectral broadening in a simple single pass geometry leads to inhomogeneous distribution of spectral components across the beam profile, and therefore to different compression factors at the beam center and periphery. The characterization of spatial-spectral structure of the beam was performed by scanning the spectral content along the x coordinate with a portable spectrometer mounted on a motorized translation stage. The measured spatial-spectral intensity map of the beam is depicted in Figure 4a, showing almost constant spectral width across the beam profile, which justifies homogeneous spectral distribution as a function of coordinate. For a more precise evaluation, we calculated the spectral overlap parameter V, as defined in [7], which serves as a quantitative measure of spatial-spectral homogeneity of the beam. The result is depicted in Figure 4b, showing the spectral overlap parameter V > 83 % across a major part of the beam, where dotted grey lines indicate the beam intensity level of 1 / e 2 . Here the intensity distribution across the beam (orange curve) was obtained by integrating the spatial-spectral map along the wavelength axis. The estimated energy contained in the beam where V > 90 % is 88.4%, corresponding to 10.14 W of average power.
Finally, the spatial beam quality of the post-compressed pulses was investigated by evaluation of beam propagation factor M 2 . In doing so, a focusing lens with f = + 300 mm was used to focus the collimated beam after compressor. The beam profile was recorded using a high resolution ( 2048 × 1536 pixel) CMOS camera (SP932U, Ophir Optronics), which was translated along the focal zone. Figure 5 shows the results of beam quality measurement in the x and y coordinates. The inset shows beam profile recorded at the focal plane (beam waist), where superimposed curves show the central cross-sections along the x and y coordinates. The dimensions of the focal spot were w x = 94 μ m and w y = 87 μ m, as evaluated at the 1 / e 2 intensity level, and were close to the calculated spot diameter of an ideal (diffraction-limited) Gaussian beam ( w 0 = 78 μ m), whereas a slight ellipticity originated from the incident amplified oscillator beam. The divergence angles of the beam in the x and y directions ( θ x = 18 . 0 mrad and θ y = 17 . 4 mrad) were evaluated from linear fits of the slopes in the far field. The computed M x 2 = 1 . 28 and M y 2 = 1 . 14 attested good spatial quality of the post-compressed pulses, which is only slightly worse than that of an amplified input beam, M x 2 = 1 . 18 , M y 2 = 1 . 11 [23].
We also characterized the performances of compression in ZnS+ZnS and ZnS+KGW configurations. Table 1 presents a brief summary and comparison of relevant post-compression parameters achieved with the examined combinations of nonlinear materials. The ZnS+ZnS configuration yielded the highest energy throughput of 80% due to minimized reflection losses, but on the other hand resulted in the longest pulses (47 fs), non-uniform spatial profile and so the lowest spatio-spectral homogeneity of the beam. Similar observations apply to ZnS+KGW configuration, which also provided the lowest transmission due to the highest reflection losses from uncoated KGW crystal at normal incidence, as a result of its large linear refractive index.

4. Conclusions

We demonstrated a proof-of-principle of simple all-solid-state post-compression setup for low energy laser pulses. The spectral broadening of 75 fs, 210 nJ pulses from an amplified 76 MHz, 15.7 W Yb:KGW oscillator was performed using several combinations of highly nonlinear bulk materials: ZnS, YAG and KGW in a single pass geometry. Among these, the broadest spectrum without beam deterioration due to the onset of self-focusing, was produced by sequential propagation in ZnS and YAG samples of 2 mm and 15 mm thickness, respectively. The spectrally broadened pulses were compressed to 37 fs by means of Gires–Tournois interferometric mirrors, which is close to the estimated Fourier transform limit (32 fs). The spatial-spectral characterization of post-compressed pulses attested almost uniform spectral distribution across the beam (the spectral overlap parameter V > 83 % ) and good beam quality ( M x 2 = 1 . 28 , M y 2 = 1 . 14 ). The measured average power of the post-compressed pulses of 11.47 W indicated relatively low (73%) energy throughput of the entire setup. However, since the energy losses originated solely due to Fresnel reflections from uncoated nonlinear materials, the energy throughput could be notably increased using anti-reflection coated samples, while the temporal intensity contrast of the post-compressed pulses could be improved using chirped mirrors with tailored dispersion characteristics for precise dispersion compensation.
Our results demonstrate that spectral broadening in highly nonlinear bulk materials could be an attractive alternative to fiber-based spectral broadening, offering virtually alignment-insensitive, low-complexity and low-cost all-solid-state arrangement for post-compression of low-energy pulses at very high laser pulse repetition rates.

Author Contributions

Conceptualization, A.D. and G.T.; methodology, V.M., J.B. and G.T.; resources, J.V.; validation, V.M. and J.B.; writing—original draft preparation, V.M. and J.B; writing—review and editing, A.D; funding acquisition, A.D. All authors have read and agreed to the published version of the manuscript.

Funding

This work has received funding from the Research Council of Lithuania (LMTLT), grant S-MIP-22-40.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Rolland, C.; Corkum, P.B. Compression of high-power optical pulses. J. Opt. Soc. Am. B 1988, 5, 641–647. [CrossRef]
  2. Mével, E.; Tcherbakoff, O.; Salin, F.; Constant, E. Extracavity compression technique for high-energy femtosecond pulses. J. Opt. Soc. Am. B 2003, 20, 105–108. [CrossRef]
  3. Nagy, T.; Simon, P.; Veisz, L. High-energy few-cycle pulses: postcompression techniques. Adv. Phys. X 2021, 6, 1845795. [CrossRef]
  4. Kim, J.I.; Kim, Y.G.; Yang, J.M.; Yoon, J.W.; Sung, J.H.; Lee, S.K.; Nam, C.H. Sub-10 fs pulse generation by post-compression for peak-power enhancement of a 100-TW Ti:Sapphire laser. Opt. Express 2022, 30, 8734–8741. [CrossRef]
  5. Tóth, S.; Nagymihály, R.S.; Seres, I.; Lehotai, L.; Csontos, J.; Tóth, L.T.; Geetha, P.P.; Somoskoi, T.; Kajla, B.; Abt, D.; Pajer, V.; Farkas, A.; Mohácsi, A.; Börzsönyi, A.; Osvay, K. Single thin-plate compression of multi-TW laser pulses to 3.9 fs. Opt. Lett. 2023, 48, 57–60. [CrossRef]
  6. Schulte, J.; Sartorius, T.; Weitenberg, J.; Vernaleken, A.; Russbueldt, P. Nonlinear pulse compression in a multi-pass cell. Opt. Lett. 2016, 41, 4511–4514. [CrossRef]
  7. Weitenberg, J.; Vernaleken, A.; Schulte, J.; Ozawa, A.;Sartorius, T.; Pervak, V.; Hoffmann, H.-D.; Udem, T.; Russbüldt, P.; Hänsch, T.W. Multi-pass-cell-based nonlinear pulse compression to 115 fs at 7.5 μJ pulse energy and 300 W average power. Opt. Express 2017, 25, 20502–20510. [CrossRef]
  8. Tsai, C.-L.; Meyer, F.; Omar, A.; Wang, Y.; Liang, A.-Y.; Lu, C.-H.; Hoffmann, M.; Yang, S.-D.; Saraceno, C.J. Efficient nonlinear compression of a mode-locked thin-disk oscillator to 27 fs at 98 W average power. Opt. Lett. 2019, 44, 4115–4118.
  9. Viotti, A.-L.; Li, C.; Arisholm, G.; Winkelmann, L.; Hartl, I.; Heyl, C.M.; Seidel, M. Few-cycle pulse generation by double-stage hybrid multi-pass multi-plate nonlinear pulse compression. Opt. Lett. 2023, 48, 984–987. [CrossRef]
  10. Seidel, M.; Arisholm, G.; Brons, J.; Pervak, V.; Pronin, O. All solid-state spectral broadening: an average and peak power scalable method for compression of ultrashort pulses. Opt. Express 2016, 24, 9412–9428. [CrossRef]
  11. Lu, C.-H.; Wu, W.-H.; Kuo, S.-H.; Guo, J.-Y.; Chen, M.-C.; Yang, S.-D.; Kung, A.H. Greater than 50 times compression of 1030 nm Yb:KGW laser pulses to single-cycle duration. Opt. Express 2019, 27, 15638–15648. [CrossRef]
  12. Seo, M.; Tsendsuren, K.; Mitra, S.; Kling, M.; Kim, D. High-contrast, intense single-cycle pulses from an all thin-solid-plate setup. Opt. Lett. 2020, 45, 367–370. [CrossRef]
  13. Hanna, M.; Guichard, F.; Daher, N.; Bournet, Q.; Délen, X.; Georges, P. Nonlinear optics in multipass cells. Laser Photon. Rev. 2021, 15, 2100220. [CrossRef]
  14. Viotti, A.-L.; Seidel, M.; Escoto, E.; Rajhans, S.; Leemans, W.P.; Hartl, I.; Heyl, C.M. Multi-pass cells for post-compression of ultrashort laser pulses. Optica 2022, 9, 197–216. [CrossRef]
  15. Fritsch, K.; Poetzlberger, M.; Pervak, V.; Brons, J.; Pronin, O. All-solid-state multipass spectral broadening to sub-20 fs. Opt. Lett. 2018, 43, 4643–4646. [CrossRef]
  16. Barbiero, G.; Wang, H.; Grassl, M.; Gröbmeyer, S.; Kimbaras, D.; Neuhaus, M.; Pervak, V.; Nubbemeyer, T.; Fattahi, H.; Kling, M.F. Efficient nonlinear compression of a thin-disk oscillator to 8.5 fs at 55 W average power. Opt. Lett. 2021, 46, 5304–5307. [CrossRef]
  17. Seidel, M.; Balla, P.; Li C.;, Arisholm, G.; Winkelmann, L.; Hartl, I.; Heyl, C.M. Factor 30 pulse compression by hybrid multipass multiplate spectral broadening. Ultrafast Science 2022, 2022, 9754919. [CrossRef]
  18. Pronin, O.; Seidel, M.; Lücking, F.; Brons, J.; Fedulova, E.; Trubetskov, M.; Pervak, V.; Apolonski, A.; Udem, T.; Krausz, F. High-power multi-megahertz source of waveform-stabilized few-cycle light. Nat. Commun. 2015, 6, 6998. [CrossRef]
  19. Nakamura, T.; Badarla, V.R.; Hashimoto, K.; Schunemann, P.G.; Ideguchi, T. Simple approach to broadband mid-infrared pulse generation with a mode-locked Yb-doped fiber laser. Opt. Lett. 2022, 47, 1790–1793. [CrossRef]
  20. Kang, D.; Otsu, T.; Tani, S.; Kobayashi, Y. Sub-10-fs pulse generation from 10 nJ Yb-fiber laser with cascaded nonlinear pulse compression. Opt. Express 2024, 32, 5214–5219. [CrossRef]
  21. Marčiulionytė, V.; Reggui, K.; Tamošauskas, G.; Dubietis, A. KGW and YVO4: two excellent nonlinear materials for high repetition rate infrared supercontinuum generation. Opt. Express 2023, 31, 20377–20386.
  22. Marčiulionytė, V.; Banys, J.; Vengelis, J.; Grigutis, R.; Tamošauskas, G.; Dubietis, A. Low-threshold supercontinuum generation in a homogeneous bulk material at 76 MHz pulse repetition rate. Opt. Lett. 2023, 48, 4609–4612.
  23. Banys, J.; Vengelis, J. Efficient single-pass and double-pass pre-chirp managed Yb-doped rod-type fiber amplifiers using Gires-Tournois interferometric mirrors. Optik 2022, 249, 168185. [CrossRef]
  24. Jansonas, G.; Budriūnas, R.; Vengris, M.; Varanavičius, A. Interferometric measurements of nonlinear refractive index in the infrared spectral range. Opt. Express 2022, 30, 30507–30524.
  25. Selivanov, A.G.; Denisov, I.A.; Kuleshov, N.V.; Yumashev, K.V. Nonlinear refractive properties of Yb3+-doped KY(WO4)2 and YVO4 laser crystals. Appl. Phys. B 2006, 83, 61–65. [CrossRef]
  26. Kabaciński, P.; Kardaś, T.M.; Stepanenko, Y.; Radzewicz, C. Nonlinear refractive index measurement by SPM-induced phase regression. Opt. Express 2019, 27, 11018–11028.
  27. Milosevic, N.; Tempea G.; Brabec, T. Optical pulse compression: Bulk media versus hollow waveguides. Opt. Lett. 2000, 25, 672–674. [CrossRef]
  28. Cornolti, F.; Lucchesi, M.; Zambon, B. Elliptic gaussian beam self-focusing in nonlinear media. Opt. Commun. 1990, 75, 129–135. [CrossRef]
  29. Fibich, G.; Ilan, B. Self-focusing of elliptic beams: an example of the failure of the aberrationless approximation. J. Opt. Soc. Am. B 2000, 17, 1749–1758. [CrossRef]
Preprints 102295 g001
Figure 1. Experimental setup for all-solid-state post-compression of low energy pulses. L1, L2, focusing lenses; M, beam steering mirrors; BS, beam splitter; WP, fused silica wedges; L3, collimating lens; GTI mirrors, Gires–Tournois interferometric mirrors for pulse compression; FS slab, fused silica slab for fine dispersion compensation; SHG-FROG, second harmonic frequency-resolved optical gating for characterization of compressed pulses, SP, spectrometer; CCD, CCD camera.
Figure 1. Experimental setup for all-solid-state post-compression of low energy pulses. L1, L2, focusing lenses; M, beam steering mirrors; BS, beam splitter; WP, fused silica wedges; L3, collimating lens; GTI mirrors, Gires–Tournois interferometric mirrors for pulse compression; FS slab, fused silica slab for fine dispersion compensation; SHG-FROG, second harmonic frequency-resolved optical gating for characterization of compressed pulses, SP, spectrometer; CCD, CCD camera.
Preprints 102295 g001
Preprints 102295 g002
Figure 2. (a) Spectra of the laser pulses after each stage of spectral broadening. (b) The input beam profile measured before the lens L1. The collimated beam profiles after propagation in combinations of (c) ZnS+ZnS, (d) ZnS+KGW and (e) ZnS+YAG.
Figure 2. (a) Spectra of the laser pulses after each stage of spectral broadening. (b) The input beam profile measured before the lens L1. The collimated beam profiles after propagation in combinations of (c) ZnS+ZnS, (d) ZnS+KGW and (e) ZnS+YAG.
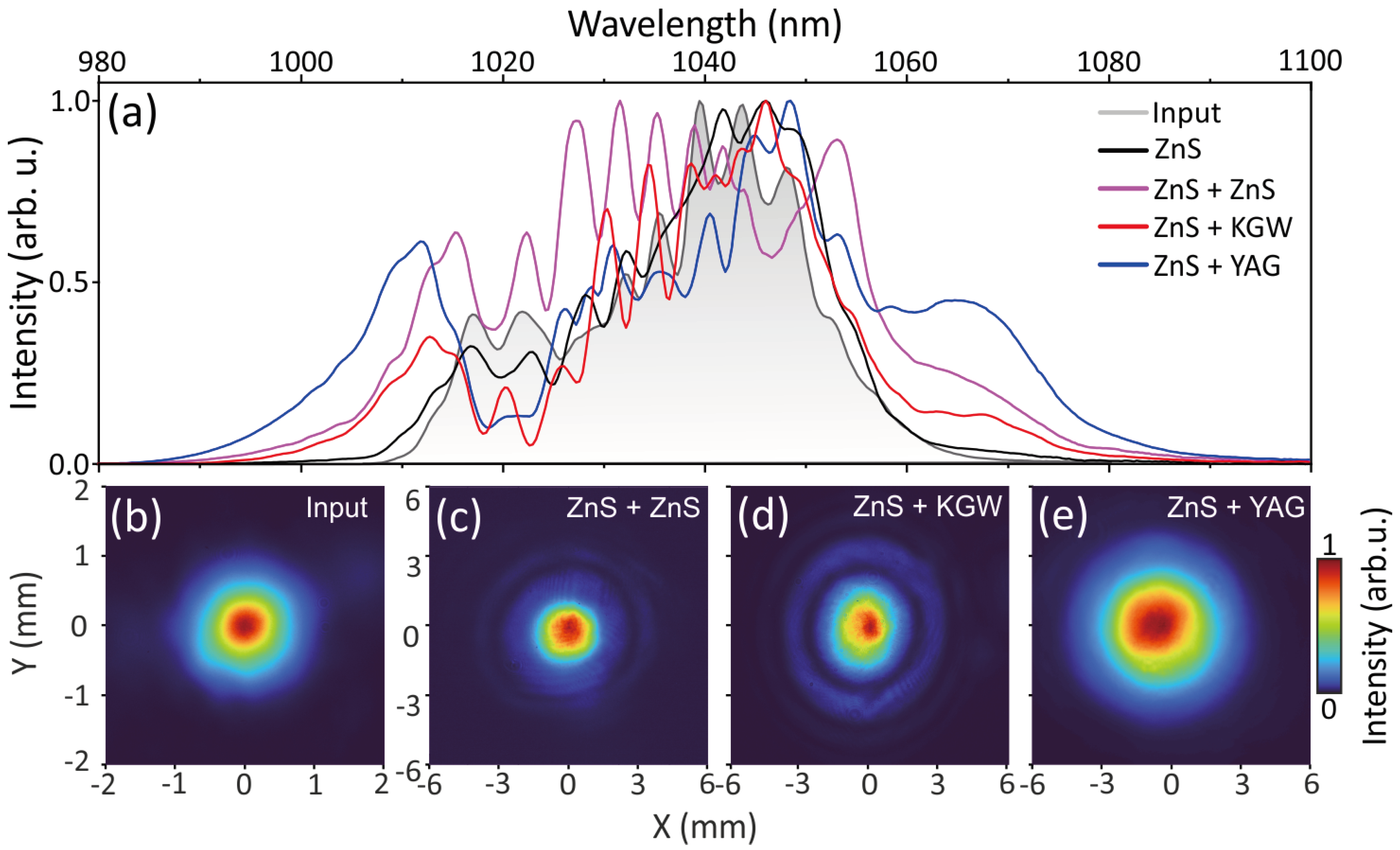
Preprints 102295 g002
Preprints 102295 g003
Figure 3. Characterization of the post-compressed pulses. (a) Measured and (b) retrieved SHG-FROG traces. (c) Measured (black solid curve) and retrieved (blue solid curve) spectra, and retrieved spectral phase (red dashed curve). (d) Retrieved temporal profile (blue solid curve) and temporal phase (red dashed curve). The temporal profiles of TL and input pulses are shown for comparison by blue and black curves, respectively.
Figure 3. Characterization of the post-compressed pulses. (a) Measured and (b) retrieved SHG-FROG traces. (c) Measured (black solid curve) and retrieved (blue solid curve) spectra, and retrieved spectral phase (red dashed curve). (d) Retrieved temporal profile (blue solid curve) and temporal phase (red dashed curve). The temporal profiles of TL and input pulses are shown for comparison by blue and black curves, respectively.
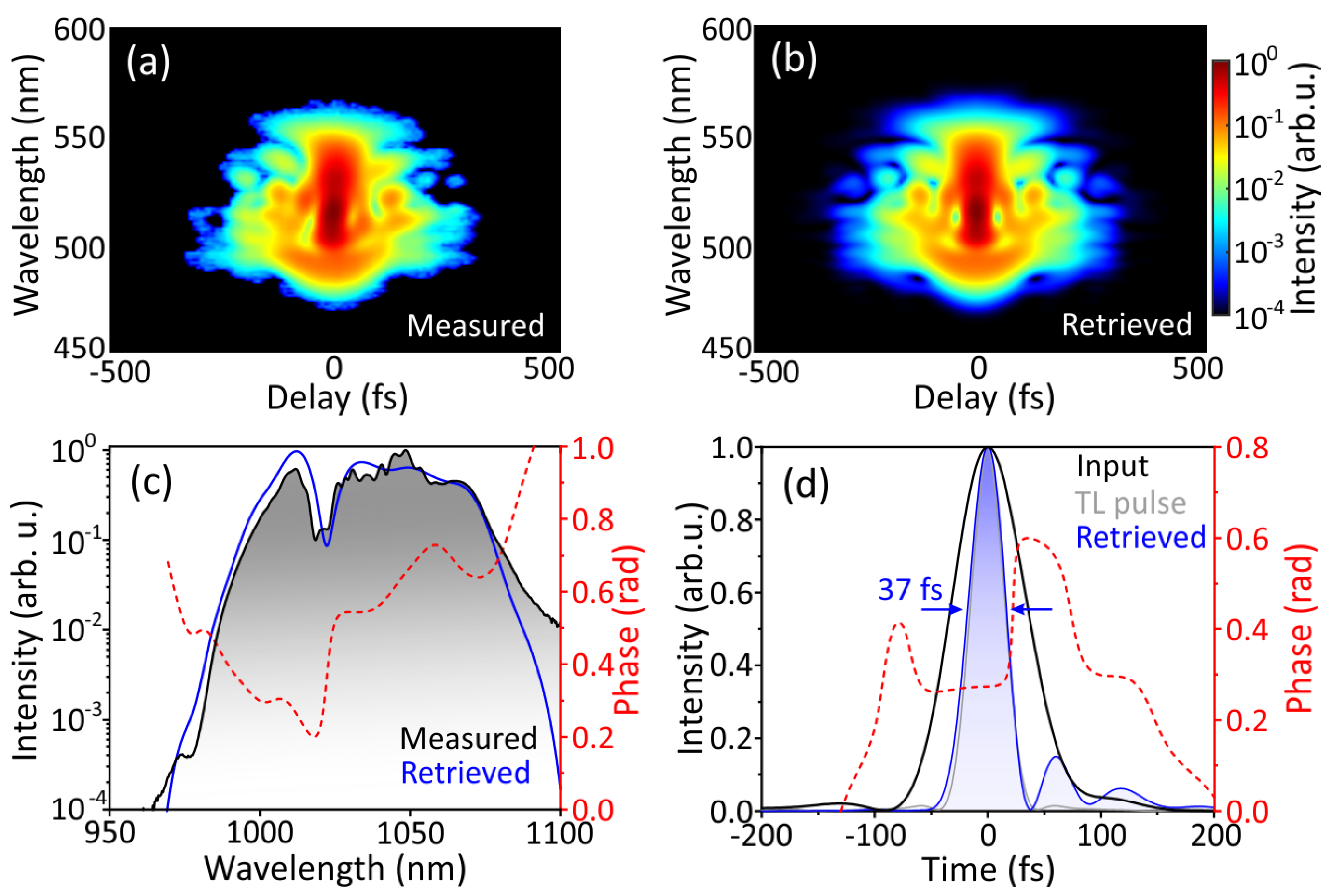
Preprints 102295 g003
Preprints 102295 g004
Figure 4. Spatial-spectral characterization of the compressed pulses. (a) Spatial-spectral homogeneity map of the output beam along the x-axis. (b) Spectral overlap parameter V (green curve) and intensity distribution over the beam profile (orange curve). Green shading denotes the area within which the beam intensity is > 1 / e 2 , as indicated by dotted gray lines.
Figure 4. Spatial-spectral characterization of the compressed pulses. (a) Spatial-spectral homogeneity map of the output beam along the x-axis. (b) Spectral overlap parameter V (green curve) and intensity distribution over the beam profile (orange curve). Green shading denotes the area within which the beam intensity is > 1 / e 2 , as indicated by dotted gray lines.
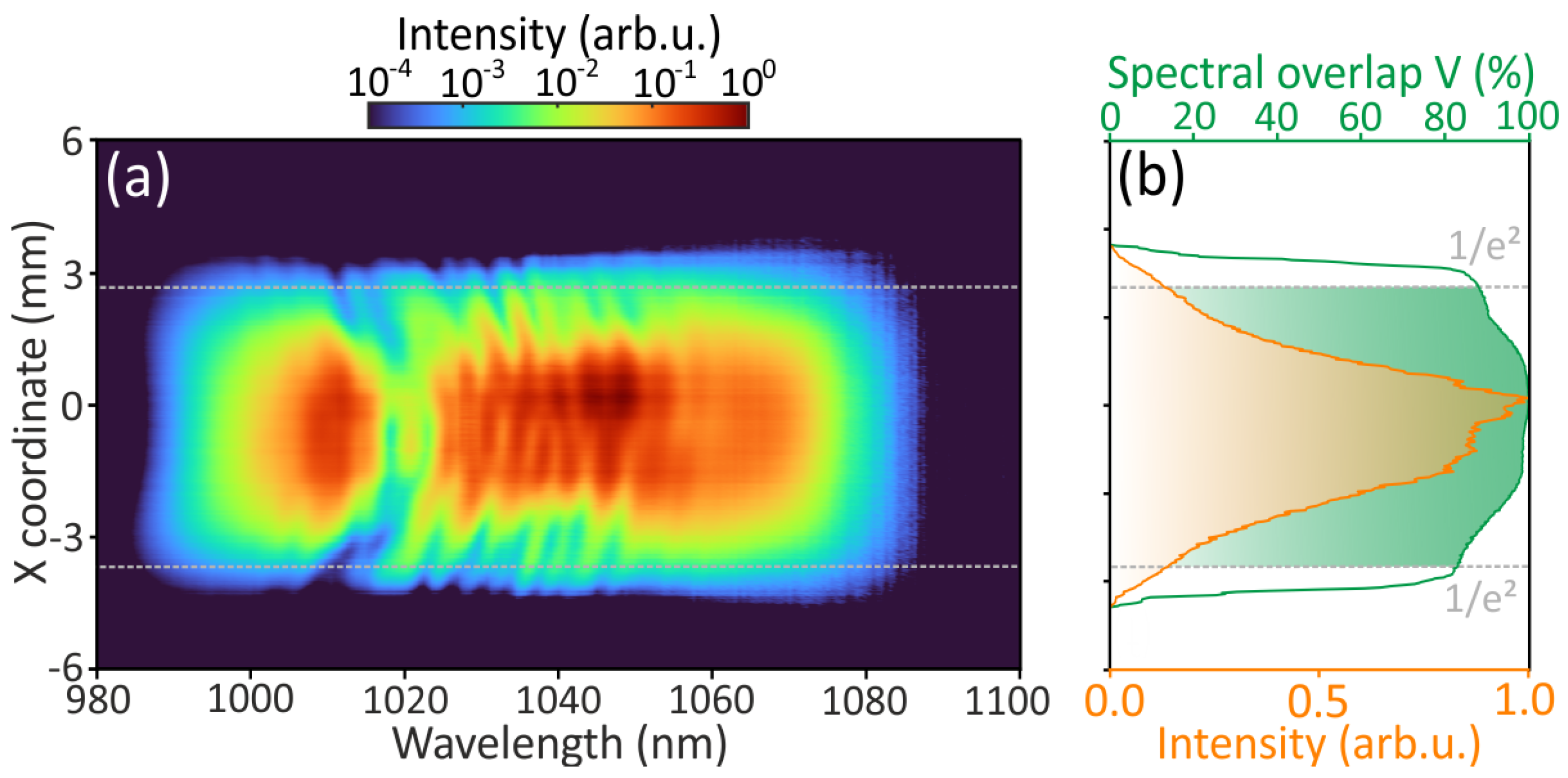
Preprints 102295 g004
Preprints 102295 g005
Figure 5. Beam quality measurement. Solid curves represent a linear fit of the slopes in the far field. The inset shows the beam profile at the beam waist.
Figure 5. Beam quality measurement. Solid curves represent a linear fit of the slopes in the far field. The inset shows the beam profile at the beam waist.
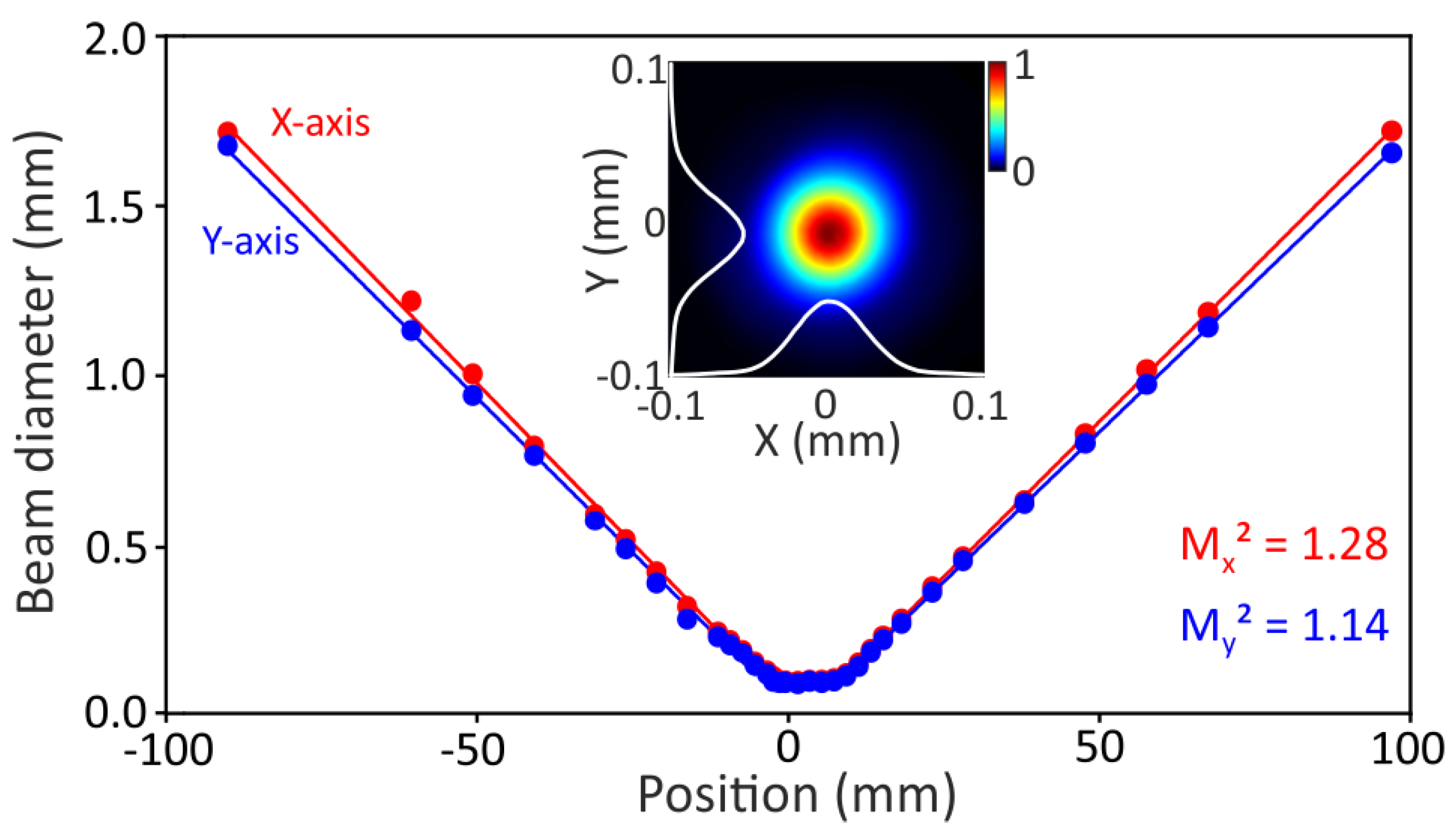
Preprints 102295 g005
Table 1. Relevant post-compression parameters achieved with the examined combinations of nonlinear materials. Pout is the average output power of the post-compressed pulses, T is energy throughput of the setup, τ TL is the duration of transform limited pulse, τ exp is the measured duration of post-compressed pulse, Ppeak is the peak power.
Table 1. Relevant post-compression parameters achieved with the examined combinations of nonlinear materials. Pout is the average output power of the post-compressed pulses, T is energy throughput of the setup, τ TL is the duration of transform limited pulse, τ exp is the measured duration of post-compressed pulse, Ppeak is the peak power.
Nonlinear Pout T τ TL τ exp Ppeak
Material W % fs fs MW
ZnS+ZnS 12.53 80 37 47 2.67
ZnS+KGW 10.70 68 39 45 2.41
ZnS+YAG 11.47 73 32 37 3.26
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated