The Elba Curves

Preprint

Article

The Elba Curves

Altmetrics

Downloads

129

Views

Comments

Elkhan B Beylarov^*,Ilyas R Hasanov

This version is not peer-reviewed

This preprints belongs to the Topic

Mathematical Modeling

Submitted:

04 April 2024

Posted:

05 April 2024

You are already at the latest version

Alerts

Abstract

This article deals with special curves similar to those known in mathematics as Lamé curves. Their equations have a certain similarity with the equations of Lamé curves. But these curves are more like ellipses in appearance. Like ellipses, they have major and minor axes. These are such curves that their major and minor semi-axis coincide with an ellipse but are different than an ellipse. The main feature of these curves is that for any triangle whose base coincides with the axis of a given curve and the vertex is on a given curve, the condition aⁿ+bⁿ=cⁿ is obtained. The number “n” is called the degree or rank of this curve. To distinguish this group of curves, we called them Elbe curves. The equations of these lines are also provided in the paper.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

Review of Literature and Other Sources

The Elbe curves are a particular case of the Lamé curve family. Gabriel Lamé (1795-1870) was a French mathematician, engineer, mechanic, and member of the Paris Academy of Sciences [1]. Lamé curves in a rectangular coordinate system have the following form:

{(\frac{x}{a})}^{m} + {(\frac{y}{b})}^{n} = 1

Here a and b are positive numbers, m, n - rational numbers.

Now let's look at some types of these curves where m and n are positive numbers.

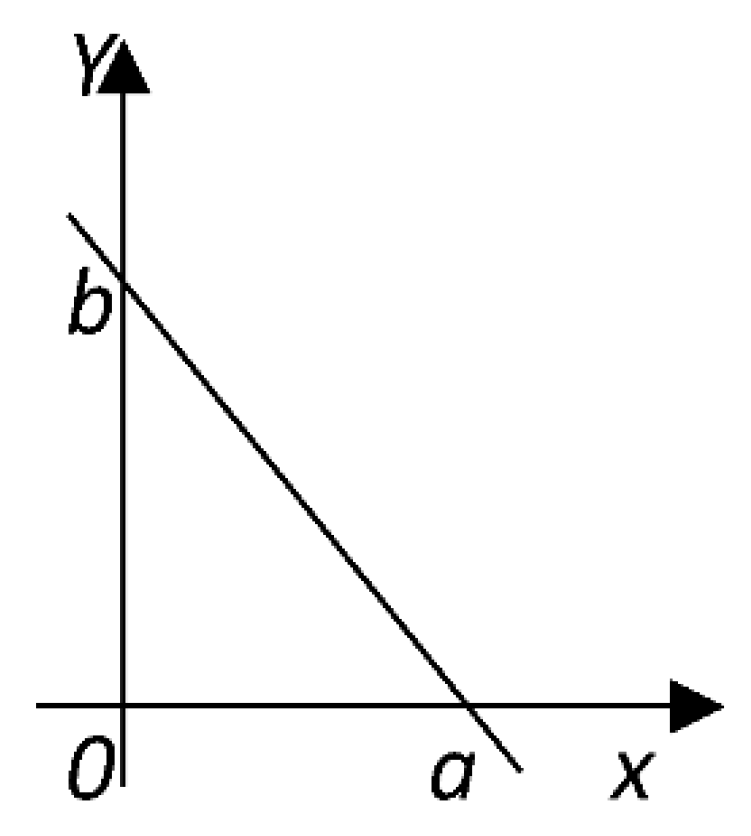
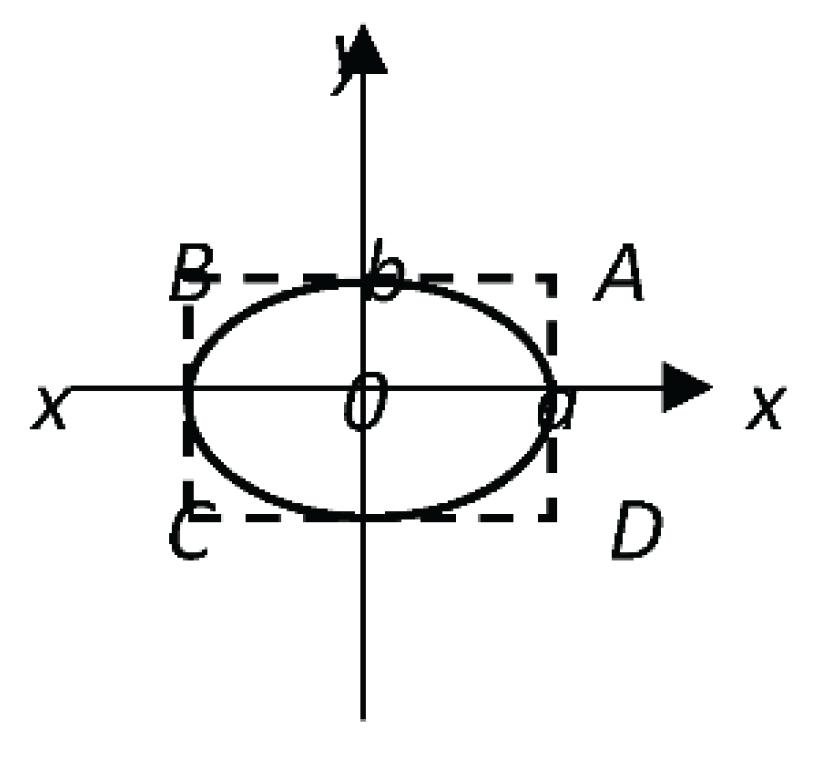
When m=n=1, a line passing through the point (a, 0) and (0, b) coordinate axes (shown in Figure 1.) comes out.
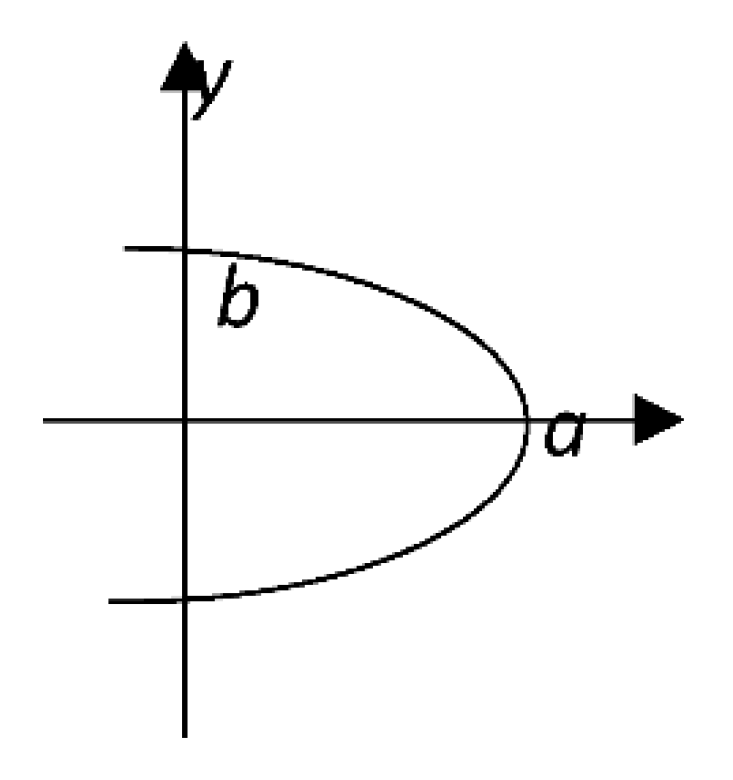
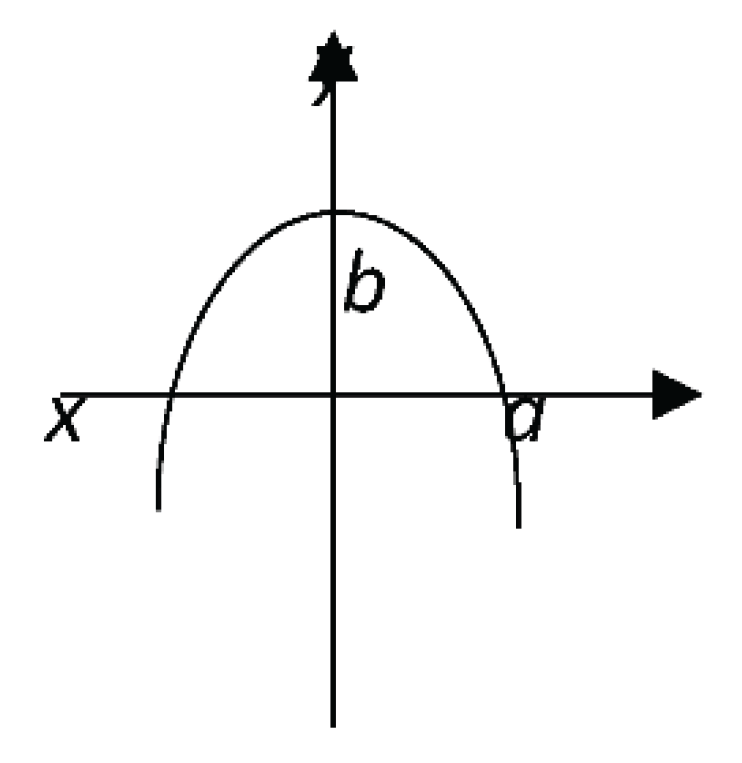
When m=1, n=2, a parabola (shown in Figure 2) comes out.
When m=2, n=1, a parabola (shown in Figure 3) comes out.
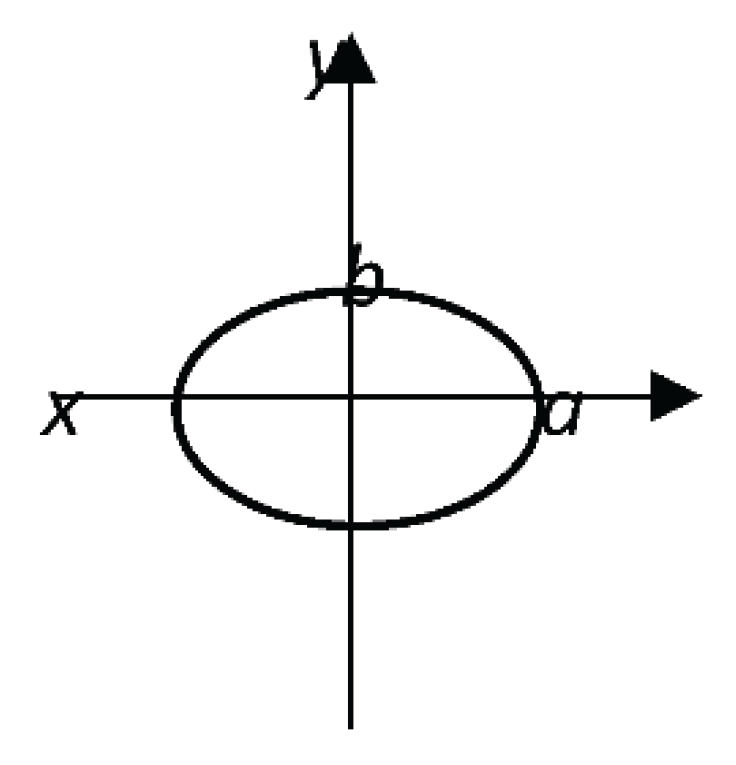
When m=2, n=2, an ellipse (shown in Figure 4) comes out [2,3].
For even values of m, n where m, n>2 an oval comes out, with axes of length 2a, 2b. If m=n, then the oval will tend to a rectangular shape for large even values: Figure 5 [4].

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Figure 5.

Although formula (1) is simple, when the parameters change, as we see, the curve radically changes its shape [5,6].

Unlike the Cassini oval [5,6], the curve is always continuous. Another property of the ellipsoidal shapes of Lamé ovals is that with different combinations of m, n, a, and b, it can have two or 4 focus ranges or none. This property is observed in the m and n values range from 1.5 to 2. The Lamé curve is widely used in architecture, design work, etc. [6]. In the Elbe curves, we are considering a=b=C, m=n. In place of x and y, there are unknowns expressing the lengths of the sides of the triangles inscribed in this curve. The base of triangle ABC, equal to “c,” lies on the OX axis. Points A and B have corresponding coordinates A(-c/2; 0), B(0; c/2). Side lengths AB=b=

\sqrt{{(\frac{c}{2} + x)}^{2} + y^{2}}

, BC=a=

\sqrt{{(\frac{c}{2} - x)}^{2} + y^{2}}

Therefore, the Elbe curve formula is:

{(\sqrt{{(\frac{c}{2} - x)}^{2} + y^{2}})}^{n} + {(\sqrt{{(\frac{c}{2} + x)}^{2} + y^{2}})}^{n} = c^{n}

General İnformation about Elba Curves

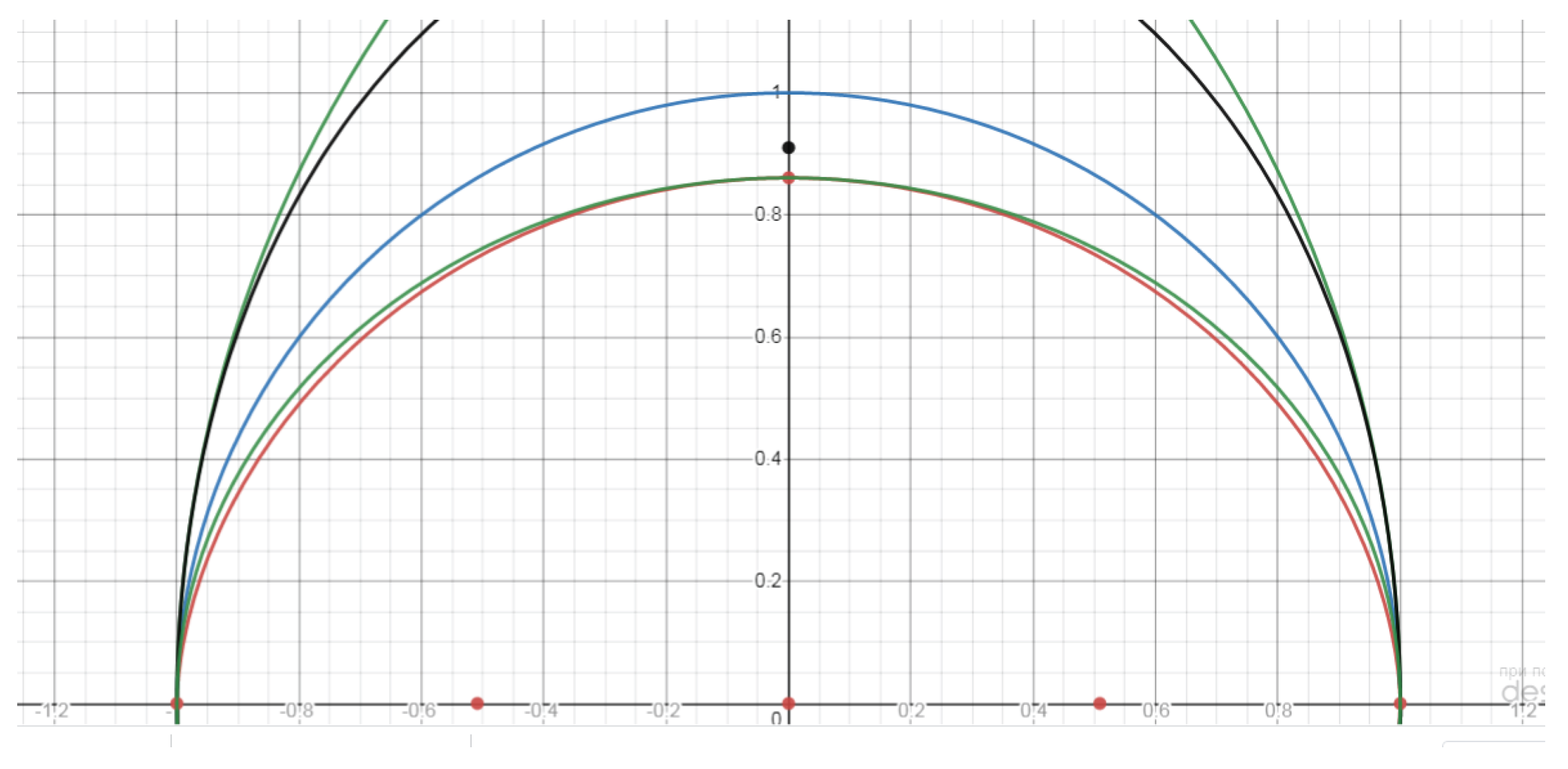
Suppose a, b, c are sides of a triangle and satisfy the condition aⁿ+bⁿ=cⁿ for 1<n<2. Then the solution of the equation (a/c)ⁿ+(b/c)ⁿ=1 with respect to a, b, c will be on the special ellipse-like curves located within a unit circle centered at the origin. We name these family of curves as the Elbe curves (Figure 1, graph 2 - ellipse, graph 3 - Elba).

{(\frac{a}{c})}^{n} + {(\frac{b}{c})}^{n} = 1

(1)

In the case of 1<n<2, the minor semi-axis of Elba curves is less than the circle's radius, and the major semi-axis is equal to the circle's radius (Figure 1, graph 3).

In the case of n=2, we get the equation of the unit circle centered at the origin. (a/c)²+(b/c)²=1. Elba coincides with the unit circle (Figure 1, graph 1).

In the case of 2<n solutions of the equation (a/c)ⁿ+(b/c)ⁿ=1 lie outside of the unit circle centered at the origin, the minor semi-axis is equal to the radius of the circle, the major semi-axis is greater than the radius of the circle, on the ellipse-like, Elba curve (Figure 2, graphs 1, 2 are the Elbe curves).

For clarity, hereafter, we will call these curves the Elba curves (Elkhan Beylarova). In Figure 1, the 1st equation is for the Elba, the 2nd is for the circle, and the 3rd is for the ellipse.

As we already mentioned, although the Elba curve looks like an ellipse with equal major and minor axes, indeed it is a different figure. This can also be seen visually by writing down the corresponding formula of the ellipse with respect to the corresponding semi-axes by observing the graphs.

The Elbe curve is also not a circular arc. This can also be proven by writing the equation of a circle passing through three points.

The angles that subtend the same chord on an arc of a circle are equal, but the angles that subtend the same chord on the Elba differ in magnitude. This is another proof that this is not an arc of a circle.

Note: a) for all right triangles obtained locating the hypotenuse on the diameter of a circle and moving the vertex on the circle, the sides and the angles adjacent to the base change, but the angle at the vertex (C=90^o) and the n's (n=2) do not change;

b) For the triangles obtained, by locating the biggest side on a circle’s diameter and moving the vertex on the Elba, the sides and all angles of the triangle change, but “n” does not change.

For all triangles inside the Elba, n’s that satisfy the condition

{(\frac{a}{c})}^{n} + {(\frac{b}{c})}^{n} = 1

are fixed.

For further clarity, all the above-mentioned points about Elba curves can also be shown on the coordinate plane.

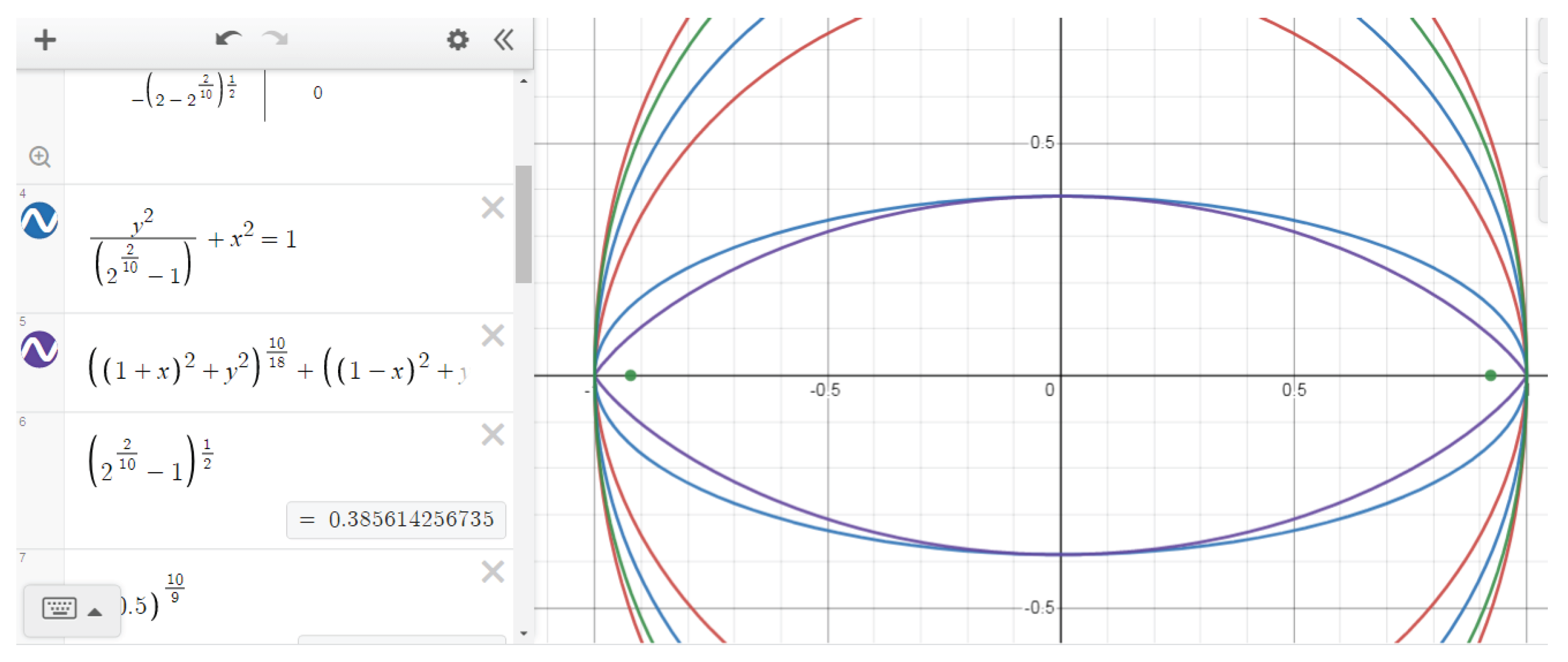
For example, to build an Elba curve for n=5/3, we would do the following.

Figure 1.

Expressing the sides of the triangle in terms of the x, y coordinates, we obtain the Elba equation and its graph for an arbitrary n in the unit circle:

{({(1 + x)}^{2} + y^{2})}^{\frac{n}{2}} + {({(1 - x)}^{2} + y^{2})}^{\frac{n}{2}} = 2^{n}

(2)

For n=2 we get an equation of the circle (Figure 1, graph 1):

{({(1 + x)}^{2} + y^{2})}^{1} + {({(1 - x)}^{2} + y^{2})}^{1} = 2^{2}

For n=5/3 we get the equation of the Elba (Figure 1, graph 3):

{({(1 + x)}^{2} + y^{2})}^{\frac{5}{6}} + {({(1 - x)}^{2} + y^{2})}^{\frac{5}{6}} = 2^{\frac{5}{3}}

The curve in the middle, very close to the Elba curve, whose semi-major axis is 1 and whose semi-minor axis is equal to the Elba's minor semi-axis, is a graph of an ellipse. Its equation is shown at the bottom of the figure (Figure 7, graph 2).

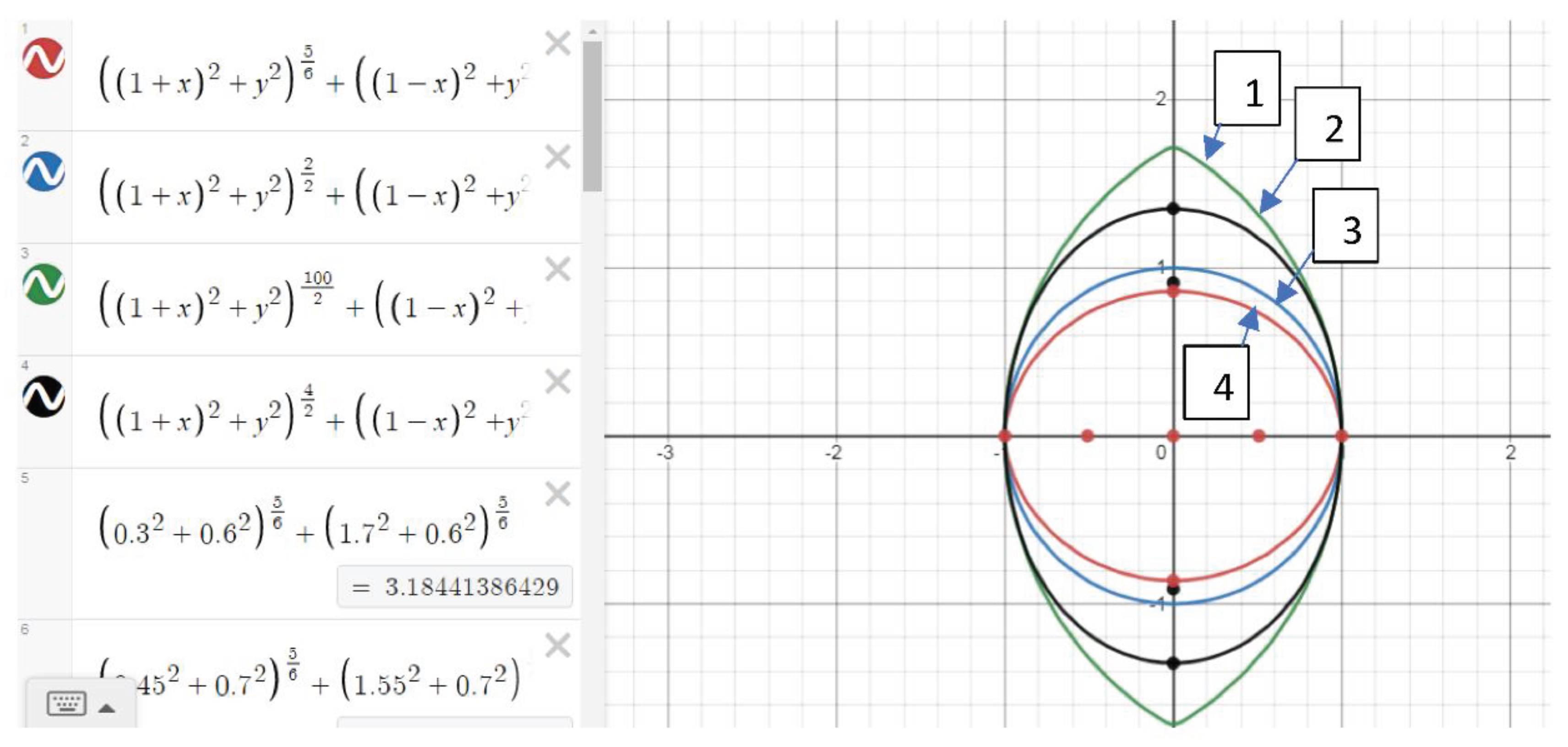
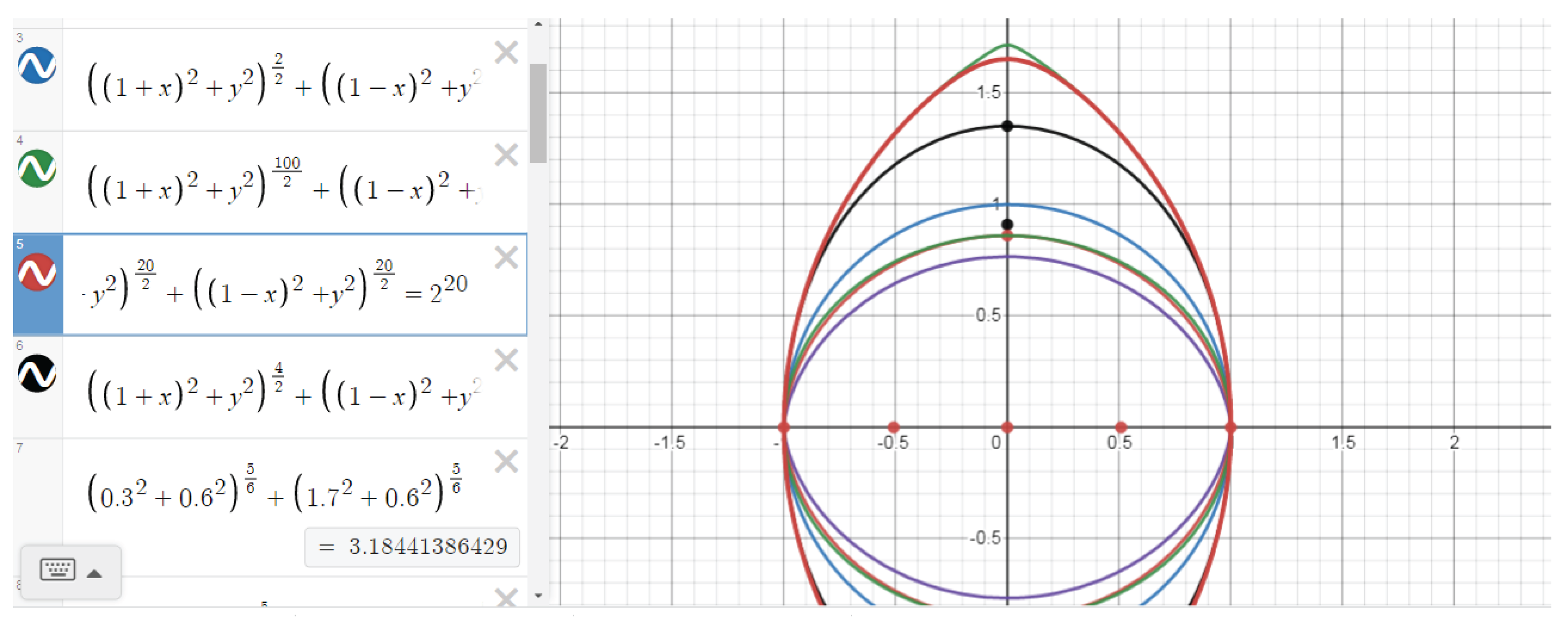
Figure 2 shows graph 1 for n=100; graph 2, for n=4, graph 3, for n=2 circle, graph 4 for n=5/3 – Elba graphs are displayed.

Figure 2.

So the circle is also a special case of the Elba with n=2.

Let us show the calculation of the minor semi-axis of the Elba.

Let's use the known equation

{(\frac{a}{c})}^{n} + {(\frac{b}{c})}^{n} = 1

For the Elba whose major semi-axis is 1 will have c=2. So,

{(\frac{a}{2})}^{n} + {(\frac{b}{2})}^{n} = 1

where a=b

{2 (\frac{a}{2})}^{n} = 1 \to {(\frac{a}{2})}^{n} = \frac{1}{2} \to \frac{a}{2} = {(\frac{1}{2})}^{\frac{1}{n}} \to a = 2 {(\frac{1}{2})}^{\frac{1}{n}} \to a = 2^{\frac{n - 1}{n}}

Therefore, for a unit circle a=b - in the case of an isosceles triangle:

a = b = 2^{\frac{n - 1}{n}}

In this case, the minor semi-axis of the Elba will be:

y_{x = 0} = {(a^{2} - 1^{2})}^{\frac{1}{2}} = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}}

(Figure 2.).

This expression can be obtained easily by assuming x=0 from the equation a²=(1+x)²+y²:

y_{x = 0}^{2} = (a^{2} - 1^{2}) h e r e y_{x = 0} = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}}

In this case, the minor semi-axis of the Elba is y_x=0, and the major semi-axis is x_y=0:

y_{x = 0} = {(a^{2} - 1^{2})}^{\frac{1}{2}} = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}} a n d x_{y = 0} = 1

For the minor semi-axis of the Elba within the unit circle, the following can be noted:

1): when n=1 it is "0";
2): In the case of 1<n<2, it is less than the radius of the unit circle, i.e., 1;
3): when n=2 it is equal to 1.
4): In the case of 2<n, it will be greater than 1 (Figure 3).

Figure 3.

Lemma 1. When dividing the sides of triangles by the largest side and multiplying by 2, since the largest side is 2, the largest value of the semi-axis on the Y axis of the Elba curves in the positive direction approaches to 3^1/2 (square root of 3) and is approximately equal to 1.73205080757.

Proof: For the largest values of N, when the sides grow and approach to the base, i.e., 2, we get an equilateral triangle. Its height will be h_y² = 2²-1²=3 or h_y = 3^1/2.

This value can be calculated similarly on an arbitrary circle.

Some İmportant Facts about Elba Curves:

For any Elba, in cases where n≠2, n≠1, and c=2, the sides of an isosceles triangle are irrational numbers. Because:

$a^{n} + a^{n} = 2^{n} \to 2 a^{n} = 2^{n} \to a^{n} = 2^{n} : 2 \to a^{n} = 2^{n - 1} \to a = 2^{\frac{(n - 1)}{n}}$

Therefore, the sides of an isosceles triangle in the Elba are irrational in all cases where the side c is an integer or a rational number.
This semi-axis is the height of the corresponding isosceles triangle, and its square is equal to the difference of the square of the side and the square of the half of the base. That is:

$y_{x = 0}^{2} = (a^{2} - 1^{2}) \to y_{x = 0} = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}}$

This means that the vertical semi-axis of an arbitrary Elba is an irrational number.
The value of the semi-axis of the Elba, along the Y-axis, increases and decreases depending on n.

Let's clarify the dependence of "n" on the vertical axis in Elba.

It is clear that,

$tg α = Y_{x = 0} v ə ya tg α = y \to tg α = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}} \to {tg}^{2} α = 2^{\frac{2 (n - 1)}{n}} - 1 \to 2^{\frac{2 (n - 1)}{n}} = {tg}^{2} α + 1$

Here, if we take the logarithm of both sides to base 2, we get:

${l o g}_{2} 2^{\frac{2 (n - 1)}{n}} = {l o g}_{2} ({t g}^{2} α + 1) \to \frac{2 (n - 1)}{n} = {l o g}_{2} ({t g}^{2} α + 1) \to 2 - \frac{2}{n} = {l o g}_{2} ({t g}^{2} α + 1) \to$

$n = \frac{2}{2 {- l o g}_{2} ({t g}^{2} α + 1)} v ə y a n = \frac{1}{1 {+ l o g}_{2} (c o s α)}$

This shows that in the case of tgα=1, n=2 is obtained, which is the case when the Elba and the circle coincide.
The circle is a special case of the Elba when n=2.

Let us consider some special cases on this issue.

For example, consider the case n=5/3. So: a ^5\3+b^5\3=c^5\3. By dividing boths sides of the equation by c^5\3 and multiplying by 2n, this triangle can be built on the diameter of a unit circle.

Figure 4.

Note (Figure 5): for n=5\3 for a triangle that satisfies the condition a ^5\3+b^5\3=c^5\3 we could write the following:

(a/c)^5/3+ (b/c)^5/3=1

a²=(1+x)²+y² (3) → a=((1+x)²+y²))^1/2

b²=(1-x)²+y² (4) → b=((1-x)²+y²))^1/2

From the difference of equations (3) and (4), we get that:

a²-b²=4x;

a²+b²=2+2x²+2y²=2(1+x²+y²)

It would be appropriate to investigate these cases for different values of x and y in the circle, ellipse, and Elba.

In Elba, which we are considering, the minor semi-axis was equidistant:

y_{x = 0} = {(2^{\frac{2 (n - 1)}{n}} - 1)}^{\frac{1}{2}}

and the semi-major axis was equal x_y=0=1. For the semi-focal distance f for the corresponding semi-axial ellipse, we get:

f = {(1 - y_{x = 0}^{2})}^{\frac{1}{2}}

(5)

For simplicity of calculations and expressions, here, without loss of generality, we can take c = 2 so that the radius of the circle under consideration and the major semi-axis of the corresponding ellipse are equal to one.

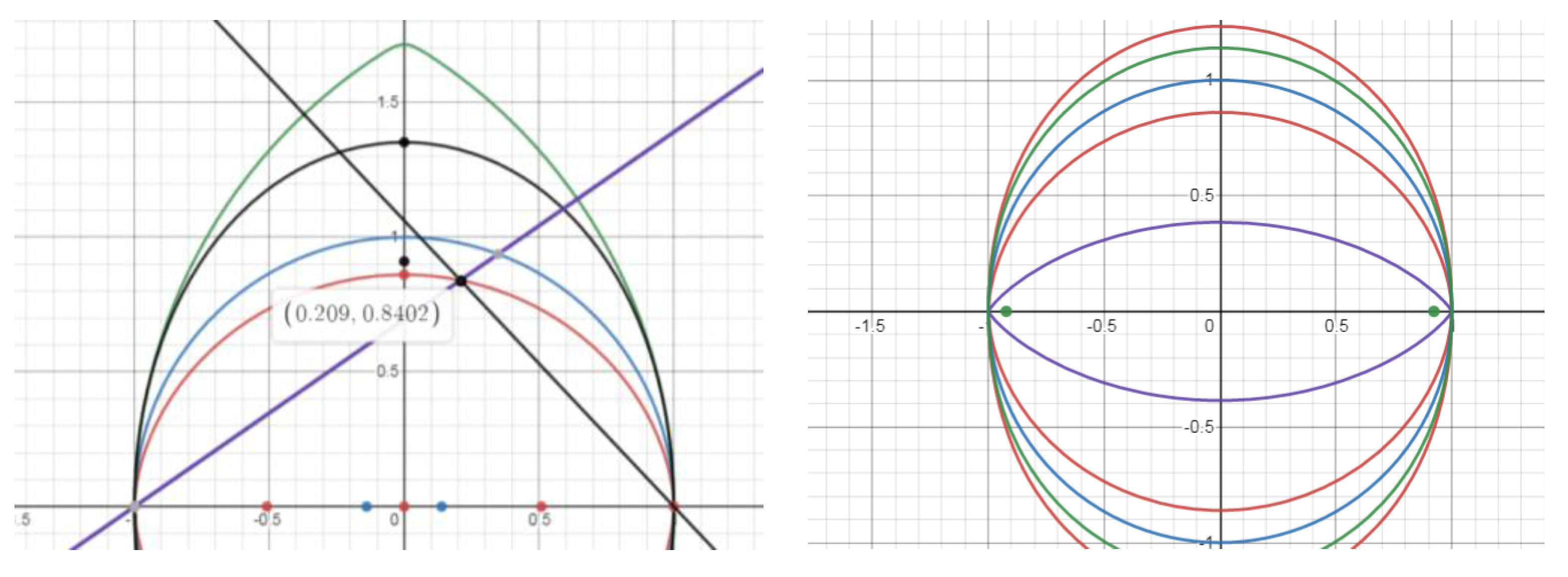
Figure 12 shows the graphical differences between the Elba curve (red) and the ellipse (green), in which the major and minor semi-axes coincide for the case of n=5/3.

Figure 5.

Figure 6 demonstrates the graphical differences between the Elba curve (blue) and the ellipse (blue), the major and minor semiaxes of which coincide, for the case of n=10/9.

Figure 6.

From a comparison of these two graphs, it can be seen that as the value of n approaches unity, the difference between the ellipse and Elba curves is more clearly observed.

As can be seen from Figure 7, as the value of “n” increases (for example, n=20 in the Figure 7, graph 2), one of the numbers a and b, or both of them (if they are close or equal to each other), approaches to "c.” Of course, since the numbers "α" and "b" are less than the number "c" and the number c remains constant, the graphs will infinitely approach to the Elbe (Figure 7, graph 1) with the largest (here n=100) “n” (Figure 7, graph 1).

Figure 7.

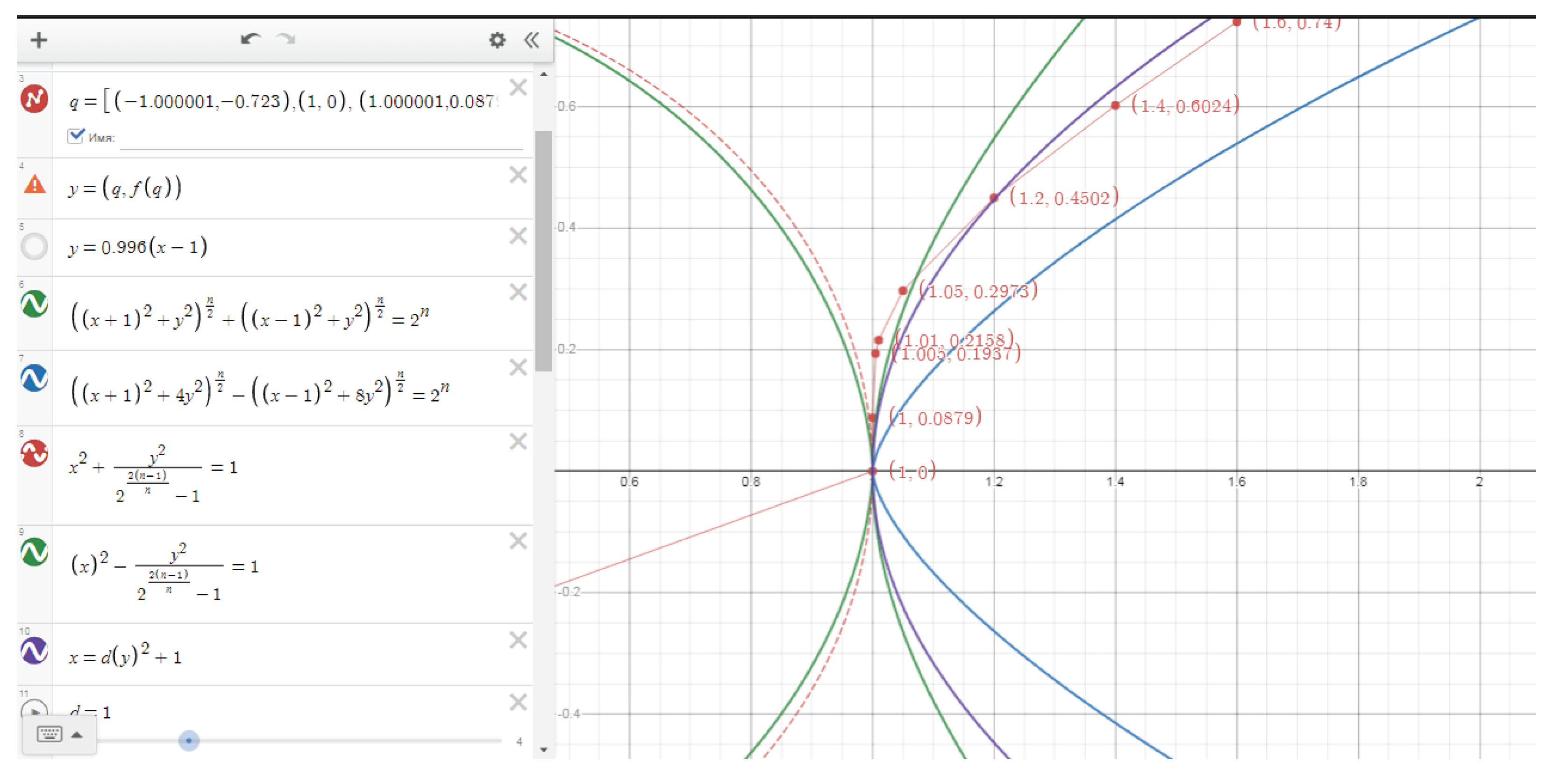
Here we would like to raise an interesting question. Figure 8 shows the formulas for transforming Elba and Ellipse into a hyperbola.

Figure 8.

Depending on the coefficients of the terms of y² in the Elba formula, the direction of the branches/sides of the curve changes. Studying these cases will reveal interesting facts.

An interesting fact is that a circle is a special case of an ellipse with equal semi-axes. At the same time, the circle is a special case of Elba when n=2. In this case, it is doubtful that there is a connection between the Elba and the ellipse. The discovery of this relation would clarify many characteristics of the Elba curves that would contribute to the solution of Fermat's theorem.

Now let's focus on a few learned facts about the circle, ellipse, and the Elba.

The study showed that:

1): In case 1<n<2, the Elba curve and the ellipse with equal semi-axes are inside the unit circle, and the Elba is inside of the ellipse;
2): in case n=2 Elba, circle and ellipse overlap each other;
3): In the case of 2<n, the ellipse is inside of the Elba, and this situation continues until the value 2<n<4.8... (this is an approximate value).
4): After the value n=4.8... (this is an approximate value), the ellipse again begins to move away from the Elba, and after a certain value, it completely goes beyond its limits.
5): It makes sense to find the logical and geometric explanation of this situation - its meaning, whether such transitions occur at higher values of n.

Although many issues related to Elbe curves have been investigated, we consider it expedient to confine ourselves to their interpretation here.

Note: The problem of proving Fermat's theorem for triangles, by applying the sines theorem shows that the equation aⁿ+ bⁿ=cⁿ and the equation sinⁿα+ sinⁿβ=sinⁿɣ are equally valid, and makes it possible and necessary to use the knowledge about triangles.

Some Formulas Related to the Elbe Curves

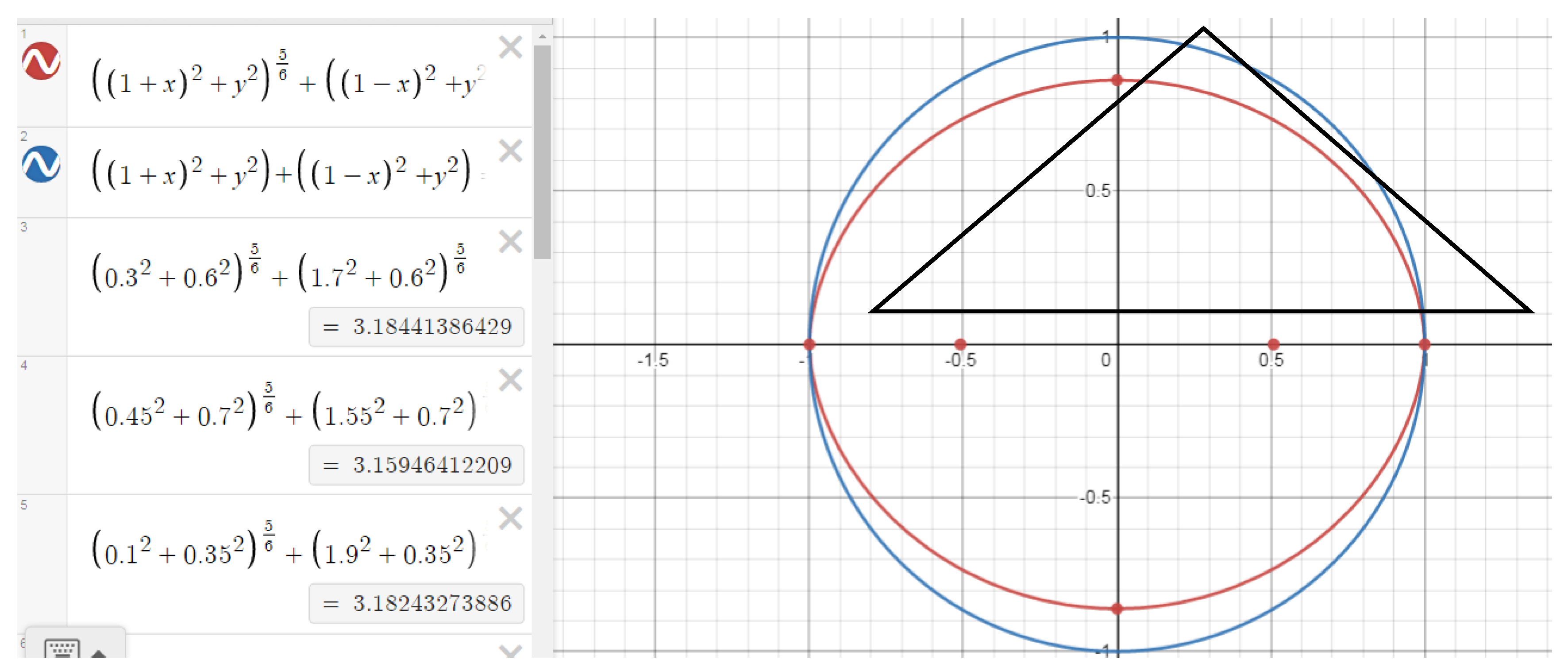
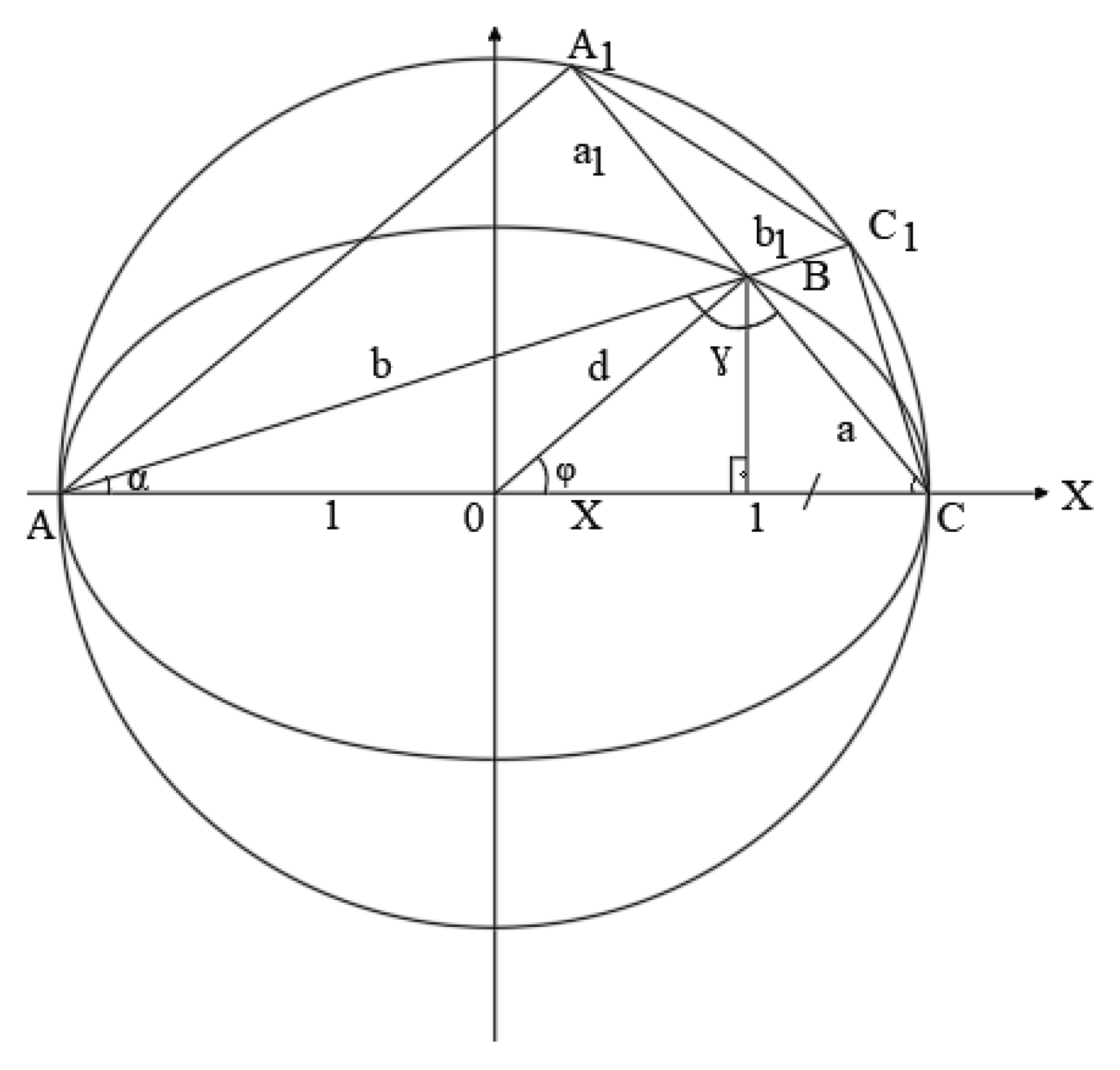
Let’s assume that the triangle ABC be inscribed in the Elbe curve (Figure 9)

Figure 9.

Point B is an arbitrary point on the curve. Points A₁ and C₁ are on the circle. These points are obtained by the intersection of BC and AB sides with a circle with the AC diameter. For simplicity, the radius of the circle is assumed to be R = 1, then C = 2R = 2. Triangles AA₁B and BC₁C are similar, since the angles are based on the same arcs. It can also be shown that ΔABC and ΔA₁BC₁ and the similarity coefficient

K = \sqrt{- c o s γ}

To do this, we write the cosine theorem for ΔABC:

c^{2} = a^{2}

b^{2} - 2 a b c o s γ

Where : \cos α = \frac{a^{2} + b^{2} - c^{2}}{2 a b} = \frac{a^{2} + b^{2} - 4}{2 a b}

(6)

Let’s assume that: a =

\sqrt{(\frac{c}{2} - {x)}^{2} + y^{2}}

b =

\sqrt{(\frac{c}{2} + {x)}^{2} + y^{2}},

then

\cos γ = \frac{(\frac{c}{2} - {x)}^{2} + y^{2} + (\frac{c}{2} + {x)}^{2} + y^{2} - c^{2}}{2 \sqrt{\begin{matrix} ((\frac{c}{2} - {x)}^{2} + y^{2}) ((\frac{c}{2} + {x)}^{2} + y^{2}) \end{matrix}}} = \frac{x^{2} + y^{2} - \frac{c^{2}}{4}}{\sqrt{\begin{matrix} ((\frac{c}{2} - {x)}^{2} + y^{2}) ((\frac{c}{2} + {x)}^{2} + y^{2}) \end{matrix}}}

(7)

With c = 2 we get:

\cos γ = \frac{x^{2} + y^{2} - 1}{\sqrt{((1 - {x)}^{2} + y^{2}) ((1 + {x)}^{2} + y^{2})}} = \frac{d^{2} - 1}{a b}

(8)

Here d = OB. On the other hand, by the theorem on chords intersecting at one point, we get:

aa₁ +bb₁ = (1+d)(1-d) = 1 – d²

(9)

Where: a₁ =

\frac{1 + d}{a},

b₁ =

\frac{1 - d}{b}

Then the similarity coefficient K = \frac{a_{1}}{b} = \frac{b_{1}}{a}; K^{2} = (\frac{1 - d^{2}}{a b}); K = \sqrt{- c o s γ}

(10)

You can also get a formula expressing d and the sides of the triangle a and b.

Using formulas (1) and (5), we have:

c o s γ = \frac{a^{2} + b^{2} - 4}{2 a b}

\frac{d^{2} - 1}{a b}

where we get:

d^{2} - 1 = \frac{a^{2} + b^{2}}{2} - 2 or d^{2} = \frac{a^{2} + b^{2}}{2} - 1 \Rightarrow d = \sqrt{\frac{a^{2} + b^{2}}{2} - 1}

(11)

Now we get a formula relating the x, y coordinates of an arbitrary point B on the Elbe curve and the angle ∠B =γ.

To do this, we use formula (8) and find an expression for sin γ. After some transformations we get:

\sin γ = \sqrt{1 - {c o s}^{2} γ} = \sqrt{1 - \frac{(x^{2} + {y^{2} - 1)}^{2}}{((1 - {x)}^{2} + y^{2}) ((1 + {x)}^{2} + y^{2})}} = \frac{2 y}{\sqrt{((1 - {x)}^{2} + y^{2}) ((1 + {x)}^{2} + y^{2})}} = \frac{2 y}{a b}

(12)

Then: ctgγ =

\frac{c o s γ}{s i n γ}

\frac{x^{2} + y^{2} - 1}{2 y}

where we get: x² + y² = 1 + 2yctgγ

(13)

We transform the last equation into the following form:

y² -2yctgγ +ctg²γ - ctg²γ = 1-х

x² +(y – ctgγ)² = 1+ ctg²γ

x^{2} + (y – ctg)^{2} = (\frac{1}{s i n γ})^{2}

(14)

The latter is the equation of a circle with center at the point 0 (0; ctgγ) and radius R =

\frac{1}{s i n γ} .

Now we get formulas expressing the coordinates (x; y) of an arbitrary point B on the curve through the angles of the triangle ABC, α and β, and sides c =2.

In ABC triangle according to the sine theorem

\frac{a}{b}

\frac{s i n α}{s i n β}

From the other side cosα =

\frac{x + 1}{b}, c o s β

\frac{1 - x}{a}

Using these formulas, you can get the following:

\frac{1 - x}{1 + x} = \frac{a}{b} \frac{c o s β}{c o s α} = \frac{s i n α}{s i n β} \frac{c o s β}{c o s α} = \frac{t g α}{t g β}

(15)

Solving the last equation in terms of x, we get the following:

х = \frac{s i n (β - α)}{s i n (β + α)} = \frac{s i n (β - α)}{s i n γ}

(16)

On the other hand, according to the sine theorem

\frac{a}{s i n α} = \frac{2}{s i n γ} \Rightarrow a = \frac{2 s i n α}{s i n γ} (17) and s i n β = \frac{y}{a} \Rightarrow y = a s i n β (18)

Substituting (12) into (13) we finally get:

y = \frac{2 s i n α s i n β}{s i n (α + β)} = \frac{2 s i n α s i n β}{s i n γ}

(19)

Now let’s set as a goal to find dependence between

\frac{a}{c} a n d \frac{b}{c}

, given n, where c = 2.

İn this case the folloüing condition is fulfilled

(\frac{a}{c})^{n} + (\frac{b}{c})^{n} = 1

(20)

Let's introduce an auxiliary angle as follows:

(\frac{a}{c})^{\frac{n}{2}} = (\frac{s i n α}{s i n γ})^{\frac{n}{2}} = c o s φ, (\frac{b}{c})^{\frac{n}{2}} = (\frac{s i n β}{s i n γ})^{\frac{n}{2}} = s i n φ

(21)

It becomes clear that in this case: cos²φ + sin²φ =

((\frac{a}{c})^{\frac{n}{2}})^{2} + ((\frac{b}{c})^{\frac{n}{2}})^{2} = 1

From formulas (21) one can get the following:

Ψ = a r c c o s ((\frac{a}{c})^{\frac{n}{2}}) = a r c s i n ((\frac{b}{c})^{\frac{n}{2}}) .

Let’s assume that

\frac{b}{c} = x, \frac{a}{c} = y .

Then we get:

\arccos (y^{\frac{n}{2}}) = a r c s i n (x^{\frac{n}{2}}) or y = \cos (a r c s i n (x^{\frac{n}{2}}))^{\frac{n}{2}}

(22)

The last formula allows us to determine for a given n and an arbitrary value x =

\frac{b}{c}

the value y =

\frac{a}{c}

References

Matematicheskaya entsiklopediya (5 volumes). (in Russian). М.: Sovetskaya entsiklopediya. 1982q. Т. 5, st.809.
Gasanov I. R. Beylarov E. B. K voprosu krivoy Ellipsa (in Russian). Young Scientist 9(456). Febrary 2023.
Ovchinnikov A. B. Algebra i geometriya v voprosakh I zadachakh.Osnovi algebary I analitechkoy geometrii. (in Russian) Изд. Стереoтип.NRSS. 2022, 288 c.İSBN978-5-9519-2839-9.
Nəsibov M.X. Qəribə əyrilər. Elmi-kütləvi ədəbiyyat. Bakı, “Maarif”.1975, 156 s.
Chebykin V.A. A ne zamakhnutsya li nam na Gabrielya nashego lame // SaPR i graphika. 2013. №8, st. 92. 94,95.
Noviye vidy ovalnikh krivikh– «rezervuarniye ovali» ovaly. Spravochnik. Injenerniy jurnal 2012, №11. st.31-35.
Edvards, G. (1980). Poslednyaya teorema Ferma. Geneticheskoe vvedenie v algebraicheskuyu teoriyu chisel. Moscow: Mir, 486. (accessed on 1.1.2023 ). Available at: http://www.ega-math.narod.ru/Books/Edwards.htm.
https://dic.academic.ru/dic.nsf/enc_mathematics/2637/%D0%9B%D0%90%D0%9C%D0%95.
https://vk.com/wall-104993817_2072.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Elba Curves

Abstract

Review of Literature and Other Sources

General İnformation about Elba Curves

Some İmportant Facts about Elba Curves:

Some Formulas Related to the Elbe Curves

References

MDPI Initiatives

Important Links

Subscribe