Prerpints.org logo
Preprint
Article

Case Study for Predicting Failures in Water Supply Networks Using Neural Networks

Altmetrics

Downloads

85

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 March 2024

Posted:

26 March 2024

You are already at the latest version

Alerts
Abstract
This study addresses the prediction of recurring failures in water supply networks, a complex and costly task, but essential for the effective maintenance of these vital infrastructures. Using historical failure data provided by Companhia de Água e Esgotos da Paraíba (CAGEPA), the research focuses on predicting the time until the next failure at specific points in the network. The authors divided the failures into two categories: Occurrences of New Faults (ONF) and Recurrences of Faults (RF). To make the predictions, they used predictive models based on Machine Learning, more specifically on MLP (Multi Layer Perceptron) neural networks. The study revealed that, by analyzing data from past failures and considering factors such as altitude, number of failures on the same street and days between failures, it is possible to achieve an accuracy greater than 80% in predicting failures within a 90-day interval. This demonstrates the feasibility of using fault history to predict future water supply outages with significant accuracy. These forecasts allow water utilities to plan and optimize their maintenance, minimizing inconvenience and losses. The article contributes to the field of water infrastructure management by suggesting that the data-driven approach can be applied in other cities or in networks of different types, such as energy or communication networks. The conclusions highlight the importance of data collection and analysis in preventing failures and optimizing water utilities’ resources.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Water distribution networks are essential infrastructures for the development of a city and its productive activities [1]. Failures in water distribution networks can bring inconvenience and losses to both the population and economic activities, industry, and agriculture [2,3]. In this context, predicting future failures or breaks in a water supply network allows the management of this network to carry out planned interventions, anticipating failures, which can reduce inconvenience and losses caused by water supply interruption [4,5,6,7].
According to information from the National Sanitation Information System (SNIS), Brazil has a Water Distribution Loss Index (WDLI) of 40.3%. This number indicates that more than 40% of treated water is lost in the distribution process. In this context, the Water and Sewage Company of Paraíba (CAGEPA) presents a WDLI of 35.4%, a value below the national average, but expressing a concerning figure: more than one-third of the water produced by the company is lost in the distribution process [8].
Predicting future failures in water supply networks is a complex and computationally expensive task, as it involves processing data with high volume and dimensionality [9]. In this context, three approaches stand out for predicting failures in this type of network: predictions based on physical models of the pipeline; Predictions based on statistical models; And predictions based on Machine Learning models. Of these three approaches, the use of Machine Learning has gained traction because it allows for the automatic identification of patterns and complex relationships among the variables linked to a water supply network [6,10].
Machine Learning-based prediction models have been employed by water supply companies to forecast failures in their networks. However, this approach requires high-dimensional and highly representative data. Such data may be scarce in terms of quantity and variety (diversity of variables) because they are highly sensitive for companies, and access to them may be limited. Data on network structure, historical failure records, spatial and meteorological data, for example, are private to water supply companies and are considered strategic for their business models, which complicates access [9,11].
According to [1,10], there are few studies involving failure prediction and optimization of corrections in water supply infrastructures. This type of operation is common in the energy sector, but few applications are known for water supply. Moreover, [3] also considers statistical results from research evaluating the condition or reliability of water distribution systems to be scarce. Additionally, according to [12], studies related to water distribution system data using recent machine learning techniques are rare.
In this context, the present research aims to predict the occurrence of failures in a water distribution network using a Machine Learning-based model and real network data, including the history of failures. This, combined with other variables, allows estimating how many days will elapse until a new failure occurs at a point in the network where previous failures have been recorded.
The present research work is organized as follows: we begin with a brief introduction to the topic, followed by a detailed presentation of the proposal and theoretical foundation. Next, we present the methodology and the development of the research. Finally, we discuss the results achieved and their implications.

2. Related Works

Failures in water supply networks can occur due to the influence of various factors, as described in the work of [13], which provides a detailed description of the main factors influencing failure mechanisms in water distribution networks. Along the same lines, the study presented by [14] also considers elements that play a determinant role in network breakdowns, taking into account information on physical, mechanical, environmental, and social components. Both works highlight the influence of failure history as an important factor for predicting new failures. This information forms the basis of our research, which considers failure history as our main predictive variable.
In the literature, there are works that address the prediction of failures in water supply networks using different approaches, but most of them utilize failure history as an important predictive variable. Some of these works employ predictive models based on Machine Learning to forecast the remaining useful life for a single pipeline in the network, as seen in [15,16,17]. Additionally, [17] uses statistical relationships between failure frequencies and weather conditions to assess the effect of climate change on future breakdowns in water supply networks.
On the other hand, we also find other works that aim to predict the probability of a failure occurring. In this line of research, we have the work of [18], which uses an adapted model from electrical networks to predict the risk of failure in water supply networks. Similarly, the work of [19] utilizes a predictive model to obtain a failure probability associated with each sample, i.e., each pipeline in the network. Based on the predicted information, the replacement of parts of the water supply network is planned.
The work of [9] aims to predict the risk of failures using AutoML based on the failure history. Similarly, [7] seeks to predict the probability of network failure. Finally, the study by [20] aims to predict the frequency of failure (failure per kilometer of the network), but it uses limited data in its model, restricting itself to data such as material, length, diameter, and installation year.
Other works deal with predicting the failure rate in water distribution mains (networks that typically distribute water between two different points with long length and diameter). This is the case with the study presented by [21]. A similar approach is taken by [10,22], although the latter applies their work to predicting failures in long-length water mains.
Unlike what is found in the literature, our work analyzes points in an urban network where there is already a history of past failures, and our prediction consists of a regression task in which the returned value indicates the number of days until the occurrence of the next failure at a particular point.

3. Problem Definition

The present work aims to predict failures in a water supply network based on its historical records of previous failures. A failure is understood as any occurrence recorded in the water supply network related to leaks, indicating a potential risk of temporary water shortage (water outage).
Accordingly, we analyze points in the water supply network where there is already a history of failures, meaning points in the network where failures are recurrent. These points are mapped based on the historical records of registered complaints, and the data from these points are subjected to a Machine Learning algorithm, a model based on Neural Network, aimed at predicting a numerical value indicating the number of days between the last registered failure and the occurrence of a new failure in the future.
With the estimated prediction of the next failure in hand, the water utility can plan maintenance activities so that this future failure can be repaired preemptively, anticipating the leak, avoiding water shortages, and minimizing inconvenience for the potentially affected population. Therefore, the predictive maintenance work can contribute to creating a positive image for the water utility among its customers.
The data used in this research is provided by the Water Supply Company CAGEPA (Water and Sewage Company of Paraíba). These are real data provided by the company regarding the recorded occurrences. These occurrences include information such as date, geographical coordinates, type, address, and other data.
For this research, data recorded in the city of Guarabira-PB was selected. The choice of this city was motivated by a recommendation from CAGEPA, as this city has the highest availability of data, with a greater number of variables available, as well as the longest data interval, extending from November 2017 to April 2023.
For clarification purposes, it is important to emphasize that failures may recur over time, meaning a failure occurring at a point in the network may be recorded again at that same point in the future. Thus, occurrences recorded within a radius of 50 meters from each other are considered a recurrence of the same failure, i.e., a repetition of a failure over time, while occurrences outside this radius are considered new independent failures. A representation of this information can be visualized in Figure 1 below:
Observing Figure 1, it is possible to visualize the occurrences recorded in the city of Guarabira-PB. In the figure, we have the map of the city and several blue dots representing the location of the failures. On the other hand, we see three highlighted points, where it is possible to perceive a central occurrence circled by a radius. This radius indicates whether other occurrences around it are new failures or recurrences of the main failure.
We can see in Figure 1 that Point A is a failure that does not have any recurrences, while Point B has only two recurrences. Finally, we see that Point C, unlike the previous ones, has several recurrences around the main failure. It is worth noting that the main failure is the oldest one, meaning it was recorded before the others.

3.1. Failure History

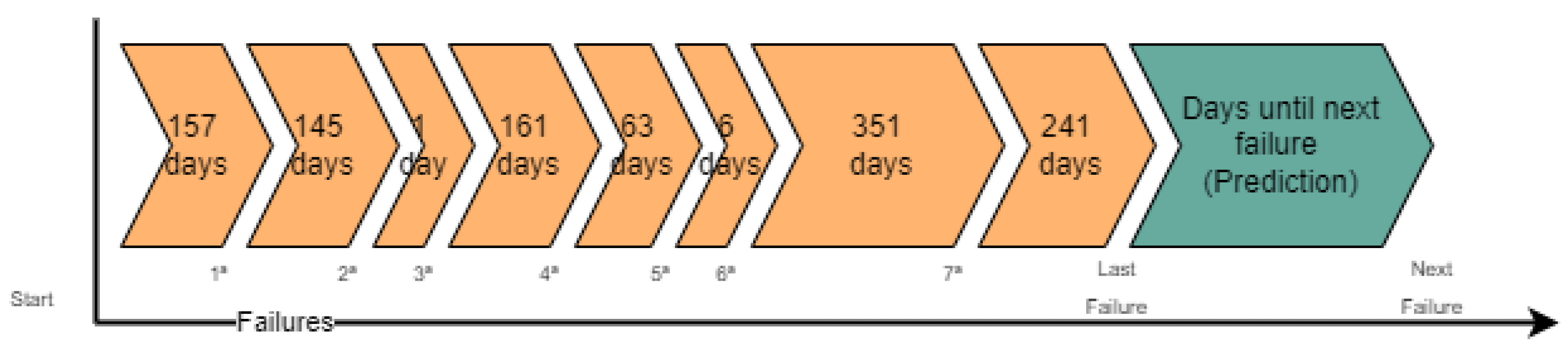
To enhance understanding of the research problem addressed in this study, Figure 2 below presents an analysis of a failure case and the arrangement of its failure history. Additionally, the figure also presents the forecast to be estimated by the Neural Network developed in this study.
Analyzing Figure 2, it is possible to visualize a point in the water supply network that experienced a recurrence of 8 failures. In the figure, we see the beginning of the monitoring, which occurred in November 2017, and the failure history presented in blocks separated by the failures that occurred at this point. For this specific case, we see that the first failure occurred 157 days after the start of monitoring, the second failure occurred 145 days after the first one, the third failure occurred only 1 day after the second one, and so on, presenting all the failures that occurred at this point in the network.
Finally, on the rightmost part of the figure, we see a blue block indicating the number of days between the last recorded failure and a new potential failure that may occur in the future. Thus, this is the prediction objective of this study: to forecast the number of days between the last recorded occurrence and an estimated future failure.

4. Materials and Methods

This research was developed to predict failures in a water supply network using real data from the same network applied to Machine Learning models. Thus, the predictive data analysis process presented in [23] was followed. Therefore, this work is structured into six main stages with their respective characteristics and artifacts generated in each one. These stages are described below in Figure 3:
According to Figure 3, the work begins with understanding the business context in which the data is embedded. It is in this stage that the objectives of analysis and prediction are defined. Next, the data collection and understanding work is carried out, with exploratory analyses aiding in understanding the information and phenomena present in the data. The third stage of the work consists of preparing the data to be used in predictive models. It is in this phase that the processes of data cleaning, variable selection, and data preparation with necessary transformations take place.
The fourth stage of the process involves the final selection of data attributes and the construction of predictive models. The fifth stage, in turn, consists of applying the constructed models to the data to obtain predictions. With the predictions made, it is possible to validate the accuracy of the model. Finally, the last stage consists of using the model with real data and its evolution.
Below, we describe how each stage described above was applied in the context of our work:
The initial two stages described in Figure 3 were carried out together, and both were developed in an immersion context within the company CAGEPA, the data provider. Understanding the business enabled a better grasp of the phenomena encountered in the exploratory analysis stage, where company experts were consulted to help uncover trends and patterns present in the data sets. After a preliminary exploration of the data, the data cleaning stage was conducted to remove attributes and values that had the potential to impair subsequent analyses.
The attribute selection stage was carried out in several phases. The CAGEPA databases used in this study have dozens of attributes, with the main one used in this work dealing with network failure occurrences and the services performed to carry out the operations of correction and recovery of these failures.
The main attributes used in this study are related to the network failure history of the company, from which the date of occurrence registration, its geographical location, its type (only occurrences of the Leak Removal type were considered), and finally, its registered address are extracted.
In addition to attributes present in the datasets provided by the company, other attributes were incorporated during the development of the work, most of which are statistical values calculated from previously existing data, such as mean, standard deviation, range, among others described below.
The attributes were divided into two types: predictor attributes and the target attribute, according to the indication of [24].
  • Target Attribute
    -
    Number of days until the occurrence of the next failure for a specific point in the network
  • Predictor Attributes
    -
    Distance to the nearest neighbor (meters)
    -
    Terrain elevation at the location where the failure was registered relative to sea level (meters)
    -
    Number of recurrences of the failure in question
    -
    Number of days since the last failure in the network
    -
    Number of days between failures in the network at the same point
    -
    Number of occurrences on the same street
    -
    Mean of the number of days between registered failures at the same point
    -
    Variance in registered failures for the same point
    -
    Standard deviation of the number of days between failures for the same point
The target attribute consists of a numeric value that expresses the number of days until the occurrence of the next failure for a specific point in the network. This value indicates the interval in days from the last known occurrence until the next failure.
The data interval used corresponds to all occurrence records in the supply network starting from January 2018 and extending until April 2023. These data consist of real records provided by the company CAGEPA, which, in addition to the occurrence dates, also provided the geographical coordinates of the occurrences. On the other hand, data such as terrain elevation, distances were calculated using the Google Maps API through the Elevation API [25].
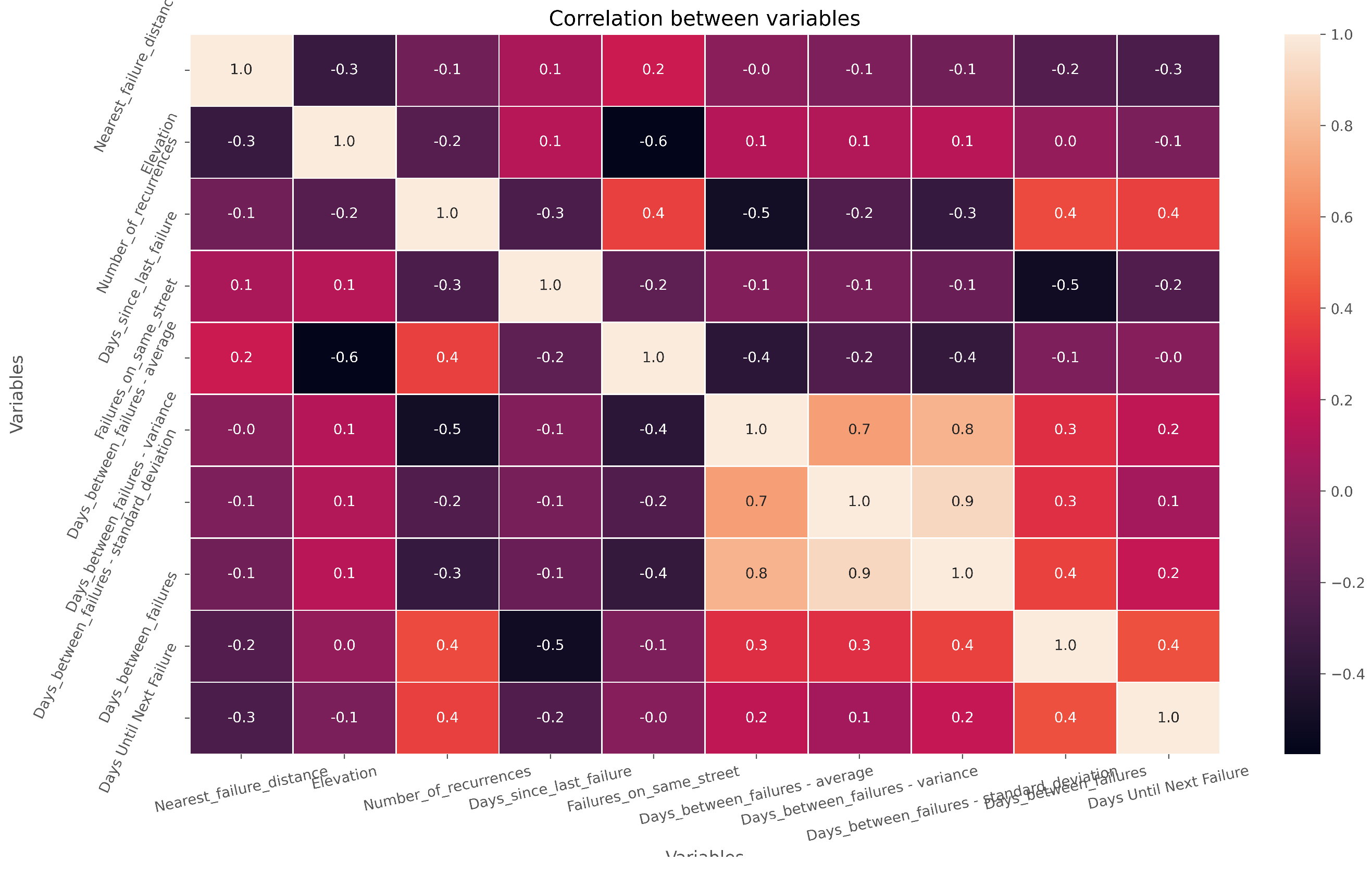
Regarding the attributes or variables used in this work, we present below the correlation values between the target attribute and each of the predictor attributes. These values are expressed in Figure 4 below, which shows the values obtained for Pearson’s Correlation between the variables.
Observing this figure, it is possible to perceive that the variables do not show strong correlation with the target attribute. Of all the analyzed attributes, only the number of recurrences and the number of days between failures show some correlation (0.4), all others present values below this measure. These values indicate that variation in the values of these variables alone does not explain the behavior of the target attribute. In other words, the number of days until the occurrence of the next failure in the network is not directly explained by the predictor variables.
From the attributes listed above, predictive models based on Multi Layer Perceptron (MLP) neural networks for the regression problem were used. In this context, this work uses manually configured models, meaning the arrangement of layers, as well as the number of neurons in each layer, are defined manually. Additionally, for comparison purposes, models with automatic configuration and Linear Regression were used, which can be used to compare the accuracy of the results. It is worth noting that the obtained values are presented and discussed in the results section.
In this stage, the process of training the predictive model occurs, meaning the model is configured and trained using labeled data with the correct response that the model should seek to achieve by correcting its training error. In this context, training occurred with a dataset of 1727 failure samples. This dataset was divided into training and testing data, the former consisting of a total of 1175 samples (corresponding to the period from January 2018 to December 2021), while the testing set consists of 552 samples spaced in time between January 2022 and April 2023.
The models used were obtained from the Scikit-Learn [26] and Keras libraries, where the MLP Regressor and Keras DNN (Deep Neural Network) models were respectively utilized. Additionally, for comparison purposes, the same data was subjected to linear regression models provided by both libraries. The results obtained are presented in the results section.
The predictive models used have different configurations: while the MLP model built using the Keras DNN library was automatically configured, the same applies to linear regression in both libraries. On the other hand, a manually configured model was built using the MLP Regressor library. This model has the following hyperparameter configuration:
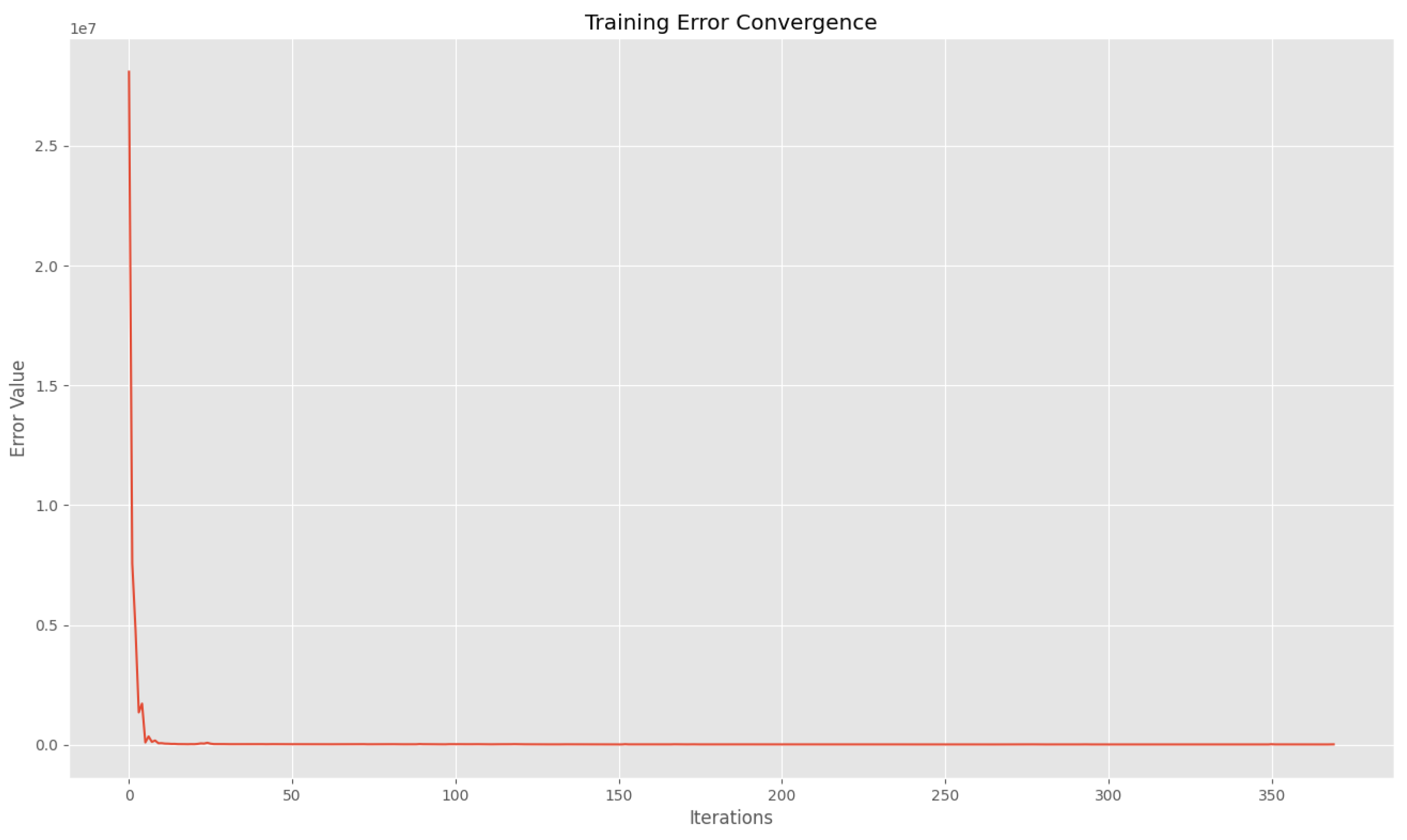
Four hidden layers containing respectively 128, 128, 648, 550 neurons in each. The activation function used was ’relu’ or rectified linear unit function. The training process occurred over 370 iterations and 100 epochs. Below, we present the convergence graph of the error in the training process.
From the models used, the last stage consists of applying new unknown data to the model and verifying the results. In other words, the model was exposed to data that it did not know, and the results obtained from this stage consist of defining the accuracy of the models used in this work. After this stage, the use and evolution of the predictive models used can be performed subsequently. The data obtained from the training and testing of the predictive models can be viewed in the Results section.

5. Results and Discussion

Predicting the occurrence of failures in a water supply network is a complex task that depends on various data, which are often inaccurate or not available in the required quantity and precision.
In this section, we present the results obtained from Machine Learning models based on MLP and Linear Regression. Initially, we will show the models used and compare them in terms of error metrics (accuracy).
Two MLP algorithms were implemented, both trained using the same dataset (Training Set). After training, both used the same data (Test Set) to make their predictions. From these predictions, it was possible to calculate the error value obtained by each of the predictive models. For comparison, the same process was performed using Linear Regression.
The Table 1 shows the error values calculated for each of the algorithms. In it, you can observe each of the models used, as well as the error values obtained from the predictions made by each model.
Observing the data in the table, we can see that the Manual MLP model obtained the best accuracy values for Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Median Absolute Error (MedAE), while the Maximum Error (MAX ERROR) value was obtained by the Automatic MLP. However, the values are very close, indicating similar accuracy in both cases.
It is worth noting that the model predicts a value corresponding to the interval of days between the last registered failure and the next failure at a given point in the network. The errors are presented in days. For example, an MAE of 33.84 for the Manual MLP means that the model is able to predict, on average, a pipeline failure with a margin of error of 33.84 days.
Given the above, we understand that the models based on Manual MLP and Automatic MLP obtained the best results. Furthermore, we noticed that the error values are close in both cases, indicating similar performance when comparing the two models. Despite being close, the performance of the Manual MLP model achieved superior performance, and for this reason, the results obtained by this model are presented below.
Given the accuracy and precision metrics achieved by the model, we present the geographical distribution of the predictions made in this study. The predictions are plotted in two graphs expressed in Figure 6.
In both Figure 6, the geographical locations of the predictions made by the Manual MLP model are presented. The colors in which each record is presented correspond to the calculated error value, where the closer to the blue color, the more accurate the prediction. On the other hand, the more yellow the point, the less accurate the prediction, meaning the higher the error value.
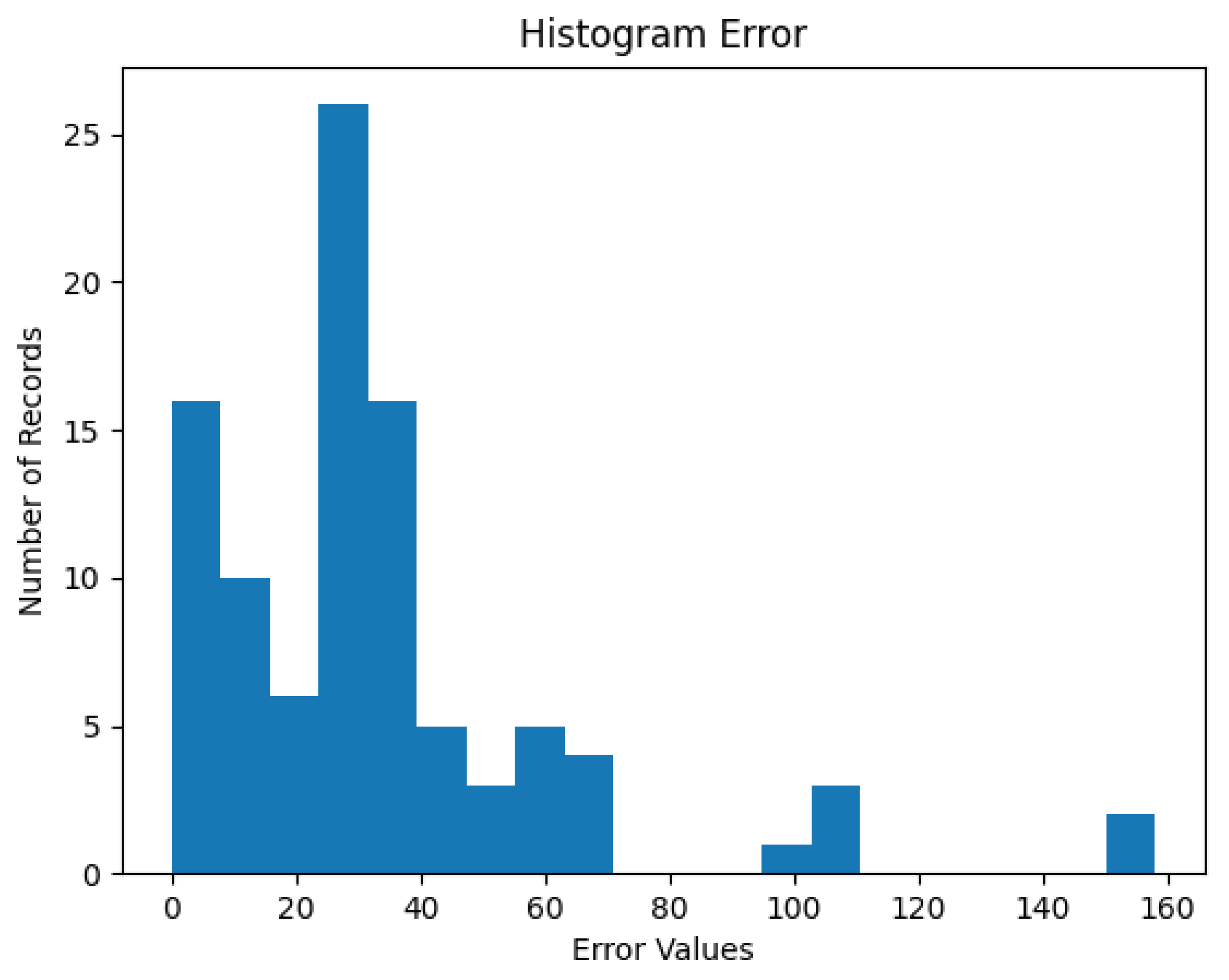
To evaluate the error obtained in the predictions of our model, let’s observe Figure 7, which presents the histogram of the error for the proposed model.
Figure 7 shows a histogram of the error obtained in the predictions of the Manual MLP model. This graph presents the distribution of error values obtained by the model. The error values indicate the number of days of discrepancy between the predicted value and the expected value. In this graph, we can see that the majority of error values are below 40 days, and that only 5 error values above 80 days were recorded.
In order to provide further clarification regarding the accuracy of the model, we analyzed the error values obtained and found that:
  • 12.37% of predictions have an error of less than 5 days
  • 21.64% of predictions have an error of less than 10 days
  • 26.80% of predictions have an error of less than 15 days
  • 57.73% of predictions have an error of less than 30 days
  • 80.41% of predictions have an error of less than 45 days
  • 87.62% of predictions have an error of less than 60 days
  • 93.81% of predictions have an error of less than 90 days
Considering the presented data, we observe that over 20% of the predictions have an error of less than 10 days, and 80% of these predictions have an error of less than 45 days. Therefore, we conclude that the predictions made provide relevant values for the decision-making process of the company, as they indicate, with a certain degree of confidence, the forecast for the day when the next break in the network will occur at a specific point.
Based on the presented results, CAGEPA can utilize the geolocation of the obtained predictions to carry out repairs on the network and preventive and/or predictive maintenance in advance (before the failure occurs), thus avoiding interruptions in the supply and inconvenience to the population. Additionally, they can optimize the mobilization of teams to carry out repairs in advance, including determining when each repair should take place and setting priorities for maintenance work.
Exactly, performing repairs after a failure occurs can lead to significant disruptions and inconvenience for customers. By using predictive maintenance based on the obtained predictions, CAGEPA can proactively address potential issues before they escalate into full-blown failures, minimizing the impact on water supply and avoiding the need for emergency repairs. This proactive approach not only improves service reliability but also reduces operational costs and enhances overall customer satisfaction.
Absolutely, planning and resource allocation are essential aspects of efficient operations for any utility company like CAGEPA. By proactively addressing potential failures based on predictive maintenance, the company can better manage its resources, optimize workforce scheduling, and ensure timely repairs without causing significant disruptions to water supply. This not only helps preserve the company’s reputation but also enhances customer satisfaction by minimizing inconvenience and ensuring reliable service delivery. Additionally, the ability to plan ahead and mitigate potential damages can lead to long-term cost savings and operational efficiencies for the company.

6. Conclusions

Given the results presented, we can conclude that it is possible to predict in advance the occurrence of failures in water supply networks using data from the network itself, focusing on the historical record of past failures.
The results show that using the history of failures as input for predictive models allows CAGEPA to predict a significant percentage of failures in its network with considerable accuracy.
As future work, it is important to predict failures in network points that do not have a history of failures. However, the type of predictive model used will likely need to be different, as well as the variables used. Additionally, this work can be expanded to be applied in other cities within the same company or in cities of different companies.
The model accuracy can be enhanced by incorporating new variables and utilizing different predictive models that may enrich the results in terms of precision. Furthermore, as a contribution to science, this work can be extrapolated and applied to other domains beyond water supply networks, such as energy supply networks, oil pipelines, communication networks, and so on.

Author Contributions

Viviano Medeiros: As the lead author, Viviano Medeiros was responsible for the overall conceptualization of the study. He led the development of the methodology, made significant contributions to the formal analysis, and was involved in the investigation process. Medeiros also took primary responsibility for drafting the original manuscript and played a key role in writing, revising, and editing the manuscript. His responsibilities extended to supervising the research project and project administration. Moisés Santos: Moisés Santos contributed equally to this work alongside Viviano Medeiros. His contributions were fundamental in conceptualizing the study and developing the methodology. Santos was also involved in the validation process, data curation, and contributed to writing, revising, and editing the manuscript. His role in obtaining resources and project funding was crucial.Alisson Brito: Alisson Brito, as the corresponding author, played an essential role in supervising the research project and project administration. His contributions included involvement in the validation process, manuscript revision, and editing, as well as significant participation in obtaining funding for the project.

Funding

This study was financed in part by the Brazilian Government Conselho Nacional de Desenvolvimento Científico e Tecnológico—Brasil (CNPQ)

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Acknowledgments

GOD

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Chatzigeorgakidis, G.; Karagiorgou, S.; Athanasiou, S.; Skiadopoulos, S. A MapReduce based k-NN joins probabilistic classifier. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Oct 2015, pp. 952–957. [CrossRef]
  2. Luo, S.; Chu, V.W.; Zhou, J.; Chen, F.; Wong, R.K.; Huang, W. A Multivariate Clustering Approach for Infrastructure Failure Predictions. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), June 2017, pp. 274–281. [CrossRef]
  3. Vališ, D.; Hasilová, K.; Forbelská, M.; Vintr, Z. Reliability modelling and analysis of water distribution network based on backpropagation recursive processes with real field data. Measurement 2020, 149, 107026. [CrossRef]
  4. Robles-Velasco, A.; Muñuzuri, J.; Onieva, L.; Cortés, P. An evolutionary fuzzy system to support the replacement policy in water supply networks: The ranking of pipes according to their failure risk. Applied Soft Computing 2021, 111, 107731. [CrossRef]
  5. Kabir, G.; Tesfamariam, S.; Loeppky, J.; Sadiq, R. Predicting water main failures: A Bayesian model updating approach. Knowledge-Based Systems 2016, 110, 144–156. [CrossRef]
  6. Giraldo-González, M.M.; Rodríguez, J.P. Comparison of Statistical and Machine Learning Models for Pipe Failure Modeling in Water Distribution Networks. Water 2020, 12. [CrossRef]
  7. Pham, Thi Minh Lanh.; Pham, Hai Ha.; Do, Nguyen Anh Thu.; Le, Dinh Hong. Proposed probabilistic models of pipe failure in water distribution system. MATEC Web Conf. 2018, 193, 02002. [CrossRef]
  8. de Informações sobre Saneamento SNIS, S.N. Diagnóstico Temático Serviços de Água e Esgoto. Gestão Técnica de Água. Technical report, Secretaria Nacional de Saneamento Ambiental - Ministério das Cidades, https://antigo.mdr.gov.br/images/stories/Arqui-vosSNSA/Arquivos_PDF/Snis/AGUA_E_ESGOTO/DIAGNOSTICO_TEMATICO_GESTAO_TECNICA_DE_AGUA_AE_SNIS-_MAI_2023.pdf, 2023. Acesso em 2023 dez. 21.
  9. Zhang, C.; Ye, Z. Water pipe failure prediction using AutoML. Facilities 2021, 39, 36–49. [CrossRef]
  10. Gorenstein, A.; Kalech, M.; Hanusch, D.F.; Hassid, S. Pipe Fault Prediction for Water Transmission Mains. Water 2020, 12. [CrossRef]
  11. Velasco, A.R.; Muñuzuri, J.; Onieva, L.; Palero, M.R. Trends and applications of machine learning in water supply networks management. Journal of Industrial Engineering and Management 2021, 14, 45–54. [CrossRef]
  12. De Clercq, D.; Smith, K.; Chou, B.; Gonzalez, A.; Kothapalle, R.; Li, C.; Dong, X.; Liu, S.; Wen, Z. Identification of urban drinking water supply patterns across 627 cities in China based on supervised and unsupervised statistical learning. Journal of Environmental Management 2018, 223, 658–667. [CrossRef]
  13. Barton, N.A.; Farewell, T.S.; Hallett, S.H.; Acland, T.F. Improving pipe failure predictions: Factors affecting pipe failure in drinking water networks. Water Research 2019, 164, 114926. [CrossRef]
  14. Fan, X.; Wang, X.; Zhang, X.; ASCE Xiong (Bill) Yu, P. Machine learning based water pipe failure prediction: The effects of engineering, geology, climate and socio-economic factors. Reliability engineering & system safety 2022, 219, 108185.
  15. Rifaai, T.M.; Abokifa, A.A.; Sela, L. Integrated approach for pipe failure prediction and condition scoring in water infrastructure systems. Reliability engineering & system safety 2022, 220, 108271.
  16. Ramírez, R.; Cobacho, R.; Torres, D.; López-Jiménez, P. Implementación de un modelo de predicción de fallos orientado a la gestión y estrategias de mantenimiento en redes de distribución de agua potable. Ingeniería del agua 2019, 23, 247–258. [CrossRef]
  17. Wols, B.; Thienen, P.v. Impact of climate on pipe failure: predictions of failures for drinking water distribution systems. European Journal of Transport and Infrastructure Research 2016, 16. [CrossRef]
  18. Zhang, C.; Wu, H.; Bie, R.; Mehmood, R.; Kos, A. Dynamic Modeling of Failure Events in Preventative Pipe Maintenance. IEEE Access 2018, 6, 12539–12550. [CrossRef]
  19. Robles-Velasco, A.; Cortés, P.; Muñuzuri, J.; Onieva, L. Prediction of pipe failures in water supply networks using logistic regression and support vector classification. Reliability Engineering & System Safety 2020, 196, 106754. [CrossRef]
  20. Kutyłowska, M. Neural network approach for failure rate prediction. Engineering Failure Analysis 2015, 47, 41–48. [CrossRef]
  21. Kabir, G.; Demissie, G.; Sadiq, R.; Tesfamariam, S. Integrating failure prediction models for water mains: Bayesian belief network based data fusion. Knowledge-Based Systems 2015, 85, 159–169. [CrossRef]
  22. Tang, K.; Parsons, D.J.; Jude, S. Comparison of automatic and guided learning for Bayesian networks to analyse pipe failures in the water distribution system. Reliability Engineering & System Safety 2019, 186, 24–36. [CrossRef]
  23. Marquesone, R. Big Data. Técnicas e tecnologias para extração de valor dos dados; Casa do Código, 2016.
  24. Faceli, K. Inteligência artificial : uma abordagem de aprendizado de máquina, second ed.; LTC: Rio de Janeiro, 2021. https://integrada.mi-nhabiblioteca.com.br/#/books/9788595154902/; ISBN: 978-85-216-3749-3.
  25. for Developers, G. Visão geral da API Elevation 2024. "Acesso em 2024 fev. 18".
  26. developers scikitlearn. 3.3. Metrics and scoring: quantifying the quality of predictions — scikit-learn.org. https://scikit-learn.org/1.3/modules/model_evaluation.html#regression-metrics, 2023. [Accessed 31-10-2023].
Preprints 102228 g001
Figure 1. Recurrent failures
Figure 1. Recurrent failures
Preprints 102228 g001
Preprints 102228 g002
Figure 2. Failure Predictions - Region of Guarabira-PB
Figure 2. Failure Predictions - Region of Guarabira-PB
Preprints 102228 g002
Preprints 102228 g003
Figure 3. Stages of Work Development
Figure 3. Stages of Work Development
Preprints 102228 g003
Preprints 102228 g004
Figure 4. Correlation between variables
Figure 4. Correlation between variables
Preprints 102228 g004
Preprints 102228 g005
Figure 5. Training Error Convergence
Figure 5. Training Error Convergence
Preprints 102228 g005
Preprints 102228 g006
Figure 6. Failure Predictions - Guarabira
Figure 6. Failure Predictions - Guarabira
Preprints 102228 g006
Preprints 102228 g007
Figure 7. Error Histogram (in days)
Figure 7. Error Histogram (in days)
Preprints 102228 g007
Table 1. Comparison of models in terms of accuracy
Table 1. Comparison of models in terms of accuracy
Error (days) MLP Manual MLP Auto. Linear Regr. KERAS DNN KERAS LR
MAE 33.84935 37.06102 45.34312 236.10285 64.07651
MSE 1981.12961 1994.35068 3762.60283 67591.47127 5740.66704
RMSE 44.50988 44.65815 61.34006 259.9836 75.76719
MedAE 28.37494 30.69204 34.8845 248.3089 74.3719
Max. Erro 158.47765 150.88351 251.06084 492.20184 217.66253
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated