Prerpints.org logo
Preprint
Article

PatchFusion: Patch-based Nonrigid Tracking and Reconstruction of Deformable Objects using a Single RGB-D Sensor

Altmetrics

Downloads

155

Views

92

Comments

0

This version is not peer-reviewed

Submitted:

26 March 2024

Posted:

27 March 2024

You are already at the latest version

Alerts
Abstract
This paper introduces PatchFusion, an innovative approach for nonrigid tracking and reconstruction of deformable objects using a single RGB-D sensor. Existing methods face challenges in accurately capturing the rapid deformations of soft and flexible objects, thereby limiting their utility in diverse scenarios. Our approach overcomes this challenge by employing a dynamic patch-based framework that adapts to rapid inter-frame motions. Firstly, patch-wise rigid transformation fields for non-overlapping patches are solved via Iterative Closest Point (ICP) by incorporating geometric features as additional similarity constraints, thereby enhancing robustness and accuracy. Secondly, deformation optimization based on a nonrigid solver is applied to refine the coarse transformation fields. In order to enable simultaneous tracking and reconstruction of deformable objects, the patch-based rigid solver is designed to run in parallel with the nonrigid solver, serving as a plug-and-play module requiring minimal modifications for integration while enabling real-time performance. Following a comprehensive evaluation, PatchFusion showcases superior performance in effectively dealing with rapid inter-frame deformations when compared to existing techniques, rendering it a promising solution with broad applicability across domains such as robotics, computer vision, and human-computer interaction.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The advent of RGB-D sensors has revolutionized computer vision applications, such as body measurements [1], 3D gaming [2] and robot navigation [3]. This kind of sensor provides a wealth of visual information by seamlessly integrating color and depth data, thereby facilitating the understanding and reconstruction of intricate objects and scenes. Of particular significance is the tracking and reconstruction of deformable objects, which present formidable challenges owing to their intricate and dynamic nature. Unlike rigid structures, deformable objects lack distinct geometric features, rendering their tracking and reconstruction a complex endeavor.
Soft tissues, fabrics, and biological structures are prime examples of deformable objects that undergo intricate shape changes, posing difficulties for conventional rigid tracking and reconstruction methods. The research interest has been growing for developing efficient 4D reconstruction schemes to capture dynamic scenes. Fusion-based methods [4,5,6,7] achieves 4D reconstruction of dynamic scenes via monocular RGB-D camera, by incrementally fusing live depth data into a canonical volume. The fusion-based reconstruction decompose the 4D representation of dynamic scenes into a canonical volumetric representation and temporarily varying deformation fields. The canonical volumetric representation is maintained and updated by integrating live depth data via Truncated Signed Distance Fields (TSDF) [8], while the deformation fields are characterized by a sparse set of rigid transformations on an embedded deformation graph (EDG) [9], and the evaluation of the transformation matrix on an arbitrary point in the whole 3D space is performed via interpolation. In order to estimate the deformation fields, a nonrigid solver including a data term and a regularization term is applied to the model-to-frame registration task. For humans and objects that move slowly, such solvers typically perform well. However, in the presence of rapid inter-frame deformations, these solvers may struggle to accurately track the motion fields, often resulting in erroneous integration of geometry and texture.
To address the aforementioned challenges, it’s crucial to note that many fusion-based methods approach nonrigid tracking by framing it as an as-rigid-as-possible optimization problem. This entails establishing an objective function that accounts for the projection data associations between a canonical frame and a live frame. Typically, these methods employ a Gauss-Newton solver iteratively within an ICP-based framework to address this optimization challenge. However, these techniques often struggle when the inter-frame deformation is significant and rapid, as iterative linearization becomes necessary during optimization. Consequently, this leads to diminished tracking accuracy, particularly when dealing with complex and fast deformations [5,6]. Another significant observation is that many nonrigid deformations can be decomposed into large rigid motions and small nonrigid deformations [10]. The presence of large rigid motions is often the primary cause of many tracking failure cases.
Accordingly, this paper introduces an innovative approach to tackle the intricate issues associated with nonrigid tracking and reconstruction of rapidly deformable objects using RGB-D data. Leveraging the depth information provided by commodity RGB-D sensor, our method aims to capture the fast deformations and shape variations of flexible object and scenes in real-time. Specifically, we introduce efficient modules to solve the embedded large rigid motions ahead of the deformation optimization for global nonrigid deformations. The two frames to be registered are initially partitioned into geometric patches, and individual rigid transformations are estimated for each patch using an improved variant of ICP [11]. This local patch-based rigid solver captures more local structural information, mitigating the influence induced by the APAP regularization term, which encourages the surface to move as rigidly as possible. This regularization term may not be compatible with the fact that some areas move relatively faster than their neighboring areas, causing fast-moving areas to be dragged by slow-moving ones. However, the solved patch-based rigid transformations may not be continuous due to abrupt motions in certain local areas. Therefore, we employ nonrigid deformation optimization to refine the coarse motion fields and obtain the finer ones. Once the final warping fields is computed, we update the TSDF values stored in each voxel of the canonical volume by warping its coordinates into the live camera frame in a nonrigid manner, thus integrating the new depth information with an averaging scheme. A comparison between the raw inputs captured by an RGB-D sensor and the temporally reconstructed results via our proposed method is presented in Figure 1. The underlying surface extracted from the canonical volume is progressively denoised and completed by fusing more registered depth data. This integration of RGB-D measurements not only enhances tracking precision but also facilitates the reconstruction of detailed surface structures, rendering it particularly suitable for applications requiring high-fidelity modeling of deformable objects.
Preprints 102293 g001
Figure 1. Comparison of raw input and our reconstruction results.
Figure 1. Comparison of raw input and our reconstruction results.
Preprints 102293 g001
The main contributions can be summarized as follows:
  • A dynamic patch-based framework, mainly consisting of two threads running in parallel that estimate motion fields in a coarse-to-fine manner, adapting to the inherent challenges posed by nonrigid deformations.
  • A patch-based rigid registration module is designed for efficiently solving a set of coarse transformation fields, which are defined and solved for each non-overlapped patch independently.
  • A deformation optimization module is employed and integrated to refine the coarse transformation fields, yielding more accurate and consistent transformation fields with the embedded deformation graph.
  • Extensive experiments demonstrate that the proposed approach is able to dynamically track and reconstruct deformable surfaces, offering a more accurate representation of their evolving shapes.
The remainder of the paper is organized as follows: Section 2 presents related works to our proposed method. An overview of definition of variables and system architecture of proposed method is presented in Section 3. The details of each module are described in Section 4. Extensive experiments and evaluations are conducted in Section 5. Finally, Section 6 concludes.

2. Related Works

2.1. Rigid Registration

Benefiting from advancements in fields such as computer vision and robotics, registration algorithms have experienced rapid development. Registration can typically be categorized into rigid [12,13] and nonrigid registrations [14,15]. In this section, we concentrate on rigid registration methods which play an important role in the coarse stage of our proposed approach. The Iterative Closest Point (ICP) algorithm [16] stands out due to its conceptual simplicity and ease of implementation. However, it encounters challenges when dealing with complex geometries featuring low overlap or significant displacements, primarily due to the difficulty in finding reasonable correspondences via closest point search. Consequently, numerous ICP variants have been proposed to address these issues, including various designs concerning correspondence matching [17,18], objective functions [11,19], and robust kernels [20]. In the context of our system’s rigid registration thread, we leverage geometric features such as normals and curvatures to enhance correspondence matching, as demonstrated in prior work [11]. These features are integrated into the objective function to improve the robustness and accuracy of the registration process.

2.2. Patch-Based Approaches for 3D Reconstruction

Patch-based methods have gained prominence in various computer vision tasks [21,22,23,24] due to their ability to handle local variations and adapt to changing environments. In the context of object tracking, patch-based approaches have been applied to both rigid and nonrigid scenarios [25]. In structure from motion, Fayad et al. [26] proposed to reconstruct the underlying surface given a monocular video by partitioning the surface into patches, each of which is reconstructed using a quadratic deformation model. In traditional reconstruction methods based on multi-view stereo, local image patches are leveraged to estimate depth information and address challenges such as occlusions and textureless regions [27,28]. In this paper, we leverage the patch-based representation for two frames to be registered and estimate patch-wise rigid motion fields for source frame, which plays an crucial role in recovering rapid inter-frame motion.

2.3. Deformable Object Tracking

Traditional approaches to object tracking often rely on rigid body assumptions, which are inadequate for capturing the complex deformations exhibited by soft and flexible materials. Recent works in deformable object tracking explore various techniques, such as shape models [21], optical flow [29], and physics-based simulations [30], to address the challenges associated with nonrigid motion. Driven by the need to track human bodies and hands, researchers have developed several methods for instances containing articulated structures by incorporating skeletons [31] or a low-dimensional parametric shape [32,33]. Although deformable object tracking with pre-scanned templates or shape priors has shown impressive performance, they usually depend on careful initialization, which restricts their applicability to more generalized scenarios. In contrast, our proposed approach is template-free, devoid of assumptions about the shape, making it readily applicable to a diverse range of scanning requirements.

2.4. RGB-D Tracking and Reconstruction

The integration of RGB-D sensors has significantly improved the accuracy and reliability of object tracking and reconstruction. Methods utilizing depth information alongside color data have been successful in handling rigid objects [34,35]. Zollhöfer et al. [4] presented the first real-time nonrigid tracking and reconstruction method based on pre-scanned mesh template. Newcombe et al. [5] developed a template-less framework that addressed the motion and geometry estimation as an optimization problem. Many following works improve the DynamicFusion algorithm with additional constraints, such as sparse 2D features[6], lighting and appearance models [7]. Moreover, Slavcheva et al. [36] proposed an novel framework for nonrigid reconstruction by level set evolution that is able to handle topology changes without correspondence search. The authors of BodyFusion [31] propose to introduce the skeletal information for tracking fast articulated motion, optimizing both the embedded node deformations and bone transformations simultaneously. Building upon this, their subsequent work, DoubleFusion [32], employs a low dimensional parametrized body model [37] to achieve robust nonrigid tracking and fusion. However, such methods heavily rely on prior knowledge of human shape, making them less suitable for general object tracking and reconstruction. Additionally, for human wearing loose clothing, extracting useful information about underlying shape and pose becomes challenging [37]. Compared with these contributions, the key property of our work is a highly efficient plug-and-play module that greatly improves the tracking accuracy and robustness of fusion-based algorithm making minimal assumption of the object shape.

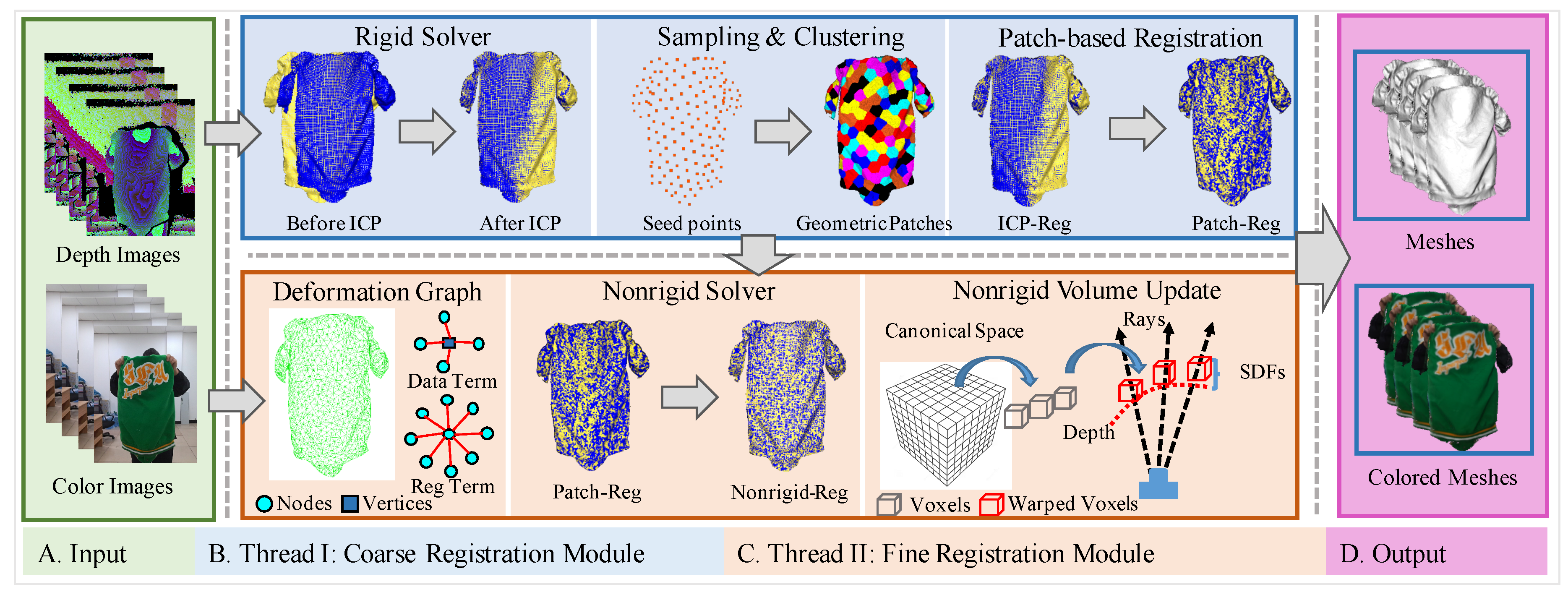
3. System Overview

3.1. Definition of Variables

In this paper, common variables are defined as follow:
  • D t - depth image at time t; C t - color image at time t.
  • u = ( v , u ) T - pixel location; u ˜ - homogeneous coordinate of u .
  • D t ( u ) - depth value at u .
  • p - continuous point in R 3 ; q - dehomogenised coordinate of p in R 2 .
  • π d - perspective projection of the depth camera.
  • π c - perspective projection of the color camera.
  • K - intrinsic matrix of depth camera.
  • T d 2 c - extrinsic matrix between depth camera and color camera.
  • T i - rigid transformation matrix of i-th node.
  • X - unknown parameter vector of all nodes.
  • x i = ( α i , β i , γ i , t i x , t i y , t i z ) T - parametrized vector of T i .
  • M t - canonical mesh at frame t; M ˜ t - warped mesh at frame t.
  • S t - rendered vertex map of M t that is predicted-to-be-visible.
  • v - vertex in R 3 from S t ; v ′ - corresponding vertex of v ; v ˜ - warped vertex of v .
  • G - embedded deformation graph consisting of nodes and edges.
  • T w 2 c - rigid transformation matrix from canonical coordinate frame to camera coordinate frame.
  • w j - influence weights; σ j - influence radius.
  • N d ( v ) - K-NN nodes of v used in data term.
  • N r ( z ) - K-NN nodes of node used in regularization term.

3.2. System Architecture

This paper presents a comprehensive approach for nonrigid tracking and reconstruction of deformable objects using data from a single RGB-D camera. Deformable objects, such as soft tissues and fabrics, exhibit intricate and dynamic deformations that pose challenges for traditional tracking and reconstruction methods. Our approach revolves around a patch-based methodology designed to dynamically adapt to the evolving shape of deformable objects. The pipeline of proposed method is depicted in Figure 2. By taking continuous depth and color images as input, our system outputs denoised meshes with high fidelity fused colors. The key components of the system consist of two parallel threads: the Thread I involves a coarse registration module, as depicted within the blue rectangular box. This thread aims at solving the patch-based transformation fields, consisting of a rigid solver for global rotation and translation, a sampling and clustering module for generating geometric patches, and a patch-based solver for individual transformations of each non-overlapping patch. The Thread II acts as an embedded deformation optimization module for the refinement of the coarse transformation fields, as depicted within the orange rectangular box. This thread involves the construction of an embedded deformation graph, a nonrigid solver based on Gauss-Newton steps, and a nonrigid volume update module. It’s worth noting that the patch-based registration is designed to run in parallel with the deformation optimization thread, enabling real-time performance and requiring minimal modifications for integration. To demonstrate the efficacy of our approach, we conduct extensive experimental evaluations comparing our method to existing techniques. The results showcase the superior performance of our RGB-D-based approach in handling fast nonrigid deformations, making it a valuable contribution to the fields of computer vision, robotics, and VR/AR content generation.

4. Methods

4.1. Preliminaries

We leverage RGB-D data to reconstruct the surface of deformable objects. The fusion of color and depth information facilitates the creation of a detailed 3D model that accurately captures the object’s shape A measurement from RGB-D sensor at time t consists of a depth map D t with depth value D t ( u ) ∈ R at each pixel location u = ( u , v ) T . The homogeneous coordinates of u is denoted by u ˜ = ( u T , 1 ) T such that p = D t ( u ) K − 1 u ˜ is the corresponding 3D point in 3D space, where p ∈ R 3 and K represents camera calibration matrix. The function q = π d ( p ) performs perspective projection of p to obtain dehomogenised coordinate.

4.2. Nonrigid Alignment as Energy Optimization

For nonrigid alignment, we adopt the embedded deformation graph (EDG) representation which is constructed and updated for each new frame [5]. A 4 × 4 rigid transform T i is assigned to each node and is parametrized through matrix exponentials based on skew-symmetric matrix theory [7], yielding fast convergence. As a result, each node has total six unknowns such that three for rotation and three for translation. For simpler notation, we stack unknowns for all nodes in a parameter vector:
X = ( x 0 T , . . . , x i T , . . . , x | Z | T ) T ,
where x i = ( α i , β i , γ i , t i x , t i y , t i z ) T with ( α i , β i , γ i ) for rotation and ( t i x , t i y , t i z ) for translation. The nonrigid alignment is formulated as a nonlinear least squares optimization problem with respect to the unknowns X . Following pioneering works [7], we define the objective based on point-to-plane data term and as-rigid-as-possible regularization term:
E t o t a l ( G , M , D t , X t ) = w d E d ( M , D t , X t ) + w r E r ( G , X t ) ,
where G denotes the node graph and M represents the canonical mesh geometry at time t − 1 . Note that G and M are updated for each subsequent frame, while time superscripts are omitted here for simplicity. D t denotes the live input depth at time t, w d and w s are balance weights for data and regularization term. E d represents a point-to-plane energy term:
E d ( M t − 1 , D t , X t ) = ∑ ( v , v ′ ) ∈ C ( n v ′ T ( v ˜ − v ′ ) ) 2 ,
where v and v ′ is a pair of correspondence, v ′ is a 3D point computed by back projecting a pixel in D t via intrinsic matrix K and n v ′ T is its normal, and C contains all correspondence pairs. The canonical vertex v is from M t − 1 , while warped vertex v ˜ is computed as follows:
v ˜ = T w 2 c ∑ j ∈ N ( v ) w j ( v , σ j ) T j t v ,
where T w 2 c represents the world-to-cam rigid transformation common to all points in canonical space, T j t is the unknown transformation matrix residing on the j-th node at time t, w j ( v , σ j ) is the weighting coefficients for neighboring nodes with pre-defined σ j controlling influence radius, and N ( v ) denotes the 4 closest neighbors of v . E r is an as-rigid-as-possible regularization term:
E r ( G , X t ) = ∑ i = 1 N Z ∑ j ∈ N ( z i ) ∥ T i t z j − T j t z j ∥ 2 2 ,
where N Z is the number of graph nodes, N ( z i ) represents the 8 closest neighbors of i-th node z i . On one hand, this regularization term prevents the motion fields from abrupt changing due to noisy depth measurements. On the other hand, only a subset of node transformations participates data term in the optimization according to the predicted-to-be-visible geometry, leaving the rest nodes unrestricted. This term plays an vital role for driving these currently invisible regions to deform as rigidly as possible.
The described nonrigid deformation objective is a nonlinear least squares problem in the unknown node transformation parameters. We employ the Gauss-Newton method that only requires first-order derivatives and exhibits quadratic convergence when close to the optimum. After linearization of X t around X t − 1 , we have the following linearized system to be solved:
J T J Δ X t = − J T r ,
where J is the Jacobian matrix evaluated at X t − 1 , Δ X t is the incremental update, and r is a residue vector.

4.3. Patch-Based Rigid Alignment

The tracking accuracy of Equation (2) is severely degenerated due to fast inter-frame motions. In such case, the initial state X t − 1 is too far from the optimum so that solving the linearized problem falls into local minima quickly. Another reason is the as-rigid-as-possible regularization term prevents the local region from deforming fast. To address this issue, we propose a novel patch-based rigid motion estimation module as a preprocessing step prior to solving Equation (2). The insight is that large inter-frame motion appears locally and rigidly which can be solved independently from the area that is far from the local area and moves relatively slowly. That is to say, the inherent motion graph is temporarily break in this preprocessing stage, facilitating the solving for fast inter-frame motion in some areas. Once the surface patching is completed on both D t − 1 and D t , patch-wise rigid ICP algorithm is applied to compute the inter-frame rigid motions for each patch. Note that, we compute the patch-wise rigid transformation fields for between adjacent depth frames instead of the warped canonical frame and current frame. The reasons are two folds. One is that we can perform this preprocessing procedure independently from the deformation optimization described in last section, opening a parallel thread for this task. Another is that resulted patch-wise motion fields between D t − 1 and D t is enough well for rigid motion compensation for deformation optimization in the following stage, though warped canonical geometry might be more smooth and complete. We adopt an improved variant version of ICP called GFOICP [11] for registering two patches from source and target frame respectively. In the context of patch-based registration, it is imperative to locate several neighboring patches in the target frame that are closest to a specific patch in the source frame. This process effectively enlarges the target patch, ensuring the preservation of valid overlaps between the patches. This dilation operation proves crucial, especially in scenarios where motion is rapid and displacements are substantial.
As shown in Figure 3, we visualize the registration results of two patches extracted from a sequence depicting waving motion, marked by red and blue boxes respectively. Two different views are employed to render the patches to be registered, with the source patch marked in yellow, the target patch in blue and the transformed source patch in red, facilitating a clearer comparison between patches before and after the registration process. Our designed patch-based registration algorithm demonstrates its effectiveness in aligning two point clouds subjected to significant displacements.

4.4. Local-to-Global Fusion

In this section, we present a mechanism for integrating locally computed, independent patch-wise rigid transformation fields into the global nonrigid deformation graph. This integration enables the system to seamlessly adapt to nonrigid deformations. The fusion process not only enhances tracking accuracy but also provides a more precise representation of the deformable object’s shape, even in scenarios characterized by rapid and complex shape changes. In addition to the transformations of individual nodes, we introduce a common rigid body transformation denoted as T w 2 c , which applies to all points in canonical space. This transformation accounts for any camera motion and factored rigid motions. Given that patch-wise transformation fields are defined and computed in live camera space, while the node transformation fields are defined and stored in canonical space, we must convert the former to the latter. This conversion process is outlined as follows:
Δ T j t v = ∑ k ∈ N ( z j ) w j ( z j ) T w 2 c − 1 T ^ k t T w 2 c v ,
where N ( z j ) represents the 4 closest patch to the j-th node z j , w j ( z j ) is similar as defined in Equation (4), and T ^ k t is the estimated rigid transformations for k-th patch obtained in last section. Instead of initializing Δ T j t as an identity transformation matrix, We employ Equation (7) to fuse and integrate patch-based motion fields, which are locally computed, into the subsequent deformation optimization process.

4.5. Implicit Surface and Rasterization

In order to reconstruct the finer geometry incrementally with more incoming depth information, we represent the underlying geometric information with the implicit surface, which is a mathematical representation in three-dimensional space define implicitly rather than explicitly. Specifically, it is described by an implicit function of the form F ( x , y , z ) = 0 , where F is a function that evaluates to zero on the surface. Point inside the surface have negative values of F, points outside have positive values, and points on the surface have zero values. This implicit representation allows for the modeling of complex shapes without explicitly defining the surface. We construct the implicit function over regular grids of 3D space following [8] using a truncated signed distance function (TSDF), denoted as S D F ( · ) . A set of descretized voxels { o i , j , k } are the sampled point in a regular grid that contains a distance value, which is initialized with depth images and subsequently updated by nonrigid registration. We assume the first depth frame defines the world coordinate system, based on which the canonical TSDF volume V is stored and update. Once the warping fields at time t is solved, we warped the voxel center o i , j , k in canonical volume nonrigidly under T w 2 c t and node-based motion fields as:
o ˜ i , j , k = T w 2 c t ∑ j ∈ N ( o i , j , k ) w j ( x ) T j t o i , j , k .
Then the signed distance values S D F ( o i , j , k ) is computed as:
S D F ( o i , j , k ) = s g n ( S D F ˜ ( o i , j , k ) ) · m i n ( | S D F ˜ ( o i , j , k ) | , t t r u n c ) ,
where t trunk represents the truncation parameter, which selectively updates voxels within a narrow shell, and S D F ˜ ( o i , j , k ) is the projective distance (along the z-axis) between the warped voxel and depth measurements D t , which is given by
S D F ˜ ( o i , j , k ) = [ o ˜ i , j , k ] z − D t ( π d ( o ˜ i , j , k ) ) .
And the updated TSDF value is given by the weighted averaging as:
S D F ′ ( o i , j , k ) = S D F ( o i , j , k ) * w ( o i , j , k ) t − 1 + S D F ˜ ( o i , j , k ) w ( o i , j , k ) t − 1 + 1 .
In order to reconstruct a colored mesh, we employ an update rule for signed distance values to update the color volume using the captured C t . Subsequently, a triangular mesh is extracted using the Marching Cubes algorithm [38] for visualization and post-processing.
Given that depth cameras can only capture a portion of the entire surface, it is advantageous to register the canonical geometry, which is predicted to be visible in the current camera coordinate frame. The advantage of this strategy avoids utilizing the entire geometry of the canonical volume, which reduces the time spent on correspondence search. Specifically, the canonical geometry is warped by the currently estimated warping fields and perspectively projected onto the live depth frame. Vertices and normals from the canonical geometry are used to shade the warped geometry. Subsequently, we rasterized the shaded geometry to produce a rendered frame denoted as S t , which stores the vertex and normal pairs of canonical geometry. This rendered frame efficiently facilitates fetching a canonical vertex v in Equation 3. Then, data association between S t and D t is computed by warping and projecting the point-normal pairs stored in S t onto the D t image plane to identify corresponding point-normal pairs according to distance and normal differences.

5. Experiments

5.1. Experiment Setup

5.1.1. Dataset

We utilize a commodity depth sensor to record sequences of dynamic scenes featuring human bodies or soft objects such as clothes or toys. In whole-body sequences, the actor stands in front of the camera at a distance of 2.0 meters to ensure capture of the entire body, facilitating rapid articulated motions. In upper-body sequences, the actor stands closer to the camera, approximately 1.2 meters away. This closer proximity enhances the accuracy of depth measurements, particularly for capturing facial details. In datasets involving clothes and objects, these items are positioned at a default distance of 1.2 meters from the camera. Additionally, we curate a dataset focusing on hand-object interactions, showcasing PatchFusion’s capability for reconstructing intricate geometry.

5.1.2. Evaluation Metrics

For evaluation purposes, reconstructing the ground truth of highly nonrigid deformable scenes poses a significant challenge. While the newly developed light stage offers a potential solution for this task, in this paper, we focus on evaluating the effectiveness of the proposed method in terms of temporal tracking accuracy. Specifically, we quantitatively assess the registration accuracy between two adjacent depth frames generated by different competing schemes. In theory, more accurate registration should lead to more precise reconstruction results. To measure the registration accuracy, we utilize an implementation in Meshlab [39], which calculates both the Root Mean Square (RMS) and maximum (MAX) values concerning the bounding box of the input point set. This allows us to gauge the performance of the proposed method quantitatively.

5.1.3. Implementation Details

Our pipeline comprises four key modules: a depth image preprocessor, a patch-based solver, a nonrigid solver, and a geometry and color volume update module. The depth image preprocessor acquires depth images via the official SDKs of the sensor and applies a bilateral filter. Each CUDA thread is dedicated to processing one pixel of the depth image to compute its 3D vertex and associated normal. This computation is performed in parallel for all pixels and takes no more than 2ms on a single GPU. We implement the rigid solver following the approach by Newcombe et al. [34], where data reduction is carried out on the GPU, and the solution of the 6x6 matrix and 6x1 vector for solving the linear system is done on the CPU. Based on the predefined sampling radius for surface patching, approximately 30-50 small patches are required to solve the rigid transformation. For the nonrigid solver, we follow the method proposed by Dou et al. [40], which involves constructing the matrix J T J and then solving the linear system J T J Δ x = − J T r . The maximum number of Gauss-Newton iterations is set to 10. However, due to the superior initialization provided by patch-based motion fields compared to solving node-based warping fields from the identity matrix, the solver typically converges in 2-3 iterations. The update of the geometry and color volume requires approximately 2-3ms per frame. By designing the patch-based solver and nonrigid solver as two major time-consuming modules running in parallel, our system achieves a processing speed of 30Hz, matching the capturing frame rate of the depth sensor. Additionally, we set the voxel size to 0.004m and the resolution of the grid to 256, forming a cube with a size of 1.024m. The sampling radius of patches is set to 0.05m, while the sampling radius of deformation nodes is set to 0.025m. We set w d = 1 and w d = 50 across all tests.

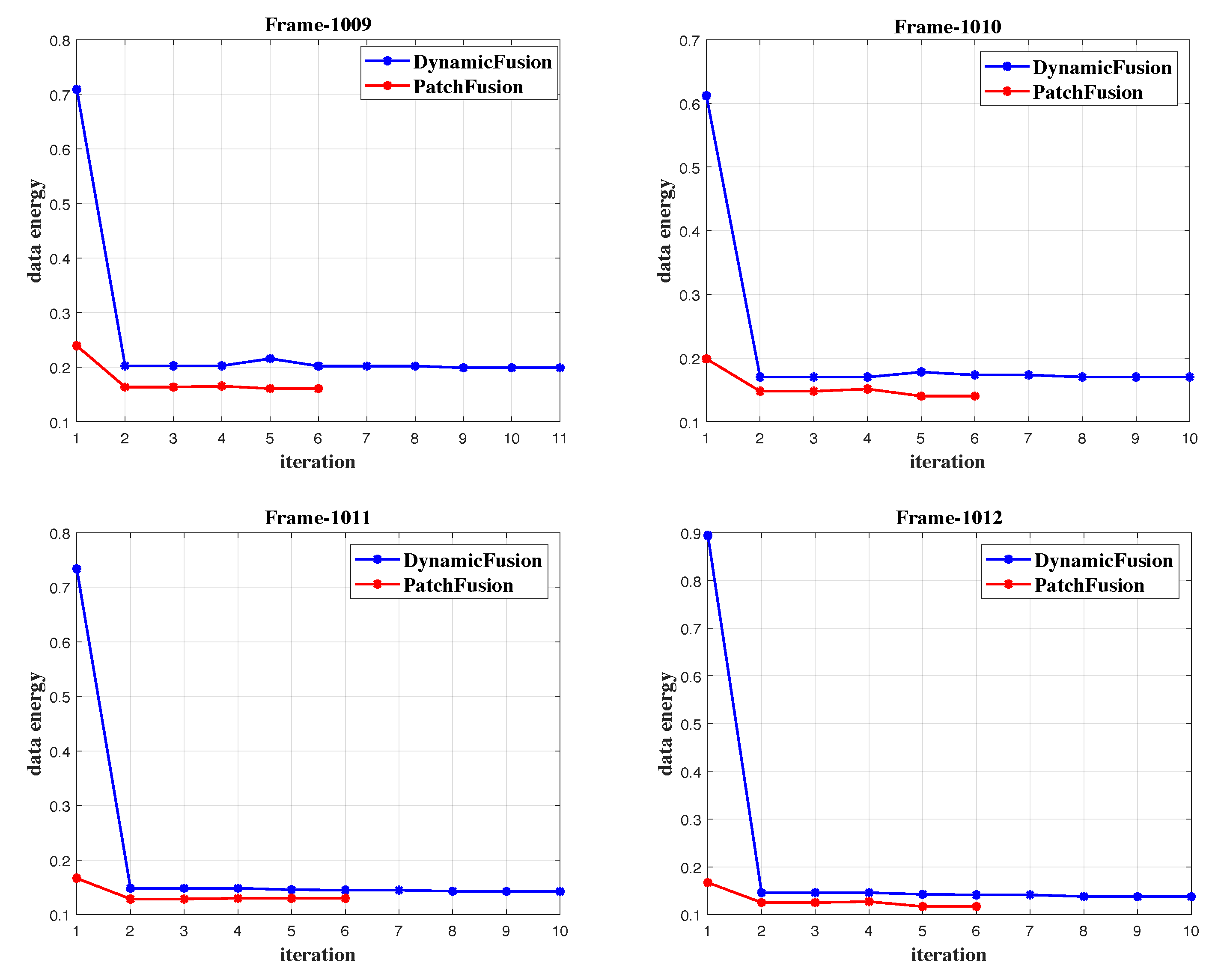
5.2. Quantative Analysis

In this section, we present a quantitative analysis of our proposed method for registering two consecutive depth frames. Evaluating the performance of our registration algorithm is crucial for assessing its accuracy and robustness in tracking-based reconstruction. We configure several competing schemes for evaluation, including rigid-ICP, nonrigid-ICP, and patch-ICP. The rigid-ICP estimates a single rigid transformation, while nonrigid-ICP involves estimating a set of rigid transformations, with the final warping fields interpolated following the implementations of DynamicFusion [5]. Patch-ICP utilizes a patch-based registration module proposed in Section 4.3. We conduct experiments on four human body sequences and two hand-interacting object sequences. Our proposed method outperforms the competing schemes with a significant improvement in both RMS and MAX errors, as reported in Table 1.

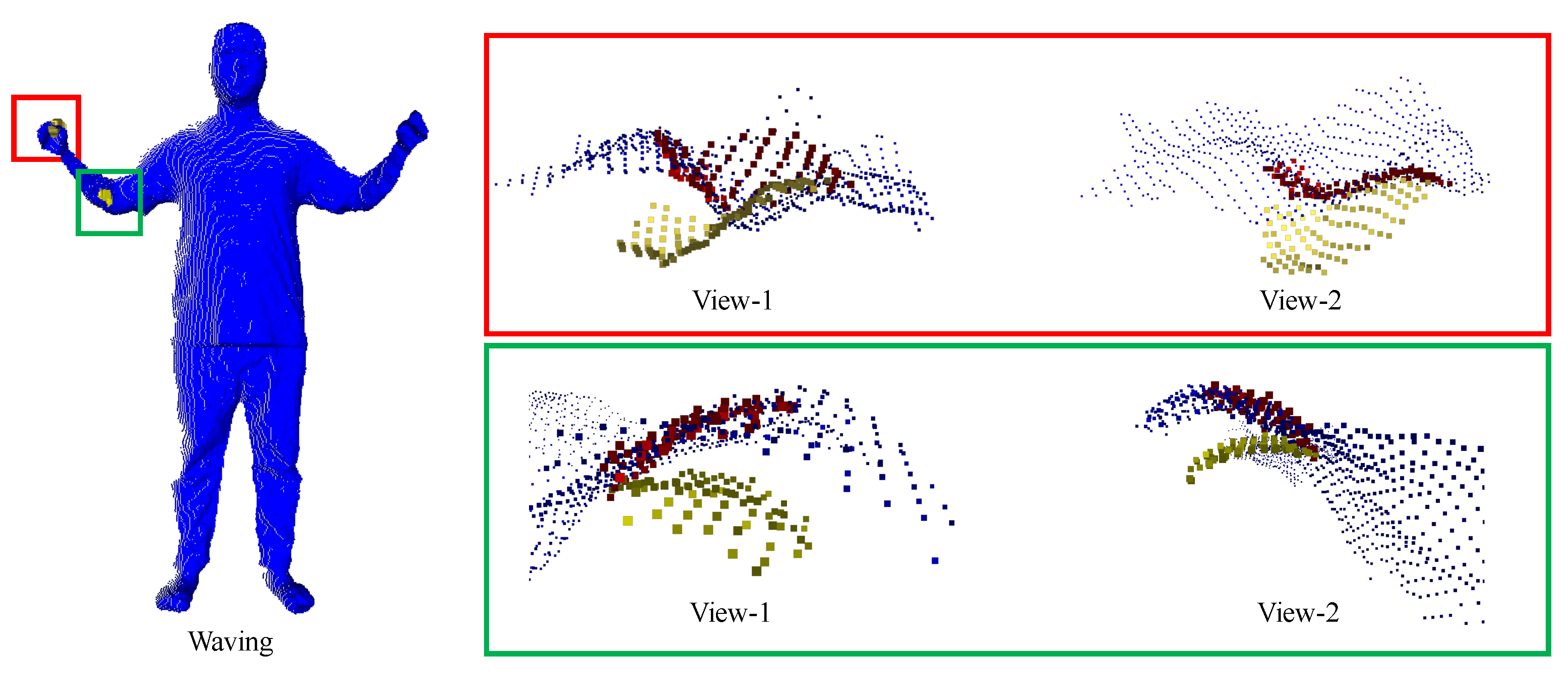
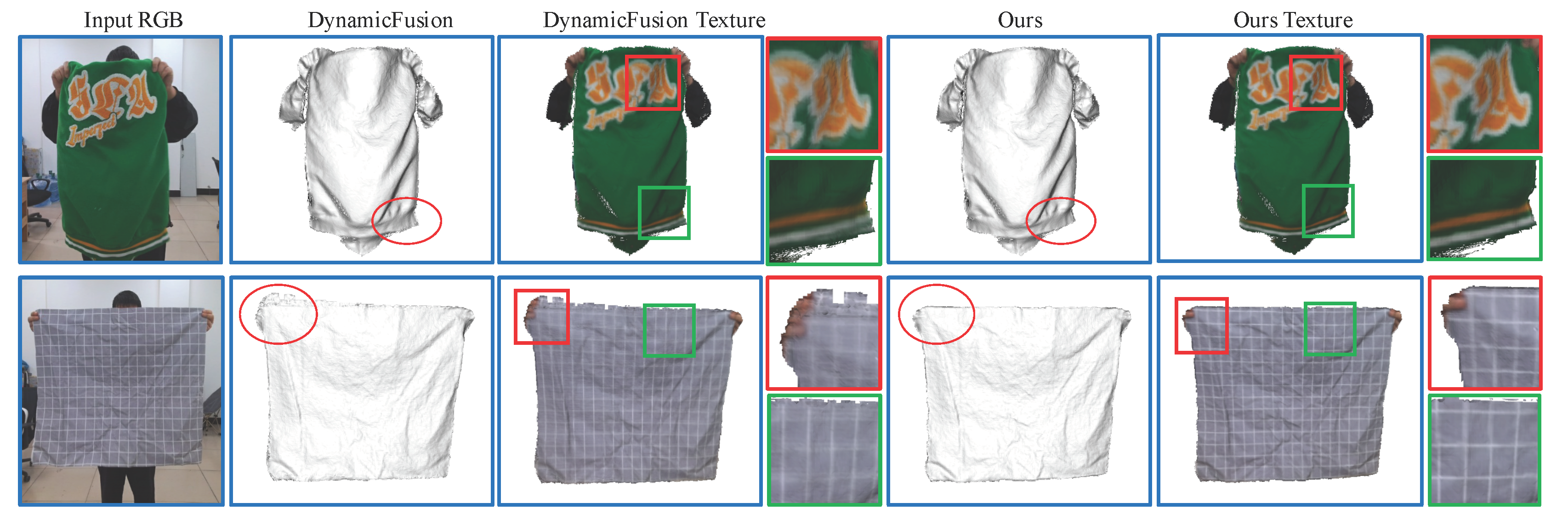
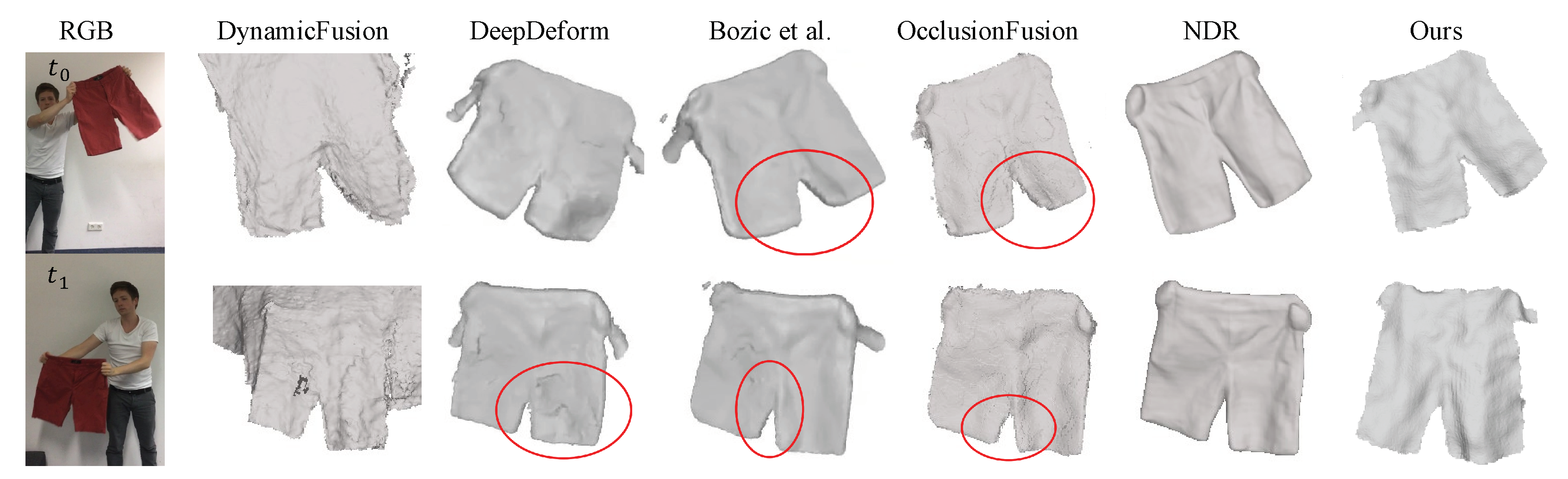
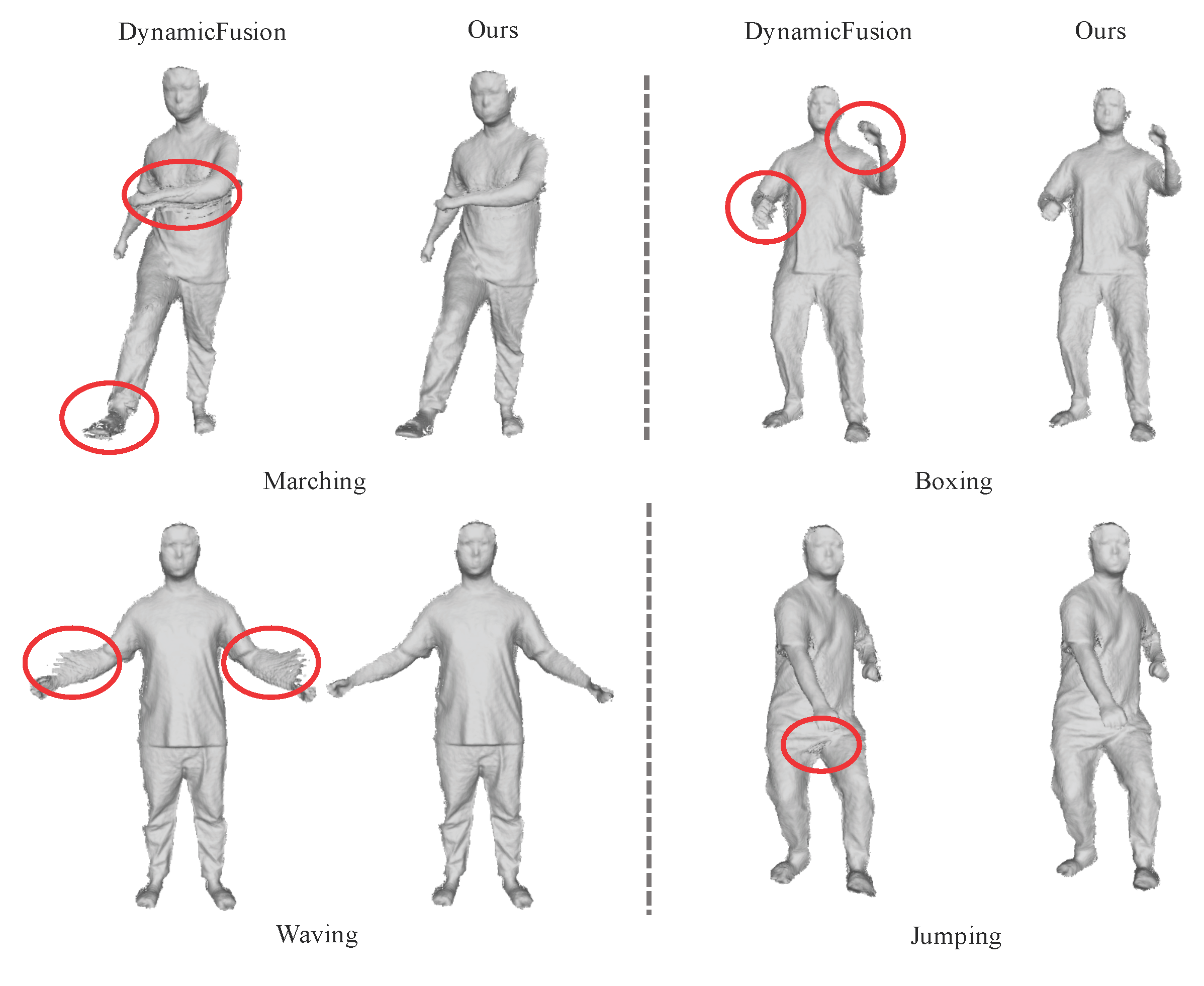
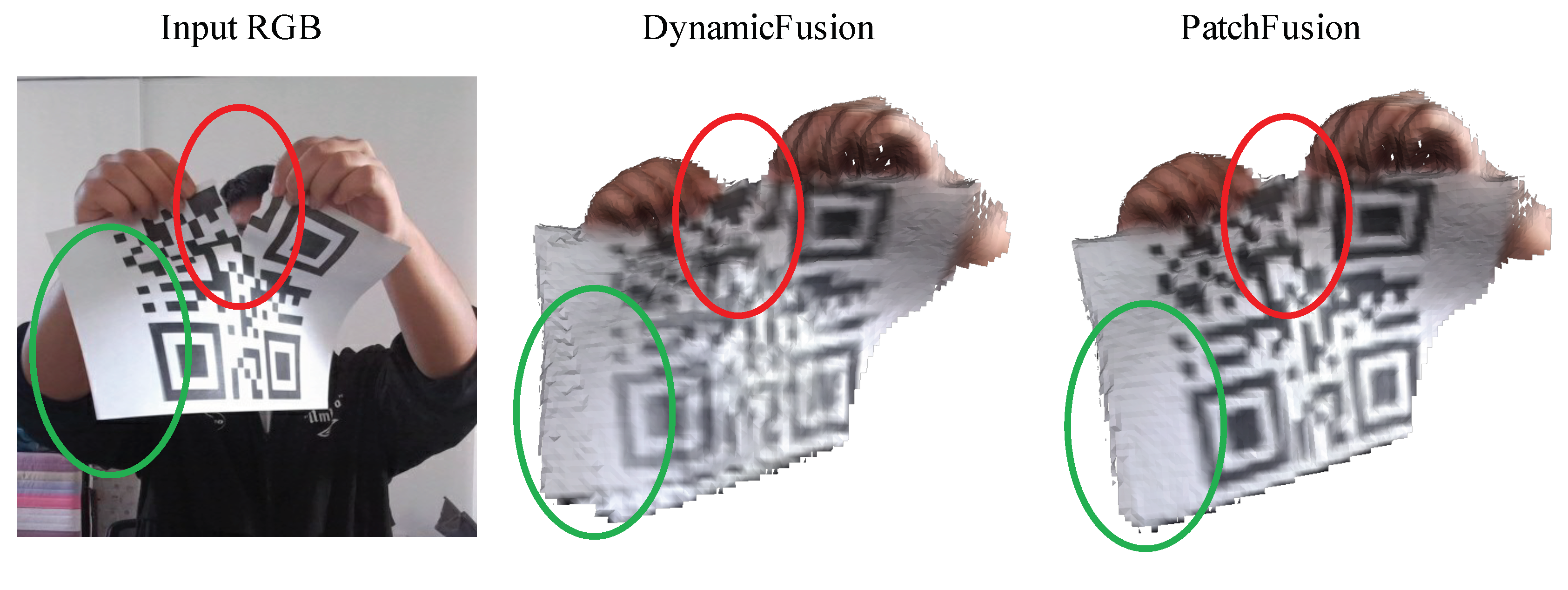
5.3. Qualitative Comparison Results

In this section, we present various dynamic scenes reconstructed using our proposed method, showcasing its improved performance and robustness, especially for fast inter-frame motions. We compare our method with several state-of-the-art RGBD-based reconstruction techniques, including DynamicFusion [5], DeepDeform [41], Bozic et al. [42], OcclusionFusion [43], and NDR [44]. Initially, we integrate the color volume update into both DynamicFusion and our proposed framework. Although both methods utilize geometric information for tracking, integrating color information into the visualization can effectively reveal tracking accuracy. By testing on two hand-interacting sequences captured by our own RGB-D sensor, our method achieves more accurate tracking results, resulting in sharper textures. As shown in Figure 4, blurry results, observed in the alphabet on the jacket and the grid texture of the tablecloth, highlight the challenges faced in tracking when capturing objects subjected to fast nonrigid deformations. Furthermore, we conduct experiments on a public dataset called DeepDeform [41], and select one of the hand-interacting object sequences for comparison with recent advances in deep learning-based reconstruction methods. As illustrated in Figure 5, our method outperforms DynamicFusion and DeepDeform in terms of tracking accuracy and the quality of reconstructed surfaces. It achieves comparable tracking robustness as Boizc et al. and NDR. While NDR produces finer geometric structures by employing high-resolution RGB cues, our method requires only depth input, making it a more lightweight solution adaptable to textureless objects. In addition to hand-interacting objects, we also conduct experiments on another crucial scenario involving deformable scenes: articulated human body datasets. We capture an avatar performing various actions, including marching, boxing, waving, and jumping. All of these actions involve fast inter-frame motions, posing significant challenges for tracking and reconstruction tasks. As depicted in Figure 6, the reconstruction results from DynamicFusion present noticeable artifacts around the arms and feet during fast motions. In contrast, our method achieves more stable reconstruction results in such scenarios.

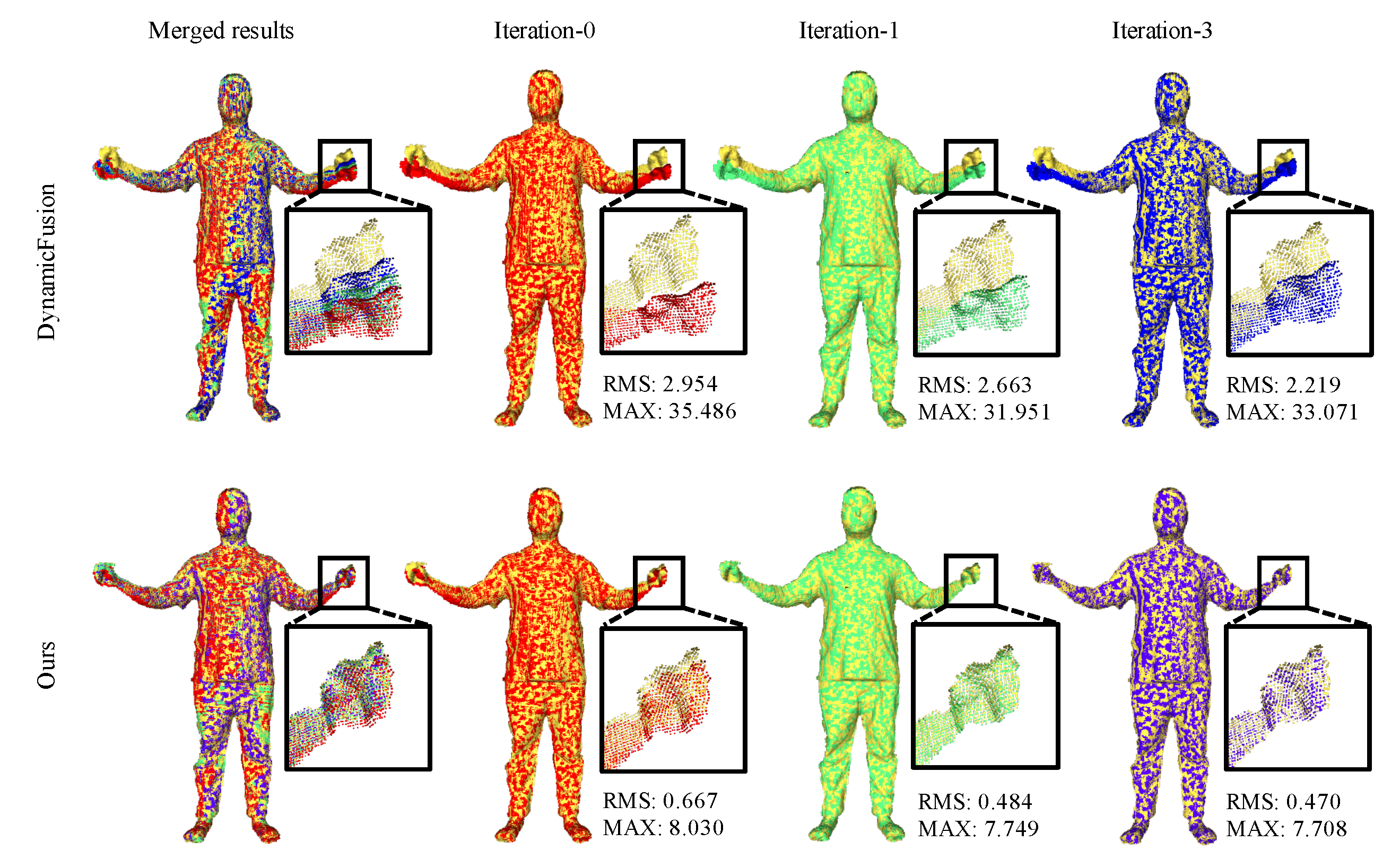
5.4. Ablations of Patch-Based Registration

In this section, we demonstrate the effectiveness of our proposed patch-based registration module compared to DynamicFusion, which only operates deformation optimization. The test sequence features a human body with rapid articulated motion around the arms, posing a challenging scenario for tracking-based reconstruction algorithms. As shown in Figure 7, the live input point set, computed by back-projecting the 2D depth frame into 3D space, is marked in yellow, while the warped point sets are computed by warping the canonical point set with the current estimated warping fields, marked by red, green, and blue respectively. We iterate over 3 outer loops, updating data associations between canonical frames and current input frames according to the newly computed warping fields, and perform Gauss-Newton steps within each outer loop with fixed data associations. The DynamicFusion algorithm struggles to recover the rapid articulated motion, leading to obvious registration errors. In Iteration-0 of DynamicFusion, the displacements mainly occur around the hands and wrists due to fast articulated motion, while the main body remains static. This discrepancy arises because the closest point search fails to find correct correspondences, causing the optimization to fall into local minima. Additionally, the As-Rigid-As-Possible (ARAP) regularization term tends to constrain the wrists and hands to move together with the static body with slight motions, leading to rapid convergence into local minima. In contrast, our proposed approach’s patch-based registration module computes coarse rigid transformations individually for each patch, fully respecting local large displacements. Furthermore, we introduce feature-based similarity in both correspondence matching and objective optimization to enhance registration robustness and accuracy. Overall, our patch-based registration module computes coarse transformation fields that roughly align the two point sets, making the refinement process of deformation optimization more robust. As observed in the bottom right inset, the two point sets align very well. Our proposed method outperforms the competing scheme with a significant improvement in both RMS and MAX errors, as reported in the figure. Additionally, we visualize the data energy versus Gauss-Newton iterations in Figure 8 for the Tablecloth sequence from frame number 1009 to 1012, comparing the convergence performance of DynamicFusion and our method. The initial registration error is dramatically reduced via our proposed patch-based registration module, thereby enabling the subsequent deformation optimization thread to achieve more accurate registration results. Furthermore, our method converges faster, typically requiring only two Gauss-Newton iterations within each outer loop, which is set to 3. However, DynamicFusion needs 3-4 iterations to meet the preset stop condition in each loop.

5.5. System Limitations and Future Work

This section discusses the limitations of our proposed method and outlines potential areas for future research. The first category of failure cases involves tracking planar objects. Since our method relies solely on geometric information and does not utilize color data, it becomes challenging to accurately track planar objects with translational motion. As illustrated in Figure 9, when attempting to track a planar object, such as a chessboard, the reconstructed texture often appears severely blurred. Another class of failure cases arises when the captured object undergoes topology changes, as depicted in Figure 10. For instance, when a paper with a QR code is torn apart, our method struggles to handle such topology changes. This challenge emerges because the canonical volume initialized by previous depth frames assumes the geometry and topology of a complete object, whereas the live capture may exhibit topology changes. Consequently, the resulting warped model maintains the same topology as the canonical geometry, leading to an inability to accurately reconstruct the gap caused by tearing.
Despite these limitations, our proposed method demonstrates superior tracking accuracy in local areas, as highlighted by the green ellipsoid, compared to existing approaches like DynamicFusion. In future work, we aim to leverage the high-resolution RGB images provided by RGB-D sensors. We plan to incorporate high-resolution cues such as sparse 2D features, dense photometric terms, and intrinsic scene parameters like albedo to enhance tracking performance. Additionally, we intend to explore existing techniques designed for topology-change-aware tracking systems [45,46] and integrate them into our method, thereby enabling its applicability in scenarios involving topology changes.

6. Conclusions

In conclusion, PatchFusion presents an innovative approach for nonrigid tracking and reconstruction of deformable objects using a single RGB-D sensor. By addressing the challenges associated with capturing rapid deformations of soft and flexible objects, PatchFusion offers a robust and accurate solution applicable across diverse scenarios. The dynamic patch-based framework, coupled with patch-wise rigid transformation fields and deformation optimization running in parallel, enables efficient tracking and reconstruction in real-time. Through comprehensive evaluation, PatchFusion demonstrates superior performance compared to existing RGB-D based reocnstruction methods especially for addressing fast inter-frame motions.

References

  1. Fuster-Guilló, A.; Azorin-Lopez, J.; Saval-Calvo, M.; Castillo-Zaragoza, J.M.; Garcia-D’Urso, N.; Fisher, R.B. RGB-D-based framework to acquire, visualize and measure the human body for dietetic treatments. Sensors 2020, 20, 3690. [Google Scholar] [CrossRef]
  2. Darwish, W.; Tang, S.; Li, W.; Chen, W. A new calibration method for commercial RGB-D sensors. Sensors 2017, 17, 1204. [Google Scholar] [CrossRef] [PubMed]
  3. Mai, C.; Chen, H.; Zeng, L.; Li, Z.; Liu, G.; Qiao, Z.; Qu, Y.; Li, L.; Li, L. A Smart Cane Based on 2D LiDAR and RGB-D Camera Sensor-Realizing Navigation and Obstacle Recognition. Sensors 2024, 24, 870. [Google Scholar] [CrossRef]
  4. Zollhöfer, M.; Nießner, M.; Izadi, S.; Rehmann, C.; Zach, C.; Fisher, M.; Wu, C.; Fitzgibbon, A.; Loop, C.; Theobalt, C.; others. Real-time non-rigid reconstruction using an RGB-D camera. ACM Transactions on Graphics (ToG) 2014, 33, 1–12. [Google Scholar] [CrossRef]
  5. Newcombe, R.A.; Fox, D.; Seitz, S.M. Dynamicfusion: Reconstruction and tracking of non-rigid scenes in real-time. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 343–352.
  6. Innmann, M.; Zollhöfer, M.; Nießner, M.; Theobalt, C.; Stamminger, M. Volumedeform: Real-time volumetric non-rigid reconstruction. European conference on computer vision. Springer, 2016, pp. 362–379.
  7. Guo, K.; Xu, F.; Yu, T.; Liu, X.; Dai, Q.; Liu, Y. Real-time geometry, albedo, and motion reconstruction using a single rgb-d camera. ACM Transactions on Graphics (ToG) 2017, 36, 1. [Google Scholar] [CrossRef]
  8. Curless, B.; Levoy, M. A volumetric method for building complex models from range images. Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, 1996, pp. 303–312.
  9. Sumner, R.W.; Schmid, J.; Pauly, M. Embedded deformation for shape manipulation. In ACM siggraph 2007 papers; 2007; p. 80–es. [Google Scholar]
  10. Yan, J.; Pollefeys, M. A factorization-based approach for articulated nonrigid shape, motion and kinematic chain recovery from video. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008, 30, 865–877. [Google Scholar] [CrossRef]
  11. He, L.; Wang, S.; Hu, Q.; Cai, Q.; Li, M.; Bai, Y.; Wu, K.; Xiang, B. GFOICP: Geometric Feature Optimized Iterative Closest Point for 3D Point Cloud Registration. IEEE Transactions on Geoscience and Remote Sensing 2023. [Google Scholar] [CrossRef]
  12. Jiang, M.; Zhang, L.; Wang, X.; Li, S.; Jiao, Y. 6D Object Pose Estimation Based on Cross-Modality Feature Fusion. Sensors 2023, 23, 8088. [Google Scholar] [CrossRef] [PubMed]
  13. Kang, C.; Geng, C.; Lin, Z.; Zhang, S.; Zhang, S.; Wang, S. Point Cloud Registration Method Based on Geometric Constraint and Transformation Evaluation. Sensors 2024, 24, 1853. [Google Scholar] [CrossRef]
  14. Hu, X.; Zhang, D.; Chen, J.; Wu, Y.; Chen, Y. Nrtnet: An unsupervised method for 3d non-rigid point cloud registration based on transformer. Sensors 2022, 22, 5128. [Google Scholar] [CrossRef]
  15. Xu, Y.; Li, J.; Du, C.; Chen, H. Nbr-net: A nonrigid bidirectional registration network for multitemporal remote sensing images. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–15. [Google Scholar] [CrossRef]
  16. Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Sensor fusion IV: control paradigms and data structures. Spie, 1992, Vol. 1611, pp. 586–606.
  17. Maken, F.A.; Ramos, F.; Ott, L. Stein ICP for uncertainty estimation in point cloud matching. IEEE robotics and automation letters 2021, 7, 1063–1070. [Google Scholar] [CrossRef]
  18. Anderson, J.D.; Raettig, R.M.; Larson, J.; Nykl, S.L.; Taylor, C.N.; Wischgoll, T. Delaunay walk for fast nearest neighbor: accelerating correspondence matching for ICP. Machine Vision and Applications 2022, 33, 31. [Google Scholar] [CrossRef]
  19. Rusinkiewicz, S. A symmetric objective function for ICP. ACM Transactions on Graphics (TOG) 2019, 38, 1–7. [Google Scholar] [CrossRef]
  20. Zhang, J.; Yao, Y.; Deng, B. Fast and robust iterative closest point. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 44, 3450–3466. [Google Scholar] [CrossRef]
  21. Cagniart, C.; Boyer, E.; Ilic, S. Free-form mesh tracking: a patch-based approach. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2010, pp. 1339–1346.
  22. Zhao, B.; Lin, W.; Lv, C. Fine-grained patch segmentation and rasterization for 3-d point cloud attribute compression. IEEE Transactions on Circuits and Systems for Video Technology 2021, 31, 4590–4602. [Google Scholar] [CrossRef]
  23. Liu, H.; Xiong, R.; Liu, D.; Ma, S.; Wu, F.; Gao, W. Image denoising via low rank regularization exploiting intra and inter patch correlation. IEEE Transactions on Circuits and Systems for Video Technology 2017, 28, 3321–3332. [Google Scholar] [CrossRef]
  24. Lee, J.H.; Ha, H.; Dong, Y.; Tong, X.; Kim, M.H. Texturefusion: High-quality texture acquisition for real-time rgb-d scanning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 1272–1280.
  25. Kwon, J.; Lee, K.M. Highly nonrigid object tracking via patch-based dynamic appearance modeling. IEEE transactions on pattern analysis and machine intelligence 2013, 35, 2427–2441. [Google Scholar] [CrossRef]
  26. Fayad, J.; Agapito, L.; Del Bue, A. Piecewise quadratic reconstruction of non-rigid surfaces from monocular sequences. European conference on computer vision. Springer, 2010, pp. 297–310.
  27. Locher, A.; Perdoch, M.; Van Gool, L. Progressive prioritized multi-view stereo. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 3244–3252.
  28. Zhang, J.; Yao, Y.; Quan, L. Learning signed distance field for multi-view surface reconstruction. 2021 IEEE. CVF International Conference on Computer Vision (ICCV), 2021, pp. 6505–6514.
  29. Huang, M.; Li, X.; Hu, J.; Peng, H.; Lyu, S. Tracking Multiple Deformable Objects in Egocentric Videos. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 1461–1471.
  30. Tang, T.; Fan, Y.; Lin, H.C.; Tomizuka, M. State estimation for deformable objects by point registration and dynamic simulation. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017, pp. 2427–2433.
  31. Yu, T.; Guo, K.; Xu, F.; Dong, Y.; Su, Z.; Zhao, J.; Li, J.; Dai, Q.; Liu, Y. Bodyfusion: Real-time capture of human motion and surface geometry using a single depth camera. Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 910–919.
  32. Yu, T.; Zheng, Z.; Guo, K.; Zhao, J.; Dai, Q.; Li, H.; Pons-Moll, G.; Liu, Y. Doublefusion: Real-time capture of human performances with inner body shapes from a single depth sensor. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 7287–7296.
  33. Zuo, X.; Wang, S.; Zheng, J.; Yu, W.; Gong, M.; Yang, R.; Cheng, L. Sparsefusion: Dynamic human avatar modeling from sparse rgbd images. IEEE Transactions on Multimedia 2020, 23, 1617–1629. [Google Scholar] [CrossRef]
  34. Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. Kinectfusion: Real-time dense surface mapping and tracking. 2011 10th IEEE international symposium on mixed and augmented reality. Ieee, 2011, pp. 127–136.
  35. Ondrúška, P.; Kohli, P.; Izadi, S. Mobilefusion: Real-time volumetric surface reconstruction and dense tracking on mobile phones. IEEE transactions on visualization and computer graphics 2015, 21, 1251–1258. [Google Scholar] [CrossRef]
  36. Slavcheva, M.; Baust, M.; Cremers, D.; Ilic, S. Killingfusion: Non-rigid 3d reconstruction without correspondences. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 1386–1395.
  37. Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graphics (Proc. SIGGRAPH Asia) 2015, 34, 248:1–248:16. [Google Scholar] [CrossRef]
  38. Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. In Seminal graphics: pioneering efforts that shaped the field; 1998; pp. 347–353.
  39. Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: an Open-Source Mesh Processing Tool. Eurographics Italian Chapter Conference; Scarano, V.; Chiara, R.D.; Erra, U., Eds. The Eurographics Association, 2008. [CrossRef]
  40. Dou, M.; Khamis, S.; Degtyarev, Y.; Davidson, P.; Fanello, S.R.; Kowdle, A.; Escolano, S.O.; Rhemann, C.; Kim, D.; Taylor, J.; others. Fusion4d: Real-time performance capture of challenging scenes. ACM Transactions on Graphics (ToG) 2016, 35, 1–13. [Google Scholar] [CrossRef]
  41. Bozic, A.; Zollhofer, M.; Theobalt, C.; Nießner, M. Deepdeform: Learning non-rigid rgb-d reconstruction with semi-supervised data. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 7002–7012.
  42. Bozic, A.; Palafox, P.; Zollhöfer, M.; Dai, A.; Thies, J.; Nießner, M. Neural non-rigid tracking. Advances in Neural Information Processing Systems 2020, 33, 18727–18737. [Google Scholar]
  43. Lin, W.; Zheng, C.; Yong, J.H.; Xu, F. Occlusionfusion: Occlusion-aware motion estimation for real-time dynamic 3d reconstruction. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 1736–1745.
  44. Cai, H.; Feng, W.; Feng, X.; Wang, Y.; Zhang, J. Neural surface reconstruction of dynamic scenes with monocular rgb-d camera. Advances in Neural Information Processing Systems 2022, 35, 967–981. [Google Scholar]
  45. Zampogiannis, K.; Fermüller, C.; Aloimonos, Y. Topology-aware non-rigid point cloud registration. IEEE Transactions on Pattern Analysis and Machine Intelligence 2019, 43, 1056–1069. [Google Scholar] [CrossRef]
  46. Li, C.; Guo, X. Topology-change-aware volumetric fusion for dynamic scene reconstruction. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XVI 16. Springer, 2020, pp. 258–274.

Short Biography of Authors

Preprints 102293 i001 Mingyuan Zhao received the M.S. degree from Tsinghua University, Beijing, China, in 2018. He is currently pursuing the Ph.D. degree with National Astronomical Observatories, Chinese Academy of Sciences, Beijing, China. His research interests include image/video/point cloud compression and processing, and 3D reconstruction.
Preprints 102293 i002 Xuexin Yu received the Ph.D. degree in astronomical technology and methods from the National Astronomical Observatories, Chinese Academy of Sciences, Beijing, China, in 2022. Currently, he is a Postdoc with the Department of Automation, Tsinghua University. His current research interests include deep learning and computer vision.
Preprints 102293 i003 Long Xu (Senior Member, IEEE) received his M.S. degree in applied mathematics from Xidian University, Xi’an, China, in 2002, and the Ph.D. degree from the Institute of Computing Technology, Chinese Academy of Sciences, Beijing, China. He was a Postdoc with the Department of Computer Science, City University of Hong Kong, the Department of Electronic Engineering, Chinese University of Hong Kong, from July Aug. 2009 to Dec. 2012. From Jan. 2013 to March 2014, he was a Postdoc with the School of Computer Engineering, Nanyang Technological University, Singapore. Currently, he is with the Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences. His research interests include image/video processing, solar radio astronomy, wavelet, machine learning, and computer vision. He was selected into the 100-Talents Plan, Chinese Academy of Sciences, 2014.
Preprints 102293 g002
Figure 2. Pipeline of proposed method.
Figure 2. Pipeline of proposed method.
Preprints 102293 g002
Preprints 102293 g003
Figure 3. Patch-wise registration based on an improved variant of ICP.
Figure 3. Patch-wise registration based on an improved variant of ICP.
Preprints 102293 g003
Preprints 102293 g004
Figure 4. Comparison results of our own captured hand-interacting objects.
Figure 4. Comparison results of our own captured hand-interacting objects.
Preprints 102293 g004
Preprints 102293 g005
Figure 5. Comparison results on a sequence from DeepDeform [41] dataset.
Figure 5. Comparison results on a sequence from DeepDeform [41] dataset.
Preprints 102293 g005
Preprints 102293 g006
Figure 6. Dynamic tracking and reconstruction results on four challenging articulated human body sequences.
Figure 6. Dynamic tracking and reconstruction results on four challenging articulated human body sequences.
Preprints 102293 g006
Preprints 102293 g007
Figure 7. Ablation results of canonical point set (source) and live input point set (target) during 3 Gauss-Newton iterations.
Figure 7. Ablation results of canonical point set (source) and live input point set (target) during 3 Gauss-Newton iterations.
Preprints 102293 g007
Preprints 102293 g008
Figure 8. Convergence analysis of four frames from Tablecloth sequence.
Figure 8. Convergence analysis of four frames from Tablecloth sequence.
Preprints 102293 g008
Preprints 102293 g009
Figure 9. Blurry results on planar object reconstruction.
Figure 9. Blurry results on planar object reconstruction.
Preprints 102293 g009
Preprints 102293 g010
Figure 10. Failure case of paper-tearing sequence due to topology change.
Figure 10. Failure case of paper-tearing sequence due to topology change.
Preprints 102293 g010
Table 1. Registration results on adjacent two frames. The best result of each sequence is marked in bold and the units of RMS and MAX errors are millimeters.
Table 1. Registration results on adjacent two frames. The best result of each sequence is marked in bold and the units of RMS and MAX errors are millimeters.
Input ICP Nonrigid-ICP Patch-ICP Ours
max↓ RMS↓ max↓ RMS↓ max↓ RMS↓ max↓ RMS↓
Marching 17.610 2.306 18.950 1.366 15.244 1.382 16.081 1.230
Boxing 23.210 3.955 19.227 1.642 22.014 1.774 20.723 1.597
Waving 33.528 3.850 20.086 1.406 18.886 1.622 17.196 1.241
Jumping 27.100 1.816 26.761 1.464 24.475 1.390 23.819 1.316
Jacket 16.127 1.817 15.895 0.911 14.460 0.939 13.663 0.869
Tablecloth 23.575 3.915 16.165 1.099 16.576 1.201 15.989 1.013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated