Preprint
Article
Atomistic Simulations of Defect Structures in Rare Earth Doped Magnesium Oxide
Altmetrics
Downloads
78
Views
64
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 March 2024
Posted:
28 March 2024
You are already at the latest version
Alerts
Abstract
Point defects induced by doping rare earth elements RE (Nd, Er) into the magnesium oxide host were investigated by classical atomistic simulations utilising the General Utility Lattice Program (GULP). Formation and association energies were calculated for the potential defect structures. Both isolated defects and defect complexes were considered. The most energetically favourable structures of defect complexes were found for rare earth doped and Li co-doped systems. The correlation between the association energy and the structure of the defect complex was investigated. The influences of Li were revealed with respect to energy and structure. The simulation results contribute to the understanding of the point defects of doped MgO and how Li influences the doping of rare earth elements in the MgO host.
Keywords:
Subject: Chemistry and Materials Science - Electronic, Optical and Magnetic Materials
1. Introduction
Magnesium oxide (MgO) has been used in a range of engineering fields such as electronics, catalysts, and medicine. Studies have been developing in both nanoparticle and bulk scales for decades.[1,2,3,4,5,6,7,8] Attributed to the symmetrical cubic crystal structure, which is the same as NaCl crystal, its potential in optical applications has drawn great research interest recently, especially in ceramics doped with rare earth elements (RE). One of the main drivers of studies on the doped polycrystalline materials is the potentially high doping concentration of optical center’s compared to single crystals, besides the relatively higher efficiency from points of both economy and energy in powder synthesis and bulk fabrication processes. Partially inspired by successful applications and developments of popular solid-state Nd doped Y3Al5O12 (YAG) laser materials, explorations on rare earth doped MgO have gained attention. But some unsolved problems rigidly impede the development of rare earth doped optical crystalline materials, such as luminescence quenching, complexities induced by co-doping, effects of doping on thermal and mechanical properties. However, our understanding and insight into the energetics and the defective structures of the rare earth dopants and co-dopants in a host are still limited. Thus, the relevant investigations are pressingly necessary.
Lithium (Li) ion was reported to contribute to the optical properties of oxide materials doped with rare earth ions, functioning as a co-activator or charge compensator. Orante Barrn[9] investigated Ce3+ doped MgO with Li as a co-dopant. Li co-doping was found to improve the luminescence intensities significantly. Li’s substitution on the Mg cation site was indicated as an essential factor that induced the improvement in optical performance, but the detailed defect structure and its formation mechanism remained unclear. Feng Gu[10] synthesised Eu: MgO nano-crystallites with the combustion method, and the photoluminescence intensity and crystallinity were enhanced after introducing Li as a co-dopant. Sivasankari[11] studied alkali co-doped (Na, K, Li) Er: MgO. The sample with Li co-dopant was found to have smaller FWHM (Full Width at Half Maximum) values, with peak profile changes in the X-ray diffraction pattern, indicating that the crystallinity was improved. Dorel Crisan et al.[12] synthesised Nd2O3 - MgO two phase systems with the chemical sol-gel method. Calculations on the mass of unit cell showed that almost no change was observed in the MgO host when introducing Nd2O3 as the impurity, meaning there was no ionic exchange. It was suggested that vacancies and ionic exchange reactions compete within the unit cell. Whether they were cation or anion vacancies, or specific ionic substitutions was not clarified. Nevertheless, it indeed indicated a particular difficulty for Nd doping into MgO. According to Oliveira[6], Li improves luminescence intensities in Nd: MgO. It was proposed that Li may provide charge compensation for neighbouring Nd. However, it was not clear how the proposed role of Li accounts for the change in the optical emissions of Nd in the sample. Nd: MgO and Er: MgO bulk transparent ceramics were investigated by Sanamyan[13] for potential laser applications. Li was found to be directly beneficial for dopants to enter the host. And Er, Li: MgO was found to exhibit better visible transparency than Nd, Li: MgO.
Due to the difficulties and complexities of characterizing defects in materials at atomic scale, using atomistic simulations, a well-established tool from a theoretical basis, which will enable us to investigate defects at atomic scale, is necessary. Various simulation methodologies have been applied for crystalline MgO[14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] as listed in Table 1. (DFT: Density Functional Theory; LDA: Local Density Approximation; GGA: Generalized Gradient Approximation; MD: Molecular Dynamics; AIMD: Ab initio Molecular Dynamics; QMC: Quantum Monte Carlo)
Intrinsic defects have been the primary research focus. There is lack of pertinent research on the topic regarding the defect chemistry of rare earth elements in crystalline MgO. In this paper, a systematic investigation of defects and defect structures was approached primarily for Nd: MgO and Nd, Li: MgO with a focus on point defects and defect complexes. A comparison with Er: MgO and Er, Li: MgO was conducted.
2. Simulation Methodology
The program employed for current simulations is the General Utility Lattice Program (GULP), which is based on classical force field methods. The original code of this program was designed for the fitting of interaction potentials to experimental data or energy surfaces. Up to date, comprehensive expansions enable it to be a general code for modelling condensed materials, solids (especially ionic materials), clusters, embedded defects and so on.[37] As for current simulations, the static lattice method[38] has been the primary simulation methodology applied and are outlined below.
In the static lattice method, interactions between atoms are modelled by a series of functions with unique parameters depending on the nature of interactions between the different atoms. An approximation in classical static/dynamical lattice theory is pairwise additivity. That is in a system containing two or more atoms, the energy of the system can be described by the interaction in pairs, summation of two body interactions.[39] In principle, the energy of a many-body systems consists of two-body interactions, three-body interactions, four-body interactions and so on. But the two-body interactions (long range Coulombic interaction and short range interations) have the largest contributions to the total energy of the systen. Therefore, under the pairwise additivity approximation, the energy of a many-body system can be expressed as:
where is the two-body interaction as a function of the distance between ions. For materials that are considered purely ionic, the lattice energy calculations contain both long-range and short-range interactions, namely, electrostatic interaction (Coulomb term), London interaction, which is also known as Van Der Waals (or called dispersion interaction for historical reasons), and repulsion term considering Pauli exclusion rules from the effects of overlapping electron densities. The lattice energy expressed by three interaction terms (two-body interations) is:
The repulsion term is expressed in the exponential Born-Mayer form, and it can be combined with the dispersive term, which is induced by interactions between the instantaneous dipole moments and their induced instantaneous dipole moments. The two short-range terms combined are known as the Buckingham potential, which was used in current calculations. The two-body Buckingham potential is mathematically expressed as:
A, and C6 are the Buckingham parameters. In practice, it is computationally impractical to include interactions between all atoms in the solid as the number of atoms are on a scale of 1023 and Buckingham interations rapidly diminish with interatomic distance. To strike a balance between efficiency and accuracy, distance cut-offs are introduced. Typically, a value of 5 - 10 Å is used. A cut-off distance of 10 Å and 12 Å were set for cation-oxygen and oxygen-oxygen potentials, respectively, in current simulations. The Ewald Summation method is employed in the calculations of electrostatic interactions due to the slow convergence of 1/r summations. The arrangement of ions in the system is then determined by energy minimization processes with respect to all relevant structure factors, unit cell parameters and atomic coordinates.[38]
Atoms are treated as point ions, with the core-shell model proposed by Dick and Overhauser[40] to account for the polarisability of ions. The shell model mimics an ion’s polarisability by defining an ion as an entity consisting of a shell and a core that interact through the spring constant . If the charges distributed on the shell of the ion are , the polarisability of the free ion can be expressed as:
The sum of the core and shell charges is equal to the formal oxidation state of respective ions. If all charges are on the core, the atom is considered to be unpolarisable. In the current simulations, the cationic core possesses formal charges, and the charge distributions of O2- are 0.869 e and -2.869 e on the core and shell, respectively. of O2- is 74.9.
As for the energy minimisation, quadratic approximation (the second-order Taylor expansion) is applied to the calculation of lattice energy:
where represents atomic coordinates. A modified Newton-Raphson method is used for energy minimization with a step search direction expressed as:
where is the modified co-efficient determined by line search, g is the gradient vector, and H-1 is the inverse of the second derivative matrix (Hessian matrix), whose calculation is the most computationally expensive step. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) hessian matrix updating scheme is used by default, as the built-in minimisation process.
Mott-Littleton (ML) method is used for calculations of defect formation energies. Atoms in the regions with different distances to the assigned defect centre are treated differently. The ML method divides the whole system studied into three regions, specifically, Region 1, Region 2b and Region 2a. Atoms in Region 1 are treated explictly. Region 2b is treated as a continuous dielectric medium. The energy is evaluated using classical continuum theory and atomic displacements are determined by bulk polarization. Region 2a is treated both atomistically and as a dielectric continuum to provide consistency between Region 1 and Region 2b[38,41,42] The radii of Region 1 and Region 2a were set to be 20 Å and 30 Å.
Calculations of lattice energy were performed as the first step for simulations. Lattice energy is the cohesive energy that keeps atoms in a crystal binding with each other. If the energy where all atoms are at an infinite distance from each other is defined as zero, then a negative value is assigned to lattice energy. Two-body Buckingham potential parameters used in current simulations are listed in Table 1, which were derived by Lewis and Catlow.[43] Li-O potential was referred from the work of Cormack, and the optimized crystal structure, calculated lattice energy and bulk modulus of Li2O using the potential agree well with other simulations and experimental results.[44,45,46] Initial structural information about the three oxide crystalline materials involved was referred from literatures.[44,45,46,47,48] The lattice energies of MgO and Nd2O3, Li2O after optimizations are shown in Table 2.
Table 2.
Buckingham Potential Parameters Used in Calculations.
| Pairwise interaction | A (eV) | ρ (Å) | C6 (eV•Å6) |
|---|---|---|---|
| Mg-O | 820.8 | 0.3242 | 0 |
| O-O | 22764 | 0.149 | 27.879 |
| Li-O | 235.1 | 0.35441 | 0 |
| Nd-O | 1379.9 | 0.3601 | 0 |
Table 3.
Calculated Lattice Energies.
| Crystalline materials | Lattice Energy per formula (eV) |
|---|---|
| MgO | -40.55 |
| Nd2O3 | -129.01 |
| Li2O | -29.67 |
3. Results and Discussions
3.1. Intrinsic Point Defects in Pristine MgO
Pristine crystalline MgO possesses a typical rock-salt structure (NaCl type) with a space group of (No. 225), as shown in Figure 1. Given the relative ionic radius difference between O2- and Mg2+, respectively 1.21 Å and 0.86 Å,[49] the structure can be described as the cations occupying the octahedral coordination site within cubic-close-packed anion arrays. Ideally, both Mg2+ and O2- ions are sitting in a perfect octahedral coordination environment. Each octahedron is connected by edge-sharing and corner-sharing with other octahedra of the same ion species. The bond length after bulk optimisation was calculated to be 2.105 Å. For undoped MgO, the intrinsic defects considered include Schottky defect and Frenkel defects, in which four basic point defects are involved. With Krӧger-Vink notations, intrinsic point defects include Mg vacancy , Mg interstitial , O vacancy , and O interstitial . Schottky and Frenkel defects are expressed as:
Table 4.
Defect Formation Energies in Pristine MgO.
| Schottky energy (per point defect) | 3.11 eV |
| FrenkelMg energy (per point defect) | 5.18 eV |
| FrenkelO energy (per point defect) | 5.04 eV |
| 22.96 eV | |
| 23.81 eV | |
| -12.60 eV | |
| -13.75 eV |
The calculated intrinsic defect formation energies per point defect are shown in Table 3. The current results are in reasonable agreement with experimental and other simulations.[16,50,51,52,53] Here, Schottky and Frenkel defect energies are calculated with completely isolated point defects. Comparatively, the Schottky defect, which consists of one and one requires less formation energy. Thus, it is considered more favourable. A more favourable Schottky intrinsic defect indicates that when a vacancy is formed in pristine MgO, another oppositely charged vacancy will be found with more probability for electrostatic compensation. As intrinsic vacancies are preferred, a further speculation can be logically arrived: substitution defects may be preferred in doped MgO. With a ccp (cubic close packed) anion array in the rock salt structure, two types of interstitial sites are available: octahedral and tetrahedral. Classically, the ratio of ion size largely impacts which site is to be occupied. So, any dopant with a size slightly larger than Mg will be more likely to occupy the octahedral site, and it becomes a substitution on Mg. Fundamentally, which sites dopants will occupy depends on the characteristics of introduced dopants, such as the effective charge or atomic size and the structure of the host material.
3.2. Point Defects and Defect Complexes in Neodymium Doped Magnesium
From the perspective of optical applications, the main purpose of doping active ions into a host material is, on the one hand, to take advantage of the unique physical properties of the host, such as thermal conductivity and intrinsic transparency; on the other hand, to take advantage of crystal field of the host. The coordination environment (such as coordination number and coordination polyhedron) plays a significant role in doped optical materials as it had been observed and studied in crystal field theory.[54] When it comes to optical centres of rare earth ions, it is known that their electronic structures are less perturbed by the structure of the host material. The 4f orbitals are often unfilled, and they are well sheltered by the outer 5s5p orbitals according to the Aufbau principle. However, the optical properties of the doped system, or the absorption and emission of dopants are still impacted by local atomic structure. The nature of doping means that the induced distortions in the host should not be ignored: that is, it is the necesssary to focus on the point defect configurations. In this section, point defects and defect complexes induced by Nd are investigated, and coordination distortions are revealed. By introducing Nd, two possible types of point defects are present, and , and their defect formation energies were calculated to be -19.53 eV and -11.37 eV, respectively. These are the two forms in which Nd can be incorporated into MgO. Two critical questions require consideration: from the point of energy, firstly, which is the more favourable way for Nd to be doped into MgO, or ? Secondly, which is the more favoured defect that exists as charge compensator with negative charges for Nd dopants: or ? To answer these questions, 23 quasi-chemical reactions were formulated under conservation and electroneutrality rules, and are listed in the Appendix. The enthalpy per rare earth doping of the reaction is considered a benchmark for quantitative evaluations of the probability of obtaining certain defect configurations practically. For example, in reaction (8)-(a), , where is the defecct formation energy of point defect, is the lattice energy of crystalline oxide. Point defects are isolated from each other at this point in the analysis. The defect reaction with the lowest enthalpy was found to involve three point defects with two Nd substitutions on Mg sites and one Mg vacancy as charge compensators, and the enthalpy was calculated to be 3.79 eV per Nd doping. Another possible charge compensator for is :
The enthalpies shown are normalised to per Nd atom doping. Magnesium vacancy is the favoured compensator for positively charged defects instead of oxygen interstitial, since its enthaply is lower as shown in reaction (8). On the other hand, in the rock salt structure of MgO, the available tetrahedral interstitial sites are the sites surrounded by four oxygen anions. So, when oxygen is placed on one of these interstitial sites, immense relaxation of the lattice then must be induced because of the large electrostatic repulsions among local anions; this is undoubtedly less favoured for a negatively charged compensator to exist naturally.
The result also indicates that Nd favours substitution on the Mg site instead of an interstitial site in the MgO host. The reactions with the lowest enthalpy changes where one and two Ndi are involved were found to be:
It is quite straightforward to see that the magnitude of the effective charge becomes higher when Ndi appears. The more Nd dopants exist in the form of interstitials, the more magnesium vacancies are needed for charge compensation, which has a positive value of formation energy. It undoubtedly increases the enthalpy of solution. Also, from the point of ionic size and effective charge, a Nd interstitial will result in more distortions to the host structure.
When point defects approach close to each other, the defect complexes can be formed. The defect complex must be considered to further determine the more favoured way to accommodate Nd dopants and the more favoured charge compensator. The mutual interactions between the point defects in a complex may influence the enthalpies of defect reactions. The way by which different configurations of defect complexes were tested is: Mg atom was placed at the origin (0, 0, 0), then substitutional or interstital point defects were placed on the availabe sites around it within a volume of 74.62 , which is the volume of one MgO unit cell. In the current context, the association energy is defined as the energy difference between the defect formation energy of a complex and the sum of the defect formation energies of those isolated point defects:
is the defect energy of the defect complex, is the defect energy of a isolated point defect, is the total number of point defects in the defect complex. The clustering of point defects is called a complex normally when , the formulation of for a pair of point defects is the same. A positive value of association energy is, as a result of this, considered unfavoured as it will increase the enthalpy when being taken into the quasi-chemical reaction. A negative value of association energy is considered favoured as it will decrease the enthalpy. It is determined mainly by the relative positions of point defects.
Defect pairs of two-point defects with oppositely effective charges where Nd dopants are involved were first considered. The lowest association energy (the highest absolute value) in each complex is listed in Table 5.
It was found in the simulations that when was intially placed at (, , ), close to the (0, 0, 0), the Nd atom moved into the vacancy position after relaxation, with a formation energy the same as (-11.37 eV). If Nd favours an interstitial site in MgO, the association energy of ( + pair is expected to be a positive value. The calculated minus value of association energy of ( + shows that the favoured way to accommodate Nd in MgO is the substitution on the Mg site instead of an interstitial site. Take the association energies of the four defect pairs of Table 4 into quasi-chemical reactions, the one of the lowest enthalpy was found to be:
It is the same set of reaction shown in reaction (8)-(a). The information that can be extracted so far according to those results is: There are great probabilities that dopant Nd exists in the form of , and that is more favoured as charge compensator rather than .
To investigate further the structures of defects in Nd: MgO, the defect complex containing three individual point defects was considered. 35 different configurations were tested to find the structure of the minimised formation energy. Initially, a magnesium vacancy was fixed at the origin, and configurations were tested by putting the other two Nd substitutions in other available Mg sites. It was found that associations between these three point defects can further reduce the normalised reaction enthalpy to 2.72 eV, a reduction of 28 % when all point defects are isolated as in reaction (8)-(a) and the relaxed structure of this defect complex is shown in Figure 2(a).
Figure 2(a) shows that both Nd substitutional defects remain an octahedral coordination polyhedron with distortions in bond angle and bond length. Figure 2(b) shows the found configuration of the highest defect energy. The interatomic distances of Nd and the distances between point defects are listed in Table 6.
Compared to undoped MgO, where the optimised Mg - O length is 2.105 Å, the mean Nd - O lengths are around 2.255 Å and 2.215 Å for configuration (a) and (b), respectively. In configuration (a), changes in Mg - O bond length can be due to the changes in the electrostatic interaction between the substitutional defect and the surrounding oxygen ions. One Nd substitutional defect possesses less effective charges than the original Mg ion, so the dominating Coulombic attraction reduces, resulting in a larger bond length. On the other hand, Nd has a larger ionic size than Mg. When placed at the Mg site, the bond length increases after relaxation to accommodate it. Two Nd dopants in Configuration (a) are closer to the Mg vacancy compared to Configuration (b), they experience more powerful electrostatic interactions with Mg vacancy, and it exerts greater distortions on the octahedral coordination. The interdopant distance Nd - Nd in Configuration (a) is 4.80 Å, which is shorter than 6.12 Å in Configuration (b). Comparisons of these two configurations show that it is enegetically favourable for Nd dopants to aggregate in Nd: MgO.
Above all, it is more probable that Nd dopants exist as substitution defects on the Mg site with Mg vacancy as the charge compensator. A defect complex is more favoured than isolated point defects. In solely Nd doped MgO, one may expect the existence of Mg vacancy near substitutional Nd dopants.
3.3. Influences of Lithium on Energetics and Defect Structures of Neodymium Doped Magnesium Oxide
According to the experimental results obtained by Dorel,[12] ionic exchange between Nd and Mg was not observed when MgO was the host. So, Nd dopants may not be successfully doped into the MgO host, or the quantity doped was too low to remain detectable. The diffuculty of doping rare earth elements into MgO was also stressed by Sannamyan.[13] Li co-doping has been experimentally proven to improve the crystallinity and optical performance in rare earth doped MgO.[6,9,10] It is important to ask a question: in which way is Li making an impact? Does Li make it easier for Nd to enter the MgO host? The standing points to view the questions here are structure and energy. A similar procedure as in Nd: MgO was conducted: defect and association energies were calculated for Nd, Li: MgO. By Li co-doping, two extra possible point defects are introduced: and , and the defect energies were calculated to be -1.23 eV and 15.89 eV, respectively. The quasic-chemical reactions for these two point defetcs in Li: MgO are as follows:
The most favourable way to accommodate Li in MgO is and compensating each other as shown in reaction (13)-(a). By comparing reaction (13)-(b) and (13)-(d), is relatively more favourable than in MgO.
Take the point defects of Nd and Li to the quasi-chemical reactions (56 possible reactions are shown in Appendix), the one of the lowest enthalpy was found to contain two Nd substitutional and two Li substitutional point defects on Mg sites:
The defect complexes considered and their respective calculated association energies are listed in Table 7.
Figure 3 shows the data points of simulation results regarding the relations between association energy and effective charge (EC) or the number of point defects (N) in defect complexes. Defect complexes containing more point defects with electroneutral effective charges are more favourable. The range of association energy is broadened by including more point defects in the complex. Ranges for a 2-, 3-, 4-point defect complex are 0.39 eV, 0.93 eV, 1.60 eV. When more point defects join the complex, more configurations become possible, increasing the range. It shows that: the range of association energy strongly depends on the relative atomic arrangements of included point defects. That is why it is necessary to conduct a systematic investigation to determine the most favourable defect structure. Depending on the specific atomic arrangement, associations can be favoured or unfavoured. This dependence on positions only occurs when the effective charge possessed by the defect complex is non-zero (-1 or +1 in the current case). The associations are always favoured when EC = 0, in both N = 2 and N = 4. With an increased N, it is more promising to find lower association energy. So far, the most potentially favourable defect complex in Nd, Li: MgO was found to be a with zero effective charges. The relative positions of the point defects included does not change the sign of association energy, but the range of the association energy of 4-point-defect complex is the largest compared to the complex with 2 or 3 point defects. The quasi-chemical reaction with the lowest enthalpy is:
Remember that in Nd: MgO, the Mg vacancy was found to be the favourable charge compensator for the Nd substitution point defect. With Li co-doping, Li substitution point defects are now playing the role of the charge compensator. Compared to the Mg vacancy with two negative effective charges and a vacant site within the crystalline lattice, the substitution by Li possesses one negative effective charge without leaving any charged vacant space, so causes less structural perturbation on the crystal structure of MgO compared to . This result shines light on why Li co-doped materials have better crystallinity.
Even though the MgO in the rock-salt structure is of high symmetry, point defects break the perfect local symmetry and result in many possible configurations. One Nd substitution defect was first fixed at the origin position (0, 0, 0). The number of possible configurations of the is then , including some double counts. That is, to put the other three cation substitutions on other available Mg sites of within a neighbouring volume of one unit cell. 280 possible configurations were tested to find the favourable defect structure of the .
The relaxed structure of the configuration with the lowest defect energy Edefect is shown in Figure 4(a). Figure 4(b) shows the configuration which has the highest defect energy found. Interatomic distances of the two configurations are listed in Table 8.
The configuration with the lower defect energy is more disordered in bond length bond angle. Li favors a position close to Nd. Compared to the enthapy of 2.72 eV obtained in reaction (12) without co-dopant, in reaction (15), incorporating Li as co-dopant reduces the enthalpy by 28 %. This result indicates that Nd can be doped into MgO more easily with Li as co-dopant from the point of energy. Structurally, firstly, the Li has a smaller ion size than Mg, which is beneficial for doping of large rare earth elements. Secondly, the relaxation of the O atom which is surrounded by four substitutional point defects causes large displacements in its position as shown in Figure 5. Two Nd substitutional point defects are located at two sides of the oxygen atom, making it an equilibrium Coulombic attraction condition, so this displacement of the O atom is mainly attributed to the two Li substitutional point defects, because of a repulsive electrostatic interaction. From the point of doping objective, the displacement of oxygen atom make more room for the accommodations of two Nd substitution dopants.
The question may be raised: What is the correlations between the defect energy of a defect complexes and their configurations – the exact atomic arranegments? Remember that the association energy in current context is defined as from equation (10) (a negative value of is favoured as it means the has a lower defect energy than , and it will decrease the reaction enthalpy) One might assume that the closer those point defects approach each other, the more associations there will be (the higher absolute value of association energy), the lower the defect energy they will have. But the relationship between configuration of defect complex and defect formation energy is not that simple even in the MgO host, which has a relatively simple crystal structure.
As shown in Figure 6, in a MgO unit cell, the arrangement for four substitutional point defects to stay distant from each other as much as possible is to put them on four diagonal corners of the cubic as in (a). Nevertheless, this configuration is more favoured than the condition where all substitutions are located on four face diagonal sites as in (b). Start from (b), moving one Li closer the other three substitutional point defects, the defect energy decreases. From selected examples, it is not clear which interatomic distance (Nd – O bond length, Nd – Nd, Nd – Li) in the defect complexes is more significant for their defect energies (or association energies). To further investigate the correlations, interatomic distances were extracted from relaxed structures of defect complexes. The interatomic distances considered include Nd – Nd, Li – Li, average Nd – Li, average Nd – O bond length and average Li – O distance (the distance between Li and the first nearest six O). The scattered data points of Eassociation vs interatomic distance are shown in Figure 7.
According to Figure 7(a), there is no apparent dependency between Eassociation and interatomic distances between two Nd dopants or two Li co-dopants in the complexes, since for each considered Nd-Nd and Li-Li distance, high or low association energies are possible as in (a). On the contrary, dependencies of Easscociation on Nd - Li, Nd - O and Li - O distances are clear in Figure 7(b) and (c). The trend lines are shown in black dashed lines. Larger average Nd - O and Li - O are favoured for associations in the cluster. A shorter average Nd-Li distance is favoured. The trend line of average Nd - O bond length has the steepest gradient. The correlations are not simply linear, no single interatomic distance solely determines the magnitude of the association energies of the defect complex. This is the great difficulty in analyzing the defect complexes. However, the results above can be used to estimate or compare association energies among defect complexes in different configurations. In other words, one may approximate the more energetically favourable defect structure by comparing average Nd - O, Li - O or Nd - Li distances.
3.4. Comparisons with Erbium Doped Magnesium Oxide
According to Sanamyan,[13] besides Nd: MgO, Li was found to have direct positive impact on the doping and optical properties of Er: MgO as well. Er, Li: MgO has better visible transparency than Nd, Li: MgO. It is meaningful to compare the doping of Er and Nd into MgO from the point of energy. Intuitively, it might be easier to dope Er than Nd, as Er possesses a smaller ionic size. Calculations were performed to investigate Er doped MgO from a theoretical aspect. Because of the unavailability of Er - O Buckingham potential parameters with the same O - O potential parameters from literature, Er - O Buckingham parameters were derived by relaxed fitting with GULP. The derivation methods of the potential parameters were outlined by Lewis and Gale.[37,55,56] The sum of least squares method was utilized to measure the fitting quality. By fitting to the experimental results,[57,58,59] the derived Er - O Buckingham parameters are A = 1381.518 eV, = 0.349 Å, C6 = 0 eV•Å6. The lattice energy of Er2O3 was calculated to be -134.97 eV, and the defect energy of and was calculated to be -14.817 eV and -23.244 eV, respectively. For Er: MgO and Er, Li: MgO, the following quasi-chemical reactions were found to possess the lowest enthalpy:
Furthermore, defect of complexes of and were considered. 35 configurations of - the same as , were tested and they were found to have the same lowest-formation-energy configuration. As for , 22 configurations were selected from the 280 configurations that were tested in the . The range of the association energies of the 280 tested configurations of is from -1.6 to 0 eV as showed in Figure 7. Based on an energy interval of 0.2 eV, in total 22 configurations of were selected, whose association energies fell within the 8 ranges from -1.6 to 0 eV. It was found that has the same favourable configuration as . The quasi-chemical reactions for Er: MgO and Er, Li: MgO of the lowest enthalpies were:
It shows that associations are also favoured in Er: MgO and Er, Li: MgO. And Li lowers down (30 %) the enthalpy for Er doping into MgO, an similar effect as in Nd: MgO. Compared to reactions (12) of Nd: MgO ( = 2.72 eV) and (15) of Nd, Li: MgO ( = 1.95 eV), doping Er into MgO host requires less energy, 2.26 eV for Er: MgO, 1.59 eV for Er, Li: MgO.
With respect to the coordination octahedra of the rare earth dopants in MgO, Figure 8 shows the information of the dopant-oxygen bond lengths of two dopant-centred octehedra in each of the doping systems. Two dopants possess the same octehedron in the respective systems. The bond length of Mg - O in the pristine MgO 2.125 Å is indicated by the black dashed line. Comparing the systems with Li and without Li, it is apparent that in Li co-doped systems, the rare earth dopants have a shorter Nd - O and Er - O bond lengths - the maximium, the mean and the minimum bond lengths. Compared to Nd, Er has the shorter bond lengths. Besides the bond lengths, a distorted octahedra of the rare earth dopants also have distorted bond angles. A method to describe the distortions of a polyhedron systematically was proposed by Baur[60], where three distortion indices (DI) were defined, bond-length distortion, bond-angle distortion and edge-length distortion (edge of the polyhedron). These distortion indices were orginally defined for tetrahedral polyhedron. For octahedral polyhedron, analogous expressions of three distortion indices are: [61]
where stands for bond length between cation atom and oxygen atom , stands for bond angle, stands for edge length of octahedral polyhedron, indicates the mean value of each quantity. The calculated DI of the dopant centred octehedra are listed in Table 9.
With the Baur’s method, RE: MgO and RE, Li: MgO have close DI of bond-length and edge-length distotions. The DI of bond-angle distortions in RE: MgO are relatively higher than in RE, Li: MgO. This is due to the high effective charges (-2) possessed by the Mg vacancy, causing large repulsions of the O atoms near the Mg vacancy. The diffence between the each quantity and the respective mean value is in an order of magnitude of -1 (0.1), so the caculated indices are in an order of magnitude of -2 (0.01). So, it is sufficient to keep the third significant figure of the numerical value when comparing degrees of distortions between octahedra. These information of the bond lengths and the distortions described above maybe useful for comparative spectroscopic studies of active RE ions in RE: MgO and RE, Li: MgO, where the local symmetries are decisive for the optical properties.
3.5. Incorporating More Li Co-Dopants
According to reaction (15), the defect complex discussed was where the quantity ratio between Nd and Li was 1:1. What will happen when more Li ions are introduced into the system? It is meaningful to consider the excess-Li condition because in the experimental practice, the mole ratio between doped Nd and Li are 1:3.[6] Based on the results obtained in the last section (reaction (13)-(a), (15) and the most favourable configuration of ), the defect complex was considered. Exrea and were placed around the most favourale configuration of . In this defect complex, there are 2 Nd atoms and 6 Li atoms (Nd: Li=1:3 or Nd, 3Li: MgO). The excess point defects were placed at the nearest neigbouring Mg sites to Nd dopants, and the excess were tested for the 8 neariest neighbouring interstitial sites to Nd dopants. The most favourable configurtion of found is shown in Figure 9 ( is normalized to per Nd dopant). The bond length and inter-atomic distances are listed in Table 10. Note that the average Nd - O bond length is 0.01 Å shorter than that of Nd, Li: MgO. The inter-dopant distance is 0.17 Å longer than that of Nd, Li: MgO. The quaisi-chemical reaction after excess-Li co-doping is shown in (19).
Compared to reaction (15), co-doping excess Li into MgO host requires extra energy of 1.42 eV per Nd dopant. Though the excess and point defects are not needed for charge compensation of Nd dopants, but they were found to have impacts on the distortion of the octahedral coordination geometry of Nd dopants. The calculated Baur DI are shown in Table 11.
Three distortion indices of octahedral coordination geometries of Nd dopants were found to decrease significantly in the excess-Li co-doping condition compared to Table 9. The reduction in the bond-length, bon-angle and edge-length distortions are 52.2 %, 76.5 % and 81.3 %, respectively. The dramatic reductions on distortion indices may be partially responsible for the experimentally observed increase in optical emission intensity by Li co-doping,[6] considering that a less distorted coordination geometry of Nd might contribute to more localized Stark levels in the 4f manifolds, which is beneficial to obtain emission with less bandwidth and increased intensity. [54,62]
4. Conclusions
The most energetically favourable structures of defect complexes in rare earth (Nd, Er) doped MgO with and without Li co-doping were found by calculations of formation energies of point defects and their defect complexes. Both rare earth dopants Nd, Er and Li co-dopants prefer substitution on Mg sites. The Li co-dopant was found to reduce the enthalpy change for rare earth dopants to be incorporated into the MgO host. provides charge compensation for the rare earth substitutional point defects, and it causes the relaxations of neighboring O atoms which help to accommodate the rare earth dopants. replacing Mg vacancy as a charge compensator may play an essential role in improving the crystallinity in co-doped materials compared to solely doped materials. Li co-doping lowers down the energy required to dope rare earth elements, Nd and Er in our case, into MgO host. In polycrystalline samples, for example, since Li encourages doping of rare earth into the host, the aggregations of dopants along the grain boundaries can be reduced. This contribution from Li would be practically meaningful for modifying concentration quenching and transparency, which are all closely related to the chemistry of grain boundaries. The correlations between the association energy and defect structure in the defect complex was investigated. The average distances between cations and the nearest oxygens and between Nd dopants and Li co-dopants were found to have a correlation with association energy. Besides interatomic distance, the breakdown of symmetry, local dipole moments, and interactions between the dipole moments may all have their roles in associations. Further studies on these physical quantities will provide deeper understanding about the association between point defects in the defect complexes. A excess-Li co-doping condition was also considered. It was found that increasing the quantity ratio between Nd and Li from 1:1 to 1:3 resulted in significant redunction of the calculated Baur Distortion Indcies. The determination of the most favourable defect structure will contribute to further investigations on the electronic structures of the doped oxides and the mechanism of how Li influences the optical properties of rare earth doped oxides will be further understood.
Author Contributions
Conceptualization, Alastair N. Cormack and Yiquan Wu; Investigation, Yanfeng Zhao, Alastair N. Cormack and Yiquan Wu; Methodology, Alastair N. Cormack; Supervision, Alastair N. Cormack and Yiquan Wu; Writing – original draft, Yanfeng Zhao; Writing – review & editing, Alastair N. Cormack and Yiquan Wu.
Acknowledgments
The topic and methodology of this work were developed by Dr. Yiquan Wu and Dr. Alastair N. Cormack. The theoretical calculations were performed using computing resources in Inamori School of Engineering at NYS College of Ceramics, Alfred University. YFZ would like to thank Dr. Doris Möncke and Dr. Alexis G. Clare for fruitful dialogues and thank Alfred University for studentships.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Quasi-Chemical Defect Reactions in Nd: MgO and Nd, Li: MgO
| Quasi-chemical reactions | per Nd dopant (eV) |
| 29.62 | |
| 29.38 | |
| 27.46 | |
| 24.35 | |
| 23.62 | |
| 22.43 | |
| 21.69 | |
| 20.51 | |
| 20.06 | |
| 18.58 | |
| 18.14 | |
| 16.22 | |
| 15.03 | |
| 14.29 | |
| 13.10 | |
| 11.18 | |
| 10.74 | |
| 10.01 | |
| 8.82 | |
| 6.89 | |
| 5.70 | |
| 4.74 | |
| 3.79 |
| 36.11 | |
| 34.19 | |
| 31.27 | |
| 31.08 | |
| 28.43 | |
| 26.79 | |
| 26.51 | |
| 26.24 | |
| 25.51 | |
| 25.32 | |
| 23.59 | |
| 23.40 | |
| 22.40 | |
| 21.95 | |
| 21.76 | |
| 21.40 | |
| 21.37 | |
| 21.03 | |
| 20.48 | |
| 19.48(4) | |
| 19.48(0) | |
| 19.11 | |
| 18.45 | |
| 18.11 | |
| 17.92 | |
| 17.56 | |
| 17.47 | |
| 17.40 | |
| 16.92 | |
| 16.53 | |
| 16.19 | |
| 16.00 | |
| 15.55 | |
| 15.51 | |
| 15.00 | |
| 13.63 | |
| 13.11 | |
| 13.08 | |
| 12.63 | |
| 12.44 | |
| 12.41 | |
| 11.71 | |
| 11.03 | |
| 10.71 | |
| 10.52 | |
| 8.82 | |
| 8.79 | |
| 8.60 | |
| 7.60 | |
| 5.68 | |
| 4.85 | |
| 4.65 | |
| 4.24 | |
| 4.09 | |
| 3.28 | |
| 2.76 |
References
- T. Kato; T. Yanagida. Optical, Scintillation and Dosimeter Properties of MgO Translucent Ceramic Doped with Cr3+. Optical Materials 2016, 54, 134–138. [Google Scholar] [CrossRef]
- T. Kato, G. Okada; T. Yanagida. Optical, scintillation and dosimeter properties of MgO transparent ceramic doped with Mn2+. Journal of the Ceramic Society of Japan 2016, 124, 559–563. [Google Scholar]
- T. Kato; G. Okada; N. Kawaguchi; T. Yanagida, Dosimeter properties of Ce-doped MgO transparent ceramics. J Lumin. 2017, 192, 316–320. [Google Scholar] [CrossRef]
- N. Kumamoto; T. Kato; N. Kawano; G. Okada; N. Kawaguchi; T. Yanagida. Scintillation and dosimeter properties of Ca-doped MgO transparent ceramics. Nucl Instrum Methods Phys Res B, 2018; 435, 313–317.
- T. Y. Fan; A. Cordova-Plaza; M. J. F. Digonnet; R. L. Byer; H. J. Shaw. Nd: MgO: LiNbO3 spectroscopy and laser devices. Journal of the Optical Society of America B, 1986; 3.
- L. C. Oliveira; E. D. Milliken; E. G. Yukihara. Development and characterization of MgO: Nd, Li synthesized by solution combustion synthesis for 2D optically stimulated luminescence dosimetry. Journal of Luminescence 2013, 133, 211–216. [Google Scholar] [CrossRef]
- M. R. Bindhu; M. Umadevi; M. Kavin Micheal, M. V. Arasu; N. Abdullah Al-Dhabi. Structural, morphological and optical properties of MgO nanoparticles for antibacterial applications. Mater Lett. 2016, 166, 19–22. [Google Scholar] [CrossRef]
- V. L. Blair; Z. D. Fleischman; L. D. Merkle; N. Ku; C. A. Moorehead. Co-precipitation of rare-earth-doped Y2O3 and MgO nanocomposites for mid-infrared solid-state lasers. Appl Opt. 2017, 56, B154–B158. [Google Scholar] [CrossRef]
- V. R. Orante-Barrn; L. C. Oliveira; J. B. Kelly, et al. Luminescence properties of MgO produced by solution combustion synthesis and doped with lanthanides and Li. J Lumin. 2011, 131, 1058–1065. [Google Scholar] [CrossRef]
- F. Gu; C. Zhong Li; H. Bo Jiang. Combustion synthesis and photoluminescence of MgO: Eu3+ nanocrystals with Li+ addition. J Cryst Growth 2006, 289, 400–404. [Google Scholar] [CrossRef]
- J. Sivasankari; S. Selvakumar Sellaiyan; S. Sankar; L. V. Devi; K. Sivaji, Structural and optical characterization of Er-alkali-metals co-doped MgO nanoparticles synthesized by solution combustion route. Physica E Low Dimens Syst Nanostruct 2017, 85, 152–159. [Google Scholar] [CrossRef]
- D. Crişan; N. Dragan, M. Crişan et al., Structural study of the MO-Nd2O3 system obtained by a sol-gel procedure. Comptes Rendus Chimie. 2018, 21, 232–246. [Google Scholar]
- T., Sanamyan; C. Cooper, G. T. Sanamyan; C. Cooper, G. Gilde; A. C. Sutorik; M. Dubinskii. Fabrication and spectroscopic properties of transparent Nd3+: MgO and Er3+: MgO ceramics. Laser Phys Lett. 2014; 11. [Google Scholar]
- B. B. Karki; G. Khanduja. Vacancy defects in MgO at high pressure. American Mineralogist 2006, 91, 511–516. [Google Scholar] [CrossRef]
- F. Gao; J.F. Hu; C. L. Yang et al, First-principles study of magnetism driven by intrinsic defects in MgO. Solid State Communications 2009, 149, 855–858. [Google Scholar] [CrossRef]
- D. Vita; M. J. Gillan; J. S. Lin, et al. Defect energetics in MgO treated by first-principles methods. Physical Review B, 1992; 46, 964–973.
- A. Gilbert; S. D. Kenny; R. Smith; E. Sanville. Ab initio study of point defects in magnesium oxide. Physical Review B 2007, 76, 184103. [Google Scholar] [CrossRef]
- Gibson; R. Haydock; J. P. LaFemina. Stability of vacancy defects in MgO: The role of charge neutrality. Physical Review B 1994,50, 2582-2592.
- E. Ertekin; L. K. Wagner; J. C. Grossman. Monte Carlo methods: Application to the F-center defect in MgO. Physical Review B 2013, 87, 155210. [Google Scholar]
- J. H. Harding; M. J. L. Sangster; A. M. Stoneham. Cation diffusion in alkaline-earth oxides. J. Phys. C: Solid State Phys. 1987, 20, 5281–5292. [Google Scholar] [CrossRef]
- L. Shluger; E. N. Heifets; J. D. Gale; C. R. A. Catlow. Theoretical simulation of localized holes in MgO. Journal of Physics: Condensed Matter 1992, 4, 5711–5722. [Google Scholar]
- J. D. Foox; E. A. Colbournf; C. R. A. Catlow. Computer simulation of alkali metal trapped hole defects in alkaline earth oxides. Journal of Physics and Chemistry of Solids.
- J. D. Foox; E. A. Colbournf; C. R. A. Catlow. Computer simulation of alkali metal trapped hole defects in alkaline earth oxides. Journal of Physics and Chemistry of Solids 1988, 49.
- Barrykunz. Characterization of fluorine-doped magnesium oxide: A computer simulation study. Journal of Physics and Chemistry of Solids, 1990; 51.
- R. Pandey; J. Zuo; A. B. Kunz. Excitonic states in pure and impurity-doped magnesium oxide. Phys. Rev. B, 1989; 39.
- T. Yokoi; M. Yoshiya. Atomistic simulations of grain boundary transformation under high pressures in MgO. Physica B: Condensed Matter 2017, 532, 2–8. [Google Scholar]
- K. Verma; B. B. Karki. First-principles simulations of MgO tilt grain boundary: Structure and vacancy formation at high pressure. American Mineralogist 2010, 95, 1035–1041. [Google Scholar] [CrossRef]
- D. S. Aidhy; P. C. Millett; D. Wolf; S. R. Phillpot; H. Huang. Kinetically driven point-defect clustering in irradiated MgO by molecular-dynamics simulation. Scr Mater. 2009, 60, 691–694. [Google Scholar] [CrossRef]
- P. Uberuaga; R. Smith; A. R. Cleave, et al. Dynamical simulations of radiation damage and defect mobility in MgO. Phys Rev. B Condens Matter Mater Phys. 2005; 71.
- N. H. De Leeuw; S. C. Parker. Molecular-dynamics simulation of MgO surfaces in liquid water using a shell-model potential for water. Physical Review B 1998, 58, 13901. [Google Scholar] [CrossRef]
- Alfè. The melting curve of MgO from first principles simulations. Physical Review Letters 2005, 94, 235701. [Google Scholar] [CrossRef]
- A. B. Belonoshko; L. S. Dubrovinsky. Molecular dynamics of NaCl (B1 and B2) and MgO (B1) melting: Two-Phase simulation. American Mineralogist 1996, 81, 303–316. [CrossRef]
- Strachan; W. A. G. Iii. Phase diagram of MgO from density-functional theory and molecular-dynamics simulations. Physical Review B 1999, 60, 15084. [Google Scholar] [CrossRef]
- G. W. Watson; E. T. Kelsey; N. H. De Leeuw; D. J. Harris; S. C. Parker. Atomistic simulation of dislocations, surfaces and interfaces in MgO. Journal of the Chemical Society - Faraday Transactions, 1996; 92, 433–438.
- Y. Zhang; Y. Lin; S. Song, et al. Study of the microstructure and antibacterial properties of MgO with doped defects. Journal of Theoretical and Computational Chemistry 2018, 17. [Google Scholar]
- A. Petersen; B. Liu; W. K. Weber; Y. Zhang. Ab initio molecular dynamics simulations of low energy recoil events in MgO. Journal of Nuclear Materials 2017, 486, 122–128. [Google Scholar] [CrossRef]
- J. D. Gale; A. L. Rohl. The General Utility Lattice Program (GULP). Mol Simul 2003, 29, 291–341. [Google Scholar] [CrossRef]
- R. A. Catlow; R. G. Bell; J. D. Gale. Computer modelling as a technique in materials chemistry. J Mater Chem 1994, 4, 4–781. [Google Scholar]
- M. T. Dove. Introduction to Lattice Dynamics. Cambridge University Press; Cambridge, 1993.
- B. G. Dick; A. W. Overhauser. Theory of the Dielectric Constants of Alkali Halide Crystals. Physical Review 1958, 112, 90–103. [Google Scholar] [CrossRef]
- Atomistic Simulations of Glasses. Edited by J. Du and A. N. Cormack; Wiley; New Jersey, 2022.
- R. J. D. Tilley. Defects in Solids. John Wiley & Sons; New Jersey, 2008.
- G. V Lewis; C. R. A. Catlow. Potential models for ionic oxides. Journal of Physics C: Solid State Physics 1985, 18, 1149. [Google Scholar] [CrossRef]
- P. Goel; N. Choudhury; S. L. Chaplot. Superionic behavior of lithium oxide Li2O: A lattice dynamics and molecular dynamics study. Phys Rev B Condens Matter Mater Phys. 2004, 70, 1–8. [Google Scholar]
- G.V. Samsonov. The Oxide Handbook. Plenum; New York, 1982.
- S. Hull; T. W. D. Farley; W. Hayes; M. T. Hutchings. The elastic properties of lithium oxide and their variation with temperature. Journal of Nuclear Materials 1988, 160, 125–134. [Google Scholar] [CrossRef]
- Cimino; P. Porta; M. Valigi. Dependence of the Lattice Parameter of Magnesium Oxide on Crystallite Size. Journal of the American Ceramic Society 1966, 49, 152–156. [Google Scholar] [CrossRef]
- M. E. Kamwaya et al. X-ray structure analysis and molecular conformation of tert-butyloxycarbonyI-L-prolylproline (Boo-Pro-Pro): errata. Refinement of the Nd2O3and Nd2O2S structures at 4 K. Acta Cryst 1982, B 38, 344.
- R. D. Shannon; C. T. Prewitt. Effective Ionic Radii in Oxides and Fluorides. Acta Cryst. B 1969, 25, 925. [Google Scholar] [CrossRef]
- 50. J. Paier; M. Marsman; K. Hummer; G. Kresse; I. C. Gerber; J. G. Angyán. Screened hybrid density functionals applied to solids. Journal of Chemical Physics, 2006; 125.
- M. J. L. Sangster; D. K. Rowell. Calculation of defect energies and volumes in some oxides. Philosophical Magazine A: Physics of Condensed Matter, Structure, Defects and Mechanical Properties 1981, 44, 613–624. [Google Scholar] [CrossRef]
- W. C. Mackrodt, R. F. Stewart. Defect properties of ionic solids. II. Point defect energies based on modified electron-gas potentials. Journal of Physics C: Solid State Physics 1979, 12, 431. [Google Scholar] [CrossRef]
- W. C. Mackrodt. Defect calculations for ionic materials in Computer Simulation of Solids. Edited by C. R. A. Catlow and W. C. Mackrodt; Springer, 1982, 173-194.
- A. Ikesue; Y. L. Aung; Voicu Lupei. Ceramic Lasers. Cambridge University Press; New York, 2013.
- G. V Lewis. Potentials: Derivation of parameters for binary oxides and their use in ternary oxides. Physica B + C 1985, 131.
- J. D. Gale. Empirical potential derivation for ionic materials. Philosophical Magazine B: Physics of Condensed Matter; Statistical Mechanics, Electronic, Optical and Magnetic Properties 1996, 73, 3–19. [Google Scholar] [CrossRef]
- Q. Guo; Y. Zhao, C. Jiang, et al. Pressure-induced cubic to monoclinic phase transformation in erbium sesquioxide Er2O3. Inorg Chem. 2007, 46, 6164–6169. [Google Scholar] [CrossRef] [PubMed]
- M. F. Berard, D. R. Wilder. Cation Self-Diffusion in Polycrystalline Y2O3 and Er2O3. Journal of the American Ceramic Society 1969, 52, 85–88. [Google Scholar] [CrossRef]
- A. Sharif; F. Chu; A. Misra; T. E. Mitchell; J. J. Petrovic. Elastic Constants of Erbia Single Crystals. Journal of the American Ceramic Society 2004, 88, 2246–2250. [Google Scholar]
- W. H. Baur. The geometry of polyhedral distortions. Predictive relationships for the phosphate group. Acta Cryst. B 1974, 30, 1195–1215. [Google Scholar] [CrossRef]
- Ertl; J. Hughes; F. Pertlik, et al. Polyhedron Distortions in Tourmaline. The Canadian Mineralogist 2002, 40, 153–162. [Google Scholar] [CrossRef]
- M. P. Hehlen; M. G. Brik; K. W. Kramer. 50th anniversary of the Judd-Ofelt theory: An experimentalist’s view of the formalism and its application. Journal of Luminescence 2013, 136, 221–239. [Google Scholar] [CrossRef]
Figure 1.
Rock-salt structure of MgO and ideal octahedral coordination.
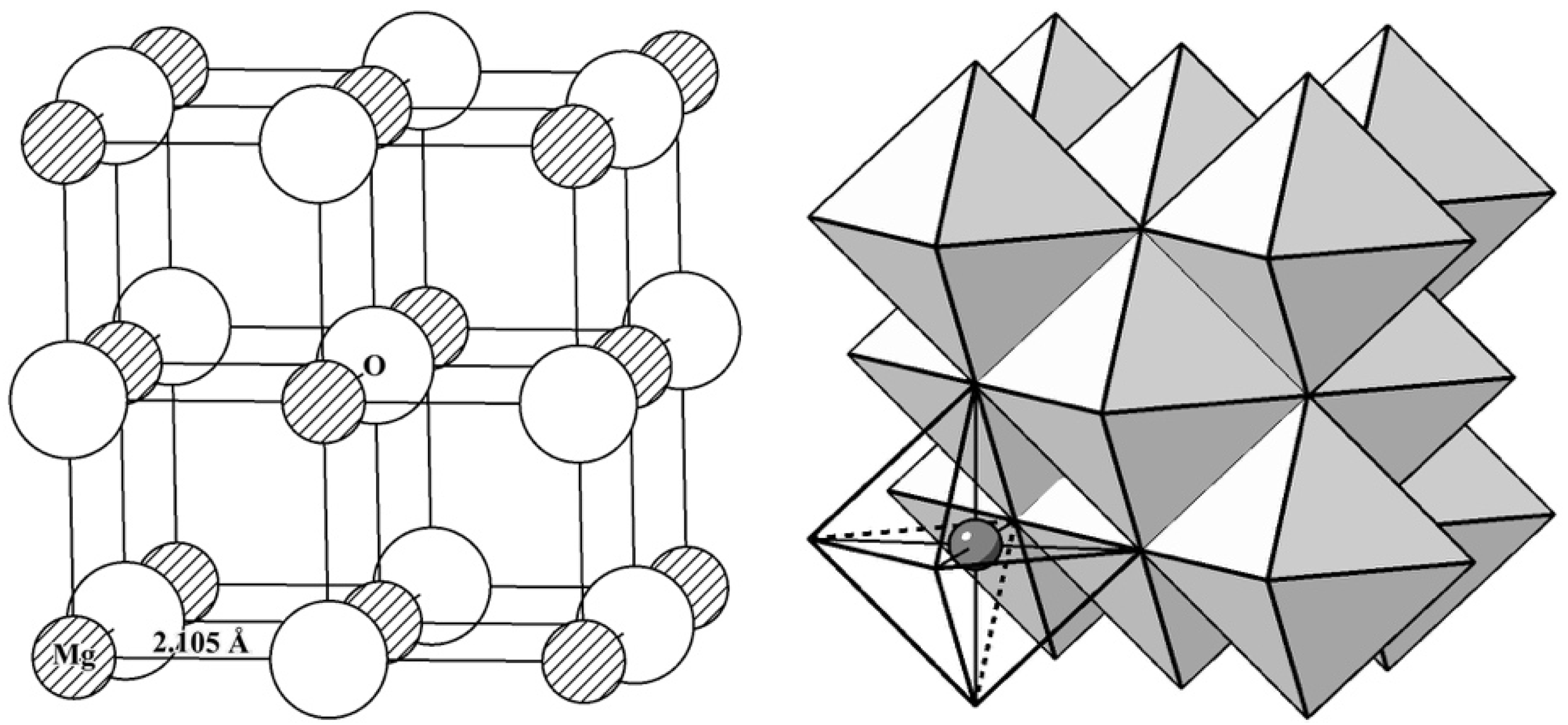
Figure 2.
Defect structure of : (a) the lowest configuration; (b) the highest configuration.
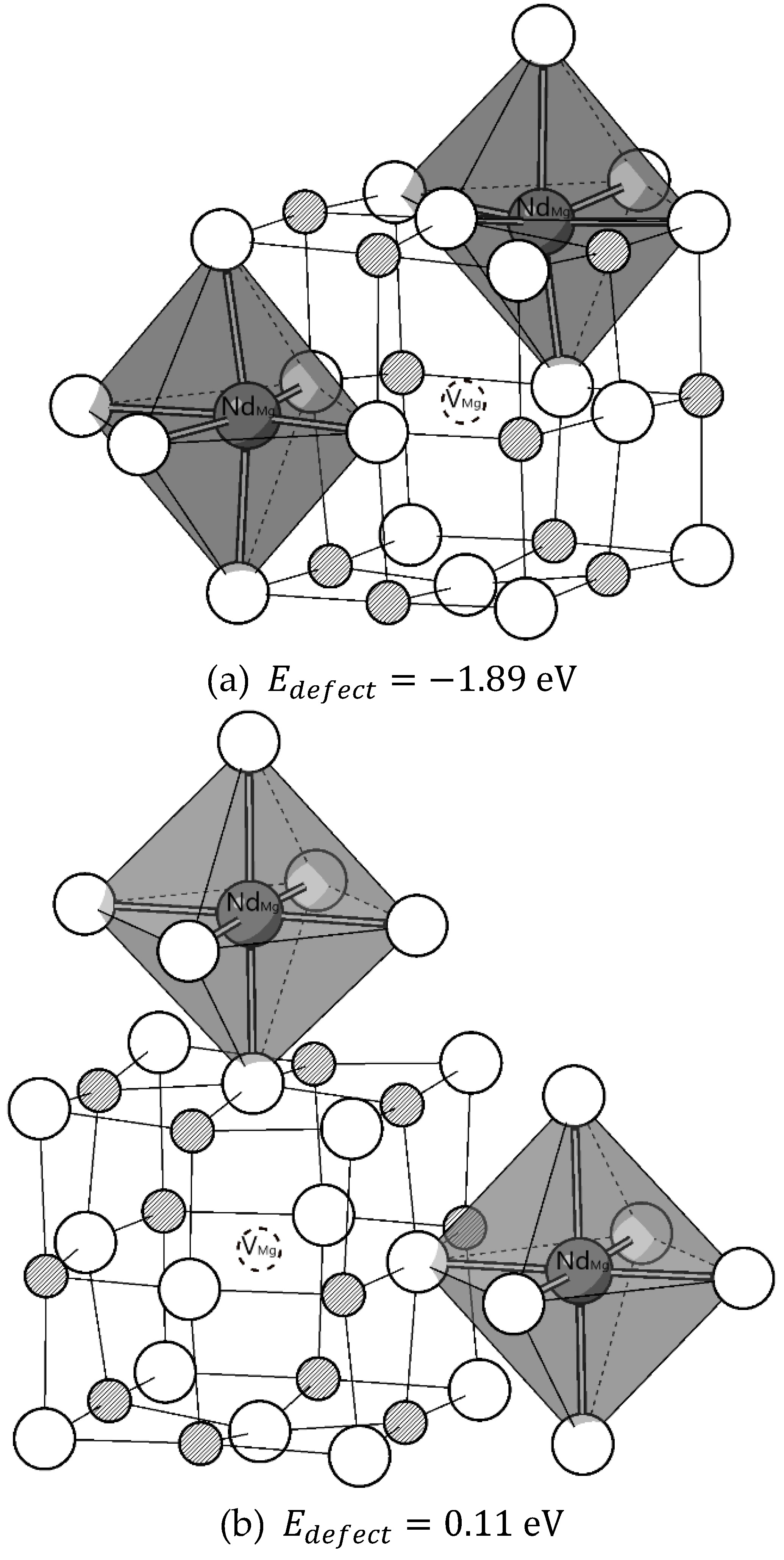
Figure 3.
Association energies of defect complex containing and : (a) Eassociation vs EC; (b) Eassociation vs N.
Figure 3.
Association energies of defect complex containing and : (a) Eassociation vs EC; (b) Eassociation vs N.
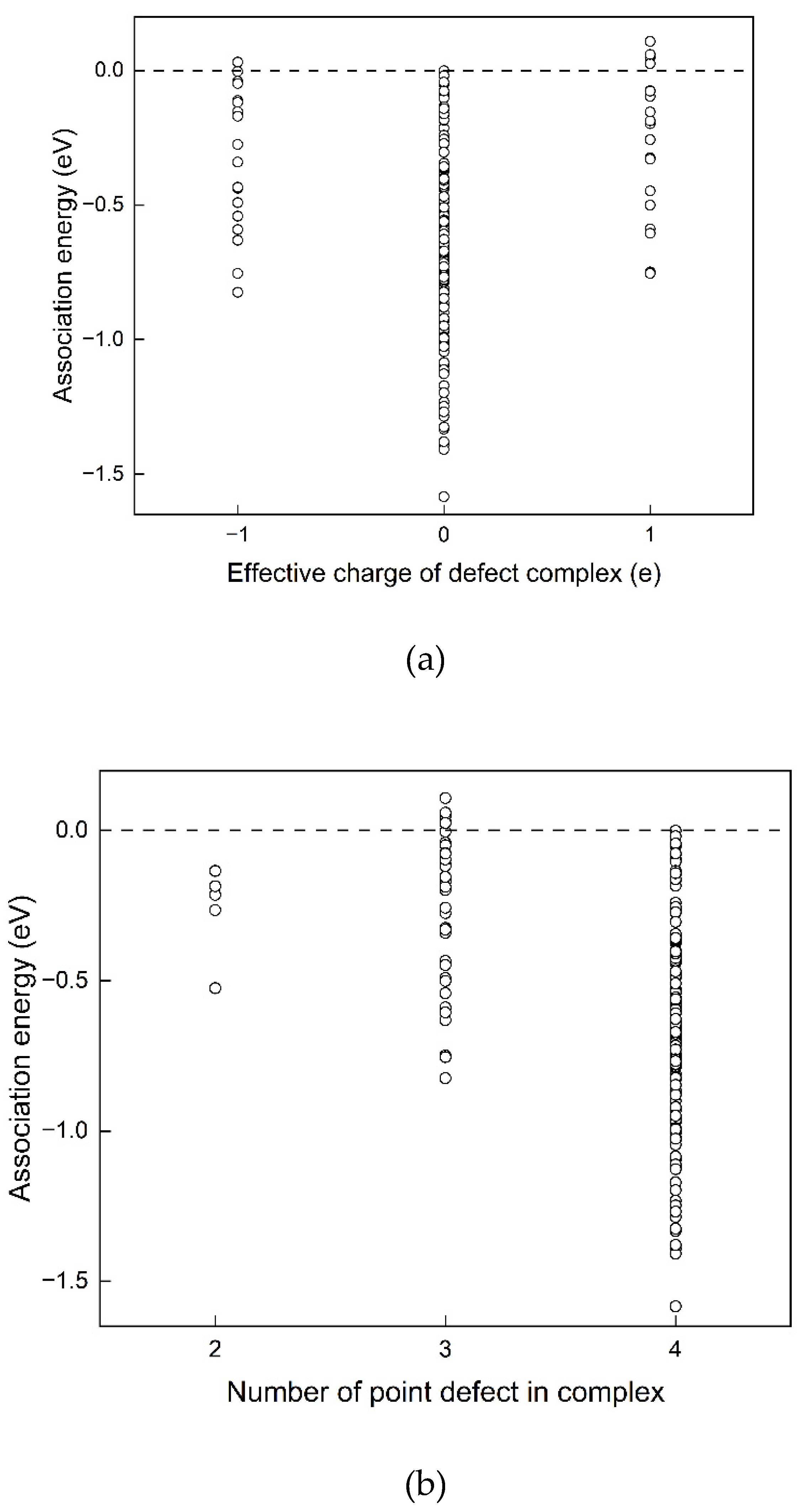
Figure 4.
Relaxed structure of : (a) the lowest Edefect configuration; (b) the highest Edefect configuration.
Figure 4.
Relaxed structure of : (a) the lowest Edefect configuration; (b) the highest Edefect configuration.
Figure 5.
Relaxed structure of from <00> and <010> directions.
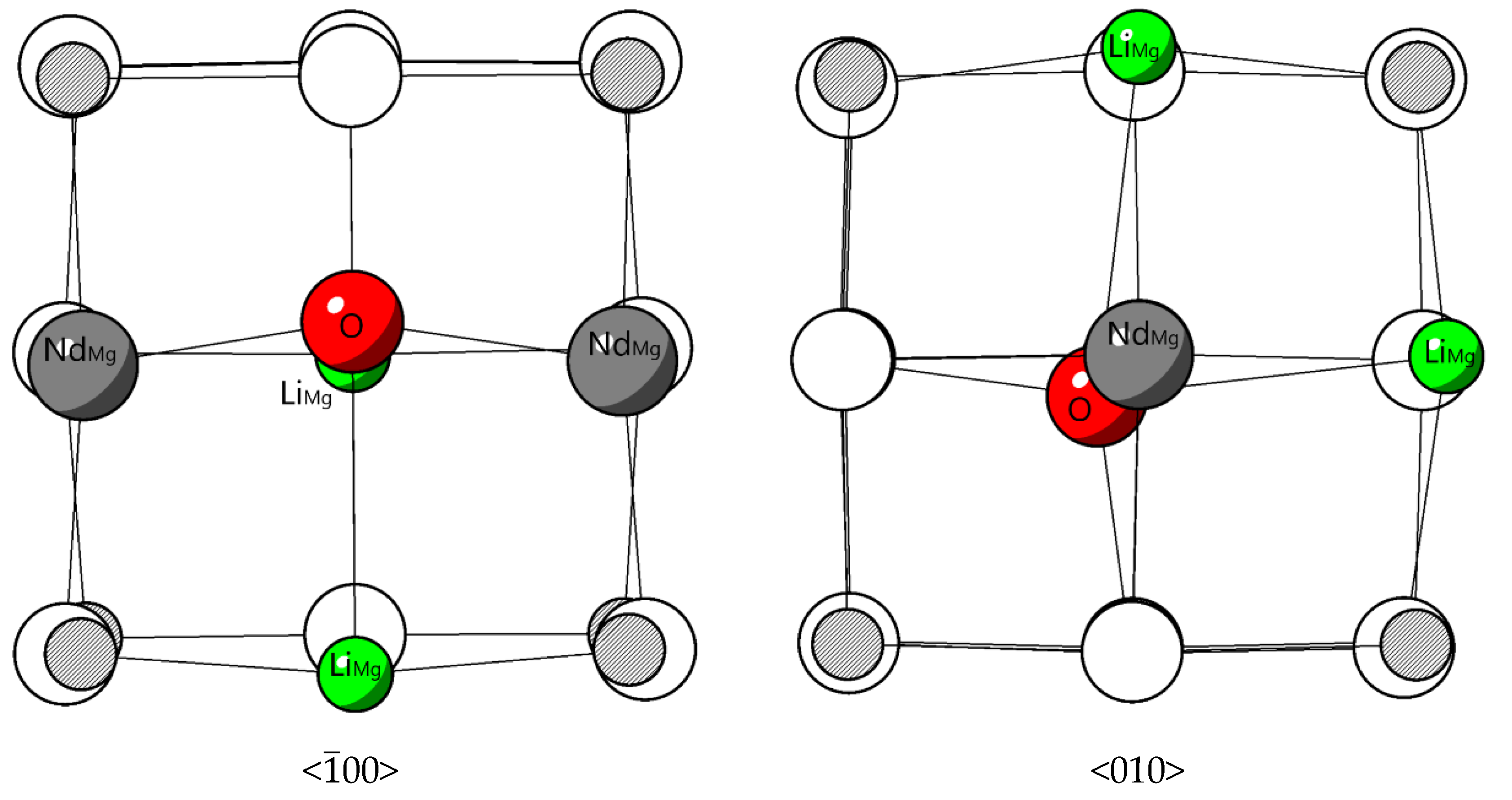
Figure 6.
Selected test positions of and their defect energies. White: O. Green: Li. Grey: Nd. Striped: Mg.
Figure 6.
Selected test positions of and their defect energies. White: O. Green: Li. Grey: Nd. Striped: Mg.
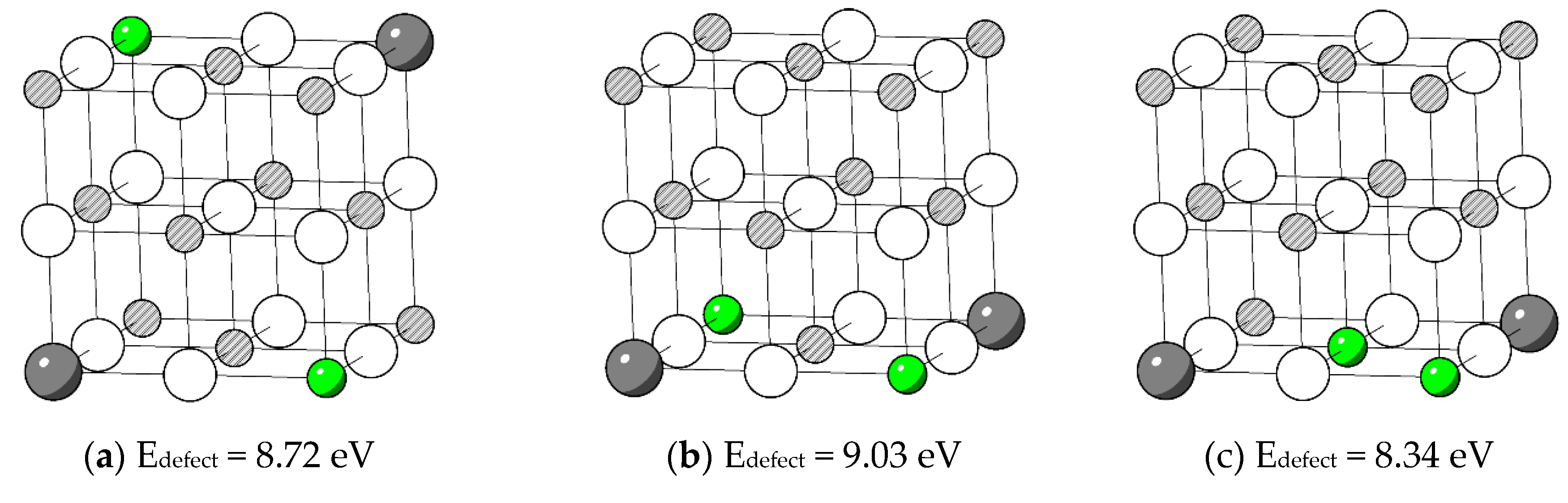
Figure 7.
Correlations between interatomic distance and association energy.
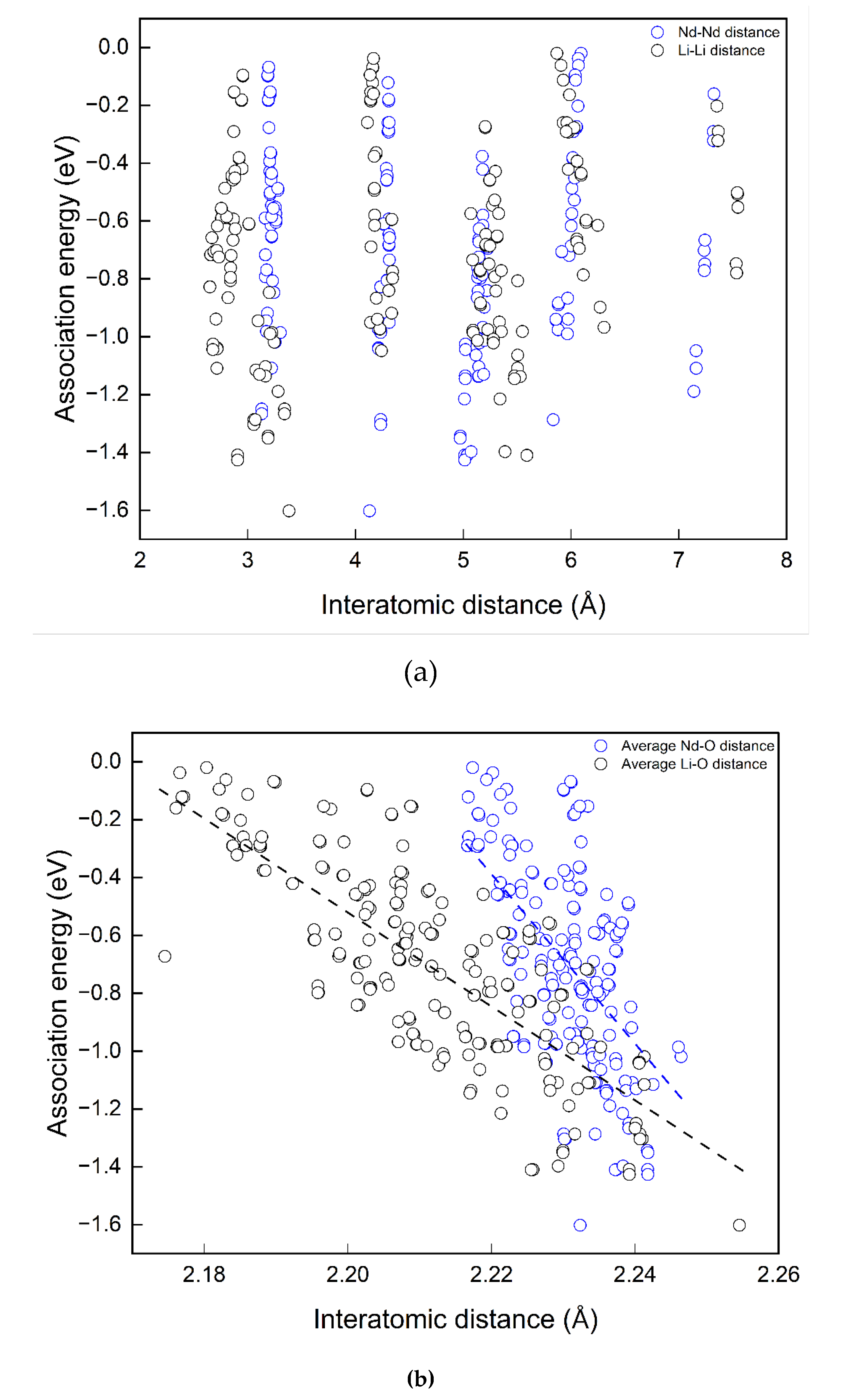
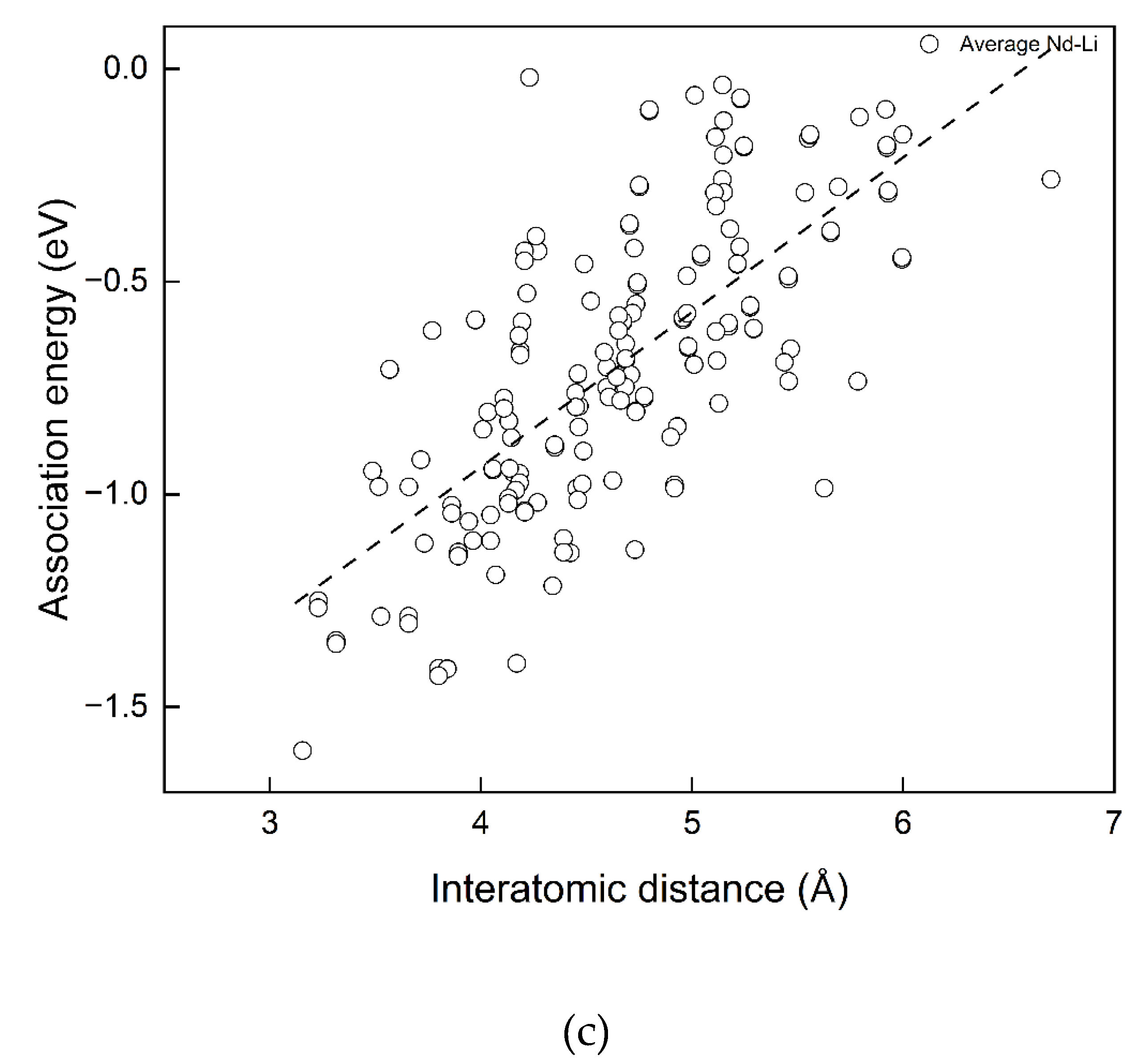
Figure 8.
Comparisons of RE-O bond lengths in RE: MgO and RE, Li: MgO. RE=Nd or Er. Grey line: Trend line.
Figure 8.
Comparisons of RE-O bond lengths in RE: MgO and RE, Li: MgO. RE=Nd or Er. Grey line: Trend line.
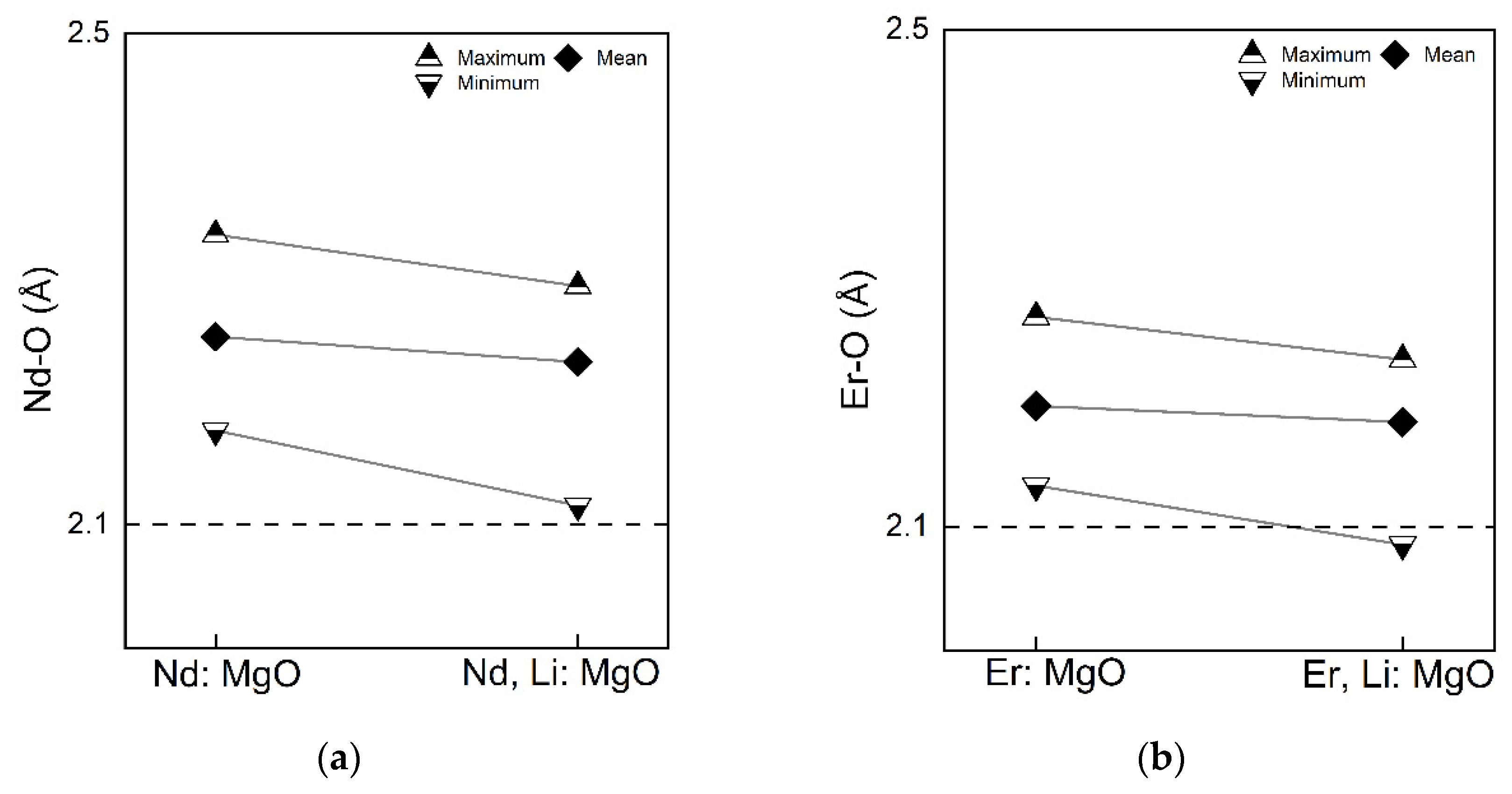
Figure 9.
The most favourable configuration of
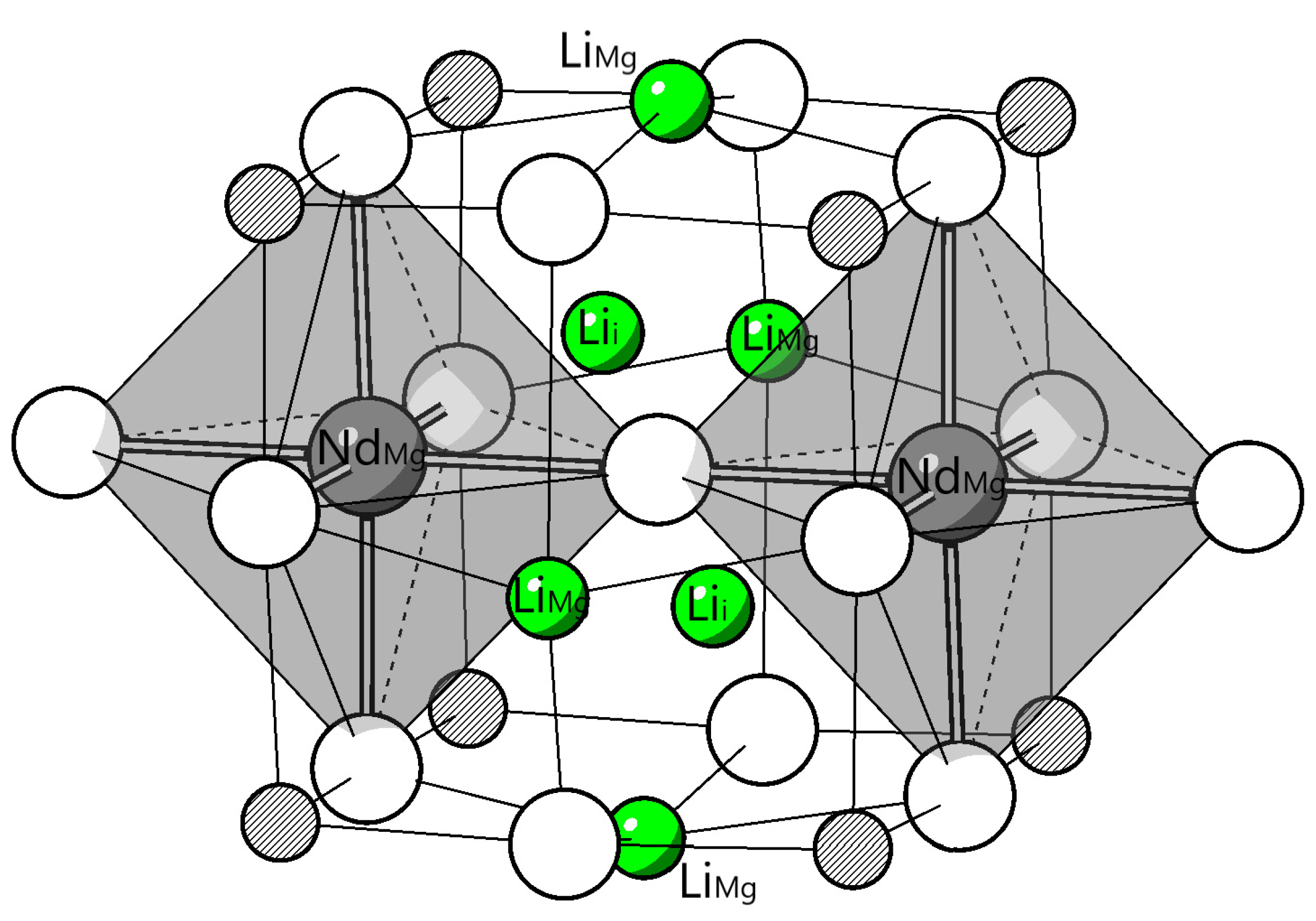
Table 1.
Topics about MgO Investigated via Simulations.
| Topic investigated | Reference | |
|---|---|---|
| Intrinsic point defects and diffusion | [14,15,16,17,18,19,20] | |
| Impurity/dopant | Alkali metal trapped hole [Li]0 | [21,22,23] |
| Fluorine F-1 | [24] | |
| S2- and Se2- | [25] | |
| Li, Al, Ti, Fe, Cu, Zn Ag | [26] | |
| Dislocations/grain boundary/surfaces/ interfaces | [27,28,29,30] | |
| Radiation damage | [31,32] | |
| Melting and phase diagram | [33,34,35] | |
| Low energy recoil events | [36] | |
Table 5.
Association Energies of Point Defect Pairs in Nd: MgO.
| Defect pair | Effective charge (e) | Association energy (eV) |
|---|---|---|
| +1 | -14.81* | |
| +1 | -4.12 | |
| -1 | -1.07 | |
| -1 | -1.63 |
*The relaxed configuration is point defect.
Table 6.
Defect structure of
| Distance | Configuration (a) (Å) | Configuration (b) (Å) |
|---|---|---|
| Average Nd-O | 2.255 | 2.215 |
| Average NdMg - VMg | 2.77 | 4.30 |
| Nd - Nd | 4.80 | 6.12 |
Table 7.
Association Energies of Defect Pairs in Nd, Li: MgO.
| Defect | Effective charge (e) | Association energy (eV) |
|---|---|---|
| 0 | -0.53 | |
| +1 | -0.77 | |
| -1 | -0.84 | |
| 0 | -1.60 |
Table 8.
Defect Structure of
| Interatomic distance | The lowest Edefect configuration (Å) | The highest Edefect configuration (Å) |
|---|---|---|
| Average Nd-O | 2.232 | 2.217 |
| Average Nd - Li | 3.154 | 4.230 |
| Nd - Nd | 4.130 | 6.093 |
| Li - Li | 3.384 | 5.868 |
Table 9.
Distortion Indices of Relaxed Octahedra in the Lowest Energy Configuration from Static Lattice Calculations.
Table 9.
Distortion Indices of Relaxed Octahedra in the Lowest Energy Configuration from Static Lattice Calculations.
| DI | Nd: MgO | Nd, Li: MgO |
| bond-length distortion | 0.024 | 0.023 |
| bond-angle distortion | 0.064 | 0.051 |
| edge-length distortion | 0.032 | 0.032 |
| DI | Er: MgO | Er, Li: MgO |
| bond-length distortion | 0.021 | 0.021 |
| bond-angle distortion | 0.052 | 0.044 |
| edge-length distortion | 0.025 | 0.026 |
Table 10.
Defect Structure of .
| Interatomic distance | (Å) |
|---|---|
| Average Nd - O | 2.223 |
| Average Nd - Li | 3.160 |
| Nd - Nd | 4.301 |
| Average Li - Li | 3.475 |
Table 11.
Distortion Indices of Relaxed Octahedra of Nd in Excess-Li Condition (Nd: Li = 1:3).
| DI | Nd, 3Li: MgO |
|---|---|
| bond-length distortion | 0.011 |
| bond-angle distortion | 0.012 |
| edge-length distortion | 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







