Preprint

Article

Smart Delivery Assignment Problem through Machine Learning and the Munkres Algorithm

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 March 2024

Posted:

28 March 2024

You are already at the latest version

Alerts

Abstract

In the realm of smart transportation and mobility, delivery organizations are continuously refining their strategies, harnessing resources and advanced analytical techniques to streamline operations, aiming to achieve optimal solutions in terms of both efficiency and cost-effectiveness. However, a persistent challenge faced by these delivery companies revolves around the effective assignment of delivery personnel to customer orders, often grappling with suboptimal assignments that lead to inefficiencies and delays. To address this issue, we propose an architecture that uses the Munkres algorithm to optimize the task assignment problem for delivery personnel with pending orders, employing different cost functions obtained with deterministic and machine learning techniques. We compared the performance of linear and polynomial regression methods to construct different cost functions represented by matrices with orders and delivery people information. Subsequently, we applied the Munkres optimization algorithm to solve the assignment problem, which optimally assigns delivery people and orders. The results demonstrate that linear regression, used to estimate distance information, can reduce estimation errors by up to 568.52 km (1.51%) for our dataset compared to other methods. Conversely, polynomial regression proves effective in constructing a superior cost function based on time information, reducing estimation errors by up to 17,143.41 minutes (11.59%) compared to alternative methods. The proposed approach aims to enhance delivery personnel allocation within the delivery sector, optimizing the efficiency of this process.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

In the rapidly evolving landscape of smart transportation, e-commerce, and logistics, the efficient management of delivery operations remains an indispensable determinant of success for delivery businesses [1]. However, within this realm, the convergence of smart transportation and mobility further complicates the equation. Smart delivery processes are confronted with a multitude of challenges, spanning from the imperative to meet increasingly demanding customer expectations for swift and reliable service to the intricate task of managing inventory levels efficiently. Additionally, the optimization of delivery routes presents a formidable challenge, necessitating consideration of dynamic variables such as traffic patterns and delivery windows. Moreover, the seamless facilitation of communication and tracking throughout the delivery journey is essential for ensuring a smooth and transparent customer experience [2,3]. These multifaceted challenges collectively underscore the pressing need for innovative logistical solutions and strategies that harness the potential of smart transportation and mobility technologies to maintain competitiveness in the ever-evolving landscape of smart e-commerce and logistics.

In this context, the use of Artificial Intelligence (AI) techniques can represent revolutionary opportunities to improve traditional approaches related to delivery, logistics, and supply chain management [4]. In particular, AI algorithms based on machine learning (ML), deep learning (DL), and reinforcement learning (RL) offer significant potential to enhance delivery processes and logistics. For example, ML algorithms can analyze vast amounts of historical delivery data to identify patterns, optimize routing, and predict demand more accurately, thereby improving the efficiency of delivery operations [4,5]. Moreover, DL models work well at processing complex data types like images and text, enabling tasks such as automatic package sorting, vehicle recognition, and natural language processing for customer inquiries [6]. On the other hand, RL algorithms can optimize decision-making in dynamic environments by learning from interactions with the delivery environment, leading to more adaptive and responsive delivery strategies [7]. These AI techniques represent a possible solution to address delivery logistics challenges.

Optimization methods also play a crucial role in improving delivery problems and logistics by efficiently allocating resources, optimizing routes, and minimizing costs [8]. Techniques such as linear programming, integer programming, and metaheuristic algorithms enable businesses to address logistics and delivery challenges such as route optimization and inventory management [9]. By mathematically modeling delivery constraints and objectives, optimization methods can help businesses make informed decisions, maximize resource utilization, and improve overall operational efficiency. These methods also facilitate dynamic adjustments to changing conditions, ensuring adaptive and responsive delivery strategies. Ultimately, optimization methods contribute to enhancing customer satisfaction, reducing delivery times, and achieving cost savings in logistics operations [10].

Over the past few years, task assignment approaches related to delivery problems have gained significant attention from various researchers. For example, in cite [11], the authors present an algorithm aimed at optimizing food delivery processes by minimizing delivery time in road networks. This approach formulates an order assignment problem as a minimum weight perfect matching task on a bipartite graph. Then, the authors employ the best-first search graph method to efficiently calculate the solution space. The authors used real data from Swiggy, the largest food-delivery company in India. This approach introduced novel concepts such as order batching and dynamic adaptation to vehicle locations to enhance the solution quality and demonstrates its effectiveness in achieving a 30% reduction in delivery time. Other works emphasize the importance of minimizing the delivery time for customer satisfaction [12]. The challenge in this respect involves stages such as order-to-vehicle assignment, order batching, and adapting to vehicle movements. To address this, the authors introduced a solution mapping the vehicle assignment problem to minimum weight perfect matching on a bipartite graph. To optimize efficiency, best-first search is utilized to construct a subgraph likely to contain the minimum matching. The algorithm enhances solution quality by considering graph batching and dynamic vehicle positions using angular distance. Extensive experiments on real food-delivery data from metropolitan cities demonstrate this approach presents substantial improvements over other strategies, including reduced food delivery time, waiting time at restaurants, and increased orders delivered per kilometer. In the work presented in [13], the authors address the challenge of online food delivery focusing on the efficient allocation of orders to drivers and route planning. For order assignment, a modified Kuhn-Munkres (Munkres) algorithm was employed to optimize matching between orders and drivers, while a machine learning classification model using eXtreme Gradient Boosting (XGBoost) predicts order batching results to prevent inappropriate matches. Additionally, a rule-based route planning method generates viable routes for drivers. Experiments conducted on real datasets from Meituan demonstrate the effectiveness of the proposed algorithm in solving the online food delivery problem, validating the performance of the classification model and the overall efficiency. In [14], the authors discuss an Autonomous Mobility-on-Demand system, which was considered an eco-friendly urban transportation service. It addresses the optimization of recharging, delivery, and repositioning tasks for shared autonomous electric vehicles through a multi-agent multi-task dynamic dispatching problem based on the Markov Decision Process. The decision-making process is divided into three subprocesses, each transformed into a mathematical problem: recharging and delivery task assignments are modeled as maximum weight matching problems of bipartite graphs while repositioning task assignment is quantified as a maximum flow problem. Algorithms such as Kuhn-Munkres and Edmond-Karp were employed to solve these problems and achieve optimal task allocation policies. In [15], a reward function balancing order income with trip satisfaction was proposed along with a state-value function estimated by Back Propagation-Deep Neural Network to assess the matching degree between vehicles and tasks. The results demonstrate significant improvements in total revenue, user waiting time reduction, and trip satisfaction through various optimization strategies such as introducing task allocation repositioning and combining charging with task repositioning.

Based on the bibliographic review presented above, it can be observed that task assignment problems are a broad field of research, which has had several developments with sundry results. In this context, the motivation of this work is to use machine learning and the Munkres optimization algorithm in a single architecture to find a feasible method to improve the assignment tasks between delivery people and orders. The synergy between Machine Learning and the Munkres Algorithm enabled us to improve delivery operations, which might have a positive impact on operational costs. Our article contributions can be summarized as follows.

We build a dataset from MAX Delivery company headquartered in Barcelona, Spain. The dataset comprises 7707 order records. Each record contains details regarding the time and coordinates of delivery personnel assigned to specific customer orders.
We used the Haversine formula to accurately calculate the distances between delivery people and customer orders. This is essential for generating an assignment matrix to solve the optimization problem related to order allocation.
We propose two different supervised machine learning methods techniques to estimate delivery time and distance for each delivery person to each customer. This is key because the dataset only contains specific data points for completed deliveries, and creating the assignment matrix requires calculating potential delivery times for all delivery person-customer combinations.
We used the Munkres Algorithm with the cost matrices obtained from the Haversine calculations, as well as the linear and polynomial regression methods. The Munkres optimization algorithm solves the task assignment problem, which optimally assigns delivery people to customer orders. The algorithm efficiently determines the best possible assignments by considering the costs associated with each assignment and guarantees an optimal solution for this task.
Finally, we compared the effectiveness of the Haversine calculations, linear regression, and polynomial regression techniques after applying the Munkres optimization algorithm to solve the task assignment problem.

2. Materials and Methods

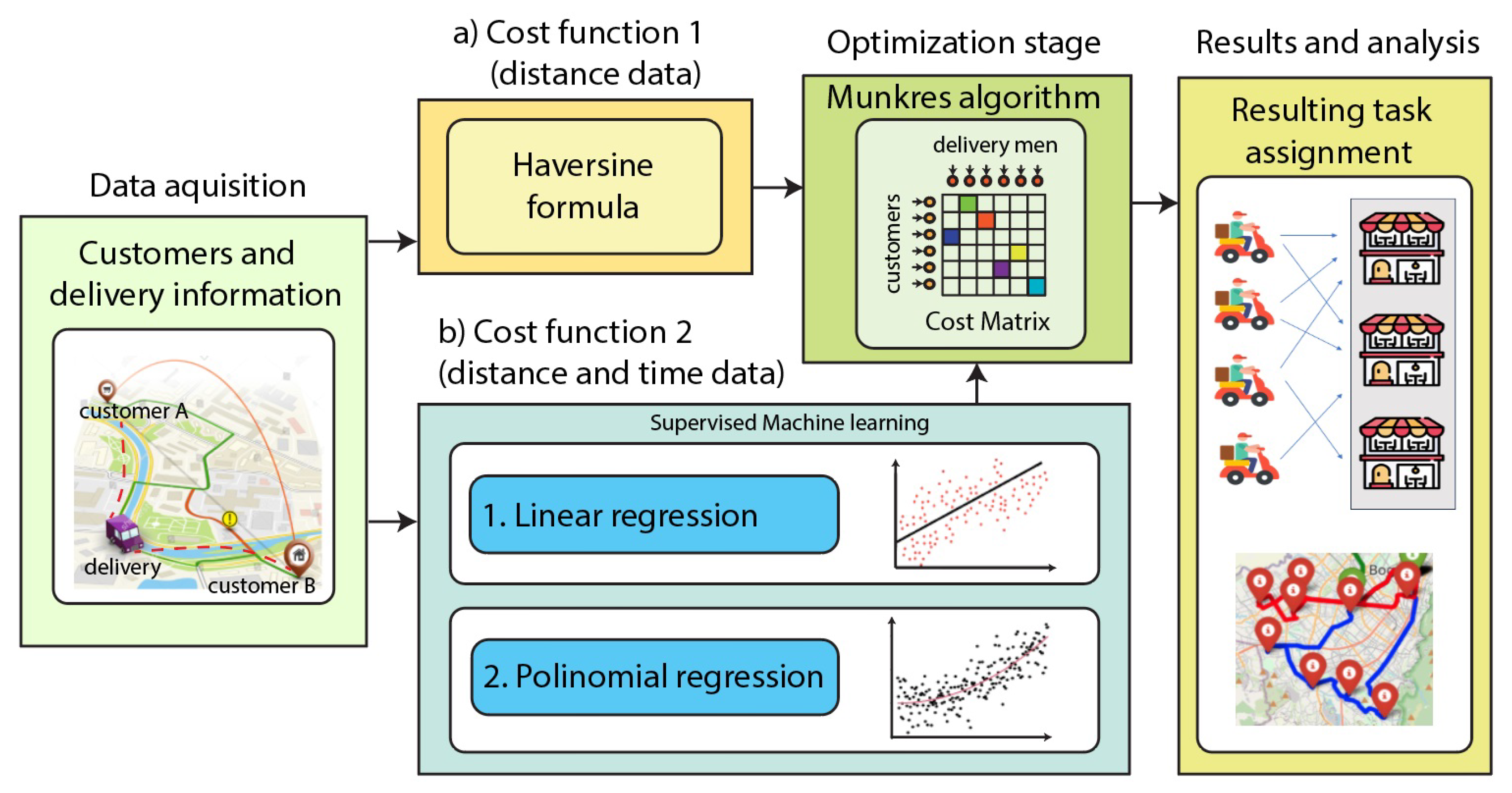
In this work, we propose the architecture presented in Figure 1, which is based on machine learning and optimization methods to improve the delivery assignment task. For this, we first create a dataset based on delivery company information called MAX Delivery from Barcelona, Spain. Then, to create a cost function to be optimized, we compared heuristics and Machine Learning methods based on Linear Regression and Polynomial Regression to model distance and time metrics. Once we estimate the cost functions, we solve the task assignment delivery problem by using the Munkres Algorithm (also known as the Hungarian method). Finally, we compare, evaluate, and present the task assignment delivery results.

2.1. Data Acquisition

For our data acquisition procedure, we sourced information from MAX Delivery, a company headquartered in Barcelona, Spain. The dataset encompasses 7707 order records, each detailing the time and coordinates of delivery personnel assigned to specific customer orders. This includes information on both the delivery person and customer coordinates, along with the time taken for each delivery. The data analyzed in this study was collected between January 1, 2023, and June 22, 2023, enabling us to compile a dataset comprising 7707 successful delivery orders. To safeguard confidentiality, all consumer and delivery person names and specific details were anonymized.

It’s important to note that our dataset provides information solely on completed deliveries and associated customer orders. However, to formulate a task assignment problem, we require a cost function represented by an assignment matrix. This matrix contains the potential cost for each delivery person to deliver to each customer. To construct this assignment matrix, we propose utilizing two distinct methods: the Haversine formula and supervised regression techniques. When employing the Haversine formula, we leverage the coordinates of each delivery person and customer to precisely compute the distance between their locations and thus complete the assignment matrix. It should be noted that while the Haversine formula accurately calculates the distance between points, determining time is more complex due to the absence of speed, trajectory, or traffic information. Consequently, any time calculations are estimations are derived from known information in our dataset using regression methods. Specifically, we utilize linear and polynomial regression to estimate the missing data in the assignment matrix of distance and time respectively.

The objective of creating the proposed assignment matrices, whether using calculated or estimated data, is to optimally assign the nearest delivery person to each customer, thereby ensuring efficient service delivery, as elaborated in subsequent sections.

2.2. Haversine Formula to Estimate Cost Matrix

The main objective of this process is to estimate the distance between the delivery people and the customer orders and generate an assignment matrix to solve the optimization problem related to the task assignment problem. To accomplish this, we calculated the distances between the delivery people and the customer orders by using the Haversine formula [16,17]. This formula utilizes the latitude and longitude information of each member of the delivery people’s fleet and the current batch of customers to calculate the distance between each of them. The Haversine formula is based on spherical trigonometry and takes into account the curvature of the Earth. It involves several steps, such as applying the Haversine formula (using radians), which computes the central angle (

θ

) between the points using the differences in latitude and longitude as indicated in Equation 1.

hav (θ) = {sin}^{2} (\frac{Δ lat}{2}) + cos ({lat}_{1}) \cdot cos ({lat}_{2}) \cdot {sin}^{2} (\frac{Δ lon}{2})

(1)

Then, we calculate the distance d by using Equation 2 using the central angle and the Earth’s radius (R), typically taken as approximately 6,371 kilometers (or 3,959 miles).

d = 2 \cdot R \cdot atan 2 (\sqrt{hav (θ)}, \sqrt{1 - hav (θ)})

(2)

The resulting value for d represents the distance between the two points along the surface of the Earth. We used this method because it is commonly used in geographic applications and navigation systems to accurately measure distances between locations. 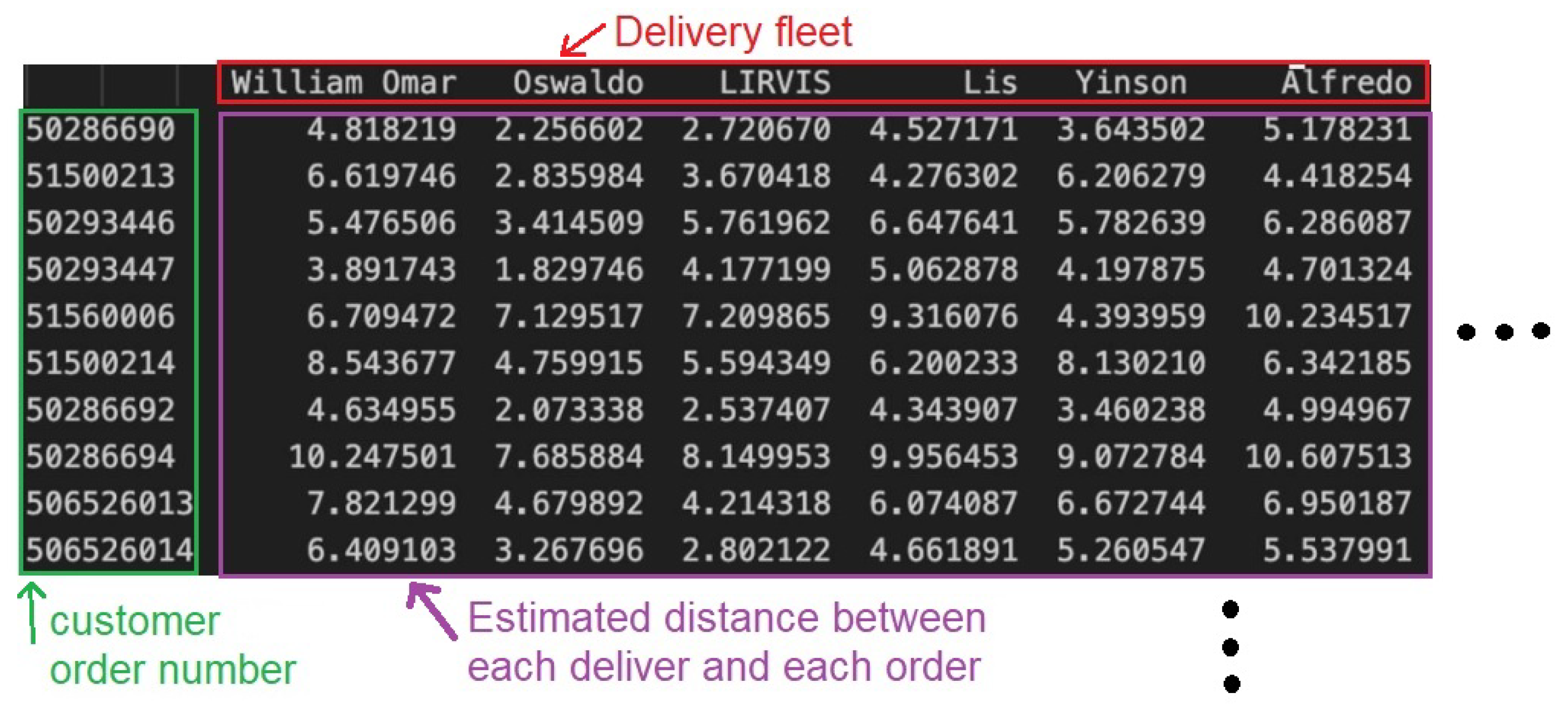The calculated distances are then used to obtain the matrix that represents the cost function used to solve the task assignment problem, which is composed of the distance between each delivery man and each customer order as illustrated in Figure 2. The matrix used during the experiments is composed of 7707 possible deliveries and 7707 customer orders.

2.3. Machine Learning to Estimate Cost Matrix

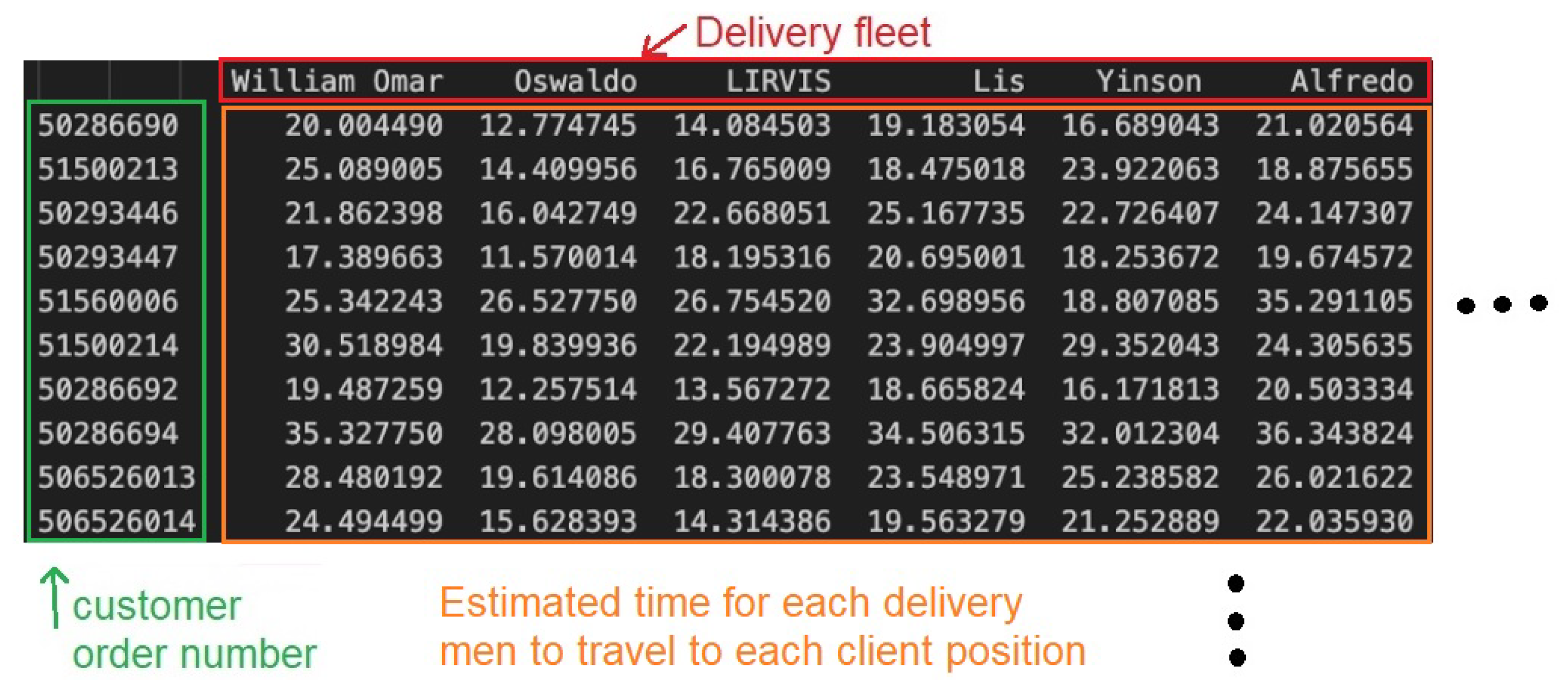
In addition to directly calculating distance with the haversine formula, we propose the use of distance and time estimations to build the cost matrix to be optimized. Since we only have specific data points for delivery persons who completed deliveries, and creating the assignment cost matrix requires calculating the potential distance and travel time for each delivery person to each customer, we utilize supervised regression-based learning models to estimate distance and delivery time. We employ two different methods to obtain an assignment matrix representing the cost function: linear regression and polynomial regression. An example of the cost matrix obtained for travel time estimation can be observed in Figure 3. We briefly explain each of the used regression methods as follows. It is worth mentioning that the matrix used during the experiments is composed of 7707 possible deliveries and 7707 customer orders.

2.3.1. Linear Regression

Linear regression is a supervised machine learning method used to model the relationship between a dependent variable and one or more independent variables. It assumes a linear relationship between the input variables and the output [18,19]. The Equation 3 represents a multiple linear regression with n independent variables.

y = b_{0} + b_{1} x_{1} + b_{2} x_{2} + \dots + b_{n} x_{n}

(3)

where y is the dependent variable,

x_{1}, x_{2}, \dots, x_{n}

are the independent variables, and

b_{1}, b_{2}, \dots, b_{n}

are the coefficients.

In the context of linear regression, the primary goal is to find the best-fitting line (or hyperplane in higher dimensions) that minimizes the error between the predicted values and the actual values in the dataset [18,19]. This is often done by minimizing a cost function, such as the Mean Squared Error (MSE), which quantifies the difference between the predicted values and the actual values [18,19]. The cost function equation measures the error between predicted and actual values as defined in Equation 4.

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} {(h_{θ} (x^{(i)}) - y^{(i)})}^{2}

(4)

where

J (θ)

represent the cost function to be optimized, m is the number of training examples,

h_{θ} (x^{(i)})

represent the predicted value for the i-th training example, and

y^{(i)}

is the actual value for the i-th training example.

Finally, Gradient descent is used to update the parameters to minimize the cost function

J (θ)

. Gradient descent is a powerful optimization algorithm that effectively addresses the optimization task in linear regression by efficiently searching for the optimal parameters that minimize the cost function

J (θ)

[18,19]. The equation that represents the update rule of the Gradient descent algorithm can be observed in Equation 5.

θ_{j} : = θ_{j} - α \frac{\partial}{\partial θ_{j}} J (θ)

(5)

where

α

is the learning rate, and the expression

\frac{\partial}{\partial θ_{j}} J (θ)

represents the partial derivative of the cost function concerning the j-th parameter. This equation iteratively updates the parameters

θ_{j}

in the direction of the steepest descent of the cost function. The gradient

\frac{\partial}{\partial θ_{j}} J (θ)

indicates the direction and magnitude of the change needed to minimize the cost function. The learning rate

α

scales this change to control the step size.

2.3.2. Polynomial Regression

Polynomial regression is a form of regression in which the relationship between the independent variables x and the dependent variable y is modeled as an n-degree polynomial [20,21]. Polynomial regression allows for a more flexible model than linear regression, as it can capture non-linear relationships between variables. However, higher-degree polynomials can lead to overfitting if not carefully controlled. The general form of a polynomial regression equation is:

y = b_{0} + b_{1} x + b_{2} x^{2} + \dots + b_{n} x^{n}

(6)

where, y is the dependent variable, x is the independent variable,

b_{0}, b_{1}, b_{2}, \dots, b_{n}

are the coefficients, and n is the degree of the polynomial. In this work, we propose the use of a quadratic polynomial regression (degree 2) as can be observed in Equation 7.

y = b_{0} + b_{1} x + b_{2} x^{2}

(7)

In polynomial regression, as in linear regression, the aim remains to minimize the cost function, typically the MSE (see Equation 4), through gradient descent (see Equation 5). However, polynomial regression introduces higher-degree polynomial terms into the hypothesis function, leading to a more complex equation for both the cost function and the gradient descent update rule. Despite these differences, the core principles of minimizing the cost function iteratively using gradient descent remain the same as indicated in Equations 4 and 5, with the mentioned adjustments to accommodate the polynomial features in the hypothesis function.

2.4. Munkres Algorithm

To effectively assign orders to delivery people while maximizing assignment efficiency, we propose the use of the Munkres Algorithm [11,22,23]. This method is also known as the Hungarian algorithm, and it is a widely used optimization algorithm for solving the assignment problem in bipartite graphs. It efficiently solves the problem of finding the optimal assignment of tasks to agents based on cost values [11,22,23]. The Munkres Algorithm is highly efficient, with a time complexity that makes it suitable for real-time and large-scale applications. Moreover, the algorithm guarantees an optimal solution to the assignment problem, ensuring that the total cost or benefit is minimized or maximized, depending on the objective function. The Munkres algorithm operates on a cost matrix representing the costs or benefits of assigning each task to each agent. Through a series of matrix operations, including row and column reductions and assignments, the algorithm efficiently identifies the optimal assignment.

The algorithm requires a cost matrix representing the costs or benefits associated with assigning tasks to agents. This cost matrix is an

n \times n

matrix, where n is the number of tasks or agents as can be observed in Equation 8.

(\begin{matrix} c_{11} & c_{12} & \dots & c_{1 n} \\ c_{21} & c_{22} & \dots & c_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ c_{n 1} & c_{n 2} & \dots & c_{n n} \end{matrix})

(8)

where

c_{i j}

represents the cost of assigning task i to agent j.

The Munkres algorithm starts by reducing each row of the cost matrix by subtracting the minimum cost in that row from all the elements in the row. This ensures that at least one zero is present in each row, as can be observed in Equation 9.

Minimize each row : {row}_{i} = {row}_{i} - \min ({row}_{i})

(9)

Similarly, each column of the cost matrix is reduced by subtracting the minimum cost in that column from all the elements in the column. This ensures that at least one zero is present in each column as can be observed in Equation 10.

Minimize each column : {column}_{j} = {column}_{j} - \min ({column}_{j})

(10)

After row and column reductions, the algorithm creates an assignment matrix, initially filled with zeros, where each zero represents an assignment of a task to an agent.

A = (\begin{matrix} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{n 1} & a_{n 2} & \dots & a_{n n} \end{matrix})

(11)

where

a_{i j} = 1

if task i is assigned to agent j, and

a_{i j} = 0

The algorithm iterates through various steps of reducing rows and columns, updating the assignment matrix, and finding augmenting paths until optimality conditions are met, ensuring that no more zeros can be chosen without violating the assignment constraints [11,22,23]. This means that each row and each column will contain exactly one zero in the assignment matrix A. Finally, the Cost of Assignment

C (A)

that represents the total cost of the assignment can be represented as stated in Equation 12.

C (A) = \sum_{i = 1}^{n} c_{i j} \cdot a_{i j}

(12)

These equations represent the core operations of the Munkres Algorithm, which iteratively reduces costs, updates the assignment matrix, and finds the optimal assignment by satisfying the optimality conditions.

3. Results

In this section, we first evaluate the results of the linear and polynomial regression algorithms used to estimate the distance and delivery time of the delivery people, thus completing the cost matrices. Subsequently, we present and compare the various outcomes obtained when solving optimization problems related to the assignment of delivery people to each potential customer. The results are presented below.

3.1. Regression Results

The results presented in Table 1 depict the performance of the proposed linear regression and polynomial regression techniques, which were trained to estimate distances and times that were used to fill the cost matrix that represents the cost function. In the case of distance estimation, polynomial regression outperforms linear regression, yielding a lower mean squared error (MSE) of 2.6 compared to 6.9 for linear regression. This translates to a substantially lower Root Mean Squared Error (RMSE) of 4.5 for polynomial regression, indicating greater accuracy in predicting distances. Similarly, for time estimation, polynomial regression achieves superior results with an MSE of 59.6 compared to 120.9 for linear regression. Consequently, the RMSE for time estimation with polynomial regression is notably lower at 7.7, showcasing its enhanced precision in predicting time durations compared to the RMSE of 11.0 for linear regression. These results suggest that polynomial regression offers better predictive capabilities for both distance and time estimation tasks compared to linear regression, demonstrating its efficacy in capturing the underlying patterns and complexities of the proposed dataset.

3.2. Task Assignment Problem Results

The results presented in Table 2 detail the performance of the proposed methods in estimating distances traveled by the delivery people after solving the task assignment problem with the Munkres algorithm. The Munkres method yields an average distance estimation of 4.55 kilometers, with a standard deviation of 3.24 kilometers, resulting in a total summation of 34956.84 kilometers. Interestingly, when combining linear regression with the Munkres method, the average estimation remains consistent at 4.55 kilometers, with a slightly reduced standard deviation of 3.23 kilometers, contributing to a marginally increased total summation of 34957.74 kilometers. Conversely, employing polynomial regression in conjunction with the Munkres method leads to a slightly higher average distance estimation of 4.62 kilometers, accompanied by a larger standard deviation of 4.49 kilometers, resulting in a total summation of 35526.26 kilometers. These findings suggest that, while both linear and polynomial regression exhibit similar average distance estimations when combined with the Munkres method, polynomial regression introduces greater variability in distance estimations, as indicated by its higher standard deviation. Notably, considering that less distance is better, the Munkres method and the linear regression combined with the Munkres method emerge as the most effective approaches when distance estimation is used to solve the assignment problem for the proposed dataset.

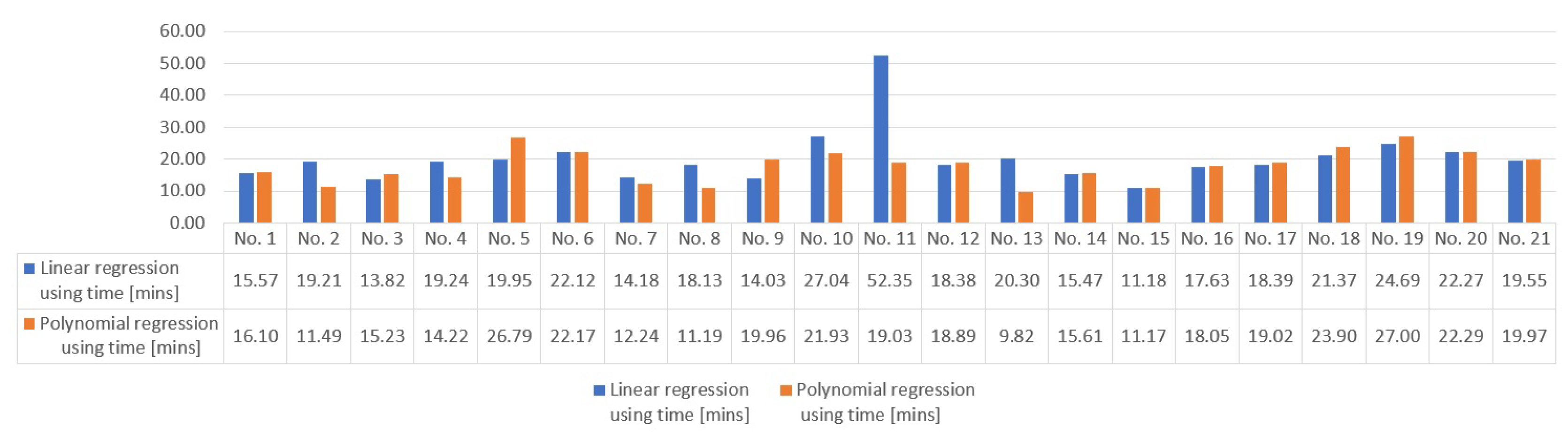
As can be observed in Table 3, for the Linear Regression method the average time estimation is 19.24 minutes, accompanied by a standard deviation of 9.12 minutes, resulting in a total summation of 147891.23 minutes. Conversely, the Polynomial Regression method yields a notably lower average time estimation of 17.01 minutes, with a reduced standard deviation of 5.25 minutes, contributing to a shorter total summation of 130747.82 minutes. These results indicate that Polynomial Regression offers more precise estimations with less variability compared to Linear Regression when we solve the task assignment problem with the Munkres method.

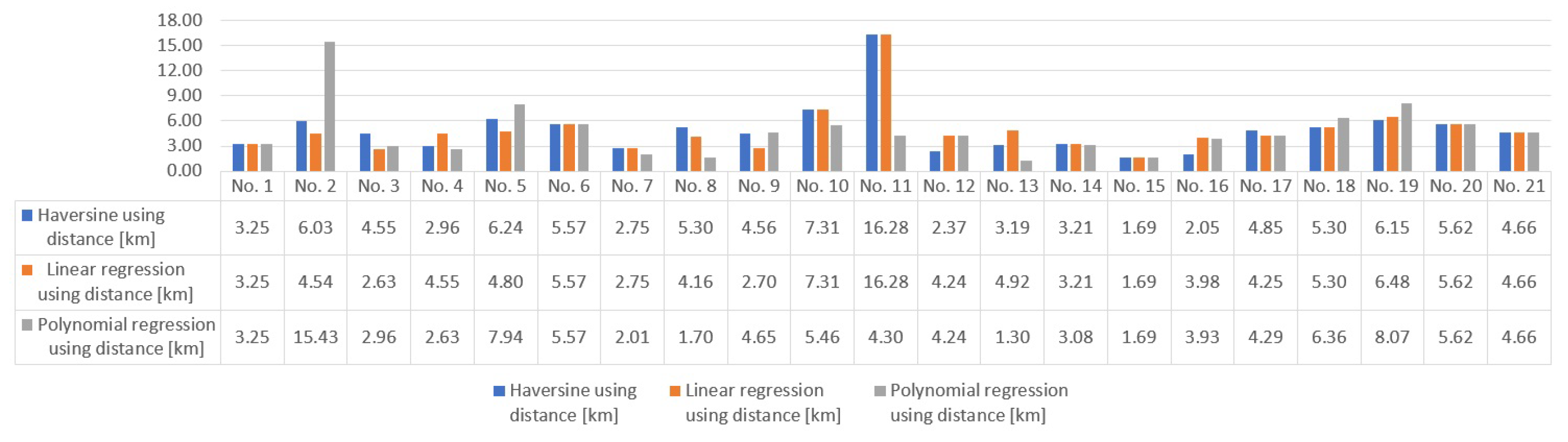
Finally, we present a sample of the results of the automatic assignment of tasks using the Munkres algorithm and the different methods of estimating the cost function in Figure 4 and Figure 5. In Figure 4, the use of distance to construct the cost matrix reveals that the best method is linear regression, with a total travel distance of 102.87 [km]. This is closely followed by the Harveysine method at 103.89 [km], and polynomial regression at 109.14 [km]. Conversely, Figure 5 illustrates that when time is utilized to formulate the cost matrix. In this case, polynomial regression emerges as the best method, resulting in a total travel time of 376.06 [min]. In contrast, the linear regression method yields a total time of 424.87 [min]. To summarize, linear regression methods demonstrate superior performance when distance estimation is utilized for our dataset, whereas polynomial regression methods excel in scenarios where time estimation is paramount.

4. Conclusions

In this work, we propose a smart delivery system to optimize the task assignment problem for delivery personnel with pending orders. The proposed approach utilizes the Munkres algorithm and various cost functions obtained through deterministic and machine-learning techniques. Linear and polynomial regression methods are compared to construct different cost functions represented by matrices with orders and delivery people information. Results show that linear regression reduces estimation errors in the distance by up to 568.52 km (1.51%) compared to other methods, while polynomial regression reduces errors in time estimation by up to 17,143.41 minutes (11.59%). The proposed smart delivery system aims to enhance delivery personnel allocation within the delivery sector, optimizing efficiency.

Author Contributions

Conceptualization, Juan Vásconez and Elias Schotborgh; Data curation, Juan Vásconez, Elias Schotborgh and Viviana Moya; Formal analysis, Juan Vásconez, Elias Schotborgh, Ingrid Vásconez, Andrea Pilco, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara; Funding acquisition, Juan Vásconez and Ingrid Vásconez; Investigation, Juan Vásconez, Elias Schotborgh, Ingrid Vásconez, Viviana Moya, Andrea Pilco, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara; Methodology, Juan Vásconez and Elias Schotborgh; Project administration, Juan Vásconez; Resources, Juan Vásconez, Elias Schotborgh, Ingrid Vásconez, Viviana Moya, Andrea Pilco, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara; Supervision, Juan Vásconez, Ingrid Vásconez, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara; Visualization, Juan Vásconez, Elias Schotborgh and Ingrid Vásconez; Writing – original draft, Juan Vásconez, Elias Schotborgh, Ingrid Vásconez, Viviana Moya, Andrea Pilco, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara; Writing – review & editing, Juan Vásconez, Ingrid Vásconez, Viviana Moya, Andrea Pilco, Oswaldo Menéndez, Robert Guamán-Rivera and Leonardo Guevara.

Acknowledgments

This work has been supported by ANID under grant Fondecyt Iniciación 11240105 and 11241171. The authors gratefully acknowledge the support provided by the Faculty of Engineering, Universidad Andres Bello, Santiago, Chile.

References

Farooq, Q.; Fu, P.; Hao, Y.; Jonathan, T.; Zhang, Y. A review of management and importance of e-commerce implementation in service delivery of private express enterprises of China. Sage Open 2019, 9, 2158244018824194. [Google Scholar] [CrossRef]
Giuffrida, N.; Fajardo-Calderin, J.; Masegosa, A.D.; Werner, F.; Steudter, M.; Pilla, F. Optimization and machine learning applied to last-mile logistics: A review. Sustainability 2022, 14, 5329. [Google Scholar] [CrossRef]
Bruni, M.E.; Fadda, E.; Fedorov, S.; Perboli, G. A machine learning optimization approach for last-mile delivery and third-party logistics. Computers & Operations Research 2023, 157, 106262. [Google Scholar]
Reis, J.; Amorim, M.; Cohen, Y.; Rodrigues, M. Artificial intelligence in service delivery systems: a systematic literature review. Trends and Innovations in Information Systems and Technologies: Volume 1 8 2020, pp. 222–233.
Gursoy, D.; Chi, O.H.; Lu, L.; Nunkoo, R. Consumers acceptance of artificially intelligent (AI) device use in service delivery. International Journal of Information Management 2019, 49, 157–169. [Google Scholar] [CrossRef]
Adak, A.; Pradhan, B.; Shukla, N.; Alamri, A. Unboxing deep learning model of food delivery service reviews using explainable artificial intelligence (XAI) technique. Foods 2022, 11, 2019. [Google Scholar] [CrossRef] [PubMed]
Jahanshahi, H.; Bozanta, A.; Cevik, M.; Kavuk, E.M.; Tosun, A.; Sonuc, S.B.; Kosucu, B.; Başar, A. A deep reinforcement learning approach for the meal delivery problem. Knowledge-Based Systems 2022, 243, 108489. [Google Scholar] [CrossRef]
Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Chen, C.Y. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm. Advanced Engineering Informatics 2022, 51, 101536. [Google Scholar] [CrossRef]
Asih, A.M.S.; Sopha, B.M.; Kriptaniadewa, G. Comparison study of metaheuristics: Empirical application of delivery problems. International Journal of Engineering Business Management 2017, 9, 1847979017743603. [Google Scholar] [CrossRef]
Tian, Z.; Zhong, R.Y.; Vatankhah Barenji, A.; Wang, Y.; Li, Z.; Rong, Y. A blockchain-based evaluation approach for customer delivery satisfaction in sustainable urban logistics. International Journal of Production Research 2021, 59, 2229–2249. [Google Scholar] [CrossRef]
Joshi, M.; Singh, A.; Ranu, S.; Bagchi, A.; Karia, P.; Kala, P. Batching and matching for food delivery in dynamic road networks. 2021 IEEE 37th international conference on data engineering (ICDE). IEEE, 2021, pp. 2099–2104.
Joshi, M.; Singh, A.; Ranu, S.; Bagchi, A.; Karia, P.; Kala, P. FoodMatch: Batching and matching for food delivery in dynamic road networks. ACM Transactions on Spatial Algorithms and Systems (TSAS) 2022, 8, 1–25. [Google Scholar] [CrossRef]
Wang, X.; Wang, L.; Wang, S.; Yu, Y.; Chen, J.f.; Zheng, J. Solving online food delivery problem via an effective hybrid algorithm with intelligent batching strategy. International Conference on Intelligent Computing. Springer, 2021, pp. 340–354.
Wang, N.; Guo, J. Multi-task dispatch of shared autonomous electric vehicles for Mobility-on-Demand services–combination of deep reinforcement learning and combinatorial optimization method. Heliyon 2022, 8. [Google Scholar] [CrossRef]
Nair, A.; Yadav, R.; Gupta, A.; Chakraborty, A.; Ranu, S.; Bagchi, A. Gigs with guarantees: Achieving fair wage for food delivery workers. arXiv, arXiv:2205.03530 2022.
Robusto, C.C. The cosine-haversine formula. The American Mathematical Monthly 1957, 64, 38–40. [Google Scholar] [CrossRef]
Basyir, M.; Nasir, M.; Suryati, S.; Mellyssa, W. Determination of nearest emergency service office using haversine formula based on android platform. EMITTER International Journal of Engineering Technology 2017, 5, 270–278. [Google Scholar] [CrossRef]
Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. Journal of Applied Science and Technology Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
Hope, T.M. Linear regression. In Machine Learning; Elsevier, 2020; pp. 67–81.
Heiberger, R.M.; Neuwirth, E.; Heiberger, R.M.; Neuwirth, E. Polynomial regression. R Through Excel: A Spreadsheet Interface for Statistics, Data Analysis, and Graphics 2009, 269–284. [Google Scholar]
Avery, M. Literature review for local polynomial regression. Unpublished manuscript 2013. [Google Scholar]
Shah, K.; Reddy, P.; Vairamuthu, S. Improvement in Hungarian algorithm for assignment problem. Artificial Intelligence and Evolutionary Algorithms in Engineering Systems: Proceedings of ICAEES 2014, Volume 1. Springer, 2015, pp. 1–8.
Sanseverino, E.R.; Ngoc, T.N.; Cardinale, M.; Vigni, V.L.; Musso, D.; Romano, P.; Viola, F. Dynamic programming and Munkres algorithm for optimal photovoltaic arrays reconfiguration. Solar Energy 2015, 122, 347–358. [Google Scholar] [CrossRef]

Figure 1. Proposed architecture for enhancing delivery assignments through Supervised Machine Learning regression techniques and the Munkres algorithm.

Figure 2. Sample of the cost matrix that represents the distance between each delivery person and each customer order. The matrix used is composed of 7707 possible deliveries and 7707 customer orders.

Figure 3. Sample of the cost matrix that represents the estimated delivery time between each delivery person and each customer order. The time estimation was realized by using linear and polynomial regression models.

Figure 4. Distance calculation after optimization procedure for a sample of 21 delivery people. a) Total Munkres distance 103.89 [km], b) Total Munkres distance 102.87 [km], c) Total Munkres distance 109.14 [km].

Figure 5. Time calculation after optimization procedure for a sample of 21 delivery people. a) Total time using linear regression of 424.87 [min], b) Total time using linear regression of 376.06 [min].

Table 1. Mean squared error (MSE) and Root Mean squared error (RMSE)

	Mean squared error (MSE)	Root Mean squared error (RMSE)
Distance estimation - linear regression	6.9 [ $m^{2}$ ]	20.3 [m]
Distance estimation - polynomial regression	2.6 [ $m^{2}$ ]	4.5 [m]
Time estimation - linear regression	120.9 [ $s^{2}$ ]	11.0 [s]
Time estimation - polynomial regression	59.6 [ $s^{2}$ ]	7.7 [s]

Table 2. Comparison results of the proposed methods to solve the task assignment problem by using distance metrics at the cost matrix.

Method	Average [km]	Standard Deviation [km]	Summation of total distance [km]
Munkres	4.55	3.24	34956.84
Linear regression + Munkres	4.55	3.23	34957.74
Polynomial regression + Munkres	4.62	4.49	35526.26

Table 3. Comparison results of the proposed methods to solve the task assignment problem by using distance metrics at the cost matrix.

	Average [minutes]	Standard Deviation [minutes]	Summation of total time [minutes]
Linear Regression + Munkres	19.24	9.12	147891.23
Polynomial Regression + Munkres	17.01	5.25	130747.82

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Smart Delivery Assignment Problem through Machine Learning and the Munkres Algorithm

Abstract

1. Introduction

2. Materials and Methods

2.1. Data Acquisition

2.2. Haversine Formula to Estimate Cost Matrix

2.3. Machine Learning to Estimate Cost Matrix

2.3.1. Linear Regression

2.3.2. Polynomial Regression

2.4. Munkres Algorithm

3. Results

3.1. Regression Results

3.2. Task Assignment Problem Results

4. Conclusions

Author Contributions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe