Prerpints.org logo
Preprint
Article

CAS Key Laboratory of Quantum Information, University of Science and Technology of China

Altmetrics

Downloads

276

Views

141

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 April 2024

Posted:

23 April 2024

You are already at the latest version

Alerts
Abstract
A challenge in building large-scale superconducting quantum processors is the precise control and manipulation of the qubit state. However, the crosstalk between the microwave control lines impedes the parallel execution of high-fidelity digital and analog quantum operations. Here, we propose and demonstrate a universal compensation protocol for calibrating the microwave signal crosstalk. We also introduce amplified error sequences to optimize the accuracy. Furthermore, we show a definitive improvement in parallel gate operations with crosstalk cancellation, demonstrating the technique's effectiveness. This work paves the way for superconducting hardware that features automated calibration of microwave crosstalk, leading to enhanced fidelities in multiqubit circuits.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology
Quantum computing is promising for solving complex problems beyond the reach of traditional computing methods [1,2,3]. Despite recent demonstrations of quantum supremacy [4,5,6,7,8,9,10], utility [11], and quantum logical error correction [12,13,14,15,16,17,18], achieving scalable quantum computing is still obstructed by numerous challenges [19]. Among these, crosstalk is well-recognized in various quantum computing systems [20,21,22,23,24,25,26,27,28]. Specifically, microwave crosstalk in superconducting circuits significantly impacts system performance by inducing unwanted quantum state transitions and gate errors [29,30,31,32]. Figure 1(a) shows such an example for transmon qubit, where the first three levels are included [33]. A microwave drive signal intended for bias qubit Q b with Rabi strength Ω b and frequency ω cr couples unintentionally to target qubit, inducing an effective Rabi strength Ω cr on the target qubit. r e i ϕ cr = Ω cr / Ω b is the complex transfer amplitude or the so-called crosstalk coefficient. Leakage occurs when the frequency ω cr of the spurious microwave signal is near resonance with the transition frequency ω ef between the first excited ( e ) and second excited ( f ) states. Gate errors manifest when ω cr is near resonance with the transition frequency ω ge between the ground ( g ) and the first excited ( f ) state. This form of interference disrupts the precise control over qubit states which is essential for accurate quantum computation and error correction. As such, the characterization and mitigation of microwave crosstalk within superconducting circuits are critical for robust and scalable quantum computing architectures.
As microwave crosstalk can always be compensated with an additional out-of-phase signal, as shown in Figure 1(a), the task translates to how one can characterize and calibrate the complex amplitude r e i ϕ cr of the crosstalk signal, so a compensation signal of the same frequency and amplitude but out-of-phase can be applied to null the crosstalk signal. Some previous works have addressed this issue, each in a particular condition. When ω cr = ω ge , a clear constructive and destructive dynamic Rabi oscillation pattern is observed when ϕ cr changes periodically [34,35], which can be used to extract r and ϕ cr . Refs. [36,37] extended this method to off-resonant case ( ω cr ≠ ω ge ) and Ref. [36] further provided an analytical formula to fit the oscillation pattern. For far-off resonance, the interference pattern of Rabi oscillation becomes invisible, and the spin-echo sequence is proposed [38] to calibrate microwave crosstalk utilizing the AC-Stark effect. Ref. [15] used the Ramsey error filter sequence to suppress leakage when ω cr is in the vicinity of ω ef . Although these schemes can cover a majority of crosstalk scenarios in the three-level subspace of transmon qubit, they are not universal and lack a unified model that governs the basic principle of the calibration procedure. Most of these schemes require at least one two-dimensional scan to obtain the final results, which makes it rather time-consuming to bring up a large quantum processor. Moreover, the sensitivity of these schemes is challenged when | ω cr − ω ge | ≫ 0 or | η | , where η = ω ef − ω ge is the anharmonicity of the superconducting qubit.
Here, we propose and demonstrate a fast and universal scheme using Ramsey-like sequences for calibrating microwave crosstalk. Given the abovementioned limitations, this work contributes to the literature mainly from three aspects. First, we propose and experimentally validate a simple two-level off-resonant driving model; this theoretical model unifies the calibrating principle for all crosstalk scenarios and provides explicit formulas to fit the experimental data. Second, instead of requiring a two-dimensional parameter scanning procedure, only multiple one-dimensional sweeps are sufficient for accurately retrieving target parameters. Third, we introduce error-amplifying sequences to improve accuracy, especially in large detuning regions. With these advancements in terms of universality, efficiency, and accuracy, our method can be readily applied to a fully automated calibration of microwave crosstalk in a large-scale quantum processor. This approach helps to utilize the full potential of contemporary noisy-intermediate-scale quantum processors.
While superconducting qubits have multiple energy levels, a two-level-system (TLS) model is adequately comprehensive for addressing the issue of microwave crosstalk. In the presence of leakage, our focus is primarily on the { e , f } subspace. Conversely, when gate errors occur, attention is directed toward the computational subspace, { g , e } . This simplification allows for a focused analysis of the phenomena critical to understanding and calibrating microwave crosstalk. Considering both the crosstalk and its compensation signals applied on a TLS, the Hamiltonian in the laboratory frame ( ℏ = 1 ) is
H = − ω TLS 2 σ z + Ω cos ω cr t + φ σ x
where σ x , y , z are Pauli matrixes, ω TLS takes the value of ω ge in the computational subpace, and ω ef in the { e , f } subspace. Ω ( φ ) is the effective drive amplitude (phase) under the action of Ω cr and Ω com . The simple trigonometric formula gives
Ω = Ω com 2 + Ω cr 2 + 2 Ω com Ω cr cos ϕ com − ϕ cr
φ = arctan Ω com sin ϕ com + Ω cr sin ϕ cr Ω com cos ϕ com + Ω cr cos ϕ cr
Moving to the rotation frame and with the rotation wave approximation, we have
H R = Δ 2 σ z + Ω 2 cos φ σ x − sin φ σ y
where, Δ = ω cr − ω TLS is the detuning between TLS and crosstalk signal. Eq. (3) is simply an off-resonant Rabi model, which we used to model all kinds of crosstalk scenarios. The effective Rabi strength Ω R = Δ 2 + Ω 2 , and the corresponding rotation axis is sin θ cos φ , sin θ sin φ , cos θ with θ = arctan Ω / Δ , see Figure 1(b).
We classify microwave crosstalk into two different types. The first type is the far-off-resonant case, Δ ≫ Ω , θ ≈ 0 ; the crosstalk mainly induces phase error that is better observed in the XY plane. We thus use the X π / 2 Ramsey-like sequence to prepare the qubit in the equatorial plane and measure it on the basis of σ y , as shown in Figure 2(a). The excited state probability P 1 of the final state is
P 1 X / 2 = A + 1 − A cos α ,
where A = 1 + sin 2 θ sin 2 φ / 2 , α = Ω R τ . Note that a simplification Δ τ = 2 n π is used to obtain the above equation so that the phase results from frame rotation can be ignored. For more general results, see supplementary material.
The second type is the resonant or near-resonant case, Δ ≪ Ω , θ ≈ π / 2 ; we use the X π Ramsey-like sequence (also shown in Figure 2(a)) to calibrate the crosstalk effect where amplitude or leakage error manifests. The probability P 1 in this case is
P 1 X = B 1 − cos α ,
where B = sin 2 θ / 2 , α = Ω R τ . We note that in principle, the X π / 2 Ramsey-like sequence can also be used for the second type, see Figure 2(b), but the X π Ramsey-like sequence provides greater contrast and sensitivity which may lead to better accuracy.
In the experiment, applying a fixed amplitude drive on the bias qubit for a duration of τ , our goal is to search for the best compensation parameters on the target qubit. To avoid two-dimensional parameter scanning and improve the experimental efficiency, we fix τ and only need two sets of data of scaning Ω com and ϕ com successively.
For the first crosstalk type, first, the compensation signal on the target qubit is fixed to Ω com = r Ω b (r is arbitrary in this step), and the experimental data of scanning its phase are fitted with Eq. (4), as shown in Figure 2(c). We obtain a crosstalk phase ϕ cr of 3.54; however, this phase is not necessarily accurate, especially when the difference between the two Rabi frequencies Ω com and Ω cr is large. At this time, the difference between ( Ω com + Ω cr ) 2 and ( Ω com − Ω cr ) 2 is negligible, and corresponds to a pair of opposite phases. Next, we set the compensation phase ϕ com = 3.54 − π , and scan r to fit with ϕ cr = 3.54 and ϕ cr = 3.54 − π , which are shown in Figure 2(d). The phase that best fits the data is the true crosstalk signal phase, and the crosstalk coefficient is extracted to 0.22 at the same time.
For the second crosstalk type, the process aligns with that shown in Figure 2(c) and (d) except for the X π Ramsey-like sequence. Figure 2(e) and (f) show an example in the leakage subspace, where ω cr is close to ω ef . Initially, we fix the compensation amplitude, and the experimental results (blue points) along with the fitting results (black solid line) for scanning the phase are depicted in Figure 2(e), where the fitted phase with Eq. (5) is 3.04. Subsequently, similar to the previous procedure, we fix the compensation phase at ϕ com = 3.04 − π and fit the experimental results with ϕ cr = 3.04 and ϕ cr = 3.04 − π , respectively, based on Eq.(5), as shown in Figure 2(f). Ultimately, we determine that the phase of the crosstalk signal is 3.04, and the crosstalk coefficient is 0.15. Finally, we note that when the crosstalk signal is exactly in resonance with the qubit frequency, the above procedure is applicable, but there is a simple method worth noting. The crosstalk coefficient r can be directly obtained by measuring Rabi oscillations as shown in Figure 2(g) and the crosstalk phase is fitted with Eq. (5) in Fig. Figure 2(h), applying the π Ramsey-like sequence as before.
In short, we use the Ramsey-like sequence X π or X π / 2 to scan the phase and the compensation amplitude separately to obtain the correct crosstalk parameters. In the case of resonance, the crosstalk coefficient is first obtained through Rabi oscillation and then the phase is fit with the sequence X π . This method is simple, efficient, and universal, so it is beneficial for fully automated calibration of microwave crosstalk in a large-scale quantum processor.
However, when the detuning is sufficiently large and not close to the anharmonicity, we observe that the experiment of sweeping the crosstalk coefficient exhibits a flat-top phenomenon near full compensation, which can also be seen in previous works. This indicates the insensitivity of the Ramsey-like experiment in the large detuning case. Therefore, we supplement the srror amplifing sequence (EAS) to fine-tune the crosstalk parameters. The pulse is depicted in Figure 3(a), where X π X − π is particularly sensitive to phase error, and X π X π can amplify amplitude error and leakage error [39]. Therefore, different pulse combinations can amplify the dominant error under different detuning conditions.
In the experiment, the frequency of the target qubit is 4799.0 MHz, and that of the bias qubit is 4699.0 MHz, with the anharmonicity of the target qubit being -232 MHz. Because the phase error is the dominant error, repeated pulse sequences X π X − π are applied to the target qubit, and the corresponding crosstalk and compensation signals are applied in a similar fashion. Following this, the excited state population P 1 of the EAS experimental result and ground state population P 0 in the Ramsey-like experiment are compared in Figure 3(b), indicating that the EAS is more sensitive to minor errors. In our experiments, due to the existence of distortion and other nonideal factors on the control lines, the parameters obtained from the EAS experiment perform better in multiqubit experiments.
Finally, to verify the effectiveness of our method, we perform individual single-qubit-gate randomized benchmarking (RB) and simultaneous RB [40,41] with and without microwave crosstalk compensation for five qubits in a 1D chain. The frequencies and anharmonicities of the five qubits are shown in Table 1. The resulting fidelities are shown in Figure 4(a), and the corresponding average standard deviation of multiple sequences repeated 30 times per sequence is shown in Figure 4(b). Microwave crosstalk causes the fidelities of some qubits in the simultaneous RB to decrease, and the average standard deviation also increases significantly. Following the above experimental process, after crosstalk compensation, the fidelities and average standard deviations of the simultaneous RBs are basically close to the levels of the individual RB, confirming the effectiveness of our method for microwave crosstalk calibration.
In summary, we introduced a rapid and universally applicable calibration method for microwave crosstalk, leveraging Ramsey-like sequences that significantly enhance calibration processes in superconducting circuits. This method circumvents the complexities of traditional calibration by implementing a simplified two-level off-resonant driving model, which standardizes calibration across various crosstalk scenarios and simplifies the extraction of target parameters through one-dimensional sweeps rather than complex two-dimensional scans. Additionally, our incorporation of error-amplifying sequences notably enhances measurement accuracy, particularly in the case of significant detuning. The validity of our method has been verified through simultaneous RB, where the fidelities are recovered to the level of individual RB. Our methodology represents a significant step forward in automating the calibration process for large-scale quantum processors. This advancement is pivotal for harnessing the capabilities of current noisy-intermediate-scale quantum processors, paving the way for more reliable and efficient quantum computing operations.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grants No. 12034018 and No. 11625419). This work is partially carried out at the USTC Center for Micro and Nanoscale Research and Fabrication.

References

  1. Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
  2. Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information; Cambridge university press, 2010. [CrossRef]
  3. Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM review 1999, 41, 303–332. [Google Scholar] [CrossRef]
  4. Hangleiter, D.; Eisert, J. Computational advantage of quantum random sampling. Review of Modern Physics 2023, 95, 035001. [Google Scholar] [CrossRef]
  5. Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; others. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
  6. Zhong, H.S.; Deng, Y.H.; Qin, J.; Wang, H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Wu, D.; Gong, S.Q.; Su, H.; others. Phase-programmable gaussian boson sampling using stimulated squeezed light. Physical Review Letters 2021, 127, 180502. [Google Scholar] [CrossRef] [PubMed]
  7. Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; others. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef] [PubMed]
  8. Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; Burkett, B.; Chen, Y.; Chen, Z.; Chiaro, B.; Collins, R.; Courtney, W.; Dunsworth, A.; Farhi, E.; Foxen, B.; Fowler, A.; Gidney, C.; Giustina, M.; Graff, R.; Guerin, K.; Habegger, S.; Harrigan, M.P.; Hartmann, M.J.; Ho, A.; Hoffmann, M.; Huang, T.; Humble, T.S.; Isakov, S.V.; Jeffrey, E.; Jiang, Z.; Kafri, D.; Kechedzhi, K.; Kelly, J.; Klimov, P.V.; Knysh, S.; Korotkov, A.; Kostritsa, F.; Landhuis, D.; Lindmark, M.; Lucero, E.; Lyakh, D.; Mandrà, S.; McClean, J.R.; McEwen, M.; Megrant, A.; Mi, X.; Michielsen, K.; Mohseni, M.; Mutus, J.; Naaman, O.; Neeley, M.; Neill, C.; Niu, M.Y.; Ostby, E.; Petukhov, A.; Platt, J.C.; Quintana, C.; Rieffel, E.G.; Roushan, P.; Rubin, N.C.; Sank, D.; Satzinger, K.J.; Smelyanskiy, V.; Sung, K.J.; Trevithick, M.D.; Vainsencher, A.; Villalonga, B.; White, T.; Yao, Z.J.; Yeh, P.; Zalcman, A.; Neven, H.; Martinis, J.M. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
  9. Zhu, Q.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; Gong, M.; Guo, C.; Guo, C.; Guo, S.; Han, L.; Hong, L.; Huang, H.L.; Huo, Y.H.; Li, L.; Li, N.; Li, S.; Li, Y.; Liang, F.; Lin, C.; Lin, J.; Qian, H.; Qiao, D.; Rong, H.; Su, H.; Sun, L.; Wang, L.; Wang, S.; Wu, D.; Wu, Y.; Xu, Y.; Yan, K.; Yang, W.; Yang, Y.; Ye, Y.; Yin, J.; Ying, C.; Yu, J.; Zha, C.; Zhang, C.; Zhang, H.; Zhang, K.; Zhang, Y.; Zhao, H.; Zhao, Y.; Zhou, L.; Lu, C.Y.; Peng, C.Z.; Zhu, X.; Pan, J.W. Quantum computational advantage via 60-qubit 24-cycle random circuit sampling. Science Bulletin 2022, 67, 240–245. [Google Scholar] [CrossRef] [PubMed]
  10. Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; Gong, M.; Guo, C.; Guo, C.; Guo, S.; Han, L.; Hong, L.; Huang, H.L.; Huo, Y.H.; Li, L.; Li, N.; Li, S.; Li, Y.; Liang, F.; Lin, C.; Lin, J.; Qian, H.; Qiao, D.; Rong, H.; Su, H.; Sun, L.; Wang, L.; Wang, S.; Wu, D.; Xu, Y.; Yan, K.; Yang, W.; Yang, Y.; Ye, Y.; Yin, J.; Ying, C.; Yu, J.; Zha, C.; Zhang, C.; Zhang, H.; Zhang, K.; Zhang, Y.; Zhao, H.; Zhao, Y.; Zhou, L.; Zhu, Q.; Lu, C.Y.; Peng, C.Z.; Zhu, X.; Pan, J.W. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Physical Review Letters 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
  11. Kim, Y.; Eddins, A.; Anand, S.; Wei, K.X.; Van Den Berg, E.; Rosenblatt, S.; Nayfeh, H.; Wu, Y.; Zaletel, M.; Temme, K.; others. Evidence for the utility of quantum computing before fault tolerance. Nature 2023, 618, 500–505. [Google Scholar] [CrossRef] [PubMed]
  12. Ryan-Anderson, C.; Bohnet, J.G.; Lee, K.; Gresh, D.; Hankin, A.; Gaebler, J.; Francois, D.; Chernoguzov, A.; Lucchetti, D.; Brown, N.C.; others. Realization of real-time fault-tolerant quantum error correction. Physical Review X 2021, 11, 041058. [Google Scholar] [CrossRef]
  13. Krinner, S.; Lacroix, N.; Remm, A.; Di Paolo, A.; Genois, E.; Leroux, C.; Hellings, C.; Lazar, S.; Swiadek, F.; Herrmann, J.; Norris, G.J.; Andersen, C.K.; Müller, M.; Blais, A.; Eichler, C.; Wallraff, A. Realizing repeated quantum error correction in a distance-three surface code. Nature 2022, 605, 669–674. [Google Scholar] [CrossRef] [PubMed]
  14. Zhao, Y.; Ye, Y.; Huang, H.L.; Zhang, Y.; Wu, D.; Guan, H.; Zhu, Q.; Wei, Z.; He, T.; Cao, S.; Chen, F.; Chung, T.H.; Deng, H.; Fan, D.; Gong, M.; Guo, C.; Guo, S.; Han, L.; Li, N.; Li, S.; Li, Y.; Liang, F.; Lin, J.; Qian, H.; Rong, H.; Su, H.; Sun, L.; Wang, S.; Wu, Y.; Xu, Y.; Ying, C.; Yu, J.; Zha, C.; Zhang, K.; Huo, Y.H.; Lu, C.Y.; Peng, C.Z.; Zhu, X.; Pan, J.W. Realization of an Error-Correcting Surface Code with Superconducting Qubits. Physical Review Letters 2022, 129, 030501. [Google Scholar] [CrossRef]
  15. Acharya, R.; Aleiner, I.; Allen, R.; Andersen, T.I.; Ansmann, M.; Arute, F.; Arya, K.; Asfaw, A.; Atalaya, J.; Babbush, R.; Bacon, D.; Bardin, J.C.; Basso, J.; Bengtsson, A.; Boixo, S.; Bortoli, G.; Bourassa, A.; Bovaird, J.; Brill, L.; Broughton, M.; Buckley, B.B.; Buell, D.A.; Burger, T.; Burkett, B.; Bushnell, N.; Chen, Y.; Chen, Z.; Chiaro, B.; Cogan, J.; Collins, R.; Conner, P.; Courtney, W.; Crook, A.L.; Curtin, B.; Debroy, D.M.; Del Toro Barba, A.; Demura, S.; Dunsworth, A.; Eppens, D.; Erickson, C.; Faoro, L.; Farhi, E.; Fatemi, R.; Flores Burgos, L.; Forati, E.; Fowler, A.G.; Foxen, B.; Giang, W.; Gidney, C.; Gilboa, D.; Giustina, M.; Grajales Dau, A.; Gross, J.A.; Habegger, S.; Hamilton, M.C.; Harrigan, M.P.; Harrington, S.D.; Higgott, O.; Hilton, J.; Hoffmann, M.; Hong, S.; Huang, T.; Huff, A.; Huggins, W.J.; Ioffe, L.B.; Isakov, S.V.; Iveland, J.; Jeffrey, E.; Jiang, Z.; Jones, C.; Juhas, P.; Kafri, D.; Kechedzhi, K.; Kelly, J.; Khattar, T.; Khezri, M.; Kieferová, M.; Kim, S.; Kitaev, A.; Klimov, P.V.; Klots, A.R.; Korotkov, A.N.; Kostritsa, F.; Kreikebaum, J.M.; Landhuis, D.; Laptev, P.; Lau, K.M.; Laws, L.; Lee, J.; Lee, K.; Lester, B.J.; Lill, A.; Liu, W.; Locharla, A.; Lucero, E.; Malone, F.D.; Marshall, J.; Martin, O.; McClean, J.R.; McCourt, T.; McEwen, M.; Megrant, A.; Meurer Costa, B.; Mi, X.; Miao, K.C.; Mohseni, M.; Montazeri, S.; Morvan, A.; Mount, E.; Mruczkiewicz, W.; Naaman, O.; Neeley, M.; Neill, C.; Nersisyan, A.; Neven, H.; Newman, M.; Ng, J.H.; Nguyen, A.; Nguyen, M.; Niu, M.Y.; O’Brien, T.E.; Opremcak, A.; Platt, J.; Petukhov, A.; Potter, R.; Pryadko, L.P.; Quintana, C.; Roushan, P.; Rubin, N.C.; Saei, N.; Sank, D.; Sankaragomathi, K.; Satzinger, K.J.; Schurkus, H.F.; Schuster, C.; Shearn, M.J.; Shorter, A.; Shvarts, V.; Skruzny, J.; Smelyanskiy, V.; Smith, W.C.; Sterling, G.; Strain, D.; Szalay, M.; Torres, A.; Vidal, G.; Villalonga, B.; Vollgraff Heidweiller, C.; White, T.; Xing, C.; Yao, Z.J.; Yeh, P.; Yoo, J.; Young, G.; Zalcman, A.; Zhang, Y.; Zhu, N. Suppressing quantum errors by scaling a surface code logical qubit. Nature 2023, 614, 676–681. [Google Scholar] [CrossRef] [PubMed]
  16. Chen, E.H.; Yoder, T.J.; Kim, Y.; Sundaresan, N.; Srinivasan, S.; Li, M.; Córcoles, A.D.; Cross, A.W.; Takita, M. Calibrated decoders for experimental quantum error correction. Physical Review Letters 2022, 128, 110504. [Google Scholar] [CrossRef] [PubMed]
  17. Bluvstein, D.; Evered, S.J.; Geim, A.A.; Li, S.H.; Zhou, H.; Manovitz, T.; Ebadi, S.; Cain, M.; Kalinowski, M.; Hangleiter, D.; others. Logical quantum processor based on reconfigurable atom arrays. Nature 2024, 626, 58–65. [Google Scholar] [CrossRef]
  18. Campbell, E. A series of fast-paced advances in Quantum Error Correction. Nature Reviews Physics 2024, 6, 160–161. [Google Scholar] [CrossRef]
  19. Córcoles, A.D.; Kandala, A.; Javadi-Abhari, A.; McClure, D.T.; Cross, A.W.; Temme, K.; Nation, P.D.; Steffen, M.; Gambetta, J.M. Challenges and Opportunities of Near-Term Quantum Computing Systems. Proceedings of the IEEE 2020, 108, 1338–1352. [Google Scholar] [CrossRef]
  20. Winick, A.; Wallman, J.J.; Emerson, J. Simulating and Mitigating Crosstalk. Physical Review Letters 2021, 126, 230502. [Google Scholar] [CrossRef]
  21. Klimov, P.V.; Bengtsson, A.; Quintana, C.; Bourassa, A.; Hong, S.; Dunsworth, A.; Satzinger, K.J.; Livingston, W.P.; Sivak, V.; Niu, M.Y.; others. Optimizing quantum gates towards the scale of logical qubits. Nature Communications 2024, 15, 2442. [Google Scholar] [CrossRef] [PubMed]
  22. Sarovar, M.; Proctor, T.; Rudinger, K.; Young, K.; Nielsen, E.; Blume-Kohout, R. Detecting crosstalk errors in quantum information processors. Quantum 2020, 4, 321. [Google Scholar] [CrossRef]
  23. Feng, L.; Huang, Y.Y.; Wu, Y.K.; Guo, W.X.; Ma, J.Y.; Yang, H.X.; Zhang, L.; Wang, Y.; Huang, C.X.; Zhang, C.; others. Realization of a crosstalk-avoided quantum network node using dual-type qubits of the same ion species. Nature Communications 2024, 15, 204. [Google Scholar] [CrossRef] [PubMed]
  24. Fang, C.; Wang, Y.; Huang, S.; Brown, K.R.; Kim, J. Crosstalk suppression in individually addressed two-qubit gates in a trapped-ion quantum computer. Physical Review Letters 2022, 129, 240504. [Google Scholar] [CrossRef] [PubMed]
  25. Debroy, D.M.; Li, M.; Huang, S.; Brown, K.R. Logical performance of 9 qubit compass codes in ion traps with crosstalk errors. Quantum Science and Technology 2020, 5, 034002. [Google Scholar] [CrossRef]
  26. Rudinger, K.; Hogle, C.W.; Naik, R.K.; Hashim, A.; Lobser, D.; Santiago, D.I.; Grace, M.D.; Nielsen, E.; Proctor, T.; Seritan, S.; others. Experimental characterization of crosstalk errors with simultaneous gate set tomography. PRX Quantum 2021, 2, 040338. [Google Scholar] [CrossRef]
  27. Wei, K.; Magesan, E.; Lauer, I.; Srinivasan, S.; Bogorin, D.F.; Carnevale, S.; Keefe, G.; Kim, Y.; Klaus, D.; Landers, W.; others. Hamiltonian engineering with multicolor drives for fast entangling gates and quantum crosstalk cancellation. Physical Review Letters 2022, 129, 060501. [Google Scholar] [CrossRef]
  28. Heinz, I.; Burkard, G. Crosstalk analysis for single-qubit and two-qubit gates in spin qubit arrays. Physical Review B 2021, 104, 045420. [Google Scholar] [CrossRef]
  29. Zhao, P.; Zhang, Y.; Li, X.; Han, J.; Xu, H.; Xue, G.; Jin, Y.; Yu, H. Spurious microwave crosstalk in floating superconducting circuits. arXiv, 2206. [Google Scholar]
  30. Wang, R.; Zhao, P.; Jin, Y.; Yu, H. Control and mitigation of microwave crosstalk effect with superconducting qubits. Applied Physics Letters 2022, 121, 152602. [Google Scholar] [CrossRef]
  31. Santos, A.C. Role of parasitic interactions and microwave crosstalk in dispersive control of two superconducting artificial atoms. Phys. Rev. A 2023, 107, 012602. [Google Scholar] [CrossRef]
  32. Tripathi, V.; Chen, H.; Khezri, M.; Yip, K.W.; Levenson-Falk, E.; Lidar, D.A. Suppression of crosstalk in superconducting qubits using dynamical decoupling. Physical Review Applied 2022, 18, 024068. [Google Scholar] [CrossRef]
  33. Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Physical Review A 2007, 76, 042319. [Google Scholar] [CrossRef]
  34. Xu, K.; Sun, Z.H.; Liu, W.; Zhang, Y.R.; Li, H.; Dong, H.; Ren, W.; Zhang, P.; Nori, F.; Zheng, D.; Fan, H.; Wang, H. Probing dynamical phase transitions with a superconducting quantum simulator. Science Advances 2020, 6, eaba4935. [Google Scholar] [CrossRef] [PubMed]
  35. Sung, Y.; Ding, L.; Braumüller, J.; Vepsäläinen, A.; Kannan, B.; Kjaergaard, M.; Greene, A.; Samach, G.O.; McNally, C.; Kim, D.; Melville, A.; Niedzielski, B.M.; Schwartz, M.E.; Yoder, J.L.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. Realization of High-Fidelity CZ and ZZ -Free iSWAP Gates with a Tunable Coupler. Physical Review X 2021, 11. [Google Scholar] [CrossRef]
  36. Yan, H.; Zhao, S.; Xiang, Z.; Wang, Z.; Yang, Z.; Xu, K.; Tian, Y.; Yu, H.; Zheng, D.; Fan, H.; Zhao, S. Calibration and cancellation of microwave crosstalk in superconducting circuits. Chinese Physics B 2023, 32, 094203. [Google Scholar] [CrossRef]
  37. High-Fidelity, Frequency-Flexible Two-Qubit Fluxonium Gates with a Transmon Coupler. Physical Review X 2023, 13, 031035–2304. [CrossRef]
  38. Nuerbolati, W.; Han, Z.; Chu, J.; Zhou, Y.; Tan, X.; Yu, Y.; Liu, S.; Yan, F. Canceling microwave crosstalk with fixed-frequency qubits. Applied Physics Letters 2022, 120, 174001. [Google Scholar] [CrossRef]
  39. Chen, Z. Metrology of Quantum Control and Measurement in Superconducting Qubits. PhD thesis, University of California, Santa Barbara, 2018.
  40. Magesan, E.; Gambetta, J.M.; Emerson, J. Characterizing quantum gates via randomized benchmarking. Physical Review A 2012, 85, 042311. [Google Scholar] [CrossRef]
  41. Gambetta, J.M.; Córcoles, A.D.; Merkel, S.T.; Johnson, B.R.; Smolin, J.A.; Chow, J.M.; Ryan, C.A.; Rigetti, C.; Poletto, S.; Ohki, T.A.; Ketchen, M.B.; Steffen, M. Characterization of addressability by simultaneous randomized benchmarking. Physical Review Letters 2012, 109, 240504. [Google Scholar] [CrossRef]
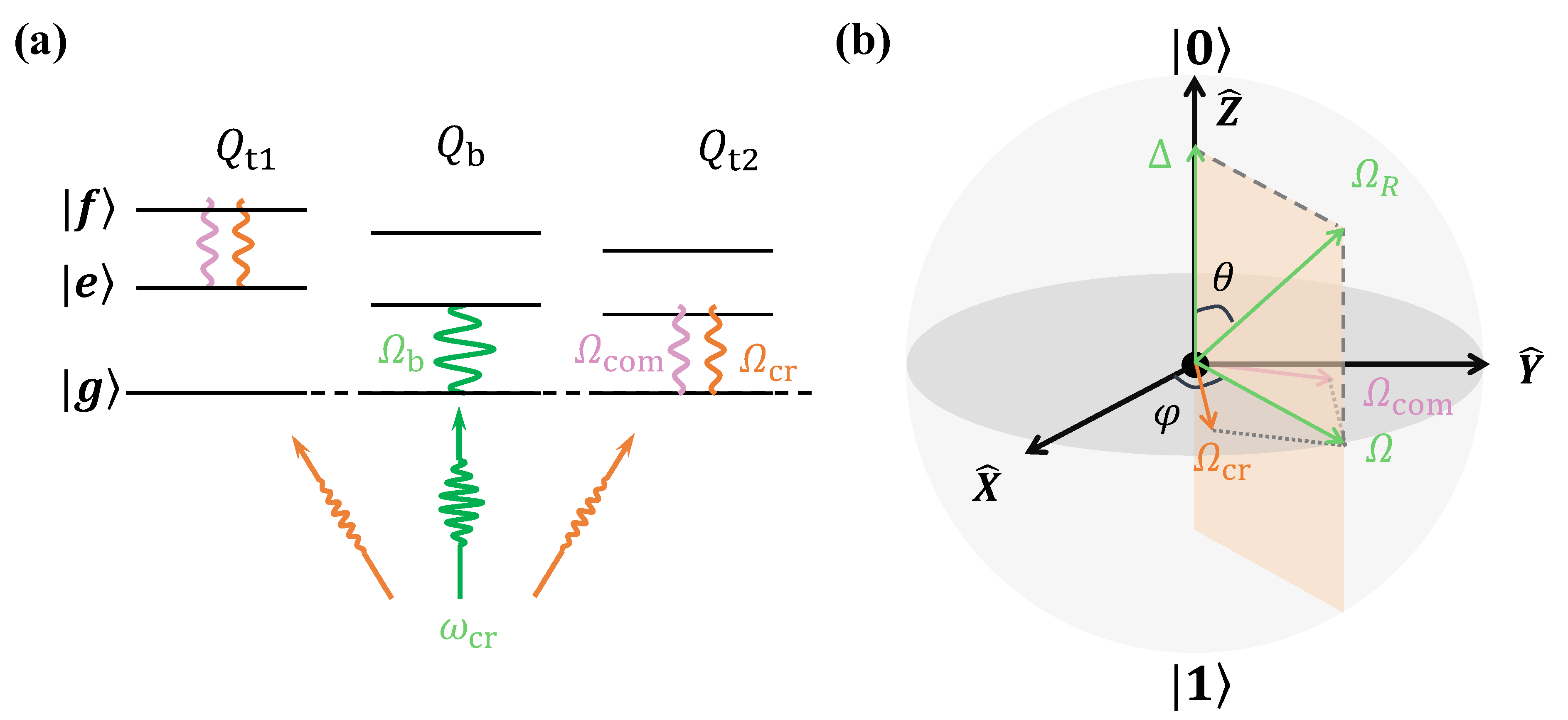
Preprints 104361 g001
Figure 1. Schematic diagram of microwave crosstalk. (a) A microwave signal of frequency ω cr intended to drive bias qubit Q b with Rabi strength Ω b , coupled unintentionally to some target qubits where a Rabi strength Ω cr is induced. To nullify this crosstalk signal Ω cr , an out-of-phase signal Ω com should be applied directly on target qubits. (b) Bloch sphere representation of off-resonant driving Hamiltonian. The control fields of Ω cr , Ω com , and Δ give effective control field Ω R with angles θ from the Z axis and φ from the X axis.
Figure 1. Schematic diagram of microwave crosstalk. (a) A microwave signal of frequency ω cr intended to drive bias qubit Q b with Rabi strength Ω b , coupled unintentionally to some target qubits where a Rabi strength Ω cr is induced. To nullify this crosstalk signal Ω cr , an out-of-phase signal Ω com should be applied directly on target qubits. (b) Bloch sphere representation of off-resonant driving Hamiltonian. The control fields of Ω cr , Ω com , and Δ give effective control field Ω R with angles θ from the Z axis and φ from the X axis.
Preprints 104361 g001
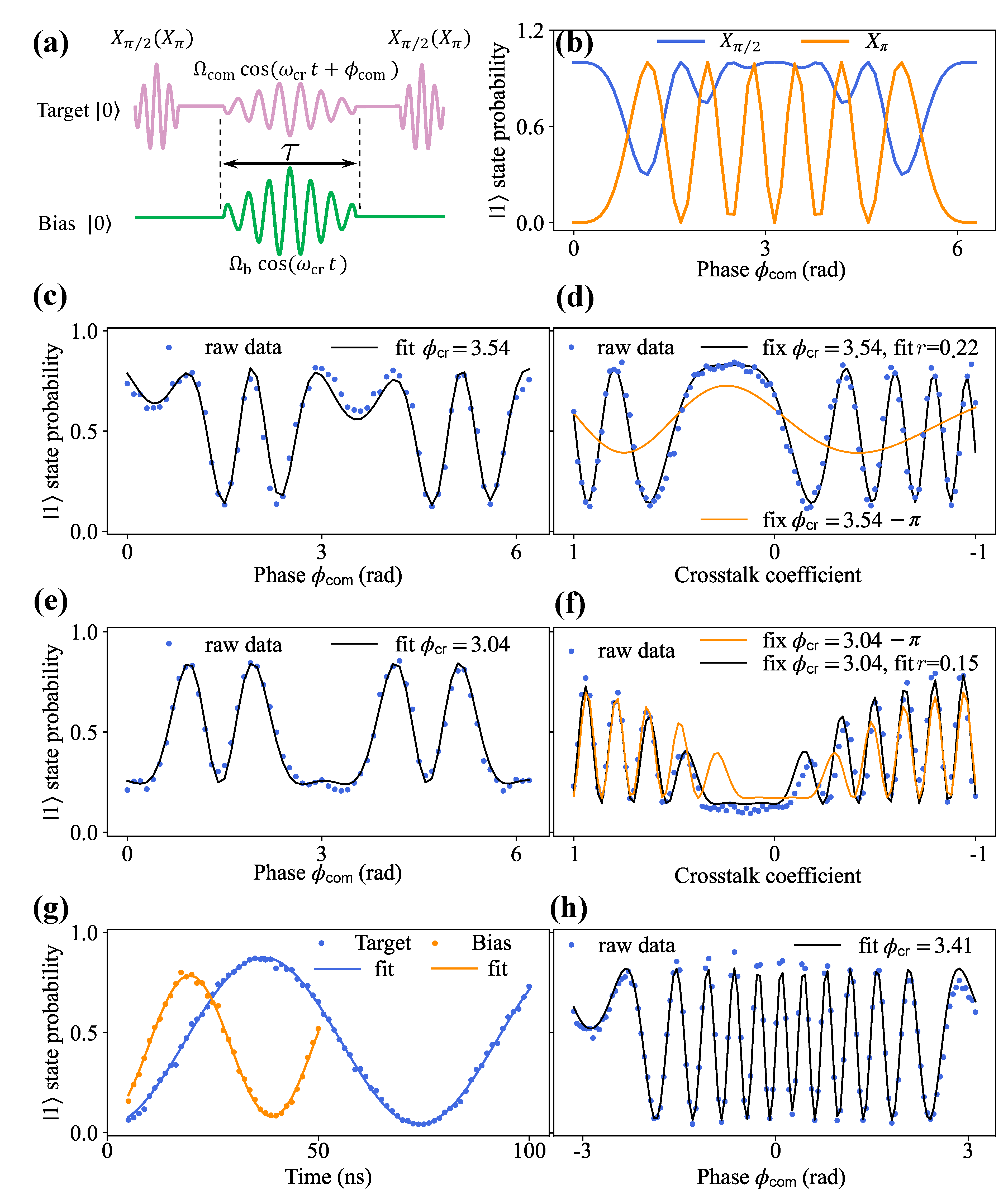
Preprints 104361 g002
Figure 2. (a) Pulse sequence for calibrating the crosstalk in the Ramsey-like experiment. The X π / 2 pulse is used for the far-off-resonance case and the X π pulse is used for the near-resonant case. (b) Simulation results for the two sequences in (a) when it is near resonance. (c), (d) Experimental results for the first type of crosstalk. (c) The fitted phase ϕ cr (black line) may not necessarily be accurate. (d) Set the phase of compensation signal ϕ com = 3.54- π . The experimental data obtained by scanning the coefficients (blue dots) are fitted with ϕ cr = 3.54 (black line) and ϕ cr = 3.54 − π (orange line), respectively. The best-fitting result indicates ϕ cr = 3.54 , and r = 0.22 . Experimental results for scanning the crosstalk compensation phase (e) and coefficient (f) for near resonances in the leakage subspace. In (f), when fixing ϕ com to 3.04 − π , the experimental data obtained by scanning the coefficients (blue dots) are fitted to ϕ cr = 3.04 (black line) and ϕ cr = 3.04 − π (orange line). The optimal fitting outcome indicates that ϕ cr is 3.04, with a corresponding coefficient of 0.15. (g) In the case of resonance, Rabi oscillations of the target qubit Ω cr / 2 π = 13.6 MHz (blue) and the bias qubit Ω b / 2 π = 25.6 MHz (orange) when driven through the bias qubit local drive line are used to extract r = Ω cr / Ω b = 0.531 . Then, the experimental results of scanning the phase are presented in (h) with blue points. The black line is fitted to Eq. (5) to extract ϕ cr .
Figure 2. (a) Pulse sequence for calibrating the crosstalk in the Ramsey-like experiment. The X π / 2 pulse is used for the far-off-resonance case and the X π pulse is used for the near-resonant case. (b) Simulation results for the two sequences in (a) when it is near resonance. (c), (d) Experimental results for the first type of crosstalk. (c) The fitted phase ϕ cr (black line) may not necessarily be accurate. (d) Set the phase of compensation signal ϕ com = 3.54- π . The experimental data obtained by scanning the coefficients (blue dots) are fitted with ϕ cr = 3.54 (black line) and ϕ cr = 3.54 − π (orange line), respectively. The best-fitting result indicates ϕ cr = 3.54 , and r = 0.22 . Experimental results for scanning the crosstalk compensation phase (e) and coefficient (f) for near resonances in the leakage subspace. In (f), when fixing ϕ com to 3.04 − π , the experimental data obtained by scanning the coefficients (blue dots) are fitted to ϕ cr = 3.04 (black line) and ϕ cr = 3.04 − π (orange line). The optimal fitting outcome indicates that ϕ cr is 3.04, with a corresponding coefficient of 0.15. (g) In the case of resonance, Rabi oscillations of the target qubit Ω cr / 2 π = 13.6 MHz (blue) and the bias qubit Ω b / 2 π = 25.6 MHz (orange) when driven through the bias qubit local drive line are used to extract r = Ω cr / Ω b = 0.531 . Then, the experimental results of scanning the phase are presented in (h) with blue points. The black line is fitted to Eq. (5) to extract ϕ cr .
Preprints 104361 g002
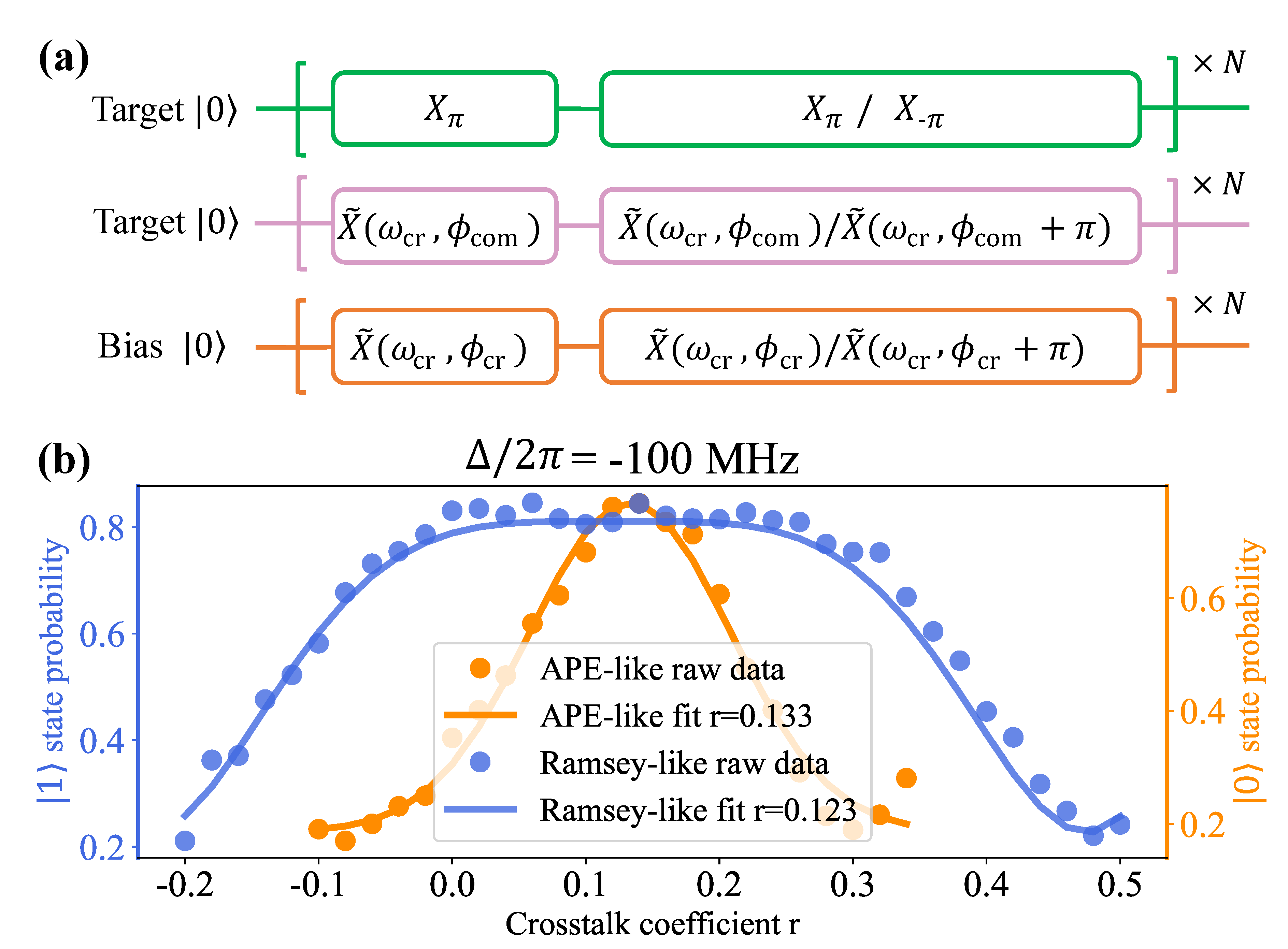
Preprints 104361 g003
Figure 3. (a) Repeated pulse sequences of EAS. In addition to applying the driving signal of its own frequency (top) to the target qubit, a compensation signal (middle) is also added. This compensation sequence changes following the pulse sequence of the bias qubit (below). (b) Comparison of the Ramsey-like sequence (blue) and EAS (orange) results for measuring the crosstalk coefficient.
Figure 3. (a) Repeated pulse sequences of EAS. In addition to applying the driving signal of its own frequency (top) to the target qubit, a compensation signal (middle) is also added. This compensation sequence changes following the pulse sequence of the bias qubit (below). (b) Comparison of the Ramsey-like sequence (blue) and EAS (orange) results for measuring the crosstalk coefficient.
Preprints 104361 g003
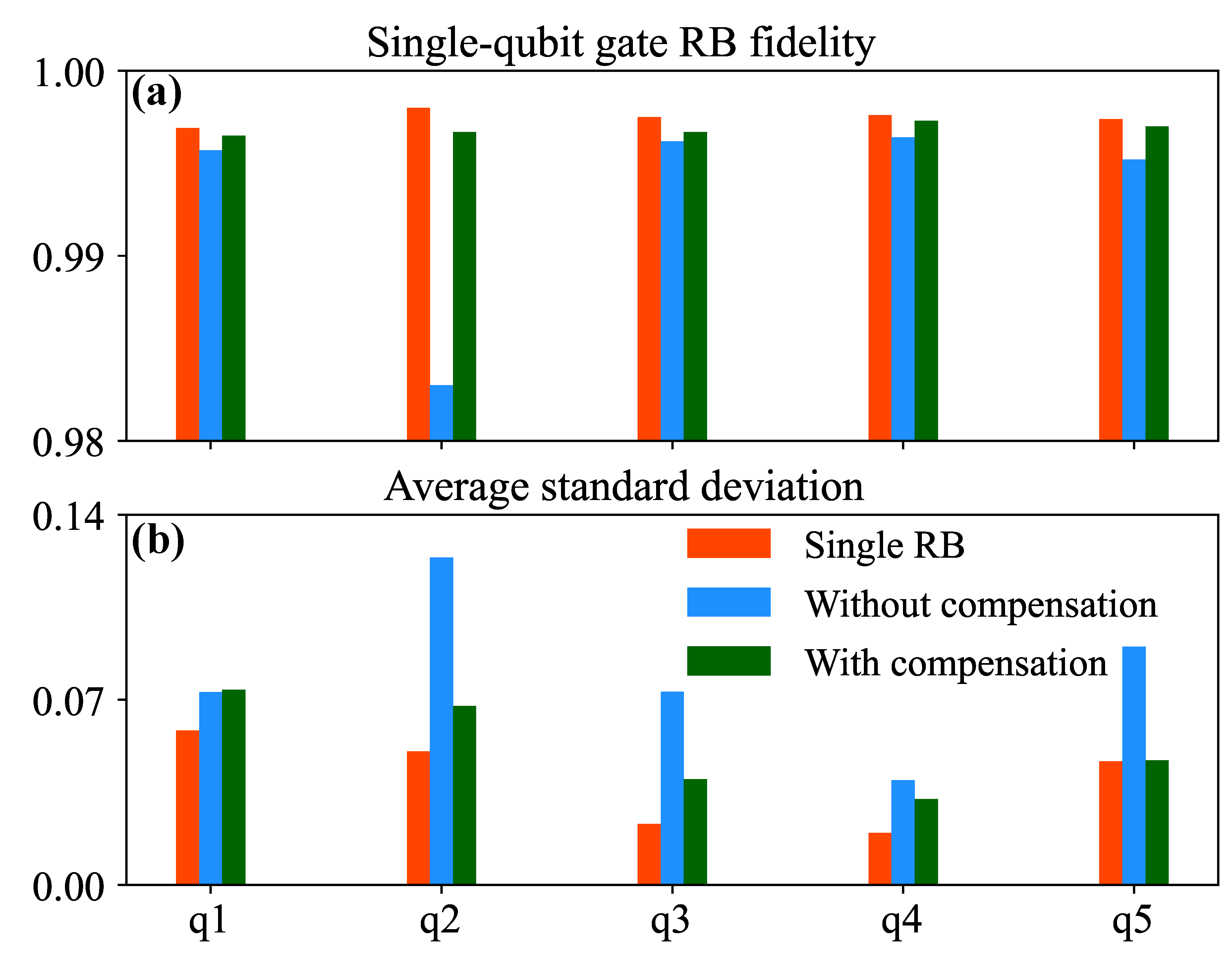
Preprints 104361 g004
Figure 4. (a) Fidelity per single-qubit gate obtained by implementing RB separately (red), simultaneously without compensation (blue) and simultaneously with compensation (green). (b) The average standard deviation of multiple sequences repeated 30 times per sequence.
Figure 4. (a) Fidelity per single-qubit gate obtained by implementing RB separately (red), simultaneously without compensation (blue) and simultaneously with compensation (green). (b) The average standard deviation of multiple sequences repeated 30 times per sequence.
Preprints 104361 g004
Table 1. The frequency and anharmonicity of five qubits.
Table 1. The frequency and anharmonicity of five qubits.
Qubit Number q1 q2 q3 q4 q5
Frequency ω ge / 2 π (MHz) 4137 4181 4524 4799 4075
Anharmonicity η / 2 π (MHz) -243 -223 -250 -228 -244
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated