Preprint
Article
Process Intensification for Enhanced Fluoride Removal and Recovery As Calcium Fluoride Using Fluidized Bed Reactor
Altmetrics
Downloads
91
Views
30
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 March 2024
Posted:
29 March 2024
You are already at the latest version
Alerts
Abstract
This study explored the feasibility of fluoride removal from simulated semiconductor industry wastewater and its recovery as calcium fluoride using fluidized bed crystallization. The continuous reactor showed best performance (>90% fluoride removal and >95% crystallization efficiency) at a calcium to fluoride ratio of 0.6 within first 40 days of continuous operation. The resulting particle size increased by more than double during this time along with a 36% increase in the seed bed height indicating deposition of CaF2 onto the silica seed. The SEM-EDX analysis showed the size and shape of the crystals formed along with high amount of Ca-F ions presence. The purity of the CaF2 crystals were determined to be 91.1% though ICP-OES analysis. Following the continuous experiment, different process improvement strategies are explored. The addition of excess amount of calcium resulted in an additional 6% fluoride removal, however, compared to this single stage process, a two-stage approach was found to be better strategy to achieve a low effluent fluoride concentration. The fluoride removal reached 94% with this two-stage approach under optimum condition of 4 + 1 h HRT combinations and a [Ca2+]/[F-] ratio of 0.55 and 0.7 for the two reactors, respectively. CFD simulation showed the impact of inlet diameter, bottom-angle shape and width and height ratio of the reactor on mixing inside reactor and possibility of further improvement in reactor performance by optimizing the FBR configuration.
Keywords:
Subject: Environmental and Earth Sciences - Water Science and Technology
1. Introduction
The sources for fluoride pollution can be both natural and anthropogenic, contributing to environmental concerns and potential health risks [1]. Natural sources include fluoride-rich minerals and rocks from which fluoride leach into water sources due to natural causes [2]. However, compared to natural sources human activities significantly causes fluoride contamination. Industrial processes, such as mining and mineral processing, aluminum and phosphate production, release fluoride into air and water [3]. Agricultural activities can also potentially release fluoride into the environment, especially when using phosphate-based fertilizers and pesticides [4]. Furthermore, burning fossil fuels—coal in particular—releases pollutants into the atmosphere that include fluoride, which can subsequently contaminate soil and water bodies [5]. In order to effectively manage and reduce fluoride pollution, it is necessary to have a thorough understanding of these diverse sources as well as how they interact with ecosystems and human health [6].
In this study, semiconductor industry wastewater is being focused on. The semiconductor industry contributes is one of major sources of fluoride pollution primarily through the use of certain chemicals and processes in semiconductor manufacturing [7]. Hydrofluoric acid (HF), one of the most commonly used chemical in semiconductor fabrication processes, and its improper handling and disposal can lead to environmental pollution. In addition, the industry also utilizes fluorinated gases, such as sulfur hexafluoride (SF6), which have strong greenhouse effects and contribute to environmental pollution [8]. Depending on the specific processes and chemicals utilized in semiconductor manufacture, the amount of fluoride present in effluent from the semiconductor industry might vary significantly [9]. Chemicals containing fluoride may be used during etching, cleaning, and polishing processes in the semiconductor manufacturing process [6].
The semiconductor industry’s own efforts to minimize its environmental impact include the development and implementation of cleaner technologies, recycling programs, and rigorous waste management practices [8,10]. Despite these efforts, proper disposal and handling of fluoride-containing chemicals remains important to reduce potential negative effects on the environment and surrounding communities. Different technologies such as adsorption, precipitation, crystallization, membrane processes (reverse osmosis, nanofiltration), electrocoagulation, electrodialysis, etc. have been predominantly used for fluoride removal [2]. Among these technologies, coagulation/precipitation of fluoride using calcium based chemicals (Ca(OH)2 and CaCl2) is a common practice including in semiconductor industry [11]. However, the sludge produced from such process contains high moisture and is difficult to be reutilized without further processing [1]. Compared with precipitation another novel process crystallization using almost same mechanism and chemicals can provide much better end product from fluoride containing wastewater treatment which can be readily utilized in other industries as raw materials.
In this regard, this study explored fluoride removal from simulated semiconductor industry wastewater using calcium fluoride crystallization. For this purpose, a fluidized bed reactor (FBR) containing silica seed was used under continuous mode of operation. Different process improvement strategies were also undertaken in order to meet the effluent standard set for fluoride by various regulatory organization. Finally, the effect of FBR configuration on fluoride removal was carried out using computational fluid dynamics (CFD) in order to explore any possibility of further improvement in the process efficiency by modifying conventional FBR.
2. Results and Discussion
2.1. Continuous FBR Performance
2.1.1. Fluoride Removal
The fluoride removal profile in FBR during its continuous operation is depicted in Figure 1a. The influent fluoride concentration to the FBR was 300 mg/L. The initial fluoride removal efficiency was low at 32% on the first day, from which it grew to reach nearly 70% during the first 10 days of reactor operation. The respective effluent fluoride concentration varied between 81-204 mg/L (Figure 1a). During this initial operation the Ca2+ to F- ratio was 0.55 which was based on the optimum ratio obtained during earlier experiment. However, as desired low effluent fluoride concentration could not be achieved at this ratio and the calcium utilization was very high, the inlet calcium concentration was increased to make the Ca2+ to F- ratio as 0.6 from 11th day onwards. With this increase in influent Ca2+ concentration a positive impact on the fluoride removal could be observed. A consistent fluoride removal efficiency of 80.7 ± 1.8% could be achieved during next 17 days of continuous reactor operation (Figure 1a). Consequently, the fluoride concentration in the reactor effluent lowered to 60 ± 6 mg/L during this time period. This positive impact of inlet Ca2+ ion increase on fluoride removal is consistent with previous studies where a high inlet calcium value correlated with better fluoride removal performance [24]. Following this period, the reactor performance showed further improvement with fluoride removal reaching 90.2 ± 1.7% during the following 22 days of FBR operation. The resulting fluoride concentration was 30 ± 8 mg/L during this period (28-50th day). From 51th day onwards the effluent the fluoride concentration gradually increased as its removal efficiency depleted. This lowering of fluoride removal can be distinguished in two stages, for the first 10 days the removal efficiency was 80.9 ± 1.4% along with an effluent F- concentration of 57.2 ± 4.2 mg/L and for the remaining 10 days these values were 73.9 ± 2.9% and 78 ± 8.9 mg/L, respectively (Figure 1a). The continuous reactor experiment showed that the FBR can successfully remove fluoride as calcium fluoride crystals, however, over a prolong period of time without replacing the seeds, the performance declined.
2.1.2. Calcium and Sulfate Profile during FBR Operation
The calcium and sulfate profile during the continuous FBR operation is shown in Figure 1b. The calcium profile showed an increasing profile during the continuous operation. Initially, the calcium utilization was very high and the effluent calcium concentration was 12-60 mg/L. Following the increase in influent calcium concentration to meet the demand of crystallization, the effluent calcium concentration also increased beyond 100 mg/L. There was a lot of fluctuations in the effluent Ca concentration during the later period of FBR operation with periodic rise in Ca concentration to as high as 150 mg/L or even 200 mg/L. The mean effluent calcium value during 11-50th day period was 96.3 mg/L with a high standard deviation (44.3). During the later period when fluoride removal performance declined a corresponding increase in the effluent calcium concentration can also be observed. The calcium concentration in the effluent stream remained above 200 mg/L and later above 300 mg/L from 55th day and 64th onwards, respectively. This increase in the Ca concentration during later period of the FBR operation could be due to accumulation of excess Ca from recycle stream as well as from the continuous CaCl2 input to the reactor. However, it needs to be mentioned here that effluent Ca values ≈300 mg/L is common in industrial processes treating fluoride containing wastewater including calcium-based fluoride precipitation methods. Hence, from the treatment point of view this isn’t unusual, but recovery and utilization of this calcium ions from effluent should be explored to further improve the process economics.
The sulfate concentration was also measured to understand its impact on fluoride removal through the calcium fluoride crystallization. Sulfate is present as co-pollutant in semiconductor industry wastewater, and can interfere with CaF2 synthesis by forming calcium sulfate. However, in this study no such interference was observed. The sulfate concentration in the FBR effluent remained almost same (401.8 ± 8.2 mg/L) throughout the reactor operation (Figure 1b). This indicate that sulfate was not removed during FBR operation and did not interfere in the CaF2 crystallization process in any way. This is important as in many cases formation of undesired CaSO4 can decrease the fluoride removal efficiency by reacting with Ca ions present inside the reactor and if precipitated along with CaF2, can reduce its purity as well.
2.1.3. Crystallization Efficiency
The fluoride speciation and CaF2 crystallization efficiency are shown in Figure 1c. The crystallization efficiency was initially low (53.9-88.1%) for first 7 days, following which the value consistently stayed above 95% during next 41 days of continuous FBR operation. From 50th day onwards along with reduction in fluoride removal efficiency, the crystallization efficiency started to decline in a gradual manner. During this phase, except for the last 5 days of FBR operation, the crystallization efficiency was >80%. The maximum crystallization efficiency value obtained in the reactor was 98.6% on 38th day of continuous reactor operation. The fluoride speciation during the reactor operation corresponds well with the crystallization efficiency results. The portion of fluoride removed as calcium fluoride fines during the initial days of FBR operation was high (25-82 mg/L) compared with the next 42 days of FBR operation during which the amount of calcium fluoride fines remained <20 mg/L or even <10 mg/L. During the initial time period (1-7 d), the amount of fluoride removed as CaF2 crystals were low (96-186 mg/L) indicating that although calcium fluoride formation was initiated in the reactor, the particles could not be retained onto the silica seed materials and they escaped the reactor along with effluent. During the best performing operating period (8-50th days) of the FBR, the concentration of CaF2 fines were much lower (<18 mg/L) than the initial phase and majority (204-284 mg/L) of the fluoride removed in the reactor went towards CaF2 crystallization (Figure 2c). However, as the FBR performance declined during the last phase of FBR operation in terms of fluoride removal, the amount of fluoride removed as crystals also reduced (≈210 mg/L). Consequently, the amount of CaF2 fines increased to >60 mg/L during this last phase of FBR operation.
This increase in CaF2 fines is the later period of continuous reactor operation is not uncommon and can be explained in two ways. The calcium concentration increases along with operating time as can be seen from the calcium profile. This increase in calcium concentration causes it to thicken and form scaling on the inner wall of the reactor. Some of the fluoride ions get captured in this calcium scaling which does not precipitate onto the silica seed rather comes out of the reactor as calcium fluoride fines. Other reason is breakdown of CaF2 scales from the deposited crystals formed over silica seeds due to shearing and tearing by upflow fluidization during continuous reactor operation over extended time period. Therefore, proper care must be taken regarding operating time of the FBR so that an optimum fluoride removal along with ideal crystal recovery could be achieved.
The seed bed height was also monitored during 70 days of continuous reactor operation and is shown in Figure 1d. As can be seen from the figure, the seed bed height grew consistently throughout the reactor operation indicating formation and growth of CaF2 crystals inside FBR. The growth rate of the seeds was at its maximum during 15 to 50 days of reactor operation which correlate well with the time period during which the other reactor performance indicators, namely fluoride removal and crystallization efficiency were at their best as well. The increase in the particle size of the seeds also showed similar pattern with 75%, 90%, 107.7% and 150.7% growth over 10-, 20-, 40- and 70-days reaction period, respectively (Figure 1d).
2.1.4. Characterization of Calcium Fluoride Crystals
Figure 2a,b depicts the SEM images of silica seed and CaF2 crystal after 70 days of continuous reactor operation. The crystal size increased by more than double from 402.7 µm in diameter of the initial silica seed to 1003 µm diameter on 70th day. The outer appearance of the crystal was smooth and the shape seems to be irregular but nearly spheroid. Similar shape of CaF2 crystal formed during fluidized bed crystallization has been previously reported [12,13]. The corresponding elemental compositions of the crystal surface is provided by EDX spectra of the initial silica seed and calcium fluoride crystals (Figure 2c,d). The initial seed contained Si, O and C, which when exposed to fluorine and calcium inside the FBR showed peaks for the presence of other elements including F, Ca, Na, Al, Cl, and S in addition to the original elements Si, C and O. The F and Ca composition in the 70 day old CaF2 crystals was 44.8 and 44.4%, respectively. This indicates the extent of deposition of CaF2 onto the silica seed. Furthermore, presence of Si was not detected in the 70th day sample which could be due to the fact that entire seed surface is covered with deposited CaF2 by such prolong reactor operation.
The XRD spectra of the calcium fluoride crystals formed inside the FBR was shown in Figure 3a. The original silica seed showed peaks at 2θ = 20.39º, 26.07º and 49.02º which are typical to the SiO2 [14]. The sample obtained after 5 h of FBR operation was more or less similar to the SiO2 as the peaks present in the diffractogram matched more with SiO2 (Figure 3a). The amount of CaF2 deposited onto the seed materials after 5 h is proportionally much smaller than silica which is reason behind detecting SiO2 in this sample. However, peak intensity for SiO2 in this sample reduced compared with original seed sample indicating that CaF2 crystallization process has started and there is other elements too in the sample along with SiO2. The characteristic peaks corresponding to the CaF2 was observed in the crystal samples obtained after 40 d reactor operation. The peaks corresponding to CaF2 that are present in this sample were at 2θ = 28º, 46.6º, 55.7º, 68.7º, 75.8º and 87.4º (JCPDS no. 87-0971) [15,16]. Formation of CaF2 with the FBR was confirmed with this XRD analysis. The XRD characterization of the CaF2 crystals also revealed the absence of calcium carbonate (CaCO3), calcium sulfate (CaSO4) or fluorapatite (Ca5(PO4)3F) in the resulting crystals. These compounds are known to precipitate during fluorine removal through fluidized bed crystallization and even some cases are the main product instead of CaF2 [14,17]. The possibility of any of these compounds’ formation in this study is completely eliminated through this XRD analysis which also in turn highlight the high purity of CaF2 formed.
The FTIR spectra obtained for silica seed material and calcium fluoride crystals obtained from different time interval is shown in Figure 3b. The broad peak at 3450 cm−1 and 1620 cm−1 represents stretching and bending vibrations of hydroxyl (–OH) group [18]. A range of small peaks at 1875 cm−1 and 2000 cm−1 could be due to the presence of C=O and C=C stretching vibrations, respectively [19]. The sharp peak at 1080 cm−1 indicates the presence of asymmetric stretching vibrations of Si−O−Si bond [20]. The C=C bending vibration is also can be seen by the peak at 830 cm−1 [21]. Other peaks at 750 cm−1 and 460 cm−1 can be attributed to the presence of sulfate and phosphate groups [18]. However, Si–O stretching vibration can also be indicated by the presence of a peak at 460 cm−1 [22]. Although, it is difficult to confirm the presence of CaF2 with FTIR spectra alone as it can only indicate presence of functional groups, some of the previous studies [18,21] have suggested that peak near 750 cm−1 is due to CaF2 presence which can be observed even in this current study too. The change in certain peak intensity following exposure to fluoride indicate role of this active group in the interaction with this fluoride. For example, peaks at 460, 830, 1080, 1875 and 2000 cm−1 showed reduced intensities for calcium fluoride crystals than silica seed, indicating role related functional groups such as Si–O, Si−O−Si, C=O and C=C have role to play in interaction of fluoride ions with silica seeds. The increase in peak intensities of OH group at 3450 cm−1 for CaF2 sample is due to presence of water in the crystals due prolong exposure to experimental conditions inside FBR.
Compositional analysis of the silica seed and CaF2 crystals obtained at the end of reactor operation was carried out using ICP-OES and the results is shown in Table 1. For this analysis, the samples are first acid digested and only the acid soluble parts are analyzed. It can be overserved from the result that the calcium and fluoride composition increased significantly from 0.34 and 1.53% in the seed material to 33.69 and 57.37% after 40 days of FBR operation. This increase in Ca and F composition in the samples directly corresponds to the reduction in silica composition from (94.81% to 2.05%) and confirms the calcium fluoride crystal formation onto the silica seed. Other elements such as sulfur, aluminum, iron, potassium, magnesium, sodium and phosphate are also present in the samples in minute quantities which may have been contributed by either the silica seed material or by the simulated wastewater used in the study. The purity of the CaF2 crystals was also calculated using this study by converting the elemental percentages to molar fraction and subtracting the impurities from CaF2 crystals (details shown in supplementary material). By this method the purity of the CaF2 crystals obtained after 70 days of FBR operation is 91.12% which is relatively high compared to many other previous studies.
Table 1.
Elemental analysis of the silica seed and calcium fluoride crystals using ICP-OES.
| Element | Silica seed (%) | CaF2 - 70 day (%) |
|---|---|---|
| Sulfate (S) | 0.14 | 0.18 |
| Aluminium (Al) | 0.34 | 0.27 |
| Calcium (Ca) | 0.34 | 53.2 |
| Fluoride (F) | 1.53 | 44.4 |
| Copper (Cu) | 0.01 | 0.00 |
| Iron (Fe) | 0.70 | 0.56 |
| Potassium (K) | 0.27 | 0.36 |
| Magnesium (Mg) | 0.12 | 0.05 |
| Sodium (Na) | 0.38 | 0.47 |
| Phosphate (P) | 0.13 | 0.00 |
| Silica (Si) | 94.81 | 0.51 |
| Zinc (Zn) | 0.04 | 0.00 |
2.2. Process Improvement Strategies
2.2.1. Effect of Increased Calcium Addition on Fluoride Removal
In order to remove the additional fluoride present in the FBR effluent, an excess amount of calcium was injected to the reactor to reach a [Ca2+]/[F-] ratio of 0.65, 0.7, 0.75 and 0.8. The results showed that with increase in the inlet calcium concentration the effluent fluoride concentration gradually decreased (Figure 4). A minimum effluent fluoride concentration of 21 mg/L was obtained for [Ca2+]/[F-] ratio of 0.8 which was 7% lower than than that obtained originally for [Ca2+]/[F-] ratio of 0.65 (Figure 4). The overall fluoride removal at this calcium concentration was 93%. It is to be noted here is that it is impossible to remove more than 95% fluoride due to the limitations associated with solubility of calcium fluoride at its high concentration [23]. Hence, if calcium is not sufficiently dissolved, it affects its reaction with fluoride and its subsequent removal. In this case, the reaction solution is saturated and no additional calcium is dissolved, so the reaction rate with fluoride drops with any further increase in influent calcium concentration. In addition, undissolved calcium can precipitate, which has been known to react with other inert substances in the solution to produce other undesired calcium compounds. Therefore, to achieve a further lower effluent fluoride concentration by increasing inlet calcium ions is not attempted in this study.
2.2.2. Performance of Two-Stage FBR for Fluoride Removal
In order to overcome the disadvantages of single-stage process to achieve a low effluent fluoride concentration, a two-stage process was designed. The two most important parameters [Ca2+]/[F-] ratio and HRT are optimized. Figure 5 shows the effect of [Ca2+]/[F-] molar ratio on fluoride removal in the second stage which was fed with fluoride (40 mg/L) containing wastewater coming out of the first reactor and had a fixed HRT of 1 h. The results showed that as the fluoride removal increased with increasing influent calcium concentration. The fluoride removal of 65% along with an effluent fluoride concentration of 14 mg/L was achieved at a [Ca2+]/[F-] ratio of 0.75 in the second stage. However, the effluent fluoride concentration as well as the fluoride removal efficiencies were almost similar for [Ca2+]/[F-] ratio of 0.65-0.8. This observation is similar to the previous findings where increase in influent concentration showed positive impact on the fluoride removal as due to common ion effect where an excessive calcium ion compared with a low fluoride concentration improves the reaction rate for calcium fluoride formation [24].
The effect of different HRT combinations for the two-stage process on fluoride removal is shown in Figure 6. The goal for this experiment is to reduce the HRT without compromising with the fluoride removal performance. A lower HRT is advantageous as more wastewater can be treated in a reactor of the same capacity, and it can be operated efficiently by reducing installation and operating costs and optimizing energy consumption. As can be seen from the figure, the 5 h + 1 h and 4 h + 1 h HRT for 1st reactor and 2nd reactor showed best results with 94.6 and 94% of fluoride removal efficiency, respectively. However, considering reduction in HRT by 1 h time in 4 h + 1 h combination, this HRT should be taken as optimum as it not only maintains same level of fluoride removal performance but also reduces overall reaction time. From the results it is clear that the HRT has a profound effect on the fluoride removal. The reduction of HRT in the first reactor reduced it’s fluoride removal capacity, which however, could be overcome in the second reactor even with just 1 h HRT. Such good performance in second reactor is due to presence of excess amount of calcium ions and relative low influent fluoride concentration compared with first reactor. For the experimental conditions with low HRT in first stage (2 and 3 h), the overall fluoride removal was not as good as the other two despite having a high HRT of 2 h in the second stage. This could be attributed to the fact that this decrease in the fluoride removal efficiency was due to insufficient reaction time between the reactants and the seeds in the reactor.
With optimization of both these parameters, it can be concludingly stated that a two-stage process is better than that of a single-stage process for fluoride removal. The addition of a second stage with fresh seeds provides for better fluoride removal opportunity as these additional seeds in the second stage increased surface area available for calcium fluoride precipitation increasing the overall removal efficiency of the system. Furthermore, by dividing the reaction for fluoride removal into two stages, sensitivity to reaction conditions can be reduced. With this reduction in reaction sensitivity, the chemical reaction can be made relatively stable even in an unstable environment, increasing the stability and efficiency of overall operation.
2.3. CFD Simulation of FBR Treating Fluoride Containing Wastewater
In order to verify the accuracy of the CFD model, attempts were made to check the similarity between experimental and model predicted increase in seed bed height during fluidization with upflow velocities. The results for this experiment are shown in Figure 7. The results showed that there was a very good similarity between the experimental and model predicted values for all the different upflow velocities except for 40 m/h when a maximum 13% variation between the two results were observed. This indicates a consistent trend by the CFD model in predicting mixing pattern inside the reactor. The somewhat deviation in results for certain values could be attributed to the difference between actual experimental condition and the assumptions made regarding them during CFD model development. For example, the shape and size of the particles are assumed to be spherical and 0.5 mm for experimental simplicity. However, in actuality the particles are of 0.3-0.7 mm in size and are of irregular shape with similarity to spherics.
In this study, CFD simulation was conducted to design a fluidized bed reactor for the purpose of maintaining the fluidized bed and proper mixing of crystals. By comparing the conditions at the bottom of the reactor with the existing reactor, it was attempted to reduce the formation of dead zones by giving the maximum angle. A dead zone refers to a place where no reaction occurs and remains stagnant, and this dead zone has a significant impact in a fluidized bed reactor. This is because the reaction does not occur within the dead zone, so the activity of the seed decreases, reducing efficiency, and the reaction rate also decreases, reducing the overall efficiency of the system [25]. Additionally, the occurrence of a dead zone within the reactor causes a non-uniform reaction. This makes it difficult to form the desired crystal product, and the stability of the process may be impaired due to inefficient use of space [26]. Therefore, it is important to minimize the dead zones in order to operate the fluidized bed reactor under optimal conditions.
The results of CFD simulation for different FBR configurations are shown in Figure 8. Form the figure it is clear that there was formation of dead zones in the FBR with original configuration, which reduced with the change of shape of the reactor to a conical bottom. In a cone shape structure, the diameter increases as it moves from the center of the lower part to upward. This contributes to maintaining the consistency of the reaction by minimizing the change in reaction conditions depending on the distance from the center to the outermost point, thus reducing the non-uniformity in the entire reaction area and reducing the possibility of forming a dead zone [25,27]. Also, the lower part of a cone shape structure stabilizes the movement of particles by receiving the force from the bottom to the top, allowing effective mixing and movement near the center [28]. Therefore, it is confirmed from this study that the cone-shaped bottom design can optimize the flow phenomenon inside FBR.
However, with reduction in inlet diameter and increase in angle of the cone shaped bottom, the dead zone increased (Figure 8b,c). This indicates that the small diameter of the inlet increases the flow rate of the fluid, making it pass through the reactor quickly, failing to secure reaction time, and reducing the available area where particles can be mixed effectively, causing the problem of particles settling in certain areas, forming a dead zone [29]. In addition, if the lower diameter of the fluidized bed reactor is small, mixing and dispersion at the inlet becomes difficult, which hinders the uniform distribution of seed particles and reactants. Therefore, it is important to select an optimal diameter by considering the flow characteristics of the inlet. Further, experimental confirmation of FBR configuration with lower angle of 12.6º and inlet diameter of 29 mm showed best fluoride removal (86.6%) which is nearly 5% more than the value obtained for original configuration.
The effect of changing reactor bottom-angle from 0° to 5°, 10° and 12.6° on reactor mixing is shown in Figure 9. The CFD simulation results clearly shows that the mixing improved with increase in bottom angle as the dead zone gradually reduces. Particularly for the configurations with 10° and 12.6° angle, the dead zone in the reactor decreased significantly. In addition, there was almost no speed deviation for both these configurations, indicating that a uniform vertical rotation flow was being formed within the reactor. These results indicate that a uniform flow of particles in the reactor will be formed to prevent precipitation of particles, and the optimal condition of 12.6°, which is the maximum angle at the bottom, was selected.
In the subsequent experiment, the inlet diameter of the reactor was reduced from 29 mm to 25 mm, 23 mm and 20 mm by keeping the bottom angle fixed at 12.6°. From the results it can be observed that the dead zone increases as the diameter of the inlet becomes smaller (Figure 10). This indicates the influence of inlet diameter on the mixing inside FBR. The principle of flow in the reactor is that the fluid flowing from the bottom rises to the top, and the rising flow moves in concentric circles in all directions and descends again along the wall [26]. Accordingly, the larger the inlet diameter, the relatively closer the distance between the bottom and the wall, so most of the relatively inflow flow descends along the wall, resulting in smooth flow. This phenomenon is reflected in the CFD results showing best mixing for wider inlet diameter. Therefore, an inlet diameter of 29 mm was chosen to be optimal for smooth particle flow inside the FBR.
The effect of width to height ratio of the reactor on proper mixing was determined using CFD and the result obtained is shown in Figure 11. The inlet diameter and bottom angle was kept fixed at 29 mm and 12.6°, respectively. The results showed that best particle mixing was best for the reactor with 1:43 width to height ratio which was the conventional reactor with a width of 50 mm and a height of 2,150 mm used during the study. The dead zone gradually increased from this first configuration to the other two reactors with width to height ratios of 1:23 and 1:15, respectively, indicating poor mixing inside such reactors. In the first reactor, smooth flow of particles can be observed due to the narrow width of the reactor (Figure 11a). In addition, it is believed that a constant fluid direction can maintain effective particle mixing by stabilizing the fluid flow at the bottom of the reactor and reducing the possibility of particle stagnation. The increase in width in other two reactor caused instability in the flow pattern. This can be more clearly observed in the third configuration with a width of 70 mm and a height of 1,040 m, where large size dead zones appeared inside the reactor due to increase in width by 20% compared to the original reactor. Moreover, it was confirmed that the maximum particle height decreased due to the increase in width despite having same amount of seed particles as the original reactor. This indicates that, at the same flow rate, the pressure at the bottom of the reactor increases as the width of the reactor increases, requiring a larger flow rate to keep the particles flowing at the same height. Therefore, in order to maintain smooth mixing of particles inside FBR, it is efficient to design the width of the reactor to be narrow. However, this drawback can be overcome by adjusting the flow rate as per the requirement based on actual reactor conditions.
3. Material and Methods
3.1. Experimental Setup
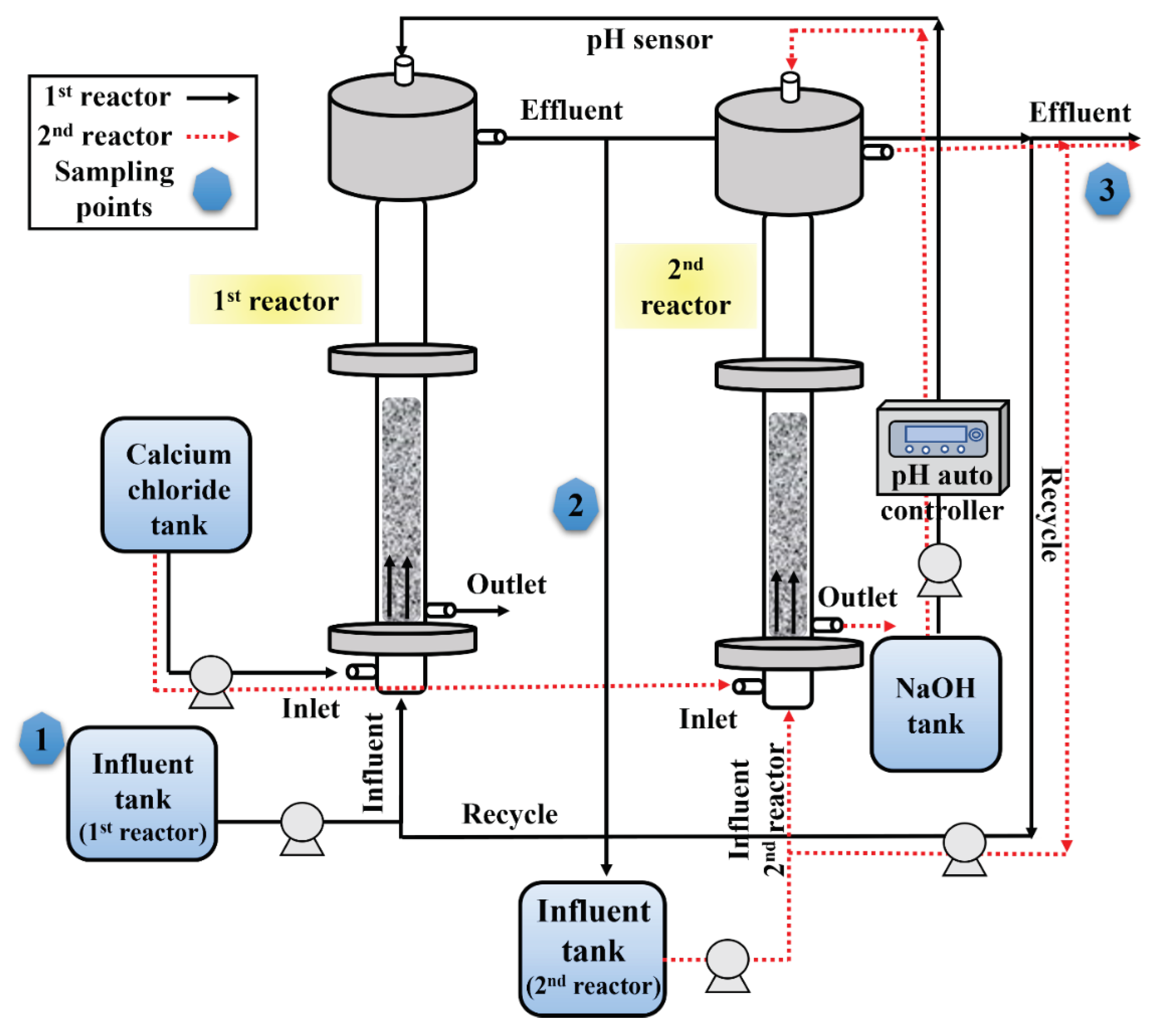
In this study, a laboratory-scale fluidized bed reactor (FBR) of 3.44 L volume was manufactured using acrylic material and used for fluoride treatment and calcium fluoride crystallization as depicted in Figure 12. The outer diameter and the height of the reactor were 50 mm and 2,150 mm, respectively. The inlet for chemical CaCl2 was installed 400 mm above the bottom of the reactor, and an outlet for CaF2 crystals was installed above this CaCl2 inlet point to enable extraction of calcium fluoride crystals. The treated water outlet is located 150 mm below the upper weir and effluent water from the reactor is discharged by natural flow. The FBR was operated in an upward flow manner to allow the seeds to flow up and down as the wastewater was injected from the bottom of the reactor. The reactor was filled with silica seeds of size 0.3~0.7 mm in diameter for the purpose of CaF2 crystallization on the seed surface during the reactor operation. In order to minimize pH fluctuations inside the reactor due to chemical reactions, pH was monitored and adjusted using a pH auto controller connected with a NaOH tank.
Afterwards, in order to improve the quality of the treated water, a two-stage process was operated (Figure 12). The second stage reactor was similar in size and shape to the first reactor including all the inlet and outlet ports. The second reactor was filled with silica seed materials of required volume. The inflow and recirculation flow to the second reactor is distinctively identified by using red dotted lines in the figure. The sampling locations for collecting samples to and from the rector(s) are shown in the figure (Figure 12).
3.2. Continuous Reactor Operation
Continuous experiments were conducted over an extended period to assess the performance of the laboratory-scale FBR. The fluoride containing simulated wastewater was introduced to the reactor at an influent flow rate of 16.5 L/day and discharged accordingly during this continuous experiment. The synthetic wastewater used in this study was similar to semiconductor industry wastewater according to Sim et al. [10] and had following characteristics: pH 2.2, conductivity 5,850 µs/cm, Fᅳ 460 mg/L, NH4+-N 11.4 mg/L, SO42- 280 mg/L, total phosphorus (TP) 2.5 mg/L, SiO2 10.3 mg/L, Al3+ 0.70 mg/L, Fe2+ 21.7 mg/L, and Mg2+ 0.1 mg/L. The HRT and upflow velocity were maintained at 5 hours and 20 m/h, respectively. These selected operating parameters are based on the optimal operating conditions derived from our prior batch experiments. A 10-fold diluted 35% CaCl2 reagent was continuously injected to the reactor at a rate of 0.29 mL/min to maintain desired calcium-to-fluoride ion ratio in the reactor. The pH was maintained to the optimal value of 6 using a pH auto controller.
To monitor fluoride removal efficiency, treated water samples were filtered once daily using a 0.45 μm GFC filter, with half of each sample being filtered. Subsequently, the fluoride ion concentration in both the unfiltered and filtered samples was measured to determine fluoride removal rates and calcium fluoride crystallization efficiency. Furthermore, to track crystal growth, the variation in seed height was monitored daily. The fluoride removal was calculated according to the following equation:
Where, F-in and F-ef are the influent and effluent fluoride concentration from FBR, respectively.
3.3. Process Improvement Strategies
Although, the continuous experiment demonstrated a very high fluoride removal, the effluent concentration could not able to reach release standard. Hence, in order to achieve further fluoride removal different strategies are undertaken. In order to check if increasing calcium concentration in the single stage process could improve the fluoride removal, influent calcium concentration was increased to meet a [Ca2+]/[F-] ratio of 0.7, 0.75 and 0.8. Later, to overcome the hurdles associated with excess calcium addition, a two-stage process (Figure 1) is envisioned. In this two-stage process, the effluent from the first reactor was used as influent for the second stage. All the other conditions including reactor configurations are same as described for the single-stage process. Different parameters key to the performance of the FBR for fluoride removal are optimized in this study. Firstly, as the influent fluoride concentration was low compared to the first reactor, the influent calcium concentration in the second reactor was optimized by varying the [Ca2+]/[F-] ratio to 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75 and 0.8. The [Ca2+]/[F-] ratio in first stage fixed was kept fixed at 0.55. In the next step, the HRT was optimized for two-stage process by varying the HRT in following manner (1st reactor + 2nd reactor): 5 h + 1 h, 4 h + 1 h, 3 h + 2 h, 3 h + 1 h, and 2 h + 2 h.
3.4. CFD Guided Optimization of FBR Configuration
CFD simulation is divided into four stages, first step of which is Geometry. Geometry is the order of creating the shape to be actually analyzed or specifying conditions in flow analysis. In general, process drawings are often inserted into files or produced in the program itself. Since it is important to implement it under realistic conditions, the governing equations and numerical techniques that apply the flow conditions such as flow speed, pressure, and temperature, and the calculation conditions such as gap width, relaxation coefficient, and variable values are entered. In addition, boundary conditions must be specified to input the physical state and information of the fluid, which is the most important setting when performing simulation. First, in this study, velocity was used as the setting for the inlet condition, and pressure was used as the setting for the discharge water outlet. The reason for setting these boundary conditions is that they are applied according to the domain of the analysis target, which is common when rotation occurs in a structure due to a strong flow.
The second step is meshing, which specifies the part of the shape to be analyzed. There are significant differences in interpretation of the grid configuration of CFD depending on its shape and size. There are three types of grids, namely hexahedral, tetrahedral and pyramidal. In this study, the polyhedral shape was used. This shape was selected because it is commonly used to accurately calculate turbulence and fluid analysis. In the case of a hexahedral other than the target shape, the numerical analysis results can produce highly accurate results, but if the structure is complex or the flow changes significantly within a short period of time, many errors may occur in the connection and formation of the lattice, which can lead to large errors in actual crystals. Changes have the potential to cause large errors. In addition, in the case of tetrahedral, it is expected that the analysis time will be somewhat long as it is mainly used in structural analysis to perform accurate calculations on the boundary layer of the structure.
Typically, increased grid density correlates with improved accuracy; however, this negatively impact by increasing analysis times, necessitating the need for careful adjustments. In this study, for efficient calculations, the overall grid size was set to 5 mm, and a relatively dense grid was placed at the inlet and outlet where rapid changes in flow are expected, as well as the flow part of the crystal, to ensure efficient analysis time and detailed flow changes. The goal was to increase accuracy and reliability by enabling accurate predictions.
The third order is physics, which specifies all conditions and equations used in flow analysis. The conditions used in this study are shown in Table 1. The equation Lagrangian-mutiphase can analyze the interaction between the solid region of the crystal and the liquid region of the wastewater in the process and the flow rate and pressure of each phase. Therefore, an equation that analyzes two or more phases simultaneously was inserted.
In the case of equations, the continuity equation and momentum equation were calculated using the k-epsilon model for turbulence generated due to strong flow velocity. This model can be considered suitable for structural fluid analysis because it is an equation that provides a good compromise in terms of accuracy and stability in general-purpose simulation. The resulting equation is as follows (Eq. 2).
Equation for kinetic energy (K):
Where, ρ is the density of the fluid, t is time, ui is the velocity component, xi is the coordinate, μ is the dynamic viscosity, μt is the turbulent viscosity, σK is the modeling constant of the turbulent viscosity, and PK is the kinetic energy.
Equation for kinetic energy consumption rate (ε):
Where, Є represents turbulence energy (dissipation), σε represents the modeling constant of turbulence energy, and C1ε and C2ε represent modeling constants. Afterwards, for particle analysis, analysis was performed using the Lagrangian method as shown in the equation below, and drag force (darg force, 𝐹𝐷), lift force (𝐹𝐿), and gravity force were considered as the forces acting on particles. The equation is as shown below (Eq. 4-6).
Where, 𝑑𝑝 and 𝐴𝑝 refer to the diameter and cross-sectional area of the particle. The particle diameter was 0.5 mm, the density was 2650 kg/m3, and it was assumed to be silica sand. 𝐶𝐷 is the drag coefficient, and 𝑎1, 𝑎2, and 𝑎3 are constants in the range of each constant 𝑅Є𝑝 number. 𝑅Є𝑝 refers to the Reynolds number of the particle.
Where, 𝑚𝑝 and 𝑢𝑝 mean the mass and speed of the particle, and Li and Ahmadi’s equation, which is a generalization of the equation called Saffman’s lift, was used. The constant K is 2.594, and 𝜌𝑝 and 𝜈𝑓 are the density of the particle and the fluid, respectively. It means kinematic viscosity coefficient.
Where, gi means force based on the law of universal gravitation.
The fourth step is to analyze the results of the actual flow inside the reactor. In general, the process of change due to flow can be confirmed in real time and predicted by analyzing the movement of a single grid.
The reactor configuration used in this study is depicted in Figure S1 along with all the dimensions. The FBR had a total height of 2,150 mm and a width of 50 mm. The silica particles were filled upto 500 mm height. The height of the lower part of the reactor was 95 mm and the fluid inlet part was 15 mm high and 29 mm in diameter. In order to verify the validity of the CFD program developed, comparative study between the experimental and model predicted results for increase in the seed bed height at different upflow velocities were conducted. The different upflow velocities used for this experiment were as follows: 10 m/h, 20 m/h, 30 m/h, 40 m/h, 50 m/h, and 60 m/h. In this numerical analysis, particle analysis was conducted after excluding energy loss due to flow rate and the possibility of crystal shape deterioration. Once the validity of the developed CFD model was established experiment was conducted to understand the effect of FBR configuration (bottom part angle and inlet diameter) on mixing inside the reactor. For this purpose, three different configurations were chosen, i.e., first existing reactor with inlet diameter of 29 mm, second a new FBR with lower angle of 12.6 degrees and inlet diameter of 29 mm, and third another FBR with a lower angle of 19.1 degrees and inlet diameter of 20 mm (Figure S2).
Further studies were conducted to find optimal design conditions using optimized CFD-DEM model. There are three design conditions that were optimized: (i) shape of the bottom of the reactor (according to the reactor bottom angle), (ii) diameter of the reactor inlet, and (iii) ratio of width to height of the reactor. For the first experiment, the bottom angle of the reactor was increased from 0° to 5°, 10° and 12.6° by keeping the inlet diameter fixed at 29 mm. Following this study, experiment was conducted to study the effect of inlet diameter by varying it from 29 mm to 25 mm, 23 mm and 20 mm. The ratio of width to height ratio was examined for three different ratios, viz, 1:43, 1:23 and 1:15. The reactor configuration for each of these experimental conditions are shown in Figure S2.
Table 1.
Conditions used for CFD flow analysis.
| Condition (unit) | Value |
|---|---|
| Liquid density (kg/m3) | 997.561 |
| Dynamic viscosity (Pa-s) | 8.8871 E-4 |
| Cp (cal/g.k) | 0.998 |
| Inlet velocity (m/s) | 4.7 E-4 |
| Temperature (°C) | 25 |
| Outlet pressure (Pa) | 0 |
| Solid density (kg/m3) | 2,650 |
| Solid diameter (mm) | 0.5 |
| Number of grains | 20000 |
| Particle count | 5000 |
3.5. Characterization of the CaF2 Crystals
The calcium fluoride crystals formed inside the FBR were characterized using different instrumental techniques, namely SEM-EDX, XRD, FTIR and ICP-OES. The SEM-EDX analysis was performed with SEM instrument (Model Vega3, Tescan) using a single calcium fluoride crystal retrieved from the FBR. The structural composition and crystallinity of the CaF2 crystals were measured using a high-resolution X-ray diffractometer (HR-XRD, Model D8 advance, Bruker), and scans were performed within the range 05° to 90°. A Fourier transform infrared spectrometer (FT-IR, Model Spectrum 3, Perkin Elmer) was used to determine the functional groups of the crystal structure. Compositional analysis of the CaF2 crystal was carried out with an inductively coupled plasma optical emission spectrometry (ICP-OES Model G8014AA, Agilent). Analysis for silica seed as control was similarly performed with all these instruments mentioned.
3.6. Analytical Methods
Analysis of ionic components including fluorine, calcium and sulfate were performed using an ion chromatograph (IC, Model Ion chromatography-mass spectrometer, Metrohm). All samples were filtered using a 0.45 μm GFC filter prior to their analysis. pH was measured using a pH meter (Model ST300, Ohaus).
4. Conclusions
The fluoride bed crystallization process applied in this study provided a very high fluoride removal over a long period of time under continuous mode of operation. Best results in terms of both fluoride removal and crystallization efficiency were achieved within 40 days of reactor operation, however, further prolongation of continuous reactor operation (beyond 50 days) resulted in declined performance. The CaF2 crystals recovered from the FBR showed high similarity with standards indicating its high purity. Further effort to improve the process efficiency through different approach showed positive outcome. Among the different methods applied, the two-stage FBR process showed promising results with effluent fluoride concentration value meeting regulatory standard of 15 mg/L. CFD based simulation technique was used to optimize the FBR configuration which showed that further improvement in reactor performance can be achieved by modifying reactor bottom shape, inlet diameter and reactor width to height ratio. These optimized configurations i.e., 12.6° bottom angle, 29 mm inlet diameter and 1:43 width to height ratio showed best mixing condition inside the FBR which could result in better reactor performance.
Funding
This work was carried out with the support of “Cooperative Research Program for Agriculture Science & Technology Development (Project No. 00219221)”, Rural Development Administration, Republic of Korea.
Acknowledgments
The authors acknowledge Hoimyung Waterzen, South Korea for providing support for ICP-OES and SEM-EDX analysis and for their help with experimental setup and fluoride containing wastewater.
References
- Wan, K.; Huang, L.; Yan, J.; Ma, B.; Huang, X.; Luo, Z.; Zhang, H.; Xiao, T. Removal of fluoride from industrial wastewater by using different adsorbents: A review. Sci. Total Environ. 2021, 773, 145535. [Google Scholar] [CrossRef]
- Lacson, C.F.Z.; Lu, M.C.; Huang, Y.H. Fluoride-containing water: A global perspective and a pursuit to sustainable water defluoridation management-An overview. J. Clean. Prod. 2021, 280, 124236. [Google Scholar] [CrossRef]
- Qiu, Y.; Ren, L.F.; Xia, L.; Shao, J.; Zhao, Y.; Van der Bruggen, B. Investigation of fluoride and silica removal from semiconductor wastewaters with a clean coagulation-ultrafiltration process. Chem. Eng. J. 2022, 438, 135562. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Cui, S.F.; Fan, R.J.; Fu, Y.Z.; Liao, Y.L.; Yang, J.Y. Distribution and superposed health risk assessment of fluorine co-effect in phosphorous chemical industrial and agricultural sources. Environ. Pollut. 2020, 262, 114249. [Google Scholar] [CrossRef]
- Li, Y.; Bi, Y.; Mi, W.; Xie, S.; Ji, L. Land-use change caused by anthropogenic activities increase fluoride and arsenic pollution in groundwater and human health risk. J. Hazard. Mater. 2021, 406, 124337. [Google Scholar] [CrossRef]
- Damtie, M.M.; Woo, Y.C.; Kim, B.; Hailemariam, R.H.; Park, K.D.; Shon, H.K.; Park, C.; Choi, J.S. Removal of fluoride in membrane-based water and wastewater treatment technologies: Performance review. J. Environ. Manage. 2019, 251, 109524. [Google Scholar] [CrossRef]
- Kim, J.; Hwang, Y.; Yoo, M.; Chen, S.; Lee, I.M. Hydrogen fluoride (HF) substance flow analysis for safe and sustainable chemical industry. Environ. Sci. Pollut. Res. 2017, 24, 25137–25145. [Google Scholar] [CrossRef]
- Ho, H.J.; Takahashi, M.; Iizuka, A. Simultaneous removal of fluoride and phosphate from semiconductor wastewater via chemical precipitation of calcium fluoride and hydroxyapatite using byproduct of recycled aggregate. Chemosphere 2023, 340, 139875. [Google Scholar] [CrossRef]
- Olejarczyk, M.; Rykowska, I.; Urbaniak, W. Management of Solid Waste Containing Fluoride—A Review. Materials 2022, 15, 3461. [Google Scholar] [CrossRef] [PubMed]
- Sim, J.; Lee, J.; Rho, H.; Park, K.D.; Choi, Y.; Kim, D.; Kim, H.; Woo, Y.C. A review of semiconductor wastewater treatment processes: Current status, challenges, and future trends. J. Clean Prod. 2023, 429, 139570. [Google Scholar] [CrossRef]
- Nath, S.K.; Dutta, R.K. Significance of calcium containing materials for defluoridation of water: a review. Desalin. Water Treat. 2015, 53, 2070–2085. [Google Scholar] [CrossRef]
- Aldaco, R.; Garea, A.; Irabien, A. Calcium fluoride recovery from fluoride wastewater in a fluidized bed reactor. Water Res. 2007, 41, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Aldaco, R.; Garea, A.; Fernández, I.; Irabien, A. Resources reduction in the fluorine industry: fluoride removal and recovery in a fluidized bed crystallizer. Clean Technol. Environ. Policy 2008, 10, 203–210. [Google Scholar] [CrossRef]
- Deng, L.; Liu, Y.; Huang, T.; Sun, T. Fluoride removal by induced crystallization using fluorapatite/calcite seed crystals. Chem. Eng. J. 2016, 287, 83–91. [Google Scholar] [CrossRef]
- Khunur, M.M.; Risdianto, A.; Mutrofin, S.; Prananto, Y.P. Synthesis of fluorite (CaF2) crystal from gypsum waste of phosphoric acid factory in silica gel. Bull. Chem. React. Eng. Catal. 2012, 7, 71–77. [Google Scholar] [CrossRef]
- Zhou, L. Preparation of calcium fluoride using phosphogypsum by orthogonal experiment. Open Chem. 2018, 16, 864–868. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.; Zhang, X.; Zhou, J.; Huang, T. Defluoridation by fluorapatite crystallization in a fluidized bed reactor under alkaline groundwater condition. J. Clean. Prod. 2020, 272, 122805. [Google Scholar] [CrossRef]
- Wang, Z.; Su, J.; Hu, X.; Ali, A.; Wu, Z. Isolation of biosynthetic crystals by microbially induced calcium carbonate precipitation and their utilization for fluoride removal from groundwater. J. Hazard. Mater. 2021, 406, 124748. [Google Scholar] [CrossRef] [PubMed]
- Azami, M.; Jalilifiroozinezhad, S.; Mozafari, M.; Rabiee, M. Synthesis and solubility of calcium fluoride/hydroxy-fluorapatite nanocrystals for dental applications. Ceram. Int. 2011, 37, 2007–2014. [Google Scholar] [CrossRef]
- Ellerbrock, R.; Stein, M.; Schaller, J. Comparing amorphous silica, short-range-ordered silicates and silicic acid species by FTIR. Sci. Rep. 2022, 12, 11708. [Google Scholar] [CrossRef]
- Gogoi, S.; Dutta, R.K. Fluoride removal by hydrothermally modified limestone powder using phosphoric acid. J. Environ. Chem. Eng. 2016, 4, 1040–1049. [Google Scholar] [CrossRef]
- Cao, J.; Yang, D.L.; Pu, Y.; Wang, D.; Wang, J.X. CaF2/SiO2 core–shell nanoparticles as novel fillers with reinforced mechanical properties and sustained fluoride ion release for dental resin composites. J. Mater. Sci. 2021, 56, 16648–16660. [Google Scholar] [CrossRef]
- Dubey, S.; Agrawal, M.; Gupta, A.B. Advances in coagulation technique for treatment of fluoride-contaminated water: a critical review. Rev. Chem. Eng. 2018, 35, 109–137. [Google Scholar] [CrossRef]
- You, S.; Cao, S.; Mo, C.; Zhang, Y.; Lu, J. Synthesis of high purity calcium fluoride from fluoride-containing wastewater. Chem. Eng. J. 2023, 453, 139733. [Google Scholar] [CrossRef]
- Xie, L.; Zhu, J.; Jiang, C. Quantitative study of mixing/segregation behaviors of binary-mixture particles in pilot-scale fluidized bed reactor. Powder Technol. 2021, 377, 103–114. [Google Scholar] [CrossRef]
- Zhang, C.; Li, S.; Wang, Z.; Shen, Y.; Wei, F. Model and experimental study of relationship between solid fraction and back-mixing in a fluidized bed. Powder Technol. 2020, 363, 146–151. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, S.; Shen, Y. CFD-DEM study of segregation and mixing characteristics under a bi-disperse solid-liquid fluidised bed. Adv. Powder Technol. 2021, 32, 4078–4095. [Google Scholar] [CrossRef]
- Feng, D.; Li, H.; Zhu, M.; Han, L.; Zhou, Y. Insight into the interaction mechanism between liquid action and cone structure in liquid-containing gas-solid spouted fluidized bed reactors. Powder Technol. 2022, 408, 117693. [Google Scholar] [CrossRef]
- Crose, M.; Zhang, W.; Tran, A.; Christofides, P.D. Multiscale three-dimensional CFD modeling for PECVD of amorphous silicon thin films. Comput. Chem. Eng. 2018, 113, 184–195. [Google Scholar] [CrossRef]
Figure 1.
Fluoride removal as calcium fluoride during continuous FBR operation. (a) Fluoride removal, (b) effluent calcium and sulfate profile, (c) calcium fluoride crystallization efficiency and (d) seed bed height and particle size profile during continuous operation.
Figure 1.
Fluoride removal as calcium fluoride during continuous FBR operation. (a) Fluoride removal, (b) effluent calcium and sulfate profile, (c) calcium fluoride crystallization efficiency and (d) seed bed height and particle size profile during continuous operation.
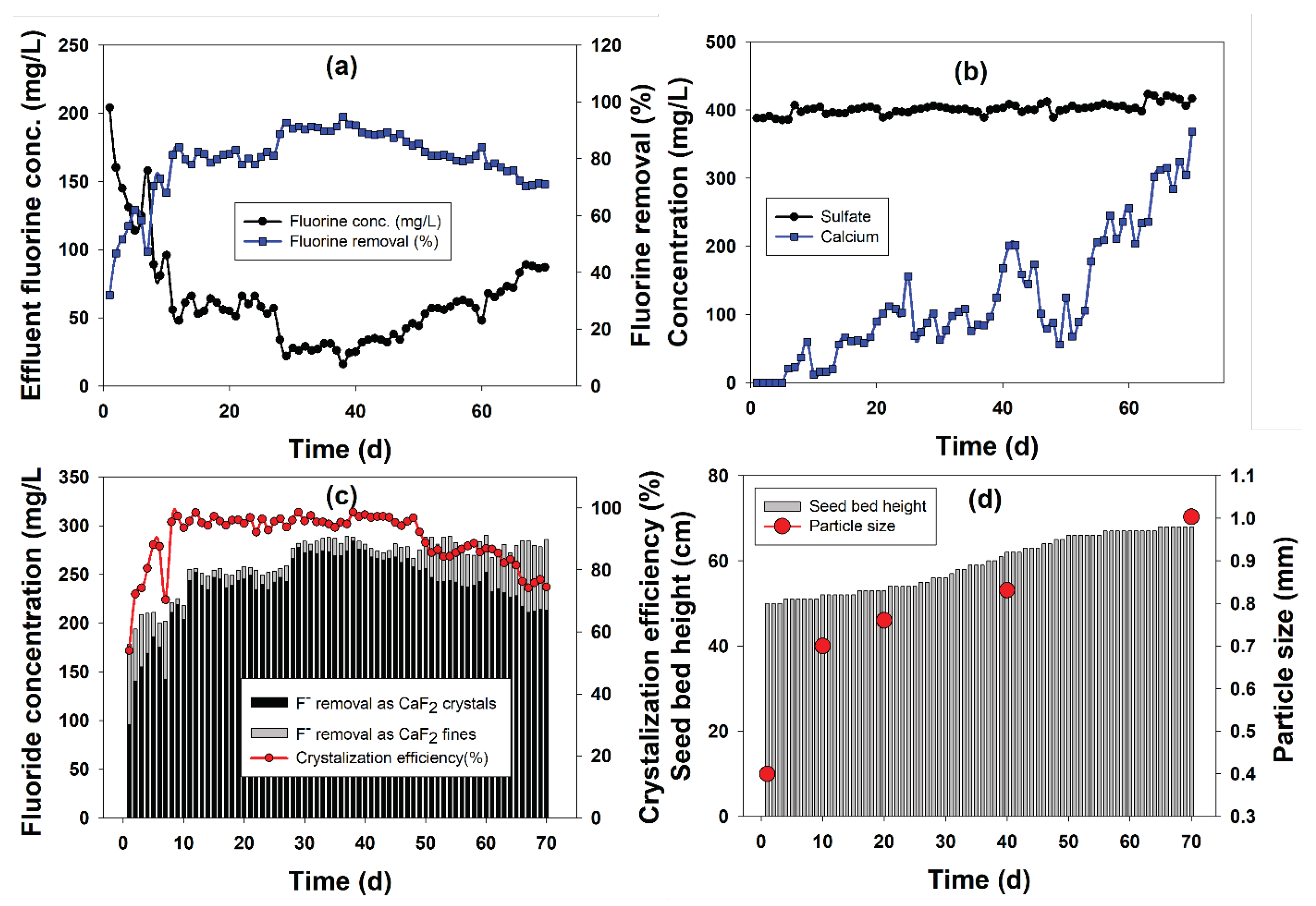
Figure 2.
SEM images (a & b) and corresponding EDX spectra (c & d) of silica seed (a & c) and calcium fluoride crystals (b & d) obtained after 70 days of FBR operation.
Figure 2.
SEM images (a & b) and corresponding EDX spectra (c & d) of silica seed (a & c) and calcium fluoride crystals (b & d) obtained after 70 days of FBR operation.
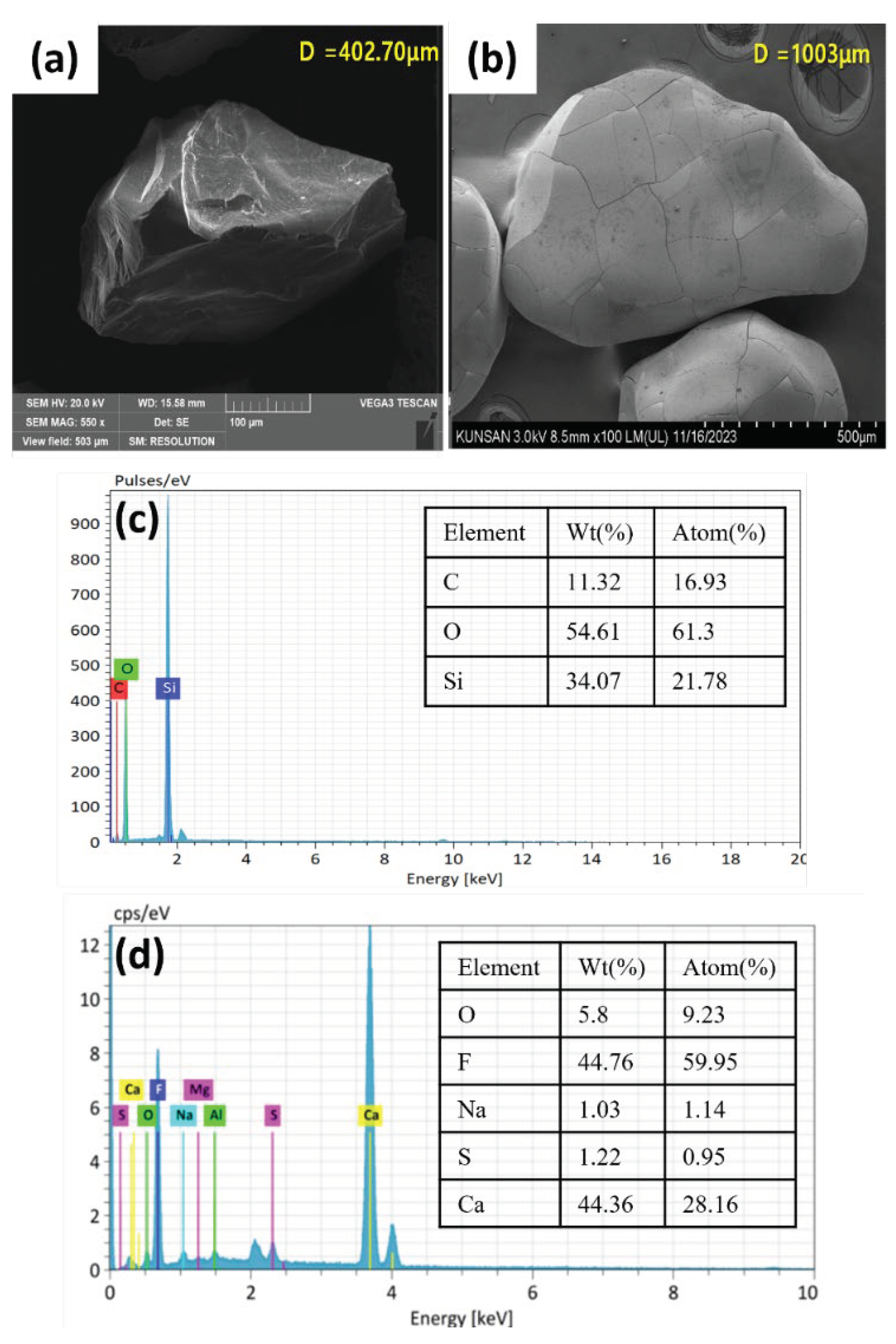
Figure 3.
(a) XRD and (b) FTIR spectra of silica seed and calcium fluoride crystals obtained after 70 days of FBR operation. .
Figure 3.
(a) XRD and (b) FTIR spectra of silica seed and calcium fluoride crystals obtained after 70 days of FBR operation. .
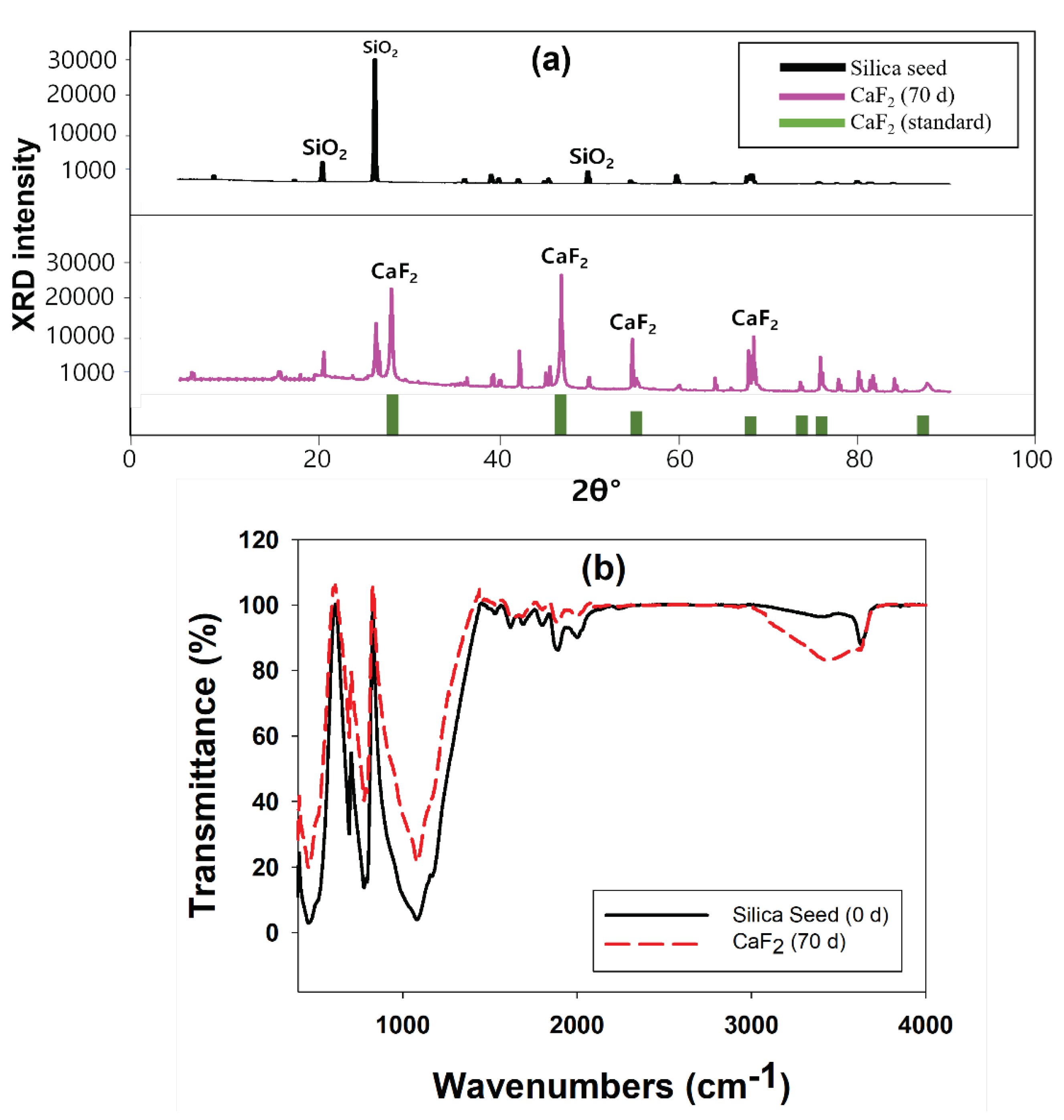
Figure 4.
Fluoride removal performance at high calcium to fluoride ratio.
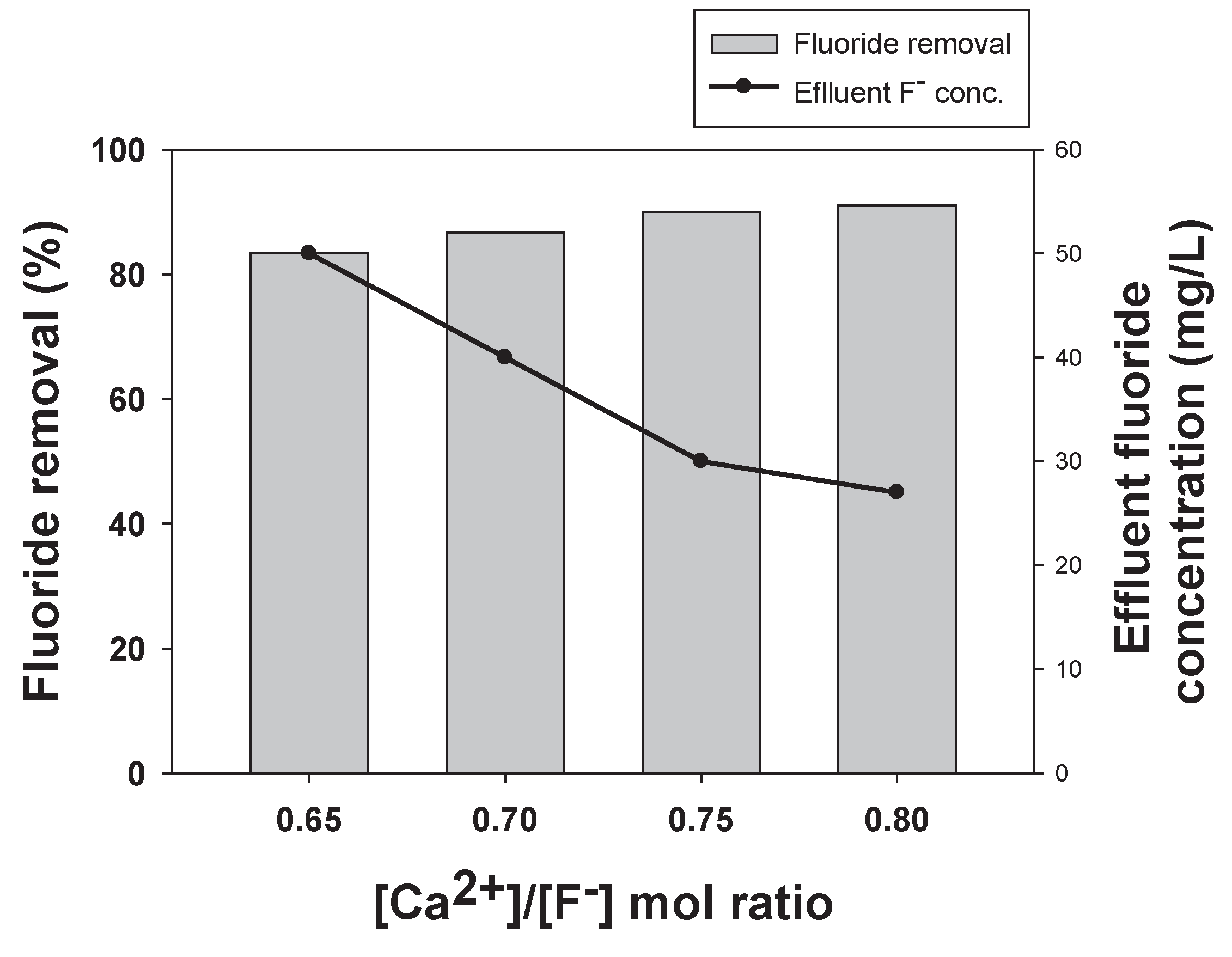
Figure 5.
Effect of calcium to fluoride ratio on fluoride removal in the second stage of two-stage process.
Figure 5.
Effect of calcium to fluoride ratio on fluoride removal in the second stage of two-stage process.
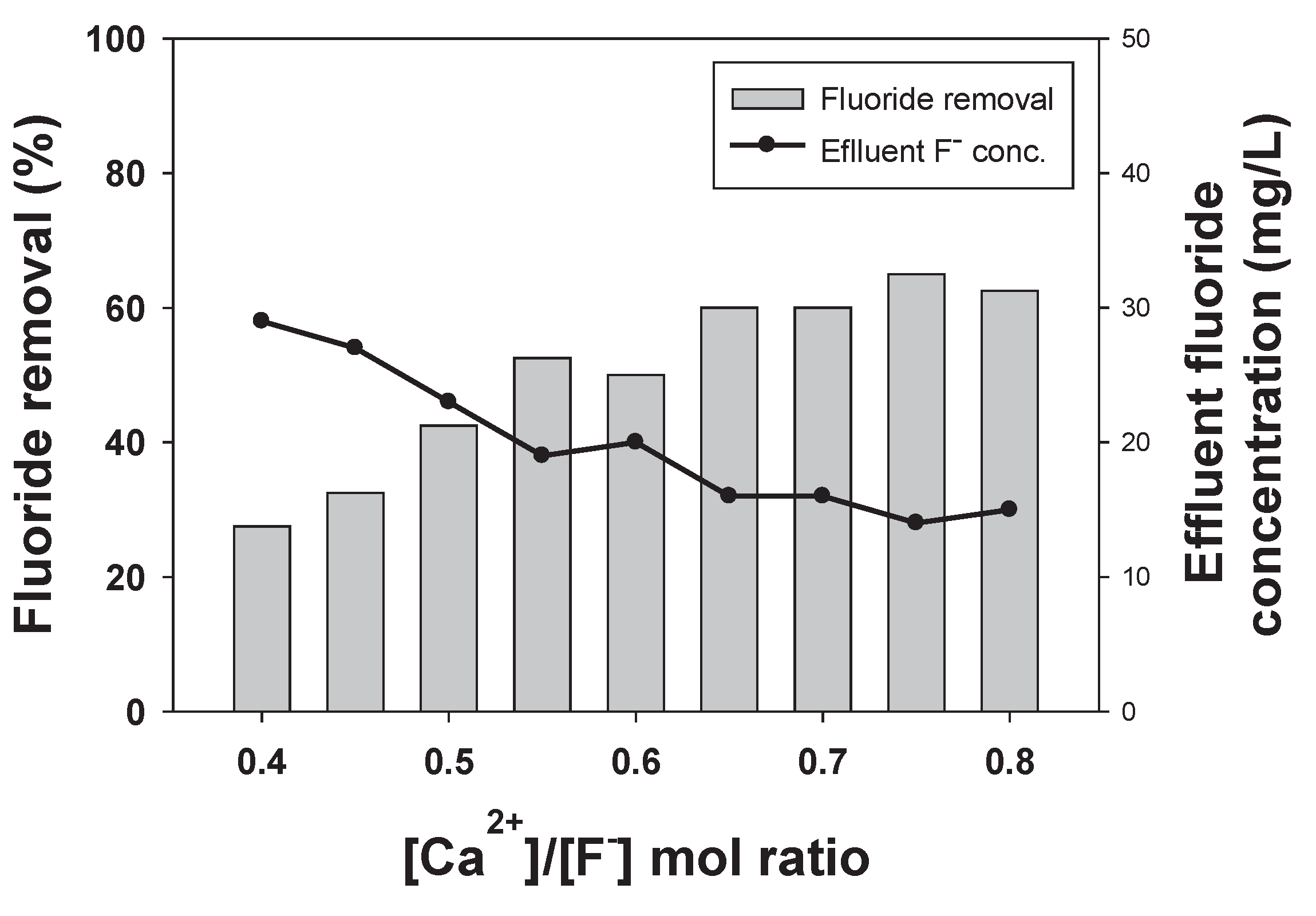
Figure 6.
Effect of different HRT combinations on fluoride removal in two-stage process.
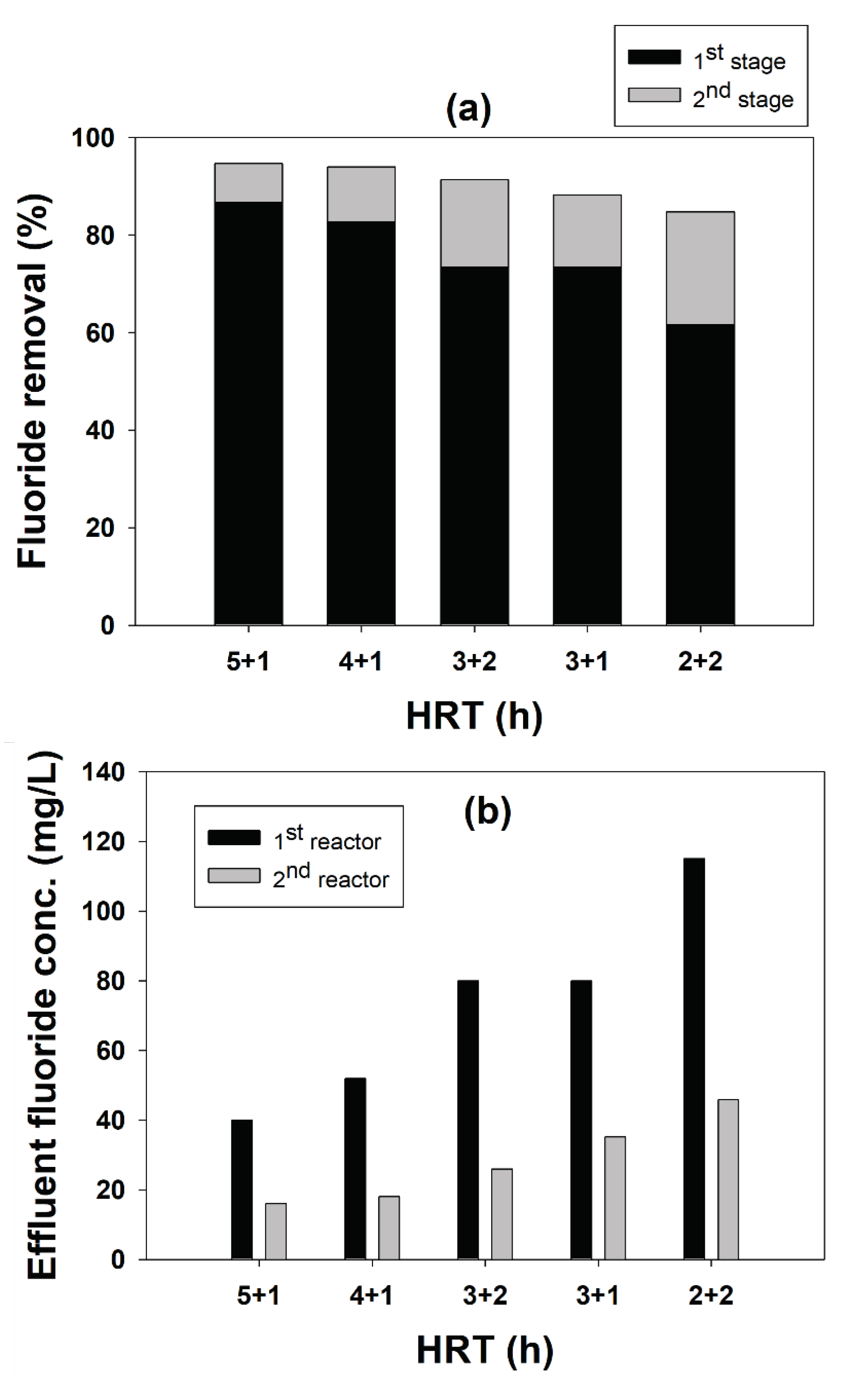
Figure 7.
Comparative study of experimental and CFD model predicted seed bed height at different upflow velocity.
Figure 7.
Comparative study of experimental and CFD model predicted seed bed height at different upflow velocity.
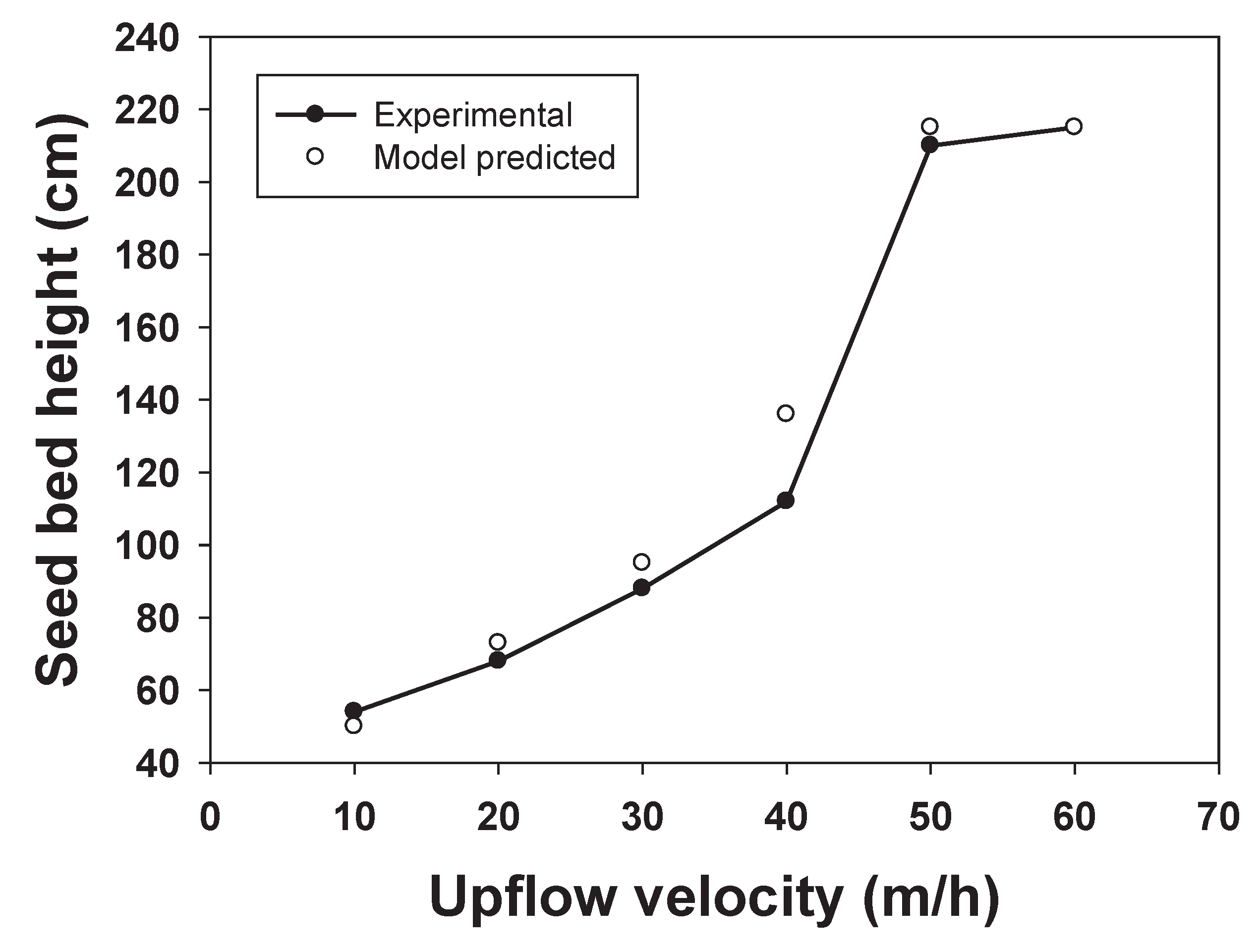
Figure 8.
Simulation results of (a) existing reactor with inlet diameter of 29 mm, (b) FBR with lower angle of 12.6 degrees and inlet diameter of 29 mm, and (c) FBR with a lower angle of 19.1 degrees and inlet diameter of 20 mm.
Figure 8.
Simulation results of (a) existing reactor with inlet diameter of 29 mm, (b) FBR with lower angle of 12.6 degrees and inlet diameter of 29 mm, and (c) FBR with a lower angle of 19.1 degrees and inlet diameter of 20 mm.
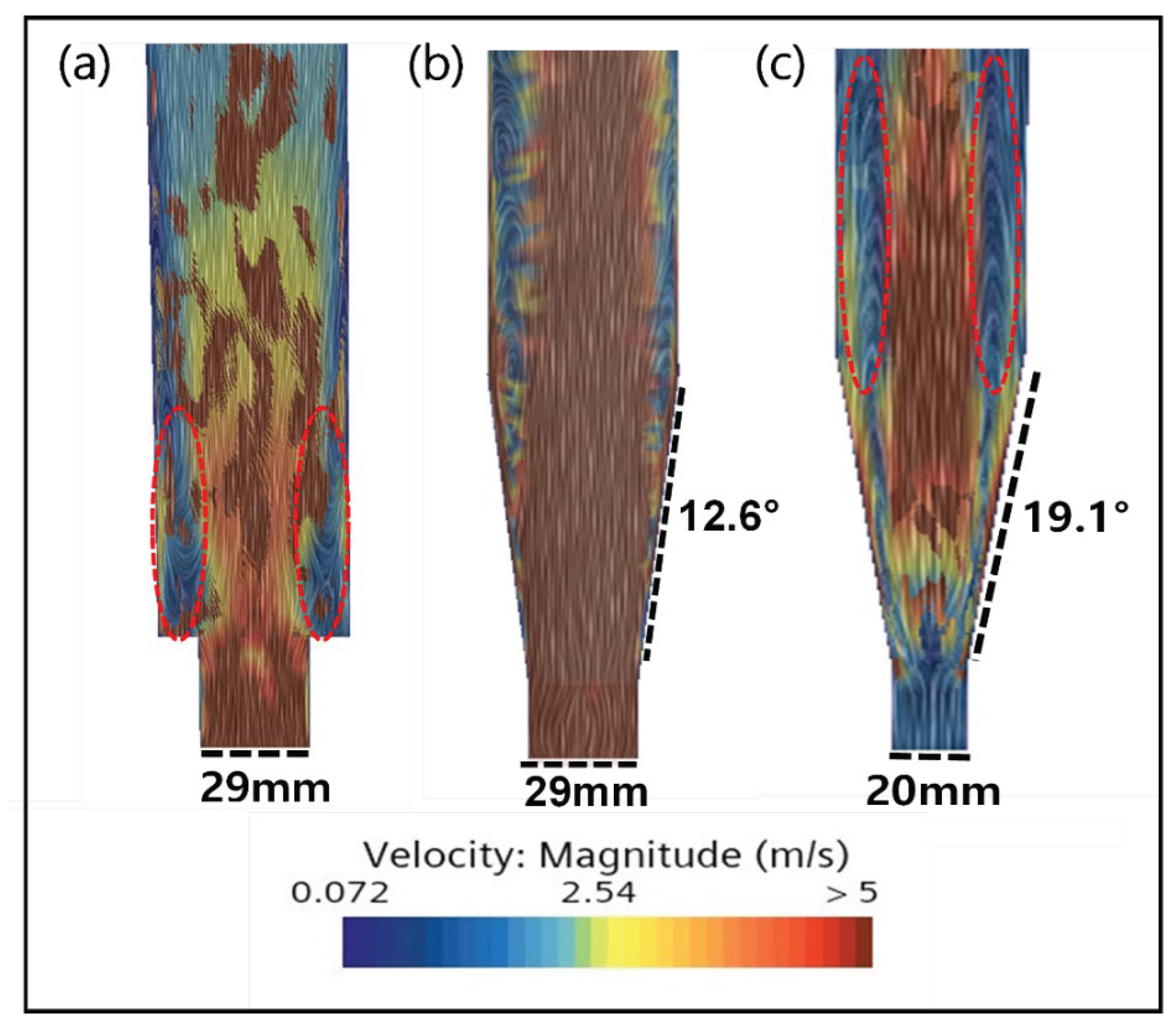
Figure 9.
Effect of bottom angle on mixing inside FBR. Simulation results for (a) 0°, (b) 5°, (c) 10° and (d)12.6° bottom angle.
Figure 9.
Effect of bottom angle on mixing inside FBR. Simulation results for (a) 0°, (b) 5°, (c) 10° and (d)12.6° bottom angle.
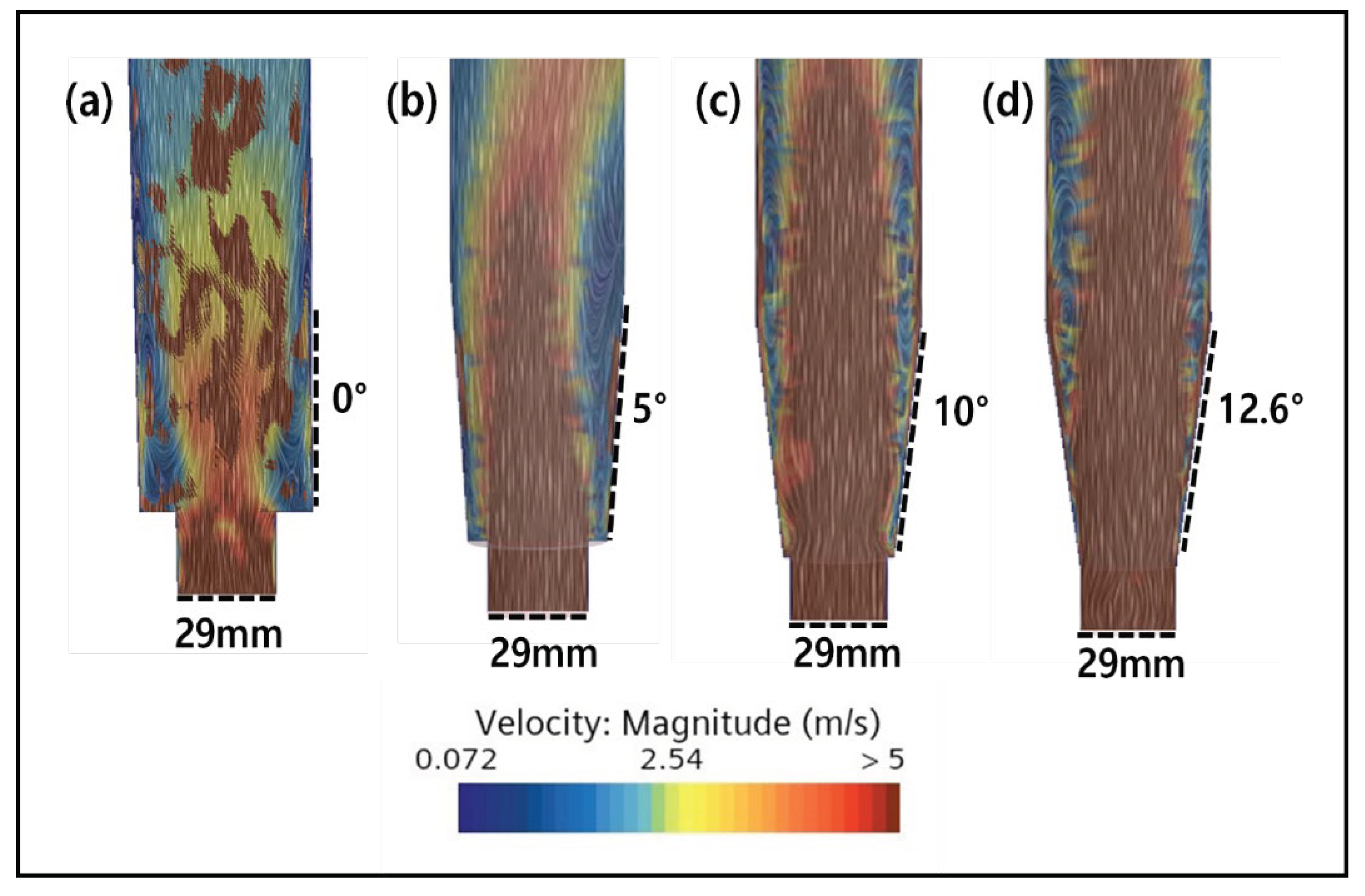
Figure 10.
Effect of inlet diameter on mixing inside FBR. Simulation results for (a) 29 mm, (b) 25 mm, (c) 23 mm and (d) 20 mm inlet diameter.
Figure 10.
Effect of inlet diameter on mixing inside FBR. Simulation results for (a) 29 mm, (b) 25 mm, (c) 23 mm and (d) 20 mm inlet diameter.
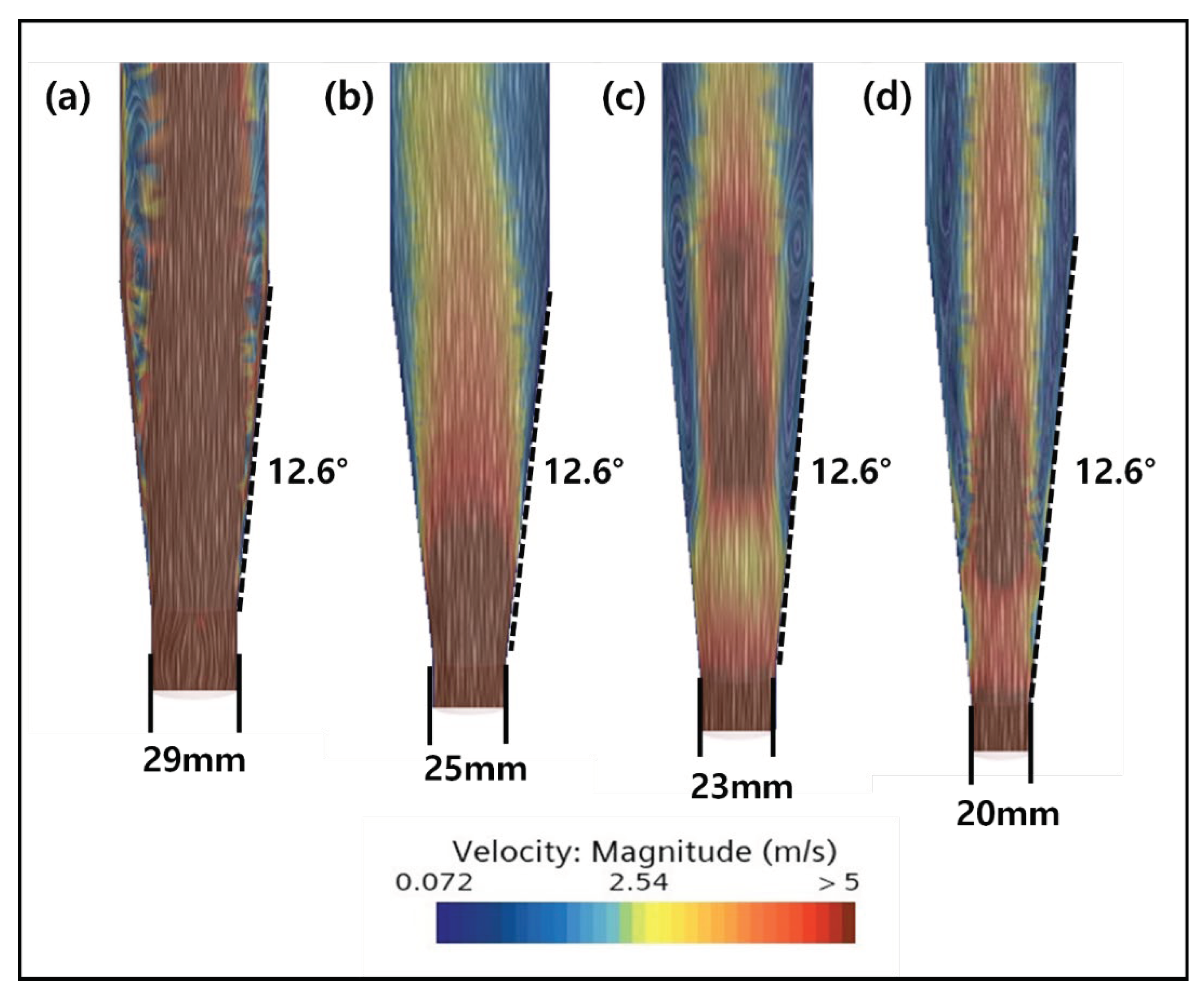
Figure 11.
Effect of width to height ratio of the reactor on mixing inside FBR. Simulation results for (a) 1:43, (b) 1:23 and (c) 1:15 ratio.
Figure 11.
Effect of width to height ratio of the reactor on mixing inside FBR. Simulation results for (a) 1:43, (b) 1:23 and (c) 1:15 ratio.
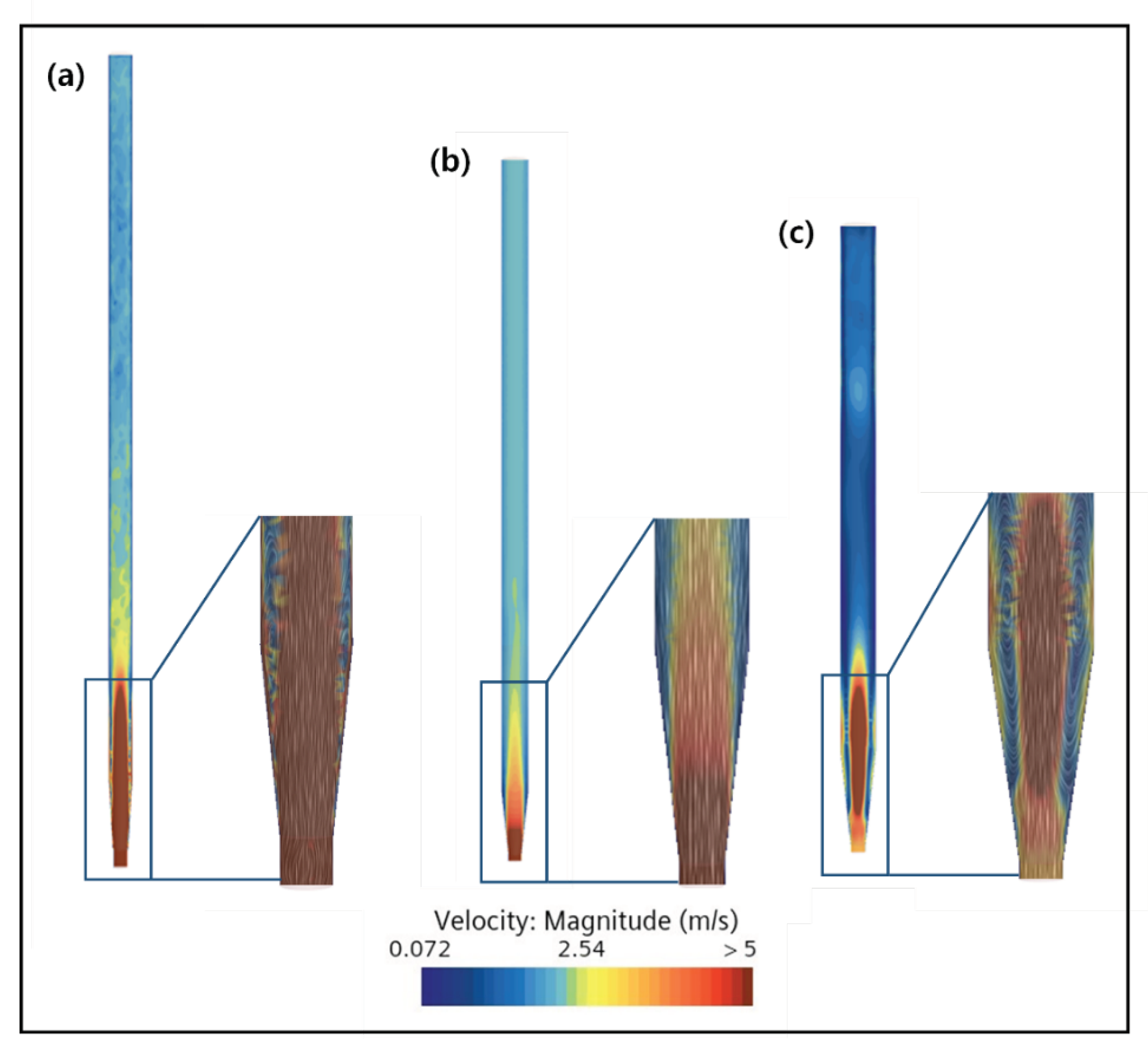
Figure 12.
Experimental setup showing single-stage and two-stage fluidized bed reactor used for continuous fluoride removal and recovery during the study.
Figure 12.
Experimental setup showing single-stage and two-stage fluidized bed reactor used for continuous fluoride removal and recovery during the study.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







