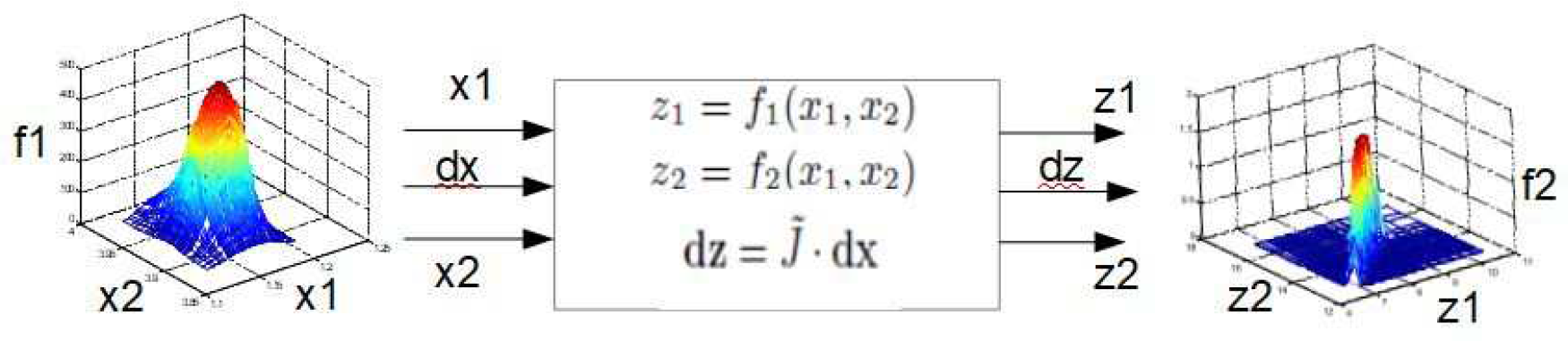Crossing Point Estimation in Human/Robot Navigation - Statistical Linearization versus Sigma-Point-Transformation

Preprint

Article

Crossing Point Estimation in Human/Robot Navigation - Statistical Linearization versus Sigma-Point-Transformation

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (7.29MB )

Rainer Heinrich Palm^*,Achim J. Lilienthal

This version is not peer-reviewed

Submitted:

27 March 2024

Posted:

28 March 2024

You are already at the latest version

Alerts

Abstract

Interactions between mobile robots and human operators in common areas require a high safety especially in terms of trajectory planning, obstacle avoidance and mutual cooperation. In this connection the crossings of planned trajectories, their uncertainty based on model fluctuations, system noise and sensor noise,play an outstanding role. This paper discusses the calculation of expected areas of interactions du ring human-robot navigation with respect to fuzzy and noisy information. Expected crossing points of possible trajectories are nonlinearily associated with positions and orientations of robot and human. The nonlinear transformation of a noisy system input, such as directions of motion of human and robot, to a system output, the expected area of intersection of their trajectories, is done by two methods: statistical linearization and the sigma-point-transformation. For both approaches fuzzy approximations are presented and the inverse problem is discussed where the input distribution parameters are computed from given output distribution parameters.

Keywords:

Subject: Computer Science and Mathematics - Robotics

1. Introduction

Planning and performing of mobile robot tasks in the presence of human operators while sharing the same workspace requires a high level of stability and safety. Research activities regarding navigation, obstacle avoidance, adaptation and collaboration between robots and human agents have been widely reported [1,2]. Multiple target tracking for robots using higher control levels in a control hierarchy are discussed in [3,4]. A human-friendly interaction between robots and humans can be obtained by human-like sensor systems [5]. A prominent role in robot navigation is the trajectory-crossing problem of robots and humans [6] and corresponding fuzzy solutions [7]. Motivations for a fuzzy solution of the intersection problem are manifold. One point is an uncertain measurement of the position and orientation of the human agent, because of which the use of a fuzzy signal and an adequate fuzzy processing seems natural [8,9]. Another aspect is the need for decreasing the computing effort in the case of complex calculations during a very small time interval. System uncertainties and observation noise lead to uncertainties of the intersection estimations. This paper deals with the one-robot one-human trajectory crossing problem whereas small uncertainties in position and orientation may lead to high uncertainties at the intersection points. Position and orientation of human and robot are nonlinearly coupled but can be linearized. In the following the linear part of the nonlinear system is considered in the analysis reported for small variations at the input [10]. In the following the "direct task" is described, meaning that the parameters of the input distribution are transformed to the output distribution parameters. The "inverse task" is also solved, meaning that for defined output distribution parameters the input parameters are calculated. In this paper two methods are outlined:

1. The statistical linearization, that linearizes the nonlinearity around the operating area ate the intersection. Means and standard deviations on the input parameters positions, orientations) are transformed through the linearized nonlinear system to obtain means and standard deviations of the output parameters position of intersection).

2. The Sigma-Point Transformation, that calculates the so-called sigma-points of the input distribution including mean and covariance of the input. The sigma-points are directly propagated through the nonlinear system [11,12,13] to obtain means and covariance of the output and, with this, the standard deviations of the output (position of intersection). The advantage of sigma-point transformation is that it captures the 1st and 2nd order statistics of a random variable, whereas the statistical linearization approximates a random variable only by its 1st order.

The paper is organized as follows. In Section 2 the general intersection problem and its analytical approach is described. Section 3 deals with the transformation/conversion of Gaussian distributions for a 2-input - 2-output system and for 6-input - 2-output system plus corresponding inverse and fuzzy solutions. In Section 4 the sigma-point approach plus inverse and fuzzy solutions is addressed. Section 5 presents simulations of the statistical sinearization and the sigma-point Transformation, to show the quality of the input-output conversion of the distributions, and the impact of different resolutions of fuzzy approximations on the accuracy of the random variable intersection. Finally, Section 6 concludes the paper with a discussion of the two different approaches and a comparison of the methods.

2. Computation of Intersections

The problem can be stated as follows:

Robot and human agent move in a common area according to their tasks or intentions. To avoid collisions, possible intersections of the paths of the agents should be predicted for both trajectory planning and on-line interactions. To accomplish this, positions, orientations and intended movements of robot and human should be estimated as accurately as needed.

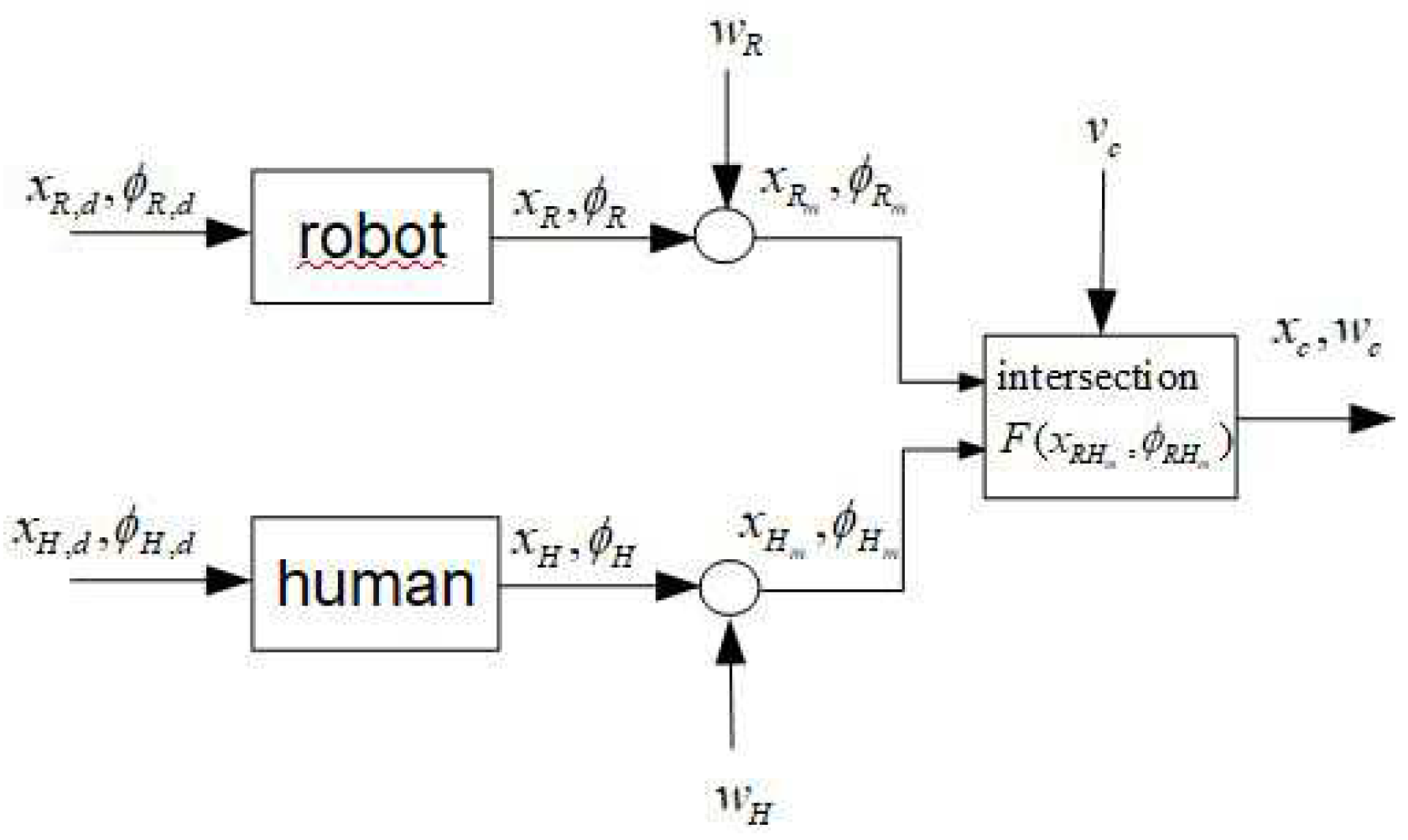
In this connection, uncertainties and noise on the random variables position/orientation

x_{R}

x_{H}

ϕ_{R}

and

ϕ_{H}

of robot and human have a great impact on the calculation of the expected intersection position

x_{c}

. The random variable

x_{c}

is calculated as the crossing point of the extension of the orientation or velocity vectors of robot and human which may change during motion depending on the task and current interaction. The task is to calculate the intersection and its uncertainty in the presence of known uncertainties of the acting agents robot and human.

System noise

w_{R}

and

w_{H}

for robot and human can be obtained from experiments. The noise

w_{c}

of the ’virtual’ intersection is composed by the nonlinear transformed noise

w_{R}

and

w_{H}

and some additional noise

v_{c}

that may come from uncertainties of the nonlinear computation of the intersection position

x_{c}

(see Figure 1). In the following, the geometrical relations are described as well as fuzzy approximations and nonlinear transformations of the random variables

x_{R}

x_{H}

ϕ_{R}

and

ϕ_{H}

2.1. Geometrical Relations

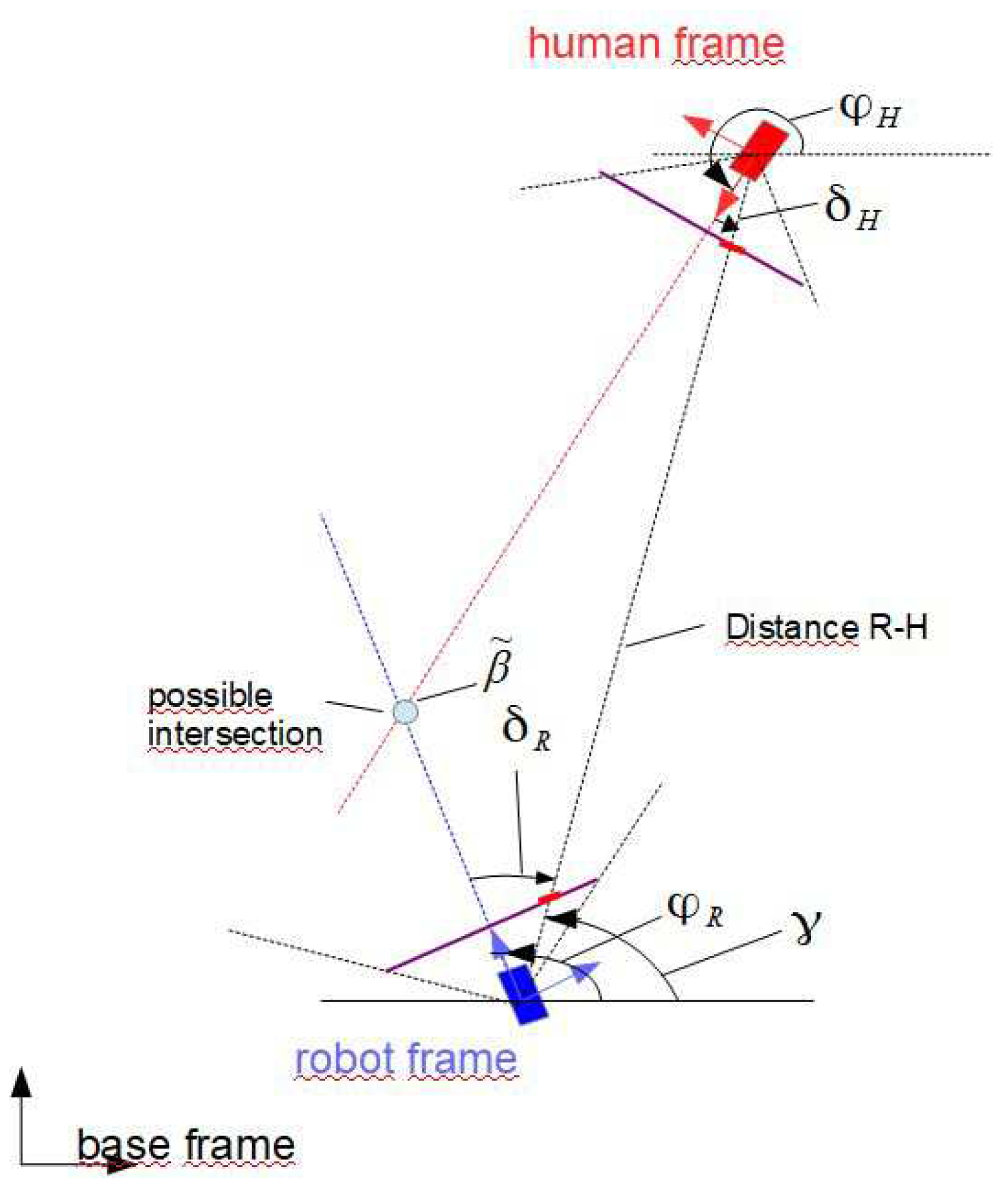
Let the intersection

(x_{c}, y_{c})

of two linear trajectories

x_{R} (t)

and

x_{H} (t)

in a plane be described by the following relations (see Figure 2)

\begin{matrix} x_{H} = x_{R} + d_{R H} cos (ϕ_{R} + δ_{R}) \\ y_{H} = y_{R} + d_{R H} sin (ϕ_{R} + δ_{R}) \\ x_{R} = x_{H} + d_{R H} cos (ϕ_{H} + δ_{H}) \\ y_{R} = y_{H} + d_{R H} sin (ϕ_{H} + δ_{H}), \end{matrix}

(1)

where

x_{H} = (x_{H}, y_{H})

and

x_{R} = (x_{R}, y_{R})

are the positions of human and robot and

ϕ_{H}

and

ϕ_{R}

are their orientation angles,

δ_{H}

and

δ_{R}

are positive angles measured from the y coordinates counterclockwise. The angle at the intersection is

\tilde{β} = π - δ_{R} - δ_{H}

. The variables

x_{H}

x_{R}

ϕ_{R}

ϕ_{H}

δ_{H}

ϕ_{H}

δ_{R}

, distance

d_{R H}

and angle

γ

are assumed to be measurable. If

ϕ_{H}

is not directly measurable then it can be computed by

ϕ_{H} = arcsin ((y_{H} - y_{R}) / d_{R H}) - δ_{H} + π

(2)

The coordinates

x_{c}

and

y_{c}

of the intersection are computed straight forward by [7]

\begin{matrix} x_{c} & = & \frac{A - B}{tan ϕ_{R} - tan ϕ_{H}} \\ y_{c} & = & \frac{A tan ϕ_{H} - B tan ϕ_{R}}{tan ϕ_{R} - tan ϕ_{H}} \\ A & = & x_{R} tan ϕ_{R} - y_{R} \\ B & = & x_{H} tan ϕ_{H} - y_{H} \end{matrix}

(3)

Rewriting (3) leads to

\begin{matrix} x_{c} & = & (x_{R} \frac{tan ϕ_{R}}{G} - y_{R} \frac{1}{G}) - (x_{H} \frac{tan ϕ_{H}}{G} - y_{H} \frac{1}{G}) \\ y_{c} & = & (x_{R} \frac{tan ϕ_{R} tan ϕ_{H}}{G} - y_{R} \frac{tan ϕ_{H}}{G}) \\ - & (x_{H} \frac{tan ϕ_{H} tan ϕ_{R}}{G} - y_{H} \frac{tan ϕ_{R}}{G}) \\ G & = & tan ϕ_{R} - tan ϕ_{H} \end{matrix}

(4)

After rearranging (4) we observe that

x_{c} = {(x_{c}, y_{c})}^{T}

is linear in

x_{R H} = {(x_{R}, y_{R}, x_{H}, y_{H})}^{T}

\begin{matrix} x_{c} = A_{R H} \cdot x_{R H} \end{matrix}

(5)

where

\begin{matrix} A_{R H} = f (ϕ_{R}, ϕ_{H}) = \\ \frac{1}{G} (\begin{matrix} tan ϕ_{R} & - 1 & - tan ϕ_{H} & 1 \\ tan ϕ_{R} tan ϕ_{H} & - tan ϕ_{H} & - tan ϕ_{R} tan ϕ_{H} & tan ϕ_{R} \end{matrix}) \end{matrix}

This notation is of advantage for further computations such as fuzzification of the intersection problem and the transformation of error distributions.

2.2. Computation of Intersections - Fuzzy Approach

The fuzzy solution presented in the following is a combination of classical analytical (crisp) methods and rule based methods in the sense of a Takagi-Sugeno fuzzy rule base.

In the following we introduce a fuzzy rule-based approximation of (5) with

n \times n

fuzzy rules

R_{i, j}

\begin{matrix} R_{i, j} : I F ϕ_{R} & = & {Φ_{R}}_{i} A N D ϕ_{H} = {Φ_{H}}_{j} \\ T H E N x_{c} & = & {A_{R H}}_{i, j} \cdot x_{R H} \end{matrix}

(6)

n - number of fuzzy terms

Φ_{R_{i}}

, and

Φ_{H_{j}}

for

ϕ_{R}

and

ϕ_{H}

with the result

\begin{matrix} x_{c} = \sum_{i, j} w_{i} (ϕ_{R}) w_{j} (ϕ_{H}) \cdot {A_{R H}}_{i, j} \cdot x_{R H} \end{matrix}

(7)

i, j = 1 . . . n

w_{i} (ϕ_{R}), w_{j} (ϕ_{H}) \in [0, 1]

are normalized membership functions with

\sum_{i} w_{i} (ϕ_{R}) = 1

and

\sum_{j} w_{j} (ϕ_{H}) = 1

Let the universes of discourse for

ϕ_{R}

and

ϕ_{H}

ϕ_{R}, ϕ_{H} \in [0, 360]

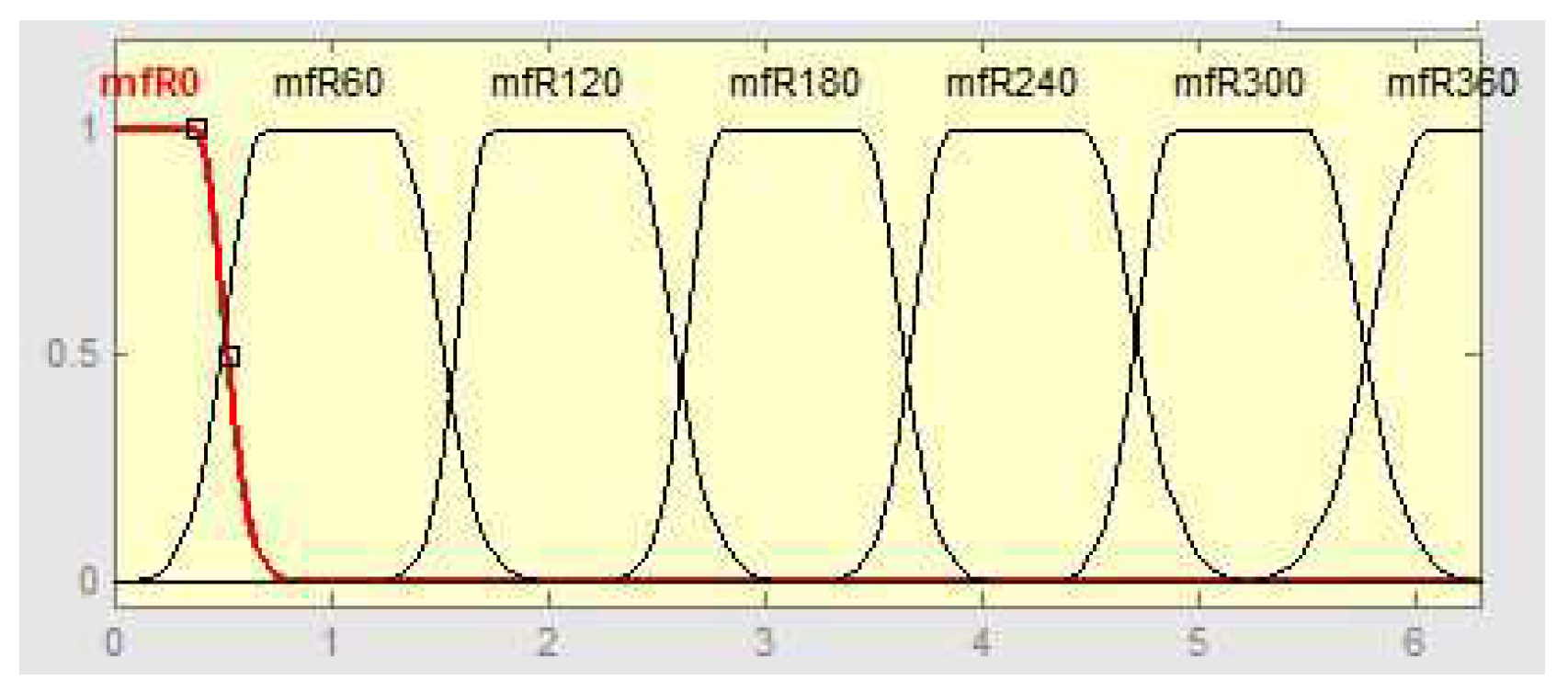
. Furthermore, let these universes of discourse be divided into n partitions (for example 6) of 60 which leads to

6 \times 6

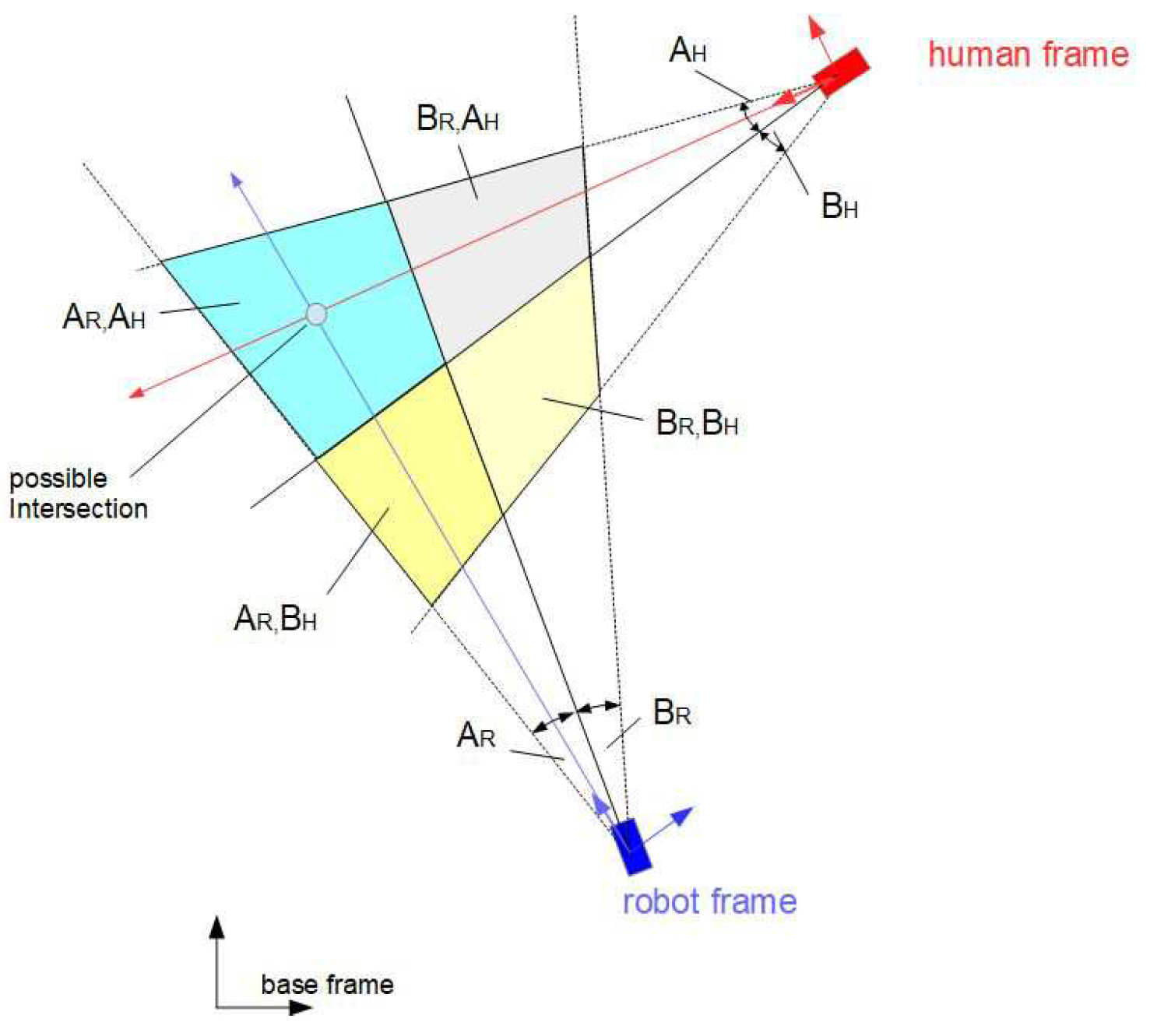
fuzzy rules. Corresponding membership functions are shown in Figure 3. It turns out that this resolution leads to a poor fuzzy approximation. The approximation quality can be improved by increasing the number of fuzzy sets which however results in a quadratic increase of the number of fuzzy rules. To avoid an "explosion" of the number of fuzzy rules being computed in one time step a set of sub-areas covering a small number of rules for each sub-area is defined. Based on the measurements of

ϕ_{R}

and

ϕ_{H}

, the appropriate sub-area is selected together with a corresponding set of rules (see Figure 4, sub-area

A_{R}, A_{H}

). With this, the number of rules to be activated at one time step of calculation is low, although the total number of rules can be high. At the borderlines between sub-areas abrupt changes may occur which can be avoided by overlapping of sub-areas.

2.3. Differential Approach

Robots and human agents usually change their positions, orientations, and velocities which requires a differential approach apart from the exact solution (4). In addition, the analysis of uncertainty and noise at

x_{c}

and the existence of noise at

ϕ_{R}

ϕ_{H}

, and

x_{R H} = {(x_{R}, y_{R}, x_{H}, y_{H})}^{T}

requires a differential strategy.

Differentiating (4) with

x_{R H} = c o n s t .

yields

\begin{matrix} {\dot{x}}_{c} = \tilde{J} \cdot \dot{ϕ} \\ \dot{ϕ} = {({\dot{ϕ}}_{R} {\dot{ϕ}}_{H})}^{T}; \tilde{J} = (\begin{matrix} {\tilde{J}}_{11} & {\tilde{J}}_{12} \\ {\tilde{J}}_{21} & {\tilde{J}}_{22} \end{matrix}) \end{matrix}

(8)

where

\begin{matrix} {\tilde{J}}_{11} & = & (\begin{matrix} - tan ϕ_{H} & 1 & tan ϕ_{H} & - 1 \end{matrix}) \frac{x_{R H}}{G^{2} \cdot {cos}^{2} ϕ_{R}} \\ {\tilde{J}}_{12} & = & (\begin{matrix} tan ϕ_{R} & - 1 & - tan ϕ_{R} & 1 \end{matrix}) \frac{x_{R H}}{G^{2} \cdot {cos}^{2} ϕ_{H}} \\ {\tilde{J}}_{21} & = & {\tilde{J}}_{11} \cdot tan ϕ_{H} \\ {\tilde{J}}_{22} & = & {\tilde{J}}_{12} \cdot tan ϕ_{R} \end{matrix}

The following sections deal with the accuracy of the computed intersection in the case of noisy orientation information (see Figure 5).

3. Transformation of Gaussian Distributions

3.1. General Assumptions

Consider a nonlinear system

z = F (x)

(9)

where the random variables

x = {(x_{1}, x_{2})}^{T}

denote the input,

z = {(z_{1}, z_{2})}^{T}

the output and F denotes a nonlinear transformation. The distribution of the uncorrelated Gaussian distributed components

x_{1}

and

x_{2}

is described by

f_{x_{1}, x_{2}} = \frac{1}{2 π σ_{x_{1}} σ_{x_{2}}} e x p (- \frac{1}{2} (\frac{e_{x_{1}}^{2}}{σ_{x_{1}}^{2}} + \frac{e_{x_{2}}^{2}}{σ_{x_{2}}^{2}}))

(10)

where

e_{x_{1}} = x_{1} - \bar{x_{1}}

\bar{x_{1}}

- mean

(x_{1})

σ_{x_{1}}

- standard deviation

x_{1}

and

e_{x_{2}} = x_{2} - \bar{x_{2}}

\bar{x_{2}}

- mean

(x_{2})

σ_{x_{2}}

- standard deviation

x_{2}

The goal is: Given the nonlinear transformation (9) and the distribution (9). Compute the output signals

z_{1}

and

z_{2}

and their distributions together with their standard deviations and the correlation coefficient. Linear systems transform Gaussian distributions linearly such that the output signals are also Gaussian distributed. This does not apply for nonlinear systems, but if the input standard deviation is small enough then a local linear transfer function can be built for which the outputs are Gaussian distributed. Suppose the the input standard devivations are small with respect to the nonlinear function then the output distribution can be written as follows

\begin{matrix} f_{z_{1}, z_{2}} = \frac{1}{2 π σ_{z_{1}} σ_{z_{2}} \sqrt{1 - ρ_{z_{12}}^{2}}} \cdot \\ e x p (- \frac{1}{2 (1 - ρ_{z_{12}}^{2})} (\frac{e_{z_{1}}^{2}}{σ_{z_{1}}^{2}} + \frac{e_{z_{2}}^{2}}{σ_{z_{2}}^{2}} - \frac{2 ρ_{z_{12}} e_{z_{1}} e_{z_{2}}}{σ_{z_{1}} σ_{z_{2}}})) \end{matrix}

(11)

ρ_{z_{12}}

- correlation coefficient.

3.2. Statistical Linearization, Two Inputs-Two Outputs

Let the nonlinear transformation

F

be described by two smooth transfer functions (see block Figure 6)

\begin{matrix} z_{1} = f_{1} (x_{1}, x_{2}) \\ z_{2} = f_{2} (x_{1}, x_{2}) \end{matrix}

(12)

where

(x_{1}, x_{2}) = (ϕ_{R}, ϕ_{H})

and

(z_{1}, z_{2}) = (x_{c}, y_{c})

Linearization of (12) yields

\begin{matrix} dz = \tilde{J} \cdot dx o r e_{z} = \tilde{J} \cdot e_{x} \end{matrix}

(13)

with

\begin{matrix} e_{z} = {(e_{z_{1}}, e_{z_{2}})}^{T} a n d e_{x} = {(e_{x_{1}}, e_{x_{2}})}^{T} \\ dz = {(d z_{1}, d z_{2})}^{T} a n d dx = {(d x_{1}, d x_{2})}^{T} \end{matrix}

(14)

\begin{matrix} \tilde{J} = (\begin{matrix} \partial f_{1} / \partial x_{1}, \partial f_{1} / \partial x_{2} \\ \partial f_{2} / \partial x_{1}, \partial f_{2} / \partial x_{2} \end{matrix}) \end{matrix}

(15)

Output Distribution

To obtain the density

f_{z_{1}, z_{2}}

(11) of the output signal, we invert (14) and substitute the entries of

e_{x}

into (10)

\begin{matrix} e_{x} = J \cdot e_{z} \end{matrix}

(16)

with

J = {\tilde{J}}^{- 1}

and

\begin{matrix} J = (\begin{matrix} J_{11} & J_{12} \\ J_{21} & J_{22} \end{matrix}) = (\begin{matrix} j_{xz} \\ j_{yz} \end{matrix}) \end{matrix}

(17)

where

j_{xz} = (J_{11}, J_{12})

and

j_{yz} = (J_{21}, J_{22})

. Entries

J_{i j}

are the result of the inversion of

\tilde{J}

. From this substitution which we get

\begin{matrix} f_{x_{1}, x_{2}} = K_{x_{1}, x_{2}} \cdot \\ e x p (- \frac{1}{2} \cdot {e_{z}}^{T} \cdot ({j_{x_{1}, z}}^{T}, {j_{x_{2}, z}}^{T}) \cdot S_{x}^{- 1} \cdot (\begin{matrix} j_{x_{1}, z} \\ j_{x_{2}, z} \end{matrix}) \cdot e_{z}) \end{matrix}

(18)

where

K_{x_{1}, x_{2}} = \frac{1}{2 π σ_{x_{1}} σ_{x_{2}}}

and

\begin{matrix} S_{x}^{- 1} = (\begin{matrix} \frac{1}{σ_{x_{1}}^{2}}, 0 \\ 0, \frac{1}{σ_{x_{2}}^{2}} \end{matrix}) \end{matrix}

(19)

The exponent of (18) is rewritten into

\begin{matrix} x p o = - \frac{1}{2} \cdot (\frac{1}{σ_{x_{1}}^{2}} {(e_{z_{1}} J_{11} + e_{z_{2}} J_{12})}^{2} \\ + \frac{1}{σ_{x_{2}}^{2}} {(e_{z_{1}} J_{21} + e_{z_{2}} J_{22})}^{2}) \end{matrix}

(20)

and furthermore

\begin{matrix} x p o = - \frac{1}{2} \cdot [e_{z_{1}}^{2} (\frac{J_{11}^{2}}{σ_{x_{1}}^{2}} + \frac{J_{21}^{2}}{σ_{x_{2}}^{2}}) + e_{z_{2}}^{2} (\frac{J_{12}^{2}}{σ_{x_{1}}^{2}} + \frac{J_{22}^{2}}{σ_{x_{2}}^{2}}) + \\ 2 \cdot e_{z_{1}} e_{z_{2}} (\frac{J_{11} J_{12}}{σ_{x_{1}}^{2}} + \frac{J_{21} J_{22}}{σ_{x_{2}}^{2}})] \end{matrix}

(21)

Let

\begin{matrix} A = (\frac{J_{11}^{2}}{σ_{x_{1}}^{2}} + \frac{J_{21}^{2}}{σ_{x_{2}}^{2}}); B = (\frac{J_{12}^{2}}{σ_{x_{1}}^{2}} + \frac{J_{22}^{2}}{σ_{x_{2}}^{2}}) \\ C = (\frac{J_{11} J_{12}}{σ_{x_{1}}^{2}} + \frac{J_{21} J_{22}}{σ_{x_{2}}^{2}}) \end{matrix}

(22)

then a comparison of xpo in (21) and the exponent in (11) yields

\begin{matrix} \frac{1}{(1 - ρ_{z_{12}}^{2})} \frac{1}{σ_{z_{1}}^{2}} = A; \frac{1}{(1 - ρ_{z_{12}}^{2})} \frac{1}{σ_{z_{2}}^{2}} = B \\ \frac{- 2 ρ_{z_{12}}}{(1 - ρ_{z_{12}}^{2})} \frac{1}{σ_{z_{1}} σ_{z_{2}}} = 2 C \end{matrix}

(23)

Standard deviations

σ_{z_{1}}

σ_{z_{2}}

and correlation coefficient

ρ_{z_{12}}

yield

\begin{matrix} ρ_{z_{12}} = - \frac{C}{\sqrt{A B}} \\ \frac{1}{σ_{z_{1}}^{2}} = A - \frac{C^{2}}{B}; \frac{1}{σ_{z_{2}}^{2}} = B - \frac{C^{2}}{A} \end{matrix}

(24)

The result is: if the parameter of the input distribution and the transfer function

F (x, y)

are known,then the output distribution parameters can be computed straight forward.

Fuzzy Solution

To save computing costs in real time we create a TS fuzzy model that is represented by the rules

R_{i j}

\begin{matrix} R_{i j} : \\ I F x_{1} = {X_{1}}_{i} A N D x_{2} = {X_{2}}_{i} \\ T H E N ρ_{z_{12}} = - \frac{C_{i j}}{\sqrt{A_{i j} B_{i j}}} \\ A N D \\ \frac{1}{σ_{z_{1}}^{2}} = A_{i j} - \frac{C_{i j}^{2}}{B_{i j}}; \\ A N D \\ \frac{1}{σ_{z_{2}}^{2}} = B_{i j} - \frac{C_{i j}^{2}}{A_{i j}} \end{matrix}

(25)

where

{X_{1}}_{i}, {X_{2}}_{i}

are fuzzy terms for

x_{1}, x_{2}

A_{i j}, B_{i j}, C_{i j}

are functions of predefined variables

x_{1} = {x_{1}}_{i}

and

x_{2} = {x_{2}}_{i}

From (25) we derive

\begin{matrix} ρ_{z_{12}} = - \sum_{i j} w_{i} (x_{1}) w_{j} (x_{2}) \frac{C_{i j}}{\sqrt{A_{i j} B_{i j}}} \\ \frac{1}{σ_{z_{1}}^{2}} = \sum_{i j} w_{i} (x_{1}) w_{j} (x_{2}) (A_{i j} - \frac{C_{i j}^{2}}{B_{i j}}) \\ \frac{1}{σ_{z_{2}}^{2}} = \sum_{i j} w_{i} (x_{1}) w_{j} (x_{2}) (B_{i j} - \frac{C_{i j}^{2}}{A_{i j}}) \end{matrix}

(26)

w_{i} (x_{1}) \in [0, 1]

and

w_{j} (x_{2}) \in [0, 1]

are weighting functions with

\sum_{i} w_{i} (x_{1}) = 1

\sum_{j} w_{j} (x_{2}) = 1

Inverse Solution

The previous paragraph discussed the direct transformation task: Let the distribution parameters of the input variable be defined, find the corresponding output parameters. However it might also be useful to solve the inverse task: Given the output parameters (standard deviation, correlation coefficient), find the corresponding input parameters. This solution of inverse task is similar to those discussed in Section 3.2. The starting point are equations (10) and (11) which describe the distributions of the inputs and outputs, respectively. Then we substitute (13) into (10) and rename the resulting exponent

x p o_{z}

into

x p o_{x}

and discuss the exponent

x p o_{x}

\begin{matrix} x p o_{x} = \frac{- 1}{2 (1 - ρ_{z_{12}}^{2})} ({e_{x}}^{T} {\tilde{J}}^{T} S_{z}^{- 1} \tilde{J} e_{x} - \frac{2 ρ_{z_{12}} e_{z_{1}} e_{z_{2}}}{σ_{z_{1}} σ_{z_{2}}}) \end{matrix}

(27)

with

\begin{matrix} S_{x}^{- 1} = (\begin{matrix} \frac{1}{σ_{z_{1}}^{2}}, 0 \\ 0, \frac{1}{σ_{z_{2}}^{2}} \end{matrix}) \end{matrix}

Now, comparing (27) with the exponent of (10) of the input density we find that the mixed term in (27) must be zero from which we obtain the correlation coefficient

ρ_{z_{12}}

and with this the standard deviations of the inputs

\begin{matrix} ρ_{z_{12}} = (\frac{{\tilde{J}}_{11} {\tilde{J}}_{12}}{σ_{z_{1}}^{2}} + \frac{{\tilde{J}}_{21} {\tilde{J}}_{22}}{σ_{z_{2}}^{2}}) \frac{σ_{z_{1}} σ_{z_{2}}}{({\tilde{J}}_{11} {\tilde{J}}_{22} + {\tilde{J}}_{12} {\tilde{J}}_{21})} \\ \frac{1}{σ_{x}^{2}} = (\frac{{\tilde{J}}_{11}^{2}}{σ_{z_{1}}^{2}} + \frac{{\tilde{J}}_{21}^{2}}{σ_{z_{2}}^{2}} - \frac{2 ρ_{z_{12}}}{σ_{z_{1}} σ_{z_{2}}} {\tilde{J}}_{11} {\tilde{J}}_{21}) / (1 - ρ_{z_{12}}^{2}) \\ \frac{1}{σ_{y}^{2}} = (\frac{{\tilde{J}}_{12}^{2}}{σ_{z_{1}}^{2}} + \frac{{\tilde{J}}_{22}^{2}}{σ_{z_{2}}^{2}} - \frac{2 ρ_{z_{12}}}{σ_{z_{1}} σ_{z_{2}}} {\tilde{J}}_{12} {\tilde{J}}_{22}) / (1 - ρ_{z_{12}}^{2}) \end{matrix}

(28)

The detailed development can be found in [14].

3.3. Six Inputs - Two Outputs

Consider again the nonlinear system

x_{c} = F (x)

(29)

In the previous subsections we assumed the positions

x_{R}

and

x_{H}

not to be currupted with noise. However taking into account the positions to be random variables, the number of inputs are 6 so that the input vector yields

x = {(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6})}^{T}

x = (ϕ_{R}, ϕ_{H}, x_{R}, y_{R}, x_{H}, y_{H})

with the output vector

x_{c} = {(x_{c}, y_{c})}^{T}

Furthermore let the uncorrelated Gaussian distributed inputs

x_{1}

...

x_{6}

be described by the 6-dim density

f_{x_{i}} = \frac{1}{{(2 π)}^{6 / 2} {| S_{x} |}^{1 / 2}} e x p (- \frac{1}{2} ({e_{x}}^{T} {S_{x}}^{- 1} e_{x}))

(30)

where

e_{x} = {({e_{x}}_{1}, {e_{x}}_{2}, . . ., {e_{x}}_{6})}^{T}

;

e_{x} = x - \bar{x}

\bar{x}

- mean(

x

S_{x}

- covariance matrix.

S_{x} = (\begin{matrix} σ_{x_{1}}^{2} & 0 & . . . & 0 \\ 0 & σ_{x_{2}}^{2} & . . . & 0 \\ . . . & . . . & . . . & . . . \\ 0 & . . . & 0 & σ_{x_{6}}^{2} \end{matrix})

According to (11) the output density is described by

\begin{matrix} f_{x_{c}, y_{c}} = \frac{1}{2 π σ_{x_{c}} σ_{y_{c}} \sqrt{1 - ρ^{2}}} \cdot \\ e x p (- \frac{1}{2 (1 - ρ^{2})} (e_{x_{c}}^{T} {S_{c}}^{- 1} e_{x_{c}} - \frac{2 ρ e_{x_{c}} e_{y_{c}}}{σ_{x_{c}} σ_{y_{c}}})) \end{matrix}

(31)

ρ

- correlation coefficient,

e_{x_{c}} = {(e_{x_{c}}, e_{y_{c}})}^{T}

After some calculations [15] we find for

ρ

\frac{1}{σ_{x_{c}}^{2}}

and

\frac{1}{σ_{y_{c}}^{2}}

\begin{matrix} ρ & = & - \frac{C}{\sqrt{A D}} \\ \frac{1}{σ_{x_{c}}^{2}} & = & A - \frac{C^{2}}{D}; \frac{1}{σ_{y_{c}}^{2}} = D - \frac{C^{2}}{A} \end{matrix}

(32)

with

\begin{matrix} A = \sum_{i = 1}^{6} \frac{1}{σ_{x_{i}}^{2}} J_{i 1}^{2}; B = \sum_{i = 1}^{6} \frac{1}{σ_{x_{i}}^{2}} J_{i 1} J_{i 2} \\ C = \sum_{i = 1}^{6} \frac{1}{σ_{x_{i}}^{2}} J_{i 1} J_{i 2}; D = \sum_{i = 1}^{6} \frac{1}{σ_{x_{i}}^{2}} J_{i 2}^{2} \end{matrix}

(33)

which is the counterpart to the 2-dim input case (24).

Inverse Solution

An inverse solution cannot be uniquely computed due to the underdetermined character of the 6-input – 2-output system. Therefore, from required variances at the intersection position (output) corresponding variances for positions and orientations of robot-human or robot-robot (input) cannot be concluded.

Fuzzy Approach

The steps to the fuzzy approach is very similar to those of the 2-input case:

- define operation points

x_{i} = {(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6})}_{i}^{T}

- compute

A_{i}

B_{i}

C_{i}

x_{i} = {(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6})}_{i}^{T}

from (33

- formulate fuzzy rules

R_{i}

according to (25) and (26),

i = 1 . . . n

The number n of rules is computed as follows:

With

l = 6

- number of fuzzy terms,

k = 6

- number of inputs, we obtain

n = l^{k} = 6^{6}

- number of rules.

This number of rules is unacceptable high. To limit n to an adequate number, one has to limit the number of inputs and/or fuzzy terms to look for the most influential variables either on heuristic or systematic way [16]. This however is not the issue to be discussed in this paper.

4. Sigma-Point-Transformation

In the following the estimation/identification of the standard deviations of possible intersection coordinates of trajectories for both robot/robot and human/robot - combinations by means of the sigma-point technique is discussed. The following method is based on the Unscented Kalman Filter technique where the intersections cannot be directly measured but predicted/computed only. Nevertheless it is possible to compute the variance of the predicted events, such as possible collisions or planned rendezvous situations, by a direct propagation of statistical parameters - the sigma-points - through the nonlinear geometrical relation which is a result of the crossing of two trajectories. Let

x = {(x_{1}, x_{2})}^{T}

- input vector,

x_{c} = {(x_{c 1}, x_{c 2})}^{T}

- output vector where for the special case

{(x_{1}, x_{2})}^{T} = {(ϕ_{R}, ϕ_{H})}^{T}

and

{(x_{c 1}, x_{c 2})}^{T} = {(x_{c}, y_{c})}^{T}

The nonlinear relation between

x

and

x_{c}

is given by (34)

x_{c} = F (x)

(34)

For the discrete case we obtain for the state

x_{c}

x_{c} (k) = F (x (k - 1) + w (k - 1))

(35)

and for the measured output

z_{c} (k)

z_{c} (k) = h (x_{c}) (k) + v (k))

(36)

where

w

and

v

are the system noise and measurement noise, respectively.

h (x_{c})

is the output nonlinearity. Let furthermore

\bar{x} (k)

- mean at time

t_{k}

P (k)

- covariance matrix

x_{0}

- initial state with known mean

μ_{0} = E (x_{0})

P_{0} (k) = E [(x_{0} - μ_{0}) {(x_{0} - μ_{0})}^{T}]

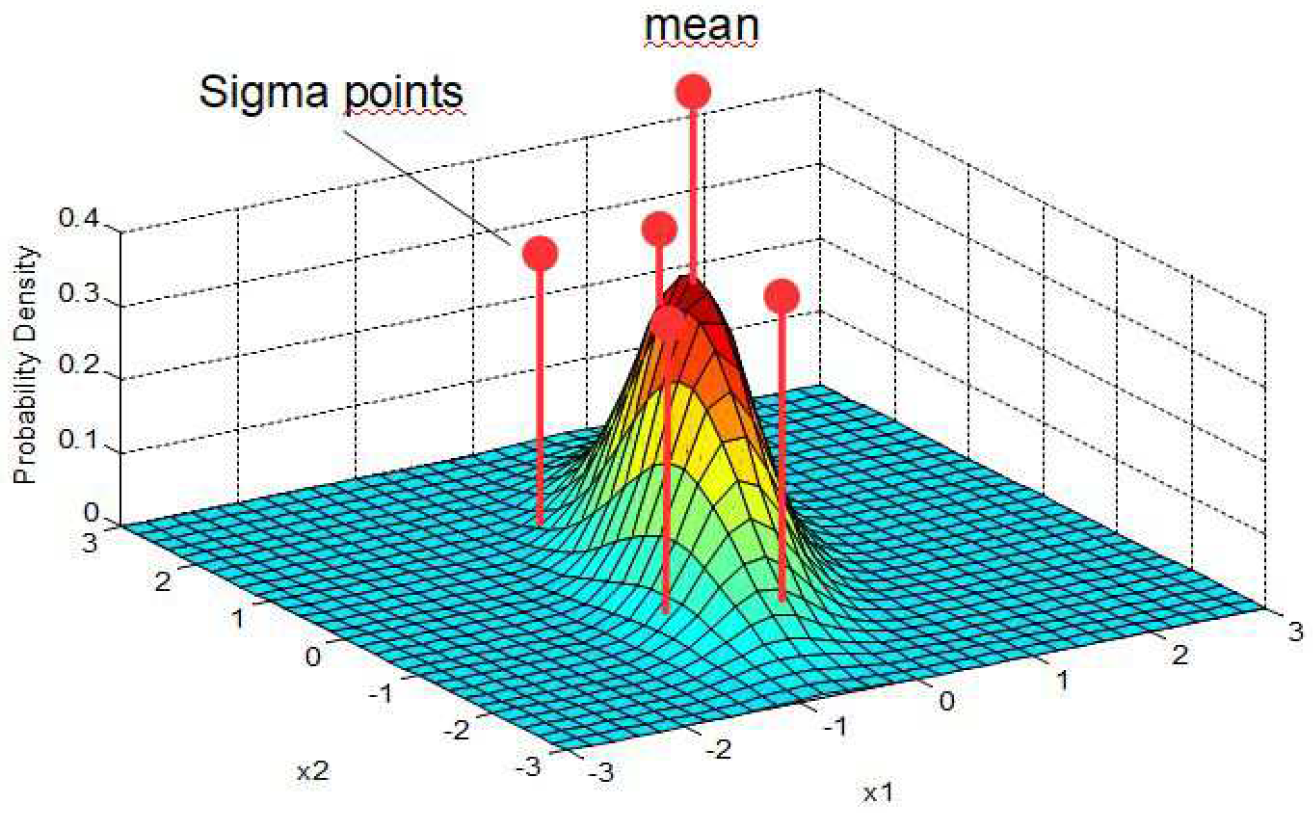
Selection of Sigma-Points

Sigma-points are selected parameters of a given error distribution of a random variable. Sigma-points lie along the major eigen-axes of the covariance matrix of the random variable. The height of each sigma-point (see Figure 7) represents its relative weight

W^{j}

used in the following selection procedure.

Let

X (k - 1)

be a set of

2 n + 1

sigma-points where n is the dimension of the state space (in our example

n = 2

X (k - 1) = {(x^{j} (k - 1), W^{j}) | j = 0 . . . 2 n}

(37)

Consider the following selection of sigma-points

\begin{matrix} x^{0} (k - 1) & = & \bar{x} (k - 1) \end{matrix}

\begin{matrix} - 1 < W^{0} < 1 \\ W^{0} & = & \frac{λ}{n + λ}; λ = α^{2} (n + κ) - n \\ x^{i} (k - 1) & = & \bar{x} (k - 1) + \sqrt{(\frac{n}{1 - W^{0}} P (k - 1))}; i = 1 . . . n \\ x^{i} (k - 1) & = & \bar{x} (k - 1) - \sqrt{(\frac{n}{1 - W^{0}} P (k - 1))}; i = (n + 1) . . . 2 n \end{matrix}

(38)

\begin{matrix} W^{j} & = & \frac{1 - W^{0}}{2 n} \end{matrix}

(39)

under the following condition

\sum_{j = 0}^{2 n} W^{j} = 1

(40)

α

and

κ

are scaling factors. A usual choice is

α = 10^{- 2}

and

κ = 0

\sqrt{\frac{n}{1 - W^{0}} P (k - 1)}

is the row/column of the matrix square root of

\frac{n}{1 - W^{0}} P

. The square root of a matrix

P

is the solution

S

for

P = S \cdot S

which is obtained by Cholesky factorization.

Model Forecast Step

To go on with the UKF, the following step is devoted to the model forecast. In this way the sigma-points

x^{j} (k)

are propagated through the nonlinear process model

x_{c}^{f, j} (k) = F (x^{j} (k - 1))

(41)

where the superscript f means "forecast". From these transformed and forecasted sigma-points the mean and covariance for the forecast value of

x_{c} (k)

\begin{matrix} x_{c}^{f} (k) & = \sum_{j = 0}^{2 n} W^{j} x_{c}^{f, j} (k) \\ P^{f} (k) & = \sum_{j = 0}^{2 n} W^{j} (x_{c}^{f, j} (k) - x_{c}^{f} (k)) {(x_{c}^{f, j} (k) - x_{c}^{f} (k))}^{T} \end{matrix}

(42)

Measurement update step

In this step the sigma-points are propagated through the nonlinear observation model

z_{c}^{f, j} (k) = h (x_{c}^{j} (k - 1))

(43)

from which we obtain mean and covariance (innovation covariance)

\begin{matrix} z_{c}^{f} (k - 1) = \sum_{j = 0}^{2 n} W^{j} z_{c}^{f, j} (k - 1) \\ C o v ({\tilde{z}}_{c}^{f} (k - 1)) = \\ \sum_{j = 0}^{2 n} W^{j} (z_{c}^{f, j} (k - 1) - z_{c}^{f} (k - 1)) \times \\ {(z_{c}^{f, j} (k - 1) - z_{c}^{f} (k - 1))}^{T} + R (k) \end{matrix}

(44)

and the cross-covariance

\begin{matrix} C o v ({\tilde{x}}_{c}^{f} (k), {\tilde{z}}_{c}^{f} (k - 1)) = \\ \sum_{j = 0}^{2 n} W^{j} (x_{c}^{f, j} (k) - x_{c}^{f} (k)) {(z_{c}^{f, j} (k - 1) - z_{c}^{f} (k - 1))}^{T} \end{matrix}

(45)

Data Assimilation Step

In this step, called the forecast information is combined with the new information from the output

z (k)

from which we obtain with the Kalman filter gain

K

{\hat{x}}_{c} (k) = x_{c}^{f} (k) + K (k) (z_{c} (k) - z_{c}^{f} (k - 1))

(46)

The gain

K

is given by

K (k) = C o v ({\tilde{x}}_{c}^{f} (k), {\tilde{z}}_{c}^{f} (k - 1)) \cdot C o v^{- 1} ({\tilde{z}}_{c}^{f} (k - 1))

(47)

and the posterior covariance is updated by

P (k) = P^{f} (k) - K (k) \cdot C o v ({\tilde{z}}_{c}^{f} (k - 1)) K^{T} (k)

(48)

Usually it is sufficient to compute mean and variance for the output/state

x_{c}

of the nonlinear static system

F (x)

. In this case it is possible to stop a further computing at eq. (42) meaning rather to calculate the transformed sigma-points

x_{c}^{f, j}

and develop the regarding output means and variances from (41) and (42). In this connection it is enough to substitute the covariance matrix

Q

into (38) instead of

P

. One advantage of the sigma-point approach prior to statistical linearization is the easy scalability to multi-dimensional random variables.

For the intersection problem there are 2 cases:

1. 2 inputs, 2 outputs (2 orientation angles, 2 crossing coordinates)

2. 6 inputs, 2 outputs (2 orientation angles and 4 position coordinates, 2 crossing coordinates)

For the statistical linearization (method 1) the step from the 2 inputs - 2 outputs case to the (6,2)-case is computationally more costly than that for the sigma-point approach (method 2), (see eqs. (20) ... (24) versus eqs. (37), (40)... (42).

Sigma-Points - Fuzzy Solutions

In order to lower the computing effort the application of TS-fuzzy interpolation may be a solution which will be shown in the following. Having a look at the 2-dimensional problem we can see a nonlinear propagation of the input sigma-points through a nonlinear function

F

. Let

x^{j}

be the 2-dimensional "input" sigma-points

x^{j} = {(x_{1}^{j}, x_{2}^{j})}^{T}

(49)

or for the special case "intersection"

x^{j} = {(ϕ_{R}^{j}, ϕ_{H}^{j})}^{T}

(50)

The propagation through

F

leads to "output" sigma-points

x_{c}^{f, j} (k) = F (x^{j} (k - 1))

(51)

or for the special case

\begin{matrix} x_{c}^{f, j} (k) & = & F (x_{1}^{j} (k - 1), x_{2}^{j} (k - 1)) = \\ F (ϕ_{R}^{j} (k - 1), ϕ_{H}^{j} (k - 1)) \end{matrix}

(52)

The special nonlinear function

F

is described by (see (5))

\begin{matrix} x_{c} = A_{R H} (ϕ_{R}, ϕ_{H}) \cdot x_{R H} \end{matrix}

(53)

where

A_{R H}

is a nonlinear matrix (6) linearly combined with the position vector

x_{R H} = {(x_{R}, y_{R}, x_{H}, y_{H})}^{T}

A fuzzification aims at

A_{R H}

\begin{matrix} F^{f u z z} (ϕ_{R}, ϕ_{H}) = A_{R H}^{f u z z} \cdot x_{R H} = \\ \sum_{l_{1}, l_{2}}^{m} w^{l_{1}} (ϕ_{R}) w^{l_{2}} (ϕ_{H}) \cdot A_{R H} (ϕ_{R}^{l_{1}}, ϕ_{H}^{l_{2}}) \cdot x_{R H} \end{matrix}

(54)

Applied to the sigma-points

(ϕ_{R}^{j}, ϕ_{H}^{j})

we get a TS fuzzy model described by the following rules

R_{l_{1}, l_{2}}

\begin{matrix} R_{l_{1}, l_{2}} : \\ I F ϕ_{R}^{j} = {Φ_{R}^{j}}_{l_{1}} A N D ϕ_{H}^{j} = {Φ_{H}^{j}}_{l_{2}} \\ T H E N x_{c}^{f, j} = A_{R H} (ϕ_{R}^{l_{1}, j}, ϕ_{H}^{l_{2}, j}) \cdot x_{R H} \end{matrix}

(55)

where

{Φ_{R}^{j}}_{l_{1}}, {Φ_{H}^{j}}_{l_{2}}

are fuzzy terms for

ϕ_{R}^{j}, ϕ_{H}^{j}

; the matrices

A_{R H}

are functions of predefined variables

ϕ_{R}^{j}

and

ϕ_{H}^{j}

. This set of rules leads to the result

\begin{matrix} x_{c}^{f, j} = F^{f u z z} (ϕ_{R}^{j}, ϕ_{H}^{j}) = \\ \sum_{l_{1}, l_{2}}^{m} w^{l_{1}} (ϕ_{R}^{j}) w^{l_{2}} (ϕ_{H}^{j}) \cdot A_{R H} (ϕ_{R}^{l_{1}, j}, ϕ_{H}^{l_{2}, j}) \cdot x_{R H} \end{matrix}

(56)

w^{l_{1}} (ϕ_{R}^{j}) \in [0, 1]

and

w^{l_{2}} (ϕ_{H}^{j}) \in [0, 1]

are weighting functions with

\sum_{l_{1}} w^{l_{1}} = 1

\sum_{l_{2}} w^{l_{2}} = 1

. The advantage of this approach is that the

l_{1} \times l_{2}

matrices

A_{R H}^{l_{1}, l_{2}, j} = A_{R H} (ϕ_{R}^{l_{1}, j}, ϕ_{H}^{l_{2}, j})

can be computed off line. Then, the calculation of mean and covariance matrix is obtained by

\begin{matrix} x_{c}^{f} (k) = \sum_{j = 0}^{2 n} W^{j} x_{c}^{f, j} (k) \\ P^{f} (k) = \sum_{j = 0}^{2 n} W^{j} {\tilde{x}}_{c}^{f, j} (k) {({\tilde{x}}_{c}^{f, j} (k))}^{T} \\ {\tilde{x}}_{c}^{f, j} = x_{c}^{f, j} - x_{c}^{f} \end{matrix}

(57)

From the covariance

P^{f}

the variances

{σ_{c}}_{x x}, {σ_{c}}_{y y}, {σ_{c}}_{x y}

can be obtained

\begin{matrix} {σ_{c}}_{x x} = E ({(x_{c}^{f} - {\bar{x}}_{c}^{f})}^{2})) \\ {σ_{c}}_{y y} = E ({(y_{c}^{f} - {\bar{y}}_{c}^{f})}^{2})) \\ {σ_{c}}_{x y} = {σ_{c}}_{y x} = E ((x_{c}^{f} - {\bar{x}}_{c}^{f}) \cdot (y_{c}^{f} - {\bar{y}}_{c}^{f})) \end{matrix}

(58)

Inverse Solution

The inverse solution for the Sigma-Point approach is much easier to get than that for the statistical linearization method. Starting from eq. (34) we build the inverse function

x = F^{- 1} (x_{c})

(59)

on the condition that

F^{- 1}

exists. Then the covariance matrix

P

is defined in correspondence to the required variances

{σ_{c}}_{x x}, {σ_{c}}_{y y}

, and

{σ_{c}}_{x y}

. The following next steps correspond to equations (34)-(42). The position vector

x_{R H}

is assumed to be known. The inversion of

F

requirers a linearization of

x_{R H}

and a starting point to obtain a stable convergence to the inverse

F^{- 1}

. The result is the mean

x

and the covariance

Q

at the input. A reliable inversion is only possible for the 2-input 2-output case.

6-Inputs 2-Outputs

This case works exactly as the 2-input 2-output case along eqs. (34)-(42) due to the fact that the computation of the Sigma-Points (38)-(40) and the propagation through the nonlinearity

F

includes automatically the input and output dimensions.

5. Simulation Results

The following simulations show results of uncertainties of predicted intersections based on statistical linearization and sigma-point-Transformation. For both methods identical parameters are employed for comparisson reasons (see Figure 2) Position/orientation of robot and human are given by

x_{R} = {(x_{R}, y_{R})}^{T} = {(2, 0)}^{T}

x_{H} = {(x_{H}, y_{H})}^{T} = {(4, 10)}^{T}

ϕ_{R} = 1.78 r a d = 102^{\circ}

ϕ_{H} = 3.69 r a d = 212^{\circ}

ϕ_{R}

and

ϕ_{H}

are corrupted by Gaussian noise with standard deviations (std) of

σ_{ϕ_{R}} = σ_{x_{1}} = 0.02

rad,

(= 1 . 1^{\circ})

σ_{ϕ_{H}} = σ_{x_{2}} = 0.02

rad,

(= 1 . 1^{\circ})

Statistical linearization

Table 1 shows a comparison of the non-fuzzy method with the fuzzy approach using sectors of

60^{\circ}, 30^{\circ}, 15^{\circ}, 7 . 5^{\circ}

of the unit circle for the orientations of robot and human. Notations in Table 2 are:

{σ_{x}}_{c}

- std-computed,

{σ_{x}}_{m}

- std-measured etc. As expected, we see that higher resolutions lead to a better match between fuzzy and analytical approach. Furthermore, the match between measured and calculated values depends on the form of membership functions (MFS). For example, low input standard deviations (0.02 rad) show a better match for Gaussian membership functions, higher input standard deviations (0.05 rad =

2 . 9^{\circ}

) require Gaussian bell shape membership functions which comes from different smoothing effects (see columns 4 and 5 in Table 2).

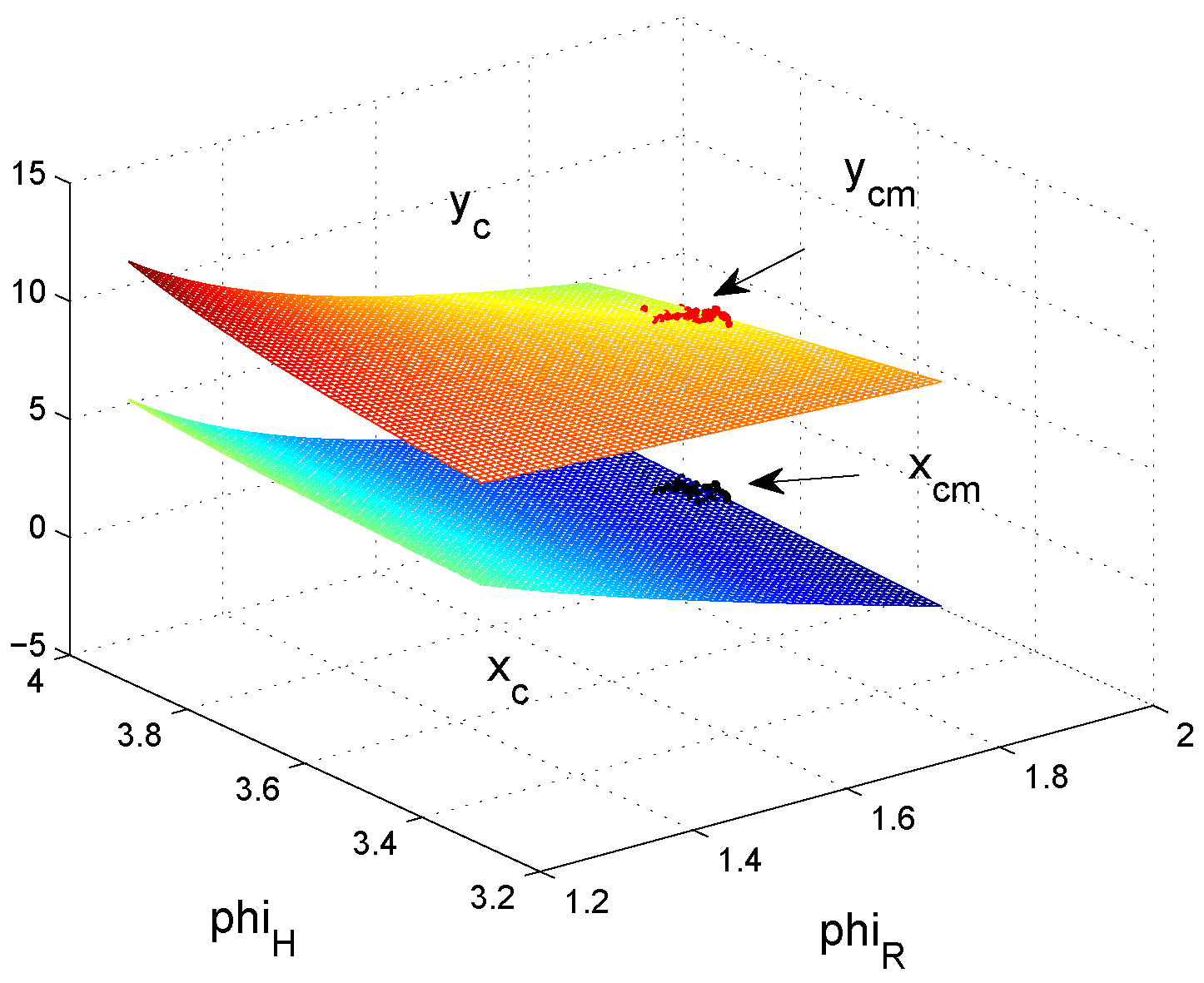
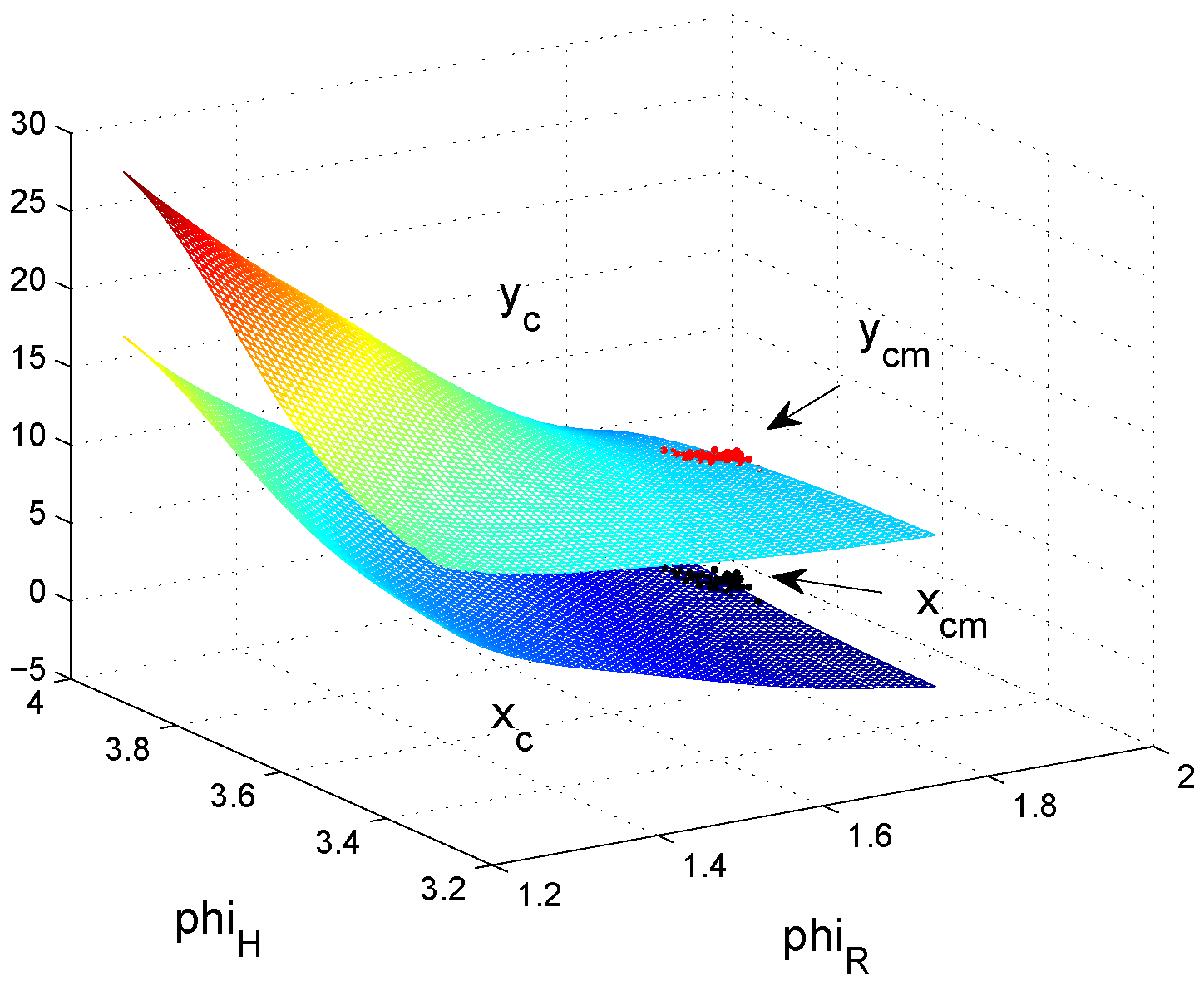
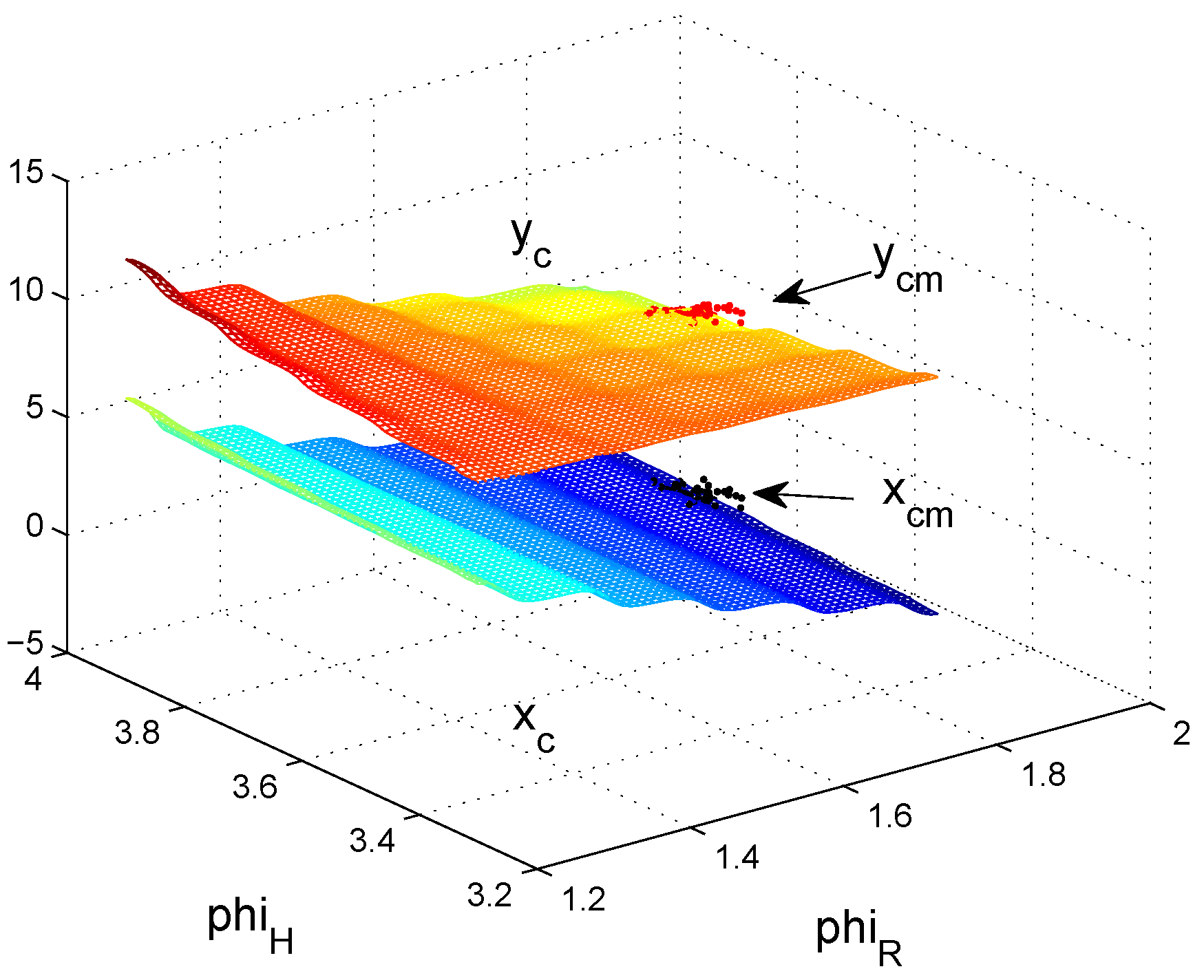
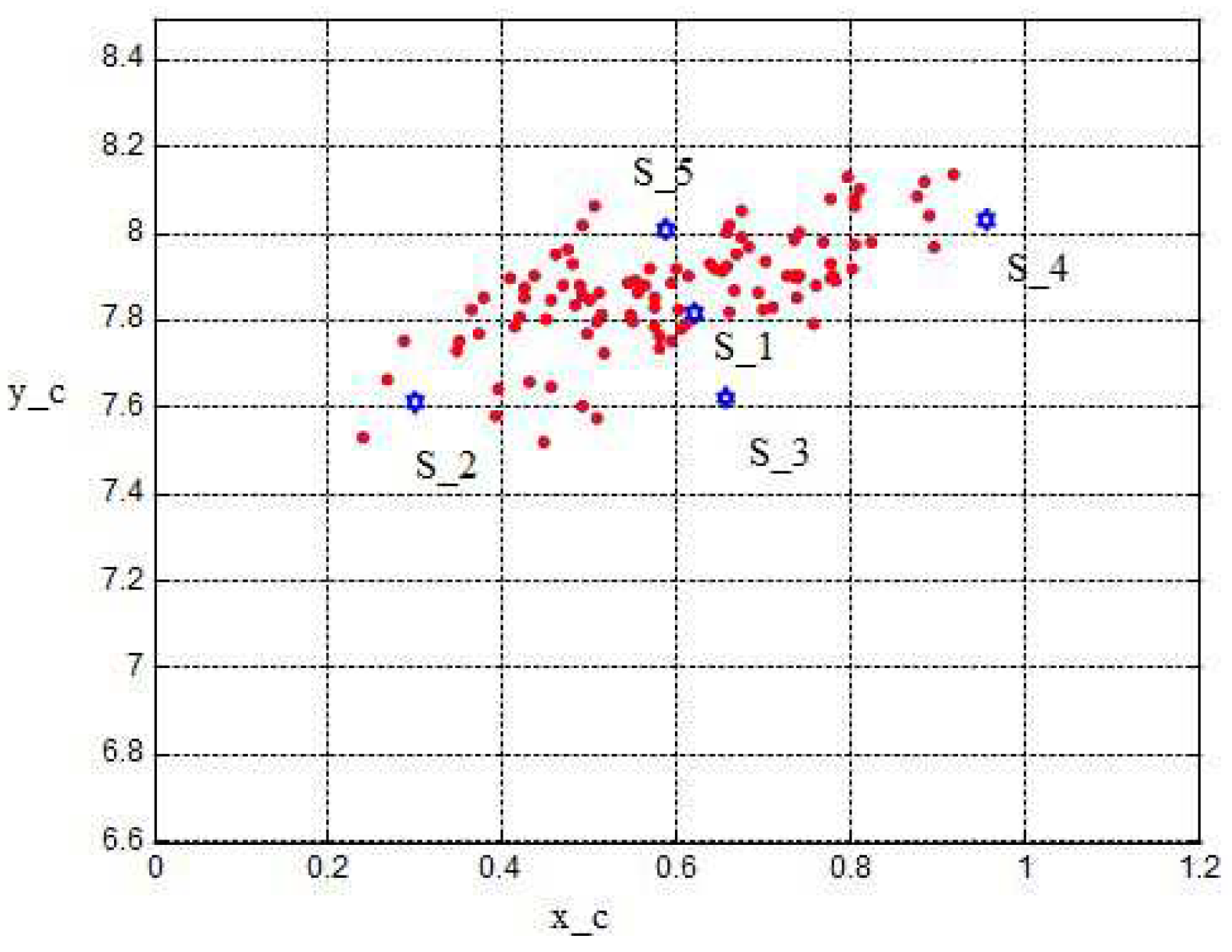
A comparison of control surfaces and corresponding measurements

x_{c m}, y_{c m}

(black and red dots) is depicted in Figure 8, Figure 9 and Figure 10. Figure 8 shows the control surface of

x_{c}

and

y_{c}

for the non-fuzzy case (4). Control surfaces of the fuzzy approximations (7) for

30^{\circ}

and

7 . 5^{\circ}

sectors are shown in Figure 9 and Figure 10. Resolution

30^{\circ}

(Figure 9) shows a very high deviation compared to the non-fuzzy approach (Figure 8) which decreases further down to resolution

7 . 5^{\circ}

(Figure 10). This explains the high differences between measured and computed standard deviations and correlation coefficients, in particular for sector sizes of

30^{\circ}

and higher.

Sigma-Point method

2-inputs - 2-outputs:

The simulation of the sigma-point method is based on a Matlab implementation of an unscented Kalman filter by [17]. The first example deals with the 2-inputs - 2-outputs case in which only the orientations are taken into account, but the disturbances of the positions of robot and human are not part of the sigma-point calculation. A comparison between the computed and measured covariance show a very good match. The same holds for the standard deviations

{σ_{x}}_{c}, {σ_{y}}_{c}

. A comparison with the statistical linearization shows a good match as well (see Table 2, rows 1 and 2).

A view at the sigma-points presents the following results: Figure 11 shows the two-dimensional distribution of the orientation angles

(ϕ_{R}

ϕ_{H})

and the corresponding sigma-points

s_{1}, . . ., s_{5}

where

s_{1}

denotes the mean value. Figure 12 shows the two-dimensional distribution of the intersection coordinates

(x_{c}, y_{c})

with the sigma-points

S_{1}, . . ., S_{5}

S_{1}

denotes the mean value and

S_{1}, . . ., S_{5}

are distributed in such a way that the

s_{i}

are transformed into

S_{i}

i = 1 . . . 5

. From both figures an optimal selection of both

s_{1}, . . ., s_{5}

and

S_{1}, . . ., S_{5}

can be observed which results in a good match of the computed and measured standard deviations

σ_{x_{c}}

6-inputs - 2-outputs:

The 6-inputs 2-outputs example shows that the additional consideration of 4 input position coordinates with

σ_{x_{R}} = 0.02

leads to similar results both for computed and measured covariances and between sigma-point method and statistical linearization (see

P (7, 7) = {σ_{x}}_{c}^{2}

P (8, 8) = {σ_{y}}_{c}^{2}

, and

c o v a r (7, 7) = {σ_{x}}_{m}^{2}

c o v a r (8, 8) = {σ_{y}}_{m}^{2}

{σ_{x}}_{c}^{2}

- computed,

{σ_{x}}_{m}^{2}

- measured variation). Table 2 shows the covariance submatrix considering the output positions only.

Computed covariance:

\begin{matrix} P & = & 10^{- 1} \times (\begin{matrix} 0.004 & - 0.000 & - 0.000 & 0.000 & - 0.000 & - 0.000 & - 0.030 & - 0.018 \\ - 0.000 & 0.004 & 0.000 & - 0.000 & - 0.000 & - 0.000 & 0.003 & - 0.017 \\ - 0.000 & 0.000 & 0.004 & 0.000 & - 0.000 & - 0.000 & 0.004 & 0.002 \\ 0.000 & - 0.000 & 0.000 & 0.004 & - 0.000 & - 0.000 & 0.001 & 0.000 \\ - 0.000 & - 0.000 & - 0.000 & - 0.000 & 0.004 & 0.000 & 0.000 & - 0.002 \\ - 0.000 & - 0.000 & - 0.000 & - 0.000 & 0.000 & 0.004 & - 0.001 & 0.004 \\ - 0.030 & 0.003 & 0.004 & 0.001 & 0.000 & - 0.001 & 0.235 & 0.127 \\ - 0.018 & - 0.017 & 0.002 & 0.000 & - 0.002 & 0.004 & 0.127 & 0.165 \end{matrix}) \\ {σ_{x}}_{c} & = & 0.153, {σ_{y}}_{c} = 0.122 \end{matrix}

(60)

Measured Covariance:

\begin{matrix} c o v a r & = & 10^{- 1} \times (\begin{matrix} 0.004 & 0.000 & 0.000 & 0.000 & 0.000 & - 0.000 & - 0.028 & - 0.020 \\ 0.000 & 0.004 & 0.000 & 0.001 & 0.000 & - 0.000 & 0.000 & - 0.020 \\ 0.000 & 0.000 & 0.004 & - 0.000 & 0.001 & - 0.001 & 0.003 & 0.001 \\ 0.000 & 0.001 & - 0.000 & 0.004 & - 0.000 & - 0.000 & - 0.000 & - 0.003 \\ 0.000 & 0.000 & 0.001 & - 0.000 & 0.005 & - 0.000 & - 0.001 & - 0.006 \\ - 0.000 & - 0.000 & - 0.001 & - 0.000 & - 0.000 & 0.005 & - 0.000 & 0.005 \\ - 0.028 & 0.000 & 0.003 & - 0.000 & - 0.001 & - 0.000 & 0.213 & 0.131 \\ - 0.020 & - 0.020 & 0.001 & - 0.003 & - 0.006 & 0.005 & 0.131 & 0.182 \end{matrix}) \\ {σ_{x}}_{c} & = & 0.145, {σ_{y}}_{c} = 0.134 \end{matrix}

(61)

2-inputs 2-outputs, direct and inverse solution

The next example shows the computation of the direct and inverse case. In the direct case we obtain again similar values between computed and measured covariances and, with this, standard deviations. The results of the inverse solution leads to similar values of the original inputs (orientations

x_{1} = ϕ_{R}, x_{2} = ϕ_{H}

), (see Table 2). Simulations of fuzzy versions showed the same similarities and can therefore be left out here.

2-inputs 2-outputs, Moving robot/human

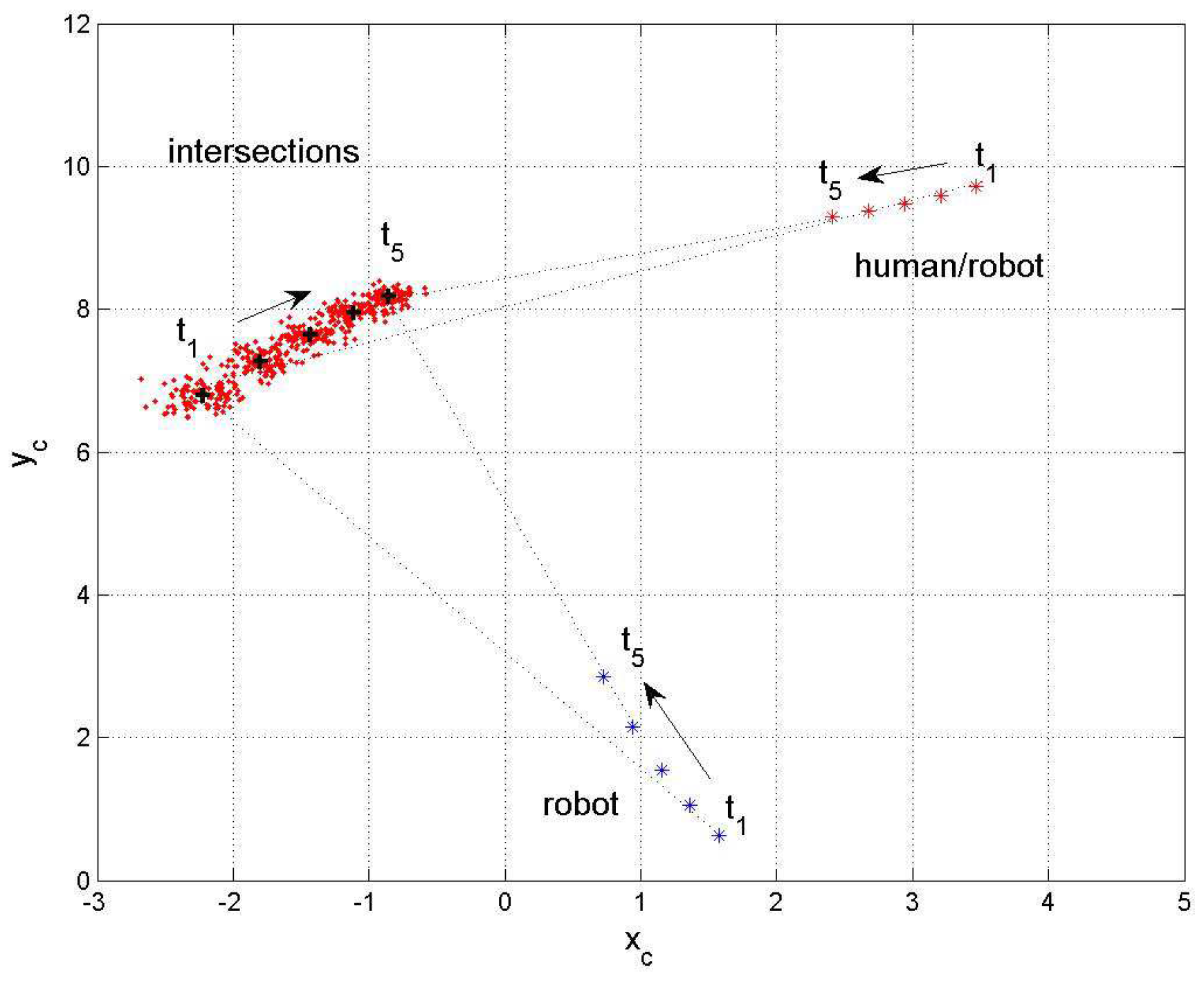
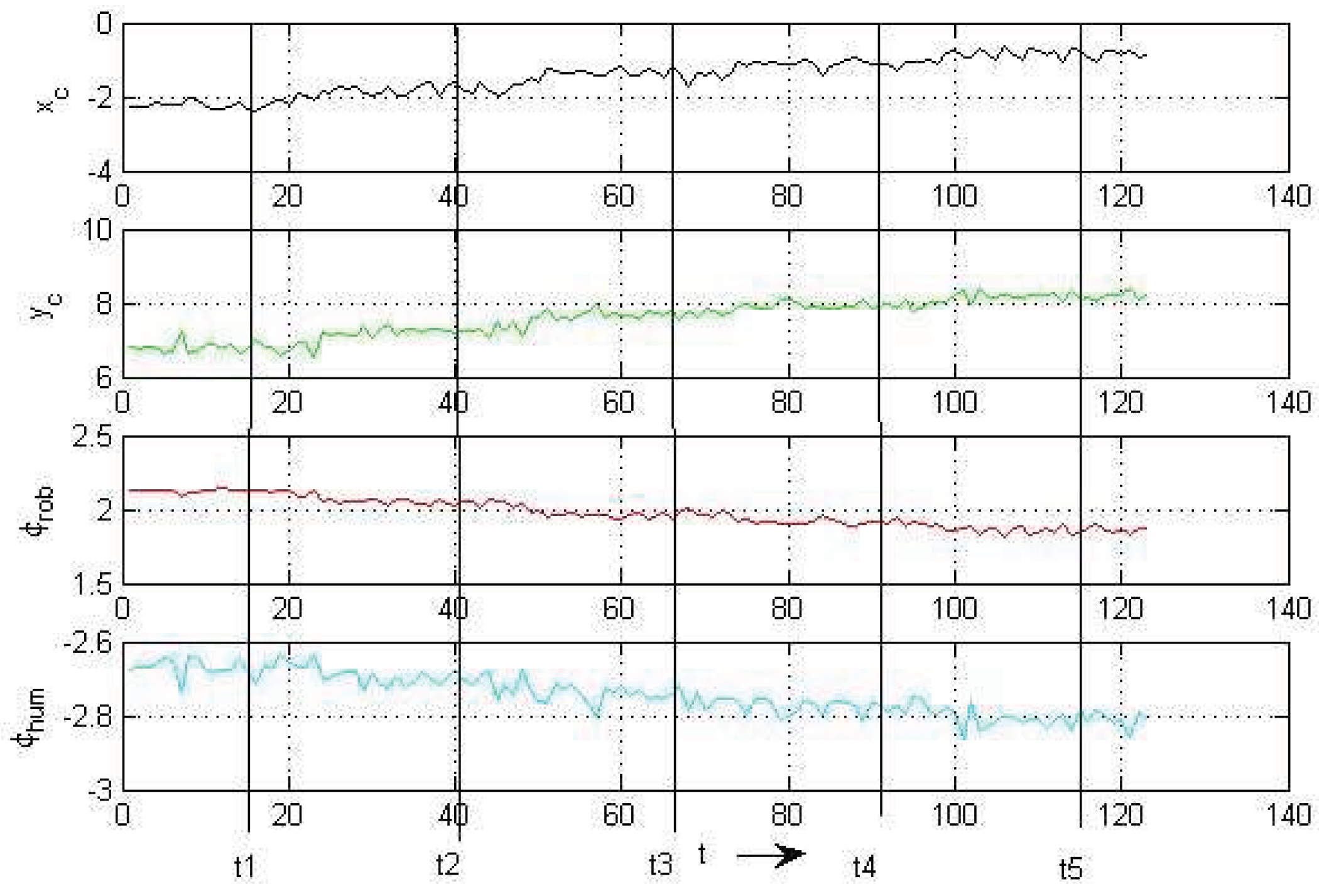
The next example deals with robot and human in motion. Figure 13 shows positions and orientations of robot and human at selected time steps

t_{1} . . . t_{5}

and the development of the corresponding intersections

x_{c}

Figure 14 shows the corresponding time plot. The time steps

t_{1} . . . t_{5}

are taken at

0.58 s, . . ., 4.58 s

with a time distance of

1 s

which are 25 time steps of 0.04s each. Robot and human start at

x_{R} = {(x_{R}, y_{R})}^{T} = {(2, 0)}^{T}

x_{H} = {(x_{H}, y_{H})}^{T} = {(4, 10)}^{T}

with the velocities

{\dot{x}}_{R} (k) = - 0.21 m / s

{\dot{y}}_{R} (1) = + 0.24 m / s

{\dot{x}}_{H} (k) = - 0.26 m / s

{\dot{y}}_{H} (1) = - 0.24 m / s

k - time step

The x components of the velocities

{\dot{x}}_{R} (k)

and

{\dot{x}}_{H} (k)

stay constant during the whole simulation.

The y components change their velocities with constant factors

\begin{matrix} {\dot{y}}_{R} (k + 1) & = & K_{R} \cdot {\dot{y}}_{R} (k) \\ {\dot{y}}_{H} (k + 1) & = & K_{H} \cdot {\dot{y}}_{H} (k) \end{matrix}

where

K_{R} = 1.2

and

K_{H} = 0.9

. The orientation angles start with

ϕ_{R} = 1.78 r a d

ϕ_{H} = 3.69 r a d

and change their values every second according to the direction of motion.

From both plots one observes an expected decrease of the output standard deviations for a mutual decrease of their distances to the regarding intersection and a good match between computed and measured values

x_{c}

(see Table 3). With the information about the distance of the robot and the standard deviation from and at the expected intersection, respectively, it becomes possible to plan either an avoidance strategy or a mutual cooperation between robot and human.

6. Summary and Conclusions

The content of this work is the prediction of encounter situations of mobile robots and human agents in shared areas by analyzing planned/intended trajectories in the presence of uncertainties and system and observation noise. In this context the problem of intersections of trajectories with respect to system uncertainties and Gaussian noise of position and orientation of the agents involved are discussed. The problem is adressed by two methods: the statistical linearization of distributions and the sigma-point-Transformation of distribution parameters. Positions and orientations of robot and human are corrupted with Gaussian noise represented by the parameters mean and standard deviation. The goal is to calculate mean and standard deviation/variation at the intersection via the nonlinear relation between positions/ orientations of robot and human on the one hand and the position of the intersection of their intended trajectories on the other hand.

This analysis is realized by statistical linearization of the nonlinear relation between the statistics of robot and human (input) and the statistics of the intersection (output). The output results are mean and standard deviation of the intersection as functions of the input parameters mean and standard deviation of positions and orientations of robot and human. This work is first carried out for 2 inputs - 2 outputs relations (2 orientations of robot/human - 2 intersection coordinates) and then for 6 inputs - 2 outputs (2 orientations and 4 position coordinates of robot/human - 2 intersection coordinates). These cases were extended to their fuzzy versions by different Takagi-Sugeno (TS) fuzzy approximations and compared with the non-fuzzy case. Up to a certain resolution the approximation works as accurate as the original non-fuzzy version. For the 2-input - 2-output case an inverse solution is derived, except the 6-input - 2-output case because of the underdetermined nature of the differential input-output relation.

The sigma-point transformation aims at transforming/propagating distribution parameters - the sigma-points - directly through nonlinearities. The transformed sigma-points are then converted into distribution parameters mean and covariance matrix. The sigma-point transformation is closely connected to the unscented Kalman filter which is used in the example of robot and human in motion. The specialty of the example is a computed virtual system output ("observation") - the intersection of two intended trajectories - where the corresponding output uncertainty is a sum of the transformed position/orientation noise and the computational uncertainty from the fuzzy approximation. In total the comparison between the computed and measured covariances show very good match and the comparison with the statistical linearization shows good coincidences as well. Both the sigma-point transformation and the differential statistical linearization scales for more than 2 variables linearly. However the computing costs for the differential approach are still higher than that for the sigma-point approach. In summary, a prediction of the accuracy of human-robot trajectories using the methods presented in this work increases the performance of human robot collaboration and human safety. In future work this method can be used for robot-human scenarios in factory workshops and for robots working in complicated environments like rescue operations in cooperation with human operators.

Author Contributions

R.P. developed the methods and implemented the simulation programs. A.L. conceived the project and gave advise and support.

Funding

This work has received funding from the European Union s Horizon 2020 research and innovation programme under grant agreement No 101017274 (DARKO).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare that they have no competing interests.

References

Khatib, O. Real-time 0bstacle avoidance for manipulators and mobile robots. IEEE Int. Conf. On Robotics and Automation,St. Loius,Missouri, 1985 1985, p. 500505.
Firl, J. Probabilistic Maneuver Recognition in Traffic Scenarios. Doctoral dissertation, KIT Karlsruhe, 2014.
W.Luo.; J.Xing.; Milan, A.; Zhang, X.; Liu, W.; Zhao, X.; Kim, T. Multiple Object Tracking: A Literature Review. Computer Vision and Pattern Recognition, arXiv 1409,7618 2014, p. 118.
J.Chen.; Wang, C.; Chou, C. Multiple target tracking in occlusion area with interacting object models in urban environments. Robotics and Autonomous Systems, Volume 103, May 2018 2018, pp. 68–82.
Kassner, M.; W.Patera.; Bulling, A. Pupil: an open source platform for pervasive eye tracking and mobile gaze-based interaction. In Proceedings of the Proceedings of the 2014 ACM international joint conference on pervasive and ubiquitous computing. ACM, 2014, pp. 1151–1160.
Bruce, J.; Wawer, J.; Vaughan, R. Human-Robot Rendezvous by Co-operative Trajectory Signals. 2015. pp. 1–2.
Palm, R.; Lilienthal, A. Fuzzy logic and control in Human-Robot Systems: geometrical and kinematic considerations. In Proceedings of the WCCI 2018: 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE). IEEE, IEEE, 2018, pp. 827–834.
R.Palm.; Driankov, D. Fuzzy inputs. Fuzzy Sets and Systems - Special issue on modern fuzzy control 1994, pp. 315–335.
L.Foulloy.; S.Galichet. Fuzzy control with fuzzy inputs. IEEE Trans. Fuzzy Systems, 11 (4) 2003, pp. 437–449.
Banelli, P. Non-Linear Transformations of Gaussians and Gaussian-Mixtures with implications on Estimation and Information Theory. IEEE Trans. on Information Theory 2013.
Julier, S.; J.K.Uhlmann. Unscented Filtering and Nonlinear Estimation. In Proceedings of the Proc. of the of the IEEE 2004, Vol.92, No.3, 2004, 2004, pp. 401–422.
R.v.d.Merwe.; E.Wan.; S.J.Julier. Sigma-Point Kalman Filters for Nonlinear Estimation and Sensor-Fusion: Applications to Integrated Navigation. In Proceedings of the Proc. of the AIAA 2004, Guidance, Navigation and Control Conference, 2004, Providence, RI, Aug 2004.
G.A.Terejanu. Unscented Kalman Filter Tutorial. Department of Computer Science and Engineering University at Buffalo 2011.
R.Palm.; Lilienthal, A. Uncertainty and Fuzzy Modeling in Human-robot Navigation. In Proceedings of the Proc. of the 11th Intern. Joint Conf. on Comp. Int. (IJCCI 2019),, IJCCI, Wien, 2019; pp. 296–305.
R.Palm.; Lilienthal, A. Fuzzy Geometric Approach to Collision Estimation Under Gaussian Noise in Human-Robot Interaction. In Proceedings of the IJCCI 2019. Studies in Computational Intelligence, vol 922. Springer, 2021, IJCCI, Cham, 2021; pp. 191–221.
J.Schaefer.; K.Strimmer. A shrinkage to large scale covariance matrix estimation and implications for functional genomics. Statistical Applications in Genetics and molecular Biology, vol. 4, iss. 1, Art. 32 2005.
Cao, Y. Learning the Unscented Kalman Filter. https://www.mathworks.com/ matlabcentral/ fileexchange/ 18217-learning-the-unscented-kalman-filter 2021.

Figure 1. Intersection principle

Figure 2. Human-robot scenario: geometry

Figure 3. Membership functions for

Δ ϕ_{R}, Δ ϕ_{H} = 0 - 360^{\circ}

Figure 3. Membership functions for

Δ ϕ_{R}, Δ ϕ_{H} = 0 - 360^{\circ}

Figure 4. Fuzzy sectors

Figure 5. Intersection with noisy orientations

Figure 6. Differential transformation

Figure 7. Sigma-points for a 2-dim Gaussian random variable

Figure 8. Control surface non-fuzzy

Figure 9. Control surface fuzzy,

30^{\circ}

Figure 9. Control surface fuzzy,

30^{\circ}

Figure 10. Control surface fuzzy,

7 . 5^{\circ}

Figure 10. Control surface fuzzy,

7 . 5^{\circ}

Figure 11.

S i g m a - P o i n t s

, input

Figure 11.

S i g m a - P o i n t s

, input

Figure 12.

S i g m a - P o i n t s

, output

Figure 12.

S i g m a - P o i n t s

, output

Figure 13. Moving robot and human

Figure 14. Time plot, robot and human

Table 1. Standard deviations, fuzzy and non-fuzzy results

input std	0.02 Gauss, bell shaped (GB)				Gauss	0.05 GB
sector size/ °	$60^{\circ}$	$30^{\circ}$	$15^{\circ}$	$7 . 5^{\circ}$	$7 . 5^{\circ}$	$7 . 5^{\circ}$
non-fuzz ${σ_{x}}_{c}$	0.143	0.140	0.138	0.125	0.144	0.366
fuzz ${σ_{x}}_{c}$	0.220	0.184	0.140	0.126	0.144	0.367
non-fuzz ${σ_{x}}_{m}$	0.160	0.144	0.138	0.126	0.142	0.368
fuzz ${σ_{x}}_{m}$	0.555	0.224	0.061	0.225	0.164	0.381
non-fuzz ${σ_{y}}_{c}$	0.128	0.132	0.123	0.114	0.124	0.303
fuzz ${σ_{y}}_{c}$	0.092	0.087	0.120	0.112	0.122	0.299
non-fuzz ${σ_{y}}_{m}$	0.134	0.120	0.123	0.113	0.129	0.310
fuzz ${σ_{y}}_{m}$	0.599	0.171	0.034	0.154	0.139	0.325
non-fuzz ${ρ_{x y}}_{c}$	0.576	0.541	0.588	0.561	0.623	0.669
fuzz ${ρ_{x y}}_{c}$	-0.263	0.272	0.478	0.506	0.592	0.592
non-fuzz ${ρ_{x y}}_{m}$	0.572	0.459	0.586	0.549	0.660	0.667
fuzz ${ρ_{x y}}_{m}$	0.380	0.575	0.990	0.711	0.635	0.592

Table 2. Covariances, standard deviations - computed and measured

Outputs	Covariance, computed	Covariance, measured	${σ_{x}}_{c}$ , comp/meas	${σ_{y}}_{c}$ , comp/meas
2 inputs	$P = (\begin{matrix} 0.0213 & 0.0114 \\ 0.0114 & 0.0159 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0264 & 0.0146 \\ 0.0146 & 0.0166 \end{matrix})$	$0.145 / 0.144$	$0.126 / 0.134$
2 inputs, stat. lin.	-	-	$0.144 / 0.142$	$0.124 / 0.129$
6 inputs	$P = (\begin{matrix} 0.0235 & 0.0127 \\ 0.0127 & 0.0165 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0213 & 0.0131 \\ 0.0131 & 0.0182 \end{matrix})$	$0.135 / 0.145$	$0.122 / 0.134$
Direct solution	$P = (\begin{matrix} 0.0234 & 0.0133 \\ 0.0133 & 0.0151 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0264 & 0.0146 \\ 0.0146 & 0.0166 \end{matrix})$	$0.152 / 0.162$	$0.128 / 128$
Inverse solution	$P = 10^{- 3} \times (\begin{matrix} 0.4666 & 0.0522 \\ 0.0522 & 0.4744 \end{matrix})$	$c o v a r = 10^{- 3} \times (\begin{matrix} 0.4841 & - 0.0190 \\ - 0.0190 & 0.396 \end{matrix})$	$0.0215 / 0.0220$	$0.0217 / 0.0190$

Table 3. Covariances, standard deviations - computed and measured, moving robot/human

Outputs	Covariance, computed	Covariance, measured	${σ_{x}}_{c}$ , comp/meas	${σ_{y}}_{c}$ , comp/meas
$t_{1}$	$P = (\begin{matrix} 0.0220 & 0.0017 \\ 0.0017 & 0.0163 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0246 & - 0.0002 \\ - 0.0002 & 0.0202 \end{matrix})$	$0.148 / 0.156$	$0.127 / 0.142$
$t_{2}$	$P = (\begin{matrix} 0.0198 & 0.0023 \\ 0.0023 & 0.0138 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0222 & 0.0018 \\ 0.0018 & 0.0153 \end{matrix})$	$0.140 / 0.148$	$0.117 / 0.123$
$t_{3}$	$P = (\begin{matrix} 0.0168 & 0.0030 \\ 0.0030 & 0.0107 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0140 & 0.0040 \\ 0.0040 & 0.0088 \end{matrix})$	$0.129 / 0.118$	$0.103 / 0.093$
$t_{4}$	$P = (\begin{matrix} 0.0151 & 0.0029 \\ 0.0029 & 0.0083 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0127 & 0.0014 \\ 0.0014 & 0.0073 \end{matrix})$	$0.122 / 0.112$	$0.091 / 0.085$
$t_{5}$	$P = (\begin{matrix} 0.0125 & 0.0023 \\ 0.0023 & 0.0061 \end{matrix})$	$c o v a r = (\begin{matrix} 0.0102 & 0.0030 \\ 0.0030 & 0.0056 \end{matrix})$	$0.112 / 0.101$	$0.078 / 0.074$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Crossing Point Estimation in Human/Robot Navigation - Statistical Linearization versus Sigma-Point-Transformation

Abstract

1. Introduction

2. Computation of Intersections

2.1. Geometrical Relations

2.2. Computation of Intersections - Fuzzy Approach

2.3. Differential Approach

3. Transformation of Gaussian Distributions

3.1. General Assumptions

3.2. Statistical Linearization, Two Inputs-Two Outputs

Output Distribution

Fuzzy Solution

Inverse Solution

3.3. Six Inputs - Two Outputs

Inverse Solution

Fuzzy Approach

4. Sigma-Point-Transformation

Selection of Sigma-Points

Model Forecast Step

Measurement update step

Data Assimilation Step

Sigma-Points - Fuzzy Solutions

Inverse Solution

6-Inputs 2-Outputs

5. Simulation Results

Statistical linearization

Sigma-Point method

6. Summary and Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe