Prerpints.org logo
Preprint
Article

Performance Evaluation of a National 7-Day Ensemble Streamflow Forecast Service for Australia

Altmetrics

Downloads

100

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 March 2024

Posted:

28 March 2024

You are already at the latest version

Alerts
Abstract
The Australian Bureau of Meteorology offers a national operational 7-day ensemble streamflow forecast service covering regions of high environmental, economic and social significance. This semi-automated service generates streamflow forecasts every morning and is seamlessly integrated into the Bureau's Hydrologic Forecasting System (HyFS). Ensemble rainfall forecasts, European Centre for Medium-Range Weather Forecasts (ECMWF) and Poor Man's Ensemble (PME), available in the Numerical Weather Prediction (NWP) suite, are used to generate these streamflow forecasts. The NWP rainfall undergoes pre-processing using the Catchment Hydrologic Pre-Processer (CHyPP) before being fed into the GR4H rainfall-runoff model, which is embedded in the Short-term Water Information Forecasting Tools (SWIFT) hydrological modelling package. The simulated streamflow is then post-processed using the Error Representation and Reduction In Stages (ERRIS). We evaluated the performance of the operational rainfall and streamflow forecasts for 96 catchments using four years of operational data between January 2020 and December 2023. Performance evaluation metrics included CRPS, relative CRPS, CRPSS, and PIT-Alpha for ensemble forecasts and NSE, PCC, MAE, KGE, PBias and RMSE and three categorical metrics CSI, FAR and POD for deterministic forecasts. The skill scores CRPS, relative CRPS, CRPSS and PIT-Alpha, gradually decreased for both rainfall and streamflow as the forecast horizon increased from Day 1 to Day 7. A similar pattern emerged for NSE, KGE, PCC, MAE and RMSE as well as the categorical metrics. Forecast performance also progressively decreased with the higher streamflow regime. Most catchments showed positive performance skills, meaning the ensemble forecast outperformed climatology. Both streamflow and rainfall forecast skills varied spatially across the country – and were generally better in the high runoff generating catchments, and poorer in the drier catchments situated in the western part of the Great Dividing Range, South Australia and mid-west of Western Australia. We did not find any association between model forecast skill and the catchment area. Our findings demonstrate that the 7-day ensemble streamflow forecasting service is robust and draws great confidence from agencies that use these forecasts to support decisions around water resources management.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

During 1997-2009, south east Australia experienced its worst drought since 1901 [1]. Known as the 'millennium drought', below-median annual rainfall was frequently observed with little recovery in intervening years during this period. In particular, observed streamflow in the Murray Darling River Basin, known as Australia's food bowl, was very low, and inflow to major reservoirs was half compared to the previous recorded minimum [2]. As a result, there was a wider societal, economic and environmental impacts [3,4]. The Federal Government passed Water Act 2007 (https://www.legislation.gov.au/Details/C2017C00151, accessed on 20th June 2023) for the future water security plan for the nation. The Bureau of Meteorology (the Bureau) was given responsibility to implement the Water Act. Among other services, streamflow forecasting at seasonal and 7-day time scale were developed as part of the water security plan [5].
A 7-day deterministic streamflow forecast service was progressively developed during 2010-15 and released by the Bureau to the public in September 2015. This was the first nationally operated continuous streamflow forecast system developed in Australia [6]. Subsequent feedback from key customers across State and Territory jurisdictions, favoured a move to ensemble, or probabilistic, forecasts. Ensemble forecasting is considered more reliable and skilful, and it can greatly benefit water resource management by providing useful information about uncertainty [7]. In response to customer needs, the Bureau progressively developed the 7-day ensemble streamflow forecasting, and released it to the public in 2020 [8]. This is a comprehensive, nation-wide service for Australia, and covers most water resources catchments of high economic value and social significance [9]. The service currently consists of 99 catchments and 208 forecast locations (Figure 1) and covers 10 out of the 13 Drainage Divisions. Catchments vary in area across the country (from 26 to 83150 km2) and are located in different hydroclimatic regions. The number of forecast locations distributed across different drainage divisions vary significantly, the selection of which was based heavily on value, little human impacts on natural flows and impact for customers – the Murray Darling division having the largest number of stations, while the South-Western Plateau, Lake Eyre Basin and North Western Plateau have no stations at all (Figure 1). Australia has a wide range of climate zones as defined by Köppen Climate Classification [10] – including tropical region in the north, temperate regions in the south, grassland and desert in the vast interior. Annual rainfall for each of the divisions vary from a 410 to 2800 mm [8]. The distribution of annual rainfall and Potential evapotranspiration (PET) varies significantly across the continent (http://www.bom.gov.au/jsp/ncc/climate_averages/rainfall/index.jsp, accessed 11 November 2023). Annual average PET is generally higher than annual average rainfall. Therefore, streamflow generation processes in most divisions are different, and are controlled by water-limited environments [11] except for the Tasmania drainage division.
There is a wide range of modelling techniques for streamflow and flood forecasting [12,13], and taking rainfall forecasts from Numerical Weather Prediction (NWP) system as an input to hydrological model for prediction is a very popular one. Ensemble streamflow forecasting has also become very popular across the world over the last decade [14,15]. There are various large-scale, continental and global, hydrological models run by communities around the world [15,16]. Global Ensemble Streamflow Forecasting and flood early warning (GloFAS) is one of the most popular forecasting systems. The U.S. Hydrologic Ensemble Forecast Service (HEFS) is run by the National Weather Service (NWS), and this service provides ensemble streamflow forecasts that seamlessly span lead times from less than 1 hour up to several years, and are spatially and temporally consistent [17]. In Canada, provincial river forecast centres deal with unique challenges in data collection, modelling and river flow forecasting due to large diversity in landscape, hydrological features across the country, and distribution of weather and extreme events at different times of the year [18]. Similar results were also found in South America, where a continental-scale hydrological model coupled with ECMWF ensemble rainfall was applied to produce streamflow forecasts up to 15 days in advance [19].
For users to fully benefit from ensemble streamflow forecasts, they need to comprehend the performance, model behaviour and forcings. Recent studies have focused on the performance evaluation of short to medium range hydrological streamflow forecasts. The quality of ensemble streamflow forecasts in the U.S. mid-Atlantic region was investigated by Siddique and Mejia [20], and they found that ensemble streamflow forecasts remain skilful for lead times of up to 7 days, and that postprocessing further increased forecast skills across lead times and spatial scales. In Canada, optimal model initial state and input configuration led to reliable short (days) and long term ( a year) streamflow forecasts [21]. In China, Liu et al. [22] demonstrated that ensemble streamflow forecasting system is skilful up to a lead time of 7 days ahead, although accuracy deteriorates as the lead time increases.
The Bureau's operational ensemble 7-day streamflow forecast service [8] now has 4 years of retrospective (archived) forecast data (January 2020 to December 2023). Performance of the overall end-to-end streamflow forecasting has not been analysed yet, and this paper presents the steps in filling this critical operational knowledge gap. Key objectives of this paper are to: (i) present the day-to-day operational monitoring and continuity of the service, (ii) perform a comprehensive evaluation of pre-processed rainfall and streamflow forecasts, and (iii) suggest possible avenues for future improvements.

2. Operational Forecast System and Model

The 7-day ensemble streamflow forecast service for Australia can be accessed through a freely available website (http://www.bom.gov.au/water/7daystreamflow/, accessed 28 February 2024). This service features forecast locations with forecasting skills and reliability that have passed specified selection criteria. While the primary emphasis is on delivering daily and hourly streamflow forecasts, the service also includes cumulative hourly streamflow and rainfall forecasts.

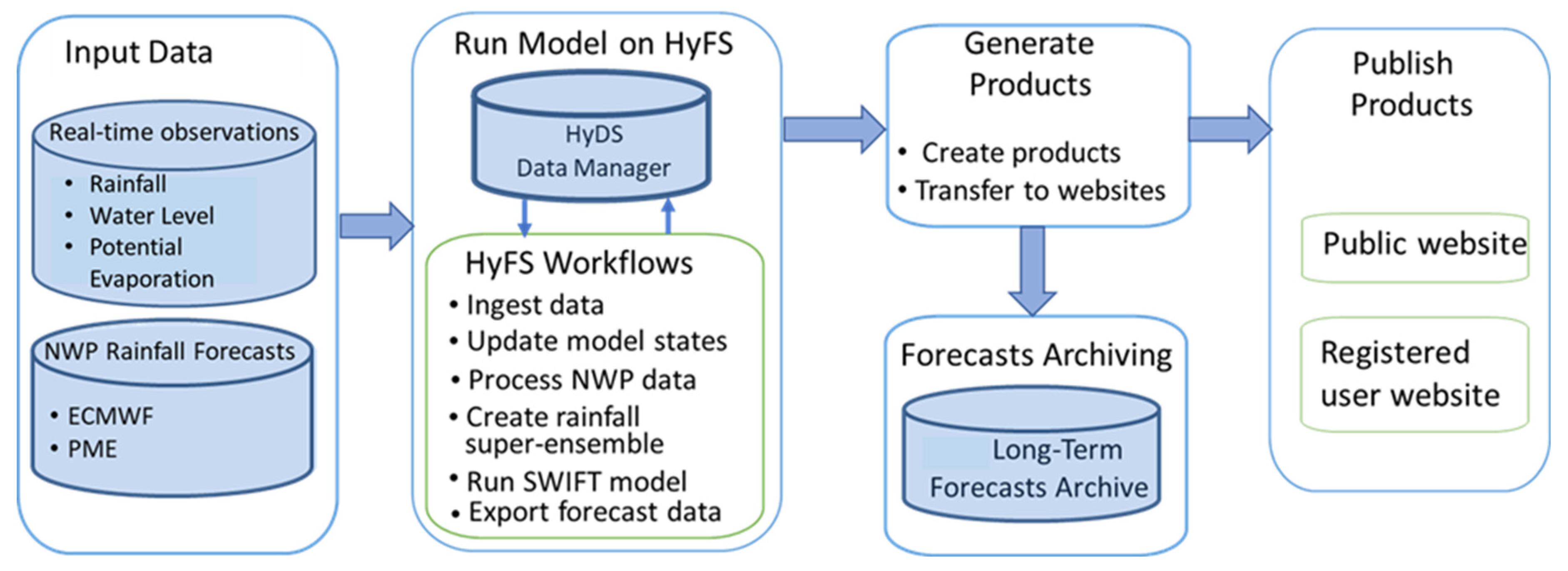
2.1. Description of the System Architecture

The forecasts are daily generated using the Bureau's Hydrological Forecasting System (HyFS). This national platform for modelling underpins flood forecasting and warning services for Australia. HyFS is a Delft-FEWS (Flood Early Warning System) based forecasting environment (https://oss.deltares.nl/web/delft-fews, accessed 20 October 2023). The system provides a comprehensive platform for management of input observations and Numerical Weather Prediction (NWP) model Quantitative Precipitation Forecasts (QPFs). It encompasses various tasks such as input data processing, forecasting and maintenance workflows, model internal state management, and forecast visualization. Publication quality plots are generated using a spatial module outside the HyFS (Figure 2) and the products are delivered to the website via the Bureau's content management system. The publication time of the forecast information to the website varies across States, but generally between 10:00AM to 12:00 Noon Australian Eastern Standard Time (AEST). An end-to-end forecast generation and publication procedure is presented in Figure 2.

2.2. Input Data

Observed rainfall and water level data are ingested into the HyFS in near-real time through the Bureau's Australian Water Resources Information System (AWRIS). Potential evapotranspiration (PET) data are extracted from the Australian Water Availability Project, AWAP [23], disaggregated to hourly and sub catchment scale, and stored in HyFS. Additionally, the Quantitative Precipitation Forecasts (QPFs) from the ECMWF and PME Numerical Weather Prediction (NWP) models' data are automatically integrated into HyFS. The ECMWF forecast rainfall is processed using the Catchment Hydrology Pre-Processor, CHyPP [24]. CHyPP generates an ensemble comprising 400 members sourced from ECMWF and merge with PME at an hourly time step for each sub-area for up to 7 days lead-time (Figure 2). Given that PME is a merged post-processed product of many global NWP products, it shows negligible improvement when CHyPP is used on it [24]. Therefore, the PME forecasts are not post-processed.

2.3. Rainfall-Runoff and Routing Model

The Short-term Water Information Forecasting Tools (SWIFT) constitute a streamflow modelling software package [25] seamlessly integrated into HyFS (Figure 2). SWIFT encompasses a variety of hydrologic models and provides a semi-distributed modelling approach – conceptual sub-areas and a node-link structure – for channel routing. Its functionality extends to modules for calibration, model initial state (hot start), ensemble forecast runs, and output error correction. Out of the available conceptual rainfall-runoff models in SWIFT GR4H, a four parameter hourly model developed by Perrin [26], was found to be most suitable for Australian applications [27]. The model calibrated parameter sets and initial state conditions were migrated and stored in HyFS for operational application. To enhance the accuracy of hydrological forecast time series, an integrated tool within SWIFT known as ERRIS (Error Representation and Reduction In Stages), developed by Li et al. [28] is used for streamflow error correction.

2.4. Operational Platform

The product generator tool produces five graphical outputs: (i) daily flow forecast, (ii) hourly flow forecast, (iii) cumulative flow forecast, (iv) cumulative rainfall forecast, and (v) forecast performance. The first four graphical products (and associated forecast data) are updated and published on the SDF website daily (http://www.bom.gov.au/water/7daystreamflow/index.shtml, accessed 22nd March 2024). The generated forecast time series is automatically archived for future analyses, and interpretation (Figure 2). Following forecast generation, selected data is packaged for downstream processing by end-users. The ensemble streamflow forecasts also serve as a guidance for the Bureau's flood forecasting service (http://www.bom.gov.au/water/floods/, accessed 8th March 2024). Operational day-to-day monitoring involves addressing issues through a systematic approach encompassing data, modelling, system and customer feedback. A designated monitoring officer logs, escalates, and resolves issues in collaboration with other experts such as software/system engineers supporting the service.

3. Performance Evaluation Methodology

Forecast quality continues to be limited by systematic and random errors from limited knowledge of initial conditions and inherent limits to represent physical processes in model structure [29,30]. Performance evaluation is generally “the process of assessing the quality of a forecast” [31] and serves as a useful tool to identify sources of errors [32,33,34]. Quantitative model performance is generally evaluated by computing metrics based on observed and forecast data. It establishes an appropriate level of confidence in a model's performance before its effective use in management and decision making. This confidence level is vital for forecasters to consider and communicate when interacting with users who rely on these forecasts. In hydrologic modelling and forecasting, observed values are used as the "point of truth" against which to assess forecast performance [35,36]. We used streamflow and rainfall (2014-16) as historical sources of "truth" to verify the model before operational release [8]. While there has been studies that presented different verification and performance evaluation metrics and diagnostic plots [37,38], we used some widely used ones for the evaluation of forecasts in ensemble and deterministic forms.

3.1. Performance Evaluation Metrics

The absence of clarity and consensus regarding criteria for defining optimal or sub-optimal forecasts can complicate the formulation, evaluation, and ultimate determination of the utility of operational forecasts. Murphy [34] defined nine forecast quantitative attributes and their relationship with different verification metrics. Additionally, 'coherence', a term used to describe whether forecasts are not, at least, worse than climatology (historical data), was also considered [39]. These cross-relationships were recently summarized by Huang and Zhao [38]. We have chosen metrics to provide a comprehensive overview of the operational forecast performance (see Appendix A). This includes all metrics used to evaluate historical performance of the model before it is used operationally [8]. Additionally, we have incorporated select supplementary metrics for a more thorough evaluation. These metrics are used for evaluating the quality of rainfall and streamflow forecasts – in ensemble, deterministic and categorical forms:
  • Deterministic: We considered median of the ensemble members and assessed the performance using the metrics – PBias, NSE, KGE, PCC, RMSE and MAE.
  • Ensemble: The metrics included were CRPS, relative CRPS, CRPSS and PIT-Alpha.
  • Categorical: Three metrics were POD, FAR, and CSI.
These metrics are widely used for assessing streamflow and rainfall prediction skills across the world [20,40,41,42,43].

3.2. Diagnostic Plots

Diagnostic plots allow visualisation of verification metrics, and they additionally provide empirical understandings of ensemble hydroclimatic forecasts [37,44]. There are generally six types of popular diagnostic plots [38,45]. Of these, we chose scatter plots, spatial maps, percentile distribution and box plots for ensemble forecasts and its deterministic form.

3.3. Forecast Data and Observations

We have chosen a full four years of dataset (from January 2020 to December 2023) for performance analysis. The hourly forecast data were accumulated to daily for performance evaluation. In line with forecast verification analyses conducted by Hapuarachchi et al. [8], we considered the most downstream locations within catchments for operational performance evaluation. The continuous hourly forecast data were unavailable for a few catchments, limiting our assessment to 96 out of 99 catchments. During the development of the service, 3 years of retrospective forecast data between 2014 to 2016 was considered for performance evaluation and hourly observed streamflow data between 1990 and 2016 was used to calculate the climatology as the reference for skill score calculation (CRPSS). Consistent with this historical approach, we maintained the same reference climatology for this research.

4. Results of Predictive Performance

We analysed performance of the models by computing the metrics as detailed in Appendix A. Decades of research and investigations consistently reveal that the ensemble mean yields results comparable to, or often better than, deterministic forecasts [7,46,47]. To comprehensively assess performance, we conducted analyses in two ways: (i) deterministic – considering only the mean of the ensemble forecasts, and (ii) ensemble –accounting for all members of the ensemble. As examples, Figure A1 (rainfall) and Figure A2 (streamflow) show the performance of two randomly selected catchments across all metrics.

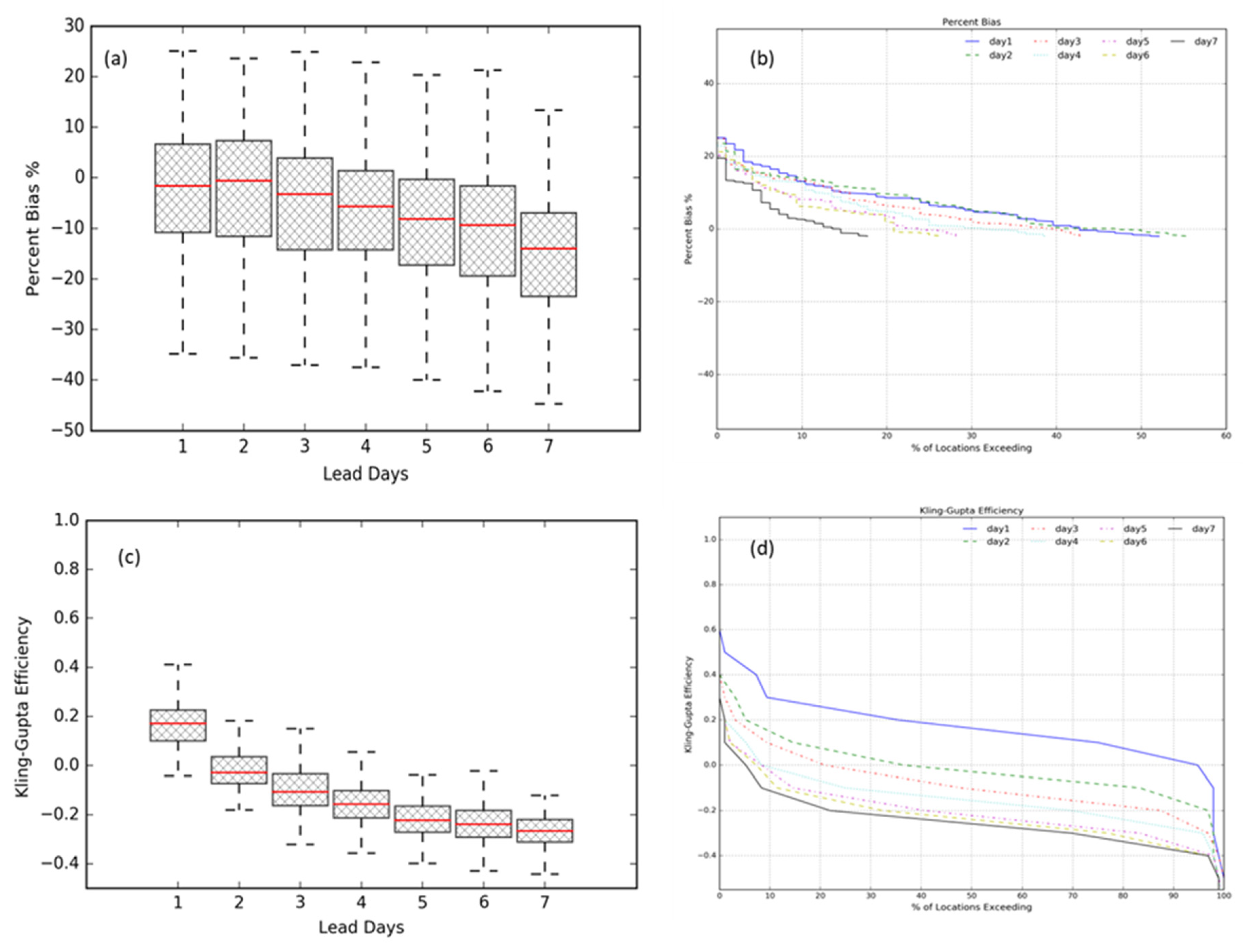
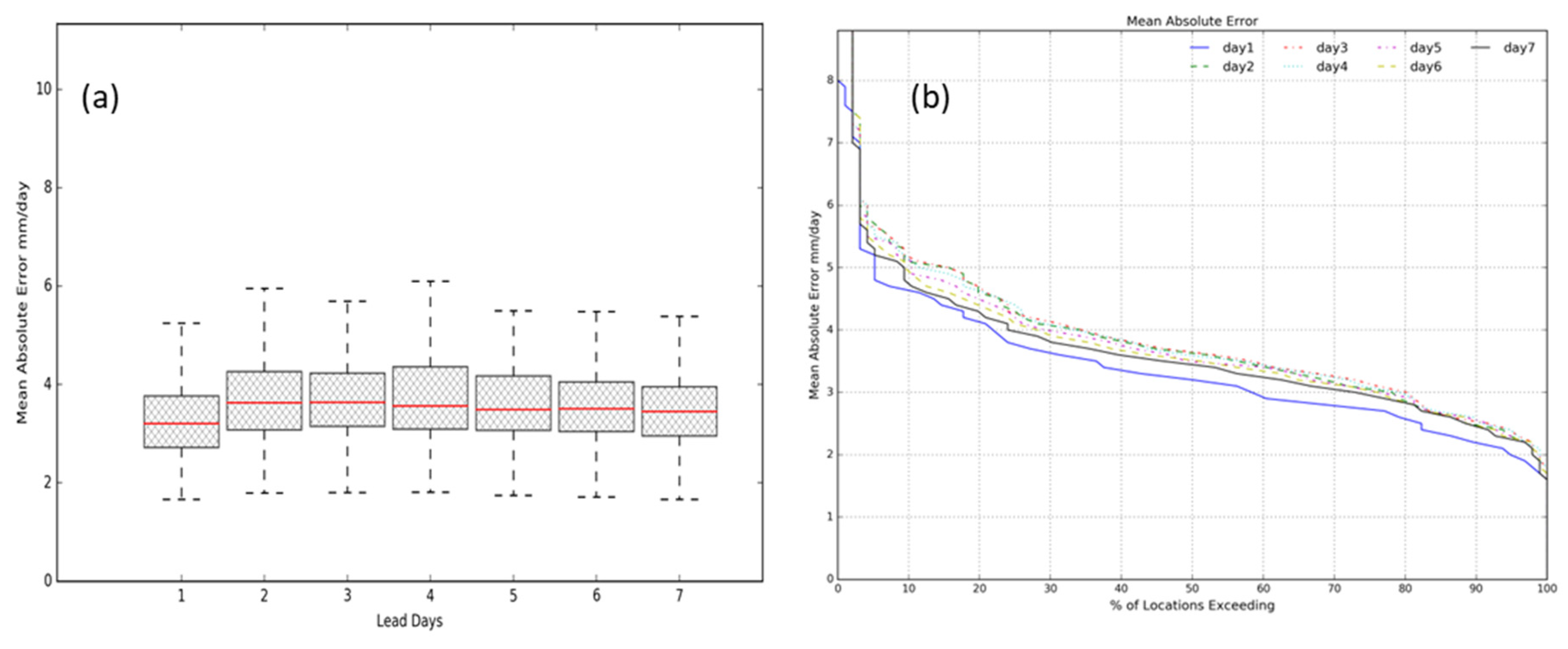
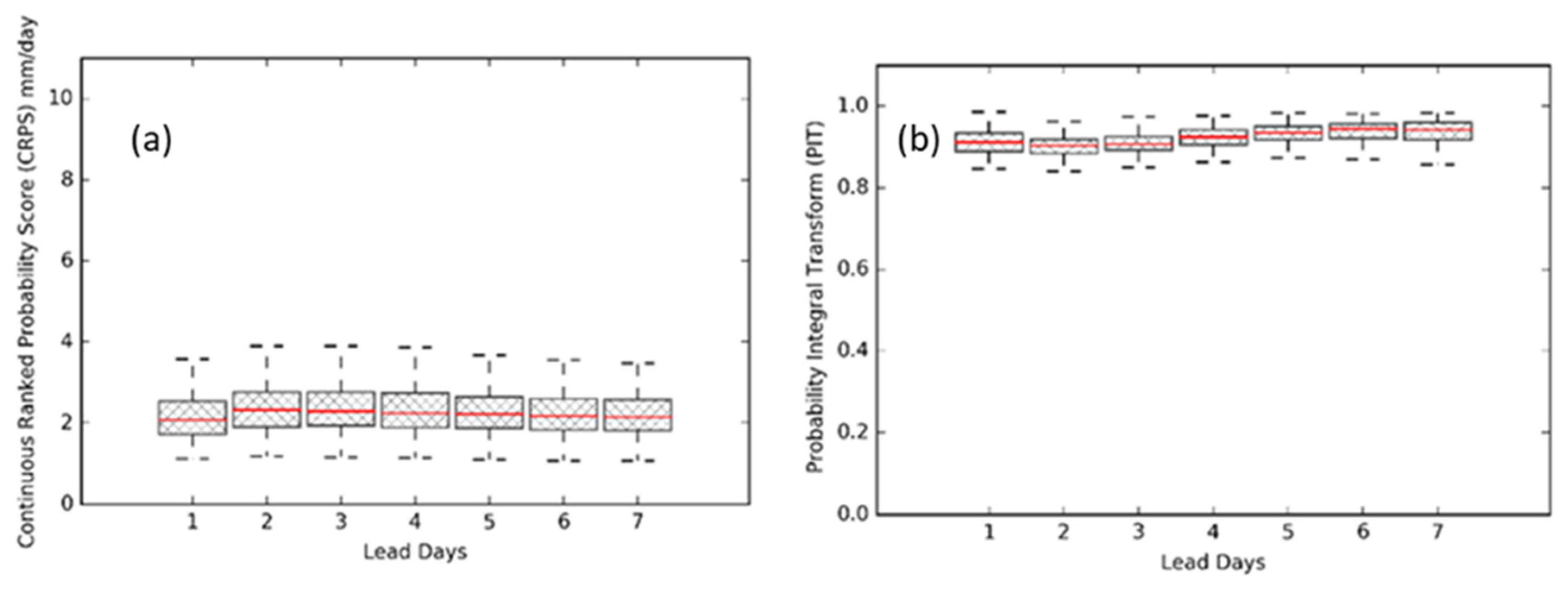
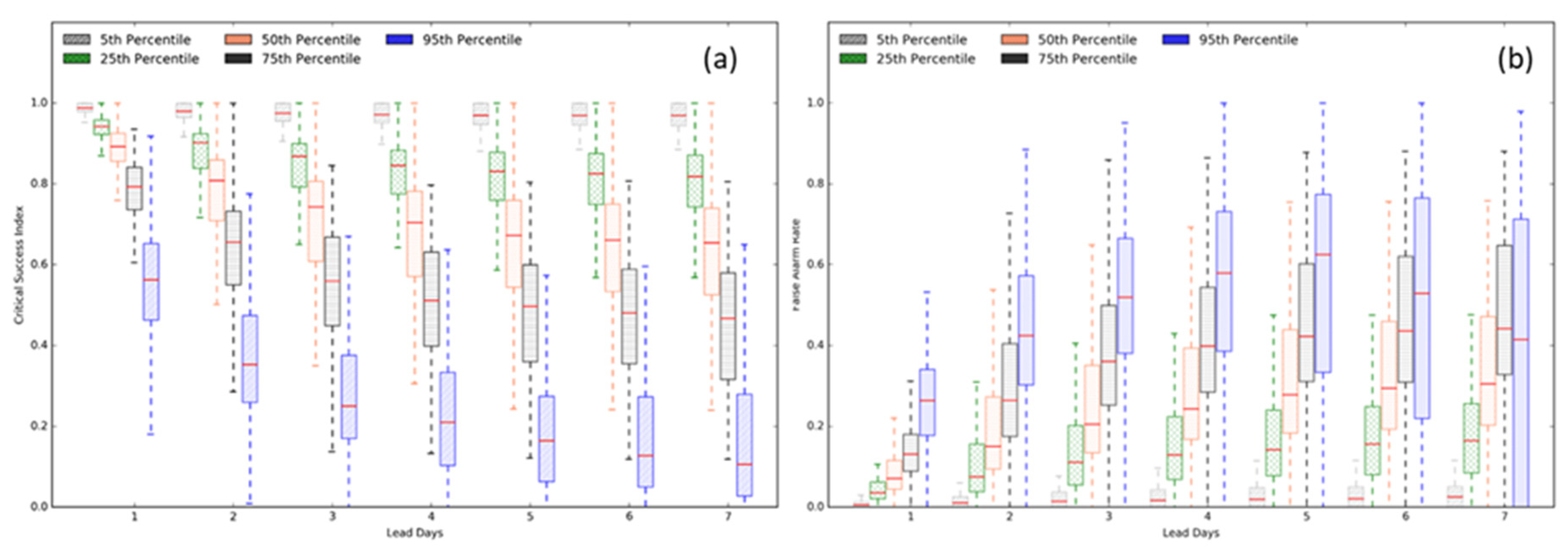
4.1. Evaluation of Rainfall Forecasts

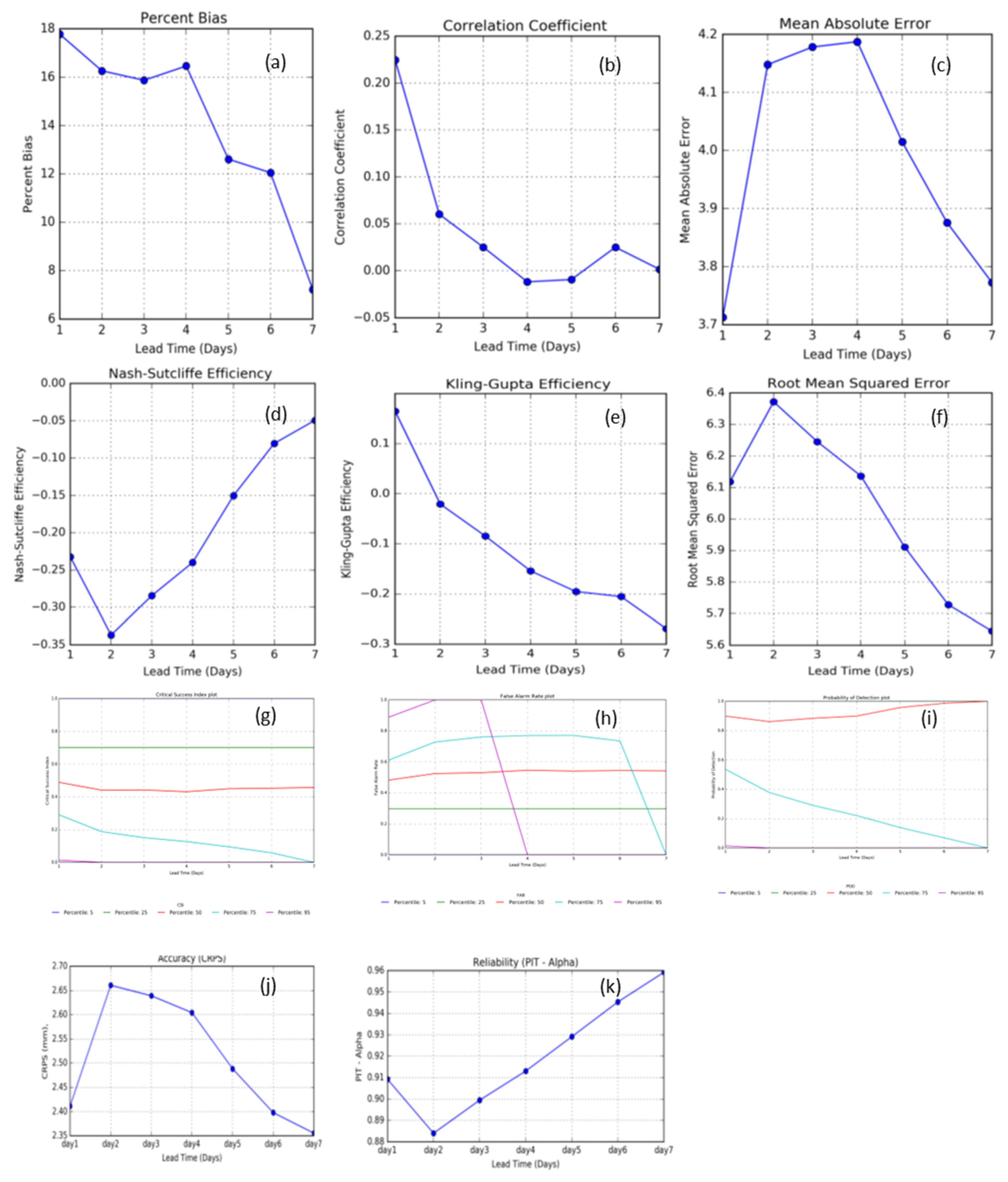
4.1.1. Performance of Ensemble Mean

In our deterministic analysis, we considered several performance metrics for deterministic analysis, including PBias, MAE and NSE, KGE, RMSE and PCC (Appendix A) across all forecast locations. The mean bias for all catchments ( n =96) approached zero, and gradually deteriorated with longer forecast horizons (Figure 3a). However, the percentile range of bias remained remarkably consistent across different forecast horizons (Day 1 to Day 7). Only about 40% and 10% of catchments had positive bias, respectively (Figure 3b). These findings closely resemble those obtained for the verification period used in developing the service [8]. The rainfall post-processor, CHyPP, played an important role in reducing bias in NWP rainfall forecasts. As anticipated based on PBias and MAE, NSE of the bias corrected forecast rainfall remained low (despite post-processing) and decreased progressively as the forecast horizon increased. Only about 95% of catchments showed positive KGE for Day 1 forecasts while this figure dropped to about 10% for the subsequent 6 days (Figure 3c). The percentile range of forecast also steadily decreased as the forecast horizon increased, with Day 1 having the largest range. Similar trends in steadily declining performance skills have been observed by other researchers – in India [48], Canada [7], China [22,49] and USA [17], just to name a few. Furthermore, when assessing rainfall forecast performance using KGE and PCC, we found relative increases, but an overall decrease as the forecast horizon extended. These patterns were consistent across both KGE and PCC metrics.
Performance of rainfall forecasts calculated using the MAE metric was similar to PBias. The median MAE was 3.3 mm/day for day 1 forecast and increased for the remaining 6 days and remained stable at around 3.7 mm/day (Figure 4a). Surprisingly, the percentile range of MAE was the largest for Day 4 and gradually decreased over the remaining three days forecasts. The MAE was greater than 5.7 mm/day or greater only for about 4% of the catchments (Figure 4b). Similar results were also evident in RMSE.
Three categorical metrics – CSI, POD and FAR – accurately evaluate the performance of rainfall forecasts across different amounts that fall within specified time frames [50,51]. These metrics have been widely used for assessment of rainfall forecasts [52,53]. In our deterministic assessment of forecast rainfall performance, we categorised the total daily amounts into 5 distinct classes – 5th, 25th, 50th, 75th and 95th percentiles (an example catchment is shown in Figure A1). Forecast performance of rainfall varied among these percentiles and also across different forecast horizons (Figure 5). The best performance was obtained from the 25th percentile range and it deteriorated for higher rainfall amounts and forecast horizons. Extreme predicted rainfall events showed minimal or no skill beyond Day 1. These findings aligned with the assessment of POD, which yielded similar results.

4.1.2. Performance of Ensemble Forecasts

We computed CRPS, relative CRPS and PIT Alpha metrics for all 96 catchments (Figure 6). Similar to that found for the deterministic form, forecast skills gradually diminished as the forecast horizon increased. The percentile range of CRPS was highest in Days 3 and 4, respectively and gradually decreased. However, the PIT Alpha was lowest for Days 2 and 3, and increased successively for the remaining Days 4-7. Our findings are similar to those verification skills from the development phase of the service [5,8]

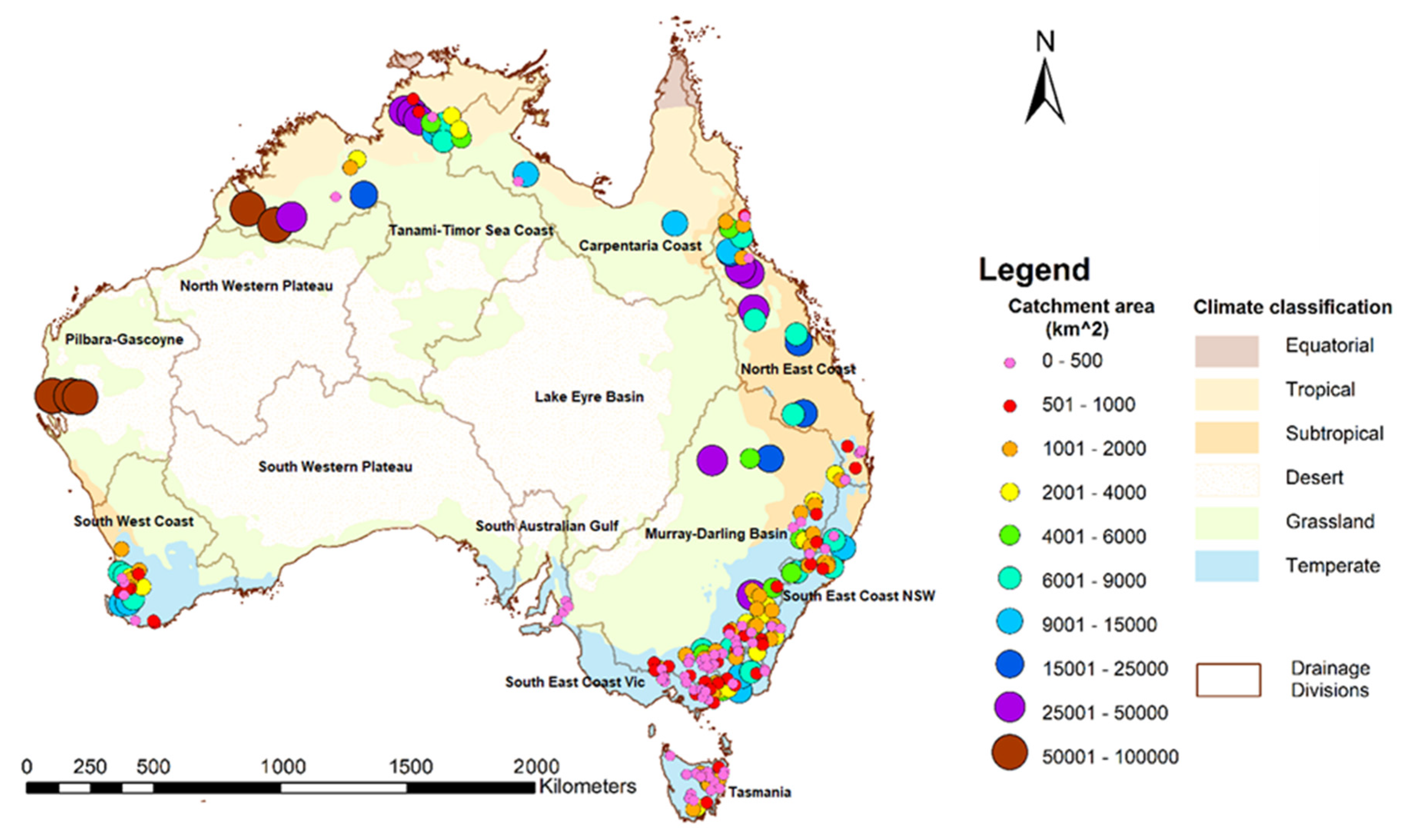
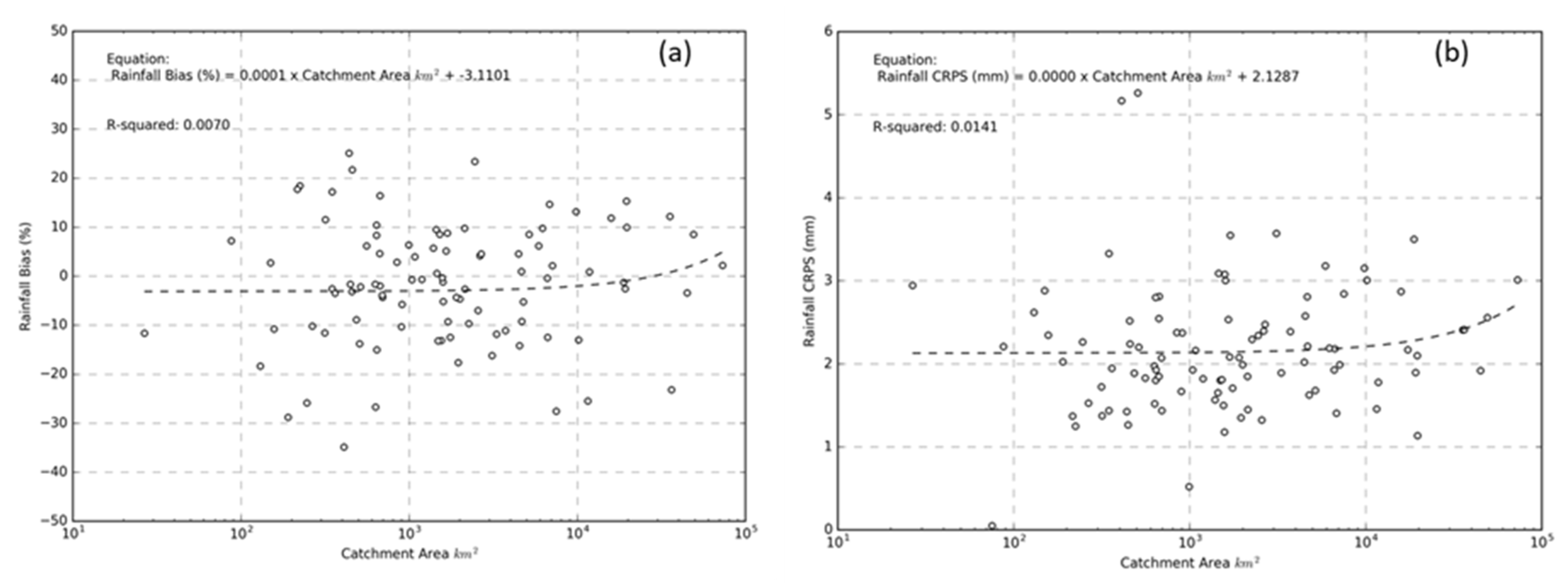
4.1.3. Skills and Catchment Areas

In addition to performance metrics and diagnostic plots, we investigated rainfall forecast skill and its association with catchment area (Figure 7). The catchment area ranges from 26 km2 to 86000 km2 (Figure 1). While there is a positive relationship between catchment area and NSE (not shown), there appeared to be no relationship with PBias, with PIT-Alpha (not shown) or with CRPS. This is in contrast to other findings across the world. For example, the national flood warning system in New Zealand, has performance skills that increase with catchment area [54].

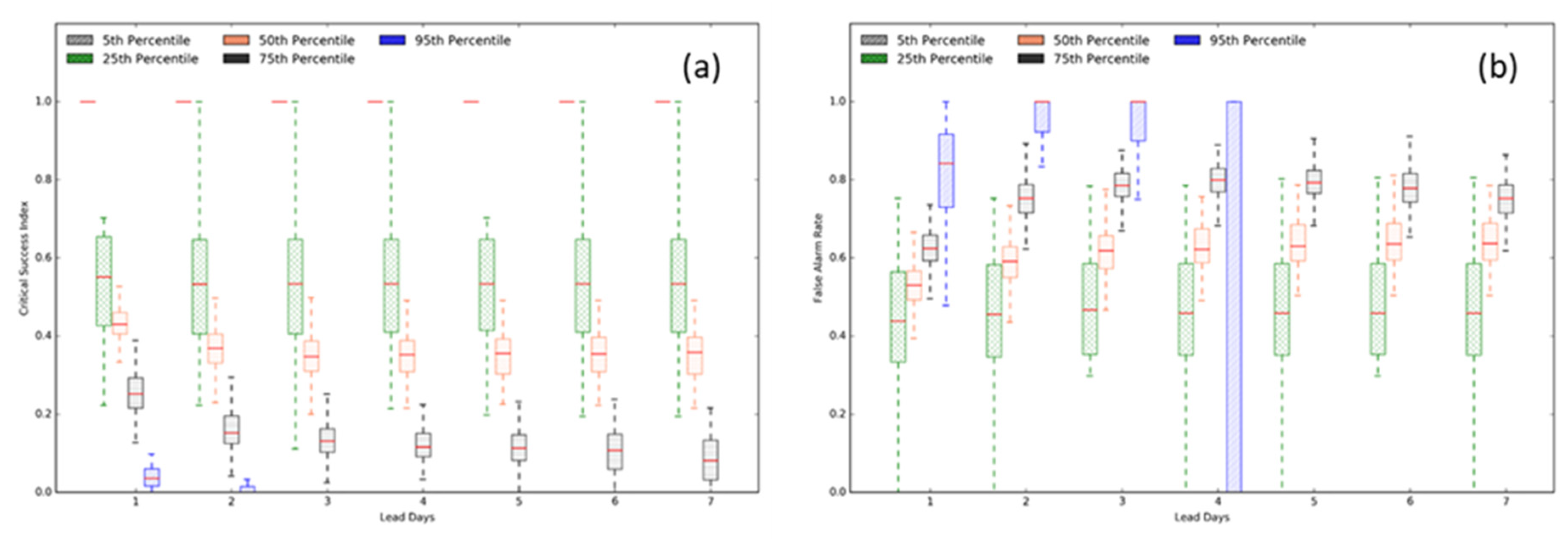
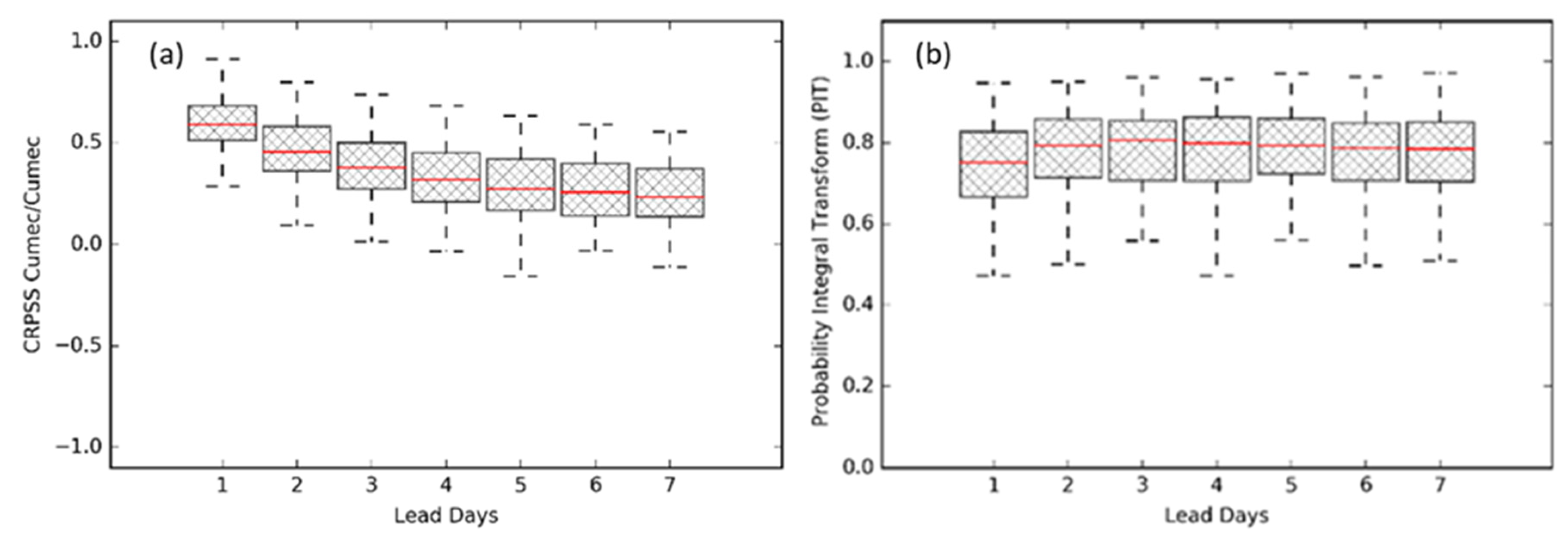
4.2. Evaluation of Streamflow Forecasts

We assessed and evaluated the 7-day ensemble streamflow forecasts using the metric as described in Appendix A and present the results in the following sections. Details of the performance metrics of a randomly selected catchment from New South Wales was shown in Figure A2.

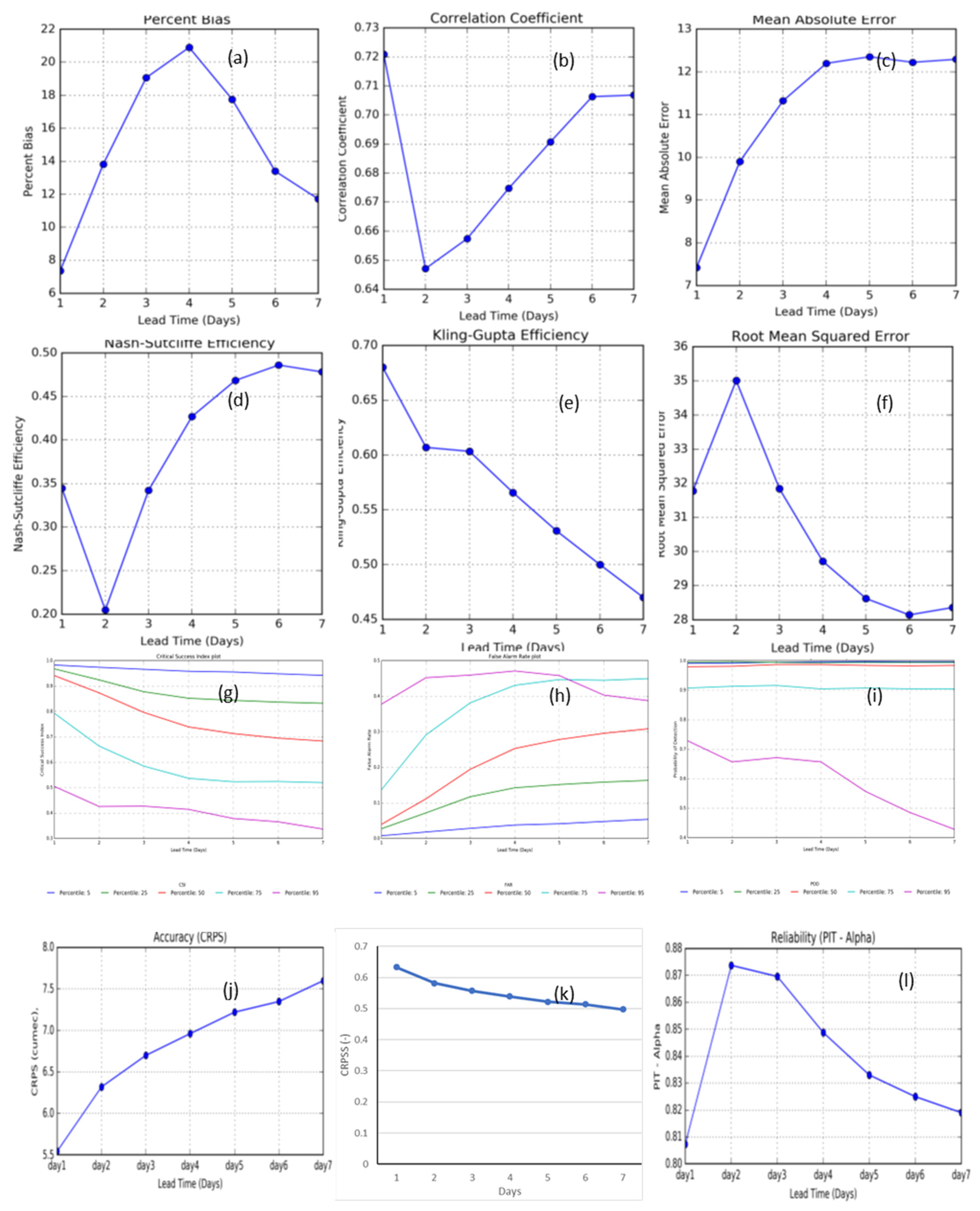
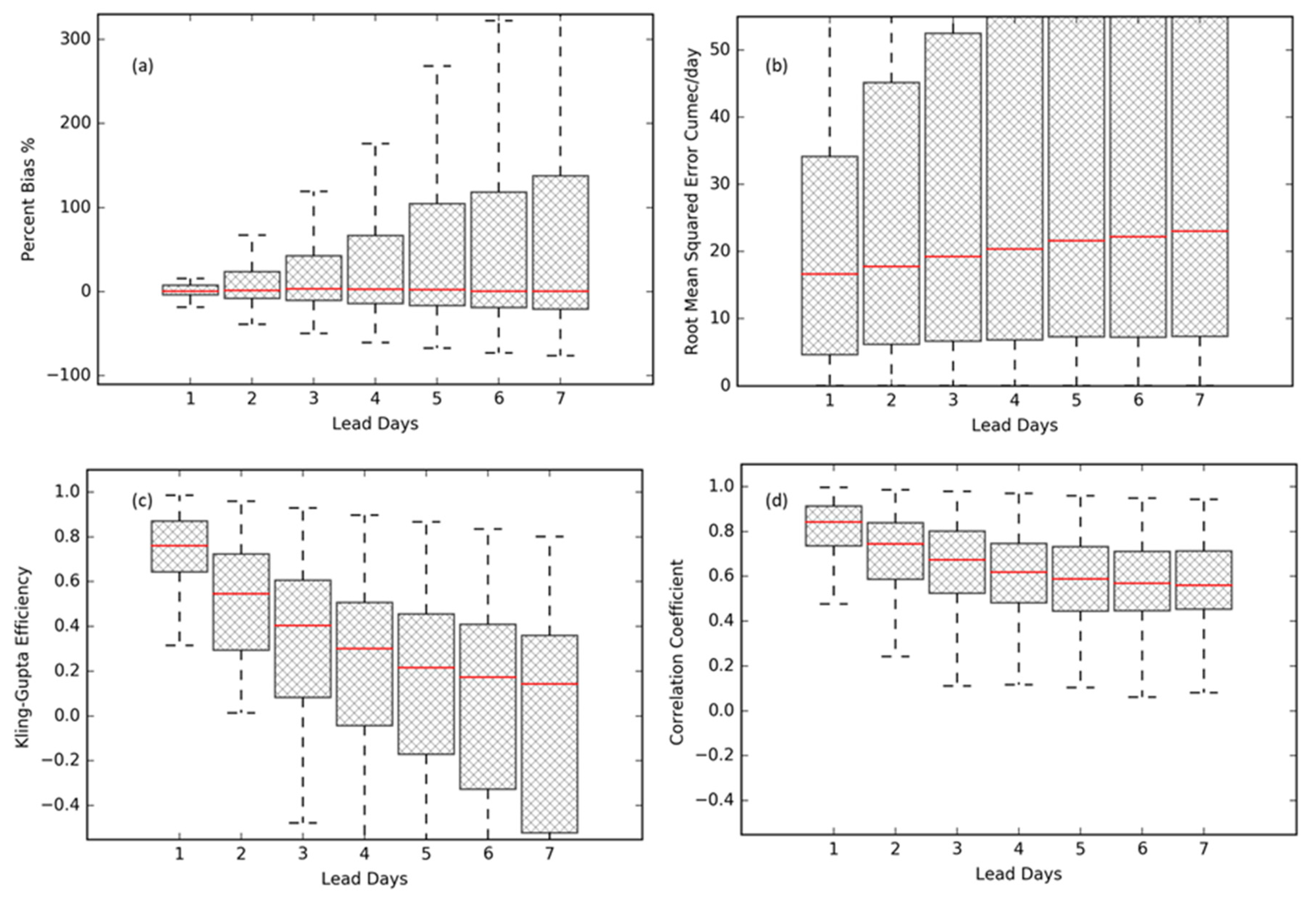
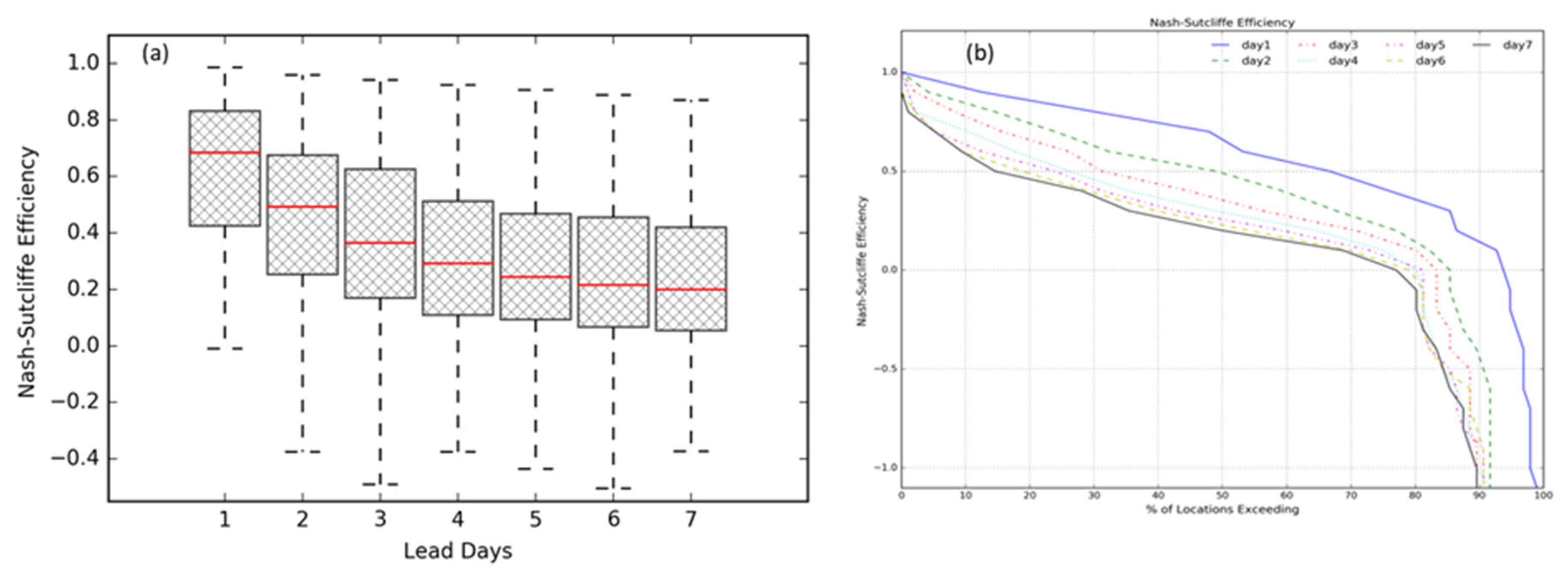
4.2.1. Performance of Ensemble Mean

Box plots of streamflow forecasting performance skills PBias, RMSE, NSE and PCC for all locations are shown in Figure 8. Skills clearly declined gradually as the forecast horizon increased from Day 1 to Day 7. The median bias for all forecast location remained very close to zero, but the percentile range increased steadily. This is different from the rainfall forecast (Figure 4a) where the median of the bias decreased over the forecast horizon and the range bound remained fairly constant. The apparent improvement in skills could be attributed to implementation of streamflow post processing [37] and the streamflow routing scheme in the SWIFT modelling system. Forecast skill using the other three metrics – RMSE, KGE and PCC, led to a similar conclusion. The performance decayed approximately exponentially as forecast horizon increased (Figure 8). However, the lower percentile bound of KGE, from Day 3 onwards, was below zero, meaning some forecast locations had no skill. Similarly, the upper bound of RMSE was very high for some catchments, indicating poorer performance.
The NSE of all catchments and forecast locations is presented in Figure 9. Similar to the other metrics, performance decreased as forecast horizon increased. Only about 25% of catchments had NSE greater than 0.6 and 0.4, respectively, for lead times 3 to 7 days. In an operational context, this performance skill is better than that found in a similar study in India using ECMWF data set as the forcing variable [48].
Categorical metrics are widely used to assess performance of streamflow and flood predictions [52,53,55,56,57]. Similar to rainfall, we classified the streamflow of different percentiles and calculated CSI, POD and FAR for all catchments (an example shown in Figure A2) for different flow regimes to further understand the model's predictive capabilities. Forecast performance progressively decreased with the higher streamflow regime and longer lead times (Figure 10). Performance of the rainfall forecast was even poorer (Figure 5) indicating that streamflow forecast skill was improved by the postprocessing error correction scheme. Another reason for poorer performance of extreme high flows could be the fewer events used in the analysis, and higher measurement uncertainty [58]. Matthews et al. [59] found similar results in Europe when comparing CRPSS of rainfall and streamflow prediction at different quantile ranges.

4.2.2. Performance of Ensemble Forecasts

Streamflow forecasting performance skills – CRPSS and PIT-Alpha again reaffirm that skills gradually decline as forecast horizon increases (Figure 11). The CRPSS skill was somewhat lower to that obtained during the development phase of the service [5,8] for Day 1 but higher for the subsequent 6 days. Few catchments had negative CRPSS skill, meaning the performance was lower than if using reference climatology. Similar results were also evident for the relative CRPS metric. The median of the PIT-Alpha score was also very similar to that obtained during the development phase of the service. However, the percentile band was much wider (Figure 11b). The streamflow forecasting skills also showed better performance than skills obtained from a similar studies conducted in USA [20], Canada [60], Europe [59], South America [19] and around the world [38]. Our findings suggest that the operational 7-day ensemble streamflow forecasting service is robust, and this provides greater confidence for end users who use or wish to use these forecasts to support water management decision making.

4.2.3. Spatial and Temporal Performance

Here we present the CRPSS and PIT-Alpha performance statistics for all 96 forecast locations for the four year evaluation period (2020 to 2023). The key idea was to identify any spatial pattern in streamflow forecasting performance skills. It was clear the model performance was poorer for the catchments in the western part of the Great Dividing Range, South Australia and mid-west of Western Australia (Figure 12). The spatial pattern of the two metrics was similar across the continent.
In addition to spatial mapping of results, we investigated regional patterns of forecast performance skills for different states and territories (jurisdictions), and present only Day 3 skills (NSE, CRPSS and PIT Alpha) in Table 1. Except for the Northern Territory, performance of only a small number of catchments at all other jurisdictions were poorer as evidenced by the deterministic, ensemble median NSE (Figure 9a). This may not represent the reality as the sample number is only 4 in Northern Territory. The maximum NSE among different jurisdictions ranged from 71% (Tasmania) to 94% (Western Australia). There were also a small number of catchments in New South Wales, Queensland and Tasmania where the CRPSS scores were negative. Most of these forecast locations had poorer NSE scores as well. The CRPSS score were greater than 20% for half of the forecast locations in Queensland, which seemed to be poorest performer among all jurisdictions. The performance skills of all forecast locations, as computed by PIT-Alpha, seemed to be better than other two metrics (Table 1). Overall, it appeared that the forecast performance of the operational service is better in Western Australia and poorer in South Australia and Queensland. Most of the underperforming locations across the continent are situated in the interior part of Australia (Figure 12). The principal reason for this poor performance could be attributed to: (i) the lower mean annual rainfall with higher inter-annual variability [61], (ii) intermittent nature of streamflow, (iii) sparse monitoring network, and (iv) poor performance of the rainfall forecasts. Overall, the performance of the system in operational setting seems to be very similar to the one obtained during development phase [8] and gives greater confidence in end-user decision making.

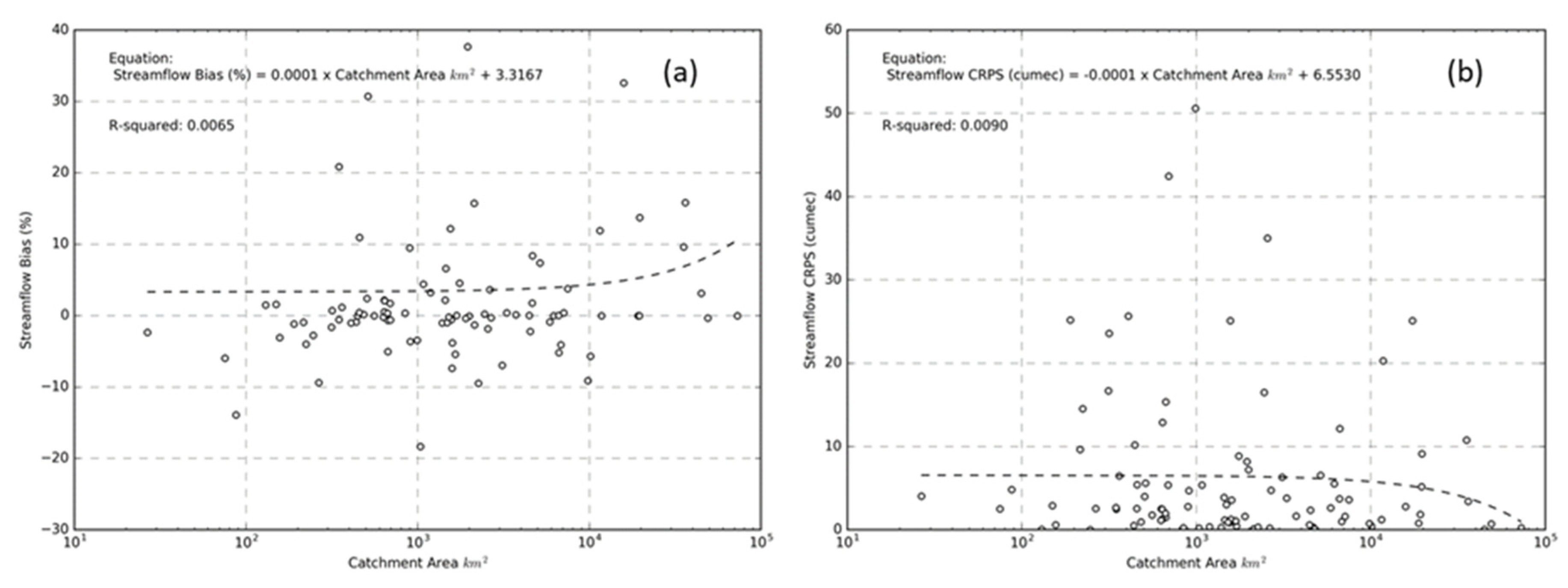
4.2.4. Performance and Catchment Area

In addition to performance metrics and diagnostic plots, we investigated streamflow forecast skill and its relationship with catchment area (Figure 13). We found there are no relationships between catchment area, NSE, PBias, PIT-Alpha, CRPS or other performance metrics. This is different from other studies around the world. For a national flood warning system in New Zealand, it was found that forecast performance skills increase with catchment area [40,54]. Similarly, in the USA, predictive flood forecasting skill of a real-time operational hydrological forecasting model had positive relationships between catchment area [20,62]. In South America, performance skills of medium range (up to 15 days) ensemble streamflow forecasts were investigated and found a positive relationship between forecast skills and catchment area [19]. Similar results were also found in China [49], but with varying relationships between geographical location and differences in climate.
A fundamental property of spatial scale in hydrology [63] is that streamflow varies less with increasing catchment area, due to averaging and smoothing effects of the complex river network. Additionally, as the catchment time of concentration (time for water to flow from the most remote point in a catchment to the outlet) increases and approaches the forecast time horizon, a larger portion of forecast streamflow volume at the catchment outlet is already in the river network, and therefore in the forecast model. In this case, skill of rainfall prediction plays a relatively lesser role as the catchment area increases. Across Australia, 50% of catchments in the 7-day streamflow forecasting service are greater than 1500 km2. There is an indication that CRPS skill score deteriorates for the catchments smaller than 1500 km2 (Figure 13b). Operationally, we implemented ERRIS to post-process hydrological model generated streamflow, and it has been proven that implementing ERRIS significantly increases forecast skill [8]. Further investigation and research in this area may reveal more about the complex relationships between forecast rainfall, flow generation processes and relationship with catchment area.

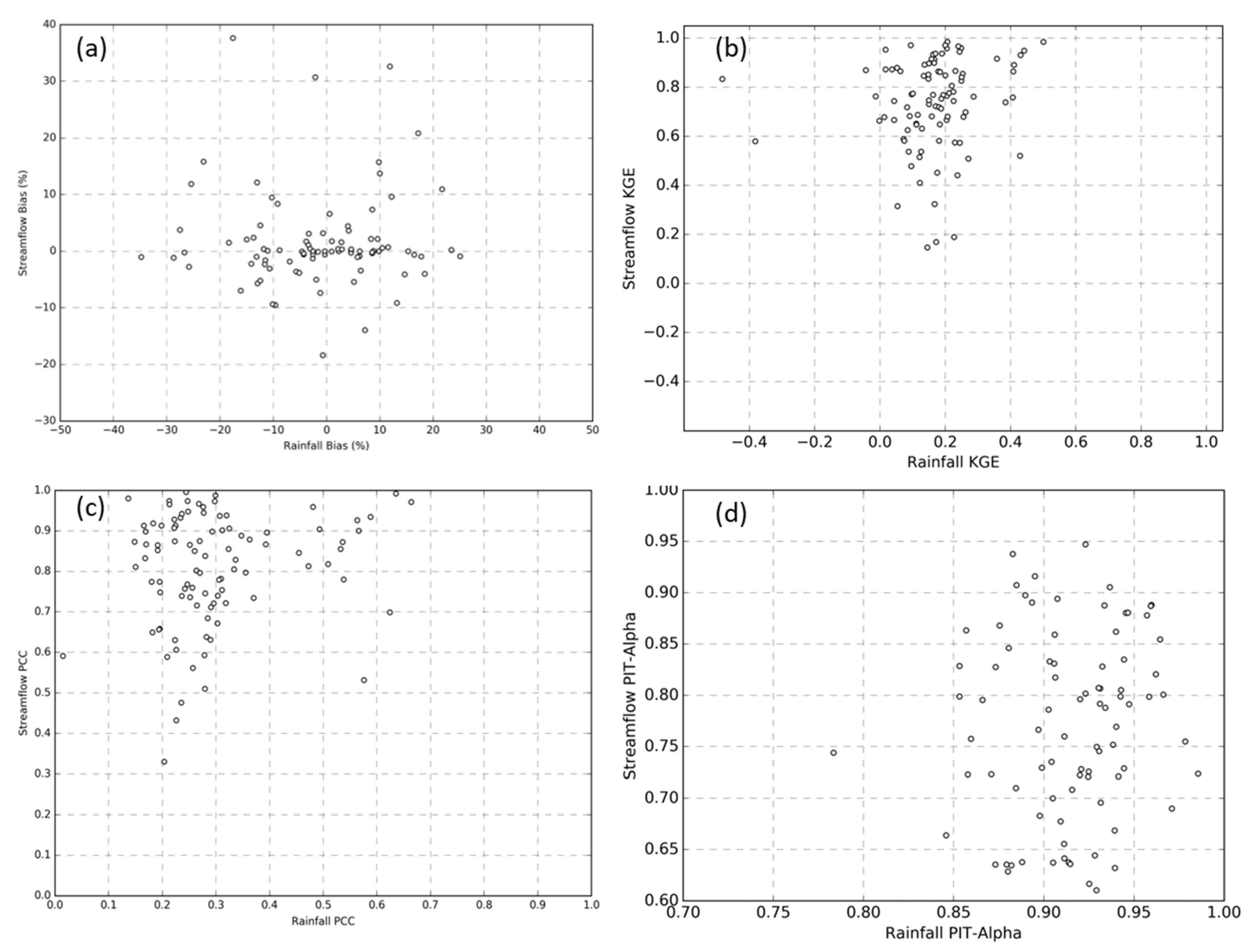
4.2.5. Comparison of Forecast Rainfall and Streamflow Forecast Metrics

We found no clear relationships between different performance evaluation metrics for both rainfall and streamflow forecasts (Figure 14). This finding is in contract to other studies around the world [7,17,22,49]. Further investigation is necessary to better understand these different findings.

5. Discussion and Future Directions

5.1. Service Expansion

Extensive customer consultation was undertaken during development of the 7-day streamflow forecasting service. More than 50 important customers across the country were consulted to identify high value catchments and forecast locations, and to help understand how the service will likely to bring most benefits to them. Due to resource constraints, some selected catchments were not ultimately not included in the service. Initiatives should be undertaken to revisit these catchments and whether forecasting service could be developed. At present the service is available only for catchments located upstream of significant infrastructure development where there is no return flow or diversion from the rivers. Research is needed to understand how infrastructure and river operations and management influence landscape water balance and how the forecasting service could be expanded to managed systems including reservoir inflows, water balance and forecast locations downstream of reservoirs.
Preprints 102470 g014
Figure 14. Scatter plots with one day lead time forecast streamflow metrics against: (a) PBias, (b) KGE, (c) PCC and (d) PIT Alpha, for all 96 forecast locations.
Figure 14. Scatter plots with one day lead time forecast streamflow metrics against: (a) PBias, (b) KGE, (c) PCC and (d) PIT Alpha, for all 96 forecast locations.
Preprints 102470 g014

5.2. Benefits and Adoption of Forecasting

Is there any benefit to using ensemble 7-day streamflow forecasts over simple climatology? The answer is yes – in terms of overall accuracy, performance and reliability. However, forecast skill varied across different regions within the country (Figure 12) and also with lead times (Figure 11). Generally, improvements in NWP rainfall forecasts lead to more accurate and reliable streamflow forecasts. However, our analysis of operational data shows that the primary source of streamflow forecast skill lies in the post-processing error correction scheme – ERRIS – and hydrological persistence, rather than in the rainfall forecasts. This finding is different from those in other parts of the world [19,20,38,59,60]. Additionally, factors such as model initial states, catchment aridity, seasonality and geographical location may also significantly influence forecast performance. It has been demonstrated that combining state updating and error correction model leads to lower streamflow forecast errors [64]. Further investigation is essential to comprehensively understand the variability of forecast skill across different flow regimes, including peak flow magnitude, timing and recession.
How can the ensemble SDF service benefit the community? By encouraging adoption of ensemble forecasts by users, and implementing these into decision-making tools. However, replacing traditional deterministic hydrological forecasts with ensemble forecasts presents challenges. A valuable scientific finding does not automatically align with end-users' decision-making [65]. Several studies have explored usability of streamflow forecasts to support decisions for reservoir operations [66,67], flood forecasting [22], water resource management [68] and hydropower generation [69,70]. One key challenge lies in the operational capacity to ingest and incorporate ensemble forecasts into water management decision support tools. Many existing tools are designed for deterministic inflow scenarios and would require significant upgrades to accommodate automated ensemble streamflow forecasts. The Bureau has been closely working with key stakeholders to increase and improve adoption of the ensemble SDF service in end-user decision-making tools. For example, forecast streamflow time series are delivered to the Murray Darling Basin Authority through File Transfer Protocol (FTP) and ingested into their ROWS system for optimal release from Hume Dam and operation of the River Murray system [71].

5.3. Understanding Forecast Skills and Uncertainties

Rainfall forecasting is very challenging due to the chaotic nature of the atmosphere [72]. Small changes in initial conditions can lead to an entirely different outcome. Modelling deficiencies further add to forecast inaccuracies, especially for longer lead times. However, ongoing improvements in NWP models, skills of rainfall forecast have increased significantly [73,74]. Skilful rainfall forecasts are now being generated by NWP models worldwide, enabling production of relatively skilful streamflow forecasts for water resource management and planning. Ensemble rainfall forecasts extending up to at least 30 days ahead are available from over five NWP models globally. Analysing rainfall data reveals that a multi-model ensemble approach enhances the predictability and reliability of these rainfall forecasts [75]. Exploring potential applications use of extended rainfall forecast data for streamflow forecasting remains an avenue for future research.
Inherent uncertainties in NWP rainfall forecasts are one of four key sources of uncertainties alongside input data, model structure, and parameters and their combinations [76]. These uncertainties vary across catchments, due to catchment characteristics, streamflow magnitude and lead time. Within the hydrological modelling community, it is widely acknowledged that the greatest uncertainty in hydrological forecasting beyond 2 to 3 days originates from rainfall input [16]. However, when considering streamflow forecasts up to 2-3 days ahead, skill primarily originates from rainfall forecasts and catchment persistence. Surprisingly, our study reveals limited skill in rainfall forecasts beyond Day 2 (Figure 3, Figure 4 and Figure 6). Notably, improvements in streamflow forecast skill were due to post-processing error corrections (Figure 8, Figure 9 and Figure 11). The role of persistence in forecast skill shows strong dependence on catchment area, network characteristics and geometric properties [77]. Although catchment area varies significantly across Australia, we observed no clear relationship with forecast skill (Figure 7 and Figure 13). Consequently, it becomes clear that the primary source of skill lies in the streamflow post-processing error correction scheme, ERRIS, with minimal contribution from rainfall forecasts and possibly persistence, or a combination of all three.
Variation in runoff and catchment area across the continent is significant, and some catchments flow only during a few months of the year [8]. There are challenges in accurately measuring low flows due to rating curve, gauging structure, or sensor issues [58]. Conversely, accuracy of high flow measurements might be limited to a specific occurrence. Our analysis revealed that streamflow forecast performance skills were notably lower high flow components (Figure 10). As we develop an ensemble flood forecasting service, it becomes crucial to evaluate high extreme flow events using longer periods of data.
In this study, we investigated the streamflow forecast skill and its geographical patterns (Figure 12, Table 1). However, research from United Kingdom [78] demonstrates that forecast skills depends on initial state, catchment characteristics and declines exponentially beyond three days. This decline is consistent with our findings, and the skills are not uniformly distributed across different hydroclimatic regions. Further investigations are necessary to understand this relationship.

5.4. Adoption for Flood Forecasting Guidance

The ensemble 7-day streamflow forecasting provides additional guidance for Bureau's current deterministic and events based flood forecasting and warning service. However, there is a growing trend toward using ensemble hydrologic forecasting to produce probabilistic flood forecasts [79]. While many aspects of ensemble forecasts for flood preparedness are still being explored, two critical points must be addressed before end-to-end adoption and operation of the ensemble forecasts are possible:
Improving accuracy and timing: improving flood forecast accuracy and skills in terms of the magnitude and timing peaks. Achieving precise predictions for flood peaks is crucial for effective preparedness and response.
Enhanced communication and support: effective communication with end-users is essential. Providing timely and actionable information to decision makers, emergency services and flood preparedness community is vital. The focus typically lies on time scales of hours to a couple of days.
Our forecast horizon is 7-days, and this is considered adequate to cover wide range of flood events, depending on factors such as catchment area, flow-generation mechanism and within-year flow distribution across Australia. The Bureau is actively working to upgrade its flood forecasting and warning service from deterministic to ensemble over the coming years. Leveraging the technology stack used for operational 7-day ensemble streamflow forecasting is vital for this service development.

6. Summary and Conclusions

The Australian Bureau of Meteorology launched its semi-automated operational 7-day ensemble forecasting service in July 2020. The service covers most of the high-value water resources across Australia, and fulfils government and stakeholder requirements.
We evaluated performance of the Bureau's operational forecasts using four years of operational output data between 2020 and 2023. Ensemble rainfall forecasts – European Centre for Medium-Range Weather Forecasts (ECMWF) and Poor Man's Ensemble (PME) – available in the Numerical Weather Prediction (NWP) suite, were taken as input to generate streamflow forecasts. The GR4H lumped rainfall-runoff model, embedded in the Short-term Water Information Forecasting Tools (SWIFT) was used to generate the streamflow forecasts. We evaluated the ensemble rainfall and streamflow forecast through CRPS, CRPSS and PIT-Alpha metrics and its deterministic form using, NSE, KGE, PCC, MAE, RMSE and categorical metrics CSI, POD and FAR. Diagnostic plots were also considered for visual inspection and empirical judgements.
We found the performance skills of the current operational ensemble streamflow forecasts remain consistent with those obtained during the development phase of the service. As we extended the forecast horizon from Day 1 to Day 7, the ensemble forecasting performance scores gradually decreased. This pattern was observed across various metrics, including CRPS, CRPSS, PIT-Alpha, NSE, KGE, PCC, MAE, RMSE, and categorical metrics like CSI, POD, and FAR. Across catchments, most results showed positive skills, indicating that the ensemble forecast outperforms climatology. Notably, there was no significant association between performance skill scores and catchment area. Spatially, streamflow and rainfall forecast skills were generally higher in the high-value water resource catchments, and lower in the western part of the Great Dividing Range, South Australia and mid-west of Western Australia. Our findings demonstrate that the 7-day streamflow forecasting service is robust, which draws confidence from stakeholders to use them to support water resources management decision making. The streamflow forecasts are already used by stakeholders and embedded into their decision-making models. The Bureau is applying similar forecasting approach to develop an integrated ensemble flood and streamflow forecasting service.

Author Contributions

M.A.B. – project administration, conceptualisation, methodology, investigation, analysis, supervision, and writing. M.M.H. – data curation, analyses, investigation, validation and visualisation. G.E.A. – spatial analyses, investigation, and visualisation. A.K. – analysis, review and validation. H.A.P.H. – analyses, review and validation. P.M.F. – project administration, resource allocation, technical editing. A.C. – project administration, resource allocation, technical editing. P.S. – systems integrity, review, edits.

Funding

The research was conducted under the Bureau's day-to-day operational and research business activities. No additional research funds were received from any external sources.

Data Availability Statement

Codes, scripts and workflows used in analysing the operational streamflow forecast data are not available to the public. The day-to-day forecast data are available to the user community upon request via the “Feedback” page of the 7-day ensemble streamflow forecast website: http:www.bom. gov.au/water/7daystreamflow/ (accessed 10th March 2024).

Acknowledgments

The SWIFT modelling system was developed through the funding from the Water Information Research and Development Alliance (WIRADA) between the Bureau and CSIRO. We sincerely thank our technical reviewers Christopher Pickett-Heaps, Urooj Khan and Biju George for their time, careful review, and valuable comments and suggestions. The large computations for this research were undertaken through the use of the National Computational Infrastructure (NCI), supported by the Australian Government.

Conflicts of Interest

We declare that the research was conducted in the absence of any commercial or financial relationships that could be interpretated as a potential conflict of interest.

Appendix A. Forecast Performance Evaluation Metrics

Streamflow data from 1990 to 2016 is used for climatological streamflow calculation. Climatological streamflow value is calculated on daily basis using the data from a 29 day window. For a given day, the climatology value is the distribution of data within the period from 2 weeks before to 2 weeks after the target day over the climatology period. Metrics were computed for each lead time – Day 1 to Day 7.
DETERMINISTIC FORECAST
PBias: This metrics estimates whether the model is consistently underestimating or overestimating streamflow. It can be positive (underestimation) or negative (overestimation) and was calculated for each lead time (in days) as:
P B i a s = ∑ i = 1 n Q i , o b s − Q i , s i m ∑ i = 1 n Q i , o b s * 100
In the above equation Q i , o b s was observed streamflow, Q i , s i m was modelled streamflow, LT was lead-time in days, and n was total number of observations.
Pearson's Correlation Coefficient (PCC): The PCC measures the linear correlation between observed and simulated time series, in our case the rainfall and streamflow respectively. It is calculated as:
P C C ∑ i = 1 n Q i , s i m − Q i , s i m ¯ Q i , o b s − Q i , o b s ¯ ∑ i = 1 n Q i , s i m − Q i , s i m ¯ 2 ∑ i = 1 n Q i , o b s − Q i , o b s ¯ 2
The value of PCC is bounded between –1 and 1 and measures the strength and direction of the relationship. When one variable changes, the other variable changes in the same direction.
Mean Absolute Error (MAE): Mean Absolute Error (MAE) is the average of the magnitude of the errors. The perfect score is zero, and was calculated by:
M A E = ∑ i = 1 n Q i , o b s − Q i , s i m n
Nash-Sutcliffe Efficiency (NSE): The Nash-Sutcliffe efficiency [80] quantifies the relative magnitude of residual variance compared to the observed streamflow variance, by:
N S E = 1 − ∑ i = 1 n Q i , o b s − Q i , s i m 2 ∑ i = 1 n Q i , o b s − Q o b s ¯ 2
In the above equation Q o b s ¯ was the mean observed streamflow. In this study, NSE is used to assess the performance of the model forecast for each of the lead time.
Kling-Gupta Efficiency (KGE): The KGE [81] performance metric is widely used in environmental and hydrologic forecasting and is defined as:
K G E = 1 − ( r − 1 ) 2 + ( α − 1 ) 2 + ( β − 1 ) 2
In the above equation r is Pearson Correlation Coefficient (Equation A2), α is a term that represents the variability of the forecast errors and is defined by the ratio of the standard deviation of the observed and predicted data ( σ s i m σ o b s ) and β is the ratio of the mean of the observed and simulated data ( μ s i m μ o b s ) respectively.
Root Mean Squire Error (RMSE): The RMSE measures the average difference between the predicted values and observed ones. It provides an estimate of how accurately the model can predict the target time series.
R M S E = 1 n ∑ i = 1 n ( Q i , s i m − Q i , o b s ) 2
ENSEMBLE FORECAST
CRPS: This metrics allows for quantitative comparison between deterministic and ensemble forecasts. It is calculated as the difference between cumulative distribution of forecast with the corresponding observation [82]. The CRPS reduces to the mean absolute error for (MAE, Equation A2) deterministic forecasts and given by:
C R P S = 1 T ∑ t = 1 T ∫ x = − ∞ x = ∞ ( F t f ( x ) − F t o ( x ) ) 2 d x
In the above equation, F t f ( x ) is the forecast cumulative distribution (CDF) probability for the tth forecast F t o ( x ) is the observed CDF probability (Heaviside function). For ensemble rainfall, the relative CRPS, as a function of catchment mean rainfall ( R ¯ ) is calculate as:
C R P S % = C R P S R ¯ X 100
CRPSS: This metric measures the relative performance of streamflow forecast and is calculated with respect to the reference forecast. It is calculated as:
C R P S S = 1 − C R P S f o r e c a s t C R P S c l i m
In the above equation, C R P S c l i m is the reference forecast, calculated from streamflow climatology period.
PIT: The Probability Integral Transform diagram (PIT) is used assess the reliability of ensemble forecasts [83]. It is the cumulative distribution function (CDF) of the forecasts F t ( f t ) evaluated at observations Q t (rainfall or streamflow) and is given by:
P I T t = F t ( Q t )
PIT is uniformly distributed for reliable forecasts and falls on the 1:1 line for a perfect forecast. To avoid visual disparity, we have used quantitative score of Kolmogorov-Smirnov Goodness (KS-D) statistic to measure the deviation of PIT values from the perfect forecast. The KS-D statistic is used to compare maximum deviation of cumulative PIT distribution from uniform distribution of the forecasts. We used PIT-Alpha [84] to compare PIT values of forecast ensemble streamflow and rainfall from all catchments:
α = 1 −   2 T ∑ t = 1 T P I T t * − t T + 1
In the above equation, P I T t * is the sorted P I T t .
CATEGORICAL METRICS
The categorical metrics for the assessment of streamflow and rainfall forecast included [85]: Probability of Detection (POD), False Alarm Ratio (FAR), and Critical Success Index (CSI). These metrics are extensively used in operational forecast assessment [52,53,55].
Probability of Detection (POD): The POD is based on the correctly identified ( X ) and missed ( Y ) number of forecast class. The value ranges from 0 to 1 and perfect score is 1.
P O D = X X + Y
False Alarm Rate (FAR): The FAR depends upon the class detected by the forecasts but not observed ( Z ) and the correctly identified ( X ) ones. The value of the metric ranges from perfect score of 0 to 1.
F A R = Z X + Z
Critical Success Index (CSI): The CSI represents the overall number for forecasts correctly produced by the model. Its value ranges from 0 to perfect score 1.
C S I = X X + Y + Z
Preprints 102470 g0a1
Figure A1. Graphical representation of forecast rainfall performance metrics of a randomly selected catchment from Tasmania: (a) PBias, (b) PCC, (c) MAE, (d) NSE, (e) KGE, (f) RMSE, (g) CSI of 5th, 25th, 50th, 75th, and 95th percentiles, (h) FAR, (i) POD, (j) CRPS and (k) PIT Alpha.
Figure A1. Graphical representation of forecast rainfall performance metrics of a randomly selected catchment from Tasmania: (a) PBias, (b) PCC, (c) MAE, (d) NSE, (e) KGE, (f) RMSE, (g) CSI of 5th, 25th, 50th, 75th, and 95th percentiles, (h) FAR, (i) POD, (j) CRPS and (k) PIT Alpha.
Preprints 102470 g0a1
Preprints 102470 g0a2
Figure A2. Graphical representation of forecast streamflow performance metrics of a randomly selected catchment from New South Wales: (a) PBias, (b) PCC, (c) MAE, (d) NSE, (e) KGE, (f) RMSE, (g) CSI of 5th, 25th, 50th, 75th and 95th percentiles, (h) FAR, (i) POD, (j) CRPS and (k) CRPSS and (l) PIT Alpha.
Figure A2. Graphical representation of forecast streamflow performance metrics of a randomly selected catchment from New South Wales: (a) PBias, (b) PCC, (c) MAE, (d) NSE, (e) KGE, (f) RMSE, (g) CSI of 5th, 25th, 50th, 75th and 95th percentiles, (h) FAR, (i) POD, (j) CRPS and (k) CRPSS and (l) PIT Alpha.
Preprints 102470 g0a2

References

  1. Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; De Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in Southeast Australia (2001-2009): Natural and Human Causes and Implications for Water Resources, Ecosystems, Economy, and Society. Water Resour. Res. 2013, 49, 1040–1057. [CrossRef]
  2. Low, K.G.; Grant, S.B.; Hamilton, A.J.; Gan, K.; Saphores, J.D.; Arora, M.; Feldman, D.L. Fighting Drought with Innovation: Melbourne’s Response to the Millennium Drought in Southeast Australia. Wiley Interdiscip. Rev. Water 2015, 2, 315–328. [CrossRef]
  3. Kirby, J.M.; Connor, J.; Ahmad, M.D.; Gao, L.; Mainuddin, M. Climate Change and Environmental Water Reallocation in the Murray-Darling Basin: Impacts on Flows, Diversions and Economic Returns to Irrigation. J. Hydrol. 2014, 518, 120–129. [CrossRef]
  4. Wang, J.; Horne, A.; Nathan, R.; Peel, M.; Neave, I. Vulnerability of Ecological Condition to the Sequencing of Wet and Dry Spells Prior to and during the Murray-Darling Basin Millennium Drought. J. Water Resour. Plan. Manag. 2018, 144. [CrossRef]
  5. Kabir, A.; Hasan, M.M.; Hapuarachchi, H.A.P.; Zhang, X.S.; Liyanage, J.; Gamage, N.; Laugesen, R.; Plastow, K.; MacDonald, A.; Bari, M.A.; et al. Evaluation of Multi-Model Rainfall Forecasts for the National 7-Day Ensemble Streamflow Forecasting Service. 2018 Hydrol. Water Resour. Symp. HWRS 2018 Water Communities 2018, 393–406.
  6. Hapuarachchi, H.A.P.; Kabir, A.; Zhang, X.S.; Kent, D.; Bari, M.A.; Tuteja, N.K.; Hasan, M.M.; Enever, D.; Shin, D.; Plastow, K.; et al. Performance Evaluation of the National 7-Day Water Forecast Service. Proc. - 22nd Int. Congr. Model. Simulation, MODSIM 2017 2017, 1815–1821. [CrossRef]
  7. Boucher, M.A.; Anctil, F.; Perreault, L.; Tremblay, D. A Comparison between Ensemble and Deterministic Hydrological Forecasts in an Operational Context. Adv. Geosci. 2011, 29, 85–94. [CrossRef]
  8. Hapuarachchi, H.A.P.; Bari, M.A.; Kabir, A.; Hasan, M.M.; Woldemeskel, F.M.; Gamage, N.; Sunter, P.D.; Zhang, X.S.; Robertson, D.E.; Bennett, J.C.; et al. Development of a National 7-Day Ensemble Streamflow Forecasting Service for Australia. Hydrol. Earth Syst. Sci. 2022, 26, 4801–4821. [CrossRef]
  9. Daley, J.; Wood, D.; Chivers, C. Regional Patterns of Australia’s Economy and Population; 2017; ISBN 9780987612151.
  10. Stern, H.; De Hoedt, G.; Ernst, J. Objective Classification of Australian Climates. Aust. Meteorol. Mag. 2000.
  11. Milly, P.C.D.; Dunne, K.A.; Vecchia, A. V. Global Pattern of Trends in Streamflow and Water Availability in a Changing Climate. Nature 2005, 438, 347–350. [CrossRef]
  12. Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J.L. Generating Ensemble Streamflow Forecasts: A Review of Methods and Approaches Over the Past 40 Years. Water Resour. Res. 2021, 57, 1–48. [CrossRef]
  13. Kumar, V.; Sharma, K.V.; Caloiero, T.; Mehta, D.J. Comprehensive Overview of Flood Modeling Approaches: A Review of Recent Advances. 2023. [CrossRef]
  14. Pappenberger, F.; Ramos, M.H.; Cloke, H.L.; Wetterhall, F.; Alfieri, L.; Bogner, K.; Mueller, A.; Salamon, P. How Do I Know If My Forecasts Are Better? Using Benchmarks in Hydrological Ensemble Prediction. J. Hydrol. 2015, 522, 697–713. [CrossRef]
  15. Wu, W.; Emerton, R.; Duan, Q.; Wood, A.W.; Wetterhall, F.; Robertson, D.E. Ensemble Flood Forecasting: Current Status and Future Opportunities. Wiley Interdiscip. Rev. Water 2020, 7. [CrossRef]
  16. Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and Global Scale Flood Forecasting Systems. Wiley Interdiscip. Rev. Water 2016, 3, 391–418. [CrossRef]
  17. Demargne, J.; Wu, L.; Regonda, S.K.; Brown, J.D.; Lee, H.; He, M.; Seo, D.J.; Hartman, R.; Herr, H.D.; Fresch, M.; et al. The Science of NOAA’s Operational Hydrologic Ensemble Forecast Service. Bull. Am. Meteorol. Soc. 2014, 95, 79–98. [CrossRef]
  18. Zahmatkesh, Z.; Jha, S.K.; Coulibaly, P.; Stadnyk, T. 17 CrossRef Citations to Date 1 Altmetric Articles An Overview of River Flood Forecasting Procedures in Canadian Watersheds. Can. Water Resour. Jouurnal 2019, 44, 219–229. [CrossRef]
  19. Siqueira, V.A.; Fan, F.M.; Paiva, R.C.D. de; Ramos, M.H.; Collischonn, W. Potential Skill of Continental-Scale, Medium-Range Ensemble Streamflow Forecasts for Flood Prediction in South America. J. Hydrol. 2020, 590, 125430. [CrossRef]
  20. Siddique, R.; Mejia, A. Ensemble Streamflow Forecasting across the U.S. Mid-Atlantic Region with a Distributed Hydrological Model Forced by GEFS Reforecasts. J. Hydrometeorol. 2017, 18, 1905–1928. [CrossRef]
  21. Mai, J.; Arsenault, R.; Tolson, B.A.; Latraverse, M.; Demeester, K. Application of Parameter Screening to Derive Optimal Initial State Adjustments for Streamflow Forecasting. Water Resour. Res. 2020, 56, 1–22. [CrossRef]
  22. Liu, L.; Ping Xu, Y.; Li Pan, S.; Xu Bai, Z. Potential Application of Hydrological Ensemble Prediction in Forecasting Floods and Its Components over the Yarlung Zangbo River Basin, China. Hydrol. Earth Syst. Sci. 2019, 23, 3335–3352. [CrossRef]
  23. Raupach, M.R.; Briggs, P.R.; Haverd, V.; King, E.A.; Paget, M.; Trudinger, C.M. The Centre for Australian Weather and Climate Research A Partnership between CSIRO and the Bureau of Meteorology Australian Water Availability Project (AWAP): CSIRO Marine and Atmospheric Research Component: Final Report for Phase 3; Canberra, 2009;
  24. Robertson, D.E.; Shrestha, D.L.; Wang, Q.J. Post-Processing Rainfall Forecasts from Numerical Weather Prediction Models for Short-Term Streamflow Forecasting. Hydrol. Earth Syst. Sci. 2013, 17, 3587–3603. [CrossRef]
  25. Perraud, J.M.; Bridgart, R.; Bennett, J.C.; Robertson, D. Swift2: High Performance Software for Short-Medium Term Ensemble Streamflow Forecasting Research and Operations. In Proceedings of the Proceedings - 21st International Congress on Modelling and Simulation, MODSIM 2015; 2015.
  26. Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003. [CrossRef]
  27. Coron, L.; Andréassian, V.; Perrin, C.; Lerat, J.; Vaze, J.; Bourqui, M.; Hendrickx, F. Crash Testing Hydrological Models in Contrasted Climate Conditions: An Experiment on 216 Australian Catchments. Water Resour. Res. 2012. [CrossRef]
  28. Li, M.; Wang, Q.J.; Bennett, J.C.; Robertson, D.E. Error Reduction and Representation in Stages (ERRIS) in Hydrological Modelling for Ensemble Streamflow Forecasting. Hydrol. Earth Syst. Sci. 2016. [CrossRef]
  29. Lucatero, D.; Madsen, H.; Refsgaard, J.C.; Kidmose, J.; Jensen, K.H. Seasonal Streamflow Forecasts in the Ahlergaarde Catchment, Denmark: The Effect of Preprocessing and Post-Processing on Skill and Statistical Consistency. Hydrol. Earth Syst. Sci. 2018, 22, 3601–3617. [CrossRef]
  30. Roy, T.; He, X.; Lin, P.; Beck, H.E.; Castro, C.; Wood, E.F. Global Evaluation of Seasonal Precipitation and Temperature Forecasts from Nmme. J. Hydrometeorol. 2020, 21, 2473–2486. [CrossRef]
  31. D. S. Wilks. Statistical Methods in the Atmospheric Sciences, Second Edition; 2007; Vol. 14; ISBN 0127519653.
  32. Manubens, N.; Caron, L.P.; Hunter, A.; Bellprat, O.; Exarchou, E.; Fučkar, N.S.; Garcia-Serrano, J.; Massonnet, F.; Ménégoz, M.; Sicardi, V.; et al. An R Package for Climate Forecast Verification. Environ. Model. Softw. 2018, 103, 29–42. [CrossRef]
  33. Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory Overview: Error Metrics for Hydrologic Modelling – A Review of Common Practices and an Open Source Library to Facilitate Use and Adoption. Environ. Model. Softw. 2019, 119, 32–48. [CrossRef]
  34. Murphy, A.H. What Is a Good Forecast? An Essay on the Nature of Goodness in Weather Forecasting. Am. Meteorol. Soc. 1993, 8, 281–293. [CrossRef]
  35. Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M.; et al. The Subseasonal to Seasonal (S2S) Prediction Project Database. Bull. Am. Meteorol. Soc. 2017, 98, 163–173. [CrossRef]
  36. Becker, E.; van den Dool, H. Probabilistic Seasonal Forecasts in the North American Multimodel Ensemble: A Baseline Skill Assessment. J. Clim. 2016, 29, 3015–3026. [CrossRef]
  37. Bennett, J.C.; Robertson, D.E.; Wang, Q.J.; Li, M.; Perraud, J.M. Propagating Reliable Estimates of Hydrological Forecast Uncertainty to Many Lead Times. J. Hydrol. 2021. [CrossRef]
  38. Huang, Z.; Zhao, T. Predictive Performance of Ensemble Hydroclimatic Forecasts: Verification Metrics, Diagnostic Plots and Forecast Attributes. Wiley Interdiscip. Rev. Water 2022, 9, 1–30. [CrossRef]
  39. Krzysztofowicz, R. Bayesian Theory of Probabilistic Forecasting via Deterministic Hydrologic Model. 1999, 35, 2739–2750. [CrossRef]
  40. McMillan, H.K.; Booker, D.J.; Cattoën, C. Validation of a National Hydrological Model. J. Hydrol. 2016, 541, 800–815. [CrossRef]
  41. Hossain, M.M.; Faisal Anwar, A.H.M.; Garg, N.; Prakash, M.; Bari, M. Monthly Rainfall Prediction at Catchment Level with the Facebook Prophet Model Using Observed and CMIP5 Decadal Data. Hydrology 2022, 9. [CrossRef]
  42. Wu, H.; Adler, R.F.; Tian, Y.; Gu, G.; Huffman, G.J. Evaluation of Quantitative Precipitation Estimations through Hydrological Modeling in IFloods River Basins. J. Hydrometeorol. 2017, 18, 529–553. [CrossRef]
  43. Piadeh, F.; Behzadian, K.; Alani, A.M. A Critical Review of Real-Time Modelling of Flood Forecasting in Urban Drainage Systems. J. Hydrol. 2022, 607, 127476. [CrossRef]
  44. Xu, J.; Ye, A.; Duan, Q.; Ma, F.; Zhou, Z. Improvement of Rank Histograms for Verifying the Reliability of Extreme Event Ensemble Forecasts. Environ. Model. Softw. 2017, 92, 152–162. [CrossRef]
  45. Yang, C.; Yuan, H.; Su, X. Bias Correction of Ensemble Precipitation Forecasts in the Improvement of Summer Streamflow Prediction Skill. J. Hydrol. 2020, 588, 124955. [CrossRef]
  46. Feng, J.; Li, J.; Zhang, J.; Liu, D.; Ding, R. The Relationship between Deterministic and Ensemble Mean Forecast Errors Revealed by Global and Local Attractor Radii. Adv. Atmos. Sci. 2019, 36, 271–278. [CrossRef]
  47. Duan, W.; Huo, Z. An Approach to Generating Mutually Independent Initial Perturbations for Ensemble Forecasts: Orthogonal Conditional Nonlinear Optimal Perturbations. J. Atmos. Sci. 2016, 73, 997–1014. [CrossRef]
  48. Singh, A.; Mondal, S.; Samal, N.; Jha, S.K. Evaluation of Precipitation Forecasts for Five-Day Streamflow Forecasting in Narmada River Basin. Hydrol. Sci. J. 2022, 00, 1–19. [CrossRef]
  49. Cai, C.; Wang, J.; Li, Z.; Shen, X.; Wen, J.; Wang, H.; Wu, C. A New Hybrid Framework for Error Correction and Uncertainty Analysis of Precipitation Forecasts with Combined Postprocessors. Water (Switzerland) 2022, 14. [CrossRef]
  50. Acharya, S.C.; Nathan, R.; Wang, Q.J.; Su, C.H.; Eizenberg, N. An Evaluation of Daily Precipitation from a Regional Atmospheric Reanalysis over Australia. Hydrol. Earth Syst. Sci. 2019, 23, 3387–3403. [CrossRef]
  51. Liu, D. A Rational Performance Criterion for Hydrological Model. J. Hydrol. 2020, 590, 125488. [CrossRef]
  52. Cai, Y.; Jin, C.; Wang, A.; Guan, D.; Wu, J.; Yuan, F.; Xu, L. Spatio-Temporal Analysis of the Accuracy of Tropical Multisatellite Precipitation Analysis 3b42 Precipitation Data in Mid-High Latitudes of China. PLoS ONE 2015, 10, 1–22. [CrossRef]
  53. Ghajarnia, N.; Liaghat, A.; Daneshkar Arasteh, P. Comparison and Evaluation of High Resolution Precipitation Estimation Products in Urmia Basin-Iran. Atmos. Res. 2015, 158–159, 50–65. [CrossRef]
  54. Cattoën, C.; Conway, J.; Fedaeff, N.; Lagrava, D.; Blackett, P.; Montgomery, K.; Shankar, U.; Carey-Smith, T.; Moore, S.; Mari, A.; et al. A National Flood Awareness System for Ungauged Catchments in Complex Topography: The Case of Development, Communication and Evaluation in New Zealand. J. Flood Risk Manag. 2022, 1–28. [CrossRef]
  55. Tian, B.; Chen, H.; Wang, J.; Xu, C.Y. Accuracy Assessment and Error Cause Analysis of GPM (V06) in Xiangjiang River Catchment. Hydrol. Res. 2021, 52, 1048–1065. [CrossRef]
  56. Tedla, H.Z.; Taye, E.F.; Walker, D.W.; Haile, A.T. Evaluation of WRF Model Rainfall Forecast Using Citizen Science in a Data-Scarce Urban Catchment: Addis Ababa, Ethiopia. J. Hydrol. Reg. Stud. 2022, 44, 101273. [CrossRef]
  57. Hossain, S.; Cloke, H.L.; Ficchì, A.; Gupta, H.; Speight, L.; Hassan, A.; Stephens, E.M. A Decision-Led Evaluation Approach for Flood Forecasting System Developments: An Application to the Global Flood Awareness System in Bangladesh. J. Flood Risk Manag. 2023, 1–22. [CrossRef]
  58. McMahon, T.A.; Peel, M.C. Uncertainty in Stage–Discharge Rating Curves: Application to Australian Hydrologic Reference Stations Data. Hydrol. Sci. J. 2019, 64, 255–275. [CrossRef]
  59. Matthews, G.; Barnard, C.; Cloke, H.; Dance, S.L.; Jurlina, T.; Mazzetti, C.; Prudhomme, C. Evaluating the Impact of Post-Processing Medium-Range Ensemble Streamflow Forecasts from the European Flood Awareness System. Hydrol. Earth Syst. Sci. 2022, 26, 2939–2968. [CrossRef]
  60. Dion, P.; Martel, J.L.; Arsenault, R. Hydrological Ensemble Forecasting Using a Multi-Model Framework. J. Hydrol. 2021, 600, 126537. [CrossRef]
  61. Dey, R.; Lewis, S.C.; Arblaster, J.M.; Abram, N.J. A Review of Past and Projected Changes in Australia’s Rainfall. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10. [CrossRef]
  62. Vivoni, E.R.; Entekhabi, D.; Bras, R.L.; Ivanov, V.Y.; Van Horne, M.P.; Grassotti, C.; Hoffman, R.N. Extending the Predictability of Hydrometeorological Flood Events Using Radar Rainfall Nowcasting. J. Hydrometeorol. 2006, 7, 660–677. [CrossRef]
  63. Oda, T.; Maksyutov, S.; Andres, R.J.; Office, A.; Technology, E.S.; Information, D.; Ridge, O.; Ridge, O. Scaling, Similarity, and the Fourth Paradigm for Hydrology. Hydrol. Earth Syst. Sci. 2019, 10, 87–107. [CrossRef]
  64. Robertson, D.E.; Bennett, J.C.; Shrestha, D.L. Assimilating Observations from Multiple Stream Gauges into Semi-Distributed Hydrological Models for Streamflow Forecasting. 2020, 1–55.
  65. Bruno Soares, M.; Dessai, S. Barriers and Enablers to the Use of Seasonal Climate Forecasts amongst Organisations in Europe. Clim. Change 2016, 137, 89–103. [CrossRef]
  66. Viel, C.; Beaulant, A.-L.; Soubeyroux, J.-M.; Céron, J.-P. How Seasonal Forecast Could Help a Decision Maker: An Example of Climate Service for Water Resource Management. Adv. Sci. Res. 2016, 13, 51–55. [CrossRef]
  67. Turner, S.W.D.; Bennett, J.C.; Robertson, D.E.; Galelli, S. Complex Relationship between Seasonal Streamflow Forecast Skill and Value in Reservoir Operations. Hydrol. Earth Syst. Sci. 2017, 21, 4841–4859. [CrossRef]
  68. Schepen, A.; Zhao, T.; Wang, Q.J.; Zhou, S.; Feikema, P. Optimising Seasonal Streamflow Forecast Lead Time for Operational Decision Making in Australia. Hydrol. Earth Syst. Sci. 2016, 20, 4117–4128. [CrossRef]
  69. Anghileri, D.; Voisin, N.; Castelletti, A.; Pianosi, F.; Nijssen, B.; Lettenmaier, D.P.; 1Institute Value of Long-Term Streamflow Forecasts to Reservoir Operations for Water Supply in Snow-Dominated River Catchments. Water Resour. Res. 2016, 52, 4209–4225. [CrossRef]
  70. Ahmad, S.K.; Hossain, F. A Web-Based Decision Support System for Smart Dam Operations Using Weather Forecasts. J. Hydroinformatics 2019, 21, 687–707. [CrossRef]
  71. Woldemeskel, F.; Kabir, A.; Hapuarachchi, P.; Bari, M. Adoption of 7-Day Streamflow Forecasting Service for Operational Decision Making in the Murray Darling Basin, Australia. Hydrol. Water Resour. Symp. (HWRS 2021), 24 August—1 Sept. 2021 2021.
  72. Lorenz, E.N. The Predictability of a Flow Which Possesses Many Scales of Motion. Tellus A Dyn. Meteorol. Oceanogr. 1969, 21, 289. [CrossRef]
  73. Cuo, L.; Pagano, T.C.; Wang, Q.J. A Review of Quantitative Precipitation Forecasts and Their Use in Short- to Medium-Range Streamflow Forecasting. J. Hydrometeorol. 2011, 12, 713–728. [CrossRef]
  74. Kalnay, E. Historical Perspective: Earlier Ensembles and Forecasting Forecast Skill. Q. J. R. Meteorol. Soc. 2019, 145, 25–34. [CrossRef]
  75. Specq, D.; Batté, L.; Déqué, M.; Ardilouze, C. Multimodel Forecasting of Precipitation at Subseasonal Timescales Over the Southwest Tropical Pacific. Earth Sp. Sci. 2020, 7. [CrossRef]
  76. Zappa, M.; Jaun, S.; Germann, U.; Walser, A.; Fundel, F. Superposition of Three Sources of Uncertainties in Operational Flood Forecasting Chains. Atmos. Res. 2011, 100, 246–262. [CrossRef]
  77. Ghimire, G.R.; Krajewski, W.F. Exploring Persistence in Streamflow Forecasting. J. Am. Water Resour. Assoc. 2020, 56, 542–550. [CrossRef]
  78. Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking Ensemble Streamflow Prediction Skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [CrossRef]
  79. Demargne, J.; Wu, L.; Regonda, S.K.; Brown, J.D.; Lee, H.; He, M.; Seo, D.J.; Hartman, R.K.; Herr, H.D.; Fresch, M.; et al. Design and Implementation of an Operational Multimodel Multiproduct Real-Time Probabilistic Streamflow Forecasting Platform. J. Hydrometeorol. 2017, 56, 91–101. [CrossRef]
  80. Nash, J.E.; Sutcliffe, J. V. River Flow Forecasting through Conceptual Models Part I - A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [CrossRef]
  81. Gupta, H.V.; Kling, H. On Typical Range, Sensitivity, and Normalization of Mean Squared Error and Nash-Sutcliffe Efficiency Type Metrics. Water Resour. Res. 2011, 47, 2–4. [CrossRef]
  82. Hersbach, H. Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems. Weather Forecast. 2000, 15, 559–570. [CrossRef]
  83. Laio, F.; Tamea, S. Verification Tools for Probabilistic Forecasts of Continuous Hydrological Variables. Hydrol. Earth Syst. Sci. 2007, 11, 1267–1277. [CrossRef]
  84. Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding Predictive Uncertainty in Hydrologic Modeling: The Challenge of Identifying Input and Structural Errors. Water Resour. Res. 2010, 46, 1–22. [CrossRef]
  85. Schaefer, J. The Critical Success Index as an Indicator of Warning Skill. Weather Forecast. 1990, 5, 570–575. [CrossRef]
Preprints 102470 g001
Figure 1. Drainage Divisions, hydroclimatic regions and forecast locations. Catchment area is shown by size and color of circles.
Figure 1. Drainage Divisions, hydroclimatic regions and forecast locations. Catchment area is shown by size and color of circles.
Preprints 102470 g001
Preprints 102470 g002
Figure 2. Flow diagram of the forecast generation and publication process for the 7-day streamflow forecast service.
Figure 2. Flow diagram of the forecast generation and publication process for the 7-day streamflow forecast service.
Preprints 102470 g002
Preprints 102470 g003
Figure 3. Rainfall forecast skill in deterministic form, all 96 catchments: (a) median PBias (%); and (b) percentage of forecast locations exceeding median bias, (c) KGE and (d) percentage of forecast locations exceeding KGE for different lead times.
Figure 3. Rainfall forecast skill in deterministic form, all 96 catchments: (a) median PBias (%); and (b) percentage of forecast locations exceeding median bias, (c) KGE and (d) percentage of forecast locations exceeding KGE for different lead times.
Preprints 102470 g003
Preprints 102470 g004
Figure 4. Median MAE (mm/day) of forecast rainfall: (a) 96 catchments; and (b) percentage of catchments exceeding median MAE for different lead times.
Figure 4. Median MAE (mm/day) of forecast rainfall: (a) 96 catchments; and (b) percentage of catchments exceeding median MAE for different lead times.
Preprints 102470 g004
Preprints 102470 g005
Figure 5. Categorical metrics of all 96 forecast locations – for different rainfall percentiles: (a) CSI and (b) FAR.
Figure 5. Categorical metrics of all 96 forecast locations – for different rainfall percentiles: (a) CSI and (b) FAR.
Preprints 102470 g005
Preprints 102470 g006
Figure 6. Box plots of rainfall forecasting skills of all 96 forecast locations: (a) CRPS, and (b) PIT-Alpha.
Figure 6. Box plots of rainfall forecasting skills of all 96 forecast locations: (a) CRPS, and (b) PIT-Alpha.
Preprints 102470 g006
Preprints 102470 g007
Figure 7. Performance of one day lead time rainfall forecast and catchment area: (a) PBias, and (b) CRPS.
Figure 7. Performance of one day lead time rainfall forecast and catchment area: (a) PBias, and (b) CRPS.
Preprints 102470 g007
Preprints 102470 g008
Figure 8. Streamflow forecast skill deterministic form: (a) Mean PBias, (b) RMSE, (c) KGE and (d) PCC, all 96 forecast locations.
Figure 8. Streamflow forecast skill deterministic form: (a) Mean PBias, (b) RMSE, (c) KGE and (d) PCC, all 96 forecast locations.
Preprints 102470 g008
Preprints 102470 g009
Figure 9. Box plots of streamflow forecasting skills of all 96 forecast locations: (a) NSE (%), and (b) percentage of catchments exceeding median NSE (%) for different lead times.
Figure 9. Box plots of streamflow forecasting skills of all 96 forecast locations: (a) NSE (%), and (b) percentage of catchments exceeding median NSE (%) for different lead times.
Preprints 102470 g009
Preprints 102470 g010
Figure 10. Categorical metrics for all 96 forecast locations – for streamflow in the 5th, 25th, 50th, 75th, and 95th percentiles: (a) CSI, and (b) FAR.
Figure 10. Categorical metrics for all 96 forecast locations – for streamflow in the 5th, 25th, 50th, 75th, and 95th percentiles: (a) CSI, and (b) FAR.
Preprints 102470 g010
Preprints 102470 g011
Figure 11. Box plots of streamflow forecasting skill (a) CRPSS (compared to mean observed flow) and (b) PIT-Alpha, all 96 forecast locations.
Figure 11. Box plots of streamflow forecasting skill (a) CRPSS (compared to mean observed flow) and (b) PIT-Alpha, all 96 forecast locations.
Preprints 102470 g011
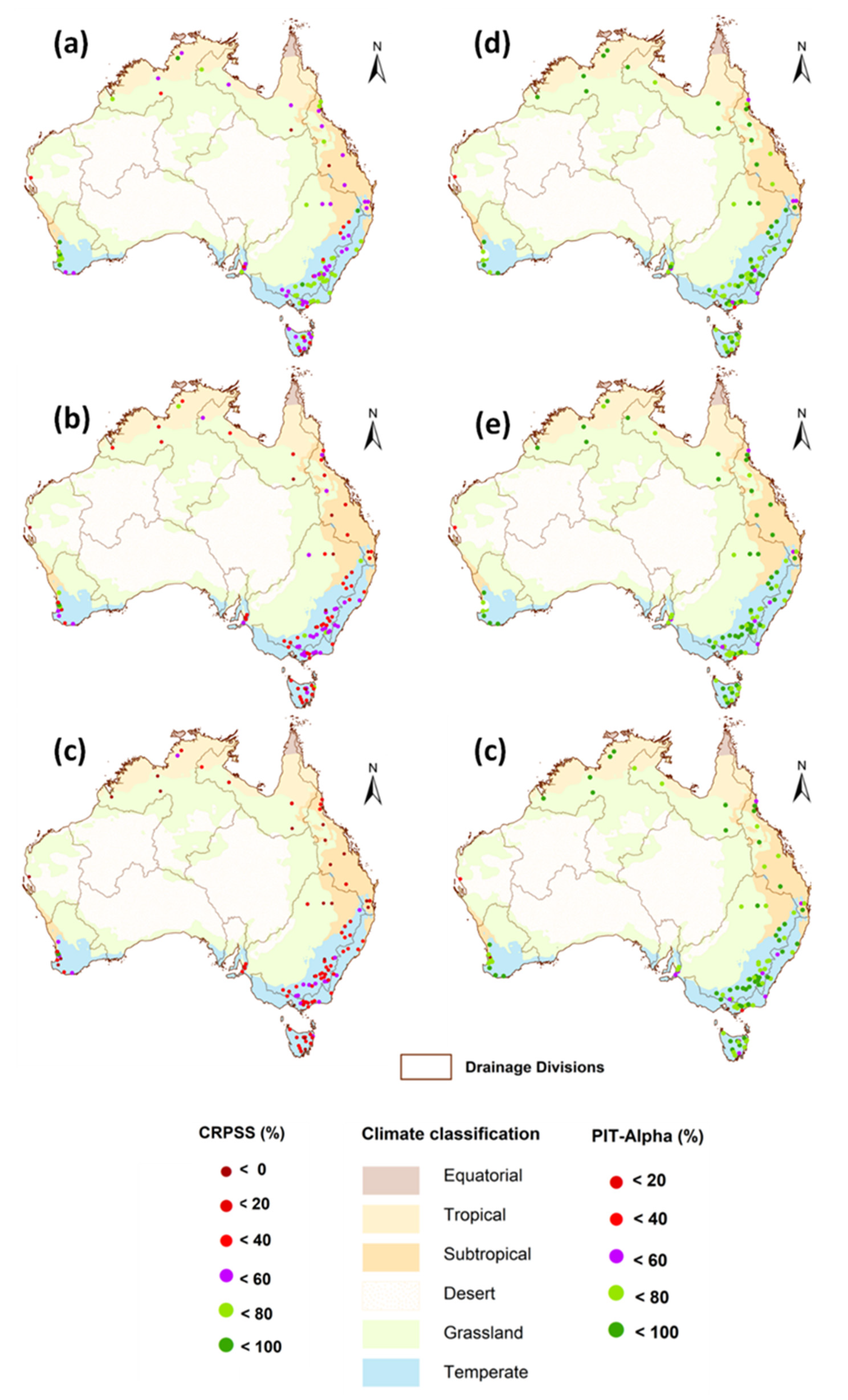
Preprints 102470 g012
Figure 12. Spatial plots of ensemble streamflow forecast skills: (a) CRPSS Day 1, (b) CRPSS Day 3, (c) CRPSS Day 7, (d) PIT Alpha Day 2, (e) PIT Alpha Day 4 and (f) PIT Alpha Day 6.
Figure 12. Spatial plots of ensemble streamflow forecast skills: (a) CRPSS Day 1, (b) CRPSS Day 3, (c) CRPSS Day 7, (d) PIT Alpha Day 2, (e) PIT Alpha Day 4 and (f) PIT Alpha Day 6.
Preprints 102470 g012
Preprints 102470 g013
Figure 13. Performance of one day lead time streamflow forecast and catchment area: (a) PBias, and (b) CRPS, all 96 forecast locations.
Figure 13. Performance of one day lead time streamflow forecast and catchment area: (a) PBias, and (b) CRPS, all 96 forecast locations.
Preprints 102470 g013
Table 1. Streamflow performance skills (NSE, CRPSS and PIT-Alpha) for different jurisdictions – forecast horizon Day 3.
Table 1. Streamflow performance skills (NSE, CRPSS and PIT-Alpha) for different jurisdictions – forecast horizon Day 3.
Jurisdiction Number of locations NSE (%) CRPSS (%) PIT-Alpha (%)
5th 50th 95th Max 5th 50th 95th Max 5th 50th 95th Max
New South Wales 28 <0 29 63 68 13 39 57 63 57 81 91 92
Northern Territory 4 43 59 88 91 29 41 65 67 70 81 85 85
Queensland 15 <0 13 82 83 <0 20 60 70 50 81 93 94
South Australia 4 <0 22 62 68 6 24 50 54 51 71 78 78
Tasmania 14 <0 43 71 71 <0 33 57 63 63 78 91 91
Victoria 19 <0 38 72 82 21 47 60 63 55 79 91 93
Western Australia 12 <0 75 88 94 12 44 84 92 45 83 91 96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated