A Dynamic Programming Approach to Collision Avoidance of Autonomous Ships

Preprint

Article

A Dynamic Programming Approach to Collision Avoidance of Autonomous Ships

Altmetrics

Downloads

113

Views

Comments

A peer-reviewed article of this preprint also exists.

Raphael Zaccone^*

This version is not peer-reviewed

Submitted:

29 March 2024

Posted:

29 March 2024

You are already at the latest version

Alerts

Abstract

The advancement of autonomous capabilities in maritime navigation has gained significant attention, with a trajectory moving from decision support systems to full autonomy. This push towards autonomy has led to extensive research focusing on collision avoidance, a critical aspect of safe navigation. Among the various possible approaches, Dynamic Programming is a promising tool for optimizing collision avoidance maneuvers. This paper presents a DP formulation for collision avoidance of autonomous vessels. We set up the problem framework, formulate it as a multi-stage decision process, define cost functions and constraints focusing on the actual requirements a marine maneuver must comply with, and propose a solution algorithm leveraging parallel computing. Additionally, we present a greedy approximation to reduce algorithm complexity. Through case studies, we demonstrate the effectiveness of the proposed approach in navigating complex scenarios, contributing to the future of autonomous maritime navigation. Through case studies, we show the efficacy of our approach in navigating complex scenarios.

Keywords:

Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity

1. Introduction

The future of navigation points toward increasing the autonomous capabilities of ships [1,2], from decision support systems to fully autonomous navigation. The framework that will guide the future of the maritime world is hinged on the classification released by the International Maritime Organization (IMO) [3], in which four incremental autonomy levels are described for the classification of autonomous ships. The push toward the development of autonomous technologies in the maritime field has created fertile ground for the research community, which has identified numerous scientific gaps in various areas typical of autonomous navigation and marine robotics, such as the development of complex guidance and control algorithms [4,5,6], collaborative control [7,8,9], situational awareness [10], path planning, and collision avoidance.

The problem of collision avoidance is to develop algorithms capable of reacting to the presence of obstacles, fixed or moving in the surrounding environment, and generating trajectories or maneuvers capable of avoiding collision, maintaining an adequate safety distance, and, when applicable, complying with the COLREG [11,12], which set the “rules of the road a ship must follow when interacting with other ships. This requirement is essential in scenarios where autonomous systems interact with human-controlled systems [13]. The scientific literature proposed various approaches to collision avoidance of marine vessels, including A* [14,15], Dijkstra’s algorithm [16,17], visibility graphs [18], rapidly-exploring random trees [19,20,21], and various population-based heuristics [22,23,24,25].

Dynamic Programming (DP) is an effective approach for solving multi-stage optimization problems. From its introduction by Bellman [26,27], DP has been successfully generalized and formulated to describe path planning problems [28]. The requirements of a collision avoidance system are the ability to effectively and efficiently represent obstacles and the surrounding environment and to determine in real-time, with low computational cost, evasive maneuvers that onboard control systems can actuate. These requirements perfectly match the potential of DP, which, in this framework, offers the possibility of a simple and effective problem description, implementation of constraints, and efficient solution schemes capable of exploiting parallelism. Despite the inherent recursive formulation of DP, very efficient solution strategies based on function memoization or tabulation [29] and leveraging parallel computation [30,31,32] have been proposed to optimize the computation efficiency. DP-based algorithms are ideal for scenarios where resources are limited and real-time computation is crucial, such as autonomous vehicles, robotics, and embedded systems, and have found application in a broad range of industrial fields, including railway transportation [33], robotics [34,35], and maritime transport. The maritime literature features various applications of DP, primarily to weather routing problems [36,37,38,39], where the objective is to determine the optimal trajectory across a space-time domain to reach the destination subject to various constraints (e.g., ship motions, sea sickness), by effectively navigating through dynamic weather conditions in compliance with various constraints.

In this article, we introduce a DP formulation of the collision avoidance problem of autonomous vessels. In Section 2, we set up the framework to describe the ship collision avoidance problem; In Section 3, we formulate the optimal path planning problem as a multi-stage decision process with a recursive definition based on Bellman’s equation; in Section 4, we describe the cost function and constraints based on the actual requirements of a collision avoidance maneuver for marine application, taking into account maneuvering limits and regulations to obtain smooth, collision-free, and COLREG compliant maneuvers. In Section 5, we propose a bottom-up solution scheme for the problem, leveraging parallel computing, while in Section 6, we further reduce the algorithm time complexity by proposing a greedy approximation of the DP problem formulated in the previous sections. Eventually, in Section 7, we test and compare the proposed algorithms against case study navigational scenarios to assess the potential of the proposed approach.

2. Collision Avoidance Framework Definition

Despite the Earth’s curvature being relevant when planning long routes, the horizon of a maneuver in a collision avoidance context is usually such that we can approximate the ship’s state space X with an Euclidean plane. At the beginning of the collision avoidance maneuver, the ship is located in

x_{s t a r t}

. We introduce the orthogonal unit vectors

e_{x}

and

e_{y}

to represent the cardinal axes of X: the unit vector

e_{x}

is aligned with the ship’s course at the beginning of the collision avoidance maneuver, while

e_{y}

points towards the ship’s starboard (right) side, so that

e_{z} = e_{x} \times e_{y}

points downwards, as per the standard convention for ship maneuverability. We will refer to any generic position

x \in S

as a waypoint. We can represent a generic maneuver or route R as a sequence of consecutive waypoints:

R = (x_{0}, x_{1}, \dots, x_{N}) = {(x_{i})}_{i = 0}^{N}

(1)

A sequence of two consecutive waypoints

s = (x, y)

is called route leg. If

s_{i} = (x_{i - 1}, x_{i})

, and we denote with “⊕” the sequence concatenation operator such that

(x, y) \oplus (y, z) = (x, y, z)

, We can represent the route R as:

R = (x_{0}, x_{1}) \oplus (x_{1}, x_{2}) \oplus \dots \oplus (x_{N - 1}, x_{N}) = s_{1} \oplus s_{2} \oplus . . . \oplus s_{N}

(2)

We introduce the notation

\vec{s} = y - x

to represent the vector connecting the start point of the leg to the endpoint. We can obtain the course change between two consecutive legs

s_{i} \in S_{i}

s_{j} \in S_{j}

S_{i}, S_{j} \subseteq \{(x, y) | x, y \in X\}

, using the function

θ : S_{i} \times S_{j} \to [0, π]

defined as follows:

θ (s_{i}, s_{j}) = arccos (\frac{\vec{s_{i}} \cdot \vec{s_{j}}}{| \vec{s_{i}} | | \vec{s_{j}} |})

(3)

Some considerations about the ship’s kinematics are also needed. Firstly, we assume the ship is moving at constant speed u. Such an assumption is reasonable since, in maritime practice, course alterations are preferred to speed reductions due to the long transients a speed alteration takes. In particular, it is common practice to avoid obstacles by altering the ship’s course and trying to keep the speed, or reducing the speed by a limited amount in the first part of the maneuver and then keeping it constant, to and slowly regaining the cruise speed after the collision risk is mitigated. Leveraging the constant speed assumption, we can easily map R to a sequence of time instants

T = {(t_{i})}_{i = 0}^{N}

. The instant

t_{i}

at which it engages the waypoint

x_{i}

is given by:

\{\begin{matrix} t_{i} = t_{i - 1} + \frac{|\vec{s_{i}}|}{u} \\ t_{0} = 0 \end{matrix}

(4)

Therefore, the instantaneous vessel position

x (t)

at time

t = t_{i} + Δ t

is given by:

x (t_{i} + Δ t) = x_{i} + u \frac{\vec{s_{i}}}{| \vec{s_{i}} |} Δ t

(5)

Moreover, since collision avoidance is about the interaction with obstacles, we need to introduce a notation and some hypotheses to describe them. First, we assume there are T obstacles in the scenario with known kinematics. We denote with

a_{m} (t) \in S

the instantaneous position of the

m^{t h}

obstacle. For this study, we will approximate the motion of the obstacles as a straight line, constant speed motion:

a_{m} (t) = a_{m} (t_{0}) + w_{m} t

(6)

Where

w_{m}

represents the speed vector of the

m^{t h}

obstacle. The proposed formulation could be generalized to any known motion law.

3. Dynamic Programming Formulation

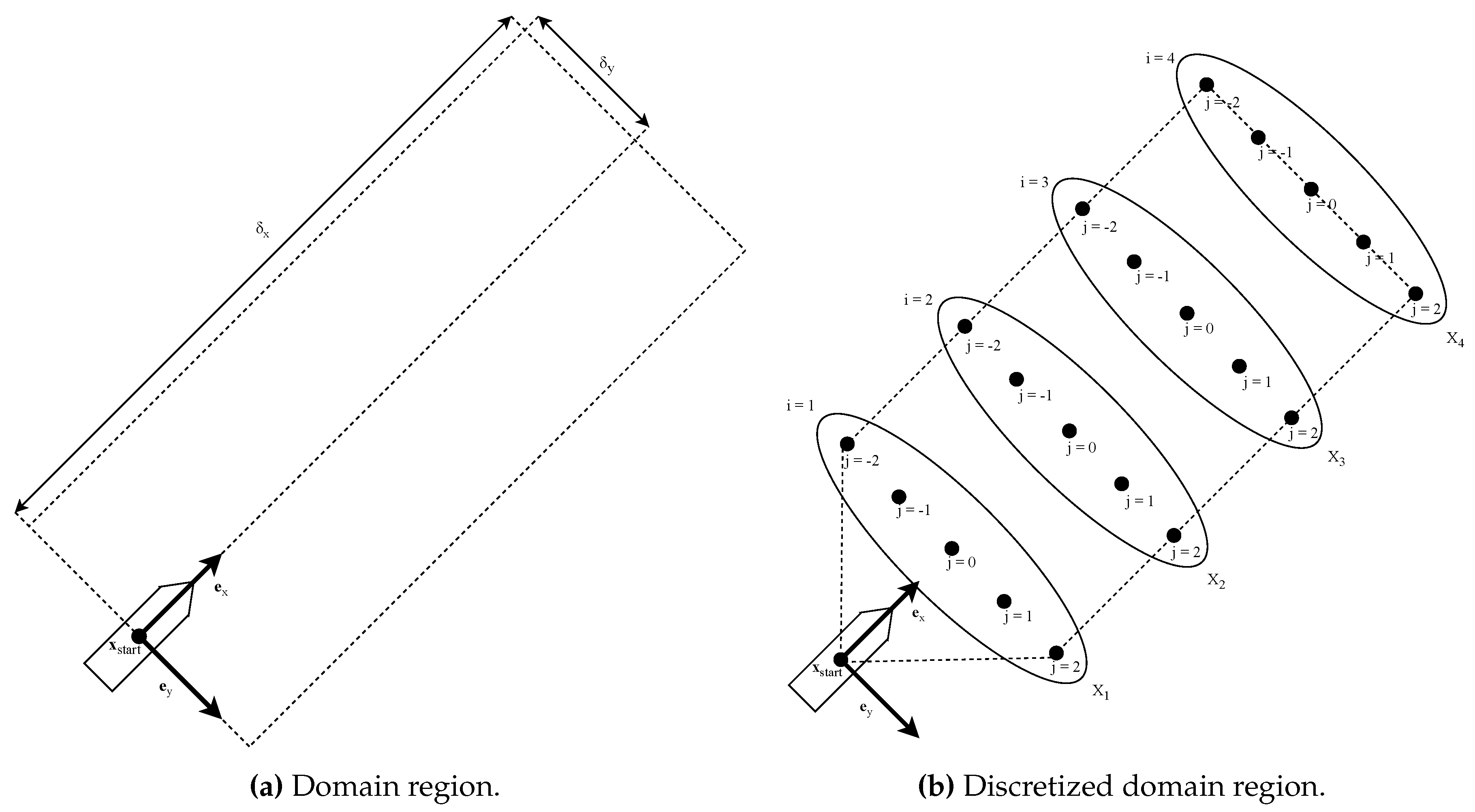
Concerning Figure 1a, let

x_{s t a r t} \in S

be the initial position of the ship, the unit vector

e_{x}

aligned with the ship’s initial course, and

e_{y}

a unit vector orthogonal to

e_{x}

and such that

e_{z} = e_{x} \times e_{y}

points downwards. Let

δ_{x}

and

δ_{y}

be the dimensions of the region in which the ship can maneuver. We introduce a discretization of the domain by defining

X_{0} = \{x_{s t a r t}\}

, and

X_{i} \subset X, i \in {1, . . ., N}

as follows:

X_{i} = \{x \in X | x = x_{s t a r t} + \frac{i}{N} δ_{x} e_{x} + \frac{j}{D} δ_{y} e_{y}, j \in {- D, \dots D}\}

(7)

Where

N, D \in N

, control the fineness of the discretization along

e_{x}

and

e_{y}

respectively, and

i, j

are the indices of the discretization. Figure 1b exemplifies a graphical representation. A route

R = {(x_{i})}_{i = 0}^{N}

is such that

x_{i} \in X_{i}

We can imagine a route

R = s_{1} \oplus s_{2} \oplus . . . \oplus s_{N}

as the result of a sequence of transitions between consecutive route legs

s_{i} = (x_{i - 1}, x_{i}) \in S_{i}

, where

S_{i} = \{s = (x, y) | x \in X_{i - 1}, y \in X_{i}\}

. In this framework, optimal route planning can be represented as finding an optimal policy in a multi-stage decision process in which the route legs represent the states. Let

J : \prod_{i = 1}^{N} S_{i} \to R

be an additively separable function expressing the cost of a route, i.e., J is such that there exists a function

c : S_{i - 1} \times S_{i} \to R

such that:

J (s_{1}, s_{2}, . . ., s_{i}) = J (s_{1}, s_{2}, . . ., s_{i - 1}) + c (s_{i - 1}, s_{i})

(8)

Let us denote

F (s_{i}) : S_{i} \to R

be the route’s cost up to the state

s_{i}

following an optimal policy. We can leverage the Bellman’s equation to define F recursively:

\{\begin{matrix} F (s_{i}) = min_{z \in S_{i - 1} | t (z, s_{i})} c (z, s_{i}) + F (z) \\ F (s_{1}) = c (s_{0}, s_{1}) \end{matrix}

(9)

Where

s_{0}

represents the state of the ship before the collision avoidance maneuver begins, and

t : S_{i - 1} \times S_{i} \to {T, F}

is a function such that

t (s_{i - 1}, s_{i}) = T

if the transition from

s_{i - 1}

s_{i}

is feasible, F otherwise.

We can analogously define the optimal predecessor function,

p : S_{i} \to S_{i - 1}

, returning the optimal predecessor state in

S_{i - 1}

for the state

s_{i} \in S_{i}

p (s_{i}) = \underset{z \in S_{i - 1} | t (z, s_{i})}{argmin} c (z, s_{i}) + F (z)

(10)

Let the recursive function

B : S_{i} \to {{(x_{k})}_{k = 0}^{i} | x_{k} \in S_{k}}

have the following form:

\{\begin{matrix} B (s_{i}) = B (p (s_{i})) \oplus s_{i} \\ B (s_{1}) = s_{1} \end{matrix}

(11)

Once we know

p (x_{i})

for all

i \in {1, . . ., N}

, the optimal solution R can be obtained backtracking the optimal decisions:

R = B (s_{N})

(12)

where:

s_{N} = \underset{s \in S_{N}}{argmin} F (s)

(13)

4. Constraints and Cost Function

The constraints are needed to formulate the function

t : S_{i - 1} \times S_{i} \to {T, F}

, identifying whether a transition is feasible. For the transition to be feasible, the next leg must begin at the end of the previous. Moreover, each transition must be such that the final result, i.e., the route, is compatible with the ship’s maneuvering capabilities, respects the COLREG, and is collision-safe. Therefore, the function t takes the following form:

t (s_{i - 1}, s_{i}) = t_{l i n k} (s_{i - 1}, s_{i}) \land t_{θ} (s_{i - 1}, s_{i}) \land t_{C O L R E G} (s_{i}) \land t_{c o l l i s i o n} (s_{i})

(14)

In particular,

t_{l i n k}

ensures the two route legs can be connected; the course change constraint function

t_{θ}

ensures the course changes along the path are compatible with ship maneuvering capabilities and good seamanship, the COLREG constraint function

t_{C O L R E G}

implements a set of rules to ensure the COLREG compliance of the own ship’s kinematics relative the other vessels’, and the collision avoidance constraint function

t_{c o l l i s i o n}

aims to guarantee an appropriate distance from the obstacles to avoid collisions safely.

4.1. Route Leg Connection

The feasibility of the transition from

s_{i - 1} \in S_{i - 1}

s_{i} \in S_{i}

is expressed by the function

t_{l i n k} : S_{i - 1} \times S_{i} \to {T, F}

. The transition is possible if the end point of the first leg is the start point of the second:

t_{l i n k} (s_{i - 1} = (\cdot, x), s_{i} = (y, \cdot)) = (x \overset{?}{=} y)

(15)

Where the symbol “·” is a placeholder for any point in the proper domain, and the operator “

\overset{?}{=}

” returning values in

{T, F}

is such that

A \overset{?}{=} B

returns T if

A = B

, F otherwise.

4.2. Course Change Constraint

We need to define a minimum and maximum threshold value for the ship’s course changes, denoted as

θ_{min}

and

θ_{max}

, respectively. The introduction of

θ_{max}

is motivated by the ship’s maneuvering capabilities and the performance of the motion control system: during a course change, the ship goes off the predefined track by a certain distance which is related to the magnitude of the course change. A large course change will push the ship too much off track, increasing the risk of collision. The reason to

θ_{min}

can be found in COLREG Rule 8(b), which requires that “Any alteration in course and/or speed to avoid collision must, if the circumstances of the case permit, be large enough to be readily apparent to another vessel observing visually or by radar; a succession of small alterations in course and/or speed must be avoided.”. We thus want to ensure that we either have course changes large enough to be apparent to an observer but not as large that the control and steering system cannot actuate them or no course change between legs. Thus, we can define

t_{θ} : S_{i - 1} \times S_{i} \to {T, F}

t_{θ} (s_{i - 1}, s_{i}) = (θ_{min} \leq θ (s_{i - 1}, s_{i}) \leq θ_{max}) \lor (θ (s_{i - 1}, s_{i}) \overset{?}{=} 0)

(16)

4.3. COLREG Compliance Constraint

COLREG is an international convention regulating several aspects of navigation, including visibility, navigation lights, and the behaviors that each ship must have in encounter situations. This last part is a set of “rules of the road” each ship has to follow when encountering other ships. The COLREG-compliant behavior can be identified by analyzing the kinematics of the ships engaging the scenario and relying on a set of if-then-else rules to assess which behavior each ship has to keep relative to the others. This action is usually called COLREG classification. Various approaches and algorithms for COLREG classification have been proposed in literature [40,41].

For this study, we will suppose we are able to determine the COLREG-compliant behavior

β_{i}

the own ship must keep relative to the

i^{t h}

dynamic obstacle in the scenario, and that

β_{i} \in C B

, where

C B

is the enumeration of all the possible behaviors:

C B = \{S O, G W, H O, A A\}

(17)

In particular, we describe the possible behaviors hereinafter:

$S O$ (Stand On): COLREG requires the target ship to maneuver to avoid a collision, so the own ship must keep its course and speed: in this case, we will neglect the presence of the target ship;
$G W$ (Give Way): The own ship must maneuver to avoid collision with the target ship, letting the latter pass ahead;
$H O$ (Head On): The own ship and the target ship are sailing on parallel and opposite routes, and the own ship must avoid the collision by turning to starboard;
$A A$ (Any Action): The own ship must take any appropriate action to avoid collision; this behavior is adopted in emergencies, such as when the target ship is expected to maneuver to avoid the collision but does not seem to initiate the evasive maneuver.

These behaviors are ensured in the solution by imposing constraints on the leg in which the own ship and the target ship cross each other’s route.

Let us assume that the ship and the target

a

cross in leg

s_{i} = (x_{i - 1}, x_{i})

, i.e., for

t \in [t_{i - 1}, t_{i}]

, and let us denote with

x_{c}

the intersection point. If

β = G W

, COLREG requires the target ship to engage

x_{c}

before the own ship; thus, we need to impose that if the own ship engages

x_{c}

during leg

s_{i}

, it does after the target has:

\begin{matrix} t_{G W} & (s_{i} = (x_{i - 1}, x_{i})) = \\ = (x_{c} \in {x (t) \in S | t \in [t_{i - 1}, t_{i}]}) \land (\frac{|x_{c} - x_{i - 1}|}{u} - \frac{|x_{c} - a (t_{i - 1})|}{| w |} > 0) \end{matrix}

(18)

β = H O

, the correct behavior is ensured by imposing that the computed path keeps the target ship on the port side of the own ship. The latter is ensured by the constraint below:

t_{H O} (s_{i}) = (\forall t \in [t_{i - 1}, t_{i}] : (a_{m} (t) - x (t)) \times \vec{s_{i}} \cdot e_{z} > 0) \lor

(19)

Eventually, the COLREG constraint function takes the following form:

\begin{matrix} t_{C O L R E G} (s_{i}) = & \forall m \in {1, . . ., T} : (β_{m} \overset{?}{=} G W \land t_{G W} (s_{i})) \lor \\ \lor (β_{m} \overset{?}{=} H O \land t_{H O} (s_{i})) \lor \\ \lor (β_{m} \in {A A, S O}) \end{matrix}

(20)

4.4. Collision Avoidance Constraint

The obstacle avoidance constraint aims to guarantee that the evasive maneuver is collision-safe. We introduce the concepts of safety distance

d_{s a f e t y}

and the Closest Point of Approach,

C P A

. The

d_{s a f e t y}

represents the distance the own ship must keep from all obstacles during an evasive maneuver to ensure safety with enough margin to account for ship dimensions and uncertainties related to the environment, control, and measurement systems. The

C P A

is the minimum distance between the center points of the own ship

x (t)

and an obstacle, whose position over time is denoted by

a_{m} (t)

, for

t \in [t_{0}, t_{N}]

. In particular, we define the

C P A_{m} (s_{i}) : S_{i} \to R

as follows:

C P A_{m} (s_{i}) = min_{t \in [t_{i} - 1, t_{i}]} |a_{m} (t) - x (t)|

(21)

Thus, if there are

T \in N

obstacles, the function

t_{c o l l i s i o n} : S_{i} \to {T, F}

checks whether a transition is collision-safe:

t_{c o l l i s i o n} (s_{i}) = \forall m \in \{1, \dots, T\} | β_{m} \neq S O : C P A_{m} (s_{i}) \geq d_{s a f e t y}

(22)

4.5. Cost Function

The definition of the cost function plays an essential role because it directly influences the geometric characteristics of the optimal path. Various approaches can be used; the proposed approach seeks the minimum control energy maneuver. In the context of this paper, control energy is related to the amplitude of the maneuvers needed to follow a path. In other words, a path with high control energy requires the ship to perform large course changes over time. To this end, we can define the transition cost c as follows:

c (s_{i - 1}, s_{i}) = θ^{2} (s_{i - 1}, s_{i})

(23)

5. Solution Scheme

This section presents a bottom-up solution scheme for the problem proposed in Section 3 based on a tabulation approach. We can divide the algorithm into two phases: the tabulation phase and the backtracking phase.

Algorithm 1 illustrates the tabulation phase. We sequentially generate the feasible states at each stage by leveraging Equation 7, while keeping track of the values of the partial optimum F and the backward link to the optimal predecessor p into proper data structures. If c and t run in constant time, the time complexity of Algorithm 1 is

O (N D^{3})

. Notice that the inner for-loop at line 6 of Algorithm 1 can be run in parallel since the loop does not mutate shared data.

Algorithm 1: Bottom-up solution scheme

$S_{1} = \emptyset$
for $j \in [- D, . . ., D]$ :
$s_{j} = (x_{s t a r t}, x_{s t a r t} + \frac{1}{N} δ_{x} e_{x} + \frac{j}{D} δ_{y} e_{y}$
$S_{1} = S_{1} \cup {s_{j}}$
$F (s_{j}) = c ((x_{s t a r t} - e_{x}, x_{s t a r t}), s_{j})$
$p (s_{j}) = N o n e$
for $i \in [2, \dots, N]$ :
$S_{i} = \emptyset$
parallel for $j \in [- D, \dots, D]$ :
$x_{j} = x_{s t a r t} + \frac{i}{N} δ_{x} e_{x} + \frac{j}{D} δ_{y} e_{y}$
for $k \in [- D, \dots, D]$ :
$x_{k} = x_{s t a r t} + \frac{i - 1}{N} δ_{x} e_{x} + \frac{k}{D} δ_{y} e_{y}$
$s_{j} = (x_{k}, x_{j})$
$T = {z \in S_{i - 1} | t (z, s_{j})}$
if $T \neq \emptyset$ :
$S_{i} = S_{i} \cup {s_{j}}$
$F (s_{j}) = {min}_{z \in T} c (z, s_{i}) + F (z)$
$p (z_{j}) = {argmin}_{z \in T} c (z, x_{i}) + F (z)$

The backtracking phase, described in Algorithm 2, reconstructs the optimal solution based on the previously tabulated backlinks returned by the best predecessor function p.

Algorithm 2: Backtracking of the optimal solution

$R = ()$
$s = {min}_{z \in S_{N}} F (z)$
while $s \neq N o n e$ :
$R = s \oplus R$
$s = p (s)$
return R

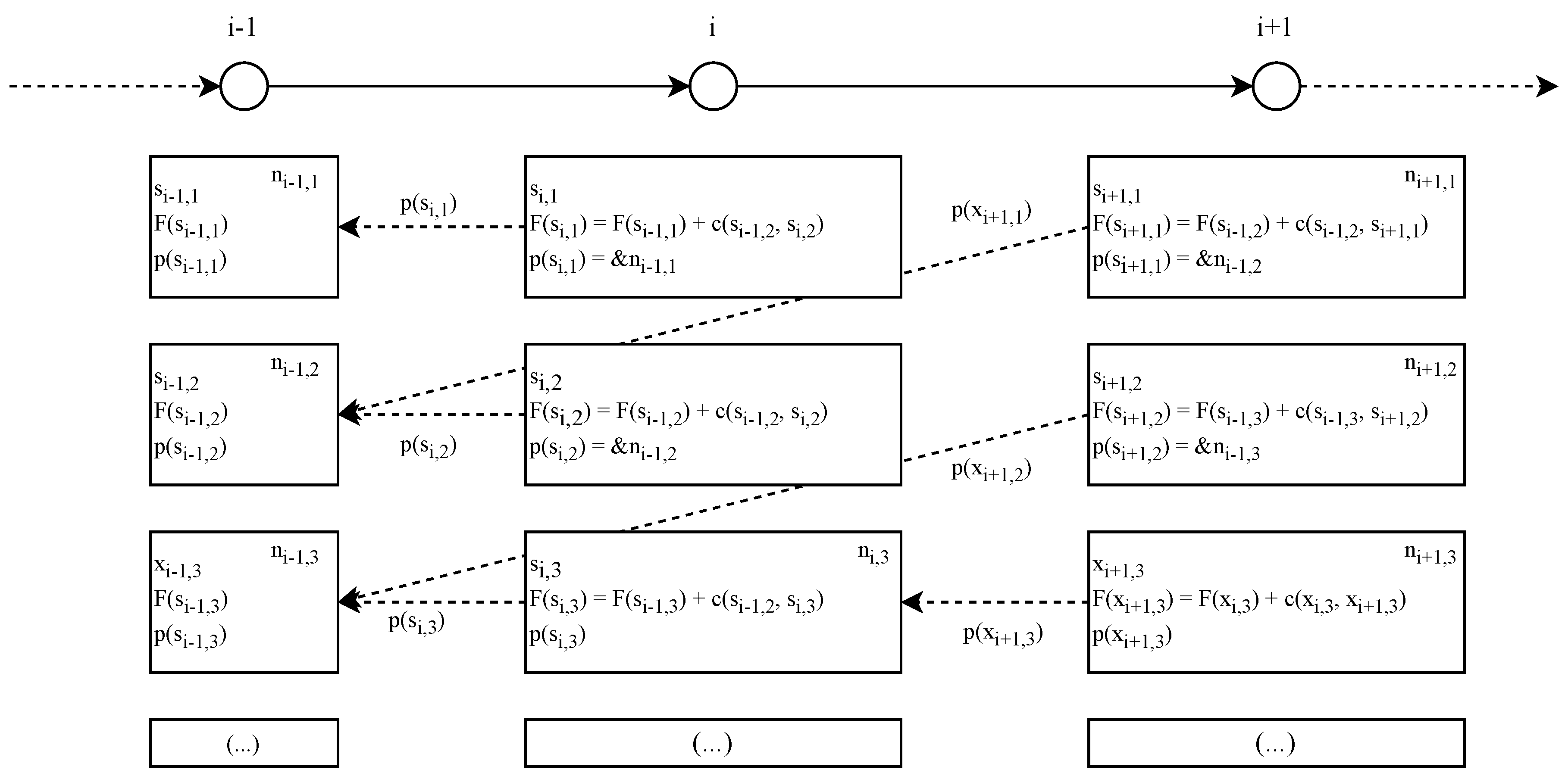
The approach described in Algorithms 1 and 2 can be implemented leveraging a tree structure, where, for each stage i and for each state j, each node

n_{i, j}

stores the state segment

s_{j} = (x, y) \in S_{i}

, the optimal cost

F (s_{j})

, and a back-link to its optimal predecessor (e.g., a pointer to its optimal predecessor node). Firstly, we create and complete the nodes of the tree according to Algorithm 1. Figure 2 shows the tree structure after Algorithm 1 is completed: each node contains the state,

s_{j}

, the optimal cost F, and points to its optimal predecessor. Secondly, we backtrack the optimal solution by selecting the node with the minimum value of F at the last stage and following the chain of backlinks, pushing the last element of

s_{j}

to the front of a list until we reach the initial state, where we push the starting point to complete the list of waypoints to be returned.

Concerning Algorithm 1, we can estimate the number of stages at each state as

{(2 D + 1)}^{2}

, i.e., the total number of transitions to be evaluated at each stage is

{(2 D + 1)}^{4}

. Since the only transitions to be evaluated are those whose initial state ends in the starting point of the final state, a proper implementation allows accessing them directly in constant time; thus, the number of evaluated transitions can be reduced to

{(2 D + 1)}^{3}

in constant time, leading to a time complexity of

O (N D^{3})

for the overall process if the cost and constraints have constant time complexity.

6. Greedy Approximation

From Equation 14, we can notice that only part of the conditions for transition feasibility depend on the state

s_{i - 1}

, as the transition cost c defined in Equation 23 does. In this section, we propose a greedy approximate dynamic programming (GADP) scheme that makes greedy decisions to reduce the number of evaluated transitions. The proposed scheme loses the capacity to find the globally optimal policy, yet it allows for reducing the time complexity of the algorithm. The basic idea is to reformulate the route

R = (x_{0}, x_{1}, . . ., x_{N})

as a sequence of transitions between consecutive states

x_{i} \in X_{i}

i \in {0, 1, . . ., N}

. In other words, we use the waypoints to represent the ship’s state rather than representing it with a leg connecting two consecutive waypoints. The greedy minimum cost at stage i is expressed by the function

F_{g} : X_{i} \to R

, while the greedy optimal predecessor is represented by the function

p_{g} : X_{i} \to X_{i - 1}

F_{g} (x_{i}) = min_{z \in S_{i - 1} | t_{g} (z, x_{i})} c_{g} (z, x_{i}) + F_{g} (z)

(24)

p_{g} (x_{i}) = \underset{z \in S_{i - 1} | t_{g} (z, x_{i})}{argmin} c_{g} (z, x_{i}) + F_{g} (z)

(25)

Where

t_{g} : X_{i - i} \times X_{i} \to {T, F}

and

c_{g} : X_{i - i} \times X_{i} \to R

greedily compute the result based on

p_{g} : X_{i} \to X_{i - 1}

t_{g} (x, y) = t ((p_{g} (x), x), (x, y))

(26)

c_{g} (x, y) = c ((p_{g} (x), x), (x, y))

(27)

Algorithm 3 shows the proposed approach. Since a whole cycle over

[- D, . . . D]

disappears in the solution scheme, we now evaluate only

{(2 D + 1)}^{2}

transition at each stage, and the time complexity required to run the algorithm drops from

O (N D^{3})

O (N D^{2})

Algorithm 3: Approximate dynamic programming bottom-up solution scheme

$S_{0} = {x_{s t a r t}}$
$F (x_{s t a r t}) = 0$
$p (x_{s t a r t}) = N o n e$
for $i \in [1, \dots, N]$ :
$S_{i} = \emptyset$
parallel for $j \in [- D, \dots, D]$ :
$x_{j} = x_{s t a r t} + \frac{i}{N} δ_{x} e_{x} + \frac{j}{D} δ_{y} e_{y}$
$T = {z \in S_{i - 1} | t_{g} (z, x_{j})}$
if $T \neq \emptyset$ :
$S_{i} = S_{i} \cup {x_{j}}$
$F_{g} (x_{i}) = {min}_{z \in T} c_{g} (z, x_{i}) + F_{g} (z)$
$p_{g} (x_{i}) = {argmin}_{z \in T} c_{g} (z, x_{i}) + F_{g} (z)$

The backtracking phase works similarly to the previous case.

7. Case Study

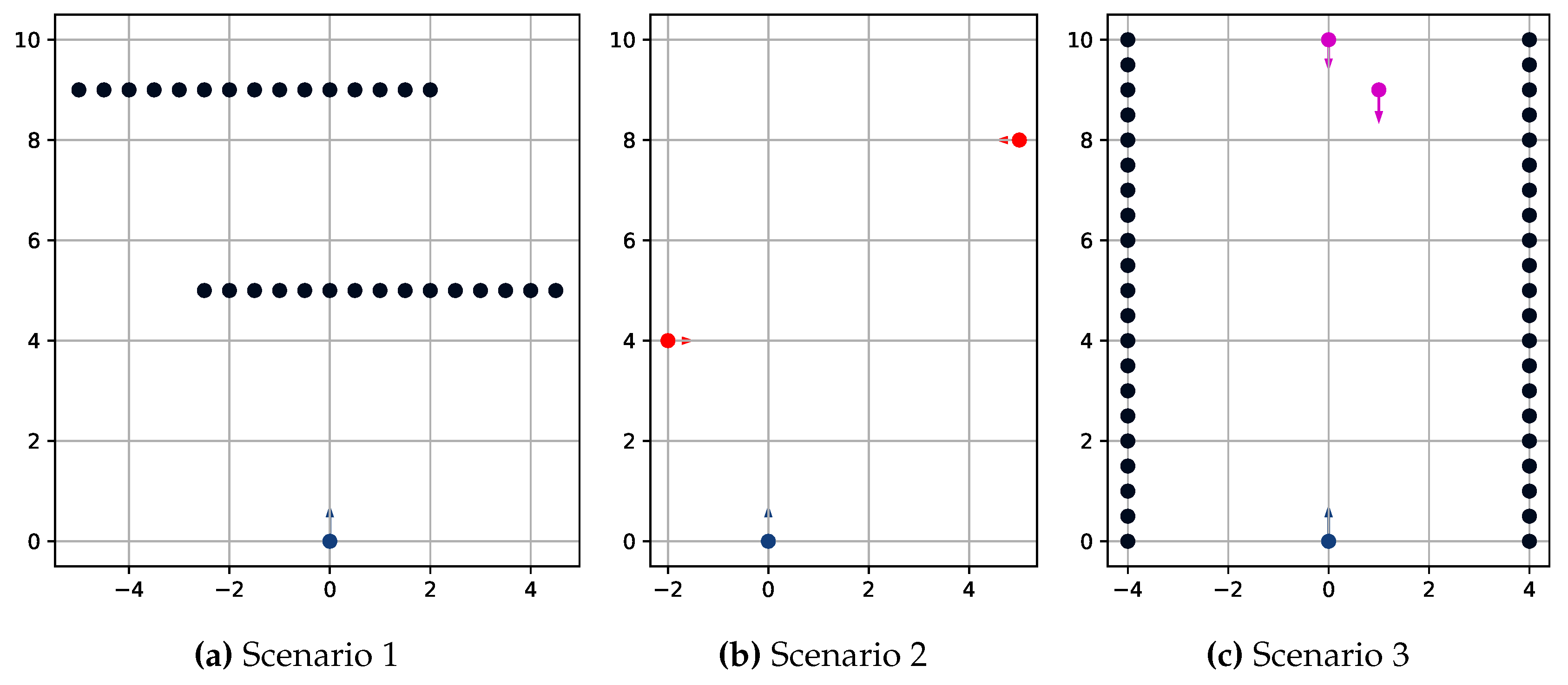
An implementation of the two proposed algorithms has been developed for testing and comparison purposes, and some test case scenarios have been designed to compare and evaluate the algorithms’ application in autonomous navigation contexts. The algorithms have been implemented in Rust language, relying on the Rayon library for parallelization. All scenarios take place in a square domain

D = [0, 10] \times [0, 10]

nautical miles, in which the own ship starts from point

(0, 0)

with heading

0^{\circ}

to reach the opposite side of the domain, i.e., any point

(10, y) \in D

Scenario 1, shown in Figure 3a, has two barriers placed at $x = 5$ and $x = 9$ nautical miles respectively, ranging in $[- 5, 2.5]$ and $[- 2.5, 5]$ . These obstacles force the own ship to maneuver between the barriers.
Scenario 2, shown in Figure 3b, features two sailboat vessels, the first starting in $(8.0, 4.5)$ with a speed of $5.0$ knots, and a heading of $270^{c i r c}$ , the second positioned at $(4, - 2)$ , with speed 6 knots and heading $90^{c i r c}$ . For both target vessels, the COLREG imposes a "give-way" behavior.
Scenario 3, shown in Figure 3c, features a double "head-on" with two target vessels starting from $(9, 1)$ and $(10, 0)$ and heading $180^{c i r c}$ and speeds of 9 and 8 knots, respectively. In addition, two fixed side barriers form a channel parallel to the x axis and 8 nautical miles wide.

To comply with the COLREG, the own ship must make only visible heading alterations, with a minimum angle of

15^{c i r c}

, while a maximum of

60^{c i r c}

turn is accepted. The algorithms perform the path optimization on a discrete computation grid defined as per Equation 7, where

N = 10

and

D = 20

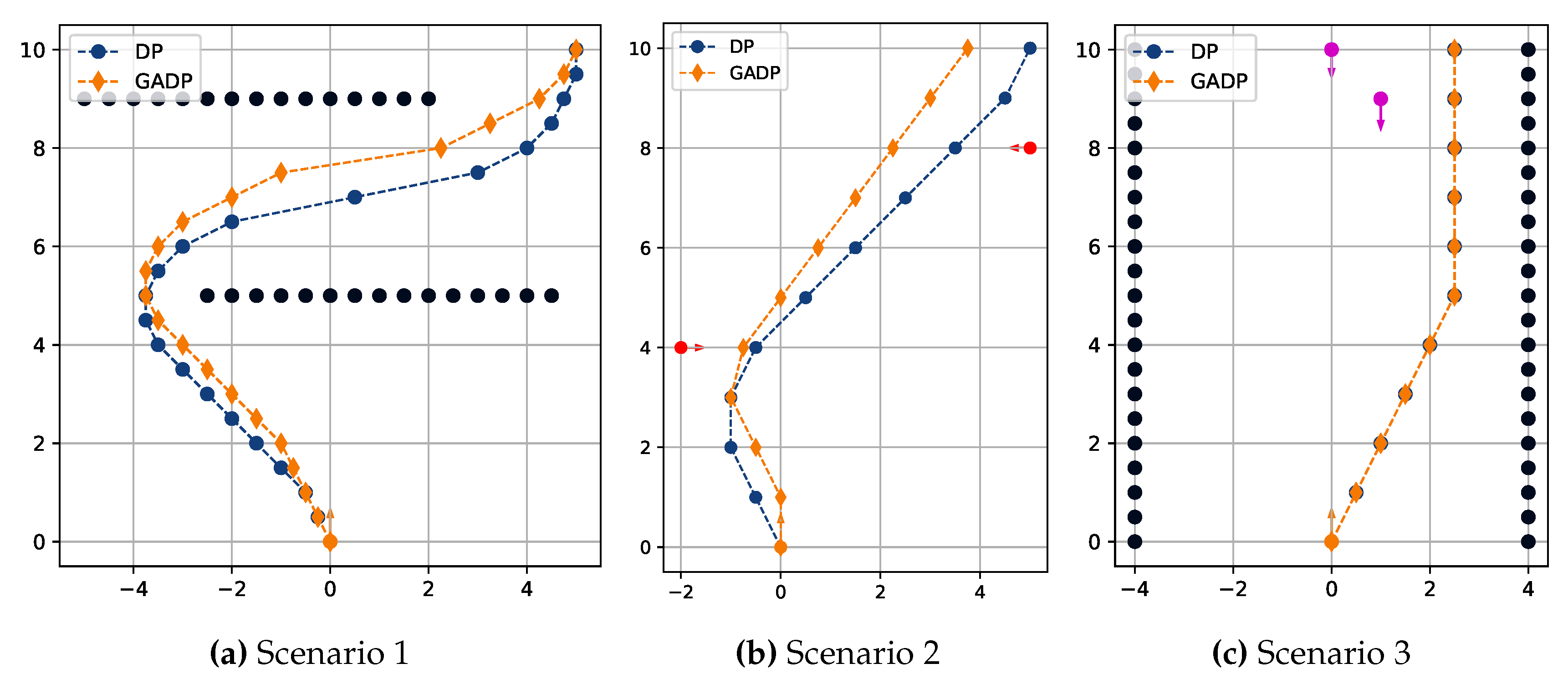
Figure 4 shows the solutions found by the two algorithms in the three proposed test scenarios. In scenarios 1 and 2 (Figure 4a,b), DP and GADP propose dissimilar trajectories; in particular, the GADP solution features more delayed direction changes. In scenario number 3 (Figure 4c), on the contrary, the solution computed by the two approaches is the same, i.e., the greedy optimum computed by GADP corresponds to the global optimum of the DP.

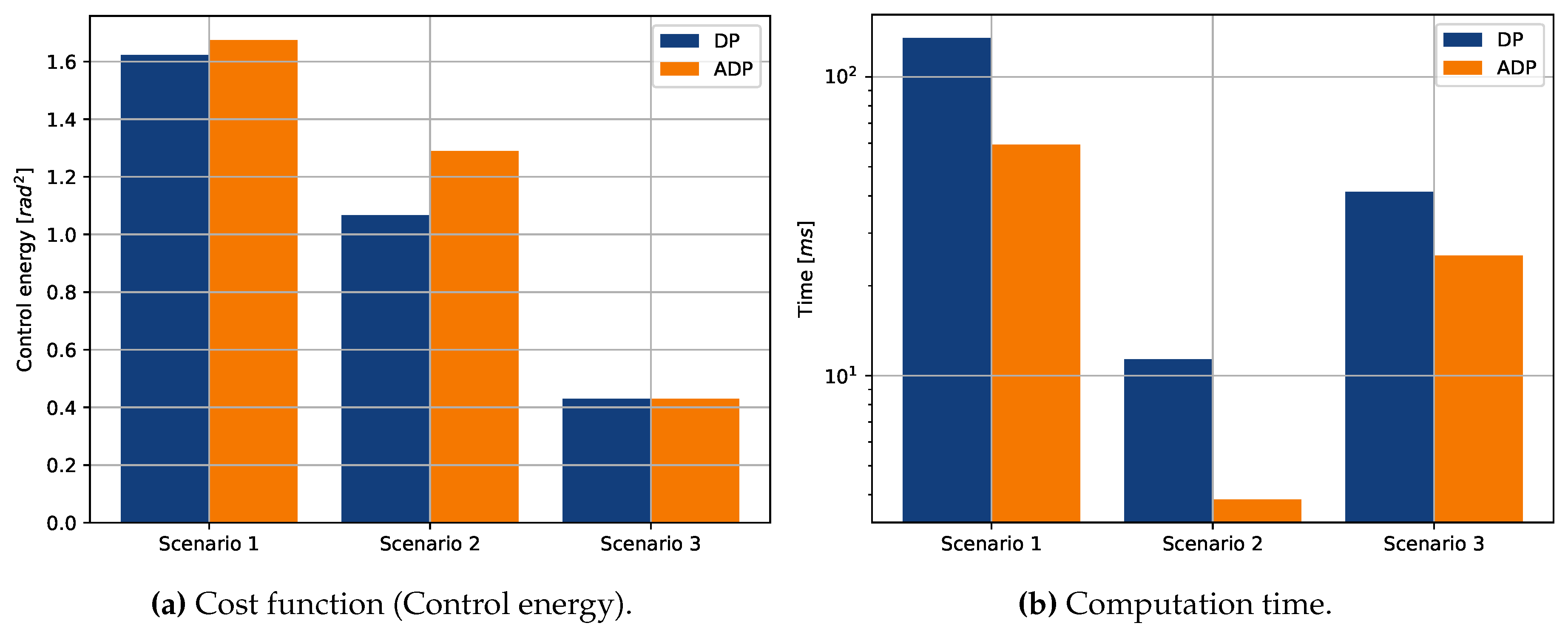
Eventually, Figure 5a,b present the value of the cost function and the computation time required to determine the solution, respectively. We can note that, at the price of a higher cost function value, the solutions determined by the GADP algorithm require less computation time.

Figure 3. Application case scenarios. Scenario 1 (3a) includes fixed obstacles only; Scenario 2 (3b) features two sailboats (in red), both requiring “give-way” behavior to the own ship (blue); Scenario 3(3b) features two head-on ships (magenta) in a narrow channel.

Figure 4. Application case scenarios solved using DP (blue) and GADP (red).

Figure 5. Cost function value (Figure 5a) and computation time (Figure 5b) comparison of the two presented algorithms.

8. Conclusions

This paper described a dynamic programming scheme for calculating evasive maneuvers of autonomous ships. We showed how the collision-free route calculation for a ship can be described by leveraging Bellman’s equation, and we described appropriate constraints to obtain a collision-safe route with features compatible with the maneuvering capabilities of a ship and compliant with collision regulations. We also proposed a greedy approximate dynamic programming (GADP) scheme that allows, using a greedy approach, to reduce the number of transitions to be evaluated for each step, consequently reducing the algorithm’s time complexity. Finally, we compared the proposed algorithms on three scenarios relevant to autonomous navigation.

Funding

This research was partially funded by European Union’s Horizon Europe under the call HORIZON-CL5-2022-D6-01 (Safe, Resilient Transport and Smart Mobility services for passengers and goods), grant number 101077026, project name SafeNav. However, the views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or Executive Agency (CINEA). Neither the European Union nor the granting authority can be held responsible.

Abbreviations

The following abbreviations are used in this manuscript:

DP	Dynamic Programming
COLREG	Convention on the International Regulations for Preventing Collisions at Sea
CPA	Closes Point of Approach
GADP	Greedy Approximate Dynamic Programming
IMO	International Maritime Organization

References

Martelli, M.; Virdis, A.; Gotta, A.; Cassarà, P.; Di Summa, M. An outlook on the future marine traffic management system for autonomous ships. IEEE Access 2021, 9, 157316–157328. [CrossRef]
Tran, H.A.; Johansen, T.A.; Negenborn, R.R. Collision avoidance of autonomous ships in inland waterways–A survey and open research problems. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2023, Vol. 2618, p. 012004.
IMO, M. Outcome of the Regulatory Scoping Exercise for the Use of Maritime Autonomous Surface Ships (MASS), 2021.
Alessandri, A.; Donnarumma, S.; Luria, G.; Martelli, M.; Vignolo, S.; Chiti, R.; Sebastiani, L. Dynamic positioning system of a vessel with conventional propulsion configuration: Modeling and simulation. Maritime Technology and Engineering, Proceedings of the MARTECH 2014.
Alessandri, A.; Donnarumma, S.; Vignolo, S.; Figari, M.; Martelli, M.; Chiti, R.; Sebastiani, L. System control design of autopilot and speed pilot for a patrol vessel by using LMIs. Towards green marine technology and transport 2015, pp. 577–583.
Singh, Y.; Bibuli, M.; Zereik, E.; Sharma, S.; Khan, A.; Sutton, R. A novel double layered hybrid multi-robot framework for guidance and navigation of unmanned surface vehicles in a practical maritime environment. Journal of Marine science and Engineering 2020, 8, 624. [CrossRef]
Bruzzone, G.; Bibuli, M.; Caccia, M.; Zereik, E. Cooperative robotic maneuvers for emergency ship towing operations. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen. IEEE, 2013, pp. 1–7.
Chen, L.; Huang, Y.; Zheng, H.; Hopman, H.; Negenborn, R. Cooperative multi-vessel systems in urban waterway networks. IEEE Transactions on Intelligent Transportation Systems 2019, 21, 3294–3307. [CrossRef]
Chen, L.; Haseltalab, A.; Garofano, V.; Negenborn, R.R. Eco-VTF: Fuel-efficient vessel train formations for all-electric autonomous ships. In Proceedings of the 2019 18th European Control Conference (ECC). IEEE, 2019, pp. 2543–2550.
Faggioni, N.; Ponzini, F.; Martelli, M. Multi-obstacle detection and tracking algorithms for the marine environment based on unsupervised learning. Ocean Engineering 2022, 266, 113034. [CrossRef]
Organization, I.M. Convention on the International Regulations for Preventing Collisions at Sea, 1972.
Burmeister, H.C.; Constapel, M. Autonomous collision avoidance at sea: A survey. Frontiers in Robotics and AI 2021, 8, 739013. [CrossRef]
Zaccone, R.; Martelli, M. Interaction between COLREG-compliant collision avoidance systems in a multiple MASS scenario. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2023, Vol. 2618, p. 012006.
Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Engineering 2018, 169, 187–201. [CrossRef]
Seo, C.; Noh, Y.; Abebe, M.; Kang, Y.J.; Park, S.; Kwon, C. Ship collision avoidance route planning using CRI-based A* algorithm. International Journal of Naval Architecture and Ocean Engineering 2023, 15, 100551. [CrossRef]
Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. Feasibility study of a constrained Dijkstra approach for optimal path planning of an unmanned surface vehicle in a dynamic maritime environment. In Proceedings of the 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC). IEEE, 2018, pp. 117–122.
Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D. Towards use of Dijkstra algorithm for optimal navigation of an unmanned surface vehicle in a real-time marine environment with results from artificial potential field 2018.
D’Amato, E.; Nardi, V.A.; Notaro, I.; Scordamaglia, V. A Visibility Graph approach for path planning and real-time collision avoidance on maritime unmanned systems. In Proceedings of the 2021 International Workshop on Metrology for the Sea; Learning to Measure Sea Health Parameters (MetroSea). IEEE, 2021, pp. 400–405.
Chiang, H.T.L.; Tapia, L. COLREG-RRT: An RRT-based COLREGS-compliant motion planner for surface vehicle navigation. IEEE Robotics and Automation Letters 2018, 3, 2024–2031. [CrossRef]
Zaccone, R.; Martelli, M. A collision avoidance algorithm for ship guidance applications. Journal of Marine Engineering & Technology 2020, 19, 62–75.
Enevoldsen, T.T.; Reinartz, C.; Galeazzi, R. COLREGs-Informed RRT* for collision avoidance of marine crafts. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021, pp. 8083–8089.
Ito, M.; Zhnng, F.; Yoshida, N. Collision avoidance control of ship with genetic algorithm. In Proceedings of the Proceedings of the 1999 IEEE International Conference on Control Applications (Cat. No. 99CH36328). IEEE, 1999, Vol. 2, pp. 1791–1796.
Kang, Y.T.; Chen, W.J.; Zhu, D.Q.; Wang, J.H.; Xie, Q.M. Collision avoidance path planning for ships by particle swarm optimization. Journal of Marine Science and Technology 2018, 26, 3.
Ning, J.; Chen, H.; Li, T.; Li, W.; Li, C. COLREGs-Compliant unmanned surface vehicles collision avoidance based on multi-objective genetic algorithm. Ieee Access 2020, 8, 190367–190377. [CrossRef]
Gao, P.; Zhou, L.; Zhao, X.; Shao, B. Research on ship collision avoidance path planning based on modified potential field ant colony algorithm. Ocean & Coastal Management 2023, 235, 106482.
Bellman, R. The theory of dynamic programming. Bulletin of the American Mathematical Society 1954, 60, 503–515. [CrossRef]
Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [CrossRef]
Jones, M.; Peet, M.M. A generalization of Bellman’s equation with application to path planning, obstacle avoidance and invariant set estimation. Automatica 2021, 127, 109510. [CrossRef]
Ayyappan, B.; Gopalan, S. A Performance and Power Characterization study of Memoization and Tabulation methods in Graph Neural Networks by assessing Dynamic Programming Workloads. In Proceedings of the 2022 6th International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE). IEEE, 2022, pp. 1–6.
Rytter, W. On efficient parallel computations for some dynamic programming problems. Theoretical Computer Science 1988, 59, 297–307. [CrossRef]
González, D.; Almeida, F.; Roda, J.; Rodriguez, C. From the theory to the tools: parallel dynamic programming. Concurrency: practice and experience 2000, 12, 21–34. [CrossRef]
Guo, Q.; Li, Z.; Song, W.; Fu, W. Parallel computing based dynamic programming algorithm of track-before-detect. Symmetry 2018, 11, 29. [CrossRef]
Mazzarello, M.; Ottaviani, E. A traffic management system for real-time traffic optimisation in railways. Transportation Research Part B: Methodological 2007, 41, 246–274. [CrossRef]
Shin, K.; McKay, N. A dynamic programming approach to trajectory planning of robotic manipulators. IEEE Transactions on Automatic Control 1986, 31, 491–500. [CrossRef]
Li, X.; Wang, L.; An, Y.; Huang, Q.L.; Cui, Y.H.; Hu, H.S. Dynamic path planning of mobile robots using adaptive dynamic programming. Expert Systems with Applications 2024, 235, 121112. [CrossRef]
Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean engineering 2018, 153, 215–224. [CrossRef]
Zaccone, R.; Figari, M.; Martelli, M. An optimization tool for ship route planning in real weather scenarios. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference. ISOPE, 2018, pp. ISOPE–I.
Zhengping, T.; Chao, J.; Xiaohai, W. Design of ship route through waterway based on dynamic programming. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 1906, p. 012001.
Choi, G.H.; Lee, W.; Kim, T.w. Voyage optimization using dynamic programming with initial quadtree based route. Journal of Computational Design and Engineering 2023, p. qwad055.
Zaccone, R.; Martelli, M.; Figari, M. A colreg-compliant ship collision avoidance algorithm. In Proceedings of the 2019 18th European Control Conference (ECC). IEEE, 2019, pp. 2530–2535.
Martelli, M.; Žuškin, S.; Zaccone, R.; Rudan, I. A COLREGs-compliant decision support tool to prevent collisions at sea. TransNav: International Journal on Marine Navigation and Safety of Sea Transportation 2023, 17. [CrossRef]

Short Biography of Authors

Raphael Zaccone received his MSc in naval architecture and marine engineering in 2013 from the University of Genoa. Subsequently, he received his PhD in 2017 with research on ship optimal weather routing, then continued his research in autonomous navigation and collision avoidance as a Post Doc. He joined the Department of Naval, Electrical, Electronic, and Telecommunications Engineering at the University of Genoa in 2019 as a Research Fellow and, from 2021, Assistant Professor. His research activities cover various areas of ship digitization and are mainly focused on developing and applying motion planning and collision avoidance algorithms for enhanced navigation, decision support, and autonomous marine vehicles. He has authored more than 35 scientific publications in international journals and conferences.

Figure 1. A representation of the domain of the collision avoidance problem (1a), and an example discretization of the domain, with

N = 4

and

D = 2

1b.

Figure 1. A representation of the domain of the collision avoidance problem (1a), and an example discretization of the domain, with

N = 4

and

D = 2

1b.

Figure 2. Tabular representation of the partial solutions in a tree structure. For each stage i and for each state j, each node

n_{i, j}

stores the state

s_{j} \in S_{i}

, the optimal cost

F (s_{j})

, and a back-link to its optimal predecessor.

Figure 2. Tabular representation of the partial solutions in a tree structure. For each stage i and for each state j, each node

n_{i, j}

stores the state

s_{j} \in S_{i}

, the optimal cost

F (s_{j})

, and a back-link to its optimal predecessor.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Dynamic Programming Approach to Collision Avoidance of Autonomous Ships

Abstract

1. Introduction

2. Collision Avoidance Framework Definition

3. Dynamic Programming Formulation

4. Constraints and Cost Function

4.1. Route Leg Connection

4.2. Course Change Constraint

4.3. COLREG Compliance Constraint

4.4. Collision Avoidance Constraint

4.5. Cost Function

5. Solution Scheme

6. Greedy Approximation

7. Case Study

8. Conclusions

Funding

Abbreviations

References

Short Biography of Authors

MDPI Initiatives

Important Links

Subscribe