Research on Aerodynamic Characteristics and Pitch Regulated Control Strategy of Coaxilcopter with Variable Rotor Spacing

This study investigates the impact of rotor spacing on the aerodynamic performance of a coaxialcopter. It has been observed that a small distance between two rotors can result in significant interaction between the propellers, consequently affecting the rotor's aerodynamic efficiency. Exploiting this characteristic, the present research introduces a coaxialcopter with variable rotor spacing. Employing finite element numerical simulations, we assess the aerodynamic behavior of this novel configuration. Through comprehensive measurements and analysis of its aerodynamic performance across varying rotor spacings from 0.1R to 1R, we validate the effectiveness of a rotor spacing control strategy for enhancing takeoff maneuvers. Our numerical simulation results reveal that the performance characteristics of both upper and lower rotor converges toward that of a single rotor as pitch ratio increases, along with the reduce of their thrust fluctuations and aerodynamic performance periodicity. Considering stable power consumption patterns and endurance performance, we analysis the interrelations binding of pitch distance of the rotors, rotational speed, and pitch angle, vis-à-vis the thrust coefficient and power coefficient. Through parameter optimization method, we demonstrate that adjusting rotor spacing offers a practical means to enhance payload capacity without increasing power input, thereby improving the efficiency, which validates the practicality and efficacy of the parameter optimization approach. Furthermore, optimizing rotor spacing for specific operational scenarios enhances overall aerodynamic performance, suggesting a viable flight control strategy for takeoff and landing conditions.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Coaxial twin rotors, characterized by their overlapping axes, opposite steering, and specific spacing, have garnered significant attention due to their inherent advantages, including a compact structure, self-balancing torque, and exceptional handling performance [1,2]. This configuration offers improved thrust efficiency while mitigating power loss attributed to tail rotor interference, making it a favored choice for various applications. However, the close proximity between coaxial rotors introduces complex aerodynamic interactions, leading to asymmetrical interferences that complicate flow field dynamics [3].

Extensive research has been conducted to analyze the aerodynamic attributes of coaxial twin rotor systems, particularly concerning rotor spacing’s impact on performance. Previous studies have employed computational fluid dynamics (CFD) calculations to investigate micro coaxial twin rotors, highlighting the significance of rotor spacing and speed on aerodynamic interference and wake boundaries [4,5]. Additionally, researchers have employed methodologies such as the sliding grid method to assess aerodynamic performance under varying rotor spacing conditions [6,7,8,9]. Similarly, aerodynamic models based on free-wake method have been established to study the influence of rotor geometric parameters on the hovering performance of coaxial twin rotors [10,11,12]. Research on coaxial rigid rotors has gradually begun in China, mainly focusing on basic research on aerodynamic characteristics, flight control strategies, and other aspects of coaxial rigid rotors [13,14,15,16]. There has been no specialized research on the issue of rotor spacing of coaxial rigid rotors.

Moreover, the effect of rotor spacing on coaxial twin rotor aerodynamics has been studied in-depth. Investigations reveal that as the pitch ratio (K_d) increases, the thrust of both upper and lower rotors tends to converge towards that of a single rotor, with a persistent 20% difference observed in the lower rotor’s thrust. However, the overall aerodynamic interference between upper and lower rotors diminishes as K_d increases, leading to a reduction in thrust fluctuation amplitude. These insights underscore the need for optimizing rotor spacing to achieve improved aerodynamic performance.

Furthermore, the significance of rotor spacing extends to the realm of aerodynamic control strategies. The study by Beijing Jiaotong University showcases a Variable Speed Semi Differential Control Mechanism that integrates speed and pitch adjustments to enhance overall control effectiveness [17]. This aligns with broader research efforts focusing on optimizing control parameters, including pitch angles and speed, to attain maximum efficiency and maneuverability [18,19,20].

Similar rotor spacing layout studies have been conducted on the aerodynamic performance of multi-rotor aircraft. Scholars have analyzed the effect of different rotor spacing on the lift of a quadcopter using a multi-layer volume grid equivalent model [21,22,23]. In addition, the aerodynamic interference of quadrotor aircraft in vertical and forward flight states has been analyzed and calculated through numerical simulation methods, providing a theoretical basis for the overall aerodynamic layout design of quadrotor aircraft [24,25,26]. The interaction between the rotor and the fuselage, as well as between the front and rear rotors, has been studied through wind tunnel tests, obtaining the variation law of the rotor lift coefficient [27,28,29,30].

In conclusion, the investigation into coaxial twin rotor aerodynamics, specifically the impact of rotor spacing on aerodynamic characteristics and control strategies, has yielded valuable insights. The understanding of rotor spacing’s influence on thrust, interference, and control strategies contributes to the development of more efficient and effective coaxial twin rotor systems. As research continues to evolve, these findings will undoubtedly shape the design, optimization, and operational strategies of future coaxial rotor configurations.

In this study, our study builds upon previous investigations by delving into the aerodynamic flow field characteristics of coaxilcopter rotors across varying pitch settings. Employing a combined control approach involving speed, rotor spacing, and pitch angle, we identify high-performance and efficiency points through parameter optimization for diverse operational scenarios.

2. Dynamic Analysis of Coaxilcopter Rotors

2.1. Dynamic Modeling of Coaxilcopter Rotors

Utilizing two rotors with opposing rotational directions and a radius of 685mm, both operating at a speed of 1000 r/min, we examine the flow field distribution of coaxial twin rotors during vertical flight, as depicted in Figure 1. For the purpose of this illustration, lateral flow disturbances and rotor flapping deformations are disregarded. The incoming air flow originates upstream with a velocity of V_c and proceeds downward. Meanwhile, V_c + w_u represents the flow velocity of the upper rotor’s wake at the plane where it intersects with the lower rotor.

In this analysis, we exclude the influences of air weight and the lower rotor’s flow field, focusing solely on the vertical flight dynamics of the upper rotor. Under these conditions, the fluid distribution can be described as follows:

\{\begin{cases} ρ A_{0} V_{c} = ρ A_{1} (V_{c} + w_{u}) \\ T_{u} = ρ A_{1} {(V_{c} + w_{u})}^{2} - ρ A_{0} {V_{c}}^{2} \\ P_{u} = p_{2} A_{1} (V_{c} + w_{u}) + \frac{ρ A_{1} {(V_{c} + w_{u})}^{3}}{2} - \frac{ρ A_{0} {V_{c}}^{3}}{2} \end{cases}

(1)

In the equation: A₀ symbolizes the area at infinity of the upper rotors, A₁ represents the segment of the upper rotor’s wake intercepted by the lower rotor, T_u signifies the thrust produced by the upper rotor, and P_u denotes the induced power of the upper rotor. Likewise, by omitting the influence of air weight and concentrating on the distribution of the rotor’s flow field, we can derive the following results:

\{\begin{cases} ρ A_{1} (V_{c} + w_{u} + v_{i l}) = ρ A_{4} (V_{c} + w_{i l}) \\ ρ A_{2} (V_{c} + v_{i l}) = ρ A_{5} (V_{c} + w_{l o}) \\ T_{l i} = ρ A_{4} {(V_{c} + w_{i l})}^{2} - ρ A {(V_{c} + v_{i u})}^{2} \\ T_{l o} = ρ A_{5} {(V_{c} + w_{l o})}^{2} - ρ A_{2} (V_{c} + v_{i u}) V_{c} \\ P_{l i} = \frac{ρ A_{4} {(V_{c} + w_{i l})}^{3}}{2} - \frac{ρ A {(V_{c} + v_{i u})}^{3}}{2} - p_{2} A (V_{c} + v_{i u}) \\ P_{l o} = \frac{ρ A_{5} {(V_{c} + w_{l o})}^{3}}{2} - \frac{ρ A_{2} (V_{c} + v_{i u}) {V_{c}}^{2}}{2} \end{cases}

(2)

In the given equation: A₄ characterizes the wake area of the lower rotor influenced by the upper rotor, while A₅ designates the wake area of the lower rotor unaffected by the upper rotor. Correspondingly, A₂ represents the unobstructed inflow area for the lower rotor. T_li denotes the thrust generated by the lower rotor in the region impacted by the upper rotor, whereas T_lo stands for the thrust produced in the zone where the lower rotor remains unaffected by the upper rotor’s presence. P_li accounts for the power consumption of the lower rotor within the area influenced by the upper rotor, and P_lo represents the power consumption within the segment where the lower rotor operates independently from the upper rotor. In essence, this can be summarized as follows:

\{\begin{cases} T_{l} = T_{l i} + T_{l o} \\ P_{l} = P_{l i} + P_{l o} \end{cases}

2.2. Evaluation Indicators for Aerodynamic Characteristics

To comprehensively assess the aerodynamic capabilities of the coaxial twin rotor system, key parameters are employed include the thrust coefficient (C_T), moment coefficient (C_M), power coefficient (C_P), besides, hover efficiency is related to the payload and hover time of multi-rotors UAV, which can be reflected by figure of metric(FM):

\{\begin{cases} C_{T} = \frac{T}{ρ A Ω^{2} R^{2}} \\ C_{M} = \frac{M}{ρ A Ω^{2} R^{3}} \\ C_{P} = \frac{P}{ρ A Ω^{3} R^{3}} \\ F M = \frac{{C_{T}}^{3 / 2}}{\sqrt{2} C_{P}} \end{cases}

In the formula, T is the rotor thrust, M is the moment or torque, P is the rotor power, Ω is the rotor speed, R is the rotor radius, ρ is the gas density, and σ_d is the rotor solidity. Once the configuration of the coaxial twin rotor system is established, the pursuit of optimized aerodynamic performance typically revolves around elevating thrust, minimizing power consumption, and enhancing overall aerodynamic efficiency.

3. Aerodynamic Characteristics of Coaxial Twin-Rotor System

The field of rotor aerodynamic performance research commonly employs methods such as the Rotating Frame of Reference and the Sliding Grid technique. Within this study, we adopt the Rotating Frame of Reference method for steady-state simulation of rotor aerodynamic behavior. Subsequently, building upon the steady-state simulation outcomes, the Sliding Grid method is employed to facilitate transient simulations.

The Rotating Frame of Reference technique entails segmenting the computational domain into three distinct zones: a static domain and two rotational domains. The rotational domain primarily encompasses grids located near the rotor. Meanwhile, the static domain accounts for the remaining area and is characterized by coarser grid sizes, a design choice that effectively minimizes computational costs.

3.1. Numerical Calculation Method

The Table 1 provided delineates the selection of initial model parameters, a process rooted in the dimensional specifications of the coaxial twin rotors’ configuration.

Subsequently, aerodynamic models are formulated. Notably, the interplay between the upper and lower rotors’ distance (d_p) and rotor radius (R) significantly influences rotor aerodynamic performance. Consequently, the pitch ratio (K_d) is introduced as a defining metric:

K_{d} = \frac{d_{p}}{R}

(3)

The computational domain assumes a comprehensive cylindrical geometry. To preempt any consequential impacts stemming from ground/ceiling/wall effects on the simulation outcomes, a judicious approach is adopted. This entails configuring the diameter of the static domain at ten times that of the rotor’s diameter, whilst enveloping the rotor within the dynamic domain, a depiction of which is showcased in Figure 2. The upper surface functions as the pressure inlet, conversely, the lower surface serves as the pressure outlet. The cylindrical surface interfaces as a boundary wall, and a deliberate interface is delineated between the dynamic and static domains.

The entire computational domain adopts a cylindrical shape. To avoid the influence of ground effects, ceiling effects, and wall effects on the simulation results, the diameter of the static domain is set to 10 times the diameter of the rotor, while the dynamic domain wraps the rotor, as shown in the Figure 2. The upper surface is the pressure inlet, the lower surface is the pressure outlet, the cylindrical surface is the wall boundary, and an interface is set between the dynamic and static domains.

In this study, the computational domain is systematically partitioned into surface grids, a meticulous approach undertaken to ensure the quality of the rotor surface meshes. To achieve this, tetrahedral cells are employed for the surface mesh, subsequently integrated into the Fluent mesh via the generation of additional tetrahedral cells. Notably, this augmentation primarily augments the density of the dynamic domain’s mesh. To accurately capture boundary layer dynamics, eight strata of boundary layers are specifically instituted upon the rotor surface. In totality, the mesh encompasses a comprehensive scale of approximately 11 million cells. The modeling methodology encompasses the deployment of both the k-ω and LES models. A critical dimension in this is the maintenance of the y+ value below 11 on the rotor wall, as showcased in Figure 3. This prerequisite is rigorously met through judicious grid refinements, ensuring compliance with stipulated requirements.

3.2. Steady State Characteristics with Variable Pitch

The influence of the pitch ratio (K_d) on the rotor system’s aerodynamic performance is effectively illustrated in Figure 4. Figure 4(a) provides the graphical depiction of the thrust(T) variation curve of the rotor system in relation to the pitch ratio K_d. Correspondingly, Figure 4(b) presents the variation curve of the rotor’s torque (M) as influenced by the pitch ratio K_d.

The investigation reveals a discernible trend in the behavior of the rotor system’s upper rotor thrust T_u concerning the pitch ratio K_d. Specifically, the upper rotor thrust initially undergoes a decline followed by an increment as the pitch ratio varies. Notably, a nadir in the upper rotor thrust is identified within the range of 0.1 to 0.3. With a pitch ratio K_d surpassing 0.6, the upper rotor’s thrust gradually aligns with that of a single rotor.

Conversely, the lower rotor thrust T_l and the cumulative total thrust T_total demonstrate an ascent proportional to the augmentation of the pitch ratio K_d. This trend persists until the pitch ratio exceeds 0.5, after which the thrust augmentation of the lower rotor becomes less prominent. However, a 20% deviation from the thrust of a singular rotor T_single persists, a divergence attributed to the interaction between the upper and lower rotors. This coupling effect engenders lower thrust relative to the single rotor configuration. In scenarios where the distance between the upper and lower rotors d_p escalates, the coupling effect between them weakens, precipitating an upsurge in the overall thrust of the rotor system.

Within the interplay of the upper and lower rotor coupling, the upper rotor registers a higher induced velocity, consequently engendering superior thrust. Meanwhile, the lower rotor experiences more pronounced tip loss, culminating in a discernible gap in thrust relative to a singular rotor configuration.

The dimensionalization of thrust and torque outputs from the coaxial rotor system facilitates the derivation of the quality factor curve and the average thrust conversion rate. This computation is predicated upon the acquired thrust coefficient and torque coefficient values. Of particular interest is the thrust conversion rate K_T, a metric that quantifies the ratio between the average thrust exerted by the upper and lower rotors and the thrust generated by an individual rotor. Mathematically, this is defined as:

K_{T} = \frac{(T_{u} + T_{l}) / 2}{T_{s i n g l e}}

(4)

Illustrated in Figure 5 (a) and 5(b), the simulation outcomes unequivocally demonstrate a pronounced alignment between the variation trend of the quality factor and that of the thrust conversion rate in the pitch ratio K_d.

Nonetheless, for instances where the pitch ratio K_d resides below 0.2, the computed average thrust conversion rate K_T assumes values beneath 0.5. This manifestation is indicative of a coaxial rotor system’s thrust registering even lower than that exhibited by an individual rotor configuration. Contrarily, as the pitch ratio exceeds 0.4, the average thrust conversion rate K_T attains values exceeding 0.8. This robust elevation effectively translates into the coaxial rotor system garnering an appreciable thrust advantage.

3.3. Transient State Characteristics with Variable Pitch

Numerical simulations of transient aerodynamic characteristics yield real-time insights into the dynamic alterations in thrust manifested by the upper and lower rotors during rotation. Extracting simulation outcomes of rotor rotations spanning two cycles across varying pitch ratios furnishes a comprehensive visualization (Figure 6). Analysis of the graphical representation underscores the periodic oscillations characterizing rotor thrust, with four distinct thrust cycles aligning per rotation cycle.

Intriguingly, as the pitch ratio K_d escalates, the mutual influence between rotors progressively wanes, precipitating a marked attenuation in the amplitude of rotor thrust fluctuations, as shown in Figure 7. Notably, this shift is paralleled by a reduction in the conspicuous periodicity inherent to rotor thrust oscillations, which gradually assumes a more stabilized profile. During transitions of the pitch ratio K_d within the range of 0.1 to 1, the upper rotor’s thrust fluctuation amplitude registers a remarkable reduction of 92.4%, while the corresponding decrease for the lower rotor attains 77.1%.

Meanwhile, the distance between the upper and lower rotors d_p substantively governs the vigor and steadiness of the vortex formations engendered by the rotor system. Augmented rotor spacing notably mitigates interference originating from proximate rotors, consequently fostering heightened vortex stability. However, with diminished rotor spacing, the proximity of neighboring rotors disturbs vortex formations, precipitating an adverse impact on the strength and stability of these vortices.

Drawing insights from Figure 8, the vortices manifest primarily in the vicinity of the rotor’s root and tip. In instances characterized by relatively modest pitch ratios K_d, the diametrically opposing directions of the upper and lower rotor vortices evoke a mutual constriction between the vortex systems of these rotors.

Remarkably, as demonstrated by Figure 9, the incremental elevation of the pitch ratio K_d progressively weakens the interaction manifesting at the root-level vortices. Notably, despite these dynamics, the aerodynamic interplay between the lower rotor and the vortex system at its tip remains influenced by the latter’s pronounced downwash velocity.

4. Optimization of Control Strategy Based on Pitch Adjustment

4.1. Correlation Analysis of Control Parameters

Alterations in the pitch ratio prompt shifts in aerodynamic attributes, including rotor thrust and moment. Notably, when viewed through the lens of actuation speed and load considerations, the advantages of adjusting rotor pitch ratio relative to changes in rotor speed become more pronounced. This underscores a notable potential for application within flight control strategies. Regarding the strategy, the evaluation criteria are centered around the Thrust coefficient and the Power coefficient. The former governs the maneuverability of the coaxial rotor system, while the latter acts as a metric for quantifying energy consumption efficiency.

Thorough investigation delves into the interrelations binding the three pivotal parameters: pitch distance of the rotors(d_p), rotational speed(n), and pitch angle(α), vis-à-vis the Thrust coefficient and Power coefficient. Derived from the outcomes from Figure 10 and Figure 11, it becomes evident that the rotational speed exerts minimal influence on both the Thrust coefficient and Power coefficient within the coaxial rotor system.

Conspicuously, the change trajectory of the Thrust coefficient, vis-à-vis alterations in the pitch ratio K_d, mirrors that of the thrust characteristics. However, a pronounced alignment manifests as both the Thrust coefficient and the Power coefficient surge proportionally in tandem with augmented pitch angles.

The findings underscore the efficacy of manipulating the pitch ratio to swiftly and seamlessly modulate thrust performance. Importantly, such adjustments yield minimal influence on the power coefficient, indicating a relatively consistent power consumption pattern and implying negligible disruptions to endurance ability. Such trait distinguishes it from conventional flight control methodologies that frequently involve altering rotational speed in drone or modifying pitch angles in helicopter, thus presenting a significant potential. Furthermore, it is noteworthy that the parameters capable of impacting aerodynamic performance do not impose mutual constraints. Instead, they can be orchestrated harmoniously to achieve elevated both in thrust performance and the overall endurance attributes. This holistic approach optimizes flight control efficacy, ultimately leading to amplified thrust and an extended operational range.

Consequently, a method for optimizing control strategies is proposed, encompassing a subsequent parameter optimization procedure tailored to the coaxial helicopter rotor model. This process capitalizes on the initial parameters, thereby facilitating the augmentation of the Thrust coefficient via pitch d_p adjustments, and the reduction of the power coefficient through precise modifications of pitch angle α, as shown in Figure 12.

4.2. Optimization Design of Control Strategy

The foundational approach to parameter optimization involves utilizing the initial parameters as the control group and contrasting them with the test parameters constituting the comparison group. The meticulous specification of these parameters is detailed presented in Table 2.

The simulation results reveal that test group D achieves a good performance of power coefficient reduction of 14.15%, and 3.02% increase in Thrust coefficient, which verifies the feasibility of the control strategy parameter optimization process.

Besides, the change of aerodynamic performance (test points A and B) is compared by changing only one parameter, saying pitch ratio or pitch angle, but the results showed that the optimization goal is not achieved. Therefore, the two parameters of pitch ratio and pitch angle (test points C and D) are changed at the same time to further analyze the change of pneumatics performance of coaxial twin rotor system under the combined action of the two parameters.

The simulation outcomes delineate a commendable performance within test group D, marked by a substantial reduction in power coefficient by 14.15%, coupled with a concurrent elevation of the Thrust coefficient by 3.02%. This outcome serves to affirm the practical feasibility of the control strategy parameter optimization process.

Furthermore, a comparative assessment is conducted concerning the alteration of aerodynamic performance (test groups A and B) in Figure 13, wherein a sole parameter, either the pitch ratio or the pitch angle, is manipulated.

Regrettably, the results underscore an inability to meet the optimization objectives. Consequently, a more nuanced approach emerges wherein both the pitch ratio and the pitch angle are concurrently adjusted (test groups C and D), thereby facilitating a comprehensive analysis of the pneumatic performance shifts inherent to the coaxial twin rotor system under the joint influence of these two parameters.

5. Experimental Verification of Rotor Aerodynamic Performance

The composition of the test platform in this article mainly includes: rotor module; the power module consists of a DC power supply, a DC brushless motor, and a speed control system; the measurement system mainly measures the speed, thrust, torque, power, and rotor spacing of the rotor. The measured data is transmitted to the computer through data acquisition software for analysis and calculation, in order to obtain the aerodynamic results of coaxial twin rotors under different blade spacing. The test platform is shown in Figure 14.

In order to verify the effect of rotor spacing on the aerodynamic interference of coaxial reversing twin rotor, the experimental and simulation values of the thrust of upper and lower rotors with rotor spacing are compared. At a speed of 1000r/min and rotor spacing of 0.1R~1R, it has been verified that the thrust of the upper and lower rotors of a coaxial twin rotor varies with blade spacing. The specific experiment is shown in Figure 15.

Compare the numerical simulation results at a speed of 1000r/min with the experimental results, as shown in Figure 16.

It can be seen that although there is a certain deviation between the numerical simulation results and the experimental results, the variation trend of thrust and torque with rotor spacing in the numerical simulation is consistent with the experimental results. Due to instrument errors in the experiment and grid accuracy in numerical simulation calculations, the maximum relative error between numerical simulation calculations and experimental results is less than 10%, which proves the effectiveness of the numerical simulation calculation method in this paper.

Similarly, experimental verification was conducted on the aerodynamic performance of each set of test points for parameter optimization, as shown in Figure 17.

It can be seen that the experimental results are still slightly larger than the simulation results, and the relative error remains within 10%. This also verifies the reliability of the parameter optimization process and results.

6. Conclusions

This study introduces a novel approach to swiftly modulate thrust performance in coaxial rotor systems by manipulating the pitch ratio, the aerodynamic performance of coaxilcopter with variable rotor spacing are explored, and the following conclusion can be drawn:

When pitch ratio K_d surpasses 0.5, both upper and lower rotor thrust converges toward that of a single rotor; the lower rotor, however, retains a persistent 20% difference. As K_d increases, the coaxial thrust gradually aligns with the double single-rotor thrust, even as the lower rotor incurs losses attributable to the upper rotor’s interaction effect.
As pitch ratio increases, thrust fluctuations in upper and lower rotors become more gradual, reducing their aerodynamic performance periodicity. In the range of pitch ratios from 0.1 to 1, thrust fluctuation amplitude decreases by 92.4% for the upper rotor and 77.1% for the lower rotor.
When the rotor spacing is set at 0.4R with a pitch angle of 7.5°, a notable 3.02% increase in the thrust coefficient and a significant 14.15% reduction in the power coefficient are observed when compared to the configuration of 0.2R pitch and a pitch angle of 10°. This observation further validates the practicality and efficacy of the parameter optimization approach.
The investigation validates the expeditious thrust modulation achievable through pitch ratio manipulation in coaxial rotor systems, maintaining both stable power consumption patterns and endurance performance.

In essence, this research propels the advancement of parameter optimization strategies for coaxial rotor systems. Through the efficacy of pitch ratio manipulation, introduction of innovative approaches, and contributions to energy-efficient flight control strategies, this study significantly enriches the field’s knowledge and possibilities.

Author Contributions

Conceptualization, W.W., Z.K. and M.Z.; methodology, M.Z.; software, Y.S.; validation, M.Z. and Q.M.; investigation, M.Z. , J.T. and Q.M.; resources, Z.K., W.W. and H.Z.; data curation, M.Z. and J.T.; writing—original draft preparation, M.Z.; writing—review and editing, Z.K. and W.W; visualization, M.Z. and Z.K.; supervision, Z.K. and W.W; project administration, W.W.; funding acquisition, Z.K., W.W. and H.Z., All authors have read and agreed to the published version of the manuscript.

Funding

This work has been funded by Beijing Natural Science Foundation, grant number 3244036; the National Key Research and Development Program, grant number 2020YFC1512500; the Shandong Postdoctora1 Science Foundation, grant number SDCX-ZG-202303052; Natural Science Foundation of Chongqing, China, grant number CSTB2022NSCQ-MSX1101.

Data Availability Statement

Data available on reasonable request from the authors.

Acknowledgments

We sincerely thank the reviewers who contributed their expertise and time on reviewing this manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Nonami, K. Prospect and Recent Research & Development for Civil Use Autonomous Unmanned Aircraft as UAV and MAV. JSDD 2007, 1, 120–128. [Google Scholar] [CrossRef]
Zhu, Z.; Zhao, Q.J.; Li, P. Unsteady flow interaction mechanism of coaxial rigid rotors in hover. Acta Aeronaut. Et Astronaut. Sin. 2016, 37, 568–578. [Google Scholar]
Yuan, M.C.; Liu, P.A.; Fan, F. Wind Tunnel Test Investigation of Coaxial Rigid Rotor Aerodynamic Interaction. J. Nanjing Univ. Aeronaut. Astronaut. 2019, 51, 257–262. [Google Scholar] [CrossRef]
Lakshminarayan, V.K.; Baeder, J.D. Computational Investigation of Microscale Coaxial-Rotor Aerodynamics in Hover. J. Aircr. 2010, 47, 940–955. [Google Scholar] [CrossRef]
Passe, B.J.; Sridharan, A.; Baeder, J.D. Computational Investigation of Coaxial Rotor Interactional Aerodynamics in Steady Forward Flight. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference; American Institute of Aeronautics and Astronautics, Dallas, TX, USA, 22 June 2015. [Google Scholar]
Lei, Y.; Ye, Y.Q.; Wang, H.D. Aerodynamic Performance Analysis of Coaxial Rotors with Different Rotor Spacing. Mach. Des. Manuf. 2023, 81–85. [Google Scholar]
Lei, Y.; Ye, Y.Q.; Wang, H.D. Study on Aerodynamic Characteristics of Coaxial Rotors UAV with Different Rotor Spacing. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 487–492. [Google Scholar] [CrossRef]
Lei, Y.; Wang, H.D.; Ye, Y.Q. Optimal analysis of rotor arrangement for a micro quadrotor aircraft. Chin. J. Comput. Mech. 2020, 37, 412–416. [Google Scholar]
Lei, Y.; Ji, Y.X.; Wang, C.W. Numerical simulation and experimental study on aerodynamics of the microcoaxial rotors. J. Exp. Fluid Mech. 2017, 31, 67–73. [Google Scholar]
Wang, Q.; Chen, M.; Wang, B.B. Effect of geometric parameters of rotor on hovering performance of caoxial rotor. J. Aerosp. Power 2014, 29, 1434–1443. [Google Scholar] [CrossRef]
Huang, S.L.; Xu, G.H.; Li, C.H. Flow Field Analysis of Coaxial Twin Rotors Based on Free Wake. J. Nanjing Univ. Aeronaut. Astronaut. 2008, 40, 721–726. [Google Scholar] [CrossRef]
Lu, C.L.; Qi, H.T.; Xu, G.H. Unsteady flow field interation of coxial rotor. J. Aerosp. Power 2019, 34, 1459–1470. [Google Scholar] [CrossRef]
Yuan`, Y.; Chen, R.L.; Li, P. Analysis of rotor control strategy for coaxial rigid rotor high-speed helicopters. J. Northwestern Polytech. Univ. 2017, 35, 915–921. [Google Scholar]
Zhang, Y. Research on Aerodynamic Interaction and Flight Characteristics of Compound Helicopter with Rigid Coaxial Rotor; Nanjing University of Aeronautics and Astronautics, 2014. [Google Scholar]
Liu, X.L.; Xu, G.H.; Shi, Y.J. Research on influence of rotor configuration on the aerodynamic characteristics of coaxial rigid rotor helicopter. Flight Dyn. 2022, 40, 41–47. [Google Scholar] [CrossRef]
Li, H.; Jia, H.; Chen, Z. Analysis and experiment on aerodynamic characteristics of coaxial rotor system. Opt. Precis. Eng. 2021, 29, 2140–2148. [Google Scholar] [CrossRef]
Dong, S.P. Design of Variable Speed Semi Differential Control Mechanism for Small Coaxial Unmanned Helicopter; Beijing Jiaotong University, 2022. [Google Scholar]
Zhang, H.L.; Qian, J.P.; Guo, C. Analysis of Aerodynamic Interference Characteristics Between Wings of Suspension Bullets Multi -Rotor Suspension Device. J. Ordnance Equip. Eng. 2021, 42, 25–29. [Google Scholar]
Liu, S. Design of the co-axial twin-rotor unmanned helicopter’s rotor and control system. Jouranl Mach. Des. 2021, 38, 84–89. [Google Scholar] [CrossRef]
Zeng, W.; Lin, Y.F.; Huang, S.L. Preliminary Experimental Research on Unsteady Aerodynamic Characteristics of Coaxial Rigid Rotor. Helicopter Techique 2017, 13–17. [Google Scholar]
Liu, X.S.; Ang, H.S.; Xiao, T.H. Analysis of rotor interference effects on quad-rotor lift in hover. Adv. Aeranautical Sci. Eng. 2014, 5, 148–153. [Google Scholar] [CrossRef]
Li, P.; Lei, B.; Zhu, J.Y. Research on Influence of Rotor Spacing on Load Characteristics of Micro Quadrotor UAVs. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 978–984. [Google Scholar] [CrossRef]
Zhao, H.; Li, X.W.; Li, L. Numerical simulation under disturbance wind and its flow control of flow field of micro rotary-wings. Chin. J. Comput. Mech. 2015, 32, 429–433. [Google Scholar]
Wang, C.; Tang, Z.F.; Xu, P. Numerical simulation of flow field and aerodynamic interference of quad-rotor UAV. Flight Dyn. 2018, 36, 83–87. [Google Scholar] [CrossRef]
Bai, Q.Q. Flow Field Analysis of Four Rotor Unmanned Aerial Vehicle in Flight; Harbin Institute of Technology, 2016. [Google Scholar]
Shen, A.; Zhou, S.D.; Wang, M. Simulation and analysis of multi-rotor UAV flow field. Flight Dyn. 2018, 36, 29–33. [Google Scholar] [CrossRef]
Hwang, J.Y.; Jung, M.K.; Kwon, O.J. Numerical Study of Aerodynamic Performance of a Multirotor Unmanned-Aerial-Vehicle Configuration. J. Aircr. 2015, 52, 839–846. [Google Scholar] [CrossRef]
Aleksandrov, D.; Penkov, I. Optimization of Lift Force of Mini Quadrotor Helicopter by Changing of Gap Size between Rotors. SSP 2013, 198, 226–231. [Google Scholar] [CrossRef]
Nguyen, D.H.; Liu, Y.; Mori, K. Experimental Study for Aerodynamic Performance of Quadrotor Helicopter. Trans. Jpn. Soc. Aero. S Sci. 2018, 61, 29–39. [Google Scholar] [CrossRef]
Luo, J.; Zhu, L.; Yan, G. Novel Quadrotor Forward-Flight Model Based on Wake Interference. AIAA J. 2015, 53, 3522–3533. [Google Scholar] [CrossRef]

Figure 1. Aerodynamic model of coaxilcopter rotors.

Figure 2. Rotor basin model and grid processing.

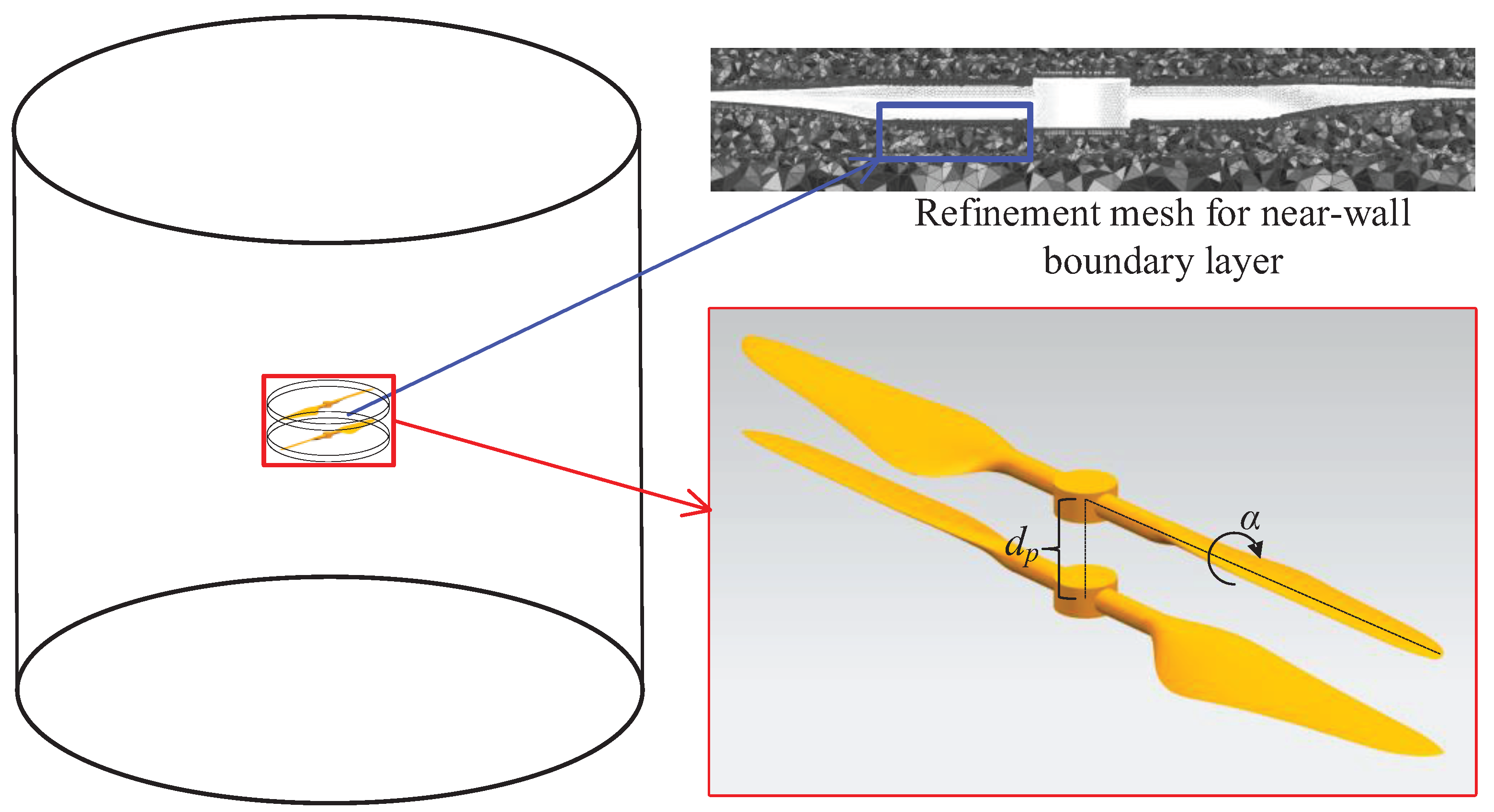
Figure 3. Wall y+ value of coxilcopter rotors.

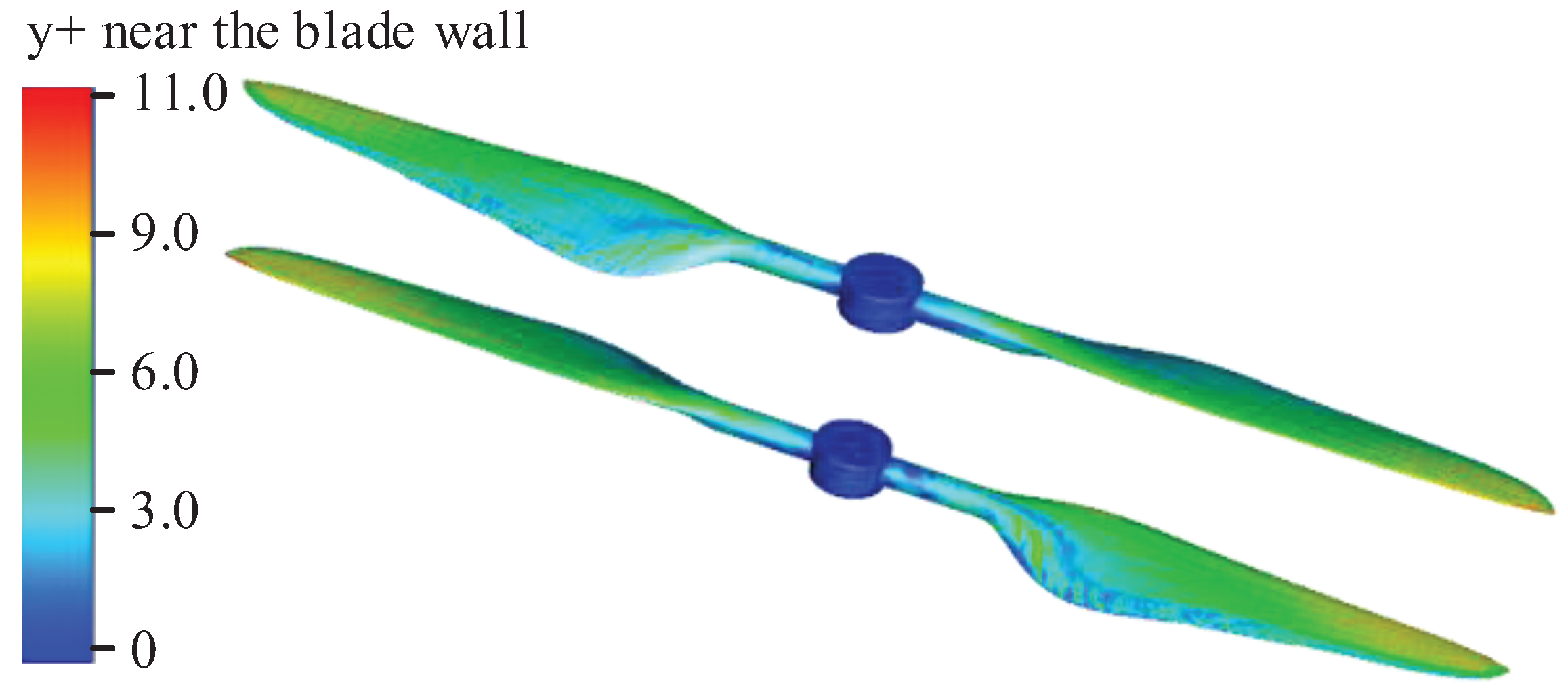
Figure 4. Steady state aerodynamic characteristics of coaxilcopter rotors.

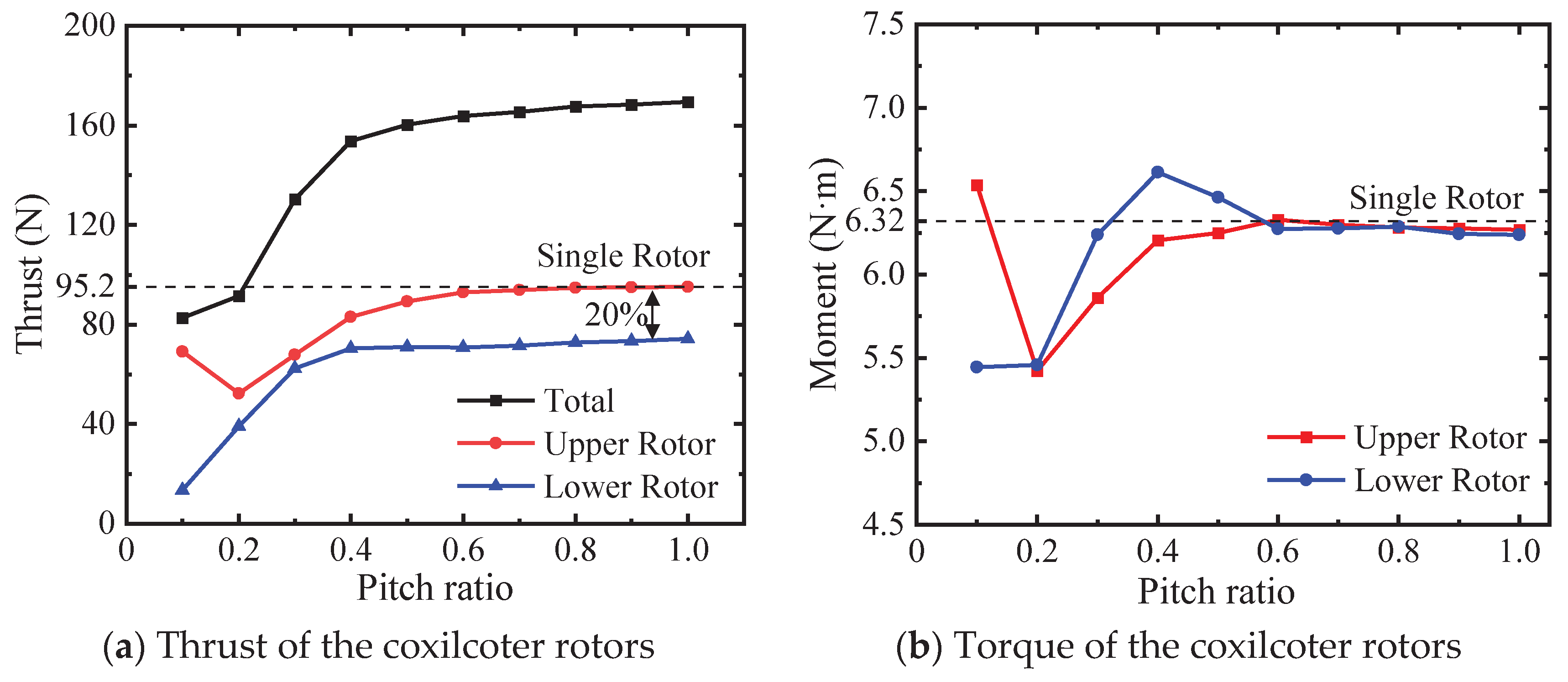
Figure 5. Steady state aerodynamic characteristics of coaxilcopter rotors.

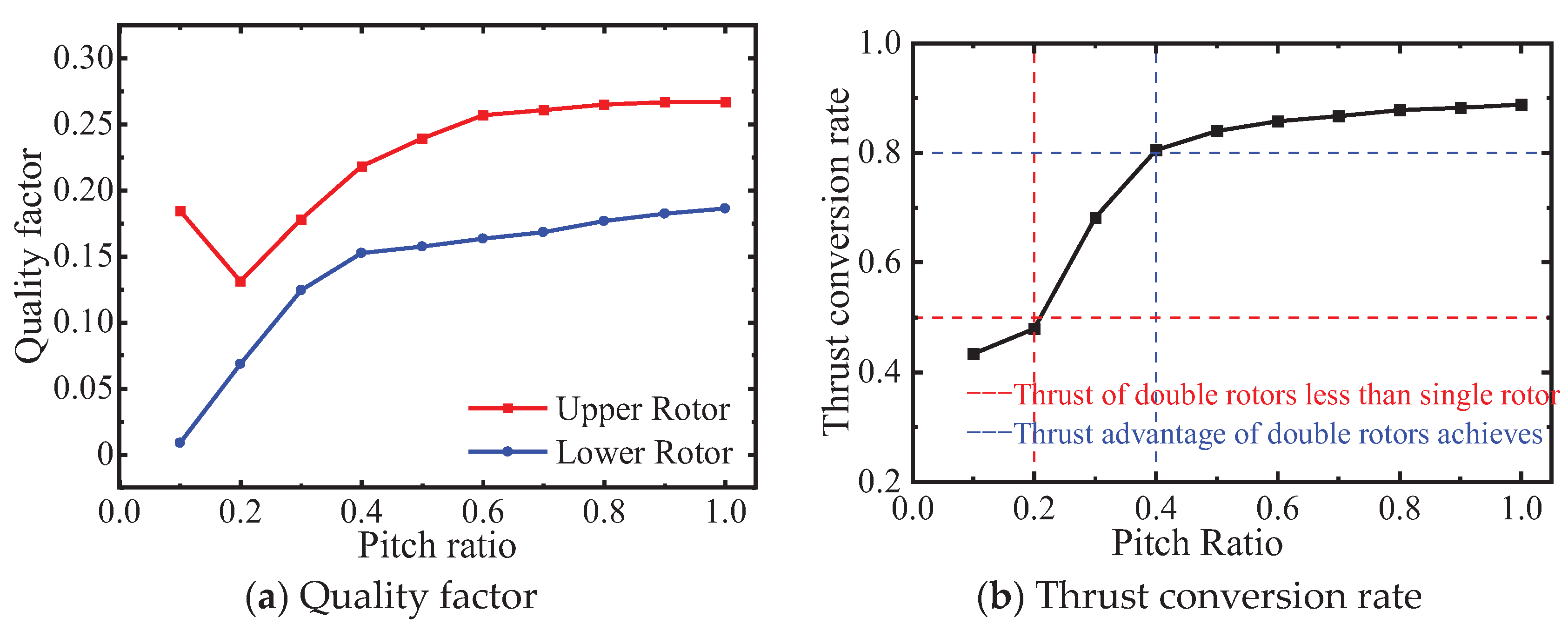
Figure 6. Transient state aerodynamic characteristics of coaxilcopter rotors.

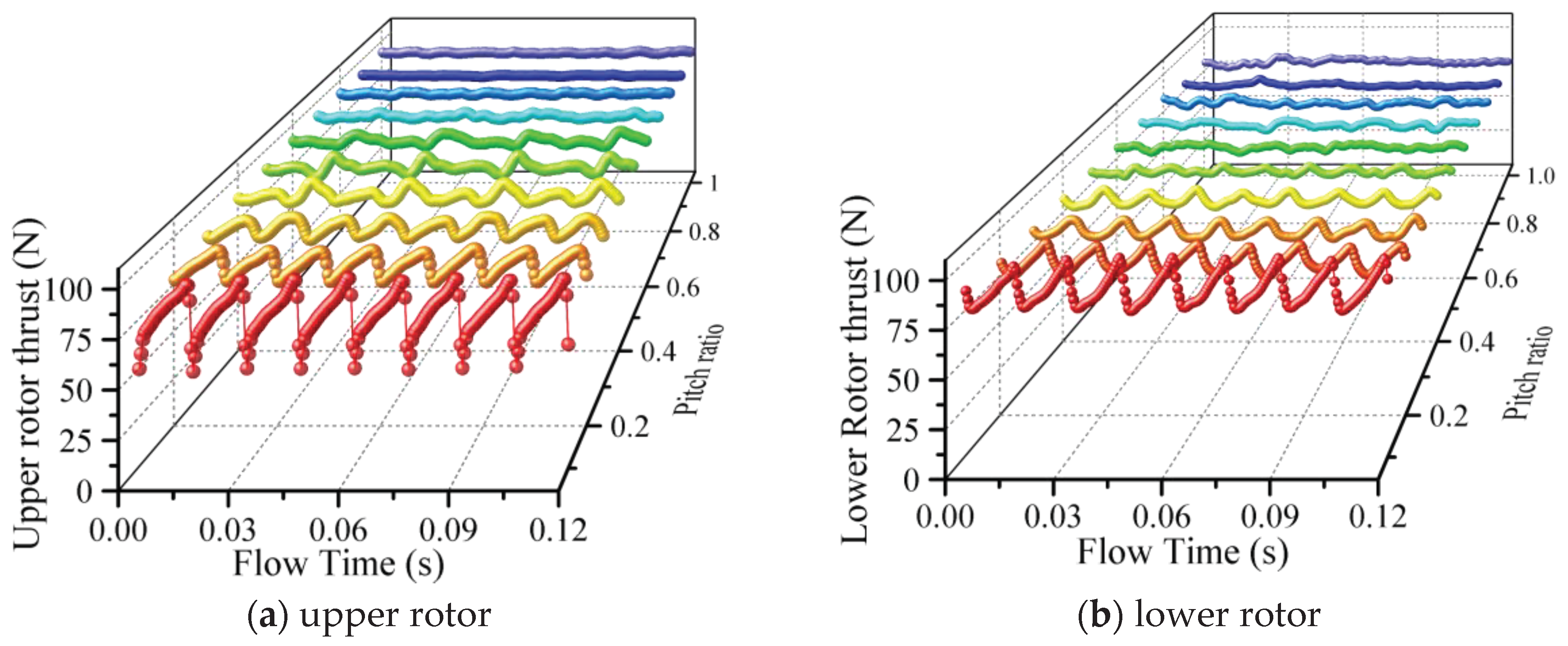
Figure 7. Average thrust of coxilcopter rotors at different pitch ratio.

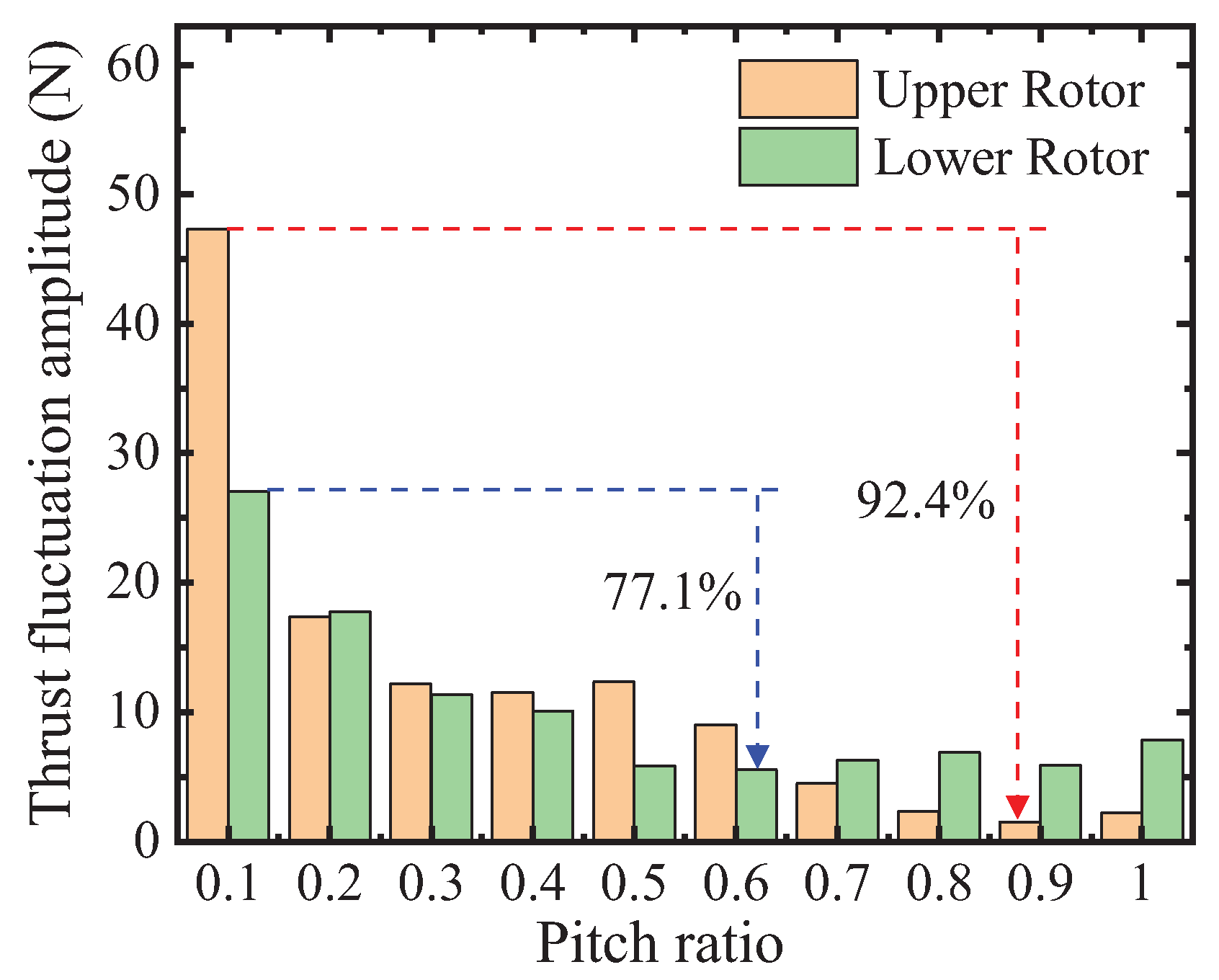
Figure 8. Vortex distribution in coaxilcopter rotors.

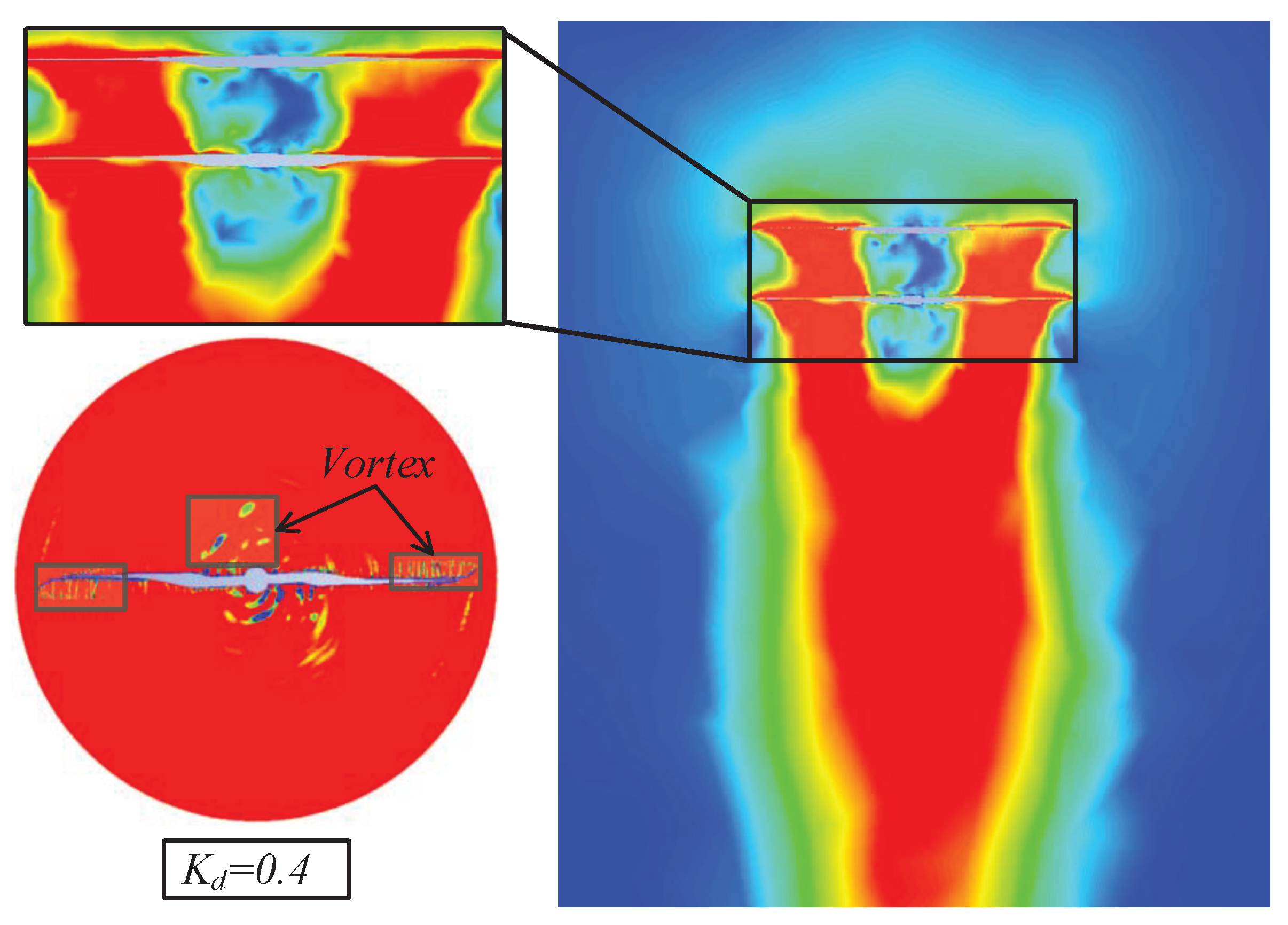
Figure 9. The comparison of vortex interference at different pitch.

Figure 10. The influence of different parameters on the thrust coefficient.

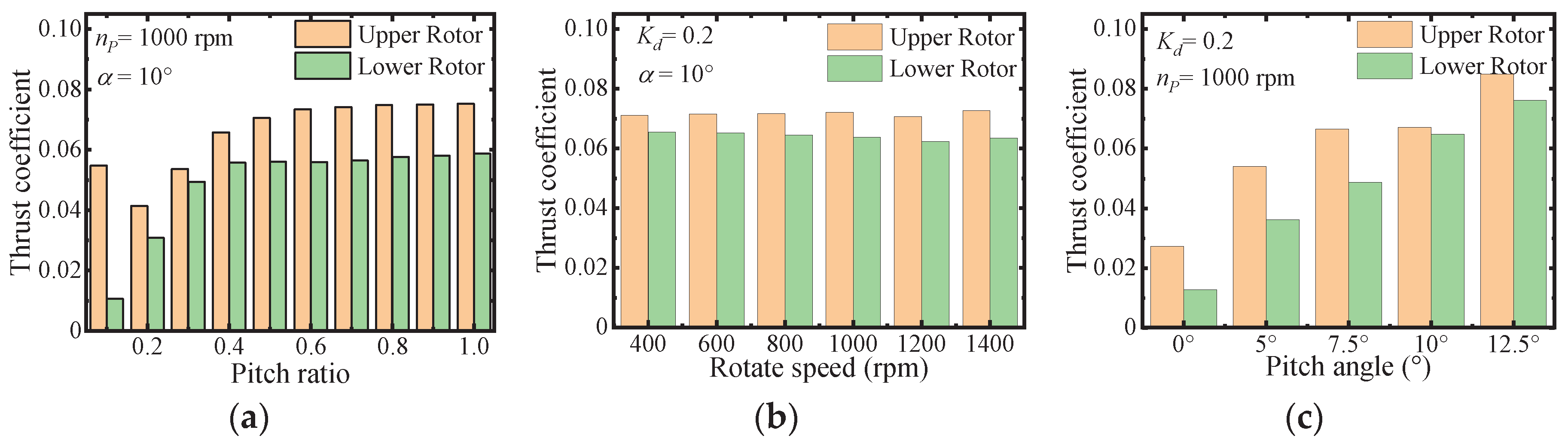
Figure 11. The influence of different parameters on the power coefficient.

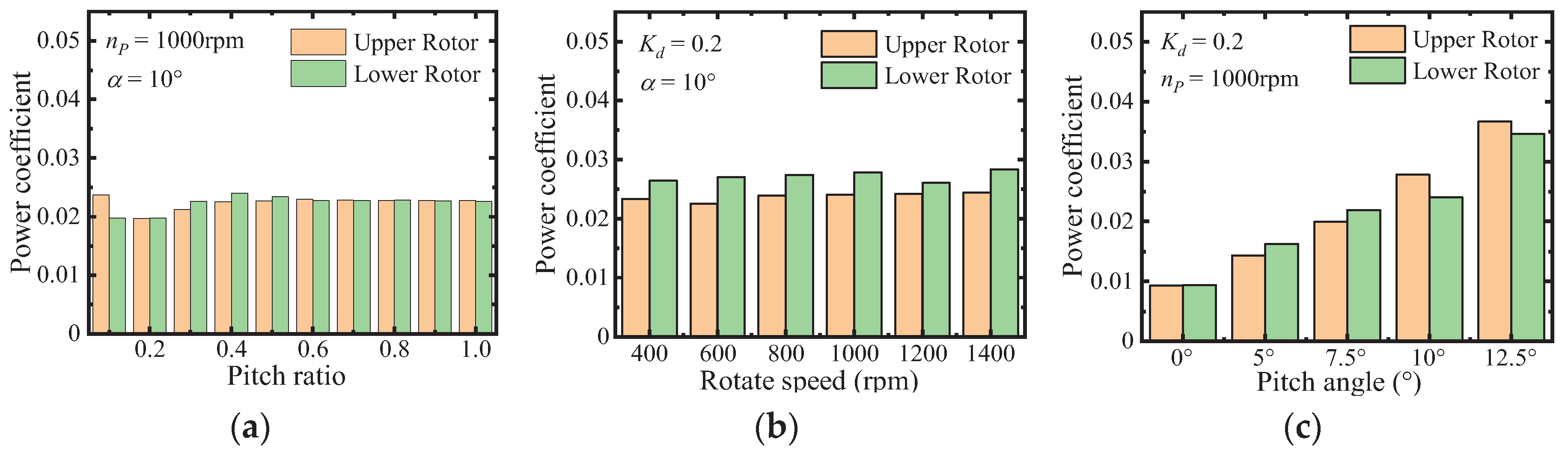
Figure 12. Workflow of parameter optimization.

Figure 13. Thrust and power coefficients of five sets of parameters.

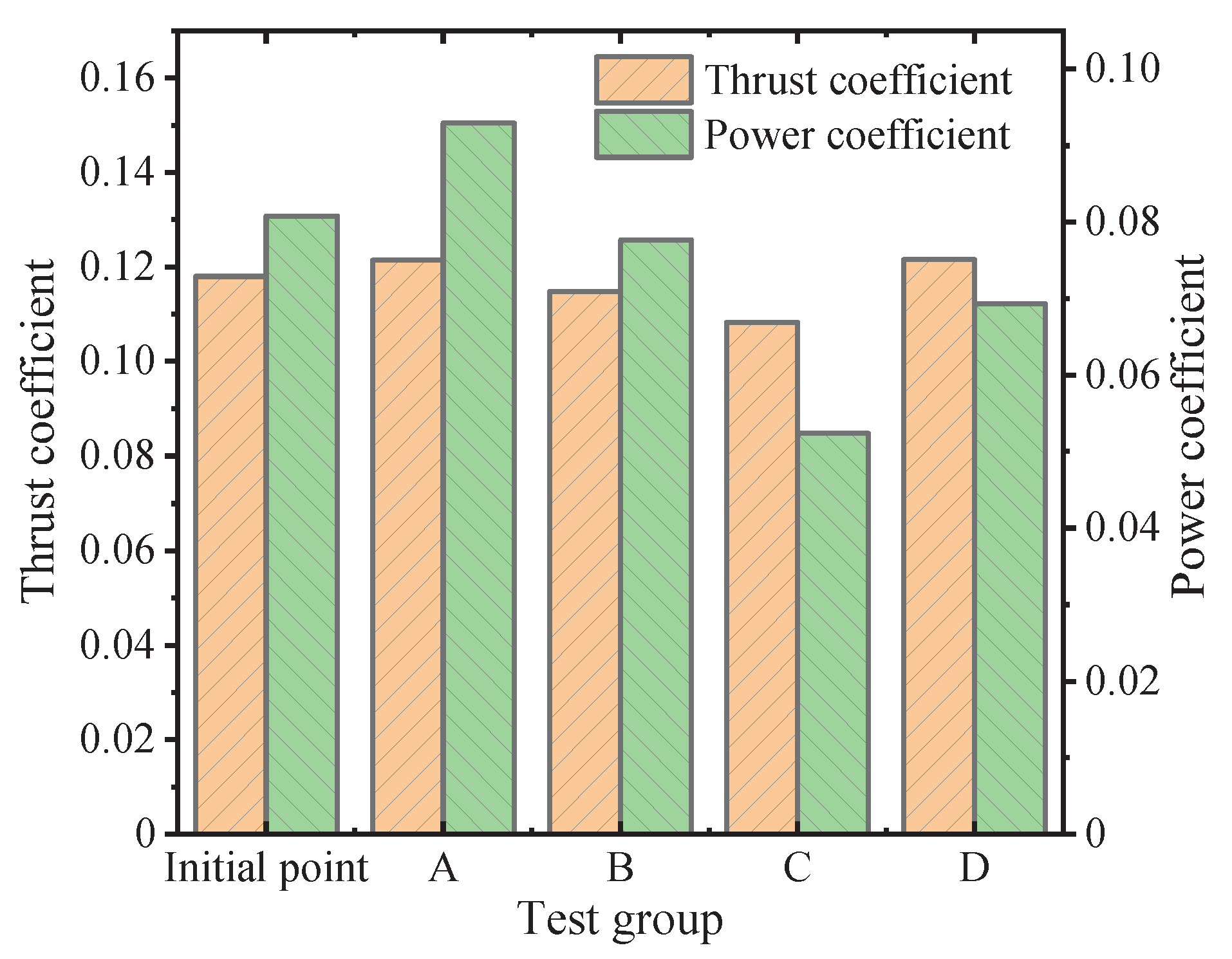
Figure 14. Test platform of coaxialcoptor rotor.

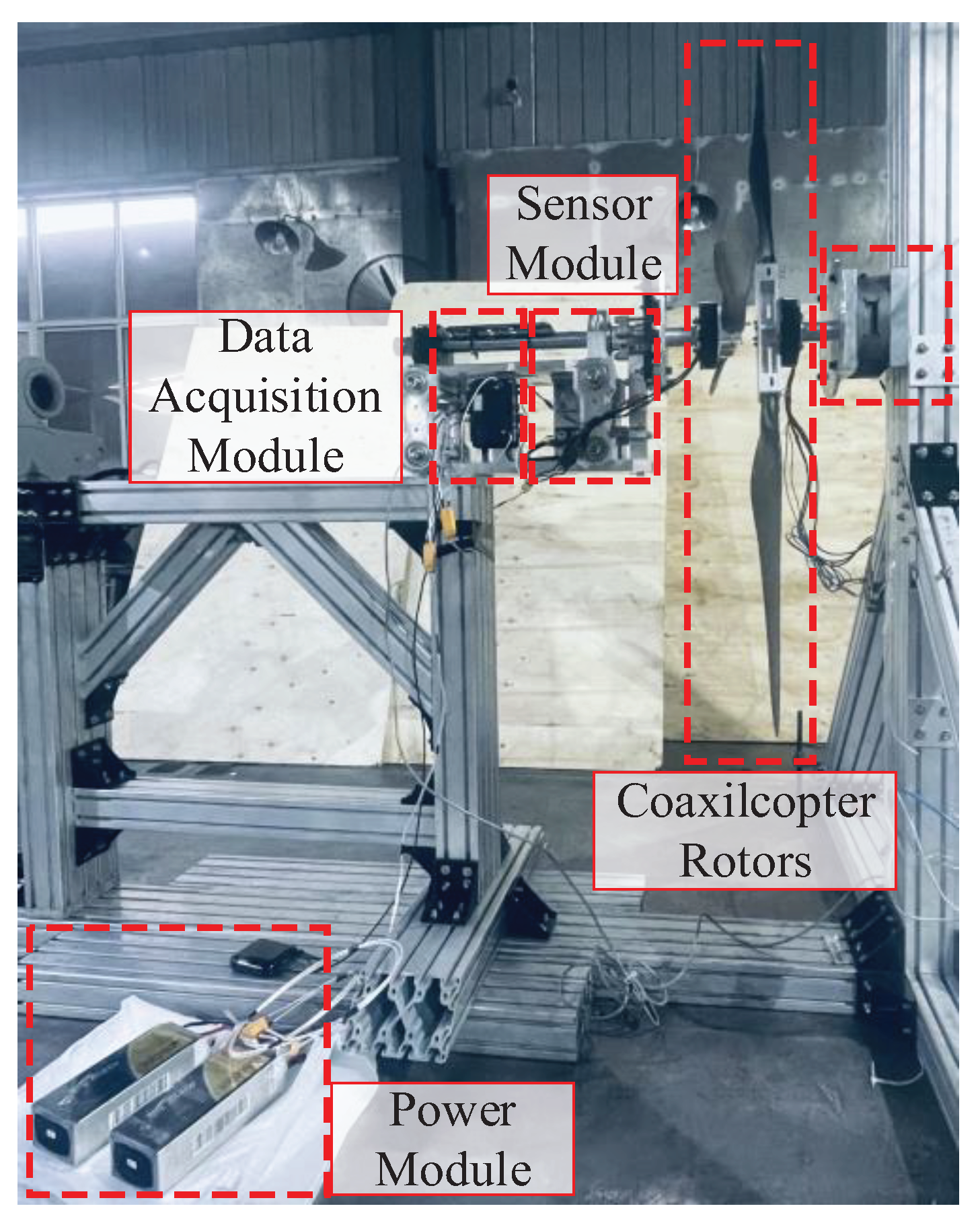
Figure 15. Aerodynamic test of coaxialcopter under different rotor spacing.

Figure 16. Comparison of simulation and experimental results of coaxialcopter rotors.

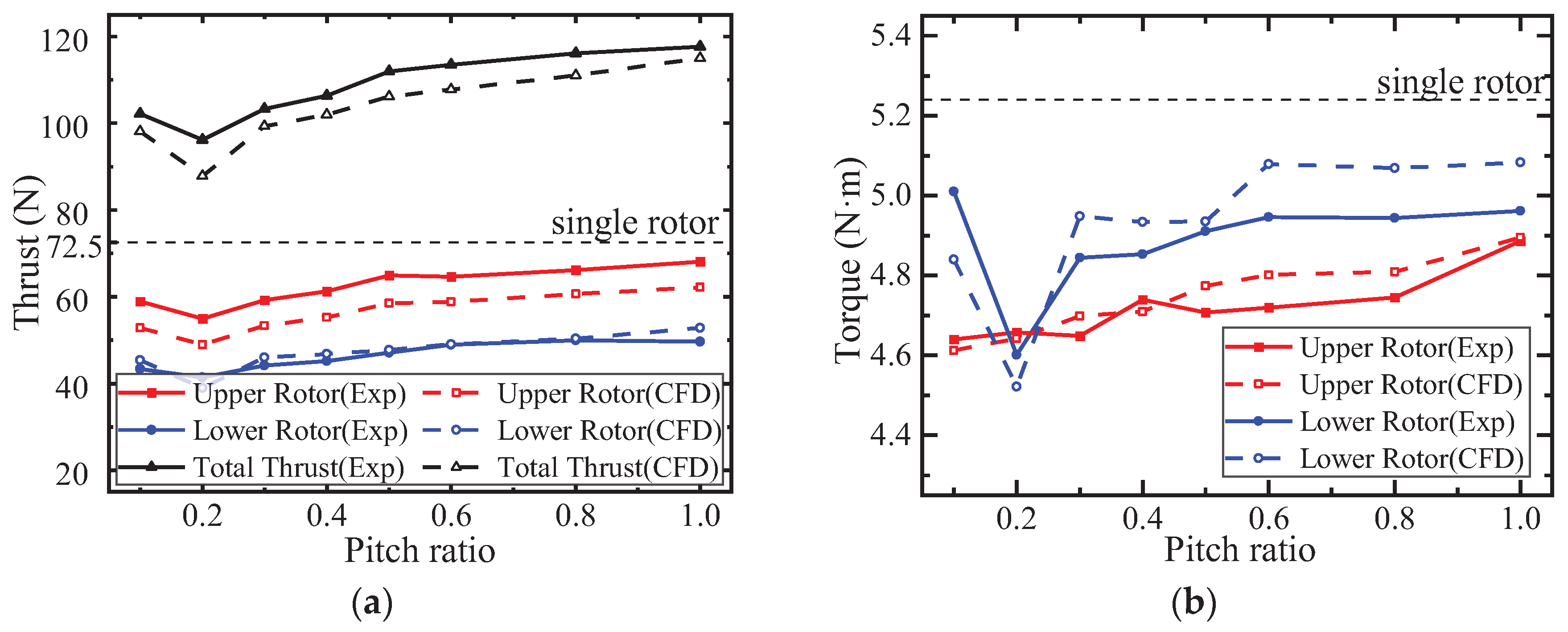
Figure 17. Comparison of simulation and experimental results for parameter optimization.

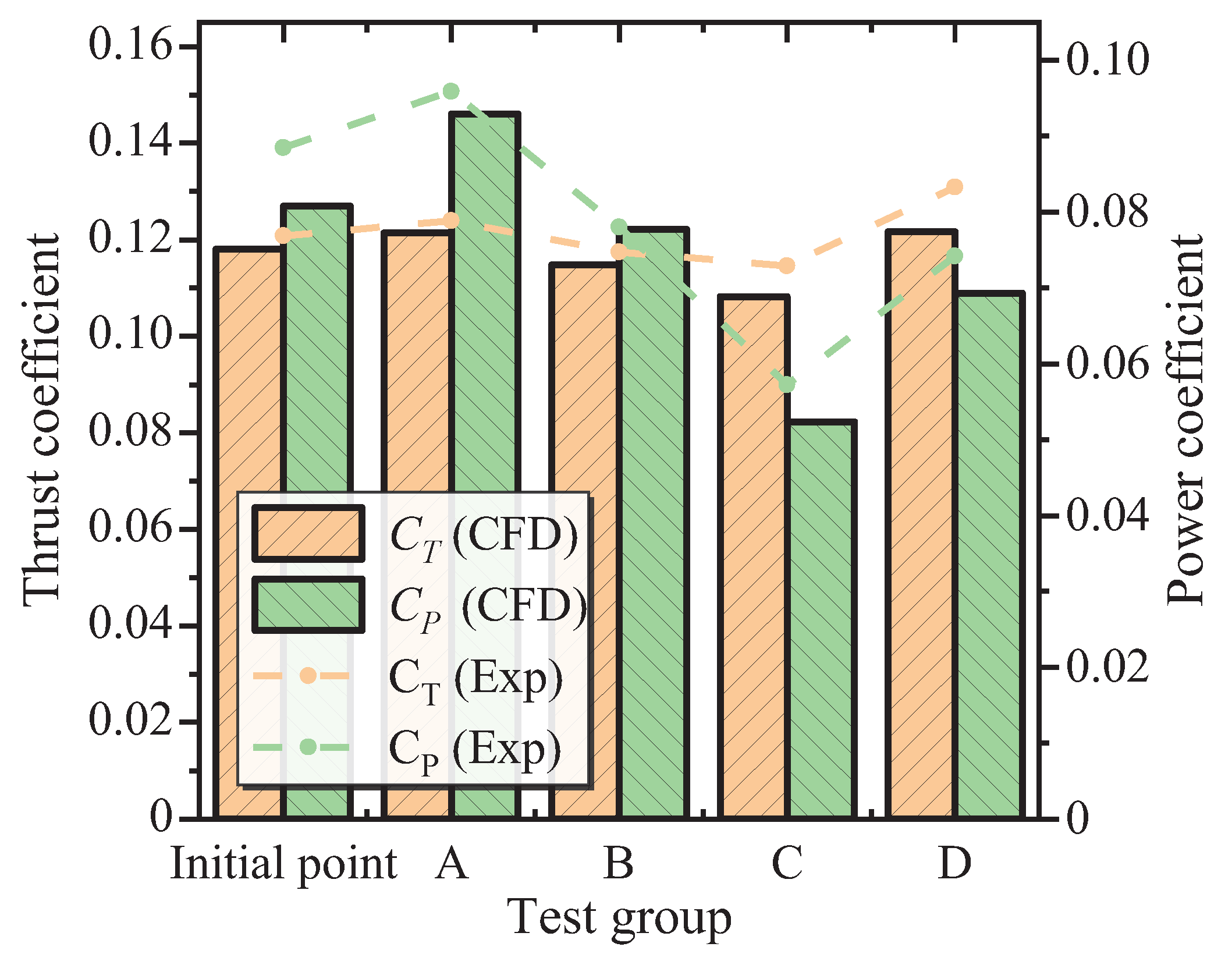
Table 1. Basic parameters of coaxialcopter rotor.

Name	Symbol	Value(unit)
Rotor radius	R	685 (mm)
Rotate speed	n_P	1000 (rpm)
Pitch angle	α	10 (°)
Pitch ratio	K_d	0.2

Table 2. Results of strategy optimization method.

Test group	Pitch ratio K_d	Pitch angle α (°)	C_T	C_P
Initial point	0.2	10	0.1180	0.0807
Test point A	0.4	10	0.1214	0.0929
Test point B	0.2	7.5	0.1148	0.0777
Test point C	0.4	5	0.1024	0.0523
Test point D	0.4	7.5	0.1216	0.0693

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer