Preprint
Article
Frictional Behavior of Chestnut (Castanea sativa Mill.) Sawn Timber for Carpentry and Mechanical Joints in Service Class 2
Altmetrics
Downloads
107
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 March 2024
Posted:
01 April 2024
You are already at the latest version
Alerts
Abstract
Wood is poised to become a material of choice for future construction. When appropriately managed, it is a renewable material with unique mechanical properties. Beyond its inherent sustainability, the use of wood has a crucial role in addressing climate change concerns due a significantly lower energy consumption and emissions during manufacturing and transportation, while simultaneously acting as a carbon sink. Thus, there has been a growing demand for hardwoods for structural applications, including Castanea sativa Mill., the focal point of this investigation. Albeit in a limited capacity, Eurocode 5-2 offers friction coefficients for softwoods, but it falls short for hardwoods which it is a gap to bridge with this research. These coefficients play a critical role in numerical simulations involving friction, enabling the optimization of joints and, by extension, the overall structural integrity. Test samples were evaluated at 18% moisture content, which is typical of Service Class 2, for various orientations of timber-to-timber and timber-to-steel friction. Considering previous friction coefficients at 12% moisture content, the linear variation was evaluated at an intermediate value of 15%. The results provide an experimental database for numerical simulations and highlight the influence of moisture content on the coefficients, which increase linearly along moisture percentages.
Keywords:
Subject: Engineering - Architecture, Building and Construction
1. Introduction
Historically, wood has been a traditional and widely used material in construction due to its abundance, ease of use and adequate mechanical properties. However, as technological advancements made steel and concrete not only more accessible but also cost-effective, these materials began to be perceived as superior alternatives due to their modern aesthetic, enhanced durability, and significantly improved fire resistance. In turn, the prominence of wood in the construction industry diminished as it was relegated to small-scale or less demanding structural applications due to concerns regarding instability, fire safety, decay, and sound transmission [1].
Currently, with the construction sector widely recognized as a major contributor to environmental degradation due to substantial material and energy consumption, greenhouse gas emissions, and waste generation, wood is experiencing a resurgence as a sustainable construction material. The favorable mechanical properties relative to its weight, the enhancement of its durability through innovative treatments and the advent of new engineered timber products, e.g., glued laminated timber (glulam), cross-laminated timber (CLT), and laminated veneer lumber (LVL), are some of the driving factors in its resurgence, besides the pursuit of sustainable development. In this regard, beyond its inherent sustainability, the use of wood has a crucial role in addressing climate change concerns due to its significantly lower embodied energy [2] and reduced CO2 emissions [3,4], while simultaneously acting as a carbon sink of approximately 1.5 t of CO2 per m3 of wood [5]. As a renewable resource originating from responsibly managed forests, wood further alleviates the pressures of raw material scarcity, highlighting its multifaceted contribution to environmental conservation.
For this investigation, chestnut wood (Castanea sativa, Mill.) was selected as this deciduous species covers more than 2.5 million hectares in Europe around the Mediterranean region, with 89% concentrated in France, Italy, Spain, Portugal, and Switzerland, in decreasing order of importance as shown in Figure 1 [6]. Several research works have underscored its ecological relevance as support for a wide variety of flora and fauna [7,8] and the European Council has included “9260 Castanea sativa woods’” in Annex 1 of the Habitats Directive [9]. Commercially, chestnut is valued both for fruit and non-wood products as well as timber. For instance, in Spain, the average total volume (with bark) of chestnut stands harvested in 2021 reached 97,878 m3 [10], mostly from the north provinces (Galicia, Asturias, Navarre and Catalonia), but also arising from the center and south of the country (Figure 1). Chestnut wood is valued for its appearance and strength; it is particularly appreciated for external use due to its natural protection against decay [11,12]; and it possesses a vast tradition of use for both structural and non-structural purposes in construction (beams, joists and traditional grain stores), woodworking, furniture, flooring, fine veneer, general joinery and poles) [11]. Nowadays, sustainability concerns have spurred a new interest in its use. In this regard, Carbone et al. [13], who investigated the market competitiveness of laminated chestnut timber products, forecasted a bright future for this type of wood while indicating the need for a targeted chestnut wood policy to significantly bolster its market penetration and growth.
In structural timber engineering, the friction properties of wood, which are the focus of this study, hold significant relevance, particularly in the design of joints and supports. The friction coefficient between wooden parts or between wood and metal connectors significantly influences the magnitude and manner of force transmission [14,15,16,17,18,19,20,21,22]. Thus, the understanding of this parameter is crucial for the analysis and simulation of both carpentry joints and mechanical connections. As with most mechanical properties of wood, friction also varies with the moisture content reached by the specimen in balance with the relative humidity and temperature of its surrounding environment. Consequently, the Eurocode 5 [23] incorporate this effect in design by establishing three services classes reflecting the environmental conditions (i.e., temperature and relative humidity of the surrounding air) to which the wood will be exposed and its eventual equilibrium moisture content:
- Service class 1: corresponds to conditions (20ºC and 65% relative humidity) where the average moisture content in most softwoods remains below 12%
- Service class 2: corresponds to conditions (20ºC and 85% relative humidity) where the average moisture content in most softwoods remains below 20%
- Service class 3: corresponds to conditions where the average moisture content in most softwoods exceeds 20%
It should be noted that although Eurocode 5 [23] identifies service classes for softwoods, the temperature and relative humidity conditions describing the different service classes and moisture contents are also applicable to hardwoods such as chestnut.
Therefore, the standards used to characterize the mechanical properties of wood stipulate testing at a specific moisture level, commonly 12%. Then, subsequent adjustments are made in calculations through the use of coefficients based on the intended service class. However, there is no European standard regarding the experimental determination of friction coefficients, but conversely, it is referenced in Table 6.1 of Eurocode 5-2 [24] for conifer timber in the context of stress-laminated deck. Specifically, values for the static friction coefficient are provided at moisture contents of ≤12% and ≥16%, with the provision that values within this range can be linearly interpolated.
Although several researchers [25,26,27] have commented on the linear variation of properties with moisture content from 8% to 20%, or until fiber saturation is reached, limited research explores the relationship between moisture content variations and friction, with investigations predominantly centered at the 12% equilibrium moisture content. Among those that do consider or provide insights on moisture content, the following studies are noteworthy:
For varying moisture content values, Argüelles et al. [26,28] reported values for the static friction coefficient ranging from 0.25 to 0.7 and for the kinetic friction coefficient within the 0.15 to 0.4 range. The coefficients increased with the moisture content of the timber-to-timber testing specimen up to saturation and remained constant beyond that point. This effect was also noticed by Kretschmann [27], who reported that the coefficients continuously increase until fiber saturation is reached. Then, the values stabilize until water is present on the surface, triggering a decrease in the coefficients due to the lubricating effect. Although for beech timber, Fu et al. [29] examined the influence of both the moisture content and wood section (i.e., tangential, diagonal, and radial) on the static and kinetic friction coefficients. Both values increased with the moisture content within the 5-30% range, but greater moisture contents are responsible for marginal increases. For the different orientations of the contact surfaces, the authors reported static friction coefficients ranging from 0.5 to 0.71 and kinetic friction coefficients ranging from 0.3 to 0.65 at 11.25% and 20% moisture levels, respectively.
Regarding timber-to-steel friction, there are a limited number of studies, predominantly focused on dynamic assessments. McKenzie et al. [19] performed an extensive examination of the kinetic friction coefficients of numerous wood species against rough and smoot steel surfaces, although chestnut was not included in the investigation. For smooth surfaces, which are common in timber connections, the study reports kinetic friction coefficients ranging from 0.1 to 0.3 for moisture content between 10% and 14%, depending on the speed of sliding. For moisture levels at fiber saturation, the values range from 0.4 to 0.64 for increasing sliding speeds. Moreover, based on the figures describing the dynamic friction included in the research, it could be inferred that the static friction values are only slightly higher than those reported for the kinetic friction.
Similarly, Kretschmann [27] noticed that the kinetic friction coefficient for smooth timber in contact with hard, smooth surfaces, such as steel, can vary from 0.3 to 0.5 in dry specimens, from 0.5 to 0.7 at intermediate moisture content, and from 0.7 to 9.9 when approaching saturation. Despite the distinct properties compared to sawn timber, it is worth mentioning the study on the friction behavior of microlaminated Picea abies against steel carried out by Dorn. [30]. The authors recorded static friction coefficient values ranging between 0.10 and 0.30 at 12% moisture content. For oven-dried specimens, these values remained mostly constant. However, for saturated specimens, the static friction coefficient increased between 74% and 123% for tests parallel to the grain and between 82% and 182% for tests perpendicular to the grain.
This research work focuses on the study of the moisture-dependent and orthotropic behavior in the assessment of both static and kinetic friction coefficients of chestnut timber. As the authors have previously conducted timber-to-timber and timber-to-steel tests at 12% moisture content [31,32], this investigation focuses on tests at Service class 2 conditions (i.e., 15% and 18%) that would ultimately allow to validate the aforementioned interpolation approach.
The enhanced understanding of friction pursued in this study aims to expand the use of Castanea sativa for structural designs involving frictional forces. Targeted applications include stressed plate bridges and walkways, timber trusses with carpentry joints, and constructions with mechanical timber-to-steel connections. The results arising from the experimental program would provide a comprehensive database to be used as an input for precise engineering calculations, such as those carried out in numerical simulations. Moreover, this investigation promotes construction sustainability by encouraging the use of less exploited materials, which entails a diversification in the range of species used in construction and thus alleviates the demand for more commonly exploited ones. Similarly, the use of more precise structural simulation and calculations would allow for a more accurate volumetric optimization of this natural resource.
2. Materials and Methods
Test samples of 105 x 50 x 25 mm were prepared from Spanish chestnut (Castanea sativa Mill.). Since the variation in moisture content changes the frictional properties of wood, the tests were carried out at two moisture contents. Firstly, at 18% moisture content, which represents Service class 2 according to Eurocode 5 [23] (e.g., structures under cover but open to the air, canopies, covered pergolas, walkways, and bridges that are either covered or protected by a wear layer, as well as indoor and enclosed swimming pools [23,25,26]). Then, at 15% moisture content (i.e., an intermediate value to the 12% moisture content used to represent the conditions of Service class 1 established in Eurocode 5 [23]). Thus, one set of specimens were stored in a condition room with a constant temperature of 20 °C and a relative humidity of 85% to ensure the hygroscopic equilibrium and the desired moisture content of 18%. Conversely, for conditioning to a humidity of 15%, a temperature of 38 °C and a humidity of 80% were set [27]. The moisture levels were checked immediately before carrying out the tests using a hygrometer and afterwards by oven drying according to EN 13183-1 [33].
In the absence of specific European standard test for determining the friction coefficient of wood and drawing upon the general recommendations provided by the American standard ASTM G115-10 [34], the authors developed and validated a test procedure based on a direct shear machine [35]. The proposed method adapts the common geotechnical equipment to facilitate the placement and contact of the surfaces to be tested (i.e., specimens were positioned in the device by their largest surface area, ensuring that sliding occurred along the longest dimension), thereby facilitating accurate experimental conditions as well as the application and recording of the necessary variables. Firstly, it allows for the application of a normal load (N) to the upper face of the specimen through a distribution plate connected to a load bridge and counter-balance device while controlling the sliding speed. Similar to other research works [31,32,36,37], this study employed a 0.5 MPa load and an 8 mm·min−1 speed to simulate conditions encountered in practice while also effectively preventing the occurrence of inertial forces. Moreover, it enables the measurement of both displacement and the necessary force (F) required to produce sliding by means of an LVDT (Linear Variable Differential Transformer) displacement and sensor load cell sensor, respectively. Therefore, the coefficient of friction (μ) is determined according to Equation (1):
wherein the proportionality constant is the friction coefficient, designated as either the static friction coefficient (μs) or kinetic friction coefficient (μk), contingent upon whether it pertains to the value at the precise moment just before sliding commences or during the ongoing relative displacement of the solids or the surfaces under examination.
F = μ x N,
Two separate experimental series were executed to evaluate the frictional behavior between pairs of materials: one set examined timber-to-timber interactions, while the other focused on timber-to-steel contacts. Moreover, to simulate the conditions of surfaces that are designed to come into contact within the joint assembly, the influence of the orthotropic nature of wood as well as the different roughness across the cutting planes was considered. As such, three distinct orthogonal axes were considered: longitudinal -L- (parallel to the fiber or grain; i.e., the axis of the tree), radial -R- (perpendicular to the grain in the radial direction and normal the growth rings), and tangential -T- (perpendicular to the grain but tangent to the growth rings) as shown in Figure 2.
Consequently, the three possible friction planes and their two respective directions of slippage were evaluated (Figure 2), ensuring a comprehensive analysis of frictional behavior under varied conditions:
- Transverse plane (perpendicular to the fiber)
- (A) predominant direction of radial sliding (sliding parallel to the radius of the growth rings)
- (B) predominant direction of tangential sliding to the growth rings
- Radial plane defined by the axis of the three and a radius of the trunk
- (C) sliding direction parallel to the fiber (i.e., radial surfaces)
- (D) sliding direction perpendicular to the fiber
- Tangential plane (tangent to the growth rings)
- (E) sliding direction parallel to the fiber (i.e., tangential surfaces)
- (F) sliding direction perpendicular to the fiber
Therefore, Figure 2 presents the array of friction pairs that reflect combinations frequently encountered in structural connections. On the one hand, timber-to-timber tests could be divided among surfaces with identical orientations: A-A, B-B, C-C, D-D, E-E, and F-F, and tests between surfaces of differing orientations: A-C, A-E, B-C, and B-E. On the other hand, timber-to-steel tests are designed as A-S, B-S, C-S, D-S, E-S, and F-S, with S indicating the steel plate. Thus, the experimental program reached a total of over 400 tests and ultimately offer significant insights into the frictional behavior.
3. Results and Discussion
3.1. Timber-to-Timber Tests with Identical Orientations
Figure 3 showcases the most illustrative graphs depicting the variation of the friction coefficient relative to the displacement for tests involving surfaces of identical orientations and friction directions, under a controlled moisture content of 18%.
The oscillations observed in Figure 3 are illustrative of the stick-slip phenomenon. However, the fluctuation manifested with reduced intensity compared to similar tests conducted at lower moisture levels [31,32]. This reduction aligns with findings by [29,38], highlighting that higher moisture weakens the stick-slip behavior between the wood surfaces. The differences between the frictional force-displacement curves of dry and wet surfaces were also observed by Fu et al. [29], who attributed them to the softening of the fibers and the decreased amplitude of the rough peaks, which led to a weakened stick-slip motion in the 5–30% moisture range. As described by Möhler and Herröder [39] in friction scenarios A and C, the sliding motion occurs continuously across the friction path and is characterized by a parabolic decrease in the horizontal force, at least in an initial segment.
Table 1 shows the friction coefficients from various sawn specimens and frictional directions grouped by friction pairs with identical orientations and a moisture content of 18%. Both, the mean value derived from the 15 tests performed for each specific pairing and the coefficient of variation (CoV) are indicated to highlight the average performance and the variability within each set.
Based on the comparison between the results presented in Table 1 and those obtained for these same orientations in a previous work [31], it becomes noticeable that moisture content significantly impacts both static and kinetic friction, overshadowing the effects of the testing orientation. This finding aligns with observations made by [29]. On average, disregarding orientation, the static friction coefficient stands at 0.70, and the kinetic friction coefficient at 0.48. Such values represent a roughly 50% increase compared to those measured at 12% moisture content. These findings are consistent with those reported by Argüelles et al. [26] (i.e., a 0.7 static friction coefficient and 0.4 kinetic friction coefficient) and Fu et al. [29] at 20% moisture content (μs = 0.5-0.71; μk = 0.3-0.65). In this experimental program, the average coefficient of variation for the different orientation test series was 7.6% for static friction and 10% for kinetic friction. Notably, the CoV for each friction pair significantly decreased by about 15 % compared to the 12% moisture tests, suggesting that increased moisture on the contact surfaces leads to less variability in friction.
3.2. Timber-to-Timber Tests with Different Orientations
Figure 4 presents some representative examples that capture the fluctuation of the friction coefficient as a function of displacement, focusing on experiments that involve surfaces with different orientations and sliding directions, conducted at a moisture content of 18%.
Similar observations apply to Figure 4 regarding the stick-slip behavior of the tested specimens. The performance of the friction pairs demonstrates a consistent relationship between displacement and friction coefficient, closely aligning with the patterns noted in scenarios of identical orientation between wood surfaces (Figure 3).
Table 2 compiles the friction coefficients from various sawn specimens and frictional directions grouped by friction pairs with identical orientations and a moisture content of 18%. A trend consistent with the earlier discussion is observed as values exhibit a notable increase compared to those at 12% moisture content [32]. Specifically, there is a 42% surge in the static friction coefficient, averaging at 0.67, and a 30% rise in the kinetic friction coefficient, averaging at 0.47. Nevertheless, the increment is less pronounced than the increase observed for samples with identical orientations, as recorded in Table 1.
The overall average values, both static and kinetic, are remarkably similar to those obtained for the same orientation at 18% moisture content and align with referenced literature from the previous section. The lack of significant variance for any specific pair could respond to a homogenizing effect of increased moisture levels. Notably, the A-C and B-E pairings continue to register the greatest friction values, a pattern consistent with observations at 12% moisture. However, no direct correlation is observed between the highest values in Table 2 and the superior frictional values arising from the friction of wood surfaces of identical orientations (Table 1). Regarding the coefficient of variation, the values decreased compared to the 12% moisture level for each tested friction pair, mirroring the trend observed for pairs of identical orientation. Nonetheless, the CoV values remained in the same range as those obtained for 18% moisture content between wood surfaces of identical orientation.
It is worth noting that the average static friction coefficient value (μs = 0.69) significantly exceeds those specified in Eurocode 5-2 [24]. For the calculation of stress-laminated deck plates consisting of sawn softwood at a moisture content greater than 16%, the design values established for the static friction coefficient are 0.45 for scenarios perpendicular to grain and 0.35 for scenarios parallel to grain. Nevertheless, this comparison should take into account the case-specificity differences regarding the type of wood and moisture content (i.e., specimens derived from Castanea sativa, a deciduous tree, conditioned at 18% moisture content). Moreover, it should be acknowledged that the values stipulated by Eurocode 5-2 [24] serve as design guidelines, factoring in safety margins to ensure structural. Thus, the proposed values by Eurocode 5-2 [24] are deliberately conservative since greater friction coefficient values are beneficial for the outcomes of the engineering calculations.
3.3. Timber-to-Steel Tests
Figure 5 showcases representative friction cases of the tests between the timber specimens at 18% moisture content and the steel plate focusing on experiments that involve different fiber orientations relative to the sliding direction.
Conversely to previous timber-to-timber tests series, Figure 5 illustrates the absence of the stick-slip phenomenon corroborating findings from other studies [29,40]. As also noted by those researchers, the increase in moisture does not introduce a pronounced inflection at the beginning of displacement. The shape of the obtained curves (Figure 5) is similar to the type B classification proposed by Möhler and Herröder [39] in which the frictional force exhibits a flat parabolic shape, indicative of a friction trajectory that either slightly decreases or, in certain instances, remains constant after reaching the peak load. Notably, in some instances, the value of friction marginally increases shortly after the sliding begins.
Table 3 details the mean values for both static and kinetic friction coefficients, accompanied by the coefficient of variation from tests involving the interaction between a steel plate and a wood specimen conditioned at 18% moisture content and sawn to exhibit a specific orientation.
Analysis of the data in the test series for the different wood orientations reveals an average static friction coefficient of 0.52 and a kinetic friction coefficient of 0.50, with coefficients of variation of 6% and 7%, respectively. Two main insights emerge from these finding:
On the one hand, there is a substantial increase in both static and kinetic friction coefficients compared to steel-wood pairs at 12% moisture content [32]. For instance, the average static coefficient exhibited a 173% rise and the kinetic coefficient a 194% surge, which closely places the kinetic value on par with the static coefficient. These substantial increases are in line with those documented by Dorn et al. [30], who conducted tests on wood against steel ranging from oven-dried to fully saturated specimens. Moreover, the obtained values fall within the range specified by Kretschmann [27] for friction of wood against hard and smooth surfaces at intermediate moisture (μk = 0.5-0.7), and are consistent with the findings reported by McKenzie et al. [41] of μk =0.4-0.64. Nonetheless, it is worth noting that this increase significantly exceeds that observed for the same moisture variation in the timber-to-timber tests, suggesting that when friction occurs against a very smooth surface, such as steel, the moisture content of the wood has a significantly major role in the friction coefficient.
On the other hand, the CoV values within each orientation are considerably lower compared to those obtained for wood specimens at 12% moisture content. Such a reduction in variability is attributed to both the increased moisture at the contact surface and the homogenizing effect of steel (i.e., the limited roughness) in the wood-steel friction dynamics.
3.4. Correlation between μk and μs
For each friction specimen pairing within the timber-to-timber test series, Figure 6a illustrates the relationship between the static friction coefficient (μs) and the kinetic friction coefficient (μk). Similarly, Figure 6b displays the average values for each friction combination. The μk/μs ratio for surfaces of identical orientation averaged 0.72, similar to the values obtained at 12% moisture content, which indicated no significant change in their relationship. For surfaces of different orientations, the μk/μs ratio was 0.69, yielding a value comparable to that of surfaces with identical orientation at 18% moisture level. This similarity suggests that the orientation of wood surfaces does not markedly affect the relationship between static and kinetic friction coefficients under the same moisture conditions.
Although no strong relationship emerged from the entire dataset, the analysis of the average values (Figure 6b) allowed for an acceptable correlation (R2 = 0.70) between static and kinetic friction coefficients (Equation (2)).
μk = 0.809μs - 0.0777 (R2 = 0.70),
Additionally, the consideration of specific friction orientations allows for improved correlations such as those shown in Equations 3 and 4 for A-C and E-E friction pairs, respectively.
For the friction pair A-C: μk = 0.98μs - 0.19 (R2 = 0.76),
For the friction pair E-E: μk = 0.89μs - 0.035 (R2 = 0.74),
A similar approach for the relationship of the static and kinetic friction coefficients of the timber-to-steel tests was followed in Figure 7a,b. The μk/μs ratio averaged 0.97, which numerically captures the behavior depicted in Figure 5 (i.e., a flat parabolic curve with a minimal reduction in the coefficient value during sliding). In this case, a notable difference is observed in the ratio compared to the values obtained at 12% moisture, which had an average of 0.83, indicating a further reduction in the differences between static and kinetic values. The greater proximity to unity reflects the absence of the initial inflection point in the registered friction behavior. This phenomenon was also noted by Fu et al. [29], who observed that the difference between μs and μk decreases with higher moisture contents.
From the average coefficients for the different timber-to-steel tests, Equation 5 shows the relationship between static and kinetic friction. The robustness of the correlation (R² = 0.96) allows for a highly reliable prediction of the kinetic coefficient from a known static coefficient, and vice versa. Moreover, the specific friction pair combinations also display strong correlations among both coefficients. It should be noted that the high degree of correlation was also identified for the 12% moisture content [32] pointing to a generalization of this observation across the entire studied moisture spectrum, as further detailed in subsequent discussions.
μk = 1.350μs - 0.199 (R2 = 0.96),
3.5. Influence of the Moisture Content on Friction Coefficients
To evaluate the validity of the linear coefficient-moisture relationships, the experimental program included a targeted series of tests at an intermediate moisture level of 15% while maintaining all other test parameters constant. The average value and coefficient of variation from 10 determinations within each friction pair combination (i.e., between wood surfaces of identical orientation, wood surfaces of different orientation, and wood and steel) of static and kinetic coefficients are displayed in Table 4, Table 5 and Table 6.
Consistent with previous observations, the CoV resembles more closely the results from the 12% moisture tests due to a lower moisture-induced homogenizing effect on the frictional behavior at this intermediate level. Nevertheless, taking into account the inherent variability of wood as a natural material, these CoV values are deemed acceptable, especially when considering those reported in the literature.
Both the static and kinetic friction coefficients fall within the range of those arising from specimens conditioned at 12% and 18% moisture content, which is in accordance with the known dependence behavior between the moisture content and the mechanical properties of wood. Certainly, the Eurocode 5-2 [24] and several researchers [25,26,27] accept that intermediate friction coefficients could be determined by linear interpolation. Therefore, taking into account the static and kinetic coefficient results obtained by the authors at 12% [31,32] and 18% moisture contents, all possible linear regressions were determined. Figure 8 and Figure 9 show these linear relationships as dotted lines colored according to each friction pair combination of the timber-to-timber and timber-to-steel tests. Moreover, to evaluate the precision of the interpolation method, the corresponding experimental results at 15% moisture content were also included in Figure 8 and Figure 9.
Aside from a few exceptions, the slopes of the linear regressions are similar for each type of friction coefficient displayed in the different figures, which is especially apparent in timber-to-steel friction cases. This observation underscores the robustness of the linear estimation approach across different materials and conditions. Moreover, Table 7 presents the interpolated friction coefficients at the 15% moisture content from each linear regression (i.e., dotted lines) in Figure 8 and Figure 9. Although, in most cases, the accuracy of the linear regression compared to the experimental value is evident from the figures, the observed error compared to the average experimental result at the same moisture content is also reported in the table.
The observed errors (Table 7), particularly in scenarios involving timber-to-steel friction, are consistently lower than the coefficients of variation recorded across all experimental tests carried out at 15% moisture content. This finding highlights the precision of the linear estimation approach within the 12-18% moisture range but also confirms its applicability to hardwoods like the sawn chestnut (Castanea sativa Mill.). Therefore, the method that originally was limited to the friction coefficient of conifers as per Eurocode 5-2 [24] proved to be significantly effective in enhancing the predictability of the frictional behavior of this particular hardwood species, which previously lacked specific and comprehensive friction coefficient data or prior testing for linear estimation accuracy.
4. Conclusions
This investigation studied the friction behavior of sawn chestnut timber. Firstly, the friction coefficient was assessed at 18% moisture content, providing insights into its performance under Service Class 2, a common scenario in wooden structures. Both static (μs) and dynamic (μk) coefficients exhibited increased values compared to those at 12% moisture content and associated with Service Class 1. The average values were μs = 0.68 and μk = 0.47 for timber-to-timber tests, and μs = 0.52 and μk = 0.5 for timber-to-steel tests. The increase was around 50% for timber-to-timber friction pairs and over 170% for timber-to-steel friction pairs compared to the 12% moisture content.
As per the particularities of the measuring equipment, the continuous evolution of the coefficient of friction relative to the displacement was graphically represented. For timber-to-timber tests, a reduction in the stick-slip phenomenon, up to its almost disappearance in some initial phases of tests, was observed due to the increased moisture. However, a clear initial peak was still noticed, albeit less pronounced than at 12% moisture content, and higher μk/μs ratios were determined. For timber-to-steel tests, there was a complete absence of the stick-slip phenomenon reported at 12% moisture content determinations. It was also noticed the lack of any peak at the onset of sliding and either the maintenance or slight increase of the friction coefficient once relative motion commenced, which resulted in a higher μk/μs ratio of 0.97.
Although the results were in line with those found by other researchers, given the limited literature available on wood friction at elevated moisture content exceeding the 12% value associated with standard testing, the direct comparison of the results was challenging, particularly for hardwood and chestnut. These new data points could be used in the same manner as the linear interpolation outlined in Eurocode 5-2 [24] for conifers. In this regard, the study confirmed the accuracy of this approach by comparing each interpolated value with the corresponding experimental result at the intermediate moisture content of 15%.
Author Contributions
Conceptualization, J.R.V.-G., P.V.-L. and D.R.-R; methodology, J.R.V.-G.; validation, formal analysis, investigation, funding acquisition, J.R.V.-G., M.M.I., P.V.-L. and D.R.-R.; writing—original draft preparation, J.R.V.-G. and D.R.-R.; writing—review and editing, supervision, J.R.V.-G., P.V.-L., and D.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Junta de Extremadura and by the European Regional Development Fund of the European Union through grants GR21163 and GR21091.
Acknowledgments
Administrative and technical support from the Forest Research Group and the Mechanical and Fluid Engineering Research Group of the University of Extremadura is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Roos, A.; Woxblom, L.; McCluskey, D. The Influence of Architects and Structural Engineers on Timber in Construction–Perceptions and Roles. Silva Fennica 2010, 44, 871–884. [Google Scholar] [CrossRef]
- Minunno, R.; O’Grady, T.; Morrison, G.M.; Gruner, R.L. Investigating the Embodied Energy and Carbon of Buildings: A Systematic Literature Review and Meta-Analysis of Life Cycle Assessments. Renewable and Sustainable Energy Reviews 2021, 143, 110935. [Google Scholar] [CrossRef]
- Tonelli, C.; Grimaudo, M. Timber Buildings and Thermal Inertia: Open Scientific Problems for Summer Behavior in Mediterranean Climate. Energy and Buildings 2014, 83, 89–95. [Google Scholar] [CrossRef]
- Martínez-Alonso, C.; Berdasco, L. Carbon Footprint of Sawn Timber Products of Castanea Sativa Mill. in the North of Spain. Journal of Cleaner Production 2015, 102, 127–135. [Google Scholar] [CrossRef]
- Arriaga, F.; Wang, X.; Íñiguez-González, G.; Llana, D.F.; Esteban, M.; Niemz, P. Mechanical Properties of Wood: A Review. Forests 2023, 14, 1202. [Google Scholar] [CrossRef]
- Conedera, M.; Tinner, W.; Krebs, P.; de Rigo, D.; Caudullo, G. Castanea Sativa in Europe: Distribution, Habitat, Usage and Threats. In European Atlas of Forest Tree Species; Publication Office of the European Union: Luxembourg, 2016. [Google Scholar]
- Rodríguez-Guitián, M.; Rigueiro, A.; Real, C.; Blanco, J.; Ferreiro da Costa, J. El Habitat” 9269 Bosques de Castanea Sativa” En El Extremo Noroccidental Iberico: Primeros Datos Sobre La Variabilidad Floristica de Los” Soutos”. Bulletin de la Société d’ Histoire Naturelle de Toulouse 2005, 141, 75–81. [Google Scholar]
- González-Varo, J.P.; López-Bao, J.V.; Guitián, J. Presence and Abundance of the Eurasian Nuthatch Sitta Europaea in Relation to the Size, Isolation and the Intensity of Management of Chestnut Woodlands in the NW Iberian Peninsula. Landscape Ecology 2008, 23, 79–89. [Google Scholar] [CrossRef]
- Council Directive 92/43/EEC On the Conservation of Natural Habitats and of Wild Fauna and Flora Available online: http://data.europa.eu/eli/dir/1992/43/2013-07-01.
- MITECO Forest Statistics Yearbook 2021; Spnanish Ministry for Ecological Transition and Demographic Challenge: Madrid, Spain, 2022.
- Vega, A.; Dieste, A.; Guaita, M.; Majada, J.; Baño, V. Modelling of the Mechanical Properties of Castanea Sativa Mill. Structural Timber by a Combination of Non-Destructive Variables and Visual Grading Parameters. Eur. J. Wood Prod. 2012, 70, 839–844. [Google Scholar] [CrossRef]
- The Chestnut Handbook: Crop & Forest Management; Beccaro, G. , Alma, A., Bounous, G., Gomes-Laranjo, J., Eds.; CRC Press: Boca Raton London New York, 2020; ISBN 978-0-429-44560-6. [Google Scholar]
- Carbone, F.; Moroni, S.; Mattioli, W.; Mazzocchi, F.; Romagnoli, M.; Portoghesi, L. Competitiveness and Competitive Advantages of Chestnut Timber Laminated Products. Annals of Forest Science 2020, 77, 51. [Google Scholar] [CrossRef]
- Villar, J.R.; Guaita, M.; Vidal, P.; Arriaga, F. Analysis of the Stress State at the Cogging Joint in Timber Structures. Biosystems Engineering 2007, 96, 79–90. [Google Scholar] [CrossRef]
- Villar, J.R.; Guaita, M.; Vidal, P. Numerical Simulation of Framed Joints in Sawn-Timber Roof Trusses. Span J Agric Res 2008, 6, 508. [Google Scholar] [CrossRef]
- Sjödin, J.; Serrano, E.; Enquist, B. An Experimental and Numerical Study of the Effect of Friction in Single Dowel Joints. Holz Roh Werkst 2008, 66, 363–372. [Google Scholar] [CrossRef]
- Koch, H.; Eisenhut, L.; Seim, W. Multi-Mode Failure of Form-Fitting Timber Connections – Experimental and Numerical Studies on the Tapered Tenon Joint. Engineering Structures 2013, 48, 727–738. [Google Scholar] [CrossRef]
- Aira, J.R.; Íñiguez-González, G.; Guaita, M.; Arriaga, F. Load Carrying Capacity of Halved and Tabled Tenoned Timber Scarf Joint. Mater Struct 2016, 49, 5343–5355. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Crespo, J.; Moya, M.; Guaita, M. Experimental and Numerical Studies of the Stress State at the Reverse Step Joint in Heavy Timber Trusses. Mater Struct 2018, 51, 17. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Vidal-López, P.; Crespo, J.; Guaita, M. Analysis of the Stress State at the Double-Step Joint in Heavy Timber Structures. Materiales de Construcción 2019, 69, e196–e196. [Google Scholar] [CrossRef]
- Domínguez, M.; Fueyo, J.G.; Villarino, A.; Anton, N. Structural Timber Connections with Dowel-Type Fasteners and Nut-Washer Fixings: Mechanical Characterization and Contribution to the Rope Effect. Materials 2021, 15, 242. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.M.M.; Leite, P.A.S.; Silva, L.D.S.; Silva, V.S.B.; Lopes, H.M. Parametric Study of Three Types of Timber Connections with Metal Fasteners Using Eurocode 5. Applied Sciences 2022, 12, 1701. [Google Scholar] [CrossRef]
- EN 1995-1-1 Eurocode 5: Design of Timber Structures - Part 1-1: General - Common Rules and Rules for Buildings; CEN: Brussels, Belgium, 2016.
- EN 1995-2 Eurocode 5: Design of Timber Structures - Part 2: Bridges; CEN: Brussels, Belgium, 2016.
- Blass, H.; Aune, P.; Choo, B.; Görlacher, R.; Grifiths, D. Timber Engineering. STEP 1: Basis of Design, Material Properties, Structural Components and Joints; Centrum Hout: Almere, Netherlands, 1995. [Google Scholar]
- Argüelles, R.; Arriaga, F.; Esteban, M.; Íñiguez, G.; Argüelles Bustillo, R. Timber Structures. Basis for Calculation [Estructuras de madera. Bases de cálculo]; AITIM. Technical Research Association of the Wood and Cork Industries: Madrid, Spain, 2013; ISBN 978-84-87381-44-7. [Google Scholar]
- Kretschmann, D.E. Wood Handbook: Wood as an Engineering Material; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- Argüelles, R.; Arriaga, F.; Esteban, M.; Íñiguez, G.; Argüelles Bustillo, R. Timber Structures. Joints [Estructuras de madera. Uniones]; AITIM. Technical Research Association of the Wood and Cork Industries: Madrid, Spain, 2015; ISBN 978-84-87381-44-7. [Google Scholar]
- Fu, W.; Guan, H.; Chen, B. Investigation on the Influence of Moisture Content and Wood Section on the Frictional Properties of Beech Wood Surface. Tribology Transactions 2021, 64, 830–840. [Google Scholar] [CrossRef]
- Dorn, M.; Habrová, K.; Koubek, R.; Serrano, E. Determination of Coefficients of Friction for Laminated Veneer Lumber on Steel under High Pressure Loads. Friction 2021, 9, 367–379. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Vidal-López, P.; Corbacho, A.J.; Moya, M. Determination of the Friction Coefficients of Chestnut (Castanea Sativa Mill.) Sawn Timber. International Agrophysics 2020, 34, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Villar-García, J.R.; Vidal-López, P.; Rodríguez-Robles, D.; Moya Ignacio, M. Friction Coefficients of Chestnut (Castanea Sativa Mill.) Sawn Timber for Numerical Simulation of Timber Joints. Forests 2022, 13, 1078. [Google Scholar] [CrossRef]
- EN 13183-1 Moisture Content of a Piece of Sawn Timber - Part 1: Determination by Oven Dry Method; CEN: Brussels, Belgium, 2002.
- ASTM G115-10 Standard Guide for Measuring and Reporting Friction Coefficients; ASTM International: West Conshohocken, PA, USA, 2018.
- Villar-García, J.R.; Vidal-López, P.; Moya Ignacio, M. Device to Perform Friction Tests between Solid Bodies. Utility Model U 201932027. 2020.
- Crespo, J.; Regueira, R.; Soilán, A.; Díez, M.R.; Guaita, M. Methodology to Determine the Coefficients of Both Static and Dynamic Friction Apply to Different Species of Wood. In Proceedings of the 1st Ibero-Latin American Congress on wood in construction (CIMAD); Coimbra, Coimbra, Portugal, 11 June 2011. [Google Scholar]
- Aira, J.R.; Arriaga, F.; Íñiguez-González, G.; Crespo, J. Static and Kinetic Friction Coefficients of Scots Pine (Pinus Sylvestris L.), Parallel and Perpendicular to Grain Direction. Materiales de Construcción 2014, 64, e030. [Google Scholar] [CrossRef]
- Berman, A.; Ducker, W.; Israelachvili, J. Experimental and Theoretical Investigations of Stick-Slip Friction Mechanisms. In Physics of Sliding Friction.; Persson, B.N.J., Tosatti, E., Eds.; NATO ASI Series; Springer: Dordrecht, Netherlands, 1996; ISBN 978-94-015-8705-1. [Google Scholar]
- Möhler, K.; Herröder, W. Range of the coefficient of friction of spruce wood rough from sawing [Obere und untere Reibbeiwerte von sägerauhem Fichtenholz]. Holz als Roh-und Werkstoff 1979, 37, 27–32. [Google Scholar] [CrossRef]
- Xu, M.; Li, L.; Wang, M.; Luo, B. Effects of Surface Roughness and Wood Grain on the Friction Coefficient of Wooden Materials for Wood–Wood Frictional Pair. Tribology Transactions 2014, 57, 871–878. [Google Scholar] [CrossRef]
- McKenzie, W.M.; Karpovich, H. The Frictional Behaviour of Wood. Wood Sci.Technol. 1968, 2, 139–152. [Google Scholar] [CrossRef]
Figure 1.
Frequency and chorology map of the distribution of Castanea sativa in Europe [6].
Figure 1.
Frequency and chorology map of the distribution of Castanea sativa in Europe [6].
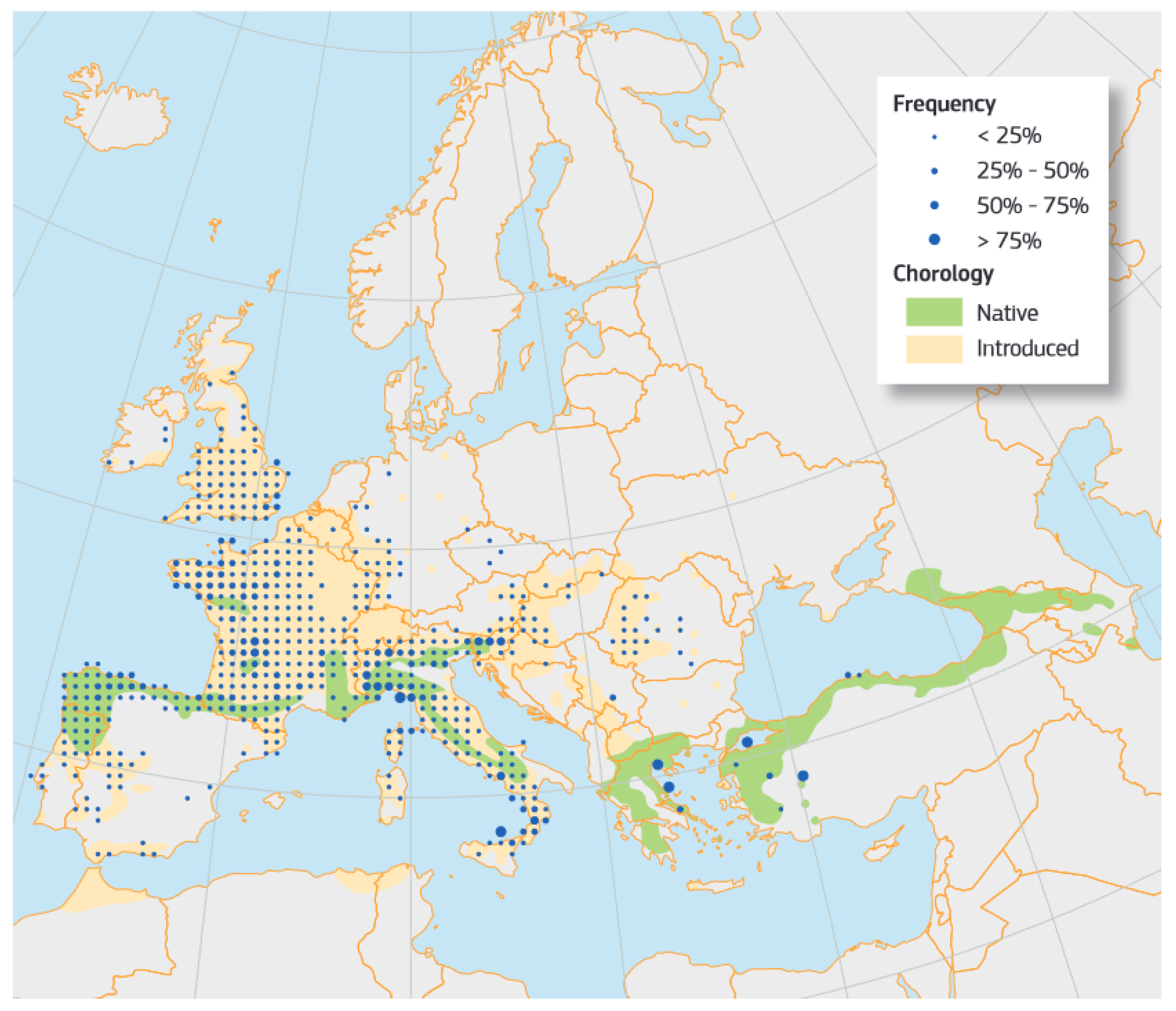
Figure 2.
Timber-to-timber and timber-to-steel friction planes for the varying anatomical directions (L, R, and T) of the specimen of wood and their respective sliding directions.
Figure 2.
Timber-to-timber and timber-to-steel friction planes for the varying anatomical directions (L, R, and T) of the specimen of wood and their respective sliding directions.
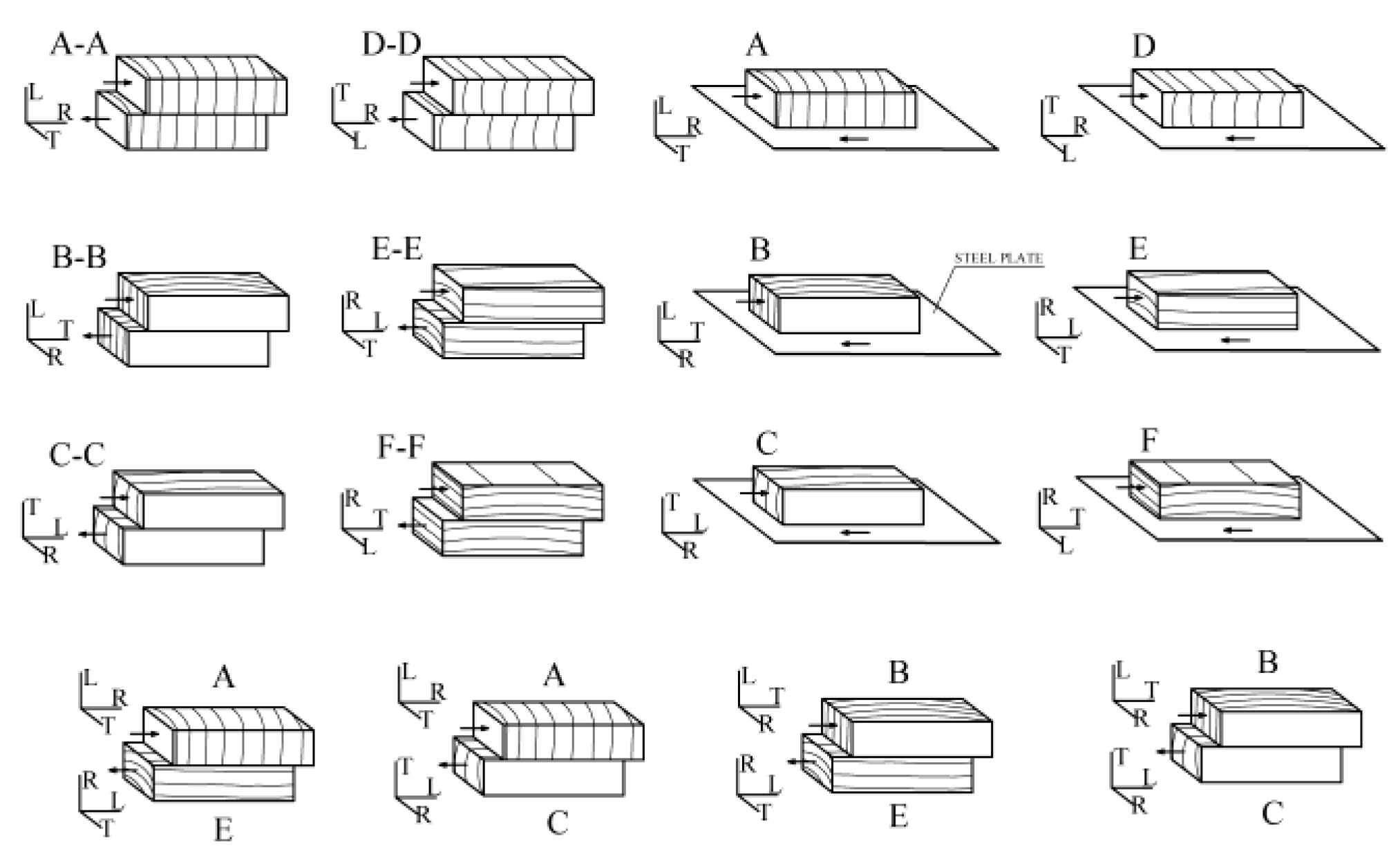
Figure 3.
Representative examples (▬ AA; ▬ BB; ▬ CC; ▬ DD; ▬ EE; ▬ FF) of the friction coefficient variation for sections with the same orientation in both specimens at a moisture content of 18%.
Figure 3.
Representative examples (▬ AA; ▬ BB; ▬ CC; ▬ DD; ▬ EE; ▬ FF) of the friction coefficient variation for sections with the same orientation in both specimens at a moisture content of 18%.
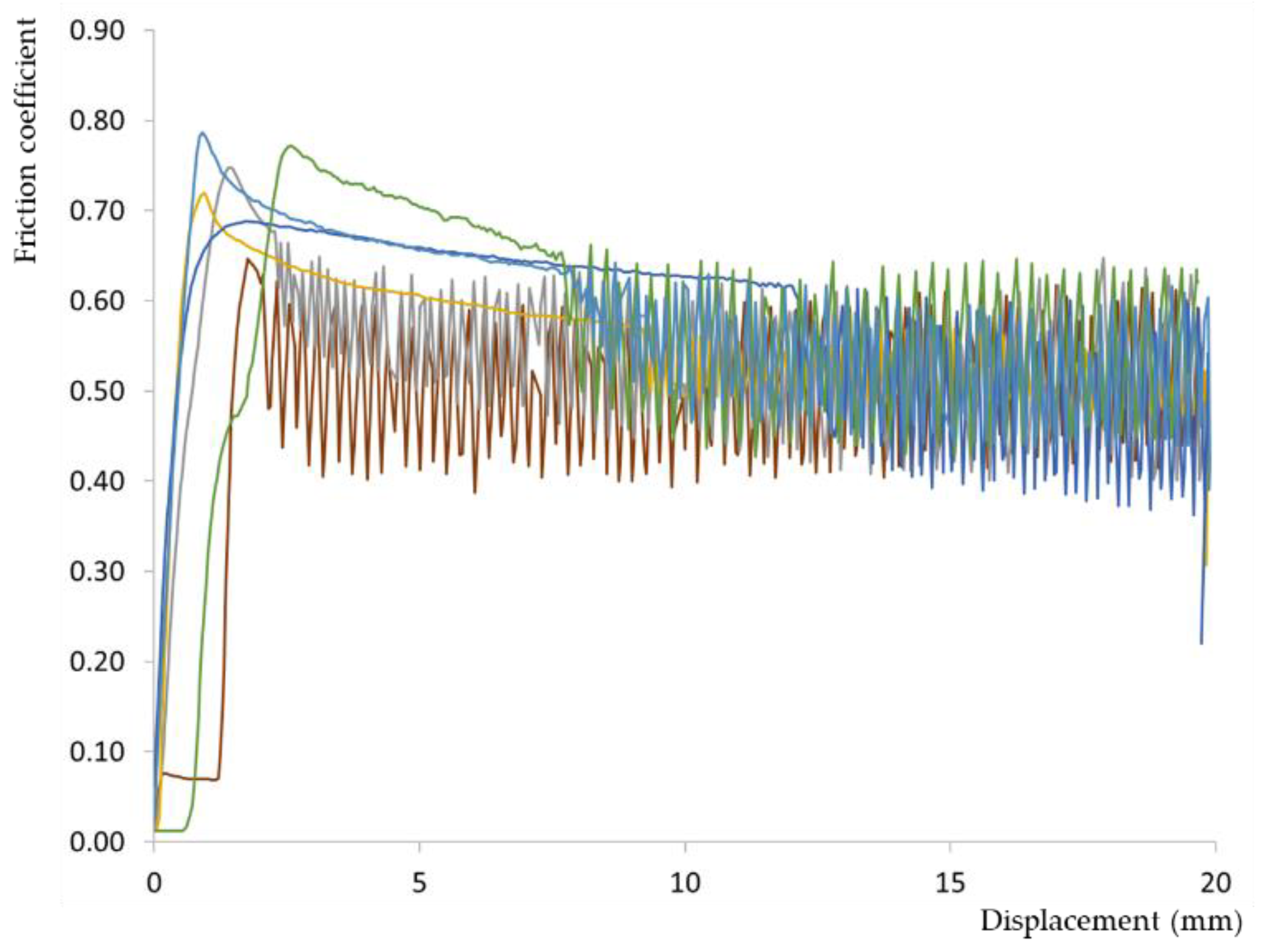
Figure 4.
Representative examples (▬ AC; ▬ AE; ▬ BC; ▬ BE) of the friction coefficient variation for specimens with different orientation at a moisture content of 18%.
Figure 4.
Representative examples (▬ AC; ▬ AE; ▬ BC; ▬ BE) of the friction coefficient variation for specimens with different orientation at a moisture content of 18%.
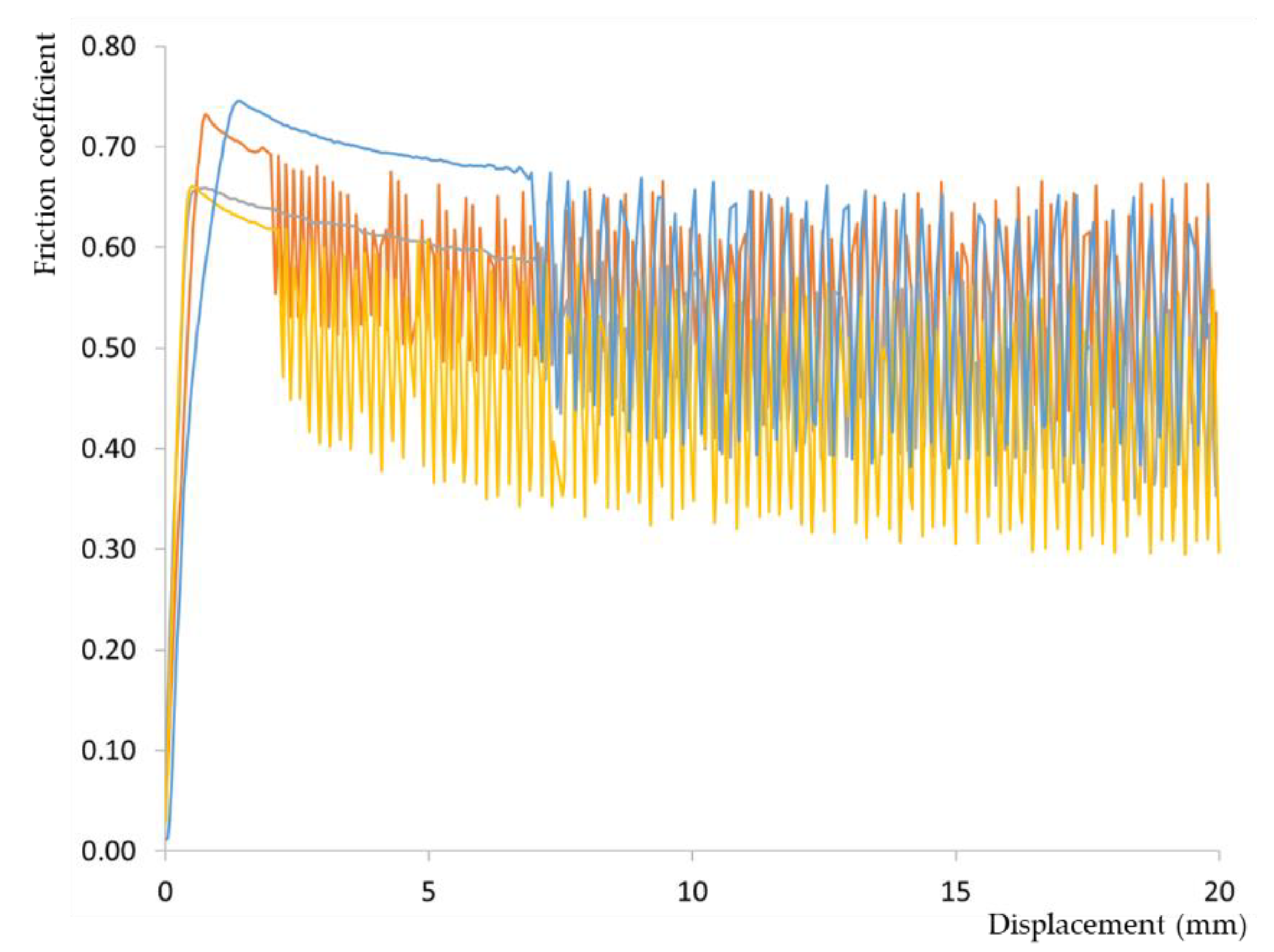
Figure 5.
Representative examples (▬ A- S; ▬ B- S; ▬ D- S; ▬ C- S; ▬ E- S; ▬ F- S) of the friction coefficient variation between the timber specimens at 18% moisture content and the steel plate.
Figure 5.
Representative examples (▬ A- S; ▬ B- S; ▬ D- S; ▬ C- S; ▬ E- S; ▬ F- S) of the friction coefficient variation between the timber specimens at 18% moisture content and the steel plate.
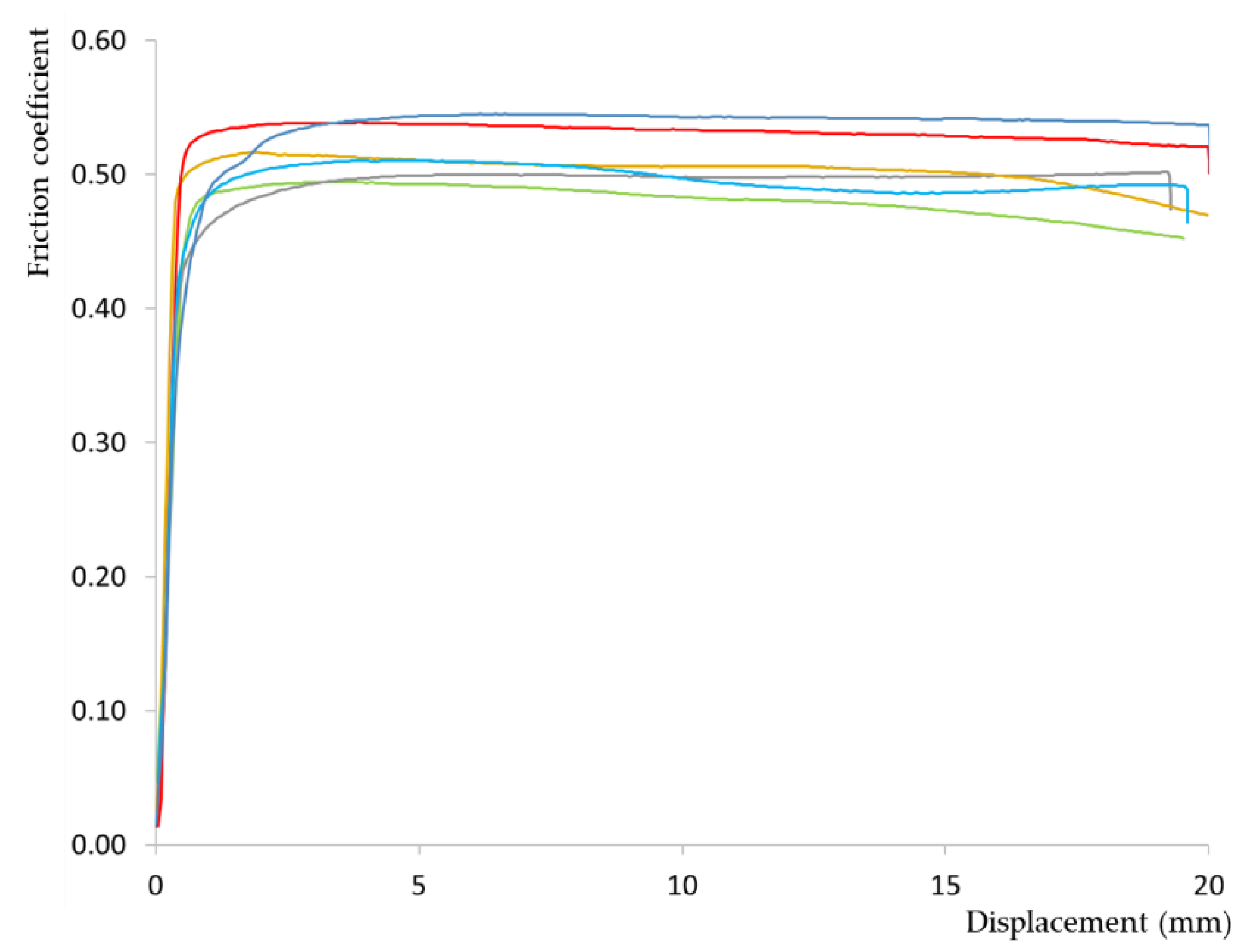
Figure 6.
Relationship between the values of μk and μs for the different timber-to-timber friction pairs (a), as well as for the mean value for each group denoted by a circle in the corresponding color (b).
Figure 6.
Relationship between the values of μk and μs for the different timber-to-timber friction pairs (a), as well as for the mean value for each group denoted by a circle in the corresponding color (b).
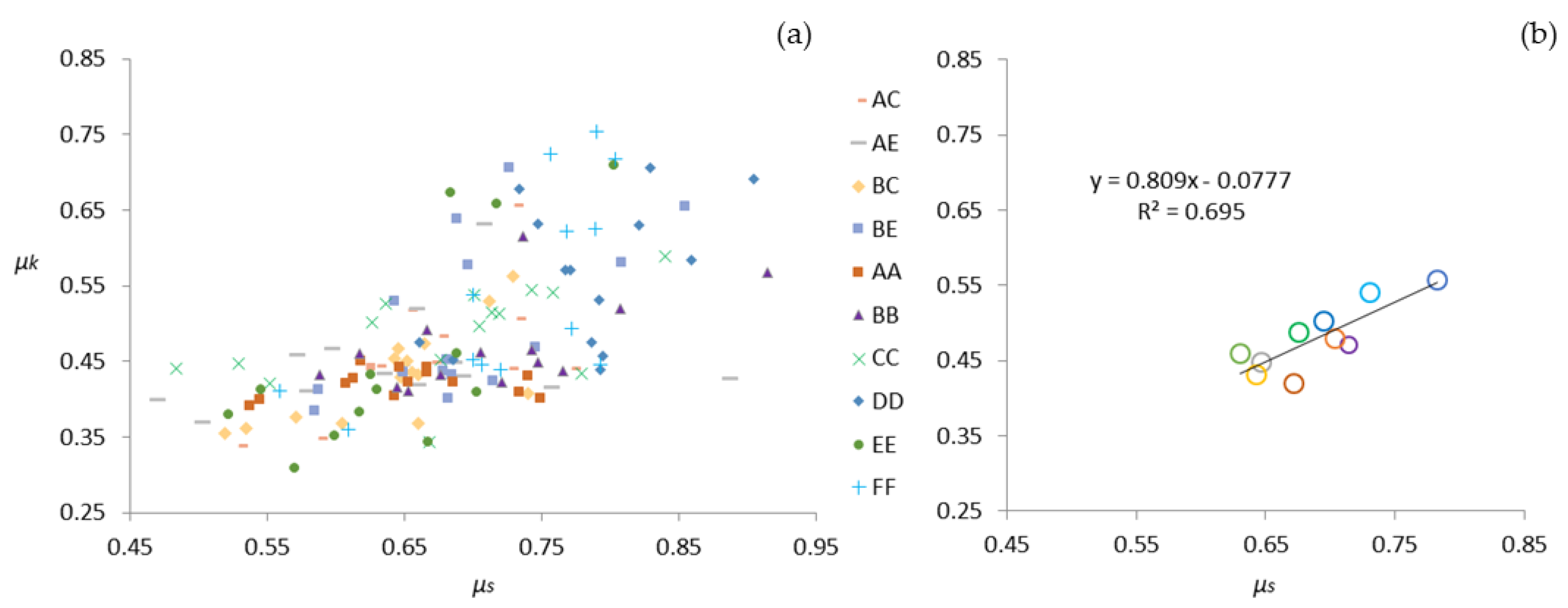
Figure 7.
Relationship between the values of μk and μs for the different timber-to-steel friction pairs (a), as well as for the mean value for each group denoted by a circle in the corresponding color (b).
Figure 7.
Relationship between the values of μk and μs for the different timber-to-steel friction pairs (a), as well as for the mean value for each group denoted by a circle in the corresponding color (b).
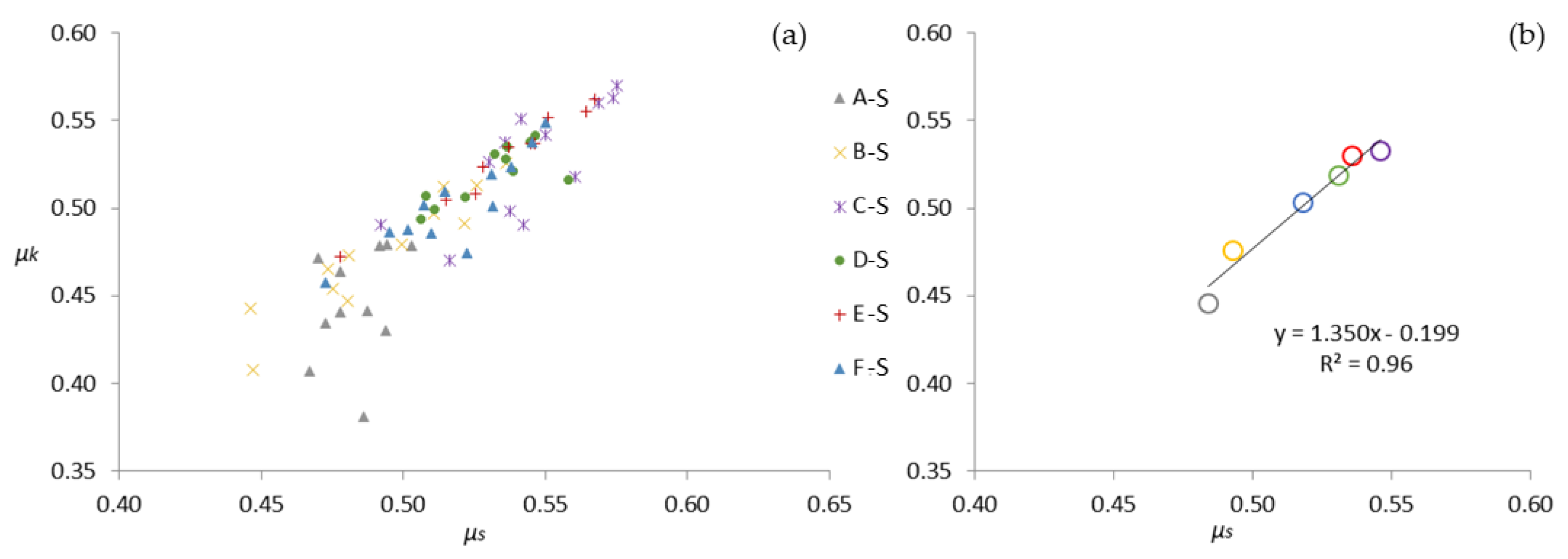
Figure 8.
For each group of timber-to-timber tests, average static (a) and kinetic (b) friction coefficient values at moisture contents of 12% (from [31,32]), 15%, and 18% as well as the linear regression between the two extreme values of the studied range.
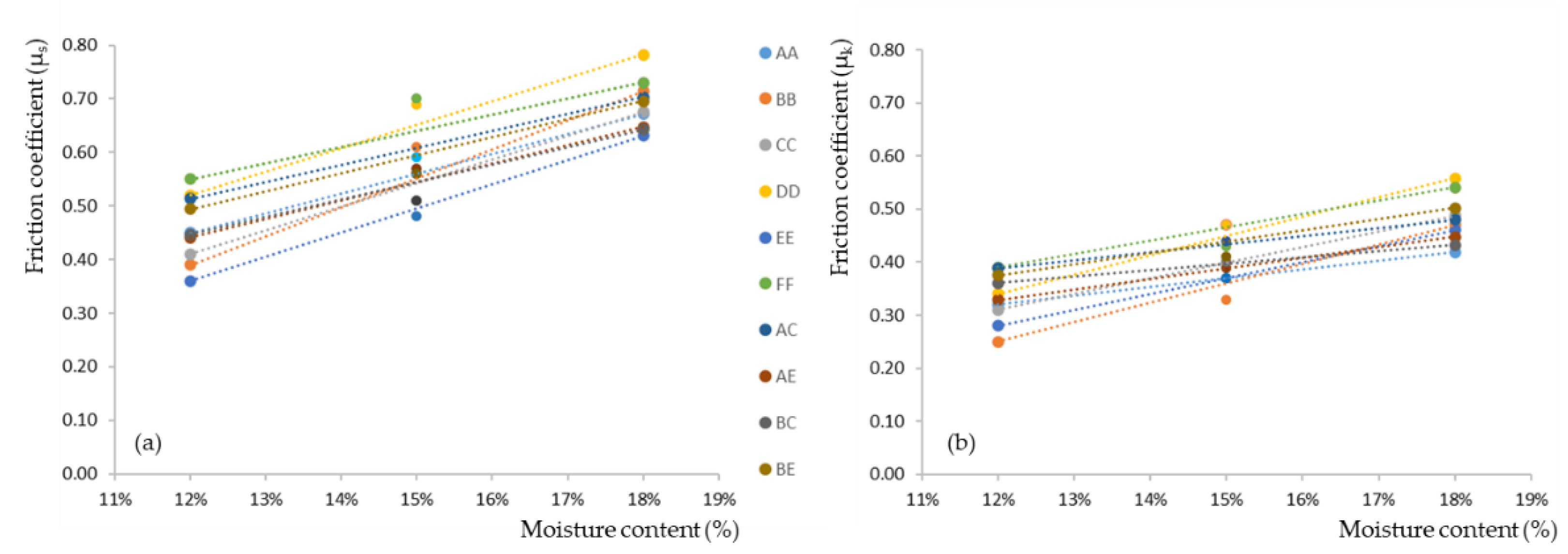
Figure 9.
For each group of timber-to-steel tests, average static (a) and kinetic (b) friction coefficient values at moisture contents of 12% (from [32]), 15%, and 18% as well as the linear regression between the two extreme values of the studied range.
Figure 9.
For each group of timber-to-steel tests, average static (a) and kinetic (b) friction coefficient values at moisture contents of 12% (from [32]), 15%, and 18% as well as the linear regression between the two extreme values of the studied range.
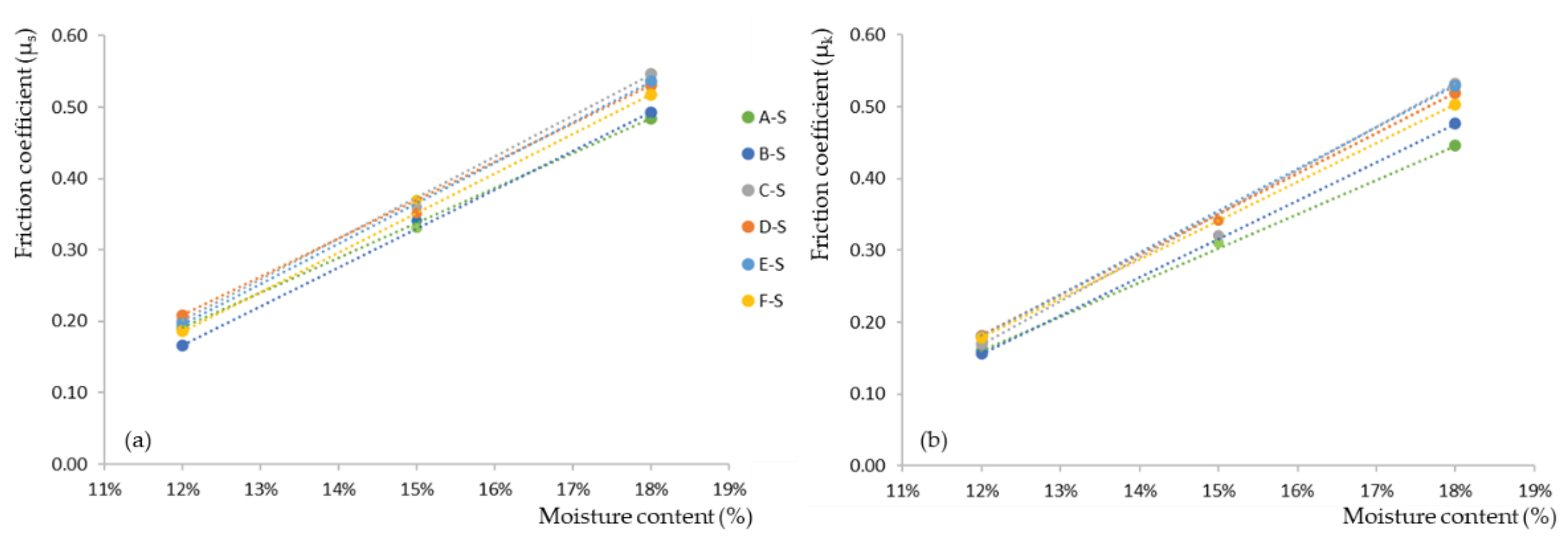
Table 1.
Friction coefficients between wood surfaces of identical orientation at 18% moisture content.
Table 1.
Friction coefficients between wood surfaces of identical orientation at 18% moisture content.
| Mean (CoV %) |
A- A | B- B | C- C | D- D | E- E | F- F |
|---|---|---|---|---|---|---|
| μs | 0.67 (15.3) |
0.71 (11.4) |
0.68 (14.4) |
0.78 (8.2) |
0.63 (13.9) |
0.73 (9.9) |
| μk | 0.42 (4.8) |
0.47 (12.7) |
0.49 (12.9) |
0.56 (16.7) |
0.46 (29.3) |
0.54 (24.6) |
Table 2.
Friction coefficients between wood surfaces of different orientation at 18% moisture content.
Table 2.
Friction coefficients between wood surfaces of different orientation at 18% moisture content.
| Mean (CoV %) |
A- C | A- E | B- C | B- E |
|---|---|---|---|---|
| μs | 0.70 (18.1) |
0.65 (15.6) |
0.64 (9.9) |
0.70 (10.3) |
| μk | 0.48 (25.7) |
0.45 (13.6) |
0.43 (14.3) |
0.50 (20.7) |
Table 3.
Friction coefficients between a wood surface at 18% moisture content and the steel plate.
| Mean (CoV %) |
A- S | B- S | C- S | D- S | E- S | F- S |
|---|---|---|---|---|---|---|
| μs | 0.48 (2.5) |
0.49 (6.1) |
0.55 (4.6) |
0.53 (3.2) |
0.54 (4.9) |
0.52 (4.4) |
| μk | 0.45 (7.2) |
0.47 (7.2) |
0.53 (7.2) |
0.52 (3.1) |
0.53 (5.2) |
0.50 (5.3) |
Table 4.
Friction coefficients between wood surfaces of identical orientation at 15% moisture content.
Table 4.
Friction coefficients between wood surfaces of identical orientation at 15% moisture content.
| Mean (CoV %) |
A- A | B- B | C- C | D- D | E- E | F- F |
|---|---|---|---|---|---|---|
| μs | 0.67 (15.3) |
0.71 (11.4) |
0.68 (14.4) |
0.78 (8.2) |
0.63 (13.9) |
0.73 (9.9) |
| μk | 0.42 (4.8) |
0.47 (12.7) |
0.49 (12.9) |
0.56 (16.7) |
0.46 (29.3) |
0.54 (24.6) |
Table 5.
Friction coefficients between wood surfaces of different orientation at 15% moisture content.
Table 5.
Friction coefficients between wood surfaces of different orientation at 15% moisture content.
| Mean (CoV %) |
A- C | A- E | B- C | B- E |
|---|---|---|---|---|
| μs | 0.56 (32.0) |
0.57 (20.9) |
0.51 (26.5) |
0.56 (17.4) |
| μk | 0.44 (16.2) |
0.39 (31.7) |
0.40 (26.3) |
0.41 (25.9) |
Table 6.
Friction coefficients between a wood surface at 15% moisture content and the steel plate.
| Mean (CoV %) |
A- S | B- S | C- S | D- S | E- S | F- S |
|---|---|---|---|---|---|---|
| μs | 0.33 (7.3) |
0.34 (17.2) |
0.36 (10.6) |
0.35 (2.9) |
0.33 (8.8) |
0.37 (17.6) |
| μk | 0.31 (8.1) |
0.31 (5.5) |
0.32 (10.2) |
0.34 (5.7) |
0.32 (5.4) |
0.32 (15.9) |
Table 7.
For each studied scenario (friction coefficients between wood surfaces of identical orientation, wood surfaces of different orientation, and wood and steel), the value of the static and kinetic friction coefficients resulting from the linear interpolation and the percentage of error relative to the experimental values at a 15% moisture content.
Table 7.
For each studied scenario (friction coefficients between wood surfaces of identical orientation, wood surfaces of different orientation, and wood and steel), the value of the static and kinetic friction coefficients resulting from the linear interpolation and the percentage of error relative to the experimental values at a 15% moisture content.
| Interpolated value (error %) |
A- A | B- B | C- C | D- D | E- E | F- F |
|---|---|---|---|---|---|---|
| μs | 0.56 | 0.55 | 0.54 | 0.65 | 0.50 | 0.64 |
| (-5.0%) | (-9.5%) | (6.4%) | (-5.7%) | (3.2%) | (-8.6%) | |
| μk | 0.37 | 0.36 | 0.40 | 0.45 | 0.37 | 0.47 |
| (-0.1%) | (9.2%) | (7.7%) | (-4.5%) | (0.0%) | (8.2%) | |
|
Interpolated value (error %) |
A- C | A- E | B- C | B- E | ||
| μs | 0.61 | 0.54 | 0.54 | 0.59 | ||
| (8.7%) | (-4.5%) | (6.8%) | (6%) | |||
| μk | 0.43 | 0.39 | 0.40 | 0.44 | ||
| (-1.2%) | (-0.4%) | (-0.9%) | (7%) | |||
|
Interpolated value (error %) |
A- S | B- S | C- S | D- S | E- S | F- S |
| μs | 0.34 | 0.33 | 0.37 | 0.37 | 0.37 | 0.35 |
| (2%) | (-3%) | (4%) | (6%) | (11%) | (-5%) | |
| μk | 0.30 | 0.32 | 0.35 | 0.35 | 0.35 | 0.34 |
| (-2%) | (2%) | (10%) | (3%) | (11%) | (6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






