Preprint
Article
Deep Reinforcement Learning for Optimizing Restricted Access Window in IEEE 802.11ah MAC Layer
Altmetrics
Downloads
121
Views
56
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 March 2024
Posted:
01 April 2024
You are already at the latest version
Alerts
Abstract
The IEEE 802.11ah standard is introduced to address the growing scale of Internet of Things (IoT) applications. To reduce contention and enhance energy efficiency within the system, the restricted access window (RAW) mechanism is introduced at the medium access control (MAC) layer to manage the significant number of stations accessing the network. However, the RAW parameters need to be appropriately determined to achieve optimal network performance. In this paper, we optimize the configuration of RAW parameters in the IEEE 802.11ah-based IoT network. We analyze and propose an RAW parameters optimization problem with the objective of improving network throughput and formulate it as a Markov decision process. To cope with the complex and dynamic network conditions, we propose a proximal policy optimization (PPO)-based deep reinforcement learning (DRL) algorithm to find the optimal RAW parameters. We construct network environments with periodic and random traffic in the NS-3 simulator to validate the performance of the proposed PPO-based RAW parameters optimization algorithm. Simulation results reveal that using the PPO-based DRL algorithm, optimal RAW parameters can be obtained under different network conditions, thereby significantly improving network throughput.
Keywords:
Subject: Computer Science and Mathematics - Computer Networks and Communications
1. Introduction
With the rapid development of Internet of Things (IoT) applications and technologies, IoT has emerged as a pivotal enabler bridging the physical and digital realms. IoT has been widely used in industry, agriculture, healthcare and other fields. Statistics show that IoT connected devices are expected to exceed 30 billion units by 2025, more than doubling from 13.8 billion in 2021 [1]. With expanding scope of applications, IoT has its own set of requirements: very low power, longer range connections, and support for a greater number of client devices per access point (AP) [2]. The fulfillment of these requirements relies on the selection of wireless communication technologies.
To meet the key requirements of IoT applications, the Wi-Fi Alliance has introduced Wi-Fi HaLow technology [3]. The Wi-Fi HaLow technology is based on the IEEE 802.11ah standard [4], operating in the unlicensed sub-1 GHz radio frequency spectrum band and utilizing narrower channels. IEEE 802.11ah is built upon the IEEE 802.11 standards with modifications for IoT applications. The physical (PHY) layer of IEEE 802.11ah is designed for long-range communication. At the medium access control (MAC) layer, novel channel access control mechanisms are introduced to facilitate access for a large number (up to 8191) of stations (STAs) and support low power consumption. Leveraging the novel features at the PHY and MAC layers, IEEE 802.11ah offers up to 100 times longer range compared to other IoT technologies, with a data rate ranging from approximately 150 kbps to a maximum of around 86.7 Mbps [4]. As shown in Figure 1, the IEEE 802.11ah-based Wi-Fi HaLow technology provides a well-balanced combination of data rate, coverage range, and energy efficiency, outperforming low-power IoT technologies such as LoRa, NB-IoT, and Zigbee [3]. Wi-Fi HaLow also features easier deployment and integration into IP networks compared to other technologies, with scalability similar to LoRa. Therefore, Wi-Fi HaLow is well-suited to meet the key requirements of IoT applications.
At the MAC layer, the restricted access window (RAW) mechanism is introduced to manage the significant number of STAs accessing the network [4]. The idea of RAW is to divide the channel time into one or more access windows, where only some of the STAs can access the channel in the designated access windows, while the others are restricted from random access. As shown in Figure 2, for STAs with certain traffic patterns, the AP divides them into one or more RAW groups during a traffic indication map (TIM) beacon interval. On the arrival of each RAW, STAs assigned to the current RAW have the right to access the channel for data transmission, while the other STAs remain dormant and cache non-urgent data until the arrival of their corresponding RAW. To further alleviate contention, each RAW is subdivided into multiple time slots with equal duration. STAs are uniformly distributed among these slots by default. During each slot, only STAs assigned to the current slot are permitted to contend for data transmission, ensuring that STAs restricted in different slots do not conflict with each other.
The operation of RAW mainly consists of two parts. One is the division of STAs into different RAW groups. The other is the configuration of RAW-related parameters, including the number of RAW groups, the number of slots in each RAW, the duration of each RAW, and the number of STAs in each RAW group. However, details about RAW parameters setting and RAW grouping are not specified in the IEEE 802.11ah standard. This allows researchers the flexibility to customize the RAW configuration to meet the specific requirements of different application scenarios. Moreover, the performance of RAW can be validated in the NS-3 simulator. In [5], the authors constructed simulation environments for IEEE 802.11ah sensor networks in the NS-3 simulator that closely resembles real-world network conditions. Through simulations, the detailed analysis of the impacts of RAW parameters (i.e., number of RAW groups, RAW group duration, and station division) on network throughput, transmission delay, and energy efficiency have been conducted in the literature. The experiments in [6] also revealed that network performance largely depends on the RAW parameters setting.
Based on this observation, some studies have focused on finding the optimal RAW parameters to improve network performance. Researchers have conducted complicated mathematical models and proposed heuristic methods to determine the optimal RAW parameters or grouping scheme [7,8,9]. However, most of the analytical models fail to consider the complexities and dynamic changes of network conditions, leading to discrepancies between the results derived by analytical models and those obtained from the NS-3 simulator. Moreover, heuristic methods for optimizing RAW parameters are often constrained by specific assumptions, such as fixed network topologies and known traffic patterns. The applicability of these methods in various scenarios requires further validation. Therefore, this paper aims to propose a flexible model-free learning method for finding the optimal RAW parameters, which is scalable, robust, light-weight, and capable of generalizing across different scenarios.
Due to the high efficiency and strong generalization capabilities, artificial intelligence (AI) methods have found broad applications in wireless networks in recent years. There is a growing number of studies employing AI methods to solve RAW parameters optimization and grouping problems. Researchers in [10] used neural networks to decide the optimal number of RAW groups and the number of slots in each RAW for given network conditions. Moreover, machine learning (ML) methods such as K-means have been used to solve grouping problems [11]. It is noteworthy that deep reinforcement learning (DRL) integrates deep learning (DL) and reinforcement learning (RL) by using deep neural networks (DNNs) to approximate value functions or optimal policies, thereby enabling the handling of high-dimensional and complex state and action spaces. DRL’s strong performance in dealing with complex and dynamic environments endows it with powerful generalization capability, making it widely applied in wireless networks for solving parameterized optimization problems such as resource allocation and scheduling [12,13]. Therefore, it is feasible to employ the DRL approach to solve RAW parameters and network performance optimization problems.
In this paper, we present a DRL method based on the proximal policy optimization (PPO) algorithm for optimizing RAW parameters in the IEEE 802.11ah-based IoT network. To the best of our knowledge, there are limited prior studies on RAW mechanism optimization using DRL-based approaches. Our study primarily focus on designing an effective DRL algorithm to find the optimal RAW parameters to enhance network throughput, and validating the feasibility of the optimized RAW parameters configuration in the NS-3 simulator. Our study can serve as a reference for applying DRL to the RAW mechanism and further extensions for optimizing other mechanisms of IEEE 802.11ah. We summarize our contributions as follows:
- Elaboration of the RAW mechanism and RAW-based channel access in the IEEE 802.11ah-based IoT network are presented to provide a more comprehensive understanding of RAW. Furthermore, mathematical analysis is presented to show significant impact of RAW parameters on network performance.
- A PPO-based DRL algorithm is designed to find the optimal RAW parameters to improve network throughput, which interacts with the network environments in the NS-3 simulator.
- Network environments with periodic and random traffic are considered in the NS-3 simulator to validate the feasibility and generalization capability of the PPO-based DRL algorithm, and the performance of the proposed algorithm is evaluated through NS-3.
The remainder of this paper is organized as follows. Prior studies on RAW-based network performance optimization and related works using AI-based methods for RAW mechanism are presented in Section 2. In Section 3, the network model considered in this paper and the operation of RAW are elaborated, throughput modeling with respect to RAW parameters is presented, and the RAW parameters optimization problem is established. The problem is reformulated as a Markov decision process (MDP), and a PPO-baed DRL algorithm for RAW parameters optimization is proposed in Section 4. In Section 5, the performance of the proposed DRL algorithm is evaluated in simulation environments built in the NS-3 simulator. Conclusions are drawn, and future studies are discussed in Section 6.
2. Related Work
2.1. Analytical Modeling for RAW Mechanism
To investigate the impact of the RAW mechanism on network performance, researchers have developed several evaluation models for the RAW-based channel access process. Typically, researchers introduce characteristics of RAW into the analytical model of the distributed coordination function (DCF) of IEEE 802.11 standards [14]. Given the known number of STAs in the network, researchers analyzed the transmission and collision probabilities in a single RAW slot. The analysis is then extended to one or multiple RAWs to derive formulas for calculating network performance metrics such as throughput, delay, and energy consumption [7,15,16]. These analytical models are validated by comparing results with those obtained from the NS-3 simulator. However, they require a series of assumptions, including saturated network traffic, ideal channel conditions, and packet loss solely caused by collisions. To obtain more accurate models, researchers further took unsaturated traffic, heterogeneous networks, signal capture, and other network conditions into account [6,17,18].
Moreover, researches investigated the impact of different RAW parameters on the network performance based on analytical models or simulation results. Authors in [19] pointed out that dividing more RAWs in a beacon interval period can reduce collision probability as the total number of competing STAs in each RAW group decreases. However, this also leads to increased delay, as larger RAW segmentations increase the probability of packet buffering. Similarly, authors in [18] stated that the more slots divided in each RAW, the fewer number of STAs competing for channel access in a single slot, thereby reducing the probability of collisions. However, the time overhead increases due to the non-cross-slot-boundary setting. Authors in [5] emphasized that a longer RAW duration generally results in better throughput. However, excessively long RAW durations perform worse in terms of latency. Moreover, the duration of a RAW should be determined based on the traffic load in each RAW group. The critical impact of RAW duration on the network performance was further discussed in [6].
2.2. Optimization in RAW Mechanism
Given the critical impact of RAW parameters on network performance, an important issue of optimizing RAW mechanism is the optimization of RAW parameters. RAW parameters include the number of RAW groups, number of slots in each RAW, duration of each RAW (which can be calculated given the slot count and slot duration), and the number of STAs in each RAW group (which can be calculated given the number of RAW groups and STAs in the network). It has been validated that the optimization of RAW parameters depends on various network variables, such as number of STAs, traffic load, and traffic patterns [5]. Most of the studies are network performance optimization-oriented, in which authors formulate RAW parameters optimization problems and obtain one or more optimal RAW parameters using various optimization methods. To jointly maximize uplink energy efficiency and delay, authors in [7] proposed an energy-delay aware window control algorithm based on the gradient descent method, enabling adaptive adjustment of slot count and slot duration according to the number of STAs in each RAW group. Similarly, the authors in [20] proposed an group-size-adaptive algorithm to determine the duration of each RAW. To cope with dynamic changes in the network size and heterogeneous traffic conditions in sensor networks with uplink traffic, authors in [21] proposed TAROA, which can adaptively adjust RAW parameters according to the current (or estimated) traffic conditions and assign STAs to different RAW groups based on the estimated transmission frequency. TAROA has been further refined in [22]. Oriented towards delay-sensitive emergency alarm sensor networks and closed-loop communication scenarios, authors in [23] proposed an RAW parameters selecting algorithm to minimize channel time-sharing consumption. Additionally, in [8], authors formulated the optimal RAW scheduling problem as an integer nonlinear programming problem with the objective of minimizing channel time at key STAs, and designed a heuristic algorithm to find the optimal RAW configurations.
Moreover, some studies focus on RAW grouping, which allocates STAs to different RAW groups based on various characteristics of STAs. According to the priority level of the STAs, authors in [24] proposed a QoS-aware priority grouping and scheduling algorithm. Considering traffic characteristics (e.g., traffic demand, mult-irate) of the STAs in heterogeneous networks, authors in [25] proposed MoROA that employs mathematical methods to solve the grouping problem and to determine the optimal RAW configurations. To achieve fairness in inter-group throughput and channel utilization, authors in [9] and [26] proposed heuristic grouping algorithms. Furthermore, in [27] and [28], authors introduced grouping strategies based on greedy algorithms and genetic algorithms, respectively.
2.3. AI-Based Methods for RAW Mechanism
It is noteworthy that in recent years, there has been a growing number of studies employing AI methods to solve RAW parameter optimization and grouping problems. Authors in [29] proposed a surrogate model for RAW performance in realistic IoT scenarios by integrating ML methods such as support vector machine and artificial neural networks (ANNs). This model accurately predicts network performance for given RAW configurations in heterogeneous networks. The predicted values can serve as inputs for real-time RAW parameters optimization algorithms, thereby enhancing algorithm accuracy. In [10], authors used ANNs to find the optimal number of RAW groups given the network size, data rate, and RAW duration. Using ML methods such as K-means, the authors implemented traffic classification and grouping schemes that can dynamically adapt to various network conditions (e.g., received signal strength, multiple rates, traffic load, and traffic arrival interval) [11,30,31,32]. In the recent study [33], the authors employed recurrent neural network based on gated recurrent units to estimate the optimal number of RAW slots, enhancing the performance in dense IEEE 802.11ah IoT network. To the best of our knowledge, there are limited prior studies using DRL methods for RAW mechanism optimization.
3. RAW Mechanism in Wireless IoT Networks
In this paper, we consider uplink data transmissions in a wireless IoT network employing the RAW mechanism. As shown in Figure 3, the network consists of one center-located AP and N randomly distributed STAs within a coverage range of several hundred meters. STAs transmit sensory data to the AP using a specific channel access control protocol. The network traffic includes periodically generated data, as well as randomly generated data following a certain probability distribution. Since the IEEE 802.11ah standard is an ideal choice for low-power IoT networks, we employ the IEEE 802.11ah-based RAW mechanism for multiple STAs access. We further describe the RAW mechanism operating in the IoT network.
3.1. Operation of the RAW Mechanism
In Section 1, we briefly introduce the idea of RAW. In this section, we elaborate on the RAW parameter set involved in RAW configuration and the channel access process based on RAW in a beacon interval. We aim to explain how key RAW parameters influence network performance at the mechanism principle level.
3.1.1. Structure of the RAW Parameter Set
The IEEE 802.11ah standard defines an information element field in the beacon frame for group-based restricted channel access, known as the RAW parameter set (RPS) [4]. RPS primarily consists of one or more RAW assignment subfields. Each RAW assignment subfield contains necessary RAW control subfields, RAW slot definition subfields, and RAW grouping subfields, for performing restricted channel access to one or multiple STAs in a RAW. According to specific requirements, elements such as RAW start time, channel indication, and periodic operation parameters subfields are conditionally present. The RAW slot definition subfield further defines the slot duration, slot count, and access restrictions between slots. As beacon frames are broadcast by the AP, STAs can learn from the related subfield of the RPS element which RAW group they belong to, as well as the number of RAW groups in a beacon interval, the number of slots in each RAW, and the duration of a single slot in each RAW. The specific rules for calculation are described as follows.
Slot duration and slot count. The formula for calculating the duration of a single slot in a RAW is as follows [4]:
Let the length of slot duration count field be y. According to the IEEE 802.11ah standard, when bits, , the maximum duration of a slot is ms, and the maximum number of slots in a RAW is . When bits, , ms, . The selection of y depends on the number of STAs in each RAW. Apparently, the duration of a RAW can be calculated as .
Slot assignment. A mapping method for allocating STAs into the corresponding slots in a RAW is defined in the IEEE 802.11ah standard [4]. It is implemented by defining a mapping function:
where x is the assosiation ID (AID) of the STA in a RAW group, is the allocation offset, which means that the first STA in the group will be allocated to the time slot, and K is the number of slots in a RAW. We provide an illustration of slot allocation in a RAW as shown in Figure 3. If , the STA with AID-1 is allocated to . The mapping function ensures a uniform distribution of STAs across slots.
Cross slot boundary. The IEEE 802.11ah standard defines restrictions on channel access across slot boundaries. STAs can access the channel either in a cross-slot-boundary way or in a non-cross-slot-boundary (NCSB) way [4]. To alleviate the hidden nodes problem and facilitate performance analysis, it is generally advisable to employs the non-cross-slot-boundary mechanism [16]. Therefore, the holding time is defined to be , where is the time required for one successful data transmission, and its expectation can be obtained through statistical analysis. With this constraint, it can be ensured that the last data transmission in the current slot has been completed by the end of slot. If the time remaining in the current slot is not sufficient for one data transmission, the STAs cache their data and wait for the arrival of the next slot to which they belong.
3.1.2. RAW-Based Channel Access and Data Transmission
The channel access and data transmission process of STAs in the IEEE 802.11ah network with RAW mechanism can be summarized as follows and shown in Figure 3.
- The STAs listen to the beacon frames broadcast by the AP, request association and authentication, and receive their AID. The AP periodically broadcasts beacon frames carrying the RPS element and informs STAs of information including their RAW group, the slot count in a RAW, and the slot duration. STAs are then assigned to different slots based on the mapping function (2).
- The STAs contend for channel access following the enhanced distributed channel access (EDCA) mechanism when their slot arrives: STAs perform carrier listening for a distributed inter-frame spacing (DIFS) time before initiating channel access. Once the channel is sensed idle, STAs start decreasing their backoff counter, and initiate channel access when their backoff counter reaches zero. If ’s backoff counter decreases to zero before ’s, initiates channel access, while suspends its backoff counter until the channel is sensed idle again.
- If the backoff counters of two or more STAs in the network decrease to zero simultaneously, these STAs attempt to access the channel at the same time, which may result in collisions. Upon encountering a collision, the STAs increase and reset their backoff counter until they reach the maximum retry limit, at which point packet loss occurs.
- STAs that successfully access the channel will transmit their data after waiting for a short inter-frame spacing (SIFS) time. A received acknowledgment (ACK) frame from the AP indicates the completion of data transmission. The time taken for one data transmission is denoted as .
The operation of the RAW mechanism elaborated above can provide a preliminary explanation at the mechanism level for the significant impact of RAW parameters on network performance: Firstly, an excessive number of STAs contending for channel access in a slot increases the probability of collisions and packet loss. Secondly, inadequate slot duration limits the amount of data STAs can transmit, thereby reducing overall throughput. Lastly, due to the NCSB mechanism, an excessive number of slots leads to frequent slot boundary switching, resulting in increased holding time overhead and buffered data. In the next subsection, we will analyze the impact of RAW parameters on network throughput at the mathematical analysis level.
3.2. Performance Modeling and RAW Parameters Optimization
Assuming that the number of RAW groups is denoted as , the number of slots in each RAW group is represented by , and the duration of a slot in each RAW group is denoted as , where . Thus, the set of number of STAs in each RAW group, the set of number of slots in each RAW, and the set of slot durations for RAW groups are represented as , , and , respectively.
The correlation between RAW parameters and network throughput can be derived based on the analytical model proposed in [14]. Given that the STAs are uniformly distributed among slots in a RAW, the number of STAs in each slot can be approximated as , and the intensity of contention in each slot is considered to be the same. Consequently, for the STAs in each slot of the i-th RAW, the probability of STAs suspending their backoff counter is defined as , indicating that the suspending probability is related to the transmission probability , the number of STAs in each slot , and the slot duration . The collision probability is denoted as .
The backoff process of a STA’s backoff counter can be analyzed using a two-dimensional Markov chain [14]. Each state during the backoff process can be represented as a probability, and the steady-state probability of each state can be further determined. According to the normalization formula, a closed-form expression for the steady-state probability of the backoff counter decreasing to zero can be obtained as , indicating that the steady-state probability at state-0 is dependent on the suspending probability , the collision probability , the given minimum size of the contention window and retry limit m. Subsequently, the transmission probability can be computed as
The collision probability is given by , and the probability that at least one STA transmits data in a slot is denoted as . Furthermore, the successful transmission probability can be represented as
The normalized slot throughput can be calculated as
where represents the average payload size of a data frame, is the time of a mini-slot in the contention window. The time for a successful data transmission and the time spent due to collision is respectively denoted as and , which are calculated in [14]. The effective time for data transmissions in a slot is . Finally, the normalized throughput of the network can be denoted by
where the duration of the beacon interval is dependent on the total duration of RAWs in one beacon interval.
According to (6), network throughput is related to the successful transmission probability, which in turn depends on the collision probability and the transmission probability. These probabilities are influenced by the number of STAs in a slot and the slot duration. Moreover, the number of RAW groups and the number of slots in a RAW jointly determine the number of STAs in a slot. Intuitively, the increasing number of RAW groups and slot divisions reduce the number of STAs per slot, thereby decreasing the collision probability. Increasing the slot duration, on the other hand, allows more time for data transmission in a slot, thereby reducing data buffering. Therefore, increasing the number of RAW groups, dividing more slots in a RAW and extending the slot duration can greatly enhance network throughput. However, excessive RAW divisions may cause more STAs to remain idle, leading to data buffering. Similarly, an excessively long slot duration may result in wasted time in networks with low traffic loads. There is a trade-off in adjusting the RAW parameters. Hence, by jointly optimizing the number of RAW groups , RAW slot counts , and slot durations with , we can formulate the network throughput maximization problem as follows:
The existing studies prefer to construct complicated analytical models of RAW, and further propose optimization methods to find the optimal RAW parameters to improve network throughput. However, solving RAW parameters optimization problems based on analytical models may lead to a high level of computational complexity or even impracticality in dynamic networks. On the one hand, these analytical models require a series of assumptions, including saturated network traffic, ideal channel conditions, and packet loss solely caused by collisions. Moreover, the analytical models do not comprehensively consider details about the RAW mechanism and channel conditions. Although some studies have refined the analytical models and taken more complex network conditions into account, this has made the analysis process more cumbersome. On the other hand, due to the mathematical or heuristic methods often involve complex rules and have not been validated in different network scenarios, their generalization ability in complex and dynamic network conditions needs to be improved.
To investigate practical network states, the IEEE 802.11ah network simulation environment is developed based on a widely used network simulator called NS-3 [5]. NS-3 is used to bulid simulation environments that closely resemble real-world network environments. The partial mechanisms of the PHY and MAC layers including the RAW mechanism are also implemented. While analytical results serve as references for optimizing RAW parameters, the simulation environment implemented by NS-3 undoubtedly provides more accurate results and can serve as a benchmark for validating these analytical results. Additionally, with the capability of handling complex and dynamic environments, DRL-based methods are well-suited for addressing RAW parameters optimization problems and demonstrate strong generalizability across various scenarios.
To determine the optimal RAW parameters in complex network environments that closely mimic real-world scenarios, we construct network environments using the NS-3 simulator, and employ the DRL-based method to decide on the RAW parameters to enhance network throughput. The specific methodology will be elaborated in the following section.
4. DRL for RAW Parameters Optimization
In this section, we propose a learning framework for optimizing RAW parameters. As depicted in the Figure 4, we set up network simulation environments in NS-3 and execute agent training in the DRL environment. The PPO algorithm [34] is employed as the specific DRL implementation algorithm in the DRL-guided NS-3 simulation framework. During training, the DRL agent receives network observations from the NS-3 simulation environment, serving as inputs to the DNNs. Each learned action (i.e., RAW parameters) are then applied as the configuration parameters for the RAW mechanism in NS-3, and a new simulation is executed to obtain an updated reward (i.e., network throughput). The DRL agent continues to receive observations from the network environment for a new training episode. Interactions between the DRL agent and the NS-3 environment continue until the DRL agent learns the optimal RAW parameters and achieves enhanced network throughput. To utilize PPO for optimizing RAW parameters to maximize network throughput, we first reformulate problem (7) as an MDP.
4.1. MDP Reformulation
Given the network conditions, we aim to optimize the RAW parameters (i.e., the number of RAW groups, the number of slots in each RAW and the slot duration in each RAW) to reduce contentions among STAs and consequently improve network throughput. To facilitate the problem formulation, the following assumptions are made for the IoT network:
- The AP collects information about the network (e.g., network size N and traffic arrival of the STAs) through management frames. Based on received packets from the STAs, network performance such as throughput and packet loss ratio can be statistically determined.
- To alleviate hidden nodes issues and collisions, STAs obey the NCSB mechanism when accessing the channel among slots.
In RL, the interaction between the agent and the environment is typically modeled as an MDP, which can be represented by a tuple , where represents the state space, represents the action space, the transition probability function represents the probability of transitioning from state s to state when action a is taken, the reward function represents the reward obtained after taking action a in state s, and is a constant discount factor. Specifically, the definitions of state, actions, reward, and observations are given as follows:
- State: The state at the current time step is defined as the throughput obtained from the current simulation statistics, denoted as . During the simulation, the AP collects the number of packets received and the payload size of each packet at the current time step to calculate the network throughput at the end of the current step.
- Action: The actions in the MDP are defined as the RAW parameters, including the number of RAW groups, the number of slots in each RAW group, and the slot duration in each RAW group. Thus, the action at step t is denoted as .
- Reward: According to the optimization objective, the reward is defined as the throughput obtained at each time step, represented as .
- Observation: The observation set is defined as the network information observable by the AP, including network size N, the set of traffic loads , and the set of traffic intervals , which can be represented as .
In the following subsection, we elaborate on the PPO algorithm for RAW parameters optimization.
4.2. PPO for Optimizing RAW Parameters
Given a policy approximator with parameters , policy-based policy gradient (PG) algorithms find the optimal to maximize the reward or value function. For a given input state , the policy network directly outputs either the action or the probability associated with the action. It then selects the appropriate action based on the probability, allowing the output action to be a continuous value. The expected value function in PG algorithms can be represented in terms of the policy parameters as
where is the stationary distribution of the Markov chain for , and denotes the Q-value of the state-action pair following the policy . The goal of PG is to find parameters that maximize by ascending he gradient of the policy. The evaluation of the policy gradient can be simplified as [36]
where the expectation is taken over all possible state-action pairs following the same policy . The policy gradient can be evaluated by sampling historical decision-making trajectories.
For each episode, all the tuples acquired by the agent can be collectively represented as a state-action trajectory resulting from the agent’s interaction with the environment over the current episode, which is denoted as . Let be the reward for a trajectory , and estimate the Q-value in (9) by . Therefore,the policy gradient in each time step can be approximated by randomly sampling , and the policy parameters can be updated as , where denotes the step size for gradient update. To reduce prediction variability and improve learning efficiency, the value function can be used as the baseline, and the advantage function is further introduced to replace .
To address high-dimensional state and action spaces while stabilizing the learning process, actor-critic (AC)-based DRL algorithms introduce a DNN with weight parameters to approximate the Q value. AC algorithms update both the policy network and the Q-value network. Specifically, at each learning step t, the actor updates the policy network by updating the policy parameters , while the critic updates the Q network by minimizing a loss function and updates the parameters by gradient ascent, where denotes the TD error. To further stabilize the training process, the deep deterministic gradient policy (DDPG) algorithm [36] utilizes two DNNs with different parameters, i.e., the online Q-network and the target Q-network . The TD error is rewritten as .
To facilitate the agent’s utilization of past experiences and improve sample efficiency, PG can be transformed into off-policy learning through the utilization of importance sampling [37]. Sample collection can be conducted under a behavior policy distinct from the target policy . To mitigate the effects of improper step size in policy optimization on training stability, the off-policy trust region policy optimization (TRPO) algorithm imposes an additional constraint on the gradient update [37], ensuring that the old and new policies do not diverge significantly. Let denote the probability ratio of the divergence between the old and new policies. TRPO maximizes the objective by applying conservative policy iteration without limiting the probability ratio to an appropriate range. This could lead to an excessively large policy update. Intuitively, a smaller deviation between the behavior policy and the target policy is better. Hence, the PPO algorithm [34] modifies the objective by constraining in a region , and penalizing changes to the policy that move away from 1. The objective in is
where denotes a distance measure in terms of the Kullback-Leibler (KL) divergence between two different probability distributions. The advantage function in the objective of problem (10) is the approximation of the actual advantage corresponding to the target policy . PPO constrains the parameters search within a region by introducing the inequality constraint in problem (10), which ensures that the KL convergence between and is bounded by . The clip function returns , and the hyper-parameter by default.
During the training of the DNNs, PPO employs fixed-length(e.g. T time steps) trajectory segments. A truncated advantage estimation is computed to replace the advantage function in problem (10) as
where . The loss function of PPO is
where is the mean squared error loss, are coefficients, S is an entropy bonus.
The PPO algorithm for optimizing RAW parameters in networks built in NS-3 is summarized in Algorithm 1. PPO utilizes two DNNs to approximate the policy networks. In each learning episode, the PPO agent runs the old/behavior policy (i.e., RAW parameters), observes network throughput obtained from the NS-3 network simulations environment for T time steps, and stores T transition tuples in the experience replay buffer. Then, it samples mini-batches of transition tuples from the replay buffer and computes advantage estimates . Subsequently, weight parameters of the target policy network are updated by using mini-batches randomly sampled from the replay buffer through importance sampling and by optimizing the surrogate loss in (12). Weight parameters of the behavior policy network are updated by . Limiting the probability ratio of the two policies ensures that the probability distribution of the output actions from the two policy networks remains similar.
The uniform grouping scheme is verified to perform better in homogeneous networks [38]. Considering the networks with periodic and random traffic in this paper, we employ the uniform grouping scheme, where STAs are evenly distributed in each RAW. Consequently, the slot duration and number of slots in each RAW group are considered to be equal. As a result, the actions of the MDP can be further simplified to the number of RAW groups, the number of slots in one RAW group, and the slot duration in one RAW group.

5. DRL-guided NS-3 Simulation
In this section, we investigate the performance of the proposed PPO-based DRL algorithm for RAW parameters optimization in networks with periodic or random traffic, which are set up in the NS-3 simulator. We firstly demonstrate the learning performance of the PPO algorithm on finding optimal RAW parameters and improving network throughput. Then, we investigate the adaptive capability of RAW parameters under dynamic network conditions such as traffic load and network size. Finally, we compare the performance of the PPO-based slot division scheme with the equal-slot-division scheme (i.e., one STA per slot) and no-slot-division scheme (i.e., only one ’slot’ in a RAW).
5.1. Simulation Setup
We set up the training environment for DRL on the Linux operating system. Specifically, we set up the DRL agent in a Python environment based on the PyTorch framework, and set up the network topology in the NS-3 simulator as depicted in Figure 3. Network conditions and simulation results are input into the PPO agent as environment states. The RAW parameters are configured based on the actions learned by the PPO agent and used for subsequent simulations in the NS-3 simulator. Throughout the training process, the PPO agent interacts numerous times with the simulated network environment set up in the NS-3 simulator.
The parameters for our network topology and the PPO agent are shown in Table 1. For analytical and simulation design purposes, we define the time step t as each fixed-duration simulation iteration performed in NS-3, where each episode consists of only one step. When performing simulations, we collect statistical information regarding network performance after every simulation iteration with a duration of 10 seconds. Note that the number of slots is in the range of according to the restriction in (1). When , the maximum slot duration is 246.14 ms, and when , the maximum slot duration is 31.1 ms. This can serve as a constraint for the agent during learning.
5.2. Learning Performance in Periodic Traffic Networks
We first consider the RAW parameters optimization in networks with periodic traffic, where all STAs are assigned to one RAW group. The action of the MDP is . In each iteration during the training process, the PPO agent observes throughput and other information from the wireless environment and employs policy to determine the RAW parameters setting for the next time step. The effectiveness of the RAW parameters is evaluated at the subsequent time step with the reward obtained from NS-3, and the RAW parameters for the following time step are determined accordingly. The PPO agent is trained through numerous interactions with network simulation environments bulit in NS-3.
5.2.1. Convergence to the Optimal RAW Parameters
We first validate the convergence performance of the PPO algorithm on a basic network topology. In the periodic traffic network, the traffic interval of all STAs is fixed (e.g., 0.1 ms). We train the PPO agent though numerous interactions with the network environment built in NS-3. The convergence performance of the PPO algorithm is shown in Figure 5, and Figure 6 demonstrates the convergence process of the PPO agent interacting with the network simulation environment in the NS-3 simulator. As the training iteration proceeds, the PPO agent learned better actions, leading to significantly increased normalized rewards obtained from interacting with the NS-3 simulation environment. After 10,000 training episodes, the reward stabilized at its maximum value. This indicates that the PPO agent has learned the optimal RAW parameters by the end of training and achieved the optimized network throughput in the periodic traffic network. We also observe the improvement of network throughput with the NS-3 simulator during the PPO agent’s training process. It can be seen in Figure 6 that the network throughput is ascending when the training process proceeds. Compared to the network throughput obtained with default settings (), the network throughput with the optimal RAW parameters obtained by PPO agent is improved by about 70%. It is evident that employing DRL method for optimizing RAW parameters is feasible, and the RAW parameters derived from learning lead to a significant enhancement in network throughput compared to default settings.
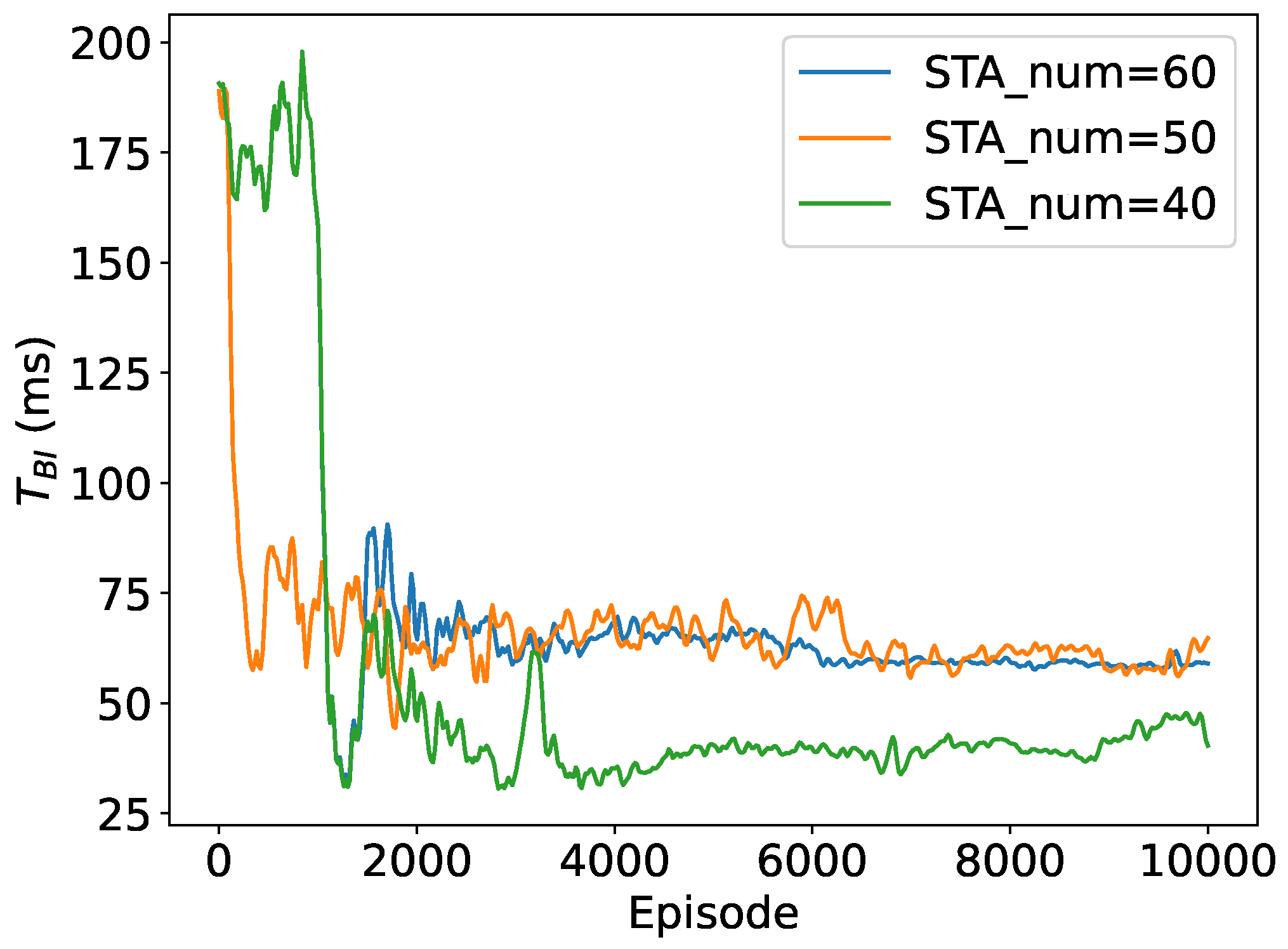
Additionally, we depict the convergence performance of the slot count within a RAW and the slot duration with different number of STAs in the network. To provide a more straightforward demonstration, we calculate the approximate duration of a beacon interval as and use beacon interval dynamics to represent variations in slot duration in the following subsections. As shown in Figure 7, both parameters converge to stable values for different network sizes, further validating the algorithm’s convergence. As the network size is relatively small, the number of slots is similar when the number of STAs in the network is 40, 50 and 60 respectively. The duration of the beacon interval increases by about 40% when the number of STAs in the network increases from 40 to 60, indicating that the slot duration is adaptively adjusting to the network size with DRL.
Figure 7.
Convergence performance of .
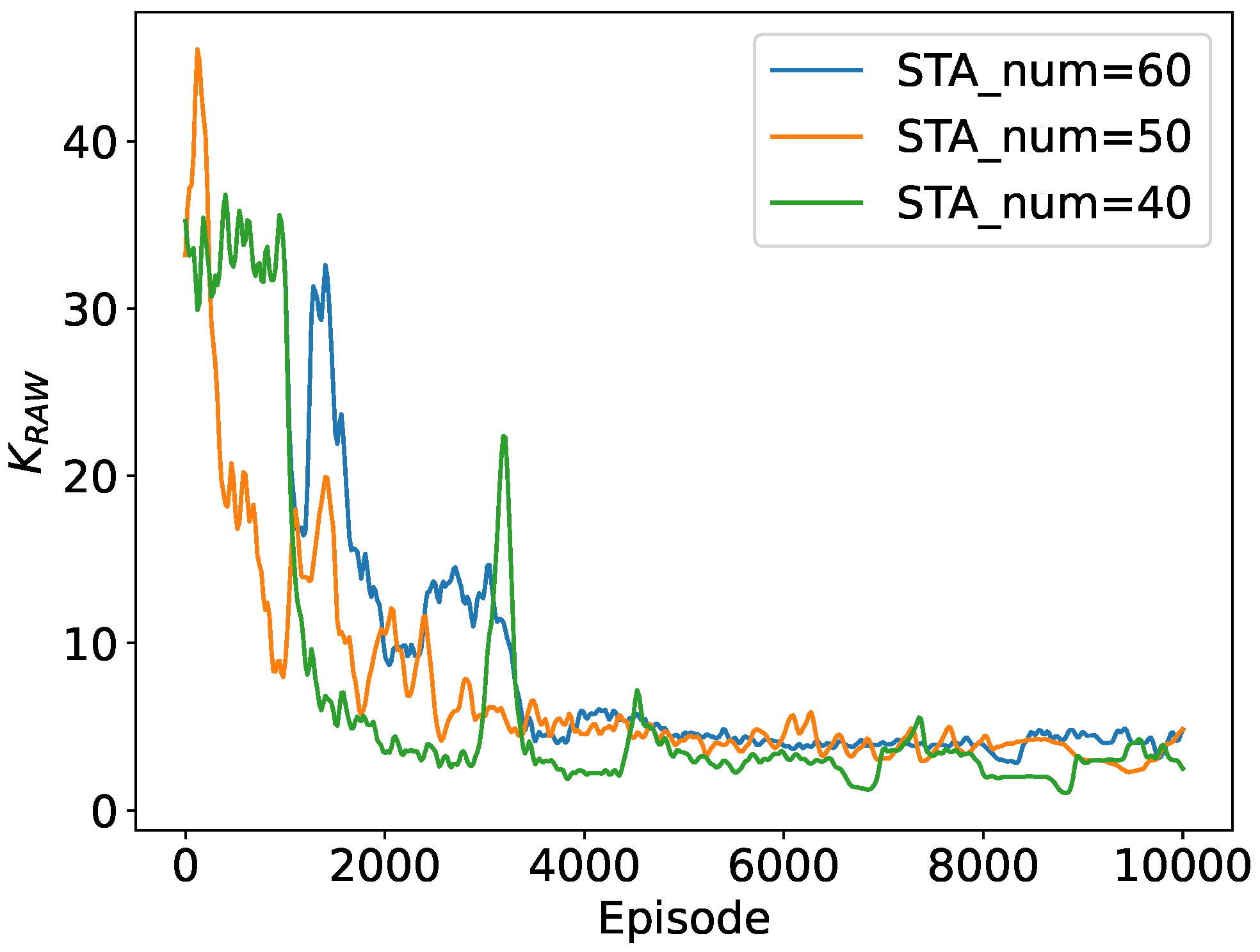
Figure 8.
Convergence performance of ().
5.2.2. Throughput Performance with Different Traffic Loads
In this section, we analyze the adaptive adjustment of RAW parameters obtained through PPO method with different network loads. We assume homogeneous traffic load 0.05 Mbps for each STA. Therefore, the traffic load in the network increases as the number of STAs in network increases. We observe the adaptive adjustments of RAW parameters and changes in network throughput as the number of STAs increases from 30 (10) to 100.
As shown in Figure 9, both the slot count and slot duration increase with the growing number of STAs and traffic load in network. The number of slots in a RAW increases stepwise with the network size and traffic load. Specifically, the slot count remains constant when the number of STAs is between 50-70 and 80-90. This is attributed to the fact that dividing fewer slots in a RAW significantly reduces contentions when the network size is small. Overall, the RAW mechanism ensures that the number of STAs in each RAW slot is not excessive. When the number of STAs in the network is less than 50, the slot duration increases significantly from to about , approximately 4 times longer, with the increasing network size and traffic load.
This trend is consistent with the changes in network throughput depicted in Figure 10. When the number of STAs in the network is less than 40, the network throughput remains unsaturated with few STAs and low traffic load in the network. As the number of STAs increases from 10 to 40, along with the ascending network traffic load, the network throughput subsequently increases from to , approximately 4 times larger. At a certain point, with number of STAs = 40, the network traffic load reaches its maximum capacity, leading to saturated network throughput under current network conditions. As the number of STAs in the network continues to increase from 40 to 90, contentions intensify, leading to a higher probability of transmission collisions. Meanwhile, when the network traffic load exceeds its capacity, constrained by the data transmission rate and the duration of a single simulation, the AP cannot handle all the traffic from STAs, resulting in a slight decrease by about 7% in network throughput. This trend is consistent with the variation of throughput with the number of STAs in IEEE 802.11 networks [14].
5.3. Learning Performance in Random Traffic Networks
To further validate the generalization ability of the proposed DRL algorithm, in this section, we modify the network conditions. While in the previous subsection, packets are transmitted at identical intervals, we now adjust the packet transmission intervals for each STA in the network. As depicted in Figure 11, the packet transmission intervals of each STA are modeled by a Poisson distribution, introducing randomness into the transmission process. Given that all STAs have the same data transmission rate, the network traffic can be considered as random. Moreover, we significantly increase the network size to emulate real-world network scales. The parameter settings are shown at Table 2. We scaled up the number of STAs in the network to exceed 150, and increase the training iterations of the PPO agent.
5.3.1. Convergence to the Optimal RAW Parameters
We first validate the convergence performance of the PPO algorithm in the new network conditions. In the random traffic network implemented in NS-3, all the STAs transmit packets at random intervals following a Poisson distribution. Additionally, the network size is larger than that in the periodic traffic network, necessitating the division of STAs into more RAW groups. Therefore, the RAW parameters to be learned include RAW group count, slot count in one RAW and slot duration in one RAW.
As shown in Figure 12, the normalized reward obtained by the PPO agent from interacting with the NS-3 simulation environment increases significantly as the training iterations progress, stabilizing at its maximum value after 17,000 training episodes. This indicates that the PPO agent can still learn the optimal RAW parameters and achieve optimized network throughput in the new network environment, i.e., the random traffic network. We also observe that as the network conditions become more complex, such as an increase in network size and random traffic arrivals, the PPO agent requires more interactions with the network simulation environment set up in NS-3. It needs to learn the optimal action selection strategy over twice as many training iterations in the random traffic network compared to the periodic traffic network.
As depicted in Figure 13, Figure 14 and Figure 15, when the number of STAs in the netwotk is 150, both the number of RAW groups and the slot duration significantly increase compared to those in a small network size, while the number of slots remains small. This implies that the PPO agent tends to divide more RAW groups rather than more slots at this network size. The convergence performance to the optimal RAW parameters obtained by the PPO agent further demonstrates the generalization capability of the proposed DRL algorithm in a complex network environment with random traffic.
5.3.2. Throughput Performance with Different Network Sizes
In this subsection, we validate and analyze the adaptive adjustment of RAW parameters obtained using the PPO algorithm under different network sizes, which is reflected by changes in the number of STAs. We increase the number of STAs from 150 to 300, a sufficiently large number to achieve saturated or oversaturated traffic load, which is suitable for validating the adjustment capability of RAW parameters and network throughput of the proposed DRL framework. We observe the adaptive changes in RAW parameters learned by the PPO agent and the network throughput obtained from the NS-3 simulation environment as the number of STAs increases. As shown in Figure 16, given that traffic load reaches saturation in large-scale networks, with the number of STAs in the network increasing from 150 to 300, the network throughput decreases by about 13%. It is evident that the increasing network size leads to intensified contention and collisions, thereby resulting in a significant decline in network throughput.
As shown in Figure 17, we observe that when the number of STAs ranges from 150 to 200, the PPO agent tends to divide STAs into roughly 3 times more RAW groups. However, when the number of STAs increases to 250-300, the agent leans towards dividing more slots (from 1 to 5) in each RAW group. We analyze that within a certain range of network sizes, simply dividing RAW groups is capable of handling the current traffic load and mitigating contention. However, as the network size grows, it becomes necessary to both divide RAW groups and more slots within each RAW group. The adaptive adjustment strategy learned by the PPO agent reduces the contention among STAs per slot, thus ensuring network throughput. Additionally, as the network size increases, the agent prefers to shorten the slot duration, consequently reducing the beacon interval duration by about 10%. We analyze that shortening the beacons broadcasting period allows the AP to schedule STAs more frequently for uplink data transmissions, thereby maintaining network throughput in intensified network conditions. We also notice that as the number of STAs increases from 60 to 150, the BI duration obtained by DRL increases from to , approximately by 66%, and the slot count increases significantly by about 3 times compared to the network size in the periodic traffic network. It is evident that as the network size scales up, contentions between STAs in the network intensify. To alleviate collisions and ensure network throughput, the PPO agent tends to dividing more slots, leading to an overall increase in the BI duration.
5.4. Throughput Comparison of Different Slot Division Schemes
To further demonstrate the improvement in network performance achieved by the PPO-based algorithm, we compare the network throughput obtained from the PPO-based slot division scheme with two baseline slot division schemes. In the no-slot division scheme, all STAs contend for channel access in the same RAW group without slot division. Conversely, in the equal-slot division scheme, each STA is allocated one slot in every RAW group, ensuring non-contention-based access where only one STA can access the channel in a slot.
The overall BI durations are the same among different slot division schemes, as determined by the BI duration learned by the PPO agent. In this case, the slot durations vary among different schemes due to different slot division methods. As depicted in Figure 18, in generally speaking, the throughput performance obtained from the NS-3 simulation environment with RAW slot division scheme learned by the PPO agent significantly outperform the two basic schemes as the number of RAW slots and slot duration adaptively adjust according to the network size. In the worst case where the number of STAs in the network is 300, the network throughput obtained from the PPO-based slot division scheme is still improved by about 80% and 1.3 times, respectively, compared to the two slot division schemes.
It can be observed that as the network size increases, contentions and collisions among STAs in the network intensify, leading to a decrease in network throughput for all three slot division schemes. However, when the number of STAs in the network is between 150 and 250, the decrease in network throughput obtained from the PPO-based slot division scheme in the NS3 simulation environment is much smaller than that of the other two schemes. This indicates that the learning-based RAW slot division scheme can maintain better network throughput than the basic slot division schemes in deteriorating network conditions. It can be verified that in the DRL-guided NS-3 simulation framework, the PPO agent can learn the optimal RAW parameters and improve the network throughput in situations of intense contention. We also observe that as the network size increases, the network performance obtained by the scheme that allocates one slot to each STA is significantly better than that of the scheme that does not divide slots within a RAW. This further validates the necessity of using the RAW grouping mechanism in large-scale networks and its improvement on network performance.
6. Conclusion
In this paper, we have proposed a PPO-based DRL algorithm for optimizing RAW parameters in the IEEE 802.11ah-based IoT network. Necessary analysis is first provided to emphasize the significant impact of RAW parameters on network throughput, and the RAW parameters optimization problem is formulated. A DRL framework interacting with the NS-3 simulator is then proposed, in which the optimization problem is reformulated as an MDP, and a PPO algorithm for RAW parameters optimization is proposed. In network environments with periodic and random traffic built in the NS-3 simulator, the performance of the proposed DRL algorithm is evaluated. Simulation results show that the PPO-based DRL scheme can obtain optimal RAW parameters under different network conditions, and achieve significantly improved network throughput compared to that of the baseline slot division schemes.
For future studies, we aim to explore the applications of DRL methods in more intricate network scenarios and optimization problems. For networks with time-varying network size and heterogeneous traffic, apart from optimizing RAW parameters, we will delve into the RAW grouping problems. The RAW grouping problems involve categorizing STAs into different RAW groups, which require optimizing grouping strategies. In this paper, we have demonstrated the capability of the DRL approach to effectively determine the optimal RAW parameters across different network environments. Consequently, the DRL approach can be extended to address the challenge of finding the optimal RAW grouping strategy. Furthermore, the dynamic nature of the network necessitates requires algorithms to perform in real-time, prompting us to further refine our algorithm.
References
- Vailshery, L.S. Internet of Things (IoT) and non-IoT active device connections worldwide from 2010 to 2025, 2022. https://www.statista.com/statistics/1101442/iot-number-of-connected-devices-worldwide/.
- Wi-Fi Alliance. Wi-Fi CERTIFIED HaLow™:Wi-Fi® for IoT applications (2021), 2021. https://www.wi-fi.org/file/wi-fi-certified-halow-wi-fi-for-iot-applications-2021.
- Wi-Fi Alliance. Wi-Fi CERTIFIED HaLow ™ Technology Overview, 2021. https://www.wi-fi.org/file/wi-ficertified-halow-technology-overview-2021.
- IEEE Standard for Information technology–Telecommunications and information exchange between systems - Local and metropolitan area networks–Specific requirements - Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 2: Sub 1 GHz License Exempt Operation. IEEE Std 802.11ah-2016 (Amendment to IEEE Std 802.11-2016, as amended by IEEE Std 802.11ai-2016) 2017, pp. 1–594.
- Tian, L.; Famaey, J.; Latré, S. Evaluation of the IEEE 802.11 ah restricted access window mechanism for dense IoT networks. In Proceedings of the 2016 IEEE 17th international symposium on a world of wireless, mobile and multimedia networks (WoWMoM). IEEE, 2016, pp. 1–9.
- Taramit, H.; Barbosa, L.O.; Haqiq, A. Energy efficiency framework for time-limited contention in the IEEE 802.11 ah standard. In Proceedings of the 2021 IEEE GlobecomWorkshops (GC Wkshps). IEEE, 2021, pp.1–6.
- Wang, Y.; Chai, K.K.; Chen, Y.; Schormans, J.; Loo, J. Energy-delay aware restricted access window with novel retransmission for IEEE 802.11 ah networks. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM). IEEE, 2016, pp. 1–6.
- Seferagi´c, A.; De Poorter, E.; Hoebeke, J. Enabling wireless closed loop communication: Optimal scheduling over IEEE 802.11 ah networks. IEEE Access 2021, 9, 9084–9100.
- Lakshmi, L.R.; Sikdar, B. Achieving fairness in IEEE 802.11 ah networks for IoT applications with different requirements. In Proceedings of the ICC 2019-2019 IEEE International Conference on Communications (ICC). IEEE, 2019, pp. 1–6.
- Mahesh, M.; Harigovindan, V. Throughput enhancement of IEEE 802.11 ah raw mechanism using ANN. In Proceedings of the 2020 First IEEE International Conference on Measurement, Instrumentation, Control and Automation (ICMICA). IEEE, 2020, pp. 1–4.
- Oliveira, E.C.; Soares, S.M.; Carvalho, M.M. K-Means Based Grouping of Stations with Dynamic AID Assignment in IEEE 802.11 ah Networks. In Proceedings of the 2022 18th International Conference on Mobility, Sensing and Networking (MSN). IEEE, 2022, pp. 134–141.
- Robaglia, B.M.; Destounis, A.; Coupechoux, M.; Tsilimantos, D. Deep reinforcement learning for scheduling uplink iot traffic with strict deadlines. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM). IEEE, 2021, pp. 1–6.
- Kumar, A.; Verma, G.; Rao, C.; Swami, A.; Segarra, S. Adaptive contention window design using deep Q-learning. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2021, pp. 4950–4954.
- Bianchi, G. Performance analysis of the IEEE 802.11 distributed coordination function. IEEE Journal on selected areas in communications 2000, 18, 535–547.
- Soares, S.M.; Carvalho, M.M. Throughput analytical modeling of IEEE 802.11 ah wireless networks. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC). IEEE, 2019, pp. 1–4.
- Zheng, L.; Ni, M.; Cai, L.; Pan, J.; Ghosh, C.; Doppler, K. Performance Analysis of Group-Synchronized DCF for Dense IEEE 802.11 Networks. IEEE Trans. Wirel. Commun. 2014, 13, 6180–6192, . [CrossRef]
- Sangeetha, U.; Babu, A. Performance analysis of IEEE 802.11 ah wireless local area network under the restricted access window-based mechanism. International Journal of Communication Systems 2019, 32.
- Taramit, H.; Camacho-Escoto, J.J.; Gomez, J.; Orozco-Barbosa, L.; Haqiq, A. Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture. Mathematics 2022, 10, 952, . [CrossRef]
- Zhao, Y.; Yilmaz, O.N.; Larmo, A. Optimizing M2M energy efficiency in IEEE 802.11 ah. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps). IEEE, 2015, pp. 1–6.
- Nawaz, N.; Hafeez, M.; Zaidi, S.A.R.; McLernon, D.C.; Ghogho, M. Throughput enhancement of restricted access window for uniform grouping scheme in IEEE 802.11 ah. In Proceedings of the 2017 IEEE international conference on communications (ICC). IEEE, 2017, pp. 1–7.
- Tian, L.; Khorov, E.; Latré, S.; Famaey, J. Real-Time Station Grouping under Dynamic Traffic for IEEE 802.11ah. Sensors 2017, 17, 1559, . [CrossRef]
- Tian, L.; Santi, S.; Latré, S.; Famaey, J. Accurate sensor traffic estimation for station grouping in highly dense IEEE 802.11 ah networks. In Proceedings of the Proceedings of the First ACM InternationalWorkshop on the Engineering of Reliable, Robust, and Secure EmbeddedWireless Sensing Systems, 2017, pp. 1–9.
- Khorov, E.; Lyakhov, A.; Nasedkin, I.; Yusupov, R.; Famaey, J.; Akyildiz, I.F. Fast and Reliable Alert Delivery in Mission-Critical Wi-Fi HaLow Sensor Networks. IEEE Access 2020, 8, 14302–14313, . [CrossRef]
- Ahmed, N.; De, D.; Hussain, M.I. A QoS-aware MAC protocol for IEEE 802.11 ah-based Internet of Things. In Proceedings of the 2018 fifteenth international conference on wireless and optical communications networks (WOCN). IEEE, 2018, pp. 1–5.
- Tian, L.; Mehari, M.; Santi, S.; Latré, S.; De Poorter, E.; Famaey, J. IEEE 802.11 ah restricted access window surrogate model for real-time station grouping. In Proceedings of the 2018 IEEE 19th International Symposium on" A World of Wireless, Mobile and Multimedia Networks"(WoWMoM). IEEE, 2018, pp. 14–22.
- Hasi, M.A.A.; Haque, M.D.; Siddik, M.A. Traffic Demand-based Grouping for Fairness among the RAW Groups of Heterogeneous Stations in IEEE802. 11ah IoT Networks. In Proceedings of the 2022 International Conference on Advancement in Electrical and Electronic Engineering (ICAEEE). IEEE, 2022, pp. 1–6.
- Chang, T.C.; Lin, C.H.; Lin, K.C.J.; Chen,W.T. Traffic-aware sensor grouping for IEEE 802.11 ah networks: Regression based analysis and design. IEEE Transactions on Mobile Computing 2018, 18, 674–687.
- Garcia-Villegas, E.; Lopez-Garcia, A.; Lopez-Aguilera, E. Genetic Algorithm-Based Grouping Strategy for IEEE 802.11ah Networks. Sensors 2023, 23, 862, . [CrossRef]
- Tian, L.; Lopez-Aguilera, E.; Garcia-Villegas, E.; Mehari, M.T.; De Poorter, E.; Latré, S.; Famaey, J. Optimizationoriented RAW modeling of IEEE 802.11 ah heterogeneous networks. IEEE Internet of Things Journal 2019, 6, 10597–10609.
- Bobba, T.S.; Bojanapally, V.S. Fair and Dynamic Channel Grouping Scheme for IEEE 802.11 ah Networks. In Proceedings of the 2020 IEEE 5th International Symposium on Telecommunication Technologies (ISTT). IEEE, 2020, pp. 105–110.
- Mahesh, M.; Pavan, B.S.; Harigovindan, V. Data rate-based grouping using machine learning to improve the aggregate throughput of IEEE 802.11 ah multi-rate IoT networks. In Proceedings of the 2020 IEEE international conference on advanced networks and telecommunications systems (ANTS). IEEE, 2020, pp.1–5.
- Ibrahim, A.; Hafez, A. Adaptive IEEE 802.11 ah MAC protocol for Optimization Collision Probability in IoT smart city data traffic Based Machine Learning models 2023.
- Pavan, B.S.; Harigovindan, V.P. GRU based optimal restricted access window mechanism for enhancing the performance of IEEE 802.11ah based IoT networks. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 16653–16665, . [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347 2017.
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems 1999, 12.
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971 2015.
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International conference on machine learning. PMLR, 2015, pp. 1889–1897.
- Kim, Y.; Hwang, G.; Um, J.; Yoo, S.; Jung, H.; Park, S. Throughput Performance Optimization of Super Dense Wireless Networks With the Renewal Access Protocol. IEEE Trans. Wirel. Commun. 2016, 15, 3440–3452, . [CrossRef]
Figure 1.
Comparison of the IEEE 802.11ah-based Wi-Fi HaLow technology with other low-power IoT technologies in terms of key aspects.
Figure 1.
Comparison of the IEEE 802.11ah-based Wi-Fi HaLow technology with other low-power IoT technologies in terms of key aspects.
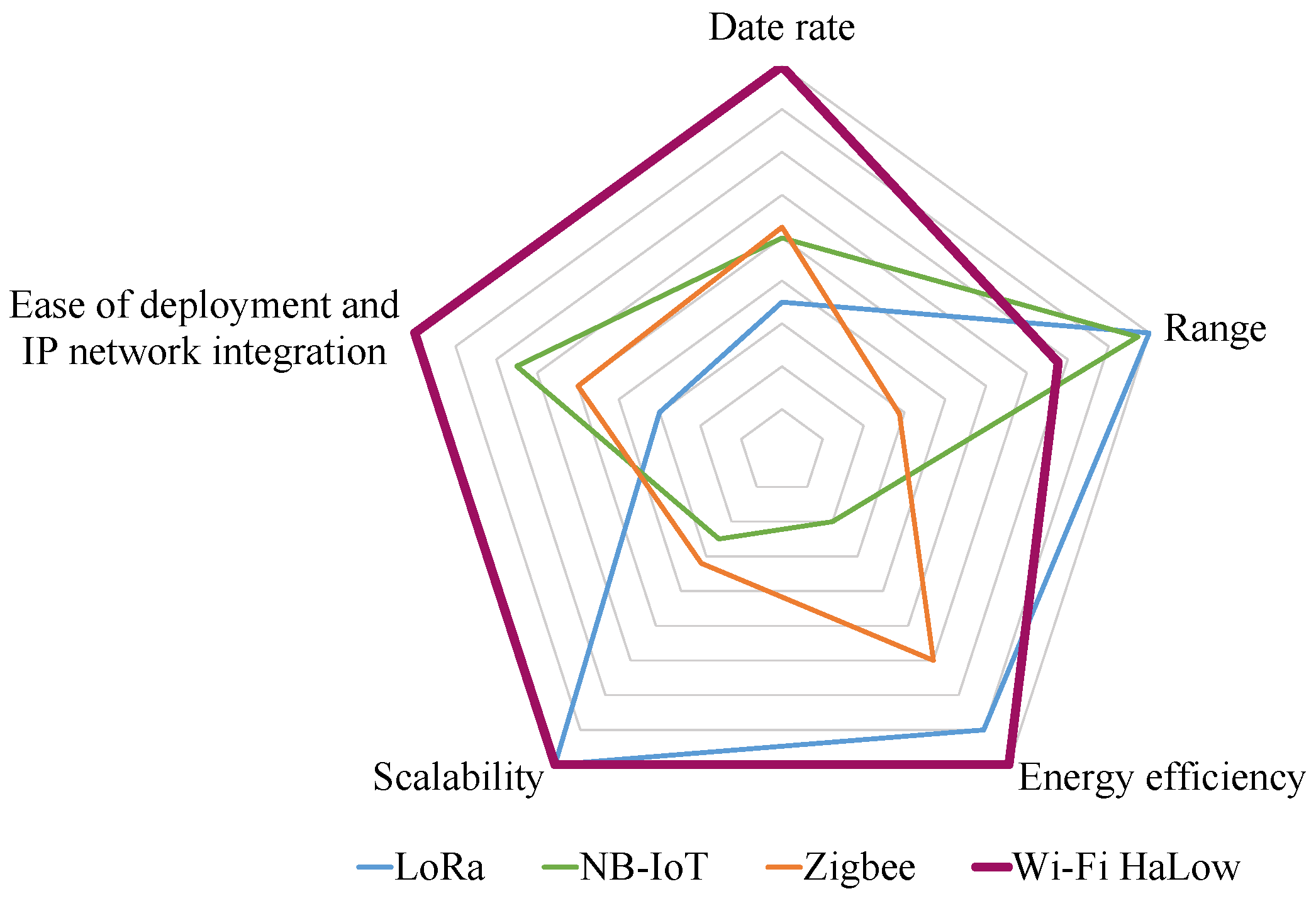
Figure 2.
A simple demonstration of RAW.
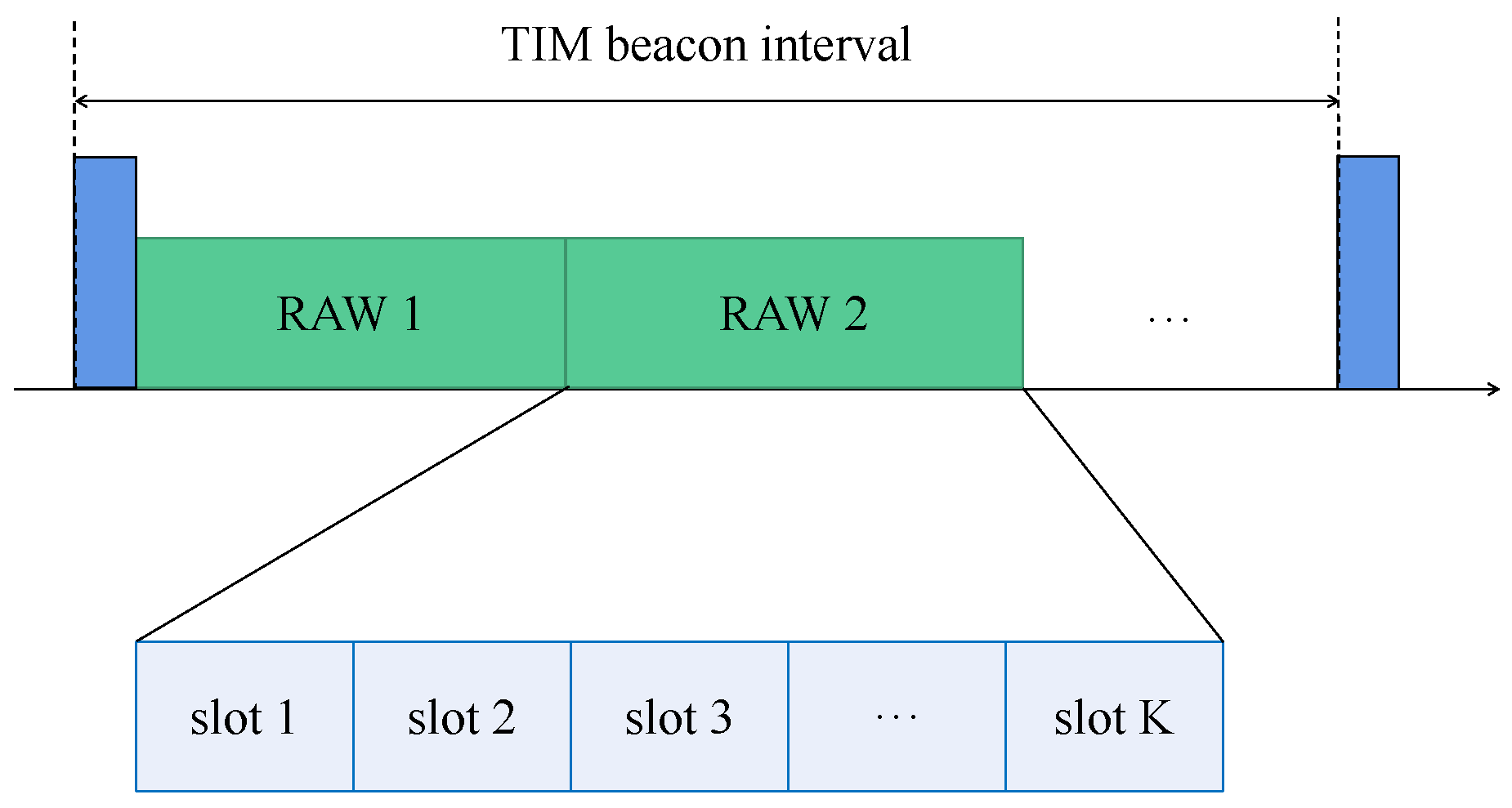
Figure 3.
The IEEE 802.11ah-based IoT network model with RAW operations.
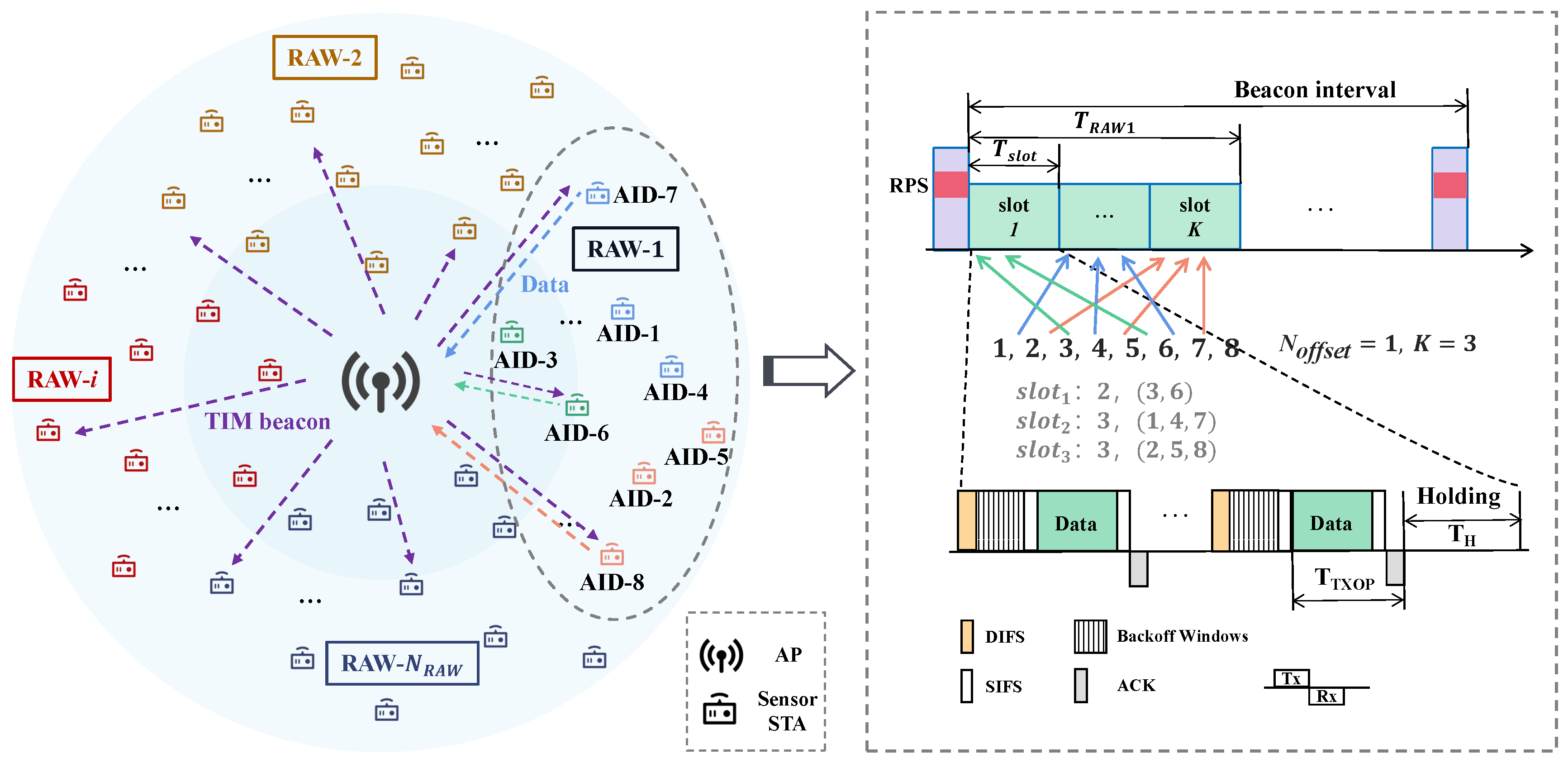
Figure 4.
DRL-guided NS-3 simulation framework for RAW parameters optimization.
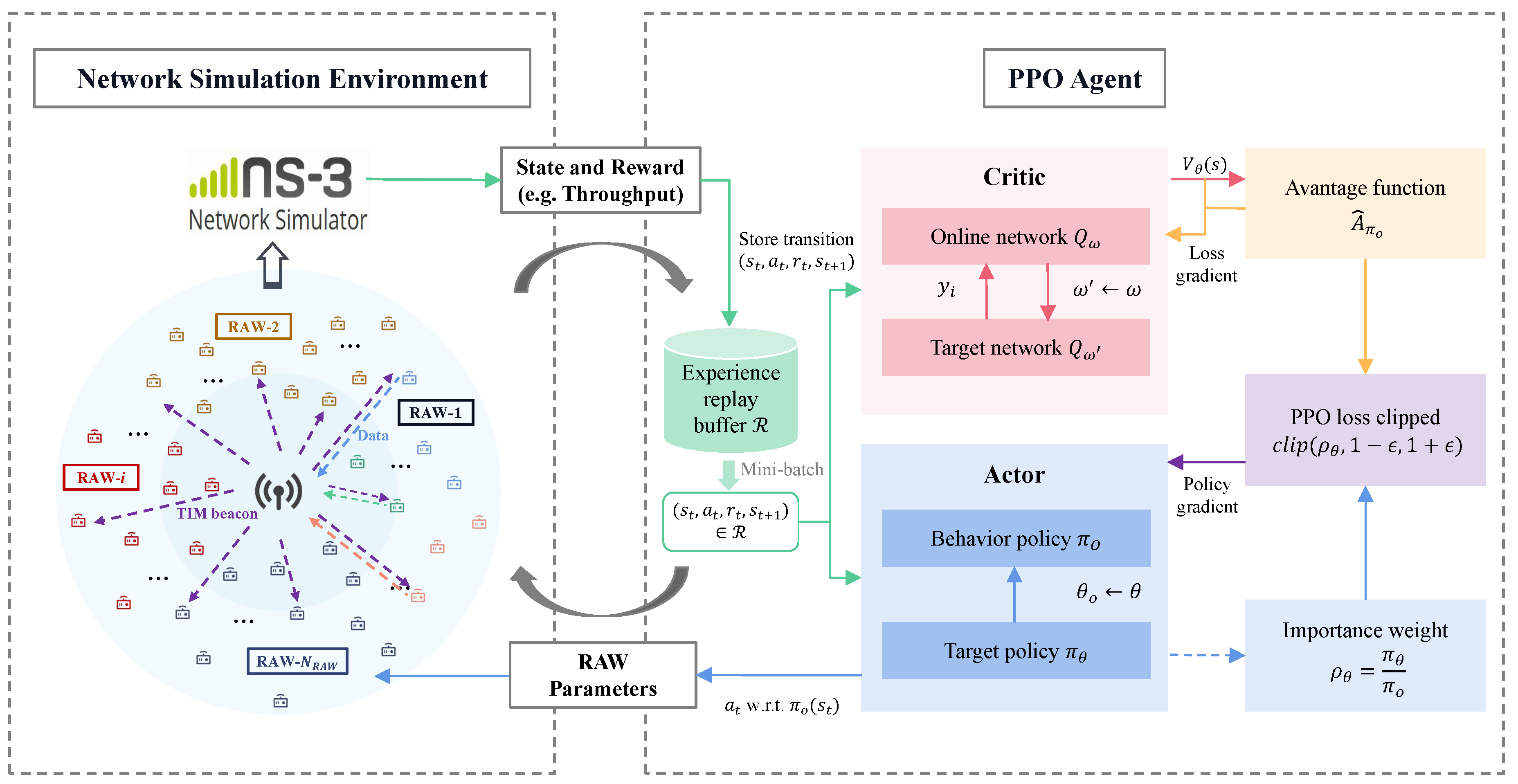
Figure 5.
Convergence performance of the PPO algorithm.
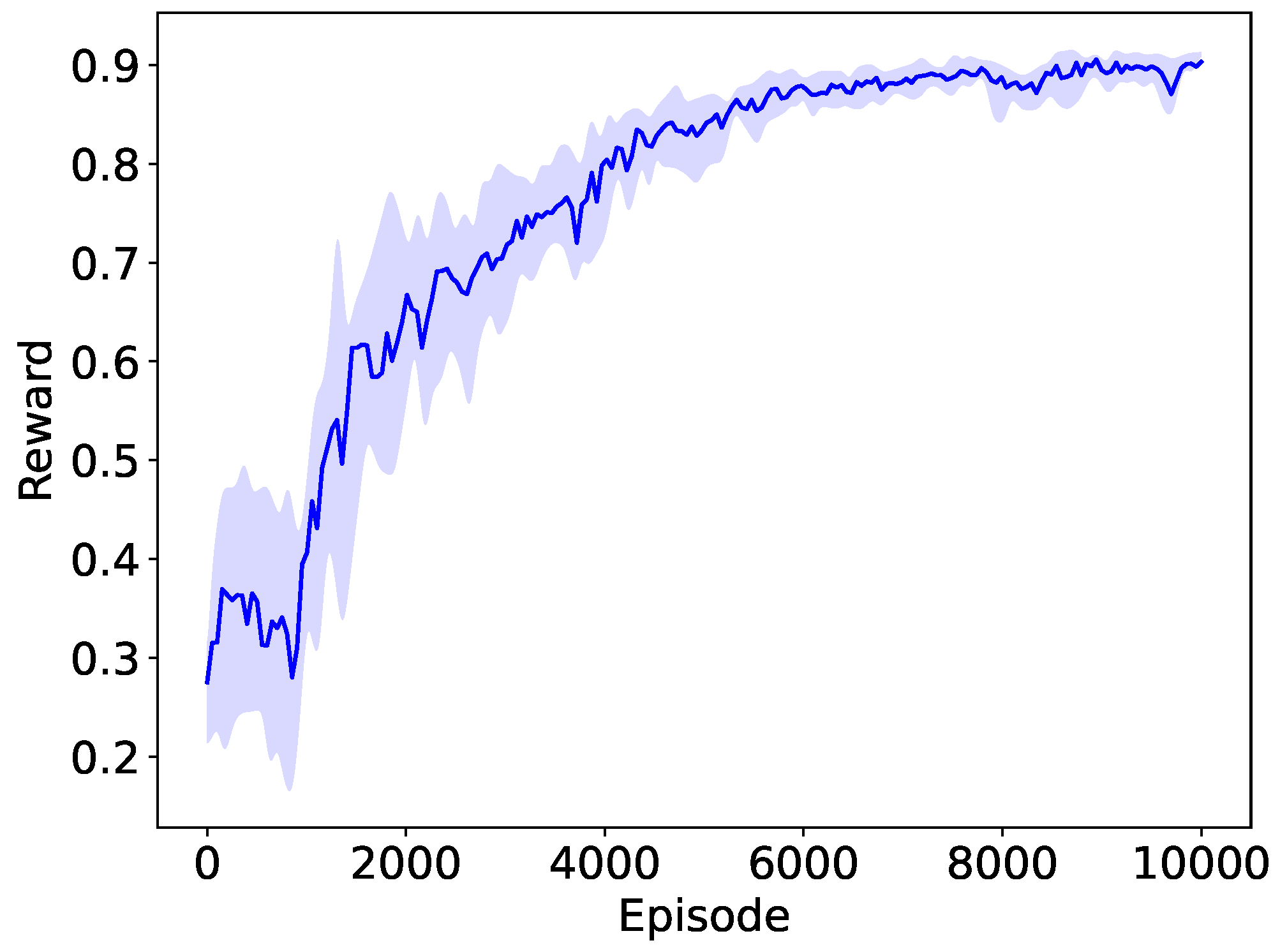
Figure 6.
Throughput ascending in NS-3 simulation environment during training episodes.
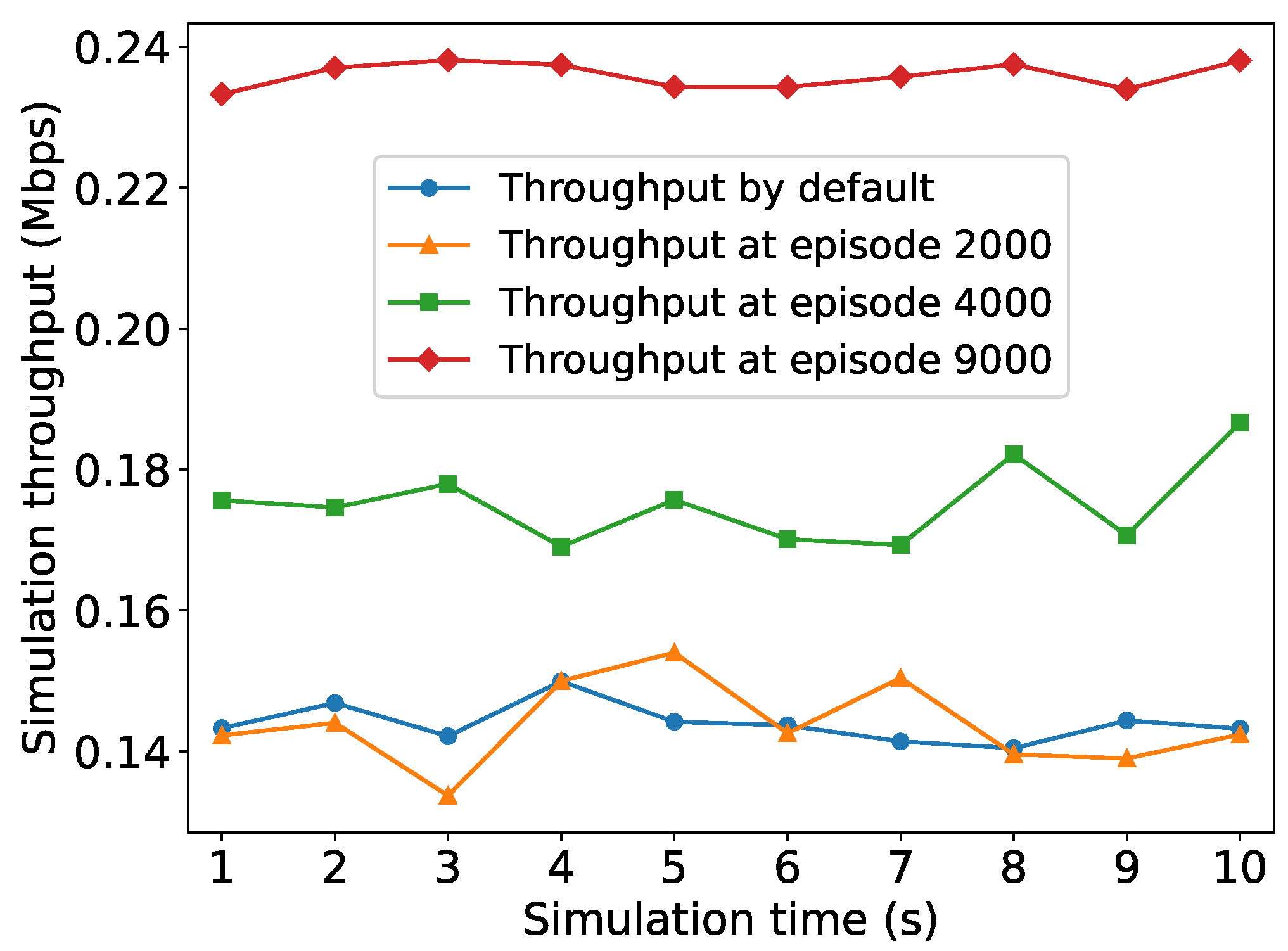
Figure 9.
Adaptive adjustment of RAW parameters with varying network traffic loads.
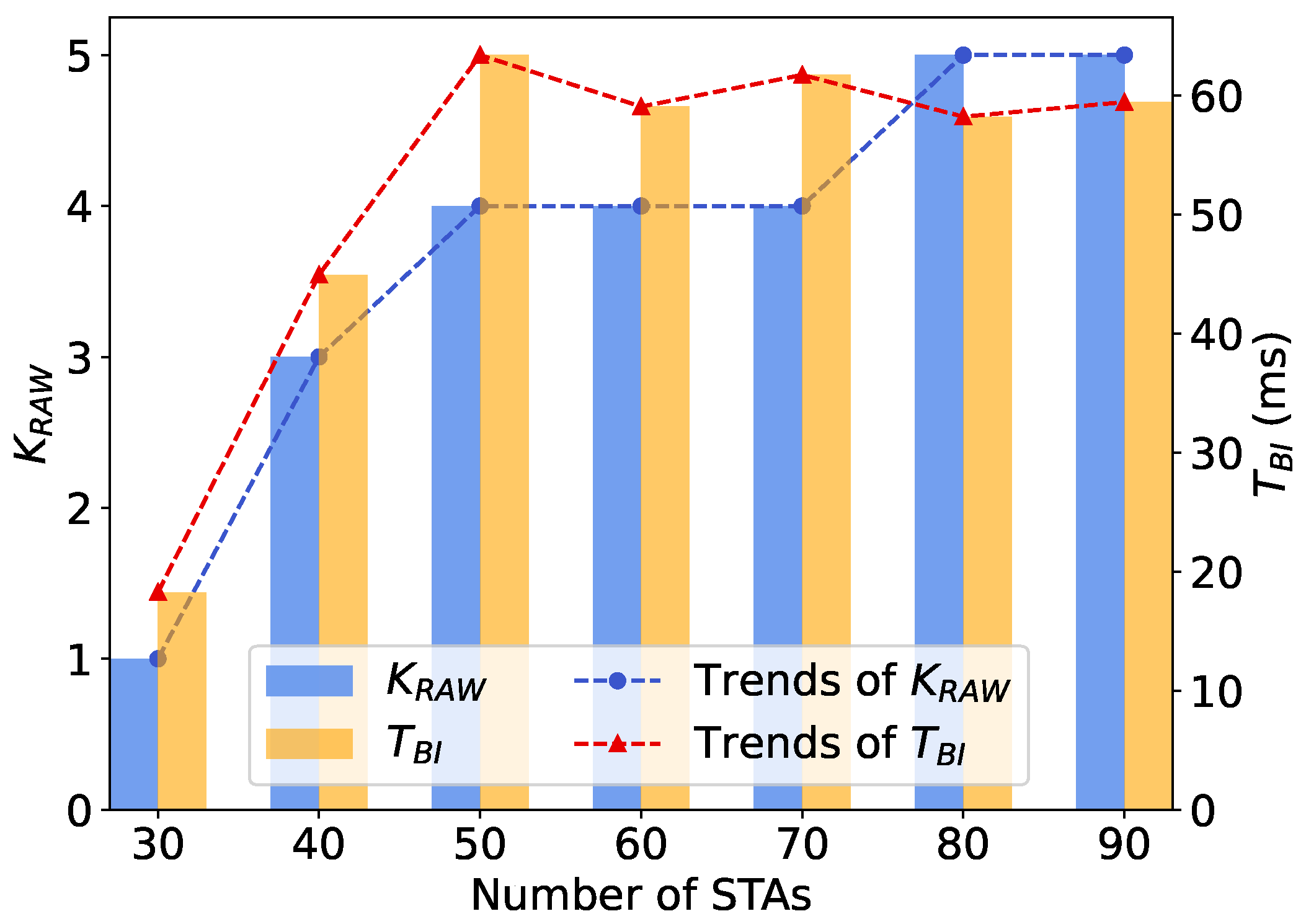
Figure 10.
Network throughput obtained by the PPO algorithm with varying network traffic loads.
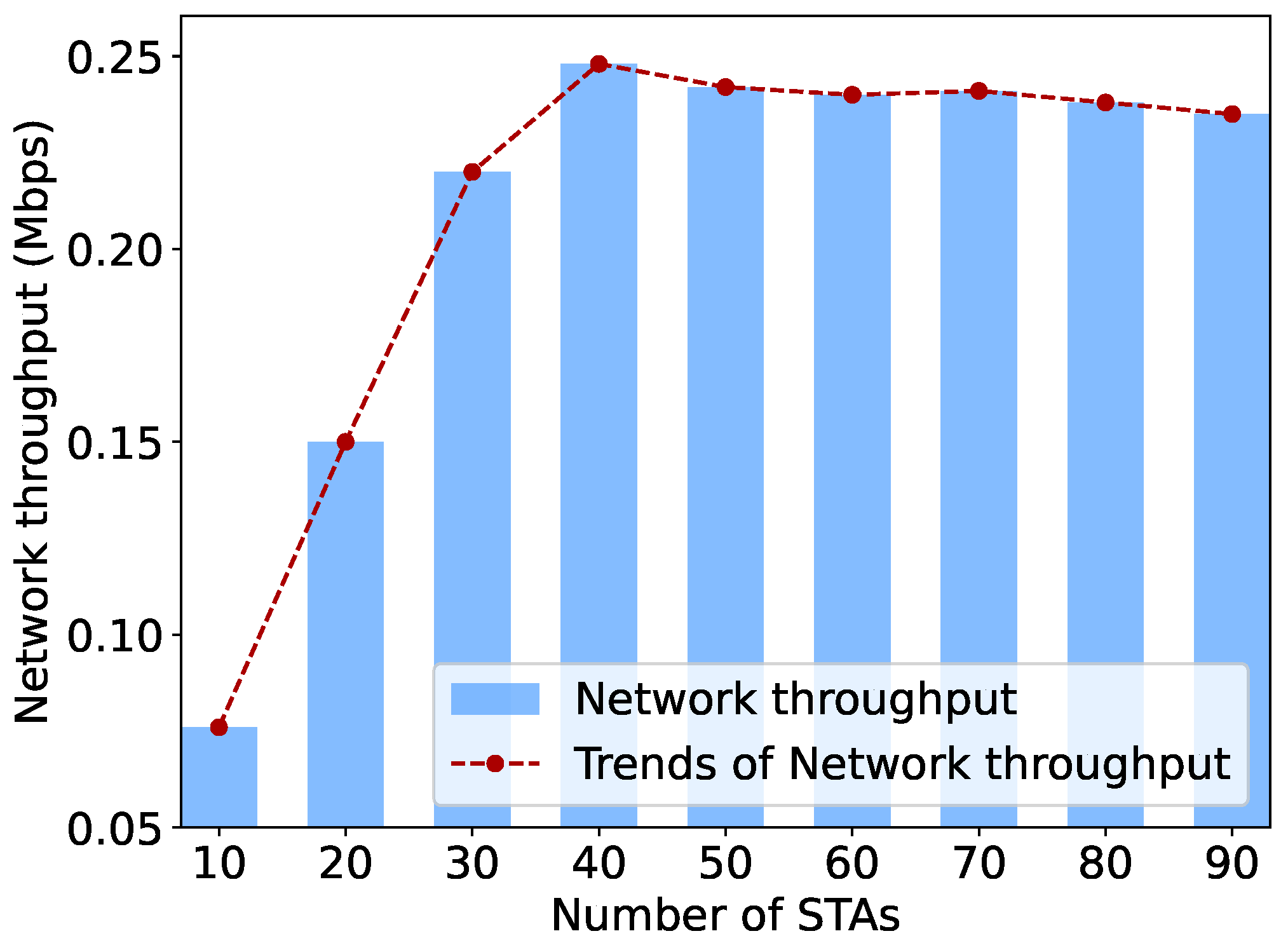
Figure 11.
Illustration of the packet transmission interval distribution of STAs in random traffic networks.
Figure 11.
Illustration of the packet transmission interval distribution of STAs in random traffic networks.
Figure 12.
Convergence performance of the PPO algorithm in random traffic networks.
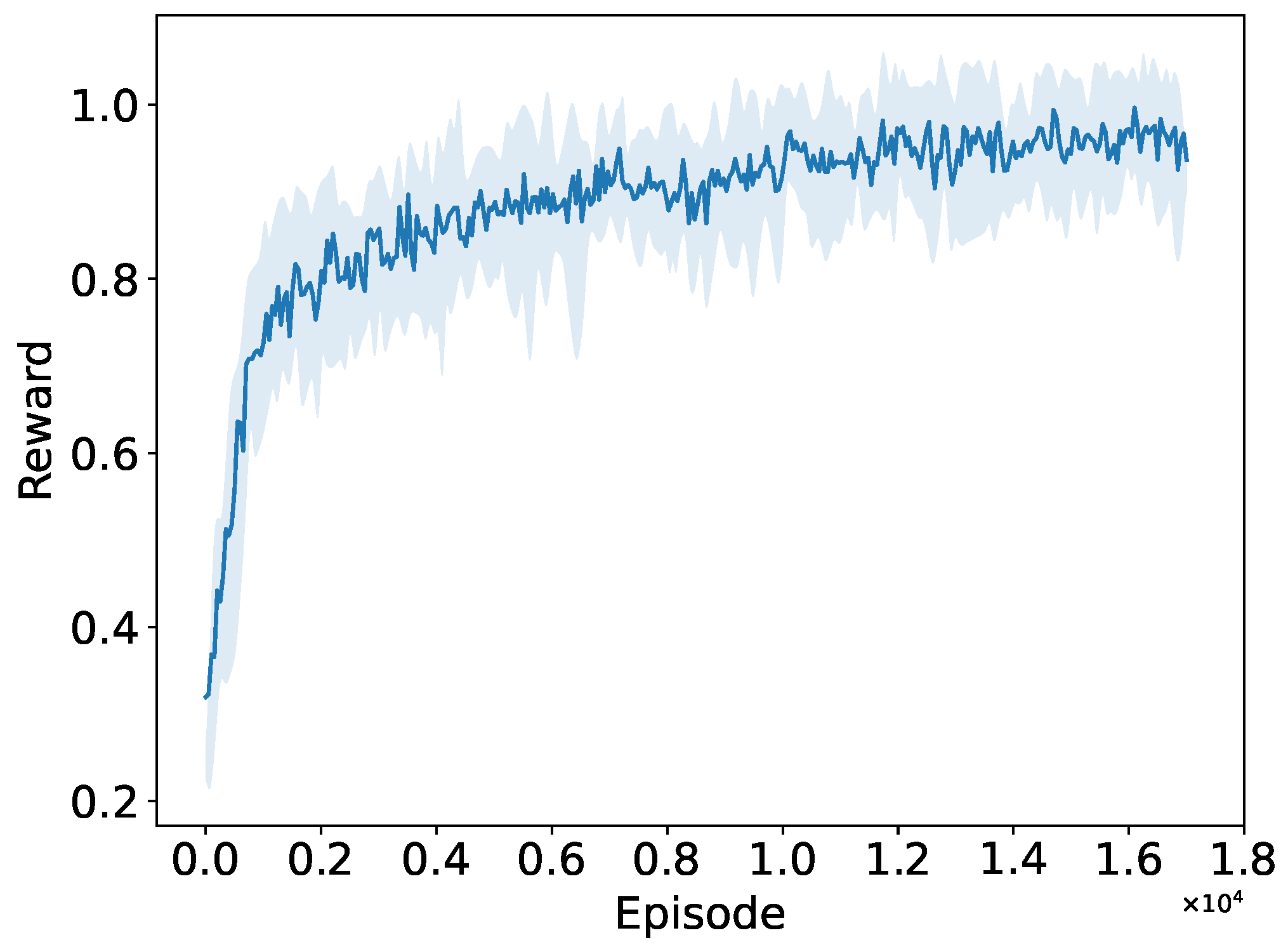
Figure 13.
Convergence performance of RAW group count .
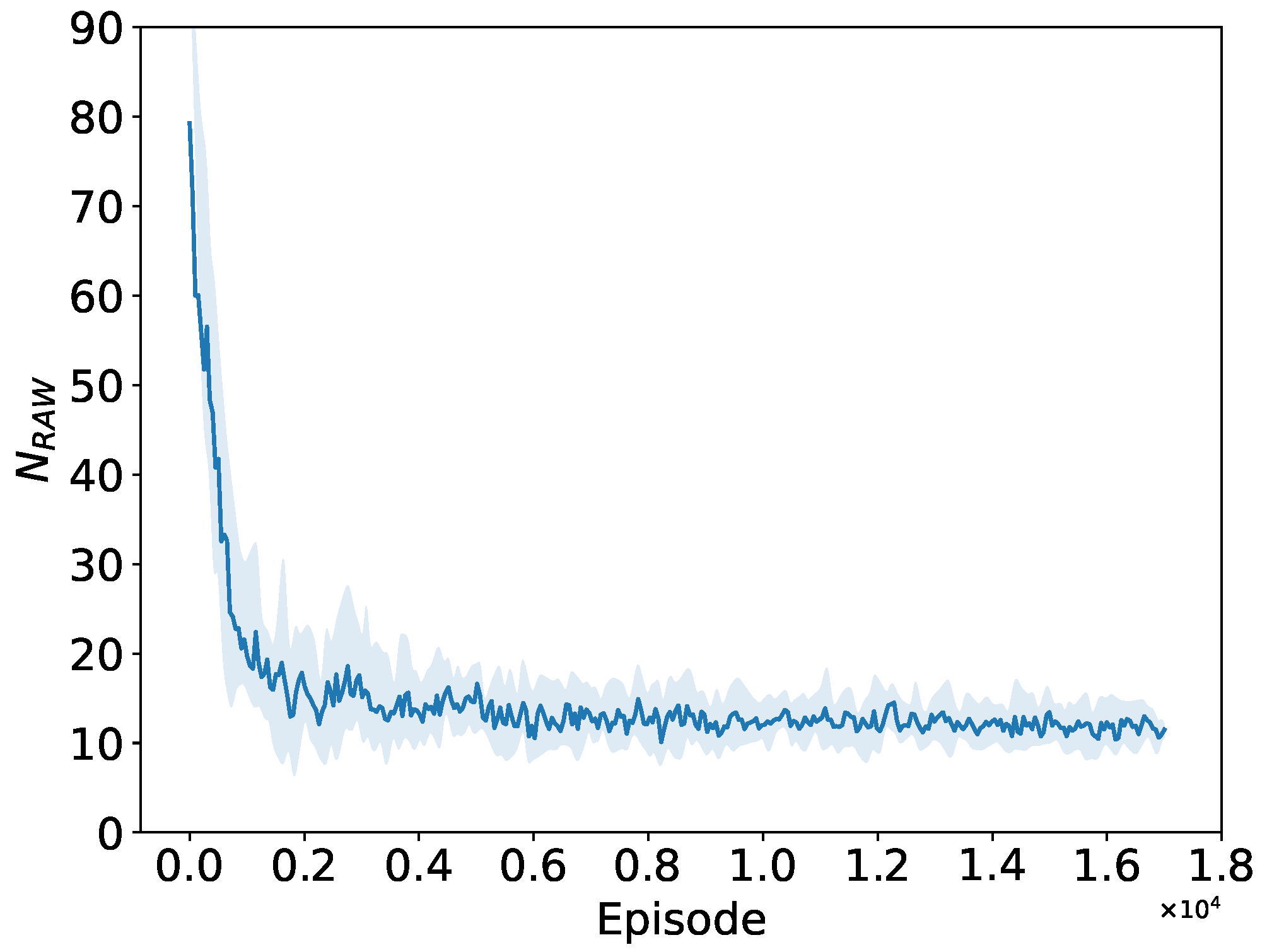
Figure 14.
Convergence performance of slot count .
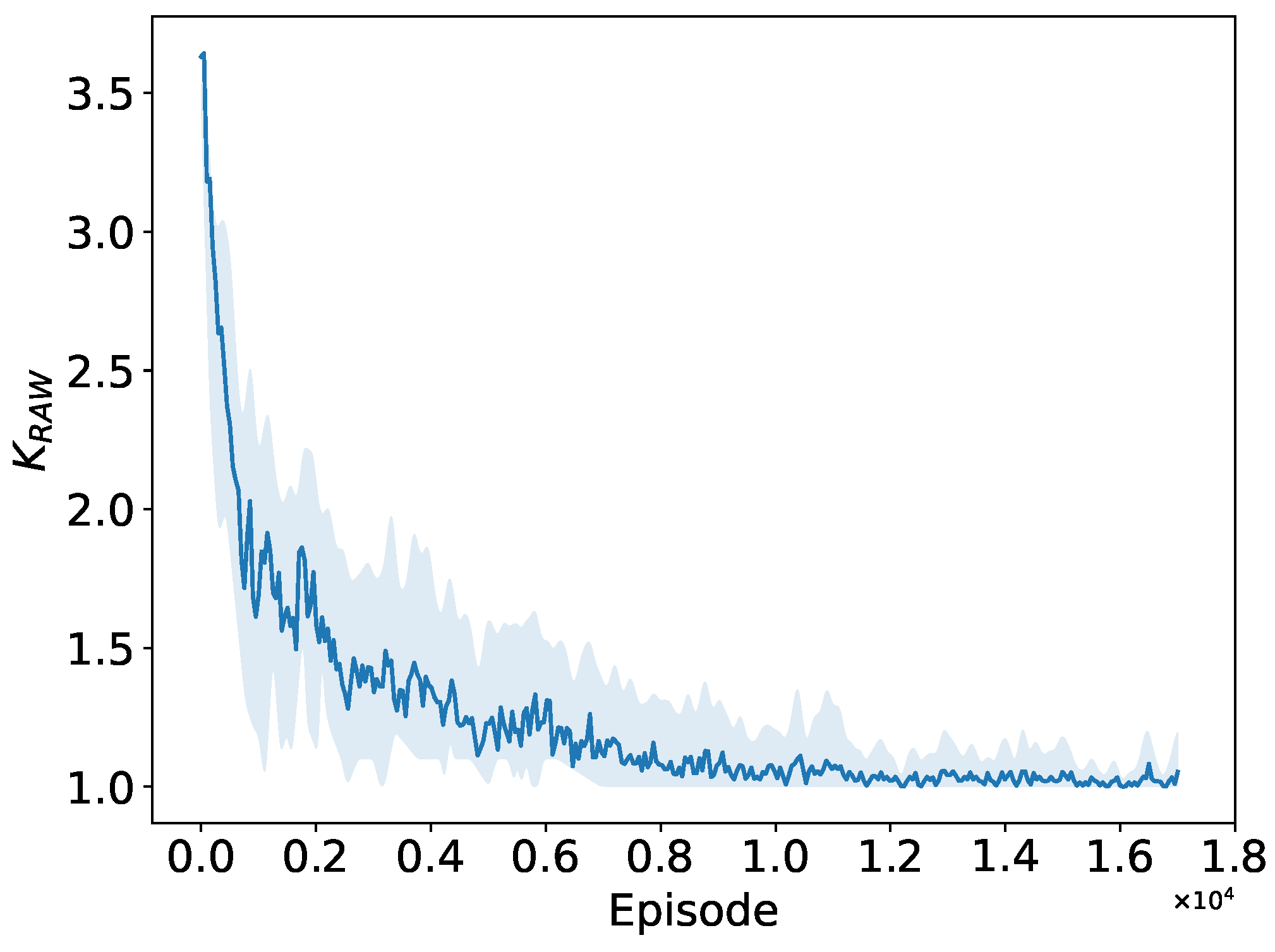
Figure 15.
Convergence performance of BI duration .
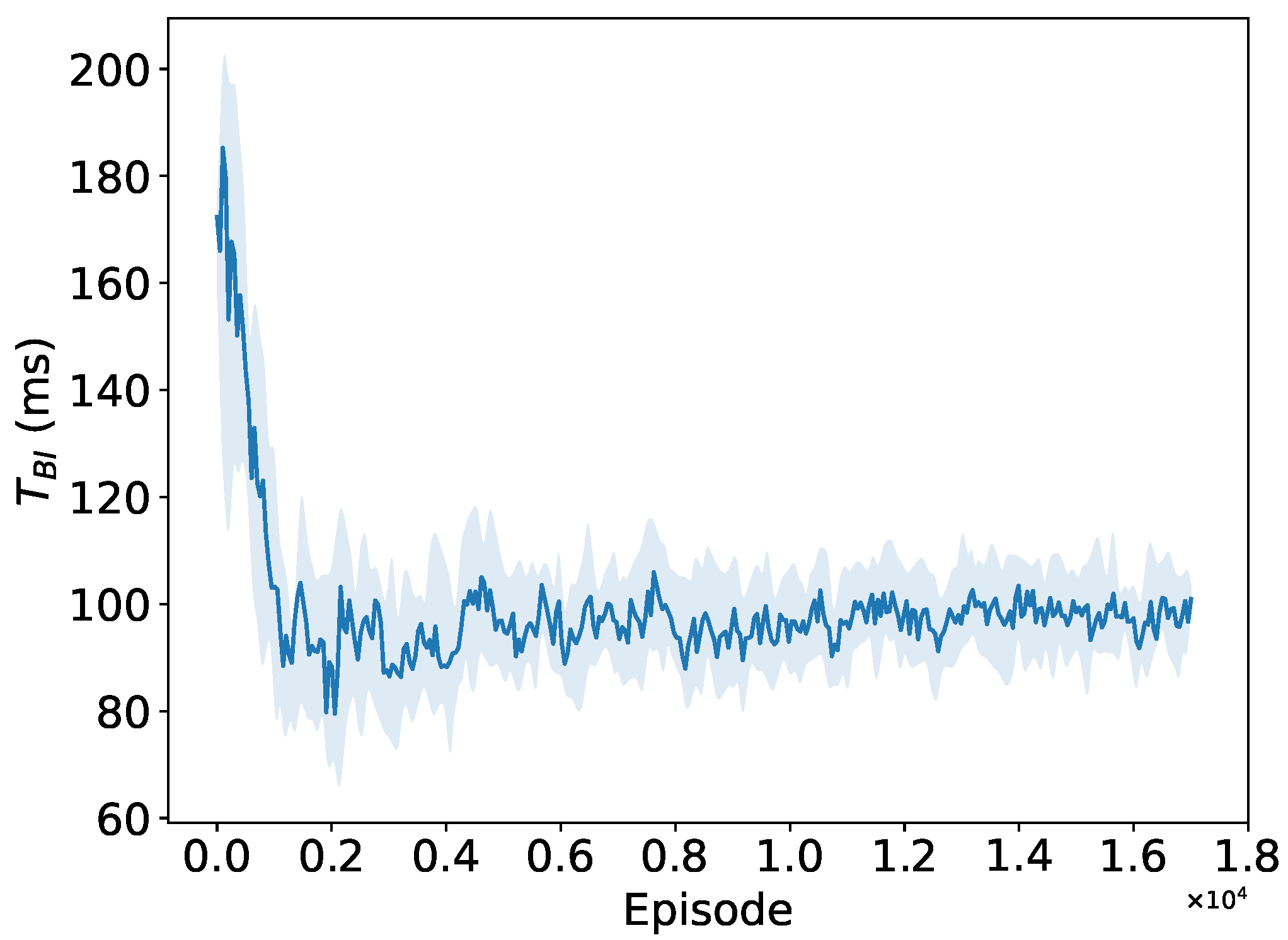
Figure 16.
Network throughput obtained by the DRL algorithm with varying network size.
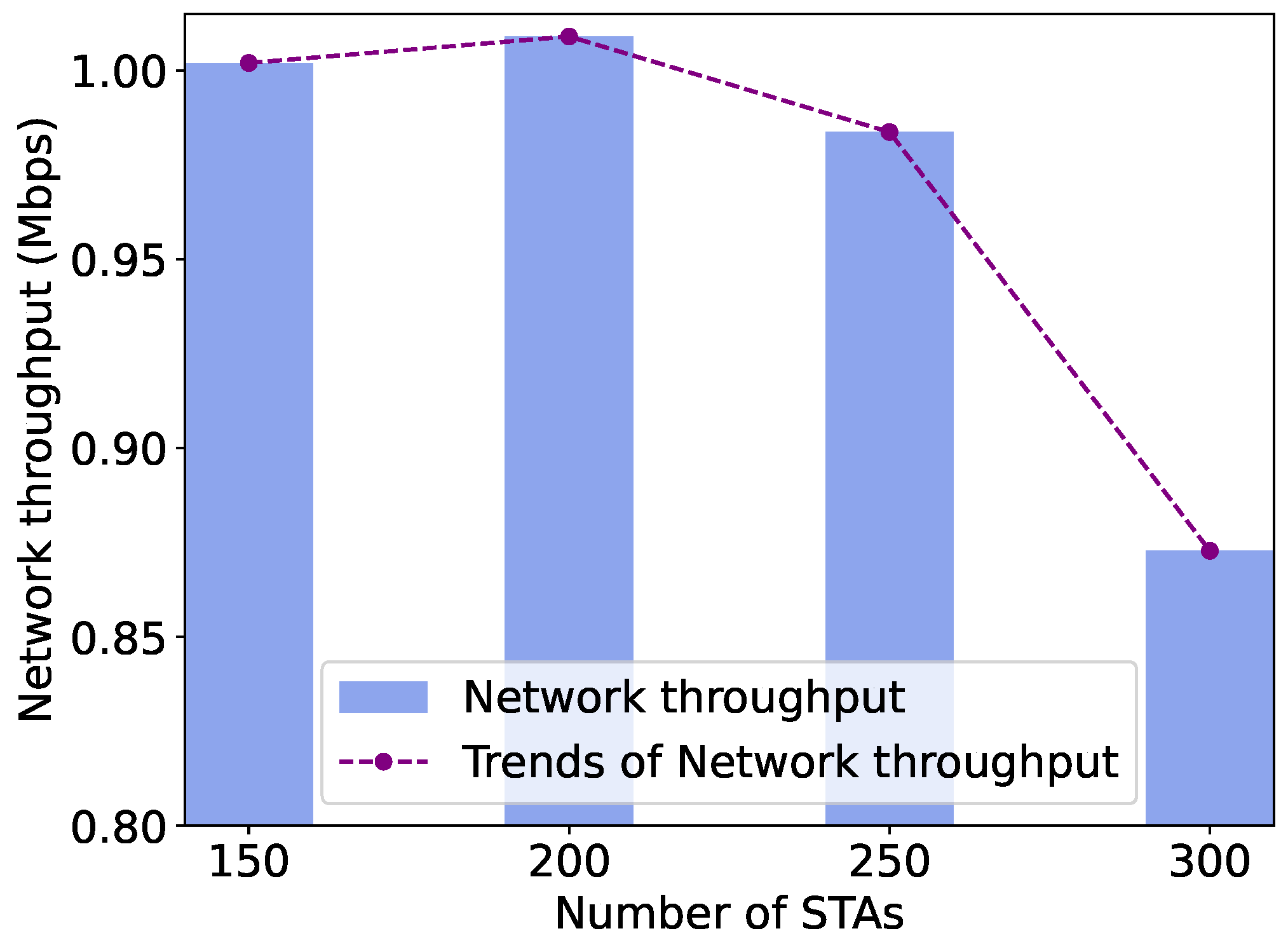
Figure 17.
Adaptive adjustment of RAW parameters with varying network size.
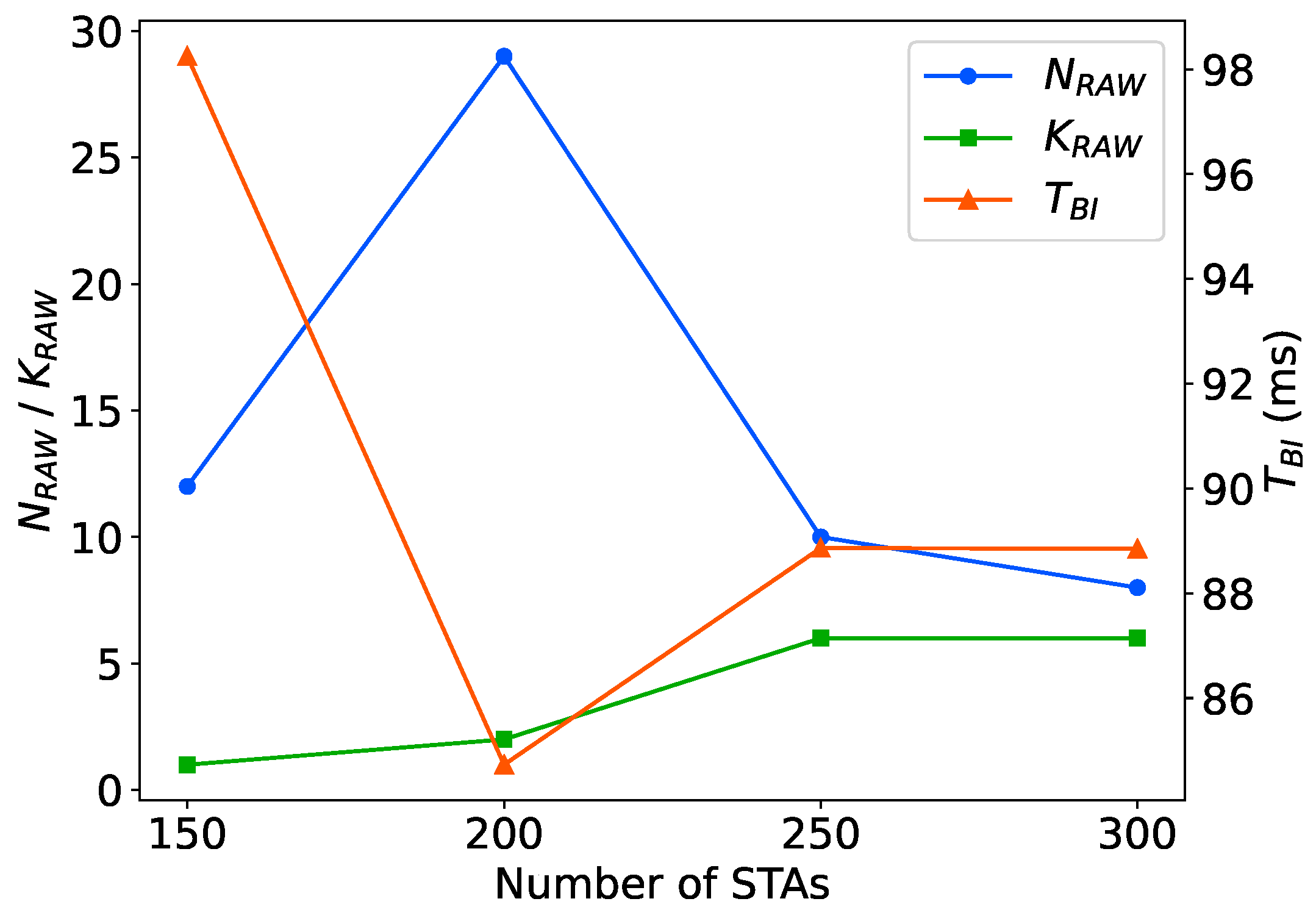
Figure 18.
Comparison of network throughput between the PPO-based slot division scheme and the baseline slot division schemes.
Figure 18.
Comparison of network throughput between the PPO-based slot division scheme and the baseline slot division schemes.
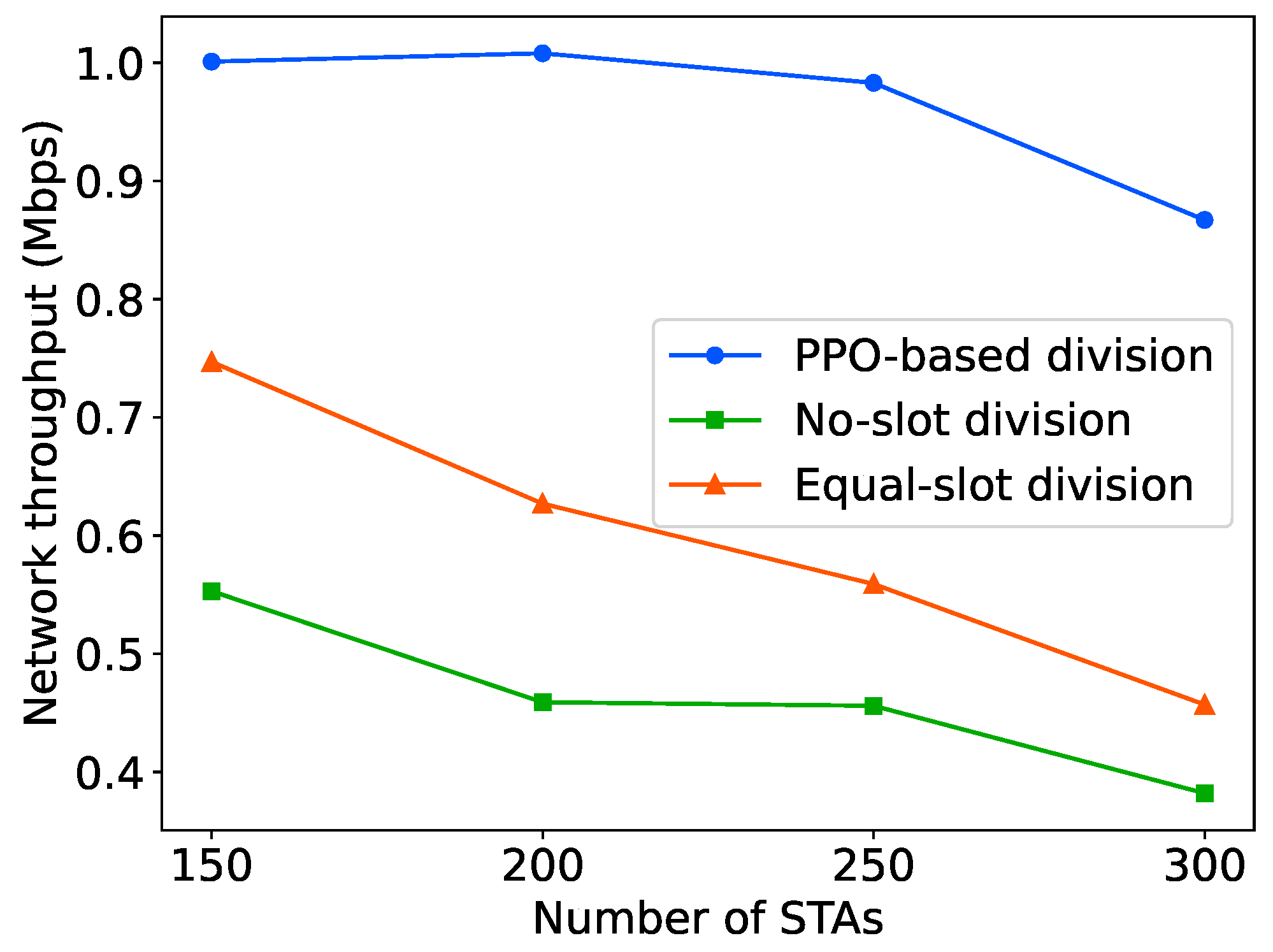
Table 1.
Parameter settings in periodic traffic networks.
| Parameters | Value |
|---|---|
| Wi-Fi channel configuration | MCS 0, 2 MHz |
| Data rate | 650 kbit/s |
| Traffic type | UDP |
| Payload size | 100 Bytes |
| Number of STAs | 60 (basic setting) |
| Number of RAW group | 1 (basic setting) |
| Coverage Radius | 300 m |
| Training episode | MAX = 10000 |
Table 2.
Parameter settings in random traffic networks.
| Parameters | Value |
|---|---|
| Wi-Fi channel configuration | MCS 0, 2 MHz |
| Data rate | 650 Kbit/s |
| Traffic type | UDP |
| Payload size | 100 Bytes |
| Number of Node | 150 (basic setting) |
| Coverage Radius | 300 m |
| Training episode | MAX = 20000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








