Preprint
Article
Enhancing Sustainable Construction: Optimization Tool for Glulam Roof Structures according to Eurocode 5
Altmetrics
Downloads
106
Views
35
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 March 2024
Posted:
01 April 2024
You are already at the latest version
Alerts
Abstract
The construction industry has a notable negative impact on the environment; thus, the promotion of the use of timber structures is an alternative to mitigate its effects. The research develops an artificial intelligence-based decision approach in the calculation of timber structures focused on the enhancement of the sustainability of roof structures. Based on the optimization carried out through genetic algorithms and the framework established in Eurocode 5, a general set of equations has been proposed for a laminated timber roof structure. The tool, which determines the most suitable roof structure for each strength class of laminated timber, allows for the determination of the dimensions of beams and purlins and their respective separations in order to minimize wood consumption. The ultimate goal is to offer multiple solutions regarding strength classes and structural designs in order to foster informed sustainable choices that promote efficient use of resources in construction.
Keywords:
Subject: Engineering - Architecture, Building and Construction
1. Introduction
Albeit its economic and social relevance, the construction sector in the European Union (EU) consumes a great amount of resources, with figures up to 50% of all extracted materials [1], and produces vast quantities of waste, accounting for 37.5% of the total [2]. Moreover, the built environment is responsible for 40% of the total energy consumption and 36% of all CO2 emissions in the EU [3].
Among some of the most commonly employed construction materials are concrete and steel. Understanding the properties and constraints of materials is essential to both the design and future construction and use; however, evaluating the environmental impact has become equally critical as climate change and sustainability concerns increase. Thus, the use of Life Cycle Assessment (LCA) databases allows for the assessment and comparison of construction materials’ environmental performance through the use of indicators such as embodied energy or CO2 emissions. For instance, the Ecoinvent database [4] indicates that steel has an embodied energy of 27.90 MJ/kg and emissions of 1.71 kg CO2/kg. Similarly, values of 0.618 MJ/kg and 0.112 kg CO2/kg are reported for concrete [4].
Nowadays, similar to other economic sectors, construction is veering towards practices within material selection, construction methods, operational efficiency, and end-of-life strategies that regard social and environmental wellbeing to further sustainability. In this regard, the European Green Deal [5] promotes the use of timber as a means to reduce the environmental pressure of the construction industry.
Although the use of timber is not new, approaches to alleviate some of the inherent limitations of wood (i.e., dimensions, strength, stability, fire resistance, etc.) through the development of wood-engineered products [6,7] and various technological advances [8,9] are propelling its current popularity. Moreover, another factor driving the increase in use is the comparatively better environmental profile with respect to other construction materials [10]. As a renewable resource, timber can be continually sourced from sustainably managed forests, which contributes to the maintenance and expansion of forested areas, thereby mitigating deforestation and promoting ecological quality [11]. Since it originates from a photosynthetic organism, uptake of carbon occurs during its growth due to biomass conversion with approximately 1.5 t CO2/m3 of wood [12]. Thus, sequestration or carbon storage could be considered in the manufacture of timber, provided that the harvested tree is used in long-life cycle products such as construction materials. Moreover, the use of timber in substitution of other more environmentally damaging materials constitutes an additional benefit in CO2 mitigation since the manufacturing emissions of the replaced construction material are avoided. After sawing, lumber is naturally or forced-dried to achieve dimensional stability and planed according to use or processing into other wood-engineered products. Undoubtedly, these operations pose a negative impact on the environment. Although precise figures vary for the different wood products, both carbon emissions and embodied energy are significantly lower in timber construction [10,13,14].
Among the wood-engineered materials, this research work focuses on glued laminated timber (also known as glulam). This construction material is composed of layers of sawn lumber bonded together, with the grain running parallel to the length of the structural element. This manufacturing allows for large spans and variable cross-sections, as well as high strength-to-weight ratios. Nevertheless, the different strength classes (e.g., from GL 20h to GL 32h for homogeneous glulam [15]) exhibit specific mechanical performances relating to the wood species. For instance, lower strength classes could be associated with softwoods (Thuja plicata, Picea sitchensis, Abies magnifica, Abies grandis, Abies concolor, Abies procera, Abies amabilis, etc.), whereas greater strength classes are connected to Pinus sylvestris, Larix decidua, Pseudotsuga menziesii, etc. [16].
In this regard, the scientific community has predominantly centered its attention on the study of a single strength class, and the interest has not been uniformly distributed among them. Conversely, it is worth mentioning the research by Baranski et al. [17], who addressed the optimization of different beam geometries as well as different qualities of glulam (i.e., GL 22h, GL 24h, GL 26h, GL 28h, GL 30h, and GL 32h).
From the literature analysis, GL 24h stands out as the most evaluated class, with a greater incidence on bending elements such as beams. In the context of structure optimization, two investigations could be highlighted. Firstly, Jelušiˇ and Kravanka [18] assessed the optimization design of timber floor joists for a given imposed load and span of the structure. Then, De Vito et al. [19], who developed a topology optimization of Douglas Fir GL 24h beams, considering the orthotropic nature of wood and the layering manufacture. Whereas Kilincarslan and Turker [20] considered the strengthening of the GL 24h spruce timber column-beam connection with carbon fiber-reinforced polymer through experimental evaluation. Wang et al. [21] evaluated the stiffness of GL 24h timber from Scotch pine beam-column joints with bolted connections and introduced a stiffness prediction method. Moreover, in the current state of transition to more sustainable materials, there are also some examples of the hybrid use of GL 24h with inert materials. Regarding the association with concrete, Fu et al. [22] studied the optimization of the bonding performance between prefabricated concrete and GL 24h timber from spruce. Similarly, Giv et al. [23] studied the effect of adhesive type on the bending behavior of the GL 24h timber-concrete composite panel. Ferrara et al. [24] conducted real-scale experiments on the mechanical performance of a GL 24h timber-concrete composite floor supported at two edges. Gomez-Ceballos et al. [25] presented a numerical method for the analysis of the mechanical behavior of GL 24 h Douglas beams reinforced with ultra-high-performance fiber-reinforced concrete. For the timber-steel conjunction, Ching et al. [26] developed a topology optimization framework for trusses made of GL 24h timber and steel that aims to reduce global warming potential.
Several authors have also assessed the GL 28h class, mostly in the context of reinforced elements such as tendons or steel bars. For instance, De Luca and Marano [27] tested the failure of pre-stressed GL 28h spruce timber reinforced with steel bars. Also for European spruce, McConnell et al. [28] tested Gl28h timber with steel tendons in post-tensioning conditions. In regards to optimization, Mam et al. [29] engaged on GL 28h bracing structures. For a timber-timber composite with glulam ribs and cross-laminated timber flanges, Suárez-Riestra et al. [30,31] tested the GL 28h from Picea abies and proposed an estimation model for the long-term behavior of the composite.
Amid the less studied strength classes, it should be mentioned the investigation carried out by Jelušič [32], who proposed an optimization approach to variable cross-section beams of GL 30h timber, as well as the research performed on GL 32h timber by Šilih et al. [33] for timber trusses and Simón-Portela [34] for an entire timber roof structure.
Despite the current clear focus on specific strength classes, the complete consideration of the strength class range within the material selection could benefit the optimization of the timber volume required for a specific structure, which is one of the objectives of this research work. In this regard, there is an extensive literature on reducing material consumption in the design of steel and concrete structures; some examples could be found in [35,36,37]. Albeit more limited, optimization approaches have also been made for timber construction such as beams [17,32,34] and trusses [18,33,38,39].
Additionally, the consideration of the use of the strength classes could also result in advantages from a sustainability standpoint since a greater variety of wood species would be considered for construction purposes. It should be noted that besides their performance and classification within a strength class, the available tree species for selection would also be motivated by their intrinsic characteristics (e.g., climatic adaptation, growing rate [34], etc.) as well as the final acquisition cost of the material. In this regard, research shows that tree species richness can enhance wood productivity while maximizing ecosystem functioning [40,41,42]. Notwithstanding, to adequately supply the increasing demand for wood as a construction material, the source material must originate from responsibly managed forests.
Therefore, the present investigation assesses the influence of glulam strength classes in timber construction. Specifically, on the design of a timber roof structure consisting of timber double-tapered beams and purlins, according to Eurocode 5 [43] requirements. To that end, an optimization tool based on genetic algorithms has been developed, and based on the results, several equations have been proposed to determine the optimal geometry (width and height) of the structural elements (beams and purlins) as well as their spatial configuration given the roof length, span, snow load, and strength class. Similarly, a general equation has been found to predict the optimum volume required for the roof structure considering the different strength classes, which would promote efficient use of resources and economic advantages while complying with structural and safety requirements.
2. Materials and Methods
2.1. Design Parameters: Material, Dimensions and Loads
A roof structure comprised of timber double tapered beams and purlins has been examined in this research work. For the assessment, six homogeneous glued laminated (glulam) timber strength classes, as defined in EN 14080 [15], have been considered: GL 20h, GL 22h, GL 24h, GL 26h, GL 28h, GL 30h and GL 32h (Table 1). This broad selection of strength classes would allow for consideration beyond the traditionally used wood species and, thus, the promotion of previously unexploited or underutilized species in timber construction.
The optimization was carried out for different timber roof dimensions. The roof length was studied at 30 m, 45 m, 60 m and 75 m; the assessed span varied from 15 m to 30 m in 1.25 m increments; and inclination angles between 5º and 10º were examined for the tapered beam. The geometry of the structural elements was also considered a variable within the experimental program. The heights of beams (Hb) and purlins (Hp) ranged from 120 to 1200 mm, with 40 mm intervals reflecting the laminate thickness. Similarly, the widths for beams (Wb) and purlins (Wp) spanned from 90 to 220 mm, adjusted in 10 mm increments. Finally, regarding the arrangement of the structural elements within the roof structure, the spacing between beams and purlins was also studied as a variable. Beam spacing (Sb) was considered within a range of 3 m to 7 m, while purlin spacing (Sp) varied from 0.625 to 1.25 meters, which was the maximum allowed separation.
Similarly, specific limits were established regarding the range of potential load conditions that the roof structure is designed to withstand. All contemplated loads were combined as established in Eurocode 1 [43] to assess the worst-case scenario in the structural integrity verification. As the roof elements fall within service class 1, a 1.25 safety factor was considered for the glulam material combined with a modification factor (kmod) of 0.9. For permanent surface loads, in addition to the self-weight of the beams and purlins that was automatically calculated during the optimization process, a dead load of 0.45 kN/m2 was also included. For variable loads, snow loads ranging from 0.4 to 3 kN/m2 were considered to accommodate typical values in different locations across the European Union [44]. It should be noted that in accordance with the Spanish Technical Building Code (also known as CTE) [45], the combination of snow and wind loads with the maintenance load is avoided due to the assumption that during extreme conditions no one would be present on the roof, thus resulting in an overestimation of the total load on the structure. Conversely, snow load values below 0.4 kN/m2 were excluded to ensure that in scenarios with negligible snow loads, the maintenance load is applied. Regarding the wind load, it was considered for a gable roof without openings in a building with a height of 5 to 7 m [46] and, since it has been proven not to affect the optimization results [34], a fixed value of 0.07 kN/m2 was employed.
2.2. Optimization
The optimization goal is to identify the most effective design for a roof structure, taking into account six different glulam strength classes that reduce timber material consumption and comply with the requirements of strength, stability, and stiffness set out in Eurocode 5 [43]. As so, initially, this method aims to balance structural performance (i.e., function and safety) with material conservation. However, it is worth mentioning that the interpretation of the outcomes across the different strength classes should also be regarded as a sustainability equalization as proponent of different strength classes represented by less exploited wood materials, which alleviates the demand of certain species promoting biodiversity.
Genetic algorithms grounded in biological evolution principles were employed to execute the optimization process. To represent different potential designs for the roof structure, an initial population of 1200 random individuals was generated. The possible dimensions (i.e., Hb, Hp, Wb, Wp, and angle) and arrangements (i.e., Sb, Sp) of beams and purlins were considered through specific values in their chromosomes. The evaluation of each design depended on the utilization rates determined within the structural calculation program developed in Matlab to verify the Eurocode 5 [43] criteria, that has been previously collected in [34] and entails:
-
Ultimate Limit States (ULS) tests
- Beam verification for shear strength (Iv ≤ 1)
- Beam verification for bending strength (Im ≤ 1)
- Beam verification in the apex zone (It,90 ≤ 1)
- Purlin verification for combined bending and shear strength.
-
Serviceability Limit States (SLS) tests
- A limit value of l/400 for the instantaneous deflection (winst)
- A limit value of l/300 for the final deflection (wfin)
- A limit value of l/225 for the net final deflection (wnetfin)
Then, the modified objective function (F(x) in Equation 1) measures the fitness of individuals in terms of volume, in m3, and applies a penalty to those that do not meet the structural safety criteria and according to the aforementioned utilization rates.
where x denotes an individual within the study population, f(x) is the objective function in terms of volume (m3), j is the number of variables under examination, Pj is the penalization term conforming to the restrictions imposed on each structural element, and Gj is the penalty parameter, with the same order of magnitude as the objective function, based on the maximum utilization ratio observed in each structural component, with j assuming values from 1 to 4:
-
G1(x) is the highest ultimate limit state utilization ratio of the beam:0 > G1(x) > 1 then, P1(G1(x)) = 3 × 10(1-G1(x));G1(x) = 1 then P1(G1(x)) = 0;G1(x) = 0 then P1(G1(x)) = 40;G1(x) > 1 then P1(G1(x)) = G1(x) × 400.
-
G2(x) is the highest serviceability limit state utilization ratio of the beam:0 > G2(x) < 1 then P2(G2(x)) = 1,8 × 10(1-G2(x));G2(x) = 1 then P2(G2(x)) = 0;G2(x) = 0 then P2(G2(x)) = 24;G2(x) > 1 then P2(G2(x)) = 60 × G2(x).
-
G3(x) is the highest ultimate limit state utilization ratio of the purlin:0 >G3(x) > 1 then P3(G3(x)) = 1.725 × 10(1-G3(x));G3(x) = 1 then P3(G3(x)) = 0;G3(x) = 0 then P3(G3(x)) = 23;G3(x) > 1 then P3(G3(x)) = G3(x) × 11.5.
-
G4(x) is the highest serviceability limit state utilization ratio of the purlin:0 >G4(x) > 1 then P4(G4(x)) = 172.5 × 10(1-G4(x));G4(x) = 1 then P4(G4(x)) = 0;G4(x) = 0 then P4(G4(x)) = 23;G4(x) > 1 then P4(G4(x)) = G4(x) × 11.5.
Then, the individuals with the lowest values are roulette-selected to be subjected to crossover (i.e., the combination of their characteristics), elitism (i.e., the retention of the fittest individuals) and mutation (i.e., the introduction of variability) operations in order to generate new individuals that replace the initial population. Respectively, values of 10%, 80% and 1% were employed for these operators. The cycle is repeated until convergence is reached, or up to a maximum set value of 50 generations. Nonetheless, convergence was always reached after 15 to 20 generations.
2.3. Statistical Analysis
A total of 1792 optimal individuals were generated based on combinations of specified values for span, depth, snow load, and strength class. A comprehensive statistical analysis was performed on the attributes of these configurations to assess, for each glulam strength class, the optimal geometry (width and height) of the structural elements (beams and purlins) comprising the roof structure as well as their spatial configuration. Additionally, the relationships among the different considered variables (i.e., snow load, span, depth, beam height and width, purlin height and width, beam spacing, and purlin spacing) as a function of the glulam strength class were examined through multiple linear regression analysis. The analysis also focused on the comparison of the optimum timber volume across different strength classes, offering a basis for making informed decisions based on both the material consumption (i.e., type and amount) and the cost-effectiveness. Therefore, several equations have been formulated to enable reliable predictions regarding the optimal volume and geometry parameters since all proposed relationships demonstrated a correlation greater than 0.95. Similarly, the normality and homoscedasticity of the residuals have been verified, confirming the validity of all predictive equations.
3. Results and Discussion
3.1. Optimal Geometry of Structural Elements and Their Spatial Configuration
3.1.1. Inclination Angle of the Double Tapered Beam
Consistently, the optimal inclination angle was 5º, the minimum for the studied range, regardless of span, snow load, and strength class. Nonetheless, it was initially hypothesized that the optimal angle might exceed the 5º considered minimum. It was assumed that an increased angle and the resulting increase in the central cross-section of the tapered beam could reduce the dimensions of the initial cross-section of the beam or allow for wider beam spacing, leading to a decrease in overall timber volume. However, a direct comparison with the findings reported by Simón-Portela [34] at a 10º inclination reveals that the reduction achieved due to the increased spacing between beams (i.e., halving the number of beams) does not compensate for the added volume due to the steeper angle. In fact, for identical loading conditions and roof dimensions, the volume at a 10º inclination is 30% greater than that at a 5º inclination. Minimal angle inclinations (< 5º) were also reported in the optimizations carried out by Baranski et al. [17] and Jelušič [32].
3.1.2. Width, Height and Spacing of Beams
The optimal beam width (Wb), in meters, could be determined using Equation 2:
where Span is expressed in meters and the Snow load is expressed in kN/m2. Coefficients A, B, and C are detailed in Table 2 categorized according to the strength class and snow load.
It is worth noting that the outcomes from Equation 2 must be rounded to the nearest tenth to further be employed in the height beam determination (Eq. 3). Thus, the resulting width of the beams has to be rounded to the closest value in 10 mm increments, with a minimum value set at 90 mm.
Although a direct comparison to other optimization research works [17,32] is not possible due to different optimization thresholds as well as material and load conditions, some commentary could be made regarding the observed patterns within the optimization results. For instance, Jelušič [32] reported that the maximum beam height-to-width ratio always ranged between 7 and 8. Conversely, for comparable strength (GL 30h) and separation, the optimization proposed in this research resulted in ratios ranging from 13.4 to 24.3, which justifies the lower beam widths arising from this investigation. Contrarily, Baranski et al. [17] limited the optimization to a maximum beam height to width ratio of 10 , whereas in the present research work, such a ratio is not restricted in order to study the complete 90 to 200 mm range with the sole limitations imposed by the structural standards. It is also worth mentioning that Baranski et al. [17] found the same width dimensions of beams to be valid for the complete strength range.
The optimal beam height (Hb), in meters, could be determined using Equation 3:
where Span and Beam width (Wb) are expressed in meters and the Snow load is expressed in kN/m2. Coefficients A, B, C, D, and E are detailed in Table 3 categorized according to the strength class and snow load.
In this case, the height of the beam must be rounded to the nearest multiple of 40, reflecting the laminate thickness, up to a maximum value of 1200 mm.
No proportional relationship was observed between the strength class and the beam height-to-span ratio since the model adjusts the height of the beam based on all geometric variables. For GL 30h, this lack of proportionality could also be observed in Jelušič [32]. In the investigation carried out by Baranski et al. [17], who studied the roof structure for a load of 0.9 kN/m2, a threshold of span/20 to span/40 was employed in the optimization. The aforementioned range is close to that resulting from this investigation, with values of beam height oscillating between span/20 and span/32.
The optimal values for the number of beams (Nb) and their spacing (Sb), in meters, could be determined using Equations 4 and 5, respectively:
where Roof length is expressed in meters and the Snow load is expressed in kN/m2. Coefficients A, B, C, and D are detailed in Table 4 categorized according to the strength class and snow load. It should be noted that the optimal number of beams must be rounded to the next integer.
In other optimization research works [17,32], the separation between beams is not subjected to optimization but has a fixed value of 4 m. Nonetheless, the results arising from this optimization point to 4 to 6 m separation for the lower snow load values and between 3 and 3.5 m for greater snow load values, both regardless of the considered strength class.
3.1.3. Width, Height and Spacing of Purlins
It was found that the width of the purlin remains unaffected by the span and snow load, as in [34], but also by the strength classes. Therefore, it could be consistently set at the optimal minimum of 90 mm. In contrast, the snow load and strength class impact the optimal height value of the purlins. Thus, for the GL 32h class, the ideal height falls between 120 and 160 mm. Whereas, for the remaining classes, the optimal height lies between 160 and 200 mm, as indicated in Table 5. As for the spacing between purlins, the optimal distance is consistently the maximum allowable, set at 1.25 m.
Example 1.
Case study of a roof structure located in an area subjected to a snow load of 1 kN/m2 with a span of 20 m and a depth of 50 m consisting of tapered-beams and purlins of glued laminated timber pertaining to GL 24h strength class.
| (from Eq. 2) | |
| (from Eq. 3) | |
| (from Eq. 4) | |
| (from Eq. 5) |
Hence, through the application of the proposed equations (Eq. 1-3), the optimal solution involves the use of 14 beams with a 5º inclination angle and cross-sectional dimensions of 90 x 840 mm spaced at intervals of 3.85 m. Whereas the optimal dimensions for purlins are 90 mm width and 160 mm height at a separation of 1.25 m. □
3.2. Optimun Timber Volume as a Function of Glulam Strength Class
Determining the optimal volume required for the construction of a timber roof structure offers relevant information regarding material usage and cost estimations. Nonetheless, it could also be used as a comparison parameter between timber materials pertaining to different strength classes since it facilitates an assessment of which strength class provides the best value in terms of material volume or cost while complying with the structural and safety requirements.
Thus, for a roof structure consisting of double tapered beams and purlins, the optimal timber volume (V), in m3, could be determined using Equation 6:
where Roof length and Span are expressed in meters and the Snow load is expressed in kN/m2. Coefficients A, B, C, D, and E are detailed in Table 6 categorized according to the strength class, snow load and span.
To provide a comprehensive analysis of the differences in timber volume across the examined strength classes, Figure 1 showcases the percentage of variation between each strength class relative to the reference class GL 32h. This comparison is calculated based on the impact of snow load and the span on the roof structure. The overview intentionally omits the factor of roof depth, as it has been determined to have negligible impact on the percentage difference between any given class and the benchmark GL 32h class.
Therefore, from a close examination of Figure 1 and in direct comparison with the reference class GL 32h, the following insights emerge:
- The selection of the GL 20h strength class roughly requires 17-20% additional volume for snow loads ranging from 0.4 to 1.0 kN/m2. For higher snow loads of 1.0 to 2 kN/m2 and 2 to 3 kN/m2, the increase in timber volume needed is about 12-15% and 10-12%, respectively.
- For the GL 22h class, an increase in timber volume of approximately 11-13% is needed for snow loads ranging from 0.4 to 0.7 kN/m2. The requirement decreases to 8-11% for loads between 0.7 to 1.8 kN/m2, 6-8% for 1.8 to 3 kN/m2 with spans of 15 to 18 m, and 3-6% for the same snow load with spans of 18 to 30 m.
- The GL 24h class demands an additional 6-8% timber volume for snow loads from 0.4 to 0.8 kN/m2, 4-6% for 0.8 to 1.8 kN/m2 with spans of 15 m to 20 m, 5-7% for 0.8 to 1.6 kN/m2 with spans of 20 to 30 m, 3-5% for 1.8 to 3.0 kN/m2 with spans of 15 to 18 m, and a minimal increase up to 3% for 1.4 to 3.0 kN/m2 with spans of 18 to 30 m.
- The GL 26h class roughly requires 6-8% additional timber volume for snow loads between 0.4 to 0.8 kN/m2, 4-6% for 0.8 to 1.2 kN/m2, 2-4% for 1.2 to 2.0 kN/m2, and a slight increase up to a 2% for snow loads of 2.0 to 3.0 kN/m2.
- For the GL 28h class, a 5-7% timber volume increase is necessary for snow loads of 0.4 to 0.8 kN/m² across spans of 15 to 27 m. A lower volume increase of 3-5% occurs for three scenarios: snow loads of 0.8 to 2 kN/m2 and spans of 15 to 25 m, 0.4 to 1.3 kN/m2 and spans of 27 to 30 m as well as for snow loads between 2.6 to 3.0 kN/m2. Moreover, it should be noted a -1% timber volume variation for snow loads of 2.0 to 2.6 kN/m2 and spans of 15 to 25 m, as well as for snow loads between 1.3 and 2.0 kN/m2 with spans of 25-30 m. The difference reaches a -2% value for snow loads of 1.3 to 2.6 kN/m2 and spans of 25 to 30 m.
- The selection of the GL 30h class requires a 4-6% increase in volume for snow loads of 0.4 to 0.6 kN/m2 and spans of 15 to 20 m, with a marginal 0-2% increase for similar snow loads across spans of 20 to 30 m as well as for snow loads of 1.0 to 2.0 kN/m2 for spans of 15 to 20 m. Whereas, for the remaining loads and spans, a decrease of up to 2% in timber volume could be achieved.
In order to analyze the aforementioned cost approach, a Spanish construction cost database [47] was employed to assess the cost of glulam timber pertaining to different strength classes. For instance, the price for 1 m3 of GL 24h timber was 1080 €, whereas 1 m3 of GL 32h timber reached 1140 €. Since GL 24 h resulted in a 5.26% lower cost, it could be inferred that for snow loads in the range of 2 to 3 kN/m2, using the GL 24h material would be desired, while for snow loads ranging from 0.4 to 2 kN/m2, the preferred decision lies in the GL 32h class. In this regard, there are numerous cases where, for snow loads greater than 2 kN/m2, cost considerations would be the sole driver in the decision due to the same timber usage for both GL 30h and GL 32h classes. Although in a smaller capacity, there are also instances following this pattern for GL 26h and GL 28h classes. Moreover, this approach should go beyond strength class and contemplate the difference in cost of different species with the suitable strength properties required for the studied strength class. Through the consideration of wood species, both within the same or a different strength class, the role of the different tree species in the ecosystem is regarded. Then, the sustainability of such derived decisions includes both material reduction and the promotion of less commonly used materials, which further biodiversity and future resilience against climate change.
Example 2.
Two worked examples initially proposed by Argüelles Álvarez and Arriaga Martitegui [48] are compared with the corresponding optimal timber volume derived from Equation 6. Specifically, example 8.1 consisting of GL 28h double tapered beams and a modification of example 6.1 focusing on purlins were employed. It should be noted that example 6.1 was modified to account for the same material and load conditions as in example 8.1. The final result for a roof structure of 20 x 45 m exposed to a snow load of 0.47 kN/m2 resulted in a GL 28h timber consumption of 39.75 m3.
Table 7 shows the calculated optimal timber volumes (Eq. 6) required for the aforementioned roof structure, while also including the volume incurred for the remaining strength classes. Moreover, the variation in the timber requirements across all strength classes is compared to the reference 39.75 m3, providing a comprehensive overview of material efficiency.
From the direct comparison for the same timber material (GL 28 h), the optimization leads to a significant reduction of 26.64% in the material volume required for the roof structure. Considering material costs [47], the reference roof incurs an expense of 43,315 €, whereas the optimized structure costs 33,243 €, representing a 10,000 € saving. Hence, the optimization results in more efficient resource use and lower construction costs without compromising structural integrity.
Similarly, the selection of timber pertaining to a different strength class also results in savings while allowing for diversification in the wood species selected or adaptation to locally available materials. Thus, such a strategy could seek economic and material efficiency but also include sustainability considerations in the decision-making process. □
Finally, to provide a simplified approach to the comparison between classes, Table 8 shows the percentage reduction between the modulus of elasticity -parallel to the grain- (Table 1) of a specific strength class and that of the GL 32h reference (RMOD) as well as the percentage reduction between the required timber volume of a specific class compared to the GL 32h reference (RVOL). As proved by the statistical analysis, the snow load range significantly explains the variability of the correlation between RVOL and RMOD (Eq. 7), with a slope approximately 1.53 times steeper for the 0.4 to 1.5 kN/m2 snow range.
4. Conclusions
This research work focused on the optimization of roof structures comprised of glulam beams and purlins of different strength classes and exposed to varying snow loads. The developed genetic algorithm tool, along with the structural calculation program, was employed to generate 1792 optimal roof structures with dimensions (i.e., roof length and span) and load conditions (i.e., snow loads below 3 kN/m2) typical of European construction. From a systematic statistical analysis, several predictive equations were proposed as a reliable method for optimizing timber roof design in accordance with Eurocode 5 [43]. Firstly, the predictive model could be used to optimize the beam width and height as well as their spatial arrangement as a function of the roof dimensions, loads, and the desired strength class. Additionally, the developed model also enabled the determination of the overall optimal timber volume required for a roof structure as a function of the strength class. Although this approach seeks the material usage reduction and economic savings, ultimately could assist in the promotion of the use of alternative wood species.
Among the findings, it was found that double tapered beams exhibited their optimal inclination angle at 5º, leading to a 30% reduction in the total timber volume used for the roof structure compared to an inclination of 10º. The optimal spacing between purlins coincided with the maximum set value, i.e., that allowed by the roofing material. This suggests an interest in considering non-traditional roofing materials as a future optimization strategy.
For structures exposed to snow loads greater than 2.5 kN/m2, a similar timber volume requirement, with at most a 3% difference, was noticed for most strength classes (GL 24h, GL 26h, GL 28h, GL 30h, and GL 32h). Thus, suggesting the existence of a broad range of wood species that effectively could rival the most commonly employed (GL 24h and GL 32h). Similarly, for snow loads greater than 1 kN/m2, GL 30h and GL 32h classes also resulted in similar consumption of timber volumes (up to a 1%). Across all strength classes, the largest differences in volume occur at span values close to 15 m and for the lower snow loads, with differences up to 20% for GL 20h compared to GL 32h. In any case, a strong relationship exists between the increase in the timber volume and the reduction in the strength class or the modulus of elasticity.
Author Contributions
Conceptualization, methodology, software, validation, investigation, data curation, writing— original draft preparation, review and editing, visualization, M.S.-P., J.R.V.-G., P.V.-L and D.R.-R.; supervision, funding acquisition, J.R.V.-G., P.V.-L and D.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Junta de Extremadura and by the European Regional Development Fund of the European Union through grants GR21163 and GR21091.
Acknowledgments
Administrative and technical support from the Forest Research Group and the Mechanical and Fluid Engineering Research Group of the University of Extremadura is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- European Commission Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. A New Circular Economy Action Plan For a Cleaner and More Competitive Europe. COM(2020) 98 Final; 2020;
- Eurostat Waste Statistics Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Waste_statistics (accessed on 6 March 2024).
- European Commission Directive (EU) 2023/1791 of the European Parliament and of the Council of 13 September 2023 on Energy Efficiency and Amending Regulation (EU) 2023/955 (Recast) (Text with EEA Relevance); 2023; Vol. 231;.
- Ecoinvent LCA Database Available online: https://ecoinvent.org/database/ (accessed on 6 March 2024).
- European Commission European Parliament Resolution of 15 January 2020 on the European Green Deal (2019/2956(RSP)); 2020;
- Ayanleye, S.; Udele, K.; Nasir, V.; Zhang, X.; Militz, H. Durability and Protection of Mass Timber Structures: A Review. Journal of Building Engineering 2022, 46, 103731. [CrossRef]
- Huang, Y.; Hu, J.; Peng, H.; Chen, J.; Wang, Y.; Zhu, R.; Yu, W.; Zhang, Y. A New Type of Engineered Wood Product: Cross-Laminated-Thick Veneers. Case Studies in Construction Materials 2024, 20, e02753. [CrossRef]
- Sandberg, D.; Kutnar, A.; Mantanis, G. Wood Modification Technologies - a Review. iForest - Biogeosciences and Forestry 2017, 10, 895. [CrossRef]
- Cabral, J.P.; Kafle, B.; Subhani, M.; Reiner, J.; Ashraf, M. Densification of Timber: A Review on the Process, Material Properties, and Application. Journal of Wood Science 2022, 68, 20. [CrossRef]
- Puettmann, M.; Pierobon, F.; Ganguly, I.; Gu, H.; Chen, C.; Liang, S.; Jones, S.; Maples, I.; Wishnie, M. Comparative LCAs of Conventional and Mass Timber Buildings in Regions with Potential for Mass Timber Penetration. Sustainability 2021, 13, 13987. [CrossRef]
- Condé, T.M.; Tonini, H.; Higuchi, N.; Higuchi, F.G.; Lima, A.J.N.; Barbosa, R.I.; dos Santos Pereira, T.; Haas, M.A. Effects of Sustainable Forest Management on Tree Diversity, Timber Volumes, and Carbon Stocks in an Ecotone Forest in the Northern Brazilian Amazon. Land Use Policy 2022, 119, 106145. [CrossRef]
- Arriaga, F.; Wang, X.; Íñiguez-González, G.; Llana, D.F.; Esteban, M.; Niemz, P. Mechanical Properties of Wood: A Review. Forests 2023, 14, 1202. [CrossRef]
- Martínez-Alonso, C.; Berdasco, L. Carbon Footprint of Sawn Timber Products of Castanea Sativa Mill. in the North of Spain. Journal of Cleaner Production 2015, 102, 127–135. [CrossRef]
- Cabral, M.R.; Blanchet, P. A State of the Art of the Overall Energy Efficiency of Wood Buildings—An Overview and Future Possibilities. Materials 2021, 14, 1848. [CrossRef]
- EN 14080 Timber Structures - Glued Laminated Timber and Glued Solid Timber - Requirements; CEN: Belgium, Brussels, 2013;
- Porteous, J.; Kermani, A. Structural Timber Design to Eurocode 5; John Wiley & Sons, 2013;
- Baranski, J.; Szolomicki, J.; Damian, K. Shape Optimization of Glulam Timber Roof Girders. In Proceedings of the World Congress on Engineering and Computer Science; 2018; Vol. 2.
- Jelušič, P.; Kravanja, S. Optimal Design and Competitive Spans of Timber Floor Joists Based on Multi-Parametric MINLP Optimization. Materials 2022, 15, 3217. [CrossRef]
- De Vito, A.F.; Vicente, W.M.; Xie, Y.M. Topology Optimization Applied to the Core of Structural Engineered Wood Product. Structures 2023, 48, 1567–1575. [CrossRef]
- Kilincarslan, S.; Simsek Turker, Y. Experimental Investigation of the Rotational Behaviour of Glulam Column-Beam Joints Reinforced with Fiber Reinforced Polymer Composites. Composite Structures 2021, 262, 113612. [CrossRef]
- Wang, X.T.; Zhu, E.C.; Niu, S.; Wang, H.J. Analysis and Test of Stiffness of Bolted Connections in Timber Structures. Construction and Building Materials 2021, 303, 124495. [CrossRef]
- Fu, Q.; Yan, L.; Thielker, N.A.; Kasal, B. Effects of Concrete Type, Concrete Surface Conditions and Wood Species on Interfacial Properties of Adhesively-Bonded Timber – Concrete Composite Joints. International Journal of Adhesion and Adhesives 2021, 107, 102859. [CrossRef]
- Giv, A.N.; Chen, Z.; Fu, Q.; Leusmann, T.; Yan, L.; Lowke, D.; Kasal, B. Bending Behavior and Bond Analysis on Adhesively Bonded Glulam-Concrete Panels Fabricated with Wet Bonding Technique. Journal of Building Engineering 2023, 76, 107140. [CrossRef]
- Ferrara, G.; Michel, L.; Ferrier, E. Flexural Behaviour of Timber-Concrete Composite Floor Systems Linearly Supported at Two Edges. Engineering Structures 2023, 281, 115782. [CrossRef]
- Gomez-Ceballos, W.G.; Gamboa-Marrufo, M.; Grondin, F. Multi-Criteria Assessment of a High-Performance Glulam through Numerical Simulation. Engineering Structures 2022, 256, 114021. [CrossRef]
- Ching, E.; Carstensen, J.V. Truss Topology Optimization of Timber–Steel Structures for Reduced Embodied Carbon Design. Engineering Structures 2022, 252, 113540. [CrossRef]
- De Luca, V.; Marano, C. Prestressed Glulam Timbers Reinforced with Steel Bars. Construction and Building Materials 2012, 30, 206–217. [CrossRef]
- McConnell, E.; McPolin, D.; Taylor, S. Post-Tensioning of Glulam Timber with Steel Tendons. Construction and Building Materials 2014, 73, 426–433. [CrossRef]
- Mam, K.; Douthe, C.; Le Roy, R.; Consigny, F. Shape Optimization of Braced Frames for Tall Timber Buildings: Influence of Semi-Rigid Connections on Design and Optimization Process. Engineering Structures 2020, 216, 110692. [CrossRef]
- Suárez-Riestra, F.; Estévez-Cimadevila, J.; Martín-Gutiérrez, E.; Otero-Chans, D. Experimental, Analytical and Numerical Vibration Analysis of Long-Span Timber-Timber Composite Floors in Self-Tensioning and Non-Tensioning Configurations. Construction and Building Materials 2019, 218, 341–350. [CrossRef]
- Suárez-Riestra, F.; Estévez-Cimadevila, J.; Martín-Gutiérrez, E.; Otero-Chans, D. Timber-Timber-Composite (TTC) Beam Long-Term Behaviour. Full Scale Experimental Campaign and Simplified Analytical Model. Construction and Building Materials 2022, 361, 129649. [CrossRef]
- Jelušič, P. Determining Optimal Designs of Timber Beams with Non-Uniform Cross-Section.; WIT Transactions on The Built Environment: Ljubljana, Slovenia, July 11 2018; Vol. 175, pp. 169–175.
- Šilih, S.; Kravanja, S.; Premrov, M. Shape and Discrete Sizing Optimization of Timber Trusses by Considering of Joint Flexibility. Advances in Engineering Software 2010, 41, 286–294. [CrossRef]
- Simón-Portela, M.; Villar-García, J.R.; Rodríguez-Robles, D.; Vidal-López, P. Optimization of Glulam Regular Double-Tapered Beams for Agroforestry Constructions. Applied Sciences 2023, 13, 5731. [CrossRef]
- Negrin, I.; Kripka, M.; Yepes, V. Design Optimization of Welded Steel Plate Girders Configured as a Hybrid Structure. Journal of Constructional Steel Research 2023, 211, 108131. [CrossRef]
- Negrin, I.; Kripka, M.; Yepes, V. Metamodel-Assisted Meta-Heuristic Design Optimization of Reinforced Concrete Frame Structures Considering Soil-Structure Interaction. Engineering Structures 2023, 293, 116657. [CrossRef]
- Gonzalez-Montellano, C.; Ramirez, A.; Gallego, E.; Ayuga, F. On the Steel Cost of Circular Flat-Bottomed Silos Designed Using the Eurocodes. Structural Engineering and Mechanics 2009, 33, 561–572. [CrossRef]
- Villar, J.R.; Vidal, P.; Fernández, M.S.; Guaita, M. Genetic Algorithm Optimisation of Heavy Timber Trusses with Dowel Joints According to Eurocode 5. Biosystems Engineering 2016, 144, 115–132. [CrossRef]
- Villar-García, J.R.; Vidal-López, P.; Rodríguez-Robles, D.; Guaita, M. Cost Optimisation of Glued Laminated Timber Roof Structures Using Genetic Algorithms. Biosystems Engineering 2019, 187, 258–277. [CrossRef]
- Baeten, L.; Bruelheide, H.; Van Der Plas, F.; Kambach, S.; Ratcliffe, S.; Jucker, T.; Allan, E.; Ampoorter, E.; Barbaro, L.; Bastias, C.C.; et al. Identifying the Tree Species Compositions That Maximize Ecosystem Functioning in European Forests. Journal of Applied Ecology 2019, 56, 733–744. [CrossRef]
- Fichtner, A.; Härdtle, W.; Li, Y.; Bruelheide, H.; Kunz, M.; Von Oheimb, G. From Competition to Facilitation: How Tree Species Respond to Neighbourhood Diversity. Ecology Letters 2017, 20, 892–900. [CrossRef]
- Vilà, M.; Vayreda, J.; Comas, L.; Ibáñez, J.J.; Mata, T.; Obón, B. Species Richness and Wood Production: A Positive Association in Mediterranean Forests. Ecology Letters 2007, 10, 241–250. [CrossRef]
- EN 1995-1-1 Eurocode 5: Design of Timber Structures - Part 1-1: General - Common Rules and Rules for Buildings; CEN: Brussels, Belgium, 2016;
- EN 1991-1-3/AC-A1 Eurocode 1: Actions on Structures - Part 3: Snow Loads; CEN: Brussels, Belgium, 2015;
- Royal Decree 314 Technical Building Code; Spanish Ministry of Housing: Madrid, Spain, 2006;
- EN 1991-1-4/AC-A1 Eurocode 1: Actions on Structures - Part 4: Wind Actions; CEN: Brussels, Belgium, 2010;
- Instituto Valenciano de la Edificación Cost Database Available online: https://bdc.f-ive.es/BDC23/1 (accessed on 5 March 2024).
- Argüelles Álvarez, R.; Arriaga Martitegui, F. Timber structures: design and calculation [Estructuras de madera: diseño y cálculo]; 1997; ISBN 978-84-87381-09-6.
Figure 1.
Timber volume variation, in percentage, between the selected strength class and the reference GL 32h class as a function of the snow load and span.
Figure 1.
Timber volume variation, in percentage, between the selected strength class and the reference GL 32h class as a function of the snow load and span.
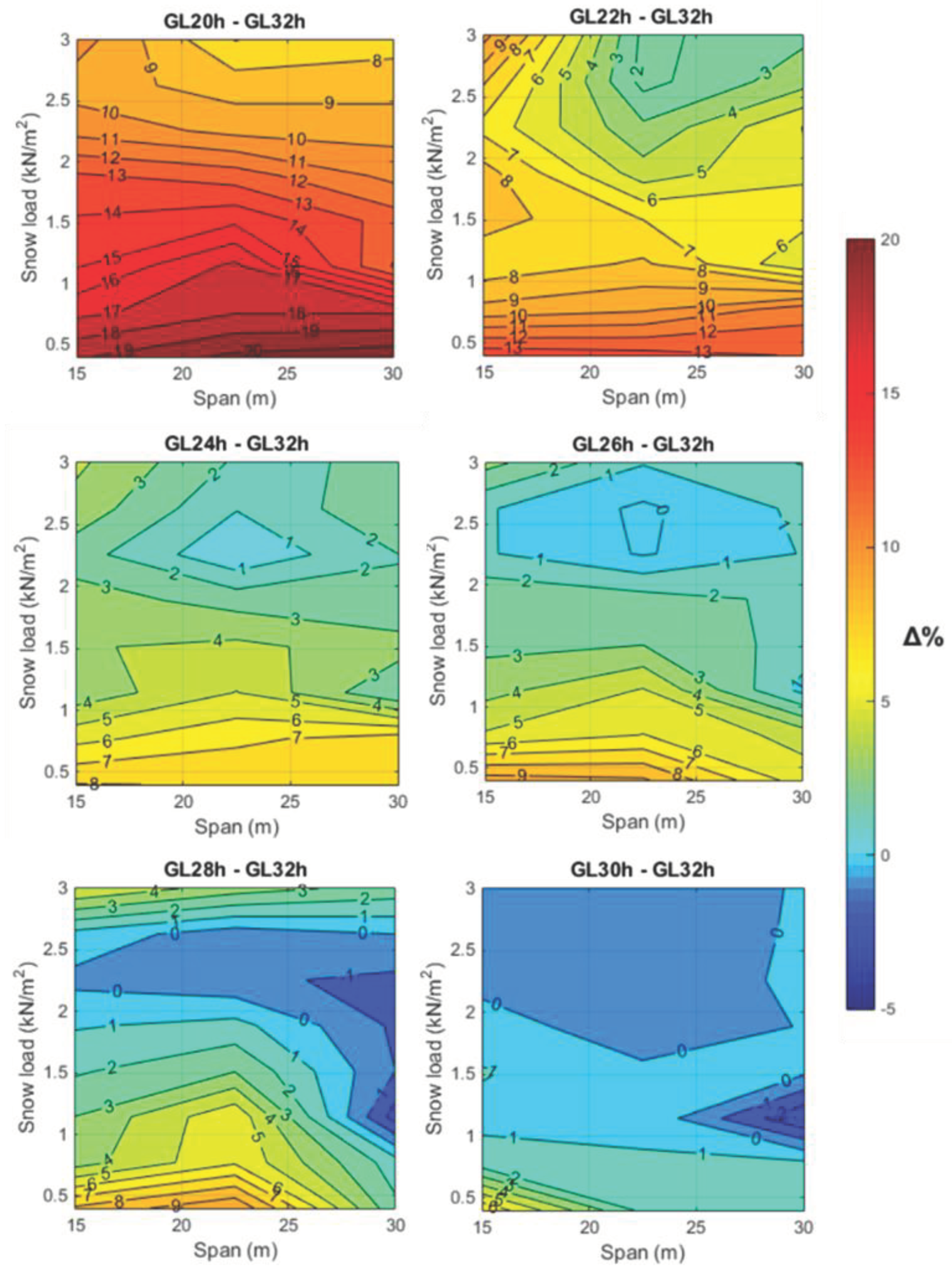
Table 1.
Characteristic properties for each homogeneous glulam strength class [15].
Table 1.
Characteristic properties for each homogeneous glulam strength class [15].
| Property | GL 20h | GL 22h | GL 24h | GL 26h | GL 28h | GL 30h | GL 32h |
|---|---|---|---|---|---|---|---|
| Bending strength (N/mm2) | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| Tensile strength -parallel to the grain- (N/mm2) | 16 | 17.6 | 19.2 | 20.8 | 22.3 | 24 | 25.6 |
| Tensile strength -perpendicular to the grain- (N/mm2) | 0.5 | ||||||
| Compression strength -parallel to the grain- (N/mm2) | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| Compression strength -perpendicular to the grain- (N/mm2) | 2.5 | ||||||
| Modulus of elasticity -parallel to the grain- (N/mm2) | 8400 | 10500 | 11500 | 12100 | 12600 | 13600 | 14200 |
| Modulus of elasticity -perpendicular to the grain- (N/mm2) | 300 | ||||||
| Density (kg/m3) | 340 | 370 | 385 | 405 | 425 | 430 | 440 |
Table 2.
Coefficients for the determination of the beam width as a function of the span, snow load, and strength class according to Equation 2.
Table 2.
Coefficients for the determination of the beam width as a function of the span, snow load, and strength class according to Equation 2.
| Strength class | Snow load range (kN/m2) | A | B | C |
|---|---|---|---|---|
| GL 20h | [0.4, 1.0] | -2.62363 | 0.08474 | 0.09558 |
| (1.0, 3.0] | -5.54945 | 0.23634 | 0.06286 | |
| GL 22h | [0.4, 1.0] | -1.92033 | 0.07653 | 0.03823 |
| (1.0, 1.8] | -3.41484 | 0.03779 | 0.12499 | |
| (1.8, 3.0] | -6.76484 | 0.38397 | 0.02239 | |
| GL 24h | [0.4, 2.4] | -3.20080 | 0.14541 | 0.02972 |
| (2.4, 3.0] | -8.5714 | 0.1154 | 0.1461 | |
| GL 26h | [0.4, 2.0] | -2.49573 | 0.12007 | 0.01960 |
| (2.0, 3.0] | -7.0249 | 0.000 | 0.1611 | |
| GL 28h | [0.4, 2.0] | -2.53236 | 0.11526 | 0.02117 |
| (2.0, 3.0] | -6.4864 | 0.00000 | 0.1511 | |
| GL 30h | [0.4, 1.6] | -1.946625 | 0.098350 | 0.009656 |
| (1.6, 3.0] | -6.19152 | 0.13680 | 0.09266 | |
| GL 32h | [0.4, 0.6] | -1.61538 | 0.07035 | 0.01870 |
| (1.4, 3.0] | -6.15110 | 0.17779 | 0.07631 |
Table 3.
Coefficients for the determination of the beam height as a function of the span, snow load, beam width, and strength class according to Equation 3.
Table 3.
Coefficients for the determination of the beam height as a function of the span, snow load, beam width, and strength class according to Equation 3.
| Strength class | Snow load range (kN/m2) | A | B | C | D | E |
|---|---|---|---|---|---|---|
| GL 20h | [0.4, 0.8] | -2437.7 | 364.9 | -387.0 | 0.0 | 1.3 |
| (0.8, 3.0] | 43.6916 | 7.7027 | -0.6686 | 1.8943 | 0.8 | |
| GL 22h | [0.4, 1.6] | -107.79 | 32.44 | 0.000 | 10.64 | 1.0 |
| (1.6, 3.0] | 44.525 | 8.276 | 0.000 | 1.516 | 0.8 | |
| GL 24h | [0.4, 2.4] | -82.268 | 30.655 | 0.000 | 9.972 | 1.0 |
| (2.4, 3.0] | 9.7869 | 0.4573 | 2.1313 | 0.1799 | 0.5 | |
| GL 26h | [0.4, 1.8] | -1195.93 | 149.32 | 0.000 | 47.62 | 1.2 |
| (2.2, 3.0] | 35.029 | 0.000 | 0.000 | 1.920 | 0.7 | |
| GL 28h | [0.4, 2.6] | -1899.6 | 255.0 | -931.2 | 152.6 | 1.3 |
| (2.6, 3.0] | -67.787 | 2.356 | 31.563 | 0.000 | 0.6 | |
| GL 30h | [0.4, 2.0] | -790.05 | 121.95 | -260.80 | 66.66 | 1.2 |
| (2.0, 3.0] | 480.66 | 0.000 | -233.57 | 23.77 | 1.0 | |
| GL 32h | [0.4, 0.6] | 227.14 | 61.13 | -1924.63 | 111.49 | 1.2 |
| (0.6, 1.4] | -143.50 | 18.99 | 138.30 | 0.000 | 0.9 | |
| (1.4, 2.4] | -565.42 | 55.17 | 220.20 | 0.000 | 1.0 | |
| (2.4, 3.0] | -1288.73 | 66.47 | 396.61 | 0.000 | 1.0 |
Table 4.
Coefficients for the determination of the number of beams as a function of the span, snow load and strength class according to Equation 4.
Table 4.
Coefficients for the determination of the number of beams as a function of the span, snow load and strength class according to Equation 4.
| Strength class | Snow load range (kN/m2) | A | B | C | D |
|---|---|---|---|---|---|
| GL 20h | [0.4, 1.0) | 1.714653 | 0.029203 | 0.003352 | 0.5 |
| [1.0, 1.4) | 1.886763 | ||||
| [1.4, 1.8) | 2.01307 | ||||
| [1.8, 2.6) | 2.079799 | ||||
| [2.6, 3.0] | 2.190146 | ||||
| GL 22h | [0.4, 0.6) | 1.387500 | 0.179969 | 0.005556 | 1.0 |
| [0.6, 1.0) | 0.227129 | ||||
| [1.0, 2.2) | 0.246142 | ||||
| [2.2, 2.8] | 0.279475 | ||||
| (2.8, 3.0] | 0.309969 | ||||
| GL 24h | [0.4, 0.6) | 2.183385 | 0.035969 | 0.003365 | 0.6 |
| [0.6, 1.0) | 0.044658 | ||||
| [1.0, 1.4) | 0.050095 | ||||
| [1.4, 1.8) | 0.053231 | ||||
| [1.8, 2.5) | 0.057995 | ||||
| [2.5, 3.0) | 0.051065 | ||||
| GL 26h | [0.4, 0.6) | -13.01695 | 0.79546 | -0.04728 | 1.4 |
| [0.6, 1.0) | 0.9864 | ||||
| [1.0, 1.4) | 1.13949 | ||||
| [1.4, 1.8) | 1.31396 | ||||
| [1.8, 3.0] | 1.49259 | ||||
| GL 28h | [0.4, 0.6) | 1.416667 | 0.175884 | 0.002162 | 1.0 |
| [0.6, 1.0) | 0.219464 | ||||
| [1.0, 1.4) | 0.245759 | ||||
| [1.4, 1.8) | 0.279462 | ||||
| (1.8, 3.0] | 0.312182 | ||||
| GL 30h | [0.4, 0.6) | -0.23722 | 0.24909 | 0.01508 | 1.1 |
| [0.6, 1.0) | 0.29747 | ||||
| [1.0, 1.4) | 0.34151 | ||||
| [1.4, 1.8) | 0.39152 | ||||
| (1.8, 3.0] | 0.43494 | ||||
| GL 32h | [0.4, 1.0) | 2.232859 | 0.041501 | 0.005099 | 0.6 |
| [1.0, 1.8) | 0.045316 | ||||
| [1.8, 3.0] | 0.050558 |
Table 5.
Optimal purlin height values as a function of the snow load and strength class.
| Strength class | Snow load range (kN/m2) | Purlin height (mm) |
|---|---|---|
| GL 20h | [0.4, 0.6] | 160 |
| (0.6, 3.0] | 200 | |
| GL 22h | [0.4, 1.6] | 160 |
| (1.6, 3.0] | 200 | |
| GL 24h | [0.4, 2.4] | 160 |
| (2.4, 3.0] | 200 | |
| GL 26h | [0.4, 2.6] | 160 |
| (2.6, 3.0] | 200 | |
| GL 28h | [0.4, 2.8] | 160 |
| (2.8, 3.0] | 200 | |
| GL 30h | [0.4, 3.0] | 160 |
| GL 32h | [0.4, 0.6] | 120 |
| (0.6, 3.0] | 160 |
Table 6.
Coefficients for the determination of the volume of timber as a function of the roof length, snow load and span according to Equation 6.
Table 6.
Coefficients for the determination of the volume of timber as a function of the roof length, snow load and span according to Equation 6.
| Strength class | Snow load range (kN/m2) | Span range (m) | A | B | C | D | E |
|---|---|---|---|---|---|---|---|
| GL 20h | [0.4, 3.0] | [15, 24] | 2.49589 | -0.39406 | -0.33466 | 0.04909 | 0.03310 |
| (24, 30] | 7.38722 | -2.81552 | 0.0000 | 0.12969 | 0.0275 | ||
| GL 22h | [0.4, 3.0] | [15, 23] | 1.06634 | -0.30129 | -0.27391 | 0.04309 | 0.02919 |
| (23, 30] | 7.26380 | -0.65811 | -0.98976 | 0.05306 | 0.06075 | ||
| GL 24h | [0.4, 3.0] | [15, 23] | 0.92186 | -0.26346 | -0.29997 | 0.03967 | 0.03067 |
| (23, 30] | 6.42904 | -0.61534 | -0.95922 | 0.04981 | 0.05996 | ||
| GL 26h | [0.4, 3.0] | [15, 22] | 0.07444 | 0.00000 | -0.39930 | 0.02437 | 0.03664 |
| (22, 29] | 5.13592 | 0.00000 | -1.12414 | 0.02561 | 0.06663 | ||
| (29, 30] | 6.0173 | 0.8492 | 0.8507 | 0.0000 | 0.0000 | ||
| GL 28h | [0.4, 2.5] | [15, 22] | 0.14786 | 0.0000 | -0.4101 | 0.02465 | 0.03664 |
| (22,30] | 4.40794 | 0.0000 | -1.05264 | 0.02806 | 0.06222 | ||
| (2.5, 3.0] | [15, 22] | -1.19404 | 0.0000 | -0.35815 | 0.01146 | 0.03943 | |
| (22,30] | 8.53219 | 0.0000 | -1.12923 | 0.0000 | 0.07523 | ||
| GL 30h | [0.4, 3.0] | [15, 23] | 1.25132 | -0.18641 | -0.35579 | 0.03370 | 0.03375 |
| (23, 30] | 5.65268 | -0.57068 | -0.97329 | 0.04615 | 0.06066 | ||
| GL 32h | [0.4, 3.0] | [15, 22] | 0.91510 | -0.20407 | -0.30354 | 0.03422 | 0.03088 |
| (22, 30] | 4.25579 | -0.50446 | -0.87409 | 0.04427 | 0.05749 |
Table 7.
Optimal timber volumes (Eq. 5) for example 2 and variation of timber consumption compared to the reference [48].
Table 7.
Optimal timber volumes (Eq. 5) for example 2 and variation of timber consumption compared to the reference [48].
| Strength class | Optimal volume (m3) | Variation (%) |
|---|---|---|
| GL 20h | 35.87 | -9.76 |
| GL 22h | 32.84 | -17.38 |
| GL 24h | 31.4 | -21.01 |
| GL 26h | 29.06 | -26.89 |
| GL 28h | 29.16 | -26.64 |
| GL 30h | 29.94 | -24.68 |
| GL 32h | 29.17 | -26.62 |
Table 8.
RMOD and RVOL values for the comparison of a strength class to the GL 32h reference class as a function of the snow load range.
Table 8.
RMOD and RVOL values for the comparison of a strength class to the GL 32h reference class as a function of the snow load range.
| Snow load range (kN/m2) | % | GL 20h | GL 22h | GL 24h | GL 26h | GL 28h | GL 30h |
|---|---|---|---|---|---|---|---|
| RMOD | 40.8 | 26.1 | 19 | 14.8 | 11.3 | 4.2 | |
| [0.4, 1.5] | RVOL | 15.9 | 9.8 | 6 | 3.2 | 2.6 | 1.1 |
| (1.5, 3.0] | RVOL | 10.2 | 5.2 | 2.7 | 1.6 | 0.7 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






