Second Moment/Order Approximations by Kernel Smoothers with Application to Volatility Estimation

Volatility estimation and quantile regression are relevant active research areas in statistics, machine learning and econometrics. In this work, we propose two procedures to estimate local variances in generic regression problems by using of kernel smoothers. The proposed schemes can be applied in multidimesional scenarios (not just for time series analysis) and easily in a multi-output framework, as well. Moreover, they allow the possibility of providing uncertainty estimation using a generic kernel smoother technique. Several numerical experiments show the benefits of the proposed methods, even comparing with benchmark techniques. One of these experiment involves a real dataset analysis.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Regression analysis can be considered as a set of methodologies for estimating the relationships between a dependent variable y (often called as ’output’ or ’response’) and a vector

x

of independent variables (often called ’input’). Essentially, the main goal in a regression problem is to obtain an approximation of the trend defined as the expected value of y given

x

, i.e.,

E [y | x]

, that is the first (non-central) moment of the conditional density

p (y | x)

. We can assert that the most complete regression problem consists of approximating the whole conditional density

p (y | x)

, whereas the simplest task in a regression problem consists of estimating only the first moment

E [y | x] = \int_{Y} y p (y | x) d y

. Intermediate scenarios appear in different applications, where other moments (higher than one) are of interest and hence are also approximated.

Volatility estimation (intended as local variance or local standard deviation) and quantile regression analysis are currently important tasks in statistics, machine learning and econometrics. The problem of the estimation of the volatility has a particular relevance in financial time series analysis, where the volatility represents the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. It is still an important active area of research [1,2,3,4]. Local linear regression methods (which can resemble a kernel smoother approach) have been already proposed for volatility estimation [5,6,7]. Quantile regression models study the relationship between an independent input vector

x

and some specific quantile or moment of the output variable y[8,9,10]. Therefore, in quantile regression analysis the goal is to estimate higher order moments of the response/output variable, given an input

x

[8,9,10,11,12,13]. It is important to remark that many advance regression methods consider a constant variance as initial assumption of the output given the input,

v a r [y | x] = σ_{e}^{2}

, i.e., it does vary with the input variable

x

[14,15]. In this work, we consider an extended approach (with respect to the assumptions used in classical regression methods) where

v a r [y | x] = v (x)

, i.e., the local variance varies with the input

x

More precisely, in this work, we propose two procedures for estimating the local variance in a regression problem and using a kernel smoother approach [15]-[16]. Note that the kernel smoother schemes contain several well-known techniques as special cases, such as the fixed radius nearest neighbours, as an example [17]. The resulting solution is non-parametric method, hence both complexity and flexibility of the solution grows with the number of data N. This ensures to have the adaquate flexibility to analyze the data.

The first proposed method is based on the Nadaraya-Watson derivation of a linear kernel smoother [14,15]. The second proposed approach draws inspiration from divisive normalization, a function grounded in the activity of brain neurons [18]. This function aims to standardize neuron activity by dividing it by the activity of neighboring neurons. It has demonstrated favorable statistical properties [19,20,21] and has been utilized in various applications [22,23].

The proposed methods can be applied to time series analysis and/or in more general regression problems where the input variables are multidimensional. Therefore, our approach can be implemented in spatial statistical modelling and any other inverse problems [10,24]. Furthermore, another advantage of the proposed scenario, is that the generalization for a multi-output scenarios can be easily designed.

From another point of view, this work gives another relevant contribution. The proposed schemes allow to perform uncertainty estimation with a generic kernel smoother technique. Indeed, a generic kernel smoother method is not generally supported by a generative probabilistic derivation that yields also an uncertainty estimation. The Gaussian processes (GPs) and relevance vector machines (RVMs) regression methods are relevant well-known and virtually unique exceptions [15,25]).

We have tested the proposed methods in five numerical experiments. Four of them involve the application of the different schemes to time series analyis, and the comparison with GARCH models which are considered benchmark techniques for volatility estimation in time series [26]. The last numerical experiment addresses a more general regression problem, with a multidimensional input variable

x

of dimension 122, considering a real (emo-soundscapes) database [27,28].

2. Approximating the Trend

Let us consider a set of N data pairs, such as

{x_{i}, y_{i}}_{i = 1}^{N}

, where

x_{i} \in R^{D}

, with

D \geq 1

, and

y_{i} \in R

. First of all, we are interested in obtaining a regression function (a.k.a.,“local mean”– trend), i.e., removing the noise in the signal obtaining an estimator

\hat{f} (x)

for all possible

x

in the input space. One possibility is to employ a linear kernel smoother. More specifically, we consider the Nadaraya-Watson estimator [14,15] that has the following form,

\begin{matrix} E [y | x] \approx \hat{f} (x) & = \\ = \sum_{n = 1}^{N} \frac{h (x, x_{n})}{\sum_{j = 1}^{N} h (x, x_{j})} y_{n} = \sum_{n = 1}^{N} φ (x, x_{n}) y_{n}, \end{matrix}

(1)

where

φ (x, x_{n}) = \frac{h (x, x_{n})}{\sum_{j = 1}^{N} h (x, x_{j})}

. Note that, by this definition, the nonlinear weights

φ (x, x_{n})

are normalized, i.e.,

\sum_{n = 1}^{N} φ (x, x_{n}) = 1, \forall x .

(2)

As an example, we could consider

h (x, z) = h (x, z | λ) = exp (- \frac{| | x - {z | |}^{2}}{λ}),

where

λ

is a parameter that should be tuned. Clearly, we have also

φ (x, z) = φ (x, z | λ) .

The form of this estimator above is quite general, and contains different other well-known methods as special cases. For instance, it contains the k-nearest neighbors algorithm (kNN) for regression as a specific case (to be more specific, the fixed-radius near neighbors algorithm). Indeed, with a specific choice of

h (x, x_{n} | λ)

(as a rectangular function), the expression above can represent the fixed-radius near neighbors estimator [15,17].

Remark 1.

The resulting regression function is flexible non-parametric method. Both complexity and flexibility of the solution grows with the number of data N.

Remark 2.

The input variables

x_{n} \in R^{D}

are vectors (

D \geq 1

), in general. Therefore, the described methods have a much wider applicability than the techniques that can be employed only for time series (where the time index is a scalar number,

x = t \in R

). Clearly, the methodologies described here can be also employed for analyzing time series. Moreover, even in a time series framework, we can obtain a prediction between two consecutive time instants. For instance, if we have a time series with daily data, with a kernel smoother we can have a prediction at each hour (or minute) within a specific day.

Learning 1 (

λ

) One possibility for tuning the parameters of the kernel functions is to use a cross-validation (CV) procedure. In this work, we have employed a leave-one-out cross-validation (LOO-CV) [14].

3. Variance Estimation Procedures

Let assume that we have already computed the trend (a.k.a., “local mean”), i.e., the regression function

\hat{f} (x)

. Here we present two methods to obtain an estimation of the local variance (or volatility) at each point

x

, which is theoretically defined as

\begin{matrix} v (x) = v a r [y | x] & = \int_{Y} {(y - E [y | x])}^{2} p (y | x) d y, \\ = E [y^{2} | x] - {(E [y | x])}^{2} . \end{matrix}

(3)

Method 1(M1) If the weights

φ (x, x_{n})

are adequate for linearly combined the outputs

y_{i}

and obtaining an proper approximation of

E [y | x]

, one can extend this idea for approximating the second non-central moment

E [y^{2} | x]

\begin{matrix} E [y^{2} | x] \approx \hat{q} (x) = \sum_{n = 1}^{N} φ (x, x_{n}) y_{n}^{2} . \end{matrix}

(4)

hence

\begin{matrix} \hat{v} (x) = \hat{q} (x) - {(\hat{f} (x))}^{2} \approx v a r [y | x], \end{matrix}

(5)

which is an estimator of theinstant variance. Note that

\hat{q (x)}

and

\hat{f} (x)

are obtained with the same weights

φ (x, x_{n}) = φ (x, x_{n} | λ),

with the same value of

λ

(obtained using a LOO-CV procedure). Thus, a variant of this procedure consists into learning another value of

λ_{2}

, i.e., obtaining other coefficients

φ_{2} (x, z) = φ_{2} (x, z | λ_{2})

, in the Eq. (4) considering the signal

y_{n}^{2}

(instead of

y_{n}

Method 2 (M2). Let us define the signal obtained as the estimated square errors

v_{n} = {(y_{n} - \hat{f} (x))}^{2}, n = 1, . . ., N .

\hat{f} (x) \approx E [y | x]

as assumed,

v_{n}

is a one-sample estimate of the variance at

x

. Then, the goal is to approximate the trend of this new signal (i.e., new output)

v_{n}

\begin{matrix} \hat{v} (x) & = \sum_{n = 1}^{N} φ_{2} (x, x_{n}) v_{n}, \end{matrix}

where we consider another parameter

λ_{2}

, i.e.,

φ_{2} (x, z) = φ_{2} (x, z | λ_{2}),

that is tuned again with LOO-CV but considering the new signal

v_{n}

. Note that

\hat{v} (x)

can be interpreted as estimation of the instant variance of the underlying signal. As alternative, also completely different kernel functions (as

φ_{2}

) can be applied (that differs for the functional form with respect to

φ

, instead just for the choice of

λ

Remark 3.

Again, as for estimating the trend, note that the two procedures above can be applied for multivariate inputs

x_{n} \in R^{D}

, and not just for scalar inputs (as in the time series).

Remark 4.

If one divides

x

\hat{v} (x)

we get a signal with uniform local variance, i.e. we have removed the (possible) heteroscedasticity. In [21], this procedure was used to define the relation kernels in the divisive normalization, and thus equalize locally the energy of neuron responses.

4. Extensions and Variants

The use of linear kernel smoothers as regression methods is not mandatory. Indeed, the ideas previously described can be employed even applying different regression methods. Below we provide some general steps in the same fashion of a pseudo-code, In order to clarify the application of possible different regression techniques:

Choose a regression method. Obtain a trend function $\hat{f} (x) \approx E [y | x]$ given the dataset ${x_{i}, y_{i}}_{i = 1}^{N}$ .
Choose one method for estimating the instance variance (between the two below):
- M1. Choose a regression method (the same of the previous step or a different one). Considering the dataset the dataset ${x_{i}, y_{i}^{2}}_{i = 1}^{N}$ and obtain $\hat{q} (x) \approx E [y^{2} | x]$ . Then, compute $\hat{v} (x) = \hat{q} (x) - {(\hat{f} (x))}^{2}$ .
- M2. Choose a regression method (the same of the previous step or a different one). Considering the dataset the dataset ${x_{i}, v_{i}}_{i = 1}^{N}$ where $v_{n} = {(y_{n} - \hat{f} (x))}^{2}$ , obtain the function $\hat{v} (x)$ .

4.1. Multi-Output Scenario and other Extensions

In a multi-output framework, we have N data pairs, such as

{x_{i}, y_{i}}_{i = 1}^{N}

, where

x_{i} \in R^{D}

, but in this case also the outputs are vectors

y_{i} \in R^{D_{Y}}

. Hence, for the local trend we have also a vectorial hidden function

\hat{f} (x) : R^{D} \to R^{D_{Y}}

for all possible

x

in the input space. Then, we could easily write

\begin{matrix} \hat{f} (x) & = \sum_{n = 1}^{N} φ (x, x_{n}) y_{n} . \end{matrix}

(6)

Regarding the estimations of local variances follow the same procedures, defining the following vectorial quantities:

\hat{q} (x) \approx E [y^{2} | x]

for M1,

\hat{v} (x) = \hat{q} (x) - {(\hat{f} (x))}^{2}

and

v_{n} = {(y_{n} - \hat{f} (x))}^{2}

for M2.

Furthermore, we could also consider different local parameters

λ

, for instance

λ_{n}

with

n = 1, . . ., N

, or more generally, with

λ = λ (x)

. In this case, we would have different coefficient functions

φ_{n} (x, x_{n})

(one for each input

x_{n}

), so that trend could be easily expressed as

\begin{matrix} \hat{f} (x) & = \sum_{n = 1}^{N} φ_{n} (x, x_{n}) y_{n} . \end{matrix}

(7)

4.2. Example of Alternative to the Kernel Smoothers for Time Series Analysis

Let us consider a time series framework, i.e., the input is a scalar time instance,

x = t \in R

, then the dataset is formed by the following pairs

{t_{i}, y_{i}}_{i = 1}^{N}

. Let also consider that the intervals,

t_{i} - t_{i - 1}

, are constant, in this case, we can skip the t index, and consider the dataset

{t_{i}, y_{i}}_{i = 1}^{N}

. In this scenario, as an alternative, one can use an autoregressive (AR) model,

\begin{matrix} y_{i} = a_{1} y_{i - 1} + a_{2} y_{i - 2} + . . . + a_{W} y_{i - W} + ϵ_{y}, \end{matrix}

(8)

where

ϵ_{y}

is a noise perturbation and the coefficients

a_{i}

, for

i = 1, . . ., W

, are obtained by a least squares (LS) minimization and the length of the temporal window W (i.e., the order of the AR filter) is obtained using a spectral information criterion (SIC) [29,30]. Then, considering the estimated coefficients

{\hat{a}}_{i}

by LS, and

\hat{W}

by SIC, we have

\begin{matrix} \hat{f} (t_{i}) = {\hat{f}}_{i} = {\hat{a}}_{1} y_{i - 1} + {\hat{a}}_{2} y_{i - 2} + . . . + {\hat{a}}_{\hat{W}} y_{i - \hat{W}} . \end{matrix}

(9)

Just as an example, in order to apply M2 for the estimating the instant variance, we can set

v_{i} = {(y_{i} - {\hat{f}}_{i})}^{2}

, and assume another AR model over

v_{i}

with window length now denoted as H,

\begin{matrix} v_{i} = b_{1} v_{i - 1} + b_{2} v_{i - 2} + . . . + b_{H} v_{i - H} + ϵ_{v}, \end{matrix}

(10)

where again the estimations

{\hat{b}}_{i}

can be obtained by LS, and

\hat{H}

by SIC. The resulting instant variance function is

\begin{matrix} v (t_{i}) = v_{i} = {\hat{b}}_{1} v_{i - 1} + {\hat{b}}_{2} v_{i - 2} + . . . + {\hat{b}}_{\hat{H}} v_{i - \hat{H}} . \end{matrix}

(11)

Clearly, the application of M1 could be performed in a similar way.

Remark 5.

The resulting estimators in this section are still a linear combination of (a portion) of the outputs. Therefore, we still have linear smoothers (or better linear filters, since only considering combinations of past samples). However, note that in Eqs. (9)-(11) the coefficients of the linear combinations are obtained by least squares (LS) method. Hence, we have a window of length W (and then H) but this differs from the use of a rectangular kernel function for two reasons: (a) the window only considers past samples; (b) the coefficients are not all equals (to the ratio 1 over the number of samples included in the window) but they are tuned by LS.

5. Numerical Experiments

5.1. Applications to Time Series

In this section, we consider 5 different numerical experiments with different (true) generating models. Here, we focus on time series (

x = t \in R

) for two main reasons: (a) first of all, for the sake of simplicity (we can easily show a realization of the data in one plot), (b) and last but not the least, we have relevant benchmark competitors such as the GARCH models [31,32,33], that we can also test. Note that GARCH models have been specifically designed for handling volatility in time series.

More specifically, in this section, we test our methodologies and different GARCH models in four easy reproducible examples. These four examples differ for the data generating model. Indeed, the data are generated as the sum of a mean function,

f (t)

, and an error term,

s (t) ε (t)

, i.e.,

\begin{matrix} y (t) & = f (t) + s (t) ε (t), ε (t) \sim N (0, 1) . \end{matrix}

(12)

where we have used the fact that we are analyzing time series, i.e.,

x = t \in R

. The functions

f (t)

and

s (t)

are deterministic, and represent for the trend and the standard deviation of the observations

y (t)

. Whereas

ε (t) \sim N (0, 1)

represent a standard Gaussian random noise. Note also that

v (t) = s {(t)}^{2}

. In order to keep the notation of the rest of the paper, note that the dataset

{t_{n}, y_{n}}_{n = 1}^{N}

will be formed by the N pairs,

x_{n} = t_{n}, y_{n} = y (t_{n}),

where

y_{n}

will be generated according to the model above. The four experiments consider:

$f (t) = sin (0.5 t)$ , $s (t) = 0.2$ .
$f (t) = t$ , $s (t) = 2 | t |$ .
$f (t) = 0.5 t^{2}$ , $s (t) = 5 sin (0.3 t)$ .
$f (t) = 0$ and $s (t)$ generated by a GARCH model.

In all cases, the generated data

y (t)

and the underlying standard deviation

s (t)

(or variance

v (t) = s {(t)}^{2}

) are known, hence we can compute errors and evaluate the performance of the used algorithms. For the application of the proposed methods we consider a nonlinear kernel function as

\begin{matrix} h (t, t_{n}) = exp (- \frac{{(t - t_{n})}^{α}}{λ}), \end{matrix}

(13)

with

α \in {1, 2, 10}

.1 The parameter

λ

is tuned by LOO-CV. We test 7 different combinations, each one mixing a specific trend approximation method with a specific variance estimation technique:

Based on kernel smoothers: we consider different regression methods based in Eqs. (1) and (13). Furthermore, for the variance estimation we consider both procedures M1 and M2 described in Section 3. More specifically:

-

KS-1-1: $α = 1$ and M1,

-

KS-1-2: $α = 1$ and M2,

-

KS-2-1: $α = 2$ and M1,

-

KS-2-2: $α = 2$ and M2,

-

KS-10-1: $α = 10$ and M1,

-

KS-10-2: $α = 10$ and M2.
Based on AR models: we apply the method described in Section 4.2, that employs two auto-regressive models, one for the trend and one for the variance, jointly with procedure M2.

Table 1 summarizes all the seven considered specific implementations. Moreover, we test several GARCH(p,q) models: GARCH(1,1), GARCH(2,2), GARCH(5,5) and GARCH(10,10) (using a Matlab implementation of GARCH models).

Remark 6.

The GARCH models work directly with the signal without trend, i.e.,

| y_{n} - {\hat{f}}_{n} |

. In order to have a fair comparison, we use a kernel smoother with

α = 2

, i.e., applying Eqs. (1)-(13) with

α = 2

(as in the KS-2 methods).

We recall that GARCH models have been specific designed for making inference in heteroscedastic time series.

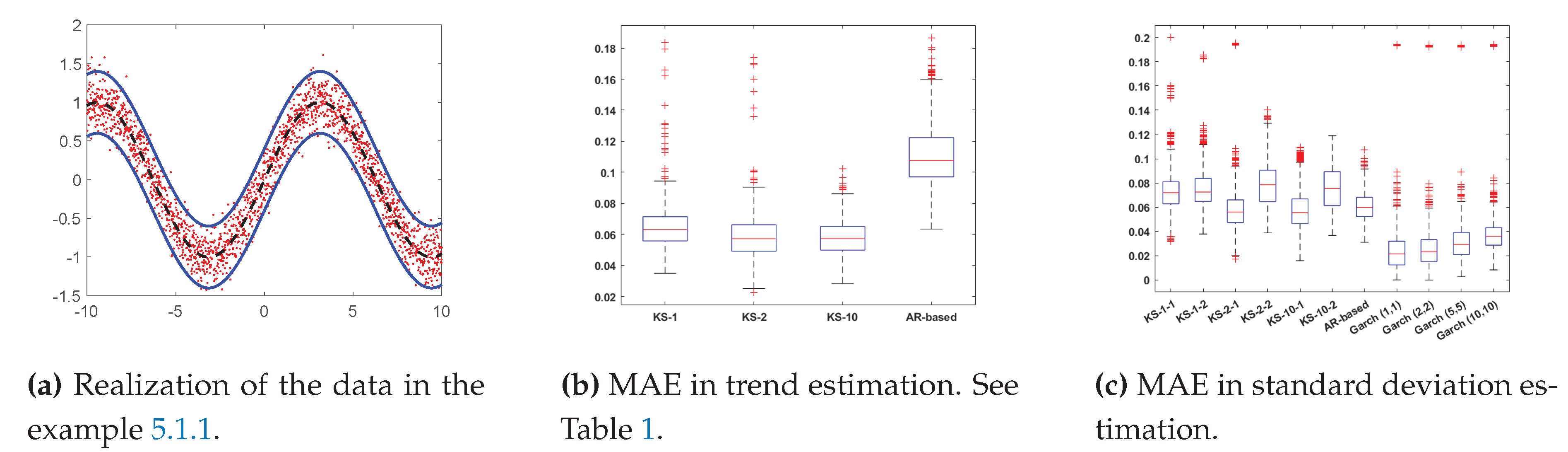
5.1.1. Experiment 1

As previously said, in this first example we consider

\begin{matrix} y (t) = sin (0.5 t) + 0.2 ε (t), ε (t) \sim N (0, 1), \end{matrix}

i.e., where

f (t) = sin (0.5 t)

and

s (t) = 0.2

( in this case we have homoscedastic series). We generate

N = 10^{4}

data with

t \in [- 10, 10]

. We apply all the algorithms, compute the mean absolute error (MAE), and repeat and average the results over

10^{4}

independent runs. Figure 1 depicts one realization of the generated data with the model above.

Results 1.Figure 1b,c provide the results in this example. Figure 1 shows the MAE obtained in estimating the trend, and Figure 1 depicts the MAE in estimating the standard deviation. In this case, regarding the trad, we see that the AR-based has an MAE higher than the rest when estimating the trend, but the other MAEs are quite similar. Similar outcomes are also obtained for approximating with the standard deviation, although the smaller MAE are provided by the GARCH models. Regarding the estimating of the standard deviation, the M1 seems to provide better results than M2, in this example.

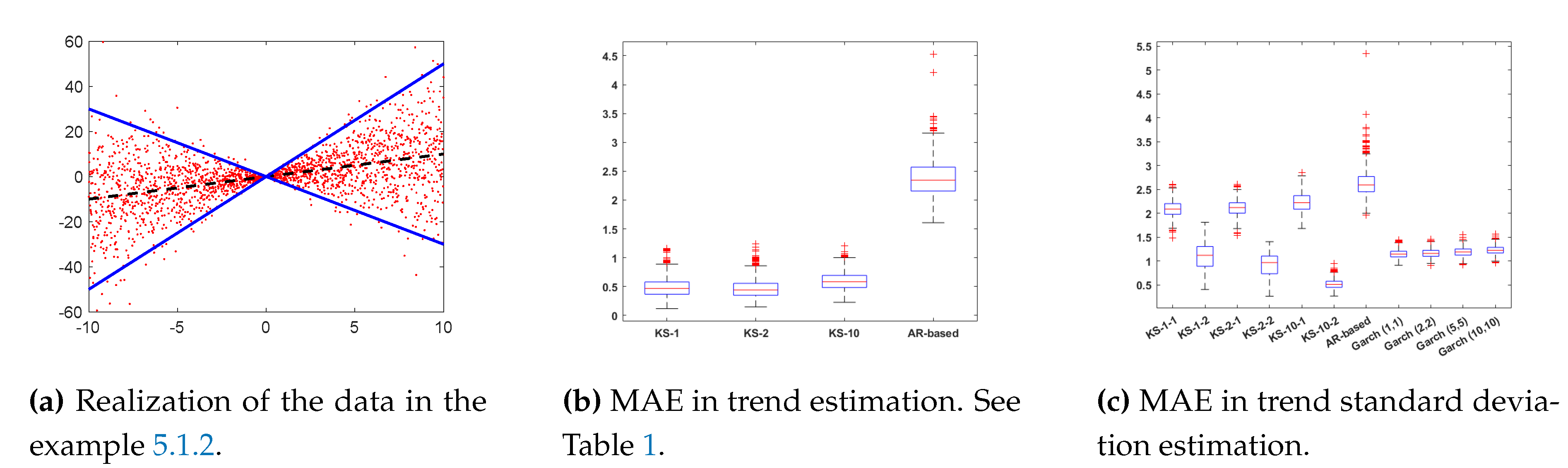
5.1.2. Experiment 2

in this second example, we consider

\begin{matrix} y (t) = t + 2 | t | ε (t), ε (t) \sim N (0, 1), \end{matrix}

where

f (t) = t

and

s (t) = 2 | t |

(i.e., in this case, we are heteroscedastic scenario). As previously, we generate

N = 10^{4}

data with

t \in [- 10, 10]

. We apply all the algorithms, compute the mean absolute error (MAE), and again we repeat and average the results over

10^{4}

independent runs. Figure 2 depicts one realization of the generated data according to the model above.

Results 2.The results are presented in Figure 2b,c. Again the MAE for the AR-based method seems to be higher than those for the rest of the algorithms when estimating the trend and standard deviation of the time series. Regarding the estimation of the standard deviation the best results are provided by the kernel methods which use the M2 (the MAE is particularly small with

α = 10

). Thus, it is remarkable that, even in this heteroscedastic scenario, the proposed methods provide similar and, in same cases, better results than GARCH models.

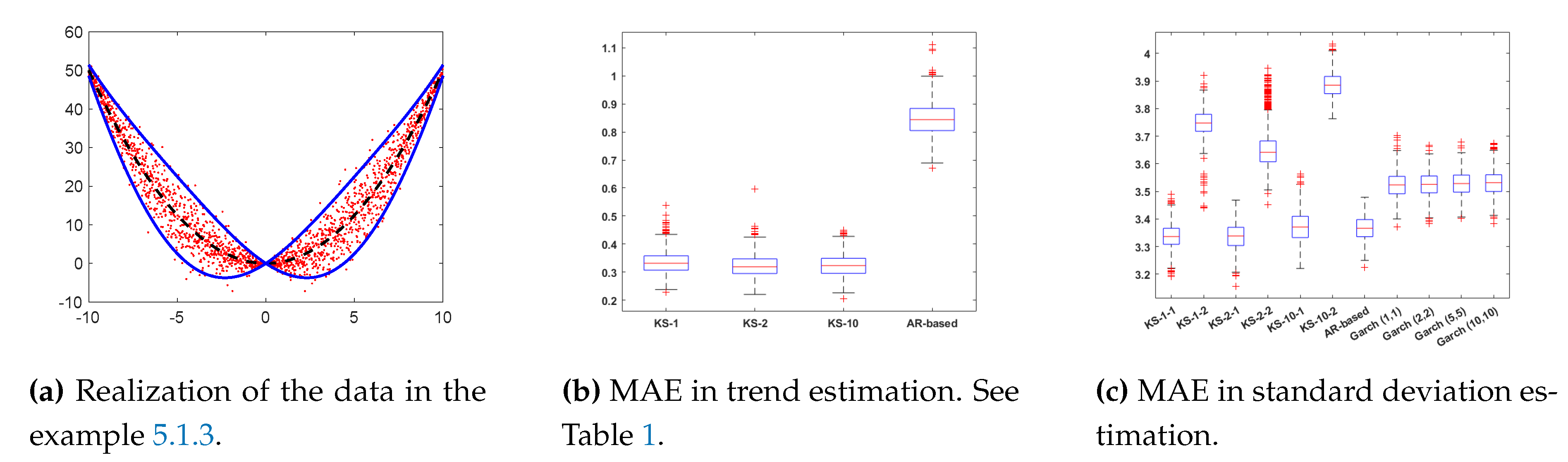
5.1.3. Experiment 3

In this third example, we consider a standard deviation that varies periodically, and a second order polynomial as a trend function, i.e.,

\begin{matrix} y (t) = 0.5 t^{2} + 5 sin (0.3 t) ε (t), ε (t) \sim N (0, 1), \end{matrix}

where

f (t) = 0.5 t^{2}

and

s (x) = 5 sin (0.3 t)

. Again, we have heterostodastic scenario. As previously, we generate

N = 10^{4}

data with

t \in [- 10, 10]

. We compute the mean absolute error (MAE), and again we repeat and average the results over

10^{4}

independent runs. Figure 3 depicts one realization of the generated data according to the described model.

Results 3.Figure 3b,c depict the box-plots of the MAE in estimating the trend and the standard deviation. As with the rest of the examples, the AR-based gives the worst results when calculating the trend of the time series, meanwhile the rest of the algorithms have very similar error values (recall that the GARCH models employ the KS-2 method for the trend estimation). However, the AR-based method provides good performance in the approximation of the standard deviation. The AR-based technique uses M2 for the variance. Moreover, for the standard deviation estimation, the methods KS-1-1-1, KS-2-1, KS-10-1 gives the smaller errors. Hence, it seems that in this case M1 works better even than GARCH models.

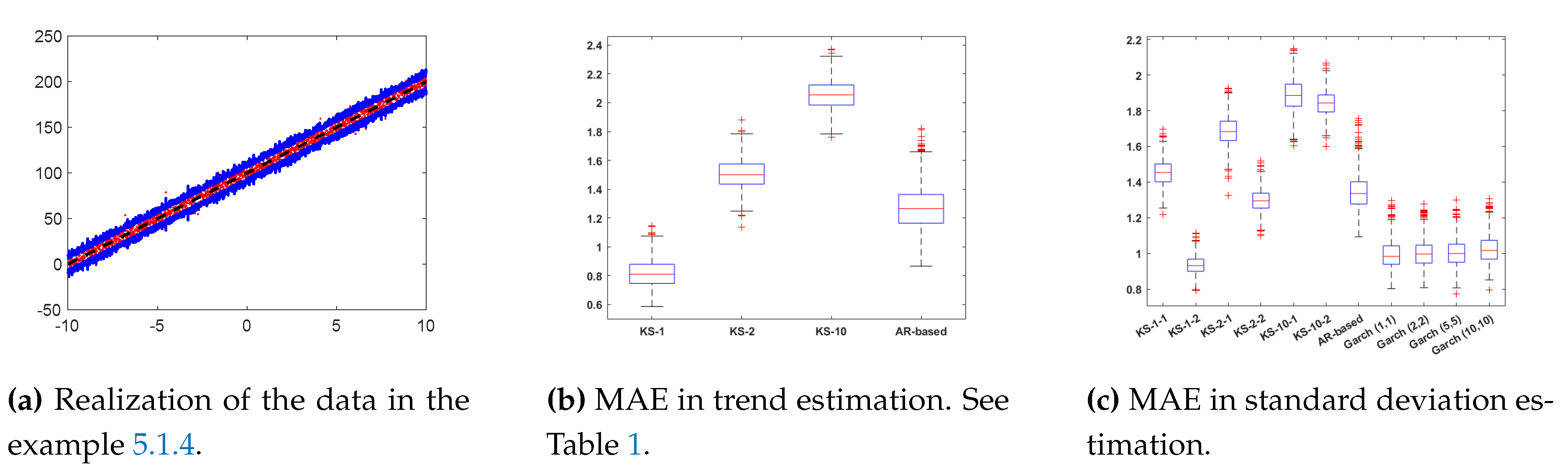
5.1.4. Experiment 4

Let us consider

\begin{matrix} y (t) & = s (t) ε (t), ε (t) \sim N (0, 1), \\ y_{t} & = s_{t} ϵ_{t} = z_{t}, \end{matrix}

i.e.,

f (t) = f_{t} = 0

, and we have denoted

z_{t} = s_{t} ϵ_{t}

. The process for the standard deviation

s_{t} = \sqrt{v_{t}}

will be a GARCH(

P, Q

), i.e.,

\begin{matrix} v_{t} = & κ + γ_{1} v_{t - 1} + \dots + γ_{P} v_{t - P} + \\ + α_{1} z_{t - 1}^{2} + \dots + α_{Q} z_{t - Q}^{2} . \end{matrix}

In this example, we generate the variance from a GARCH(

2, 3

)

\begin{matrix} v_{t} = & 2 + 0.2 \cdot v_{t - 1} + 0.1 \cdot v_{t - 2} + 0.2 \cdot z_{t - 1}^{2} + \\ + 0.2 \cdot z_{t - 2}^{2} + 0.2 \cdot z_{t - 3}^{2} \end{matrix}

(14)

Clearly, again, it is a heterostodastic scenario. we generate

N = 10^{4}

data and apply the different techniques. We compute the mean absolute error (MAE), and we repeat and average the results over

10^{4}

independent runs. One realization of the generated data is given in Figure 4. Note that the trend is linear but the volatility presents very fast changes since it generated by a GARCH(2,3) model (see blue line in Figure 4).

Results 4.The results for this example are presented in Figure 4b,c. The best performance in the estimation of

s (t)

are obtained by KS-1-2 and all the GARCH models (as expected in this case). The AR-based and KS-2-2 also provided close values of MAE. In this example, clearly M2 outperforms M1. We remark that, even in this scenario that is particularly favorable for the GARCH models, all the proposed methods provide competitive results. The highest (hence worst) MAEs values are given by the KS with

α = 10

which is a quite extreme tuning/choice of this parameter, specially when the volatility follows an autoregressive rule. Indeed, a Laplacian kernel with

α = 1

is more adequate in this framework. For further considerations see [15].

5.1.5. Final Comments about the Applications to Time Series

All the proposed methods based on kernel smoothers (KS) and M1, M2 always provide competitive results (with closer or smaller MAE values) with respect to the benchemark algorithms such as GARCH methods, which have been specifically designed for the estimation of the standard deviation in time series.

These numerical experiments show that the proposed M1 and M2 can even outperform GARCH models the estimation of the standard deviation in time series. The GARCH models seems to provide more robust results when the signal has been generated truly by a GARCH model in Section 5.1.4 and, surprisingly, in the homoscedasticscenario in Section 5.1.1. The methods based on kernel smoothers virtually outperform the AR-based due to the fact that they incorporate the “future samples” in their estimators. A rectangular window, including both past and future samples, should improve the performance of the AR-based method.

5.2. Application in Higher input Dimension: Real Data on Soundscape Emotions

GARCH models have been specifically designed for estimating the volatility in time series, hence

x = t \in R

. However, the methods proposed in this work can be applied to problems with multidimensional inputs

x \in R^{D}

with

D \geq 1

More specifically, here we focus on analyzing a soundscape emotion database. In the last decade, soundscapes have become one of the most active topics in acoustics. In fact, the number of related research projects and scientific articles grows exponentially [34,35,36]. In urban planning and environmental acoustics, the general scheme consists of (a) soundscapes recording, (b) computing of acoustic and psychoacoustic indicators of the signals, (c) including other context indicators (e.g. visual information [37]), and (d) ranking of soundscapes audio signals employing emotional descriptors. Finally, the model can be developed [24].

Here, we consider the emo-soundscapes database (EMO) [27,28], where

N = 1200

and

D = 122

, i.e.,

x \in R^{122}

, which is the largest available soundscape database with annotations of emotion labels, and also the most recent, up to now [27,38]. Among the 122 audio features that form the inputs

x

, we can distingush three main groups of features of the audio signals: psychoacoustic features, time-domain features and frequency-domain features. The output y that we consider is called arousal. For further information, the complete database can be found at https://metacreation.net/emo-soundscapes/. We employ again a kernel function of type

h (x, z) = h (x, z | λ) = exp (- \frac{| | x - {z | |}^{α}}{λ}),

with

α = 2

. Therefore, considering the EMO database

{x_{i}, y_{i}}_{i = 1}^{1200}

We apply M1 and M2 and CV-LOO for tuning

λ

. The MAE in estimating the trend is

0.0388

obtained with an optimal parameter

λ^{*} = 0.12

. Moreover, in both cases, we find a sensible increase of the volatility of the output in the last half of the samples, for i from 621 to 1213. This could be an interesting result, that should be discussed with experts on the field and in the EMO database.

6. Conclusions

In this work, we have proposed two methods for estimating the instant/local variance in regression problems based on kernel smoothers. From another point of view, this work can be also seen as a way to perform quantile regression (at least, a second order quantile regression) using kernel smoothers.

With respect to other procedures given in the literature, the proposed methods have a much wider applicability than other techniques, since they can be employed only for time series, as the well-known GARCH models (where the time index is a scalar number,

x = t \in R

). Indeed, the proposed schemes can be employed with multidimensional input variables

x_{n} \in R^{D}

. Moreover, the proposed techniques can be also applied to time series (

D = 1

) and also can obtain a prediction between two consecutive time instants (i.e., with an higher resolution that the received data). More generally, estimation of the local variance can given at any the training data

x_{i}

but also in any generic test input

x

Furthermore, analyzing time series, the numerical simulations have shown that the proposed schemes provides competitive results even with respect to GARCH models (which are specifically design for analyzing time series). An application to real data and multidimensional inputs (with dimension 122) have been also provided. As a future research line, we plan to design kernel smoother functions with local parameters

λ

, or more generally with

λ = λ (x)

, to better handle the heteroscedasticity. Moreover, the application to multioutput scenarios can be designed and considered.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org

Acknowledgments

This work was partially supported by the Young Researchers R&D Project, ref. num. F861 (AUTO-BA- GRAPH) funded by Community of Madrid and Rey Juan Carlos University, the Agencia Estatal de Investigación AEI (project SP-GRAPH, ref. num. PID2019-105032GB-I00) and by MICIIN/FEDER/UE, Spain under Grant PID2020-118071GB-I00.

Conflicts of Interest

The authors declare no conflict of interest.

References

Engle, R. Risk and volatility: Econometric models and financial practice. American Economic Review 2004, 94, 405–420. [Google Scholar] [CrossRef]
Chang, C.; McAleer, M.; Tansuchat, R. Modelling long memory volatility in agricultural commodity futures returns. Annals of Financial Economics 2012, 7, 1250010. [Google Scholar] [CrossRef]
Dedi, L.; Yavas, B. Return and volatility spillovers in equity markets: An investigation using various GARCH methodologies. Cogent Economics & Finance 2016, 4, 1266788. [Google Scholar]
Ibrahim, B.; Elamer, A.; Alasker, T.; Mohamed, M.; Abdou, H. Volatility contagion between cryptocurrencies, gold and stock markets pre-and-during COVID-19: evidence using DCC-GARCH and cascade-correlation network. Financial Innovation 2024, 10, 104. [Google Scholar] [CrossRef]
FAN, J.; YAO, Q. Efficient estimation of conditional variance functions in stochastic regression. Biometrika 1998, 85, 645–660. [Google Scholar] [CrossRef]
Yu, K.; Jones, M.C. Likelihood-Based Local Linear Estimation of the Conditional Variance Function. Journal of the American Statistical Association 2004, 99, 139–144. [Google Scholar] [CrossRef]
Ruppert, D.; Wand, M.P.; Holst, U.; Hössjer, O. Local Polynomial Variance-Function Estimation. Technometrics 1997, 39, 262–273. [Google Scholar] [CrossRef]
Cheng, H. Second Order Model with Composite Quantile Regression. Journal of Physics: Conference Series 2023, 2437, 012070. [Google Scholar] [CrossRef]
Huang, A.Y.; Peng, S.P.; Li, F.; Ke, C.J. Volatility forecasting of exchange rate by quantile regression. International Review of Economics and Finance 2011, 20, 591–606. [Google Scholar] [CrossRef]
Martino, L.; Llorente, F.; Curbelo, E.; López-Santiago, J.; Míguez, J. Automatic Tempered Posterior Distributions for Bayesian Inversion Problems. Mathematics 2021, 9. [Google Scholar] [CrossRef]
Baur, D.G.; Dimpfl, T. A quantile regression approach to estimate the variance of financial returns. Journal of Financial Econometrics 2019, 17, 616–644. [Google Scholar] [CrossRef]
Chronopoulos, I.C.; Raftapostolos, A.; Kapetanios, G. Forecasting Value-at-Risk using deep neural network quantile regression. Journal of Financial Econometrics 2023. [Google Scholar] [CrossRef]
Huang, Q.; Zhang, H.; Chen, J.; He, M. Quantile regression models and their applications: a review. Journal of Biometrics & Biostatistics 2017, 8, 1–6. [Google Scholar]
Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer, 2006.
Martino, L.; Read, J. Joint introduction to Gaussian Processes and Relevance Vector Machines with Connections to Kalman filtering and other Kernel Smoothers. Information Fusion 2021, 74, 17–38. [Google Scholar] [CrossRef]
Altman, N.S. Kernel Smoothing of Data With Correlated Errors. Journal of the American Statistical Association 1990, 85, 749–759. [Google Scholar] [CrossRef]
Bentley, J.L.; Stanat, D.F.; Williams, E.H. The complexity of finding fixed-radius near neighbors. Information Processing Letters 1977, 6, 209–212. [Google Scholar] [CrossRef]
Carandini, M.; Heeger, D. Normalization as a canonical neural computation. Nat. Rev. Neurosci. 2012, 13, 51–62. [Google Scholar] [CrossRef] [PubMed]
Malo, J.; Laparra, V. Psychophysically tuned divisive normalization approximately factorizes the PDF of natural images. Neural computation 2010, 22, 3179–3206. [Google Scholar] [CrossRef]
Ballé, J.; Laparra, V.; Simoncelli, E. Density modeling of images using a generalized normalization transformation. 2016. 4th International Conference on Learning Representations, ICLR 2016 ; Conference date: 02-05-2016 Through 04-05-2016.
Laparra, V.; Ballé., J.; Berardino, A.; Simoncelli, E. Perceptual image quality assessment using a normalized Laplacian pyramid. In Proceedings of the Proc. Human Vis. Elect. Im., 2016, Vol. 2016, pp. 1–6.
Laparra, V.; Berardino, A.; Ballé, J.; Simoncelli, E. Perceptually optimized image rendering. Journal of the Optical Society of America A 2017, 34, 1511. [Google Scholar] [CrossRef] [PubMed]
Hernendez-Camara, P.; Vila-Tomas, J.; Laparra, V.; Malo, J. Neural networks with divisive normalization for image segmentation. Pattern Recognition Letters 2023, 173, 64–71. [Google Scholar] [CrossRef]
Millan-Castillo, R.S.; Martino, L.; Morgado, E.; Llorente, F. An Exhaustive Variable Selection Study for Linear Models of Soundscape Emotions: Rankings and Gibbs Analysis. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2022, 30, 2460–2474. [Google Scholar] [CrossRef]
Rasmussen, C.E.; Williams, C.K.I. Gaussian processes for machine learning; MIT Press, 2006; pp. 1–248.
Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 1986, 31, 307–327. [Google Scholar] [CrossRef]
Fan, J.; Thorogood, M.; Pasquier, P. Emo-soundscapes: A dataset for soundscape emotion recognition. In Proceedings of the 2017 Seventh international conference on affective computing and intelligent interaction (ACII). IEEE; 2017; pp. 196–201. [Google Scholar]
Fonseca, E.; Pons Puig, J.; Favory, X.; Font Corbera, F.; Bogdanov, D.; Ferraro, A.; Oramas, S.; Porter, A.; Serra, X. Freesound datasets: a platform for the creation of open audio datasets. In Proceedings of the Hu X, Cunningham SJ, Turnbull D, Duan Z, editors. Proceedings of the 18th ISMIR Conference; pp. 201723–272017486.
Martino, L.; San Millan-Castillo, R.; Morgado, E. Spectral information criterion for automatic elbow detection. Expert Systems with Applications 2023, 231, 120705. [Google Scholar] [CrossRef]
Morgado, E.; Martino, L.; Millan-Castillo, R.S. Universal and automatic elbow detection for learning the effective number of components in model selection problems. Digital Signal Processing 2023, 140, 104103. [Google Scholar] [CrossRef]
Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 1986, 31, 307–327. [Google Scholar] [CrossRef]
Hansen, P.R.; Lunde, A. A forecast comparison of volatility models: does anything beat a GARCH (1, 1)? Journal of Applied Econometrics 2005, 20, 873–889. [Google Scholar] [CrossRef]
Trapero, J.R.; Cardos, M.; Kourentzes, N. Empirical safety stock estimation based on kernel and GARCH models. Omega 2019, 84, 199–211. [Google Scholar] [CrossRef]
Aletta, F.; Xiao, J. What are the current priorities and challenges for (urban) soundscape research? Challenges 2018, 9, 16. [Google Scholar] [CrossRef]
Lundén, P.; Hurtig, M. On urban soundscape mapping: A computer can predict the outcome of soundscape assessments. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering, Vol. 253; 2016; pp. 2017–2024. [Google Scholar]
Lionello, M.; Aletta, F.; Kang, J. A systematic review of prediction models for the experience of urban soundscapes. Applied Acoustics 2020, 170, 107479. [Google Scholar] [CrossRef]
Axelsson, O.; Nilsson, M.E.; Berglund, B. A principal components model of soundscape perception. The Journal of the Acoustical Society of America 2010, 128, 2836–2846. [Google Scholar] [CrossRef] [PubMed]

The value

α = 1

is the minimum possible value if we desire to have a suitable

L_{p}

distance (with

p = α

), satisfying all the properties of a distance. The choice of

α = 2

is just in order to consider the typical Euclidean distance. For bigger values of

α

, we set

α = 10

also for avoiding possible numerical problems.

Figure 1. (a) A realization of the data (red dots) generated by the model in Section 5.1.1; the function

f (t)

is shown dashed black line and the two continue blue lines depict

f (t) \pm 2 s (t)

(containing approx. 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.1.

Figure 1. (a) A realization of the data (red dots) generated by the model in Section 5.1.1; the function

f (t)

is shown dashed black line and the two continue blue lines depict

f (t) \pm 2 s (t)

(containing approx. 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.1.

Figure 2. (a) A realization of the data (red dots) generated by the model in Section 5.1.2; the function

f (t)

is shown dashed black line and the two continuous blue lines depict

f (t) \pm 2 s (t)

(containing approximately 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.2.

Figure 2. (a) A realization of the data (red dots) generated by the model in Section 5.1.2; the function

f (t)

is shown dashed black line and the two continuous blue lines depict

f (t) \pm 2 s (t)

(containing approximately 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.2.

Figure 3. (a) A realization of the data (red dots) generated by the model in Section 5.1.3; the function

f (t)

is shown as a dashed black line and the two continuous blue lines depict

f (t) \pm 2 s (t)

(containing approximately 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.3.

Figure 3. (a) A realization of the data (red dots) generated by the model in Section 5.1.3; the function

f (t)

is shown as a dashed black line and the two continuous blue lines depict

f (t) \pm 2 s (t)

(containing approximately 95% of the probability mass). (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.3.

Figure 4. (a) A realization of the data (red dots) generated by the model in Section 5.1.4. The linear trend

f (t) = t

is shown as a dashed black line. Whereas the two continuous blue lines depict

f (t) \pm 2 s (t)

where

s (t)

is generated by a GARCH model. (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.4.

Figure 4. (a) A realization of the data (red dots) generated by the model in Section 5.1.4. The linear trend

f (t) = t

is shown as a dashed black line. Whereas the two continuous blue lines depict

f (t) \pm 2 s (t)

where

s (t)

is generated by a GARCH model. (b)-(c) Box-plots of the MAEs of the different algorithms of the experiment in Section 5.1.4.

Table 1. Proposed methods (specific implementations) tested in the numerical experiments.

Method	KS-1-1	KS-1-2	KS-2-1	KS-2-2	KS-10-1	KS-10-2	AR-based
For trend estimation	Eqs. (1)-(12), $α = 1$		Eqs. (1)-(12), $α = 2$		Eqs. (1)-(12), $α = 10$		AR - Section 4.2
For variance estimation	M1	M2	M1	M2	M1	M2	AR and M2 - Section 4.2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Second Moment/Order Approximations by Kernel Smoothers with Application to Volatility Estimation

Abstract

1. Introduction

2. Approximating the Trend

3. Variance Estimation Procedures

4. Extensions and Variants

4.1. Multi-Output Scenario and other Extensions

4.2. Example of Alternative to the Kernel Smoothers for Time Series Analysis

5. Numerical Experiments

5.1. Applications to Time Series

5.1.1. Experiment 1

5.1.2. Experiment 2

5.1.3. Experiment 3

5.1.4. Experiment 4

5.1.5. Final Comments about the Applications to Time Series

5.2. Application in Higher input Dimension: Real Data on Soundscape Emotions

6. Conclusions

Supplementary Materials

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe