Submitted:
31 March 2024
Posted:
01 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
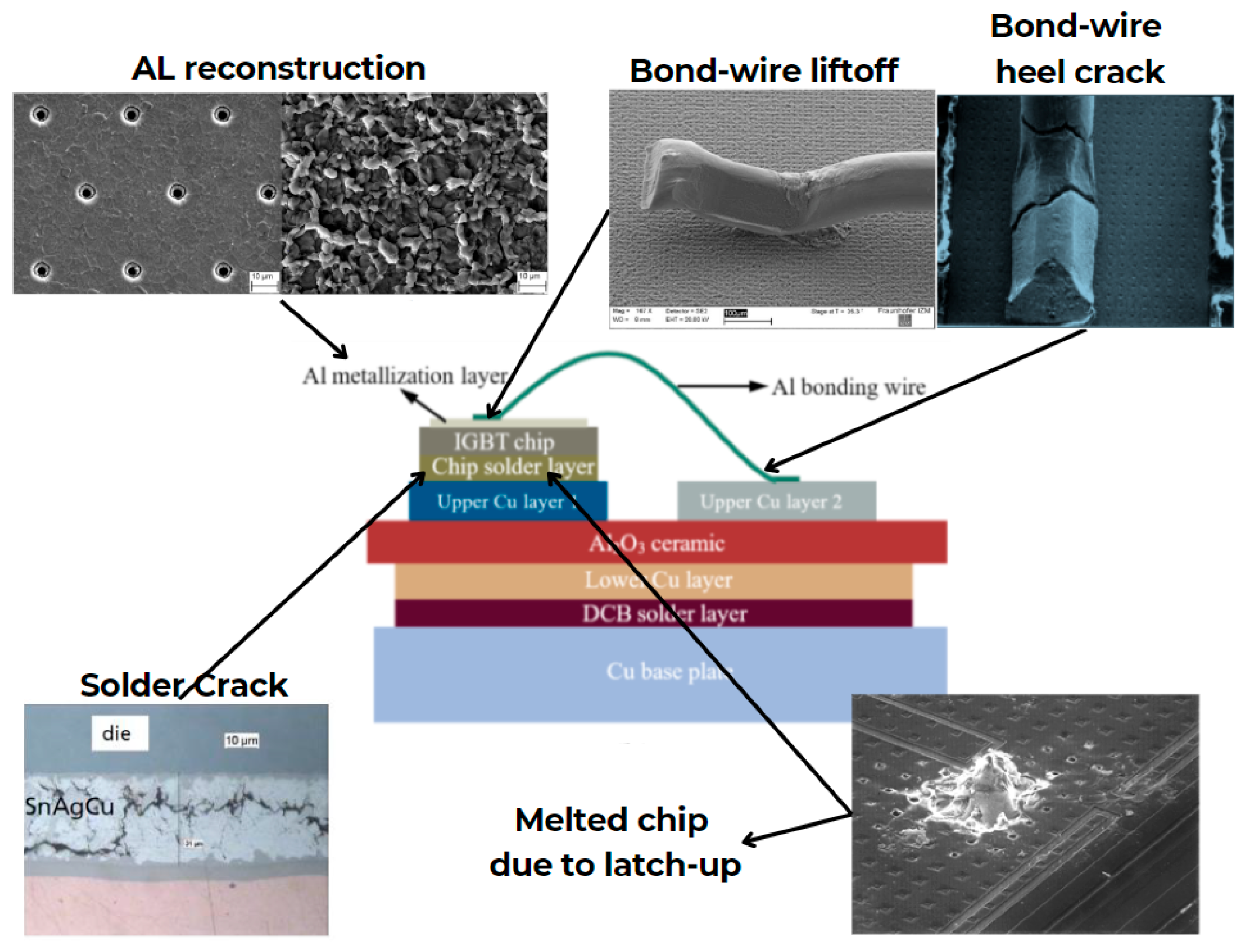
2. Mathematical Equation of the Grain Boundary Grooving
3. Case of Evaporation/Condensation [51,52]
4. Diffusion Case [53]
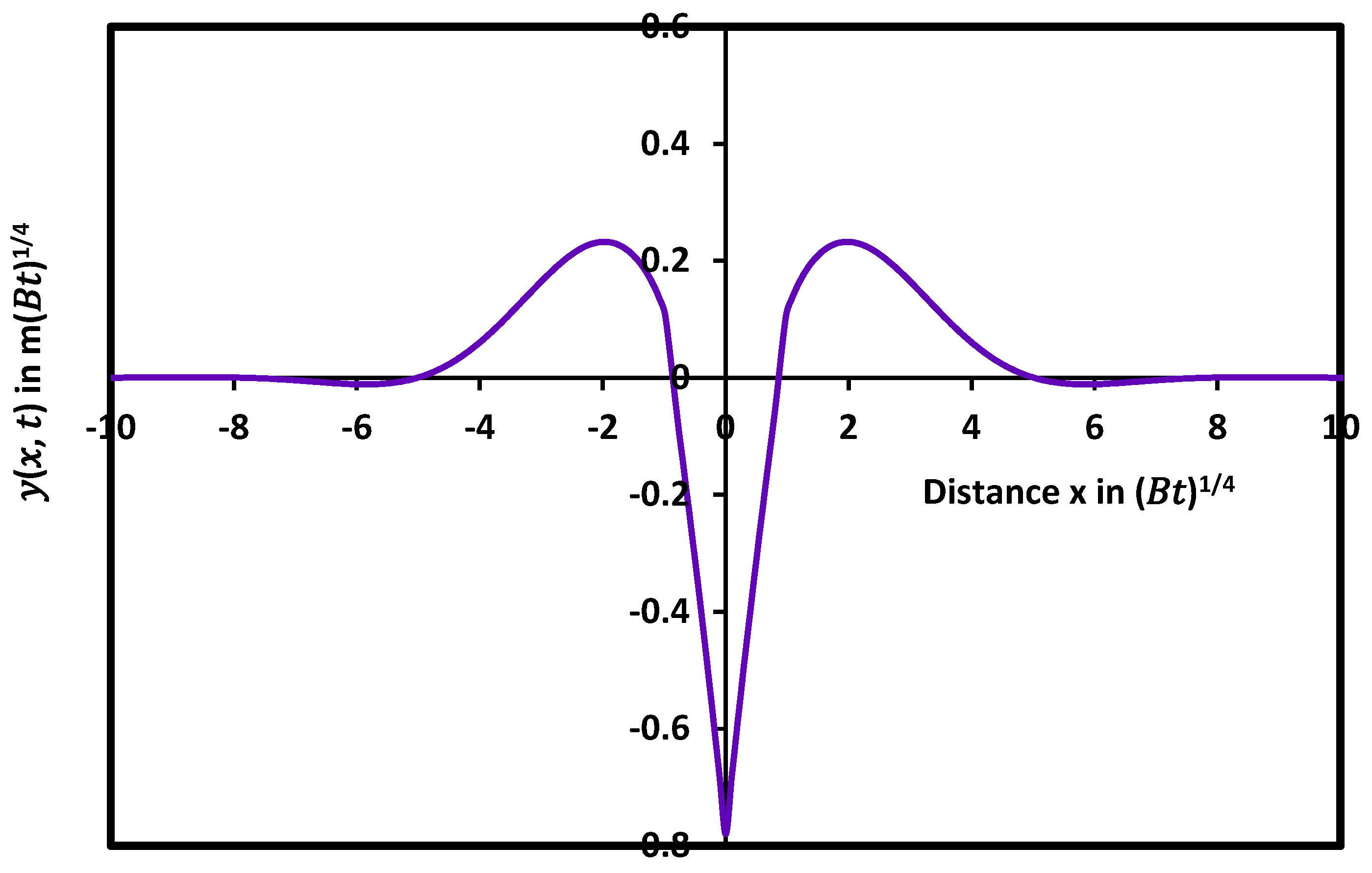
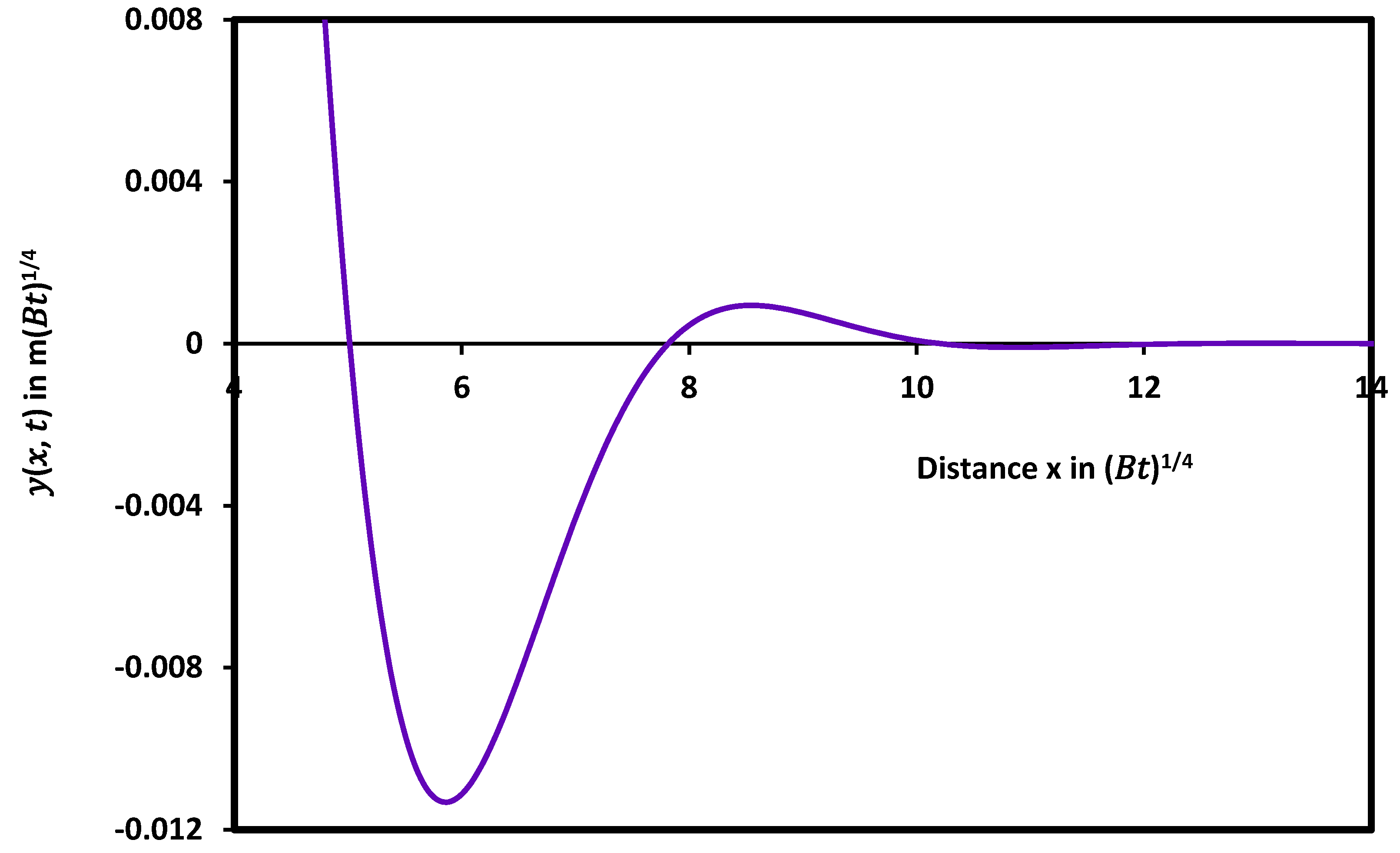
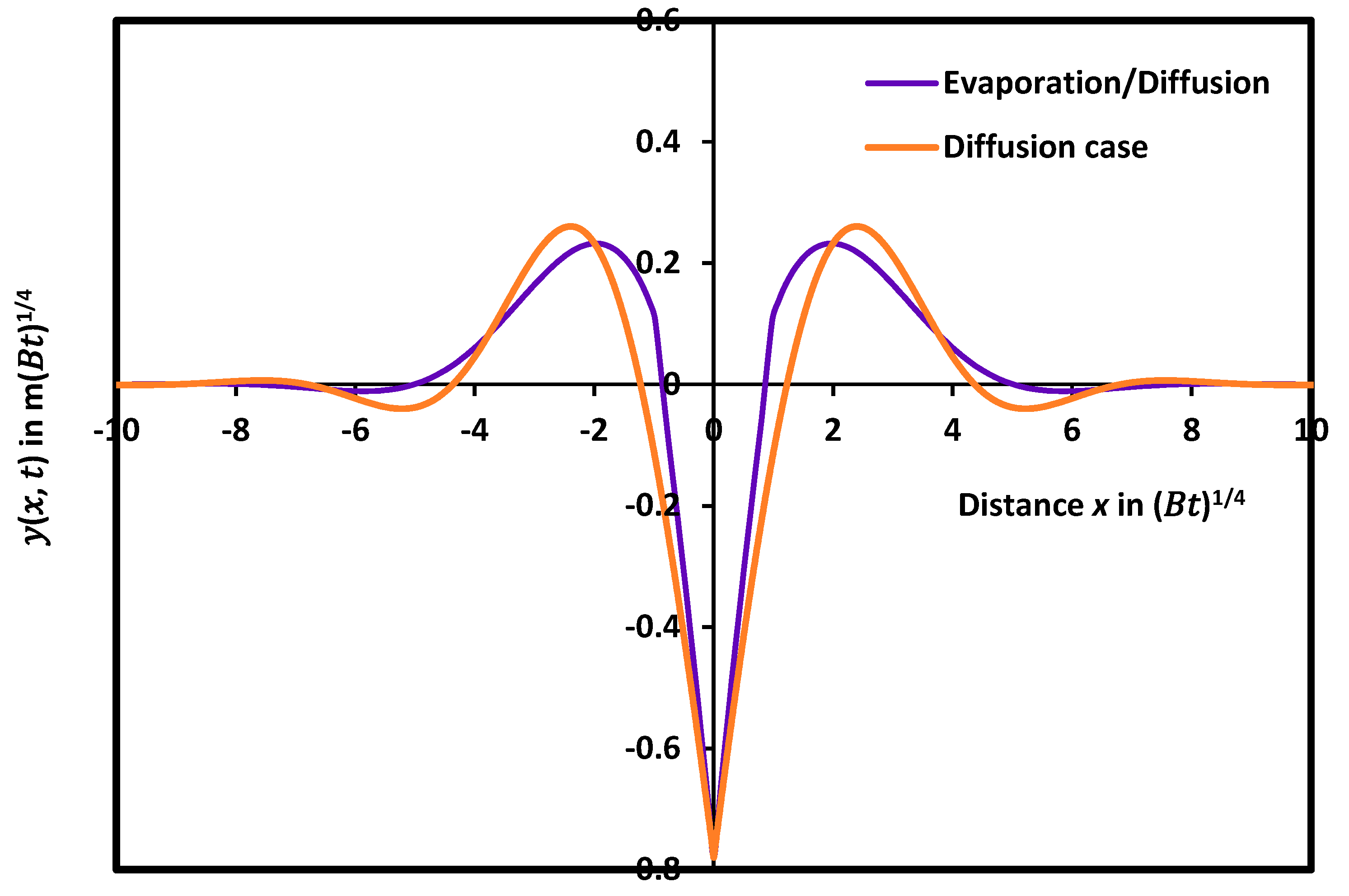
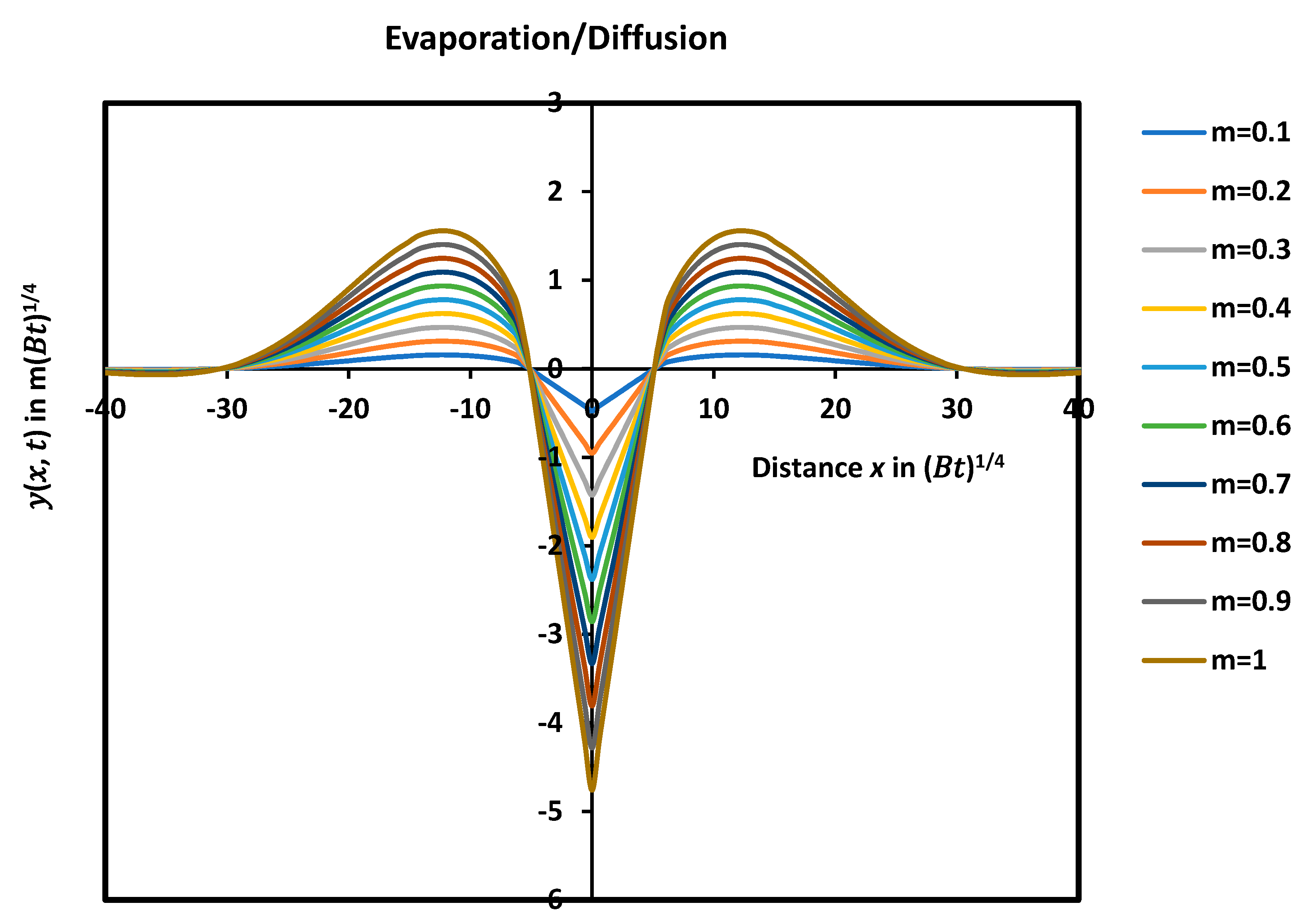
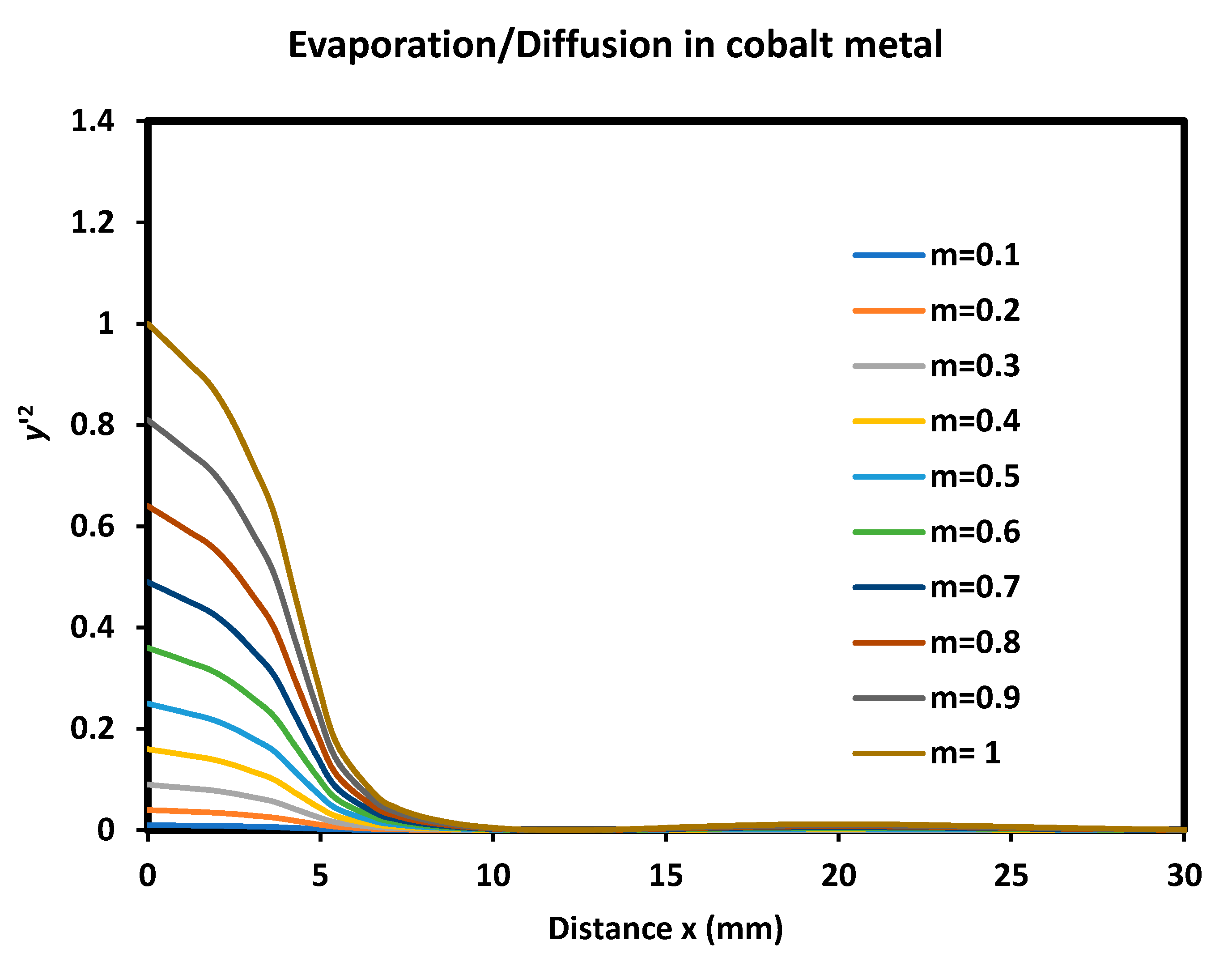
5. Study of the Combination of Evaporation/Condensation and Diffusion Cases
Mathematical Resolution of the Combined Cases
7. Analytical Solution by Using the Series Development
7. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- 1. First case for u
- 2. Second case for
References
- Zibo Chen, Alex Q. Huang, Extreme high efficiency enabled by silicon carbide (SiC) power devices, Materials Science in Semiconductor Processing, 2024, 172. [CrossRef]
- J. Millán, P. Godignon, X. Perpiñà, A. Pérez-Tomás, J. Rebollo, A survey of wide bandgap power semiconductor devices, IEEE Trans. Power Electron., 2014, 29 (5), 2155-2163.
- X. Li, et al. Achieving zero switching loss in silicon carbide MOSFET, IEEE Trans. Power Electron., 2019, 34 (12), 12193-12199.
- Cui, T., Mukherjee, S., Sudeep, P.M. et al. Fatigue of graphene. Nat. Mater. 2020, 19, 405–411. [CrossRef]
- Mughrabi, H. Fatigue, an everlasting materials problem - still en vogue, Proc. Eng., 2010, 2, 3-26.
- Sangid, M.D. The physics of fatigue crack initiation, Int. J. Fatigue, 2013, 57, 58-72.
- Zhang, Y. , Udrea, F. & Wang, H. Multidimensional device architectures for efficient power electronics. Nat Electron 2022, 5, 723–734. [Google Scholar] [CrossRef]
- Jin, Q., Guo, T., Pérez, N. et al. On-Chip Micro Temperature Controllers Based on Freestanding Thermoelectric Nano Films for Low-Power Electronics. Nano-Micro Lett., 2024, 16, 126. [CrossRef]
- Zhou, F., Gong, H., Xiao, M. et al. An avalanche-and-surge robust ultrawide-bandgap heterojunction for power electronics. Nat Commun, 2023, 14, 4459. [CrossRef]
- Antoniou, M., Udrea, F. & Bauer, F. Robustness of superjunction structures against cosmic ray induced breakdown. Solid State Electron. 2010, 54, 385–391. [Google Scholar] [CrossRef]
- Zhou, X., Howell-Clark, J. R., Guo, Z., Hitchcock, C. W. & Chow, T. P. Performance limits of vertical GaN of conventional doped pn and natural polarization superjunction devices. Appl. Phys. Lett. 2019, 115, 112104.
- Kaplar, R. J. et al. Review—ultra-wide-bandgap algan power electronic devices. ECS J. Solid State Sci. Technol. 2016, 6, Q3061.
- Mokarian Zanjani, S., Sadeghi, S., Shahalizad, A. et al. An investigation on the cyclic temperature-dependent performance behaviors of ultrabright air-stable QLEDs. Sci Rep, 2023, 13, 12713. [CrossRef]
- Mullins, W. W. Theory of thermal grooving. Journal of Applied Physics, 1957, 28 (3), 333-339.
- Mullins, W. W. The effect of thermal grooving on grain boundary motion, Acta Metallurgica, 1958, 6 (6), 414-427.
- Mullins, W. W. Grain boundary grooving by volume diffusion. Transactions of the Metallurgical Society of AIME, 1960, 218, 354-361.
- N. Klein, Electrical Breakdown in Solids, Advances in Electronics and Electron Physics, Academic Press, Volume 26, 1969, Pages 309-424, Editor(s): L. Marton. [CrossRef]
- Lee, C., Kort-Kamp, W.J.M., Yu, H. et al. Grooved electrodes for high-power-density fuel cells. Nat Energy, 2023, 8, 685–694. [CrossRef]
- Hui Ren, Guisheng Zou, Qiang Jia, Zhongyang Deng, Chengjie Du, Wengan Wang, Lei Liu, Thermal stress reduction strategy for high-temperature power electronics with Ag sintering, Microelectronics Reliability, 2021, Volume 127, 114379. [CrossRef]
- Liu, H.; Xue, S.; Tao, Y.; Long, W.; Zhong, S. Design and solderability characterization of novel Au–30Ga solder for high-temperature packaging, J. Mater. Sci. Mater. Electron., 2020, 31 (3), 2514-2522.
- Xin Wang, Chunling Xu, Aoshuang Zhai, Ming Liu, Xiao Huang, Kai Tian, Xuekun Luo, Chenguang Liu, Zhihui Tang, Zhenye Zhao, Effect of surface stress concentration control and surface material strengthening on the fatigue performance of shot-peened single-crystal superalloy, Journal of Alloys and Compounds, 2023, 933, 167796. [CrossRef]
- J. Sun, S. Yang, H. Yuan, Assessment of thermo-mechanical fatigue in a nickel-based single-crystal superalloy CMSX-4 accounting for temperature gradient effects, Mater. Sci. Eng. A, 2021, 809 , 140918. [CrossRef]
- Ge, Z.; Xie, G.; Segersäll, M. et al., Influence of Ru on the thermomechanical fatigue deformation behavior of a single crystal superalloy, Int. J. Fatigue, 2022, 156 , 106634,. [CrossRef]
- Zhang, Z., Xu, L., Qu, T. et al. Diffusion metamaterials. Nat Rev Phys, 2023, 5, 218–235. [CrossRef]
- Narayana, S. & Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett., 2012, 108, 214303.
- Guenneau, S., Petiteau, D., Zerrad, M., Amra, C. & Puvirajesinghe, T. Transformed Fourier and Fick equations for the control of heat and mass diffusion. AIP Adv., 2015, 5, 053404.
- Hu, H. et al. Observation of topological edge states in thermal diffusion. Adv. Mater., 2022, 34, 2202257.
- Xuwei Zhuang, Aibing Zhang, Baolin Wang & Ji Wang, Thermal and diffusion induced stresses of layered electrodes in the lithium-ion battery under galvanostatic charging, Journal of Thermal Stresses, 2023, 46(12), 1313-1328. [CrossRef]
- Xue Mei Luo, Bin Zhang, Guang Ping Zhang, Fatigue of metals at nanoscale: Metal thin films and conductive interconnects for flexible device application, Nano Materials Science, 2019, 1(3), 198-207. [CrossRef]
- Eberl, C. et al. Ultra high-cycle fatigue in pure Al thin films and line structures, Mater. Sci. Eng., A, 2006, 421 (1–2) , pp. 68-76.
- Schwaiger, R.; Kraft, O. Size effects in the fatigue behavior of thin Ag films, Acta Mater., 2003, 51 (1), 195-206.
- Chason, E., et al., Stress in thin films and coatings: Current status, challenges, and prospects. Journal of Vacuum Science & Technology A, 2018, 36 (2), 020801.
- Doerner, M.F.; Nix, W.D. Stresses and deformation processes in thin films on substrates, Crit. Rev. Solid State Mater. Sci., 1988, 14 (3), 225-268. [CrossRef]
- Nix, W.D. Mechanical properties of thin films, Metall. Trans. A, 1989, 20 (11) , 2217-2245. [CrossRef]
- Kaiser, N. Review of the fundamentals of thin-film growth, Appl. Opt., 2002, 41 (16) , 3053-3060. [CrossRef]
- Zhang, H.; Wong, H. Coupled grooving and migration of inclined grain boundaries: regime I. Acta Materialia, 2002, 50, 1983–1994.
- Bouville, M.; Dongzhi, C.; Srolovitz, D. J. Grain-boundary grooving and agglomeration of alloy thin films with a slowdiffusing species. Physical Review Letters, 2007, 98 (8), 1-3.
- Bouville, M. Effect of grain shape on the agglomeration of polycrystalline thin films. Applied Physics Letters, 2007, 90, no.6, Article ID 061904, 3 pages.
- Genin, F. Y.; Mullins, W. W.; Wynblatt, P. The effect of stress on grain-boundary grooving, Acta Metall. 1993, 41, 3541-3547.
- Hackney, S. A. Grain-boundary grooving at Þnite grain size, Scripta Metall. 1988, 22, 1731.
- Klinger, L.; Glickman, E.; Fradkov, V.; Mullins, W.W.; Bauer, C. Extension of thermal grooving for arbitrary grain-boundary ßux. J. Appl. Phys. 1995, 78, 3833–3838. [Google Scholar] [CrossRef]
- Klinger, L.; Glickman, E.; Fradkov, V.; Mullins, W.W.; C. Bauer, Effect of surface and grain-boundary diffusion on interconnect reliability. Mater. Res. Soc. Symp. Proc. 1995, 391, 295, 1995.
- Brokman, A. K. R.; Mullins W.W.; Vilenkin, A.J. Analysis of boundary motion in thin films. Scripta Metallurgica et Materialia, 1995, 32 (9), 1341-1346.
- Stone, H. A.; Aziz, M. J.; Margetis, D. Grooving of a grain boundary by evaporation–condensation below the roughening, Journal of Applied Physics, 2005, 97, 113535-1-6.
- Tritscher, P. An integrable fourth-order nonlinear evolution equation applied to surface redistribution due to capillary. J. Austral. Math. Soc. Ser. B, 1997, 38, 518-541.
- Hristov, J.; Multiple integral-balance method: Basic idea and an example with Mullin’s model of thermal grooving, Thermal Science, 2017, 21 (3), 1555-1560. [CrossRef]
- Hristov, J. ; Fourth-order fractional diffusion model of thermal grooving: integral approach to approximate closed form solution of the Mullins model. Math. Model. Nat. Phenom. 2018, 13 (6), 2018. 14p. [Google Scholar] [CrossRef]
- Tritscher, P.; Broadbridge, P. Grain boundary grooving by surface diffusion: an analytic nonlinear model for a symmetric groove. Proc. Roy. Soc. London A, 1995, 450, 569–587.
- Schwartz, L.W.; Roy, R.V. Theoretical and numerical results for spin coating of viscous liquids. Phys. Fluids 2004, 16(3), 569–584. [Google Scholar] [CrossRef]
- Mullins, W. W.; Sekerka, R. F. Morphological Stability of a Particle Growing by Diffusion or Heat Flow. J. Appl. Phys. 1963, 34, pp. 323–329. https://link.springer.com/chapter/10.1007/978-3-642-59938-5_4.
- Hamieh, T.; Khatir, Z.; Ibrahim, A. Analytical Solutions to the Problem of the Grain Groove Profile. Nanoscience & Technology: Open Access, 2018. [CrossRef]
- Hamieh, T.; Khatir, Z.; Ibrahim, A. New solution of the partial differential equation of the grain groove profile problem in the case of evaporation/condensation. Scientific Reports, 2019, 9 (1), 1-17. [CrossRef]
- Hamieh, T.; Ibrahim, A.; Khatir, Z. Thermal Fatigue Effect on the Grain Groove Profile in the Case of Diffusion in Thin Polycrystalline Films of Power Electronic Devices. Micromachines, 2023, 14, 1781. [CrossRef]
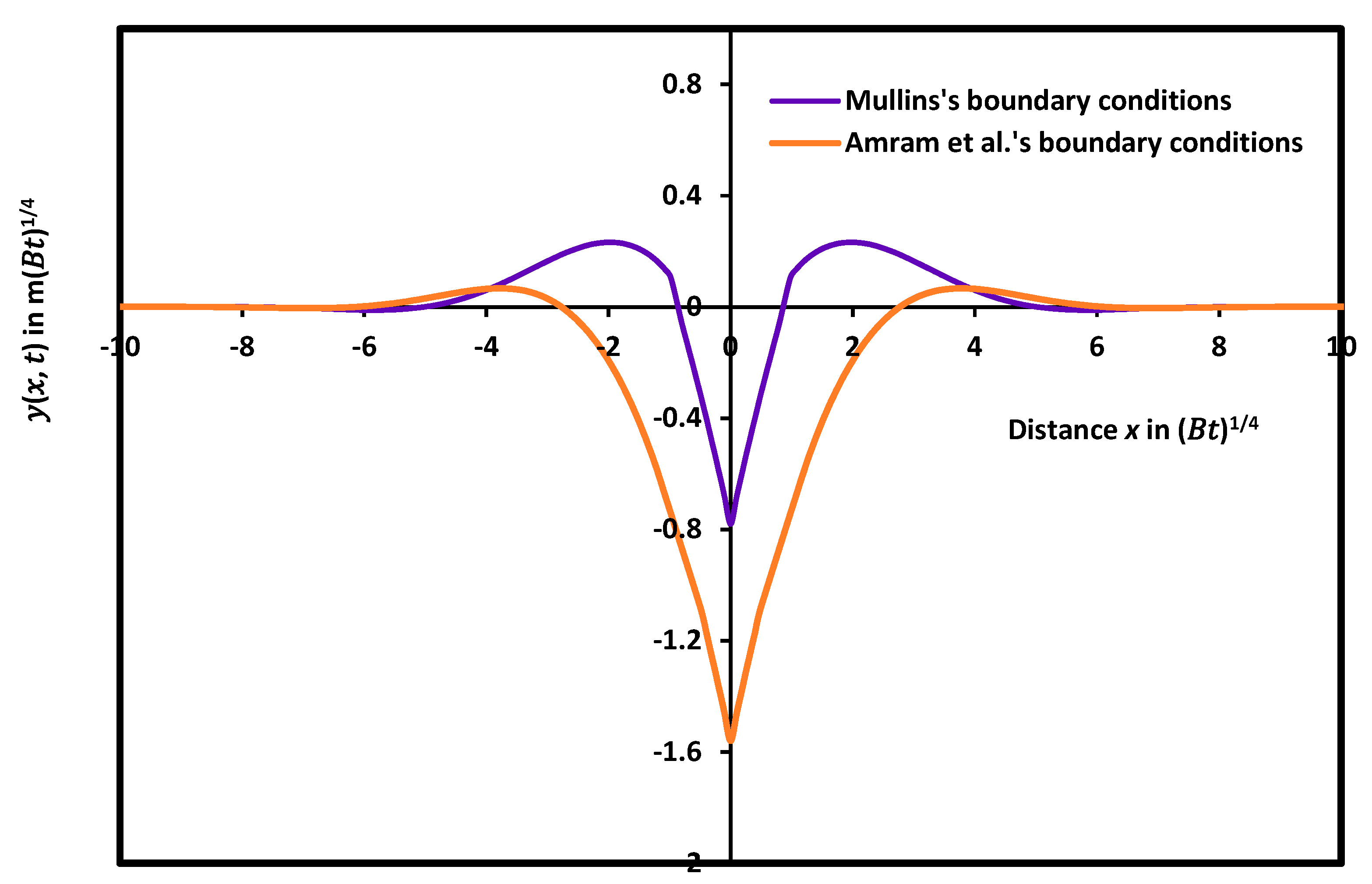
- D. Amram, L. Klinger, N. Gazit, H. Gluska, E. Rabkin, Grain boundary grooving in thin films revisited: The role of interface diffusion, Acta Materialia, 2014, 69, 386-396. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




