Preprint
Article
Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems
Altmetrics
Downloads
74
Views
31
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 March 2024
Posted:
02 April 2024
You are already at the latest version
Alerts
Abstract
Major (exo)planetary and satellite bodies seem to concentrate at intermediate areas of the radial 1
distributions of all the objects orbiting in each (sub)system. We show that angular-momentum transport during secular evolution of (exo)planets and satellites necessarily results in the observed intermediate accumulation of the massive objects. We quantify the ‘middle’ as the mean of mean motions (orbital angular velocities) when three or more massive objects are involved. Radial evolution of the orbits is expected to be halted when the survivors settle near mean-motion resonances and angular-momentum transfer between them ceases (gravitational Landau damping). This dynamical behavior is opposite in direction to what has been theorized for viscous and magnetized accretion disks, in which gas spreads out and away from either side of any conceivable intermediate area. We present angular momentum transfer simulations in few-body systems, and we calculate the tidal dissipation timescales and the physical properties of the mean tidal field in planetary and satellite (sub)systems.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
An inspection of planetary and satellite orbital data in the solar system1 reveals that major objects seem to cluster at intermediate areas of the radial distributions of orbiting bodies, and only smaller objects are found in the inner and the outer regions of these subsystems. The same arrangement of massive objects is usually seen in multiplanet extrasolar systems as well. Keeping in mind that there may be more undetected planets farther out in these systems, some examples presently are: HD 10180 [42], Kepler-80 and 90 [60], TRAPPIST-1 [19,27], HR 8832 [9,32,65], K2-138 [12,41], Kepler-11 [39], and even the four-planet systems of Kepler-223 [49] and GJ 876 [48,57]. Despite being a clue pertaining to the processes of massive planet and large satellite formation and evolution, this conspicuous property has not been discussed in the past, and there have been no ideas about how we could possibly exploit it to learn from it.
Our approach to the problem has been single-minded from the outset. It was apparent to us that such large bodies have moved toward one another during early evolution, perhaps as soon as a few large solid cores emerged in these subsystems and the accretion disks dissipated away. In such a case, there must exist a generic physical mechanism (a global tidal field) that drives angular-momentum redistribution, but eventually further migration is hindered when this mechanism ceases to operate. In this work, we formulate such a secular mechanism (gravitational Landau damping of the tidal field) that relies on first principles and requires no additional conditions in order to operate. Some related calculations, commonly involving continuous fluids or collisionless systems with at least particles, have been carried out by other researchers in the past [2,25,45,54,55,56,63]. The differences that we point out below concern the details of evolution of just a few (4-7) major bodies and the physical interpretation of the results.
In § 2, we describe the dynamical evolution of two interacting Keplerian fluid elements through nonequilibrium states that leads to a runaway dynamical instability. This analysis is applicable to magnetized accretion disks, but not to planets or satellites in which the integral of circulation is not conserved (not even approximately—these systems are topologically not simply-connected). In § 3, we describe the secular evolution of large individual gravitating bodies in Keplerian orbits around a central mass and under the influence of tidal dissipation which leads to body clustering. In § 4, we discuss our results in the context of planet and satellite evolution.
Quite a few technical details are deferred to three self-contained appendices. In Appendix A, we describe few-body systems evolving by exchanging angular momentum and lowering their total mechanical energies. In Appendix B, we formulate a self-consistent calculation of the charactiristic tidal dissipation time and the corresponding radial velocity fluctuations in such systems. In Appendix C, we analyze gravitational Landau damping of the tidal field in few-body systems, a unique mechanism responsible for settling of the bodies near mean-motion resonances over times comparable to , where they no longer exchange substantial amounts of angular momentum and so they send the global tidal field to oblivion.
2. Dynamical Evolution of Interacting Keplerian Fluid Elements
Balbus and Hawley [2] introduced a mechanical analog of the magnetorotational instability (MRI) in gaseous accretion disks, two mass elements and in circular Keplerian orbits around a central mass with radii and , respectively. The mass elements are connected by a weak spring with constant k (representing a magnetic-field line) whose role is to allow for angular momentum transfer between the elements. When perturbed under the constraint of constant total angular momentum,2 this model behaves just like gaseous accretion disks under the influence of viscosity [45], except that the instability is now dynamical: the masses move apart and their displacements reduce the total free energy of the system [17], leading to a runaway [1,2,13,14].
We use the phase-transition formalism [17] to describe the evolution of this system out of equilibrium: if a perturbation lowers the free energy () while preserving the total angular momentum (), the system will transition to a new nonequilibrium state of lower energy; whereas if , the system will just oscillate about the initial equilibrium state characterized by total energy and total angular momentum . We assume that the initial equilibrium orbits are perturbed by small displacements and . Then the conservation of total angular momentum relates the displacements to first order by the equation
where and are the equilibium azimuthal velocities, and the change in free energy to first order is found to be
where , and and are the mean motions (orbital angular velocities) of the masses in their equilibrium state. The change in potential energy of the spring, , is of second order and is omitted from equation (2). It is now apparent that for , then and . The masses move apart and the resulting nonequilibrium configuration is unstable to continuing disengagement that will reduce further the free energy of the system.
The above dynamical instability (a mechanical analog of the MRI) does not operate in planetary and satellite systems. It is strictly applicable to perfect fluids in which circulation and angular momentum are both conserved [17]. Conservation of circulation is implicit in the above model; it can be readily seen in equation (1) assuming that the mass elements are axisymmetric rings with equal masses, in which case the equation takes the equivalent form
to first order in the displacements.
In viscous unmagnetized disks, dissipative stresses destroy circulation slowly and the instability is then secular [45]. In stellar and particle systems, there is no conservation law of circulation and equation (3) is invalid, even in approximate form, because all the elements of the stress tensor introduce gradients of comparable magnitude into the Jeans equations of motion [3,7,17]. Therefore, the evolution of multiple planetary and satellite bodies requires a different mathematical approach, though still constrained by the applicable conservation laws of energy and angular momentum.
3. Secular Evolution of Interacting Planets and Satellites
Ostriker and Gunn [54] studied the secular evolution of a dynamically stable, uniformly-rotating pulsar subject to angular momentum and energy losses due to emission of multipolar radiation. Evolution takes place slowly over timescales much longer than the dynamical time (the rotation period) of the object. In this model, the pulsar is thought of as transitioning between quasistatic equilibrium states (the Dedekind ellipsoids [10]) in which it maintains its uniform rotation albeit with a slowly changing angular velocity . Here, ‘slowly’ is quantified by the condition that
Under a series of assumptions, the strongest of which is inequality (4), Ostriker and Gunn [54] proved that the losses in angular momentum L and rotational kinetic energy E are related by the equation
where the time derivatives are both implicitly negative. The use of E for rotational kinetic energy (their Equation (7)) has caused some indiscretions in the literature. For example, Page and Thorne [55] call E the ‘energy-at-infinity’ (which is kinetic after all) and equation (5) ‘universal’ despite having derived it under their assumption iv(a), which is essentially equivalent to condition (4); whereas Papaloizou [56] calls E the ‘orbital energy’ of a planet in the context of the same quasistatic approximation.
Below, we also use equation (5) to follow the secular evolution of planets and satellites losing kinetic energy slowly due to the action of dissipative processes induced by a global tidal field. First, we revisit the approach of Papaloizou [56] whose calculation is correct but his conclusion is wrong. Then, we formulate the same problem as a variation of the free energy of the system [17] undergoing quasistatic out-of-equilibrium evolution away from its initial equilibrium state.
3.1. Papaloizou Approach
We consider two gravitating bodies with masses and orbiting around a central mass in nearly circular Keplerian orbits with radii and , respectively. We assume that tides due to M during orbit circularization are dissipated in the interiors of the bodies, causing small amounts of kinetic energy to be converted to heat H. The slow rate of dissipation is given by
Here, ‘slow’ is defined by inequality (4) and by the condition that
where T is the total orbital kinetic energy of the bodies. Then the evolution of the system is described by a sequence of quasistatic equilibrium states that are accessible to the bodies because equation (6) together with energy conservation guarantee that the total mechanical energy E of the bodies will decrease in time ().
The mechanical energy and angular momentum contents of each body are related by
where and is the mean motion of body . Since , then for the Keplerian orbits. Under the quasistatic assumption (4), a relation analogous to equation (5) is also applicable here, in the form
The factor of appears because represents the mechanical energy of each body which is implicitly negative (, where G is the Newtonian gravitational constant). The negative sign cannot be absorbed in equations (8) and (9) because, unlike in equation (5) above, here the individual terms and have opposite signs.
Conservation of total angular momentum is expressed by the equation
and total energy conservation for the system gives
Using equations (9), we rewrite equation (10) in the form
Thus, after considerable deliberations of the details, we have arrived at the equations adopted by Papaloizou [56].
It is obvious from equations (11) and (12) that, as the system evolves quasistatically, the mechanical energy of one body will increase and that of the other body will decrease; but the overall change in will be a decrease by an amount of , allowing for the system to proceed to a neighboring quasi-equilibrium state. In the absence of a model for , it is not prudent to solve these equations for the energy rates in order to deduce the details of the evolution. It is more sensible to examine the changes in angular momentum of the bodies: Combining equations (9)-(11), we find that
where and . We see now that the inner body 1 will gain angular momentum and will move outward, while the outer body 2 will lose angular momentum and will move inward. Overall, the two bodies will converge toward an intermediate orbit in which they would both share the total angular momentum equally.
Surprisingly, convergence toward the intermediate orbit with the average angular momentum does not occur in three or more orbiting bodies (Appendix A), where a new ‘critical orbit’ emerges, characterized by a mean motion , the average of the initial mean motions of the bodies. But in these systems, convergence toward this critical orbit will not continue unscathed, if two-body encounters set in and upset the quasistatic evolution. For the same reason, this orbit is in principle secularly unstable, but a body placed on it will remain in place for a long time, provided that another orbiting body does not come close. These results are established in Appendix A, and their significance and repercussions are discussed in § 4.
3.2. Free-Energy Variational Approach
We formulate briefly the problem studied in § 3.1 as a variation of the free energy of the system of two bodies with masses () orbiting around a central mass and stepping out of equilibrium and into a new state while still obeying conditions (4), (7), and (9). The two bodies can move on to such a (generally nonequilibrium) state only if this state is characterized by lower free energy () and the same total angular momentum (). The total mechanical energy plays the role of the free energy function [17] here, thus we have
and
Combining these two relations with equations (9) in the form , we find that
For (implying that the initial Keplerian radii obey ), we find that and , respectively. Thus, in order for the system to begin its search for a new equilibrium state of lower free energy, the inner body will move outward and the outer body will move inward.
4. Summary and Discussion
4.1. Summary
We have used the conservation laws of energy and angular momentum to describe and contrast the dynamical evolution of two interacting mass elements in a gaseous accretion disk and the secular evolution of massive planets and large satellites. Both types of subsystems were assumed to exhibit Keplerian orbital profiles around a dominant central mass and to exchange angular momentum via weak tidal torques. But evolution takes different paths in these two cases, and the reason is the (non)conservation of circulation. In perfect-fluid disks (§ 2), circulation is conserved and the mechanical analog of the MRI suffers a dynamical instability, as was first described by Balbus and Hawley [2]; whereas in (extra)solar multi-body subsystems (§ 3), there is no analogous conservation law and dissipative evolution proceeds secularly via a sequence of quasistatic equilibrium configurations [54] or via nonequilibrium states, both of which progressively lower the total mechanical energy of the (sub)system.
4.2. Global Mean-Motion Resonances
Extending the analytical work of Papaloizou [56] to more than two orbiting bodies, we show in Appendix A that tidal dissipation induced by the central mass leads to clustering of multi-body systems generally toward the mean of their initial mean motions , where and .3 Although secularly unstable, this critical orbit may host a massive body for a long time, at least comparable to the dissipation time that characterizes this part of the evolution of the system ( is quantified in Appendix B). A close encounter with another body can clear out the critical orbit, if the interaction between the two bodies continues unimpeded for a long enough time (Appendix A). Convergence of major bodies toward an intermediate region of the radial distribution of orbiting bodies should not come as a surprise, as it is observed in quite a few solar subsystems (gaseous giants, Galilean moons, and Saturnian and Uranian moons4) and many exoplanetary systems (§ 1); they all show an unmistaken clustering of several (4-7) massive bodies at intermediate orbital locations clustered around the critical orbit with mean motion .
The next question is, where and how does such radial convergence of orbiting bodies stop? After all, the observed massive planets and satellites seem to be currently on very long-lived, if not secularly stable orbits, with no pair evolving toward an intermediate orbit. So the clustering process must be quelled somehow before the objects begin interacting strongly via close paired encounters. The seminal paper of Goldreich [25] provided a substantial part of the answer long ago: Goldreich [25] showed that several ‘special cases of commensurable mean motions [of satellites] are not disrupted by tidal forces.’ This means that when some of the more massive satellites of the gaseous giants reach near mean-motion resonances (MMRs), their angular momenta do not vary tidally any more, thus the satellites maintain their orbital elements in long-lasting dynamical configurations (see also Appendix C for gravitational Landau damping of the mean tidal field when all massive bodies lie near MMRs).
The most massive body must play an important role in the above process because it is the one that evolves tidally slower than all the other bodies; so, it must be the body that lays out the resonant structure of the global tidal field for the entire (sub)system (Appendix C). When other massive bodies reach nearby global MMRs, their further evolution is impeded because the most massive body does not affect them tidally any longer; and they also refrain from interacting with smaller orbiting bodies in the system. In this setting, the tidal field will be thus severely damped and the remaining low-mass objects trying slowly to converge will also be hampered, either because they encounter global MMRs, or they are simply too far away from the resonating massive bodies. In the end, the entire system will appear to be relaxed (no more substantial imbalances from exchanges of angular momentum) with all of its members lying in or near global MMRs and the mean tidal field erased since the major bodies no longer contribute to it. At present, this is what is actually observed in all (exo)planetary and satellite subsystems.
At this point, we should clarify what we perceive differently in reference to the volumes of work carried out about (mostly local) MMRs5 to date [12,21,25,39,43,48,51,53,57,58,69,70]: We argue that multi-body resonances are not a local phenomenon; ‘principal MMRs’ (1:k and k:1, where ) are global in each system, and their locations are set by the most massive object that used to dominate the mean tidal field affecting the entire system; and secondary global MMRs of the form p:q () are also bound to lie at in-between locations. In such a global layout, it is not helpful to focus on the relative deviations of orbital elements from exact nearby MMRs and devise arbitrary thresholds for objects to be or not to be locked in resonance. Though unfortunately, we recognize this to be the current state of affairs in studies of phase angles of local MMRs between near-neighbors: for instance, the Earth is not thought to be in the 1:12 global MMR of Jupiter because its orbital period is 4.2 days longer than the exact resonant value of 361.05 d; and its phase angle would have to circulate slowly relative to the phase of Jupiter, so the same pattern would only repeat once every 87 years (see section “Coincidental Near MMRs” in the citation of footnote 5 for the same argument). This is not the right way of thinking about global resonances in the mean tidal field of our solar system (that is severely damped presently). We defer further discussion of this rather complicated issue to Appendix C.
4.3. The Critical Orbit in Solar Subsystems
The main result of this work has ramifications beyond the particular systems that we study. The orbits of the planets and satellites all have Keplerian radial profiles. The Keplerian profile is just a special case of a power law, a profile with no critical or inflection points, a property that makes it relatively simple, but also totally featureless.
But now, the dynamics of multiple bodies evolving by applying torques and exchanging angular momentum has given us a critical point in this profile, the mean of the initial mean motions , or equivalently, the harmonic mean of the orbital periods (, where we take ), viz.
Given , the critical orbital radius can be determined from Kepler’s third law. We note however that not many bodies are expected to occupy the critical orbits in their subsystems because all bodies may have a priori circularized their orbits at or near MMRs—unless of course the critical orbit coincides with an MMR, in which case the chances of finding a body there improve considerably (see § 4.4 below).
Our planetary system and Jupiter’s satellite subsystem each contain dominant adjacent orbiting bodies, the gaseous giant planets and the Galilean moons, respectively. For the gaseous giants, we find that
so Saturn has settled just wide of the critical orbit as we see it presently. For the Galilean moons, we find that at present
so Europa was trapped into the renowned Laplace resonance (LR) and could not expand its orbit farther out. We did not include inner low-mass bodies in these estimates for an obvious reason; their fates were fully determined by weak tidal forces exerted on them by the distant massive bodies, so they can be viewed as passive receivers of tiny amounts of angular momentum having slowly worked their way outward and toward the common goal. The Earth, in particular, may have taken angular momentum from nearby Mars, preventing the outward movement of this tiny planet.
For the Earth, it is interesting to examine where our planet finally settled at the end of the orbital evolution of the gaseous giants: our planet is currently orbiting just wide of the 1:12 principal MMR of Jupiter (as already mentioned, its orbital period is only 4.2 d longer). It may not be surprising that the planet did not settle at the center of the 1:12 MMR. During secular evolution, it was only gaining angular momentum, working its way outward toward the common goal. Such slightly wider orbits are observed in many exoplanets as well [21,39]. Those inner ones with orbital periods shorter than may be understood along the same line of reasoning, as having moved outward during evolution (but see also Refs. [4,40] discussing this issue).
4.4. The Critical Orbit in Exoplanets
In extrasolar systems, K2-138 [12,41] presents a transparent example of a planet on a critical orbit. For the six planets known in this system, we find that
so planet d is effectively occupying the critical orbit. All planets are near global MMRs as determined from the orbital period of the largest planet e. In order of increasing orbital periods, these are 2:7, 3:7, 2:3 1:1, 3:2, 5:1, for planets b-g, respectively. In planets b-f, all adjacent pairs have local period ratios 3/2 [12]; and the outermost planet g resides in a higher-order harmonic ratio, i.e., . The resonant chain is global, though not fully packed. If it were fully packed, then no planet would occupy the hypothetical ‘8-planet’ critical orbit ().
Another example with the critical orbit being occupied is the TRAPPIST-1 system with seven planets in a very compact configuration ( AU; [19,27]). We find that
so planet d lies on the critical orbit. All planets are near global MMRs as determined from the orbital period of the largest planet g. In order of increasing orbital periods, these are 1:8, 1:5, 1:3, 1:2, 3:4, 1:1, 3:2, for planets b-h, respectively. More details on how such systems came to be are included in Appendix C.
Author Contributions
D.M.C. and D.K. have worked on all aspects of the problems. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
NASA and NSF support over the years is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GLD | Gravitational Landau Damping |
| LD | Landau Damping |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| MRI | Magnetorotational Instability |
Appendix A. Angular Momentum Transfer Between Multiple Bodies
Appendix A.1. Three Bodies
We consider three bodies with equal masses () orbiting around a cental mass in Keplerian orbits as illustrated schematically in Figure A1. The mean motions obey the inequality . We assume that the dissipation rate is the same in all bodies and we use equation (13) to calculate the initial transfer of angular momentum between pairs. We have
and
The total orbital angular momentum of the system is indeed conserved; adding these three equations and simplifying, we obtain
Since , then it becomes clear that and , so and will converge toward . For body , we rewrite equation (A2) as
We find that if and only if is orbiting at the average value of the mean motions and (i.e., if ), which, by a property of the arithmetic mean of terms of a sequence, is also equal to the mean of the mean motions
in such a case, facilitates the transfer of angular momentum between and without being subjected to a net gain or loss in . Then, acts as a ‘forward-biased conduit’ that transfers angular momentum exclusively from to .
Figure A1.
Schematic diagram of three bodies in conjunction with equal masses () orbiting around (black arrows) a central mass at radii with periods . The asterisk denotes the location of the mean of their mean motions . The blue arrows indicate how the orbits will evolve initially via exchanges of angular momentum between the bodies.
Figure A1.
Schematic diagram of three bodies in conjunction with equal masses () orbiting around (black arrows) a central mass at radii with periods . The asterisk denotes the location of the mean of their mean motions . The blue arrows indicate how the orbits will evolve initially via exchanges of angular momentum between the bodies.
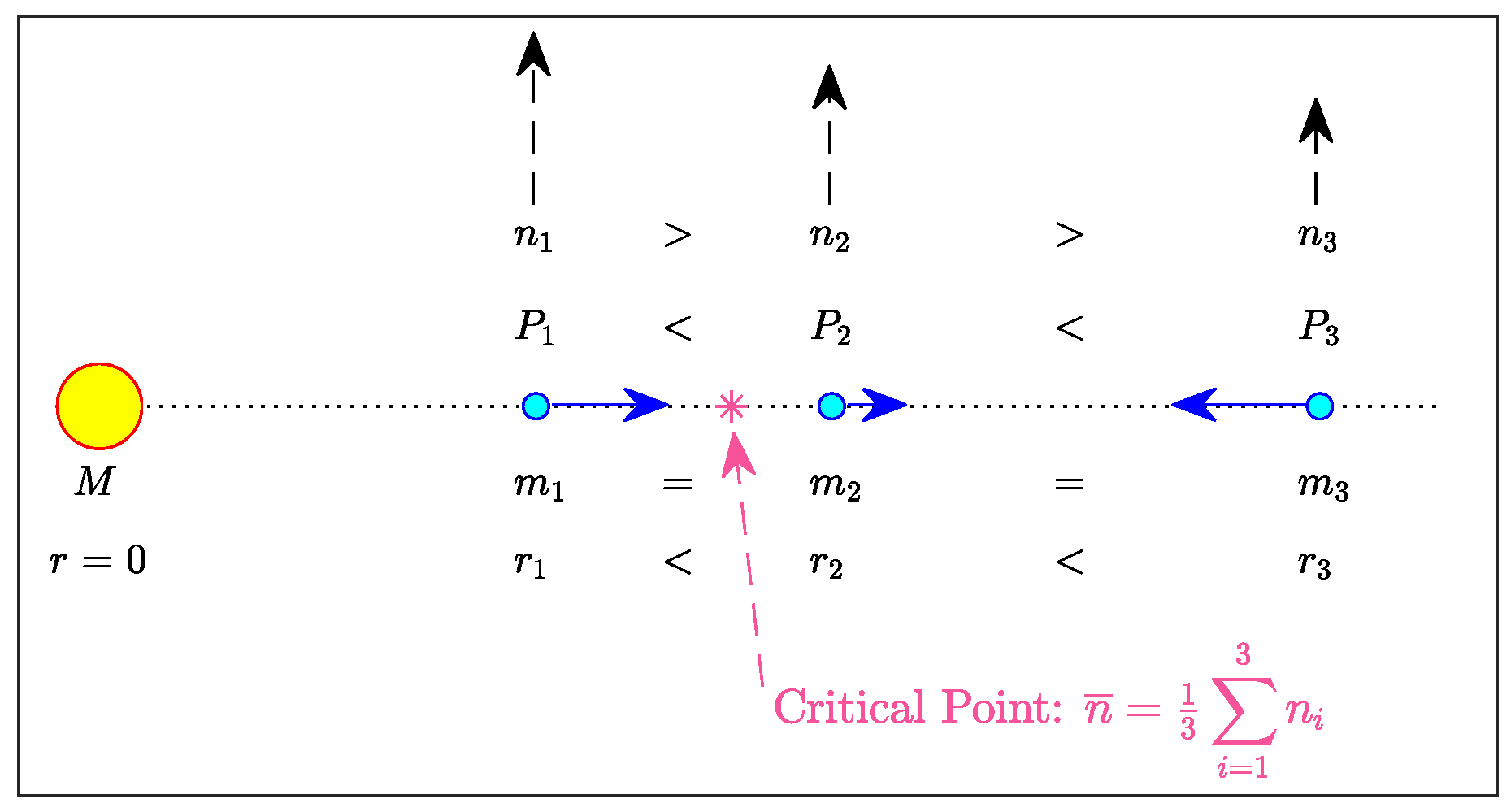
Figure A2.
Time evolution of the angular momenta of 3 equal-mass bodies with initial conditions , , , (Keplerian orbits), and . Time is measured in units of , where Q is the effective tidal dissipation function and P is the orbital period (; Appendix B). This early evolution does not depend on the chosen timestep. Body 2 starts with and . The total angular momentum of the system is conserved and .
Figure A2.
Time evolution of the angular momenta of 3 equal-mass bodies with initial conditions , , , (Keplerian orbits), and . Time is measured in units of , where Q is the effective tidal dissipation function and P is the orbital period (; Appendix B). This early evolution does not depend on the chosen timestep. Body 2 starts with and . The total angular momentum of the system is conserved and .
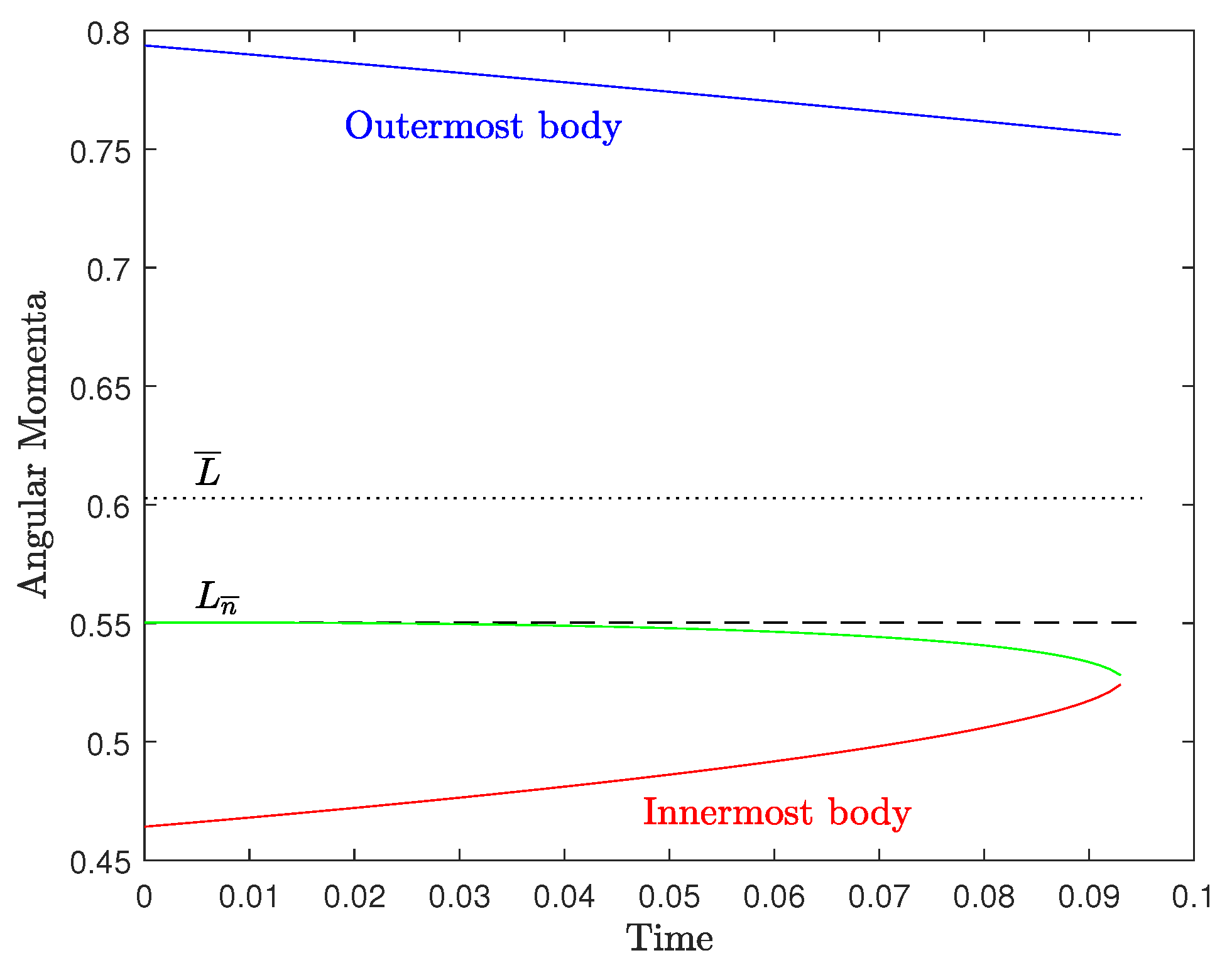
Furthermore, if (as shown in Figure A1), then (equation (A5)) and the orbit of will expand; whereas the opposite will occur for . Thus, this critical orbit characterized by is secularly unstable, but a body placed on it may survive for a long time, until it undergoes a close encounter with another approaching body. This is shown in Figure A2 that depicts the evolution of 3 equal-mass bodies in Keplerian orbits with initial conditions , , and .
Figure A3.
As in Figure A2, but for 4 equal-mass bodies with initial conditions , , , , and .
Figure A3.
As in Figure A2, but for 4 equal-mass bodies with initial conditions , , , , and .
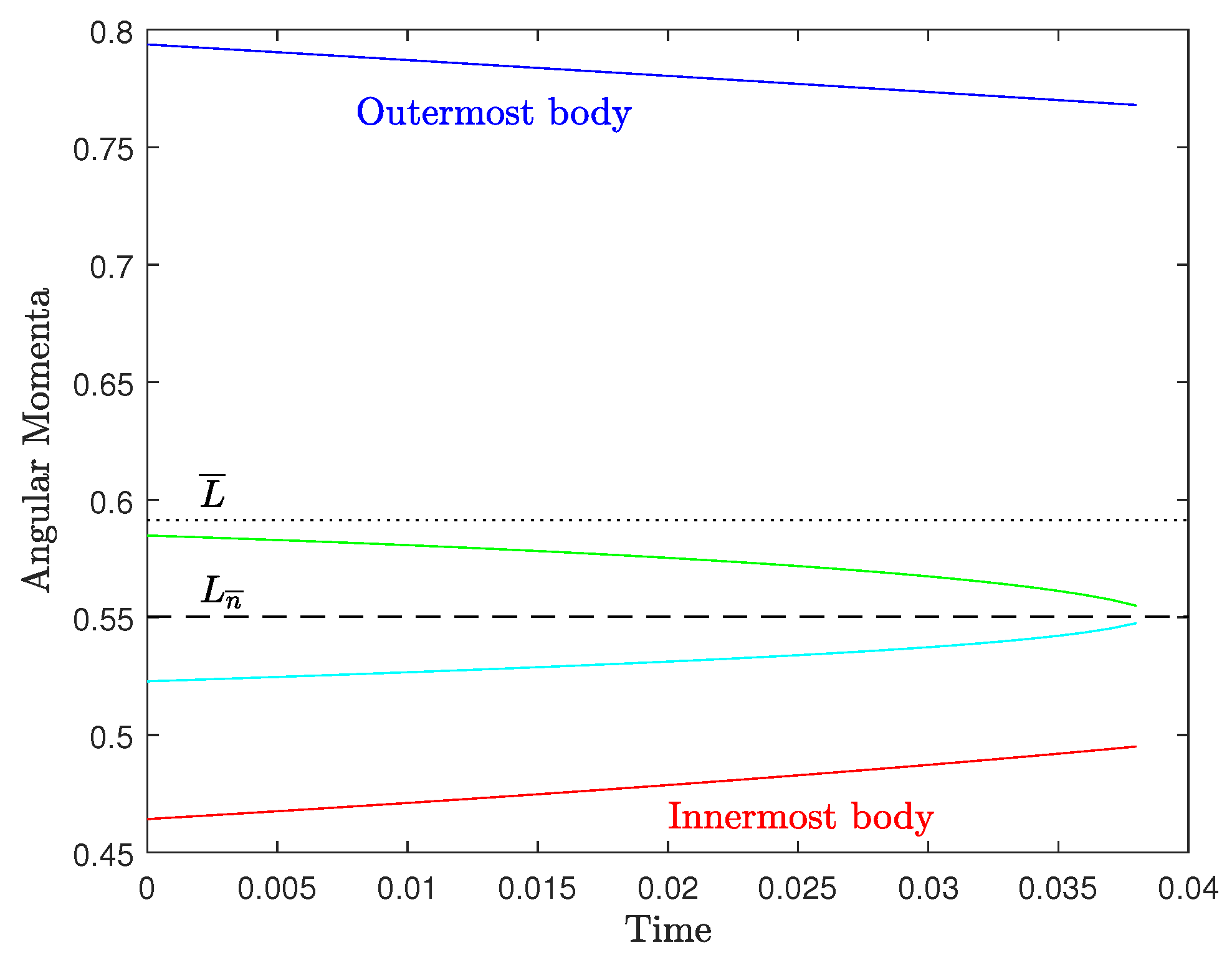
Figure A4.
As in Figure A2, but for 5 equal-mass bodies with initial conditions , , , , and .
Figure A4.
As in Figure A2, but for 5 equal-mass bodies with initial conditions , , , , and .
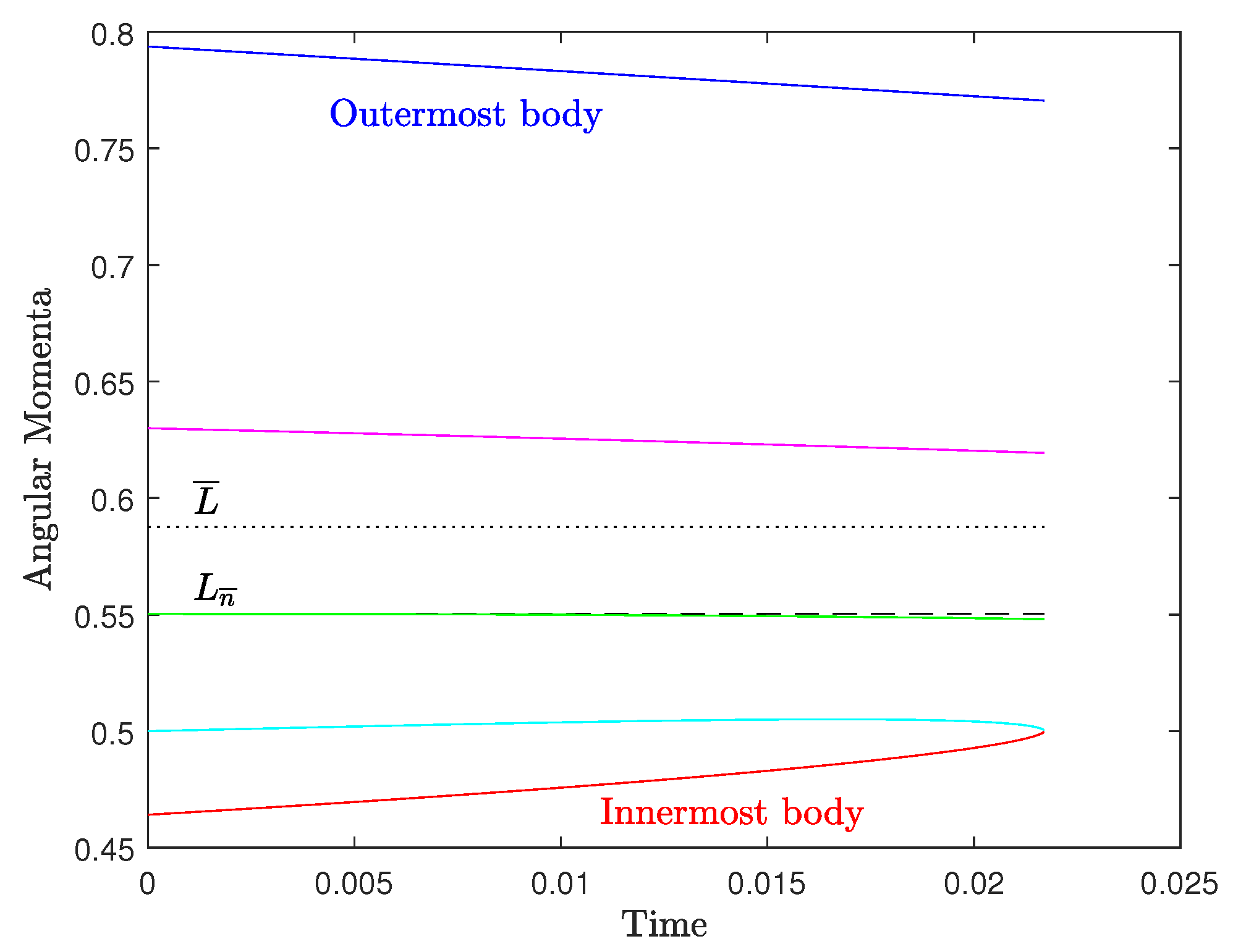
Figure A5.
Long-term () evolution of the angular momenta of the 4 equal-mass bodies shown in Figure A3. Close encounters between pairs and triplets are dependent on the chosen timestep .
Figure A5.
Long-term () evolution of the angular momenta of the 4 equal-mass bodies shown in Figure A3. Close encounters between pairs and triplets are dependent on the chosen timestep .
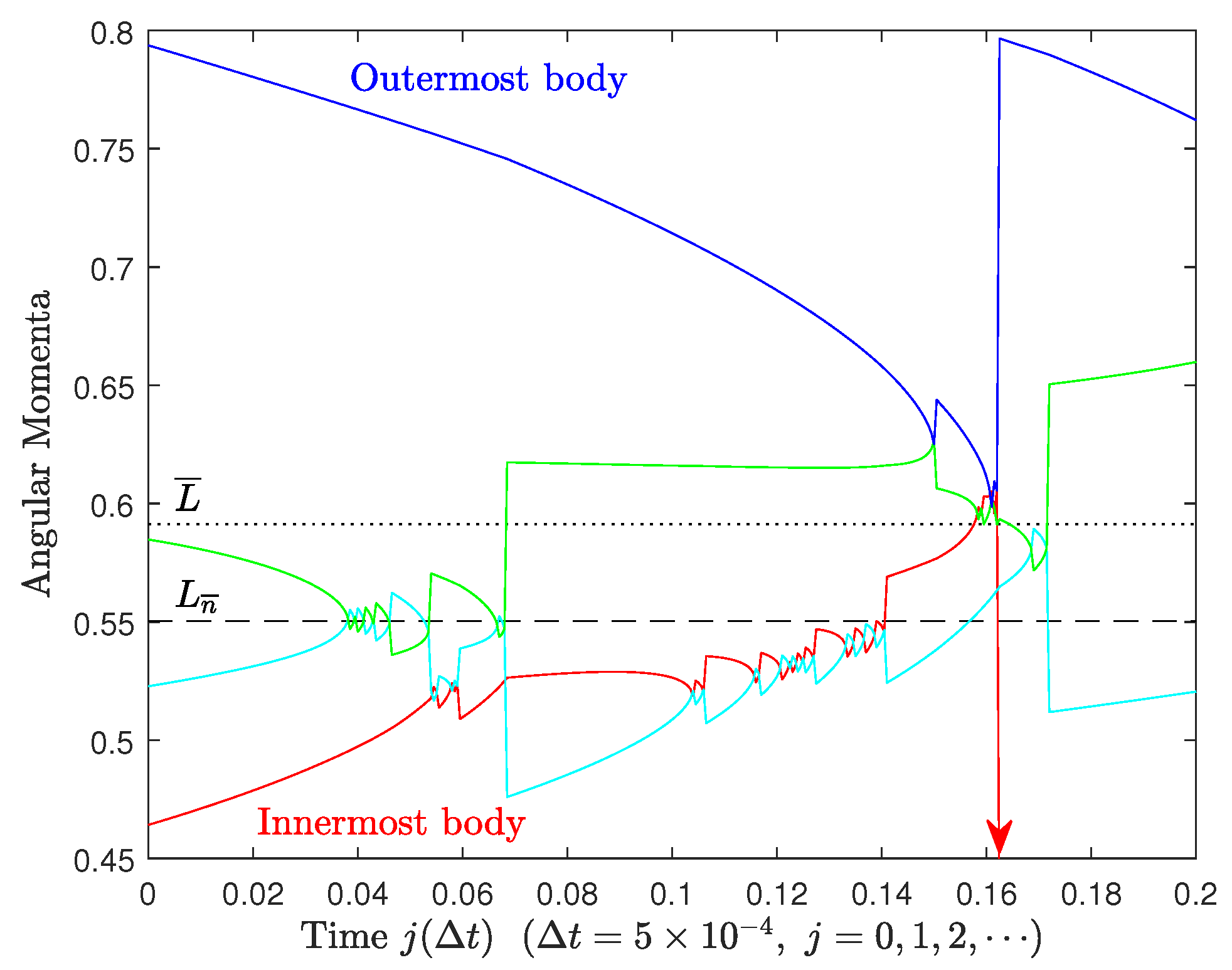
Figure A6.
Long-term () evolution of the angular momenta of the 5 equal-mass bodies shown in Figure A4. Close encounters between pairs and triplets are dependent on the chosen timestep .
Figure A6.
Long-term () evolution of the angular momenta of the 5 equal-mass bodies shown in Figure A4. Close encounters between pairs and triplets are dependent on the chosen timestep .
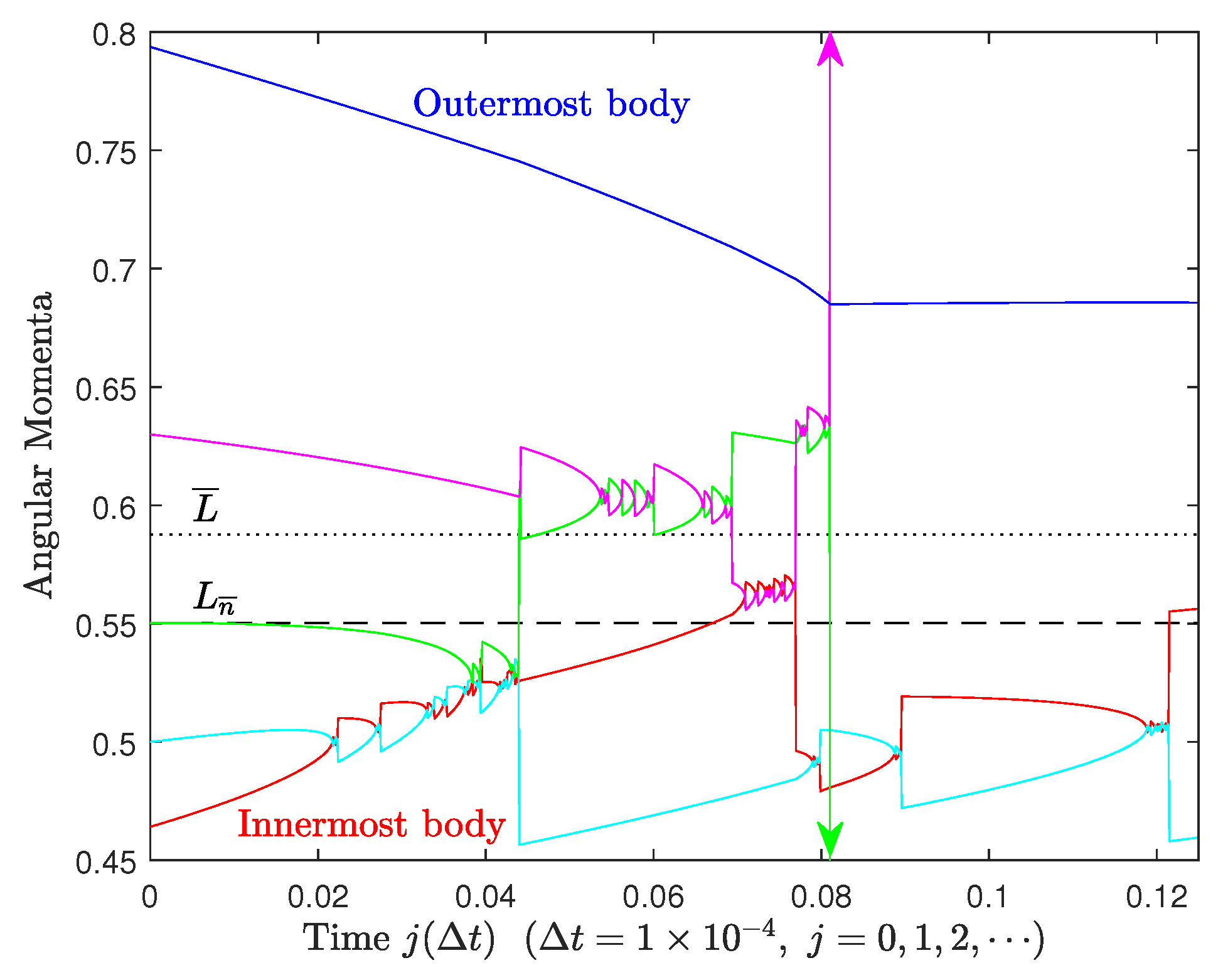
Appendix A.2. Four Bodies
As can be seen in Figure A3 and Figure A4, the same behavior and conclusions can be deduced for four (or more) equal-mass orbiting bodies for the times before paired interactions begin to occur. As one or two bodies may reach near the critical orbit with mean motion , the remaining bodies will continue exchanging smaller amounts of angular momentum. Left unimpeded, this process will lead to orbit coalescence (possibly after ejection of some closely interacting pairs; see Figure A5 and Figure A6), and this is why in (extra)solar subsystems there must be another mechanism to quell or severely depress angular momentum transfer before the orbits merge. As was discussed in § 4, we believe that such a mechanism has been discovered by Goldreich [25] long ago.
Referring back to the results depicted in Figure A3, it is important to investigate the early behavior of the two intermediate bodies (2 and 3) lying near the critical orbit with in a four-body system, when paired interactions between nearest neighbors are not too strong yet. (This is because the two most famous subsystems in our solar system, the gaseous giant planets and the Galilean satellites of Jupiter, both contain four major bodies each.) In the case, we find for intermediate bodies 2 and 3 that
and
We see that a sufficient condition for is that ; and a sufficient condition for is that . In this case, bodies 2 and 3 will initially converge toward one another irrespective of the location of . In a variety of cases however, the four major bodies are expected to have formed at some relative distances from one another, and may just as well have initially fallen between and . Then the two intermediate bodies 2 and 3 will converge toward , as seen in Figure A3.
Appendix A.3. Five Bodies
Here we investigate the critical orbit with in the case of 5 interacting bodies. In a four-body configuration, we place initially a fifth body with and at the critical orbit of the other four bodies 1-4, so that
The mean remains unchanged for the 5 bodies. After some tedious algebra, the angular momentum change of the added body is found to be proportional to three cyclic factors, viz.
where all positive definite factors have been dropped for the sake of convenience. We see that the initial condition is not sufficient for the fifth body to be in an equilibrium orbit with , but another condition must also be met. If is set to zero, the above 3 factors determine the additional condition for to be the average of any of the specific 3 pairs of mean motions (1,2 or 2,3 or 1,3). Each of these averages is cyclically equivalent to yet another average between mean motions (1,2→3,4; 2,3→4,1; and 1,3→4,2), for a total of 6 combinations between any two paired mean motions. The first two averages (1,2 and 3,4) cannot occur, but the remaining four combinations are viable.
Any one of the four viable conditions, along with , is sufficient for the fifth body to be initially in equilibrium. Such an equilibrium state is unstable due to interaction of the fifth body with any other body that may come close in the long run. But this state can be long-lived if the nearest neighbors take a long time to approach the fifth body. An example of the entire process, complete with two- and three-body interactions at later times, is shown in Figure A4 and Figure A6, respectively, in which the initial setup of the 4 mean motions is symmetric about the fifth mean motion .
Appendix A.4. Time Evolution of the Critical Orbit
The only constant plotted for reference in the figures above is the mean angular momentum . The corresponding mean motion of this ‘intermediate’ Keplerian orbit is also constant in time. This orbit is far less important for systems with 4 or more bodies, and for 3 bodies one of which occupies initially the critical orbit (Figure A3, Figure A4 and Figure A2, respectively). On the other hand, the important critical orbit with initial values and does not remain constant in time; it relocates slowly toward the constant intermediate orbit with (this is not shown in the figures).
As the critical orbit moves toward the constant intermediate orbit, its angular momentum always increases and its mean motion always decreases in a Keplerian setting. That is, schematically,
and
Proving one of these inequalities is not a trivial matter (the other one follows immediately for Keplerian rotation). With the help of Mathematica, we have shown that inequality (A12) is an identity for and bodies, so an inductive proof may be possible.
Appendix B. Dissipation Timescale, Velocity Fluctuations, and Related Scales
Appendix B.1. Dissipation Timescale
We estimate the dissipation timescale for interacting bodies such as massive planets and large satellites. We begin with the Kolmogorov microscales, in which viscosity dominates and a small part of the kinetic energy is converted to heat. Although these microscales are used to describe diffusion in fluids, the equations are relevant to our problem as well because they imply a Reynolds number of [35], a value that is appropriate for stellar systems and multiple bodies evolving quasistatically under the influence of weak tidal interactions. For , the square of the dissipation time is
where is the kinematic viscosity coefficient and is the specific (per unit mass) energy dissipation rate. These quantities are related by , where is the symmetric strain-rate tensor that appears in the equations of motion [3]. Thus, in equation (A13) is the root mean square value of the reciprocal terms . This property allows us to estimate and from the macroscopic scales of interest6 (one cycle with orbital period P) without altering the microscopic gradients of the strains that literally do all the work. For the viscosity coefficient with dimensions of area over time, we write for one cycle that
where r and P are the orbital radius and orbital period, respectively; and for the specific energy dissipation rate with dimensions of power per unit mass, we write
where and is the distorted mass in which dissipation occurs in each cycle (i.e., the mass of the tidal bulges in a body). Combining equations (A13)-(A15), we find that
We relate to the effective specific tidal dissipation function Q [26,46,52] by estimating the kinetic energy loss of mass over one cycle P, viz.
where is the orbital kinetic energy of mass and is a dimensionless function. Here we assume that the rotational kinetic energy of is negligible compared to . Equation (A17) implies that
and substitution into equation (A16) gives
or
where we have used . These equations may be useful for estimating dissipation times (where ), but they do not provide clear physical insight. For this reason, we recast equation (A16) in the form
where is the orbital angular momentum of bulge mass , and for an average energy dissipation rate of (taking now ), we find that
where and are the corresponding specific quantities, respectively. We see now that is the time it takes to dissipate a part of the energy at constant bulge angular momentum L; or in microscales, the time to dissipate a part of the specific energy at constant specific angular momentum ℓ.
Equation (A22) can also be recast in the familiar form
where is the orbital moment of inertia of mass and
is the geometric mean of the two characteristic frequencies of the problem. Equation (A23) justifies the presence of the factor of 1/2 in equations (A21) and (A22) above; whereas equation (A24) shows how the dissipation couples to orbital dynamics and regulates the energy loss of the tidal bulges during quasistatic evolution. Clearly, the geometric mean places more weight to , the much shorter one of the two frequencies. This is seen also in the equivalent relation , where and .
Appendix B.2. Velocity Fluctuations
We relate the tidal dissipation function Q to the characteristic velocity of small-scale fluctutions which, for , is given by [35]
Using equations (A13), (A18), (A20) and (A25), we find that
or, in terms of the long azimuthal angle ,
where is the orbital velocity. Equation (A27) corresponds to equation (A19) above; divided by , it gives an estimate of the number of orbits
in one dissipation time, albeit for fixed .
Appendix B.3. Integral Length
The remaining scale in our problem, the so-called integral length scale l [67], derives from the above scales. For , we find that
This l is not the tiny length scale over which energy is dissipated;7 it is an observable macroscopic length scale of the bulk kinetic energy of the bulges, some of which will be transferred to the much smaller dissipative scales over times comparable to . Its importance lies in the fact that the dissipation rate () is primarily determined at this length scale via equation (A31), and not by the corresponding microscale of the ‘turbulent regime’ [23].
Using equations (A26), (A27), and (A31), we find that
and that
Perhaps a simpler interpretation derived from equation (A32) (divide both sides by ) is that is the cumulative area that will be swept by the radius vector of a body after k orbits having taken place over one dissipation time (equation (A28)). The large value of is characteristic of the largest motions of the turbulent flows [50] in the bulk of an orbiting body, which explains the relation in our astrophysical setting. It is also worth noting that, in this setting, , i.e., the geometric mean of the two extreme turbulent scales describes the rms value of the orbital radius of the body.
Appendix B.4. Damping Rate
The damping rate (dimension [time]−1) of a wave-like perturbation on the surface of an incompressible fluid was derived by Landau and Lifshitz [37] in their study of gravity waves of amplitude A, wavelength , and frequency , where is the kinematic viscosity coefficient. Their calculation appears to differ from the calculation above in two subtle respects: (a) Landau and Lifshitz [37] define as the coefficient of the decay of the amplitude A, not of the specific energy (equation (A29)); and (b) they purport to calculate dissipation of the total mechanical energy, not only of the kinetic energy.
Concerning difference (a), a relation between and our is obtained by comparing the decay of the damped wave’s energy at any time t, viz.
so that the damping rate of the amplitude A is
Difference (b) above is more subtle because it does not seem to affect the scales of the problem; for example, using our notation and differentiating with respect to t, we find from the definition of and equation (A34) that
so there is no difference between the two results. The reason is that despite the discussion preceding equation (25.3) in Ref. [37], the energy they used is actually one-half of the mechanical energy of the perturbation, so the kinetic energy of the wave was actually used in their calculation as well.
Appendix B.5. Remarks on Protostellar Disks
We note that Kepler’s third law was not used in the above calculations, so was not assumed to necessarily be the equilibrium value, which is also fitting for the variational principle used in § 3.2 above. In both cases, however, the bodies obey the two quasistatic conditions (4) and (7) or, equivalently, that .
The above dissipation time should be accounted for in planetary and satellite systems after the gaseous accretion disk has dispersed because torques from the disk are expected to interfere in the early evolution of these bodies. Most protostars (∼90%) lose their inner disks after about 3-8 Myr [28,30], although some young stars apparently lose them within the first 1 Myr of their lifetimes, and some older stars are found with inner disks after about 8-16 Myr. These timescales are shorter than the times over which terrestrial planet formation was completed in our solar system (30-100 Myr; [66]). Owing to the soft dependence of on seen in equation (A20), all of the above times are longer than the dissipation times of interacting solar subsystems, so there is ample time available for the solar nebula and gaseous protosatellite disks to disperse; and for the few (usually 4-7) developing massive cores to complete their accretion processes, differentiate themselves from their surroundings [66], and begin their next phase of quasistatic evolution driven by their own mean tidal field, in the absence of other external torques. What occurs in this latter phase (after disk dispersal), and the fate of the mean tidal field itself are the subjects of Appendix C.
Appendix C. Landau Damping of Tidal Waves near Mean-Motion Resonances
Goldreich [25] studied local mean-motion resonances (MMRs) between pairs of satellites and found that the resonant configurations are not disturbed by tidal forces. This treatment confirmed that the tidal field created by the massive bodies in each (sub)system seems to be absent when the bodies all settle near MMRs. But these local paired calculations did not provide a reason for the absence of the field. Nor could they, because MMRs are a global phenomenon that takes place over the entire (sub)system. Goldreich [25] could not imagine that the underlying field is nowadays severely curtailed or dispersed altogether, so he hypothesized that the resonant body pairs may regulate the transfer of angular momentum in ways that maintain their resonant configurations. Of course, this cannot be the case; the results in Appendix A show that each body, resonant or not, receives and distributes angular momentum based on the conservation of the total amount and the small dissipation rate. So no body is capable of regulating transfer globally, although the most massive body will be perturbed much less, solely on the basis of its larger inertia.
Thus, we think that the most massive body is responsible for laying out the global resonant structure of the (sub)system, just as it provides the largest part of the tidal field for its near-neighbors. It becomes apparent that when other massive bodies also encounter principal MMRs of the most massive body (§ 4.2), they will no longer contribute to the mean tidal field that they helped create in the first place, which, in turn, would be severely damped. Once the mean field (the collective mode of radial oscillations) is damped thus, there is no mechanism to get it back. Minor bodies can no longer exchange angular momentum efficiently, thus they will also relax near global MMRs.
Based on the above picture, we sought an physical explanation for the freezing of radial motions in Landau damping (LD) [36], an analogous effect that takes place in electrons in a plasma. Gravitational Landau damping (GLD) has already been applied to stellar systems [7,33,44,64], but not to the few-body (4-7) systems that we envision. Thus, the historical trend in calendar time shows dramatic leaps from electrons in the 1940s, down to galaxy stars in the 1960s, and down again to 4-7 (extra)solar-system bodies presently.
To justify the leap down to just a few bodies, we argue as follows: There is no element in the derivation of LD that requires a large number of particles. Furthermore, the fundamental assumption of a collisionless system is easier satisfied by few bodies as compared to stars or electrons. All that is required is a confinement mechanism, whether this be ionic Coulomb attraction in a plasma, or central gravitational attraction in a galaxy or in a few-body system. The first astrophysical studies made the connection between stellar systems and electronic plasmas because of the large numbers of ‘particles’ involved in both systems (also GLD operates only at wavelengths that are stable to the Jeans instability; [7,31,63]); and they discovered that very small regions of the phase space of stellar systems contain the important particles (the so-called ‘resonant particles’) with speeds comparable to the phase velocity of the tidal wave.
Appendix C.1. Damping Mechanism
A complete satisfactory physical interpretation of LD was lacking until recently, although the outcome is no longer disputed. In plasmas, LD has been verified experimentally [11,20] and by simulations [34]; it is also used to stabilize electron beams in accelerators ([29] and references therein). Recently, following the tradition of Dawson [18], the seminal works of Ryutov [59] and Wesson [68] gave clear descriptions of LD using only real variables, and their derivations make the physics behind the damping mechanism of the mean field much better understood. On the other hand, some detailed descriptions using complex variables are found in influential books on plasma physics [5,8,22,62]; although such convoluted mathematical treatments may obscure the physics behind the effect.
The damping mechanism in plasmas and stellar systems opearates as follows. Resonant particles gain energy from the mean field and become nonresonant, i.e., they move at speeds substantially higher than the phase velocity of the mean wave. Then, other slower-moving particles become resonant and they also gain energy from the field. The process continues until the field is robbed of its energy and dissipates away. This mechanism cannot work in exactly the same fashion in few-body systems because of the small number of ‘particles’ involved. Instead, the mean field is weakened every time a massive body becomes resonant (i.e., it ‘levitates’ at the top of a wave crest), and the mean tidal field disappears altogether when the few major bodies all end up near resonances, where they no longer support collective tidal interactions.
In what follows, we adopt the treatments of the linear LD by Trigger et al. [63] and Fitzpatrick [22], two resources providing clear physical insights, and we customize their analyses to the few-body gravitating systems of interest. We provide four theoretical derivations related to GLD that are illuminating despite the mild use of complex variables; they complement nicely the real-value calculations recommended above [18,59,68]. First, we derive the characteristic screening length (analogous to the plasma Debye length [5,8]) for few-body systems (§ C.2). Second, we verify that this screening length is formally applicable to planetary (sub)systems, and we quantify the GLD rate [63] for Jeans-stable waves (§ C.3). Third, we show a crucial elementary proof [22,62], that bodies near the phase speed of such a wave will interact strongly with the wave; thus, they are the ones participating in substantial energy exchanges and causing linear LD (§ C.4). Fourth, we describe the longitudinal oscillations of a single body, initially in phase with the tidal wave, and trapped in a potential trough of the decaying tidal field (§ C.5). Finally, we close with an application of the results to two important four-body subsystems in our solar system, the gaseous giant planets and the Galilean moons of Jupiter (§ C.6).
Appendix C.2. Jeans Wavenumber and Hill Radius
GLD operates at short wavelenths , where k is the wavenumber. The question is how short. With an eye on GLD in stellar systems, Binney and Tremaine [7] determined the condition that for standing waves to be necessarily damped (there are no travelling waves in the system),8 where is the critical Jeans wavenumber defined by the equation
where is the gravitational (Jeans) frequency and is the velocity dispersion of stars.
For the few-body systems of interest, there is no predetermined Jeans wavelength, although we know empirically that the systems are dynamically stable, so they are not in any danger of suffering the dynamical Jeans instability. We need however to determine a threshold akin to . We proceed as follows: In plasma physics, the Debye length is used to determine the volume inside which the field of one electron dominates relative to the mean field produced by all electrons. In our case, an analogous screening length is the Hill radius h [61], viz.
where r is the orbital radius, M is the central mass, and m is the mass of an orbiting body. Although not a systemic constant, h is a fair description of the sphere of gravitational influence around individual orbiting bodies.
It turns out that the above two scales are reciprocal. To show this, we need to redefine our concepts of Jeans frequency and velocity dispersion for few bodies with in Keplerian orbits about central mass M. We adopt the usual Keplerian orbital parameters, i.e., and , where G is the gravitational constant. The Keplerian orbital frequency is naturally the de facto gravitational frequency in this case, i.e.,
We also use the radial derivative of the given above, i.e., , , and . Then, combining these equations, we find that
and then equation (A35) gives
Another important relation is obtained when we transform the Jeans frequency that dictates the zeroth-order tidal field to a corresponding Hill frequency localized to individual bodies. Combining equations (A36) and (A37), we find that
As will be seen below, the factor of 3 in this relation is significant. For later reference, AU and yr for Jupiter in our planetary system now; and Mm and d for Ganymede in Jupiter’s satellite subsystem now.
Appendix C.3. Regimes of Jeans Instability and Gravitational Landau Damping
The above relations describe fundamental parameters that appear in the dispersion relation and the Landau damping rate for few-body systems. The same parameters have also been derived for a stellar system by Trigger et al. [63] (hereafter TEvS) in a fundamental piece of work that has been flying under the radar of the astronomical community for 20 years. In particular:
- (a)
- TEvS considered an ‘infinite’ self-gravitating collection of masses with uniform density , in which case the Hill frequency is a constant defined by the equation
- (b)
- This idealized system contains two species of particles with masses m and . To rewrite as a ‘global’ quantity, we imagine a spherical volume of radius r containing a mass M (smaller masses are neglected) with mean density , in which case we obtainor , which is the same as equation (A40) for few-body systems. Now it becomes evident why we used here the symbol for the frequency (TEvS call it ), just as we did in § C.2 above. The need for radius r to be taken around a mass M stems from the peculiarities of this infinite uniform self-gravitating model (any mass M can be a central mass in its vicinity, where the geometry then becomes spherically symmetric).
- (c)
-
The linear stability analysis of this Jeans-like model also establishes the local ‘Debye length’ D, viz.which TEvS call the Debye-Jeans radius, although they point out that this D is not related to screening (a minor oversight that neglects the role of the Hill radius in gravitating bodies). Here is the thermal velocity of fast particles belonging to the m-species in 3 dimensions. In one dimension, the velocity dispersion will then beand then we find that
- (d)
- Collisions between heavy and light particles must be included in the TEvS model, otherwise the number of particles is not conserved. On the other hand, few-body systems are collisionless in the long run (some ejections of lower-mass bodies by the massive bodies are expected in early evolution); thus, for our application, we reduce the equations of TEvS to the limit of zero collision frequency ().
- (e)
-
The TEvS dispersion relation in the limit of (their Equation (15)) readswhere k is the wavenumber andof a radial mode with frequency . The function is given bywhere, in our case, , with the asymptotic behavior
1. Classical Jeans Instability Regime.—For , when collisions are retained (that is, for in equation (A47)), equation (A48) can be integrated along the real axis. The dispersion relation takes the f-dependent form of Equation (19) in TEvS. In the limit of , this form reduces to the dispersion relation
Evidently, the two-species model exhibits the classical Jeans instability for long-wavelength modes (), provided that the characteristic ‘sound speed’ is defined as
In comparison to the few-body system of § C.2 with parameter set , the two-species Jeans model then shows the following parametric relations:
2. Gravitational Landau Damping Regime.—For and for short wavelengths , equations (A46), (A47) and (A49) combine to give
in the limit of . These are the Landau-like modes and they are all damping since for . For wave amplitudes , the damping rate () is
For the few-body systems of interest, and the damping rate takes the form
Thus, in this model, the damping rate is proportional to the local Hill frequency (equation (A40)); whereas in the TEvS two-species infinite model, is proportional to the constant frequency (equation (A41)). In both models, waves with very short wavelengths ( or ) are damped at much higher rates (). On the other hand, waves with and wavelengths stable to Jeans modes of size
tend to persist for the longest times. In § C.6, we describe an application of this result to the gaseous giant planets in our solar system and the Galilean satellites of Jupiter.
Appendix C.4. Bodies Interacting with their Collective Tidal Field
A one-dimensional radial tidal field generated by a few massive gravitating bodies is described by the equation
where is the amplitude (dimension of [acceleration]), k is the radial wavenumber, and is the frequency of the wave. Any of the major bodies in this field feels an acceleration due to the collective influence of the other massive bodies of the same form, viz.
In the absence of the field, a body initially at with initial radial velocity will move to , and we can introduce the initial conditions to the perturbation by substituting the zeroth-order solution into the exponential term of equation (A58) [22,62], viz.
Integrating in time, we find for the radial velocity that
For initial radial velocities of bodies that are close to the wave’s phase velocity
we resolve the indeterminate form in the last bracket of equation (A60) by de L’Hospital’s rule, and we find that
Thus, bodies with velocities close to (resonant bodies) will be subjected to linear velocity perturbations that grow in time. They will lose energy to the wave or gain energy from the wave, and they are responsible for the overall damping of the wave when it occurs eventually. This explains why in all related calculations, the damping rate depends on the negative slope of the distribution function evaluated at (e.g., [68]). But it does not explain why wave damping predominates wave growth, as the perturbed bodies may gain or lose energy in their interactions with the wave depending on their phases.
More detailed considerations are needed in order to understand the damping of the mean field. Following the clear descriptions given by [22] and [68], we make the following important points for plasma fields, and then for tidal fields:
- (a)
- It is certainly not the case that slightly faster-moving bodies will lose energy and slightly slower-moving bodies will gain energy from the wave, as is commonly quoted. This misconception invalidates the analogy with the famous example of a surfer riding an ocean wave. Whether a resonant body will gain or lose energy depends on the phase of the wave upon energy exchange. In other words, a radially oscillating body trapped within its Hill radius with radial veclocity near the wave’s phase velocity will rob the wave of some of its energy only if its oscillation is in phase with the wave (see § C.5 below).
- (b)
- (c)
- Considering only resonant bodies starting with velocities , if they gain energy, they will move away from resonance; whereas if they lose energy, they will move closer to the resonant velocity . The end result is that the latter bodies interact more efficiently with the wave and, on average, the field gains energy from bodies with . The opposite holds for bodies with for which the gainers are more efficient and the field is damped.
- (d)
- In a Maxwellian radial velocity distribution (even a sparse one with just 4-7 bodies), or in any other distribution with a roughly similar (bell-shaped) profile, there will be more bodies with ; thus on average, the wave will have to push on most of them and it will be damped. It is for this reason that the negative gradient of the distribution function at determines the damping rate [68].
We note that items (c) and (d) above are not as dominant in few-body systems because few bodies have another mechanism available to them (settling into MMRs) in order to stop contributing to the mean tidal field, thereby undermining it to a large extent. We describe GLD occurring in just a few gravitating bodies in § C.5 and § C.6 below.
Figure A7.
Schematic diagram of a body of mass m trapped in a trough of the potential due to the standing tidal wave described in § C.4 above. The body starts at with relative velocity in the wave frame. As it is settling toward (exact resonance), it bounces back and forth radially between turning points of opposite phases, such as the points indicated by blue circles.
Figure A7.
Schematic diagram of a body of mass m trapped in a trough of the potential due to the standing tidal wave described in § C.4 above. The body starts at with relative velocity in the wave frame. As it is settling toward (exact resonance), it bounces back and forth radially between turning points of opposite phases, such as the points indicated by blue circles.
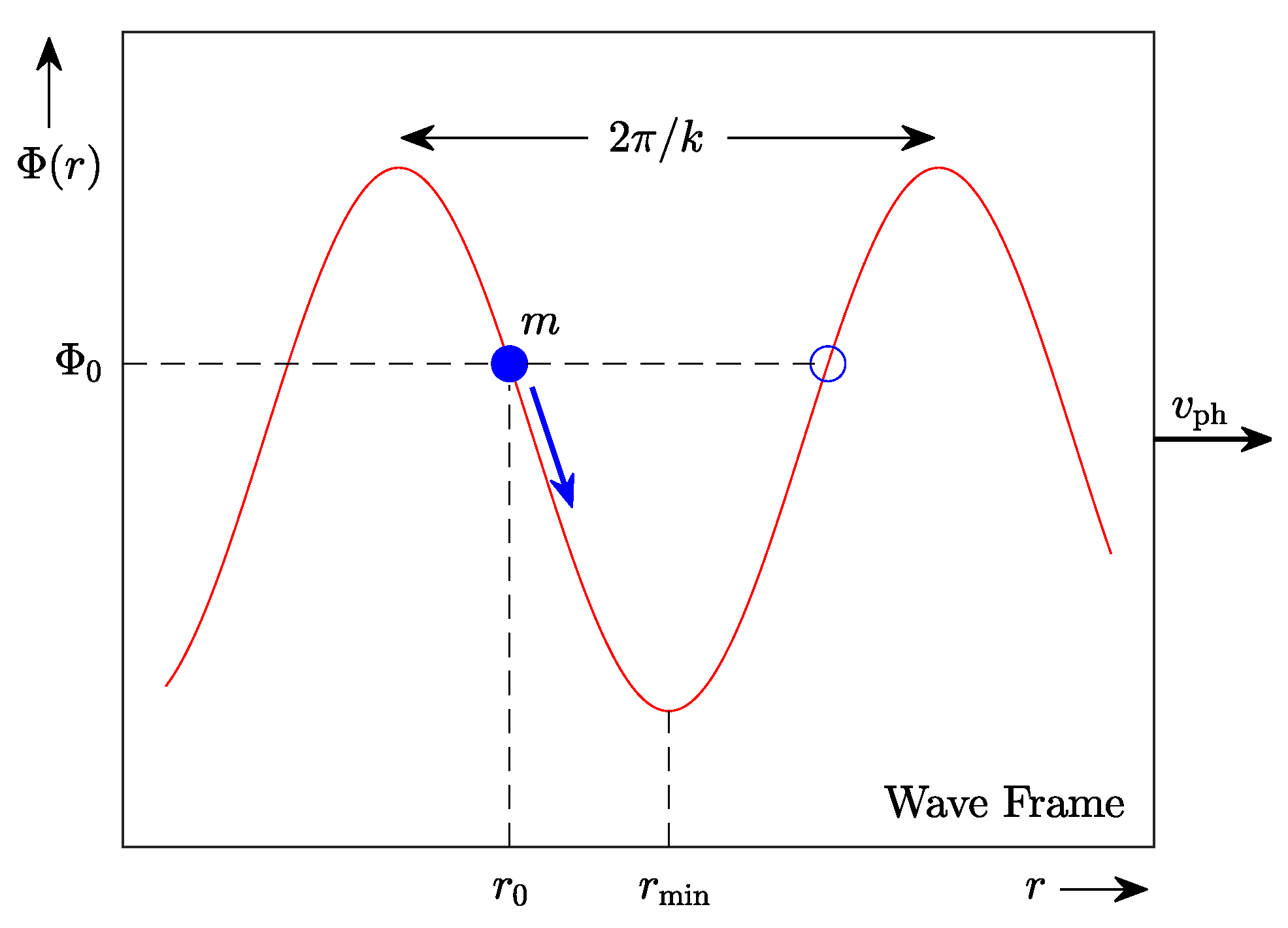
Appendix C.5. A Resonant Body Trapped in the Tidal Potential
Consider a resonant body, initially at , trapped in a trough of the mean tidal potential of a standing tidal wave, in a reference frame that moves with the phase velocity of the wave (e.g., [62]), as shown in Figure A7. The turning points of the potential are specified by the value . The body will bounce around the potential minimum at according to the harmonic oscillator equation
with , , and solution
where the amplitude . Any small amount of dissipation (such that ) in equation (A63) will modify the amplitude A in equation (A64) to and will drive toward zero and and the radius . When the body manages to relax at , it will levitate—i.e., it will keep moving with the wave without gaining or losing energy or angular momentum. When the massive bodies in a few-body system all relax near such potential minima, then the mean field will be damped out. This is how the tidal field is weakened and is finally dispersed, when all major bodies no longer contribute to it.
For the wave described by equation (A57), the frequency of the bounce is . The characteristic period of the bounce then is , i.e., it becomes longer as the wave amplitude decays in time. For this reason, the bouncing body should always be found near at times (long after the tidal wave has effectively dissipated).
For the longest and slower-damped modes with (i.e., ), then and the bounce frequency is . In this limit, the maximum period of the bounce is (characteristic values were given in § C.2 for the radial movements of Jupiter and Ganymede). It turns out that is of the orbital period of each body; and the corresponding wavelengths from equation (A56) are
for Jupiter and Ganymede, respectively. These values will be used in the applications of § C.6 below.
In general, the relaxed bodies in a system in which the tidal field has been damped are not expected to be found all in phase because of the radial bouncing around in their potential troughs that preceded their settling to noninteracting orbits. We have experienced this situation first-hand in the work of Goldreich [25] who found only 7 pairs of satellites of the gaseous giants having related phase angles. In expanding the search for mean-motion resonances in (exo)planetary subsystems, we need to search, not only for approximate resonant scalings of the orbital-period ratios and the phase angles, but for spatial wavelength-dependent scalings as well. To do the latter part, we need first to obtain an estimate of the longest wavelength of the mean tidal field long gone (see, e.g., equation (A56)); but this may not be a difficult task, as is demonstrated in § C.6 below and in the recent study of the multiplanetary system of HD 110067 [16].
Appendix C.6. Signatures of Tidal Fields Long Gone
Imprints.—According to the results of our study, major planets in our solar system and massive moons in satellite subsystems moved around in their collective tidal fields until they got caught in potential troughs, where they settled near potential minima and contributed to the damping of the field. Damping occurred because most, if not all, bodies developed radial speeds equal to the phase velocity of the longitudinal wave. In such a levitating configuration, tidal interactions ceased and the wave was severely and permanently suppressed.
In this case, there must be imprints left over in the presently settled orbits of major bodies, signatures of a tidal dissipative evolution that took place in the distant past. Some imprints were found by Goldreich [25] in the phase angles of some resonant satellite pairs and in the Laplace phase of the three innermost Galilean moons. Below, we pursue additional evidence in the characteristic wavelengths of the long-gone tidal fields.
Wavelengths.—We search for the most obvious imprints of GLD in solar-system subsystems. As we pointed out long ago, the orbital radii of the 3 innermost terrestrial planets and the 3 outermost gaseous giants are obviously in arithmetic progression, in clear contradiction with the geometric progression favored across all planetary orbits by the empirical Titius-Bode rule [15,38]. This old observation fits quite well in the present context of equidistant potential minima in the expired solar tidal field.
In order to search for radial regularities in the current orbits of solar-system bodies, we need to have some prior knowledge about the longest wavelength of the long-gone tidal field. Equation (A56) is a suitable starting point, but this is not the regularity condition we seek for the following reason: Neighboring massive bodies cannot generally settle into adjacent potential minima (§ C.5) because their Hill spheres would then intersect. Therefore, nearest-neighboring bodies must generally be separated by at least two wavelengths of the tidal field. Thus, we define , the minimum separation between adjacent bodies, by the equation
where h is the Hill radius of the most massive body in the subsystem. Then, for the wavelengths of the tidal fields of the gaseous giant planets and the Galilean satellites given in equation (A65), we find that the minimum separations are
and
respectively. We apply, in turn, these estimates to the corresponding solar subsystems below.
Gaseous Giants.—We consider the gaseous giant planets in our solar system. It is well-known that their orbital radii are ∼ 5, 10, 20, and 30 AU, respectively. If these four massive planets are largely responsible for the damping of the collective wave during dissipative evolution in the past, then they must have finally settled near the bottoms of what used to be wave troughs of the standing tidal wave that pushed them around for a time.
This is clearly confirmed by the present-day orbital radii of the gas giants. Using the 4.5 AU minimum separation (equation (A67)), we find that relative to Jupiter ( AU), the outer three gaseous giants settled at about 2, 6, and 11 wavelengths away; the predicted radii are
to be compared with the actual semimajor axes of 9.58, 19.2, and 30.1 AU, respectively (relative deviations %). So Jupiter and Saturn are confirmed to be adjacent neighbors and Kepler’s third law gives an orbital period ratio of with a relative deviation of only 2%. On the other hand, the precise ratio of orbital radii is 1.842, and Kepler’s third law then gives a period ratio of precisely. It becomes obvious then that this is a pristine resonant subsystem with the four gaseous giants having settled (at increasing orbital periods) near the 1:1, 5:2, 7:1, and 14:1 MMRs of Jupiter, with Uranus showing the largest relative deviation of ∼1% in both semimajor axis and orbital period.
Galilean Moons.—Next we consider the four Galilean moons of Jupiter (Io, Europa, Ganymede, and Callisto) in some detail. Their orbital radii are
respectively. Using the 0.4 Gm minimum separation found for Ganymede (equation (A68)), we find that Europa is 2 wavelengths inward and Callisto is 4 wavelengths outward of Ganymede. The precision of this orbital configuration is astounding by astronomical measures. It has not been quoted or discussed in the past because a physical model such as GLD of the tidal field was lacking.
On the other hand, Io appears to have settled at 3.25 wavelengths inward of Ganymede and its location reveals that it is adjacent to Europa. (The number of wavelengths is not an integer probably because Io was locked into the LR early on, and its radial motions were suppressed.) Although not expected, this ∼1 separation is permitted because, owing to their smaller masses, the Hill radii of Io and Europa are much smaller than that of Ganymede (by factors of 0.33 and 0.43, respectively). Thus, although these smaller moons are adjacent neighbors, their Hill spheres do not at all intersect.
Scaled to the orbital radius of Io ( Gm), the orbital radii of the 4 Galilean moons are
respectively. (Small moon Europa is necessarily a bit off of 1.5 in this linear scale for the reason noted in § 4—it was also locked into the LR early on.) Thus, counting out by +0.5 from Io occupying wave trough #1, the next three Galilean moons have settled very close to the potential minima of tidal-wave troughs #2, 4, and 8. This is how the LR is realized in the spatial dimension of the long-gone tidal field, but only in conjunction with Kepler’s third law which must be valid for the observed spatial layout to be confirmed as resonant: in particular, relative to the orbit of Io, the Keplerian period ratios are for Europa and for Ganymede, completing thus the LR.
Callisto, the outermost massive moon,9 is famous for not participating in the 1:2:4 LR of the innermost three moons, and having to settle down to the 7:3 global MMR relative to the most massive moon Ganymede [53]. From the spatial sequence (A71), we get for Callisto and Ganymede and a period ratio of with a relative deviation of 3.5%. On the other hand, the precise observed ratio of semimajor axes is 1.759, in which case Kepler’s third law then gives a period ratio of exactly.
Finally, we note that Callisto could not have settled closer to Ganymede than , as presently observed. With Callisto at the or potential minimum (orbital radius of 1.27 Gm and 1.47 Gm, respectively), the Hill spheres of the two major moons would overlap. At the potential minimum (radius 1.67 Gm), the Hill spheres would not overlap, but Callisto would then occupy the 2:1 global MMR of Ganymede, extending thus the Laplace chain to 4 moons. Such configuration has never been observed in the solar system or in extrasolar systems [16], so it seems that the 2:1 MMR (following immediately past 1:1, with no body in-between) must be vacant in all systems.
We believe that the prospect of being in the 2:1 global MMR is precisely what made the orbit at from Ganymede unreachable to Callisto. There is ample evidence (but no proof or explanation) in the satellite subsystems of our solar system and in exoplanetary systems that the 1:2 global MMR is strictly ‘forbidden’ [16], unless it is a building block of a Laplace triple chain (see, e.g., GJ 876; [48,57]), or the in-between 3:2 resonant orbit is also occupied (HD 110067; [43]). Investigation of this important empirical discovery is just beginning (see also [16,24,47]).
References
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214.
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1.
- Batchelor, G. K. 2000, An Introduction to Fluid Dynamics (Cambridge: Cambridge Univ. Press), pp. 147, 153.
- Batygin, K., & Morbidelli, A. 2013, AJ, 145, 1.
- Bellan, P. M. 2006, Fundamentals of Plasma Physics (Cambridge: Cambridge Univ. Press), p. 155.
- Bernstein, I. B., Greene, J. M., & Kruskal, M. D. 1957, Phys. Rev., 108, 546.
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton Univ. Press), pp. 347, 412, 437-439, 677.
- Bittencourt, J. A. 2004, Fundamentals of Plasma Physics (New York: Springer), p. 500.
- Bonfanti, A., & Gillon, M. 2020, A&A, 635, A6.
- Chandrasekhar, S. 1969, Ellipsoidal Figures of Equilibrium (New Haven: Yale Univ. Press), pp. 71, 124.
- Chen, C. H. K., Klein, K. G., & Howes, G. G. 2019, Nature Comm., 10, 740.
- Christiansen, J. L., Crossfield, I. J. M., Barentsen, G., et al. 2018, AJ, 155, 57.
- Christodoulou, D. M., Contopoulos, J., & Kazanas, D. 1996, ApJ, 462, 865.
- Christodoulou, D. M., Contopoulos, J., & Kazanas, D. 2003, ApJ, 586, 372.
- Christodoulou, D. M., & Kazanas, D. 2017, RAA, 17, 129.
- Christodoulou, D. M., & Kazanas, D. 2023, RNAAS, 7, 275.
- Christodoulou, D. M., Kazanas, D., Shlosman, I., & Tohline, J. E. 1995, ApJ, 446, 472.
- Dawson, J. 1961, Phys. of Fluids, 4, 869.
- Delrez, L., Gillon, M., Triaud, A. H. M. J., et al. 2018, MNRAS, 475, 3577.
- Doveil, F., Escande, D. F., & Macor, A. 2005, Phys. Rev. Lett., 94, 085003.
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146.
- Fitzpatrick, R. 2015, Plasma Physics (Boca Raton: CRC Press), pp. 229-241.
- George, W. K. 2013, Lectures in Turbulence for the 21st Century, http://www.turbulence-online.com/publication.html, pp. 64-66.
- Gerlach, E. & Haghighipour, N. 2012, Celest. Mech. Dyn. Astr., 113, 35.
- Goldreich, P. 1965, MNRAS, 130, 159.
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375.
- Grimm, S. L., Demory, B.-O., Gillon, M., et al. 2018, A&A, 613, A68.
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153.
- Herr, W. 2014, in Proceedings of the CAS-CERN Accelerator School: Advanced Accelerator Physics, ed. W. Herr (Geneva: CERN), p. 377.
- Hillenbrand, L. A. 2008, in A Decade of Extrasolar Planets Around Normal Stars, STScI Symp. Ser. 19, ed. M. Livio, K. Sahu, & J. Valenti (Cambridge: Cambridge Univ. Press), p. 84.
- Jeans, J. H. 1902, Phil. Trans. Royal Soc. London, 199, 1.
- Johnson, M. C., Endl, M., Cochran, W. D., et al. 2016, ApJ, 821, 74.
- Kandrup, H. E. 1998, ApJ, 500, 120.
- Klimas, A. J., Viñas, A. F., & Araneda, J. A. 2017, J. Plasma Phys., 83, 905830405.
- Landahl, M. T., & Mollo-Christensen, E. 1992, Turbulence and Random Processes in Fluid Mechanics (Cambridge: Cambridge Univ. Press), p. 10.
- Landau, L. 1946, J. of Physics, 10, 25 (English translation).
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics, 2nd English edition, Translated by J. B. Sykes & W. H. Reid (Oxford: Pergamon Press), pp. 31-33, 92-93.
- Laskar, J. 2000, Phys. Rev. Lett., 84, 3240.
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8.
- Lithwick, Y., & Wu, Y. 2012, ApJL, 756, L11.
- Lopez, T. A., Barros, S. C. C., Santerne, A., et al. 2019, A&A, 631, A90.
- Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112.
- Luque, R., Osborn, H. P., Leleu, A., et al. 2023, Nature, 623, 932.
- Lynden-Bell, D. 1962, MNRAS, 124, 279.
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603.
- MacDonald, G. J. F. 1964, Rev. Geophys., 2, 467.
- Martí, J. G., Giuppone, C. A., & Beaugé, C. 2013, MNRAS, 433, 928.
- Millholland, S., Laughlin, G., Teske, J., et al. 2018, AJ, 155, 106.
- Mills, S. M., Fabrycky, D. C., Migaszewski, C., et al. 2016, Nature, 533, 509.
- Mora, D. O., & Obligado, M. 2020, Exp. Fluids, 61, 199.
- Morbidelli, A. 2002, Modern Celestial Mechanics (Boca Raton: CRC Press).
- Munk, W. H., & MacDonald, G. J. F. 1960, The Rotation of the Earth (Cambridge: Cambridge Univ. Press).
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge Univ. Press).
- Ostriker, J. P., & Gunn, J. E. 1969, ApJ, 157, 1395.
- Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499.
- Papaloizou, J. C. B. 2011, Celest. Mech. Dyn. Astr., 111, 83.
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890.
- Roy, A. E., & Ovenden, M. W. 1954, MNRAS, 114, 232.
- Ryutov, D. D. 1999, Plasma Phys. Control. Fusion, 41, A1.
- Shallue, C. J., & Vanderburg, A. 2018, AJ, 155, 94.
- Souami, D., Cresson, J., Biernacki, C., & Pierret, F. 2020, MNRAS, 496, 4287.
- Stix, T. H. 1992, Waves in Plasmas (New York: Springer-Verlag), pp. 169-193.
- Trigger, S. A., Ershkovich, A. I., van Heijst, G. J. F., & Schram, P. P. J. M. 2004, Phys. Rev. E, 69, 066403 (TEvS).
- Vandervoort, P. O. 2003, MNRAS, 339, 537.
- Vogt, S. S., Burt, J., Meschiari, S., et al. 2015, ApJ, 814, 12.
- Wadhwa, M., & Russell, S. S. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S.S. Russell (Tucson: Univ. Arizona Press), p. 995.
- Wang, H., & George, W. K. 2002, J. Fluid Mech., 459, 429.
- Wesson, J. 2015, Phys. of Plasmas, 22, 022519.
- Wisdom, J. 1980, AJ, 85, 1122.
- Wisdom, J. 1986, Cel. Mech., 38, 175.
| 1 | |
| 2 | Constant circulation would be more precise, although the two integrals of motion are equivalent in axisymmetric fluid systems. |
| 3 | In contrast, two orbiting bodies converge toward an intermediate orbit with angular momentum (§ 3.1). |
| 4 | Neptune’s primordial satellite system was obliterated by the arrival and retrograde capture of Triton, so it is not structurally comparable to the satellite systems of the other gaseous giants. |
| 5 | Page https://en.wikipedia.org/wiki/Orbital_resonance contains a comprehensive empirical summary of orbital MMRs along with a listing of hyperlinks to ∼100 professional citations. |
| 6 | |
| 7 | Defined as , the microscopic length over which energy dissipation takes place is then found to be or, equivalently, . |
| 8 | |
| 9 | Callisto is the third most massive moon in the solar system behind Ganymdede and Saturn’s Titan. Its mass is 72.6% of Ganymede’s and 80.0% of Titan’s. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





