Continuous Power Management of Decentralized DC Microgrid Based on Transitional Operation Modes under System Uncertainty and Sensor Failure

In this paper, a continuous power management for a decentralized DC microgrid (DCMG) is proposed to achieve voltage regulation and power balance even under system uncertainty and voltage sensor failure. The DCMG system achieves a continuous power management through only the primary controller to reduce the computational burden of each power agent. To enhance the reliability and resilience of the DCMG system under voltage sensor failure, a DC bus voltage (DCV) sensor fault detection algorithm is proposed. In this algorithm, the DCV sensor failure is detected by comparing the measured DCV with the estimated DCV. When the power agent identifies the DCV sensor failure, it changes the operation properly according to the proposed control mode decision algorithm to maintain the stability of the DCMG system. When uncertain conditions such as the power variation of the distributed generations, sudden grid disconnection, DCV sensor failure, electricity price change, and critical battery status occur, the DCMG system is changed to transitional operation modes. These transitional operation modes are employed to transmit the power agent information to other agents without digital communication links (DCLs) and to accomplish power sharing even under such uncertain conditions. In the transitional operation modes of the DCMG system, the DCV levels are temporarily shifted to an appropriate level, enabling each power agent to detect the uncertainty conditions, and subsequently to determine its operation modes based on the DCV levels. Simulation and experimental results under different test conditions confirm the reliability and effectiveness of the proposed control scheme.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Interest in sustainable and renewable energy is increasing due to environmental problems such as greenhouse gas emissions and fossil fuel depletion [1,2]. With the increasing demand for cleaner energy, the microgrid system has been emerged as a promising solution for the generation and distribution of electrical energy. By using the microgrid, the distributed generations based on renewable energy sources, utility grid, energy storage systems (ESSs), and loads are interconnected efficiently and reliably to overcome the limitation caused by the intermittent nature of renewable energy sources, which provides a sustainable alternative to the conventional power grid [3,4,5]. By harnessing diverse renewable energy sources, microgrid contributes to reduce carbon footprint and enhance energy resilience. The microgrid system which is efficient and robust for the use of distributed energy sources is usually composed of ESSs, loads, and distributed generations such as the wind turbine and photovoltaic (PV) [6].

Generally, the microgrid is divided into DC microgrid, AC microgrid (ACMG), and AC/DC hybrid microgrid [7]. Among these structures, DCMG stands out for its simplicity and efficiency. Unlike AC/DC hybrid and AC microgrids, the DCMG minimizes unnecessary power conversion stages and avoids problems such as synchronization, harmonics, and reactive power [8,9,10,11]. Furthermore, in the DCMG system, DC energy sources such as fuel cells, PV, and ESSs like supercapacitors or batteries are easily interconnected [12].

According to the configuration of the DCL, the control scheme for the DCMG system is categorized into three main types: centralized control, distributed control, and decentralized control [13,14,15]. The centralized control determines the operation modes of each power agent by a central controller that communicates with all the power agents via DCLs [16,17]. The distributed control also uses DCL to communicate with adjacent power agents. However, in the distributed control, all the power agents determine the proper operation modes with limited DCL to adjacent power agents without relying on a central controller [18,19]. It is worth mentioning that the transmission time delay caused by the DCL which is unavoidable in both the distributed and centralized controls, might negatively impact the efficiency and stability of the DCMG system [3]. A decentralized control scheme can be employed as an alternative way to solve this weakness. In the decentralized control scheme, only local measurements such as the DCV are used without any DCL between power agents to determine the operation modes of the DCMG system properly [20]. In addition, the power agents operate independently in the decentralized DCMG system without the use of any DCL, which significantly increases the flexibility, simplicity, and scalability of the microgrid system [21,22].

Generally, the DCV is utilized as global information for each power agent in the decentralized DCMG system [23,24,25,26]. If the DCV is decreasing from the nominal DCV value, it indicates that the supply power to the DC bus is less than the demand power. In contrast, if the DCV is increasing from the nominal DCV value, it means that there is surplus power in the DCMG system. Traditionally, the droop control method is utilized in the decentralized DCMG system to control the DCV at the nominal value [27,28,29,30,31]. In the study [29], the power balance of the DCMG system is achieved based on the voltage–current (V-I) droop controller according to the DCV level. To overcome the weakness of the DCV fluctuation in this scheme, the researchers in [31,32] proposed the use of an integral term in the secondary controller for ensuring the DCV restoration to the nominal value. In these methods, the secondary control is utilized to regulate the DCV to the nominal value while the primary control is employed to maintain the power balance in the decentralized DCMG system. Although the voltage fluctuation problem caused by the droop controller is mitigated by combining the primary and secondary controls, there still exists a computational burden in the above methods. Moreover, it is desirable to consider a method to enhance the system reliability even under the sensor device failure.

To operate the DC microgrid efficiently, several sensors are utilized to provide feedback signals for real-time monitoring and control systems. It is worth mentioning that the information from these sensors plays a significant role, especially in the decentralized DCMG system to determine the control modes of each power agent because of the absence of the DCLs between the power agents. The sensor failure of abnormality leads to discrepancies in data interpretation among power agents, potentially resulting in suboptimal system operation, or even instability in an extreme case [33,34]. To overcome such sensor failure, the researchers in the studies [35,36] presented a fault tolerant control by hardware redundancy. In those methods, additional sensors are equipped as redundancy hardware to deal with sensor faults. In spite of the reliability enhancement against sensor failures, these approaches obviously increase the system cost. On the other hand, a fault detection and isolation controller is proposed for the distributed DCMG system via an adaptive high-gain observer to detect different types of sensor failure [37]. The research in [38] proposed a H_∞ observer for DC-DC converters to compensate for the current and voltage sensor faults. However, it is difficult to implement those control schemes for the decentralized DCMG system because the DCLs between the power agents are absent in the decentralized DCMG.

Motivated by this concern, this study presents a continuous power management of a decentralized DCMG system based on the transitional operation modes under system uncertainty and sensor failure to improve the system reliability. To achieve a continuous power balance as well as voltage stabilization even under several uncertain conditions such as the power variation of the distributed generation, the grid disconnection, and critical battery status, the transitional operation modes are employed to transmit the power agent information to others without DCLs. In these transitional operation modes of the DCMG system, the DCV levels are temporarily adjusted to a proper level. In addition, to minimize the electricity price, the proposed scheme determines the operation modes of power agents by considering the electricity price conditions in grid-connected mode. It is important to mention that the proposed control scheme uses only the primary control to achieve the DCV restoration, which significantly reduces the computational burden.

To monitor the abnormality of the DCV sensor, all the power agents estimate the DCV by using the observer in the proposed scheme. In all power agents, the proposed DCV sensor fault detection algorithm is implemented to detect the DCV sensor fault by comparing the estimated DCV with the measured DCV. Under normal conditions without the DCV sensor failure, the proposed power management scheme achieves both voltage regulation and power balance by using the estimated DCV. However, when the DCV sensor failure occurs in any power agent, the operation modes of each agent are changed properly based on the proposed control mode decision algorithms to ensure continuous power management even under DCV sensor fault. The main contributions of this paper can be summarized as follows:

(i): The proposed decentralized control scheme achieves a continuous power management based on the transitional operation modes under system uncertainty and sensor failure, which greatly improves the system reliability. In addition, both voltage regulation and power sharing are accomplished by using only the primary controller to reduce the computational burden.
(ii): Even under uncertain conditions such as the power variation of the distributed generation, the grid disconnection, the electricity price change, and critical battery status, the proposed decentralized DCMG system ensures voltage stabilization as well as the power balance by using the transitional operation modes without DCLs. Once an uncertain condition occurs, the DCV levels are temporarily adjusted to a proper level in transitional operation modes, and then, the power agents determine their operation modes based on the DCV levels.
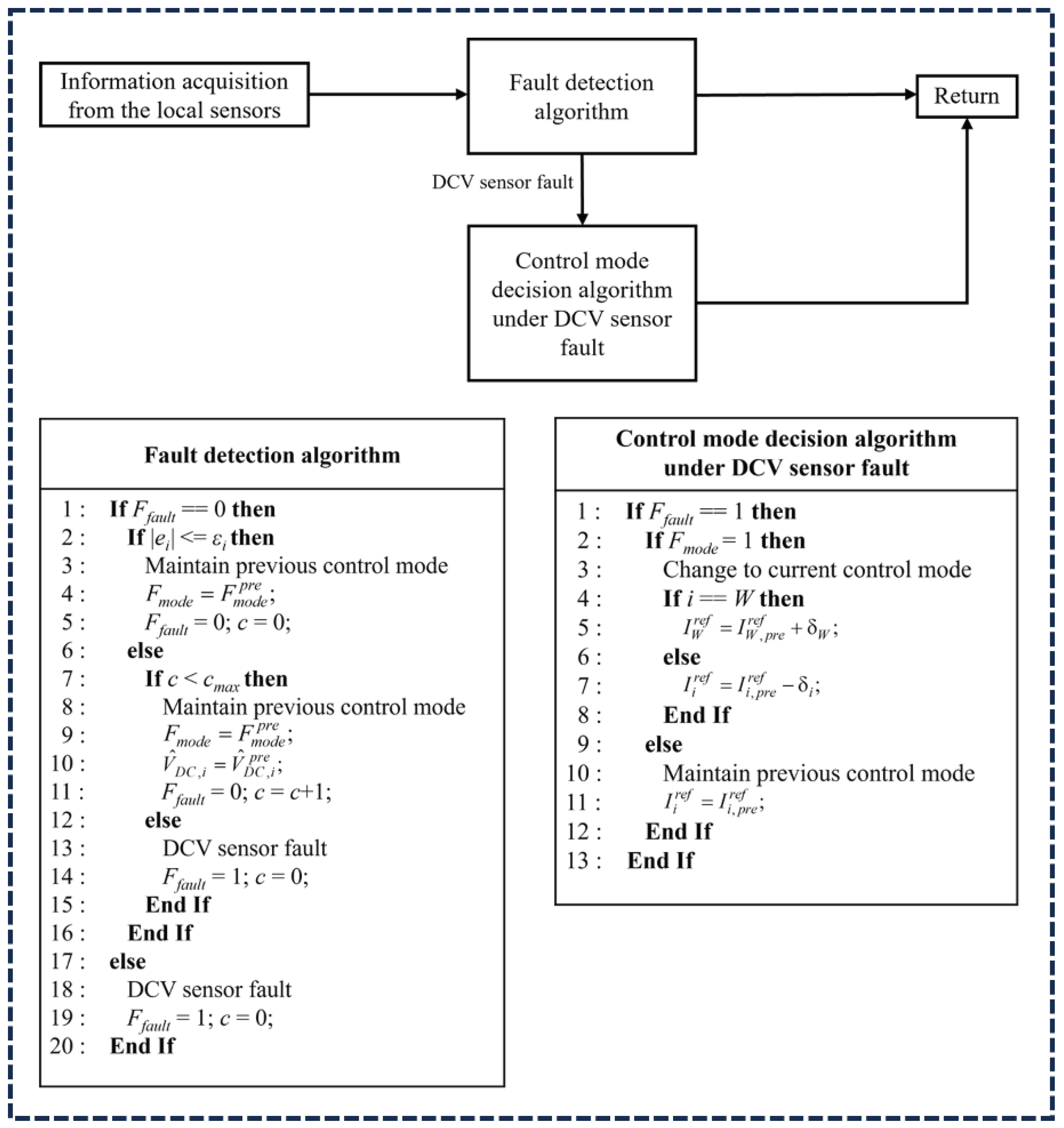
(iii): To enhance the reliability of the DCMG system, the DCV sensor fault detection algorithm continuously monitors the abnormality of the DCV sensor in the proposed scheme. Under normal conditions without the DCV sensor failure, the proposed scheme achieves both voltage regulation and power balance. When the DCV sensor failure occurs in a power agent, the proposed control mode decision algorithm properly changes the operation of the power agent into the current control mode for seamless power management. In addition, the proposed scheme can stably work even under multiple DCV sensor faults in more than one power agent at the same time if there exists a normal DCV sensor in a DCMG system.

This paper is organized as follows: Section 2 describes the system configuration of a DCMG and decentralized control scheme. Section 3 explains the control strategy of power agents in normal conditions, the control strategy under the DCV sensor fault, and transitional operation modes of power agents. Section 4 and Section 5 show the simulation and experimental results of the decentralized DCMG system under various conditions to validate the proposed control schemes. Finally, Section 6 provides the conclusion of this paper.

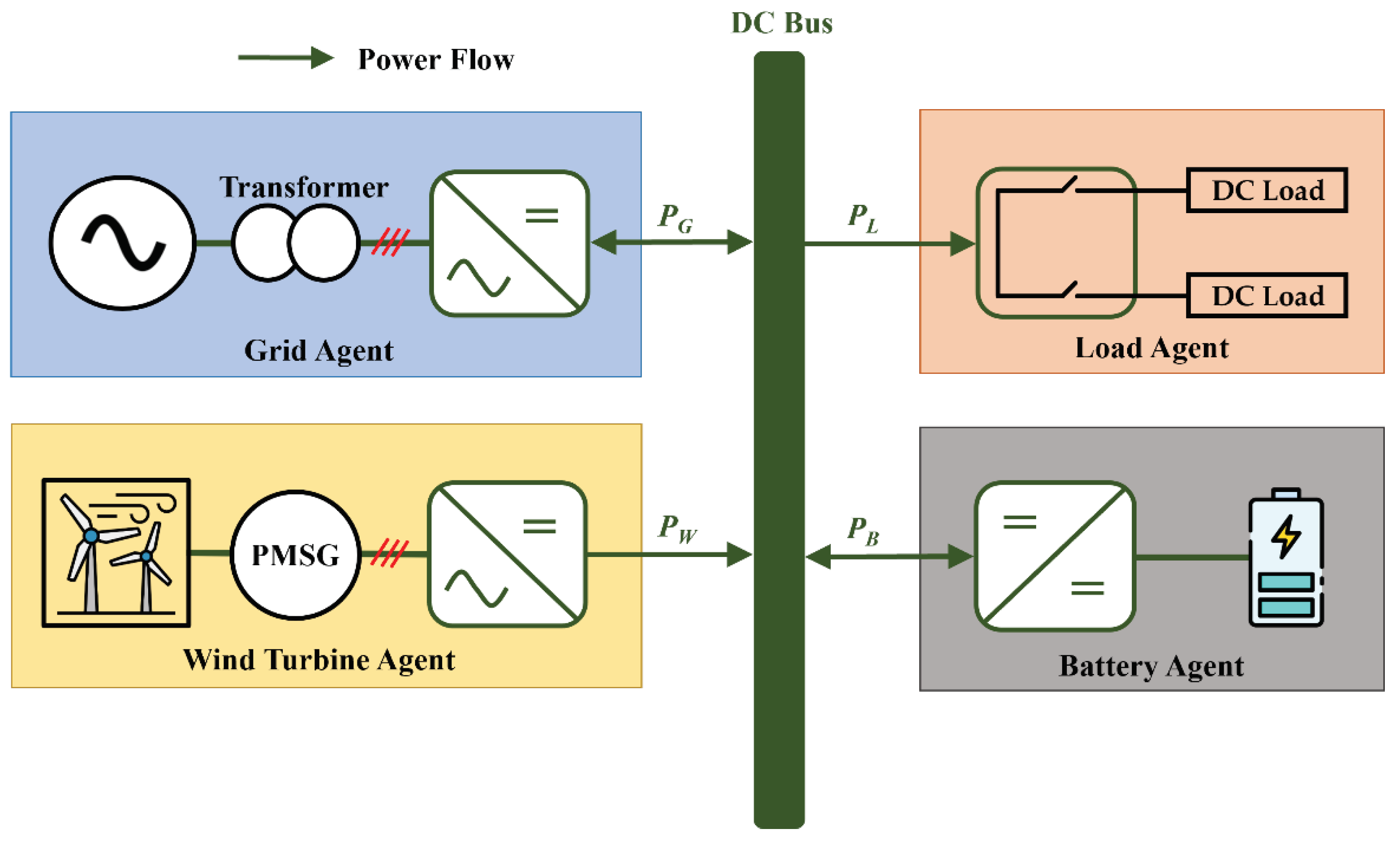
2. System Configuration of a DCMG and Decentralized Control Scheme

Figure 1 shows the system configuration of a decentralized DCMG that consists of four power agents: a grid agent, a wind turbine agent, a load agent, and a battery agent. The grid agent connects the main grid to the DC bus through a transformer and an AC/DC bidirectional converter. The wind turbine agent connects the wind turbine to the DC bus, in which the mechanical energy from the turbine is converted into electrical energy through a permanent magnet synchronous generator (PMSG) and an AC/DC unidirectional converter. The battery agent connects the battery to the DC bus through a DC/DC bidirectional converter. The load agent consists of DC loads which are directly connected to the DC bus.

In this DCMG system, both the grid and battery agents are capable of transferring bidirectional power, by supplying the power into the DC bus or absorbing the power from the DC bus. On the other hand, the wind turbine agent has only unidirectional power flow by supplying the power to the DC bus. The load agent only absorbs the power from the DC bus. As shown in Figure 1,

P_{G}

P_{L}

P_{W}

, and

P_{B}

represent the power flow of the grid, load, wind turbine, and battery agents, respectively. In this paper, positive power values (

+

) represent that the power agent absorbs the power from the DC bus. On the contrary, negative power values (

-

) represent that the power agent supplies the power to the DC bus.

Figure 2 shows the simplified structure for the power converter of agent i which consists of a switch module, inductor

L_{i}

, capacitor

C_{i}

, and virtual resistance

R_{L i}

for the grid, wind, and battery agents. In this figure, i denotes each agent, i.e.,

i =

G, W, and B representing the grid, wind, and battery agents, respectively. The dynamic model of the power converter in Figure is derived by applying Kirchhoff’s law as follows:

\frac{d V_{D C, i}}{d t} = \frac{I_{i}^{o u t}}{C_{i}} - \frac{V_{D C, i}}{R_{L i} C_{i}}

(1)

where

V_{D C, i}

and

I_{i}^{o u t}

denote the DCV measured from the sensor and converter output current of agent

i

, respectively. It is worth mentioning that the resistance

R_{L i}

for each power agent

i

, is connected in parallel to produce the total equivalent resistance

R_{L}

at the DC bus of the DCMG system. This yields the relation as follows:

\frac{1}{R_{L}} = \sum \frac{1}{R_{L i}}

(2)

where

R_{L}

is the total equivalent load of the DCMG system.

3. Control Strategy and Transition Operations of Power Agents under Emergency Conditions

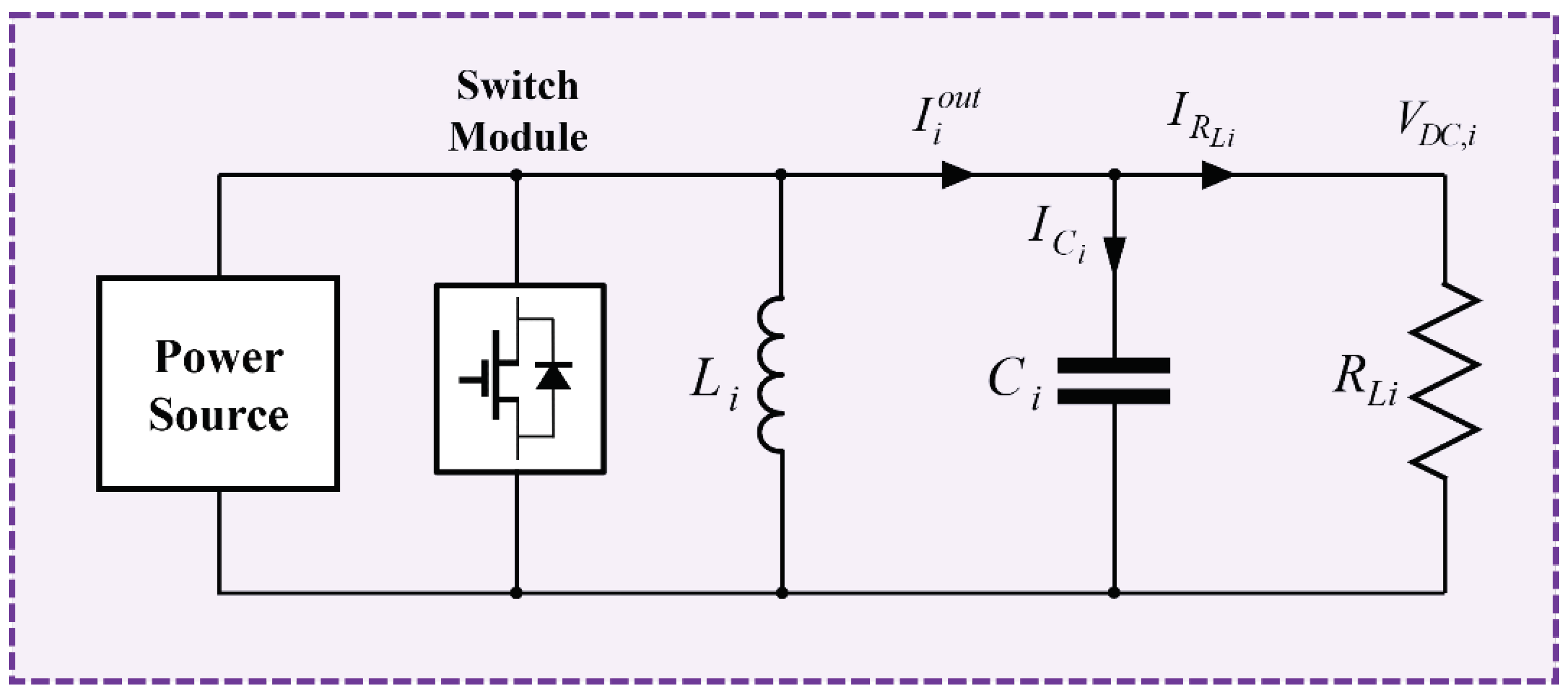
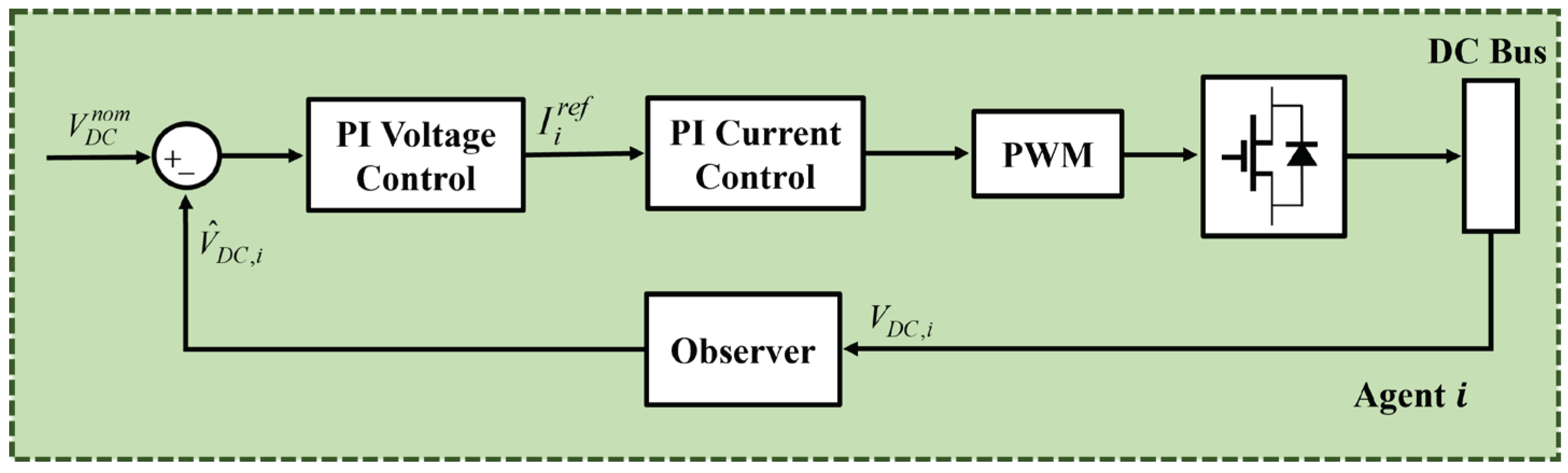
3.1. Control Strategy of Power Agents

Figure 3 shows the control block diagram of agent

i

in the decentralized DCMG system. Compared to the conventional voltage droop controllers [30,31], the proposed control scheme only utilizes the primary controller to reduce the computational burden. The primary controller consists of the voltage control and current control. In the proposed control scheme, in order to maintain the power balance even in the circumstance of emergency conditions, the DCV sensor fault in agent

i

is detected, which is described in detail in Subsection 3.2. For this purpose, the DCV of agent

i

is estimated by the observer in the proposed control scheme. The agent

i

regulates the DCV by the proportional-integral (PI) controllers using the estimated DCV value. In addition, the estimated DCV is also used to detect the DCV sensor fault for the purpose of guaranteeing the power balance. From (1), the DCV of agent

i

can be estimated as

{\dot{\hat{V}}}_{D C, i} = \frac{I_{i}^{o u t}}{C_{i}} - \frac{{\hat{V}}_{D C, i}}{C_{i} R_{L i}} + N_{i} (V_{D C, i} - {\hat{V}}_{D C, i})

(3)

where

{\hat{V}}_{D C, i}

is the estimated DCV value and

N_{i}

is observer gain.

To ensure the power balance, the decentralized DCMG system in this study uses nine steady-state operation modes as shown in Table 1 under normal conditions without any DCV sensor fault. In each operation, the control modes of the power agent

i

are determined according to the criterion that only one power agent regulates the DCV at each instant. When the DCMG system is subject to change of the operation modes caused by uncertain conditions such as power variation and system uncertainty, the transition operation modes are used to identify the power agent that regulates the DCV. The transition operation modes are described in detail in Subsection 3.3. The control modes of the power agent

i

are separated into two types: the voltage control and current control modes. The voltage control mode which is implemented as shown in Figure 3, is employed to regulate the DCV. In contrast, the current control mode is realized by only the PI current controller.

Nine steady-state operation modes in Table 1 are explained in detail.

Operating mode NO₁: This mode occurs in the high electricity price when the sum of maximum discharging battery power and wind power is higher than load demand. The grid agent regulates the DCV at the nominal value V_nom by GVCM_inv (Grid agent Voltage Control Mode by Inverter operation). The battery agent operates in BCCM_dis (Battery Current Control Mode by Discharging operation), and the wind agent operates in the maximum power point tracking (MPPT) mode.

Operating mode NO₂: This mode occurs in the high electricity price when the sum of maximum discharging battery power and wind power is lower than load demand. In this situation, to guarantee the power balance, the grid agent supplies the power to the DC bus even under high electricity price condition by regulating the DCV at V_nom. The grid agent works in GVCM_con (Grid agent Voltage Control Mode by Converter operation), the battery agent operates in BCCM_dis, and the wind turbine agent operates in the MPPT mode.

Operating mode NO₃: This mode occurs in the normal electricity price when the sum of maximum charging battery power and load demand is less than the wind power. In this case, to ensure the power balance, the grid agent absorbs the power from the DC bus by regulating the DCV at V_nom. The grid agent operates in GVCM_inv, the battery agent operates in BCCM_char (Battery Current Control Mode by Charging operation), and the wind turbine agent operates in the MPPT mode.

Operating mode NO₄: This mode occurs in the normal electricity price when the sum of maximum charging battery power and load demand is higher than the wind power. The grid agent regulates the DCV at V_nom by GVCM_con. The battery agent and the wind turbine agent operate in BCCM_char and the MPPT mode, respectively.

Operating mode NO₅: This mode occurs in the normal electricity price when the battery state-of-charge (SOC) level is in maximum and the wind power is lower than the load demand. This mode also occurs in the high electricity price when the battery SOC level is in minimum and the wind power is lower than the load demand. In both situations, the grid agent regulates the DCV at V_nom by GVCM_con while the battery and wind turbine agents operate in the IDLE and the MPPT modes, respectively.

Operating mode NO₆: This mode occurs in the normal electricity price when the battery SOC level is in maximum and the wind power is higher than load demand. This mode also occurs in the high electricity price when the battery SOC level is in minimum and the wind power is higher than load demand. In both situations, the grid agent regulates the DCV by GVCM_inv. The battery agent operates in the IDLE mode, and the wind turbine agent operates in the MPPT mode.

Operating mode NO₇: This mode occurs in the islanded mode when the wind power is less than the sum of the load demand and maximum charging power of the battery. The battery agent operates in BVCM (Battery Voltage Control Mode) to regulate the DCV at V_nom while the wind turbine agent operates in the MPPT mode.

Operating mode NO₈: This mode occurs in the islanded mode when the sum of the battery maximum charging power and the load demand is lower than the wind power. In this situation, the wind turbine agent operates in VCM (Voltage Control Mode) to regulate the DCV at V_nom while the battery agent operates in BCCM_char.

Operating mode NO₉: This mode occurs in the islanded mode when the battery SOC level is in maximum, and the wind turbine power is higher than the load demand. The wind turbine agent operates in VCM to regulate DCV at V_nom and the battery agent operates in the IDLE mode.

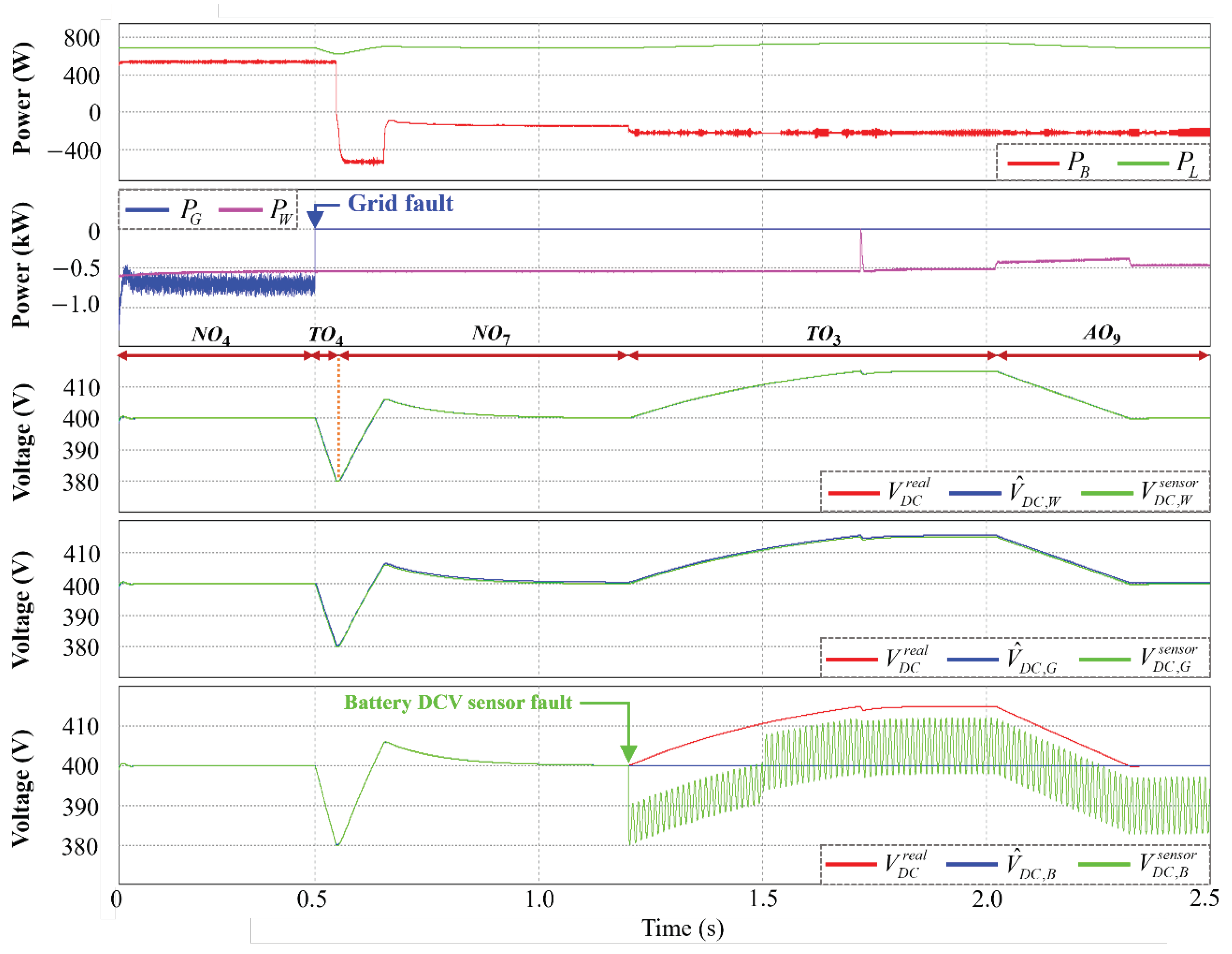
3.2. Control Strategy under DCV Sensor Fault

Figure 4 shows the DCV sensor fault detection and control mode decision algorithms of agent i under the DCV sensor fault. In these algorithms, e_i,

ε_{i}

, c, c_max,

{\hat{V}}_{D C, i}^{p r e}

I_{i}^{r e f}

, and

I_{i, p r e}^{r e f}

represent the difference between

V_{D C, i}

and

{\hat{V}}_{D C, i}

, specified threshold value, the counter, the specified threshold of the counter, the previous value of

{\hat{V}}_{D C, i}

, the reference current of agent i, and the previous value of

I_{i}^{r e f}

, respectively. The variable F_fault denotes a fault flag which is used to indicate that the DCV sensor in agent

i

has a fault. When the DCV sensor has a fault, the variable F_fault is set to one. Otherwise, it is reset to zero. Also, the variable F_mode represents a control mode flag which is used to indicate the control mode of agent i before the DCV sensor fault. If the control mode of agent i was the voltage control mode before the DCV sensor fault, the variable F_mode is set to one. Otherwise, it is reset to zero.

In the proposed control scheme, when F_fault is equal to zero, the system compares

e_{i}

with

ε_{i}

to investigate the normal operation of the DCV sensor. When

e_{i}

is larger than

ε_{i}

, the counter is utilized to count this event. When the counter c is less than c_max, the counter c is increased and

{\hat{V}}_{D C, i}

is replaced with

{\hat{V}}_{D C, i}^{p r e}

. However, if the counter c is greater than c_max, the fault detection algorithm confirms the DCV sensor fault in power agent i. As soon as the DCV sensor fault is identified, the fault detection algorithm sets the flag F_fault to one. Then, the control mode decision algorithm of agent i is executed to guarantee the system stability even in the DCV sensor fault by determining a proper operation mode.

In the control mode decision algorithm, the transition operations to the current control mode depend on the previous operations of the power agent having the DCV sensor fault. If the DCV sensor failure occurs in the power agent that does not regulate the DCV, it still maintains the operation of the current control mode with

I_{i}^{r e f}

set to the previous current reference

I_{i, p r e}^{r e f}

. On the other hand, if the DCV sensor failure occurs in the power agent i that regulates the DCV, the other power agent should take the role of regulating the DCV. For this purpose, the power agent operation is shifted to the current control mode with the current reference change.

In case that the DCV sensor fault occurs in the grid or battery agent that regulates the DCV, the current reference

I_{i}^{r e f}

is shifted to negative by subtracting a small positive value

δ_{i}

from the previous current reference

I_{i, p r e}^{r e f}

. Because more power is supplied to the DC bus, the DCV level is continuously increased. As a result, by detecting this DCV transition, the other power agents can regulate the DCV after the transition operation mode.

In case that the DCV sensor fault occurs in the wind turbine agent that regulates the DCV, the current reference

I_{W}^{r e f}

of the wind turbine agent is shifted to positive by adding a small positive value

δ_{W}

to the previous current reference

I_{W, p r e}^{r e f}

. Because the power supplied to the DC bus is reduced, the DCV level is decreasing. By detecting this DCV transition, the other power agents can regulate the DCV after the transition operation mode.

To ensure both the voltage regulation and power balance even under the DCV sensor fault, Table 2 shows additional steady-state operation modes for a decentralized DCMG system according to the DCV sensor fault. During normal operation without any sensor fault, the DCMG system operates in one of the steady-state operation modes listed in Table 1. Under the DCV sensor fault, the DCMG system operation is changed to one of the additional steady-state modes in Table 2 after the transition operation modes which will be explained in the next subsection.

Nine additional steady-state operation modes in Table 2 are explained in detail. The operation mode transition from the normal operation in Table 1 to the additional operation in Table 2, caused by the DCV sensor faults will be described in Figure 5.

Operation mode AO₁: In this mode, the battery agent operates in BVCM to regulate the DCV at V_nom. The wind turbine agent operates in the MPPT mode and the grid agent operates in GCCM_inv (Grid Current Control Mode by Inverter operation).

Operation mode AO₂: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in BCCM_dis and the grid agent operates in GCCM_inv.

Operation mode AO₃: In this mode, the battery agent operates in BVCM to regulate DCV at V_nom. The wind agent operates in the MPPT mode and the grid agent operates in GCCM_con (Grid Current Control Mode by Converter operation).

Operation mode AO₄: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in BCCM_dis and the grid agent operates in GCCM_con.

Operation mode AO₅: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in BCCM_char and the grid agent operates in GCCM_inv.

Operation mode AO₆: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in BCCM_char and the grid agent operates in GCCM_con.

Operation mode AO₇: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in the IDLE mode and the grid agent operates in GCCM_con.

Operation mode AO₈: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in the IDLE mode and the grid agent operates in GCCM_inv.

Operation mode AO₉: In this mode, the wind turbine agent operates in VCM to regulate DCV at V_nom. The battery agent operates in BCCM_dis.

Figure 5 shows the operation mode transitions caused by the DCV sensor fault, in which the DCV sensor fault of the battery, wind turbine, and grid agents is denoted by the variables

F_{B}

F_{W}

, and

F_{G}

, respectively. The maximum and minimum SOC levels of the battery agent are denoted by

S O C_{B}^{H}

and

S O C_{B}^{L}

, respectively. The variables

F_{B}

F_{W}

, and

F_{G}

are represented as

\begin{array}{c} F_{i} = 1, if the DCV sensor fault occurs in power agent i \\ F_{i} = 0, Otherwise \\ for i = B, W, G . \end{array}

(4)

Similarly, two variables to denote the battery SOC status are defined as

\begin{array}{c} F_{B H} = 1, if S O C_{B} = S O C_{B}^{H} \\ F_{B H} = 0, Otherwise \end{array}

(5)

\begin{array}{c} F_{B L} = 1, if S O C_{B} = S O C_{B}^{L} \\ F_{B L} = 0, Otherwise \end{array}

(6)

where

S O C_{B}

denotes the battery SOC.

If the DCV sensor failures occur when the DCMG system operates in the normal operation mode NO₁, the DCMG operation is changed to additional operation modes as shown in Figure 5a. During the operation of NO₁, if the DCV sensor failure occurs in the battery agent (F_B=1) or the wind turbine agent (F_W=1) or both the battery and wind turbine agents ((F_B=1)&(F_W=1)), the DCMG system still maintains NO₁ because the battery and the wind turbine agents did not regulate the DCV before the sensor fault. If the grid (F_G=1) or both the grid and wind turbine agents ((F_G=1)&(F_W=1)) have the DCV sensor fault, the DCMG system operation is changed to mode AO₁. The grid agent changes the control mode from GVCM_inv in NO₁ into GCCM_inv in AO₁ according to Figure 4. In this case, the battery agent operates in BVCM to regulate the DCV. Finally, if both the grid and battery agents ((F_G=1)&(F_B=1)) have the DCV sensor fault, only the wind turbine agent can regulate the DCV. As a result, the DCMG system is changed to mode AO₂.

Figure 5b, Figure 5c, and Figure 5d show the transition to additional operation modes of the DCMG system when the DCV sensor fault occurs during the normal DCMG system operation in NO₂, NO₃, and NO₄, respectively. These figures show similar behavior with Figure 5a according to the location of the DCV sensor fault. However, under each DCV sensor fault, the destination of additional operation modes is quite different. In the normal operation modes NO₂, NO₃, and NO₄, the grid agent regulates the DCV either in converter or inverter operation. Even in the case of (F_B=1) or (F_W=1) or ((F_B=1)&(F_W=1)), the DCMG system still maintains the previous operations NO₂, NO₃, and NO₄, respectively, as shown in Figure 5b, Figure 5c, and Figure 5d because the grid agent can still regulate the DCV. If the DCV sensor fault occurs in the grid agent, (F_G=1) or ((F_G=1)&(F_W=1)), the DCV regulation is achieved by the battery agent, which results in the transition into additional operation modes AO₃, AO₁, and AO₃, respectively, in Figure 5b, Figure 5c, and Figure 5d. If the DCV sensor failure occurs in the grid agent and battery agent at the same time ((F_G=1)&(F_B=1)), only the wind turbine agent is able to regulate the DCV. Then, by transition into additional operation modes AO₄, AO₅, and AO₆, respectively, the wind turbine agent regulates the DCV in VCM, and other power agents operate in the current control mode.

Figure 5e shows the operation mode transition from NO₅ caused by the DCV sensor faults. As we mentioned before, NO₅ occurs in the normal electricity price when the battery SOC level is in maximum and the wind power is lower than the load demand. This mode also occurs in the high electricity price when the battery SOC level is in minimum and the wind power is lower than the load demand. If the DCV sensor fault does not occur in the grid agent, the DCMG system maintains mode NO₅. In the condition of [(F_BH=1)&(F_G=1)] or [(F_G=1)&(F_B=1)], the DCMG system is changed from NO₅ to AO₇. In the first condition, the battery agent operates in the IDLE because it can not absorb charging power. In the second condition, because the grid and battery agents can not regulate the DCV, the wind turbine agent operates in VCM to regulate the DCV, which results in AO₇. In the condition of [(F_BL=1)&{(F_G=1) or ((F_G=1)&(F_W=1))}], the DCMG system is changed from NO₅ to AO₃. This condition represents the case that the DCV sensor fault occurs in the grid agent, or both the grid and wind turbine agents when the battery SOC level is in a minimum. In either case, the battery agent works in BVCM to regulate the DCV with charging, which results in AO₃.

Figure 5f has a similar structure as Figure 5e. While the grid agent starts with GVCM_con in the normal operation mode of NO₅ in Figure 5e, it starts with GVCM_inv in NO₆ in Figure 5f. Unless the DCV sensor fault occurs in the grid agent, the DCMG system maintains mode NO₆. Depending on the battery SOC condition and the DCV sensor fault locations, this normal operation mode is shifted to AO₈ or AO₁, respectively. In AO₁, the battery agent regulates the DCV in BVCM. If the battery agent is not available to regulate the DCV because of the SOC condition or DCV sensor fault, the wind turbine agent is used in VCM, instead.

Figure 5g shows the operation mode transition caused by the DCV sensor faults when the DCMG system operates in NO₇. If the DCV sensor of the battery agent is operating normally regardless of whether the DCV sensor fault occurs in the grid or wind turbine agent, the DCMG system maintains NO₇. However, when the battery agent has a DCV sensor fault, i.e., (F_B=1), only the wind turbine agent can regulate the DCV in VCM. Then, the DCMG system is changed to AO₉ or NO₈ depending on the power relation of the wind power and load demand.

Figure 5h shows the transition of the DCMG system when the DCV sensor fault occurs during the normal operation of NO₈. Unless the DCV sensor failure occurs in the wind turbine agent, the DCMG system maintains NO₈. If the wind turbine agent has a DCV sensor fault (F_W=1), the battery agent regulates the DCV in BVCM, which results in the change of the DCMG operation to NO₇.

Finally, Figure 5i shows the operation mode transition from NO₉ caused by the DCV sensor fault. Since only the wind turbine agent is operating in NO₉, the DCMG system maintains NO₉, if the DCV sensor of the wind turbine agent does not have a fault.

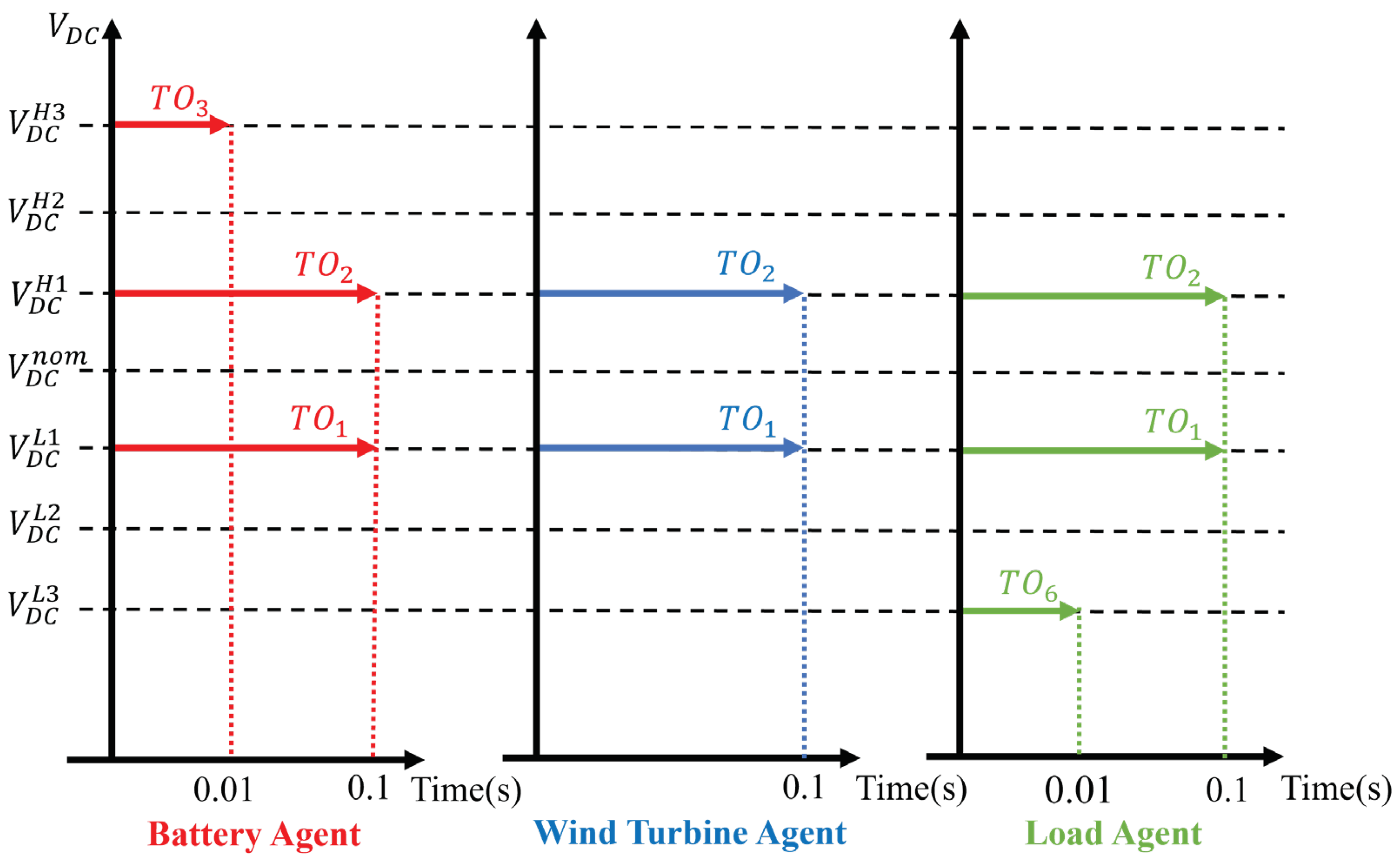
3.3. Transitional Operation Modes of Power Agents

In the proposed DCMG system, all power agents determine the operation modes by detecting the information of the DCV level without DCLs. When certain transient conditions are introduced into the DCMG system, the power agent in the DCMG system temporarily shifts the DCV value to different levels during a predetermined time. During this predetermined time, all the power agents appropriately change the operation mode during the transient periods before the DCMG system returns to another steady-state operation mode.

Table 3 lists the transition operation modes which are introduced into the DCMG system due to the DCMG system uncertainty. This Table also shows the power agents which activate each transition operation mode and resultant actions. In this Table, V_L₁, V_L₂, and V_L₃ denote the first, second, and third low level DCV, respectively, and V_H₁, V_H₂, and V_H₃ denote the first, second, and third high level DCV, respectively.

When the event such as the electricity price change from normal to high, or the grid agent reconnection from a fault with a high electricity price happens, the DCMG system temporarily uses the transition operation mode TO₁. In the mode TO₁, the grid agent regulates the DCV to V_L₁ to inform this event to other power agents. Figure 6 shows the detection of the transition operation modes by each power agent. In Figure 6, the horizontal axis represents the time required for transition operation detection, the vertical axis represents the DCV levels for different transition operations, and the color indicates the power agents to detect the transition operation. As the DCV level reaches V_L₁, and lasts during 0.1 s, the other power agents such as the battery, wind turbine, and load agent identify this event, and changes their operation appropriately. After 0.5 s from the instant that the DCV reaches V_L₁, the grid agent regulates the DCV back to the nominal value V_nom.

When the event such as the electricity price change from high to normal, or the grid agent reconnection from a fault with the normal electricity price happens, the DCMG system temporarily uses the transition operation mode TO₂. In TO₂, the grid agent regulates the DCV to V_H₁ to inform this event to other power agents. As shown in Figure 6, as the DCV level reaches V_H₁, and lasts during 0.1 s, the other power agents identify this event, and change their operation appropriately. After 0.6 s from the instant that the DCV reaches V_H₁, the grid agent regulates the DCV back to the V_nom.

In an islanded mode of the DCMG system, if the battery agent is in critical condition such as the maximum battery SOC_B, the DCV is increasing because the battery agent cannot absorb power. After the DCV reaches V_H₃, the wind turbine agent maintains the DCV to V_H₃ during 0.3 s with the transition operation mode TO₃. After 0.01 s from the instant that the DCV reaches V_H₃, the battery agent identifies this event to change the operation appropriately. After 0.3 s, the wind turbine agent regulates the DCV to V_nom again. This transition operation mode TO₃ is also initiated by the grid agent when the grid agent operating in GVCM_inv is disconnected from the DCMG system, or the grid agent has a DCV sensor fault.

The transition operation mode TO₄ is triggered by the grid agent when the grid agent operating in GVCM_con has a fault. The transition operation mode TO₄ is also activated when the wind power is decreased in an islanded mode. In this situation, because the supplied power is less than the load demand, the DCV is decreasing. If the battery agent detects that the DCV level is maintained lower than V_L₂ more than 0.01 s, as shown in Table 3, the battery agent acknowledges this event. Then, the battery agent changes the operation to BVCM to regulate the DCV back to V_nom.

When the grid agent is in emergency conditions such as a grid fault in high electricity price or the DCV sensor fault, the DCV is increasing due to surplus power, which triggers the transition operation mode TO₅. As the DCV level is maintained higher than V_H₂ more than 0.01 s, the battery agent acknowledges this event, and changes the operation to BVCM to regulate the DCV back to V_nom.

When the DCMG system is in an islanded mode, SOC_B reaches the minimum level, and the generated power of the wind turbine is less than the load demand, the DCV is decreased to the critical value of V_L₃. After 0.01 s from the instant the DCV reaches V_L₃, the load shedding is started.

4. Simulation Results

In this section, the reliability and feasibility of the proposed control scheme are evaluated through the simulations of a decentralized DCMG system using the PSIM software. The simulations are conducted considering several uncertain operating conditions such as the DCV sensor fault, grid fault, the minimum or maximum battery SOC level, the agent power variation, and the electricity price change of the grid. The system parameters of a decentralized DCMG system are shown in Table 4. In this table, PMSG denotes a permanent magnet synchronous generator, and LCL denotes an inductive-capacitive-inductive filter of the utility grid agent.

4.1. Transition between Grid-Connected Mode and Islanded Mode under DCV Sensor Fault

Figure 7 shows the simulation results in the case of the transition between the grid-connected mode and islanded mode under the battery DCV sensor fault. In this figure,

{\hat{V}}_{D C, i}

(for I = G, W, and B) is the estimated DCV value in each power agent,

V_{D C, i}^{s e n s o r}

is the measured DCV by the sensor in each power agent, and

V_{D C}^{r e a l}

is the actual DCV value. In this simulation, the DCMG system starts in mode NO₄ which is one of the grid-connected modes. In this mode, the grid agent operates in GVCM_con to regulate the DCV at V_nom, the battery agent operates in BCCM_char, and the wind turbine agent operates in the MPPT mode. At t= 0.5 s, the grid fault occurs, which causes the change of DCMG system operation from the grid-connected mode NO₄ to islanded mode TO₄. Because the supplied power is less than the load demand, the DCV is reduced. If the battery agent detects that the DCV level is maintained lower than V_L₂ more than 0.01 s, as shown in Table 3, the battery agent acknowledges the grid disconnection from the DCMG. Then, the battery agent changes the operation from BCCM_char to BVCM to regulate the DCV back to V_nom, and the entire DCMG system operation is changed from TO₄ to NO₇.

At t=1.2 s, when the DCV is regulated by the battery agent, the battery DCV sensor fault occurs. As soon as the battery agent identifies the DCV sensor fault, it is shifted to the current control mode by the proposed fault detection and control mode decision algorithms as shown in Figure 4. By using the proposed scheme, the battery agent increases the DCV by supplying more power to the DC bus. If the DCV level reaches V_H₃, the wind turbine agent maintains the DCV to V_H₃ during 0.3 s. As a result, the DCMG system is changed from NO₇ to TO₃. After 0.3 s from the instant that the DCV reaches V_H₃, the wind turbine agent regulates the DCV back to V_nom and the resultant DCMG system operation is changed from TO₃ to AO₉.

It is confirmed from this simulation result that the battery agent can still supply power to the DC bus in a current control mode even if the battery agent has a DCV sensor fault, which clearly demonstrates that the proposed control scheme ensures power sharing and seamless power management even in abnormal system conditions.

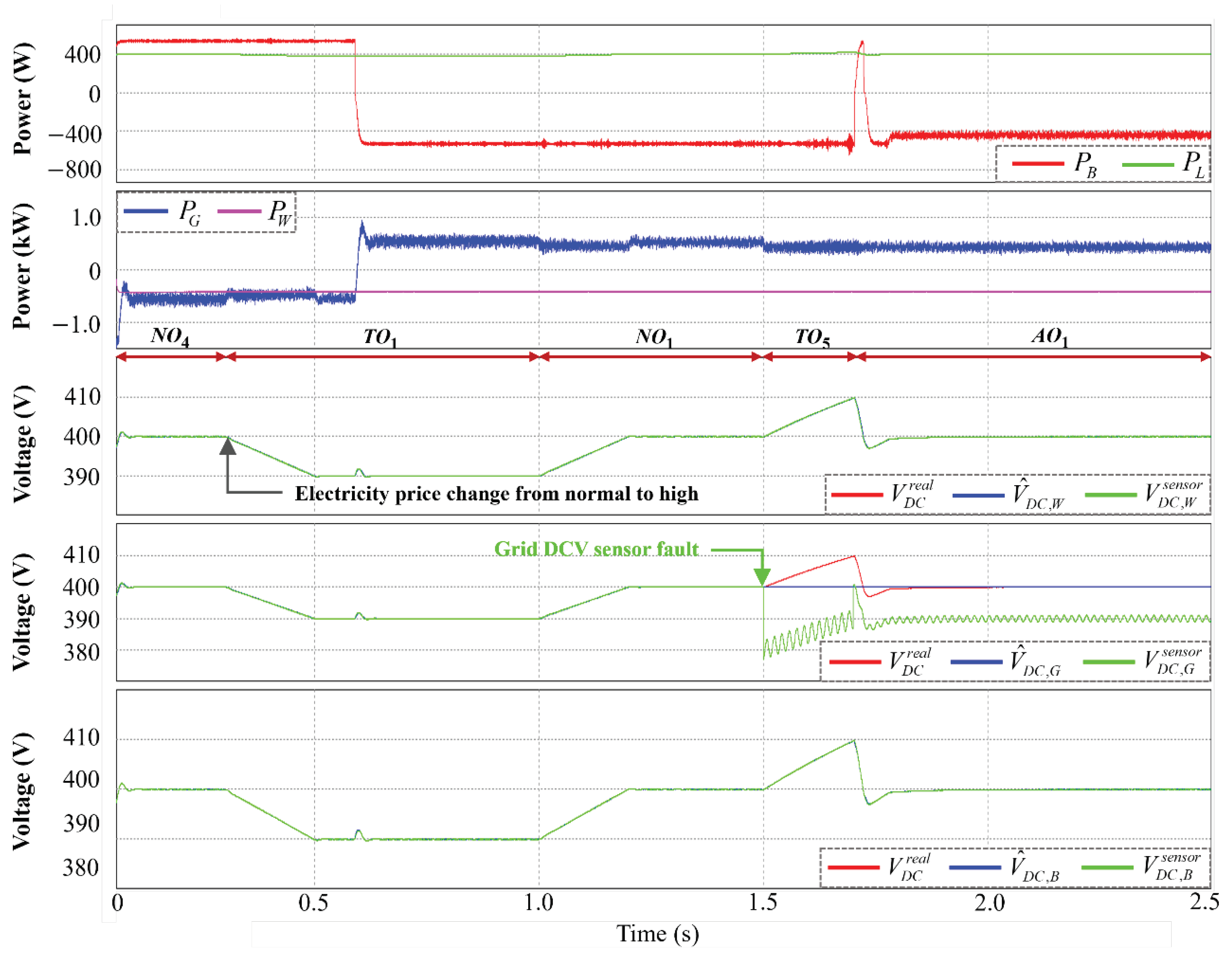
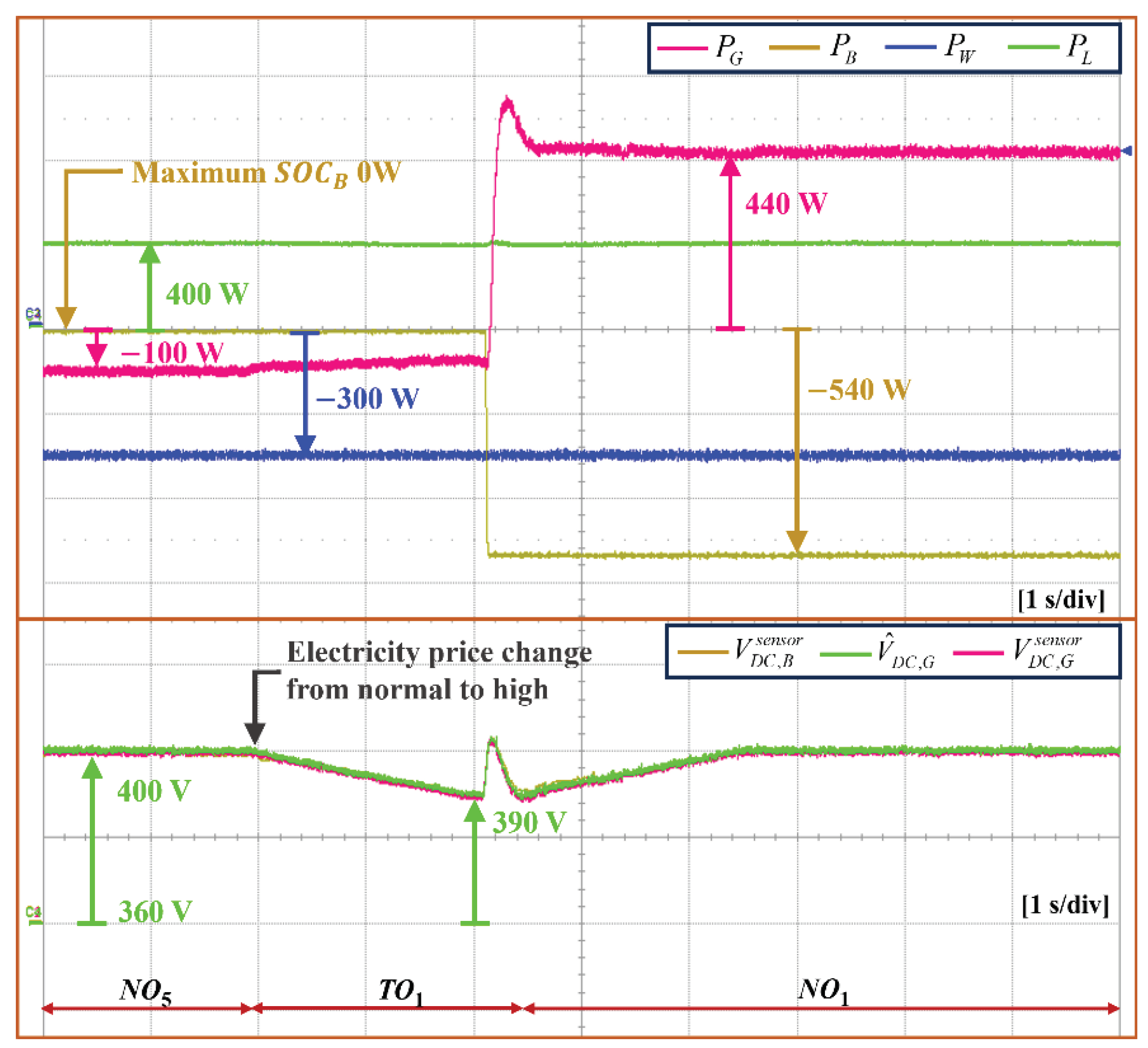
4.2. Transition from Normal to High Electricity Price Condition under DCV Sensor Fault

Figure 8 shows the simulation results in the case of electricity price change from normal to high under the grid DCV sensor fault. The DCMG system initially works in NO₄ at the normal electricity price. In this mode, the grid agent operates in GVCM_con to regulate the DCV at V_nom, the battery agent operates in BCCM_char, and the wind turbine agent operates in the MPPT mode. At t=0.3 s, when the electricity price is changed from normal to high, the grid agent regulates the DCV to V_L₁ in order that the other agents recognize the electricity price change. As a result, the DCMG system is changed from NO₄ to TO₁. After 0.1 s from the instant that the DCV reaches V_L₁, the battery and wind turbine agents detect this event. Then, the battery agent changes the operation from BCCM_char to BCCM_dis to supply power to the DC bus, which causes the grid agent to change from GVCM_con to GVCM_inv. After 0.5 s from the instant that the DCV reaches V_L₁, the grid agent regulates the DCV back to V_nom, and the entire DCMG system operation is changed from TO₁ to NO₁.

At t=1.5 s, when the grid DCV sensor fault occurs, the operation mode of the grid agent is changed to the current control mode as soon as its DCV sensor fault is detected as shown in Figure 4. As a result, the DCMG system is changed from NO₁ to TO₅. According to the proposed fault detection and control mode decision algorithms, the grid agent increases the DCV by supplying more power to the DC bus. When the battery agent detects that the DCV level is maintained higher than V_H₂ more than 0.01 s, the battery agent recognizes the grid DCV sensor fault. Then, the battery agent changes the operation from BCCM_dis to BVCM to regulate the DCV back to V_nom, and the DCMG system operation is changed from TO₅ to AO₁. This simulation result also validates continuous power sharing in the presence of the DCV sensor fault in the grid agent.

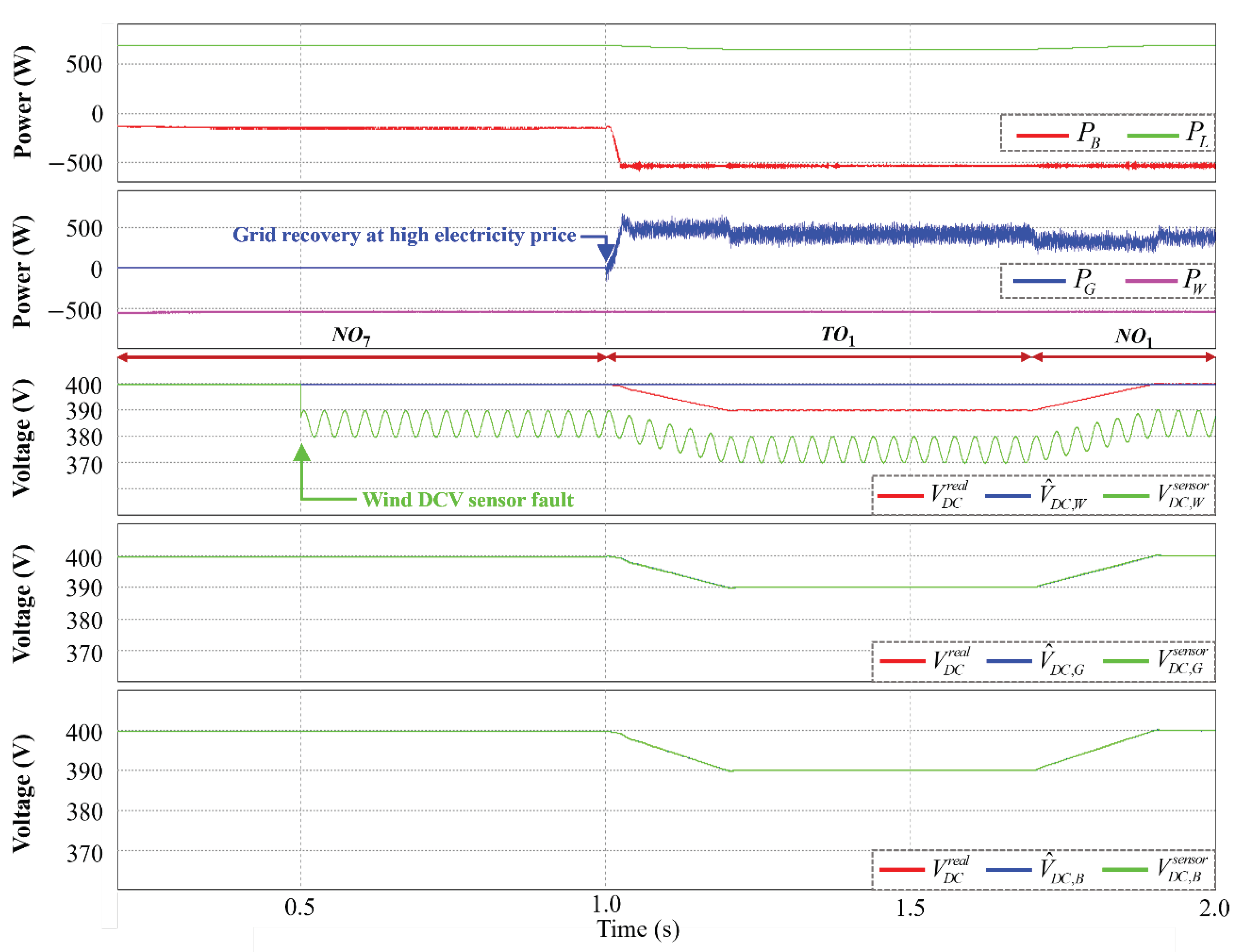
4.3. Grid Recovery with High Electricity Price Condition under DCV Sensor Fault

Figure 9 shows the simulation results in the case of grid reconnection at high electricity price under the wind turbine DCV sensor fault. It is assumed that the DCMG system starts in mode NO₇ which is one of the islanded modes. In this mode, the battery agent operates in BVCM to regulate the DCV at V_nom and the wind turbine agent operates in the MPPT mode. At t=0.5 s, the DCV sensor failure occurs in the wind turbine agent. However, the DCMG system maintains mode NO₇ because the wind turbine agent did not regulate the DCV. In this situation, the wind turbine agent continues operating in the MPPT mode with

I_{W}^{r e f} = I_{W, p r e}^{r e f}

as shown in Figure 4.

At t=1.0 s, when the grid agent reconnects at a high electricity price, the grid agent works in GVCM_inv to regulate the DCV to V_L₁, and the DCMG system is changed from NO₇ to TO₁. After 0.1 s from the instant that the DCV reaches V_L₁, the battery and wind turbine agents detect the grid agent reconnection at a high electricity price. Then, the battery agent changes the operation from BVCM to BCCM_dis to supply the power to the DC bus. After 0.5 s from the instant that the DCV reaches V_L₁, the grid agent regulates the DCV back to V_nom, and the entire DCMG system operation is changed from TO₁ to NO₁. This simulation result also proves a continuous power sharing under the DCV sensor fault in the wind turbine agent.

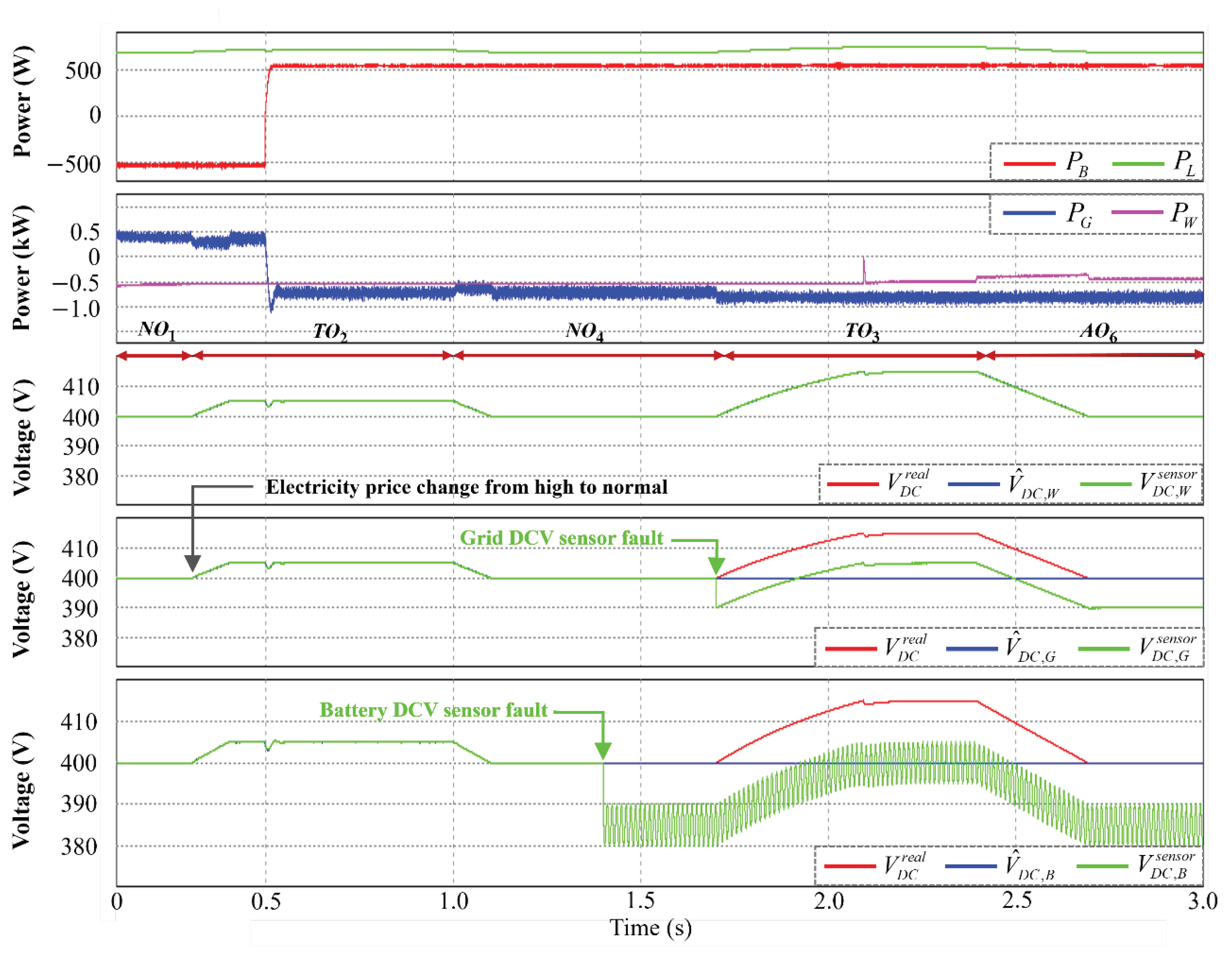
4.4. Transition from High to Normal Electricity Price Condition under DCV Sensor Fault

Figure 10 shows the simulation results in the case of electricity price change from high to normal under the grid and battery DCV sensor faults. In this simulation, the DCMG system initially operates at NO₁ with a high electricity price. In this mode, the grid agent operates in GVCM_inv to regulate the DCV at V_nom, the battery agent operates in BCCM_dis, and the wind turbine agent operates in the MPPT mode.

At t=0.3 s, when the electricity price is changed from high to normal, the grid agent regulates the DCV to V_H₁, and the DCMG system is changed from NO₁ to TO₂. After 0.1 s from the instant that the DCV reaches V_H₁, the battery and wind turbine agents detect the electricity price change from high to normal. Then, the battery agent changes the operation from BCCM_dis to BCCM_char to absorb the power from the DC bus, which causes the grid agent to change the operation from GVCM_inv to GVCM_con. After 0.6 s from that instant the DCV reaches V_H₁, the grid agent regulates the DCV back to V_nom, and the DCMG system is changed from TO₂ to NO₄.

At t=1.4 s, the DCV sensor fault occurs in the battery agent. The DCMG system maintains NO₄ because the battery agent did not regulate the DCV. In this case, the battery agent maintains the previous operation BCCM_char with

I_{B}^{r e f} = I_{B, p r e}^{r e f}

as shown in Figure 4.

At t=1.7 s, the DCV sensor fault happens in the grid agent which is regulating the DCV to V_nom. As soon as the grid agent detects the DCV sensor fault, the grid agent operation is shifted to the current control mode by the proposed scheme, which results in the DCMG operation change from NO₄ to TO₃. In this mode, the grid agent increases the DCV by supplying more power to the DC bus. If the battery agent detects that the DCV level is maintained higher than V_H₂ more than 0.01 s, the battery agent acknowledges the grid DCV sensor fault. However, the battery agent cannot regulate the DCV due to its DCV sensor fault. In this case, the DCV level further increases more than V_H₂. As soon as the DCV reaches V_H₃, the wind turbine agent maintains the DCV to V_H₃ during 0.3 s. After 0.3 s from the instant that the DCV reaches V_H₃, the wind turbine agent regulates the DCV back to V_nom, and the entire DCMG system operation is changed from TO₃ to AO₆. This simulation result shows that the proposed scheme ensures seamless power management even in the circumstance of multiple DCV sensor faults.

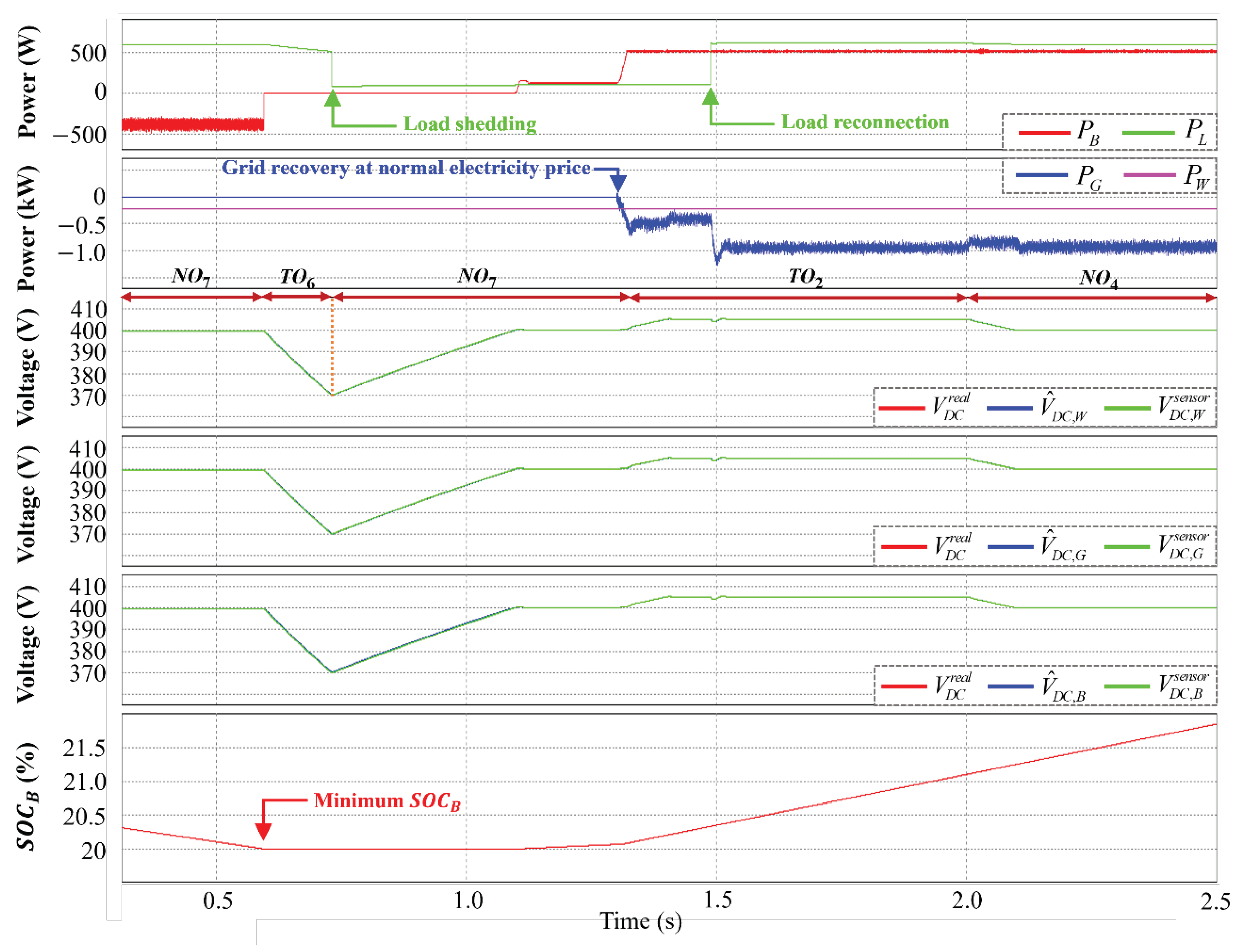
4.5. Case of Minimum Battery SOC Level

Figure 11 shows the simulation results in the case of load shedding when the battery SOC level reaches the minimum value. In this simulation, the DCMG system starts in mode NO₇ which is one of the islanded modes. In this mode, the wind power is less than the load demand, which causes the battery agent to operate in BVCM by discharging mode to maintain the DCV at V_nom.

At t=0.6 s, when the battery SOC level reaches the minimum value, the battery agent changes the operation from BVCM to the IDLE mode, and the DCMG system is changed from NO₇ to TO₆. Because the supplied power is less than the load demand, the DCV drops rapidly. If the load agent detects that the DCV level is maintained lower than V_L₃ more than 0.01 s, as shown in Table 3, the load agent recognizes the supplied power is less than the load demand. As a result, the load shedding is activated to prevent the DCMG system collapse in these emergency conditions. When the DCV becomes higher than V_nom as a result of load shedding, the battery agent operation is changed from the IDLE to BVCM to regulate the DCV back to V_nom, which changes the DCMG system operation from TO₆ to NO₇.

At t=1.3 s, as the grid agent is reconnected to the DCMG system at normal electricity price, the grid agent operates in GVCM_con to regulate the DCV to V_H₁, and the DCMG operation is changed from NO₇ to TO₂. After 0.1 s from the instant that the DCV reaches V_H₁, the battery, wind turbine, and load agents recognize the grid reconnection at normal electricity price. Then, the battery agent changes the operation from BVCM to BCCM_char and the load reconnection starts. After 0.6 s from the instant that the DCV reaches V_H₁, the grid agent regulates the DCV back to V_nom, and the entire DCMG system operation is changed from TO₂ to NO₄.

5. Experimental Results

An experimental hardware setup for a decentralized DCMG system which is depicted in Figure 12 is employed to confirm the reliability and feasibility of the proposed control scheme. To construct a decentralized DCMG system, four power agents such as the wind turbine, battery, utility grid, and load agents are used with the system parameters in Table 4. The wind turbine agent is composed of an AC/DC unidirectional converter for transmitting power to the DC bus and a wind turbine emulator consisting of a PMSG, a mechanically coupled induction motor, and an AC motor control panel. The battery agent employs an interleaved bidirectional DC/DC converter to connect the battery with the DC bus. The utility grid agent is composed of a three-phase main grid, a bidirectional AC/DC converter with an LCL filter, and a Y-Δ transformer. A digital signal processor (DSP) TMS320F28335 is used to realize the proposed control scheme for a decentralized DCMG system. The experimental tests are conducted under five different conditions: electricity price change from normal to high, the DCV sensor fault in the grid-connected mode, transition between grid-connected mode and islanded mode, minimum SOC_B level in the islanded mode, and the DCV sensor fault in the islanded mode.

5.1. Transition from Normal to High Electricity Price Condition in Grid-Connected Mode

Figure 13 shows the experimental results in the case of the electricity price change from high to normal in grid-connected mode. In this experiment, the DCMG system starts in mode NO₅ which is one of the grid-connected modes and SOC_B is at the maximum level. In this mode, the grid agent operates in GVCM_con to regulate the DCV to V_nom, the wind turbine agent operates in the MPPT mode, and the battery agent operates in the IDLE mode.

When the electricity price is changed from normal to high, the grid agent regulates the DCV to V_L₁ in order that the other agents recognize the electricity price change. As a result, the DCMG system operation is changed from NO₅ to TO₁. After 0.1 s from the instant that the DCV reaches V_L₁, the battery and wind turbine agents detect the electricity price change from normal to high. Then, the battery agent changes the operation from the IDLE mode to BCCM_dis to supply power to the DC bus, which makes the grid agent to change operation from GVCM_con to GVCM_inv. After 0.5 s from the instant the DCV reaches V_L₁, the grid agent regulates the DCV back to V_nom, and the entire DCMG system operation is changed from TO₁ to NO₁. This experimental result clearly shows voltage stabilization as well as a good power balance by a decentralized control method without any DCLs.

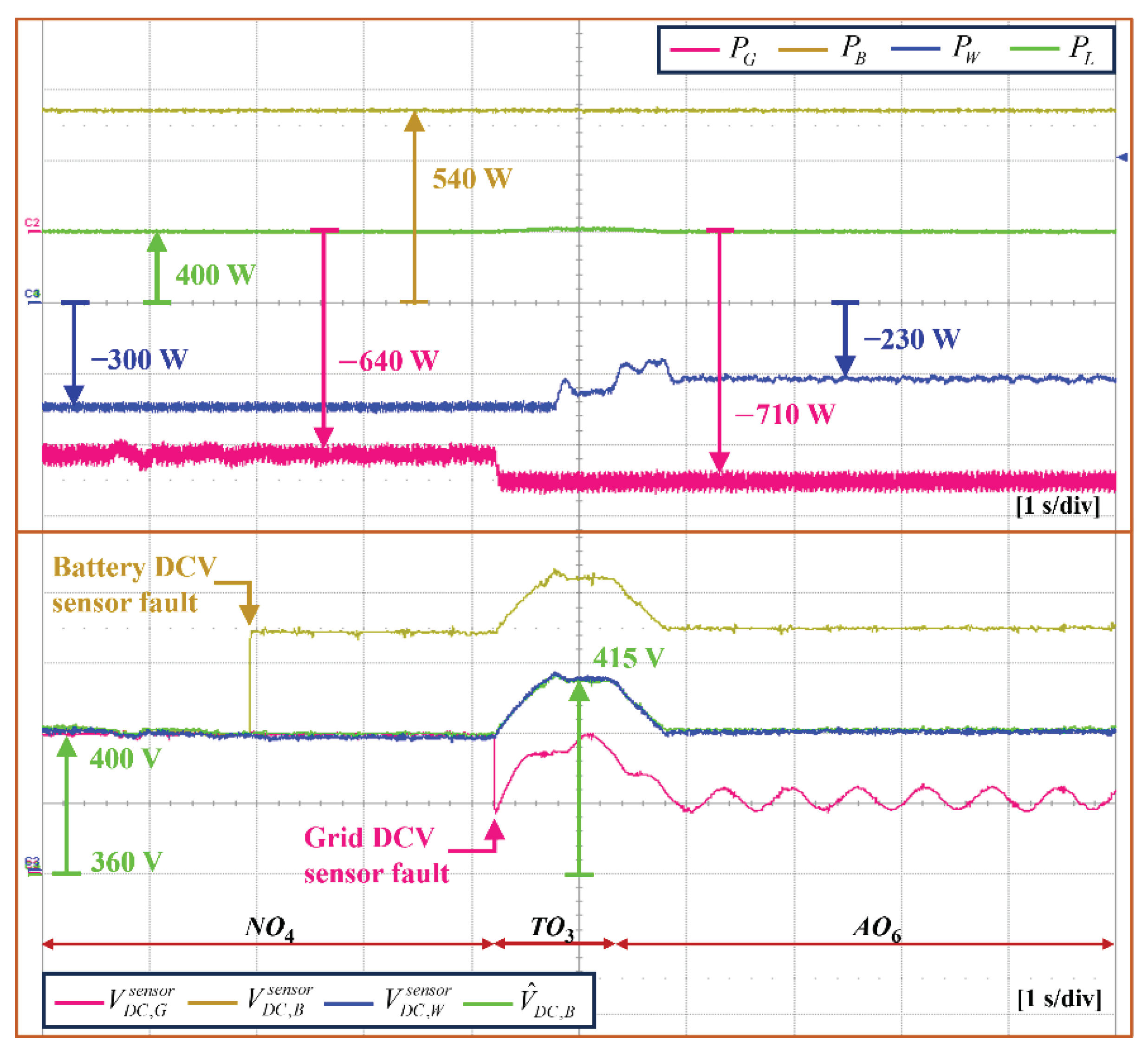
5.2. Grid-connected Mode under DCV Sensor Fault

Figure 14 shows the experimental results for the grid-connected mode under the grid and battery DCV sensor faults. In this test, the DCMG system initially operates in NO₄ with the normal electricity price condition. In this mode, the grid agent operates in GVCM_con to regulate the DCV at V_nom, while the wind turbine and battery agents operate in the MPPT and BCCM_char, respectively.

When a DCV sensor fault first occurs in the battery agent, the DCMG system maintains NO₄ because the battery agent did not regulate the DCV. In this situation, the battery operation is still BCCM_char with

I_{B}^{r e f} = I_{B, p r e}^{r e f}

as shown in Figure 4. When the grid agent which is regulating the DC bus has a sensor fault, the grid agent operation mode is changed to GCCM_con, and the DCMG system operation is changed from NO₄ to TO₃. Similar to Figure 10, the DCV increases rapidly in this case because the grid agent supplies more power to the DC bus. If the battery agent detects that the DCV level is maintained higher than V_H₂ more than 0.01 s, the battery agent acknowledges the grid DCV sensor fault. However, the battery agent cannot regulate the DCV due to its DCV sensor fault. In this case, the DCV level further increases more than V_H₂. As soon as the DCV reaches V_H₃, the wind turbine agent operates in VCM to maintain the DCV to V_H₃. After 0.3 s from the instant that the DCV reaches V_H₃, the wind turbine agent regulates the DCV back to V_nom, and the DCMG system operation is changed from TO₃ to AO₆. This experimental result shows the same behaviors with the simulation in Figure 10, which verifies that the proposed control scheme achieves both the power balance and voltage stabilization even under multiple DCV sensor faults.

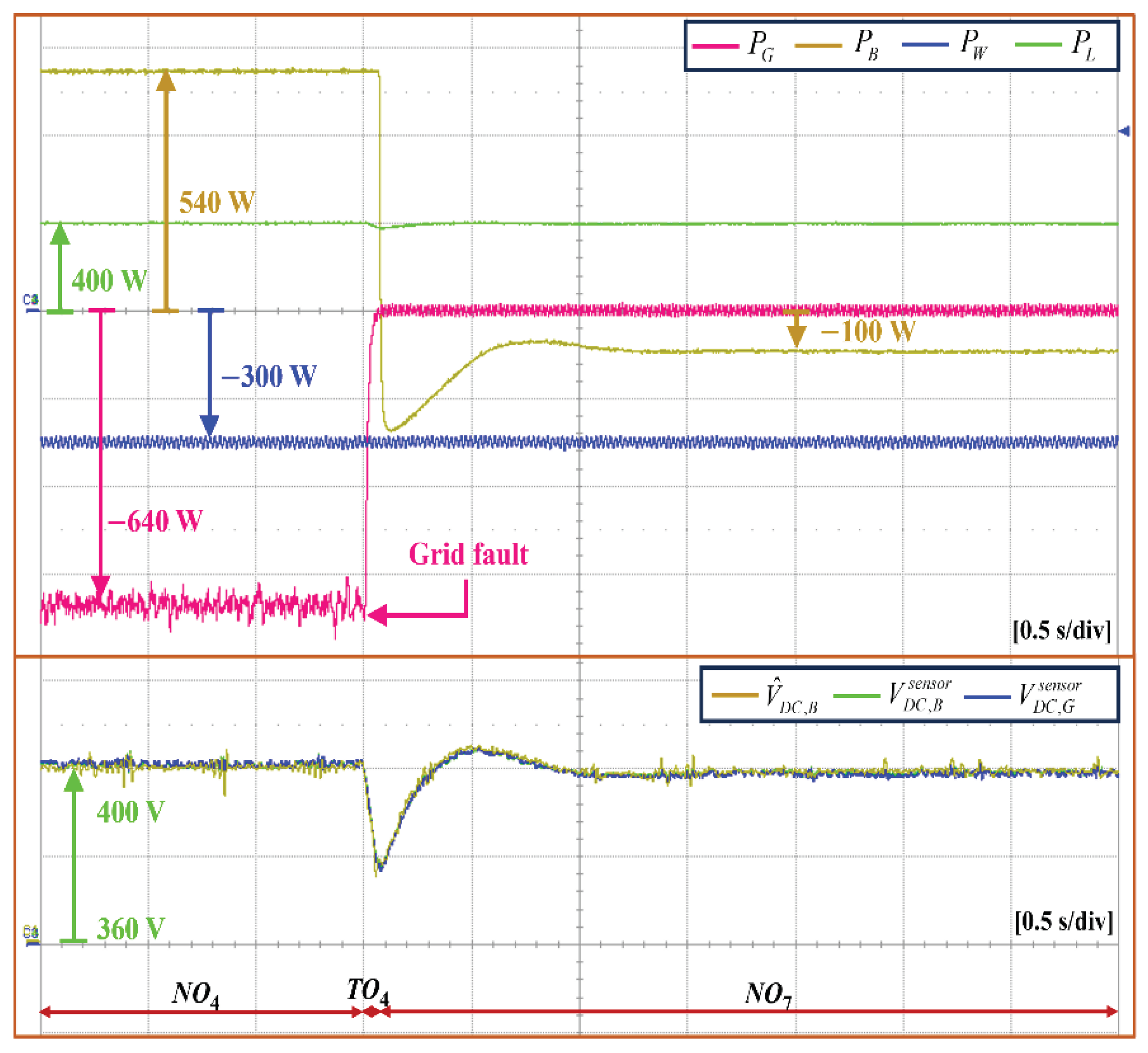
5.3. Transition between Grid-Connected Mode and Islanded Mode

Figure 15 shows the experimental results for the transition from the grid-connected mode to the islanded mode. Initially, the DCMG system operates in NO₄ which is one of the grid-connected modes. In this mode, the grid agent operates in GVCM_con to regulate the DCV to V_nom, while the wind turbine and battery agents operate in the MPPT mode and BCCM_char, respectively.

When the grid is disconnected from the DCMG, it causes the change of the DCMG system operation from the grid-connected mode NO₄ to islanded mode TO₄. The DCV decreases rapidly because the supplied power is less than the demand power. If the battery agent detects that the DCV level is maintained lower than V_L₂ more than 0.01 s, the battery agent acknowledges the grid disconnection from the DCMG system. Then, the battery agent changes the operation from BCCM_char to BVCM to regulate the DCV back to V_nom, and the entire DCMG system operation is changed from TO₄ to NO₇.

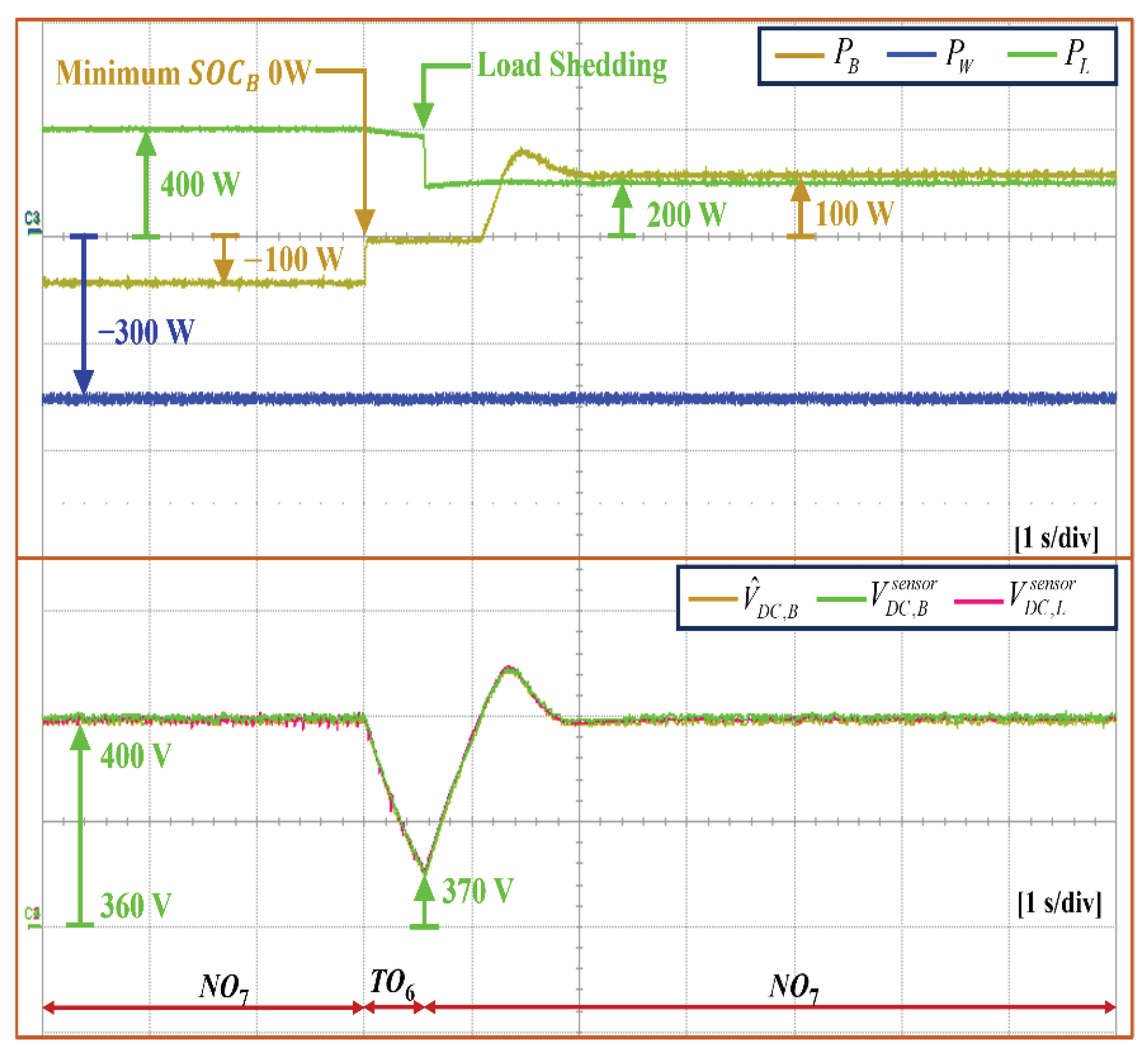
5.4. Islanded Mode under Minimum Battery SOC Level

Figure 16 shows the experimental result in the case of load shedding when the battery SOC level reaches the minimum value. The DCMG system starts in mode NO₇ which is one of the islanded modes. In this mode, the battery agent supplies the power to the DC bus to regulate the DCV in BVCM because the wind power is less than the load demand. When the battery SOC level reaches the minimum value, the battery agent changes the operation from BVCM to the IDLE mode, and the DCMG system is changed from NO₇ to TO₆. The DCV is decreased rapidly because the supplied power is less than the demand power. After 0.01 s from the instant that the DCV is lower than V_L₃, the load agent detects the supplied power is less than the demand, then the load shedding is activated to prevent the DCMG system collapse in this emergency condition. When the DCV becomes higher than V_nom, because the supplied power is higher than the demand, the battery agent operation is changed from the IDLE to BVCM to regulate the DCV back to V_nom, which changes the DCMG system operation from TO₆ to NO₇.

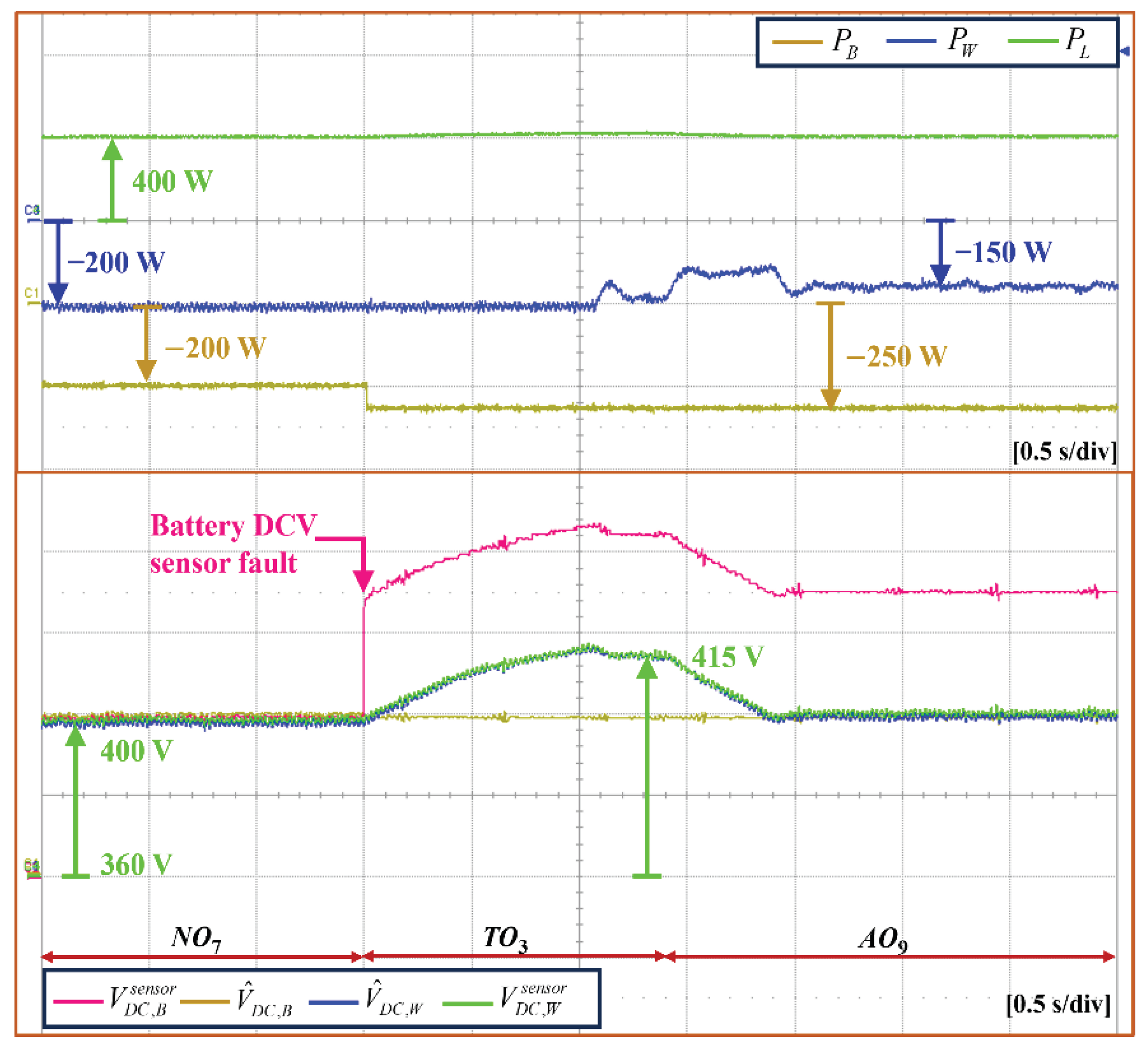
5.5. Islanded Mode under DCV Sensor Fault

Figure 17 shows the experimental result for the islanded mode under the battery DCV sensor fault. Initially, the DCMG system starts in mode NO₇ which is one of the islanded modes. In this mode, the battery agent supplies the power to the DC bus to regulate the DCV in BVCM because the wind power is less than the load demand. When the battery DCV sensor fault occurs, the battery agent identifies the DCV sensor fault. Then, the battery agent changes the operation to the current control mode. By using the proposed scheme, the battery agent increases the DCV, and the DCMG system is changed from NO₇ to TO₃. When the DCV reaches V_H₃, the wind turbine agent regulates the DCV to V_H₃ by VCM. After 0.3 s from the instant that the DCV reaches V_H₃, the wind turbine agent regulates the DCV back to V_nom, and the DCMG system operation is changed from TO₃ to AO₉.

6. Conclusions

This study has proposed a continuous power management of a decentralized DCMG based on the transitional operation modes under system uncertainty and sensor failure. The power agents in the decentralized DCMG system utilize only the primary controller to achieve both the voltage regulation and power sharing with reduced computational burden. To improve the reliability of the DCMG system, the abnormality of the DCV sensor is monitored by the proposed DCV sensor fault detection algorithm, in which all the power agents estimate the DCV by using the observer and compare the estimated DCV with the measured DCV. If the power agent identifies the DCV sensor failure, it modifies the operation mode appropriately to ensure the stability of the DCMG system in accordance with the proposed control mode decision algorithm under the DCV sensor fault. By using the proposed algorithms, the DCMG system maintains the operation without system collapse even with multiple sensor failures, if only one sensor operates normally.

To achieve a continuous power balance as well as the voltage stabilization even under several uncertain conditions such as the power variation of the distributed generation, sudden grid disconnection, and critical battery status, the DCMG system uses the transitional operation modes to transmit the information to other power agents without using DCLs in this study. In the transitional operation modes, the DCV levels are temporarily shifted to an appropriate level during the predetermined time. Based on the DCV levels, each power agent determines its operation mode after detecting the uncertain conditions. The reliability and effectiveness of the proposed control scheme have been demonstrated by the simulation and experimental results under various test conditions.

Author Contributions

The primary idea of the control structure of the DC microgrid and the entire system were developed by S.-B.J., D.T.T., M.A.M.J., M.K., and K.-H.K.. The research was conducted and numerical data was analyzed by S.-B.J., D.T.T., and M.A.M.J. under the guidance of K.-H.K.. S.-B.J., D.T.T., M.A.M.J., M.K., and K.-H.K. worked together in preparing the manuscript. The published version of the manuscript has been read and agreed upon by all authors.

Funding

This study has been conducted with the support of the Korea Institute of Industrial Technology as “Development of core technologies of AI based self-power generation and charging for next-generation mobility (KITECH EH-24-0003)”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

BCCM_char BCCM_dis BVCM	Battery Current Control Mode by charging operation Battery Current Control Mode by discharging operation Battery Voltage Control Mode
GCCM_con	Grid agent Current Control Mode by converter operation
GCCM_inv	Grid agent Current Control Mode by inverter operation
GVCM_con	Grid agent Voltage Control Mode by converter operation
GVCM_inv LCL	Grid agent Voltage Control Mode by inverter operation Inductive-Capacitive-Inductive
MPPT	Maximum Power Point Tracking
PMSG VCM	Permanent Magnet Synchronous Generator Wind turbine agent Voltage Control Mode

References

Ogunrinde, O.; Shittu, E.; Dhanda, K.K. Investing in renewable energy: Reconciling regional policy with renewable energy growth. IEEE Eng. Manag. Rev. 2018, 46, 103–111. [Google Scholar] [CrossRef]
Qazi, A.; Hussain, F.; Rahim, N.A.; Hardaker, G.; Alghazzawi, D.; Shaban, K.; Haruna, K. Towards sustainable energy: A systematic review of renewable energy sources, technologies, and public opinions. IEEE Access 2019, 7, 63837–63851. [Google Scholar] [CrossRef]
Dugan, R.C. Challenges in considering distributed generation in the analysis and design of distribution system. 2008 IEEE Power and Energy Society General Meeting – Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburg, USA, 2008. [Google Scholar] [CrossRef]
Huang, S.-J.; Hsieh, C.-W.; Wan, H.-H. Confirming the permissible capacity of distributed generation for grid-connected distribution feeders. IEEE Trans. Power Syst. 2015, 30, 540–541. [Google Scholar] [CrossRef]
Su, S.-Y.; Lu, C.-N.; Chang, R.-F.; Guillermo, G.-A. Distributed generation interconnection planning: A wind power case study. IEEE Trans. Smart Grid 2011, 2, 181–188. [Google Scholar] [CrossRef]
Mohanty, S.; Bhanja, A.; Gautam, S.P.; Chittathuru, D.; Dash, S.K.; Mangaraj, M.; Chinthaginjala, R.; Alamri, A.M. Review of a comprehensive analysis of planning, functionality, control, and protection for direct current microgrids. Sustainability 2023, 15, 15405. [Google Scholar] [CrossRef]
Cabana-Jiménez, K.; Candelo-Becerra, J.E.; Sousa Santos, V. Comprehensive analysis of microgrids configurations and topologies. Sustainability 2022, 14, 1056. [Google Scholar] [CrossRef]
Kumar, D.; Zare, F.; Ghosh, A. DC microgrid technology: System architectures, AC grid interfaces, grounding schemes, power quality, communication networks, applications, and standardizations aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
Santoro, D.; Delmonte, N.; Simonazzi, M.; Toscani, A.; Rocchi, N.; Sozzi, G.; Cova, P.; Menozzi, R. Local power distribution—A review of nanogrid architectures, control strategies, and converters. Sustainability 2023, 15, 2759. [Google Scholar] [CrossRef]
Keshavarzi, D.; Farjah, E.; Ghanbari, T. Hybrid DC circuit breaker and fault current limiter with optional interruption capability. IEEE Trans. Power Electron. 2018, 33, 2330–2338. [Google Scholar] [CrossRef]
Lotfi, H.; Khodaei, A. AC versus DC microgrid planning. IEEE Trans. Smart Grid 2017, 8, 296–304. [Google Scholar] [CrossRef]
Zhou, L.; Zhang, Y.; Lin, X.; Li, C.; Cai, Z.; Yang, P. Optimal sizing of PV and BESS for a smart household considering different price mechanisms. IEEE Access 2018, 6, 41050–41059. [Google Scholar] [CrossRef]
Al-Ismail, F.S. DC microgrid planning, operation, and control: A comprehensive review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
Saleh, M.; Esa, Y.; Hariri, M.E.; Mohamed, A. Impact of information and communication technology limitations on microgrid operation. Energies 2019, 12, 2926. [Google Scholar] [CrossRef]
Abbasi, M.; Abbasi, E.; Li, L.; Aguilera, R.P.; Lu, D.; Wang, F. Review on the microgrid concept, structures, components, communication systems, and control methods. Energies 2023, 16, 484. [Google Scholar] [CrossRef]
Van Nguyen, T.; Kim, K.-H. Power flow control strategy and reliable DC-link voltage restoration for DC microgrid under grid fault conditions. Sustainability 2019, 11, 3781. [Google Scholar] [CrossRef]
Mehdi, M.; Kim, C.-H.; Saad, M. Robust centralized control for DC islanded microgrid considering communication network delay. IEEE Access 2020, 8, 77765–77778. [Google Scholar] [CrossRef]
Yu, Y.; Liu, G.-P.; Huang, Y.; Guerrero, J.M. Distributed data-driven secondary regulation for the conflict between voltage recovery and accurate current sharing in DC microgrids. IEEE Trans. Power Electron. 2023, 38, 9617–9634. [Google Scholar] [CrossRef]
Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cárdenas-Dobson, R.; Martínez-Gómez, M.; Sáez, D. Distributed control strategies for microgrids: An overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
Li, Q.; Chen, F.; Chen, M.; Guerrero, J.M.; Abbott, D. Agent-based decentralized control method for islanded microgrids. IEEE Trans. Smart Grid 2016, 7, 637–649. [Google Scholar] [CrossRef]
Bani-Ahmed, A.; Rashidi, M.; Nasiri, A.; Hosseini, H. Reliability analysis of a decentralized microgrid control architecture. IEEE Trans. Smart Grid 2019, 10, 3910–3918. [Google Scholar] [CrossRef]
Gu, Y.; Xiang, X.; Li, W.; He, X. Mode-adaptive decentralized control for renewable DC microgrid with enhanced reliability and flexibility. IEEE Trans. Power Electron. 2014, 29, 5072–5080. [Google Scholar] [CrossRef]
Wang, C.; Duan, J.; Fan, B.; Yang, Q.; Liu, W. Decentralized high-performance control of DC microgrids. IEEE Trans. Smart Grid 2019, 10, 3355–3363. [Google Scholar] [CrossRef]
Xia, Y.; Yu, M.; Tao, X.; Peng, Y.; Wei, W. Decentralized control for parallel bidirectional power converters of a grid-connected DC microgrid. IECON 2016 - 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 2016. [Google Scholar] [CrossRef]
Xu, L.; Chen, D. Control and operation of a DC microgrid with variable generation and energy storage. IEEE Trans. Power Delivery 2011, 26, 2513–2522. [Google Scholar] [CrossRef]
Chen, D.; Xu, L.; Yao, L. DC voltage variation based autonomous control of DC microgrids. IEEE Trans. Power Delivery 2013, 28, 637–648. [Google Scholar] [CrossRef]
Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and stability analysis of islanded DC microgrids under droop control. IEEE Trans. Power Electron. 2015, 30, 4597–4607. [Google Scholar] [CrossRef]
Li, X.; Guo, L.; Zhang, S.; Wang, C.; Li, Y.W.; Chen, A.; Feng, Y. Observer-based DC voltage droop and current feed-forward control of a DC microgrid. IEEE Trans. Smart Grid 2018, 9, 5207–5216. [Google Scholar] [CrossRef]
Gao, F.; Bozhko, S.; Costabeber, A.; Patel, C.; Wheeler, P.; Hill, C. I.; Asher, G. Comparative stability analysis of droop control approaches in voltage-source-converter-based DC microgrids. IEEE Trans. Power Electron. 2017, 32, 2395–2415. [Google Scholar] [CrossRef]
Jabbar, M.A.M.; Tran, D.T.; Kim, K.-H. Decentralized power flow control strategy using transition operations of DC-bus voltage for detection of uncertain DC microgrid operations. Sustainability 2023, 15, 11635. [Google Scholar] [CrossRef]
Habibullah, A.F.; Kim, K.-H. Decentralized power management of DC microgrid based on adaptive droop control with constant voltage regulation. IEEE Access 2022, 10, 129490–129504. [Google Scholar] [CrossRef]
Tran, D.T.; Kim, M.; Kim, K.-H. Seamless power management for decentralized DC microgrid under voltage sensor faults. IEEE Access 2023, 11, 74627–74640. [Google Scholar] [CrossRef]
Dehkordi, N.M.; Moussavi, S.Z. Distributed resilient adaptive control of islanded microgrids under sensor/actuator faults. IEEE Trans. Smart Grid 2020, 11, 2699–2708. [Google Scholar] [CrossRef]
Oritz-matos, L.; Zea, L.B.G.; Gonzalez-sanchez, J.W. A methodology of sensor fault-tolerant control on a hierarchical control for hybrid microgrids. IEEE Access 2023, 11, 58078–58098. [Google Scholar] [CrossRef]
Chandra, M.V.S.S.; Mohapatro, S. Hybrid sensor fault tolerant control of low voltage DC microgrid. IEEE Trans. Ind. Appl 2024, 60, 1705–1715. [Google Scholar] [CrossRef]
Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Yang, C.; Gao, C.; Liu, Y.; Liu, Z.; Ji, R. Fault diagnosis methodology of redundant closed-loop feedback control systems: Subsea blowout preventer system as a case study. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1618–1629. [Google Scholar] [CrossRef]
Jessen, K.; Soltani, M.; Hajizadeh, A. Sensor fault detection for line regulating converters supplying constant power loads in DC microgrids. 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems, Dubrovnik, Croatia, 2020. [Google Scholar] [CrossRef]
Huang, M.; Ding, L.; Li, W.; Chen, C.Y.; Liu, Z. Distributed observer-based H∞ fault-tolerant control for DC microgrids with sensor fault. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1659–1670. [Google Scholar] [CrossRef]

Figure 1. System configuration of DCMG.

Figure 2. Simplified structure for power converter of agent

i

Figure 2. Simplified structure for power converter of agent

i

Figure 3. Control block diagram of agent

i

Figure 3. Control block diagram of agent

i

Figure 4. DCV sensor fault detection and control mode decision algorithms of agent

i

under DCV sensor fault.

Figure 4. DCV sensor fault detection and control mode decision algorithms of agent

i

under DCV sensor fault.

Figure 5. Operation mode transition caused by the DCV sensor faults. (a) From mode NO₁; (b) From mode NO₂; (c) From mode NO₃; (d) From mode NO₄; (e) From mode NO₅; (f) From mode NO₆; (g) From mode NO₇; (h) From mode NO₈; (i) From mode NO₉.

Figure 6. Transition operation detection by each agent.

Figure 7. Simulation results in case of the transition between grid-connected mode and islanded mode under the battery DCV sensor fault.

Figure 8. Simulation results in case of electricity price change from normal to high under the grid DCV sensor fault.

Figure 9. Simulation results in case of grid reconnection with high electricity price under the wind turbine DCV sensor fault.

Figure 10. Simulation results in case of electricity price change from high to normal under the grid and battery DCV sensor faults.

Figure 11. Simulation results in case of load shedding when the battery SOC level reaches the minimum value.

Figure 12. Experimental hardware setup for a decentralized DCMG.

Figure 13. Experimental results for the transition of electricity price condition from normal to high in grid-connected mode.

Figure 14. Experimental results for grid-connected mode under the grid and battery DCV sensor faults.

Figure 15. Experimental results for transition from grid-connected mode to islanded mode.

Figure 16. Experimental results for islanded mode when the battery SOC level reaches the minimum value.

Figure 17. Experimental results for islanded mode under the battery DCV sensor fault.

Table 1. Steady-state operation modes.

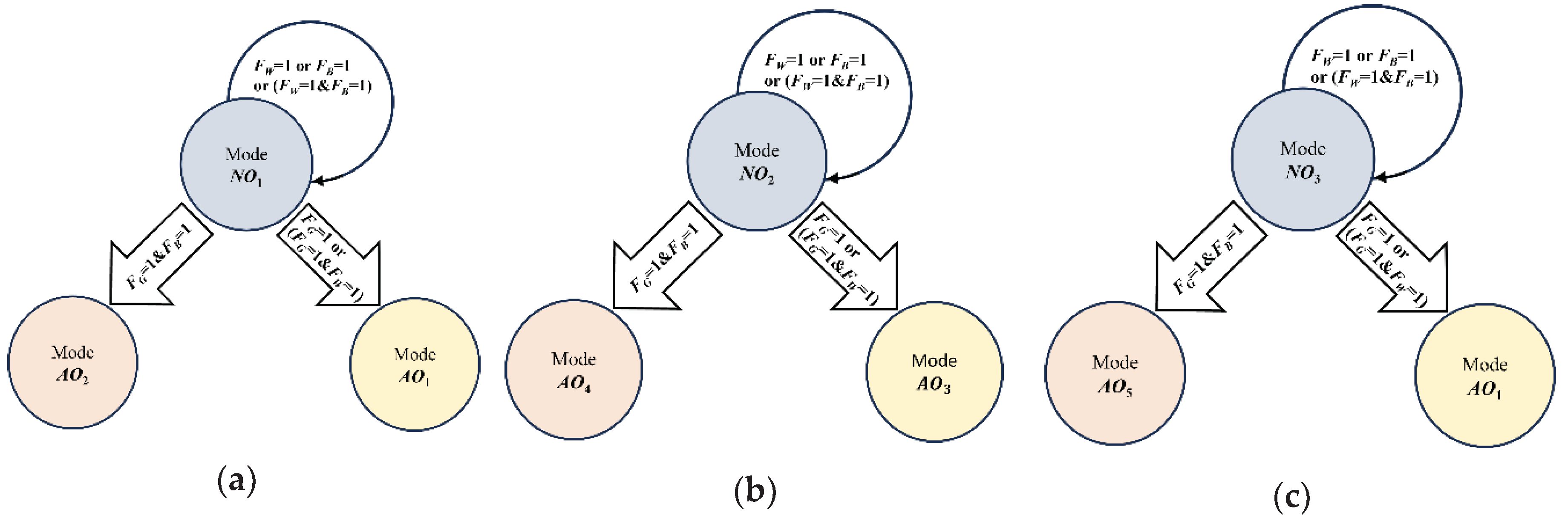
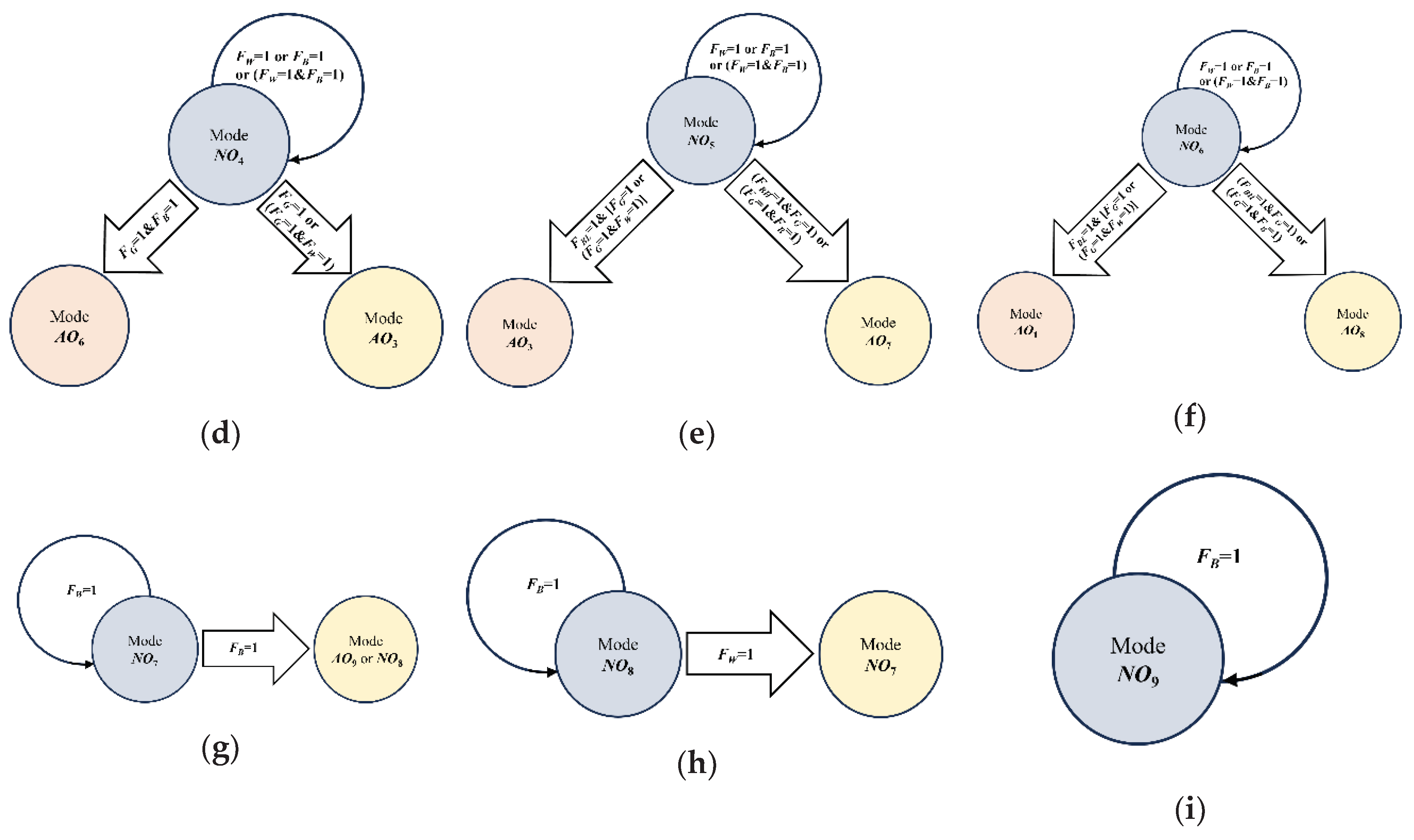
Mode	Battery Agent	Wind Turbine Agent	Grid Agent	Load Agent
NO₁	BCCM_dis	MPPT	GVCM_inv	NOR
NO₂	BCCM_dis	MPPT	GVCM_con	NOR
NO₃	BCCM_char	MPPT	GVCM_inv	NOR
NO₄	BCCM_char	MPPT	GVCM_con	NOR
NO₅	IDLE	MPPT	GVCM_con	NOR
NO₆	IDLE	MPPT	GVCM_inv	NOR
NO₇	BVCM	MPPT	Fault	NOR
NO₈	BCCM_char	VCM	Fault	NOR
NO₉	IDLE	VCM	Fault	NOR

Table 2. Additional steady-state operation modes according to DCV sensor fault.

Mode	Battery Agent	Wind Turbine Agent	Grid Agent	Load Agent
AO₁	BVCM	MPPT	GCCM_inv	NOR
AO₂	BCCM_dis	VCM	GCCM_inv	NOR
AO₃	BVCM	MPPT	GCCM_con	NOR
AO₄	BCCM_dis	VCM	GCCM_con	NOR
AO₅	BCCM_char	VCM	GCCM_inv	NOR
AO₆	BCCM_char	VCM	GCCM_con	NOR
AO₇	IDLE	VCM	GCCM_con	NOR
AO₈	IDLE	VCM	GCCM_inv	NOR
AO₉	BCCM_dis	VCM	Fault	NOR

Table 3. Power agents to activate each transition operation.

Mode	Grid Agent	Wind Turbine Agent	Battery Agent	Agent Action
TO₁	✔			▪ Grid agent activates TO₁. ▪ Grid agent regulates DCV to V_L₁. ▪ If DCV level reaches V_L₁, grid agent maintains DCV to V_L₁ during 0.5 s. ▪ As DCV level reaches V_L₁, and lasts during 0.1 s, other power agents identify this event, and change their operations.
TO₂	✔			▪ Grid agent activates TO₂. ▪ Grid agent regulates DCV to V_H₁. ▪ If DCV level reaches V_H₁, grid agent maintains DCV to V_H₁ during 0.6 s. ▪ As DCV level reaches V_H₁, and lasts during 0.1 s, other power agents identify this event, and change their operations.
TO₃	✔		✔	▪ Grid or battery agent activates TO₃. ▪ DCV is increasing due to surplus power. ▪ If DCV level reaches V_H₃, wind turbine agent maintains DCV to V_H₃ during 0.3 s. ▪ As DCV level reaches V_H₃, and lasts during 0.01 s, battery agent identifies this event, and changes its operations.
TO₄	✔	✔		▪ Grid or wind turbine agent activates TO₄. ▪ DCV is decreasing due to deficiency power. ▪ If battery agent detects that DCV level is maintained lower than V_L₂ more than 0.01 s, battery operation is changed to BVCM.
TO₅	✔			▪ Grid agent activates TO₅. ▪ DCV is increasing due to surplus power. ▪ If battery agent detects that DCV level is maintained higher than V_H₂ more than 0.01 s, battery operation is changed to BVCM.
TO₆	✔	✔	✔	▪ All power agent activate TO₆. ▪ DCV is decreasing due to deficiency power. ▪ If load agent detects that DCV level is maintained lower than V_L₃ more than 0.01 s, load shedding mode is activated.

Table 4. System parameters of DCMG system.

Power Agents	Parameters	Value
Battery agent	Minimum SOC ( $S O C_{B}^{L}$ ) Maximum SOC ( $S O C_{B}^{H}$ ) Maximum discharging power Maximum charging power Maximum voltage Rated capacity Converter filter inductance L	20 % 90 % $-$ 540 W 540 W 180 V 25 Ah 7 mH
Grid agent	Transformer Υ/Δ Grid frequency Grid voltage Filter capacitance of LCL filter Inverter-side inductance of LCL filter Grid-side inductance of LCL filter	380/220 V 60 Hz 220 V 4.5 μF 1.7 mH 1.7 mH
Wind turbine agent	PMSG number of poles PMSG inertia PMSG stator resistance PMSG dq-axis inductance PMSG flux linkage Converter filter inductance	6 0.111 kgm² 0.64 Ω 0.82 mH 0.18 Wb 7 mH
Load agent	Power of load 1 Power of load 2 Power of load 3 Priority level : load 1 > load 2 > load 3	200 W 200 W 200 W -
DC bus	Nominal DCV (V_nom) First level of high DCV (V_H₁) Second level of high DCV (V_H₂) Third level of high DCV (V_H₃) First level of low DCV (V_L₁) Second level of low DCV (V_L₂) Third level of low DCV (V_L₃) Capacitance	400 V 405 V 410 V 415 V 390 V 380 V 370 V 4 mF

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Continuous Power Management of Decentralized DC Microgrid Based on Transitional Operation Modes under System Uncertainty and Sensor Failure

Abstract

1. Introduction

2. System Configuration of a DCMG and Decentralized Control Scheme

3. Control Strategy and Transition Operations of Power Agents under Emergency Conditions

3.1. Control Strategy of Power Agents

3.2. Control Strategy under DCV Sensor Fault

3.3. Transitional Operation Modes of Power Agents

4. Simulation Results

4.1. Transition between Grid-Connected Mode and Islanded Mode under DCV Sensor Fault

4.2. Transition from Normal to High Electricity Price Condition under DCV Sensor Fault

4.3. Grid Recovery with High Electricity Price Condition under DCV Sensor Fault

4.4. Transition from High to Normal Electricity Price Condition under DCV Sensor Fault

4.5. Case of Minimum Battery SOC Level

5. Experimental Results

5.1. Transition from Normal to High Electricity Price Condition in Grid-Connected Mode

5.2. Grid-connected Mode under DCV Sensor Fault

5.3. Transition between Grid-Connected Mode and Islanded Mode

5.4. Islanded Mode under Minimum Battery SOC Level

5.5. Islanded Mode under DCV Sensor Fault

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe