Prerpints.org logo
Preprint
Article

Design of an Axial-type Magnetic Gear with Auxiliary Flux-enhancing Structure

Altmetrics

Downloads

101

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 April 2024

Posted:

02 April 2024

You are already at the latest version

Alerts
Abstract
In this paper, a new axial-type magnetic gear with auxiliary flux-enhancing structure (AFS-AMG) is proposed. Compared to conventional AFS-AMG, it has the higher torque density and higher permanent magnet (PM) utilization factor. Firstly, the design rules and operating principles of proposed AFS-AMG are elaborated. Then, the mapping relation between the radial-type magnetic gears (RMGs) and AMGs are elucidated. Compared to its counterpart in RMGs, AFS-AMGs achieve small size. Then, the geometrical parameters of AFS-AMGs are optimized to obtain the better electromagnetic performances, where the torque density per volume and per PM volume is adopted as the evaluation standard. Finally, three different AMG topologies are constructed in finite element analysis (FEA) software for comparison. It is proven that the AFS-AMG has the largest torque density per volume and per PM volume.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The mechanical gearbox is the cornerstone of variable-speed transmission systems, playing a pivotal role in aligning the torque and rotational velocity between the prime mover and the driven load. Its widespread adoption is attributed to its exceptional torque density and versatile gear ratios. However, the reliance on physical contact for power transmission in mechanical gears introduces significant tribological challenges. These challenges manifest as elevated costs associated with lubrication, cooling, and maintenance [1]. Empirical evidence underscores the fact that tooth abrasion critically undermines the reliability of mechanical gears, often emerging as a primary cause of system failures [2]. This vulnerability significantly restricts their application in industries such as food, pharmaceuticals, and chemicals, where the operational environment demands higher standards of cleanliness and system integrity. In situations where a clear separation between power input and output is required, mechanical gears may not meet these strict requirements.
Magnetic gears (MGs) are emerging as superior alternatives to traditional mechanical gearboxes, offering a host of benefits that include higher efficiency, reduced noise, and intrinsic self-protection features [3,4]. These advantages stem from MGs’ ability to inherently provide overload protection through the physical separation of input and output rotors, a critical feature that significantly enhances transmission reliability [5]. Unlike mechanical gears, which rely on the direct meshing of teeth on the master and slave wheels for motion and power transmission, MGs utilize the coupling of magnetic fields between permanent magnets affixed to these wheels, a principle that is also finding applications in the design of electric motors, such as the permanent-magnet field-modulation machines [6,7]. The initial phase of MG research focused on developing magnetic gear topologies by drawing parallels with the traditional designs of mechanical gears. This foundational work has led to the development of a diverse array of MG types over the past two decades. Classifying MGs by their operating principles reveals a variety including coaxial permanent-magnet (PM) coaxial MGs, reluctance MGs [8], cycloidal MGs [9], and planetary MGs [10]. When categorized by structural characteristics, the range expands to radial-type magnetic gears (RMGs), axial-type magnetic gears (AMGs), linear MGs [11], and tubular MGs [12]. Notably, RMGs and AMGs have attracted significant research interest for their potential to directly replace mechanical gearboxes in practical engineering applications. While RMGs are celebrated for their adaptability, certain applications may find them less suitable due to strict spatial constraints. In these instances, AMGs present an advantageous alternative, boasting higher torque density and a reduced axial length compared to RMGs [13]. The distinction between Axial Magnetic Gears (AMGs) and Radial Magnetic Gears (RMGs) is primarily rooted in the orientation of permanent magnet magnetization and the nature of their coupling surfaces. Specifically, RMGs feature magnets that are magnetized in the radial direction and utilize the radial outer circular surface for coupling. Conversely, AMGs employ an axial magnetization direction, with coupling occurring at the axial outer end surface. This fundamental difference renders AMGs particularly advantageous in applications where weight reduction is paramount, such as in aerospace technologies [14].
The historical development of AMGs was marked by a significant milestone in 1987 when Tsurumoto K. and Kikuchi S. introduced an axial magnetic gear with an involute shaped permanent magnet, arranged in a circular pattern on a base disc, achieving a 3:1 gear ratio using SmCo5 permanent magnets. This design was revolutionary in that it transitioned the coupling region from a radial to an axial cross-section [15], subsequently undergoing further optimizations by Tsurumoto K. [16,17]. The application of axial magnetic gears, particularly in centrifugal equipment as investigated by Klaui [18] and Meisberger [19], has demonstrated the potential to achieve high torque densities through experimental testing. Innovations aimed at enhancing torque density have included the development of a flux-focusing axial magnetic gear, although this design was challenged by the issue of flux leakage [20,21]. An alternative approach involved employing a Halbach array to augment torque density [22]. Afsari’s introduction of a magneto-resistive linkage-type axial magnetic gear presented a design that not only reduced the number of required permanent magnets but also aimed to enhance gear reliability [23]. Despite these advancements, the design faced limitations in significantly boosting gear torque and exhibited magnetic leakage in slower-rotating rotors. Furthermore, the performance evaluation of AMGs necessitates the construction of complex three-dimensional models, a process that is notably time-consuming and has thus limited the proliferation of research and development in this area [24,25]. The axial-direction force exerted by AMGs also poses substantial challenges to their fabrication, complicating the design process further. Another overarching concern for both types of magnetic gears is the extensive reliance on permanent magnets (PMs), which considerably inflates manufacturing costs due to the materials used.
In addressing the limitations identified in existing Axial Magnetic Gear (AMG) designs—namely, the insufficient improvement in torque density and the consequential cost implications stemming from the extensive use of permanent magnets (PMs)—this paper introduces a innovative approach. We propose the integration of an iron-made flux-enhancing plate to the exterior of AMGs, a novel addition designed to significantly elevate the output torque. This innovative concept is meticulously analyzed through the examination of flux path variations, pre and post the implementation of the auxiliary flux-enhancing plane, elucidating the underlying principle of flux enhancement.
Subsequently, the performance metrics of three distinct AMG configurations are rigorously compared to demonstrate the superiority of our proposed structure. This comparison not only showcases the enhanced torque density achieved through our design but also highlights an unprecedented improvement in the PM utilization factor. By ingeniously augmenting the magnetic flux efficiency within the gear system, our approach effectively mitigates the challenges associated with high PM usage, thereby addressing both the performance and cost-efficiency concerns.

2. Structure Configuration

2.1. Design Rules and Operating Principle

The proposed auxiliary flux-enhancing structural axial-type magnetic gear (AFS-AMG) contains four planes, and its structure is depicted in Figure 1.
Two rotors are those with surface-mounted PMs on them, and the one with less PM pieces is the high-speed rotor, while the one with more PM pieces is the low-speed rotor. High-speed rotors are radially magnetised and low-speed rotors are tangentially magnetised.
The first and third plane from the left to the right are steady planes, and they formed as one stator component. The PMs on the high-speed rotor are magnetized on the axial direction, while the PMs on the low-speed rotor are magnetized on the circumferential direction. The two rotors are composed of iron and PMs, while the modulator consists of an iron block and non-magnetic parts, which modulate the internal magnetic field. The left auxiliary surface and auxiliary teeth are made of iron with magnetic conductivity. This structure forms a three-layer air gap, with the air gap near the high-speed rotor termed the high-speed rotor air gap, and the air gap near the low-speed rotor referred to as the low-speed rotor air gap. The air gap near the auxiliary teeth is called the auxiliary surface air gap.
For AFS-AMGs, its air-gap region has a thin disk shape, and its torque generation method is different from that of RMGs. Hence, to analyze its torque generation mechanism, the AFS-AMG is divided into several slices on the radial direction, and each slice is spread on the circumferential direction on a plane. Hence, the analysis of AFS-AMG can be simplified into analyzing a linear magnetic gear, as depicted in Figure 2.
Since there are a lot of harmonics in AFS-AMGs, the magnetic permeance method is adopted for qualitative analysis of a specific slice in the AFS-AMG. First, the magnetomotive force (MMF) of the low-speed rotor Flow and air-gap permeance Λ can be written into Fourier series form:
F low ( θ , t ) = ∑ i = 1 , 3 , 5 ∞ F low , i cos i P low θ − i 2 π P low Ω low 60 t
Λ ( θ ) = Λ 0 + ∑ j = 1 , 3 , 5 ∞ Λ j cos j Q mod θ
where F low , i is the amplitude of i th harmonic in MMF; Λ j is the amplitude of jth harmonic in the permeance; P low and Ω low are the pole-pair number and rotating speed of the low-speed rotor, respectively. Q mod is the number of modulator pieces.
Then, the air-gap magnetic flux density B can then be expressed as the product of F and Λ [26] :
B r ( θ , t ) = F low ( θ , t ) · Λ ( θ ) = ∑ i = 1 , 3 , 5 ∞ Λ 0 F low , i cos i P low θ − i 2 π P low Ω low 60 t + 1 2 F low , i Λ j cos i P low + j Q mod θ − i 2 π P low Ω low 60 t + 1 2 F low , i Λ j cos i P low − j Q mod θ + i 2 π P low Ω low 60 t
Due to the modulation effect of the modulator. The order of each harmonic magnetic density contained in the air gap of AMGs can be expressed by the following equation::
p n , k = | n p + k n m | n = 1 , 3 , 5 , … , ∞ k = 0 , ± 1 , ± 2 , ± 3 , … , ± ∞
where p is the number of magnetic poles of the permanent magnet of the high-speed rotor or low-speed rotor, and n m is the number of modulation blocks of the modulator. When the modulator is stationary, the rotation speed of the harmonic magnetic density contained in the air gap magnetic density of the AMG is:
Ω n , k = n p n p + k n m Ω
where Ω is the mechanical rotation speed of the high-speed rotor or low-speed rotor. It can be seen from the above equation, the speed of rotation of the space harmonic density is different from the speed of rotation of the rotor carrying the PMs through the modulation of the modulator.
Then, observed from the high-speed rotor side, to produce a steady electromagnetic torque, the pole-pair number of highspeed rotor PMs P high should satisfy [27]:
P high = i P low − j Q mod
where i and j should be 1 to maximize the transmitted torque. Therefore, we have:
P high = Q mod − P low
Additionally, since the auxiliary flux-enhancing plane serves as a complementary structure for the magnetic flux to form a shorter loop, its tooth number Q teeth should be equal to the number of modulator pieces, namely:
Q teeth = Q mod
Next, based on the law of conservation of energy, the rotating speed and output torque relations between the highspeed and low-speed rotor satisfy:
T high T low = − P high P low
Ω high Ω low = − P low P high
where T high and T low are the electromagnetic torques on the high-speed and low-speed rotor, respectively. Ω high and Ω l o w are the rotating speeds of the high-speed and low-speed rotor, respectively.
Besides, AFS-AMGs’ gear ratio G is defined as:
G = P high P low
Figure 3 illustrates the magnetic flux density and flux line distribution on a given slice of AMGs with and without the auxiliary plane simulated in finite element analysis (FEA) software. It can be observed that without the auxiliary plane, the magnetic flux path passes through the air region several times to form a close loop. Since the permeability of air is much lower than that of the iron, the magnetic reluctance of the whole loop is very large, leading to a small magnetic flux density on the air gap. However, when the auxiliary plane is added to the outside of the spoke-type PMs, the corresponding flux line changes to pass through a path with smaller reluctance. Hence, the magnetic flux density on the air gap increases, leading to a larger electromagnetic torque.

2.2. Flux-Enhancing Effect of Extra Modulator

The flux-enhancing effect of the auxiliary plane can also be llustrated by the imaginary flux line path, as shown in Figure 4. The auxiliary plane acts as a pivotal element in enhancing the magnetic flux within the system, thereby contributing to its overall efficiency and effectiveness. Additionally, the displacement angle between the auxiliary olane and modulator θ shift , as defined in Figure 4, should be equal o for a maximum torque generation purpose [28].

2.3. Evolution of AMGs

The inherent architectures of AMGs are fundamentally derived from their RMGs counterparts, as delineated in Table 1 [29]. The fundamental operational principles of AMGs and RMGs bear similarities, yet their distinctions are primarily manifested in two critical aspects. Initially, the orientation of magnetic flux density diverges between the two gear types: in AMGs, the principal magnetic flux pathways are aligned axially, whereas in RMGs, these pathways are oriented radially. This difference in magnetic flux orientation is pivotal as it influences the design and operational efficiency of the gears. Secondly, the configuration of the rotors in AMGs is arranged axially, facilitating a multi-plane structural design that is inherently suited for accommodating additional layers without significantly compromising the gear’s compactness. This axial distribution is advantageous for integrating multiple operational planes within a single gear system, enhancing its functionality and potential applications. Conversely, the incorporation of auxiliary structures in RMGs results in a substantial increase in the gear’s overall dimensions, making it less feasible for applications requiring compactness. Hence, the implementation of a flux-enhancing plane is particularly efficacious for AMGs, as it maximizes the impact of magnetic flux enhancement within the gear’s operational framework.

3. Optimization Process

There are two important indexes for the evaluation of AFS-AMGs, namely the torque density with respect to the total volume τ V − total , and torque density with respect to the volume of PMs τ ¯ V P P M . They can be defined as [30]:
τ V − total = T low π R out 2 − R in 2 L
τ V − P M = T l o w V P M
where R in and R out are the inner and outer radii of the AFSAMG, respectively. L is the axial length of the AFS-AMG, and V P M is the total volume of PMs in the AFS-AMG.
Given the substantial computational demands of executing a single instance of AFS-AMG in FEA software, the application of a genetic algorithm-based optimization method for AFS-AMGs is rendered impractical. Consequently, the paper opts for a parameter sweep method for the optimization process. This approach involves the sequential optimization of the geometrical parameters associated with AFS-AMGs. By methodically altering each parameter within a specified range and evaluating the resulting performance metrics, the optimal configuration can be identified with greater efficiency and less computational expense.

3.1. Pole-Pair Combination Selection

To make AMGs with different pole-pair combinations comparable to one another, the gear ratio range is settled at the first stage. Since gear ratio G should not be integer to avoid large torque ripple [31,32], its value is set within the range between four to five in this paper. Additionally, since iron bars are required to inserted between each circumferentially-magnetized PMs, Plow cannot be too large to prevent manufacture difficulties. Hence, the possible pole-pair combinations for AFS-AMGs are listed in Table 2. Figure 5 depicts the electromagnetic torque waveforms on the low-speed rotor of AFS-AMG with different pole-pair combinations with the same geometrical size. Since the volume of the whole AFS-AMG and PMs do not change with the pole-pair combination variation, it is enough to use Tlow as the judgement standard. It can be observed that 4-19 pole-pair combination has the largest torque, and a relatively low torque ripple. Hence, the 4-19 pole-pair combination of AFS-AMGs is chosen for further geometrical parameter optimization.

3.2. Air-Gap Length Optimization

Another point of concern within the design of AFS-AMG systems pertains to the optimization of the air-gap length, denoted as T air . An excessively large T air significantly elevates the magnetic reluctance, consequently diminishing the torque density of the system. Conversely, a minimal T air complicates the manufacturing process and substantially amplifies the axial force exerted between each plane, potentially compromising structural integrity. To streamline both design and manufacturing processes, the air-gap lengths between the four planes within the AFS-AMG configurations are uniformly established.
As illustrated in Figure 6, the variation of the total tangential torque, τ V total , along with the axial-direction force on the modulator, F z , as functions of the air-gap length, are presented. Given that the volume of the permanent magnets (PM) remains constant irrespective of variations in air-gap length, the PM-related torque, τ V P M , is not depicted. The graphical analysis reveals a decline in both τ V total and F z with the increment of air-gap length. For this study, an air-gap length of 0.6 mm is selected as an optimal compromise, considering factors such as manufacturing precision and the material strength of the modulator in practical engineering applications. This decision highlights the important balance between achieving high performance and maintaining ease of manufacturing and durability in AFS-AMG system design.

3.3. PM and Modulator Thickness Optimization

The thickness of PMs plays a crucial role in determining the magnitude of MMF, which, in turn, significantly impacts the magnetic flux density across the air gap, as delineated in Equation (3). Moreover, the thickness of the modulator pieces and the auxiliary plane teeth critically influences the extent of magnetic saturation within the silicon steel. This saturation level is a key determinant of the torque density in AFS-AMGs. To streamline the optimization procedure, we propose equalizing the thicknesses of the circumferentially-magnetized PMs located on the low-speed rotor and the axially-magnetized PMs. This unified thickness parameter is denoted as T P M . Similarly, to facilitate a simplified optimization framework, the thicknesses of the modulator pieces and the auxiliary plane teeth are also standardized and represented by T mod .
Figure 7 depicts the variations of torque density per volume and torque density per PM volume with respect to T P M and T mod . It can be observed that the variation trend of τ V total and τ V P M are in conflict with one another. For instance, the peak value of τ V total occurs when the value of T P M is 12 mm , but the peak value of τ V P M occurs when the value of T P M is 5 mm . Hence, a trade off must be made to balance the conflict of τ V total and τ V P M . In this paper, the AFS-AMG with T P M = 7 mm , T mod = 5 mm is selected, where τ V total = 147 . 1 Nm · L − 1 and τ V P M = 781 . 5 Nm · L − 1 .

3.4. Back Iron Thickness Optimization

The thickness of back iron of the high-speed rotor and auxiliary plane will influence the magnetic saturation, which further affect the electromagnetic torque. To simplify the optimization process, the thickness of the back iron of the high-speed rotor and auxiliary plane are set equal, which is represented by T iron . Figure 8 depicts the variations of torque density per volume and torque density per PM volume with respect to T iron . It can be observed that the variation trends of and τ V P M are in conflict with each other. However, the increasing gradient of becomes smaller when the value of T iron is above 9 mm . Hence, in this paper, T iron is set as 9 mm .

3.5. High-Speed Rotor PM Arc Angle Ratio Optimization

For the PMs on the low-speed rotor, they are adjacent with the silicon steel part to form a complete plane. If these PMs and silicon steel are not stuck with each other tightly, the mechanical strength of the low-speed rotor will be affected. However, the PMs on the high-speed rotor are stuck to the back iron, so there could be intervals between each PM block. The arc angle ratio γ of the high-speed rotor PMs is defined as:
γ = α 2 π / P h i g h
Figure 9 depicts the variations of torque density per volume and torque density per PM volume with respect to the arc angle ratio γ . It can be observed that the variation trend of τ V total and τ V P M are in conflict with one another. The decreasing trend of τ V total becomes prominent when γ is above 0.9 , while the increasing trend of becomes indistinctive when γ is above 0.9 . Hence, γ is chosen as 0.9 in this paper.

4. Electromagnetic Performance Evaluation

To prove the superiority of the AFS-AMG, three AMGs with the same inner and outer radii, similar PM and silicon steel amount are constructed in FEA software JMAG to compare their performances, whose parameters are provided in Table 3. The MG input torque is on the high-speed shaft, therefore the output power is:
T l o w Ω l o w = T h i g h Ω h i g h − P l o s s
where the bracketed torque and power loss terms denote that they are functions of the high-speed rotor input speed Ω h i g h .The loss within the AMG can be separated into:
P loss = P core + P eddy
where P core is the iron core loss and P eddy is the eddy current loss.
The following formula can be used to calculate the core loss, which includes the eddy current loss and hysteresis loss caused by the laminated structure of electrical steel sheets [33]:
P c o r e = ∑ ∫ V A e ( n f ) 2 B m 2 + A h ( n f ) B m 2 ) d ν
where A e and A h represent the eddy current loss and hysteresis loss coefficients, respectively. The magnetic flux frequency is denoted by f, and B m represents the harmonic magnetic flux density.
The calculation of eddy current loss is very important because the generation of eddy current loss can lead to thermal demagnetization. The eddy current loss of PM can be expressed as the integral of the eddy current density [34]:
P e d d y = 1 σ ∫ J e d d y · J e d d y * d V
Here, σ represents the conductivity of each material, J e d d y represents the eddy current density, and V represents the volume of the material.
The efficiency was calculated by using :
Efficiency ( η ) = P out P out + P loss × 100
where P out is the output power and P loss is the power loss.
The corresponding simulation result values are provided in Table 4.
In the study of AMGs, particularly in analyzing their performance metrics, it’s essential to consider the iron losses and permanent magnet (PM) eddy current losses as pivotal factors affecting overall efficiency. Figure 10 compares the performance of the AMGs visually. Among the different configurations examined, AMG(a) exhibits the highest iron and PM eddy current losses, with values reaching 27.15W and 75.86W, respectively. In contrast, AMG(c) demonstrates a significant reduction in both iron and PM eddy current losses, recorded at 14.25W and 31.58W, respectively, thus offering an improvement over AMG(a). The most efficient configuration in terms of minimizing losses is found in AMG(b), where the iron and PM eddy current losses are identical to those in AMG(c), at 14.25W and 31.58W, respectively. When evaluating the overall efficiency, AMG(a) ranks the lowest with an efficiency of 97.36%. Meanwhile, AMG(c) achieves a higher efficiency of 99.2%, which is only slightly below the efficiency of AMG(b) at 99.45%.
The air gap density of an AMG contains not only the radial and tangential components, but also the axial component.The axial component of the air gap density (axial air gap density) is the most important component of the air gap density and has the greatest influence on the torque capacity of an AMG.Based on the air gap density distribution of an axial magnetic gear and using the Maxwell stress tensor method to calculate the torque, the torque and axial force of an AMG can be expressed as:
T = ( R o 2 − R i 2 ) 2 μ 0 ∫ R i R o ∫ 0 2 π B z z , r , θ B θ ( z , r , θ ) d θ d r
F = ( R o − R i ) 2 μ 0 ∫ R i R o ∫ 0 2 π ( B z 2 z , r , θ − B θ 2 ( z , r , θ ) ) d θ d r
where, μ 0 is the vacuum permeability; B z ( z , r , θ ) and B θ ( z , r , θ ) are the axial and tangential components of the air gap magnetic density at different radii in the axial magnetic gear, respectively. R 0 and R i are the inner and outer diameters of the axial magnetic gear, respectively.
Of course, the torque and axial force of the high speed rotor are only related to the magnetic density distribution in the air gap of the high speed rotor, and the torque and axial force of the low speed rotor are only related to the magnetic density distribution in the air gap of the low speed rotor. Since the air gap magnetic density at different radii of axial magnetic gear is not the same, in order to simplify the calculation of AMG torque, the air gap magnetic density at the average radius R a is used to replace the air gap magnetic density at different radii, where the calculation formula of the AMG torque and axial force can be converted to:
T = ( R o 2 − R i 2 ) R a 2 μ 0 ∫ 0 2 π B z z , R a , θ B θ ( z , R a , θ ) d θ
F = ( R o − R i ) R a 2 μ 0 ∫ 0 2 π ( B z 2 z , R a , θ − B θ 2 ( z , R a , θ ) ) d θ
The axial component B z ( z , r , θ ) and the tangential component B θ ( z , r , θ ) of the air gap magnetic density at the mean radius Rm are expressed as follows:
B z z , R a , θ = ∑ n = 1 , 2 , 3 + ∞ b z n z , R a cos n θ − φ z n
B θ z , R a , θ = ∑ n = 1 , 2 , 3 + ∞ b θ n z , R a cos n θ − φ θ n
where, b z n and b θ n are Fourier coefficients; φ z n and φ θ n are the initial angles of the axial and tangential components of each harmonic wave flux density contained in the air gap flux density at radius R a , respectively.
So, the calculation formula of the AMG torque can be expressed as:
T = π ( R o 2 − R i 2 ) R a 2 μ 0 ∑ n = 1 , 2 , 3 + ∞ b z n z , R a b θ n z , R a cos φ z n − φ θ n
F = π R o − R i R a 2 μ 0 ∑ n = 1 , 2 , 3 + ∞ b z n z , R a 2 − b θ n z , R a 2
The electromagnetic torque waveforms on the low-speed rotor for the three AMGs are depicted in Figure 11. It can be observed that the AFS-AMG (c) has the largest torque density per PM volume. The PM utilization factor of AFS-AMG is 2.15 times of that in AMG (a), and 1.40 times of that in AMG (b). Additionally, AFS-AMG has a higher efficiency compared with conventional AMGs, namely AMG (a).
The axial component magnetic flux density distributions on the air region between the auxiliary plane and low-speed rotor and their corresponding Fast Fourier Transform (FFT) of the AMG (b) and (c) with the radius being 60 mm are depicted in Figure 12. It can be observed that for AMG (c), namely the AFS-AMG, the amplitudes of working harmonics, namely 4th and 19th harmonics, are much larger than that in AMG (b), leading to a torque increase.
The magnetic field distribution of the proposed AMG viewed from the less-PM face and more-PM face is shown in Figure 13. It can be observed that the back iron is more easily saturated on the less-PM side, while the auxiliary plane has lower magnetic field density.
Figure 14 illustrates the axial forces exerted on all components of the AMG, encompassing both the low-speed rotor and the high-speed rotor. Notably, the axial force experienced by the low-speed rotor is relatively significant, reaching 2960 N. Consequently, the axial forces acting on the magnetic steel (N-pole) and the back iron are computed separately for a detailed analysis. Given that the North pole comprises four pieces of magnetic steel, the axial force exerted on each piece is approximately 400 N. This value falls within the tolerance limits of the manufacturing process, indicating its feasibility. In contrast, the average axial force on the high-speed rotor is quantified at around 123 N, a comparatively lower value. This discrepancy is attributed to the minimal variation in the magnetic field associated with the low-speed rotor.
The attraction between the two rotors is accompanied by strain on the modular-poles. To analyze the results, the stress and strain on the modular poles were calculated using FEA based on equations (2) and (3).
stress ( f ) = F / A
stress ( y ) = δ / L
Stress is defined as the force per unit area, where F is the applied force and A is the area. Strain, on the other hand, is the elongation per unit length, where δ is the modified length and L is the existing length. The analysis results are presented in Figure 15, which shows that the stress on the modular-pole is 2 . 218 e + 07 N / m ∧ 2 , a value that is below the yield force ( 6 . 204 e + 08 N / m ∧ 2 ) of the material used in the modular-pole. The strain is approximately 0 . 018 mm . The air gap between the modular-pole and the two rotors is 0 . 6 mm . The analysis results indicate that the deformation rate of the magnetic gear is within the allowable range.

5. Conclusions

In this paper, a novel AFS-AMG is proposed, which has two rotating components: one is composed of axially-magnetized PMs, and another one is composed of circumferentially-magnetized PMs. Inspired by the structural innovation in RMGs, an auxiliary flux-enhancing slide is introduced in AMGs to decrease the magnetic reluctance in the flux path, the proposed AFS-AMG has a higher torque density per volume (181.14 Nm/L) and per PM volume (809.6 Nm/L), and a higher efficiency compared to conventional AMG structures. The PM utilization factor of AFS-AMG is twice compared with conventional AMG structure.The simulation results show that the magnetic field distribution of the magnetic gear is reasonable, and the stress on the modulation pole is within a reasonable range.

6. Outlook

Although some aspects of axial magnetic gearing have been investigated in this paper, there are many issues that need to be investigated in greater depth, which can be summarised in the following two areas:
(1) Prototyping and Experimental Validation: While simulation results are promising, the next step involves prototyping and rigorous testing under real-world conditions. This will provide invaluable data on the performance, durability, and potential limitations of the AFS-AMG, guiding further refinements.
(2) Temperature field analysis: This paper does not analyze the temperature field of the AFS-AMG, and further accurate calculation of the temperature field is required. These factors should be comprehensively considered in order to better establish and apply the transmission system of the AFS-AMG.

Author Contributions

Conceptualization, F.L.; methodology, F.L.; software, F.L.; validation, H.Z.; resources, F.L.; data curation, H.Z.; writing---original draft preparation, F.L.;writing---review and editing, F.L.; visualization, X.S.; supervision, H.Z.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the Guangdong Basic and Applied Basic Research Foundation under Project 2022A1515110361, University Innovation Project in Guangdong Province Supported by Guangdong Provincial Department of Education Project 2023KTSCX172 and Guangzhou-HKUST(GZ) Joint Funding Program 2024A03J0618.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Li, K.; Bird, J.Z. A review of the volumetric torque density of rotary magnetic gear designs. In Proceedings of the 2018 XIII international conference on electrical machines (ICEM). IEEE, 2018, pp. 2016–2022. [CrossRef]
  2. Ribrant, J.; Bertling, L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005. In Proceedings of the 2007 IEEE power engineering society general meeting. IEEE, 2007, pp. 1–8. [CrossRef]
  3. Zhao, H.; Liu, C.; Song, Z.; Yu, J. A fast optimization scheme of coaxial magnetic gears based on exact analytical model considering magnetic saturation. IEEE Transactions on Industry Applications 2020, 57, 437–447. [CrossRef]
  4. Rasmussen, P.O.; Andersen, T.O.; Jorgensen, F.T.; Nielsen, O. Development of a high-performance magnetic gear. IEEE transactions on industry applications 2005, 41, 764–770. [CrossRef]
  5. Aloeyi, E.F.; Shoaei, A.; Wang, Q. A hybrid coaxial magnetic gear using flux-focusing halbach permanent magnet arrangement. In Proceedings of the 2023 IEEE 14th International Conference on Power Electronics and Drive Systems (PEDS). IEEE, 2023, pp. 1–6. [CrossRef]
  6. Zhao, H.; Liu, C.; Dong, Z.; Huang, R.; Li, X. Design and optimization of a magnetic-geared direct-drive machine with V-shaped permanent magnets for ship propulsion. IEEE Transactions on Transportation Electrification 2021, 8, 1619–1633. [CrossRef]
  7. Li, X.; Wei, Z.; Zhao, Y.; Wang, X.; Hua, W. Design and analysis of surface-mounted permanent-magnet field-modulation machine for achieving high power factor. IEEE Transactions on Industrial Electronics 2023. [CrossRef]
  8. Aiso, K.; Akatsu, K.; Aoyama, Y. A novel reluctance magnetic gear for high-speed motor. IEEE Transactions on Industry Applications 2019, 55, 2690–2699. [CrossRef]
  9. Jørgensen, F.T.; Andersen, T.O.; Rasmussen, P.O. The cycloid permanent magnetic gear. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting. IEEE, 2006, Vol. 1, pp. 373–378. [CrossRef]
  10. Huang, C.C.; Tsai, M.C.; Dorrell, D.G.; Lin, B.J. Development of a magnetic planetary gearbox. IEEE Transactions on Magnetics 2008, 44, 403–412. [CrossRef]
  11. Atallah, K.; Wang, J.; Howe, D. A high-performance linear magnetic gear. Journal of Applied Physics 2005, 97. [CrossRef]
  12. Pakdelian, S.; Frank, N.W.; Toliyat, H.A. Magnetic design aspects of the trans-rotary magnetic gear. IEEE transactions on energy conversion 2014, 30, 41–50. [CrossRef]
  13. Chen, Y.; Fu, W.N.; Ho, S.L.; Liu, H. A quantitative comparison analysis of radial-flux, transverse-flux, and axial-flux magnetic gears. IEEE Transactions on Magnetics 2014, 50, 1–4. [CrossRef]
  14. Tsurumoto, K.; Kikuchi, S. A new magnetic gear using permanent magnet. IEEE Transactions on Magnetics 1987, 23, 3622–3624. [CrossRef]
  15. Tsurumoto, K. Power transmission of magnetic gear using common meshing and insensibility to center distance. IEEE Translation Journal on Magnetics in Japan 1988, 3, 588–589. [CrossRef]
  16. Tsurumoto, K. Some considerations on the improvement of performance characteristics of magnetic gear. IEEE Translation Journal on Magnetics in Japan 1989, 4, 576–582. [CrossRef]
  17. Kläui, E. Electrodynamic transmission and a centrifugal pump with a transmission of this kind, 2001. US Patent 6,217,298.
  18. Meisberger, A. Magnetic gear and centrifuge having a magnetic gear, 2002. US Patent 6,440,055.
  19. Zhu, D.; Yang, F.; Du, Y.; Xiao, F.; Ling, Z. An axial-field flux-modulated magnetic gear. IEEE Transactions on Applied Superconductivity 2016, 26, 1–5. [CrossRef]
  20. Acharya, V.M.; Bird, J.Z.; Calvin, M. A flux focusing axial magnetic gear. IEEE transactions on magnetics 2013, 49, 4092–4095. [CrossRef]
  21. Kouhshahi, M.B.; Bird, J.Z.; Acharya, V.M.; Li, K.; Calvin, M.; Williams, W.; Modaresahmadi, S. An axial flux focusing magnetically geared generator for low input speed applications. IEEE Transactions on Industry Applications 2019, 56, 138–147. [CrossRef]
  22. Hu, F.; Zhou, Y.; Cui, H.; Liu, X. Spectrum analysis and optimization of the axial magnetic gear with Halbach permanent magnet arrays. Energies 2019, 12, 2003. [CrossRef]
  23. Afsari, S. Optimal design and analysis of a novel reluctance axial flux magnetic gear. Scientia Iranica 2022, 29, 1573–1580. [CrossRef]
  24. Afsari, S.A.; Heydari, H.; Dianati, B. Cogging torque mitigation in axial flux magnetic gear system based on skew effects using an improved quasi 3-D analytical method. IEEE Transactions on Magnetics 2015, 51, 1–11. [CrossRef]
  25. Acharya, V.M.; Bird, J.Z.; Calvin, M. A flux focusing axial magnetic gear. IEEE transactions on magnetics 2013, 49, 4092–4095. [CrossRef]
  26. Li, X.; Shen, F.; Yu, S.; Xue, Z. Flux-regulation principle and performance analysis of a novel axial partitioned stator hybrid-excitation flux-switching machine using parallel magnetic circuit. IEEE Transactions on Industrial Electronics 2020, 68, 6560–6573. [CrossRef]
  27. Atallah, K.; Howe, D. A novel high-performance magnetic gear. IEEE Transactions on magnetics 2001, 37, 2844–2846. [CrossRef]
  28. Zhao, H.; Liu, C.; Song, Z.; Wang, W.; Lubin, T. A dual-modulator magnetic-geared machine for tidal-power generation. IEEE Transactions on Magnetics 2020, 56, 1–7. [CrossRef]
  29. Zhang, X.; Liu, X.; Chen, Z. A novel dual-flux-modulator coaxial magnetic gear for high torque capability. IEEE transactions on energy conversion 2017, 33, 682–691. [CrossRef]
  30. Gardner, M.C.; Johnson, M.; Toliyat, H.A. Comparison of surface permanent magnet coaxial and cycloidal radial flux magnetic gears. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE). IEEE, 2018, pp. 5005–5012. [CrossRef]
  31. Praslicka, B.; Gardner, M.C.; Johnson, M.; Toliyat, H.A. Review and analysis of coaxial magnetic gear pole pair count selection effects. IEEE Journal of Emerging and Selected Topics in Power Electronics 2021, 10, 1813–1822. [CrossRef]
  32. Nielsen, S.S.; Wong, H.Y.; Baninajar, H.; Bird, J.Z.; Rasmussen, P.O. Pole and segment combination in concentric magnetic gears: Vibrations and acoustic signature. IEEE Transactions on Energy Conversion 2022, 37, 1644–1654. [CrossRef]
  33. Tian, Y.; Liu, G.; Zhao, W.; Ji, J. Design and analysis of coaxial magnetic gears considering rotor losses. IEEE Transactions on Magnetics 2015, 51, 1–4. [CrossRef]
  34. Chen, Q.; Liang, D.; Jia, S.; Wan, X. Analysis of multi-phase and multi-layer factional-slot concentrated-winding on PM eddy current loss considering axial segmentation and load operation. IEEE Transactions on Magnetics 2018, 54, 1–6. [CrossRef]
Preprints 102794 g001
Figure 1. Explosive view of the proposed AFS-AMG.
Figure 1. Explosive view of the proposed AFS-AMG.
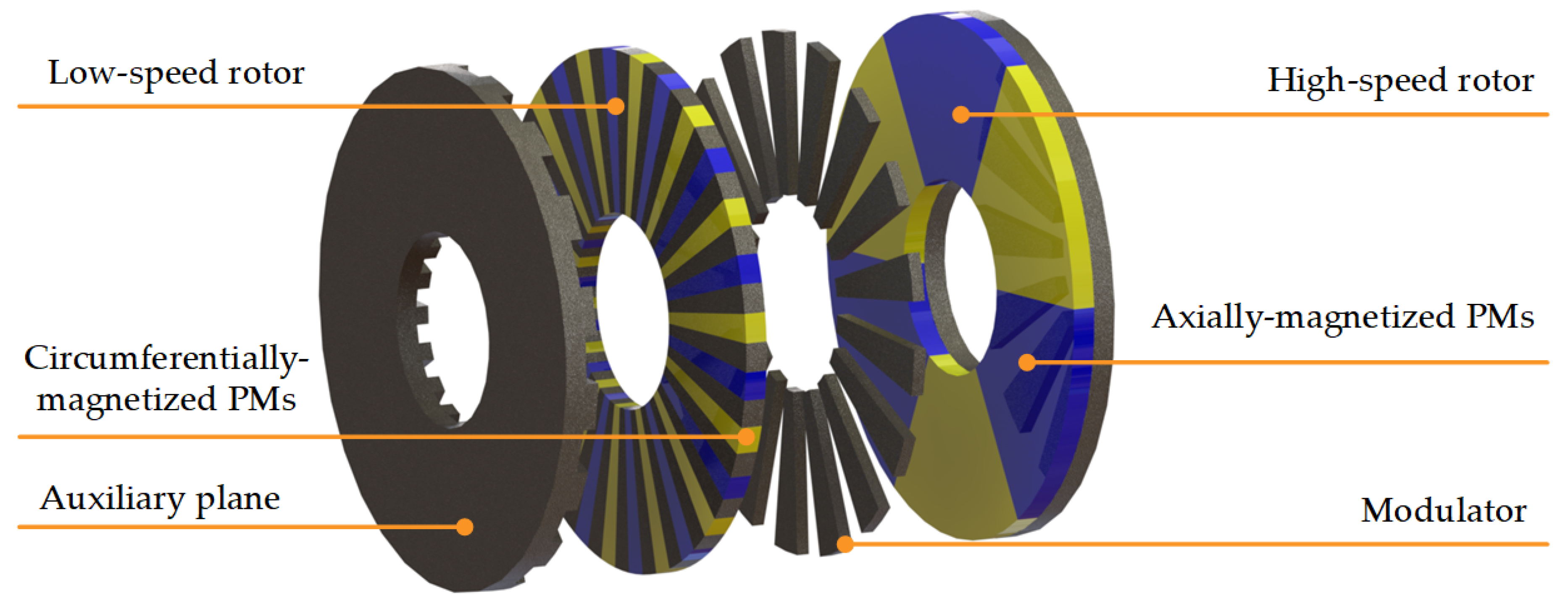
Preprints 102794 g001
Preprints 102794 g002
Figure 2. Analysis simplification of the AFS-AMG.
Figure 2. Analysis simplification of the AFS-AMG.
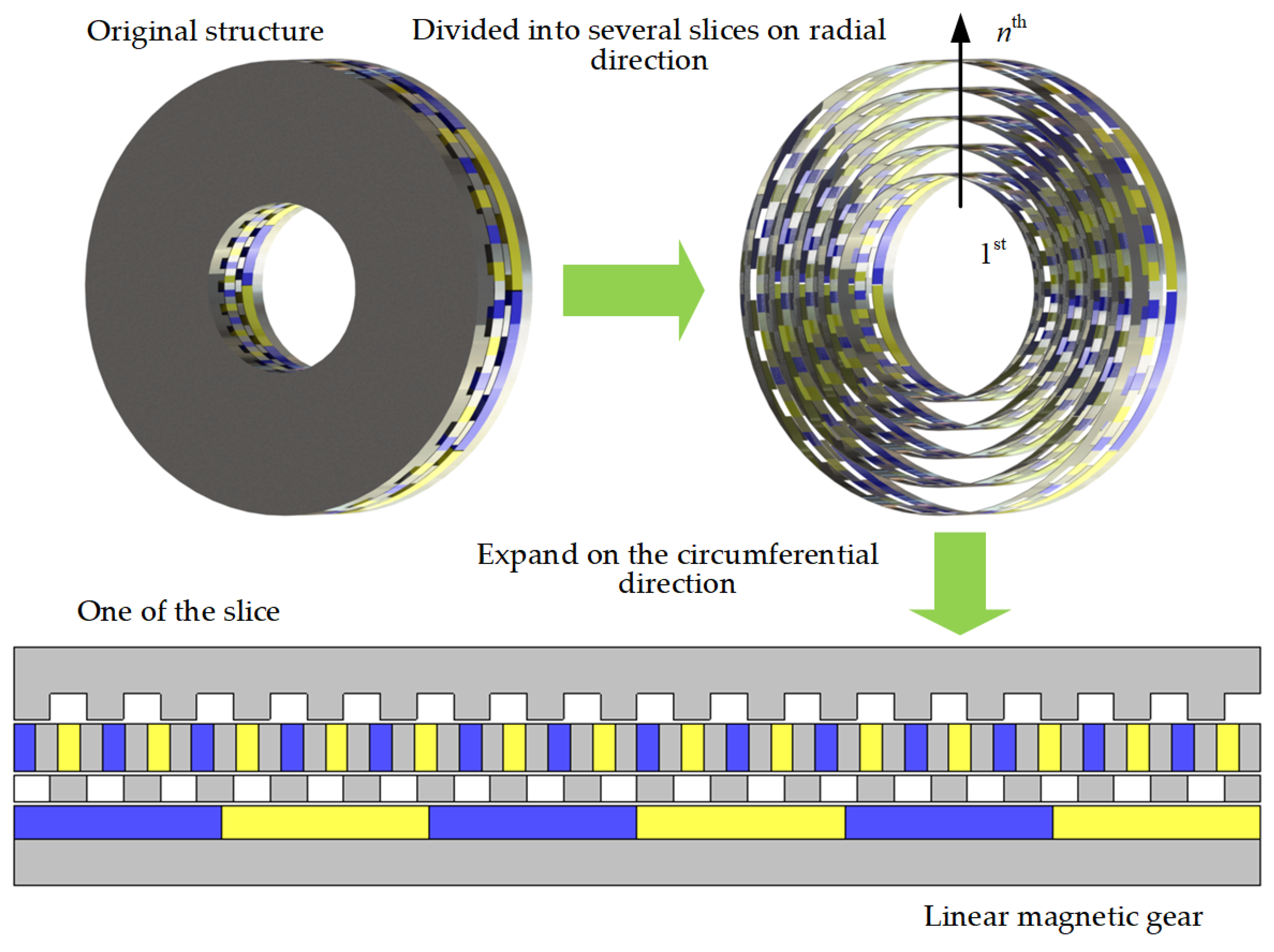
Preprints 102794 g002
Preprints 102794 g003
Figure 3. The magnetic flux density distribution of the AFS-AMG with and without the auxiliary plane.
Figure 3. The magnetic flux density distribution of the AFS-AMG with and without the auxiliary plane.
Preprints 102794 g003
Preprints 102794 g004
Figure 4. The magnetic flux path illustration of the AFS-AMG with and without the auxiliary plane.
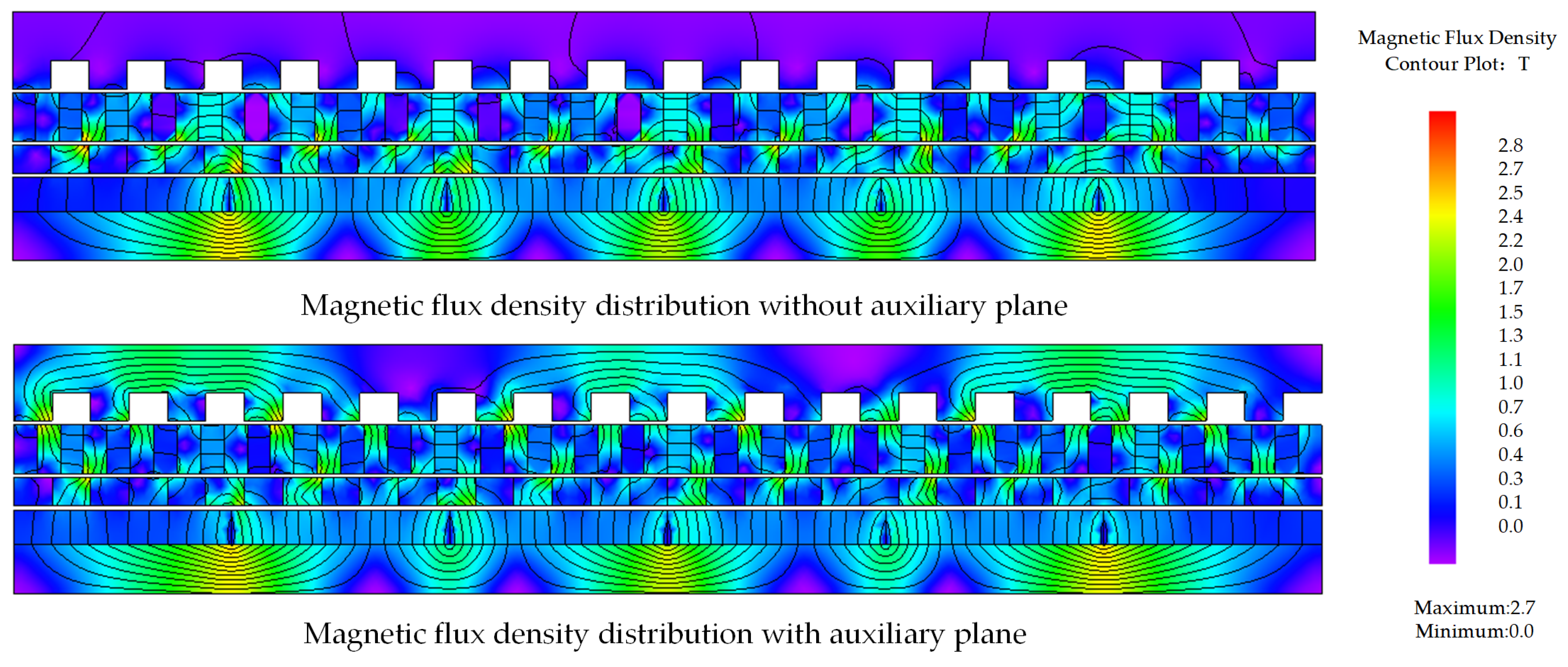
Figure 4. The magnetic flux path illustration of the AFS-AMG with and without the auxiliary plane.
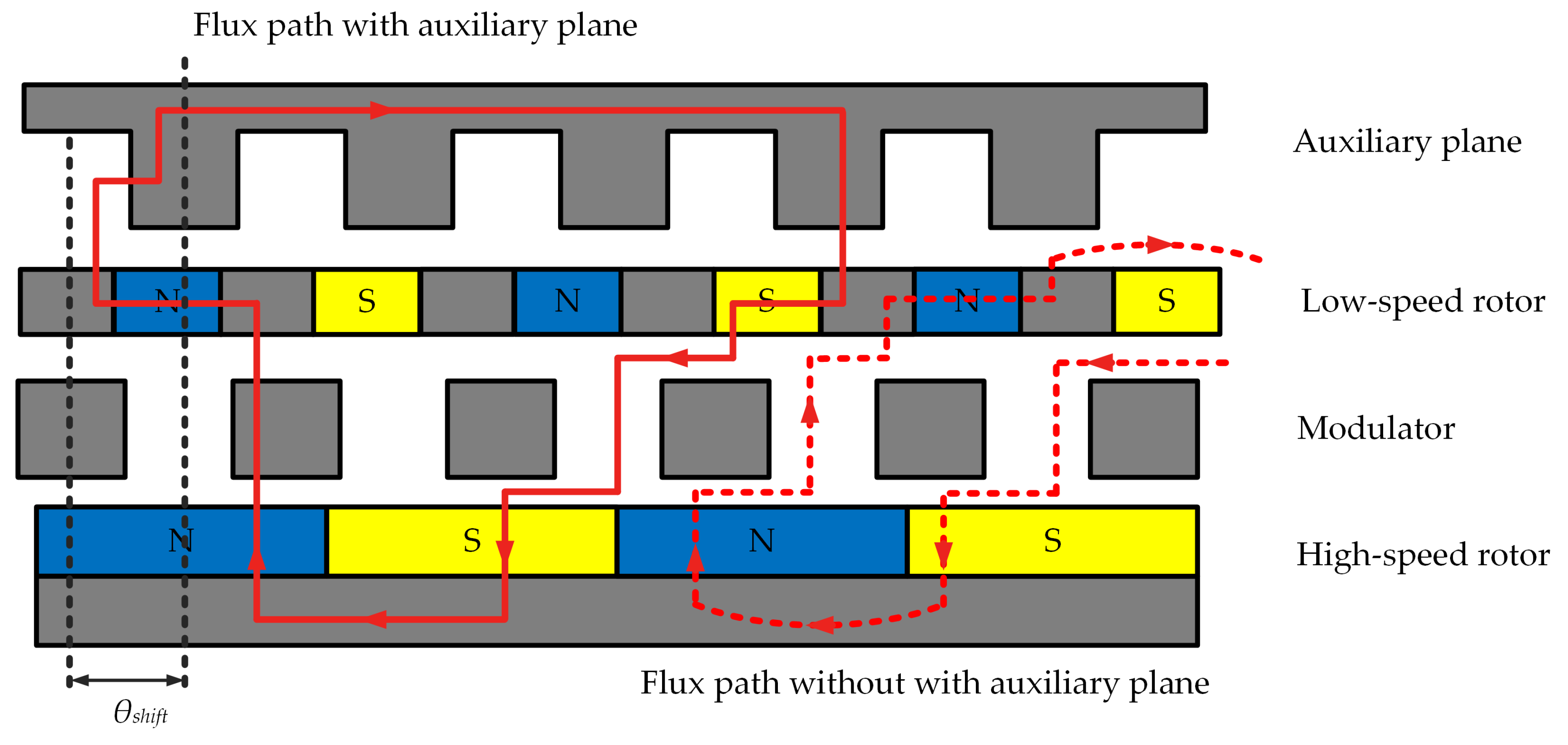
Preprints 102794 g004
Preprints 102794 g005
Figure 5. The torque waveforms on the low-speed rotor of AFS-AMGs with different pole-pair combinations.
Figure 5. The torque waveforms on the low-speed rotor of AFS-AMGs with different pole-pair combinations.
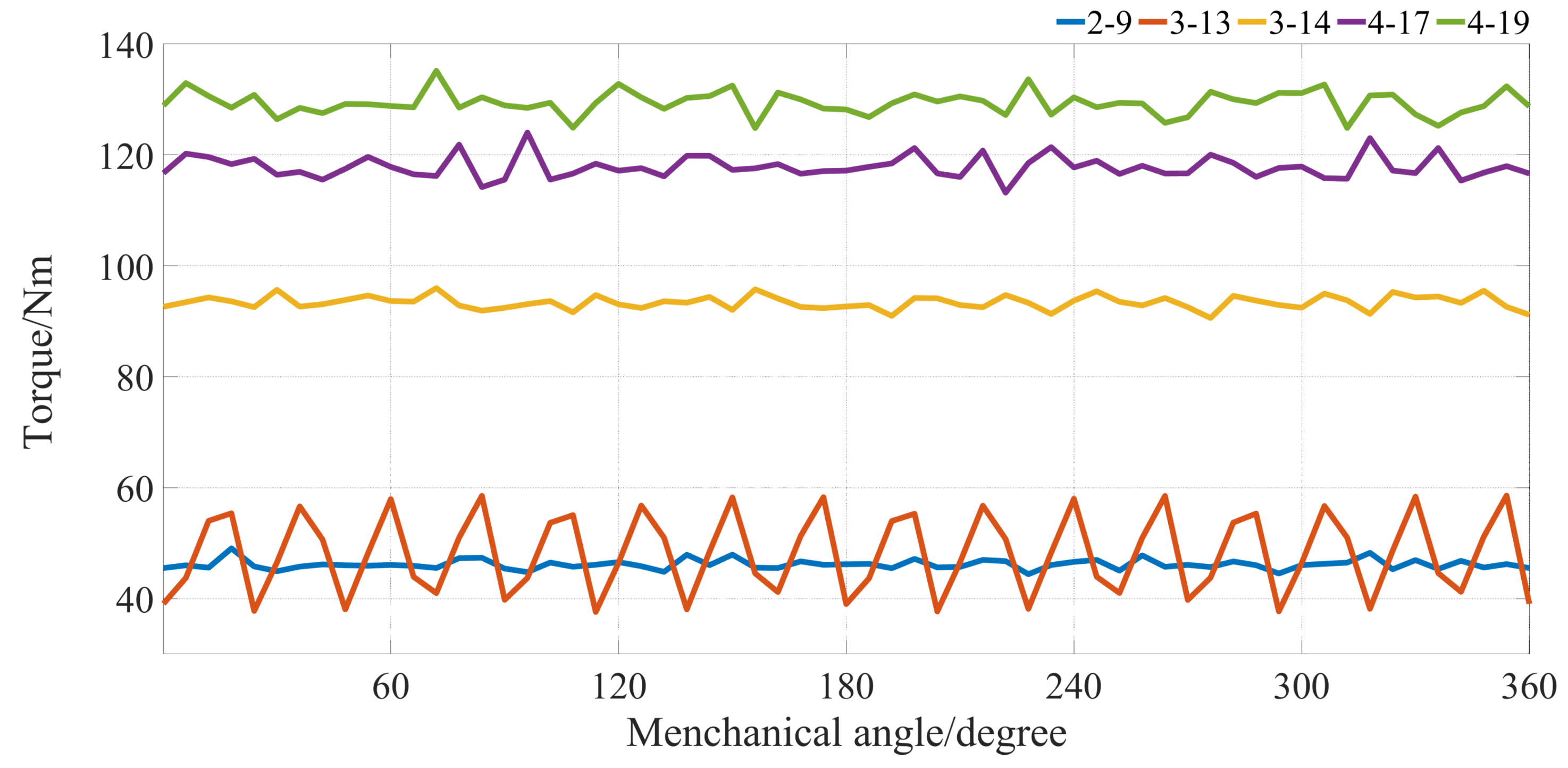
Preprints 102794 g005
Preprints 102794 g006
Figure 6. Variation of torque density per volume and axial-direction force on the modulator with respect to air-gap length in AFS-AMGs.
Figure 6. Variation of torque density per volume and axial-direction force on the modulator with respect to air-gap length in AFS-AMGs.
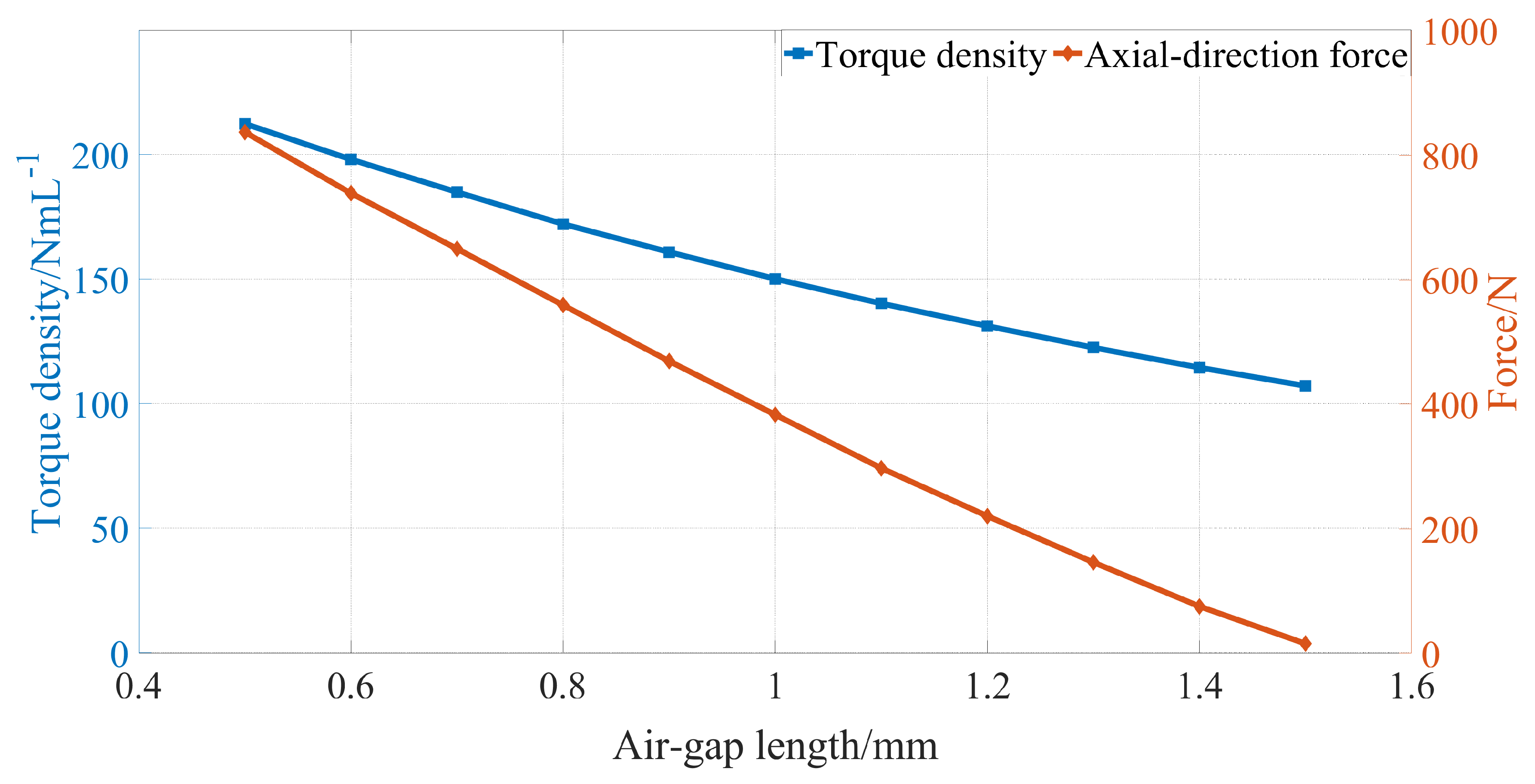
Preprints 102794 g006
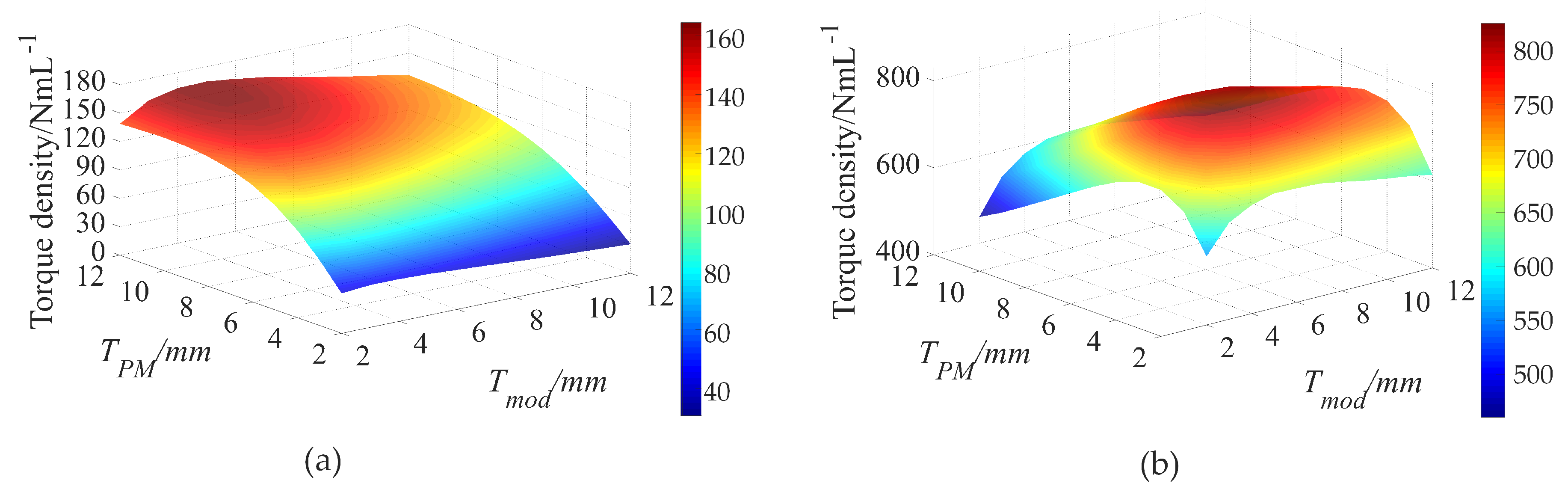
Preprints 102794 g007
Figure 7. Variation of torque density with respect to the thickness of modulator teeth and PMs: (a) τ V total ; (b) τ V P M .
Figure 7. Variation of torque density with respect to the thickness of modulator teeth and PMs: (a) τ V total ; (b) τ V P M .
Preprints 102794 g007
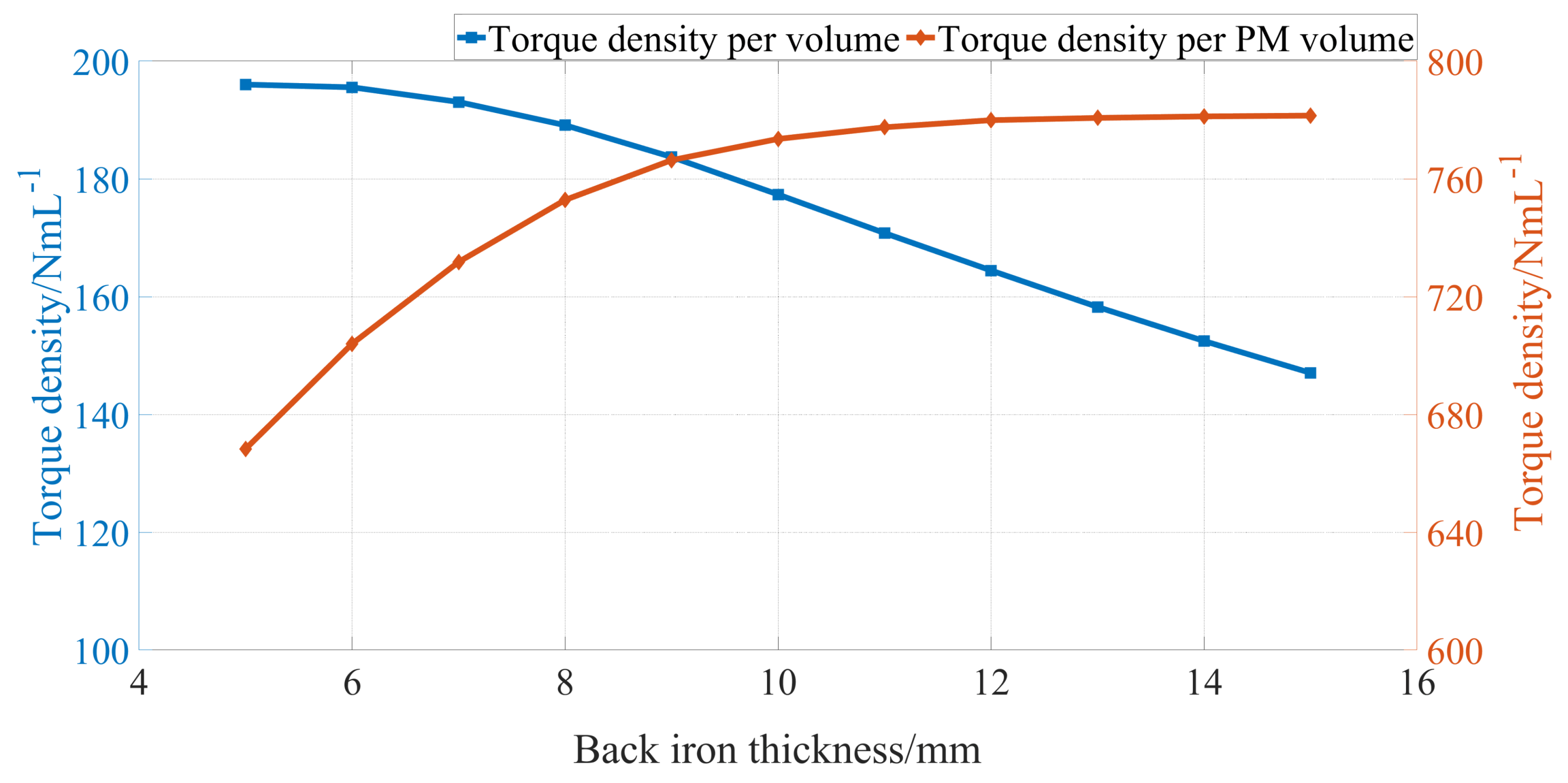
Preprints 102794 g008
Figure 8. Variation of torque density with respect to the thickness of back iron in AFS-AMGs.
Figure 8. Variation of torque density with respect to the thickness of back iron in AFS-AMGs.
Preprints 102794 g008
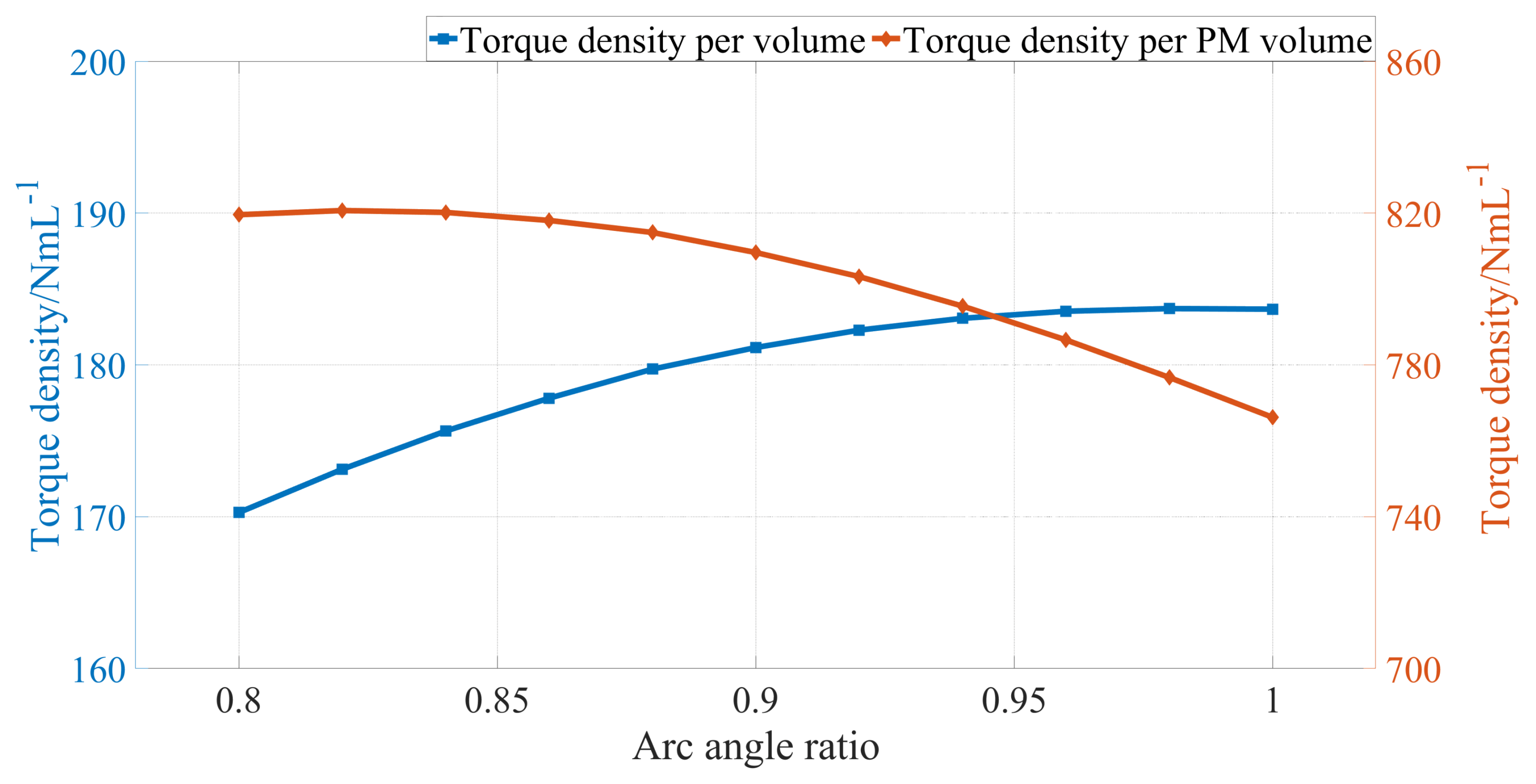
Preprints 102794 g009
Figure 9. Variation of torque density per PM volume with respect to PMs’ arc angle ratio on the high-speed rotor in AFS-AMGs.
Figure 9. Variation of torque density per PM volume with respect to PMs’ arc angle ratio on the high-speed rotor in AFS-AMGs.
Preprints 102794 g009
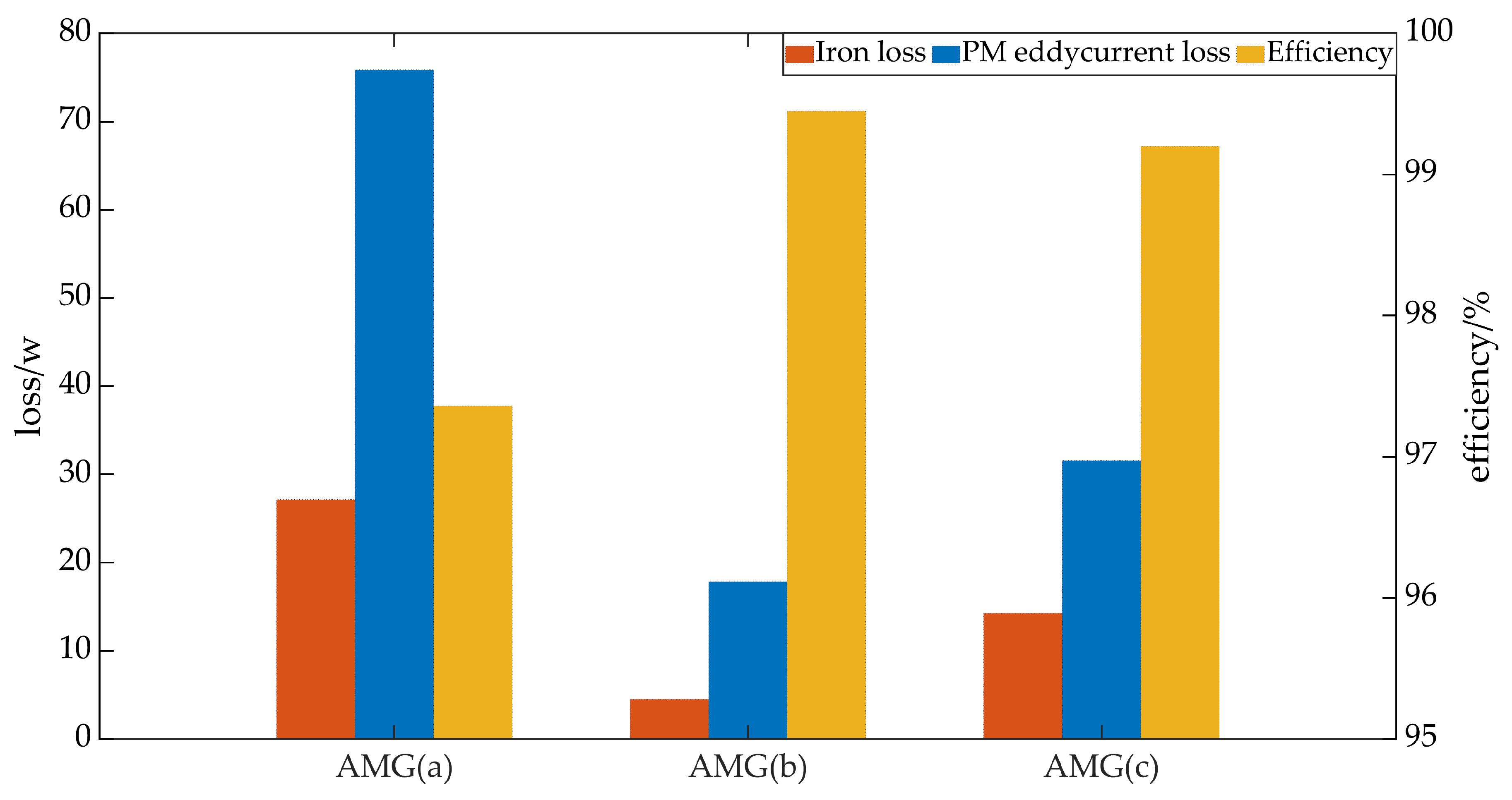
Preprints 102794 g010
Figure 10. Comparison of the three different AMGs.
Figure 10. Comparison of the three different AMGs.
Preprints 102794 g010
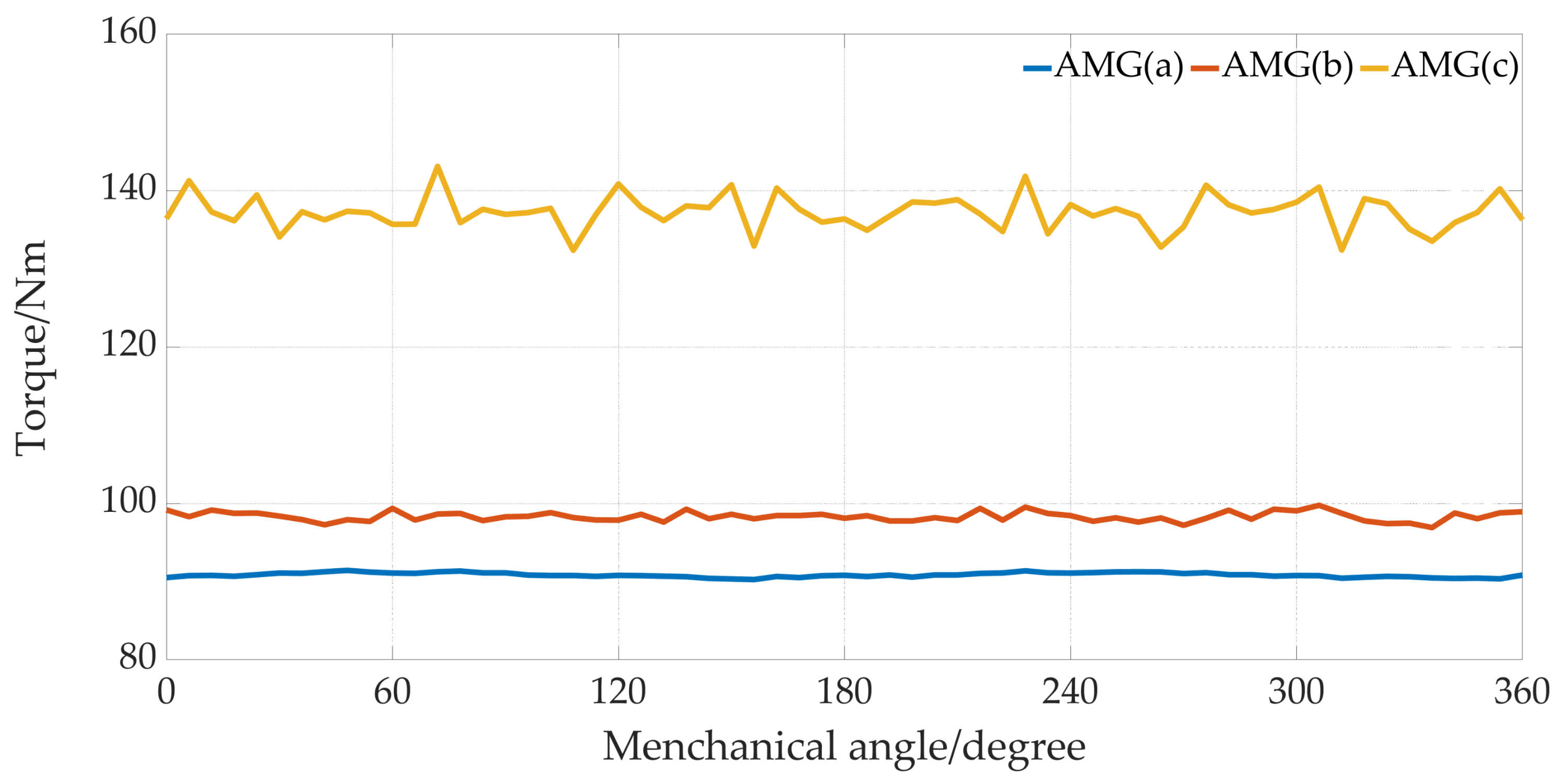
Preprints 102794 g011
Figure 11. Torque waveforms of the three different AMGs.
Figure 11. Torque waveforms of the three different AMGs.
Preprints 102794 g011
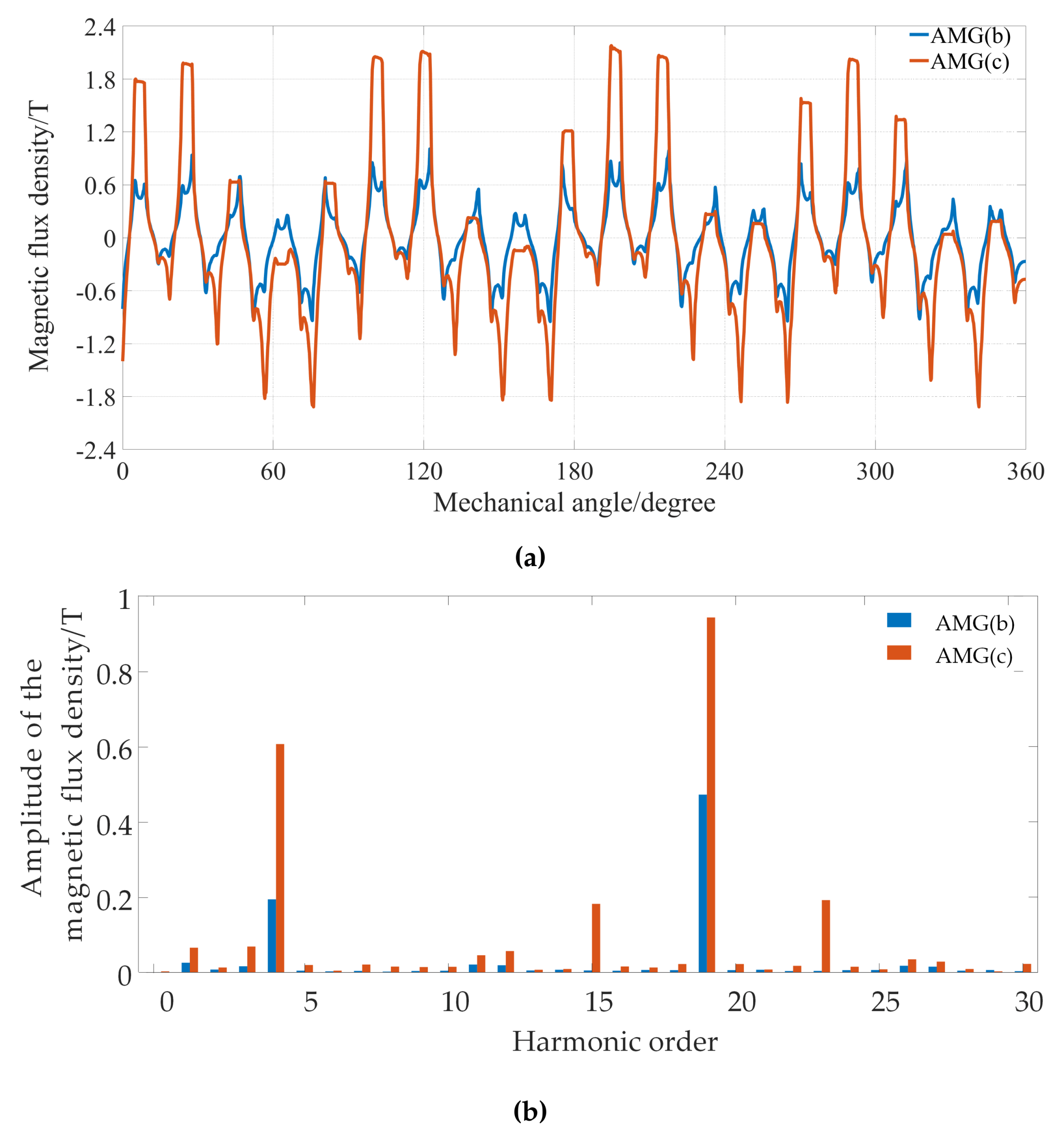
Preprints 102794 g012
Figure 12. Magnetic flux density distribution on the circumferential direction with radius being 60 mm: (a) Axial component; (b) the corresponding FFT.
Figure 12. Magnetic flux density distribution on the circumferential direction with radius being 60 mm: (a) Axial component; (b) the corresponding FFT.
Preprints 102794 g012
Preprints 102794 g013
Figure 13. Magnetic field distribution of the proposed AMG: (a)From less-PM face; (b) From more-PM face.
Figure 13. Magnetic field distribution of the proposed AMG: (a)From less-PM face; (b) From more-PM face.
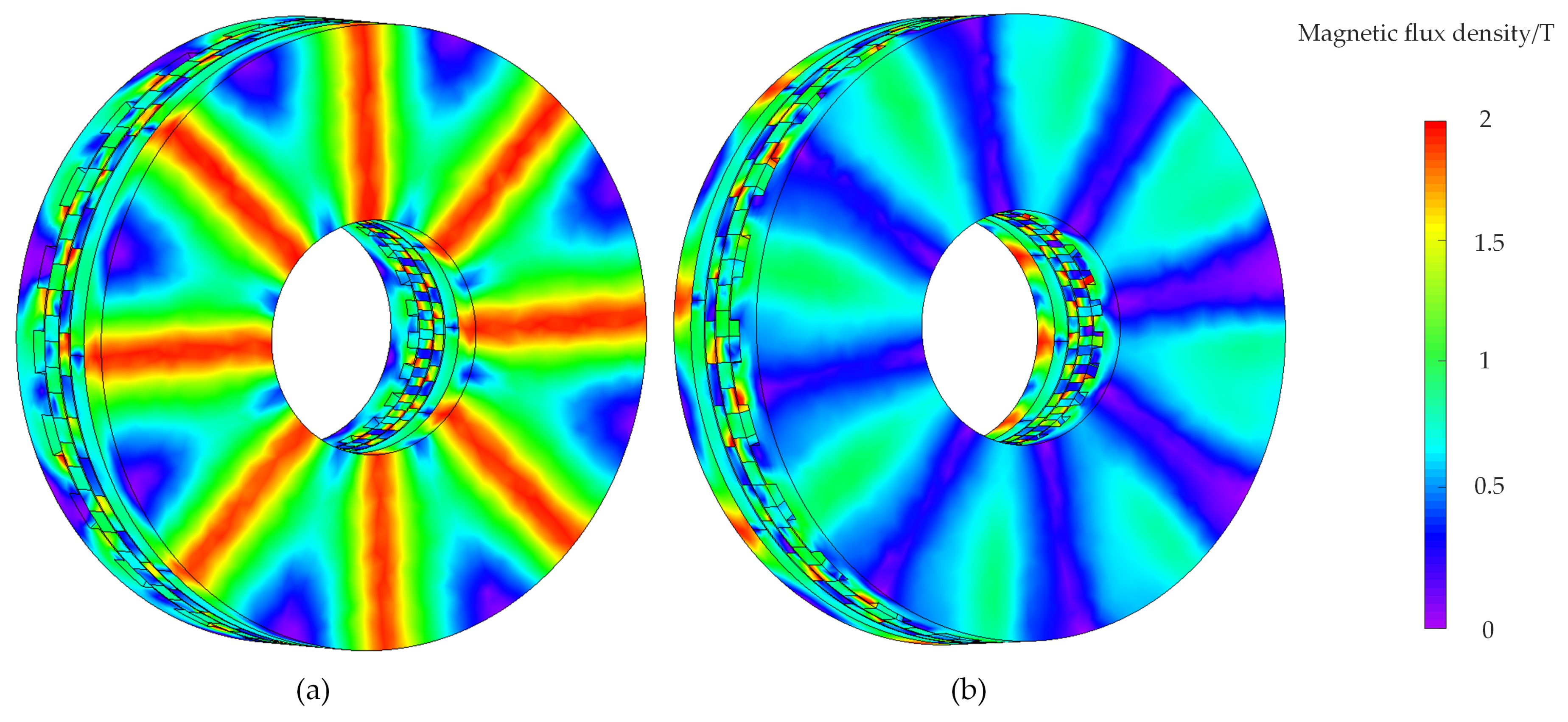
Preprints 102794 g013
Preprints 102794 g014
Figure 14. Axial force of the proposed AMG.
Figure 14. Axial force of the proposed AMG.
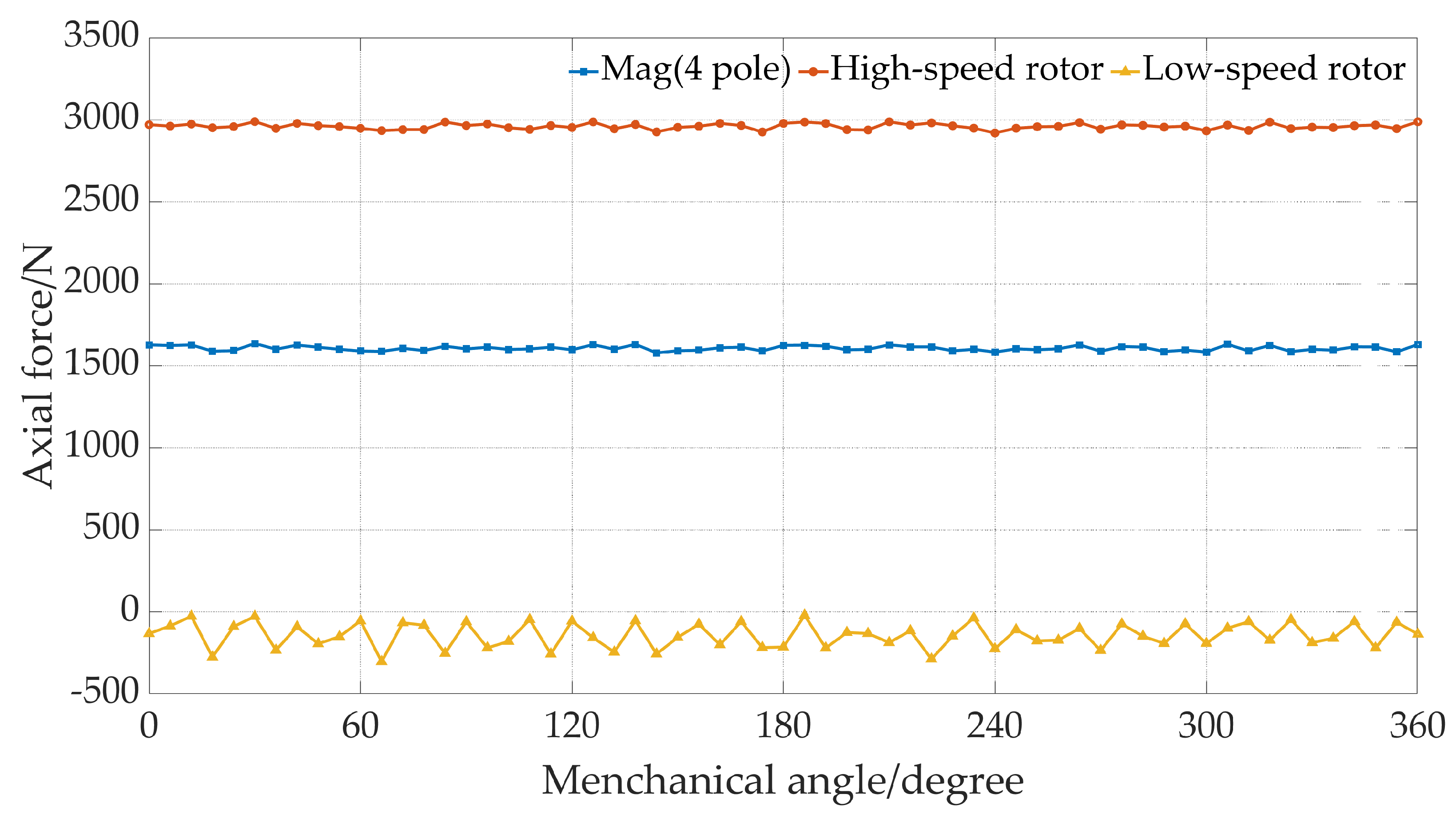
Preprints 102794 g014
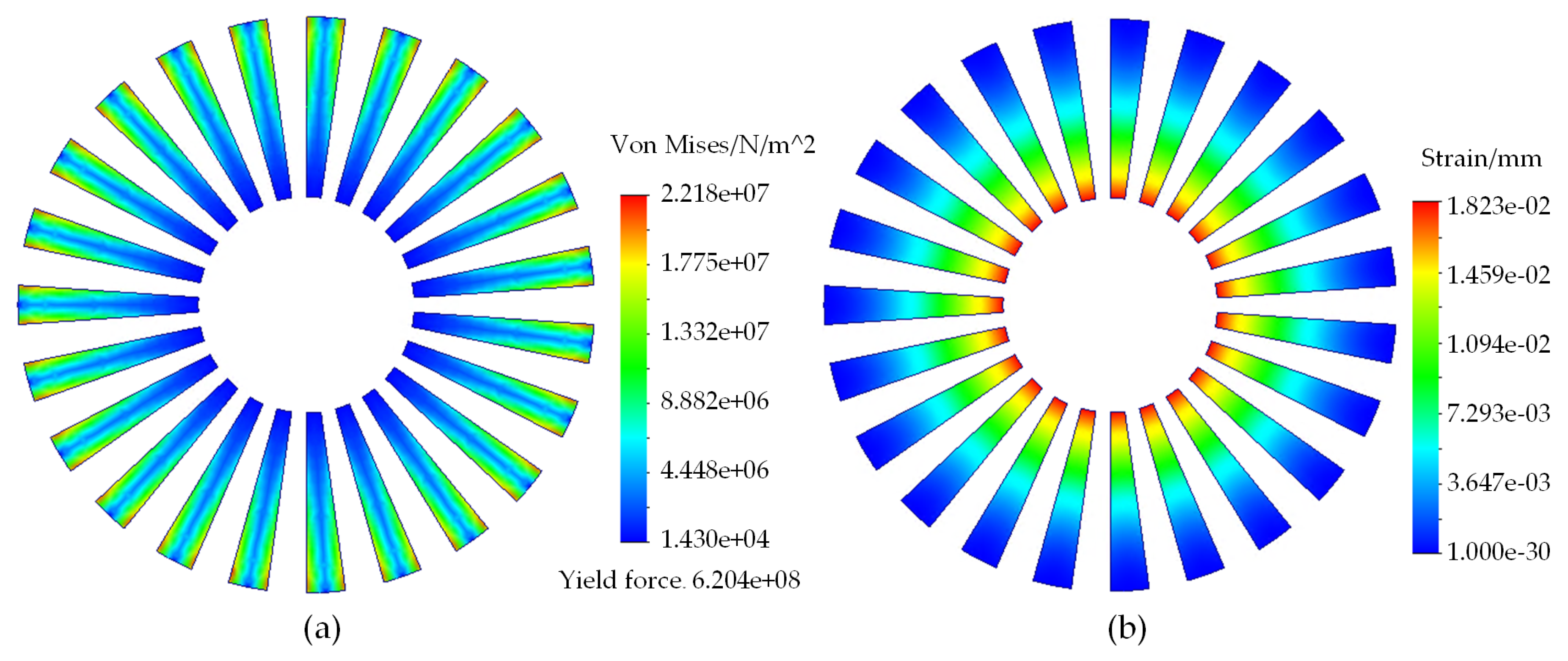
Preprints 102794 g015
Figure 15. Stress analysis of modulator teeth: (a) Stress; (b) Strain.
Figure 15. Stress analysis of modulator teeth: (a) Stress; (b) Strain.
Preprints 102794 g015
Table 1. Mapping relations between RMGs and AMGs.
Table 1. Mapping relations between RMGs and AMGs.
RMG AMG
(a) Preprints 102794 i001 Preprints 102794 i002
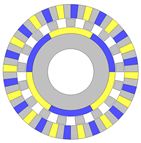(b) Preprints 102794 i003 Preprints 102794 i004
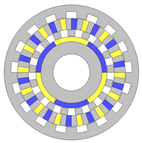(c) Preprints 102794 i005 Preprints 102794 i006
Table 2. Possible pole-pair combinations of AFS-AMGs.
Table 2. Possible pole-pair combinations of AFS-AMGs.
P h i g h P l o w G
2 9 4.5
3 13,14 4.33,4.67
4 17,19 4.25,4.75
Table 3. Mapping relations between RMGs and AMGs.
Table 3. Mapping relations between RMGs and AMGs.
Symbol Parameter Value
P low Low-speed rotor PM pole pairs number 19
P high High-speed rotor PM pole pairs number 4
Q Modulation pieces number 23
R out Outer radius of the AFS-AMG 80 mm
R in Inner radius of the AFS-AMG 30 mm
T air Air-gap length 0.6 mm
T P M Thickness of PMs on low-speed and high-speed rotors 7 mm
T mod Thickness of modulator pieces and auxiliary plane teeth 5 mm
T iron Thickness of the back iron of high-speed rotor and auxiliary plane 9 mm
γ Arc angle ratio of high-speed rotor PMs 0.9
Ω low Rotating speed of low-speed rotor 400 r/min
Ω high Rotating speed of high-speed rotor 1900 r/min
Table 4. Simulation result values of the AMGs.
Table 4. Simulation result values of the AMGs.
Symbol AMG (a) AMG (b) AMG (c)
T low / Nm 90.85 98.32 137.09
τ V total / Nm · L − 1 135.51 194.87 181.14
τ V P M / Nm · L − 1 375.56 580.53 809.60
Torque ripple / % 1.28 2.89 7.82
Iron loss/W 27.15 4.53 14.25
PM eddy current loss/W 75.86 17.86 31.58
Efficiency/% 97.36 99.45 99.20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated