Preprint
Article
How a Thermodynamic Version of the Friedmann Equation Appears to Solve the Early Galaxy Formation Problem
Altmetrics
Downloads
86
Views
77
Comments
0
This version is not peer-reviewed
Submitted:
31 March 2024
Posted:
02 April 2024
You are already at the latest version
Alerts
Abstract
Based on our recent thermodynamic formulation of the Friedmann equation, we demon- strate how the age of the universe must be approximately 14.6 billion years. This is about 800 million years older than predicted by the Λ-CDM model and therefore greatly alleviates the early galaxy formation problem.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. The Cosmic Age in Cosmology
It is well known that, in cosmology, the age of the universe at any point in time must simply be , and then the current age of the universe becomes , as pointed out, for example, by Melia and Shevchuk [1]. However, this formula still results in a very wide uncertainty in cosmic age, due to the significant uncertainty in present in both Melia’s cosmology and in -CDM cosmology. The uncertainty in arises both from measurement difficulties and from the Hubble tension uncertainty. Considering the Hubble tension, within one standard deviation ranges from km/s/Mpc to km/s/Mpc, as calculated from seven recent measurement studies of which we will show. This wide range of values leads to a cosmic age estimate range of about to billion years.
In the -CDM model, the estimated cosmic age is further adjusted according to the assumption that the universe has expanded faster than the speed of light. Of interest, in the special case where and , the -CDM estimated cosmic age coincidentally matches that predicted by models, namely , as recently pointed out by Kutschera and Dyrda [2]. So, it is clear that large uncertainties in cosmic age estimates due to measurement errors in , as well as the Hubble tension itself [3], result when using only in isolation. Moreover, in the -CDM model, one also uses inputs other than , including cosmological redshifts, to estimate the cosmic age; their best current age estimate is Gyr [4]. Their small uncertainty in this number is surprising, to say the least.
Recently, Haug and Tatum demonstrated [5] that the Friedmann equation [6] can be written in thermodynamic form:
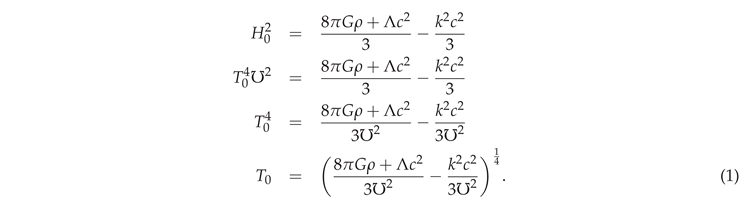
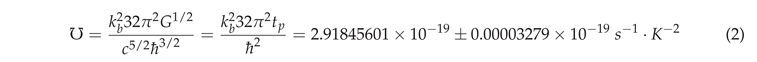
The only uncertainty in this constant comes from the uncertainty in G, as the other constants are exact according to the NIST CODATA 2018 standard. When working with our particular sub-class of cosmology model, one can set .
Our thermodynamic formulation of the Friedmann equation is a result based on many years of work by multiple researchers, starting with Tatum et. al [9] in 2015. Their cosmic temperature formula linked the CMB temperature, given as:
with the Hubble constant at any cosmic time, , according to . So, is the Hubble radius at cosmic time t. The same formula was later derived from the Stefan-Boltzmann law; see Haug and Wojnow [10,11]. As our sub-class of cosmology must have and also , equation (3) can naturally also be re-written as:
where is the cosmic time as it evolves. Solving for gives:
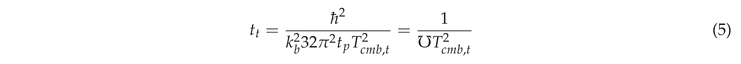
We also must have:
In the flat space critical Friedmann solution, one sets and and we then have:
This is as expected, and a well-known result. From the work of Tatum et al. [7,8], we also must have:
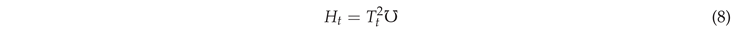
So, our critical Friedmann solution can also be expressed as:
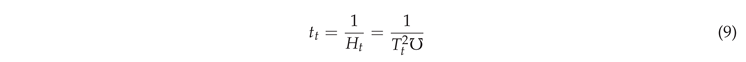
And, for the current spatially-flat epoch of the universe, we also have:
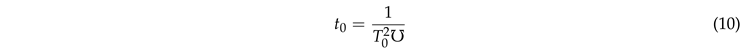
Since has been measured much more precisely than , this leads to a much more accurate estimate of current cosmic age, as shown in Table 1. If had been measured with the same precision as the current CMB temperature, one could have also obtained the same precision in (when one ignores the Hubble tension, which we claim to have solved; see [12,13]). The justification for such precision is explained in [7]. Given this background, please see Table 1 and Table 2.
In models, one can now estimate the current cosmic age much more precisely by adopting our thermodynamic Friedmann equation; see [5]. In the Melia sub-class of model [1], without our thermodynamic Friedmann equation, there is greater uncertainty in its estimate of the cosmic age, ranging from about 13.2 to 14.8 billion years. In sharp contrast, based on four recent CMB studies, we can now constrain the cosmic age to slightly greater than 14.6 billion years, with very high precision. See again Table 1. This is largely due to the current high precision (i.e., low uncertainty) in current CMB temperature measurements.
Tatum and Haug [25] were first to derive a 14.6 billion year cosmic age estimate from their new cosmological model, when calibrating their redshift prediction formula using all 580 type Ia supernova redshifts in the Union2 database. This shows that our particular sub-class of model is internally consistent, because it is also consistent with our thermodynamic form of the Friedmann equation.
It is worth mentioning here that Haug and Tatum [12] also solved the Hubble tension by using the Union2 supernova redshift database. We initially started with a mere guess for , but then employed intelligent algorithms, such as the well-known bisection method and the Newton-Raphson method, in order to minimize errors between predicted and observed redshift values. When applying this new approach to predicted redshifts using the formula: , we found: . This level of precision surpasses that of any other study, and yields a cosmological time of years. Our particular solution to the Hubble tension, and its alignment with our thermodynamic form of the Friedmann equation, produces the same cosmic time estimate when using as that when using the CMB temperature measurement directly. It is important to note that the original Friedmann equation, and now its thermodynamic counterpart, are, at a deeper level, essentially the same equation. They are based on two different observations, either current CMB temperature or , but are now coupled by an exact mathematical relationship (using our Upsilon composite constant) that has been overlooked in other cosmological models.
2. Two Cosmological Redshift Formulas and Their Implications
In general, for multiple different models, we have , as pointed out by Lima et al. [26]. In our thermodynamic Friedmann equation, it is clear that one must have , which is consistent with observational studies [27] indicating that must be close to zero. So, we now assume . This leads to the cosmological redshift formula in our particular sub-class of cosmology, when setting (i.e., flat space cosmology); one must have:
Which, when solved for , brings us back to the well-tested relation. If, instead, we want to have , then our thermodynamic Friedmann equation tells us that we also must have:
which leads to , which we have recently shown does not appear to be consistent with observations. In making this discovery, we claim to have resolved the Hubble tension; see again [12]. It is important to note here that we now have both a new redshift formula and a new cosmological framework providing exact inter-relationships between , , z, and even the Planck scale [9,11,13].
3. What Modern Telescopes Have Revealed About the Earliest Galaxies and Their Supermassive Black Holes
Modern telescopes, most notably the James Webb Space Telescope (JWST), have revealed numerous early galaxy surprises with respect to expectations based on the Lambda-CDM cosmology model and our current understanding of the physics of galaxy formation. The most distant galaxies, particularly those with redshifts of , appear shockingly different from previous expectations. Their combined unexpected features have given rise to what has been called the “early galaxy problem.” They present a severe challenge to Lambda-CDM cosmology and our previous theories and simulations of early galaxy formation.
Before the most modern space telescopes became available, the prevailing theory of galaxy evolution was the “Hierarchical Model.” The idea was that modern galaxy formation could only occur as a piecemeal process of gradually-accumulating evolutionary building blocks over many billions of years. However, in recent years, large galaxies with modern features could already be seen by 3-6 billion years of cosmic age. This discovery was one of the first indications that the Hierarchical Model theory must be incorrect. In addition, it has gradually become apparent that supermassive black holes (SMBHs) are more ubiquitous and fundamental as “seeds” for galaxy formation than previously thought.
The JWST confirmed these growing suspicions about the early universe and elucidated a number of surprising features of the highest redshift galaxies. These galaxies are found to be far more mature in appearance than previously expected for age. Their bulk mass and brightness is already much greater than expected [28,29,30]. Interestingly, they also tend to be ultracompact, having diameters roughly several hundred to one thousand times smaller than that of the Milky Way [31,32]. The oldest among them, having redshifts greater than 9, also have much lower ratios of their star mass to that of their SMBH. In mature galaxies, such as the Milky Way, this ratio is usually about 1000 to 1. However, very early galaxies tend to have much smaller ratios, less than 100 to perhaps as low as roughly 1 to 1. The very early SMBHs of one study [33] were typically at least 10-100 times smaller than the active galactic nuclei of quasars. Such findings suggest that these considerably smaller early SMBHs might act as initial “seeds” for galaxy star formation and bursty activity by some sort of positive feedback loop. It has also been proposed that larger SMBH “seeds” might even form by “direct collapse” from gargantuan clouds of primordial hydrogen gas [34].
Given the surprising degree of apparent maturity of the earliest visible galaxies, one must ask to what degree the early galaxy problem could be the result of some yet-undiscovered flaw in the Lambda-CDM cosmic age estimate of roughly 13.8 billion years, as opposed to an incomplete understanding of the physics of early galaxy and/or SMBH formation. While the discussion so far has focused on new concepts of early galaxy and SMBH formation (which can be “tested" in sophisticated computer simulations), the question with respect to cosmic age must also be recognized as highly model-dependent. A different cosmology model will naturally calculate a different cosmic age. Could it be that 13.8 billion years is in need of correction in favor of allowing for a longer time interval between the Big Bang and the appearance of the first galaxies?
Precise calculation of cosmic age has everything to do with having the correct redshift formulae with respect to time-dependent cosmic temperature, radius and cosmological distance. That having the correct redshift formula is crucial to the calculation of cosmic age, is already well-known in the literature. A recent example is offered by Gupta [35]. By adopting a different (“hybrid”) redshift formula, Gupta stretches the cosmic age to 26.7 billion years, thus allowing “enough time to form massive galaxies” (his words).
In Section 2, we demonstrated the importance of having the correct redshift formula and methodology. In particular, we showed how the standard cosmological formula could be underestimating cosmic age by a significant degree. In our previous publications wherein we have offered a Hubble tension solution [12,13], we have already shown how such a formula can, conversely, overestimate a local Hubble constant value derived from a database of supernova redshifts.
4. How the Stefan-Boltzmann Law is Inextricably Linked with Our Thermodynamic Friedmann Equation
The Stefan-Boltzmann luminosity from a black body is directly linked to the Stefan-Boltzmann law and is given by:
where is the Stefan-Boltzmann constant, defined as , and T is the temperature of the black body.
Here, we will demonstrate that we can recover the Stefan-Boltzmann law from the relationship between the past and current Friedmann critical density of the universe. The critical Friedmann density of the universe (which also plays a central role in Melia’s cosmology as well as in the -CDM model) is given by the classical Friedmann equation:
Since the Haug-Tatum model largely relies upon the mathematical coupling between the current CMB temperature and the value, namely, by 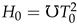 , we can substitute in the above equation:
, we can substitute in the above equation:
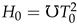 , we can substitute in the above equation:
, we can substitute in the above equation: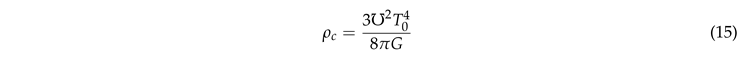
In addition, using as discussed in Section 2, and the same critical density formula for past epochs of the universe, within cosmology, we must have:
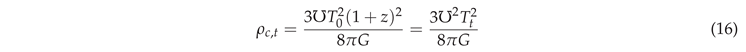
Furthermore, in a growing black hole model, we must also have:
so we must have :
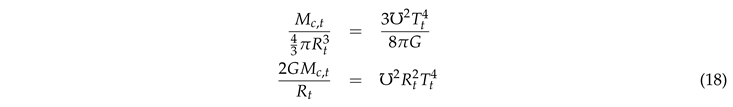
The Upsilon constant is given by 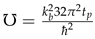 so, by squaring,
so, by squaring, 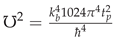 and remembering , we have:
and remembering , we have:
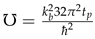 so, by squaring,
so, by squaring, 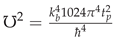 and remembering , we have:
and remembering , we have: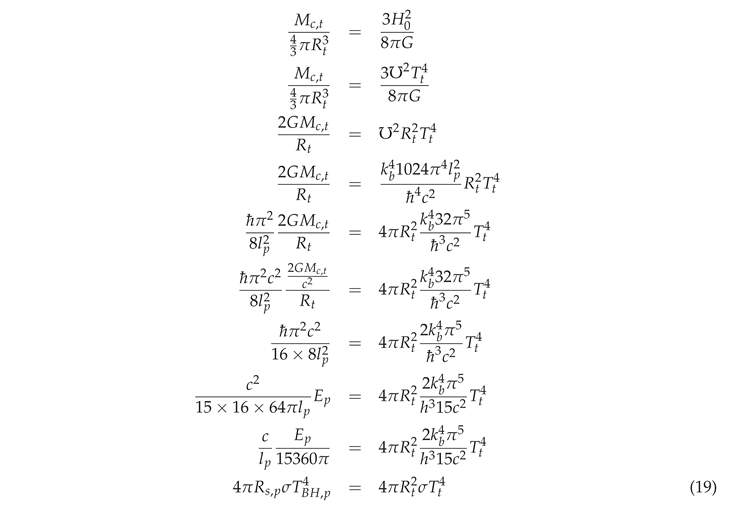
Where is the internal luminosity of a Planck mass Schwarzschild black hole, and and . This means that we must always have:
The above results show that we have recovered the Stefan-Boltzmann luminosity from our thermodynamic Friedmann equation. This is to be expected, since the thermodynamic Friedmann equation relies upon the CMB temperature coupling to the Hubble constant, as first indicated by Tatum et al. [9] in 2015. Later, in 2023, Haug and Wojnow [10,11] used the Stefan-Boltzmann law to derive the same basic relationships. Thus, we believe that our thermodynamic Friedmann formula is always consistent with the Stefan-Boltzmann law. Can any other cosmological model make a similar claim? We invite proponents of other models and proponents of the -CDM model to discuss our results and compare them with their own models.
Since we must have:
The above results can also be proven in a much simpler way. From Section 2 we know we must have:
If we want to satisfy , which basically has been confirmed by observations, this means that we must also have:
This would imply that we must have:
So, mathematically, we have determined that the internal black hole luminosity must remain constant across all Schwarzschild black holes (and possibly other types of black holes). This naturally does not imply that the internal temperature (CMB) is the same during the growth of the black hole Hubble sphere. A smaller radius corresponds to an earlier epoch of the universe when the CMB temperature was higher. However, the internal luminosity remains constant when measured at because the shorter radius is precisely offset by the higher temperature. This finding aligns with Haug and Wojnow’s [36] derivation, which began from a different angle since the thermodynamic Friedmann equation had not yet been invented at the time of their investigation. They also found that what they termed CMB luminosity surprisingly remains constant in growing black hole cosmology. Thus, while the temperature and radius change as the universe expands, the internal luminosity remains unchanged (at radius ). If we, instead, were to assume:
This would lead to :
which would require a modification of the Stefan-Boltzmann law, which we think would be highly unlikely to hold against observations. It would also require that we have , which does not seem to fit current observations in favor of .
Again, we invite proponents of other models and proponents of the -CDM model to discuss our results and compare them with their own models.
5. Summary and Conclusions
We have demonstrated how our particular sub-class of model, in conjunction with our thermodynamic form of the Friedmann equation, leads to an estimated cosmic age of approximately 14.6 billion years. This suggests that the universe is about 800 million years older than estimated by standard cosmology model proponents. Thus, this cosmic age extension potentially solves the early galaxy formation problem related to recent observations made by the James Webb Space Telescope. Furthermore, use of our thermodynamic Friedmann equation also results in significantly higher precision in cosmic age estimates, in comparison to those given using only the standard Friedmann equation and in isolation. In our view, this new approach to calculating cosmic age with high precision is revolutionary and has potentially important implications for the early universe. Nevertheless, we recommend that the astrophysics community scrutinize our model over time and form their own opinion.
References
- F. Melia and Shevchuk A. S. H. The rh=ct universe. Monthly Notices of the Royal Astronomical Society, 419:2579, 2012. [CrossRef]
- M. Kutschera and Dyrda M. Coincidence of universe age in Λ-cdm and Milne cosmologies. arXiv:astro-ph/0605175, 2006. [CrossRef]
- E. Valentino et. al. In the realm of the Hubble tension – a review of solutions. Classical and Quantum Gravity, 38:153001, 2021. [CrossRef]
- D. et. al Valcin. The age of the universe with globular clusters: reducing systematic uncertainties. Journal of Cosmology and Astroparticle Physics, 2021:017, 2021. [CrossRef]
- E. G. Haug and E. T. Tatum. Friedmann type equations in thermodynamic form lead to much tighter constraints on the critical density of the universe. https://www.preprints.org/manuscript/202403.1241/v2, /: URL https, 2024.
- A. Friedmann. Über die krüng des raumes. Zeitschrift für Physik, 10:377, 1922. [CrossRef]
- E. T. Tatum, E. G. EHaug, and S. Wojnow. High precision Hubble constant determinations based upon a new theoretical relationship between CMB temperature and H0. Hal archive, 2023. [Google Scholar]
- E. T. Tatum. Upsilon constants and their usefulness in Planck scale quantum cosmology. Journal of Modern Physics, 15:167, 2024. [CrossRef]
- E. T. Tatum, U. V. S. Seshavatharam, and S. Lakshminarayana. The basics of flat space cosmology. International Journal of Astronomy and Astrophysics, 5:116, 2015. [Google Scholar] [CrossRef]
- E. G. Haug and S. Wojnow. How to predict the temperature of the CMB directly using the Hubble parameter and the Planck scale using the Stefan-Boltzman law. Research Square, Pre-print, under consideration by journal, 2023. [CrossRef]
- E. G. Haug. CMB, Hawking, Planck, and Hubble scale relations consistent with recent quantization of general relativity theory. International Journal of Theoretical Physics, 63(57), 2024. [CrossRef]
- E. G. Haug and E. T. Tatum. Solving the Hubble tension by extracting current CMB temperature from the Union2 supernova database. Hal archive, /: URL https, 2024.
- E. G. Haug and E. T. Tatum. Planck length from cosmological redshifts solves the Hubble tension. ResearchGate.org 2024. [CrossRef]
- S. Dhal, S. Singh, K. Konar, and R. K. Paul. Calculation of cosmic microwave background radiation parameters using cobe/firas dataset. Experimental Astronomy (2023), 612:86, 2023. [Google Scholar] [CrossRef]
- D. J. Fixsen. The temperature of the cosmic microwave background. The Astrophysical Journal, 707:916, 2009. [CrossRef]
- P. Noterdaeme, P. Petitjean, R. Srianand, C . Ledoux, and S. López. The evolution of the cosmic microwave background temperature. Astronomy and Astrophysics 526, 2011. [CrossRef]
- D. J. Fixsen et. al. The temperature of the cosmic microwave background at 10 ghz. The Astrophysical Journal, 612:86, 2004. [CrossRef]
- Y. S. Murakami et. al Leveraging SN Ia spectroscopic similarity to improve the measurement of H0. arXiv:2306.00070, arXiv:2306.00070.
- T. de Jaeger, L. Galbany, A. G. Riess, B. E. Stahl, B. J. Shappee, A. V. Filippenko, and Zheng W. A 5 percent measurment of the Hubble–Lamaîte constant from Type II supernovae. Monthly Notices of the Royal Astronomical Society, 51:4620, 2022. [Google Scholar] [CrossRef]
- A. G. Riess et. al. A comprehensive measurement of the local value of the Hubble constant with 1 km s-1 mpc-1 uncertainty from the Hubble space telescope and the sh0es team. The Astrophysical Journal 934, 2021. [CrossRef]
- N. Aghanim et. al. Planck Collaboration; Aghanim. Planck 2018 results. vi. cosmological parameters. Astronomy & Astrophysics 641, 2020. [CrossRef]
- A. Sneppen, D. Watson, D. Poznanski, O. Just, A. Bauswein, and R. Wojtak. Measuring the hubble constant with kilonovae using the expanding photosphere method. Astronomy and Astrophysics, 678, 2023. [Google Scholar] [CrossRef]
- L. Balkenhol et. al. Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3g 2018 TT, TE, and EE dataset. Physical Review D, 108:023510, 2023. [CrossRef]
- P. L. Kelly et. al. Constraints on the Hubble constant from supernova Refsdal’s reappearance. Science, 380:6649, 202. [CrossRef]
- E. T. Tatum and E. G. Haug. Extracting a cosmic age of 14.6 billion years from all 580 type Ia supernova redshifts in the Union2 database. ResearchGate.org 2024. [CrossRef]
- J. A. S. Lima, A. I. Silva, and S. M. Viegas. Is the radiation temperature±redshift relation of the standard cosmology in accordance with the data? Monthly Notices of the Royal Astronomical Society, 312:747, 2000. [Google Scholar] [CrossRef]
- D.A. Riechers, A. Weiss, and F. et al. Walter. Microwave background temperature at a redshift of 6.34 from H2O absorption. Nature 602:58, 2022. [CrossRef]
- L. J. Furtak et. al. A supermassive black hole in the early universe growing in the shadows. arXiv:2308.05735 2023, arXiv:2308.05735, 2023. [CrossRef]
- A. Ferrara and P. Pallottini, and A . Dayal. On the stunning abundance of super-early, luminous galaxies revealed by JWST. Monthly Notices of the Royal Astronomical Society, 522:3986, 2023. [CrossRef]
- Y. Harikane et. al . Pure spectroscopic constraints on uv luminosity functions and cosmic star formation history from 25 galaxies at zspec =8.61-13.20 confirmed with jwst/nirspec. Astrophysics Journal, 960:56, 2023. [CrossRef]
- J. E. Greene et. al . Uncover spectroscopy confirms a surprising ubiquity of agn in red galaxies at z>5. arXiv:2309.05714 2023, arXiv:2309.05714, 2023. [CrossRef]
- J. F. Baggen et. al. Sizes and mass profiles of candidate massive galaxies discovered by JWST at 7<z<9: Evidence for very early formation of the central –100pc of present-day ellipticals. The Astrophysical Journal Letters 955, 2023. [CrossRef]
- F. Pacucci et. al . JWST ceers and jades active galaxies at z=4-7 violate the local m.–m. relation at >3σ: Implications for low-mass black holes and seeding models. Astrophysics Journal 957, 2023. [CrossRef]
- x, J. Silk et. al. Which came first: Supermassive black holes or galaxies? insights from jwst. The Astrophysical Journal Letters, 961, 2024. [Google Scholar] [CrossRef]
- R. P. Gupta. JWST early universe observations and λcdm cosmology. Monthly Notices of the Royal Astronomical Society 524:3385, 2023. [CrossRef]
- E. G. Haug and S. Wojnow. The blackbody CMB temperature, luminosity, and their relation to black hole cosmology, compared to Bekenstein-Hawking luminosity. Hal archive, 2024.
Table 1.
This table compares cosmic age estimates using the thermodynamic form of the critical Friedmann equation. One can therefore choose between using or the current CMB temperature for these estimates; as the current CMB temperature is measured much more precisely, that was our choice.
Table 1.
This table compares cosmic age estimates using the thermodynamic form of the critical Friedmann equation. One can therefore choose between using or the current CMB temperature for these estimates; as the current CMB temperature is measured much more precisely, that was our choice.
| CMB study : | CMB measurement : | Cosmic age estimates using |
|---|---|---|
| thermodynamic critical Friedmann equation: | ||
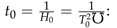 |
||
| 2023: Dhal et. al [14] : | years | |
| 2009: Fixsen et. al [15] : | years | |
| 2011: Noterdaeme et. al [16] : | years | |
| 2004: Fixsen et. al [17] : | years |
Table 2.
This table compares estimated cosmic ages when one relies on the standard equation, using precision in conjunction with critical density Friedmann assumptions. Furthermore, the current wide range of cosmic age uncertainty must come not only from lower precision in measuring the Hubble constant alone, but from the Hubble tension uncertainty as well.
Table 2.
This table compares estimated cosmic ages when one relies on the standard equation, using precision in conjunction with critical density Friedmann assumptions. Furthermore, the current wide range of cosmic age uncertainty must come not only from lower precision in measuring the Hubble constant alone, but from the Hubble tension uncertainty as well.
| Study : | estimate : | Current cosmic age estimates |
|---|---|---|
| using and critical density | ||
| Friedmann assumptions: | ||
| 2023: Murakami et al. [18] : | years | |
| 2022: Jaeger et. al [19]: | years | |
| 2021: Riess et al. [20] : | years | |
| 2021: Planck Collaboration [21] : | years | |
| 2023: Sneppen et. al [22] : | years | |
| 2023: Balkenhol et. al [23] : | years | |
| 2023: Kelly et. al [24]: | years |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated