Optimal Selection of Distribution, Power and Type of Luminaires for Street Lighting Designs Using Multi-criteria Decision

Preprint

Article

Optimal Selection of Distribution, Power and Type of Luminaires for Street Lighting Designs Using Multi-criteria Decision

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Nataly Gabriela Valencia Pavón^*,

Alexander Aguila Téllez^*

Edwin Marcelo Garcia

Javier Arturo Rojas Urbano,

Narayanan K

Nataly Gabriela Valencia Pavón^*,

Alexander Aguila Téllez^*

Edwin Marcelo Garcia

Javier Arturo Rojas Urbano,

Narayanan K

This version is not peer-reviewed

Submitted:

31 March 2024

Posted:

02 April 2024

You are already at the latest version

Alerts

Abstract

This article introduces an innovative design method for public lighting systems that surpasses the limitations of conventional approaches, which rely on predefined lamp characteristics and spatial arrangement. By employing a multi-criteria decision algorithm, our study proposes an optimal design methodology considering several key aspects, including the distance between lamps, their type, power, and light distribution. The goal is to achieve optimal illumination that enhances visibility on public roads for drivers and pedestrians while simultaneously minimizing glare, installation costs and maximizing energy efficiency. The proposed methodology is implemented through an algorithm developed in Matlab, with results validated through simulations in Dialux. This information is used to construct a decision matrix, assessed using the CRITIC method across 180 different scenarios within a specific case study. The findings demonstrate the effectiveness of multi-criteria decision-making as a tool for significantly improving the planning and design of lighting in public illumination systems, allowing for selecting the optimal combination of parameters that ensure the best lighting conditions.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

A lighting system provides an artificial light source to facilitate the performance of daily activities in the absence of natural light sources or when their influence on the workspace is minimal [18]. The utility of these systems is commonly defined by the illumination level (E), which determines the light intensity on the work plane. Therefore, the design of lighting systems is based on determining the number of lamps and their distribution in the workspace to achieve the required illumination level, a procedure known as the lumen method [9,12].

When discussing street lighting, the performance of a lighting system is not only measured in terms of illumination level but also must take into account factors that affect comfort and functionality for the user [10,11,19]. The illumination level must be ensured at the eye level of pedestrians as well as at the sight level of drivers. It is important to maintain visibility across the entire path and prevent the lamp from dazzling people’s vision. Therefore, illumination uniformity (Uo) and glare index (UGR) are included as performance parameters of lighting [23,25].

Another factor currently considered is energy efficiency. Street lighting is widely used both night and day to enhance visibility in areas with little to no natural light. Since artificial light sources that consume electrical energy are used, they can account for 21% to 40% of energy consumption in buildings in developing countries and up to 15% in industrialized countries [14,17]. This mode of operation also affects the cost of operation and maintenance, which is covered by public administration and can amount to a significant value [8,20].

It can be observed that the design of lighting requires meeting various criteria to ensure utility, comfort, and feasibility, making it not only a technical issue but also an economic one [5,7,15]. These issues can be analyzed by applying multi-criteria mathematical models or using heuristic algorithms; the difference between them is that the first strategy allows for an exact solution, while the second yields an approximate solution. Moreover, by using multi-criteria models, the influence of each criterion on the design can be evaluated, allowing for the inclusion of optimization [22].

Currently, research has been conducted where multi-criteria models are applied to the design of street lighting systems, tunnels, and indoor spaces, as developed by [6,13,14,20,24], where multi-criteria models are implemented for the problem, while the use of genetic algorithms is explored in the works of [11,15,16,21] y [26]. These studies differ in their optimization objectives and the number of criteria considered. Figure 1 summarizes these studies’ basic information, identifying the issue’s current state. Most studies use multi-criteria models with various techniques for solving or simplifying their resolution. Each project has its own optimization function, but largely they coincide in improving energy efficiency. All lighting projects comply with constraints related to the level and uniformity of illumination; some consider electrical power in the cost calculation, while others incorporate user feedback.

This article presents an optimized public lighting design method using a multi-criteria decision algorithm. It optimizes the spacing of lamps, type, power, and distribution based on the criteria: illumination level, light dispersion, glare, installation costs, and energy efficiency. Unlike other works, this design includes the effect of pavement type, and the costs include the effect of the lamps’ lifespan; finally, the CRITIC method is used to normalise the decision matrix.

1.1. Public Lighting Design Procedure

The design of street lighting consists of having an adequate level of illuminance in a working plane that considers visibility for drivers as well as for pedestrians; this is achieved by means of lamps suspended on poles along the street, then, the design consists of determining the location of the lamp (h and s) and the spacing along the street (D), according to the scheme shown in the figure below Figure 2.

1.1.1. Determination of h and s

Mounting height (h) is employed to control glare, such that a greater height results in a lesser glare effect, thereby enhancing visibility by moving the light fixtures away from the normal line of sight. Additionally, height aids in determining the luminous performance and the distribution of light from the fixture. Regulations have standardized height based on the maximum intensity of the lamp, as seen in Table 1. This standardization also facilitates the construction of poles on which they are mounted, though height can be increased if needed to improve uniformity.

For the overhang (s), it is conditioned that it must not exceed one-fourth of the mounting height or one-fourth of the roadway width, leading to the establishment of the Equation (1).

s = m a x \{h / 4; w / 4\}

(1)

1.1.2. Determination of D

The calculation is performed based on the total light output of the lamps and the average illuminance required. These terms are related by Equation (2), as expressed in [1].

D = \frac{b * M}{E_{a v} * W} * U

(2)

Where:

D = spacing between adjacent lamps, in [m].

b = light output of the lamp, in [lx].

M = maintenance factor, commonly a value of 0.85 is used.

E_{a v}

= maintained average illuminance, in [Lm].

W = width of the roadway.

U = Utilization factor.

The value b depends on the lamp type used in the design and is a specification provided by the manufacturer; Uis quantified based on the lamp’s type and location, with standardized values determined by the ratio of transverse distance to mounting height [1]. The value of

E_{a v}

is determined using Equation (3).

E_{a v} = L_{a v} \cdot F_{E / L}

(3)

Where:

L_{a v}

= Average luminance required on the roadway, in

[c d / m^{2}]

F_{E / L}

= Illumination to luminance ratio, in

[\frac{l x}{c d / m^{2}}]

The value of

L_{a v}

is standardized according to the classification of roads based on their usage. For this work, the values established in [1] have been considered, as they align with other international standards such as [2,3], design manuals like [4], and are used in the works of [8,10,11,12]. Table 2 presents the values for roads considered as major routes, classified as Group A, which have been taken into account for this work.

F_{E / L}

responds to the light distribution capacity of a luminaire and the type of surface to be illuminated, defining the values shown in Table 3. For Group A roads, the use of cut-off lamps is recommended, so only the first row would be considered, highlighting the need to predefine the type of surface considered in the design, namely, the type of pavement of the street to be illuminated.

The utilization factor (U) can be selected based on the ratio

\frac{w - s}{h}

nd the wattage of the lamp being used, as [2] provides tables from which the value can be chosen. Once the D value is calculated, the lighting distribution is evaluated such that the calculated value is used for unilateral and opposite bilateral cases, whereas for staggered bilateral (D) is doubled, as illustrated in Figure 3.

2. Materials and Methods

To evaluate the application of multi-criteria decision-making in the design of public lighting systems, this study focuses on a 2-lane public road without a median, each lane being 13.5 [m] wide with a total length of 2 [km]. The maximum speed on the road is 50 [km/h], categorizing it as group A2. Decision variables identified include the type of pavement, type of lamp, lamp wattage, and lighting distribution, with their values and relationships schematically represented in Figure 4, resulting in 180 scenarios.

Regarding the criteria, parameters that define the quality of illumination as well as the economic aspect of the design have been considered, including average luminance, uniformity, uniformity index, surface-sensation ratio, vertical illuminance, efficiency, installation cost, and operating cost. The values of the lighting quality parameters will be determined by simulation, thus eliminating the need to define an objective function, while for the economic parameters, the objective functions are defined in Equations (4) and (5).

C_{i n s} = N_{l a m p} * (P_{l a m p} + ((P_{i n s} / 6) * h))

(4)

C_{o p} = N_{l a m p} * (P_{k W h} * P t_{k W} * 12 * 365 / E f) + N_{l a m p} * (P_{l a m p} / V U_{l a m p})

(5)

Where:

$C_{i n s}$ = installation cost of the design.
$C_{o p}$ = operation and maintenance cost.
$N_{l a m p}$ = number of lamps.
$P_{l a m p}$ = unit price of a lamp.
$P_{i n s}$ = installation price per lamp on a 6 [m] pole.
h = height of the pole for the lamp.
$P_{k W h}$ = price of electrical energy consumption per $[k W h]$ .
$P t_{k W}$ = lamp power in $[k W]$ .
$E f$ = lamp efficiency.
$V U_{l a m p}$ = lifespan of a lamp.

2.1. Public Lighting Design

For each scenario, the procedure described in Section 1.1 is applied, determining the mounting height, overhang, and spacing between lamps for each scenario. In this study, the effect of pavement type is included, as the reflection of light emitted by the lamps varies depending on the material. This can be quantified using the reflection coefficient with Equation (6) and the values from Table 4.

E_{a v}^{'} = E_{a v} * C r

(6)

Where:

$E_{a v}$ = maintained average illuminance, in $[L m]$ .
$C r$ = reflection coefficient.

The design is carried out through an algorithm developed in MATLAB, the flowchart of which can be seen in Figure 5. The algorithm relies on nested loops that facilitate the selection of different values for each variable and define indicators for selecting parameters and conducting the required iterative calculations; the program’s output is a matrix that indicates the values of D, h, and s for each scenario.

2.2. Public Lighting Simulation

To obtain the lighting criteria for each scenario, simulations are performed using the DIALux Evo software. Figure 6 shows the software’s workspace views; in the "Road" tab, the characteristics of the road to be simulated are defined, with the road surface parameter Q0 used to set the reflection coefficient, and the classification of the road is selected in the validation field. The lamp and its distribution are chosen in the "Luminaire Selection" tab, and the values of D, h, and s are entered. The results are graphically presented through isolux curves on the road model and the numerical results are in a table.

2.3. Multi-Criteria Analysis

Multi-criteria decision-making methods enable the ranking of alternatives in problems where a decision depends on multiple criteria, ensuring that the decision is explicit, rational, and efficient. The method establishes a mathematical optimization model with a set of criteria or objective functions( F) and a set of variables (X), whose combination of elements defines the set of scenarios (A) as indicated below [27,28,29]:

F (X) = [F_{1} (X), F_{2} (X), . . ., F_{n} (X)]

(7)

X = [x_{1}, x_{2}, . . ., x_{m}]

(8)

A (X) = [A_{1} (X), A_{2} (X), . . ., A_{i} (X)]

(9)

Where

A_{i} (X)

is the element representing the i-th combination among the elements of X. For each element of A, every element of F is evaluated in the respective combination of elements of X, and the obtained results are organized in a matrix known as the decision matrix, as shown in Equation (10).

D = [\begin{matrix} F_{1} (A_{1}) & F_{1} (A_{2}) & F_{1} (A_{3}) & . . . & F_{1} (A_{i}) \\ F_{2} (A_{1}) & F_{2} (A_{2}) & F_{2} (A_{3}) & . . . & F_{2} (A_{i}) \\ . . . & . . . & . . . & . . . & . . . \\ F_{n} (A_{1}) & F_{n} (A_{2}) & F_{n} (A_{3}) & . . . & F_{n} (A_{i}) \end{matrix}]

(10)

From the decision matrix, the decision vector P is obtained, whose values result from the weighted sum of the values for each scenario, utilizing Equation (12). The weights of the criteria

W_{n}

are determined through statistical techniques, and the highest value in the set P indicates the optimal scenario for the multi-criteria problem.

P_{i} = \sum_{p = 1}^{i} \sum_{q = 1}^{n} (W_{q} D_{p q})

(11)

A_{o p t} = m a x \{P\}

(12)

For this article, the decision matrix is formed with the results obtained in Section 2.1 and Section 2.2, obtaining a matrix of 8x180. To determine the optimal scenario, the CRITIC method is used to calculate the weights of each criterion (

w_{j}

) using the Equations (13)–(15); this method uses the variance of each criterion (

σ_{j}

) and its correlation (

r_{j k}

). The matrix values are updated using the Equation (13) [13].

w_{j} = σ_{j} * \sum_{k = 1}^{n} (1 - r_{j k})

(13)

r_{j k} = \frac{c o v (j, k)}{σ_{j} * σ_{k}}

(14)

σ_{j} = \sqrt{\frac{\sum_{i = 1}^{m} {(x_{i j} - (\sum_{i = 1}^{m} (x_{j k}) / m))}^{2}}{m - 1}}

(15)

m_{i j} = \frac{x_{i j} - x m i n_{i j}}{x m a x_{i j} - x m i n_{i j}}

(16)

m_{i j} = \frac{x m a x_{i j} - x_{i j}}{x m a x_{i j} - x m i n_{i j}}

(17)

Before calculating the weights, it is necessary to normalize the values of the decision matrix. For this, range normalization is used, which considers the minimum and maximum values, defining Equations (16) and (17) for a benefit or cost criterion, respectively. This process is carried out through an algorithm in MATLAB, whose flowchart can be seen in Figure 7, which takes the decision matrix as input, determines the minimum and maximum for each criterion, normalizes them, calculates the weight for each variable, and finally returns the normalized matrix and the decision vector, identifying the maximum.

3. Results

According to the procedure explained in Section 2.1, the MATLAB algorithm is executed with the data of the proposed street in Section 2; for each scenario, the data shown in Table 5 are obtained. For example, the results obtained for three scenarios are shown, where sodium vapour lamps of 100 W are used on the street with black asphalt, and the arrangement of the lamps along the street is changed. This allows for clearly identifying the scenario’s variable combination and the values obtained for the calculable criteria. The data are obtained for all 180 scenarios where LED and metal halide lamps are used, thus defining the decision matrix.

With this information, the simulation of each scenario is carried out to obtain the quality parameters of public lighting, as explained in Section 2.2. In Figure 8, the results from DIALux are shown, along with the three-dimensional view displaying the isolux curves and the arrangement of the lamps. For each simulation, it was ensured that the parameters meet the minimum standards set in [3]. Regarding illumination, the design process consistently yielded good parameters; in some scenarios, adjustments were made only to the lamp height.

Quality lighting parameters are added to Table 5 to complete the decision matrix. In Table 6, the decision matrix for the first 3 scenarios is shown, including only the values corresponding to the criteria, which are the ones influencing the multicriteria algorithm.

Upon this decision matrix, the CRITIC method is applied. Firstly, the values are normalized, wherein it is defined that installation and operation criteria are of a cost nature, while all others are of a benefit nature. Thus, the optimal scenario corresponds to the maximum of the weighted sums. The normalized data of the 8 criteria for the 180 scenarios can be observed in Figure 9, which facilitates the visualization of the decision matrix. It can be seen that there is no uniform pattern of behavior in the obtained data.

The optimal scenario corresponds to the one with the best conditions regarding all criteria, i.e., the one with the highest weighted sum value. As observed in Figure 10, the best scenarios correspond to those with LED lamps of 150 W, installed at a height of 7.5 m, with a protrusion of 3.4 m in a bilateral opposite disposition. The highest among all stands out for having pavement made of cement pavers. These results strengthen the trend of transitioning to LED lamps, not only for efficiency and environmental contribution but also because they collectively represent the best option for public lighting.

Next, the best scenario is analyzed with respect to a single criterion, considering the average luminance. According to Figure 11, the best scenario is number 168, which entails 400 W LED lamps installed at a height of 7.5 m, with a protrusion of 3.4 m in a bilateral opposite disposition, and polished concrete pavement. Regarding this criterion, scenario 150 ranks second.

In Figure 12, the results regarding illuminance uniformity are presented. The best scenario is number 138, which involves using 150 W LED lamps installed at the height of 6 m, with a protrusion of 3.4 m in a bilateral opposite disposition, and grey asphalt pavement. Regarding this criterion, scenario 150 once again ranks second.

In Figure 13, the results regarding the economic component, i.e., the installation and operation costs associated with the public lighting design, can be observed. It is found that the scenario with the lowest installation cost is number 148, where 150 W LED lamps are used at a height of 7.5 m in a unilateral disposition. Scenario 150 ranks 15th. Regarding this parameter, it can be noted that most scenarios have the same value because only the installation cost based on the pole height was considered, a value repeated in several designs.

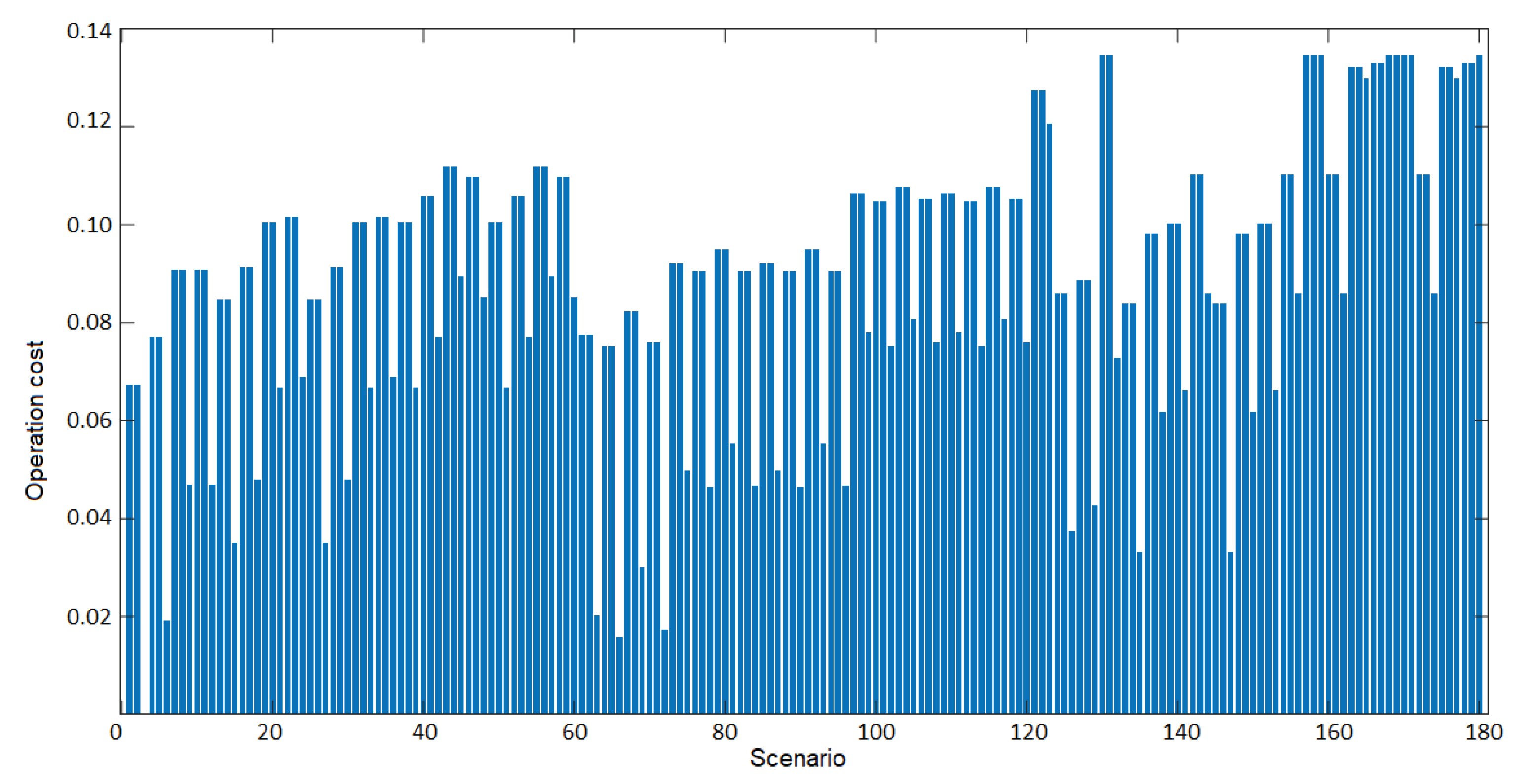
If only the operating cost is considered, scenario 3 has the lowest cost, while scenario 150 is ranked 26th. The analysis with respect to individual criteria further clarifies the conception of street lighting design as a multi-criteria analysis problem, where one must optimize according to different criteria to determine the best scenario.

Figure 14. Operating cost results

4. Conclusions

The design of street lighting should not only consider the average luminance level in the driver’s plane of view as it was traditionally done, but should also consider all aspects that involve lighting and economic comfort. Therefore, it is necessary to adapt the traditional design strategies to a multi-criteria analysis and optimization approach, thus obtaining a more complete design.

A multi-criteria algorithm has been developed to design street lighting, obtaining a complete tool that can be used from the planning stage of a street because one of the variables involved is the type of pavement so that the material that leads to the optimal design can be chosen. The use of this variable is one of the aspects to highlight in this work because, according to the literature review, it has not been taken into account in most similar works, so a strategy is given to include it not only in the design but also in the validation by means of DIALux.

The validation of the designs made with the lumen or traditional method observed that the design always allows obtaining an adequate level of average luminance and uniformity within the regulations. However, it was necessary to adjust the installation height in several scenarios because there was glare, especially on surfaces with higher reflection coefficients. This aspect is very important to consider in scenarios where a type of pavement has already been predefined since it is not convenient to choose high-power lamps or to install them at low heights.

The results obtained show that public lighting lamps should be preferable with LED technology, which not only implies a contribution to energy efficiency and, therefore, environmental contribution but also represents a favourable scenario as they are the starting point towards the optimal operational and economical design, becoming the recommendation for new lighting projects or replacement in projects already installed.

Funding

This research received no external funding.

References

Ministerio De Industrias y Productividad, “Reglamento Técnico Ecuatoriano Rte Inen 069 (1R) Alumbrado Público,” 2013. [Online]. Disponible en línea: url http://www.normalizacion.gob.ec/wpcontent/uploads/downloads/2015/02/RTE-069-1R.pdf.
International Electrotechnical Commission, IEC Standards.
Illuminating Engineering Society, IES Standards.
ENERGEX and Ergon Energy. "Public Lighting Design Manual.", 2021.
M. Beccali, M. Bonomolo, V. Lo Brano, G. Ciulla, V. Di Dio, F. Massaro, and S. Favuzza, "Energy Saving and User Satisfaction for a New Advanced Public Lighting System," *Energy Conversion and Management*, 195, 943–957, 2019. [CrossRef]
R. Carli, M. Dotoli, and R. Pellegrino, "A Decision-Making Tool for Energy Efficiency Optimization of Street Lighting," *Computers and Operations Research*, 96, 223–235, 2018. [CrossRef]
F. Cassol, P. S. Schneider, F. H. R. França, and A. J. Silva Neto, "Multi-Objective Optimization as a New Approach to Illumination Design of Interior Spaces," *Building and Environment*, 46(2), 331–338, 2011. [CrossRef]
C. W. Chu, W. C. Chao, C. C. Yang, P. J. Wu, C. Y. Chen, Y. P. Kuo, and L. L. Lee, "Optimal Design of LED Street Lighting with Road Conditions," *Proceedings - 2016 3rd International Conference on Computing Measurement Control and Sensor Network, CMCSN 2016*, 1, 9–11, 2017.
M. Fesanghary, S. Asadi, and Z. W. Geem, "Design of Low-Emission and Energy-Efficient Residential Buildings Using a Multi-Objective Optimization Algorithm," *Building and Environment*, 49(1), 245–250, 2012. [CrossRef]
D. Gómez-Lorente, O. Rabaza, A. Espín Estrella, and A. Peña-García, "A New Methodology for Calculating Roadway Lighting Design Based on a Multi-Objective Evolutionary Algorithm," *Expert Systems with Applications*, 40(6), 2156–2164, 2013. [CrossRef]
V. Gueorgiev, "Optimization of Lighting Distribution in Road Lighting Luminaires," *2018 20th International Symposium on Electrical Apparatus and Technologies, SIELA 2018 - Proceedings*, 2018.
D. M. Keith, "Roadway Lighting Design for Optimization of UPD, STV and Uplight," *Journal of the Illuminating Engineering Society*, 29(2), 15–23, 2000. [CrossRef]
S. G. Li, G. Tu, and Q. Zhou, "An Optimal Design Model for Tunnel Lighting Systems," *Optik*, 226(P1), 165660, 2021.
E. N. D. Madias, L. T. Doulos, P. A. Kontaxis, and F. V. Topalis, "A Decision Support System for Techno-Economic Evaluation of Indoor Lighting Systems with LED Luminaires," *Operational Research*, 21(2), 1403–1422, 2021. [CrossRef]
P. Mandal, D. Dey, and B. Roy, "Indoor Lighting Optimization: A Comparative Study between Grid Search Optimization and Particle Swarm Optimization," *Journal of Optics (India)*, 48(3), 429–441, 2019. [CrossRef]
B. Mattoni, P. Gori, and F. Bisegna, "A Step towards the Optimization of the Indoor Luminous Environment by Genetic Algorithms," *Indoor and Built Environment*, 26(5), 590–607, 2017. [CrossRef]
M. A. Nelson, B. P. Anderson, and H. Cai, "Selection Methods and Procedure for Evaluation of LED Roadway Luminaires," *LEUKOS - Journal of Illuminating Engineering Society of North America*, 13(3), 159–175, 2017. [CrossRef]
A. Pachamanov and D. Pachamanova, "Optimization of the Light Distribution of Luminaries for Tunnel and Street Lighting," *Engineering Optimization*, 40(1), 47–65, 2008.
A. Peña-García, "Sustainable Tunnel Lighting: One Decade of Proposals, Advances and Open Points," *Tunnelling and Underground Space Technology*, 119(September 2021), 2022.
Y. Qu, A. Clausen, and B. N. Jørgensen, "A Multi-Objective Optimization Platform for Artificial Lighting System in Commercial Greenhouses," *Energy Informatics*, 4(Suppl 2), 2021. [CrossRef]
O. Rabaza, D. Gómez-Lorente, A. M. Pozo, and F. Pérez-Ocón, "Application of a Differential Evolution Algorithm in the Design of Public Lighting Installations Maximizing Energy Efficiency," *LEUKOS - Journal of Illuminating Engineering Society of North America*, 16(3), 217–227, 2020. [CrossRef]
Y. Shen and G. Ge, "Multi-Objective Particle Swarm Optimization Based on Fuzzy Optimality," *IEEE Access*, 7, 101513–101526, 2019. [CrossRef]
P. L. Sikdar and P. K. G. Thakurta, "An Energy Efficient Street Lighting Framework: ANN-Based Approach," *Innovations in Systems and Software Engineering*, 17(2), 131–139, 2021. [CrossRef]
C. Villa and R. Labayrade, "Multi-Objective Optimisation of Lighting Installations Taking into Account User Preferences - A Pilot Study," *Lighting Research and Technology*, 45(2), 176–196, 2013. [CrossRef]
M. Zalesinska and M. Gorczewska, "Comparative Study of Lighting Quality and Energy Efficiency for Various Road Lighting Situations," *Proceedings of 2016 IEEE Lighting Conference of the Visegrad Countries, Lumen V4 2016*, 1–5, 2016.
J. Zou and L. Li, "Optimization of Luminous Intensity Distribution of Roadway Lighting Luminaire Based on Genetic Algorithm," *Proceedings - 2010 2nd WRI Global Congress on Intelligent Systems, GCIS 2010*, 1, 327–330, 2010.
Hamed Taherdoost and Mitra Madanchian. 2023. "Multi-Criteria Decision Making (MCDM) Methods and Concepts." Encyclopedia 3, no. 1: 77-87. [CrossRef]
Ponce, D.; Aguila Téllez, A.; Krishnan, N. "Optimal Selection of Conductors in Distribution System Designs Using Multi-Criteria Decision". Energies 2023, 16, 7167. [Google Scholar] [CrossRef]
Rengel, A.; Téllez, A.A.; Ortiz, L.; Ruiz, M. Optimal Insertion of Energy Storage Systems Considering the Economic Dispatch and the Minimization of Energy Not Supplied. Energies 2023, 16, 2593. [Google Scholar] [CrossRef]

Figure 1. Comparative Table of Similar Works

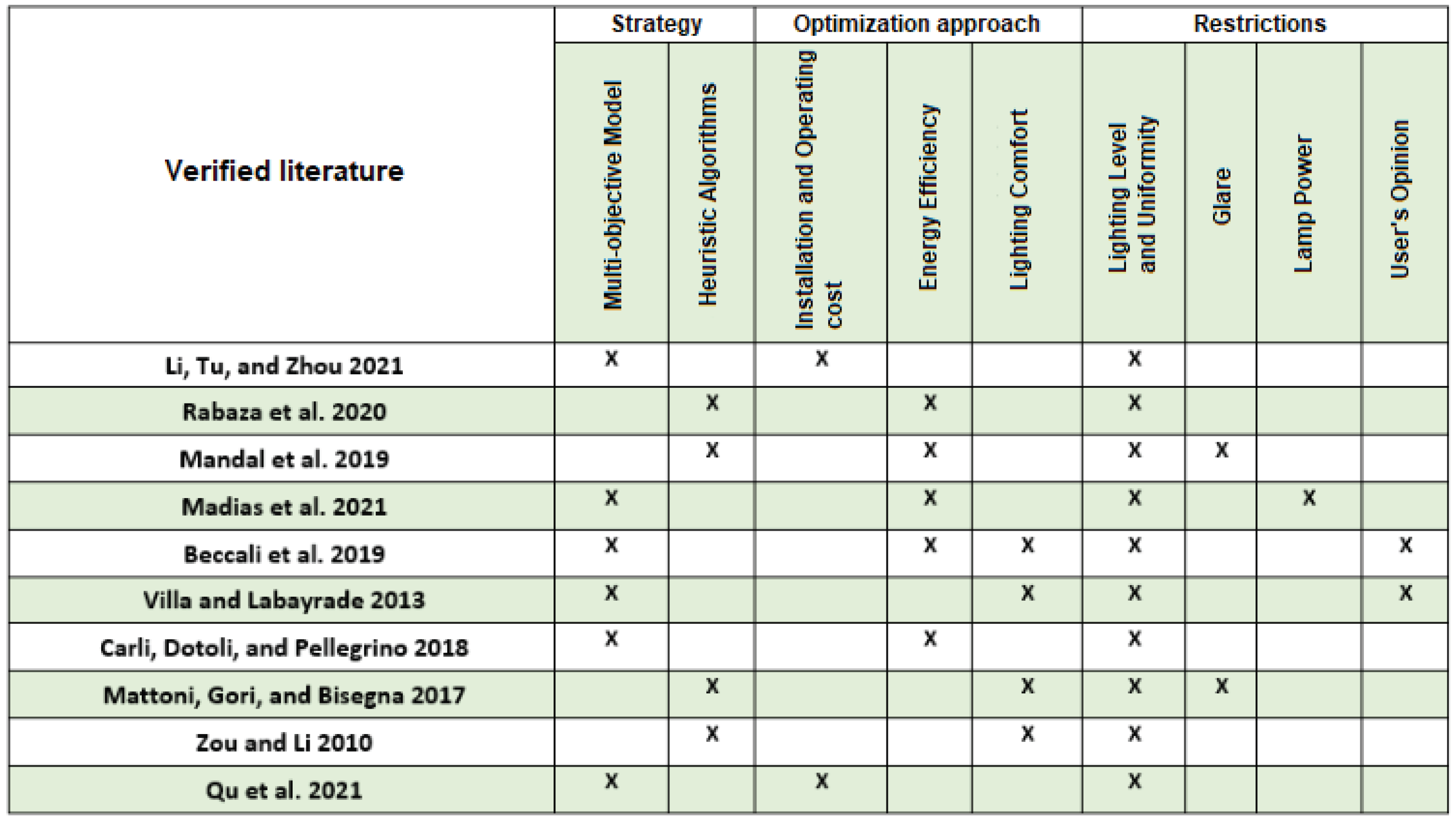
Figure 2. Variables involved in public lighting

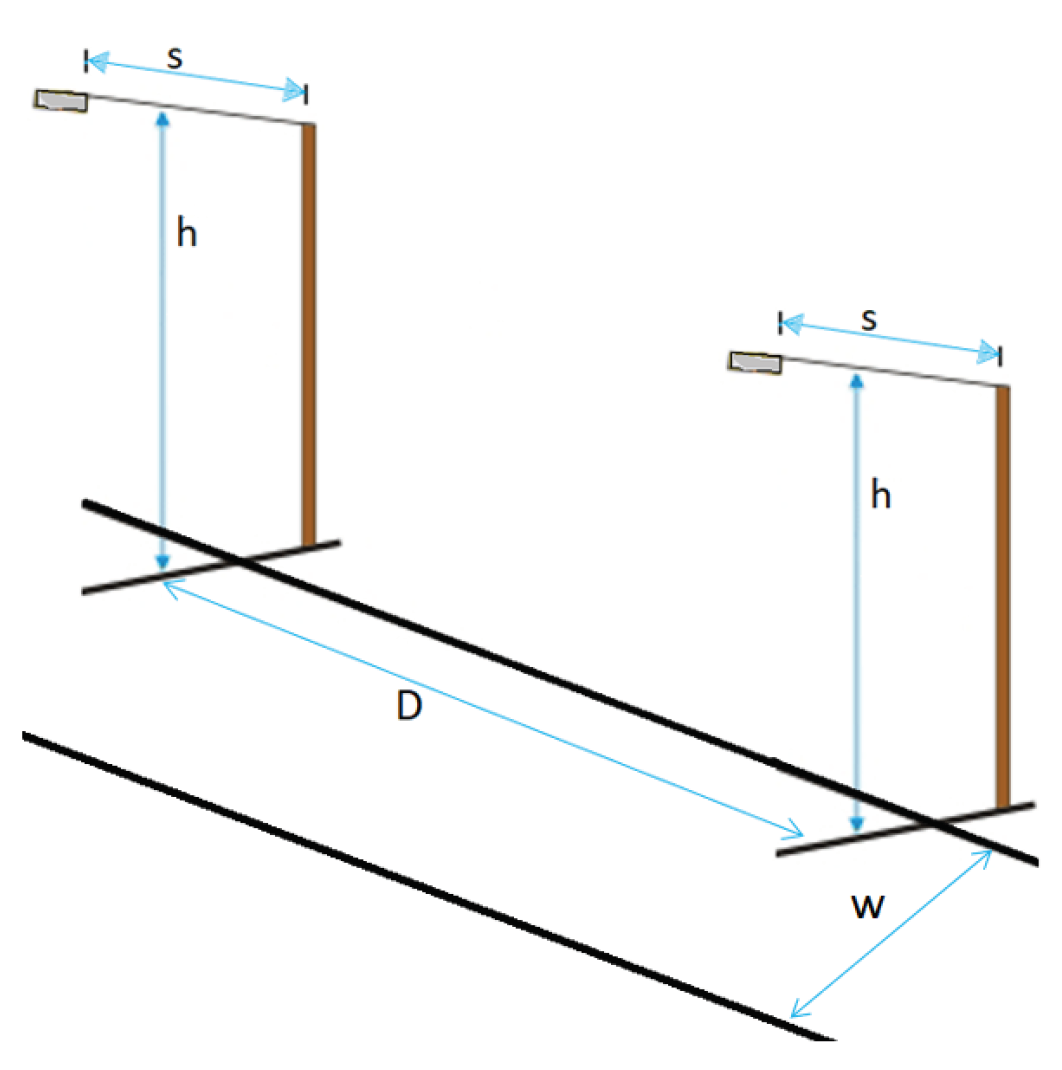
Figure 3. Distribution of public lighting

Figure 4. Design variables and their relationship

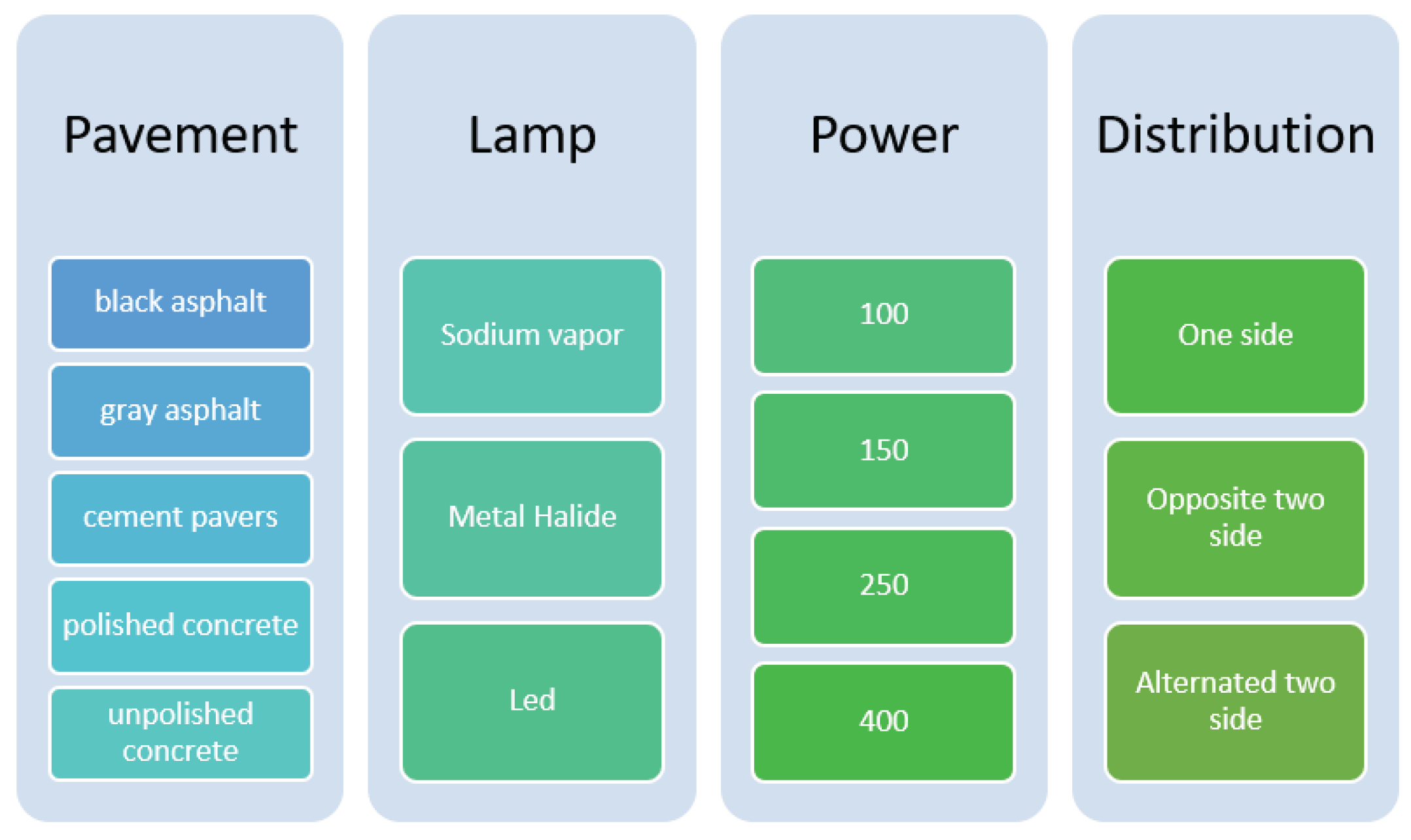
Figure 5. Flowchart for Public Lighting Design

Figure 6. Working windows in DIALux evo.

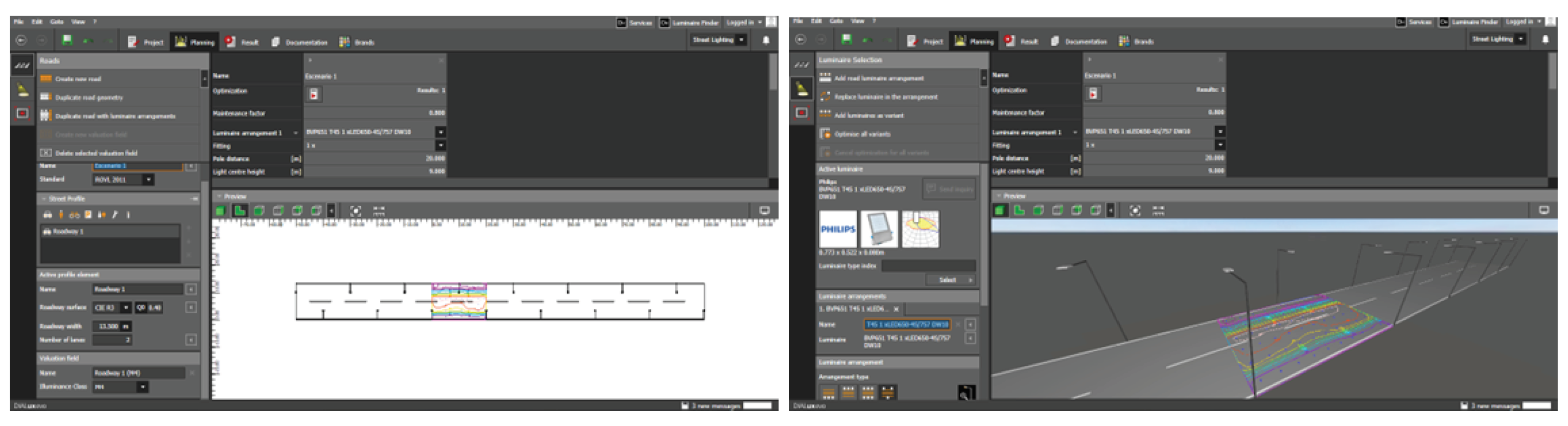
Figure 7. CRITIC flow chart

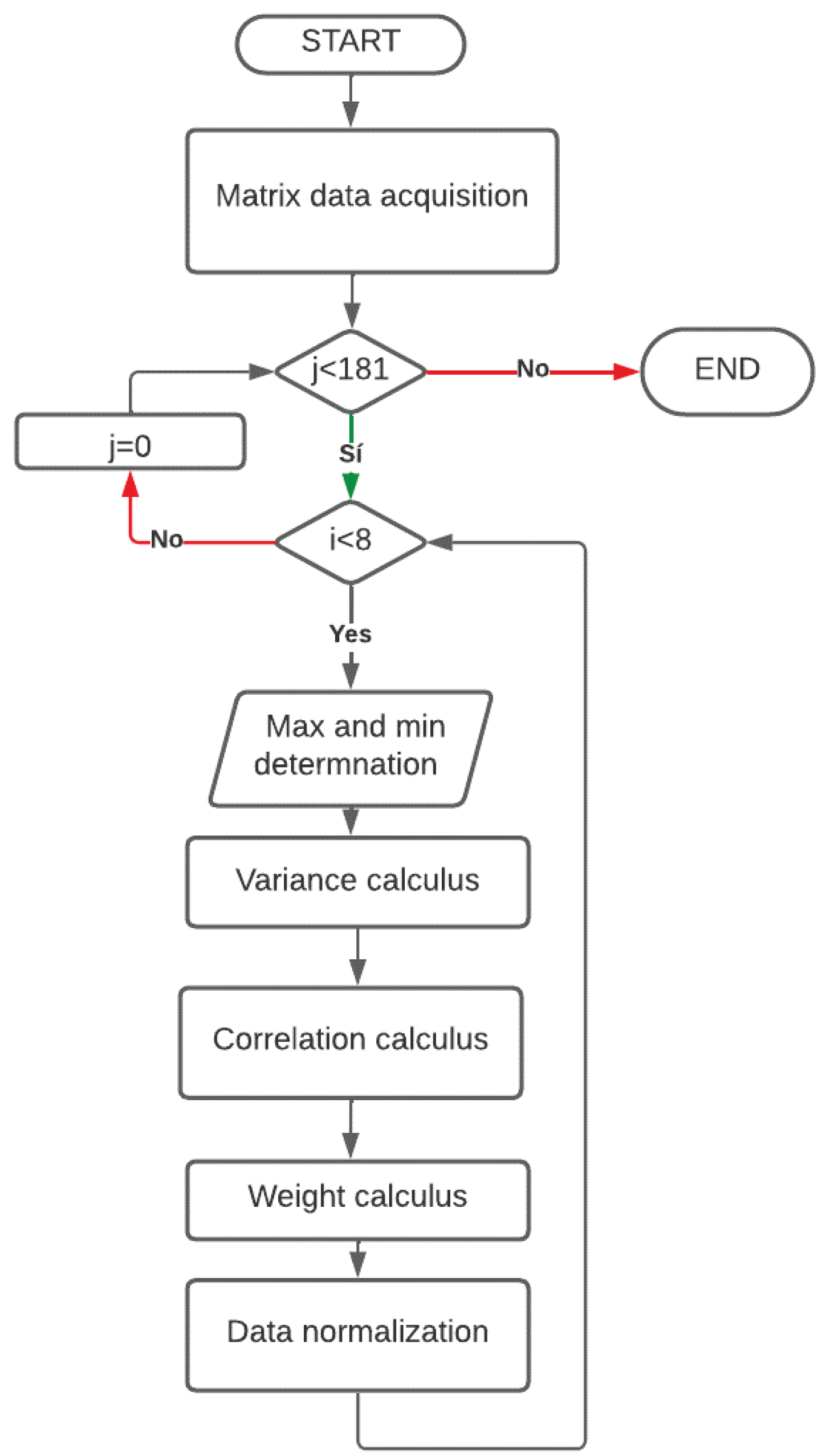
Figure 8. Results obtained with DIALux

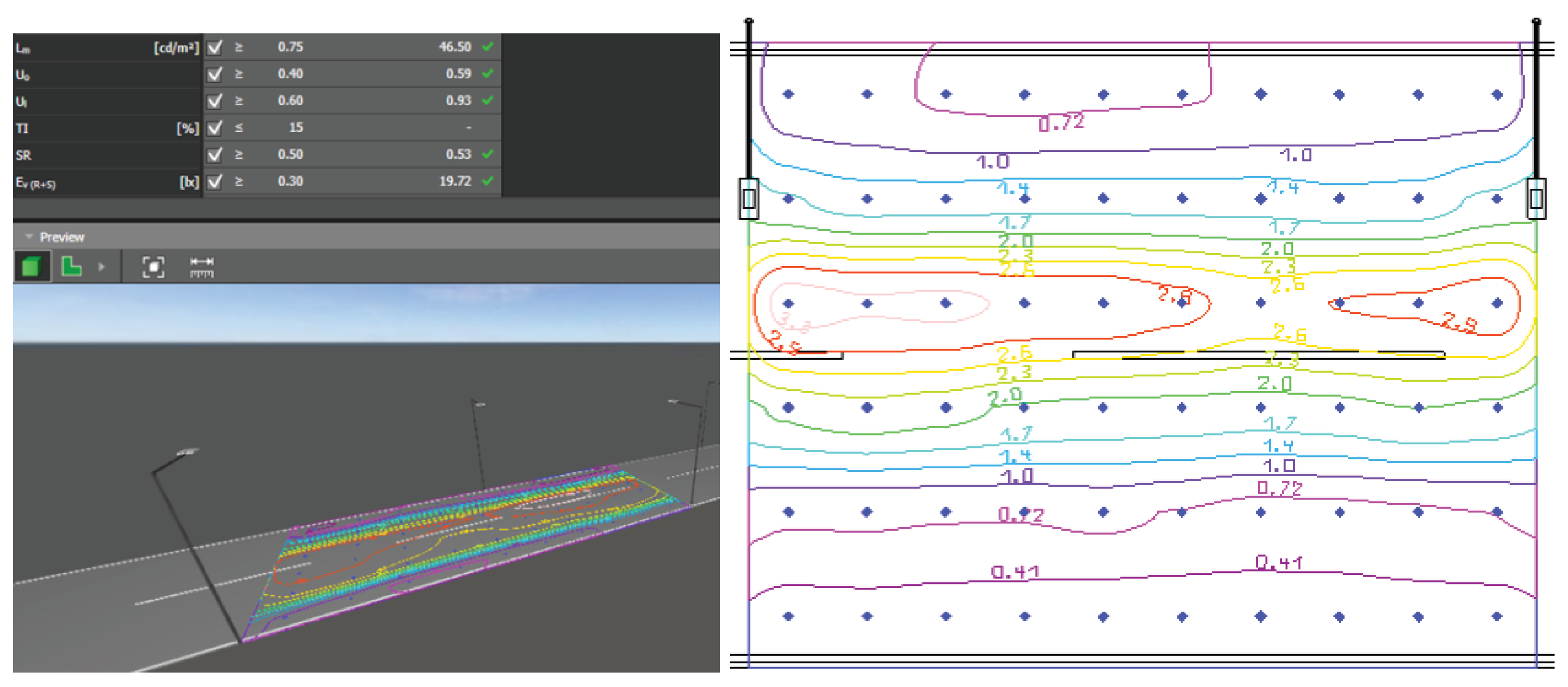
Figure 9. Graphical representation of the normalized decision matrix

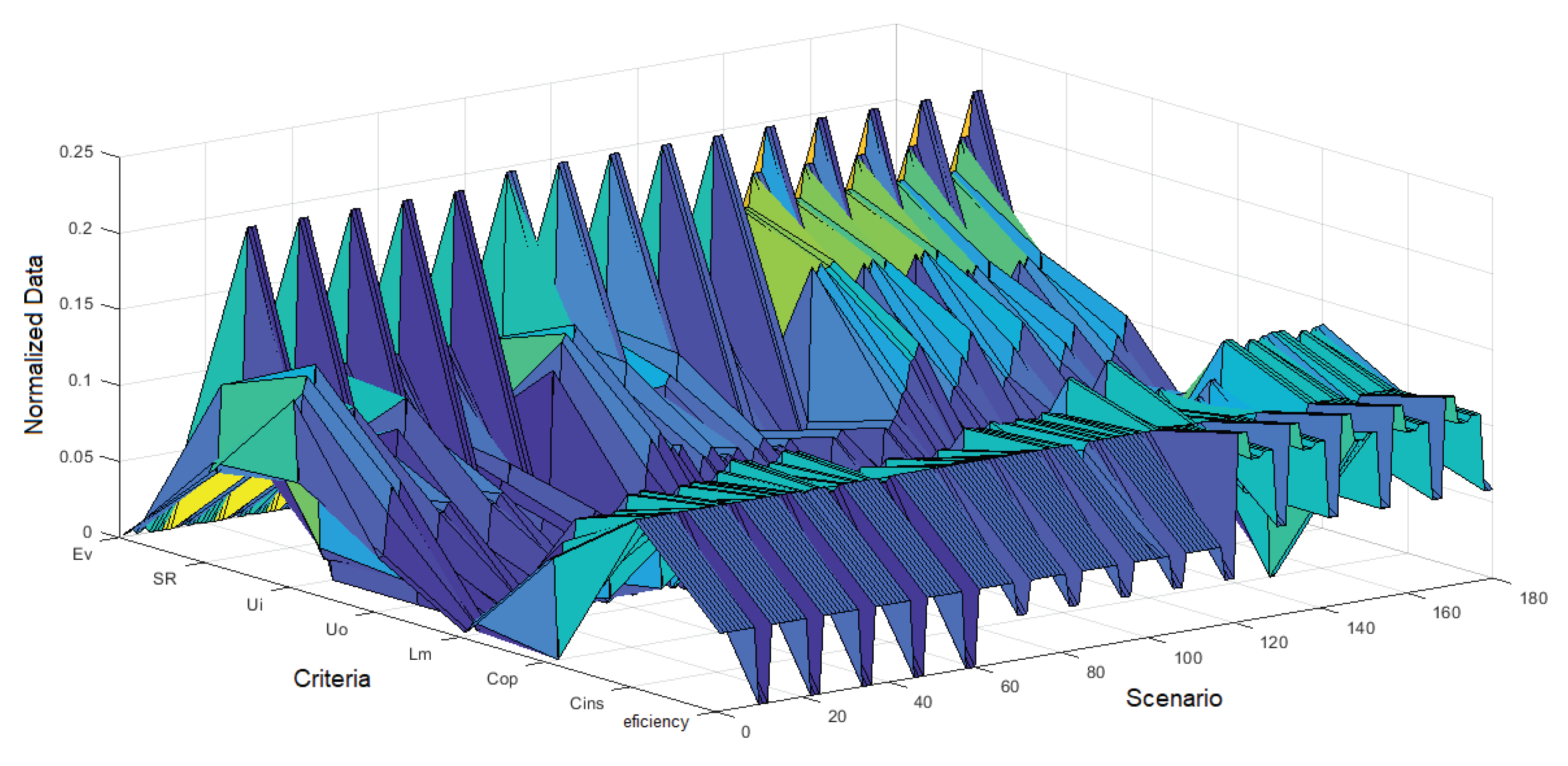
Figure 10. Weighted sum results

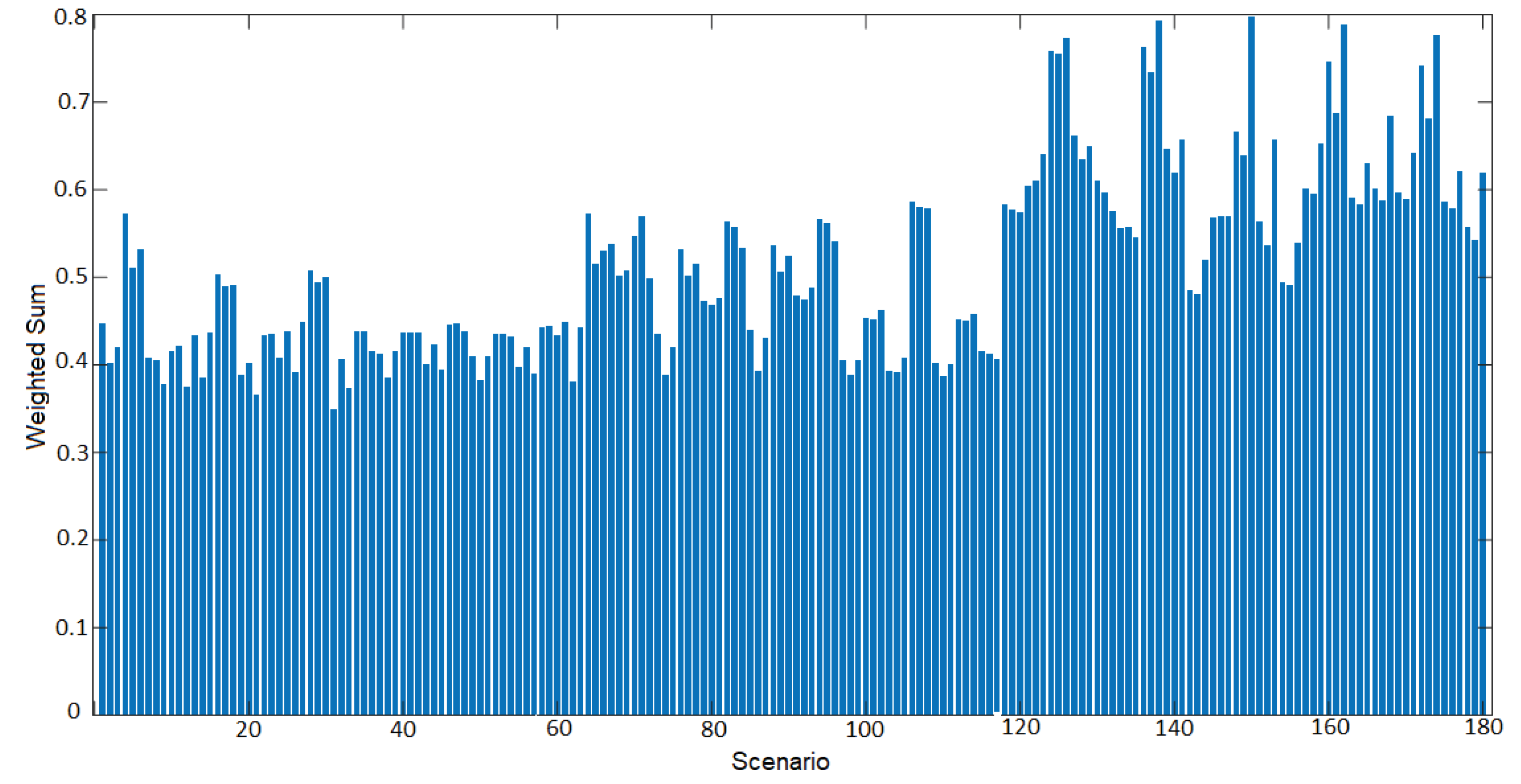
Figure 11. Illuminance Results (Lm)

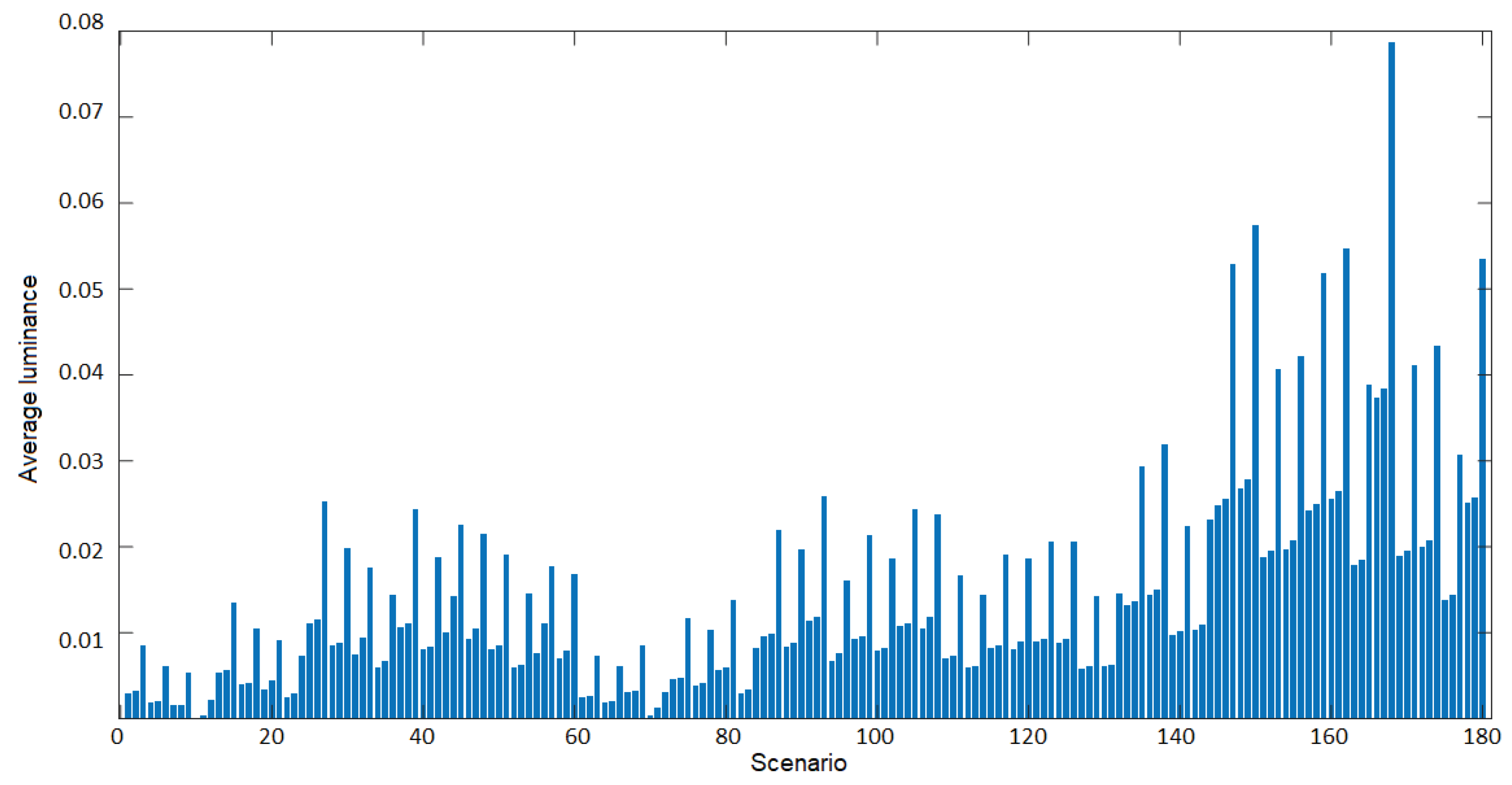
Figure 12. Economic component results (Uo)

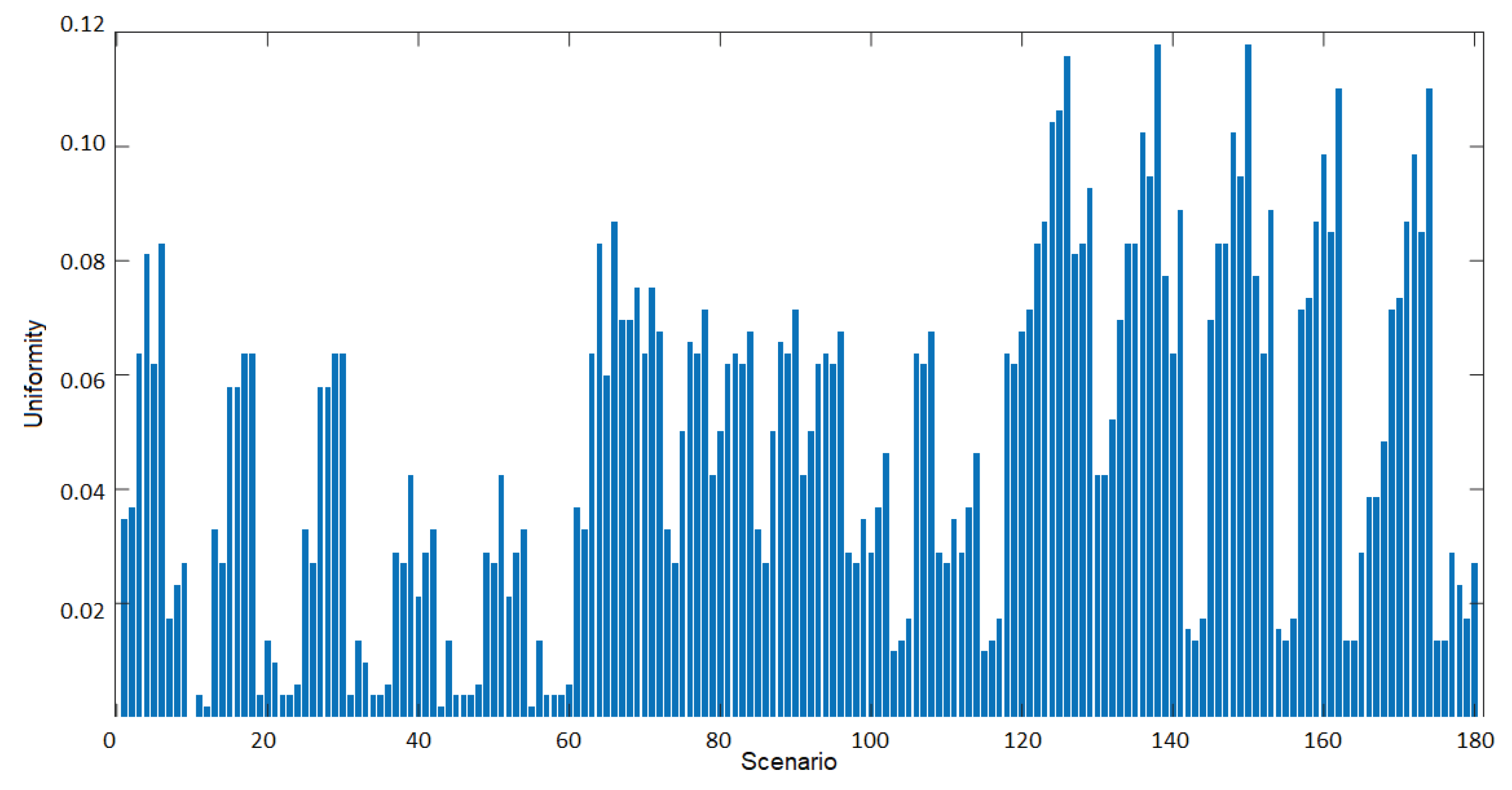
Figure 13. Installation cost results

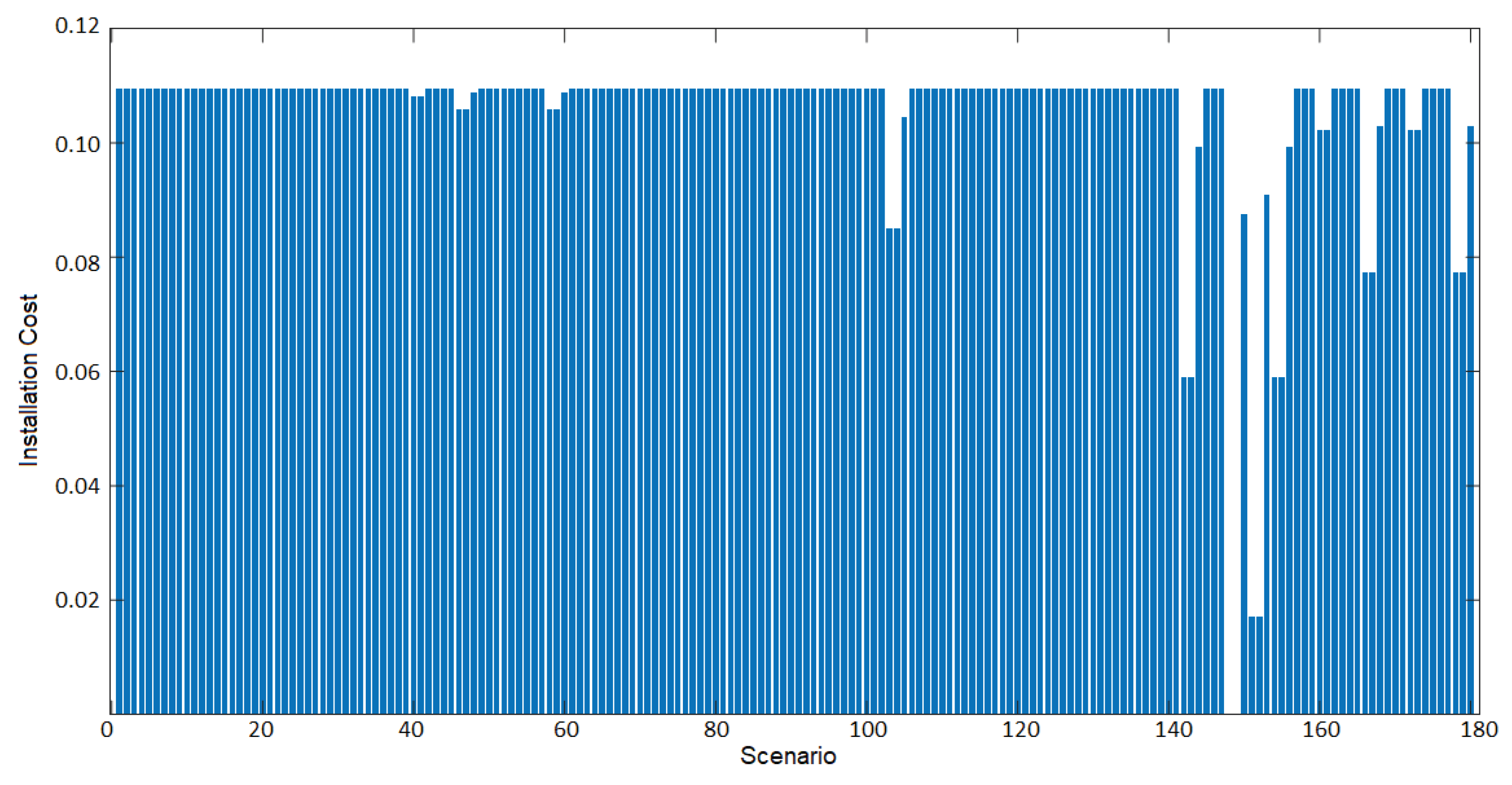
Table 1. Minimum Mounting Height,

[m]

Table 1. Minimum Mounting Height,

[m]

Maximum Intensity $[c d]$	Cut-off Luminaire	Semi Cut-off Luminaire	Non Cut-off Luminaire
Up to 1000	6	6	6
From 1000 to 2000	7.5	7.5	7.5
From 2000 to 4500	7.5	7.5	-
From 4500 to 6000	7.5	7.5	-
Over 6000	9	9	-

Adapted from [2]

Table 2. Recommended Values for Public Lighting.

Group	Type of Road	$L_{a v}$ [cd/ $m^{2}$ ]
A1	Highways. Speed limit over 70 km/h.	1.5
A2	Major roads (arterials). Speed limit from 55 to 70 km/h.	1.0
A3	Direct routes through urban areas. Speed limit 55 km/h.	0.75
A4	Link roads connecting direct routes with suburban roads.	0.5

Adapted from [2]

Table 3. Conversion of Luminance to Illumination,

F_{E / L} [\frac{l x}{c d / m^{2}}]

Table 3. Conversion of Luminance to Illumination,

F_{E / L} [\frac{l x}{c d / m^{2}}]

Type of Luminaire	Dark Surface	Medium Surface	Light Surface
Cut off (C)	24	18	12
Semi cut off (SC)	18	13	9
Non cut off (NC)	15	10	7

Adapted from [2]

Table 4. Reflection Coefficient.

Type of Pavement	Black Asphalt	Grey Asphalt	Cement Cobblestones	Polished Concrete	Unpolished Concrete
Cr	0.1	0.2	0.35	0.5	0.4

Table 5. Results of public lighting design.

Variables/Criterion	Scenario 1	Scenario 2	Scenario 3
Lamp Type	Sodium vapor	Sodium vapor	Sodium vapor
Power [W]	100	100	100
Pavement	Black asphalt	Black asphalt	Black asphalt
Height [m]	6	6	6
Protrusion [m]	3.4	3.4	3.4
Arrangement	Unilateral	Alternating Bilateral	Opposite Bilateral
Spacing [m]	17	34	17
Lamps	119	238	238
Efficiency	80	80	80
Installation	5572.77	11145.54	11145.54
Operation	59941585	119883171	119883171

Table 6. Results of public lighting design.

Criterion	Scenario 1	Scenario 2	Scenario 3
Efficiency	80	80	80
Installation	5572.77	11145.54	11145.54
Operation	59941585	119883171	119883171
Lm	1.86	1.93	3.87
Uo	0.18	0.19	0.33
Ui	0.76	0.42	0.78
SR	0.3	0.31	0.3
Ev	0.51	0.6	1.37

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimal Selection of Distribution, Power and Type of Luminaires for Street Lighting Designs Using Multi-criteria Decision

Abstract

1. Introduction

1.1. Public Lighting Design Procedure

1.1.1. Determination of h and s

1.1.2. Determination of D

2. Materials and Methods

2.1. Public Lighting Design

2.2. Public Lighting Simulation

2.3. Multi-Criteria Analysis

3. Results

4. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe