Prerpints.org logo
Preprint
Article

Comparing the Mechanical Properties of Rice Cells and Proto-plasts under PEG6000 Drought Stress Using Double Resonator Piezoelectric Cytometry

Altmetrics

Downloads

124

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 April 2024

Posted:

02 April 2024

You are already at the latest version

Alerts
Abstract
Plant cells' ability to withstand abiotic stress is strongly linked to modifications in their mechanical characteristics. Nevertheless, the lack of a workable method for consistently tracking plant cell mechanical properties severely restricts our comprehension of the mechanical alterations in plant cells under stress. With Polyethylene Glycol (PEG6000), we created a drought-like environment, and we used the Double Resonator Piezoelectric Cytometry (DRPC) method to dynamically and non-invasively track changes in the stress (ΔS) created and viscoelasticity (storage modulus G' and loss modulus G") of protoplasts and suspension cells of rice during drought stress. The findings demonstrate that, rice suspension cells and protoplasts react mechanically differently to 5%–15% PEG6000 stress, implying distinct resistance mechanisms. However, neither of them can withstand 25% PEG6000 stress, they respond mechanically similarly to 25% PEG6000 stress. The results of DRPC are further corroborated by the morphological alterations of rice cells and protoplasts observed under an optical microscope. To sum up, the DRPC technique functions as a precise cellular mechanical sensor and offers novel research tools for the evaluation of plant cell adversity and differentiating between the mechanical reactions of cells and protoplasts under abiotic stress.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

Water deficit has a major have a major effect on rice, an important cereal crop. In response to drought stress, proline and glycine levels in plant cells rise and influence cellular metabolism [1]. The dynamics of the cell wall are crucial when drought stress is applied to rice cells [2,3], particularly in the processes of cell wall remodeling and synthesis. Research shows that plants can thicken their cell walls during drought stress by depositing lignin and hemicellulose, which improves secondary walls [4,5,6]. Furthermore, cell wall flexibility may rise or fall as a result of dryness [7,8]. Cell wall elasticity and drought tolerance were found to be correlated in studies comparing elastic moduli under drought stress in six types of radiata pine and common bean [9,10]. Increased peroxidase activity and cell wall hardening in rice seedling roots may be related, according to research by Chuan Chi Lin and colleagues [11]. The plasma membrane is an excellent medium for detecting and transferring mechanical pressures because it is located between the cytoskeleton and the cell wall [12,13]. When plants experience drought stress, their plasma membrane’s composition varies and its integrity is compromised [14,15]. Plant growth and environmental adaptability depend on the dynamic plant cytoskeleton’s ability to quickly modify tissue stability and dynamics in response to both internal and external stimuli [16]. Actin filaments and microtubule proteins display depolymerization and polymerization processes when subjected to a drought stress. Actin filaments (AFs) and microtubules (MTs) control cell rigidity and energy dissipation [17]. Moreover, once they become active, early indicators of drought stress such as Ca2+, reactive oxygen species (ROS), ion channels, kinases, and phosphatases [18] may cause structural and functional modifications to the cytoskeleton, plasma membrane, and cell wall, changing the mechanical characteristics of plant cells. Unfortunately, there aren’t many effective detection methods available for following the dynamic changes in the mechanical properties of plant cells right now. Plant cells would maintain mechanical homeostasis, or “mechanostasis”, wherein the strength of the cell wall and the magnitude of turgor are in balance [19]. During cell growth or under abiotic stress, both cell wall’s mechanical properties and turgor would either maintain a new mechnostatsis or undergoing adaptive changes.
However, it is experimentally challenging to track and separate the effects of turgor and cell wall’s mechanical properties, in particular under abiotic stress, the cells would loss its turgor and generate a negative turgor pressure [20], there is no appropriate method to measure negative turgor pressure at cellular level. The hydrostatic pressure (or turgor pressure P) relates to the tensile stress (σ) generated within the wall for an idealized spherical plant cell according to Eqn. 1[21].
σ = P R 2 h   ⇔   P = 2 h R
where R and h are the radius of the cell, and thickness of the cell wall respectively. There is currently no method available to measure either turgor pressure P or tensile stress (σ) in a non-invasive and continuous manner (Table 1 [22,23,24,25,26,27]). Thus, there is great need to develop some new technique to monitor the changes in cells’ generated forces and viscoelasticity of plant cells under development and various stresses.
A technique based on quartz crystal for measuring minute masses is called QCM (Quartz Crystal Microbalance). QCM sensors are characterized by their high sensitivity, non-destructive, and real-time measurements [26]. QCM was used by Mei Zeng et al. [28] to track the dynamic processes of rice cell adhesion to PLL-poly (3-PBA)/Au and salt stress treatment with NaCl in real-time. QCM-d technology was employed by Chen et al. [29] to track the dynamic viscoelastic alterations of tobacco BY-2 cells at varying mannitol concentrations. However, these studies only provided semi-quantitative information about cells’ viscoelasticity by using cell viscoelastic index (CIV), and no information about cellular force was given. Recently, we developed the Double Resonator Piezoelectric Cytometry (DRPC) technique [30], which monitors and measures the forces generated by cells and cells’ viscoelastic moduli using two different crystals of AT and BT cuts with the same frequency and surface morphology. It is based on the acoustic wave principle that surface stress exerted on the AT and BT chips would affect the elastic moduli which are related to their second-order and third order elastic constants as well as the cutting angle φ (angle of rotation about the crystallographic x-axis), and therefore their frequencies. AT and BT cuts, their rotation angles are 35˚15’ and -49˚respectively. The cells’ viscoelastic parameters are then calculated by treating the viscoelastic load as an additional acoustic impedance by measuring changes in the crystal’s frequency and motional resistance or bandwidth.
Our team has applied the DRPC technique for tracking the dynamic adhesion of H9C2 cells and evaluating the two cardiovascular medications on H9C2 cardiomyocytes’ contractile properties [31], for distinguishing between necrosis and apoptosis of HeLa cells based on their respective cyto-mechanical characteristics [32]. In this work, DRPC chips were used to monitor the dynamic changes in cellular forces and cells’ viscoelastic moduli of both rice cells and rice protoplasts in real-time under the treatments of varying concentrations of Polyethylene Glycol (PEG6000) to simulate drought stress. This research explored the possibilities of the DRPC technique in studying the dynamic changes in cell wall-plasma membrane-cytoskeleton continuum and is expected to offer a novel research tool for investigating the stress resistance of plant cells.

2. Materials and Methods

2.1. Materials and Major Reagents/Instruments

Rice Material: Seeds of Oryza sativa L. japonica cv. Experimental apparatus: QCA922 eight-channel quartz crystal microbalance (Seiko-EG&G, Japan); AT and BT-cut crystals of 5 MHz and 9 MHz with gold electrodes were used in the experiments; the quartz crystal blanks were made by Hangzhou Zhongjing Electronic Technology Co., Ltd.) and the gold coatings were deposited by Beijing Chenjing Electronic Co., Ltd.

2.2. Sample Preparation

Preparation of Rice Suspension Cells: A plant incubator was set to a dark temperature of 25°C and 60% humidity, seeds were sterilized and injected onto solid culture medium. Following the development of callus tissue and the enlargement of the lower hypocotyl, the callus tissue was moved to liquid culture medium and positioned in a shaking bed with a constant temperature of 25°C and a rotation speed of 130 rpm/min for dark cultivation. Before being used, cells were passed through a 300-400 mesh screen and then counted.
Preparation of Rice Protoplasts: After the rice suspension cells were prepared as previously described, they were put in a confocal glass dish and agitated at a rate of 60 rpm/min while being treated to a dark enzymatic digestion at 25°C. A large number of fully rounded rice protoplasts were revealed by a microscope after around five hours, after being passed through a 400-500 mesh sieve.

2.3. Quantitative Measurements of Surface Stress Generated by Plant Cells and their Viscoelastic Moduli using DRPC Technology

Detailed theoretical background and methods of DRPC were introduced in our previous publication [30]. Here we briefly introduced the DRPC technique and its extension for the study of plant cells. The frequency change Δf caused by cell adhesion and various stimuli is typically in the range of a few hundred Hz, which is much smaller than the frequency f0 of the quartz crystal (typically 5 MHz or 9 MHz), i.e., Δ f/f0 << 1. Consequently, the observed total relative frequency shift can be explained by the following linear perturbations of the quartz crystal: cells generated surface stress, cell mass, and viscoelasticity.
Δ f / f 0 = Δ f s / f 0 + Δ f m / f 0 + Δ f v i s c o / f 0
As a result of the shear waves’ penetration depth to the cells is much smaller than that of the cells itself, cells can be thought of as a semi-infinite viscoelastic load. The following equations are relative frequency shifts induced by surface stress cells exerted on the quartz crystal chips (ΔS), mass of the cells (Δm) and cells’ viscoelastic parameters; while K and µq are stress coefficient and elastic modulus, both of which are cut dependent. ρq is quartz density which is cut independent, and Zq= ρ q µ q is the acoustic impedance of the quartz.
Δ f s f 0 = K Δ S t q ,   Δ f m f 0 = − 2 f 0 Δ m ρ q μ q , Δ f v i s c o f 0 = − ( π Z q ) − 1 ρ c G * − G ' / 2
Therefore, Equation 2 can be expressed as:
Δ f / f 0 = K Δ S / t q − ( ρ q μ q ) − 1 2 f 0 Δ m + π − 1 ρ c G * − G ' / 2
Apply equation 3 to AT and BT cuts, we have
Δ f A T / f 0 A T = K A T Δ S / t q A T − ( ρ q μ q A T ) − 1 2 f 0 A T Δ m + π − 1 I m ( ρ c G ' + i G ”
Δ f B T / f 0 B T = K B T Δ S / t q B T − ( ρ q μ q B T ) − 1 2 f 0 B T Δ m + π − 1 I m ( ρ c G ' + i G ”
Given the assumed frequencies of AT-cut and BT-cut crystals are equal, f0AT=f0BT=f0, and taking into account the correlation between quartz crystal thickness tq, crystal frequency, and elastic modulus:
t q = 0.5 f 0 − 1 ( ρ q / μ q ) − 0.5
Combine equations (4)-(6) and under the condition of f0AT=f0BT=f0, the contributions of cells’ mass and viscoelastic terms of eqns. (4) and (5) can be canceled, resulting in equation (7) illustrating the dynamic change in surface stress exerted by the cells.
ΔSt= f0-1(KAT-KBT)-1(ΔftATtqAT-ΔftBTtqBT)
Here, the stress coefficients of AT-cut and BT-cut quartz crystals are KAT = 2.75×10-l2 cm2 dyn-1, KBT = -2.65 ×10-l2 cm² dyn⁻¹; the thickness of AT-cut and BT-cut quartz crystals, tqAT and tqBT, are both related to the frequencies of AT- and BT-cut crystals; f0 is the resonant frequency of AT-cut and BT-cut quartz crystals; ΔftAT and ΔftBT are the frequency shifts of AT-cut and BT-cut quartz crystals with respect to their reference points (stable values in the culture medium) at any given time (t).
When f0AT=f0BT=9 MHz, tq9MAT=0.0185 cm, tq9MBT=0.0282 cm, Equation (7) can be simplified to:
ΔS=380.8ΔfAT-582.2ΔfBT
When f0AT=f0BT=5 MHz, tq5MAT=0.03328 cm, tq5MBT=0.05098 cm, Equation (7) can be simplified to:
ΔS=1230.4ΔfAT-1878.5ΔfBT
Hz is the unit of ΔfAT and ΔfBT, while dyne/cm is the unit of ΔS. When ΔS is positive, means that the cells are enlarged and they are in a tensile state, (e.g., under hydrostatic pressure or turgor pressure). When ΔS is negative, the plant cells are in a contractile state and that they are producing compressive stress. The above equations (7)-(9) are derived under the conditions that cells’ mass, viscoelasticity and generated surface stress are constantly changing, whereas the cells’ medium is maintained unchanged, however, during the abiotic stresses, the density, viscosity and viscoelasticity of the media would change depending on what types of stresses are, for drought stress as simulated by PEG6000 solutions, the viscoelasticity of the media would change. In this case, an additional term characterizing the viscoelasticity of PEG6000 can be added to the inside of the second brackets of eqn. (4) and (5), eventually; would still produce the same equations of eqns. (7)-(9).
Furthermore, real-time cell viscoelasticity monitoring is possible using the DRPC approach. The frequency shift Δf subtracted from the total frequency shift from the contribution induced by surface stress, change in either half-bandwidth (Γ) or motional resistance (ΔR) relative to their values in air can be used to determine the storage modulus (G’) and loss modulus (G”) of the cells. Specific relationships are as follows
G = π 2 Z q 2 ρ c f 0 2 ( Δ R 2 16 π 2 L q 2 − ∆ f 2 )
G = − Z q 2 f R 2 ρ c L q f 0 2
The quartz crystal’s impedance, Zq, is 8.84 × 105 g/cm⋅s for AT cut crystal, ρc is the cells’ density, which is taken to be the same as that of water. Lq, which is regarded as a constant, is the quartz crystal’s measured inductance while submerged in the medium.

2.4. Dynamic Monitoring of the Mechanical Properties of Rice Cells under Different Concentrations of PEG6000 Stress Using DRPC

9 MHz AT-cut and BT-cut chips were cleaned by following the procedure described by Mei Zeng et al. [28], then the chips were surface-modified with 1% PDADMAC at 25°C for 30 minutes under dark conditions, followed by rinsing with deionized water and drying with nitrogen gas. The modified chips were assembled with cleaned Teflon pools to form the detection chambers, and 500 μL of medium was added to each of the chambers. The detection chambers were connected to a QCA-922 instrument to monitor the changes in frequencies and motional resistances of the 9 MHz AT-cut and BT-cut chips. Once the frequency and resistance values became stable, 200 μL of a mixture of culture medium containing 50,000 cells was added to each of the chambers, and the data was recorded at this stage for 3 hours by the instrument. Then, the PEG6000 stock solution was added to the chambers to achieve a volume percentage of PEG6000 in the system of 5%, 10%, 15%, and 25%, respectively, and the changes in resistance and frequency were continuously monitored. The control group were the same except for without adding the rice cells and was followed the same steps as the experimental group.

2.5. Dynamic Monitoring of the Mechanical Properties of Rice Protoplasts under Different Concentrations of PEG6000 Stress Using DRPC

In the experiment involving rice protoplasts, 5 MHz chips were used as the substrates for the attachments of the protoplasts, and all other experimental steps were the same as in section 2.4.

2.6. Microscopic Observations of the Morphologies of Rice Cells and Protoplasts under Different Concentrations of PEG6000 Stress

To observe the cell morphologies at different concentrations, cells or protoplasts were attached to a 12-well plate following the same method as described in section 2.4. Solutions of PEG6000 ranging from 0% to 25% (2 mL) were added to each well. The plates were kept at 25°C in the dark for 1 hour, and the cell morphologies at each concentration were observed using a Lumascope 720 microscope.

3. Results

3.1. The Mechanical Changes of Rice Cells under Different Concentrations of PEG6000 Stress Concentrations

Figure 1 shows the frequency and resistance changes of AT and BT-cut quartz crystal chips during the adhesions of rice cells followed by the treatments of different PEG6000 stress concentrations. Upon the introduction of roughly 50,000 cells, ΔF decreased and ΔR increased as the cells adhered to the quartz crystal chip. The cells induced DRPC chips’ responses showed a sudden decrease in ΔF followed by an increase, and a sharp increase in ΔR followed by a decrease, upon the addition of 5%-25% PEG6000 stresses. Moreover, the variations in ΔF and ΔR progressively increased as the concentration rose. The stress (ΔS) produced by the cells under 5%-25% PEG6000 stress can be calculated using Formula (8) in accordance with the DRPC [30] principles, as seen in Figure 2. The cells exerted compressive stress first, followed by exerting tensile stress, as seen by the rapid rebound of ΔS to a positive value following an initial fall to a negative value under 5%-15% PEG6000 stresses. Furthermore, under 5%-15% PEG6000 stresses, the compressive stress that the cells exerted increased with the PEG6000 concentration, as did the time it took for ΔS to rebound to a positive value. When the cells were subjected to 25% PEG6000 stress, ΔS dropped to a negative value, reached its maximum absolute value, and finally it did not return to a positive value. And the cells exerted greater immediate compressive stress.
Furthermore, curves showing the changes over time of storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) under 5%-25% PEG6000 stresses were generated using equations (10) and (11), as shown in Figure 3. The DRPC technique also allows for real-time monitoring of cell viscoelasticity. It is clear that rice cells’ storage modulus (G’) and loss modulus (G”) showed the tendency of first increasing and then decreasing under 5%-25% PEG6000 stresses. Moreover, under all the PEG6000 stresses, a shift in the cells’ state from a viscoelastic gel state to a more solid state as indicated by the general decrease in the loss tangent. The findings of the variations in the association between the mechanical parameters of rice cells at varying PEG6000 stress concentrations are shown in Figure 4. Overall, there is a linear relationship between the modulus and the stress that the cells produce within a specific range, and there is also a linear relationship between the storage and loss moduli within the same intervals.

3.2. Mechanical Changes of Rice Protoplasts under Different Concentrations of PEG6000 Stress

Figure 5 shows the frequency and resistance changes (ΔF and ΔR) of AT and BT-cut quartz crystal chips during the adhesions of rice protoplasts followed by the treatments of different PEG6000 stress concentrations. Upon the addition of roughly 50,000 protoplasts, ΔF dropped and ΔR rose during the adhesions of the protoplasts. The protoplasts induced DRPC responses under 5% -15% PEG6000 stresses demonstrate an initial decrease in ΔF and increase in ΔR, then they became relatively stable. However, the protoplasts induced DRPC responses show only a brief and sudden drop in ΔF and increase in ΔR, then both ΔF and ΔR recovered significantly under the treatments of 25% PEG6000. Based on the DRPC concept, the stress variations (ΔS) produced by protoplasts under 5%-25% PEG6000 stresses were calculated using Equation (9), which were presented in Figure 6. The stress ΔS produced by protoplasts under 5%-15% PEG6000 stresses first dropped to negative values and then progressively recovered, suggesting that protoplasts first produced gradually increased compressive stress that gradually reduced over time. The stress ΔS generated by protoplasts declined to negative levels and did not fully recover under 25% PEG6000 stress. This suggests that under 25% PEG6000 stress, protoplasts maintain their contractile state while continually producing compressive stress.
The protoplasts’ viscoelastic parameters were also calculated using Equations (10) and (11), we presented the time-dependent curves of the protoplasts’ storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) under 5%-25% PEG6000 stresses in Figure 7. The results show that, under 5% PEG6000 stress, protoplasts first became stiffer and then soften, changing from a viscoelastic gel-like state to a more solid state. The storage modulus (G’) of the protoplasts increased and then slightly decreased, the loss modulus (G”) increased and then remained almost constant, and the loss tangent (G”/G’) decreased and then remained essentially unchanged. The results show that under 10%-15% PEG6000 stresses, protoplasts’ storage modulus (G’) and loss modulus (G”) increased and then decreased, while the loss tangent (G”/G’) decreased at first and then significantly increased. This suggests that protoplasts first stiffen and then significantly soften, moving from a viscoelastic gel-like state to a more solid state and finally reversed to a more fluid-like state.
Under the stress of 25% PEG6000, the storage modulus (G’) and loss modulus (G″) of the protoplasts decreased more obviously after their initial increasing; and the loss tangent (G″/G’) decreased momently to close to 0 then stayed almost unchanged, indicating that the protoplasts transformed to a nearly solid-like state and remained unchanged. The correlated changes in the mechanical parameters of rice protoplasts under the stress of different PEG6000 concentrations are displayed in Figure 8. Overall, within a specific range, the relationship between modulus and the stress produced by protoplasts is linear. Within the same range, the relationship between storage modulus and loss modulus is linear.

3.3. Comparison of Mechanical Properties of Rice Cells and Protoplasts under Different Concentrations of PEG6000 Stress

As illustrated in Figure 9, we contrasted the maximal force and moduli changes generated by cells and protoplasts prior to and following a 5%-25% PEG6000 stress. Compared to cells, protoplasts show larger maximum changes in force and moduli before and after being subjected to the stress under the same PEG6000 concentrations. Furthermore, the stress produced by protoplasts and cells both increased with the increase of PEG6000 concentration, but the moduli G’ and G″ don’t appear to follow the predictable patterns, suggesting a more complicated influence on moduli fluctuations. The mechanical characteristics of rice cells and protoplasts at various PEG6000 stress concentrations were then subjected to linear regression analysis, as shown in Table 2. Overall, there are stronger relationships among the mechanical properties of rice cells than protoplasts for limited time regions.

3.4. Morphological Changes in Rice Cells and Protoplasts under Different Concentrations of PEG6000 Stress

Using an Olympus inverted fluorescent microscope, the morphological changes of rice cells and protoplasts adhering on laser confocal plates before and one hour after the additions of different concentrations of PEG6000 were detected, as shown in Figure 10. Both cells and protoplasts in their first states (Figure 10a and e) showed strong, well-formed structures. The morphologies of both cells and protoplasts appeared to be largely intact under 5% PEG6000 stress (Figure 10b and f), with many tiny particles developing within the cells and abnormalities along the protoplast membranes with disordered cytoplasmic structures. Under the stress of 15% PEG6000, both cells and protoplasts collapsed (Figure 10c and g). Ultimately, both cells and protoplasts experienced significant dehydration and distortion under 25% PEG6000 stress (Figure 10d and h).

4. Discussion

In this study, we investigated the mechanical characteristics of rice cells and protoplasts under PEG6000-simulated drought stress by our newly developed DRPC technique, and the results showed that the mechanical responses of the cells and protoplasts during the drought stress adaptation varied. We discovered that under 5%–15% PEG6000 stress, the changes in mechanical characteristics of cells and protoplasts varied. The cells displayed a brief compressive stress that was succeeded by a slow onset of tensile stress. Cell dehydration was ascribed for this, as it caused a sharp drop in turgor pressure and momentary compressive stress. Tensile stress was produced by the stretching of Hechtian strands between the cell wall and plasma membrane in protoplasts, which had shrunk as a result of water loss. According to Elizabeth S. Haswell et al.’s description of the molecular pathways by which plants perceive and react to osmotic challenges, most protoplasts separate from the cell wall during the process of plasmolysis, but the Hechtian strands still remained to connect the plasma membrane and the cell wall [33]. Thus, membrane tension can be raised by protoplast’s expansion as well as its shrinking. On the other hand, protoplasts lacking of cell wall do not produce significant tensile stress under the same stress circumstances because of the missing of the Hechtian threads. The volume impact caused by drought stress may be the reason for the initial increase and subsequent decrease in compressive stress produced by protoplasts. Traction force microscopy was used by Liu Y et al. [34] to quantify the traction force that animal cells exert on a substrate. They discovered that, in the presence of excessive osmolarity, traction force first increased and subsequently declined, with cell traction force fluctuating in response to volume variations. Michael P. Murrell et al.’s research [35] revealed that lipid droplets scattered over pliable substrates generate strong traction forces. Using a micro-rheometer, Durand-Smet et al. [36] examined the rheology of individual protoplasts and animal cells and discovered that both showed mild power-law rheology. Therefore, these research findings provide scientific justification for our parallel comparisons between protoplasts and animal cells. During the late stages of stress, we observed that protoplasts showed a progressive decrease in compressive stress, indicating a sluggish recovery of volume. This conclusion is in line with the findings of Chloé Roffay et al. 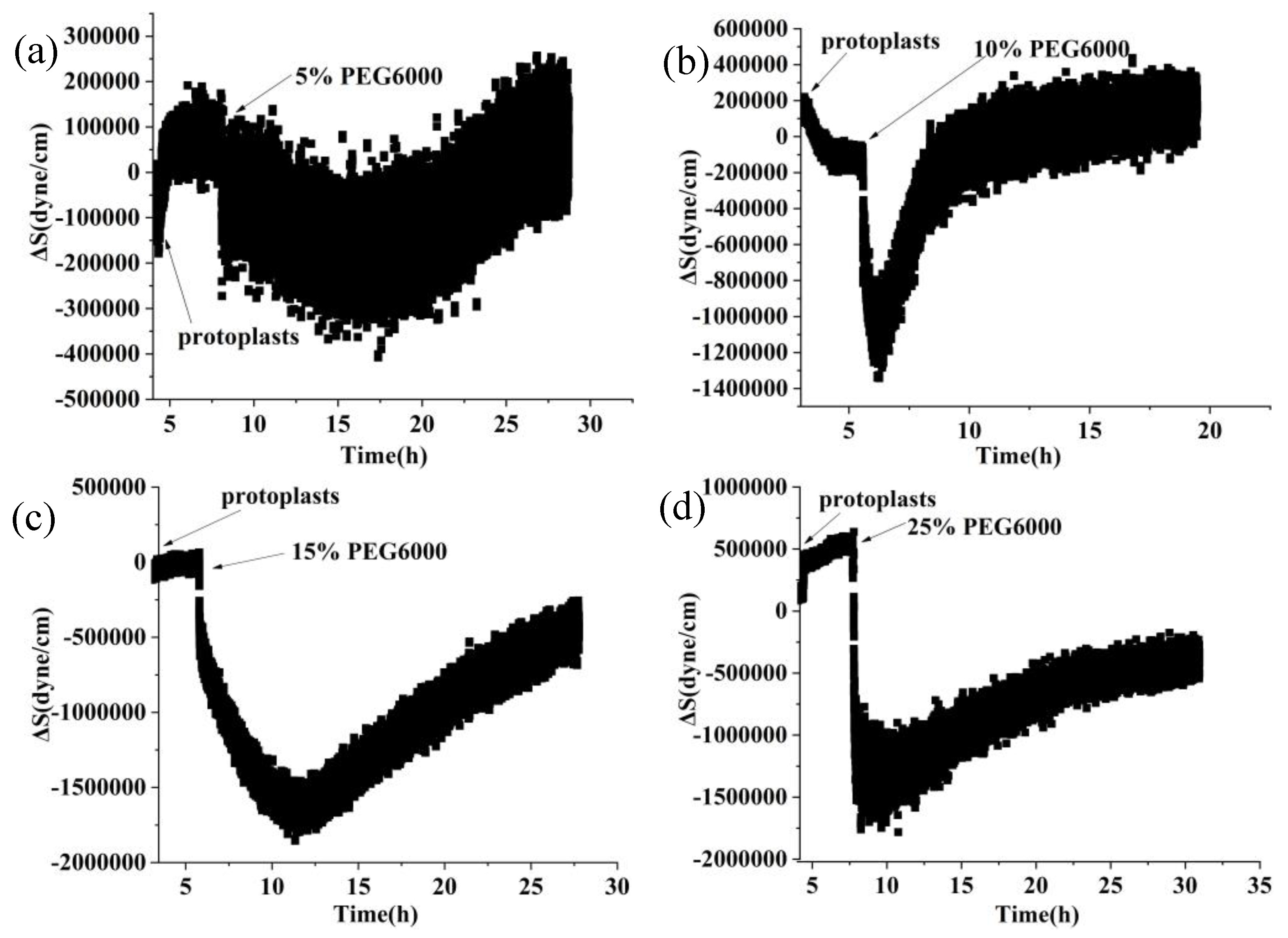[37], who observed incomplete restoration even after several hours and sluggish volume recovery in cells under acute hypertonic stress. The differences in stress resistance between walled cells and protoplasts lacking the cell wall may also be reflected in the varying response rates of cells and protoplasts to the same stress. Under unfavorable stress conditions, cells react quickly, but protoplasts react more slowly.
Moreover, a substantial amount of evidence suggests that abiotic stresses cause the cytoskeletal network to reorganize [38,39,40,41]. The tensegrity model [42] states that actin filaments dominate tensile stress and microtubules dominate compressive stress. According to An-Shan Hsiao et al. [43], rice cells that express intrinsic disordered proteins (RePRP) attach to actin filaments in water-deficient circumstances, thereby decreasing the amount of actin filaments and reorienting the microtubule network through the binding of microtubule proteins. This implies a reduction in the tensile stress dominated by actin filaments, and ΔS is mainly dominated by compressive stress produced by microtubules. Actin filaments in plant cells have been seen to depolymerize and subsequently reassemble under high osmotic stress [44,45], suggesting a progressive restoration of actin filament-dominated tensile stress and a gradual reduction in compressive stress. Consistent with our observations under the microscope, we observed that the changes in the mechanical properties of cells and protoplasts under 25% PEG6000 stress were similar. This suggests that at this concentration, both cells and protoplasts may experience strong contractions, which could lead to possible breaking of Hechtian strands and/or the disruption of the cytoskeletal network; resulting in irreversible damages to these cellular structures and neither the cells nor the protoplasts could withstand the 25% PEG6000 stress. We observed that the cells and protoplasts underwent severe deformations at 25% PEG6000 concentration by optical microscope, which supported our cyto-mechanical test results. It has been reported that the stress generated by cells is positively correlated with turgor pressure and cell radius, and negatively correlated with cell wall thickness [21]. Assuming that the turgor pressures generated by rice cells and wall-removed protoplasts are the same, as the cell wall thickness is much larger than that of the plasma membrane cortex, the measured stress generated by protoplasts should be much greater than that of the walled cells. 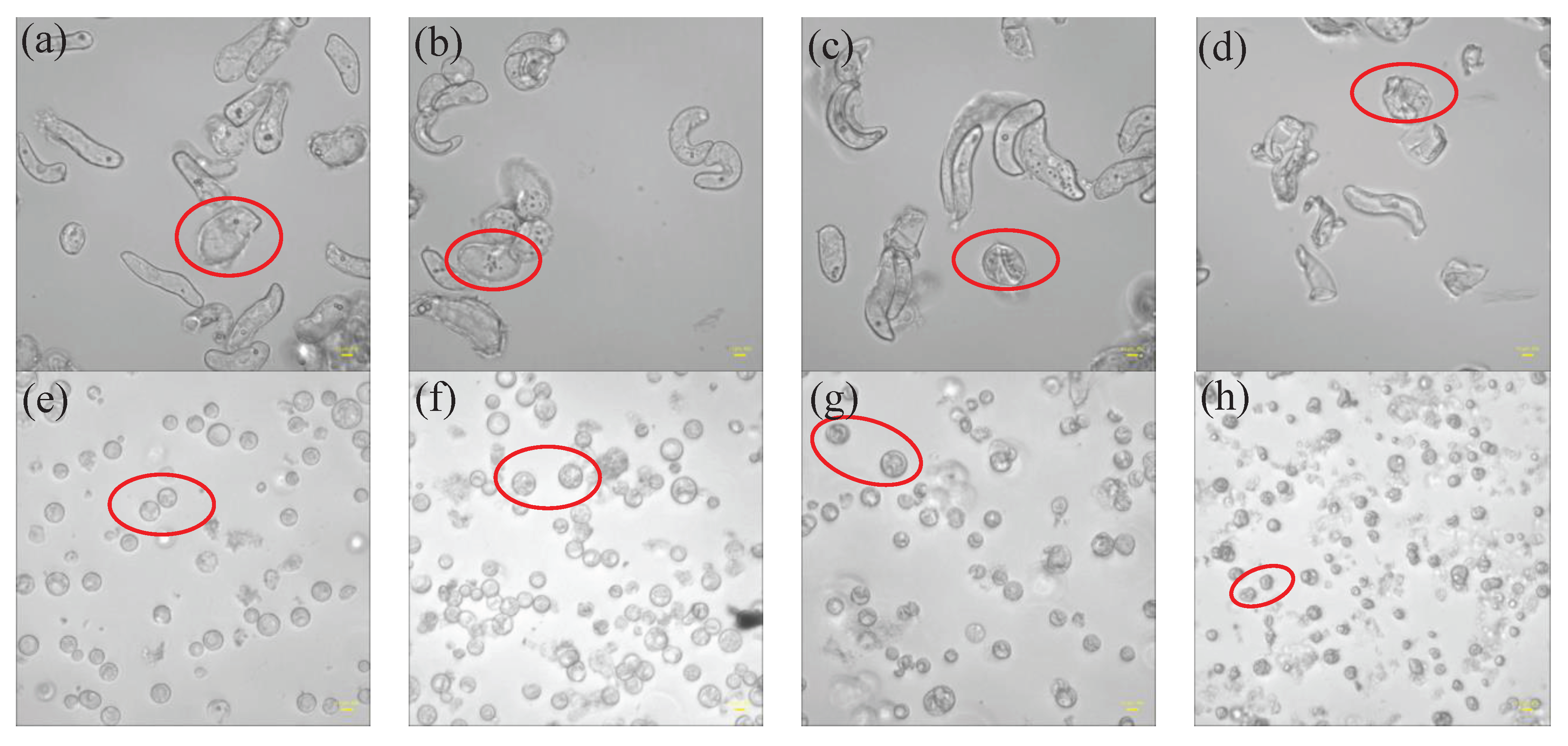This was exactly observed as shown in Figure 9. In addition, under the same stress conditions, the maximum stress generated by cells is greater than that of protoplasts, and both increased with the increase of stress concentration. These are in line with that the observed changes in cell morphologies also increased with the increase of stress concentration, further confirmed the reliability of DRPC technology.
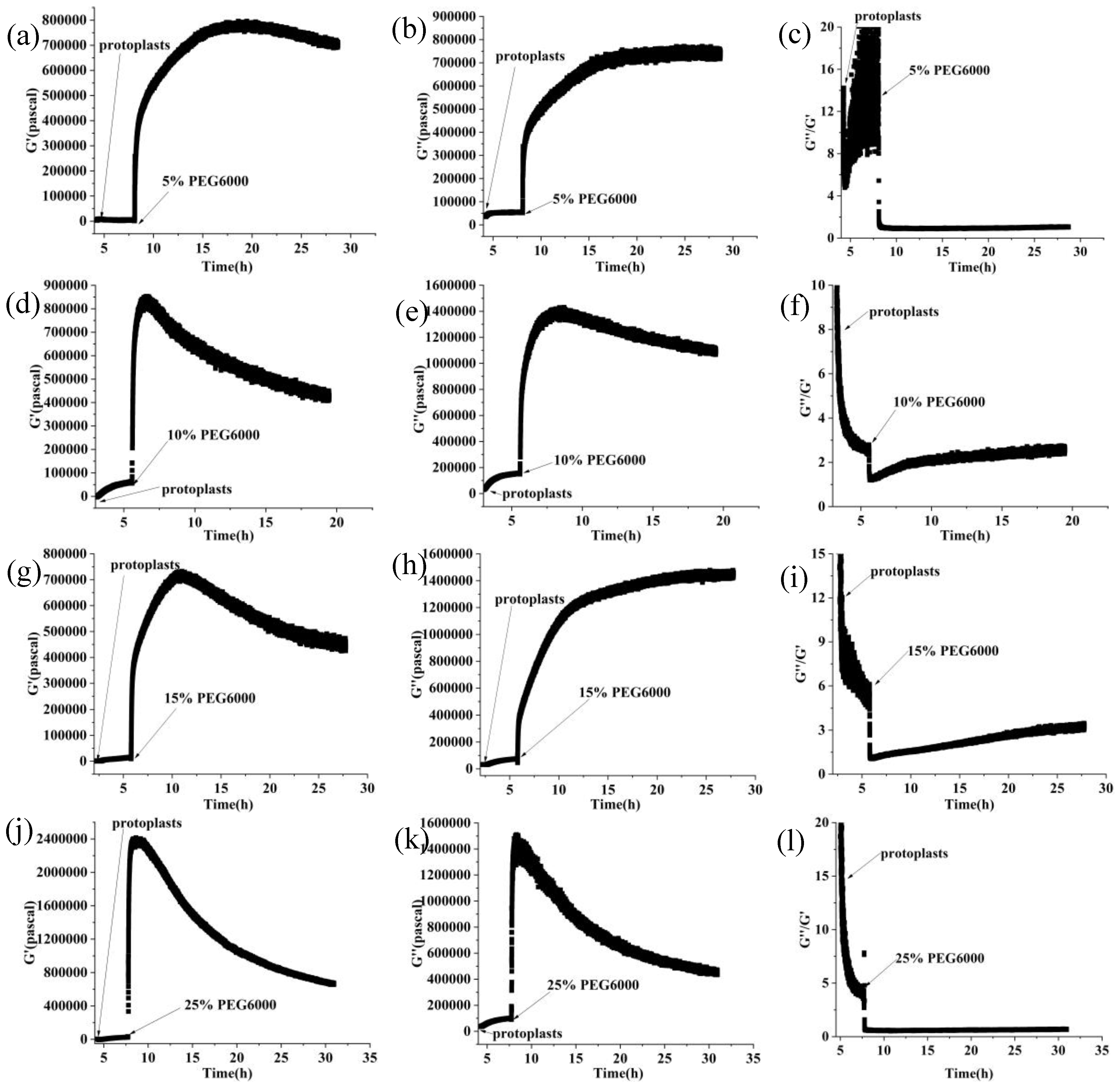
Under the stress of 5%-25% PEG6000 concentrations, we investigated and compared the changes in cellular viscoelasticity of protoplasts and rice cells. The findings demonstrated a quick increase and subsequent decrease in the cell storage modulus. This could be connected to how drought stress causes plant cells to produce reactive oxygen species (ROS) and Ca2+. According to related research, ROS and peroxidases can form crosslinks with glycoproteins in the cell wall and phenolic chemicals, which can cause the cell wall to harden. When ROS levels stay high, OH- radicals are formed, which lead to polymer disintegration and loosening of the cell wall due to swelling proteins [3,46], just as we observed that many granular substances were produced inside the cells under PEG6000 stress, while there were absent in the protoplasts(cf. Figure 10). This indicates the regulatory role of substances such as ROS and peroxidase in the cell wall’s viscoelasticity. Furthermore, plant cells have the ability to create acidic microdomains, which induces cell wall loosening, or Ca2+-pectic acid crosslinking, which promotes cell wall hardness [47]. Because of the quick production of ROS and Ca2+, rice cells under drought stress quickly stiffen and then soften, illustrating the cell wall’s malleability in the process of plant cell resistance [2]. Moreover, it has been reported that bacterial cells treated with strong osmotic pressure for 30 seconds thicken their cell wall, which thins down an hour later [48]. This process can also occur in plant cells, causing a brief stiffening and then relaxing accompanied with a drop in ΔS and then an increase of ΔS. According to our findings, protoplasts’ storage modulus progressively rises before falling, maybe as a result of cytoskeletal and volume modifications brought on by drought stress. After applying osmotic stress to stem cells, Ming Guo et al. [49] found a strong and reliable correlation between stem cell stiffness and cell volume that is, as cell volume falls, cell stiffness rises. The study by Leah Ginsberg et al. 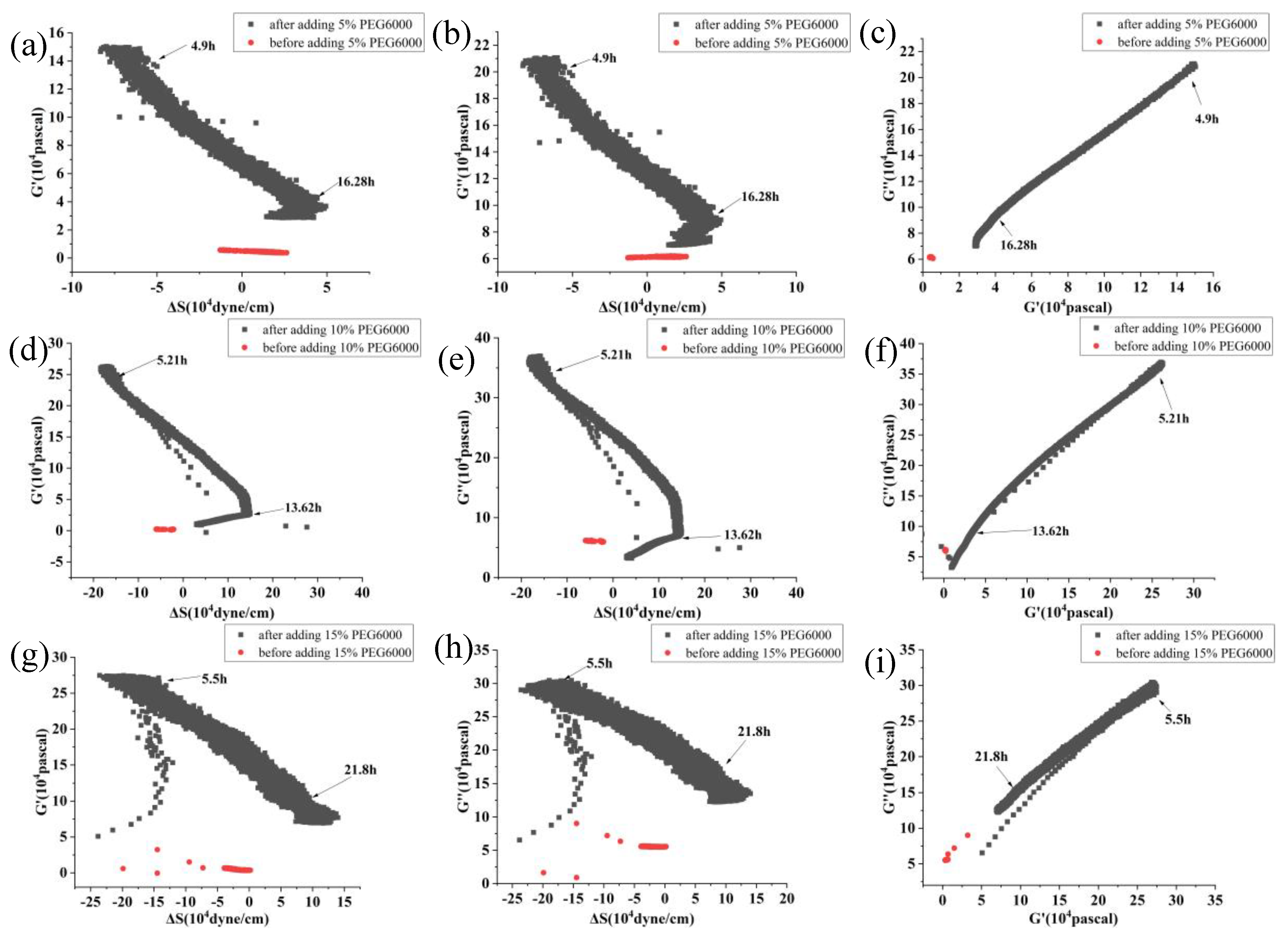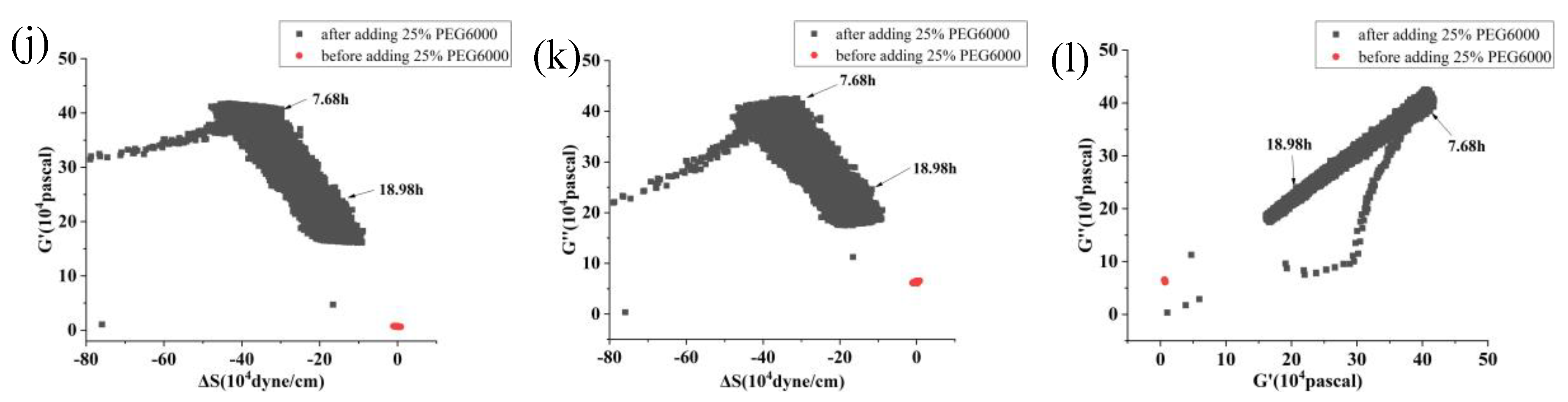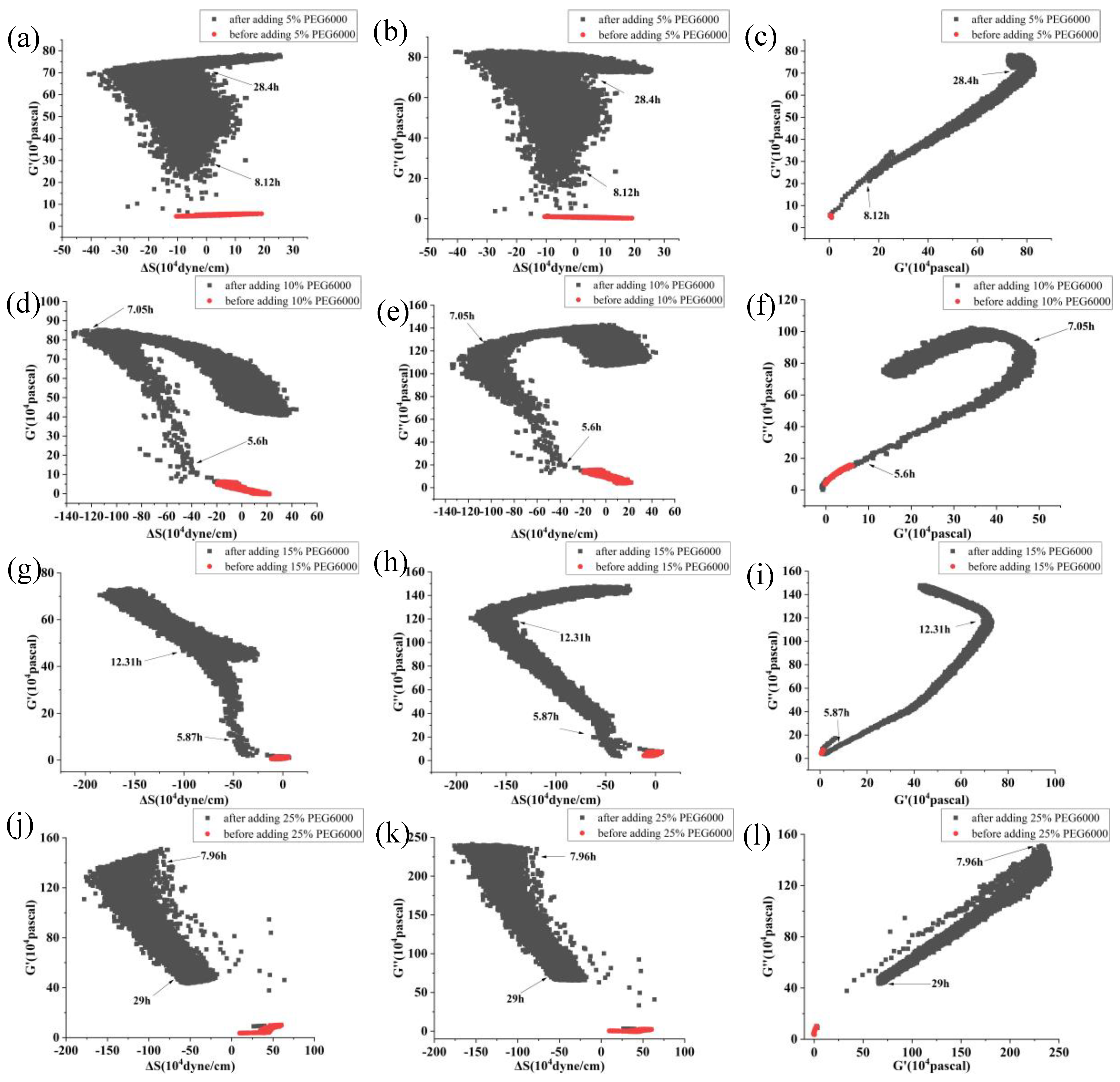[17] demonstrates that the cytoskeleton plays a major role in determining the stiffness and dissipation energy of tobacco cells during indentation. They discovered that the MT network contributes nearly twice as much stiffness as the AF network. According to the shift in the loss tangent, cells experience a tendency to transition to a more solid state when under drought stress, whilst protoplasts show a tendency to move to a more fluid-like state. This could imply that plant cells’ inflexible cell wall construction is essential for their ability to withstand environmental stress. Furthermore, compared to protoplasts, our findings show much stronger links among the mechanical parameters of rice cells (cf. Figure 4 and Figure 8). The existence of cell wall would provide plant cells with a more integrative structure to resist and adapt to various abiotic stresses. This emphasizes the significance of intact cell wall-plasma membrane perception of physical stresses to some extent [50].

5. Conclusions

In order to dynamically and non-destructively determine the mechanical characteristics of rice cells and protoplasts under 5%-25% PEG6000 stress, this study used our newly developed Double Resonator Piezoelectric Cytometry (DRPC) approach. The outcomes demonstrated that under 5%-15% PEG6000 stress, the mechanical performance of cells and protoplasts varied considerably. At first, compressive stress was seen in both cells and protoplasts; however, cells generated compressive stress at a greater rate than protoplasts did. Tensile stress was then slowly observed in the cells; however, it was almost absent from the protoplasts. Furthermore, there was an early rise and then a decline in the elastic modulus and loss modulus of cells and protoplasts. While the loss tangent of protoplasts showed an initial decrease followed by an increase, the loss tangent of cells generally declined. Similar alterations were seen in the mechanical characteristics of both the cells and protoplasts under the stress of 25% PEG6000. It is worth noting that the maximum stresses produced by cells under the stress of 5%-25% PEG6000 were smaller than that of the protoplasts, and the maximum stresses produced by both of them increased with the increase of PEG6000 concentration. Moreover, the morphological changes of rice cells and protoplasts observed by optical microscopy further confirmed the results of DRPC. In summary, the changes in the cells generated stress and viscoelastic moduli of rice cells and protoplasts under the stress of different concentrations of PEG6000 reflect the differences in mechanical properties of rice cells before and after wall removal. The results show that DRPC technology is expected to provide biomechanical information for studying the changes of plant cells under various unfavorable stress conditions, and provide a novel tool for the study of plant stress physiology at cellular level.

Author Contributions

Conceptualization, Y.Y. and T.Z; methodology, Y.Y., T. Z.; software Y.Y. and Y.Z.; validation, Y.Y. and T.Z.; formal analysis, Y.Y., W.P and C.T; investigation, Y.Y.; resources. T.Z; data curation, Y.Y; writing original draft preparation, Y.Y.; writing review and editing, T.Z; visualization, Y.Y., Y.Z. and Z.K; supervision, T.Z.; project administration, T. Z. funding acquisition, T.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (31870933).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Acknowledgments

The authors would like to thank all of the reviewers who participated in the article.

Conflicts of Interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

References

  1. Matysik J, Alia, Bhalu B, et al. Molecular mechanisms of quenching of reactive oxygen species by proline under stress in plants[J]. Current Science, 2002: 525-532.
  2. Ganie S A, Ahammed G J. Dynamics of cell wall structure and related genomic resources for drought tolerance in rice[J]. Plant cell reports, 2021, 40: 437-459.
  3. Tenhaken R. Cell wall remodeling under abiotic stress[J]. Frontiers in plant science, 2015, 5: 771.
  4. Gall H L, Philippe F, Domon J M, et al. Cell wall metabolism in response to abiotic stress[J]. Plants, 2015, 4(1): 112-166.
  5. Moura J C M S, Bonine C A V, de Oliveira Fernandes Viana J, et al. Abiotic and biotic stresses and changes in the lignin content and composition in plants[J]. Journal of integrative plant biology, 2010, 52(4): 360-376.
  6. Zheng M, Meng Y, Yang C, et al. Protein expression changes during cotton fiber elongation in response to drought stress and recovery[J]. Proteomics, 2014, 14(15): 1776-1795.
  7. Hessini K, Martínez J P, Gandour M, et al. Effect of water stress on growth, osmotic adjustment, cell wall elasticity and water-use efficiency in Spartina alterniflora[J]. Environmental and Experimental Botany, 2009, 67(2): 312-319.
  8. Clifford S C, Arndt S K, Corlett J E, et al. The role of solute accumulation, osmotic adjustment and changes in cell wall elasticity in drought tolerance in Ziziphus mauritiana (Lamk.) [J]. Journal of Experimental Botany, 1998, 49(323): 967-977.
  9. De Diego N, Sampedro M C, Barrio R J, et al. Solute accumulation and elastic modulus changes in six radiata pine breeds exposed to drought[J]. Tree physiology, 2013, 33(1): 69-80.
  10. Martínez J P, Silva H, Ledent J F, et al. Effect of drought stress on the osmotic adjustment, cell wall elasticity and cell volume of six cultivars of common beans (Phaseolus vulgaris L.) [J]. European journal of agronomy, 2007, 26(1): 30-38. [CrossRef]
  11. Lin C C, Kao C H. Osmotic stress-induced changes in cell wall peroxidase activity and hydrogen peroxide level in roots of rice seedlings[J]. Plant Growth Regulation, 2002, 37: 177-184.
  12. Frachisse J M, Thomine S, Allain J M. Calcium and plasma membrane force-gated ion channels behind development[J]. Current Opinion in Plant Biology, 2020, 53: 57-64.
  13. Couchoud M, Der C, Girodet S, et al. Drought stress stimulates endocytosis and modifies membrane lipid order of rhizodermal cells of Medicago truncatula in a genotype-dependent manner[J]. BMC plant biology, 2019, 19: 1-14.
  14. Sharma P, Lakra N, Goyal A, et al. Drought and heat stress mediated activation of lipid signaling in plants: a critical review[J]. Frontiers in Plant Science, 2023, 14: 1216835.
  15. ElBasyoni I, Saadalla M, Baenziger S, et al. Cell membrane stability and association mapping for drought and heat tolerance in a worldwide wheat collection[J]. Sustainability, 2017, 9(9): 1606.
  16. Wang X, Mao T. Understanding the functions and mechanisms of plant cytoskeleton in response to environmental signals[J]. Current opinion in plant biology, 2019, 52: 86-96.
  17. Ginsberg L, McDonald R, Lin Q, et al. Cell wall and cytoskeletal contributions in single cell biomechanics of Nicotiana tabacum[J]. Quantitative Plant Biology, 2022, 3: e1.
  18. Mohanta T K, Bashir T, Hashem A, et al. Early events in plant abiotic stress signaling: interplay between calcium, reactive oxygen species and phytohormones[J]. Journal of Plant Growth Regulation, 2018, 37: 1033-1049. [CrossRef]
  19. Codjoe J M, Miller K, Haswell E S. Plant cell mechanobiology: greater than the sum of its parts[J]. The Plant Cell, 2022, 34(1): 129-145.
  20. Ding Y, Zhang Y, Zheng Q S, et al. Pressure–volume curves: revisiting the impact of negative turgor during cell collapse by literature review and simulations of cell micromechanics[J]. New Phytologist, 2014, 203(2): 378-387.
  21. Nakayama H, Koga H, Long Y, et al. Looking beyond the gene network–metabolic and mechanical cell drivers of leaf morphogenesis[J]. Journal of Cell Science, 2022, 135(8): jcs259611.
  22. Knoblauch J, Mullendore D L, Jensen K H, et al. Pico gauges for minimally invasive intracellular hydrostatic pressure measurements[J]. Plant physiology, 2014, 166(3): 1271-1279.
  23. Bidhendi A J, Geitmann A. Methods to quantify primary plant cell wall mechanics[J]. Journal of Experimental Botany, 2019, 70(14): 3615-3648.
  24. Vahabi S, Salman B N, Javanmard A. Atomic force microscopy application in biological research: a review study[J]. Iranian journal of medical sciences, 2013, 38(2): 76.
  25. Pu J, Putnis C V, Wang L. Elsayad K, Werner S, Gallemí M, et al. Mapping the subcellular mechanical properties of live cells in tissues with fluorescence emission–Brillouin imaging[J]. Science signaling, 2016, 9(435): rs5-rs5.
  26. Zhou T, Marx K A, Dewilde A H, et al. Dynamic cell adhesion and viscoelastic signatures distinguish normal from malignant human mammary cells using quartz crystal microbalance[J]. Analytical Biochemistry, 2012, 421(1): 164-171.
  27. Bufi N, Durand-Smet P, Asnacios A. Single-cell mechanics: The parallel plates technique[M]//Methods in cell biology. Academic Press, 2015, 125: 187-209.
  28. Zeng M, Zhou T, Su Z, et al. Electrochemically prepared poly (L-lysine) and 3-hydroxyphenylboronic acid composite as a conventional adhesion material for rice suspension cells[J]. Electrochemistry Communications, 2020, 115: 106737.
  29. Chen Z, Zhou T, Hu J, et al. Quartz crystal microbalance with dissipation monitoring of Dynamic viscoelastic changes of tobacco BY-2 cells under different osmotic conditions[J]. Biosensors, 2021, 11(5): 136.
  30. Zhou T, Huang J, Xiong L, et al. Real-Time Quantification of Cell Mechanics and Functions by Double Resonator Piezoelectric Cytometry–Theory and Study of Cellular Adhesion of HUVECs[J]. Advanced Materials Interfaces, 2023: 2300048.
  31. Zhou Z, Peng H, Li J, et al. Real-time monitoring of the contractile properties of H9C2 cardiomyocytes by double resonator piezoelectric cytometry[J]. Analytical Methods, 2023.
  32. Li W, Li J, Wu Y, et al. A novel method in identifying pyroptosis and apoptosis based on the double resonator piezoelectric cytometry technology[J]. Biosensors, 2023, 13(3): 356.
  33. Haswell E S, Verslues P E. The ongoing search for the molecular basis of plant osmosensing[J]. Journal of General Physiology, 2015, 145(5): 389-394.
  34. Liu Y, Wu W, Feng S, et al. Dynamic response of the cell traction force to osmotic shock[J]. Microsystems & Nanoengineering, 2023, 9(1): 131.
  35. Murrell M P, Voituriez R, Joanny J F, et al. Liposome adhesion generates traction stress[J]. Nature Physics, 2014, 10(2): 163-169.
  36. Durand-Smet P, Chastrette N, Guiroy A, et al. A comparative mechanical analysis of plant and animal cells reveals convergence across kingdoms[J]. Biophysical journal, 2014, 107(10): 2237-2244.
  37. Roffay C, Molinard G, Kim K, et al. Passive coupling of membrane tension and cell volume during active response of cells to osmosis[J]. Proceedings of the National Academy of Sciences, 2021, 118(47): e2103228118.
  38. Blume Y B, Krasylenko Y A, Yemets A I. The role of the plant cytoskeleton in phytohormone signaling under abiotic and biotic stresses[J]. Mechanism of plant hormone signaling under stress, 2017, 2: 127-185.
  39. Quezada E H, Arthikala M K, Nanjareddy K. Cytoskeleton in abiotic stress signaling[M]//Mitigation of plant abiotic stress by microorganisms. Academic Press, 2022: 347-371.
  40. Balcerowicz M. A new order through disorder: Intrinsically disordered proteins reshape the cytoskeleton under drought stress[J]. 2020.
  41. Śniegowska-Świerk K, Dubas E, Rapacz M. Drought-induced changes in the actin cytoskeleton of barley (Hordeum vulgare L.) leaves[J]. Acta physiologiae plantarum, 2015, 37: 1-13. [CrossRef]
  42. Wang N, Naruse K, Stamenović D, et al. Mechanical behavior in living cells consistent with the tensegrity model[J]. Proceedings of the National Academy of Sciences, 2001, 98(14): 7765-7770.
  43. Hsiao A S, Wang K, Ho T H D. An intrinsically disordered protein interacts with the cytoskeleton for adaptive root growth under stress[J]. Plant Physiology, 2020, 183(2): 570-587.
  44. Komis G, Apostolakos P, Galatis B. Hyperosmotic stress-induced actin filament reorganization in leaf cells of Chlorophyton comosum[J]. Journal of experimental botany, 2002, 53(375): 1699-1710.
  45. Kumar S, Jeevaraj T, Yunus M H, et al. The plant cytoskeleton takes center stage in abiotic stress responses and resilience[J]. Plant, Cell & Environment, 2023, 46(1): 5-22.
  46. Novaković L, Guo T, Bacic A, et al. Hitting the wall—Sensing and signaling pathways involved in plant cell wall remodeling in response to abiotic stress[J]. Plants, 2018, 7(4): 89.
  47. Voxeur A, Höfte H. Cell wall integrity signaling in plants: “To grow or not to grow that’s the question” [J]. Glycobiology, 2016, 26(9): 950-960.
  48. Ene I V, Walker L A, Schiavone M, et al. Cell wall remodeling enzymes modulate fungal cell wall elasticity and osmotic stress resistance[J]. MBio, 2015, 6(4): 10.1128/mbio. 00986-15.
  49. Guo M, Pegoraro A F, Mao A, et al. Cell volume change through water efflux impacts cell stiffness and stem cell fate[J]. Proceedings of the National Academy of Sciences, 2017, 114(41): E8618-E8627.
  50. Vaahtera L, Schulz J, Hamann T. Cell wall integrity maintenance during plant development and interaction with the environment[J]. Nature plants, 2019, 5(9): 924-932.
Preprints 102827 g001
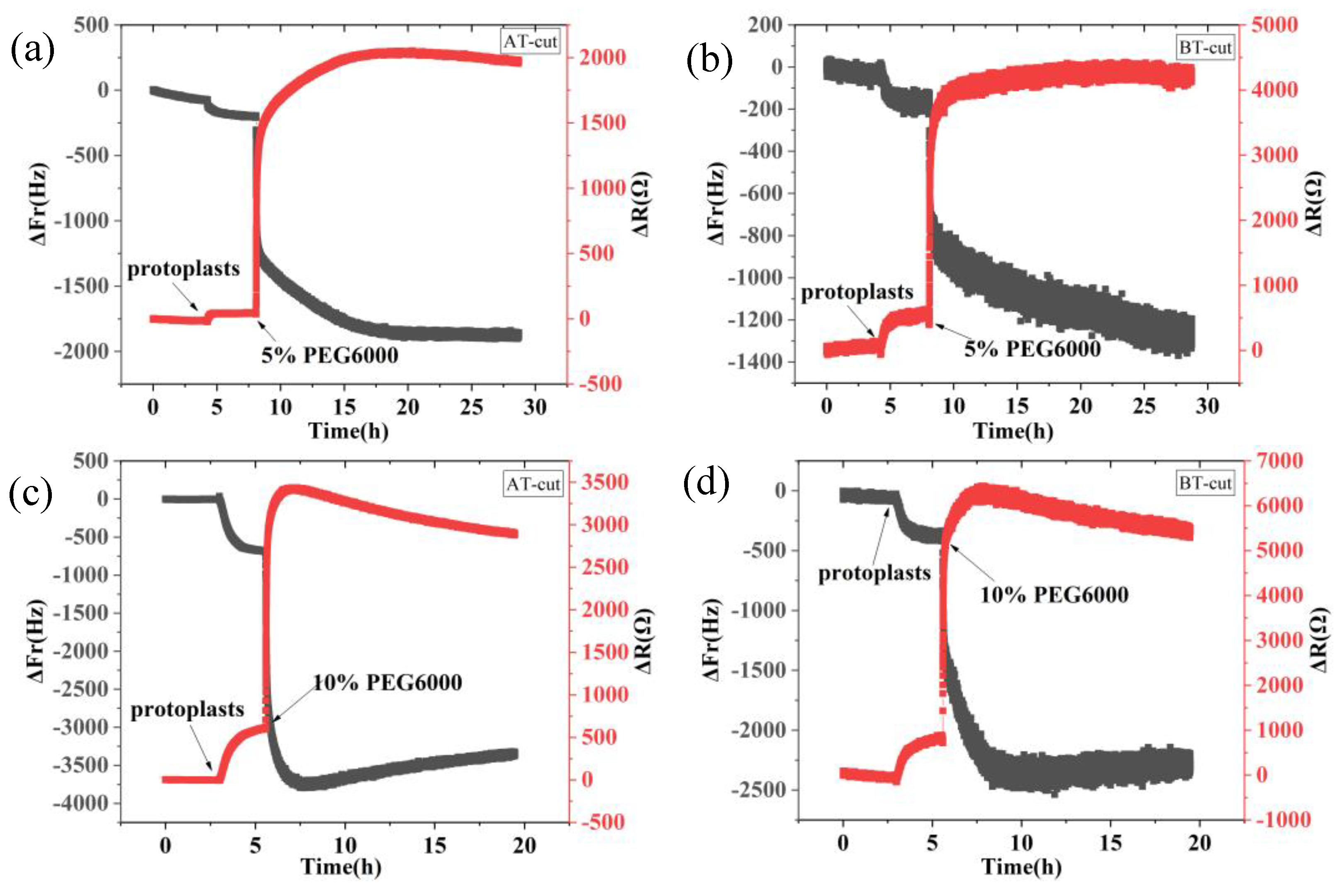
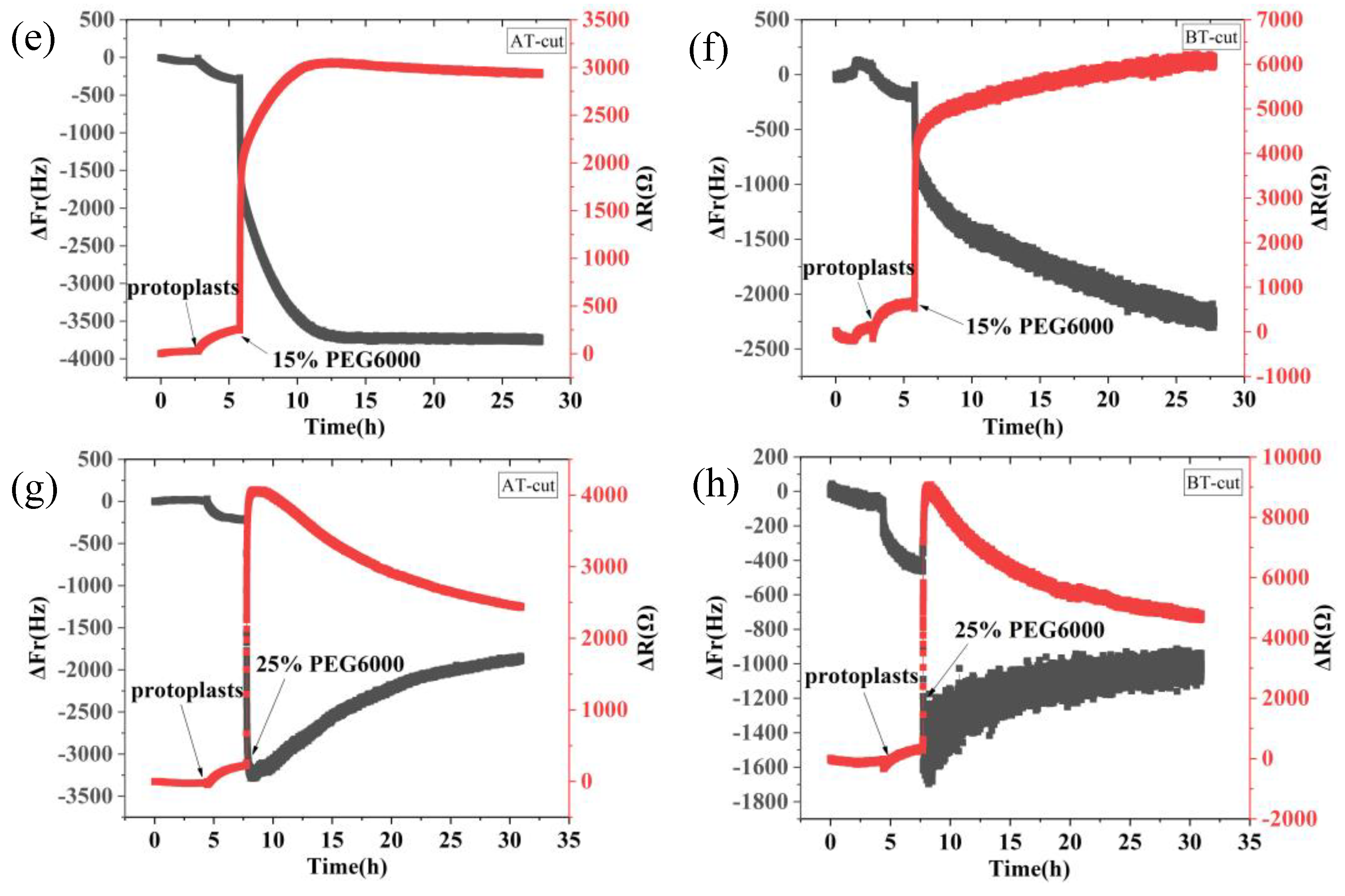
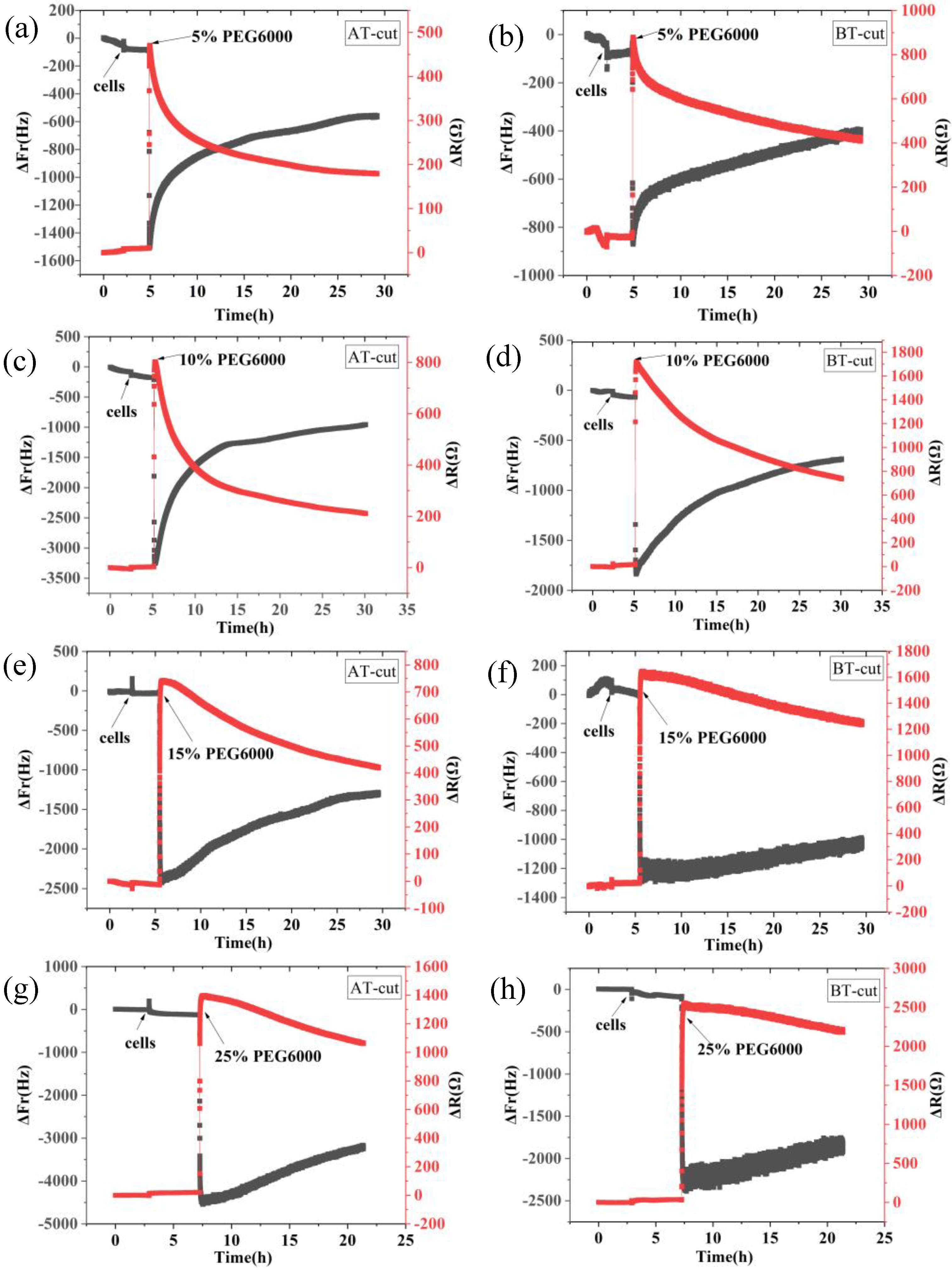
Figure 1. 9 MHz DRPC tracking of frequency-resistance alterations brought on by rice cells under varying PEG6000 stress concentrations. 5% PEG6000 in (a, b), 10% PEG6000 in (c, d), 15% PEG6000 in (e, f), and 25% PEG6000 in (g, h).
Figure 1. 9 MHz DRPC tracking of frequency-resistance alterations brought on by rice cells under varying PEG6000 stress concentrations. 5% PEG6000 in (a, b), 10% PEG6000 in (c, d), 15% PEG6000 in (e, f), and 25% PEG6000 in (g, h).
Preprints 102827 g001
Preprints 102827 g002
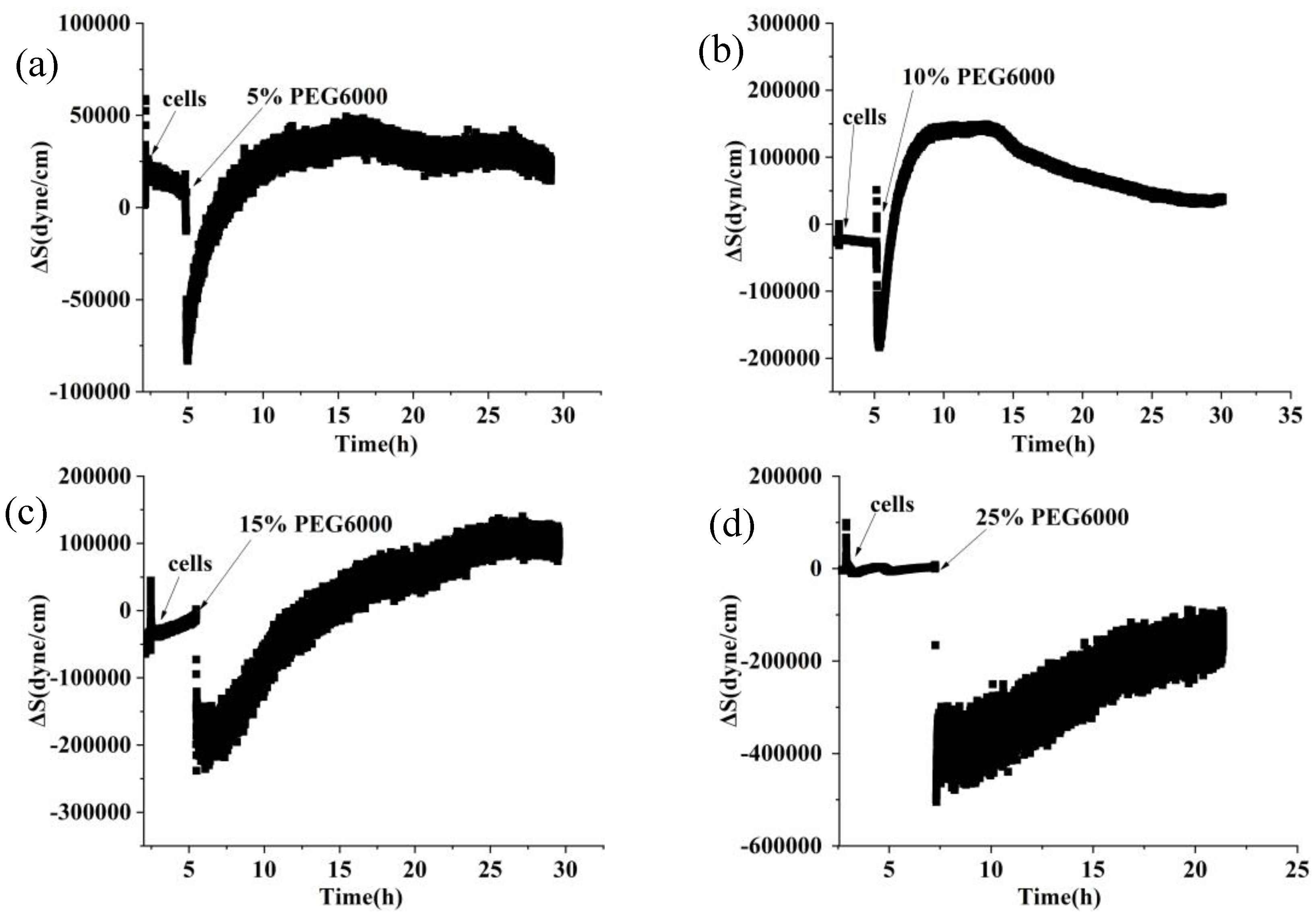
Figure 2. 9 MHz DRPC tracking of stress (ΔS) variations produced by rice cells under various PEG6000 stress concentrations. PEG 6000 percentages are as follows: a: 5%, b: 10%, c: 15%, and d: 25%.
Figure 2. 9 MHz DRPC tracking of stress (ΔS) variations produced by rice cells under various PEG6000 stress concentrations. PEG 6000 percentages are as follows: a: 5%, b: 10%, c: 15%, and d: 25%.
Preprints 102827 g002
Preprints 102827 g003aPreprints 102827 g003b
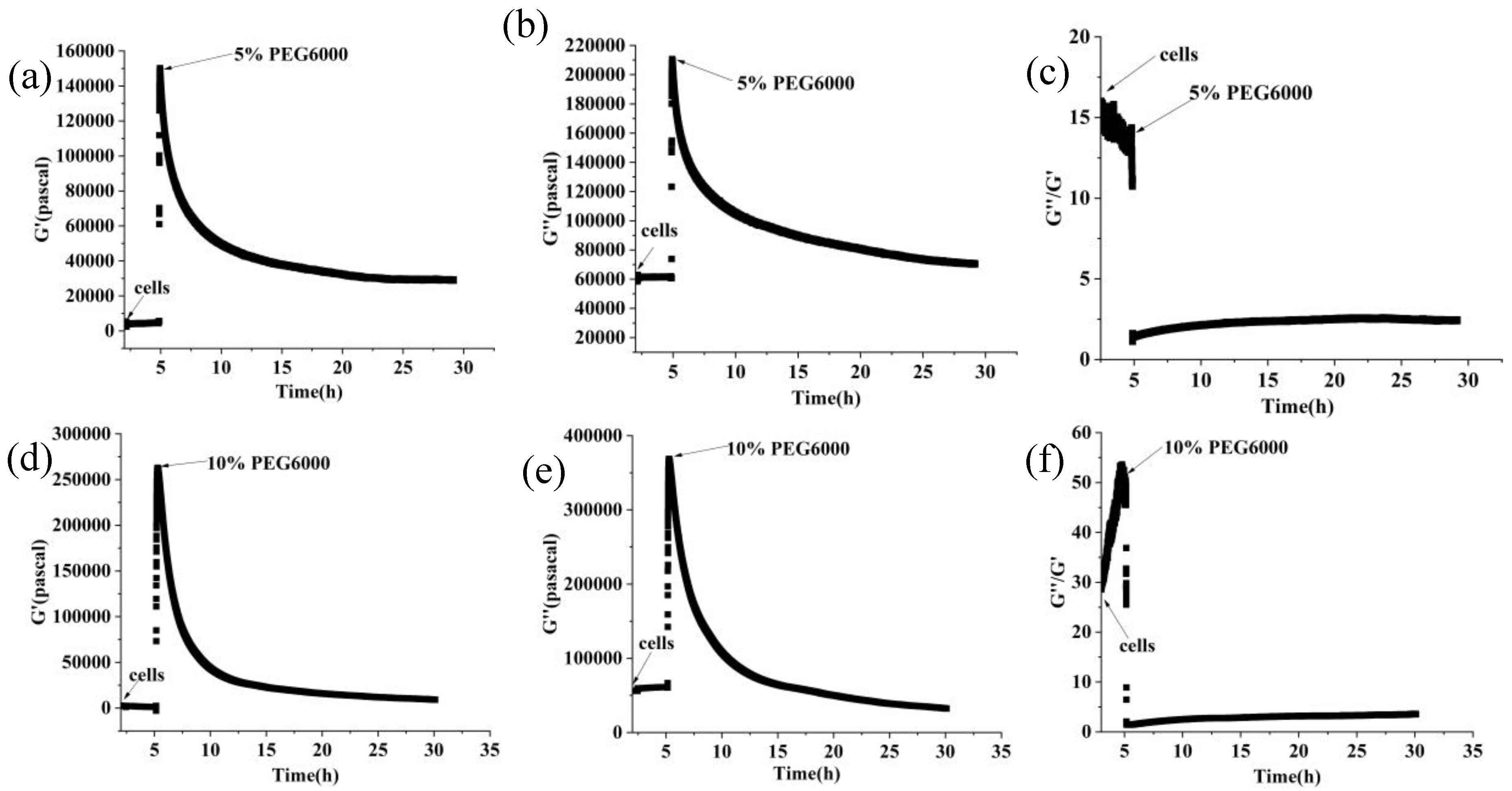
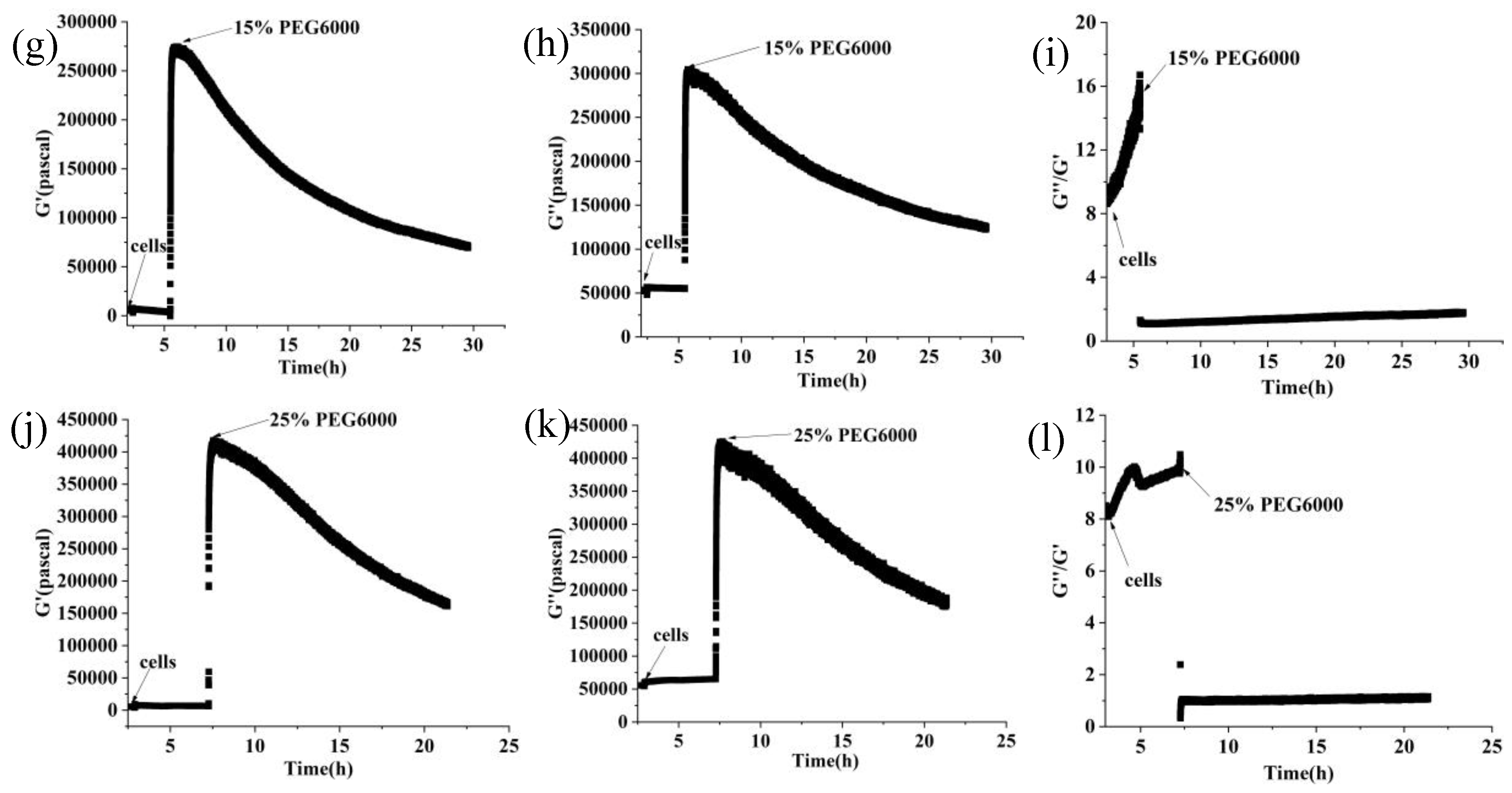
Figure 3. Changes in storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) of rice cells under different concentrations of PEG6000 stress monitored by 5 MHz DRPC technique. (a, d, g, j): G’, (b, e, h, k): G”, (c, f, i, l): G”/G’. (a, b, c):5% PEG6000, (d, e, f):10% PEG6000, (g, h, i):15% PEG6000, (j, k, l):25% PEG6000.
Figure 3. Changes in storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) of rice cells under different concentrations of PEG6000 stress monitored by 5 MHz DRPC technique. (a, d, g, j): G’, (b, e, h, k): G”, (c, f, i, l): G”/G’. (a, b, c):5% PEG6000, (d, e, f):10% PEG6000, (g, h, i):15% PEG6000, (j, k, l):25% PEG6000.
Preprints 102827 g003aPreprints 102827 g003b
Preprints 102827 g004aPreprints 102827 g004b
Figure 4. Correlations among the mechanical parameters of rice cells under the stress of different concentrations of PEG6000. Relationships between G’ and ΔS are shown in (a, d, g, j), G” and ΔS are shown in (b, e, h, k), and G” and G’ are shown in (c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Figure 4. Correlations among the mechanical parameters of rice cells under the stress of different concentrations of PEG6000. Relationships between G’ and ΔS are shown in (a, d, g, j), G” and ΔS are shown in (b, e, h, k), and G” and G’ are shown in (c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Preprints 102827 g004aPreprints 102827 g004b
Preprints 102827 g005aPreprints 102827 g005b
Figure 5. 5 MHz DRPC tracking of frequency-resistance shifts brought about by rice protoplasts under varying PEG6000 stress concentrations. 5% PEG6000 in (a, b), 10% PEG6000 in (c, d), 15% PEG6000 in (e, f), and 25% PEG6000 in (g, h).
Figure 5. 5 MHz DRPC tracking of frequency-resistance shifts brought about by rice protoplasts under varying PEG6000 stress concentrations. 5% PEG6000 in (a, b), 10% PEG6000 in (c, d), 15% PEG6000 in (e, f), and 25% PEG6000 in (g, h).
Preprints 102827 g005aPreprints 102827 g005b
Preprints 102827 g006
Figure 6. 5 MHz DRPC tracking of stress (ΔS) variations produced by rice protoplasts at various PEG6000 stress concentrations. PEG 6000 concentrations: a: 5%, b: 10%, c: 15%, and d: 25%.
Figure 6. 5 MHz DRPC tracking of stress (ΔS) variations produced by rice protoplasts at various PEG6000 stress concentrations. PEG 6000 concentrations: a: 5%, b: 10%, c: 15%, and d: 25%.
Preprints 102827 g006
Preprints 102827 g007
Figure 7. Variations in rice protoplasts’ storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) under the stress of different PEG6000 concentrations were tracked using 5 MHz DRPC technique. G’: (a, d, g, j), G”: (b, e, h, k), G”/G’ :(c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Figure 7. Variations in rice protoplasts’ storage modulus (G’), loss modulus (G”), and loss tangent (G”/G’) under the stress of different PEG6000 concentrations were tracked using 5 MHz DRPC technique. G’: (a, d, g, j), G”: (b, e, h, k), G”/G’ :(c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Preprints 102827 g007
Preprints 102827 g008
Figure 8. Correlations among the mechanical parameters of rice protoplasts under the stress of different concentrations of PEG6000. Relationships between G’ and ΔS are shown in (a, d, g, j), G” and ΔS are shown in (b, e, h, k), and G” and G’ are shown in (c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Figure 8. Correlations among the mechanical parameters of rice protoplasts under the stress of different concentrations of PEG6000. Relationships between G’ and ΔS are shown in (a, d, g, j), G” and ΔS are shown in (b, e, h, k), and G” and G’ are shown in (c, f, i, l). PEG6000 concentrations: (a, b, c): 5%; (d, e, f): 10%; (g, h, i): 15%; (j, k, l): 25%.
Preprints 102827 g008
Preprints 102827 g009
Figure 9. Comparisons of the mechanical properties of protoplasts and rice cells at varying PEG6000 stress concentrations. (a): ΔS , (b): G’ , (c): G”.
Figure 9. Comparisons of the mechanical properties of protoplasts and rice cells at varying PEG6000 stress concentrations. (a): ΔS , (b): G’ , (c): G”.
Preprints 102827 g009
Preprints 102827 g010
Figure 10. Morphologies of rice cells and protoplasts under the stress of different PEG6000 concentrations (scale bar: 10 μm). (a, b, c, d): Cells; (e, f, g, h): Protoplasts. (b, f): 5% PEG6000, (c, g): 15% PEG6000, (d, h): 25% PEG6000, and (a, e): blank control.
Figure 10. Morphologies of rice cells and protoplasts under the stress of different PEG6000 concentrations (scale bar: 10 μm). (a, b, c, d): Cells; (e, f, g, h): Protoplasts. (b, f): 5% PEG6000, (c, g): 15% PEG6000, (d, h): 25% PEG6000, and (a, e): blank control.
Preprints 102827 g010
Table 1. A comparison of main functions of existing plant cell mechanics methods.
Table 1. A comparison of main functions of existing plant cell mechanics methods.
Method/instrument Cell
Viscoelasticity		 Cellular force Simultaneous measurement of cellular force and viscoelasticity Nondestructive long-term Single cell cell cluster
Pico gauges _ + _ _ + _
Indentation techniques + _ _ _ + -
Atomic force microscopy, AFM + + - _ + -
Brillouin scattering microscopy, BSM + _ _ + + -
Quartz Crystal Microbalance, QCM + _ _ + + +
Parallel plate rheometer, PPR + + - _ + _
Table 2. Relationships among mechanical parameters of rice cells and protoplasts at various PEG6000 stress concentrations as determined by linear regressions.
Table 2. Relationships among mechanical parameters of rice cells and protoplasts at various PEG6000 stress concentrations as determined by linear regressions.
Concentration of PEG6000 G’-ΔS G”-ΔS G”-G’
slope R2 Time region(h) slope R2 Time region(h) slope R2 Time region(h)
cells 5% -0.8577 0.9739 5.03-13.6 -0.8972 0.9688 5.03-13.6 1.0482 0.9981 5.03-13.6
10% -0.6484 0.9927 5.17-10.43 -0.7641 0.9784 5.17-10.43 1.1838 0.9947 5.17-10.43
15% -0.6054 0.9764 5.63-18.82 -0.4849 0.9601 5.63-18.82 0.8062 0.9961 5.63-18.82
25% -0.8934 0.9146 7.31-21.36 -0.8029 0.8758 7.31-21.36 0.9157 0.9939 7.31-21.36
protoplasts 5% -0.1944 0.7186 16.02-28.7 0.1184 0.7316 16.02-28.7 0.7932 0.9839 8.19-16.02
10% -0.1340 0.8998 6.23-8.64 0.2411 0.8425 6.23-8.64 1.2517 0.9330 8.72-19.42
15% -0.4370 0.9468 5.52-9.72 -0.6866 0.9684 5.52-9.72 2.2203 0.9866 6.00-10.7
25% -1.5380 0.9128 9.15-29.64 -0.7824 0.8732 9.15-29.64 0.5317 0.9923 7.96-29.58
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated