Preprint

Article

Determination of Critical Damage Size of Inclined Waterproof Coal Pillar under Asymmetric Load

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 April 2024

Posted:

02 April 2024

You are already at the latest version

Alerts

Abstract

Quantitative determination of the critical size of inclined coal pillar in old goaf water affected area is of great significance for water damage prevention and safe mining. The critical size of inclined waterproof coal pillar is derived by using theoretical analysis, numerical calculation and field engineering practice for the stability of the waterproof coal pillar in old goaf water affected area of 1303 working face of Dananhu I mine in Xinjiang region. Firstly, a force model of inclined waterproof coal pillar was established to reveal the law that the critical size of the coal pillar increases with the increase of coal seam inclination under the action of asymmetric load. Then, numerical simulation was applied to reveal the dynamic evolution process of plastic deformation-destabilization-destruction of section coal pillar under the influence of mining and single-side water pressure, and the critical size of waterproof coal pillar in study area was determined to be 19.09m. Finally, measures such as pumping and pressure relief and slurry reinforcement were adopted to reduce the deformation rate of the roadway on side of waterproof coal pillar, which ensured the stability of the coal pillar and roadway and the safe recovery of the working face.

Keywords:

Subject: Engineering - Mining and Mineral Processing

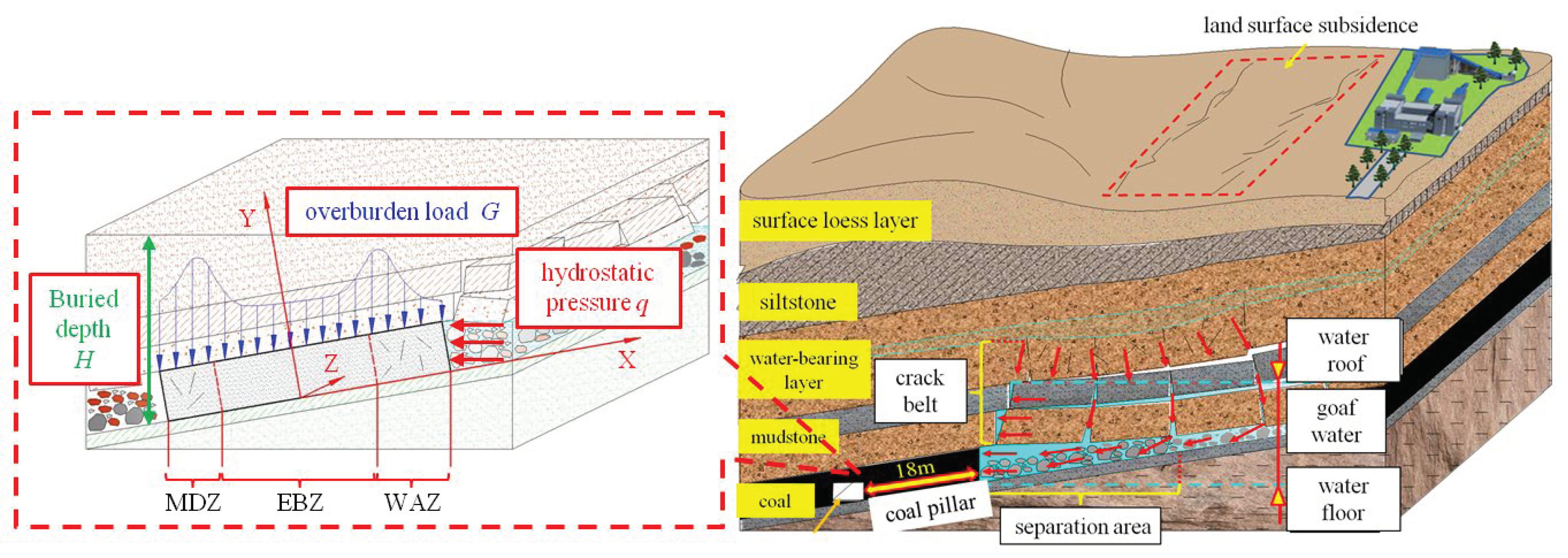
1. Introduction

Over 60% of China’s electricity is generated through the combustion of coal, making the secure and efficient extraction of coal resources vital to the nation’s economic development. One key aspect of ensuring the safety of coal mining operations is the rational design and stability control of coal pillars [1,2,3,4]. Additionally, given China’s complex underground hydrological conditions, with up to 25 billion tons of coal reserves affected by water, the design of many coal pillars must not only consider the safe bearing of overlying strata loads and the stability of surrounding roadways but also the prevention of water-related hazards in voids left by coal extraction [5,6]. However, coal pillars, as underground support structures, are inherently fraught with complexities due to their geological formation and the presence of numerous fractures [7,8,9]. Human-induced disturbances, such as mining activities, can easily weaken these structures internally [10,11]. When the load-bearing capacity of a coal pillar reaches its yield limit, catastrophic events like structural collapse are highly likely, resulting in significant economic losses and potentially even loss of life [12,13,14].

To address these issues, numerous scholars have conducted extensive research on waterproof coal pillars, yielding significant findings. For example, theories like load estimation methods have been used to analyze the characteristics of overlying strata loads on coal pillars, focusing on these loads as the primary source of instability and elucidating the mechanisms behind pillar failure [15,16]. For example, by drawing on the two-zone constraint theory, the water barrier coal pillar is divided into three parts of the central elastic zone and the plastic zone on both sides, and using the relevant theory of elastic mechanics, the critical size formula of the elastic zone of the coal pillar in near horizontal coal seam under the combined effect of uniform load and water pressure is derived [17,18,19,20]. For example, using the theory of hydrodynamics and multiple regression [21,22,23], we analyze the reasonable width of the water barrier coal pillar under the influence of different types of faults, and derive the formula for calculating the size of the water barrier coal pillar when the fault dip angle is large and small [24,25,26,27]. For example, neural networks and improved numerical calculation algorithms have been employed for reasonable analysis and prediction of coal pillar dimensions [28,29].The analysis of the influence of the overburden collapse process and the development characteristics of the water-conducting fracture zone on the stability of the water barrier pillar is given by means of physically similar simulation [30,31,32,33,34,35]. In recent years, with the popular development of computer, numerical simulation has gradually become a new means to study the size of waterproof coal pillar [36,37,38,39,40]. Many scholars mostly use the seepage and deformation theory to establish the numerical model of solid-flow coupling in the coal seam mining process to reveal the stress evolution law of coal pillars of different widths under the influence of water and mining, which is used as the basis for the size of water barrier pillars [41,42,43,44].

Despite these advancements, current research rarely addresses the impact of coal seam inclination on the form of coal pillars or explores the stress characteristics at different locations within the pillars. This paper, therefore, focuses on the asymmetrical loading on inclined coal pillars caused by their angle of inclination. It examines the stress patterns and critical instability characteristics of the elastic barrier zone in inclined pillars, studies the dynamic evolution of plastic deformation-instability-failure of the inclined waterproof coal pillar under the influence of mining activities and unilateral water pressure, and establishes expressions for the critical failure dimensions of the inclined coal pillar under unilateral hydrostatic pressure. This provides a reference for the stability research of inclined coal pillars in similar geological conditions and offers scientific theoretical support for the prevention of disasters caused by underground space instability.

2. Mechanics Modeling

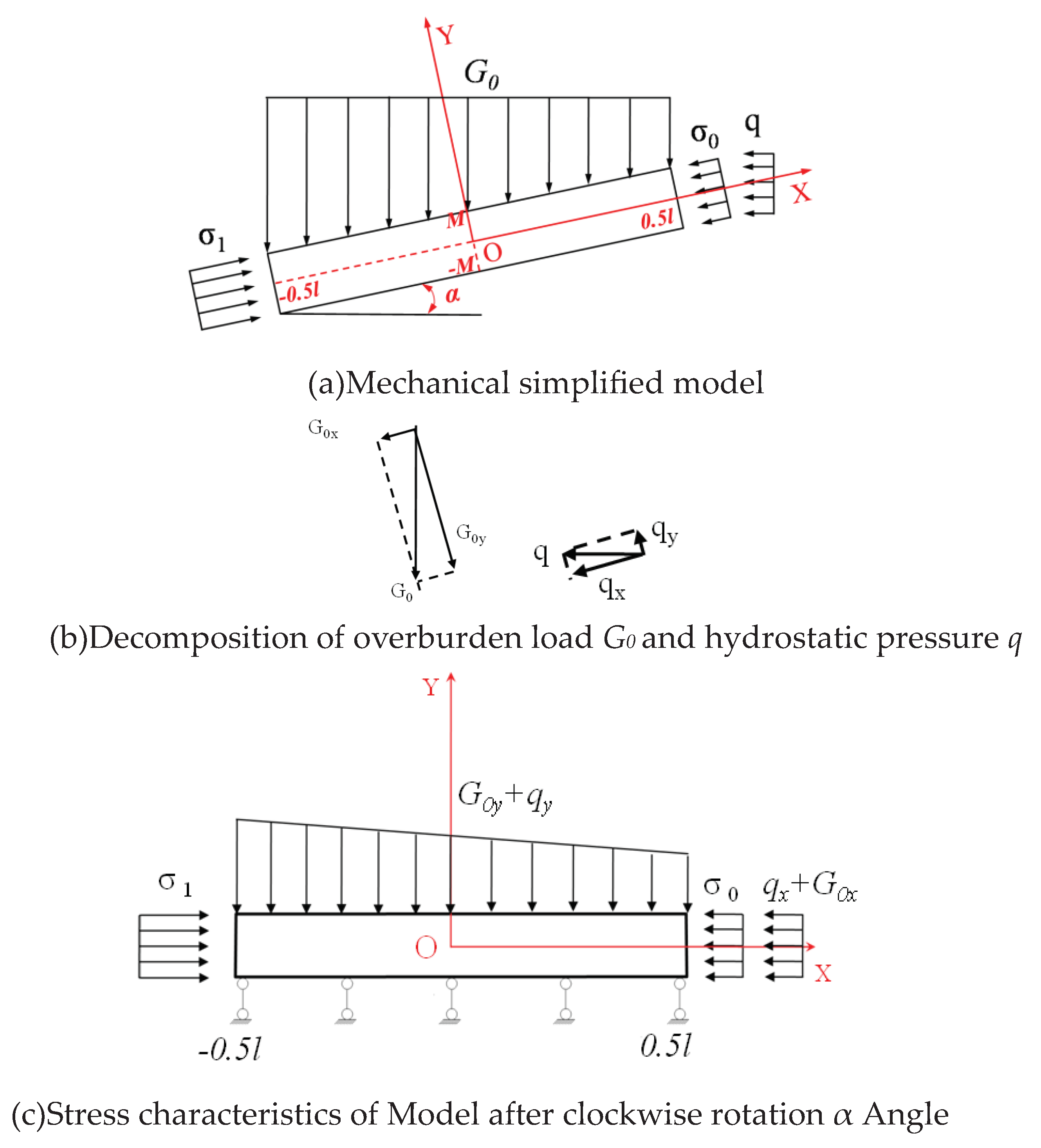
2.1. Force Analysis of Inclined Waterproof Coal Pillar

Artificial mining disturbance is the key factor to break the balance of stress between the coal pillar and its surrounding rock and lead to the formation of old goaf water. In the actual production process, with the back mining of two working faces and the gradual generation of old goaf water in the mining area, both ends of the water barrier coal pillar will be affected by the support pressure, and one side will also be affected by old goaf water, which will certainly produce stress concentration in both sides of the coal pillar. When the degree of stress concentration exceeds the bearing capacity of the coal pillar body, the internal joint fracture of the coal pillar will gradually expand, resulting in the transformation of the structure of both sides of the coal pillar from elastomeric to plastic body. When the plastic zone on both sides expands to penetration, the coal pillar will lose its load-bearing and water-insulation capacity.

In this process, as the force characteristics along the direction of roadway advancement in the coal pillar change minimally, the cross-section of a coal pillar is typically the focus of study. This reveals that the ends of a coal pillar bear more load, leading to more fracture development and a transition from an elastic to a plastic state. Closer to the middle of the pillar, the overlying strata load approaches the original rock stress, resulting in less transformation between elastic and plastic states in the coal pillar.

Therefore, in this paper, the coal pillar under the influence of water addition in the mining area is divided into the mining disturbance zone (MDZ), the elastic barrier zone(EBZ) and the water pressure affected zone(WAZ), as Fig1 shown. In this figure, G is the overburden load (vertical direction) under mining disturbance; q is the hydrostatic pressure value on one side of the coal pillar; α is thsse inclination angle of the coal seam; H is the height from the middle of the elastic zone of the coal pillar to the ground surface.

2.2. Determination of the Critical Length of the Elastic Barrier Zone

From the instability process of the overburden load on inclined pillars, it’s inferred that the cross-sectional structure of an inclined pillar can be simplified into shorter mining-disturbed zones at both ends and a longer central elastic zone (EBZ). Since the bearing capacity of the plastic zones on both sides is compromised, the central elastic body should be the main focus of the study. Since the force direction in the elastic barrier area of the waterproof pillar is mainly concentrated in the XOY plane (Figure 1), and the force characteristics of the tangent plane perpendicular to the Z axis (parallel to the XOY plane) are similar, the force state of the coal pillarcan be simplified to a plane problem for solution [14].

Assuming that the length of the elastic barrier zone(EBZ) is l, the overburden load of coal pillar is G₀, and the hydrostatic pressure q is constant after crossing the water pressure influence zone, a simplified model of the elastic barrier zone mechanics can be obtained, as shown in Figure 2a.

When X-axis is the horizontal direction and Y-axis is the vertical direction, then σ₀ is the horizontal constraint between the coal body in the elastic zone and the water pressure influence zone;σ₁ is the horizontal constraint between the coal body in the elastic zone and the recovery disturbance zone; q is the hydrostatic pressure value after crossing the plastic zone of the coal pillar; α is the dip angle of the coal seam. It is known from the literature [8,14] that under the near horizontal coal seam conditions, the residual support pressure on the elastic zone of the coal pillar can be approximated as constant as K₁γH, where K₁ is the stress concentration coefficient of the elastic zone (generally half of the maximum stress concentration coefficient).

Through the above elaboration, we can analysis stress characteristics in the elastic barrier zone of inclined waterproof coal pillar. As shown in Figure 2b, G₀ can be decomposed into G_0x and G_0y, q can be decomposed into q_x and q_y. So stress of G_0x and q_x is horizon vector, stress of G_0y and q_y is vertical vector. Thus,

G_{0} = - K_{1} γ (H - x \sin α)

(1)

G_{0 y} = - K_{1} γ (H - x \sin α) c o s α

(2)

G_{0 x} = - K_{1} γ (H - x \sin α) s i n α

(3)

q_{x} = - |q| \cos α

(4)

q_{y} = |q| \sin α

(5)

Because the vertical stress of EBZ does not change along with the change of Y axis direction stress, G₀ is constant.

Thus, using semi-inverse solution of elastic mechanicsto can solve this problem.

In Figure 2a:

σ_{y} = G_{0 y} + q_{y} = \frac{K_{1} γ \sin 2 α}{2} x + (|q| s i n α - K_{1} γ H \cos α)

(6)

To simplify the calculation,definition:

A = \frac{K_{1} γ \sin 2 α}{2}

B = |q| \sin α - K_{1} γ H \cos α

Therefore, according to the equilibrium differential equation

σ_{y} = \frac{\partial^{2} f (x, y)}{\partial x^{2}}

By integrating Equation (6), the stress function can be obtained:

f (x, y) = \int σ_{y} d y = \frac{A}{6} x^{3} + \frac{B}{2} x^{2} + f_{1} (y) x + f_{2} (y)

(7)

We can find that f₁(y) and f₂(y) are functions of the unknown parameter y. In order for the stress function f(x,y) to hold, the compatibility equation should be satisfied:

\frac{\partial^{4} f (x, y)}{\partial x^{4}} + 2 \frac{\partial^{4} f (x, y)}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} f (x, y)}{\partial y^{4}} = 0

(8)

Eq. (7) is substituted into Eq. (8) to obtain:

x \frac{\partial^{4} f_{1} (y)}{\partial y^{4}} + \frac{\partial^{4} f_{2} (y)}{\partial y^{4}} = 0

(9)

Since x ∈ [-0.5l,0.5l], taking different values of x and substituting it into Eq. (4), simplifying it gives:

\frac{\partial^{4} f_{1} (y)}{\partial y^{4}} = 0

\frac{\partial^{4} f_{2} (y)}{\partial y^{4}} = 0

Therefore, the expressions of f₁(y) and f₂(y) can be obtained:

f_{1} (y) = C_{1} y^{3} + C_{2} y^{2} + C_{3} y + C_{4}

(10)

f_{2} (y) = D_{1} y^{3} + D_{2} y^{2} + D_{3} y + D_{4}

(11)

And substituting Eq. (10) and Eq. (11) into Eq. (7), it is apparent that:

\begin{matrix} f (x, y) = \frac{A}{6} x^{3} + \frac{B}{2} x^{2} + x (C_{1} y^{3} + C_{2} y^{2} + C_{3} y + C_{4}) \\ + (D_{1} y^{3} + D_{2} y^{2} + D_{3} y + D_{4}) \end{matrix}

(12)

This leads to:

σ_{x} = \frac{\partial^{2} f (x, y)}{\partial y^{2}} = 6 C_{1} x y + 2 C_{2} x + 6 D_{1} y + 2 D_{2}

(13)

σ_{y} = \frac{\partial^{2} f (x, y)}{\partial x^{2}} = A x + B

(14)

τ_{x y} = - \frac{\partial^{2} f (x, y)}{\partial x \partial y} = - (3 C_{1} y^{2} + 2 C_{2} y + C_{3})

(15)

As the elastic zone of coal pillar is in critical equilibrium, and there is a large interlayer friction between coal and rock seams, so:

σ_{1} = - (σ_{0} + q_{x} + G_{0 x})

(16)

Based on this simplified calculation, the symmetry of the mechanical model is therefore considered first. As shown in Figure 2c, since the bottom of the coal pillar can be regarded as a fixed end constraint, the load on the elastic barrier zone of the water barrier coal pillar is symmetric along the XOZ side, so it should satisfy σ_x(-y) = σ_x(y), σ_y(-y) = σ_y(y), -τ_xy(y) = τ_xy(-y). Substituting into equations (13)-(15) yields C₁=D₁=C₃=0.

At this point, considering the boundary conditions, as shown in Figure 2c, at the boundary x = -0.5l, it is obtained that:

σ_{x} (- 0.5 l) = - C_{2} l + 2 D_{2} = - (σ_{0} + q_{x} + G_{0 x})

(17)

At the boundary x = 0.5l, it follows that:

σ_{x} (0.5 l) = C_{2} l + 2 D_{2} = σ_{0} + q_{x} + G_{0 x}

(18)

The union of (17) and (18) is solved by D₂ = 0,

C_{2} = \frac{σ_{0} + q_{x} + G_{0 x}}{l}

, and combined with equations (13)-(15) we get:

σ_{x} = 2 \frac{σ_{0} + q_{x} + G_{0 x}}{l} x

(19)

σ_{y} = G_{0 y} + q_{y}

(20)

τ_{x y} = - 2 \frac{σ_{0} + q_{x} + G_{0 x}}{l} y

(21)

in the formula, x∈[-0.5l,0.5l], y∈[-0.5M,0.5M].

Since the force in the horizontal direction of the coal pillar (with the coordinate axis as the reference system) is symmetrical along the Y-axis and the object has been assumed to be a uniform medium, the horizontal combined stress at the point O at its form center should be 0 and should only be subjected to the pressure in the vertical direction. At this time, x=0 and y=0 are substituted into equations (19)-(21), and σ_x and τ_xy are both 0, thus verifying the accuracy and reasonableness of the above equation.

The magnitude of the principal stress at any point within the elastic barrier of the coal pillar can be obtained by combining the elastodynamic principal stress relationship equation.

At this point, considering the underground engineering problem, the damage of the surrounding rock is suitable for analysis using the Mohr–Coulomb criterion, so the expression for the stress at it critical damage is introduced.

σ_{1} = \frac{1 + \sin φ}{1 - \sin φ} σ_{3} + \frac{2 c \cos φ}{1 - \sin φ}

(22)

Where, c is the cohesion of coal body and φ is the friction angle within the coal body.

At this time, the critical size of the elastic barrier zone can be obtained by substituting any point σ_x, σ_y, τ_xy, at the boundary of the waterproof pillar into equation (22) and connecting vertical (19)-(21).To simplify the calculation,The boundary point (0,0.5M) is substituted as shown in Figure 2c, x=0 and y=0.5M (M is the thickness of the coal seam).well sorted:

l = \frac{2 M (K_{1} γ H \sin α + |q| c o s α + |σ_{0}|)}{\sqrt{|{[4 c \cos φ + 2 (|q| \sin α - K_{1} γ H \cos α) \sin φ]}^{2} - {(|q| \sin α - K_{1} γ H \cos α)}^{2}|}}

(23)

Where, according to the Cullen Moore criterion, it is obtained that

σ_{0} = \frac{1 - \sin φ}{1 + \sin φ} K γ H - \frac{2 c \cos φ}{1 + \sin φ}

(24)

Equation (23) is the expression of the critical size of the elastic barrier zone of the inclined coal pillar (inclination angle α) under the influence of water pressure q and recovery disturbance (to reflect the directionality of the force more intuitively, the force in the negative direction with the coordinate axis is therefore added to the absolute value).

And when the coal seam dip angle is 0°, it is known that sinα = 0 and cosα = 1.The critical size l of the barrier zone in the middle of the waterproof coal pillar of the horizontal coal seam can be obtained by bringing in equation (23):

l^{'} = \frac{2 M (|q| + |σ_{0}|)}{\sqrt{|{(4 c \cos φ - 2 K_{1} γ H \sin φ)}^{2} - {(K_{1} γ H)}^{2}|}}

(25)

2.3. Calculation of the Critical Length of the Elastic Barrier

It can be deduced that based on the characteristics of the overburden load on the inclined waterproof coal pillar, combined with the functional relationships between various physical parameters and the above derivation process, it is apparent that:

(1): The numerator of equation (22), K₁γHsinα+|q|cosα+|σ₀|, is exactly the main stress σ_x applied to both sides of the boundary of the elastic barrier zone of the coal pillar, and the denominator, |q|sinα-K₁γHcosα, is the main stress σ_y applied to the upper boundary of the elastic zone of the coal pillar, while the rest are the mechanical parameters of the coal pillar and its dip angle. It can be seen that the critical length of the central barrier zone is closely related to the principal stress σ_x in the inclination of the elastic zone of the coal pillar, the principal stress σ_y in the vertical direction and the inclination angle of the coal seam.
(2): By analysing equations (19)-(21) and comparing them with equation (23), we can see that when the dip angle of the seam is 0°, the forces at the bottom angle of the pillar are equal and maximum, and damage can occur at any position at the bottom of the pillar. When the inclination angle α is not 0°, the internal stresses in the pillar are greater at the corners, but the stresses at the lowest horizontal part of the pillar (e.g., the lower left corner of the pillar in Figure 2a) are the greatest, and σ_x, σ_y and τ_xy are the maximum values at this time. Therefore, when the load on the inclined coal pillar exceeds its limit, the lowest horizontal bottom angle of the pillar should be the most vulnerable to damage.
(3): In the range of inclination angle α ∈ [0°, 90°], as the inclination angle increases, the load given to the coal pillar by the residual support pressure G₀ along the inclination of the seam gradually increases, while the load perpendicular to the coal pillar gradually decreases, i.e., σ_x is proportional to the inclination angle α, and σ_y is inversely proportional to the inclination angle α. Combined with equation (23), we can obtain that the critical size of the elastic barrier zone of the water barrier coal pillar presents a characteristic proportional to the inclination angle of the coal seam.
(4): The destructive effect of water on the coal pillar is mainly reflected in two aspects. On the one hand is the pressure effect on the coal pillar, as can be seen from equations (23) -(25), with the increase of water pressure q, mainly reflected in the influence of the main stress σ_x on the tendency of the coal pillar, and the greater the water pressure, the greater the critical length. The other side is that the physical and mechanical properties of the coal rock body under water immersion will be significantly reduced, which will also affect the determination of the critical length of the elastic barrier zone of the water barrier coal pillar.

2.4. Determination of the Critical Size of MDZ and WAZ

Determining the length of mining disturbance zone(MDZ) and water pressure affected zone(WIZ) is l₁ and l₀.There are extremely well established results to draw on for the study of the critical size of the coal pillars disturbed by mining at the working face. The literature [7,8] gives an expression for the critical size of the water barrier coal pillar mining disturbance zone (MDZ) by applying the Cullen-Moore criterion and has been tested in a wide range of applications.

l_{1} = \frac{M}{2 f λ} \ln |\frac{f K_{1} γ H + c}{(λ - 1) f c \cot φ + c}|

(26)

Where, f is the friction factor between the top and bottom of the coal seam, generally f=tanφ/4; λ is the lateral pressure coefficient, generally taking the value of 2.5.

As for the formula for calculating the length of the water pressure affected zone in inclined coal seams, the literature [22] combined theoretical and empirical formulas and gave its ratio to the length of the recovery disturbance zone.

\frac{l_{1}}{l_{0}} = \frac{\cos (δ + α)}{\cos (δ - α)}

(27)

Where, α is the coal pillar inclination angle; δ is the rock seam movement angle.

Therefore, the final combined equations (23)-(27) can be obtained as the critical length of water barrier coal pillar in inclined coal seam:

\begin{array}{l} L = l_{1} + l + l_{0} \\ = [1 + \frac{\cos (δ - α)}{\cos (δ + α)}] \frac{M}{2 f λ} \ln |\frac{f K_{1} γ H + c}{(λ - 1) f c \cot φ + c}| + \frac{2 M (K_{1} γ H \sin α + |q| c o s α + |σ_{0}|)}{\sqrt{|{[4 c \cos φ + 2 (|q| \sin α - K_{1} γ H \cos α) \sin φ]}^{2} - {(|q| \sin α - K_{1} γ H \cos α)}^{2}|}} \end{array}

(28)

3. Application of Critical Size Calculation for Water Barrier Coal Pillars

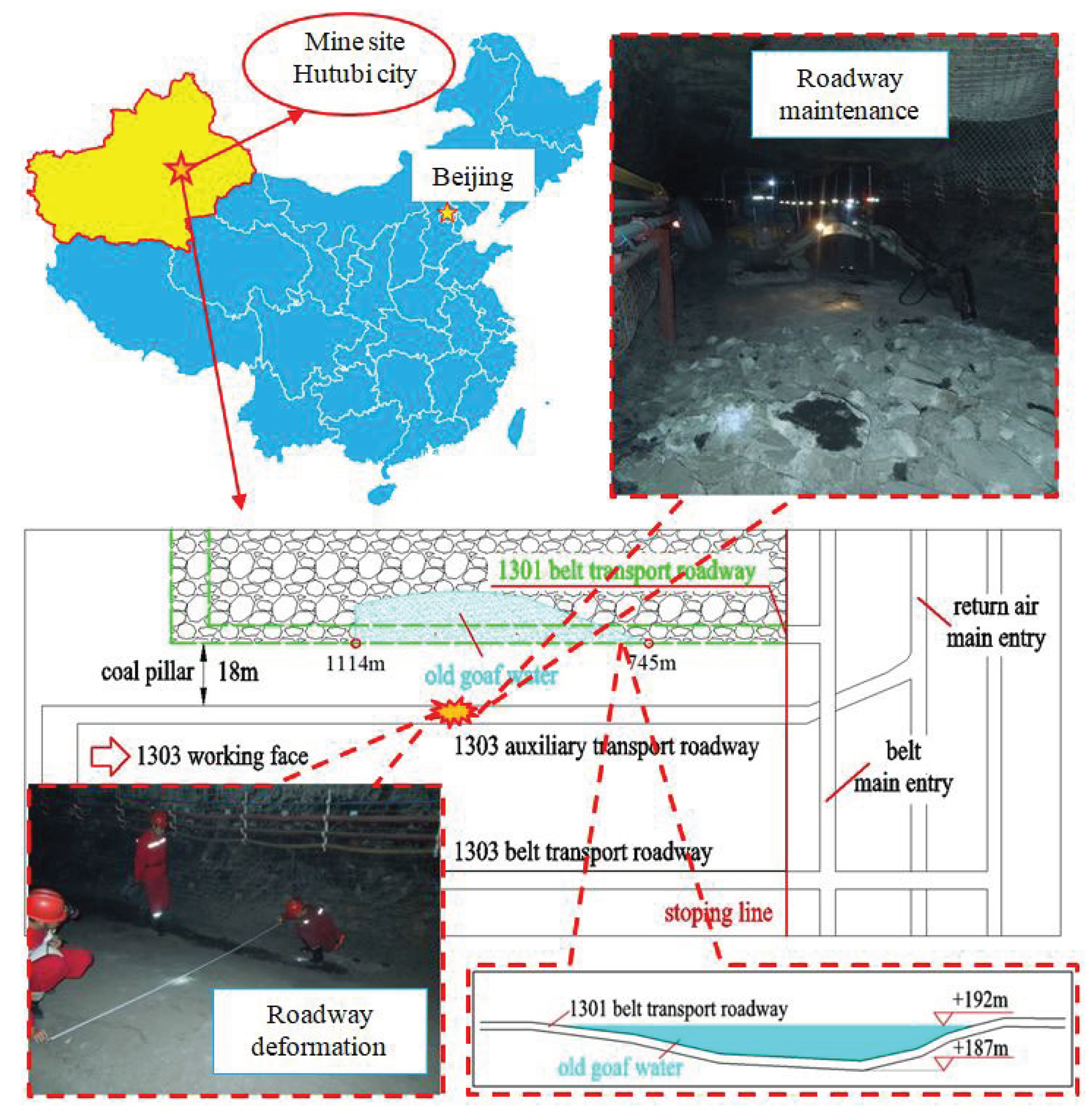
3.1. Project Overview of the Study Area

The 18m coal pillar is left between the empty area of 1301 working face and the auxiliary transport roadway of the current 1303 working face in Dananhu I mine. As a result of the fissures generated by the mining disturbance during the mining process of the upper section (1301 working face), part of the coal pillar in the section (745-1114 m section from the return wind tunnel) is affected by the water accumulation in the mining void area (Figure 3), whose accumulation elevation is +209m and is non-flow dynamic, and the maximum hydrostatic pressure is 0.26MPa. Therefore, it is important to determine the limit of stability of the water-insulated coal pillar, so as to predict whether the existing pillar can ensure the safe recovery of the working face under the influence of water.

Through multiple means, including field collection, coal rock sampling experiments and physically similar simulations, the relevant parameters required for the waterproof coal pillar calculation were finally obtained (as shown in Table 1)

3.2. Calculation of the Critical Size of the Waterproof Coal Pillar in the Study Area

Substituting the above parameters into equation (26), we can get the critical size l₁ of 2.95m for the disturbance zone of waterproof coal pillar retrieval. and then from equation (27), we can get the critical size l₀ of 4.95m for the water pressure influence zone.

Substituting the above dimensional results and related parameters into equation (24), the stress σ₀ at the junction of the plastic and elastic zones can be obtained as 6.921 MPa.

Finally, by substituting all the relevant parameters into equation (23), the critical size l of the elastic barrier zone of the coal pillar in the limit state:

\begin{matrix} l = \frac{2 M (K_{1} γ H \sin α + |q| c o s α + |σ_{0}|)}{\sqrt{|{[4 c \cos φ + 2 (|q| \sin α - K_{1} γ H \cos α) \sin φ]}^{2} - {(|q| \sin α - K_{1} γ H \cos α)}^{2}|}} \\ = \frac{2 \times 6 . 5 \times (2 \times \frac{24 . 5 \times 255 . 5}{10^{3}} \times 0 . 208 + 0 . 26 \times 0 . 978 + 6 . 921)}{\sqrt{|{[4 \times 1 . 92 \times 0 . 8878 + 2 \times (0 . 26 \times 0 . 208 - 2 \times \frac{24 . 5 \times 255 . 5}{10^{3}} \times 0 . 978) \times 0 . 46]}^{2} - {(0 . 26 \times 0 . 208 - 2 \times \frac{24 . 5 \times 255 . 5}{10^{3}} \times 0 . 978)}^{2}|}} = 11 . 19 m \end{matrix}

Therefore, in the limit state, the critical size of the inclined state waterproof coal pillar is:

L= l₁+ l+ l₀=2.95+11.19+ 4.95=19.09m

And when the coal seam inclination angle α is assumed to be 0°, the critical dimensions of the elastic barrier zone l’ and the water pressure influence zone l’0 of the horizontal state coal pillar can be obtained by substituting equations (25) and (27) as follows:

\begin{matrix} l' = \frac{2 M (|q| + |σ_{0}|)}{\sqrt{|{(4 c \cos φ - 2 K_{1} γ H \sin φ)}^{2} - {(K_{1} γ H)}^{2}|}} \\ = \frac{2 \times 6.5 \times (0.26 + 6.921)}{\sqrt{|{(4 \times 1.92 \times 0.8878 - 2 \times 2 \times \frac{24.5 \times 255.5}{10^{3}} \times 0.46)}^{2} - {(2 \times \frac{24.5 \times 255.5}{10^{3}})}^{2}|}} = 7.76 m \end{matrix}

l'_{0} = \frac{\cos (δ - 0 °)}{\cos (δ + 0 °)} = l_{1} = 2. 95 m

At this time, the critical size of the horizontal state waterproof coal pillar is

L’= l’₁+ l+ l’₀=2.95+7.76+2.95=13.66m

Therefore, taking the geological conditions of Dananhu I mine as the benchmark (excluding the coal seam inclination), the theoretical limit size is 13.66m when the coal seam inclination angle α is assumed to be 0° to leave the water barrier coal pillar; with the coal seam inclination angle α of 12° to leave the water barrier coal pillar, the width of coal pillar is 19.09m, an increase of 29%. The coal seam inclination angle has an extremely important influence on the retention of coal pillars. The width of the coal pillar left at the project site is 18m, which is close to the limit size, so it is necessary to take corresponding protective measures for the coal pillar and the surrounding roadway.

4. Elastic-Plastic Evolution of the Waterproof Coal Pillar in the Study Area

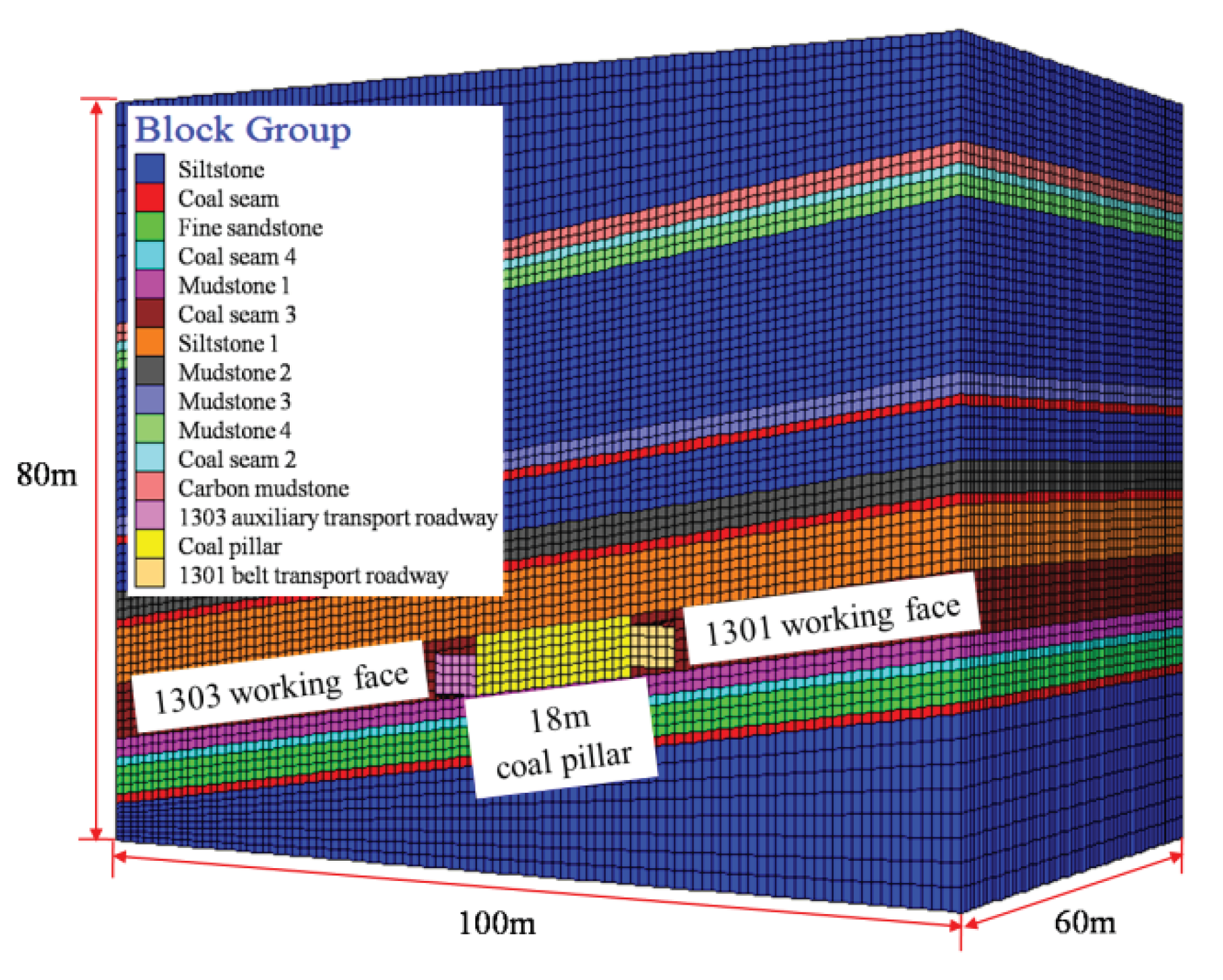
4.1. Numerical Modeling of the Study Area

Flac3D was used to study the elastic-plastic evolution process of the inclined coal pillar under the action of asymmetric load. Based on the geological conditions of the Dananhu I mine, a numerical calculation model was established, as shown in Figure 4. Based on the field exploration and rock mechanics experiments, the relevant mechanical parameters were optimised and assigned, and the physical and mechanical parameters of each rock seam are shown in Table 2.

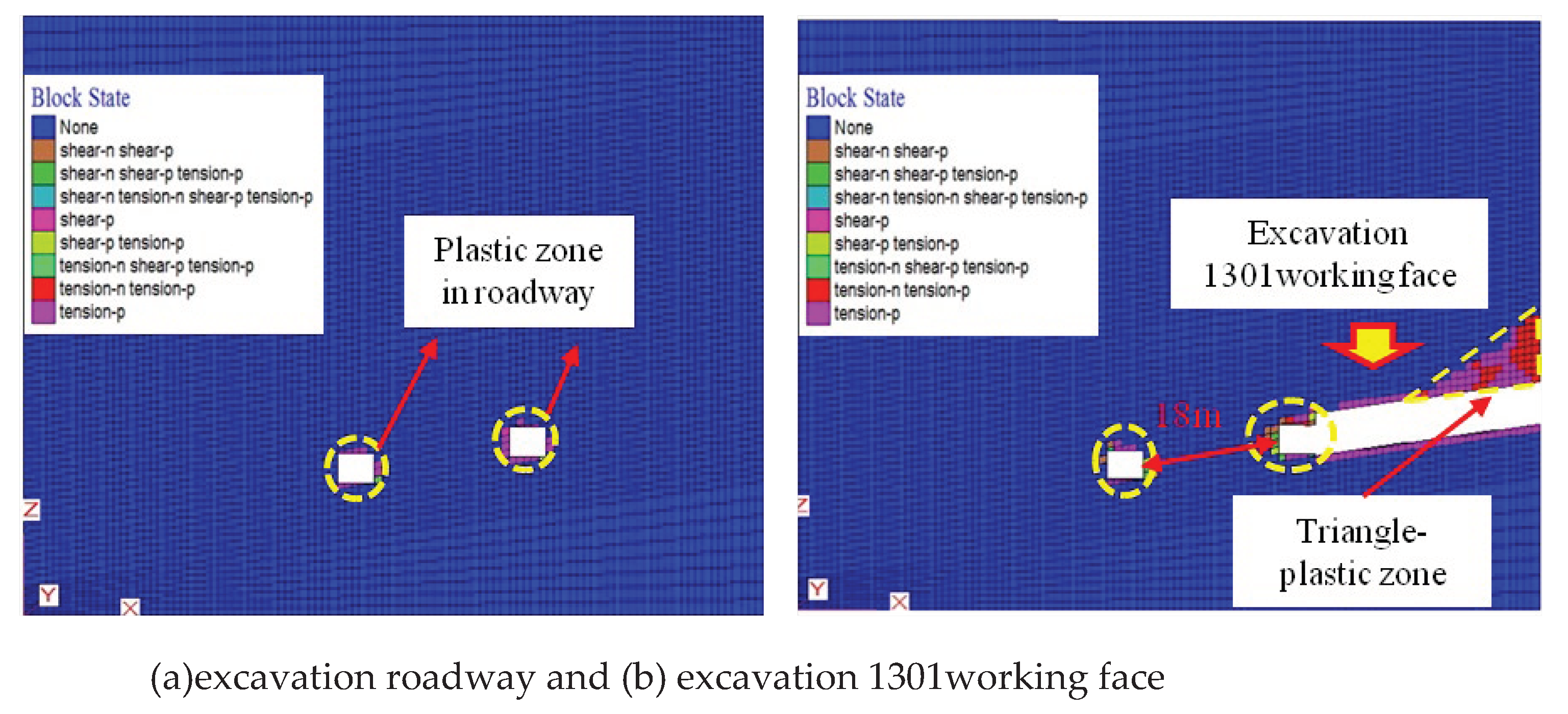
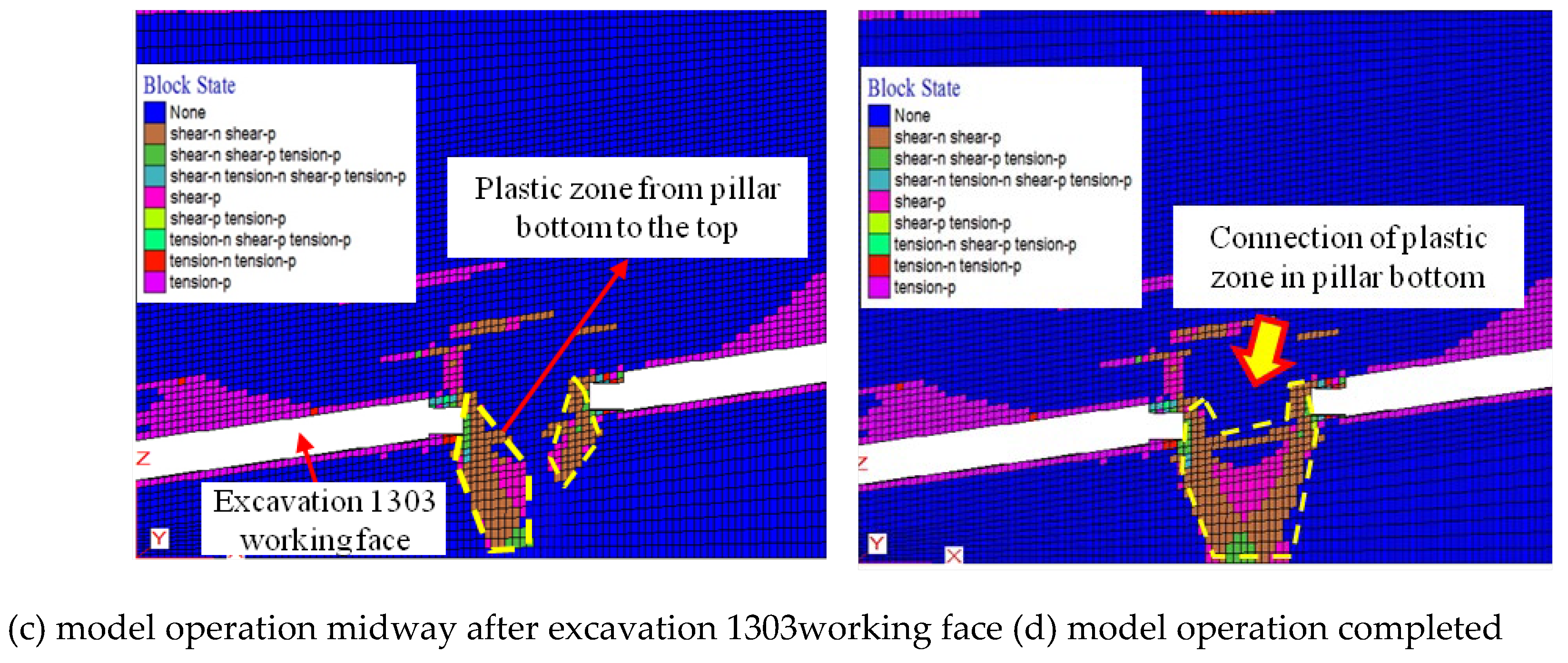
4.2. Fracture Evolution and Plastic Zone Formation Process in the Coal Pillar

Under such conditions, internal fissures in the coal pillar will gradually develop and expand, resulting in a reduction in the overall strength of the pillar and local plastic deformation. In the case of inclined coal pillar, due to the influence of its inclination angle, the force in the coal pillar will not be symmetrically distributed along its center line, which will certainly lead to stress concentration in some areas of the coal pillar and eventually the strength deterioration will occur first in the stress concentration area.

Figure 5 reflects the evolution of the transformation of the elastic and plastic zones within the inclined waterproof coal pillar during the mining process, as can be seen from the figure:

(1) From Figure 5a to Figure 5b, it can be seen that with the retrieval of the upper section working face (1301 working face) and the excavation of the roadway in this section, the internal stress equilibrium of the coal pillar is broken, and the roof plate of the 01 working face mining goaf area is broken, forming residual supporting pressure along the coal seam tendency, and finally a triangular plastic zone appears in the upper right corner of Figure 5b. At this time, the coal pillar was in a unilateral loaded state, and the fissures in the surrounding rock of the roadway on the loaded side extended and expanded, so the loose range of the surrounding rock of the roadway on the side of the coal pillar in the mining void area was about 1m larger than that of the roadway on the other side of the coal pillar, but at this time, most areas of the coal pillar were still elastic zones, indicating that the internal fissures of the coal pillar were less developed and had good stability under the unilateral loaded state.

(2) The change process from Figure 5c to Figure 5d shows that when the working face of this section (03 working face) is retrieved, the coal pillar is in the loaded state on both sides, at this time, the coal pillar is changed from unilateral pressure to pressure on both sides, and the range of its plastic zone on both sides is further increased. However, due to the influence of the coal seam inclination angle, the loading on both sides of the coal pillar is not symmetrical, which leads to the lower left corner of the coal pillar becoming the residual support pressure concentration area, at this time, the residual support pressure not only affects the stability of the coal pillar, but also by the transfer along the coal seam floor, plus the coal seam floor is mudstone with low strength, so it leads to the obvious development of fissures in the lower left corner of the coal pillar and the formation of a large plastic zone, which eventually gradually This is also consistent with the theoretical calculation of the location of the first damage to the coal pillar. This is also consistent with the theoretical calculation where the coal pillar was first damaged. During the whole process of fracture evolution and plastic zone formation, the fractures in the surrounding rock of the roadway on both sides of the coal pillar also expanded to a certain extent, which led to a significant increase in the loosening of the roadway, indicating that the stability of the roadway was also significantly reduced under the influence of mining disturbance.

(3) In the numerical simulation, the plastic zone of the coal pillar base plate is penetrated, so the plastic penetration zone will easily become the old goaf water seepage channel and eventually induce water damage. Therefore, it is necessary to carry out corresponding old goaf water prevention and coal pillar reinforcement measures in advance to ensure the safe recovery of the working face.

5. Engineering Practice

In view of the weakening of the coal pillar by the old goaf water and the characteristic that the bottom angle of the coal pillar is most easily damaged due to the inclination angle, the secondary reinforcement of the water barrier coal pillar is carried out by means of pumping and pressure relief and grouting reinforcement in the area of serious deformation of the coal pillar.

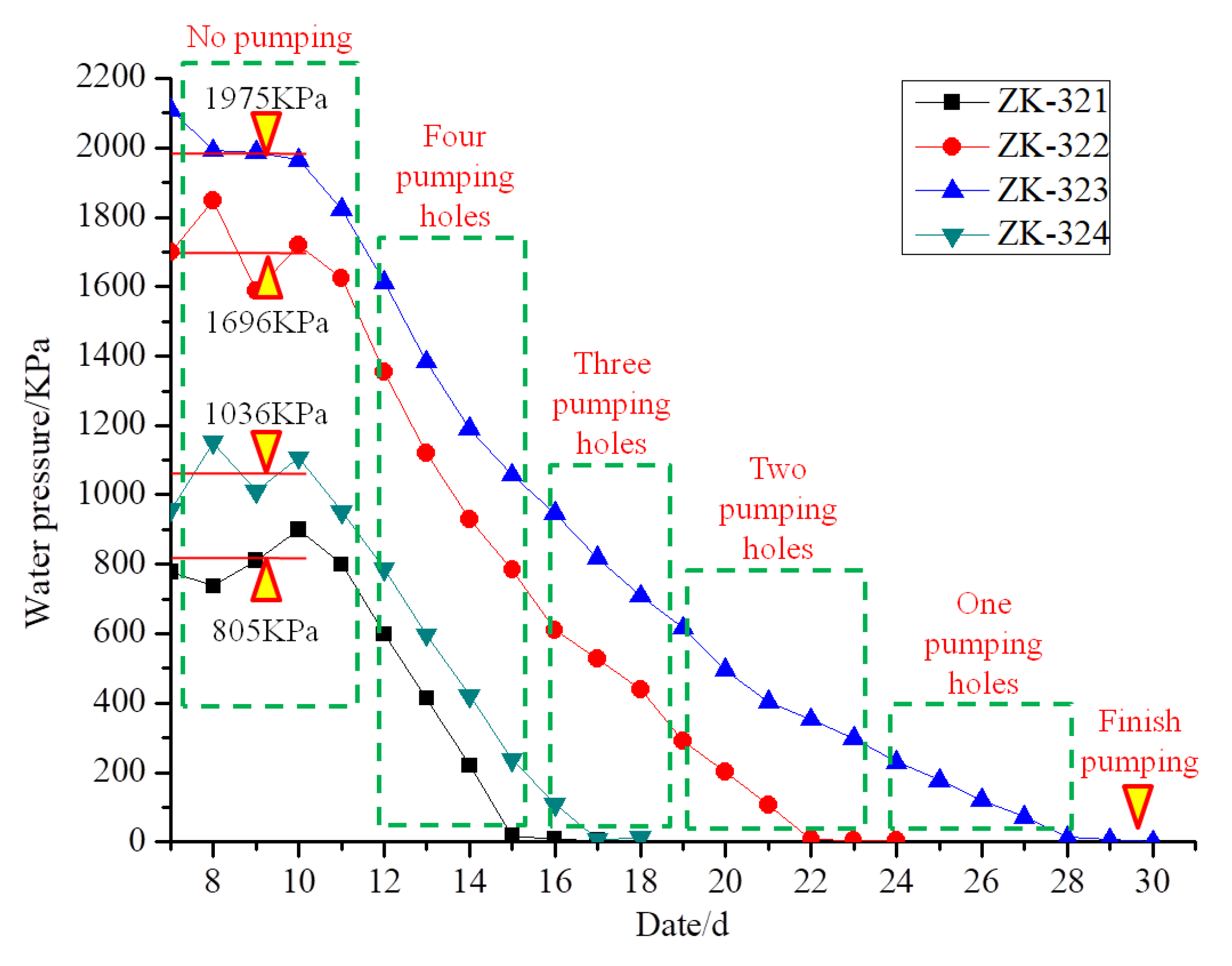
5.1. Pumping and Pressure Relief

In order to achieve the pumping and pressure relief, four pumping holes were constructed from 11 September in the water pressure affected area between 745m and 1114m in the 1303 auxiliary transport roadway (the horizontal elevation of the roadway in this area is between 183-202m) to carry out the water pumping and pressure relief works in the mining area. The locations of the four pumping holes are shown in Table 3.

The water pressure of the old goaf water measured by the borehole during the pumping process is shown in Figure 6. As can be seen from the graph, the rate of decrease in water pressure shows a gradual decrease in the process of decreasing the volume of water in the old goaf water. This is due to the fact that as the pumping works progress, the water pressure measured in each borehole also approaches 0 in turn, and therefore when a borehole is completed pumping and sealed (1m concrete seal), the total daily volume of water pumped out will decrease. Ultimately, as at October 2016, a total of 12,222m³ of water had been pumped from the Dananhu I Mine and the water pressure measured at the completion of the works was 0.028MPa, indicating that this area contains only a very small amount of old goaf water.

5.2. Grouting Reinforcement

Due to the obvious bottom drum and flaky gang phenomenon in the 1303 auxiliary transport roadway in the old goaf water affected area during the workface retrieval process, especially the bottom plate drums out obviously near the coal pillar side, as shown in Figure 7a. Therefore, in order to reduce the further expansion of the plastic deformation area of the water barrier coal pillar, polyimine gum grease was injected into the serious plastic deformation area on the coal pillar side of the tunnel, so as to achieve the purpose of closing the fissures in the surrounding rock and ensuring the structural stability of the coal pillar, as shown in Figure 7b.

As the bottom corner of the coal pillar is the starting point of plastic deformation expansion, a 42mm diameter borehole with a depth of 5m was constructed along a 45° downward direction from the coal pillar gang to inject marisan. The polyimine gum grease resin was mixed with the catalyst at a ratio of 1:1 and then injected into the coal pillar using a special polyimine gum grease grouting pump at a pressure of 8.0-18.0MPa.

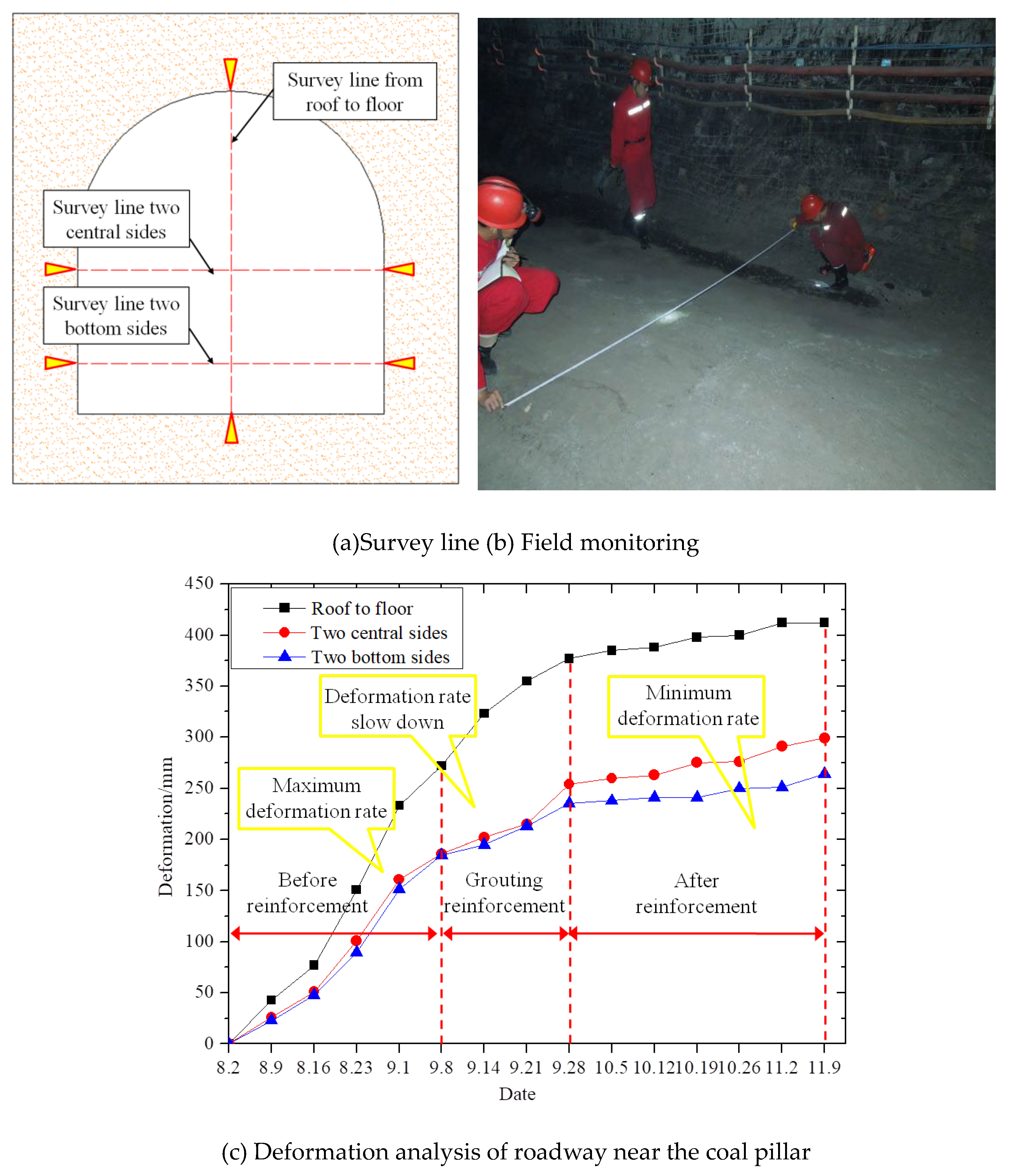
5.3. Effectiveness Test

Figure 8 reveals the deformation pattern of the surrounding rock of the coal pillar in the old goaf water affected area after taking corresponding measures. The deformation of the top and bottom plates of the roadway near the coal pillar and the two sides of the roadway were analysed in chronological order, and the overall deformation rate of the coal pillar side of the roadway showed a decreasing trend. The second stage was the period of pumping and pressure relief and polyimine gum grease injection (8 September-28 September), when the three deformation rates of the roadway were significantly reduced, including 5.6mm/d for the top and bottom plates, 3.5mm/d for the central two sides and 2.5mm/d for the lower two sides; the last stage was the post-reinforcement monitoring period (29 September-9 November), when the three deformation rates of the roadway were significantly reduced. The last stage was the post-reinforcement monitoring period (29 September-9 November), when the deformation in all three directions of the roadway was smaller, with an average of 0.84mm/d.

Through the above analysis, it can be concluded that the old void water control and coal pillar reinforcement measures have effectively curbed the expansion of coal pillar and roadway surrounding rock deformation, thus ensuring the safe recovery of the working face.

6. Conclusions

Xinjiang, as a key energy base in China’s “Belt and Road” development plan, has many coal seams that are inclined and often affected by groundwater. If mines fail to control the stability of inclined waterproof coal pillars, serious safety accidents are highly likely. Therefore, this paper conducts a mechanical analysis and numerical simulation study on the stability characteristics of the inclined waterproof coal pillar in Xinjiang mining areas under the influence of old goaf water. The findings are crucial for the safe extraction of coal resources and the promotion of stable energy supply. The specific research outcomes include:

(1) Establishing a mechanical model for the elastic barrier zone of the inclined waterproof coal pillar, and deriving expressions for the critical dimension under the asymmetric loading. The study indicates that the limit dimension of inclined section coal pillar is significantly influenced by the angle of inclination. In scenarios where other geological factors remain constant, the critical dimensions of the elastic barrier zone in inclined section coal pillar show a direct proportional relationship with the coal seam inclination. Taking the geological conditions of the Dananhu I mine as an example, the critical width of the waterproof coal pillar at a 12° inclination increases by 30% compared to when the inclination is 0°.

(2) Through numerical simulations, the evolution of the elastic-plastic zones in coal pillars in inclined sections under multiple mining disturbances is analyzed. Combined with mechanical analysis, it is found that the lowest bottom angle of the coal pillar is the first to experience failure. Numerical simulation experiments show that fractures first develop and expand at the lowest point of the pillar, leading to widespread plastic yielding, after which the plastic zone at this bottom corner extends along the floor of the coal seam towards the other bottom corner, eventually creating a channel for old goaf water seepage through the interconnected plastic zone at both bottom corners of the pillar.

(3) The study also analyzed how stress concentration in the bottom corner regions of the coal pillar, caused by overburden, is key to triggering the deterioration of pillar structural stability. Based on this, methods such as pumping water to relieve pressure and grouting to reinforce the coal pillar are used to enhance the stability of the inclined waterproof coal pillar. Field practice has shown that these measures significantly reduce the deformation rate of the coal pillar side roadway, indicating that when the coal pillar is at their critical dimensions, appropriate old goaf water prevention and stability reinforcement measures can effectively restrain the deformation of the coal pillar and surrounding rock in roadways, thus ensuring the safe extraction of the workface.

Funding

This work was supported by the Major Program of the National Natural Science Foundation of China, Grant number 52394191

Author contributions

Data curation, Pengfei Shan; Formal analysis, Helong Gu; Funding acquisition, Xingping Lai; Project administration, Wenhua Yang; Software, Xiaoqian Yuchi and Helong Gu; Validation, Pengfei Shan; Writing – original draft, Xiaoqian Yuchi; Writing – review & editing, Xingping Lai and Xiaoqian Yuchi.

Ethics Approval

The authors declare that this article does not involve human or animal experiments and does not require ethics approval.

Consent to publish

All authors have read and agreed to the published version of the manuscript.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Acknowledgment

A special acknowledgement should be shown to the anonymous reviewers for their constructive and valuable comments. Thank them for their guidance in their busy schedule.

Conflict of interest

The authors declare no conflict of interest.

References

Dong, S.N. Some key scientific problems on water hazards frequently happened in China’s coal mines. Journal of China Coal Society 2010, 35, 66–71. [Google Scholar]
Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. Journal of China Coal Society 2019, 44, 1283–1305. [Google Scholar]
Li, A.; Ma, Q.; Lian, Y.; Ma, L.; Mu, Q.; Chen, J. Numerical simulation and experimental study on floor failure mechanism of typical working face in thick coal seam in Chenghe mining area of Weibei, China. Environ. Earth Sci. 2020, 79, 1–22. [Google Scholar] [CrossRef]
Dong, L.; Tong, X.; Ma, J. Quantitative Investigation of Tomographic Effects in Abnormal Regions of Complex Structures. Engineering 2020, 7, 1011–1022. [Google Scholar] [CrossRef]
Liu, R.; He, Y.; Zhao, Y.; Jiang, X.; Ren, S. Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal. Appl. Sci. 2020, 10, 3555. [Google Scholar] [CrossRef]
Michieka, N.M. Energy and the Environment: The Relationship Between Coal Production and the Environment in China. Nat. Resour. Res. 2013, 23, 285–298. [Google Scholar] [CrossRef]
Sun, J.P.; Qian, X.H. Analysis of coal mine accidents in China during 2004-2015. Industry and Mine Automation 2016, 42, 1–5. [Google Scholar]
Xue, Y.; Ranjith, P.G.; Dang, F.; Liu, J.; Wang, S.; Xia, T.; Gao, Y. Analysis of Deformation, Permeability and Energy Evolution Characteristics of Coal Mass Around Borehole After Excavation. Nat. Resour. Res. 2020, 29, 3159–3177. [Google Scholar] [CrossRef]
Dong, L.; Hu, Q.; Tong, X.; Liu, Y. Velocity-Free MS/AE Source Location Method for Three-Dimensional Hole-Containing Structures. Engineering 2020, 6, 827–834. [Google Scholar] [CrossRef]
Dong, L.; Chen, Y.; Sun, D.; Zhang, Y. Implications for rock instability precursors and principal stress direction from rock acoustic experiments. Int. J. Min. Sci. Technol. 2021, 31, 789–798. [Google Scholar] [CrossRef]
Dong, L.; Tong, X.; Hu, Q.; Tao, Q. Empty region identification method and experimental verification for the two-dimensional complex structure. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2021, 147, 104885. [Google Scholar] [CrossRef]
Shang, H.F.; Ning, J.G.; Hu, S.C. Field and numerical investigations of gate road system failure under an irregular residual coal pillar in close-distance coal seams. Energy Science Engineering 2019, 7, 2720–2740. [Google Scholar] [CrossRef]
Shi, W.G.; Zhang, J.F.; Zhang, H.M. , et al. Structural Division and Determination of Rational Width for Waterproof Partition Coal Pillar. Chinese Journal of Rock Mechanics and Engineering 2017, 36, 1227–1237. [Google Scholar]
Cai, M.F. Key theories and technologies for surrounding rock stability and ground control in deep mining. Journal of Mining and Strata Control Engineering 2020, 02, 5–13. [Google Scholar]
Rezaei, M.; Hossaini, M.F.; Majdi, A. A time-independent energy model to determine the height of destressed zone above the mined panel in longwall coal mining. Tunn. Undergr. Space Technol. 2015, 47, 81–92. [Google Scholar] [CrossRef]
Shi, L.; Wang, Y.; Qiu, M.; Han, L.; Zhao, Y. Research on the required width of a fault waterproof coal pillar based on underground pressure control theory. Arab. J. Geosci. 2019, 12, 1–14. [Google Scholar] [CrossRef]
Mu, H.W.; Bao, Y.S.; Song, D.Z. , et al. Investigation of strong strata behaviors in the close-distance multi-seam coal pillar mining. Shock and Vibration 2021, 42, 1–14. [Google Scholar]
Xia, B.; Jia, J.; Yu, B.; Zhang, X.; Li, X. Coupling effects of coal pillars of thick coal seams in large-space stopes and hard stratum on mine pressure. Int. J. Min. Sci. Technol. 2017, 27, 965–972. [Google Scholar] [CrossRef]
Bukowski, P. Water hazard assessment in active shafs in upper Silesian coal basin mines. Mine Water Environ 2011, 30, 302–311. [Google Scholar] [CrossRef]
Wang, R.; Bai, J.-B.; Yan, S.; Chang, Z.-G.; Wang, X.-Y. An innovative approach to theoretical analysis of partitioned width & stability of strip pillar in strip mining. Int. J. Rock Mech. Min. Sci. 2020, 129, 104301. [Google Scholar] [CrossRef]
Liang, W.; Zhao, G.; Wang, X. , et al. Assessing the rock burst risk for deep shafts via distance-based multi-criteria decision making approaches with hesitant fuzzy information. Eng. Geol. 2019, 260, 105211. [Google Scholar]
Wang, S.; Li, X.; Wang, D. Mining-induced void distribution and application in the hydro-thermal investigation and control of an underground coal fire: A case study. Process. Saf. Environ. Prot. 2016, 102, 734–756. [Google Scholar] [CrossRef]
Yang, H.; Guo, Z.; Chen, D.; Wang, C.; Zhang, F.; Du, Z. Study on Reasonable Roadway Position of Working Face under Strip Coal Pillar in Rock Burst Mine. Shock. Vib. 2020, 2020, 1–21. [Google Scholar] [CrossRef]
Chen, Y.; Zhao, G.; Wang, S.; Wu, H.; Wang, S. A case study on the height of a water-flow fracture zone above undersea mining: Sanshandao Gold Mine, China. Environ. Earth Sci. 2019, 78, 122. [Google Scholar] [CrossRef]
Frith, R.; Reed, G. Limitations and potential design risks when applying empirically derived coal pillar strength equations to real-life mine stability problems. Int. J. Min. Sci. Technol. 2018, 29, 17–25. [Google Scholar] [CrossRef]
Bo, L.; Chen, Y.L. Risk Assessment of Coal Floor Water Inrush from Underlying Aquifers Based on GRA–AHP and Its Application. Eng. Geol. 2016, 34, 143–154. [Google Scholar]
Tan, Y.L.; Yu, F.H.; Chen, L. A new approach for predicting bedding separation of roof strata in underground coal mines. International Journal of Rock Mechanics and Mining Sciences 2013, 61, 183–188. [Google Scholar] [CrossRef]
Wang, R.; Yan, S.; Bai, J. , et al. Theoretical analysis of damaged width & instability mechanism of rib pillar in open-pit high wall mining. Advances in Civil Engineering 2019, 2019, 6328702. [Google Scholar]
Yu, W.; Wang, W.; Wu, G.; Yu, X.; Peng, W. Three Zones and Support Technique for Large Section Incline Shaft Crossing Goaf. Geotech. Geol. Eng. 2017, 35, 1921–1931. [Google Scholar] [CrossRef]
Yu, W.; Wang, W.; Wu, G.; Yu, X.; Peng, W. Three Zones and Support Technique for Large Section Incline Shaft Crossing Goaf. Geotech. Geol. Eng. 2017, 35, 1921–1931. [Google Scholar] [CrossRef]
Liu, R.; Ren, S.; Fan, J.; Wu, F.; William, N.T. The air-flow structure and gas dispersion behavior in gas tunnel construction through bench cut method. Therm. Sci. 2019, 23, 1417–1424. [Google Scholar] [CrossRef]
Wang, G.; Wu, M.; Wang, R.; Xu, H.; Song, X. Height of the mining-induced fractured zone above a coal face. Eng. Geol. 2017, 216, 140–152. [Google Scholar] [CrossRef]
Sun, W.; Zhang, S.; Guo, W.; Liu, W. Physical Simulation of High-Pressure Water Inrush Through the Floor of a Deep Mine. Mine Water Environ. 2017, 36, 542–549. [Google Scholar] [CrossRef]
Wang, S.; Huang, L.; Li, X. Analysis of rock burst triggered by hard rock fragmentation using a conical pick under high uniaxial stress. Tunn. Undergr. Space Technol 2020, 96, 103195. [Google Scholar] [CrossRef]
Zhang, S.; Guo, W.; Li, Y.; Sun, W.; Yin, D. Experimental Simulation of Fault Water Inrush Channel Evolution in a Coal Mine Floor. Mine Water Environ. 2017, 36, 443–451. [Google Scholar] [CrossRef]
Yu, Y.; Deng, K.-Z.; Luo, Y.; Chen, S.-E.; Zhuang, H.-F. An improved method for long-term stability evaluation of strip mining and pillar design. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2018, 107, 25–30. [Google Scholar] [CrossRef]
Liu, R. ; H. Yi; Zhao, Y.F., et al. Tunnel Construction Ventilation Frequency-control Based on Radial Basis Function Neural Network. Automation in Construction 2020, 118, 103293. [Google Scholar]
Xie, X. ; X. B. L; Shang, X., et al. Prediction of height of water flowing fractured zone based on PCA-BP neural networks model. China Saf. Sci. J. 2017, 27, 100–105. [Google Scholar]
Liu, B.; He, L.; Luo, L.P. Numerical Modeling on Fluid-Solid Coupling for the Water Proof Coal Pillar Design. Journal of Mining & Safety Engineering 2009, 26, 445–449. [Google Scholar]
Russell, F.; Guy, R. Coal pillar design when considered a reinforcement problem rather than a suspension problem. Min Sci Technol. 2018, 28, 11–19. [Google Scholar]
Liang, W.; Zhao, G.; Wu, H.; Chen, Y. Assessing the risk degree of goafs by employing hybrid TODIM method under uncertainty. Bull. Eng. Geol. Environ. 2018, 78, 3767–3782. [Google Scholar] [CrossRef]
Meng, X.; Liu, W.; Mu, D. Influence Analysis of Mining’s Effect on Failure Characteristics of a Coal Seam Floor with Faults: A Numerical Simulation Case Study in the Zhaolou Coal Mine. Mine Water Environ. 2018, 37, 754–762. [Google Scholar] [CrossRef]
Wang, Z.Q.; Chen, C.F.; Wang, L. , et al. Research on Reasonable Size of Waterproof Pillar in Mining Inclined Coal Seam. Journal of Mining & Safety Engineering, 2013, 30, 735–738. [Google Scholar]
Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. Journal of China Coal Society 2019, 44, 1283–1305. [Google Scholar]
Meng, Z.; Shi, X.; Li, G. Deformation, failure and permeability of coal-bearing strata during longwall mining. Eng. Geol. 2016, 208, 69–80. [Google Scholar] [CrossRef]
Dong, S.N. Some key scientific problems on water hazards frequently happened in China’s coal mines. Journal of China Coal Society 2010, 35, 66–71. [Google Scholar]
Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. Journal of China Coal Society 2019, 44, 1283–1305. [Google Scholar]

Figure 1. Overburden load of inclined waterproof coal pillar.

Figure 2. mechanical model of elastic barrier zone of inclined waterproof coal pillar.

Figure 3. 1303 Working face mining schematic diagram.

Figure 4. Numerical calculation model.

Figure 5. Evolution process of elastic-plastic zone in waterproof coal pillar after mining influence.

Figure 6. Water pressure measurement curve after pumping.

Figure 7. Grouting reinforcement by polyimine gum grease.

Figure 8. Effectiveness test of roadway near the coal pillar.

Table 1. Physical and mechanical parameters of coal pillar in Dananhu I mine.

Elastic zone stress concentration factor K₁	Plastic zone tress concentration factor K	Dip angle of coal seam (°)	Coal seam thickness (m)	Rock volume force γ(KN/m³)	Buried depth H(m)
2	4	12	6.5	24.5	255.5
Internal friction angle ϕ(°)	Cohesion c(MPa)	Poisson ratio υ₀	Maximum hydrostatic pressure q(MPa)	Strata movement angleδ (°)	Friction factor f
27.4	1.92	0.36	0.26	50	0.129

Table 2. Physical and mechanical parameters of the layers of Dananhu I Mine.

layer	compressive strength (MPa)	rock density (kg/m³)	bulk modulus (GPa)	shear modulus (GPa)	internal friction angle ϕ(°)	cohesion c (MPa)	poisson ratio υ₀
Siltstone	1.46	2360	7.8	2.8	29.9	5.35	0.29
Fine sandstone	1.33	2259	6.8	2.4	30	4.2	0.34
Siltstone	1.46	2360	7.8	2.8	29.9	5.35	0.29
Coal seam	0.48	1370	4.4	0.5	27.4	1.92	0.36
Mudstone	1.37	2397	6.07	1.37	29	3.07	0.28
Carbon mudstone	1.35	2400	6.8	1.9	28.6	4.07	0.28

Table 3. Layout position of pumping hole and drilling parameters in gob water affected area.

pumping holes	horizontal elevation	hole position near return air roadway	drilling parameters
ZK-321	201m	818m	drilling depth is 19m, drilling diameter is 52mm
ZK-322	192m	891m
ZK-323	187m	964m
ZK-324	199m	1037m

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer