Prerpints.org logo
Preprint
Article

Forecasting the Power Generation Mix in Italy Based on Grey Markov Models

Altmetrics

Downloads

114

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 April 2024

Posted:

02 April 2024

You are already at the latest version

Alerts
Abstract
This study considers an application of the first-order Grey Markov Model to foresee the values of Italian power generation in relation to the available energy sources. The model is used to fit data from the Italian energy system from 2000 to 2022. The integration of Markovian error introduces a random element to the model, which is able now to capture inherent uncertainties and misalignments between the Grey model predictions and the real data. This application provides valuable insights for strategic planning in the energy sector and future developments. The results show good accuracy of the predictions, which provides powerful information for the effective implementation of energy policies concerning the evolution of energy demand in the country. Despite advancements, Italy’s 2032 energy mix will still significantly rely on fossil fuels, emphasizing the need for sustained efforts beyond 2032 to enhance sustainability.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Grey Systems Theory (GST) was initiated by Julong Deng in 1982 [1] and further developed in [2]. It represents an approach aimed at forecasting systems characterized by small sample sizes and poor information. This methodology excels in managing systems where only fragments of information are known by identifying, unearthing, and refining the valuable data present. Grey systems theory has proven to be an effective strategy for handling uncertainty in information. In applied sciences, it’s common to encounter systems that are not fully understood and are supported by minimal data sets and vague information, highlighting the need to apply this theory.
Since its inception, GST has witnessed consistent expansion in terms of cross-disciplinary applications and in the diversity of its methodologies. In particular, the proposal of novel approaches and techniques for addressing data that are unknown, incomplete, or inadequate is at the core of recent developments.GST has been employed across a broad spectrum of fields, for example, in predictive scientometrics [3], energy and environmental emissions [4,5], materials science [6], engineering disciplines [7], the development of electric vehicles [8], environmental studies [9], management of water leaks [10], within the fields of economics and social sciences [11], and additional examples are illustrated in [12,13].
Generally, the Grey model G ( M , N ) comprises M-order partial differential equations and N variables. The principle of grey modelling is founded on the assumption that a process’s underlying mechanisms can be abstracted by a specific, standard partial differential equation, which mirrors the method’s degree of complexity. The estimation of model parameters is conducted through the analysis of accident data. This modelling framework is distinguished by its ability to use just four pieces of data to project future events [14]. In the literature, two single-variable grey models are predominantly utilized: the first-order G ( 1 , 1 ) and the second-order G ( 2 , 1 ) .
In practice, observed data are frequently subject to various random influences, leading to data series that exhibit unpredictability and volatility. The G M ( 1 , 1 ) forecasting model is an effective tool for data sequences with minimal data, but it struggles with sequences that exhibit significant fluctuations [15]. To overcome this issue and to increase forecast precision, the Grey Markov Chain Model M C G M ( 1 , 1 ) was created to correct the residual errors produced by G M ( 1 , 1 ) . This model merges the first-order single-variable G M ( 1 , 1 ) grey forecasting model with a Markov-chain ( M C ) model that adjusts for residuals [16,17]. This integration of models has been widely applied to datasets that are small in size but characterized by randomness and fluctuation [18,19,20]. The core concept behind the M C G M ( 1 , 1 ) model involves identifying discrete states for the residual errors from G M ( 1 , 1 ) and computing Markov probability transition matrices to grasp the statistical properties of these random residuals. Subsequently, adjustments are made based on these Markov matrices to refine the forecasting accuracy of the original G M ( 1 , 1 ) model.
In this article, we have chosen to retrace the steps of the model described above for forecasting the energy mix of primary energy consumption for Italy up to 2032.
The importance of this topic lies in the strategic planning and policy-making to meet environmental goals and energy security. Forecasting the energy mix enables the assessment of future energy scenarios, including the adoption of renewable energy sources, and helps in evaluating their impact on carbon emissions reduction and energy security. A recent application study to the Australian framework is discussed in [21].
For Italy, as part of the European Union (EU), forecasting the energy mix is crucial for aligning with the EU’s ambitious targets for reducing greenhouse gas emissions and increasing the share of renewable energy in total energy consumption by 2030 and beyond. Understanding the future energy mix aids in planning for the necessary infrastructure developments, such as grid upgrades and energy storage solutions, to accommodate an increased share of variable renewable energy sources like wind and solar power, see e.g. [22].
Moreover, forecasting the energy mix is essential for identifying potential challenges and opportunities within the energy transition. For instance, it can highlight the need for Italy to diversify its energy sources to reduce dependence on imported fossil fuels, thus enhancing energy security. It also allows for the identification of economic opportunities related to the energy transition, including job creation in the renewable energy sector and potential for technological innovation.
Furthermore, an accurate forecast of the energy mix is vital for ensuring the reliability and stability of the energy supply. As Italy moves towards a more sustainable energy system, understanding the balance between supply and demand, the integration of renewable energy and the role of energy efficiency becomes increasingly important. This insight is critical for maintaining a stable energy supply while meeting environmental targets.
In conclusion, forecasting the energy mix is of paramount importance for Italy as it navigates its energy transition. It supports strategic planning, policy development, and infrastructure investment decisions aimed at achieving a sustainable, secure, and competitive energy system.
Given the absence of prior applications of this model for this specific purpose in the literature, we have endeavoured to outline its implementation steps towards the applied results.
This study provides an insightful look into Italy’s future energy composition, using a forecasting model that integrates the Grey system theory with Markov chains to address the uncertainties in energy prediction. The obtained results reveal a significant trend towards the adoption of renewable energy sources while indicating that fossil fuels will still play a dominant role in Italy’s energy mix by 2030. This dual dependence underscores the complexity of transitioning to a sustainable energy framework and highlights the critical need for Italy to enhance its efforts in renewable energy development. The results serve as a call to action for policymakers, suggesting that while strides are being made towards a greener energy future, more aggressive policies and investments are required to reduce fossil fuel dependency significantly. This study not only sheds light on the potential energy landscape of Italy in the coming years but also emphasizes the importance of innovative forecasting techniques in planning and policy-making for energy transition.
The paper is organised as follows. In Section 2, we present the model. Specifically, in the SubSection 2.1, we illustrate the steps of the Grey Model GM(1,1), and in the SubSection 2.2, we explain how to apply the Markov chain for error adjustment. Subsequently, in Section 3, we introduce our case study focused on forecasting the consumption of primary energy from each energy source for Italy until 2032 and in Section 4 the conclusions of our work are given.

2. The Model

The GM(1,1) model employs a first-order differential equation to describe the forecasting target, and it stands as a primary tool in grey system forecasting. Additionally, the enhanced MCGM(1,1) approach, merging the principles of the GM(1,1) model with those of the Markov chain, delivers improved statistical assessments for datasets that demonstrate significant fluctuations.

2.1. GM(1,1) Model

The GM(1,1) model is widely recognized for its ability to generate reliable short-term forecasts using a limited dataset of non-negative values. In this section, we will discuss the steps required to implement this model.
Let X ( 0 ) be the vector representing the original data sequence containing n observations:
X ( 0 ) = ( x 1 ( 0 ) , x 2 ( 0 ) , . . . , x n ( 0 ) ) T .
Firstly, we perform a one-time accumulated generating operation in the following way
x k ( 1 ) = ∑ i = 1 k x i ( 0 ) , k = 1 , 2 , … , n ,
in order to create the X ( 1 ) array
X ( 1 ) = ( x 1 ( 1 ) , x 2 ( 1 ) , . . . , x k ( 1 ) , . . . , x n ( 1 ) ) T .
It should be observed that the first element of vector in Eq. (1) corresponds to the first element of vector in Eq.(2), symbolically represented as x 1 ( 0 ) = x 1 ( 1 ) .
Then, set Z ( 1 ) = ( z 2 ( 1 ) , z 3 ( 1 ) , . . . , z n ( 1 ) ) be the vector of background values computed as follows:
z k ( 1 ) = x k ( 1 ) + x k − 1 ( 1 ) 2 , k = 2 , … , n .
This is equivalent to stating that the general element z k ( 1 ) is the arithmetic mean of the two neighbouring data points.
The G M ( 1 , 1 ) equation is defined as follows
x k ( 0 ) + a z k ( 1 ) = b
where a is the developing coefficient and b is the Grey effect.
Next, the cumulative values x 1 ( 1 ) , x 2 ( 1 ) , … , x n ( 1 ) can be approximated by the first-order Grey differential equation
d X ( 1 ) d t + a X ( 1 ) = b ,
Based on the principles of Least Square Estimation (LSE), the estimation of parameters a ^ and b ^ can proceed in the following manner:
[ a ^ , b ^ ] T = ( B T B ) − 1 B T y ,
where
B = − z 2 ( 1 ) 1 − z 3 ( 1 ) 1 ⋮ ⋮ − z n ( 1 ) 1 , y = x 2 ( 0 ) x 3 ( 0 ) ⋮ x n ( 0 ) .
To calculate an estimate of the Standard Error ( S E ) associated with the parameters a ^ and b ^ we compute
S E 2 = V a r ^ a ^ b ^ = ∑ k = 1 n x k ( 0 ) − x ^ k ( 0 ) 2 n − 2 ( B T B ) − 1 ,
Finally, the solution of [6] led us to the time response function
x ^ k ( 1 ) = x 1 ( 0 ) − b ^ a ^ e − a ^ ( k − 1 ) + b ^ a ^ , k = 1 , 2 , …
Therefore, the predicted values of X ( 0 ) are:
x ^ k ( 0 ) = x ^ k ( 1 ) − x ^ k − 1 ( 1 ) = 1 − e a ^ x 1 ( 0 ) − b ^ a ^ e − a ^ ( k − 1 ) , k = 2 , … ,
given the assumption that the first value is known, that is x ^ 1 ( 0 ) = x 1 ( 0 ) .

2.2. Markov Chain Residual Modification

Observed data often fluctuate due to various random influences. Consequently, accurate forecasts with the GM(1,1) model are difficult to obtain. To overcome this problem, we integrate a Markov-chain approach to refine the residual errors. In particular, the MCGM(1,1) model merges the grey forecasting approach of GM(1,1) with a Markov-chain mechanism to adjust for residual errors. The core concept behind the MCGM(1,1) involves first identifying discrete states for the residual errors from GM(1,1), then calculating Markov probability transition matrices to understand the statistical behaviour of these residuals, and finally applying corrections based on these matrices. This process enhances the original forecasting accuracy of the GM(1,1) model. The step-by-step residual modification is described in the current section.
First, we define which residuals to be used. There are examples in the literature that show the use of absolute errors [23] and others that show the use of relative errors [20,24]. In our investigation, we focus on relative errors represented in the form
r ε k = x ^ k ( 0 ) − x k ( 0 ) x k ( 0 ) , k = 1 , 2 , … , n .
Let ε k = ( ε 1 , ε 2 , . . . , ε n ) be the chosen series of residual values, ε m i n be the minimum and ε m a x be the maximum. We split the range of residuals [ ε m i n , ε m a x ] into q intervals of the same length. The generic interval is denoted by
r w = ε m i n + ( w − 1 ) ε m a x − ε m i n q ; ε m i n + w ε m a x − ε m i n q , w = 1 , … , q .
Each of them is assumed to be a state. In particular, state 1 is the interval with the lower bound equal to ε m i n , and state q is the one with ε m a x as the upper bound.
This means that the sequence of residual values is converted into a sequence of states assuming values in the set E = { r 1 , r 2 , … , r q } . The state of residual ε k depends on which interval belongs to. The specific number of state divisions is not rigidly defined; rather, it is determined based on comprehensive factors such as the sample size and the error range of the fit [25]. Classifying them into 3 to 5 states is typically deemed suitable [26].
Now, take c w as the notation for the representative value of each state r w , w = 1 , 2 , … , q whose lower bound is l w and upper bound is u w . In some circumstances, simple choices are considered. For example, the formula proposed in [23] is a weighted average of the lower and upper bounds of the intervals:
c w = α w l w + ( 1 − α w ) u w , w = 1 , 2 , … , q ,
where α w are the weights that can be assigned to the extremes of each interval. In general, various choices are possible by producing statistical estimations of the representative values of the states of the Markov process. This is commonly done in diverse application settings, see for example [27,28]. Accordingly, we consider the following estimation formula:
c w = ∑ k = 1 n 1 { ε k ∈ r w } · ( ε k ) ∑ k = 1 n 1 { ε k ∈ r w } .
The next assumption is to consider this series of states as generated by a Markov chain { R k } k ∈ N . Hence, for every time k ∈ N , it results that
P [ R k + 1 = c j | R k = c i , R k − 1 = c h , . . . ] = P [ R k + 1 = c j | R k = c i ] = : p i j ≡ p i j ( 1 ) .
The above probabilities define the so-called one-step transition probability matrix, P = ( p i j ) i , j ∈ E .
Now, we introduce the transition probability matrix P ( m ) as an q × q matrix with elements p i j ( m ) , where i and j denote the rows and columns respectively, and m counts the number of the steps. Indeed, P ( m ) is called the m-steps transition probability matrix and represents the m-th power of the matrix P .
P ( m ) = p 11 ( m ) p 12 ( m ) ⋯ p 1 q ( m ) p 21 ( m ) p 22 ( m ) ⋯ p 2 q ( m ) ⋮ ⋮ ⋱ ⋮ p q 1 ( m ) p q 2 ( m ) ⋯ p q q ( m )
According to the Markov chain assumption, it results that
p i j ( m ) = P [ R k + m = c j | R k = c i ] .
Each element p i j ( m ) represents the probability of R k + m = c j given that R k = c i , i.e. the residual process transits from state c i to state c j in m steps. The one-step transition probability matrix is estimated as follows:
p i j ( 1 ) = t i j ( 1 ) t i , i , j = 1 , 2 , … , q .
The term t i j ( 1 ) represents the total number of transitions from the i-th to the j-th state after m = 1 step, and t i is the count of occurrences of state i within the residual sequence. To obtain the m-step transition matrix, the one-step matrix is raised to the m-th power.
Each row in P ( m ) has elements that sum to one. If the sum of a row’s elements for state i is nil because we never observed a residual belonging to the i-th interval r i , one choice could be to directly assign p i i ( 1 ) = 1 . This choice implies that state r i functions as an absorbing state.
Due to limited data, another problem may arise in the application of this model. It may be possible that a state of the process is only visited once and at the last observation of the time series of the residuals. In this eventuality, we are unable to estimate the transition probabilities over the row of the transition matrix which corresponds to the considered state. Here, the choice to characterize that state as an absorbing one poses a major risk when forecasting over a time span exceeding the observation time. In such a scenario, rendering state r i absorbing exclusively dictates the predictions, thereby introducing distortions. This is because it is unrealistic to assume that the process remains in the residual state r i until the end of the predictive interval.
Therefore, our recommendation is to assign to each element over the row an equal probability. This equates to the random initialization of errors within the system, subsequently allowing them to develop following the observed frequencies via the Markovian framework.
For example, this is equivalent to saying that for a number of states equal to r = 4 , each row element would be equal to 0.25 . In this way, when the chain reaches this particular state, it will not be absorbed by the starting state and it will be equally likely to reach in the next visit any other state.
The Markov chain method is employed to adjust the initial values obtained from the GM(1,1) model predictions revising it by adding the effect of a predicted residual. We can now describe this procedure, as follows.
Let us assume that at the current time k the residual process is in the state i, that is ε k ∈ r i = [ l i , u i ] . The GM(1,1) model produces forecasting x ^ k + m ( 0 ) of the variable x ( 0 ) for future times k + m , m = 0 , 1 , 2 … . These forecasts are adjusted according to the formula
x ^ ^ k + m ( 0 ) = x ^ k + m ( 0 ) ( 1 − ε ^ k ( m ) ) , k = 1 , 2 , ⋯ , n .
The prediction ε ^ k ( m ) can be computed conditionally on the state of the residual process R k . Thus, if the residual at time k is in state r i , the prediction is given by:
ε ^ k ( m ) = p i 1 ( m ) c 1 + p i 2 ( m ) c 2 + ⋯ + p i r ( m ) c r , k = 1 , 2 , ⋯ , n .
The prediction formula (20) expresses a m-steps forecasting.
Thus, for m = 0 , we obtain a contemporary adjustment according to the state r i given by the relation
x ^ ^ k ( 0 ) = x ^ k ( 0 ) ( 1 − c i ) , k = 1 , 2 , ⋯ , n .
which is obtained setting m = 0 into (20) and (21). Hence, the Markov chain corrects the initial prediction according to the representative value of the residual state at time k.
For m = 1 and for the residual at time k being at state r i , we obtain
x ^ ^ k + 1 ( 0 ) = x ^ k + 1 ( 0 ) ( 1 − ε ^ k ( 1 ) ) = x ^ k + 1 ( 0 ) ( 1 − ∑ j = 1 q p i j c j ) , k = 1 , 2 , ⋯ , n .
In this case, the GM(1,1) forecast x ^ k + 1 ( 0 ) is corrected according to the factor 1 − ∑ j = 1 q p i j c j which contains the expected value of the residual process at next time conditionally on the occupancy of the state r i at current time k.
In general, as m varies the model gives predictions for any future time k + m .

3. Case Study

The transition towards a sustainable and diversified energy mix is a critical challenge and opportunity for countries worldwide. Italy, with its unique geographical, economic, and social landscape, presents an intriguing case for examining how future energy consumption patterns might evolve. This case study delves into forecasting Italy’s primary energy consumption mix-up to the year 2032, employing the innovative Grey Markov Model MCGM(1,1).
The data for our study were collected from the comprehensive database of "Our World in Data" (https://ourworldindata.org/), renowned for its extensive global energy statistics. This rich dataset provided us with annual figures of primary energy consumption across various sources in Italy, measured in terawatt-hours (TWh), spanning from the year 2000 to 2022. The energy sources detailed in this dataset include Biofuel, Coal, Gas, Hydro, Nuclear, Oil, Solar, and Wind.
Table 1 presents data on primary energy consumption across various sources measured in terawatt-hours for the years 2000 through 2022. Each row represents a year, showing how much energy was consumed from each source during that year. Starting from 2000, when reliance on traditional sources like Coal, Gas, and Oil was predominant, there has been a noticeable diversification and increase in renewable energy sources over the years. For instance, Solar and Wind energy consumption started from nearly negligible amounts in 2000 but show significant growth, indicating a shift towards more sustainable energy sources. Notably, Nuclear energy consumption remains at zero. Following the Chernobyl disaster in 1986, Italy held a referendum in 1987, which resulted in the decision to discontinue the use of nuclear power for energy production. The table is a comprehensive depiction of the evolving energy landscape, highlighting the gradual transition from fossil fuels to renewable energy sources.
Primary energy is the energy that is produced when a source is burned in its raw form. It includes the energy required by the end user in the form of electricity, transportation and heating, as well as inefficiencies and energy lost during the conversion of raw materials into a usable form. Since renewable sources are reported in terms of their electricity output, they are corrected by the ‘substitution method’ for efficiency losses in fossil fuels [29]. It attempts to match non-fossil energy sources to the inputs that would be required if they were generated from fossil fuels. To this end, energy generation from non-fossil sources has been divided by a standard ‘thermal efficiency factor’ by Energy Institute [30]. In this way, it is reliable to compare inefficient fossil fuel inputs to renewable energy sources, which do not have this inefficiency.
In our analysis, we will not use the data referring to biofuel from 2000 to 2003 because they contain zero values which would affect the results unrealistically.
For illustrative purposes, let us revisit all the stages of the previously described model, employing data related to the coal energy consumption in terawatt-hours and set them as the following vector
X ( 0 ) = ( 145.580 , 154.697 , 159.678 , 172.299 , 193.013 , 191.534 , 193.911 , 189.848 , 183.701 , 143.823 , 159.028 , 178.270 , 182.733 , 157.403 , 153.447 , 143.395 , 127.732 , 111.904 , 102.567 , 77.534 , 59.253 , 65.182 , 84.773 ) T .
The vector containing the cumulative values is
X ( 1 ) = ( 145.580 , 300.277 , 459.955 , 632.254 , 825.267 , 1016.801 , 1210.712 , 1400.56 , 1584.261 , 1728.084 , 1887.112 , 2065.382 , 2248.115 , 2405.518 , 2558.965 , 2702.36 , 2830.092 , 2941.996 , 3044.563 , 3122.097 , 3181.35 , 3246.532 , 3331.305 ) T ,
and consequently we compute
Z ( 1 ) = ( 222.9285 , 380.116 , 546.1045 , 728.7605 , 921.034 , 1113.7565 , 1305.636 , 1492.4105 , 1656.1725 , 1807.598 , 1976.247 , 2156.7485 , 2326.8165 , 2482.2415 , 2630.6625 , 2766.226 , 2886.044 , 2993.2795 , 3083.33 , 3151.7235 , 3213.941 , 3288.9185 ) T .
To estimate the parameters a ^ and b ^ , we use the following matrices:
B = − 222.9285 1 − 380.116 1 ⋮ ⋮ − 3288.9185 1 , y = 154.697 159.678 ⋮ 84.773 .
Using Eq. (7) we get the estimation of the developing coefficient a ^ = 0.034 and the Grey effect b ^ = 210.598 . Meanwhile, we use Eq. (9), to compute the Standard Errors obtaining S E ( a ^ ) = 0.006 and S E ( b ^ ) = 13.320 .
Wanting to get a forecast up to 2032, which is ten years ahead of the last available data, we use Eq. (10) to get the cumulated values x ^ k ( 1 ) and Eq. (11) to get the predicted values x ^ k ( 0 ) . The results of the GM(1,1) model are shown in Table 2. Moreover, in Figure 1, coal primary and predicted energy consumption in terawatt-hours are plotted. It shows that the prediction starts with the initial available data, rises up, and follows an exponential behaviour.
Now, let us proceed with the correction of predictions through the Markov chain. Consider the initial data and compute the relative errors utilizing Eq. (12). Results are recorded in Table 2. In this series, the minimum is ε m i n = − 23.466 and the maximum is ε m a x = 80.454 . Now, we split the range of residuals [ − 23.466 , 80.454 ] into r = 4 intervals and assume each one to be a state
State 1 = [ − 23.466 , 2.514 ] , State 2 = ( 2.514 , 28.494 ] , State 3 = ( 28.494 , 54.474 ] , State 4 = ( 54.474 , 80.454 ] .
In the last column of the Table 2, states are assigned based on the interval each relative error falls into. From Eq. (15), the centers of each state are: c 1 = − 11.974 , c 2 = 12.490 , c 3 = 36.692 , c 4 = 69.54 .
Subsequently, the one-step transition probability matrix is computed through Eq. (19)
P ( 1 ) = 0.833 0.167 0 0 0.4 0.4 0.2 0 0 0.5 0 0.5 0 0.5 0 0.5 .
For example, the value 0.833 represents the probability of reaching state 1 given that the chain at the previous step was in state 1; 0.167 stands for the probability of reaching state 2 given that the chain was previously in state 1. Raising the matrix to the m-th power makes it possible to obtain the m-steps transition matrix. From the matrix in Eq. (29), we obtain the following stationary distribution
π = 0.632 0.263 0.053 0.052 .
Since we know all the real values referred to the years 2000-2022, for these years we use the one-step transition probability matrix updating the state i in Eq. (21). Whereas for the years 2023-2032 we used the state i = 2 , that is the last known state, and the matrix raised to the m − th power. Finally, once all the adjustments ε ^ k ( 1 ) are computed, Eq. (20) is used to get the adjusted GM(1,1) predictions from 2001 to 2032. See Table 2 for the results referring to the years of the sample and Table 3 for the prediction from 2023 to 2032. Figure 2 summarizes the coal primary and predicted energy consumption in terawatt-hours through the GM(1,1) model before and after the Marvokian adjustment. The dashed vertical line separates the years of our sample from the years related to the forecast. To its left, as we have previously explained, the one-step transition matrix was used, updating the forecast with the observed value each time, while on the right, the forecast was made starting from the last observed value, using the m-step transition matrix. Compared to the forecast made with the Grey Model, the Markovian correction allows for predictions that follow the trend of the observed data, enhancing the predictive capability.
All the previously described steps were repeated for each energy source, obtaining the predictions from 2023 to 2032. It should be noted that in the cases of Biofuel and Solar, it was not possible to calculate the representative values for all states because some states were never reached, as the relative errors pertained only to certain states. To overcome this problem, we employed Change Point analysis to identify the optimal point at which to truncate each data series [31]. The truncation point was determined to be in the year 2010 for Biofuel and in 2011 for Solar. After implementing these modifications, we were able to determine the representative values for each state and retrace all prior steps. In Table 4 all the GM(1,1) adjusted predictions are shown for all the energy sources while in Table 5 the estimates together with the Standard Errors (provided in parenthesis) of the developing coefficient and the Grey effect for each energy source are provided.
Table 5 contains the data relating to the estimate and the Standard Error of the developing coefficient and the Grey effect for each energy source.
The predictions highlight a steady increase in solar and wind energy, reflecting a global shift towards more sustainable and renewable energy sources. Biofuel predictions also show a consistent yet slight increase, indicating a modest contribution to Italy’s energy mix. Coal consumption, on the other hand, is forecasted to decline, echoing the broader transition away from fossil fuels. The forecast for gas and oil consumption suggests a decrease, aligning with efforts to reduce carbon emissions and dependency on non-renewable energy sources. Hydroenergy consumption shows minor fluctuations, indicating stability in its contribution to the energy mix.

4. Conclusions

In this comprehensive study, we introduced and applied the Grey Markov Model GM(1,1) integrated with Markov Chain Residual Modification to forecast Italy’s power generation mix-up to the year 2032. This approach allowed us to incorporate both the uncertainty inherent in historical data and its fluctuating nature, providing a more accurate prediction model for Italy’s energy future.
Our findings reveal a significant potential for renewable energy sources to increase their share in Italy’s energy mix, indicating a gradual decrease in reliance on fossil fuels. This transition aligns with global efforts towards more sustainable and environmentally friendly energy production methods. Notably, the model demonstrated high accuracy in predictions, affirming the integration of Grey systems and Markov chains as a robust method for forecasting in the energy sector.
The insights garnered from this study underscore the necessity for Italy’s energy policymakers to further encourage and invest in renewable energy sources. Strategic planning should incorporate the predicted shifts in energy production types, emphasizing sustainability and energy independence. Additionally, the model’s predictions can serve as a guide for adjusting current policies and devising new regulations to support the anticipated changes in the energy sector.
While this study offers valuable forecasts and insights, it also opens several avenues for future research:
  • Extending the model to other countries and regions to compare and contrast energy mix transitions on a global scale.
  • Incorporating additional variables such as technological advancements, policy changes, and economic factors that could impact the power generation mix.
  • Exploring the potential impacts of increased renewable energy adoption on grid stability, energy prices, and environmental outcomes.
In conclusion, the application of Grey Markov Models to forecast Italy’s power generation mix presents a promising tool for energy researchers and policymakers alike. By understanding future trends, Italy can better prepare for a sustainable energy future, reducing carbon emissions and fostering a resilient energy system. Further research in this area will undoubtedly refine these predictions and contribute to the global knowledge base on energy forecasting methodologies.

Author Contributions

Conceptualization, G.D.; methodology, G.D. and V.V; software, V.V.; validation, G.D., A.K. and V.V.; formal analysis, V.V.; investigation, V.V.; resources, G.D. and A.K.; data curation, V.V.; writing—original draft preparation, G.D., A.K. and V.V.; writing—review and editing, X.X.; visualization, V.V.; supervision, G.D. and A.K.; project administration, G.D.; funding acquisition, G.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the program MUR PRIN 2022 n. 2022 ETEHRM "Stochastic models and techniques for the management of wind farms and power systems".

Informed Consent Statement

Not applicable.

Data Availability Statement

The data for this study were collected from the comprehensive database of "Our World in Data" (https://ourworldindata.org/).

Acknowledgments

V.V. expresses her profound gratitude to the University of Piraeus, particularly the Department of Statistics and Insurance Science, for their exceptional support and hospitality during the visiting period.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Deng, J.L. Control problems of grey system. System & Control Letters 1982, 1, 288–294. [Google Scholar]
  2. Julong, D.; others. Introduction to grey system theory. The Journal of grey system 1989, 1, 1–24. [Google Scholar]
  3. Javed, S.A.; Liu, S. Evaluation of outpatient satisfaction and service quality of Pakistani healthcare projects: application of a novel synthetic grey incidence analysis model. Grey Systems: Theory and Application 2018, 8, 462–480. [Google Scholar] [CrossRef]
  4. Ma, X.; Lu, H.; Ma, M.; Wu, L.; Cai, Y. Urban natural gas consumption forecasting by novel wavelet-kernelized grey system model. Engineering Applications of Artificial Intelligence 2023, 119, 105773. [Google Scholar] [CrossRef]
  5. Raheem, I.; Mubarak, N.M.; Karri, R.R.; Manoj, T.; Ibrahim, S.M.; Mazari, S.A.; Nizamuddin, S. Forecasting of energy consumption by G20 countries using an adjacent accumulation grey model. Scientific Reports 2022, 12, 13417. [Google Scholar] [CrossRef]
  6. Wang, Y.; Gao, Y.; Sun, L.; Li, Y.; Zheng, B.; Zhai, W. Effect of physical properties of Cu-Ni-graphite composites on tribological characteristics by grey correlation analysis. Results in Physics 2017, 7, 263–271. [Google Scholar] [CrossRef]
  7. Tao, L.; Liang, A.; Xie, N.; Liu, S. Grey system theory in engineering: a bibliometrics and visualization analysis. Grey Systems: Theory and Application 2022, 12, 723–743. [Google Scholar] [CrossRef]
  8. Candra, C.S. Evaluation of barriers to electric vehicle adoption in Indonesia through grey ordinal priority approach. International Journal of Grey Systems 2022, 2, 38–56. [Google Scholar] [CrossRef]
  9. Tseng, M.L. Using linguistic preferences and grey relational analysis to evaluate the environmental knowledge management capacity. Expert systems with applications 2010, 37, 70–81. [Google Scholar] [CrossRef]
  10. Jing, K.; Zhi-Hong, Z. Time prediction model for pipeline leakage based on grey relational analysis. Physics Procedia 2012, 25, 2019–2024. [Google Scholar] [CrossRef]
  11. Delcea, C.; Cotfas, L.A. Advancements of grey systems theory in economics and social sciences; Springer, 2023.
  12. Delcea, C.; Javed, S.A.; Florescu, M.S.; Ioanas, C.; Cotfas, L.A. 35 years of grey system theory in economics and education. Kybernetes 2023. [Google Scholar] [CrossRef]
  13. Sifeng, L. Memorabilia of the establishment and development of grey system theory (1982–2021). Grey Systems 2022, 12, 701–702. [Google Scholar]
  14. Al-shanini, A.; Ahmad, A.; Khan, F.; Oladokun, O.; Nor, S.H.M. Alternative prediction models for data scarce environment. In Computer Aided Chemical Engineering; Elsevier, 2015; Vol. 37, pp. 665–670.
  15. Deng, J. Gray decision and prediction. Huazhong University of Science and Technology Press, Wuhan, 1986. [Google Scholar]
  16. Huang, M.; He, Y.; Cen, H. Predictive analysis on electric-power supply and demand in China. Renewable Energy 2007, 32, 1165–1174. [Google Scholar] [CrossRef]
  17. He, Y.; Bao, Y. Grey-Markov forecasting model and its application. System Engineering-Theory & Practice 1992, 9, 59–63. [Google Scholar]
  18. Morcous, G.; Lounis, Z. Maintenance optimization of infrastructure networks using genetic algorithms. Automation in construction 2005, 14, 129–142. [Google Scholar] [CrossRef]
  19. Li, G.D.; Yamaguchi, D.; Nagai, M. A GM (1, 1)–Markov chain combined model with an application to predict the number of Chinese international airlines. Technological Forecasting and Social Change 2007, 74, 1465–1481. [Google Scholar] [CrossRef]
  20. Sun, X.; Sun, W.; Wang, J.; Zhang, Y.; Gao, Y. Using a Grey–Markov model optimized by Cuckoo search algorithm to forecast the annual foreign tourist arrivals to China. Tourism Management 2016, 52, 369–379. [Google Scholar] [CrossRef]
  21. De Rosa, L.; Castro, R. Forecasting and assessment of the 2030 australian electricity mix paths towards energy transition. Energy 2020, 205, 118020. [Google Scholar] [CrossRef]
  22. Álvarez-Arroyo, C.; Vergine, S.; D’Amico, G.; Escaño, J.M.; Alvarado-Barrios, L. Dynamic optimisation of unbalanced distribution network management by model predictive control with Markov reward processes. Heliyon 2024, 10. [Google Scholar] [CrossRef]
  23. Hu, Y.C.; Jiang, P.; Chiu, Y.J.; Tsai, J.F. A novel grey prediction model combining markov chain with functional-link net and its application to foreign tourist forecasting. Information 2017, 8, 126. [Google Scholar] [CrossRef]
  24. Zhan-Li, M.; Jin-Hua, S. Application of Grey-Markov model in forecasting fire accidents. Procedia Engineering 2011, 11, 314–318. [Google Scholar] [CrossRef]
  25. Guan, J.; Feng, Y.; Ying, M. Decomposition of quantum Markov chains and its applications. Journal of Computer and System Sciences 2018, 95, 55–68. [Google Scholar] [CrossRef]
  26. Jia, Z.q.; Zhou, Z.f.; Zhang, H.j.; Li, B.; Zhang, Y.x. Forecast of coal consumption in Gansu Province based on Grey-Markov chain model. Energy 2020, 199, 117444. [Google Scholar] [CrossRef]
  27. D’Amico, G.; Di Biase, G.; Manca, R. Income inequality dynamic measurement of Markov models: Application to some European countries. Economic Modelling 2012, 29, 1598–1602. [Google Scholar] [CrossRef]
  28. Barbu, V.S.; D’amico, G.; De Blasis, R. Novel advancements in the Markov chain stock model: analysis and inference. Annals of Finance 2017, 13, 125–152. [Google Scholar] [CrossRef]
  29. Ritchie, H.; Rosado, P. What’s the difference between direct and substituted primary energy? Our World in Data 2021. https://ourworldindata.org/energy-substitution-method.
  30. Energy Institute. Statistical Review of World Energy, 2023.
  31. Kalligeris, E.N.; Karagrigoriou, A.; Parpoula, C. On stochastic dynamic modeling of incidence data. The International Journal of Biostatistics 2023. [Google Scholar] [CrossRef]
Preprints 102897 g001
Figure 1. Coal primary energy consumption observed values and predictions in terawatt-hours.
Figure 1. Coal primary energy consumption observed values and predictions in terawatt-hours.
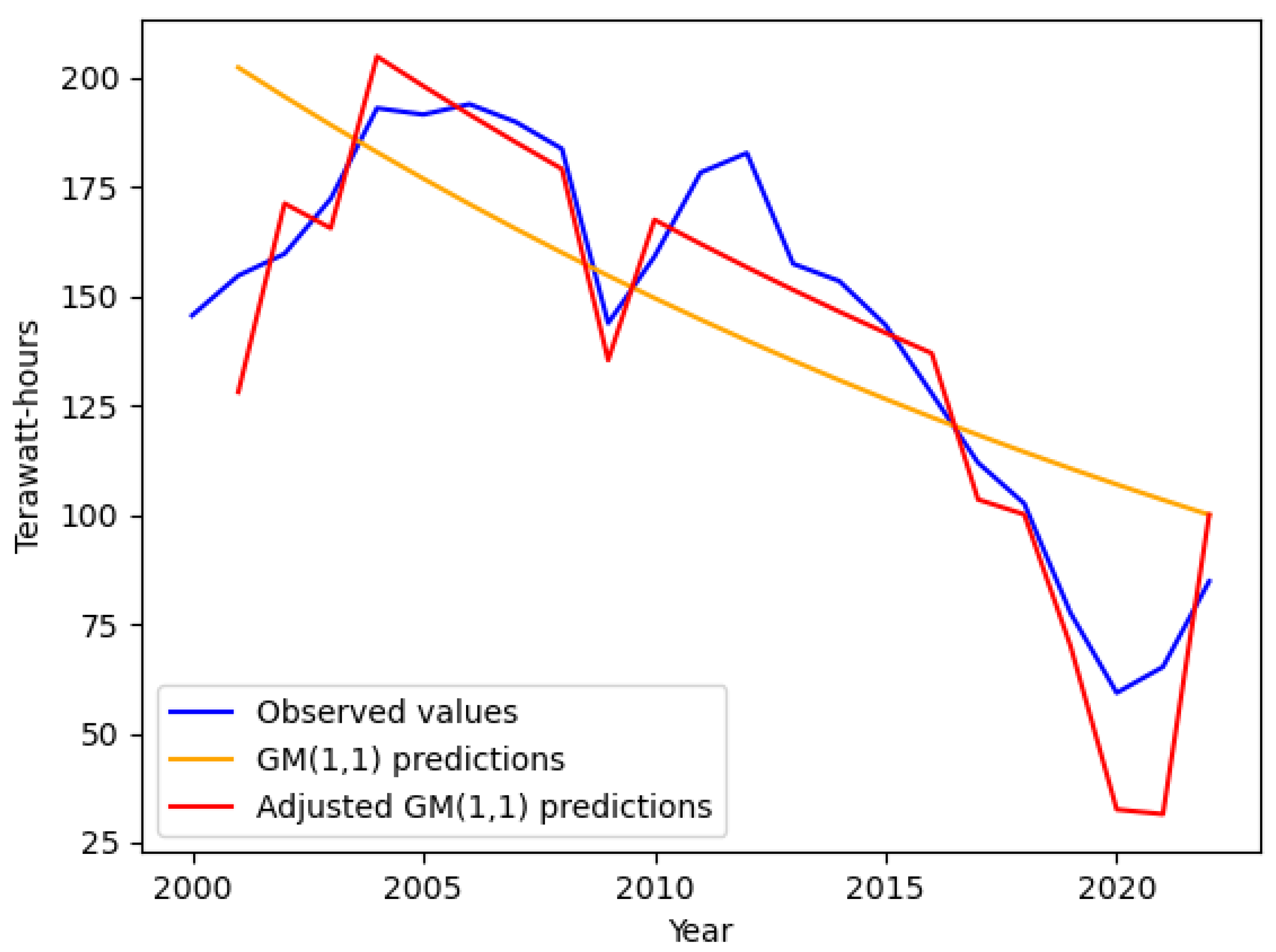
Preprints 102897 g001
Preprints 102897 g002
Figure 2. Coal primary and predicted energy consumption in terawatt-hours through GM(1,1) model before and after the adjustment.
Figure 2. Coal primary and predicted energy consumption in terawatt-hours through GM(1,1) model before and after the adjustment.
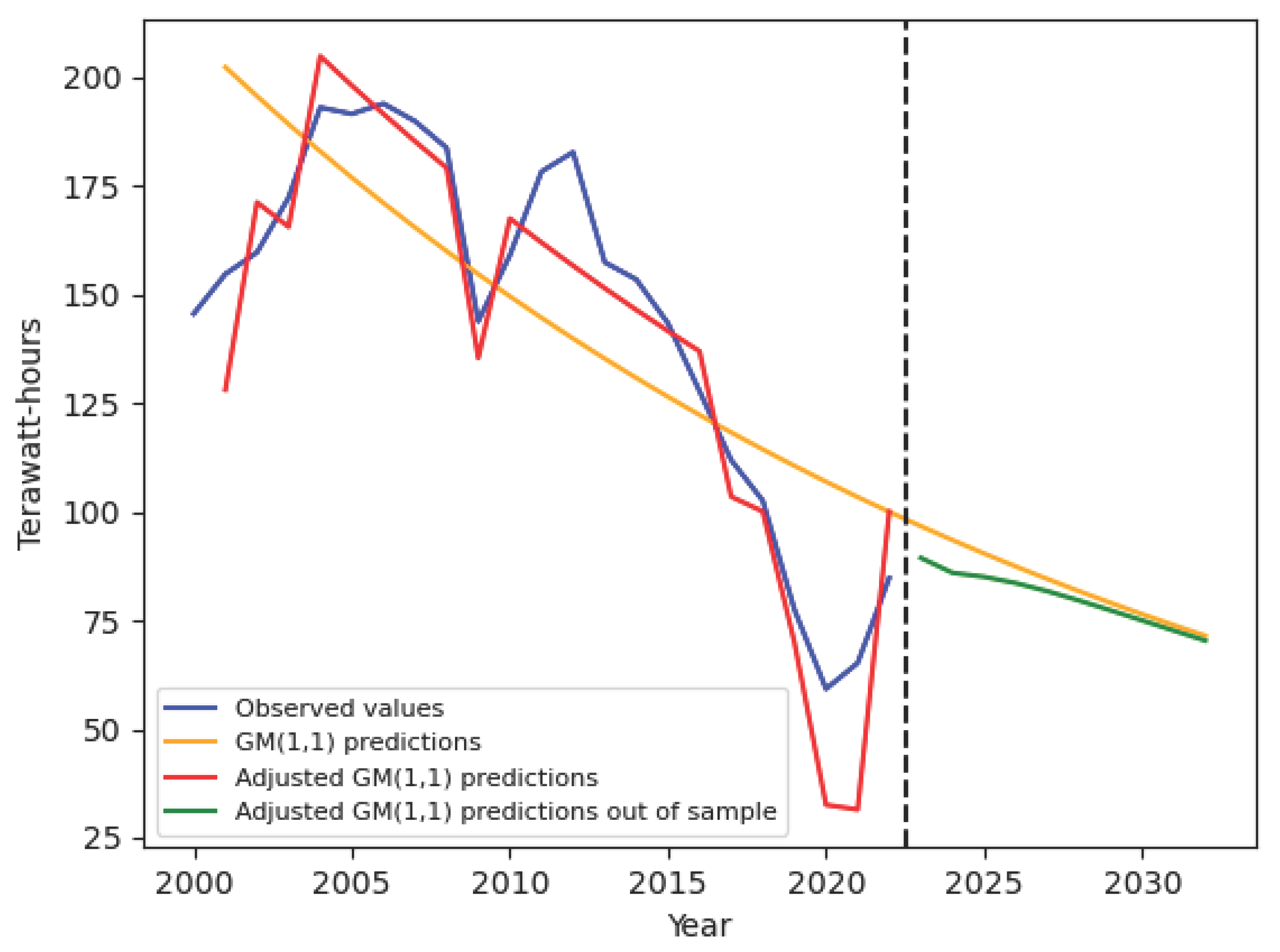
Preprints 102897 g002
Table 1. Primary energy consumption in terawatt-hours by source.
Table 1. Primary energy consumption in terawatt-hours by source.
Year Biofuel Coal Gas Hydro Nuclear Oil Solar Wind
2000 0 145.580 678.785 130.699 0 1124.703 0.053 1.665
2001 0 154.697 680.646 137.521 0 1102.603 0.056 3.464
2002 0 159.678 676.029 115.349 0 1106.428 0.061 4.098
2003 0 172.299 745.332 106.348 0 1095.877 0.070 4.228
2004 2.754 193.013 773.418 122.003 0 1072.420 0.084 5.322
2005 1.933 191.534 827.695 103.275 0 1039.467 0.089 6.709
2006 2.178 193.911 810.588 105.263 0 1038.177 0.100 8.454
2007 1.977 189.848 814.561 92.788 0 1005.712 0.110 11.407
2008 7.983 183.701 808.515 116.963 0 946.612 0.542 13.660
2009 12.885 143.823 743.176 137.228 0 875.992 1.891 18.273
2010 15.864 159.028 791.499 141.879 0 853.391 5.289 25.330
2011 15.672 178.270 742.161 126.410 0 828.881 29.782 27.190
2012 17.494 182.733 713.566 114.819 0 772.214 51.718 36.761
2013 14.687 157.403 667.404 143.831 0 706.480 58.838 40.601
2014 12.546 153.447 589.716 158.604 0 671.279 60.430 41.119
2015 15.486 143.395 643.154 122.631 0 710.444 61.783 39.974
2016 15.401 127.732 675.458 113.592 0 704.790 59.174 47.353
2017 15.610 111.904 715.788 96.335 0 713.695 64.876 47.216
2018 15.979 102.567 692.141 129.177 0 730.328 59.936 46.873
2019 9.359 77.534 707.906 122.194 0 709.052 62.443 53.252
2020 13.227 59.253 676.252 125.100 0 585.492 65.504 49.273
2021 13.822 65.182 723.737 118.766 0 652.068 65.519 54.760
2022 12.217 84.773 652.692 73.416 0 686.015 71.749 53.870
Table 2. Error analysis, state assignment and adjusted prediction for the primary energy coal consumption in terawatt-hours from 2000 to 2022.
Table 2. Error analysis, state assignment and adjusted prediction for the primary energy coal consumption in terawatt-hours from 2000 to 2022.
Year Observed value GM(1,1) prediction Absolute residual Relative error States Residual Adjustment Adjusted GM(1,1) prediction
k x k ( 0 ) x ^ k ( 0 ) a ε k r ε k w ε ^ k ( 0 ) x ^ ^ k ( 0 )
2001 154.697 202.299 47.602 30.771 3 -36.692 128.071
2002 159.678 195.623 35.945 22.511 2 -12.490 171.190
2003 172.299 189.167 16.868 9.790 2 -12.490 165.540
2004 193.013 182.924 10.089 -5.227 1 11.974 204.828
2005 191.534 176.887 14.647 -7.647 1 11.974 198.068
2006 193.911 171.049 22.862 -11.79 1 11.974 191.531
2007 189.848 165.404 24.444 -12.875 1 11.974 185.210
2008 183.701 159.945 23.756 -12.932 1 11.974 179.098
2009 143.823 154.667 10.844 7.540 2 -12.490 135.349
2010 159.028 149.562 9.466 -5.952 1 11.974 167.472
2011 178.27 144.627 33.643 -18.872 1 11.974 161.945
2012 182.733 139.853 42.880 -23.466 1 11.974 156.600
2013 157.403 135.238 22.165 -14.082 1 11.974 151.432
2014 153.447 130.775 22.672 -14.775 1 11.974 146.434
2015 143.395 126.459 16.936 -11.811 1 11.974 141.602
2016 127.732 122.285 5.447 -4.264 1 11.974 136.928
2017 111.904 118.250 6.346 5.671 2 -12.490 103.481
2018 102.567 114.347 11.780 11.485 2 -12.490 100.065
2019 77.534 110.573 33.039 42.613 3 -36.692 70.002
2020 59.253 106.924 47.671 80.454 4 -69.540 32.569
2021 65.182 103.395 38.213 58.626 4 -69.540 31.495
2022 84.773 99.983 15.210 17.942 2 -12.490 87.495
Table 3. Adjusted prediction of coal primary energy consumption in terawatt-hours from 2023 to 2032.
Table 3. Adjusted prediction of coal primary energy consumption in terawatt-hours from 2023 to 2032.
Year GM(1,1) prediction Residual Adjustment Adjusted GM(1,1) prediction
k x ^ k ( 0 ) ε ^ k ( m ) x ^ ^ k ( 0 )
2023 96.683 -7.545 89.389
2024 93.493 -8.062 85.955
2025 90.407 -5.951 85.027
2026 87.424 -4.378 83.596
2027 84.538 -3.329 81.724
2028 81.748 -2.639 79.591
2029 79.050 -2.185 77.323
2030 76.442 -1.887 74.999
2031 73.919 -1.691 72.669
2032 71.479 -1.562 70.363
Table 4. Primary energy consumption prediction in Italy in terawatt-hours from 2023 to 2032.
Table 4. Primary energy consumption prediction in Italy in terawatt-hours from 2023 to 2032.
Year Biofuel Coal Gas Hydro Oil Solar Wind
2023 11.461 89.389 694.271 94.266 573.561 70.008 76.235
2024 12.234 85.955 669.458 110.202 548.961 72.172 83.317
2025 11.370 85.027 675.409 111.143 537.014 73.477 91.057
2026 11.212 83.596 664.983 110.941 525.465 75.121 99.517
2027 10.991 81.724 663.762 110.773 512.196 76.688 108.762
2028 10.709 79.591 657.744 110.583 497.767 78.346 118.867
2029 10.471 77.323 654.454 110.387 482.989 80.010 129.910
2030 10.231 74.999 649.780 110.192 468.365 81.726 141.979
2031 9.995 72.669 645.926 109.997 454.118 83.469 155.169
2032 9.766 70.363 641.687 109.802 440.312 85.256 169.584
Table 5. Estimate and the associated Standard Error of the developing coefficient and the Grey effect for each energy source.
Table 5. Estimate and the associated Standard Error of the developing coefficient and the Grey effect for each energy source.
Year Biofuel Coal Gas Hydro Oil Solar Wind
a ^ 0.023 0.034 0.006 0.002 0.031 -0.021 -0.089
(0.008) (0.006) (0.003) (0.005) (0.001) (0.003) (0.010)
b ^ 16.745 210.598 777.177 121.821 1198.075 54.432 10.875
(0.922) (13.320) (26.369) (8.766) (24.775) (1.170) (2.765)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated