Preprint
Article
Numerical Coupling between a FEM Code and the FVM Code OpenFOAM by Using the MED Library
Altmetrics
Downloads
109
Views
43
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 April 2024
Posted:
03 April 2024
You are already at the latest version
Alerts
Abstract
This paper investigates a numerical code coupling technique to tackle multi-physics and multi-scale simulations using state-of-the-art software packages that typically address some specific modeling domain. The coupling considers the in-house FEM code, FEMuS, and the FVM code OpenFOAM, by exploiting the MED library from the SALOME platform. The present approach is tested on a buoyancy-driven fluid flow within a square cavity, where the buoyancy force constitutes the coupling term. In uncoupled scenarios, momentum and temperature equations are solved both in FEM and FVM codes without data exchange. In the coupled setting, only the OpenFOAM velocity and the FEMuS temperature fields are solved separately and shared at each time step (or vice versa). The MED library handles the coupling with the addition of suitable ad-hoc data structures that perform the field transfer between codes. Different Rayleigh numbers are investigated, comparing the outcomes of coupled and uncoupled cases with reference literature results. Additionally, a boundary data transfer application is presented to extend the capabilities of the coupling algorithm to coupled applications with separate domains. In this problem, the two domains share interfaces and boundary values on specific fields as fluxes are exchanged between the two numerical codes.
Keywords:
Subject: Engineering - Energy and Fuel Technology
1. Introduction
In the last few decades, the performance increase of computational tools has gained more and more attention from the scientific community. In Computational Fluid Dynamics (CFD), accuracy and efficiency remain challenging, especially when dealing with complex systems. Thus, interest in using multi-scale and multi-physics numerical tools to conduct complex and realistic simulations has grown. The evaluation of the whole system requires a modeling effort for all the various scales and interactions associated with its different components together with the development of numerical tools capable of analyzing phenomena across multiple scales and physics [1,2,3].
Nowadays, several computational codes have been developed to solve problems involving different engineering aspects, from physics (at every scale), chemistry, biology to mathematics. In this context, the concept of High-Performance Computing (HPC) assumes a central role as it enables the possibility to address complex and sophisticated problems by using additional computational power.
On the other hand, the simulation of very complex systems is still challenging due to the different phenomena scales. For this reason, the existing codes are developed to address, in general, only a family of problems. For instance, we can find, in the open-source framework, a plethora of simulation software that can tackle a subset of the physical systems we are interested in. We can refer to codes such as OpenFOAM [4], TrioCFD [5], and code_Saturne [6] for fluid-dynamics simulations. These codes can solve the Navier-Stokes equations, in their incompressible and compressible variations, multiphase flow, turbulence phenomena (at different scales, through RANS, LES or DNS), and so on. Several solvers are available in the thermomechanical field, including elasticity problems and fracture propagation. Among them, we can mention Code-Aster [7] or TFEL/MFront [8]. Codes such as Dragon/Donjon have been developed to tackle neutronic problems. Additionally, other open-source FEM-based numerical platforms such as libMesh [9], Deal-II [10], and FEniCS [11] are widely used to solve generic PDE problems.
For the simulation of highly complex problems, the capability of modeling different physics coming from various application domains is necessary. However, none of the cited codes can manage the full complexity of any given physics phenomena. Two main strategies have been explored to simulate these complex multi-scale and multi-physics problems. One way is to develop a new numerical code to model all the relevant physical phenomena. This strategy is commonly referred to as monolithic approach. Alternatively, one can choose to couple existing and validated codes. This second approach is a technique that can integrate multiple codes to leverage their respective strengths and enhance simulation capabilities. For instance, we can think about the simulation of a nuclear reactor, for which every physics is tightly coupled to all the others (i.e., the neutronics, the thermal-hydraulics, the heat exchange, and thermal-mechanics behavior, and possibly the presence of multiphase issue). The code coupling technique can be a reasonable strategy to exploit the different code peculiarities and avoid the necessity to develop a new computational tool that incorporates all the necessary features. By doing so, we can benefit from using codes that have already been extensively validated and from their expertise developed over many years. Therefore, this strategy focuses on a framework suitable coupling between different codes by exchanging efficiently output and input data (i.e., directly coupling the codes in memory and not through writing and reading from external files) [12].
This paper presents a coupling strategy by exploiting the open-source MED and MEDCoupling library to link the in-house FEMuS code with the well-established OpenFOAM software. FEMuS is a multigrid finite element code that contains solvers for many different physical problems [13]. We use two multi-physics examples to show the code coupling methodology, where some physical output variables are taken from the first code and are considered input data for the second code and vice-versa.
The paper is organized as follows. A brief introduction to the computational environment and an insight into the two codes adopted for this work is given in the next section. Then, the coupling strategy for the involved codes is introduced with a detailed description of the numerical algorithm. Finally, two examples of numerical code coupling between FEMuS and OpenFOAM are discussed: a coupled application with the exchange of volumetric fields and another where the exchange is limited to some boundary fields. Numerical results are provided and compared with literature data of the same physical problems performed with the monolithic approach.
2. The NumericalPlatform Environment
A numerical platform has been developed at the Department of Industrial Engineering of the University of Bologna to enhance numerical codes’ portability and communication. The NumericPlatform [14] for engineering applications is based on PDE models in the field of FEM (Finite Element Methods) and FVM (Finite Volume Methods). The platform integrates different physical models that deal with fluids and solids using finite elements (FE) and finite volumes (FV) discretization techniques. It also provides for the coupling of algebraic and differential PDE models implemented on different domains, typical of system and CFD simulations for multiscale coupling. The purpose of the platform is to create a numerical environment for multiphysics and multiscale simulations, such as nuclear reactor systems, through the FEMuS computational capabilities and communication with other solvers. This latter feature of coupling and data exchange allows exploiting the code’s strengths in simulating different physical aspects, avoiding the necessity to write new solvers for physics that are not (yet) supported and instead making use of highly validated ones, saving time and resources that are crucial when dealing with highly complex simulations.
The NumericPlatform has been developed with several environments for different levels of users: one suitable for the development and coupling of the FEMuS in-house code and another ready for the deployment of engineering applications. In the latter case, this environment provides data entry for input/output using CAD/Mesh Generators and visualization/post-processing with tools typical of the SALOME [15] computational platform (i.e., Paraview [16]). In particular, the input/output data are managed by the MED and HDF5 libraries. Implementations of the PDE models on FE and FV discretization are available from different codes. Among others, the OpenFOAM and FEMuS libraries, which have been augmented with a suitable set of routines supporting the MED libraries usage paradigm, are the codes of interest for this application.
In the following, brief introductions on the finite element FEMuS and finite volume OpenFOAM codes are given, as well as on the SALOME platform and the MED library functionalities.
2.1. FEM Code: FEMuS
The Numeric Platform computational environment revolves around the in-house multigrid finite element library FEMuS, a C++ code exploiting different open-source libraries, such as PETSc [17] for linear algebra and LibMesh [9] for the creation and handling of a hierarchy of meshes. It contains several solvers for the incompressible Navier-Stokes equations, heat transfer, Fluid-Structure Interaction, multiphase flows, and optimal control with the adjoint method [13]. The FEMuS code has, among others, the advantage of easy implementation of new models by directly encoding the constitutive equations, suitably discretized according to the FEM paradigm, through direct C++ code. This approach streamlines the process of integrating novel formulations, enhancing the versatility and adaptability of the simulation framework. For example, an anisotropic four-parameter turbulence model has been implemented, including nonlinear thermal models for the closure of the turbulent heat flux, to simulate low Prandtl number fluids with the RANS methodology. In this framework, it is possible to effectively simulate new physical phenomena like the complex dynamics of turbulent flows in non-conventional fluids such as liquid metals. Interested readers can find further FEMuS solvers and applications in [18,19,20,21,22,23].
Apart from its solver capabilities, the FEMuS library has been extended to support the coupling of the finite element library outcomes with external codes with a MED-compatible C++ interface relying on the SALOME platform.
2.2. FVM Code: OpenFOAM
The OpenFOAM software is a well-known open-source and object-oriented C++ library mainly developed for computational fluid dynamic simulation purposes, separately maintained by ESI and the OpenFOAM foundation [4]. Its versatility, scalability, and extensive suite of solvers and libraries make it one of the most used codes in computational frameworks, enhancing researchers and engineers to simulate a wide range of phenomena with relatively high fidelity. OpenFOAM offers a comprehensive and robust platform for modeling complex fluid dynamics scenarios across several disciplines, ranging from aerodynamics and multiphase flows to turbulence and the intricate interplay of heat transfer phenomena. Its modular architecture ensures strong adaptability, allowing expert users to integrate new modules, functionalities, and models tailored to their research needs. Moreover, the active and engaged community surrounding OpenFOAM fosters a collaborative environment for developing new ideas and solving problems. This collective effort ensures continual development and optimization, keeping the code at the forefront of scientific research and engineering innovation while providing access to community resources such as tutorials and user-contributed enhancements.
The OpenFOAM software package exploits the well-known Finite Volume modeling technique (FVM), widely adopted in the numerical modeling of fluid flow. By implementing library routines for linear systems discretization, the computational domain is divided into discrete elements, commonly referred to as cells, where the system(s) of PDEs is solved. In addition to its solver capabilities, the software is distributed with auxiliary tools for static and dynamic mesh manipulations, library functions for pre/post-processing, and utilities for the parallelization of the computational effort.
2.3. The MED and MEDCoupling Library from the SALOME Platform
A coupling procedure has been implemented by leveraging the MED and MEDCoupling libraries to exploit the FEM and FVM strengths, enhancing the result accuracy. This library is a specific module of the SALOME platform for data retrieving, manipulation and sharing at a memory level, thereby avoiding the slowness connected to the use of on-disk files. The MED library is a low-level implementation of an abstraction layer for data structures that can be manipulated and stored in the HDF5 format. The MEDCoupling library, on the other hand, is one of the available modules of the SALOME platform environment and the core library on which this coupling work relies on. It leverages on the MED coupling for the exchange format and implements algorithms for the distribution and interpolation of fields.
SALOME is a numerical platform developed by CEA and EDF with the aim to provide an advanced open-source platform for Computer Aided Engineering (CAE) purposes [24]. This platform is equipped with several modules (GUI, Shaper, Geometry, Mesh, Fields, YACS, HexaBlock, Homard, ADAO, EFICAS, JobManager, ParaViS, SOLVERLAB, etc.) able to handle every step of the simulation process and the integration of external codes. In fact, the platform is envisioned by its authors as “a powerful open source parametric CAD modeler, a multi-algorithm mesh generator/editor, a computational code supervisor, and many data analysis and processing tools”[15].
Here, we are mainly interested in exploiting the MESH module of SALOME for the mesh creation (exported in MED format), as well as its communication capabilities and ability to handle meshes and fields. To achieve this, we can leverage the MED-file library module, a C++ library designed for reading and writing MED files. Additionally, the SALOME environment offers additional capabilities targeted to coupling procedures. These include the supervisor, which generates simulation workflows connecting the different computational units, and the FIELDS and MEDCoupling library. The latter plays a significant role in data communication by providing powerful tools for the manipulation of input and output data resulting from simulations performing data movement, analysis, conversion, and optimization. Among its functionalities, the crucial ones are reading/writing from/to files, aggregating and exchanging data, performing interpolation, format conversion, and renumbering or partitioning data for multiprocess workflows. In the following, we will refer to the MED and MEDCoupling libraries with only the MED name for simplicity.
3. Coupling Procedure through the MED Library
This section explains in detail the coupling approach implemented between the two CFD codes, FEMuS and OpenFOAM that will be used for the numerical demonstrations in the following sections. This procedure can easily be generalized to additional software with minimum modifications, mainly by translating the internal data structures into the MED format. It is essential to point out that this framework scales optimally with the number of computational codes that are connected: adding a new library implies the development of a single wrapper of its data fields in the MED coupling format instead of developing specific procedures to couple the new code to each of the other libraries in the platform. In other words, the coupling strategy follows a hub-and-spoke model instead of a point-to-point approach that would require a significant effort to add new software. A schematic example of the two coupling models is reported in Figure 1.
The coupling application implements three different classes designed for data transfer and synchronization. The first class acts as the intermediary between OpenFOAM and the MED library by extracting the numerical field data from the internal data structures into an object compatible with the MED format. This class is the interface OpenFOAM-MED that we named of_interface. Similarly, the second class, femus_interface, is the interface between FEMuS and the MED library, enabling the use of the numerical field data within the FEMuS framework. Finally, the third class, namely med_class, is responsible for managing the operations within the MED library itself. It includes tasks such as data storage, retrieval, and data manipulation. An additional feature available in this class is the possibility to interpolate a field insisting on a mesh to a different mesh discretization.
In the following, we generally refer to Code 1 and Code 2: the reader can interchangeably substitute them with FEMuS and OpenFOAM. Figure 2 illustrates the coupling procedure. At the supervisor level, the main function manages the interaction between the two codes and their associated interface structures with specific solver functions. Firstly, it manages the initialization and setup of both Code 1 and Code 2, ensuring they are correctly configured and ready to interact. This involves initializing the two problems and the respective interface structures including an exchange mesh and its numerical fields. Moreover, the supervisor function manages the synchronization of the simulation time steps between Code 1 and Code 2. This enforces that both codes progress together to maintain consistency in the coupled simulation. At each time step, the supervisor coordinates the exchange of fields, updating solutions, and monitoring convergence criteria.
This framework can be exploited in various simulations involving coupling between volume or boundary fields. For simulations requiring volume field transfer, the application allows the exchange of numerical data representing physical quantities distributed in the whole computational domain. On the other hand, simulations involving boundary field transfer focus on the interaction between different physical domains or interfaces within the computational domain. By transferring boundary conditions, forces, or constraints between Code 1 and Code 2, we can simulate complex fluid-structure interactions, conjugate heat transfer processes, and multi-phase flow phenomena. For both these two types of coupling, the main structure of the algorithm remains consistent. In the following sections, the algorithm implemented is described.
3.1. Coupling Algorithm
As illustrated in Algorithm 1, in the initial step of the coupling process, both Code 1 and Code 2 are required to generate a mesh copy in MED format corresponding to the computational domain (or a portion of it). Both interface classes of Code 1 and Code 2 feature a function named init_interface(), used for extracting essential information to recreate the mesh in MED format. This function assigns the interface name for reference at the supervisor level and retrieves the mesh connectivity, coordinates, and mapping data necessary to link the data structure of the code mesh with that of the MED mesh. Since the FEMuS code employs Finite Element Method (FEM) and handles biquadratic fields, its mesh is biquadratic. However, for coupling with the OpenFOAM problem, which operates with linear meshes, the interface to the MED coupling implements a linear mesh. Therefore, holding the information from the original biquadratic mesh, we extract the data to create a corresponding linear mesh for the FEMuS coupling interface. Once the interface classes have stored the necessary information, the MED library can generate a copy of the mesh in MED format. The function responsible for managing the creation of the mesh is called create_mesh(), and it belongs to the med_class class.
At this stage, both codes have their respective copies of the mesh in MED format. Following the creation of meshes, both codes initialize the fields to be exchanged. We have implemented two distinct functions within the med_class, that are init_med_field_on_nodes() and init_med_field_on_cells(). The first creates and initializes a MED format field of type MEDCoupling::MEDCouplingFieldDouble on mesh nodes, setting it to zero. In contrast, the other function performs a similar operation but targets mesh cells instead of nodes.
In these functions, an array of type MEDCoupling::DataArrayDouble is generated for each field that is required by the specific coupling procedure. This format enables the MED library to effectively set the values of the MED field based on the stored data.
Both codes have now completed the initialization at the supervisor level through their dedicated functions within their respective classes. Moreover, the interfaces for the data transfer have been configured with their corresponding MED mesh copies and MED fields. At the supervisor level, the process can start the time loop.
The time loop begins with the execution of the solver functions within Code 1, which are responsible for solving the system of governing equations of the specific physics being modeled. Once Code 1 has completed its computations and obtained a solution, the internal fields are transferred to the corresponding MED fields. This transfer process involves a sequence of functions. Firstly, the interface class of Code 1 uses the function get_field_from_Code1() to extract the solution of the field from Code 1. Next, within the med_class class, two functions are employed: fill_med_array(), which sets the field values into the corresponding DataArrayDouble, and update_med_field(), which sets the array into the MED field.
At this step, a projection function can be used when a source field from Code 1 has to be interpolated from the source mesh to a target grid suitable for Code 2. The MED library provides a range of functions tailored to this functionality. It is important to highlight that the interpolation functions are available for (e.g., cell-wise) and (e.g., node-wise) fields, both targeting intensive or extensive fields.
 |
These interpolation algorithms can combine different field types, e.g. it is possible to interpolate from to , from to , from to , and from to . In this application, a to interpolation scheme is employed, requiring that both fields from FEMuS and OpenFOAM be represented as cell-wise fields. Given that FEMuS uses biquadratic fields, it becomes necessary to convert the solution into a cell-wise field. To achieve this conversion, an interpolation algorithm specifically designed for converting (biquadratic field) to field is employed after the extraction of the solution from FEMuS. Therefore, the interpolation() function from med_class is called. This function is used to interpolate the MED field from Code 1 to a MED field over a MED mesh of Code 2. The MED field interpolated over the mesh of Code 2 is now available (directly in memory) as a MED object. With an inverse process, it can be stored as the solution of Code 2 using the interface function set_field_to_Code2(). In the scenario where Code 2 is FEMuS, an interpolation algorithm from to field must be used before calling the set_field_to_Code2() function. This is necessary to ensure compatibility between the cell-wise field format required by the coupling framework and the biquadratic solution format required by FEMuS.
With the solution provided by Code 1, Code 2 can proceed to solve its specific physics. Once the solution of the system of equations in Code 2 is obtained, it provides the field to be exchanged back to Code 1 using a mechanism analogous to the previous one. The interface function get_field_from_Code2() is called to extract solution from Code 2, while fill_med_array() and update_med_field() are employed to set the solution of the Code 2 into the corresponding MED field. Then the interpolation() function is used to interpolate the MED field from Code 2 to the target MED field associated with Code 1. Finally, this interpolated field is written into Code 1 using the set_field_to_Code1() routine.
Once Code 1 receives the solution from Code 2, the data exchange between the two codes is completed. With both codes now equipped with the necessary fields, the time loop can proceed to the next time iteration at the supervisor level. This iterative process is repeated at each time step until the end of the simulation.
4. Numerical Results
In this section, we present two numerical examples that show the capabilities of the algorithm described above. The idea is to analyze two different aspects of the data transfer between numerical codes. Specifically, volume and boundary field transfer are investigated since both situations represent realistic applications. The first example is a buoyant-driven cavity where different codes solve the velocity and temperature fields, while the second one is a conjugate heat transfer problem between two different domains where temperature and heat flux are exchanged. For both applications, the mathematical problem is described with appropriate boundary conditions, and the numerical results are compared with literature reference data for the same application setting.
4.1. Buoyant Driven Cavity
In the following section, a first numerical application is presented to show the simulation results of a code coupling procedure between volume fields, taking reference data from the literature as a benchmark. The simulation setting is depicted in Figure 3, where a square cavity is considered as the numerical domain for the resolution of Navier-Stokes and temperature equations. In this case, we can consider a Newtonian and incompressible fluid for which a two-dimensional setting has been investigated. In particular, these equations are coupled though the buoyancy term. Therefore, considering the velocity , the pressure p and the temperature T, we have
where is the kinematic viscosity, the density, the coefficient of thermal expansion, the thermal diffusivity, the reference temperature and Q the volumetric thermal source. We recall that represents the divergence operator, ∇ is the gradient, while the Laplacian. For all the presented tests, a laminar behavior of the flow has been considered.
Regarding the boundary condition, we impose a no-slip boundary condition for the velocity field at every boundary edge. For the energy equation, both Dirichlet and Neumann boundary conditions are used. In particular, we impose the temperature on two opposite edges, creating a hot and a cold wall, while on the remaining edges, an insulation condition has been imposed, according to Figure 3. Furthermore, the volumetric thermal source Q was set to zero for every numerical simulation.
As we know from the literature, the form of the solution to this problem depends on the non-dimensional Rayleigh number that is defined as , where L is the reference length of the domain. Referring to Figure 3, we have . Moreover, the reference temperature is set to the mean value between and for every specific simulation. The numerical tests have been performed for different numbers, ranging from up to and compared with reference data. Specifically, this problem has been described in several works [25,26,27,28,29].
Regarding the numerical approach, four different approaches are presented and analyzed. Two simulations have been performed by solving the system of equations (1) considering a monolithic solution with the FEMuS code (F) and OpenFOAM (), taken as reference. The other two cases use the code coupling technique: in the first case (), the temperature is solved in FEMuS and the velocity in OpenFOAM, and vice-versa in the second case (). In the two latter procedures, we recall that the coupling between the codes takes place through two terms in the equations: the buoyancy term, which requires the temperature field in the momentum equation, and the advection term in the energy equation, which is computed via the velocity field coming from the momentum equation. This is a necessary condition for the cases and to satisfy the problem described in (1). In particular, the field transfer is performed considering the volumetric value of the specific field, so for each cell of the target mesh, the field is interpolated from the source mesh by using the MED structures described in the previous section. The entire volumetric field is transferred between the two codes, adopting the same discretization for the domain, even if the FEM codes consider biquadratic quadrilateral elements while the FVM code uses linear quadrilateral elements.
4.1.1. Volume Data Transfer Algorithm
Following Algorithm 1, we outline the procedure employed for the coupling application involving volume data transfer. In both coupling cases and , the init_interface() and create_mesh() are used to create a MED mesh object of the entire domain. The FEMuS problem can use either a 2D or a 3D mesh, according to the problem dimension. In contrast, OpenFOAM can handle only 3D meshes, even for 2D problems. Since we are addressing this latter mesh dimension in this context, the volume mesh used by FEMuS consists of a 2D computational grid. Consequently, the MED meshes employed in this scenario consider a 2D mesh for FEMuS and a 3D mesh for OpenFOAM with a single cell across the third dimension.
The initialization of MED fields over the MED meshes involves calling the routine init_med_field_on_cells() to initialize a cell-wise temperature field and a cell-wise velocity field for both codes throughout the entire computational domain. We name the temperature field over MED meshes as temp_P0_2Dmesh for FEMuS and temp_P0_3Dmesh for OpenFOAM. Similarly, the velocity field is denoted by vel_P0_2Dmesh and vel_P0_3Dmesh for FEMuS and OpenFOAM, respectively.
We describe the algorithm for the coupling case since the case is entirely similar but with the fields swapped. Once the time loop is started, FEMuS first solves the temperature equation as described in (1). Then, the get_field_from_femus() function is called to extract the temperature solution. Given that FEMuS solves for a biquadratic temperature field, an interpolation from to is performed to correctly pass the data to OpenFOAM, which works with fields. Following this, the fill_med_array() and update_med_field() functions are used to set the temp_P0_2Dmesh field. At this point, the interpolation() routine is used to interpolate temp_P0_2Dmesh into the MED mesh from OpenFOAM to obtain the target MED field temp_P0_3Dmesh. The function set_field_to_OpenFOAM() set the interpolated field into the OpenFOAM temperature field, used to compute the buoyancy term within the Navier-Stokes equation. Once OpenFOAM has solved the system of equations, the velocity field is extracted using get_field_from_OpenFOAM() routine and set to the vel_P0_3Dmesh field. Then, the interpolation function computes the vel_P0_2Dmesh to be passed to the FEMuS code. This field must be first interpolated using the to interpolation scheme and then written into the velocity field of FEMuS using the routine set_field_to_femus(). In the following time iteration, FEMuS uses this updated velocity field in the advection term of the temperature equation.
4.1.2. Simulations Results
The numerical fields resulting from the computation have been non-dimensionalized with the following
where represents the Dirichlet boundary condition for the temperature on the cold wall. Naturally, by considering these new variables such as the non-dimensional temperature , the non-homogeneous Dirichlet boundary conditions change their specific values: on the cold wall we now have , while on the hot one, we have . Therefore, the numerical results are described by using only the non-dimensionalized variables.
In Figure 4, Figure 5, Figure 6 and Figure 7 isolines of the contour of the velocity magnitude (), the non-dimensional velocity components () and the non-dimensional temperature () are reported for four numbers (from up to ) for the two coupling algorithms ( and ). Reference results of the physical field contours can be widely found in the literature for this kind of problem. For this reason, the interested reader can refer to [29] and references therein. For every case of number, the contour isolines are in agreement with those in the literature.
In Table 1 a grid convergence analysis is reported for the maximum value of the component evaluated at , for the case of . In particular, three types of grid size have been investigated, corresponding respectively to 400, 1600, and 6400 elements (), for each of the four simulation setups. The four simulations show the same convergence behavior, with a similar value for the finest grid solution. A comparison with [12] for the same simulations has been reported since we have used the same grid refinement. It can be noticed that our results are consistent with the ones already published.
In Table 2 and Table 3, we report the maximum value of the non-dimensional velocity components, and evaluated respectively at the planes and with different numbers and compare them with the same data taken from the literature.
In general, a good agreement can be noticed for the maximum value of the non-dimensional velocity components. For the case of , however, a slight difference is present concerning other literature data, although the four simulations presented in this work exhibit values close to each other.
In Figure 8 and Figure 9 the non-dimensional velocity components and the non-dimensional temperature are reported for every type of the four simulations (F, , , ) and for every number. A comparison with literature data from [29], symbolized with circular markers, is also highlighted. Specifically, these plots refer to the variables’ behavior at specific points in the domain: the line for the component and the line for the component and the temperature .
Regarding the latter variable, the plotted domain is restricted to (apart from ) since the literature data con be found only this interval. Moreover, for the same , a good agreement with reference data published in [29] is present for every case and every type of simulation, including both coupled algorithms. For this reason, we do not provide a zoom on specific regions of the non-dimensional temperature plot since the lines of the four simulations are almost overlapping. The same trend can also be seen for the component, while some discrepancy can be noticed for the component in the case of . On the other hand, each of our simulations seems to produce the same numerical solution, confirming the goodness of the simulations and coupling procedure. We provide a zoom of the plot in the region close to the maximum/minimum of the velocity components to better highlight the slight differences between the four simulations and the literature results.
4.2. Conjugate Heat Transfer (CHT)
In this section, we present the second application implemented to test the data transfer between a FVM code and a FEM code in the domain defined by Figure 10. This test aims to investigate the data transfer through a boundary that connects these two domains. In this context, we analyze a Conjugate Heat Transfer problem that describes a thermal exchange between two regions of different materials. In particular, we consider the heat exchange through a physical boundary between a solid and a fluid region. This kind of application finds significant attention in several scientific and engineering applications, such as solar heating [30], heat exchange [31] and nuclear energy production [32].
The solid is modeled as a two-dimensional isotropic material with constant material properties. Two domains are considered where different equations are solved. The first region represents a solid domain in which only the temperature equation has been solved, while in the second region, the momentum and temperature equations are solved for a buoyant fluid, employing the same system of equation described in (1). The only parameter which describes the temperature distribution in the solid is the thermal diffusivity , which is defined as
where k is the thermal conductivity and the thermal capacity of the solid domain. Therefore, the heat equation in the solid reads as
We recall that in the following discussion, the physical field has been non-dimensionalized, thus, the temperature field T is transformed into the corresponding by using (2).
The peculiarity of this kind of physical setup is the mutual exchange of the boundary conditions values at the interface between the two regions. At the common interface, the fluid problem is equipped with a non-homogeneous Dirichlet boundary condition while the solid problem uses a non-homogeneous Neumann boundary condition. Specifically, the temperature field in the solid at the boundary is used as the boundary condition for the fluid region, while the heat flux computed at the same interface for the fluid region is the boundary condition for the temperature equation of the solid.
Therefore, for the solid, two homogenous Neumann boundary conditions have been imposed for the top and bottom boundaries as a fixed temperature is imposed on one lateral side (the cold wall). Otherwise, on the opposite wall (interface), a computed in the fluid region is imposed at every time step.
Regarding the fluid region, the boundary conditions for the velocity field are the same as the cavity configuration presented in the previous section. For the temperature field, the top and bottom walls are described with a homogeneous boundary condition, while the other two boundaries are equipped with a fixed temperature field. When, in one side, a non-dimensional temperature is fixed (hot wall), the interface has a changing temperature field in agreement to the solution of the temperature equation in the solid region. A schematic representation of the direction for the exchanging of physical quantities can be seen in Figure 10. Here, the grey-colored solid region is graphically separated from the fluid one with a dashed line, through which the flux (wavy line, ) and the temperature (solid line, ) are exchanged.
4.2.1. Boundary Data Transfer Algorithm
The method used for the coupling application involving boundary data transfer follows a procedure similar to the algorithm described in paragraph 4.1.1. In this scenario, we aim to couple the boundary between the solid and the fluid region within a 2D problem. Hence, the interface structures consist of a 1D mesh for FEMuS and a 2D mesh for OpenFOAM. After the interfaces and the meshes are created, the fields to be exchanged are initialized. In this instance, the fields to be transferred between the codes are the temperature at the boundary and the wall heat flux through the same boundary. Thus, we generate two MED fields for storing FEMuS data: a cell-wise heat flux field (qs_P0_1Dmesh) and a temperature field (temp_P0_1Dmesh). Similarly, corresponding MED fields are initialized for OpenFOAM: qs_P0_2Dmesh and temp_P0_2Dmesh.
At the beginning of the time loop, OpenFOAM solves the governing equation for the fluid and the temperature equation. It then computes the wall heat flux to be transferred to FEMuS. The qs_P0_2Dmesh is first extracted from the solution of OpenFOAM with the function get_field_from_OpenFOAM() and then stored in a MED field over the corresponding mesh. The heat flux provided by OpenFOAM is interpolated over the target mesh to obtain the target field qs_P0_1Dmesh. This field is then written into the FEMuS solver as a non-homogeneous Neumann boundary condition using the set_field_to_femus() routine. It is worth noting that the to interpolation is needed before the solution is written into the boundary since the field provided by OpenFOAM has a cell-wise approximation. The updated boundary condition is then used by FEMuS to solve the temperature equation within the solid domain, as described in (4). After obtaining the temperature solution in the solid, the get_field_from_femus() function is invoked to retrieve the solution at the boundary domain. With the inverse mapping this solution is first converted into a field and then interpolated over the OpenFOAM boundary to yield the temp_P0_2Dmesh field. This field is used as a Dirichlet boundary condition for OpenFOAM as the boundary temperature is updated using the set_field_to_OpenFOAM() routine. At this stage, control is turned back to OpenFOAM, where it continues the task of solving its equations in the following time step.
4.2.2. Simulations Results
A schematic representation of the physical configuration is reported in Figure 10, where the mutual exchange of the boundary conditions at the interface is depicted. Note that the fluid region is described by a squared cavity of dimension . In this work, two geometric configurations are considered to take into account the solid region with thickness of and , where l is the length side of the cavity. The physical and geometrical configuration have been implemented following the work of Basak et al. [33], with the idea of reproducing numerical results described in literature.
Several physical and geometrical configurations have been analyzed in [33], changing the number, the number, the conductivity ratio K, the solid wall thickness t and its geometrical position (hot side or cold side). Regarding K, this parameter is defined as the ratio between solid and fluid thermal conductivity as
where the subscripts s and f refer to solid and fluid regions, respectively.
We present the numerical simulation of these tests considering only a few configurations. In particular, the number has been considered fixed and equal to , while two numbers have been considered ( and ). Three values of K have been investigated, equal to , and . Concerning the solid wall position, only one configuration has been taken into account, where the solid represents the cold side of the physical domain.
Regarding the initial condition for the temperature field, it is worth noting that two different thermal conductivity are present in the whole simulated region (fluid + solid) for which we have that . Therefore, the linear behavior of the temperature distribution between cold and hot walls, which is the initial condition, has to take into account two different with two different region widths. In our simulation, we fix the initial temperature as
where represents the initial temperature on the interface and is equal to , with and the width of the two regions. Naturally, Equation (6) arises from the well-known solution of the temperature distribution inside a wall with two different regions, but no advection. Considering the boundary conditions on , which reads on the cold wall (solid) and on the hot wall (fluid), this initial condition ensures that the temperature flux is always with the right sign, i.e., the thermal flux passes through the common boundary from the fluid to the solid region.
In Figure 11, Figure 12 and Figure 13, the contour of the non-dimensional temperature and the velocity stream function are reported for the simulated cases. Considering the non-dimensional temperature, we can notice a different behavior for the isolines with different conductivity ratios K. When , the largest part of the temperature gradient is located in the solid region, while for values of , the same consideration can be drawn for the fluid region. Naturally, increasing the number, we re-obtain the classical temperature isolines of a buoyant cavity, where the isolines distribution still follows the previous discussion of the conductivity ratio K. These considerations can be applied also in the case of a solid wall thickness equal to .
Regarding the velocity stream function , the major difference can be noticed between the simulations with a different number: for the order of magnitude is lower than one while for we reach values up to 8. Also, the conductivity ratio K influences this value, for which an increase of K produces an increase in the stream function magnitude.
In Figure 14, the local Nusselt number on the interface is reported for the case of the solid wall thickness equal to . This parameter has been computed as the normal gradient of the non-dimensional temperature on the interface and represents the total ratio between the convective and the conductive heat transfer over the boundary interface. In particular, we have
A comparison with reference literature data is reported with the white circular markers (data from [33]) and the gray markers obtained with the boundary data algorithm presented in this work. A good agreement can be noticed for every reported case. A slight overestimation concerning the literature data is obtained for the case with and .
5. Conclusions
In this work an algorithm for the numerical coupling of a Finite Volume code (OpenFOAM) and a Finite Element code (FEMuS) is presented by using an external library (MED). The code coupling relies on volumetric and boundary data exchange over the simulated domain without using external files. The algorithm is suitable for multiphysics simulations where different codes with different fields of application can be coupled based on their specific field features.
Specifically, we have presented two types of data exchange: a volume and a boundary data transfer. The volume coupling considers the volume transfer data in a buoyant-driven cavity problem. The boundary coupling cosider a conjugate heat transfer problem between a solid and a fluid. In the first application, we tested the code coupling through the buoyancy term in the momentum equation, while in the second application, the coupling was performed by considering the thermal boundary condition on the interface between the two regions. For the buoyant cavity application, the coupling has been performed in two ways, firstly solving the momentum equation in OpenFOAM and temperature in FEMuS and then switching the equation to solve between the two codes. Both simulation results of the two applications show good agreement with the same applications already presented in the literature. Future works will investigate the capability of the presented algorithm to exchange additional physics, such as turbulence modeling with the aim of enhancing the OpenFOAM models with specific thermal turbulence models available in the FEMuS code.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Drikakis, D.; Frank, M.; Tabor, G. Multiscale computational fluid dynamics. Energies 2019, 12, 3272. [Google Scholar] [CrossRef]
- Groen, D.; Zasada, S.J.; Coveney, P.V. Survey of multiscale and multiphysics applications and communities. Computing in Science & Engineering 2013, 16, 34–43. [Google Scholar] [CrossRef]
- Cordero, M.E.; Uribe, S.; Zárate, L.G.; Rangel, R.N.; Regalado-Méndez, A.; Reyes, E.P. CFD Modelling of Coupled Multiphysics-Multiscale Engineering Cases. Comput. Fluid Dyn.-Basic Instruments Appl. Sci, 2018. [Google Scholar]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International workshop on coupled methods in numerical dynamics; 2007; Volume 1000, pp. 1–20. [Google Scholar]
- Angeli, P.E.; Bieder, U.; Fauchet, G. Overview of the TrioCFD code: Main features, VetV procedures and typical applications to nuclear engineering. In Proceedings of the NURETH 16-16th International Topical Meeting on Nuclear Reactor Thermalhydraulics; 2015. [Google Scholar]
- Archambeau, F.; Méchitoua, N.; Sakiz, M. Code Saturne: A finite volume code for the computation of turbulent incompressible flows-Industrial applications. International Journal on Finite Volumes 2004, 1. [Google Scholar]
- Levesque, J. The Code Aster: a product for mechanical engineers; Le Code Aster: un produit pour les mecaniciens des structures. Epure 1998. [Google Scholar]
- Helfer, T.; Michel, B.; Proix, J.M.; Salvo, M.; Sercombe, J.; Casella, M. Introducing the open-source mfront code generator: Application to mechanical behaviours and material knowledge management within the PLEIADES fuel element modelling platform. 70, 994–1023. [CrossRef]
- Kirk, B.S.; Peterson, J.W.; Stogner, R.H.; Carey, G.F. libMesh: A C++ Library for Parallel Adaptive Mesh Refinement/Coarsening Simulations. Engineering with Computers 2006, 22, 237–254. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal. II—a general-purpose object-oriented finite element library. ACM Transactions on Mathematical Software (TOMS) 2007, 33, 24-es. [Google Scholar] [CrossRef]
- Alnæs, M.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G. The FEniCS project version 1.5. Archive of numerical software 2015, 3. [Google Scholar]
- Da Vià, R. Development of a computational platform for the simulation of low Prandtl number turbulent flows. PhD thesis, University of Bologna, 2019.
- Barbi, G.; Bornia, G.; Cerroni, D.; Cervone, A.; Chierici, A.; Chirco, L.; Da Vià, R.; Giovacchini, V.; Manservisi, S.; Scardovelli, R. FEMuS-Platform: A numerical platform for multiscale and multiphysics code coupling. In Proceedings of the 9th International Conference on Computational Methods for Coupled Problems in Science and Engineering, COUPLED PROBLEMS 2021. International Center for Numerical Methods in Engineering, 2021, pp. 1–12.
- Numeric Platform. https://github.com/FemusPlatform/NumericPlatform.
- SALOME. https://www.salome-platform.org/?page_id=23, 2023.
- Ahrens, J.; Geveci, B.; Law, C.; Hansen, C.; Johnson, C. 36-paraview: An end-user tool for large-data visualization. The visualization handbook 2005, 717, 50038–1. [Google Scholar]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Benson, S.; Brown, J.; Brune, P.; Buschelman, K.; Constantinescu, E.M.; Dalcin, L.; Dener, A.; et al. PETSc Web page. https://petsc.org/, 2023.
- Chierici, A.; Giovacchini, V.; Manservisi, S. ANALYSIS AND NUMERICAL RESULTS FOR BOUNDARY OPTIMAL CONTROL PROBLEMS APPLIED TO TURBULENT BUOYANT FLOWS. International Journal of Numerical Analysis & Modeling 2022, 19. [Google Scholar]
- Chirco, L.; Manservisi, S. An optimal control approach to a fluid-structure interaction parameter estimation problem with inequality constraints. Computers & Fluids 2021, 226, 104999. [Google Scholar] [CrossRef]
- Da Vià, R.; Giovacchini, V.; Manservisi, S. A Logarithmic Turbulent Heat Transfer Model in Applications with Liquid Metals for Pr = 0.01–0.025. Applied Sciences 2020, 10. [Google Scholar] [CrossRef]
- Da Vià, R.; Manservisi, S. Numerical simulation of forced and mixed convection turbulent liquid sodium flow over a vertical backward facing step with a four parameter turbulence model. International Journal of Heat and Mass Transfer 2019, 135, 591–603. [Google Scholar] [CrossRef]
- Barbi, G.; Cervone, A.; Chierici, A.; Chirco, L.; Da Vià, R.; Franceschini, F.; Giovacchini, V.; Manservisi, S. SIMULATION OF TALL-3D EXPERIMENTAL FACILITY WITH A MULTISCALE AND MULTIPHYSICS COMPUTATIONAL PLATFORM. In Proceedings of the 9th International Conference on Computational Methods for Coupled Problems in Science and Engineering, COUPLED PROBLEMS 2021. International Center for Numerical Methods in Engineering, 2021, Vol. 1, pp. 1–12.
- Chirco, L.; Da Vià, R.; Manservisi, S. VOF evaluation of the surface tension by using variational representation and Galerkin interpolation projection. Journal of Computational Physics 2019, 395, 537–562. [Google Scholar] [CrossRef]
- Ribes, A.; Caremoli, C. Salome platform component model for numerical simulation. In Proceedings of the 31st annual international computer software and applications conference (COMPSAC 2007). IEEE, 2007, Vol. 2, pp. 553–564.
- de Vahl Davis, G. Natural convection of air in a square cavity: a benchmark numerical solution. International Journal for numerical methods in fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Manzari, M. An explicit finite element algorithm for convection heat transfer problems. International Journal of Numerical Methods for Heat & Fluid Flow 1999, 9, 860–877. [Google Scholar] [CrossRef]
- Massarotti, N.; Nithiarasu, P.; Zienkiewicz, O. Characteristic-based-split (CBS) algorithm for incompressible flow problems with heat transfer. International Journal of Numerical Methods for Heat & Fluid Flow 1998, 8, 969–990. [Google Scholar] [CrossRef]
- Mayne, D.A.; Usmani, A.S.; Crapper, M. h-adaptive finite element solution of high Rayleigh number thermally driven cavity problem. International Journal of Numerical Methods for Heat & Fluid Flow 2000, 10, 598–615. [Google Scholar] [CrossRef]
- D.C., W.; B.S.V., P.; G.W., W. A new benchmark quality solution for the buoyancy-driven cavity by discrete singular convolution. Numerical Heat Transfer: Part B: Fundamentals 2001, 40, 199–228. [CrossRef]
- Pangavhane, D.R.; Sawhney, R.; Sarsavadia, P. Design, development and performance testing of a new natural convection solar dryer. Energy 2002, 27, 579–590. [Google Scholar] [CrossRef]
- Fitzgerald, S.D.; Woods, A.W. Transient natural ventilation of a room with a distributed heat source. Journal of Fluid Mechanics 2007, 591, 21–42. [Google Scholar] [CrossRef]
- Espinosa, F.; Avila, R.; Cervantes, J.; Solorio, F. Numerical simulation of simultaneous freezing–melting problems with natural convection. Nuclear engineering and design 2004, 232, 145–155. [Google Scholar] [CrossRef]
- Basak, T.; Anandalakshmi, R.; Singh, A.K. Heatline analysis on thermal management with conjugate natural convection in a square cavity. Chemical engineering science 2013, 93, 67–90. [Google Scholar] [CrossRef]
Figure 1.
Coupling strategy models: point-to-point on the left and hub-and-spoke on the right.
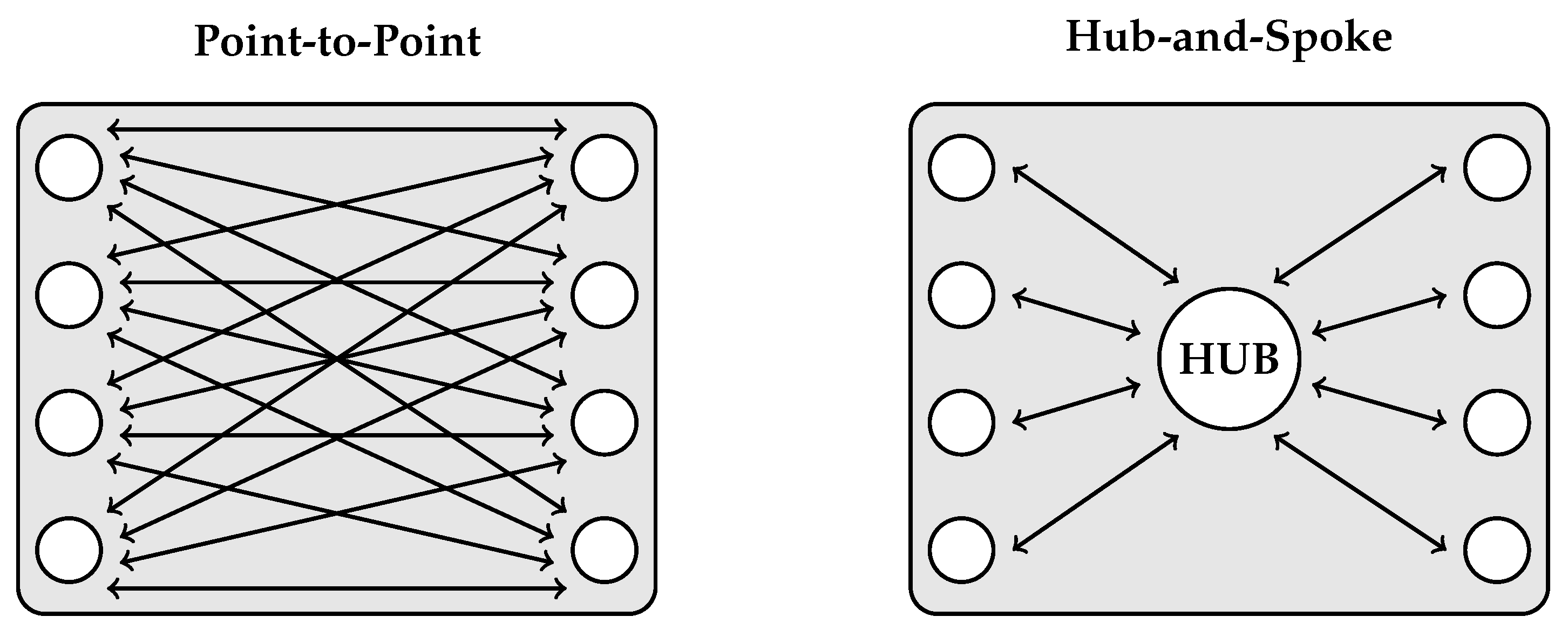
Figure 2.
Coupling procedure scheme.
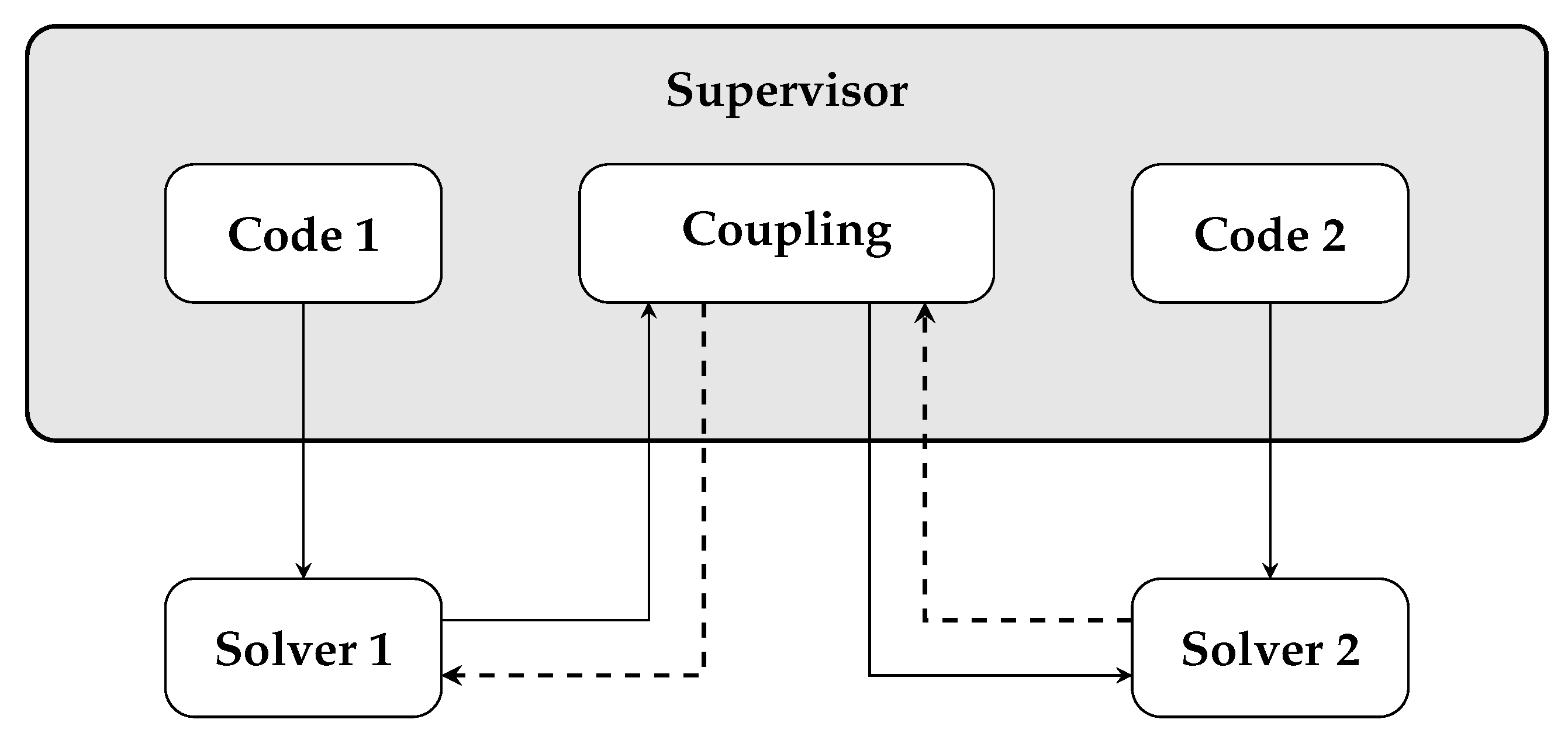
Figure 3.
Geometry of the buoyant cavity problem with boundary conditions for the temperature field.
Figure 3.
Geometry of the buoyant cavity problem with boundary conditions for the temperature field.
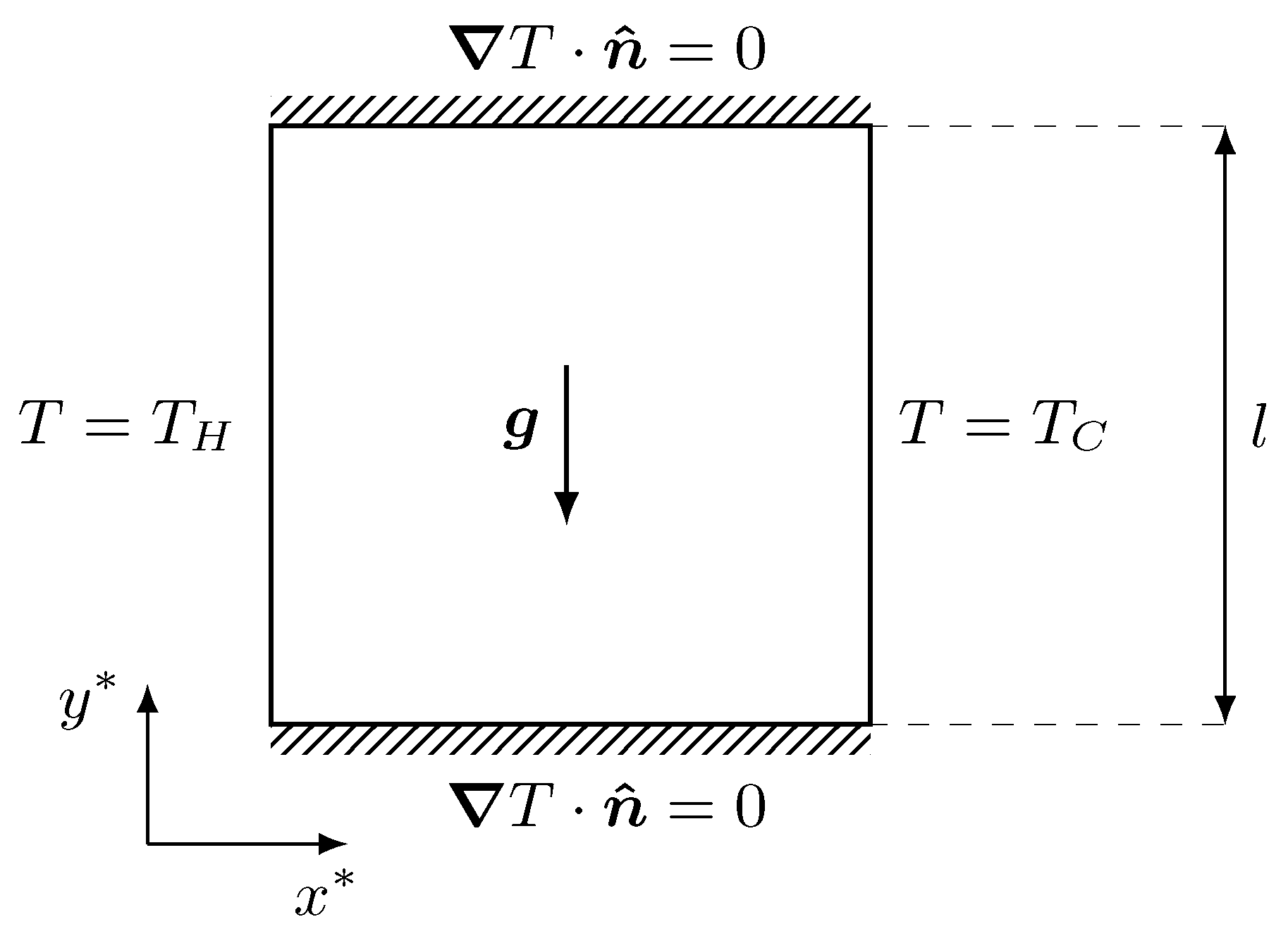
Figure 4.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
Figure 4.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
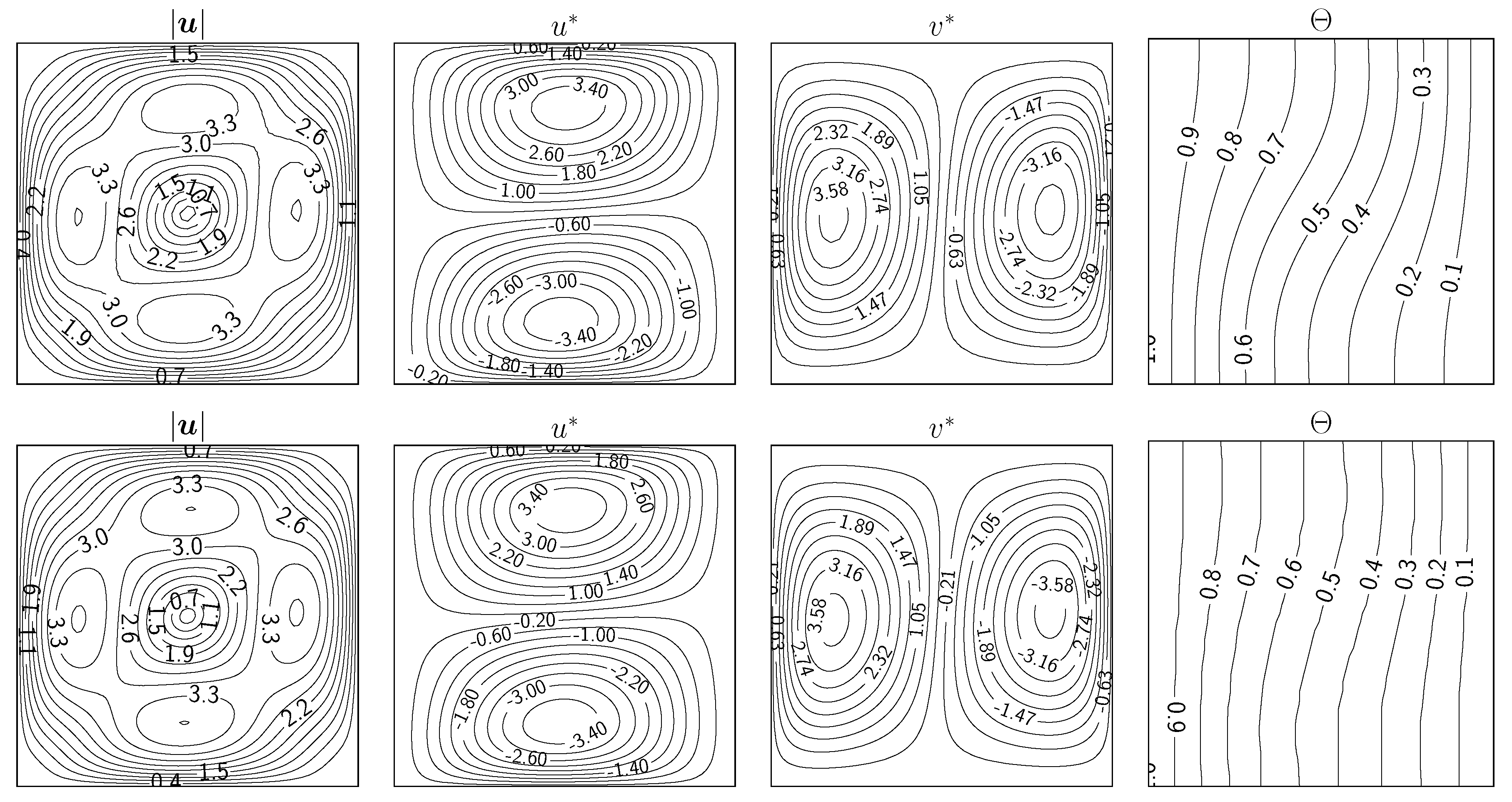
Figure 5.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
Figure 5.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
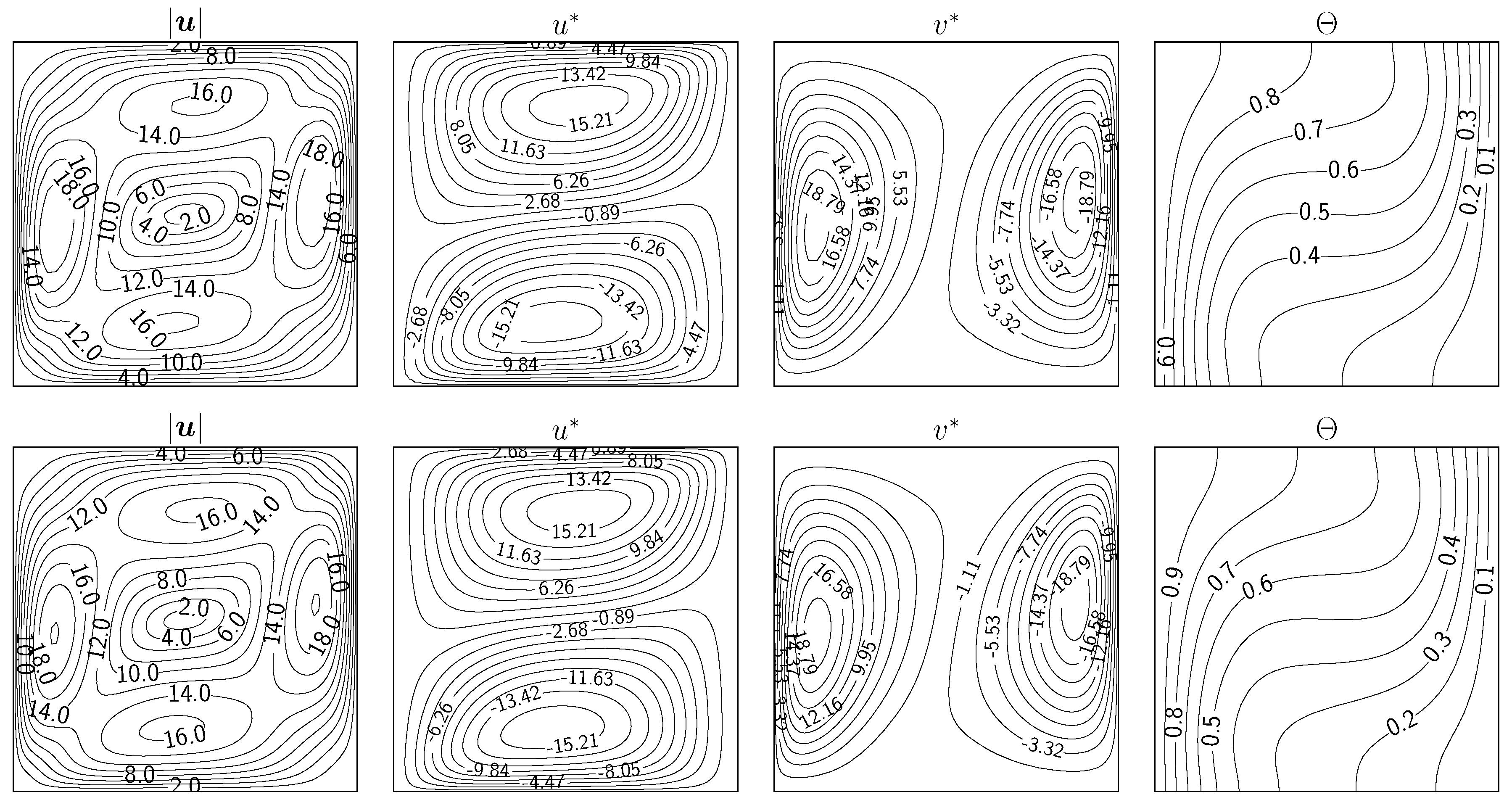
Figure 6.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature . Coupling algorithm (top) and (bottom) for the case with .
Figure 6.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature . Coupling algorithm (top) and (bottom) for the case with .
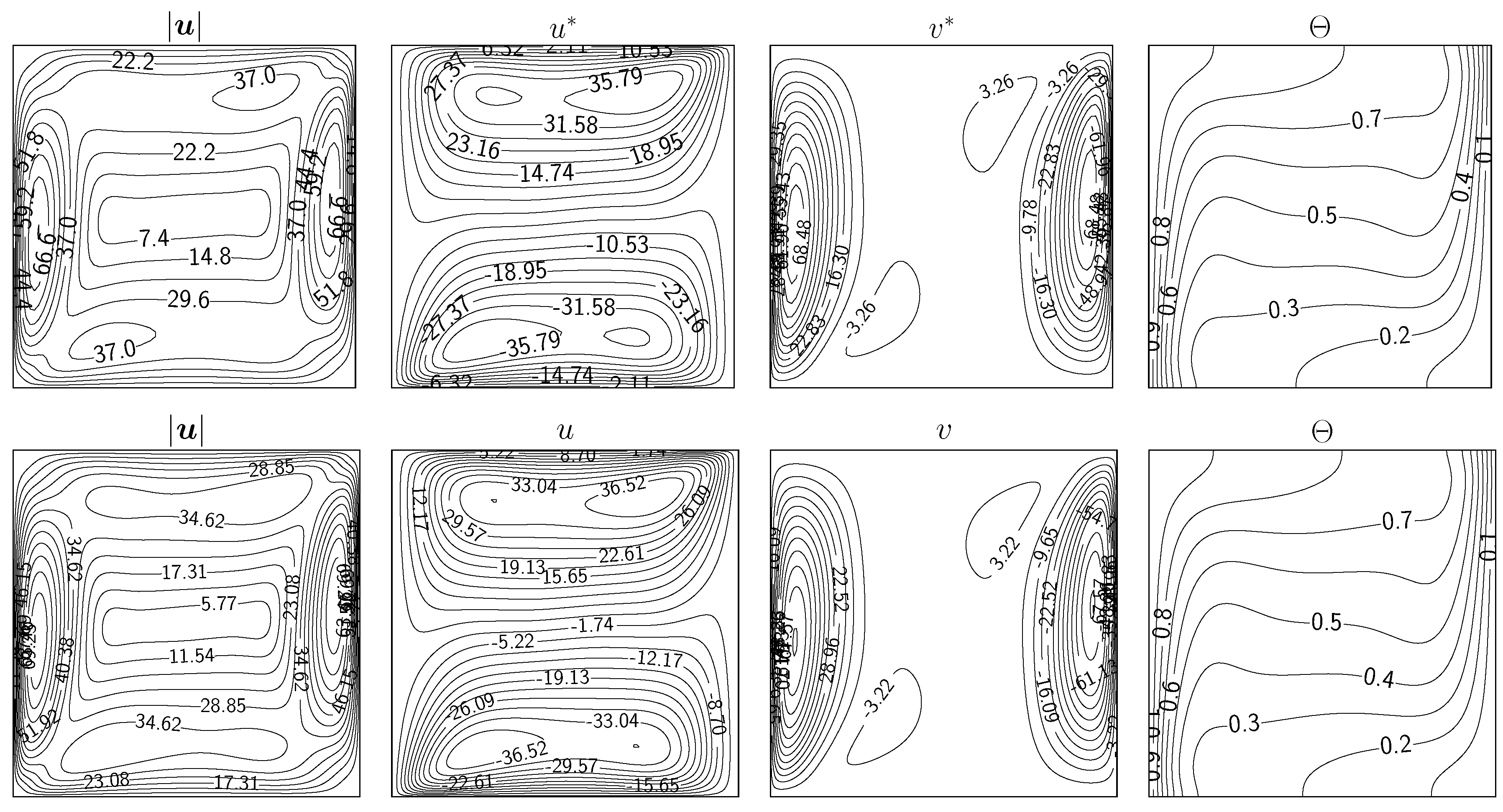
Figure 7.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
Figure 7.
From left to right, the contour of velocity magnitude, non-dimensional velocity components and non-dimensional temperature. Coupling algorithm (top) and (bottom) for the case with .
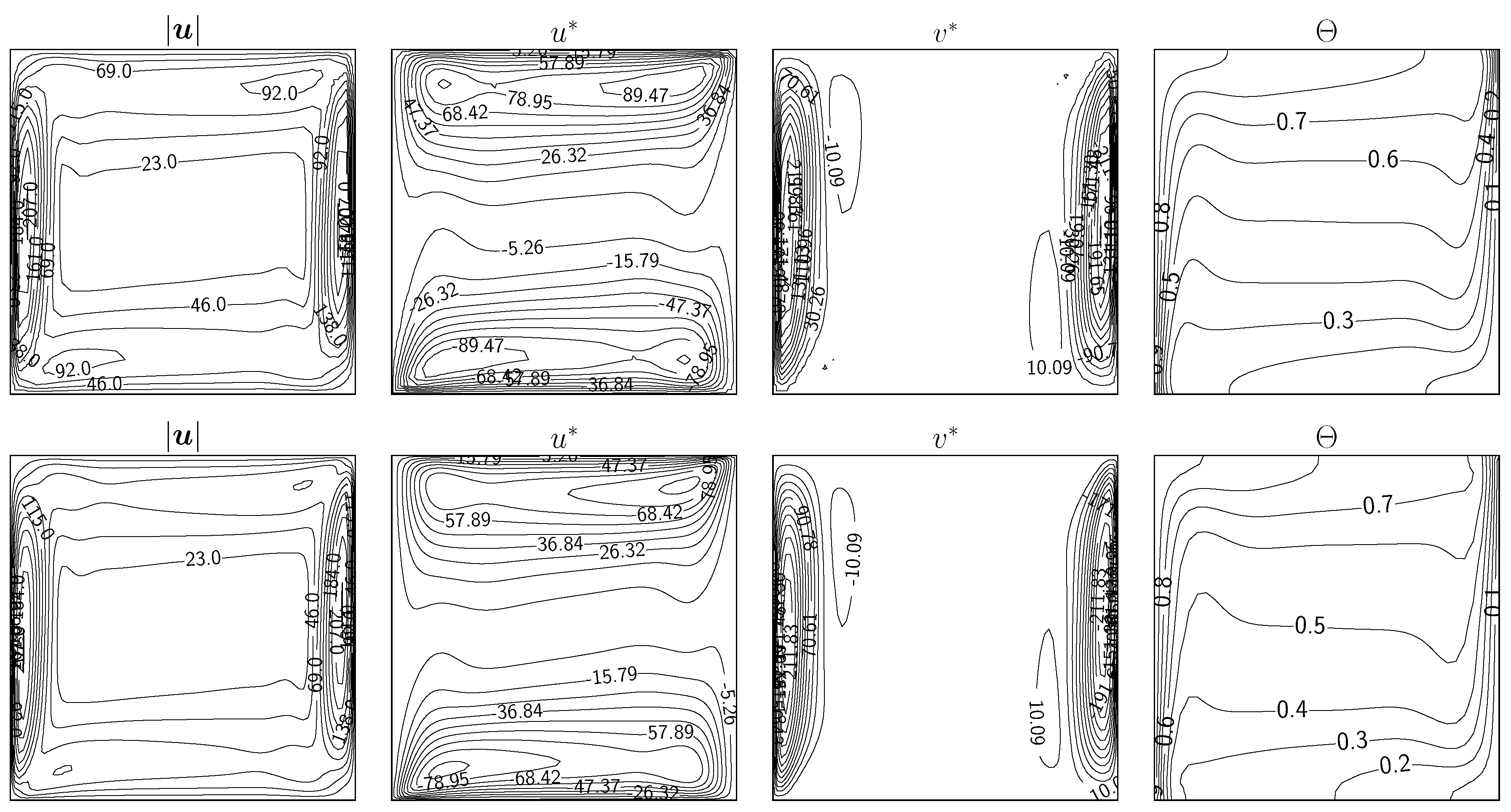
Figure 8.
Non-dimensional temperature (at , top) and non-dimensional components (at , middle) and (at , bottom) for the four types of simulations (F, , and ) with a comparison with literature data from [29] (circular markers). Case with on the left and on the right.
Figure 8.
Non-dimensional temperature (at , top) and non-dimensional components (at , middle) and (at , bottom) for the four types of simulations (F, , and ) with a comparison with literature data from [29] (circular markers). Case with on the left and on the right.
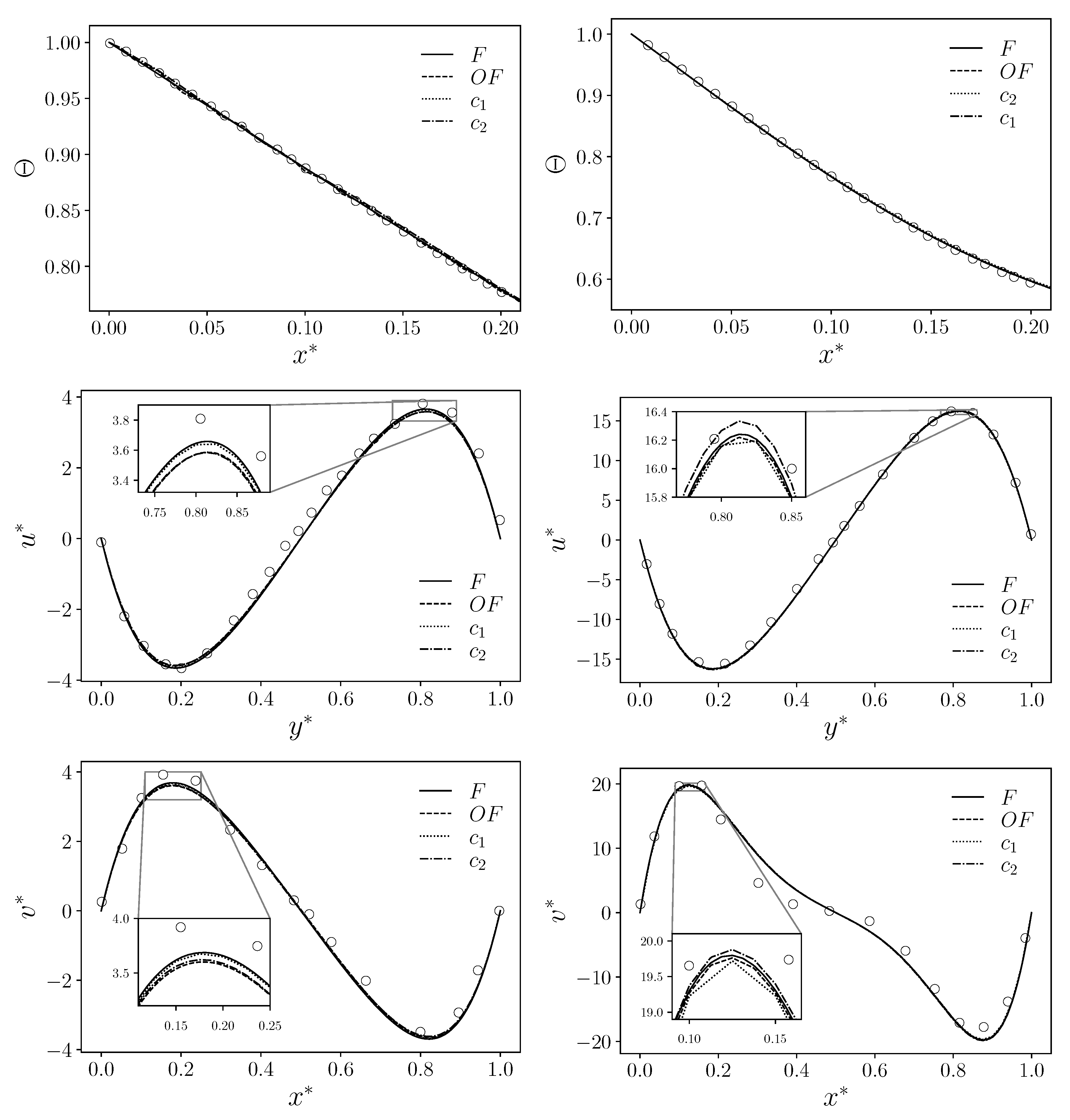
Figure 9.
Non-dimensional temperature (at , top) and non-dimensional components (at , middle) and (at , bottom) for the four types of simulations (F, , and ) with a comparison with literature data from [29] (circular markers). Case with on the left and on the right.
Figure 9.
Non-dimensional temperature (at , top) and non-dimensional components (at , middle) and (at , bottom) for the four types of simulations (F, , and ) with a comparison with literature data from [29] (circular markers). Case with on the left and on the right.
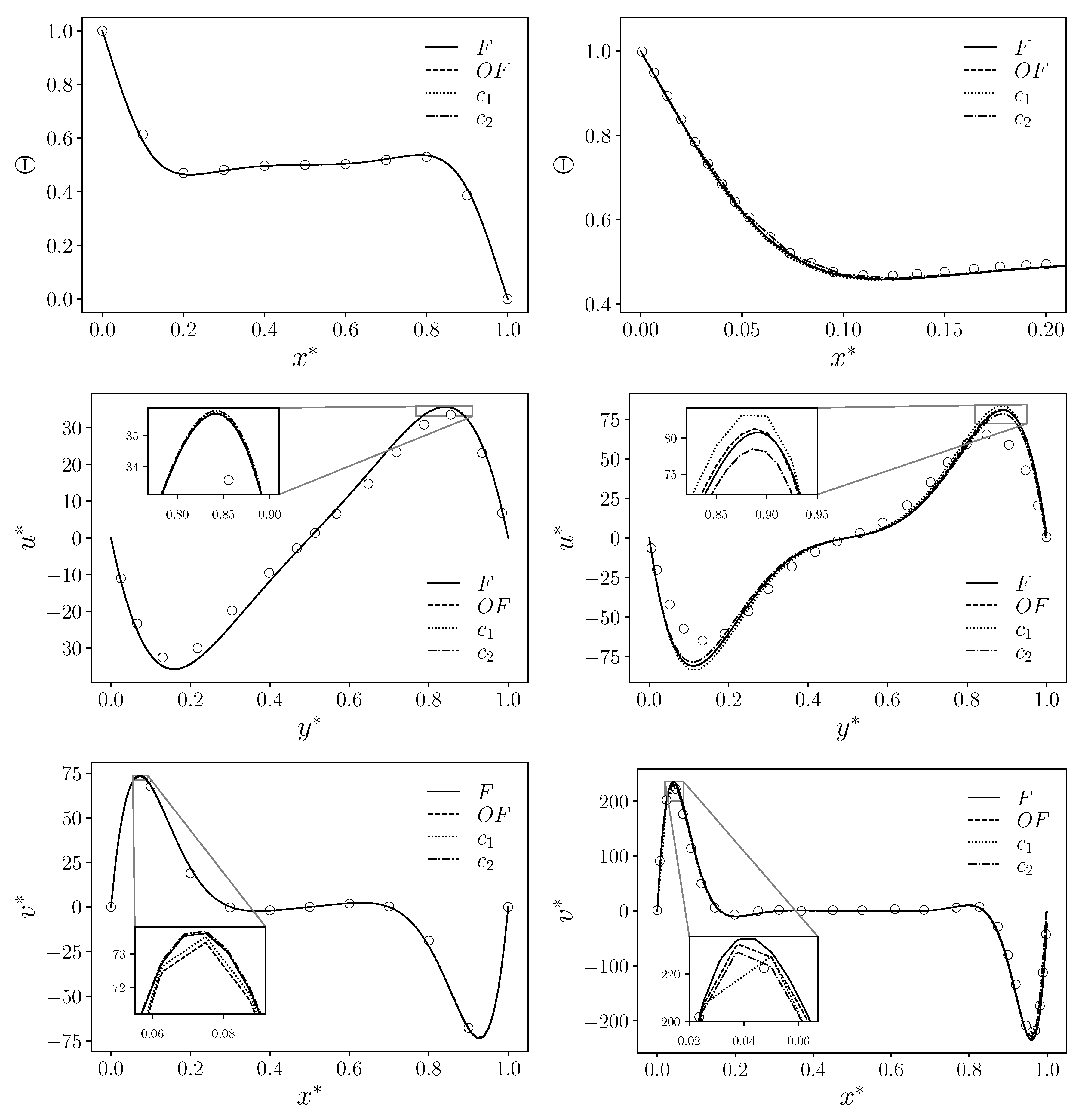
Figure 10.
Geometrical configurations of the CHT problem: on the left the domain with the solid wall thickness equal to , on the right equal to .
Figure 10.
Geometrical configurations of the CHT problem: on the left the domain with the solid wall thickness equal to , on the right equal to .
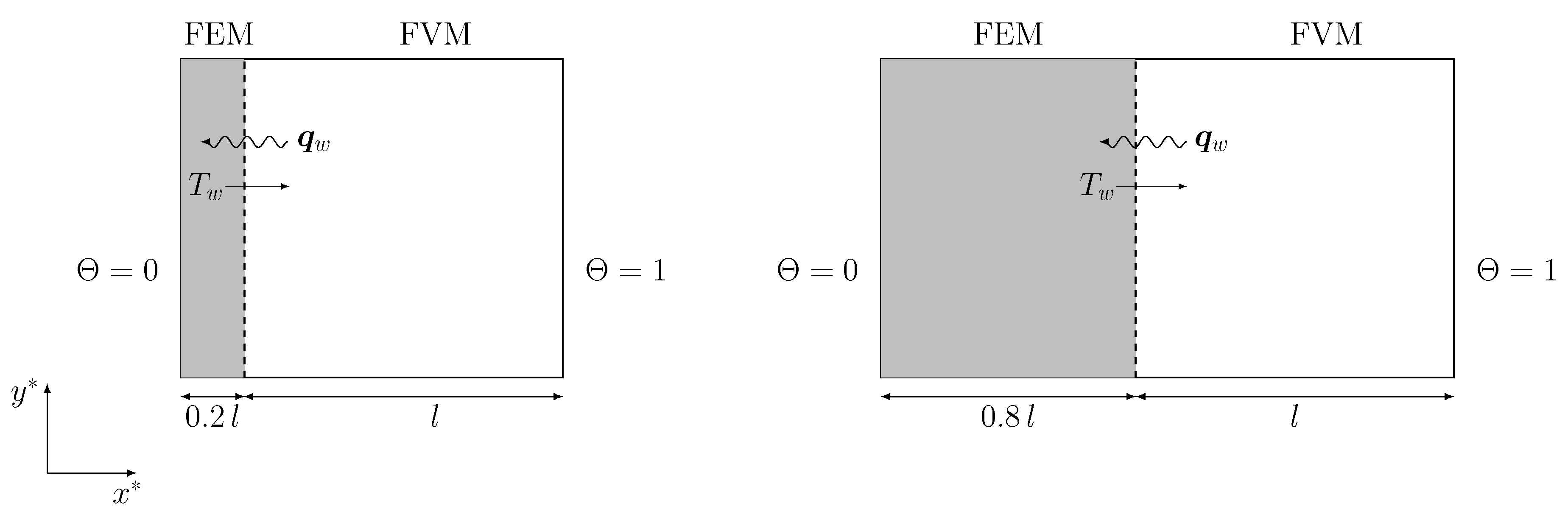
Figure 11.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
Figure 11.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
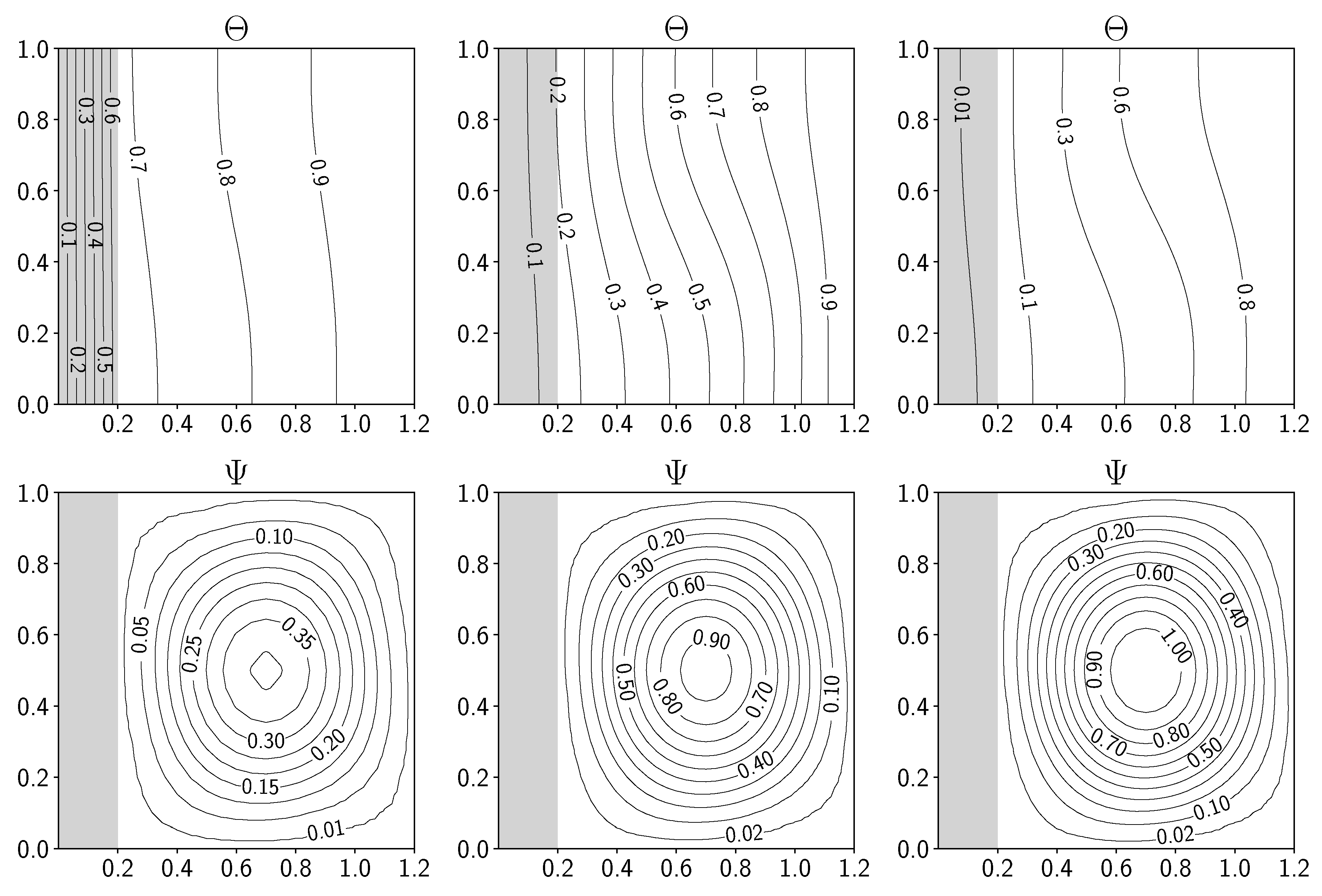
Figure 12.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
Figure 12.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
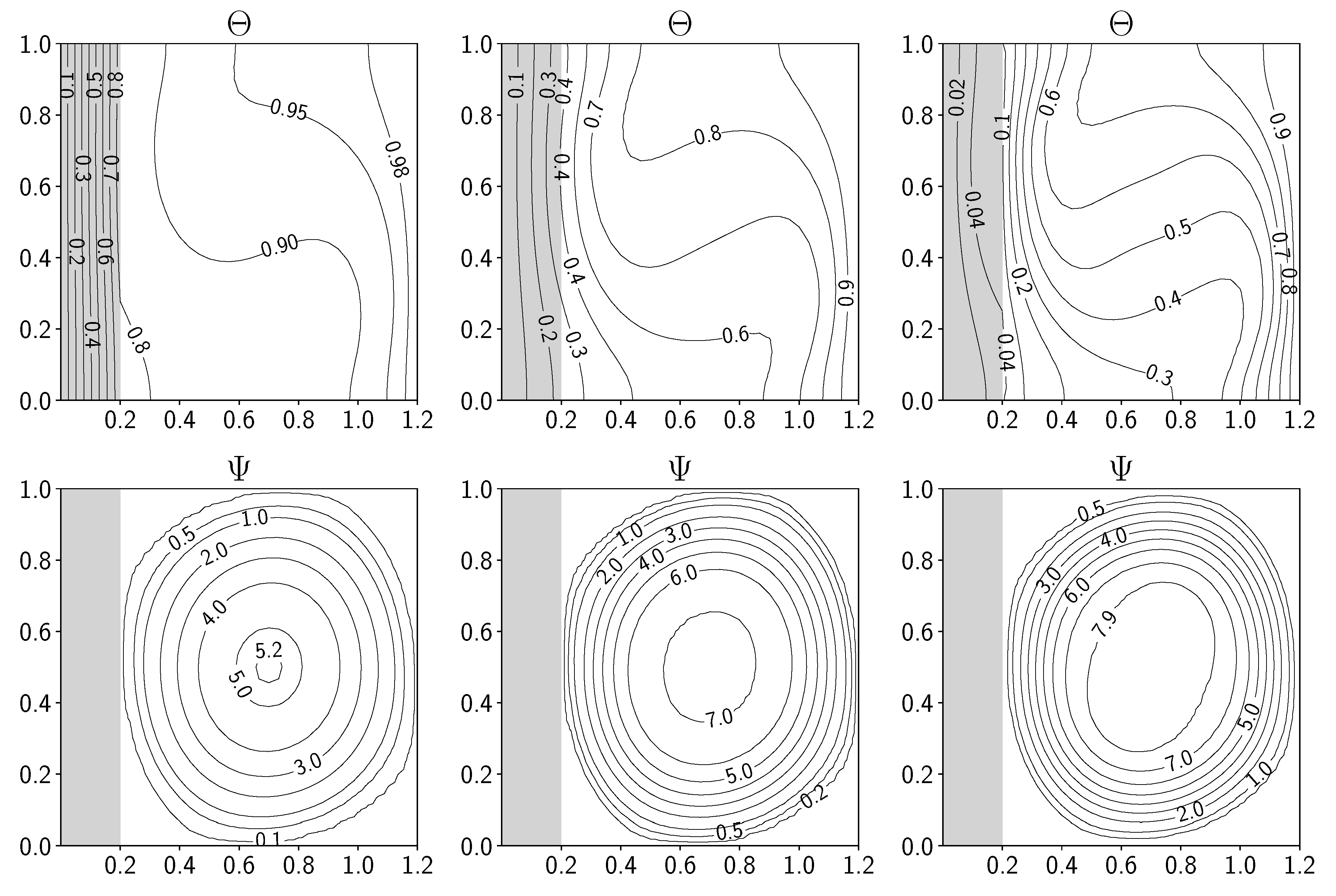
Figure 13.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
Figure 13.
Simulations with solid thickness and . From left to right contour of non-dimensional temperature (top) and velocity stream function (bottom) for , 1, 10.
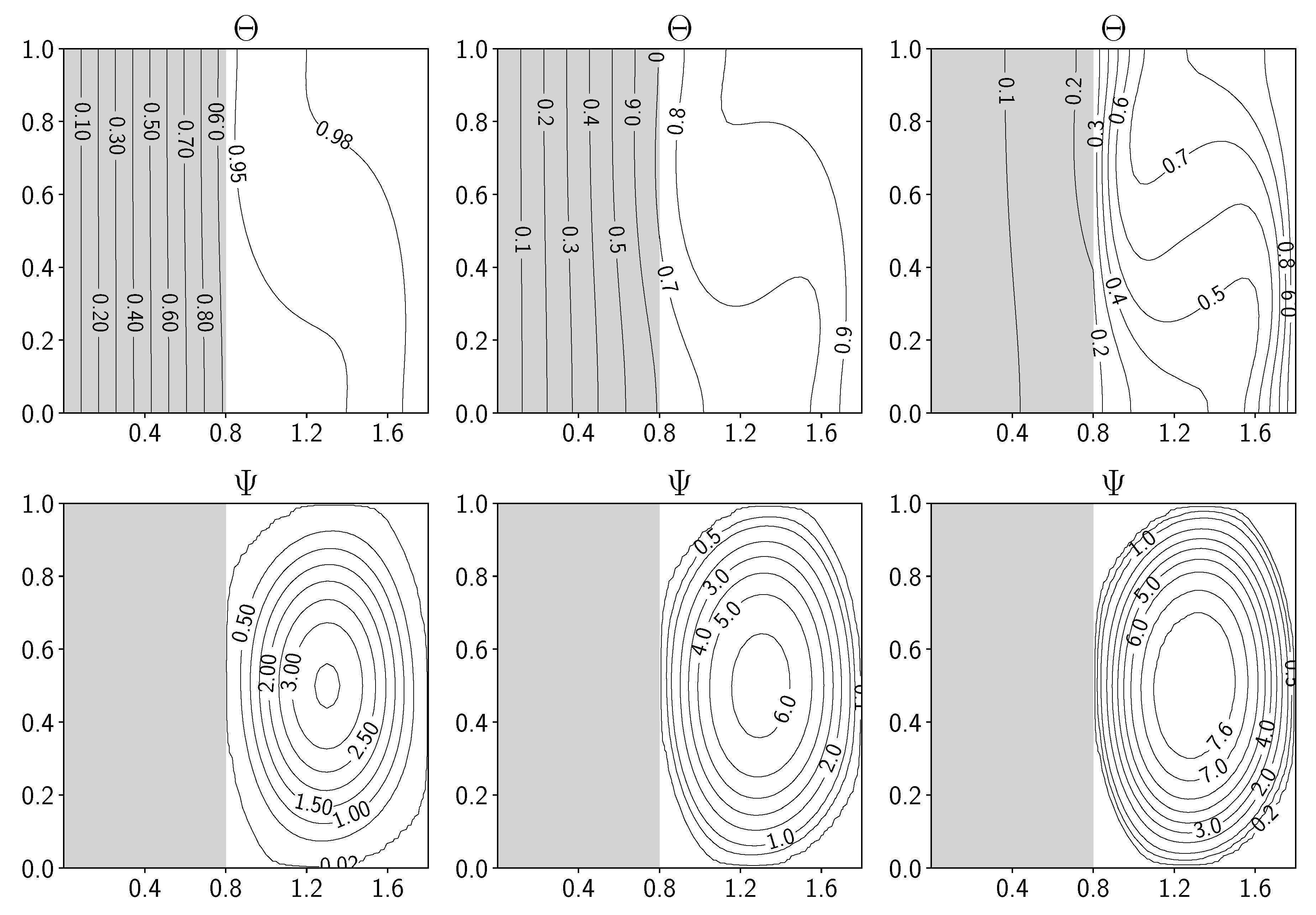
Figure 14.
Local boundary Nusselt number for the case with solid thickness : gray markers are the simulations with on top ( on the left and on the right), on the bottom ( on the left and on the right). A comparison with data from [33] is reported (white circular markers).
Figure 14.
Local boundary Nusselt number for the case with solid thickness : gray markers are the simulations with on top ( on the left and on the right), on the bottom ( on the left and on the right). A comparison with data from [33] is reported (white circular markers).
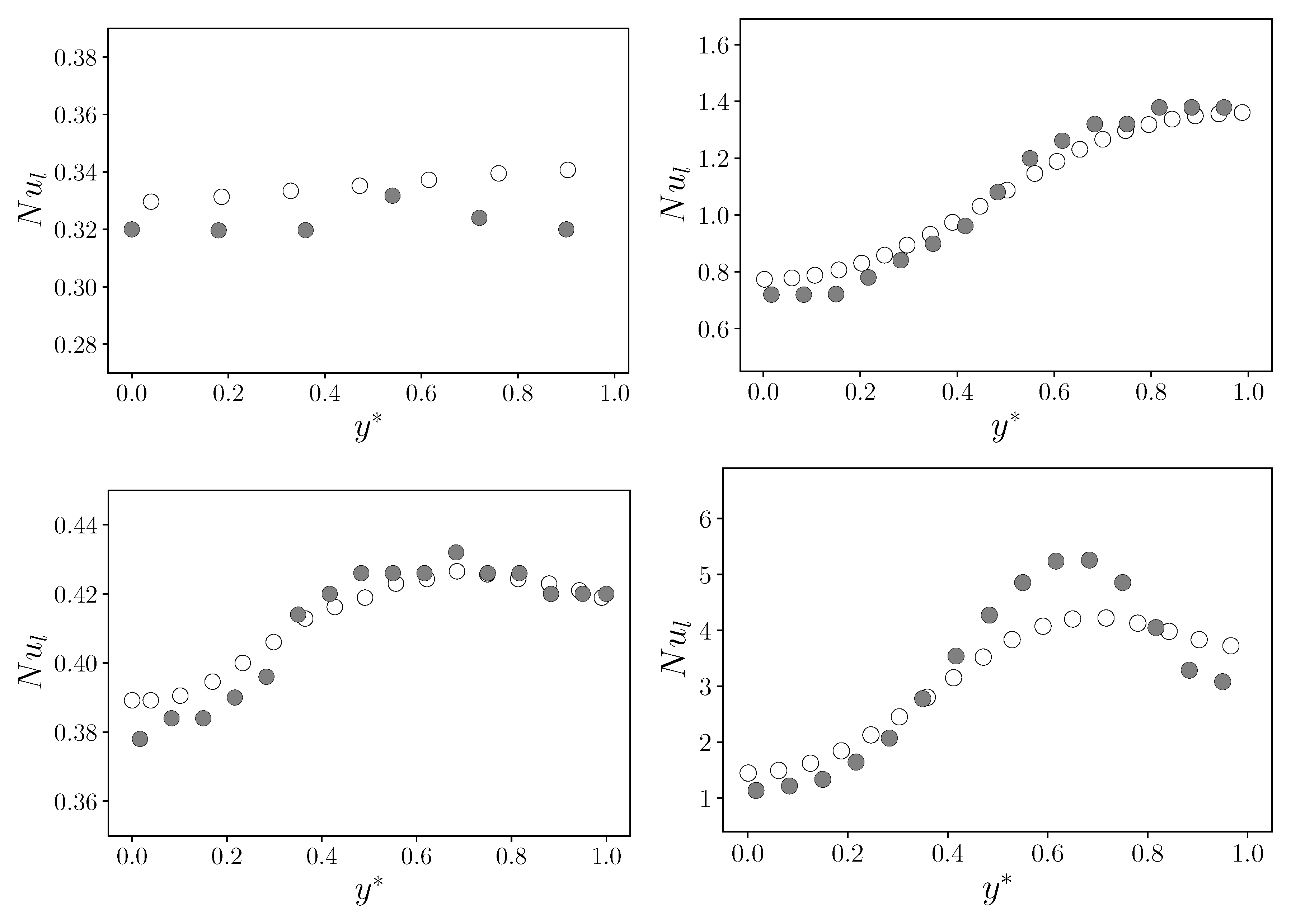
Table 1.
Grid convergence of the value at for the case with , and comparison with the same data of [12], for three different level of discretisation.
Table 1.
Grid convergence of the value at for the case with , and comparison with the same data of [12], for three different level of discretisation.
| F | [12] | ||||
|---|---|---|---|---|---|
| 73.639 | 65.186 | 66.789 | 71.908 | 73.241 | |
| 73.615 | 72.470 | 73.140 | 73.244 | 73.189 | |
| 73.617 | 73.337 | 73.515 | 73.681 | 73.168 |
Table 2.
Maximum value of -component at , for different numbers and comparison with literature data.
Table 2.
Maximum value of -component at , for different numbers and comparison with literature data.
| F | [25] | [26] | [28] | [29] | ||||
|---|---|---|---|---|---|---|---|---|
| 3.66 | 3.59 | 3.64 | 3.70 | 3.63 | 3.68 | 3.65 | 3.49 | |
| 16.24 | 16.22 | 16.19 | 16.33 | 16.18 | 16.10 | 16.18 | 16.12 | |
| 35.70 | 35.71 | 35.75 | 35.80 | 34.81 | 34.00 | 34.77 | 33.39 | |
| 80.79 | 81.03 | 83.16 | 78.47 | 65.33 | 65.40 | 64.69 | 65.40 |
Table 3.
Maximum value of -component at , for different numbers and comparison with literature data.
Table 3.
Maximum value of -component at , for different numbers and comparison with literature data.
| F | [25] | [26] | [27] | [28] | [29] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 3.69 | 3.60 | 3.68 | 3.73 | 3.68 | 3.73 | 3.69 | 3.70 | 3.69 | |
| 19.80 | 19.76 | 19.72 | 19.88 | 19.51 | 19.90 | 19.63 | 19.62 | 19.76 | |
| 73.62 | 73.34 | 73.52 | 73.68 | 68.22 | 70.00 | 68.85 | 68.69 | 70.63 | |
| 234.80 | 234.66 | 227.41 | 229.06 | 216.75 | 228.00 | 221.60 | 220.83 | 227.11 |
Table 4.
Average Nusselt number with different conductivity ratios K, varying the number and wall thickness t. A comparison with results from [33] is also reported.
Table 4.
Average Nusselt number with different conductivity ratios K, varying the number and wall thickness t. A comparison with results from [33] is also reported.
| [33] | [33] | [33] | ||||
| 0.332 | 0.335 | 0.898 | 0.890 | 1.08 | 1.08 | |
| 0.412 | 0.412 | 1.897 | 1.907 | 3.269 | 3.162 | |
| [33] | [33] | [33] | ||||
| 0.118 | 0.117 | 0.850 | 0.851 | 2.556 | 2.578 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








