Prerpints.org logo
Preprint
Article

On an Aggregated Estimate for Human Mobility Regularities through Movement Trends and Population Density

Altmetrics

Downloads

84

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 April 2024

Posted:

03 April 2024

You are already at the latest version

Alerts
Abstract
This article introduces an analytical framework that interprets individual measures of entropy-based mobility derived from mobile phone data. We explore and analyze two widely recognized entropy metrics: random entropy and uncorrelated Shannon entropy. These metrics are estimated through collective variables of human mobility, including movement trends and population density. By employing a collisional model, we establish statistical relationships between entropy measures and mobility variables. Furthermore, our research addresses three primary objectives: firstly, validating the model; secondly, exploring correlations between aggregated mobility and entropy measures in comparison to five economic indicators; and finally, demonstrating the utility of entropy measures. Specifically, we provide an effective population density estimate that offers a more realistic understanding of social interactions. This estimation takes into account both movement regularities and intensity, utilizing real-time data analysis conducted during the peak period of the Covid-19 pandemic.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

MSC:  82D30; 82D05; 70F99; 91D10; 91D20

1. Introduction

Human mobility and its regularity is an important and interdisciplinary research field and many theoretical studies have explored it at both individual and group levels [1,2,3].
Human mobility exhibits both random and regular patterns, reflecting a complex interplay of social interactions. Entropy offers a means to quantify these patterns [4,5,6], particularly in the context of understanding employees’ and consumers’ mobility behaviors. The economic significance of these insights is considerable, as mobility patterns serve as powerful predictors of consumer behavior and commercial activity [7,8].
Our analytical framework aims to provide an interpretation of individual measures of entropy-based mobility as obtained from mobile phone data [9,10]. We introduce and analyze the well-known random entropy and uncorrelated Shannon entropy, and estimate them through collective variables of human mobility such as movement trends and population density. We adopt a collisional model that allows us to establish statistical relationships between entropy measures and mobility variables.
We focus our data analysis on US state-level mobile phone data, utilizing measures such as radius of gyration and mobility entropy to characterize movement patterns. User location datasets can be used to study and model user mobility behaviors [11,12,13,14]. The time period of the early CoViD-19 pandemic is particularly interesting as mobility restrictions and other social distancing interventions were implemented to mitigate the spread of the disease. These measures had significant impacts on economic activities, amplifying the effects of changes in mobility behaviors on social, economic, and demographic trends and patterns [15,16,17,18].
We define a novel approach to the measurement of population density, one of the most fundamental properties of urban areas. Many research works have looked at the relationship between the density, mobility, productivity, and urban development of a region(s) [19]. Population-weighted density captures density as perceived by a randomly chosen individual and is meant to measure average "experienced" density, as popularized in economics [20,21]. We propose an adjustment factor to population density defined in terms of the mobility patterns of a region. By using mobility and demographic data information, we observe how the proposed entropy-weighted population density suggests that people perceive interactions as more effective when there is frequent movement with low irregularity.
Finally, we investigate how mobility constraints influence employment, consumer choices, and market dynamics. Human movement patterns are strongly associated with regional socioeconomic indicators [22,23,24,25]. Mobile phone data can be used as a proxy to evaluate the density, activity, and social characteristics of a population [26,27,28]. The economic and social shock presented by abrupt or intense changes of human mobility and population density has reshaped perceptions of individuals and organizations about work and occupations. Employment rate, for example, is known to be strongly related to aggregate measures of consumer spending [29,30] especially during times of crisis. Our analysis sheds light on the role of entropy measures of human mobility in economic analyses, contributing to the literature of mathematical modeling of consumer behaviors in relation to mobility regularities [31,32,33]. We provide an epidemiological model for the effective reproduction number in combination with entropy-based metrics of human mobility and we reveal relationships between economic indicators and mobility-based variables, underscoring how economic activity and human movement are intertwined.

2. Methods & Models

Entropy is a significant, widely used and above all successful measure for quantifying in-homogeneity, impurity, complexity and uncertainty or unpredictability. We are interested in the entropy of a person’s large-scale motion. This metric tracks how erratic or how predictable a person’s movement is. Lower entropy implies higher predictability, meaning that an individual’s time spent at all locations is highly predictable. Conversely, high entropy implies that predicting the time an individual spends in some location(s) is difficult.
Random entropy measures the uncertainty of an individual’s next location assuming that this individual’s movement is completely random among L possible locations, and is estimated from data as:
E [ S ^ rand ] = 〈 log L i 〉 N
which captures the predictability of each user by assuming that the person’s whereabouts are uniformly distributed among L i distinct locations.
Uncorrelated entropy, on the other hand, is based on Shannon entropy: if the individual’s movement among N possible locations follows a certain probability distribution, the uncorrelated entropy is then estimated from data as:
E [ S ^ unc ] = − ∑ k = 1 L i p k log p k N
where L i is, again, the number of distinct locations by each of the individuals, i = 1 … N , and where p k is the frequency of the user’s visit to their k-th location (k is the index of all locations that the user visits). Shannon entropy is high when an individual performs many different trips from a variety of origins and destinations; it is low when he performs a small number of recurring trips. The uncorrelated Shannon entropy takes into account the number of different locations visited as well as the proportion of time spent at each location. Since the entropy of the distribution of time spent at a location is no lower than that of a uniform distribution, one has that E [ S ^ unc ] ≤ E [ S ^ rand ] , where the equality holds when the process is completely random.
Definition 1
(collisional assumption). Let individuals be point particles in a container of area A that interact with the borders of the container and otherwise move freely. Let the container be of such a shape as to ensure chaotic motion of the particles.
We start with the analytical estimation of random entropy through a configurational approach:
Proposition 1
(Configurational Entropy). Let A be an area in which N non-interacting individuals randomly move. Let δ = N / A be the population density. In the configurational case, the random entropy can be computed as:
S R = ln δ o δ
where δ o is a characteristic density (typically, N individuals per unit area).
Proof. 
The proposition is proved in Appendix A □
Note that the configurational entropy depends only on the population density. The presumed areal equidistribution of individuals implicit in the definition of S R reminds one of the random entropy E [ S ^ rand ] in eq.(1).
Human mobility encompasses various activities, such as commuting to work, shopping, or socializing, which collectively contribute to the dynamic fabric of human interactions within a given community or region. So, it would be desirable to have an entropy that would include both velocity and density as independent variables.
Proposition 2
(Informational Entropy). Let N be the number of individuals in an area. Let the state of the set of individuals be represented by a point in 4 N − dimensional phase space. The principle of maximum entropy yields
S U = 1 + ln δ o δ μ 2 μ o 2
where μ is the mobility and μ o is the minimal resolvable velocity.
Proof. 
The proposition is proved in Appendix B □
In a sense, S U is a better measure of the entropy than S R , since it takes into account spatiotemporal patterns in mobility. They are equivalent (up to a constant) only if the mobility distribution is unchanging in space and time.

3. Results

In this section we discuss three main objectives of the research. First, we provide evidence concerning the relation between entropy as directly estimated and reported from datasets and the entropy calculated from mobility data using the configurational and informational entropies. Second, we illustrate how to calculate a novel measure of the population density as “experienced” based on the entropy. Third, we highlight statistical evidence about the relationship between mobility regularities and certain macroscopic economic indicators. Finally, we provide a real-time epidemiological estimation of the effective reproduction number in relation with mobility patterns of regularities.

3.1. Entropy in Human Mobility

We have used data provided by Camber Systems database [34] that reports the random and uncorrelated Shannon entropies at the length scale of meters. Real-time user locations are collected using the global positioning system (GPS), call detail record logs (CDR) and wireless-LAN (WLAN). Recording human activities can yield high-fidelity proxies of socio-economic development and well-being. However mobility data have their biases and limitations. For example, these data can be more representative of a younger and more affluent population while underrepresenting those living in rural areas.
We use data provided by Camber Systems database [34] which offers estimates for random entropy, uncorrelated (Shannon) Entropy, and radius of gyration (RoG). The latter, RoG, measures how far an individual moves from its trajectory’s center of mass. We will identify RoG as a measure of mobility μ .
We now describe the two branches which compose the human mobility in our collisional model: mobility (RoG) and population density.
  • Mobility is the average distance traveled by an individual. In the data it is represented by the median radius of gyration in meters of devices which stayed in one location overnight. This metric provides a summary of travel that incorporates both the number of trips and the distance of each trip. The radius of gyration r g ( u ) for user u, is calculated by first taking the root mean squared distance of a user’s location from their trajectory’s center of gravity averaged over a given time window.1 It is interpreted as the characteristic distance traveled by user during a day 2. The individual radius of gyration is different from the average travel distance, because an individual moving in a comparatively confined space will have a small radius of gyration even if a large distance is covered. The aggregated radius of gyration R o G is reported for a group of devices in a geohash-7 granularity of about 153 meters by 153 meters; for every user u, one generates their home region A as the region in which they spend the most time in their location set. Then, one aggregate this value across a population in a given region to provide an average and percentiles. This is the metric used in the CamberSystem [34] database. In practice, the radius of gyration represents a way to describe human mobility as an aggregated measure of human movements. It can be taken as measure of mean velocity μ in our collisional model and μ o is the displacement resolution which determines the minimal movement that can be detected in a geohash area in a day.
  • The second aspect of human mobility in our collisional model is the number of individuals that can interact in a region. Despite its simplicity, population density δ is quite difficult to estimate, since we should map the number of individuals in an effective region of interaction. Most economic agents are more concentrated in space than gross population density measures suggest. For these reasons, the informational entropy is just an approximation of the uncorrelated entropy since we cannot know the exact value of the urban population density. As a consequence, we cannot directly use the population density reported by the US Census Bureau [35], which is calculated in terms of the area of a geographic region rather than the effective area in which people interact. We use the population weighted density of [42] from Table 1: it represents the population density that the average person experiences [43]. It is often more representative of the effective interaction region standard census estimate [44].
As a consequence, while the human movement trend data μ is a reliable mobility predictor for entropy, the population density δ cannot be measured with the same precision and frequency as movement trends.
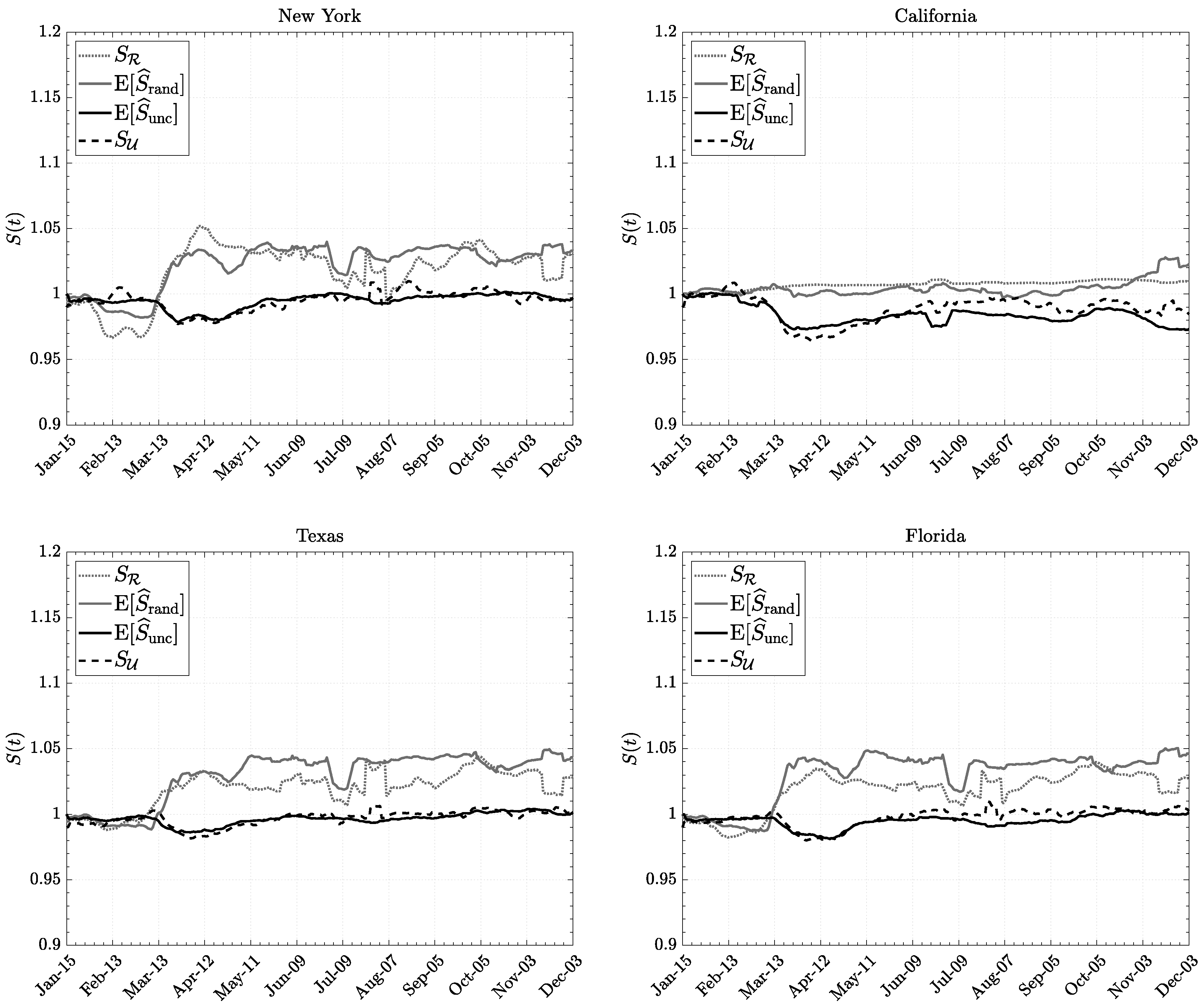
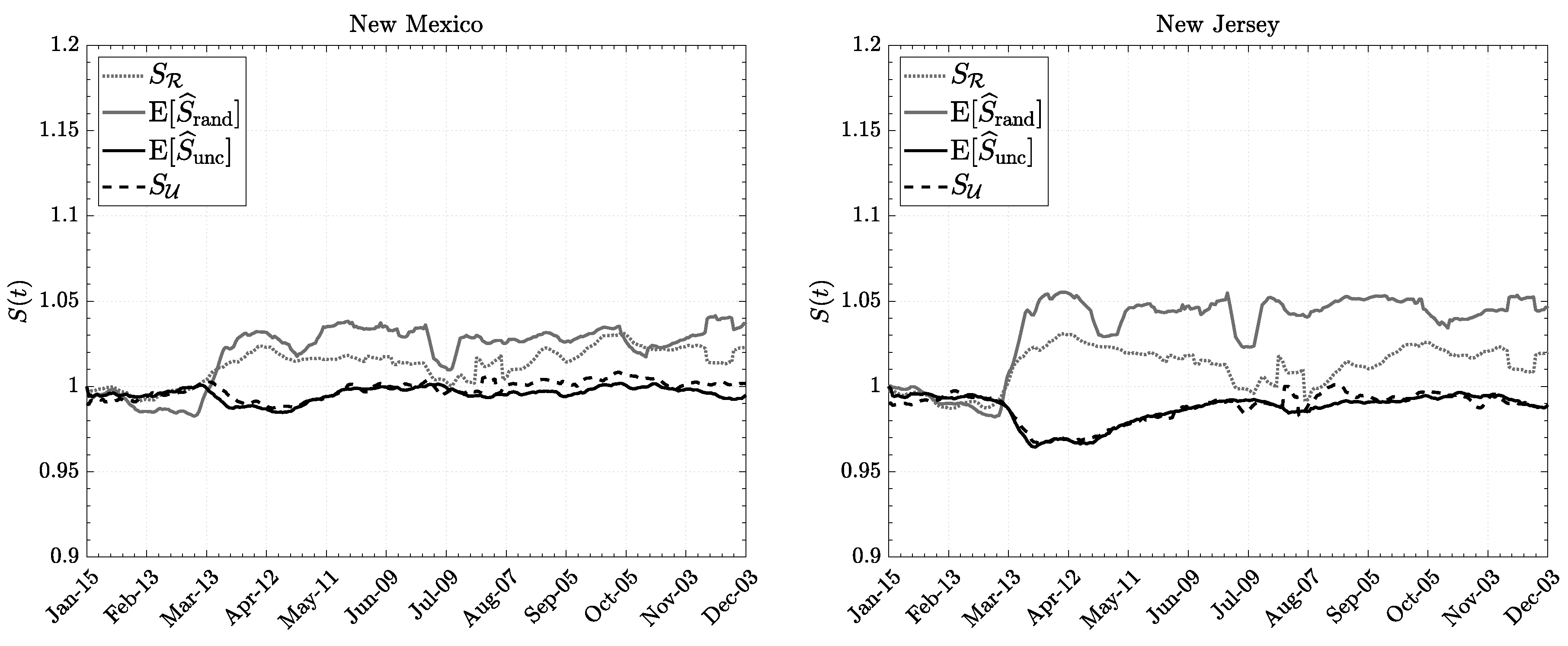
We show in Figure 1 and Figure 2 the various measures of entropy in certain US states. We notice that the estimate uncorrelated entropy E [ S ^ unc ] is well approximated by the informational entropy S U expressed via human mobility variables. On the other hand, the random entropy E [ S ^ rand ] is only roughly approximated by the configurational entropy, since this relies on stronger assumptions and on the estimate of population density only, which is a quite crude measure. Nevertheless, it follows a similar trend in states where the population is more evenly distributed.
However, in every case reported, we notice a change after the beginning of March 2020: the random entropy has increased while the uncorrelated entropy exhibits the opposite trend. A possible interpretation is that, after the Covid-19 outbreak individuals increased the number of stops (visited more distinct locations), but at the same time they have moved less uniformly among different locations they have to stop at. This possibly reflects the fact that people kept moving but spent more time in important places like essential workplaces, and less time in visiting non-necessary locations (bars, restaurants etc...). Over the course of a year the uncorrelated Shannon entropy have recovered its original value, while the random Shannon entropy has maintained is new mean value. This suggests that the density of active individuals has diminished, possibly because of social and economic downturns and reduction in production activities and consumption behaviors.

3.2. Population Density Estimate

The ordinary gross population density is defined as population divided by (land) area. This is a flawed measure since it deals with large geographic entities such as counties, states, and countries rather than smaller structured regions such as cities. As an economic measure, population density needs to accommodate the fact that most economic agents live in a more concentrated space than gross population density measures suggest. The two basic issues with average population density calculations are the arbitrariness of defining borders and the fact that average population density focuses on the density of the average plot of land, not the density observed by the average person.
There several ways to correct for the arbitrariness of defining borders, territorial characteristics, and people distribution in a region. The focus is to produce a sort of “perceived” population density. For example, the population weighted density, proposed by [43,45], is a family of methods that weight the value of density by their corresponding population size in the aggregation process. In particular, to gain perspective on the densities at which people live, the population-weighted is derived from the densities of all the census tracts included within the boundary of the Core-based statistical area. In the specific case of the United States, we have used the regular population density [35] and other weighted population density metrics at sub-national (state) level for the year 2020, as retrieved via the WorldPop dataset [42]. Following the Shannon (uncorrelated) entropy as from phone-data as [34], the perceived population density is:
d ^ ew = d 0 μ 2 μ o 2 exp { 1 − E [ S ^ unc ] }
where we have interpreted d 0 is the number of individuals that one can count in a random geohash, which is the same as the gross density from the census bureau, i.e. the number of people per km 2 of land area. In Table 2 we show the various adjustment criteria for the census population density. The first column shows the typical measure of population density as number of persons divided by the nominal surface area of the sate. The second column represents the two entropy-weighted population density as computed by eq.(5). The last two columns report two other popular approaches to adjust and weight the population density. The first uses population divided by land area adjusted for geographic characteristics, see [46]. The last column represents the population weighted density based on weighted median, as suggested by [43], which is more strongly related to the size of the urban area.
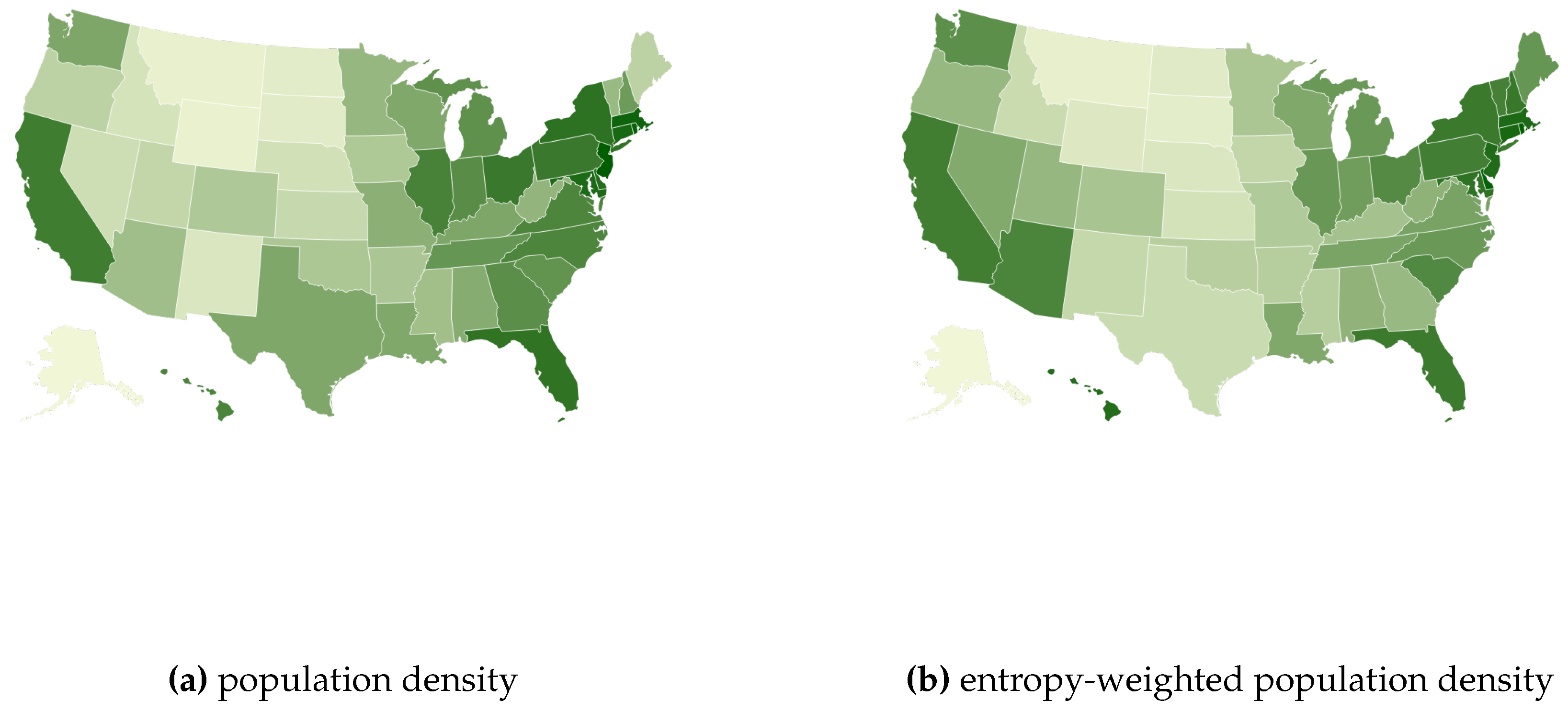
In Figure 3 we show two population density maps: the gross population density and the Shannon entropy-weighted population density. The latter differs from the former by a correction factor which takes into account both the amount of movement and the diversity of mobility. For a similar surface area and population, the experienced density is higher for regions where people tend to move more with high regularity (low entropy). The correction factor for random entropy only takes into account movement regularity. So, the entropy-weighted population density indicates that individuals perceive the interaction to be more effective if people move a lot with a low degree of confusion: in areas with irregular movements, individuals may encounter others less frequently, leading to a perception of lower population density. Conversely, in areas with more regular movements, encounters with others may be more frequent, leading to a perception of higher population density. Moreover, in areas with more irregular movements, individuals may have less predictable spatial relationships with others, which can decrease their perception of population density [47,48,49].
However, our estimate must be used with caution since it depends on the quality of its components and the assumptions behind the model that establish the relationship between mobility variables. More work is required to provide a more systematic study of the impact of different ways to define the average velocity μ , which here we denote as the radius of gyration. Other alternatives are possible, such as the mean square displacement and the straight-line distance, which define different types of movement trends. Moreover, other definitions of entropy are also possible; for example, the real entropy is a metric that not only uses the frequency of visitation but also considers the order and the time spent in visited locations, thus capturing more complete spatiotemporal features of mobility patterns [3,4,50]. The take-home message is that even if the actual population density remains constant, the perception of crowding can vary based on the intensity and irregularity of movements.

3.3. Economic Activity, Mobility Patterns and Epidemiological Evolution

In this final section, we aim to highlight several stylized facts and empirical evidence concerning patterns of mobility and various socio-economic indicators, such as short-term regional income, employment rates, and other socio-economic factors [51,52,53]. We examine the correlations between aggregated mobility and entropic measures vis-à-vis five socio-economic indicators. 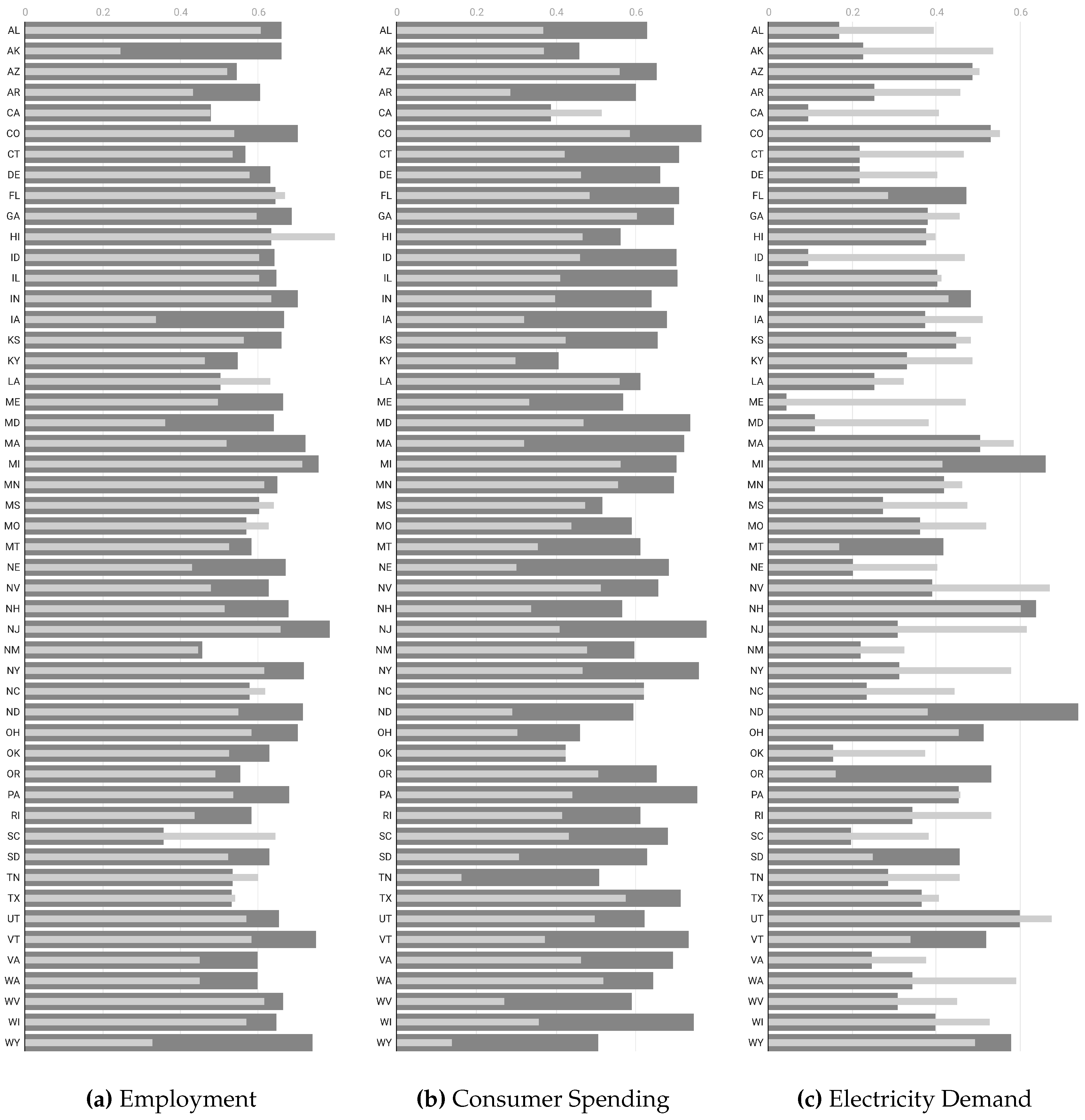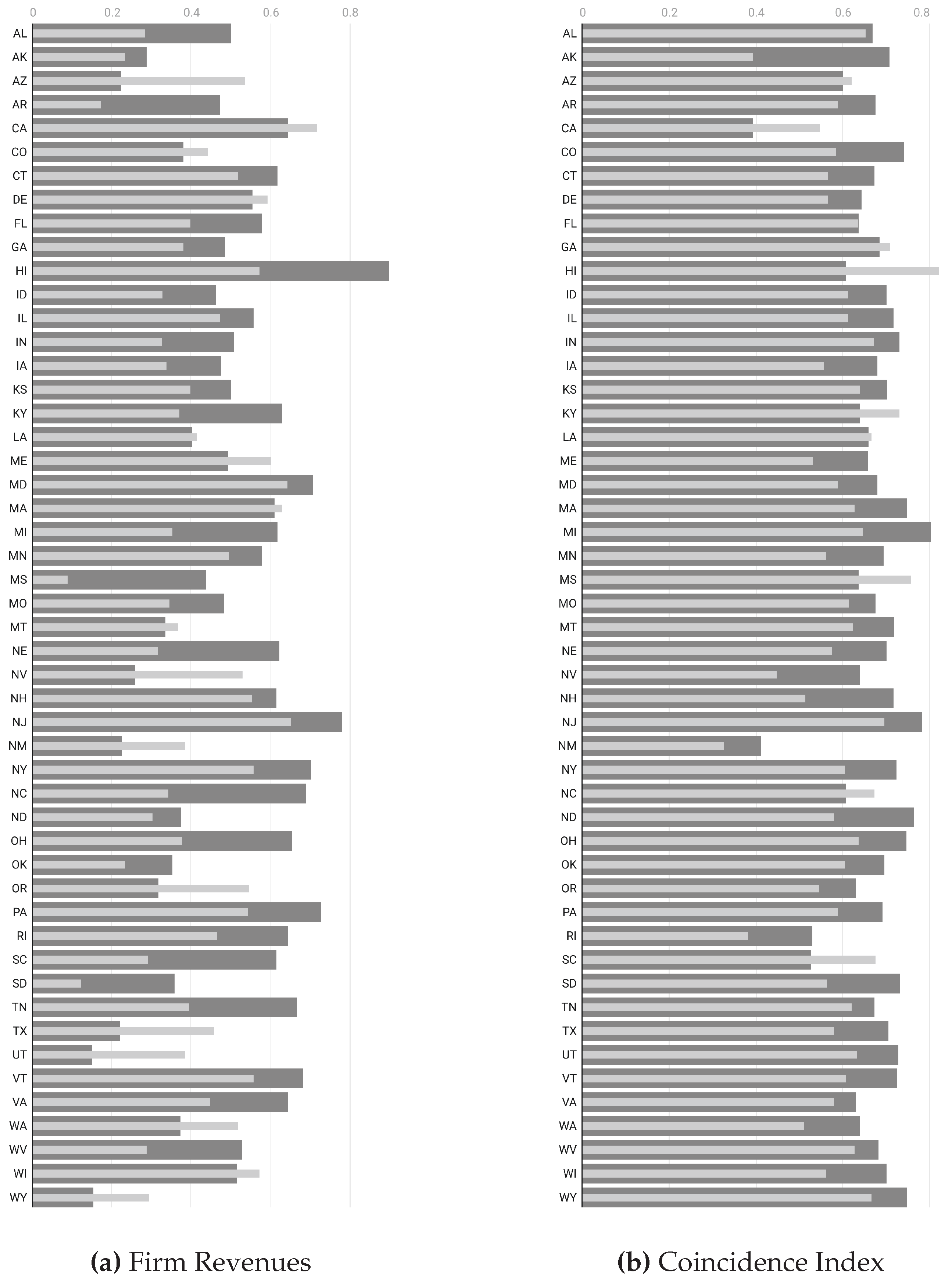As case study, we select some daily and monthly regional economical indicators which have been already analyzed in the research of the short-term impact of Covid-19 epidemic on the economy [54,55,56,57]. We have used 5 economic indicators: employment, consumer spending, electricity production, firms revenues and the coincidence index.
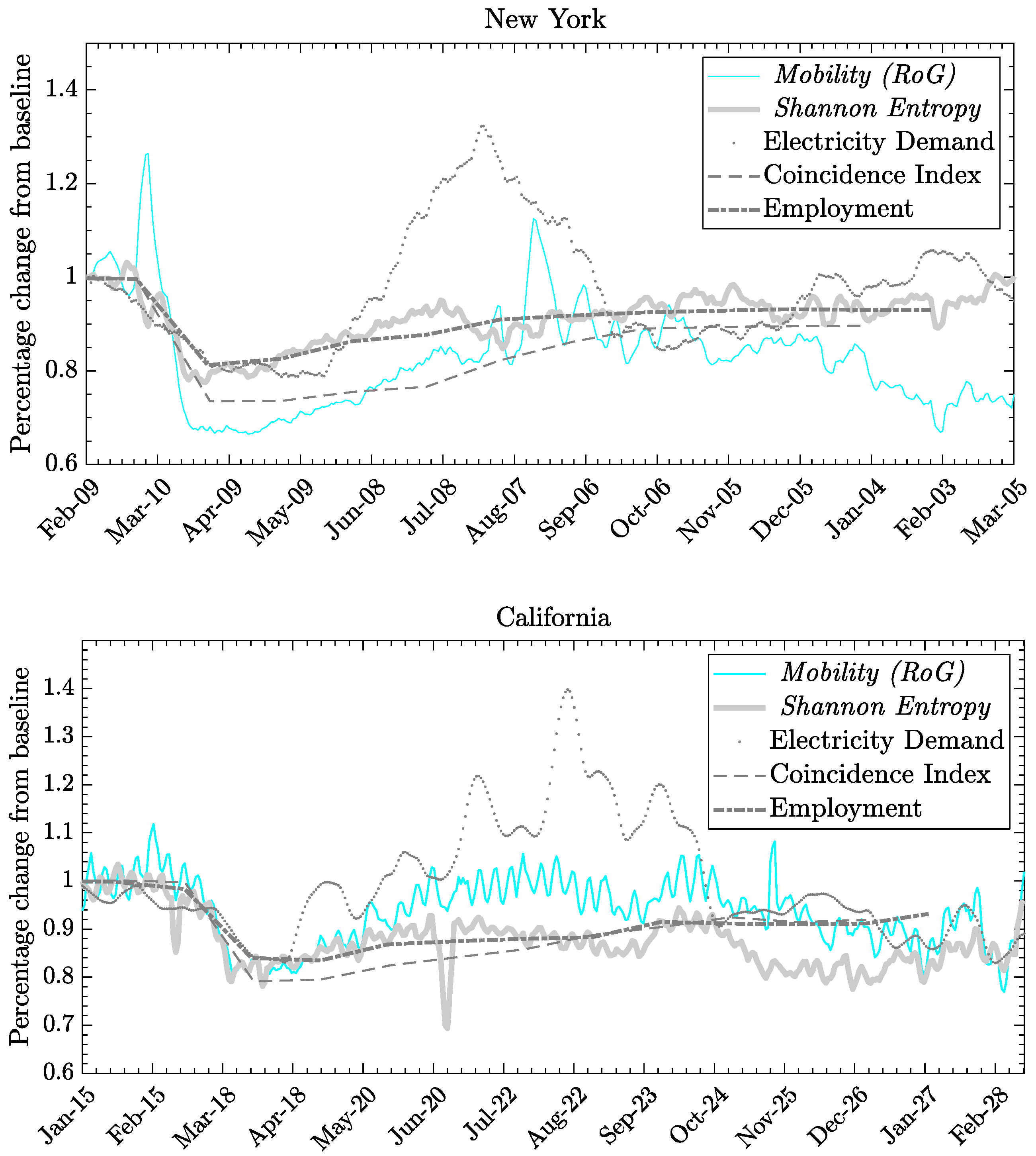
In Figure 4, we illustrate that economic indicators shown in the plot appear to be better aligned with entropy rather than mobility, especially for U.S. states like New York and others where entropy and mobility exhibit opposite trends at the beginning of 2021. In states such as California, where the two mobility indicators show similar trends, the correlations between mobility and economic indexes are more indistinguishable.
At this point, we can assess the statistical measures that determine the association of these indicators against mobility and entropy variables for each state. We accomplish this by measuring the linear relationship through the correlation coefficient, thereby highlighting the aggregated extent to which each of the economic time series moves together with mobility and entropy. We demonstrate that some of the economic series are more strongly correlated with entropy compared to solely mobility. We attribute this to the varying information content in each economic variable and to the fact that entropy embodies more complex information than just mobility. While this may be advantageous for certain economic indicators, it may not hold true for others. In particular, we investigate the relationship between each of the selected economic indexes versus the mobility and entropy variables for each of the 50 U.S. states, as reported in Figure 5.
We observe that entropy is systematically highly correlated with employment and the coincident index compared to mobility in almost all states. Conversely, mobility (such as RoG) shows a higher correlation with energy demand. As for the impacts on the labor market, employment rates in the United States fell dramatically during the first months of 2020 as the repercussions of the CoVid-19 pandemic reverberated through the labor market. However, the pandemic-related economic pause and lockdown differently affected the employment opportunities of individuals working in different sectors. In particular, regions with economies relying on the movement of people (such as tourism) faced substantially higher unemployment at the end of 2020 than regions with core industries based on the movement of information. Population mobility is closely related to consumer decisions regarding what to buy, how much to buy, and when to buy among many goods and services. Consumers not only satisfy their own needs but also determine the quantity and types of goods and services ultimately produced. The production of these goods and services creates jobs in all sectors of the economy. From a consumer spending perspective, we have selected only high-frequency data related to electricity demand. This indicator measures how much electricity each end-use sector consumes and the varying effects of COVID-19 mitigation efforts on the sectors. We have used data on demand for electricity as reported by the International Energy Agency (IEA) [38] of regional electricity production in megawatt-hours units. Ultimately, we have selected the monthly coincident index for each of the 50 states as produced by the Federal Reserve Bank of Philadelphia [39]. The coincident indexes combine four state-level indicators to summarize current economic conditions in a single statistic. These indexes are monthly indicators of economic activity for each of the 50 U.S. states, based on a composite of four widely available data series on state conditions: total non-farm payroll employment, the unemployment rate, average hours worked in manufacturing, and real wages and salary disbursements.
We summarize all the results above in terms of an overall analysis as reported in table Table 3 where we have computed the median correlations and their confidence intervals. We observe that Entropy shows a significantly higher degree of correlation against employment and coincidence index than mobility. This may be due to the more complex nature of the entropy which accounts for mobility together with other social distances measures as indicator of regularity of locations patterns. Meanwhile mobility is more strongly correlated with energy demand, and this can be due to the fact that the consumption of electricity is more sensitive to a change in movements of individuals rather then some sort of regularity of those.
Building upon the empirical findings, we can lay the foundation for a mathematical model that links epidemic trends to human mobility and social distancing behaviors. These factors, in turn, both influence and are influenced by social and economic activities. In this context, it’s important to note that informational entropy serves as a crucial variable in determining the effective reproduction number of an epidemic. The reproduction number R t has been estimated via a renewal epidemic model as developed in [59,60]. The human mobility regularity pattern influences the epidemiological evolution as follows:
Proposition 3.
The evolution of the effective reproduction number can be written in terms of uncorrelated Shannon entropy S through the following delayed equation:
R t + τ = s t γ t R 0 e Δ S t
where τ is a delay variable that accounts for the typical time it takes to observe newly generated positive test, R 0 denotes the basic reproduction number, s t represents the fraction of susceptible individuals respect to the initial time t = 0 , γ t represents the infection transmissibility factor, and finally, Δ S t = 1 2 ( S t − S 0 ) is the Shannon entropy (half) difference respect to its initial value S 0 at time t = 0 .
Proof. 
The proposition is proved in Appendix C □
From the previous proposition, we can see that the condition Δ S t > 0 will result in a positive contribution of the entropy to an increase of the effective reproduction number. Conversely, the condition Δ S t < 0 will contribute to a decrease of the effective reproduction number. If Δ S t = 0 the value of the effective reproduction will change uniquely in relation to the susceptible population and infection transmissibility. As a consequence, keeping all the other variables constant, the more regular human movement becomes, the lower the reproduction number is.
Using a methodology similar to the epidemiological-mobility approach as in Proposition 3 , we can imagine to create a quantitative relationship between macro-economic costs and an entropy-based measure of collective human mobility. This will imply to assess the implications of changes in human mobility patterns through a hypothetical macro-economic indicator C = f ( ω , L ) , where L encompasses various mobility variables like movement trends, population density, and societal interaction patterns. Conversely, the variable ω represents a pure economic factor, capturing the specificity (elasticity) of the economic indicator and its sensitivity to changes in mobility and interactions within region-specific demographic, social, and economic contexts. However, due to the complexity of the subject, our empirical exercise represents only a qualitative and preliminary investigation for such mathematical foundation.
In conclusion, we have focused our research study on establishing a robust and quantitative description of population mobility, laying the groundwork for further and more rigorous studies that can connect socio-economic indicators to mobility patterns. An exhaustive explanation of the empirical results goes beyond the purpose of the work, but could lead to an interesting discussion in behavioral and transportation economics to better understand how spatial cognition shapes mobility patterns [47,61,62,63].

4. Final Remarks

Regarding patterns of mobility, entropy serves as a valuable metric for quantifying the level of disorder or randomness within human movement behaviors. As individuals traverse various locations and engage in different activities, the entropy of their mobility patterns provides insight into the diversity and unpredictability of their movements. Higher entropy values suggest greater variability and less predictability in mobility patterns, whereas lower entropy values indicate more structured and predictable behaviors. Moreover, entropy-based metrics are proposed as potential candidates for macroscopic connections between human mobility patterns and economic activity. Consequently, by analyzing entropy in mobility patterns, researchers can discern underlying trends and dynamics, facilitating a deeper understanding of human behavior and informing decision-making processes in various domains such as urban planning, transportation, and public health.
This work has contributed to show that entropy, as measure of the diversity of mobility, exhibits a stronger relation with certain economic indicators as also seen in [12]. In addition, our theoretical framework is able to provide a more reliable estimate of perceived population density through a weight factor which takes into account both regularities and intensity of movements. We have explored the relationship between mobility, entropy, and various economic variables. Understanding this correlation could be valuable for developing region-specific mitigation policies that effectively balance epidemic control and economic stability.
While we do not claim to offer an exhaustive model for mobility patterns and population behaviors, we view our work as a starting point for quantitatively representing the connection between human movement trends and regularities with demographic and economic indicators. The significance of our contribution lies in the fact that entropy encapsulates various aspects of social movement trends and has the potential to serve as a straightforward mobility indicator for policymakers. As future work, we aim to expand the model to incorporate more detailed individual behavior information, such as travel trajectories and time spent in specific locations. Achieving this will require overcoming our model’s assumption that individuals’ movements are uncorrelated, thereby enhancing the reliability of describing dynamic socio-economic phenomena driven by mobility trends.

Author Contributions

Conceptualization, F.V., D.L.; methodology, F.V., D.L.; software, F.V.; validation, F.V., D.L.; formal analysis, F.V., D.L.; investigation, F.V., D.L.; resources, F.V., D.L.; data curation, F.V.; writing—original draft preparation, F.V., D.L. ; writing—review and editing, F.V., D.L.; visualization, F.V. ; supervision, F.V., D.L.; project administration, F.V., D.L.. All authors have read and agreed to the published version of the manuscript.

Funding

F.V. has received a support for the work funded by UCAJEDI Investments in the Future project managed by the National Research Agency (ANR) with the reference number ANR-15-IDEX-01. D.L. has received financial support through NIH sub-award GMO:240910 PO: 0000003121.

Data Availability Statement

The mobility datasets presented in this article are not readily available because it was accessible only for a time limitation for the period during the covid19 pandemic. Requests to access the datasets should be directed to Camber System [34]. The demographic data presented in the study are openly available in Census Bureau and World Pop Hub at [42,44]. Finally economic data presented in the study are openly available in Economic Tracker at [37], in U.S. energy information administration [38] and in the Federal Reserve Bank at [39].

Acknowledgments

F.V. wants to acknowledge to be a member of GNAMPA-INdAM.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
RoG Radius of Gyration
PWD-M Population Weighted Density based on weighted median
GPS global positioning system
CDR call detail record

Appendix A. Proof of Proposition 1

Proof. 
The effective area allowed for a single individual is A = L 2 so that the configurational space is:
A N = A N ,
where A is the area of the region in which the population is considered. So, the Boltzmann entropy under constant mobility expansion is
S B = k log A N A 0 N
= k N log A A 0 ,
where A 0 is a characteristic area, often the unit area. Consequently, the configurational entropy in terms of the Boltzmann picture is
S R = 1 k N S B ≈ ln A A 0
= ln δ o δ ,
where δ o = N A 0 . □

Appendix B. Proof of Proposition 2

We consider N individuals in a 2 dimensional region. Canonical coordinates and momenta are p = ( p 1 … p 2 N ) , q = ( q 1 … q 2 N ) so that every point in the 4 N dimensional phase-space k ( p , q ) corresponds to a possible state of the social system. The volume measure of the phase-space is defined as:
d Γ = 1 c ∏ i = 1 2 N d p i d q i
where c = ( m 2 μ 0 2 π A 0 ) N is a dimensionful constant. The probability for the system to occupy the state k is ρ ( k ) . Entropy determines the phase space volume of available states. Assuming that one only knows the values of a finite set of macroscopic variables, the principle of maximum entropy (a sort of special case of Occam’s razor) dictates that one should choose the distribution ρ consistent with those values that has the largest entropy.
S G = k B ∫ R 4 N − ρ log ρ d Γ − λ 1 2 ∫ R 4 N p 2 m 2 ρ d Γ − N μ 2 − λ 2 ∫ R 4 N ρ d Γ − 1
where the second and the third constraint terms account for enforcing the root mean square velocity and for enforcing normalization respectively. Maximizing the entropy is equivalent to the minimization of the information about the system.
The maximization of entropy under constrains provide the value of the Lagrange multipliers ( λ 1 , λ 2 ) :
0 = δ S = ∫ R 4 N − log ρ − 1 − λ 1 2 m 2 p 2 − λ 2 δ ρ d Γ
After some calculations we find that
ρ = e − ( 1 + λ 2 ) − λ 1 2 p 2 m 2
meanwhile from constraints we get the value of the multipliers:
∫ R 4 N p 2 m 2 ρ d Γ = N μ 2 ⇒ λ 1 = 1 μ
∫ R 4 N ρ d Γ = 1 ⇒ m 2 π λ 1 2 N 1 c ∫ V d q = e 1 + λ 2
The last integral A N = ∫ V d q represents the configurational spatial entropy which can be calculated as in eq.(A1) which summarizes that we are considering point particles that only interact with the walls. Therefore, we can write
S G = − 〈 ln ρ 〉 = − − ( 1 + λ 2 ) − λ 1 2 p 2 m 2 = 1 + λ 2 + λ 1 2 p 2 m 2 = ln m 2 π λ 1 2 N A N c − λ 1 2 e − ( 1 + λ 2 ) ∂ ∂ λ 1 2 ∫ R 2 N e − λ 1 2 p 2 m 2 d p
where the last integral is equal to ( m 2 π / λ 1 2 ) N . Finally, after minor algebraic manipulations, we get the uncorrelated Shannon entropy in terms of social mobility variables as:
S U = S G / ( k B N ) = 2 log μ μ o + log δ o δ + 1 .
We explicitly see the dependence of the entropy on mobility and population density, where δ o = N / A 0 is a characteristic density and μ 0 is a characteristic speed.

Appendix C. Proof of Proposition 3

Directly from the result in [59], the effective reproduction number written is written as:
R ( t + τ ) = R 0 n s ( t ) n s ( t 0 ) η ( t ) η ( t 0 ) 1 − λ ( t ) 1 − λ ( t 0 ) δ ( t 0 ) δ ( t ) μ ( t ) μ ( t 0 ) ,
where the time delay τ is the generative infectious time which takes into account the typical time to generate positive test results. For simplicity, we define s t = n s ( t ) n s ( t 0 ) the fraction of susceptible population n s ( t ) respect to an initial value, γ t = η ( t ) η ( t 0 ) 1 − λ ( t ) 1 − λ ( t 0 ) is the infection transmissibility factor which depend on the viral transmissibility ratio η ( t ) / η ( t 0 ) multiplied by the tracing efficiency γ t = 1 − λ ( t ) 1 − λ ( t 0 ) . As regarding with the mobility variables, we have made use of the fact that the population density δ is inversely proportional to the squared distance between individuals as used in [59], meanwhile μ ( t ) has the usual meaning of movement trend as in the present text. We now exploit the result in Proposition 2 to use the entropy in the place of human mobility variable δ and μ , so that we can write:
ln μ ( t ) δ ( t ) δ ( t 0 ) μ ( t 0 ) 2 = S t − S 0
then inserting the previous expression in the eq.(A13), we obtain the thesis of the proposition. References

References

  1. Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Physics Reports 2018, 734, 1–74. [Google Scholar] [CrossRef]
  2. Gallotti, R.; Bazzani, A.; Degli Esposti, M.; Rambaldi, S. Entropic measures of individual mobility patterns. Journal of Statistical Mechanics: Theory and Experiment 2013, 2013, P10022. [Google Scholar] [CrossRef]
  3. Osgood, N.D.; Paul, T.; Stanley, K.G.; Qian, W. A theoretical basis for entropy-scaling effects in human mobility patterns. PloS one 2016, 11, e0161630. [Google Scholar] [CrossRef] [PubMed]
  4. Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
  5. Lu, X.; Wetter, E.; Bharti, N.; Tatem, A.J.; Bengtsson, L. Approaching the limit of predictability in human mobility. Scientific reports 2013, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
  6. Kulkarni, V.; Mahalunkar, A.; Garbinato, B.; Kelleher, J.D. Examining the limits of predictability of human mobility. Entropy 2019, 21, 432. [Google Scholar] [CrossRef] [PubMed]
  7. Lesser, J.A.; Lusch, R.F. Entropy and the prediction of consumer behavior. Behavioral Science 1988, 33, 282–291. [Google Scholar] [CrossRef]
  8. Xu, J.; Shen, H.; Wyer Jr, R.S. Does the distance between us matter? Influences of physical proximity to others on consumer choice. Journal of Consumer Psychology 2012, 22, 418–423. [Google Scholar] [CrossRef]
  9. Blondel, V.D.; Decuyper, A.; Krings, G. A survey of results on mobile phone datasets analysis. EPJ data science 2015, 4, 1–55. [Google Scholar] [CrossRef]
  10. Luca, M.; Barlacchi, G.; Lepri, B.; Pappalardo, L. A survey on deep learning for human mobility. ACM Computing Surveys (CSUR) 2021, 55, 1–44. [Google Scholar] [CrossRef]
  11. Cintia, P.; Fadda, D.; Giannotti, F.; Pappalardo, L.; Rossetti, G.; Pedreschi, D.; Rinzivillo, S.; Bonato, P.; Fabbri, F.; Penone, F.; et al. The relationship between human mobility and viral transmissibility during the COVID-19 epidemics in Italy. arXiv, 2020; arXiv:2006.03141. [Google Scholar]
  12. Pappalardo, L.; Vanhoof, M.; Gabrielli, L.; Smoreda, Z.; Pedreschi, D.; Giannotti, F. An analytical framework to nowcast well-being using mobile phone data. International Journal of Data Science and Analytics 2016, 2, 75–92. [Google Scholar] [CrossRef]
  13. Luca, M.; Barlacchi, G.; Lepri, B.; Pappalardo, L. Deep Learning for Human Mobility: a Survey on Data and Models. arXiv, 2020; arXiv:2012.02825. [Google Scholar]
  14. Bonato, P.; Cintia, P.; Fabbri, F.; Fadda, D.; Giannotti, F.; Lopalco, P.L.; Mazzilli, S.; Nanni, M.; Pappalardo, L.; Pedreschi, D.; et al. Mobile phone data analytics against the covid-19 epidemics in italy: flow diversity and local job markets during the national lockdown. arXiv, 2020; arXiv:2004.11278. [Google Scholar]
  15. Tommaso, F.; Leonardo, G.; Fabio, V.; Alessandro, C.; Mattia, G.; Francesco, L.; Severin, R.; Giorgio, F.; Mauro, N.; Andrea, R. On the employment and health impact of the COVID-19 shock on Italian regions: a value chain approach. Regional Studies 2024, 58, 490–506. [Google Scholar] [CrossRef]
  16. Reissl, S.; Caiani, A.; Lamperti, F.; Guerini, M.; Vanni, F.; Fagiolo, G.; Ferraresi, T.; Ghezzi, L.; Napoletano, M.; Roventini, A. Assessing the Economic Impact of Lockdowns in Italy: A Computational Input–Output Approach. Industrial and Corporate Change 2022, 31, 358–409, https://academic.oup.com/icc/articlepdf/ 31/2/358/43219115/dtac003.pdf. [Google Scholar] [CrossRef]
  17. Clemente, G.P.; Grassi, R.; Rizzini, G. The effect of the pandemic on complex socio-economic systems: community detection induced by communicability. Soft Computing, 2023; 1–23. [Google Scholar]
  18. Ye, Y.; Cao, Z.; Dajun Zeng, D.; Zhang, Q. Supply chain loss from easing COVID-19 restrictions: an evolutionary economic-epidemiological modelling study. Proceedings of the Royal Society A 2024, 480, 20230803. [Google Scholar] [CrossRef]
  19. Rappaport, J. A productivity model of city crowdedness. Journal of Urban Economics 2008, 63, 715–722. [Google Scholar] [CrossRef]
  20. Glaeser, E.L.; Kahn, M.E. Sprawl and urban growth. Harvard Institute of Economic Research. Handbook of regional and urban economics 2004, 4, 2481–2527. [Google Scholar]
  21. Carozzi, F. Urban density and COVID-19. IZA discussion paper 2020. [Google Scholar] [CrossRef]
  22. Brodeur, A.; Gray, D.M.; Islam, A.; Bhuiyan, S. A Literature Review of the Economics of COVID-19. IZA Discussion Paper 2020. [Google Scholar] [CrossRef]
  23. Papageorge, N.W.; Zahn, M.V.; Belot, M.; Van den Broek-Altenburg, E.; Choi, S.; Jamison, J.C.; Tripodi, E. Socio-demographic factors associated with self-protecting behavior during the Covid-19 pandemic. Journal of Population Economics, 2020; 1–48. [Google Scholar]
  24. Basurto, A.; Dawid, H.; Harting, P.; Hepp, J.; Kohlweyer, D. Economic and epidemic implications of virus containment policies: insights from agent-based simulations. Bielefeld Working Papers in Economics and Management 2020. [Google Scholar] [CrossRef]
  25. Avery, C.; Bossert, W.; Clark, A.; Ellison, G.; Ellison, S.F. An Economist’s Guide to Epidemiology Models of Infectious Disease. Journal of Economic Perspectives 2020, 34, 79–104. [Google Scholar] [CrossRef]
  26. Ji, Y.; et al. Understanding human mobility patterns through mobile phone records: a cross-cultural study. PhD thesis, Massachusetts Institute of Technology, 2011.
  27. Salat, H.; Smoreda, Z.; Schläpfer, M. A method to estimate population densities and electricity consumption from mobile phone data in developing countries. PloS one 2020, 15, e0235224. [Google Scholar] [CrossRef] [PubMed]
  28. Järv, O.; Tenkanen, H.; Toivonen, T. Enhancing spatial accuracy of mobile phone data using multi-temporal dasymetric interpolation. International Journal of Geographical Information Science 2017, 31, 1630–1651. [Google Scholar] [CrossRef]
  29. Krumme, C.; Llorente, A.; Cebrian, M.; Moro, E.; et al. The predictability of consumer visitation patterns. Scientific reports 2013, 3, 1–5. [Google Scholar] [CrossRef] [PubMed]
  30. Dynarski, M.; Sheffrin, S.M. Consumption and unemployment. The Quarterly Journal of Economics 1987, 102, 411–428. [Google Scholar] [CrossRef]
  31. Jakimowicz, A. The Role of Entropy in the Development of Economics. Entropy 2020, 22. [Google Scholar] [CrossRef] [PubMed]
  32. Rosser Jr, J.B. Econophysics and the entropic foundations of economics. Entropy 2021, 23, 1286. [Google Scholar] [CrossRef] [PubMed]
  33. Ermilov, M.M.; Surkova, L.E.; Samoletov, R.V. Mathematical modeling of consumer behavior, taking into account entropy. In Frontier information technology and systems research in cooperative economics; Springer, 2020; pp. 269–278.
  34. CamberSystems. Social Distancing Reporter, 12/20/2020. available at https://covid19.cambersystems.com.
  35. U.S. Census Bureau. 2010 Census. U.S. Department of Commerce, 2011. available at https://www.census.gov/library/visualizations/2012/dec/c2010sr-01-density.html.
  36. Edwards, R.; Bondarenko, M.; Tatem, A.; Sorichetta, A. Unconstrained national Population Weighted Density in 2000, 2005, 2010, 2015 and 2020 ( 1km resolution ), 2021.
  37. Opportunity Insights Team. Opportunity Insights Economic Tracker Data, 2021. available at https://tracktherecovery.org/.
  38. Administration, U.E.I. EIA-930, Hourly and Daily Balancing Authority Operations Report. U.S. Energy Information Administration, 2021. available at https://www.eia.gov/beta/electricity/gridmonitor/dashboard/electric_overview/US48/US48.
  39. Philadelphia, F.R.B. State Coincident Indexes. Federal Reserve Bank of Philadelphia, 2021. available at https://www.philadelphiafed.org/surveys-and-data/regional-economic-analysis/state-coincident-indexes.
  40. Liao, Y.; Yeh, S.; Jeuken, G.S. From individual to collective behaviours: exploring population heterogeneity of human mobility based on social media data. EPJ Data Science 2019, 8, 34. [Google Scholar] [CrossRef]
  41. Liu, T.; Yang, Z.; Zhao, Y.; Wu, C.; Zhou, Z.; Liu, Y. Temporal understanding of human mobility: A multi-time scale analysis. PloS one 2018, 13, e0207697. [Google Scholar] [CrossRef]
  42. Robin Edwards, Maksym Bondarenko, A. J.T.; Sorichetta., A. Unconstrained subnational Population Weighted Density in 2000, 2005, 2010, 2015 and 2020 ( 1km resolution ). [CrossRef]
  43. Ottensmann, J.R. On population-weighted density. Available at SSRN 3119965 2018. [Google Scholar] [CrossRef]
  44. U.S. Bureau Labor Statistics, B. U.S. Bureau Labor Statistics, B. Job Flexibilities and Work Schedules 2017-2018 Data from the American Time Use Survey, 2019. www.bls.gov/tus/data.html.
  45. Craig, J. Averaging population density. Demography 1984, 21, 405–412. [Google Scholar] [CrossRef] [PubMed]
  46. Henderson, J.V.; Storeygard, A.; Weil, D.N. Quality-adjusted population density. Bravo Working Paper 2020. [Google Scholar]
  47. Otterbring, T.; Folwarczny, M.; Tan, L.K. Populated places and conspicuous consumption: high population density cues predict consumers’ luxury-linked brand attitudes. Frontiers in Psychology 2021, 12, 728903. [Google Scholar] [CrossRef] [PubMed]
  48. Plane, D.A.; Mu, W. A people-based density perspective on physical/virtual world spaces in the microcosmic city. Land use policy 2021, 111, 104462. [Google Scholar] [CrossRef]
  49. Başkan, A.H.; Zorba, E.; Bayrakdar, A. Impact of the population density on quality of life. Journal of Human Sciences 2017, 14, 506–518. [Google Scholar] [CrossRef]
  50. Smolak, K.; Siła-Nowicka, K.; Delvenne, J.C.; Wierzbiński, M.; Rohm, W. The impact of human mobility data scales and processing on movement predictability. Scientific Reports 2021, 11, 15177. [Google Scholar] [CrossRef] [PubMed]
  51. Bonaccorsi, G.; Pierri, F.; Cinelli, M.; Flori, A.; Galeazzi, A.; Porcelli, F.; Schmidt, A.L.; Valensise, C.M.; Scala, A.; Quattrociocchi, W.; et al. Economic and social consequences of human mobility restrictions under COVID-19. Proceedings of the National Academy of Sciences 2020, 117, 15530–15535. [Google Scholar] [CrossRef] [PubMed]
  52. Weill, J.A.; Stigler, M.; Deschenes, O.; Springborn, M.R. Social distancing responses to COVID-19 emergency declarations strongly differentiated by income. Proceedings of the National Academy of Sciences 2020, 117, 19658–19660. [Google Scholar] [CrossRef]
  53. Pepe, E.; Bajardi, P.; Gauvin, L.; Privitera, F.; Lake, B.; Cattuto, C.; Tizzoni, M. COVID-19 outbreak response, a dataset to assess mobility changes in Italy following national lockdown. Scientific data 2020, 7, 1–7. [Google Scholar] [CrossRef]
  54. Flaschel, P.; Galanis, G.; Tavani, D.; Veneziani, R. Pandemics and aggregate demand: A framework for policy analysis. CAMA Working Paper 2021. [Google Scholar] [CrossRef]
  55. Reissl, S.; Caiani, A.; Lamperti, F.; Guerini, M.; Vanni, F.; Fagiolo, G.; Ferraresi, T.; Ghezzi, L.; Napoletano, M.; Roventini, A. Assessing the economic effects of lockdowns in Italy: a dynamic Input-Output approach. LEM Working Paper Series 2021. [Google Scholar] [CrossRef]
  56. Guerrieri, V.; Lorenzoni, G.; Straub, L.; Werning, I. Macroeconomic implications of COVID-19: Can negative supply shocks cause demand shortages? Technical report, National Bureau of Economic Research, 2020.
  57. Gene, F.; Jameson, A.C.; Isaac, A.N.; Emma, C.N.; Paul, D.R. Unemployment Rates During the COVID-19 Pandemic: In Brief. Technical Report R46554, Congressional Research Service (CRS)., 2021.
  58. of Labor Statistics, B. Economy at a Glance. United States Department of Labor, 2021. available at https://www.bls.gov/eag/home.htm.
  59. Vanni, F.; Lambert, D.; Palatella, L.; Grigolini, P. On the use of aggregated human mobility data to estimate the reproduction number. Scientific reports 2021, 11, 23286. [Google Scholar] [CrossRef] [PubMed]
  60. Palatella, L.; Vanni, F.; Lambert, D. A phenomenological estimate of the true scale of CoViD-19 from primary data. Chaos, Solitons & Fractals, 2021; 110854. [Google Scholar]
  61. Barbosa, H.; Hazarie, S.; Dickinson, B.; Bassolas, A.; Frank, A.; Kautz, H.; Sadilek, A.; Ramasco, J.J.; Ghoshal, G. Uncovering the socioeconomic facets of human mobility. Scientific reports 2021, 11, 8616. [Google Scholar] [CrossRef] [PubMed]
  62. Luh, S.; Kannan, R.; Schmidt, T.J.; Kober, T. Behavior matters: A systematic review of representing consumer mobility choices in energy models. Energy Research & Social Science 2022, 90, 102596. [Google Scholar]
  63. Pappalardo, L.; Manley, E.; Sekara, V.; Alessandretti, L. Future directions in human mobility science. Nature computational science 2023, 3, 588–600. [Google Scholar] [CrossRef]
1
The radius of gyration is defined as r g ( u ) = 1 L i ( u ) ∑ i = 1 L i ( u ) ( r i ( u ) − r ¯ ( u ) ) 2 where r i ( u ) represents the i = 1 … L i ( u ) positions recorded for the device u and r ¯ ( u ) is the center of mass of the trajectory.
2
Note that the radius of gyration for purely diffusive motion obeys r g ( t ) ∼ t [40,41].
Preprints 102914 g001
Figure 1. Entropies of individuals’ movements in 2020 for New York, California, Texas, and Florida. The time series have been rescaled by their values at beginning of the observation period. Data courtesy of Camber Systems [34] and U.S. Census Bureau U.S. Census Bureau [35].
Figure 1. Entropies of individuals’ movements in 2020 for New York, California, Texas, and Florida. The time series have been rescaled by their values at beginning of the observation period. Data courtesy of Camber Systems [34] and U.S. Census Bureau U.S. Census Bureau [35].
Preprints 102914 g001
Preprints 102914 g002
Figure 2. Comparison between the various implementations of the entropy of individuals’ movements. Data courtesy of Camber Systems [34] and U.S. Census Bureau U.S. Census Bureau [35] for New Mexico (a state with an evenly distributed population) and New Jersey (a state with an unevenly distributed population.)
Figure 2. Comparison between the various implementations of the entropy of individuals’ movements. Data courtesy of Camber Systems [34] and U.S. Census Bureau U.S. Census Bureau [35] for New Mexico (a state with an evenly distributed population) and New Jersey (a state with an unevenly distributed population.)
Preprints 102914 g002
Preprints 102914 g003
Figure 3. Comparison between the standard population density: people per unit area (a) and the population density weighted by the Shannon entropy correction factor (b).
Figure 3. Comparison between the standard population density: people per unit area (a) and the population density weighted by the Shannon entropy correction factor (b).
Preprints 102914 g003
Preprints 102914 g004
Figure 4. The economic indicators are reported monthly. Data courtesy of Camber Systems CamberSystems [34], U.S. Bureau of labor statistics of Labor Statistics [58], Federal Reserve Bank of Philadelphia [39] and Electricity demand EIA [38], for mobility, labor, economic and energy data respectively.
Figure 4. The economic indicators are reported monthly. Data courtesy of Camber Systems CamberSystems [34], U.S. Bureau of labor statistics of Labor Statistics [58], Federal Reserve Bank of Philadelphia [39] and Electricity demand EIA [38], for mobility, labor, economic and energy data respectively.
Preprints 102914 g004
Preprints 102914 g005
Figure 5. Correlation coefficient for each state between each economic indicator and the RoG mobility (light thin bars) and uncorrelated entropy (dark thick bars) for three different economic indicators: (a) employment rate, (b) consumer spending and (c) energy consumption. Longer bars indicate a stronger correlation between the time series.
Figure 5. Correlation coefficient for each state between each economic indicator and the RoG mobility (light thin bars) and uncorrelated entropy (dark thick bars) for three different economic indicators: (a) employment rate, (b) consumer spending and (c) energy consumption. Longer bars indicate a stronger correlation between the time series.
Preprints 102914 g005
Preprints 102914 g006
Figure 6. Correlation coefficient for each state between each economic indicator and the RoG mobility (light thin bars) and uncorrelated entropy (dark thick bars) for two different economic indicators: (a) Firms’ revenues and (b) Coincidence index. Longer bars indicate a stronger correlation between the time series.
Figure 6. Correlation coefficient for each state between each economic indicator and the RoG mobility (light thin bars) and uncorrelated entropy (dark thick bars) for two different economic indicators: (a) Firms’ revenues and (b) Coincidence index. Longer bars indicate a stronger correlation between the time series.
Preprints 102914 g006
Table 1. Data Repositories at state US level
Table 1. Data Repositories at state US level
Human Mobility Data
Camber Systems Social Distancing Reporter [34]- Entropy, RoG & Devices (daily)
U.S. Census Bureau [35] - Populaton density (annual)
World Pop Hub [36] - Population weighted density (annual)
Economic Data
Economic Tracker [37] - Employment, Consumer Spending & Firms Revenue (daily)
U.S. Energy Information Administration [38] - Energy Demand and Production (daily)
Federal Reserve Bank of Philadelphia [39] - Coincidence index (monthly)
Table 2. State population density estimates for the year 2020
Table 2. State population density estimates for the year 2020
State Population Density (d)
Census[35] Entropy-weighted Adjusted [35] PWD-M [42]
New Jersey 466.3 474.0 785.4 1713.7
Rhode Island 395.6 1403.7 455.3 1403.3
Massachusetts 341.2 524.9 552.4 1275.1
Connecticut 284.3 688.3 371.4 916.8
Maryland 240.5 228.1 453.4 1580.6
Delaware 193.0 1061.5 259.8 977.0
New York 159.4 67.5 1323.0 3132.5
Florida 154.6 57.0 286.4 1345.3
Pennsylvania 110.5 43.1 276.0 980.6
Ohio 110.5 31.7 228.2 935.5
California 97.9 43.9 329.1 2873.6
Illinois 88.1 22.0 410.6 1676.6
Hawaii 85.1 350.7 250.6 2342.3
Virginia 83.5 17.4 286.8 1152.1
North Carolina 83.3 21.7 150.6 516.8
Indiana 72.6 19.8 138.1 824.6
Georgia 71.3 11.7 204.4 710.8
Michigan 68.2 21.6 201.3 857.4
South Carolina 66.1 33.0 97.5 483.7
Tennessee 63.9 16.8 123.7 513.1
New Hampshire 58.6 117.4 95.4 307.8
Washington 44.2 28.3 129.5 1489.4
Kentucky 43.7 9.5 91.3 474.9
Texas 42.9 4.8 245.4 1626.6
Louisiana 41.5 15.1 97.2 646.2
Wisconsin 41.5 15.0 112.5 849.3
Alabama 37.4 12.8 64.2 346.1
Missouri 34.5 7.7 113.9 853.2
West Virginia 28.8 13.1 44.8 220.4
Minnesota 27.3 8.5 128.9 981.6
Vermont 26.1 41.4 34.1 124.5
Arizona 24.7 37.6 76.0 1887.7
Mississippi 24.5 7.1 37.3 243.3
Arkansas 22.4 7.1 40.8 372.5
Oklahoma 22.3 6.9 73.2 736.2
Iowa 21.8 5.6 43.7 816.1
Colorado 21.5 9.0 121.2 1783.1
Oregon 17.0 11.9 76.9 1639.1
Maine 16.8 23.4 37.4 134.8
Utah 15.1 12.0 135.2 1907.0
Kansas 13.8 3.5 64.9 1032.3
Nevada 10.8 14.7 64.4 3016.4
Nebraska 9.7 2.7 71.0 1246.8
Idaho 8.3 4.7 35.1 1137.8
New Mexico 6.7 5.4 24.9 1058.6
South Dakota 4.5 1.8 12.5 677.2
North Dakota 4.3 2.1 9.6 878.1
Montana 2.8 1.4 6.9 515.4
Wyoming 2.3 2.4 3.3 694.3
Alaska 0.5 0.5 5.6 687.6
Table 3. Correlation coefficient among all the 50 US states. Median values of the correlation coefficient and their 10th and 90th percentiles.
Table 3. Correlation coefficient among all the 50 US states. Median values of the correlation coefficient and their 10th and 90th percentiles.
Indicator (RoG) Mobility C.I. (Shannon) Entropy C.I.
Employment 0.55 [0.43, 0.64] 0.64 [0.53, 0.72]
Consumer Spending 0.43 [0.29,0.56] 0.65 [0.48, 0.74]
Electricity Demand 0.46 [0.32,0.59] 0.36 [0.16, 0.56]
Firms Revenue 0.51 [0.24,0.69] 0.34 [0.26, 0.60]
Coincident index 0.61 [0.51, 0.69] 0.69 [0.61, 0.75]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated