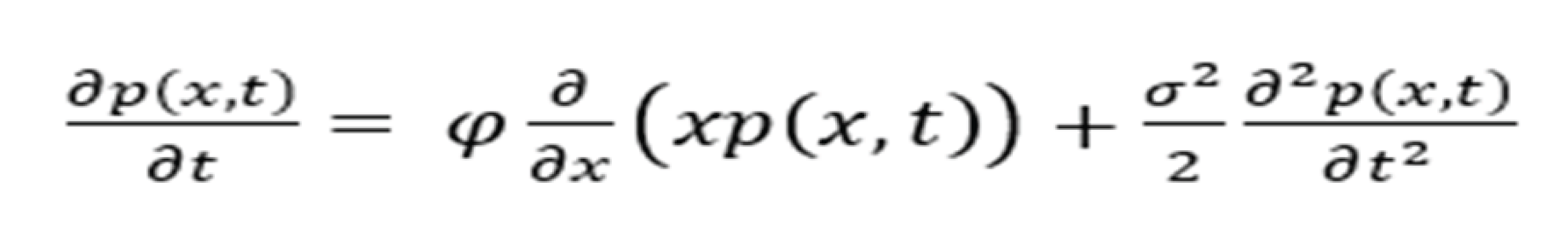Preprint

Article

Unfolding the Third Approximation of The Time‐Dependent Controller’s Designed Parameter (TDCDP) of Fokker Planck Kolmogorov (FPK) Probability Density Function(PDF)

Altmetrics

Downloads

Views

Comments

Dr Ismail A Mageed^*

This version is not peer-reviewed

Submitted:

03 April 2024

Posted:

03 April 2024

You are already at the latest version

Alerts

Abstract

A difficult open problem that has never been fully resolved in the literature to date is the behaviour of the (TDCDP) third approximation. As a giant step towards modern control theory, this cutting-edge paper will advance control theory and other relevant inter-disciplinary subjects. Because control theory is important in industry and engineering, this study will be especially beneficial to anyone working in these disciplines who wish to understand more about recent advances in control theory settings. In contrast, the wealth of applications of Fokker Planck Kolmogorov (FPK) equations numerous disciplines As a result, the study instantly gains more taste and credibility. At the end of the paper, there are several challenging open problems, some concluding remarks, and recommendations for further investigation.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

Introduction

It is possible to equationally view the closed-loop system [1,2,3,4,5,6,7] by:

d x_{t} = - φ x_{t} d t + σ d W_{t}

(1)

The system’s state is represented by

x_{t}

, TDCDP is denoted by

φ

> 0

, the Weiner process is defined by

W_{t}

, and

σ > 0

Fokker Planck Kolmogorov equation is:

(2)

The PDF,

p (x, t)

solves (2), with

p (x, t) = \sqrt (\frac{φ}{π σ^{2} (1 - e^{- 2 φ t})}) e^{(- \frac{φ {(x - x_{0} e^{- φ t})}^{2}}{π σ^{2} (1 - e^{- 2 φ t})})}

(3)

x_{0}

defines the initial value of

x_{t}

φ (t) = \frac{W_{0} (- \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}})}{2 t} + \frac{t σ^{2}}{2 r (t)}

(4)

Provided that

W_{0}

is the Lambert W function [8] and

r (t)

defines a time-dependent variance function. Figure 1 (c.f., [7]) visualizes

x_{t}

W_{0}

is defined as [8]:.

W_{0} (z) = \sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}

(5)

Where

z

is any complex number and it is satisfied when

z

is real. Also, for real values of

z

W_{0} (z)

satisfies:

\frac{d W_{0} (z)}{d z} = \frac{W_{0} (z)}{z (1 + W_{0} (z))}

(6)

The following theorem is essential to obtain the main results of section two.

Preliminary Theorem (PT) [9]

Let f be a function that is defined and differentiable on an open interval (c,d).

If f^{'} (x) > (<) 0 \forall x \in (c, d), then f increases (decreases) on (c, d)

(7)

This paper’s contributions are:

Solving for the first time ever, the TDCDP’s third approximation.
Introducing up-to-date, unsolved issues.

The current work reads: The methodology is highlighted in section two. Section three provides results and discussion. Section four discusses some emerging research questions with future research pathways.

Methodology

Notably, a mathematical approach is undertaken to calculate the threshold based on the preliminary theorem(see Equation (7)). More potentially, calculus and more advanced algebraic forms are utilized to uncover TDCDP’s time-dependent lower bound. Looking at the bigger picture, this discovery will lead to a contemporary control theory rather than being limited within the traditional classical frames.

This current paper provides the full answer, by solving the , but yet there are still numerous unexplored applications. This will put the research community into more spacious frontiers of thoughtful innovation.

Communicating (4), and (5), we arrive at the

n^{t h}

approximation of TDCDP, namely,

φ_{n} (t)

φ_{n} (t, r (t)) = \frac{\sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}}{2 t} + \frac{t σ^{2}}{2 r (t)}, z = - \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}}

(8)

Results and Discussion

Define

φ_{3} (t, r (t)) = \frac{(z - z^{2} + \frac{3}{2} z^{3})}{2 t} + \frac{t σ^{2}}{2 r (t)}

(9)

, z (c.f., (8))

Theorem 1 For

φ_{3}

of (9) satisfies:

φ_{3} (t, r (t)) > - (\frac{σ^{2}}{r (t)} + \frac{t σ^{4}}{{(r (t))}^{2}} + \frac{3 t^{2} σ^{6}}{{2 (r (t))}^{3}}) + \frac{t σ^{2}}{2 r (t)}

(10)

ii)

φ_{3} (t, r (t))

is temporally forever increasing(decreasing), whenever

\frac{σ^{2}}{{(r (t))}^{2}} (r - t r^{.}) - (e^{- \frac{t σ^{2}}{r (t)}} (\frac{σ^{4}}{{(r (t))}^{2}} + \frac{{t σ}^{4} r^{.}}{{(r (t))}^{3}} - \frac{σ^{2} r^{.}}{{(r (t))}^{2}}) + e^{- \frac{2 t σ^{2}}{r (t)}} (\frac{σ^{4}}{{(r (t))}^{2}} - \frac{{2 t σ}^{4} r^{.}}{{(r (t))}^{3}} - \frac{2 t σ^{6}}{{(r (t))}^{3}} + \frac{2 t^{2} σ^{6} r^{.}}{{(r (t))}^{4}}) + e^{- \frac{3 t σ^{2}}{r (t)}} (\frac{{3 t σ}^{6}}{{(r (t))}^{3}} - \frac{9 {t^{2} σ}^{6} r^{.}}{2 {(r (t))}^{4}} - \frac{9 {t^{2} σ}^{8}}{2 {(r (t))}^{4}} + \frac{9 {t^{3} σ}^{8} r^{.}}{2 {(r (t))}^{5}})) > (< 0), . = \frac{d}{d t}

(11)

Proof

(i) Clearly,

φ_{3} (t, r (t))

(c.f., (9)) read:

φ_{3} (t, r (t)) = - \frac{1}{2} (\frac{σ^{2}}{r (t)} e^{- γ} + \frac{{t σ}^{4}}{{(r (t))}^{2}} e^{- 2 γ} + \frac{3 {t^{2} σ}^{6}}{{2 (r (t))}^{3}} e^{- 3 γ}) + \frac{t σ^{2}}{2 r (t)}, γ = \frac{t σ^{2}}{r (t)}

(12)

Thus,

φ_{3} (t, r (t))

- \frac{1}{2}

(\frac{σ^{2}}{r (t)} e^{- γ} + \frac{{t σ}^{4}}{{(r (t))}^{2}} e^{- 2 γ} + \frac{3 {t^{2} σ}^{6}}{{2 (r (t))}^{3}} e^{- 3 γ}) + \frac{t σ^{2}}{2 r (t)}

> - \frac{1}{2}

(\frac{σ^{2}}{r (t)} + \frac{{t σ}^{4}}{{(r (t))}^{2}} + \frac{3 {t^{2} σ}^{6}}{{2 (r (t))}^{3}}) + \frac{t σ^{2}}{2 r (t)}

(Since,

e^{- γ} < 1)

> -

(\frac{σ^{2}}{r (t)} + \frac{{t σ}^{4}}{{(r (t))}^{2}} + \frac{3 {t^{2} σ}^{6}}{{2 (r (t))}^{3}}) + \frac{t σ^{2}}{2 r (t)}

(ii) Communicating the preliminary theorem,

φ_{3} (t, r (t)) is forever increasing (decreasing) in t if and only if \frac{d φ_{3} (t, r (t))}{d t} > (< 0)

(13)

respectively

Following some lengthy mathematical steps, we arrive at the desired result in (11).

Define

r (t) = σ^{2}

(14)

(c.f., (8))

This established the following theorem.

Theorem 2 For

φ_{n} (t, r (t))

(c.f., (14)), it holds that:

φ_{3} (t, σ^{2}) = - \frac{1}{2} (e^{- 3 t}) (e^{2 t} + {t e}^{t} + \frac{3}{2} t^{2}) + \frac{t}{2}

(15)

ii)

φ_{3} (t, σ^{2}) = 0 has a real root within the unit interval

(16)

iii)

φ_{3} (t, σ^{2})

is forever increasing in

t

Proof

We have,

φ_{3} (t, r (t)) (c . f ., (9))

It is implied that:

{r (t) = σ}^{2} ⟹ z = - t e^{- t}

(17)

Thus,

φ_{3} (t, σ^{2}) = \frac{(- t e^{- t} - t^{2} e^{- 2 t} - \frac{3}{2} t^{3} e^{- 3 t})}{2 t} + \frac{t}{2} = - \frac{1}{2} (e^{- 3 t}) (e^{2 t} + {t e}^{t} + \frac{3}{2} t^{2}) + \frac{t}{2}

(18)

Looking at (14), (i) is immediate.

ii) Let

φ_{3} (t, σ^{2}) = 0

Therefore,

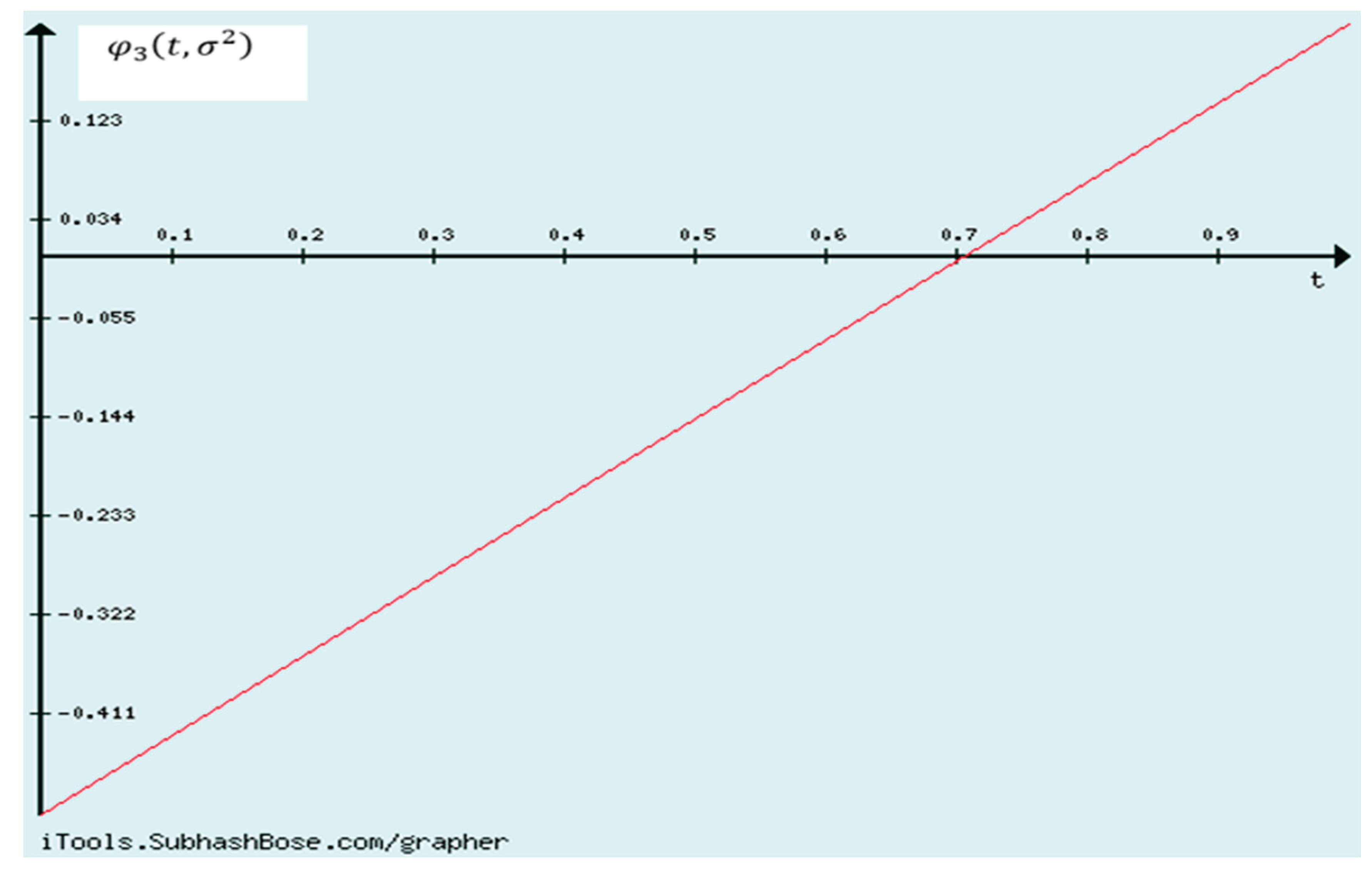
This can be visualized by checking that

φ_{3} (0, σ^{2}) = - 0.5, φ_{3} (1, σ^{2}) = 0.2110523365

(19)

Looking at Figure 2, it is evident that the root of

φ_{3} (t, σ^{2}) = 0

, will be floating between

0.7, a n d 0.8 \in [0,1] .

Communicating mathematical analysis, (ii) follows.

(iii)

\frac{d φ_{3} (t, σ^{2})}{d t} = (\frac{1}{2} + \frac{1}{2} e^{- 3 t} (e^{2 t} + 2 t e^{t} + \frac{9}{2} t^{2} + 3 t - e^{t}))

(10)

Therefore,

\frac{d φ_{3} (t, σ^{2})}{d t} > 0 ⟺ (\frac{1}{2} + \frac{1}{2} e^{- 3 t} (e^{2 t} + 2 t e^{t} + \frac{9}{2} t^{2} + 3 t - e^{t})) > 0

(11)

(\frac{1}{2} + \frac{1}{2} e^{- 3 t} (e^{2 t} + 2 t e^{t} + \frac{9}{2} t^{2} + 3 t - e^{t})) > 0

(12)

Equivalently,

e^{3 t} + e^{2 t} + 2 t e^{t} + \frac{9}{2} t^{2} > 3 t + e^{t}

(13)

Mathematically speaking, since

t > 0

e^{3 t} + e^{2 t} + 2 t e^{t}

\frac{9}{2} t^{2} >

e^{t}

t + t + t = 3 t + e^{t}

Hence, (iii) is immediate by engaging the preliminary theorem.

On a different note,

{l i m}_{t \to \infty} φ_{3} (t, σ^{2}) = {l i m}_{t \to \infty} (\frac{(- t e^{- t} - t^{2} e^{- 2 t} - \frac{3}{2} t^{3} e^{- 3 t})}{2 t} + \frac{t}{2}) = \infty

(14)

Which consolidates the forever increasability of

φ_{3} (t, σ^{2})

t

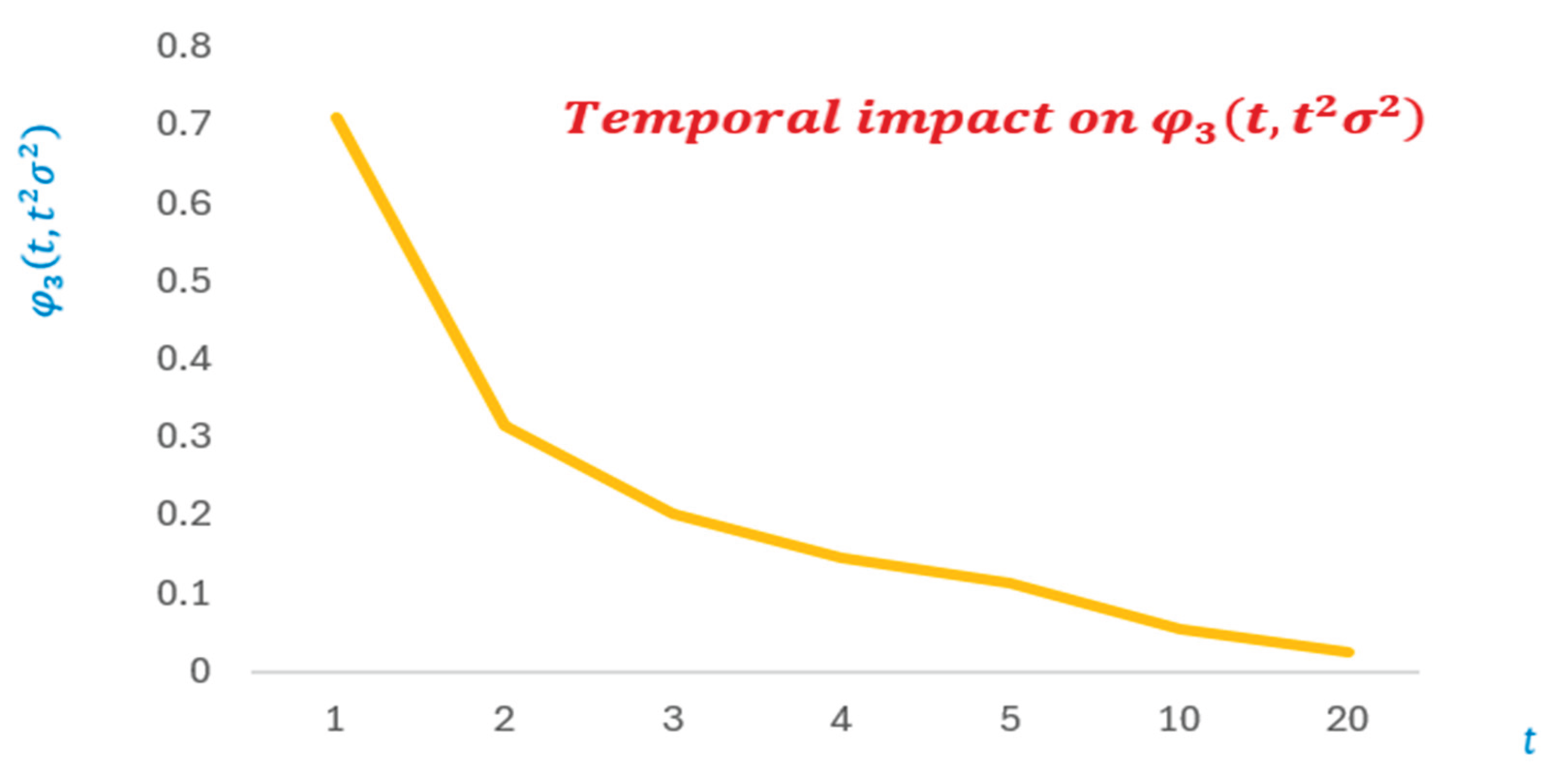
Having a close look at another case,

φ_{3} (t, {t^{2} σ}^{2})

, it can be easily shown by Figure 3, that

φ_{3} (t, {t^{2} σ}^{2})

decreases drastically as time increases. Moreover,

{l i m}_{t \to \infty} φ_{3} (t, {t^{2} σ}^{2}) = 0

(15)

Conclusion and Future Research

The third approximation of the TDCDP,

φ_{3} (t, r (t))

, has been examined in this explanation. More opportunely, this research has brought attention to a few suggested open issues:

Open Problem 1

Can we solve the ever- challenging open problem of finding the upper bound of

φ_{3} (t, r (t))

(c.f.(10)). It is expected that this upper bound, if existed, will be time-dependent?

Open Problem 2

Is it possible mathematically wise to unlock the most challenging open problem ever in uncovering the TDCDP’s fourth, fifth, sixth… approximations. The proposed open challenges will be solved in the next phase of research, which will also look at further extensions of FPK theory to additional multidisciplinary areas of human understanding.

References

I.A.Mageed, Threshold and Upper Bound for The Controller’s Designed Parameter of Fokker Planck Kolmogorov Probability Density Function with Applications to Cryptocurrency. Int J Med Net, 2(3),2024, 01-06. https://www.opastpublishers.
Hotz, A.; Skelton, R.E. Covariance control theory. Int. J. Control. 1987, 46, 13–32. [Google Scholar] [CrossRef]
K. J. Åström, Introduction to Stochastic Control Theory, Courier Corporation: North Chelmsford, MA, USA, (2012).
Ren, M.; Zhang, Q.; Zhang, J. An introductory survey of probability density function control. Syst. Sci. Control. Eng. 2019, 7, 158–170. [Google Scholar] [CrossRef]
H. Wang, Bounded Dynamic Stochastic Systems: Modelling and Control, Springer Science & Business Media: Berlin/Heidelberg, Germany, (2012).
S.M. Ross, et al., “Stochastic Processes, ” Wiley: New York, NY, USA, (1996).
I.A. Mageed, et al., Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov (FPK) Equation to System Control, Modelling and Simulation. In2023 28th International Conference on Automation and Computing (ICAC) (2023)1-6.
I.Mezo, Lambert W Function: Its Generalizations and Applications, Chapman and Hall/CRC: London, UK, (2022).
Gapeev, P.V.; Kort, P.M.; Lavrutich, M.N.; Thijssen, J.J.J. Optimal Double Stopping Problems for Maxima and Minima of Geometric Brownian Motions. Methodol. Comput. Appl. Probab. 2022, 24, 789–813. [Google Scholar] [CrossRef]
I.A. Mageed, D.D. Kouvatsos, The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold, In ICORES (2021)153-160.
I.A. Mageed, Q. I.A. Mageed, Q.Zhang, Information Geometry? Exercises de Styles. electronic Journal of Computer Science and Information Technology, (2022) 9-14.
Barreiro-Gomez, J.; Tembine, H. Mean-Field-Type Games for Engineers; Taylor & Francis Ltd: London, United Kingdom, 2021; ISBN 9781003098607. [Google Scholar]
T. Elsaesser, The mind-game film, In The Mind-Game Film, Routledge, (2021) 89-112.
Li, C.; Liu, Q.; Zhou, Z.; Buss, M.; Liu, F. Off-Policy Risk-Sensitive Reinforcement Learning-Based Constrained Robust Optimal Control. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 53, 2478–2491. [Google Scholar] [CrossRef]
Huang, J.; Qiu, Z.; Wang, S.; Wu, Z. A Unified Relation Analysis of Linear-Quadratic Mean-Field Game, Team and Control. IEEE Trans. Autom. Control. 2023, PP, 1–8. [Google Scholar] [CrossRef]
Carmona, R. The influence of economic research on financial mathematics: Evidence from the last 25 years. Finance Stochastics 2021, 26, 85–101. [Google Scholar] [CrossRef]
Li, Z.; Reppen, A.M.; Sircar, R. A Mean Field Games Model for Cryptocurrency Mining. Manag. Sci. 2023. [Google Scholar] [CrossRef]

Figure 1.

Figure 2. Roots of

φ_{3} (t, σ^{2}) = 0

Figure 2. Roots of

φ_{3} (t, σ^{2}) = 0

Figure 3.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.