Prerpints.org logo
Preprint
Article

A New Type of Hydraulic Clutch with Magnetorheological Fluid: Theory and Experiment

Altmetrics

Downloads

110

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 April 2024

Posted:

03 April 2024

You are already at the latest version

Alerts
Abstract
The paper presents a new type of hydraulic clutch operating with magnetorheological (MR) fluids and the results achieved from both theoretical analysis and experimental measurement. The hy-draulic clutch system of its own design with MR working fluid and a rotating magnetic field lo-cated is designed. The principle of this clutch is to use a rotating magnetic field created by an al-ternating current electromagnet to set the MR fluid in motion. In the tests of the hydraulic clutch with a rotating magnetic field, MR fluid produced on their own, consisting of solid iron particles of various diameters mixed with a silicone oil, are used as working fluids. The rheological properties of MR fluids are assessed on the basis of tests carried out with a Brookfield DV2T rheometer equipped with a magnetic device for generating the magnetic field of its own design. The char-acteristics of the hydraulic clutch with MR working fluid and the rotating magnetic field are tested on a specially built test stand. As a result of the research, it has been found that the torque transmitted by the clutch is the greater, the higher the rotational speed of the magnetic field and the lower the rotational speed of the beaker in which the working fluid is placed, and that the greatest torque occurs for the working fluid with the highest iron content. Based on the analysis of the structure and characteristics of the clutch in which the magnetic field is used, it has been shown that the design of the developed clutch is similar to that of an induction clutch, and its characteristics correspond to the characteristics of the eddy current clutch. Therefore, the proposed new clutch working with MR fluid and the rotating magnetic field can be applied to stationary power transmission system similarly to an eddy current clutch.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

One of mostly commonly used in machine components includes mechanical clutches. The clutches perform a number of tasks in drive systems, e.g. connecting and disconnecting shafts, overload protection, enabling or improving start-up, and equalizing loads during operation of multi-motor drives. Due to that, perfecting the clutch design is a desirable direction in the development of machines, as it has a significant impact on increasing the durability and improving the functionality of machines. The driving and driven parts of the clutch are connected to each other with a connector – permanently or allowing slippage. Particularly in slipping clutches, a fluid or a magnetic field may act as a connector. Hydraulic clutches whose connector is a fluid are built in either a viscous or hydrodynamic variant [1,2,3]. In typical viscous clutches, the torque is transmitted as a result of friction caused by shear stresses in the working fluid located in the working gap formed by the driving part and the driven part of the clutch [4,5,6,7]. In classic magnetic clutches, the magnetic field is used to induce an electric current, and thus generate magnetic forces between the torque-transmitting parts of the clutch [8].
The working fluids used in hydraulic clutches are usually hydraulic oils. However, clutches which use fluids with rheological properties controlled by electric current are already used [9,10,11,12]. There are two types of the aforementioned fluids: magnetorheological fluids (MR) and electrorheological fluids, wherein the MR fluids are the ones that are used more frequently, due to the fact that the shear stresses obtained in MR fluids are 20 to 50 times higher than in electrorheological fluids [13]. MR fluids are two-phase mixtures or colloids, which change their rheological properties under the influence of a magnetic field [14,15,16]. The solid phase of the MR consists of particles made of ferromagnetic materials such as cobalt, iron, iron alloys, and oxides of these metals. MR fluids whose solid particles have a diameter of several dozen nanometers are also known as ferrofluids or ferro-colloids. Their liquid phase is usually silicon oil, due to the fact that temperature has little effect on the rheological properties of this oil. MR fluids also contain chemical compounds which prevent solid phase sedimentation and particle aggregation. Apart from clutches, MR fluids are used as working fluids in various machine components [17,18], mainly in vibration dampers [19,20,21,22], electrohydraulic servo control systems [23,24], cantilever sandwich beams [25], and seals [26]. The main advantages those determine the technical use of these fluids are: the ability to control shear stresses in the fluid using electric current, and the short reaction time of the liquid to a change in the magnetic field (this allows for high dynamics of the controlled component). The relevant literature provides different theories regarding the impact of the rotating magnetic field on the MR fluid placed in the beaker, wherein theoretical considerations apply only to ferro-colloids. The forces, which influence the phenomena occurring in a ferro-colloids placed in a rotating magnetic field, include magnetic interaction, intermolecular attraction, surface tension, centrifugal force, viscosity, friction and gravity. The magnetic field is determined by the three following vector quantities: magnetic induction B → , magnetic field intensity H → and magnetization J → . These three are related by the dependency B → = μ 0 H → + J → , where the coefficient μ 0 signifies the magnetic permeability of free space.
According to the authors of publications [27,28], there are two possible ways that magnetization J → of ferro-colloid particles reacts to a rotating magnetic field. These two ways are called the Neel mechanism and the Brawn mechanism. For smaller particles which cannot freely rotate within the fluid due to a greater resistance to movement, the magnetization vector rotates inside the particle. This manner of magnetization is called the Neel mechanism. The Brawn mechanism is related to the Brawn motion of solid particles within a fluid. The Neel mechanism occurs if the colloid consists of solid iron particles with a diameter smaller than 0.0085 μm, while the Brawn mechanism occurs when the colloid consists of solid iron particles with a diameter larger than 0.0085 μm. However, it should be noted that this does not represent a general rule. For ferro-colloid solid particles made of cobalt, the limiting particle diameter is 0.004 μm. Under the influence of a rotating magnetic field, larger ferro-colloid particles rotate freely within the fluid, with an angular velocity ω of the rotation of the magnetic field. The base fluid in the immediate vicinity of the solid particles rotates as well, so each ferro-colloid particle becomes the center of a microscopic vortex. All particles rotate at the same angular velocity ω, which means that there is no macroscopic movement of the ferro-colloid, and only the outermost fluid particles (at the walls of the beaker) move. The rotating magnetic field affects the macroscopic motion of the ferro-colloid only when the magnetic field is non-uniform. However, for a larger volume of ferro-colloid to move, additional conditions must be met regarding the diameter and concentration of solid particles and the viscosity of the base fluid. A similar interpretation of the influence of the rotating magnetic field on the movement of ferro-colloid is presented in article [29]. In a stationary magnetic field, the magnetization vector J → is collinear with the magnetic field intensity vector H → . During the rotation of the magnetic field, the collinearity of these vectors can also be maintained for small solid ferro-colloid particles. Then, the magnetization vector J → rotates freely with the solid particles in the base fluid. On the other hand, in large particles, when the magnetic field intensity vector H → rotates with angular velocity ω, the magnetization vector J → remains behind the vector H → and is shifted by a certain lag angle. As a result of the lag angle, the vector product J → × H → has a value other than zero and creates a torque M influencing the motion of particles in the rotating magnetic field. The solid particles rotate slower than the magnetic field because their movement is inhibited by the viscous forces of the fluid.
The authors of publication [30] proposed the "magnetic pole model". Their assumption is that each volume element in a homogenous ferro-colloid can be assigned a magnetization vector J → dependent on the concentration of solid particles and the lag angle α, in relation to the rotating magnetic field H → dependent on the resistance caused by viscous forces. In the presence of a rotating magnetic field, the torque (resulting from vector product J → × H → ) induces rotation in the volume element, causing it to rotate with the rotation speed of the magnetic field ω. However, for bulk rotation of the ferro-colloid to occur, there must be in homogeneities in the ferro-colloid in the value
or the angle α. Then, a pair of mutually interacting magnets are created. As a result, one of these magnets pulls the other, which causes the whole volume of the ferro-colloid to rotate in the beaker with the speed of ω. During experimental research [29,30,31,32,33] on the behavior of various ferro-colloids placed in a beaker affected by a magnetic field rotating with an angular velocity ω, it has been found that ferro-colloid solid particles rotate within the base fluid with an angular velocity of ω. This causes the base fluid to rotate around these particles at a speed lower than the angular velocity ω. Depending on the test conditions and the existing in homogeneities: the magnetic field, magnetization, particle concentration, friction coefficient and viscosity of the base fluid, it is possible that the entire ferro-colloid volume will move with an angular velocity lower than ω. Wherein, the ferro-colloid may rotate in the ω direction, against the ω direction, or macroscopic vortices may occur. The rotation speed of the ferro-colloid depends on the angular velocity ω, the magnetic field intensity, the location of the magnetic field, the size of solid particles and their magnetization. A thin ferro-colloid ring may appear near the beaker’s wall, rotating at an angular velocity much lower than ω. After adding an immiscible fluid to the ferro-colloid, one could observe the formation of a convex or concave meniscus as a result of the rotation of the magnetic field.
The effect of a rotating magnetic field on ferro-colloids is confirmed in work [33], which examines the behavior of a ferro-colloid drop placed in an alcohol solution with simultaneously applied rotating and DC axial magnetic fields. Observing the placement of ferrofluid in a fluid reveals various distinctive patterns. The publications [34,35] present research results on the behavior of ferro-colloids under the influence of a rotating magnetic field, utilizing a Brookfield rheometer. The rheometer spindle is immersed in a stationary beaker filled with a ferro-colloid; the beaker is affected by a rotating magnetic field generated by the stator winding of a three-phase induction motor. It has been found that the torque acting on the rheometer spindle depends on the angular velocity of rotation of the magnetic field, the magnetic field intensity and the magnetization of the ferro-colloid particles. The study [29] also considers the possibility of increasing the efficiency of a hydrodynamic torque converter filled with ferro-colloid as a working fluid, placed inside the winding stator of a three-phase induction motor.
However, as expected, there was no increase in the angular velocity of the output shaft of the hydrodynamic torque converter as a result of the impact of the rotating magnetic field on the ferro-colloid. The article introduces a novel construction concept for a hydraulic clutch (HCMR) incorporating a MR fluid This concept involves the application of a rotating magnetic field to induce the rotation of the MR fluid, consequently transmitting torque through friction against the beaker walls. The developed HCMR is at the “technology demonstration” stage.

2. Tests of the Hydraulic Clutch with MR Fluid

2.2. Construction of a Hydraulic Clutch with MR Fluid

On the input shaft of the HCMR there is an electromagnet that generates a rotating magnetic field. The electromagnet is built using the winding stators of a three-phase induction motor. Slip rings and brushes power the electromagnet. Inside the electromagnet there is a beaker containing the MR fluid, connected to the output shaft. The input and output shafts are mounted in the housing. The HCMR structure is shown in Figure 1. The HCMR works in the following manner. A rotating magnetic field is created in the electromagnet. During clutch operation, the angular velocity ω of the magnetic field rotation ω is added to the angular velocity ω1 of the input shaft rotation. The magnetic field rotating with an angular velocity “ω + ω1”sets the MR fluid in rotation. As a consequence of friction against the beaker walls, the fluid rotates the beaker (and the output shaft connected to it) with an angular velocity ω2.

2.3. Tested MR Fluids

In-house manufactured fluids are used in the HCMR tests. The fluids consist of solid iron particles in the form of spherical powder of various diameters, mixed with silicone oil. Laboratory sieves with mesh dimensions specified in the ISO 3310-1 standard are used in order to isolate solid particles of the required diameter. Given the brief duration of the tests, no anti-corrosion additives or additives aimed at reducing sedimentation and aggregation of MR fluids are utilized. The data concerning the composition of the tested MR fluids are presented in Table 1. The fluids with the composition shown in Table 2 are prepared with different weight concentration ratio ϕ of solid particles, marked with digital symbols. The full name of the MR fluid used in testing consists of the type of the fluid (depending on the size of the solid particles, A or B) and the symbol of the fluid (depending on the weight concentration ratio of solid particles, from 1 to 5). Thus, “A1” signifies a fluid whose particle size is 3.5 μm to 6.5μm, and ϕ = 50%, as can be seen from Table 1 and Table 2.

2.3. Testing the Rheological Properties of MR Fluids

In order to assess the rheological properties of MR fluids in the absence or in the presence of a magnetic field, a special test stand is constructed, as shown in Figure 2. The test stand consists of a Brookfield DV2T rheometer and an internally designed magnetic device with an electromagnet generating a magnetic field. The magnetic device is presented in Figure 3. The change in magnetic induction B in the MR fluid is achieved by supplying power to the electromagnet coil using an Array 3645A electric power supply with adjustable voltage. Measurements of magnetic induction in the MR fluid are performed with the Smart Magnetic Sensor SMS 102. The PC is equipped with Brookfield DV2T rheometer software used to record the time course of the measured values. The waveforms are saved as files in the computer’s memory. In order to obtain the values of the torque Mr loading the rheometer spindle, which are consistent with the rheometer manufacturer’s recommendations, several variants of the magnetic device design are created and tested. The test conditions and the dimensions of the magnetic device determined during the tests are presented in Table 3. The relative measurement error of the measured quantities such as: angular velocity ωr and torque Mr of the rheometer, voltage U and current intensity I of the electric power supply, magnetic induction B and the fluid temperature T are less than 1%. Due to the specific structure of the magnetic device whose steel spindle rotates in a magnetic field, the occurrence of eddy currents is taken into account, as they brake the spindle. Based on the test results conducted without MR fluids in the magnetic device's container, the relative measurement error of the torque Mr caused by eddy currents is estimated to be less than 5% over the entire range of tests.
Figure 4 shows an example of the dependence of the spindle’s torque movement resistance Mr on the magnetic induction B for fluids A1 and B1. The comparison of the waveforms shown in Figure 4 with the waveforms obtained for MR fluids, such as MR 132 AD [36], shows that the waveforms obtained for the A1 fluid are the most similar, while the waveforms obtained for the B2 fluid are the most distant from the waveforms typical for MR fluids. The reason for these discrepancies is the homogeneity of the fluids during testing, which is related to the fluids’ structure. MR fluids containing small-diameter iron particles, such as fluid A1, are more homogeneous and under the influence of a magnetic field the iron particles do not move quickly, as the resistance to their movement in the oil is greater than the magnetic forces. On the other hand, iron particles with a larger diameter, such as the ones in fluid B2, are more strongly attracted to the electromagnet poles and they move much faster towards the beaker walls. This means that, during tests, the fluid containing more oil remains at the rheometer spindle, and therefore the influence of the magnetic field on the rotational movement of the spindle decreases. Figure 5 shows an example of the dependences of the torque Mr on ωr for fluid A5 and various values of magnetic induction B. As can be seen from Figure 5, in the case of fluid A, the value of the torque Mr increases both with the increase in angular velocity ωr and magnetic induction B. As the concentration of iron particles in fluid A increases, a corresponding increase in the torque value Mr is observed. As the magnetic induction increases, the angle of inclination between the approximating line and the positive ωr -axis increases. As the angular velocity ωr increases, so does the value of the torque Mr in the absence of a magnetic field.

2.4. Test stand for the hydraulic clutch with MR fluid

2.5. Phenomena Occurring during Operation of the Hydraulic Clutch with MR Fluid

During the tests of the operation of the clutch with a rotating magnetic field with fluids A and B, it is noticeable that after generating a rotating magnetic field with a constant angular velocity ω, the beaker is initially stationary. In the first seconds after turning on the rotating magnetic field, wrinkles appear on the surface of the fluid, Figure 7a. If the liquid is not well mixed, a rotating ring of solid particles may appear on the walls of the beaker, Figure 7b. The emergence of wrinkles on the surface of the MR fluid, depicted in Figure 7, suggests the influence of surface tension forces at the interface between two mediums: the MR fluid with magnetic properties and the non-magnetic air [31]. After a while, the fluid at the bottom of the beaker starts to rotate with the beaker, assuming a hexagonal shape, Figure 8. Polygon shaped deformations of fluids can also be observed for single-phase fluids [37]. Similar regular deformations during rotation also occur for gases. Such a phenomenon was noticed at Saturn's north pole during space probe missions such as Voyager 1, Voyager 2 and Cassini [38]. The occurrence of deformations is linked to various factors, including the emergence of secondary flows propelled by centrifugal force, meridional circulation within the fluid, and the development of Görtler vortices as the fluid flows along the walls [39,40].
After the beaker’s rotation speed ω2 increases to the maximum value ω2max, the free surface of the fluid in the beaker is arranged as for a potential vortex, assuming a parabolic shape, Figure 9. The maximum rotation speed of the beaker ω2max is always lower than the angular rotation speed of the magnetic field ω. Braking the beaker in the presence of a rotating magnetic field causes a decrease in the rotational speed ω2 of the beaker and an increase in the value of the braking torque M. When the beaker reaches the maximum centrifugation speed and the magnetic field is turned off, the fluid rapidly spreads onto the walls of the beakers, Figure 10.

2.6. Test Results of the Characteristics of the Hydraulic Clutch with MR Fluid

The HCMR characteristics are tested for a predetermined volume V of the MR fluid in the beaker. Figure 11 shows a diagram of the dependence of the angular velocity ω2 of the HCMR output shaft on the angular velocity of the magnetic field rotation ω, when the beaker contains the B5 fluid and is not braked. It can be observed from Figure 11 that in the absence of the braking torque there is a linear relationship between the angular velocity ω2 of the HCMR output shaft and the rotational speed of the magnetic field ω. The slip s = (ω–ω2)/ω is almost constant and its average value is 0.66. For instance, in Figure 12 and Figure 13, the relationship between torque M and angular velocity of the output shaft ω2 is illustrated for fluids A and B. The vessel was gradually decelerated using a friction brake at ω = 300 rad/s. Figure 12 shows the measurement points and approximation lines. Figure 12 shows that as the torque M decreases, the angular velocity ω2 increases linearly. Higher torque values occur for fluid A1 than for fluid B1, which appears to be associated with the factor the fact that smaller particle diameter results in a higher concentration of Fe in fluid A1 compared to fluid B1 within the same volume, and the viscoplastic properties of fluid A1 contribute to increased adhesion to the vessel walls compared to fluid B1. Figure 13 shows the dependences of M on ω2. In order to increase readability of Figure 13, especially for higher angular velocity values ω2, the measurement points are omitted and only the approximating lines are shown. The influence of the mass of iron contained in the MR fluid on the dependence of the torque M on the angular velocity ω2 is also clearly visible in Figure 13. The greater the mass fraction ϕ, and therefore the mass of iron in the fluid B in the beaker, the greater the torque M.
Figure 14 and Figure 15 show the dependence of the torque Mmax (shown in Figure 12) on the angular velocity for selected fluids A and B, depending on the rotational speed of the magnetic field ω. The dependence of the torque Mmax on the angular velocity ω (presented in Figure 14 and Figure 15) for selected A and B fluids is increasing, wherein the higher the angular velocity ω, the smaller the increase in the torque Mmax. Figure 16 shows the dependence of the torque Mmax on the volume V of the A1 fluid placed in the beaker, for magnetic field rotational speed ω = 200 rad/s. Figure 16 shows the significant influence of the mass of iron contained in the MR fluid on the dependence of the torque Mmax on the volume V of the MR fluid. It should be noted that the dependence of the torque Mmax on the volume V of the MR fluid is not linear, but regressive.

3. Characteristics of the Hydraulic Clutch with MR Fluid

3.1. Operating Method of the Hydraulic Clutch with MR Fluid

Conducting a theoretical analysis of HCMR operation poses challenges due to the presence of magnetic forces alongside the forces typically encountered in hydraulic clutches during their operation. Furthermore, the interplay of these forces induces localized changes in density through the phase separation of the MR fluid. The reduction in the angular velocity ω2 of the HCMR output shaft, as the torque value increases, takes place within the rotating magnetic field. This decrease primarily stems from the combined effects of centrifugal, gravitational, and magnetic forces. The decrease is also slightly dependent on different forces, such as: intermolecular forces, buoyancy and surface tension. The observation that the MR fluid in a rotating beaker, subjected to a magnetic field, takes on a free surface resembling a paraboloid (Figure 9), and subsequently spreads onto the beaker walls after the magnetic field is deactivated (Figure 10), provides evidence that the radial magnetic forces acting on solid particles of the MR fluid are smaller but comparable in magnitude to centrifugal forces. The influence of gravity is not significant due to the small amount of fluid in the vessel and therefore its low level. During the operation of the HCMR, the magnetic field, the MR fluid and the beaker move in rotation. The rotating magnetic field attracts solid particles, which in turn transfer the rotational motion to the beaker walls using friction forces due to the forces pressing the liquid against the beaker walls. The attracted particles move in relation to each other, and their movement is determined by Bingham’s viscous-plastic fluid model as shown in Figure 17 [41].
Figure 18 shows the rotating magnetic field is shown as the pole of a rotating magnet. When the angular velocities of the beaker ω2 and the field rotation ω are equal, the magnetic force acts along the radius of the beaker, because the beaker’s movement is not relative to the pole, Figure 18a. Centrifugal force Fo also acts along the radius. The lack of circumferential force means that the friction force between the MR fluid and the beaker wall does not occur, and there is no torque M acting on the fluid and the beaker. When the angular velocity ω2 of the beaker decreases due to braking, falling below the rotational speed ω of the magnetic field, the magnetic pole surpasses the cluster of solid particles. The movement of these particles toward the pole is impeded by viscous forces resulting from tangential stresses in the MR fluid. Then, as presented in Figure 18b, the magnetic force Fm deflects from the radius and can be divided into the circumferential component of the magnetic force Fm1 and the radial component of the magnetic force Fm2. Such deflection of the magnetic force from the radius is also found during the operation of a powder clutch, on the basis of the observation of the arrangement of solid particle chains in the working gap [8]. The circumferential force Fm1 creates a torque acting on the MR fluid ring, while the axial force Fm2 reduces the centrifugal force Fo. The reduction of the centrifugal force Fo by the force Fm2 is evident from the observation that, following the disappearance of the magnetic field during the beaker's rotation, the MR fluid influences the walls of the beaker, Figure 10. Simultaneously, the MR fluid moves toward the pole of the magnetic field and is pressed against the beaker wall as a result of the resultant forces Fo- Fm2. Simultaneously, the MR fluid, moving towards the magnetic field's pole, is pressed against the beaker wall due to the resultant force Fo- Fm2. This results in a friction force F on the beaker walls, generating a torque M on the beaker axis. This torque, equal in value but opposite in direction, acts as a braking force on the beaker. Further reduction of the speed of the beaker ω2 causes an increase in the force F whose value is proportional to the difference in rotational speeds (ω–ω2) due to the occurrence of viscous forces; at the same time, it causes a decrease in the centrifugal force Fo pressing the MR fluid ring against the beaker. In the case of lower beaker velocities ω2, the force (Fo–Fm2) is too small to transfer the rotational motion of the MR fluid ring to the beaker movement, so that the HCMR stops operating properly.

3.2. Comparison of the Hydraulic Clutch with MR Fluid to Other Clutches

In order to classify the HCMR, it has been compared to other clutches which utilize a magnetic field, such as: induction clutches, eddy current clutches, magnetic particle clutches, viscous clutches with MR fluid, electromagnetic friction-type clutches and magnetic clutches. The structure of HCMR is similar to induction clutches, while its operating principle is similar to magnetic clutches with electromagnets. It can also be regarded as a combination of a viscous clutch, where shear stresses in the MR fluid are altered using a magnetic field, and a hydrodynamic clutch in which a magnetic field acts on the fluid instead of blades. Based on the data from publications [8, 42–44], Figure 19 shows characteristics of clutches which use the influence of a magnetic field. The comparison of Figure 19 and Figure 12 shows that HCMR’s characteristics is similar to characteristics of eddy current clutches. Therefore, the proposed new clutch working with MR fluid and the rotating magnetic field can be applied to stationary power transmission system similarly to eddy current clutches. The advantages of clutches with a rotating magnetic field, as well as other clutches using magnetic fields operating in drive systems, include controllability, high durability, and the absence of a rigid connection between the driving and driven parts. This characteristic makes the drive system shafts insensitive to misalignment.

4. Conclusions

On the basis of the considerations regarding HCMR, the following general conclusions have been drawn:
(1) The literature review shows that the rotating magnetic field can cause macroscopic rotation of the MR fluid with a rotational speed lower than the rotational speed of the magnetic field. Whether such a movement will occur and what its direction will be depends on a number of factors related to the properties of the MR fluid and operating conditions. Due to the complexity of the phenomena occurring, no single model has been developed so far to explain the causes of rotation of the MR fluid in a rotating magnetic field. Most authors believe that the shape of the model is significantly impacted by the inhomogeneities in the MR fluid affected by the rotating magnetic field.
(2) The impact of the magnetic field on the rheological properties of MR fluids with varying sizes of iron particles, assessed using a customized rheometer with a magnetic device, can be accurately determined for MR fluids with iron particles having diameters not exceeding 6.5 μm. Iron particles with a larger diameter exhibit a stronger attraction towards the poles of the electromagnet situated outside the measuring gap. This results in a reduction of the iron content in the vicinity of the rheometer spindle, thereby limiting the influence of the magnetic field on the measured torque. Therefore, other measurement methods should be sought for MR fluids with larger iron particles.
(3) In the absence of a load on the HCMR output shaft, the angular velocity of the beaker containing the MR fluid exhibits a linear dependence on the angular velocity of the magnetic field. However, during shaft braking, the torque transmitted by the clutch increases with higher angular velocity of the magnetic field and lower angular velocity of the beaker. The highest torque occurs for MR fluids with the highest iron content and solid particles with dimensions ranging from 3.5 to 6.5 μm.
(4) HCMR characteristics are similar to characteristics of eddy current clutches and result mainly from the combined action of magnetic and centrifugal forces on the MR fluid. The solid particles of the MR fluid are attracted by the rotating magnetic field and simultaneously pressed against the walls of the beaker, mainly due to the influence of centrifugal forces. The rotational motion of the beaker is induced by the friction force generated due to the applied pressure. The magnitude of the friction force, which propels the rotation of the beaker, increases with the greater difference between the rotational speed of the magnetic field and that of the beaker. The viscous-plastic properties of the MR fluid cause the solid particles of the MR fluid to be slower than the rotation of the magnetic field.
It is finally remarked here that further research regarding HCMR should aim to design, construct and test a clutch prototype and to select MR fluids with the optimal size and shape of solid particles so that the proposed system can be applicable to several types of the hydraulic control systems in real environment subjected to various uncertainties such as time-varying temperature.

Author Contributions

Conceptualization, K.M. and I.M.; methodology, K.O. and A.O.; validation, K.M., A.O., and A.M.; formal analysis, K.M and I.M.; investigation, K.M.; resources, A.M.; data curation, A.O., K.O. and Z.K.; writing—original draft preparation, Z.K.; writing—review and editing, K.O., Z.K. and A.K., S.B.C.; visualization, K.O. and A.O; supervision, S.B.C.; project administration, S.B.C. All authors have read and agreed to the published version of the manuscript.

Funding

The authors received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no potential conflict of interest with respect to the research, authorship, and publication of this article.

References

  1. Musiałek, I.; Kęsy, Z.; Kęsy, A.; Kim, G. W.; Choi, S. B. Mathematical modelling and experimental validation of hybrid clutch combined with two modes: hydraulic and electrorheological fluid mode. Smart Mater. Struct. 2020, 30, 1–13. [CrossRef]
  2. Olszak, A.; Osowski, K.; Kęsy, Z.; Kęsy, A. Modelling and testing of a hydrodynamic clutch filled with electrorheological fluid in varying degree. J. Intell. Mater. Syst. Struct. 2019, 30, 649–660. [CrossRef]
  3. Olszak, A.; Osowski, K.; Kesy, A.; Kesy Z. Experimental researches of hydraulic clutches with smart fluids. Int. Rev. Mech. Eng. 2016, 10, 364–372. [CrossRef]
  4. Olszak, A.; Osowski, K.; Motyl, P.; Mędrek, G.; Zwolak, J.; Kęsy, A.; Kęsy, Z.; Choi, S. B. Selection of materials used in viscous clutch with ER fluid working in special conditions. Front. Mater. 2019, 6, 1–13. [CrossRef]
  5. Tung, S. C.; Lindol, J. L. Modeling torque converter clutch viscous damper performance. SAE Technical Paper 1985, 850459. [CrossRef]
  6. Naito, G.; Yaguchi, E.; Matuda, T.; Asahi, M.; Nakata, T.; Inokuchi, I. New electronically controlled torque split 4WD system for improving cornering performance. SAE Technical Paper 1990, 900556. [CrossRef]
  7. Chirico, D. Development and perspectives of the automotive industry. ATA – Ingegneria Automotoristica 1990, 43.
  8. Vorobyeva, T. M. Electromagnetic clutches and couplings; Pergamon Press: Oxford, 1965; 82.
  9. Kęsy, Z.; Mędrek, G.; Olszak, A.; Osowski, K.; Kęsy, A. Electrorheological fluid based clutches and brake. Encyclopedia of Smart Materials 2022, 5, 171–186. [CrossRef]
  10. Olszak, A.; Osowski, K.; Kęsy, Z.; Kęsy, A. Investigation of hydrodynamic clutch with MR fluid. J. Intell. Mater. Syst. Struct. 2018, 30, 155–168. [CrossRef]
  11. Choi, S. B.; Hong, S. R.; Cheong, C. C.; Park Y. K. Comparison of field-controlled characteristics between ER and MR clutches. J. Intell. Mater. Syst. Struct. 1999, 10, 615–619. [CrossRef]
  12. Choi, S. B.; Lee, D. Y. Rotational motion control of a washing machine using electrorheological clutches and brakes. Proc. Inst. Mech. Eng., Part C 2005, 219, 627–637. [CrossRef]
  13. Musiałek, I.; Migus, M.; Osowski, K.; Olszak, A.; Kęsy, Z.; Kęsy, A.; Kim, G. W.; Choi, S. B. Analysis of a combined clutch with an electrorheological fluid. Smart Mater. Struct. 2020, 29, 1–12. [CrossRef]
  14. Carlson, D. J. MR fluids and devices in the real world. Int. J. Mod. Phys. B 2005, 19, 1463–1470. [CrossRef]
  15. Genc, S.; Phule, P. P. Rheological properties of magnetorheological fluids. Smart Mater. Struct. 2002, 11, 140–146.
  16. Sapiński, B.; Horak W. Rheological properties of MR fluids recommended for use in shock absorbers. Acta Mech. Autom. 2013, 7, 107–110. [CrossRef]
  17. Do, X. P.; Choi, S. B. Magnetorheological fluid based devices reported in 2013–2018: mini-review and comment on structural configurations. Front. Mater. 2019, 6, 1–8. [CrossRef]
  18. Carlson, J. D.; Catanzarite, D. M.; St. Clair, K. A. Commercial magneto–rheological fluid devices. Int. J. Mod. Phys. B 1996, 10, 2857–2865. [CrossRef]
  19. Gołdasz, J.; Sapiński, B. Insight into magnetorheological shock absorbers; Springer International Publishing: Switzerland, 2015; 251.
  20. Cruze, D.; Latha, H.; Arunraj, E.; Jebadurai, V. S.; Sarala, L. A review on optimal design of magneto-rheological damper. International Journal of Mechanical and Production Engineering Research and Development, 2018, 8, 569–578.
  21. Sapiński, B.; Rosół, M. MR damper performance for shock isolation. Journal of Theoretical and Applied Mechanics 2007, 45, 133–145.
  22. Milecki, A. Using of magnetorheological and electrgheological fluids in electrohydraulic servo control system. Hydraulics and Pneumatics 1998, 5, 16–25.
  23. Hu, G.; Liao, M.; Li, W. Analysis of a compact annular-radial orifice flow magnetorheological valve and evaluation of its performance. J. Intell. Mater. Syst. Struct. 2017, 28, 1322–1333. [CrossRef]
  24. Choi, S. B.; Choi, W. Y. Position control of a cylinder using a hydraulic bridge circuit with ER valves. J. Dyn. Sys. Meas. Control. 2000, 122, 201–209. [CrossRef]
  25. Lara-Prieto, V.; Parkin, R.; Jackson, M.; Silberschmidt, V.; Kęsy, Z. Vibration characteristics of MR cantilever sandwich beams: experimental study. Smart Mater. Struct. 2009, 19, 1–9. [CrossRef]
  26. Horak, W.; Szczęch, M. Numerical simulation and experimental validation of the critical pressure value in ferromagnetic fluid seals. IEEE Transactions on Magnetics 2017, 53, 1–1. [CrossRef]
  27. Wohlfarth, E. P. Ferromagnetic materials. North-Holland Publishing Company: Amsterdam, 1980.
  28. Bashtovoy, V. G.; Berkovsky, B. M.; Vislovich, A. N. Introduction to thermomechanics of magnetic fluids. Institute for High Temperatures: Moscov, 1988.
  29. Anton, I.; Vekas, L.; Potencz, I.; Suciu, E. Ferrofluid flow under the influence of rotating magnetic fields. IEEE Transactions on Magnetism 1980, 16, 283–287. [CrossRef]
  30. Rosensweig, R. E. Ferrohydrodynamics. Cambridge University Press: Cambridge, 1985.
  31. Mailfert, L.; Martinet, A. Flow regimes for a magnetic suspension under a rotating magnetic field. Journal de Phisique 1973, 34, 197–201. [CrossRef]
  32. Moskowitz, R.; Rosensweig, R. E. Nonmechanical torque-driven flow of a ferromagnetic fluid by an electromagnetic field.. Appl. Phys. Lett. 1967, 11, 301–303. [CrossRef]
  33. Lorenz, C.; Zahn, M. Hele-shaw ferrohydrodynamics for rotating and dc axial magnetic fields. Phys. Fluids. 2003, 15, S4–S4. [CrossRef]
  34. Rhodes, S.; He, X.; Elborai, S.; Lee S. H.; Zahn, M. Magnetic fluid behavior in uniform DC, AC, and rotating magnetic fields. Journal of Electrostatics 2006, 64, 513–519. [CrossRef]
  35. Rosenthal, A. D.; Rinaldi, C.; Franklin, T.; Zahn, M. Torque measurements in spin-up flow of ferrofluids. Journal of Fluids Engineering Transactions of the ASME 2004, 126, 196–205. [CrossRef]
  36. Zschunke, F.; Rivas, R.; Brunn P. O. Temperature behavior of magnetorheological fluids. Applied Rheology 2005, 15, 116–121. [CrossRef]
  37. Jansson, T. R. N.; Haspang, M. P.; Jensen, K. H.; Hersen, P.; Bohr, T. Polygons on a rotating fluid surface. Phys. Rev. Lett. 2006, 96, 174502-1–174502-4. [CrossRef]
  38. Godfrey, D. A. A hexagonal feature around Saturn’s north pole. Icarus 1988, 76, 335–356. [CrossRef]
  39. Saric, W. S. Gortler vortices. Annu. Rev. Fluid Mech. 1994, 26, 379–409. [CrossRef]
  40. Floryan, J. M.; Saric, W. Stability of gortler vortices in boundary layers. AIAA Journal 1982, 20, 316–323. [CrossRef]
  41. Whorlow, R. W. Rheological techniques. Second Edition, Ellis Horwood Limited, 1992.
  42. Post, R. S. Permanent magnet coupling fundamentals. AISE Steel Technology 1999, 11, 54–57.
  43. Gosline, A. H.; Campion, G.; Hayward, V. On the use of eddy current brakes as tunable, fast turn-on viscous dampers for haptic rendering. Proc. Eurohaptics 2006, 2006, 229–234.
  44. Kęsy, Z.; Kęsy, A. Performance assessment of new brake actuator with magneto– rheological working fluid. Int. Rev. Mech. Eng. 2007, 1, 691–696.
Preprints 103004 g001
Figure 1. HMCR construction scheme: 1 – coil, 2 – bearings, 3 – output shaft, 4 – beaker, 5 – MR fluid, 6 – stator of a three-phase induction motor, 7 – slip rings, 8 – input shaft, 9 – bearings housing.
Figure 1. HMCR construction scheme: 1 – coil, 2 – bearings, 3 – output shaft, 4 – beaker, 5 – MR fluid, 6 – stator of a three-phase induction motor, 7 – slip rings, 8 – input shaft, 9 – bearings housing.
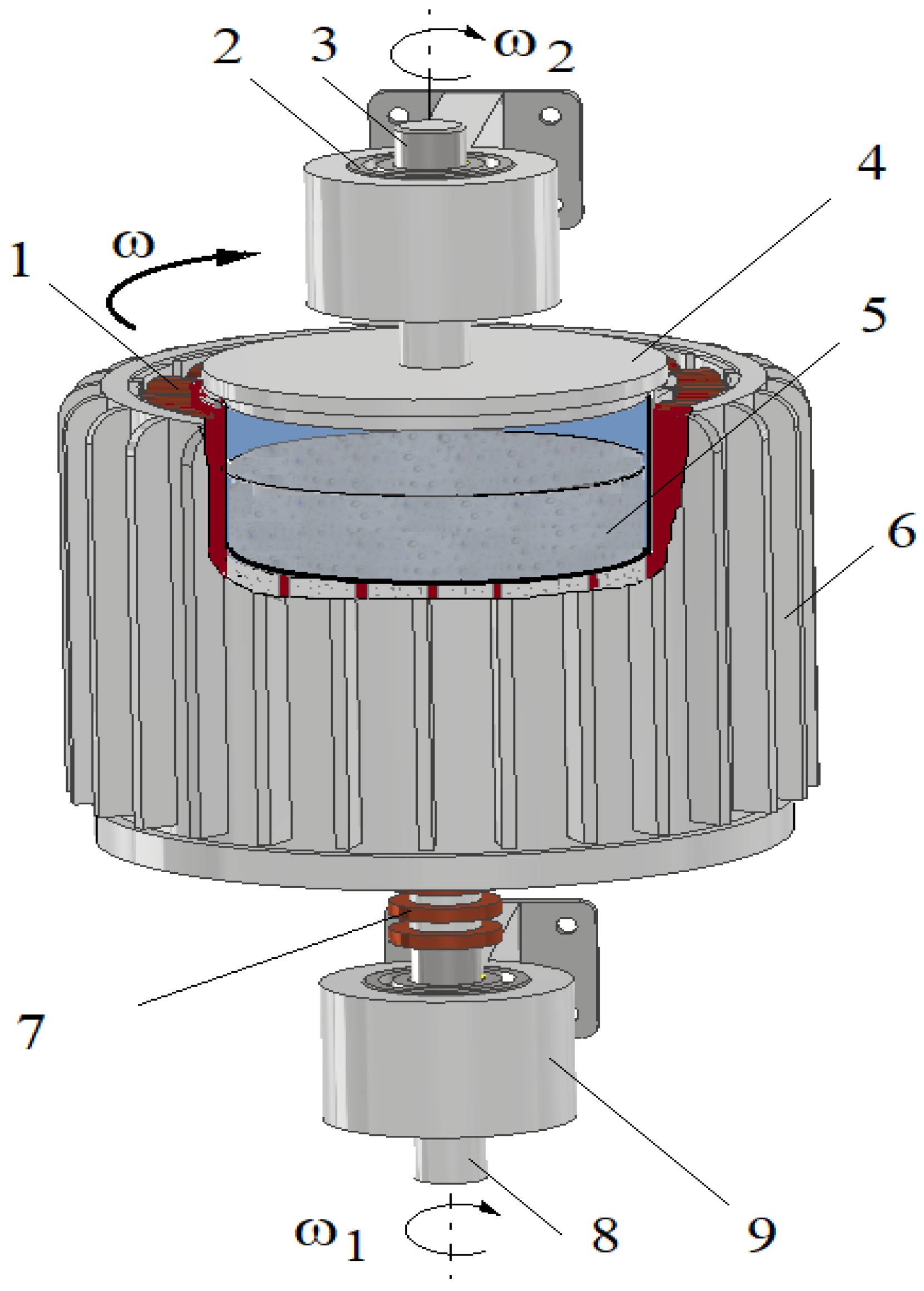
Preprints 103004 g001
Preprints 103004 g002
Figure 2. View of the station used for testing the rheological properties of the MR fluid: 1 – PC, 2 – rheometer, 3 – electric power supply, 4 – magnetic device.
Figure 2. View of the station used for testing the rheological properties of the MR fluid: 1 – PC, 2 – rheometer, 3 – electric power supply, 4 – magnetic device.
Preprints 103004 g002
Preprints 103004 g003
Figure 3. Magnetic device used to test the MR fluid: 1 – beaker with MR fluid, 2 – electromagnet coil, 3 – magnetic circuit.
Figure 3. Magnetic device used to test the MR fluid: 1 – beaker with MR fluid, 2 – electromagnet coil, 3 – magnetic circuit.
Preprints 103004 g003
Preprints 103004 g004
Figure 4. The dependence of the torque Mr on magnetic induction B for fluids A1 and B1 and for ωr = 2 rad/s.
Figure 4. The dependence of the torque Mr on magnetic induction B for fluids A1 and B1 and for ωr = 2 rad/s.
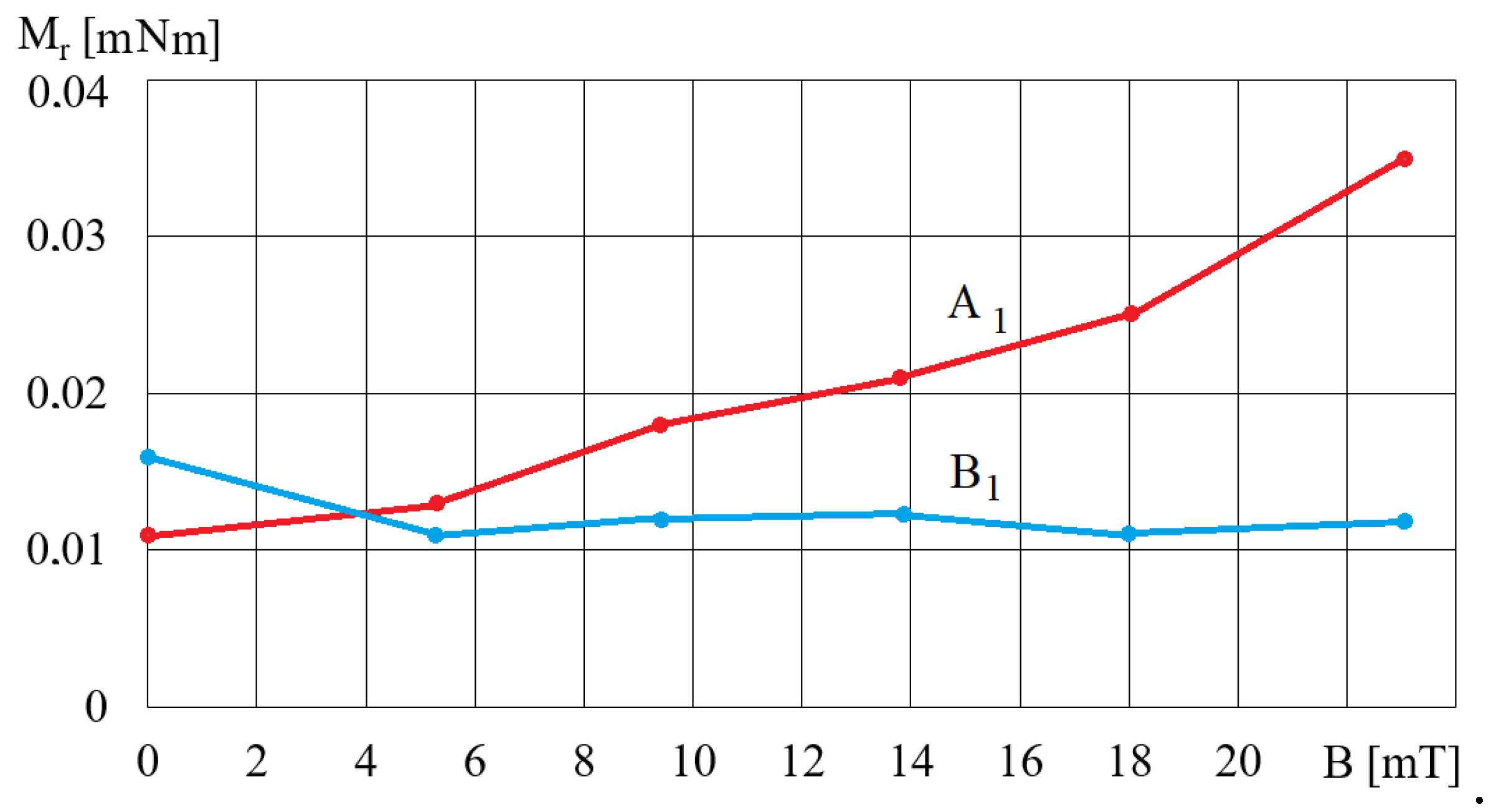
Preprints 103004 g004
Preprints 103004 g005
Figure 5. Dependences of the torque Mr on ωr for fluid A5 and different values of B.
Figure 5. Dependences of the torque Mr on ωr for fluid A5 and different values of B.
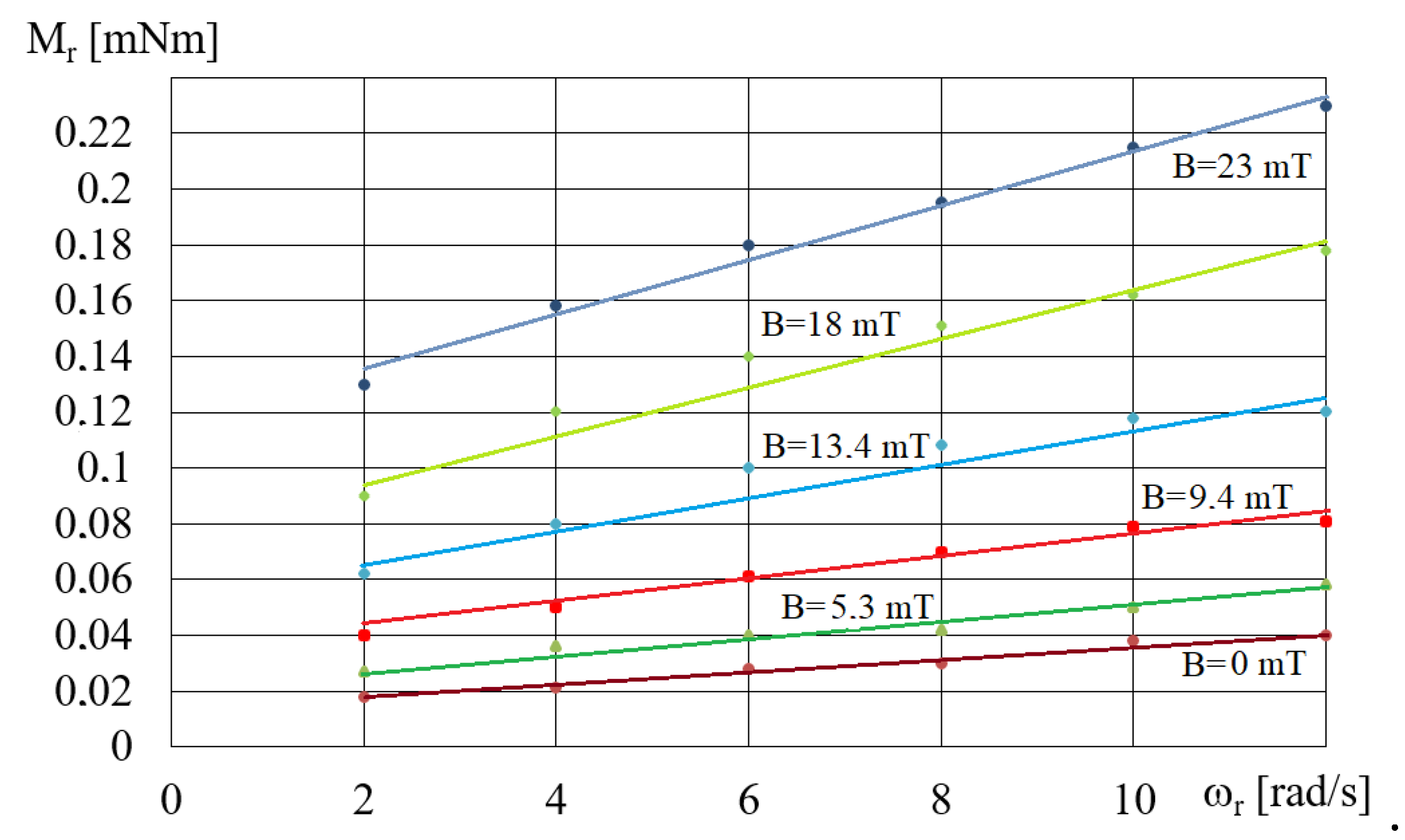
Preprints 103004 g005
Preprints 103004 g006
Figure 6. HCMR test stand: a – construction scheme: 1 – stator of a three-phase induction motor, 2 – beaker, 3 – beaker bearing, 4 – torque meter, 5 – output shaft, 6 – brake, 7 – rotational speed meter, 8 – clutch, 9 – MR fluid, 10–frame; b – view.
Figure 6. HCMR test stand: a – construction scheme: 1 – stator of a three-phase induction motor, 2 – beaker, 3 – beaker bearing, 4 – torque meter, 5 – output shaft, 6 – brake, 7 – rotational speed meter, 8 – clutch, 9 – MR fluid, 10–frame; b – view.
Preprints 103004 g006
Preprints 103004 g007
Figure 7. View of the B3 fluid surface at HCMR start-up for ω = 240 rad/s: a – wrinkles, b – ring of swirling fluid.
Figure 7. View of the B3 fluid surface at HCMR start-up for ω = 240 rad/s: a – wrinkles, b – ring of swirling fluid.
Preprints 103004 g007
Preprints 103004 g008
Figure 8. View of a hexagon formed by the rotation of the MR fluid for B3 fluid and ω = 240 rad/s.
Figure 8. View of a hexagon formed by the rotation of the MR fluid for B3 fluid and ω = 240 rad/s.
Preprints 103004 g008
Preprints 103004 g009
Figure 9. View of the potential vortex in fluid B2.
Figure 9. View of the potential vortex in fluid B2.
Preprints 103004 g009
Preprints 103004 g010
Figure 10. View of the B2 fluid spread evenly on the beaker walls.
Figure 10. View of the B2 fluid spread evenly on the beaker walls.
Preprints 103004 g010
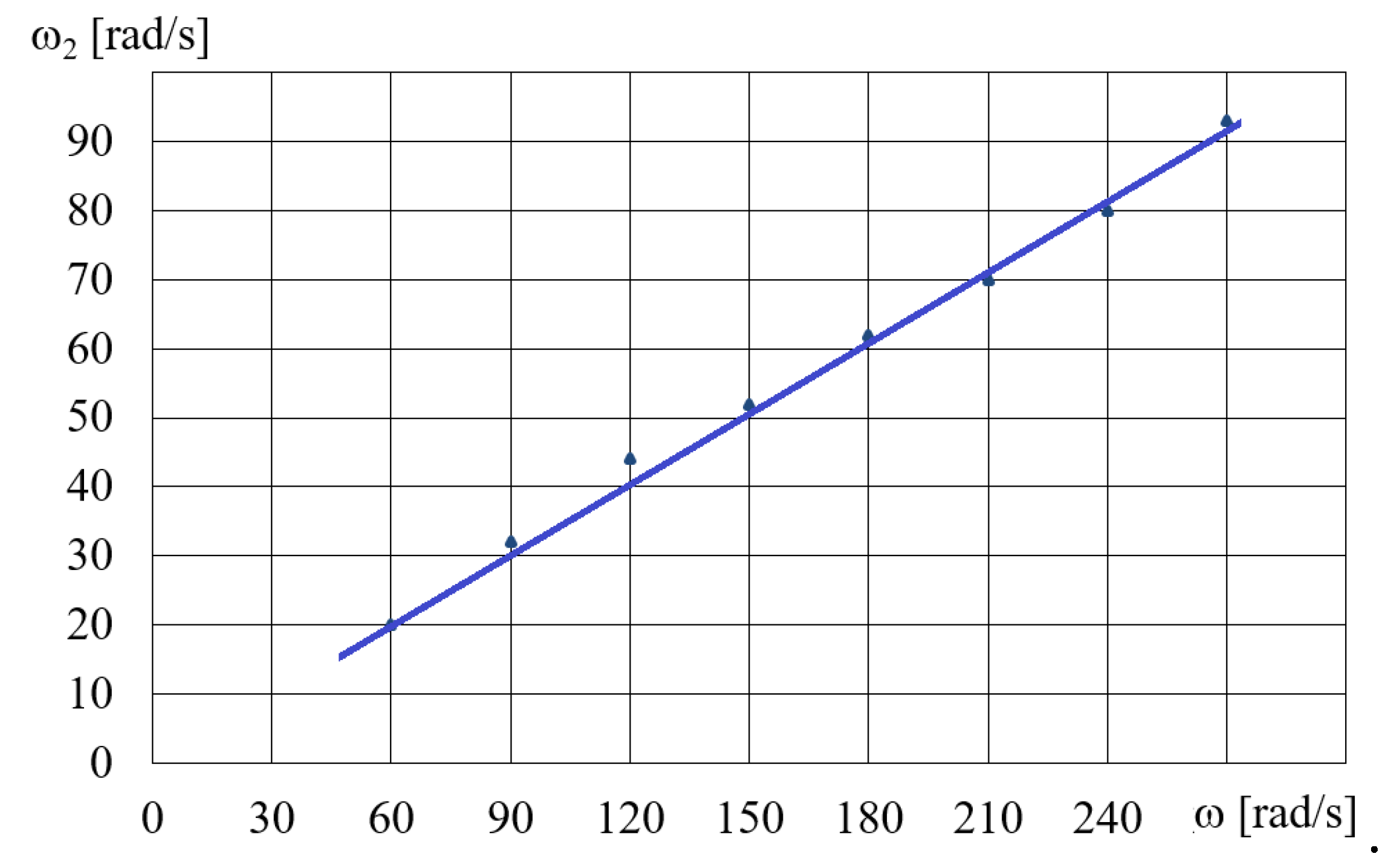
Preprints 103004 g011
Figure 11. Dependences of angular velocity ω2 on angular velocity ω for the fluid B5and fluid volume V = 75 cm3.
Figure 11. Dependences of angular velocity ω2 on angular velocity ω for the fluid B5and fluid volume V = 75 cm3.
Preprints 103004 g011
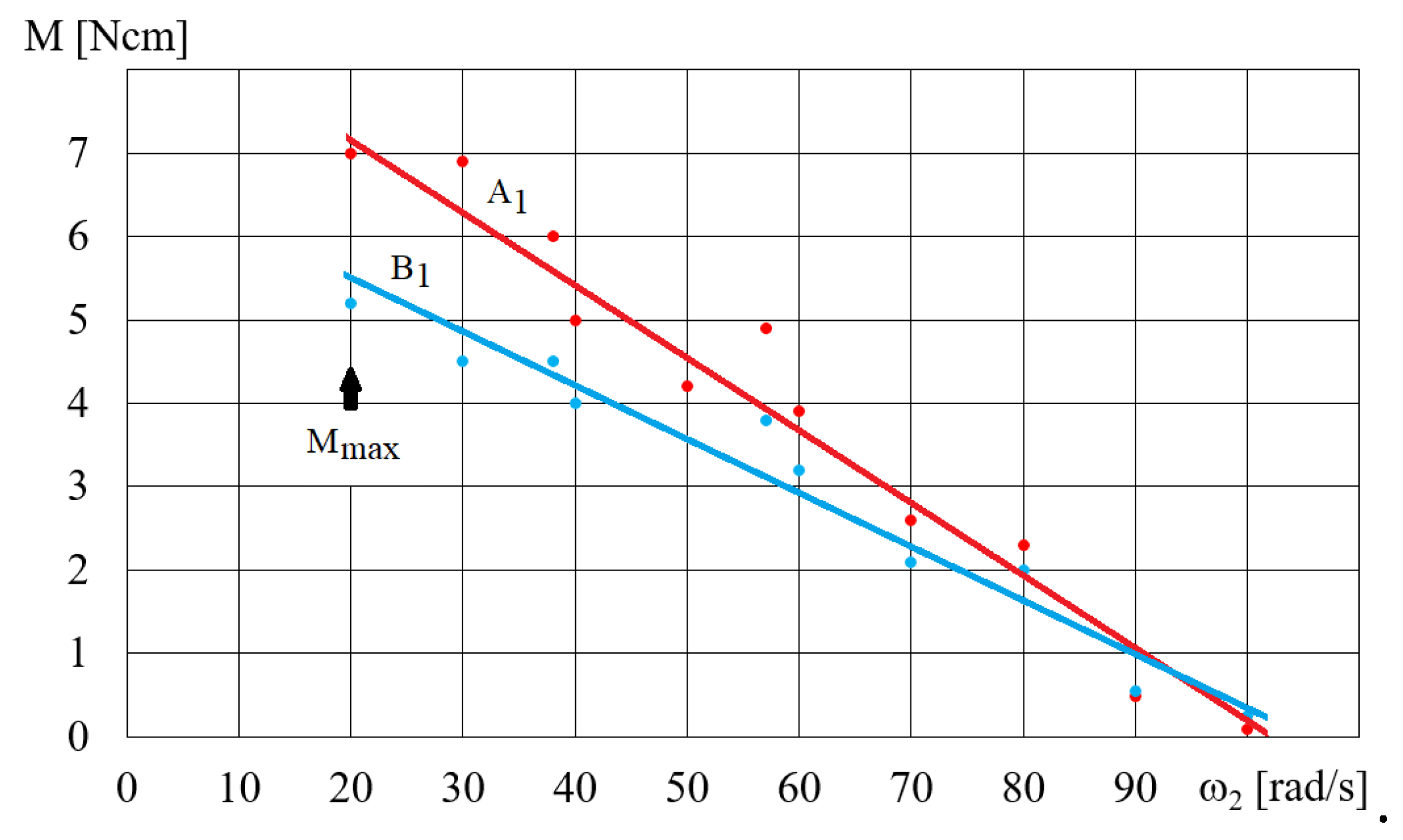
Preprints 103004 g012
Figure 12. Dependence of the torque M on the angular velocityω2 for fluids A1 and B1, ω = 300 rad/s, V = 75 cm3.
Figure 12. Dependence of the torque M on the angular velocityω2 for fluids A1 and B1, ω = 300 rad/s, V = 75 cm3.
Preprints 103004 g012
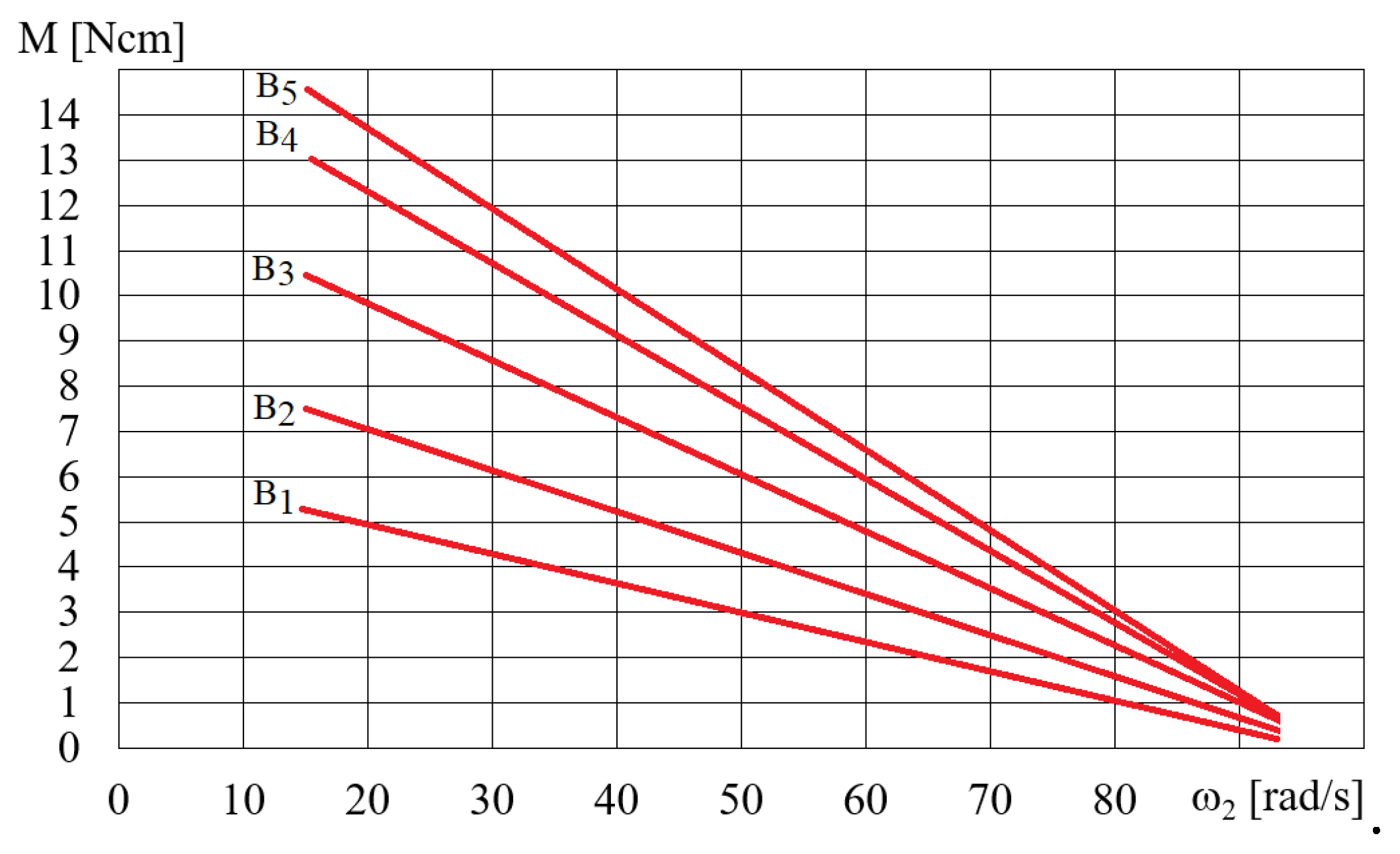
Preprints 103004 g013
Figure 13. Dependence of the torque M on the angular velocityω2 for fluid B for ω = 300 rad/s, V = 75 cm3.
Figure 13. Dependence of the torque M on the angular velocityω2 for fluid B for ω = 300 rad/s, V = 75 cm3.
Preprints 103004 g013
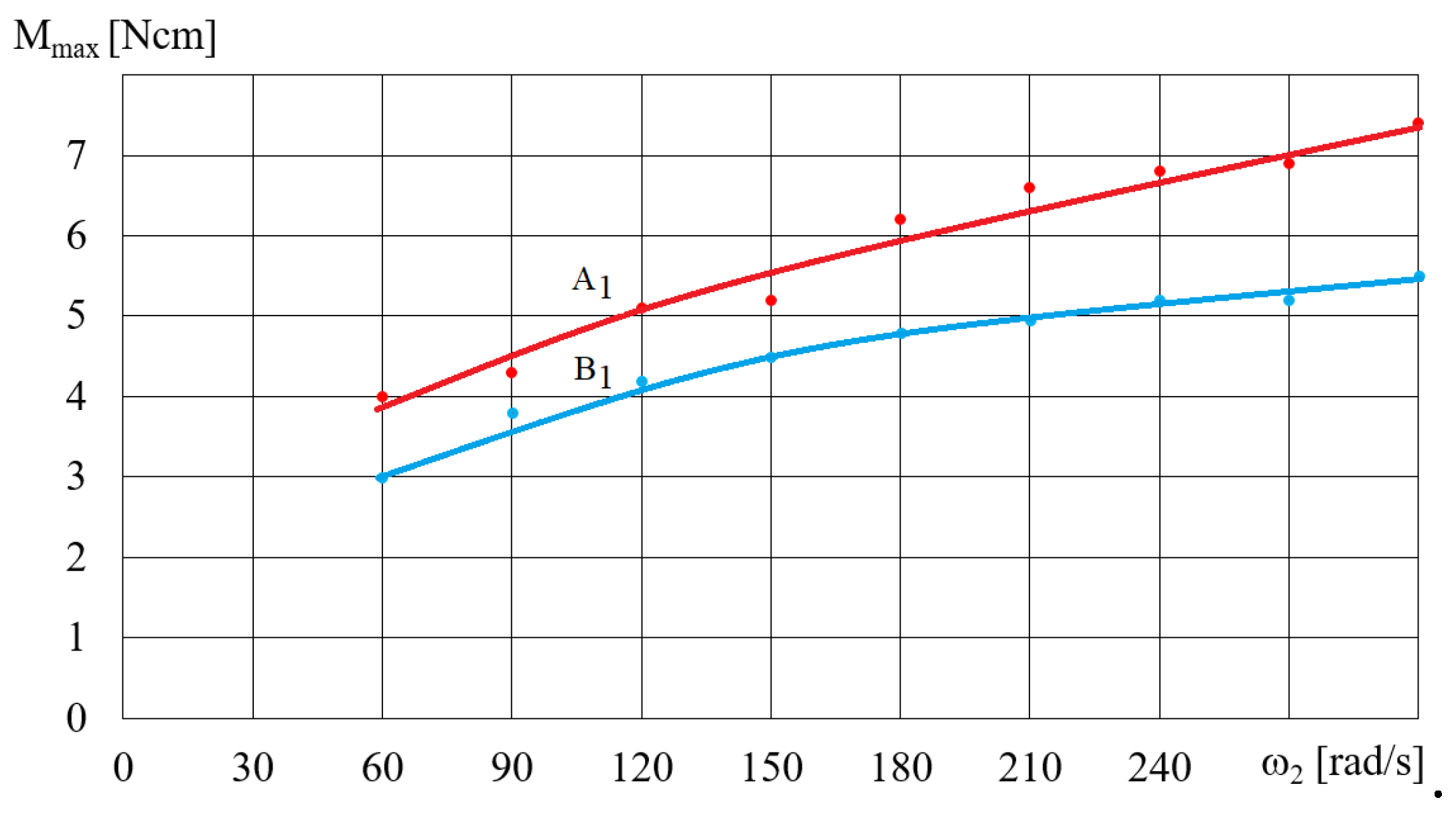
Preprints 103004 g014
Figure 14. Dependence of the torque M on the angular velocityω2for fluid B for ω = 300 rad/s, V = 75 cm3.
Figure 14. Dependence of the torque M on the angular velocityω2for fluid B for ω = 300 rad/s, V = 75 cm3.
Preprints 103004 g014
Preprints 103004 g015
Figure 15. Dependence of the torque Mmax on angular velocity ω for fluids A4 and B4, V = 75 cm3.
Figure 15. Dependence of the torque Mmax on angular velocity ω for fluids A4 and B4, V = 75 cm3.
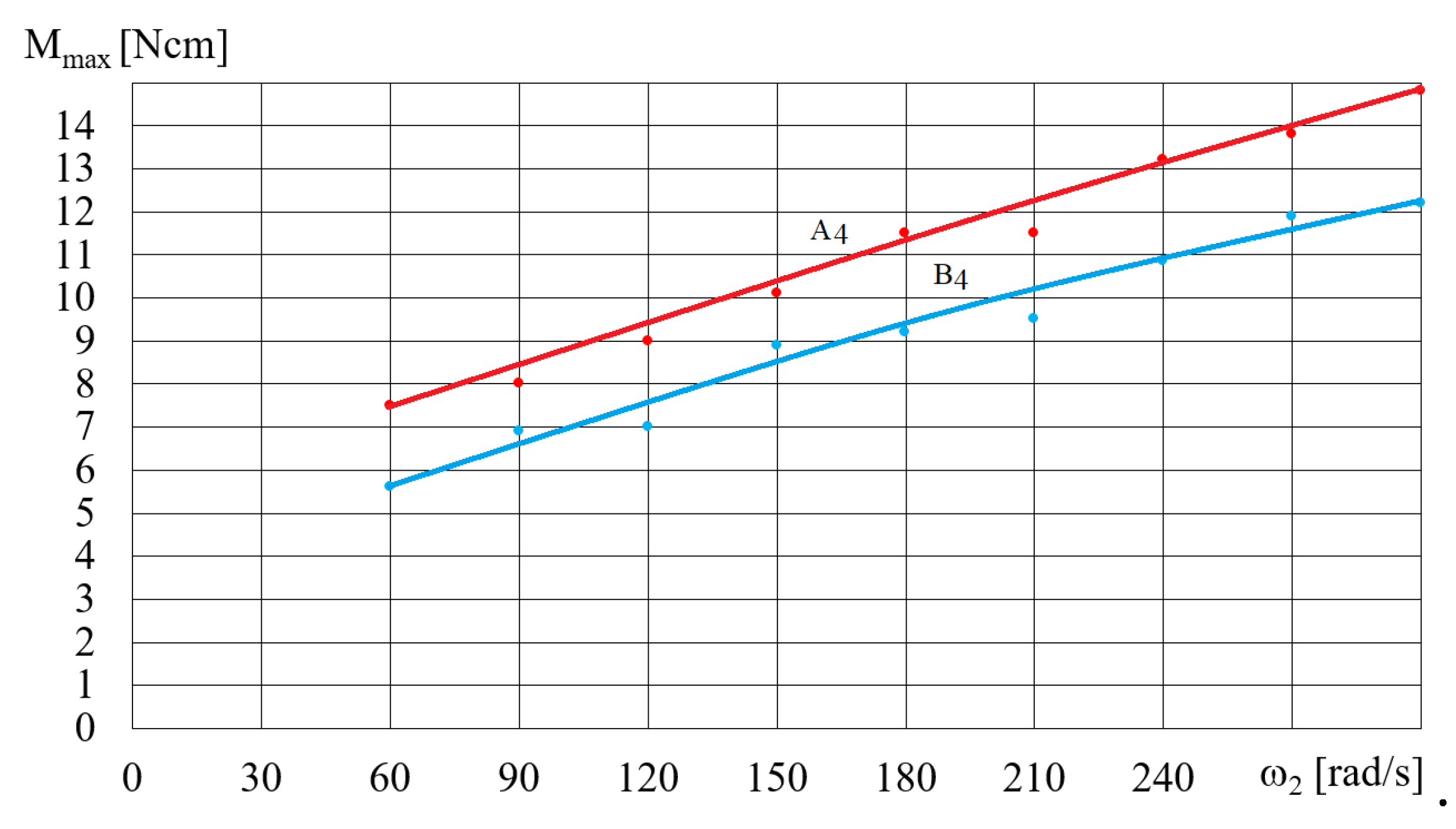
Preprints 103004 g015
Preprints 103004 g016
Figure 16. Dependence of the torque Mmax on the volume V of the fluid A1for ω = 200 rad/s.
Figure 16. Dependence of the torque Mmax on the volume V of the fluid A1for ω = 200 rad/s.
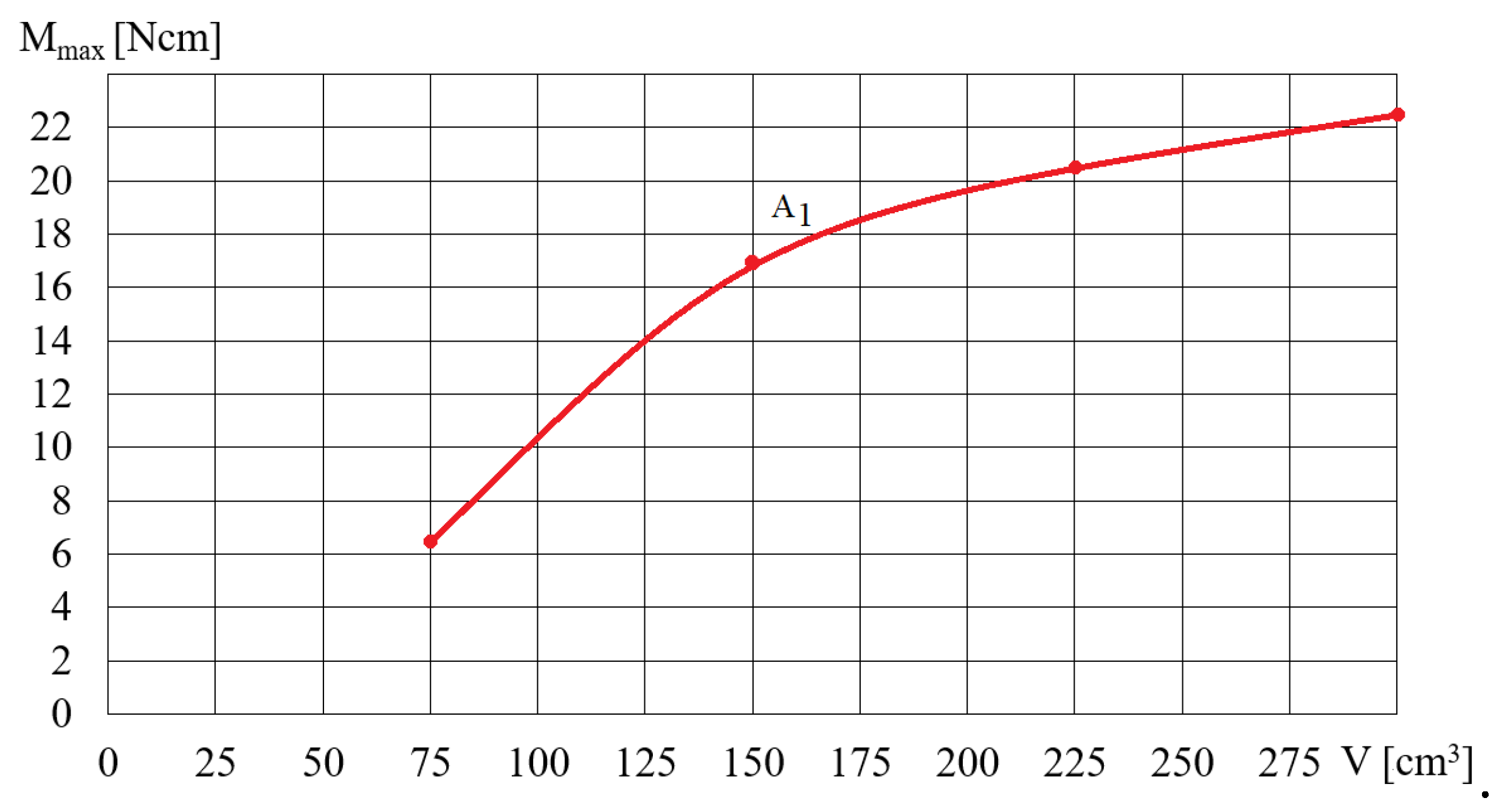
Preprints 103004 g016
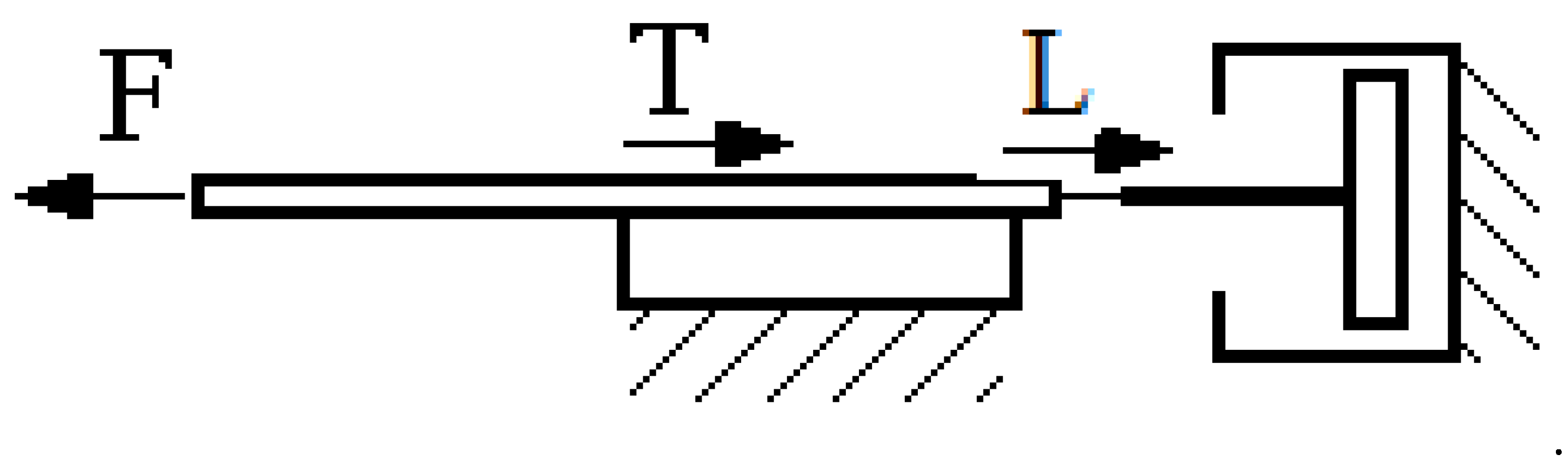
Preprints 103004 g017
Figure 17. Viscous-plastic model of Bingham’s fluid: F – force acting on particles, T – friction force, L – viscous force.
Figure 17. Viscous-plastic model of Bingham’s fluid: F – force acting on particles, T – friction force, L – viscous force.
Preprints 103004 g017
Preprints 103004 g018
Figure 18. Forces acting on the MR fluid and the beaker during HCMR operation: a – ω2 = ω; 1 – beaker wall, 2 – magnet, 3 –MR fluid pulled by the magnet, 4 – a ring of MR fluid; b – ω2<ω.
Figure 18. Forces acting on the MR fluid and the beaker during HCMR operation: a – ω2 = ω; 1 – beaker wall, 2 – magnet, 3 –MR fluid pulled by the magnet, 4 – a ring of MR fluid; b – ω2<ω.
Preprints 103004 g018
Preprints 103004 g019
Figure 19. Characteristics of clutches using the influence of a magnetic field: 1 – electromagnetic friction-type clutches, 2 – induction clutches, 3 –viscous clutches with MR fluid, 4 –magnetic particle clutches, 5 – eddy current clutches.
Figure 19. Characteristics of clutches using the influence of a magnetic field: 1 – electromagnetic friction-type clutches, 2 – induction clutches, 3 –viscous clutches with MR fluid, 4 –magnetic particle clutches, 5 – eddy current clutches.
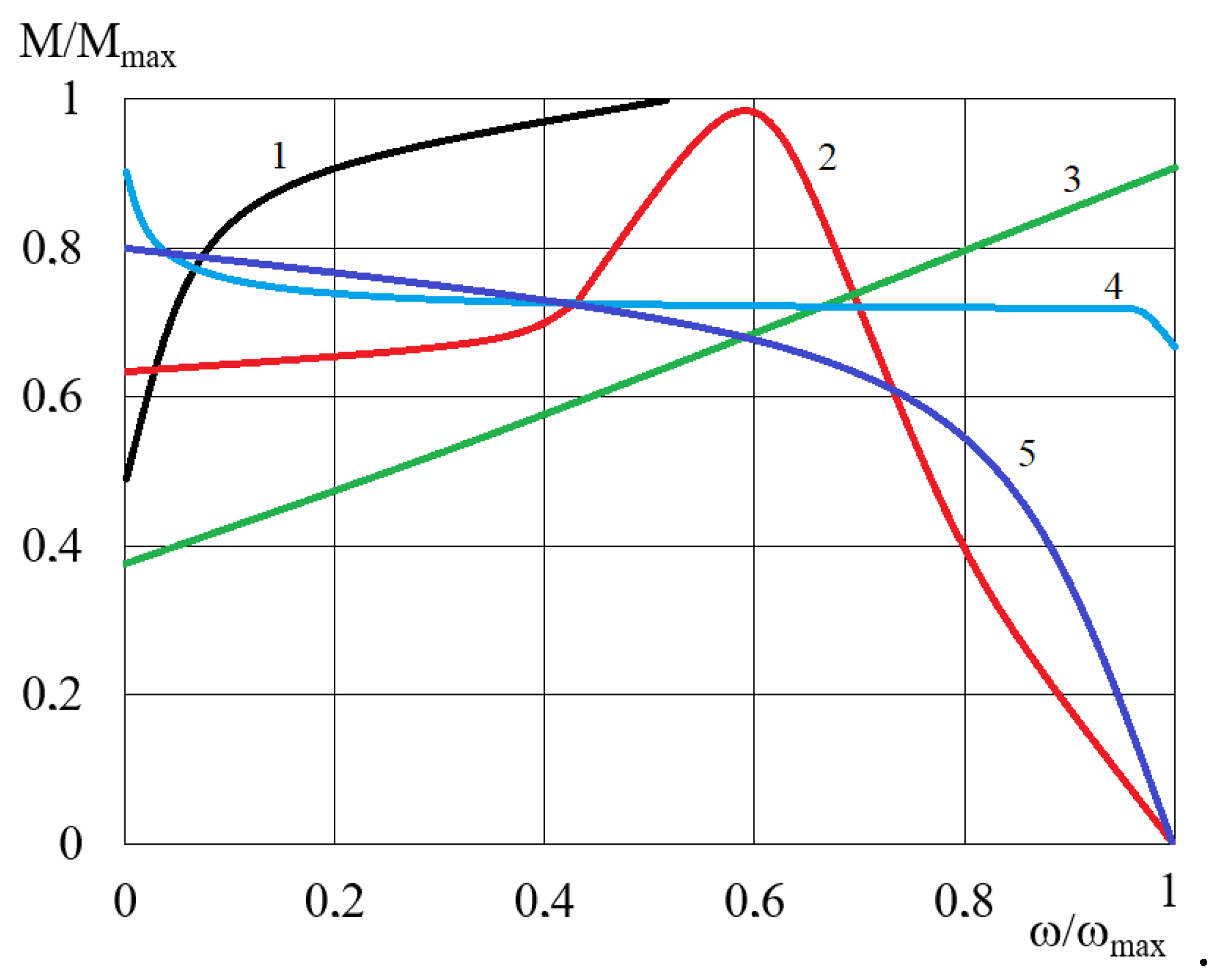
Preprints 103004 g019
Table 1. Names and composition of the in-house manufactured MR fluids.
Table 1. Names and composition of the in-house manufactured MR fluids.
Name Fe particles’ size Base fluid
A From 3.5 μm to 6.5μm Silicon oil OL.111
B From 100 μm to 150μm Silicon oil OL.111
Table 2. The weight concentration ratio in the tested MR fluids.
Table 2. The weight concentration ratio in the tested MR fluids.
Symbol Density [g/cm3] Weight concentration ratio of solid particles ϕ [%]
1 1.69 0.50
2 2.01 0.60
3 2.30 0.67
4 2.56 0.72
5 2.79 0.75
Table 3. Dimensions of the magnetic device for the rheometer Brookfield DV2T.
Table 3. Dimensions of the magnetic device for the rheometer Brookfield DV2T.
Parameter Value
Spindle radius RV-07 (7) 2.1 mm
Internal radius of the tank opening 3.25 mm
Maximum spindle immersion depth 35 mm
Length of the electromagnet core 276 mm
Cross-section of the electromagnet core 24 mm x 12 mm
Wire diameter and number of turns of the electromagnet coil 0.25 mm x 850
Spindle angular velocity range 2 rad/s–10 rad/s
MR fluid temperature during testing 25 o C
Table 4. Data regarding the components of the test stand.
Table 4. Data regarding the components of the test stand.
Component Designation
Frequency converter LG SV008iC5-1F
Engine stator 230 V 0.75 kW
Brake MH1
Temperature sensor NTC 215
Angular velocity meter Measure Me MT522
Torque gauge MT1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated