Preprint
Article
Fractal Dimension of Generalized Rényian Entropy With Potential Fractal Dimension Applications to Smart Cities
Altmetrics
Downloads
157
Views
40
Comments
0
This version is not peer-reviewed
Submitted:
03 April 2024
Posted:
04 April 2024
You are already at the latest version
Alerts
Abstract
The fractal dimension of is identified in this paper. More importantly, the undertaken research has shown how affects the Koch snowflake . The study has demonstrated the existence of negative values of (Koch snowflake), which connects to a considerable number of extremely intriguing mathematical and physical research areas. The information-theoretic impact on the Sierpiniski Gasket dimension , which corresponds to , was treated in a more fundamental way. Notably, the credibility of this current study adds to the existing kThe fractal dimension of is identified in this paper. More importantly, the undertaken research has shown how affects the Koch snowflake . The study has demonstrated the existence of negative values of (Koch snowflake), which connects to a considerable number of extremely intriguing mathematical and physical research areas. The information-theoretic impact on the Sierpiniski Gasket dimension , which corresponds to , was treated in a more fundamental way. Notably, the credibility of this current study adds to the existing knowledge for the information- theoretic fractal dimensions. On another applicative note, this paper offers some potential applications of fractal dimension to smart cities. The investigation of the threshold theorems for and in terms of the triad is part of the next study phase. Additionally, investigating the newly obtained 's corresponding arbitrary Sierpinski Gasket for the first time.applicative note, this paper offers some potential applications of fractal dimension to smart cities. The investigation of the threshold theorems for and in terms of the triad is part of the next study phase. Additionally, investigating the newly obtained 's corresponding arbitrary Sierpinski Gasket for the first time.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Introduction
The Shannonian entropic measure, [1] reads:
The probability of the event is given by the equation . This entropy, defines the concept of information in information theory.
Most importantly, Generalized Rényian Entropy of order and namely to read as
With and
Notably, as and for reduces to the Rényian Entropy [3] of order
And for, reduces to the Shannonian entropic formula (1.1).
Entropy and fractal dimension are related because entropy is a statistical measure of complexity in spatial dimensions. Fractals measure a pattern’s ability to fill space because of its distinctive scaling behaviour. This connection aids in our comprehension of the complex interrelationship between information theory and pattern geometry [4,5,6,7,8,9]. Lewis Fry Richardson investigated in [10] how the length of the stiff stick used to measure coastlines can affect the measured length of the shoreline. Mandelbrot referenced this earlier research in [10,11,12].
There are numerous formal mathematical definitions that can be used to study fractal dimension). One formulation of this kind establishes relationships between ), the scaling factor (𝜀), and the number of sticks () required to cover a coastline. These formulas help quantify the complexity and scaling properties of fractal patterns in spatial dimensions. An area of Arizona’s Grand Canyon is reproduced with the help of the GNU Image Manipulation Programme and Google Earth satellite images. These tools can be used to paint portraits or create various depictions of the aspects of the canyon, as seen in Figure 1 (c.f., [12]).
It is possible to see how painted portraits were created by using Google Earth satellite photographs of a section of the Grand Canyon in Arizona. Figure 2 and Figure 3 show how the . of the canyon’s rim was determined by using the ruler tool in Google Earth to set a reference length of 6 km. While Figure 3 shows the simultaneous decline of . and 𝜀, Figure 2 shows the abrupt heavy-tailed declination that 𝜀 (an additional variable) experiences in response to the continuous growth of (a variable).
Section 2 of the present work mind map reviews earlier research on the connection between entropy and , with an emphasis on Shannon and Rényi entropies. It also explains how entropy principles can be used to get . This review of earlier research sheds light on the fractal dimension’s entropic genesis. Section 3 of the paper is dedicated to deriving new results and presenting a numerical analysis that strongly supports the idea that the logarithmic base has a substantial impact on the behavior of the Koch snowflakes. This section focuses on explaining and demonstrating how different values of the logarithmic base influence the behavior of the fractal dimension in the context of the Koch snowflake. Section 4 addresses the significant impact of fractal dimension on smart cities. Section 5 covers the conclusion and future work.
2. Materials and Methods
For occurrences with equal probabilities, that is, , an exposition of for some entropic formulae, see [1,3,13,14].
[12] reads:
Rényian dimension, [14] reads:
3. Results and Discussion
Theorem 1:
For, it holds that:
Proof:
Engaging (2.3), it is implied that
Engaging (2.1) and (2.2), the proof follows.□
Corollary 2
satisfies:
- 1.
- 2.
Proof:
Taking the limit of (c.f., (2.3)) as
This proves 1.
The proof of 2 is immediate by (2.3) and the well-known formula:
Notably, by changing the indices of the generalised dimensions, we can observe how they affect the behaviour of s.□
Consequently,
Clearly, is significantly impacted by. For vanishes and starts to negatively decrease immensely for Unexpectedly, tends to infinity as approaches 1, as visualized by Figure 4. As progresses to increase, the corresponding significantly decreases, which is shown by Figure 5. As expected, as increases, will tend to zero. Notably, the attained negative values of are physically interpreted by the measurements of the degrees of emptiness in an empty set, non-conclusion, model architectures with various sorts of inhomogeneity non scattered particle distributions are described as being empty (lacunar).
More interestingly, the Sierpiniski Gasket (SG) fractal dimension follows by putting N = 3 and 𝜀 = 1/2.
Engaging (2.3), one gets:
In the following experiment, the information theoretic impact of the non-extensive parameter will be addressed.
Obviously,is significantly impacted by. The none-extensivity of the parameter enforces to increase drastically as it can be visualized by Figure 6 that as approaches unity tends to infinity. Notably, lies in the extensivity domain, which physically translates to short-range interactions.
4. Applications to Smart Cities:
Local or microscopic chaos and global or macroscopic disorder are the two types of chaos covered by chaos theory [16]. Local chaos is mostly investigated by dissipative structure theory and synergetic theory since it primarily deals with the relationships and interconnections within a system. Chaos theory, on the other hand, focuses specifically on global chaos, which is described as deterministic patterns and behaviours that arise from complex systems.
[16] looked at the growth of smart cities, particularly in China, and stressed how evaluation and planning may suffer from a lack of a basic understanding of smart city systems. Consequently, [14] offered a complete framework for assessing and regulating the operations of smart cities that considers smart gadgets, ICT, and the dynamics of development. It also implied that the self-organizing system theory could potentially be able to accommodate for the complexity of smart cities.
Smart systems [16] are made up of several interrelated parts, including systems for energy, ICT, economics, security, and institutional culture. As smart city systems are developed, these systems, which are driven by internal institutional culture and ICT mechanisms, evolve from simple smart cell components to more complex entities. Figure 7 (c.f., [16]) demonstrates how these open systems interact with the outside world to exchange information and energy to create a full self-organizing framework.
The entire functioning and quality of service provided by an urban road network are directly influenced by its structural features [17]. Because fractal theory is self-similar and scale invariant, it can be used to examine urban road networks. To evaluate and enhance urban road networks, this research computes and examines nine Harbin districts’ five fractal dimensions, as well as their relationships to area, population, road length, and building density.
Figure 8(c.f., [17]) portrays the map of Harbin, a Chinese city. The main urban area of Harbin has a total of 12,800 roads and the combined length of these roads is 9757.934 kilometres.
Data including the road network map, area, population, building area, road number, and building number were collected for 9 districts in Harbin, China, to compute the road work’s [17]. Shape files were utilised for downloading the information about the metropolitan road network from Open Street Map (OSM). Figure 9 illustrates how this information will be utilised to examine the fractal characteristics of the Harbin Road network.
In their research, [17] measured five different types of fractal dimensions using images in BMP file format (.bmp). The images in question had a black backdrop with white elements that represented roads and boundaries on them. Figure 10 illustrates the conversion of nine maps into the appropriate BMP format with varied sizes (width and height) and a resolution of 500 dpi from the GIS software-generated shape file data.
The urban climate is influenced by various factors [18] and understanding them can help mitigate heat stress in the context of urbanization and climate change. In a study focusing on European cities, it was found that the Urban Heat Island (UHI) phenomenon is influenced by city size, fractality (complexity of urban form), and anisometry (degree of stretching). According to the study, UHI intensity decreases with anisometry and rises with city size and fractal dimension. Smaller, dispersed, and stretched cities are considered preferable for mitigating UHI, although trade-offs must be made considering the positive effects of large cities.
The UHI was determined by the researchers [18] using land cover data and temperature data from remote sensing. The disparity between the mean temperature inside an urban cluster and the mean temperature outside is how they characterised the severity of the urban heat island (UHI). The study examined how the size, fractality, and anisometry of the city clusters affect the UHI during the summer of 2006–2013, focusing on the 5,000 largest urban clusters in Europe.
- Multiplying the number of cells in a city cluster by the area of each cell yields the city size . Due to Zipf’s law, which states that there are many small cities and few large ones, the logarithm of city is used to reduce the skewness in the data.
- To measure the fractal dimension of city clusters, [18] used the box counting method, which involves counting the number of square boxes needed to cover the structure. Figure 11a–c of the study shows three examples of city clusters with different sizes and levels of fractality, illustrating the concept visually. The box-counting method is used to calculate of city clusters, which provides a measure of their compactness. By analyzing the linear regressions of the log-log scale plots of box-counting results, the slopes of the lines estimate the fractal dimensions, indicating that cities with larger values are generally more compact in shape.
- Anisometry of a city cluster is the degree of deviation of a city from a circular shape. It is computed using the main axis to minor axis ratio of the city cluster’s equivalent ellipse. A higher value of anisometry indicates that the city is more elongated or stretched in shape, as illustrated by the example of Belgrade in Figure 11a–c (c.f., [18]).
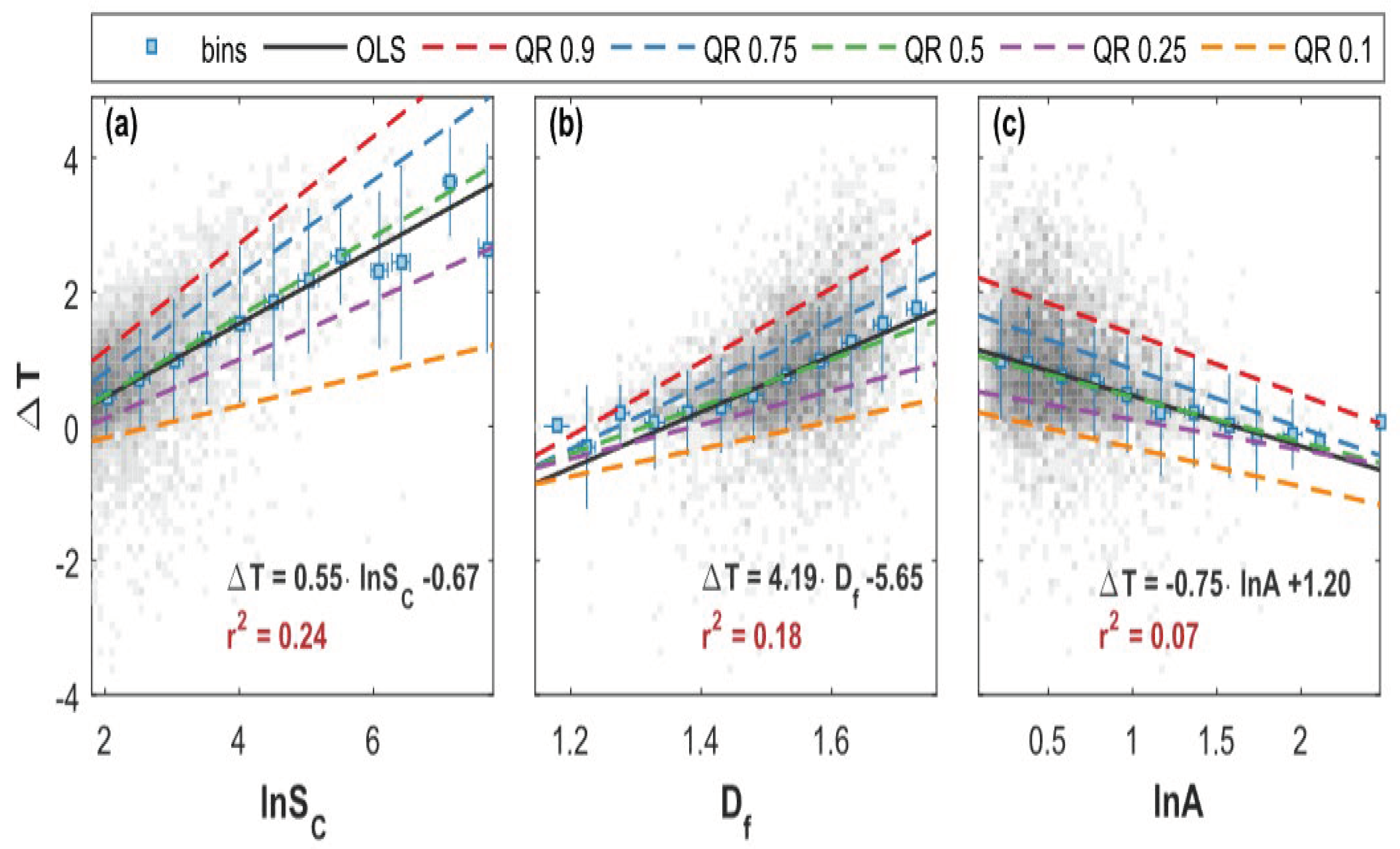
Scatterplots in Figure 12 (c.f., [18]) show the associations between three parameters and the midday UHI intensity in the setting. The UHI intensity increases with city growth, as seen in Figure 12a, with an increase in UHI intensity of roughly 0.4 °C occurring for every doubling of city size. Moreover, there is a substantial correlation between population size and UHI intensity [18]. Quantile regressions also show heteroscedasticity, which suggests a stronger dispersion of UHI severity among major cities. The association between and UHI intensity is seen in Figure 12b. The findings reveal that more compact cities often have larger UHI effects, with an average UHI intensity rise of about 2 °C as increases. Additionally, in Figure 12c, it is observed that the UHI intensity decreases with increasing anisometry, with more circular cities exhibiting higher UHI intensities.
5. Conclusion and Future Work
On a very strong note, this current study adds to the existing knowledge, based on only one single paper in literature [9], where the undertaken research was mainly of the fractal dimensions of the very basic Shannonian entropic form. More importantly, this paper extends the Information Theoretic Fractal Geometry (ITFG) to the highest level, by obtaining , as a potential generalization to [9]. It is worth noting that the first author of the current paper has published two seminal papers(see, [21,22]) to set the cornerstones of ITFG based on the theory of both Ismail’s Second and Fourth Entropies, namely () and (). Potentially, and are considered as ultimate generalization to numerous entropy measures within the literature. Based on these consolidated facts, the current paper provides another ground-breaking discovery that adds to ITFG. The study has shown the existence of negative values of, which links to very interesting mathematical and physical avenues of research. More fundamentally, the information-theoretic impact on Sierpiniski Gasket dimension of that corresponds to was addressed. The influential impact of fractal dimension to advance smart cities was overviewed. Future work involves finding the fractal dimension of available entropies in the literature [19,20] to draw a detailed comparison between these derived fractal dimensions, which will open new grounds towards a revolutionary ITFG. The next research phase includes the exploration of the threshold theorems for and in terms of more potentially, exploring for a first-time ever the corresponding arbitrary Sierpinski Gasket for the newly derived. On another applicative note, more applications of fractal dimension to smart cities, engineering and other interdisciplinary themes of research will be addressed.
References
- Shannon, C.E. A mathematical theory of communication. The Bell system technical journal, 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Bhat A H, Baig M A K. Some Coding Theorems on Generalized Reyni’s Entropy of Order α and Type β. International Journal of Applied Mathematics and Information Sciences Letters. 2016, 5, 13–19.
- Rényi, A. (1961). On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability: Contributions to the Theory of Statistics (Vol. 4; pp. 547-562).
- Mageed IA, Zhang Q. An Introductory Survey of Entropy Applications to Information Theory, Queuing Theory, Engineering, Computer Science, and Statistical Mechanics. In2022 27th International Conference on Automation and Computing (ICAC) 2022 Sep 1 (pp. 1-6). IEEE.
- Mageed IA, Zhang Q. An Information Theoretic Unified Global Theory for a Stable M/G/1 Queue With Potential Maximum Entropy Applications to Energy Works. In 2022 Global Energy Conference (GEC) 2022 Oct 26 (pp. 300-305). IEEE.
- Mageed, Ismail A, and Bhat Ashiq H. Generalized Z-Entropy (Gze) and Fractal Dimensions. Appl. Math. Inf. Sci. 2022, 16, 829–834. [CrossRef]
- Sagan, H. (1994). Space - Filling Curves. Berlin: Springer-Verlag. Page 156. ISBN 0-387-94265-3.
- Vicsek, T. (1992). Fractal growth phenomena. Singapore New Jersey: World Scientific. ISBN 978- 981-02-0668-0.
- Sparavigna, A.C. Fractional differentiation-based image processing. arXiv 2009, arXiv:0910. 2381. [Google Scholar]
- Mandelbrot, B.B. (1983). The fractal geometry of nature. Macmillan. ISBN 978-0-7167-1186-5.
- Harte, D. (2001). Multifractals. London: Chapman & Hall. ISBN 978-1-58488-154-4.
- Sparavigna, A.C. (2016). Entropies and fractal dimensions. Philica. Hal-01377975f. 0137. [Google Scholar]
- Ott, E. Attractor dimensions. Scholarpedia 2008, 3, 2110. [Google Scholar] [CrossRef]
- Mageed IA, Zhang Q. The Rényian-Tsallisian Formalisms of the Stable M/G/1 Queue with Heavy Tails Entropian Threshold Theorems for the Squared Coefficient of Variation. electronic Journal of Computer Science and Information Technology. 2023, 9, 7–14.
- Mageed IA, Zhang Q. Inductive Inferences of Z-Entropy Formalism (ZEF) Stable M/G/1 Queue with Heavy Tails. In2022 27th International Conference on Automation and Computing (ICAC) 2022 Sep 1 (pp. 1-6). IEEE.
- Yan J, Liu J, Tseng FM. An evaluation system based on the self-organizing system framework of smart cities: A case study of smart transportation systems in China. Technological Forecasting and Social Change. 2020, 153, 119371.
- Deng H, Wen W, Zhang W. Analysis of Road Networks Features of Urban Municipal District Based on Fractal Dimension. ISPRS International Journal of Geo-Information. 2023, 12, 188.
- Zhou B, Rybski D, Kropp JP. The role of city size and urban form in the surface urban heat island. Scientific reports. 2017, 7, 4791.
- Bhat, A. H, Siddiqui, N. A, et al. Generalization of Renyi’s Entropy and its Application in Source Coding. Appl. Math. Inf. Sci. 2023, 17, 941–948.
- Bhat, A. H., & Baig, M. A. K. Characterization of new two parametric generalized useful information measure. Journal of Information Science Theory and Practice 2016, 4, 64–74.
- A. Mageed, Fractal Dimension(Df) Theory of Ismail’s Second Entropy(HIq) with Potential Fractal Applications to ChatGPT, Distributed Ledger Technologies(DLTs) and Image Processing(IP), IEEE international conference on Computers& Applications(ICCA 2023)The British University in Egypt, (2023).
- A. Mageed, Fractal Dimension(Df) of Ismail’s Fourth Entropy(HIV(𝑞,𝑎1,𝑎2,…,𝑎𝑘)) with Fractal Applications to Algorithms, Haptics, and Transportation, IEEE international conference on Computers& Applications (ICCA 2023)The British University in Egypt.
Figure 1.
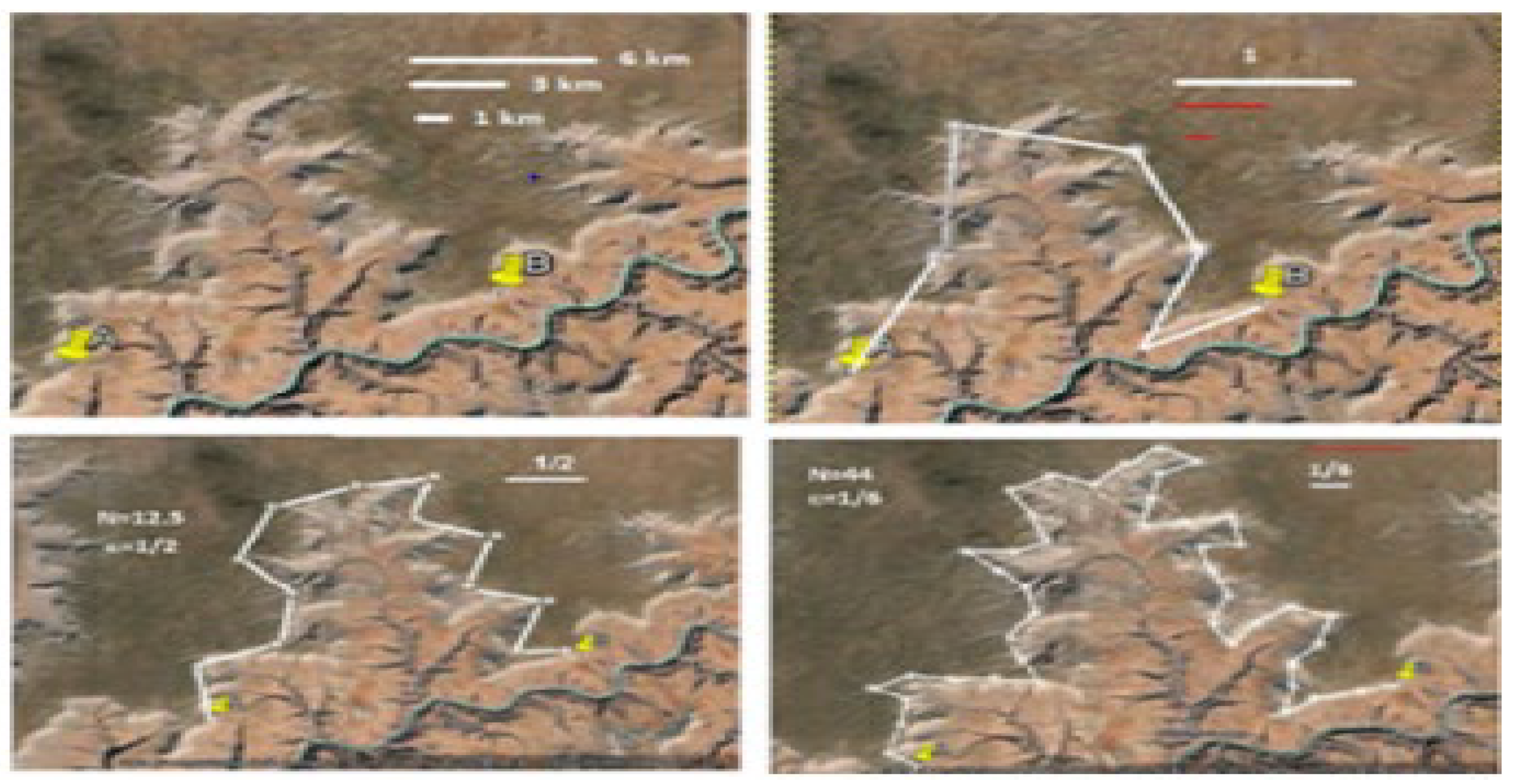
Figure 2.

Figure 3.
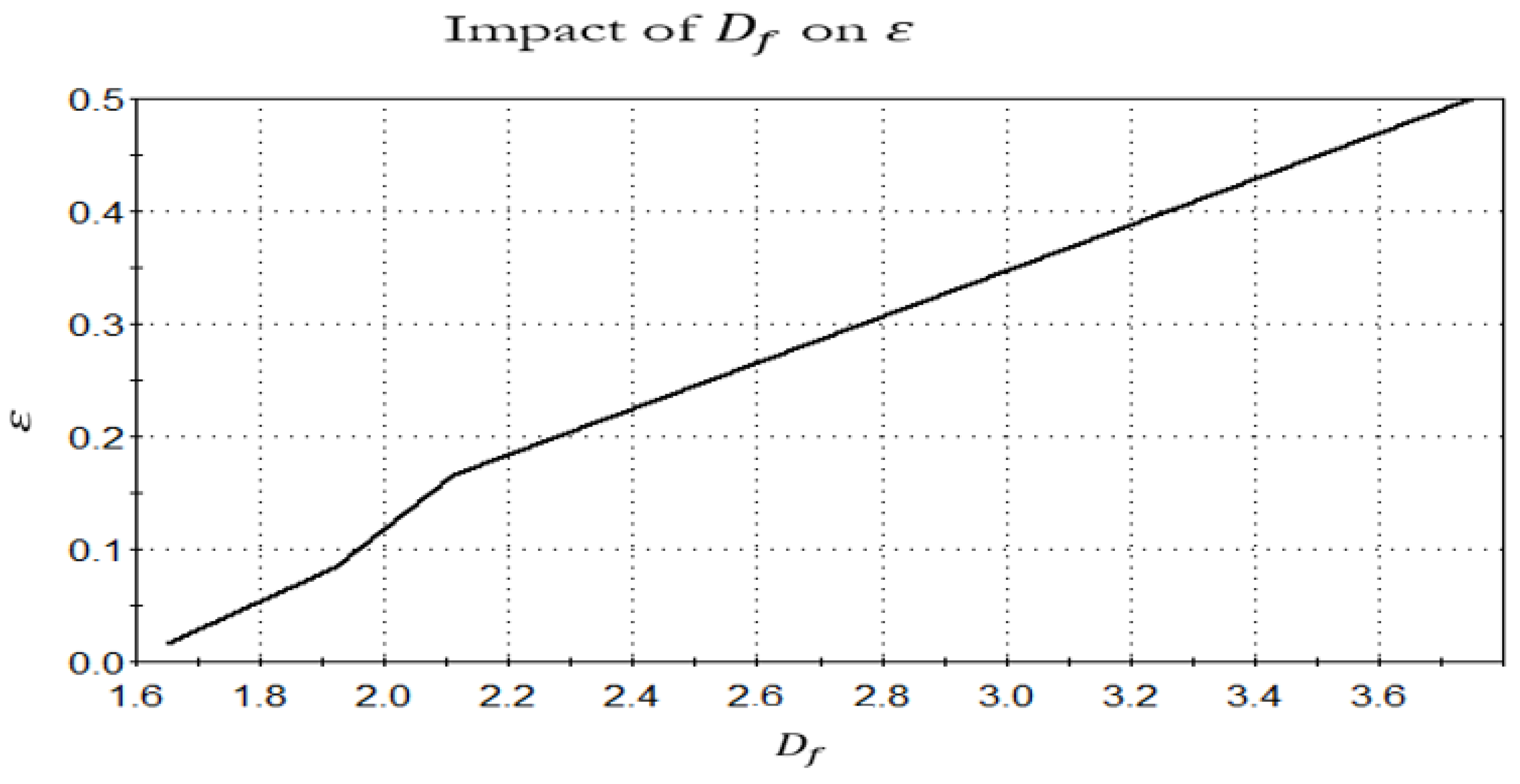
Figure 4.
The impact of the logarithmic base D on,
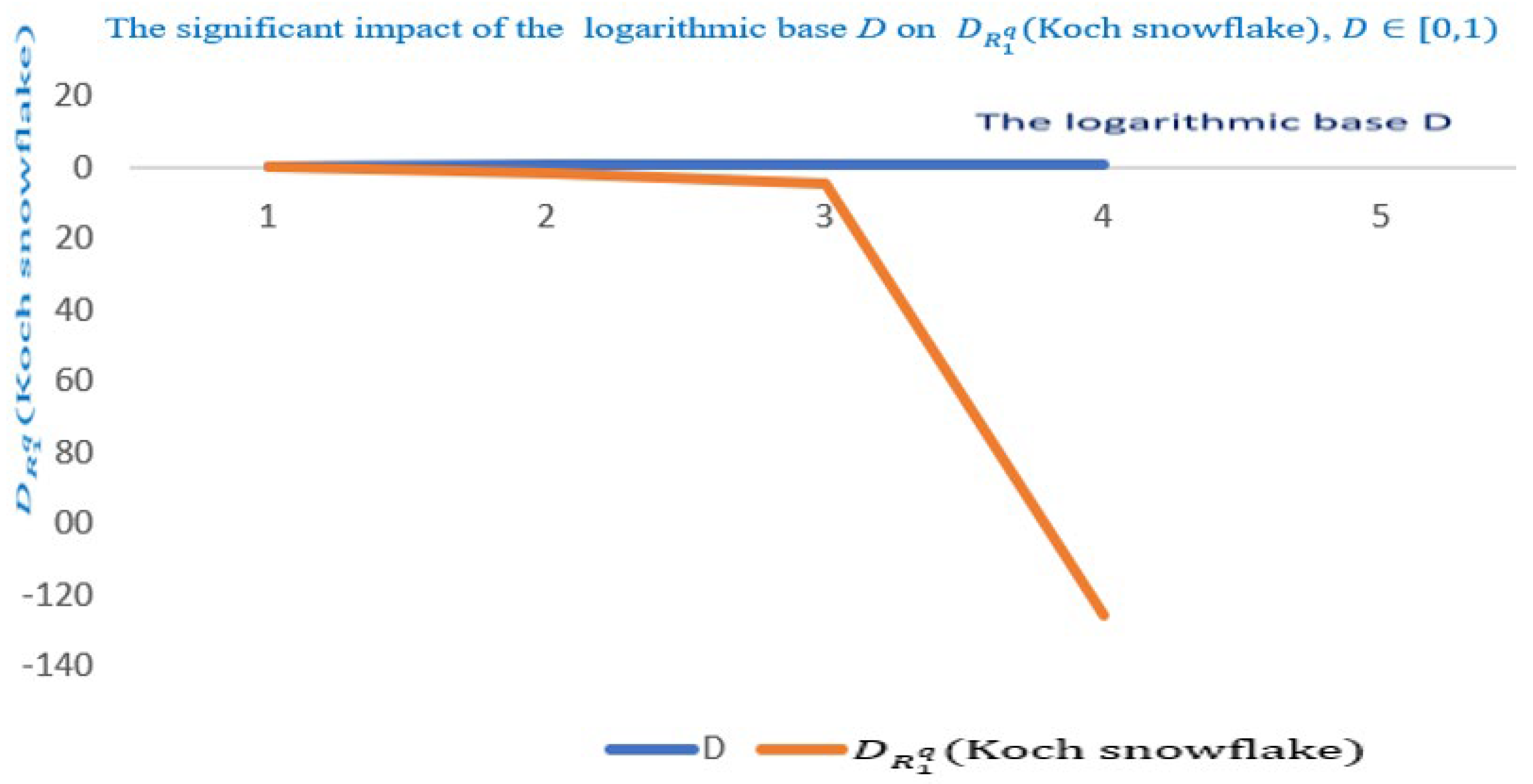
Figure 5.
A portrait on how the logarithmic base D impacts,
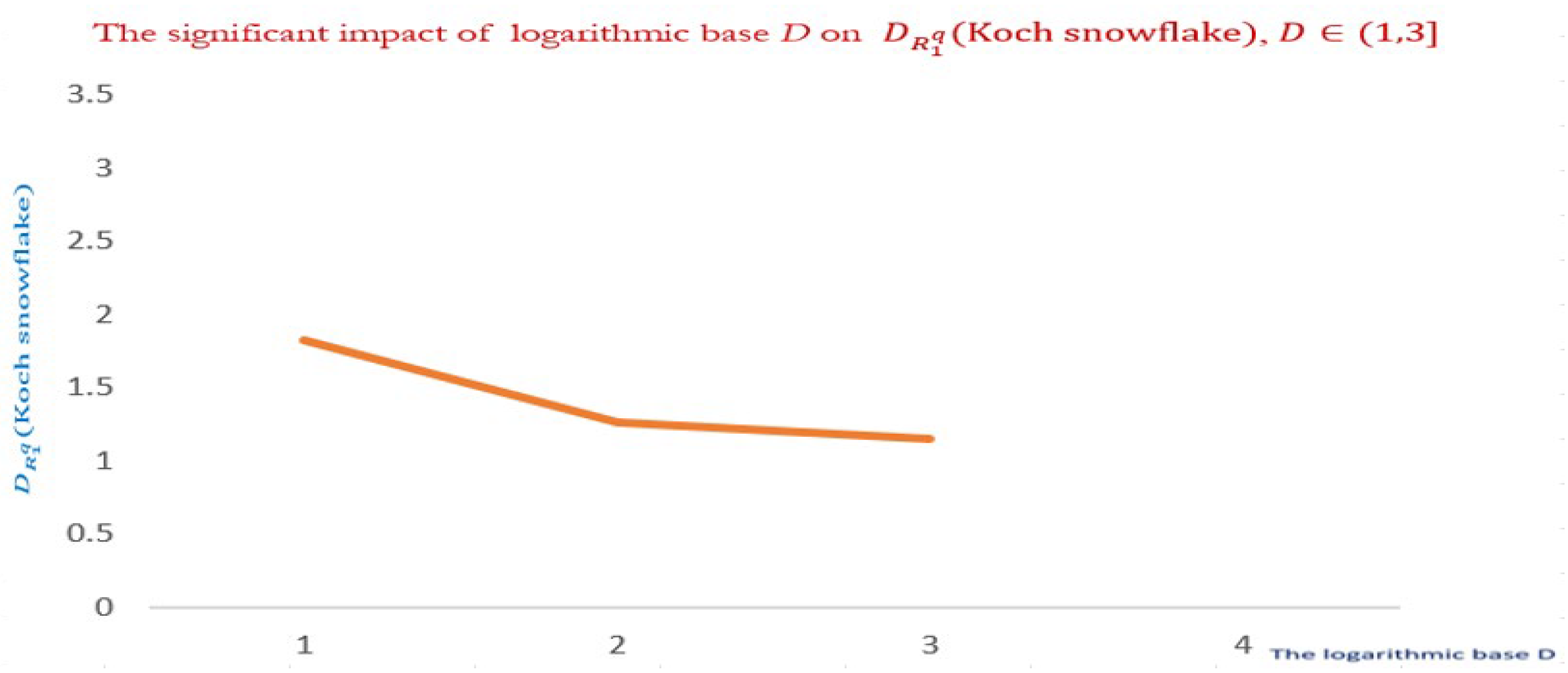
Figure 6.
How .

Figure 7.
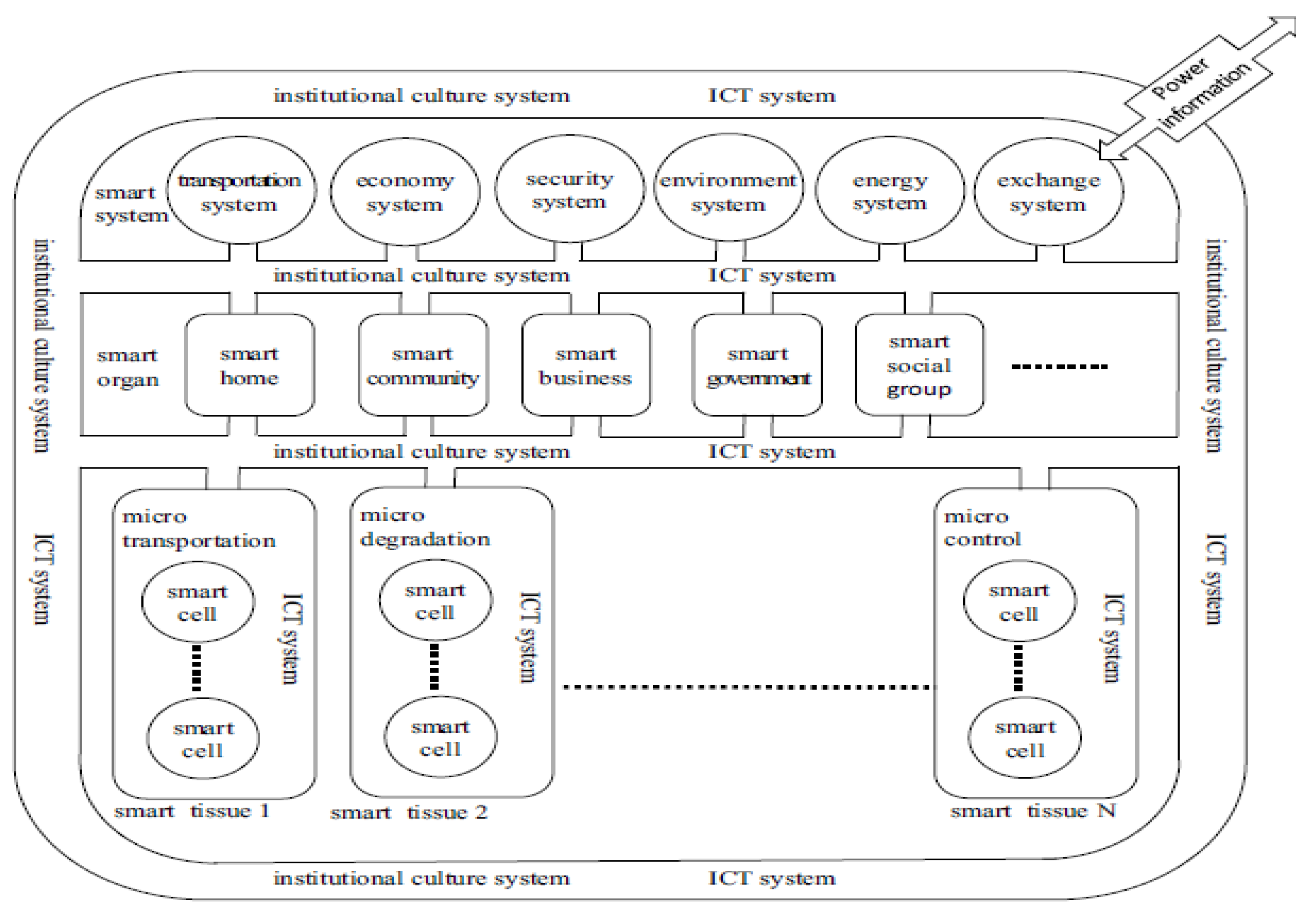
Figure 8.
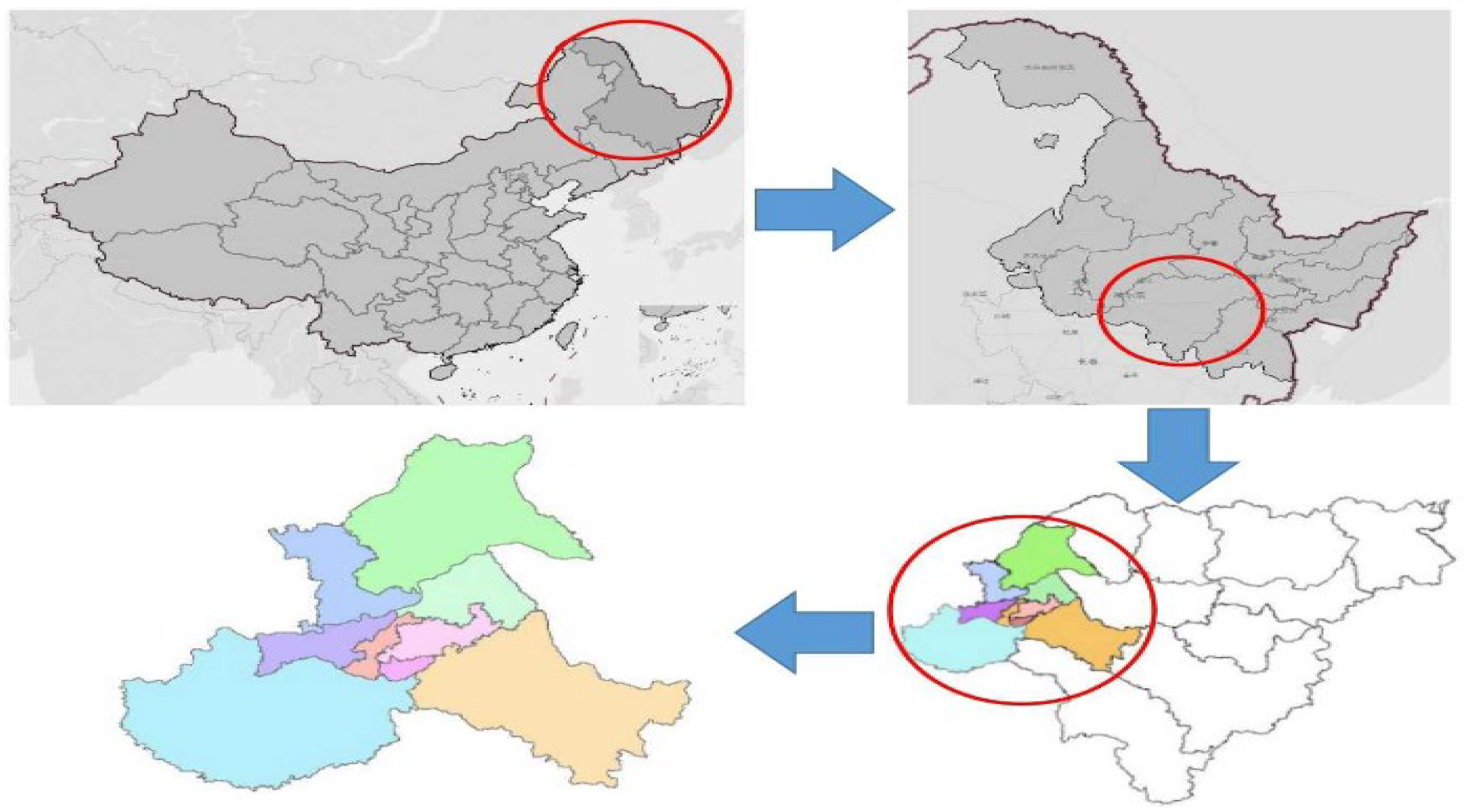
Figure 9.
The core districts have more roads and intersections, whereas as we move away from the city centre, there are less roads and crossroads. By examining the data from the road network, it is possible to observe this spatial pattern of road distribution, which has consequences for urban and transportation development in Harbin [17].
Figure 9.
The core districts have more roads and intersections, whereas as we move away from the city centre, there are less roads and crossroads. By examining the data from the road network, it is possible to observe this spatial pattern of road distribution, which has consequences for urban and transportation development in Harbin [17].

Figure 10.
The road maps of these districts have been digitally represented with a high level of detail and clarity, allowing for precise analysis and visualization of the road infrastructure in those areas [17].
Figure 10.
The road maps of these districts have been digitally represented with a high level of detail and clarity, allowing for precise analysis and visualization of the road infrastructure in those areas [17].

Figure 11.
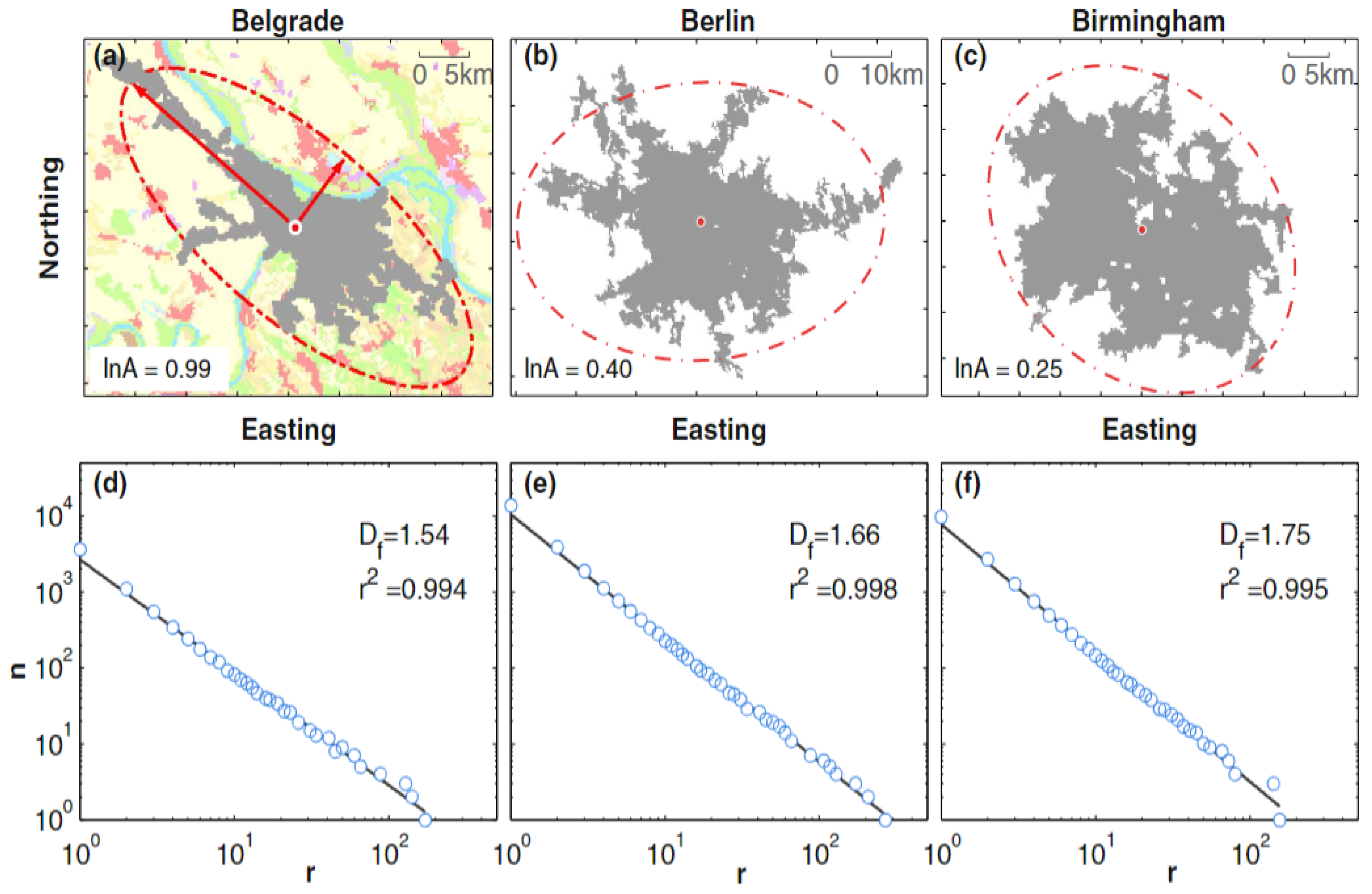
Figure 12.
The UHI intensity is analysed using quantile regressions and ordinary least square regression, with the results visualized through linear regressions and quantile regressions. The quantile regressions provide slopes for different quantiles, indicating the varying impact of the factors on UHI intensity [18].
Figure 12.
The UHI intensity is analysed using quantile regressions and ordinary least square regression, with the results visualized through linear regressions and quantile regressions. The quantile regressions provide slopes for different quantiles, indicating the varying impact of the factors on UHI intensity [18].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






