Prerpints.org logo
Preprint
Article

A Temporal Difference and Cross-variate Fusion Network for Multivariate Time Series Classification

Altmetrics

Downloads

135

Views

51

Comments

0

This version is not peer-reviewed

Submitted:

04 April 2024

Posted:

04 April 2024

You are already at the latest version

Alerts
Abstract
Multivariate Time Series Classification (MTSC) is one of most important tasks in time series analysis, aiding in activities such as human motion recognition and medical diagnostics. Existing methods for MTSC do not explicitly model temporal differences and generalize the idea of temporal difference into a efficient temporal module. Additionally, existing methods are not yet able to capture cross-variable relationships well during network training. As a result, they are unable to achieve convincing feature representation, leading to suboptimal classification accuracy. In this paper, we propose a novel MTSC model called Temporal Difference and Cross-variate Fusion Network (TDCFN), which integrates a two-stream differential LSTM network and a cross-variate feature extraction network to enhance feature representation. TDCFN achieves superior classification accuracy by capturing dynamic temporal evolution and inter-variable relationships. The experimental results show that TDCFN can achieve competitive performance with state-of-the-art multivariate time series classification approaches.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

0. Introduction

Time series are widely used in many important areas of human life, including manufacturing, healthcare, biology, multimedia, climate science, action recognition and speech recognition[1]. In recent years, with the advancement of sensors and data storage technologies, data mining of time-series data has gradually attracted widespread attention. The analysis of these time-series data scan be categorized as time series classification[2], prediction[3], clustering[4], anomaly detection[5], etc. Time series classification task, that we are concerned with, as one of the basic problems of time series analysis, can help people to determine the events that have occurred by recognizing the labels of the series recordings, such as human motion recognition[6] and activity recognition[7] in sports, as well as the diagnosis based on electrocardiogram (ECG), electroencephalogram (EEG) and Magnetoencephalography (MEG), which are bioelectronics analyses in medicine[8], estimation of sea state in meteorology[9], and many other fields. In fact, most of these problems essentially belong to multivariate time series classification (MTSC). Compared with univariate time series classification (UTSC)[10], the data to be analyzed in MTSC task typically comprise a set of co-evolving time series simultaneously recorded by a group of sensors over time. Intuitively, this data composition better reflects real-life scenarios. With the characteristics of multivariate, MTSC has more system information and better performance in determining the type of event. For instance, it can determine a patient’s heartbeat type and machine operation. For example, Figure 1 depicts an example sample from the BasicMotions multivariate time series dataset, showcasing the 3D accelerometer and gyroscope data collected while participants engage in four activities using a smartwatch(specifically, this sample corresponds to the ’walking’ activity). However, improving the accuracy of MTSC efficiently remains a challenging problem.
In recent years, there has been extensive research on MTS classification methods, various methods have been proposed, and resulting some notable achievements. In traditional approaches, most methods are pattern-based, which can be classified into distance-based methods[11,12,13,14,15], feature-based methods[16,17,18] and ensemble methods[19,20]. Although traditional methods have improved the accuracy to some extent, the methods are time consuming because they require a large amount of data preprocessing and feature engineering task. For example, shapelets based approaches for MTSC require the computation of a large number of candidate patterns, which may lead to inefficient training and poor model performance. In addition, ensemble models also require multiple classifiers leading to complex modelling, high computational complexity and long training times.
With the brilliant success of deep learning (DL) in Computer Vision (CV)[21] and Natural Language Processing (NLP) fields[22], researchers have started to try to solve the MTSC problems by utilizing the excellent feature extraction capability of deep neural networks. Among numerous neural network models, convolutional neural network (CNN) and recurrent neural network (RNN), as popular deep learning frameworks, have been widely used in MTSC tasks. CNNs have shown promising results in time series classification due to their excellent local feature extraction, such as Multi-Channel CNN (MC-CNN)[23] and Multi-scale Convolutional Neural Network (MSCNN)[24]. Recurrent neural networks are able to capture sequence dependencies and naturally support temporal classification tasks. [25] used a hierarchical recurrent neural network for skeleton-based action recognition, which divides the human skeleton based on its body structure into the network divides the human skeleton based on the human body structure into five parts, and then divides them into five sub-networks, fuses the representations of the skeleton sequences in the sub-networks to form higher-level inputs, and finally feeds them into a single-layer perceptual machine for classification. [26] attempted to use a dual-network based model that incorporates Long Short-Term Memory (LSTM) and Fully Convolutional Networks (FCN) to jointly capture the features of MTS.
However, existing studies do not model the inter-variable relationships well in their models, and the temporal information also fades away during the feature extraction process. In addition, the existing RNN models do not explicitly model the temporal difference information of the time series, which may contain information about the dynamic evolution within the multivariate data. By modelling the temporal difference information of MTS, we can exploit the rich information provided by sequence segments with large temporal differences to extract more discriminative feature representations to support downstream classification tasks.
Therefore, this paper proposes a novel multivariate time-series classification model, which is a dual-network-based model consisting of a two-stream differential LSTM network and a cross-variate feature extraction network. Through the two-stream differential LSTM, the dynamic evolution information of the time series data is fused with the original information, which jointly guides the gating mechanism and the time series dependency extraction of the RNN network. The cross-variate feature extraction network based on depth-separable convolution is used to process sequences, channels and variables to achieve better feature extraction of inter-variate relationships. Our contributions are as follows:
  • We propose a novel multivariate time series classification network called Temporal Difference and Cross-variate Fusion Network(TDCFN) to enhance the feature representation capability and improve the classification accuracy of the MTSC task through the combination of two-stream Diff-LSTM and cross-variate feature extraction network, which simultaneously models temporal features and inter-variable features.
  • We obtain the input of LSTM by preprocessing the time series data into differential and source data, with a focus on extracting the temporal features by transforming the LSTM into a two-stream model, which takes advantage of the dynamic evolution of the time series.
  • We capture the dependencies between variables and learn the information representation through a cross-variate features extracting network module to generate latent features.
  • We perform extensive experiments on MTS benchmark datasets. Experiments on ten benchmark datasets show that TDCFN outperforms state-of-the-art strategies on the MTSC task.

1. Related Works

1.1. Pattern-Based Multivariate Time Series Classification Algorithm

Distance-based methods, which typically use Euclidean distance (ED) or dynamic time warping (DTW) distance between time series pairs as a similarity measure, use traditional classifiers (e.g., SVM and NN) to classify MTSs. NN-DTW is proposed in [15], which combines DTW and NN classifiers, and has been shown to be a very strong baseline. The effectiveness of distance-based approaches is directly influenced by the choice of distance measures, which requires professional design of appropriate distances.
Feature-based methods classify time series by identifying words patterns[16] or shapelet patterns[17,18] in the time series. Such methods were originally proposed for UTS classification, but can be easily transformed and directly applied to MTS classification. However, the use of these feature-based methods heavily relies on the knowledge of domain experts and requires extensive preprocessing and feature engineering works[27]. Thus, applying feature-based methods to different time series datasets can be challenging.
Ensemble-based approaches achieve classification by ensembling multiple classifiers that focus on different perspectives[19,20]. The final classification result is obtained through weighted voting. Such models greatly improve the classification efficiency of traditional methods.

1.2. DL-Based Multivariate Time Series Classification Algorithm

Deep learning algorithms, which do not require complex data preprocessing or extensive feature engineering, can solve the problems of traditional methods. Specifically, deep learning methods have shown promising results for TSC. For instance, OS-CNN [28] uses Conv1D to extract local features of time series, while ROCKET and MiniROCKET employs numerous stochastic convolutional kernel transformations to extract features relevant to TSC[29,30]. InceptionTime [31] utilises inception structures to investigate multiscale time series representations. Wang et al. developed a technique based on recurrent neural networks and proposed the Adaptive Differential Evolution (ADE) algorithm to derive classifiers for time series[32]. Subsequently, there have been attempts to use a dual-network-based model, which consists of a local-feature extraction network and a relation extraction network in parallel. MLSTM-FCN uses a combined LSTM layer and an FCN layer augmented by squeezing and excitation modules to extract time series features from MTS and a softmax layer is then applied to predict the labels[26]. [33] proposed RAN, a residual attention net that consists of a ResNet-based feature network and a transformer-based relation network. This approach also shows promising performance on UCR datasets. A robust temporal feature network (RTFN) is proposed for extracting features in time series classification[34]. The network consists of a temporal feature network (TFN) with a residual structure, multiple convolutional layers, and a long short-term memory (LSTM) based attention network (LSTMaN). However, existing research fails to adequately capture the relationships between variables and overlook the explicit modeling of temporal differences in time series data. In next section, we will propose TDCFNet, which help us to harness the valuable insights from sequence segments with significant temporal difference and cross-variate relationship, enabling the extraction of more discriminative features to bolster subsequent classification tasks.

2. Method

2.1. Problem Statement

Given a set of multivariate time series X = X 1 , X 2 , X 3 , … , X N of N instances, we have multivariate time series data X i = x 1 , x 2 , x 3 , … , x T ∈ R T × D , where T denotes the total sampling length of the sequence, and D is the number of variables of each sampling point X i , which can be expressed as a matrix as follows:
X i = x ( 1 , 1 ∣ i ) x ( 2 , 1 ∣ i ) x ( T , 1 ∣ i ) x ( 1 , 2 ∣ i ) x ( 2 , 2 ∣ i ) ⋯ x ( T , 2 ∣ i ) ⋮ ⋱ ⋮ x ( 1 , D ∣ i ) x ( 2 , D ∣ i ) ⋯ x ( T , D ∣ i )
Note that univariate time series data are situations where D equals 1, while multivariate time series data are situations where D exceeds 1.
The goal of TSC is to accurately predict the class labels y = 1 , 2 , 3 , … , c from class c. Therefore, we construct a classifier F, thus we have:
y ^ i = F X i
where y ^ i ∈ { 1 , 2 , … , c } . F can be trained by minimising the discrepancy between the predicted class y ^ i and the ground-truth class y i . Here, we adopt a cross entropy loss which is a commonly used loss function for multi-class classification to reflect this discrepancy.

2.2. Model Architecture Overview

The proposed model framework is illustrated in Figure 2 It comprises of three components: the two Stream Diff-LSTM module, for extracting time-series features that contain information about dynamic differential changes, the cross-variate feature extraction network module, for extracting relational feature representations between variables, the feature fusion and multi-class classification module, which fuses the features of the first two components and passes the combined results to a fully connected layer for classification learning. To understand the algorithmic process of our model better, we present the pseudo-code as shown in Algorithm 1. In the following, we describe the implementation details of each part in detail.
Algorithm 1:The pseudo-code of TDCFN.
1. Input: A set of Multivariate time series X
2. Output: The probability P of each category
3. Initialize: Parameters of TDCFN
4. Forward Pass:
5. Obtain two levels of temporal feature representations H , H ^ by applying Two Stream Diff-LSTM on X
6. Compute the output X e m b e d using the embedding layer: X e m b e d = F e m b e d d i n g X i
7. Compute the cross-variate feature extraction network module output F by applying depthwisen, channel-wise and dimension-wise convolutions and skip connection operations: F = F d i m F c h a n n e l F d e p t h X e m b e d + X e m b e d
8. Acquire feature P L S T M and P C F N by global average pooling operation on ( H , H ^ ) and F respectively
9. Concatenate P L S T M and P C F N and obtain F c o n
10. Fed F c o n into fully connected layers to obtain the low-dimensional embedding
11. Apply softmax function to obtain the probability distribution P
12. Backward Pass:
13. Compute the loss using the predicted probabilities and the ground truth labels
14. Perform backpropagation to update the parameters of the entire network

2.3. Two Stream Diff-LSTM Module

The Recurrent Neural Network (RNN) is presently the most widely used deep neural network framework for processing sequence data. Unlike traditional feed-forward deep neural network models, RNN networks preserve the internal hidden state in the constituent network cells to handle sequential dependencies in capturing sequences. The standard RNN network expresses the update of the hidden state h as:
h t = g U h t − 1 + W X t
where g represents a smooth and bounded activation function, such as the sigmoid function. W denotes the weight parameters from the input layer to the hidden layer at time step t. X t represents the input received by the model at time at time step t. U stands for the weight parameters of the hidden layer corresponding to time step t − 1 , while h t and h ( t − 1 ) denote the hidden state from the current time step t and previous time step t − 1 respectively.
The Long Short-Term Memory (LSTM) network is a variant of Recurrent Neural Networks (RNNs) that aims to address the issue of long-term dependencies in traditional RNNs. It is a more sophisticated RNN model unit. Similar to RNNs, LSTM is composed of memory cells that store information about the input sequence. However, LSTM uses gate units to control the flow of information in and out of the memory cells. The structure of the LSTM memory cell is illustrated in Figure 3. Let x t denote the input sequence at the current time step, and m represents the number of variables. h t ∈ R n denotes the hidden state of the LSTM cell, and n is a hyperparameter of the LSTM model indicating the number of storage cells in the hidden layer. i t ∈ R n denotes the input gate of the storage cell, f t ∈ R n denotes the forgetting gate of the storage cell, and it is the output gate. g t ∈ R n is the intermediate computation of c t and c t ∈ R n denotes the main information of the storage cell. W and U are trainable parameters. σ and tanh denote the sigmoid activation function and the tanh activation function, respectively. ⊙ denote the elementwise product operation.The LSTM memory cell can be implemented as the following equation:
f t = σ W f · h t − 1 , x t + b f
k t = c t − 1 ⊙ f t
i t = σ W i · h t − 1 , x t + b i
g t = tanh W g · h t − 1 , x t + b g
j t = g t ⊙ i t
c t = j t + k t
o t = σ W o · h t − 1 , x t + b o
h t = tanh ( c t ) ⊙ o t
Two-Stream Network is a common approach in deep learning. Inspired by the Two-Stream CNN proposed by Karpathy et.al [35] and the Temporal Difference Network proposed by [36], we try to adapt the LSTM to Two Stream Diff-LSTM. Figure 4 shows our Two Stream Diff-LSTM cell structure. As shown in the figure, the traditional LSTM cell is extended into a two-stream network, including the difference stream and the original stream. In the difference stream, the feature representation of the difference is obtained by processing the difference time series with the update equation of LSTM. Given the time series x = x 1 , x 2 , x 3 , … , x N , we preprocess the time series to obtain the difference time series x ^ = x ^ 1 , x ^ 2 , x ^ 3 , … , x ^ N , in the following way:
x ^ t = 0 , if t = 1 x t − x t − 1 , if t = 2 , 3 , … , N
where x t , x ^ t , x t − 1 ∈ R D . After the difference processing, we obtain the temporal input containing information about the dynamic changes in the temporal dimension, which is important for learning temporal feature representation. Next, we use it to guide the operation of the gate mechanism of the LSTM in the difference stream, updating the cell as a way to model using (4)–(11). Specifically, for each time step of the difference data x ^ t , we compute the state of the hidden layer of the cell h ^ t considered as a differential temporal feature describing dynamically changing information in the temporal dimension.
At the same time, we use this feature to guide the LSTM update of the original stream. Specifically, for the data x ^ t at each time step, we utilized h ^ t and the hidden layer h ^ t − 1 of the previous time step to participate in the learning of the LSTM cell’s representation by guiding the operation of the LSTM’s gate mechanism, including the input gate, forget gate, and the output gate, and updating the cell’s state. The original flow is formulated as follows:
f t = σ W f · h t − 1 , h ^ t , x t + b f
i t = σ W i · h t − 1 , h ^ t , x t + b i
o t = σ W o · h t − 1 , h ^ t , x t + b o
Eventually, we obtained two levels of temporal feature representations H = h 1 , h 2 , h 3 , … , h n and H ^ = h ^ 1 , h ^ 2 , h ^ 3 , … , h ^ n , where n is a hyperparameter of the LSTM model indicating the number of storage cells in the hidden layer.

2.4. Cross-Variate Feature Extraction Network Module

In this convolution module, we use the idea of depthwise separable convolution architecture [38] to implement the modelling of relationships across variables to extract temporal features. The key idea behind depthwise separable convolution is to split feature learning. The convolutional operation is decomposed into two distinct steps: the depthwise convolution and the pointwise convolution. In the depthwise convolution, each channel of the input is convolved separately, preserving the depth dimension. This operation allows for spatial convolution to be performed without altering the depth of the input. The resulting output from the depthwise convolution is then passed through the pointwise convolution, where 1 × 1 convolutions are applied to adjust the number of input channels from the depthwise convolution to a desired new channel depth. The purpose of this architecture is to perform independent computations for each channel, allowing different representations of the data to be learned within each channel, which can better capture the complex relationships and characteristics of the data. Therefore, we use this idea of separate and independent representation learning to help us process time series.
First, we apply the input MTS to the embedding layer of the 1D convolution with padding. The embedding layer is able to effectively transform the input sequence data into embedding vectors with more advanced representation capabilities through the convolutional embedding process. This transformation can help neural networks to better understand and process sequence data. After embedding, the number of channels of the output tensor and the number of features per channel provide another multilevel representation of features, simultaneously, we preserve the temporal sequence of data across multivariate dimensions, as follows:
X e m b e d = F e m b e d d i n g X i ∈ R D × C × L
where D is the number of dimensions, L denotes the number of channels and L represents the length after embedding.
Then, inspired by the depthwise separable convolution architecture, we further decompose the convolutional operation into three distinct steps: depthwise, dimension-wise, and channel-wise convolutions. Specially, each step is implemented using group convolution, which divides the input channels into multiple groups, allowing for parallel processing of feature maps within each group. This parallelization strategy not only reduces computational complexity but also enhances feature diversity and representation capability.
In detail, firstly the depthwise convolution treats each dimension independently, performing convolutions along the temporal dimension while preserving the channels and depth dimensions. This step allows for capturing temporal patterns across different channels. Following the depthwise convolution, the channel-wise convolution focuses on convolving across the channel direction. This operation ensures that features are extracted efficiently within each channel while maintaining temporal coherence. Lastly, the dimension-wise convolution applies convolutions along the dimensions, enabling the model to capture inter-variate dependencies and interactions. This step enhances the model’s ability to learn complex relationships between different dimensions, leading to improved representation learning. Importantly, residual connections are incorporated by connecting the output of the last step to the final output, allowing the network to learn identity mappings more easily and effectively learn features. The structure is illustrated in Figure 5.
F = F d i m F c h a n n e l F d e p t h X e m b e d + X e m b e d
By breaking down the convolutional operation into these three steps, our model can effectively extract multi-level features from the input data, incorporating temporal, dimensional, and channel-wise information. This comprehensive feature extraction process contributes to the model’s robustness and performance across various tasks.

2.5. Feature Fusion and Multi-Class Classification Module

We fuse the features obtained from the previous two modules as inputs to the classification module. First, we use F p o o l represents the global average pooling operation, applied to the output of the two modules respectively, as follows:
P L S T M = F p o o l H , H ^
P C F N = F p o o l F
Then, we concatenate the pooling result P L S T M and P C F N to obtain the fuse feature F c o n , which can be represented as follows:
F c o n = C o n c a t P L S T M , P C F N
where C o n c a t ( · ) is the concatenate operation. Finally, we fed F c o n into a fully connected layer and softmax function to do the multi-classify task. We used the cross-entropy loss function to train our model.

3. Experimental Results and Analysis

3.1. Dataset

The dataset we choose is the latest UEA multivariate time series classification archive [37], to evaluate the performance of the proposed model. The UEA multivariate time series classification archive, which serves as our benchmark,collects data from various real-world application domains, including ECG, EEG/MEG signal, Human Motion Recognition(Motion) , Human Activity Recognition (HAR), Audio Spectra (AS), and Other. The datasets vary in length from 8 (PEMS-SF) to 3000 (MOTORIMAGERY), in dimension from 2 (AtrialFibrilation, PenDigits) to 963 (PEMSSF), and in category from 2 (MotorImagery) to 39 (Phoneme). And the train sizes range from 12 (StandwalkJump) to 7494 (PenDigits). The details of the datasets are shown in Table 1.

3.2. Evaluation Metrics

This paper evaluates the performance of our proposed model and some other MSTC algorithms for each dataset using classification accuracy, average accuracy, and the number of Wins/Ties as evaluation metrics.
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn.

3.3. Experimental Performance

We evaluate our proposed method against eight benchmark approaches commonly used in multivariate time series classification. These benchmarks include traditional distance-based classifiers, recent models such as the bag-of-patterns approach as well as a deep learning method. Here are the details of the benchmark methods we consider:
  • 1NN-ED and 1NN-ED(norm): These classifiers are traditional distance-based model, which utilize the one-nearest neighbor algorithm with Euclidean distance, both with and without data normalization. The Euclidean distance metric measures the straight-line distance between two points in a multidimensional space. This baseline method is widely used in time series classification tasks due to its simplicity and effectiveness.
  • 1NN-DTW-i and 1NN-DTW-i(norm): These classifiers are traditional distance-based model,which employ dimension-independent Dynamic Time Warping (DTW) with and without normalization. The DTW algorithm computes distances based on the sum of DTW distances for each dimension of the time series data. DTW is a flexible and robust measure that accounts for variations in the temporal alignment of sequences, making it suitable for time series classification tasks.
  • 1NN-DTW-D and 1NN-DTW-D(norm): These classifiers are traditional distance-based model, which utilize dimension-dependent Dynamic Time Warping (DTW-D) with and without normalization. Unlike the dimension-independent DTW approach, DTW-D directly computes the DTW distance based on multidimensional points, rather than treating each dimension separately. This variant of DTW is particularly useful when the dimensions of the time series data are interdependent and require joint consideration during distance computation.
  • WEASEL+MUSE: This framework is feature-based model based on the bag-of-patterns (BOP) approach and represents the latest advancement in multivariate time series classification[16].
  • MLSTM-FCN: This algorithm is one of state-of-the-art deep learning based framework designed for multivariate time series classification. The model architecture includes an LSTM layer, stacked CNN layers, and a Squeeze-and-Excitation block for feature extraction. We utilize the source code provided by the authors and execute the approach using default parameter settings, as described in the original work[26].
We evaluate the performance of each method based on three key metrics: classification accuracy, average accuracy, and the frequency of Wins/Ties across different datasets. The results are summarized in Table 2. Notably, TDCFN demonstrates superior classification accuracy, outperforming other methods on 11 datasets. Furthermore, TDCFN achieves the highest average classification accuracy, reaching 0.67. Regarding the number of Wins/Ties, TDCFN exhibits 11 instances of Wins/Ties, while ensemble model WEASEL+MUSE records 4 Wins/Ties. These results underline the effectiveness and robustness of TDCFN compared to alternative methods.
Specifically, our model outperforms or achieves comparable accuracy scores to existing methods across various datasets, demonstrating its effectiveness in multivariate time series classification tasks. For instance, on the AF dataset, our TDCFN model achieved a notable accuracy improvement compared to traditional methods such as ED-1NN and DTW-1NN-D. While the WEASEL+MUSE algorithm attained a higher accuracy score of 0.333, our TDCFN model demonstrated a significant enhancement with an accuracy of 0.400. This indicates the effectiveness of our model in capturing complex patterns within the AF dataset, which may involve intricate temporal dynamics and cross-variate interactions. Similarly, on the CT dataset, our TDCFN model showcased substantial improvement over other algorithms, achieving an accuracy score of 0.986. Although the WEASEL+MUSE algorithm also attained a high accuracy score of 0.990, our TDCFN model demonstrated competitive performance, outperforming conventional methods like ED-1NN and DTW-1NN-I. This suggests that our model effectively captures the distinctive characteristics of the CT dataset, which may involve nuanced temporal variations and inter-variable dependencies.Moreover, on the FD dataset, our TDCFN model exhibited significant advancement in accuracy compared to baseline methods. With an accuracy score of 0.566, our model surpassed the performance of ED-1NN and DTW-1NN-D, indicating its capability to discern subtle patterns and anomalies within the FD dataset, which might encompass diverse temporal patterns and complex interrelations among variables. Additionally, on the HMD dataset, our TDCFN model demonstrated remarkable accuracy enhancement, achieving a score of 0.391. While the WEASEL+MUSE algorithm also performed well with an accuracy of 0.365, our TDCFN model showcased superior performance compared to conventional methods like ED-1NN and DTW-1NN-D. This suggests that our model effectively captures the unique characteristics of the HMD dataset, which may involve intricate temporal structures and cross-variate dependencies inherent in human motion data.
Furthermore, in this experiment, we observed the loss reduction during the training process. By plotting the training loss curves for these datasets, we can clearly see a continuous decrease in the model’s loss, indicating effective convergence on these datasets. These observations provide strong evidence for the validity of our model and the stability of the training process. Figure 6 illustrates the results obtained from the two datasets.

3.4. Ablation Experiments

The above experiments show that TDCFN is a feasible solution for the MTSC. Moreover, ablation experiments are essential in assessing the individual contributions of components within a model. In our study, we conducted ablation experiments to investigate the impact of removing two key modules from our model: the Two Stream Diff-LSTM module and the Cross-variate feature extraction network module. Table 3 shows the three comparisons of the ablation experiments.
  • Multilayer Perceptron(MLP) Classifier: In this ablation experiment, we constructed a model comprising solely a fully connected layer classifier, which is also called Multilayer Perceptron(MLP) Classifier, devoid of any additional feature extraction or processing modules. This experiment aims to serve as a baseline comparison to evaluate the significance of the feature extraction components present in the full TDCFN model.
  • Without Two Stream Diff-LSTM module: This experiment involved removing the Two Stream Diff-LSTM module, which is responsible for capturing temporal features containing dynamic differential information. By conducting this ablation experiment, we aimed to understand the influence of this module on the overall performance of the model.
  • Without Cross-variate feature extraction network module: In this experiment, we excluded the Cross-variate feature extraction network module, which is designed to extract relational features among variables. The purpose was to assess the significance of this module in enhancing the model’s ability to capture inter-variable relationships and representation.
Through these ablation experiments, we aimed to gain insights into the individual contributions of each module to the overall performance of our model. This analysis helps validate the effectiveness of our model design choices and provides guidance for further refinement and optimization. The experimental details are shown in Table 3. The table presents experimental results across different types of datasets, including ECG, HAR, AS, EEG/MEG, and Motion. The observed results demonstrate that our model outperforms all other configurations across all types of datasets. The average accuracy rate further corroborates the effectiveness of our model, achieving the highest average accuracy across all dataset types.
Across all datasets, we observed consistent improvements in classification accuracy when incorporating both the Two Stream Diff-LSTM and Cross-variate feature extraction network into our TDCFN model. For instance, on the AF dataset, which represents ECG data, the TDCFN model achieved a significantly higher accuracy of 0.400 compared to alternative configurations. This underscores the crucial role played by both the Two Stream Diff-LSTM and Cross-variate feature extraction network in effectively capturing temporal dynamics and cross-variate dependencies inherent in ECG signals. Similarly, on the BM dataset (HAR), our TDCFN model attained perfect accuracy (1.000), outperforming all alternative configurations. This highlights the indispensability of the proposed model architecture in accurately discerning complex human activity patterns, which may involve intricate temporal sequences and inter-variable relationships.
Overall, the ablation study results demonstrate the pivotal role played by the Two Stream Diff-LSTM and Cross-variate feature extraction network in enhancing the classification performance of our proposed TDCFN model across diverse multivariate time series datasets. Our ablation study provides valuable insights into the efficacy of individual model components and highlights the robustness of our approach in addressing complex time series classification tasks.

4. Conclusion

In this article, we proposed a novel deep learning algorithm for multivariate time series classification task, named TDCFN. The key idea of TDCFN is to fuse two stream Diff-LSTM and cross-variate feature extraction network, aiming to leverage both temporal dynamics and inter-variable relationships in multivariate time series data. Through extensive experiments on various benchmark datasets, we demonstrated the effectiveness and robustness of TDCFN in capturing complex patterns and making accurate predictions across different application domains. Furthermore, we conducted ablation studies to analyze the contributions of each component in our model. TDCFN presents a promising solution for multivariate time series classification, offering a comprehensive framework that effectively integrates temporal dynamics and inter-variable relationships.

References

  1. Bagnall A, Lines J, Bostrom A, et al. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances[J]. Data mining and knowledge discovery, 2017, 31: 606-660. [CrossRef]
  2. Du M, Wei Y, Zheng X, et al. Multi-feature based network for multivariate time series classification[J]. Information Sciences, 2023, 639: 119009. [CrossRef]
  3. Fan J, Zhang K, Huang Y, et al. Parallel spatio-temporal attention-based TCN for multivariate time series prediction[J]. Neural Computing and Applications, 2023, 35(18): 13109-13118. [CrossRef]
  4. Singhal A, Seborg D E. Clustering multivariate time-series data[J]. Journal of Chemometrics: A Journal of the Chemometrics Society, 2005, 19(8): 427-438.
  5. Blázquez-García A, Conde A, Mori U, et al. A review on outlier/anomaly detection in time series data[J]. ACM Computing Surveys (CSUR), 2021, 54(3): 1-33. [CrossRef]
  6. Qin Z, Zhang Y, Meng S, et al. Imaging and fusing time series for wearable sensor-based human activity recognition[J]. Information Fusion, 2020, 53: 80-87. [CrossRef]
  7. Yang J, Nguyen M N, San P P, et al. Deep convolutional neural networks on multichannel time series for human activity recognition[C]//Ijcai. 2015, 15: 3995-4001.
  8. Hasasneh A, Kampel N, Sripad P, et al. Deep learning approach for automatic classification of ocular and cardiac artifacts in meg data[J]. Journal of Engineering, 2018, 2018. [CrossRef]
  9. Cheng X, Li G, Ellefsen A L, et al. A novel densely connected convolutional neural network for sea-state estimation using ship motion data[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 5984-5993. [CrossRef]
  10. Zhao B, Lu H, Chen S, et al. Convolutional neural networks for time series classification[J]. Journal of Systems Engineering and Electronics, 2017, 28(1): 162-169. [CrossRef]
  11. Seto S, Zhang W, Zhou Y. Multivariate time series classification using dynamic time warping template selection for human activity recognition[C]//2015 IEEE symposium series on computational intelligence. IEEE, 2015: 1399-1406.
  12. Abanda A, Mori U, Lozano J A. A review on distance based time series classification[J]. Data Mining and Knowledge Discovery, 2019, 33(2): 378-412. [CrossRef]
  13. Sharabiani A, Darabi H, Rezaei A, et al. Efficient classification of long time series by 3-d dynamic time warping[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(10): 2688-2703. [CrossRef]
  14. Chen Y, Hu B, Keogh E, et al. Dtw-d: Time series semi-supervised learning from a single example[C]//Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. 2013: 383-391.
  15. Rakthanmanon T, Keogh E. Data mining a trillion time series subsequences under dynamic time warping[C]//Twenty-Third International Joint Conference on Artificial Intelligence. 2013.
  16. Schäfer P, Leser U. Multivariate time series classification with WEASEL+ MUSE[J]. arXiv:1711.11343, 2017.
  17. Li G, Choi B, Xu J, et al. Shapenet: A shapelet-neural network approach for multivariate time series classification[C]//Proceedings of the AAAI conference on artificial intelligence. 2021, 35(9): 8375-8383.
  18. Ma Q, Zhuang W, Cottrell G. Triple-shapelet networks for time series classification[C]//2019 IEEE International Conference on Data Mining (ICDM). IEEE, 2019: 1246-1251.
  19. Lines J, Taylor S, Bagnall A. Hive-cote: The hierarchical vote collective of transformation-based ensembles for time series classification[C]//2016 IEEE 16th international conference on data mining (ICDM). IEEE, 2016: 1041-1046.
  20. Middlehurst M, Large J, Flynn M, et al. HIVE-COTE 2.0: A new meta ensemble for time series classification[J]. Machine Learning, 2021, 110(11): 3211-3243. [CrossRef]
  21. Voulodimos A, Doulamis N, Doulamis A, et al. Deep learning for computer vision: A brief review[J]. Computational intelligence and neuroscience, 2018, 2018. [CrossRef]
  22. Otter D W, Medina J R, Kalita J K. A survey of the usages of deep learning for natural language processing[J]. IEEE transactions on neural networks and learning systems, 2020, 32(2): 604-624. [CrossRef]
  23. Zheng Y, Liu Q, Chen E, et al. Exploiting multi-channels deep convolutional neural networks for multivariate time series classification[J]. Frontiers of Computer Science, 2016, 10: 96-112. [CrossRef]
  24. Cui Z, Chen W, Chen Y. Multi-scale convolutional neural networks for time series classification[J]. arXiv:1603.06995, 2016.
  25. Du Y, Wang W, Wang L. Hierarchical recurrent neural network for skeleton based action recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1110-1118.
  26. Karim F, Majumdar S, Darabi H, et al. Multivariate LSTM-FCNs for time series classification[J]. Neural networks, 2019, 116: 237-245. [CrossRef]
  27. Wang Z, Yan W, Oates T. Time series classification from scratch with deep neural networks: A strong baseline[C]//2017 International joint conference on neural networks (IJCNN). IEEE, 2017: 1578-1585.
  28. Tang W, Long G, Liu L, et al. Rethinking 1d-cnn for time series classification: A stronger baseline[J]. arXiv:2002.10061, 2020: 1-7.
  29. Dempster A, Petitjean F, Webb G I. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels[J]. Data Mining and Knowledge Discovery, 2020, 34(5): 1454-1495.
  30. Dempster A, Schmidt D F, Webb G I. Minirocket: A very fast (almost) deterministic transform for time series classification[C]//Proceedings of the 27th ACM SIGKDD conference on knowledge discovery & data mining. 2021: 248-257.
  31. Ismail Fawaz H, Lucas B, Forestier G, et al. Inceptiontime: Finding alexnet for time series classification[J]. Data Mining and Knowledge Discovery, 2020, 34(6): 1936-1962. [CrossRef]
  32. Wang L, Wang Z, Liu S. An effective multivariate time series classification approach using echo state network and adaptive differential evolution algorithm[J]. Expert Systems with Applications, 2016, 43: 237-249. [CrossRef]
  33. Huang S H, Lingjie X, Congwei J. Residual attention net for superior cross-domain time sequence modeling[J]. arXiv:2001.04077, 2020.
  34. Xiao Z, Xu X, Xing H, et al. RTFN: A robust temporal feature network for time series classification[J]. Information sciences, 2021, 571: 65-86. [CrossRef]
  35. Karpathy A, Toderici G, Shetty S, et al. Large-scale video classification with convolutional neural networks[C]//Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. 2014: 1725-1732.
  36. Wang L, Tong Z, Ji B, et al. Tdn: Temporal difference networks for efficient action recognition[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021: 1895-1904.
  37. Bagnall A, Dau H A, Lines J, et al. The UEA multivariate time series classification archive, 2018[J]. arXiv:1811.00075, 2018.
  38. Howard A G, Zhu M, Chen B, et al. Mobilenets: Efficient convolutional neural networks for mobile vision applications[J]. arXiv:1704.04861, 2017.
Preprints 103099 g001
Figure 1. A Single Sample from the Multivariate Time Series Dataset BasicMotions with 100 time steps and 6 variables.
Figure 1. A Single Sample from the Multivariate Time Series Dataset BasicMotions with 100 time steps and 6 variables.
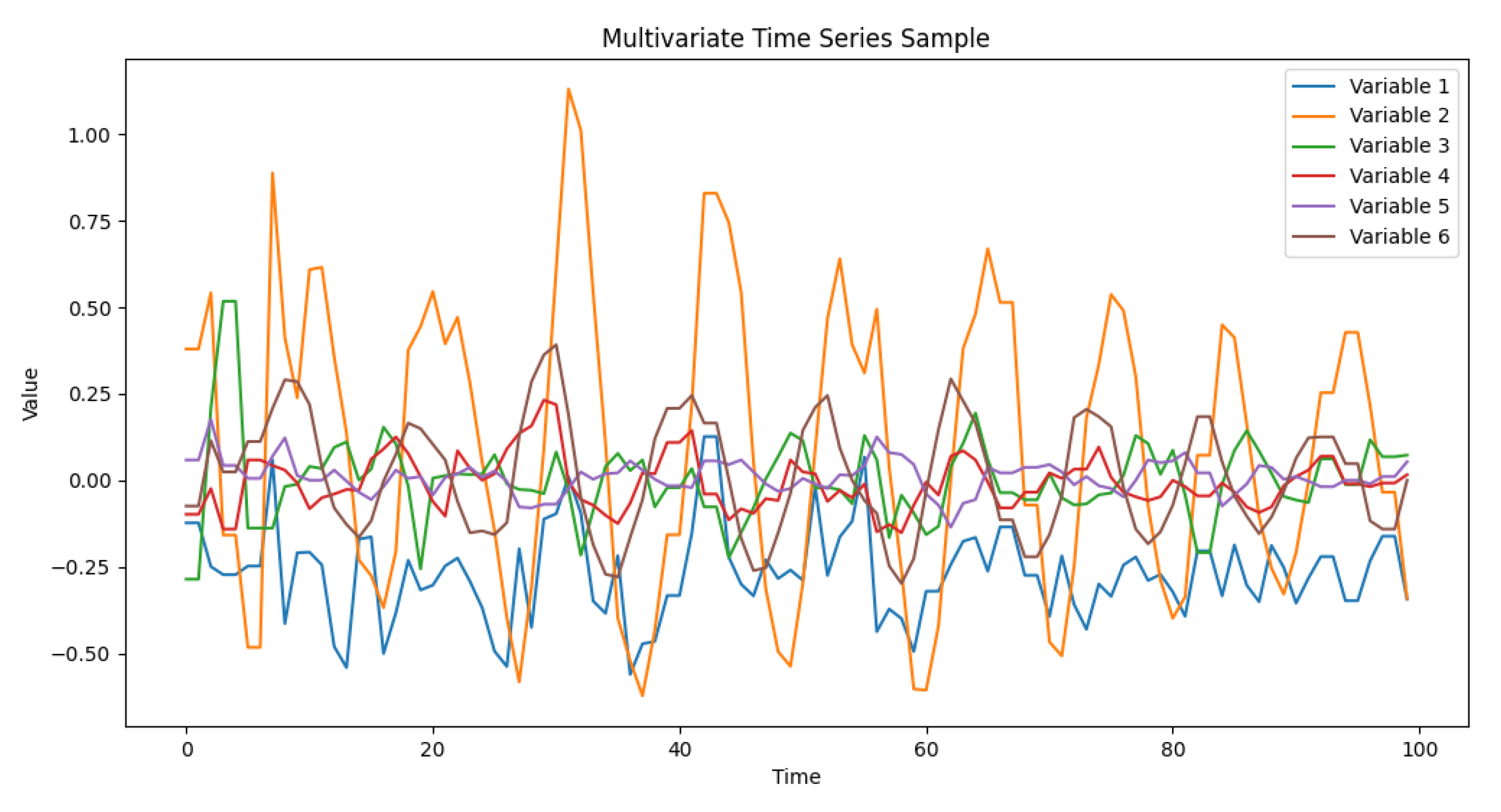
Preprints 103099 g001
Preprints 103099 g002
Figure 2. TDCFN Architecture Overview.
Figure 2. TDCFN Architecture Overview.
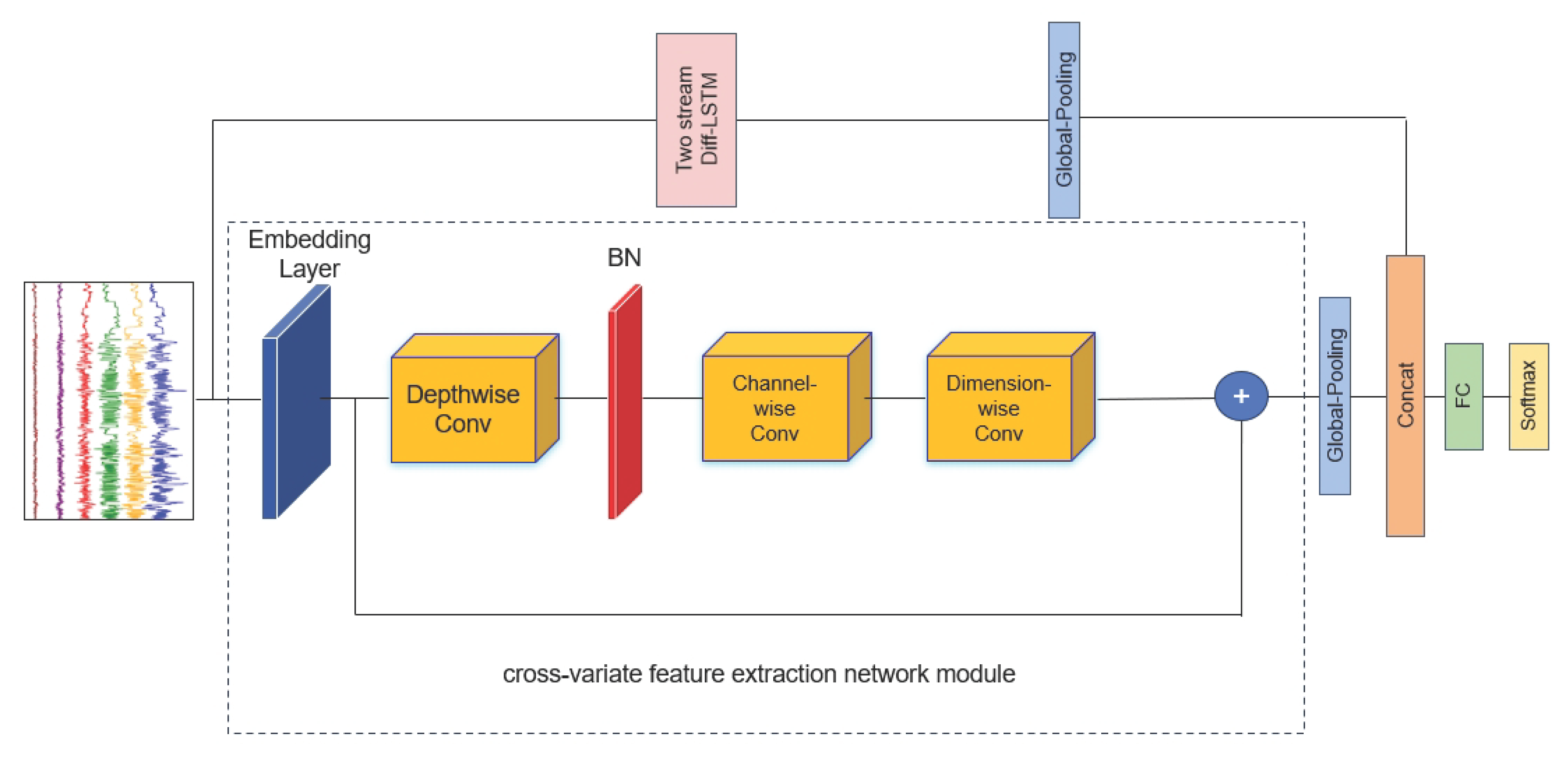
Preprints 103099 g002
Preprints 103099 g003
Figure 3. A LSTM memory cell.
Figure 3. A LSTM memory cell.
Preprints 103099 g003
Preprints 103099 g004
Figure 4. Two stream Diff-LSTM memory cell.
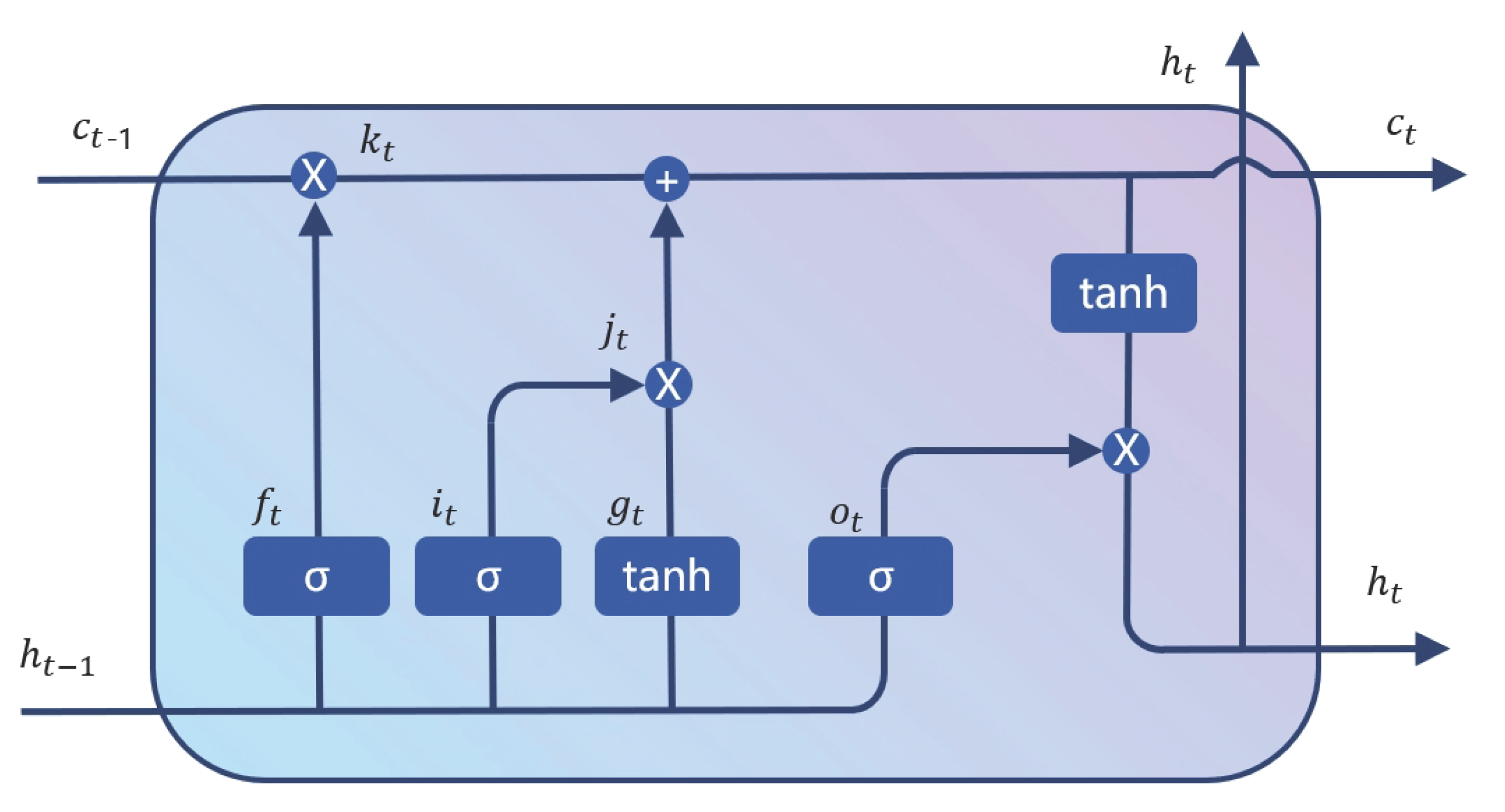
Figure 4. Two stream Diff-LSTM memory cell.
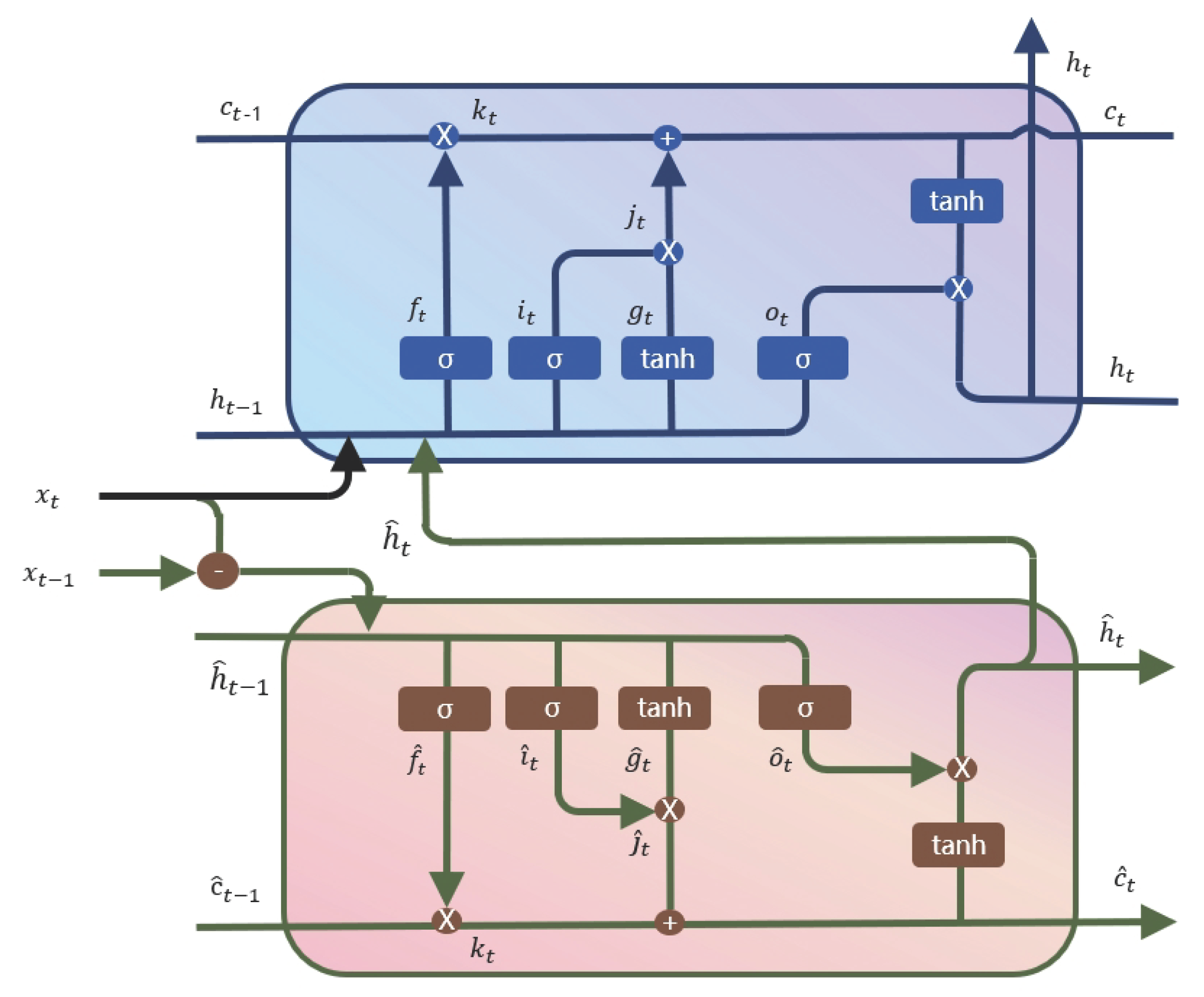
Preprints 103099 g004
Preprints 103099 g005
Figure 5. cross-variate feature extraction network.
Figure 5. cross-variate feature extraction network.
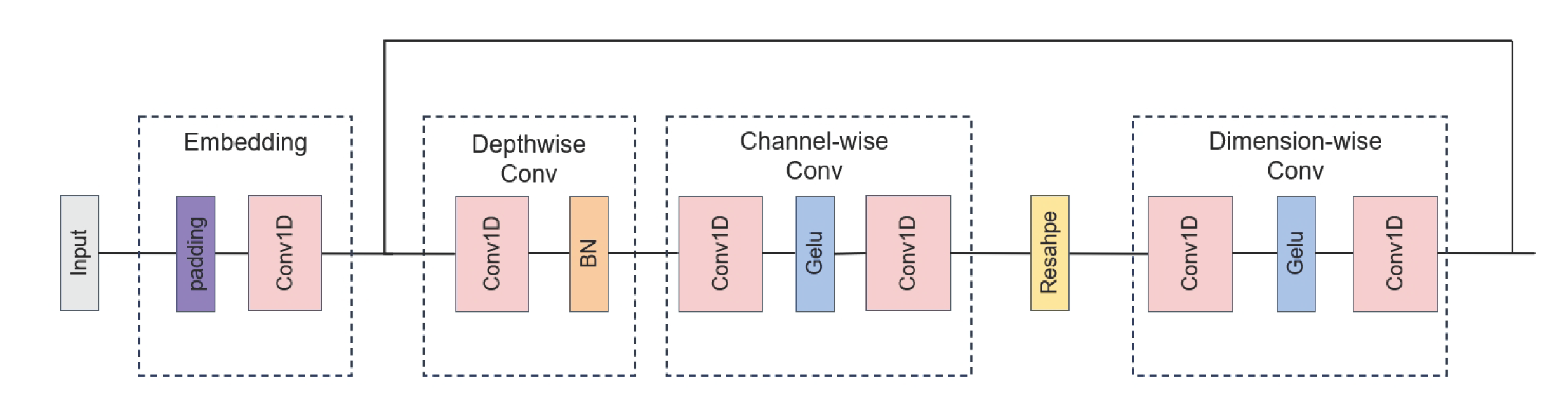
Preprints 103099 g005
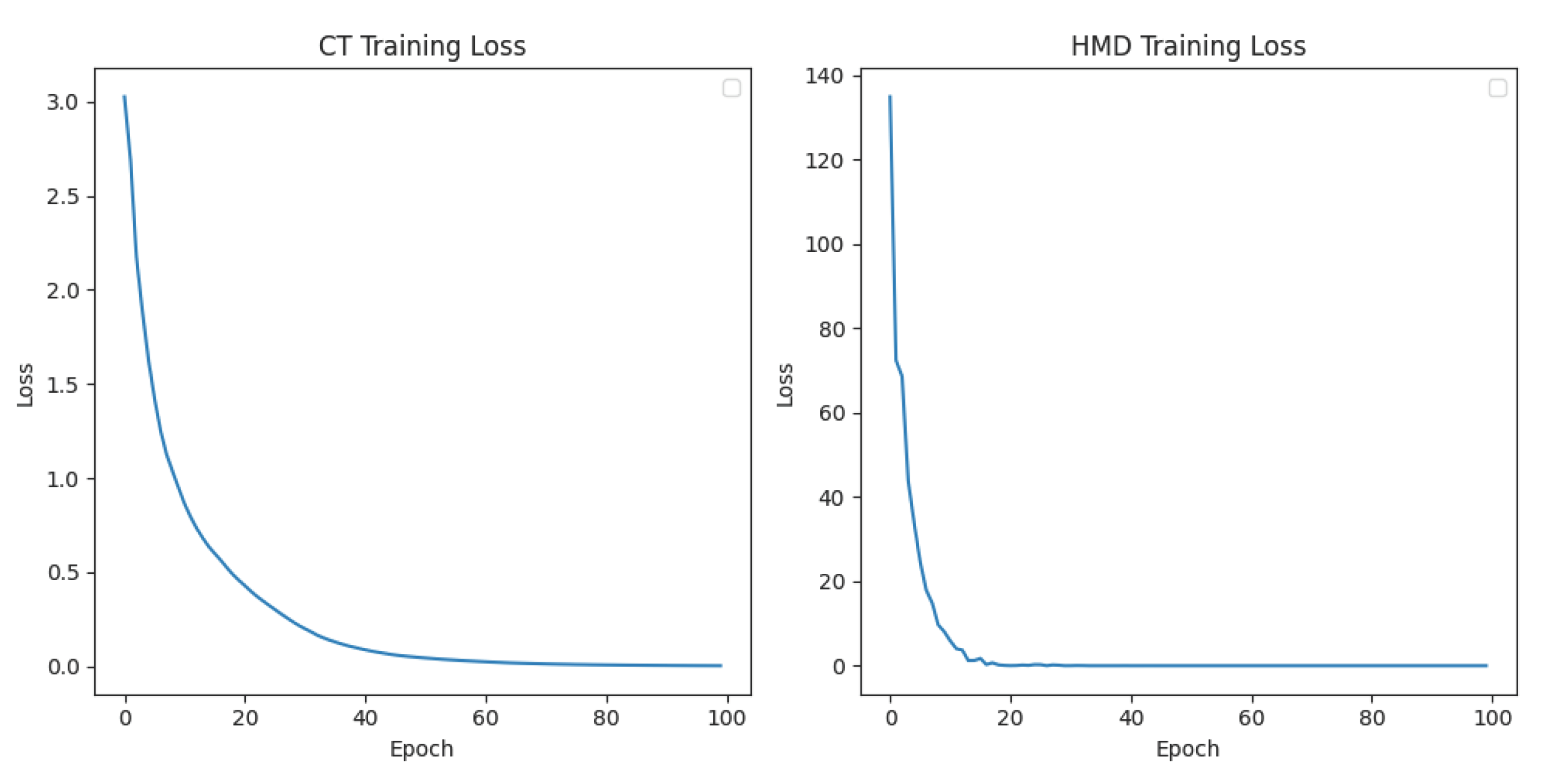
Preprints 103099 g006
Figure 6. The loss curves of datasets.
Figure 6. The loss curves of datasets.
Preprints 103099 g006
Table 1. Characteristics of the MTSC datasets.
Table 1. Characteristics of the MTSC datasets.
Dataset(Abbreviation) Train Test Number of dimensions Series Length Number of classes Type
ArticularyWordRecognition (AWR) 275 300 9 144 25 Motion
AtrialFibrillation (AF) 15 15 2 640 3 ECG
BasicMotions (BM) 40 40 6 100 4 HAR
CharacterTrajectories (CT) 1422 1436 3 182 20 Motion
FaceDetection (FD) 5890 3524 144 62 2 EEG/MEG
HandMovementDirection (HMD) 160 74 10 400 4 EEG/MEG
Heartbeat (HB) 204 205 61 405 2 AS
MotorImagery (MI) 278 100 64 3000 2 EEG/MEG
NATOPS (NATO) 180 180 24 51 6 HAR
PEMS-SF (PEMS) 267 173 963 144 7 Other
PenDigits(PD) 7494 3498 2 8 10 Motion
Phoneme(PM) 3315 3353 11 217 39 AS
SelfRegulationSCP2 (SRS2) 200 180 7 1152 2 EEG/MEG
StandWalkJump (SWJ) 12 15 4 2500 3 ECG
Table 2. Performance comparisonn of classification accuracy in UEA multivariate time series datasets.
Table 2. Performance comparisonn of classification accuracy in UEA multivariate time series datasets.
Dataset Algorithm
ED-1NN ED-1NN(norm) DTW-1NN-I DTW-1NN-I(norm) DTW-1NN-D DTW-1NN-D(norm) WEASEL+MUSE MLSTM-FCN TDCFN
AWR 0.970 0.970 0.980 0.980 0.987 0.987 0 . 990 0.973 0.970
AF 0.267 0.267 0.267 0.267 0.200 0.220 0.333 0.267 0 . 400
BM 0.675 0.676 1 . 000 1 . 000 0.975 0.975 1 . 000 0.950 1 . 000
CT 0.964 0.964 0.969 0.969 0 . 990 0.989 0 . 990 0.985 0.986
FD 0.519 0.519 0.513 0.500 0.529 0.529 0.545 0.545 0 . 566
HMD 0.279 0.278 0.306 0.306 0.231 0.231 0.365 0.365 0 . 391
HB 0.620 0.619 0.659 0.658 0.717 0.717 0.727 0.663 0 . 756
MI 0.510 0.510 0.390 N/A 0.500 0.500 0.500 0.510 0 . 550
NATO 0.860 0.850 0.850 0.850 0.883 0.883 0.870 0.889 0 . 939
PEMS 0.705 0.705 0.734 0.734 0.711 0.711 N/A 0.699 0 . 763
PD 0.973 0.973 0.939 0.939 0.977 0.977 0.948 0.978 0 . 979
PM 0.104 0.104 0.151 0.151 0.151 0.151 0 . 190 0.110 0.131
SRS2 0.483 0.483 0.533 0.533 0.539 0.539 0.460 0.472 0 . 555
SWJ 0.200 0.200 0.333 0.333 0.200 0.200 0.333 0.067 0 . 400
AVG ACC 0.580 0.579 0.616 0.587 0.613 0.614 0.589 0.605 0 . 670
Wins/Ties 0 0 1 1 1 0 4 0 11
Table 3. Ablation study in UEA multivariate time series datasets.
Table 3. Ablation study in UEA multivariate time series datasets.
Dataset Type Algorithm
MLP classifier without Two Stream Diff-LSTM without Cross-variate feature extraction network TDCFN
AF ECG 0.266 0.266 0.333 0 . 400
BM HAR 0.675 0.975 0.750 1 . 000
HB AS 0.663 0.687 0.682 0 . 756
MI EEG/MEG 0.51 0.54 0.51 0 . 550
PD Motion 0.778 0.973 0.964 0 . 979
AVG ACC 0.578 0.688 0.647 0.737
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated