Preprint
Article
Precise Inverse Kinematic Calculation of the Center of Gravity for Bipedal Walking Robots
Altmetrics
Downloads
103
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
04 April 2024
Posted:
04 April 2024
You are already at the latest version
Alerts
Abstract
Walking of humanoid robots is dependent on precise tracking of the center of gravity and foot trajectories. Trajectory tracking is achieved by mobilizing the robot joints to produce the correct trajectory. Errors are being occurred because of assumptions on tracking the center of gravity and the foot trajectories. In this study, a numerical algorithm has been developed that produces an exact and single kinematic solution in which the center of gravity and foot trajectories can be tracked with the desired precision. The effectiveness of the algorithm was examined with a dynamic simulation and compared with the method given in the literature The main highlight of this study, using the presented algorithm, the robot can walk even if the position of its center of gravity is lower than its hips, resulting tracking error was smaller than reported in the literature.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Humanoid robots have a similar joint structure to humans and are expected to perform actions usually performed by humans. Having robots with human-like mobility which do not require changes in work environments in the industry, space, service, and health sectors can increase the quality of life of people. Humanoid robots have now become advanced enough to be used in industrial settings[1,2,3]. These robots mainly consist of two parts. The bottom part which consists of two legs connected to the pelvis and carries the trunk is responsible for locomotion. The upper body, which is connected to two arms and contains a central computer, sensors, and a power supply, performs the tasks assigned to the robot. This study focuses on the locomotion of the bottom part consisting of two legs and a pelvis piece.
Humanoid robots move via gravity, contact forces, and torques applied to their joints [4]. For the process of walking, first, planning is made for gait and steps [5,6,7]. In this process, the trajectories of the center of gravity (CoG) of the robot and its feet are obtained. When the robot is expected to walk based on its CoG, the inverted pendulum method is used [8]. For walking based on foot positions, the cart-table model is used [9]. In both methods, the zero-moment point (ZMP) is used as the point of contact between the fixed foot and the floor [10]. Inverse kinematics methods are used to move the limbs to the desired position in the workspace, whereas forward kinematics methods are used to move them in the joint space [11]. In the second step, inverse kinematics calculations are made so that the robot can follow these trajectories. When the foot and pelvis positions are known, joint angles can be calculated using the inverse kinematics method. Analytical or numerical approaches can be used for these calculations [12,13,14,15,16,17].
However, this does not guarantee the tracking of the CoG of the robot at the desired precision level. The CoG is in the middle of the connection points of the two legs of the robot or at a higher position [18,19,20,21,22,23,24,25]. The position of the CoG is calculated before the robot starts its motion. Throughout the motion, the difference between the position of the pelvis and the position of the CoG is assumed to be fixed [9]. Another assumption is that the CoG of the robot is fixed in reference to the supporting leg [26].
When the position of the CoG is not calculated precisely, the deviations in the position of the CoG caused by contact forces prevent the locomotion of the robot [27]. The methods used in the literature to solve this problem are listed in the following paragraph.
In a previous study, the feet of the robot were made larger [28]. To increase the accuracy of calculation, in addition to CoG and foot trajectories, analyses requiring the hip position, hip trajectory, and orientation trajectories were carried out [20,29]. When the weight of the foot constitutes a higher proportion of the total weight of the robot, the foot that is in motion has a greater influence on the locomotive dynamics of the robot. To mitigate this effect, the method of modeling the moving foot as a pendulum was used. Nevertheless, there were still errors in the tracking of the CoG, and the movements of the robot were restricted due to the aforementioned assumptions [30].
In applications, it is aimed to ensure that the controller moves the robot within the desired tolerances against these errors. The smallest achievable error was found as 0.18 m with the inverse dynamics control method [31] and 0.03-0.4 m with the non-linear optimization control method [32].
In this study, for the precise tracking of the position of the CoG, an iterative method of calculating joint angles was developed. The method can calculate the position of the CoG at a precision of 0.001 m or lower. As a result of calculations, a single solution is given. There is no need to select the optimum solution from among multiple solutions. It is sufficient to know only the CoG and the trajectories of the feet.
Rest of the study is organized as follows. Section 2 gives information on used robot in the study. In section 3, the kinematics of the robot is explained. Dynamics of the robot is given in Section 4. Section 5 gives explanation on calculation of CoG and zero moment point equations. The main subject of the study, the algorithm, is explained in Section 6 with equations and pseudo code. Initial values and result trajectories are also given. In Section 7, the simulation model and parameters of the study are presented. The results of the study are discussed in Section 8. The study is finalized by representing the conclusions in Section 9.
2. Materials and Methods
2.1. Robot Structure
The robot reported in this study is the numerical model of the ITU Biped bipedal walking robot [33]. The rotational axes of 3 motors are placed at the hip joint so that they intersect at a single point, while the rotational axes of 2 motors are placed at the ankle joint so that they intersect at a single point. The joint types and positions of the robot are shown in Figure 1.
In Figure 1, is the inertial coordinate system, is the base coordinate system, is the starting point for movement, is the pelvis length, and is the pelvis height of the robot. is the hip point of the left leg, is the foot coordinate system, and are the joint angles of the right leg. To increase readability, the hip point of the right leg and the joint angles of the left leg weren’t shown in Figure 1. and are the link lengths of the robot.
2.2. Robot Kinematics
The Denavit-Hartenberg (DH) [34] method is used for kinematic calculations. The link transformation table is presented in Table 1.
Equations 1-4 present the link transformation matrices for an inertial reference frame.
Transformation matrix of according to is given in Equation 2. The calculation for the left foot is made by writing in the second row and fourth column.
The joint transformation matrix can be written with Equation 3.
After these expressions, the position and orientation of the foot can be calculated based on the 0th coordinate system as given in Equation 4.
Here, the left side of the equation is obtained by the placement of the values in the DH matrix. Its right side includes the position and orientation values of the foot obtained in the 0th coordinate system. When the reciprocal of the left side of the equation is taken, the chain from the foot to the hip is obtained. If both sides are multiplied by the matrix , the transformation matrix from the ankle to the hip can be obtained [35].
As 2 coordinate systems intersect at the ankle, and 3 intersect at the hip, the value of the knee joint is obtained based on the matrix that is formed. According to this, inverse kinematic calculations can be made using the expressions in Equations 5-10.
The forward kinematics of the robot can be calculated using Equation 11.
This expression denotes the orientation and position matrix of the robot in an inertial frame of reference according to the joint angles used as inputs.
2.3. Robot Dynamics
The dynamics of the robot are obtained using the linear inverted pendulum method. In the 3-dimensional linear inverted pendulum model (3DLIPM) shown in Figure 2, the desired surface equation is reached by setting and . As the height of the inverted pendulum, is taken as a constant.
After making these arrangements, the differential equations that define the system can be given with Equations 12 and 13.
Step positions are set in a matrix , as given in Eq. 14. The trajectory of the CoG is obtained as the output.
Using Equations 12-14, for a step length of 0.3 m (), a step width of 0.065 () m, and a CoG height of 0.45 m (, the trajectory of the CoG is found as shown in Figure 3. When the foot position is taken as a reference, the height of the hip of the robot in this case is 0.826 m. The step height is 0.075 m (). The foot trajectories are continuous up to the second derivation [36].
In Figure 3, the robot starts its movement by taking a step with its right leg. It walks for a total of 6 steps and stops.
2.4. CoG and ZMP Calculations
The ITU Biped has a six axis force-torque sensor at its ankle. ZMP was indirectly measured by using the parameters shown in Figure 4.
Because no torque will be generated in parallel with the foot plane according to the definition of the ZMP [10], the position of the ZMP based on the reaction on the sensor created by the force and moment at the ZMP is calculated using Equations 15 and 16.
The robot has a right leg, a left leg, and a pelvis. The symbolic locations of CoG are shown in Figure 5.
In the algorithm, the CoG of the robot is calculated using the positions of the CoG given in Figure 5 in Equation 17.
2.6. Converging Center of Gravity Algorithm
For the precise calculation of the position of the CoG, first, joint angles are calculated using the current positions. Using these angles, the CoG of the robot is calculated. The vector from the current position of the CoG to the reference position of the CoG is found using Equation 18.
To calculate the unit vector of this vector, Equation 19 is utilized.
Using Equation 20, the hip connected to the foot that is in contact with the floor is moved to a new position by multiplying the unit vector by a certain coefficient (0.001 in this study).
The hip connected to the foot in motion is also moved accordingly. The joint angles and the CoG of the robot are calculated again based on these new hip positions. This process continues until the difference between the reference and current positions of the CoG becomes smaller than the desired value. In our study, the error margin is taken as 0.001 m. The calculation is first made for the fixed foot. Afterward, the indices of the fixed and moving feet are changed, the foot in motion is assumed to be fixed, and the hips are moved. In this way, the masses and positions of all robot components are utilized.
The pseudo-code of the process is given in Table 2.
In this method, first, the error between the reference and current positions of the CoG is calculated.
Figure 6 displays the graphical representation of the legs of the robot. The right leg is shown in blue, and the left leg is shown in red. The CoG at the beginning of the trajectory calculations is named the current CoG and is shown as a blue cross. The reference CoG position is named the target CoG and is shown as a green asterisk.
2.7. Simulation Model
A dynamic model in which the limb angles calculated using this algorithm are used as inputs is obtained as in Figure 8 using the MATLAB SimScape MultiBody [37]. The foot positions in the gait of the robot are predetermined. To define contact with the floor, the “Spatial Contact Force” [38] block of the SimScape MultiBody that defines contact between spherical and planar surfaces is used. The “Inertia Sensor” component in the MATLAB Multibody [39] was used to measure the actual CoG of the mechanism in the simulation. The parameters that are used in the study are presented in Table 3.
The joint angles of the left and right legs are input to the model. The model applies trajectories to the robot. ZMP and CoG are calculated in the model. Since the floor is flat and the CoG height of the robot is constant in the simulation, only the x and y components of the ZMP and CoG are plotted.
3. Results
Two simulations have been run that use the same walking parameters. The CCGD algorithm has been used in the first simulation. Joint angles have been calculated with the CCGD algorithm for precise tracking of the CoG in each position in the trajectory. In the second simulation, the CoG has been calculated before the movement starts. The vector is assumed to be constant between the pelvis and the CoG. Both simulations have been run as open-loop. Neither a balancer nor a controller has been used.
The poses of the robot with and without CCGD are presented in Figure 9. As seen in Figure 9 (a), the robot is able to follow the trajectory without falling when CCGD is used. In the case when CCGD is not used, shown in Figure 9 (b), the robot is unable to preserve its stance and falls by losing its balance after taking its fourth step.
Figure 10 shows the reference ZMP and CoG trajectory, as well as the trajectories of the CoG obtained with and without CCGD comparatively. While the result of the simulation run with CCGD is compatible with the reference CoG, the trajectory calculated without CCGD starts to deviate after the second step and results in the robot falling at the fourth step. The starting points of motion are very close to each other. There is sliding in the feet during motion as only 4 points contact the floor. This explains the errors observed on the trajectories along the x and y axes.
Calculation times of this method are also obtained. In a computer equipped with Windows 10 Pro 22H2, Core i7 2700, 16GB memory, and 240GB SSD hardware and running MATLAB R2023b, the calculation time for the first value on the trajectory is 0.001662 s, while this time for the following calculations is 0.000414 s. This shows that it is possible to make calculations 2415 times per second. Accordingly, the calculation method that is developed here can calculate joint angles according to a given CoG and foot trajectories at the desired level of precision in the real-time control of bipedal walking robots.
The results of the simulation with and without CCGD are given in Figure 11 and Figure 12 respectively.
It can be seen in Figure 11, which presents the result of the simulation run with CCGD, that the ZMP values and CoG trajectory are in good agreement. Due to the hysteresis in contact forces, the ZMP values show deviations. However, because these values stay within the support geometry, the robot does not fall and can complete its walk.
In the result of the simulation run without CCGD in Figure 12, on the other hand, although the CoG and ZMP values are compatible in the first 2 steps, they deviate after this point, and the trajectory showing the robot fall is seen in the fourth step as a result of the disruption of this compatibility in the third step.
In addition, CoG tracking error values of CCGD algorithm is illustrated in Figure 13 below.
Figure 13 displays the errors between the calculated and simulated CoG position values. The greatest error value was 0.0559 m, the smallest error value was 9.6353e-4 m, and the average error value was 0.0238 m.
4. Conclusions
The variation of limb positions by using the unit vector of the vector between the target and reference centers of gravity, rather than joint angles, allows the precise determination of the CoG. Using this method, the robot can walk on an even surface without needing any feedback or control.
There is no need for the CoG of the robot to be higher than the hip level. Therefore, there is no need to design the legs as very light components and the trunk as a heavy component. Using the CCGD algorithm, the robot can walk even if the position of its CoG is lower than its hips.
This method has advantages over the methods in the literature mentioned in the article. The model developed in the study allowed tracking the trajectory of the CoG with a 0.0238 m error in the numerical simulation.
Author Contributions
All authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the
corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Optimus (robot). Available online: https://En.Wikipedia.Org/Wiki/Optimus_(Robot) (accessed on 15 March 2024).
- Agility Robotics. Available online: https://Agilityrobotics.Com/ (accessed on 15 March 2024).
- Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; Kajita, S.; Morisawa, M.; Kumagai, I.; Kanehiro, F. Humanoid Robot HRP-5P: An Electrically Actuated Humanoid Robot with High-Power and Wide-Range Joints. IEEE Robot Autom Lett 2019, 4, pp–1431. [Google Scholar] [CrossRef]
- Sugihara, T.; Morisawa, M. A Survey: Dynamics of Humanoid Robots. Advanced Robotics, 2020, 34, 21–22. [Google Scholar] [CrossRef]
- Rokbani, N.; Cherif, A.; Alimi, A.M. Toward Intelligent Biped-Humanoids Gaits Generation. In Humanoid Robots.Ben Choi, Intech. Rijeka, Croatia, 2009. pp. 259-272. [CrossRef]
- Chevallereau, C.; Razavi, H.; Six, D.; Aoustin, Y.; Grizzle, J. Self-Synchronization and Self-Stabilization of 3D Bipedal Walking Gaits. Rob Auton Syst 2018, 100, pp–43. [Google Scholar] [CrossRef]
- Yin, C.; Zhu, J.; Xu, H. Walking Gait Planning And Stability Control. In Humanoid Robots.Ben Choi, Intech. Rijeka, Croatia, 2009. pp. 297-332. [CrossRef]
- Tang, Z.; Er, M.J. Humanoid 3D Gait Generation Based on Inverted Pendulum Model. 22nd IEEE International Symposium on Intelligent Control, ISIC 2007. Part of IEEE Multi-conference on Systems and Control. [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped Walking Pattern Generation by Using Preview Control of Zero-Moment Point. Proc IEEE Int Conf Robot Autom 2003, 2, pp–1620. [Google Scholar] [CrossRef]
- Vukobratovic, M.; Borovac, B. Zero-Moment Point - Thirty Five Years of Its Life. 2012, 1, pp. 1. [CrossRef]
- Lavor, C.; Xambó-Descamps, S.; Zaplana, I. Robot Kinematics. SpringerBriefs in Mathematics. [CrossRef]
- Maalouf, N.; Elhajj, I.H. ; Shammas, · Elie; Daniel Asmar, · Biomimetic Energy-Based Humanoid Gait Design. [CrossRef]
- Kobayashi, T.; Sekiyama, K.; Hasegawa, Y.; Aoyama, T.; Fukuda, T. Virtual-Dynamics-Based Reference Gait Speed Generator for Limit-Cycle-Based Bipedal Gait. ROBOMECH Journal 2018, 5, 18. [Google Scholar] [CrossRef]
- Alba, M.; Prada, J.C.G.; Meneses, J.; Rubio, H. Center of Percussion and Gait Design of Biped Robots. Mech Mach Theory 2010, 45, 1681–1693. [Google Scholar] [CrossRef]
- Lim, I.S.; Kwon, O.; Park, J.H. Gait Optimization of Biped Robots Based on Human Motion Analysis. Rob Auton Syst 2014, 62, 229–240. [Google Scholar] [CrossRef]
- Atmeh, G.; Subbarao, K. A Neuro-Dynamic Walking Engine for Humanoid Robots. Rob Auton Syst 2018, 110, pp–124. [Google Scholar] [CrossRef]
- Hildebrandt, A.-C.; Ritt, K.; Wahrmann, D.; Wittmann, R.; Sygulla, F.; Seiwald, P.; Rixen, D.; Buschmann, T. Torso Height Optimization for Bipedal Locomotion. 2018. [Google Scholar] [CrossRef]
- Khomariah, N.E.; Pramadihanto, D.; Dewanto, R.S. FLoW Bipedal Robot: Walking Pattern Generation. Proceedings - 2015 International Electronics Symposium: Emerging Technology in Electronic and Information, IES 2015, 78. [CrossRef]
- Park, I.W.; Kim, J.Y.; Lee, J.; Oh, J.H. Online Free Walking Trajectory Generation for Biped Humanoid Robot KHR-3(HUBO). Proc IEEE Int Conf Robot Autom 2006, 2006, pp–1231. [Google Scholar] [CrossRef]
- Mandava, R.K.; Vundavilli, P.R. Forward and Inverse Kinematic Based Full Body Gait Generation of Biped Robot. International Conference on Electrical, Electronics, and Optimization Techniques, ICEEOT 2016, 3301. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Z.; Chen, Y. Bipedal Walking Pattern Generation and Control for Humanoid Robot with Bivariate Stability Margin Optimization. Advances in Mechanical Engineering 2018, 10, 2018. [Google Scholar] [CrossRef]
- Olcay, T.; Özkurt, A. Design and Walking Pattern Generation of a Biped Robot. Turkish Journal of Electrical Engineering and Computer Sciences 2017, 25, pp–761. [Google Scholar] [CrossRef]
- Carpentier, J.; Tonneau, S.; Naveau, M.; Stasse, O.; Mansard, N. A Versatile and Efficient Pattern Generator for Generalized Legged Locomotion. Proc IEEE Int Conf Robot Autom, 3555. [Google Scholar] [CrossRef]
- Chae, H.-S. Development of the Modeling for Biped Robot Using Inverse Kinematics. WSEAS Transactions on Systems, 2004, 3, 9, pp. 2788–2792.
- Tevatia, G.; Schaal, S. Inverse Kinematics for Humanoid Robots. Proceedings-IEEE International Conference on Robotics and Automation 2000, 1, pp–294. [Google Scholar] [CrossRef]
- Efrain, O.; Ponce, R.; Mansard, N.; Souères, P.; Ramos, O.E.; Soù, P. Whole-Body Motion Integrating the Capture Point in the Operational Space Inverse Dynamics Control. IEEE-RAS International Conference on Humanoid Robots. [CrossRef]
- Shibata, M.; Natori, T. Impact Force Reduction for Biped Robot Based on Decoupling COG Control Scheme, 6th International Workshop on Advanced Motion Control. Proceedings (Cat. No.00TH8494), Nagoya, Japan, 2000, pp. [CrossRef]
- Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. undefined 2011, 27, pp–984. [Google Scholar] [CrossRef]
- Bajrami, X.; Dermaku, A.; Likaj, R.; Demaku, N.; Kikaj, A.; Maloku, S.; Kikaj, D. Trajectory Planning and Inverse Kinematics Solver for Real Biped Robot with 10 DOF-s. IFAC-PapersOnLine 2016, 49, pp–88. [Google Scholar] [CrossRef]
- Buschmann, T.; Lohmeier, S.; Bachmayer, M.; Ulbrich, H.; Pfeiffer, F. A Collocation Method for Real-Time Walking Pattern Generation. IEEE-RAS International Conference on Humanoid Robots, 6. [CrossRef]
- Nakanishi, J.; Mistry, M.; Schaal, S. Inverse Dynamics Control with Floating Base and Constraints. Proc IEEE Int Conf Robot Autom, 1942. [Google Scholar] [CrossRef]
- Clever, D.; Hu, Y.; Mombaur, K. Humanoid Gait Generation in Complex Environments Based on Template Models and Optimality Principles Learned from Human Beings. 2018, 37, pp. 37. [CrossRef]
- Bayraktaroğlu, Z.Y.; Acar, M.; Gerçek, A.; TAN, N.M. Design and Development of the I.T.U. Biped Robot. GAZI UNIVERSITY JOURNAL OF SCIENCE 2018, 31, pp–251. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J Appl Mech 1955, 22, pp–215. [Google Scholar] [CrossRef]
- Ali, M.A.; Park, H.A.; Lee, C.S.G. Closed-Form Inverse Kinematic Joint Solution for Humanoid Robots. IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, IROS 2010 - Conference Proceedings. [CrossRef]
- Yapıcı, K.O. 14 Serbestlik Dereceli İki Ayaklı Bir Robotun Dinamik Yürüme Hareketinin Kontrolü. Master Thessis, ITU Science and Technology Institute: İstanbul, 2008.
- Simscape Multibody. Available online: https://Www.Mathworks.Com/Products/Simscape-Multibody.html (accessed on 15 March 2024).
- Spatial Contact Force. Available online: https://www.mathworks.com/help/sm/ref/Spatialcontactforce.html?SearchHighlight=spatial%20contact&s_tid=srchtitle_support_results_1_spatial%20contact (accessed on 15 March 2024).
- Inertia Sensor. Available online: https://www.mathworks.com/help/sm/ref/Inertiasensor.html?S_tid=srchtitle_site_search_1_inertia%20sensor (accessed on 15 March 2024).
Figure 1.
Joint angles and basic dimensions of the robot.
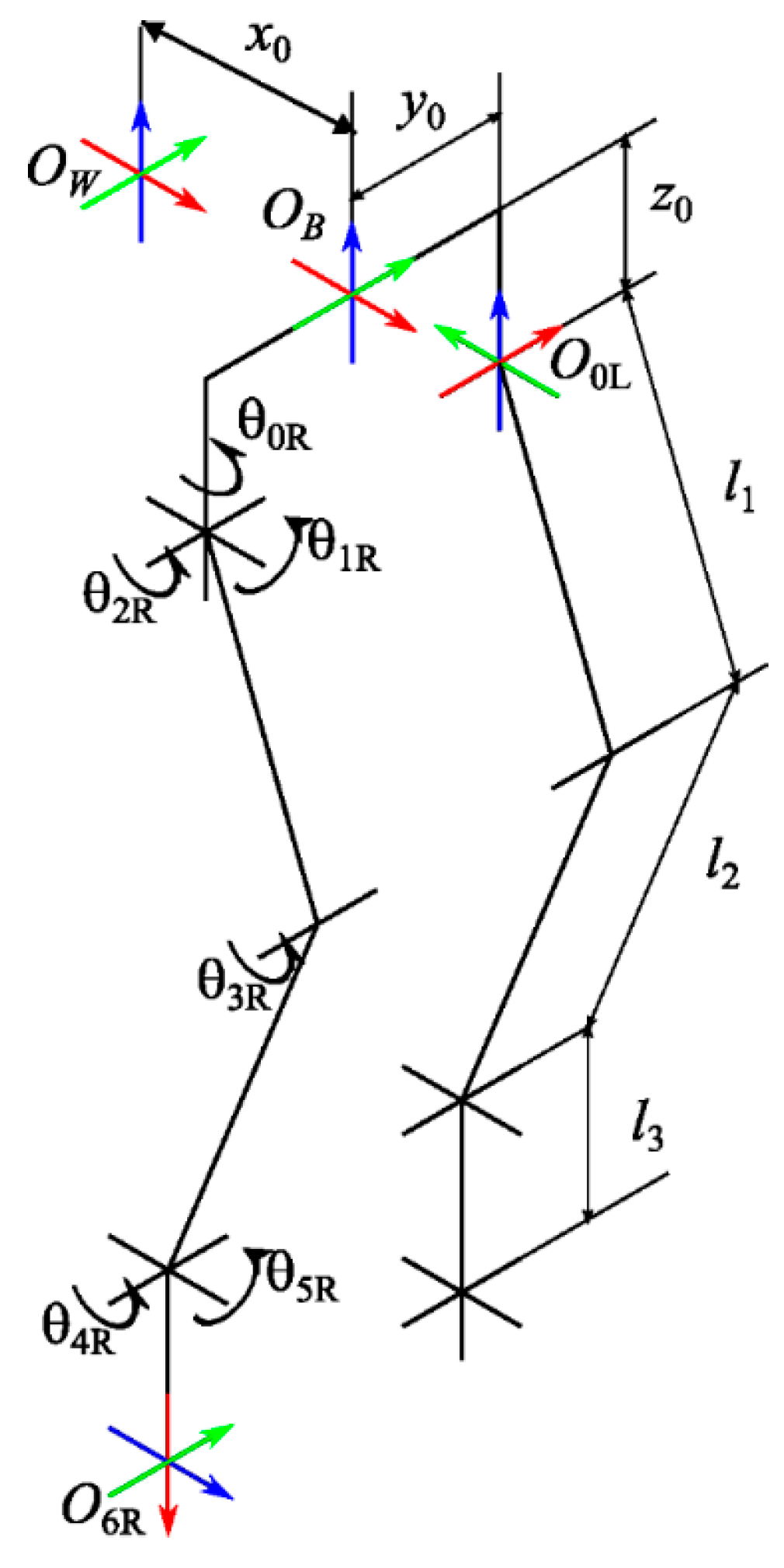
Figure 2.
3-dimensional linear inverted pendulum model (3DLIPM).
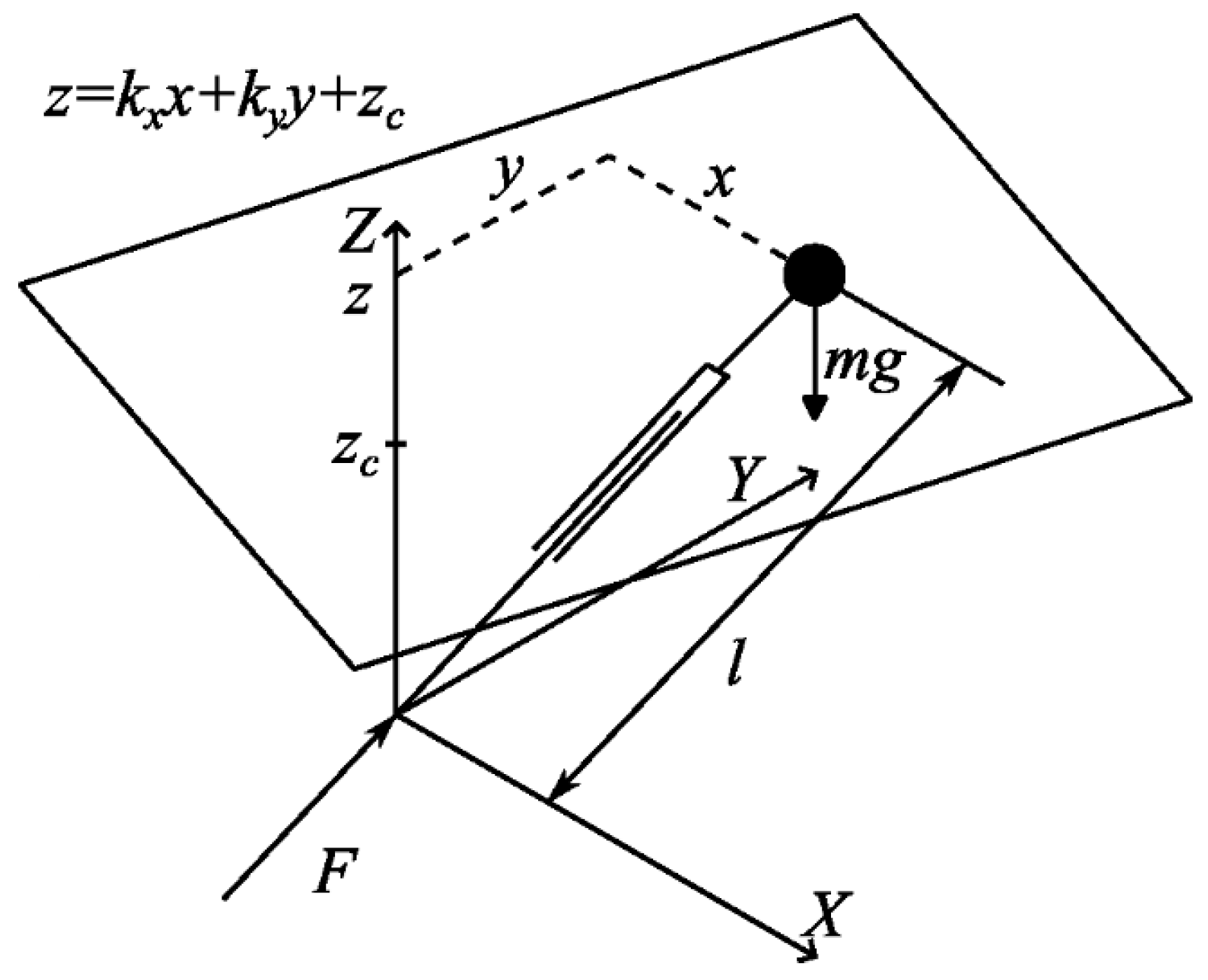
Figure 3.
Trajectory of the CoG and fixed foot positions.
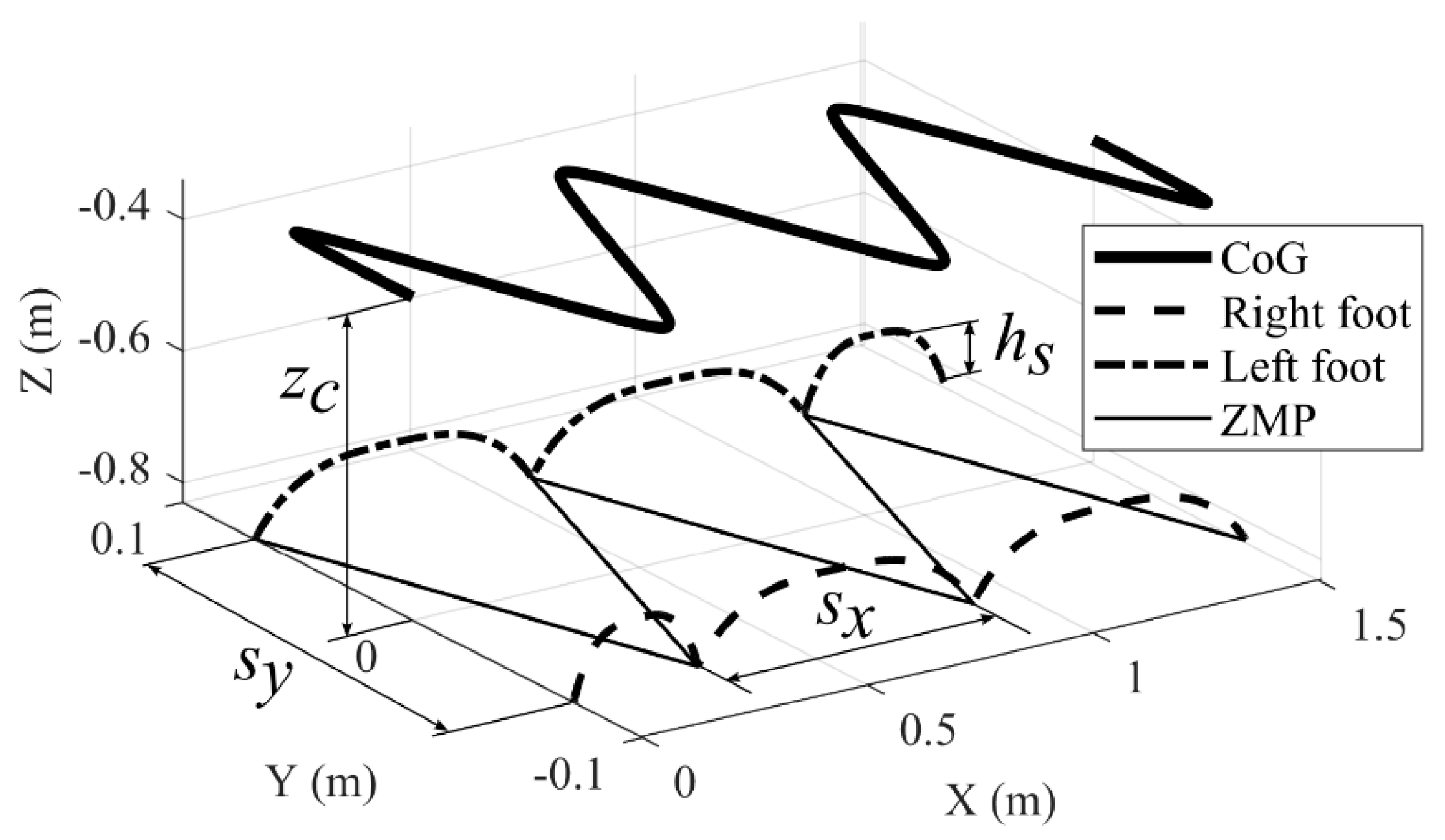
Figure 4.
Parameters used in ZMP calculations.
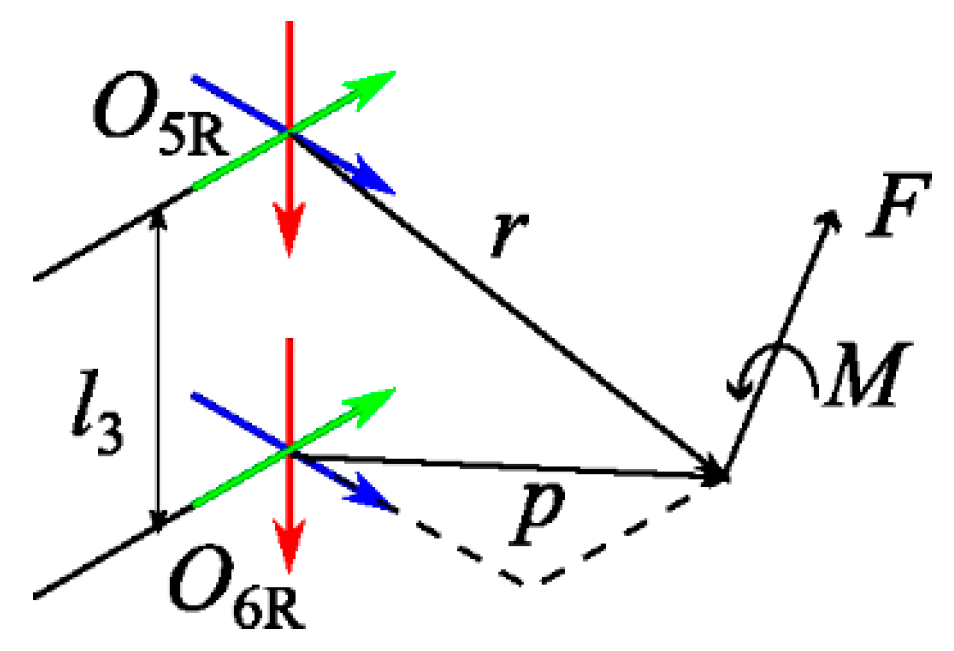
Figure 5.
CoG locations of different assemblies of the robot on the ITU Biped CAD model
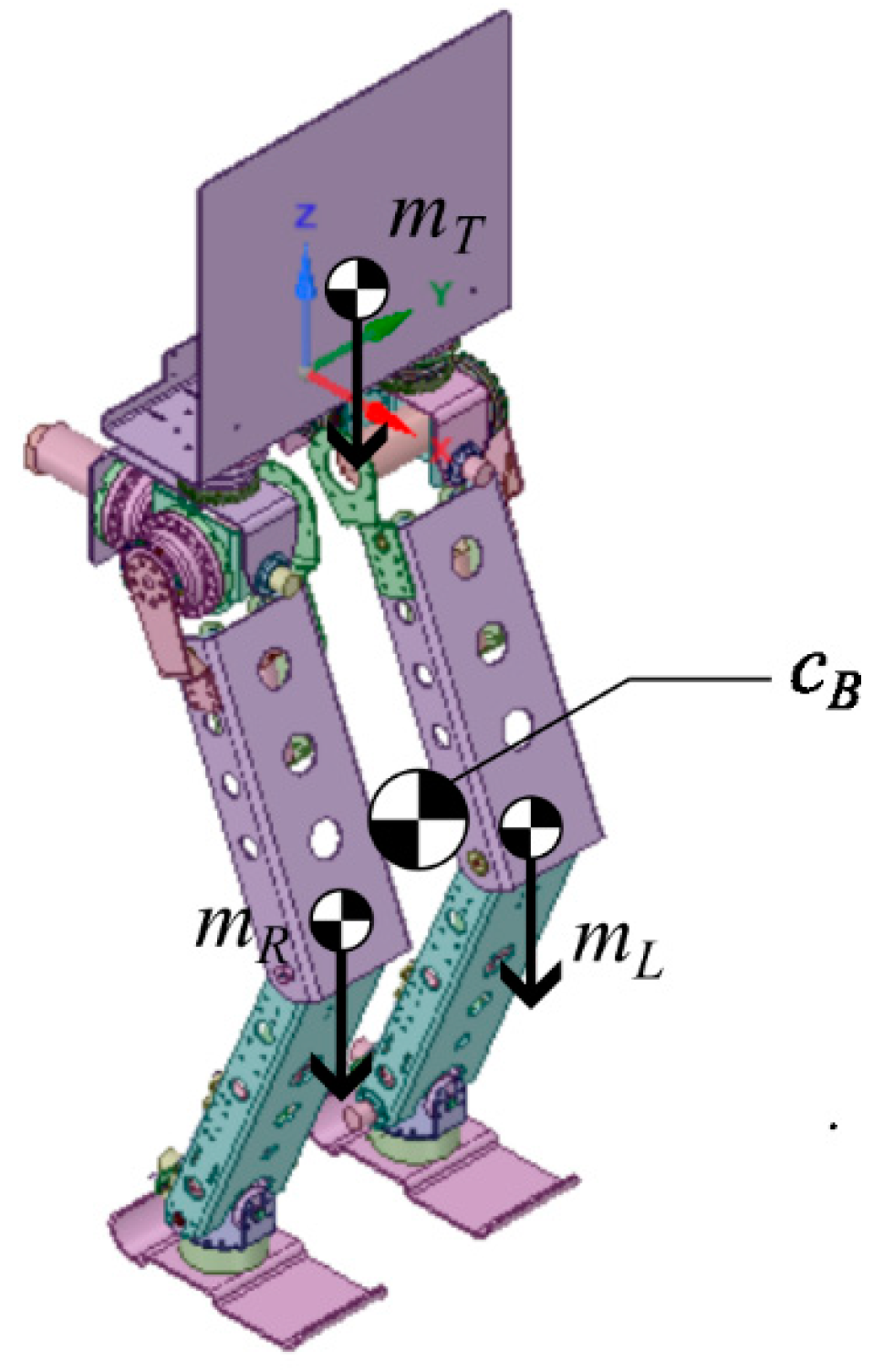
Figure 6.
Graphical presentation of the robot and its CoG.
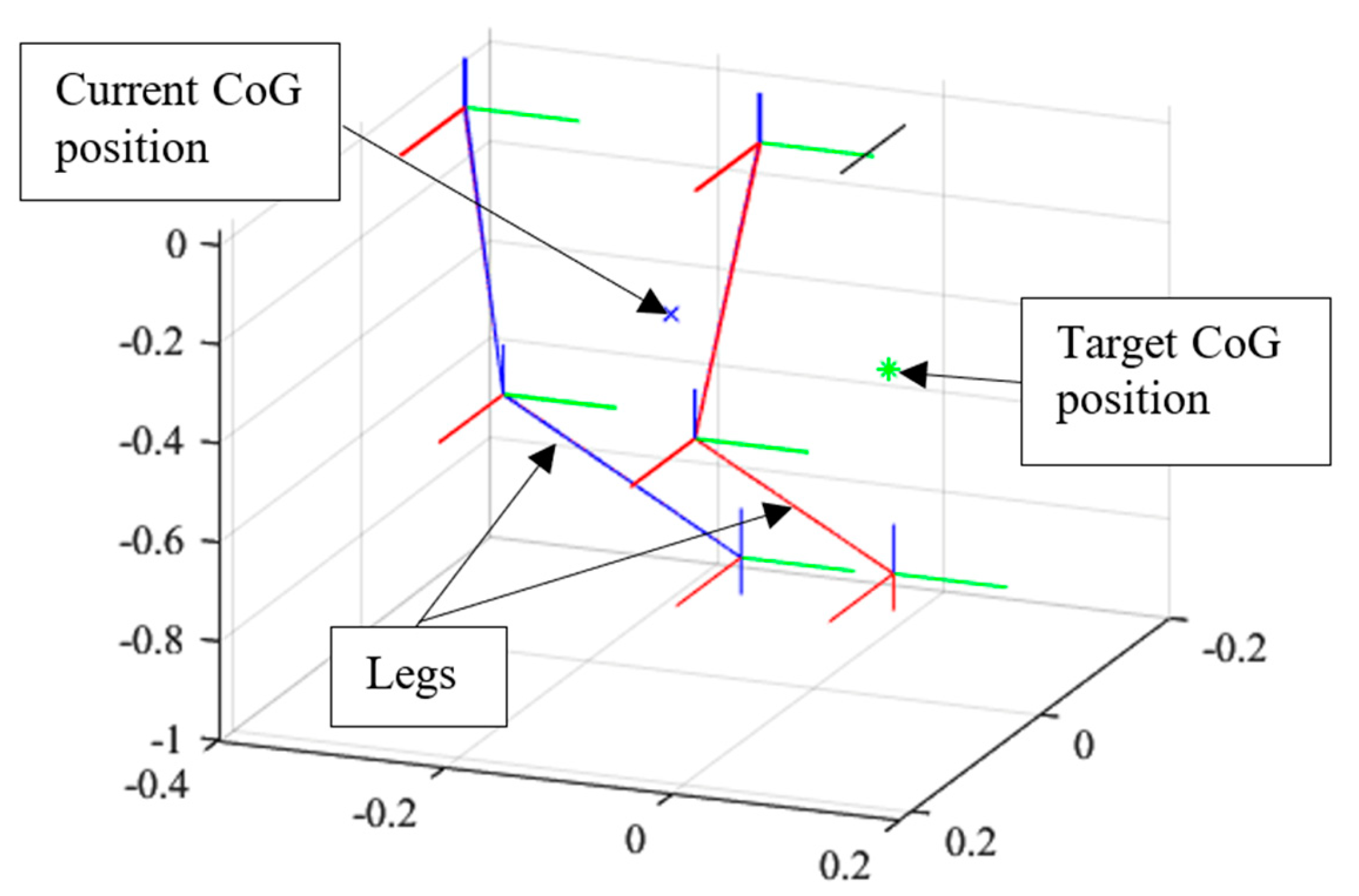
Figure 7.
CoG trajectory created by the Converging CoG Difference algorithm.
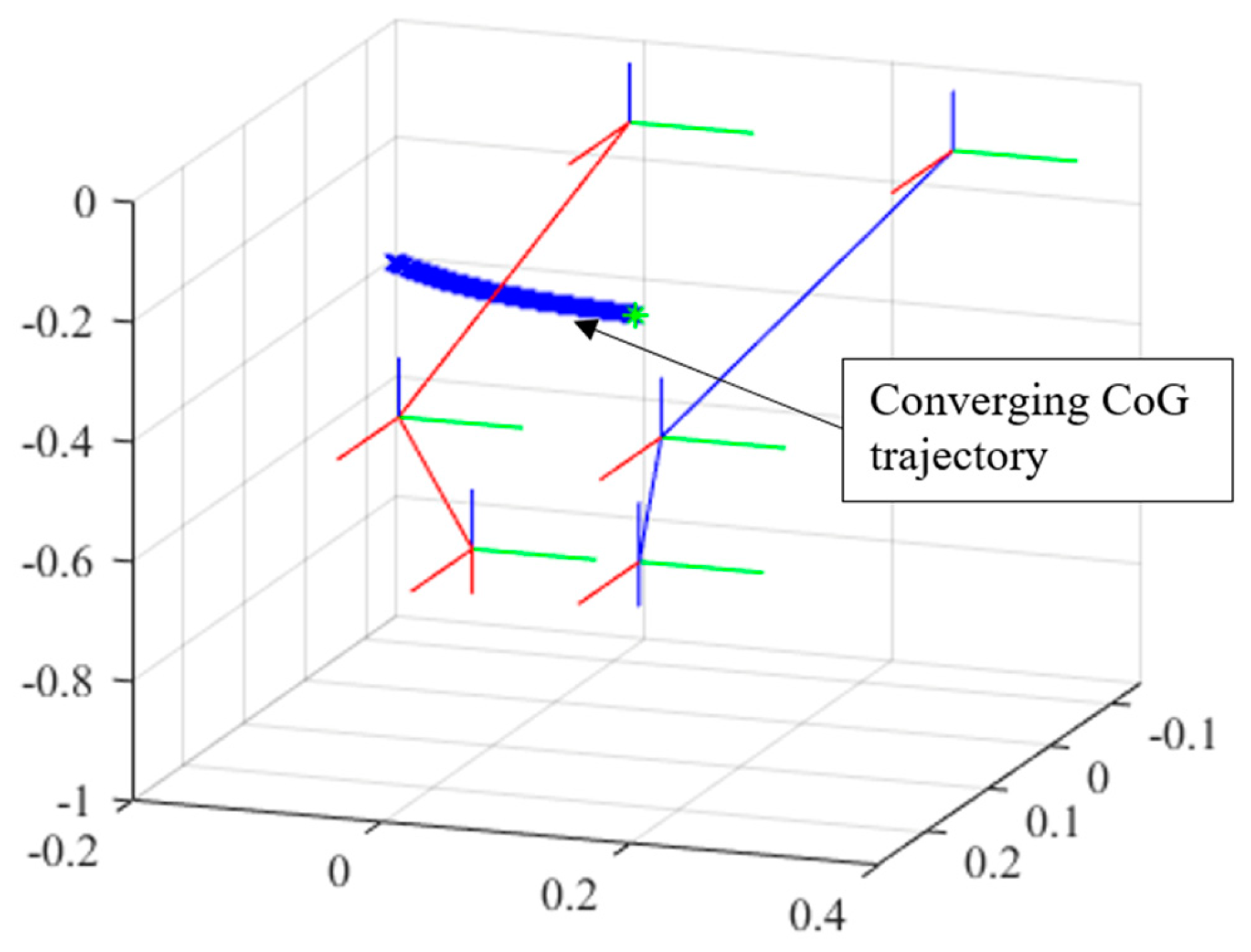
Figure 8.
Simulink model diagram.

Figure 9.
Simulation steps: (a) the CCGD , (b) constant pelvis to CoG reference.
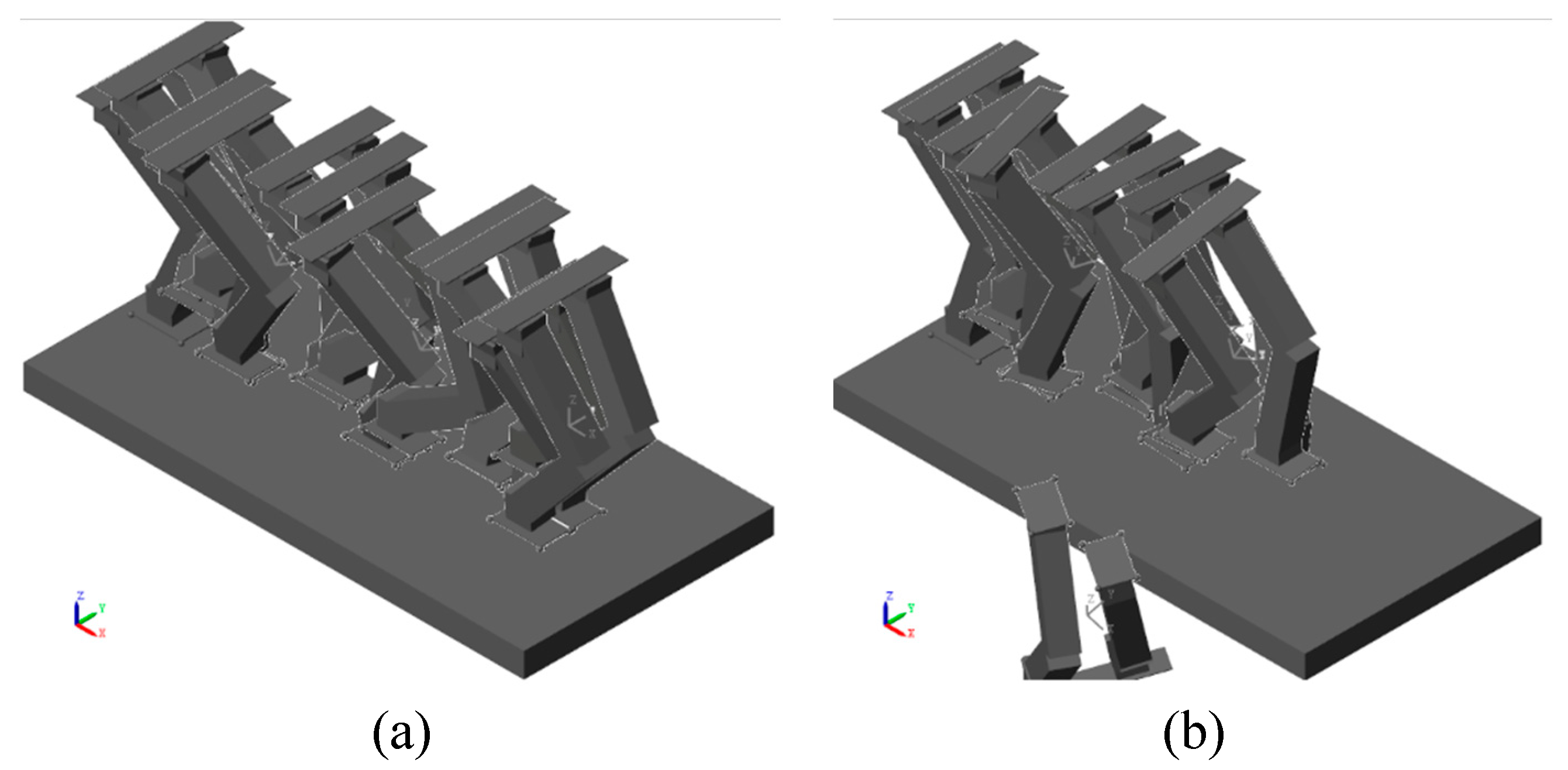
Figure 10.
Calculated and simulated trajectories.
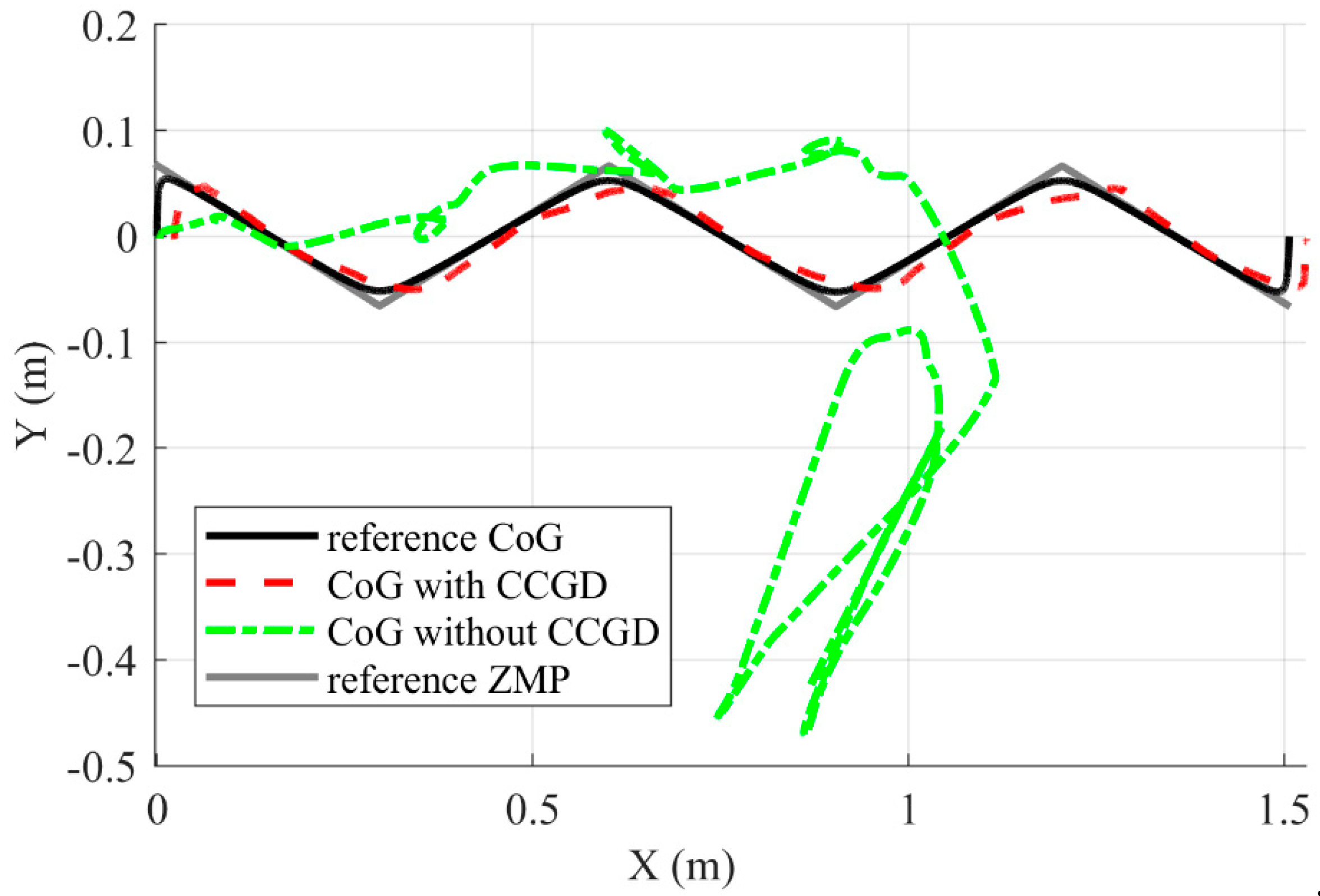
Figure 11.
Result of simulation with CCGD.
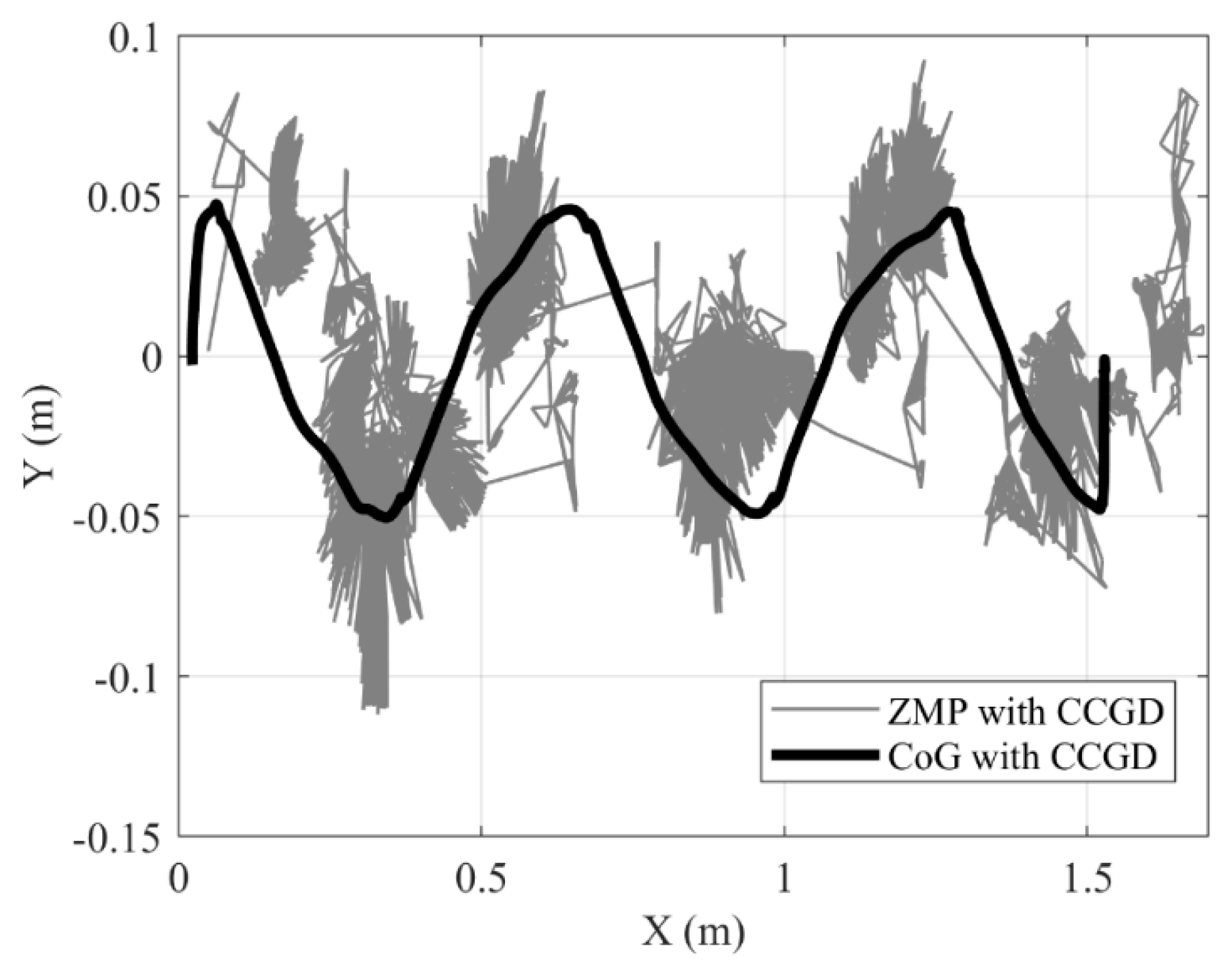
Figure 12.
Result of simulation without CCGD.
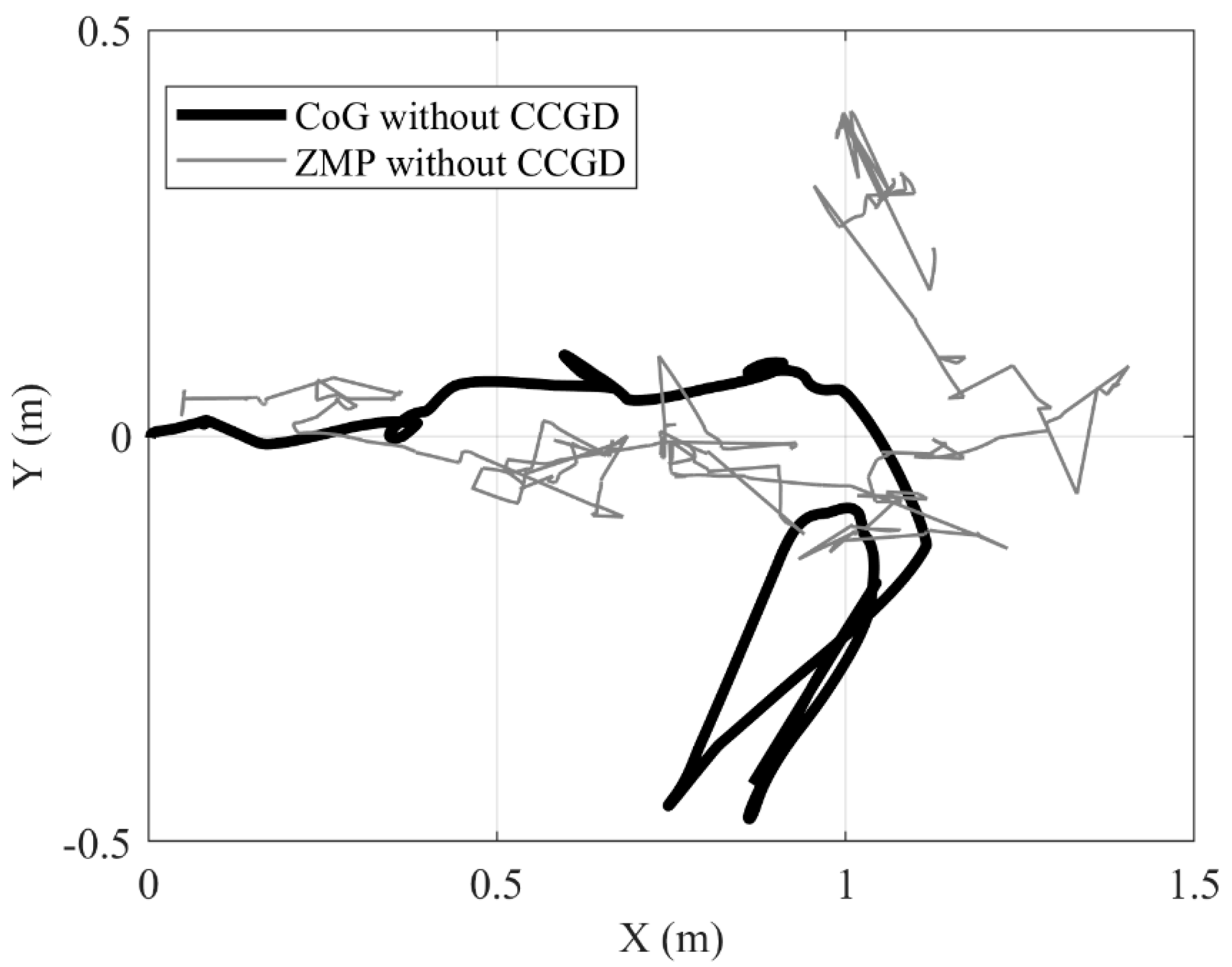
Figure 13.
CoG tracking error values of CCGD algorithm.
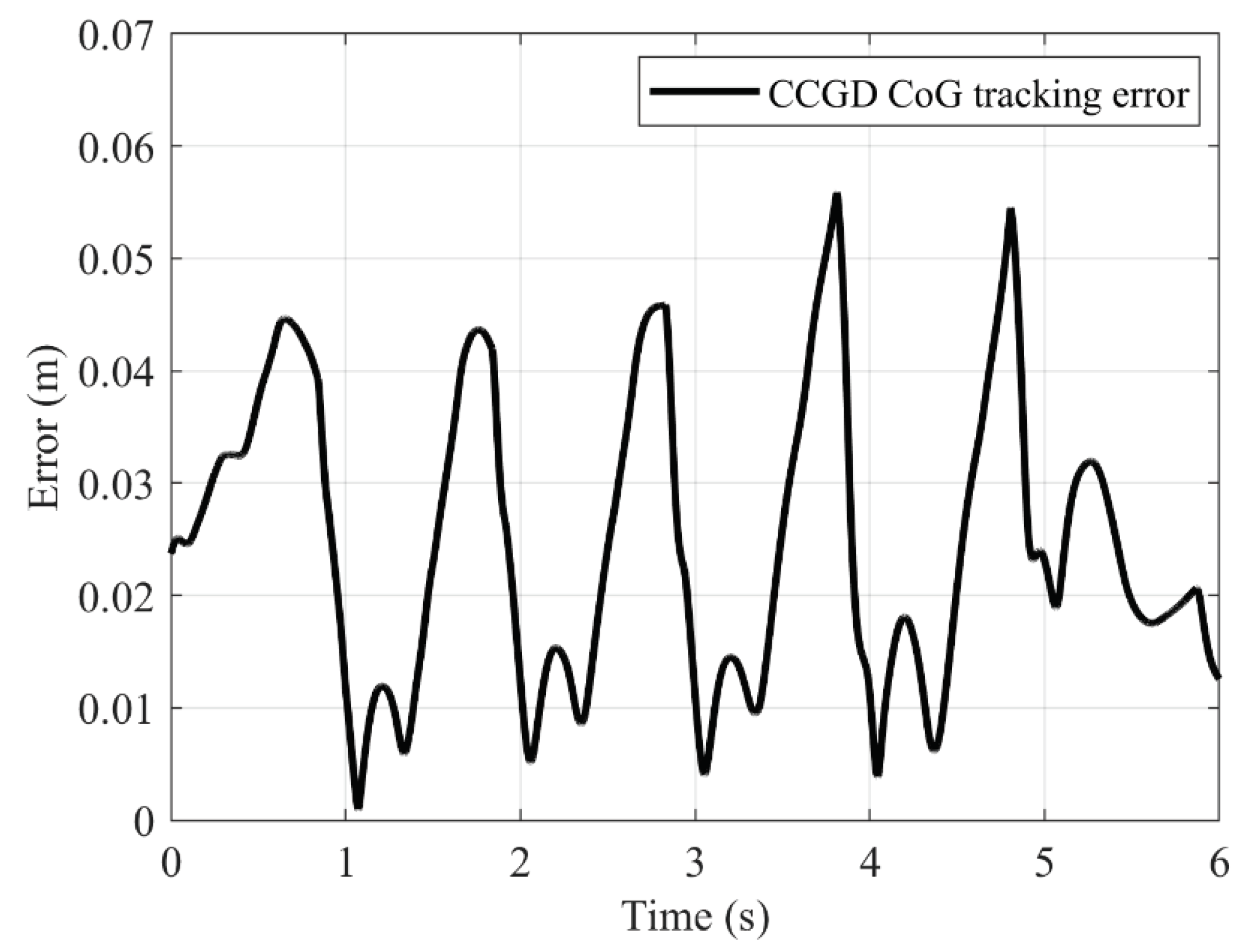
Table 1.
Link transformation table according to the DH method.
| Joint no. | ||||
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | ||
| 3 | 0 | 0 | ||
| 4 | 0 | 0 | ||
| 5 | 0 | 0 | ||
| 6 | 0 | 0 |
Table 2.
Converging Center of Gravity Algorithm (CCGD).
| Algorithm | |||
| 1 | : | fixed ⇐ 1 | |
| 2 | : | moving ⇐ 2 | |
| 3 | : | For each point in CoG_Traj | |
| 4 | : | ⇐ point (1) | |
| 5 | : | ⇐ point (2) | |
| 6 | : | ||
| 7 | : | While | |
| 8 | : | (Eq. 17) | |
| 9 | : | (Eq. 18) | |
| 10 | : | (Eq. 19) | |
| 11 | : | (Eq. 20) | |
| 12 | : | ||
| 13 | : | (Eqs. 5-10) | |
| 14 | : | (Eq. 17) | |
| 15 | : | (Eq. 18) | |
| 16 | : | If< | |
| 17 | : | Save joint angles | |
| 18 | : | Else | |
| 19 | : | (Eq. 11) | |
| 20 | : | Continue cycle | |
| 21 | : | End if | |
| 22 | : | transitory ⇐ j | |
| 23 | : | j ⇐ i | |
| 24 | : | i ⇐transitory | |
| 25 | : | End while | |
| 26 | : | End for | |
Table 3.
Study parameters.
| Parameter | Value | Unit | Explanation |
| 0.3 | m | Step length | |
| 0.065 | m | Distance between feet | |
| 0.075 | m | Step height | |
| 0.01 | m | Contact sphere radius | |
| 6.00E+04 | N/m | Contact rigidity | |
| 6.00E+03 | Ns/m | Contact dampening ratio | |
| 0.001 | m | Precision of calculation | |
| 0.001 | Unit vector magnitude coef. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






