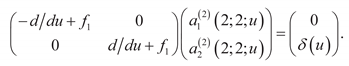1. Introduction
The analysis of the accuracy of results (usually called “responses”) computed by models relies fundamentally on the functional derivatives (usually called “sensitivities”) of the respective model responses with respect to the parameters in the respective computational model. Such sensitivities are needed for many purposes, including: (i) understanding the model by ranking the importance of the various parameters; (ii) performing “reduced-order modeling” by eliminating unimportant parameters and/or processes; (iii) quantifying the uncertainties induced in a model response due to model parameter uncertainties; (iv) performing “model validation,” by comparing computations to experiments to address the question “does the model represent reality?” (v) prioritizing improvements in the model; (vi) performing data assimilation and model calibration as part of forward “predictive modeling” to obtain best-estimate predicted results with reduced predicted uncertainties; (vii) performing inverse “predictive modeling”; (viii) designing and optimizing the system.
Response sensitivities are computed by using either deterministic or statistical methods. The simplest deterministic method for computing response sensitivities is to use finite-difference schemes in conjunction with re-computations using the model with “judiciously chosen” altered parameter values. Evidently, such methods can at best compute approximate values of a very limited number of sensitivities. Deterministic methods that can compute more exactly the values of first-order sensitivities include the “Green’s function method” [
1], the “forward sensitivity analysis methodology” [
2], and the “direct method” [
3], which rely on analytical or numerical differentiation of the computational model under investigation to compute local response sensitivities exactly. However, for a computational model comprising many parameters, the conventional deterministic methods become impractical for computing sensitivities higher than first-order because they are subject to the “curse of dimensionality,” a term coined by Belmann [
4] to describe phenomena in which the number of computations increases exponentially in the respective phase-space. In the particular case of sensitivity analysis using conventional deterministic methods, the number of large-scale computations increases exponentially in the phase-space of model parameter as the order of sensitivities increases.
The alternatives to “deterministic methods” are the “statistical methods”, which construct an approximate response distribution (often called “response surface”) in the parameters space, and subsequently use scatter plots, regression, rank transformation, correlations, and so-called “partial correlation analysis,” in order to identify approximate expectation values, variances and covariances for the responses. These statistical quantities are subsequently used to construct quantities that play the role of (approximate) first-order response sensitivities. Thus, statistical methods commence with “uncertainty analysis” and subsequently attempt an approximate “sensitivity analysis” of the approximately computed model response (called a “response surface”) in the phase-space of the parameters under consideration. The currently popular statistical methods for uncertainty and sensitivity analysis are broadly categorized as sampling-based methods [
5,
6], variance-based methods [
7,
8], and Bayesian methods [
9]. Various variants of the statistical methods for uncertainty and sensitivity analysis are reviewed in the book edited by Saltarelli et al. [
10]. The main advantage of using statistical methods for uncertainty and sensitivity analysis is that they are conceptually easy to implement. On the other hand, statistical methods for uncertainty and sensitivity analysis have three major inherent practical drawbacks, as follows:
- (i)
Even first-order sensitivities cannot be computed exactly.
- (ii)
Statistical methods are (also) subject to the curse of dimensionality and have not been developed for producing second- and higher-order sensitivities.
- (iii)
Since the response sensitivities and parameter uncertainties are amalgamated, inherently and inseparably, within the results produced by statistical methods, improvements in parameter uncertainties cannot be directly propagated to improve response uncertainties; rather, the entire set of simulations and statistical post-processing must be repeated anew.
- (iv)
A “fool-proof” statistical method for analyzing correctly models involving highly correlated parameters does not seem to exist currently, so that particular care must be used when interpreting regression results obtained using such models.
It is known that the “adjoint method of sensitivity analysis” has been the most efficient method for computing exactly first-order sensitivities, since it requires a single large-scale (adjoint) computation for computing all of the first-order sensitivities, regardless of the number of model parameters. The idea underlying the computation of response sensitivities with respect to model parameters using adjoint operators was first used by Wigner [
11] to analyze first-order perturbations in nuclear reactor physics and shielding models based on the
linear neutron transport (or diffusion) equation, as subsequently described in textbooks on these subjects [
12,
13,
14,
15,
16]. Cacuci [
2] is credited (see, e.g., [
17,
18]) for having conceived the rigorous “1
st-order adjoint sensitivity analysis methodology” for generic large-scale
nonlinear (as opposed to linearized) systems involving generic operator responses and having introduced these principles to the earth, atmospheric and other sciences.
Cacuci [
19,
20] has extended his 1
st-order adjoint sensitivity analysis methodology to enable the comprehensive computation of 2
nd-order sensitivities of model responses to model parameters (including imprecisely known domain boundaries and interfaces) for large-scale linear and nonlinear systems. The 2
nd-order adjoint sensitivity analysis methodology for linear systems was applied [
21] to compute exactly the 21,976 first-order sensitivities and 482,944,576 second-order sensitivities (of which 241,483,276 are distinct from each other) for an OECD/NEA reactor physics benchmark [
22]. This benchmark is modeled by the neutron transport equation involving 21,976 uncertain parameters, the solving of which is representative of “large-scale computations.” The neutron transport equation was solved using the software package PARTISN [
23] in conjunction with the MENDF71X cross section library [
24], which comprises 618-group cross sections based on ENDF/B-VII.1 nuclear data [
25]. The spontaneous fission source was computed using the code SOURCES4C [
26]. This work has demonstrated that, contrary to the widely held belief that second- and higher-order sensitivities are negligeable for reactor physics systems, many 2
nd-order sensitivities of the OECD benchmark’s response to the benchmark’s uncertain parameters were much larger than the largest 1
st-order ones. This finding has motivated the investigation of the largest 3
rd-order sensitivities, many of which were found to be even larger than the 2
nd-order ones. Subsequently, the mathematical framework for determining and computing the 4
th-order sensitivities was developed, and many of these were found to be larger than the 3
rd-order ones. This sequence of findings has motivated the development by Cacuci [
27] of the “n
th-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems” (abbreviated as “n
th-CASAM-L”), which was developed specifically for linear systems because important model responses produced by such systems are various Lagrangian functionals which depend simultaneously on both the forward and adjoint state functions governing the respective linear system. Among the most important such responses are the Raleigh quotient for computing eigenvalues and/or separation constants when solving partial differential equations, and the Schwinger functional for first-order “normalization-free” solutions [
28,
29]. These functionals play a fundamental role in optimization and control procedures, derivation of numerical methods for solving equations (differential, integral, integro-differential), etc.
In parallel with developing the n
th-CASAM-L, Cacuci [
30] has also developed the
nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Nonlinear Systems (n
th-CASAM-N). Just like the n
th-CASAM-L, the n
th-CASAM-N is also formulated in linearly increasing higher-dimensional Hilbert spaces (as opposed to exponentially increasing parameter-dimensional spaces), thus overcoming the curse of dimensionality in sensitivity analysis of nonlinear systems, enabling the most efficient computation of exactly-determined expressions of arbitrarily high-order sensitivities of generic nonlinear system responses with respect to model parameters, uncertain boundaries and internal interfaces in the model’s phase-space.
Recently, Cacuci [
31] has introduced the “Second-Order
Function/
Feature
Adjoint
Sensitivity
Analysis
Methodology for
Nonlinear Systems” (2
nd-FASAM-N), which enables a considerable reduction (by comparison to the 2
nd-CASAM-N) of the number of large-scale computations needed to compute the second-order sensitivities of a model response with respect to the model parameters, thereby becoming the most efficient methodology known for computing second-order sensitivities exactly. Paralleling the construction of the 2
nd-FASAM-N, this work introduces the “First- and Second-Order
Function/
Feature
Adjoint
Sensitivity
Analysis
Methodology for Response-Coupled Adjoint/Forward Linear Systems” (1
st and 2
nd-FASAM-L). The mathematical methodology of the 1
st-FASAM-L is presented in
Section 3, while the mathematical methodology of the 2
nd-FASAM-L is presented in
Section 4. The application of the 1
st-FASAM-L and the 2
nd-FASAM-L is illustrated in
Section 5 by means of a simplified yet representative energy-dependent neutron-slowing down model which is fundamental importance to reactor physics and design [
32,
33,
34]. The concluding discussion presented in
Section 6 prepares the ground for the subsequent generalization of the present work to enable the most efficient possible computation of exact sensitivities of any (arbitrarily-high) order with respect to “feature functions” of model parameters and, hence, to the model’s parameters.
2. Mathematical Modeling of Response-Coupled Linear Forward and Adjoint Systems
The generic mathematical model considered in this work is fundamentally the same as was considered in [
27], but with the major difference that functions (‘features”) of the primary model parameters will be generically identified within the model. The
primary model parameters will be denoted as
,…,
, where the subscript “
TP” indicates “
Total number of
Primary Parameters;” the qualifier “primary” indicates that these parameters do not depend on any other parameters within the model. These model parameters are considered to include imprecisely known geometrical parameters that characterize the physical system’s boundaries in the phase-space of the model’s independent variables. These boundaries depend on the physical system’s geometrical dimensions, which may be imprecisely known because of manufacturing tolerances. In practice, these primary model parameters are subject to uncertainties. It will be convenient to consider that these parameters are components of a “vector of
primary parameters” denoted as
, where
denotes the TP-dimensional subset of the set of real scalars. For subsequent developments, matrices and vectors will be denoted using capital and lower-case bold letters, respectively. The symbol “
” will be used to denote “is defined as” or “is by definition equal to.” Transposition will be indicated by a dagger
superscript. The nominal parameter values will be denoted as
; the superscript “0” will be used throughout this work to denote “nominal” or “mean” values.
The model is considered to comprise independent variables which will be denoted as , and are considered to be the components of a -dimensional column vector denoted as , where the sub/superscript “” denotes the “Total number of Independent variables.” The vector of independent variables is considered to be defined on a phase-space domain, denoted as , , the boundaries of which may depend on some of the model parameters . The lower boundary-point of an independent variable is denoted as (e.g., the inner radius of a sphere or cylinder, the lower range of an energy-variable, the initial time-value, etc.), while the corresponding upper boundary-point is denoted as (e.g., the outer radius of a sphere or cylinder, the upper range of an energy-variable, the final time-value, etc.). A typical example of boundary conditions that depend on imprecisely-known parameters that pertain to the geometry of the model and also to parameters that pertain to the material properties of the respective model occur when modeling particle diffusion within a medium, the boundaries of which are facing vacuum. For such models, the boundary conditions for the respective state (dependent) variables (i.e., particle flux and/or current) are imposed not on the physical boundary but on the “extrapolated boundary” of the respective spatial domain. The “extrapolated boundary” depends both on the imprecisely known physical dimensions of the medium’s domain/extent and also on the medium’s properties, i.e., atomic number densities and microscopic transport cross sections. The boundary of , which will be denoted as , comprises the set of all of the endpoints of the respective intervals on which the components of are defined, i.e., .
The mathematical model that underlies the numerical evaluation of a process and/or state of a physical system comprises equations that relate the system's independent variables and parameters to the system's state/dependent variables. A
linear physical system can generally be modeled by a system of coupled operator-equations as follows:
In Equation (1), the vector is a -dimensional column vector of dependent variables and where the sub/superscript “” denotes the “Total (number of) Dependent variables.” The functions , denote the system’s “dependent variables” (also called “state functions”). The matrix , has dimensions . The components are operators that act linearly on the dependent variables and also depend (in general, nonlinearly) on the uncertain model parameters . Furthermore, the vector is a -dimensional vector having components , which are real-valued functions of (some of) the primary model parameters . The quantity denotes the total number of such functions which appear exclusively in the definition of the model’s underlying equations. Such functions customarily appear in models in the form of correlations that describe “features” of the system under consideration, such as material properties, flow regimes. etc. Usually, the number of functions is considerably smaller than the total number of model parameters, i.e., . For example, the numerical model (Cacuci and Fang, 2023) of the OECD/NEA reactor physics benchmark (Valentine 2006) comprises 21,976 uncertain primary model parameters (including microscopic cross sections and isotopic number densities) but the neutron transport equation, which is solved to determine the neutron flux distribution within the benchmark, does not use these primary parameters directly but instead uses just several hundreds of “group-averaged macroscopic cross sections” which are functions/features of the microscopic cross sections and isotopic number densities (which in turn are uncertain quantities that would be components of the vector of primary model parameters). In particular, a component may simply be one of the primary model parameters , i.e., .
The -dimensional column vector , having components , denotes inhomogeneous source terms, which usually depend nonlinearly on the uncertain parameters . Since the right-side of Equation (1) may contain distributions, the equality in this equation is considered to hold in the weak (i.e., “distributional”) sense. Similarly, all of the equalities that involve differential equations in this work will be considered to hold in the distributional sense.
When
contains differential operators, a set of boundary and initial conditions which define the domain of
must also be given. Since the complete mathematical model is considered to be linear in
, the boundary and/or initial conditions needed to define the domain of
must also be linear in
. Such linear boundary and initial conditions are represented in the following operator form:
In Equation (2), the quantity denotes a matrix of dimensions having components denoted as , which are operators that act linearly on and nonlinearly on the components of ; the quantity denotes the total number of boundary and initial conditions. The -dimensional column vector comprises components that are operators which, in general, act nonlinearly on the components of .
Physical problems modeled by linear systems and/or operators are naturally defined in Hilbert spaces. The dependent variables
, for the physical system represented by Eqs. (1) and (2) are considered to be square-integrable functions of the independent variables and are considered to belong to a Hilbert space which will be denoted as
, where the subscript “zero” denotes “zeroth-level“ or “original.” Higher-level Hilbert spaces, which will be denoted as
and
, will also be used in this work. The Hilbert space
is considered to be endowed with the following inner product, denoted as
, between two elements
and
:
The “dot” in Equation (3) indicates the “scalar product of two vectors,” which is defined as follows:
The product-notation in Equation (3) denotes the respective multiple integrals.
The linear operator
is considered to admit an adjoint operator, which will be denoted as
and which is defined through the following relation for a vector
In Equation (5), the formal adjoint operator
is the
matrix comprising elements
which are obtained by transposing the formal adjoints of the forward operators
. Hence, the system adjoint to the linear system represented by (1) and (2) can generally be represented as follows:
When the forward operator comprises differential operators, the operations (e.g., integration by parts) that implement the transition from the left-side to the right side of Equation (5) give rise to boundary terms which are collectively called the “bilinear concomitant.” The domain of is determined by selecting adjoint boundary and/or initial conditions so as to ensure that the adjoint system is well-posed mathematically. It is also desirable that the selected adjoint boundary conditions should cause the bilinear concomitant to vanish when implemented in Equation (5) together with the forward boundary conditions given in Equation (2). The adjoint boundary conditions thus selected are represented in operator form by Equation (7).
The relationship shown in Equation (5), which is the basis for defining the adjoint operator, also provides the following fundamental “reciprocity-like” relation between the sources of the forward and the adjoint equations, i.e. Eqs. (1) and (6), respectively:
The functional on the right-side of Equation (8) represents a “detector response”, i.e., a reaction-rate between the particles and the medium represented by which is equivalent to the “number of counts” of particles incident on a detector of particles that “measures” the particle flux . In view of the relation provided in (8), the vector-valued source term in the adjoint equation Equation (6) is usually associated with the “result of interest” to be measured and/or computed, which is customarily called the system’s “response.” In particular, if and , then , which means that, in such a case, the right-side of Equation (8) provides the value of the ith-dependent variable (particle flux, temperature, velocity, etc.) at the point in phase-space where the respective measurement is performed.
The results computed using a mathematical model are customarily called “model responses” (or “system responses” or “objective functions” or “indices of performance”). For linear physical systems, the system’s response may depend not only on the model’s state-functions and on the system parameters but may simultaneously also depend on the adjoint state function. As has been discussed by Cacuci [
27,
30], any response of a linear system can be formally represented (using expansions or interpolation, if necessary) and fundamentally analyzed in terms of the following generic integral representation:
where
is a suitably differentiable nonlinear function of
, and
. The integral representation of the response provided in Equation (9) can represent “averaged” and/or “point-valued” quantities in the phase-space of independent variables. For example, if
represents the computation or the measurement (which would be a “detector-response”) of a quantity of interest at a point
in the phase-space of independent variables, then
would contain a Dirac-delta functional of the form
. Responses that represent “differentials/derivatives of quantities” would contain derivatives of Dirac-delta functionals in the definition of
. The vector
, having components
, which appears among the arguments of the function
, represents functions of primary parameters that often appear solely in the definition of the response but do not appear in the mathematical definition of the model, i.e., in Eqs. (1), (2), (6) and (7). The quantity
denotes the total number of such functions which appear exclusively in the definition of the model’s response. Evidently, the response will depend directly and/or indirectly (through the “feature”-functions) on all of the primary model parameters. This fact has been indicated in Equation (9) by using the vector-valued function
as an argument in the definition of the response
to represent the concatenation of all of the “features” of the model and response under consideration. The vector
of “model features” is thus defined as follows:
As defined in Equation (10), the quantity denotes the total number of “feature functions of the model’s parameters” which appear in the definition of the nonlinear model’s underlying equations and response.
Solving Eqs. (1) and (2), at the nominal (or mean) values, denoted as , of the model parameters, yields the nominal forward solution, which will be denoted as . Solving Eqs. (6) and (7) at the nominal values, , of the model parameters yields the nominal adjoint solution, which will be denoted as . The nominal value of the response, , is determined by using the nominal parameter values , the nominal value of the forward state function, and the nominal value of the adjoint state function.
The definition provided by Equation (9) implies that the model response
depends on the components of the feature function
, and would therefore admit a Taylor-series expansion around the nominal value
, having the following form:
where
. The “sensitivities of the model response with respect to the (feature) functions” are naturally defined as being the functional derivatives of
with respect to the components (“features”)
of
. The notation
indicates that the quantity enclosed within the braces is to be evaluated at the nominal values
. Since
, the computations of the functional derivatives of
with respect to the functions
, which appear in Equation (11), will be considerably less expensive computationally than the computation of the functional derivatives involved in the Taylor-series of the response with respect to the model parameters. The functional derivatives of the response with respect to the parameters can be obtained from the functional derivatives of the response with respect to the “feature” functions
by simply using the chain rule, i.e.:
and so on. The evaluation/computation of the functional derivatives
,
, etc., does not require computations involving the model, and is therefore computationally trivial by comparison to the evaluation of the functional derivatives (“sensitivities”) of the response with respect to either the functions (“features”)
or the model parameters
.
The range of validity of the Taylor-series shown in Equation (11) is defined by its radius of convergence. The accuracy −as opposed to the “validity”− of the Taylor-series in predicting the value of the response at an arbitrary point in the phase-space of model parameters depends on the order of sensitivities retained in the Taylor-expansion: the higher the respective order, the more accurate the respective response value predicted by the Taylor-series. In the particular cases when the response happens to be a polynomial function of the “feature” functions , the Taylor series represented by Equation (11) is finite and exactly represents the respective model response.
In turn, the functions
can also be formally expanded in a multivariate Taylor-series around the nominal (mean) parameter values
, namely:
The choice of feature functions is not unique but can be tailored by the user to the problem at hand. The two most important guiding principles for constructing the feature functions based on the primary parameters are as follows:
- (i)
As will be shown below in
Section 4 while establishing the mathematical framework underlying the 2
nd-FASAM-L, the number of large-scale computations needed to determine the numerical value of the second-order sensitivities is proportional to the number of first-order sensitivities of the model’s response with respect to the feature functions
fi(α). Consequently, it is important to minimize the number of feature functions
fi(α), while ensuring that all of the primary model parameters are considered within the expressions constructed for the feature functions
fi(α). In the extreme case when some primary parameters,
αj, cannot be grouped into the expressions of the feature functions
fi(α), each of the respective primary model parameters
αj becomes a feature function
fj(α).
- (ii)
The expressions of the features functions fi(α) must be independent of the model’s state functions; they must be exact, closed-form, scalar-valued functions of the primary model parameters αj, so the exact expressions of the derivatives of fi(α) with respect to the primary model parameters αj can be obtained analytically (with “pencil and paper”) and, hence, inexpensively from a computational standpoint. The motivation for this requirement is to ensure that the numerical determination of the subsequent derivatives of the features functions fi(α) with respect to the primary model parameters αj becomes trivial computationally.
The domain of validity of the Taylor-series in Equation (13) is defined by its own radius of convergence. Of course, in the extreme case when no feature function can be constructed, the feature functions will be the primary parameters themselves, in which case the n
th-FASAM-L methodology becomes identical to the previously established n
th-CASAM-L methodology [
27].
3. The First-Order Function/Feature Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward and Adjoint Linear Systems (1st-FASAM-L)
The “
First-Order
Function/Feature
Adjoint
Sensitivity
Analysis
Methodology for Response-Coupled Forward/Adjoint
Linear Systems” (1
st-FASAM-L) aims at enabling the most efficient computation of the first-order sensitivities of a generic model response of the form
with respect to the components of the “features” function
. In preparation for subsequent generalizations towards establishing the generic pattern for computing sensitivities of arbitrarily high-order, the function
will be called the “
1st-level forward/adjoint function” and the system of equations satisfied by this function (which is obtained by concatenating the original forward and adjoint equations together with their respective boundary/initial conditions) will be called “
the 1st-Level Forward/Adjoint System (1st-LFAS)” and will be re-written in the following concatenated matrix-form:
where the following definitions were used:
In the list of arguments of the matrix , the argument “” indicates that this square matrix comprises four component sub-matrices, as indicated in Equation (16). Similarly, the argument “2” that appears in the block-vectors , , and indicates that each of these column block-vectors comprises two sub-vectors as components. Also, throughout this work, the quantity “” will be used to denote either a vector or a matrix with zero-valued components, depending on the context. For example, the vector “” in Equation (15) is considered to have as many components as the vector . On the other hand, the quantity “” which appears in Equation (16) may represent either a (sub) matrix or a vector of the requisite dimensions.
The nominal (or mean) parameter values, , are considered to be known, but these values will differ from the true values , which are unknown, by variations , where . The parameter variations will induce variations in the vector-valued function , around the nominal value , and will also induce variations and , respectively, around the nominal solution through the equations underlying the model. All of these variations will induce variations in the model response , in a neighborhood around , where is a real-valued scalar.
Formally, the first-order sensitivities of the response
with respect to the components of the feature function
are provided by the first-order Gateaux (G-)variation of
at the phase-space point
, which is defined as follows:
where the following definitions were used:
In general, the G-variation
is nonlinear in the variations
,
and/or
. In such cases, the partial functional Gateaux (G-)derivatives of the response
with respect to the functions
do not exist, which implies that the response sensitivities to the model parameters do not exist, either. Therefore, it will be henceforth assumed in this work that
is
linear in the respective variations, so the corresponding partial G-derivatives exist and
is actually the first-order
G-differential of the response. The usual numerical methods (e.g., Newton’s method and variants thereof) for solving the equations underlying the model also require the existence of the first-order G-derivatives of the original model equations; these will also be assumed to exist. When the 1
st-order G-derivatives exists, the G-differential
can be written as follows:
In Equation (20), the “direct-effect” term
comprises only dependencies on
and is defined as follows:
The following convention/definition was used in Equation (21):
The above convention implies that:
(a) For
:
(b) For
:
(c) For
:
(d) For
:
The notation on the left-side of Equation (22) represents the inner product between two vectors, but the symbol “()” which indicates “transposition” has been omitted in order to keep the notation as simple as possible. “Daggers” indicating transposition will also be omitted in other inner products, whenever possible, while avoiding ambiguities.
In Equation (20), the “indirect-effect” term
depends only on the variations
in the state functions, and is defined as follows:
In Eqs. (21) and (27), the notation has been used to indicate that the quantity within the brackets is to be evaluated at the nominal values of the parameters and state functions. This simplified notation is justified by the fact that when the parameters take on their nominal values, it implicitly means that the corresponding state functions also take on their corresponding nominal values. This simplified notation will be used throughout this work.
The direct-effect term can be computed after having solved the forward system modeled by Eqs. (1) and (2), as well as the adjoint system modeled by Eqs. (6) and (7), to obtain the nominal values of the forward and adjoint dependent variables.
On the other hand, the indirect-effect term
defined in Equation (27) can be quantified only after having determined the variations
in the state functions of the 1
st-Level Forward/Adjoint System (1
st-LFAS). The variations
are obtained as the solutions of the system of equations obtained by taking the first-order G-differentials of the 1
st-LFAS defined by Eqs. (14) and (15), which are obtained by definition as follows:
Carrying out the differentiations with respect to
in the above equations and setting
in the resulting expressions yields the following matrix-vector equations:
where:
In order to keep the notation as simple as possible in Eqs. (30)‒(37), the differentials with respect to the various components of the feature function have all been written in the form , keeping in mind the convention/notation introduced in Equation (22). The system of equations comprising Eqs. (30) and (31) will be called the “1st-Level Variational Sensitivity System (1st-LVSS)” and its solution, , will be called the “1st-level variational sensitivity function,” which is indicated by the superscript “(1)”. The solution, , of the 1st-LVSS will be a function of the components of the vector of variations . In principle, therefore, if the response sensitivities with respect to the components of the feature function are of interest, then the 1st-LVSS would need to be solved as many times as there are components in the variational features-function . On the other hand, if the response sensitivities with respect to the primary parameters are of interest, then the 1st-LVSS would need to be solved as many times as there are primary parameters. Solving the 1st-LVSS involves “large-scale computations.”
On the other hand, solving the 1
st-LVSS can be avoided altogether by using the ideas underlying the “adjoint sensitivity analysis methodology” originally conceived by Cacuci [
2] and subsequently generalized by Cacuci [
27,
30] to enable the computation of arbitrarily high-order response sensitivities with respect to primary model parameters for both linear and nonlinear models. Thus, the need for solving repeatedly the 1
st-LVSS for every variation in the components of the feature function (or for every variation in the model’s parameters) is eliminated by expressing the indirect-effect term
defined in Equation (27) in terms of the solutions of the “
1st-Level Adjoint Sensitivity System” (1
st-LASS), which will be constructed by implementing the following sequence of steps:
Introduce a Hilbert space, denoted as
, comprising vector-valued elements of the form
, where the components
,
, are square-integrable functions. Consider further that this Hilbert space is endowed with an inner product denoted as
between two elements,
,
, which is defined as follows:
In the Hilbert
, form the inner product of Equation (30) with a yet undefined vector-valued function
to obtain the following relation:
Using the definition of the adjoint operator in the Hilbert space
, recast the left-side of Equation (39) as follows:
where
denotes the bilinear concomitant defined on the phase-space boundary
, and where
is the operator formally adjoint to
, i.e.,
Require the first term on right-side of Equation (40) to represent the indirect-effect term defined in Equation (27),by imposing the following relation:
where:
Implement the boundary conditions represented by Equation (31) into Equation (40) and eliminate the remaining unknown boundary-values of the function
from the expression of the bilinear concomitant
by selecting appropriate boundary conditions for the function
, to ensure that Equation (42) is well-posed while being independent of
unknown values of
and of
. The boundary conditions thus chosen for the function
can be represented in operator form as follows:
The selection of the boundary conditions for represented by Equation (44) eliminates the appearance of the unknown values of in and reduces this bilinear concomitant to a residual quantity that contains boundary terms involving only known values of , , , and . This residual quantity will be denoted as . In general, this residual quantity does not automatically vanish, although it may do so occasionally.
The system of equations comprising Equation (42) together with the boundary conditions represented Equation (44) will be called the 1st-Level Adjoint Sensitivity System (1st-LASS). The solution of the 1st-LASS will be called the 1st-level adjoint sensitivity function. The 1st-LASS is called “first-level” (as opposed to “first-order”) because it does not contain any differential or functional-derivatives, but its solution, , will be used below to compute the first-order sensitivities of the response with respect to the components of the feature function .
Using Equation (39) together with the forward and adjoint boundary conditions represented by Eqs. (31) and (44) in Equation (40) reduces the latter to the following relation:
In view of Eqs. (27) and (42), the first term on the right-side of Equation (45) represents the indirect-effect term
. It therefore follows from Equation (45) that the indirect-effect term can be expressed in terms of the 1
st-level adjoint sensitivity function
as follows:
As indicated by the identity shown in Equation (46), the variations
and
have been eliminated from the original expression of the indirect-effect term, which now depends on the 1
st-level adjoint sensitivity function
. Adding the expression obtained in Equation (46) with the expression for the direct-effect term defined in Equation (21) yields, according to Equation (20) the following expression for the total 1
st-order sensitivity
of the response
with respect to the components of the feature function
:
The identity which appears in Equation (47) emphasizes the fact that the variations and , which are expensive to compute, have been eliminated from the final expressions of the 1st-order sensitivities of the response with respect to the components , of the features functions. The dependence on the variations and has been replaced in the expression of by the dependence on the 1st-level adjoint sensitivity function . It is very important to note that the 1st-LASS is independent of variations in the components of the feature function and is consequently also independent of any variations in the primary model parameters. Hence, the 1st-LASS needs to be solved only once to determine the 1st-level adjoint sensitivity function . Subsequently, the “indirect-effect term” is computed efficiently and exactly by simply performing the integrations required to compute the inner product over the adjoint function , as indicated on the right-side of Equation (47). Solving the 1st-Level Adjoint Sensitivity System (1st-LASS) requires the same computational effort as solving the original coupled linear system, entailing the following operations: (i) inverting (i.e., solving) the left-side of the original adjoint equation with the source to obtain the 1st-level adjoint sensitivity function ; and (ii) inverting the left-side of the original forward equation with the source to obtain the 1st-level adjoint sensitivity function .
The 1
st-order sensitivities
,
, can be expressed as an integral over the independent variables as follows:
In particular, if the residual bilinear concomitant is non-zero, the functions would contain suitably defined Dirac delta-functionals for expressing the respective non-zero boundary terms as volume-integrals over the phase-space of the independent variables. Dirac-delta functionals would also be used in the expression of to represent terms containing the derivatives of the boundary end-points with respect to the model and/or response parameters.
The response sensitivities with respect to the primary model parameters would be obtained by using the expression obtained in Equation (48) in conjunction with the “chain rule” of differentiation provided in Equation (12).
It is important to compare the results produced by the 1
st-FASAM-L (for obtaining the sensitivities of the model response with respect to the model’s features) with the 1
st-CASAM (the
1st-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems) methodology, which provides the expressions of the responses sensitivities directly with respect to the model’s primary parameters. Recall that the 1
st-CASAM-L [
27] yields the following expression for the 1
st-order sensitivities of the response with respect to the primary model parameters:
The same 1
st-level adjoint sensitivity function, denoted as
, appears in Equation (49) as well as in Equation (48). Therefore, the same number of “large-scale computations” (which are needed to solve the 1
st-LASS to determine the 1
st-level adjoint sensitivity function) is needed for obtaining either the response sensitivities with respect to the components,
,
, of the feature function
using the c, or for obtaining the response sensitivities directly with respect to the primary model parameters
,
, by using the 1
st-CASAM-L. The use of the 1
st-CASAM-L would also require performing a number of
integrations to compute all of the response sensitivities with respect to the primary parameters; in contradistinction, the use of the 1
st-FASAM-L would require only
integrations (
) to compute all of the response sensitivities with respect to the components
of the feature function. Since integrations using quadrature-scheme are significantly less expensive computationally by comparison to solving systems of equations (e.g., the original equations underlying the model and the 1
st-LASS), the computational savings provided by the use of the 1
st-FASAM-L is small by comparison to using the 1
st-CASAM-L. However, this conclusion is valid only for the computation of 1
st-order sensitivities. As will be shown in
Section 4, below, the computational savings are significantly larger when computing the second-order sensitivities by using the 2
nd-FASAM-L rather than using the 2
nd-CASAM-L (or any other method).
4. The Second-Order Function/Feature Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward and Adjoint Linear Systems (2nd-FASAM-L)
The “Second-Order Function/Feature Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems“ (2nd-FASAM-L) determines the 2nd-order sensitivities of the response with respect to the components of the “feature” function by conceptually considering that the first-order sensitivities , which were obtained in Equation (48), are “model responses.” Consequently, the 2nd-order sensitivities are obtained as the “1st-order sensitivities of the 1st-order sensitivities” by applying the concepts underlying 1st-FASAM to each 1st-order sensitivity , , which depends on both the vector , which comprises the original state variables, as well as on the 1st-level adjoint function .
To establish the pattern underlying the computation of sensitivities of arbitrarily high-order, it is useful to introduce a systematic classification of the systems of equations that will underly the computation of the sensitivities of various orders. As has been shown in the Section 2.1, above, the 1
st-order response sensitivities
depend on the original state functions
and on the 1
st-level adjoint sensitivity function
. The system of equations satisfied by these functions will be called “
the 2nd-Level Forward/Adjoint System (2nd-LFAS)” and will be re-written in the following concatenated form:
where the following definitions were used:
The notation used for the matrix indicates the following characteristics: (i) the superscript “2” indicates “2nd-level”; (ii) the argument “” indicates that this square matrix comprises 4x4=16 component sub-matrices. Similarly, the argument “22” that appears in the block-vectors , and indicates that each of these column block-vectors comprises four sub-vectors as components.
The first-order G-differential of a first-order sensitivity
,
, is obtained by definition as follows:
The direct-effect term
in Equation (54) is defined as follows
and can be computed immediately. The indirect-effect term
in Equation (54) depends on the 2
nd-level variational sensitivity function
and is defined as follows:
where:
Evidently, the functions
and
are needed in order to evaluate the above indirect-effect term. These functions are the solutions of the system of equations obtained by taking the first-G-differential of the 2
nd-LFAS defined by Eqs. (52) and (53). Applying the definition of the first G-differential the 2
nd-LFAS yields the following
2nd-Level Variational Sensitivity System (2nd-LVSS)” for the
2nd-Level variational sensitivity function :
Carrying out the differentiation with respect to
in Eqs. (58) and (59), and setting
in the resulting expressions yields the following 2
nd-LVSS:
where the following definitions were used:
The matrix depends only the system’s response and is responsible for coupling the forward and adjoint systems. Although the forward and adjoint systems are coupled, they could nevertheless be solved successively rather than simultaneously, because the matrix is block-diagonal. All of the components of the matrices and vectors underlying the 2nd-LVSS are to be computed at nominal parameter and state function values, as indicated in Eqs. (60) and (61).
Computing the indirect-effect term by solving the 2nd-LVSS would require at least large-scale computations (to solve the 2nd-LVSS) for every component of the feature function .
The need for solving the 2
nd-LVSS will be circumvented by deriving an alternative expression for the indirect-effect term
, as defined in Equation (56), in which the second-level
variational function
will be replaced by a 2
nd-level
adjoint function which is independent of variations in the model parameter and state functions. This 2
nd-level adjoint function will be the solution of a 2
nd-Level Adjoint Sensitivity System (2
nd-LASS), which will be constructed by using the same principles as employed for deriving the 1
st-LASS. The 2
nd-LASS is constructed in a Hilbert space, denoted as
, which will comprise as elements block-vectors of the same form as
, i.e., a vector in
has the generic structure
, comprising four vector-valued components of the form
. The inner product between two elements,
and
, of this Hilbert space, will be denoted as
and is defined as follows:
Note that there are distinct indirect-effect terms . Each of these indirect-effect terms will serve as a “source” for a “2nd-Level Adjoint Sensitivity System (2nd-LASS)” that will be constructed by applying the same sequence of steps that were used in Section 2.1, above, to construct the 1st-LASS. This implies that a distinct 2nd-level adjoint sensitivity function, of the form , , corresponding to each distinct indirect-effect term, will be needed for constructing each of the corresponding 2nd-LASS, as follows:
For each
, form the inner product in the Hilbert space
of Equation (60) with a yet undefined function
to obtain the following relation:
Using the definition of the adjoint operator in the Hilbert space
, recast the left-side of Equation (68) as follows:
where
denotes the bilinear concomitant defined on the phase-space boundary
and where
is the operator formally adjoint to
.
The first term on right-side of Equation (69) is now required to represent the indirect-effect term
defined in Equation (56). This requirement is satisfied by recalling Equation (57) and imposing the following relation on each function
,
:
The definition of the vector
will now be completed by selecting boundary conditions which will be represented in operator form as follows:
The boundary conditions represented by Equation (71) are selected so as to satisfy the following requirements: (a) these boundary conditions together with Equation (70) constitute a well posed problem for the functions ; (b) the implementation in Equation (69) of these boundary conditions together with those provided in Equation (61) eliminates all of the unknown values of the functions and in the expression of the bilinear concomitant . This bilinear concomitant may vanish after these boundary conditions are implemented, but if it does not, it will be reduced to a residual quantity which will be denoted as and which will comprise only known values of , , and .
The system of equations represented by Equation (70) together with the boundary conditions represented by Equation (71) constitute the 2nd-Level Adjoint Sensitivity System (2nd-LASS). The solution of the 2nd-LASS, i.e., the four-component vector , , will be called the 2nd-level adjoint sensitivity function. It is important to note that the 2nd-LASS is independent of any variations, , in the components of the feature function and, hence, is independent of any parameter variations, , as well.
The equations underlying the 2
nd-LASS, represented by Eqs. (70), (71), together with the equations underlying the 2
nd-LVSS, represented by Eqs. (60) and (61), are now employed in Equation (69) in conjunction with Equation (56) to obtain the following expression for the indirect-effect term
in terms of the 2
nd-level adjoint sensitivity functions
, for
:
As the last equality (identity) in Equation (72) indicates, the 2nd-level variational sensitivity function has been eliminated from appearing in the expression of the indirect-effect term, having been replaced by the 2nd-level adjoint sensitivity function , for each .
Inserting the expressions that define the vector
from Equation (63)‒(65) into Equation (72) and adding the resulting expression for the indirect-effect term to the expression of the direct-effect term given in Equation (54) yields the following expression for the total second-order G-differential of the response
:
where
denotes the
2nd-order partial sensitivity of the response
with respect to the components
of the feature function
, evaluated at the nominal parameter values
, and has the following expression for
:
Since the
2nd-LASS is independent of variations in the components of the feature-functions (and, hence, variations in the model parameters), the exact computation of all of the partial second-order sensitivities
requires at most
large-scale (adjoint) computations using the 2
nd-LASS. When the 2
nd-LASS is solved
-times, the “off-diagonal” 2
nd-order mixed sensitivities
will be computed twice, in two different ways, using two distinct 2
nd-level adjoint sensitivity functions, thereby providing an independent intrinsic (numerical) verification that the 1
st- and 2
nd-order response sensitivities with respect to the components of the feature functions are computed accurately. In component form, the equations comprising the 2
nd-LASS are solved, for each
, in the following order:
Dirac delta-functionals may need to be used in Equation (74) in order to express in integral form the eventual non-zero residual terms in the residual bilinear concomitant and/or the terms containing derivatives with respect to the lower- and upper-boundary points. Ultimately, the expression of the partial second-order sensitivities
obtained in Equation (74) is written in the following integral form, which mirrors Equation (48):
The computation of the partial second-order sensitivities using Equation (74) requires quadratures for performing the integrations over the four components of the 2nd-level adjoint sensitivity function , which are obtained by solving the 2nd-LASS for . Thus, obtaining all of the second-order sensitivities with respect to the components of the feature function requires performing at most large-scale computations for solving the 2nd-LASS.
By comparison, if the 2
nd-CASAM-L [
27] had been applied to compute the second-order sensitivities of the response directly with respect to the model parameters,
(instead of
) large-scale computations for solving the corresponding 2
nd-LASS would have been required, where
denotes the total number of primary model parameters. Since
, fewer large-scale computations are needed when using the 2
nd-FASAM-L rather than the 2
nd-CASAM-L. Notably, the left-sides of the 2
nd-LASS to be solved within the 2
nd-FASAM-L are the same as those to be solved within the 2
nd-CASAM-L. However, the source terms on the right-sides of these 2
nd-LASS are different from each other: there are as many source-terms on the right-sides as there are components of the feature function within the 2
nd-FASAM-L, and there are as many right-side sources as there are primary model parameters within the 2
nd-CASAM-L.
5. Illustrative High-Order Feature Adjoint Sensitivity Analysis of Energy-Dependent Particle Detector Response
The application of the n
th-FASAM-L methodology will be illustrated in this Section by considering the simplified model of the distribution in the asymptotic energy range of neutrons produced by a source of neutrons placed in an isotropic medium comprising a homogeneous mixture of “
M” non-fissionable materials having constant (i.e., energy-independent) properties. For simplicity, but without diminishing the applicability of the n
th-FASAM-L methodology, this medium is considered to be infinitely large. The simplified neutron transport equation that models the energy-distributions of neutrons in such materials is called the “neutron slowing-down equation” and is written using the neutron
lethargy (rather than the neutron energy) as the independent variable, which is denoted as “
u” and is defined as follows:
, where
denotes the energy-variable and
denotes the highest energy in the system. Thus, the neutron slowing-down model [
32,
33,
34] for the energy-distribution of the neutron flux in a homogeneous mixture of non-fissionable materials of infinite extent takes on the following drastically simplified form of the neutron transport balance equation:
The quantities which appear in Equation (80) are defined below.
- (1)
The lethargy-dependent neutron flux is denoted as ; denotes a cut-off lethargy, usually taken to be the lethargy that corresponds to the thermal neutron energy (ca. 0.0024 electron-volts).
- (2)
The macroscopic elastic scattering cross section for the homogeneous mixture of “
M” materials is denoted as
and is defined as follows:
where
denotes the elastic scattering cross section of material “
i”, and where the atomic or molecular number density of material “
i” is denoted as
and is defined as follows:
, where
is Avogadro’s number
, while
and
denote the respective material’s mass number and density.
- (3)
The average gain in lethargy of a neutron per collision is denoted as
and is defined as follows for the homogeneous mixture:
- (4)
The macroscopic absorption cross section is denoted as
and is defined as follows for the homogeneous mixture:
where
, denotes the microscopic radiative-capture cross section of material “
i”.
- (5)
The macroscopic total cross section is denoted as
and is defined as follows for the homogeneous mixture:
- (6)
The source
is considered to be a simplified “spontaneous fission” source stemming from fissionable actinides, such as
239Pu and
240Pu, emitting monoenergetic neutrons at the highest energy (i.e., zero lethargy). Such a source is comprised within the OECD/NEA polyethylene-reflected plutonium (PERP) OECD/NEA reactor physics benchmark [
21,
22] which can be modeled by the following simplified expression:
where the superscript “
S” indicates “source;” the subscript index
k=1 indicates material properties pertaining to the isotope
239Pu; the subscript index
k=2 indicates material properties pertaining to the isotope
240Pu;
denotes the decay constant;
denotes the atomic density of the respective actinide;
denotes the spontaneous fission branching ratio;
denotes the average number of neutrons per spontaneous fission;
denotes a function of parameters used in a Watt’s fission spectrum to approximate the spontaneous fission neutron spectrum of the respective actinide. The detailed forms of the parameters
are unimportant for illustrating the application of the n
th-FASAM-L methodology. The nominal values for these imprecisely known parameters are available from a library file contained in SOURCES4C [
26].
The response considered for the above neutron slowing-down model is the reaction rate, denoted as
, of neutrons of energy
that would be measured by a detector characterized by an interaction cross section
, where
denotes the atomic or molecular number density of the detector’s material while
denotes the detector’s microscopic interaction cross section. Mathematically, the detector’s reaction rate can be represented by the following functional of the neutron flux
:
For this “source-detector” model, the following primary model parameters are subject to experimental uncertainties:
(i) the atomic number densities ; the microscopic radiative-capture cross section ; the scattering cross section , for each material “i”, , included in the homogeneous mixture;
(ii) the source parameters ,, , , , for k=1,2;
(iii) the atomic density and the microscopic interaction cross section that characterize the detector’s material.
These above primary parameters are considered to constitute the components of a “vector of primary model parameters” defined as follows:
On the other hand, the structure of the computational model comprising Eqs. (80), (81) and (87) suggests that the components
of the feature function
can be defined as follows:
Solving Eqs. (80) and (81) while using the definitions introduced in Equation (89) yields the following expression for the flux
in terms of the components
of the feature function
:
In terms of the components
of the feature function
, the model’s response takes on the following expression:
As Equation (91) indicates, the model response can be considered to depend directly on primary model parameters. Alternatively, the model response can be considered to depend directly on 3 feature functions and only indirectly (through the 3 feature functions) on the primary model parameters. In the former consideration/interpretation, the response sensitivities to the primary model parameters will be obtained by applying the nth-CASAM-L methodology. In the later consideration/interpretation, the response sensitivities to the primary model parameters will be obtained by applying the nth-FASAM-L methodology, which will involve two stages, as follows: the response sensitivities with respect to the feature functions will be obtained in the first stage, while the subsequent computation of the response sensitivities to the primary model parameters will be performed in the second stage, by using the response sensitivities with respect to the feature functions obtained in the first stage. The computational distinctions that stem from these differing considerations/interpretations within the nth-CASAM-L methodology versus the nth-FASAM-L methodology will become evident in the remainder of this Section by means of using the illustrative neutron slowing-down model, which is representative of the general situation for any linear system.
According to the “reciprocity relation” for linear systems highlighted in Equation (8), the detector response defined in Equation (87) can be alternatively expressed in terms of the solution of the “adjoint slowing-down model”, i.e., the model that would be adjoint to the forward slowing-down model represented by Eqs. (80) and (81). The “adjoint slowing-down model” is constructed in the Hilbert space
of all square-integrable functions
,
endowed with the following inner product, denoted as
:
Using the inner product
defined in Equation (92), the adjoint slowing-down model is constructed by the usual procedure, namely: (i) construct the inner product of Equation (80) with a function
; (ii) integrate by parts the resulting relation so as to transfer the differential operation from the forward function
onto the adjoint function
; (iii) use the initial condition provided in Equation (81) and eliminate the unknown function
by choosing the final-value condition
; (iv) choose the source for the resulting adjoint slowing-down model so as to satisfy the reciprocity relation shown in Equation (8). The result of these operations is the following adjoint slowing down model for the adjoint slowing-down function
:
In terms of the adjoint slowing-down function
, the detector response takes on the following alternative expression:
The correctness of the alternative expression for the detector response provided in Equation (95) can be readily verified by solving the adjoint slowing down equation to obtain the following closed form expression for the adjoint slowing-down function
:
and subsequently inserting the above expression into Equation (95) to obtain the same final result as was obtained in Equation (91) in terms of the forward slowing-down flux
.
5.1. First-Order Adjoint Sensitivity Analysis: 1st-FASAM-L Versus 1st-CASAM-L
In this Subsection, the computation of the first-order sensitivities of the response with respect to the primary model parameters will first be demonstrated by using the 1st-FASAM-L. Subsequently, the same first-order sensitivities will be obtained by using the 1st-CASAM-L and the two alternative paths will be compared to each other, showing that the same expressions are obtained for the respective sensitivities, as expected. Although the computational efforts are not identical, they are comparable in terms of efficiency, with a slight advantage for the 1st-FASAM-L methodology.
5.1.1. Application of the 1st-FASAM-L
The 1
st-FASAM-L will be applied to the neutron slowing-down paradigm illustrative model by following the principles outlined in
Section 3. In this case, the model response is written in terms of the feature functions as follows:
where the flux
is the solution of the
1st-Level Forward/Adjoint System (1st-LFAS) comprising Eqs. (80) and (81), where Equation (80) is written in terms of the feature functions as follows:
The first-order sensitivities of the response
with respect to the components of the feature function
are provided by the first-order Gateaux (G-)variation
of
, for variations
and
around the phase-space point
, as shown in Equation (18), to obtain:
where the “direct-effect” term
and, respectively, the “indirect-effect” term
are defined as follows:
The “1
st-level variational sensitivity function”
is obtained as the solution of the “1
st-Level Variational Sensitivity System (1
st-LVSS)” obtained by taking the first-order G-differentials of the 1
st-LFAS defined by Eqs. (98) and (81), which are derived as shown in Eqs. (28) and (29), to obtain:
Carrying out the differentiations with respect to
in the above equations and setting
in the resulting expressions yields the following 1
st-LVSS:
For further reference, the closed-form solution of the above 1
st-LVSS has the following expression:
In principle, the above expression for
could be used in Equation (101) to obtain the value if the indirect-effect term. In practice, however, the 1
st-LVSS cannot be solved analytically so the closed form expression of
is not available. Consequently, rather than (numerically) solve repeatedly the 1
st-LVSS for every possible variation induced by the primary parameters in the component feature functions, the alternative route to determining the expression of the indirect-effect term is to develop the 1
st-Level Adjoint sensitivity System (1
st-LASS) by following the procedure described in
Section 3. The Hilbert space, denoted as
, appropriate for this illustrative model is the space of all square-integrable functions endowed with the following inner product, denoted as
, between two elements,
,
, belonging to this Hilbert space:
In this particular instance, the Hilbert space coincides with the original Hilbert space used for the original forward and adjoint slowing down models. More generally, similar situations occur when the response depends either just on the forward or just on the adjoint state function(s).
Using Equation (107), construct in the Hilbert space
the inner product of Equation (104) with a square-integrable function
to obtain the following relation:
Using the definition of the adjoint operator in the Hilbert space
, which in this case amounts to integration by parts of the left-side of Equation (108), obtain the following relation:
Require the first term on right-side of Equation (109) to represent the indirect-effect term defined in Equation (101), to obtain the following relation:
Implement the boundary conditions represented by Equation (105) into Equation (109) and eliminate the unknown boundary-value
from this relation by imposing the following boundary condition:
The system of equations comprising Equation (110) together with the boundary condition represented Equation (111) is the 1st-Level Adjoint Sensitivity System (1st-LASS) and its solution is the 1st-level adjoint sensitivity function.
Using Equation (101), together with the equations underlying the 1
st-LASS and 1
st-LVSS in Equation (108) reduces the latter to the following expression for the indirect-effect term:
Adding the expression obtained in Equation (112) with the expression for the direct-effect term defined in Equation (100) yields the following expression for the total 1
st-order variation
of the response
with respect to the components of the feature function
:
The identity which appears in Equation (113) emphasizes the fact that “1st-level variational sensitivity function” , which is expensive to compute, has been eliminated from the final expression of the 1st-order total variation , being replaced by the dependence on the 1st-level adjoint sensitivity function , which is independent of variations in the components of the feature function and is consequently also independent of any variations in the primary model parameters. Hence, the 1st-LASS needs to be solved only once to determine the 1st-level adjoint sensitivity function , which requires the same amount of computational effort as solving the original forward system for the function .
The expressions of the sensitivities of the response
with respect to the components of the feature function
are given by the expressions that multiply the respective components of
in Equation (113), namely:
The above expressions are to be evaluated at the nominal parameter values but the indication has been omitted for simplicity.
Solving the 1
st-LASS yields the following closed-form expression for the 1
st-level adjoint sensitivity function
:
where the Heaviside functional has the usual meaning, namely:
and
.
Inserting the expression obtained in Equation (117) into Eqs. (114)‒(116) yields the following closed-form expressions for the sensitivities of the response
with respect to the components of the feature function
:
The correctness of the expressions obtained in Eqs. (118)‒(120) can be verified by directly differentiating the closed-form expression given in Equation (91).
Alternatively, the 1st-FASAM-L methodology could have been applied to the alternative expression, in terms of the adjoint slowing-down function, for the detector response provided in Equation (95). It can be verified that the final expressions for the response sensitivities with respect to the feature functions , , obtained by using Equation (95) as the starting point in conjunction with the adjoint slowing-down model are the same as obtained in Eqs. (118)‒(120).
The expressions of the first-order sensitivities of the response
with respect to the primary model parameters
,
, as defined in Equation (88), are obtained by using the expressions obtained in Eqs. (118)‒(120) in conjunction with the chain rule of differentiation of the compound functions
,
. Note that the feature function
depends only on the parameters that characterize the detector, so the first-order sensitivities of the response
with respect to the primary model parameters
and
can be readily obtained by using Equation (120), as follows:
Similarly, the primary model parameters
that characterize the neutron source distribution only appear through the definition of the feature function
. It therefore follows that the first-order sensitivities of the response
with respect to these primary model parameters are obtained as follows:
On the other hand, the primary model parameters
that characterize the composition of the homogenized material in which the neutrons slow-down appear through the definitions of both feature functions
and
. It therefore follows that the first-order sensitivities of the response
with respect to these primary model parameters are obtained as follows:
The explicit differentiations in Eqs. (128)‒(130) are straightforward to perform, but are too lengthy to be presented here and are not material to applying the principles of the 1st-FASAM-L methodology.
In summary, the application of the 1st-FASAM-L to compute the first-order sensitivities of the response with respect to the primary model parameters , , requires the following computations:
One “large-scale” computation to solve the 1st-LASS to obtain the 1st-level adjoint sensitivity function .
Three “quadratures”, as indicated in Eqs. (114)‒(116), involving the 1st-level adjoint sensitivity function to obtain the three sensitivities of the response with respect to the components , , of the feature function . These computations are inexpensive.
Chain-rule type differentiations using the definitions of the components , of the feature function , and the three sensitivities obtained in Eqs. (114)‒(116). These computations are inexpensive.
5.1.2. Application of the 1st-CASAM-L
The application of the 1
st-CASAM-L methodology will yield the first-order response sensitivities directly with respect to the primary model parameters. These sensitivities will be obtained by determining the first-order Gateaux (G-) variation
of the response
as for variations
and
around the phase-space point
, using the definition provided in Equation (87), to obtain:
where the “direct-effect” term
and, respectively, the “indirect-effect” term
are defined as follows:
The “1
st-level variational sensitivity function”
is obtained as the solution of the “1
st-Level Variational Sensitivity System (1
st-LVSS)” obtained by taking the first-order G-differentials of the 1
st-LFAS defined by Eqs. (80) and (81) to obtain:
Carrying out the differentiations with respect to
in the above equations and setting
in the resulting expressions yields the following 1
st-LVSS:
To avoid solving the above the 1
st-LVSS repeatedly, for every possible variation in the primary parameters, the appearance of the function
will be eliminated for the expression of the indirect-effect term by replacing it with the solution of the 1
st-Level Adjoint Sensitivity System (1
st-LASS) which will be constructed in the Hilbert space
, as before: use Equation (107) to form the inner product of Equation (136) with a square-integrable function
to obtain the following relation:
Integration by parts of the left-side of Equation (138) yields the following relation:
Requiring the first term on right-side of Equation (139) to represent the indirect-effect term defined in Equation (133) yields the following relation:
Eliminate the unknown boundary-value
from Equation (139) by imposing the following boundary condition:
The system of equations comprising Eqs. (140) and (141) is the
1st-Level Adjoint Sensitivity System (1
st-LASS) and its solution
is the
1st-level adjoint sensitivity function. As already shown in the general 1
st-FASAM methodology presented in
Section 3, the 1
st-LASS which arises within the framework of the 1
st-CASAM-L is identical to the 1
st-LASS that arises within the 1
st-FASAM methodology, which is the reason underlying the use of the same notation for the 1
st-level adjoint sensitivity function, namely
, in both cases.
Implementing the equations underlying the 1
st-LASS and 1
st-LVSS into Equation (138) and recalling the expression of the indirect-effect term provided in Equation (133) yields the following expression for the indirect-effect term:
Adding the expression obtained in Equation (142) with the expression for the direct-effect term defined in Equation (132) yields the following expression for the total 1
st-order variation
of the response
with respect to the components of the feature function
:
The identity which appears in Equation (143) emphasizes the fact that “1st-level variational sensitivity function” , which is expensive to compute, has been eliminated from the final expression of the 1st-order total variation , being replaced by the dependence on the 1st-level adjoint sensitivity function , which is independent of any variations in the primary model parameters. Hence, the 1st-LASS needs to be solved only once to determine the 1st-level adjoint sensitivity function , which requires the same amount of computational effort as solving the original forward system for the function .
The expressions of the first-order sensitivities of the response
with respect to the primary model parameters are the expressions that multiply the corresponding parameter variations
in Equation (143). In particular, the (two) first-order sensitivities of the response
with respect to the primary model parameters underlying the detector’s interaction cross section arise solely from the direct-effect term and have the following expressions:
The above expressions are to be evaluated at the nominal parameter values but the indication has been omitted for simplicity. As expected, the above expressions are identical to the corresponding expressions obtained using the 1st-FASAM-L, as provided in Eqs. (121) and (122), respectively.
The first-order sensitivities of the response
with respect to the primary model parameters underlying the spontaneous fission source arise solely from the first term on the right-side of Equation (143) and have the following expressions in terms of the 1
st-level adjoint sensitivity function
:
As expected, the above expressions are identical to the corresponding expressions obtained using the 1st-FASAM-L, as provided in Eqs. (123)‒(127), respectively.
The first-order sensitivities of the response
with respect to the primary model parameters
that characterize the composition of the homogenized material in which the neutrons slow-down arise from both the first and the second terms on the right-side of Equation (143) and have the following expressions in terms of the 1
st-level adjoint sensitivity function
:
As expected, the above expressions are identical to the corresponding expressions obtained using the 1st-FASAM-L, as provided in Eqs. (128)‒(130), respectively.
In summary, the application of the 1st-CASAM-L to compute the first-order sensitivities of the response with respect to the primary model parameters , , requires the following computations:
One “large-scale” computation to solve the 1st-LASS to obtain the 1st-level adjoint sensitivity function . As has been already remarked, this 1st-LASS is exactly the same as the 1st-LASS needed within the 1st-FASAM-L methodology for computing the first-order sensitivities of the response with respect to the components , , of the feature function .
A total of “quadratures” involving the 1st-level adjoint sensitivity function to obtain numerically the sensitivities of the response with respect to the primary model parameters , . These numerical computations are inexpensive by comparison to solving the 1st-LASS but are more expensive than performing “chain-rule”-type differentiation “on paper,” as performed if applying the 1st-FASAM-L. Hence, the 1st-FASAM-L methodology enjoys a slight computational advantage over the 1st-CASAM-L methodology.
5.2. Second-Order Adjoint Sensitivity Analysis: 2nd-FASAM-L Versus 2nd-CASAM-L
In this Subsection, the computation of the first-order sensitivities of the response with respect to the primary model parameters will first be demonstrated by using the 2nd-FASAM-L. Subsequently, the same first-order sensitivities will be obtained by using the 2nd-CASAM-L and the two alternative paths will be compared to each other, showing that the same expressions are obtained for the respective sensitivities, as expected. Both the 2nd-FASAM-L and the 2nd-CASAM-L methodologies obtain the second-order sensitivities by considering the first-order G-differential of each of the first-order sensitivities. Therefore, the 2nd-FASAM-L methodology will provide significant computational advantages by comparison to the 2nd-CASAM-L methodology the since it will require at most 3 large-scale computations, i.e., the same number of large-scale computations as the number of components , , of the feature function . In contradistinction, the 2nd-CASAM-L methodology will require one large-scale (adjoint) computation for each primary model parameter , , amounting to a total of number of large-scale computations.
5.2.1. Application of the 2nd-FASAM-L
As has been shown in
Section 4, the 2
nd-FASAM-L methodology generically determines the 2
nd-order sensitivities
of the response with respect to the components of the “feature” function
by conceptually considering that the first-order sensitivities
, are “model responses.” Consequently, the 2
nd-order sensitivities are obtained as the “1
st-order sensitivities of the 1
st-order sensitivities” by applying the concepts underlying 1
st-FASAM to each 1
st-order sensitivity
,
.
5.2.1.1. Second-Order Sensitivities Stemming From
The above principles will be applied to the first-order sensitivity
expressed by Equation (114) to obtain the second-order sensitivities of the form
,
. The argument “1” in the notation
indicates that this sensitivity is with respect to the
first component, namely
, of the feature function
, while also depending on the functions
and
. These functions are the solutions of the “2
nd-Level Forward/Adjoint System (2
nd-LFAS)” which is obtained by concatenating the original 1
st-Level Forward/Adjoint System (1st-LFAS) with the 1
st-Level Adjoint Sensitivity System (1
st-LASS), cf. Eqs. (98), (81), (110) and (111), as reproduced below:
The first-order G-differential of
is obtained from Equation (114), by definition, as follows:
Note that the first-order G-differential consists solely of the “indirect-effect term”; there is no “direct-effect” term since there is no explicit dependence on variations .
The variational functions
and
are the solutions of the system of equations obtained by taking the first-G-differential of the 2
nd-LFAS. Applying the definition of the first G-differential to the equations underlying the 2
nd-LFAS yields the following 2
nd-Level Variational Sensitivity System (2
nd-LVSS)” for the 2
nd-level variational sensitivity function
:
The above 2
nd-LVSS would need to be solved repeatedly, for every possible variation in the feature functions
,
. This need is circumvented by deriving an alternative expression for
, in which the 2
nd-level variational function
is replaced by a 2
nd-level adjoint sensitivity function which will be independent of variations in the feature functions
,
. This 2
nd-level adjoint sensitivity function will be the solution of a 2
nd-Level Adjoint Sensitivity System (2nd-LASS) to be constructed below by following the steps generally outlined in
Section 5, in a Hilbert space, denoted as
, which is endowed with the following inner product, denoted as
, between two elements,
and
:
Using Equation(161) to form the inner product in the Hilbert space
of the 2
nd-LVSS, cf. Eqs. (158) and (159), with a yet undefined function
yields the following relation:
The above relation holds for the nominal parameter values, but the notation has been omitted, for simplicity.
Using the definition of the adjoint operator in the Hilbert space
, which amounts to integration by parts, recast the left-side of Equation (162) into the form below:
The first two terms on right-side of Equation (163) are now required to represent the G-differential
defined in Equation (157), which yields the following relations:
The definition of the vector
will now be completed by selecting boundary conditions so as to eliminate the unknown values
and
in Equation (163). This is accomplished by imposing the following boundary conditions:
The system of equations represented by Eqs. (164) and (165) constitute the 2nd-Level Adjoint Sensitivity System (2nd-LASS) for the 2nd-level adjoint sensitivity function . It is important to note that the 2nd-LASS is independent of any variations, , in the components of the feature function and, hence, is independent of any parameter variations, , as well.
The equations underlying the 2
nd-LASS, together with the equations underlying the 2nd-LVSS, are now employed in Equation(162), in conjunction with Equation (163), to obtain the following expression for the G-differential
in terms of the 2nd-level adjoint sensitivity function
:
As the last equality (identity) in Equation (166) indicates, the 2
nd-level variational sensitivity function
has been eliminated from the final expression of the G-differential
, having been replaced by the 2
nd-level adjoint sensitivity function
. Identifying in Equation (166) the expressions that multiply the variations
,
, yields the following expressions for the second-order sensitivities of the response
with respect to the components of the feature function
:
The 2
nd-LASS can be solved to obtain the following closed-form expressions for the components of the 2
nd-level adjoint sensitivity function
;
Inserting the expressions obtained in Eqs. (170) and (171) into Eqs. (167)‒(169) and performing the respective integrations yields the following expressions for the respective second-order sensitivities:
The correctness of the expressions obtained in Eqs. (172)‒(174) can be verified by directly differentiating the closed-form expressions provided in Eqs. (118)‒(120).
5.2.1.2. Second-Order Sensitivities Stemming From
Applying the procedure used in the previous Subsection to the first-order sensitivity expressed by Equation (115) will provide the second-order sensitivities of the form , . The argument “2” in the notation indicates that this sensitivity is with respect to the second component, namely , of the feature function . Remarkably, this sensitivity does not depend on the forward function but only depends on the 1st-level adjoint sensitivity function . As previously discussed, these functions are the solutions of the “2nd-Level Forward/Adjoint System (2nd-LFAS).”
The first-order G-differential of
is obtained by applying its definition to Equation (115), as follows:
As indicated in Equation (175), the first-order G-differential
consists solely of the indirect-effect term which depends on the 1
st-level variational function
. As before, the need for computing this variational function is circumvented by constructing a 2
nd-Level Adjoint Sensitivity System (2
nd-LASS) for a 2
nd-level adjoint sensitivity function
, by implementing the same steps as outlined above for obtaining the 2
nd-order sensitivities that stem from the first-order sensitivity
, namely Eqs. (162)‒(165). These steps will not be repeated here in detail; they lead to the following 2
nd-LASS for 2
nd-level adjoint sensitivity function
:
Solving the 2
nd-LASS defined by Eqs. (176) and (177) yields the following closed-form expressions for the components of the 2
nd-level adjoint sensitivity function
:
.
The alternative expression of the G-differential
in terms of the 2
nd-level adjoint sensitivity function
has the following form (which is obtained by implementing the same steps as those leading to Equation (166), above):
Identifying in Equation (179) the expressions that multiply the variations
,
, yields the following second-order sensitivities of the response
with respect to the components of the feature function
:
Inserting the expression obtained for
in Equation (178) into Eqs. (180) and (182), and performing the respective integrations yields the following expressions for the respective second-order sensitivities:
The correctness of the expressions obtained in Eqs. (183) and (184) can be verified by directly differentiating accordingly the closed-form expressions given in Eqs. (118)‒(120).
5.2.1.3. Second-Order Sensitivities Stemming From
Applying the above principles to the first-order sensitivity obtained in Equation (116) will provide the second-order sensitivities of the form , . The argument “3” in the notation indicates that this sensitivity is with respect to the third component, namely , of the feature function . Notably, this sensitivity depends on the forward function but does not depend on the 1st-level adjoint sensitivity function .
The first-order G-differential of
is obtained, by definition, as follows:
Note that the first-order G-differential
consists solely of the indirect-effect term. As before, the need for computing the variational function
is circumvented by constructing a 2
nd-Level Adjoint Sensitivity System (2
nd-LASS) for a 2
nd-level adjoint sensitivity function
, by implementing the same steps were used for obtaining the previous 2
nd-order sensitivities. These steps lead to the following 2
nd-LASS for 2
nd-level adjoint sensitivity function
:
Solving the 2
nd-LASS defined by Eqs. (186) and (187) yields the following closed-form expressions for the components of the 2
nd-level adjoint sensitivity function
:
In terms of the 2
nd-level adjoint sensitivity function
the alternative expression of the G-differential
has the following form (which is obtained by implementing the same steps as those leading to Equation (166), above):
Identifying in Equation (189) the expressions that multiply the variations
,
, yields the following second-order sensitivities of the response
with respect to the components of the feature function
:
Inserting the expression obtained for
in Equation (188) into Eqs. (190) and (191), and performing the respective integrations yields the following expressions for the respective second-order sensitivities:
The correctness of the expressions obtained in Eqs. (193) and (194) can be verified by directly differentiating the closed-form expressions given in Eqs. (118)‒(120).
Summarizing the results obtained in Subsection 5.2.1 leads to the following conclusions:
The second-order sensitivities , , of the model response with respect to the three features components , , of the feature function are obtained by performing 3 “large-scale” computations to solve the 3 corresponding 2nd-LASS which all have the same left-side but have differing sources on their right-sides. The source-term for each of these 2nd-LASS corresponds to one of the 3 first-order sensitivities. Thus, computing the second-order sensitivities requires as many “large-scale” computations as there are non-zero first-order sensitivities, i.e., at most as many “large-scale” computations as there are components , , of the feature function .
The mixed second-order sensitivities , , are computed twice, involving distinct 2nd-level adjoint sensitivity functions. Therefore, the symmetry property provides an intrinsic mechanism for verifying the accuracy of the computations of the respective 2nd-level adjoint sensitivity functions.
The unmixed second order sensitivities , are computed just once.
5.2.2. Application of the 2nd-CASAM-L
The principles underlying the application of the 2nd-CASAM-L methodology are the same as those underlying the 2nd-FASAM-L methodology: both methodologies obtain the second-order sensitivities by considering the first-order G-differential of each of the first-order sensitivities. As has been shown in the foregoing, the 2nd-FASAM-L methodology requires at most 3 large-scale computations (i.e., the same number of large-scale computations as the number of components , , of the feature function ) for solving the three 2nd-Level Adjoint Sensitivity Systems that arise by considering the three first-order sensitivities of the detector response with respect to the three components of the feature function . In contradistinction, the 2nd-CASAM-L methodology requires one large-scale (adjoint) computation for each primary model parameter , , amounting to a total of number of large-scale computations. The specific computations are described below.
5.2.2.1. Second-Order Sensitivities Stemming from the First-Order Sensitivities with Respect to the Medium’s Material Properties
The expressions of the first-order sensitivities of the detector response with respect to the material properties (i.e., microscopic cross sections and atomic number densities) of the medium in which the neutrons are slowing-down (i.e., losing energy or, equivalently, gaining lethargy) are provided in Eqs. (151)‒(153). These expressions have the following generic form:
where
,
,
, and
The second-order sensitivities stemming from the first-order sensitivities represented by Equation (195) are obtained from the first G-differential of this equation, which has the following expression, by definition, for each
:
where:
The direct-effect term can be computed immediately, since all quantities are known. The indirect-effect term can be computed, in principle, after solving the 2
nd-LVSS to obtain the 2
nd-level variational sensitivity function
. As has been repeatedly discussed in the foregoing, solving the 2
nd-LVSS is expensive computationally, so this variational function is replaced in the expression of the indirect-effect term by a 2
nd-level adjoint sensitivity function, by following the same steps as outlined in
Section 5.2.1. Since there are
first-order sensitivities of the form
,
there will be
distinct 2
nd-level adjoint sensitivity functions, one corresponding to each first-order sensitivity. These
distinct 2
nd-level adjoint sensitivity functions will be the solutions of the corresponding
distinct 2
nd-Level Adjoint Sensitivity Systems (2
nd-LASS). Each of these
2
nd-LASS will have a distinct source-term on the right-side (each distinct source stemming from the corresponding first-order sensitivities of the form
), but all of these
2
nd-LASS will have the same left-sides, which will have the same form as the left-side of the 2
nd-LASS needed previously, in Subsection 5.2.1 for the computations of the 2
nd-order sensitivities of the response with respect to the components of the feature functions, cf. Equation (164), (176), and (186). Since the left-sides of these 2
nd-LASS represent the (differential) operators that need to be inverted, the actual inversion of these operators needs to be performed once only, and the inverted operator should be stored; subsequently, the inverted operator can be used
times, operating on
distinct source terms, to compute the respective
distinct 2
nd-level adjoint sensitivity functions.
5.2.2.2. Second-Order Sensitivities Stemming from the First-Order Sensitivities with Respect to the Source Properties
The expressions of the first-order sensitivities of the detector response with respect to the parameters that characterize the source which emits the neutrons into the medium are provided in Eqs. (146)‒(150). These expressions have the following generic form:
where:
The second-order sensitivities stemming from the first-order sensitivities represented by Equation (202) are obtained from the first G-differential of this relation, which has the following expression, by definition, for each
;
:
where:
The direct-effect term can be computed immediately, since all quantities are known. The indirect-effect term can be computed, in principle, after solving the 2
nd-LVSS to obtain the 2
nd-level variational sensitivity function
, but this path is expensive computationally, so this variational function is replaced in the expression of the indirect-effect term by a 2
nd-level adjoint sensitivity function, by following the same steps as outlined in
Section 5.2.1. Since there are 10 first-order sensitivities of the form
,
;
, there will be 10 distinct 2
nd-level adjoint sensitivity functions, one corresponding to each first-order sensitivity. Thus, there will be 10 distinct 2
nd-Level Adjoint Sensitivity Systems (2
nd-LASS) to be solved, each having a distinct source-term on the right-side, but all of them having the same left-sides as the left-side of the 2
nd-LASS needed previously, in Subsection 5.2.1 for the computations of the 2
nd-order sensitivities of the response with respect to the components of the feature functions, namely Eqs. (164), (176), and (186).
5.2.2.3 Second-Order Sensitivities Stemming from the First-Order Sensitivities with Respect to the Detector Properties
The expressions of the first-order sensitivities of the detector response with respect to the detector’s material properties (i.e., microscopic cross section and atomic number density) are provided in Eqs. (144) and (145). These expressions have the following generic form:
where:
The second-order sensitivities stemming from the first-order sensitivities represented by Equation (211) are obtained by determining the first G-differential of this relation, which has the following expression, by definition, for each
:
where:
The direct-effect term can be computed immediately, since all quantities are known. The indirect-effect term can be computed, in principle, after solving the 2
nd-LVSS to obtain the 2
nd-level variational sensitivity function
, but this path is expensive computationally. As before, this variational function is replaced in the expression of the indirect-effect term by a 2
nd-level adjoint sensitivity function, by following the same steps as outlined in
Section 5.2.1. Since there are 2 first-order sensitivities of the form
,
, there will be 2 distinct 2
nd-level adjoint sensitivity functions, one corresponding to each first-order sensitivity. As before, the two 2
nd-LASS to be solved have distinct source-terms on their right-sides, but both have the same left-sides as the left-side of the 2
nd-LASS needed previously, as in Eqs. (164), (176), and (186).
In summary, the results discussed in Subsection 5.2.2 indicate that computing the 2nd-order sensitivities of the model response directly with respect to the primary model parameters, , by applying the 2nd-CASAM-L methodology requires one large-scale (adjoint) computation for each primary model parameter , amounting to a total of number of large-scale computations for solving the respective 2nd-LASS. All of these 2nd-LASS have the same left-side (which is also the same as needed for computing the 2nd-order sensitivities of the response with respect to the feature functions by applying the 2nd-FASAM-L) but have differing sources on their right-sides. The unmixed second order sensitivities , are computed just once. The mixed second order sensitivities , , are computed twice, involving distinct 2nd-level adjoint sensitivity functions. Therefore, the symmetry property provides an intrinsic mechanism for verifying the accuracy of the computations of the respective 2nd-level adjoint sensitivity functions.