Prerpints.org logo
Preprint
Article

Correctness Verification of Mutual Exclusion Algorithms by Model Checking

Altmetrics

Downloads

121

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 April 2024

Posted:

05 April 2024

You are already at the latest version

Alerts
Abstract
Mutual exclusion algorithms are at the heart of concurrent, distributed/parallel, real-time and operating systems. It is well-known that such algorithms are very difficult to analyze and in the literature different conjectures about starvation-freedom and the number of by-passes (also said the overtaking factor), which in turn affects the (hopefully) bounded waiting time that a process competing for entering the critical section has to suffer before accessing the shared resource, have been formulated for specific algorithms. This paper proposes a novel modelling approach based on Timed Automata and the Uppaal toolset, which proves effective for studying all the properties of a mutual exclusion algorithm for N≥2 processes, by exhaustive model checking. Although the approach, as already confirmed by similar experiments reported in the literature, is not scalable due to state explosion problems, and can be practically applied until N≤5, it is of great value for revealing true properties of analyzed algorithms. For dimensions N>5 the statistical model checker of Uppaal can be used which, although based on simulations, can confirm properties by estimations and probabilities. The paper describes the proposed modelling and verification method and applies it to several mutual exclusion algorithms, thus retrieving known properties but also showing new results about properties often studied only by peer-review and intuitive reasoning.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

Mutual exclusion (ME) [1,2] is a fundamental problem in the concurrent, distributed, real-time programming domains [3,4,5,6,7]. It can stated as follows. We have a software system with N ≥ 2 processes which compete for the use of a shared resource R . For predictability and deterministic evolution of the system behavior, only one process at a time should be allowed to be in use of the resource. The code executed by the process when it is using the resource constitutes its atomic critical section. Other properties of a ME algorithm include: (a) progress, that is a process competing for accessing the resource eventually gets the permission to use the resource; (b) absence of deadlocks; (c) no process should experiment starvation, in other terms a competing process should not suffer from an unbounded waiting, or an unbounded number of by-passes/overtakings from other competing processes.
ME solutions typically can be provided by a high-level or low-level abstraction context. High-level ME mechanisms can directly be provided by a programming language (e.g., Java) and accompanying library, and include semaphores, locks or monitor constructs [8]. Such solutions, though, ultimately depend on the mechanisms implemented in the underlying Operating Systems. Primitive ME solutions are required to give support to high-level mechanisms. Primitive ME solutions can be based on specialized hardware mechanisms, e.g., machine instructions like test-and-set, or they can be designed as pure software algorithms which depend on a (hopefully) few shared variables and a purposely designed, often ingenious, protocol which establishes the entry and exit code sections which processes have to obey respectively for competing and entering the resource and for releasing the resource at the end of the critical section.
This paper focusses on pure software ME primitive algorithms, whose properties can be very difficult to assess. In the literature, such algorithms are normally studied by peer-review and intuitive reasoning. More structured tools are represented by theorem provers [9] which can need a not easy formal mathematical representation of the algorithms and their data variables. Theorem provers, though, can be unable to reason on the time dimension of an ME solution.
This paper proposes an original modelling and verification approach based on the Timed Automata [10] and the Uppaal toolbox [11] which enable an automatic assessment of the properties of an ME algorithm through exhaustive model checking. Although the approach necessarily is not scalable due to the state explosion problems which inevitably intervene when considering a number of processes N > 5 , it is of great practical value for detecting true properties of ME solutions and to go beyond conjectures often formulated in the literature, particularly about the number of by-passes a process can be affected when competing together with its peers.
The paper significantly extends preliminary work and results of the authors as reported in two conference papers [12,13]. Differences from the previous authors’ work are as follows.
  • The modelling and verification method is completely re-designed and its semantics and transformation on to the Timed Automata of Uppaal clarified.
  • The novel approach is applied to several ME algorithms proposed in the literature, thus retrieving known results and properties but also, sometimes, discovering new features about specific ME solutions.
  • Both exhaustive model checking (MC) and statistical model checking (SMC) [14,15] can be exploited for property checking. Although SMC is based on simulations, properties of an ME algorithm for N ﹥ 5 processes can be extrapolated by estimations and probability, thus furnishing further arguments to the indications emerged by the exhaustive verification work accomplished until N ＝ 5 processes.
The paper is structured as follows. Section 2 presents an overview of the basic concepts of Timed Automata and Uppaal modelling. Section 3 describes the proposed modelling and verification method for mutual exclusion algorithms, and its semantic transformation on to Uppaal. Section 4 demonstrates by several examples the application and the experimental verification work carried out by using the proposed approach on representative mutual exclusion algorithms. Both the atomic and the week memory models are considered. The inter-play between the exhaustive model checking and the statistical model checking activities is clarified. Section 5, finally, concludes the paper and indicates some on-going and future work.

2. An Overview of Uppaal Timed Automata Modelling

Uppaal [15] is a popular modelling and verification toolbox for concurrent/distributed real-time systems. Power and flexibility of Uppaal derive from the adoption of a high-level version of Timed Automata (TA) [10] which are formal concurrent entities with an easy to understand graphical formulation. A model consists of a network of interacting TA. Interactions are based on unicast and broadcast channels and on global data of primitive types like integers and bools, plus structs and arrays. Unicast channels ensure two-way synchronizations in couples of TA (also said template processes, or parameterizable processes). The sender process of a unicast channel transmits (!) a signal toward a single receiver. The sender, though, gets blocked until the receiver is ready to receive (?) and vice versa (rendezvous). The synchronization does not carry any data or parameters which can easily be provided through the mediation of some global data variables. After the synchronization, both the sender and receiver resume their concurrent execution. Broadcast channels, instead, enable one-way synchronizations, where a single sender can synchronize with zero, one or multiple receivers. In other terms, the sender of a broadcast channel never blocks. Uppaal models are time-sensitive. The passage of time is controlled by clocks. A clock can be reset. A clock measures the time units elapsed from its last reset. All the clocks of a model grow according to the same rate. Time is assumed to be dense. A process automaton consists of locations linked by directed edges annotated by guarded commands. A location denotes a local state where the automaton can remain for a certain amount of time (including zero or possibly infinite time units). A normal location (see the NCS location in Figure 1) denotes a state where the automaton can stay for an arbitrary time. An invariant, that is a logical condition, e.g., based on a clock constraint, can restrict the permanence of the automaton in a normal location. In this case the location has to be abandoned before its invariant is up to become false. An urgent location (see locations with the internal U in Figure 3) has to be exited immediately, without time passage. A committed location (see the initial location with the internal C in Figure 2) is similar to an urgent location. However, Uppaal gives priority to committed locations which will be exited before the urgent ones. Among a same group of committed or urgent locations, the exit order is non-deterministic. A guarded command is composed of three optional attributes: a guard (a logical condition based on clock and/or data constraints) which is true by default when it is missing; a channel synchronization operation (? or !); an update component, that is a comma separated sequence of variable assignments and clock resets. A void command denotes a spontaneous edge. A spontaneous edge originating from a normal location, can be taken at any time, also after an infinite amount of time, that is the edge can possibly not taken at all. A guarded command represents the unit of concurrency of the Uppaal modelling language. When a channel synchronization involves two or more locations in different automata, a joint instantaneous exiting of the corresponding locations will occur. Semantics of Uppaal prescribes, in a joint synchronization in multiple automata, that the update operations in the sender precede the updates of the receivers (the order of the receiver updates is defined in the system declaration section).
Unicast and broadcast channels can be declared to be urgent. In this case, an enabled command involving an urgent synchronization, will be executed before any time passage. However, the order of exiting from multiple simultaneous urgent locations and normal locations with an exiting edge annotated with an enabled guard and an urgent synchronization is non-deterministic.
A distinguishing feature of the Uppaal modelling language which contributes to the creation of compact models is the possibility of exploiting C-like functions (see Algorithm 5 for an example) for defining the guard and/or the update components of commands.
The formal semantics of a Uppaal model can be defined by a Timed Transition System (TTS) defined as ( S , s 0 , → ) where S is a set of execution states of the model, s 0 is the initial state and → denotes the state relation which moves the current state to the next one. Two basic relations exist: the delay transition and the action transition. An action transition represents an instantaneous state change, e.g., tied to a joint synchronization in multiple automata. All the action transitions enabled in the current system state will be executed before time advancement. When no more actions exist to be executed at current time, the system time can be increased of a quantity δ whose amount is constrained by the fact of not falsifying any invariant in the whole model. The amount δ is added to all the model clock valuations. A particular model execution is represented by a sequence of delay/action transitions.
The Uppaal model checker (here refereed as U-MC), accepts a query formula (see Table 1 for examples) expressed according to a subset of the Timed Computational Tree Logic (TCTL) [11], builds the TTS of the model, referred to as the model state graph, and navigates the graph to prove/disprove the query. A query captures a property to be checked. Properties can be of safety (checking that a bad state is never reached) or liveness (checking that a good state is eventually reached) nature. A counterexample (said a diagnostic trace) can be built by U-MC to reproduce a sequence of transitions (events) which the modeler can analyze, in the symbolic simulator, to detect why a given formula was satisfied or not satisfied by the state graph. Nodes (execution states) of the state graph are made up of two parts: a data part, and a time zone. The time zone represents, by a system of clock inequalities, all the possible (also infinite) time instants for reaching the given state. A node of the state graph is actually an equivalence class: it represents all the states having the same data, and whose occurrence times are solutions of the time zone inequality system. Each arc exiting from a state node and linking to a next state node is labelled with the delay or action transition which causes it.
Complexity of the state graph is exponential in the number of clocks. However, it is not the absolute number of clocks used in the model which matters, but rather the maximum number of simultaneous active clocks, that is the maximum parallelism degree of the model. An active clock is one which is currently used in an invariant or in a constraint in a guard. The number of active clocks affects the complexity of the state graph. In addition, the memory demand critically increases as more data variables are introduced by the modeler. Another measure of the state graph complexity is represented by the degree of action interleaving (partial-order), mirrored by the number of exiting arcs from a state node. The Uppaal model checker (U-MC) navigates the state graph by exploring all the possible execution paths, and then the action interleavings, which originate from the initial state node.
In the last years Uppaal was equipped also of a Statistical Model Checker (U-SMC) [14,15] which does not build the state graph but uses instead simulations for estimating properties. The memory consumption of U-SMC is linear with the model requirements. U-SMC gives the modeler the possibility of interpreting the basic TA as Stochastic Timed Automata. To a normal location the rate of a negative exponential probability distribution can be attached, which is sampled to furnish the dwell time for remaining in the location. In the case a normal location is provided of an invariant on a clock x of the type x ≤ b , where b is the maximal time the automaton can stay in the location, and an exiting edge with a guard like x ≥ a , with a ≤ b , under U-MC the automaton can exit the location at any time non-deterministically chosen in the dense interval [ a , b ] . Under U-SMC a delay is sampled by a uniform probability distribution in the same interval, which constitutes the dwell time before abandoning the location. U-SMC supports queries written in the Metric Interval Temporal Logic (MITL) [15] (see Table 2 for examples). As a simple example, U-SMC can estimate the probability of an event occurrence by executing a certain number of simulations (whose amount can be automatically inferred), each one lasting after an assigned time limit, and counting how many times the event occurs in the various runs, divided by the total number of runs. As a further benefit, U-SMC can accumulate data from a simulation so as to display them graphically thus favoring a better understanding of a dynamic behavior.
Uppaal Timed Automata are used in this work to model and analyze mutual exclusion algorithms by model checking. A key feature offered by Uppaal is the possibility of investigating the effects of time on the behavior of such algorithms.

3. A Modelling Method for Mutual Exclusion Algorithms

Mutual exclusion algorithms can be studied according to two memory models: the common strong memory model (SMM) and the Weak Memory Model (WMM) [6]. According to SMM, the write and read operations issued by processes on a memory cell are atomic. In the WMM model, though, a memory cell under writing can be simultaneously read by other processes and a non-deterministic value can be achieved (flickering). In this paper both models will be considered.
In the following, N processes identified by unique numbers from 1 to N, compete for the use of a shared resource. The abstract code structure of the generic Process(i) is assumed to be a never ending loop as in Algorithm 1.
Algorithm 1. General code structure of a process involved with mutual exclusion.
global shared communication variables
Process(i):
local variables of the process
loop
  NCS //Non Critical Section
  Entry
  CS //Critical Section
  Exit
end-loop
In the NCS section the process does something unrelated from the shared resource. More in particular, the duration of NCS is arbitrary and can include 0 time units (the NCS is immediately abandoned) and infinite time units (in the NCS the process can block or terminate). Process i follows a specific protocol for accessing the resource. The Entry part is what is called the competing part. The process signals its interest in accessing the resource. However, it has to wait until the process gets the grant to actually access the resource. The Exit part consists of the final operations which the process execute to let partners be informed it has finished with this access to the resource.
Both the Entry and the Exit code sections depend on and make use of the global and shared communication variables. On the other hand, each process owns some private, inaccessible to other processes, local variables. The original design of a mutual exclusion algorithm concerns devising a minimal number of shared communication variables whose use is capable of ensuring the mutual exclusion and the related properties.
A correct mutual exclusion algorithm should guarantee the following properties are fulfilled.
  • (safety) Absence of deadlocks in the processes attempting to use the shared resource.
  • (safety) At any time, only one process should be allowed to enter its critical section.
  • (bounded liveness) A competing process eventually enters its critical section. In other terms, the waiting time for a competing process should be finite and hopefully small. Equivalently, the number of by-passes or the overtaking factor which a waiting process experiments from other competing processes should be bounded. This property also expresses, for a competing process, the absence of starvation.
  • (liveness) A process in its non-critical section should never impede a competing process to enter its critical section.

3.1. Uppaal Modelling Method

Mutual exclusion (ME) algorithms normally do not make any assumption about the time duration of the operations in the Entry, the Exit and the CS sections (see Algorithm 1). In the proposed Uppaal method for a generic process (see Figure 1), all the elementary operations are modelled by urgent locations, thus having a 0 duration. The consequence is a high-degree of interleaving or partial-order in the nodes of the state graph, particularly when the number N of processes increases. A significant degree of interleaving complicates the generation and the navigation of the state graph during the model checking. These considerations suggested a refinement of the ME modelling method as follows. First, the execution of the Entry actions, although they are continuously executed (busy-waiting) in the physical process, perhaps running on a separate processor/core, in the Uppaal model can be conveniently postponed (lazy modelling) until there is an “evidence” that changes in the shared communication variables occurred which require the process to actually check if it really can prosecute toward the critical section or not. All of this in no case introduces changes in the logic of the ME algorithm, but it can reduce the burden of an excessive interleaving degree in the model.
In Figure 1, the ME model-dependent t r y ( ) boolean function is introduced, which returns true if something is changed in the shared communication variables which motivates the process to execute the Entry actions. If the guess expressed by try(), for non-determinism and concurrent execution with partner processes, would result in a failure, that is the process has still to continue waiting in the competing state, the BW location will be re-entered. If instead the Entry actions end with a success, the process continues by entering its critical section. It is worth noting that BW is immediately exited at any time the optimistic try() function returns true. Toward this, a (fictitious) signal sent over the urgent and broadcast channel s y n c h is used. Note that no receiver exists for this asynchronous message.
The CS section (see Algorithm 1) is purposely modelled as a normal location with a dwell time of exactly 1 time unit (see the invariant x ≤ 1 on CS and the guard x ≥ 1 on the edge exiting the location CS). The use of an unitary duration for any critical section makes the model time-sensitive, facilitates the prediction of the overtaking factor (see later in this paper) and does not affect the mutual exclusion algorithm evolution. On the other hand, the CS behavior can naturally break possible zeno-cycles [16], that is those infinite sequences of events executed in 0 time, which could arise in a model with a lot of urgent actions.
The non-critical section NCS is instead modelled as a normal location with a spontaneous exiting edge. As a consequence, NCS can be abandoned in 0 time units or the process automaton can remain in it also an infinite number of time units. The last situation models the process which can be stopped into NCS.
Special care is required in the modelling of the actions of both the Entry and the Exit sections. Under both the Strong Memory Model (SMM) and the Weak Memory Model (WMM) it is fundamental to realize that individual shared communication variables must be set (written) or get (read) in separated edges of the Uppaal process model. All of this mirrors the fact that each single shared communication variable has to be accessed from a different memory location. As a consequence, a condition based on multiple shared variables has to be split and its result calculated by evaluating separately its basic components. This way the evaluation of the condition can be correctly affected by the non-determinism and interleaving of the various processes. The situation is different for local variables of a process. Such variables can be supposed to be held in separate registers so that multiple local variables can be operated in a single edge command without errors.
The above mentioned constraints on the use of shared communication variables, do not apply in the formulation of the try() function body, where the goal is to “rapidly” predict, e.g., that the process can possibly enter its critical section. It has to be stressed, though, that a true result of try() expresses only an optimistic prediction which can be falsified in the actual non-deterministic execution of the Entry actions.
As one can see from Figure 1, the initial location of a process model is represented by NCS. The overall model with N process instances can be initialized by a Bootstrap automaton (see Figure 2) whose initial location is marked as committed so as to be sure, through the initialize() function, all the global shared data get initialized before any process starts executing. After the execution of the initialize() function, the Bootstrap moves to a final normal location without exits thus disconnecting from the model.

3.2. Predicting the Overtaking Factor

In the model of Figure 1 time can advance not only because the CS location has one time unit duration but also because of the unpredictable staying of the process into the NCS. The interplay of CS/NCS timing is a key factor for predicting the number of overtakings. Since all the processes are identical, one of them can be elected for measuring the overtakings. Let it be denoted by tp (target process, by default the process 1). Some common global declarations of a mutual exclusion Uppaal model are the following:
const int N=…; //the number of processes
typedef int [1,N] pid; //the type of process unique identifiers
const pid tp=1; //target process example
clock x[pid]; //one clock per process
The clock x[tp] is reset as soon as the target process starts competing. The following reset(i) function can be used for this purpose:
void reset(const pid i){
if(i==tp) x[tp]=0;
}//reset
After its reset, x[tp] grows as other competing processes enter their critical sections. Since the unitary duration of the location CS (see Figure 1), the maximal value reached by x[tp] measured before entering its CS, can furnish the number of overtakings. Such a number coincides with the number of CSs executed by competing processes before the tp process is allowed to enter its CS.
Semantic correctness of this approach, despite the timing introduced by NCS, can be stated as in the following. Of course, by design, a mutual exclusion algorithm is expected to ensure a finite number of overtakings to be suffered by any process and also by the tp process. Let ∆ t p be the finite amount of time that the (competing) tp process has to wait before entering its CS. Let tc be a competing process which gets its CS before tp, and then enters its NCS which is finally abandoned after a time ∆ t c , when a new competition for tc is started. In the case ∆ t c ≥ ∆ t p it necessarily follows that the process tp eventually enters its CS and a new competition phase is then launched. Would instead be ∆ t c < ∆ t p , this means that the time spent by tc into its NCS naturally occurs, by concurrency/parallelism, as part of the time spent for waiting by tp, mirrored by the clock valuation x[tp]. Therefore, the time behavior of processes into NCS does not forbit the correct detection of the maximal number of overtakings by observing the clock x[tp].
An important consequence of the mutual exclusion property and of the choice of the target process tp for observing the number of overtakings, is that, at any moment of the model verification, despite the number N of the processes, at most two clocks can be active: that of the process tp and the one of the competing process which is allowed to enter its critical section.

3.3. Model Checking and TCTL Queries

A basic set of TCTL [11] queries which can be used to study a mutual exclusion algorithm expressed in Uppaal according to the general process model of Figure 1, are suggested in Table 1.
The 1st query of Table 1 asks if it is always true (A[]) or invariantly, that in all the states of the state graph there is no deadlock. The 2nd query checks if, invariantly, the number of processes that are in the CS location is always less than or equal to 1 (the fundamental mutual exclusion property). The 3rd query based on the l e a d s − t o operator − − > [11], states that starting from the BW location, it inevitably follows that the process enters its CS. The 4th existential query (E<>) verifies that a process in the NCS does not forbid another process to be in the CS. The 5th query, finally, asks to quantify the maximal number of overtakings suffered by the chosen target process. Different locations, not necessarily the BW, can be chosen for observing the suprema value of x[tp]. For example, a (urgent) location just before entering the CS could be adopted as well.

3.4. Statistical Model Checking and MITL Queries

The basic process model in Figure 1 can easily be adapted for it to be exploited also under the Uppaal Statistical Model Checker (U-SMC) [15]. Basically, the possibility of time not advancing in the NCS location can be avoided by attaching to NCS the rate of an exponential probability distribution function which can conveniently be established as m u = 1.0 / E O F , where EOF is the expected overtaking factor. Some MITL queries useful for checking the model of a mutual exclusion algorithm through simulations, are proposed in Table 2. It is to be anticipated, though, that it can be difficult, in simulation, to observe the effective number of overtakings. This is because U-SMC, during a simulation, follows a particular execution path of the actions interleaving, whereas the model checker analyzes all the possible paths.
The query 1 of Table 2 asks U-SMC to estimate, using an inferred number of simulation runs each lasting 10000 time units, the occurrence probability of the event “is there any state in which the number of processes in CS is greater than 1?”. U-SMC proposes a confidence interval (by default with the confidence degree 95%) for the event probability. Of course, the confidence interval should indicate an almost impossible event. With the default parameters setting of U-SMC [15], a typical “impossible” event is witnessed by the interval [ 0,0.0981446 ] . Similarly, an almost “certain” event is denoted by a confidence interval of [ 0.901855,1 ] . The 2nd query monitors the number of processes simultaneously in CS in a simulation, e.g., lasting 100 time units. Following the query execution, U-SMC can show graphically the accumulated data. The 3rd query quantifies the probability of a process, e.g., the tp, to effectively enter its critical section. Such a query is expected to suggest an almost sure event. The 4th and 5th queries ask U-SMC to quantify the confidence interval of the probability that the target process experiments a number of overtakings respectively greater than the expected bound (an event which should be impossible) or that such a number is always found to be less than the expected bound (an event which should be certain).

4. Modelling and Analysis of Mutual Exclusion Algorithms

The following reports several modelling examples and their analysis results. Presented models are examples of scientific models [17], in the sense that they are aimed at permitting reasoning on and semantic interpretation of the selected mutual exclusion algorithms. They differ from engineering models where a formal system model is preliminarily prepared and analyzed toward a physical implementation. All the presented experiments were carried out using the latest version Uppaal 5.0.0, 64 bit, running on a Win11 Pro desktop platform, Dell XPS 8940, Intel i7-10700 (8 physical cores), CPU@2.90 GHz, 32GB RAM.

4.1. Solutions for Two Processes

The mutual exclusion problem for two processes was solved in the sixties of the previous century by T.J. Dekker [3]. This algorithm was improved by G.L. Peterson in [19].

4.1.1. The Dekker’s Algorithm

It is based on the following shared communication variables:
bool flag[2], int[1,2] turn
The flag array is initialized to all false. The initial value of turn can be either 1 or 2. The generic process i (1 or 2) is shown in Algorithm 2, where the Entry and Exit code sections are clearly recognizable. The local constant j denotes the partner process. Each process sets the value of its own f l a g [ ] , which can be checked by the partner. When a process wants to compete for the use of the resource, it sets its flag[] variable to true. The value of t u r n ultimately decides which process actually enters its critical section. When a process exits from its CS, it gives the turn to the partner and puts its flag[] to false to state it is, at the moment, not interested in the resource. Despite its apparent simplicity, the understanding of the Entry section can be difficult. Non-determinism, in fact, is at the heart of the algorithm behavior. The Uppaal model of the Process(i) is depicted in Figure 3, where the try() function (see Figure 1) was directly expanded. The Process automaton has only one parameter: c o n s t p i d i . The use of the p i d typedef enables N instances (here N = 2 ) of the Process automaton to be created at the system bootstrap time, and the various instances are distinguished by Process(1) and Process(2).
The behavior of the algorithm can be preliminarily visually inspected by animating the Uppaal model in the symbolic simulator, which is the typical tool for debugging model errors. Effectively one “can see” the two processes never enter simultaneously their CS. In addition, would the partner be in the busy-waiting location BW, when the current process exits its CS, the waiting process can be unblocked by receiving its turn. Things, though, can be more complicate with respect to what intuitively emerges from the animation.
Algorithm 2. Dekker’s Process(i).
Process(i):
local constant: int j=3-i;
while(true){
    NCS;
    flag[i]=true;
    while( flag[j] ){
        if( turn==j ){
            flag[i]=false;
            wait-until( turn==i );
            flag[i]=true;
        }
    }
    CS;
    turn=j;
    flag[i]=false;
}
Properties verification can be assessed through the model checker. Effectively, the Dekker model is deadlock free (query 1 of Table 1). In addition, the fundamental mutual exclusion property (query 2 of Table 1) is satisfied. This property was accompanied by the assessment that both Process(1) and Process(2) can effectively enter the CS with the two existential queries which are satisfied:
E<> Process(1).CS
E<> Process(2).CS
Also the liveness property checked by query 4 of Table 1 is satisfied. However, the query 3 of Table 1 as well as the query:
Process(1).W --> Process(1).CS
are not satisfied. In reality this property is tied to the fact that the model in Figure 3 has a zeno-cycle (see the loop from W to itself: b[j] followed by k!=j, which can be executed an infinite number of times and in 0 time). The query 5 of Table 1 furnishes, whatever is the target process, an overtaking factor of 1.
As a final remark, it should be observed that zeno-cycles (equivalent to a mechanical perpetual motion) can exist int the model but not in the physical reality where operations have necessarily a non-zero execution time, provided an adequate time resolution level is adopted.

4.1.2. The Peterson’s Algorithm for Two Processes

A more elegant and compact solution to the mutual exclusion problem for two processes was proposed by G.L. Peterson in [19]. Using the same shared data as in the Dekker’s algorithm and the same initializations, the pseudo-code of the algorithm and its Uppaal model are shown respectively in Algorithm 3 and Figure 4.
Algorithm 3. Peterson’s Process(i).
Process(i):
local constant: int j=3-i;
while(true){
    NCS;
    flag[i]=true;
    turn=j;
    wait-until(!flag[j] || turn==i);
    CS;
    flag[i]=false;
}
The Peterson algorithm was find be fully correct from all the queries of Table 1, with an overtaking factor of 1. What is interesting, in the Peterson model, is that it does not have any zeno-cycle by construction. In the algorithm, a process i in busy-waiting finishes waiting as soon as the partner process j is not interested in the use of the resource or the turn is assigned to i. Any one of these conditions commands the exiting of the process i from BW. On the other hand, when a process exits its CS, in the case it immediately starts again competing, not only signals this by setting its flag[] to true but also assigns the turn to the partner which, if it is in BW, immediately gets unblocked while the first process certainly waits in its BW.

4.2. Solutions for N ≥ 2

Processes
Several algorithms are reported in the literature. In the following, a subset of representative algorithms is considered and their properties thoroughly studied using the modelling and verification method proposed in this paper.

4.2.1. The Dijkstra’s Algorithm

The first solution to the mutual exclusion problem for N ≥ 2 processes, numbered from 1 to N, was proposed by E.W. Dijkstra in [18]. The algorithm is based on the following shared variables:
bool[1..N] b, c; int k
The initial value of k, 1 ≤ k ≤ N , is immaterial. If Process(i) enters its CS, k holds the value i. Process(i) modifies the values b[i] and c[i] which are inspected by the other processes. Arrays b[] and c[] are initialized to all true. The algorithm, reproduced as in [18], is shown in Algorithm 4. Informal arguments about its (not trivial) correctness were discussed in [18].
The Uppaal model of Algorithm 4 is depicted in Figure 5, whereas the adopted try() function is shown in Algorithm 5. As one can see, try() returns true if, optimistically, Process(i) could proceed toward its CS. After a true value of try(), the exact actions of the Entry section of Algorithm 4 are executed. Since in Li3 the value of b[k] has to be checked, first the value of k is read into the (at the moment free) local variable j, then the value of b[j] is consulted. From Li3 the model always comes back to BW. To reduce the burden of the model checker operation, each time BW or NCS are re-entered, the local value of j is reset to 1. From Li4, if all the c[j], 1 ≤ j ≤ N , j ! = i , are true, the process moves to its CS.
Algorithm 4. The E.W. Dijkstra algorithm for the N ≥ 2 processes
Process(i):
local int j;
LiO: b[i] := false;
Lil:     if k # i then
Li2:         begin c[i] := true;
Li3             if b[k] then k:=i;
                        go to Lil
                end
            else
Li4:             begin c[i] := false;
                            for j := 1 step 1 until N do
                            if j # i and not c[j] then go to Lil
                    end;
                critical section;
                c[i] := true; bill := true;
                remainder of the cycle in which stopping is allowed;
                go to LiO
Algorithm 5. try() function of Figure 5.
bool try(){
        int j;
        if( k!=i ){
            return false;
        }
        else{
            for( j=1; j<=N; ++j )
                if( j!=i && !c[j] )
                    return false;
        }
        return true;
}//try
The model in Figure 5 was investigated for N varying from 2 to 5. It emerged that the model satisfies the properties of absence of deadlocks and that of the mutual exclusion (queries 1 and 2 of Table 1). In addition a different behavior emerged of Process(1) from the other processes. Process(1) satisfies query 3 but not the other processes. The query 4 was also not verified whatever is the target process. The overtaking factor, yet for N = 3 , is unbounded (undefined) for processes i>1. This result, mentioned, e.g., in [20], complies with the implicit assumption in the design of the Algorithm 4, that processes are expected to compete rather infrequently, as it may occur in some applications.

4.2.2. The Knuth’s Algorithm

This algorithm was proposed in [20] as an attempt to improve the Dijkstra’s solution described in [18]. It is based on the following shared communication variables:
int[1,N] control; int k
both initialized to 0. A process i signals to the partners about its status by writing a value in {0,1,2} in its control[i] variable. The value 0 mirrors the process is not interested in the CS. The value 1 means the process wants to compete for the resource, thus starting the Entry section of Algorithm 1. Finally, the value 2 mirrors the process is up to enter its CS. The algorithm is reproduced in Algorithm 6. The meaning of the f o r at line L1 is to use first the indices from k down to 1, by step -1, then to use the indices from N down to 1 step -1. It should be noted that initially, when k=0, only the second part of the f o r from N down to 1 is executed.
Algorithm 6. The Knuth’s algorithm for N ≥ 2 processes
Process(i):
begin int j;
    L0: control[i]=1;
    L1: for j=k step -1 until 1, N step -1 until 1 do
                    begin if j==i then go to L2;
                        if control[j]!=0 then go to L1;
                end;
    L2: control[i]=2;
                for j=N step -1 until 1 do
                    if j!=i && (control[j]==2) then go to L0;
    L3: k=i;
                critical_section;
                k=if i==1 then N else i-1;
    L4: control[i]=0;
                remainder of the cycle in which stopping is allowed;
                go to L0;
end
The Uppaal model corresponding to Algorithm 6 is shown in Figure 6. The busy-waiting location coincides with L1. The try() function is reported in Algorithm 7, and basically executes the actions from L1 to L2 without state changes. The decrement function dec(j) is also shown in Algorithm 7.
Algorithm 7. The try() and dec() functions of the Uppaal model in Figure 6.
bool try(){
    int j;
    if(k>=i && i>=1){
        for(j=k; j>i; --j)
            if(control[j]!=0) return false;
    }
    else{ //k<i<=N
        for(j=N; j>i; --j)
            if(control[j]!=0) return false;
    }
    for(j=N; j>=1; --j)
        if(j!=i && control[j]==2) return false;
    return true;
}//try

int dec(int j){
    if(k>0) return (j==1)?N:j-1;
    return j-1;
}//dec
Correctness of the intricate Knuth’s algorithm was informally discussed in [20], where it was predicted an overtaking factor of 2 N − 1 − 1 .
The Uppaal model of Figure 6 was extensively analyzed by model checking, with N ranging from 2 to 5. Queries 1, 2 and 4 of Table 1 were found satisfied. In particular, the query 1 about the absence of deadlocks which requires the complete generation of the state graph, in the case N = 5 terminates after 265 sec with a RAM peak of 5GB. Query 3 of Table 1, stating that a competing process in L1 eventually reaches the CS location, was found to be not satisfied. This last property testifies the existence of a zeno-cycle in the Entry part. By using our proposed time-sensitive model, it emerged that the number of observed overtakings, for varying N , is reported as in the Table 3.
From the Table 3 it emerges a linear number of overtakings N − 1 , not 2 N − 1 − 1 . The same results were observed on the more expensive Knuth’s model where the location L1 of Figure 6 is turned urgent and the try() function is ignored, thus there is the maximum degree of interleavings required by the algorithm in Algorithm 6. On the adapted model for U-SMC, the query 4 of Table 2:
Pr[<=10000](<>Process(tp).L1 && x[tp]>(N-1))
launched, e.g., for N = 10 , proposes the confidence interval of an almost impossible event.

4.2.3. The de Bruijn’s Algorithm

N.G. de Bruijn suggested in [21] an improvement to the Knuth’s algorithm which consisted in a replacement of the three lines of the L3 instructions of Algorithm 6 with the following:
L3: critical_section;
if control[k]==0 || k==i then k= if k==1 then N else k-1;
In addition, the initial value of k is no longer 0 but it can be any process identifier.
As a consequence of the above modifications, the new algorithm should ensure a bound on the overtakings of 1 2 N N − 1 .   The Uppaal model of the de Bruijn algorithm is shown in Figure 7.
Model checking the de Bruijn model confirmed exactly the same basic properties as the Knuth’s model. The observed overtakings vs. N are shown in Table 4.
By increasing N, it seems the overtakings tends to be (slightly) smaller than 1 2 N N − 1 . On the adapted model for U-SMC, the query:
Pr[<=10000](<>Process(tp).L1 && x[tp]>(N*(N-1)/2))
for varying values of N, responds the event is almost impossible.

4.2.4. The Eisenberg & McGuire Algorithm

A further improvement of the Knuth’s algorithm was proposed by Eisenberg & McGuire in [22]. It uses the same shared variables and the same initializations as in de Bruijn’s algorithm (see Section 4.2.3). The new algorithm (see Algorithm 8) is committed to provide a linear overtaking factor of N − 1 .
Algorithm 8. The Eisenberg & McGuire’s algorithm for N ≥ 2 processes.
Process(i):
begin int j;
    L0: control[i]=1;
    L1: for j=k step 1 until N, 1 step 1 until k do
            begin
                if j==i then go to L2;
                if control[j]!=0 then go to L1;
            end;
    L2: control[i]=2;
        for j=1 step 1 until N do
            if j!=i && (control[j]==2) then go to L0;
    L3: if control[k]!=0 && k!=i then go to L0;
    L4: k=i;
        critical_section;
    L5: for j=k step 1 until N, 1 step 1 until k do
                if j!=k and control[j]!=0 then
                    begin
                        k=j;
                        go to L6;
                    end;
    L6: control[i]=0;
            remainder of the cycle;
            go to L0;
end
The Uppaal model of the Eisenberg & McGuire’s algorithm is depicted in Figure 8. The try() function was adjusted in a straightforward way according to steps from L1 to L3 of Algorithm 8. All the basic properties as in the Knuth and de Bruijn algorithms are satisfied. In addition, the liveness query (absence of starvation):
Process(1).L1 --> Process(1).CS
is now satisfied too. Table 5 reports the overtakings vs. N for the new algorithm, which confirms the expected trend of N − 1 .
In the case N = 5 , the query 5 of Table 1 terminated in 147 sec with a RAM peak of about 5 GB.
The analysis using the Uppaal Statistical Model Checker of the model of Figure 8, adapted for simulation, confirmed, for N = 10 , an estimation of the maximum value of the overtaking factor to be 9.
In the light of the model checking work, the Eisenberg & McGuire’s algorithm confirmed its superior character w.r.t. to both the de Bruijn and the Knuth algorithms, because it fulfills all the mutual exclusion properties and exhibits an overtaking factor, as expected, of N − 1 . The algorithm is often indicated (see, e.g., [8]) as a reference for a correct and preferable mutual exclusion solution.

4.2.5. The Generalized Peterson’s Algorithm

The Peterson’s algorithm (see Section 4.1.2) for two processes was generalized by his author to N ≥ 2 processes as follows. Processes have the unique numbers from 1 to N. There is a ladder of N − 1 levels, numbered from 1 to L = N − 1 . Each process who wants to enter the critical section has to climb the ladder. The first process who reaches the last level, grants the right to use the resource. A process moves to the next level provided all the other processes occupy previous levels (competing processes or they are not interested in the use of the resource) (that is: ( ∀ k!=i, q[k]<j), or when another process enters its same level (that is: turn[j]!=i). The algorithm is reported in Algorithm 9. It is based on the global shared variables:
int[0,N] q[1,N]; int[1,N] turn[1,N-1]
Algorithm 9. The Peterson’s solution for N ≥ 2 processes.
Process(i):
local int j;
while(true){
    NCS;
    for j=1 step 1 until N-1 do
        begin
            q[i]=j; turn[j]=i;
            wait-until( ∀ k!=i, q[k]<j) or (turn[j]!=i));
        end;
        CS;
        q[i]=0;
}
The corresponding Uppaal model is reported in Figure 9. The try() function is simply the following:
bool try(){
return (forall(k:pid)(k==i || q[k]<j) || turn[j]!=i);
}//try
Queries from 1 to 4 of Table 1 are satisfied. In particular, the query 1 which checks for the absence of deadlocks, in the case N = 5 , ends in 102 sec with a memory peak of 2.3 GB.
processes.
Table 6 collects the overtaking factor for N ranging from 2 to 5. It emerged an overtaking bound of 1 2 N N − 1 . This result agrees with that reported in [2] but not with the papers [23,24] which claimed the bound to be N − 1 .
The correct and expected behavior of the algorithm for N>5 was confirmed by using the queries of Table 2 on the model of Figure 9 preliminarily adapted for the statistical model checker.

4.2.6. The Block & Woo Algorithm

This algorithm was proposed in [25] with the aim to improve the behavior of the generalized Peterson’s algorithm. Using the same variable names as in the Peterson’s algorithm, the new shared variables are as follows:
bool q[1,N]; int[1,N] turn[1,N]
The array q[] instead of holding process ids now contains bool values (0 or 1). In addition, the ladder has here N levels, not N-1. Differently from the Peterson’s solution, where a process has to reach the last level of the ladder for entering its CS, in the Block & Woo algorithm (see Algorithm 10) a process can achieve the grant when it obtains a level “high enough” with respect to the number of the competing processes. Would this number be m , the process goes into its C S when it reaches the level m . The Uppaal model corresponding to Algorithm 10 is depicted in Figure 10.
Algorithm 10. The Block & Woo algorithm for N ≥ 2 processes.
Process i: int j;
while(true){
    NCS;
    j = 0;
    q[i] =1;
    repeat
        j = j+1
        turn[j] =i;
        wait-until (turn[j]!=i) or ( ∑ k = 1 N q k ≤ j )
    until (turn[j]==i)
    CS;
    q[i] =0;
}
The adopted try() function of Figure 10 is the following:
bool try(){
return turn[j]!=i || (sum(k:pid)q[k])<=j;
}//try
Model checking the Block & Woo algorithm for N ≤ 4 and using the queries of Table 1, confirmed it satisfies all the basic properties of a mutual exclusion algorithm. In addition, the solution does not have zeno-cycles and its overtaking factor was found to be 1 2 N N − 1 in agreement with the evaluation provided by the authors in [25]. This number coincides with that we have found for the generalized Peterson’s algorithm (see Section 4.2.5) so the new algorithm does not seem a real improvement. Using the adapted model for statistical model checking, all the queries in Table 2 confirmed the qualitative and quantitative behavior of the algorithm also for N > 4 .

4.2.7. The Aravind & Hesselink Algorithm

This algorithm was proposed in [9] as a more efficient extension of the generalized Peterson’s algorithm (see Section 4.2.5). The algorithm is very interesting, although it is more heavy to analyze under model checking than either the Peterson’s algorithm or the Block&Woo’s algorithm. Its properties were assessed in [9] using the PVS theorem prover.
The algorithm behaviour can be summarized by using the “children party metaphor” with N children. The party room hosts N corners identified by the numbers from 0 to N − 1 . At his arrival, a child reaches the corner N − 1 . When a child at corner l e v e l finds in the room there are no more than k children (not counting itself), he/she can move to the corner k , provided k < l e v e l . Reaching the corner 0 represents the entering of the critical section. At the corner 0 there is a table where to pick a piece of cake to eat in the garden. A child can come back from the garden to the room if he/she feels to eat more cake. A chair is available at each corner l e v e l > 0 , which a child can occupy. However, any child present at the same corner can climb the chair, thus possibly pushing a previous occupant. A pushed child then reaches the corner l e v e l − 1 .
What it is expensive in the algorithm is the children re-counting phase. The algorithm is based on the following shared data:
bool act[1,N]; pid turn[0,N-1];
which receive their default values at the initialization time. An abstract formulation of the algorithm is shown in Algorithm 11. An Uppaal model corresponding to Algorithm 11 is portrayed in Figure 11.
Algorithm 11. The Aravind & Hesselink algorithm for mutual exclusion.
Process(i):
local variables: int[0,N-1] level; bool bb; pid q; int[0,N-1] card;
while(true){
    NCS;
    act[i]=true; level=N-1;
    while(level>0){
        card=N-1-|{q,1<=q<=N : !act[q]}|; //number of not CS interested processes
        if(card<level){ level=card; bb=false; }
        else if(!bb){ turn[level]=i; bb=true; card=|{q,1<=q<=N, q!=i && act[q]}|; }
        else if(turn[level]!=i){ level--; bb=false; }
    }
    CS;
    act[i]=false;
}
The try() function for the model of Figure 11 is:
bool try(){
return level==0 || N-1-(sum(q:pid)!act[q])<level || !bb || turn[level]!=i;
}//try
Since the use of many global and local variables in the model of Figure 11, there is a state explosion even for N = 4 . For N=2 and N=3 all the TCTL queries from 1 to 4 of Table 1 were found satisfied. Query 5 suggested a N − 1 overtaking factor, which exactly confirms the authors prediction in [9]. For this model, the MITL queries in Table 2 were useful to investigate the algorithm behavior, on the adapted model for U-SMC, for N>=4. More in particular, all the responses to Table 2 queries confirmed the expectations, with a bound on the overtakings of N − 1 . As an example, for N = 10 , Figure 12 reports the result generated by U-SMC for the query 2 of Table 2. To give an idea of the wall-clock time required by some U-SMC queries, the query 4 of Table 2 furnishes the indication of an impossible event after 29 runs and 62 sec.

4.2.8. Solutions under the Weak Memory Model

It has been pointed out, e.g., in [6,9], that the hypothesis of a RAM memory with atomic read/write operations is today almost ideal, especially when one considers the use of personal devices with multi-port memories [26]. In these cases, it can happen that multiple reads can occur during a write operation on a given memory cell. The effect of multiple readers on a same memory cell holding a shared variable v a r to which the value v has to be assigned, can be modelled by returning a non-deterministic value (flickering) belonging to the type of v a r .
The presence of flickering in the model of a mutual exclusion algorithm increases the non-determinism and partial-order in the state graph, which complicates the model checking exploration. As a consequence, not only the algorithm becomes more heavy to analyse, but it could lose its properties.
All the algorithms for N ≥ 2 processes previously studied in this paper, were also checked under flickering. Only the generalized Peterson’s algorithm, the Block & Woo’s algorithm and the Aravind & Hesselink’s algorithm were found robust and safe also under the weak memory model. For brevity, the following only considers the Araving & Hesseling’s algorithm/model modified with flickering (see Figure 13). As always, in the Uppaal model of Figure 13, guards of edge commands are shown in green, the non-deterministic selection of a value belonging to its type is depicted in yellow, the update actions appear in blue.
As an example of flickering, when the Process(i) automaton leaves its NCS in Figure 13, it has, among the other actions, to set (write) its act[i] shared variable to the true value. Due to flickering, though, first a non-deterministic assignment of a value belonging to int[0,1] (the integers equivalent of false and true) is anticipated, which is then followed by the correct assignment of act[i]=true. This way it is perfectly possible, for non-determinism, that a reader can achieve the value defined by the flickering and not the right value.
The model of Figure 13 was analyzed by exhaustive model checking for N in [2,3] and by statistical model checking for N in [4,10]. It was found to be correct from all the TCTL and MITL queries respectively of Table 1 and Table 2. What it is interesting, the bounded overtaking factor was confirmed to be N − 1 as in the normal case without flickering. For the above properties, the Aravind & Hesselink’s algorithm emerged as one of the most safe and efficient mutual exclusion algorithms.

5. Conclusions

Reasoning on a concurrent/parallel software system [4,5,6] can be very complex. The origin of this difficulty stands in the non-determinism and action interleaving which dominate the evolution of the system. All of this can jeopardize the human intuition and peer-review normally adopted to predict the properties of a concurrent system.
This paper proposes an original approach based on formal modelling for the automated analysis of mutual-exclusion algorithms, which are at the heart of concurrent/parallel, real-time and operating systems. The approach is based on the Timed Automata [10] as implemented in the popular and continually evolved Uppaal toolbox [11]. The major limitation of the proposed method is the well-known state explosion problem, which arises in complex algorithms which makes use of or generate too many data. As an example, solutions like the Lamport’s bakery algorithm [27] which grants the access to the critical section on the basis of an ever increasing service number, is difficult to handle by the exhaustive model checking. It could be studied by the statistical model checker. The state explosion restriction forbids, even for addressable algorithms, the analysis when the number N of the involved processes is greater than 5. Another reason for having chosen Uppaal for the experiments, rests on the fact that the tool also provides a statistical model checker [14,15] which does not build the model state graph but instead relies on simulations and stochastic behavior. This way, the tool permits an exploration of the properties of a complex algorithm by estimating event probabilities which can be of great practical value by providing further arguments about the correctness of a given algorithm for not trivial values of N .
The paper applies the proposed modelling and verification approach to several algorithms defined in the literature, of which known results are retrieved and confirmed but also, in some cases, unexpected results emerge, for example about the bounded degree of the overtaking which a competing and waiting process can suffer before getting the grant to enter its critical section.
The paper investigates the mutual exclusion algorithms from the point of view of the classic memory model with read/write atomic operations. However, the modelling and verification aspects when the weak memory model is adopted, that is when multiple readers can simultaneous access an under writing memory cell with the uncertainty (flickering) [6,9] which accompanies the reading process, are also investigated.
Prosecution of the research will address the following points. First to apply the proposed approach to other mutual exclusion algorithms. Second to optimize the implementation of the approach and deepen the differences from alternative methods like the theorem provers which normally are unable to deal with the timing aspects. Third to exploit parallel simulation [28] for studying large models on a multi-core machine.

References

  1. Lamport, L. The mutual exclusion problem: part I---a theory of interprocess communication. In Concurrency: the Works of Leslie Lamport; 2019, pp. 227–245.
  2. Raynal, M. Algorithms for mutual exclusion, 1986, MIT Press.
  3. Dijkstra, E.W. Co-operating sequential processes. In Programming languages: NATO Advanced Study Institute: lectures given at a three weeks Summer School held in Villard-le-Lans, 1966, ed. by F. Genuys, pp. 43–112, Academic Press Inc.
  4. Raynal, M. Concurrent programming: algorithms, principles, and foundations 2012, Springer Science & Business Media.
  5. Misra, J. A foundation of parallel programming. In Constructive Methods in Computing Science: International Summer School directed by FL Bauer, M. Broy, EW Dijkstra, CAR Hoare, 1989, pp. 397–445, Springer Berlin Heidelberg.
  6. Lamport, L. On interprocess communication. Distributed Computing 1986, 1, 77–101. [Google Scholar] [CrossRef]
  7. Nigro, L.; Cicirelli, F. Formal modeling and verification of embedded real-time systems: An approach and practical tool based on Constraint Time Petri Nets. Mathematics 2024, 12, 812. [Google Scholar] [CrossRef]
  8. Silbershatz, A.; Galvin, P.B.; Gagne, G. Operating System Concepts, 2018, 10th Edition, Wiley.
  9. Aravind, A.A.; Hesselink, W.H. A queue based mutual exclusion algorithm. Acta Informatica 2009, 46, 73–86. [Google Scholar] [CrossRef]
  10. Alur, R.; Dill, D.L. A theory of timed automata. Theoretical Computer Science 1994, 126, 183–235. [Google Scholar] [CrossRef]
  11. Behrmann, G.; David, A. , Larsen, K.G. A tutorial on UPPAAL. In: M. Bernardo, F. Corradini (Eds.), Formal Methods for the Design of Real-Time Systems 2004, LNCS 3185, Springer, pp. 200–236.
  12. Cicirelli, F.; Nigro, L. Modelling and verification of mutual exclusion algorithms. IEEE/ACM 20th International Symposium on Distributed Simulation and Real Time Applications (DS-RT), IEEE, 2016, pp. 136–144.
  13. Cicirelli, F.; Nigro, L.; Sciammarella, P.F. Model checking mutual exclusion algorithms using Uppaal. In Proc. of 5th Computer Science On-Line Conference, 2016, Springer.
  14. Agha, G.; Palmskog, K. A Survey of Statistical Model Checking. ACM Trans. Model. Comput. Simul. 2018, 28, 6:1–6:39. [Google Scholar] [CrossRef]
  15. David, A.; Larsen, K.G.; Legay, A.; Mikucionis, M.; Poulsen, D.B. Uppaal SMC tutorial. Int. J. Softw. Tools Technol. Transf. 2015, 17, 397–415. [Google Scholar] [CrossRef]
  16. Bowman, H.; Gomez, R.; Su, L. A tool for the syntactic detection of zeno-timelocks in Timed Automata. Electron. Notes Theor. Comput. Sci. 2005, 139, 25–47. [Google Scholar] [CrossRef]
  17. Lee, E.A. Modeling in engineering and science. Communications of the ACM 2018, 62, 35–36. [Google Scholar] [CrossRef]
  18. Dijkstra, E.W. Solution of a problem in concurrent programming control. Communications of the ACM 1965, 8, 569. [Google Scholar] [CrossRef]
  19. Peterson, G.L. Myths about the mutual exclusion problem. Information Processing Letters 1981, 12, 115–116. [Google Scholar] [CrossRef]
  20. Knuth, D.E. Additional comments on a problem in concurrent programming control. Communications of the ACM 1966, 9, 321–322. [Google Scholar] [CrossRef]
  21. de Bruijn, N.G. Additional comments on a problem in concurrent programming control. Communications of the ACM 1967, 10, 137–138. [Google Scholar] [CrossRef]
  22. Eisenberg, M.A.; McGuire, M.R. Further comments on Dijkstra’s concurrent programming control problem. Communications of the ACM 1972, 15, 999. [Google Scholar] [CrossRef]
  23. Kowalttowski, T.; Palma, A. Another solution of the mutual exclusion problem. Information Processing Letters 1984, 19, 145–146. [Google Scholar] [CrossRef]
  24. Hofri, M. Proof of a mutual exclusion algorithm – A ‘Class’ic example. ACM SIGOPS OSR 1990, 24, 18–22. [Google Scholar] [CrossRef]
  25. Block, K.; Woo, T.K. A more efficient generalization of Peterson’s mutual exclusion algorithm. Information Processing Letters 1990, 35, 219–222. [Google Scholar] [CrossRef]
  26. Frenzel, L.E. Dual-port SRAM accelerates smart-phone development. Electronic Design 2004.
  27. Lamport, L. A new solution of Dijkstra’s concurrent programming problem. Comm. of ACM 1974, 17, 453–455. [Google Scholar] [CrossRef]
  28. Nigro, L. Parallel Theatre: An actor framework in Java for high performance computing. Simulation Modelling Practice and Theory 2021, 106, 102189. [Google Scholar] [CrossRef]
Preprints 103022 g001
Figure 1. Proposed abstract Uppaal model for a mutual exclusion process.
Figure 1. Proposed abstract Uppaal model for a mutual exclusion process.
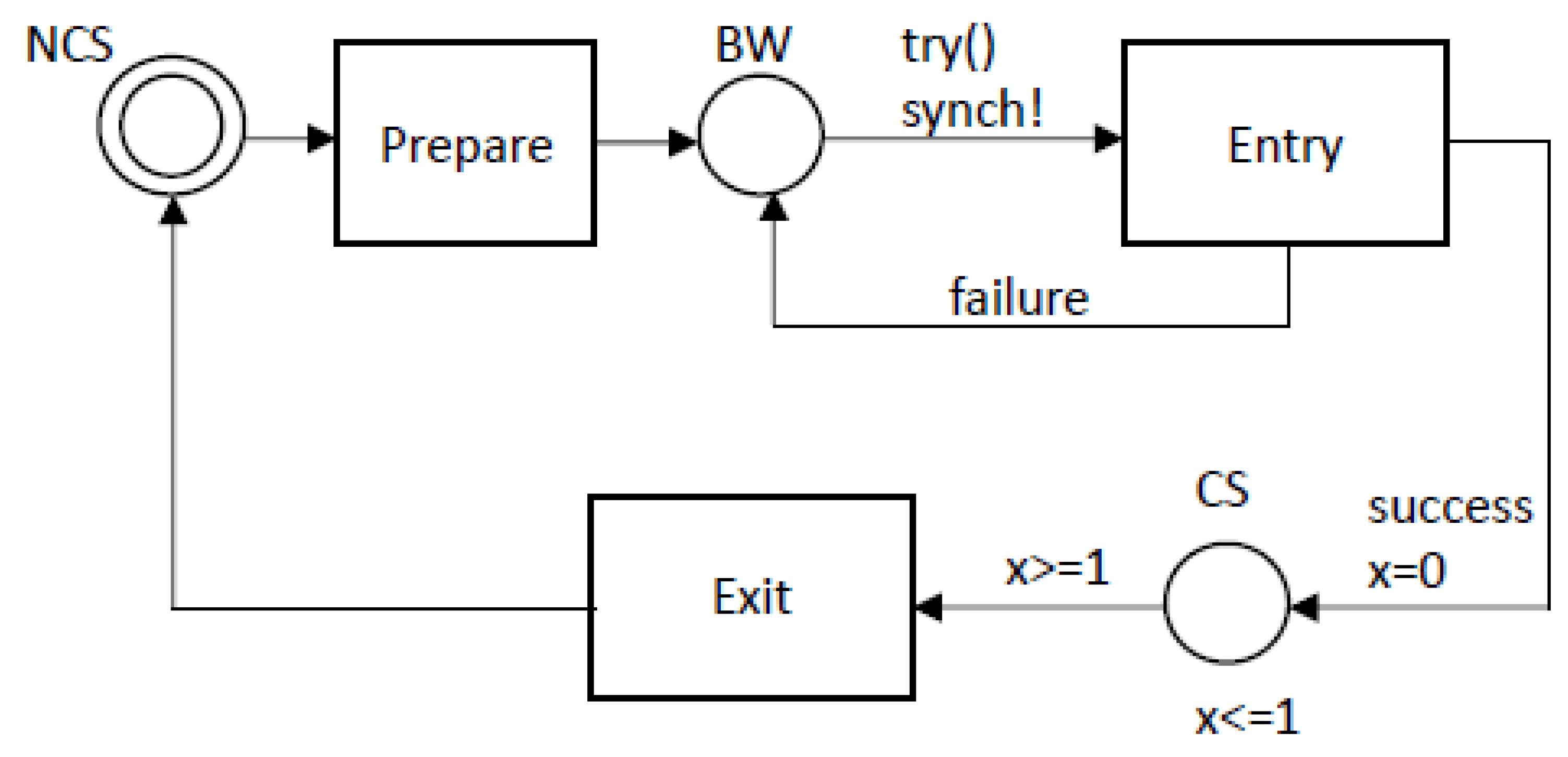
Preprints 103022 g001
Preprints 103022 g002
Figure 2. The Bootstrap automaton.
Figure 2. The Bootstrap automaton.
Preprints 103022 g002
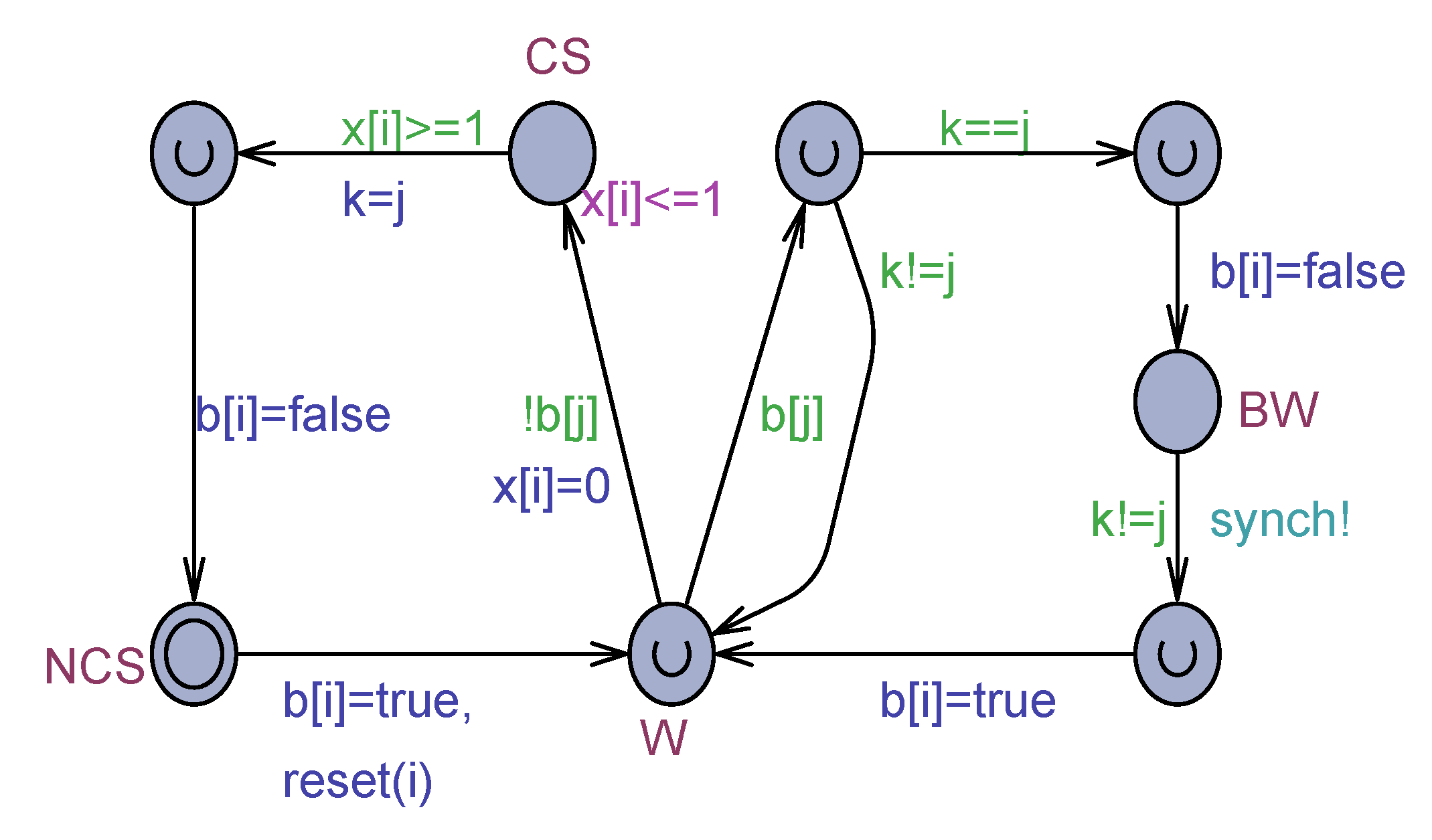
Preprints 103022 g003
Figure 3. Uppaal model of the Dekker’s Process(i).
Figure 3. Uppaal model of the Dekker’s Process(i).
Preprints 103022 g003
Preprints 103022 g004
Figure 4. Uppaal model of the Peterson’s Process(i).
Figure 4. Uppaal model of the Peterson’s Process(i).
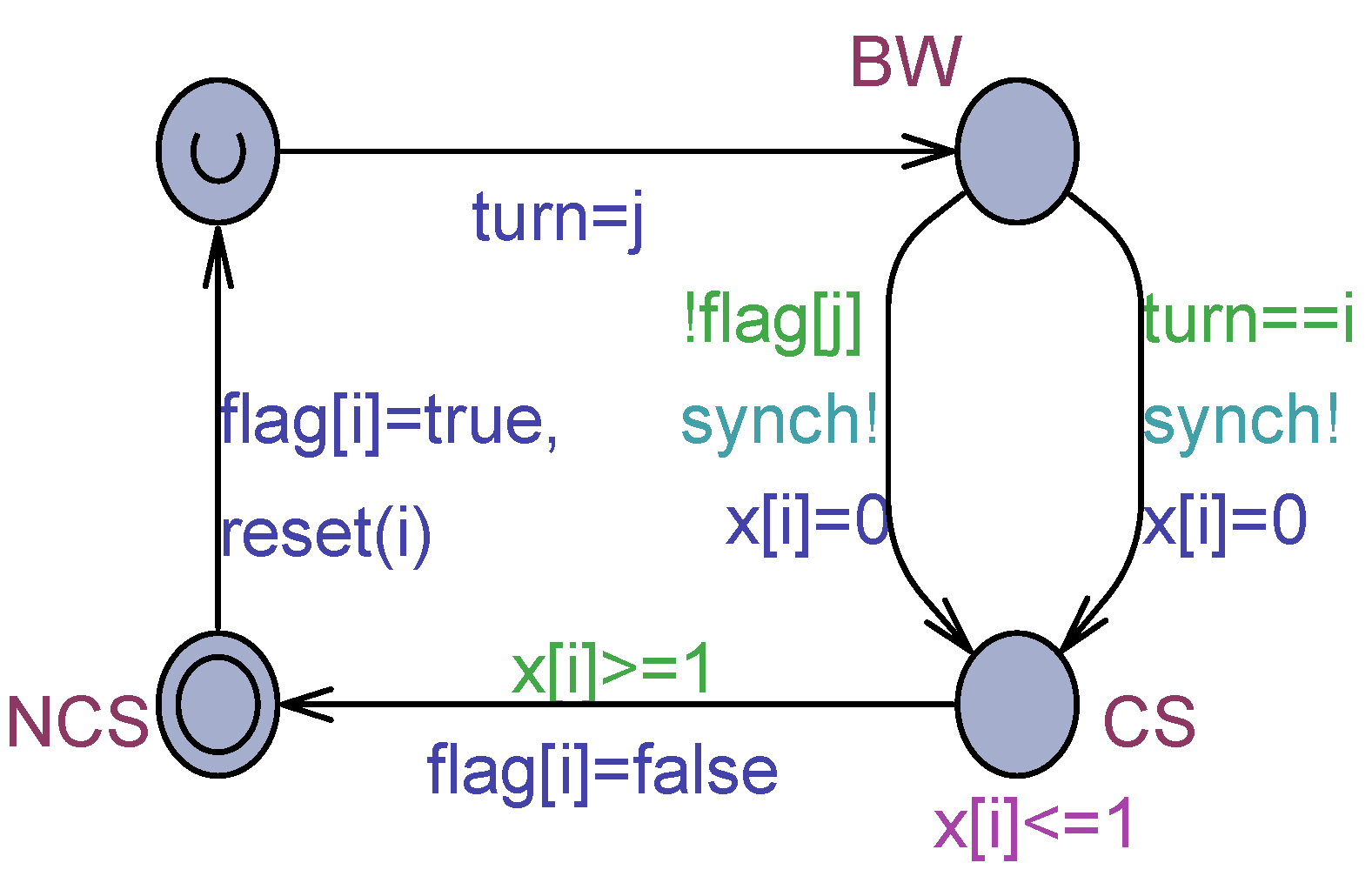
Preprints 103022 g004
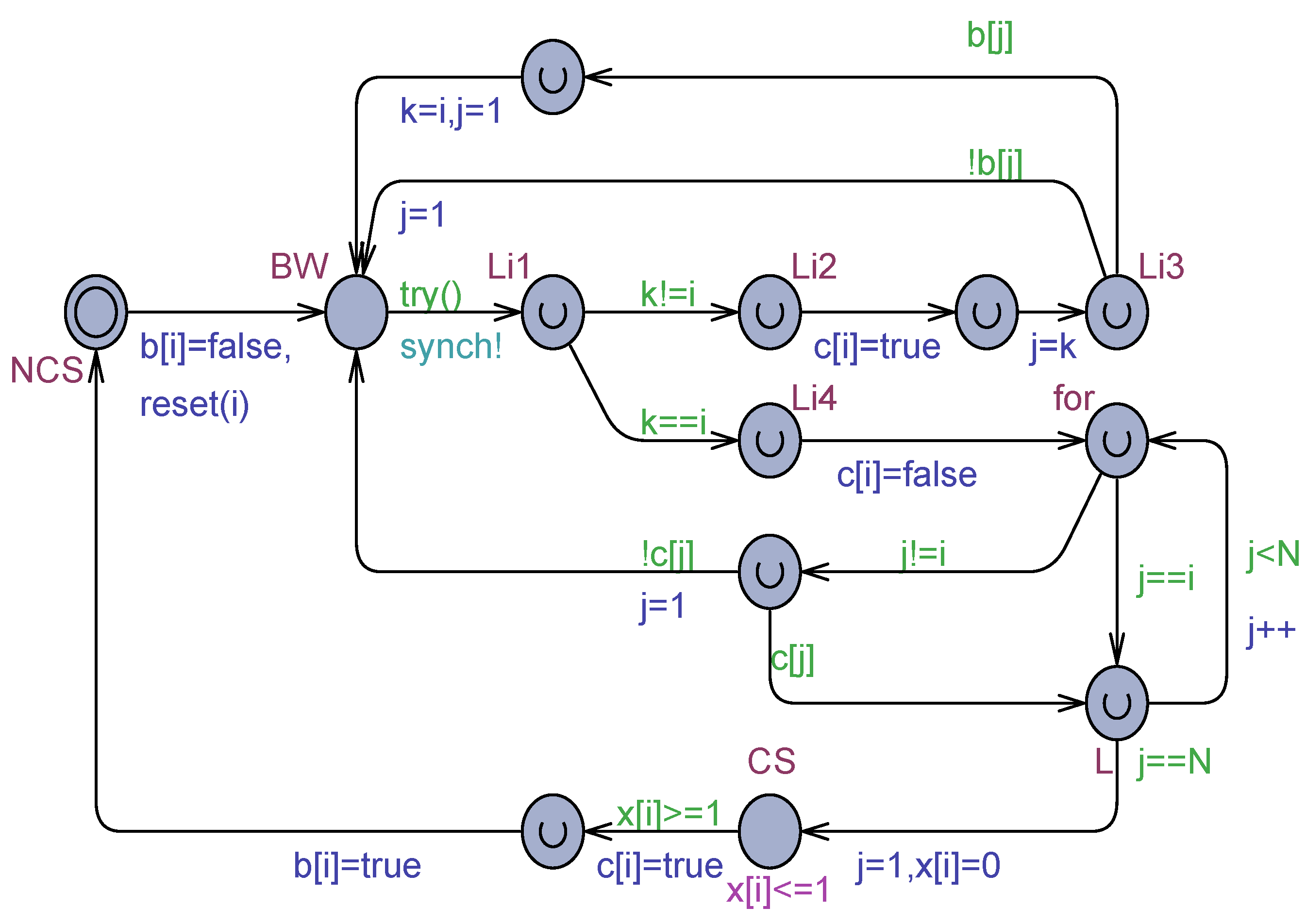
Preprints 103022 g005
Figure 5. Uppaal model for the Dijkstra’s algorithm.
Figure 5. Uppaal model for the Dijkstra’s algorithm.
Preprints 103022 g005
Preprints 103022 g006
Figure 6. Uppaal model of the Knuth’s algorithm of Algorithm 6.
Figure 6. Uppaal model of the Knuth’s algorithm of Algorithm 6.
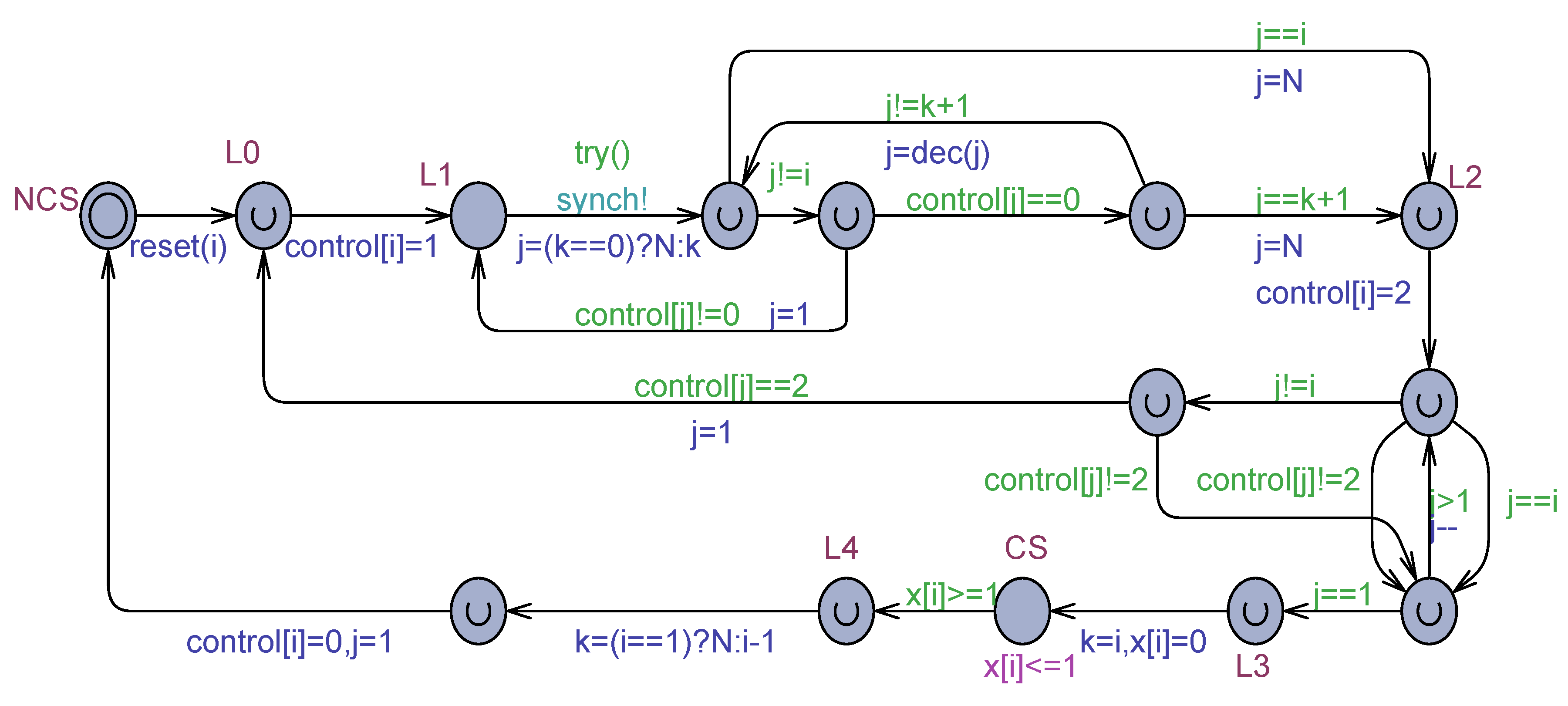
Preprints 103022 g006
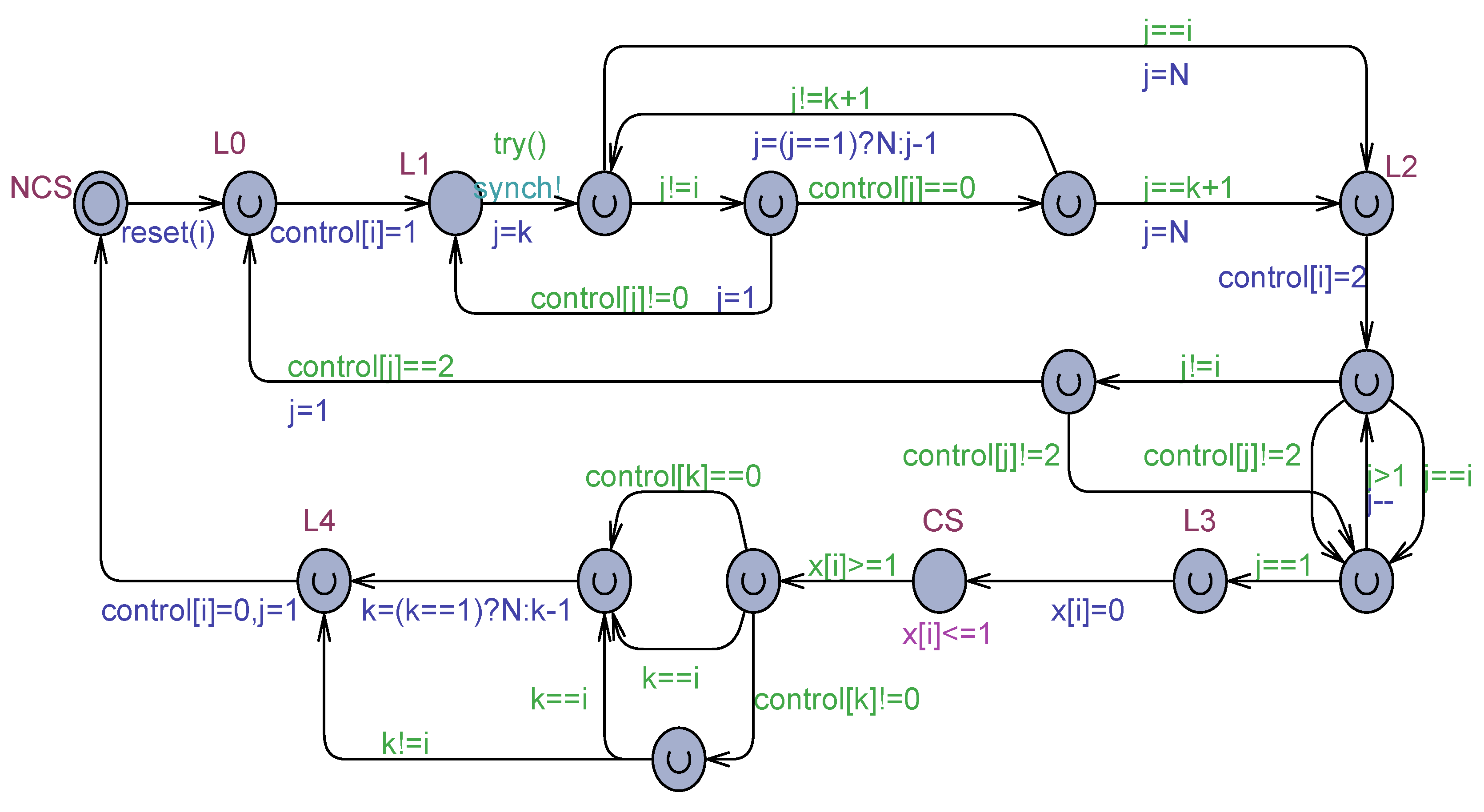
Preprints 103022 g007
Figure 7. Uppaal model of the de Bruijn’s algorithm.
Figure 7. Uppaal model of the de Bruijn’s algorithm.
Preprints 103022 g007
Preprints 103022 g008
Figure 8. Uppaal model of the de Eisenberg & McGuire’s algorithm.
Figure 8. Uppaal model of the de Eisenberg & McGuire’s algorithm.
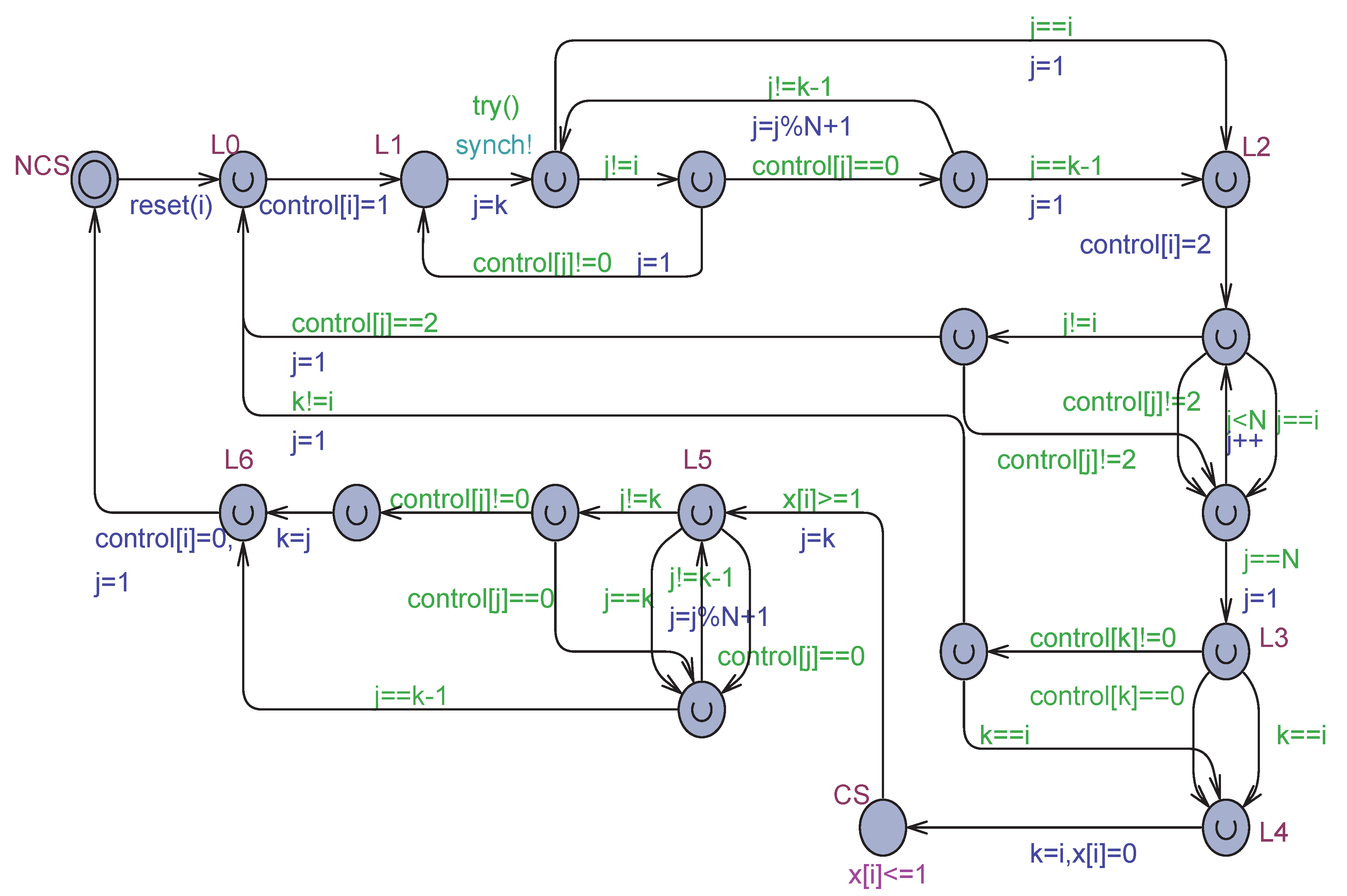
Preprints 103022 g008
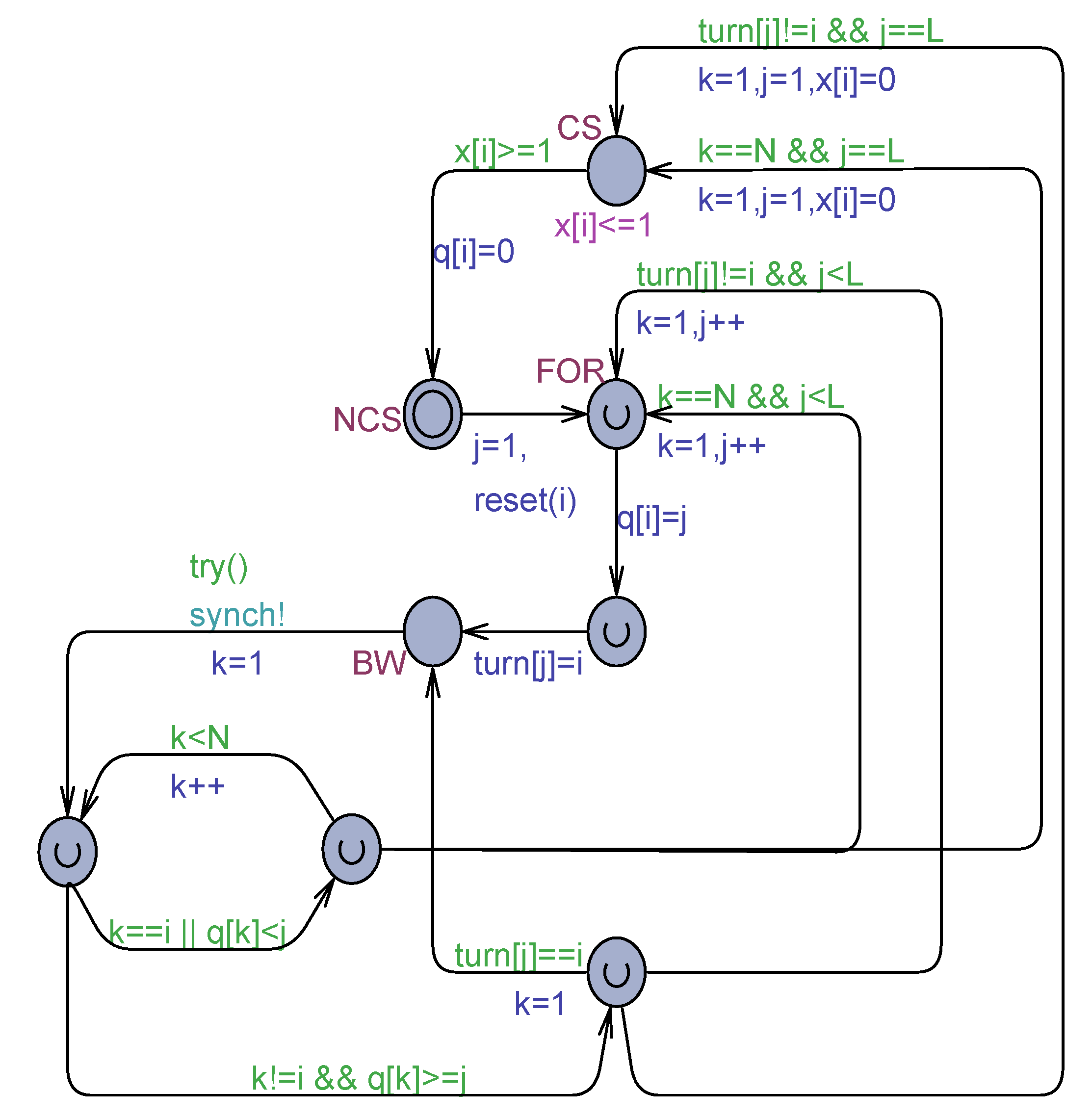
Preprints 103022 g009
Figure 9. Uppaal model for the Peterson’s algorithm for N ≥ 2
Figure 9. Uppaal model for the Peterson’s algorithm for N ≥ 2
Preprints 103022 g009
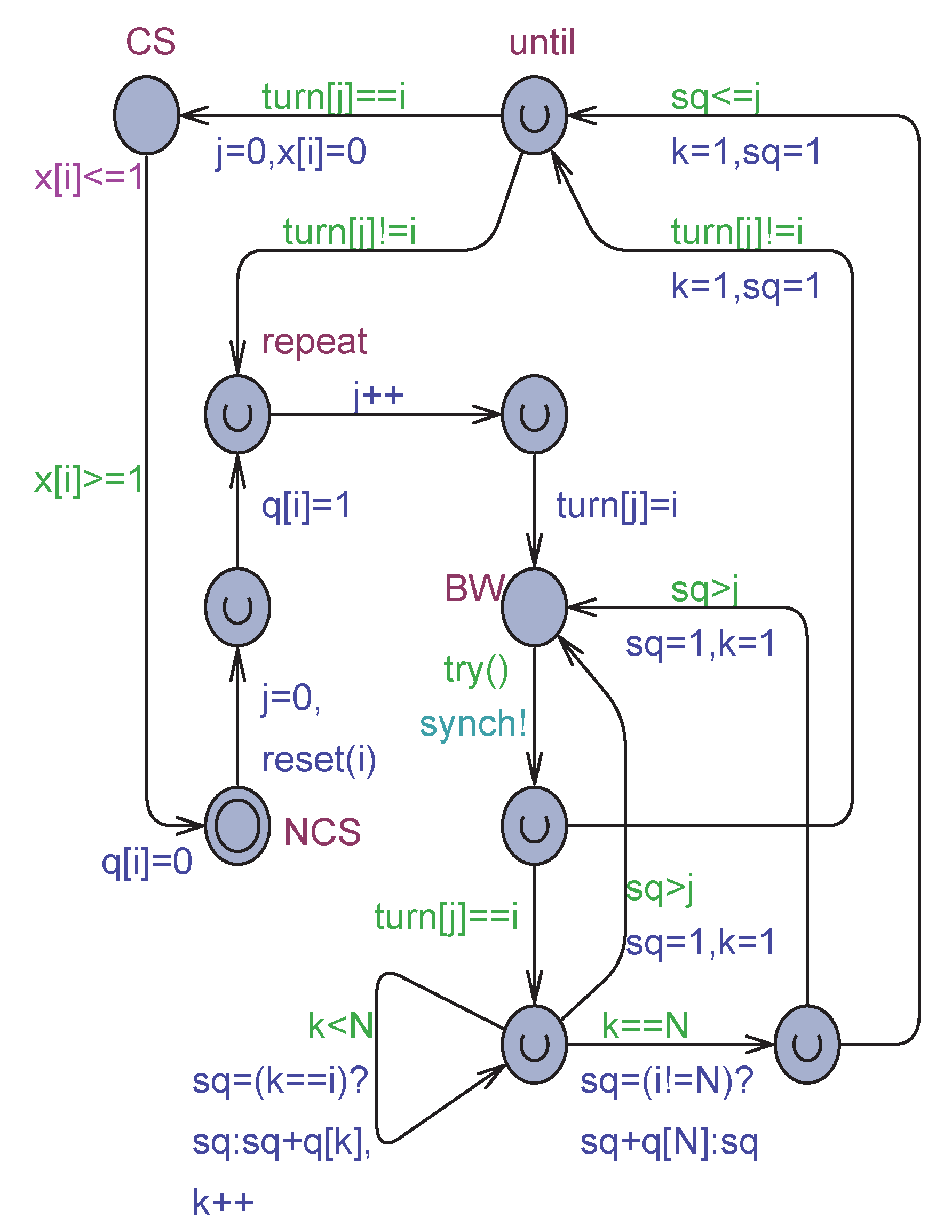
Preprints 103022 g010
Figure 10. Uppaal model for the Block & Woo algorithm for N ≥ 2 processes.
Figure 10. Uppaal model for the Block & Woo algorithm for N ≥ 2 processes.
Preprints 103022 g010
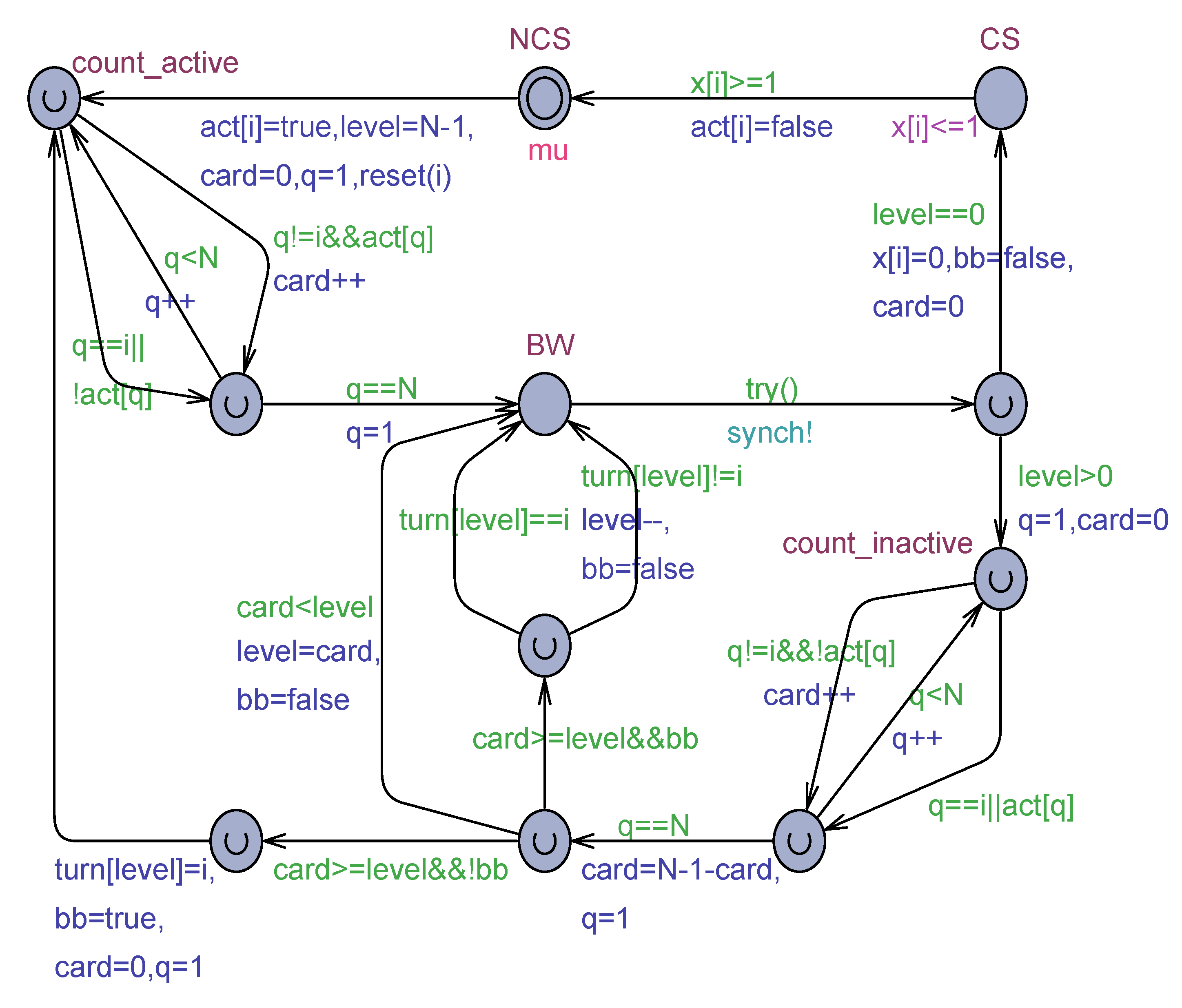
Preprints 103022 g011
Figure 11. Uppaal model for the Aravind & Hesselink algorithm for N ≥ 2 processes.
Figure 11. Uppaal model for the Aravind & Hesselink algorithm for N ≥ 2 processes.
Preprints 103022 g011
Preprints 103022 g012
Figure 12. Number of processes, vs. time, simultaneously found in their CS for N = 10 .
Figure 12. Number of processes, vs. time, simultaneously found in their CS for N = 10 .
Preprints 103022 g012
Preprints 103022 g013
Figure 13. The Uppaal model of the Aravind & Hesselink algorithm under weak memory model and flickering.
Figure 13. The Uppaal model of the Aravind & Hesselink algorithm under weak memory model and flickering.
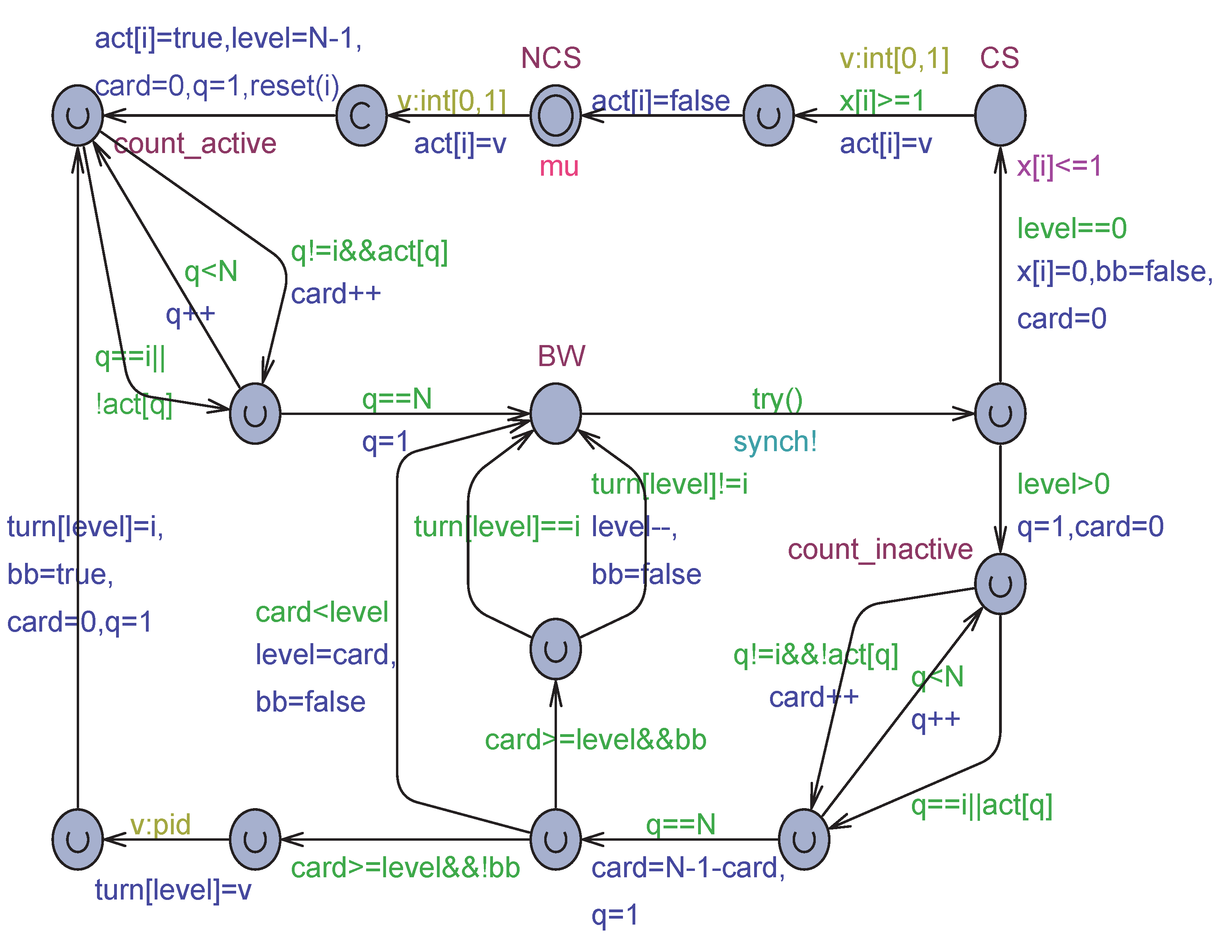
Preprints 103022 g013
Table 1. Some TCTL queries for checking a modelled mutual exclusion algorithm.
Table 1. Some TCTL queries for checking a modelled mutual exclusion algorithm.
# TCTL query Property
1 A[] !deadlock Absence of deadlocks.
2 A[] (sum(i:pid)Process(i).CS)<=1 At most one process can be in its critical section (CS).
3 Process(tp).BW − − > Process(tp).CS A process in BW eventually enters the critical section.
4 E<> Process(1).NCS && Process(2).CS A process in NCS does not forbid another process from entering the CS.
5 sup{ Process(tp).BW } : x[tp] The suprema value of the overtaking factor.
Table 2. Some MITL queries for monitoring the overtaking factor.
Table 2. Some MITL queries for monitoring the overtaking factor.
# MITL query Property
1 Pr[<=10000](<>(sum(i:pid)Process(i).CS)>1) Probability that more than one process can be in CS.
2 simulate[<=100]{sum(i:pid)Process(i).CS} Monitoring the number of processes simultaneously in CS in a simulation of 100 time units.
3 Pr[<=1000](<>Process(tp).CS) Probability that a process can actually enter its CS.
4 Pr[<=10000](<>Process(tp).BW &&
x[tp]>expected-value)		 Probability that the overtaking factor (x[tp]) can be found greater than the expected-value.
5 Pr[<=10000]([] Process(tp).NCS ||
x[tp]<=expected-value)		 Probability that x[tp] is always found less than or equal its expected-value.
Table 3. Observed overtakings vs. N for the Knuth’s algorithm.
Table 3. Observed overtakings vs. N for the Knuth’s algorithm.
N ov
2 1
3 2
4 3
5 4
Table 4. Observed overtakings vs. N for the de Bruijn’s algorithm.
Table 4. Observed overtakings vs. N for the de Bruijn’s algorithm.
N ov
2 1
3 3
4 5
5 7
Table 5. Observed overtakings vs. N for the Eisenberg & McGuire’s algorithm.
Table 5. Observed overtakings vs. N for the Eisenberg & McGuire’s algorithm.
N ov
2 1
3 2
4 3
5 4
Table 6. Observed overtakings vs. N for the generalized Peterson’s algorithm.
Table 6. Observed overtakings vs. N for the generalized Peterson’s algorithm.
N ov
2 1
3 3
4 6
5 10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated