Preprint
Article
Vector Optical Bullets in Dielectric Media: Polarization Structures and Group Velocity Effects
Altmetrics
Downloads
191
Views
51
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 April 2024
Posted:
08 April 2024
You are already at the latest version
Alerts
Abstract
Theoretical studies on the generation of nondiffracting and nondispersive light pulses and their experimental implementation are one of the renowned problems within electromagnetics. Current technologies enable creation of short-duration pulses of a few cycles with high power and fluency. An application of these techniques to the field of nondiffracting and nondispersive pulses requires a proper mathematical description of highly focused vector pulses. In this work, we study vector optical bullets in a dielectric medium with different polarization structures: linear, azimuthal, and radial. We report the differences caused by the vector model compared to the scalar model. We analyze effects caused by superluminal, subluminal, or even negative group velocity on properties of vector optical bullets inside a dielectric material.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
Engineering of structured light is on the rise nowadays due to the wide range of possible applications and benefits not only within optics, but also within physics in general [1]. This interest is caused by a large degree of controllable phenomena such as optical traction [2,3], optical spinning [4], self-healing [5], imaging [6] and nondiffractive nondispersive propagation [7].
The diffraction of light beams is one of the obstacles in the way of laser communication, information transfer, and long-distance laser interactions. As the beam propagates, its spatial components experience dephasing due to diffraction, so the spatial profile is distorted: the size increases and the intensity drops [8,9,10]. The nondiffracting beam is a beam that circumvents diffraction spreading through constructive interference in a zone called the Bessel zone. The most well-known example of such a beam is the Bessel beam [11,12]. However, other beams are also known- the elliptical Mathieu [13], the parabolic Weber [14], or the Airy beam [15]. These examples propagate infinitely large distances and possess infinite energy, however, giving them a Gaussian envelope results in finite energy optical beams resisting diffractive spreading over finite distances [16].
Moving to pulsed beams [17], yet another obstacle appears for long-distance laser applications. Due to the dispersion of the material, the phase velocities of different temporal components with different wavelengths are not the same [8]. For this reason, they propagate differently [18], so the pulse experiences dispersive broadening and other shape distortions [19]. This was found to be overcome using the nonmonochromatic superposition of nondiffracting beams with a predefined spatiotemporal dispersion within the pulse [20,21]. Joint dispersion and diffraction resistance of such pulsed fields has allowed to call them optical bullets. Among such examples of pulsed nondiffracting and nondispersing beams are pulsed Bessel beams [22], focus wave mode [23], and X-waves [24,25,26] and spatio temporal light sheets [27,28], which got their extension to the elliptical and parabolical X-waves [29] and to the nonlinear optics [30,31].
Yet another degree of freedom, which becomes more noticeable within the field of structured light, is the polarization of the electromagnetic field. This advance is constantly increasing since the realization that inhomogeneous polarization enables a sharper focus of light [32,33], which can be conveniently understood using a multipolar description of light [34,35], valid also for pulsed fields [36]. As the numerical aperture increases, the scalar description of the optical field becomes invalid [37,38,39,40]. Even for linearly polarized light, a noticeable longitudinal component appears and even detectable cross-polarization is observed [41]. The longitudinal component is especially noticeable in radially and azimuthally polarized light [42], which is created using polarization controllable optical elements [43,44].
The concept of an inhomogeneously polarized nondiffracting beam was successfully introduced by Bouchal [45], although some insight into the topic was already present in the book by Stratton [46] and the method of construction of such polarized structures is discussed in great detail by Morse [47]. The extension of the concept of nondiffracting X-waves from the scalar domain to the vector domain was introduced [48] and extended to vortical properties with an arbitrary frequency spectrum [49]. Vector light sheets of nondiffracting light were also recently studied, [50,51]. Moreover, vector parabolical, elliptical optical bullets were considered [52,53]. These advances are especially interesting, given the applications of pulsed beams polarized radially and azimuthally for material processing [54,55], together with the applications of nondiffracting beams [56,57].
We have already investigated highly nonparaxial vector Bessel-X pulses [58], introducing analytical expressions and revealing novel properties introduced by inhomogeneous polarization. In this work, we move on to the investigation of another type of optical bullets - vector focus wave modes, which are generalizations of the X-waves and Bessel-X pulses inside a dielectric dispersive medium. For this purpose, we selected one of the glass materials and analyzed the dispersion relation of the spatiotemporal spectra [21]. The general expression of the spatiotemporal spectra describes the cone angles of forward propagating Bessel beams that result in the pulsed signal propagating in the Bessel zone with controllable velocity V, which can be superluminar [59,60], subluminar [61], or even negative (i.e. propagate backward) [25]. These conditions may require high cone angles of superposed Bessel beams, so a valid vector description is required. We introduce to the optical bullets this vector description and study electromagnetic structure of resulting pulsed fields in a glass, relating the duration to the transverse size of the beam, central frequency and propagation velocity of the optical bullet.
2. Materials and Methods
Nondiffracting and nondispersive wave packets usually are introduced within the frame of the cylindrical coordinate system and are perceived as a coherent superposition of monochromatic solutions of the respective cylindrical coordinate system. For such a coherent superposition to have nondiffracting and nondispersive properties, the wave vectors and frequencies within the wave packet have to correlate with each other. This requirement results in a wide range of different wave packets that are resistant to diffraction and dispersion. In this work, our aim is to investigate the so-called optical bullets, which are characterized by the following relation:
where is the z component of the wave vector , is the transverse component of the wave vector, is the wave frequency, c is the speed of light, n is the refractive index of the material, is the angle between the z axis and the vector, V is the group velocity of the focus wave mode, and is the propagation constant. This dependency introduces the spatial-temporal relationship between the wave vector and the wave frequency. It can be visually perceived as the angular dispersion law for different frequencies:
Substituting the relation between the vector k and the frequency of the wave into the general expression of the superposition of monochromatic waves results in the following integral expression:
where and m is the topological charge of the focus wave mode, are cylindrical coordinates.
The scalar focus wave modes are well known and have been studied. Our aim here is to construct their vector counterparts. Vectorial solutions of the Maxwell equations are constructed from solutions of scalar wave equations using the method given in Reference [46,47]
where ∇ is a nabla operator and is a predefined vector [47]. Applying this operation to Equation (3) leads to the following expressions for transverse electric (TE) optical bullets:
and transverse magnetic (TM) optical bullets:
Vector functions and are basis vector functions of cylindrical coordinate systems obtained from Equation (4). Their exact expressions and physical interpretations depend on the choice of the vector .
When , the expressions resulting for and are
where is the first derivative of the Bessel function of the m-th order. This expression describes an azimuthally polarized Bessel vortex beam.
This expression describes a radially polarized Bessel vortex beam, compare with Ref [45].
When , the resulting expressions for and are
where is the unit vector of the Cartesian coordinate system. This expression describes a linearly polarized (in the y-direction) Bessel vortex beam.
where is the second order derivative of the Bessel function of the m-th order. This expression describes a linearly polarized (in the x direction) Bessel vortex beam, see Reference [45] for a slightly different definition.
Substitution of these four different basis functions into Equations (5, 6) gives integral expressions for vector optical bullets inside a dielectric material. The selection of the vector gives us azimuthally and radially polarized optical bullets, and the selection of the vector gives us linearly polarized (in the y and x directions) optical bullets. In general, these expressions cannot be analytically integrated, but integration can be performed under some strict conditions. For example, in the vacuum, when and the spectral envelope has a particular expression
then the integrals from Equations (5, 6) can be analytically evaluated to azimuthally and radially polarized pulsed Bessel-X vortices [58].
3. Vector Optical Bullets in Dielectric Material
In this section, we systematically investigate and present a comparison of linearly polarized optical bullets with their radially/azimuthally polarized counterparts in the dielectric material. We selected a BK7 glass for this investigation, but note that these steps can be easily applied to any other material whose dispersion can be described using a Sellmeier formula [62]. The angular dispersion of the focus wave modes is described by Equation (2). The properties of such dispersion curves have already been extensively studied in the literature, see Reference [21], so we shall briefly recall them without diving into the problematics.
An example of angular dispersion curves for BK7 glass is shown in Figure 1 for a few selections of group velocities and parameters . In the first case, we select a positive value of and change the group velocity values . As a result, we observe the angular dispersion that increases monotonically with frequency. The main feature of these dependencies is that the range of frequencies where the optical bullet exists changes with velocity; see Figure 1a. In the second case, we select one particular negative value of to plot the angular dispersions for 5 different values of the group velocity, see Figure 1b. This case is especially interesting as a demonstration of the rich and complex dependencies of the angular dispersion. Moreover, for some values, we observe monotonically decreasing angles for single-wave components, which after reaching the inflection point start to increase. At a particular value of the group velocity , the inflection point touches the frequency axis. A further change in the group velocity results in the dispersion curve splitting into two parts; see Figure 1b. In the last example, we selected a negative group velocity to show the possibility of creating a backward propagating optical bullet inside the dielectric material; see Figure 1c and plot dispersion curves for a selection of parameters .
Before proceeding to the analysis of numerical simulations, we note that the situation depicted in Figure 1b is the most interesting and most studied in the literature, as for the scalar optical bullets, the rich dynamics of spatiotemporal profiles is observed. Usually, the optical bullets have a spatial profile that resembles the capital Latin letter X; for this reason, the optical bullets are very often called mistakenly X-waves or Bessel-X pulses, although the latter solutions are obtained as a particular case of the focus wave modes with parameter and very specific and distinct expressions of the spectral envelope . Yet another example of the transformations in the spatiotemporal profile of the nondiffracting and nondispersive focus wave mode is the change to the capital Latin letter O, caused by specific angular dispersion due to which the peripheral intensities merge together; see References [21,24,63].
Motivated by this particular case having great attention in the literature we select one particular angular dispersion curve from the Figure 1b, when and , as this is the case with most changes in the spatiotemporal profile of the vector optical bullet. For this study, we introduce the rectangular shape of the spectral envelope , where
where the is the spectral width of the rectangular spectral envelope, is the central frequency of the wave packet. For the rectangular spectral envelope, the spectral width can be related to the temporal duration using the expression [64].
In further numerical simulations, we numerically integrate Equations (5, 6) using the aforementioned expression for the spectral envelope. For our convenience, we select one particular value of the pulse duration fs and two particular values of the central frequency, one giving us an example of the so-called X spatiotemporal profile, and another giving us an example of the so-called O spatiotemporal profile.
We start our simulations by choosing , which gives us two linearly polarized optical bullets. The case of the transverse electric optical bullet(the main component is the y component). We present the results in Figure 2. The longitudinal intensity profile of the vector optical bullet is depicted in Figure 2a. We note a distinct cross profile, which is the cause of the most used name for the optical bullets, and a clear resemblance to the capital X letter is observed. In Figure 2b we depict the total intensity profile of the transverse electric optical bullet in the plane. The streamlines depict the orientation of the electric field. In Figure 2c-e, we demonstrate individual electric field components of the vector optical bullet. The component x is absent due to the transversality of the electric field with respect to . The main dominant component is the y component, and the main effect of vectorization of the scalar optical bullet is the appearance of the z component, see Figure 2e.
In the next numerical simulation, we turn our attention to the transverse magnetic focus wave mode, see Figure 3. The intensity distribution of the transverse magnetic optical bullet in the longitudinal plane is presented in Figure 3a. Due to the selection of the central carrier frequency , in both cases we end up with relatively moderate angles of the angular dispersion curve. For this reason, the electric intensity distribution in Figure 3a is similar to the one in Figure 2a. The main difference is revealed in Figure 3b, where the transverse intensity distribution is depicted together with the streamlines with the electric field. As one can see, the transverse magnetic optical bullet is polarized in the x direction. A closer look at the individual electric field components, see Figure 3c-e, shows that the dominating electric field component is the x component, the z component is present as in the previous case, but it is rotated by 90 degrees. The most notable change is the presence of the cross-polarized (y component), which is diminishingly small due to the rather modest angles of the angular dispersion curve.
We start our investigation of inhomogeneously polarized optical bullets () by analyzing the case of azimuthally polarized optical pulse for this purpose we use Equation (7). and obtain individual electric field components by integration of Equation (5). As in the previous case, we chose the same parameters to obtain an azimuthally polarized optical pulse with the X letter in the longitudinal plane, see Figure 4.
First, we note a hollow center of the optical pulse (see Figure 4a), which is caused by the presence of a polarization singularity on the optical axis of the optical bullet. In this polarization, the singularity is visualized in Figure 4b, and is common for azimuthally polarized beams. The presence of this structure results in the x and y components being rotated 90 degrees with respect to each other, see Figure 4c, d. The intensity structure of the azimuthally polarized optical bullet contains a number of concentric rings with clockwise and counterclockwise pace of the electric field rotation; see Figure 4b. Changes in the orientation of the azimuthally polarized light are caused by different phases on concentric rings when moving away from the center of the beam. As expected, the longitudinal component is absent in this case, see Figure 4e.
The next case, which we study, is the radially polarized optical bullet. We obtain individual electric field components using Equation (8) which we use to integrate Equation (6). For consistency, the set of parameters is the same in this integral as in previous cases.
The numerical results are given in Figure 5. The longitudinal intensity distribution of the radially polarized optical bullet largely resembles the previous case - we observe the presence of the onaxis intensity minima, though the intensity never reaches zero here, see Figure 5a. The intensity distribution in the transverse plane together with the depiction of the polarization state is given in Figure 5b. We observe here the presence of the polarization singularity: the electric field lines are not defined in the very center of the beam and are oriented either away or towards the center of the beam. Oscillations in the orientations are caused by phase changes in the concentric intensity structure of the radially polarized optical bullet. This behavior is well known and expected and is caused by the intensity distributions of the x and y components, see Figure 5c, d. The x component of the radially polarized optical pulse is rotated 90 degrees compared to the x component of the azimuthally polarized pulse; see Figure 4c. The y component also rotates 90 degrees; see Figure 5d. Most notably, we observe the appearance of the longitudinally polarized z component; see Figure 5e. The presence of the nonzero z component causes the region of the onaxis polarization singularity to become somewhat less pronounced. As the maximum value of the z component reaches 10 % of the maximum intensity on the axis.
Our next aim is to investigate the set of parameters for which the longitudinal shape of the optical bullet is expected to change from the capital Latin letter X to the capital Latin letter O. For ease of comparison, the dispersion curve, which we investigate, is the same as previously, see Figure 1b, curve (2), but the central frequency has now decreased. This change will lead to larger spatial angles in the optical bullet, and thus we expect vectorial properties to become more pronounced.
We start the verification of this claim by repeating numerical simulations of the linearly polarized optical bullet using Equations (5, 6). The linearly polarized transverse electric optical bullet is presented in Figure 6. We immediately notice the changes in the longitudinal intensity distribution; see Figure 6a. Long-range peripheral arms similar to the X shape are no longer present, compared to Figure 2a. Although the spatial extent of the central part is smaller now and we observe a large number of needle-like structures when we move away from the center, we can deduce a rhombus-like area with approximately same levels of intensity; see Figure 6a. This becomes especially obvious when we turn our attention to the intensity levels of approximately 20 % of the normalized value. Although this rhombus shape has sharp corners, it can be seen as a distorted O-shaped. Thus, we can conclude that the spatiotemporal shape of the vector optical bullet experiences the same changes as reported for scalar optical pulses [21,24].
The transverse intensity distribution of the linearly polarized optical bullet is given for this case in Figure 6b. The electric field lines in this plane are expectedly oriented along the y direction. However, the intensity distribution of the total electric field has some signs of nonuniformity, with the tendency to have higher intensities in the direction of the electric field. In the expected manner for the transverse electric optical bullet, no x component is present, see Figure 6c. The dominant electric field component is the y component; see Figure 6d. When we plot the longitudinal electric field component, see Figure 6e, we recognize the cause of the nonuniformity in the total electric field. The maximum value of the z component reaches 10 % of the intensity of the y component. This increase in the relative strength of the longitudinal component is mainly caused by changes in the central frequency of the optical pulse, compared to Figure 2e.
In the next set of simulations we move on to investigate the transverse magnetic linearly polarized optical bullet; see Figure 7. The longitudinal intensity distribution is given in Figure 7a. As in the case of the transverse electric optical bullet, in this case, we observe a disappearance of the pronounced X shape in the intensity profile, compared to Figure 3a. This behavior is expected because of the change in the central frequency of the optical pulse. The transverse intensity distribution is depicted in Figure 7b together with the streamlines depicting the orientation of the electric field. We note the appearance of some inhomogeneity in the flow of the electric field, compared to Figure 6b. There are some particular points in the regions of vanishingly low intensity when the electric field is not oriented along the x-axis anymore. This behavior is expected when one notices the presence of the component y in the Equation (10).
The intensity distributions of the individual electric field components are given in Figure 7c-e. As expected, the x component of the electric field is the strongest; see Figure 7c. Most notably, we observe the appearance of a vanishingly small y component; see Figure 7d. Its maximum value reaches the single percent digits compared to the dominant x component. The longitudinal component reaches 10 % of the value of the x component. This behavior is comparable to the case of the transverse electric optical bullet; see Figure 6e.
We investigate radially and azimuthally polarized optical bullets of the O type using the same set of parameters as we did in the case of linearly polarized FWM. An example of the azimuthally polarized optical bullet for this particular case is given in Figure 8. The longitudinal intensity distribution is shown in Figure 8a. As expected, no z-component is present in the beam; see Equation (7), for this reason the optical pulse has a void-like intensity structure with no axial intensity. In particular, the general shape of the transverse intensity distribution is a distinct rhombus-like shape, resembling the capital Latin letter O, compared to Figure 4a. The transverse intensity distribution now represents a large number of concentric rings with oscillating direction of clockwise and counterclockwise electric field rotation; see Figure 8b. As the change in the central frequency has resulted in the increase of spatial angles of the individual Bessel beams, creating a optical bullet, the focus wave mode became more spatially confined, see Figure 8c, d. The individual electric field components are spatially oriented in the same way as in the previous case; see Figure 4c, d, but a finer structure with larger number of rings has appeared. As expected, no z components are present; see Figure 8e.
The situation depicting the radially polarized optical bullet is given in Figure 9. The longitudinal intensity distribution, given in Figure 9a, resembles the intensity distribution of azimuthally polarized FWM; see Figure 8a, with a noticeable difference. The axial intensity is no longer zero and is on a level comparable to the general pattern of the beam. This can be especially noticed in the transverse intensity distribution of the electric field shown in Figure 9b. The central part of the beam is not hollow anymore, though we observe a polarization singularity with star-like flow of the electric field streamlines. Due to the phase jumps in the adjacent concentric rings, the orientation of the electric field is changing from inwards to outwards; see Figure 9b. The individual components of the electric field are shown in Figure 9c-e. As expected, the two strongest field components are the x and y components; see Figure 9c, d and compared to the previous case, in Figure 5c, d. The longitudinal component became stronger, when compared to the previous case, please note the change in the colorbar values; see Figure 5e and Figure 9e.
Lastly, we proceed to the investigation of very specific optical bullets with the spatial dispersion dependence depicted in Figure 1c. We recall here that these dependencies were obtained from Equation (1), when requiring that the longitudinal components of the wave vector remain positive, i.e. describe the forward propagating conical beams, whereas the group velocity V of the optical bullet is negative, thus the result of the superposition of the forward propagating waves is a backward propagating optical pulse. For this study, we choose one particular set of parameters, see Figure 1c, curve (1). We note that this specific condition requires rather large spatial angles of the individual components (up to ) and additionally restricts the temporal frequencies for which backward propagation of the pulse is possible.
Once again, we use Equation (9) to evaluate the linearly polarized transverse electric optical bullets, see Equation (5). The results of the numerical simulations are given in Figure 10. The longitudinal intensity distribution of the transverse electric optical bullet is given in Figure 10a. Note that, because of the relatively high spatial angles, we had to decrease the transverse scale in all subsequent figures. The general shape of the optical bullet is of the O type. The area of approximately the same intensity level has a distinct rhombus-like shape. However, the most pronounced effect is observed in the transverse intensity distribution; see Figure 10b. The concentric ring-like structure that was observed in previous cases, see Figure 2b and Figure 6b is not present anymore. This change can be understood by looking at the intensity patterns of individual electric field components; see Figure 10c-e. No x component is present, but the longitudinal component of the field is the strongest due to the high spatial angles of the individual plane waves; see Figure 1c.
The linearly polarized transverse magnetic optical bullet for this particular case is evaluated and presented in Figure 11. The most noticeable difference for the backward propagating TM mode compared to the TE mode can be seen in Figure 11a. The transverse beam size is considerably larger in this case, but the longitudinal dimension is the same. The changes are even more pronounced in the transverse pattern of the optical bullet at its center; see Figure 11b. The streamlines representing the electric field are not oriented along the x-axis anymore, compared to the previous cases, see Figure 3b and Figure 7b. The intensity distribution is not symmetrical anymore with respect to the beam center but is elongated along the x-axis. This behavior is a direct manifestation of high spatial frequencies comprising the backward-propagating FWHM. In a similar fashion, linearly polarized light is elongated along the direction of polarization in high numerical aperture systems. Moreover, from the flow of the electric field lines, we conclude that the notable cross-polarized component is present., see Figure 11b. The individual components of the electric field are given in Figure 11c-e. The x-polarized component is no longer symmetric, though the concentric rings system is observable in the beam profile. For this particular case, we observe the strongest cross-polarized y component from all the considered cases; see Figure 11d. Its maximum value is even comparable to that longitudinally polarized in Figure 11e. The general shapes of these individual components are in line with expectations. We see that the longitudinal component is elongated along the direction of polarization and that the cross-polarized component has two perpendicular splits in its concentric ring pattern.
We consider the inhomogeneously polarized backwards propagating optical bullets with the case of azimuthal polarization; see Figure 12. The longitudinal intensity distribution is given in Figure 12a. Compared to previously investigated cases, the most distinct effect caused by spatiotemporal dispersion is the change of the transverse sizes and observation of the general shape of O-type; see Figure 12a. In the transverse plane, we see a large number of concentric rings with clockwise and counterclockwise directions of the electric field flow; see Figure 12b.
The longitudinal field component for azimuthal polarization is zero, and the x and y components are of the same strength, and intensity distributions with one notable difference being a 90 degree rotation with respect to each other; see Figure 12c-e.
The radially polarized backward-propagating optical bullet is depicted in Figure 13. Here, we observe a distinct difference to the azimuthally polarized optical bullet and compare Figure 12a and Figure 13a. Whereas the central part of the azimuthally polarized optical bullet is hollow because of the presence of azimuthal phase singularity, the central part of the radially polarized optical bullet is the brightest one. The transverse intensity distribution depicts the same trend - the central part still contains the star-like radial polarization singularity, but the intensity is still highest at its very core; see Figure 13b. The solution to this riddle is presented in Figure 13c-e, where the individual electric field components of the optical pulse are given. The x and y components are comparable to each other and rotated by 90 degrees in respect to one another; see Figure 13c, d. However, in reverse to the previous cases, the strongest electric field component is the longitudinal one; see Figure 13e. This behavior is expected due to the choice of the central frequency in the optical pulse, causing the appearance of high spatial angles . Under these conditions, the radial polarization becomes strongly focused, which in return causes the appearance of very tight small spots with longitudinal polarization [32].
We summarize the investigation of these three particular cases by investigating the effects that the choice of group velocities V and the propagation constant has on the spatiotemporal parameters of the optical bullets, such as effective beam width in transverse and longitudinal directions. In the case of uniform beam shapes, such as a Gaussian beam or similar modes, the question of the beam width definition is pretty straightforward. The full width at half maximum of the intensity is the most commonly used within the field. However, in our case, the complex vectorial nature together with a rich ring-like structure observed in the variously polarized pulses suggests to look at alternative definitions for the beam width. One of the alternatives that is very efficient at accounting for peripheral parts of the complex optical beams is the so-called second-moment definition.
where is the radial coordinate in the plane under consideration and is the total intensity of the electric field.
As we have concluded from three cases investigated in the previous part, the spatiotemporal dependence between frequencies, individual cone angles (see Figure 1) strongly affects intensity distributions both of individual electric field components and total electric field for vector optical bullets. Therefore, it is natural to ask ourselves whether these effects can be qualified using standard metrics, such as beam length. In this numerical experiment, we keep the same duration () for all cases and change the central frequency of the pulse. We consider linearly polarized TE and TM optical bullets along with radially and azimuthally polarized ones. The transverse beam width is evaluated together with the longitudinal extent of the optical pulse using two different definitions: FWHM and second moment.
The beam widths of the optical pulses using the FWHM definition are given in Figure 14a. First, we note that for particular parameters and the FWHM beam width behaves very distinctly: the beam width first decreases, up to central frequencies of , then increases to the maximum value of at frequency . A further increase in the carrier frequency results in a monotonically decreasing beam size. This behavior can be understood by looking at Figure 1b, curve (2). The spike in FWHM dependency occurs at the same frequency when the spatial angles are rather small. When the spatial angles increase, we obtain optical pulses with small transverse sizes. Most notably, the linearly polarized modes have, for this case, indistinguishable beam width; see Figure 14a, red curves. The same applies to the radially and azimuthally polarized beams, though they are larger than the linearly polarized optical bullets. For this particular case, the spatial angles are rather modest, so the difference between the azimuthal and radial polarizations is vanishingly small, as is the case between the linearly polarized TM and TE optical bullets.
We also investigate the beam sizes of the backward propagating focus wave modes, where and , see Figure 14a, blue curves. In our previous investigation, we observed the most notable differences between polarizations in this case. As a result, we observe that the FWHM beam-width dependencies are separate for all different cases of vector FWMs. Most notably, the radial polarization becomes comparable in the beam sizes to the linearly polarized TE FWM, as the frequency increases. This is an expected outcome because it is well known that radial polarization could even result in a tighter focal spot than linear polarization [32]. Radial polarization has beam sizes smaller than those of the linearly polarized TM mode; see Figure 14a. The largest beam sizes are observed for the azimuthally polarized FWHM.
The next metric is the definition of the second moment of the beam width. This metric usually has the characteristic of artificially increasing importance of peripheral parts of the beam. It represents the radial distance weighted intensity; therefore, if the intensity drops moving away from the center of the beam slower than the square of the radial distance, it might result in larger beam sizes than those obtained using the FWHM definition. The result of the numerical estimate of this beam width for the same set of parameters is given in Figure 14b. We immediately notice differences in the general trend of the beam-width dependencies of the carrier frequency. Whereas the FWHM beam width was monotonically decreasing for four cases out of eight, the second-moment beam width depends on the carrier frequency non-monotonically. For small carrier frequencies, it starts to increase to some particular value and then drops. In this case, the linear polarization has the largest beam width. These subtle differences that occur at smaller carrier frequencies are observable for the four cases considered here. Moving to the case of backward propagating FWM, see Figure 14b, blue curves, we note yet another tendency: the beam widths defined using the second order moment of the beam behave differently than those defined using the FWHM definition; compare to Figure 14a. This means that even though the beam is above the 50 percent level is larger, the total intensity in the beam drops a lot faster than the radial coordinate for smaller carrier frequencies. The fact that the second-moment beamwidth increases with increasing central frequency indicates that significant side lobes become present in the vector FWMs.
The longitudinal beam size has also been investigated. The result did not show any change in that size across all investigated frequencies, and for the sake of brevity, figures covering this claim are not provided. In the case of and , the longitudinal beam size remains constant at using the FWHM definition for all polarizations investigated. For the case of and , the longitudinal beam size remains constant at for all the investigated scenarios. Using the definition of second-moment beam size, we have determined the following constant longitudinal beam lengths: for and , and for and .
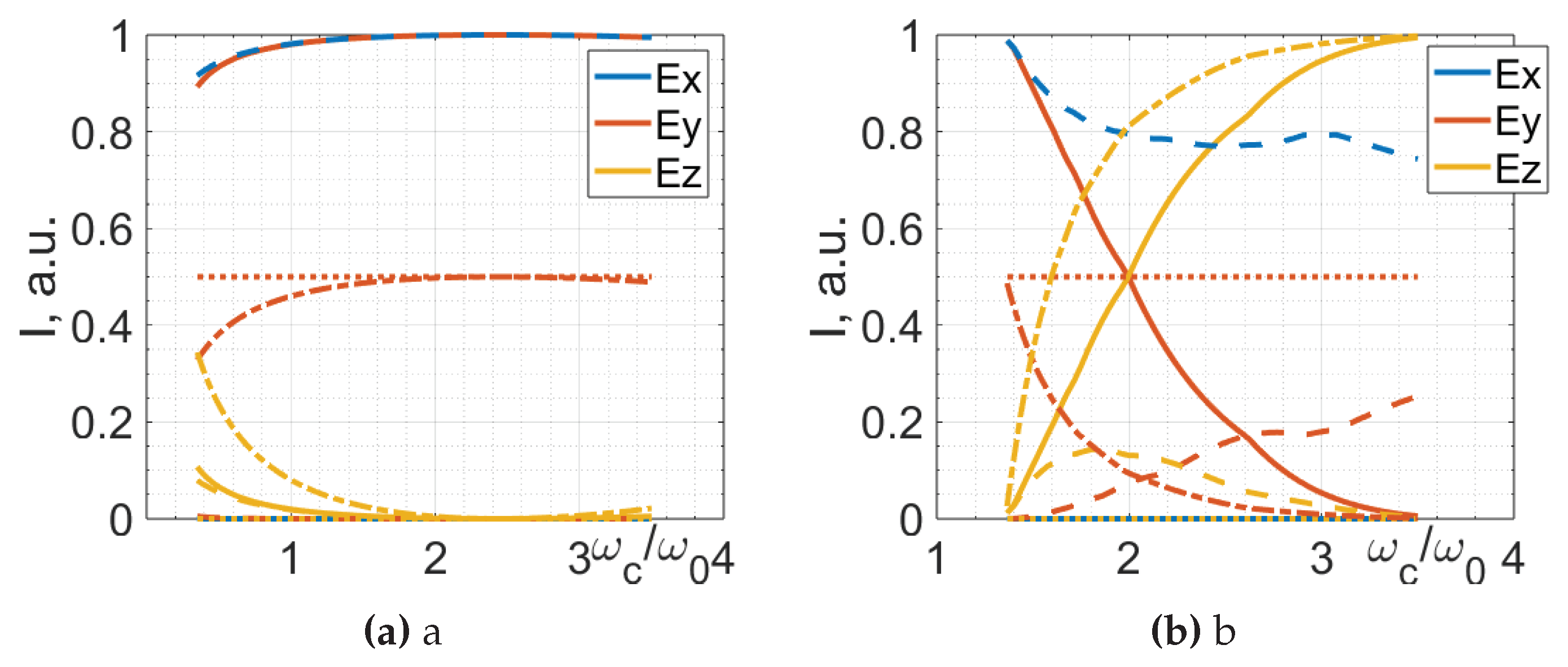
Another key point of interest in this investigation is the relative strengths of the intensity of individual electric field components for different frequencies. In Figure 15a, we give these dependencies for and . The solid lines represent the linear TE polarization and the dashed line represents the linear TM polarization. For linear polarization, with lower frequency values, we can see that the z component has an intensity of up to 10%. With increasing frequency, the z component of the electric field decreases and, around the value of , the z component approaches 0. For the TE polarization, the y component is nonexistent; for the TM polarization, the x component is nonexistent. The azimuthal polarization has constant x- and y-components of equal proportions at all frequencies tested, without a z component of the electric field. Radial polarization has the z component for low frequencies, which decreases rapidly with increasing frequency, see Figure 15a.
In the case where the vector FWM propagates backwards, that is, and , the dependencies of the normalized intensities of the individual components are more pronounced. The linear TE optical bullet and radially polarized FWM have strong z-components of the electric fields that increase with increasing frequency. On the other hand, the linear TM polarization has a strong x component of the electric field, but with increasing frequency, the maximal intensities of the y and z electric field components start to dominate, see Figure 15b. From the frequencies of , the intensity of the z component of the electric field slowly decreases, resulting in the increase of the y component. The azimuthally polarized FWM shows steady and equally strong x and y components at all tested frequencies, as expected. The radially polarized FWM has the strongest z electric field component, which increases rapidly with increasing frequency, see Figure 15b.
4. Discussion and Conclusions
We have introduced the vector formalism to the concept of nondiffracting and nondispersing optical bullets within a dielectric material. Vector optical bullets for different polarizations were introduced: linear polarization, azimuthal polarization, and radial polarization. Two different propagation velocities V were chosen to showcase the wide variety of spatiotemporal dispersions of vector optical bullets, one positive and one negative (i.e. backward propagating). The first value of the group velocity V was chosen because it enforces a particularly interesting dispersion, with cone angles that extend from small paraxial (i.e. scalar description is valid) to larger values, which require now a proper vector treatment of the electric field.
For this particular velocity, we selected two different values of central frequencies, showcasing two possible situations: one giving the so-called X spatiotemporal profile and another giving the so-called O spatiotemporal profile. We can conclude that the spatiotemporal shape of the vector optical bullet experiences the same changes as reported for scalar optical pulses with differences arising from nonzero longitudinal and cross-polarization components. In the expected manner, high cone angles result in a vector description of the vector FWM, also demonstrating distinct distances between polarizations.
For the second case, when the forward propagating superposition of Bessel beams creates within the Bessel zone a backward propagating pulse of negative velocity V, we observed the most notable differences in the properties of vector optical bullets within the dielectric material. Due to the highly nonparaxial nature of such exotic waves, the longitudinal component is quite noticeable in the TE and TM polarized optical bullets, most notable is the appearance of relatively large cross-polarized component in the linearly polarized TM mode. As expected no differences did appear in the azimuthally polarized optical bullet, but the radially polarized wave was most affected - the longitudinal electric field component dominates the intensity pattern.
Lastly, we have studied how polarization and spatio-temporal dispersion influence beam sizes of the optical bullets in the focal plane. For this we have used two distinct metrics - the full width half maximum and the second-order moment of the beam. As expected, the FWHM beam size gradually increases, where the central frequency and the group velocity allow the angular dispersion curve to touch the frequency axis. This has been shown using two different methods to calculate the beam size: the full width at half maximum and the method of the second moment. For the optical bullets with negative group velocity the FWHM beam sizes monotonically increase as we move along the dispersion curve to higher cone angles of the spatial components. The second metric is well known for its sensitivity to the side lobe energy, so this parameter has revealed a complex dynamics within the optical bullets showcasing a competition between the main spike of the signal and the side lobes.
We also investigated the normalized maximal intensities of each component for the linear, radial, and azimuthal polarizations of the TE and TM for the negative and positive group velocity values. The behaviors are found to be very different for these aforementioned cases. The most notable difference was caused by rather high spatial angles in the backwards propagating optical bullets, as we investigate various carrier frequencies.
Author Contributions
Conceptualization, S. O.; methodology, S. O. and A. G.; software, A. G. and K. L.; validation, K. L.; formal analysis, S. O. and K. L.; investigation, A. G. and K. L.; resources, S. O.; data curation, K. L.; writing—original draft preparation, S. O. and K. L.; writing—review and editing, S. O. and K. L.; visualization, K. L.; supervision, S. O.; project administration, S. O.; funding acquisition, S. O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the Research Council of Lithuania (LMTLT) via agreement No. [S-MIP-23-71].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data will be made available upon request.
Acknowledgments
This work is dedicated to the memory of Professor Algis Petras Piskarskas (1942-2022), who was a mentor, colleague, a pioneer and a leader in the field of optics.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FWM | Focus Wave Modes |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
| FWHM | Full Width Half Maximum |
References
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; others. Roadmap on structured light. Journal of Optics 2016, 19, 013001. [Google Scholar] [CrossRef]
- Shvedov, V.; Davoyan, A.R.; Hnatovsky, C.; Engheta, N.; Krolikowski, W. A long-range polarization-controlled optical tractor beam. Nature photonics 2014, 8, 846–850. [Google Scholar] [CrossRef]
- Mitri, F.; Li, R.; Guo, L.; Ding, C. Optical tractor Bessel polarized beams. Journal of Quantitative Spectroscopy and Radiative Transfer 2017, 187, 97–115. [Google Scholar] [CrossRef]
- Friese, M.E.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optical alignment and spinning of laser-trapped microscopic particles. Nature 1998, 394, 348–350. [Google Scholar] [CrossRef]
- Milione, G.; Dudley, A.; Nguyen, T.A.; Chakraborty, O.; Karimi, E.; Forbes, A.; Alfano, R.R. Measuring the self-healing of the spatially inhomogeneous states of polarization of vector Bessel beams. Journal of Optics 2015, 17, 035617. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nature methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.X.; He, H.; Tang, H.; Wong, K.K. Non-diffracting light wave: Fundamentals and biomedical applications. Frontiers in Physics 2021, 9, 698343. [Google Scholar] [CrossRef]
- Akhmanov, S.A.; Nikitin, S.Y. Physical optics; Oxford University Press, 1997.
- Vesperinas, M.N. Scattering and diffraction in physical optics; World Scientific Publishing Company, 2006.
- Bennett, C.A. Principles of physical optics; John Wiley & Sons, 2022.
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. JOSA A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Gori, F.; Guattari, G.; Padovani, C. Bessel-gauss beams. Optics communications 1987, 64, 491–495. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Optics letters 2000, 25, 1493–1495. [Google Scholar] [CrossRef] [PubMed]
- López-Mariscal, C.; Bandres, M.A.; Gutiérrez-Vega, J.C.; Chávez-Cerda, S. Observation of parabolic nondiffracting optical fields. Optics express 2005, 13, 2364–2369. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.; Broky, J.; Dogariu, A.; Christodoulides, D. Observation of accelerating Airy beams. Physical Review Letters 2007, 99, 213901. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Bandres, M.A. Helmholtz–gauss waves. JOSA A 2005, 22, 289–298. [Google Scholar] [CrossRef]
- Shen, Y.; Zhan, Q.; Wright, L.G.; Christodoulides, D.N.; Wise, F.W.; Willner, A.E.; Zou, K.h.; Zhao, Z.; Porras, M.A.; Chong, A.; others. Roadmap on spatiotemporal light fields. Journal of Optics 2023, 25, 093001. [Google Scholar] [CrossRef]
- Orlov, S.; Gajauskaite, A.; Juršėnas, A. Propagation of vector nondiffracting and nondispersive pulsed beams through an air-dielectric planar interface. Procedia CIRP 2018, 74, 585–588. [Google Scholar] [CrossRef]
- Hodgson, J.N. Optical absorption and dispersion in solids; Springer Science & Business Media, 2012.
- Orlov, S.; Piskarskas, A.; Stabinis, A. Localized optical subcycle pulses in dispersive media. Optics letters 2002, 27, 2167–2169. [Google Scholar] [CrossRef] [PubMed]
- Orlov, S.; Stabinis, A. Angular dispersion of diffraction-free optical pulses in dispersive medium. Optics communications 2004, 240, 1–8. [Google Scholar] [CrossRef]
- Saari, P.; Sõnajalg, H. Pulsed bessel beams. Laser Physics 1997, 7, 32–39. [Google Scholar]
- Reivelt, K.; Saari, P. Optical generation of focus wave modes. JOSA A 2000, 17, 1785–1790. [Google Scholar] [CrossRef] [PubMed]
- Porras, M.A.; Valiulis, G.; Di Trapani, P. Unified description of Bessel X waves with cone dispersion and tilted pulses. Physical Review E 2003, 68, 016613. [Google Scholar] [CrossRef]
- Zapata-Rodríguez, C.J.; Porras, M.A. X-wave bullets with negative group velocity in vacuum. Optics letters 2006, 31, 3532–3534. [Google Scholar] [CrossRef]
- Salem, M.A.; Bağcı, H. Reflection and transmission of normally incident full-vector X waves on planar interfaces. JOSA A 2012, 29, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Kondakci, H.E.; Abouraddy, A.F. Diffraction-free space–time light sheets. Nature Photonics 2017, 11, 733–740. [Google Scholar] [CrossRef]
- Yessenov, M.; Hall, L.A.; Schepler, K.L.; Abouraddy, A.F. Space-time wave packets. Advances in Optics and Photonics 2022, 14, 455–570. [Google Scholar] [CrossRef]
- Davila-Rodriguez, J.; Gutiérrez-Vega, J.C. Helical Mathieu and parabolic localized pulses. JOSA A 2007, 24, 3449–3455. [Google Scholar] [CrossRef] [PubMed]
- Butkus, R.; Orlov, S.; Piskarskas, A.; Smilgevicius, V.; Stabinis, A. Phase matching of optical X-waves in nonlinear crystals. Optics communications 2005, 244, 411–421. [Google Scholar] [CrossRef]
- Orlov, S.; Stabinis, A.; Smilgevicius, V.; Valiulis, G.; Piskarskas, A. Parametric excitation of X-waves by downconversion of Bessel beams in nonlinear crystals. Optics letters 2007, 32, 68–70. [Google Scholar] [CrossRef] [PubMed]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Physical review letters 2003, 91, 233901. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. The focus of light—linear polarization breaks the rotational symmetry of the focal spot. Journal of modern optics 2003, 50, 1917–1926. [Google Scholar]
- Orlov, S.; Peschel, U.; Bauer, T.; Banzer, P. Analytical expansion of highly focused vector beams into vector spherical harmonics and its application to Mie scattering. Physical Review A 2012, 85, 063825. [Google Scholar] [CrossRef]
- Orlov, S.; Berškys, J. Vector-spherical-harmonics representation of vector complex source beams carrying vortices. Physical Review A 2020, 102, 063532. [Google Scholar] [CrossRef]
- Gonoskov, I.; Aiello, A.; Heugel, S.; Leuchs, G. Dipole pulse theory: Maximizing the field amplitude from 4 π focused laser pulses. Physical Review A 2012, 86, 053836. [Google Scholar] [CrossRef]
- Orlov, S.; Peschel, U. Complex source beam: A tool to describe highly focused vector beams analytically. Physical Review A 2010, 82, 063820. [Google Scholar] [CrossRef]
- Orlov, S.; Banzer, P. Vectorial complex-source vortex beams. Physical Review A 2014, 90, 023832. [Google Scholar] [CrossRef]
- Mitri, F. Superposition of nonparaxial vectorial complex-source spherically focused beams: Axial Poynting singularity and reverse propagation. Physical Review A 2016, 94, 023801. [Google Scholar] [CrossRef]
- Gutiérrez-Cuevas, R.; Moore, N.J.; Alonso, M.A. Lorenz-Mie scattering of focused light via complex focus fields: An analytic treatment. Physical Review A 2018, 97, 053848. [Google Scholar] [CrossRef]
- Bauer, T.; Orlov, S.; Peschel, U.; Banzer, P.; Leuchs, G. Nanointerferometric amplitude and phase reconstruction of tightly focused vector beams. Nature Photonics 2014, 8, 23–27. [Google Scholar] [CrossRef]
- Oron, R.; Blit, S.; Davidson, N.; Friesem, A.A.; Bomzon, Z.; Hasman, E. The formation of laser beams with pure azimuthal or radial polarization. Applied Physics Letters 2000, 77, 3322–3324. [Google Scholar] [CrossRef]
- Machavariani, G.; Lumer, Y.; Moshe, I.; Meir, A.; Jackel, S. Spatially-variable retardation plate for efficient generation of radially-and azimuthally-polarized beams. Optics Communications 2008, 281, 732–738. [Google Scholar] [CrossRef]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G.; Gertus, T. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass. Applied Physics Letters 2011, 98, 201101. [Google Scholar] [CrossRef]
- Bouchal, Z.; Olivík, M. Non-diffractive vector Bessel beams. Journal of Modern Optics 1995, 42, 1555–1566. [Google Scholar] [CrossRef]
- Stratton, J.; Antennas, I. P. Society, Electromagnetic Theory, 2007.
- Morse, P.; Feshbach, H. Methods of theoretical physics, number 2 tom. International series in pure and applied physics (McGraw-Hill, 1953), 1953. [Google Scholar]
- Salem, M.A.; Bağcı, H. Energy flow characteristics of vector X-waves. Optics express 2011, 19, 8526–8532. [Google Scholar] [CrossRef] [PubMed]
- Ornigotti, M.; Conti, C.; Szameit, A. Universal form of the carrier frequency of scalar and vector paraxial X waves with orbital angular momentum and arbitrary frequency spectrum. Physical Review A 2015, 92, 043801. [Google Scholar] [CrossRef]
- Diouf, M.; Harling, M.; Yessenov, M.; Hall, L.A.; Abouraddy, A.F.; Toussaint, K.C. Space-time vector light sheets. Optics Express 2021, 29, 37225–37233. [Google Scholar] [CrossRef] [PubMed]
- Yessenov, M.; Chen, Z.; Lavery, M.P.; Abouraddy, A.F. Vector space-time wave packets. Optics Letters 2022, 47, 4131–4134. [Google Scholar] [CrossRef]
- Gotovski, P.; Orlov, S. Parabolic Vector Focus Wave Modes. Journal of Laser Micro Nanoengineering 2019, 14, 25–31. [Google Scholar]
- Vosylius, V.; Orlov, S. Vector Focus Wave Modes with Elliptic Cross-Section. Journal of Laser Micro Nanoengineering 2019, 14, 74–80. [Google Scholar]
- Meier, M.; Romano, V.; Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Applied Physics A 2007, 86, 329–334. [Google Scholar] [CrossRef]
- Kraus, M.; Ahmed, M.A.; Michalowski, A.; Voss, A.; Weber, R.; Graf, T. Microdrilling in steel using ultrashort pulsed laser beams with radial and azimuthal polarization. Optics express 2010, 18, 22305–22313. [Google Scholar] [CrossRef]
- Bhuyan, M.; Courvoisier, F.; Lacourt, P.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Applied Physics Letters 2010, 97, 081102. [Google Scholar] [CrossRef]
- Duocastella, M.; Arnold, C.B. Bessel and annular beams for materials processing. Laser & Photonics Reviews 2012, 6, 607–621. [Google Scholar]
- Laurinavičius, K.; Orlov, S.; Gajauskaitė, A. Azimuthally and Radially polarized pulsed Bessel-X vortices. Optik 2022, 270, 169998. [Google Scholar] [CrossRef]
- Zamboni-Rached, M.; Recami, E.; Hernández-Figueroa, H.E. New localized Superluminal solutions to the wave equations with finite total energies and arbitrary frequencies. The European Physical Journal D-Atomic, Molecular, Optical and Plasma Physics 2002, 21, 217–228. [Google Scholar] [CrossRef]
- Valtna, H.; Reivelt, K.; Saari, P. Methods for generating wideband localized waves of superluminal group velocity. Optics communications 2007, 278, 1–7. [Google Scholar] [CrossRef]
- Kondakci, H.E.; Abouraddy, A.F. Optical space-time wave packets having arbitrary group velocities in free space. Nature communications 2019, 10, 929. [Google Scholar] [CrossRef]
- Nikogosyan, D.N. Properties of optical and laser-related materials: a handbook; 2003.
- Porras, M.A.; Parola, A.; Di Trapani, P. Nonlinear unbalanced O waves: nonsolitary, conical light bullets in nonlinear dissipative media. JOSA B 2005, 22, 1406–1413. [Google Scholar] [CrossRef]
- Stabinis, A.P.; Valiulis, G. Ultratrumpųjų šviesos impulsų netiesinė optika. Vilniaus universitetas 2008. [Google Scholar]
Figure 1.
(a) Angular dispersion of the optical bullet inside the BK7 glass, when , and : (1), (2), (3), 1 (4), (5). (b) Angular dispersion of the optical bullet within the BK7 glass, when , and : (1), (2), (3), (4), (5), (c) Angular dispersion of the optical bullet within the BK7 glass, when , and : (1), (2), (3), (4), (5). The frequency is normalized to the value of PHz
Figure 1.
(a) Angular dispersion of the optical bullet inside the BK7 glass, when , and : (1), (2), (3), 1 (4), (5). (b) Angular dispersion of the optical bullet within the BK7 glass, when , and : (1), (2), (3), (4), (5), (c) Angular dispersion of the optical bullet within the BK7 glass, when , and : (1), (2), (3), (4), (5). The frequency is normalized to the value of PHz
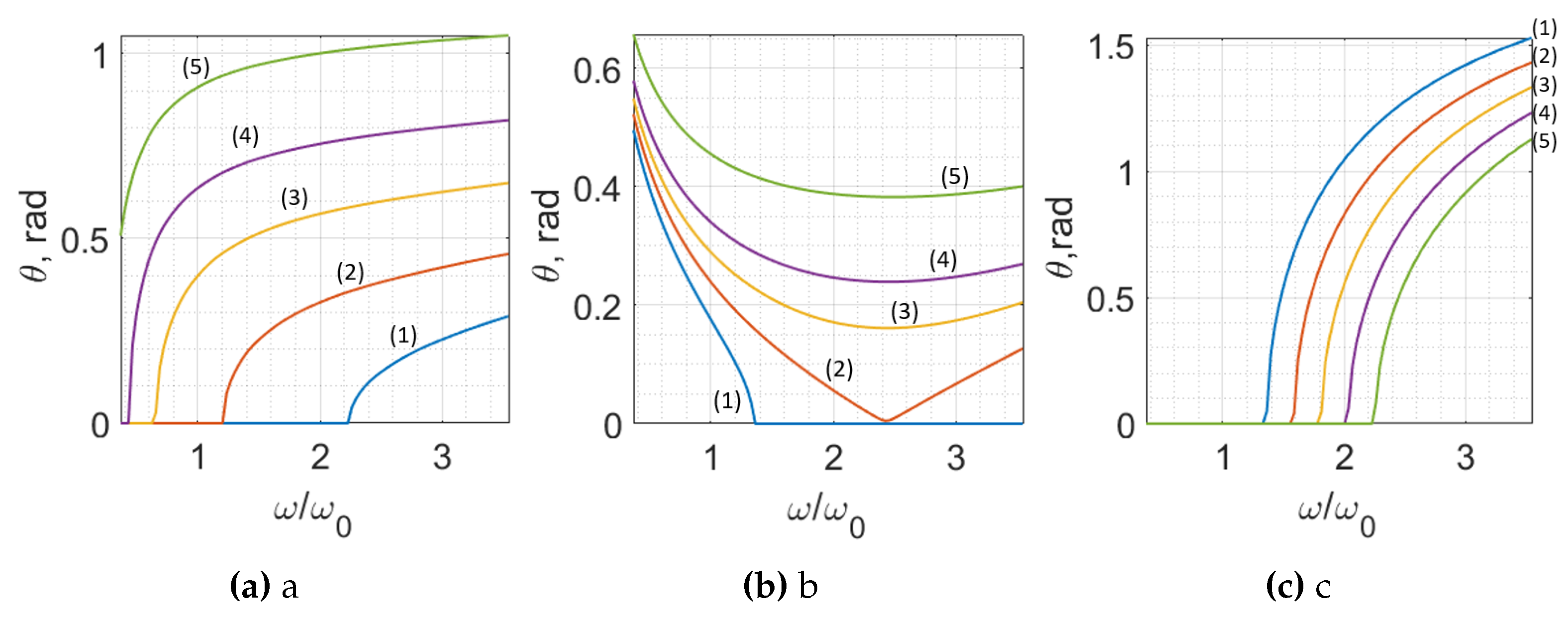
Figure 2.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
Figure 2.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
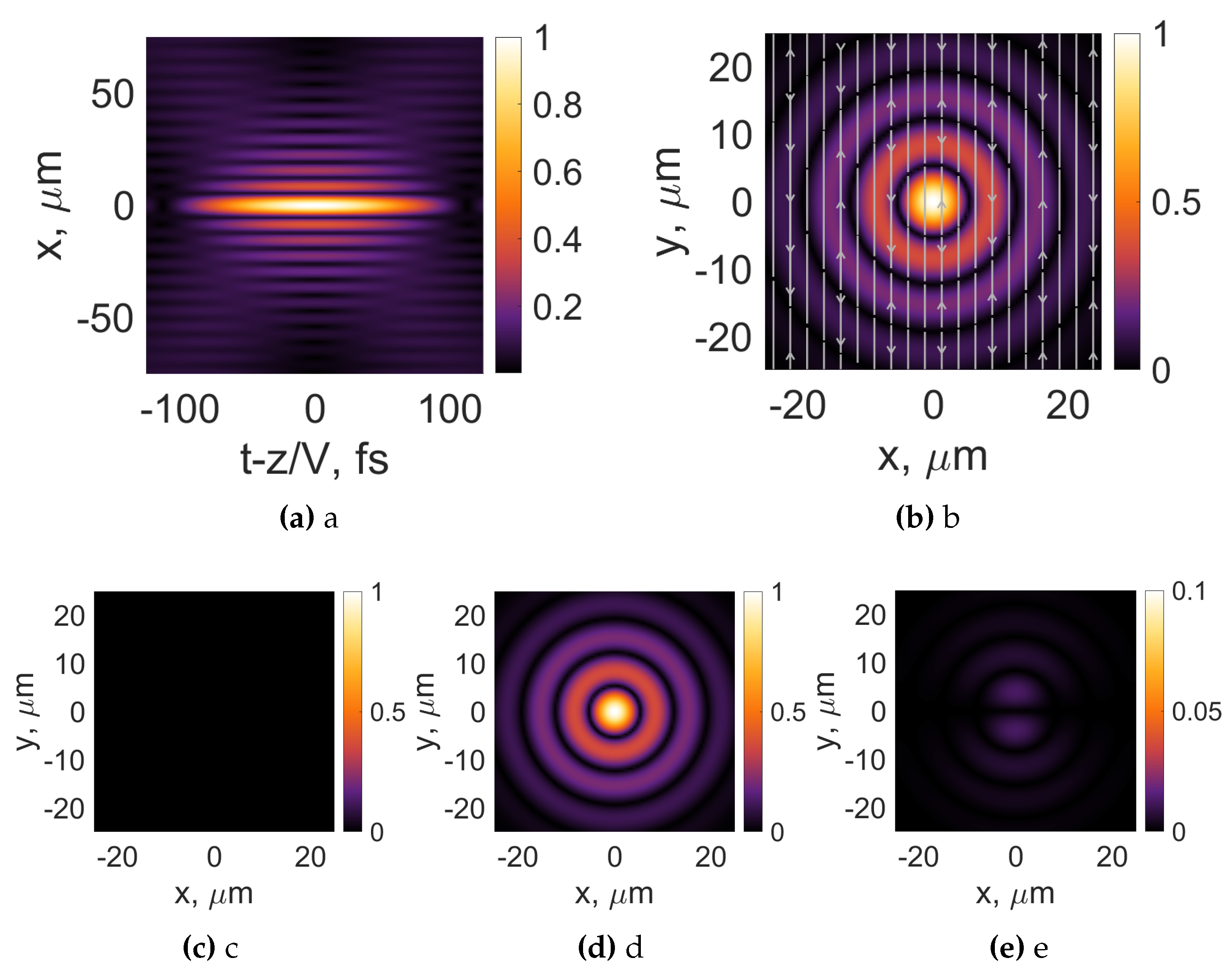
Figure 3.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
Figure 3.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
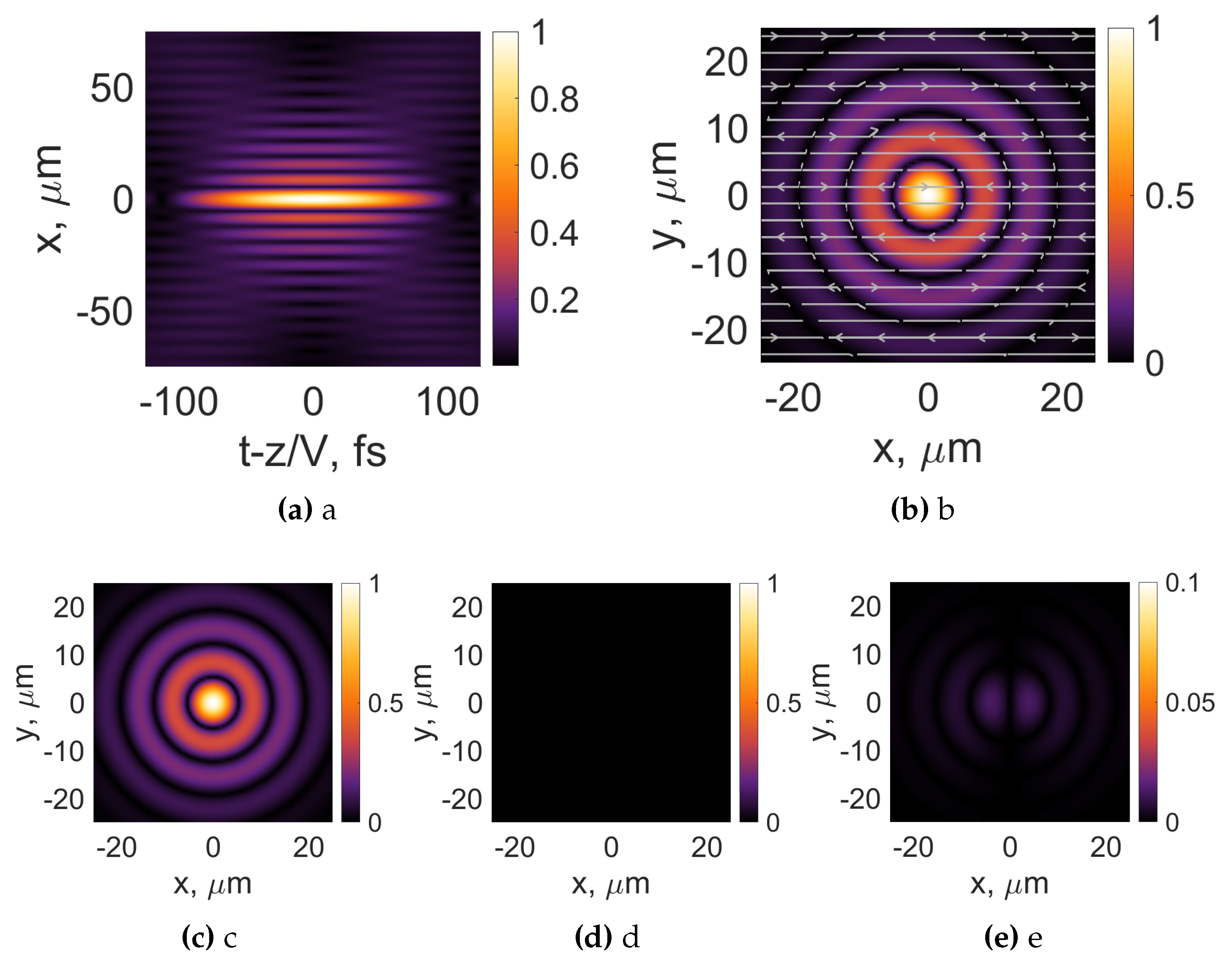
Figure 4.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
Figure 4.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .

Figure 5.
Intensity distributions of radially polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency . Topological charge , pulse duration , , .
Figure 5.
Intensity distributions of radially polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency . Topological charge , pulse duration , , .
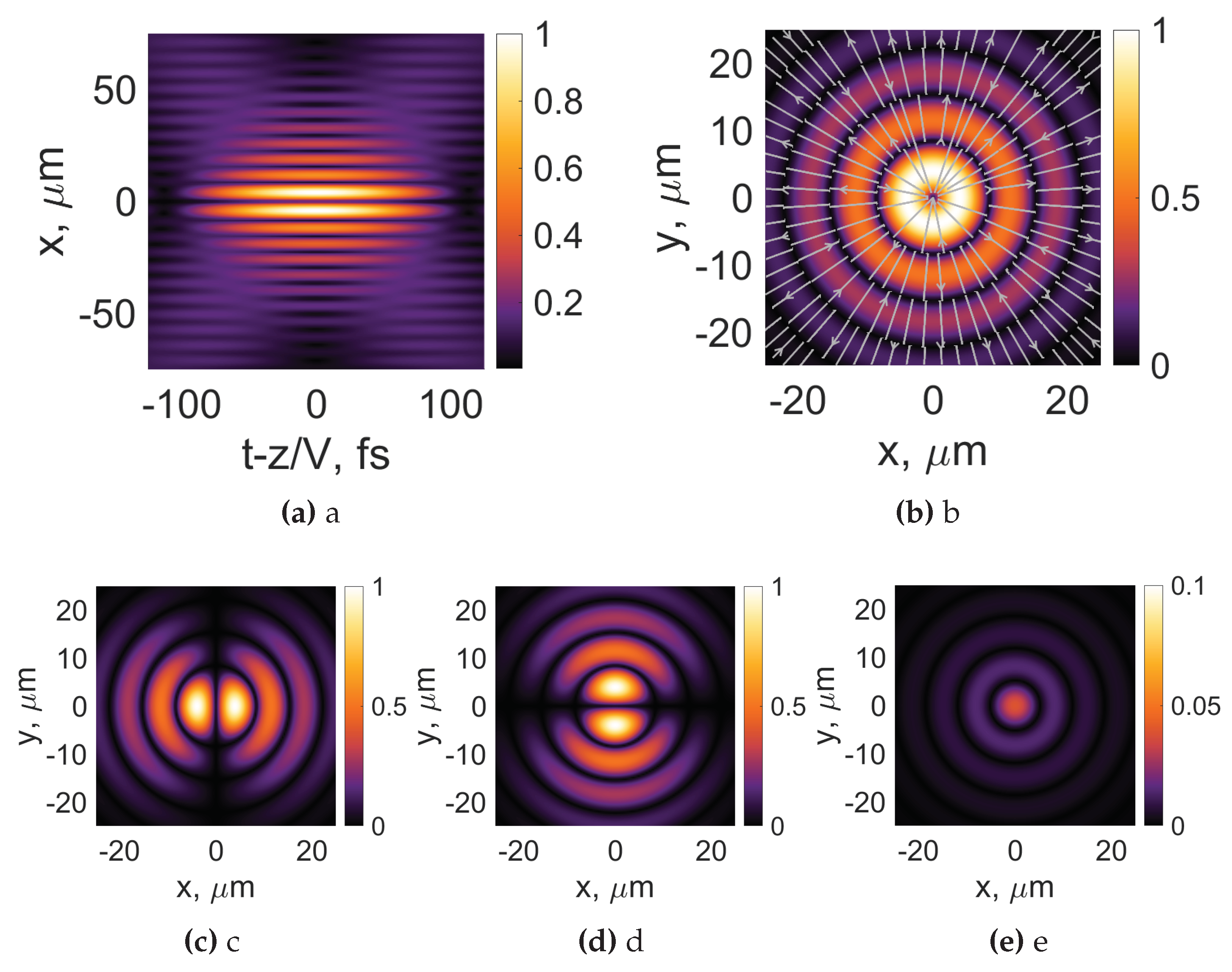
Figure 6.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
Figure 6.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
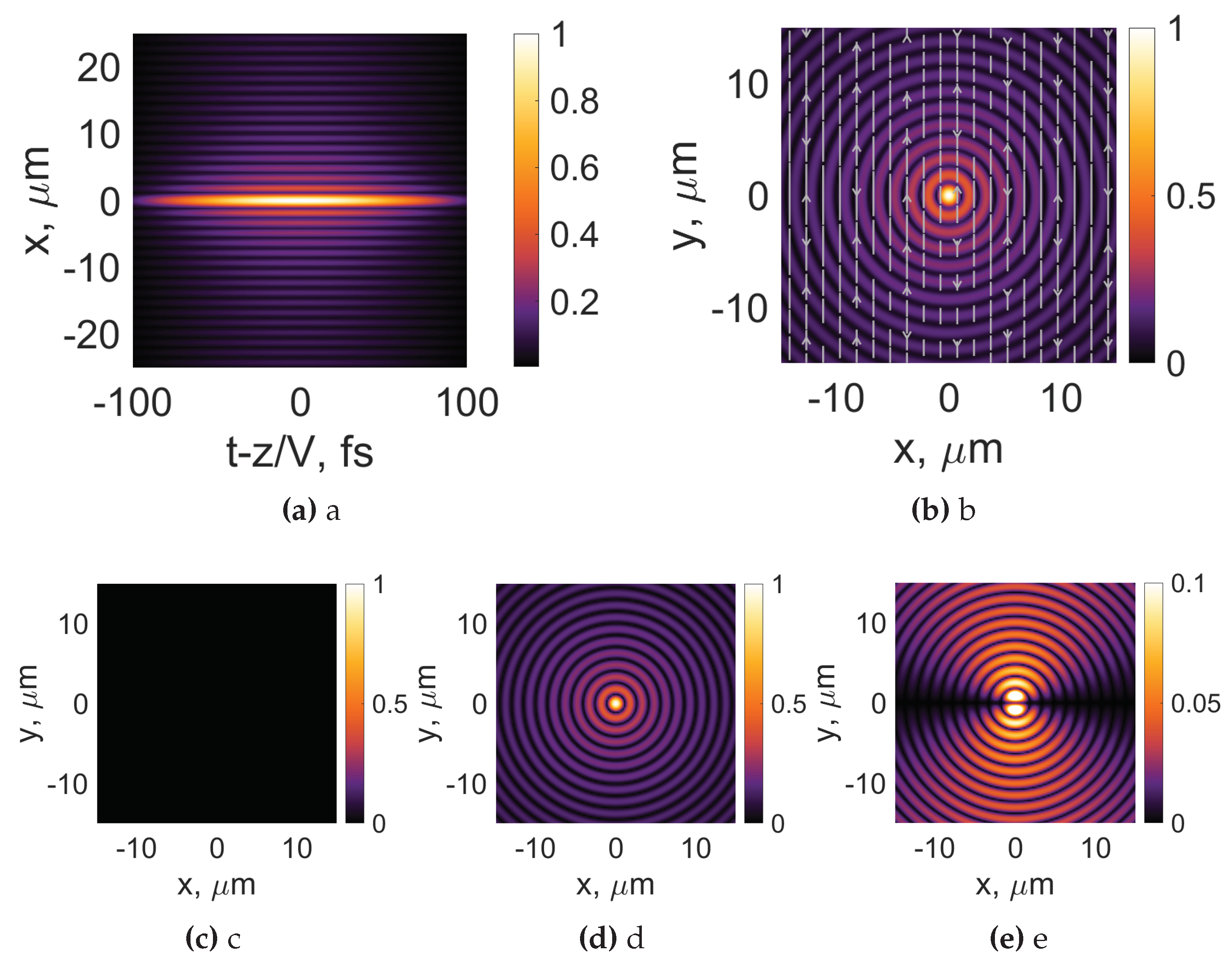
Figure 7.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
Figure 7.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. The frequency Hz. Topological charge , pulse duration , , .
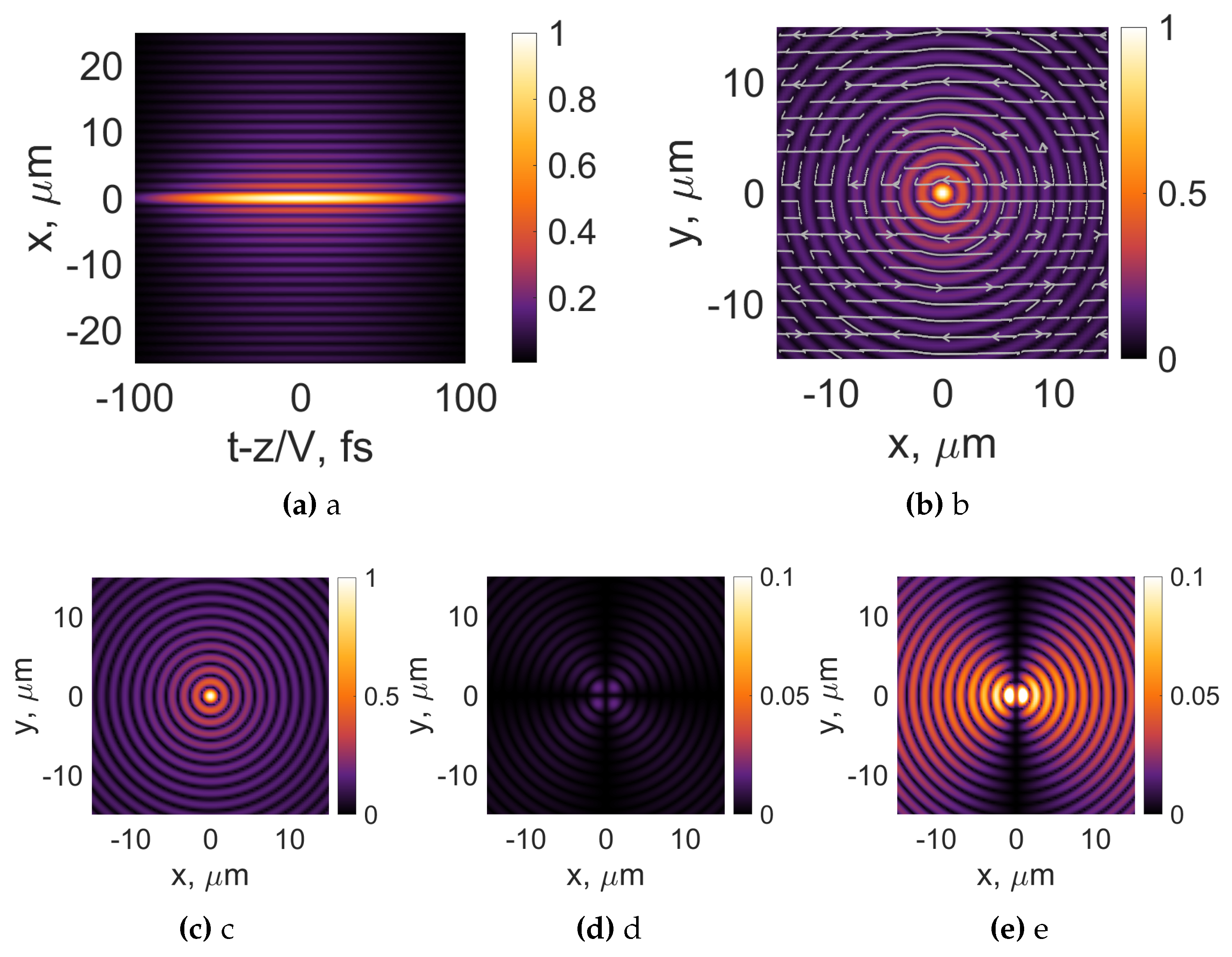
Figure 8.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
Figure 8.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
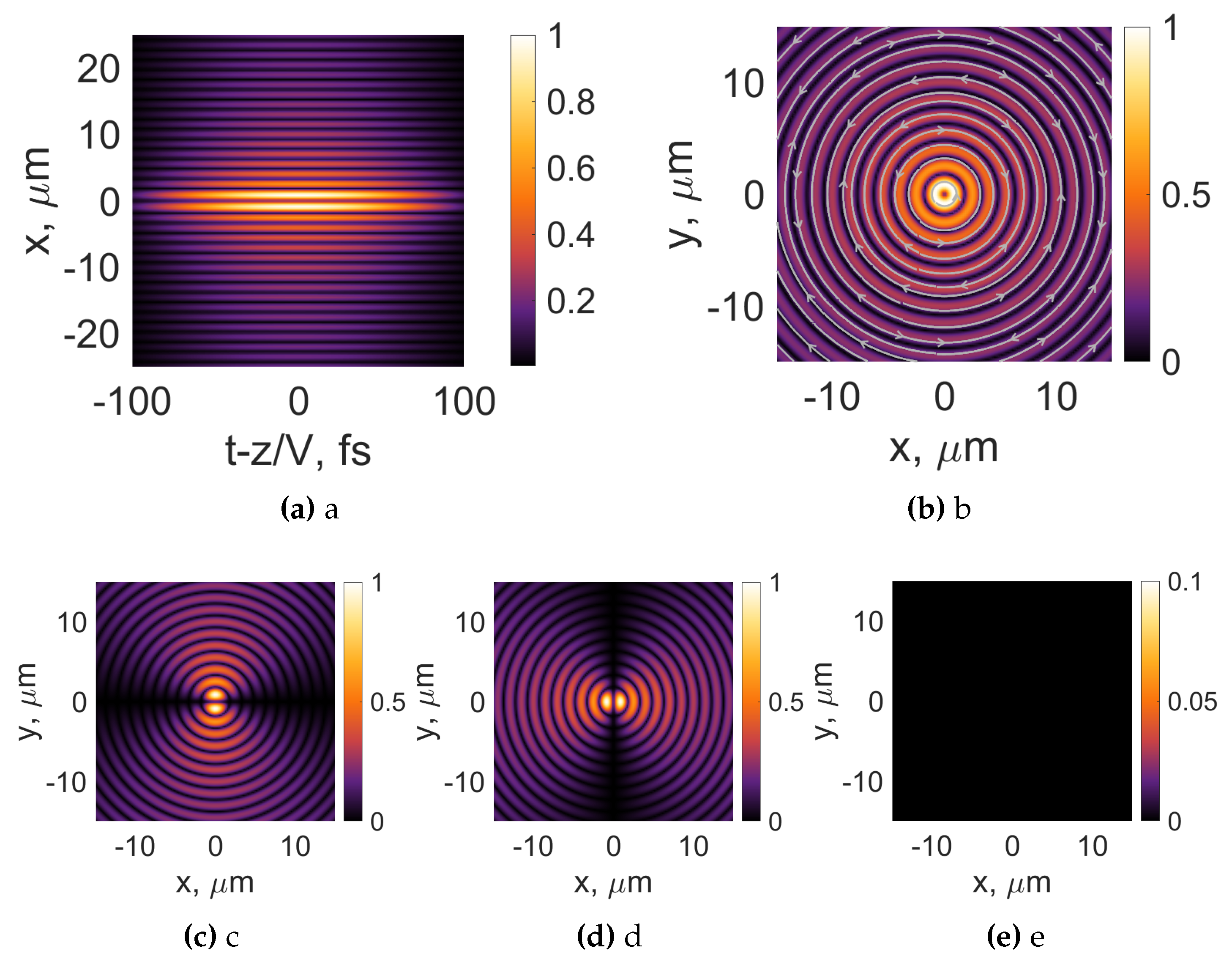
Figure 9.
Intensity distributions of radially polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
Figure 9.
Intensity distributions of radially polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)) in the transverse plane. The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , pulse duration , , .
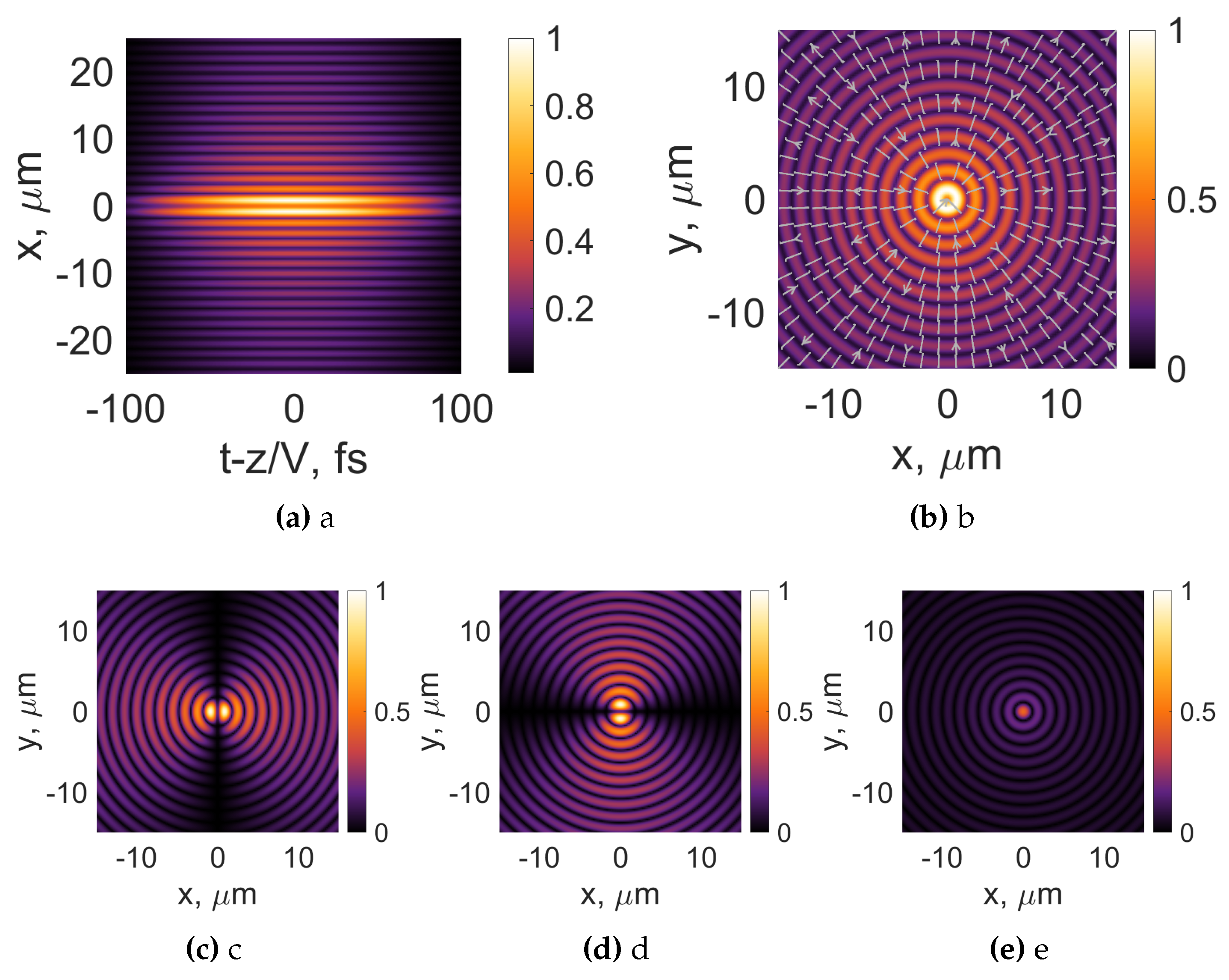
Figure 10.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
Figure 10.
Intensity distributions of transverse electric (TE) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
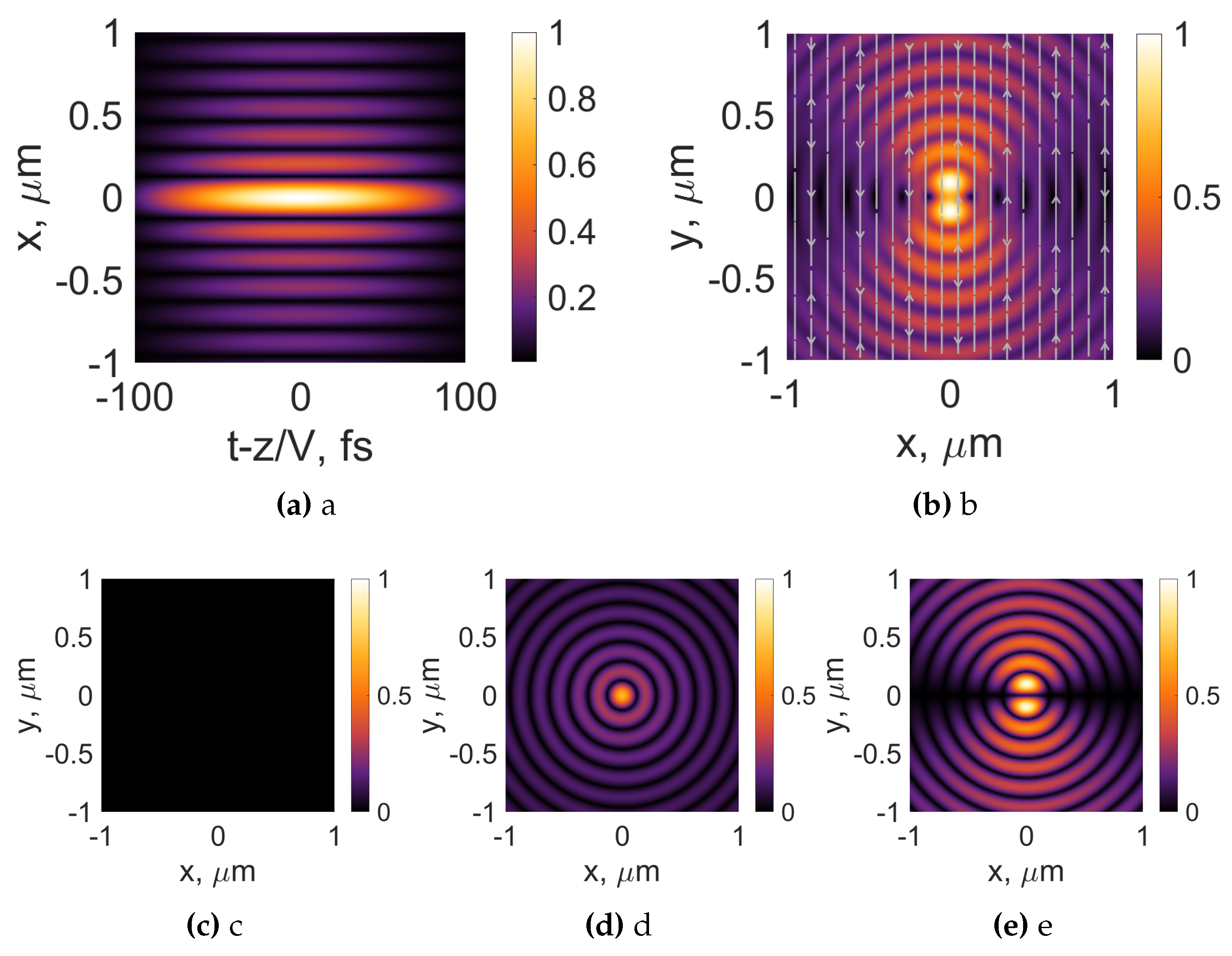
Figure 11.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
Figure 11.
Intensity distributions of transverse magnetic (TM) linearly polarized Bessel-X pulses and its individual components(, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
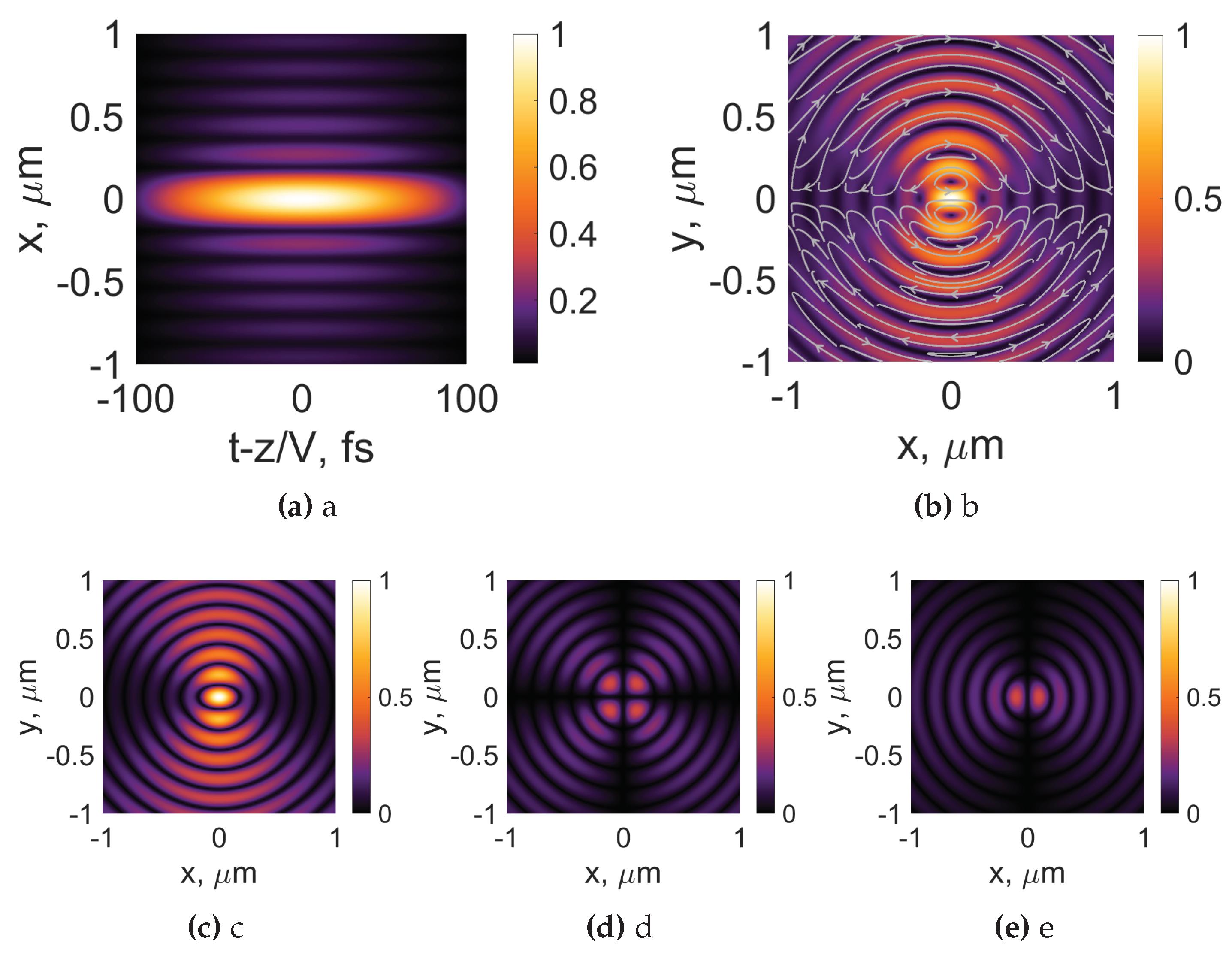
Figure 12.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components (, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
Figure 12.
Intensity distributions of azimuthally polarized Bessel-X pulses and its individual components (, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
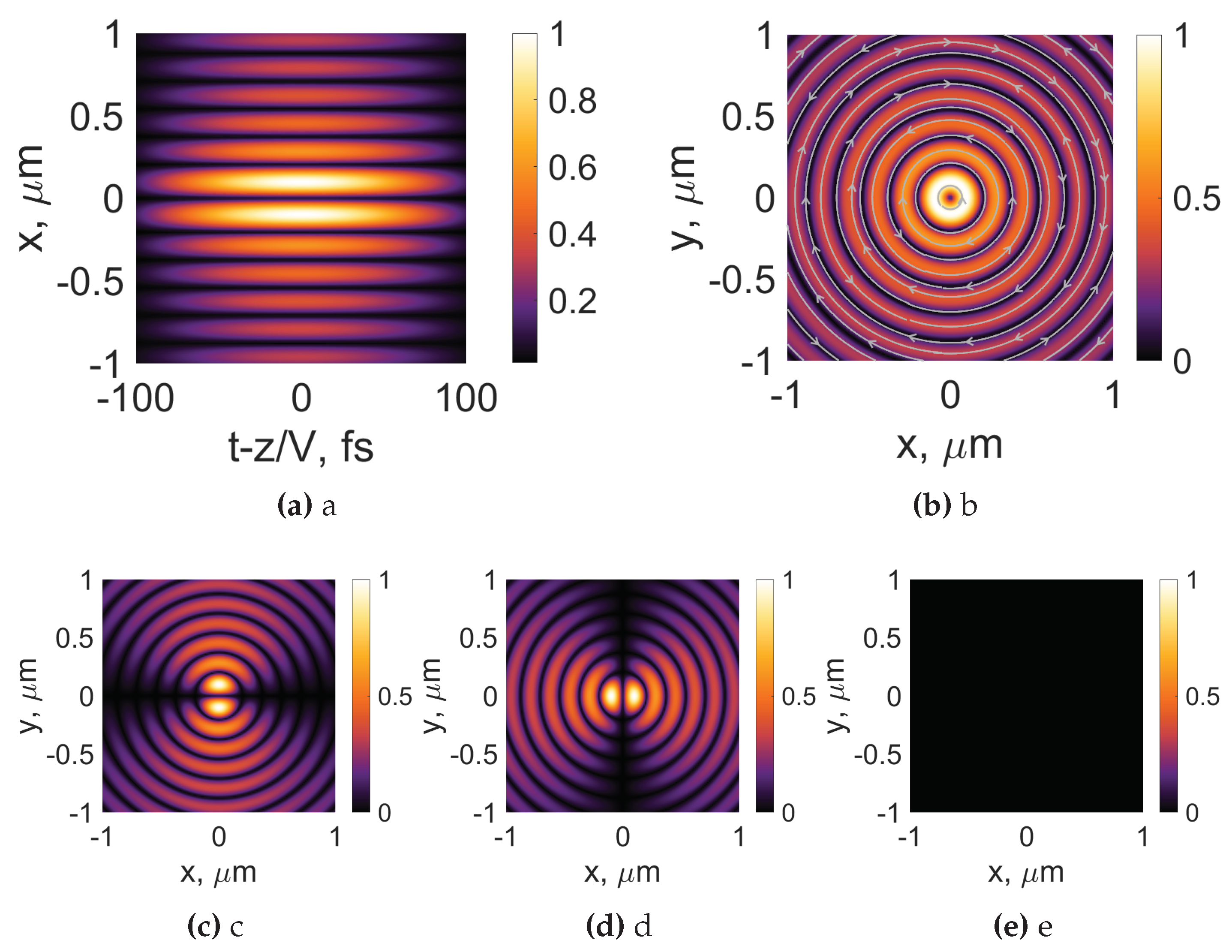
Figure 13.
Intensity distributions of radially polarized Bessel-X pulses and its individual components (, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
Figure 13.
Intensity distributions of radially polarized Bessel-X pulses and its individual components (, (c), , (d), , (e)). The white arrows represent the orientation of the electric field. Frequency Hz. Topological charge , , , .
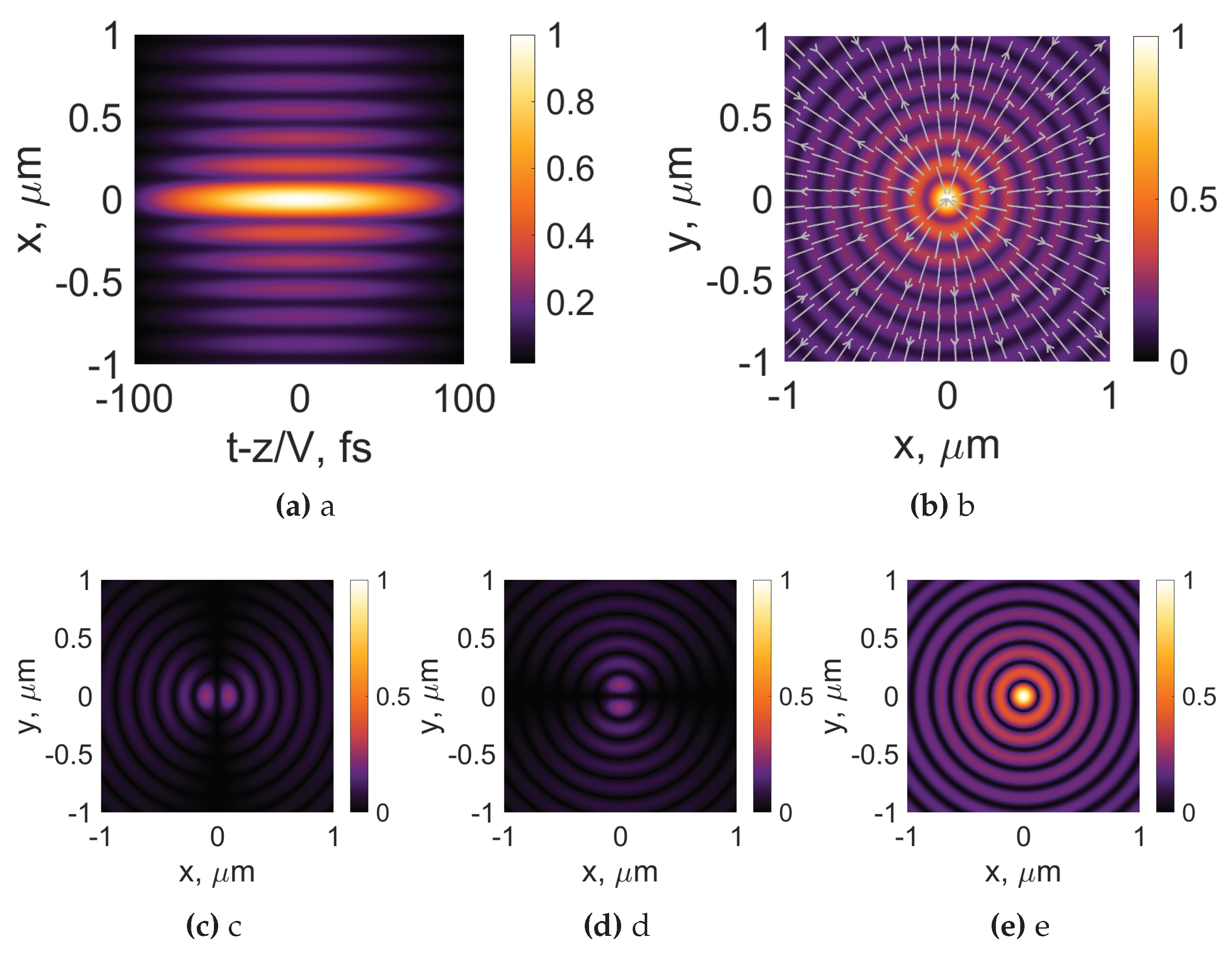
Figure 14.
Dependencies of FWHM (a) and second-moment (b) pulse widths in BK7 glass for different values of frequency for linear, azimuthal and radial polarizations. The red color represents , and the blue color . Topological charge , .
Figure 14.
Dependencies of FWHM (a) and second-moment (b) pulse widths in BK7 glass for different values of frequency for linear, azimuthal and radial polarizations. The red color represents , and the blue color . Topological charge , .
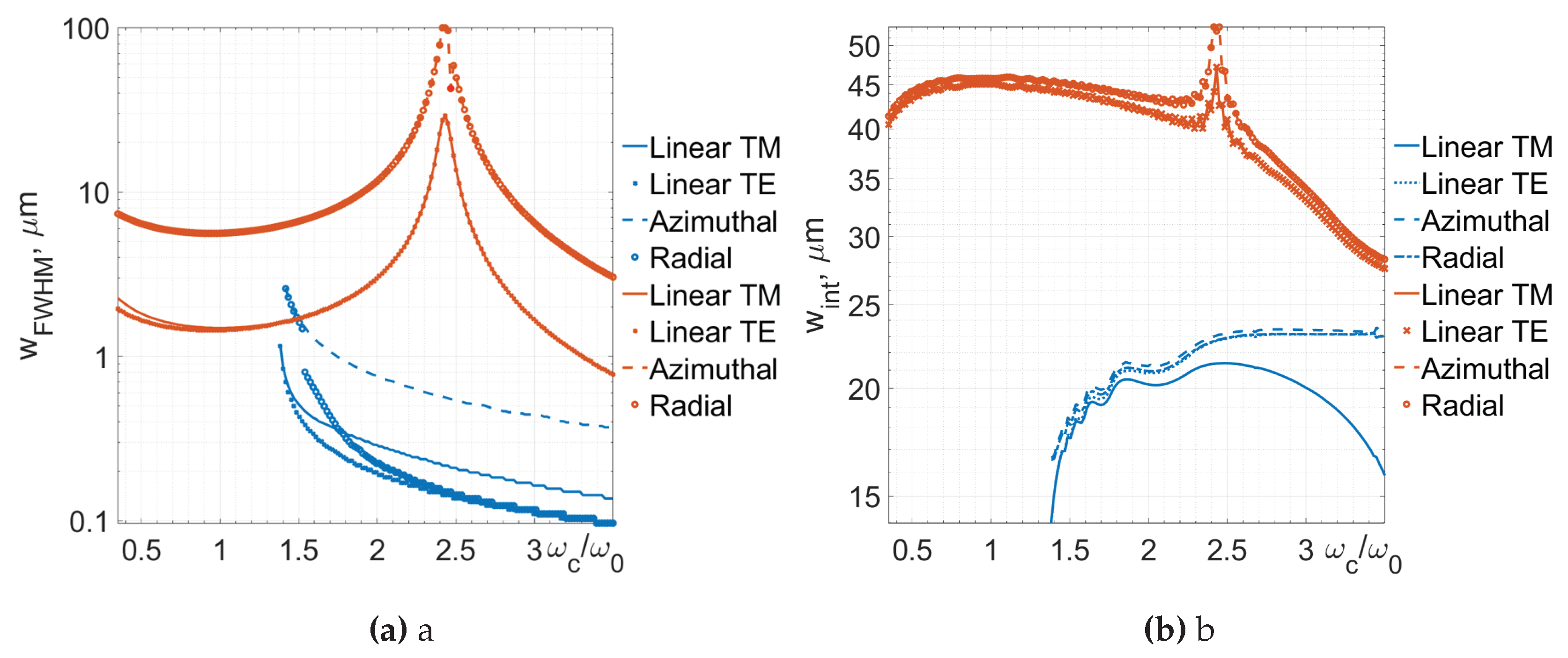
Figure 15.
Normalized intensities of individual components of FWM pulses ( - blue, - red, - green). Topological charge , pulse duration . For the cases: (a) , , (b) , . The solid line represents the linear polarization of TE, the dashed line represents the linear polarization of TM, the dotted line represents the azimuthal polarization, and the dashed-dotted line represents the radial polarization.
Figure 15.
Normalized intensities of individual components of FWM pulses ( - blue, - red, - green). Topological charge , pulse duration . For the cases: (a) , , (b) , . The solid line represents the linear polarization of TE, the dashed line represents the linear polarization of TM, the dotted line represents the azimuthal polarization, and the dashed-dotted line represents the radial polarization.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





