Preprint
Article
Wastewater-Based Epidemiology for SARS-CoV-2 in Northern Italy: A Spatiotemporal Model
Altmetrics
Downloads
143
Views
91
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (8.46MB )
This version is not peer-reviewed
Preprints on COVID-19 and SARS-CoV-2
Submitted:
08 April 2024
Posted:
08 April 2024
You are already at the latest version
Alerts
Abstract
The study investigated the application of Wastewater-Based Epidemiology (WBE) as a tool for monitoring SARS-CoV-2 prevalence in a city in Northern Italy from October 2021 to May 2023. Starting from a widely applied deterministic model, this study proposed a variation to take into account population characteristics and virus biodegradation in the sewer network. The model calculated virus loads and corresponding COVID-19 cases over time in different areas of the city and was validated with healthcare data while considering viral mutations, vaccinations, and testing variability. The correlation between the predicted and reported cases was high across the three waves that occurred in the considered period, demonstrating the model’s capacity to predict relevant fluctuations in the number of cases. Population characteristics did not substantially influence the predicted and reported infection rates. Conversely, biodegradation significantly reduced the virus load reaching the wastewater treatment plant, resulting in a 30% reduction in the total virus load produced in the study area. This approach can be applied for comparing virus load values across cities with varying population demographics and sewer network structures, enhancing the comparability of WBE data for effective surveillance and intervention strategies.
Keywords:
Subject: Public Health and Healthcare - Public, Environmental and Occupational Health
1. Introduction
The global effort against the COVID-19 pandemic has underscored the need for innovative and robust surveillance methods to track the prevalence of SARS-CoV-2, the causative agent of COVID-19, within communities. Wastewater-based epidemiology (WBE) has emerged as a valuable tool for the proactive and scalable monitoring of viral presence in populations [1] and several countries have successfully implemented WBE as a complementary surveillance system to clinical testing [2,3]. This surveillance method not only aids in the early detection and prevention of disease outbreaks but also enables timely public health interventions such as targeted testing, contact tracing, and resource allocation [1,2]. Several studies [4,5] emphasize the importance of environmental surveillance as an early warning system to detect viral levels in the population and identify outbreaks before cases are reported to the healthcare system.
Recently, the application of this method as a complementary approach to clinical surveillance has become even more important given the reduction in recorded tests and the widespread occurrence of asymptomatic or mildly symptomatic cases [6]. Indeed, wastewater serves as a collective pool of genetic material shed by an entire community, providing insights into the prevalence of SARS-CoV-2, including asymptomatic and presymptomatic cases [1,2,7]. Advances in the monitoring of SARS-CoV-2 in wastewater have been significant, with molecular techniques such as quantitative reverse transcription‒polymerase chain reaction (qRT-PCR) playing a pivotal role in the accurate quantification of viral RNA [1,3].
Italy, one of the hardest hit countries, has been monitoring urban sewage since July 2020 as part of a pilot study: the “SARI project” (Epidemiological Surveillance for SARS-CoV-2 in urban sewage in Italy), coordinated by the National Institute for Public Health and involving a network composed of regions, wastewater service providers, regional environmental protection agencies and local health authorities [8].
On March 17, 2021, the European Commission recommended that EU member states begin monitoring SARS-CoV-2 in wastewater by October 1, 2021 [9]. Therefore, since October 2021, in Italy, existing research activities within the SARI project have been transformed into a surveillance system, with two main focuses: analysing the trend of SARS-CoV-2 in urban wastewaters to predict epidemiological trends in the population and studying the spread of SARS-CoV-2 variants over time [8].
Following the principles of WBE and focusing on the surveillance objective defined by the SARI project, this study aims to predict the temporal and spatial distribution of COVID-19 cases starting from SARS-CoV-2 detection in the main wastewater treatment plant (WWTP) of a medium-sized city in northern Italy.
This interest aligns with several studies conducted in many other countries, where various modelling techniques have been employed in the development of WBE for COVID-19 surveillance [10], including regression [5,11], artificial intelligence [12,13], and deterministic models [3,14,15,16,17].
In the present study, a deterministic model was applied: the equation upon which the model was based was initially proposed by Ahmed [14] and subsequently employed in various other studies [3,15,16,17]. The equation was adapted to integrate a spatial component: the proposed model enables the calculation of the spatial and temporal distribution of COVID-19 cases by adjusting SARS-CoV-2 RNA concentration data at the WWTP to take into account virus biodegradation effects.
The model aimed to accurately simulate the biodegradation of the virus along the sewer network via an approach similar to that employed by McCall et al. [18]. This estimate, together with the characteristics of the population and its geographical distribution, allowed us to determine the virus load produced in each zone within the study area and the corresponding number of new cases over time.
This approach proposes a methodology that can be effectively implemented in multiple cities where WBE is conducted. This methodology enables a reliable comparison of virus load values measured at WWTPs among cities characterized by different population demographics and sewer network distributions.
The performance of the model was evaluated by comparing the estimated cases with those recorded by the regional healthcare system and considering various relevant health variables for interpreting the results.
2. Materials and Methods
2.1. Study Area and Population Analysis
The study was conducted based on measurements detected at the main WWTP in Bologna, the capital of the Emilia-Romagna region in northern Italy. The plant is located in the north of Bologna and serves the city and neighboring municipalities, catering to a capacity of 800,000 population equivalents.
The study area was defined as the area served by the WWTP. The study was conducted at the submunicipal level; therefore, the municipalities were divided into census sections [19], which are already widely used for statistical analyses. Only Bologna was divided into statistical areas [20] since these areas are more extensive and offer more recent data than census sections [19].
A three-step selection process was followed to define the areas (i.e., census sections and statistical areas) belonging to the study area. First, the study area was delineated as the union of the areas that are encompassed by or intersect the catchment area served by the sewer network. Additionally, those areas that were enclosed by the previously selected areas were included. Finally, from the selected areas, those that were primarily associated with another treatment facility were excluded. The resulting study area encompasses nearly all the statistical areas of Bologna and part of the census sections of the neighboring municipalities. (Figure 1).
The study population is an estimate of the individuals domiciled in the study area, obtained by multiplying the number of residents [19,20] by a coefficient derived from the data in the Regional Assistance Registry, representing the ratio between the domiciled and resident populations at the municipality level. (Table S1)
2.2. Virus Concentration and Wastewater Flow Rate at the WWTP
The concentration of SARS-CoV-2 RNA [GC/L] and the effluent flow rate [m3/day] observed at the inlet of the WWTP were obtained from a data-sharing platform within the network of the SARI project. The study period was chosen according to the availability of concentration data and ranged from 13/10/2021 (the first day of sampling) to 24/05/2023. The measurements were conducted weekly or twice a week, with an irregular frequency, resulting in a total of 165 data points throughout the entire period.
Samples were collected, processed for determination of virus concentration and subjected to RNA extraction following the reference analytical protocol established for the SARI project [21]. Wastewater composite samples of 100 ml were collected over a 24-hour period. A 50 ml aliquot was frozen and constituted the "archive sample" to be retained for any further determinations. The second 50 ml aliquot was immediately processed or stored at a refrigerated temperature (-20°C) until the analysis was conducted, for a maximum of 24 - 48 h.
The wastewater sample concentration was determined with a PEG/NaCl protocol using the method published by Wu et al. [22]. SARS-CoV-2 analysis included, as an initial step, cell lysis with guanidine isothiocyanate followed by the extraction of genetic material based on the adhesion of nucleic acids on magnetic silica performed using the MiniMag/eGeneUP (bioMerieux) platform with a final volume of 100 µl for RNA elution. The quantitative detection of SARS-CoV-2 was performed by real-time RT-qPCR in accordance with the EU 2021/472 Recommendation [9]. The quantitative determination of SARS-CoV-2 was based on ORF-1ab (nps 14), with Murine Norovirus used as a control virus during the analysis.
The mean (1.79 105 [GC/L]), median (0.83 105 [GC/L]), and maximum (1.10 106 [GC/L]) concentrations of SARS-CoV-2 RNA measured at the WWTP (Figure S2,Table S2) fell within the range (102-105 [GC/L] with maximum values exceeding 106 [GC/L]) found in the literature [4,5,23,24].
In combined sewer systems, such as the one described in the present study, intense rainfall events can lead to a significant dilution of the SARS-CoV-2 RNA concentration in the sewer, as well as fluctuations in flow velocity and other parameters. Therefore, concentration data collected when the flow rate exceeded the 90th percentile of values recorded in 2022 (156.5 103 [m3/day]) were treated as outliers and thus removed [11](Table S3,Figure S3). In support of this method, the correlation between the effluent flow values measured at the WWTP inlet and the cumulative daily precipitation values [25] measured by monitoring stations in Bologna and neighboring municipalities was analysed. The highest correlation (Pearson 0.88) was observed when considering the cumulative daily precipitation of the day preceding the flow measurement. This could be attributed to evening rains that reach the WWTP after several hours, contributing to the cumulative effluent flow on the following day.
The daily load of SARS-CoV-2 RNA at the inlet of the WWTP [GC/day] was obtained by multiplying the observed values (after removing outliers) of the SARS-CoV-2 RNA concentration by the effluent flow rate. Subsequently, the historical time series of the daily load of SARS-CoV-2 RNA was processed using the locally estimated scatterplot smoothing (LOESS) method [26]. This was done with a dual purpose: first, to transform the historical series into one with a daily regular data interval based on irregularly measured data points, and second, to smooth the values to obtain a signal purified from potential measurement errors (Figure S4). The LOESS method was implemented in Python [27], considering 11 neighboring data points for the local value estimation as in Rauch et al. [11].
2.3. Health Data
The Local Health Authority of Bologna provided daily cases of COVID-19 within the statistical areas and census sections in which the subjects were isolated.
For each patient, the following information was available: census section or statistical area of isolation, presence of symptoms and onset of symptoms date if symptomatic, date of the swab test, diagnosis date (i.e., date when a positive case is officially recorded in the healthcare system), admission date and discharge date in case of hospitalization, final outcome (i.e., whether the individual recovered or deceased), final outcome date, and cause of death if deceased.
The model presented in this article was implemented to estimate new daily cases. Therefore, data on newly reported daily cases from the healthcare system were selected to evaluate the model’s performance. The decision to estimate new daily cases instead of active cases was made by recognizing that the duration of an infected individual’s classification as an active case is likely to be more uncertain, varying significantly from person to person, and influenced by prevailing COVID-19 regulations (e.g., a confirmatory test was not always required to confirm the end of the infection period).
To reduce individual variability, the date of symptoms onset (or the date of the swab test if asymptomatic) was taken as the reference date for defining a new case, hospitalization, or death reported by the healthcare system. This was considered the best reference date for comparing predicted and reported cases due to the correspondence of the onset of symptoms with the peak of SARS-CoV-2 excretion in feces [15,28,29].
Daily city-level data on tests and vaccines (second and third doses) were provided by the Local Health Authority of Bologna. An analysis of these health variables was performed to interpret the model results.
2.4. Model Equation
The model was based on an equation employed in previous studies [3,14,15,16,17] for modelling the relationship between the SARS-CoV-2 concentration at WWTPs and the number of COVID-19 cases. This equation was adapted by integrating two different factors to consider the spatial component. This adjustment was made to obtain a more accurate estimate of virus biodegradation and, consequently, to derive the actual contributions of SARS-CoV-2 RNA from different areas within the catchment and thus predict the corresponding number of COVID-19 cases.
A virus biodegradation factor and a population-based coefficient were introduced in the equation to differentiate the contribution of each area to the observed concentration at the WWTP. Both of these factors were calculated for each area.
The daily load of SARS-CoV-2 at the inlet of the WWTP [GC/day] was set equal to the sum of the daily virus load generated by each area, which was reduced by accounting for virus biodegradation along the sewer network and refined by incorporating the population-based coefficient associated with the population of each area (Eq. 1).
Where CW (t) is the measured concentration of SARS-CoV-2 RNA at the inlet of the WWTP [GC/L], QW (t) is the wastewater flow rate at the inlet of the WWTP [L/day] (CW (t) multiplied by QW(t) represents the daily load of SARS-CoV-2 RNA [GC/day] as derived in Section 2.2), Sh is the fecal shedding rate (i.e., number of SARS-CoV-2 RNA genomic copies per gram of feces produced by each infected individual) [GC/g], Mf is the mass of feces produced per inhabitant per day [g/(inhabitant · day], i represents the area within municipality, Pi is the population in the area i [inhabitant], k is the biodegradation constant [h-1], ϴi is the hydraulic residence time for the area i [h], Wi is the population-based coefficient characteristic of each area i [adim.] and IR(t) [adim.] is the average infection rate (i.e., number of cases divided by population) across the entire study area, and it is the unknown variable of the equation (the methodology followed to derive the equation is detailed in the Supplementary material, Section S3). Once IR(t) was determined, the number of cases in each area over time (ci) was derived (Eq. 2).
The model output consisted of the number of predicted cases per day for each census section or statistical area included in the study area. However, when comparing the predicted and reported cases, the results were aggregated in grouped areas. The municipal boundaries were used to group the census sections, while for Bologna, a proximity criterion was adopted to group some statistical areas together. This approach aimed to increase the population size within each comparison zone, thereby enhancing statistical significance when observing spatial variability in cases. The 88 statistical areas within the city of Bologna were therefore grouped into 59 areas, ensuring that none had fewer than 2000 residents, while the aggregation of census sections by municipality resulted in zones with more than 2700 inhabitants (Figure S1,Table S12).
The infection rate for each grouped area over time IRj(t) was then obtained (Eq. 3).
Where cj represents the number of cases in each grouped area, Pj is the total population of the grouped area and Wj is the population-based coefficient for grouped areas (weighted average of Wi based on population size).
2.4.1. Population-Based Coefficient
The population-based coefficient (Wi) allowed to consider for each area the following population characteristics in the prediction of cases: age, sex, family size [19,20] and comorbidities. Comorbidity data were provided by the Local Health Authority of Bologna and were obtained from different databases related to the years 2021-2022 (hospital discharge forms [SDO], territorial pharmaceutical care [AFT], direct dispensing drugs [FED] and specific pathology).
The Wi coefficient, which is constant over time and variable across space, was defined as the ratio between a specific infection rate for area i (Ai) and the infection rate for the entire study area (ATOT) (Eq. 4). To establish Ai and ATOT, Poisson regression was employed, and the regression coefficients (β0,β1,..βn) were derived from a study conducted in the municipality of Bologna from February 2020 to November 2021 [30] (Table S4). The variables (x1, x2… xn) were calculated for each area and represent the fractions of the population belonging to the following classes: age (0-21, 21-65, >65), sex (M/F), family size (1, 2, 3, >3), and comorbidities (hypertension, diabetes and the “other comorbidities” considered in the study [30]).
2.4.2. Fecal Shedding Rate and Mass of Feces
Two average values of the fecal shedding rate (Sh) were calculated considering data from the Delta and Omicron variants across six different communities in the USA [31]. The population-weighted average shedding rates for the Delta and Omicron variants incorporated into the model were 108.658 and 107.813, respectively (Table S6).
Considering the evolution of the virus from the Delta variant to the Omicron variant in December 2021 (Figure 7), the shedding rate for the Delta variant was applied until December 19th, while that for the Omicron variant was applied from January 3rd onwards, and a combination of the two values was used for the last two weeks of December (Table S8). The daily wet mass of feces (Mf) produced by each individual was assumed to be 128 [g/(inhabitant· day)] [32].
2.4.3. Biodegradation
The biodegradation of the virus along the sewer network was modelled with a first-order kinetics (Eq. S5) [33,34,35]. The biodegradation constant (k) was calculated based on values found in experiments [4] conducted under conditions most similar to those of the present study. The values were adjusted for the observed temperatures in the sewer network of Bologna (12°C, 16°C, 20°C) [36] according to a linear equation (Eq. 5) [33,35]. The linear coefficient (m) and intercept (q) were calculated based on the literature values of k and temperature (T) [4], after which the k values corresponding to the observed temperatures of Bologna were determined. The three derived k values (0.097, 0.101, and 0.104 [h-1]) were incorporated into the model, varying with the time of the year (Table S9).
The hydraulic residence time (ϴi) for each area was estimated by dividing the effective distance (Di), i.e., the distance calculated along the network from the centroid of each area to the WWTP, by the flow velocity of wastewater along the sewer network (v).
Di was determined by applying the Dijkstra algorithm [37] to measure the shortest path along the sewer network from each area’s centroid to the WWTP (using the GeoPandas library (version 0.13.2) in Python).
2.5. Uncertainty and Sensitivity Analysis
To calculate the model uncertainty, the Li et al. [3] error propagation formula was employed, where the uncertainty is expressed as the relative standard deviation (RSD). The formula incorporates the relative standard deviations of each model’s parameter. These uncertainty values were derived from the literature (Section S4).
The total number of cases is included in the formula because the uncertainty associated with the shedding rate and the mass of faces of each individual decreases as the number of infected individuals increases: beyond 10 cases, the impact of these uncertainty values on the total uncertainty becomes limited [3].
The uncertainty associated with the model results varied from 0.81 RSD to 0.33 RSD depending on the total number of infected individuals in the area.
The unknown variable (IR(t)) exhibited a linear dependency on all model parameters except k and ϴ. Therefore, a 1% variation in one of the parameters resulted in a corresponding variation in IR(t) of ±1%, while for a 1% increase in k or ϴ, the corresponding increase in IR(t) was 0.35%. (Eq. S9)
3. Results
3.1. Effect of Biodegradation
More than half of the considered areas were located within an effective distance range of 10 to 18 km from the WWTP (corresponding hydraulic residence time: 3.5 - 6 h). The virus load produced in these areas decreased by 30 - 45% along the path in the sewer network due to biodegradation. Virus loss was highly significant (60 - 70%) for the areas with the greatest effective distance (> 30km) from the WWTP (Table 1,Figure 2). However, in these areas, the population density was very low.
The ratio between the SARS-CoV-2 RNA load measured at the WWTP and that generated in the areas of the basin before being introduced into the sewer system and thus biodegraded is independent of time and can be expressed as (Eq. 6):
At 16 °C, the ratio was 0.694, and this value slightly decreased as k increased. Therefore, the virus load detected at the WWTP was approximately 70% of that actually produced in the study area.
Starting from the estimation of biodegradation, the contribution of each area to the virus load detected at the WWTP was evaluated, and indicators were created to better understand the significance of biodegradation and virus production in the different areas (Section S5.1).
The contribution of hospitals in terms of the viral load discharged into the sewer system and detected at the WWTP during the study period was evaluated based on the number of hospitalized individuals. While the ratio of COVID-19 patients hospitalized to the total number of cases reported in the entire study area was very low (0.03), this value was much greater (i.e., 42, 14 and 4) when referring only to the cases reported in the three statistical areas of Bologna where hospitals were located. From these coefficients, the virus load generated in each area with hospitals and contributing to the virus load detected at the WWTP was estimated, considering biodegradation. For the area where the hospital with the highest number of COVID-19 patients was located, this predicted contribution ranged from 0.014% without considering hospitalized subjects to 1% considering hospitalized subjects (Table S13).
3.2. Predicted and Reported Infection Rates in the Study Area
The predicted and reported daily IR(t) trends over the study area were compared throughout the entire study period (Figure 3). The reported IR(t) was obtained as the daily sum of the reported COVID-19 cases in the area relative to the date of symptom onset or the date of the swab test (Section 2.3), smoothed with a simple moving average over 7 days and divided by the total population within the study area. The mean absolute error between the predicted and reported IR(t) over the entire study period was 54 cases over 100000 inhabitants and the Spearman correlation coefficient was 0.599.
The time period was divided based on the trend of the reported cases to better compare the predicted and reported data. The transition dates were chosen to correspond to the relative minima of reported cases, with the exception of the beginning of the first wave, for which the shift between the Delta and Omicron variants was chosen. This approach defined three waves and an ’off-waves’ period (Table 2).
The correlation was consistently high across the three waves but notably lower during the ’off-waves’ period. During the first wave, the predicted and reported cases were quite similar, with an underestimation falling within the uncertainty range (mean absolute percentage error of 0.3), while an overestimation by the model was observed in the subsequent waves.
The temporal trends of total tests and reported cases were very similar, showing a high correlation (Spearman 0.87). For both tests and cases, the values during the first wave were significantly greater than those observed in the subsequent waves, whereas the positivity rate (i.e., the proportion of positive cases among tests conducted) showed a less pronounced difference between the first and subsequent waves, and its trend was more similar to that of the hospitalizations. (Figure 4)
Furthermore, to evaluate the early warning capacity of the system, the time lag between the virus load at the WWTP and the number of active cases reported over time was investigated. The diagnosis date was considered the reference date for active cases, corresponding to the date when a positive case was officially recorded in the healthcare system. The maximum correlation (Spearman coefficient = 0.70) was observed when comparing the virus load data with the curve of the active cases recorded 9 days later, suggesting a time lag of 9 days.
3.3. Spatial Comparison of the Predicted and Reported Cases in Each Grouped Area
The comparison between the predicted and reported cases in the grouped areas revealed a medium/high accuracy of the model in estimating the spatial distribution of the cases (Figure 5). Particularly, in the first wave, the error rate was low, with an average mean absolute percentage error across all the areas of 0.18 (min: 0.01, max: 0.20), while in subsequent waves, the error rate increased due to the greater gap between the predicted and reported daily IR(t) trends (Table S12).
However, the model failed to accurately capture the spatial variation in IRj(t) (Figure 6). In fact, the standard deviation of the predicted IRj(t) among different areas was an order of magnitude lower than that associated with the reported IRj(t). The minimal variations in the predicted IRj(t) across different grouped areas are due to the similarity in the values of the population-based coefficient Wj (max =1.024, min = 0.983, standard deviation= 0.009) (Table S14).
The standard deviation of Wj was low since the regression coefficients used to determine Wj were very low (max = 0.329, min = -0.008) (Table S4). In addition, population characteristics were very similar among the different areas (Table S5).
The uncertainty associated with the daily estimation of IRj(t) in each area was calculated (Section 2.5). Since the uncertainty depends on the number of cases (the lower the number of cases is, the greater the uncertainty is), its value varied from one area to another and was greater than that calculated in the temporal analysis. Starting from the uncertainty value, the upper and lower limits associated with the estimation of IRj(t) in each area were computed (Figure 6).
Only throughout the first wave and off-wave periods, the reported values of IRj(t) remained within the range of uncertainty associated with the predicted IRj(t), while during the second and third waves, the reported IRj(t) only partially overlapped with the uncertainty range.
The spatial variation in the reported IRj(t) did not exhibit consistency over time; across different areas, the IRj(t) values deviated differently from the mean, displaying both higher and lower values over time (Figure S7). Indeed, across the three distinct waves and in the off-waves period, only 21 out of 67 areas (31%) demonstrated consistent temporal variations. Of these, 11 areas consistently exhibited IRj(t) values above the mean, while 10 areas consistently exhibited values below the mean. However, for 46 areas, the variation was not consistent over time.
Upon comprehensive analysis of the three waves and the off-waves, considering the variation in IRj(t) relative to the mean, 31 areas (46%) demonstrated concordance between the predicted and reported variations in IRj(t), while this was not observed in 36 areas.
4. Discussion
4.1. Model Parameters
The faecal shedding rate (Sh), the wet mass of faeces (Mf) and the biodegradation constant (k) were assumed from the literature since site-specific data for these parameters were not available. The shedding rate exhibited significant variability, ranging from 103 to 109 [GC/g] [3,16,29,31]. This variability was attributed to the estimation method, which can be at the individual level [3,40] or at the population level (retrospectively determined based on observed concentrations at WWTPs and positive cases) [16,31]. Additionally, shedding depends on factors such as population characteristics (e.g., sex, age, ethnic group [31] and health status [3]), viral variants or subvariants [31], symptoms exhibited and disease stage [41,42].
Given the considerable variability in shedding values, two values were selected specifically for the variants prevalent during the study period (Delta and Omicron) [31]. Moreover, we averaged the shedding values calculated across diverse and numerous populations to account for interindividual shedding variability.
Prasek et al. [31] considered a six-day sum of reported cases appropriate for representing the number of infected individuals contributing to the daily virus load in wastewater. Therefore, the shedding coefficients derived from Prasek et al. [31] were included in the model as daily average values. This allowed to consider that the cases contributing to the concentration at the WWTP were not only new daily cases but also active cases with a high shedding rate, i.e., cases occurring within the six days surrounding the day of the measured value [15,43]. The value chosen for the daily wet mass of feces produced by each individual represents the median of the data collected across various communities in many countries over an extended period (1934-2011) [32].
The value of the biodegradation constant varies depending on the sewer network type (combined or separate system), wastewater temperature and pressure [18,23,44], initial virus concentration [18,33] and structure [34], and other effluent parameters, such as suspended solids [45], biofilm [46], BOD and pH. The values of k in the literature range from 0.004 [h-1] [33] to 0.120 [h-1] [4],as determined through experiments conducted under specific conditions. In the present study, the value for the biodegradation constant was derived from an article [4] that closely matched our conditions: the k value was determined by analysing fluctuations in virus concentration over short intervals of time, and the virus was naturally present in the collected wastewater without any additional introduction. In fact, SARS-CoV-2 shed in feces may contain intact virus, compromised capsid virus, and free nucleic acids; thus, the rapid decay of SARS-CoV-2 RNA observed in the study [4] reflects the decay of all three of these viral RNA sources typically found in naturally contaminated wastewater. Notably, an improvement and potential future development of the model will involve deriving site-specific values for the described parameters.
4.2. Effect of the Biodegradation and Contribution of Each Area
The impact of biodegradation on reducing the viral load reaching the WWTP was assessed by estimating the reduction between the viral load generated from each area and that detected at the WWTP. The maximum reduction reached 70%, with an average reduction of approximately 30%, indicating the substantial influence of biodegradation on reducing the virus load in the sewer network.
In addition, the virus load [GC/day] produced in the entire study area over time, removing the effects of biodegradation and the geographic distribution of the population, was determined (Eq. 6) to allow the comparison of this parameter across different cities. According to the literature, the normalized value at WWTP can be obtained by dividing the measured load by the total population served by the plant [47]. Our approach offers a more precise normalization method, considering the actual distance of the population from the WWTP.
Furthermore, in pursuit of monitoring and early warning goals, indicators were developed that assess the impact of population density and biodegradation on the virus load detected at the WWTP. These indicators revealed that densely populated areas, even those located far from the WWTP, substantially contributed to the virus load at the WWTP. However, the contribution of distant areas was mitigated by elevated biodegradation values. This led to the identification of potential monitoring points.
Moreover, the hospital contributions to the viral load during the study period were retrospectively calculated. Indeed, the contribution of each area estimated by the model relies on the population domiciled within the area, thus not accounting for the possibility that infected individuals may be located in different areas. The contribution of each hospital to the total viral load at the WWTP was deemed negligible, whereas the individual contribution of each hospital was significant compared to the contribution of the area in which it is located
4.3. Health Variables Analysis to Compare the Predicted and Reported Infection Rates
In interpreting the results of the comparison between reported and predicted COVID-19 cases, it is crucial to consider that the reported number of positive cases in the health surveillance system was affected by an error arising from the presence of numerous positive individuals who were not identified. This number of unreported cases varied over the study period due to a combination of factors, e.g., changes in the number of tests conducted and in isolation protocols, vaccine efficacy in reducing symptoms, milder variants and the psychological impact on individuals [6].
Identifying an appropriate period for comparing predicted and reported cases was challenging. Ideally, validation should be performed when the number of unreported cases is as low as possible. However, no quantitative data about underreporting were available. Hence, a qualitative analysis of health variables that may have influenced the number of reported and predicted cases over time was conducted to better understand the comparison between them: time trends in vaccination rates, testing and subvariants were examined across the entire population of the study area.
From October 2021 to March 2022, the number of individuals who received the third dose increased from 0% to 60% of the total resident population, peaking in December 2021 and January 2022. The increase in individuals receiving the third dose might have played a role in the decrease in the number of reported cases in the waves following the first wave. Indeed, approximately 15 days after the administration of the third dose, individuals might have been less susceptible to severe outcomes, potentially impacting the detection of cases.
The decrease in the number of tests recorded since late January 2022 (Figure 4) could be attributed in part to the introduction of rapid self-diagnostic tests, implemented starting on January 19 in the Emilia Romagna region. According to the positivity rate, it is evident that if the number of tests conducted during the three waves had been equivalent, there would likely have been more reported cases than those actually recorded in the second and third waves. This supports the hypothesis that underreporting was greater during these waves. This hypothesis seems to also be supported by the hospitalization curve. In fact, the ratio between hospitalizations and new cases during January 2022 was the lowest of the entire period (2%), suggesting a greater number of unreported cases in the other waves.
Moreover, a transition from the Delta variant to the Omicron variant (BA.1) was observed during the study period. According to rapid regional surveys [48], the presence of the Omicron variant in the population increased exponentially in December 2021, overtaking the Delta variant between the penultimate week and last week of the month. This transition was followed by further variations within the Omicron lineage (BA.2, BA.4, BA.5, BA.2.75, BQ1, and XBB) [48] (Figure 7). An increase in COVID-19 cases was observed concurrently with variant or lineage variations (Figure 3, Figure 7), in agreement with other studies [6,49]. Furthermore, milder fluctuations in predicted and reported cases in the months from October to December 2022 coincided with minor variations in Omicron lineages.
Figure 7.
Percentage of SARS-CoV-2 variant lineages over time obtained from regional surveys [48].
Figure 7.
Percentage of SARS-CoV-2 variant lineages over time obtained from regional surveys [48].
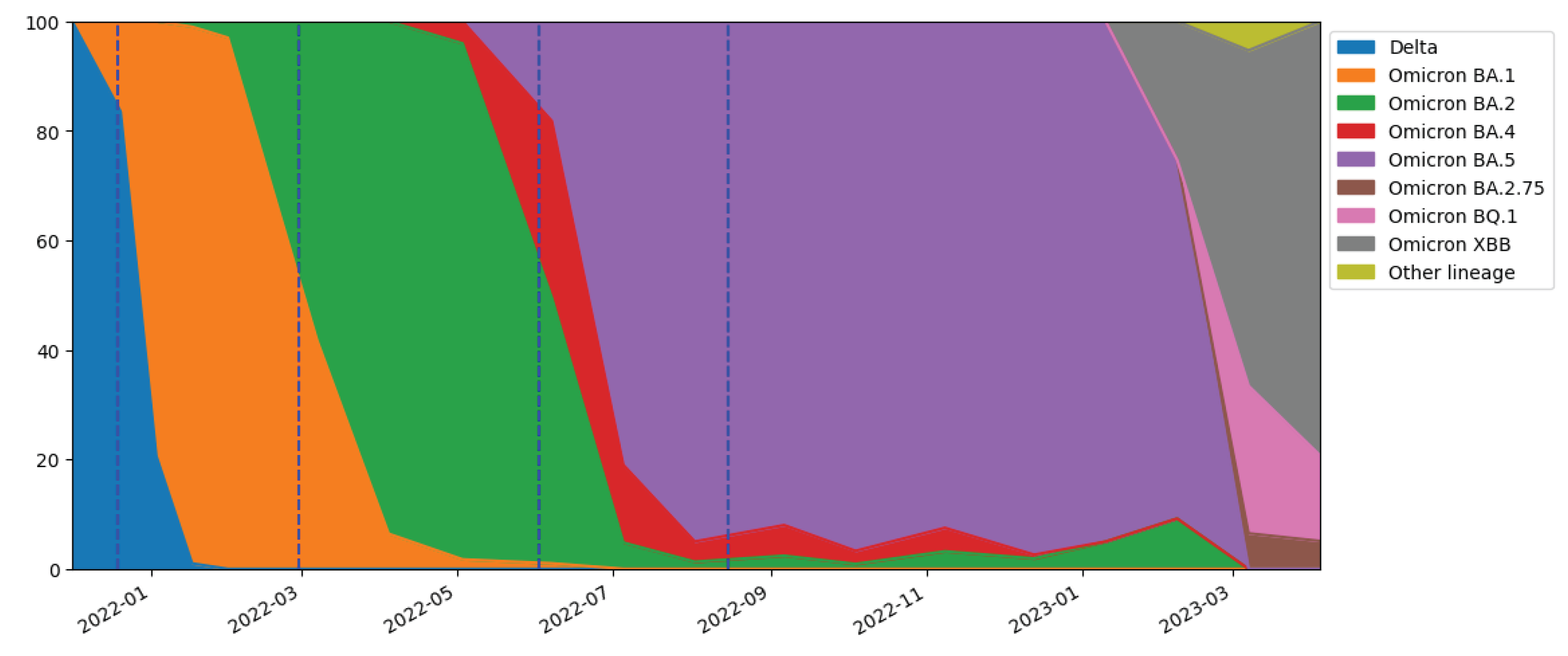
It is important to emphasize that the shedding values employed in the model [31] were related only to Delta and Omicron variants (mainly BA.1). Therefore, the model overestimation in the second and third waves might also be attributed to a change in shedding due to the shift from Omicron BA.1 to BA.2 and from Omicron BA.2 to BA.4/BA.5, respectively. In fact, the shedding related to the BA.1 subvariant is likely lower than that related to Delta, Omicron BA.2 and BA.5 [49]. However, this overestimation does not fully justify the magnitude of the difference observed between the predicted and reported cases.
In conclusion, the most reliable period for accurate validation of the model could be from October 2021 until the end of February 2022, when the number of cases underreported was likely the lowest. According to the reported and predicted cases during this period, the model underestimated the number of cases reported by the healthcare system. This discrepancy, although within the uncertainty interval, is still noteworthy and may be attributable to the use of parameters from the literature, such as the fecal shedding rate.
4.4. Spatial Comparison of the Predicted and Reported Cases in Each Grouped Area
The temporal inconsistency in the variation in the reported IRj within the same area indicates that a random effect could have caused the increase in cases in one area rather than another. Furthermore, in the areas where the variation in the reported IRj remained consistent over time, other factors such as deprivation and obesity indices [50] may need to be considered to explain the variability in IRj. Additionally, a limitation of the proposed approach is the use of an estimate of the population domiciled in each area (Section 2.1) for calculating the reported IRj. In summary, the model accurately predicted the spatial distribution of cases because the reported IRj exhibited minimal variations among the different grouped areas. Consequently, the distribution of reported cases across the areas was primarily influenced by the population size of each area, which also determines the distribution of predicted cases.
5. Conclusions
The presented model aimed to correlate the virus concentration at the WWTP with the number of COVID-19 cases in the respective catchment area. This approach was based on previous models that either omitted biodegradation [14,15,16,17] or treated it as a uniform factor across the catchment area [3]. Our approach involved a detailed consideration of biodegradation along the sewer system, with a similar approach to that of McCall et al. [18] but with an additional step: associating the biodegradation factor with population distribution and characteristics.
By applying the model to data from the main WWTP of Bologna, daily COVID-19 cases for each census section or statistical area served by the WWTP were estimated. To assess the model’s performance, the predicted cases were compared with those reported by the healthcare system. The results were first analysed by comparing the predicted and reported infection rates over time and then by examining the variation in reported and predicted cases in different areas.
The model demonstrated satisfactory results, predicting the trend of reported cases over time and space well. The model slightly underestimated the reported cases during the first COVID-19 wave analysed and overestimated the number of reported cases during subsequent waves. Nevertheless, the correlation between the two datasets was consistently high across the three waves, demonstrating the model’s capacity to predict the relevant waves and the significant increases in the number of cases.
The inclusion of biodegradation in the model equation significantly improved case estimates, enabling the calculation of the decrease in virus load along the sewer network from each area to the WWTP. Conversely, no substantial variation in the final result was obtained by adding the population-based coefficient.
The model estimated that biodegradation significantly reduced the virus load reaching the WWTP, resulting in a 30% reduction in the total virus load produced in the study area. The approach used in the present study allows for the comparison of data from WWTPs in different cities by normalizing the detected values for virus biodegradation and the geographic distribution of the population.
The model demonstrated its reliability as a valuable tool for early warning systems, offering a complementary approach to clinical surveillance, especially given the reduction in reported cases and tests by the healthcare system. Furthermore, the model can provide an indication of the magnitude of underreported cases. Additionally, a time lag of 9 days was observed between the variations in the SARS-CoV-2 load at the WWTP and the changes in the trend of the reported active cases.
Notably, potential modifications to the parameters can be easily implemented to improve the accuracy of the model and can be obtained through the collection of additional site-specific information and measurements (e.g., sewer flow velocity and biodegradation constant). In particular, an important future development could involve calculating the faecal shedding rate parameter on-site and over time to obtain shedding values specific to the demographic characteristics of the population and to virus subvariants on which the model is applied.
Moreover the model could be optimized by placing sampling and measurement points along the sewer network. This would improve precision and reliability in the estimation of cases for various areas and could help identify local differences in infection rates. Additionally, the model can be easily integrated into an online dashboard, enhancing accessibility and immediacy for public health operators. Finally, the model could be adapted for surveillance of other viruses or chemicals, making it a versatile tool for monitoring and preventing the effects of diverse viruses or substances on the population.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1: Resident and domiciled population in the study area; Table S2: Statistics of SARS-CoV-2 RNA concentration at the WWTP; Table S3: Statistics of wastewater flow rate at the WWTP; Table S4: Variables and estimates from the Global Poisson regression model; Table S5: Statistics of population characteristics; Table S6: Shedding rate values; Table S7: Variation of the spread of Delta and Omicron variants and sub-variants; Table S8: Shedding values depending on the period; Table S9: Biodegradation rate constant values varying with temperature and time of year; Table S10: Parameters in the error propagation formula; Table S11: Uncertainty associated with IR(t) varying with the number of cases; Table S12: For each grouped area: population domiciled in the area, number of reported and predicted cases and percentage contribution of the area to the detected value of SARS-CoV-2 at the WWTP; Table S13: Contribution of hospitals in terms of viral load detected at the WWTP during the study period; Table S14: Statistics of the daily average reported and predicted infection rate and of the population-based coefficient; Figure S1: Map of areas and grouped areas included in the study; Figure S2: SARS-CoV-2 RNA concentration at the WWTP; Figure S3: Wastewater flow rate at the WWTP; Figure S4: Daily load of SARS-CoV-2 RNA at the inlet of the WWTP; Figure S5: Maps of the 3 indicators; Figure S6: Maps of the statistical areas of Bologna, considering hospitalized COVID-19 individuals; Figure S7: Infection rate variation across grouped areas during the study period. Equation S1, S2, S3, S4, S5, S6, S7: Equations used to derive the model equation; Equation S8: Error propagation formula; Equation S9: Normalized local sensitivity analysis; Equation S10, S11, S12: Equations of the three indicators; Equation S13: hospitals coefficient;.
Author Contributions
Conceptualization, M.F., L.V. G.B., A.C. and A.R.; methodology, M.F. and L.V.; software, M.F.; validation, M.F. and L.V.; formal analysis, M.F. and L.V.; investigation, M.F., L.V., F.A., L.D.L., F.F., E.M., M.G.M. and L.M.; resources, L.D.L., M.G.M., L.M., V.P., G.B., P.P., A.C. and A.R.; data curation, M.F., L.V., L.D.L., F.F., E.M. and L.M.; writing—original draft preparation, M.F., L.V., M.G.M. and A.C.; writing—review and editing, M.F., L.V., F.F., C.F., E.M., M.G.M. A.C. and A.R.; visualization, M.F. and L.V.; supervision, C.F., M.G.M., V.P., G.B., P.P., A.C. and A.R.; project administration, M.G.M., A.C. and A.R.; funding acquisition, G.B. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded within the EU Project “EC G.A. NO. 060701/2021/864481/SUB/ENV.C2 -Support to the member states to establish national systems, local collection points, and digital infrastructure for monitoring covid 19 and its variants in waste waters”, and the Project “Epidemiologia delle acque reflue: implementazione del sistema di sorveglianza per l’identificazione precoce di agenti patogeni, con particolare riferimento al Sars-CoV2”, promoted by the Italian Ministry of Health (PROGRAMMA CCM 2020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Databases and information system: https://www.istat.it/en/analysis-and-products/databases; Statistical areas of Bologna: https://opendata.comune.bologna.it/explore/dataset/aree-statistiche/information/; dext3r: https://simc.arpae.it/dext3r.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Corchis-Scott, R.; Geng, Q.; Seth, R.; Ray, R.; Beg, M. R.; Biswas, N.; Charron, L.; Drouillard, K. D.; D’Souza, R.; Heath, D. D.; Houser, C.; Lawal, F.; McGinlay, J.; Menard, S. L.; Porter, L. A.; Rawlings, D.; Scholl, M. L.; Siu, K. W. M.; Tong, Y.; Weisener, C. G.; Wilhelm, S. W.; McKay, R. M. L. Averting an Outbreak of SARS-CoV-2 in a University Residence Hall through Wastewater Surveillance. Microbiology Spectrum 2021, 9 (2). [CrossRef]
- Bertels, X.; Demeyer, P.; Van Den Bogaert, S.; Boogaerts, T.; Van Nuijs, A. L. N.; Delputte, P.; Lahousse, L. Factors influencing SARS-CoV-2 RNA concentrations in wastewater up to the sampling stage: A systematic review. Science of the Total Environment 2022, 820, 153290. [CrossRef]
- Li, X.; Zhang, S.; Shi, J.; Luby, S. P.; Jiang, G. Uncertainties in estimating SARS-CoV-2 prevalence by wastewater-based epidemiology. Chemical Engineering Journal 2021, 415, 129039. [CrossRef]
- Weidhaas, J.; Aanderud, Z. T.; Roper, D. K.; VanDerslice, J.; Gaddis, E.; Ostermiller, J.; Hoffman, K.; Jamal, R.; Heck, P. E.; Zhang, Y.; Torgersen, K. T.; Laan, J. V.; LaCross, N. Correlation of SARS-CoV-2 RNA in wastewater with COVID-19 disease burden in sewersheds. Science of the Total Environment 2021, 775, 145790. [CrossRef]
- Robotto, A.; Lembo, D.; Quaglino, P.; Brizio, E.; Polato, D.; Civra, A.; Cusato, J.; Di Perri, G. Wastewater-based SARS-CoV-2 environmental monitoring for Piedmont, Italy. Environmental Research 2022, 203, 111901. [CrossRef]
- Baldovin, T.; Amoruso, I.; Fonzo, M.; Bertoncello, C.; Groppi, V.; Pitter, G.; Russo, F.; Baldo, V. Trends in SARS-CoV-2 clinically confirmed cases and viral load in wastewater: A critical alignment for Padua city (NE Italy). Heliyon 2023, 9 (10), e20571. [CrossRef]
- McMahan, C. S.; Self, S.; Rennert, L.; Kalbaugh, C. A.; Kriebel, P. D.; Graves, D.; Colby, C.; Deaver, B. J. A.; Popat, S. C.; Karanfil, P. T.; Freedman, P. D. L. COVID-19 wastewater epidemiology: a model to estimate infected populations. The Lancet Planetary Health 2021, 5 (12), e874–e881. [CrossRef]
- La Rosa, G.; Iaconelli, M.; Veneri, C.; Mancini, P.; Ferraro, G. B.; Brandtner, D.; Lucentini, L.; Bonadonna, L.; Rossi, M.; Grigioni, M.; Suffredini, E. The rapid spread of SARS-COV-2 Omicron variant in Italy reflected early through wastewater surveillance. Science of the Total Environment 2022, 837, 155767. [CrossRef]
- EUR-LEX - 32021H0472 - EN - EUR-LEX. https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32021H0472&qid=1628798981209.
- Ciannella, S.; González-Fernández, C.; Gómez-Pastora, J. Recent progress on wastewater-based epidemiology for COVID-19 surveillance: A systematic review of analytical procedures and epidemiological modeling. Science of the Total Environment 2023, 878, 162953. [CrossRef]
- Rauch, W.; Schenk, H.; Insam, H.; Markt, R.; Kreuzinger, N. Data modelling recipes for SARS-CoV-2 wastewater-based epidemiology. Environmental Research 2022, 214, 113809. [CrossRef]
- Morvan, M.; Lo Jacomo, A.; Souque, C.; Wade, M. J.; Hoffmann, T.; Pouwels, K. B.; Lilley, C.; Singer, A. C.; Porter, J.; Evens, N.; Walker, D. L.; Bunce, J. T.; Engeli, A.; Grimsley, J. M. S.; O’Reilly, K.; Danon, L. An analysis of 45 large-scale wastewater sites in England to estimate SARS-CoV-2 community prevalence. Nature Communications 2022, 13 (1). [CrossRef]
- Jiang, G.; Wu, J.; Weidhaas, J.; Li, X.; Chen, Y.; Mueller, J. F.; Li, J.; Kumar, M.; Zhou, X.; Arora, S.; Haramoto, E.; Sherchan, S.; Orive, G.; Lertxundi, U.; Honda, R.; Kitajima, M.; Jackson, G. Artificial neural network-based estimation of COVID-19 case numbers and effective reproduction rate using wastewater-based epidemiology. Water Research 2022, 218, 118451. [CrossRef]
- Ahmed, W.; Angel, N.; Edson, J.; Bibby, K.; Bivins, A.; O’Brien, J.; Choi, P. M.; Kitajima, M.; Simpson, S. L.; Li, J.; Tscharke, B. J.; Verhagen, R.; Smith, W.; Zaugg, J.; Dierens, L.; Hugenholtz, P.; Thomas, K. V.; Mueller, J. F. First confirmed detection of SARS-CoV-2 in untreated wastewater in Australia: A proof of concept for the wastewater surveillance of COVID-19 in the community. Science of the Total Environment 2020, 728, 138764. [CrossRef]
- Prasek, S. M.; Pepper, I. L.; Innes, G. K.; Slinski, S.; Ruedas, M.; Sánchez, A. C.; Brierley, P.; Betancourt, W. Q.; Stark, E. R.; Foster, A. R.; Betts-Childress, N. D.; Schmitz, B. W. Population level SARS-CoV-2 fecal shedding rates determined via wastewater-based epidemiology. Science of the Total Environment 2022, 838, 156535. [CrossRef]
- Schmitz, B. W.; Innes, G. K.; Prasek, S. M.; Betancourt, W. Q.; Stark, E. R.; Foster, A. R.; Abraham, A. G.; Gerba, C. P.; Pepper, I. L. Enumerating asymptomatic COVID-19 cases and estimating SARS-CoV-2 fecal shedding rates via wastewater-based epidemiology. Science of the Total Environment 2021, 801, 149794. [CrossRef]
- Wani, H.; Menon, S.; Desai, D.; Dsouza, N.; Bhathena, Z.; Desai, N. B.; Rose, J. B.; Shrivastava, S. Wastewater-Based Epidemiology of SARS-CoV-2: Assessing Prevalence and Correlation with Clinical Cases. Food and Environmental Virology 2023, 15 (2), 131–143. [CrossRef]
- McCall, C.; Fang, Z.; Li, D.; Czubai, A. J.; Juan, A.; LaTurner, Z. W.; Ensor, K. B.; Hopkins, L.; Bedient, P. B.; Stadler, L. B. Modeling SARS-CoV-2 RNA degradation in small and large sewersheds. Environmental Science 2022, 8 (2), 290–300. [CrossRef]
- Databases and information system. https://www.istat.it/en/analysis-and-products/databases.
- Statistical areas of Bologna. https://opendata.comune.bologna.it/explore/dataset/aree-statistiche/information/.
- La Rosa, G.; Bonadonna, L.; Suffredini, E. Protocollo della Sorveglianza di SARS-CoV-2 in reflui urbani (SARI) - rev. 3. Zenodo 2022. [CrossRef]
- Wu, F.; Zhang, J.; Xiao, A.; Gu, X.; Lee, W. L.; Armas, F.; Kauffman, K. M.; Hanage, W. P.; Matus, M.; Ghaeli, N.; Endo, N.; Duvallet, C.; Poyet, M.; Moniz, K.; Washburne, A. D.; Erickson, T.; Chai, P. R.; Thompson, J. R.; Alm, E. J. SARS-CoV-2 Titers in Wastewater Are Higher than Expected from Clinically Confirmed Cases. MSystems 2020, 5 (4). [CrossRef]
- Ahmed, W.; Bertsch, P. M.; Bibby, K.; Haramoto, E.; Hewitt, J.; Huygens, F.; Gyawali, P.; Korajkic, A.; Riddell, S.; Sherchan, S. P.; Simpson, S. L.; Sirikanchana, K.; Symonds, E. M.; Verhagen, R.; Vasan, S. S.; Kitajima, M.; Bivins, A. Decay of SARS-CoV-2 and surrogate murine hepatitis virus RNA in untreated wastewater to inform application in wastewater-based epidemiology. Environmental Research 2020, 191, 110092. [CrossRef]
- La Rosa, G.; Mancini, P.; Ferraro, G. B.; Veneri, C.; Iaconelli, M.; Bonadonna, L.; Lucentini, L.; Suffredini, E. SARS-CoV-2 has been circulating in northern Italy since December 2019: Evidence from environmental monitoring. Science of the Total Environment 2021, 750, 141711. [CrossRef]
- dext3r. https://simc.arpae.it/dext3r.
- Cleveland, W. S.; Devlin, S. J. Locally Weighted Regression: An approach to regression analysis by local fitting. Journal of the American Statistical Association 1988, 83 (403), 596–610. [CrossRef]
- Cappellari, M.; McDermid, R. M.; Alatalo, K.; Blitz, L.; Bois, M.; Bournaud, F.; Bureau, M.; Crocker, A. F.; Davies, R. L.; Davis, T. A.; De Zeeuw, P. T.; Duc, P.; Emsellem, É.; Khochfar, S.; Krajnović, D.; Küntschner, H.; Morganti, R.; Naab, T.; Oosterloo, T.; Sarzi, M.; Scott, N.; Serra, P.; Weijmans, A.-M.; Young, L. M. The ATLAS3D project – XX. Mass–size and mass–σ distributions of early-type galaxies: bulge fraction drives kinematics, mass-to-light ratio, molecular gas fraction and stellar initial mass function. Monthly Notices of the Royal Astronomical Society 2013, 432 (3), 1862–1893. [CrossRef]
- Benefield, A. E.; Skrip, L. A.; Clement, A.; Althouse, R. A.; Chang, S.; Althouse , B. M. SARS-CoV-2 viral load peaks prior to symptom onset: a systematic review and individual-pooled analysis of coronavirus viral load from 66 studies. medRxiv (Cold Spring Harbor Laboratory) 2020. [CrossRef]
- Foladori, P.; Cutrupi, F.; Segata, N.; Manara, S.; Pinto, F.; Malpei, F.; Bruni, L.; La Rosa, G. SARS-CoV-2 from faeces to wastewater treatment: What do we know? A review. Science of the Total Environment 2020, 743, 140444. [CrossRef]
- Zeleke, A. J.; Miglio, R.; Palumbo, P.; Malaguti, E.; Chiari, L.; Due, U. Spatiotemporal heterogeneity of SARS-CoV-2 diffusion at the city level using geographically weighted Poisson regression model: The case of Bologna, Italy. Geospatial Health 2022, 17 (2). [CrossRef]
- Prasek, S. M.; Pepper, I. L.; Innes, G. K.; Slinski, S.; Betancourt, W. Q.; Foster, A. R.; Yaglom, H.; Porter, W. T.; Engelthaler, D. M.; Schmitz, B. W. Variant-specific SARS-CoV-2 shedding rates in wastewater. Science of the Total Environment 2023, 857, 159165. [CrossRef]
- Rose, C.; Parker, A.; Jefferson, B.; Cartmell, E. The Characterization of feces and Urine: A review of the literature to inform advanced Treatment technology. Critical Reviews in Environmental Science and Technology 2015, 45 (17), 1827–1879. [CrossRef]
- Bivins, A.; Greaves, J.; Fischer, R. J.; Yinda, K. C.; Ahmed, W.; Kitajima, M.; Munster, V. J.; Bibby, K. Persistence of SARS-COV-2 in water and wastewater. Environmental Science and Technology Letters 2020, 7 (12), 937–942. [CrossRef]
- Yang, S.; Dong, Q.; Li, S.; Zhao, C.; Kang, X.; Ren, D.; Xu, C.; Zhou, X. H.; Peng, L.; Sun, L.; Zhao, J.; Yang, J.; Han, T.; Liu, Y.; Qian, Y.; Liu, Y.; Huang, X.; Qu, J. Persistence of SARS-CoV-2 RNA in wastewater after the end of the COVID-19 epidemics. Journal of Hazardous Materials 2022, 429, 128358. [CrossRef]
- Silverman, A. I.; Boehm, A. B. Systematic Review and Meta-Analysis of the persistence and disinfection of human coronaviruses and their viral surrogates in water and wastewater. Environmental Science and Technology Letters 2020, 7 (8), 544–553. [CrossRef]
- Cipolla, S. S.; Maglionico, M. Heat Recovery from Urban Wastewater: Analysis of the Variability of Flow Rate and Temperature in the Sewer of Bologna, Italy. Energy Procedia 2014, 45, 288–297. [CrossRef]
- Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. Introduction to algorithms; MIT Press, 2001.
- Compagni, R. D.; Polesel, F.; Von Borries, K. J. F.; Zhang, Z.; Turolla, A.; Antonelli, M.; Vezzaro, L. Modelling micropollutant fate in sewer systems – A new systematic approach to support conceptual model construction based on in-sewer hydraulic retention time. Journal of Environmental Management 2019, 246, 141–149. [CrossRef]
- Bareš, V.; Jirák, J.; Pollert, J. Spatial and temporal variation of turbulence characteristics in combined sewer flow. Flow Measurement and Instrumentation 2008, 19 (3–4), 145–154. [CrossRef]
- Zhang, Y.; Cen, M.; Hu, M.; Du, L.; Hu, W.; Kim, J. J.; Dai, N. Prevalence and persistent shedding of fecal SARS-COV-2 RNA in patients with COVID-19 infection: a systematic review and meta-analysis. Clinical and Translational Gastroenterology 2021, 12 (4), e00343. [CrossRef]
- Natarajan, A.; Zlitni, S.; Brooks, E. F.; Vance, S. E.; Dahlen, A.; Hedlin, H.; Park, R.; Han, A. X.; Schmidtke, D. T.; Verma, R.; Jacobson, K.; Parsonnet, J.; Bonilla, H.; Singh, U.; Pinsky, B. A.; Andrews, J. R.; Jagannathan, P.; Bhatt, A. S. Gastrointestinal symptoms and fecal shedding of SARS-CoV-2 RNA suggest prolonged gastrointestinal infection. Med 2022, 3 (6), 371-387.e9. [CrossRef]
- Cheung, K.; Hung, I.; Chan, P. P. Y.; Lung, K.-C.; Tso, E. Y.; Liu, R.; Ng, Y. Y.; Chu, M. Y.; Chung, T. W.-H.; Tam, A. R.; Yip, C. C.-Y.; Leung, K. H.; Fung, A. Y. F.; Zhang, R. R.; Lin, Y.; Cheng, H. M.; Zhang, A. J.; To, K. K.; Chan, K. H.; Yuen, K. Y.; Leung, W. K. Gastrointestinal manifestations of SARS-COV-2 infection and virus load in fecal samples from a Hong Kong cohort: systematic review and meta-analysis. Gastroenterology 2020, 159 (1), 81–95. [CrossRef]
- Cavany, S.; Bivins, A.; Wu, Z.; North, D.; Bibby, K.; Perkins, A. Inferring SARS-CoV-2 RNA shedding into wastewater relative to the time of infection. Epidemiology and Infection 2022, 150. [CrossRef]
- Hart, O. E.; Halden, R. U. Computational analysis of SARS-CoV-2/COVID-19 surveillance by wastewater-based epidemiology locally and globally: Feasibility, economy, opportunities and challenges. Science of the Total Environment 2020, 730, 138875. [CrossRef]
- Petala, M.; Dafou, D.; Kostoglou, M.; Karapantsios, Th. D.; Kanata, Ε.; Chatziefstathiou, A.; Sakaveli, F.; Kotoulas, K.; Arsenakis, M.; Roilides, E.; Metallidis, S.; Papa, A.; Stylianidis, E.; Papadopoulos, A. M.; Papaioannou, N. A physicochemical model for rationalizing SARS-CoV-2 concentration in sewage. Case study: The city of Thessaloniki in Greece. Science of the Total Environment 2021, 755, 142855. [CrossRef]
- Li, J.; Ahmed, W.; Metcalfe, S.; Smith, W.; Choi, P. M.; Jackson, G.; Cen, X.; Zheng, M.; Simpson, S.; Thomas, K. V.; Mueller, J. F.; Thai, P. K. Impact of sewer biofilms on fate of SARS-CoV-2 RNA and wastewater surveillance. Nature Water 2023, 1 (3), 272–280. [CrossRef]
- Verani, M.; Federigi, I.; Muzio, S.; Lauretani, G.; Calà, P.; Mancuso, F.; Salvadori, R.; Valentini, C.; La Rosa, G.; Suffredini, E.; Carducci, A. Calibration of Methods for SARS-CoV-2 Environmental Surveillance: A Case Study from Northwest Tuscany. International Journal of Environmental Research and Public Health 2022, 19 (24), 16588. [CrossRef]
- EpiCentro. Sorveglianza genomica del virus SARS-CoV-2 e delle sue varianti di interesse in sanità pubblica in Italia. https://www.epicentro.iss.it/coronavirus/sars-cov-2-monitoraggio-varianti.
- Rector, A.; Bloemen, M.; Thijssen, M.; Delang, L.; Raymenants, J.; Thibaut, J.; Pussig, B.; Fondu, L.; Aertgeerts, B.; Van Ranst, M.; Van Geet, C.; Arnout, J.; Wollants, E. Monitoring of SARS-CoV-2 concentration and circulation of variants of concern in wastewater of Leuven, Belgium. Journal of Medical Virology 2023, 95 (2). [CrossRef]
- Ho, J. S.-Y.; Fernando, D.; Chan, M. Y.; Sia, C. Obesity in COVID-19: A Systematic review and Meta-analysis. Annals Academy of Medicine Singapore 2020, 49 (12), 996–1008. [CrossRef]
Figure 1.
Map of the study area (orange) divided into census sections and statistical areas (delineated in gray). Representation of the wastewater treatment plant (WWTP) (red triangle), sewer network (blue), catchment area (light blue), names and boundaries of the municipalities (black).
Figure 1.
Map of the study area (orange) divided into census sections and statistical areas (delineated in gray). Representation of the wastewater treatment plant (WWTP) (red triangle), sewer network (blue), catchment area (light blue), names and boundaries of the municipalities (black).
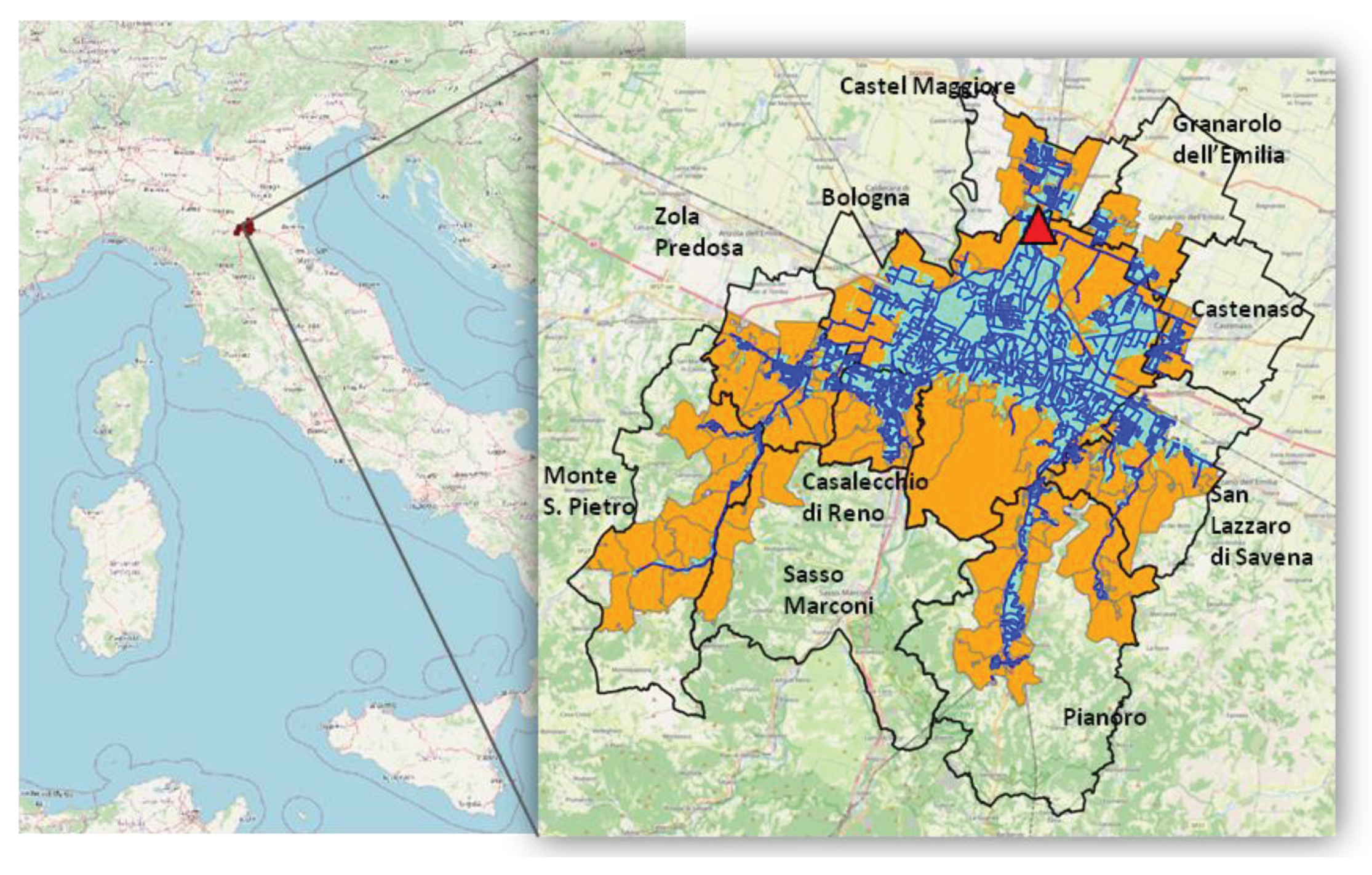
Figure 2.
A) Map of biodegradation in the study area, WWTP (red triangle). B) Frequency distribution of biodegradation in the study area. Biodegradation is expressed as a 1-e-kϴi percentage, calculated with k = 0.101 (T= 16°C).
Figure 2.
A) Map of biodegradation in the study area, WWTP (red triangle). B) Frequency distribution of biodegradation in the study area. Biodegradation is expressed as a 1-e-kϴi percentage, calculated with k = 0.101 (T= 16°C).
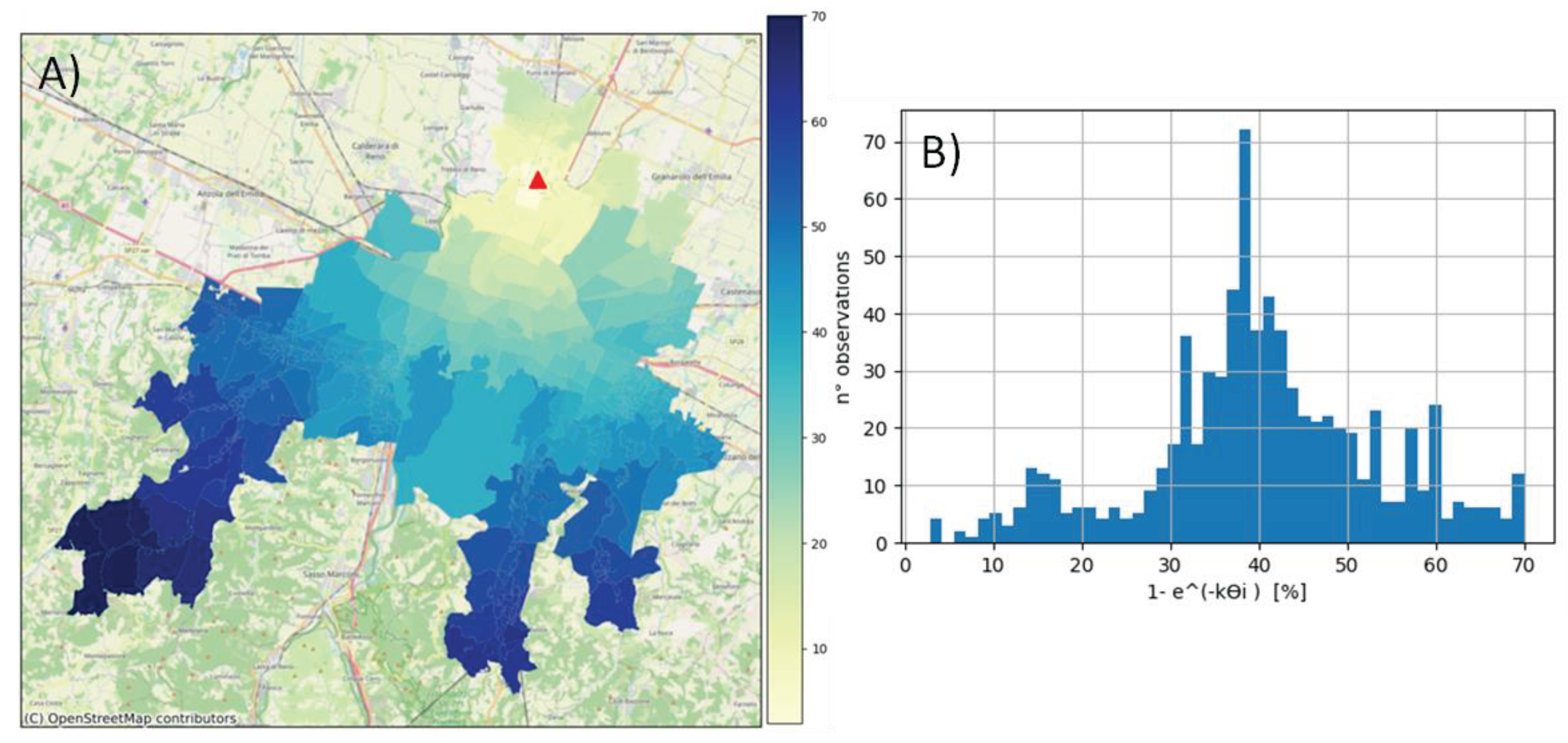
Figure 3.
Predicted (blue) and reported (orange) infection rate IR(t) across the entire study area and the uncertainty interval (RSD) (light blue) associated with the predicted IR(t).
Figure 3.
Predicted (blue) and reported (orange) infection rate IR(t) across the entire study area and the uncertainty interval (RSD) (light blue) associated with the predicted IR(t).
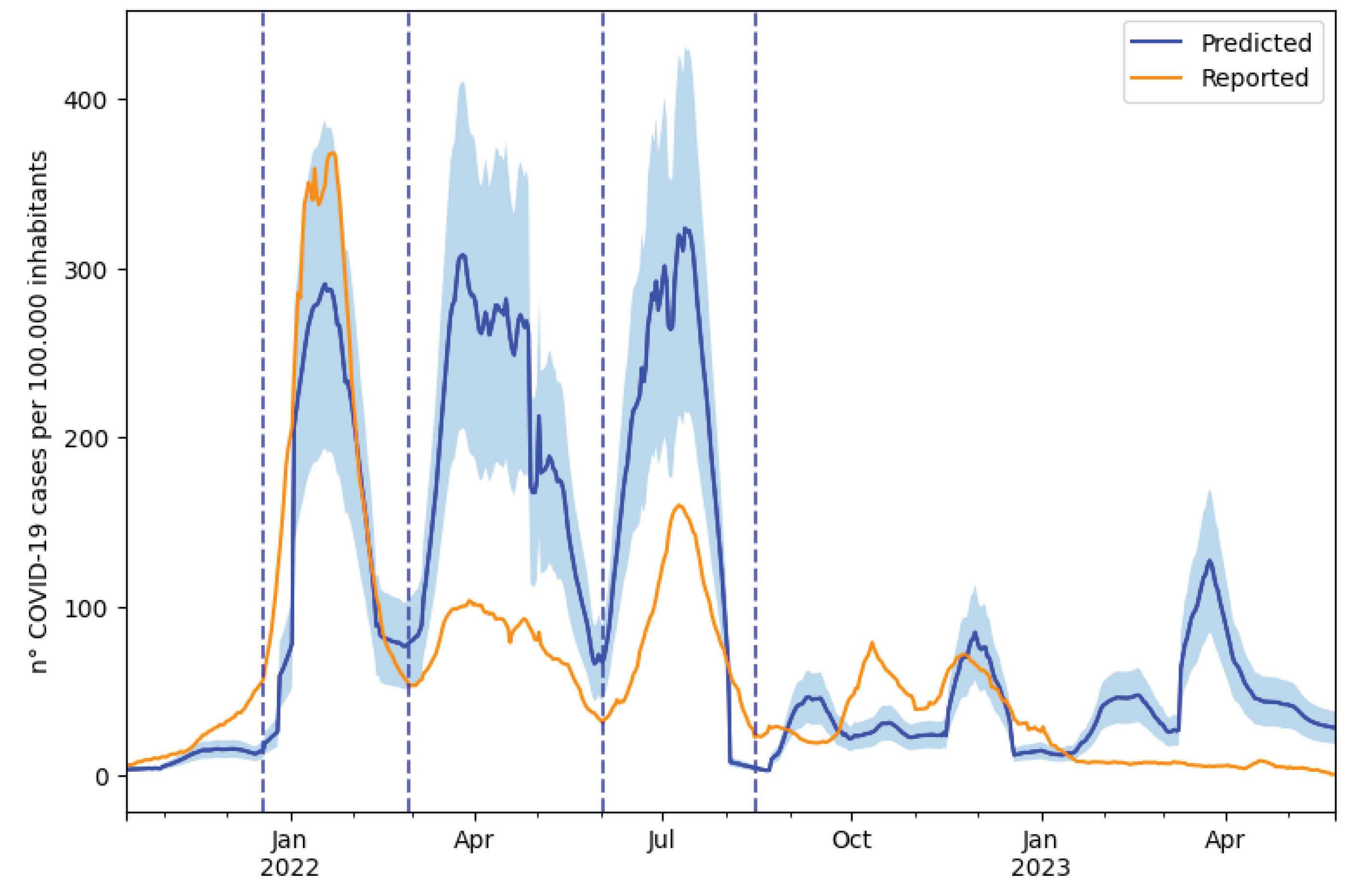
Figure 4.
Tests: Daily reported tests across the entire study area per 100000 inhabitants averaged with a simple moving average (SMA) over 7 days. Positivity rate: Weekly average of positive cases among tests conducted. To calculate the positivity rate, the date on which the test was conducted was taken as the reference date for both tests and cases. Reported cases: reported daily COVID-19 cases over 100000 inhabitants averaged with a simple moving average (SMA) over 7 days (reported IR(t)). Hospitalizations: weekly sum of COVID-19 hospitalizations. Both reported cases and hospitalizations are represented based on the symptom onset date if symptomatic or the date of the test in asymptomatic cases.
Figure 4.
Tests: Daily reported tests across the entire study area per 100000 inhabitants averaged with a simple moving average (SMA) over 7 days. Positivity rate: Weekly average of positive cases among tests conducted. To calculate the positivity rate, the date on which the test was conducted was taken as the reference date for both tests and cases. Reported cases: reported daily COVID-19 cases over 100000 inhabitants averaged with a simple moving average (SMA) over 7 days (reported IR(t)). Hospitalizations: weekly sum of COVID-19 hospitalizations. Both reported cases and hospitalizations are represented based on the symptom onset date if symptomatic or the date of the test in asymptomatic cases.
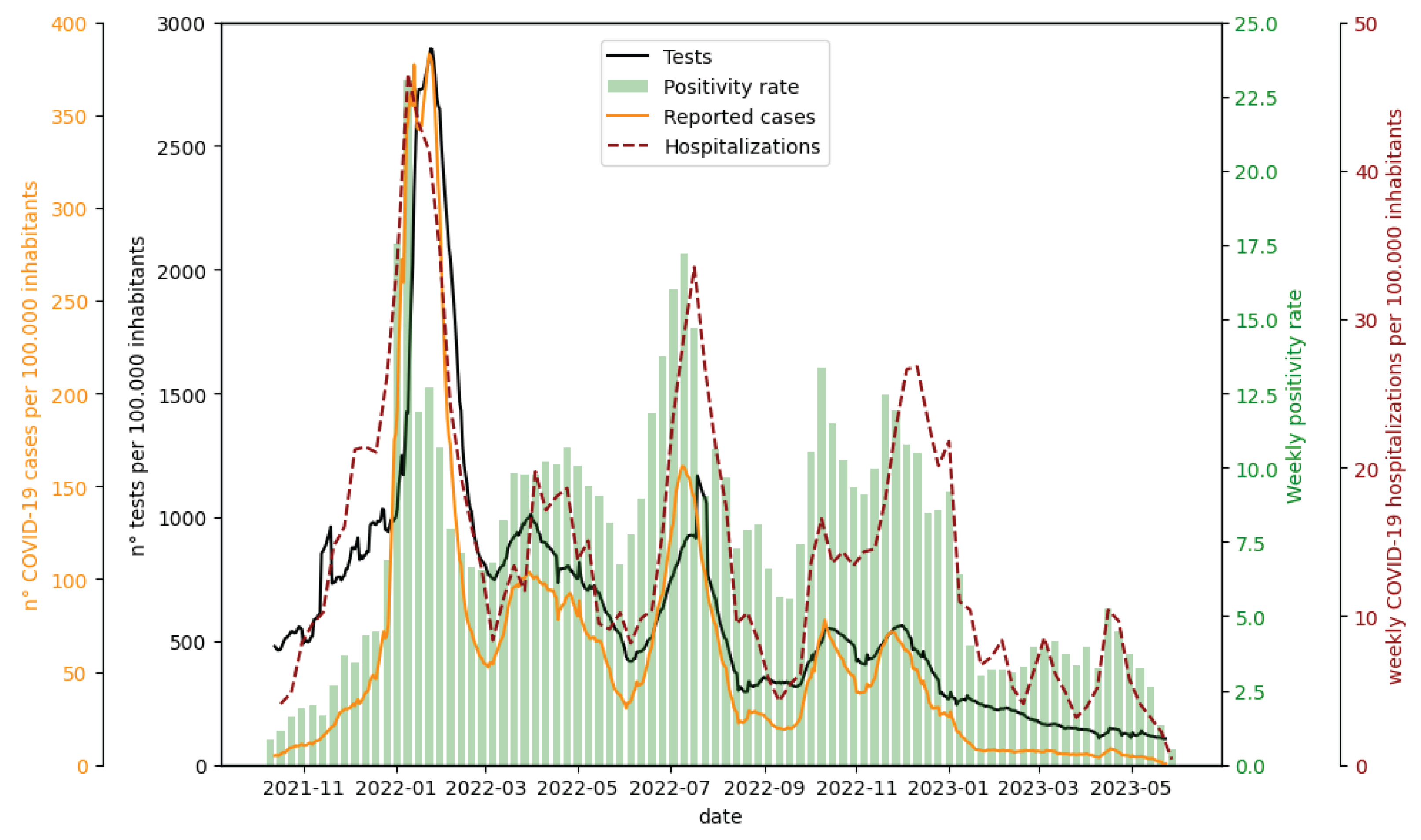
Figure 5.
Maps of predicted total cases (A) and reported total cases (B) during the first wave in different grouped areas.
Figure 5.
Maps of predicted total cases (A) and reported total cases (B) during the first wave in different grouped areas.
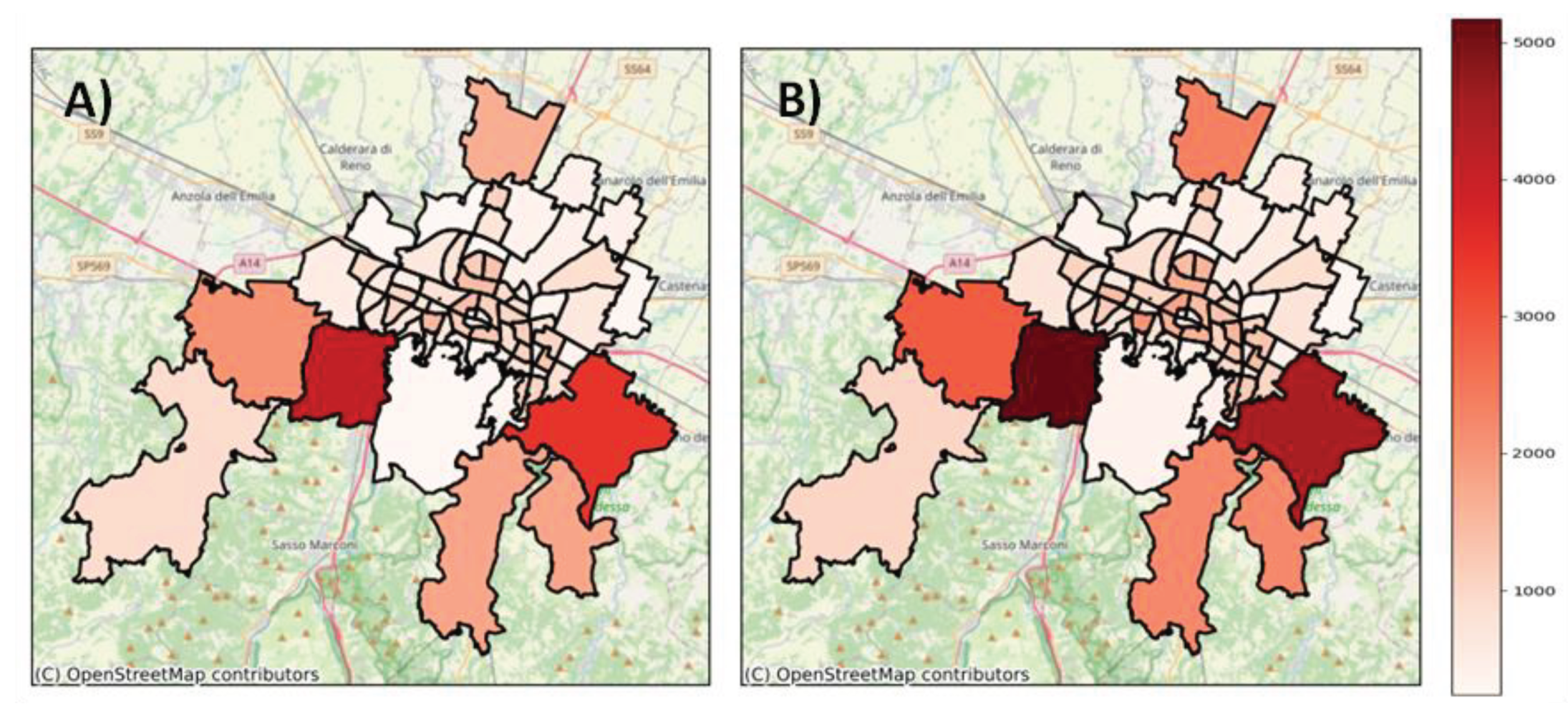
Figure 6.
Box plot of the daily average reported and predicted infection rates (IRj), along with the lower and upper uncertainty bounds associated with the daily average predicted IRj. The IRj is expressed as daily average cases per 1000 inhabitants over the wave and in the grouped area (for each box plot, one data point for each grouped area and for each wave is represented).
Figure 6.
Box plot of the daily average reported and predicted infection rates (IRj), along with the lower and upper uncertainty bounds associated with the daily average predicted IRj. The IRj is expressed as daily average cases per 1000 inhabitants over the wave and in the grouped area (for each box plot, one data point for each grouped area and for each wave is represented).
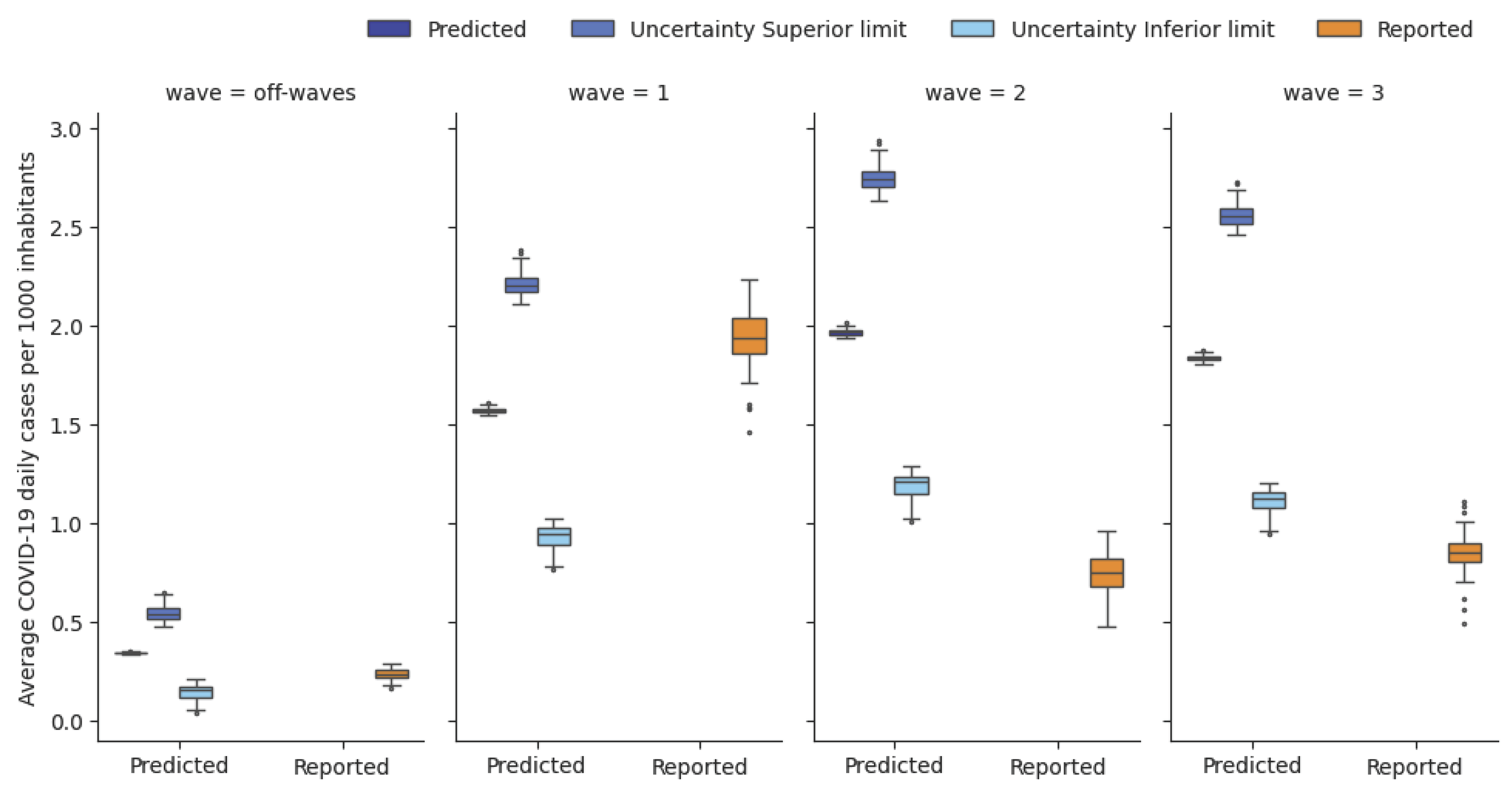
Table 1.
Maximum, minimum, median, standard deviation, 25th percentile and 75th percentile values of the following: linear distance of centroids from the WWTP [km], effective distance (calculated along the sewer network) of centroids from the WWTP (Di [km]), hydraulic residence time (ϴi [h]), and biodegradation (1- e-kϴi [%]) varying with the biodegradation constant k.
Table 1.
Maximum, minimum, median, standard deviation, 25th percentile and 75th percentile values of the following: linear distance of centroids from the WWTP [km], effective distance (calculated along the sewer network) of centroids from the WWTP (Di [km]), hydraulic residence time (ϴi [h]), and biodegradation (1- e-kϴi [%]) varying with the biodegradation constant k.
| max | min | median | st.dev. | 25% | 75% | |
|---|---|---|---|---|---|---|
| Linear distance i [km] | 26.7 | 0.5 | 10.9 | 4.7 | 8.7 | 13.3 |
| Di [km] | 34.4 | 0.8 | 14.5 | 6.6 | 11.8 | 18.8 |
| ϴi [h] | 11.9 | 0.3 | 5.0 | 2.3 | 4.1 | 6.5 |
| 1- e-kϴi [%], k = 0.097[h-1] | 68.6 | 2.8 | 38.6 | 13.0 | 32.8 | 46.9 |
| 1- e-kϴi [%], k = 0.101 [h-1] | 70.0 | 2.9 | 39.8 | 13.2 | 33.8 | 48.3 |
| 1- e-kϴi [%], k = 0.104 [h-1] | 71.1 | 3.0 | 40.7 | 13.4 | 34.6 | 49.3 |
Table 2.
Mean absolute error (MAE), mean absolute percentage error (MAPE) and Spearman correlation coefficient between predicted and reported IR(t) in different time intervals (first, second and third waves, off-waves period and entire study period).
Table 2.
Mean absolute error (MAE), mean absolute percentage error (MAPE) and Spearman correlation coefficient between predicted and reported IR(t) in different time intervals (first, second and third waves, off-waves period and entire study period).
| 1° wave (2021-12-19 - 2022-02-28) | 2° wave (2022-03-01 - 2022-06-02) | 3° wave (2022-06-03 - 2022-08-15) | off-waves (2021-10-13 - 2021-12-19 and 2022-08-15- 2023-05-24) | Entire study period (2021-10-13 - 2023-05-24) | |
|---|---|---|---|---|---|
| MAE | 47 | 120 | 109 | 26 | 54 |
| MAPE | 0.3 | 1.5 | 1.3 | 3.6 | 2.5 |
| Spearman | 0.858 | 0.954 | 0.897 | -0.223 | 0.599 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






