Preprint
Article
ECHO: Energy-Efficient Computation Harnessing Online Arithmetic – a MSDF-Based Accelerator for DNN Inference
Altmetrics
Downloads
110
Views
31
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 April 2024
Posted:
08 April 2024
You are already at the latest version
Alerts
Abstract
Deep Neural Network (DNN) inference demands substantial computing power, resulting in significant energy consumption. A large number of negative output activations in convolution layers are rendered zero due to the invocation of the ReLU activation function. This results in a substantial number of unnecessary computations that consume significant amounts of energy. This paper presents ECHO: Energy-efficient Computation Harnessing Onilne Arithmetic - A MSDF-based accelerator for DNN inference, designed for computation pruning, utilizing an unconventional arithmetic paradigm known as online/ most-significant digit first (MSDF) arithmetic which performs computations in a digit-serial manner. The MSDF digital serial computation of online arithmetic enables overlapped computation of successive operations leading to substantial performance improvements. The online arithmetic, coupled with a negative output detection scheme, facilitates early and precise recognition of negative outputs. This, in turn, allows for the timely termination of unnecessary computations, resulting in a reduction of energy consumption. The implemented design has been realized on the Xilinx Virtex-7 VU3P FPGA and subjected to a comprehensive evaluation through a rigorous comparative analysis involving widely used performance metrics. Experimental results demonstrate promising power and throughput improvements compared to contemporary methods. In particular, the proposed design achieved an average improvement in power consumption of up to 81%, 82.9%, and 40.6% for VGG-16, ResNet-18, and ResNet-50 workloads compared to the conventional bit-serial design, respectively. Furthermore, significant average speedups of 2.39×, 2.6×, and 2.42 were observed when comparing the proposed design to conventional bit-serial designs for VGG-16, ResNet-18, and ResNet-50 models respectively.
Keywords:
Subject: Computer Science and Mathematics - Hardware and Architecture
1. Introduction
Since their inception, deep neural networks (DNNs) have demonstrated remarkable performance and have been recognized as state-of-the-art methods, achieving near-human performance in various applications such as image processing [1], pattern recognition [2], bioinformatics [3], natural language processing [4], etc., among others. The efficacy of DNNs becomes particularly evident in scenarios involving vast amounts of data with subtle features that may not be easily discernible by humans. This positions DNNs as invaluable tools to address evolving data processing needs. It is widely observed that the number of layers significantly influences the performance of the network [5]. DNNs, consisting of more layers, often lead to enhanced feature extraction capabilities. However, it is essential to acknowledge that deeper networks typically demand a larger number of parameters, consequently requiring more extensive computational resources and memory capacity for effective training and inference.
DNN training and inference demands significant computing power, leading to the consumption of considerable energy resources. In a study presented in [6], it was estimated that dynamic power consumption, training a 176 billion parameter language model consumes metric tonnes of . This environmental impact underscores the urgency of optimizing DNN implementations, a concern that has gained widespread attention from the research community [7,8]. Addressing these challenges is crucial to strike a balance between the power and environmental costs associated with deploying DNNs for various applications.
In their fundamental structure, DNNs rely on basic mathematical operations such as addition and multiplication, culminating in the multiply-accumulate (MAC) operation. These MAC operations can constitute approximately of the total computations in convolutional neural networks (CNNs) [9]. The configuration and arrangement of MAC units depend on the size and structure of the DNN. For instance, the pioneering DNN in the ImageNet challenge, which surpassed human-level accuracy and is known as the ResNet model with 152 layers, necessitates GMAC operations and 60 million weights [10,11]. Typically, processing a single input sample in a DNN demands approximately one billion MAC operations [12]. This highlights the potential for substantial reductions in computational demands by enhancing the efficiency of MAC operations. In this context, researchers have suggested to prune the computations by replacing floating point numbers with fixed point, with minimal or no loss in accuracy [13,14]. Another plausible approach involves minimizing the bit precision used during MAC operations [15], an avenue extensively explored within the area of approximate computing [16]. Research indicates that implementing approximate computing techniques in DNNs can result in power savings, for training and inference, of up to [17]. However, many of these approximate computing methods often compromise accuracy, which may not be suitable for some critical applications. Consequently, devising methodologies that enhance DNN computation efficiency without compromising output accuracy becomes crucial.
A typical CNN comprises several convolution and fully-connected layers such as VGG-16 as shown in Figure 1. In such CNN models, the convolution layers typically serve the purpose of complex feature extraction and the fully-connected layers perform the classification task using the complex features extracted from the convolution layers. During inference, these layers execute MAC operations on the input utilizing trained weights to produce a distinct feature representation as the output [4]. These layers, cascaded in a certain configuration, can approximate a target function. While convolution and fully-connected layers are adept at representing linear functions, they cannot directly cater to the applications requiring nonlinear representations. To introduce non-linearity into the DNN model, the outputs of these layers undergo processing via a nonlinear operator known as an activation function [18]. Since every output value must pass through an activation function, selecting the appropriate one holds significant impact over the performance of DNNs [19].
Rectified Linear Unit (ReLU) is among the most employed activation functions in modern DNNs [20]. The simplicity and piece-wise linearity of ReLU contribute to faster learning capability and stability in values when utilizing gradient-descent methods [18]. The ReLU function, as shown in Figure 2, acts as a filter that outputs the same input for positive input values and outputs zero for negative inputs. This implies that precision in output is crucial only when the input is a positive value. The input to a ReLU function typically originates from the output of a fully-connected or convolution layer in the DNN, involving a substantial number of MAC operations [12]. It is indicated in [21] that a significant proportion, ranging from to of ReLU inputs in DNNs are negative. Consequently, a considerable amount of high-precision computation in DNNs is discarded, as output elements are reduced to zero after the ReLU function. The early detection of these negative values has the potential to curtail the energy expended on high-precision MAC operations, ultimately leading to a more efficient DNN implementation.
To this end, we propose ECHO: Energy-efficient Computing Harnessing Online Arithmetic - A MSDF-based accelerator for DNN inference, aimed at computation pruning at the arithmetic level. ECHO leverages an unconventional arithmetic paradigm, i.e., online, or most-significant digit first (MSDF) arithmetic which works in a digit-serial manner, taking inputs and producing output from most-significant to least-significant side. The MSDF nature of online arithmetic-based computation units combined with a negative output detection scheme can aid in the accurate detection of negative outputs at an early stage which results in promising computation and energy savings. The experimental results demonstrate that the ECHO showcases promising power and throughput improvements compared to contemporary methods.
The rest of the paper is organized as follows. Section 2 presents a comprehensive review of the relevant literature. Section 3 presents an overview of online arithmetic-based computation units and the details of the proposed design. The evaluation and results of the proposed methodology has been presented in Section 4, followed by the conclusion in Section 5.
2. Related Works
Over the past decade, researchers have extensively addressed challenges in DNN acceleration and proposed solutions such as DaDianNao [22], Stripes [23], Bit-Pragmatic [24], Cnvlutin [25], Tetris [26], etc. Bit-Pragmatic [24], is designed to leverage the bit information content of activation values. The architecture employs bit-serial computation of activation values using sparse encoding to skip computations for zero bits. By avoiding unnecessary computations for zero bits in activation values, Bit-Pragmatic achieves performance and energy improvements. On the other hand, Cnvlutin [25] aimed to eliminate unnecessary multiplications when the input is zero, leading to improved performance and energy efficiency. The architecture of Cnvlutin incorporates hierarchical data-parallel compute units and dispatchers that dynamically organize input neurons, skipping these unnecessary multiplications, to ensure the efficient utilization of computing units, thereby keeping them busy to achieve superior resource utilization.
Problems such as unnecessary computations and the varying precision requirements across different layers of CNNs have been thoroughly discussed in the literature [27,28]. These computations can contribute to increased energy consumption and resource demands in accelerator designs. To tackle these challenges, researchers have investigated designing domain-specific architectures specifically tailored to accelerate the computation of convolution operations in deep neural networks [29,30]. To reduce the number of MAC operations in DNNs, the work in [31] noted that neighboring elements within the output feature map often display similarity. By leveraging this insight, they achieved a reduction in MAC operations with loss in accuracy. In reference to [32], the introduction of processing units equipped with an approximate processing mode resulted in substantial improvements in energy efficiency, ranging from to . However, these gains in energy efficiency were achieved at a cost of drop in accuracy. This trade-off between energy efficiency and accuracy highlights the potential benefits of approximate processing modes in achieving energy savings but underscores the need to carefully balance these gains with the desired level of accuracy in DNN computations.
In recent years, there has been a growing trend towards implementing DNN acceleration and evaluation designs using bit-serial arithmetic circuits [23,33,34,35,36]. This shift is motivated by several factors: (1) reducing computational complexity and required communication bandwidth, (2) accommodating the variable data precision needs of different deep learning networks and within the layers of a network, (3) easily varying compute precision using bit-serial designs by adjusting the number of compute cycles in a DNN model evaluation, and (4) enhancing energy and resource utilization through early detection of negative results, thereby terminating ineffective computations yielding negative results.
One notable contribution in this direction is Stripes [23], recognized as a pioneering work that employs bit-serial multipliers instead of conventional parallel multipliers in its accelerator architecture to address challenges related to power and throughput. In a similar context, UNPU [33] builds upon the Stripes architecture by incorporating look-up tables (LUTs) to store inputs for reuse multiple times during the computation of an input feature map. These advancements mark significant progress in the research towards more efficient and effective CNN acceleration.
These accelerators are designed to enhance the performance of DNN computations through dedicated hardware implementations. However, it is important to note that none of these hardware accelerators have explicitly focused on the potential for computation pruning through early detection of negative outputs for ReLU activation functions. The aspect of efficiently handling and optimizing ReLU computations, especially in terms of early detection and pruning of negative values, remains an area where further exploration and development could potentially lead to improvements in efficiency and resource utilization.
Most modern CNNs commonly employ ReLU as an activation function, which filters out negative results from convolutions and replaces them with zeros. Studies [37,38,39] indicate that modern CNNs produce approximately - negative outputs, resulting in a significant power wastage on unnecessary computations. Traditional CNN acceleration designs typically perform the ReLU activation separately after completing the convolution operations. Existing solutions involve special digit encoding schemes like those in [38,39] or intricate circuit designs [37,40] to determine whether the result is negative. SnaPEA [37] aims to reduce the computation of a convolutional layer followed by a ReLU activation layer by identifying negative outputs early in the process. However, it is important to note that SnaPEA introduces some complexities. It requires reordering parameters and maintaining indices to match input activations with the reordered parameters correctly. Additionally, in predictive mode, SnaPEA necessitates several profiling and optimization passes to determine speculative parameters, adding an extra layer of complexity to the implementation. MSDF arithmetic operations have also emerged as a valuable approach for early detection of negative activations [40,41]. Shuvo et al. [40] introduced a novel circuit implementation for convolution where negative results can be detected early, allowing subsequent termination of corresponding operations. Similarly, USPE [42] and PredictiveNet [43] propose splitting values statistically into most significant bits and least significant bits for early negative detection. Other works in this avenue include [44,45,46]. However, existing methods for early detection of negative activations often rely on digit encoding schemes, prediction using a threshold, or complex circuitry, which may introduce errors or increase overhead.
3. Materials and Methods
A convolution layer in a neural network processes an input image by applying a set of M 3D kernels in a sliding window fashion. A standard CNN-based classifier model is generally composed of two main modules: the feature extraction module and the classification module. The feature extraction module typically comprises stacks of convolution, activation, and pooling layers. On the other hand, the classification module contains stacks of fully connected layers. Activation functions, which introduce non-linearity, are strategically placed either after the convolution layer or the pooling layer to enhance the model’s representation power and enable it to capture complex patterns and features in the data. In typical convolution layers of CNNs, the computation involves a series of MAC operations to compute the output feature maps. Each MAC operation entails multiplying corresponding elements of the kernel and input feature maps and summing up the results. The convolution operation carried out in a CNN layer can be described by a simple weighted sum or Sum of Products (SOP) equation, as follows:
In the given equation, represents the output of layer l, w is the kernel with dimensions , and x denotes the input of the convolution. Notably, it can be observed from the equation that for any pair , the kernel w remains constant while the input x changes in accordance with the sliding window operation. This characteristic of convolution presents the opportunity for weight stationarity in the dataflow architecture of convolution layers.
3.1. Online Arithmetic
In online arithmetic, computations of input operands and output flow in a digit-by-digit manner from the most significant to the least significant position, meaning that inputs are processed and outputs are generated digit-by-digit from left to right (LR) [47]. The algorithms are designed such that to produce the digit of the result, digits of the corresponding input operands are required, as illustrated in Figure 3. Here, is referred to as the online delay, which varies for different arithmetic operations and is typically a small integer (ranging from 1 to 4). To generate the most significant output first, online arithmetic leverages a redundant number system, making the cycle time independent of working precision. One notable advantage of online arithmetic is the ability to pipeline the execution of dependent operations. As soon as the most significant digit (MSD) of the predecessor unit is generated, the successive unit can initiate computation [48]. This stands in contrast to conventional digit-serial arithmetic, where all digits must be known to start computation. While it is possible to have overlapped/pipelined computation with conventional digit-serial arithmetic in either MSDF or least significant digit first (LSDF) manner, it becomes challenging when arithmetic operations, such as division (MSDF), are followed by multiplication (LSDF). Since online arithmetic always computes in the MSDF manner, overlapped computation of dependent operations is consistently feasible. This property enhances the efficiency and parallelization capabilities of online arithmetic.
The property of generating outputs based on partial input information in online computation negates the need to store intermediate results. Instead, these results can be immediately consumed in subsequent computations. Consequently, this leads to a reduction in the number of read/write operations from/to memory, resulting in lower memory traffic and subsequent energy savings [49].
To facilitate generating outputs based on partial input information, online computation relies on flexibility in computing digits. This is achieved by employing a redundant digit number system. In this study, a signed digit (SD) redundant number system is utilized, where numbers are represented in a radix-(r) format that offers more than r values for representing a given value. Specifically, a symmetric radix-2 redundant digit set of is used. To ensure compatibility, the online modules work with fractional numbers, simplifying operand alignment. In this system, the first digit of the operand carries a weight of , and at a given iteration j, the digit is represented by two bits, namely and . The numerical value of the digit is computed by subtracting () the and bits as shown in relation (2).
The input and outputs are given as (3) and (4) respectively.
where j represents the iteration index and the subscript i denote the digit index. In a given online algorithm, the execution spans cycles. The algorithm processes a single digit input for n iterations. After cycles of providing the first input digit, it generates a single output digit in each subsequent iteration. This approach emphasizes digit-level processing and output generation, contributing to the overall efficiency of online computation.
3.1.1. Online Multiplier (OLM)
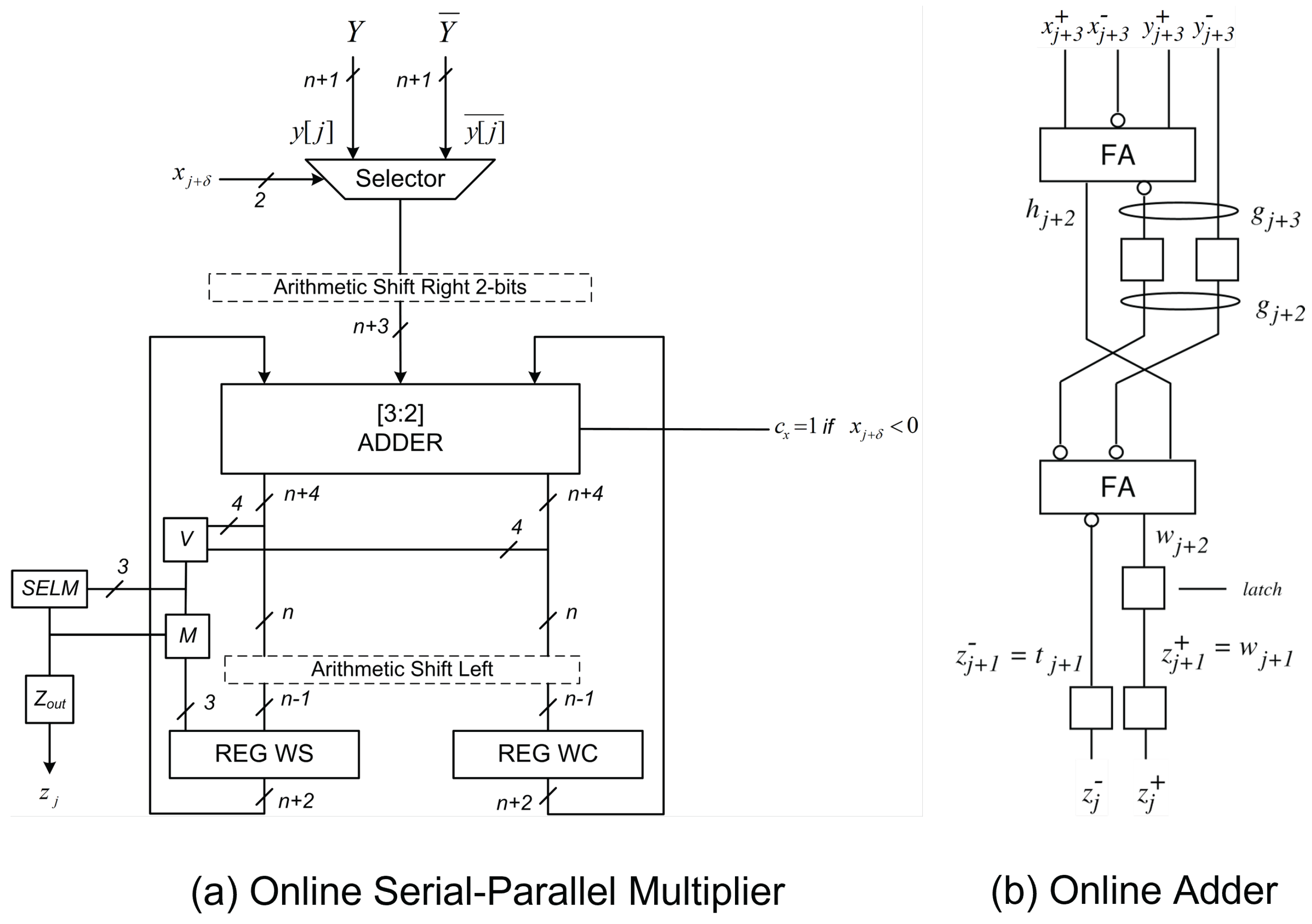
In most CNN designs, the convolution during inference involves multiplying a constant weight kernel with the input image in a sliding window fashion. This characteristic implies that the kernel matrix must be used multiple times for the convolution operation. In this context, an online multiplier with one operand in parallel and the other in a serial manner can be advantageous, allowing the weight kernel to be employed in parallel while the input is fed in a serial manner. In this study, a non-pipelined serial-parallel multiplier, as presented in [50] and depicted in Figure 4(a), is used. The multiplier generates its output in a MSDF fashion after an online delay of cycles. The serial input and output in each cycle are represented as (3) and (4), respectively, while the constant weight is represented as:
The pseudocode of the non-pipelined radix-2 serial-parallel online multiplier is shown in Algorithm 1. Additional details related to the recurrence stage and selection function of the serial-parallel online multiplier are presented in [50].
| Algorithm 1 Serial-Parallel Online Multiplication |
|
3.1.2. Online Adder (OLA)
As the multipliers utilized in this study produce outputs in an MSDF fashion, an adder with a similar capability is essential for computing the SOP. In this context, a digit-serial online adder, which takes both inputs and generates its output in an MSDF fashion, is employed. This choice facilitates digit-level pipelining in the proposed SOP design and contributes to the early detection and subsequent termination of negative activations. The online adder, with an online delay of , follows a straightforward construction, as illustrated in Figure 4(b). Further details and relevant derivations can be found in [51].
3.2. Proposed Design
This section provides a detailed overview of the architecture of ECHO, which is built upon online computation units featuring early detection and termination capabilities for negative outputs. The arrangement of computation units within the processing engine (PE) of the proposed design, along with the techniques for identifying and terminating ineffective convolutions (resulting in negative outputs), is thoroughly discussed.
3.2.1. Processing Engine Architecture
Each processing engine (PE), as illustrated in Figure 5, is equipped with online serial-parallel multipliers, succeeded by a reduction tree comprising online adders. This configuration is designed to compute a convolution, as outlined in Eq. 1, on an input channel or feature map. The input pixel is serially fed in a digit-by-digit manner, while the kernel pixel is concurrently fed in parallel, as indicated by the different arrows in Figure 5.
Each multiplier in the PE is responsible for the multiplication of one pixel in the convolution window with the corresponding pixel in the same feature map of the convolution kernel. Therefore, all the pixels are processed in parallel. The number of cycles required for a PE to generate its output can be calculated as follows
where and are the online delays of online multiplier and adder respectively, is the number of reduction tree stages required to generate the SOP of the multipliers, and is the precision of the SOP result generated by a PE. is calculated as follows.
3.2.2. Early Detection and Termination of Negative Computations
Convolution operation in CNN models can be referred as multiple channel multiple kernel (MCMK) convolution, where the term channel corresponds to the input feature maps and kernel corresponds to the convolution kernel. However, a multiple channel single kernel (MCSK) convolution is carried out repeatedly using several kernels to generate the output of a convolution layer. A basic MCSK convolution in a CNN can be described by the following equation.
Where, represents the output at position in the output feature map, denote the input, and denotes the weight. The innermost double summation term performs the convolution for the input feature map, N denotes the number of input feature maps, and b denotes the bias.
In most designs of CNN accelerators, the focus is often on achieving faster and more efficient generation of the SOP. However, only a limited number of works explore the potential for early assessment of negative values in the activation layer, particularly for ReLU. Early detection, and the subsequent termination of computation, of negative activations poses a significant challenge in accelerators based on conventional arithmetic. For example, in conventional bit-serial multipliers, the multiplicand is processed in parallel, while the multiplier is processed serially. In each iteration, a partial product is generated and stored in a register. This partial product is then shifted into appropriate positions before being added to other partial products to obtain the final product. Typically, an accumulator or a series of adders, such as carry-save adders or ripple-carry adders, are employed to perform this reduction. In the case of convolution, an additional level of reduction, aimed at generating the sum of multiplications (see the innermost double summation in (8)), is required to obtain the output pixel. Moreover, if there are more than one input feature maps, another level of reduction, responsible for adding the SOPs across N input feature maps, is needed to compute the SOP as depicted by the outermost summation in (8). In conventional bit-serial multipliers, determining the most significant bit and identifying the polarity of the result requires waiting until all partial products have been generated and added to the previous partial sums. Among the limited works addressing the early detection of negative activations, some utilize either a digit encoding scheme or an estimation technique for early negative detection [39], while others focus on complex circuit designs such as carry propagation shift register (CPSR) in [40].
The challenge of early detection and termination of negative activations can be effectively addressed by leveraging the inherent capability of online arithmetic to generate output digits in a MSDF manner. ECHO facilitates the detection and the subsequent termination of negative activation computation within p cycles, where and represents the number of cycles needed to compute the complete result. This is achieved by monitoring and comparing the output digits. The process of detecting negative activations and subsequently terminating the relevant computation is outlined in Algorithm 2.
| Algorithm 2 Early detection and termination of negative activations in ECHO |
|
1.35
|
The ReLU unit is equipped with registers to store the output and bits, representing the positive and negative output digits of the SOP in redundant number representation. During each iteration, the new digits are concatenated, as indicated in Algorithm 2, with their corresponding previous digits. As soon as the value of drops below the value of , indicating a negative output, a termination signal is generated by the control unit, and the computation of the respective SOP is terminated. This simple procedure, aided by the inherent MSDF nature of online arithmetic, of early detection and termination of negative outputs can save a significant number of computation cycles required for a convolution operation resulting in a negative number, leading to substantial energy savings.
3.2.3. Accelerator Design
The overall architecture of ECHO is depicted in Figure 6. It consists of multiple PEs arranged in a 2D array, where each column in the array contains N PEs. The convolution kernels and input activations stored in the DRAM, are pre-loaded into the weight buffers (WB) and activation buffers (AB) using the activation and weight interconnect. The activations and weights are then forwarded via the same interconnect to the PE array for computation. The results of the computations are written back to the DRAM using the memory manager in the central controller. The output of each column is fed serially to a corresponding decision unit in the central controller where the polarity of the output activation is determined dynamically. If the output digit is determined to be negative, a termination signal is generated which is propagated to the corresponding column resulting in the subsequent termination of the computation in that column. The various signals and data lines are color-coded in Figure 6, and the description of the color coding can be found in Figure 7. By design, the proposed accelerator architecture supports input tiling by the invocation of N PEs in each column. However, the number of columns in the accelerator array can be determined on the basis of the architecture of the CNN and the target hardware. The number of cycles required to generate the result of a convolution can be calculated as
Where is the number of reduction tree stages required to add the SOP results of N input feature maps to generate the final output of the convolution. is the precision of the final SOP result of the convolution.
The central controller, as shown in Figure 7, consists of memory manager block and several decision units dedicated for each column in the accelerator array. At the end of each convolution SOP computation, the central controller generates signals (see DRAM read signal in Figure 7) for new input activations and/or weights to be loaded into the activation and weight buffers respectively. The decision unit blocks in the central controller receive the respective column output digits serially (indicated by black arrows in Figure 7), and generate a column termination signal (indicated by red arrow in Figure 7) when the column output is detected to be negative.
The design of the decision unit is presented in Figure 7. The decision unit consists of a comparator where a comparison between the and redundant digits is carried out. Moreover, it also contains registers to store the redundant output digits of the respective column. In case of a convolution resulting in a positive output, these registers are populated for and then forwarded to the memory manager block to be written back to the DRAM. The counter block keeps the count of the so that the final positive result is forwarded to the DRAM. This is done by the invocation of the multiplexers for each register i.e., when the are elapsed, the counter triggers the selection signal of the multiplexer to route the value stored in the registers to the memory manager. However, in the event of a convolution resulting in a negative value, the comparator generates a column termination signal, as indicated by red arrow in Figure 7, which subsequently terminates the computation of the respective column. Moreover, the column termination signal is also used as the reset signal for the registers and counter in the decision unit, thereby selecting the multiplexer input connected to 0 subsequently forwarding a 0 value to the memory manager.
The following Section 4 contains details on the experiments conducted to ascertain the performance of the proposed design on modern CNNs and also performs a comparison of the proposed design with contemporary designs.
4. Experimental Results
To evaluate and compare the performance of the proposed design, we conduct experimental evaluation using two baseline designs, 1) Baseline-1: conventional bit-serial accelerator design based on UNPU accelerator [33], 2) Baseline-2: online arithmetic-based design without the capability to early-detect and terminate the ineffective negative computations. For a fair comparison, both the baseline designs use the same accelerator array layout as ECHO. We evaluate ECHO on VGG-16 [52] and ResNet [11] workloads. The layer-wise architecture of the CNN models is presented in Table 1. As mentioned in the table, each of the CNNs contain several convolution layer blocks, where the convolution layers within the blocks have the same number of convolution kernels (M) and the output feature map dimensions (). It is also worth noting that while VGG-16 contains a maxpooling layer after every convolution block, the ResNet-18 CNN performs down-sampling by a strided () convolution in the first convolution layer in each block of layers except for the maxpooling layer after C1.
We used pre-trained VGG-16, ResNet-18, and ResNet-50 models obtained from torchvision [53] for our experiments. For the evaluation, we used 1000 images from the validation set of ImageNet database [10]. The RTL of the proposed and baseline accelerators are designed and functionally verified using Xilinx Vivado 2018.2. The implementation and evaluation is carried out on Xilinix Vertix-7 VU3P FPGA.
Table 2 and Table 3 present the layer-wise comparative results for inference time, power consumption, and speedup for VGG-16 and ResNet-18 networks respectively. It is worth noting that, for VGG-16 workload, the online arithmetic-based design without the early negative detection capability (Baseline-2), outperforms the conventional bit-serial design (Baseline-1). The baseline-2 design, on average, achieves improvement in inference time compared to the baseline-1 design. It also consumes less power and improved speedup in computation compared to the baseline-1 design which underscores the superior capability of the online arithmetic-based DNN accelerator designs. Similarly, ECHO achieves and improved inference time, consumes and less power, and also achieves and improved speedup compared to the baseline-1 and baseline-2 designs, respectively, for VGG-16 network.
Similarly, for ResNet-18 model, as indicated in Table 3, ECHO achieves and improved inference time, consumes and less power, achieves and higher throughput, and also achieves and improved speedup compared to the baseline-1 and baseline-2 designs.
Figure 8 presents the runtimes of ECHO compared to the baseline methods. From the figures, it can be noted that the accelerator design based on online arithmetic (Baseline-2) outperforms the conventional bit-serial design (Baseline-1) even without the capability of early detection of the negative outputs, which emphasizes the superiority of the online arithmetic-based designs over the conventional bit-serial designs. As shown in Figure 8a, ECHO showcases mean improvements of and in runtime compared to baseline-1 and baseline-2 designs respectively, for the VGG-16 workloads. Similarly, as shown in Figure 8b, ECHO achieves and improvements in runtime on ResNet-18 workloads compared to baseline-1 and baseline-2 designs respectively. These average runtime improvements lead to average speedups of and for VGG-16 and ResNet-18 CNN models, respectively, compared to conventional bit-serial design. Similarly, compared to online arithmetic-based design without the capability of early detection negative outputs (baseline-2), ECHO achieves an average speedup of and for VGG-16 and ResNet-18 workloads, respectively. The faster runtimes of ECHO do not only result due to the efficient design of the online arithmetic-based processing elements, but also due to the large number of negative output activations which in-turn helps in terminating the ineffective computations resulting in substantial power and energy savings.
The power consumption is related to the execution time as well as the utilization of resources in the accelerator. The proposed early detection and termination of negative output activations can result in substantial improvements in power consumption. Figure 9 shows the layer-wise power consumption of ECHO compared to the baseline designs. For VGG-16 model, as shown in Figure 9a, ECHO achieves and improvements in power consumption compared to baseline-1 and baseline-2 designs respectively. Similarly, as depicted in Figure 9b, ECHO shows significant improvements of and in power consumption for ResNet-18 workloads compared to baseline-1 and baseline-2 designs respectively.
A comparison of the FPGA implementation of ECHO with the conventional bit-serial design (Baseline-1) and online arithmetic design without the early negative detection capability (Baseline-2) is presented in Table 4. All the designs in these experiments were evaluated on a 100MHz frequency. It can be observed from the comparative results that the logic resource and BRAM utilization for ECHO is marginally higher than those for the Baseline-1 design. However, ECHO achieves , , and higher throughput compared to the Baseline-1 design for VGG-16, ResNet-18, and ResNet-50 CNN workloads respectively. Similarly, ECHO achieves , , and improvement in latency/image for VGG-16, ResNet-18, and ResNet-50 workloads, respectively, compared to baseline-1 design. We also implemented ECHO without the early detection and termination capability (Baseline-2) on FPGA and achieved a throughput improvement of , , and for VGG-16, ResNet-18, and ResNet-50 workloads respectively. Moreover, ECHO also achieved a , , and improvement in latency for VGG-16, ResNet-18, and ResNet-50 models compared to Baseline-2 design. ECHO exhibits improved power consumption due to the use of the proposed method of early detection of the negative results. In particular, for VGG-16 model, ECHO achieved improvements of and compared to baseline-1 and baseline-2 designs respectively. The proposed design shows similar improvements of and , compared to baseline-1 and baseline-2 designs respectively, for ResNet-18 workload. ECHO achieved and less power consumption for ResNet-50 model, compared to baseline-1 and baseline-2 designs respectively.
Similar to the comparison with the baseline designs, a comparison of the proposed design with previous methods is also conducted for VGG-16, ResNet-18, and ResNet-50 workloads. The comparative results are presented in Table 5. For VGG-16 workload, the proposed design achieves , , , and superior performance in-terms of peak throughput compared to NEURAghe [54,55,56], and Caffeine [57], respectively. In-terms of energy efficiency, ECHO achieved and improvement in energy efficiency compared to NEURAghe [54] and OPU [56], respectively. Similarly, the proposed design outperformed NEURAghe [54] and [58] by and in-terms of peak throughput performance for ResNet-18 workload. ECHO also achieved superior energy efficiency of compared to for [54] and for [58]. For ResNet-50 network, the proposed design achieved and superior results in-terms of peak throughput and energy efficiency, respectively. However, besides the promising performance in context to the comparative results stated earlier, the proposed design utilizes slightly large number of logic resources compared to its contemporary counterparts. Another area for future research and exploration in this avenue lies in the lightweight design of the online arithmetic-based compute units, where a compact design may help in reducing the area/logic resource overhead experienced in the present design.
5. Conclusion
This research introduces ECHO - A DNN hardware accelerator focused on computation pruning through the use of online arithmetic. ECHO effectively addresses the challenge of early detection of negative activations in ReLU-based DNNs, showcasing substantial improvements in power efficiency and throughput for VGG-16, ResNet-18, ResNet-50 workloads. Compared to existing methods, the proposed design demonstrates superior performance with mean throughput improvements of , , and for VGG-16, ResNet-18, and ResNet-50 respectively. With regards to energy efficiency, ECHO achieved superior energy efficiencies () of , , and for VGG-16, ResNet-18, and ResNet-50 workloads. Moreover, ECHO achieved average improvements in power consumption of up to , , and for VGG-16, ResNet-18, and ResNet-50 workloads compared to the conventional bit-serial design, respectively. Furthermore, significant average speedups of , , and were observed when comparing the proposed design to conventional bit-serial designs for VGG-16, ResNet-18, and ResNet-50 models respectively. Additionally, ECHO outperforms online arithmetic-based designs without early detection, achieving average speedups of and for VGG-16 and ResNet-18 workloads. These findings underscore the potential of the proposed hardware accelerator in enhancing the efficiency of computing convolution in deep neural networks during inference.
Author Contributions
Conceptualization, Muhammad Sohail Ibrahim and Muhammad Usman; methodology, Muhammad Sohail Ibrahim; software, Muhammad Sohail Ibrahim and Muhammad Usman; validation, Jeong-A Lee and Muhammad Usman; formal analysis, Muhammad Sohail Ibrahim; investigation, Muhammad Sohail Ibrahim and Muhammad Usman; writing—original draft preparation, Muhammad Sohail Ibrahim; writing—review and editing, Muhammad Sohail Ibrahim, Muhammad Usman, and Jeong-A Lee; visualization, Muhammad Sohail Ibrahim; supervision, Jeong-A Lee.
Acknowledgments
This research was supported by Basic Science Research Program funded by the Ministry of Education through the National Research Foundation of Korea (NRF-2020R1I1A3063857). The EDA tool was supported by the IC Design Education Center (IDEC), Korea.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, G.; Xu, Z.; Li, J.; Yang, J.; Zeng, T.; Qi, G.J. CTCNet: A CNN-transformer cooperation network for face image super-resolution. IEEE Transactions on Image Processing 2023, 32, 1978–1991. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Wang, X.; Liu, X.; Liu, Q.; Song, J.; Sebe, N.; Kim, B. Explainable deep learning for efficient and robust pattern recognition: A survey of recent developments. Pattern Recognition 2021, 120, 108102. [Google Scholar] [CrossRef]
- Usman, M.; Khan, S.; Park, S.; Lee, J.A. AoP-LSE: Antioxidant Proteins Classification Using Deep Latent Space Encoding of Sequence Features. Current Issues in Molecular Biology 2021, 43, 1489–1501. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Kwon, H.; Chatarasi, P.; Pellauer, M.; Parashar, A.; Sarkar, V.; Krishna, T. Understanding reuse, performance, and hardware cost of dnn dataflow: A data-centric approach. Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, 2019, pp. 754–768.
- Gupta, U.; Jiang, D.; Balandat, M.; Wu, C.J. TOWARDS GREEN, ACCURATE, AND EFFICIENT AI MODELS THROUGH MULTI-OBJECTIVE OPTIMIZATION. Workshop paper at Tackling Climate Change with Machine Learning, ICLR 2023.
- Narayanan, D.; Harlap, A.; Phanishayee, A.; Seshadri, V.; Devanur, N.R.; Ganger, G.R.; Gibbons, P.B.; Zaharia, M. PipeDream: Generalized pipeline parallelism for DNN training. Proceedings of the 27th ACM Symposium on Operating Systems Principles, 2019, pp. 1–15.
- Deng, C.; Liao, S.; Xie, Y.; Parhi, K.K.; Qian, X.; Yuan, B. PermDNN: Efficient compressed DNN architecture with permuted diagonal matrices. 2018 51st Annual IEEE/ACM international symposium on microarchitecture (MICRO). IEEE, 2018, pp. 189–202.
- Jain, S.; Venkataramani, S.; Srinivasan, V.; Choi, J.; Chuang, P.; Chang, L. Compensated-DNN: Energy efficient low-precision deep neural networks by compensating quantization errors. Proceedings of the 55th Annual Design Automation Conference, 2018, pp. 1–6.
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- Hanif, M.A.; Javed, M.U.; Hafiz, R.; Rehman, S.; Shafique, M. Hardware–Software Approximations for Deep Neural Networks. Approximate Circuits: Methodologies and CAD 2019, pp. 269–288.
- Zhang, S.; Mao, W.; Wang, Z. An efficient accelerator based on lightweight deformable 3D-CNN for video super-resolution. IEEE Transactions on Circuits and Systems I: Regular Papers 2023.
- Lo, C.Y.; Sham, C.W. Energy efficient fixed-point inference system of convolutional neural network. 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS). IEEE, 2020, pp. 403–406.
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. European conference on computer vision. Springer, 2016, pp. 525–542.
- Agrawal, A.; Choi, J.; Gopalakrishnan, K.; Gupta, S.; Nair, R.; Oh, J.; Prener, D.A.; Shukla, S.; Srinivasan, V.; Sura, Z. Approximate computing: Challenges and opportunities. 2016 IEEE International Conference on Rebooting Computing (ICRC). IEEE, 2016, pp. 1–8.
- Liu, B.; Wang, Z.; Guo, S.; Yu, H.; Gong, Y.; Yang, J.; Shi, L. An energy-efficient voice activity detector using deep neural networks and approximate computing. Microelectronics Journal 2019, 87, 12–21. [Google Scholar] [CrossRef]
- Szandała, T. Review and comparison of commonly used activation functions for deep neural networks. Bio-inspired neurocomputing 2021, pp. 203–224.
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022. [Google Scholar] [CrossRef]
- Cao, J.; Pang, Y.; Li, X.; Liang, J. Randomly translational activation inspired by the input distributions of ReLU. Neurocomputing 2018, 275, 859–868. [Google Scholar] [CrossRef]
- Shi, S.; Chu, X. Speeding up convolutional neural networks by exploiting the sparsity of rectifier units. arXiv preprint 2017, arXiv:1704.07724. [Google Scholar]
- Luo, T.; Liu, S.; Li, L.; Wang, Y.; Zhang, S.; Chen, T.; Xu, Z.; Temam, O.; Chen, Y. DaDianNao: A neural network supercomputer. IEEE Transactions on Computers 2016, 66, 73–88. [Google Scholar] [CrossRef]
- Judd, P.; Albericio, J.; Hetherington, T.; Aamodt, T.M.; Moshovos, A. Stripes: Bit-serial deep neural network computing. 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). IEEE, 2016, pp. 1–12.
- Albericio, J.; Delmás, A.; Judd, P.; Sharify, S.; O’Leary, G.; Genov, R.; Moshovos, A. Bit-Pragmatic Deep Neural Network Computing. 2017 50th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), 2017, pp. 382–394.
- Albericio, J.; Judd, P.; Hetherington, T.; Aamodt, T.; Jerger, N.E.; Moshovos, A. Cnvlutin: Ineffectual-neuron-free deep neural network computing. ACM SIGARCH Computer Architecture News 2016, 44, 1–13. [Google Scholar] [CrossRef]
- Gao, M.; Pu, J.; Yang, X.; Horowitz, M.; Kozyrakis, C. Tetris: Scalable and efficient neural network acceleration with 3d memory. Proceedings of the Twenty-Second International Conference on Architectural Support for Programming Languages and Operating Systems, 2017, pp. 751–764.
- Judd, P.; Albericio, J.; Hetherington, T.; Aamodt, T.; Jerger, N.E.; Urtasun, R.; Moshovos, A. Proteus: Exploiting precision variability in deep neural networks. Parallel Computing 2018, 73, 40–51. [Google Scholar] [CrossRef]
- Shin, S.; Boo, Y.; Sung, W. Fixed-point optimization of deep neural networks with adaptive step size retraining. 2017 IEEE International conference on acoustics, speech and signal processing (ICASSP). IEEE, 2017, pp. 1203–1207.
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D. A domain-specific architecture for deep neural networks. Communications of the ACM 2018, 61, 50–59. [Google Scholar] [CrossRef]
- Juracy, L.R.; Garibotti, R.; Moraes, F.G.; others. From CNN to DNN Hardware Accelerators: A Survey on Design, Exploration, Simulation, and Frameworks. Foundations and Trends® in Electronic Design Automation 2023, 13, 270–344. [Google Scholar] [CrossRef]
- Shomron, G.; Weiser, U. Spatial correlation and value prediction in convolutional neural networks. IEEE Computer Architecture Letters 2018, 18, 10–13. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T.; Tian, Y.; Yuan, F.; Xu, Q. ApproxANN: An approximate computing framework for artificial neural network. 2015 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE, 2015, pp. 701–706.
- Lee, J.; Kim, C.; Kang, S.; Shin, D.; Kim, S.; Yoo, H.J. UNPU: An energy-efficient deep neural network accelerator with fully variable weight bit precision. IEEE Journal of Solid-State Circuits 2018, 54, 173–185. [Google Scholar] [CrossRef]
- Hsu, L.C.; Chiu, C.T.; Lin, K.T.; Chou, H.H.; Pu, Y.Y. ESSA: An energy-Aware bit-Serial streaming deep convolutional neural network accelerator. Journal of Systems Architecture 2020, 111, 101831. [Google Scholar] [CrossRef]
- Isobe, S.; Tomioka, Y. Low-bit Quantized CNN Acceleration based on Bit-serial Dot Product Unit with Zero-bit Skip. 2020 Eighth International Symposium on Computing and Networking (CANDAR). IEEE, 2020, pp. 141–145.
- Li, A.; Mo, H.; Zhu, W.; Li, Q.; Yin, S.; Wei, S.; Liu, L. BitCluster: Fine-Grained Weight Quantization for Load-Balanced Bit-Serial Neural Network Accelerators. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2022, 41, 4747–4757. [Google Scholar] [CrossRef]
- Akhlaghi, V.; Yazdanbakhsh, A.; Samadi, K.; Gupta, R.K.; Esmaeilzadeh, H. Snapea: Predictive early activation for reducing computation in deep convolutional neural networks. 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA). IEEE, 2018, pp. 662–673.
- Lee, D.; Kang, S.; Choi, K. ComPEND: Computation Pruning through Early Negative Detection for ReLU in a deep neural network accelerator. Proceedings of the 2018 International Conference on Supercomputing, 2018, pp. 139–148.
- Kim, N.; Park, H.; Lee, D.; Kang, S.; Lee, J.; Choi, K. ComPreEND: Computation Pruning through Predictive Early Negative Detection for ReLU in a Deep Neural Network Accelerator. IEEE Transactions on Computers 2021. [Google Scholar] [CrossRef]
- Shuvo, M.K.; Thompson, D.E.; Wang, H. MSB-First Distributed Arithmetic Circuit for Convolution Neural Network Computation. 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS). IEEE, 2020, pp. 399–402.
- Karadeniz, M.B.; Altun, M. TALIPOT: Energy-Efficient DNN Booster Employing Hybrid Bit Parallel-Serial Processing in MSB-First Fashion. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2021, 41, 2714–2727. [Google Scholar] [CrossRef]
- Song, M.; Zhao, J.; Hu, Y.; Zhang, J.; Li, T. Prediction based execution on deep neural networks. 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA). IEEE, 2018, pp. 752–763.
- Lin, Y.; Sakr, C.; Kim, Y.; Shanbhag, N. PredictiveNet: An energy-efficient convolutional neural network via zero prediction. 2017 IEEE international symposium on circuits and systems (ISCAS). IEEE, 2017, pp. 1–4.
- Asadikouhanjani, M.; Ko, S.B. A novel architecture for early detection of negative output features in deep neural network accelerators. IEEE Transactions on Circuits and Systems II: Express Briefs 2020, 67, 3332–3336. [Google Scholar] [CrossRef]
- Suresh, B.; Pillai, K.; Kalsi, G.S.; Abuhatzera, A.; Subramoney, S. Early Prediction of DNN Activation Using Hierarchical Computations. Mathematics 2021, 9, 3130. [Google Scholar] [CrossRef]
- Pan, Y.; Yu, J.; Lukefahr, A.; Das, R.; Mahlke, S. BitSET: Bit-Serial Early Termination for Computation Reduction in Convolutional Neural Networks. ACM Transactions on Embedded Computing Systems 2023, 22, 1–24. [Google Scholar] [CrossRef]
- Ercegovac, M.D. On-Line Arithmetic: An Overview. Real-Time Signal Processing VII; Bromley, K., Ed. International Society for Optics and Photonics, SPIE, 1984, Vol. 0495, pp. 86 – 93.
- Usman, M.; Lee, J.A.; Ercegovac, M.D. Multiplier with reduced activities and minimized interconnect for inner product arrays. 2021 55th Asilomar Conference on Signals, Systems, and Computers. IEEE, 2021, pp. 1–5.
- Ibrahim, M.S.; Usman, M.; Nisar, M.Z.; Lee, J.A. DSLOT-NN: Digit-Serial Left-to-Right Neural Network Accelerator. 2023 26th Euromicro Conference on Digital System Design (DSD). IEEE, 2023, pp. 686–692.
- Usman, M. ; D. Ercegovac, M.; Lee, J.A. Low-Latency Online Multiplier with Reduced Activities and Minimized Interconnect for Inner Product Arrays. Journal of Signal Processing Systems, 2003; 1–20. [Google Scholar]
- Ercegovac, M.D.; Lang, T. Digital arithmetic; Elsevier, 2004.
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv preprint 2014, arXiv:1409.1556. [Google Scholar]
- Marcel, S.; Rodriguez, Y. Torchvision the machine-vision package of torch. Proceedings of the 18th ACM international conference on Multimedia, 2010, pp. 1485–1488.
- Meloni, P.; Capotondi, A.; Deriu, G.; Brian, M.; Conti, F.; Rossi, D.; Raffo, L.; Benini, L. NEURAghe: Exploiting CPU-FPGA synergies for efficient and flexible CNN inference acceleration on Zynq SoCs. ACM Transactions on Reconfigurable Technology and Systems (TRETS) 2018, 11, 1–24. [Google Scholar] [CrossRef]
- Li, G.; Liu, Z.; Li, F.; Cheng, J. Block convolution: toward memory-efficient inference of large-scale CNNs on FPGA. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2021, 41, 1436–1447. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, C.; Zhao, T.; Wang, K.; He, L. OPU: An FPGA-based overlay processor for convolutional neural networks. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2019, 28, 35–47. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, G.; Fang, Z.; Zhou, P.; Pan, P.; Cong, J. Caffeine: Toward Uniformed Representation and Acceleration for Deep Convolutional Neural Networks. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2019, 38, 2072–2085. [Google Scholar] [CrossRef]
- Xie, X.; Lin, J.; Wang, Z.; Wei, J. An efficient and flexible accelerator design for sparse convolutional neural networks. IEEE Transactions on Circuits and Systems I: Regular Papers 2021, 68, 2936–2949. [Google Scholar] [CrossRef]
Figure 1.
A typical convolution neural network - VGG-16
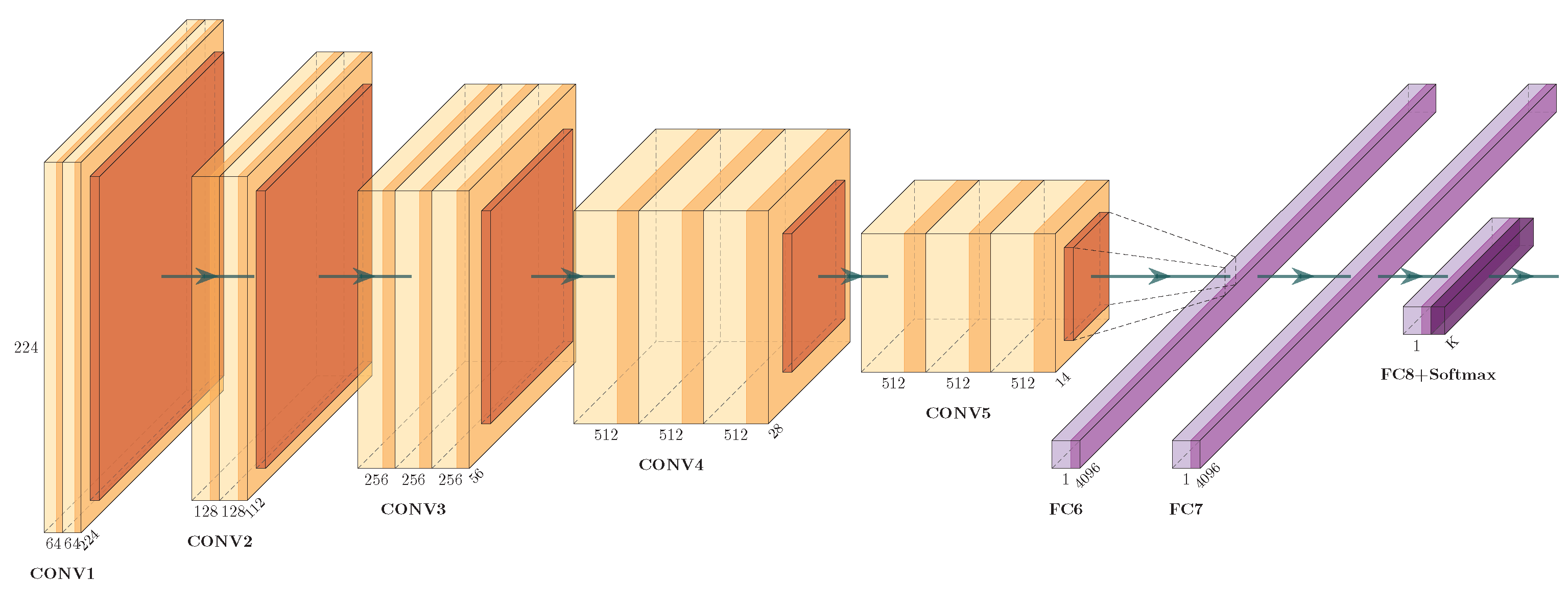
Figure 2.
The Rectified Linear Unit (ReLU) activation function
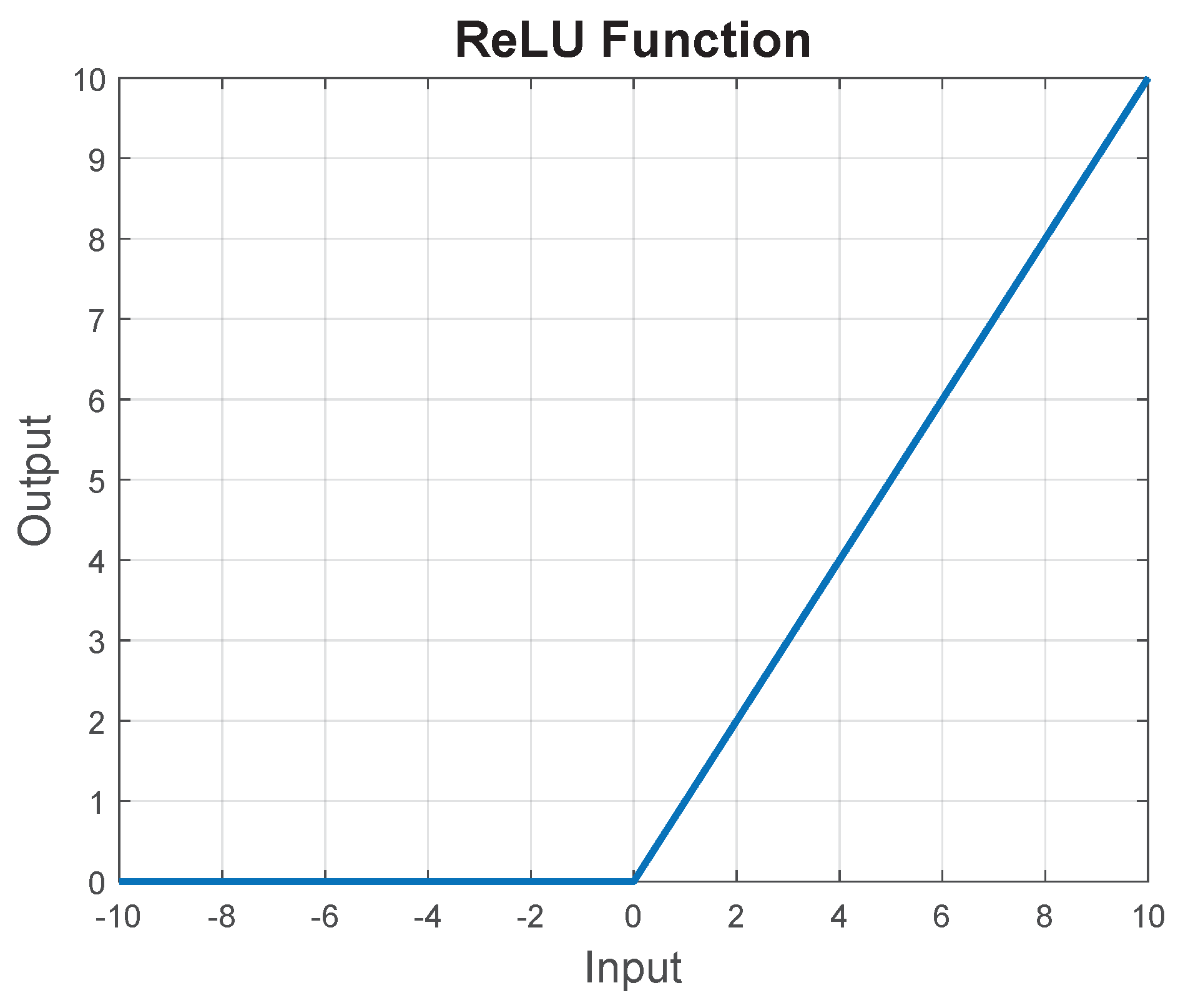
Figure 3.
Timing characteristics of online operation with .
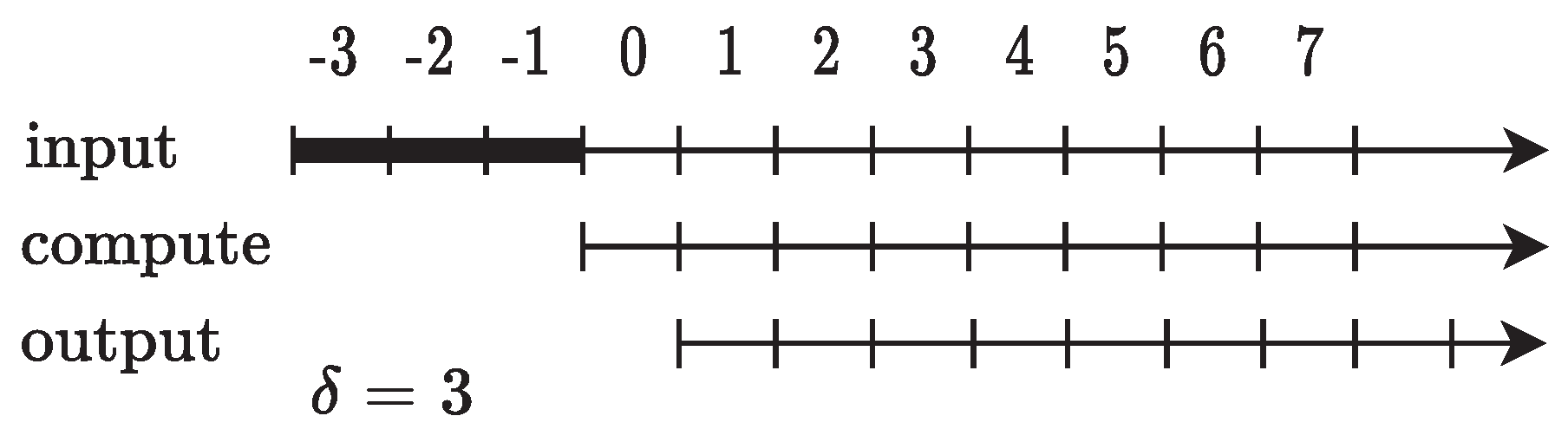
Figure 5.
Processing engine architecture of ECHO. Each PE contains multipliers where each multiplier accepts a bit-serial (input feature) and a parallel (kernel pixel) input.
Figure 5.
Processing engine architecture of ECHO. Each PE contains multipliers where each multiplier accepts a bit-serial (input feature) and a parallel (kernel pixel) input.
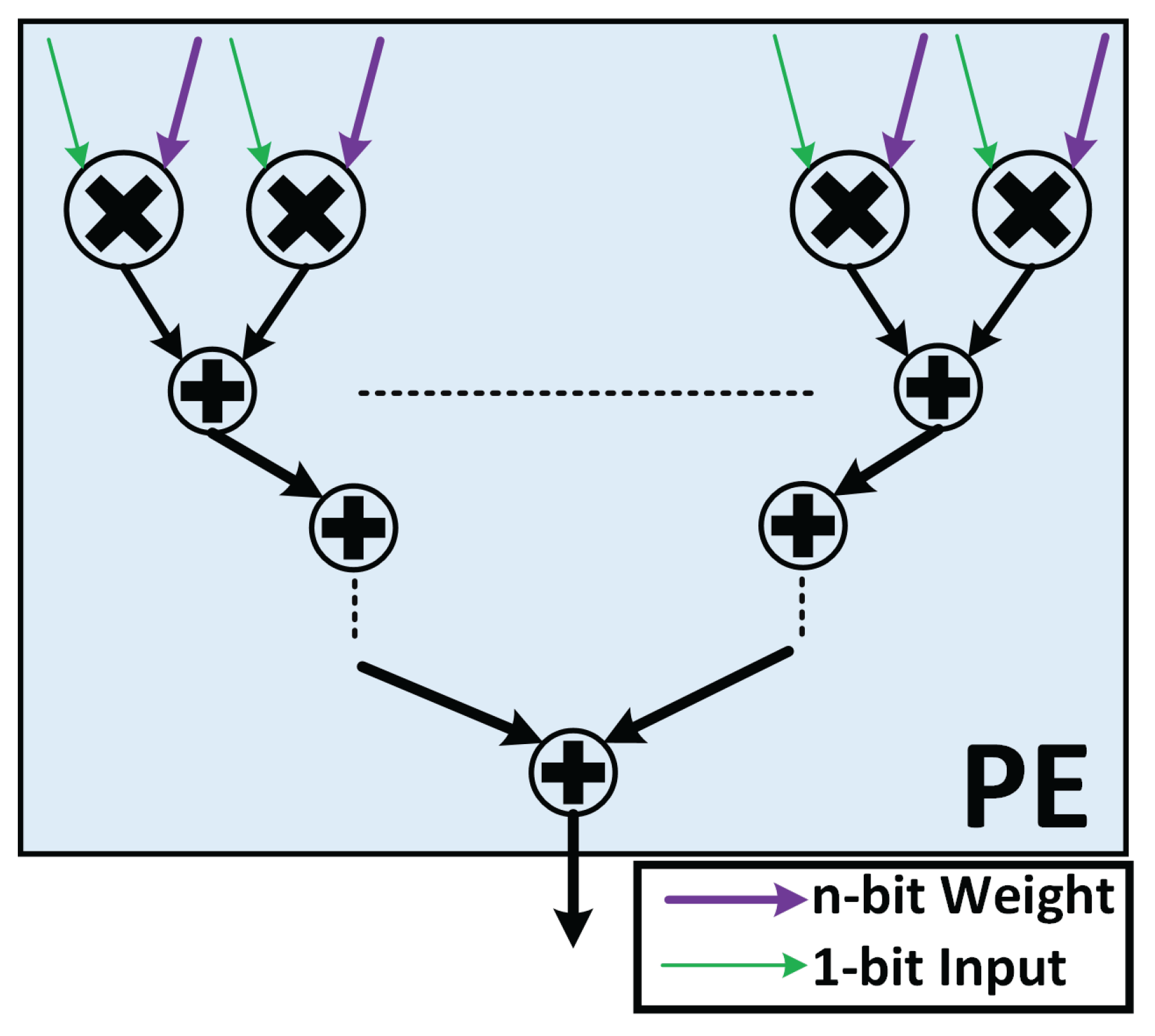
Figure 6.
Architecture of ECHO for a convolution layer. Each column is equipped with N PEs to facilitate the input channels, while each column of PE is followed by an online arithmetic-based reduction tree for the generation of the final SOP. The central controller block generates the termination signals and also controls the dataflow to and from the weight buffers (WB) and activation buffers (AB).
Figure 6.
Architecture of ECHO for a convolution layer. Each column is equipped with N PEs to facilitate the input channels, while each column of PE is followed by an online arithmetic-based reduction tree for the generation of the final SOP. The central controller block generates the termination signals and also controls the dataflow to and from the weight buffers (WB) and activation buffers (AB).
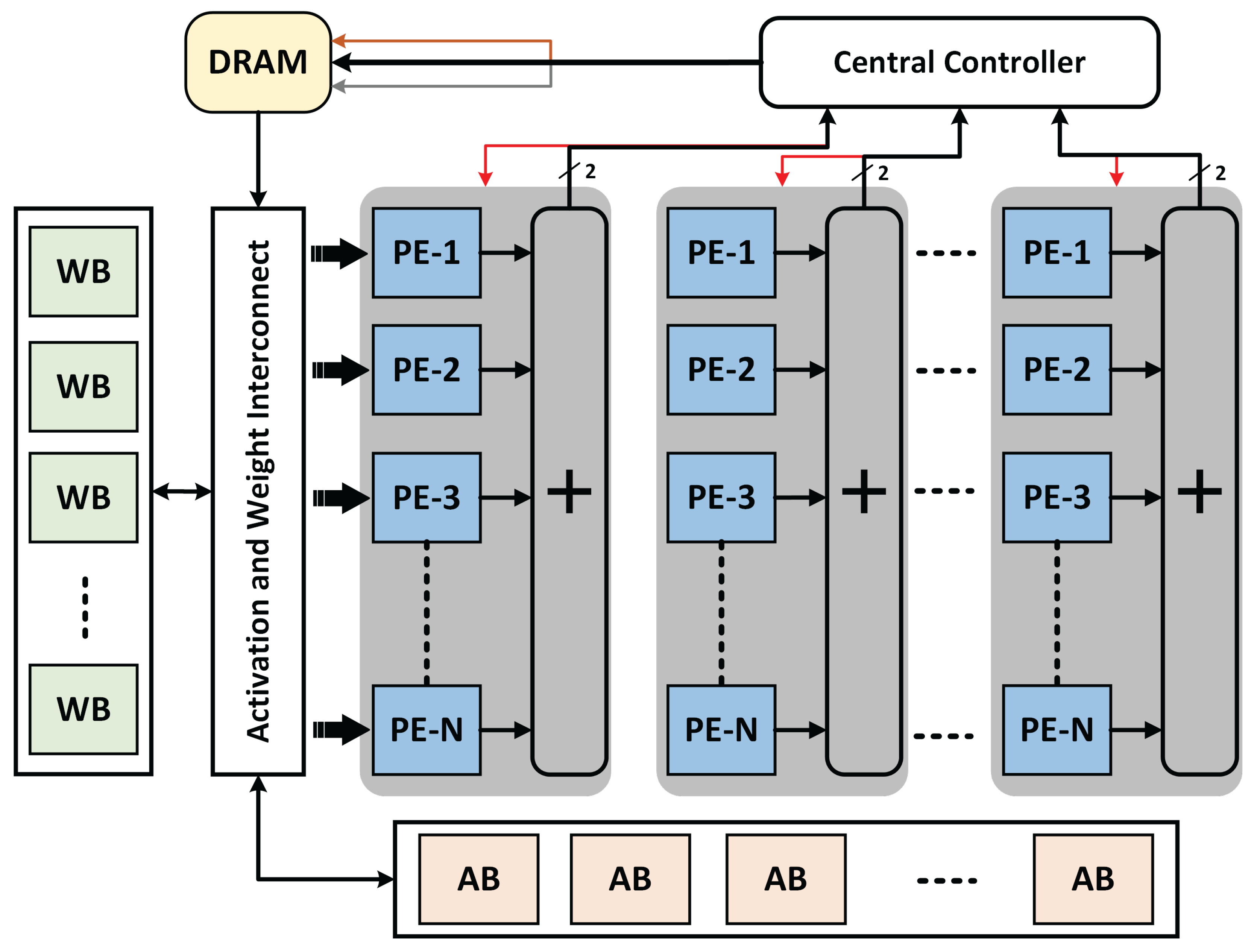
Figure 7.
Central Controller and Decision Unit in ECHO
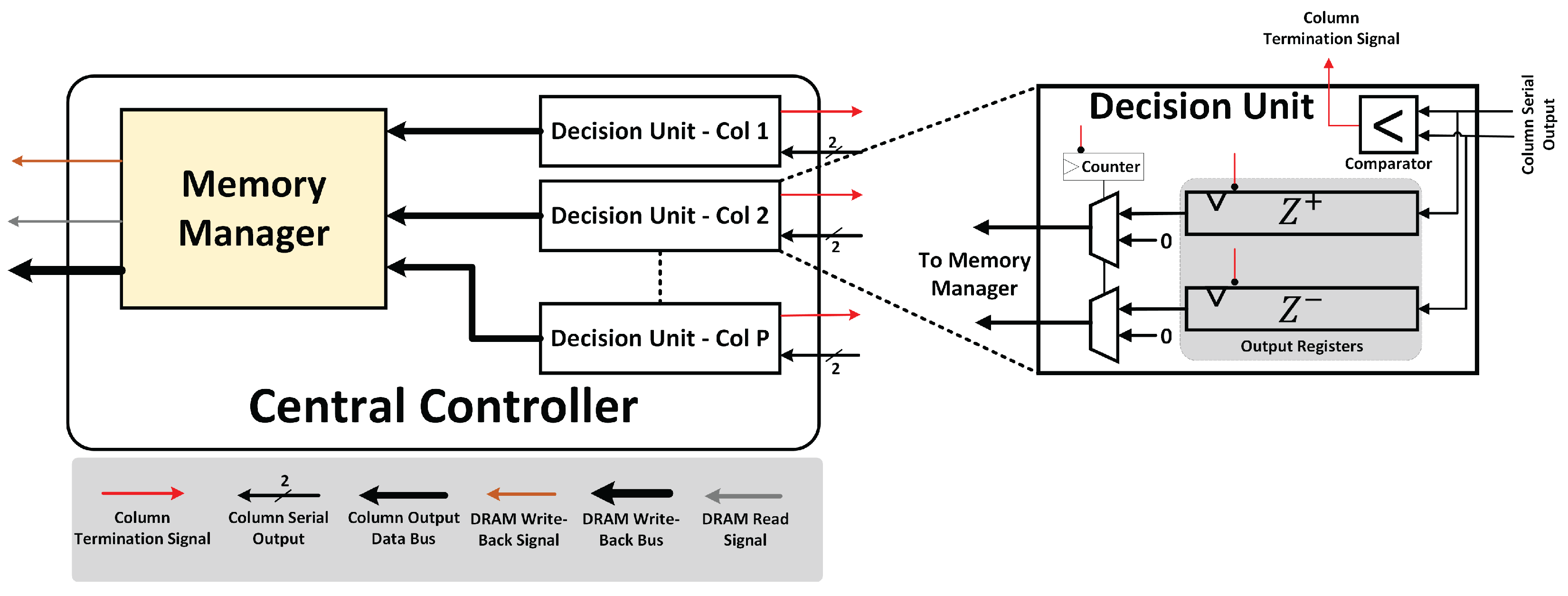
Figure 8.
Runtimes of the convolution layers for the proposed method with the baseline designs. The proposed design achieved mean runtime improvements of 58.16% and 61.6% compared to conventional bit-serial design (Baseline-1) for VGG-16 and ResNet-18 workloads respectively.
Figure 8.
Runtimes of the convolution layers for the proposed method with the baseline designs. The proposed design achieved mean runtime improvements of 58.16% and 61.6% compared to conventional bit-serial design (Baseline-1) for VGG-16 and ResNet-18 workloads respectively.
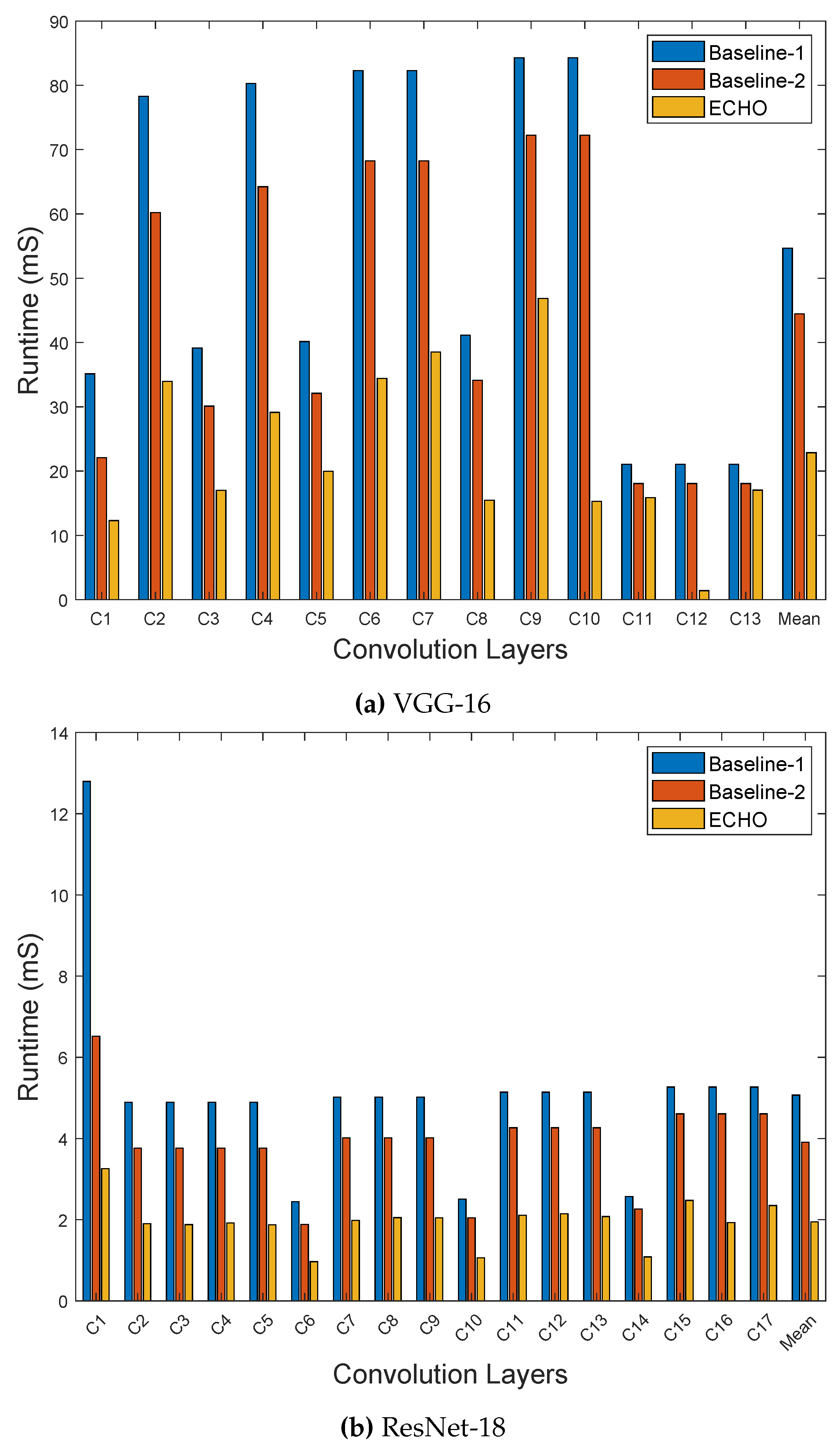
Figure 9.
Power consumption of the proposed design with the baseline designs. The proposed design achieved and mean reduction in power consumption compared to conventional bit-serial design (Baseline-1) for VGG-16 and ResNet-18 workloads respectively.
Figure 9.
Power consumption of the proposed design with the baseline designs. The proposed design achieved and mean reduction in power consumption compared to conventional bit-serial design (Baseline-1) for VGG-16 and ResNet-18 workloads respectively.
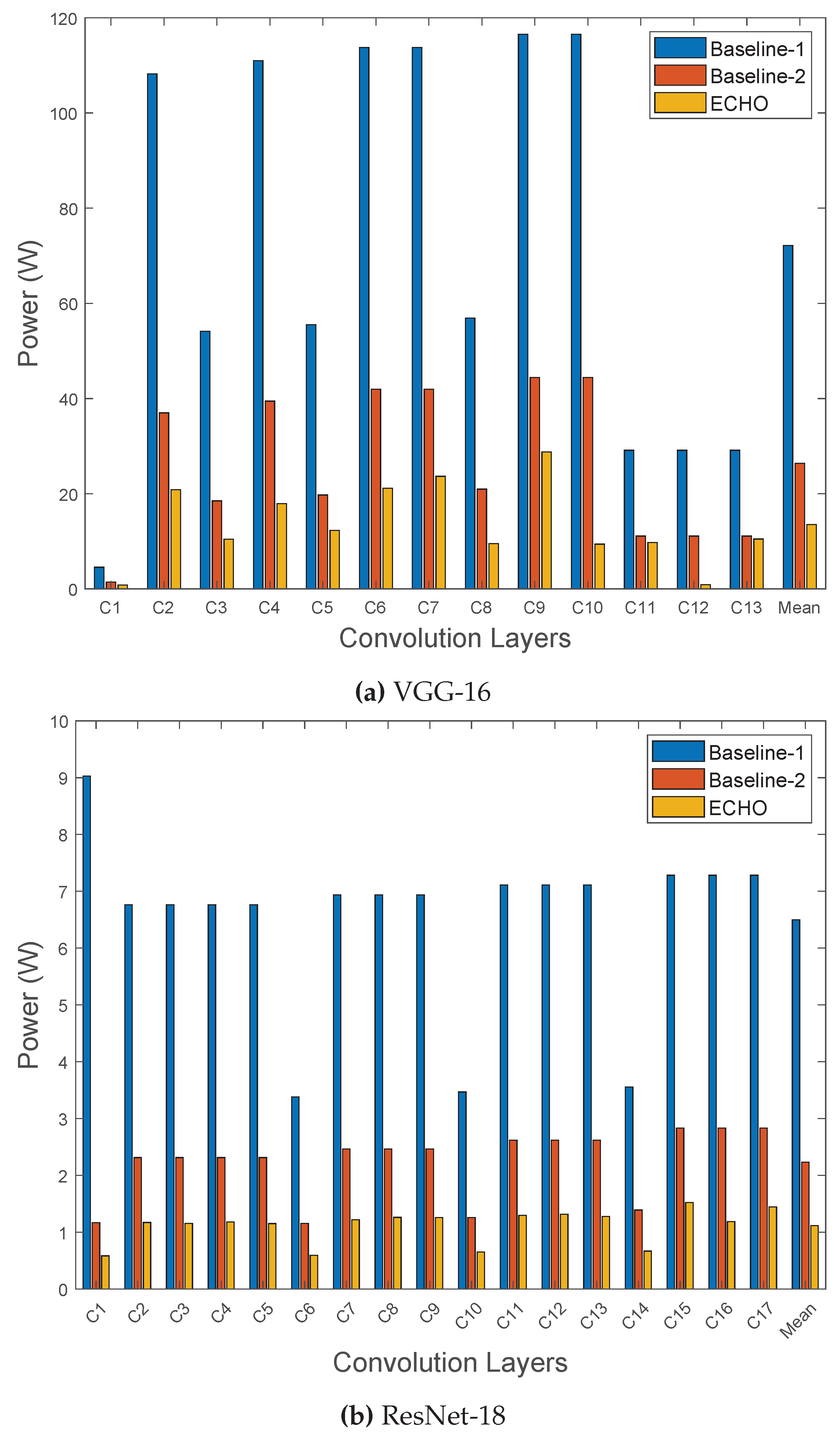
Table 1.
Convolution layer architecture of VGG-16 and ResNet networks. Where M denotes the number of kernels (number of output feature maps) and denotes the dimensions of the output feature maps.
Table 1.
Convolution layer architecture of VGG-16 and ResNet networks. Where M denotes the number of kernels (number of output feature maps) and denotes the dimensions of the output feature maps.
| Network | Layer | Kernel Size | M | |
|---|---|---|---|---|
| VGG-16 | C1-C2 | 64 | ||
| C3-C4 | 128 | |||
| C5-C7 | 256 | |||
| C8-C10 | 512 | |||
| C11-C13 | 512 | |||
| ResNet-18 | C1 | 64 | ||
| C2-C5 | 64 | |||
| C6-C9 | 128 | |||
| C10-C13 | 256 | |||
| C14-C17 | 512 | |||
| ResNet-50 | C1 | 64 | ||
| C2-x |
|
64, 256 | ||
| C3-x | 128, 512 | |||
| C4-x | 256, 1024 | |||
| C5-x | 512, 2048 |
Table 2.
Comparison of per layer inference time, power consumption, throughput, and speedup for the convolution layers of VGG-16 network.
Table 2.
Comparison of per layer inference time, power consumption, throughput, and speedup for the convolution layers of VGG-16 network.
| Layer | Inference Time (mS) | Power (W) | Speedup | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO | |
| C1 | 35.12 | 22.8 | 12.29 | 4.55 | 1.44 | 0.81 | 1 | 1.54 | 2.86 |
| C2 | 78.27 | 60.21 | 33.95 | 108.2 | 36.99 | 20.86 | 1 | 1.3 | 2.31 |
| C3 | 39.13 | 30.10 | 16.99 | 54.10 | 18.5 | 10.44 | 1 | 1.3 | 2.3 |
| C4 | 80.28 | 64.22 | 29.14 | 110.98 | 39.46 | 17.90 | 1 | 1.25 | 2.75 |
| C5 | 40.14 | 32.11 | 19.98 | 55.49 | 19.73 | 12.27 | 1 | 1.25 | 2.01 |
| C6 | 82.28 | 68.24 | 34.42 | 113.75 | 41.92 | 21.14 | 1 | 1.21 | 2.39 |
| C7 | 82.28 | 68.24 | 38.51 | 113.75 | 41.92 | 23.66 | 1 | 1.21 | 2.14 |
| C8 | 41.14 | 34.12 | 15.49 | 56.87 | 20.96 | 9.51 | 1 | 1.21 | 2.67 |
| C9 | 84.29 | 72.25 | 46.86 | 116.53 | 44.39 | 28.79 | 1 | 1.16 | 1.79 |
| C10 | 84.29 | 72.25 | 15.30 | 116.53 | 44.39 | 9.40 | 1 | 1.16 | 5.51 |
| C11 | 21.07 | 18.06 | 15.86 | 29.13 | 11.09 | 9.74 | 1 | 1.16 | 1.33 |
| C12 | 21.07 | 18.06 | 1.41 | 29.13 | 11.09 | 0.86 | 1 | 1.16 | 14.92 |
| C13 | 21.07 | 18.06 | 17.04 | 29.13 | 11.09 | 10.47 | 1 | 1.16 | 1.24 |
| Mean | 54.65 | 44.46 | 22.87 | 72.16 | 26.38 | 13.53 | 1 | 1.23 | 2.39 |
Table 3.
Comparison of per layer inference time, power consumption, throughput, and speedup for the convolution layers of ResNet-18 Model.
Table 3.
Comparison of per layer inference time, power consumption, throughput, and speedup for the convolution layers of ResNet-18 Model.
| Layer | Inference Time (mS) | Power (W) | Speedup (×) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO | |
| C1 | 12.79 | 6.52 | 3.25 | 9.02 | 1.16 | 0.58 | 1 | 1.96 | 3.93 |
| C2 | 4.89 | 3.76 | 1.9 | 6.76 | 2.31 | 1.16 | 1 | 1.3 | 2.57 |
| C3 | 4.89 | 3.76 | 1.88 | 6.76 | 2.31 | 1.15 | 1 | 1.3 | 2.6 |
| C4 | 4.89 | 3.76 | 1.91 | 6.76 | 2.31 | 1.17 | 1 | 1.3 | 2.56 |
| C5 | 4.89 | 3.76 | 1.87 | 6.76 | 2.31 | 1.15 | 1 | 1.3 | 2.61 |
| C6 | 2.44 | 1.88 | 0.96 | 3.38 | 1.15 | 0.59 | 1 | 1.29 | 2.54 |
| C7 | 5.01 | 4.01 | 1.98 | 6.93 | 2.46 | 1.21 | 1 | 1.24 | 2.53 |
| C8 | 5.01 | 4.01 | 2.05 | 6.93 | 2.46 | 1.26 | 1 | 1.24 | 2.44 |
| C9 | 5.01 | 4.01 | 2.04 | 6.93 | 2.46 | 1.25 | 1 | 1.24 | 2.45 |
| C10 | 2.5 | 2.04 | 1.06 | 3.46 | 1.25 | 0.65 | 1 | 1.22 | 2.35 |
| C11 | 5.14 | 4.26 | 2.1 | 7.1 | 2.62 | 1.29 | 1 | 1.2 | 2.44 |
| C12 | 5.14 | 4.26 | 2.14 | 7.1 | 2.62 | 1.31 | 1 | 1.2 | 2.4 |
| C13 | 5.14 | 4.26 | 2.07 | 7.1 | 2.62 | 1.27 | 1 | 1.2 | 2.48 |
| C14 | 2.57 | 2.26 | 1.08 | 3.55 | 1.39 | 0.66 | 1 | 1.13 | 2.37 |
| C15 | 5.26 | 4.6 | 2.47 | 7.28 | 2.83 | 1.52 | 1 | 1.14 | 2.12 |
| C16 | 5.26 | 4.6 | 1.92 | 7.28 | 2.83 | 1.18 | 1 | 1.14 | 2.73 |
| C17 | 5.26 | 4.6 | 2.35 | 7.28 | 2.83 | 1.44 | 1 | 1.14 | 2.23 |
| Mean | 5.06 | 3.9 | 1.94 | 6.49 | 2.23 | 1.11 | 1 | 1.29 | 2.6 |
Table 4.
Comparison of FPGA implementation of the proposed design with the conventional bit-serial design (Baseline-1) online arithmetic design without the early negative detection capability (Baseline-2). The FPGA device used for this experiment is Xilinx Ultrascale+ Vertix-7 VU3P. The Peak Throughput and Latency per Image have been mentioned in GOPS and ms respectively.
Table 4.
Comparison of FPGA implementation of the proposed design with the conventional bit-serial design (Baseline-1) online arithmetic design without the early negative detection capability (Baseline-2). The FPGA device used for this experiment is Xilinx Ultrascale+ Vertix-7 VU3P. The Peak Throughput and Latency per Image have been mentioned in GOPS and ms respectively.
| Model | VGG-16 | ResNet-18 | ResNet-50 | ||||||
| Design | Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO | Baseline-1 | Baseline-2 | ECHO |
| Frequency (MHz) | 100 | 100 | 100 | ||||||
| Logic Utilization | 238K (27.6%) |
315K (36.54%) |
238K (27.6%) |
315K (36.54%) |
238K (27.6%) |
315K (36.54%) |
|||
| BRAM Utilization | 83 (11.4%) |
84 (11.54%) |
83 (11.4%) |
84 (11.54%) |
83 (11.4%) |
84 (11.54%) |
|||
| Mean Power (W) | 72.16 | 26.38 | 13.53 | 6.49 | 2.23 | 1.11 | 9.63 | 11.5 | 5.72 |
| Peak Throughput (GOPS) | 47.3 | 61.4 | 655 | 47.3 | 61.4 | 123 | 39.01 | 61.4 | 128.7 |
| Latency per Image (ms) | 710.5 | 578.03 | 297.3 | 86.2 | 66.4 | 33.1 | 366.7 | 464.01 | 231.03 |
| Average Speedup (×) | 1 | 1.23 | 2.39 | 1 | 1.29 | 2.6 | 1 | 1.21 | 2.42 |
Table 5.
Comparison with previous works.
| Models | VGG-16 | ResNet-18 | ResNet-50 | |||||||
| Designs | NEURAghe [54] | [55] | OPU [56] | Caffeine [57] | ECHO | NEURAghe [54] | [58] | ECHO | [58] | ECHO |
| Device | Zynq Z7045 |
Zynq ZC706 |
Zynq XC7Z100 |
VX690t | VU3P | Zynq Z7045 |
Arria10 SX660 |
VU3P | Arria10 SX660 |
VU3P |
| Frequency (MHz) | 140 | 150 | 200 | 150 | 100 | 140 | 170 | 100 | 170 | 100 |
| Logic Utilization | 100K | - | - | - | 315K | 100K | 102.6K | 315K | 102.6K | 315K |
| BRAM Utilization | 320 | 1090 | 1510 | 2940 | 84 | 320 | 465 | 84 | 465 | 84 |
| Peak Throughput (GOPS) | 169 | 374.98 | 397 | 636 | 655 | 58 | 89.29 | 123 | 90.19 | 128.7 |
| Energy Efficiency (GOPS/W) | 16.9 | - | 24.06 | - | 48.41 | 5.8 | 19.41 | 21.58 | 19.61 | 22.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated