Prerpints.org logo
Preprint
Article

Hydrostatic Equation of State of BCC Bi by Direct Solving the Partition Function

Altmetrics

Downloads

96

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 April 2024

Posted:

09 April 2024

You are already at the latest version

Alerts
Abstract
Body-centered cubic bismuth (Bi) is considered an enticing pressure marker, and therefore it is highly desirable to command its accurate equation of state (EOS). However, significant discrepancies are noted among the previous experimental EOSs. In the present work, the EOS up to 300 GPa is theoretically obtained by direct solving the partition function via a direct integral approach (DIA). The calculated results nearly reproduce the hydrostatic experimental measurements below 75 GPa, and the deviations from the measurements gradually get larger with increasing pressure. Based on the ensemble theory of equilibrium state, DIA works with high precision particularly in high-pressure conditions, so the hydrostatic EOS presented in this work is expected to be a reliable pressure standard.
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

Metal bismuth (Bi), crystalizing in a rhombohedral structure at ambient conditions, undergoes a series of pressure-induced transitions in sequence of rhombohedral phase → monoclinic phase → body-centered tetragonal phase → body-centered cubic (bcc) phase [1,2,3,4,5,6,7]. All these room temperature transition points are clear and have been widely used as pressure calibration. Especially, bcc Bi is enticing as an internal pressure standard because (i) it is stable over a wide pressure range (7.7 - 299 GPa) [7,8,9,10]; (ii) it has the highest atomic number of any non-radioactive element, bringing about strong x-ray diffraction signals; (iii) its bulk modulus (35.2 - 58.9 GPa [10,11]) is much smaller than that of most other pressure standards (such as Ta 194 GPa [12], Au 167 GPa [13], and W 310 GPa [14]), giving rise to larger volume change under the same pressure. So, bcc Bi as pressure calibration is expected to improve the pressure measurements in high-pressure researches. However, high-pressure (> 50 GPa) experimental investigations on the equation of state (EOS) of bcc Bi are very limited, and only four [8,9,10,11] experiments were reported in the last two decades. What’s more, among these measured EOSs, significant discrepancies are noted particularly in high pressure range. We think two aspects should be mainly considered about this disparity.
First, evaluations of pressure in static research depend strongly on a secondary pressure scale that the values may be quite different by different scales for the same one experiment. For example, Akahama et al. [10] pointed out that if the Au pressure scale promoted by Jamieson et al. [15] was used to calibrate the pressure in their experiment for the EOS of Bi, the determined pressures above 30 GPa would be observably smaller than that evaluated from the Pt gauge of Holmes et al. [16], and with increasing compression, the difference rises constantly high up to ~ 20 GPa around 150 GPa. In 2023, Campbell et al. [9] conducted quasi-hydrostatic high-pressure investigations for Bi, and showed that the EOS over 100 GPa presents apparent difference when two neon scales promoted respectively by themselves and by Dewaele et al. [17] were used to calibrate the pressure that the discrepancy reaches ~ 10 GPa around 250 GPa. Obviously, the accuracy of the pressures determined in static experiments relies intimately on the precision of the adopted calibrants. In fact, currently available pressure standards were primitively originated from fitting, or further extrapolating limited measurements with empirical equations, such as Vinet [18,19], third-order Birch-Murnaghan [20,21], AP2 [22,23] and so on. As is known that empirical functions were usually built on a limited physics basis, the evaluated pressures are always disparate using different equations or even using the same equation [24,25], the predicted results may be significantly diverse with different input data. So, most pressure scales at present are not unified and the discrepancies generally present more and more with increasing pressure.
To obtain quasi-hydrostatic pressures, it is typically required to load samples with a pressure transmitting medium (PTM) in diamond anvil cell (DAC) experiments. Whereas, Bi itself with low yield/shear strength [26] is regarded as a good PTM, and in some of previous static high-pressure researches for the EOS of Bi no other PTM was used, counting on Bi itself to redistribute the anisotropic stress. It was revealed that with no additional PTM the uniaxial stress component in the compressed sample Bi was relatively small [8,9,10,11], but non-negligible deviatoric stresses were found in the concurrently compressed pressure markers, which may arouse significant errors for the determination of pressure. For example, a very recent experiment conducted in 2023 by Storm et al. [8] without any other PTM showed that a correction for the pressure (279 GPa) evaluated from the used Au gauge due to non-hydrostatic effect reaches 39 GPa, meaning that a relative indeterminacy of 13% at ~ 300 GPa exists in their reported Bi EOS. It should be pointed out that the non-hydrostatic effect on different pressure scales is different hinging on their inherent incompressibility. For example, pressure corrections due to gradient stress for the Pt calibrant used in the experiments of Ref. [10] and the Cu scale used in Ref. [8] were significantly smaller than that for the just mentioned Au in Ref. [8]. So, the second factor accounting for the inconsistence between previous experimental EOS of bcc Bi is the different degrees of non-hydrostatic effect on the pressure markers in terms of if additional PTM and what pressure scales were used in the experiments.
As mentioned above, high-pressure experimental EOSs of bcc Bi are controversial at present, and it is necessary to confront this issue in a theoretical way. In fact, the ensemble theory offers a promising avenue for accurate EOSs of condensed matters as long as the partition function (PF) or free energy (FE) is calculated precisely. It is known that exact solving the PF involving a 3N-fold configurational integral far exceeds the capability of current computer technologies, so the EOS of bcc Bi has never been calculated by direct solving the PF at the level of first principles calculating the interatomic energies. Recently, a direct integral approach (DIA) to the PF with ultrahigh precision and efficiency was established by Ning et al. [27], and has been successfully used to calculate the EOS of solid copper [27], iridium [28], argon [29], and 2-D materials [30], and reproduce the phase transition of crystal vanadium [31], zirconium [32], and aluminum [33]. In particular, a very recent work on the high-temperature and simultaneously high-pressure EOS of tungsten [34] showed that compared with available static compression experiments, all the deviations of the calculated results by DIA were within or comparable to the uncertainty of the experiments. In this work, DIA is applied to calculate the PF of crystal bcc Bi and further the hydrostatic room temperature EOS up to 300 GPa. Details for the implementation of DIA are elaborated in section 2. Careful comparisons and discussions of the calculated results with available experiments are presented respectively in section 3 and 4, and the final section is the conclusion.

2. Materials and Methods

For a crystal containing N atoms confined within volume V at temperature T, the atoms are regarded as N point particles with cartesian coordinate q N = q 1 , q 2 , ⋯ q N , and the total energy, U q N , as the function of q N can be computed by quantum mechanics. With the knowledge of U q N , the PF of the system reads.
Z = 1 N ! 2 π m β h 2 3 2 N ∫ d q N e − β U q N = 1 N ! 2 π m β h 2 3 2 N Q
where h is the Planck constant and β = 1 / k B T with k B the Boltzmann constant. If the configurational integral Q = ∫ d q N e − β U q N is solved, the pressure (P) is,
P = 1 β ∂ l n Z ∂ V
Helmholtz FE (F) is,
F = − 1 β l n Z
and any other thermodynamic quantities can be obtained.
For a crystal with all the N atoms placed in their lattice sites Q N = Q 1 , Q 2 , ⋯ , Q N and with the total potential energy U 0 ( Q N ) , we first introduce a transformation [27],
q ′ N = q N − Q N ,   U ′ q ′ N = U q N − U 0 Q N ,
where q ’ N represents the displacements of atoms away from their equilibrium positions. Then, the configurational integral Q is expressed as
Q = e − β U 0 ∫ d q ′ N e − β U ′ q ′ N
According to DIA [27], the above 3N-fold integral could be approximated as
Q = e − β U 0 ∏ i = 1 N ( L i x L i y L i z )
with the effective length
L i x = ∫ e − β U ′ 0 ⋯ q i x ′   ⋯ 0 d q i x ′
L i y = ∫ e − β U ′ 0 ⋯ q i y ′   ⋯ 0 d q i y ′
and
L i z = ∫ e − β U ′ 0 ⋯ q i z ′ ⋯ 0 d q i z ′
where q i x ’ ( q i y ’ or q i z ’ ) is the x (y or z) coordinate of the ith atom moving away off its ideal lattice site along with the other two degrees of freedom of the atom and all the other atoms fixed.
For crystal bcc Bi, all the atoms are equivalent and, therefore, the configurational integral Q in Equation (6) turns into
Q = e − β U 0 L x L y L z N
Clearly, if orientations [100], [010], and [001] are selected as the axes of a Cartesian system, then L x , L y and L z are equal, so that
Q = e − β U 0 L x 3 N
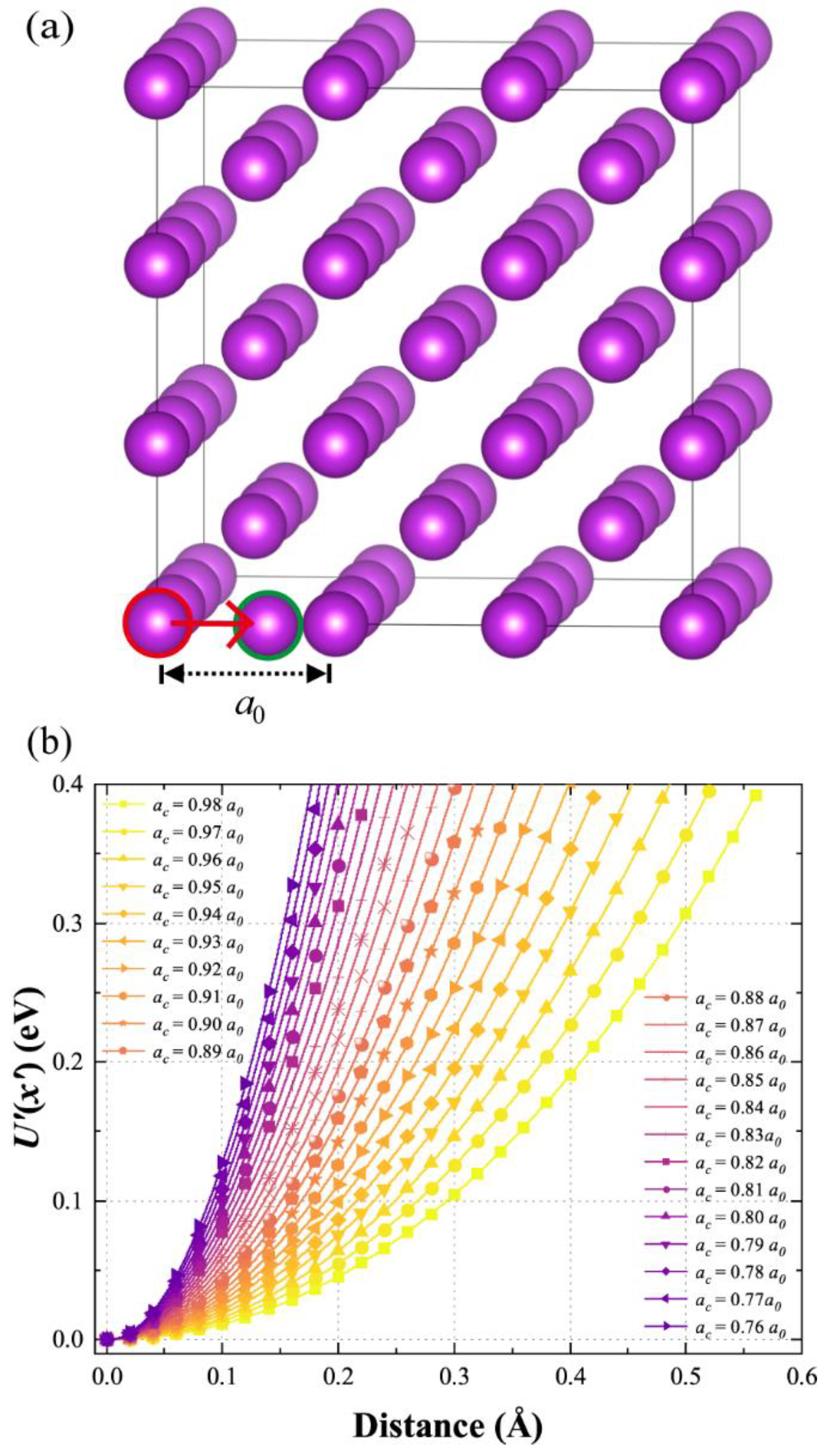
To implement the calculations, we constructed a 3 × 3 × 3 supercell containing 54 atoms arranged in a bcc structure. First, the system was fully relaxed to make the stresses survived by the atoms isotropic that the optimized lattice constant is a0 (Figure 1a) and the total energy U 0 . Then, an arbitrary atom (in the red circle) was moved away along the [100] direction step by step with an interval of 0.02 Å. At each step, the total energy of the system U ( x ) was calculated with the lattice and all the atoms frozen. The completed U ’ x ’ = U x − U 0 (Figure 1(b)) was smoothed by cubic spline interpolation algorithm [35]. Furthermore, L x was calculated via Equation (7) and the corresponding PF could be obtained based on Equations (9) and (1). Changing the volume of the supercell by enlarging or shrinking the lattice constant a0 and repeating the above process without optimizing the supercell, a series of U 0 and U ’ x ’ as a function of the volume can be achieved (Figure 1b). Accordingly, room temperature PF vs V and further the corresponding P-V relationship could be obtained by Equation (2).
All the above calculations were completed by the density functional theory (DFT), and performed in the Vienna Ab initio Simulation Package (VASP) [36,37], in which the projector augmented wave (PAW) pseudopotential [38,39] with 6s26p3 as the valence states was adopted for describing the electron-ion interactions, and the generalized gradient approximation (GGA) parametrized by Perdew-Burke-Ernzerhof (PBE) [40] was employed to consider the exchange-correlation interactions of the electrons. In the first step of optimizing the structure, the forces acted on each atom were less than 0.02 eV/Å when the relaxation was converged. For the calculations of the total energies, electron self-consistent tolerance was 2 × 10-6 eV, which is fine enough regarding to the integration in Equation (7). A Γ-centered 11 × 11 × 11 uniform k-mesh was set to sample the Brillouin zone by the Monkhorst-Pack scheme and the tetrahedron method with Blöchl corrections was adopted to determine the electron orbital partial occupancy with the plane-wave cut-off energy of 350 eV. Convergence tests of all these parameters were performed for the structure with the smallest volume (ac = 0.76 a0) that the fluctuation of the total energy was less than 10-3 eV/atom. Unquestionably, the precision of the calculated total energies for the structures with larger volumes would not degrade under the same parameters.

3. Results

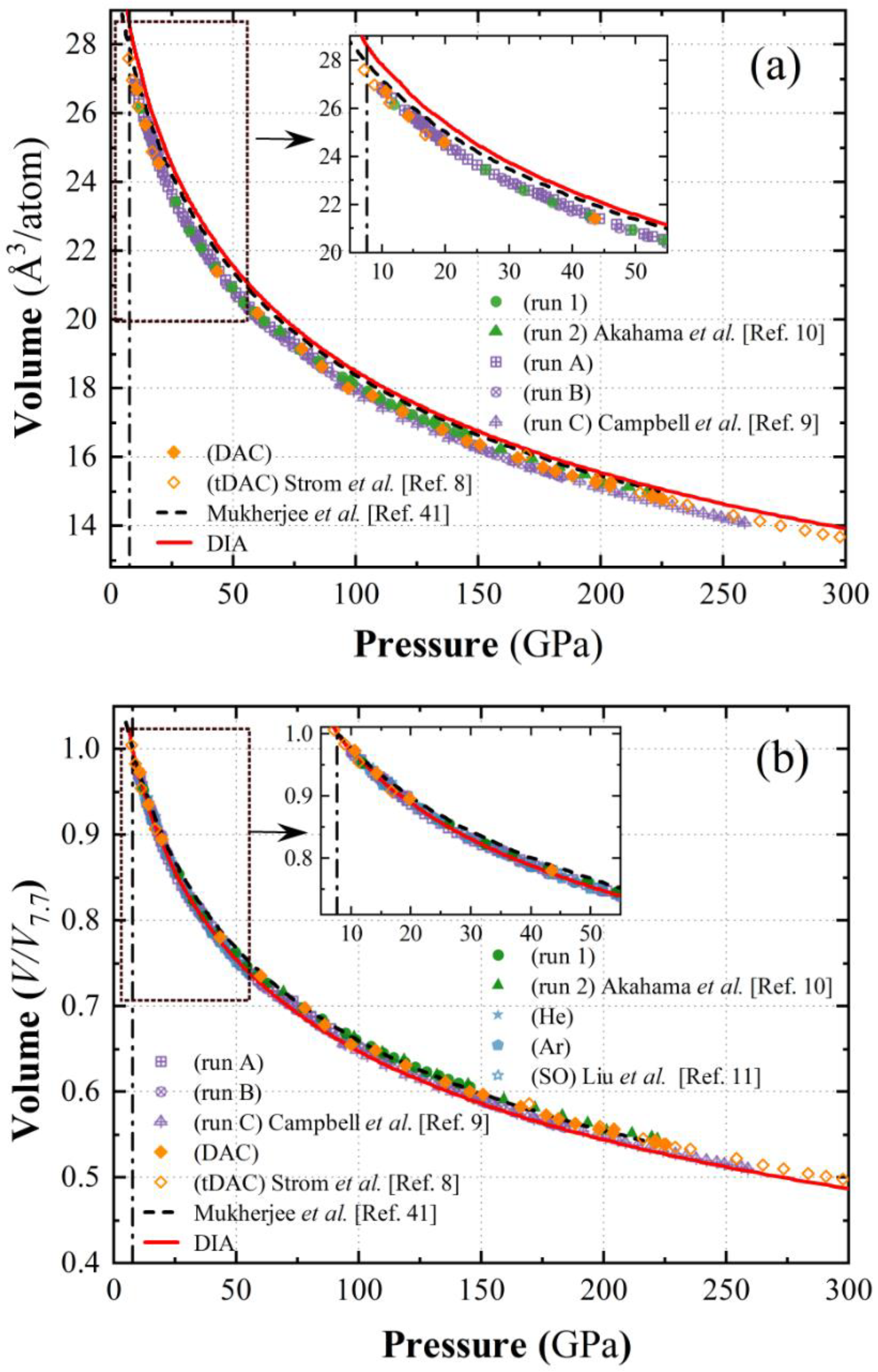
The calculated data of the isothermal EOS of bcc Bi at 300 K are listed in Table 1. The P-V curve as well as four sets of experimental measurements [8,9,10,11] and the theoretical results (up to 220 GPa) by Mukherjee et al. [41] under Debye model (DM) are displayed in Figure 2. As indicated in Figure 2a that the GGA functional usually tend to overestimate lattice constants, the calculated volumes from both DIA and DM at given pressure are consistently larger than the experimental measurements. To avoid this systematic offset, relative volume vs pressure is usually used in previous works [42,43,44] to implement the comparisons between theoretical calculations and experimental results and is also adopted in the present work. Since bcc Bi was recognized to emerge at 7.7 GPa [7,8,11,41], relative volume V/V7.7 with V7.7 the atomic volume at 7.7 GPa was used to express the EOS (Figure 2b), and all the discussions start from 7.7 GPa in this work. Under the same value of V/V7.7, deviations of the calculated pressure from DIA (PDIA), or DM (PDM) with the experimental measurements (PExp) are exhibited in Figure 3.
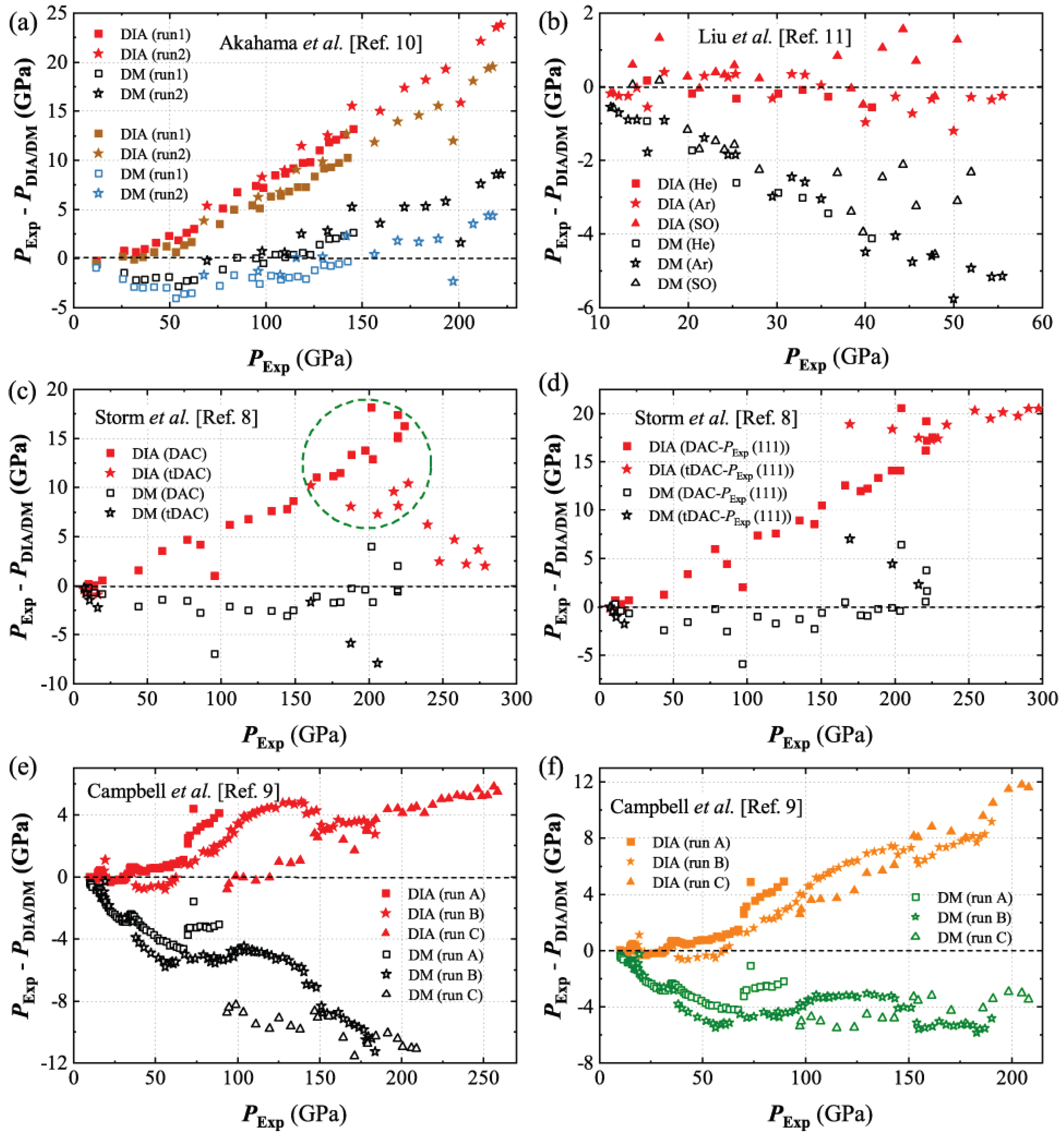
In 2002, Akahama et al. [10] carried out two sets of experiments in conventional DACs, and measured the unit cell volumes of Bi up to 145 and 222 GPa, respectively. Compared with PExp, PDIA manifests consistently smaller in the whole pressure range, and the difference, PExp - PDIA, increases gradually with increasing pressure up to 23.8 GPa (red symbols in Figure 3a) at the highest compression, corresponding to a relative error ((PExp - PDIA)/ PExp) of ~ 11%. On the other hand, PDM presents much closer to PExp in the high-pressure scope (> 70 GPa) (black symbols in Figure 3a). In fact, the Pt pressure scale of Holmes et al. [16] used in this experiment has been revealed to overestimate pressures [47]. As the authors of Ref. [10] pointed out that if Au calibration of Jamieson et al. [15] was adopted to evaluate the pressures, the values would be lower than that estimated from Holmes’ Pt, and the highest pressure in their first experimental run would be 128.9 GPa (instead of 145 GPa), which is less than PDIA by only ~ 3 GPa, while smaller than PDM by ~ 13 GPa. Considering that systematic errors arising from the selected pressure scale may exist in the Bi EOS of Akahama et al., we re-calibrate the pressures in Ref. [10] with the latest Pt standard established by Fratanduono et al. [45] in 2021. As shown by the brown symbols in Figure 3a, the re-calibrated pressures are indeed smaller than that evaluated from Holmes’ Pt, and the largest difference between PDIA and the re-determined pressure reduces to 19.5 GPa, corresponding to the relative error of 9%. Comparatively, average difference between PDM and the re-estimated pressure displays much smaller with the average relative deviation (|PExp - PDM|/ PExp) of only 2.7% (blue symbols in Figure 3a).
In 2013, Liu et al. [11] inspected the influence of different PTMs on the EOS of Bi using a DAC, and found the measured results up to 55 GPa were consistent with each other when He, Ar, and silicone oil (SO) PTM were used. As shown in Figure 3(b), the three sets of extremely self-consistent experimental data under different PTMs are nearly reproduced by DIA, and the differences between PDIA and PExp fluctuate around zero in the experimental condition with average |PExp - PDIA| of only 0.48 GPa, which is entirely within the uncertainty of PExp arising from the used ruby pressure scale in the experiments. On the other hand, PDM deviates PExp more and more with increasing pressure, and the relative error (|PExp - PDM|/ PExp) reaches ~ 9.3% at the highest compression.
In 2023, Storm et al. [8] conducted diffraction studies of Bi up to 298 GPa using both conventional and toroidal DAC (tDAC) to investigate the EOS without additional PTM. As the red squares in Figure 3c showed, the difference between PDIA and the PExp (0 - 224 GPa) completed in the conventional DAC increases with increasing pressure, and the largest relative error reaches about 7%. While, the difference between PDIA and the PExp (red stars in Figure 3c) at higher compression range (160 - 280 GPa) performed in a tDAC decreases with increasing pressure, leading to a systematic error of larger than 10 GPa (in the green dashed circle) around 200 GPa. This uncertainty of the pressures is mainly a consequence of markedly different degrees of non-hydrostatic effect on the Cu [46] and Au [45] pressure scales used in their respective DAC and tDAC experimental runs, since if only the x-ray diffraction peaks of (111) lattice plane, least affected by uniaxial stress, of the Cu and Au were selected to determine the pressures, the just mentioned systematic errors would disappear as that indicated in Figure 3d. Comparatively, the calculated results by DM (black symbols in Figure 3c,d) agree well with these non-hydrostatic measurements.
Almost at the same time as Storm et al. [8], Campbell et al. [9] reported three data sets on the compression of Bi in a DAC in a neon PTM, up to a maximum pressure of about 260 GPa. As shown by the red symbols in Figure 3e, PDIA agrees very well with PExp below 75 GPa, over which PDIA deviates from PExp gradually up to 5.8 GPa. Meanwhile, DM manifests worse than DIA as indicated by the black symbols in Figure 3e. It should be pointed out that in the first two experimental runs (run A and run B) of Ref. [9], the used Cu pressure scale [48] by Dewaele et al. was promoted essentially to only 153 GPa, so the PExp over 153 GPa in the run B measurements (16.8 - 184 GPa) are extrapolated results. Besides, this Cu calibration determined by a ruby scale [48] was indicated to underestimate pressures [49,50]. To inspect these queries, we re-calibrate the pressures of experimental run A and run B of Ref. [9] with the latest Cu calibration proposed by Fratanduono et al. [46] in 2020. As shown by the orange squares and stars in Figure 3f, above ~ 100 GPa, the recalibrated pressures are indeed larger than that estimated by the scale of Dewaele et al. [48], and the maximum re-estimated pressure in experimental run B is 190.4 GPa (instead of 184 GPa). The difference between PDIA and the re-evaluated pressure increases with increasing pressure gradually up to 9.2 GPa. Pressures in the run C experiment of Ref. [9] were determined by a neon EOS established by the authors based on the compression data measured in their run B experiment, in which neon and Cu were concurrently compressed, and the corresponding pressures were calibrated by the Cu EOS of Dewaele et al. [48]. So the PExp over 153 GPa in the run C measurements (93.8 - 258.7 GPa) of Ref. [9] were also extended results, which are actually not recommended. As the authors of Ref. [9] said if the pressures in their run C measurements were calibrated by the neon EOS promoted by Dewaele et al. [17], the pressures will be higher. As shown by the orange triangles in Figure 3f, since the neon EOS of Ref. [17] was proposed to 209 GPa, recalibration with this neon scale for the pressures in the run C experiment of Ref. [9] is just to 209 GPa. The difference between PDIA and the re-calibrated pressures increases with increasing pressure gradually up to 11.8 GPa, corresponding to a relative error ((PExp - PDIA)/ PExp) of 5.8%, which is two times larger than that displayed in Figure 3e. Comparatively, PDM is much closer to the re-calibrated pressures in pressure range of over 100 GPa with the largest deviation of only ~ 6 GPa.

4. Discussion

It is noted that after re-calibrating the pressures of Ref. [9] by the latest Cu pressure scale of Fratanduono et al. [46], the difference between PDIA and the re-estimated pressures (orange squares and stars in Figure 3f) below 200 GPa is very approximate to that between PDIA and PExp of Ref. [8] (red squares in Figure 3d), where the pressure calibration is also the latest Cu EOS of Fratanduono et al. [46]. This indicates that the apparent difference between originally reported EOS of bcc Bi by Storm et al. [8] and Campbell et al. [9] is mainly caused by the systematic errors inherent in the different Cu EOSs of Dewaele et al. [48] and Fratanduono et al. [46], although minor difference of the hydrostatic (or non-hydrostatic) conditions in the two experiments should be also concerned since PDIA nearly reproduces the low-pressure experimental measurements (< 75 GPa) of Ref. [9], while deviates from the measurements of Ref. [8] gradually with increasing pressure.
Similarly, after re-calibrating the pressures in Ref. [10] with the latest Pt pressure scale proposed by Fratanduono et al. [45], the difference between PDIA and the re-evaluated pressures (brown symbols in Figure 3a) is nearly the same with that between PDIA and PExp of Ref. [8] (red squares in Figure 3d). So, if the Cu [46] and Pt [45] pressure scale both promoted by Fratanduono et al. are self-consistent, it can be concluded that the experimental EOSs of bcc Bi up to 200 GPa are nearly converged so far.
Whereas, as shown by the brown symbols in Figure 3a, red squares in Figure 3d and orange symbols in Figure 3f, the calculated results by DIA still display gradually increasing deviations from these re-calibrated experimental data, and the relative difference reaches about 7% at 200 GPa. It should be pointed out that both the Cu [46] and Pt [45] pressure scale by Fratanduono et al. were established via reducing the ramp compressed stress-density data to the room temperature isothermal one, so the accuracy of the Cu [46] and Pt [45] EOS is strongly dependent on the reduction method. For the thermodynamic model used in Ref. [45] and [46], on the one hand, the thermal energy caused by the plastic work heating in the ramp compression were determined from the Debye integral, which is strongly related to the selection of the expression of the Grüneisen parameter. On the other hand, the Grüneisen parameters for the Cu [46] and Pt [45] were treated as simply volume dependent, but they are actually both volume and temperature dependent. As a result, these approximations may cause large deviations in the reduced isotherms of the Cu [46] and Pt [45] EOS, particularly at high pressures.
What worth mentioning is that large uniaxial stress component was observed in the pressure marker Au used in the tDAC experiments of Ref. [8], so the corresponding measured pressures are seriously non-hydrostatic, and should be very different from the ones under hydrostatic conditions. As discussed in the last paragraph of section 3, pressure measurements over 153 GPa in Ref. [9] are extended results, which are actually not recommended. So, the experimental EOS of bcc Bi over 200 GPa is needed to be re-inspected in future.
It is observed that in low pressure range, DM displays much worse than DIA in terms of all the PExp showed in Figure 3. As presented in Ref. [41] that the calculated Debye temperature for Bi is smaller than 300 K below ~ 100 GPa, so DM is probably not a good approximation in 0 - 100 GPa regarding to the EOS of bcc Bi. In addition, DM works actually within the framework of harmonic approximation, which is whereas suggested to be effective on the systems with atomic volume smaller than 20 Å3/atom, beyond which the accuracy of harmonic approximation gets lower and lower with increasing atomic volume [51]. As the calculations of Ref. [41] showed, below 69 GPa, the atomic volume of bcc Bi is larger than 20 Å3/atom. These may account for the worse agreement of the calculated results by DM with the experimental measurements in low pressure range.
As a contrast to DM, calculations by DIA agree better with all the experimental measurements at low pressures, especially with Ref. [9] and [11] displaying better hydrostatic conditions, which indicates the reliability of DIA since low-pressure measurements in static experiments are out of question so far. In fact, with the same function describing the potential energy of materials, DIA has been rigorously confirmed by corresponding molecular dynamic simulations as very accurate for the EOS calculations of condensed matters [27]. DIA working without any artificial or empirical parameters is universally applicable to any solids, and its accuracy tends to increase with decreasing atomic volume. So, the high-pressure predictions by DIA are expected to be accurate.

5. Conclusions

By direct solving the partition function, we obtained the room temperature isothermal EOS of bcc Bi. The deviations of the calculated results from the hydrostatic experimental measurements could be negligible below 75 GPa, while gradually get larger in higher pressure range, which may be caused by the inaccuracy of the pressure standard used in high-pressure conditions. Compared with the non-hydrostatic experiments, the deviations of the calculated pressures gradually increase with increasing pressure, revealing the fact that the non-hydrostatic experiments cannot be well described by the theory of equilibrium statistics. In conclusion, the EOS provided in the present work is expected to be a believable standard for future static pressure measurements.

Author Contributions

Conceptualization, Yue-Yue Tian, Bo-Yuan Ning, Hui-Fen Zhang and Xi-Jing Ning; Data curation, Yue-Yue Tian, Hui-Fen Zhang and Xi-Jing Ning; Formal analysis, Yue-Yue Tian, Hui-Fen Zhang and Xi-Jing Ning; Methodology, Bo-Yuan Ning and Xi-Jing Ning; Project administration, Yue-Yue Tian, Hui-Fen Zhang and Xi-Jing Ning; Software, Bo-Yuan Ning; Writing – original draft, Yue-Yue Tian; Writing – review & editing, Yue-Yue Tian, Hui-Fen Zhang and Xi-Jing Ning. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Data is contained within the article.

Acknowledgments

We gratefully acknowledge Hongzhiwei technology (Shanghai) Co., Ltd. for providing the computation resources.

Conflicts of Interest

The authors have no conflicts of interest.

References

  1. Yaoita, K.; Tsuji, K.; Katayama, Y.; Imai, M.; Chen, J.-Q.; Kikegawa, T.; Shimomura, O. The structure of liquid bismuth under pressure. J. Non-Cryst. Solids 1992, 150, 25–28. [Google Scholar] [CrossRef]
  2. McMahon, M.I.; Degtyareva, O.; Nelmes, R.J. Ba-IV-type incommensurate crystal structure in group-V metals. Phys. Rev. Lett. 2000, 85, 4896–4899. [Google Scholar] [CrossRef] [PubMed]
  3. Duff, R.E.; Minshall, F.S. Investigation of a Shock-Induced Transition in Bismuth. Phys. Rev. 1957, 108, 1207–1212. [Google Scholar] [CrossRef]
  4. Aoki, K.; Fujiwara, S.; Kusakabe, M. Stability of the bcc structure of bismuth at high pressure. J. Phys. Soc. Jpn. 1982, 51, 3826–3830. [Google Scholar] [CrossRef]
  5. Degtyareva, O.; McMahon, M.I.; Nelmes, R.J. High-pressure structural studies of group-15 elements. High Pressure Res. 2004, 24, 319–356. [Google Scholar] [CrossRef]
  6. Ono, S. High-pressure phase transition of bismuth. High Pressure Res. 2018, 38, 414–421. [Google Scholar] [CrossRef]
  7. Husband, R.J.; O’Bannon, E.F.; Liermann, H.-P.; Lipp, M.J.; Méndez, A.S.J.; Konôpková, Z.; McBride, E.E.; Evans, W.J.; Jenei, Z. Compression-rate dependence of pressure-induced phase transitions in Bi. Sci Rep 2021, 11, 14859. [Google Scholar] [CrossRef] [PubMed]
  8. Storm, C.V.; McHardy, J.D.; Duff, M.J.; MacLeod, S.G.; O’Bannon, E.F., III; McMahon, M.I. The stress state in bismuth to 298 GPa and its use as a pressure transmitting medium and pressure marker at multi-megabar pressures. J. Appl. Phys. 2023, 133, 245904. [Google Scholar] [CrossRef]
  9. Campbell, D.J.; Sneed, D.T.; O’Bannon, E.F.; Söderlind, P.; Jenei, Z. Refined room-temperature equation of state of Bi up to 260 GPa. Phys. Rev. B 2023, 107, 224104. [Google Scholar] [CrossRef]
  10. Akahama, Y.; Kawamura, H.; Singh, A.K. Equation of state of bismuth to 222 GPa and comparison of gold and platinum pressure scales to 145 GPa. J. Appl. Phys. 2002, 92, 5892–5897. [Google Scholar] [CrossRef]
  11. Liu, L.; Song, H.X.; Geng, H.Y.; Bi, Y.; Xu, J.-a.; Li, X.; Li, Y.; Liu, J. Compressive behaviors of bcc bismuth up to 55 GPa. Phys. Status. Solidi. (b) 2013, 250, 1398–1403. [Google Scholar] [CrossRef]
  12. Katahara, K.W.; Manghnani, M.H.; Fisher, E.S. Pressure derivatives of the elastic moduli of niobium and tantalum. J. Appl. Phys. 1976, 47, 434–439. [Google Scholar] [CrossRef]
  13. Holzapfel, W.B.; Hartwig, M.; Sievers, W. Equations of state for Cu, Ag, and Au for wide ranges in temperature and pressure up to 500 GPa and above. J. Phys. Chem. Ref. Data 2001, 30, 515–529. [Google Scholar] [CrossRef]
  14. Qi, X.; Cai, N.; Wang, S.; Li, B. Thermoelastic properties of tungsten at simultaneous high pressure and temperature. J. Appl. Phys. 2020, 128, 105105. [Google Scholar] [CrossRef]
  15. Jamieson, J.; Fritz, J.N.; Manghanani, M.H. Adv. Earth Planet. Sci. 1980, 12, 27.
  16. Holmes, N.C.; Moriarty, J.A.; Gathers, G.R.; Nellis, W.J. The equation of state of platinum to 660 GPa (6.6 Mbar). J. Appl. Phys. 1989; 66, 2962–2967. [Google Scholar] [CrossRef]
  17. Dewaele, A.; Datchi, F.; Loubeyre, P.; Mezouar, M. High pressure-high temperature equations of state of neon and diamond. Phys. Rev. B 2008, 77, 094106. [Google Scholar] [CrossRef]
  18. Vinet, P.; Ferrante, J.; Rose, J.H.; Smith, J.R. Compressibility of solids. J. Geophys. Res. Solid Earth 1987, 92, 9319–9325. [Google Scholar] [CrossRef]
  19. Vinet, P.; Ferrante, J.; Smith, J.R.; Rose, J.H. A universal equation of state for solids. J. Phys. C: Solid State Phys. 1986, 19, L467. [Google Scholar] [CrossRef]
  20. Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. Solid Earth 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
  21. Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
  22. Holzapfel, W.B. Equations of state for solids under strong compression. High Pressure Res. 1998, 16, 81–126. [Google Scholar] [CrossRef]
  23. Holzapfel, W.B. Physics of solids under strong compression. Rep. Prog. Phys. 1996, 59, 29. [Google Scholar] [CrossRef]
  24. Gaurav, S.; Sharma, B.S.; Sharma, S.B.; Upadhyaya, S.C. Analysis of equations of state for solids under high compressions. Physica B 2002, 322, 328–339. [Google Scholar] [CrossRef]
  25. Burakovsky, L.; Burakovsky, N.; Cawkwell, M.J.; Preston, D.L.; Errandonea, D.; Simak, S.I. Ab initio phase diagram of iridium. Phys. Rev. B 2016, 94, 094112. [Google Scholar] [CrossRef]
  26. Gutiérrez, G.; Menéndez-Proupin, E.; Singh, A.K. Elastic properties of the bcc structure of bismuth at high pressure. J. Appl. Phys. 2006, 99, 103504. [Google Scholar] [CrossRef]
  27. Ning, B.-Y.; Gong, L.-C.; Weng, T.-C.; Ning, X.-J. Efficient approaches to solutions of partition function for condensed matters. J. Phys.: Condens. Matter 2021, 33, 115901. [Google Scholar] [CrossRef] [PubMed]
  28. Han, J.; Shi, L.-Q.; Wang, N.; Zhang, H.-F.; Peng, S.-M. Equation of state of Iridium: from insight of ensemble theory. J. Phys.: Condens. Matter 2022, 34, 465702. [Google Scholar] [CrossRef] [PubMed]
  29. Gong, L.-C.; Ning, B.-Y.; Weng, T.-C.; Ning, X.-J. Comparison of Two Efficient Methods for Calculating Partition Functions. Entropy 2019, 21, 1050. [Google Scholar] [CrossRef]
  30. Liu, Y.-P.; Ning, B.-Y.; Gong, L.-C.; Weng, T.-C.; Ning, X.-J. A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate. Nanomaterials 2019, 9, 978. [Google Scholar] [CrossRef]
  31. Ning, B.-Y.; Ning, X.-J. Pressure-induced structural phase transition of vanadium: a revisit from the perspective of ensemble theory. J. Phys.: Condens. Matter 2022, 34, 425404. [Google Scholar] [CrossRef]
  32. Ning, B.-Y. Pressure-induced structural phase transitions of zirconium: an ab initio study based on statistical ensemble theory. J. Phys.: Condens. Matter 2022, 34, 505402. [Google Scholar] [CrossRef] [PubMed]
  33. Ning, B.-Y.; Zhang, L.-Y. An ab initio study of structural phase transitions of crystalline aluminium under ultrahigh pressures based on ensemble theory. Comput. Mater. Sci. 2023, 218, 111960. [Google Scholar] [CrossRef]
  34. Tian, Y.-Y.; Ning, B.-Y.; Zhang, H.-F.; Ning, X.-J. Equation of state for tungsten obtained by direct solving the partition function. J. Appl. Phys. 2024, 135, 015102. [Google Scholar] [CrossRef]
  35. Dierckx, P. An algorithm for smoothing, differentiation and integration of experimental data using spline functions. J. Comput. Appl. Math. 1975, 1, 165–184. [Google Scholar] [CrossRef]
  36. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  37. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  38. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  39. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  40. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  41. Mukherjee, D.; Sahoo, B.D.; Joshi, K.D.; Gupta, S.C. On equation of state, elastic, and lattice dynamic stability of bcc bismuth under high pressure: Ab-initio calculations. J. Appl. Phys. 2014, 115, 053702. [Google Scholar] [CrossRef]
  42. Xiang, S.; Xi, F.; Bi, Y.; Xu, J.a.; Geng, H.; Cai, L.; Jing, F.; Liu, J. Ab initio thermodynamics beyond the quasiharmonic approximation: W as a prototype. Phys. Rev. B 2010, 81, 014301. [Google Scholar] [CrossRef]
  43. Wang, Y.; Chen, D.; Zhang, X. Calculated Equation of State of Al, Cu, Ta, Mo, and W to 1000 GPa. Phys. Rev. Lett. 2000, 84, 3220–3223. [Google Scholar] [CrossRef] [PubMed]
  44. Burakovsky, L.; Burakovsky, N.; Preston, D.; Simak, S. Systematics of the Third Row Transition Metal Melting: The HCP Metals Rhenium and Osmium. Crystals 2018, 8, 243. [Google Scholar] [CrossRef]
  45. Fratanduono, D.E.; Millot, M.; Braun, D.G.; Ali, S.J.; Fernandez-Pañella, A.; Seagle, C.T.; Davis, J.-P.; Brown, J.L.; Akahama, Y.; Kraus, R.G.; et al. Establishing gold and platinum standards to 1 terapascal using shockless compression. Science 2021, 372, 1063–1068. [Google Scholar] [CrossRef] [PubMed]
  46. Fratanduono, D.E.; Smith, R.F.; Ali, S.J.; Braun, D.G.; Fernandez-Pañella, A.; Zhang, S.; Kraus, R.G.; Coppari, F.; McNaney, J.M.; Marshall, M.C.; et al. Probing the solid phase of noble metal copper at terapascal conditions. Phys. Rev. Lett. 2020, 124, 015701. [Google Scholar] [CrossRef] [PubMed]
  47. Jin, K.; Wu, Q.; Geng, H.; Li, X.; Cai, L.; Zhou, X. Pressure-volume-temperature equations of state of Au and Pt up to 300 GPa and 3000 K: internally consistent pressure scales. High Pressure Res. 2011, 31, 560–580. [Google Scholar] [CrossRef]
  48. Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef]
  49. Dorogokupets, P.I.; Oganov, A.R. Ruby, metals, and MgO as alternative pressure scales: A semiempirical description of shock-wave, ultrasonic, X-ray, and thermochemical data at high temperatures and pressures. Phys. Rev. B 2007, 75, 024115. [Google Scholar] [CrossRef]
  50. Sokolova, T.S.; Dorogokupets, P.I.; Litasov, K.D. Self-consistent pressure scales based on the equations of state for ruby, diamond, MgO, B2-NaCl, as well as Au, Pt, and other metals to 4 Mbar and 3000 K. Russ. Geol. Geophys. 2013, 54, 181–199. [Google Scholar] [CrossRef]
  51. Gong, L.-C.; Ning, B.-Y.; Ming, C.; Weng, T.-C.; Ning, X.-J. How accurate for phonon models to predict the thermodynamics properties of crystals. J. Phys.: Condens. Matter 2021, 33, 085901. [Google Scholar] [CrossRef]
Preprints 103285 g001
Figure 1. (color online) A 3 × 3 × 3 supercell of bcc Bi with optimized lattice constant a0, in which an arbitrary atom in the red circle is moved along the [100] direction (red arrow) step by step until its final position labeled in the green circle to obtain U ’ x ’ (a); dependence of U ’ x ’ on the distance of the moved atom away from its equilibrium potion x ’ under a series of volumes with lattice constant ac changed from 0.76 a0 to 0.98 a0 (b).
Figure 1. (color online) A 3 × 3 × 3 supercell of bcc Bi with optimized lattice constant a0, in which an arbitrary atom in the red circle is moved along the [100] direction (red arrow) step by step until its final position labeled in the green circle to obtain U ’ x ’ (a); dependence of U ’ x ’ on the distance of the moved atom away from its equilibrium potion x ’ under a series of volumes with lattice constant ac changed from 0.76 a0 to 0.98 a0 (b).
Preprints 103285 g001
Preprints 103285 g002
Figure 2. (color online) Absolute volume (V) (a) and relative volume (V/V7.7) (b) vs pressure of bcc Bi with V7.7 the volume under 7.7 GPa at 300 K. The red solid and black dashed lines are the calculated curves by DIA and Debye model [41], respectively. The measurements in two experimental runs performed in 2002 by Akahama et al. [10] are respectively represented by the green dots (run 1) and triangles (run 2). In 2023, Campbell et al. [9] provided three sets of compressed data denoted by the purple squares (run A), circles (run B) and triangles (run C). The orange solid and open diamonds represent the two sets of experimental measurements conducted in a conventional and toroidal DAC (tDAC) by Storm et al. [8] in 2023. Liu et al. [11] in 2013 investigated the EOS of Bi using He, Ar and silicone oil (SO) as the PTM, and the corresponding measurements are shown by the blue solid stars (He), pentagons (Ar) and open stars (SO), respectively, which is not exhibited in (a) because absolute volumes of Bi were not presented in their work. Since bcc Bi was recognized to emerge at 7.7 GPa (marked by the vertical dash dotted line in (a) and (b)), all the discussions in the context start from 7.7 GPa.
Figure 2. (color online) Absolute volume (V) (a) and relative volume (V/V7.7) (b) vs pressure of bcc Bi with V7.7 the volume under 7.7 GPa at 300 K. The red solid and black dashed lines are the calculated curves by DIA and Debye model [41], respectively. The measurements in two experimental runs performed in 2002 by Akahama et al. [10] are respectively represented by the green dots (run 1) and triangles (run 2). In 2023, Campbell et al. [9] provided three sets of compressed data denoted by the purple squares (run A), circles (run B) and triangles (run C). The orange solid and open diamonds represent the two sets of experimental measurements conducted in a conventional and toroidal DAC (tDAC) by Storm et al. [8] in 2023. Liu et al. [11] in 2013 investigated the EOS of Bi using He, Ar and silicone oil (SO) as the PTM, and the corresponding measurements are shown by the blue solid stars (He), pentagons (Ar) and open stars (SO), respectively, which is not exhibited in (a) because absolute volumes of Bi were not presented in their work. Since bcc Bi was recognized to emerge at 7.7 GPa (marked by the vertical dash dotted line in (a) and (b)), all the discussions in the context start from 7.7 GPa.
Preprints 103285 g002
Preprints 103285 g003
Figure 3. Under the same value of V/V7.7, differences between the calculated pressure from DIA (PDIA) or Debye model (PDM) with the in situ experimental measurement (PExp) by Akahama et al. [10], Liu et al. [11], Storm et al. [8], and Campbell et al. [9] are displayed as the red or black symbols in (a), (b), (c) and (e), respectively. After the pressures in Ref. [10] are re-evaluated using the latest Pt scale proposed by Fratanduono et al. [45], the deviations between PDIA or PDM with the re-calibrated pressures are displayed in (a) by the brown or blue symbols, respectively. If the x-ray diffraction peaks of only the (111) lattice plane of the used Cu and Au pressure markers are selected to determine the pressures (labeled by PExp (111)) in Ref. [8], the deviations of PDIA or PDM with PExp (111) are displayed in (d). For the pressures in the first two experimental runs (run A and run B) and the third one (run C) of Ref. [9], recalibrating was performed with the latest Cu pressure gauge of Fratanduono et al. [46] and the neon EOS of Dewaele et al. [17], respectively, and the deviations of PDIA or PDM with the re-estimated pressures are represented by the corresponding orange and green symbols in (f).
Figure 3. Under the same value of V/V7.7, differences between the calculated pressure from DIA (PDIA) or Debye model (PDM) with the in situ experimental measurement (PExp) by Akahama et al. [10], Liu et al. [11], Storm et al. [8], and Campbell et al. [9] are displayed as the red or black symbols in (a), (b), (c) and (e), respectively. After the pressures in Ref. [10] are re-evaluated using the latest Pt scale proposed by Fratanduono et al. [45], the deviations between PDIA or PDM with the re-calibrated pressures are displayed in (a) by the brown or blue symbols, respectively. If the x-ray diffraction peaks of only the (111) lattice plane of the used Cu and Au pressure markers are selected to determine the pressures (labeled by PExp (111)) in Ref. [8], the deviations of PDIA or PDM with PExp (111) are displayed in (d). For the pressures in the first two experimental runs (run A and run B) and the third one (run C) of Ref. [9], recalibrating was performed with the latest Cu pressure gauge of Fratanduono et al. [46] and the neon EOS of Dewaele et al. [17], respectively, and the deviations of PDIA or PDM with the re-estimated pressures are represented by the corresponding orange and green symbols in (f).
Preprints 103285 g003
Table 1. Relative volume (V/V7.7) as a function of pressure (in GPa). V7.7 is the calculated atomic volume (28.58 Å3/atom) of bcc Bi under 7.7 GPa at 300 K.
Table 1. Relative volume (V/V7.7) as a function of pressure (in GPa). V7.7 is the calculated atomic volume (28.58 Å3/atom) of bcc Bi under 7.7 GPa at 300 K.
P V
7.7 1.0000
10 0.9728
20 0.8891
30 0.8311
40 0.7890
50 0.7545
60 0.7265
70 0.7026
80 0.6819
90 0.6637
100 0.6474
110 0.6328
120 0.6197
130 0.6077
140 0.5965
150 0.5862
160 0.5766
170 0.5677
180 0.5593
190 0.5515
200 0.5441
210 0.5370
220 0.5303
230 0.5240
240 0.5180
250 0.5122
260 0.5068
270 0.5015
280 0.4965
290 0.4916
300 0.4870
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated