Prerpints.org logo
Preprint
Article

User Anxiety-aware Electric Vehicle Charging Scheduling: An Episodic Deep Reinforcement Learning Approach

Altmetrics

Downloads

125

Views

141

Comments

0

This version is not peer-reviewed

Electric Vehicles Energy Management, 2nd Volume

Submitted:

05 April 2024

Posted:

09 April 2024

You are already at the latest version

Alerts
Abstract
The transportation industry is rapidly transitioning from Internal Combustion Engine (ICE) based vehicles to Electric Vehicles (EVs) to promote clean energy. However, large-scale adoption of EVs can compromise the reliability of the power grids by introducing large uncertainty in the demand. Demand response with a controlled charge scheduling strategy for EVs can mitigate such issues. In this paper, a deep reinforcement learning- based charge scheduling strategy is developed for individual EVs by considering user’s dynamic driving behavior and charging preferences. The temporal dynamics of user’s anxiety about charging the EV battery is rigorously addressed. A dynamic weight allocation technique is applied to continuously tune user’s priority for charging and cost-saving with respect to charging duration. The sequential charging control problem is formulated as a Markov decision process, and an episodic approach to the deep deterministic policy gradient (DDPG) algorithm with target policy smoothing and delayed policy update techniques is applied to develop the optimal charge scheduling strategy. A real-world dataset that captures user’s driving behavior, such as arrival time, departure time, and charging duration, is utilized in this study. The extensive simulation results reveal the effectiveness of the proposed algorithm in minimizing energy cost while satisfying user’s charging requirements.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

I. Introduction

High renewable energy penetration and transportation electrification are the keys to building a secure and sustainable energy infrastructure due to their potential for reducing carbon emission and dependency on fossil fuels [1]. Many countries are adopting this potential as an initiative to promote their fuel efficiency and emission standards. For instance, the United States has outlined its target to increase the national Electric Vehicles (EV) sales shares to 50% by 2030 [2]. This is also reflected in the increasing trend of global sales of EVs in recent years. International Energy Agency (IEA) reported that there was a 41% growth in new EV registrations in the year 2020 alone, undeterred by the pandemic-related worldwide downturn in car sales [3]. Although EVs offer numerous environmental benefits, large-scale adoption of EVs may pose severe impacts on power grids due to the large and undesirable peaks in the load [4]. Enhancing the generation capacity and network restructuring can be a proactive measure. However, this solution requires substantial infrastructure investments and is a time-consuming approach that is unable to cope with the rapid growth of EV adoption in the transportation industry. Another feasible yet cost-effective solution is adopting the Demand Response (DR) programs that enable EV users to coordinate their charging schedules in response to time-varying electricity prices [5]. With a readily available Vehicle-to-Grid (V2G) technology [6], EV users can also incentivize themselves by supplying energy to the grid and thus can contribute to the supply/demand balance for the grid.
Time-varying electricity pricing is a widely adopted DR strategy that helps enhance grid reliability and reduce high generation cost caused by peak demand. Contrary to traditional flat-rate pricing, where customers are charged at the same rate throughout the day, time-varying pricing (TVP) allows the utilities to offer variable rates to their customers at different times of the day depending on total demand, supply, and other critical factors. TVP incentivizes the users to shift their demand from peak hours to off-peak hours and thus, reduce their energy costs as well as reduce the unwanted spikes in the load curve. Utilities offer a variety of TVP programs to their customers, among which Time-of-use (TOU) [7] is the most common pricing program, where the day is divided into two or three consecutive blocks of hours based on peak, off-peak, and mid-peak periods. In TOU, the prices vary from one block to another. Therefore, it is less reflective of the volatile nature of the wholesale electricity prices. In critical-peak-pricing (CPP), utilities use their load forecasting capability and identify a ‘critical event’ when the price increases dramatically due to deterrent system conditions or weather. Usually, these events are identified and communicated to the users at least a day in advance and are only applied up to 18 times per calendar year [8]. Both TOU and CPP are known in advance, and hence, customers can plan their energy usage accordingly. Another pricing program that closely follows the wholesale energy market is Real-time-pricing (RTP) [9]. In RTP, prices vary hourly (sometimes sub-hourly) to reflect the real-time fluctuations in the wholesale market due to variations in demand, supply, generator failure, etc. 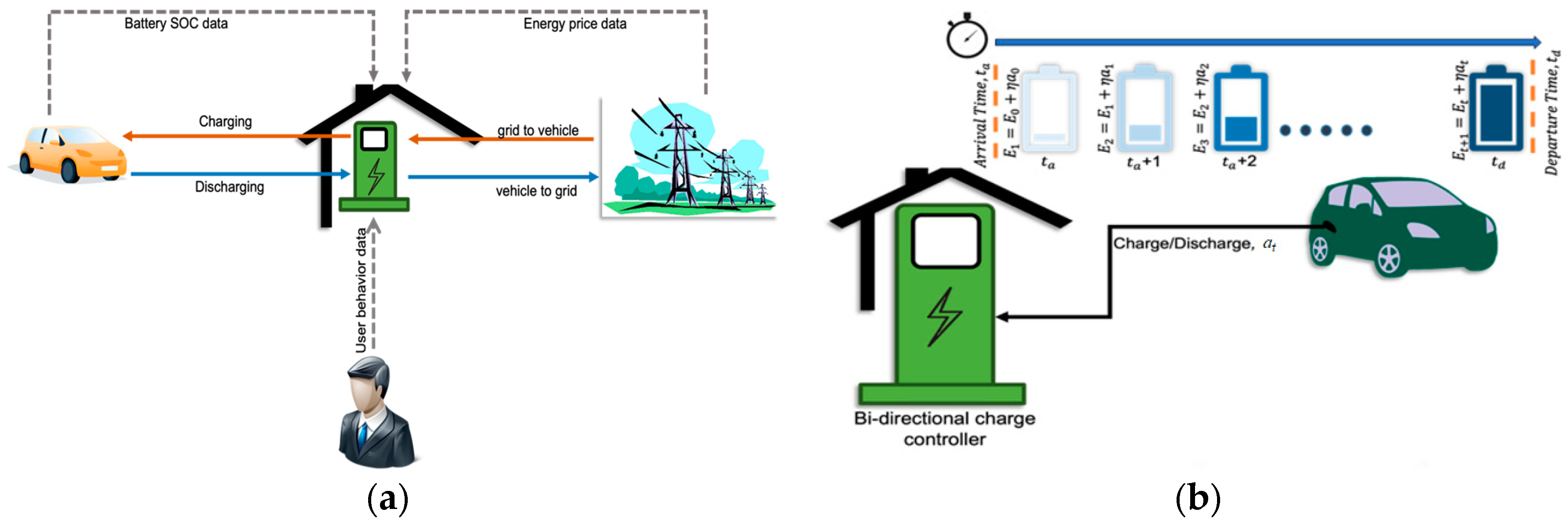Although RTP is yet to be adopted by many utility companies, pilot projects run by several utilities, such as Commonwealth Edison Company (ComEd) and Georgia Power, have proven its economical and practical viability for efficient energy management [10,11]. RTP can be cleared day-ahead or every hour. EV users can respond to the hourly variable pricing signal by navigating their charging demand. Therefore, this paper considers that an hourly day-ahead pricing signal is available to the EV user. Additionally, we consider the grid to be bi-directional with net metering arrangements [12] to facilitate V2G technology. V2G allows the users to inject surplus energy of their EV batteries into the grid. Net metering is required to realize V2G as it enables bidirectional trading of energy between EV users and the grid [13].
An efficient charge scheduling strategy should meet the requirements of both EV users and utility companies. From the EV users’ perspective, the requirements consist of meeting their charging demand and meanwhile minimizing charging costs. From the utility’s perspective, the requirements include ‘peak shaving’ during peak hours and ‘valley filling’ during off-peak hours to facilitate the operation and increase the reliability of the grid. Therefore, an appropriate DR program that can meet these requirements is necessary to accommodate the large-scale adoption of EVs. By implementing an effective charging control strategy, EV users can benefit themselves and help the grid by responding to the pricing signal. On the flip side of the coin, the uncertainties pertaining to the user’s driving behavior, i.e., random arrival and departure times of EVs to and from a charging station, need to be addressed rigorously to develop a charging control scheme. Moreover, users’ sporadic charging preferences and time-varying energy prices of the utilities also need to be accounted for by an effective solution.
Reinforcement Learning (RL) has been used in many studies as the solution method for optimal charge scheduling of EVs. In general, RL helps to learn the policy of selecting the best action in a given environment. An on-policy RL algorithm such as state-action-reward-state-action (SARSA) [14] is used in [15] where discrete state and action spaces are considered. However, a discrete state space limits the actual representation of a real-world charging environment. Reference [16] uses Hyperopia SARSA (HSA), where a linear function approximator is used to evaluate the charging actions. Another deficiency of on-policy RL is that the same policy is used for decision-making and evaluation, which potentially limits exploration of the RL agent. To overcome this, off-policy RL leverages experiences generated by random policies facilitating better simulations of real-world scenarios. Off-policy RL, such as Q-learning [17], is used to derive optimal charging strategy for EVs, focusing on various objectives, such as minimizing the charging cost, maximizing EV user’s revenue, satisfying charging demand, and balancing the grid load [18,19,20,21]. However, Q-learning inherently suffers in real-world scenarios where the state and action spaces are large and continuous. Moreover, both SARSA and Q-learning suffer from limited approximation capability in the case of policy evaluation, such as action-value estimation.
Recent successes of Deep Reinforcement Learning (DRL) [22,23] have inspired many researchers to address the problem of EV charge scheduling using DRL. Reference [24] applies Deep Q-Learning (DQN) to minimize electricity bill and user’s range anxiety. User’s range anxiety, defined as the difference between the current and the desired battery energy, is applied at the departure time. Reference [25] uses Kernel Density Estimation (KDE) to approximate variables related to charger usage patterns, such as arrival time, charging duration, and charging amount from real-world data. However, in both [24] and [25], the EV charge scheduling problem is solved using DQN considering discrete charging rates as action space. DQN can only handle discrete action space and, therefore, are not suitable for the problems where continuous action space is required. Authors in [26] address this issue by formulating the problem as a Constrained Markov Decision Process (CMDP) and derive a continuous charge scheduling strategy using Constrained Policy Optimization (CPO) [27]. User’s range anxiety is handled using the constraints and a cost function. However, this work disregards user’s anxiety during the charging periods, which is an essential factor when determining an optimal charging strategy. Reference [28] uses continuous soft actor-critic (SAC) algorithm to learn an optimal charging control strategy. The reward function includes three types of sensitivity coefficients based on user’s preference that requires manual tuning. Reference [29] also considers continuous charging actions and proposes a Control Deep Deterministic Policy Gradient (CDDPG) algorithm to learn the optimal charging policy. This algorithm uses two replay memories: one to store all the experiences generated before the end of an episode and the other to store only the last experience of an episode. Experiences are then sampled from both memories to train the model. While the performance is favorable, sampling from two different replay memories introduces biased updates that consequently affect the learning performance. To ensure that the unbiased sampling property of RL is maintained, the importance-sampling technique can be implemented [30].
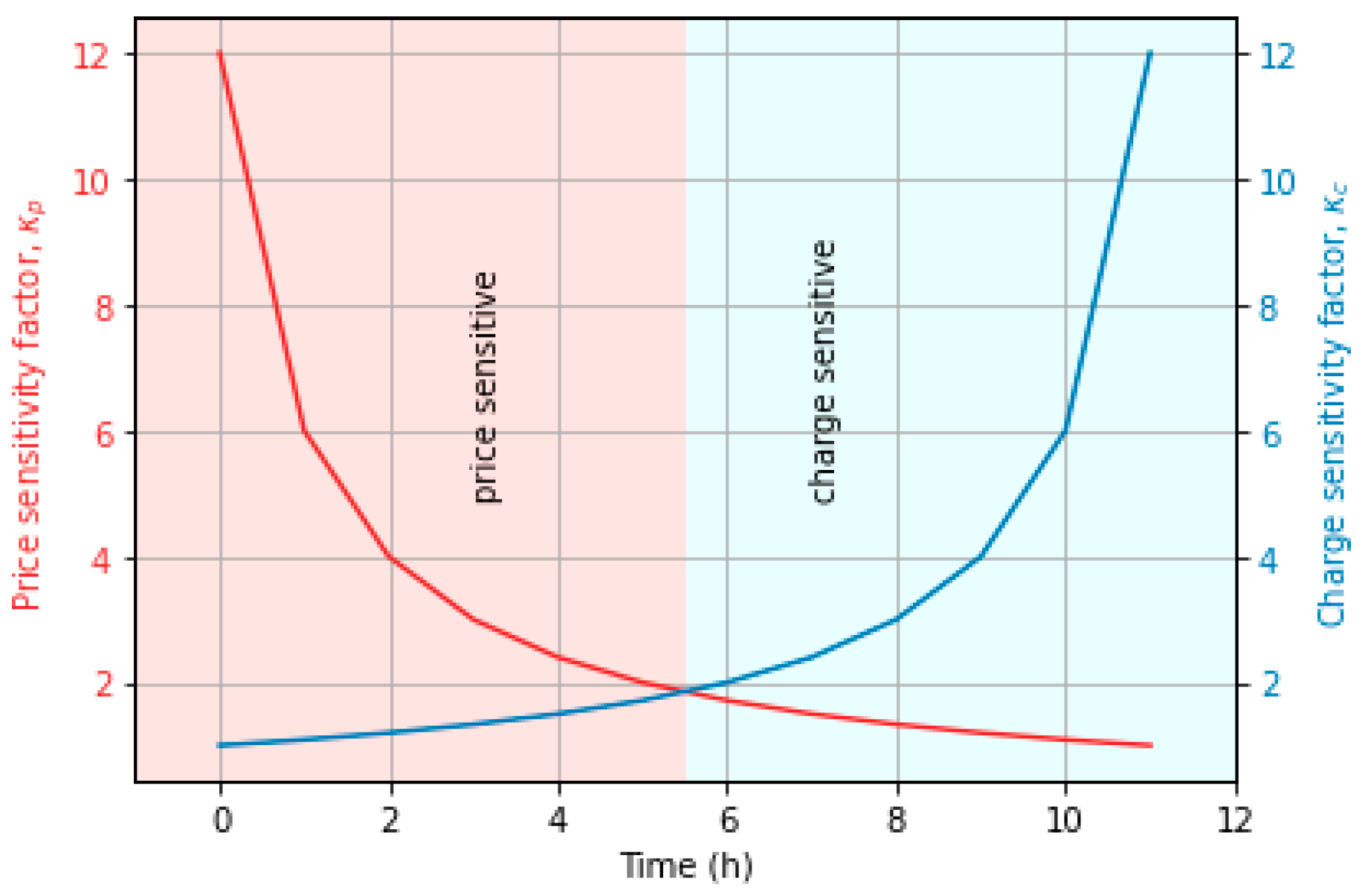
Despite the promising outcomes, the preceding methods lack a few critical aspects when determining the charge scheduling strategy. Firstly, the influence of the remaining charging duration is ignored in the literature when defining user’s anxiety. More specifically, the variation of user’s anxiety with time is not addressed. In our work, we address this variation by defining an anxiety function not only in terms of uncharged battery energy but also in terms of the remaining charging duration. Secondly, the previous works used manually tuned constant coefficients to represent user’s preference for meeting energy demand over minimizing energy cost. In a practical scenario, a user is naturally more inclined to minimize energy cost during the first few hours of the charging duration. As it approaches the departure time, the importance of charging the battery to satisfy the energy requirement increases when compared to minimizing cost. Using constant coefficients cannot account for this scenario effectively. Thus, we introduce a dynamic weight allocation technique to address this issue and avoid the need for manual tuning of coefficients. Thirdly, the randomness of user’s driving behavior, such as arrival time, departure time, etc., was modeled by using a normal distribution in most studies. However, the distribution was defined based on assumptions that may fail to reflect the unpredictability in the real-world. In this paper, a real-world dataset is utilized to extract key information, such as arrival time, departure time, charging duration, and battery SOC.
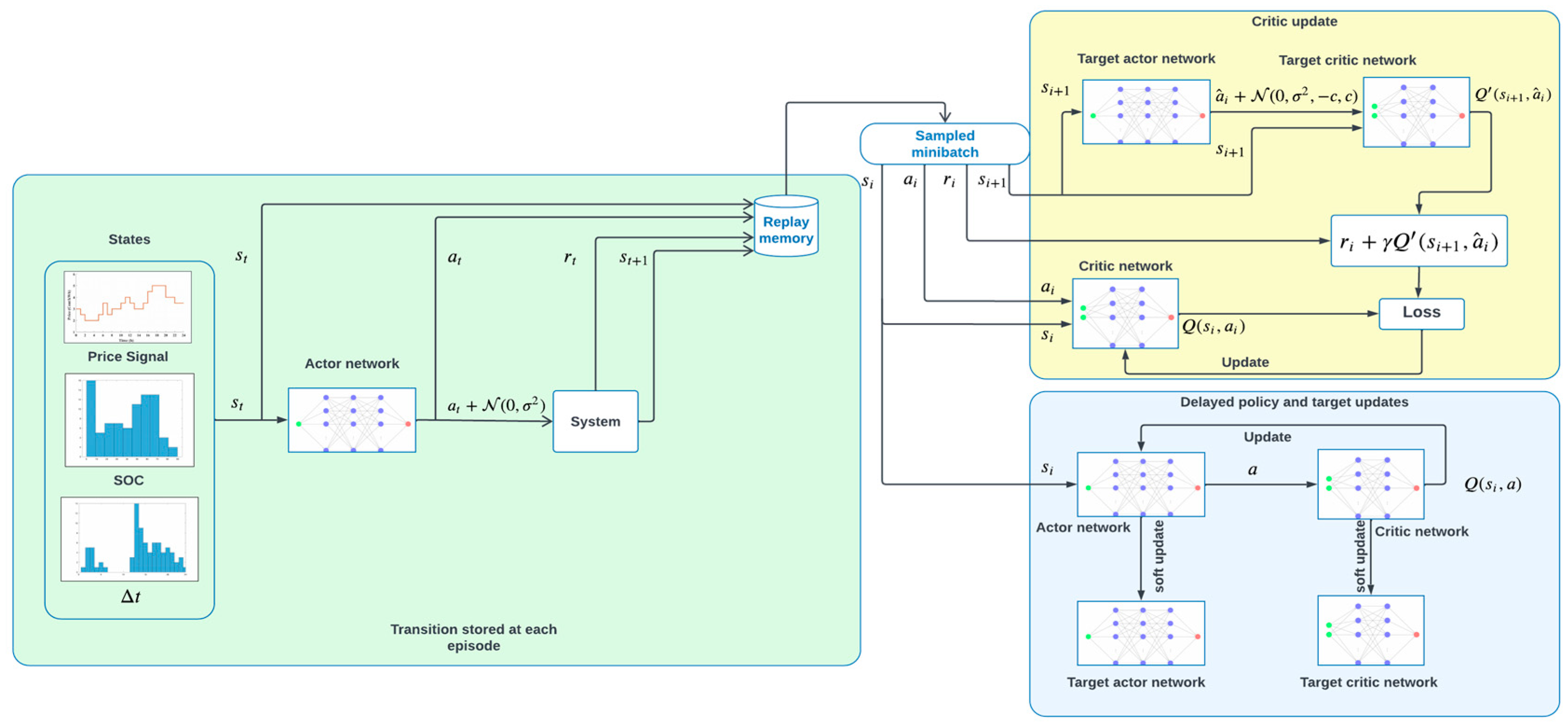
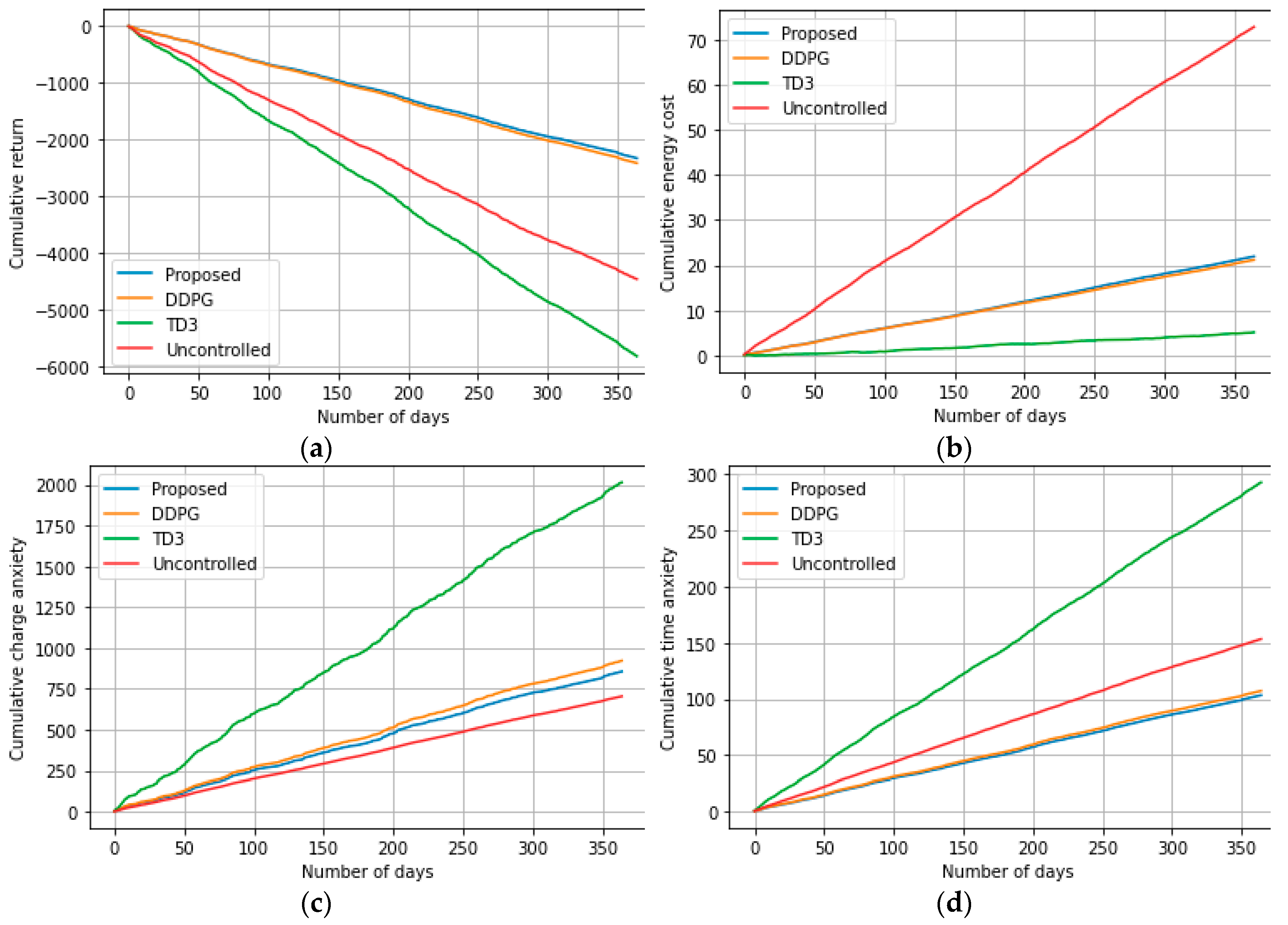
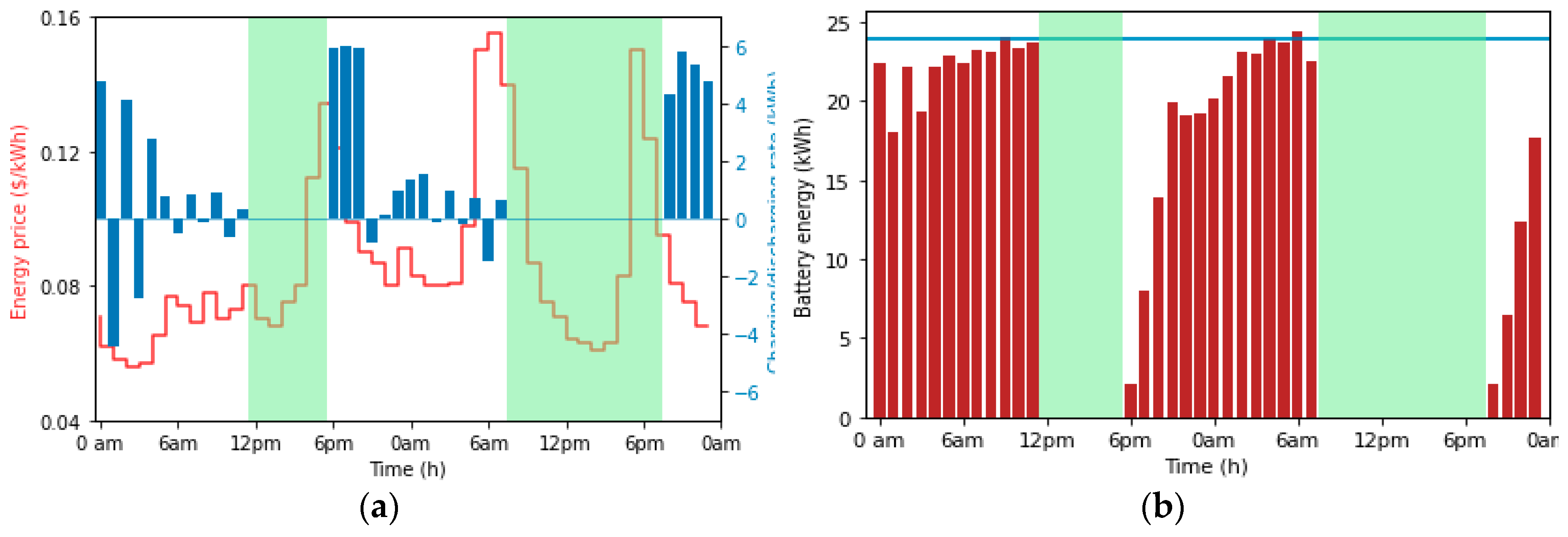
In this work, the anxiety is applied during the entire time horizon of the charging duration to address the influence of time on user’s anxiety. 2) A dynamic weight allocation technique is used to implement the time-varying importance of the components of the reward function. Upon arrival, the weight of energy cost is the highest, and the weight of the anxiety components is the lowest. In sharp contrast, at departure, the weight of the energy cost is the lowest, and the weight of the anxiety components is the highest. 3) This paper proposes an episodic approach to the widely used Deep Deterministic Policy Gradient (DDPG) algorithm [31], in which each episode corresponds to the complete charging duration between the arrival and departure times. 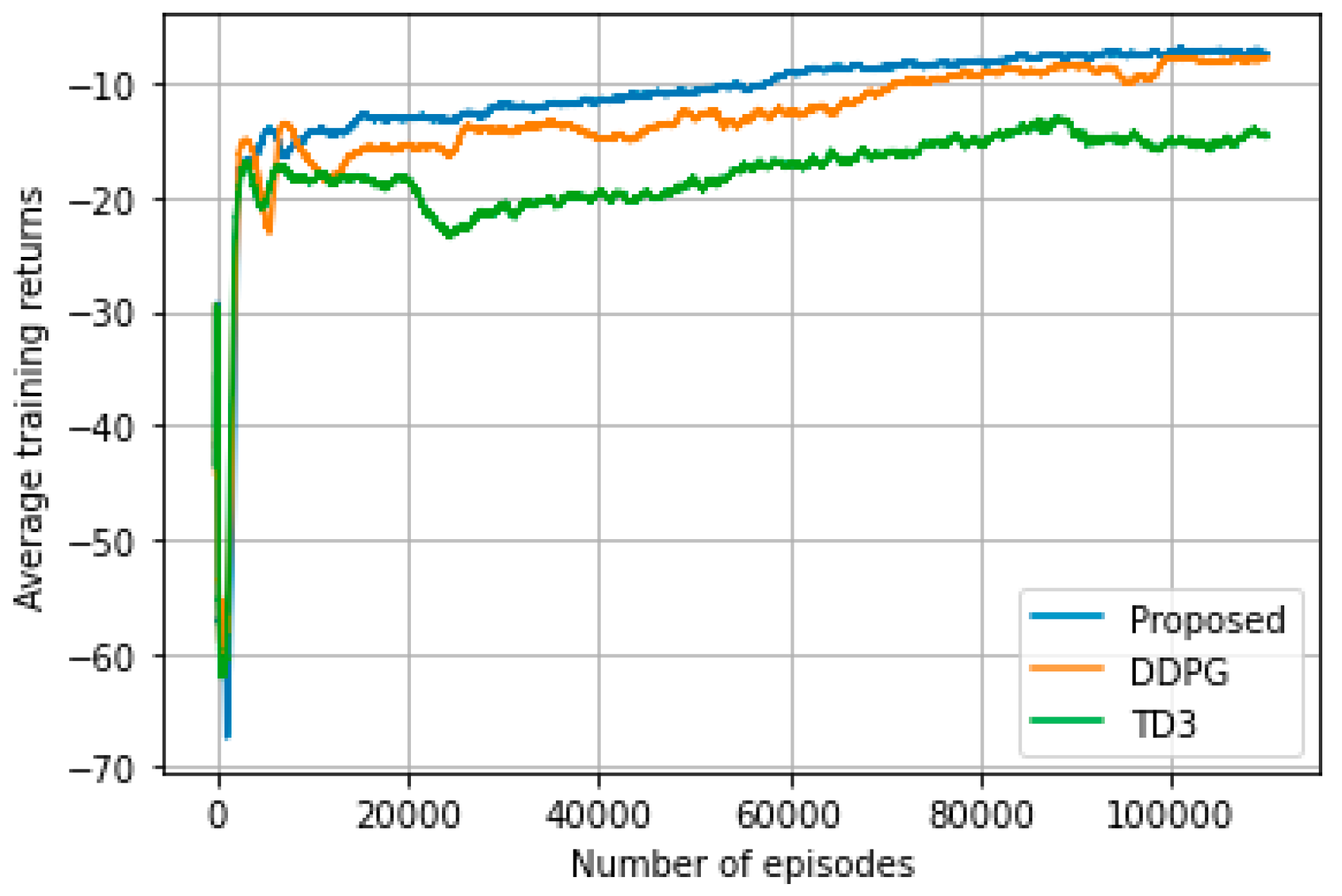Moreover, this paper incorporates target policy smoothing and delayed policy update techniques from the Twin Delayed DDPG (TD3) algorithm [32] to address the inherent instability and overfitting problems of the DDPG algorithm. 4) Finally, a real-world dataset is used to derive a realistic model for user's random driving behavior, such as arrival time, departure time, and battery SOC. The performance is compared with two state-of-the-art DRL algorithms: DDPG and TD3. The simulation results exhibit the effectiveness of the proposed algorithm in terms of energy cost minimization and energy demand satisfaction.
The objective of this paper is to develop a charge scheduling strategy that ensures the maximum battery SOC by the time of departure, while minimizing the energy costs through a controlled and dynamic decision-making technique. To obtain the optimal strategy for EV charging control, we propose a model-free DRL-based algorithm. The main contributions of this article are as follows. 1) User’s anxiety is redefined in terms of the remaining energy and the remaining charging duration. More specifically, user’s anxiety consists of two components: a) the difference between the present battery SOC and the target SOC, and b) the ratio of the difference between the present battery SOC and the target SOC to the remaining charging duration. Unlike the previously mentioned studies, in which the anxiety was applied only on the departure time.
The rest of the paper is structured as follows: Section II discusses the system model and a detailed MDP formulation. In Section III, a brief background of DRL followed by the proposed algorithm is presented. In Section IV, performance evaluation of the proposed algorithm along with detailed analysis of the results is provided. Finally, Section V concludes this paper.

II. System Model and Problem Formulation

A. EV Charge Scheduling Model

An overall system model is presented in Figure 1. This paper focuses on deriving an EV charging control strategy for home energy management, i.e., we only consider the charging period when the EV is parked at home. Figure 1a illustrates the information and power flow between the components of the system. Day-ahead pricing signal and user’s driving data, such as arrival time and departure time, are stored and processed by the bidirectional home charge controller. The vehicle’s battery SOC is received by the charge controller in real-time. The gray dotted lines represent the unidirectional information flow that is received and processed by the charge controller. This information potentially serves as the state variables of the MDP, which is described in a later subsection. Based on the information, the charge controller makes charging or discharging decisions for the EV. The solid lines represent the power flow. Figure 1b illustrates the sequential charging and discharging setup for one specific charging period. The total charging period is essentially the hourly time difference between the arrival time and the next departure time of an EV. We consider hourly charging time intervals or time steps and define the remaining charging duration ∆t according to the following equation:
∆ t =   t d − t ,   f o r t a ≤ t < t d ,
in which t a and t d denote the arrive time and departure time, respectively. Specifically, the remaining charging duration ∆t equals the total charging period when the EV is connected to the charger or at arrival time ta. Further, ∆t decreases by one hour at each time step until the charging period ends, and ∆t reduces to 1 at the last hour before the departure time t d . Since hourly time steps are considered, ∆t is a discrete variable whose value can range from 1 to 24 hours. In real-world scenarios, ∆t typically ranges from 1 to 14 hours based on the realistic vehicle data set used in this study [34].
Each EV has two charging modes: G2V and V2G. The battery dynamics are described as follows:
E t + 1 = E t + η a t ,   f o r E   ∈ ( 0 ,   C ) ,
in which E t is the stored energy of the EV battery, η is the charging/discharging efficiency factor of the EV battery, and a t is the charging/discharging power determined by the control algorithm at time t. Specifically, a t is positive and η is less than 1 when the battery is being charged, and at is negative and η is greater than 1 for battery discharging. Further,
is limited by the battery capacity C. Battery SOC, s o c t   at time t is the ratio of the current stored battery energy E t and the rated capacity of the battery C [33], which can be expressed as follows:
<!-- MathType@Translator@5@5@MathML2 (no namespace).tdl@MathML 2.0 (no namespace)@ -->
E t .
Then, based on (2), the dynamics in the state of charge can be described by the following equation:
s o c t + 1 = s o c t + η E t C ,   f o r s o c   ∈ ( 0 ,   1 ) .
At each time step, a bill is generated when the battery is charged, i.e., when a t is positive, and revenue is generated when discharged, i.e., when a t is negative. We consider this scenario based on the net metering arrangement where a bi- directional meter measures both the incoming and outgoing electricity for G2V and V2G modes, respectively. We denote this bill/revenue for charging/discharging energy at time t as ξ t and calculate it using the equation below:
ξ t = p t a t ,
in which p t denotes the energy price at time t. User’s anxiety due to uncharged battery energy at each time step is defined by the absolute deficit in the present SOC from the user’s target SOC. Therefore, user’s charge anxiety ϕ t is defined as follows:
ϕ t = s o c t a r g e t − s o c t + .
Intuitively, user’s anxiety is proportional to the difference between the target SOC and the current SOC. However, we notice that user’s anxiety also varies with time, in the sense that it is inversely proportional to the remaining charging duration ∆t. This is because the user tends to be more anxious when the remaining charging duration is less compared to when the remaining charging duration is more even at the same SOC level. With this insight, we define this anxiety as user’s time anxiety ψ t   as follows:
ψ t = s o c t a r g e t − s o c t + ∆ t .
The charging control model aims to minimize individual EV user’s electricity cost, charge anxiety, and time anxiety. However, the randomness of critical parameters, such as user’s driving and charging behavior, user’s charging preference, and time-varying prices, prevent us from applying a direct optimization rule to our model. In the following subsection, we develop an MDP-based formulation for the proposed charging control model to address this issue.

B. MDP Formulation

The problem of EV charge scheduling can be viewed as a sequential decision-making problem where the environment is partially random, and MDP provides effective mathematical modeling for such problems. We formulate the model from the previous subsection as a finite MDP with discrete time steps. Specifically, at each time step, the charge controller observes the environment state s t , takes an action a t that controls the charging/discharging power, receives a reward r t for that action from the environment, and moves to a new state s t + 1 . This process is repeated until the charging period is complete. In this paper, we define the MDP model with 5-tuples {S, A, P, R, γ} where S represents the state space of the environment, A represents the continuous action space, P is the state transition probability, R is the immediate reward function, and γ is the discount factor. The details about the MDP are presented in the following.
State: We include the vehicle’s battery SOC, electricity price, and user’s driving behavior as the state variables. More specifically, the state of our EV charge scheduling agent at time t is defined as s t a 3-tuple state-space represented by the following,
s t = s o c t ,   p t ,   ∆ t   a n d s t ∈ S ,
in which s o c t denotes battery SOC at time t, pt denotes per unit price of energy at time t, and ∆t denotes the remaining charging duration from time t to departure time t d as described in (1). Note that ∆t encapsulates the user’s driving behavior (arrival time and departure time).
2) Action: The action a t is the charging/discharging power at time t. We define the action as a continuous variable for fine-grained control and limit the variable as the following to represent the real-world charging scenario.
E m a x d i s ≤ a t ≤ E m a x c h ,
where E m a x d i s and E m a x c h are maximum dischargeable and chargeable energy in one hour, respectively (note that E m a x d i s is negative and E m a x c h is positive). The action is positive when the vehicle is charging or in G2V mode and negative when the vehicle is discharging or in V2G mode.
3) Transition Probability: The transition probability of an MDP represents the dynamics of an environment with randomness pertaining to the environment and the state variables. The transition from state s t to s t + 1 is governed by the transition probability P s t + 1 | s t ,   a t . For the EV charge scheduling problem, the transition probability is influenced by the action a t , the battery dynamics from (4), charging duration modeled in (1), and the randomness of hourly electricity price. Random arrival and departure time and unpredictable charging preference of the user affect the charging duration and battery SOC. Therefore, we adopt a model-free approach to solve the MDP, where the agent learns the dynamics of the environment by continuously optimizing its policy.
4) Reward: Reward is the immediate response from the environment for the transition from one state to another state by executing an action. In this work, we consider user’s energy cost from (5), charge anxiety from (6), and time anxiety from (7) to formulate the reward function. The reward r t at time t is defined by the following equation:
r t = − κ p ∆ t ξ t + κ c ∆ t ϕ t + κ c ∆ t ψ t ,
where κp and κc are the price sensitivity factor and the charge sensitivity factor, respectively, which represent user’s sensitivity towards electricity price, charge anxiety, and time anxiety. Intuitively, a large electricity bill and a significant uncharged battery energy should yield the least reward. However, in practice, some users are likely to tolerate large uncharged energy to avoid higher charging cost. The variations of such preferences can be handled by using the sensitivity factors. In contrast to other studies [24,25], where these factors were constant or manually tuned, we propose a dynamic weight allocation technique to tune the weights between the components automatically. More specifically, we define κp and κc as the following functions of remaining charging duration ∆t, such that their values change with time within the total charging duration without the need for manual tuning:
κ p ∆ t = ∆ t i n i ∆ t i n i − ∆ t + 1
κ c ∆ t = ∆ t i n i ∆ t
All components are normalized to ensure the same scale and κp, κc ϵ [1, ∆ t i n i ], in which ∆ t i n i = t d − t a , i.e., the initial charging duration when EV arrives.
We consider that the user is more sensitive to reducing energy cost during the first half of the charging duration and more sensitive to satisfying charging demand during the last half of the charging duration. Figure 2 depicts the scenario where both the price and charge sensitivity factors vary with time but in opposite directions. Based on the compared values of the sensitivity factors in Figure 2, the total charging period can be divided into two time zones: 1) a price-sensitive zone and 2) a charge-sensitive zone. In the price-sensitive zone, the price sensitivity factor κp is greater than the charge sensitivity factor κc, which represents the case that the user is more sensitive to the price of the electricity than the anxiety. As time approaches the departure time, the price-sensitivity factor decreases, and the charge-sensitivity factor increases. In the charge-sensitive zone, the charge-sensitivity factor κc is greater than the price sensitivity factor κp, which represents that case that the user is more sensitive to the uncharged battery SOC and anxiety than the price.
5) Objective Function: The charging/discharging action executed under a given state is evaluated using the action- value function. The action-value, Q π ( s , a ) is the expected total discounted reward, starting from a state s , taking an action a , and then following a policy π . The term action-value is referred to as Q-value for brevity in the rest of the paper. Q-value is calculated using (12).
Q π s , a = E π ∑ k = 0 ∞ γ k r t + k + 1 | s t = s ,   a t = a
where π represents the charging/discharging policy that maps the system state to the action. γ ϵ [ 0,1 ] denotes the discount factor that balances the importance between the immediate reward and future rewards. γ = 0 represents a myopic policy where only the immediate reward is considered to calculate the Q-value, while γ = 1 represents a most farsighted policy where all the future rewards and the immediate reward is of equal importance.
The objective of the EV charging control problem is to generate the optimal policy π that maximizes the Q-value. Therefore, the optimization problem is formulated as
Q * s , a = max π ⁡ Q π s , a
in which Q * s , a represents the optimal Q-value.

III. Proposed Approach

In this section, we provide a brief discussion on state-of-the-art RL algorithms and their suitability for the EV charge scheduling application. The later subsection presents the proposed approach and the developed algorithm.

A. Preliminaries

When considering the most suitable RL algorithm for the formulated EV charge scheduling problem, the algorithm’s ability to operate on a large and continuous action space is stressed. While many of the fundamental RL algorithms are suitable for discrete actions of the agent, DDPG can handle applications with large and continuous state and action spaces. DDPG adopts an actor-critic setup where the agent concurrently learns the Q-values using the Q-learning method in a critic network Q (note that Q was used in the previous section to denote Q-values and is reused here to denote the critic network in accordance with literatures) and a policy by using the policy gradient methods, i.e., SARSA in an actor network µ. Additionally, DDPG utilizes a target critic network to calculate the loss function and a target policy network to calculate an action that maximizes the Q-value of the target critic network. The loss functions used in DDPG are given below:
L c r i t i c = E R + γ Q ' s t + 1 , μ ' s t + 1 − Q s t ,   a t 2
L a c t o r = E Q s t ,   μ s t ,
in which Q′ and µ′ are the target critic and the target actor networks, respectively. Also, DDPG addresses the issue of having highly correlated data by using replay memory and the issue of moving target by implementing a soft update of the target weights. In this article, we adopt the principle of DDPG algorithm, with a few key improvements that are presented in the next subsection.

B. The Proposed Algorithm

An episodic update is employed in the proposed algorithm. Conventionally, in DDPG, all the network parameters are updated at each step. Therefore, each transition of an episode occurs by following a newer policy. Specifically, if an episode is of length L, updating at each time step causes each transition within that episode to be generated by following L different policies. Consequently, each policy corresponds to only one transition that is stored in the replay memory. Note that having more examples from a similar policy increases exploration. Hence, in the proposed algorithm, instead of updating at each step, we update the network parameters after the completion of an entire episode. This approach results in generating more examples by following the same policy. Moreover, this helps improve the exploration of the agent because, in this case, the agent is taking actions using the same policy at different steps of the episode.
DDPG uses Temporal Difference updates, where the Q-value of a state is estimated based on the projected Q-values of the subsequent states. This generates a residual error that eventually accumulates to a large amount as the number of iterations increases. Due to the resulting estimation error, the variance in value estimation increases proportionally as the error. Since the actor, critic, and target networks are updated simultaneously, the errors due to the high variance result in highly divergent behavior. Therefore, a delay is implemented to the policy update to allow the critic network to minimize the residual error and to become stable [32]. The delay causes the policy network to update less frequently than the critic network. Thus, the policy network uses the Q-values with a lower variance, resulting in better convergence.
In the case of continuous action space, the actions with very close values typically have similar Q-values for a given state. If the Q-values are not similar for close action values for a given state, then the agent will always be implicitly dictated to pick the action for which the function approximator (neural network) returns the highest Q-value and thus may never explore the action values that are closer. This eventually leads to an overfitting issue, especially for a deterministic policy. To avoid this, we implement target policy smoothing as suggested by Reference [32] by adding a small Gaussian perturbation (the term ϵ in Figure 3 and Algorithm 1) around the action so that all the actions within this small area would have similar Q-values. The perturbation is limited to a very small region (specified by the term c for the truncated Gaussian distribution of ϵ in Figure 3 and Algorithm 1) around the action. Further, the action is clipped to ensure that it remains within the range of valid action values.
Algorithm 1 summarizes the implementation of policies with delayed update and target policy smoothing. At first, actor, critic, and target networks are initialized with random parameters θ Q ,   θ μ ,   θ Q ' , and θ μ ' , respectively. The environment is reset at the beginning of each episode, providing an initial state. Random actions are chosen during the first few steps to conduct exploration. After that, action is selected according to the actor policy and then added with an exploration with random perturbation, μ s t | θ μ + ϵ ,   ϵ ~ N 0 ,   σ 2 . This action is executed to generate an immediate reward and the next state. Such transitions are continuously stored into a replay memory D in a first-in-first-out (FIFO) manner. After each episode, a sample mini batch of transitions is selected randomly to update critic networks with the target policy smoothing technique. The actor and target network updates are delayed to minimize the variance in the target critic’s estimations. A schematic diagram of the proposed algorithm is illustrated in Figure 3.
Preprints 103183 i001
One key difference between the proposed algorithm and DDPG together with TD3 is the episodic update. In DDPG, the networks are updated at each time step. In TD3, the critic networks are updated at each time step, and the actor and target network updates are delayed. Whereas in the proposed algorithm, the networks are updated after each episode. This way, each example of an episode is generated under the same policy which potentially increases exploration and consequently results in better convergence. Additionally, the target policy smoothing and delayed policy update techniques are not present in DDPG but in TD3. TD3 also uses two critic networks and two corresponding target networks. However, in our proposed algorithm, we only use a single critic network and a corresponding target network to optimize the resource requirement. The extensive simulation results presented in the next section show that greater control performance can be achieved using the proposed algorithm than using DDPG and TD3.

IV. Performance Evaluation

In this section, we evaluate the performance of our proposed algorithm through extensive simulations. First, the experimental settings that include preprocessing of real data, simulation setup, and benchmarks are presented. The following subsection presents a comparison with different benchmarks in terms of convergence. After that, the performance of the proposed algorithm is evaluated in terms of the cumulative reward over one year. The algorithm is further compared with the benchmarks in terms of satisfying user’s energy demand. Finally, the effect of the charging control strategy on minimizing electricity cost and satisfying charging demand are demonstrated in detail.

A. Experimental Settings

1) Real-world Data Preprocessing: Information such as arrival time, departure time, and battery SOC are critical for an effective EV charge scheduling strategy. We aim to acquire this information by utilizing a real-world dataset instead of using hypothetical scenarios to provide a more practical solution. We consider a large-scale real-world dataset [34] that represents energy consumption data of 383 personal cars in Ann Arbor, Michigan, USA. This diverse fleet consists of 264 gasoline vehicles, 92 hybrid electric vehicles (HEVs), and 27 PHEV/EVs. The data for the PHEV/EVs are used for our research. Specifically, this time-series dataset includes GPS signals, such as latitude and longitude, OBD-II data, such as speed and engine RPM, and battery usage data, such as battery SOC, current, and voltage on a millisecond time scale. Note that the data acquisition was performed only when the vehicles were driven from November 2017 to November 2018. We estimate a probabilistic model to extract the information related to the arrival time, the departure time, and the battery SOC of the PHEV/EVs. To extract the required information from the data, we perform data preprocessing in the following steps. 1) We consider the daily home charging scenarios. Therefore, the arrival time, the departure time, and the battery SOC at the arrival time are simply the last clock time, the first clock time, and the SOC at the last clock time of each day, respectively. 2) A closer observation of the data extracted from the previous step reveals that the vehicles were not driven using battery on some days. This is reasonable because PHEVs can also be operated by gasoline. Although this does not affect the arrival and departure times, it fails to represent an accurate scenario of battery SOC at arrival time. Additionally, we noticed that some days the vehicles were driven for a very short time, i.e., 2 minutes or less. This largely affects the distribution of arrival time and departure time. Therefore, to ensure the relevance of the real data, we discard the gasoline-driven days and the short trip days. Finally, we fit the processed data into a truncated normal distribution. The mean and standard deviation of arrival time are 21:00 and 2 hours, respectively, and bounded by 17:00 and 24:00 (these values are rounded to integer hours as the time step for the formulated problem is on an hourly basis). For departure time, the mean and standard deviation are 11:00 and 5 hours, respectively, with the boundary of 5:00 and 16:00. Battery SOC is represented by the fraction of the total capacity of the battery C, and its mean and standard deviation are 40% and 20% respectively, which is bounded by 0% and 80%. The distribution of arrival time, departure time, and battery SOC is summarized in Table 1.
We utilize the day-ahead wholesale electricity market clearing price as the electricity pricing data because the retail price is linked with the day-ahead wholesale market price in the real-time pricing mechanism. Since the majority of the energy transaction is cleared in the day-ahead market, the day-ahead price is a good indicator of the real-time retail price. Therefore, day-ahead prices are used in this study. More specifically, we utilize the day-ahead energy price from Midwest Independent Transmission System Operator (MISO), the same power grid operator that serves Michigan, Ann Arbor area.
2) Simulation Setup: The Nissan Leaf is considered to be the representative EV with a rated battery capacity of 24 kWh and a maximum chargeable/dischargeable energy of 6 kWh per hour for our experiment. The action space boundaries are calculated by normalizing the maximum chargeable/ dischargeable energy with respect to the battery capacity. Therefore, the action space ranges between -.25 and .25. We assume that the user requires the EV to be fully charged at the departure time; therefore, the target SOC is set to 1, which represents 100% SOC level. During training, two different network structures are used for policy optimization and value estimation. More specifically, we used three hidden layers of sizes 1000, 500, and 200 for the actor or policy network and two hidden layers of sizes 400 and 200 for the critic network. The corresponding target networks are of similar sizes. After each episode, the critic network is updated for K = 28 times, and the policy network is updated for 14 times. The training was conducted for 110,000 episodes. The overall training setup is summarized in Table 2.
3) Benchmark: When selecting the benchmarks to evaluate the proposed method, the efficiency and stability of an algorithm are the key factors. The two most widely used DRL-based algorithms are DDPG and TD3 because of the stability they exhibit in many applications. Many literatures adopt DDPG and TD3 as their benchmarks due to these features, and likewise, we select DDPG and TD3 algorithms as the benchmark to evaluate our proposed method. Additionally, we also compare our algorithm to traditional scenario where the user does not adopt any control strategy.
a) DDPG: In DDPG, the actor and critic networks and their corresponding target networks are updated at each time step of an episode. No policy delay is implemented, and the Gaussian perturbation is not added to the action.
b) TD3: TD3 uses one actor network and two critic networks. Similar to the proposed approach, a policy delay and a small Gaussian perturbation is implemented. However, in TD3, the critic networks are updated at each time step, and the actor and target networks are updated by considering policy delay (generally every two timesteps). In contrast, the proposed method updates the networks after every episode.
c) Uncontrolled charging: The proposed algorithm is further compared with the scenario where the user adopts no charging control schemes. This is the traditional and myopic scenario where the EV is charged at a maximum allowable rate until the battery SOC reaches the target SOC. Once reaching the target SOC, the charging is ended. Also, in uncontrolled charging, there is no discharging action to support the V2G applications.
All the experiments are conducted on a workstation with an 8-core Intel Core i7-7700 CPU @ 3.60GHz, and the methods are implemented using Python 3.6 and TensorFlow 2.6.0.

B. Comparison with Benchmarks

1) Training Performance: The convergence of the proposed algorithm is compared to those of the DDPG and TD3 in terms of average training returns in Figure 4. As illustrated in Figure 4, the average training return is relatively low during the initial phase, but as the number of episodes increases, the reward also increases. This is true for the proposed approach and the two benchmark approaches. However, the proposed algorithm reaches convergence relatively faster than the benchmarks. The proposed algorithm reaches convergence at around 80,000 episodes, whereas both DDPG and TD3 reach convergence at around 105,000 episodes. The proposed algorithm’s convergence level is also the highest among the three algorithms. Figure 4 indicates that the average training return of the proposed algorithm converges to approximately -7, whereas DDPG and TD3 converge to roughly -8 and -15, respectively. The overall convergence comparisons reveal the effectiveness of the proposed algorithm in terms of faster and higher convergence compared with DDPG and TD3.
2) Testing Performance: After the training phase, the actor networks are used to determine the charging/ discharging actions, which are then used to obtain a real-time charge scheduling strategy for the EV. We use one year of the real-world dataset to evaluate the performance of the proposed algorithm and compare it with the benchmarks. First, the cumulative reward for one year is considered as the metric for performance evaluation. Cumulative reward consists of the accumulated daily return, energy cost, charge anxiety, and time anxiety for one year. Intuitively, the algorithm with the highest cumulative return or the lowest cumulative energy cost, charge anxiety, and time anxiety is performing better than the others. The cumulative return is calculated by R = ∑ m = 1 365 ∑ t r t . The cumulative energy cost is calculated by C = ∑ m = 1 365 ∑ t ξ t . The cumulative charge anxiety and the cumulative time anxiety are given by A 1 = ∑ m = 1 365 ∑ t ϕ t and A 2 = ∑ m = 1 365 ∑ t ψ t , respectively. Figure 5 illustrates the comparison between the proposed algorithm and the benchmarks in terms of cumulative return (Figure 5a), energy cost (Figure 5b), charge anxiety (Figure 5c) and time anxiety (Figure 5d).
The numerical comparisons of the cumulative rewards over a year are further presented in Table 3. As demonstrated in Figure 5 and Table 3, the proposed algorithm shows better performance in terms of total return and time anxiety than those of the DDPG and TD3. According to Figure 5b, TD3 generates the lowest energy cost. However, TD3 fails to meet the charging demand significantly as shown in Figures 5c and 5d. Although the cumulative energy costs using the proposed algorithm and the DDPG are almost similar, the overall performance of the proposed algorithm is better than DDPG as illustrated in Figure 5a. Note that the charge anxiety is the lowest in the uncontrolled charging scenario. This is reasonable because the battery is always charged to its full capacity in uncontrolled charging. Moreover, for simplicity, we ignore the self-discharging of the battery when calculating the charge anxiety and time anxiety. Nevertheless, among all the algorithms compared in this section, the cumulative energy cost for one year is significantly higher when uncontrolled charging is adopted.
The performance of the proposed algorithm is further evaluated in terms of satisfying the user’s energy demand. We analyze the vehicle’s SOC at the time of departure for one year and calculate the average error. Here, the error indicates the difference between the vehicle’s SOC at the departure time and user’s target SOC. The distribution of the error is presented in Table IV along with mean percentage error for one year. From Table IV, it can be seen that the proposed algorithm satisfies user’s charging demand more effectively than the benchmarks. The mean departure-time SOC for one year is over 98% in the case of the proposed algorithm with a standard deviation of 2.1%. Whereas, in the case of DDPG, the mean departure-time SOC is around 93% and in the case of TD3, the mean is the lowest (72%).
Table 4. Departure-time soc and mean percentage error.
Table 4. Departure-time soc and mean percentage error.
Proposed DDPG TD3
Mean SOC 0.984 0.934 0.72
Standard deviation of SOC 0.021 0.008 0.044
Mean percentage error 3% 6% 28%

C. Charge Scheduling

To demonstrate the charge scheduling strategy of the pro- posed algorithm, a 48-hour charge/discharge schedule of an individual EV in response to the dynamic energy price is presented in Figure 6. The areas in green of Figures 6a and 6b indicate the time periods when the EV is not at home. It can be observed from Figure 6a that the EV is charging when the price is low and discharging when the price is high. Also, from Figures 6a and 6b, we can see that at the time of arrival, if the battery energy is too low, the EV is charged aggressively to meet the demand, and if the initial SOC is high, the EV is discharged to reduce energy cost.

V. Introduction

In this paper, the problem of EV charge scheduling is solved using a DRL-based method. The relationship between charging time and user’s anxiety is rigorously addressed in the reward function during the MDP formulation of the problem. A dynamic weight allocation technique is also introduced to represent user’s time-varying priorities for cost minimization and demand requirement. An episodic approach to the DDPG algorithm, along with target policy smoothing and delayed policy update techniques, are developed. A real-world dataset is utilized to validate a practical and optimal charging control strategy. The effectiveness of the proposed algorithm is demonstrated through extensive simulation results using the real data from different perspectives. The simulation results demonstrate that the algorithm can attain the maximum battery SOC at departure time while minimizing energy costs. Although the results make the feasibility of the proposed algorithm promising, the study is based on a few assumptions which are aimed to be discussed in the future work of the authors.
Although some research work incorporates battery degradation model in their problem formulation, the reasoning behind such models needs to be studied more extensively in terms of EV batteries before utilizing them in the reward function. For the conciseness of our work, we refrained from adding the battery degradation research in this paper. However, battery degradation due to the rapid and frequent charging-discharging cycles needs to be studied extensively, and incorporating this into the problem formulation would make the problem more realistic.

References

  1. Sioshansi, R.; Denholm, P. Emissions Impacts and Benefits of Plug-In Hybrid Electric Vehicles and Vehicle-to-Grid Services. Environ. Sci. Technol. 2009, 43, 1199–1204. [CrossRef]
  2. Fact sheet: President Biden announces steps to drive American leadership forward on clean cars and trucks,” https://www.aeaweb.org/ forum/2049/biden-executive-strengthening-american-leadership-trucks, accessed: 2022-04-26.
  3. Global EV outlook 2021. https://www.iea.org/reports/ global-ev-outlook-2021, accessed: 2022-01-31.
  4. Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [CrossRef]
  5. Rassaei, F.; Soh, W.-S.; Chua, K.-C. Demand Response for Residential Electric Vehicles With Random Usage Patterns in Smart Grids. IEEE Trans. Sustain. Energy 2015, 6, 1367–1376. [CrossRef]
  6. Kempton, W.; Tomić, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [CrossRef]
  7. Celebi, E.; Fuller, J.D. Time-of-Use Pricing in Electricity Markets Under Different Market Structures. IEEE Trans. Power Syst. 2012, 27, 1170–1181. [CrossRef]
  8. “Critical peak pricing-San Diego Gas & Electric,” https://www. sdge.com/businesses/savings-center/energy-management-programs/ demand-response/critical-peak-pricing, accessed: 2022-03-04.
  9. H. Allcott, “Real time pricing and electricity markets,” Harvard University, vol. 7, 2009.
  10. Star A., M. Isaacson, L. Kotewa, and M. Ozog, “Real-time pricing is the real deal: An analysis of the energy impacts of residential real-time pricing,” in Proceedings of the ACEEE, 2006, pp. 316–327.
  11. Faruqui and S. Sergici, “Pricing programs: time-of-use and real time,” Encyclopedia of Energy Engineering, p. 18, 2007.
  12. Poullikkas, G. Kourtis, and I. Hadjipaschalis, “A review of net metering mechanism for electricity renewable energy sources,” International Journal of Energy and Environment (Print), vol. 4, 2013.
  13. S. Huecker, “Community and virtual net metering: Overcoming barriers to distributed generation,” 2013.
  14. G. A. Rummery and M. Niranjan, On-line Q-learning using connectionist systems. Citeseer, 1994, vol. 37.
  15. Chis A., J. Lunde´n, and V. Koivunen, “Scheduling of plug-in electric vehicle battery charging with price prediction,” in IEEE PES ISGT Europe 2013. IEEE, 2013, pp. 1–5.
  16. Wang, S.; Bi, S.; Zhang, Y.J.A. Reinforcement Learning for Real-Time Pricing and Scheduling Control in EV Charging Stations. IEEE Trans. Ind. Informatics 2019, 17, 849–859. [CrossRef]
  17. J. Watkins and P. Dayan, “Q-learning,” Machine learning, vol. 8, no. 3, pp. 279–292, 1992.
  18. Ko, H.; Pack, S.; Leung, V.C.M. Mobility-Aware Vehicle-to-Grid Control Algorithm in Microgrids. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2165–2174. [CrossRef]
  19. Q. Dang, D. Wu, and B. Boulet, “A q-learning based charging scheduling scheme for electric vehicles,” in 2019 IEEE Transportation Electrification Conference and Expo (ITEC). IEEE, 2019, pp. 1–5.
  20. Hou, L.; S. Ma, J. Yan, C. Wang, and J. Y. Yu, “Reinforcement mechanism design for electric vehicle demand response in microgrid charging stations,” in 2020 International Joint Conference on Neural Networks (IJCNN). IEEE, 2020, pp. 1–8.
  21. Mhaisen, N.; N. Fetais, and A. Massoud, “Real-time scheduling for electric vehicles charging/discharging using reinforcement learning,” in 2020 IEEE International Conference on Informatics, IoT, and Enabling Technologies (ICIoT). IEEE, 2020, pp. 1–6.
  22. Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [CrossRef]
  23. Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [CrossRef]
  24. Wan, Z.; Li, H.; He, H.L.H.; Prokhorov, D. Model-Free Real-Time EV Charging Scheduling Based on Deep Reinforcement Learning. IEEE Trans. Smart Grid 2018, 10, 5246–5257. [CrossRef]
  25. Lee, J.; Lee, E.; Kim, J. Electric Vehicle Charging and Discharging Algorithm Based on Reinforcement Learning with Data-Driven Approach in Dynamic Pricing Scheme. Energies 2020, 13, 1950. [CrossRef]
  26. Li, H.; Wan, Z.; He, H. Constrained EV Charging Scheduling Based on Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 11, 2427–2439. [CrossRef]
  27. Ge, Y.; Zhu, F.; Ling, X.; Liu, Q. Safe Q-Learning Method Based on Constrained Markov Decision Processes. IEEE Access 2019, 7, 165007–165017. [CrossRef]
  28. Yan, L.; Chen, X.; Zhou, J.; Chen, Y.; Wen, J. Deep Reinforcement Learning for Continuous Electric Vehicles Charging Control With Dynamic User Behaviors. IEEE Trans. Smart Grid 2021, 12, 5124–5134. [CrossRef]
  29. Zhang, F.; Yang, Q.; An, D. CDDPG: A Deep-Reinforcement-Learning-Based Approach for Electric Vehicle Charging Control. IEEE Internet Things J. 2020, 8, 3075–3087. [CrossRef]
  30. Hou, Y.; L. Liu, Q. Wei, X. Xu, and C. Chen, “A novel DDPG method with prioritized experience replay,” in 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2017, pp. 316–321.
  31. T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, Silver, and D. Wierstra, “Continuous control with deep reinforcement learning,” 2019.
  32. S. Fujimoto, H. van Hoof, and D. Meger, “Addressing function approximation error in actor-critic methods,” in Proceedings of the 35th International Conference on Machine Learning, ser. Proceedings of Machine Learning Research, J. Dy and A. Krause, Eds., vol. 80. PMLR, 10–15 Jul 2018, pp. 1587–1596.
  33. Zhang, M.; Fan, X. Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electr. Veh. J. 2020, 11, 23. [CrossRef]
  34. Oh, G.; Leblanc, D.J.; Peng, H. Vehicle Energy Dataset (VED), A Large-Scale Dataset for Vehicle Energy Consumption Research. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3302–3312. [CrossRef]

Short Biography of Authors

Ishtiaque Zaman received the B.Sc. degree in electrical and telecommunications engineering from North South University, Dhaka, Bangladesh in 2011, the M.S. degree in electrical engineering from Lamar University, USA, in 2017, and the Ph.D. degree in electrical engineering in Texas Tech University, USA in 2022. He worked as an Engineering Development Group Intern at MathWorks, Inc, USA during the fall and summer of 2018 and 2020, respectively, where he developed and automated hardware-in-the-loop simulation workflow of electrical components for efficient deployment. His research interests include machine learning and deep learning technologies and their applications in energy management, smart grid, renewable energy, and load forecasting.
Shamsul Arefeen received the B.Sc. degree in electrical and electronics engineering from Islamic University of Technology, Dhaka, Bangladesh in 2003, the M.S. degree in electrical engineering from Texas Tech University, USA, in 2018, and the Ph.D. degree in electrical engineering in Texas Tech University, USA in 2022. He is currently an Assistant Professor at SUNY Morrisville. He was a part-time instructor of freshmen engineering courses on computational thinking and data science at Texas Tech University. He worked as a graduate intern at National Renewable Energy Laboratory (NREL), USA, during the summer of 2021, where he contributed to the development of bifacial radiance software for bifacial photovoltaic performance modeling. His research interests include renewable energy systems, electric vehicles, smart grid, machine learning and deep learning.
S. L. S. Chetty Vasanth received the B. Tech. degree in electrical and electronics engineering from SRM Institute of Science and Technology, Chennai, India, in 2021. He is currently pursuing a M.S. degree in electrical engineering at Texas Tech University, USA in 2023. Additionally, he is working as a graduate student assistant for engineering courses on control systems analysis and electrical circuits. His research interests include renewable energy systems, smart grid, power electronics, machine learning and power systems.
Tim Dallas is a senior member of IEEE. He received the B.A. degree in physics from the University of Chicago, USA, in 1991 and the M.S degree in physics and the Ph.D. degree in applied physics from Texas Tech University, USA, in 1993 and 1996, respectively. He worked as a Senior Technology and Applications Engineer for ISI Lithography, TX, USA from 1997 to 1998 and was a Post-doctoral Research Fellow in Chemical Engineering at the University of Texas, Austin, USA, from 1998 to 1999, prior to his faculty appointment at Texas Tech University in 1999. He is currently a Professor with the Department of Electrical and Computer Engineering at Texas Tech University. His research interests include microelectromechanical systems, nanotechnology, solar energy, and engineering education. He developed educational technologies for deployment to under-served regions of the world. His research group has developed MEMS-based educational technologies that have been commercialized, expanding dissemination. Dr. Dallas served as an Associate Editor of IEEE Transactions on Education.
Miao He (S’08, M’13, SM’18) received the B.S. degree from Nanjing Univ. of Posts and Telecom. in 2005, the M.S. degree from the Tsinghua University in 2008, and the Ph.D. degree from Arizona State University in 2013, all in Electrical Engineering. He joined the faculty of Texas Tech University in 2013 and is now an associate professor at the Department of Electrical and Computer Engineering. His research interests include deep learning applied to modeling, control, and optimization of smart grids, power networks, and renewable energy.
Preprints 103183 g001
Figure 1. (a) System model and (b) Sequential charging/discharging set up for one charging period.
Figure 1. (a) System model and (b) Sequential charging/discharging set up for one charging period.
Preprints 103183 g001
Preprints 103183 g002
Figure 2. Price Sensitivity and Charge Sensitivity Factor for a 12-hour Charging Period.
Figure 2. Price Sensitivity and Charge Sensitivity Factor for a 12-hour Charging Period.
Preprints 103183 g002
Preprints 103183 g003
Figure 3. Schematic diagram of the proposed algorithm.
Figure 3. Schematic diagram of the proposed algorithm.
Preprints 103183 g003
Preprints 103183 g004
Figure 4. Comparison of convergence during training.
Figure 4. Comparison of convergence during training.
Preprints 103183 g004
Preprints 103183 g005
Figure 5. (a) Cumulative total return, (b) Cumulative energy cost, (c) Cumulative charge anxiety, and (d) Cumulative time anxiety.
Figure 5. (a) Cumulative total return, (b) Cumulative energy cost, (c) Cumulative charge anxiety, and (d) Cumulative time anxiety.
Preprints 103183 g005
Preprints 103183 g006
Figure 6. (a) 48-hour charge/discharge scheduling in response to dynamic energy price and (b) Battery energy due to charging/discharging.
Figure 6. (a) 48-hour charge/discharge scheduling in response to dynamic energy price and (b) Battery energy due to charging/discharging.
Preprints 103183 g006
Table 1. User’s driving behavior.
Table 1. User’s driving behavior.
Parameters Distributions Boundaries
Arrival Time N (21, 22) [17, 24]
Departure Time N (11, 52) [5, 16]
Battery SOC N (0.4C, (0.2C)2) [0, 0.8C]
Table 2. Training Hyperparameters.
Table 2. Training Hyperparameters.
Parameter Value
Number of critic updates, K 28
Number of policy and target updates, K/2 14
Discount factor, γ 0.99
Learning rate 0.00001
Soft update factor, τ 0.99
Replay memory size, D 108
minibatch size 120
Table 3. Numerical comparison of the rewards.
Table 3. Numerical comparison of the rewards.
Total return Energy cost Charge anxiety Time anxiety
Proposed −2334.77 21.91 855.83 103.27
DDPG −2420.82 21.15 922.02 107.16
TD3 −5819.73 5.09 2013.63 292.75
Uncontrolled −4462.19 72.83 703.96 153.26
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated