Preprint
Article
Fatigue Crack Propagation of 51CrV4 Steels for Leaf Springs Suspensions of Railway Freight Wagons
Altmetrics
Downloads
92
Views
36
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 April 2024
Posted:
09 April 2024
You are already at the latest version
Alerts
Abstract
Leaf springs are critical components for the railway vehicle safety in which they are installed. Although these components are produced in high-strength alloyed steel and designed to operate under cyclic loading conditions in the high-cyclic fatigue region, their failure is still possible to occur and hence lead to economic and human catastrophes. The aim of this document is precisely to characterise the mechanical crack growth behaviour of the 51CrV4 spring steel representative of leaf springs under cyclic conditions, that is, crack propagation in mode I. The common fatigue crack growth prediction models (Paris and Walker) considering the effect of stress ratio and parameters such as propagation threshold, critical stress intensity factor and crack closure ratio are also determined using statistical methods, which resulted in good approximations with respect to the experimental results. Lastly, the fracture surfaces under the different test conditions were analysed using SEM, with no significant differences to declare. As a result of this research work, it is expected that the developed properties and fatigue crack growth prediction models can assist design and maintenance engineers in understanding fatigue behaviour in the initiation and propagation phase of cracks in leaf springs for railway freight wagons.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
The industry provides a wide range of spring steels with variable properties for a variety of technological applications. The chromium-vanadium alloyed steel, 51CrV4 steel grade, has been used for the design of industry machinery components and suspension elements of road and rail vehicles [1,2,3]. In the rail freight sector, 51CrV4 steel grade is usually found in leaf springs due to its high mechanical strength to static and fatigue loadings [4,5].
Leaf springs, as critical components for vehicle safety, are often designed for an infinite life, however, occasionally fatigue fracture occurs in these components (see Figure 1). Since this component is designed to operate in the high-cyclic fatigue regime, the fatigue phenomenon is expected to be governed mostly by surface crack initiation mechanisms. Nevertheless, to maximize the availability of the vehicle fleet, inspection and maintenance periods of the components need to be optimized. Then, the optimization of the intervention strategy can be done by knowing the percentage of life associated with the crack propagation life. Furthermore, fatigue failure of suspension elements can lead to derailment of rolling stock, leading to economic losses. Then, the optimization of the intervention strategy can be done by knowing the percentage of life associated with the crack propagation life. Furthermore, fatigue failure of suspension elements can lead to rolling stock derailment, hence leading to economic losses [6].
Different types of investigations have been carried out in order to understand the resistance to the fatigue crack growth in leaf springs. These studies were carried out at both the material level and the component level.
The investigation regarding fracture resistance properties in leaf springs is of great importance, not only due to their quasi-brittle behaviour [4], but also because thermal and mechanical treatments can significantly change these properties. For example, the number of cycles for fatigue failure tends to be higher when the tempering temperature increases [4,7]. These variations may be greater if a superficial shot peening treatment is applied. When this mechanical treatment is applied, the fatigue crack can start from internal inclusions (oxides, carbides) or surface defects (due to its high surface roughness [8,9]), which hence changes both the number of cycles for failure and threshold propagation limit [10,11,12]. Concerning fracture toughness, this material property tends to progressively decrease with the decrease in tempering temperature, but has an inverse evolution in relation to the hardness of the material [11,13,14].
Regarding the quenching treatment, increasing the quenching temperature from 840 to 920 oC, it was observed in [11] an increase in the speed rate of crack propagation, in the regime II of propagation, for the propagation mode I. Not only that, the quenching and tempering process affect crack propagation behaviour. According to investigations carried out on low-alloy bainitic steel (51CrV4), the effect of heat treatment is beneficial for the propagation threshold value [15]. Testing a 51CrV4 low-alloy bainitic steel for different stress ratios and propagation directions, a significant influence was found for both cases in propagation regime I, however, this effect starts being irrelevant as the crack enters in the propagation regime II.
Via scanning electron microscopy (SEM), transgranular fracture surfaces were observed. In these fractures surfaces, secondary cracks and fracture micro-mechanism especially due to facet cleavage were observed [7,11,16]. Additionally, reduced-sized ductile-dimples were observed. Regarding the development of fatigue striations, their visualization is not frequently observed, however, when they were observed in martensitic steels, on a very small scale. According to [7], the fatigue striations had a quite reduced spacing (around 1 m).
Concerning the type of fracture surface frequently observed in 51CrV4 steel, the fatigue crack propagation process is transgranular, because in cases where intergranular fracture surfaces were observed in leaf springs, these cracks were originated essentially due to the occurrence of corrosion pitting that promoted environmental embrittlement, and hence cracks propagated between grain boundaries [17].
Thus, combining the material complexity (associated with the production of leaf springs) with the importance of structural safety that these components have, in this research, the crack growth analysis in cyclic conditions of spring steel for parabolic springs applied to rail freight is carried out. Regardless of the leaf spring geometry, fracture surfaces observed in leaf springs tend to exhibit a perpendicular propagation direction to the maximum principal stress, showing that crack propagation is perfectly defined by mode I propagation direction (crack propagation perpendicular to the loading) [10,16,17,18,19,20,21,22]. Thus, the fatigue crack growth properties of the material are determined only for mode I, using compact tension (CT) specimens. Initially, the Paris law for propagation regime II and the threshold law for propagation regime I are determined via the least-squares method for distinct stress ratios. Additionally, the crack closure effect was analysed via the crack closure ratio. The fatigue crack growth analysis was extended using Walker’s model to represent a full-range relationship. In this full-range model, Walker’s parameter was used to combine propagation behaviour in regimes I and II under distinct stress ratios. At last, a fracture surface analysis using scanning electron microscopy (SEM), is performed. The effect of the stress ratio is evaluated on the topography of the sampled surfaces.
The crack propagation properties and crack propagation curves determined and developed in this research are essential for understanding the crack propagation behaviour in chromium-vanadium alloyed steel, 51CrV4. Furthermore, it is expected that the properties obtained from the analyses carried out in this document can be used in further damage-tolerant approaches along with numerical simulations to predict the fatigue life of leaf springs, with the aim of avoiding serious losses associated with the failure of suspension elements, namely leaf springs.
2. Fatigue Crack Growth
After the fatigue crack initiation stage is reached, the fatigue crack with a macro-size propagates steadily until reaching its critical size, leading to its structural failure. This steady crack growth has been described in terms of controlled-failure assumptions from Fracture Mechanics theory. In the case of materials exhibiting a linear elastic behaviour or a low amount of plasticity around the crack tip, the LEFM (Linear Elastic Fracture Mechanics) is applicable. LEFM suggests that the stress-state at the crack tip be represented by the stress intensity factor, K.
2.1. Fatigue Crack Propagation Behaviour
Under cyclic loadings, the LEFM is still suitable for the fatigue crack propagation analysis, if the stress intensity factor range, , is assumed. The subcritical crack propagation behaviour (regime II) of spring steel is well represented [12,22,23,24] by Paris’s law (equation (1)) [25,26], such that
where, C and m are material constants determined by experimental data. The stress intensity factor range, , defined at a cycle and related to stress range, , and crack length, a, is given by equation (2)
with Y denoting a geometrical parameter.
Besides regime II, when the value of is low enough, equation (1) may be not suitable to describe the propagation rate. Under these conditions, the crack propagation regime is identified as regime I, where a threshold value for may be observed, which means if is inferior than the threshold stress intensity factor range, , no crack propagation is observed. In this regime, a power law (equation (3)) is used to predict the relationship for several steels, including spring steels [10], such that
with and denoting the respective regressors, also determined by experimental data.
On the other hand, at propagation regime III, when the maximum stress intensity factor value approximates the critical stress intensity factor, or the fracture toughness, , a fast acceleration of crack propagation is observed, leading rapidly to the collapse.
2.2. Mean Stress Effect
As mean stress has a significant influence on fatigue life approaches, it is also expected that this variable influences the fatigue crack growth. Increasing the mean stress, the crack propagation rate, , tends to increase in all regimes, but with less impact in regime II. At regime III, as this regime is dependent on the fracture toughness of the material, substantial shifts in the crack propagation rate occur. However, regime I is the most affected region, highlighting the high influence of mean stress in the threshold stress intensity factor range, beyond the material dependence.
Several models taking into account the mean stress effect and fracture materials properties have been proposed based on equation (1). Walker adapted equation (1) for different stress ratio, at regime II [27], such that
where denotes an equivalent value of the stress intensity factor range, and the coefficient and the exponent are fitted to experimental data. which varies between 0.3 and 1 for most metals, but has typical values around 0.5 [27]. is dependent on material and is directly related to the stress ratio effect, indicating a higher influence of in fatigue crack growth behaviour for lower values. In the absence of experimental data, Walker’s parameter may be estimated from the ultimate tensile strength, , of the material by the following equation [28]
In addition to the Walker model, Forman combined the mean stress effect with regimes II and III [29,30], resulting in (equation(6)), with
where and are also empirical parameters fitted by available experimental data.
Along with the wide applicability of the Walker model (equation 4), and the importance of regime I of crack propagation, Walker combined both regimes I and II, which resulted in
in which being described as a function of , such that
results in a new Walker’s equation, that is independent of the value of chosen, such that
where the only parameters to be determined are and . Notice that in equation (9), is a known value determined previously via equation (8) using different data, which was obtained for different stress ratios.
2.3. Crack Closure
The importance of crack closure was identified by Elber [31] showing that a fatigue crack may be closed even under tensile loading. Residual compressive deformation in the vicinity of the crack tip is responsible for the reduction of crack tip driving force, causing the contact of crack faces before the minimum loading is reached. The crack closure is often accounted as a closure ratio, U, indicating the portion of loading in which the crack is open, as
with denoting that there is no closure effect and denoting a large closure effect. In equation (10), is and may be seen as the effective crack driving force, and that is less or equal to the nominal crack tip driving force . is the stress intensity factor in the opening, which may be equal to or slightly greater than , designated as the closure stress intensity factor.
The literature reports that the crack closure effect may have a greater interest in regime I of fatigue crack propagation. Many advances in the crack closure theory have been developed, such as plasticity-, oxide-, or roughness-induced closure [32,33]. The plasticity-induced closure theory considers the cyclic plastic zone at the crack tip and also a wake of plasticity in deformed material along crack faces. This model is mathematically expressed by Newman Closure’s equation (11), isolating the quantity of from equation (10) [34]
3. Material and Experimental Procedure
3.1. Chemical Composition and Microstructure
The steel under investigation is the chromium-vanadium alloyed steel 51CrV4 with an average carbon content of roughly 0.50 % as presented in Table 1. Being this steel grade standardised to be quenched at 850 °C (40 min) in an oil bath, and then tempered at 450 °C for 90 min, the 51CrV4 steel (as received) exhibited a tempered martensite microstructure with retained austenite (white phases) [12] as shown in Figure 2.
3.2. Material and Specimen Geometry
In terms of mechanical strength under monotonic loading conditions, the statistical values were obtained in the proper tests presented in the reference [4], which followed the ISO 6892-1[35] standards as presented in Table 2. The results refer to a batch of several specimens obtained from different spring leaves in their longitudinal and transverse directions. Table 2 shows a spring steel with high mechanical strength, = 1271.48 MPa and = 1438.5 MPa, but with low (conventional) ductility at fracture, = 7.53 %. This spring steel grade exhibited a Vickers hardness of 447 HV (corresponding ≈ 45 HRC).
Regarding the analysis of the fatigue crack propagation behaviour, the propagation tests are carried out in propagation mode I, following the guidelines in the ASTM E647 standard [36]. Compact tension (CT) specimens are manufactured according to the guidelines ASTM E647 standard [36], resulting in the geometry specimen with a milled surface illustrated in Figure 3.
The CT geometry is manufactured ensuring that the thickness, B, should be within the interval range, , with W denoting the maximum horizontal length that the crack can achieve. The initial crack, , measured from the loading line, is considered to be greater than , such that the calculation of the stress intensity factor, K, is not affected by the small variations in the location and dimensions of the loading pin holes. The elasticity condition, , with , denoting the maximum stress intensity factor applied during the test, is also guaranteed. Table 3 presents the average and standard dimensions of specimens used in the experimental campaign, where the nomenclature is in accordance with the ASTM E647 standard [36] and can be viewed in Figure 3.
Each specimen was obtained from different leaves belonging to distinct leaf springs. Since it is impossible to test CT specimens whose crack propagates perpendicularly to the longitudinal direction of the longitudinal axis of the leaf, as it is normally verified in fracture surfaces of leaf springs [18,19], CT specimens were manufactured in the other directions. Thus, any effect associated with the direction of manufactured specimens in the crack propagation behaviour can be detected and then extrapolated to the crack propagation behaviour through the thickness direction. Specimens identified as LT denote that the crack propagates through the transversal direction of the leaf. On the other hand, specimens marked as TL denote the face of crack propagation through the longitudinal direction of the leaf’s axis. Figure 4 illustrates the directions from which the samples were taken and the respective labels.
The sample marking system is in accordance with the batch and leaf from which the sample (first and second character) was taken, the crack propagation directions, TL and LT, are identified by the third and fourth characters. The fifth parameter is used to identify samples obtained by the same batch, same crack propagation direction and tested under the same stress ratio conditions. The last three characters (sixth to octave) are identifiers of the stress ratio used in the test (stress ratio of 0.1, 0.3, 0.5 and 0.7).
3.3. Apparatus and Experimental Procedure
Concerning the apparatus, the design of the grips, fixtures, and loading pins for testing CT specimens made of high-strength steels followed the ASTM E647 standard [36]. The fatigue crack propagation tests were carried out in a MTS 810 testing machine equipped with a MTS clevis gripping system to measure the crack opening displacement.
Fatigue crack propagation tests were made to obtain the properties of crack growth in different load ratios, = 0.1, 0.3, 0.5, and 0.7, along the propagation regimes I, II, and III. Firstly, the crack propagation phase II is investigated until the unstable propagation failure and thus both behaviours in regime II and III are gathered from a single test. The determination of the critical stress intensity factor, , is made considering the critical crack length, , corresponding to the value of 95 % of the crack length in the failure . Posterior fatigue crack propagation tests are performed to determine the threshold stress intensity range, . The procedure consists of reducing progressively the applied value of until the stabilisation phase of by the continuum evaluation of the crack propagation rate value, .
Before the initiation of proper fatigue crack growth tests, a pre-crack of 10 mm (approximately) is made in each CT specimen in fatigue conditions with a sinusoidal waveform cyclic loading at a frequency of 12 Hz. The average value measured for the initial crack was mm. The proper tests were made until the fracture under conditions of constant force amplitude and controlled increasing . The testing control was made using software integrated with the MTS system and managed by FlexTest console. The crack length measurement is made by the compliance method according to the ASTM E647 standard [36]. Regarding the stress intensity factor range, is calculated using the dimensionless crack length, , such that
where . The determination of is made considering the incremental polynomial method [36], which involves the fitting of a second-order polynomial curve for a set of successive points, with n denoting the number of points. The gathered data is still used to determine the crack closure effect associated with the material. Its determination is verified by computing the crack opening force value via the compliance offset method.
3.4. Statistical Techniques
The fatigue crack growth models presented in this paper are usually calibrated using linear regression methods, whose parameters are estimated by the ordinary least-squares method [37] as suggested by the ASTM E647 standard [36]. Thus, the linear response function, with the vector of independent variables and the vector of dependent variables is written as
where the estimators is given as:
and the estimator is explicitly determined considering , and the sample average values for dependent variable, , and independent variable, , such that
Notice that in the cases where the material response function is described with a power law, the logarithm is applied to the random variables.
4. Results and Discussion
The results obtained will be assessed and discussed throughout this section. Initially, the fatigue crack growth characterization is made considering the propagation regime II (assuming Paris law (equation (1)), analysing the effect of the rolling direction and the stress ratio, as well as the crack closure effect. Then the properties and are determined. Finally, the calibration of the fatigue crack propagation model using the Walker model ((equations (4) and (7)) are considered.
4.1. Rolling Direction Effect
Analysing the different directions of the tested specimens, LT and TL, as shown in Figure 4, it is observed that LT specimens tend to exhibit a greater value of C, however, LT specimens appeared to have a lower rate propagation speed as presented in Table 4. The regression analysis of equation (1) revealed for TL specimens, a coefficient C = 3.526E-08 ± 1.827E-08 (mm/cycle) MPa and an exponent m = 2.299 ± 0.1377, whereas for specimens manufactured in LT direction were obtained C =7.534E-08 ± 3.761E-08 (mm/cycle) MPa and m = 2.006 ± 0.1249. The effect of parameters C and m are visible in Figure 5.
Analysing the data presented in Table 4, one verifies that despite the existence of differences associated with the direction of the CT specimens, the differences are significant, rounding 53% for the C coefficient and 15% for the exponent m. These differences may be also associated with some variation in the mechanical properties. Thus, the following analysis will be performed considering the combined crack growth properties independent of the testing direction of the material.
4.2. Stress Ratio Effect and Crack Closure
The variation of the crack propagation rate in regime II with the evolution of for different is illustrated in Figure 6. For the stress ratios of 0.1 and 0.3, an increase in the value of the coefficient C and m with the stress ratio is observed, however for the higher ratios, 0.5 and 0.7, the propagation rate was lower. According to the regression model (equation (1)), the coefficients C and exponents m were very close. For , the material exhibited a coefficient C = 7.65E-08 and exponent and for , the material exhibited a coefficient C = 7.33E-08 and exponent . In the case of the stress ratio of 0.5, the material exhibited a higher value of C, 8.78E-08, but the slope was slightly lower than 1.90. On the other hand, for , a value of C = 4.39E-08 and a were determined. Table 5 presents in the second and third columns the summary of Paris’ law values obtained for different stress ratios (see first column). Comparing the results obtained for the stress ratio of 0.1, with the tests carried out in [11], a slope value m is slightly lower than 2.025 in relation to 2.40. In contrast, Slightly higher values for C are verified (7.65E-08 and 4.96E-08 (mm/cycle) MPa).
Taking into account this proximity, it is expected that the stress ratio effect is low on the chromium-vanadium spring steel for cracks propagating in regime II. The stress ratio effect on the propagation rate can be explained by the crack closure effect at the crack tip. The average closure ratio, , (given by equation (10)), indicates that there is only an 8 % reduction in the crack tip driving force associated with plasticity located at the crack tip, which might explain the low sensitivity to the stress ratio effect on the crack tip. Figure 7 depicts the average value and respective standard deviations measured for the crack closure ratio for stress ratios 0.1 and 0.3.
4.3. Critical Stress Intensity Factor
The critical stress intensity factor, , is calculated considering the largest crack length measured at the failure. The average value found for was MPa (see Table 5). Considering the condition , with a yield strength of 1271.48 MPa and a thickness of 10 mm, the determined value of = 138.37 MPa does not correspond to the plane strain fracture toughness, ( MPa). Besides, in the literature, usual values for high-strength steels can reach 65 MPa [38,39] and steels with Rockwell C hardness of 45 HRC can assume values between 50 and 70 MPa [13].
4.4. Threshold Stress Intensity Factor Range
The procedure for the determination of is illustrated in Figure 8. According to the gathered data presented in Figure 8, is the value of for the moment that , which corresponds to the crack length that stops to propagate, which results in a of 6.92 MPa for (very close to the observed in [40] (5 MPa)), 5.78, and 5.39 MPa for and 0.5, respectively. In [41,42], the same steel grade was tested for a (with a 10 mm thick specimen), for a martensitic material (without tempering) and for a steel grade with a ferrite/pearlitic microstructure. The values obtained of 4 and 11.2 MPa in [41,42], for martensitic and ferritic/pearlitic microstructure, respectively, validate the obtained result (6.92 MPa) for our material.
Since the threshold value is determined, it is possible to estimate a power curve law to predict the relationship in the regime I, as written in equation (3). The regression method applied in equation (3) results for each = 1.5225E-06, = 1.6122E-06, and = 2.1803E-06 (mm/cycle) MPa . Regarding the exponents regressors, = 1.0112, = 0.9321, and = 0.7310 (summarized in Table 5). The average values for power curve law are respectively MPa, = 1.7717E-07 ± 3.5671E-07 (mm/cycle) MPa and .
From the comparison between and obtained for different stress ratios in regime I as illustrated in Figure 9, for lower values, the slope of crack propagation rate tends to be greater. Nevertheless, for higher ratios, in addition to the crack starting propagating for lower values, after the propagation begins, the crack always has a superior crack propagation rate. Graphically, Figure 9 shows that there is a good fitting in the initial zone after the crack begins propagating. However, for greater than 10 MPa, there is an increase in the crack propagation rate. This deviation might be associated with the beginning of the propagation regime II, whereby equation (3) is no longer valid.
4.5. Global Fatigue Crack Propagation Model
The results previously presented showed a low crack closure effect for the different analysed stress ratios. Considering this result, a global fatigue crack propagation model considering the different stress ratios is then calibrated. Initially, the data is calibrated according to Paris law (equation (1)), resulting in the curve illustrated in Figure 6. The calibration of the parameters for the equation (1) resulted in a coefficient C = 5.99E-08 and an exponent , with a coefficient of determination, of . Visually, it is verified in Figure 10 that the points of greatest scatter are associated with the zone with the highest crack growth rate for most stress intensity ratios. Considering this scatter, Figure 10 also presents the respective straight-line confidence bands for one times the standard deviation of the .
Although the model presents an average curve for the stress ratios analysed, the Walker model given by the equation (4) is normally used to represent the fatigue crack growth as a function of the stress ratio. Usually, the parameter is determined using data in propagation regime II, however, as the specimen tested under has exhibited a lower crack propagation rate when compared to 0.3 and 0.1, the Walker parameter, , is not possible to be obtained from (4). Thus, equation (8) is considered to determine . The described linear least squares regression method is considered ( and ), resulting in , MPa with a . Extrapolating the equation (8) for stress ratio values of -1, we obtain a value of MPa, which is very close to the result obtained in [10], of MPa, validating the accuracy of the equation model (8) and results obtained.
Figure 11 illustrates the regression obtained from the equation (8) and the respective propagation threshold points obtained previously. Comparing the experimental with the one obtained via equation (5), which results in a value of = 0.5941 for MPa, it is verified that the value determined from equation (8) of 0.5767 is in satisfactory agreement.
Once is determined, the Walker model written in equation (4) results via the least-squares method in the coefficient = 3.47E-08 and in the exponent = 2.16, with a coefficient of determination of , as shown in Figure 12. Figure 12 shows a greater scatter of the data obtained for ratios of 0.5 and 0.7, however, all points are contained in the grey area (illustrated in darker blue in Figure 12), corresponding to the prediction curves for one times the standard deviation of the propagation rate, , with regards to the average value, . The red and blue areas correspond to predictions considering once and twice the standard deviation of the parameters C and m, respectively denoted as and . Data are presented in Table 6.
Extending the Walker’s model (4) up to regime I (see equation (7)), results in the coefficient = 5.78E-08 and with a coefficient of determination , as illustrated in Figure 13. It turns out that stress intensity ratio data of 0.1, 0.3, and 0.5 for higher strain intensity ranges are better fitted by equation (9), except for the ratio of 0.7. However, as the stress intensity factor range decreases, there is a greater deviation of the experimental results concerning the equation model (9). Also, Figure 13 suggests that the conservative prediction curve should be given by the mean curve plus 1 times the standard deviation for both lower and strain higher intensity ranges instead of the prediction curves considering once and twice the standard deviation of and .
The data referring to the equation (4) and equation (9) models are presented in Table 6 together with the results obtained by regression to the global model given by the Paris’ law (equation (1)). According to the data presented in Table 6, it can be seen that the value of m given by Walker’s model considering only the propagation region II is closer to the value obtained by Paris’ law with the global data. However, for the C parameter, Walker’s model considering the zone close to the propagation threshold is closer than that obtained by the Paris law.
4.6. Fracture Surface Analysis
SEM technology allowed to analyse of the fracture surfaces from the initiation, up to unstable fracture zones. Four samples corresponding to a stress ratio of 0.1 and 0.5 according to the LT and TL propagation systems were considered for the analysis. Figure 14 illustrates an initial pre-crack of around 1 mm in front of . According to Figure 14 , no significant changes in the crack surface transition between pre-crack and the fatigue crack growth testing are visible which is an excellent indication of the proper selection of the pre-cracking loading level.
The effect of the propagation direction of the CT specimens is analysed considering two samples (manufactured in the LT and TL directions) tested at of 0.1 (see Figure 15). In general, there are no significant differences to point out between the specimens. Both specimens feature some large cleavage facets with identical dimensions. Furthermore, micro-cracks can be observed in multiple directions in relation to the propagation direction for both specimens. This similarity in behaviour is then reflected by the material behaviour response in the Paris curves (Figure 6) and in the respective Paris law exponent coefficients (equation (1)).
With regard to the stress ratio effect, two specimens tested under a stress ratio of 0.1 and 0.5 were selected. Figure 16 shows the comparison of crack propagation paths from the pre-crack initiation zone to the initiation moment of the crack unstable propagation for an x100 magnification.
Comparing both fracture surfaces along the crack propagation path, it is verified that the pre-crack zone tends to present a rougher fracture surface, compared to the stable propagation zone as illustrated in Figure 17 at 1 and 6 mm. The rougher surface at 1 mm crack length is associated with the test speed which is higher than the proper testing speed due to the need for rapid generation of a pre-crack.
Additionally, the stable crack propagation zone from 3 up to 20 mm exhibits a smoother fracture surface. For lower stress ratio ( = 0.1), the surface appears to be slightly rougher in contrast to CT specimens tested at = 0.5. After 20 mm, the fracture surface of the specimen tested at = 0.1 starts to be rougher. This trend is easily visible from the micrographs of Figure 17 at 6 mm. From a crack length of 20 mm in Figure 16 begins to indicate a change in the fracture surface topography, becoming rougher in both specimens. This change is associated with the increase in crack propagation rate in regime III, not showing significant differences for different stress ratios as verified in Figure 16 at 21 mm. In this zone (nº5) the appearance of ductile dimples with small dimensions is quite visible [16].
Increasing the magnification in x200k, one can state that propagation occurs essentially at the transgranular level, with cleavage micro-mechanisms being the cause in the pre-crack initiation zone, crack propagation, stable, and unstable cracks. For the entire propagation zone analysed, no fatigue striations with dimensions of the order of 10 m were identified. Figure 18, picture zone 3, shows the existence of a longitudinal crack which was formed by the decohesion of the metallic matrix with the non-metallic slender inclusion. These small crack geometries are often found on specimens manufactured with the TL propagation system.
Additionally, from Figure 16, a greater number of darker spots appear in specimen tested at = 0.1. These are cleavage facets, indicating that for lower stress ratios, there is a greater likelihood for cleavage facets to form (see Figure 18). Still, for specimen tested at = 0.1, in Figure 18 - position 16 mm, it is observed the existence of cleavage micro-cracks of approximately 20 m within the facets. Moving to the unstable crack propagation zone (21 mm), the appearance of ductile dimples was verified for the specimen tested for = 0.5.
5. Conclusions
The propagation behaviour of fatigue cracks in chromium-vanadium steel was analysed for several stress ratios using CT specimens obtained from the LT and TL directions of suspension spring leaves.The propagation behaviour in regime II was initially analysed according to the Paris law, one verified a low effect of the stress ratio. This low difference can be explained essentially by the high value of crack closure ratio, , and statistically by the coefficient of determination obtained for the global Paris regression model taking into account all stress ratios, , for a C = 5.99E-08 ± 1.98E-08 (mm/cycle) MPa and m = 2.10 ± 0.09. The results were monitored until the moment of failure, making it possible to estimate the value of the critical stress intensity factor, resulting in = 138.37 ± 2.61 MPa.
In a second phase, the propagation threshold value was determined for the stress ratios of 0.1, 0.3, and 0.5, verifying a clear effect of the stress ratio associated with the propagation threshold with values of 6.92, 5.78, and 5.39 MPa, respectively. The propagation law parameters for regime I were determined for each stress ratio, obtaining an average value of = 1.77E-08±3.57E-07 MPa and = 0.89 ± 0.14.
Since the material exhibits a strong influence on the stress intensity factor in propagation regime I, Walker’s model was used to describe crack growth in regimes I and II. The Walker parameter was determined by its relation to the propagation threshold, resulting in = 0.5767. Initially, the parameters of the Walker’s model for regime II are considered, such that the value obtained for and were respectively 3.47E-08 ± 1.32E-08 mm/cycle and 2.16 ± 0.09, with a . Then, Walker’s model contemplating the two propagation regimes was used, resulting in a = 5.78E-08 ± 1.43E-08 (mm/cycle) MPa and = 1.43 ± 0.05, with a . In fact, the introduction of the propagation region I changes the value of m from 2.16 to 1.43 moving away from the value obtained for the Paris law and increasing the coefficient C from 3.47E-08 to 5.78E-08, approaching the value obtained from the Paris’ law.
Finally, an analysis of the fracture surfaces of the specimens was carried out. The effect of the manufacturing direction of the specimens and the stress intensity ratio were evaluated. In general, the fracture surface analysis showed that the crack propagation process occurs predominantly in a transgranular way with micro-cleavage processes and without visible fatigue striations. From the analysis made for the LT and TL propagation systems, no significant differences were revealed, which is also demonstrated by the coefficients and exponents obtained by the Paris law. However, the presence of slender small cracks caused by the decohesion of the metallic matrix interface with the non-metallic inclusion was verified for the TL specimens. Comparing the evaluated stress ratios, it was verified that the fracture surface topographies of specimens tested at = 0.1 tend to be rougher than specimens tested at = 0.5. In addition, for = 0.1 specimens present a greater amount of larger size cleavage facets, making it possible to observe for some a very smooth surface, which indicates the crack closure occurrence. Other aspects such as micro-cleavage cracks (with 20 m) and ductile dimples were sporadically observed.
Author Contributions
Conceptualization, Gomes V.M.G.; methodology, Gomes V.M.G. and Lesiuk G. ; software, Gomes V.M.G. and Lesiuk G.; validation, Gomes V.M.G., Lesiuk G. and de Jesus A.M.P.; formal analysis, Gomes V.M.G.; investigation, Gomes V.M.G. and Lesiuk G.; resources, Lesiuk G., Correia J.A.F.O. and de Jesus A.M.P.; data curation, Gomes V.M.G. and Lesiuk G.; writing—original draft preparation, Gomes V.M.G.; writing—review and editing, Gomes V.M.G., Lesiuk G., Correia J.A.F.O. and de Jesus A.M.P.; visualization, Gomes V.M.G., Lesiuk G. and de Jesus A.M.P.; supervision, Lesiuk G., Correia J.A.F.O. and de Jesus A.M.P.; project administration, de Jesus A.M.P.; funding acquisition, Lesiuk G., Correia J.A.F.O. and de Jesus A.M.P.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
The authors also want to express a special thanks to the Doctoral Programme iRail - Innovation in Railway Systems and Technologies funded by the Portuguese Foundation for Science and Technology, IP (FCT) through the PhD grant (PD/BD/143141/2019); and the following Research Projects: FERROVIA 4.0, with reference POCI-01-0247-FEDER-046111, co-financed by the European Regional Development Fund (ERDF), through the Operational Programme for Competitiveness and Internationalization (COMPETE 2020), under the PORTUGAL 2020 Partnership Agreement; SMARTWAGONS - DEVELOPMENT OF PRODUCTION CAPACITY IN PORTUGAL OF SMART WAGONS FOR FREIGHT with reference nr. C644940527-00000048, investment project nr.27 from the Incentive System to Mobilising Agendas for Business Innovation, funded by the Recovery and Resilience Plan and by European Funds NextGeneration EU; and PRODUCING RAILWAY ROLLING STOCK IN PORTUGAL, with reference nr. C645644454-00000065, investment project nr. 55 from the Incentive System to Mobilising Agendas for Business Innovation, funded by the Recovery and Resilience Plan and by European Funds NextGeneration EU.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Hy. , Hu, Jd., Li, J. et al. Effect of tempering temperature on microstructure and mechanical properties of AISI 6150 steel. J. Cent. South Univ. 2013, 20, 866–870. [Google Scholar] [CrossRef]
- Brnic, J. , Brcic, M., Krscanski, S., Canadija, M., Niu, J. Analysis of materials of similar mechanical behavior and similar industrial assignment. Procedia Manufacturing 2019, 37, 207–213. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z.; Hou, J.; Thrush, S. J.; Barber, G. C. , Zou, Q., Yang, H.; Qiu, F., Tribological behavior of heat treated AISI 6150 steel. Journal of Materials Research and Technology 2020, 9, 12293–12307. [Google Scholar] [CrossRef]
- Gomes, V.M.G.; Souto, C.D. S; Correia, J. A.; de Jesus, A.M.P. Monotonic and Fatigue Behaviour of the 51CrV4 Steel with Application in Leaf Springs of Railway Rolling Stock. Metals 2024, 14(3), 266. [Google Scholar] [CrossRef]
- Malikoutsakis, M.; Gakias, C.; Makris, I.; Kinzel, P.; Müller, E.; Pappa, M.; Savaidis, G. n the effects of heat and surface treatment on the fatigue performance of high-strength leaf springs. In MATEC Web of Conferences. EDP Sciences 2021, 349, 04007. [Google Scholar] [CrossRef]
- Federal Department of the Environment, Transport, Energy and Communications DETEC. Derailment in Daillens VD. Report according to RID 1.8.5.4 2016 http://www.otif.org/fileadmin/user_upload/otif_verlinkte_files/05_gef_guet/07_rid_verweis/1.8.5.2/Switzerland_2015_04_25_E.pdf.
- Žužek, B.; Sedlacek, M.; Podgornik, B. Effect of segregations on mechanical properties and crack propagation in spring steel. Frattura ed Integrità Strutturale, 2015; 9. [Google Scholar] [CrossRef]
- Llaneza, V.; Belzunce, F. ; Study of the effects produced by shot peening on the surface of quenched and tempered steels: roughness, residual stresses and work hardening. Applied Surface Science 2015, 356, 475–485. [Google Scholar] [CrossRef]
- Soady, K.A. Life assessment methodologies incorporating shot peening process effects: mechanistic consideration of residual stresses and strain hardening: Part 1 – effect of shot peening on fatigue resistance. Materials Science and Technology 2013, 29, 637–651. [Google Scholar] [CrossRef]
- Gubeljak, N.; Predan, J.; Senčič, B.; Chapetti, M. D. The Crack Initiation and Propagation in threshold regime and SN curves of High Strength Spring Steels. In IOP Conference Series: Materials Science and Engineering, 2016; 119, 012024. [Google Scholar] [CrossRef]
- Lai, C.; Huang, W.; Li, S.; Liu, T.; Lv, R.; Tang, X.; Yu, J. Effects of quenching and tempering heat treatment on microstructure, mechanical properties, and fatigue crack growth behavior of 51CrV4 spring steel. In IOP Conference Series: Materials Science and Engineering, 2021; 8, 096514. [Google Scholar] [CrossRef]
- Lee, C. S.; Lee, K. A.; Li, D. M.; Yoo, S. J.; Nam, W. J. Microstructural influence on fatigue properties of a high-strength spring steel. Materials Science and Engineering: A, 1998; 241, 30–37. [Google Scholar] [CrossRef]
- Senčič, B.; Šolić, S.; Leskovšek, V. Fracture toughness–Charpy impact test–Rockwell hardness regression based model for 51CrV4 spring steel. Materials science and technology 2014, 30(12), 1500–1505. [Google Scholar] [CrossRef]
- Šolić, S.; Senčič, B.; Leskovšek, V. Influence of heat treatment on mechanical properties of 51CrV4 high strength spring steel. International heat treatment and surface engineering 2014, 7, 92–98. [Google Scholar] [CrossRef]
- Lambers, H. G.; Gorny, B.; Tschumak, S.; Maier, H. J.; Canadinc, D. Crack growth behavior of low-alloy bainitic 51CrV4 steel. Procedia Engineering 2010, 2, 1373–1382. [Google Scholar] [CrossRef]
- Cheng, G.; Chen, K.; Zhang, Y.; Chen, Y. The fracture of two-layer leaf spring: Experiments and simulation. Engineering Failure Analysis; 2021, 133, 105971. [Google Scholar] [CrossRef]
- James, M. N.; Hattingh, D. G.; Matthews, L. Embrittlement failure of 51CrV4 leaf springs. Engineering Failure Analysis; 2022, 139, 106517. [Google Scholar] [CrossRef]
- Infante, V.; Freitas, M.; Baptista, R. Failure analysis of a parabolic spring belonging to a railway wagon. International Journal of Fatigue 2022, 140, 106526. [Google Scholar] [CrossRef]
- Gomes, V.; Correia, J.; Calçada, R.; Barbosa, R.; de Jesus, A. Fatigue in trapezoidal leaf springs of suspensions in two-axle wagons—An overview and simulation. In Structural Integrity and Fatigue Failure Analysis; Lesiuk, G., Szata, M., Blazejewski, W., de Jesus, A.M., Correia, J.A., Eds.; VCMF 2020 Structural Integrity: 2022; Volume 25, pp. 97–114. [CrossRef]
- Ali, N.; Riantoni, R.; Putra, T. E.; Husin, H. The fracture of two-layer leaf spring: Experiments and simulation. IOP conference series: materials science and engineering. IOP Publishing, 2022; 541, 012046. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, J.; Yang, X.; Zhu, Z.; Liu, S. Failure analysis on the collapse of leaf spring steels during cold-punching. Engineering Failure Analysis, 2010; 17, 971–978. [Google Scholar] [CrossRef]
- Ceyhanli, U. T.; Bozca, M. Experimental and numerical analysis of the static strength and fatigue life reliability of parabolic leaf springs in heavy commercial trucks. Advances in Mechanical Engineering, 2020; 12, 1687814020941956. [Google Scholar] [CrossRef]
- Melander, A.; Larsson, M. The effect of stress amplitude on the cause of fatigue crack initiation in a spring steel. International Journal of Fatigue, 2020; 15, 119–131. [Google Scholar] [CrossRef]
- Wu, S. C.; Li, C. H.; Luo, Y.; Zhang, H. O.; Kang, G. Z. A uniaxial tensile behavior based fatigue crack growth model. International Journal of Fatigue; 2020, 131, 105324. [Google Scholar] [CrossRef]
- Paris, P. C.; Gomez, M. P.; Anderson, W. E. A rational analytic theory of fatigue. The Trend in Engineering; 1961, 13(1), 9-14, https://imechanica.org/files/1961%20Paris%20Gomez%20Anderson%20A%20rational%20analytic%20theory%20of%20fatigue.pdf. /: 13(1), 9-14, https.
- Paris, P. C.; Erdogan, F. A critical analysis of crack propagation laws. Journal of Basic Engineering; 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Dowling, N. E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture and Fatigue, 2nd ed.; Publisher: New Jersey, United States of America: Prentice-Hall Inc, 1999. [Google Scholar]
- Dowling, N. E.; Calhoun, C. A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue & Fracture of Engineering Materials & Structures, 2008; 32, 163–179. [Google Scholar] [CrossRef]
- Forman, R. G.; Kearney, V. E. Engle. R. M. Numerical analysis of crack propagation in cyclic-loaded structures. J. Basic Eng. 1967; 89, 459. [Google Scholar] [CrossRef]
- Mínguez, J. Foreman’s crack growth rate equation and the safety conditions of cracked structures. Engineering fracture mechanics, 1994; 48, 663–672. [Google Scholar] [CrossRef]
- Elber, W. Fatigue crack closure under cyclic tension. Enginnering Fracture Mechanics, 1970; 2, 37–45. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Publisher: Cambridge University Press, 1998. [Google Scholar]
- Maierhofer, J.; Gänser, H. P.; Pippan, R. Modified Kitagawa–Takahashi diagram accounting for finite notch depths. International Journal of Fatigue; 2015, 70, 503–509. [Google Scholar] [CrossRef]
- Newman Jr, J. C. A crack opening stress equation for fatigue crack growth. International Journal of Fracture; 1984, 24, 131–135. [Google Scholar] [CrossRef]
- ISO 6892-1, Metallic materials-tensile testing-Part 1: Method of test at ambient temperature. European Committee for Standardization, Brussels, 2009.
- ASTM E647, Standard test method for measurement of fatigue crack growth rates. American Society for Testing and Materials 2000, 2000 03.01, 591. [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; 6th ed.; Publisher: Wiley, 2013. [Google Scholar]
- Gubeljak, N.; Predan, J.; Senčič, B.; Chapetti, M. D. Effect of residual stresses and inclusion size on fatigue resistance of parabolic steel springs. Materials Testing, 2014; 56, 312–317. [Google Scholar] [CrossRef]
- Lancaster, J. The technical background. Engineering Catastrophes. Materials Testing, 2005; 139–189. [Google Scholar] [CrossRef]
- Chapetti, M. D.; Senčič, B.; Gubeljak, N. Fracture mechanics analysis of a fatigue failure of a parabolic spring. Matéria (Rio de Janeiro) 2023, 28, e20230115. [Google Scholar] [CrossRef]
- Schramm, B.; Richard, H. A.; Kullmer, G. Theoretical, experimental and numerical investigations on crack growth in fracture mechanical graded structures. Engineering Fracture Mechanics; 2023, 167, 188–200. [Google Scholar] [CrossRef]
- Schramm, B.; Richard, H. A. Crack propagation in fracture mechanical graded structures. Frattura ed Integrità Strutturale, 2015; 9. [Google Scholar] [CrossRef]
Figure 1.
Fatigue fracture of the master spring leaf of a parabolic leaf spring.

Figure 2.
Typical microstructure of the chromium-vanadium alloyed steel for all tested specimens [4].
Figure 2.
Typical microstructure of the chromium-vanadium alloyed steel for all tested specimens [4].

Figure 3.
Geometry of the compact tension specimen used to evaluate the crack growth propagation under mode I fatigue loading.
Figure 3.
Geometry of the compact tension specimen used to evaluate the crack growth propagation under mode I fatigue loading.
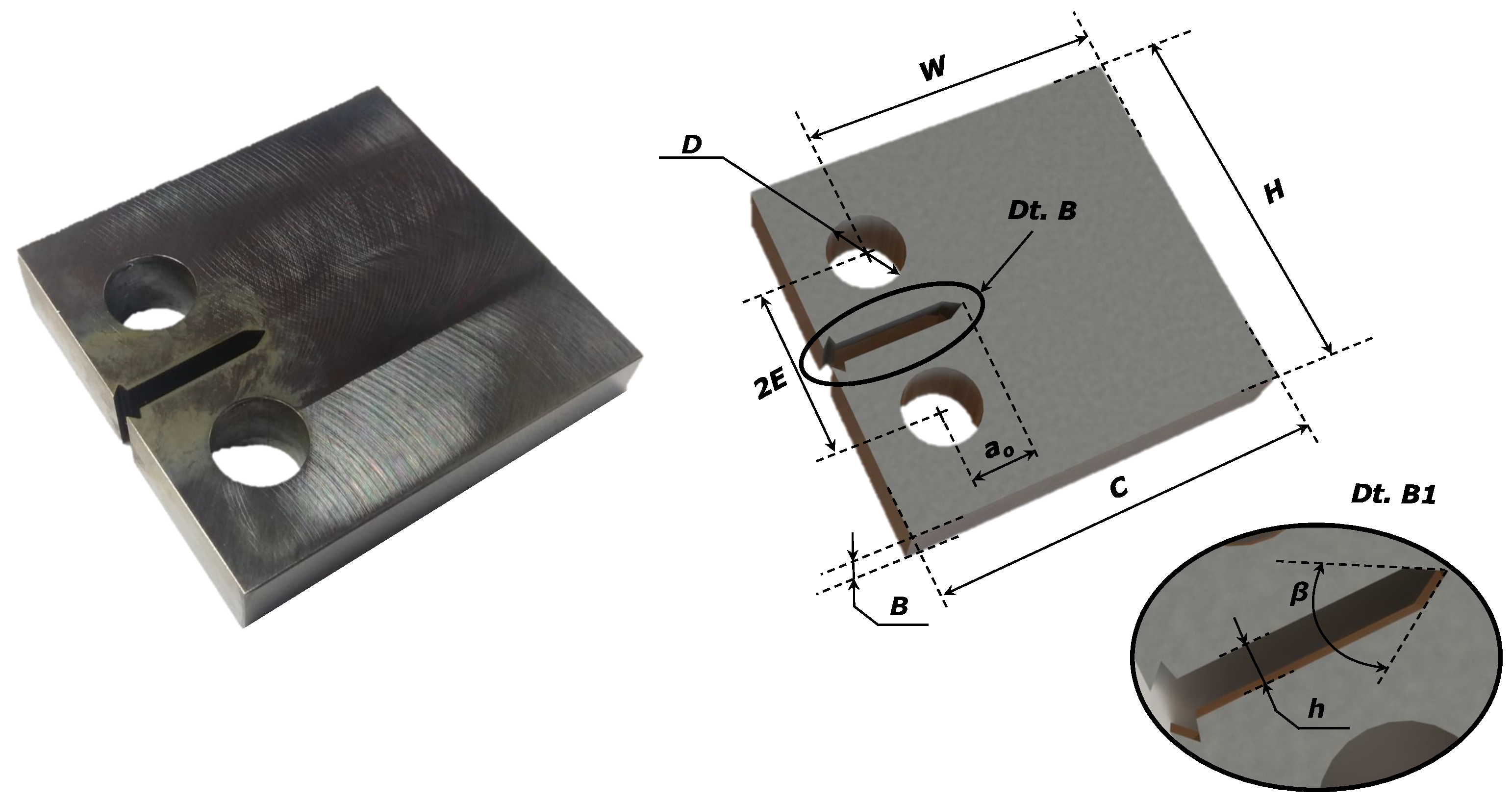
Figure 4.
Illustration of the directions from which samples were taken according to the LT and TL labels.
Figure 4.
Illustration of the directions from which samples were taken according to the LT and TL labels.
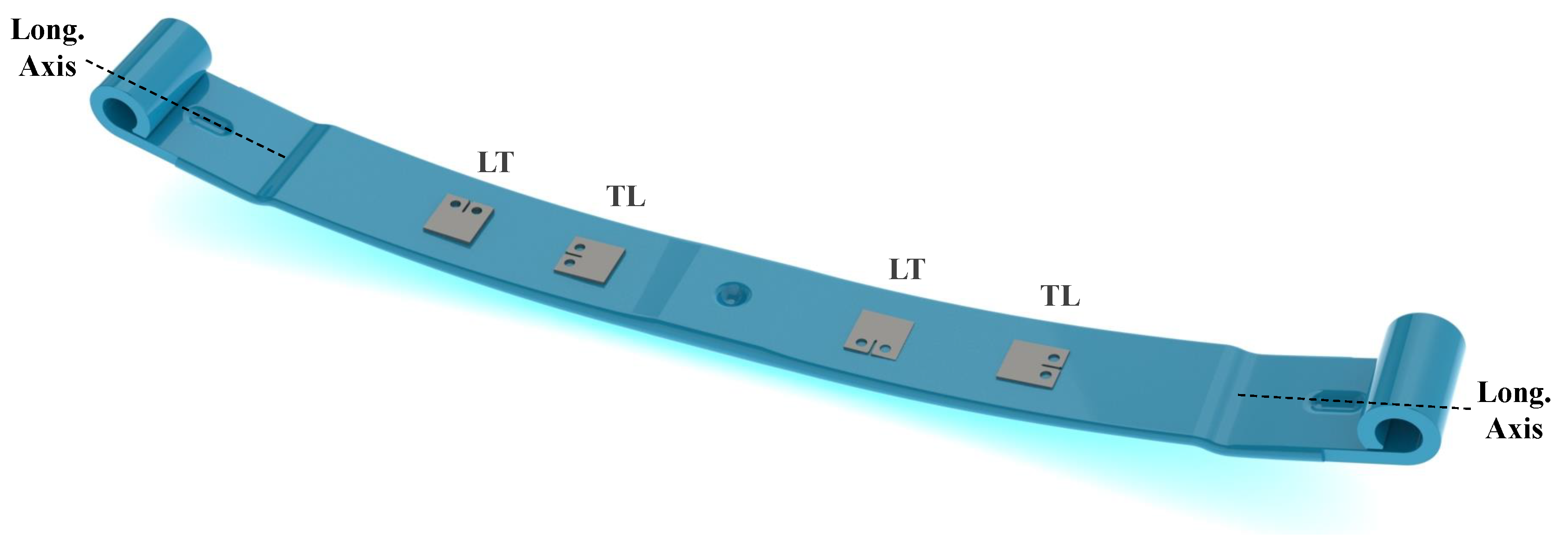
Figure 5.
Influence of the rolling direction in the crack propagation rate in propagation regime II.
Figure 5.
Influence of the rolling direction in the crack propagation rate in propagation regime II.

Figure 6.
Variation of the crack propagation rate in propagation regime II in relation to the applied stress intensity factor range for different stress intensity ratios.
Figure 6.
Variation of the crack propagation rate in propagation regime II in relation to the applied stress intensity factor range for different stress intensity ratios.
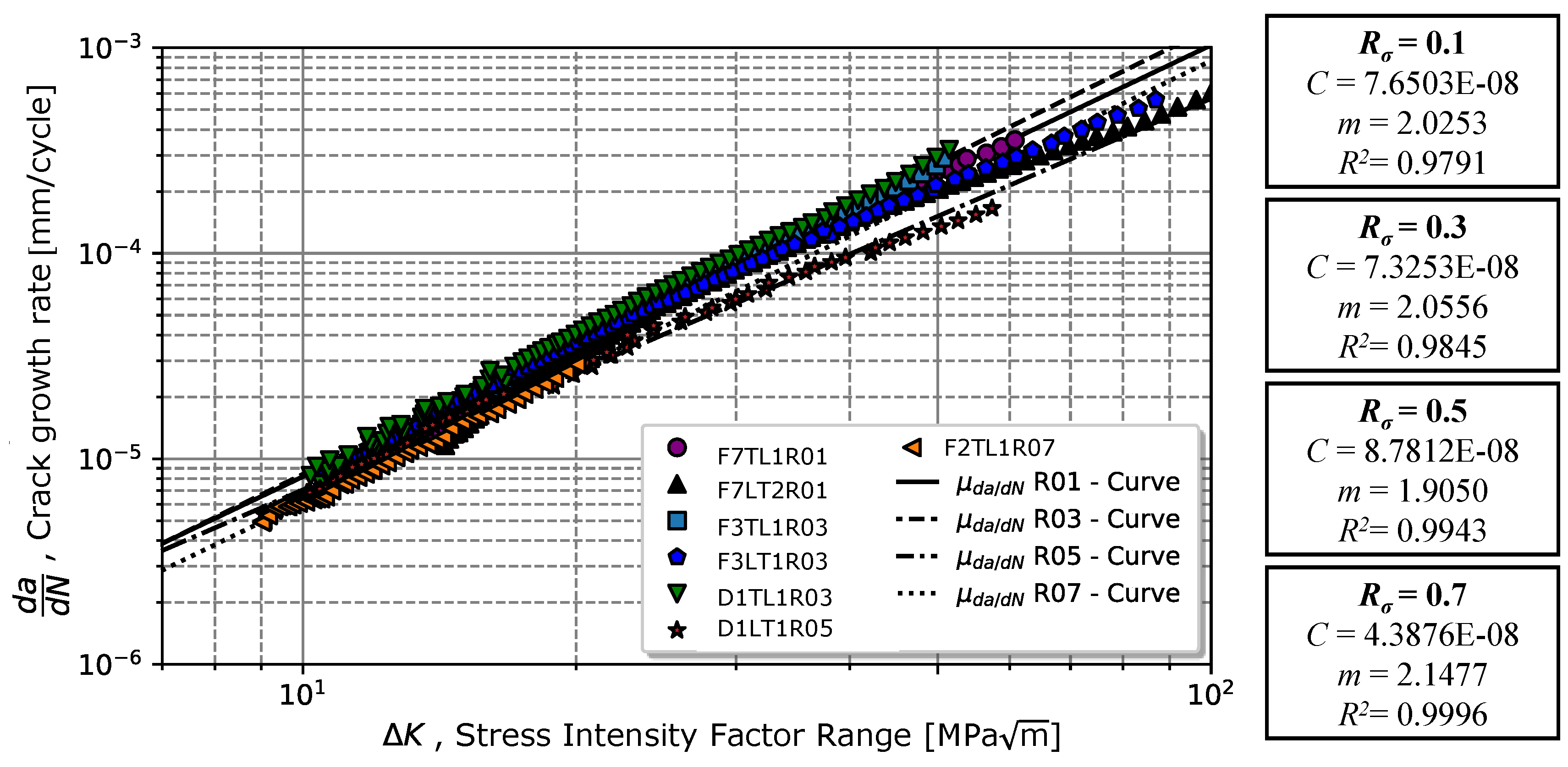
Figure 7.
Average value of the crack closure ratio and respective standard deviation determined throughout the fatigue crack propagation tests.
Figure 7.
Average value of the crack closure ratio and respective standard deviation determined throughout the fatigue crack propagation tests.

Figure 8.
Determination of the threshold of stress intensity factor range from the analysis of the variation of stress intensity factor range throughout the crack growth fatigue testing.
Figure 8.
Determination of the threshold of stress intensity factor range from the analysis of the variation of stress intensity factor range throughout the crack growth fatigue testing.
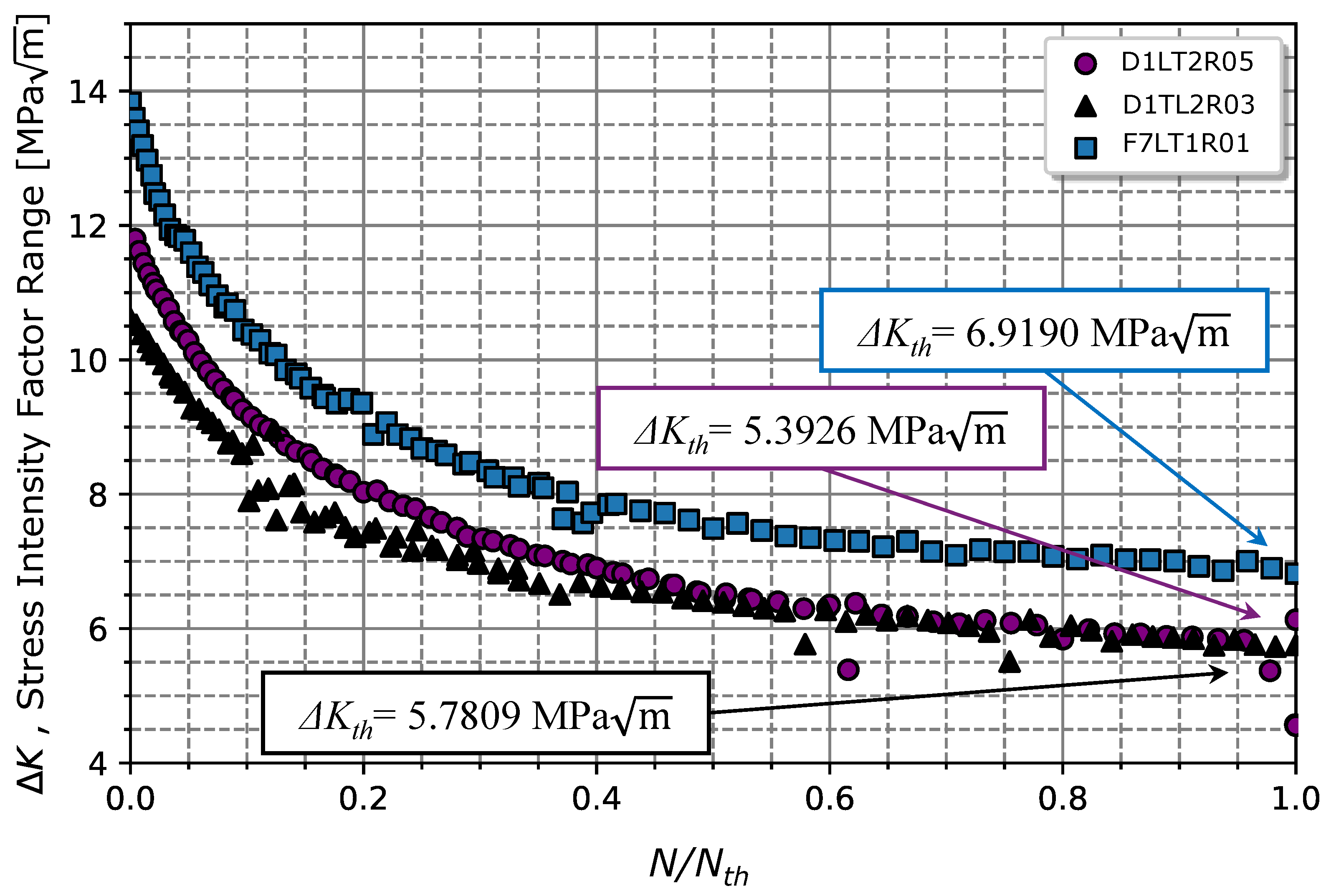
Figure 9.
Effect of the stress ratio in the propagation threshold and the crack propagation model for regime I according to the equation (3) .
Figure 9.
Effect of the stress ratio in the propagation threshold and the crack propagation model for regime I according to the equation (3) .
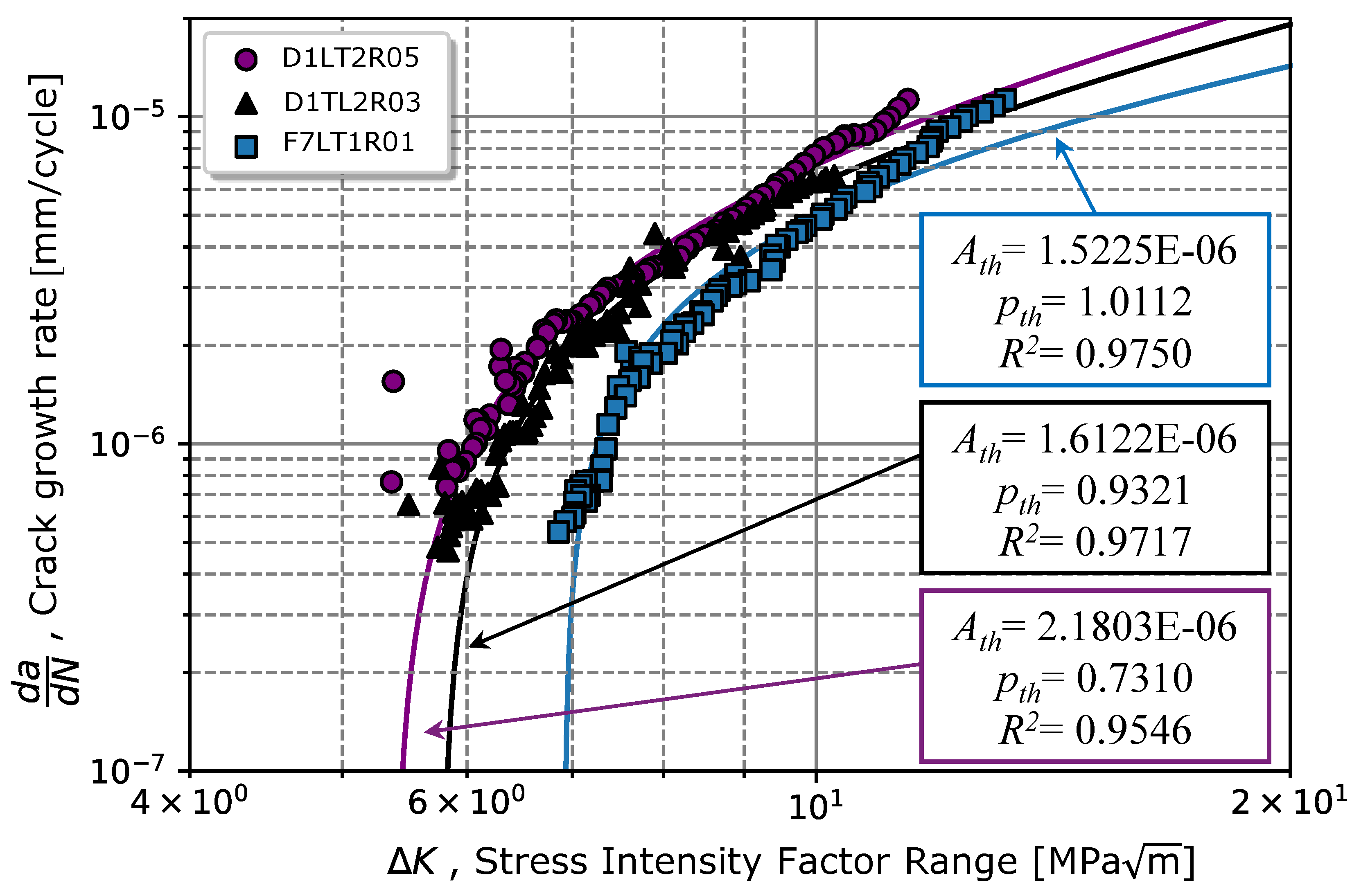
Figure 10.
Global curve representing the variation of the crack propagation rate in the propagation regime II for several stress ratios and the respective standard deviation.
Figure 10.
Global curve representing the variation of the crack propagation rate in the propagation regime II for several stress ratios and the respective standard deviation.
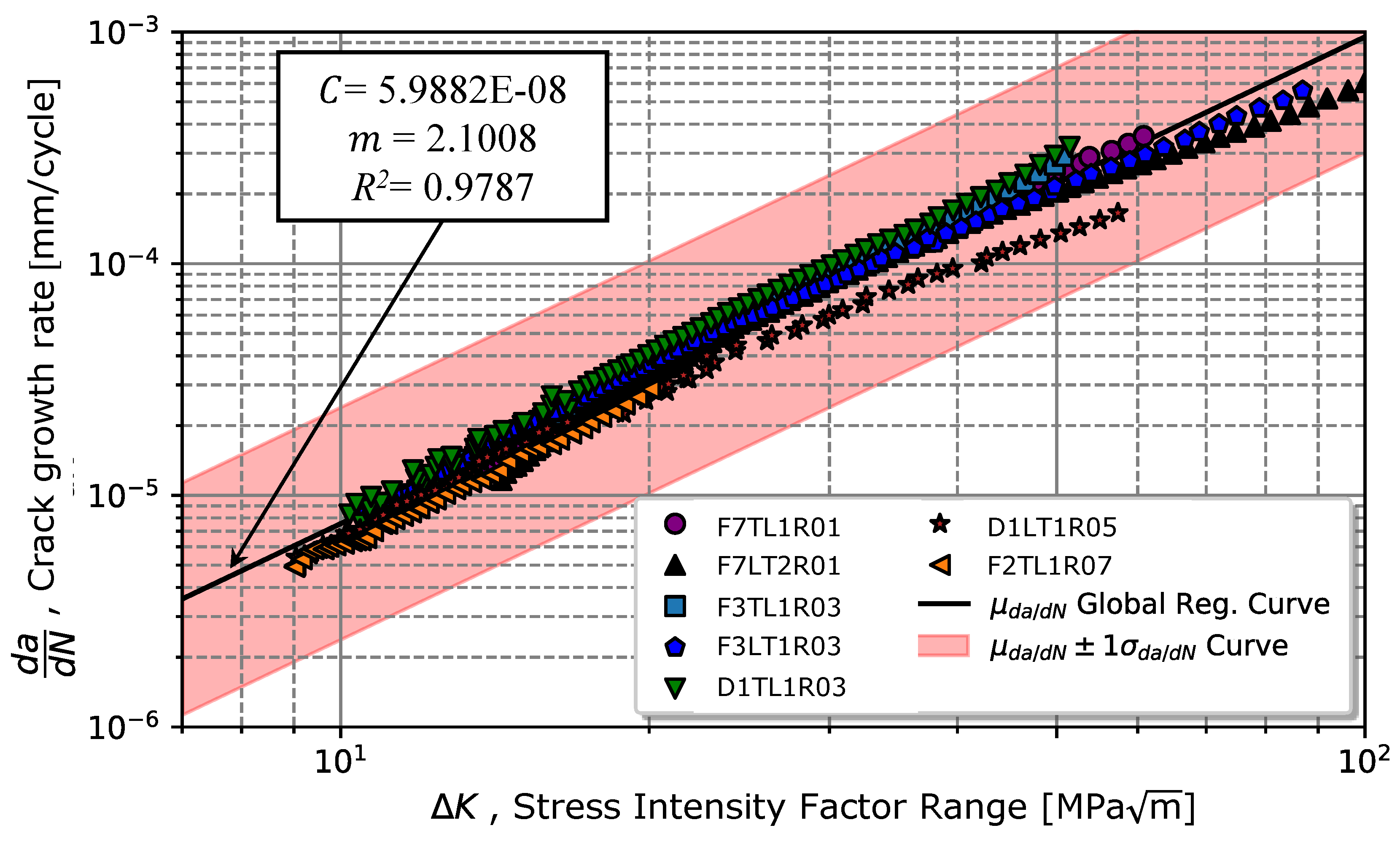
Figure 11.
Relationship for determining the Walker’s parameter, , in accordance with the equation (8).
Figure 11.
Relationship for determining the Walker’s parameter, , in accordance with the equation (8).
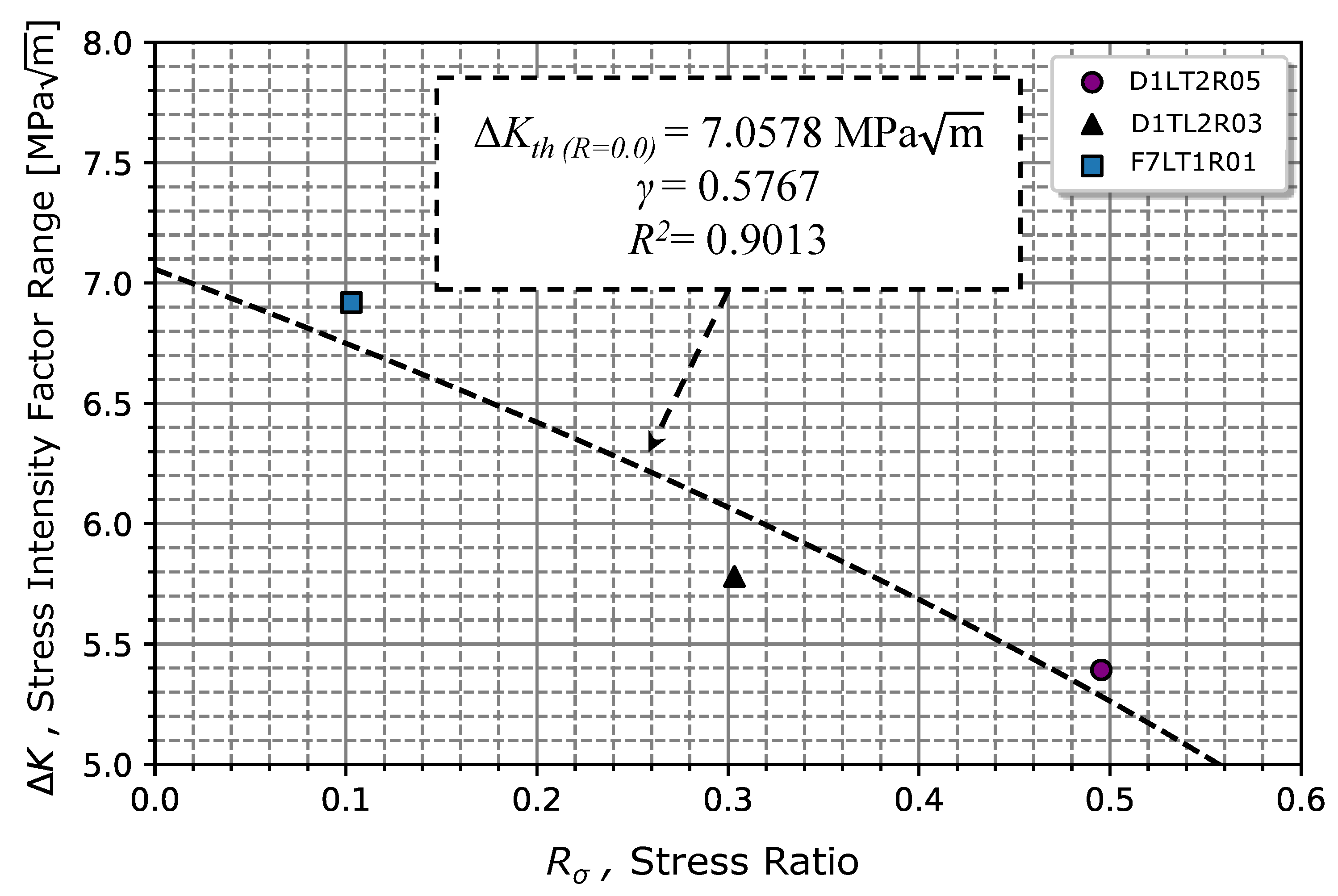
Figure 12.
Representation of the Walker’s model (equation (4)) for different stress intensity factor ratios.
Figure 12.
Representation of the Walker’s model (equation (4)) for different stress intensity factor ratios.
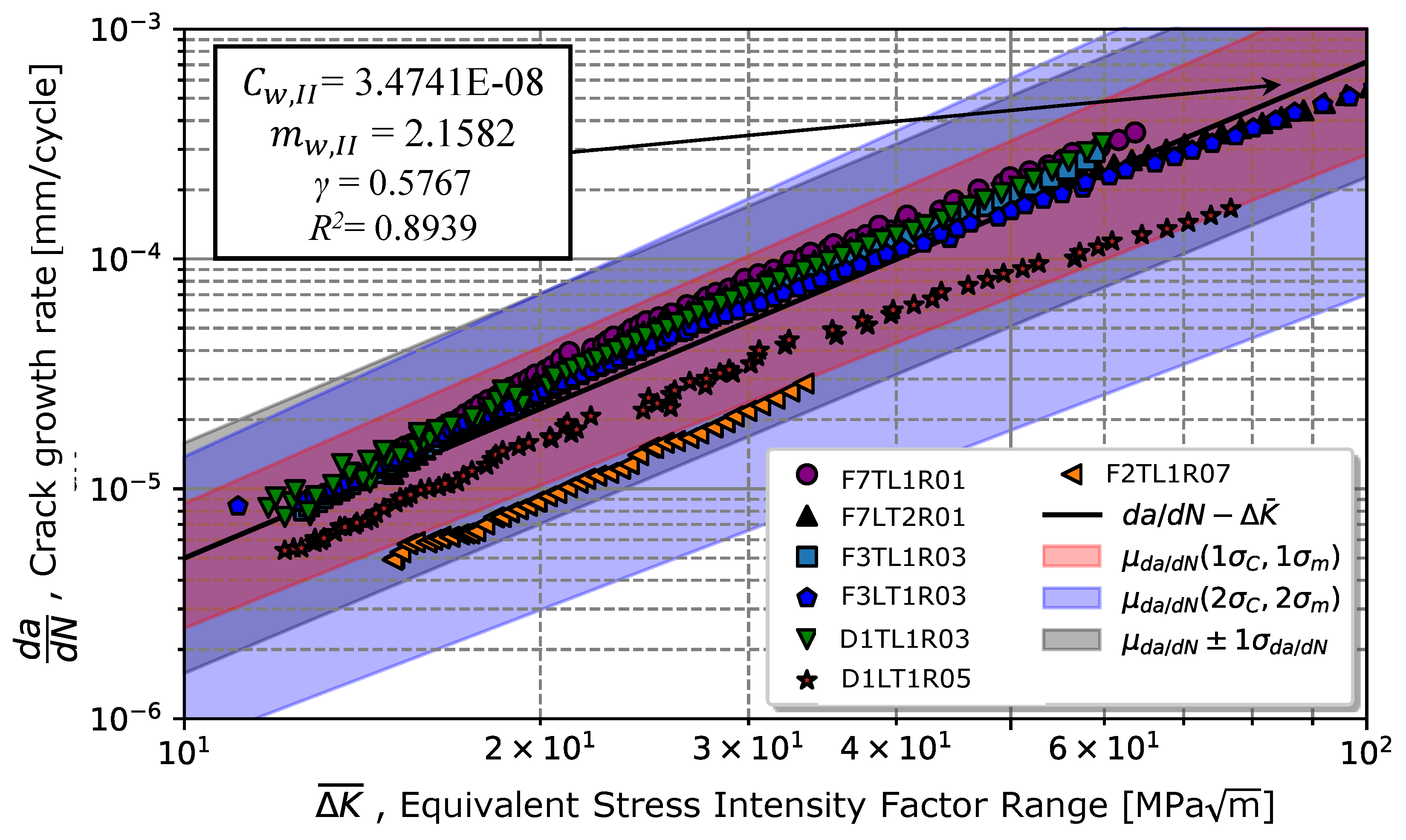
Figure 13.
Representation of the Walker’s model (equation (9)) for different stress intensity factor ratios.
Figure 13.
Representation of the Walker’s model (equation (9)) for different stress intensity factor ratios.

Figure 14.
Illustration of a pre-crack size for an x40 magnification.

Figure 15.
Comparison between fracture surface paths of specimens obtained from LT and TL directions for an x500 magnification ( = 0.1).
Figure 15.
Comparison between fracture surface paths of specimens obtained from LT and TL directions for an x500 magnification ( = 0.1).
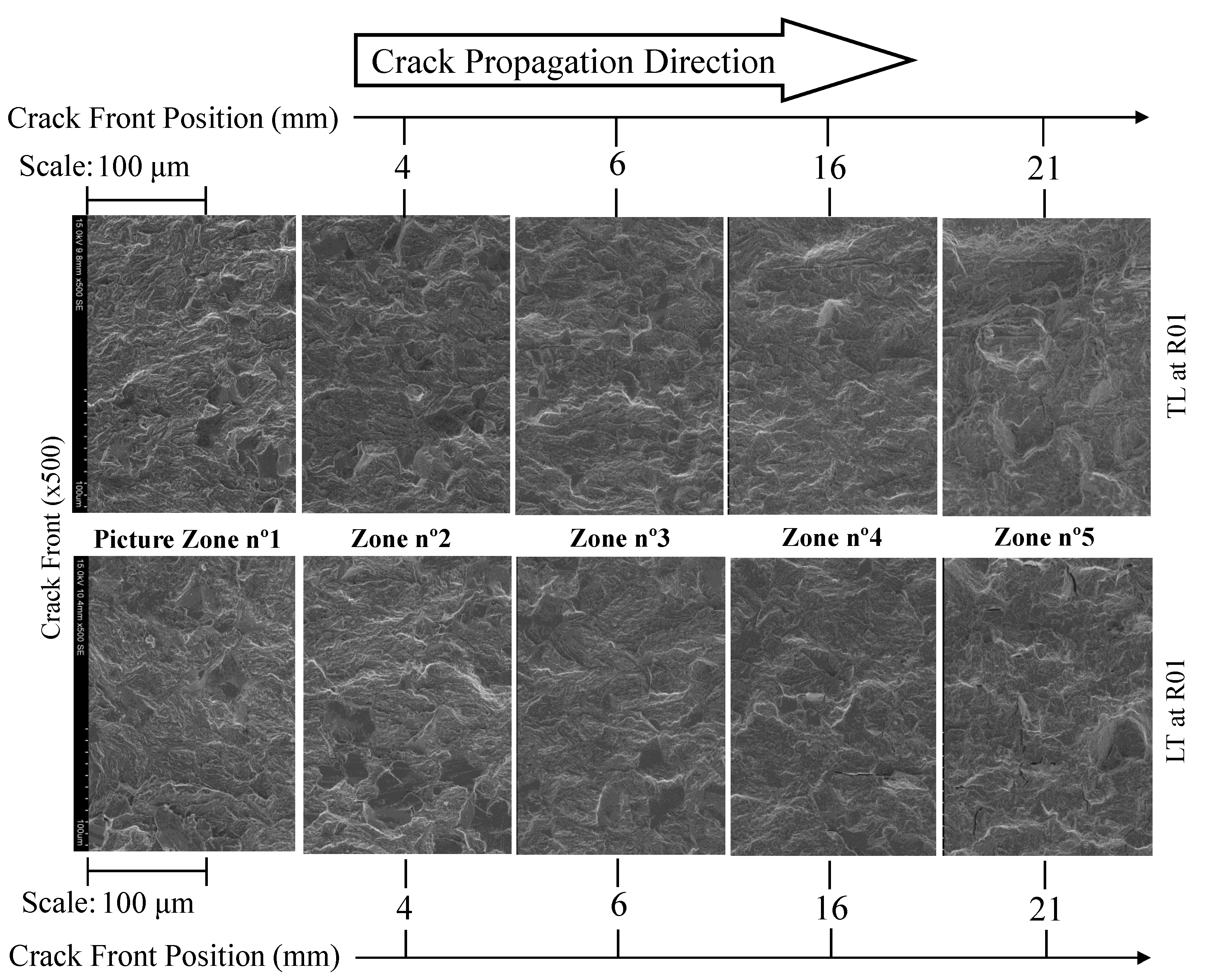
Figure 16.
Crack propagation path from the pre-crack initiation zone to the unstable propagation moment for an x100 magnification ( = 0.1 and 0.5).
Figure 16.
Crack propagation path from the pre-crack initiation zone to the unstable propagation moment for an x100 magnification ( = 0.1 and 0.5).

Figure 17.
Topography comparison of fracture surfaces from the initiation zone to the unstable propagation zone for = 0.1 and 0.5.
Figure 17.
Topography comparison of fracture surfaces from the initiation zone to the unstable propagation zone for = 0.1 and 0.5.

Figure 18.
Magnification of the crack propagation path from the pre-crack initiation zone to the beginning moment of unstable propagation for an x2.00k magnification ( = 0.1 and 0.5).
Figure 18.
Magnification of the crack propagation path from the pre-crack initiation zone to the beginning moment of unstable propagation for an x2.00k magnification ( = 0.1 and 0.5).

Table 1.
Standard chemical composition of 51CrV4 steel grade in % wt.
| Material | C | Si | Mn | Cr | V | S | Pb | Fe |
|---|---|---|---|---|---|---|---|---|
| 51CrV4 (1.815) | 0.47-0.55 | ≤0.40 | 0.70-1.10 | 0.90-1.20 | ≤0.10-0.25 | ≤0.025 | ≤0.025 | 96.45-97.38 |
Table 2.
Monotonic mechanical properties obtained of the chromium-vanadium alloyed steel, 51CrV4 [4].
Table 2.
Monotonic mechanical properties obtained of the chromium-vanadium alloyed steel, 51CrV4 [4].
| E | |||||
|---|---|---|---|---|---|
| [GPa] | [MPa] | [MPa] | [%] | [%] | |
| Average | 7.53 | 34.69 | |||
| Std. Dev. [] | |||||
| DIN 51CrV4 (1.8159) | 200 | 1200 | 1350-1650 | 6 | 30 |
Table 3.
Average dimensions of CT specimens used in fatigue crack growth testing according to ASTM E647 standard [36].
Table 3.
Average dimensions of CT specimens used in fatigue crack growth testing according to ASTM E647 standard [36].
| [mm] | W [mm] | B [mm] | H [mm] | C [mm] | h [mm] | D [mm] | d [mm] | [deg] |
|---|---|---|---|---|---|---|---|---|
| 10.20 | 35.04 | 9.95 | 47.99 | 49.98 | 2.56 | 21.95 | 10.01 | 60 |
| ± 0.31 | ± 0.07 | ± 0.04 | ± 0.03 | ± 0.03 | ± 0.09 | ± 0.10 | ± 0.04 |
Table 4.
Comparison of Paris law parameters for LT and TL propagation directions.
| C (LT) [(mm/cycle) MPa ] | C (TL) [(mm/cycle) MPa ] | m (LT) | m (TL) | |
|---|---|---|---|---|
| 0.1 | 8.8364E-08 | 4.1781E-08 | 1.9653 | 2.2343 |
| 0.3 | 8.3013E-08 | 4.2025E-08 | 2.0087 | 2.2522 |
| 0.5 | 8.7819E-08 | - | 1.9050 | - |
| 0.7 | 5.9891E-08 | - | 1.7109 | - |
| Average | 7.534E-08 | 3.526E-08 | 2.006 | 2.299 |
| ± Std. | 3.761E-08 | 1.827E-08 | 0.1249 | 0.1377 |
Table 5.
Property values that quantify the propagation phase in regimes I, II, and III for different stress ratios.
Table 5.
Property values that quantify the propagation phase in regimes I, II, and III for different stress ratios.
| C | |||||||
|---|---|---|---|---|---|---|---|
| [(mm/cycle) MPa] | [MPa] | [mm] | [MPa] | [(mm/cycle) MPa] | |||
| 0.1 | 7.6503E-08 | 2.0253 | 137.57 | 28.94 | 6.919 | 2.180E-06 | 0.7310 |
| 0.3 | 7.3253E-08 | 2.0556 | 139.86 | 29.00 | 5.781 | 1.612E-06 | 0.9310 |
| 0.5 | 8.781E-08 | 1.9050 | 134.48 | 29.03 | 5.393 | 1.523E-06 | 1.0112 |
| 0.7 | 4.3876E-08 | 2.1477 | 137.97 | 28.82 | - | - | - |
| Average | 5.9882E-08 | 2.1008 | 138.37 | 28.95 | 6.0308 | 1.7717E-06 | 0.891 |
| ± Std. | 1.9760E-08 | 0.0910 | 2.61 | 0.08 | 0.7933 | 3.5671E-07 | 0.1444 |
Table 6.
Comparison of the properties that identify the propagation phase in regime I and II given by the equation models (1), (4), and (9).
| Equation | C [(mm/cycle) MPa] | m | |||
|---|---|---|---|---|---|
| 0.5767 | Walker (4) | Average | 3.4741E-08 | 2.1582 | 0.8939 |
| ± Std. | 1.3215E-08 | 0.0978 | |||
| Walker (9) | Average | 5.7773E-08 | 1.4316 | 0.9134 | |
| ± Std. | 1.4316E-08 | 0.0548 | |||
| N.D | Paris (1) | Average | 5.9882E-08 | 2.1008 | 0.9787 |
| ± Std. | 1.9760E-08 | 0.0910 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









