Prerpints.org logo
Preprint
Article

Exploring the Influencing Factors of Dietary Transition towards Vegetarianism in Korea’s Southern Provinces.

Altmetrics

Downloads

163

Views

82

Comments

0

This version is not peer-reviewed

Consumer Behaviour and Healthy Food Consumption

Submitted:

09 April 2024

Posted:

10 April 2024

You are already at the latest version

Alerts
Abstract
This study explores the elements that influence consumer vegetarian diet choices in parts of South Korean provinces. The study examines these explanatory variables: ethical-animal-welfare, health, environment, social issues , mood-emotion, and religious-beliefs with vegetarianism serving as the dependent variable. The Likert scale data from 264 respondents were analyzed using logistic regression analysis. Results show that health, ethical-animal-welfare ideals as well as environmental concerns emerge as significant variables influencing the decision to embrace a vegetarian diet. This shows that consumers (international students) in Korea are becoming more aware of and concerned about health, ethical and sustainable dietary choices. Secondly, health plays a crucial role in the vegetarian diet selection, indicating that health-conscious people are more inclined to choose a vegetarian lifestyle. Religious belief and mood have various degrees of influence on the vegetarian diet decision. The findings of this study have consequences for consumer behavior, marketing managers, and decision-makers. Businesses in the food industry, in particular, can gain from catering to the needs and tastes of consumers that prioritize ethical-animal welfare ideals, as well as those that value health and environmental sustainability. Creating and advertising vegetarian and vegan choices in local restaurants can effectively attract and serve this specific target demographic.
Keywords: 
Subject: Social Sciences  -   Behavior Sciences

1. Introduction

Consumer behavior and decision-making processes have a significant impact on market trends and industries. One prominent feature of consumer behavior is the growing interest in and acceptance of vegetarian diets. This study investigates the variables that motivate people to gravitate towards vegetarian diets, exploring the intricate process behind their decision-making. Understanding consumer behavior and decision-making processes toward vegetarian dietary choices is critical for businesses and marketers aiming to cater to this growing segment of the population, from personal beliefs and health concerns to environmental and ethical concerns. Businesses may build effective strategies to address the needs and tastes of this increasing consumer segment by understanding the motivations and decision-making factors that push individuals to embrace a vegetarian lifestyle.Over the last few years, there has been a noticeable shift in advanced economies towards lowering meat consumption and adopting vegetarian eating options. According to Google Trends, interest in ‘veganism’ has surged seven times between 2014 and 2019 (Ngo et al. 2021) [1]. According to the Korea Vegetarian Union (KVU), the number of ethical vegans in South Korea has reached roughly 500,000, with approximately 1.5 million people adopting plant-based diets. This increase in numbers is especially striking given the traditional significance of communal meals and the value of shared dining experiences in developing intimate ties and emotional bonding in Korean culture. Thus, choosing vegetarianism may be viewed as breaking from the non-vegetarian norm, as demonstrated by studies conducted by Ngo et al. (2021) and Taebum & In-Jin (2015) [2].
Notwithstanding the possible environmental and health benefits of lowering meat consumption, it appears that the public is primarily concerned with the health benefits alone. A street intercept study in which participants were asked an unprompted question on methods to protect the environment backs up this observation. Surprisingly, 60% of respondents named transportation options as a way to preserve the environment, while just 3% mentioned the impact of nutrition (Joyce et al.,. 2012). The factors that influence the shift in dietary practice toward a vegetarian diet among foreign students in South Korea’s southern provinces might have consequences for consumer behavior and marketing strategies in the country. Hence, this study explores the factors influencing the transition in dietary practice toward a vegetarian diet among foreign students in South Korea’s southern provinces. Marketers in South Korea might adapt their approaches to meet the changing dietary preferences of international students through understanding the ethical/welfare, social peer/family influence, religious/cultural, health, awareness/convenience and environmental factors that influence their decisions. Marketers may engage with this consumer segment and promote vegetarian products and services in an appealing manner by catering to these factors and effectively communicating the benefits of vegetarian options.
This study distributed questionnaire which utilized a five-point Likert scale to explore the influencing factors that motivate vegetarian dietary decision among 264 respondents who are mostly foreign students living in the Southern provinces of Korea. The prominent factors examined are six in number based on previous literature (Ngo et al. 2021). While health, ethical-animal welfare, social-peer influence, religious-cultural belief, mood and environmental factors serve as the predictor variables, vegetarian decision, a dichotomous (binary) dummy variable construct from the respondents who practice vegetarianism and those who consume conventional diets serve as the dependent variable (Joyce et al.,. 2012) [3].
Employing the binary logistic regression technique in the empirical analysis, the results show that out of the six factors explored, two motivating variables that predict consumer behaviour towards vegetarian dietary choice namely health factor and ethical/animal welfare variables presented statistically significant relationships at the 1% and 2% levels respectively. A robustness test is conducted using a multivariate regression analysis to explore the impact of the motivating factors towards vegetarian diet decision. The results are consistent with that observed from the logistic regression technique.The variables of health and ethical/animal welfare are robust and shows statistically significant relationship at the 1% and 2% levels respectively. The environmental factor however shows a weak relationship at a statistical significance level of 10%.
This finding has both policy and practical implications for businesses and marketing managers in the food/consumer segments of the market in Korea. First off, the increased awareness of the health benefits of a vegetarian diet opens up more opportunities for marketers to promote and sell vegetarian food products or services that emphasize their nutritional benefits. To attract health-conscious consumers, marketers might highlight health benefits such as lower risk of certain diseases and weight management. Using communication that stresses the nutritional worth and excellent health consequences of vegetarian diet options can help with increased sales and revenue generation.
Secondly, ethical/animal welfare considerations can have a significant impact on consumer behavior in South Korea. Individuals who emphasize these issues may opt for a vegetarian diet to align their eating habits with their ideals of compassion for animals and the environment. They may deliberately seek for things branded as cruelty-free or made with ethical and sustainable practices. Understanding this consumer segment and their motivations might help marketers cater to their needs and preferences.
Lastly, advertising strategies can be designed to target consumers that prioritize ethics and animal welfare. In their marketing communications, businesses can emphasize their commitment to animal welfare and ethical standards. This can include displaying certifications, collaborating with animal rights groups, or using transparent sourcing approaches. Marketers can attract consumers who are specifically looking for products that align with their moral principles by promoting these ideals.
The remaining part of this study are presented under literature review, research methodology, empirical analysis and conclusion.

2. Literature Review

Research has suggested a connection between reduced meat intake and life expectancy; however, further investigation is required to establish causality due to methodology constraints. One difficulty is defining and categorizing groups based on meat consumption, as persons who consume meat less than once a week are frequently deemed non-vegetarian for analysis purposes [4].
Moreover, because many self-described vegetarians still consume meat, some research rely on self-reported vegetarian status, which may not adequately reflect actual eating patterns. A study carried out in the United States, for instance, discovered that, while self-described vegetarians had healthier overall diets than non-vegetarians, a majority of self-described vegetarians reported ingesting red meat, chicken, or fish based on a two-day food recollection [5].
These quantitative inadequacies limit the capacity to detect differences between vegetarians and non-vegetarians, and the association between reduced meat consumption and longevity may be stronger than the results suggest [4]. What is more, the beneficial changes reported in health outcomes may be due to the use of plant-based meals rather than just the removal of animal-based foods [4].
According to thorough assessments over the past few years, the top triggers for adopting a vegetarian diet are, in descending order of prevalence, ethical considerations for animal welfare, good health, environment, and religion [6,7]. Additionally, there are significant intergenerational disparities in the motivations for choosing a vegetarian diet. Consumers between 41 to 60 are more inclined to highlight health-related concerns, whereas younger generations favor ethical and environmental grounds [8]. Juvenile vegetarianism is most commonly encouraged for factors related to health, animal welfare, and the environment, according to [9]. Evidently, there are two primary groups of consumers and persons that practice vegetarianism, depending on their objectives. According to research by [10,11,12], the main reasons vegetarians opt to eliminate meat are to receive certain health benefits or lose weight. In contrast, ethical vegetarians see giving up meat as a moral need motivated by the desire to stop harming animals used for food or other purposes [13,14].
The majority of the current study on plant-based diets has been fixated on ethical and health implications. In a study employing surveys, Lea et al. [15] looked into the challenges and potential advantages of following a plant-based diet. They also held target group discussions to examine the disadvantages and advantages especially associated with plant-based foods [16]. Convenience and simplicity of preparation emerged as key hurdles in the focus groups’ discussion among a variety of factors highlighted [16]. Lack of awareness was identified as the main barrier to consuming a plant-based diet, with 42% of participants saying they needed more information [15], notably on nutrition and how to prepare plant-based meals.
Other often noted obstacles included a lack of enthusiasm in changing one’s diet and worries about other family members unwillingness to do the same. It was shown that female respondents were less inclined to concur that humans were designed to eat meat. Regarding perceived advantages, the majority (79%) recognized that a plant-based diet may have positive health effects, such as lowering cholesterol levels, while 70% concurred that it may avoid diseases generally [15].
When questioned about the advantages of a plant-based diet, male participants in a survey of university students tended to highlight health benefits. With the exception of 8% of female participants who listed the less harm to animals as a positive, this trend was also seen among them [17]. The survey also revealed that people switching to plant-based diets did not seem to be doing so primarily for environmental concerns.
Extant research investigated whether the Theory of Planned Behavior [18] and the Transtheoretical Model [19] might be used to predict the intention to switch to a plant-based diet. They suggested that encouraging a plant-based diet would work well as a preventative measure for chronic illnesses [17]. The decision-making process for consuming more fruits and vegetables as opposed to switching to a plant-based diet was found to be different, the researchers noted. They also saw differences in views toward a plant-based diet depending on a person’s gender and stage of transition. The implications of these findings for consumer behavior initiatives are important since people who are already at the contemplation stage may not be easily persuaded by certain stimuli or health experts’ advice. However, educating people about the advantages of a plant-based diet and addressing sentiments about obtaining plant-based protein, which were common concerns for both males and females could prove beneficial [17].

2.1. Hypothesis Development

According to the Theory of Planned Behavior (TPB), attitudes are judged based on the strength of behavioral beliefs and serve as predictors of behaviors. These attitudes rooted in beliefs and have the capacity to influence behavioral intentions [20]. The “attitude towards behavior” hypothesis, as proposed by [21], investigates how customers not only act but also include their emotions and beliefs about the cues that activate behavioral intentions.
According to some research, morally driven vegetarianism comprises a specific way of life, with vegetarianism playing a role in identity formation [22,23,24]. The moral status of animals and the rationale for inflicting them grief and pain are central to ethical debates [25,26]. The ethical/animal welfare research community presents two perspectives broadly identified as the “biological functioning” school and the “feelings” school. One group believes that animal welfare is primarily concerned with the physical health and well-being of animals, whilst the other believes that animal welfare is more concerned with the psychological well-being and feelings of animals [1], As a result, any assessment of welfare should take into account scientific facts regarding animals’ feelings derived from their structure, functions, and behavior. Failure to establish conditions that allow these traits to be expressed might lead to unfavorable sentiments in the animals [27]. Animal welfare is a prominent variable in various studies relevant to vegetarian decision-making [6,8,9]. Furthermore, labeling animals as “food animals” alters the impressions of their intelligence and attractiveness, lowering moral worries about eating them [28,29,30]. The rejection of using animals for food has been emphasized as a key difference between vegetarians/vegans and omnivores [31,32].
H1
Ethical and animal welfare has a significant impact on vegetarian diet decision.
Previous study reveals that vegetarianism and veganism are mostly motivated by ethical and health concerns. Beardsworth and Keil [33] underline the fundamental difficulties around food that are relevant to vegetarianism. These include the trade-off between food for energy and health and food that can cause illness, the balance between gustatory pleasure and probable discomfort or illness produced by specific foods, and the ethical quandary of consuming food needed for healthy living and at the same time, that which requires the slaughter of animals. Omnivores prefer to stress the good health benefits and satisfaction obtained from eating meat, whereas vegetarians tend to focus on the negative health effects. Health is a relevant motivation for vegetarian/vegan diets. A meatless diet is perceived as healthier, especially by vegetarians/vegans. Consequently, they expect an improvement in their health status by maintaining or changing to a meatless diet [33,34,35,36].
H2
Health concerns has a significant impact on vegetarian diet decision.
Regarding social and peer interactions, the study conducted by Hirschler [37] emphasizes the problems that vegans experience in social situations, notably with family members. While family attitudes might range from extreme rejection to adopting a vegetarian or vegan diet themselves, the vegans interviewed perceive these relationships as difficult. According to Hirschler, vegetarians/vegans can persuade family members and friends to accept or even change their dietary preferences. Beardsworth and Keil [38] examine difficulties between parents and vegetarian children in particular, as parents may interpret the child’s vegetarianism as a rejection of their own eating choices and may resist supporting the youngster. According to Nezlek et al. [39], vegetarians are more likely to have vegetarian friends and partners, highlighting the significance of dietary preferences in vegetarian social ties. Mylan [40] examines hurdles to lowering meat consumption and identifies social punishments such as dissatisfaction of others or constraints on attending social occasions.
H3
Social group have a significant impact on vegetarian diet decision.
According to Pimentel and Pimentel [41], the current food pattern widespread in North America is environmentally unsustainable. They back up their assertion with their own study findings and Department of Agriculture data. According to their calculations, creating an identical quantity of protein from meat requires 11 times more fossil fuel than producing an equivalent amount of protein from vegetables. Furthermore, the synthesis of animal protein requires 100 times more water than the creation of vegetable protein. The majority of this water demand comes from crop cultivation and animal feed, with agricultural irrigation accounting for 85% of freshwater consumption. The authors believe that present animal-based diets, together with population expansion, constitute a challenge to the sustainable use of natural resources. The opinion that a vegetarian diet has a smaller environmental impact was the only significant factor distinguishing vegetarians from non-vegetarians in a study on the influences of vegetarianism conducted by Kalof et-al. [42]. Vegetarianism’s health and animal welfare benefits, on the other hand, did not reveal significant variation. The market today provides a variety of commercial channels that sell “health foods,” “wholefoods,” and, more recently, “organic foods” grown without chemicals, pesticides, or artificial fertilizers, which put environmental concerns over food productivity [43]. According to Hoek et al. [44], a “vegetarian-oriented consumerism” that addresses ethical and environmental issues is emerging. Furthermore, according to Allen Fox [45], a vegetarian economy contributes to “ecosystem health” by lowering pollution, intensive farming, and land degradation caused by grazing, which benefits both developed and developing countries. Hence, vegetarians’ psychological well-being can be improved by being aware of their role to the future of the world according to Wilson et al. [46].
H4
Environmental concerns has a significant impact on vegetarian diet decision.
Religion can influence food decisions by providing social support. Religious communities provide a forum for people who share common values, interests, and activities to interact while building larger social networks and getting more social support [47]. Religious beliefs are frequently acknowledged as a guiding impact on people’s ethical and moral eating choices [48]. Many people who follow specific religious traditions are vehemently opposed to the killing of animals for human interests. There are dietary limitations in several religions, particularly addressing the use of meat [49,50]. Religious motivation, according to Peek et al. [51], is associated with a higher level of support for animal rights.
H5
Religious beliefs have a significant impact on vegetarian diet decision.
A cross-sectional study involving a large sample of men from the Avon Longitudinal Study of Parents and Children discovered that vegetarian men had a higher prevalence of depressive symptoms even after controlling for potential confounding factors like family history of depression, education level, age, ethnic origins, and alcohol and tobacco consumption [52]. Similarly, in another cross-sectional study of 15-year-old Norwegian and Swedish students, those who ate less meat had a higher risk of depression, even after controlling for physical characteristics, health status, family situation, social status, exercise habits, and alcohol and tobacco consumption [53]. Furthermore, a cross-sectional study in Germany found that vegan adults had a greater prevalence of depressive disorders, anxiety disorders, and somatoform disorders, even after controlling for socio-demographic factors [54].
H6
Mood has a significant impact on vegetarian diet decision.

2.2. Conceptual Model

Based on prior research findings, this study propose a conceptual model captured in Figure 1, in which the six predictor variables are projected to have a significant influence on Vegetarian Decisions.

3. Research Methodology

By constructing a questionnaire based on theoretical foundations and prior investigations, this study consolidated data on factors influencing participants’ choice of a vegetarian diet. The questionnaire used a five-point Likert scale (ranging from Strongly Disagree to Strongly Agree) and was administered through an online survey using Google Forms. Internet interviews were chosen due to their suitability for sensitive topics and the potential bias faced by individuals with vegetarian diets. Participants may feel more comfortable expressing their opinions online, benefiting from the anonymity provided. Additionally, online surveys are cost-effective and allow access to hard-to-reach groups, including those engaged in expert forums. The majority of surveys were conducted through vegetarian groups on platforms such as Kakao, Facebook, and Whatsapp, leveraging their large visitor base.
Data Collection and Analysis
From various universities student communities in the Southern Provinces of Korea, the author sourced motivations for vegetarian dietary choice and 264 foreign student participants responded through the disseminated google form questionnaire. The scale was verified using IBM SPSS 23.0 software, with a significance level of 0.05 considered statistically significant. Descriptive statistical analysis was performed on the data, followed by checks for reliability using Cronbach Alpha coefficients. Exploratory Factor Analysis (EFA) was conducted to reduce and summarize the data while assessing the reliability of the variables. Correlation analysis was employed to evaluate the suitability of factors before including them in the regression model. Subsequently, a binary logistic regression analysis was conducted to examine the factors influencing vegetarian choice decisions in the population of foreign students in the Southern Provinces of Korea. Additionally, a robustness test was performed using multivariate regression analysis to explore variations in the vegetarian diet decisions of this population.

4. Results.

4.1. Descriptive Analysis

GENDER
Frequency Percent Valid Percent Cumulative Percent
Valid I prefer not to say 4 1.5 1.5 1.5
MALE 124 47 47 48.5
FEMALE 136 51.5 51.5 100
Total 264 100 100
Overall, the data was collected from 264 respondents. While 124 students representing 47% of the population identified as the male gender, 136 students representing 51.5% identified as female gender whereas 4 students representing 1.5% of the respondents prefer not to identify as any gender.
Do you consider yourself a vegetarian or a vegan?
Frequency Percent Valid Percent Cumulative Percent
Valid NO 211 79.9 79.9 79.9
YES 53 20.1 20.1 100
Total 264 100 100
Out of 264 respondents, only 53 representing 20.1% identified as vegetarian or vegan. Vegetarian in this case includes Lacto, Lacto-Ovo, Ovo, and Vegan as defined above. However, 211 respondents representing 80% of the population identified as non-vegetarians.
Weight
Frequency Percent Valid Percent Cumulative Percent
Valid 0 1 0.4 0.4 0.4
40 - 50 kg 17 6.4 6.4 6.8
50 - 60 kg 50 18.9 18.9 25.8
60 - 70 kg 133 50.4 50.4 76.1
70 - 80 kg 2 0.8 0.8 76.9
80 -90 kg 41 15.5 15.5 92.4
90 - 100 kg 15 5.7 5.7 98.1
100 - 120 kg 3 1.1 1.1 99.2
120 - 130 kg 2 0.8 0.8 100
Total 264 100 100
Majority of the respondents weigh between 60 to 70kg representing 50.4% while 15.5% of the entire respondents fall in the weight range of 80 to 90kg. Respondents weighing above 100kg are 5 representing only 2% of the entire sample whereas 17 students representing 6% of the sample weigh from 40 to 50kg.
Height
Frequency Percent Valid Percent Cumulative Percent
Valid 120 -130 cm 3 1.1 1.1 1.1
130 - 140 cm 10 3.8 3.8 4.9
140 - 150 cm 10 3.8 3.8 8.7
150 - 160 cm 87 33 33 41.7
160 - 170 cm 108 40.9 40.9 82.6
170 - 180 cm 38 14.4 14.4 97
180 - 190 cm 8 3 3 100
Total 264 100 100
In terms of height, 108 students representing 41% of the sample are 1.6m to 1.7m tall. 46 students are taller than 1.7m representing 17.4% of the population while 110 students representing 41.7% are shorter than 1.6m.

4.2. Evaluation of Research Model for Analysis

Table 1. Cronbach’s Alpha Reliability Statistics.
Table 1. Cronbach’s Alpha Reliability Statistics.
S/No. Variable Cronbach’s Coefficients No. of Items
1 ANIMAL WELFARE 0.803 3
2 SOCIAL 0.840 3
3 HEALTH 0.898 4
4 ENVIRONMENT 0.935 9
5 MOOD 0.906 5
6 RELIGION 0.730 3
TOTAL MEAN = 0.852 27
Animal welfare, Social peer, Health, Environment, Mood, and Religion variables have acceptable internal consistency (0.9 > α > 0.7).
The Kaiser-Meyer-Olkin (KMO) measure of sampling adequacy is 0.946 which is above the recommended value of 0.6. Equally, the Bartlett’s Test of Sphericity is significant as presented in Table 2 below.
Variable Extraction using Principal Component Analysis
Table 4. Pearson Correlations Matrix.
Table 4. Pearson Correlations Matrix.
Preprints 103470 i001
Overall, all the variables show positive and statistical significant correlations with vegetarian decision except for religion and health. High correlations did not manifest among the independent variables as well.

4.3. Binary Logistic Regression Analysis

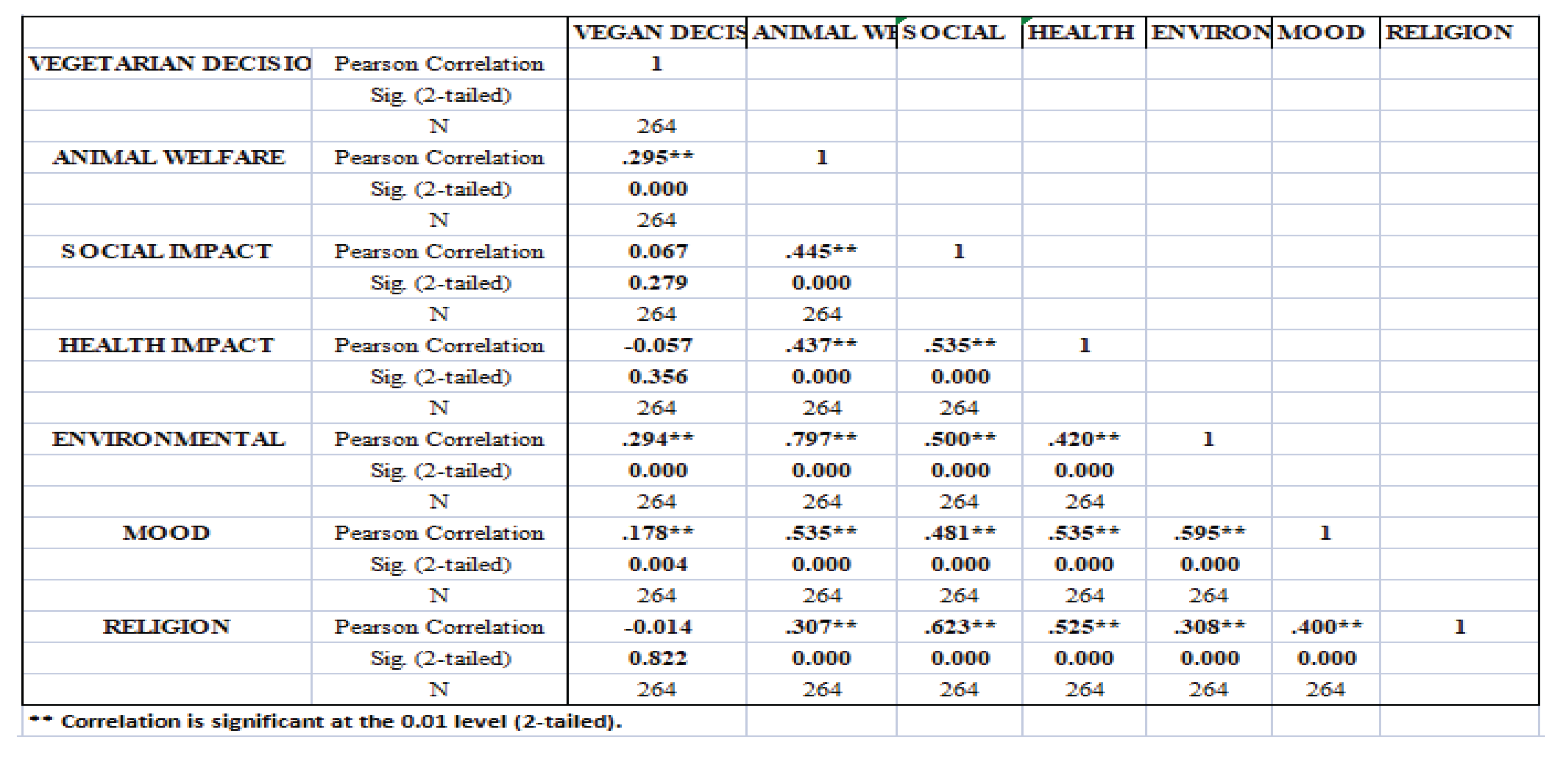
In Table 5, the Case Processing Summary indicates that all 264 cases in the dataset were included in the logistic regression analysis, and there were no missing cases or unselected cases.
In Table 6, the purpose of encoding the dependent variable is to represent the different categories or responses numerically so that they can be used in the logistic regression analysis. By assigning the internal values of 0 and 1 to the original values, the logistic regression model can estimate the relationship between the predictors (independent variables) and the likelihood of the dependent variable being “YES” based on the given encoding.
In Table 7, “I prefer not to say” is the reference category, indicated by a frequency of 4. The parameter coding for this category is (1.000, .000), which means that when compared to the reference category, there is no difference in the parameter estimates for this category. “MALE” has a frequency of 124. The parameter coding for this category is (.000, 1.000), indicating that when compared to the reference category (“I prefer not to say”), the parameter estimate for this category is 1.000.
“FEMALE” has a frequency of 136. The parameter coding for this category is (.000, .000), indicating that when compared to the reference category (“I prefer not to say”), there is no difference in the parameter estimates for this category.
These parameter codings allow the logistic regression model to estimate the effects of each category of the categorical variable on the likelihood of the dependent variable being “YES” (as encoded earlier).
The “Omnibus Tests of Model Coefficients” in Table 8 presents the results of the omnibus tests conducted on the coefficients of the logistic regression model.
The chi-square statistic is a measure of the overall goodness-of-fit of the logistic regression model. In this table, the chi-square value is 51.010.
The degrees of freedom (df) represent the number of parameters estimated in the model. In this case, there are 8 degrees of freedom.
The significance level(Sig), also known as p-value, indicates the probability of observing the obtained chi-square value or a more extreme value under the null hypothesis of no relationship between the predictors and the dependent variable. In this analysis, the p-value is reported as .000, which means the obtained chi-square value is statistically significant at the chosen significance level.
Therefore, the omnibus tests of model coefficients suggest that the logistic regression model, as a whole, is statistically significant in predicting the dependent variable. The chi-square test indicates that the observed relationship between the predictors and the dependent variable is unlikely to have occurred by chance alone. Therefore, there is evidence to support the conclusion that the predictors included in the model have a significant influence on the likelihood of the dependent variable being “YES” (as encoded earlier).
Table 9 shows the “Model Summary” which provides information about the fit and predictive ability of the logistic regression model. The step (1) number indicates the iteration of the model. In this case, there is only one step included in the model.
The -2 log likelihood is a measure of the overall fit of the logistic regression model. It represents the log of the likelihood function multiplied by -2, and lower values indicate a better fit. In this analysis, the -2 log likelihood value is 213.756.
The Cox & Snell R Square is a measure of the proportion of variance in the dependent variable( vegetarian decision) that is accounted for by the logistic regression model. It ranges from 0 to 1, with higher values indicating a better fit. In this analysis, the Cox & Snell R Square is reported as .176, indicating that the model explains approximately 17.6% of the variance in the dependent variable.
The Nagelkerke R Square is an adjusted version of the Cox & Snell R Square, which takes into account the number of predictors and the sample size. It also ranges from 0 to 1, with higher values indicating a better fit. In this analysis, the Nagelkerke R Square is reported as .277, suggesting that the model explains approximately 27.7% of the variance in the dependent variable.
Additionally, estimation process terminated after 6 iterations because the parameter estimates changed by less than .001. This indicates that the model has reached a stable state and further iterations are not necessary. The logistic regression model shows a reasonably good fit based on the -2 log likelihood value. The Cox & Snell R Square and Nagelkerke R Square values suggest that the model explains a moderate amount of the variance in the dependent variable ranging from 17.6% to 27.7%. However, it is circumspect to note that the model may not capture all factors influencing the dependent variable, and there may be unexplained variance.
Table 10 presents The “Hosmer and Lemeshow Test” which is used to assess the goodness-of-fit of a logistic regression model by comparing the observed and expected frequencies of the dependent variable across groups defined by predicted probabilities. The step number indicates the iteration of the model. In this case, there is only one step included in the model. The chi-square statistic is calculated based on the differences between the observed and expected frequencies in the groups. In this analysis, the chi-square value is 7.742. The degrees of freedom represent the number of categories minus the number of estimated parameters. In this case, there are 8 degrees of freedom. The significance level, also known as p-value, indicates the probability of observing the obtained chi-square value or a more extreme value under the null hypothesis of good fit. In this analysis, the p-value is reported as .459, which is above the conventional threshold of .05. The Hosmer and Lemeshow Test assesses whether there is evidence of a lack of fit between the observed and expected frequencies in the logistic regression model. In this case, the test yields a non-significant result with a p-value of .459. This suggests that there is no significant lack of fit, indicating that the observed and expected frequencies are consistent with each other and the model provides a good fit to the data.
Table 11 presents the “Variables in the Equation” and gives information about the coefficients, standard errors, Wald statistics, degrees of freedom, p-values, and odds ratios of the variables included in the logistic regression equation.
The logistic regression result describes the association between the independent factors (GENDER, RELIGION, MOOD, ENVIRONMENT, HEALTH, SOCIAL, ANIMAL WELFARE) and the dependent variable (Vegetarian diet decision).
In the logistic regression analysis output, the coefficient for the variable “ANIMAL WELFARE” is 0.713, with a standard error of 0.307. The Wald statistic value is 5.398, and the related p-value is 0.020. This suggests that the variable “ANIMAL WELFARE” has a statistically significant association with the decision to pursue a vegetarian diet. The odds ratio (Exp(B)) is 2.041, which suggests that for every one-unit increase in the “ANIMAL WELFARE” variable, the odds of adopting a vegetarian diet rise by nearly 104.1%. The 95% confidence interval for the odds ratio ranges from 1.118 to 3.725.
From the results of the analysis, variable “HEALTH” has a coefficient of -0.683 and a standard error of 0.221. The Wald statistic value is 9.58, with a p-value of 0.002 correspondingly. This suggests that the variable “HEALTH” has a highly significant association with the decision of becoming vegetarian. The odds ratio (Exp(B)) is 0.505, which implies a one-unit increase in the “HEALTH” variable reduces the likelihood of selecting a vegetarian diet by approximately 49.5%. The odds ratio has a 95% confidence interval of 0.328 to 0.778. These findings imply that the perceived value of health, as well as concern for animal welfare, have a major impact on the decision to eat a vegetarian diet. Higher perceived health advantages are connected with a lower likelihood of eating vegetarian, but greater concern for animal welfare is associated with a higher likelihood of eating vegetarian.
The results show that the variable “ENVIRONMENT” has a coefficient of 0.518 and a standard error of 0.325. The Wald statistic is 2.547, and the associated p-value is 0.11. This implies that, at the standard significance level p < 0.05, the factor “ENVIRONMENT” has no statistically significant link with the decision to follow a vegetarian diet. The odds ratio (Exp(B)) is 1.679, indicating that a one-unit increase in the “ENVIRONMENT” variable increases the likelihood of adopting a vegetarian diet by about 67.9%. However, it cannot be inferred that this association is statistically significant because the p-value is more than 0.05. However, the variable “SOCIAL Peer” has a coefficient of -0.076 and a standard error of 0.203. The Wald statistic is 0.141, and the associated p-value is 0.707. This means that the variable “SOCIAL” has no statistically significant link with the decision to eat a vegetarian diet. The odds ratio (Exp(B)) is 0.927, indicating that a one-unit increase in the “SOCIAL” variable reduces the likelihood of selecting a vegetarian diet by approximately 7.3%. However, since the p-value is greater than 0.05, the relationship is not considered statistically significant. When it comes to the variable “RELIGION”, the results show that it has a coefficient of 0.075 and a standard error of 0.165. The Wald statistic is 0.207, and the associated p-value is 0.649. This means that the variable “RELIGION” has no statistically significant link with the decision to eat a vegetarian diet. The odds ratio (Exp(B)) is 1.078, showing that a one-unit increase in the “RELIGION” variable increases the probabilities of adopting a vegetarian diet by 7.8%. The association, however, is not statistically significant because the p-value is bigger than 0.05. Lastly, the variable “MOOD” has a coefficient of 0.371 and a standard error of 0.235. The Wald statistic is 2.499, and the associated p-value is 0.114. This implies that the variable “MOOD” has no statistically significant link with the decision to eat a vegetarian diet. The odds ratio (Exp(B)) is 1.45, indicating that a one-unit increase in the “MOOD” variable increases the likelihood of selecting a vegetarian diet by about 45%. The association, however, is not statistically significant because the p-value is bigger than 0.05. It seems that the factors ENVIRONMENT, SOCIAL, RELIGION, and MOOD do not have a statistically significant link with the decision to follow a vegetarian diet, according to the logistic regression analysis.

4.4. Robustness Test

Multivariate Regression Analysis:
Model Summary
Model R R Square Adjusted R Square Std. Error of the Estimate Durbin-Watson
1 .392(a) 0.153 0.134 0.374 1.397
a Predictors: (Constant), RELIGION, ANIMAL WELFARE, MOOD, HEALTH, SOCIAL PEER, ENVIRONMENT
b Dependent Variable: Do you consider yourself a vegetarian or a vegan?(Vegetarian in this case includes Lacto, Lacto-Ovo, Ovo, and Vegan as defined above.)
The correlation coefficient (R) is 0.392, indicating a moderate positive correlation between the predictors and the dependent variable. The coefficient of determination (R Square) is 0.153, indicating that approximately 15.3% of the variance in the dependent variable can be explained by the predictors in the model. The adjusted R Square is 0.134, which takes into account the number of predictors in the model. It suggests that approximately 13.4% of the variance in the dependent variable is explained by the predictors, adjusted for the model’s complexity. The standard error of the estimate is 0.374, which represents the average distance between the observed values and the predicted values. The Durbin-Watson statistic is 1.397, which is close to 2.0. It indicates that there is no significant autocorrelation present in the residuals. Therefore the model accounts for a moderate amount of variance in the dependent variable, but there may be other factors not included in the model that also contribute to the prediction. The absence of autocorrelation suggests that the residuals are independent and do not exhibit any systematic pattern.
ANOVA
Model Sum of Squares df Mean Square F Sig.
1 Regression 6.495 6 1.082 7.757 .000
Residual 35.865 257 0.14
Total 42.36 263
a Dependent Variable: Do you consider yourself a vegetarian or a vegan?(Vegetarian in this case includes Lacto, Lacto-Ovo, Ovo, and Vegan as defined above.)
b Predictors: (Constant), RELIGION, ANIMAL WELFARE, MOOD, HEALTH, SOCIAL, ENVIRONMENT
The regression component accounts for 6.495 units of variation, with 6 degrees of freedom. The mean square is 1.082. The F-statistic is 7.757, and the associated p-value is 0.000. This indicates that the regression model is statistically significant in predicting the dependent variable. The residual component accounts for 35.865 units of variation, with 257 degrees of freedom. The mean square is 0.140. The total variation in the dependent variable is 42.360 units, with a total of 263 degrees of freedom. Overall, the significant F-statistic suggests that the independent variables (Religion, ANIMAL Welfare, Mood, Health, Social peer, Environment) collectively have a significant impact on predicting the dependent variable (considering oneself as a vegetarian or a vegan).
Coefficients
Variables Unstandardized Coefficients Standardized Coefficients t Sig. Collinearity Statistics
B Std. Error Beta Tolerance VIF
(Constant) -0.113 0.099 -1.14 0.255
Animal Welfare 0.083** 0.035 0.229 2.366 0.019 0.351 2.848
Social Peer -0.004 0.027 -0.011 -0.134 0.894 0.482 2.073
Health -0.095*** 0.028 -0.266 -3.465 0.001 0.561 1.784
Environment 0.065* 0.039 0.17 1.656 0.099 0.311 3.217
Mood 0.040 0.027 0.116 1.48 0.14 0.534 1.873
Religion -0.011 0.022 -0.037 -0.477 0.633 0.554 1.805
*,** and *** represent statistical significance at 10%, 5% and 1% respectively.
The regression output provides information about the coefficients of the independent variables (Animal Welfare, Social peer, Health, Environment, Mood, and Religion) and their relationship with the dependent variable (Vegetarian Decision). The Collinearity Statistics suggest that there is no significant issue with multicollinearity in the model. The predictor variables demonstrate acceptable levels of independence from each other, which strengthens the reliability of the regression coefficients and their interpretations. The coefficients represent the estimated effect of each independent variable on the dependent variable, while the standardized coefficients (Beta) provide a measure of the relative importance of each independent variable in predicting the dependent variable. In this model:
Animal Welfare has a positive coefficient of 0.083, indicating that an increase in ethical and animal welfare considerations is associated with a higher likelihood of considering oneself a vegetarian. This coefficient is statistically significant (p < 0.05), suggesting a meaningful impact.
Social peer influence variable(family and friends) has a small negative coefficient of -0.004, suggesting a weak negative relationship with the likelihood of being a vegetarian. However, this coefficient is not statistically significant (p > 0.05), indicating that Social connections may not have a significant effect.
Health has a negative coefficient of -0.095, indicating that higher Health concerns are associated with a lower likelihood of being a vegetarian. This coefficient is statistically significant (p < 0.001), indicating a significant impact. Students might worry that the complete exclusion of conventional animal proteins might weigh on their health.
The environmental variable has a positive coefficient of 0.065, suggesting that greater environmental concerns are associated with a higher likelihood of being a vegetarian. However, this coefficient is not statistically significant (p > 0.05), indicating that the relationship may not be significant.
The mood variable has a positive coefficient of 0.040, suggesting a small positive relationship with the likelihood of being a vegetarian. However, this coefficient is not statistically significant (p > 0.05), indicating that Mood may not have a significant effect.
Religion has a small negative coefficient of -0.011, suggesting a weak negative relationship with the likelihood of being a vegetarian. However, this coefficient is not statistically significant (p > 0.05), indicating that Religion may not have a significant effect.
Overall, the regression analysis indicates that animal welfare and health are major factors determining the likelihood of being a vegetarian. However, it is crucial to stress that the importance and degree of these associations should be taken with caution, taking into account the study’s specific context and constraints.

4.5. Study Limitations

Firstly, this study acknowledges the fact that data from internet sources may be subject to sampling bias. Because the sample does not represent the full population of consumers in the Southern Provinces of Korea, the results may not be generalizable to a larger population. Also due to the fact that the study focused on international students alone, the findings may not be applicable to other populations, such as local students or international students in other geographical regions. The cultural, social, and educational factors unique to Southern provinces of South Korea may have an impact on the outcomes. Secondly, because online surveys rely on voluntary participation, self-selection bias occurs. Individuals who choose to engage may have different qualities or beliefs than those who do not. This could have an impact on the findings’ representativeness and generalizability. Thirdly, because Likert-scale data is based on self-reporting, it is susceptible to response bias. Participants’ responses may be socially desirable or influenced by their current mood or circumstances, resulting in erroneous or biased results.
Again, there may be minimal control over the survey participants’ environment and settings. Distractions, external influences, or insufficient attention to survey questions could all have an impact on the quality and reliability of the responses.
Finally, International students in Korea come from a variety of cultural backgrounds and may have varied degrees of English ability. Cultural nuances and language difficulties may influence the usage of Likert scale items and the interpretation of queries, potentially affecting the accuracy.

5. Conclusion

This study looked at the elements that influence the dietary transition to vegetarianism among foreign students in South Korea’s southern provinces, concentrating on, religion, mood, environment, health, social pressure, and ethical-animal welfare concerns. The logistic regression analysis revealed important insights into the correlations between these characteristics and the likelihood of respondents selecting a vegetarian diet.
The study’s findings have substantial consequences for Korean consumer behavior, marketing managers, and decision-makers. The findings underscored the importance of ethical-animal welfare concerns, as well as health, ecological, social-psychological, and religious views in determining the decision to adopt a vegetarian diet. This indicates that there is a growing awareness and attention to ethical and sustainable eating choices among international students in Korea. For marketing managers and decision-makers in the food industry, this study underscores the importance of catering to the needs and preferences of consumers who prioritize environmental sustainability, and animal welfare. Creating and promoting vegetarian and vegan options in local restaurants and food enterprises could attract and appeal to this specific target demographic.
Secondly, the study found that health was a crucial factor influencing the decision to follow a vegetarian diet. This research suggests that health-conscious people, including students from other countries, are more likely to eat vegetarian given the appealing health benefits of such dietary options. Marketing and educational campaigns emphasizing the health benefits of vegetarianism could effectively target and attract this demographic. Furthermore, having nutritious and well-balanced vegetarian food alternatives in campus cafeterias and other food outlets might promote health-conscious students’ dietary preferences. In addition, the study found that gender, religion, and mood all had varying levels of influence on the decision to follow a vegetarian diet. Understanding these elements can assist marketing managers and decision-makers in tailoring their strategy to certain demographic and psychographic categories. Consideration of overseas students’ religious views and cultural backgrounds, for example, might inspire the development of marketing messages and campaigns that resonate with their values and beliefs. Recognizing the significance of mood and emotions in dietary decisions can also inform the design of promotional activities that appeal to the target audience’s emotional needs and aspirations.
In general, this study contributes to our awareness of the factors that influence vegetarian diet decisions among international students in South Korean provinces. The implications of this research for consumer behavior, marketing managers, and decision-makers result in the ability to cater to the preferences and demands of a growing sector of health-conscious, ecologically sensitive, and ethically motivated consumers. Organizations and decision-makers in South Korea can effectively meet the demands of this target market and contribute to a sustainable and healthier food culture in the region by aligning their approaches, product offerings, and advertising campaigns with the identified factors influencing the vegetarian dietary choices.

References

  1. Ngo, V.Q.T.; Vo, T.A.D.; Ngo, A.P.; Nguyen, D.M.A.; Le, M.T.; To, T.P.L.; Nguyen, T.T.P. Factors Influencing on Consumer’s Decision on Vegetarian Diets in Vietnam. The Journal of Asian Finance, Economics and Business 2021, 8, 485–495. [Google Scholar] [CrossRef]
  2. Taebum, Y.; In-Jin, Y. Becoming a vegetarian in Korea: The sociocultural implications of vegetarian diets in Korean society. Korea Journal 2015, 55, 111–135. [Google Scholar] [CrossRef]
  3. Joyce, A.; Dixon, S.; Comfort, J.; Hallett, J. Reducing the Environmental Impact of Dietary Choice: Perspectives from a Behavioral and Social Change Approach. Journal of Environmental and Public Health 2012, 2012, 978672. [Google Scholar] [CrossRef]
  4. Singh, P.N.; Sabate, J.; Fraser, G.E. Does low meat consumption increase life expectancy in humans? The American Journal of Clinical Nutrition. 2003, 78 (supplement 3), 526S–532S. [Google Scholar] [CrossRef] [PubMed]
  5. Haddad, E.H.; Tanzman, J.S. What do vegetarians in the United States eat? American Journal of Clinical Nutrition. 2003, 78 (supplement 3), 626S–632S. [Google Scholar] [CrossRef]
  6. Rosenfeld, D.L. The psychology of vegetarianism: Recent advances and future directions. Appetite, 2018, 131, 125–138. [Google Scholar] [CrossRef]
  7. Rosenfeld, D.L. Why some choose the vegetarian option: Are all ethical motivations the same? Motivation and Emotion 2019, 43, 400–411. [Google Scholar] [CrossRef]
  8. Pribis, P.; Pencak, R.C.; Grajales, T. Beliefs and attitudes toward vegetarian lifestyle across generations. Nutrients 2010, 2, 523–531. [Google Scholar] [CrossRef]
  9. Worsley, A.; Skrzypiec, G. Teenage vegetarianism: prevalence, social and cognitive contexts. Appetite 1998, 30, 151–170. [Google Scholar] [CrossRef] [PubMed]
  10. Key, T.; Appleby, P.N.; Rosell, M.S. Health effects of vegetarian and vegan diets. Proceedings of the Nutrition Society 2006, 65, 35–41. [Google Scholar] [CrossRef]
  11. Kim, H.J.; Houser, R.F. Two small surveys, 25 years apart, investigating motivations of dietary choice in 2 groups of vegetarians in the Boston area. Journal of the American Dietetic Association 1999, 99, 598–601. [Google Scholar] [CrossRef] [PubMed]
  12. Wilson, S.M.; Weatherall, A.; Butler, C. A rhetorical approach to discussions about health and vegetarianism. Journal of Health Psychology 2004, 9, 567–581. [Google Scholar] [CrossRef] [PubMed]
  13. Fessler, D.M.T.; Arguello, A.P.; Mekdara, J.M.; Macias, R. Disgust sensitivity and meat consumption: A test of an emotivist account of moral vegetarianism. Appetite 2003, 41, 312–341. [Google Scholar] [CrossRef] [PubMed]
  14. Jabs, J.; Devine, C.M.; Sobal, J. Model of the process of adopting vegetarian diets: Health vegetarians and ethical vegetarians. Journal of Nutrition Education 1998, 30, 196–202. [Google Scholar] [CrossRef]
  15. Lea, E.J.; Crawford, D.; Worsley, A. Public views of the benefits and barriers to the consumption of a plant-based diet. European Journal of Clinical Nutrition. 2006, 60, 828–837. [Google Scholar] [CrossRef] [PubMed]
  16. Lea, E.; Worsley, A.; Crawford, D. Australian adult consumers’ beliefs about plant foods: a qualitative study. Health Education and Behavior. 2005, 32, 795–808. [Google Scholar] [CrossRef] [PubMed]
  17. Wyker, B.A.; Davison, K.K. Behavioral change theories can inform the prediction of young adults’ adoption of a plant-based diet. Journal of Nutrition Education and Behavior. 2010, 42, 168–177. [Google Scholar] [CrossRef] [PubMed]
  18. Ajzen, I. The theory of planned behavior. Organizational Behavior and Human Decision Processes. 1991, 50, 179–211. [Google Scholar] [CrossRef]
  19. Prochaska, J.O.; DiClemente, C.C. Stages and processes of self-change of smoking: toward an integrative model of change. Journal of Consulting and Clinical Psychology. 1983, 51, 390–395. [Google Scholar] [CrossRef]
  20. Clare D’Souza, Anne Renée Brouwer, Stephen Singaraju,Veganism: Theory of planned behaviour, ethical concerns and the moderating role of catalytic experiences. Journal of Retailing and Consumer Services 2022, 66, 102952. [CrossRef]
  21. Icek Ajzen. The theory of planned behavior, Organizational Behavior and Human Decision Processes, Volume 50, Issue 2, 1991, Pages 179-211, ISSN 0749-5978. [CrossRef]
  22. Fox, N.; Ward, K.J. You are what you eat? Vegetarianism, health and identity. Soc. Sci. Med. 2008, 66, 2585–2595. [Google Scholar] [CrossRef] [PubMed]
  23. Sneijder, P.; Te-Molder, H. Normalizing ideological food choice and eating practices. Identity work in online discussions on veganism. Appetite 2009, 52, 621–630. [Google Scholar] [PubMed]
  24. Nezlek, J.B.; Forestell, C.A. Vegetarianism as a social identity. Curr. Opin. Food Sci. 2020, 33, 45–51. [Google Scholar] [CrossRef]
  25. Hsiao, T. In defense of eating meat. J. Agric. Environ. Ethics 2015, 28, 277–291. [Google Scholar] [CrossRef]
  26. Erd˝os, L. Veganism versus meat-eating, and the myth of “root capacity”: A response to Hsiao. J. Agric. Environ. Ethics 2015, 28, 1139–1144. [Google Scholar] [CrossRef]
  27. Duncan, I.J.H. (2005). Science-based assessment of animal welfare: farm animals. Department of Animal and Poultry Science, University of Guelph, Guelph, Ontario N1G 2W1, Canada. UK.
  28. Joy, M. Why We Love Dogs, Eat Pigs, and Wear Cows: An Introduction to Carnism; Red Wheel: Newburyport, MA, USA, 2011. Red Wheel: Newburyport, MA, USA, 2011.
  29. Bratanova, B.; Loughnan, S.; Bastian, B. The effect of categorization as food on the perceived moral standing of animals. Appetite 2011, 57, 193–196. [Google Scholar] [CrossRef] [PubMed]
  30. Loughnan, S.; Bratanova, B.; Puvia, E. The Meat Paradox: How are we able to love animals and love eating animals. Mind Italia 2011, 1, 15–18. [Google Scholar]
  31. Rothgerber, H. Underlying differences between conscientious omnivores and vegetarians in the evaluation of meat and animals. Appetite 2015, 87, 251–258. [Google Scholar] [CrossRef]
  32. Piazza, J.; Ruby, M.B.; Loughnan, S.; Luong, M.; Kulik, J.; Watkins, H.M.; Seigerman, M. Rationalizing meat consumption. The 4Ns. Appetite 2015, 91, 114–128. [Google Scholar] [CrossRef]
  33. Beardsworth, A.D.; Keil, E.T. Vegetarianism, veganism, and meat avoidance: Recent trends and findings. Br. Food J. 1991, 93, 19–24. [Google Scholar] [CrossRef]
  34. Ruby, M.B. Vegetarianism. A blossoming field of study. Appetite 2012, 58, 141–150. [Google Scholar] [CrossRef]
  35. Fox, N.; Ward, K. Health, ethics and environment: A qualitative study of vegetarian motivations. Appetite 2008, 50, 422–429. [Google Scholar] [CrossRef] [PubMed]
  36. Rozin, P.; Markwith, M.; Stoess, C. Moralization and becoming a vegetarian: The transformation of preferences into values and the recruitment of disgust. Psychol. Sci. 1997, 8, 67–73. [CrossRef]
  37. Hirschler, C.A. “What pushed me over the edge was a deer hunter”: Being Vegan in North America. Soc. Anim. 2011, 19, 156–174. [Google Scholar] [CrossRef]
  38. Beardsworth, A.; Keil, T. The vegetarian option: Varieties, conversions, motives and careers. Sociol. Rev. 1992, 40, 253–293. [Google Scholar] [CrossRef]
  39. Nezlek, J.B.; Cypryanska, M.; Forestell, C.A. Dietary Similarity of Friends and Lovers: Vegetarianism, Omnivorism, and Personal Relationships. J. Soc. Psychol. 2020, 1–7. [Google Scholar] [CrossRef]
  40. Mylan, J. Sustainable consumption in everyday life: A qualitative study of UK consumer experiences of meat reduction. Sustainability 2018, 10, 2307. [Google Scholar] [CrossRef]
  41. Pimentel, D.; Pimentel, M. Sustainability of meat-based and plant-based diets and the environment. American Journal of Clinical Nutrition. 2003, 78, 660S–663S. [Google Scholar] [CrossRef] [PubMed]
  42. Kalof, Dietz, Stern, & Guagnano L. Kalof, T. Dietz, P.C. Stern, G.A. Guagnano Social psychological and structural influences on vegetarian beliefs. Rural Sociology 1999, 64, 500–511. [Google Scholar] [CrossRef]
  43. Coveney, J. (2000). Food, morals, and meaning: The pleasure and anxiety of eating. Psychology Press.
  44. Hoek, A.C.; Luning, P.A.; Stafleu, A.; de Graaf, C. Food-related lifestyle and health attitudes of Dutch vegetarians, non-vegetarian consumers of meat substitutes, and meat consumers. Appetite 2004, 42, 265–272. [Google Scholar] [CrossRef]
  45. Fox, M.A. The contribution of vegetarianism to ecosystem health. Ecosystem Health 1999, 5, 70–74. [Google Scholar] [CrossRef]
  46. Wilson, M.S.; Weatherall, A.; Butler, C. A rhetorical approach to discussions about health and vegetarianism. Journal of Health Psychology 2004, 9, 567–581. [Google Scholar] [CrossRef]
  47. Ellison, C.G. Race, religious involvement and depressive symptomatology in a southeastern U.S. community. Social Science and Medicine 1995, 40, 1561–1572. [Google Scholar] [CrossRef]
  48. Lindeman, M.; Väänänen, M. Measurement of ethical food choice motives. Appetite 2000, 34, 55–59. [Google Scholar] [CrossRef]
  49. Karen Hye-Cheon Kim, WM. Alex Mcintosh, Karen, S. Kubena & Jeffery Sobal Religion, Social Support, Food-Related Social Support, Diet, Nutrition, and Anthropometrics in Older Adults. Ecology of Food and Nutrition 2008, 47, 205–228. [Google Scholar] [CrossRef]
  50. Ockerman, H.W.; Nxumalo, D.J. Reported reasons for meat avoidance. Outlook on Agriculture 1998, 27, 41–45. [Google Scholar] [CrossRef]
  51. Peek, C.W.; Konty, M.A.; Frazier, T.E. Religion and ideological support for social movements: The case of animal rights. Journal for the Scientific Study of Religion 1997, 429–439. [Google Scholar] [CrossRef]
  52. Hibbeln, J.R.; Northstone, K.; Evans, J.; Golding, J. Vegetarian diets and depressive symptoms among men. J. Affect. Disord. 2018, 225, 13–17. [Google Scholar] [CrossRef]
  53. Larsson, C.L.; Klock, K.S.; Åstrøm, A.N.; Haugejorden, O.; Johansson, G. Lifestyle-related characteristics of young low-meat consumers and omnivores in Sweden and Norway. J. Adolesc. Health. 2002, 31, 190–198. [Google Scholar] [CrossRef]
  54. Goldberg, M.; Carton, M.; Descatha, A.; Leclerc, A.; Roquelaure, Y.; Santin, G.; Zins, M. , CONSTANCES Team CONSTANCES: A general prospective population-based cohort for occupational and environmental epidemiology: Cohort profile. Occup. Environ. Med. 2016, 74, 66–71. [Google Scholar] [CrossRef]
Preprints 103470 g001
Figure 1. Conceptual Model.
Figure 1. Conceptual Model.
Preprints 103470 g001
Table 2. KMO and Bartlett’s Test.
Table 2. KMO and Bartlett’s Test.
Kaiser-Meyer-Olkin Measure of Sampling Adequacy 0.946
Bartlett’s Test of Sphericity Approx. Chi-Square 6072.281
df 351
Sig. 0.000
Table 3. Rotated Component Matrix.
Table 3. Rotated Component Matrix.
ITEMS Component
1 2 3 4 5 6
ANIMAL WELFARE1 0.761
AMIMAL WELFARE2 0.771
ANIMAL WELFARE3 0.816
SOCIAL 1 0.714
SOCIAL 2 0.690
SOCIAL 3 0.742
HEALTH 1 0.804
HEALTH 2 0.841
HEALTH3 0.719
HEALTH4 0.734
ENVIRONMENT1 0.505
ENVIRONMENT2 0.683
ENVIRONMENT3 0.858
ENVIRONMENT4 0.828
ENVIRONMENT5 0.842
ENVIRONMENT6 0.833
ENVIRONMENT7 0.817
ENVIRONMENT8 0.838
ENVIRONMENT9 0.736
MOODAWARENESS1 0.797
MOODAWARENESS2 0.729
MOODAWARENESS3 0.793
MOODAWARENESS4 0.748
MOODAWARENESS5 0.707
RELIGION1 0.607
RELIGION2 0.523
RELIGION3 0.816
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
Rotation converged in 8 iterations.
Table 5. Case Processing Summary.
Table 5. Case Processing Summary.
Unweighted Cases N Percent
Selected Cases Included in Analysis 264 100
Missing Cases 0 0
Total 264 100
Unselected Cases 0 0
Total 264 100
If weight is in effect, see classification table for the total number of cases.
Table 6. Dependent Variable Encoding.
Table 6. Dependent Variable Encoding.
Original Value Internal Value
NO 0
YES 1
Table 7. Categorical Variables Codings.
Table 7. Categorical Variables Codings.
Frequency Parameter coding
(1) (2)
GENDER I prefer not to say 4 1 0
MALE 124 0 1
FEMALE 136 0 0
Table 8. Omnibus Tests of Model Coefficients.
Table 8. Omnibus Tests of Model Coefficients.
Chi-square df Sig.
Step 1 Step 51.010 8 0.000
Block 51.010 8 0.000
Model 51.010 8 0.000
Table 9. Model Summary.
Table 9. Model Summary.
Step -2 Log likelihood Cox & Snell R Square Nagelkerke R Square
1 213.756a 0.176 0.277
a Estimation terminated at iteration number 6 because parameter estimates changed by less than .001.
Table 10. Hosmer and Lemeshow Test.
Table 10. Hosmer and Lemeshow Test.
Step Chi-square df Sig.
1 7.742 8.000 0.459
Table 11. Variables in the Equation.
Table 11. Variables in the Equation.
B S.E. Wald df Sig. Exp(B) 95% C.I.for EXP(B)
Lower Upper
Step 1(a) GENDER - - 5.276 2 0.072 - - -
GENDER(1) 2.098 1.199 3.062 1 0.08 8.151 0.777 85.474
GENDER(2) -0.471 0.37 1.618 1 0.203 0.625 0.302 1.29
RELIGION 0.075 0.165 0.207 1 0.649 1.078 0.78 1.491
MOOD 0.371 0.235 2.499 1 0.114 1.45 0.915 2.298
ENVIRONMENT 0.518 0.325 2.547 1 0.11 1.679 0.889 3.174
HEALTH -0.683*** 0.221 9.58 1 0.002 0.505 0.328 0.778
SOCIAL -0.076 0.203 0.141 1 0.707 0.927 0.623 1.379
ANIMAL WELFARE 0.713** 0.307 5.398 1 0.020 2.041 1.118 3.725
Constant -5.157*** 1.087 22.517 1 0.000 0.006 - -
a Variable(s) entered on step 1: GENDER, RELIGION, MOOD, ENVIRONMENT, HEALTH, SOCIAL, ANIMAL WELFARE.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated